(立方体的展开图)
正方体11种平面展开图(精心整理)
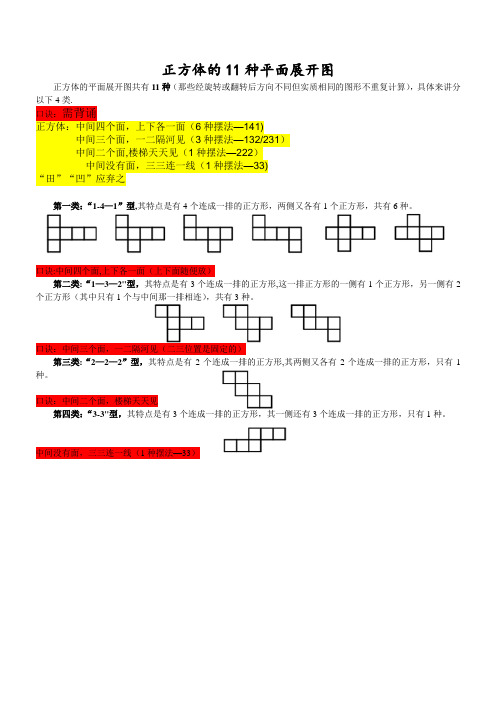
正方体的11种平面展开图
正方体的平面展开图共有11种(那些经旋转或翻转后方向不同但实质相同的图形不重复计算),具体来讲分以下4类.
口诀:需背诵
正方体:中间四个面,上下各一面(6种摆法—141)
中间三个面,一二隔河见(3种摆法—132/231)
中间二个面,楼梯天天见(1种摆法—222)
中间没有面,三三连一线(1种摆法—33)
“田”“凹”应弃之
第一类:“1-4—1”型,其特点是有4个连成一排的正方形,两侧又各有1个正方形,共有6种。
口诀:中间四个面,上下各一面(上下面随便放)
第二类:“1—3—2"型,其特点是有3个连成一排的正方形,这一排正方形的一侧有1个正方形,另一侧有2个正方形(其中只有1个与中间那一排相连),共有3种。
口诀:中间三个面,一二隔河见(二三位置是固定的)
第三类:“2—2—2”型,其特点是有2个连成一排的正方形,其两侧又各有2个连成一排的正方形,只有1种。
口诀:中间二个面,楼梯天天见
第四类:“3-3"型,其特点是有3个连成一排的正方形,其一侧还有3个连成一排的正方形,只有1种。
中间没有面,三三连一线(1种摆法—33)。
正方体11种平面展开图(精心整理)

正方体的11种平面展开图
正方体的平面展开图共有11种(那些经旋转或翻转后方向不同但实质相同的图形不重复计算),具体来讲分以下4类。
口诀:需背诵
正方体:中间四个面,上下各一面(6种摆法-141)
中间三个面,一二隔河见(3种摆法-132/231)
中间二个面,楼梯天天见(1种摆法-222)
中间没有面,三三连一线(1种摆法-33)
“田”“凹”应弃之
第一类:“1—4—1”型,其特点是有4个连成一排的正方形,两侧又各有1个正方形,共有6种。
口诀:中间四个面,上下各一面(上下面随便放)
第二类:“1—3—2”型,其特点是有3个连成一排的正方形,这一排正方形的一侧有1个正方形,另一侧有2个正方形(其中只有1个与中间那一排相连),共有3种。
口诀:中间三个面,一二隔河见(二三位置是固定的)
第三类:“2—2—2”型,其特点是有2个连成一排的正方形,其两侧又各有2个连成一排的正方形,只有1种。
口诀:中间二个面,楼梯天天见
第四类:“3—3”型,其特点是有3个连成一排的正方形,其一侧还有3个连成一排的正方形,只有1种。
中间没有面,三三连一线(1种摆法-33)。
正方体11种平面展开图(精心整理)

精品文档
.
正方体的11种平面展开图
正方体的平面展开图共有11种(那些经旋转或翻转后方向不同但实质相同的图形不重复计算),具体来讲分以下4类。
口诀:需背诵
正方体:中间四个面,上下各一面(6种摆法-141)
中间三个面,一二隔河见(3种摆法-132/231)
中间二个面,楼梯天天见(1种摆法-222)
中间没有面,三三连一线(1种摆法-33)
“田”“凹”应弃之
第一类:“1—4—1”型,其特点是有4个连成一排的正方形,两侧又各有1个正方形,共有6种。
口诀:中间四个面,上下各一面(上下面随便放)
第二类:“1—3—2”型,其特点是有3个连成一排的正方形,这一排正方形的一侧有1个正方形,另一侧有2个正方形(其中只有1个与中间那一排相连),共有3种。
口诀:中间三个面,一二隔河见(二三位置是固定的)
第三类:“2—2—2”型,其特点是有2个连成一排的正方形,其两侧又各有2个连成一排的正方形,只有1种。
口诀:中间二个面,楼梯天天见
第四类:“3—3”型,其特点是有3个连成一排的正方形,其一侧还有3个连成一排的正方形,只有1种。
中间没有面,三三连一线(1种摆法-33)。
正方体11种平面展开图(精心整理)

正方体的11种平面睁开图之杨若古兰创作正方体的平面睁开图共有11种(那些经扭转或翻转后方向分歧但实质不异的图形不反复计算),具体来讲分以下4类.
口诀:需背诵
正方体:两头四个面,上下各一面(6种摆法-141)
两头三个面,一二隔河见(3种摆法-132/231)
两头二个面,楼梯天天见(1种摆法-222)
两头没有面,三三连一线(1种摆法-33)
“田”“凹”应弃之
第一类:“1—4—1”型,其特点是有4个连成一排的正方形,两侧又各有1个正方形,共有6种.
口诀:两头四个面,上下各一面(上上面随便放)
第二类:“1—3—2”型,其特点是有3个连成一排的正方形,这一排正方形的一侧有1个正方形,另一侧有2个正方形(其中只要1个与两头那一排相连),共有3种.
口诀:两头三个面,一二隔河见(二三地位是固定的)
第三类:“2—2—2”型,其特点是有2个连成一排的正方形,其两侧又各有2个连成一排的正方形,只要1种.
口诀:两头二个面,楼梯天天见
第四类:“3—3”型,其特点是有3个连成一排的正方形,其一侧还有3个连成一排的正方形,只要1种.
两头没有面,三三连一线(1种摆法-33)。
立方体及其展开图

检查完整性
确保展开图完整地展示了 立方体的所有面和结构特 征,没有遗漏或错误。
03
立方体的几何性质
立方体的体积
总结词
立方体的体积是其边长的三次方。
详细描述
立方体的体积是其长、宽、高三个维度的乘积,即V=a^3,其中a是立方体的 边长。
立方体展开图的定义
01
立方体展开图是指将一个完整的 立方体进行展开,将其表面完全 展平在平面上的图形。
02
立方体展开图是立体几何中一个 重要的概念,它有助于我们更好 地理解三维空间中的几何形状和 结构。
立方体展开图的种类
1-4-1型
一个面作为底面,四个 面与底面相邻,一个面
与底面相对。
1-3-2型
一个面作为底面,三个 面与底面相邻,两个面
与底面相对。
2-2-2型
3-3型
两个面作为底面,两个面 与其中一个底面相邻,两 个面与另一个底面相对。
三个面作为底面,每个 面都与另外两个面相邻。
立方体展开图的绘制方法
01
02
03
确定展开方向
根据需要选择合适的展开 方向,确保图形在平面上 能够完全展开。
绘制展开图
对未来研究的展望
深入探索
01
未来可以进一步研究立方体及其展开图的性质和特点,如探讨
不同展开方式的几何特征和性质。
应用拓展
02
探索立方体及其展开图在更多领域的应用,如机器人学、计算
机图形学和虚拟现实技术等。
跨学科研究
03
结合其他学科,如物理学、生物学和心理学等,从不同角度研
究立方体及其展开图,以揭示其更深层次的本质和意义。
正方体11种平面展开图(精心整理)

正方体的11种平面展开图
正方体的平面展开图共有11种(经旋转或翻转后方向不同但实质相同的图形不重复计算),具体来讲分以下4类:
口诀:需背诵
正方体:中间四个面,上下各一面(6种摆法-141)
中间三个面,一二隔河见(3种摆法-132/231)
中间二个面,楼梯天天见(1种摆法-222)
中间没有面,三三连一线(1种摆法-33)
“田”“凹”应弃之
第一类:“1—4—1”型,其特点是有4个连成一排的正方形,两侧又各有1个正方形,共有6种。
口诀:中间四个面,上下各一面(上下面随便放)
第二类:“1—3—2”型,其特点是有3个连成一排的正方形,这一排正方形的一侧有1个正方形,另一侧有2个正方形(其中只有1个与中间那一排相连),共有3种。
口诀:中间三个面,一二隔河见(二三位置是固定的)
第三类:“2—2—2”型,其特点是有2个连成一排的正方形,其两侧又各有2个连成一排的正方
形,只有1种。
口诀:中间二个面,楼梯天天见
第四类:“3—3”型,其特点是有3个连成一排的正方形,其一侧还有3个连成一排的正方形,只有1种。
中间没有面,三三连一线(1种摆法-33)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
硕博教育VIP课堂辅导讲义
学员姓名:科目:数学年级:七年级授课日期:
授课时段:总课时:授课时长:剩余课时:
课题
教学目标
重点、难点
考点及考试要
求
教学内容
棱锥与棱柱
棱柱:有两个面互相平行,其余各面都是四边形,并且每相邻两
个四边形的公共边都互相平行。
棱柱中两个互相平行的面,叫做棱柱的底面.棱柱中除两个底面以
外的其余各个面都叫做棱柱的侧面.棱柱中两个侧面的公共边叫做
棱柱的侧棱.棱柱中侧面与底面的公共顶点叫做棱柱的顶点.
底面是三角形、四边形、五边形……的棱柱分别叫做三棱柱、
四棱柱、五棱柱……
棱锥:有一个面是多边形,其余各面是有一个公共点的三角形。
这个多边形叫做棱锥的底面,其余各面叫做棱锥的侧面;
相邻侧面的公共边叫做棱锥的侧棱,各侧面的公共顶点叫做棱
锥的顶点,顶点到底面的距离叫棱锥的高.
棱锥的底面可以是三角形、四边形、五边形……我们把这
样的棱锥分别叫做三棱锥、四棱锥、五棱锥……
从不同的方向看立体图形:
当我们从某一角度观察一个物体时,所看到的图象叫做物体的一个视图,从正面观察得到的视图叫做主视图或正视图,从上面观察得到的视图叫做俯视图,从左边观察得到的视图叫做左视图.
主视图、俯视图、左视图三者合在一起叫做物体的三视图.
常见立体图形展开图(牢记)三棱锥
长方体
正方体展开图分类
正方体:第一类,中间四连方,两侧各一个,共六种。
第二类,中间三连方,两侧各有一、二个,共三种。
第三类,中间二连方,两侧各有二个,只有一种。
第四类,两排各三个,只有一种。
初一数学立体图形的展开图习题精选
一、选择题
1.圆锥的侧面展开图是________________.
2.三棱柱的侧面展开图是__________________.
4.想一想:将左边的图形折成一个立方体,右边的四个立方体哪一个是由左边的图形折成的?
5.如图所示,下列图形中,不是正方体的展开图是()
6.如图所示的立方体,如果把它展开,可以是下列图形中的()
二、填空题
1.如图所示,用字母M表示与A相对的面,请在下面的正方体展开图中填写相应的字母.
2.如图所示的是长方体的展开图,若A面在前面,则()面会在上面,若从
右面看是面C,而D在后面,则()面会在上面.
3.如图是一个正方体纸盒的展开图,当折成纸盒时,与点1重合的点是
_________.
三、解答题
1.填空题
(1)七棱往有____个顶点,有____条棱,有______个侧面.
(2)圆锥体的底面是_________形,圆锥体的侧面的平面展开图是
_______形.
(3)在图中是正方体展开图的有_________.
(4)一个圆形薄铁,刚好做成两个无底圆锥形容器,则这个圆形薄铁
的周长恰好是无底圆锥底面周长的________.
2.判断题
(1)如图中,①是②的表面展开图.()
(2)长方体的表面展开图只有一种.()
(3)由于圆锥体可以由直角三角形旋转得到,所以圆锥体的侧面展开图也可以是三角形.()
(4)圆锥体的侧面展开图只有一种.()
3.选择题
(1)如图是一个三边相等的三角形,三边的中点用虚线连接,如果将三角形沿虚线向上
折叠,得到的立体图形是()
A.三棱柱 B.三棱锥C.正方体 D.圆锥
(2)三棱柱中棱的条数是()
A.三条 B.六条 C.八条 D.九条
(3)八棱柱有()面.
A.2个 B.8个 C.10个 D.12个
4.如图,右图是左图表面的展开图,右图已有两个面标出是长方体的下面和右面,请你在右图中把长方体的其他面标出来.
5.如图,是由几个小正方体所组成的几何体,请画出这个几何体的三视图.
6.如图是由些大小相同的小正方体组成的简单几何体的主视图和俯视图.(1)请你画出这个几何体的一种左视图;
(2)若组成这个几何体的小正方体的块数为n,你写出n的所有可能值.
7.如图是一个正方体的展开图,每个面都标注了字母.
(1)如果面A在多面体的底部,上面是哪一个面?
(2)如果F在前面,从左看是面B,上面是哪一面?
(3)从右面看到面C,面D在后面,上面是哪一面?
课后作业
学生对本次课评价
○特别满意○满意○一般○差
学生签字:
教师对学生的评价
1、学生上次作业评价:○好○较好○一般○差
2、学生本次上课情况评价:○好○较好○一般○差
3、对学生本次学习情况的如实反馈及建议:
教师签字:
家长的意见或建议
家长签字:。
