随机过程1(1.1)
清华大学随机过程答案1
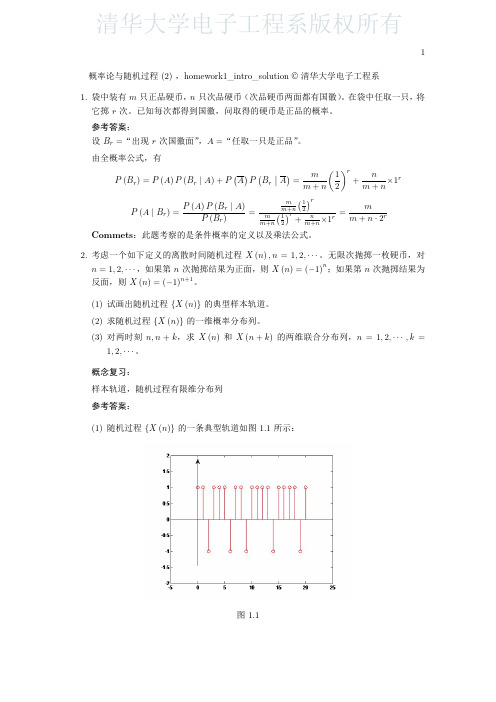
3. 质点在直线上做随机运动,即在 t = 1, 2, 3, · · · 时质点可以在 x 轴上往右或往左做一个 单位距离的随机游动。若往右移动一个单位距离的概率为 p,往左移动一个单位距离的 概率为 q,即 P {ξ (i) = +1} = p,P {ξ (i) = −1} = q,p + q = 1,且各次游动是相互统 ∑n 计独立的。经过 n 次游走,质点所处的位置为 ηn = η (n) = ξi。
参考答案:
(1) V = a 时,一条样本轨道为典型的正弦曲线。 2
(2) ξ (0) = 0,fξ(0)(x) = δ(x);ξ (π/2ω) = V ,其概率密度同 V 一样。
(π) ξ
4ω
=
V
√ 2
,
fξ(
π 4ω
)
(x)
=
√ 2 a
,
0
<
0, 其他
xHale Waihona Puke <√a 2() 5π
ξ 4ω
=
V
−
√ 2
n
pmqn−m = pn − qn。
m=0
m
∑n
解法二:因各次游走是相互统计独立的,则 E [η (n)] = E[ξi] = (p − q)n。
i=1
清华大学电子工程系版权所有
3
(2) 假设 n1 < n2,
Rηη (n1, n2) = E [η (n1) η (n2)] = E {η (n1) [η (n1) + η (n2) − η (n1)]} = E[η (n1)]2 + E [η (n1)] E [η (n2) − η (n1)] = {E [η (n1)]}2 + V ar [η (n1)] + (p − q)2n1 (n2 − n1) = (p − q)2n21 + n1V ar [ξi] + (p − q)2n1 (n2 − n1) = (p − q)2n1n2 + n1[1 − (p − q)2]
第1章 随机过程

1.3 随机过程的数字特征
随机过程的集合平均 (Ensemble average)
随机过程就是由多个(无穷多个)随机变量按照一定的排列规则组成的; 完整描述随机过程的最完美方法是确定其联合概率密度函数; 如果随机过程的概率密度函数已确定,可根据其直接计算数字特征; 如果能够得到大量的样本,则数字特征也可根据样本的集合平均进行计算。
School of Civil Engineering Harbin Institute of Technology
1.1 为什么要研究和学习随机过程(续)
结构设计
现在设计中如何考虑不确定性?
荷
载
结
构 响 为什么需要学习随机振动
应
结构自重 活荷载 地 风 震
构件尺寸 材料特性
静力响应 地震响应 风致振动
Division of Disaster Mitigation and Bridge Engineering
School of Civil Engineering Harbin Institute of Technology
1.1 为什么要研究和学习随机过程(续)
教材与参考书
从数学观点 :是随机过程理论在振动领域的应用,它是概率统计
方法与结构动力学相结合的产物。
哈尔滨工业大学 土木工程学院 防灾减灾与桥梁工程学科组
Division of Disaster Mitigation and Bridge Engineering
School of Civil Engineering Harbin Institute of Technology
1.2 随机过程的定义和分类
由于随机过程可由一系列随机变量描述,对于任意{t1 , t2 ,
随机过程习题和答案

一、1.1设二维随机变量(,)的联合概率密度函数为: 试求:在时,求。
解:当时, = =1.2 设离散型随机变量X 服从几何分布:试求的特征函数,并以此求其期望与方差。
解:所以:2.1 袋中红球,每隔单位时间从袋中有一个白球,两个任取一球后放回,对每 对应随机变量一个确定的t⎪⎩⎪⎨⎧=时取得白球如果对时取得红球如果对t e t tt X t 3)(.维分布函数族试求这个随机过程的一2.2 设随机过程,其中是常数,与是相互独立的随机变量,服从区间上的均匀分布,服从瑞利分布,其概率密度为试证明为宽平稳过程。
解:(1)与无关 (2),所以 (3)只与时间间隔有关,所以为宽平稳过程。
2.3是随机变量,且,其中设随机过程U t U t X 2cos )(=求:,.5)(5)(==U D U E.321)方差函数)协方差函数;()均值函数;((2.4是其中,设有两个随机过程U Ut t Y Ut t X ,)()(32==.5)(=U D 随机变量,且数。
试求它们的互协方差函2.5,试求随机过程是两个随机变量设B At t X B A 3)(,,+=的均值),(+∞-∞=∈T t 相互独若函数和自相关函数B A ,.),()(),2,0(~),4,1(~,21t t R t m U B N A X X 及则且立为多少?3.1一队学生顺次等候体检。
设每人体检所需的时间服从均值为2分钟的指数分布并且与其他人所需时间相互独立,则1小时内平均有多少学生接受过体检?在这1小时内最多有40名学生接受过体检的概率是多少(设学生非常多,医生不会空闲)解:令()N t 表示(0,)t 时间内的体检人数,则()N t 为参数为30的poisson 过程。
以小时为单位。
则((1))30E N =。
40300(30)((1)40)!k k P N e k -=≤=∑。
3.2在某公共汽车起点站有两路公共汽车。
乘客乘坐1,2路公共汽车的强度分别为1λ,2λ,当1路公共汽车有1N 人乘坐后出发;2路公共汽车在有2N 人乘坐后出发。
1.随机过程概论

{ X (t ) , t (,) } 是一随机过程 . 状态空间 I (,) . 样本函数空间 X { cos πt , t } .
H 发生
x( t )
x( t ) t
x( t ,T ) x( t )
1 1 1
T 发生
o
t t x( t , H )
1
2
x( t , T ) x( t ) x( t , H )
Ft
1 , t 2 ,, t n
( x1 , x2 ,, xn ) Ft ( xk ) , t1 , t 2 ,, t n T , n 1 ,
k 1
k
n
则称 X (t ) 具有独立性 , 或称 X (t ) 是独立过程 .
随机过程的独立性是指其在不同的时刻互不影响 , 一维分布
t1 , t 2 T .
当 A~N (0,1), B~U (0,2) 且 A, B 相互独立时 ,
EA 0,
EA2 DA ( EA)2 1,
EB 1,
EB 2 DB ( EB)2 4 3 ,
E ( AB ) EA EB 0,
所以可得
m X ( t ) t EA EB 1 , RX (t1 , t 2 ) t1t 2 EA2 ( t1 t 2 ) E ( AB) EB 2 t1t 2 4 3 , t1 , t 2 T .
o
称为统计平均或集平均 . 均值函数 m X ( t ) 表示了随机过程 X ( t ) 在各个时刻的摆动中心 .
X ( t ) 的二阶原点矩和二阶中 心矩分别记为
2 ΨX ( t ) EX 2 ( t ) 2 2 2 X ( t ) E[ X ( t ) m X ( t )]2 Ψ X (t ) m X (t )
《随机过程》孙文昌

设{Xt : t ∈ T }是随机过程, 对任意t1, · · · , tn ∈ T 以及(x1, · · · , xn) ∈ Rn, 记随机变 量Xt1, · · · , Xtn的n维联合分布函数为
Ft1,···,tn (x1, · · · , xn) = P (Xt1 < x1, · · · , Xtn < xn) 当n和tk变化时, 得到一族分布函数:
p(x) = 1 ∫ e−itxφ(x)dx. 2π R
对于随机向量(ξ1, · · · , ξn), 它的特征函数定义为
φ(t1, · · · , tn) = Eei(t1ξ1+···+tnξn).
定理 1.8 连续性定理.
(i). 若分布函数列Fn(x)弱收敛于分布函数F (x), 则相应的特征函数列φn(t) 收敛于相应的 特征函数φ(t), 且在t的任一有限区间内该收敛是一致的.
例 1.1 在研究生物群体的增长问题时,为了描述群体的发展或演变过程, 就要在每一 时刻t记录群体的数量xt, 每一xt是随机变量. 假设我们从t = 0开始连续地观测, 则{xt, t ∈ [0, +∞)}就是一个随机过程.
例 1.2 在海浪分析中,需要观测在固定点上海平面的垂直振动.设xt表示在固定点上, 于时刻t海平面相对于平均平面的高度, 则xt是随机变量,而{xt, t ∈ [0, +∞)}是随机过程.
函数, 即对任何x ∈ R,
{ω : ξ(ω) < x} ∈ F ,
则称ξ(ω)为(实)随机变量. 若ξ1(ω)和ξ2(ω)都是实随机变量, 则ξ(ω) = ξ1(ω) + iξ2(ω)称为复随机变量.
第一章 随机过程的一般理论
随机过程的基本概念与应用

随机过程的基本概念与应用随机过程是概率论中研究一系列随机事件在时间上的演化规律的重要分支。
它在各个领域都有着广泛的应用,在通信、控制、金融、生物、物理等方面都发挥着重要作用。
一、随机过程的基本概念1.1 随机过程的定义随机过程是指一组随机变量${X_t}$,其中$t$表示时间,$X_t$表示在时间$t$时刻随机变量的取值。
随机过程是随机变量的函数族,常用记号为${X_t:t\in T}$。
其中$t$取遍$T$所表示的时间集合,$T$可以是实数集、整数集或其他有限或无限集合。
1.2 随机过程的分类随机过程根据其时间变化的连续性与离散性可以分为连续时间随机过程和离散时间随机过程两种。
连续时间随机过程是指随机变量在时间上是连续的,如布朗运动、泊松过程等。
离散时间随机过程是指随机变量在时间上是离散的,如马尔可夫过程、随机游走等。
1.3 随机过程的性质随机过程具有多种性质,包括平稳性、独立性、齐次性等。
其中比较重要的平稳性是指在时间平移下,随机过程的统计性质保持不变,即一个随机过程是平稳的,当且仅当对于任意$t_1,t_2$,其一阶矩和二阶矩不随时间变化而改变。
例如,设随机过程${X_t:t\geq 0}$的均值为$\mu$,方差为$\sigma^2$,则其平稳性条件为:$$\mathbb{E}[X_t]=\mu, \ \forall t\geq 0$$$$\mathbb{E}[(X_s-\mu)(X_t-\mu)]=\sigma^2, \ \forall s,t\geq 0$$二、随机过程的应用随机过程在许多领域中都有着广泛的应用。
以下列举其中几个典型应用。
2.1 通信领域随机过程在通信领域中是必不可少的工具。
通信信号可以看作是一种随时间变化的随机过程,而信道则可看作是一种将输入信号映射成输出信号的随机过程。
因此,随机过程在信号调制、信噪比估计、编码等方面都有着广泛的应用。
2.2 控制领域在控制领域中,随机过程被广泛用于表示、建模和分析控制系统的动态特性。
随机过程习题及答案

随机过程习题及答案第二章随机过程分析1.1学习指导1.1.1要点随机过程分析的要点主要包括随机过程的概念、分布函数、概率密度函数、数字特征、通信系统中常见的几种重要随机过程的统计特性。
1.随机过程的概念随机过程是一类随时间作随机变化的过程,它不能用确切的时间函数描述。
可从两种不同角度理解:对应不同随机试验结果的时间过程的集合,随机过程是随机变量概念的延伸。
2.随机过程的分布函数和概率密度函数如果ξ(t )是一个随机过程,则其在时刻t 1取值ξ(t 1)是一个随机变量。
ξ(t 1)小于或等于某一数值x 1的概率为P [ξ(t 1)≤x 1],随机过程ξ(t )的一维分布函数为F 1(x 1,t 1)=P [ξ(t 1)≤x 1](2-1)如果F 1(x 1,t 1)的偏导数存在,则ξ(t )的一维概率密度函数为对于任意时刻t 1和t 2,把ξ(t 1)≤x 1和ξ(t 2)≤x 2同时成立的概率称为随机过程?(t )的二维分布函数。
如果存在,则称f 2(x 1,x 2;t 1,t 2)为随机过程?(t )的二维概率密度函数。
对于任意时刻t 1,t 2,…,t n ,把 {}n 12n 12n 1122n n ()(),(), ,() (2 - 5)=≤≤≤F x x x t t t P t x t x t x ξξξ,,,;,,,称为随机过程?(t )的n 维分布函数。
如果存在,则称f n (x 1,x 2,…,x n ;t 1,t 2,…,t n )为随机过程?(t )的n 维概率密度函数。
3.随机过程的数字特征随机过程的数字特征主要包括均值、方差、自相关函数、协方差函数和互相关函数。
随机过程?(t )在任意给定时刻t 的取值?(t )是一个随机变量,其均值为其中,f 1(x ,t )为?(t )的概率密度函数。
随机过程?(t )的均值是时间的确定函数,记作a (t ),它表示随机过程?(t )的n 个样本函数曲线的摆动中心。
什么是随机过程(一)

什么是随机过程(一)引言概述:随机过程是概率论和数学统计学中的重要概念,用于描述随机事件在时间和空间上的演化规律。
它在实际问题建模和分析中具有广泛的应用,涵盖了大量的领域,如通信系统、金融市场、生物学等。
本文将介绍随机过程的基本概念和特征,并探讨其在实际中的应用。
正文:1. 随机过程的定义1.1 随机过程的基本概念1.2 随机变量与随机过程的关系1.3 不同类型的随机过程(如离散随机过程、连续随机过程等)2. 随机过程的特征2.1 随机过程的时间域特征2.2 随机过程的统计特征2.3 随机过程的独立性和相关性2.4 随机过程的平稳性2.5 随机过程的马尔可夫性质3. 随机过程的应用3.1 通信系统中的随机过程3.2 金融市场中的随机过程3.3 生物学中的随机过程3.4 物理学中的随机过程3.5 工程控制中的随机过程4. 随机过程的建模和分析方法4.1 马尔可夫链模型4.2 随机演化方程模型4.3 随机微分方程模型4.4 随机过程的仿真方法4.5 随机过程的参数估计方法5. 随机过程的未来发展5.1 随机过程在人工智能中的应用5.2 随机过程在时空数据分析中的应用5.3 随机过程在大数据分析中的应用5.4 新兴领域中的随机过程研究5.5 随机过程理论与实际应用的结合总结:本文介绍了随机过程的定义、特征和应用,并讨论了随机过程的建模和分析方法。
随机过程作为概率论和数学统计学的重要分支,具有广泛的应用前景。
随着人工智能和大数据分析的发展,随机过程在各个领域中的应用将进一步扩展。
值得期待的是,未来随机过程理论和实际应用的结合将推动该领域的进一步发展。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例5.利用掷一枚硬币的试验定义一个随机过程
X
(t)
cos t ,出现正面
2t,
出现反面
0 t
称{Xt,t=0,1,2,….,} 是随机过程.
以上4个例子的共同特点是: 对某参数集中的任意一个参数t,就有一个 随机变量X(t)与之对应.
随机过程定义
设(Ω,F,P)为一概率空间,T为一参数集,T R,
若对每一 t ∈T,均有定义在(Ω,F,P)上的一个 随机变量X(ω,t),(ω∈Ω)与之对应,
1, x1 3
2x2 3
( x1 2x2 )
例4.利用重复掷硬币的试验定义一个随机过程
X
(t)
cos t ,出现正面
2t,
出现反面
0 t
出现正面与反面的概率相等.
⑴ 求X(t)的一维分布函数F(1/2; x),F(1; x).
⑵ 求X(t) 的二维分布函数F(1/2,1; x1,x2).
E(A Bt1)(A Bt2 ) 1 t1t2
所以协方差矩阵为
M 11tt11t22
1 t1t2 1 t22
而( X(t1), X(t2) ) 的均值向量为 μ=(0, 0) 所以该S.P.的二维分布为
(X (t1) X (t2)) ~ N(, M ),t1 0,t2 0
3.对每一个确定的ω0∈Ω,X(ω0,t)是定义在T上的普通 函数. 记为 x(ω0,t), 称为为随机过程的一个样本函数. 也称轨道或实现.样本函数的图形称为样本曲线.
X(t)
例1的样本曲线与状态
状态X(t0)=4
样本曲线x1(t) x1(t)
状态X(t0)=5
t
样本曲线x2(t) x2(t)
t t0 状态空间S={0,1,2,….}, T=[0,+∞)
解 对任意的t≥0, X(t)=A+Bt, 有题意知X(t)是正态分布. 又 E[X(t)]=0, D[X(t)]=1+t2
所以S.P.的一维分布为X(t) ~N(0,1+t2)
又对任意的t1≥0, t2≥0, X(t1)=A+Bt1 ~N(0,1+t12), X(t2)=A+Bt2 ~N(0,1+t22),
F (t1,t2; x1, x2)=P(X(t1) ≤x1, X(t2) ≤x2 ), x1, x2∈R
为随机过程{X(t),t∈T}的二维分布函数.
3. n维分布函数
对任意固定的t1,t2, …,tn∈T, X (t1) ,X (t2),…, X (tn)为n个随机变量.称其联合分布函数
F (t1,t2 ,…,tn ; x1, x2,…, xn) = P(X(t1) ≤x1, X(t2) ≤x2 … X(tn) ≤xn )
4
4 2
由于函数x 2 V的反函数为V h(x) 2x, 2
其导数为h(x) 2,则利用公式
f
X(
3 4
)
(
x)
fV
(h(
x)) 0
h(
x)
0 h(x) 1 其它
2
0
2
0
0 2x 1 其它
2 x0 2 其它
例3. 设S.P.X(t) Acost,t 0其中A具有以下概率分布
P(A i) 1 ,i 1,2,3. 3
试求 (1)该S.P.的一维分布函数 F( , x), F( , x)
4
2
(2)该S.P.的二维分布函数
F (0,
3
; x1, x2 )
解(1)Q X ( ) Acos 2 A,
则称X(ω,t)为(Ω,F,P)上的一个随机过程(S.P.)
记{X(ω,t), ω∈Ω,t∈T},
简记{X(t),t∈T},或X(t).
T称为参数集或参数空间, t称为参数,一般表 示时间或空间. 参数集通常有以下形式: ⑴ T={0,1,2,…}或 T= {…-2,-1,0,1,2,…} ⑵ T=[a,b],其中a 可以为-∞, b可以为+∞.
例2 的样本曲线与状态
X(t) X(t) Acos(t )
状态X(t0)
样本曲线x1(t)
t0
状态X(t0)
t 样本曲线x2(t)
状态空间S=[-A,A],参数集T=[-∞,+ ∞]
X(t)
例3 的样本曲线与状态
70
60
50
状态X(t0)=40
40
30
状态X(t0)=25
20
状态X(t0)=18
随机过程是概率论的深入和发展. 它是研究客观世界中随机演变过程的规律性的 学科.
随机过程的理论与方法在自动控制、雷达与通信、 生物工程、天文气象、地质能源、社会科学及工 程技术、经济管理等许多领域有着极为广泛的应 用。
课程任务
掌握随机过程的基本概念.
掌握随机过程的基本理论和分析方法.
具备处理随机现象的思想与方法.
x1 x2,…, xn ∈R 为随机过程{X(t),t∈T}的n维分布函数.
有限维分布函数族定义
称随机过程{X(t),t∈T}的一维分布函数,二维 分布函数,…,n维分布函数,…,的全体 为随机 过程的有限维分布函数族.
注: 有限维分布函数族能够描述随机过程的 统计特性.
有限维分布函数族的性质
对称性 设i1,i2, ,in是1,2, , n的任意一个排列,则
具有应用随机过程的理论和方法来分析问题和 解决问题的能力.
基本内容
随机过程基本概念 随机分析 平稳过程 马尔科夫过程(链)
教材 《随机过程》张卓奎 陈慧婵 西安电子科技大学出版社 2003 《随机过程同步学习指导》 张卓奎 陈慧婵
西安电子科技大学出版社 2004
参考教材 1.《随机过程》毛用才 胡奇英 西安电子科技大学出版社 1998 2.《随机过程理论》 周荫清 电子工业出版社 第二版 2006 3.《 An introduction to stochastic processes 》
随机过程 Stochasstic processes
西安电子科技大学 教师宋月
E-mail songyue25@
引言
本课程的研究对象
概率论主要是以一个或有限个随机变量为研究 对象的. 随着科学技术的不断发展,人们发现几乎一切可 观察现象都具有随机性. 必须对一些随机现象的变化过程进行研究.即需 要研究无穷多个随机变量
P(
A
x1,
A 2
x2
)
P( A x1, A 2x2 )
P( A x1) P( A 2x2 )
x1 2x2 x1 2x2
0,
Leabharlann 1,
3 2
,
3
x1 1
1 x1 2 (x1 2x2 ) 或 2 x1 3
2x2 1 1 2x2 2 2 2x2 3
F (ti1 , ti2 , , tin ; xi1 , xi2 , , xin )
F(t1,t2, ,tn; x1, x2, , xn )
相容性 设m<n,则
F(t1,t2, ,tm; x1, x2, , xm ) F(t1,t2, ,tm,tm1, ,tn; x1, x2, , xm,, )
例2. 具有随机初位相的简谐波
X(t) Acos(t )
其中A ω为常数,φ服从[0,2π]上的均匀分布.
由于初位相的随机性,在某时刻t=t0, X(t0)是一个随机变量.
若要观察任一时刻t的波形,则需要用一族随机变量 X(t)描述. 则称{X(t),t∈[0 ,+∞)}为随机过程.
例3.生物群体的增长问题.以Xt表示在时刻t某种 生物群体的个数,则对每一个固定的t,Xt是一 个随机变量.
Edward P.C. kao Thomson 2003
第一章 随机过程的基本概念
● 随机过程的定义及其有限维分布函数族 ● 随机过程的数字特征 ● 几类重要的随机过程
重点 随机过程的定义、数字特征、正态过程、 Poisson过程.
要求(1)准确理解随机过程的定义,熟悉研究 随机过程的方法.
(2)熟练求出样本函数、有限维分布、 数字特征、特征函数.
10
样本曲线x1(t) 样本曲线x2(t)
样本曲线x3(t)
t
0 24 …
t0
状态空间S={0,1,2,….}, T=[0,24,……)
4.根据参数集与状态空间离散与否,随机过程可分为
●离散参数,离散状态的随机过程 (例3) ● 离散参数,连续状态的随机过程 (例4) ● 连续参数,离散状态的随机过程 (例1) ● 连续参数,连续状态的随机过程 (例2) 参数集为离散的随机过程也称为随机序列, 或时间序列.
难点 有限维分布和Poisson过程.
§1 随机过程的定义
例1. 考察 [0,t0]时间内某网站收到的访问次数X(t0), 则X(t0)是一个随机变量.
如果要长时间内该网站的访问次数, 则需要让t 变化起来,即t趋于无穷大,则 X(t)是一族随机变量.
此时X(t) 是与时间有关系的随机变量,称 {X(t), t∈[0,∞)}是随机过程.
即
1 1
( X (t1)
X (t2 )) ( A
B)
t1
t2
由A,B独立知, (A,B)服从二维正态分布
(定理 正态变量的线性变换是正态变量)
page24 定理1.5.3(3)
