正弦三角函数查询表(0°-90°)
角函数表查询

(1)特殊角三角函数值sin0=0sin30=sin45= 二分之根号2sin60=?? 二分之根号3sin90=1cos0=1cos30=?? 二分之根号3cos45= 二分之根号2cos60=cos90=0tan0=0tan30= 三分之根号3tan45=1tan60= 根号3tan90=无cot0=无cot30= 根号3cot45=1cot60= 三分之根号3cot90=0(2)0°~90°的任意角的三角函数值,查三角函数表。
(见下)(3)锐角三角函数值的变化情况(i)锐角三角函数值都是正值(ii)当角度在0°~90°间变化时,正弦值随着角度的增大(或减小)而增大(或减小)余弦值随着角度的增大(或减小)而减小(或增大)正切值随着角度的增大(或减小)而增大(或减小)余切值随着角度的增大(或减小)而减小(或增大)(iii)当角度在0°≤α≤90°间变化时,0≤sinα≤1, 1≥cosα≥0,当角度在0°<α<90°间变化时,tanα>0, cotα>0.“锐角三角函数”属于三角学,是《数学课程标准》中“空间与图形”领域的重要内容。
从《数学课程标准》看,中学数学把三角学内容分成两个部分,第一部分放在义务教育第三学段,第二部分放在高中阶段。
在义务教育第三学段,主要研究锐角三角函数和解直角三角形的内容,本套教科书安排了一章的内容,就是本章“锐角三角函数”。
在高中阶段的三角内容是三角学的主体部分,包括解斜三角形、三角函数、反三角函数和简单的三角方程。
无论是从内容上看,还是从思考问题的方法上看,前一部分都是后一部分的重要基础,掌握锐角三角函数的概念和解直角三角形的方法,是学习三角函数和解斜三角形的重要准备。
附:三角函数值表sin0=0,sin15=(√6-√2)/4 ,sin30=1/2,sin45=√2/2,sin60=√3/2,sin75=(√6+√2)/2 ,sin90=1,sin105=√2/2*(√3/2+1/2) sin120=√3/2sin135=√2/2sin150=1/2sin165=(√6-√2)/4sin180=0sin270=-1sin360=0sin1= sin2= sin3=sin4= sin5= sin6=sin7= sin8= sin9=sin10= sin11= sin12=sin13= sin14= sin15=sin16= sin17= sin18=sin19=0. sin20=0. sin21= sin22= sin23= sin24=sin25= sin26= sin27=sin28= sin29= sin30=sin31= sin32= sin33=sin34= sin35= sin36=0.sin40=0. sin41=0. sin42= sin43= sin44= sin45=sin46= sin47= sin48=sin49= sin50= sin51=sin52= sin53= sin54=sin55= sin56=0. sin57=0. sin58= sin59= sin60=0. sin61= sin62=0. sin63= sin64= sin65=0. sin66= sin67=0. sin68= sin69=0. sin70= sin71= sin72=sin73=0. sin74= sin75=0. sin76=0. sin77=0. sin78= sin79= sin80= sin81=sin82=0. sin83= sin84= sin85= sin86= sin87=0. sin88=0. sin89=0.sin90=1cos1=0. cos2=0. cos3=0. cos4= cos5= cos6=cos7= cos8=0. cos9=cos13=0. cos14=0. cos15=0. cos16= cos17=0. cos18=cos19= cos20= cos21=0.cos22= cos23=0. cos24=cos25=0. cos26= cos27=cos28= cos29= cos30=0.cos31= cos32= cos33=cos34=0. cos35= cos36=cos37= cos38= cos39=cos40= cos41= cos42=cos43= cos44= cos45=cos46= cos47= cos48=cos49=0. cos50=0. cos51=0. cos52= cos53= cos54=0.cos55=0. cos56= cos57=0. cos58= cos59= cos60=cos61= cos62= cos63=0.cos64= cos65= cos66=0.cos67= cos68=0. cos69=cos70=0. cos71= cos72=cos73= cos74= cos75=cos79= cos80= cos81=cos82= cos83= cos84=cos85= cos86= cos87=cos88= cos89=cos90=0tan1= tan2= tan3=tan4= tan5= tan6=tan7= tan8= tan9=tan10= tan11= tan12=tan13=0. tan14= tan15=0. tan16=0. tan17= tan18=tan19= tan20= tan21=0.tan22=0. tan23=0. tan24=0. tan25=0. tan26=0. tan27=0. tan28= tan29= tan30=0.tan31=0. tan32=0. tan33=0. tan34=0. tan35=0. tan36=0. tan37= tan38= tan39=0.tan40=0. tan41=0. tan42=0. tan43= tan44=0. tan45=0. tan46= tan47= tan48=tan49= tan50= tan51=tan52= tan53=1. tan54=tan55= tan56=1. tan57=1.tan58=1. tan59=1. tan60=1.tan61=1. tan62=1. tan63=tan64= tan65= tan66=tan67= tan68=2. tan69=2.tan70=2. tan71= tan72=tan73=3. tan74= tan75=3.tan76= tan77= tan78=tan79= tan80= tan81=tan82= tan83= tan84=tan85= tan86= tan87=tan88= tan89=tan90=无取值容量620KW,功率因数,视在功率542KVA,无功功率应该是多少?有公式吗?悬赏分:0 - 离问题结束还有5 天22 小时无功功率是怎样算出来的?提问者:2007xinwei2007 - 经理四级视在功率=(有功功率的平方+无功功率的平方)开根号有功功率=视在功率×功率因数在本计算中P有功=S视在×cosφ=542×=Q无功=√(542×542-×=或者根据cosφ求出sinφ 得出φ=37 sinφ=Q=S× sinφ=542×=回答者:womyn5 - 千总五级7-3 17:59。
0到90度的特殊三角函数值表

0到90度的特殊三角函数值表
(原创版)
目录
1.特殊三角函数值表的定义和意义
2.0 到 90 度的正弦、余弦、正切函数值
3.记忆方法和应用场景
正文
【1.特殊三角函数值表的定义和意义】
特殊三角函数值表是一个数学工具,用于查找 0 到 90 度之间正弦、余弦、正切等函数的值。
这些值在解决许多实际问题中非常有用,尤其是在工程、物理和数学等领域。
【2.0 到 90 度的正弦、余弦、正切函数值】
在 0 到 90 度的范围内,正弦、余弦和正切函数的值可以通过查表获得。
这些值是固定的,可以通过记忆或查询表格来获得。
- 正弦函数(Sine,sin):在 0 到 90 度的范围内,正弦函数的值从 0 增加到 1,然后减少到 -1,最后回到 0。
- 余弦函数(Cosine,cos):在 0 到 90 度的范围内,余弦函数的值从 1 减少到 0,然后增加到 1,最后回到 0。
- 正切函数(Tangent,tan):在 0 到 90 度的范围内,正切函数的值从 0 增加到无穷大,然后减少到负无穷大,最后回到 0。
【3.记忆方法和应用场景】
记忆这些函数值有多种方法,比如使用记忆口诀或通过图像记忆。
在实际应用中,特殊三角函数值表常用于解决各种计算问题,比如计算角度、计算三角形的边长等。
总的来说,特殊三角函数值表是一个非常有用的数学工具,对于解决许多实际问题非常有帮助。
特殊直角三角形函数表

特殊直角三角形函数表三角函数是数学中重要的概念之一,它在解决几何问题、物理问题和工程问题中起着重要的作用。
在三角函数中,特殊直角三角形是一类具有特殊角度的三角形,其角度值相对简单,具有一些特殊的性质。
本文将为读者提供一张特殊直角三角形函数表,旨在帮助读者更好地理解和应用相关的三角函数。
特殊直角三角形包括正弦三角形、余弦三角形和切线三角形。
下面是它们的函数表:正弦三角形:角度(度)正弦值0° 030° 1/245° √2/260°√3/290° 1余弦三角形:角度(度)余弦值0° 130° √3/245° √2/260° 1/290° 0切线三角形:角度(度)正切值0° 030° √3/345° 160° √390° -从上表可以看出,正弦三角形的正弦值从0到1逐渐增大,而余弦三角形的余弦值则相反,从1逐渐减小到0。
切线三角形的正切值在0°到90°之间是递增的,而在90°时则为无穷大。
这些特殊直角三角形的函数值具有一些规律和性质。
例如,在正弦三角形中,30°、45°和60°三个角的正弦值正好是一个等差数列,这是因为它们的边长比例相同。
同样,在余弦三角形中,这三个角的余弦值也构成一个等差数列。
这些规律和性质在解决各种三角函数问题时具有重要的指导作用。
除了上表中所列举的特殊直角三角形函数值,我们还可以通过基本三角函数的定义和性质推导得出其他角度的函数值。
例如,正弦函数是一个奇函数,因此可以根据角度的正负确定函数值的正负。
余弦函数是一个偶函数,也具有类似的性质。
切线函数则是一个周期为180°的函数。
特殊直角三角形函数表是数学学习和应用中的一项重要工具,它能够帮助我们快速准确地计算和理解三角函数的一些特殊值。
三角函数值对照表
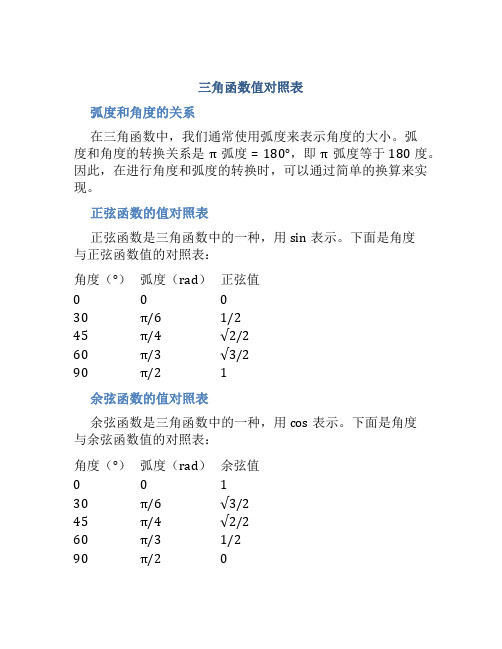
三角函数值对照表
弧度和角度的关系
在三角函数中,我们通常使用弧度来表示角度的大小。
弧
度和角度的转换关系是π 弧度 = 180°,即π 弧度等于180度。
因此,在进行角度和弧度的转换时,可以通过简单的换算来实现。
正弦函数的值对照表
正弦函数是三角函数中的一种,用sin表示。
下面是角度
与正弦函数值的对照表:
角度(°)弧度(rad)正弦值
000
30π/61/2
45π/4√2/2
60π/3√3/2
90π/21
余弦函数的值对照表
余弦函数是三角函数中的一种,用cos表示。
下面是角度
与余弦函数值的对照表:
角度(°)弧度(rad)余弦值
001
30π/6√3/2
45π/4√2/2
60π/31/2
90π/20
正切函数的值对照表
正切函数是三角函数中的一种,用tan表示。
下面是角度与正切函数值的对照表:
角度(°)弧度(rad)正切值
000
30π/6√3/3
45π/41
60π/3√3
90π/2未定义
总结
通过以上对照表可以清晰地显示出不同角度下三角函数的值,对于理解三角函数在不同角度下的表现具有重要意义,也方便我们在数学计算中的应用。
熟练掌握三角函数值的对照表有助于提高数学运算效率,希望对您有所帮助。
常用角度的三角函数值表

常用角度的三角函数值表1. 介绍三角函数是数学中的基本概念之一,它们用来描述在直角三角形中的角度与边长之间的关系。
常用的三角函数包括正弦函数、余弦函数和正切函数。
这些函数在不同的角度下取得不同的值,我们可以通过角度的改变来观察三角函数的变化规律。
2. 正弦函数正弦函数(Sine function)是指一个角所对最长边与斜边的比值。
在三角函数值表中,我们可以列举出一些常用角度对应的正弦函数值,如下所示:角度正弦函数值0°030°0.545°0.70760°0.86690° 1……正弦函数的取值范围在-1到1之间,当角度为0°时,正弦函数的值为0;当角度为90°时,正弦函数的值为1;当角度为180°时,正弦函数的值又变为0,依此类推。
3. 余弦函数余弦函数(Cosine function)是指一个角所对的邻边与斜边的比值。
下面是一些常用角度对应的余弦函数值:角度余弦函数值0° 130°0.86645°0.70760°0.590°0……余弦函数的取值范围也是在-1到1之间,当角度为0°时,余弦函数的值为1;当角度为90°时,余弦函数的值为0;当角度为180°时,余弦函数的值又变为1,以此类推。
4. 正切函数正切函数(Tangent function)是指一个角所对的最长边与邻边的比值。
下面是一些常用角度对应的正切函数值:角度正切函数值0°030°0.57745° 160° 1.73290°无穷大……正切函数的取值范围是无穷大到无穷小,当角度为0°时,正切函数的值为0;当角度接近90°时,正切函数的值趋近于无穷大;当角度为180°时,正切函数的值又回到无穷大的状态。
5. 三角函数图像在二维平面直角坐标系中,我们可以通过绘制三角函数的图像来更直观地理解它们的变化规律。
三角函数表查询

(1)特殊角三角函数值sin0=0sin30=0.5sin45=0.7071 二分之根号2sin60=0.8660 二分之根号3sin90=1cos0=1cos30=0.866025404 二分之根号3cos45=0.707106781 二分之根号2cos60=0.5cos90=0tan0=0tan30=0.577350269 三分之根号3tan45=1tan60=1.732050808 根号3tan90=无cot0=无cot30=1.732050808 根号3cot45=1cot60=0.577350269 三分之根号3cot90=0(2)0°~90°的任意角的三角函数值,查三角函数表。
(见下)(3)锐角三角函数值的变化情况(i)锐角三角函数值都是正值(ii)当角度在0°~90°间变化时,正弦值随着角度的增大(或减小)而增大(或减小)余弦值随着角度的增大(或减小)而减小(或增大)正切值随着角度的增大(或减小)而增大(或减小)余切值随着角度的增大(或减小)而减小(或增大)(iii)当角度在0°≤α≤90°间变化时,0≤sinα≤1, 1≥cosα≥0,当角度在0°<α<90°间变化时,tanα>0, cotα>0.“锐角三角函数”属于三角学,是《数学课程标准》中“空间与图形”领域的重要内容。
从《数学课程标准》看,中学数学把三角学内容分成两个部分,第一部分放在义务教育第三学段,第二部分放在高中阶段。
在义务教育第三学段,主要研究锐角三角函数和解直角三角形的内容,本套教科书安排了一章的内容,就是本章“锐角三角函数”。
在高中阶段的三角内容是三角学的主体部分,包括解斜三角形、三角函数、反三角函数和简单的三角方程。
无论是从内容上看,还是从思考问题的方法上看,前一部分都是后一部分的重要基础,掌握锐角三角函数的概念和解直角三角形的方法,是学习三角函数和解斜三角形的重要准备。
常用三角函数表值查表

常用三角函数表值查表在数学和物理学中,三角函数是一组描述角度和长度关系的函数。
常用的三角函数包括正弦函数(sine)、余弦函数(cosine)和正切函数(tangent)。
这些函数在各种科学和工程领域中经常被使用,因此了解它们的数值表值是很有用的。
本文将提供常用三角函数的表值,帮助读者快速查找常见角度的三角函数值。
以下是常见角度的正弦、余弦和正切值的表格:角度正弦值余弦值正切值0°01030°1/2√3/2√3/345°√2/2√2/2160°√3/21/2√390°10undefined120°√3/2-1/2-√3135°√2/2-√2/2-1150°1/2-√3/2-√3/3180°0-10通过查阅上述表格,我们可以快速获得常见角度的三角函数表值。
需要注意的是,在表格中有一些特殊的角度,如90°和180°,它们的正弦值和余弦值分别为1和-1,而正切值在这些角度处是未定义的。
调用三角函数时,我们通常会使用弧度而不是角度作为输入参数。
下面的表格列出了一些常见角度对应的弧度值:角度弧度0°0 30°π/6 45°π/4 60°π/3 90°π/2 120°2π/3 135°3π/4 150°5π/6 180°π通过将角度转换为弧度,我们可以使用标准的数学函数库来计算三角函数的值。
常用的编程语言通常提供了这些函数,例如Python中的math库和JavaScript中的Math对象。
除了上述常见角度的三角函数值之外,我们还可以通过使用三角函数的性质来计算其他角度的值。
例如,正弦函数是一个周期函数,其周期为360°或2π弧度。
因此,对于角度θ,我们可以使用以下公式计算正弦函数的值:sin(θ) = sin(θ mod 360°)其中。
三角函数表查询

(1)特殊角三角函数值sin0=0sin30=sin45= 二分之根号2sin60=?? 二分之根号3sin90=1cos0=1cos30=?? 二分之根号3cos45= 二分之根号2cos60=cos90=0tan0=0tan30= 三分之根号3tan45=1tan60= 根号3tan90=无cot0=无cot30= 根号3cot45=1cot60= 三分之根号3cot90=0(2)0°~90°的任意角的三角函数值,查三角函数表。
(见下)(3)锐角三角函数值的变化情况(i)锐角三角函数值都是正值(ii)当角度在0°~90°间变化时,正弦值随着角度的增大(或减小)而增大(或减小)余弦值随着角度的增大(或减小)而减小(或增大)正切值随着角度的增大(或减小)而增大(或减小)余切值随着角度的增大(或减小)而减小(或增大)(iii)当角度在0°≤α≤90°间变化时,0≤sinα≤1, 1≥cosα≥0,当角度在0°<α<90°间变化时,tanα>0, cotα>0.“锐角三角函数”属于三角学,是《数学课程标准》中“空间与图形”领域的重要内容。
从《数学课程标准》看,中学数学把三角学内容分成两个部分,第一部分放在义务教育第三学段,第二部分放在高中阶段。
在义务教育第三学段,主要研究锐角三角函数和解直角三角形的内容,本套教科书安排了一章的内容,就是本章“锐角三角函数”。
在高中阶段的三角内容是三角学的主体部分,包括解斜三角形、三角函数、反三角函数和简单的三角方程。
无论是从内容上看,还是从思考问题的方法上看,前一部分都是后一部分的重要基础,掌握锐角三角函数的概念和解直角三角形的方法,是学习三角函数和解斜三角形的重要准备。
附:三角函数值表sin0=0,sin15=(√6-√2)/4 ,sin30=1/2,sin45=√2/2,sin60=√3/2,sin75=(√6+√2)/2 ,sin90=1,sin105=√2/2*(√3/2+1/2) sin120=√3/2sin135=√2/2sin150=1/2sin165=(√6-√2)/4sin180=0sin270=-1sin360=0sin1= sin2= sin3=sin4= sin5= sin6=sin7= sin8= sin9=sin10= sin11= sin12=sin13= sin14= sin15=sin16= sin17= sin18=sin19=0. sin20=0. sin21= sin22= sin23= sin24=sin25= sin26= sin27=sin28= sin29= sin30=sin31= sin32= sin33=sin34= sin35= sin36=0.sin40=0. sin41=0. sin42= sin43= sin44= sin45=sin46= sin47= sin48=sin49= sin50= sin51=sin52= sin53= sin54=sin55= sin56=0. sin57=0. sin58= sin59= sin60=0. sin61= sin62=0. sin63= sin64= sin65=0. sin66= sin67=0. sin68= sin69=0. sin70= sin71= sin72=sin73=0. sin74= sin75=0. sin76=0. sin77=0. sin78= sin79= sin80= sin81=sin82=0. sin83= sin84= sin85= sin86= sin87=0. sin88=0. sin89=0.sin90=1cos1=0. cos2=0. cos3=0. cos4= cos5= cos6=cos7= cos8=0. cos9=cos13=0. cos14=0. cos15=0. cos16= cos17=0. cos18=cos19= cos20= cos21=0.cos22= cos23=0. cos24=cos25=0. cos26= cos27=cos28= cos29= cos30=0.cos31= cos32= cos33=cos34=0. cos35= cos36=cos37= cos38= cos39=cos40= cos41= cos42=cos43= cos44= cos45=cos46= cos47= cos48=cos49=0. cos50=0. cos51=0. cos52= cos53= cos54=0.cos55=0. cos56= cos57=0. cos58= cos59= cos60=cos61= cos62= cos63=0.cos64= cos65= cos66=0.cos67= cos68=0. cos69=cos70=0. cos71= cos72=cos73= cos74= cos75=cos79= cos80= cos81=cos82= cos83= cos84=cos85= cos86= cos87=cos88= cos89=cos90=0tan1= tan2= tan3=tan4= tan5= tan6=tan7= tan8= tan9=tan10= tan11= tan12=tan13=0. tan14= tan15=0. tan16=0. tan17= tan18=tan19= tan20= tan21=0.tan22=0. tan23=0. tan24=0. tan25=0. tan26=0. tan27=0. tan28= tan29= tan30=0.tan31=0. tan32=0. tan33=0. tan34=0. tan35=0. tan36=0. tan37= tan38= tan39=0.tan40=0. tan41=0. tan42=0. tan43= tan44=0. tan45=0. tan46= tan47= tan48=tan49= tan50= tan51=tan52= tan53=1. tan54=tan55= tan56=1. tan57=1.tan58=1. tan59=1. tan60=1.tan61=1. tan62=1. tan63=tan64= tan65= tan66=tan67= tan68=2. tan69=2.tan70=2. tan71= tan72=tan73=3. tan74= tan75=3.tan76= tan77= tan78=tan79= tan80= tan81=tan82= tan83= tan84=tan85= tan86= tan87=tan88= tan89=tan90=无取值容量620KW,功率因数,视在功率542KVA,无功功率应该是多少有公式吗悬赏分:0 - 离问题结束还有 5 天 22 小时无功功率是怎样算出来的提问者: 2007xinwei2007 - 经理四级视在功率=(有功功率的平方+无功功率的平方)开根号有功功率=视在功率×功率因数在本计算中 P有功=S视在×cosφ=542×=Q无功=√(542×542-×=或者根据cosφ求出sinφ 得出φ=37 sinφ=Q=S× sinφ=542×=回答者:womyn5 - 千总五级 7-3 17:59。
三角函数表

(2)0°~90°的任意角的三角函数值,查三角函数表。
(见下)(3)锐角三角函数值的变化情况(i)锐角三角函数值都是正值(ii)当角度在0°~90°间变化时,正弦值随着角度的增大(或减小)而增大(或减小)余弦值随着角度的增大(或减小)而减小(或增大)正切值随着角度的增大(或减小)而增大(或减小)余切值随着角度的增大(或减小)而减小(或增大)(iii)当角度在0°≤α≤90°间变化时,0≤sinα≤1, 1≥cosα≥0,当角度在0°<α<90°间变化时,tanα>0, cotα>0.“锐角三角函数”属于三角学,是《数学课程标准》中“空间与图形”领域的重要内容。
从《数学课程标准》看,中学数学把三角学内容分成两个部分,第一部分放在义务教育第三学段,第二部分放在高中阶段。
在义务教育第三学段,主要研究锐角三角函数和解直角三角形的内容,本套教科书安排了一章的内容,就是本章“锐角三角函数”。
在高中阶段的三角内容是三角学的主体部分,包括解斜三角形、三角函数、反三角函数和简单的三角方程。
无论是从内容上看,还是从思考问题的方法上看,前一部分都是后一部分的重要基础,掌握锐角三角函数的概念和解直角三角形的方法,是学习三角函数和解斜三角形的重要准备。
附:三角函数值表sin0=0,sin15=(√6-√2)/4 ,sin30=1/2,sin45=√2/2,sin60=√3/2,sin75=(√6+√2)/2 ,sin90=1,sin105=√2/2*(√3/2+1/2)sin120=√3/2sin135=√2/2sin150=1/2sin165=(√6-√2)/4sin180=0sin270=-1sin360=0sin1=0.01745240643728351 sin2=0.03489949670250097 sin3=0.05233595624294383 sin4=0.0697564737441253 sin5=0.08715574274765816 sin6=0.10452846326765346sin7=0.12186934340514747 sin8=0.13917310096006544 sin9=0.15643446504023087 sin10=0.17364817766693033 sin11=0.1908089953765448 sin12=0.20791169081775931 sin13=0.22495105434386497 sin14=0.24192189559966773 sin15=0.25881904510252074 sin16=0.27563735581699916 sin17=0.2923717047227367 sin18=0.3090169943749474 sin19=0.3255681544571567 sin20=0.3420201433256687 sin21=0.35836794954530027 sin22=0.374606593415912 sin23=0.3907311284892737 sin24=0.40673664307580015 sin25=0.42261826174069944 sin26=0.4383711467890774 sin27=0.45399049973954675 sin28=0.4694715627858908 sin29=0.48480962024633706 sin30=0.49999999999999994 sin31=0.5150380749100542 sin32=0.5299192642332049 sin33=0.544639035015027sin34=0.5591929034707468 sin35=0.573576436351046 sin36=0.5877852522924731sin37=0.6018150231520483 sin38=0.6156614753256583 sin39=0.6293203910498375 sin40=0.6427876096865392 sin41=0.6560590289905073 sin42=0.6691306063588582 sin43=0.6819983600624985 sin44=0.6946583704589972 sin45=0.7071067811865475 sin46=0.7193398003386511 sin47=0.7313537016191705 sin48=0.7431448254773941 sin49=0.7547095802227719 sin50=0.766044443118978 sin51=0.7771459614569708sin52=0.7880107536067219 sin53=0.7986355100472928 sin54=0.8090169943749474 sin55=0.8191520442889918 sin56=0.8290375725550417 sin57=0.8386705679454239 sin58=0.848048096156426 sin59=0.8571673007021122 sin60=0.8660254037844386sin61=0.8746197071393957 sin62=0.8829475928589269 sin63=0.8910065241883678 sin64=0.898794046299167 sin65=0.9063077870366499 sin66=0.9135454576426009sin67=0.9205048534524404 sin68=0.9271838545667873 sin69=0.9335804264972017 sin70=0.9396926207859083 sin71=0.9455185755993167 sin72=0.9510565162951535 sin73=0.9563047559630354 sin74=0.9612616959383189 sin75=0.9659258262890683 sin76=0.9702957262759965 sin77=0.9743700647852352 sin78=0.9781476007338057 sin79=0.981627183447664 sin80=0.984807753012208 sin81=0.9876883405951378sin82=0.9902680687415704 sin83=0.992546151641322 sin84=0.9945218953682733sin85=0.9961946980917455 sin86=0.9975640502598242 sin87=0.9986295347545738sin88=0.9993908270190958 sin89=0.9998476951563913sin90=1cos1=0.9998476951563913 cos2=0.9993908270190958 cos3=0.9986295347545738cos4=0.9975640502598242 cos5=0.9961946980917455 cos6=0.9945218953682733cos7=0.992546151641322 cos8=0.9902680687415704 cos9=0.9876883405951378cos10=0.984807753012208 cos11=0.981627183447664 cos12=0.9781476007338057cos13=0.9743700647852352 cos14=0.9702957262759965 cos15=0.9659258262890683cos16=0.9612616959383189 cos17=0.9563047559630355 cos18=0.9510565162951535cos19=0.9455185755993168 cos20=0.9396926207859084 cos21=0.9335804264972017cos22=0.9271838545667874 cos23=0.9205048534524404 cos24=0.9135454576426009cos25=0.9063077870366499 cos26=0.898794046299167 cos27=0.8910065241883679cos28=0.882947592858927 cos29=0.8746197071393957 cos30=0.8660254037844387cos31=0.8571673007021123 cos32=0.848048096156426 cos33=0.838670567945424cos34=0.8290375725550417 cos35=0.8191520442889918 cos36=0.8090169943749474cos37=0.7986355100472928 cos38=0.7880107536067219 cos39=0.7771459614569709cos40=0.766044443118978 cos41=0.754709580222772 cos42=0.7431448254773942cos43=0.7313537016191705 cos44=0.7193398003386512 cos45=0.7071067811865476cos46=0.6946583704589974 cos47=0.6819983600624985 cos48=0.6691306063588582cos49=0.6560590289905074 cos50=0.6427876096865394 cos51=0.6293203910498375cos52=0.6156614753256583 cos53=0.6018150231520484 cos54=0.5877852522924731cos55=0.5735764363510462 cos56=0.5591929034707468 cos57=0.5446390350150272cos58=0.5299192642332049 cos59=0.5150380749100544 cos60=0.5000000000000001cos61=0.4848096202463371 cos62=0.46947156278589086 cos63=0.4539904997395468 cos64=0.43837114678907746 cos65=0.42261826174069944 cos66=0.4067366430758004 cos67=0.3907311284892737 cos68=0.3746065934159122 cos69=0.35836794954530015 cos70=0.3420201433256688 cos71=0.32556815445715675 cos72=0.30901699437494745 cos73=0.29237170472273677 cos74=0.27563735581699916 cos75=0.25881904510252074 cos76=0.24192189559966767 cos77=0.22495105434386514 cos78=0.20791169081775923 cos79=0.19080899537654491 cos80=0.17364817766693041 cos81=0.15643446504023092 cos82=0.13917310096006546 cos83=0.12186934340514749 cos84=0.10452846326765346 cos85=0.08715574274765836 cos86=0.06975647374412523 cos87=0.052335956242943966 cos88=0.03489949670250108 cos89=0.0174524064372836cos90=0tan1=0.017455064928217585 tan2=0.03492076949174773 tan3=0.052407779283041196 tan4=0.06992681194351041 tan5=0.08748866352592401 tan6=0.10510423526567646tan7=0.1227845609029046 tan8=0.14054083470239145 tan9=0.15838444032453627tan10=0.17632698070846497 tan11=0.19438030913771848 tan12=0.2125565616700221tan13=0.2308681911255631 tan14=0.24932800284318068 tan15=0.2679491924311227 tan16=0.2867453857588079 tan17=0.30573068145866033 tan18=0.3249196962329063 tan19=0.34432761328966527 tan20=0.36397023426620234 tan21=0.3838640350354158 tan22=0.4040262258351568 tan23=0.4244748162096047 tan24=0.4452286853085361 tan25=0.4663076581549986 tan26=0.4877325885658614 tan27=0.5095254494944288 tan28=0.5317094316614788 tan29=0.554309051452769 tan30=0.5773502691896257 tan31=0.6008606190275604 tan32=0.6248693519093275 tan33=0.6494075931975104 tan34=0.6745085168424265 tan35=0.7002075382097097 tan36=0.7265425280053609 tan37=0.7535540501027942 tan38=0.7812856265067174 tan39=0.8097840331950072 tan40=0.8390996311772799 tan41=0.8692867378162267 tan42=0.9004040442978399 tan43=0.9325150861376618 tan44=0.9656887748070739 tan45=0.9999999999999999 tan46=1.0355303137905693 tan47=1.0723687100246826 tan48=1.1106125148291927 tan49=1.1503684072210092 tan50=1.19175359259421 tan51=1.234897156535051tan52=1.2799416321930785 tan53=1.3270448216204098 tan54=1.3763819204711733 tan55=1.4281480067421144 tan56=1.4825609685127403 tan57=1.5398649638145827 tan58=1.6003345290410506 tan59=1.6642794823505173 tan60=1.7320508075688767 tan61=1.8040477552714235 tan62=1.8807264653463318 tan63=1.9626105055051503 tan64=2.050303841579296 tan65=2.1445069205095586 tan66=2.246036773904215tan67=2.355852365823753 tan68=2.4750868534162946 tan69=2.6050890646938023 tan70=2.7474774194546216 tan71=2.904210877675822 tan72=3.0776835371752526 tan73=3.2708526184841404 tan74=3.4874144438409087 tan75=3.7320508075688776 tan76=4.0107809335358455 tan77=4.331475874284153 tan78=4.704630109478456tan79=5.144554015970307 tan80=5.671281819617707 tan81=6.313751514675041tan82=7.115369722384207 tan83=8.144346427974593 tan84=9.514364454222587tan85=11.43005230276132 tan86=14.300666256711942 tan87=19.08113668772816tan88=28.636253282915515 tan89=57.289961630759144tan90=无取值。
常用的三角函数值对照表

常用的三角函数值对照表
正弦函数(Sine Function)
正弦函数是三角函数中的一种,通常用sin表示。
在数学中,正弦函数的定义如下:
$$ \\sin(\\theta) = \\frac{对边}{斜边} $$
下表是常用角度的正弦值对照表:
角度(度)0°30°45°60°90°
正弦值00.50.7070.8661
余弦函数(Cosine Function)
余弦函数是三角函数中的一种,通常用cos表示。
在数学中,余弦函数的定义如下:
$$ \\cos(\\theta) = \\frac{邻边}{斜边} $$
下表是常用角度的余弦值对照表:
角度(度)0°30°45°60°90°
余弦值10.8660.7070.50
正切函数(Tangent Function)
正切函数是三角函数中的一种,通常用tan表示。
在数学中,正切函数的定义如下:
$$ \\tan(\\theta) = \\frac{对边}{邻边} $$
下表是常用角度的正切值对照表:
角度(度)0°30°45°60°90°
正切值00.5771 1.732∞
以上是常用的三角函数值对照表,这些数值在解决各种数学和物理问题中经常会被用到。
三角函数是数学中非常重要的概念,对于理解波动、振动、周期性等现象具有重要意义。
希望这份对照表能帮助您更好地理解和应用三角函数。
