《概率论与随机过程》第1章习题
清华大学随机过程答案1
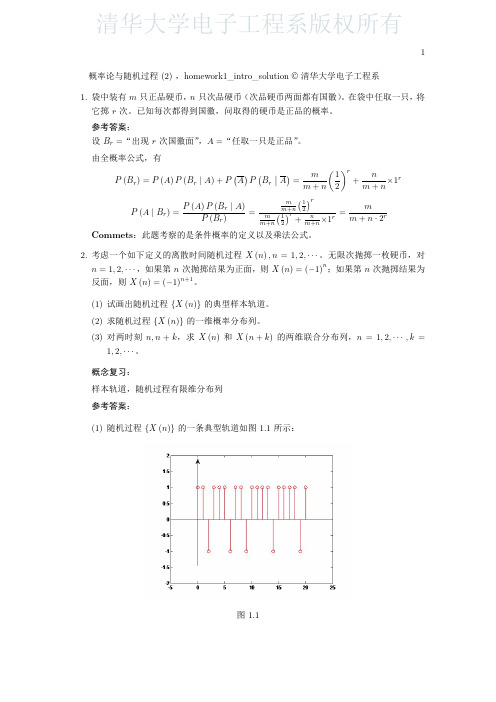
3. 质点在直线上做随机运动,即在 t = 1, 2, 3, · · · 时质点可以在 x 轴上往右或往左做一个 单位距离的随机游动。若往右移动一个单位距离的概率为 p,往左移动一个单位距离的 概率为 q,即 P {ξ (i) = +1} = p,P {ξ (i) = −1} = q,p + q = 1,且各次游动是相互统 ∑n 计独立的。经过 n 次游走,质点所处的位置为 ηn = η (n) = ξi。
参考答案:
(1) V = a 时,一条样本轨道为典型的正弦曲线。 2
(2) ξ (0) = 0,fξ(0)(x) = δ(x);ξ (π/2ω) = V ,其概率密度同 V 一样。
(π) ξ
4ω
=
V
√ 2
,
fξ(
π 4ω
)
(x)
=
√ 2 a
,
0
<
0, 其他
xHale Waihona Puke <√a 2() 5π
ξ 4ω
=
V
−
√ 2
n
pmqn−m = pn − qn。
m=0
m
∑n
解法二:因各次游走是相互统计独立的,则 E [η (n)] = E[ξi] = (p − q)n。
i=1
清华大学电子工程系版权所有
3
(2) 假设 n1 < n2,
Rηη (n1, n2) = E [η (n1) η (n2)] = E {η (n1) [η (n1) + η (n2) − η (n1)]} = E[η (n1)]2 + E [η (n1)] E [η (n2) − η (n1)] = {E [η (n1)]}2 + V ar [η (n1)] + (p − q)2n1 (n2 − n1) = (p − q)2n21 + n1V ar [ξi] + (p − q)2n1 (n2 − n1) = (p − q)2n1n2 + n1[1 − (p − q)2]
概率论与数理统计第一章

第一章测试题一、选择题1•设A, B, C为任意三个事件,则与A 一定互不相容的事件为(A)A B C (B)A B一AC (C)ABC (D)2. 对于任意二事件A和B,与A B二B不等价的是(A)A B (B)B A (C) AB 二(D)AB = ■-A P(A) :: P(A B)C. P(A) P(AB)4 .设0 :: P A ::1 , 0 :. P B -1 ,A事件A与B互不相容C.事件A与B相互对立5 .对于任意两事件A与B ,A P A -P BC. PA -P ABB. P(A)乞P(A B)D. P(A)ZP(AB)P(A B) + P(AB)=1,贝U()B.事件A与B相互独立D.事件A与B互不独立B. P A -P B P ABD. P A PA - P AB6. 若A、B互斥,且P A 0,P B 0,则下列式子成立的是( )A P(AB)=P(A) B. P(BA)>0C. P(AB) = P(A)P(B)D. P(BA)=O7. 设A、B、C 为三个事件,已知P(B A)=0.6,P(C AB )=0.4,则P(BC〔A) =()A 0.3 B. 0.24 C. 0.5 D. 0.218 .设A , B是两个随机事件,且0<P(A)v1 , P(B)>0, P(B| A) = P(B| A),则必有3•设A、B是任意两个事件, A B,P B 0,则下列不等式中成立的是((A) P(A| B) =P(A| B) (B) P(A|B) = P(A|B)()(A) P(A| B) =P(A| B) (B) P(A|B) = P(A|B)(C) P(AB) =P(A)P(B) (D ) P(AB) = P(A)P(B)9•设A,B,C是三个相互独立的随机事件,且0<P(C)v1。
则在下列给定的四对事件中不相互独立的是()(A)LB 与 C ( B)AC 与 C ( C)M TB与 C ( D)AB 与C10•设A, B, C三个事件两两独立,则A, B, C相互独立的充要条件是()(A) A与BC独立 (B) AB与A+C独立 (C) AB与AC独立 (D) A+B与A+C独立11 •将一枚均匀的硬币独立地掷三次,记事件A= “正、反面都出现”,B= “正面最多出现一次”,C= “反面最多出现一次”,则下面结论中不正确的是( ) (A) A与B独立 (B) B与C独立(C) A与C独立 (D) B C与A独立12.进行一系列独立重复试验,每次试验成功的概率为p,则在成功2次之前已经失败3次的概率为()(A)4p(1-p)3(B) C;p2(1-p)3(C) (1-p)3( D) 4p2(1-p)3二、选择题1•设A, B, C 为三个事件,且P(AoB) =0.9,P(AUBOC) =0.97,则P(AB_C) = _________ .2. 设10件产品中有4件不合格品,从中任取两件,已知所取两件产品中有一件是不合格品,另一件也是不合格品的概率为 _______ .3. 随机地向半圆0 ::: y :::•.. 2ax - x2 (a为正常数)内掷一点,点落在半圆内任何区域的概率与区域的面积成正比,则原点和该点的连线与x轴的夹角小于二的概率4为______ .4. 设随机事件A, B及其和事件A-B的概率分别是0.4, 0.3, 0.6,若B表示B的对立事件,则积事件AB的概率P(AB) = _______ .5. 某市有50住户订日报,有65:住户订晚报,有85住户至少订这两种报纸(C) P(AB) =P(A)P(B) (D ) P(AB) = P(A)P(B)中的一种,则同时订这两种报纸的住户的百分比是 ________ .6. 三台机器相互独立运转,设第一,第二,第三台机器不发生故障的概率依次为0.9, 0.8, 0.7,则这三台机器中至少有一台发生故障的概率__________ .7. 电路由元件A与两个并联元件B, C串联而成,若A, B, C损坏与否相互独立,且它们损坏的概率依次为0.3, 0.2, 0.1,则电路断路的概率是__________ .8. 甲乙两人投篮,命中率分别为0.7, 0.6,每人投三次,则甲比乙进球多的概率1 i 19. 三人独立破译一密码,他们能单独译出的概率分别为 -,1,-,则此密码被译5 3 4出的概率_____ .10. 设A, B是任意两个随机事件,则P{( A - B)(A - B)(A - B)(A - B)} = _____________ 11已知A、B 两事件满足条件P(AB )=P(AB ),且P(A) = p,则P(B) = ____________1 312.已知P(A)二P(B)二P(C)二,P(AB)二P(BC) =0,P(AC)二,贝U A,B,C 都不发4 16生的概率为___________三、计算题1. 一袋中装有10个球,其中3个黑球7个白球,每次从中任取一球,然后放回,求下列事件的概率:(1) 若取3次,A={3个球都是黑球};⑵若取10次,B={10次中恰好取到3次黑球},C={10次中能取到黑球};(3)若未取到黑球就一直取下去,直到取到黑球为止,D={恰好取3次},E={至少取3次}.2. 有两箱同种类的零件,第一箱内装50只,其中10只一等品,第二箱内装30只,其中18只一等品.今从两箱中任意挑出一箱,然后从该箱中取零件2次, 每次任取一只,作不放回抽样.求(1) 第一次取到的零件是一等品的概率;(2) 已知第一次取到的零件是一等品的条件下,第二次取到的也是一等品的概率.3. 设10件产品中有3件次品,7件正品,现每次从中任取一件,取后不放回.试求下列事件的概率.(1) 第三次取到次品;(2) 第三次才取到次品;(3) 已知前两次没有取到次品,第三次取到次品;4. 从过去的资料得知,在出口罐头导致索赔事件中,有50%是质量问题,30%是数量短缺问题,20%是包装问题。
《随机过程》课后习题解答
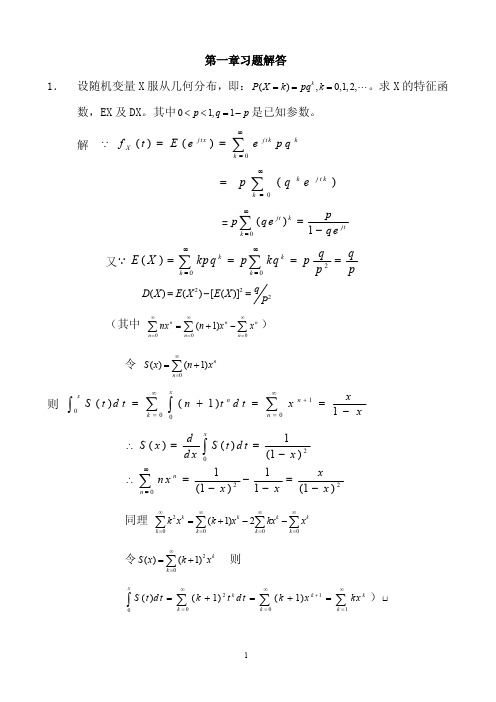
( k 0, 2, n )
1 为一特征函数,并求它所对应的随机变量的分布。 1 t2
n n i
f (t
i 1 k 1
tk )i k
5
=
i 1 k 1
n
n
i k
1 (ti tk )
2
i 1 k 1
n
n
e jti e jti e jti {1 ( jtk )(1 jtk )} n n e jtk e e i k jti = i 1 k 1 e n(1 jtk ) e
1 n n n j ( ti tk ) l ] i k = [e n i 1 k 1 l 1
(2) (3)
其期望和方差; 证明对具有相同的参数的 b 的 分布,关于参数 p 具有可加性。
解 (1)设 X 服从 ( p , b ) 分布,则
f X (t ) e jtx
0
b p p 1 bx x e dx ( p )
bp ( p)
x
0
p 1 ( jt b ) x
i k
1 M 2
0
ti t k } ) ( M 1max{ i , j n
且 f (t ) 连续 f (0) 1 (2) f (t )
f (t ) 为特征函数
1 1 1 1 1 [ ] 2 2 1 t 1 ( jt ) 2 1 jt 1 jt
3
fZ(k)() t (1 )kk! jk (1 jt)(k1)
E (Z k ) 1 (k ) f Z (0) ( 1) k k ! k j
n
随机过程第一章习题答案

随机过程 第一章 习题答案
1.方法一: F (t ; x) P{ X (t ) x} P{ X sin t x} 当t k 时,P{ X (t ) 0} 1,其中k为整数,
k 当t 时,
x x sin t (i)若 sin t 0, F (t ; x) P{ X } ( x) dx sin t x 1 1 1 1 x 2 f (t ; x) ( ) exp{ ( )} sin t sin t sin t 2 2 sin t x x x sin t (ii )若 sin t 0, F (t ; x) P{ X } 1 P{ X } 1 ( x)dx sin t sin t 1 1 1 x 2 f (t ; x) Fx' (t ; x) exp{ ( )} sin t 2 2 sin t 1 1 x 2 f (t ; x) exp{ ( ) }, k 为整数。 2 sin t 2 sin t
时,k为整数,有 X
一维分布密度为:f (t ; x) 当t= k
时,k为整数,有P{ X (t ) 0} 1
1 1 Xt x}=P{e } e Xt x 1 1 1 =P{Xt ln }=P{Xt ln x}=P{X ln x}=1-P{X ln x} x t t 1 11 1 1 f (t ; x) Fx' (t ; x) f ( ln x)( ) f ( ln x) t t x tx t 2.F(t;x)=P{X(t) x}=P{e Xt x}=P{
方法二: X N(0,1) EX=0,EX 2 =DX=1 EX(t)=E(Xsin t)=sin tEX 0 k N(0 , sin 2 t) 1 1 x 2 exp{ ( ) }, x 2 sin t 2 sin t DX (t ) D(Xsin t) (sin t) 2 DX sin 2 t 当t
概率论与随机过程第1章习题

《概率论与随机过程》第1章习题(总5页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--《概率论与随机过程》第一章习题1. 写出下列随机试验的样本空间。
(1) 记录一个小班一次数学考试的平均分数(设以百分制记分)。
(2) 同时掷三颗骰子,记录三颗骰子点数之和。
(3) 10只产品中有3只是次品,每次从其中取一只(取出后不放回),直到将3只次品都取出,记录抽取的次数。
(4) 生产产品直到得到10件正品,记录生产产品的总件数。
(5) 一个小组有A ,B ,C ,D ,E5个人,要选正副小组长各一人(一个人不能兼二个职务),观察选举的结果。
(6) 甲乙二人下棋一局,观察棋赛的结果。
(7) 一口袋中有许多红色、白色、蓝色乒乓球,在其中任意取4只,观察它们具有哪几种颜色。
(8) 对某工厂出厂的产品进行检查,合格的盖上“正品”,不合格的盖上“次品”,如连续查出二个次品就停止检查,或检查4个产品就停止检查,记录检查的结果。
(9) 有A ,B ,C 三只盒子,a ,b ,c 三只球,将三只球装入三只盒子中,使每只盒子装一只球,观察装球的情况。
(10)测量一汽车通过给定点的速度。
(11)将一尺之棰折成三段,观察各段的长度。
2. 设A ,B ,C 为三事件,用A ,B ,C 的运算关系表示下列事件。
(1) A 发生,B 与C 不发生。
(2) A 与B 都发生,而C 不发生。
(3) A ,B ,C 都发生。
(4) A ,B ,C 中至少有一个发生。
(5) A ,B ,C 都不发生。
(6) A ,B ,C 中至多于一个发生。
(7) A ,B ,C 中至多于二个发生。
(8) A ,B ,C 中至少有二个发生。
3. 设{}10,2,1, =S ,{}4,3,2=A ,{}5,4,3=B ,{}7,6,5=C ,具体写出下列各等式 (1)B A 。
(2)B A ⋃。
(3)B A 。
浙江大学《概率论、数理统计与随机过程》课后习题答案第一章

1解:该试验的结果有9个:(0,a ),(0,b ),(0,c ),(1,a ),(1,b ),(1,c ),(2,a ),(2,b ),(2,c )。
所以,(1)试验的样本空间共有9个样本点。
(2)事件A 包含3个结果:不吸烟的身体健康者,少量吸烟的身体健康者,吸烟较多的身体健康者。
即A 所包含的样本点为(0,a ),(1,a ),(2,a )。
(3)事件B 包含3个结果:不吸烟的身体健康者,不吸烟的身体一般者,不吸烟的身体有病者。
即B 所包含的样本点为(0,a ),(0,b ),(0,c )。
2、解 (4)(1)ABBC AC 或ABC ABC ABC ABC ; (5)(2)ABBC AC (6)(提示:题目等价于A ,B ,C 至少有2个发生,与(1)相似); (7)(3)ABC ABC ABC ;(8)(4)AB C 或ABC ;(9)(提示:A ,B ,C 至少有一个发生,或者A B C ,,不同时发生);3(1)错。
依题得,但,故A 、B 可能相容。
(2)错。
举反例 (3)错。
举反例 (4)对。
证明:由,知,即A 和B 交非空,故A 和B 一()()()()0=-+=B A p B p A p AB p 空集≠B A ()6.0=A p ()7.0=B p ()()()()()3.03.1>-=-+=B A p B A p B p A p AB p定相容。
4、解(1)因为A B ,不相容,所以A B ,至少有一发生的概率为:()()()=0.3+0.6=0.9P A B P A P B =+(2) A B , 都不发生的概率为:()1()10.90.1P A B P A B =-=-= ;(3)A 不发生同时B 发生可表示为:AB ,又因为A B ,不相容,于是()()0.6P A B P B == ;5解:由题知,. 因得,故A,B,C 都不发生的概率为.6、解 设A ={“两次均为红球”},B ={“恰有1个红球”},C ={“第二次是红球”} 若是放回抽样,每次抽到红球的概率是:810,抽不到红球的概率是:210,则 (1)88()0.641010P A =⨯=; ()3.0=BC AC AB p ()05.0=ABC P ()()()()()ABC p BC p AC p AB p BC AC AB p 2-++= ()()()()4.023.0=+=++ABC p BC p AC p AB p ()()C B A p C B A p -=1()()()()()()()()[]ABC p BC p AC p AB p C p B p A p +++-++-=1()05.04.02.11+--=15.0=(2)88()210.321010P B =⨯⨯-=(); (3)由于每次抽样的样本空间一样,所以:8()0.810P C == 若是不放回抽样,则(1)2821028()45C P A C ==;(2)118221016()45C C P B C ==; (3)111187282104()5A A A A P C A +==。
随机过程第一章习题解答

第一章习题解答1. 设随机变量X 服从几何分布,即:(),0,1,2,k P X k pq k ===。
求X 的特征函数,EX 及DX 。
其中01,1p q p <<=-是已知参数。
解()()jtxjtk k X k f t E ee pq ∞===∑ 0()k jtkk p q e∞==∑ =0()1jt kjt k pp qe qe∞==-∑ 又20()kk k k q q E X kpq p kq pp p∞∞======∑∑ 222()()[()]q D X E X E X P =-=(其中 00(1)nnn n n n nxn x x ∞∞∞====+-∑∑∑)令 0()(1)n n S x n x ∞==+∑则 1000()(1)1xxnn k n x S t dt n tdt xx∞∞+===+==-∑∑⎰⎰ 202201()()(1)11(1)1(1)xn n dS x S t dt dxx xnx x x x ∞=∴==-∴=-=---⎰∑同理 2(1)2kkkk k k k k k x k x kx x ∞∞∞∞=====+--∑∑∑∑令20()(1)k k S x k x ∞==+∑ 则211()(1)(1)xkk k k k k S t dt k t dt k xkx ∞∞∞+====+=+=∑∑∑⎰)2、(1) 求参数为(,)p b 的Γ分布的特征函数,其概率密度函数为1,0()0,0()0,0p p bxb x e x p x b p p x --⎧>⎪=>>Γ⎨⎪≤⎩(2) 其期望和方差;(3) 证明对具有相同的参数的b 的Γ分布,关于参数p 具有可加性。
解 (1)设X 服从(,)p b Γ分布,则10()()p jtxp bxX b f t ex e dx p ∞--=Γ⎰ 1()0()p p jt b x b x e dx p ∞--=Γ⎰101()()()()(1)p u p p p p p b e u b u jt b x du jt p b jt b jt b∞----==Γ---⎰ 10(())x p p e x dx ∞--Γ=⎰ (2)'1()(0)X p E X f j b∴== 2''221(1)()(0)X p p E X f j b+==222()()()PD XE X E X b ∴=== (4) 若(,)i i X p b Γ 1,2i = 则121212()()()()(1)P P X X X X jt f t f t f t b-++==-1212(,)Y X X P P b ∴=+Γ+同理可得:()()iiP X b f t b jt∑=∑-3、设ln (),()(k Z F X E Z k =并求是常数)。
概率论_第一章_习题

第一章随机事件及其概率1.2设{ EMBED Equation.DSMT4 |A、、表示三个随机事件,试将下列事件用、、表示出来:(1)仅发生;(2)、、都发生;(3)、、都不发生;(4)、、不都发生;(5)不发生,且、中至少有一事件发生;(6)、、中至少有一事件发生;(7)、、中恰有一事件发生;(8)、、中至少有二事件发生;(9)、、中最多有一事件发生。
解:(1);(2);(3);(4);(5);(6);(7);(8)或者;(9)或者或者1.4电话号码由7个数字组成,每个数字可以是中的任一个数字(但第一个数字不能是0),求电话号码是由完全不同的数字组成的概率。
解:基本事件的总数(即7位电话号码的总数)为,而由完全不同的数字组成的电话号码的个数为,于是所求概率1.5把10本书任意地放在书架上,求其中指定的3本放在一起的概率。
解:10本书共有种排法。
指定的三本放在一起有种排法,把这三本看作一个整体与剩下的7本书又有种排法,因此所求的概率1.7在桥牌比赛中,把52张牌任意的分发给东、南、西、北四家(每家13张牌),求北家13张牌中:(1)恰有5张黑桃、4张红心、3张方块、1张草花的概率;(2)恰有大牌A、K、Q、J各一张,其余为小牌的概率。
解:基本事件的总数。
(1)事件(北家的13张牌中恰有5张黑桃,4张红心,3张方块,1张草花)包含的基本事件数,于是,所求的概率。
(2)事件(北家的13张牌中恰有大牌A、K、Q、J各一张,其余为小牌)包含的基本事件数,于是,所求的概率。
1.9同时掷四个均匀的骰子,求下列事件的概率:(1)——四个骰子的点数各不相同;(2)——恰有两个骰子的点数相同;(3)——四个骰子的点数两两相同,但两对的点数不同;(4)——恰有三个骰子的点数相同;(5)——四个骰子的点数都相同。
解:同时投掷四个均匀的骰子,出现的点数共有种。
(1)事件包含的事件个数,于是;(2)事件包含的事件个数,于是;(3)事件包含的事件个数,于是;(4)事件包含的事件个数,于是;(5)事件包含的事件个数,于是1.13某工厂生产的一批产品共100个,其中有5个次品。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《概率论与随机过程》第一章习题1.写出下列随机试验的样本空间。
(1)记录一个小班一次数学考试的平均分数(设以百分制记分)。
(2)同时掷三颗骰子,记录三颗骰子点数之和。
(3)10只产品中有3只是次品,每次从其中取一只(取出后不放回),直到将3只次品都取出,记录抽取的次数。
(4)生产产品直到得到10件正品,记录生产产品的总件数。
(5)一个小组有A,B,C,D,E5个人,要选正副小组长各一人(一个人不能兼二个职务),观察选举的结果。
(6)甲乙二人下棋一局,观察棋赛的结果。
(7)一口袋中有许多红色、白色、蓝色乒乓球,在其中任意取4只,观察它们具有哪几种颜色。
(8)对某工厂出厂的产品进行检查,合格的盖上“正品”,不合格的盖上“次品”,如连续查出二个次品就停止检查,或检查4个产品就停止检查,记录检查的结果。
(9)有A,B,C三只盒子,a,b,c三只球,将三只球装入三只盒子中,使每只盒子装一只球,观察装球的情况。
(10)测量一汽车通过给定点的速度。
(11)将一尺之棰折成三段,观察各段的长度。
2.设A,B,C为三事件,用A,B,C的运算关系表示下列事件。
(1)A发生,B与C不发生。
(2)A与B都发生,而C不发生。
(3)A,B,C都发生。
(4)A,B,C中至少有一个发生。
(5)A,B,C都不发生。
(6)A,B,C中至多于一个发生。
(7)A,B,C中至多于二个发生。
(8)A,B,C中至少有二个发生。
3. 设{}10,2,1, =S ,{}4,3,2=A ,{}5,4,3=B ,{}7,6,5=C ,具体写出下列各等式 (1)B A 。
(2)B A ⋃。
(3)B A 。
(4) BC A 。
(5))(C B A ⋃。
4. 设{}20≤≤=x x S ,⎭⎬⎫⎩⎨⎧≤<=121x x A ,⎭⎬⎫⎩⎨⎧<≤=2341x x B ,具体写出下列各式。
(1)B A ⋃。
(2)B A ⋃。
(3)B A 。
(4) B A 。
5. 设A ,B ,C 是三事件,且41)()()(===C P B P A P ,0)()(==CB P AB P ,1)(=AC P ,求A ,B ,C 至少有一个发生的概率。
6. 在1500个产品中有400个次品,1100个正品,任意取200个。
(1) 求恰有90个次品的概率。
(2) 至少有2个次品的概率。
7.(1)在房间里有500个人,问至少有一个人的生日是10月1日的概率是多少(设一年以365天计算)(2)在房间里有4个人,问至少有二个人的生日在同一个月的概率是多少8. 一盒子中有4只次品晶体管,6只正品晶体管,随机地抽取一只测试,直到4只次品管子都找到为止。
求第4只次品管子在下列情况发现的概率。
(1) 在第5次测试发现。
(2) 在第10次测试发现。
9. 甲、乙位于二个城市,考察这二个城市六月份下雨的情况。
以A ,B 分别表示甲,乙二城市出现雨天这一事件。
根据以往的气象记录已知4.0)()(==B P A P ,28.0)(=AB P ,求)/(B A P ,)/(A B P 及)(B A P ⋃。
10. 已知在10只晶体管中有2只次品,在其中取二次,每次随机地取一只,作不放回抽样,求下列事件的概率。
(1) 二只都是正品。
(2) 二只都是次品。
(3) 一只是正品,一只是次品。
(4) 第二次取出的是次品。
11. 某人忘记了电话号码的最后一个数字,因而随意地拨号,求他拨号不超过三次而接通所需的电话的概率是多少如果已知最后一个数字是奇数,那么此概率是多少12. 某工厂中,机器321,,B B B 分别生产产品总数的25%,35%和40%。
它们生产的产品中分别有5%,4%,2%的次品,将这些产品混在一起,今随机地取一只产品,发现是次品。
问这一次品是机器321,,B B B 生产的概率分别是多少13. 将二信息分别编码为A 和B 传送出去,接收站接收时,A 被误收作B 的概率为,而B 被误收作A 的概率为。
信息A 与信息B 传送的频繁程度为2:1。
若接收站收到的信息是A ,问原发信息是A 的概率是多少14. 如图所示1,2,3,4,5,6表示继电器接点。
假设每一继电器接点闭合的概率为p ,且设各继电器接点闭合与否相互独立。
求L 至R 连通的概率是多少L R15. 对飞机进行三次独立的射击,第一次射击的命中率为,第二次为,第三次为。
飞机击中一次而被击落的概率为,击中二次而被击落的概率为,若被击中三次则飞机必然被击落,求射击三次而击落飞机的概率。
16. 一袋中有5只乒乓球,编号为1,2,3,4,5,在其中同时取三只。
以X 表示取出的三只球中的最大号码,写出随机变量X 的概率质函数。
17. (1)设随机变量X 的概率质函数为!}{k a k X P kλ==,0,,2,1,0>=λ k 为常数,试确定常数a 。
(2) 设随机变量X 的概率质函数为Na k X P ==}{,1N ,,2,1,0k -= ,试确定常数a 。
18. 设事件A 在每一次试验中发生的概率为,当A 发生不少于3次时,指示灯发出信号。
(1)进行了5次独立试验,求指示灯发出信号的概率。
(2)进行了7次独立试验,求指示灯发出信号的概率。
19. 一电话交换机每分钟的呼唤次数服从参数为4的泊松分布,求:(1)每分钟恰有8次呼唤的概率。
(2)每分钟的呼唤次数大于10的概率。
20. 设随机变量X 的分布函数为⎪⎩⎪⎨⎧<≥-=-.0,0,0,1)(x x e x F x (1) 求}3{},2{>≤X P X P , (2)求概率密度)(x f 。
21. 一工厂生产的电子管的寿命X (以小时计)服从参数为160=μ,σ的正态分布,若要求80.0}200120{≥≤<X P ,允许σ最大为多少22. 设随机变量X 的概率质函数为求2X Y =的概率质函数。
23. 设X 的概率密度为⎪⎩⎪⎨⎧<<=其它,00,2)(2ππx x x f ,求sinX Y =的概率密度。
24. 设随机变量(X ,Y )的概率密度为⎪⎩⎪⎨⎧≤≤≤≤+=其它.,0,20,10,3),(2y x xy x y x f 求}1{≥+Y X P 。
25. 设X 和Y 是两个相互独立的随机变量,其概率密度分别为⎩⎨⎧≤≤=其它.,0,10,1)(x x f X ⎪⎩⎪⎨⎧≤>=-.000)(y ,,y ,e y f y Y 试求随机变量Z=X+Y 的概率密度。
26. 设随机变量(X ,Y )的概率密度为),2exp(21),(2222σπσy x y x f +-=+∞<<∞-+∞<<-∞y x ,。
求22Y X Z +=的概率密度。
27. 设某种型号的电子管的寿命(以小时计)近似地服从)20,160(2N 分布,随机地选取4只,求其中没有一只寿命小于180 小时的概率。
28. 设随机变量X 的概率质量函数为求)(),(),(53X E X E X E 22+。
29. 设X 服从二项分布,其概率质量函数为{}.10.,,2,1,0,)1(<<=-⎪⎪⎭⎫ ⎝⎛==-p n k p p k n k X P k n k 求)(X E 和)(X D 。
30. 设X 服从泊松分布,其概率质量函数为{}.0,,2,1,0,!>===-λλλk k e k X P k 求)(X E 和)(X D 。
31. 设X 服从均匀分布,其概率密度函数为⎪⎩⎪⎨⎧<<-=,其它0,,1)(,b x a a b x f 求)(X E 和)(X D 。
32. 设X 服从正态分布,其概率密度函数为()+∞<<∞->⎥⎥⎦⎤⎢⎢⎣⎡-=x x f ,02-x exp 21)(22σσμσπ,。
求)(X E 和)(X D 。
33. 有3只球,4只盒子,盒子的编号为1,2,3,4。
将球独立地,随机地放入4只盒子中去。
以X 表示其中至少有一只球的盒子的最小号码(例如X=3表示第1号,第二号盒子是空的,第三只盒子至少有一只球),试求E [X],D[X]。
34. 对于任意两个随机变量X ,Y ,证明下式成立:(1) ),(2)()()(Y X Cov Y D X D Y X D ++=+;(2) )()()(),(Y E X E XY E Y X Cov -=。
35. 设随机变量X 的概率密度函数为⎪⎩⎪⎨⎧≤>=-000x ,x ,e f(x)x 。
求(1)Y=2X ,(2)x e Y 2-=的数学期望。
36. 设随机变量(X ,Y )的概率密度函数为⎩⎨⎧<<<<=其它,,x,y ,x K,y)f(x,0010 试确定出常数K ,并求)XY (E 。
37. 已知正常男性成人血液中,每一毫升白细胞数平均是7300,均方差是700。
利用契比雪夫不等式估计每毫升含白细胞数在5200~9400之间的概率。
38. 设随机变量X 的概率密度函数为⎪⎩⎪⎨⎧≤>=-000x ,x ,e )x (f x λλ,其中0>λ为常数。
求)(X E 和)(X D 。
39. 设随机变量X 的概率密度函数为⎪⎩⎪⎨⎧≤>-=0,00),2exp()(222x x x x x f σσ,其中0>σ为常数。
求)(X E 和)(X D 。
40. 设随机变量X 的概率质量函数为{}1-==k pq k X P , ,,k 21=。
其中p q ,p -=<<110为常数,则称X 服从参数为p 的几何分布。
试求)(X E 和)(X D 。
41. 设随机变量(X ,Y)的概率密度函数为.202081≤≤≤≤+=y ,x ,)y x ()y ,x (f 。
求)(X E 、)Y (E 、)Y ,X (Cov 。
42. 计算机在进行加法时,对每个加数取整(取为接近于它的整数),设所有的取整误差是相互独立的,且它们都在(,)上服从均匀分布。
(1) 若将1500个数相加,问误差总和的绝对值超过15的概率是多少(2) 几个数可加在一起使得误差总和的绝对值小于10的概率为43. (1)一个复杂的系统,由100个相互独立起作用的部件所组成。
在整个运行期间每个部件损坏的概率。
为了使整个系统起作用,至少必需有85个部件工作,求整个系统工作的概率。
(2)一个复杂的系统,由n 个相互独立起作用的部件所组成。
每个部件的可靠性(即部件工作的概率)为。
且必须至少有80%部件工作才能使整个系统工作,问n 至少为多少才能使系统的可靠性为。
44. 某个单位设置一电话总机,共有200架电话分机。
设每个电话分机有5%的时间要使用外线通话,假定每个分机是否使用外线通话是相互独立的。
