最新ansys屈曲分析练习模型
(ANSYS屈曲分析)

7.1 特征值屈曲分析的步骤 7.2 构件的特征值屈曲分析 7.3 结构的特征值屈曲分析
第7章 结构弹性稳定分析
结构失稳或结构屈曲: 当结构所受载荷达到某一值时,若增加一微小的 增量,则结构的平衡位形将发生很大的改变,这种现 象叫做结构失稳或结构屈曲。 结构稳定问题一般分为两类: ★第一类失稳:又称平衡分岔失稳、分枝点失稳、特 征值屈曲分析。结构失稳时相应的荷载可称为屈曲荷 载、临界荷载、压屈荷载或平衡分枝荷载。 ★第二类失稳:结构失稳时,平衡状态不发生质变, 也称极值点失稳。结构失稳时相应的荷载称为极限荷 载或压溃荷载。 ●跳跃失稳:当荷载达到某值时,结构平衡状态发生 一明显的跳跃,突然过渡到非邻近的另一具有较大位 移的平衡状态。可归入第二类失稳。
7.1 特征值屈曲分析的步骤--查看结果
⑴ 列表显示所有屈曲荷载系数 命令格式:SET,LIST SET栏对应的数据为模态数阶次,TIME/FREQ栏对应的数据 为该阶模态的特征值,即屈曲荷载系数。荷载步均为1,但每个 模态都为一个子步,以便结果处理。 ⑵ 定义查看模态阶次 命令格式:SET,1,SBSTEP ⑶ 显示该阶屈曲模态形状 命令格式:PLDISP ⑷ 显示该阶屈曲模态相对应力分布 命令格式:PLNSOL或PLESOL等。 模态形状归一化处理,位移不表示真实的变形。 直接获取第N阶屈曲模态的特征值(屈曲荷载系数): *get,freqN,mode,N,freq 其中FREQN为用户定义的变量,存放第N阶模态的屈曲荷载系 数,其余为既定标识符。
第7章 结构弹性稳定分析
★结构弹性稳定分析=第一类稳定问题 ANSYS特征值屈曲分析(Buckling Analysis)。 ★第二类稳定问题 ANSYS结构静力非线性分析,无论前屈曲平衡状态 或后屈曲平衡状态均可一次求得,即“全过程分析”。 这里介绍ANSYS特征值屈曲分析的相关技术。在本 章中如无特殊说明,单独使用的 “ 屈曲分析 ” 均指 “ 特 征值屈曲分析”。
ansys 屈曲分析详细过程

KD KG F
非线性屈曲分析的流程图如下:
图 2 非线性屈曲分析流程图
2
3、非线性方程组求解方法 (1)增量法 增量法的实质是用分段线性的折线去代替非线性曲线。增量法求解时将荷载
分成许多级荷载增量,每次施加一个荷载增量。在一个荷载增量中假定刚度矩阵 保持不变,在不同的荷载增量中,刚度矩阵可以有不同的数值,并与应力应变关 系相对应。
QSV QH / (1 y2 ) 和QSP QH y / (1 y2 ) 其中,y=df (x) / dx,当单元足够小时,可采用y y / y
图 3 曲梁均布荷载等效与分解
3
5、问题的描述 矩形截面圆弧拱桥,在梁上受均布荷载,荷载及截面尺寸如图 1 所示,要求
用 ANSYS 进行拱圈的非线性屈曲分析,求极限荷载。本作业进行了圆弧拱的弹 性屈曲分析和非线性屈曲分析,分线性分析时引入初始几何缺陷。
题目:跨径 L=89m,矢跨比 f/L=1/5 的圆弧拱,梁高 h/L=1/30,梁宽 b/L=1/15 求:1.弹性屈曲荷载; 2.非线性极限承载能力。
ansys结构屈曲分析

退出求解器
命令: 命令:finish GUI:close the : solution menu
ANSYS 结构屈曲分析 二 结构屈曲分析的基本步骤
(3)扩展解:无论采取哪种特征值提取方法,如果想要得到屈曲模 )扩展解:无论采取哪种特征值提取方法, 态的形状,就必须执行扩展解。 态的形状,就必须执行扩展解。可以 把扩展解简单理解为将屈曲 模态的形状写入结果文件。具体操作步骤如下: 模态的形状写入结果文件。具体操作步骤如下:
注意二: 注意二: 材料的弹性模量 EX必须定义。
ANSYS 结构屈曲分析 二 结构屈曲分析的基本步骤
(2)获得静力解:与一般静力解类似,但需注意以下几点: )获得静力解:与一般静力解类似,但需注意以下几点:
注意一: 注意一:
必须激活预应力影响。 必须激活预应力影响。
注意二: 注意二:
通常只需施加一个单位荷 载即可。当施加单位荷载 载即可。 时,求解得到的特征值就 表示临界荷载, 表示临界荷载,施加非单 位荷载时, 位荷载时,求解得到的特 征值乘以施加的载荷就得 到临界荷载; 到临界荷载;
• 命令:mxpand,nmode,,,elcalc • GUI:main menu 〉solution 〉loads step opts 〉 expasionpass 〉single modes 〉expand modes
扩展求解
• 命令:solve • GUI:main menu 〉solution 〉solve 〉current LS
列出现在所有的屈曲荷载因子
命令:set,list 命令 GUI: mian menu 〉 general postproc 〉results summary
读取指定的模态来显示屈曲模态形状
AnsysMechanical屈曲分析技术

AnsysMechanical屈曲分析技术1. 屈曲分析的基本概念当受拉杆件的应力达到屈服极限或强度极限时,将引起塑性变形或断裂。
这些是由于强度不足所引起的失效。
在工程中,我们会注意到当细长杆件受压时,表现出与强度失效完全不同的性质。
当杆件受压超过某一临界值时,再增加压力,杆件会产生很大的完全变形,最终折断。
内燃机配气机构中的挺杆,空气压缩机,蒸汽机的连杆等都是这样的受压构件。
日常生活中,我们也有很多这样的经验。
此时如果根据拉压杆件的强度公式进行校核,会发现此时杆件所受的压应力远小于屈服极限或强度极限。
此时,我们说结构丧失了稳定性,属于结构稳定性分析的范畴。
同样,对于薄板结构(如筒仓,钢塔),也同样存在受压载荷作用下的稳定性问题。
稳定性问题根据失稳发生的区域又分为整体稳定性与局部稳定性。
国内外的设计规程规范详细地规定了稳定性设计的技术指标,从结构设计方面保证了结构在稳定性方面的技术要求,如《钢结构设计标准GB50017-2010》、《空间网格结构技术规程JGJ7-2010》等。
对于非标构件,使用有限元校核也提出了明确的方法。
初始缺陷的施加是稳定性分析中一个重要的环节,我们看到《钢结构设计标准GB50017-2010》中给出了确定方法。
试验方法和有限元方法的结合广泛应用在强度设计和稳定性设计中。
2. ANSYS Mechanical屈曲分析下图是一端固定,另一端受压的柱子,当F增加到一个临界值后,此时如果有一个侧向的扰动,柱子顶端会产生很大的横向变形,此时结构处于不稳定状态。
对于理想的无缺陷的杆件,F的临界值对应右图的分支点,对应于ANSYS Mechanical中的特征值屈曲分析。
实际结构中,由于存在制造,安装误差,或者材料局部有缺陷,并不能达到分支点失稳,而是在极限载荷位置即丧失稳定性,此时需要使用ANSYS Mechanical的非线性屈曲分析。
3. ANSYS Mechanical特征值屈曲分析ANSYS Mechanical特征值屈曲是一种形式的线性扰动分析,上游的静力分析模型可以是线性的,也可以是非线性的。
ansys 屈曲分析详细过程

非线性屈曲分析的流程图如下:
图 2 非线性屈曲分析流程图
2
3、非线性方程组求解方法 (1)增量法 增量法的实质是用分段线性的折线去代替非线性曲线。增量法求解时将荷载
分成许多级荷载增量,每次施加一个荷载增量。在一个荷载增量中假定刚度矩阵 保持不变,在不同的荷载增量中,刚度矩阵可以有不同的数值,并与应力应变关 系相对应。
图 4 荷载及拱的几何尺寸示意
几何尺寸: f/L=1/5, H/L=1/30,B/图L=图1图/15
L=89m,f=17.8m,H=2.97m,B=5.93m,R=64.5m
材料性能:拱圈采用 C40 混凝土,弹性模量为 32500MPa,泊松比为 0.3。
在 ANSYS 中进行建模分析,初始荷载为 q=100000kN/m 其过程如下:
0.5
K2
58.9
90.4
93.4
86.7
64.0
根据表 1 查得:
K2 90.4
故其理论弹性屈曲荷载为:
qcr
K2
EI x l3
3.25104 1 5933.33 2966.673
90.4
12 890003
5.38107
N
m
2、拱的弹性屈曲与非线性屈曲 对于一般的特征值屈曲分析,主要是在平衡状态,考虑到轴向力或者中面内
力对弯曲变形的影响,由最小势能原理,结构弹性屈曲分析归结为求解特征值问 题:
KD KG 0
通过特征值分析求得的解有特征值和特征向量,特征值就是临界荷载系数, 特征向量是临界荷载系数对应的屈曲模态。
特征值屈曲分析的流程图如下:
1
图 1 弹性屈曲分析流程图
非线性屈曲分析是考虑结构平衡受扰动(初始缺陷、荷载扰动)的非线性静 力分析,该分析是一直加载到结构极限承载状态的全过程分析,分析中可以综合 考虑材料塑性和几何非线性。结构非线性屈曲分析归结为求解矩阵方程:
ansys屈曲分析

3.1 几何非线性3.1.1 大应变效应一个结构的总刚度依赖于它的组成部件(单元)的方向和单刚。
当一个单元的结点经历位移后,那个单元对总体结构刚度的贡献可以以两种方式改变。
首先,如果这个单元的形状改变,它的单元刚度将改变(图3-1(a))。
其次,如果这个单元的取向改变,它的局部刚度转化到全局部件的变换也将改变(图3-1(b))。
小的变形和小的应变分析假定位移小到足够使所得到的刚度改变无足轻重。
这种刚度不变假定意味着使用基于最初几何形状的结构刚度的一次迭代足以计算出小变形分析中的位移(什么时候使用“小”变形和应变依赖于特定分析中要求的精度等级)。
相反,大应变分析考虑由单元的形状和取向改变导致的刚度改变。
因为刚度受位移影响,且反之亦然,所以在大应变分析中需要迭代求解来得到正确的位移。
通过发出 NLGEOM,ON(GUI路径Main Menu>Solution>Analysis Options),来激活大应变效应。
这种效应改变单元的形状和取向,且还随单元转动表面载荷。
(集中载荷和惯性载荷保持它们最初的方向。
)在大多数实体单元(包括所有的大应变和超弹性单元),以及部分的壳单元中大应变特性是可用的。
在ANSYS/Linear Plus程序中大应变效应是不可用的。
图3-1 大应变和大转动大应变过程对单元所承受的总旋度或应变没有理论限制。
(某些ANSYS单元类型将受到总应变的实际限制──参看下面。
)然而,应限制应变增量以保持精度。
因此,总载荷应当被分成几个较小的步,这可用〔 NSUBST, DELTIM, AUTOTS〕命令自动实现(通过GUI路径 MainMenu>Solution>Time/Frequent)。
无论何时如果系统是非保守系统,如在模型中有塑性或摩擦,或者有多个大位移解存在,如具有突然转换现象,使用小的载荷增量具有双重重要性。
3.1.2 应力-应变在大应变求解中,所有应力─应变输入和结果将依据真实应力和真实(或对数)应变(一维时,真实应变将表示为ε=Ln(l/l) 。
ANSYS WORKBENCH 11.0线性屈曲分析

ANSYS WORKBENCH 11.0培训教程(DS)第七章线性屈曲分析本章概述•在本章中将讲述DS中的线性屈曲分析的应用.–在DS中,进行线性屈曲分析类似于应力分析.–假设用户在此之前已经讨论过第四章线性静力结构分析的内容.•本章所讨论的性能通常适用于ANSYS DesignSpace Entra licenses及更高licenses.–许多本章当中所讨论的选项需要更高级别的licenses,但这些都没有直接的指出.–简谐和非线性静态结构分析在此没有讨论,但是在相关章节当中会有介绍.屈曲分析的背景•许多结构需要估计结构的稳定性。
细长柱、压缩部件、以及真空容器都是需要考虑稳定性的例子.•在不稳定(屈曲)开始时,结构在本质上没有变化的载荷作用下(超过一个很小的动荡)在x方向上的位移{∆x}会有一个很大的改变.F FStable Unstable…屈曲分析的背景•特征值或线性屈曲分析预测的是理想线弹性结构的理论屈曲强度(分歧点).•特征值方程决定了结构的分歧点.教科书上相应的方法近似于线弹性屈曲分析方法.–Euler柱的特征值屈曲方法与经典的Euler方法匹配.…屈曲分析的背景•然而,非理想和非线性行为阻止许多真实的结构达到它们理论上的弹性屈曲强度。
线性屈曲通常产生非保守的结果, 应当谨慎使用.–把屈曲当成苏打水罐:•材料响应是非弹性的。
需要考虑几何非线性的影响,接触也是需要的。
因此这些类型的非线性行为都不被考虑.•在苏打水罐上的小的瑕疵,例如一个小的缺陷,将会影响响应并且使模型不对称.然而,这些小的瑕疵在线性屈曲分析中不予考虑.…屈曲分析的背景•尽管屈曲分析是非保守的,但是也有许多优点:–它比非线性屈曲计算省时,并且应当作第一步计算来评估临界载荷(屈曲开始时的载荷).–线性屈曲分析可以用来作为决定产生什么样的屈曲模型形状的设计工具.•结构可能发生屈曲的方法可以作为设计中的向导…线性屈曲分析基础•对于线性屈曲分析,下面的特征值方法用来得到屈曲载荷乘子λi 和屈曲模态ψi :这个结论在分析中有一些相对的假设:–[K]和[S] 是常量:•假设为线弹性材料行为•应用小变形理论,并且不包括非线性特性•基于载荷{F}的响应是一个线性的关于λi 的函数–附加的约束条件:•不允许非零位移约束或热载荷•在DS 中涉及到应用线性屈曲分析,记住这些假设是很重要的.[][](){}0=+i i S K ψλB. 屈曲分析步骤•线性屈曲分析步骤与线性静力分析很相似,因此不是每个步骤都详细介绍.其中的黄色斜体的步骤是屈曲分析的特殊步骤.–生成几何体–分配材料属性–定义接触(假如需要的话)–定义网格控制(可选择的)–定义载荷和约束–定义屈曲结果–求解模型–查看结果…几何模型和材料属性•与线性静力分析类似,任何DS支持的类型的几何体都可以使用:–实体–壳体(定义适当厚度)–线(定义适当的截面形状)•对于线模型仅有屈曲模态和位移结果是可以得到的.•对于材料特性,最少需要定义杨氏模量和泊松比ANSYS License AvailabilityDesignSpace Entra xDesignSpace xProfessional xStructural xMechanical/Multiphysics x…接触对•屈曲分析中可以定义接触对.但是,由于这是一个纯粹的线性分析,因此接触行为不同于非线性接触类型:•以下各方面需要重点注意:–Pinball 范围将影响一些接触类型–所有非线性接触类型被简化为“绑定”或“不分离”接触.•没有分离的接触在屈曲分析中带有警告,因为它在切向没有刚度.这将产生许多过剩的屈曲模态.如果合适的话,考虑应用绑定接触来代替.ANSYS License AvailabilityDesignSpace Entra DesignSpace x Professional x Initially Touching Inside Pinball Region Outside Pinball Region BondedBondedBonded Free No Separation No Separation No Separation Free RoughBondedFree Free FrictionlessNo SeparationFree FreeContact Type Linear Buckling Analysis…载荷和约束•至少要施加一个能够引起屈曲的结构载荷到模型上:–所有的结构载荷都要乘上载荷系数来决定屈曲载荷.因此不支持不成比例或常值的载荷(参考下一张幻灯片)–允许刚性约束(即无位移约束)–允许无热载荷–仅有压缩的约束是非线性,因此不推荐使用在屈曲分析中•结构可以是全约束–在模型中可以施加刚性位移.确定模型上的约束适当.ANSYS License AvailabilityDesignSpace Entra xDesignSpace xProfessional x…载荷和约束•假如施加常值和成比例的载荷则需要给出特殊的指定.–用户可以重复屈曲分析,调整可变载荷直到载荷乘数为1.0或接近1.0.–讨论一个柱子在自重W O和表面集中力A作用下的例子.可以通过重复计算,调整A的值直到λ= 1.0.ANSYS License AvailabilityDesignSpace Entra xDesignSpace xProfessional x…需求结果•许多屈曲分析的选项与静力分析选项相似.但是当在求解下拉菜单下的屈曲分析工具被选择时DS会分辨并执行屈曲分析:–屈曲工具在求解下拉菜单下增加了另一个菜单.–详细的屈曲菜单允许用户指定屈曲模态的阶数.缺省的时候只计算第一阶屈曲模态.增加模态阶数会增加计算时间.但是,通常只有少数屈曲模态是希望的.ANSYS License AvailabilityDesignSpace Entra xDesignSpace xProfessional x Although most users are only concerned with the first buckling mode, it is generally a good idea to request the first 2 or 3 buckling modes. There may be closely-space buckling modes, so this would tell the user if the model may be susceptible to more than one failure mode.…需求结果•需要求解的结果位于屈曲菜单下:–屈曲分析的模态受控于在屈曲菜单下有详细介绍的模态阶数–应力,应变或某方向的位移等附加结果可以在屈曲下拉菜单下指定•如果已指定,则每阶屈曲模态的应力,应变或位移结果都会得到•假如一个模型的应力和应变已经得到,那么另外的计算也是需要的.–在“Solution”下拉菜单下没有结果直接被指定.ANSYS License AvailabilityDesignSpace Entra xDesignSpace xProfessional xStructural x…求解选项•求解下拉菜单提供了详细的将要执行分析的类型–对于屈曲分析,求解下拉菜单的详细选项通常都不需要改变.•在大多情况下,“Solver Type”通常在默认的“ProgramControlled”选项的左边.它仅仅控制在初始静力分析中的求解器而不是屈曲求解方法.•“Weak springs”也意味着初始的静力分析.•屈曲分析不支持“Large Deflection”.–“Analysis Type”在线性屈曲分析情况下可以显示“Buckling”.ANSYS License AvailabilityDesignSpace Entra xDesignSpace xProfessional x…求解模型•设定好模型以后,可以像其它分析一样选择Slove按钮求解屈曲分析.–对于同一个模型,线性屈曲分析比静力分析要耗费很多时间.这是因为此时静力分析和屈曲分析同时进行.–求解下拉菜单的Worksheet工具条提供了详细的计算输出,包括使用内存的大小以及多少阶模态已经扩展了.–假如在求解完成后应力或应变或再多的屈曲模态需要考虑,那么需要一个新的求解.ANSYS License AvailabilityDesignSpace Entra xDesignSpace xProfessional x…观察结果•求解结束可以观察屈曲的模态–每一阶屈曲模态的的乘子都有详细的描述.载荷乘子与真实载荷的乘积代表临界载荷.–屈曲模态代表相对体积而不是绝对尺寸.但是这些可以用来判定失效的模态的形状.ANSYS License AvailabilityDesignSpace Entra xDesignSpace xProfessional x…观察结果•屈曲载荷乘子(λ)的说明:–下面的塔模型被求解了两次. 首先施加一单位载荷.第二次施加了所希望的载荷(见下页)…观察结果屈曲载荷乘子(λ)的说明Load Unit ad BucklingLo _*λ=λLoadActual ad BucklingLo _=•第一个算例,屈曲载荷乘子(λ)就是屈曲载荷•第二个算例,屈曲载荷乘子(λ)可以解释为安全因子。
ANSYS屈曲分析

/prep7
/title,buckling of a bar with hinged solves
et,1,beam3
r,1,0.25,52083e-7,.5
mp,ex,1,30e6
mp,prxy,1,0.3
n,1
n,11,,100
prod,4,2,,,U2,,,-1,1,1 !2号变量乘-1作为4号变量
/AXLAB,X,U !x轴用U标注,默认为TIME
/AXLAB,Y,F(N) !x轴用F(N)标注,默认为VALUE
/xrange,4 !指定x轴的范围
finish
!特征值屈曲分析(线性)
/solu
antype,buckle !屈曲分析
bucopt,lanb,1 !使用莱布尼兹法扩展模态,提取特征值数为1阶
mxpand,1 !扩展一阶模态
solve
finish
!施加初始扰动
/post1
fill
e,1,2
egen,10,1,1 !复制单元,10为复制次数,包括本身;1节点增量;1复制元素
finish
!静力求解
/solu
antype,static
pstres,on !打开预应力效应
d,1,all
f,11,fy,-1
solve
nlgeom,on !打开大变形
kbc,0 !斜坡载荷
nsubst,100 !定义子步数
arclen,on,2 !采用弧长法,半径最大为2
outres,,1 !控制输出所有子步结果
f,11,fy,-40 !施加载荷40,线性屈曲分析得到预测载荷38.553
基于ANSYS的轴心受压杆屈曲分析(很好很全)

基于ANSYS的轴心受压柱屈曲分析吕辉哈尔滨工程大学航天与建筑工程学院摘要:为了了解和掌握轴心受压柱特征值屈曲和非线性屈曲差异,以及考虑在屈曲分析中划分不同单元数量对分析结果的影响,选取适当的单元数量,利用有限元软件ANSYS对结构进行分析。
初步了解特征值屈曲与非线性屈曲所得结果差异。
在此基础上进行了多例轴心受压柱的仿真模拟分析,同时考虑不同长细比对屈曲分析结果的影响,掌握了长细比变化对轴心受压柱特征值屈曲和非线性屈曲的计算结果的影响规律。
提出工程中应尽量采取非线性屈曲分析,并在分析中采取正确的分析方法。
关键词:ANSYS仿真模拟;轴心受压柱;单元数量;特征值屈曲;非线性屈曲The analysis of axial-compressed column bucklingbased on ANSYSLv HuiHarbin Engineering University, College of Aerospace and Civil EngineeringAbstracts: The finite element software ANSYS is used to understand and master the diffierences between axial-compressed column buckling and nonlinear buckling, and to consider different numbers of modules`s impact on analysis results in buckling analysis, and choose the appropriate element numebrs. The differences of the results of eigenvalue buckling and nonlinear buckling is preliminary understood. Based that, simulation analysis of a number of cases of axial-compressed column is made, meanwhile different slenderness ratio`s impact on buckling analysis is taken into account, so the impact by variable slenderness ratio on the results of axial-compressed column buckling and nonlinear buckling is unterstood. So the nonlinear buckling analysis in the project is proposed,and the right analysis method should be taken.Key words:ANSYS Simulation; axial-compressed column; the number of element; eigenvalue buckling; nonlinear buckling引言:随着计算机的发展人类实现了一个又一个的突破,大大提高了产品开发、设计、分析和制造的效率和产品性能。
ANSYS经典案例在Workbench中实现之薄壁结构的屈曲与后屈曲分析

文章来源:安世亚太官方订阅号(搜索:peraglobal)案例背景屈曲分析对于一个成功的结构设计,尤其是包含壳和梁的结构,是至关重要的。
虽然线性特征值屈曲分析相对直接与简便,但是也有其自身缺点:因为实际屈曲过程是一个非线性(大变形)过程,如果不能考虑结构非线性,分析只能得到近似结果,另外线性屈曲分析对于结构后屈曲分析无能为力。
非线性屈曲分析过程较为复杂,同时可能需要多次尝试才能得到较为可信的结果,但是由于其不存在线性屈曲分析的局限性,所以工程上倾向通过非线性屈曲来评价结构的稳定性。
实际中,工程师很难判断结构究竟何时开始发生屈曲。
从工程和科研角度看,人们在整个屈曲过程中,最感兴趣的阶段其实是结构将要产生大变形,但是尚未产生较大变形的阶段,有时结构甚至还未产生变形,因为此时对应的载荷是结构的临界屈曲载荷。
非线性屈曲分析可以很好得在这方面提供工程意义上的指导。
非线性屈曲分析通过使用以下一些方法,控制整个仿真计算的收敛性,达到用户的工程需求:1 非线性稳定性控制(nonlinearstabilization)该方法可以应对屈曲分析中的局部和整体不稳定性,并且可以与其它非线性控制技术联合使用进行仿真(弧长法除外);2 弧长法该方法只能处理力载荷下的结构整体失稳。
3 将稳态分析处理成“准静态”的动力学问题该方法通过使用动力学效应防止计算发散,但是具体操作较为复杂。
本案例通过承受外部静水压力载荷的周向加强筋圆柱薄壁结构,说明如何通过仿真分析,预测结构的屈曲载荷和后屈曲状态,同时介绍控制非线性屈曲分析中,控制计算收敛性的方法。
问题描述圆柱薄壁的材料为2024-T3铝合金,由五层横截面为Z型的周向加强筋支撑,圆柱薄壁两端由两个厚盖板(厚度为25mm)密封,并分别由一个L型的铆接条加固。
圆柱薄壁承受外部均匀压强,从而使圆柱薄壁上两个Z型加强筋之间的局部屈曲,最终导致结构失效。
尺寸(mm)圆柱薄壁截面半径355.69圆柱薄壁深度431.8圆柱薄壁厚度 1.034盖板半径380盖板厚度25Z型加强筋厚度0.843L型铆接条厚度 1.64Z型加强筋横截面尺寸如下图所示:图1 Z型加强筋横截面形状及尺寸L型铆接条横截面尺寸为19*19mm,厚度为1.64mm。
【ANSYS】屈曲分析

!设置记录结果数,100000 !设置视角 !更改任务名 !进入前处理 !设置单元类型,Shell181,单元类型号,1 !定义实常数,厚度,2.286mm !定义材料密度,2736kg/m3 !定义弹性模量,0.7311GPa !定义泊松比,0.3249 !定义热膨胀系数,22.32e-6 !定义参考温度为,0℃ !建立矩形 !定义线条划分长度,10mm !划分面网格 !选择线,2:2:4 !选择线条上的点 !定义节点边界条件,约束所有自由度 !定义载荷,温度,1℃
!选择静态分析 !打开预应力
!选择屈曲分
ANSYS 圆管屈曲分析实验报告1

圆管屈曲分析实验报告1、问题描述图1为一薄壁圆管,壁厚为0.216m,直径为4m,高度为21.6m。
圆管的材料弹性模量为210Gpa,泊松比为0.3。
圆管两端面受约束,试分析此薄壁圆管侧壁四周受压情况下的屈曲临界载荷。
图1 薄壁圆管模型2、问题分析2.1、什么是模态及本题的模态阶数选取模态是机械结构的固有振动特性,每一个模态具有特定的固有频率、阻尼比和模态振型。
通过模态分析可以得出物体在某一易受影响的频率范围内各阶主要模态的特性,就可以预知结构在此频段内,在外部或内部各种振源作用下实际振动反应。
因此,模态分析是结构动态设计及设备的故障诊断的重要方法。
一个物体有很多固有振动频率(理论上是无穷多个),按照从小到大的顺序,第一个就叫一阶固有频率,以此类推。
模态的阶数对应固有频率阶数。
一般,低阶模态刚度相对比较弱,在同样量级的激励作用下,响应会相对所占的权值大一些,所以工程上低阶模态比较受关注,理论上低阶模态理论也相对成熟。
且用有限元进行模态分析计算,阶数越高,误差越大。
此题中分析对象比较简单,所以选取前5模态进行分析已经满足工程需要。
2.2、网格单元的选取此薄壁圆管由于壁厚远远小于直径,均匀壁厚,材料结构简单,所以单元类型可以选用shell 93—八节点结构壳单元。
2.3、网格划分类型的选取有限元分析的精度和效率与单元的密度和几何形状有密切关系,按照相应的误差准则和网格疏密程度,应该避免网格的畸形,因此,划分网格时,应尽量采用映射网格模式划分。
本题中,圆管形状规则,采取映射网格进行划分。
3、解题步骤3.1、建立工作文件名及工作标题选择Utility Menu→File→Change Jobname ,出现Change Jobname对话框,在Enter new jobname输入栏中输入工作文件名Tube, 点OK完成设置。
选择Utility Menu→File→Change Title,出现Change Title对话框,在输入栏中输入Buckling of a tube, 点OK, 完成设置。
Ansys第21例非线性屈曲分析实例

Ansys第21例⾮线性屈曲分析实例第21例⾮线性屈曲分析实例—悬臂梁本例通过计算悬臂梁的临界载荷,介绍了利⽤ANSYS进⾏⾮线性屈曲分析的⽅法、步骤和过程。
21.1⾮线性屈曲分析过程1.建⽴模型⾮线性屈曲分析的建模过程与其他分析相似,包括选择单元类型、定义单元实常数、定义材料特性、定义横截⾯、建⽴⼏何模型和划分⽹格等。
2.求解(1)进⼊求解器。
(2)指定分析类型。
⾮线性屈曲分析属于⾮线性静⼒学分析。
(3)定义分析选项。
激活⼤变形效应。
(4)施加初始⼏何缺陷或初始扰动。
可以先进⾏线性屈曲分析,将分析所得到的屈曲模态形状乘以⼀个较⼩的系数后作为初始扰动施加到结构上,本例即采⽤该⽅法。
(5)施加载荷。
所施加的载荷应⽐预测值⾼10%⼀21%。
(6)定义载荷步选项。
(7)设置弧长法。
(8)求解。
3.查看结果在POST26时间历程后处理器中,建⽴载荷和位移关系曲线,从⽽确定结构的临界载荷。
21.2问题描述及解析解图21-1 (a)所⽰为⼀悬臂梁,图21-1 (b)为梁的横横截⾯形状,分析其在集中⼒P作⽤下的临界载荷。
已知截⾯各尺⼨分别为H=50mm、h=43mm、B=35mm、b=32mm,梁的长度L=1m。
钢的弹性模量E=2xl011N/m2,泊松⽐p=0.3。
图21-1⼯⼦悬臂梁21.3分析步骤21.3.1改变任务名拾取菜单Utility Menu→File→Change Jobname,弹出如图21-2所⽰的对话框,在“[/FJLNAM]”⽂本框中输⼊EXAMPLE21,单击“OK”按钮。
21.3.2选择单元类型拾取菜单Main Menu→Preprocessor→Element Type→Add/Edit/Delete,弹出如图21-3所⽰的对话框,单击“Add.”按钮,弹出如图21-4所⽰的对话框,在左侧列表中选“Structural Beam”,在右侧列表中选“3 node 189”,单击“OK”按钮,返回到如图21-3所⽰的对话框,单击“Close”按钮。
一个屈曲分析实例
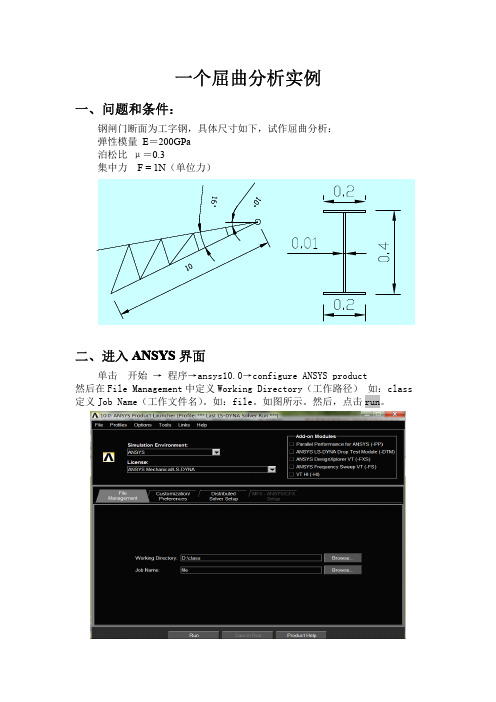
一个屈曲分析实例一、问题和条件:钢闸门断面为工字钢,具体尺寸如下,试作屈曲分析:弹性模量E=200GPa泊松比μ=0.3集中力F=1N(单位力)二、进入ANSYS界面单击开始→程序→ansys10.0→configure ANSYS product然后在File Management中定义Working Directory(工作路径)如:class 定义Job Name(工作文件名)。
如:file。
如图所示。
然后,点击run。
三、定义单元及材料1新建单元类型运行主菜单Preprocessor→Element Type→Add/Edit/Delete(新建/编辑/删除单元类型)命令,接着在对话框中单击“Add”按钮新建单元类型。
2定义单元类型因为beam188单元适合于分析柔性梁结构,支持弹性,蠕变和塑性模型的计算。
先选择单元为beam,接着选择3D2node188,然后单击“OK”按钮确定,完成单元类型的选择。
3关闭单元类型对话框回到单元类型对话框,已经新建了beam单元,单击对话框中“Close”按钮关闭对话框。
4定义截面形状及参数运行主菜单Preprocessor→Sections→Beam→Common sections命令,接着在对话框中sub-type中选择“工”字钢断面,在下面的尺寸中分别填入:W1=0.2,W2=0.2,W3=0.4,t1=0.01,t2=0.01,t3=0.01,点击OK结束。
5设置材料属性运行主菜单Preprocessor→Material props→Material Models(材料属性)命令。
选择材料属性命令后,系统会显示材料属性设置对话框。
6设置杨氏弹性模量与泊松比在材料属性设置对话框右侧依次选择Structural→Linear→Elastic→Isotropic。
完成选择命令后,接着在对话框中EX杨氏弹性模量输入2e11,PPXY泊松比输入0.3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ansys屈曲分析练习模型:边界条件:底端固定几何:长为100mm,截面:10mm×10mm 惯性矩:Izz=833.333材料性质:E=2.0e5MPa,v=0.3分析压力的临界值分析过程:特征值屈曲分析方法:1、建立关键点1(0 0 0),2(0 100 0)2、在关键点1、2之间建立直线3、定义单元类型(Beam3)4、定义单元常数5、定义材料属性6、定义网格大小,指定单元边长为107、划分网格(首先此处应该做一次模态分析,有模态数据文件,后出来才可以看屈曲模态。
)8、定义分析类型(static)9、激活预应力效应。
要进行屈曲分析,必须激活预应力效应。
10、施加位移约束(关键点1固定)11、施加集中荷载,Fy=-1N12、求解13、结束求解,14、重新定义分析类型(Eigen Buckling)15、设置屈曲分析选项,提取1阶模态(菜单路径:Solution-->Analysis Type-->Analysis options16、求解,结束后退出17、解的展开1)设置expansion pass “on”2)设置展开模态为1(Load Step Options>ExpansionsPass>Single Expand>Expand Modes3)重新求解18、查看结果(临界载荷和屈曲模态等)二、非线性分析方法前8步与上述过程相同9、设置分析控制(主要黄色高亮部分区域需要修改)10、施加位移约束(关键点1固定)11、施加集中荷载,Fy=-50000N,Fx=-250N12、求解13、查看变形和位移14、定义时间-历史变量1)进入时间历程后处理器(TimeHist Postproc)2)在弹出的对话框中选择左上角的+号,添加一个监控变量(节点2的Y方向位移)15、查看位移-载荷曲线屈曲分析是一种用于确定结构开始变得不稳定时的临介荷载和屈曲结构发生屈曲响应时的模态形状的技术。
ANSYS提供两种结构屈曲荷载和屈曲模态分析方法:非线性屈曲分析和特征值屈曲分析。
非线性屈曲分析是在大变形效应开关打开的情况下的一种非线性静力学分析,该分析过程一直进行到结构的极限荷载或最大荷载。
非线性屈曲分析的方法是,逐步地施加一个恒定的荷载增量,直到解开始发散为止。
尤其重要的是,要一个足够小的荷载增量,来使荷载达到预期的临界屈曲荷载。
若荷载增量太大,则屈曲分析所得到的屈曲荷载就可能不准确,在这种情况下打开自动时间步长功能,有助于避免这类问题,打开自动时间步长功能,ANSYS程序将自动寻找屈曲荷载。
特征值屈曲分析步骤为:1.建模2.获得静力解:与一般静力学分析过程一致,但必须激活预应力影响,通常只施加一个单位荷载就行了3.获得特征屈曲解:A.进入求解B.定义分析类型C.定义分析选项D.定义荷载步选项E.求解4.扩展解之后就可以察看结果了示例1:! ansys 7.0 有限元分析实用教程! 3.命令流求解! ANSYS命令流:! Eigenvalue BucklingFINISH ! 这两行命令清除当前数据 /CLEAR/TITLE,Eigenvalue Buckling Analysis/PREP7 ! 进入前处理器ET,1,BEAM3 ! 选择单元R,1,100,833.333,10 ! 定义实常数MP,EX,1,200000 ! 弹性模量MP,PRXY,1,0.3 ! 泊松比K,1,0,0 !创建梁实体模型K,2,0,100L,1,2 !创建直线ESIZE,10 ! 单元边长为1mmLMESH,ALL,ALL ! 划分网格FINISH ! 退出前处理!屈曲特征值部分/SOLU !进入求解ANTYPE,STATIC ! 在进行屈服分析之前,ANSYS需要从静态分析提取数据PSTRES,ON ! 屈服分析中采用预应力DK,1,ALL ! 定义约束FK,2,FY,-1 ! 顶部施加载荷SOLVE ! 求解FINISH ! 退出求解/SOLU ! 重新进入求解模型进行屈服分析ANTYPE,BUCKLE ! 屈服分析类型BUCOPT,LANB,1 ! 1阶模态,子空间法SOLVE ! 求解FINISH ! 退出求解/SOLU ! 重新进入求解展开模态EXPASS,ON ! 模态展开打开MXPAND,1 ! 定义需要展开的阶数SOLVE ! 求解FINISH ! 退出求解/POST1 ! 进入通用后处理SET,LIST ! 列出特征值求解结果SET,LAST ! 入感兴趣阶数模态结果 PLDISP ! 显示变形后图形!NonLinear Buckling !非线性分析部分FINISH !这两行命令清除当前数据/CLEAR/TITLE, Nonlinear Buckling Analysis/PREP7 ! 进入前处理ET,1,BEAM3 ! 选择单元MP,EX,1,200000 ! 弹性模量MP,PRXY,1,0.3 ! 泊松比R,1,100,833.333,10 ! 定义实常数K,1,0,0,0 ! 底端节点K,2,0,100,0 ! 顶点L,1,2 ! 连成线ESIZE,1 ! 网格尺寸参数设定LMESH,ALL ! 划分网格FINISH ! 退出前处理/SOLU ! 进入求解ANTYPE,STATIC ! 静态分析类型(非屈服分析) NLGEOM,ON ! 打开非线性大变形设置OUTRES,ALL,ALL ! 选择输出数据NSUBST,20 ! 5个子步加载NEQIT,1000 ! 20步迭代AUTOTS,ON ! 自动时间步长LNSRCH,ON ! 激活线搜索选项/ESHAPE,1 ! 显示二维状态下变形图DK,1,ALL,0 ! 约束底部节点FK,2,FY,-50000 ! 顶部载荷稍微比特征值分析结果大 FK,2,FX,-250 ! 施加水平扰动载荷SOLVE ! 求解FINISH ! 退出求解/POST26 ! 进入时间-历程后处理器RFORCE,2,1,F,Y ! 2# 变量表示力NSOL,3,2,U,Y ! 3# 变量表示y 方向位移XVAR,2 ! 将x 轴显示2#变量PLVAR,3 ! y轴显示3#变量数据/AXLAB,Y,DEFLECTION ! 修改y 轴标签/AXLAB,X,LOAD ! 修改x 轴标签/REPLOT ! 重新显示图形示例2:!悬臂梁受端部轴向压力作用的屈曲分析!先进行静力分析,在进行特征值屈曲分析,最后进行非线性分析!静力分析fini/cle/filname,beam-flexure/tittle,beam-flexure/prep7*set,f1,-1e6 ! 设置轴向压力荷载参数et,1,beam189mp,dens,1,7.85e3 ! 设置材料参数mp,ex,1,2.06e11mp,nuxy,1,0.2sectype,1,beam,I,,2 ! 设置截面参数secoffset,centsecdata,0.15,0.15,0.25,0.015,0.015,0.015,0,0,0,0k,1,0k,2,2.5,0k,3,1.25,1lstr,1,2latt,1,,1,,3,,1lesize,1,,,10lmesh,1/view,1,1,1,1/eshape,1.0dk,1,,,,0,all,fk,2,fx,f1 ! 施加关键点压力finish/soluantype,0eqslv,spar ! 求解器设置稀疏矩阵直接法 pstres,on ! 打开预应力开关solvefinish!特征值屈曲分析/soluantype,1bucopt,lanb,6,0 ! 取前六阶模态分析mxpand,6,0,0,1,0.001solvefinish/post1*do,i,1,6set,ipldisp,i*enddo*get,freq1,mode,1,freqfinish!非线性屈曲分析/config,nres,200 ! 只记录两百步的结果/prep7tb,biso,1,1,2 ! 定义材料非线性tbtemp,0tbdata,,2.0e8,0upgeom,0.01,1,1,'beam-flexure','rst'! 对有限元模型进行一阶模态的位移结果0.01 倍的修改 save,beam-flexure,dbfinishresu,beam-flexure,db/soluantype,0nlgeom,1 ! 打开大变形outres,all,allarclen,1,0 ! 弧长法设置arctrm,l ! 弧长法终止准则达到第一个峰值时终止计算nsubst,200,,,1fk,2,fx,f1*freq1!fk,2,fx,f1*freq1*1.2 ! 将轴向压力值放大,放大系数为第一阶模态的主频solvefinish问题描述一根直的细长悬臂梁,一端固定一端自由。
在自由端施加载荷。
本模型做特征值屈曲分析,并进行非线性载荷和变形研究。
研究目标为确定梁发生分支点失稳(标志为侧向的大位移)的临界载荷。
问题特性参数本例使用如下材料特性:杨氏模量=1.0X10e4psi泊松比=0.0本例使用如下的几何特性:L=100inH=5inB=2in本例的载荷为:P=1lb问题示意图特征值屈曲分析是线性化的计算过程,通常用于弹性结构。
屈曲一般发生在小于特征值屈曲分析得到的临界载荷时。
这种分析比完全的非线性屈曲分析需要的求解时间要少。
用户还可以做非线性载荷和位移研究,这时用弧长法确定临界载荷。
对于更通用的分析,一般要进行崩溃分析。
在模型中有缺陷时一定要做非线性崩溃分析,因为此时模型不会表现出屈曲。
可以通过使用特征值分析求解的特征向量来添加缺陷。
特征向量是最接近于实际屈曲模态在预测值。
添加的缺陷应该比梁的标准厚度要小。
缺陷删除了载荷-位移曲线的突变部分。
通常情况下,缺陷最大不小于10%的梁厚度。
UPGEOM命令在前一步分析的基础上添加位移并更新变形的几何特征。
第一步:设置分析名称和图形选项1.选择菜单Utility Menu>File>Change Title。
2.输入“Lateral Torsional Buckling Analysis”并单击OK。
3.确认PowerGraphics正在运行。
选择菜单Utility Menu>lotCtrls>Style>Hidden-Line Options。
确认PowerGraphics选项打开并单击OK。
4.将Graphical Solution Tracking打开。
选择菜单Main Menu>Solution>-Load Step Opts-Output Ctrls>Grph Solu Track并确认对话框中radio按钮设置为ON。
