1-2常见的晶体结构
第二章 晶体学基本理论

2.7.1 倒易点阵定义
倒易点阵: 是用 a*. b*和c*基矢量描述的三维空间,与a.b.c描
述的正空间互为倒易
倒易点阵满足 a*b=a*c=b*a=b*c=c*.a=c*.b=0---(1) a*a = b*b = c*.c =1--- (2)
第四十二页,共55页
2.7.1 倒易点阵定义
这些空间位向性质完全相同的晶面属于同族等同晶 面,用{hkl}表示
例如:立方晶系中
{ 1 0 0 } ( 1 0 0 ) ( 0 1 0 ) ( 0 0 1 )
{ 1 1 1 } ( 1 1 1 ) ( 1 1 1 ) ( 1 1 1 ) ( 1 1 1 )
第二十八页,共55页
晶向指数的确定
由原点o指向任意一个倒易结点所连接的矢量hakblchkl为整数倒易矢量的方向垂直正点阵的hkl面或平行于晶面的法线hkl晶体点阵经过倒易变换建立相应的倒易点阵晶体中的晶面与其对应倒易点阵结点的关系立方晶系倒易点阵示意图立方晶系倒易点阵100110010001011021020120121101102uvw倒易结点的指数用它所代表的晶面的面指数表示272倒易点阵的性质则正点阵中的晶面在倒易点阵中可以用一个倒易结点表示273倒易点阵的几何意义正点阵中的一组平行晶面hkl相当于倒易点阵中的一个该组晶面间距的倒数
上还有一个阵点,
阵点坐标 000 , 110,101,011
22 2 2 22
第十七页,共55页
强调:晶体结构和空间点阵的区别
空间点阵是晶体中质点排列的几何学抽象,用以 描述和分析晶体结构的周期性和对称性,由于各阵点 的周围环境相同,它只能有14中类型
晶体结构是晶体中实际质点(原子、离子或 分子)的具体排列情况,它们能组成各种类型的 排列,实际存在的晶体结构是无限的
苏州大学-材料科学基础-1-2:晶体结构

1 0,0, 2 1 1 ,0, 2 2
1 1 0, , 2 2 1 1 1 , , 2 2 2 1 0, ,0 2
0,0,0
1 ,0,0 2
1 1 , ,0 2 2
材料科学基础
Fundamental of Materials Science
问题:
① 日常生活中使用的茶杯、餐具是什么材料制作的?材料具有何 种性能才能满足使用要求?
② 电子仪表内不同元件之间需要用材料连接起来,以实现每个元
件的功能,试考虑选择何种材料恰当?
③ 选择飞机机翼材料时应考虑哪些主要的性能?
例3 以NaCl晶胞为例,说明等径球面心立方紧密堆积中
的八面体和四面体空隙的位置和数量,并计算其空间 利用率。
2 化学组成与晶体结构的关系
2.1 质点的相对大小
——内在因素对晶体结构的影响
2.2 配位数与配位多面体
一个原子(或离子)周围同种原子(或异号离子)的数目。 ——原子(或离子)的配位数(CN)
1.000~0.73 CsCl 2 KF RbCl PbBr 0.732~0.41 SrS 4 SrSe MgO NaBr LiCl 0.414~0.22 MgTe 5 BeTe
NaCl型
ZnS型
晶体结构的马德隆常数
结构类 型
A
EL
NaCl
1.7476
CsCl
1.7627
立方 ZnS
1.6381
ZnS NaCl
同种元素结合成晶体时,因其电负性相同,形成非极性共价键; 异种元素结合成晶体时,随着两元素电负性差值增大,键的极性逐渐增强。
1 2 离子键 (%) 1 exp X A X B 4
1-2 第一章 晶体的结构(配位数、几种重要的晶体结构)

体积和配位数(举例 体积和配位数 举例) 举例
• • • • •
简立方 体心立方 面心立方 氯化铯( 氯化铯(CsCl) ) 氯化钠
12
简立方
配位数:? 配位数:6
V= a3
13
体心立方
V = ? /2 a3 原胞? 原胞?
配位数:? 配位数:? 8
14
面心立方
a3 V = ? /4 原胞? 原胞?
8 c/a = ? 3 7
fcc(立方密堆) (立方密堆)
8 c/a = ? 3
A B C ABCABC
8
堆积比( 结构 结构) 堆积比(fcc结构)
a
• fcc:每个晶胞共 个原子 :每个晶胞共4个原子 • 顶角原子:共8个原子,每 个原子, 顶角原子: 个原子 个顶角原子8个晶胞共享 个晶胞共享, 个顶角原子 个晶胞共享, 相当于每个晶胞1个顶角原 相当于每个晶胞 个顶角原 子 • 面上原子:共6个原子,每 面上原子: 个原子, 个原子 2a 个面上原子2个晶胞共享 个晶胞共享, 个面上原子 个晶胞共享, rmax = 4 相当于每个晶胞3个原子 相当于每个晶胞 个原子 4 3 4 × πrmax • 堆积比:硬球体积与整个体 堆积比: 2π 3 堆积比 = = 积之比 3 a 6
c
πa 3 / 3 2a 3 = 2π / 6 堆积比= 堆积比 ?
3 2 V = 6 × ( a )× 4 8 a = 3 3
3
a
2a
3
4 a 刚球所占体积 = (3 + 2 + 1)× π = πa 3 3 2
27
Structures: hcp
• Crystals c/a • He 1.633 • Be 1.581 • Mg 1.623 • Ti 1.586 • Crystals c/a • Zn 1.861 • Co 1.622 • Cd 1.996 • Zr 1.594
常见的晶体结构及其原胞晶胞

§1-2 常见的晶体结构及其原胞、晶胞1) 简单晶体的简单立方(simple cubic, sc) 它所构成的晶格为布喇菲格子。
例如氧、硫固体。
基元为单一原子结构的晶体叫简单晶体。
其特点有: 三个基矢互相垂直(),重复间距相等,为a,亦称晶格常数。
其晶胞=原胞;体积= ;配位数(第一近邻数) =6。
(见图1-7)图1-7简单立方堆积与简单立方结构单元2) 简单晶体的体心立方( body-centered cubic, bcc ) , 例如,Li,K,Na,Rb,Cs,αFe,Cr,Mo,W,Ta,Ba等。
其特点有:晶胞基矢, 并且,其惯用原胞基矢由从一顶点指向另外三个体心点的矢量构成:(见图1-9 b)(1-2)其体积为;配位数=8;(见图1-8)图1-8体心立方堆积与体心立方结构单元图1-9简单立方晶胞(a)与体心立方晶胞、惯用原胞(b)3) 简单晶体的面心立方( face-centered cubic, fcc ) , 例如,Cu,Ag,Au,Ni,Pd,Pt,Ne, Ar, Xe, Rn, Ca, Sr, Al等。
晶胞基矢,并且每面中心有一格点, 其原胞基矢由从一顶点指向另外三个面心点的矢量构成(见图1-10 b):(1-3)其体积=;配位数=12。
,(见图1-10)图1-10面心立方结构(晶胞)(a)与面心立方惯用原胞(b)4) NaCl结构(Sodium Chloride structure),复式面心立方(互为fcc),配位数=6(图1-11 a)。
表1-1 NaCl结构晶体的常数5) CsCl结构(Cesuim Chloride structure),复式简单立方(互为sc),配位数=8(图1-11 b)。
表1-2 CsCl结构晶体的常数图1-11 NaCl结构和CsCl结构6) 金刚石结构(Diamond structure), 两套fcc格子相互沿对角线位移1/4处套合。
常见晶体结构

常见晶体结构
FCC和HCP ➢配位数是一样的 ➢间隙相对大小是一样的 ➢间隙数和原子数比是一样的 ➢堆垛密度(致密度)是一样的
0.155R<100>
常见晶体结构
三、常见晶体结构及其几何特征
4 常见晶体的堆垛方式 任何晶体都可以看成由任给的{hkl}原子面一层一层堆垛而成的。 主要讨论FCC和HCP的密排面的堆垛次序。
➢这里,“最邻近”是就同种元素的原子 相比较而言,而配位数则是一个原子周 围的各元素的最近邻原子数之和。 ➢ 配位数通常用 CN 表示。例如, CN 12 表示配位数为12。
体心立方结构 CN8常见晶 Nhomakorabea结构四 面 体 配 位4
立方 体配
位 8
常见晶体结构
八 面 体 配 位6
十 四 面 体 配 位 12
体中的原子看成是有一定直径的刚球,则紧密系 数可以用刚球所占空间的体积百分数来表示。
以一个晶胞为例,致密度就等于晶胞中原子所 占体积与晶胞体积之比 即: 致密度 =晶胞中原子所占体积之和/晶胞的体积。
=nv/V n: 晶胞原子数 v:每个原子所占的体积 V: 晶胞的体积
常见晶体结构
三、常见晶体结构及其几何特征
1 常见晶体结构 (1)体心立方结构 简写为BCC 例如:V Nb Ta Cr Mo W (2)面心立方结构 简写为FCC 例如:Al Cu Ag Au (3)密排六方结构 简写为HCP 例如:-Ti -Zr -Hf
常见晶体结构
2 几何特征 2.1 配位数 简写CN 一个原子周围最邻近的原子数 ➢ 纯元素金属 这些最邻近的原子到所论原子的距离是相等的 ➢ 多元素晶体 不同元素的最邻近原子到所论原子的距离不一定相等
晶体的结构和结晶

2.晶胞:晶体中有代表性的最胞 的三个棱边的尺 寸 a、b、c。用 埃(Å)表示。
1Å=10-8cm 各棱间的夹角用
、、表示。
晶体的结构和结晶
四、三种典型的晶体结构: 体心立方、面心立方、密排六方。
晶体的结构和结晶
晶体的结构和结晶
晶体的结构和结晶
▪ 密排六方晶格
晶格常数:底面边长 a 和高 c,
c/a=1.633
原子半径:r = 1 a
2 原子个数:6 配位数: 12 致密度:0.74 常见金属: Mg、Zn、 Be、Cd等
晶体的结构和结晶
§ 1-2 实际金属的晶体结构
一、 多晶体结构和亚结构 单晶体:晶体材料内部原子规律排列,位向不发 生改变的晶体。 多晶体:由许多晶格位向不同的小晶体构成的晶 体结构,称为多晶体。
位错上半部分原子受压,下半部分原子受拉。离位 错线越近晶格畸变越大,应力越大。
晶体的结构和结晶
▪ 位错密度:单位体积位错线总长度。
▪ = L/V(cm/cm3或1/cm2)
▪ 金属的位错密度为104~1012/cm2 ▪ 位错对性能的影响:以位错线为中心的管道区周
围晶格都发生了畸变,从而阻碍位错的运动,使 材料的强度提高。由于线缺陷的影响面比点缺陷 大的多,因此对材料性能的影响也大的多。 ▪ 减少或增加位错密度都可以提高金属的强度。
A
C B
D
晶界
晶体的结构和结晶
亚晶界
三、合金的晶体结构
1.几个重要概念:
▪ 合金:由两种或两种以上的金属或金属与非金属 元素组成的具有金属特性的物质叫合金。
▪ 组元:组成合金的独立的最基本的单元(一般是 一种元素或一种稳定的化合物)。
机械工程材料(第二版)课后习题答案

2-1常见的金属晶体结构有哪几种?它们的原子排列和晶格常数有什么特点?-Fe、-Fe、Al、Cu、Ni、Cr、V、Mg、Zn各属何种结构?答:常见晶体结构有3种:⑴体心立方:-Fe、Cr、V⑵面心立方:-Fe、Al、Cu、Ni⑶密排六方:Mg、Zn2---7为何单晶体具有各向异性,而多晶体在一般情况下不显示出各向异性?答:因为单晶体内各个方向上原子排列密度不同,造成原子间结合力不同,因而表现出各向异性;而多晶体是由很多个单晶体所组成,它在各个方向上的力相互抵消平衡,因而表现各向同性。
第三章作业3-2 如果其它条件相同,试比较在下列铸造条件下,所得铸件晶粒的大小;⑴金属模浇注与砂模浇注;⑵高温浇注与低温浇注;⑶铸成薄壁件与铸成厚壁件;⑷浇注时采用振动与不采用振动;⑸厚大铸件的表面部分与中心部分。
答:晶粒大小:⑴金属模浇注的晶粒小⑵低温浇注的晶粒小⑶铸成薄壁件的晶粒小⑷采用振动的晶粒小⑸厚大铸件表面部分的晶粒小第四章作业4-4 在常温下为什么细晶粒金属强度高,且塑性、韧性也好?试用多晶体塑性变形的特点予以解释。
答:晶粒细小而均匀,不仅常温下强度较高,而且塑性和韧性也较好,即强韧性好。
原因是:(1)强度高:Hall-Petch公式。
晶界越多,越难滑移。
(2)塑性好:晶粒越多,变形均匀而分散,减少应力集中。
(3)韧性好:晶粒越细,晶界越曲折,裂纹越不易传播。
4-6 生产中加工长的精密细杠(或轴)时,常在半精加工后,将将丝杠吊挂起来并用木锤沿全长轻击几遍在吊挂7~15天,然后再精加工。
试解释这样做的目的及其原因?答:这叫时效处理一般是在工件热处理之后进行原因用木锤轻击是为了尽快消除工件内部应力减少成品形变应力吊起来,是细长工件的一种存放形式吊个7天,让工件释放应力的时间,轴越粗放的时间越长。
4-8 钨在1000℃变形加工,锡在室温下变形加工,请说明它们是热加工还是冷加工(钨熔点是3410℃,锡熔点是232℃)?答:W、Sn的最低再结晶温度分别为:TR(W) =(0.4~0.5)×(3410+273)-273 =(1200~1568)(℃)>1000℃TR(Sn) =(0.4~0.5)×(232+273)-273 =(-71~-20)(℃) <25℃所以W在1000℃时为冷加工,Sn在室温下为热加工4-9 用下列三种方法制造齿轮,哪一种比较理想?为什么?(1)用厚钢板切出圆饼,再加工成齿轮;(2)由粗钢棒切下圆饼,再加工成齿轮;(3)由圆棒锻成圆饼,再加工成齿轮。
晶体结构的类型分类

晶体结构的类型分类晶体是由原子、离子或分子按照一定的规则排列而成的固体物质。
晶体结构的类型分类是根据晶体中原子、离子或分子的排列方式和空间群的不同来进行的。
不同的晶体结构类型具有不同的物理和化学性质,对于研究晶体的性质和应用具有重要的意义。
本文将介绍几种常见的晶体结构类型分类。
1. 离子晶体结构离子晶体结构是由正负离子按照一定的比例和排列方式组成的晶体。
离子晶体结构可以分为两种类型:离子-离子晶体和离子-极化离子晶体。
离子-离子晶体是由正负离子按照一定的比例排列而成的,如氯化钠晶体。
离子-极化离子晶体是由正负离子和极化离子按照一定的比例排列而成的,如氯化钾晶体。
2. 原子晶体结构原子晶体结构是由原子按照一定的规则排列而成的晶体。
原子晶体结构可以分为两种类型:金属晶体和共价晶体。
金属晶体是由金属原子按照一定的规则排列而成的,如铁晶体。
共价晶体是由非金属原子按照一定的规则排列而成的,如硅晶体。
3. 分子晶体结构分子晶体结构是由分子按照一定的规则排列而成的晶体。
分子晶体结构可以分为两种类型:分子-分子晶体和分子-离子晶体。
分子-分子晶体是由分子按照一定的比例排列而成的,如葡萄糖晶体。
分子-离子晶体是由分子和离子按照一定的比例排列而成的,如氯化铵晶体。
4. 复合晶体结构复合晶体结构是由不同类型的原子、离子或分子按照一定的规则排列而成的晶体。
复合晶体结构可以分为两种类型:复合离子晶体和复合分子晶体。
复合离子晶体是由不同类型的离子按照一定的比例排列而成的,如硫酸铜铵晶体。
复合分子晶体是由不同类型的分子按照一定的比例排列而成的,如葡萄糖-脱氧核糖晶体。
总结:晶体结构的类型分类包括离子晶体结构、原子晶体结构、分子晶体结构和复合晶体结构。
不同类型的晶体结构具有不同的物理和化学性质,对于研究晶体的性质和应用具有重要的意义。
通过对晶体结构的分类和研究,可以深入了解晶体的组成和性质,为晶体材料的设计和应用提供理论基础。
1-2 金属的晶体结构

c
a3
a1
a2
六方晶系晶向指数的确定
解析法: 用三轴坐标先求出待标晶向的三个指数U,V,W, 再利用下列三轴与四轴坐标系晶向指数的关系, 换算出四周坐标系的晶向。
1 u 2U V 3 1 v 2V U 3 t (u v ) w W
3种典型金属的晶体结构
刚球模型 晶胞原子数 原子半径 配位数和 原子堆垛顺序 致密度
体心 立方
CN=8 k=0.68
ABABAB…
面心 立方
CN=12 k=0.74
ABCABC…
密排 六方
CN=12 k=0.74
ABABAB…
四、晶向指数和晶面指数
晶面——晶体结构中,由一系列原子所构成的平面。
晶向——晶体中任意两个原子中心之间连线所指的
八面体间隙rB=0.414rA 有6个 四面体间隙rB=0.225rA 有12个
描述晶胞从以下几个方面: 晶胞中原子的排列方式 (原子所处的位置) 点阵参数 (晶格常数和晶轴间夹角) 晶胞中原子数 原子半径 R(原子的半径)(和点阵常数关系) 配位数 和致密度 密排方向和密排面 晶体结构中间隙 (大小和数量) 原子的堆垛方式
1 1 x , y ,z 1 2 2
[1 1 2]
例一、已知某过原点晶向上一点的坐标为1、1.5、2,
求该直线的晶向指数。 将三坐标值化为最小整数加方括弧得[234]。
[234]
例二、已知晶向指数为[110],
画出该晶向。
找出1、1、0坐标点,连接 原点与该点的直线即所
常见九种典型的晶体结构
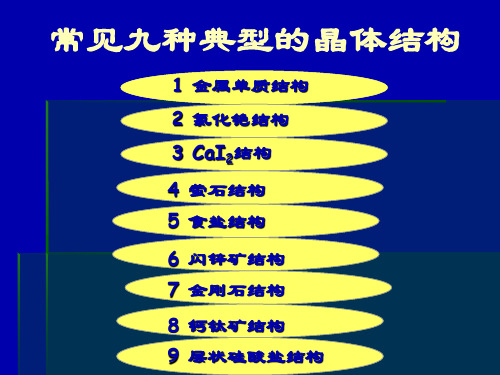
反萤石型结构
球键图
阳离子四面体配位 阴离子立方体配位
反萤石型结构可看作:阴离子做立方最紧密堆积,阳离 子充填在全部的四面体空隙中。
结构类型 物质名称 萤石(CaF2)
萤石型结 氯化锶(SrCl2)
构
氯化钡(BaCl2)
氟化铅(PbF2)
氧化钾(K2O)
反萤石型 结构
氧化钠(Na2O)
氧化锂(Li2O)
闪锌矿的晶体结构:球键图(左)、配位多面体连接图(右)
结构中,S2- 和Zn2+配位数都是4,配位多面体都 是四面体。四面体共角顶相联。
从图可看出,[SZn4] 四面体([ZnS4] 四面体 也是一样)共角顶联成的 四面体基元层与[111]方 向垂直。
由于S2-和Zn2+都呈配位四面体,所以闪锌矿只用一种配位 多面体结构形式表达(S和Zn互换是一样的)。
(Fe3+(Fe2+Fe3+)2O4)。
当结构中四、八面体孔隙被A2+和B3+无序占据时, 叫混合尖晶石结构,代表晶相是镁铁矿(Fe, Mg)3O4。
具有尖晶石型结构的部分物质
Fe3O4 VMn2O4 NiAl2O4 NiGa2O4 Co3S4 TiZn2O4 γ-Fe2O3 LiTi2O4 CoAl2O4 MgGa2O4 NiCo2S4 VZn2O4 MnFe2O4 MnTi2O4 ZnAl2O4 MnGa2O4 Fe2SiO4 SnMg2O4 MgFe2O4 ZnCr2O4 Co3O4 ZnIn2S4 Ni2SiO4 TiMg2O4 Ti Fe2O4 CoCr2O4 GeCo2O4 MgIn2O4 Co2SiO4 WNa2O4 LiMn2O4 CuMn2O4 VCo2O4 CuV2S4 Mg2SiO4 CdIn2O4
机械工程材料(第二版)课后习题答案

2-1常见的金属晶体结构有哪几种?它们的原子排列和晶格常数有什么特点?-Fe、-Fe、Al、Cu、Ni、Cr、V、Mg、Zn各属何种结构?答:常见晶体结构有3种:⑴体心立方:-Fe、Cr、V⑵面心立方:-Fe、Al、Cu、Ni⑶密排六方:Mg、Zn2---7为何单晶体具有各向异性,而多晶体在一般情况下不显示出各向异性?答:因为单晶体内各个方向上原子排列密度不同,造成原子间结合力不同,因而表现出各向异性;而多晶体是由很多个单晶体所组成,它在各个方向上的力相互抵消平衡,因而表现各向同性。
第三章作业3-2 如果其它条件相同,试比较在下列铸造条件下,所得铸件晶粒的大小;⑴金属模浇注与砂模浇注;⑵高温浇注与低温浇注;⑶铸成薄壁件与铸成厚壁件;⑷浇注时采用振动与不采用振动;⑸厚大铸件的表面部分与中心部分。
答:晶粒大小:⑴金属模浇注的晶粒小⑵低温浇注的晶粒小⑶铸成薄壁件的晶粒小⑷采用振动的晶粒小⑸厚大铸件表面部分的晶粒小第四章作业4-4 在常温下为什么细晶粒金属强度高,且塑性、韧性也好?试用多晶体塑性变形的特点予以解释。
答:晶粒细小而均匀,不仅常温下强度较高,而且塑性和韧性也较好,即强韧性好。
原因是:(1)强度高:Hall-Petch公式。
晶界越多,越难滑移。
(2)塑性好:晶粒越多,变形均匀而分散,减少应力集中。
(3)韧性好:晶粒越细,晶界越曲折,裂纹越不易传播。
4-6 生产中加工长的精密细杠(或轴)时,常在半精加工后,将将丝杠吊挂起来并用木锤沿全长轻击几遍在吊挂7~15天,然后再精加工。
试解释这样做的目的及其原因?答:这叫时效处理一般是在工件热处理之后进行原因用木锤轻击是为了尽快消除工件内部应力减少成品形变应力吊起来,是细长工件的一种存放形式吊个7天,让工件释放应力的时间,轴越粗放的时间越长。
4-8 钨在1000℃变形加工,锡在室温下变形加工,请说明它们是热加工还是冷加工(钨熔点是3410℃,锡熔点是232℃)?答:W、Sn的最低再结晶温度分别为:TR(W) =(0.4~0.5)×(3410+273)-273 =(1200~1568)(℃)>1000℃TR(Sn) =(0.4~0.5)×(232+273)-273 =(-71~-20)(℃) <25℃所以W在1000℃时为冷加工,Sn在室温下为热加工4-9 用下列三种方法制造齿轮,哪一种比较理想?为什么?(1)用厚钢板切出圆饼,再加工成齿轮;(2)由粗钢棒切下圆饼,再加工成齿轮;(3)由圆棒锻成圆饼,再加工成齿轮。
1-2常见的晶体结构及其原胞、晶胞

1-2常见的晶体结构及其原胞、晶胞§1-2 常见的晶体结构及其原胞、晶胞1) 简单晶体的简单⽴⽅(simple cubic, sc) 它所构成的晶格为布喇菲格⼦。
例如氧、硫固体。
基元为单⼀原⼦结构的晶体叫简单晶体。
其特点有: 三个基⽮互相垂直(),重复间距相等,为a,亦称晶格常数。
其晶胞=原胞;体积= ;配位数(第⼀近邻数) =6。
(见图1-7)图1-7简单⽴⽅堆积与简单⽴⽅结构单元2) 简单晶体的体⼼⽴⽅( body-centered cubic, bcc ) , 例如,Li,K,Na,Rb,Cs,αFe,Cr,Mo,W,Ta,Ba等。
其特点有:晶胞基⽮, 并且,其惯⽤原胞基⽮由从⼀顶点指向另外三个体⼼点的⽮量构成:(见图1-9 b)(1-2)其体积为;配位数=8;(见图1-8)图1-8体⼼⽴⽅堆积与体⼼⽴⽅结构单元图1-9简单⽴⽅晶胞(a)与体⼼⽴⽅晶胞、惯⽤原胞(b)3) 简单晶体的⾯⼼⽴⽅( face-centered cubic, fcc ) , 例如,Cu,Ag,Au,Ni,Pd,Pt,Ne, Ar, Xe, Rn, Ca, Sr, Al等。
晶胞基⽮,并且每⾯中⼼有⼀格点, 其原胞基⽮由从⼀顶点指向另外三个⾯⼼点的⽮量构成(见图1-10 b):(1-3)其体积=;配位数=12。
,(见图1-10)图1-10⾯⼼⽴⽅结构(晶胞)(a)与⾯⼼⽴⽅惯⽤原胞(b)4) NaCl结构(Sodium Chloride structure),复式⾯⼼⽴⽅(互为fcc),配位数=6(图1-11 a)。
表1-1 NaCl结构晶体的常数5) CsCl结构(Cesuim Chloride structure),复式简单⽴⽅(互为sc),配位数=8(图1-11 b)。
表1-2 CsCl结构晶体的常数图1-11 NaCl结构和CsCl结构6) ⾦刚⽯结构(Diamond structure), 两套fcc格⼦相互沿对⾓线位移1/4处套合。
-常见晶体结构举例

1. 面心立方(fcc) ------Cu、Al、Ni、Pb、
Au、Rh(铑)等 (GT002) 致密度η(又称空间利用率):晶体中原子 所占体积与晶体总体积之比。 配位数:晶体中一个原子最近邻的原子数。 (注意:不是格点数) 例如:Cu 配位数=12,惯用原胞包含格点数=4 最近邻原子间距=?
思考题: 如果材料由半径为r和R的两种粒子球组 成,其配位数是否会大于12?
9. 钙钛矿结构 例如,BaTiO3,SrTiO3 O1,O2,O3的周围“环境”不同, 钙钛矿结构由五个SC子格子套构而成。 (GT017,GT018)
5. 氯化铯(CsCl)结构 Cs+,Cl-离子分别为简立方(SC)子 格子,二子格子体心套构。 B格子=SC 配位数=? 6. NaCl结构 Na+,Cl-分别为fcc子格子,沿立方边位 移a/2套构而成。 (GT016b)
注
意
不同晶体结构的Cu.NaCl,金刚石结构, 闪锌矿结构等,它们的B格子均为fcc, 所以,B格子的种类数大大少于晶体结
hcp的排列方式为AB,AB,…… 密排面垂直于棱柱高c轴。 fcc的排列方式为ABC,ABC,…… 密排面垂直于体对角线。 (GT003, 模型) hcp和fcc均为配位数为12的密堆积,
可能给我们什么启示?
8. 纤维锌矿结构(六角硫化锌结构) 两个hcp套构而成。 例如,ZnO, ZnS。 (模型)
构的种类数。
7. 六方密排结构(h c p)---Mg、Be、Cd等 (模型)(GT003) 惯用原胞是以正六边形为底的直角棱柱。 晶格常数是正六边形的边长a和柱高c. 密堆积:如果晶体由全同的一种粒子组成, 而粒子被看成是小圆球,这些小圆球最紧 密的堆积状态。此时它有最大的配位数- --12。 有最大配位数12的排列方式称为密堆积。 基元内原子数=2 惯用原胞体积是初基原胞体积的3倍
实际金属的晶体结构

实际金属的晶体结构金属的晶体结构是指由金属原子组成的周期性排列的三维结构。
金属晶体具有许多独特的特征和性质,这些特征和性质与金属原子的三维排列有关。
下面将介绍几种常见的金属晶体结构。
1.简单立方晶体结构(SC):简单立方晶体结构是最简单的晶体结构之一,也是最稀有的金属晶体结构之一、每个金属原子都处于一个立方体角上,每个原子周围有六个邻近原子。
简单立方晶体常见于稀有金属如钠、银等。
2.面心立方晶体结构(FCC):面心立方晶体结构是最常见的金属晶体结构之一,许多常见的金属如铝、铜、金等都采用该结构。
每个金属原子都处于一个立方体的顶点和立方体每个面的中心,每个原子周围有12个邻近原子。
面心立方结构的密堆率为0.743.体心立方晶体结构(BCC):体心立方晶体结构是另一种常见的金属晶体结构,一些金属如铁、钢等采用该结构。
每个金属原子都处于一个立方体的顶点和立方体中心,每个原子周围有8个邻近原子,体心立方结构的密堆率为0.684.密堆排列晶体结构(HCP):密堆排列晶体结构是另一种常见的金属晶体结构,钛、锆等金属常见于该结构。
每个金属原子都处于一个六角形基面的顶点和基面两侧的空间,每个原子周围有12个邻近原子。
密堆排列结构的密堆率为0.74此外,还有一些金属具有其他特殊的晶体结构,例如钻石立方晶体结构、金刚石晶体结构等。
这些结构都与金属原子之间的相互作用力和排列方式有关。
金属的晶体结构对其性质具有重要影响。
例如,面心立方结构的金属具有优良的塑性和导电性,因为金属原子的排列方式使得原子在晶体中能够相对自由地滑动。
相比之下,体心立方结构的金属则具有较高的硬度和较强的磁性。
这些不同的晶体结构直接影响到金属的导电性、热传导性、密度、力学性能等性质。
总之,金属的晶体结构是由金属原子周期性排列而成的三维结构。
不同的金属晶体结构具有不同的特征和性质,进一步影响到金属的性能和用途。
了解金属的晶体结构对于研究和应用金属材料具有重要的意义。
材料科学基础第一章2-1典型的晶体结构及几何特征
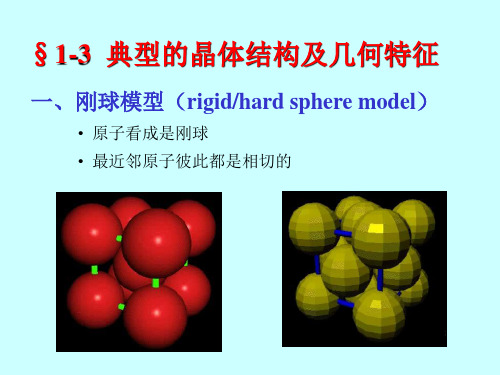
与相邻的8个晶胞共有,每个晶胞
实际上只占其1/8;位于晶胞棱上
的原子为相邻的4个晶胞所共有;
每个面心原子为相邻两个晶胞共
有;而晶胞中心原子为晶胞所独
有。
• FCC结构每个晶胞中的原子数:
1
1
8 6 4
8
2
1、FCC 面心立方
配位数
• 配位数是指晶体结构中任一原子周围
( )
3
4
3
4r 3
2
2、HCP 密排六方
••
•
• 原子半径:
上下底面的中心原子与周围六个
顶角上的原子相切
1
2 = , =
2
• 每个晶胞中的原子数:
1
1
12 2 3 6
6
2
•
••
•
•
•
•
•
••
•
•
••
2、HCP 密排六方
• 配位数:
C.N.= 6 + 3×2 =12
最邻近的原子数。常用CN
(coordination number)表示。
• 对于多元素晶体,“最近邻”是同种原
子比较而言,配位数是一个原子周围的
各元素的最近邻原子数之和。
• 晶体结构中每个原子的配位数愈大,
晶体中的原子排列就愈紧密。
• •
•
•
•
• • • •
•
•
•
•
•ห้องสมุดไป่ตู้
• FCC结构的配位数:
A面、B面、C面上各4个,等同点, 4×3=12
• 堆垛密度
2
c
3
常见的金属晶体结构

第二章作业2-1 常见的金属晶体结构有哪几种?它们的原子排列和晶格常数有什么特点?V、Mg、Zn 各属何种结构?答:常见晶体结构有 3 种:⑴体心立方:-Fe、Cr、V ⑵面心立方:-Fe、Al、Cu、Ni ⑶密排六方:Mg、Zn -Fe、-Fe、Al、Cu、Ni、Cr、2---7 为何单晶体具有各向异性,而多晶体在一般情况下不显示出各向异性?答:因为单晶体内各个方向上原子排列密度不同,造成原子间结合力不同,因而表现出各向异性;而多晶体是由很多个单晶体所组成,它在各个方向上的力相互抵消平衡,因而表现各向同性。
第三章作业3-2 如果其它条件相同,试比较在下列铸造条件下,所得铸件晶粒的大小;⑴金属模浇注与砂模浇注;⑵高温浇注与低温浇注;⑶铸成薄壁件与铸成厚壁件;⑷浇注时采用振动与不采用振动;⑸厚大铸件的表面部分与中心部分。
答:晶粒大小:⑴金属模浇注的晶粒小⑵低温浇注的晶粒小⑶铸成薄壁件的晶粒小⑷采用振动的晶粒小⑸厚大铸件表面部分的晶粒小第四章作业4-4 在常温下为什么细晶粒金属强度高,且塑性、韧性也好?试用多晶体塑性变形的特点予以解释。
答:晶粒细小而均匀,不仅常温下强度较高,而且塑性和韧性也较好,即强韧性好。
原因是:(1)强度高:Hall-Petch 公式。
晶界越多,越难滑移。
(2)塑性好:晶粒越多,变形均匀而分散,减少应力集中。
(3)韧性好:晶粒越细,晶界越曲折,裂纹越不易传播。
4-6 生产中加工长的精密细杠(或轴)时,常在半精加工后,将将丝杠吊挂起来并用木锤沿全长轻击几遍在吊挂7~15 天,然后再精加工。
试解释这样做的目的及其原因?答:这叫时效处理一般是在工件热处理之后进行原因用木锤轻击是为了尽快消除工件内部应力减少成品形变应力吊起来,是细长工件的一种存放形式吊个7 天,让工件释放应力的时间,轴越粗放的时间越长。
4-8 钨在1000℃变形加工,锡在室温下变形加工,请说明它们是热加工还是冷加工(钨熔点是3410℃,锡熔点是232℃)?答:W、Sn 的最低再结晶温度分别为: TR(W) =(0.4~0.5)×(3410+273)-273 =(1200~1568)(℃)>1000℃ TR(Sn) =(0.4~0.5)×(232+273)-273 =(-71~-20)(℃) <25℃所以W 在1000℃时为冷加工,Sn 在室温下为热加工4-9 用下列三种方法制造齿轮,哪一种比较理想?为什么?(1)用厚钢板切出圆饼,再加工成齿轮;(2)由粗钢棒切下圆饼,再加工成齿轮;(3)由圆棒锻成圆饼,再加工成齿轮。
常见九种典型的晶体结构

尖晶石通式是A2+B3+2O4,表示二价阳离子A占据了 晶胞四面体空隙,三价阳离子B占据八面体空隙,此即尖晶 石结构,代表是尖晶石 MgAl2O4 。
当结构中的四面体空隙被B3+占据,而八面体空隙则被 B3+和A2+各占一半,即有分子式B3+ A2+B3+ 2O4时,这 种结构叫做反尖晶石结构,代表物质磁铁矿
从图可看出, SZn4 四 面体 ZnS4 四面体也是 一样 共角顶联成的四面 体基元层与 111 方向垂 直。
由于S2-和Zn2+都呈配位四面体,所以闪锌矿只用一种配位多 面体结构形式表达 S和Zn互换是一样的 。
如果将闪锌矿结构中的Zn和S都变成C,则结构变成金刚石
结构 Fd3m 。
具有闪锌矿型结构的物质
▪ 层电荷的来源
1 来源于四面体片的 Al->Si替代。这时,与配 平电荷的层间阳离子距离 较近,称之为“近电”。
记为 Xt
2 来源于八面体片的 Mg->Al替代。这时,于配 平电荷的层间阳离子距离 较远,称之为“远电”。
记为 Xo
▪ 层电荷的分布
在晶胞所示范围 内,每个单面只有 -0.33价的电荷。
2.51A, 上面的4个 为3.24A
2 TiO6 八面 体中,Ti亦不在 中心位置。
▪ 以上两个原因导致晶体的对称降低,由原来的立 方原始格子降低为四方原始格子。空间群Pm3m P4mm。从而晶体具有了极性 具有极轴 ,这是 导致其铁电性的最根本原因。
8 尖晶石结构
Spinel ,AB2O4
萤石晶胞中存在平行于 111 面的离子堆积层,因此, 萤石具有{111}完全解理。
阳离子配位四面体的连接:共棱联结形成的萤石结构。 晶胞中由8个 FCa4 共棱连接而成,而且四面体的每根棱 都被共用了。
常见的晶体结构高中化学

常见的晶体结构高中化学晶体是由原子、分子或离子等按照一定的规则排列组成的固体物质。
晶体结构是指晶体中原子、分子或离子的排列方式和空间位置的有序性。
以下是一些常见的晶体结构:1.立方晶系:立方晶系是最简单的晶体结构类型,具有最高的对称性。
立方晶系包括以下几种晶体结构:-简单立方结构:最简单的晶体结构,如钠金属。
-面心立方结构:每个立方格点上除了原子所在的角点外,还有一个原子位于正方形面的中心,如铝、铜等。
-体心立方结构:每个立方格点上除了原子所在的角点外,还有一个原子位于立方体的中心,如铁、锂等。
-体心立方密堆结构:在体心立方结构的基础上,每个体心立方顶点上还有各自的三个原子,如铬、铤等。
2.六方晶系:六方晶系的晶体结构相对复杂,具有六重轴对称性。
六方晶系包括以下几种晶体结构:-六方最密堆积结构:最密堆积的晶体结构,如铝合金、硬质合金等。
3.正交晶系:正交晶系的晶体结构具有三个相互垂直的轴和互相垂直的面,没有对称轴。
正交晶系包括以下几种晶体结构:-基心正交结构:每个顶点上有原子以外,还有一个原子位于底面的中点,如锌等。
-面心正交结构:每个顶点上原子以外,还有一个原子位于两个邻接底面的中点和两个对称角上的原子,如镍。
4.单斜晶系:单斜晶系的晶体结构具有一个二重轴和一组不对称的轴,没有对称轴。
单斜晶系包括以下几种晶体结构:-单斜底心结构:每个顶点上有原子以外,还有一个原子位于两个底面的中点,如铅、镀镍等。
5.斜方晶系:斜方晶系的晶体结构没有对称轴,具有两个相等且垂直的轴。
-斜方单斜结构:具有一个反射面,如黄铁矿、菱铁矿等。
6.三斜晶系:三斜晶系的晶体结构没有对称轴,也没有垂直的轴。
三斜晶系包括以下几种晶体结构:-无底心三斜结构:没有底心原子,如铜酸亚锌等。
这些晶体结构是根据晶体的对称性进行分类的,每一种晶体结构都有其独特的排列方式和空间位置。
通过研究晶体结构,可以揭示物质的物理和化学性质以及材料的制备和应用方面的特点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图2-44 四面体的共顶、共面和共棱联结 (中心正离子间的距离为:1:0.58:0.33)
图2-44 八面体的共顶、共面和共棱联结(中心正幻离灯子片间1的1 距离为: 1:0.71:0.58)
二、典型金属的晶体结构
3.点阵常数与原子半径
R 2R
R RR
a0
a0 2R
a0
a0
2 2R 3
R 2R
R
a0
a0
2 2R 2
SC
BCC
FCC
*HCP点阵常数与原子半径
a0 2R
c0 2
2a 4 3
2R 3
C0/2 C0
2R 2R
C0/2
HCP
4.一个晶胞中占有的原子数
第二节 常见的晶体结构
晶体化学基本原理 典型金属的晶体结构 常见无机化合物晶体结构
一、晶体化学基本原理
1. 原子半径与离子半径
有效半径: 在晶体结构中原子或离子处于相接触时的半径
离子晶体中,正负离子相接触的中心距,即为正负离子 的半径之和 ;共价键化合物的晶体中,两个相邻键合的 中心距,即是两个原子的共价半径之和。在纯金属的晶 体中,两个相邻原子中心距的一半,就是金属原子半径。
于从邻近的正离子配给该负离子各静电键强度的总
和。
SZ n
第三规则 在配位结构中,配位多面体共用棱,特别是共用面 的存在会降低这个结构的稳定性。图2-44四面体和 八面体的共顶、共面和共棱联结
第四规则
在晶体中有一种以上的正离子,那么高电价正离子的 低配位数多面体之间尽可能彼此互不结合的趋势。
第五规则
Rbcc )2
( a0 4
)2
( a0 2
)2
5 rin 4 a0 Rbcc
a0/4
rin Rbcc
a0/2
5 3
Rbcc
Rbcc
rin 5 1 0.291
Rbcc
3
octahedral sites
bcc 4Rbcc 3a0
a0/4
rin Rbcc
a0/2
rin
1 2
a0
Rbcc
23 3
值
r r
0.000 ~ 0.155
正离子的 负离子多面体的形状 配位数
2
直线形
实例 干冰CO2
0.155 ~
3
0.225
三角形
B2O3
0.225 ~
4
0.414
四面体
SiO2, GeO2
0.414 ~
6
0.732
0.732 ~
8
1.000
1.000以上
12
八面体 立方体 立方八面体
NaCl, MgO,
(2
R
fc c
)
Center of tetrahedron, o,
oD = (3/4)DE
A D
B
3
rin oD Rfcc 4 DE Rfcc
2Rfcc
32
3
rin 2 3 R fcc R fcc ( 2 1)R fcc
o
C
A
E
B
rin 3 1 0.225
R fcc
2
晶体结构中的空隙位(2): bcc
Octahedral sites: Face and edge center sites
6 1 12 1 6
2
4
面心和棱中点
Tetrahedral sites
bcc
a/4
a
6 4 1 12 2
侧面中心线1/4和3/4处
Tetrahedral site2 ZrO2, CaF2,
CsCl
Cu
4Rfcc 2a0
C
D
Tetrahedron
DE
2 3
(2
R
fc c
)
Center of tetrahedron, o,
oD = (3/4)DE
A D
B
3
rin oD Rfcc 4 DE Rfcc
2Rfcc
32
3
rin 2 3 R fcc R fcc ( 2 1)R fcc
1.原子紧密堆积方式
简单立方结构sc (ABCABC…)
体心 bcc 结构 (ABCABC…)
2
2 3
d0
面 心立方紧密堆积 (ABCABC…)
Unit cell
六方 紧密堆积hcp (ABAB…)
2.原子的配位数与空隙
简单立方结构中原子的配位数为6,体心立方
结构中原子的配位数为8。
密排六方结构中原子的配位数 密排六方结构中原子的配位数为12
Rbcc
Rbcc
rin 2 3 1 0.155
Rbcc
3
晶体结构中的空隙位(3): hcp
Octahedral sites:
6
×
×
晶体结构中的空隙位(3): hcp
Tetrahedral sites
×
×
7c 8
1c
××
8
2 6 2 1 2 3 12 3
5c 8
3c 8
棱和中心线的1/4和3/4处
2.球体紧密堆积原理
离子晶体和原子晶体中原子和离子在结构中堆积相 当于球体相互作最紧密堆积。晶体的紧密堆积有两 种:如纯金属晶体的等大球体最紧密堆积和离子作 不等大球体的紧密堆积。
等大球体紧密堆积方式(球体代表原子)
ABC AB
四 面 体 空 隙 和八 面 体 空 隙 数
八面体空 隙
四面体空隙
o
C
A
E
B
rin 3 1 0.225
R fcc
2
r 2 1 0.414 R
2r
a0 2 2R
4. 鲍林规则
第一规则
在正离子周围,形成一个负离子配位多面体,正负 离子间的距离取决于它们的半径之和,而配位数取 决于它们的半径之比。
第二规则(静电价规则)
在一个稳定的晶体结构中,每一个负离子的电价等
Octahedron
Tetrahedron
Interstitials
3. 原子和离子的配位数
指在晶体结构中,该原子或离子的周围与它直接相邻结 合的原子个数或所有异号离子的个数
原子或离子的周围与它直接相邻结合的原子或离子的中心 联线所构成的多面体,称为原子或离子的配位多面体
正负离子半径比值与配位数的关系
每个球周围有8个四面体 空隙,6个八面体空隙。 n个等径球堆积时,其 四面体空隙数为8n/4=2n, 八面体空隙数为6n/6=n
面 心立方紧密堆积 Face-centered cubic (ABCABC…)
Unit cell
六方 紧密堆积hcp (ABAB…)
Close-packed hexagonal
面心立方结构中原子的配位数为12
晶体结构中的间隙位(1): fcc
Octahedral sites
Tetrahedral sites
Cube and edge center sites
112 1 4
8
4
2r
a0 2 2R
fcc 4Rfcc 2a0
C
D
Tetrahedron
DE
2 3
