2015高考数学专题复习:函数图像
2015高考数学一轮总复习课件:2.7 函数的图像

规范解答:函数为奇函数,∴图像关于原点对称,排除 A;令 y=0,
π
πk
得 cos 6x=0,∴6x=2+kπ(k∈Z),x=12+6π(k∈Z),函数的
π 零点有无穷多个,排除 C,且 y 轴右侧第一个零点为 x=12;又函数 y
π =2x-2-x 为增函数,当 0<x<12时,y=2x-2-x>0,cos 6x>0,
第二十六页,编辑于星期五:十二点 三十一分。
(2)在同一坐标系中作出函数 y=f(x)与 y=mx 的图像,如图.由图像知,当 y= mx 与 f(x)=-x2+4x-3(1<x<3)有两个公共点时,方程 f(x)=mx 有四 个不同的实数根.(8 分)
由直线 y=mx 与 y=-x2+4x-3(1<x<3)相切,即 mx=-x2+4x-3,x2 +(m-4)x+3=0 有两个相等实根,得 Δ=(m-4)2-4×3=0,∴m=4-2 3, (10 分)
|x2-1| x+1,x≤-1或x>1,
规范解答:∵函数
y=
x-1
= -x-1,-1<x<1,
函数
y=kx-2
的图
|x2-1| 像恒过点(0,-2),作出函数 y= x-1 的图像,根据图像易知,当两个
第二十五页,编辑于星期五:十二点 三十一分。
规范解答:(1)∵f(x)=|x2-4x+3|
(x-2)2-1,x∈(-∞,1]∪[3,+∞),
=
(2 分)
-(x-2)2+1,x∈(1,3),
作出图像如图所示. 由图可知,函数 f(x)在区间[1,2],[3,+∞)上单调递增, 在(-∞,1],[2,3]上单调递减.(6 分)
第九页,编辑于星期五:十二点 三十一分。
1 2.(教材改编)函数 f(x)=x-x 的图像关于 (C)
2015高考数学第一轮复习函数的图象

2.当0<a<1时,在同一坐标系中,函数y=a-x与y=logax的图 象是( )
【解析】选C.y=a-x=( 1 )x,由0<a<1知,
1 故选C. >1, a a
3.函数y=f(x)为偶函数,则函数y=f(x+1)的一条对称轴是____.
【解析】≧y=f(x)的对称轴为x=0,
左移 又 y f x y f x 1, 一个单位
(4)可先去掉绝对值号化成分段函数,再分段画出函数的图象.
【规范解答】(1)将函数y=log2x的图象向左平移一个单位,再 将x轴下方的部分沿x轴翻折上去,即可得到函数y=|log2(x+1)|
的图象,如图.
(2)作出函数 y ( 1 ) x 的图象,保留 y ( 1 ) x 图象中x≥0的部
a
x 1 从而得出函数 g x log 1 1 在区间(-1,+≦)上递增, x 1 a 且当x=0时,g x log 1 1 0, 即图象过原点, 0 1 a
均在相应定义域是减函数,
分析A,B,C,D四个答案,只有C满足要求.
考向 3
函数图象的应用
【典例3】已知函数f(x)=x|m-x|(x∈R),且f(4)=0. (1)求实数m的值. (2)作出函数f(x)的图象并判断其零点个数. (3)根据图象指出f(x)的单调递减区间. (4)根据图象写出不等式f(x)>0的解集.
利用上述方法,排除、筛选错误与正确的选项.
【提醒】注意联系基本函数图象的模型,当选项无法排除时,
代特殊值,或从某些量上寻找突破口.
【加固训练】若函数f(x)=ax(a>0,a≠1)为增函数,那么
g x log 1
2015年高考数学复习学案:正切函数的图像和性质
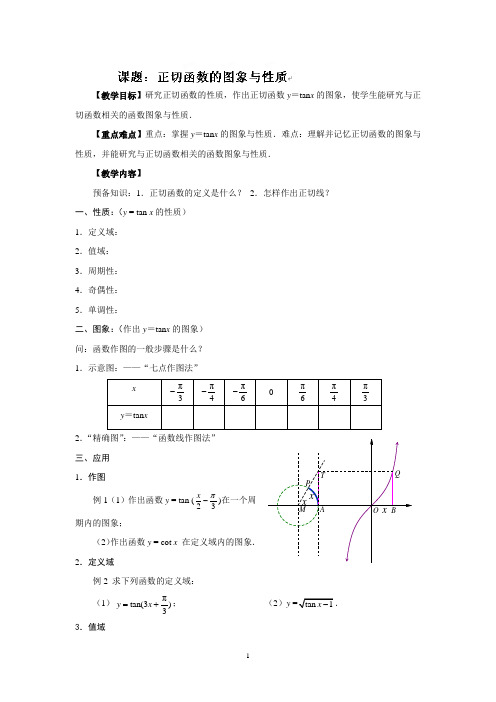
【教学目标】研究正切函数的性质,作出正切函数y =tan x 的图象,使学生能研究与正切函数相关的函数图象与性质.【重点难点】重点:掌握y =tan x 的图象与性质.难点:理解并记忆正切函数的图象与性质,并能研究与正切函数相关的函数图象与性质.【教学内容】预备知识:1.正切函数的定义是什么? 2.怎样作出正切线? 一、性质:(y = tan x 的性质) 1.定义域: 2.值域: 3.周期性: 4.奇偶性: 5.单调性:二、图象:(作出y =tan x 的图象) 问:函数作图的一般步骤是什么? 1.示意图:——“七点作图法”2.“精确图”:——“函数线作图法” 三、应用 1.作图例1(1)作出函数y = tan (23x π-)在一个周期内的图象;(2)作出函数y = cot x 在定义域内的图象. 2.定义域例2 求下列函数的定义域: (1)πtan(3)3y x =+; (2)y 3.值域例3 求下列函数的值域:(1)y = tan x(π6≤x≤2π3);(2)y = tan (2x-π3)(0≤x≤π2).4.周期性例4 求下列函数的最小正周期:(1)f(x) = 5tan (35x-π3);(2)f(x) = tan x- cot x.5.奇偶性例5判下列函数的奇偶性:(1)f(x) = cos x · tan x;(2)f(x)= cos ( tan x ) .6.单调性例6 求下列函数的单调增区间:(1)y = 3tan (π23x-) ;(2)y = tan (-x ) .【小结作业】1.填空题:(1)函数πtan()26xy=+的定义域为________________,值域为____________,单调增区间为___________________.(2)函数y = tan 2x(-π12≤x≤π3)值域为__________________.(3)函数f(x) = tan x+cot x的定义域为________________,值域为________________,最小正周期为____________.(4)将tan1,tan2,tan3,tan4由小到大排列:________<_______<_______<_______.2.作出函数y = 2tan (π23x-)在一个周期内的图象.。
2015高考总复习数学(文)课件:3.5 函数的图象

答案:B
(2)若函数 y=f(x)(x∈R)满足 f(x+2)=f(x),且 x∈[-1,1]时,
f(x)=|x|,则函数 y=f(x)(x∈R)的图象与函数 y=log3|x|的图象的
交点个数为( A.2 个 C.4 个 ) B.3 个 D.无数个
解析:由已知条件可作出函数 f(x)及 y=log3|x|的图象,如 图 3-5-2,由图象可得其交点的个数为 4 个.故选 C.
考点 3
利用图象判断根的分布
例 3:(1)(2012 年辽宁)设函数 f(x)(x∈R)满足 f(-x)=f(x),
f(x)=f(2-x),且当 x∈[0,1]时,f(x)=x3.又函数 g(x)=|xcos(πx)|,
则函数
1 3 h(x)=g(x)-f(x)在-2,2上的零点个数为(
π 2sinx+4与①②都必须经过收缩变换才可能重合.
答案:①②
【互动探究】 2.将函数 y=2x 的图象按向量 a 平移后得到函数 y=2x+6 的图象,给出以下四个命题: ①a 的坐标可以是(-3,0); ②a 的坐标可以是(0,6); ③a 的坐标可以是(-3,0)或(0,6); ④a 的坐标可以有无数种情况. 其中是真命题的个数是( D ) A.1 个 B.2 个 C.3 个 D.4 个
的图象;去掉 y=f(x)在 y 轴左边的图象,作与右边对称的图象,
即得到 f(|x|)的图象;将 y=f(x)在 x 轴下边的图象翻上去(关于 x
轴对称),即得到|f(x)|的图象.
答案:D
(2)若两个函数的图象经过若干次平移后能够重合,则称这 两个函数为“同形”函数.给出下列四个函数:①f1(x)=sinx+
1.函数图象的作图方法 以解析式表示的函数作图象的方法有两种,即列表描点法
2015高考数学一轮课件:2-7函数的图象

题型一 函数图象的变换
【例 1】
函数 f(x)=3loxg13x
x≤1, x>1,
则 y=f(1-x)的
图象是( )
第十八页,编辑于星期五:十三点 十三分。
[解析] 画出 y=f(x)的图象,再作其关于 y 轴对称的图象, 得到 y=f(-x)的图象,再将所得图象向右平移 1 个单位,得到 y =f[-(x-1)]=f(-x+1)的图象,故选 C.
答案:B
第二十八页,编辑于星期五:十三点 十三分。
题型三 函数图象的应用
【例 3】 函数 f(x)=(12)|x-1|+2cosπx(-2≤x≤4)的所有零点 之和等于( )
A.2 C.6
B.4 D.8
第二十九页,编辑于星期五:十三点 十三分。
[解析] 由 f(x)=(12)|x-1|+2cosπx=0, 得(12)|x-1|=-2cosπx, 令 g(x)=(12)|x-1|(-2≤x≤4), h(x)=-2cosπx(-2≤x≤4), 又因为 g(x)=(12)|x-1|=212x-x1-,1,-12≤≤xx≤<41,.
[变式 2] (2014·浙江杭州一模)已知函数 f(x)的图象如图所 示,则 f(x)的解析式可能是( )
A.f(x)=x2-2ln |x| B.f(x)=x2-ln |x| C.f(x)=|x|-2ln |x| D.f(x)=|x|-ln |x|
第二十七页,编辑于星期五:十三点 十三分。
解析:由函数图象可得,函数 f(x)为偶函数,且 x>0 时,函 数 f(x)的单调性为先减后增,最小值为正,极小值点小于 1,分 别对选项中各个函数求导,并求其导函数等于 0 的正根,可分别 得 1, 22,2,1,由此可得仅函数 f(x)=x2-ln |x|符合条件,故应 选 B.
2015届高三数学第一轮复习课件:2.7函数的图像

(2)要使函数
y
|x2-1| = x-1 =
x+1(x<-1或x>1), -x-1(-1≤x<1)
与直
线 y=kx-2 恰好有两个交点,如图,因为 y=kx-2 过
第十三页,编辑于星期五:八点 五十一分。
定点 B(0,-2). 所以 0<k<1 或1<k<kBA=4,所以 k 的取值范围为(0,
§2.7 函数的图象
1.在实际情境中,会根据不同的需要选择图象法、列 表法、解析法表示函数.
2.掌握基本初等函数的图象,会运用函数图象理解和 研究函数的性质.
一、函数的图象 1.函数图象的作法主要有描点连线法、图象变换法. 描点连线法作图的一般步骤为__列表__、__描点__、__连线 __.熟悉函数图象的作法后可以不要列表这一步,直接
第一页,编辑于星期五:八点 五十一分。
边算边描点.
2.函数在某区间上的单调性决定了函数图象在这个区
间上的大致变化趋势,结合图象对解决问题很有帮助.
函数
函数的图象
f(x)=kx+b
f(x)=kx(k≠0)
第二页,编辑于星期五:八点 五十一分。
函数
f(x)=|x-a|
函数的图象
1.y=|f(x)|的图象是将 y=f(x)的图象在 x 轴下方的 部分以 x 轴为对称轴翻折到 x 轴上方,其余部分不变而得到 的.而 y=f(|x|)的图象是将 y=f(x),x≥0 的部分作出, 再利用偶函数的图象关于 y 轴对称,作出 x<0 的图象而得
B 根据函数的解析式识别函数图象,要从定义域、值 域、单调性、奇偶性等方面入手,结合给出的函数图象进行 全面分析,有时可结合部分特殊函数值,进行辅助推断,这 是解决函数图象识别类试题的基本方法.
2015届高考数学教材知识点函数的图像复习导学案

2015届高考数学教材知识点函数的图像复习导学案【学习目标】1.掌握作函数图像的两种基本方法:描点法和图像变换法.2.了解图像的平移变换、伸缩变换、对称变换,能利用函数的图像研究函数的性质,以达到识图、作图、用图的目的.预习案1.函数图像的三种变换(1)平移变换y =f(x)的图像向左平移a(a>0)个单位,得到的图像;y=f(x -b)(b>0)的图像可由y=f(x)的图像而得到;y=f(x)的图像向下平移b(b>0)个单位,得到的图像;y=f(x)+b(b>0)的图像可由y=f(x)的图像而得到.总之,对于平移变换,记忆口诀为:左加右减,上加下减.(2)对称变换y=f(-x)与y=f(x)的图像关于对称;y=-f(x)与y=f(x)的图像关于对称;y =-f(-x)与y=f(x)的图像关于对称;y=|f(x)|的图像可将y=f(x)的图像在x轴下方的部分,其余部分不变而得到;y=f(|x|)的图像可先作出y=f(x)当x≥0时的图像,再作关于y轴的对称.(3)伸缩变换y=f(ax)(a>0)的图像,可将y=f(x)的图像上所有点的坐标变为原来的倍,坐标而得到.y=af(x)的图像,可将y =f(x)的图像上所有点的坐标不变,坐标伸长为原来的.2.几个重要结论(1)若f(m+x)=f(m-x)恒成立,则y=f(x)的图像关于直线对称.(2)设函数y=f(x)定义在实数集上,则函数y=f(x-m)与y=f(m-x)(m>0)的图像关于直线对称.(3)若f(a+x)=f(b-x),对任意x∈R恒成立,则y=f(x)的图像关于x=a +b2对称.(4)函数y=f(a+x)与函数y=f(b-x)的图像关于x=b-a2对称.【预习自测】 1.函数y=lg|x-1|的图像大致为()2.函数y=1-1x-1的图像是3.当0<a<1时,在同一坐标系中,函数y=a-x与y=logax的图像是 ()4.要得到函数y=8•2-x的图像,只需将函数y=的图像 ()A.向右平移3个单位 B.向左平移3个单位C.向右平移8个单位 D.向左平移8个单位5.设函数f(x)=|x+1|+|x-a|的图像关于直线x=1对称,则a的值为 ()A.3B.2 C.1 D.-1 探究案题型一利用变换作图例1.作出下列函数的图像.(1)f(x)=x1+|x|; (2)f(x)=|lg|x-1||.探究1.作出下列函数的图像.(1)y=2x+2;(2)y=x+2x-1; (3)y=(12)|x| ; (4)y=|log2x-1|.题型二知式选图或知图选式问题例2.函数f(x)的部分图像如图所示,则函数f(x)的解析式是 ()A.f(x)=x+sinx B.f(x)=cosxx C.f(x)=xcosx D.f(x)=x•(x-π2)•(x-3π2)探究2.(1)函数y=x2-2sinx的图像大致是 () (2)(2013•衡水调研卷)函数y=x+sin|x|,x∈的大致图像是 () 题型三函数图像的对称性例3.(1)已知f(x)=ln(1-x),函数g(x)的图像与f(x)的图像关于点(1,0)对称,则g(x)的解析式为(2)设函数y=f(x)的定义域为实数集R,则函数y=f(x-1)与y=f(1-x)的图像关于 ()A.直线y=0对称 B.直线x=0对称 C.直线y=1对称 D.直线x=1对称探究3.(1)已知函数f(2x+1)是奇函数,则函数y=f(2x)的图像关于下列哪个点成中心对称 () A.(1,0) B.(-1,0) C.(12,0) D.(-12,0) ()(2)求证:函数f(x)满足对任意x,都有f(a-x)=f(a+x),则函数f(x)的图像关于直线x=a对称.题型四函数图像的应用例4.(1)函数f(x)=|4x-x2|-a恰有三个零点,则a=________. (2)不等式log2(-x)<x+1的解集为__________.探究4.若直线y=x+m和曲线y=1-x2有两个不同的交点,则m的取值范围是________.我的学习总结:(1)我对知识的总结 .(2)我对数学思想及方法的总结。
2015高考数学配套课件:2-9 函数的图像

课前自助餐
授人以渔
自助餐
课时作业
第二页,编辑于星期五:十五点 七分。
高考调研
新课标版 ·高三数学(文)
请注意!
高考对函数图像的考查形式多样,命题形式主要有由函数的 性质及解析式、选图;由函数的图像来研究函数的性质、图像的 变换、数形结合解决问题等,其重点是基本初等函数的图像以及 函数的性质在图像上的直观体现.
课前自助餐
授人以渔
自助餐
课时作业
第八页,编辑于星期五:十五点 七分。
高考调研
新课标版 ·高三数学(文)
1.函数 y=log2|x|的图像大致是( )
答案 C 解析 函数 y=log2|x|为偶函数,作出 x>0 时 y=log2x 的图像, 图像关于 y 轴对称,应选 C.
课前自助餐
授人以渔
自助餐
高考调研
新课标版 ·高三数学(文)
思考题 2 函数 y=x+cosx 的大致图像是( )
课前自助餐
授人以渔
自助餐
课时作业
第二十九页,编辑于星期五:十五点 七分。
高考调研
新课标版 ·高三数学(文)
【解析】 ∵y′=1-sinx≥0,∴函数 y=x+cosx 为增函 数,排除 C.
又当 x=0 时,y=1,排除 A, 当 x=π2时,y=π2,排除 D.∴选 B. 【答案】 B
课前自助餐
授人以渔
自助餐
课时作业
第五页,编辑于星期五:十五点 七分。
高考调研
新课标版 ·高三数学(文)
(2)对称变换 y=f(-x)与 y=f(x)的图像关于 y轴 对称; y=-f(x)与 y=f(x)的图像关于 x轴 对称; y=-f(-x)与 y=f(x)的图像关于 原点 对称; y=|f(x)|的图像可将 y=f(x)的图像在 x 轴下方的部分折到x轴 上方 ,其余部分不变而得到; y=f(|x|)的图像可先作出 y=f(x)当 x≥0 时的图像,再作关于 y 轴的对称.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015高考数学专题复习:函数图像
1、判断函数图像依据: 1.基本函数图像特征: 2.奇偶性: 3.导数单调性: 4.特殊点: 5.定义域:
6.函数之间大小关系:
7.平移变换
2、指出下列函数与()x f y =的图像之间的关系: 1.()1-=x f y 2.()2-=x f y 3.()x f y -= 4.()x f y -= 5.()x f y --= 6.()x f y =
7.()
x f y = 8.()x f y -=
练习:已知()()()()⎩⎨
⎧≤<≤≤-=10...........
01.sin x x x x x f π,作出下列函数图像: 1.()1-=x f y 2.()2-=x f y 3.()x f y -= 4.()x f y -=
5.()x f y --=
6.()x f y =
7.()x f y =
8.()
x f y -=
1.函数)(x f y =与函数()x g y =的图像如右图所示,则函数()()x g x f y ⋅=的图像可能是下面的( )
2.()y f x =的图像如图所示,则()y f x =的解析式可能为 ( ) A.()cos f x x x =-- B.()sin f x x x =-- C.()||cos f x x x = D.()||sin f x x x =
3.(山东)函数
sin x
y
x
=,
(,0)(0,)x ππ∈-的图像可能是下列图像中的 ( )
4.(13山东)函数x x x y sin cos +=的图像大致为 ( )
5.(山东)函数x
x x
y --=
226cos 的图像大致为 ( )
6.函数()x
x x f 2log =的图像大致是 ( )
7.下列四个图像可能是函数10ln |1|
1
x y x +=
+图像的是 ( )
8.函数||
x y a =与sin y ax =(0a >且1a ≠)在同一直角坐标系下的图像可能是 ( )
9.函数sin ln sin x x y x x -⎛⎫
=
⎪+⎝⎭
的图像大致是 ( )
10.在同一个坐标系中画出函数,sin x
y a y ax ==的部分图像,其中01a a >≠且,则下列所给图像
中可能正确的是 ( )
11.函数()2
1x e x f -=的部分图像大致是 ( )
12.已知函数|ln |
1
()||x f x e x x
=--
,则函数(1)y f x =+的大致图像为 ( )
13.函数lg
=y 1
|1|
x +的大致图像为 ( )
14.函数x x
y cos 1
⋅=
在坐标原点附近的图像是 ( )
15.函数)10(1||log )(<<+=a x x f a 的图像大致为 ( )
16.函数3log 3
x
y =的图像大致是 ( )
17.函数)(log )(b x x f a +=的图像如右图,b a ,为常数,则函数b a x g x
+=)(的大致图像是 ( )
18.已知函数()=x f 2,(10)
,(01)
x x x x --≤≤⎧⎪⎨
<≤⎪⎩,则下列的图像错误的是 ( )
19.(08山东)函数ln cos ()2
2
y x x π
π
=-
<<
的图像是 ( )
20.(山东)函数2sin 2
x
y x =
-的图像大致是 ( ) A B C. D.
21.(山东)函数2
2x y x =-的图像大致是 ( )
22.函数()2tan 22f x x x ππ⎛⎫
=-- ⎪⎝⎭
在,上的图像大致为 ( )
23.(1)已知21,[1,0),
()1,[0,1],
x x f x x x +∈-⎧=⎨+∈⎩则下列函数的图像错误的是 ( )
(A))1(-x f 的图像 (B))(x f -的图像 (C)|)(|x f 的图像 (D)|)(|x f 的图像
(2)函数sin ,[,]y x x x ππ=+∈-的大致图像是 ( )
24.设函数()22
-=x x g ,()()()()()()⎪⎩
⎪⎨⎧≥-<++=x g x x x g x g x x x g x f ,,4)(,求()x f 的值域
25.已知函数()()()()()()()()()()()
⎩⎨⎧<≥=-=-=x g x f x f x g x f x g x F x x x g x x f ,,,2,232,则()x F 的最大值为
26.函数{}c b a ,,min 表示取c b a ,,中最小的值,则函数{}
x x x
-+10,2,2min 的值域为
27.设函数()(,)y f x =-∞+∞在内有定义,对于给定的正数k ,定义函数:()()()
()()()⎩
⎨⎧≤>=K x f x f K x f x x f K ..2,
取函数||
()x f x a -=()1>a ,当a
K 1=时,函数()x f K 的单调递减的是
28.对任意实数b a ,定义运算“⊗”:,1,
, 1.
b a b a b a a b -≥⎧⊗=⎨-<⎩设2()(1)(4)f x x x =-⊗+,若函数
()y f x k =+的图像与x 轴恰有三个不同交点,则k 的取值范围是 ( )
A.()1,2-
B.[]1,0
C.[)0,2-
D.[)1,2-
29.已知函数()⎪⎩⎪⎨⎧≤+->=0
,40
,2
x x x x x x f ,若()1-≥ax x f 恒成立,则实数a 的取值范围是
30.已知函数()()()()⎩⎨⎧>≤=k x f k
k x f x f x F )( )(,当()21,2==-k x f x
时,作图并求函数值域
31.用{}min ,b a 表示b a ,两数中的最小值,若函数(){}
t x x x f +=,min 的图像关于直线2
1
-
=x 对称, 则t 的值为 ( )
A .2-
B .2
C .1-
D .1
()()()()()()()()()()()()()()()()()()()()()()C
A C A D
B A A A D A
C
D A D C C D D C D A 222120191817.161514.13.12.11.10.9.8.7.6.5.43.2.1()()()()()
()(]()(][)()()[]()()D D F A D 3121,0300,629.281,0,1276,267277225,20,4924,23⎥⎦
⎤
⎝⎛-∞+-∞--=-+∞⎥⎦
⎤
⎢
⎣⎡-,。
