独立性检验的思想及应用(1)

合集下载

《独立性检验的基本思想及其初步应用(第1课时)》教学设计

1.1.2 独立性检验的基本思想及其初步应用第一课时(谷杨华)一、教学目标1.核心素养通过学习独立性检验的基本思想及其初步应用，初步形成基本的数据分析能力,培养数学运算能力.2.学习目标（1）1.1.1.1 了解分类变量的概念（2）1.1.1.2 了解等高条形图、列联表概念，学会用列联表、等高条形图直观判断分类变量的关系（3）1.1.1.3 了解独立性检验基本思想，初步学会用独立性检验的基本思想判断分类变量的关系3.学习重点了解独立性检验基本思想，初步学会用独立性检验的基本思想判断分类变量的关系4.学习难点了解独立性检验基本思想，初步学会用独立性检验的基本思想判断分类变量的关系二、教学设计（一）课前设计1.预习任务任务1阅读教材P10－P12，思考什么是分类变量，列联表如何画？任务2有哪些方法可以直观判断两个分类变量是否有关系？2.预习自测1.下列不是分类变量的是()A.近视B.身高C.血压D.药物反应解：B.判断一个量是否是分类变量,只需看变量的不同值是否表示个体的不同类别,A,C,D选项的不同值都可以表示个体的不同类别,只有B选项的不同值不表示个体的不同类别.2.下面是一个22⨯列联表则表中a,b A. 94,96 B. 52,50 C. 52,54 D. 54,52 解：C（二）课堂设计 1.知识回顾（1）线性回归方程：∧∧∧+=a x b y ，其中:1122211()()()n niii ii i nniii i x x y y x y nx yb x x xnx∧====---==--∑∑∑∑，a ∧=x b ∧-y（2）回归分析：是对具有相关关系的两个变量进行的统计分析的一种常用方法. （3）线性回归模型：y bx a e =++其中a 和b 为模型的未知参数，e 称为随机误差. 2.问题探究问题探究一什么是分类变量？●活动一理论研究，概念学习—分类变量在现实生活中，会遇到各种各样的变量，如果要研究它们之间的关系，观察下面两组变量，分析在取不同的值时表示的个体有何差异？变量的不同“值”表示个体所属的不同类别，像这样的变量成为分类变量. （1）分类变量也称为属性变量或定性变量，它的不同值表示个体所属的不同类别. （2）分类变量的取值一定是离散的，如性别只取男、女两个值.（3）可以把分类变量的不同取值用数字表示，如用0表示男，1表示女，这是性别变量就成了取值为0和1的随机变量，但这些数字的大小没有意义. 分类变量是大量存在的，例如是否吸烟，宗教信仰，国籍等问题探究二如何研究两个分类变量之间是否有关系？在日常生活中，我们常常关心两个分类变量之间是否有关系.例如，吸烟与患肺癌是否有关系？性别是否对喜欢数学课程有影响？ ●活动一实例探究，引出问题例1 为调查吸烟是否对肺癌有影响，某肿瘤研究所随机地调查了9965人，得到如下结果：表格 1那么吸烟是否对患肺癌有影响？估计吸烟者与不吸烟者患病的可能性差异？●活动二实例探究，引出概念 1.列联表类似于上面的表格这样列出两个分类变量的频数表，称为列联表.即列联表是两个或者两个以上分类变量的频数表，书中仅限于研究两个分类变量的列联表，并且每个分类变量只取两个值，这样的列联表成为2×2列联表.一般的，假设有两个分类变量X 和Y ，它们的取值分别为{}21,x x 和{}21,y y ，其样本频数列联表为：1y 2y总计1x a bb a + 2xcd d c + 总计c a +b d +d c b a +++其中d c b a +++是样本容量. ●活动三利用旧知，研究问题利用频率分布表判断;由患肺癌在吸烟者与不吸烟者中的频率差异可粗略估计吸烟对患肺癌有影响; ●活动四学习新知，对比研究与表格相比，图形更能直观的反映出两个分类变量间是否相互影响，我们常用等高条形图展示列联表数据的频率特征. 2.等高条形图利用等高条形图来分析两个分类变量之间是否具有相关关系，可以形象、直观地反映两个分类变量之间的总体状态和差异大小，进而判断它们之间是否具有相关关系.（1）绘制等高条形图时，列联表的行对应的是高度，两行的数据不相等，但对应的条形图的高度是相同的；两行的数据对应不同的颜色.（2）等高条形图中由两个高度相同的矩形，每一个矩形中都有两种颜色，观察下方颜色区域的高度，如果两个高度相差比较明显，就判断两个分类变量之间有关系.下图是吸烟与是否患肺癌的等高条形图0%10%20%30%40%50%60%70%80%90%100%不吸烟吸烟患肺癌不患肺癌由条形图可以发现，在吸烟样本中，患肺癌的频率要高些，因此直观上可以认为吸烟更容易引发肺癌.例2 在调查的480名男人中有38人患色盲，520名女人中有6名患色盲，试利用图形来判断色盲与性别是否有关？【知识点：分类变量，等高条形图】详解根据题目给出的数据作出如下的列联表：色盲不色盲总计男38442480女6514520总计44956 1 000根据列联表作出相应的等高条形图：从等高条形图来看在男人中患色盲的比例要比在女人中患色盲的比例大得多，因而，我们认为性别与患色盲是有关系的.点拨:利用数形结合的思想，借助等高条形图来判断两个分类变量是否相关是判断变量相关的常见方法之一.一般地，在等高条形图中，aa＋b 与cc＋d相差越大，两个分类变量有关系的可能性就越大.问题探究三如何从统计学方面研究两个分类变量之间是否有关系？重点、难点知识★▲通过数据和图形分析，我们得到的直观判断是“吸烟和患肺癌有关”那么这种判断是否可靠？我们通过统计分析回答这个问题.为研究的一般性,在列联表中用字母代替数字为了回答上述问题，我们先假设H：吸烟与患肺癌没有关系,那么吸烟样本中不患肺癌的比例应该与不吸烟样本中相应的比例差不多，即：dc cb a a +≈+，即bc ad ≈. 因此，bc ad -越小，说明吸烟与患肺癌之间关系越弱；bc ad -越大，说明吸烟与患肺癌之间关系越强.为了使不同样本容量的数据有统一的评判标准，构造一个随机变量()()()()()22n ad bc K a b c d a c b d -=++++ （1）（其中n a b c d =+++为样本容量.）若0H 成立，即“吸烟与患肺癌没有关系”，则2K 应该很小. 根据表1中的数据，利用公式（1）计算得到2K 的观测值为632.5691987421487817)209942497775(99652≈⨯⨯⨯⨯-⨯=k这个值到底能告诉我们什么呢？统计学家经过研究后发现，在0H 成立的情况下， 2( 6.635)0.01P K ≥≈ （2）在0H 成立的情况下，2K 的观测值大于6.635的概率非常小，近似为0.010，是个小概率事件.现在2K 的观测值632.56≈k ，远远大于635.6，所以有理由断定0H 不成立，即认为“吸烟与患肺癌有关系”.但这种判断会犯错误，犯错误的概率不会超过010.0.上面这种利用随机变量2K 来确定是否能以一定把握认为“两个分类变量有关系”的方法，称为两个分类变量的独立性检验. 3.课堂总结【知识梳理】(1)变量的不用“值”表示个体所属的不同类别，像这样的变量成为分类变量. (2)列出两个分类变量的频数表，称为列联表.(3)设0H ：吸烟与患肺癌没有关系,那么吸烟样本中不患肺癌的比例应该与不吸烟样本中相应的比例差不多，即：dc cb a a +≈+，即bc ad ≈. 因此，bc ad -越小，说明吸烟与患肺癌之间关系越弱；bc ad -越大，说明吸烟与患肺癌之间关系越强.为了使不同样本容量的数据有统一的评判标准，构造一个随机变量()()()()()22n ad bc K a b c d a c b d -=++++ （1）（其中n a b c d =+++为样本容量.）若0H 成立，即“吸烟与患肺癌没有关系”，则2K 应该很小.【重难点突破】(1)列联表与等高条形图列联表由两个分类变量之间频率大小差异说明这两个变量之间是否有关联关系，而利用等高条形图能形象直观地反映它们之间的差异，进而推断它们之间是否具有关联关系.一般地，在等高条形图中，a a ＋b 与cc ＋d 相差越大，两个分类变量有关系的可能性就越大.(2)利用等高条形图判断两个分类变量是否有关的步骤：4.随堂检测1.独立性检验中，可以粗略地判断两个分类变量是否有关的是（） A. 残差B. 等高条形图C.假设检验的思想D.以上都不对【知识点：独立性检验】解: B.2.分类变量X 和Y 的列联表如下，则（）A. ad bc -越小，说明X 与Y 的关系越弱B. ad bc -越大，说明X 与Y 的关系越强C. 2()ad bc -越大，说明X 与Y 的关系越强 D. 2()ad bc -越接近于0，说明X 与Y 关系越强【知识点：独立性检验】解：C 2K 越大， 2()ad bc -越大, 犯错误的概率的越小，说明X 与Y 的关系越强. 3..在一次独立性检验中，得出2×2列联表如下：最后发现，两个分类变量x 和y 没有任何关系，则m 的可能值是（） A.200 B.720 C.100 D.180 【知识点：独立性检验】解：B 分类变量x 和y 没有任何的关系，所以，得到720=m ，故选B. 4.在一个2×2列联表中，由其数据计算得到K 2的观测值k ＝13.097，则其两个变量间有关系的可能性为( ) A.99.9% B.95% C.90% D.0 附表：【知识点：独立性检验】解：A 因为所求的213.09710.828k ，故可能性为99.9%，所以选A.5.某校为了研究学生的性别和对待某一活动的态度(支持和不支持两种态度)的关系，运用2×2列联表进行独立性检验，经计算K 2＝7.069，则至少有 _的把握认为“学生性别与是否支持该活动有关系”. 附：【知识点：独立性检验】解：99﹪ （三）课后作业基础型自主突破 1.下面说法正确的是( )A.统计方法的特点是统计推断准确、有效B.独立性检验的基本思想类似于数学上的反证法C.任何两个分类变量有关系的可信度都可以通过查表得到D.不能从等高条形图中看出两个分类变量是否相关【知识点：独立性检验】解：B2.观察下列各图，其中两个分类变量x ，y 之间关系最强的是( )【知识点：独立性检验】解：D3.确定结论“X 与Y 有关系”的可信度为95℅时，则随机变量2k 的观测值k 必须（） A.大于828.10 B.大于841.3 C.小于635.6 D.大于706.2 【知识点：独立性检验】解：B 通过表中的数据可知可信度为95℅时2 3.841kP （K 2≥k 0） 0.05 0.025 0.010 0.005 0.001 k 03.8415.0246.6357.87910.8284. 想要检验是否喜欢参加体育活动是不是与性别有关，应该检验( ) A.H 0：男性喜欢参加体育活动 B.H 0：女性不喜欢参加体育活动 C.H 0：喜欢参加体育活动与性别有关 D.H 0：喜欢参加体育活动与性别无关【知识点：独立性检验】解： D5.对分类变量X 与Y 的随机变量2K 的观测值K ,说法正确的是（ ) A .K 越大，" X 与Y 有关系”可信程度越小; B . K 越小，" X 与Y 有关系”可信程度越小; C . K 越接近于0，" X 与Y 无关”程度越小 D . K 越大，" X 与Y 无关”程度越大【知识点：独立性检验】解： B能力型师生共研6.若有%9.99的把握说事件A 与事件B 有关，那么具体算出的2K 的观测值k 一定满足（）A.828.10>kB.828.10<kC.635.6>kD.635.6<k 【知识点：独立性检验】解： A7.假设有两个分类变量X 和Y ，它们的值域分别为{x 1，x 2}和{y 1，y 2}，其2×2列联表为：(D ) A.a ＝5，b ＝4，c ＝3，d ＝2 B.a ＝5，b ＝3，c ＝4，d ＝2 C.a ＝2，b ＝3，c ＝4，d ＝5 D.a ＝3，b ＝2，c ＝4，d ＝5 【知识点：独立性检验】解： D8.某校为了研究学生的性别和对待某一活动的态度(支持与不支持)的关系，运用2⨯2列联表进行独立性检验，经计算K 2=7.069，则所得到的统计学结论为：有把握认为“学生性别与支持该活动有关系”【知识点：独立性检验】解： 99％【解析】根据6.6357.06910.828<<，所以犯错误率低于1%，所以应该有99%的把握，认为“学生性别与支持该活动有关系” ，探究型多维突破9.某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示：(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少？抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少？ (2)试运用独立性检验的思想方法点拨：学生的学习积极性与对待班级工作的态度是否有关系？并说明理由.(参考下表)【知识点：独立性检验,古典概型】解:(1)积极参加班级工作的学生有24人,总人数为50人,概率为25125024=；不太主动参加班级工作且学习积极性一般的学生有19人,概率为5019.(2)5.111315026242524)761918(5022≈=⨯⨯⨯⨯-⨯⨯=K , ∵828.102>K ,∴有%9.99的把握说学习积极性与对待班级工作的态度有关系.10.2016年夏季奥运会将在巴西里约热内卢举行，体育频道为了解某地区关于奥运会直播的收视情况，随机抽取了100名观众进行调查，其中40岁以上的观众有55名，下面是根据调查结果绘制的观众准备平均每天收看奥运会直播时间的频率分布表(时间：分钟)：将每天准备收看奥运会直播的时间不低于80分钟的观众称为“奥运迷”，已知“奥运迷”中有10名40岁以上的观众.（1）根据已知条件完成下面的22⨯列联表，并据此资料你是否有认为“奥运迷”与年龄有关？（2）将每天准备收看奥运会直播不低于100分钟的观众称为“超级奥运迷”，已知“超级奥运迷”中有2名40岁以上的观众，若从“超级奥运迷”中任意选取2人，求至少有1名40岁以上的观众的概率.【知识点：独立性检验,概率统计】解：（1）由频率分布表可知，在轴取的100人中，“奥运迷”有25人，从完成22⨯列联表如下：因为3.030 3.841<，所以没有“奥运迷”与年龄有关.（2）由频率分布表可知，“超级奥运迷”有5人，从而所有可能结果所组成的基本事件空间为：()()()()()()()()()(){}12132311122122313212,,,,,,,,,,,,,,,,,,,a a a a a a a b a b a b a b a b a b b b Ω=其中i a 表示男性，1,2,3,i i b =表示女性，1,2i =.Ω由10个基本事件组成，且是等可能的，用A 表示事件“任意选2人，至少有1名40岁以上观众”，则()()()()()()(){}11122122313212,,,,,,,,,,,,,A a b a b a b a b a b a b b b =，即事件A 包含7个基本事（四）自助餐1.在等高条形图中，下列哪两个比值相差越大，要推断的论述成立的可能性就越大( )A.a a ＋b 与dc ＋d B.c a ＋b 与a c ＋d C.a a ＋b 与c c ＋d D.a a ＋b 与c b ＋c【知识点：独立性检验】解： C2.为了调查中学生近视情况，某校150名男生中有80名近视，140名女生中有70名近视.在检验这些中学生眼睛近视是否与性别有关时用什么方法最有说服力（） A.平均数 B.方差 C.回归分析 D.独立性检验【知识点：独立性检验】解： D 本例考查学生眼睛的“近视”与“性别”两件事情之间是否存在相关性，从给出的数据可以列出22⨯列联表，所以适合用独立性检验.3.在一个2×2列联表中，由其数据计算得K 2的观测值k ＝7.097，则这两个变量间有关系的可能性为（）A.99%B.99.5%C.99.9%D.无关系【知识点：独立性检验】解： A 由表格数据可知k ＝7.097>6.635，所以这两个变量间有关系的可能性为99%4.某疾病研究所想知道吸烟与患肺病是否有关，于是随机抽取1000名成年人调查是否抽烟及是否患有肺病得到22⨯列联表，经计算得231.52=K ，已知在假设吸烟与患肺病无关的前提条件下，01.0)635.6(,05.0)841.3(22=≥=≥K P K P .则该研究所可以（）A.有%95以上的把握认为“吸烟与患肺病有关”B.有%95以上的把握认为“吸烟与患肺病无关”C.有%99以上的把握认为“吸烟与患肺病有关”D.有%99以上的把握认为“吸烟与患肺病无关” 【知识点：独立性检验】解： A 因为2 5.231 3.841K =>,而2( 3.841)0.05P K ≥=,故有有%95以上的把握认为“吸烟与患肺病有关”5.2016年3月9日至15日，谷歌人工智能系统“阿尔法”迎战围棋冠军李世石，最终结果“阿尔法”以总比分4比1战胜李世石.许多人认为这场比赛是人类的胜利，也有许多人持反对意见，有网友为此进行了调查，在参加调查的2548名男性中有1560名持反对意见， 2452名女性中有1200名持反对意见，在运用这些数据说明“性别”对判断“人机大战是人类的胜利”是否有关系时，应采用的统计方法是（） A.茎叶图 B.分层抽样 C.独立性检验 D.回归直线方程【知识点：独立性检验】解:C 这是独立性检验，因为这里有两个分类变量，一个是性别分为男女，一个是意见分为支持和反对，这样就构成一个22⨯联表，用独立性检验来验证“人机大战是人类的胜利”是否有关系.6.某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量之间的关系，随机抽查52名中学生，得到统计数据如表1至表4，这与性别有关联的可能性最大的变量是（）A.成绩B.视力C.智商D.阅读量【知识点：独立性检验】解：D由表中数据可得：表1:()25262210140.00916362032K⨯⨯-⨯=≈⨯⨯⨯；表2:()25242012161.76916362032K⨯⨯-⨯=≈⨯⨯⨯；表3:()2528241281.316362032K⨯⨯-⨯=≈⨯⨯⨯；表4:()25214302623.4816362032K⨯⨯-⨯=≈⨯⨯⨯.其中23.48最大,所以阅读量与性别有关联的可能性最大.7.如下表是对于喜欢足球与否的统计列联表依据表中的数据，得到2K.【知识点：独立性检验】解：228542122854.77245406817k⨯-⨯==⨯⨯⨯.8.若由一个2×2列联表中的数据计算得K2的观测值k＝4.013，那么在犯错误的概率不超过________的前提下认为两个变量之间有关系.【知识点：独立性检验】解：0.05 因随机变量K2的观测值k＝4.013＞3.841，因此，在犯错误的概率不超过0.05的前提下，认为两个变量之间有关系.9.如果K2的观测值为6.645，可以认为“x与y无关”的可信度是________.【知识点：独立性检验】解：1%10.某学校对该校学生作了一项调查发现:在平时的模拟考试中,性格内向的学生426人中332人在考前心情紧张,性格外向的学生594人中有213人在考前心情紧张,作出等高条形图,利用图形判断考前心情紧张与性格类别是否有关系.【知识点：独立性检验】解：作列联表如下:性格内向性格外向总计考前心情紧张332 213 545考前心情不紧张94 381 475总计426 594 1020 相应的等高条形图如图所示:图中阴影部分表示考前心情紧张与考前心情不紧张中性格内向的比例,从图中可以看出考前心情紧张的样本中性格内向占的比例比考前心情不紧张样本中性格内向占的比例大,可以认为考前紧张与性格类型有关.11.甲、乙两所学校高三年级分别有1200人，1000人，为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况，采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩，并作出了频数分布统计表如下：（1）计算x，y的值；（2）若规定考试成绩在[120,150]内为优秀，请分别估计两所学校数学成绩的优秀率；（3）根据以上统计数据完成2×2列联表，并判断是否有90%的把握认为两所学校的数学成绩有差异.【知识点：独立性检验，分层抽样，概率统计】解：（1）x＝10，y＝7；（2）甲乙分别为；25%，40%（3）见解析.试题分析：（1）由题为分层抽样，可确定出甲乙两个学校分别抽取的人数，然后结合频数表，可求出x，y的值；（2）由题给出了优秀的标准，结合给出的表格，可分别求甲乙学校的数学成绩的优秀率，（即由每个学校优秀的人数除以它们的人数）；（3）由题为独立性检验；可先做出二列联表，再代入独立性检验的公式，求出2K，对应参考值可下结论.试题解析：（1）甲校抽取人，乙校抽取人，故x＝10，y＝7，（240%.（3）表格填写如图，k2＞2.706又因为1－0.10＝0.9，故有90%的把握认为两个学校的数学成绩有差异.。

独立性检验的基本思想及其初步应用

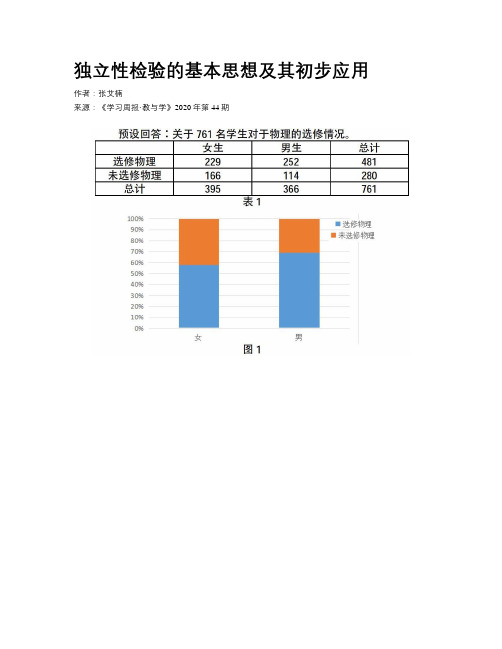
独立性检验的基本思想及其初步应用作者：张艾楠来源：《学习周报·教与学》2020年第44期一、教学目标：1.通过生活中实际问题的探究，理解独立性检验的基本思想，明确独立性检验的基本步骤，会对两个分类变量进行独立性检验，并能利用独立性检验的基本思想来解决实际问题。

2.通过探究高中生选修物理与性别是否有关系引出独立性检验的问题，借助样本数据的列联表分析独立性检验的实施步骤。

3.通过本节课的学习，加强数学与现实生活的联系。

以科学的态度评价两个分类变量有关系的可能性。

培养学生运用所学知识，解决实际问题的能力。

教学中适当地利用学生合作與交流，使学生在学习的同时，体会与他人合作的重要性。

二、教学重点：通过案例的分析研究，展现统计中数据分析的全过程。

让学生体会独立性检验的基本思想，掌握独立性检验的一般步骤;三、教学难点：独立性检验过程中的获得及其意义的理解。

四、教学方法：问题化和探究式教学五、教学手段：多媒体，pad六、教学过程：（一）创设情境课前预习（小组讨论，合作探究）：在之前的学习中，我们研究过两个变量的相关性及它们之间的线性回归方程。

这里再给出几个例子，吸烟与患慢性气管炎是否有关？秃顶和患心脏病是否有关？爱好运动与性别是否有关？上述例子中的各个变量与之前学习过的变量不太一样，变量吸烟我们可以按吸烟与不吸烟分类，性别我们可以按男女分类，变量的不同值表示个体所属的不同类别，像这样的变量，我们叫分类变量。

分类变量不一定只能分两类，比如职业，这个变量就有很多的结果，高中阶段我们只研究具有两个结果的分类变量。

观察下面这个例子：为了迎接2020年的新高考改革，在高一下学期的时候对全年级的761名学生选修物理、化学、生物、政治、历史和地理的情况进行了调查，这里给出全年级同学选修物理的情况。

请同学们自己整理数据并回答下列问题。

问题1：你能否设计一个方法，使得上述的统计结果更加直观？问题2：你能否设计出一个方案，来判断高中生选修物理是否与性别有关？问题3：请同学们以小组为单位，搜集你们感兴趣的分类变量的相关数据，并用你设计的方案来判断你所研究的分类变量之间是否存在一定的关系。

独立性检验思想及应用

独立性检验思想及应用独立性检验（Independence Test）是统计学中用于研究两个或多个分类变量之间是否存在关联的方法。

它基于假设显著性检验的思想，通过计算观察值与期望值之间的差异程度，来判断两个变量是否独立。

在实际应用中，独立性检验经常用于确定两个变量是否相互影响或存在某种联系，以及在实验设计、社会科学研究、生物学研究等领域中的数据分析。

独立性检验的基本思想是基于对观察样本的期望值进行比较，来推断两个或多个分类变量是否存在关联。

在进行独立性检验时，常用的统计方法包括卡方检验（Chi-square Test）、Fisher精确检验（Fisher's Exact Test）和logistic回归分析（Logistic Regression）等。

卡方检验是独立性检验中最常用的方法之一。

它基于卡方统计量的分布特性，通过计算观测频数与期望频数之间的差异，来判断两个或多个分类变量之间的关联性。

卡方检验的原理是比较观测频数与期望频数之间的差异是否显著，若差异显著，则表明两个变量之间存在关联。

Fisher精确检验是一种非参数的检验方法，用于较小样本量且存在预期频数很低的情况。

它通过穷举计算所有可能的观测结果，来计算出在给定的边际总和下，观测频数与期望频数之差异的概率。

Fisher精确检验在小样本研究中经常被使用，特别是用于研究罕见事件的相关性。

logistic回归分析是一种广义线性模型，可用于分析二分类变量的关联性。

它将自变量的线性组合通过logistic函数转换为估计概率，从而实现对二分类变量之间的关系进行研究。

logistic回归分析在独立性检验领域中常用的方法包括二分类变量的logistic回归、多分类变量的logistic回归和多项式logistic回归等。

独立性检验在很多领域都有广泛的应用。

在医学研究中，独立性检验可以用于分析某种疾病的发病率与多个危险因素之间的关联性，以及评估治疗方法对疾病预后的影响；在社会科学研究中，独立性检验可以用于分析社会经济因素与人群特征之间的关联，以及评估政策改革对社会发展的影响；在生物学研究中，独立性检验可以用于分析基因型与表型之间的关联，以及评估不同基因型对遗传疾病的易感性等。

独立性检验的基本思想及其初步应用

如果“吸烟与患肺癌没有关系”，那么吸烟样
本中不患肺癌的比例应该与不吸烟样本中相应的比
例差不多.
所以
a a+
b

c
c +d
,
所以 a c + d ca + b,
ad bc
即 ad bc 0.
︱ad-bc︱越小，说明吸烟与患肺癌之间的关系越弱;
︱ad-bc︱越大，说明吸烟与患肺癌之间的关系越强.
患心脏病患其他病总计
秃顶
214
175
389
不秃顶
451
597
1 048
总计
665
772
1 437
(1)相应的等高条形图如下所示，
不患心脏病患心脏病
秃顶
不秃顶
由图可认为秃顶与患心脏病有关系
吸烟与患肺癌列联表（单位：人）
不患肺癌
患肺癌
总计
不吸烟
7 775
42
7 817
吸烟
2 099
49
2 148
总计
9 874
91
9 965
在不吸烟者中患肺癌的比重是__0_._5_4_%_,
在吸烟者中患肺癌的比重是__2_._2_8_%_.
说明：吸烟者和不吸烟者患肺癌的可能性存在差异，吸烟者患肺癌的可能性大.
K2
（n ad bc）2
(a b)(c d )(a c)(b d )
临界值表：
P ( K 2 k 0 ) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828

独立性检验基本思想及应用

独立性检验基本思想及应用独立性检验是一种用于确定两个变量之间是否存在关联的统计方法。

其基本思想是通过比较观察到的数据与预期的数据之间的差异来推断这两个变量之间的关系。

独立性检验的应用非常广泛。

在社会科学中，独立性检验常被用于研究两个分类变量之间是否存在关联，例如性别和职业、教育水平和政治倾向等。

在医学研究中，独立性检验也可以用来检查某种治疗方法是否与疾病的发展有关，以及风险因素和某种疾病之间的关系。

此外，独立性检验还被广泛应用于市场调查、品牌定位以及质量控制等领域。

独立性检验的基本思想是建立一个零假设（H0）和一个备择假设（H1）。

零假设认为两个变量是独立的，即它们之间没有关联；备择假设则认为两个变量之间存在关联。

独立性检验的步骤可以分为以下几步：1. 收集数据：需要收集两个分类变量的数据，例如通过问卷调查或观察获得数据。

2. 建立列联表：将数据整理成列联表形式，列联表是一种用于描述两个或多个分类变量之间关系的矩阵。

表格的行表示一个变量的不同类别，列表示另一个变量的不同类别，表格中的每个单元格表示两个类别的交叉数量。

3. 计算期望频数：在独立性检验中，我们假设两个变量是独立的，因此可以基于各类别的边际总数以及样本总数来计算期望频数。

期望频数是在两个变量独立情况下，各个类别的交叉数量。

4. 计算卡方统计量：卡方统计量用于衡量观察到的数据与期望数据之间的差异程度。

计算公式为：χ2 = Σ（（观察频数- 期望频数）^2 / 期望频数）。

其中，Σ表示对所有单元格进行求和。

5. 设定显著性水平：显著性水平α为决策的临界点，用于决定是否拒绝零假设。

通常，α的常见选择为0.05或0.01。

6. 判断和解释结果：根据计算出的卡方统计量与临界值进行比较，如果计算出的卡方值大于临界值，拒绝零假设，认为两个变量之间存在关联；反之，接受零假设，认为两个变量是独立的。

独立性检验的结果常常以卡方统计量和p值的形式呈现。

p值是在零假设成立的条件下，观察到的数据与期望数据之间差异的概率。

独立性检验的基本思想及其初步应用

§3.2独立性检验的基本思想及其初步应用学习目标 1.了解独立性检验的基本思想、方法及其简单应用.2.理解判断两个分类变量是否有关系的常用方法、独立性检验中K2的含义及其实施步骤（重、难点）.知识点1两个分类变量之间关联关系的定性分析1.分类变量变量的不同“值”表示个体所属的不同类别，像这样的变量称为分类变量.这里的“变量”和“值”都应作为“广义”的变量和值进行理解，它们取的不一定是具体的数值.2.列联表列出的两个分类变量的频数表，称为列联表.假设两个分类变量X和Y，它们的可能取值分别为{x1，x2}和{y1，y2}，其样本频数列联表（也称为2×2列联表）为：y1y2总计x1 a b a＋bx2 c d c＋d总计a＋c b＋d a＋b＋c＋d3.两个分类变量之间关联关系的定性分析的方法（1）频率分析法：通过对样本的每个分类变量的不同类别事件发生的频率大小进行比较来分析分类变量之间是否有关联关系.通常通过列联表列出两个分类变量的频数表来进行分析.（2）图形分析法：与表格相比，图形更能直观地反映出两个分类变量间是否互相影响，常用等高条形图展示列联表数据的频率特征.【预习评价】（1）下面是一个2×2列联表：y1y2总计x1 a 2173x282533总计 b 46则表中a，b处的值分别为（）A.94，96B.52，50C.52，60D.54，52（2）根据如图所示的等高条形图可知吸烟与患肺病关系（填“有”或“没有”）.知识点2独立性检验1.定义：利用随机变量K2来判断“两个分类变量有关系”的方法称为独立性检验.2.K2＝n（ad－bc）2（a＋b）（c＋d）（a＋c）（b＋d），其中n＝a＋b＋c＋d.3.独立性检验的具体做法（1）根据实际问题的需要确定容许推断“两个分类变量有关系”犯错误概率的上界α，然后查表确定临界值k0.（2）利用公式计算随机变量K2的观测值k.（3）如果k≥k0，就推断“X与Y有关系”，这种推断犯错误的概率不超过α，否则就认为在犯错误的概率不超过α的前提下不能推断“X与Y有关系”，或者在样本数据中没有发现足够证据支持结论“X与Y有关系”.【预习评价】（1）在吸烟与患肺病这两个分类变量是否相关的判断中，下列说法中正确的是（）①若K2的观测值k＞6.635，则在犯错误的概率不超过0.01的前提下，认为吸烟与患肺病有关系，那么在100个吸烟的人中必有99人患有肺病；②从独立性检验可知在在犯错误的概率不超过0.01前提下，认为吸烟与患肺病有关系时，我们说若某人吸烟，则他有99%的可能患有肺病；③从统计量中得知在犯错误的概率不超过0.05的前提下认为吸烟与患肺病有关系，是指有5%的可能性使得推断出现错误.A.①B.①③C.③D.②（2）某班主任对全班50名学生进行了作业量的调查，数据如下表：认为作业量大认为作业量不大总计男生18927女生81523总计262450则推断“学生的性别与认为作业量大有关”这种推断犯错误的概率不超过（）A.0.01B.0.005C.0.025D.0.001题型一利用等高条形图判断两个分类变量是否有关系【例1】为考察某种药物预防疾病的效果进行动物试验，得到如下列联表：患病未患病总计服用药104555未服用药203050总计3075105试用等高条形图分析服用药和患病之间是否有关系.规律方法（1）本题采用数形结合法通过条形图直观地看出差异，得出结论. （2）应用等高条形图判断两变量是否相关的方法在等高条形图中，可以估计满足条件X＝x1的个体中具有Y＝y1的个体所占的比例aa＋b，也可以估计满足条件X＝x2的个体中具有Y＝y1的个体所占的比例cc＋d.“两个比例的值相差越大，H1成立的可能性就越大.”【训练1】网络对现代人的生活影响较大，尤其是对青少年，为了解网络对中学生学习成绩的影响，某地区教育主管部门从辖区初中生中随机抽取了1 000人调查，发现其中经常上网的有200人，这200人中有80人期末考试不及格，而另外800人中有120人不及格.利用图形判断学生经常上网与学习成绩有关吗？方向1 有关“相关的检验”【例2－1】某校对学生课外活动进行调查，结果整理成下表：用你所学过的知识进行分析，能否在犯错误的概率不超过0.005的前提下，认为“喜欢体育还是文娱与性别有关系”？方向2有关“无关的检验”【例2－2】为了探究学生选报文、理科是否与对外语的兴趣有关，某同学调查了361名高二在校学生，调查结果如下：理科对外语有兴趣的有138人，无兴趣的有98人，文科对外语有兴趣的有73人，无兴趣的有52人.分析学生选报文、理科与对外语的兴趣是否有关？规律方法（1）独立性检验的关注点在2×2列联表中，如果两个分类变量没有关系，则应满足ad－bc≈0，因此|ad －bc|越小，关系越弱；|ad－bc|越大，关系越强.（2）独立性检验的具体做法①根据实际问题的需要确定允许推断“两个分类变量有关系”犯错误的概率的上界α，然后查表确定临界值k0.②利用公式K2＝n（ad－bc）2（a＋b）（c＋d）（a＋c）（b＋d）计算随机变量K2的观测值k.③如果k＞k0，推断“X与Y有关系”这种推断犯错误的概率不超过α；否则，就认为在犯错误的概率不超过α的前提下不能推断“X与Y有关系”，或者在样本数据中没有发现足够的证据支持结论“X与Y有关系”.【训练2】打鼾不仅影响别人休息，而且可能与患某种疾病有关.下表是一次调查所得的数据：根据独立性检验，能否在犯错误的概率不超过0.001的前提下认为每一晚都打鼾与患心脏病有关系？题型三独立性检验的综合应用【例3】某高校共有学生15 000人，其中男生10 500人，女生4 500人.为调查该校学生每周平均体育运动时间的情况，采用分层抽样的方法，收集300位学生每周平均体育运动时间（单位：时）的样本数据.（1）应收集多少位女生的样本数据？（2）根据这300个样本数据，得到学生每周平均体育运动时间的频率分布直方图（如图），其中样本数据的分组区间为[0，2]，（2，4]，（4，6]，（6，8]，（8，10]，（10，12].估计该校学生每周平均体育运动时间超过4小时的概率.（3）在样本数据中，有60位女生的每周平均体育运动时间超过4小时，请完成每周平均体育运动时间与性别列联表，并判断是否认为“该校学生的每周平均体育运动时间与性别有关”.附：P（K2≥k0）0.1000.0500.0100.005k0 2.706 3.841 6.6357.879K2＝n（ad－bc）2（a＋b）（c＋d）（a＋c）（b＋d）.规律方法（1）解答此类题目的关键在于正确利用K2＝n（ad－bc）2计算k的值，再用它与临界值k0的大小作比（a＋b）（c＋d）（a＋c）（b＋d）较来判断假设检验是否成立，从而使问题得到解决.（2）此类题目规律性强，解题比较格式化，填表计算分析比较即可，要熟悉其计算流程，不难理解掌握.【训练3】某校高三年级在一次全年级的大型考试中，数学成绩优秀和非优秀的学生中，物理、化学、总分成绩优秀的人数如下表所示，能否在犯错误的概率不超过0.001的前提下认为数学成绩优秀与物理、化学、总分成绩优秀有关系？物理优秀化学优秀总分优秀数学优秀228225267数学非优秀14315699注：该年级在此次考试中数学成绩优秀的有360人，非优秀的有880人.课堂达标1.观察下列各图，其中两个分类变量x，y之间关系最强的是（）2.某同学寒假期间对其30位亲属的饮食习惯进行了一次调查，列出了如下2×2列联表：偏爱蔬菜偏爱肉类总计50岁以下 4 8 12 50岁以上 16 2 18 总计201030则可以说其亲属的饮食习惯与年龄有关的把握为（） A.90%B.95%C.99%D.99.9%3.为了判断高中学生的文理科选修是否与性别有关系，随机调查了50名学生，得到如下2×2列联表：理科文科男 13 10 女720已知P （K 2≥3.841）≈0.05，P （K 2≥5.024）≈0.025.根据表中数据，得到K 2的观测值k ＝50×（13×20－10×7）223×27×20×30≈4.844.可认为选修文理科与性别有关系的可能性不低于 . 4.根据下表计算：不看电视看电视男 37 85 女35143K 2的观测值k ≈ （保留3位小数）.5.在109个人身上试验某种药物预防感冒的作用，得到如下列联表：感冒未感冒总计服用药1146 57 未服用药 213152总计3277109则有多大把握认为该药有效？课堂小结1.列联表与等高条形图列联表由两个分类变量之间频率大小差异说明这两个变量之间是否有关联关系，而利用等高条形图能形象直观地反映它们之间的差异，进而推断它们之间是否具有关联关系.2.对独立性检验思想的理解独立性检验的基本思想类似于数学中的反证法.先假设“两个分类变量没有关系”成立，计算随机变量K2的值，如果K2值很大，说明假设不合理.K2越大，两个分类变量有关系的可能性越大.基础过关1.对两个分类变量A，B的下列说法中正确的个数为（）①A与B无关，即A与B互不影响；②A与B关系越密切，则K2的值就越大；③K2的大小是判定A与B是否相关的唯一依据A.0B.1C.2D.32.高二第二学期期中考试，按照甲、乙两个班学生的数学成绩优秀和及格统计人数后，得到如下列联表：优秀及格总计甲班113445乙班83745总计197190则随机变量K2的观测值约为（）A.0.600B.0.828C.2.712D.6.0043.考察棉花种子经过处理跟生病之间的关系得到下表数据：种子处理种子未处理总计根据以上数据，可得出（）A.种子是否经过处理跟是否生病有关B.种子是否经过处理跟是否生病无关C.种子是否经过处理决定是否生病D.以上都是错误的4.2013年6月11日，中国的“神舟十号”发射成功，由此许多人认为中国进入了航天强国之列，也有许多人持反对意见，为此进行了调查.在参加调查的3 648名男性公民与3 432名女性公民中，持反对意见的男性有1 843人、女性有1 672人，在运用这些数据说明中国“神十”发射成功是否与中国进入航天强国有关系时，用下列最具说服力.①回归直线方程；②平均数与方差；③独立性检验.5.为了解高中生作文成绩与课外阅读量之间的关系，某研究机构随机抽取了60名高中生，通过问卷调查，得到以下数据：由以上数据，计算得到K2的观测值k≈9.643，根据临界值表，以下说法正确的是（填序号）.①没有充足的理由认为课外阅读量大与作文成绩优秀有关；②有0.5%的把握认为课外阅读量大与作文成绩优秀有关；③有99.9%的把握认为课外阅读量大与作文成绩优秀有关；④有99.5%的把握认为课外阅读量大与作文成绩优秀有关.6.在研究某种药物对“H1N1”病毒的治疗效果时，进行动物试验，得到以下数据，对150只动物服用药物，其中132只动物存活，18只动物死亡，对照组150只动物进行常规治疗，其中114只动物存活，36只动物死亡.（1）根据以上数据建立一个2×2列联表；（2）试问该种药物对治疗“H1N1”病毒是否有效？7.在一次恶劣天气的飞行航程中调查男女乘客在飞机上晕机的情况如下表所示，根据此资料是否能在犯错误的概率不超过0.05的前提下认为在恶劣天气飞行中男人比女人更容易晕机？能力提升8.利用独立性检验来考察两个分类变量X和Y是否有关系时，通过查阅下表来确定“X与Y有关系”的可信程度.如果K2≥5.024，那么就有把握认为“X与Y有关系”的百分比为（）A.25%B.75%C.2.5%D.97.5%9.某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量的关系，随机抽查了52名中学生，得到统计数据如表1至表4，则与性别有关联的可能性最大的变量是（）表1表2表3表4A.成绩B.视力C.智商D.阅读量10.下表是关于男婴与女婴出生时间调查的列联表：那么，A＝，B＝，C＝，D＝，E＝.11.在研究性别与吃零食这两个分类变量是否有关系时，下列说法中正确的是（填序号）.①若K2的观测值k＝6.635，则我们在犯错误的概率不超过0.01的前提下认为吃零食与性别有关系，那么在100个吃零食的人中必有99人是女性；②由独立性检验可知在犯错误的概率不超过0.01的前提下认为吃零食与性别有关系时，如果某人吃零食，那么此人是女性的可能性为99%；③由独立性检验可知在犯错误的概率不超过0.01的前提下认为吃零食与性别有关系时，是指每进行100次这样的推断，平均有1次推断错误.12.随着生活水平的提高，人们的休闲方式也发生了变化.某机构随机调查了n 个人，其中男性占调查人数的25.已知男性中有一半的人的休闲方式是运动，而女性中只有13的人的休闲方式是运动. （1）完成下列2×2列联表：（2）若在犯错误的概率不超过0.05的前提下，可认为“性别与休闲方式有关”，那么本次被调查的人数至少有多少？（3）根据（2）的结论，本次被调查的人中，至少有多少人的休闲方式是运动？ 13.（选做题）某学校为了解该校高三年级学生在市一练考试的数学成绩情况，随机从该校高三文科与理科各抽取50名学生的数学成绩，作出频率分布直方图如图，规定考试成绩在[120，150]内为优秀.（1）由以上频率分布直方图填写下列2×2列联表.若按是否优秀来判断，是否有99%的把握认为该校的文理科数学成绩有差异.文科理科总计优秀非优秀总计5050100（2）某高校派出2名教授对该校随机抽取的学生成绩中一练数学成绩在140分以上的学生进行自主招生面试，每位教授至少面试一人，每位学生只能被一位教授面试.若甲教授面试的学生人数为ξ，求ξ的分布列和均值.。

独立性检验的基本思想及其初步应用

P(K2≥k0） 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k0
0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
小结：回顾我们分析“吸烟对患肺癌是否有影响”这个案例的过程：我们是如何判断两个分类变量是否有关系？ 1.提出假设H0：两个分类变量没有关系； 2.写出2×2列联表，并由K2的公式计算其观测值k ； 3.作出推断：确定临界值k0，通过观测值k与k0比较作出判断；
利用频率判断概率是否相等
利用统计量的观测值与临界值比较
利用等高条形图直观判断有关利用小概率事件发生给出“判
系
断有关系”犯错误的概率
【例】在某医院，因为患心脏病而住院的665名男性病人中，有 214人秃顶，而另外772名不是因为患心脏病而住院的男性病人中有175人秃顶. （1）利用图形判断秃顶与患心脏病是否有关系；（2）能否在犯错误的概率不超过0.01的前提下认为秃顶与患心脏病有关系？
（1）若k≥k0，认为k很大，推断H0不成立，从而有 [1-P(K2≥k0)]×100%的把握认为“两个分类变量有关系”，即：在犯错误的概率不超过P(K2≥k0)的前提下认为“两个分类变量有关系”；（2）若k<k0，认为k很小，无法拒绝H0 ，即：样本观测数据没有足够证据证明“两个分类变量有关系”.
总计 7 817 2 148 9 965
依据两个分类变量的取值，列出的频数分布表我们称为 2×2列联表
列分类（Y）
未发生数（y1）
行分
甲（x1）
a
类（X）
乙（x2）
c

独立性检验的基本思想及其初步应用(一)

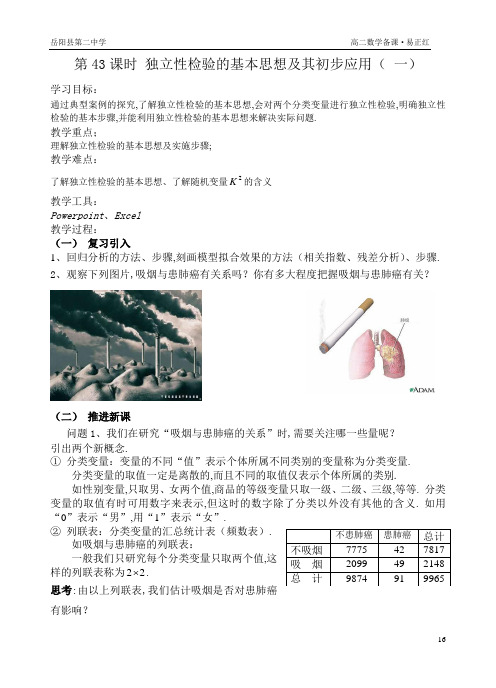
第43课时独立性检验的基本思想及其初步应用（一）学习目标：通过典型案例的探究,了解独立性检验的基本思想,会对两个分类变量进行独立性检验,明确独立性检验的基本步骤,并能利用独立性检验的基本思想来解决实际问题.教学重点；理解独立性检验的基本思想及实施步骤;教学难点：了解独立性检验的基本思想、了解随机变量2K的含义教学工具：Powerpoint、Excel教学过程：（一）复习引入1、回归分析的方法、步骤,刻画模型拟合效果的方法（相关指数、残差分析）、步骤.2、观察下列图片,吸烟与患肺癌有关系吗？你有多大程度把握吸烟与患肺癌有关？（二）推进新课问题1、我们在研究“吸烟与患肺癌的关系”时,需要关注哪一些量呢？引出两个新概念.①分类变量：变量的不同“值”表示个体所属不同类别的变量称为分类变量.分类变量的取值一定是离散的,而且不同的取值仅表示个体所属的类别.如性别变量,只取男、女两个值,商品的等级变量只取一级、二级、三级,等等. 分类变量的取值有时可用数字来表示,但这时的数字除了分类以外没有其他的含义. 如用“0”表示“男”,用“1”表示“女”.②列联表：分类变量的汇总统计表（频数表）.如吸烟与患肺癌的列联表：一般我们只研究每个分类变量只取两个值,这样的列联表称为22.思考:由以上列联表,我们估计吸烟是否对患肺癌有影响？方法一：①在不吸烟者中患肺癌的比例为0.54%；②在吸烟者中患肺癌的比例为2.28%. 因此,直观上可以得到结论：吸烟群体和不吸烟群体患肺癌的可能性存在差异. 方法二：我们还能够从图形中得到吸烟与患肺癌之间的关系吗？如右图,是等高条形图展示列联表数据的频率特征,其中浅色条的高分别表示不吸烟和吸烟样本中不患肺癌的频率；两个深色条的高分别表示不吸烟和吸烟样本中患肺癌的频率.比较两个深色条的高可以发现,在吸烟样本中患肺癌的频率要高一些,因此直观上可以认为吸烟更容易引发肺癌.通过数据和图形分析,我们得到的直观判断是1H ：吸烟和患肺癌有关,那么这种判断是否可靠呢？思考：我们能够从多大程度上认为吸烟与患肺癌之间有关系呢?为了解决上述问题,我们先假设1H 不成立,即 0H ：吸烟与患肺癌没有关系.设事件A 表示不吸烟,事件B 表示不患肺癌,则“吸烟与患肺癌没有关系”等价于“吸烟与患肺癌相互独立”,由事件相互独立性性质,则“不吸烟与不患肺癌也是相互独立”的,即假设0H 成立等价于 ()()()P AB P A P B =由表可知,a 恰好为事件AB 发生的频数；a b +和a c +恰好分别为事件A 和事件B发生的频数,由于频率近似于概率,所以()()()P AB P A P B =成立时应该有 n c a n b a n a +⨯+≈,其中d c b a n +++=为样本容量,即))(()(c a b a a d c b a ++≈+++ 即bc ad ≈也就是说0H ： “吸烟与患肺癌没有关系”成立的充要条件是bc ad ≈,那么这个式子到底能从量上告诉我们什么,怎样来进一步刻画？我们知道bc ad ≈,也就是说bc ad ,的值很接近,那么||ad bc -应该非常接近于0,于是有：问题：||ad bc -的大小说明什么问题？||ad bc -越小,说明0H 成立,即吸烟与患肺癌之间关系越弱； ||ad bc -越大,说明0H 不成立,即1H 成立,吸烟与患肺癌之间有关系.为了使不同样本容量的数据有统一的评判标准,基于上述分析,我们构造一个随机变量22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++为样本容量.重新审视问题：若0H ：吸烟与患肺癌没有关系成立,则2K 应该很小.由上公式计算得到2K 的观测值为29965(777549422099)56.63278172148987491k ⨯-⨯=≈⨯⨯⨯ 这个值到底能告诉我们什么呢？显然,2K 的观测值“很大”,我们有理由认为0H 不成立,即1H 成立,吸烟与患肺癌之间有关系.值得注意的是“很大”是一个什么标准,在样本测量中必须有一个标准——临界值！于是统计学家经过研究发现,在0H 成立的情况下,2( 6.635)0.010.P K ≥≈(小概率事件,发生概率不到5%的事件)这里临界值为6.635,即在0H 成立的情况下,2K 的观测值大于6.635的概率非常小,近似于0.010,是一个小概率事件.也就是说,正常情况下(0H 成立的情况下)2K 的观测值有(以大概率)99%的时候小于6.635.到此,我们就明白了,2K ＝56.632≥6.635,发生了一个小概率事件,违背了正常情况(0H 成立),所以1H 成立,吸烟与患肺癌之间有关系.上面的过程实际上借助于随机变量2K 的观测值k ,建立了一个判断0H 是否成立的规则：如果 6.635k ≥,就判断0H 不成立,即吸烟与患肺癌有关系；否则就判断0H 成立,即吸烟与患肺癌没有关系.在该规则下,把结论“0H 成立”错判成“0H 不成立”的概率不会超过2( 6.635)0.010.P K ≥≈,即有99%的把握认为0H 不成立.知识形成1、分类变量：变量的不同“值”表示个体所属不同类别的变量称为分类变量.分类变量的取值一定是离散的,而且不同的取值仅表示个体所属的类别. 2、列联表：分类变量的汇总统计表（频数表）. 如吸烟与患肺癌的列联表.一般我们只研究每个分类变量只取两个值,这样的列联表称为22⨯.3、独立性检验：这种利用随机变量2K 来确定是否能以给定把握认为“两个分类变量有关系”的方法,称为两个分类变量的独立性检验.4、独立性检验基本思想的形成过程：第一步:提出假设检验问题0H:吸烟与患肺癌没有关系↔ 1H :吸烟与患肺癌有关系;第二步：选择检验的指标22()K ()()()()n ad bc a b c d a c b d -=++++（它越小,原假设“H 0：吸烟与患肺癌没有关系”成立的可能性越大；它越大,备择假设“H 1：吸烟与患肺癌有关系”成立的可能性越大;（三）典例分析1、已知分类变量的列联表如下：和Y X 则下列说法正确的是（ C ）A bc ad -越小,说明Y 和X 关系越弱B bc ad -越大,说明Y 和X 关系越强C 2)(bc ad -越大,说明Y 和X 关系越强D 2)(bc ad -越接近于0,说明Y 和X 关系越强2、根据右边等高条形图,可知男女性别与患色盲有关系（填“有”或“没有”） 3、统计假设:0H )()()(B P A P AB P ⋅=成立时,有以下判断：①)()()(B P A P B A P ⋅=;②)()()(B P A P B A P ⋅=;③)()()(BP A P B A P ⋅=其中真命题的个数是（ C ） A 1 B 2 C 3 D 03、某大学要研究性别与职称（教授与副教授）之间是否有关系,你认为应该收集哪些数据女教授的人数,男教授的人数,女副教授的人数,男副教授的人数 .4、为了调查高中生的数学成绩和物理成绩的关系,在某校随机抽取部分学生调查,得到如下两个图表：根据以下图表,完成以下列联表5、在研究新措施对防治猪白痢是否有效时,得观测结果如上表右,试作出二维条形图并判断新措施对防治猪白痢是否有效？解：作出二维条形图如下图所示,从二维条形图中,可以估计在新措施中的死亡数所占的比例为15018,在对照组中死亡数所占的比例为15036,二者的差值为15018|1503615018|=-,差别很大,因此从二维条形图中我们可以看出新措施对防治猪白痢是有效的.（四）课时小结1、独立性检验的基本思想；2、独立性检验的操作步骤；3、了解2×2列联表的意义与能识别二维条形图和等高条形图. （五）作业 P 97练习。

《独立性检验的基本思想及其初步应用(第1课时)》导学案

§1.2.1 独立性检验的基本思想及其初步应用1.通过探究“吸烟是否与患肺癌有关系”引出独立性检验的问题，并借助样本数据的列联表、柱形图和条形图展示在吸烟者中患肺癌的比例比不吸烟者中患肺癌的比例高，让学生亲身体验独立性检验的必要性;2.会根据22K.⨯列联表求统计量2重点：理解独立性检验的基本思想及实施步骤.难点：了解独立性检验的基本思想、了解随机变量的含义.【知识链接】（预习教材，找出疑惑之处）复习1：回归分析的方法、步骤，刻画模型拟合效果的方法（相关指数、残差分析）、步骤.【学习过程】※学习探究新知一：1.分类变量：.2.22⨯列联表：.试试：你能列举出几个分类变量吗？探究任务：吸烟与患肺癌的关系1.由列联表可粗略的看出：(1)不吸烟者有患肺癌;(2)不吸烟者有患肺癌.因此，直观上课的结论：.2.用三维柱柱图和二维条形图直观反映:(1)根据列联表的数据,作出三维柱形图:由上图可以直观地看出,吸烟与患肺癌.(2) 根据列联表的数据,作出二维条形图:由上图可以直观地看出,吸烟与患肺癌.根据列联表的数据,作出等高条形图:由上图可以直观地看出,吸烟与患肺癌.反思：（独立性检验的必要性）通过数据和图形,我们得到的直观印象是患肺癌有关.那是否有一定的把握认为“吸烟与患肺癌有关”呢？新知二：统计量2K吸烟与患肺癌列联表H：吸烟与患肺癌没关系，则在吸烟者和不吸烟者中患肺癌不患肺癌者的假设相应比例.因此，越小，说明吸烟与患肺癌之间关系；反之，.2K=※ 典型例题例1 吸烟与患肺癌列联表求2K .※ 动手试试练1. 性别与喜欢数学课程列联表：求K .【学习反思】 ※ 学习小结1. 分类变量： .2. 22 列联表： .3. 统计量2K ： .。

36741_《独立性检验的基本思想及其应用》同步练习1

3.2独立性检验的基本思想及其初步应用A卷（课堂针对训练六）1.2双基再现1．★下列变量中不是分类变量的是（）A．近视B．成绩C．性别D．饮酒2．★★下列说法中错误的是（）A．有时可以把分类变量的不同取值用数字表示，但这时的数字除了分类以外没有其它含义B．在统计学中，独立性检验就是检验两个分类变量是否有关系的一种方法C．在进行独立性检验时，可以先利用三维柱形图和二维条形图粗略地判断两个分类变量是否有关系D．通过三维柱形图和二维条形可以精确的给出所得结论的可靠程度3．★★某高校《统计》课程的教师随机给出了选该课程的一些情况，具体数据如下：为了判断选修统计专业是否与性别有关，根据表中数据，得2 4.844K≈，因为2 3.841K>，所以可以判定选修统计专业与性别有关.那么这种判断出错的可能性为（）A．5%B．95%C．1%D．99%4．★★某大学要研究性别与职称之间是否有关系，你认为该收集哪些数据？5．★★在三维柱形图中，主对角线的两个柱形高度的乘积bc相关越大，X与Y有关系的可能性就.6．★★★为了探究电离辐射的剂量与人体的受损程度是否有关，用两种不同的剂量的电离辐射照射小白鼠.在照射14天内的结果如下：进行统计分析时的统计假设是变式活学7．★★★（教材1.2例1变式）研究人员选取170名青年男女大学生的样本，对他（她）们进行一种心理测验，发现有60名女生对该心理的最后一个题目的反应是：作肯定的18名，否定42名；男生110名在相同的项目上作出肯定的有22名，否定的有88名.请问性别与态度之间是否存在某种关系？请分别用图形与独立性检验的方法进行判断.8．★★★★(教材1.2例1变式)在研究某种新措施对猪白痢的防治效果问题时，得到了以下治猪白痢是否有效？实践演练9．★★★★如何对草莓、橙子、桃子、苹果、梨等5种水果进行分类？10．★★★★★在调查的480名男人中有38名患有色盲，520名女人中有6名患有色盲，分别利用图形和独立性检验的方法来判断色盲与性别是否有关？你所得到的结论在什么范围内有效？。

独立检验基本思想一

定量变量：变量的取值表示特定个体的特定的含义，定量变量：变量的取值表示特定个体的特定的含义，不同取值之间的运算也有特定的含义。不同取值之间的运算也有特定的含义。
一个红铃虫的产卵数和温度，一个红铃虫的产卵数和温度，就是两个定量变量。王明的身高是180cm ，李铁的身高是李铁的身高是175cm。说明张明比李立高王明的身高是。说明张明比李立高(180-175)cm 定量变量的数字特征如均值和方差都有实际的意义。定量变量的数字特征如均值和方差都有实际的意义。分类变量则不同，性别变量的两个不同值之间的大小没有意义，分类变量则不同，性别变量的两个不同值之间的大小没有意义，性别变量的均值和方差也没有意义。值和方差也没有意义。
独立性检验的基本思想及其基本应用 1
在现实生活中，会遇到各种各样的变量，在现实生活中，会遇到各种各样的变量，并需要研究他们之间的关系。并需要研究他们之间的关系。观察下面的两种变量，分析他们取不同”值时表示的两种变量，分析他们取不同值”时表示的个体有何差异？个体有何差异？
I. 国籍、宗教信仰、出生的月份、国籍、宗教信仰、性别、出生的月份、一个人是否吸烟；一个人是否吸烟； II. 成绩、身高、年龄、某班同学学生的百成绩、身高、年龄、米成绩；
5月31 日是世界无烟日。有关医学研究表明，许多疾病，例如:心脏病，癌症，脑血管病，慢性阻塞性肺病都与吸烟有关，吸烟已成为继高血压之后的第二号全球杀手。这些疾病与吸烟有关的结论是怎样得出的呢？我们来看下面的问题。
某医疗机构为了了解呼吸道疾病与吸烟是否有关，经行了一次抽样调查。否有关，经行了一次抽样调查。共调查了 515 个成年人，其中吸烟者个成年人，其中吸烟者220 人，不吸烟调查结果是：吸烟的220 人中有者295 人。调查结果是：吸烟的 37 人患呼吸道疾病简称患病，183人未患人患呼吸道疾病(简称患病简称患病)，人未患呼吸道疾病（简称未患病）；不吸烟的295 呼吸道疾病（简称未患病）；不吸烟的）；不吸烟的人中有21 人患病，人未患病人未患病。人中有人患病，274人未患病。

独立性检验的基本思想及初步应用教案

独立性检验的基本思想及初步应用一、教学目标1. 让学生理解独立性检验的基本思想，掌握独立性检验的步骤和应用。

2. 培养学生运用独立性检验解决实际问题的能力，提高学生的数据分析素养。

3. 引导学生运用数学软件或计算器进行独立性检验，培养学生的操作能力。

二、教学内容1. 独立性检验的基本思想（1）理解独立性检验的定义和作用。

（2）掌握独立性检验的基本步骤：提出假设、构造检验统计量、确定显著性水平、计算临界值、做出结论。

2. 独立性检验的初步应用（1）学会运用独立性检验解决实际问题，如判断两个分类变量是否独立。

（2）学会运用数学软件或计算器进行独立性检验，提高数据分析能力。

三、教学重点与难点1. 教学重点：（1）独立性检验的基本思想及步骤。

（2）独立性检验在实际问题中的应用。

（3）运用数学软件或计算器进行独立性检验。

2. 教学难点：（1）独立性检验步骤中构造检验统计量的方法。

（2）如何正确选择显著性水平。

四、教学方法与手段1. 教学方法：（1）讲授法：讲解独立性检验的基本思想和步骤。

（2）案例教学法：分析实际问题，引导学生运用独立性检验。

（3）实践操作法：让学生运用数学软件或计算器进行独立性检验。

2. 教学手段：（1）多媒体课件：展示独立性检验的基本思想和步骤。

（2）数学软件或计算器：让学生进行实际操作。

五、教学过程1. 导入新课：通过一个实际问题引入独立性检验的概念，激发学生的兴趣。

2. 讲解独立性检验的基本思想：讲解独立性检验的定义、作用和基本步骤，让学生理解独立性检验的基本思想。

3. 案例分析：分析一个实际问题，引导学生运用独立性检验，体会独立性检验在解决实际问题中的应用。

4. 实践操作：让学生运用数学软件或计算器进行独立性检验，培养学生的操作能力。

5. 总结与反思：总结本节课的主要内容，让学生巩固所学知识，并思考如何更好地运用独立性检验解决实际问题。

六、教学拓展1. 引导学生探讨独立性检验在实际应用中的局限性，如样本量对检验结果的影响。

独立性检验的基本思想在生活中的应用

独立性检验的基本思想在生活中的应用224100 江苏省盐城市大丰区南阳中学潘锦明独立性检验在日常生活中有广泛的应用，解决该类问题的关键是理解独立性检验的基本思想、熟记公式,准确的运算。

具体地讲要注意以下几个方面。

1.独立性检验的基本思想：① 独立性检验的必要性（为什么不能只凭列联表的数据和图形下结论？）：列联表中的数据是样本数据，它只是总体的代表，具有随机性，故需要用列联表检验的方法确认所得结论在多大程度上适用于总体.②独立性检验的原理（与反证法类似）：反证法假设检验要证明结论A 备择假设H 1在A 不成立的前提下进行推理在H 1不成立的条件下，即H 0成立的条件下进行推理推出矛盾，意味着结论A 成立推出有利于H 1成立的小概率事件（概率不超过α的事件）发生，意味着H 1成立的可能性（可能性为（1－α））很大没有找到矛盾，不能对A 下任何结论，即反证法不成功推出有利于H 1成立的小概率事件不发生，接受原假设 ③独立性检验的基本步骤为：第一步：找相关数据，作出列联表（以吸烟与患肺癌为例）；第二步：提出假设检验问题H 0：吸烟与患肺癌没有关系↔ H 1：吸烟与患肺癌有关系。

第三步：选择检验的指标22()K ()()()()n ad bc a b c d a c b d -=++++,用K 2来确定结论“X 与 Y 有关系”的可信程度.（它越小，原假设“H 0：吸烟与患肺癌没有关系”成立的可能性越大；它越大，备择假设“H 1：吸烟与患肺癌有关系”成立的可能性越大.强调：在熟练掌握了两个分类变量的独立性检验方法之后，可直接计算的值解决实际问题，而没有必要画相应的图形，但是图形的直观性也不可忽视.2.应用举例例1. 有人发现了一个有趣的现象，中国人的邮箱名称里含有数字的比较多，而外国人邮箱名称里含有数字的比较少.为了研究国籍和邮箱名称里是否含有数字的关系，他收集了124个邮箱名称，其中中国人的70个，外国人的54个，中国人的邮箱中有43个含数字，外国人的邮箱中有27个含数字.（1）根据以上数据建立一个2×2的列联表；（2）他发现在这组数据中，外国人邮箱名称里含数字的也不少，他不能断定国籍和邮箱名称里含有数字是否有关，你能帮他判断一下吗？分析：按题中数据建列联表，然后根据列联表数据求出k 值，即可判定.不患肺癌患肺癌总计不吸烟 7775 42 7817 吸烟 209949 2148 总计 9874 91 9965（.由表中数据得=2K 201.660645470)21273343(1242≈⨯⨯⨯⨯-⨯⨯，因为024.5>k ，所以有理由认为假设“国籍和邮箱名称里是否含有数字无关”是不合理的，即有005.97的把握认为“国籍和邮箱名称里是否含有数字有关”.评注：独立性检验类似于反证法，其一般步骤为：第一步：首先假设两个分类变量几乎没有关系（几乎独立）；第二步：求随机变量k 的值；第三步.判断两个分类变量有关的把握（即概率）有多大.例2. 针对时下的“韩剧热”，某校团委对“学生性别和是否喜欢韩剧是否有关”作了一次调查，其中女生人数是男生人数的21，男生喜欢韩剧的人数占男生人数的61，女生喜欢韩剧人数占女生人数的32. （1）若有0095的把握认为是否喜欢韩剧和性别有关，则男生至少有多少人；（2）若没有充分的证据显示是否喜欢韩剧和性别有关，则男生至多有多少人. 分析：有0095的把握认为回答结果对错和性别有关，说明841.3>k ，没有充分的证据显示回答结果对错和性别有关，说明706.2≤k .设出男生人数，并用它分别表示各类别人数，代入2K 的计算公式，建立不等式求解即可.解：x （1）若有0095的把握认为回答结果的对错和性别有关，则841.3>k ，由841.38322)66365(2322>=⋅⋅⋅⨯-⨯=x x x x x x x x x x K ，解得24.10>x ， ∵6,2xx 为整数，∴若有0095的把握认为回答结果的对错和性别有关，则男生至少有12人；（2）没有充分的证据显示回答结果的对错和性别有关，则706.2≤k ，由706.28322)66365(2322≤=⋅⋅⋅⨯-⨯=x x x x x x x x x x K ，解得216.7≤x ，∵6,2xx 为整数，∴若没有充分的证据显示回答结果的对错和性别有关，则男生至多有6人.评注：这是一个独立性检验的创新问题，解答时要注意理解“至少”、“至多”的含义. 通过上面几例，大家是否已体会到了回归分析和独立性检验思想方法的应用的广泛性和重要性.其实，这两种思想方法并不神秘，你身边有很多问题可信手拈来，用它们处理，这一点还请同学们多思考、勤尝试.练习：1、为了研究某种新药的副作用（如恶心等），给50位患者服用此新药，另外50名患者服用安慰剂，得到下列实验数据：请问服用新药是否可产生副作用？2、某大型企业人力资源部为了研究企业员工工作积极性和对待企业改革的关系，随机抽取了189名员工进行调查，其中支持企业改革的调查者中，工作积极的54人，工作一般的32人，而不太赞成企业改革的调查者中，工作积极的40人，工作一般的63人.(1) 根据以上数据建立一个22⨯的列联表；(2) 对于人力资源部的研究项目，根据以上数据可以认为企业的全体员工对待企业改革的态度与其工作积极性是否有关系？练习答案：1、解：提出假设0H ：服用新药与产生副作用之间没有关系由已知数据可以求得63.686.781195050435461510022>=⨯⨯⨯⨯-⨯⨯=）（K所以有99%的把握认为新药与产生副作用是相关联的.0H ：企业的全体员工对待企业改革的态度与其工作积极性无关.根据（1）中列联表的数据，可以求得879.7759.101038695943240635418922>≈⨯⨯⨯⨯-⨯⨯=）（K所以有99.5%的把握认为抽样员工对待企业改革的态度与其工作积极性是有关的.从而可以认为企业的全体员工对待企业改革的态度与其工作积极性是有关的.。

3.2独立性检验的思想及应用(一)

列联表
0.54% 在不吸烟者中患肺癌的比重是_______ 在不吸烟者中患肺癌的比重是_______ 2.28% 在吸烟者中患肺癌的比重是_______ 在吸烟者中患肺癌的比重是_______ 结论:吸烟者和不吸烟者患肺癌的可能性存在差异. 结论:吸烟者和不吸烟者患肺癌的可能性存在差异.
不吸烟吸烟总计
不患肺癌 7775 2099 9874
患肺癌 42 49 91
总计 7817 2148 9965
等高条形图
1.0 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.0 不吸烟患肺癌不患肺癌吸烟
我们通过分析数据和图形, 我们通过分析数据和图形 , 得到的直观判断吸烟和患肺癌有关" 是 " 吸烟和患肺癌有关 " , 那么这种判断是否可靠呢?这需要用统计观点来考察这个问题. 靠呢?这需要用统计观点来考察这个问题.
独立性检验
利用随机变量K 判断" 利用随机变量 2判断"两个分类变量有关的方法称为独立性检验独立性检验. 系"的方法称为独立性检验. 反证法原理与独立性检验原理的比较反证法原理独立性检验原理在假设H0下,如果推出一个矛盾, 如果推出一个矛盾, 就证明假设H0不成立. 不成立. 在假设H0下,如果推出一个小概率事件, 不成立. 事件,就说明H0不成立.
例如,吸烟是否与患肺癌有关系吗? 例如,吸烟是否与患肺癌有关系吗?
探究
为了研究吸烟是否对肺癌有影响, 为了研究吸烟是否对肺癌有影响,某肿瘤研究所随机地调查了9965 9965人得到如下结果(单位: 地调查了9965人,得到如下结果(单位:人) 不吸烟吸烟总计不患肺癌 7775 2099 9874 患肺癌 42 49 91 总计 7817 2148 9965

独立性检验的基本思想及其初步应用》

独立性检验的基本思想及其初步应用》生更加直观地理解两个分类变量之间的关系。

问题2：根据三维柱形图和二维条形图，你能否看出吸烟者和不吸烟者患肺癌的比例有何不同？二、独立性检验的基本思想1、独立性检验的基本思想：独立性检验是用来检验两个分类变量是否有关系的一种统计方法。

如果两个分类变量是独立的，那么它们之间是没有关系的；如果两个分类变量不独立，则它们之间是有关系的。

2、独立性检验的步骤：1）列出列联表；2）计算期望频数；3）计算卡方值；4）查表得出显著性水平；5）判断两个分类变量是否有关系。

三、K2检验的计算公式1、K2检验的计算公式：K2=∑(Oi-Ei)²/Ei其中，Oi为观察频数，Ei为期望频数。

2、K2检验的含义：K2检验的值越大，观察频数与期望频数的差距越大，两个分类变量之间的关系就越显著。

四、独立性检验的应用举例1、应用举例：1）医学研究：调查吸烟是否对患肺癌有影响；2）社会调查：调查男女是否对某一品牌的喜好程度有影响；3）市场调查：调查年龄与消费金额是否有关系。

2、独立性检验的应用：通过独立性检验，可以判断两个分类变量是否有关系，从而为我们提供科学的依据，进行合理的决策。

教学反思：本节课通过生动的例子和图表，引入了独立性检验的基本概念和思想。

通过对K2检验公式的介绍，让学生了解了如何计算卡方值。

同时，通过应用举例，让学生了解了独立性检验的实际应用。

在教学过程中，教师注重启发学生的思维，让学生在合作探究中主动掌握知识，达到了预期的教学目标。

练1、在某医院，665名男性病人中，214人秃顶，而在772名非心脏病男性病人中，175人秃顶。

能否以99%的置信度认为“秃顶与患心脏病”有关系？思考1、为调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老年人，结果如下：性别。

是否需要志愿者需要。

不需要男性。

30.170女性。

373.271）估计该地区老年人中需要志愿者提供帮助的比例；2）能否以99%的置信度认为该地区的老年人是否需要志愿者提供帮助与性别有关系？思考2、某研究小组为了研究中学生的身体发育情况，在某学校随机抽出20名15至16周岁的男生，将他们的身高和体重制成2×2列联表，根据列联表的数据，能否以95%的置信度认为该学校15至16周岁的男生的身高和体重之间有关系？课后作业：课本第18页第1题和第2题。