SAS中的描述性统计过程
几种描述性统计分分析的SAS过程

几种描述性统计分分析的SAS过程描述性统计是统计学中的一种方法,用于总结和描述数据集的主要特征。
它有助于了解数据的整体分布、偏差和离散性等。
SAS(统计分析系统)是一种流行的统计软件,具有丰富的分析功能。
以下是几种常用的SAS过程,用于执行描述性统计分析。
1.PROCMEANS:PROCMEANS是一种计算统计指标的SAS过程,包括均值、总和、最小值、最大值、标准差等。
可以使用该过程对数值变量进行描述性统计,并在输出中显示这些统计指标。
可以通过指定多个变量和分组变量来计算针对不同子组的统计指标。
该过程还可以生成频数和百分比。
2.PROCFREQ:PROCFREQ是一种用于计算分类变量频数和百分比的SAS过程。
它可以计算每个类别的频数,并使用该信息生成频数表。
该过程还可以计算两个或更多分类变量之间的交叉频数表,并计算出每个类别的百分比。
3.PROCUNIVARIATE:PROCUNIVARIATE是一种用于执行单变量分析的SAS过程。
它可以计算变量的均值、标准差、峰度、偏度等统计指标。
该过程可以绘制直方图、箱线图、正态检验图和PP图等,以帮助理解数据的分布特征。
还可以执行分位数分析、离散度分析和异常值识别等。
4.PROCCORR:PROCCORR是一种用于计算变量之间相关性的SAS过程。
它可以计算变量间的皮尔逊相关系数,并使用协方差矩阵和相关系数矩阵来描述变量之间的线性关系。
该过程还可以绘制散点图矩阵和相关系数图,以直观地显示变量之间的关系。
5.PROCGLM:PROCGLM是一种用于执行多因素方差分析的SAS过程。
它可以根据自变量的水平和交互作用来分解因变量的方差,并进行显著性检验。
该过程可以计算组间差异的F值和p值,并生成方差分析表。
PROCGLM还支持使用协变量进行调整的方差分析,以控制对方差的影响。
以上是几种常用的SAS过程,用于执行描述性统计分析。
每个过程都有各自的功能和输出,可以根据数据和分析需求选择合适的过程。
SAS学习系列11.-对数据做简单的描述统计

11. 对数据做简单的描述统计(一)使用proc means描述数据用proc means过程步,可以对数据做简单的描述统计,包括:非缺省值个数、均值、标准差、最大值、最小值等。
基本语法:PROC MEANS data = 数据集<可选项>;V AR 变量列表;CLASS 分组变量;<BY 变量;><WEIGHT 变量;> (加权平均的权数)<FREQ 变量;> (相应观测出现的频数)说明:(1)可选项“MAXDEC = n”用来指定输出结果的小数位数;(2)默认是对数据集的所有数值变量的非缺省值做描述统计,若想包含缺省值,加上可选项“MISSING”;(3)V AR语句指定要做描述统计的变量;CLASS语句指定按分组变量对数据进行分组分别做描述统计;BY语句同CLASS语句(需要事先按BY变量排好序);(4)默认输出非缺省值个数、均值、标准差、最大值、最小值;也可以自己指定需要输出的描述统计量:MAX ——最大值;MIN——最小值;MEAN——均值;MEDIAN——中位数;MODE——众数;N——非缺省值个数;NMISS——缺省值个数;RANGE——极差;STDDEV——标准差;SUM——累和;例1 鲜花销售的数据(C:\MyRawData\Flowers.dat),变量包括顾客ID,销售日期,petunias,snapdragons,marigolds三种花的销量:读取数据,计算新变量销售月份month,并使用proc sort按照月份排序,并使用proc means的by语句来按照月份描述数据。
代码:data sales;infile'c:\MyRawData\Flowers.dat';input CustID $ @9SaleDate MMDDYY10.Petunia SnapDragon Marigold;Month = MONTH(SaleDate);proc sort data = sales;by Month;/* Calculate means by Month for flower sales; */proc means data = sales MAXDEC = 0;by Month;var Petunia SnapDragon Marigold;title'Summary of Flower Sales by Month';run;运行结果:(二)使用统计量有时候需要将统计量存入新数据集,以便进一步做数据分析,或者与原数据集合并。
sas第八章 描述性统计过程
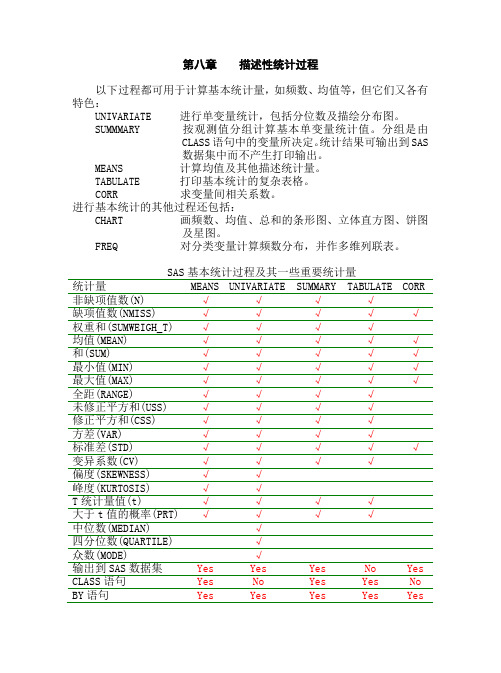
第八章描述性统计过程以下过程都可用于计算基本统计量,如频数、均值等,但它们又各有特色:UNIVARIATE 进行单变量统计,包括分位数及描绘分布图。
SUMMMARY 按观测值分组计算基本单变量统计值。
分组是由CLASS语句中的变量所决定。
统计结果可输出到SAS数据集中而不产生打印输出。
MEANS 计算均值及其他描述统计量。
TABULATE 打印基本统计的复杂表格。
CORR 求变量间相关系数。
进行基本统计的其他过程还包括:CHART 画频数、均值、总和的条形图、立体直方图、饼图及星图。
FREQ 对分类变量计算频数分布,并作多维列联表。
SAS基本统计过程及其一些重要统计量统计量MEANS UNIVARIATE SUMMARY TABULATE CORR 非缺项值数(N) √√√√缺项值数(NMISS) √√√√√权重和(SUMWEIGH_T) √√√√均值(MEAN) √√√√√和(SUM) √√√√√最小值(MIN) √√√√√最大值(MAX) √√√√√全距(RANGE) √√√√未修正平方和(USS) √√√√修正平方和(CSS) √√√√方差(VAR) √√√√标准差(STD) √√√√√变异系数(CV) √√√√偏度(SKEWNESS) √√峰度(KURTOSIS) √√T统计量值(t) √√√√大于t值的概率(PRT) √√√√中位数(MEDIAN) √四分位数(QUARTILE) √众数(MODE) √输出到SAS数据集Yes Yes Yes No Yes CLASS语句Yes No Yes Yes No BY语句Yes Yes Yes Yes Yes第一节 MEANS 过程MEANS过程对数值变量给出简单的描述性统计。
例: 数据集SCORE含有学生三门课程的成绩(见SORT过程),用MEANS 过程可得到: PROC MEANS DATA=SCORE;MEANS过程由下列语句控制:PROC MEANS [选择项];VAR 变量表;BY 变量表;CLASS 变量表;FREQ 变量;WEIGHT 变量;ID 变量表;OUTPUT [选择项];除PROC语句之外的其他语句均为可选语句。
SAS数据分析常用操作指南

SAS数据分析常用操作指南在当今数据驱动的时代,数据分析成为了企业决策、科学研究等领域的重要手段。
SAS 作为一款功能强大的数据分析软件,被广泛应用于各个行业。
本文将为您介绍 SAS 数据分析中的一些常用操作,帮助您更好地处理和分析数据。
一、数据导入与导出数据是分析的基础,首先要将数据导入到 SAS 中。
SAS 支持多种数据格式的导入,如 CSV、Excel、TXT 等。
以下是常见的导入方法:1、通过`PROC IMPORT` 过程导入 CSV 文件```sasPROC IMPORT DATAFILE='your_filecsv'OUT=your_datasetDBMS=CSV REPLACE;RUN;```在上述代码中,将`'your_filecsv'`替换为实际的 CSV 文件路径,`your_dataset` 替换为要创建的数据集名称。
2、从 Excel 文件导入```sasPROC IMPORT DATAFILE='your_filexlsx'OUT=your_datasetDBMS=XLSX REPLACE;RUN;```导出数据同样重要,以便将分析结果分享给他人。
可以使用`PROC EXPORT` 过程将数据集导出为不同格式,例如:```sasPROC EXPORT DATA=your_datasetOUTFILE='your_filecsv'DBMS=CSV REPLACE;RUN;```二、数据清洗与预处理导入的数据往往存在缺失值、异常值等问题,需要进行清洗和预处理。
1、处理缺失值可以使用`PROC MEANS` 过程查看数据集中变量的缺失情况,然后根据具体情况选择合适的处理方法,如删除包含缺失值的观测、用均值或中位数填充等。
2、异常值检测通过绘制箱线图或计算统计量(如均值、标准差)来检测异常值。
对于异常值,可以选择删除或进行修正。
3、数据标准化/归一化为了消除不同变量量纲的影响,常常需要对数据进行标准化或归一化处理。
SAS的基本统计分析

SAS的基本统计分析SAS(统计分析系统)是一种广泛使用的统计分析软件,被广泛应用于数据分析和建模。
它提供了各种强大的统计分析功能,包括描述性统计、推断统计、回归分析、多元分析等。
在本文中,我们将介绍SAS的一些基本统计分析功能。
1.描述性统计分析:描述性统计是对数据集的基本特征进行分析和总结。
SAS提供了各种描述性统计分析功能,包括计算均值、中位数、百分位数、方差、标准差等。
例如,我们可以使用SAS的`MEANS`过程计算数据集中的变量的均值和标准差。
2.推断统计分析:推断统计分析是根据样本数据推断总体的参数估计和假设检验。
SAS提供了一系列的推断统计分析功能,包括参数估计、置信区间估计、假设检验等。
例如,我们可以使用SAS的`TTEST`过程进行两个样本的t检验,或者使用`ANOV`过程进行方差分析。
3.回归分析:回归分析用于研究自变量与因变量之间的关系,并建立预测模型。
在SAS中,我们可以使用`REG`过程进行回归分析。
该过程提供了许多回归模型,如一元线性回归、多元线性回归、逻辑回归等。
我们可以通过回归分析来了解变量之间的关系,发现影响因变量的重要因素,并进行预测。
4.多元分析:多元分析是一种分析多个自变量对因变量的影响的方法。
SAS提供了多种多元分析的方法,如多元方差分析(MANOVA)、主成分分析(PCA)、因子分析等。
我们可以使用SAS的`GLM`过程进行多元方差分析,或者使用`FACTOR`过程进行因子分析。
5.时间序列分析:时间序列分析是一种对时间相关数据进行建模和预测的方法。
SAS提供了一些时间序列分析的功能,如自回归移动平均模型(ARMA)、自回归积分移动平均模型(ARIMA)等。
我们可以使用SAS的`ARIMA`过程进行时间序列分析,拟合ARIMA模型并进行预测。
6.非参数统计分析:非参数统计分析是一种不需要对总体进行任何假设的统计分析方法。
SAS提供了一些非参数统计分析的功能,如Wilcoxon秩和检验、Kruskal-Wallis检验等。
Ch5 SAS基本统计过程 mean uni ttest npar

DF 16 13.8
t Value Pr > |t| 1.81 0.0885 1.85 0.0859
看此表之前应先看下面的方差齐性检验表,由于两组资料 总体方差齐同( P=0.8735,两组资料总体方差齐同),故看 “Equal”一行的结果 :t=1.81,p=0.0885;如果方差不齐, 则看“Unequal”一行的结果。
PROC MEANS [options] [statistics-keywords]; VAR variables; CLASS variables;
该过程除PROC语句(下划线部分)是必须的外,其它的语 句都是可选的。
彭斌
Slide 2
1).PROC MEANS语句
PROC MEANS [options] [statistic-keywords];
彭斌
Slide 17
绘制直方图
➢ 程序语句: PROC UNIVARIATE data= student; Histogram height ; RUN;
➢ 语句选项: 1、拟合正态曲线 Histogram height / normal ; 2、指定直方图的组中值 Histogram height / midpoints=35 40 45 50 55 60 65 70;
左边表中是对应的百分位数;上面表中是极值情况, 列出 5个最大值和5个最小值.
彭斌
Slide 15
(2) 用univariate过程对身高变量进行正态性检验 程序如下: PROC UNIVARIATE data= student normal; VAR height ; RUN;
在这PROC语句中添加选项“normal”即可。
彭斌
Slide 12
SAS描述性统计

统计程式
MEANS过程 MEANS过程
统计程式
例题4.1,进入SAS的显示管理系统,在编辑窗口输入程式: 例题4.1,进入SAS的显示管理系统,在编辑窗口输入程式: 4.1,进入SAS的显示管理系统 ex; 9;输入一个数据集,其中一个变量长度为9 data ex;length name$ 9;输入一个数据集,其中一个变量长度为9 t1- @@; input name sex$ group$ t1-t3 @@;将数据行中的数分别赋给几个变量 Cards; Cards; wangdong 1 1 90 70 60 xueping 2 2 85 95 88 输入一组数据行 让其他SAS SAS语句使用 zhouhua 1 1 77 84 69 heyan 1 2 95 78 88 让其他SAS语句使用 hufang 1 2 78 77 69 zhangqun 1 1 93 91 89 ; maxdec=2;将数据集EX EX中的观测值进行简单描述性统计 proc means maxdec=2;将数据集EX中的观测值进行简单描述性统计 t1-t3; group;按组别将t1 t2、t3中的值分类统计 t1、 var t1-t3;class group;按组别将t1、t2、t3中的值分类统计 maxdec=4; proc means mean std cv maxdec=4;需要描述的变量 t1-t3; group;run; 按组别将t1 t2、t3值的分析结果打印 t1、 var t1-t3; class group;run; 按组别将t1、t2、t3值的分析结果打印
统计程式
MEANS过程 MEANS过程
统计程式
例题4.3,进入SAS的显示管理系统,在编辑窗口输入程式: 例题4.3,进入SAS的显示管理系统,在编辑窗口输入程式: 4.3,进入SAS的显示管理系统 ex; @@;d=xdata ex; input x y @@;d=x-y; Cards; Cards; 11.3 15 15 13.5 12.8 10 11 12 13 12.3 14 13.8 14 13.5 13.5 12 14.7 11.4 13.8 12 ; std; y; proc means n mean std; var x y; prt; d;run; proc means n mean std t prt; var d;run; 程式中的第一个proc means作 的简单的描述性统计, 程式中的第一个proc means作x与y的简单的描述性统计, 第二个proc means作 的总体均值差为0的显著性检验。 第二个proc means作x与y的总体均值差为0的显著性检验。
sas描述性统计分析

28
27
26
散点图
25
24
23
22
21 女 20 1900 1920 1940 1960 1980 2000 男
定性变量的图表示:饼图 定性变量(或属性变量,分类变量 )不能点出直方图、散点图或茎 叶图,但可以描绘出它们各类的 比例。
饼图
定性变量的图表示:条形图
从每一条可以看出讲各种语言的 实际人数,而且分别给出了每 个语种中母语和日常使用的人 数(在图中并排放置)。条形 图显示比例不如饼图直观。
数据的“尺度”
另一个常用的尺度统计量为(样本)标 准差 (standard deviation) 。度量样 本中各数值到均值距离的一种平均。 标准差实际上是方差 (variance) 的平方 根。如果记样本中的观测值为 x1,…,xn,则样本方差为
数据的“尺度”
两个均值一样,但右边的要 “胖”些,方差为左边的一 倍
描述性统计分析
East China JiaoTong University
如 同 给 人 画 像 一 样
数 据 的 描 述
在对数据进行深入加工之前,总 应该对数据有所印象。 可以借助于图形和简单的运算, 来了解数据的一些特征。 由于数据是从总体中产生的,其 特征也反映了总体的特征。对 数据的描述也是对其总体的一 个近似的描述。
其中茎叶图中茎的单位为10cm,而叶子单位为1cm。比如,由于 第一行茎为150cm,因此叶子中的九个数字001223344代表九个数 目150、150、151、152、152、153、153、154、154cm等。每 行左边有一个频数(比如第一行有9个数目,第二行有17个等等); 可以看出最长的一行为从165cm到169cm的一段(有35个数)。
数据分析(SAS描述性统计分析过程)

var
变量列表 ;
by
变量列表 ;
freq
变量 ;
weight 变量 ;
id
变量列表 ;
output <out=输出数据集名> <统计量关键字=变量名列表> <pctlpts= 百分位数 pctlpre=变量前缀名 pctlname=变量后缀名>;
run;
proc uiate过程旳主要控制语句如下:
proc means(5)
SAS程序 data examp1; input x @@; cards; 70.4 72.0 76.5 74.3 76.5 77.6 67.3 72.0 75.0 74.3 73.5 79.5 73.5 74.7 65.0 76.5 81.6 75.4 72.7 72.7 67.2 76.5 72.7 70.4 77.2 68.8 67.3 67.3 67.3 72.7 75.8 73.5 75.0 72.7 73.5 73.5 72.7 81.6 70.3 74.3 73.5 79.5 70.4 76.5 72.7 77.2 84.3 75.0 76.5 70.4 ; proc means data=examp1 n mean cv skewness kurtosis range median ; var x; run;
mode sumwgt max min range median t prt clm lclm uclm
众数,出现频数最高旳数 权数和 最大值 最小值 极差,max—min 中间值 总体均值等于0旳t统计量 t分布旳双尾p值 置信度上限和下限
置信度下限
置信度上限
kurtosis
对尾部陡平旳度量——峰度
------Quantile-----Percent Observed Estimated
如何用SAS进行统计分析

如何用SAS进行统计分析SAS(统计分析系统)是一种用于数据分析和统计建模的软件工具。
它提供了一系列功能和程序,用于数据处理、统计分析、预测建模、图形展示和报告生成等。
本文将介绍如何使用SAS进行统计分析,涵盖数据导入、数据清洗、描述性统计分析、假设检验、回归分析和聚类分析等内容。
1. 数据导入和数据清洗在使用SAS进行统计分析之前,你需要将待分析的数据导入到SAS软件中。
SAS支持多种数据格式,包括CSV、Excel、Access等。
你可以使用SAS提供的PROC IMPORT过程将数据导入到SAS的数据集中。
导入数据后,你需要对数据进行清洗。
数据清洗的目的是去除数据中的错误、缺失或异常值,以确保数据的质量。
你可以使用SAS的数据步骤(DATA STEP)来处理数据,例如删除缺失值、填补缺失值、去除异常值等。
2. 描述性统计分析描述性统计分析是对数据进行总结和描述的过程。
它包括计算数据的中心趋势(均值、中位数、众数)、数据的离散程度(标准差、方差、极差)、数据的分布形态(偏度、峰度)等。
在SAS中,你可以使用PROC MEANS过程进行描述性统计分析。
该过程可以计算多个变量的均值、标准差、最小值、最大值、中位数等统计指标。
此外,你还可以使用PROC UNIVARIATE过程计算数据的偏度、峰度等统计值,并绘制直方图和箱线图来展示数据的分布情况。
3. 假设检验假设检验是对样本数据进行推断性统计分析的一种方法。
它用于判断观察到的样本差异是否显著,从而对总体参数进行推断。
在SAS中,你可以使用PROC TTEST过程进行双样本t检验、单样本t检验和相关样本t检验等。
此外,PROC ANOVA过程可以用于方差分析,PROC FREQ过程可以用于卡方检验。
4. 回归分析回归分析是研究因变量与自变量之间关系的一种统计分析方法。
它用于预测和解释因变量的变化,并评估自变量对因变量的影响程度。
在SAS中,你可以使用PROC REG过程进行简单线性回归分析和多元线性回归分析。
实验报告3—— SAS描述统计分析

实验报告实验项目名称SAS描述统计分析所属课程名称现代统计软件实验类型验证性实验实验日期2014-10-28班级学号姓名成绩实验报告说明1.实验项目名称:要用最简练的语言反映实验的内容。
要求与实验指导书中相一致。
2.实验类型:一般需说明是验证型实验还是设计型实验,是创新型实验还是综合型实验。
3.实验目的与要求:目的要明确,要抓住重点,符合实验指导书中的要求。
4.实验原理:简要说明本实验项目所涉及的理论知识。
5.实验环境:实验用的软硬件环境(配置)。
6.实验方案设计(思路、步骤和方法等):这是实验报告极其重要的内容。
概括整个实验过程。
对于操作型实验,要写明依据何种原理、操作方法进行实验,要写明需要经过哪几个步骤来实现其操作。
对于设计型和综合型实验,在上述内容基础上还应该画出流程图、设计思路和设计方法,再配以相应的文字说明。
对于创新型实验,还应注明其创新点、特色。
7.实验过程(实验中涉及的记录、数据、分析):写明上述实验方案的具体实施,包括实验过程中的记录、数据和相应的分析(原程序、程序运行结果、结果分析解释)。
8.结论(结果):即根据实验过程中所见到的现象和测得的数据,做出结论。
9.小结:对本次实验的心得体会、思考和建议。
10.指导教师评语及成绩:指导教师依据学生的实际报告内容,用简练语言给出本次实验报告的评价和价值。
注意:∙每次实验开始时,交上一次的实验报告。
∙实验报告文档命名规则:“实验序号”+“_”+ “班级”+“_”+“学号”+“姓名”+“_”+ “.doc”例如:管信11班的张军同学学号为:2011312299 本次实验为第2次实验即:实验二、SAS编程基础;则实验报告文件名应为:实验二_管信11 _2011312299_张军.doc 。
几种描述性统计分分析 的SAS过程

2. PROC UNIVARIATE过程 过程
此过程除可完成PROC MEANS过程类似的一些分析外,还具有计 算数据的分位数、绘制茎叶图和QQ图、对数据进行正态性检验等功能。 基本语句: 基本语句 PROC UNIVARIATE options; VAR variables; OUTPUT OUT=dataset name keyword=name … ; RUN; 说明: 说明 (a) “options”部分的选项包括: (i) DATA=SAS dataset name: 指定欲分析的SAS数据集名称; (ii) PLOT: 要求对所分析的各变量的观测值产生一个茎叶图和一 个正态QQ图; (iii) NORMAL: 要求对各变量的观测值作做正态性检验并输出检 验统计量的观测值及检验p-值(n<=2000, W检验;n>2000, Kolmogorov-Smirnov检验)。
4. PROC CORR过程 过程
该过程主要用于计算SAS数据集中各数值变量间的协方差矩阵和 相关系数(包括Pearson相关系数阵和Spearman相关系数阵)矩阵, 并且在各对变量的相关系数下的括号中给出检验响应相关系数是否为零 的检验p-值。此外,此过程还自动输出一些描述性统计量(如各变量的 均值、标准差等等)。 基本语句为: 基本语句为: PROC CORR options; VAR variables; WITH varibles; RUN; 说明: 说明 (a) 第一句中“options”可包括如下选项: (i) DATA=SAS dataset name 指定所分析的SAS数据集; (ii) PEARSON: 要求输出Pearson相关系数矩阵;
3. PROC Cቤተ መጻሕፍቲ ባይዱPABILITY过程 过程
SAS中的描述性统计过程

SAS中的描述性统计过程SAS是一种强大的统计分析软件,提供了丰富的描述性统计分析过程。
这些过程可以帮助统计分析师对数据进行总体的描述和了解。
下面将详细介绍SAS中的描述性统计过程及其应用。
一、数据准备在进行描述性统计之前,需要准备数据。
SAS可以导入各种格式的数据集,如SAS数据集、CSV文件、Excel文件等。
导入数据后,可以使用SAS的数据步骤对数据进行预处理,包括数据清洗、缺失值处理、变量转换等。
这样可以确保数据的质量和完整性。
二、数据探索1.频数统计SAS提供了PROCFREQ过程来计算变量的频数、百分比和交叉表。
可以使用该过程来了解变量的分布情况、缺失值情况和数据异常情况。
通过频数统计,可以发现数据集中的异常值或需要进一步处理的特殊情况。
2.描述性统计SAS中的PROCMEANS和PROCSUMMARY过程可计算变量的均值、标准差、最大值、最小值、中位数等描述性统计量。
这些统计量可以帮助我们了解数据的中心趋势、离散程度和分布情况。
此外,我们还可以使用PROCUNIVARIATE过程来绘制直方图、箱线图和正态概率图,以更直观地了解数据的分布情况。
3.相关分析SAS提供了PROCCORR过程来计算变量之间的相关系数。
通过相关分析,可以了解变量之间的线性关系强度和方向。
PROCCORR还可以生成相关矩阵和散点图,帮助我们观察变量之间的关系。
4.排序和排名SAS提供了PROCRANK过程来对变量进行排序和排名。
排序可以帮助我们找出变量中的异常值或极端值。
排名可以用于对变量进行等级分类,如将考试成绩按照从高到低进行排名。
5.缺失值处理SAS提供了多种方法来处理缺失值,如删除带有缺失值的观测、使用均值或中位数代替缺失值、使用插补方法进行缺失值估计等。
可以使用PROCMEANS、PROCUNIVARIATE和PROCMI过程对缺失值进行处理。
三、数据汇总和报告1.数据表汇总SAS中的PROCTABULATE和PROCREPORT过程可以生成数据表和报告。
sas各过程笔记描述性统计线性回归logistic回归生存分析判别分析聚类分析主成分分析因子分析
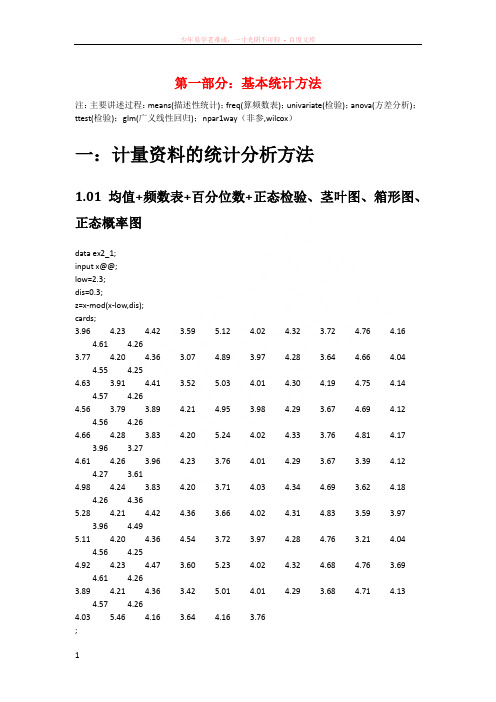
第一部分:基本统计方法注:主要讲述过程:means(描述性统计);freq(算频数表);univariate(检验);anova(方差分析);ttest(检验);glm(广义线性回归);npar1way(非参,wilcox)一:计量资料的统计分析方法1.01均值+频数表+百分位数+正态检验、茎叶图、箱形图、正态概率图data ex2_1;input x@@;low=2.3;dis=0.3;z=x-mod(x-low,dis);cards;3.964.23 4.42 3.595.12 4.02 4.32 3.72 4.76 4.164.61 4.263.774.20 4.36 3.07 4.89 3.97 4.28 3.64 4.66 4.044.55 4.254.63 3.91 4.41 3.525.03 4.01 4.30 4.19 4.75 4.144.57 4.264.56 3.79 3.89 4.21 4.95 3.98 4.29 3.67 4.69 4.124.56 4.264.66 4.28 3.83 4.205.24 4.02 4.33 3.76 4.81 4.173.96 3.274.61 4.26 3.96 4.23 3.76 4.01 4.29 3.67 3.39 4.124.27 3.614.98 4.24 3.83 4.20 3.71 4.03 4.34 4.69 3.62 4.184.26 4.365.28 4.21 4.42 4.36 3.66 4.02 4.31 4.83 3.59 3.973.964.495.11 4.20 4.36 4.54 3.72 3.97 4.28 4.76 3.21 4.044.56 4.254.92 4.23 4.47 3.605.23 4.02 4.32 4.68 4.76 3.694.61 4.263.894.21 4.36 3.425.01 4.01 4.29 3.68 4.71 4.134.57 4.264.035.46 4.16 3.64 4.16 3.76;/*freq语句,算频数表*/proc freq;tables z;run;proc means data=ex2_1n mean std stderr clm;var x;run;data ex2_1;input x f@@;cards;3.07 23.27 33.47 93.67 143.87 224.07 304.27 214.47 154.67 104.87 65.07 45.27 2;run;proc means;freq f;var x;run;/*把freq f改成weight f就是把f当权重或频数来算,f则在0,1之间*//*计算x的95%的置信区间*/proc univariate data=ex2_1;var x;output out=pctpctlpre=ppctlpts=2.5 97.5;run;proc print data=pct;run;/*正态检验、茎叶图、箱形图、正态概率图*/proc univariate data=ex2_1normalplot;var x;run;/*Extreme Observation显示的值是最小的5个极值和最大的5个极值*/1.02几何均值data ex2_5;input x f@@;y=log10(x);cards;10 420 340 1080 10160 11320 15640 141280 2;proc means noprint;/*调用means过程,不显示结果*/var y;freq f;output out=b/*结果输出到数据集b中*/mean=logmean;/*把数据集b中均数的变量名mean改为logmean*/run;data c;/*新建数据集c*/set b;/*调用数据集b*/g=10**logmean;/*计算变量logmean的反对数,该值就是x的几何均数,将该值赋值给变量g*/ proc print data=c;var g;run;/*这个是计算平通平均数的值*/proc means data=ex2_5;var x;freq f;run;1.03已知均值和方差求置信区间-单样本+单样本与总体/*单样本*/data ex3_2;n=10;mean=166.95;std=3.64;t=tinv(0.975,n-1);pts=t*std/sqrt(n);lclm=mean-pts;uclm=mean+pts;proc print;var lclm uclm;run;/*单样本与总体均值*/data ex3_5;n=36;/*样本量*/s_m=130.83;/*样本均值*/std=25.74;/*样本标准差*/p_m=140;/*总体均值*/df=n-1;/*自由度*/t=(s_m-p_m)/(std/sqrt(n));p=(1-probt(abs(t),df))*2;/*根据t值计算p值*/run;proc print;var t p;run;1.06双样本均值相等检验+两组分开+两组一起算+两组样本量不同/*双样本分开算*/data ex3_4;n1=29;n2=32;m1=20.10;m2=16.89;s1=7.02;s2=8.46;ss1=s1**2*(n1-1);ss2=s2**2*(n2-1);sc2=(ss1+ss2)/(n1+n2-2);se=sqrt(sc2*(1/n1+1/n2));t=tinv(0.975,n1+n2-2);lclm=(m1-m2)-t*se;uclm=(m1-m2)+t*se;proc print;var t se lclm uclm;run;/*双样本相减后再算*//*用MEANS作配对资料两个样本均数比较的t检验*/data ex3_6;input x1 x2 @@;d=x1-x2;cards;0.840 0.5800.591 0.5090.674 0.5000.632 0.3160.687 0.3370.978 0.5170.750 0.4540.730 0.5121.200 0.9970.870 0.506;proc means t prt;var d;run;/*用UNIVARIATE过程作配对资料两样本均数比较的t检验*/ proc univariate data=ex3_6;var d;run;/*双样本两组样本量不同*/data ex3_7;input x@@;if _n_<21 then c=1;/*当观测数小于21时,变量c的值为1,表示试验组*/else c=2;/*其余变量c的值为2,表示对照组*/cards;-0.70 -5.60 2.00 2.80 0.70 3.50 4.00 5.80 7.10 -0.502.50 -1.60 1.703.00 0.404.50 4.60 2.50 6.00 -1.403.70 6.50 5.00 5.20 0.80 0.20 0.60 3.40 6.60 -1.106.00 3.80 2.00 1.60 2.00 2.20 1.20 3.10 1.70 -2.00;proc ttest;/*调用ttest过程*/var x;/*定义分析变量为x*/class c;/*定义分组变量为c*/run;1.08-1.13anova方差分析过程+一维分组+二维分组+三维分组/*只有一组分组因素*/data ex4_2;input x c @@;cards;3.53 1 2.42 2 2.86 3 0.89 44.59 1 3.36 2 2.28 3 1.06 44.34 1 4.32 2 2.39 3 1.08 42.66 1 2.34 2 2.28 3 1.27 43.59 1 2.68 2 2.48 3 1.63 43.13 1 2.95 2 2.28 3 1.89 43.30 1 2.36 2 3.48 3 1.31 44.04 1 2.56 2 2.42 3 2.51 43.53 1 2.52 2 2.41 3 1.88 43.56 1 2.27 2 2.66 3 1.41 43.85 1 2.98 2 3.29 3 3.19 44.07 1 3.72 2 2.70 3 1.92 41.37 12.65 2 2.66 3 0.94 43.93 1 2.22 2 3.68 3 2.11 42.33 1 2.90 2 2.65 3 2.81 42.98 1 1.98 2 2.66 3 1.98 44.00 1 2.63 2 2.32 3 1.74 43.55 1 2.86 2 2.61 3 2.16 42.64 1 2.93 23.64 3 3.37 42.56 1 2.17 2 2.58 3 2.97 43.50 1 2.72 2 3.65 3 1.69 43.25 1 1.56 2 3.21 3 1.19 42.96 13.11 2 2.23 3 2.17 44.30 1 1.81 2 2.32 3 2.28 43.52 1 1.77 2 2.68 3 1.72 43.93 1 2.80 2 3.04 3 2.47 44.19 1 3.57 2 2.81 3 1.02 42.96 1 2.97 23.02 3 2.52 44.16 1 4.02 2 1.97 3 2.10 42.59 1 2.31 2 1.68 33.71 4;proc anova;/*调用anova过程*/class c;/*定义分组变量为c*/model x=c;/*定义模型,分析g对x的影响*/means c/dunnett;/*用LSD法对多组均数过行两两比较*/means c/hovtest;/*作方差齐性检验,默认levene法,p值大于0.05,则认为是g组方差相等*/run;quit;/*有两组分组因素*/data ex4_4;input x a b@@;cards;0.82 1 10.65 2 10.51 3 10.73 1 20.54 2 20.23 3 20.43 1 30.34 2 30.28 3 30.41 1 40.21 2 40.31 3 40.68 1 50.43 2 50.24 3 5;proc anova;class a b;/*定义分组变量a和b*/model x=a b;/*定义模型,分析a和b对x影响*/means a/snk;/*用SNK法对变量a的多组均数进行两两比较*/run;quit;1.15嵌套设计资料的方差分析glm过程一级因素+二组因素/*嵌套设计资料的方差分析*/data ex11_6;input x a b @@;cards;82 1 184 1 191 1 288 1 285 1 383 1 365 2 461 2 462 2 559 2 556 2 660 2 671 3 767 3 775 3 878 3 885 3 989 3 9;proc glm;/*调用glm过程*/class a b;/*定义分组变量为a和b*/model x=a a(b);/*定义模型,以a为一组因素,b为二级因素*/run;quit;1.17重复测量资料的方差分析data ex12_2;input t1 t2 g@@;/*确定变量名称,t1和t2分别为两个时间点的分析变量,g为处理因素变量,b为区组变量*/cards;130 114 1124 110 1136 126 1128 116 1122 102 1118 100 1116 98 1138 122 1126 108 1124 106 1118 124 2132 122 2134 132 2114 96 2118 124 2128 118 2118 116 2132 122 2120 124 2134 128 2;proc glm;/*调用glm过程*/class g;/*定义分组变量g*/model t1 t2=g;/*定义模型,分析g对变量t1和t2的影响*/repeated time 2/*命名重复因子为time,有2个水平*/contrast(1)/*表示以第一时间点为对照点*//summary;/*考察不同时间点与对照时间点比较的结果*/run;quit;data ex12_3;input t0-t4 g@@;cards;120 108 112 120 117 1118 109 115 126 123 1119 112 119 124 118 1121 112 119 126 120 1127 121 127 133 126 1121 120 118 131 137 2122 121 119 129 133 2128 129 126 135 142 2117 115 111 123 131 2118 114 116 123 133 2131 119 118 135 129 3129 128 121 148 132 3123 123 120 143 136 3123 121 116 145 126 3125 124 118 142 130 3;proc glm;class g;model t0-t4=g;repeated time 5/*命名重复因子为time,有2个水平*/contrast(1);run;quit;二:计数资料的统计分析方法2.1四格表资料的卡方检验data ex7_1;input r c f@@;/*确定变量名称,r为行变量,c为列变量,f为频数变量*/ cards;1 1 991 2 52 1 752 2 21;proc freq;/*调用freq过程*/weight f;/*定义f为频数变量*/tables r*c/*作r*c的列联表*//chisq/*对列联表作卡方检验*/expected;/*输出每个格的理论频数*/run;2.5阳性事件发生的概率(二项分布)data ex6_1;do x=6 to 8;/*建立循环,变量x从6到8*/p1=probbnml(0.7,10,x);/*计算二项分布随机变量不大于x的概率*/p2=probbnml(0.7,10,x-1);/*计算二项分布随机变量不大于x-1的概率*/p=p1-p2;*/计算出现x的概率*/output;/*结果输出*/end;proc print;var x p;run;2.6正态分布法计算总体率的可信区间data ex6_3;n=100;x=55;p=x/n;sp=sqrt(p*(1-p)/n);u=probit(0.975);usp=u*sp;lclm=p-usp;uclm=p+usp;proc print;var n p sp lclm uclm;run;2.7样本率与总体率的比较(直接法——单侧检验)data ex6_4;d=probbnml(0.55,10,8);p=1-d;proc print;var p;run;2.8样本率与总体率的比较(直接法——双侧检验)data ex6_5;p01=probbnml(0.6,10,9);p02=probbnml(0.6,10,8);p0=p01-p02;/*计算出现9的概率*/do i=0to10;/*建立循环,变量i从0到10*/p11=probbnml(0.6,10,i);p12=probbnml(0.6,10,i-1);p1=p11-p12;/*计算出现i的概率*/if i=0then p1=p11; /*定义出现0的概率*/if p1<=p0 then output; /*如果出现i的概率小于出现9的概率,则保留在数据集中*/ end;proc means sum;var p1;run;2.9两个样本率比较的z检验data ex6_7;n1=120;n2=110;x1=36;x2=22;p1=x1/n1;p2=x2/n2;pc=(x1+x2)/(n1+n2);/*计算合并发生率*/sp=sqrt(pc*(1-pc)*(1/n1+1/n2));/*计算两个率相差的标准误差*/u=(p1-p2)/sp;/*计算u值*/p=(1-probnorm(abs(u)))*2;/*计算p值*/format u p 5.4;/*输出格式为小数点后保留4位*/proc print;var pc sp u p;run;2.10.Poisson分布的样本均数与总体均数比较(直接法)data ex6_12;n=120;/*确定样本例数*/pai=0.008; /*确定总体率*/lam=n*pai; /*计算总体均数lamda*/x=4; /*确定实际发生数*/p=1-poisson(lam,x-1);/*计算实际发生数所对应的概率*/proc print;var lam p;run;2.11 Poisson分布的样本均数与总体均数比较(正态近似法)data ex6_12;n=25000;/*样本量*/x=123; /*样本均数*/pi=0.003; /*确定总体率*/lam=n*pi; /*计算总体均数*/u=(x-lam)/sqrt(lam*(1-pi)); /*计算u值*/p=1-probnorm(abs(u)); /*计算u值所对应的p值*/proc print;var lam u p;run;2.14负二项分布的参数估计data ex6_16;input x f@@;cards;0 301 142 83 44 25 06 2;proc univariate;var x;freq f;output out=mv2var=v;run;data k;set mv2;k=mu**2/(v-mu);proc print;var mu k;run;三、非参数统计方法3.2单个样本中位数和总体中位数比较data ex8_2;input x1@@;median=45.30;/*假设中位数为45.30*/d=x1-median; /*计算x1和假设中位数的差值*/cards;44.21 45.30 46.39 49.47 51.05 53.1653.26 54.37 57.16 67.37 71.05 87.37;proc univariate; /*调用univariate过程度*/var d;run;proc means median; /*调用means过程计算x1实际的中位数*/var x1;run;3.3两个独立样本比较的Wilcoxon秩和检验(R对应函数wilcox.test())data ex8_3;input x c @@;/*确定变量名称,x、c分别为分析变量和分组变量(类别多于两类一样的写法)*/2.78 13.23 14.20 14.87 15.12 16.21 17.18 18.05 18.56 19.60 13.23 23.50 24.04 24.15 24.28 24.34 24.47 24.64 24.75 24.82 24.95 25.10 2;proc npar1way wilcoxon;/*调用npar1way过程,进行wilcoxon分析*/var x;/*定义分析变量为x*/class c;/*定义分组变量为c*/run;3.4等级资料的两样本比较data ex8_4;input c g f@@;/*确定变量名称,f为频数,c为分类,g为要分析的变量(分类多种类似)*/ cards;1 1 11 2 81 3 161 4 101 5 42 1 22 2 232 3 112 5 0;proc npar1way wilcoxon;/*调用npar1way过程,进行wilcoxon分析*/freq f;/*确定频数变量为f*/var g;/*定义分析变量g*/class c;/*定义分组变量c*/run;第二部分:多元统计分析方法注:主要讲述过程:reg(回归),corr(相关分析),nlin(对数曲线回归),logistic(逻辑回归),phreg(条件logistic回归分析+cox回归),life test(生存分析),discrim(判别分析),stepdisc(逐步回归),cluster(聚类),varclus(指标聚类),princomp(主成分分析),factor(因子分析),cancorr(典型相关分析)一:回归和相关分析1.1两个变量的直线回归分析data ex9_1;input x y;/*确定变量名称*/cards;13 3.5411 3.019 3.096 2.488 2.5610 3.3612 3.187 2.65;proc reg;/*调用reg过程*/model y=x;/*定义模型,以y为应变量,以x为自变量*//*在model语句后面加上选项,得到一些有用的统计量,常用的有:stb(输出标准化偏回归系数)、p(输出每个观测的实际值、预测值和残差)、cli(输出每个观测预测值均数的双侧95%置信区间)、clm(输出每个观测预测值的双侧95%置信范围)*//*例如:model y=x /stb p cli */plot y*x;/*画出散点图*/run;1.2两个变量的直线相关分析data ex9_5;input x y;cards;43 217.2274 316.1851 231.1158 220.9650 254.7065 293.8454 263.2857 271.7367 263.4669 276.5380 341.1548 261.0038 213.2085 315.1254 252.08;proc corr;/*若要求作spearman相关分析,则可以写成proc corr spearman */ var x y;run;/*得到一个相关系数矩阵*/1.4加权直线加回data ex9_9;input x y;w=1/(x*x); /*设置权重变量w*/cards;0.11 4.000.12 5.100.21 9.500.30 9.000.34 17.200.44 14.000.56 18.900.60 29.400.69 22.100.80 41.50;proc reg;weight w;/*定义权重变量w*/model y=x;/*定义模型,以y为因变量,以x为自变量*/run;1.5两个直线回归系数的比较data ex9_12;input x y c@@;cards;13 3.54 111 3.01 19 3.09 16 2.48 18 2.56 110 3.36 112 3.18 17 2.65 110 3.01 29 2.83 211 2.92 212 3.09 215 3.98 216 3.89 28 2.21 27 2.39 210 2.74 215 3.36 2;proc glm;class c;model y=x c x*c;/*定义模型,分析x、c以及x和c的交互作用对y的影响,即判断两总体直线回归系数是否相同*/run;proc glm;class c;model y=x c;/*上一步已排除协变量的影响,然后再分析两分析变量是否来自同一总体*/run;1.6两个变量的对数曲线回归data ex9_13;input x y;cards;0.005 34.110.050 57.990.500 94.495.000 128.5025.000 169.98;proc nlin;/*调用nlin过程*/parms a=0 b=0; /*定义初始值*/model y=a+b*log10(x); /*定义对数模型,以y为因变以量,x为自变量*/ run;1.7两个变量的指数曲线回归分析data ex9_14;input x y;cards;2 545 507 4510 3714 3519 2526 2031 1634 1838 1345 852 1153 860 465 6;proc nlin;parms a=4 b=0.03;/*定义初始值*/model y=exp(a+b*x);/*定义指数模型,以y为因变量,x为自变量*/run;1.8多元回归data ex15_1;input x1-x4 y@@;/*确定变量名称,x1,x2,x3,x4分别为自变量,y为应变量*/ cards;5.68 1.90 4.53 8.20 11.203.79 1.64 7.32 6.90 8.806.02 3.56 6.95 10.80 12.304.85 1.075.88 8.30 11.604.60 2.32 4.05 7.50 13.406.05 0.64 1.42 13.60 18.304.90 8.50 12.60 8.50 11.107.08 3.00 6.75 11.50 12.103.85 2.11 16.28 7.90 9.604.65 0.63 6.59 7.10 8.404.59 1.97 3.61 8.70 9.304.29 1.97 6.61 7.80 10.607.97 1.93 7.57 9.90 8.406.19 1.18 1.42 6.90 9.606.13 2.06 10.35 10.50 10.905.71 1.78 8.53 8.00 10.106.40 2.40 4.53 10.30 14.806.06 3.67 12.797.10 9.105.09 1.03 2.53 8.90 10.806.13 1.71 5.28 9.90 10.205.78 3.36 2.96 8.00 13.605.43 1.13 4.31 11.30 14.906.50 6.21 3.47 12.30 16.007.98 7.92 3.37 9.80 13.2011.54 10.89 1.20 10.50 20.005.84 0.92 8.616.40 13.303.84 1.20 6.45 9.60 10.40;proc reg;model y=x1-x4;/*也可以写成model y=x1 x2 x3 x4;*/run;1.9逐步回归data ex12_2;input x1-x4 y@@;cards;5.68 1.90 4.53 8.20 11.203.79 1.64 7.32 6.90 8.806.02 3.56 6.95 10.80 12.304.85 1.075.88 8.30 11.604.60 2.32 4.05 7.50 13.406.05 0.64 1.42 13.60 18.304.90 8.50 12.60 8.50 11.107.08 3.00 6.75 11.50 12.103.85 2.11 16.28 7.90 9.604.65 0.63 6.59 7.10 8.404.59 1.97 3.61 8.70 9.304.29 1.97 6.61 7.80 10.607.97 1.93 7.57 9.90 8.406.19 1.18 1.42 6.90 9.606.13 2.06 10.35 10.50 10.905.71 1.78 8.53 8.00 10.106.40 2.40 4.53 10.30 14.806.06 3.67 12.797.10 9.105.09 1.03 2.53 8.90 10.806.13 1.71 5.28 9.90 10.205.78 3.36 2.96 8.00 13.605.43 1.13 4.31 11.30 14.906.50 6.21 3.47 12.30 16.007.98 7.92 3.37 9.80 13.2011.54 10.89 1.20 10.50 20.005.84 0.92 8.616.40 13.303.84 1.20 6.45 9.60 10.40;proc reg;model y=x1-x4/selection=stepwise/*定义模型,以y因变量,x1-x4为变量进行多元回归分析*/ sle=0.10/*定义入先变量的界值*/sls=0.10;/*定义剔除变量的界值*/run;三:logistic回归3.1 两个变量logistic回归分析data ex16_1;input y x1 x2 f@@;/*确定变量名称,y为发病情况,x1为吸烟情况,x2为饮酒情况,f为发生频数*/cards;1 0 0 631 0 1 631 1 0 441 1 1 2650 0 0 1360 0 1 1070 1 0 570 1 1 151;proc logistic;/*调用logistic过程*/freq f;/*定义频数变量f*/model y=x1 x2;/*定义模型,以y为因变量,x1和x2为自变量*/run;3.2 1:M配对资料的条件logistic回归分析data ex16_3;input i y x1-x6 @@;/*确定变量名称,i为区组变量,y为病人情况,1为病例,0为对照,x1-x6为危险因素*/t=2-y;/*定义时间变量*/cards;1 1 3 5 1 1 1 01 0 1 1 1 3 3 01 0 1 1 1 3 3 02 1 13 1 1 3 02 0 1 1 13 2 02 0 1 2 13 2 03 1 14 1 3 2 03 0 1 5 1 3 2 03 0 14 1 3 2 04 1 1 4 1 2 1 14 0 2 1 1 3 2 05 1 2 4 2 3 2 0 5 0 1 2 1 3 3 05 0 2 3 1 3 2 06 1 1 3 1 3 2 1 6 0 1 2 1 3 2 06 0 1 3 2 3 3 07 1 2 1 1 3 2 1 7 0 1 1 1 3 3 07 0 1 1 1 3 3 08 1 1 2 3 2 2 0 8 0 1 5 1 3 2 08 0 1 2 1 3 1 09 1 3 4 3 3 2 0 9 0 1 1 1 3 3 09 0 1 4 1 3 1 010 1 1 4 1 3 3 1 10 0 1 4 1 3 3 010 0 1 2 1 3 1 011 1 3 4 1 3 2 0 11 0 3 4 1 3 1 011 0 1 5 1 3 1 012 1 1 4 3 3 3 0 12 0 1 5 1 3 2 012 0 1 5 1 3 3 013 1 1 4 1 3 2 0 13 0 1 1 1 3 1 013 0 1 1 1 3 2 014 1 1 3 1 3 2 1 14 0 1 1 1 3 1 014 0 1 2 1 3 3 015 1 1 4 1 3 2 0 15 0 1 5 1 3 3 015 0 1 5 1 3 3 016 1 1 4 2 3 1 0 16 0 2 1 1 3 3 016 0 1 1 3 3 2 017 1 2 3 1 3 2 0 17 0 1 1 2 3 2 017 0 1 2 1 3 2 018 1 1 4 1 3 2 0 18 0 1 1 1 2 1 0 18 0 1 2 1 3 2 019 0 1 1 1 2 1 019 0 2 2 2 3 1 020 1 1 4 2 3 2 120 0 1 5 1 3 3 020 0 1 4 1 3 2 021 1 1 5 1 2 1 021 0 1 4 1 3 2 021 0 1 2 1 3 2 122 1 1 2 2 3 1 022 0 1 2 1 3 2 022 0 1 1 1 3 3 023 1 1 3 1 2 2 023 0 1 1 1 3 1 123 0 1 1 2 3 2 124 1 1 2 2 3 2 124 0 1 1 1 3 2 024 0 1 1 2 3 2 025 1 1 4 1 1 1 125 0 1 1 1 3 2 025 0 1 1 1 3 3 0;proc phreg;/*调用phreg过程*/model t*y(0)=x1-x6/*定义模型,以t为时间变量,y为截尾变量,x1-x6为自变量*//selection=stepwise/*选择逐步回归方法筛选变量*/sle=0.1sls=0.1/*入选和剔除的界值均为0.1*/ties=discrete;/*用离散logistic模型替代比例危险模型*/strata i;/*定义区组变量*/run;2.3 应变量为多分类资料的logistic回归data ex16_5;input x1 x2 y f;/*x1是两个社区,x2是性别,Y是获取健康知识途径(传统大众媒介=1,网络=2,社区宣传=3,f为频数)*/cards;0 0 1 200 0 2 350 0 3 260 1 1 100 1 2 270 1 3 571 0 1 421 02 171 1 1 161 12 121 1 3 26;proc logistic;freq f;/*定义频数变量为f*/model y(ref='3')/*定义模型,以y为因变量,ref语句指时参照的类别为“社区宣传”,最后得到结果均为与“社区宣传”相对应*/=x1 x2/*定义x1和x2为自变量*//link=glogit;/*指定多分类应变量回归模型*/run;四:生存分析4.1乘积极限法估计生存率,例17-2甲、乙两种手术方法的生存率估计data ex17_2;input t d@@;/*确定变量名称,t为时间变量,d为截尾变量*/cards;1 13 15 15 15 16 16 16 17 18 110 110 114 017 119 020 022 026 034 134 044 159 1;proc lifetest;/*调用lifetest过程*/time t*d(0);/*定义模型,以t为时间变量,d为截尾变量,变量值为0表示截尾数据*/ run;4.2寿命表法估计生存率data ex17_3;input t d f@@;cards;0 0 00 1 4561 0 391 1 2262 0 222 1 1523 0 233 1 1714 0 244 1 1355 0 1075 1 1256 0 1336 1 837 0 1027 1 748 0 688 1 519 0 649 1 4210 0 4510 1 4311 0 5311 1 3412 0 3312 1 1813 0 2714 0 3314 1 615 0 2015 1 0;proc lifetest method=life/*调用lifetest过程,指定用寿命表法估计生存率*/ width=1;/*表示每间隔1估计生存率*/freq f;/*表示以f为频数变量*/time t*d(0);/*定义模型,以t为时间变量,d为截尾变量,变量值为0表示截尾数据*/ run;4.3生存曲线比较的log-rank检验及制作生存曲线data ex17_4;input t d g @@;cards;1 1 13 1 15 1 15 1 15 1 16 1 16 1 16 1 17 1 18 1 110 1 110 1 114 0 117 1 119 0 120 0 122 0 126 0 131 0 134 1 134 0 144 1 159 1 11 1 21 1 22 1 23 1 23 1 24 1 24 1 24 1 26 1 26 1 28 1 29 1 29 1 210 1 211 1 212 1 213 1 215 1 217 1 218 1 2;proc lifetest plot=(s);/*调用lifetest过程并做生存曲线图*/ time t*d(0);strata g;/*定义变量g为分组变量*/run;4.4.cox回归分析data ex17_5;input x1-x6 t y @@;cards;54 0 0 1 1 0 52 057 0 1 0 0 0 51 058 0 0 0 1 1 35 143 1 1 1 1 0 103 048 0 1 0 0 0 7 140 0 1 0 0 0 60 044 0 1 0 0 0 58 036 0 0 0 1 1 29 139 1 1 1 0 1 70 042 0 1 0 0 1 67 042 0 1 0 0 0 66 042 1 0 1 1 0 87 051 1 1 1 0 0 85 049 1 1 1 0 1 76 0 52 1 1 1 0 1 74 0 48 1 1 1 0 0 63 0 54 1 0 1 1 1 101 0 38 0 1 0 0 0 100 0 40 1 1 1 0 1 66 1 38 0 0 0 1 0 93 0 19 0 0 0 1 0 24 1 67 1 0 1 1 0 93 0 37 0 0 1 1 0 90 0 43 1 0 0 1 0 15 149 0 0 0 1 0 3 150 1 1 1 1 1 87 0 53 1 1 1 0 0 120 0 32 1 1 1 0 0 120 0 46 0 1 0 0 1 120 043 1 0 1 1 0 120 044 1 0 1 1 0 120 0 62 0 0 0 1 0 120 0 40 1 1 1 0 1 40 1 50 1 0 0 1 0 26 1 33 1 1 0 0 0 120 0 57 1 1 1 0 0 120 0 48 1 0 0 1 0 120 0 28 0 0 0 1 0 3 1 54 1 0 1 1 0 120 1 35 0 1 0 1 1 7 1 47 0 0 0 1 0 18 1 49 1 0 1 1 0 120 0 43 0 1 0 0 0 120 0 48 1 1 0 0 0 15 1 44 0 0 0 1 0 4 1 60 1 1 1 0 0 120 0 40 0 0 0 1 0 16 1 32 0 1 0 0 1 24 1 44 0 0 0 1 1 19 1 48 1 0 0 1 0 120 0 72 0 1 0 1 0 24 1 42 0 0 0 1 0 2 1 63 1 0 1 1 0 120 0 55 0 1 1 0 0 12 1 39 0 0 0 1 0 5 1 44 0 0 0 1 0 120 074 0 0 0 1 1 7 161 0 1 0 1 0 40 145 1 0 1 1 0 108 038 0 1 0 0 0 24 162 0 0 0 1 0 16 1;proc phreg;model t*y(1)=x1-x6/*定义模型,以t为时间变量,y为截尾变量,变量值1表示截尾数据,x1-x6为危险因素*//selection=stepwisesle=0.05sls=0.05;run;五:判别和聚类分析5.1判别分析data ex18_4;input x1-x4 g; /*确定变量名称,x1-x4为用于进行判别分析的指标,g为分组变量*/ cards;6.0 -11.5 19 90 1-11.0 -18.5 25 -36 390.2 -17.0 17 3 2-4.0 -15.0 13 54 10.0 -14.0 20 35 20.5 -11.5 19 37 3-10.0 -19.0 21 -42 30.0 -23.0 5 -35 120.0 -22.0 8 -20 3-100.0 -21.4 7 -15 1-100.0 -21.5 15 -40 213.0 -17.2 18 2 2-5.0 -18.5 15 18 110.0 -18.0 14 50 1-8.0 -14.0 16 56 10.6 -13.0 26 21 3-40.0 -20.0 22 -50 3;proc discrim;class g;/*定义分组变量为g*/var x1-x4;/*定义用于分析的指标变量为x1-x4*/run;(结果横向是真实值,竖向的预测值)5.2逐步判别分析data ex18_5;input x1-x4 g;cards;6.0 -11.5 19 90 1-11.0 -18.5 25 -36 390.2 -17.0 17 3 2-4.0 -15.0 13 54 10.0 -14.0 20 35 20.5 -11.5 19 37 3-10.0 -19.0 21 -42 30.0 -23.0 5 -35 120.0 -22.0 8 -20 3-100.0 -21.4 7 -15 1-100.0 -21.5 15 -40 213.0 -17.2 18 2 2-5.0 -18.5 15 18 110.0 -18.0 14 50 1-8.0 -14.0 16 56 10.6 -13.0 26 21 3-40.0 -20.0 22 -50 3;proc stepdisc /*调用stepdisc过程*/slentry=0.2/*确定入选标准为0.2*/slstay=0.3;/*确定剔除标准为0.3*/class g;/*定义分组变量为g*/var x1-x4;/*定义用于分析的指标变量为x1-x4*/run;(筛选出变量后,调用discrim过程对筛选出的变量作判别分析,即先做5.2再做5.1)5.3作样品聚类和指标聚类data ex19_3;input x1-x9;cards;46 25 5 2138 1.68 0.35 8.11 4 4 35 12 20 3510 2.76 1.43 6.84 3 3 52 25 20 2784 2.19 0.54 4.11 3 3 32 7 20 2451 1.93 0.47 11.45 9 6 38 22 0 3247 2.56 0.80 11.68 5 5 51 31 30 3710 2.92 0.37 11.60 2 2 40 9 10 3194 2.51 0.40 11.40 5 5 34 17 20 4658 3.67 0.46 11.35 3 3 50 29 0 5019 3.95 0.47 13.45 10 8 42 20 20 7482 5.89 0.12 13.11 0 0 57 30 15 3800 2.99 0.19 10.76 2 236 15 20 2478 1.95 0.25 10.00 0 037 12 0 3827 3.01 0.82 10.50 4 4 52 32 0 2984 2.35 0.16 11.15 3 3 52 32 10 3749 2.95 0.72 11.45 11 10 42 27 30 4941 3.89 0.73 13.80 7 6 44 27 20 3948 3.11 0.33 13.65 16 14 40 21 5 3360 2.64 0.37 11.40 0 0 38 21 5 2936 2.31 0.69 11.40 1 1 44 27 20 6851 5.39 0.99 12.28 7 6 43 27 0 3926 3.09 0.47 11.95 0 0 26 10 3 4381 3.45 0.52 11.80 7 5 37 18 20 7142 5.62 0.85 11.81 5 5 28 9 20 2612 2.06 0.37 11.65 1 1 25 9 30 2638 2.08 0.78 12.25 1 1 34 14 20 4322 3.40 0.41 15.00 5 5 50 32 20 2862 2.25 0.69 8.80 2 2;proc cluster/*调用cluster过程*/method=average;/*采用类平均法进行聚类*/var x1-x9;/*定义用于分析的指标变量x1-x9*/run;proc treegraphics haxis=axis1 horizontal;/*调用tree过程输出聚类图,并将图横向输出*/ run;/*对各个指标聚类,即对9个变量聚类*/proc varclus;/*调用varclus过程*/var x1-x9;/*定义用于分析的指标变量x1-x9*/run;六、主成分分析和因子分析6.1主成分分析data ex20_1;input x1-x6;cards;92 77 80 95 99 12697 75 77 80 95 12595 80 70 78 89 12075 75 73 88 98 11092 68 72 79 88 11390 85 80 70 78 10372 93 75 77 80 10088 70 76 72 81 10264 70 69 85 93 10570 73 70 87 84 10078 69 75 73 89 9778 72 71 68 75 9675 64 63 76 73 9284 66 77 55 65 7670 64 51 60 67 8858 72 75 62 52 7582 73 40 50 48 6145 65 42 47 43 60;proc princomp;/*调用princomp过程,对6个变量做主成分分析,结果包括主成分累积贡献率,特征向量矩阵*/run;6.2因子分析data ex20_2;input x1-x9;cards;4.34 389 99.06 1.23 25.46 93.15 3.56 97.51 61.663.45 271 88.28 0.85 23.55 94.31 2.44 97.94 73.334.38 385 103.97 1.21 26.54 92.53 4.02 98.484.18 377 99.48 1.19 26.89 93.86 2.92 99.41 63.164.32 378 102.01 1.19 27.63 93.18 1.99 99.71 80.004.13 349 97.55 1.10 27.34 90.63 4.38 99.03 63.164.57 361 91.66 1.14 24.89 90.60 2.73 99.69 73.534.31 209 62.18 0.52 31.74 91.67 3.65 99.48 61.114.06 425 83.27 0.93 26.56 93.81 3.09 99.48 70.734.43 458 92.39 0.95 24.26 91.12 4.21 99.76 79.074.13 496 95.43 1.03 28.75 93.43 3.50 99.10 80.494.10 514 92.99 1.07 26.31 93.24 4.22 100.00 78.954.11 490 80.90 0.97 26.90 93.68 4.97 99.77 80.533.53 344 79.66 0.68 31.87 94.77 3.59 100.00 81.974.16 508 90.98 1.01 29.43 95.75 2.77 98.72 62.864.17 545 92.98 1.08 26.92 94.89 3.14 99.41 82.354.16 507 95.10 1.01 25.82 94.41 2.80 99.35 60.614.86 540 93.17 1.07 27.59 93.47 2.77 99.80 70.215.06 552 84.38 1.10 27.56 95.15 3.10 98.63 69.234.03 453 72.69 0.90 26.03 91.94 4.50 99.05 60.424.15 529 86.53 1.05 22.40 91.52 3.84 98.58 68.423.94 515 91.01 1.02 25.44 94.88 2.56 99.36 73.914.12 552 89.14 1.10 25.70 92.65 3.87 95.52 66.674.42 597 90.18 1.18 26.94 93.03 3.76 99.28 73.813.05 437 78.81 0.87 23.05 94.46 4.03 96.223.94 477 87.34 0.95 26.78 91.784.57 94.28 87.344.14 638 88.57 1.27 26.53 95.16 1.67 94.50 91.673.87 583 89.82 1.16 22.66 93.43 3.55 94.49 89.074.08 552 90.19 1.10 22.53 90.36 3.47 97.88 87.144.14 551 90.81 1.09 23.06 91.65 2.47 97.72 87.134.04 574 81.36 1.14 26.65 93.74 1.61 98.20 93.023.93 515 76.87 1.02 23.88 93.82 3.09 95.46 88.373.90 555 80.58 1.10 23.08 94.38 2.06 96.82 91.793.62 554 87.21 1.10 22.50 92.43 3.22 97.16 87.773.75 586 90.31 1.12 23.73 92.47 2.07 97.74 93.893.77 627 86.47 1.24 23.22 91.17 3.40 98.98 89.80;proc factor/*调用factor过程*/n=4;/*确定因子数为4,如果不写就默认为3*/run;proc factorn=4rotate=quartimax;/*因子旋转的方法为四次方最大正交旋转*/run;七、典型相关分析data ex21_1;input x1-x4 y1-y4;cards;1210 120.1 23.8 61.0 10.2 66.3 2.01 2.731210 120.7 23.4 59.8 11.3 67.6 1.92 2.711040 121.2 22.9 59.0 10.1 66.5 1.92 2.601620 121.5 24.6 59.5 9.5 67.8 1.95 2.641690 122.5 24.4 60.7 11.0 69.2 2.08 2.641150 122.7 27.2 64.5 10.5 69.1 2.19 2.841460 123.3 24.9 58.4 10.5 69.0 2.01 2.72 1190 123.4 21.8 59.0 10.6 67.4 1.90 2.71 1840 123.9 23.5 60.2 9.6 67.1 2.00 2.84 1250 124.5 25.2 63.0 11.2 67.8 2.05 2.78 1480 124.8 22.3 58.1 10.7 67.9 2.05 2.73 1310 124.9 22.0 58.0 10.5 67.8 1.98 2.68 1660 125.3 24.7 60.0 10.8 69.3 1.95 2.80 1580 125.6 22.8 59.0 9.4 69.1 2.00 2.65 1460 125.8 25.7 61.0 10.2 69.6 1.95 2.70 1240 126.0 30.2 68.0 9.2 67.1 2.14 2.88 1100 126.2 25.2 60.5 9.8 68.4 1.98 2.72 1250 126.8 23.6 58.5 10.2 67.5 1.94 2.74 1270 127.1 23.0 57.7 10.8 69.8 1.90 2.78 1300 127.6 24.3 59.0 10.3 67.9 1.93 2.84 1350 127.7 24.1 60.0 11.0 69.7 2.03 2.77 1250 128.3 21.6 55.5 10.4 68.5 1.83 2.70 1720 128.5 27.1 62.0 11.4 71.2 2.03 2.75 1480 128.5 22.6 57.4 10.0 67.3 2.04 2.83 1380 129.4 24.9 60.5 11.5 69.8 2.04 2.76 1170 129.0 26.7 63.7 9.6 67.4 2.13 2.98 1640 129.8 26.1 62.0 9.8 71.0 2.00 2.84 1640 131.6 28.7 62.8 9.7 70.7 1.89 2.89 1150 130.2 25.0 58.6 10.5 71.8 1.96 2.78 1430 130.5 26.1 60.7 10.8 68.6 2.05 2.77 1150 130.6 23.4 54.4 11.8 69.2 1.96 2.78 1150 131.4 25.5 63.2 10.2 70.4 2.05 2.84 1320 131.6 25.6 58.9 10.9 70.2 2.06 2.86 1360 131.7 27.4 62.0 10.9 73.5 1.99 2.70 1460 132.0 26.3 61.5 11.1 71.2 2.17 2.13 1380 132.2 25.7 61.4 10.1 70.1 1.96 2.83 1300 132.5 24.5 57.0 10.8 71.8 2.02 2.84 1220 132.7 27.0 61.3 10.1 72.2 2.08 2.80 1320 132.9 25.2 60.5 11.2 73.1 2.01 2.73 1910 133.1 30.1 67.0 9.0 87.1 2.15 2.97 1800 133.5 26.5 62.5 9.8 71.7 2.07 2.82 1560 133.6 24.8 58.5 10.3 72.2 1.93 2.79 1840 134.0 26.0 60.5 10.4 73.0 1.98 2.74 1470 134.3 28.2 62.0 11.3 87.2 2.66 4.03 1590 134.4 25.5 60.7 9.6 69.9 1.99 2.81 1430 134.1 26.6 63.0 11.2 72.2 2.06 2.90 1760 134.6 32.5 66.0 9.9 87.4 2.61 2.98 1470 135.3 27.9 61.8 10.1 73.3 2.20 2.78 1580 135.6 28.1 65.8 9.8 73.1 2.05 2.891840 137.1 27.6 62.8 9.5 72.4 2.11 2.91 1810 137.4 28.3 62.5 9.4 74.2 2.06 3.00 1850 138.1 29.5 62.4 9.7 72.3 2.12 4.02 2120 140.0 34.9 68.8 9.5 87.9 2.74 4.15 1760 140.7 32.0 64.4 10.2 74.0 2.17 4.05 1800 141.0 32.5 63.8 9.5 88.2 2.65 4.08 1260 141.7 29.1 65.0 9.7 88.2 2.68 2.90 1860 142.4 19.3 70.0 10.1 89.6 2.71 4.06 1800 144.7 27.0 58.3 10.8 74.8 2.10 2.82 1470 136.8 26.3 61.4 10.0 72.2 2.07 2.93 1260 121.1 22.9 59.0 10.6 66.3 2.05 2.76 1570 132.7 25.3 58.6 11.5 73.6 2.16 2.78 1290 125.0 25.7 60.5 10.1 68.8 2.00 2.69 1580 133.2 27.3 60.7 9.6 71.7 2.11 2.85 1690 132.8 28.6 64.7 9.6 72.9 2.19 4.08 1670 131.6 25.4 59.7 10.6 69.8 2.14 2.76 1300 133.1 25.9 58.0 10.1 69.7 2.12 2.83 1610 134.0 25.8 59.6 9.4 70.8 2.10 2.88 1580 134.3 26.3 61.2 10.2 72.2 2.14 2.84 1570 129.1 27.7 62.2 11.1 72.9 2.09 2.93 1660 140.1 32.1 67.0 9.3 87.1 2.15 4.03 1040 132.6 27.9 62.0 10.3 72.5 2.08 2.81 1290 128.3 23.6 58.5 9.3 69.0 1.97 2.76 1980 145.8 34.5 68.0 9.8 89.7 2.68 4.25 1210 133.3 25.6 61.5 9.9 71.0 2.11 2.82 1300 134.3 25.6 61.0 10.5 73.2 2.02 2.83 1310 138.1 27.8 61.2 9.9 73.5 2.09 2.78 1590 135.6 25.9 59.6 9.6 72.8 2.10 2.91 1270 128.3 24.1 58.5 10.3 69.2 1.92 2.77 1310 129.7 24.7 61.7 10.1 69.4 2.03 2.80 2280 143.6 37.6 70.0 9.7 88.8 2.17 4.18 1580 136.6 32.3 67.2 10.3 87.1 2.66 4.04 2370 147.4 38.8 73.0 10.8 90.7 2.82 4.38 ;proc cancorr;/*调用cancorr过程*/var x1-x4;/*定义一组变组变量*/with y1-y3;/*定义另一组变量*/run;。
医学统计学:SAS实验-统计描述

算第一层和交叉层的统计量。 • FREQ过程也可以将结果输出到SAS数据集中。
FREQ过程由下列语句控制:
Proc freq [选择项];
Tables 请求式┅[/选择项];
Weight 变量;
By
变量表;
Output [选择项];
FREQ过程——可以生成单向和多向的频数表和 交叉表。
MEANS过程——用来对数据集中的数值变量计 算简单的描述统计量( N、Mean、Std Dev、 Minimum、Maximum)。
• SUMMARY过程——用来计算单个变量的基本统计 量,它和MEANS过程的不同之处在于该过程不在 OUTPUT窗口输出结果,除非加上命令PRINT,而 MEANS过程总是在OUTPUT窗口输出。
173.6 175.3 178.4 181.5 170.5 176.4 170.8 171.8 180.7 170.7
173.8 164.4 170.0 175.0 177.7 171.4 162.9 179.0 174.9 178.3
174.5 174.3 170.4 173.2 174.5 173.7 173.4 173.9 172.9 177.9
171.2 177.1 170.7 173.6 167.2 170.7 174.7 171.8 167.3 174.8
168.5 178.7 177.3 165.9 174.0 170.2 169.5 172.1 178.2 170.9
171.3 176.1 169.7 177.9 171.1 179.3 183.5 168.5 175.5 175.9
**语句的简单说明**
• Tables语句
sas系统proc univariate过程

sas系统proc univariate过程1. 介绍SAS(Statistical Analysis System)是统计分析系统,是业界广泛使用的数据分析工具之一。
SAS提供了多个过程(PROC)来处理和分析数据,其中之一是Proc Univariate过程。
本文将详细介绍SAS系统中的Proc Univariate过程的相关内容。
2. Proc Univariate过程的作用Proc Univariate过程用于对数据进行单变量分析,主要目的是研究单个变量的统计特征和分布情况。
该过程可用于描述变量的中心位置、离散程度、分布形状等统计指标,同时还能生成各种图形以帮助进一步分析数据。
3. 使用方法使用Proc Univariate过程需要先导入相关的数据,以下是使用Proc Univariate 的基本示例代码:PROC UNIVARIATE DATA=data;VAR variable;HISTOGRAM;QQPLOT;RUN;在此示例中,data代表数据集的名称,variable代表需要分析的变量名。
使用VAR 语句指定需要分析的变量。
HISTOGRAM和QQPLOT是两个示例输出图形,代表直方图和正态概率图(Q-Q plot)。
4. 常见输出使用Proc Univariate过程后,会生成多个输出,包括描述性统计指标、分位数、图形等。
4.1 描述性统计指标描述性统计指标可以用于描述变量的中心位置、离散程度等,常见的统计指标包括:•平均值(Mean)•中位数(Median)•众数(Mode)•标准差(Standard Deviation)•方差(Variance)•偏度(Skewness)•峰度(Kurtosis)4.2 分位数分位数是将数据分成若干部分的统计量,常见的分位数包括:•中位数(50%分位数)•四分位数(25%和75%分位数)•百分位数(例如10%、90%分位数)4.3 图形Proc Univariate过程还可以生成多种图形,用于帮助分析数据的分布情况,常见的图形包括:•直方图(Histogram)•密度曲线图(Density Plot)•箱线图(Box Plot)•正态概率图(Q-Q Plot)•生存曲线(Survival Plot)5. 实际应用案例以下是一个使用Proc Univariate过程的实际案例,以探究某公司员工的薪资分布情况:PROC UNIVARIATE DATA=employees;VAR salary;HISTOGRAM;QQPLOT;MEANS;RUN;在该案例中,employees是包含员工数据的数据集,salary是需要分析的薪资变量。
实验三 SAS描述统计分析

实验三SAS描述统计分析对数据进行频数统计、计算特征统计量和将数据图形化的过程称为描述统计。
其目的是为了揭示数据的集中趋势、分散程度和数据分布形态,展示极端数据,最后做出说明现象本质的初步结论。
用图形对数据进行描述性统计分析具有直观、鲜明、形象、便捷等特点,在表达统计数据时可以给人留下深刻的印象。
统计图形的种类很多,利用SAS可以方便的绘制常用的统计图形。
3.1 实验目的掌握使用SAS对数据作描述性统计分析的方法。
掌握SAS/GRAPH所提供的常用图形功能,能用SAS的统计图形对数据进行描述性统计分析。
3.2 实验内容一、用INSIGHT计算统计量、绘制统计图形二、用“分析家”计算统计量、绘制统计图形三、编程实现描述性统计(MEANS、UNIVARIATE、FREQ过程)、编程绘制统计图(GPLOT 和GCHART过程)3.3 实验指导一、用INSIGHT计算统计量【实验3-1】按性别分别计算SASHELP.CLASS中身高的均值、标准差、中位数和其它四分位数,简单分析学生身高的状况。
1. 在INSIGHT中打开数据集在菜单中选择“Solution(解决方案)”→“Analysis(分析)”→“Interactive Data Analysis (交互式数据分析)”,打开“SAS/INSIGHT Open”对话框,在对话框中选择数据集:SASHELP.CLASS,单击“Open(打开)”按钮,即可在INSIGHT中打开数据窗口,如图3-1左所示。
2. 用Distribution菜单项计算统计量(1) 选择菜单“Analyze(分析)”→“Distribution (Y)(分布)”,打开“Distribution (Y)”对话框。
在数据集CLASS的变量列表中,选择height,然后单击“Y”按钮,height被选为分析变量,选择sex,然后单击“Group”按钮,sex被选为分组变量,如图3-1右所示。
proc means置信区间

proc means置信区间
proc means是SAS(统计分析系统)中用于生成描述性统计信息的过程。
它可以计算均值、中位数、标准差、最小值、最大值和置信区间等统计量。
置信区间是用来估计总体参数的区间估计,它可以帮助我们评估参数估计的精确度和可靠性。
在使用proc means计算置信区间时,我们可以通过在语句中使用CLM(Confidence Limits for Mean)选项来指定置信水平。
例如,如果我们想要计算均值的95%置信区间,我们可以使用以下语句:
sas.
proc means data=mydata mean clm;
var myvariable;
run;
在这个例子中,我们使用了mean选项来计算均值,并使用了
clm选项来生成置信区间。
默认情况下,proc means会计算95%的置信区间,但我们也可以通过在clm选项后面指定其他置信水平来计算不同置信水平的置信区间。
需要注意的是,置信区间的计算依赖于样本数据的分布和样本量,因此在解释置信区间的时候,我们需要考虑到这些因素。
通常情况下,置信区间越窄,我们对总体参数的估计就越精确。
综上所述,使用proc means计算置信区间可以帮助我们对总体参数进行区间估计,从而更好地理解数据的特征和总体特征的估计范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
SAS中的描述性统计过程(2012-08-01 18:07:01)▼分类:数据分析挖掘标签:杂谈SAS中的描述性统计过程描述性统计指标的计算可以用四个不同的过程来实现,它们分别是means过程、summary过程、univariate过程以及tabulate过程。
它们在功能范围和具体的操作方法上存在一定的差别,下面我们大概了解一下它们的异同点。
相同点:他们均可计算出均数、标准差、方差、标准误、总和、加权值的总和、最大值、最小值、全距、校正的和未校正的离差平方和、变异系数、样本分布位置的t检验统计量、遗漏数据和有效数据个数等,均可应用by语句将样本分割为若干个更小的样本,以便分别进行分析。
不同点:(1)means过程、summary过程、univariate过程可以计算样本的偏度(skewness)和峰度(kurtosis),而tabulate过程不计算这些统计量;(2)univariate过程可以计算出样本的众数(mode),其它三个过程不计算众数;(3)summary过程执行后不会自动给出分析的结果,须引用output语句和print过程来显示分析结果,而其它三个过程则会自动显示分析的结果;(4)univariate过程具有统计制图的功能,其它三个过程则没有;(5)tabulate过程不产生输出资料文件(存储各种输出数据的文件),其它三个均产生输出资料文件。
统计制图的过程均可以实现对样本分布特征的图形表示,一般情况下可以使用的有chart过程、plot过程、gchart过程和gplot过程。
大家有没有发现前两个和后两个只有一个字母‘g’(代表graph)的差别,其实它们之间(只差一个字母g的过程之间)的统计描述功能是相同的,区别仅在于绘制出的图形的复杂和美观程度。
chart过程和plot过程绘制的图形类似于我们用文本字符堆积起来的图形,只能概括地反映出资料分布的大体形状,实际上这两个过程绘制的图形并不能称之为图形,因为他根本就没有涉及一般意义上图形的任何一种元素(如颜色、分辨率等)。
而gchart过程和gplot过程给出的是真正意义上的图形,可以用很多的语句和选项来控制图形的各方面的性质和特征。
chart和gchart与plot和gplot的区别则体现在不同的作图功能,前两个过程可以绘制出的图形主要有条形图(包括横条和竖条)、圆图、环形图和星形图等,后两个过程通常用一个记录中的两个变量值表示点的坐标来绘制图形,如散点图和线图等。
描述性统计过程的一般格式1. means过程的一般格式proc means选项列表;by变量名称(分组变量);class变量名称(分组变量);freq变量名称(数值变量,用以表示相应记录出现的频数)weight变量名称(数值变量,用以表示相应记录的权重系数)var变量名称(待分析的数值变量);run;Proc means语句后的选项主要用来指定所要计算的统计量,默认情况下,Means过程会给出频数、均数、标准差、最大值和最小值等,其余统计量的计算均需要在选项中指定。
class语句所指定的分组变量用来进行分组,而by语句所指定的分组变量是用来将数据分为若干个更小的样本,以便SAS分别在各小样本内进行各自独立的处理。
freq语句和weight语句分别引导代表记录出现频数和权重系数的数值变量。
var语句引导所要进行分析的所有变量的列表,SAS将对var语句所引导的所有变量分别进行描述性统计分析。
summary过程的一般格式proc summary选项列表;by变量名称(分组变量);class变量名称(分组变量);freq变量名称(数值变量,用以表示相应记录出现的频数)weight变量名称(数值变量,用以表示相应记录的权重系数)output <out=数据集名> <统计量关键字=自定义变量名>var变量名称(待分析的数值变量);run;summary过程的格式和means过程可以说是完全相同的,各条语句和选项的含义也是相同的,包括在means过程中未列出的output语句也可以应用于means过程,只是此语句在summary过程应用较多(这样才能将分析结果显示出来),所以才将其列入一般格式中。
output语句用来对分析结果输出为数据文件进行控制,其后的选项可有可无,若无则SAS按照默认方式进行。
“out=数据集名”用来定义输出数据文件的文件名称,文件名的格式和数据步中数据文件名相同。
“统计量关键字=自定义变量名”用来自定义输出数据文件中各种统计量的变量名称,前者是系统定义的(和proc语句后选项中的统计量关键字完全相同),必须正确无误,后者可自行定义。
默认状态下输出统计量只有频数、均数、标准差、最大值和最小值,在默认状态不能满足需要时这一选项则是必需的。
univariate过程的一般格式proc univariate选项列表;by变量名称(分组变量);class变量名称(分组变量);freq变量名称(数值变量,用以表示相应记录出现的频数)weight变量名称(数值变量,用以表示相应记录的权重系数)histogram变量名称/选项列表output <out=数据集名> <统计量关键字=自定义变量名>pctlpts=<百分位数…><指定需要的百分位数>pctlpre=<新变量名列><指定所需百分位数对应的输出变量名>var变量名称(待分析的数值变量);run;univariate过程和以上两个过程的格式非常相似,相同的语句和选项其含义也相同,所不同的是某些统计量只能在univariate过程中计算(如众数),以及univariate过程中所具有的绘图功能。
histogram 语句即用来指示SAS对其后所指定的变量绘制直方图,其后的选项用来指示SAS添加不同类型的拟合图形(如正态分布的分布密度曲线)。
tabulate过程的一般格式proc tabulate选项列表;by变量名称(分组变量);class变量名称(分组变量);freq变量名称(数值变量,用以表示相应记录出现的频数)weight变量名称(数值变量,用以表示相应记录的权重系数)table <<页变量表达式>,<行变量表达式>,<列变量表达式>></表格选项>var变量名称(待分析的数值变量,统计量列入相应的表单元格);run;tabulate过程和上述几个过程的格式也基本相似,相同的语句和选项也代表相同的含义。
最大的不同也是tabulate过程中最为重要的是table语句,他用来定义表格的具体格式以及表格中所要包括的统计量。
gchart过程的一般格式proc gchart选项列表;图形关键词变量名称/选项列表run;proc gplot选项列表;bubble散点图表达式bubble2散点图表达式plot散点图表达式plot2散点图表达式run;从gplot过程的一般格式中我们就可看出,此过程只能绘制两种类型的图形,bubble语句指示SAS绘制泡状散点图,plot语句指示SAS绘制点状散点图。
bubble2语句和plot2语句指示SAS在同一区域内(bubble2和bubble在同一区域,plot2和plot在同一区域)绘制第二个图形,两者的横坐标相同(同一变量),纵坐标分别位于左右两侧(可以是同一变量,也可以是两个不同的变量)。
散点图表达式的一般形式为:(1)bubble和bubble2语句:纵坐标变量名*横坐标变量名=泡尺寸变量名(变量值以泡的大小表示),三者均应为数值变量;(2)plot和plot2语句:纵坐标变量名*横坐标变量名<=n/分类变量名>,此处等号及其后的部分可以省略,此时SAS以默认的散点类型绘制散点图;若等号后为n(n为正整数,是散点类型的编号),SAS则以指定的编号对应的散点类型绘制散点图;若等号后为分类变量名(可为字符型或数值型,为数值型时作为离散型变量处理,每一个值将被当作一个类别),此变量的具体值(或与每个具体值对应的图形)将被作为散点用来绘制散点图。
chart过程和plot过程的一般格式及各选项使用方法分别与gchart过程和gplot过程是基本相同的,不同之处仅在于后两者中涉及到有关三维和图形元素(颜色等)的语句和选项在前两者中是无效的。
例如vbar3d语句在chart过程中无效,bubble语句在plot过程中无效。
其余的语句和选项使用方法完全相同,所以在掌握了gchart过程和gplot过程后,chart过程和plot过程你会不学自通。
(三)描述性统计关键字及其含义SAS中可计算的描述性统计量多达二十余种,大部分可在以上介绍的前四个过程中计算,个别统计量在某些过程中不能计算,大家需要注意,要不然系统显示错误信息时还不知道是怎么回事。
我经常遇到这种情况,系统提示错误(此类提示信息显示在log窗口中)时总是摸不着头脑,费半天劲才能搞明白。
没办法,摸着石头过河嘛!不过这样也并非一无是处,最起码可以积累很多使用经验。
下表(表2.2)列出SAS中可以计算的所有描述性统计量关键字及其含义,供大家使用时参考。
表2.2 SAS中可以计算的描述性统计量关键字及其含义关键字所代表的含义n 有效数据记录数.. . nmiss 缺失数据记录数mean 均数std 标准差stderr 标准误var 方差median 中位数mode 众数cv 变异系数max 最大值min 最小值range 全距sum 总计sumwgt 加权值总计css 校正的离均差平方和uss 未校正的离均差平方和clm 可信限(上下界值)lclm 可信限下侧界值uclm 可信限上侧界值skew(skewness)偏度kurt(kurtosis)峰度t 分布位置假设检验之t统计量probt 上述t统计量对应的概率值.. .q1 第一四分位数q3 第三四分位数qrange 四分位数间距p1 第一百分位数p5 第五百分位数p10 第十百分位数p90 第九十百分位数p95 第九十五百分位数p99 第九十九百分位数分享:。
