网络图中的六个时间参数
双代号网络图六个时间参数的简易计算方法

双代号网络图六个时间参数的简易计算方法
一、非常有用的要点:
任何一个工作总时差≥自由时差
自由时差等于各时间间隔的最小值(这点对六时参数的计算非常用用) 关键线路上相邻工作的时间间隔为零,且自由时差=总时差
在网络计划中,计算工期是根据终点节点的最早完成时间的最大值
二、双代号网络图六时参数总结的计算步骤(比书上简单多了)
① ②
t 过程
步骤一:
1.A 上再做A 下
2.做的方向从起始工作往结束工作方向;
3.起点的A 上=0,下一个的A 上=前一个的A 下;当遇到多指向时,要取数值大的A 下
4.A 下=A 上+t 过程(时间)
步骤二:
1.B 下再做B 上
2.做的方向从结束点往开始点
3.结束点B 下=T (需要的总时间=结束工作节点中最大的A 下)
结束点B 上=T-t 过程(时间)
关键工作:总时差最小的工作
最迟开始时间—最早开始时间(min )
最迟完成时间—最早完成时间(min )
4.B下=前一个的B上(这里的前一个是从终点起算的);遇到多指出去的时,取数值小的B上
B上=B下—t过程(时间)
步骤三:总时差=B
上—A
上
=B
下
—A
下
如果不相等,你就是算错了
步骤四:自由时差=紧后工作A
上(取最小的)—本工作A
下
例:
总结起来四句话:
1.最早时间从起点开始,最早开始=紧前最早结束的max值;
2.最迟时间总终点开始,最迟完成=紧后最迟开始的min值;
3.总时差=最迟-最早;
4.自由时差=紧后最早开始的min值-最早开始
注:总时差=自由时差+紧后总时差的min值。
网络图中的六个时间参数.doc

2.网络图中的六个时间参数(重点)网络图中的时间参数主要有六个:最早开始时间;最早完成时间;最迟开始时间;最迟完成时间;总时差和自由时差。
各时间参数的含义如下。
(1)工作最早开始时间ESii(EarliestStartTime)——是指在其所有紧前工作全部完成后,本工作有可能开始的最早时刻。
(2)工作最早完成时间EFii(EarliestFinishTime)——是指在其所有紧前工作全部完成后,本工作有可能完成的最早时刻。
工作的最早完成时间等于工作最早开始时间与其持续时间之和。
(3)工作最迟完成时间LFii(LatestFinishTime)——是指在不影响整个任务按期完成的前提下,本工作必须完成的最迟时刻。
(4)工作最迟开始时间LSii(LatestStartTime)——是指在不影响整个任务按期完成的前提下,本工作必须开始的最迟时刻。
工作的最迟开始时间等于工作最迟完成时间与其持续时间之差。
(5)总时差TFii(TotalFloatTime)——是指在不影响总工期的前提下,本工作可以利用的机动时间。
(6)自由时差FFii(FreeFloatTime)——是指在不影响其紧后工作最早开始时间的前提下,本工作可以利用的机动时间。
3.双代号网络图中时间参数的计算(1)时间参数计算数学模型:下面取一网络片断(图9-24)作为计算简图。
令整个计划的开始时间为第0天,则:工作最早开始时间等于其紧前工作最早完成时间的最大值。
令整个计划的总工期为一常数,则:工作最迟完成时间等于其紧后工作最迟开始时间的最小值。
在网络计划中,总时差最小的工作为关键工作。
特别地,当网络计划的计划工期等于计算工期时,总时差为零的工作就是关键工作。
由于工作的自由时差是总时差的构成部分,所以,当工作的总时差为零时,其自由时差必然为零。
即:如果网络计划中工作数量比较多,一般用项目管理软件进行计算。
如果数量不多也可用手工进行计算。
(2)计算步骤。
网络时间参数计算
2020/5/14
四.关键线路的确定方法: 1.分析线路进行确定; 2.通过计算时间参数进行确定; 3.破圈法:
关键线路走最长的线路,逢圈保留最长线路。 例如以下两例:
2020年5月14日星期四
建筑施工组织与管理
10
2020年5月14日星期四
建筑施工组织与管理
3
2-4工序:LS2-4=[ LS4-7,LS5-9]min-5=[8,11]min-5=3;
2-3工序:LS2-3=5-3=2;
2-6工序:LS2-6=9-4=5;
1-2工序:LS1-2=[ LS2-3,LS2-4,LS2-6]min-2
=[2,3,5]min-2=0
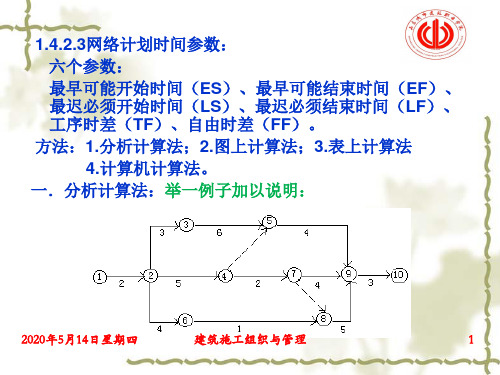
1.4.2.3网络计划时间参数:
六个参数:
最早可能开始时间(ES)、最早可能结束时间(EF)、 最迟必须开始时间(LS)、最迟必须结束时间(LF)、 工序时差(TF)、自由时差(FF)。
方法:1.分析计算法;2.图上计算法;3.表上计算法
4.计算机计算法。
一.分析计算法:举一例子加以说明:
2020年5月14日星期四
通过以上原理可以得到: ESjk=[ESji+tij]max=[ EFij]max。
3.计算最迟必须开始时间(LS): 逆算:LSij=T-[∑tjk]max-tij=[LSjk]min- tij 9-10工序:LS9-10=18-3=15; 5-9工序:LS5-9=15-4=11; 7-9工序:LS7-9=15-4=11; 8-9工序;LS8-9=15-5=10; 4-7工序:LS4-7=[ LS7-9,LS8-9]min-2=[11,10]min-2=8; 6-8工序:LS6-8=10-1=9; 3-5工序:LS3-5=11-6=5;
双代号网络图六个参数的两种简易计算方法及实例分析

双代号网络图计算方法是每年建造师考试中的必考题,小到选择题、大到案例分析题,笔者在此总结2种计算方法,并附实例,供大家参考学习,互相交流,考出好成绩。
双代号网络图计算方法一一、要点:任何一个工作总时差≥自由时差自由时差等于各时间间隔的最小值(这点对六时参数的计算非常用用)关键线路上相邻工作的时间间隔为零,且自由时差=总时差最迟开始时间—最早开始时间(最小)关键工作:总时差最小的工作最迟完成时间—最早完成时间(最小)在网络计划中,计算工期是根据终点节点的最早完成时间的最大值二、双代号网络图六时参数我总结的计算步骤(比书上简单得多)①②t过程做题次序: 1 4 5 ES LS TF2 3 6 FS LF FF步骤一:1、A 上再做A 下23、起点的A 上=0,下一个的A 上A 上 4、A 下=A 上+t 过程(时间)步骤二:1、 B 下再做B 上2、 做的方向从结束点往开始点3、 结束点B 下=T (需要的总时间=结束工作节点中最大的A 下)结束点B 上=T-t 过程(时间)4、B 下=前一个的B 上(这里的前一个是从终点起算的) 遇到多指出去的时,取数值小的B 上B 上=B 下—t 过程(时间)步骤三:总时差=B 上—A 上=B 下—A 下 如果不相等,你就是算错了步骤四:自由时差=紧后工作A 上(取最小的)—本工作A 下=紧后工作的最早开始时间—本工作的最迟开始时间 (有多个紧后工作的取最小值) 例:双代号网络图计算方法二一、双代号网络图6个时间参数的计算方法(图上计算法)从左向右累加,多个紧前取大,计算最早开始结束;从右到左累减,多个紧后取小,计算最迟结束开始。
紧后左上-自己右下=自由时差。
上方之差或下方之差是总时差。
计算某工作总时差的简单方法:①找出关键线路,计算总工期;②找出经过该工作的所有线路,求出最长的时间③该工作总时差=总工期-②二、双代号时标网络图双代号时标网络计划是以时间坐标为尺度编制的网络计划,以实箭线表示工作,以虚箭线表示虚工作,以波形线表示工作的自由时差。
双代号网络计划时间参数的计算方法

双代号网络计划时间参数的计算方法自认为对双代号网络图的知识掌握的差不多,也能够理解;只是在遇到这六个时间参数的时候,还是有些发怵,今天重新把这六个参数捋了捋,总结如下:1、最早开始时间、最早完成时间:从网络计划的起点节点开始,顺着箭头方向依次进行;以网络计划起点为开始节点的工作,当未规定其最早开始时间时,其最早开始时间为零;有多个紧前工作的工作,其最早开始时间等于其紧前工作最早完成时间的最大值。
2、最迟开始时间、最迟完成时间:从网络计划的终点节点开始,顺着箭头方向依次进行;以网络终点节点为完成节点的工作,其最迟完成时间等于网络计划的计划工期,即要先找出关键线路,求出计划总工期作为最后一项工作的最迟完成时间;有多个紧后工作的工作,其最迟完成时间等于其紧后工作最迟开始时间的最小值。
3、总时差:不影响总工期的时差,等于该工作最迟完成时间与最早完成时间之差,或该工作最迟开始时间与最早开始时间之差;总时差最小的工作为关键工作,当网络计划的计划工期等于计算工期时,总时差为零的工作就是关键工作;同一条线路上的总时差相等(同一条线路都可以共用的时间,谁用了是谁的,不影响总工期)。
4、自由时差不影响紧后工作的时间;对于有多个紧后工作的工作,其自由时差等于本工作之紧后工作最早开始时间-本工作最早完成时间所得之差的最小值;无紧后工作的工作,也就是以网络计划重点节点为完成节点的工作,其自由时差等于计划工期与本工作最早完成时间之差;对于网络计划中以重点节点为完成节点的工作,其自由时差与总时差相等;只有一项紧前工作的紧前工作,该紧前工作的自由时差为0;自由时差小于等于总时差,总时差为零自由时差必为0 。
呵呵,本来想用通俗的语言解释一下,可写下来还是有点绕,我觉得这东西贵在理解,好像只是专家们为了考试罗列了一些概念,把简单的问题弄复杂了;没办法为了考试,慢慢理解吧。
二、搭接网络计划时间参数的计算单代号搭接网络计划时间参数的计算与前述单代号网络计划和双代号网络计划时间参数的计算原理基本相同。
双代号网络图六个时间参数的简易计算方法

双代号网络图六个时间参数的简易计算方法、非常有用的要点:任何一个工作总时差》自由时差自由时差等于各时间间隔的最小值(这点对六时参数的计算非常用用)关键线路上相邻工作的时间间隔为零,且自由时差=总时差「最迟开始时间一最早开始时间(min)关键工作:总时差最小的工作VL最迟完成时间一最早完成时间(min)在网络计划中,计算工期是根据终点节点的最早完成时间的最大值、双代号网络图六时参数总结的计算步骤(比书上简单多了)① -------------- > ②t过程步骤一:1. A上再做A下2 .做的方向从起始工作往结束工作方向;3. 起点的A上=0,下一个的A上二前一个的A下;当遇到多指向时,要取数值大的A下4. A下=人上+t过程(时间)步骤二:1. B下再做B上2. 做的方向从结束点往开始点3. 结束点B T=T(需要的总时间=结束工作节点中最大的A下)结束点B ±=T-t过程(时间)4. B下二前一个的B上(这里的前一个是从终点起算的);遇到多指出去的时,取数值小的B 做题次序:上B上=B下一t过程(时间)步骤三:总时差=B上一A上=B下一A下如果不相等,你就是算错了步骤四:自由时差二紧后工作A上(取最小的)一本工作A下例:紧后工作A上有9和11取小值9,?=9-9 (本工作的A下)=0总结起来四句话:1. 最早时间从起点开始,最早开始=紧前最早结束的max值;2. 最迟时间总终点开始,最迟完成二紧后最迟开始的min值;3. 总时差=最迟一最早;4. 自由时差二紧后最早开始的min值一最早开始注:总时差=自由时差+紧后总时差的min值。
双代号网络图6个时间参数的计算方法
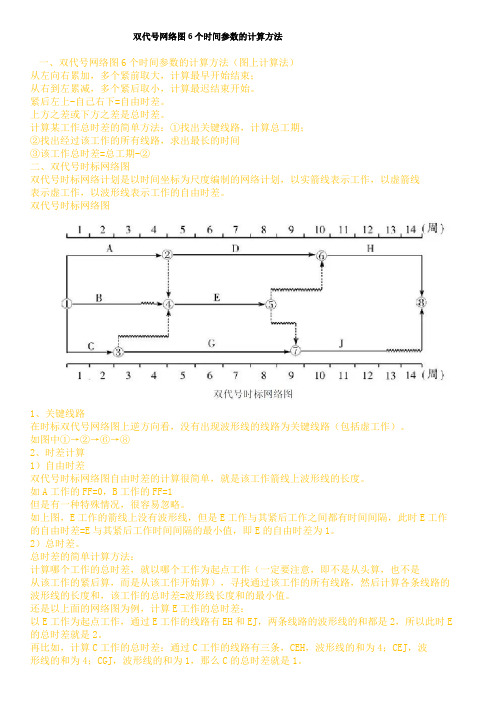
双代号网络图6个时间参数的计算方法一、双代号网络图6个时间参数的计算方法(图上计算法)从左向右累加,多个紧前取大,计算最早开始结束;从右到左累减,多个紧后取小,计算最迟结束开始。
紧后左上-自己右下=自由时差。
上方之差或下方之差是总时差。
计算某工作总时差的简单方法:①找出关键线路,计算总工期;②找出经过该工作的所有线路,求出最长的时间③该工作总时差=总工期-②二、双代号时标网络图双代号时标网络计划是以时间坐标为尺度编制的网络计划,以实箭线表示工作,以虚箭线表示虚工作,以波形线表示工作的自由时差。
双代号时标网络图1、关键线路在时标双代号网络图上逆方向看,没有出现波形线的线路为关键线路(包括虚工作)。
如图中①→②→⑥→⑧2、时差计算1)自由时差双代号时标网络图自由时差的计算很简单,就是该工作箭线上波形线的长度。
如A工作的FF=0,B工作的FF=1但是有一种特殊情况,很容易忽略。
如上图,E工作的箭线上没有波形线,但是E工作与其紧后工作之间都有时间间隔,此时E工作的自由时差=E与其紧后工作时间间隔的最小值,即E的自由时差为1。
2)总时差。
总时差的简单计算方法:计算哪个工作的总时差,就以哪个工作为起点工作(一定要注意,即不是从头算,也不是从该工作的紧后算,而是从该工作开始算),寻找通过该工作的所有线路,然后计算各条线路的波形线的长度和,该工作的总时差=波形线长度和的最小值。
还是以上面的网络图为例,计算E工作的总时差:以E工作为起点工作,通过E工作的线路有EH和EJ,两条线路的波形线的和都是2,所以此时E 的总时差就是2。
再比如,计算C工作的总时差:通过C工作的线路有三条,CEH,波形线的和为4;CEJ,波形线的和为4;CGJ,波形线的和为1,那么C的总时差就是1。
网络图中的六个时间参数

2.网络图中的六个时间参数(重点)网络图中的时间参数主要有六个:最早开始时间;最早完成时间;最迟开始时间;最迟完成时间;总时差和自由时差。
各时间参数的含义如下。
(1)工作最早开始时间ESii(EarliestStartTime)——是指在其所有紧前工作全部完成后,本工作有可能开始的最早时刻。
(2)工作最早完成时间EFii(EarliestFinishTime)——是指在其所有紧前工作全部完成后,本工作有可能完成的最早时刻。
工作的最早完成时间等于工作最早开始时间与其持续时间之和。
(3)工作最迟完成时间LFii(LatestFinishTime)——是指在不影响整个任务按期完成的前提下,本工作必须完成的最迟时刻。
(4)工作最迟开始时间LSii(LatestStartTime)——是指在不影响整个任务按期完成的前提下,本工作必须开始的最迟时刻。
工作的最迟开始时间等于工作最迟完成时间与其持续时间之差。
(5)总时差TFii(TotalFloatTime)——是指在不影响总工期的前提下,本工作可以利用的机动时间。
(6)自由时差FFii(FreeFloatTime)——是指在不影响其紧后工作最早开始时间的前提下,本工作可以利用的机动时间。
3.双代号网络图中时间参数的计算(1)时间参数计算数学模型:下面取一网络片断(图9-24)作为计算简图。
令整个计划的开始时间为第0天,则:工作最早开始时间等于其紧前工作最早完成时间的最大值。
令整个计划的总工期为一常数,则:工作最迟完成时间等于其紧后工作最迟开始时间的最小值。
在网络计划中,总时差最小的工作为关键工作。
特别地,当网络计划的计划工期等于计算工期时,总时差为零的工作就是关键工作。
由于工作的自由时差是总时差的构成部分,所以,当工作的总时差为零时,其自由时差必然为零。
即:如果网络计划中工作数量比较多,一般用项目管理软件进行计算。
如果数量不多也可用手工进行计算。
(2)计算步骤。
双代号网络图六个时间参数的简易计算方法[规整]
![双代号网络图六个时间参数的简易计算方法[规整]](https://img.taocdn.com/s3/m/020fa59aa1116c175f0e7cd184254b35eefd1abd.png)
双代号网络图六个时间参数的简易计算方法
一、非常有用的要点:
任何一个工作总时差≥自由时差
自由时差等于各时间间隔的最小值(这点对六时参数的计算非常用用)关键线路上相邻工作的时间间隔为零,且自由时差=
总时差
关键工作:总时差最小的工作
最迟开始时间—最早开始时间(min )
最迟完成时间—最早完成时间(min )
在网络计划中,计算工期是根据终点节点的最早完成时间的最大值二、双代号网络图六时参数总结的计算步骤(比书上简单多了)
①
②
t 过程
步骤一:
1.A 上再做A 下
2.做的方向从起始工作往结束工作方向;
3.起点的A 上=0,下一个的A 上=前一个的A 下;当遇到多指向时,要取数值大的A
下
4.A 下=A 上+t 过程(时间)
步骤二:
1.B 下再做B 上
2.做的方向从结束点往开始点
3.结束点B 下=T (需要的总时间=结束工作节点中最大的A 下)
结束点B上=T-t过程(时间)
4.B下=前一个的B上(这里的前一个是从终点起算的);遇到多指出去的时,取数值小的B上
B上=B下—t过程(时间)
步骤三:总时差=B上—A上=B下—A下
如果不相等,你就是算错了
步骤四:自由时差=紧后工作A上(取最小的)—本工作A下
例:
总结起来四句话:
1.最早时间从起点开始,最早开始=紧前最早结束的max值;
2.最迟时间总终点开始,最迟完成=紧后最迟开始的min值;
3.总时差=最迟-最早;
4.自由时差=紧后最早开始的min值-最早开始
注:总时差=自由时差+紧后总时差的min值。
双代号网络图六个时间参数计算口诀

双代号收集图六个时光参数盘算口诀(技能)
工作最早时光的盘算: 顺着箭线,取大值
工作最迟时光的盘算:逆着箭线,取小值
总时差:最迟开减最早开
自由时差:后早开减本早完
1.工作最早时光的盘算(包含工作最早开端时光和工作最早完成时光):“顺着箭线盘算,依次取大”(最早开端时光--取紧前工作最
早完成时光的最大值), 肇端结点工作最早开端时光为0. 用最早开端时光加中断时光就是该工作的最早完成时光.
2.收集筹划工期的盘算:终点节点的最早完成时光最大值就是该收集
筹划的盘算工期,一般以这个筹划工期为请求工期.
3.工作最迟时光的盘算(包含工作最迟完成时光和最迟开端时光):“逆着箭线盘算,依次取小”(最迟完成时光--取紧后工作最迟开端时光的最小值).与终点节点相连的最后一个工作的最早完成时光(盘算
工期)就是最后一个工作的最迟完成时光.用最迟完成时光减去工作的
中断时光就是该工作的最迟开端时光.
4.总时差:“最迟开减最早开”(最迟开端时光减最早开端时光或者
最迟完成时光减最早完成时光).留意这里都是“最迟减最早”.每个工作都有总时差,最小的总时差是零,我们经常说总时差为零的工作是“没有总时差”.
5.自由时差:“后早开减本早完”(紧后工作的最早开端时光减本工作的最早完成时光).自由时差老是小于.最多等于总时差,不会大于总时差.。
工程项目管理的六个参数

一、最早开始时间(ES)最早开始时间是指在不影响后续工作的情况下,某项工作可以开始的最早时间。
ES 是计算网络图时间参数的基础,其计算方法如下:1. 以网络图起点为起点,ES=0;2. 对于每项工作,其ES等于所有紧前工作的ES加上该工作的持续时间;3. 对于网络图终点,其ES等于该工作的ES。
二、最早结束时间(EF)最早结束时间是指在不影响后续工作的情况下,某项工作可以结束的最早时间。
EF 的计算方法如下:1. 以网络图起点为起点,EF=0;2. 对于每项工作,其EF等于该工作的ES加上该工作的持续时间;3. 对于网络图终点,其EF等于该工作的EF。
三、最迟开始时间(LS)最迟开始时间是指在不影响项目总工期的情况下,某项工作可以开始的最晚时间。
LS的计算方法如下:1. 以网络图终点为终点,LS等于该工作的LF;2. 对于每项工作,其LS等于紧后工作的LS减去该工作的持续时间;3. 对于网络图起点,其LS等于0。
四、最迟结束时间(LF)最迟结束时间是指在不影响项目总工期的情况下,某项工作可以结束的最晚时间。
LF的计算方法如下:1. 以网络图终点为终点,LF等于该工作的EF;2. 对于每项工作,其LF等于紧后工作的LF减去该工作的持续时间;3. 对于网络图起点,其LF等于0。
五、总时差(TF)总时差是指在不影响项目总工期的情况下,某项工作可以推迟的时间。
TF的计算方法如下:1. 对于每项工作,其TF等于该工作的LF减去EF;2. 对于网络图起点,其TF等于0;3. 对于网络图终点,其TF等于0。
六、自由时差(FF)自由时差是指在不影响紧后工作最早开始时间的情况下,某项工作可以推迟的时间。
FF的计算方法如下:1. 对于每项工作,其FF等于紧后工作的ES减去该工作的EF;2. 对于网络图起点,其FF等于0;3. 对于网络图终点,其FF等于0。
通过计算这六个参数,工程项目管理者可以更好地掌握项目进度、成本、质量等关键信息,从而确保项目顺利实施、高效完成。
双代号网络计划图中计算6个时间参数帮助记忆的口诀

双代号网络计划图中计算6个时间参数帮助记忆的口诀双代号网络计划图中计算6个时间参数帮助记忆的口诀工作最早时间的计算: 顺着箭线,取大值工作最迟时间的计算:逆着箭线,取小值总时差:最迟减最早自由时差:后早始减本早完1.工作最早时间的计算(包括工作最早开始时间和工作最早完成时间):“顺着箭线计算,依次取大”(最早开始时间--取紧前工作最早完成时间的最大值),起始结点工作最早开始时间为0。
用最早开始时间加持续时间就是该工作的最早完成时间。
2.网络计划工期的计算:终点节点的最早完成时间最大值就是该网络计划的计算工期,一般以这个计划工期为要求工期。
3.工作最迟时间的计算(包括工作最迟完成时间和最迟开始时间):“逆着箭线计算,依次取小”(最迟完成时间--取紧后工作最迟开始时间的最小值)。
与终点节点相连的最后一个工作的最早完成时间(计算工期)就是最后一个工作的最迟完成时间。
用最迟完成时间减去工作的持续时间就是该工作的最迟开始时间。
4.总时差:“最迟减最早”(最迟开始时间减最早开始时间或者最迟完成时间减最早完成时间)。
注意这里都是“最迟减最早”。
每个工作都有总时差,最小的总时差是零,我们经常说总时差为零的工作是“没有总时差”。
5.自由时差:“后早始减本早完”(紧后工作的最早开始时间减本工作的最早完成时间)。
自由时差总是小于、最多等于总时差,不会大于总时差。
建筑施工,双代号网络图怎么快速求总时差和自由时差,一步步推,考试中这么弄太耽误时间了求关键线路的最快的方法是用标号法。
总时差等于最迟开始时间-最早开始时间=最迟完成时间-最早完成时间自由时差小于等于总时差自由时差等于紧后工作的最早开始时间减本工作的最早完成时间所得差值的最小值。
时标网络:计算哪个工作的总时差,就以哪个工作为起点工作,寻找通过该工作的所有线路,然后计算各条线路的波形线的长度和,波形线长度和的最小值就是该工作的总时差双代号网络:计算哪个工作的总时差,就寻找通过该工作的所有线路,然后计算各条线路的长度和,与工期分别相减,其中的最小值就是该工作的总时差。
网络图中六个时参数

网络图中六个时参数————————————————————————————————作者:————————————————————————————————日期:2.网络图中的六个时间参数(重点)网络图中的时间参数主要有六个:最早开始时间;最早完成时间;最迟开始时间;最迟完成时间;总时差和自由时差。
各时间参数的含义如下。
(1)工作最早开始时间ESii(EarliestStartTime)——是指在其所有紧前工作全部完成后,本工作有可能开始的最早时刻。
(2)工作最早完成时间EFii(EarliestFinishTime)——是指在其所有紧前工作全部完成后,本工作有可能完成的最早时刻。
工作的最早完成时间等于工作最早开始时间与其持续时间之和。
(3)工作最迟完成时间LFii(LatestFinishTime)——是指在不影响整个任务按期完成的前提下,本工作必须完成的最迟时刻。
(4)工作最迟开始时间LSii(LatestStartTime)——是指在不影响整个任务按期完成的前提下,本工作必须开始的最迟时刻。
工作的最迟开始时间等于工作最迟完成时间与其持续时间之差。
(5)总时差TFii(TotalFloatTime)——是指在不影响总工期的前提下,本工作可以利用的机动时间。
(6)自由时差FFii(FreeFloatTime)——是指在不影响其紧后工作最早开始时间的前提下,本工作可以利用的机动时间。
3.双代号网络图中时间参数的计算(1)时间参数计算数学模型:下面取一网络片断(图9-24)作为计算简图。
令整个计划的开始时间为第0天,则:工作最早开始时间等于其紧前工作最早完成时间的最大值。
令整个计划的总工期为一常数,则:工作最迟完成时间等于其紧后工作最迟开始时间的最小值。
在网络计划中,总时差最小的工作为关键工作。
特别地,当网络计划的计划工期等于计算工期时,总时差为零的工作就是关键工作。
由于工作的自由时差是总时差的构成部分,所以,当工作的总时差为零时,其自由时差必然为零。
双代号网络图六个时间参数计算口诀

双代号网络图六个时间参数计算口诀
(技巧)工作最早时间的计算:
顺着箭线,取大值
工作最迟时间的计算:
逆着箭线,取小值
总时差:
最迟开减最早开
自由时差:
后早开减本早完
1.工作最早时间的计算(包括工作最早开始时间和工作最早完成时间):
“顺着箭线计算,依次取大”(最早开始时间--取紧前工作最早完成时间的最大值),起始结点工作最早开始时间为0。
用最早开始时间加持续时间就是该工作的最早完成时间。
2.网络计划工期的计算:
终点节点的最早完成时间最大值就是该网络计划的计算工期,一般以这个计划工期为要求工期。
3.工作最迟时间的计算(包括工作最迟完成时间和最迟开始时间):
“逆着箭线计算,依次取小”(最迟完成时间--取紧后工作最迟开始时间的最小值)。
与终点节点相连的最后一个工作的最早完成时间(计算工期)就是最后一个工作的最迟完成时间。
用最迟完成时间减去工作的持续时间就是该工作的最迟开始时间。
4.总时差:
1/ 2
“最迟开减最早开”(最迟开始时间减最早开始时间或者最迟完成时间减最早完成时间)。
注意这里都是“最迟减最早”。
每个工作都有总时差,最小的总时差是零,我们经常说总时差为零的工作是“没有总时差”。
5.自由时差:
“后早开减本早完”(紧后工作的最早开始时间减本工作的最早完成时间)。
自由时差总是小于、最多等于总时差,不会大于总时差。
2/ 2。
双代号网络图6个时间参数简单计算方法

双代号网络图6个时间参数简单计算方法双代号网络图(也称为双代号网)是一种用来表达工程项目或生产流程中各个活动之间的先后关系的工具。
它通过使用箭头来表示活动,箭头的方向表示活动的先后顺序,箭头上的时间参数表示活动的开始时间和持续时间。
在双代号网络图中,有六个重要的时间参数,分别是:最早开始时间(ES)、最早结束时间(EF)、最晚开始时间(LS)、最晚结束时间(LF)、总时差(TF)和自由时差(FF)。
1. 最早开始时间(Early Start,ES):指一个活动可以开始的最早时间。
对于一个活动,它的最早开始时间等于它的前驱活动的最早结束时间(EF)。
2. 最早结束时间(Early Finish,EF):指一个活动结束的最早时间。
对于一个活动,它的最早结束时间等于最早开始时间(ES)加上该活动的持续时间(D)。
3. 最晚开始时间(Late Start,LS):指一个活动可以开始的最晚时间。
对于一个活动,它的最晚开始时间等于它的后继活动的最早开始时间(ES)减去该活动的持续时间(D)。
4. 最晚结束时间(Late Finish,LF):指一个活动结束的最晚时间。
对于一个活动,它的最晚结束时间等于它的后继活动的最早开始时间(ES)减去15. 总时差(Total Float,TF):指一个活动可以延迟的最长时间,而不会导致项目整体工期延长。
总时差等于最晚开始时间(LS)减去最早开始时间(ES),或等于最晚结束时间(LF)减去最早结束时间(EF)。
6. 自由时差(Free Float,FF):指一个活动可以延迟的最长时间,而不会导致后续活动受到延迟的影响。
自由时差等于后继活动的最早开始时间(ES)减去该活动的最早结束时间(EF)减去1计算这六个时间参数的方法如下:1.计算最早开始时间(ES)和最早结束时间(EF):根据箭头的方向,从左往右依次确定每个活动的最早开始时间和最早结束时间。
对于第一个活动,最早开始时间为0,最早结束时间为持续时间(D)。
双代号网络图六个时间参数的简易计算

关于盘算双代号收集图的标题用图上盘算法盘算如图所示双代号收集图的各项时光参数(六时标注)肯定症结路线.症结工作和总工期.注:个中工作F的最迟完成时光为盘算工期17 其自由时差为17-12=5(盘算工期-F的最早完成时光,因F后没有紧后工作了;H后也没有紧后工作了)双代号收集图是运用较为广泛的一种收集筹划情势.它是以箭线及其两头节点的编号暗示工作的收集图.双代号收集图中的盘算重要有六个时光参数:ES:最早开端时光,指各项工作紧前工作全体完成后,本工作最有可能开端的时刻;EF:最早完成时光,指各项紧前工作全体完成后,本工作有可能完成的最早时刻LF:最迟完成时光,不影响全部收集筹划工期完成的前提下,本工作的最迟完成时光;LS:最迟开端时光,指不影响全部收集筹划工期完成的前提下,本工作最迟开端时光;TF:总时差,指不影响筹划工期的前提下,本工作可以运用的灵活时光;FF:自由时差,不影响紧后工作最早开端的前提下,本工作可以运用的灵活时光.双代号收集图时光参数的盘算一般采取图上盘算法.下面用例题进行讲授.例题:试盘算下面双代号收集图中,求工作C的总时差?早时光盘算:ES,假如该工作与开端节点相连,最早开端时光为0,即A的最早开端时光ES=0;EF,最早停止时光等于该工作的最早开端+中断时光,即A的最早停止EF为0+5=5;假如工作有紧前工作的时刻,最早开端等于紧前工作的最早停止取大值,即B的最早开端FS=5,同理最早停止EF为5+6=11,而E工作的最早开端ES为B.C工作最早停止(11.8)取大值为11.迟时光盘算:LF,假如该工作与停止节点相连,最迟停止时光为盘算工期23,即F的最迟停止时光LF=23;LS,最迟开端时光等于最迟停止时光减去中断时光,即LS=LF-D;假如工作有紧后工作,最迟停止时光等于紧后工作最迟开端时光取小值.时差盘算: FF,自由时差=(紧后工作的ES-本工作的EF);TF,总时差=(紧后工作的LS-本工作的ES)或者=(紧后工作的LF-本工作的EF).该题解析:则C工作的总时差为3.。
双代号网络图时间参数计算技巧
双代号网络图作为工程项目进度管理中,是最常用的工作进度安排方法,也是工程注册类执业考试中必考内容,对它的掌握程度,决定了实务考试的通过概率大小。
双代号网络图时间参数主要为6个时间参数(最早开始时间、最早完成时间、最迟开始时间、最迟完成时间、总时差和自由时差)的计算,按计算方法可以分为:1、节点计算法2、工作计算法3、表格计算法节点计算法最适合初学者,其计算方法简单、快速。
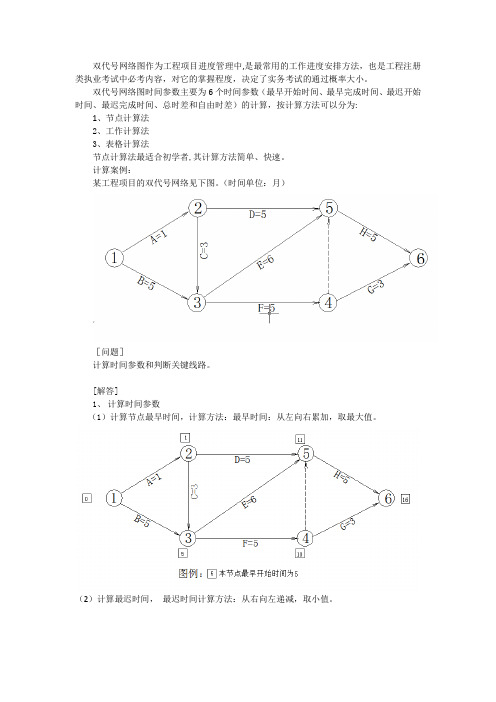
计算案例:某工程项目的双代号网络见下图。
(时间单位:月)[问题]计算时间参数和判断关键线路。
[解答]1、计算时间参数(1)计算节点最早时间,计算方法:最早时间:从左向右累加,取最大值。
(2)计算最迟时间,最迟时间计算方法:从右向左递减,取小值。
2、计算工作的六个时间参数自由时差:该工作在不影响其紧后工作最早开始时间的情况下所具有的机动时间。
总时差:该工作在不影响总工期情况下所具有的机动时间.通过前面计算节点的最早和最迟时间,可以先确定工作的最早开始时间和最迟完成时间,根据工作持续时间,计算出最早完成时间和最迟开始时间,以F工作为例,计算F工作的4个参数(以工作计算法标示)如下:注:EF=ES+工作持续时间LF=LS+工作持续时间接下来计算F工作的总时差TF,在工作计算法中,总时差TF=LS-ES或LF—EF,在节点计算法,总时差TF可以紧后工作的最迟时间—本工作的最早完成时间,或者是紧后工作最迟时间—最早时间,以F工作为例计算它的TF:接下来计算F工作的自由时差FF,根据定义:该工作在不影响其紧后工作最早开始时间的情况下所具有的机动时间,自由时差FF=紧后工作最早(或最小)开始时间—本工作最早完成时间ES,以F工作为例,F的紧后工作为G和H,G工作的最早开始时间为10(即4节点的最早时间),H工作的最早开始时间为11(即5节点的最早时间),G工作的时间最小,所以F的自由时差FF=G工作的最早开始时间ES—F工作的最早完成时间EF:最后计算所有工作的时间参数如图:通过上图我们得知:(1)关键线路为1-3-5-6,计算工期为16个月。
双代号网络图六个参数计算方法
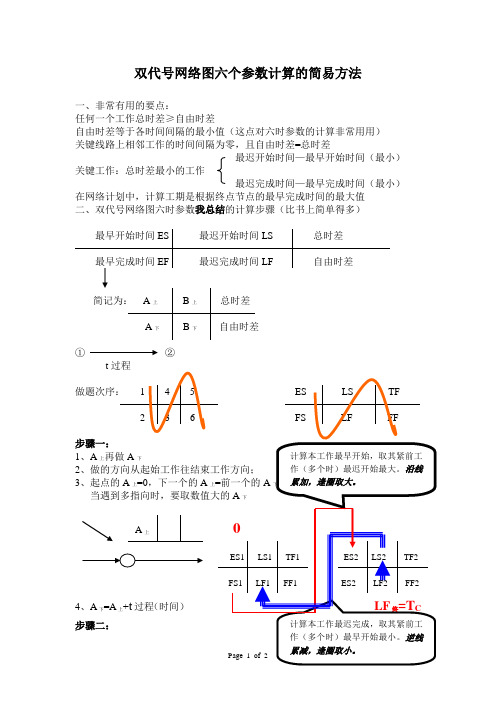
双代号网络图六个参数计算的简易方法
一、非常有用的要点:
任何一个工作总时差≥自由时差
自由时差等于各时间间隔的最小值(这点对六时参数的计算非常用用)
关键线路上相邻工作的时间间隔为零,且自由时差=总时差
最迟开始时间—最早开始时间(最小)关键工作:总时差最小的工作
最迟完成时间—最早完成时间(最小)在网络计划中,计算工期是根据终点节点的最早完成时间的最大值
二、双代号网络图六时参数我总结的计算步骤(比书上简单得多)
①②
t过程
做题次序: 1 4 5 ES LS TF
2 3 6 FS LF FF
步骤一:
1、A上再做A下
2
3、起点的A上=0,下一个的A上
A上
4、A下=A上+t过程(时间)
步骤二:
Page 2 of 2 1、 B 下再做B 上
2、 做的方向从结束点往开始点
3、 结束点B 下=T (需要的总时间=结束工作节点中最大的A 下)
结束点B 上=T-t 过程(时间)
4、B 下=前一个的B 上(这里的前一个是从终点起算的)
遇到多指出去的时,取数值小的B 上
B 上=B 下—t 过程(时间)
步骤三:
总时差=B
上—A 上=B 下—A 下
如果不相等,你就是算错了
步骤四:
自由时差=紧后工作A 上(取最小的)—本工作A 下
=紧后工作的最早开始时间—本工作的最迟开始时间
(有多个紧后工作的取最小值)
例:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.网络图中的六个时间参数(重点)
网络图中的时间参数主要有六个:最早开始时间;最早完成时间;最迟开始时间;最迟完成时间;总时差和自由时差。
各时间参数的含义如下。
(1)工作最早开始时间ESii(EarliestStartTime)——是指在其所有紧前工作全部完成后,本工作有可能开始的最早时刻。
(2)工作最早完成时间EFii(EarliestFinishTime)——是指在其所有紧前工作全部完成后,本工作有可能完成的最早时刻。
工作的最早完成时间等于工作最早开始时间与其持续时间之和。
(3)工作最迟完成时间LFii(LatestFinishTime)——是指在不影响整个任务按期完成的前提下,本工作必须完成的最迟时刻。
(4)工作最迟开始时间LSii(LatestStartTime)——是指在不影响整个任务按期完成的前提下,本工作必须开始的最迟时刻。
工作的最迟开始时间等于工作最迟完成时间与其持续时间之差。
(5)总时差TFii(TotalFloatTime)——是指在不影响总工期的前提下,本工作可以利用的机动时间。
(6)自由时差FFii(FreeFloatTime)——是指在不影响其紧后工作最早开始时间的前提下,本工作可以利用的机动时间。
3.双代号网络图中时间参数的计算
(1)时间参数计算数学模型:
下面取一网络片断(图9-24)作为计算简图。
令整个计划的开始时间为第0天,则:
工作最早开始时间等于其紧前工作最早完成时间的最大值。
令整个计划的总工期为一常数,则:
工作最迟完成时间等于其紧后工作最迟开始时间的最小值。
在网络计划中,总时差最小的工作为关键工作。
特别地,当网络计划的计划工期等于计算工期时,总时差为零的工作就是关键工作。
由于工作的自由时差是总时差的构成部分,所以,当工作的总时差为零时,其自由时差必然为零。
即:
如果网络计划中工作数量比较多,一般用项目管理软件进行计算。
如果数量不多也可用手工进行计算。
(2)计算步骤。
时间参数的计算方法很多,可人工计算,也可通过计算机计算。
手工计算一般采用图上计算法或表上计算法。
不管采用哪种方法,其计算步骤大致相同,具体步骤为:
1)计算工作的最早时间。
工作的最早时间是从左向右逐项工作进行计算。
先定计划的开始时间,网络图中的起始节点一般取相对时间为第0天,则第一项工作的最早开始
时间为第0天,将它与第一项工作的持续时间相加,即为该工作的最早完成时间。
逐项进行计算,一直算到最后一项工作,其最早完成时间即为该计划的计算工期。
2)确定网络计划的计划工期。
如果项目的总工期没有特殊的规定,一般取项目的计划工期为计算工期。
3)计算工作的最迟时间。
工作的最迟时间是从右向左逐项进行计算。
先定计划工期,最后一项工作的完成时间即为所定的计划工期时间,将它与其持续时间相减,即为最后一项工作的最迟开始时间。
逆方向逐项进行计算,一直算到第一项工作。
4)计算工作的总时差。
每一工作的最迟时间与最早时间之差,即为该工作的总时差。
5)计算工作的自由时差。
某一工作的自由时差为其紧后工作的最早开始时间最小值减去本工作的最早完成时间。
6)确定网络计划中的关键线路。
总时差为零的工作为关键工作,将这些关键工作首尾相连在一起即为关键线路,一般用粗箭线或双箭线表示。
其计算结果如图9-25所示,将各参数按规定标至网络图上。
节点法:
沿线累加,逢圈取大
逆线累减,逢圈取小。
