怎样作圆的内接正五边形(精)
正五边形尺规作图的画法及其他

正五边形尺规作图的画法及其他正五边形的画法圆内接正五边形的画法如下:1、作一个圆,设它的圆心为O;2、作圆的两条互相垂直的直径AZ和XY;3、作OY的中点M;4、以点M为圆心,MA为半径作圆,交OX于点N;5、以点A为圆心,AN为半径,在圆上连续截取等弧,使弦AB=BC=CD=DE=AN,则五边形ABCDE即为正五边形。
以上两种图形的作法运用了所求图形边长与已知的线段长度的关系,用构造直角三角形的方法作出与所求图形的边长相等的线段,从而作出整个图形,这是尺规作图中常用的一种方法——等线段法,即用已知图形的线段作出与所求图形边长相等的线段。
正多边形的尺规作图是大家感兴趣的.正三边形很好做;正四边形稍难一点;正六边形也很好做;正五边形就更难一点,但人们也找到了正五边形的直规作图方法.确实,有的困难一些,有的容易一些.正七边形的尺规作图是容易一些,还是困难一些呢?人们很久很久未找到作正七边形的办法,这一事实本身就说明作正七边形不容易;一直未找到这种作法,也使人怀疑:究竟用尺规能否作出正七边形来?数学不容许有这样的判断:至今一直没有人找到正七边形的尺规作图方法来,所以断言它是不能用尺规作出的.人们迅速地解决了正三、四、五、六边形的尺规作图问题,却在正七边形面前止步了:究竟能作不能作,得不出结论来.这个悬案一直悬而未决两千余年.17世纪的费马,就是我们在前面已两次提到了的那个法国业余数学家,他研究了形如Fi(i为右下角标)=22i(底数2指数2的i次幂)+1的数.费马的一个著名猜想是,当n≥3时,不定方程xn+yn=zn没有正整数解.现在他又猜测Fi 都是素数,对于i=0,1,2,3,4时,容易算出来相应的Fi:F0=3,F1=5,F2=17,F3=257,F4=65 537验证一下,这五个数的确是素数.F5=225+1是否素数呢?仅这么一个问题就差不多一百年之后才有了一个结论,伟大的欧拉发现它竟不是素数,因而,伟大的费马这回可是猜错了!F5是两素数之积:F5=641×6 700 417.当然,这一事例多少也说明:判断一个较大的数是否素数也决不是件简单的事,不然,何以需要等近百年?何以需要欧拉这样的人来解决问题?更奇怪的是,不仅F5不是素数,F6,F7也不是素数,F8,F9,F10,F11等还不是素数,甚至,对于F14也能判断它不是素数,但是它的任何真因数还不知道.至今,人们还只知F0,F1,F2,F3,F4这样5个数是素数.由于除此而外还未发现其他素数,于是人们产生了一个与费马的猜想大相径庭的猜想,形如22i+1的素数只有有限个.但对此也未能加以证明.当然,形如Fi=22i+1的素数被称为费马素数.由于素数分解的艰难,不仅对形如Fi=22i+1的数的一般结论很难做出,而且具体分解某个Fi也不是一件简单的事.更加令人惊奇的事情发生在距欧拉发现F5不是素数之后的60多年,一位德国数学家高斯,在他仅20岁左右之时发现,当正多边形的边数是费马素数时是可以尺规作图的,他发现了更一般的结论:正n边形可尺规作图的充分且必要的条件是n=2k(2的k次幂)或2k×p1×p2×…×ps,(1,2…s为右下角标)其中,p1,p2,…,ps是费马素数.正7边形可否尺规作图呢?否!因为7是素数,但不是费马素数.倒是正17边形可尺规作图,高斯最初的一项成就就是作出了正17边形.根据高斯的理论,还有一位德国格丁根大学教授作了正257边形.就这样,一个悬而未决两千余年的古老几何问题得到了圆满的解决,而这一问题解决的过程是如此的蹊跷,它竟与一个没有猜对的猜想相关连.正17边形被用最简单的圆规和直尺作出来了,而正多边形可以换个角度被视为是对圆的等分,那么这也相当于仅用圆规和直尺对圆作了17等分,其图形更觉完美、好看.高斯本人对此也颇为欣赏,由此引导他走上数学道路(他早期曾在语言学与数学之间犹豫过),而且在他逝后的墓碑上就镌刻着一个正17边形图案.高斯把问题是解决得如此彻底,以致有了高斯的定理,我们对于早已知道如何具体作图的正三边形、正五边形,还进而知道了它们为什么能用尺规作图,就因为3和5都是费马素数(3=F0,5=F1);对于很久以来未找到办法来作出的正七边形,乃至于正11边形、正13边形,现在我们能有把握地说,它们不可能由尺规作图,因为7、11、13都不是费马素数;对于正257边形、正65 537边形,即使我们不知道具体如何作,可是理论上我们已经知道它们是可尺规作图的;此外,为什么正四边形、正六边形可尺规作图呢?因为4=22,因为6=2·3而3=F0.。
正五边形尺规作图的画法及其他(精品)

正五边形尺规作图的画法与其他正五边形的画法第一种:圆内接正五边形的画法如下:1、作一个圆,设它的圆心为O;2、作圆的两条互相垂直的直径AZ和XY;3、作OY的中点M;4、以点M为圆心,MA为半径作圆,交OX于点N;5、以点A为圆心,AN为半径,在圆上连续截取等弧,使弦AB=BC=CD=DE=AN,则五边形ABCDE即为正五边形.第二种作法:1. 以O为圆心,半径长为R画圆,并作互相垂直的直径MN和AP;2. 平分半径OM于K,得OK=KM;3. 以K为圆心,KA为半径画弧与ON交于H, AH即为正五边形的边长;4. 以AH为弦长,在圆周上截得A、B、C、D、E各点,顺次连结这些点.五边形ABCDE即为所求.第三种:圆内接正五边形的画法如下:1、作一个圆,设它的圆心为O;2、作圆的两条互相垂直的直径AZ和XY;3、作OY的中点M;4、以点M为圆心,MA为半径作圆,交OX于点N;5、以点A为圆心,AN为半径,在圆上连续截取等弧,使弦AB=BC=CD=DE=AN,则五边形ABCDE即为正五边形.以上两种图形的作法运用了所求图形边长与已知的线段长度的关系,用构造直角三角形的方法作出与所求图形的边长相等的线段,从而作出整个图形,这是尺规作图中常用的一种方法——等线段法,即用已知图形的线段作出与所求图形边长相等的线段.正多边形的尺规作图是大家感兴趣的.正三边形很好做;正四边形稍难一点;正六边形也很好做;正五边形就更难一点,但人们也找到了正五边形的直规作图方法.确实,有的困难一些,有的容易一些.正七边形的尺规作图是容易一些,还是困难一些呢?人们很久很久未找到作正七边形的办法,这一事实本身就说明作正七边形不容易;一直未找到这种作法,也使人怀疑:究竟用尺规能否作出正七边形来?数学不容许有这样的判断:至今一直没有人找到正七边形的尺规作图方法来,所以断言它是不能用尺规作出的.人们迅速地解决了正三、四、五、六边形的尺规作图问题,却在正七边形面前止步了:究竟能作不能作,得不出结论来.这个悬案一直悬而未决两千余年.17世纪的费马,就是我们在前面已两次提到了的那个法国业余数学家,他研究了形如Fi 〔i为右下角标〕=22i〔底数2指数2的i次幂〕+1 的数.费马的一个著名猜想是,当n≥3时,不定方程xn+yn=zn没有正整数解.现在他又猜测Fi都是素数,对于i=0,1,2,3,4时,容易算出来相应的Fi:F0=3,F1=5,F2=17,F3=257,F4=65 537验证一下,这五个数的确是素数.F5=225+1是否素数呢?仅这么一个问题就差不多一百年之后才有了一个结论,伟大的欧拉发现它竟不是素数,因而,伟大的费马这回可是猜错了!F5是两素数之积:F5=641×6 700 417.当然,这一事例多少也说明:判断一个较大的数是否素数也决不是件简单的事,不然,何以需要等近百年?何以需要欧拉这样的人来解决问题?更奇怪的是,不仅F5不是素数,F6,F7也不是素数,F8,F9,F10,F11等还不是素数,甚至,对于F14也能判断它不是素数,但是它的任何真因数还不知道.至今,人们还只知F0,F1,F2,F3,F4这样5个数是素数.由于除此而外还未发现其他素数,于是人们产生了一个与费马的猜想大相径庭的猜想,形如22i+1的素数只有有限个.但对此也未能加以证明.当然,形如Fi=22i+1的素数被称为费马素数.由于素数分解的艰难,不仅对形如Fi=22i+1的数的一般结论很难做出,而且具体分解某个Fi也不是一件简单的事.更加令人惊奇的事情发生在距欧拉发现F5不是素数之后的60多年,一位德国数学家高斯,在他仅20岁左右之时发现,当正多边形的边数是费马素数时是可以尺规作图的,他发现了更一般的结论:正n 边形可尺规作图的充分且必要的条件是n=2k〔2的k次幂〕或2k×p1×p2×…×ps,〔1,2…s为右下角标〕其中,p1,p2,…,ps是费马素数.正7边形可否尺规作图呢?否!因为7是素数,但不是费马素数.倒是正17边形可尺规作图,高斯最初的一项成就就是作出了正17边形.根据高斯的理论,还有一位德国格丁根大学教授作了正257边形.就这样,一个悬而未决两千余年的古老几何问题得到了圆满的解决,而这一问题解决的过程是如此的蹊跷,它竟与一个没有猜对的猜想相关连.正17边形被用最简单的圆规和直尺作出来了,而正多边形可以换个角度被视为是对圆的等分,那么这也相当于仅用圆规和直尺对圆作了17等分,其图形更觉完美、好看.高斯本人对此也颇为欣赏,由此引导他走上数学道路<他早期曾在语言学与数学之间犹豫过>,而且在他逝后的墓碑上就镌刻着一个正17边形图案.高斯把问题是解决得如此彻底,以致有了高斯的定理,我们对于早已知道如何具体作图的正三边形、正五边形,还进而知道了它们为什么能用尺规作图,就因为3和5都是费马素数<3=F0,5=F1>;对于很久以来未找到办法来作出的正七边形,乃至于正11边形、正 13边形,现在我们能有把握地说,它们不可能由尺规作图,因为7、11、13都不是费马素数;对于正257边形、正65 537边形,即使我们不知道具体如何作,可是理论上我们已经知道它们是可尺规作图的;此外,为什么正四边形、正六边形可尺规作图呢?因为4=22,因为6= 2· 3而 3=F0.。
正五边形尺规作图的画法及其他

正五边形尺规作图的画法及其他正五边形的画法圆内接正五边形的画法如下:1、作一个圆,设它的圆心为O;2、作圆的两条互相垂直的直径AZ和XY;3、作OY的中点M;4、以点M为圆心,MA为半径作圆,交OX于点N;5、以点A为圆心,AN为半径,在圆上连续截取等弧,使弦AB=BC=CD=DE=AN,则五边形ABCDE即为正五边形。
以上两种图形的作法运用了所求图形边长与已知的线段长度的关系,用构造直角三角形的方法作出与所求图形的边长相等的线段,从而作出整个图形,这是尺规作图中常用的一种方法——等线段法,即用已知图形的线段作出与所求图形边长相等的线段。
正多边形的尺规作图是大家感兴趣的.正三边形很好做;正四边形稍难一点;正六边形也很好做;正五边形就更难一点,但人们也找到了正五边形的直规作图方法.确实,有的困难一些,有的容易一些.正七边形的尺规作图是容易一些,还是困难一些呢?人们很久很久未找到作正七边形的办法,这一事实本身就说明作正七边形不容易;一直未找到这种作法,也使人怀疑:究竟用尺规能否作出正七边形来?数学不容许有这样的判断:至今一直没有人找到正七边形的尺规作图方法来,所以断言它是不能用尺规作出的.人们迅速地解决了正三、四、五、六边形的尺规作图问题,却在正七边形面前止步了:究竟能作不能作,得不出结论来.这个悬案一直悬而未决两千余年.17世纪的费马,就是我们在前面已两次提到了的那个法国业余数学家,他研究了形如Fi (i为右下角标)=22i(底数2指数2的i次幂)+1 的数.费马的一个著名猜想是,当n≥3时,不定方程xn+yn=zn没有正整数解.现在他又猜测Fi都是素数,对于i=0,1,2,3,4时,容易算出来相应的Fi:F0=3,F1=5,F2=17,F3=257,F4=65 537验证一下,这五个数的确是素数.F5=225+1是否素数呢?仅这么一个问题就差不多一百年之后才有了一个结论,伟大的欧拉发现它竟不是素数,因而,伟大的费马这回可是猜错了!F5是两素数之积:F5=641×6 700 417.当然,这一事例多少也说明:判断一个较大的数是否素数也决不是件简单的事,不然,何以需要等近百年?何以需要欧拉这样的人来解决问题?更奇怪的是,不仅F5不是素数,F6,F7也不是素数,F8,F9,F10,F11等还不是素数,甚至,对于F14也能判断它不是素数,但是它的任何真因数还不知道.至今,人们还只知F0,F1,F2,F3,F4这样5个数是素数.由于除此而外还未发现其他素数,于是人们产生了一个与费马的猜想大相径庭的猜想,形如22i+1的素数只有有限个.但对此也未能加以证明.当然,形如Fi=22i+1的素数被称为费马素数.由于素数分解的艰难,不仅对形如Fi=22i+1的数的一般结论很难做出,而且具体分解某个Fi也不是一件简单的事.更加令人惊奇的事情发生在距欧拉发现F5不是素数之后的60多年,一位德国数学家高斯,在他仅20岁左右之时发现,当正多边形的边数是费马素数时是可以尺规作图的,他发现了更一般的结论:正n边形可尺规作图的充分且必要的条件是n=2k(2的k次幂)或2k×p1×p2×…×ps,(1,2…s为右下角标)其中,p1,p2,…,ps是费马素数.正7边形可否尺规作图呢?否!因为7是素数,但不是费马素数.倒是正17边形可尺规作图,高斯最初的一项成就就是作出了正17边形.根据高斯的理论,还有一位德国格丁根大学教授作了正257边形.就这样,一个悬而未决两千余年的古老几何问题得到了圆满的解决,而这一问题解决的过程是如此的蹊跷,它竟与一个没有猜对的猜想相关连.正17边形被用最简单的圆规和直尺作出来了,而正多边形可以换个角度被视为是对圆的等分,那么这也相当于仅用圆规和直尺对圆作了17等分,其图形更觉完美、好看.高斯本人对此也颇为欣赏,由此引导他走上数学道路(他早期曾在语言学与数学之间犹豫过),而且在他逝后的墓碑上就镌刻着一个正17边形图案.高斯把问题是解决得如此彻底,以致有了高斯的定理,我们对于早已知道如何具体作图的正三边形、正五边形,还进而知道了它们为什么能用尺规作图,就因为3和5都是费马素数(3=F0,5=F1);对于很久以来未找到办法来作出的正七边形,乃至于正11边形、正 13边形,现在我们能有把握地说,它们不可能由尺规作图,因为7、11、13都不是费马素数;对于正257边形、正65 537边形,即使我们不知道具体如何作,可是理论上我们已经知道它们是可尺规作图的;此外,为什么正四边形、正六边形可尺规作图呢?因为4=22,因为6= 2· 3而 3=F0.。
正五边形尺规作图的画法及其他

正五边形尺规作图的画法及其他正五边形的画法圆内接正五边形的画法如下:1、作一个圆,设它的圆心为O;2、作圆的两条互相垂直的直径AZ和XY;3、作OY的中点M;4、以点M为圆心,MA为半径作圆,交OX于点N;5、以点A为圆心,AN为半径,在圆上连续截取等弧,使弦AB=BC=CD=DE=AN,则五边形ABCDE即为正五边形。
以上两种图形的作法运用了所求图形边长与已知的线段长度的关系,用构造直角三角形的方法作出与所求图形的边长相等的线段,从而作出整个图形,这是尺规作图中常用的一种方法——等线段法,即用已知图形的线段作出与所求图形边长相等的线段。
正多边形的尺规作图是大家感兴趣的.正三边形很好做;正四边形稍难一点;正六边形也很好做;正五边形就更难一点,但人们也找到了正五边形的直规作图方法.确实,有的困难一些,有的容易一些.正七边形的尺规作图是容易一些,还是困难一些呢?人们很久很久未找到作正七边形的办法,这一事实本身就说明作正七边形不容易;一直未找到这种作法,也使人怀疑:究竟用尺规能否作出正七边形来?数学不容许有这样的判断:至今一直没有人找到正七边形的尺规作图方法来,所以断言它是不能用尺规作出的.人们迅速地解决了正三、四、五、六边形的尺规作图问题,却在正七边形面前止步了:究竟能作不能作,得不出结论来.这个悬案一直悬而未决两千余年.17世纪的费马,就是我们在前面已两次提到了的那个法国业余数学家,他研究了形如Fi (i为右下角标)=22i(底数2指数2的i次幂)+1 的数.费马的一个著名猜想是,当 n≥3时,不定方程xn+yn=zn没有正整数解.现在他又猜测Fi都是素数,对于i=0,1,2,3,4时,容易算出来相应的Fi:F0=3,F1=5,F2=17,F3=257,F4=65 537验证一下,这五个数的确是素数.F5=225+1是否素数呢?仅这么一个问题就差不多一百年之后才有了一个结论,伟大的欧拉发现它竟不是素数,因而,伟大的费马这回可是猜错了!F5是两素数之积:F5=641×6 700 417.当然,这一事例多少也说明:判断一个较大的数是否素数也决不是件简单的事,不然,何以需要等近百年?何以需要欧拉这样的人来解决问题?更奇怪的是,不仅F5不是素数,F6,F7也不是素数,F8,F9,F10,F11等还不是素数,甚至,对于F14也能判断它不是素数,但是它的任何真因数还不知道.至今,人们还只知F0,F1,F2,F3,F4这样5个数是素数.由于除此而外还未发现其他素数,于是人们产生了一个与费马的猜想大相径庭的猜想,形如22i+1的素数只有有限个.但对此也未能加以证明.当然,形如Fi=22i+1的素数被称为费马素数.由于素数分解的艰难,不仅对形如Fi=22i+1的数的一般结论很难做出,而且具体分解某个Fi也不是一件简单的事.更加令人惊奇的事情发生在距欧拉发现F5不是素数之后的60多年,一位德国数学家高斯,在他仅20岁左右之时发现,当正多边形的边数是费马素数时是可以尺规作图的,他发现了更一般的结论:正n边形可尺规作图的充分且必要的条件是n=2k(2的k次幂)或 2k×p1×p2×…×ps,(1,2…s为右下角标)其中,p1,p2,…,ps是费马素数.正7边形可否尺规作图呢?否!因为7是素数,但不是费马素数.倒是正17边形可尺规作图,高斯最初的一项成就就是作出了正17边形.根据高斯的理论,还有一位德国格丁根大学教授作了正257边形.就这样,一个悬而未决两千余年的古老几何问题得到了圆满的解决,而这一问题解决的过程是如此的蹊跷,它竟与一个没有猜对的猜想相关连.正17边形被用最简单的圆规和直尺作出来了,而正多边形可以换个角度被视为是对圆的等分,那么这也相当于仅用圆规和直尺对圆作了17等分,其图形更觉完美、好看.高斯本人对此也颇为欣赏,由此引导他走上数学道路(他早期曾在语言学与数学之间犹豫过),而且在他逝后的墓碑上就镌刻着一个正17边形图案.高斯把问题是解决得如此彻底,以致有了高斯的定理,我们对于早已知道如何具体作图的正三边形、正五边形,还进而知道了它们为什么能用尺规作图,就因为3和5都是费马素数(3=F0,5=F1);对于很久以来未找到办法来作出的正七边形,乃至于正11边形、正 13边形,现在我们能有把握地说,它们不可能由尺规作图,因为7、11、13都不是费马素数;对于正257边形、正65 537边形,即使我们不知道具体如何作,可是理论上我们已经知道它们是可尺规作图的;此外,为什么正四边形、正六边形可尺规作图呢?因为4=22,因为 6= 2·3而 3=F0.THANKS致力为企业和个人提供合同协议,策划案计划书,学习课件等等打造全网一站式需求欢迎您的下载,资料仅供参考。
初中数学知识点总结:圆内接正五边形知识点及平面直角坐标系

初中数学知识点总结:圆内接正五边形知识点及平面直角坐标系顾名思义,圆内接正五边形指内接于圆的正五边形。
圆内接正五边形圆内接正五边形的定义与性质圆内接正五边形的每一条边相等(即圆的每一条弦相等),每个角均为108°,每个角在圆内所对的优弧相等。
圆内接正五边形的尺规作图(1)以O为圆心,定长R为半径画圆,并作相互垂直的直径MN和 AP. (2)平分半径ON,得OK=KN. (3)以 K为圆心,KA为半径画弧与OM交于 H, AH即为正五边形的边长. (4)以AH为弦长,在圆周上截得A、B、C、D、E各点,顺次连接这些点即得正五边形。
正五边形的内角和求法由于五边形的内角和可看为3个三角形的内角和,所以,3×180°=540°正五边形的内角求法据上一条“正五边形的内角和求法”可知道,正五边形的内角和为540°。
往下拓展:由于正五边形的五个角均相等,且五边形的内角和为540°;所以正五边形的每个内角均为540°÷5=108°我们学习的圆内接正五边形知识要领虽然不多,但都是重点要点。
平面直角坐标系下面是对平面直角坐标系的内容学习,盼望同学们很好的掌控下面的内容。
平面直角坐标系平面直角坐标系:在平面内画两条相互垂直、原点重合的数轴,组成平面直角坐标系。
水平的数轴称为*轴或横轴,竖直的数轴称为y轴或纵轴,两坐标轴的交点为平面直角坐标系的原点。
平面直角坐标系的要素:①在同一平面②两条数轴③相互垂直④原点重合三个规定:①正方向的规定横轴取向右为正方向,纵轴取向上为正方向②单位长度的规定;一般状况,横轴、纵轴单位长度相同;实际有时也可不同,但同一数轴上需要相同。
③象限的规定:右上为第一象限、左上为第二象限、左下为第三象限、右下为第四象限。
相信上面对平面直角坐标系知识的讲解学习,同学们已经能很好的掌控了吧,盼望同学们都能考试胜利。
1.8 圆内接正五边形
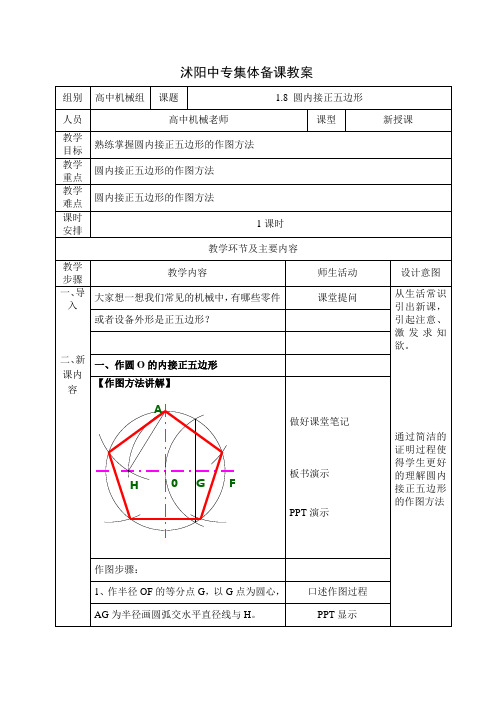
二、课堂练习 三、 总 结 1、作圆 O 的内接正五边形
查漏补缺 学生示范、课堂讲解
【小结】 本节课学习了圆内接正五边形的方 归纳本课所学的内容。 明确本节课 程的重要知 法,希望课后及时巩固所学内容。 识要点。 板 书 设 计 课 后 作 教 学 反 思 1.8 圆内接正五边形 一、作圆 O 的内接正五边形 二、证明过程
2、以 AH 为半径,分圆周为五等分,顺序 连接各等分点即可。 二、证明过程 为什么 AH 就是正五边形的边长呢? 【讲解】 求证:圆内接正五边形的边长 L=AH,已知 Sin36°=(√10-2√5)/4 证明: 设圆 O 的半径为 R 则 L=2RSin36°=R(√10-2√5)/2 ∵在△AOG 中 AG=R√5 在△AOH 中 AH=√AO² +0H² =R(√10-2√5)/2 =L 通过简洁的 证明过程使 得学生更好 的理解圆内 接正五边形 的作法原理 PPT 演示 口述证明过程
二、 一、作圆 O 的内接正五边形 新 课内 【作图方法讲解】 容 A 做好课堂笔记 通过简洁的 证明过程使 得学生更好 的理解圆内 接正五边形 的作图方法
H
0
G
F
板书演示
PPT 演示
作图步骤: 1、作半径 OF 的等分点 G,以 G 点为圆心, AG 为半径画圆弧交水平直径线与 H。 口述作图过程 PPT 显示
练习册习题
沭阳中专集体备课教案
组别 人员 教学 目标 教学 重点 教学 难点 课时 安排 高中机械组 课题 高中机械老师 熟练掌握圆内接正五边形的作图方法 圆内接正五边形的作图方法 圆内接正五边形的作图方法 1 课时 教学环节及主要内容 教学 教学内容 步骤 一、 大家想一想我们常见的机械中, 导 有哪些零件 入 或者设备外形是正五边形? 师生活动 课堂提问 设计意图 从生活常识 引出新课, 引起注意、 激 发 求知 欲。 1.8 圆内接正五边形 课型 新授课
风景园林设计专业《作圆的内接正多(n)边形5》

作圆的内接正多〔n〕边形技能目标能够熟练地利用外接圆作内接正多边形圆内接正多边形一般是将圆周几等分,然后各点依次连线做出正多边形。
常见的正多边形有三边形、四边形、五边形、六边形和七边形。
一、圆内接正三角形如图2.9所示,过圆心做垂直的两直线,以一条直径的端点为圆心,以圆半径为半径作圆弧与圆相交两点,把这两点分图2.9圆内接正三角形别与直径的另一端点相连接,既得到内接正三角形。
二、圆内接正四边形作图方法如图2.10:〔1〕用45°三角板斜边过圆心作直径交圆周于1、3点;〔2〕移动三角板,用直角边作垂线14和12;〔3〕用丁字尺画23和34两直线。
三、 圆内接正五边形作图方法如图2.11:〔1〕作OB 的垂直平分线交OB 于点P ; 〔2〕以P 为圆心,PC 长为半径画弧交直径AB 于点H ; 〔3〕CH 即为五边形的边长,等分圆周得五等分点C 、E 、G 、K 、F ;〔4〕连接圆周各等分点,即为正五边形。
四、 圆内接正六边形方法一:用圆规作图分别以圆在水平直径上的两处交点A 、D 为圆心,以圆的半径R 作圆弧,与圆交于B 、F 、E 、C 点,依次连接A 、B 、C 、D 、E 、F 点即得圆内接正六边形。
如图2.12〔a 〕图2.11 圆的内接正五边形图2.10 圆内接正四边形方法二:用三角板作图以60º三角板的短直角边靠着丁字尺,过圆的水平直径与圆周的交点作平行线,画出四条斜边,再连接上下水平边,即得圆内接正六边形。
如图2.12〔b〕〔a〕〔b〕图2.12 圆内接正六边形五、圆内接正七边形将直径AK等分为七等分,以A点为圆心,AK为半径作弧,交水平中心线于点S,延长连线S2、S4、S6,与圆周交得点G、F、E,再作出它们的对称点B、C、D,依次连接即可作出圆内接正七边形〔图2.13〕。
图2.13 圆内接正七边形小结。
作圆内接正五边形
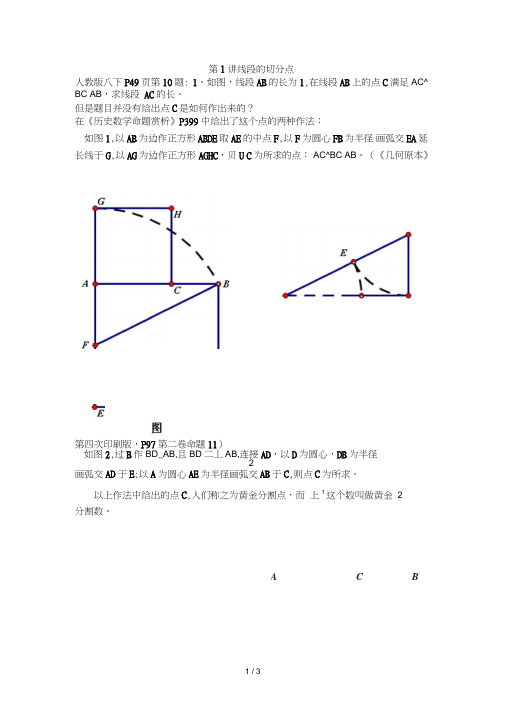
第1讲线段的切分点人教版八下P49页第10题: 1、如图,线段AB的长为1,在线段AB上的点C满足AC^ BC AB,求线段AC的长。
但是题目并没有给出点C是如何作出来的?在《历史数学命题赏析》P399中给出了这个点的两种作法:如图1,以AB为边作正方形ABDE取AE的中点F,以F为圆心FB为半径画弧交EA延长线于G,以AG为边作正方形AGHC,贝U C为所求的点:AC^BC AB。
(《几何原本》第四次印刷版,P97第二卷命题11)如图2,过B作BD_AB,且BD二丄AB,连接AD,以D为圆心,DB为半径2画弧交AD于E;以A为圆心AE为半径画弧交AB于C,则点C为所求。
以上作法中给出的点C,人们称之为黄金分割点,而上1这个数叫做黄金2分割数。
A C B第2讲弦切角、切割线定理1、弦切角及弦切角定理顶点在圆上,一条边与圆相交而另一条边与圆相切的角叫做弦切角。
弦切角定理弦切角等于它所夹的弧所对的圆周角已知:.BAC是。
O的弦切角,AC与。
O相切,BAC所夹的弧是弧AB , APB 是弧AB 所对的圆周角求证:.BAC 二.APB分析:类似于圆周角与圆心的三种位置关系,弦切角与圆心得位置关系也有三种:圆心在弦AB上;圆心在弦切角.BAC的外部;圆心在弦切角.BAC的内部。
2、切割线定理从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段的比例中项。
已知:如图,P为。
O外一点,PA是。
O的切线,切点为A , PT是。
O的割线, PT交O O于点B、C。
求证:PA^PB PC切割线定理的逆定理如图,P为。
O外一点,A是。
O上一点,,PT是。
O的割线,PT 交O O 于点B、C。
PA—PB PC求证:PA是O O 的切线P TP第3讲底角为72的等腰三角形作一个等腰三角形,两个底角都等于顶角的两倍作法:取任意线段AB , C为黄金分割点,以A为圆心,AB为半径作圆A,在圆内作线段BD=AC,连接AD,CD则厶ABD为所求。
尺规作图正五边形

尺规作图正五边形
[正五边形的画法]
圆内接正五边形的画法如下:
①以O为圆心,定长R为半径画圆,并作互相垂直的直径MN和 AP.
②②平分半径ON,得OK=KN.
③③以 K为圆心,KA为半径画弧与 OM交于 H, AH即为正五边形的
边长.
④④以AH为弦长,在圆周上截得A,B,C,D,E各点,顺次连接这些点即
得正五边形.
⑤已知边长作正五边形的近似画法如下:
⑥①作线段AB等于定长l,并分别以A,B为圆心,已知长l为半径画
弧与AB的中垂线交于K.
⑦②以K为圆心,取AB的2/3长度为半径向外侧取C点,使CK=2/3AB
⑧③以 C为圆心,已知边长 AB为半径画弧,分别与前两弧相交于
M,N.
⑨④顺次连接A,B,N,C,M各点即近似作得所要求的正五边形.
在圆内作一个正三角形
先画个圆O。
半径为R
在圆上取任意一点P圆心。
半径仍为R做弧。
与圆O相交与AB两点。
AB是正三角形的两个顶点了。
再以A为圆心,半径仍为R做弧。
与圆O又有两个交点。
其中一个肯定为第1次做弧的圆心P。
还有个设为Q
以Q为圆心。
半径为R作弧。
与圆O有两个交点。
一个为A,另一个为C
则三角形ABC为正三角形。
正五边形的画法

、[正五边形的画法]圆内接正五边形的画法如下:1、任作一圆O2、任作圆O中互相垂直的两直径AB、CD3、作OD的垂直平分线交OD于E4、以E为圆心,EA长为半径作弧,交CD于F5、在圆O上顺序作弦AG=GH=HM=MN=NA=AF则得正五边形AGHMN已知边长作正五边形的近似画法如下:①作线段AB等于定长l,并分别以A,B为圆心,已知长l为半径画弧与AB的中垂线交于K.②以K为圆心,取AB的2/3长度为半径向外侧取C点,使CK=2/3AB③以C为圆心,已知边长AB为半径画弧,分别与前两弧相交于M,N.④顺次连接A,B,N,C,M各点即近似作得所要求的正五边形.正多边形的尺规作图是大家感兴趣的.正三边形很好做;正四边形稍难一点;正六边形也很好做;正五边形就更难一点,但人们也找到了正五边形的直规作图方法.确实,有的困难一些,有的容易一些.正七边形的尺规作图是容易一些,还是困难一些呢?人们很久很久未找到作正七边形的办法,这一事实本身就说明作正七边形不容易;一直未找到这种作法,也使人怀疑:究竟用尺规能否作出正七边形来?数学不容许有这样的判断:至今一直没有人找到正七边形的尺规作图方法来,所以断言它是不能用尺规作出的.人们迅速地解决了正三、四、五、六边形的尺规作图问题,却在正七边形面前止步了:究竟能作不能作,得不出结论来.这个悬案一直悬而未决两千余年.17世纪的费马,就是我们在前面已两次提到了的那个法国业余数学家,他研究了形如Fi (i为右下角标)=22i(底数2指数2的i次幂)+1 的数.费马的一个著名猜想是,当n≥3时,不定方程xn+yn=zn没有正整数解.现在他又猜测Fi都是素数,对于i=0,1,2,3,4时,容易算出来相应的Fi:F0=3,F1=5,F2=17,F3=257,F4=65 537验证一下,这五个数的确是素数.F5=225+1是否素数呢?仅这么一个问题就差不多一百年之后才有了一个结论,伟大的欧拉发现它竟不是素数,因而,伟大的费马这回可是猜错了!F5是两素数之积:F5=641×6 700 417.当然,这一事例多少也说明:判断一个较大的数是否素数也决不是件简单的事,不然,何以需要等近百年?何以需要欧拉这样的人来解决问题?更奇怪的是,不仅F5不是素数,F6,F7也不是素数,F8,F9,F10,F11等还不是素数,甚至,对于F14也能判断它不是素数,但是它的任何真因数还不知道.至今,人们还只知F0,F1,F2,F3,F4这样5个数是素数.由于除此而外还未发现其他素数,于是人们产生了一个与费马的猜想大相径庭的猜想,形如22i+1的素数只有有限个.但对此也未能加以证明.当然,形如Fi=22i+1的素数被称为费马素数.由于素数分解的艰难,不仅对形如Fi=22i+1的数的一般结论很难做出,而且具体分解某个Fi也不是一件简单的事.更加令人惊奇的事情发生在距欧拉发现F5不是素数之后的60多年,一位德国数学家高斯,在他仅20岁左右之时发现,当正多边形的边数是费马素数时是可以尺规作图的,他发现了更一般的结论:正n边形可尺规作图的充分且必要的条件是n=2k(2的k次幂)或2k×p1×p2×…×ps,(1,2…s为右下角标)其中,p1,p2,…,ps是费马素数.正7边形可否尺规作图呢?否!因为7是素数,但不是费马素数.倒是正17边形可尺规作图,高斯最初的一项成就就是作出了正17边形.根据高斯的理论,还有一位德国格丁根大学教授作了正257边形.就这样,一个悬而未决两千余年的古老几何问题得到了圆满的解决,而这一问题解决的过程是如此的蹊跷,它竟与一个没有猜对的猜想相关连.正17边形被用最简单的圆规和直尺作出来了,而正多边形可以换个角度被视为是对圆的等分,那么这也相当于仅用圆规和直尺对圆作了17等分,其图形更觉完美、好看.高斯本人对此也颇为欣赏,由此引导他走上数学道路(他早期曾在语言学与数学之间犹豫过),而且在他逝后的墓碑上就镌刻着一个正17边形图案.高斯把问题是解决得如此彻底,以致有了高斯的定理,我们对于早已知道如何具体作图的正三边形、正五边形,还进而知道了它们为什么能用尺规作图,就因为3和5都是费马素数(3=F0,5=F1);对于很久以来未找到办法来作出的正七边形,乃至于正11边形、正13边形,现在我们能有把握地说,它们不可能由尺规作图,因为7、11、13都不是费马素数;对于正257边形、正65 537边形,即使我们不知道具体如何作,可是理论上我们已经知道它们是可尺规作图的;此外,为什么正四边形、正六边形可尺规作图呢?因为4=22,因为6= 2· 3而3=F0.费马数费马数是以数学家费马命名一组自然数,具有形式:其中 n 为非负整数。
九年级数学上册第3章正五边形尺规作图的画法及延伸(青岛版)

正五边形尺规作图的画法及延伸圆内接正五边形的画法如下:(1)作一个圆,设它的圆心为O;(2)作圆的两条互相垂直的直径AZ和XY;(3)作OY的中点M;(4)以点M为圆心,MA为半径作圆,交OX于点N;有MA=MN.(5)以点A为圆心,AN为半径,在圆上连续截取等弧,使AB=BC=CD=DE=AN。
(6)连接AE.则五边形ABCDE即为正五边形。
证明:设圆的半径为R,由上述正五边形的作法可知:()22222AN AO ON AO AM MO=+=+-∴110252-AN R=.由于半径为R的正五边形的边长a=AN,所以五边形ABCDE即为正五边形。
以上作法运用了所求图形边长与已知的线段长度的关系,用构造直角三角形的方法作出与所求图形的边长相等的线段,从而作出整个图形,这是尺规作图中常用的一种方法——等线段法,即用已知图形的线段作出与所求图形边长相等的线段。
正多边形的尺规作图是大家感兴趣的.正三边形很好做;正四边形稍难一点;正六边形也很好做;正五边形就更难一点,但人们也找到了正五边形的尺规作图方法.那正七边形的尺规作图是容易一些,还是困难一些呢?人们很久很久未找到作正七边形的办法,这一事实本身就说明作正七边形不容易;一直未找到这种作法,也使人怀疑:用尺规究竟能否作出正七边形来?数学不容许有这样的判断:即“至今一直没有人找到正七边形的尺规作图方法来,所以断言它是不能用尺规作出的.”人们迅速地解决了正三、四、五、六边形的尺规作图问题,却在正七边形面前止步了:究竟能作不能作,得不出结论来.这个悬案一直悬而未决两千余年.17世纪的费马,就是我们在前面已两次提到了的那个法国业余数学家,他研究了形如221ii F =+的数.费马的一个著名猜想是,当 n≥3时,不定方程xn +yn =zn 没有正整数解.现在他又猜测Fi 都是素数,对于i =0,1,2,3,4时,容易算出来相应的Fi : F0=3,F1=5,F2=17,F3=257,F4=65 537验证一下,这五个数的确是素数.F5=225+1是否素数呢?仅这么一个问题就差不多一百年之后才有了一个结论,伟大的欧拉发现它竟不是素数,因而,伟大的费马这回可是猜错了!F 5是两素数之积:F 5=641×6 700 417.当然,这一事例多少也说明:判断一个较大的数是否素数也决不是件简单的事,不然,何以需要等近百年?何以需要欧拉这样的人来解决问题?更奇怪的是,不仅F5不是素数,F6,F7也不是素数,F8,F9,F10,F11等还不是素数,甚至,对于F14也能判断它不是素数,但是它的任何真因数还不知道.至今,人们还只知F0,F1,F2,F3,F4这样5个数是素数.由于除此而外还未发现其他素数,于是人们产生了一个与费马的猜想大相径庭的猜想,形如22i +1的素数只有有限个.但对此也未能加以证明.当然,形如Fi=22i+1的素数被称为费马素数.由于素数分解的艰难,不仅对形如Fi=22i+1的数的一般结论很难做出,而且具体分解某个Fi 也不是一件简单的事.更加令人惊奇的事情发生在距欧拉发现F5不是素数之后的60多年,一位德国数学家高斯,在他仅20岁左右之时发现,当正多边形的边数是费马素数时是可以尺规作图的,他发现了更一般的结论:正n 边形可尺规作图的充分且必要的条件是n=2k (2的k 次幂)或 2k×p1×p2×…×ps ,(1,2…s 为右下角标)其中,p1,p2,…,ps 是费马素数.正7边形可否尺规作图呢?否!因为7是素数,但不是费马素数.倒是正17边形可尺规作图,高斯最初的一项成就就是作出了正17边形.根据高斯的理论,还有一位德国格丁根大学教授作了正257边形.就这样,一个悬而未决两千余年的古老几何问题得到了圆满的解决,而这一问题解决的过程是如此的蹊跷,它竟与一个没有猜对的猜想相关连.正17边形被用最简单的圆规和直尺作出来了,而正多边形可以换个角度被视为是对圆的等分,那么这也相当于仅用圆规和直尺对圆作了17等分,其图形更觉完美、好看.高斯本人对此也颇为欣赏,由此引导他走上数学道路(他早期曾在语言学与数学之间犹豫过),而且在他逝后的墓碑上就镌刻着一个正17边形图案.高斯把问题是解决得如此彻底,以致有了高斯的定理,我们对于早已知道如何具体作图的正三边形、正五边形,还进而知道了它们为什么能用尺规作图,就因为3和5都是费马素数(3=F0,5=F1);对于很久以来未找到办法来作出的正七边形,乃至于正11边形、正13边形,现在我们能有把握地说,它们不可能由尺规作图,因为7、11、13都不是费马素数;对于正257边形、正65 537边形,即使我们不知道具体如何作,可是理论上我们已经知道它们是可尺规作图的;此外,为什么正四边形、正六边形可尺规作图呢?因为4=22,因为6= 2· 3而3=F0.。
正五边形的画法

正五边形尺规作图的画法及其他正五边形的画法圆内接正五边形的画法如下:1、作一个圆,设它的圆心为O;2、作圆的两条互相垂直的直径AZ和XY;3、作OY的中点M;4、以点M为圆心,MA为半径作圆,交OX于点N;5、以点A为圆心,AN为半径,在圆上连续截取等弧,使弦AB=BC=CD=DE=AN,则五边形ABCDE即为正五边形。
以上两种图形的作法运用了所求图形边长与已知的线段长度的关系,用构造直角三角形的方法作出与所求图形的边长相等的线段,从而作出整个图形,这是尺规作图中常用的一种方法——等线段法,即用已知图形的线段作出与所求图形边长相等的线段。
正多边形的尺规作图是大家感兴趣的.正三边形很好做;正四边形稍难一点;正六边形也很好做;正五边形就更难一点,但人们也找到了正五边形的直规作图方法.确实,有的困难一些,有的容易一些.正七边形的尺规作图是容易一些,还是困难一些呢?人们很久很久未找到作正七边形的办法,这一事实本身就说明作正七边形不容易;一直未找到这种作法,也使人怀疑:究竟用尺规能否作出正七边形来?数学不容许有这样的判断:至今一直没有人找到正七边形的尺规作图方法来,所以断言它是不能用尺规作出的.人们迅速地解决了正三、四、五、六边形的尺规作图问题,却在正七边形面前止步了:究竟能作不能作,得不出结论来.这个悬案一直悬而未决两千余年.17世纪的费马,就是我们在前面已两次提到了的那个法国业余数学家,他研究了形如Fi (i为右下角标)=22i(底数2指数2的i次幂)+1 的数.费马的一个著名猜想是,当n≥3时,不定方程xn+yn=zn没有正整数解.现在他又猜测Fi都是素数,对于i=0,1,2,3,4时,容易算出来相应的Fi:F0=3,F1=5,F2=17,F3=257,F4=65 537验证一下,这五个数的确是素数.F5=225+1是否素数呢?仅这么一个问题就差不多一百年之后才有了一个结论,伟大的欧拉发现它竟不是素数,因而,伟大的费马这回可是猜错了!F5是两素数之积:F5=641×6 700 417.当然,这一事例多少也说明:判断一个较大的数是否素数也决不是件简单的事,不然,何以需要等近百年?何以需要欧拉这样的人来解决问题?更奇怪的是,不仅F5不是素数,F6,F7也不是素数,F8,F9,F10,F11等还不是素数,甚至,对于F14也能判断它不是素数,但是它的任何真因数还不知道.至今,人们还只知F0,F1,F2,F3,F4这样5个数是素数.由于除此而外还未发现其他素数,于是人们产生了一个与费马的猜想大相径庭的猜想,形如22i+1的素数只有有限个.但对此也未能加以证明.当然,形如Fi=22i+1的素数被称为费马素数.由于素数分解的艰难,不仅对形如Fi=22i+1的数的一般结论很难做出,而且具体分解某个Fi也不是一件简单的事.更加令人惊奇的事情发生在距欧拉发现F5不是素数之后的60多年,一位德国数学家高斯,在他仅20岁左右之时发现,当正多边形的边数是费马素数时是可以尺规作图的,他发现了更一般的结论:正n边形可尺规作图的充分且必要的条件是n=2k(2的k次幂)或2k×p1×p2×…×ps,(1,2…s为右下角标)其中,p1,p2,…,ps是费马素数.正7边形可否尺规作图呢?否!因为7是素数,但不是费马素数.倒是正17边形可尺规作图,高斯最初的一项成就就是作出了正17边形.根据高斯的理论,还有一位德国格丁根大学教授作了正257边形.就这样,一个悬而未决两千余年的古老几何问题得到了圆满的解决,而这一问题解决的过程是如此的蹊跷,它竟与一个没有猜对的猜想相关连.正17边形被用最简单的圆规和直尺作出来了,而正多边形可以换个角度被视为是对圆的等分,那么这也相当于仅用圆规和直尺对圆作了17等分,其图形更觉完美、好看.高斯本人对此也颇为欣赏,由此引导他走上数学道路(他早期曾在语言学与数学之间犹豫过),而且在他逝后的墓碑上就镌刻着一个正17边形图案.高斯把问题是解决得如此彻底,以致有了高斯的定理,我们对于早已知道如何具体作图的正三边形、正五边形,还进而知道了它们为什么能用尺规作图,就因为3和5都是费马素数(3=F0,5=F1);对于很久以来未找到办法来作出的正七边形,乃至于正11边形、正 13边形,现在我们能有把握地说,它们不可能由尺规作图,因为7、11、13都不是费马素数;对于正257边形、正65 537边形,即使我们不知道具体如何作,可是理论上我们已经知道它们是可尺规作图的;此外,为什么正四边形、正六边形可尺规作图呢?因为4=22,因为6= 2· 3而 3=F0.。
圆内接正五边形边长与半径关系

圆内接正五边形边长与半径关系1. 引言:圆里的五边形大家好,今天咱们聊聊一个有趣的话题——圆内接正五边形的边长和半径之间的关系。
哎,别急着打瞌睡,这可是个挺有意思的事儿呢。
想象一下,你在画一个完美的圆,接着在圆里头安置一个正五边形。
你知道吗?这个正五边形的边长和圆的半径之间有着不一般的关系呢。
要是你学过一点点几何,或者对这些数学小秘密感兴趣,那这篇文章肯定会让你觉得有点小惊喜!2. 正五边形的秘密2.1 正五边形的基本特征首先,咱们得了解一下正五边形。
正五边形,那可不是什么普通的五边形,它的五条边都是一样长的,五个角也是一模一样的。
想象一下,一个漂亮的五边形,边边角角都非常对称,不会有一边长一边短,或者一个角大一个角小的尴尬情况。
就像一个小小的完美雕塑,真是太妙了!2.2 内接五边形的妙处当这个正五边形内接在一个圆里,它的每一个顶点都恰好在圆的边上。
这时,五边形的边长和圆的半径之间有个奇妙的关系。
这就像你做蛋糕时,把蛋糕底和边的比例调整得刚刚好一样,这种关系也能让你心中产生一种‘哇,原来如此’的感觉。
3. 边长与半径的关系3.1 数学上的描述现在来点专业的。
要找出正五边形的边长和圆的半径的关系,咱们可以用一个叫做“正五边形内接圆的半径公式”。
如果你对这些公式感到陌生,别担心,公式看起来有点复杂,但只要弄懂了它,真是会让你有一种豁然开朗的感觉。
具体来说,边长和半径之间的关系可以用一个漂亮的三角函数公式来描述:边长等于半径乘以一个叫做“正弦函数”的东西。
3.2 公式的实际应用简单来说,公式是这样:边长等于半径乘以“正弦36度”的值。
‘哇塞’,这听起来是不是有点难以置信?不过,别担心,数学上说得通的东西,咱们现实中也能通过一些计算和图形来验证。
就像你在餐馆里点菜,看菜单上写的各种菜名,实际尝试后才知道哪个味道最好一样,通过这些公式,咱们能搞懂圆内五边形的边长和半径之间的关系。
4. 结尾:数学的趣味总的来说,虽然这话题听起来有点“高深莫测”,但只要咱们好好理解,实际上挺有趣的。
半径为r的内接正五边形边心距

半径为r的内接正五边形边心距半径为r的内接正五边形边心距---------------------------------内接正五边形是几何图形中的一种图形,它的定义是一个由五条相等的直线构成的正多边形,且每条边都与另一条边的中点相连。
内接正五边形由半径为r的圆内接而成,其中心距也就是两个顶点之间的距离,是内接正五边形的一个重要参数。
### 一、内接正五边形定义内接正五边形是一种正多边形,它由五条相等的直线构成,且每条边都与另一条边的中点相连。
这种多边形的特点是,所有的外角均为108°,并且它的面积与半径r成正比。
### 二、内接正五边形的特性内接正五边形具有以下特性:1. 所有的外角均为108°;2. 内角均为36°;3. 内接正五边形面积与半径r成正比;4. 每条边心距均相等;5. 每条对角线的长度均为2r;6. 中心到任意一顶点的距离均为r√10/2。
### 三、内接正五边形的计算公式由于内接正五边形的特性,可以用以下公式来求出其中心距:$$a=\sqrt{5r^2-\frac{5}{4}r^2}=\frac{3}{2}r$$其中,a表示中心距,r表示半径。
通过这个公式可以求出内接正五边形的中心距。
### 四、应用场景内接正五边形由于其特殊的几何特性,广泛应用于各行各业。
例如:1. 内接正五边形常用于木工、家具、建筑装饰、建筑加固、建筑几何布局及其他工业领域;2. 内接正五边形在医学领域也有广泛应用,例如在医学成像中常常用于诊断星形血管病变;3. 在数学教学中,内接正五边形常常作为例子用于说明多边形的特性以及几何几率的应用。
### 五、总结以上就是半径为r的内接正五边形的特性以及相关的应用场景。
通过本文可以了解到,内接正五边形不仅具有独特的几何特性,而且也广泛应用于各行各业。
