流体力学第八章 修改 1讲解
流体力学第八章(Fluid Mechanics)

2nd – Year Fluid Mechanics, Faculty of Engineering and Computing, Curtin University FLUID MECHANICS 230For Second-Year Chemical, Civil and Mechanical EngineeringFLUID MECHANICS LECTURE NOTESCHAPTER 8 FLOW OVER IMMERSED BODY8.1 IntroductionWe have discussed pipe flow in Chapter 6, which is internal flow because the fluid is confined within well-defined boundaries. This chapter deals with external flows, i.e. flows over bodies immersed in the fluid. Typical examples of external flows include the flow of water over a submarine (Figure 8-1a) or a fish (Figure 8-1b), the flow of air over an aircraft (Figure 8-1c).(a)(b) (c)Figure 8-1 Examples; a) submarine; b) fish; c) aircraft;The fluid forces (drag and lift) on the immersed bodies are of important considerations in practice. In this chapter, we will learn the fundamentals of drag and lift, as well as the methods for determining and optimising these forces in engineering applications.8.2 Drag and liftAs shown in Figure 8-2, the forces exerted on the surface of an aerofoil by the fluid include the pressure force (Figure 8-2a) and the viscous force (Figure 8-2b). The results of these forces are the net drag force F D and lift force F L (Figure 8-2c). Taking a small element dA on the aerofoil surface in Figure 8-2c, we can decompose the pressure force (PdA ) and viscous force (dA w τ) into x-direction force dF x and y-direction force dF y , as shown in Figure 8-2d,θτθsin )(cos )(dA PdA dF w x += θτθcos )(sin )(dA PdA dF w y +−=.Integrating dF x and dF y along the surface, we can calculate the drag and lift forces as, dA dA P dF F w x D ∫∫∫+==θτθsin cos (E8-1) ∫∫∫+−==dA dA P dF F w y L θτθcos sin . (E8-2)Equations E8-1 and E8-2 reveals that 1) both shear stress and pressure contribute to the drag and lift. In the case of drag, the former is called friction drag ; the later is called pressure drag ;2) to calculate drag and lift, sufficient knowledge are required on three aspects: the body shape as it determines the distribution of θ; the distribution of pressure P and the distribution of shear stress w τ along the surface.Practically, it is very difficult to obtain the distribution of pressure and shear stress. Therefore, E8-1 and E8-2 are generally not very useful. To make it easy for engineers, dimensionless coefficients are often used instead. These dimensionless numbers are called drag coefficient C D and lift coefficient C L , defined as A V F C D D 22ρ= (E8-3) A V F C L L 22ρ= (E8-4) where A is projected (or frontal) area, i.e. the project area of the body in the flow direction.Figure 8-2 Forces on an aerofoil [1]: a) pressure force; b) viscous force; c). resultant drag andlift; d) pressure and viscous forces on a small surface area dA in (c), plotted in an x-y coordination system.8.3 The boundary layer8.3.1 Hydraulician and hydrodynamicistFor a fundamental understanding on the cause of drag and lift, we must have a good understanding on the boundary layer concept. Let’s start with some historical background on two groups of fluid mechanicians who developed two different approaches in dealing with problems of fluid mechanics by late 19th century.One is the group of hydraulicians, focused on experiments and attempted to generalise useful design equations from experimental data. This group developed the filed of experimental hydraulics, delivering empirical solutions with little theoretical content. The other is the group of hydrodynamicists, who focused on differential equations describing flows and tried to apply them to practical problems. In order to solve these differential equations, the fluid was assumed to have zero viscosity and constant density. This group developed the filed of theoretical hydrodynamics, seeking pure theoretical solutions based on ideal-fluid flows.The ideal-fluid solutions of hydrodynamicists agreed well with the observations of flows did not involve solid surface, e.g. tides, however did not agree with observed behaviours in the problems that concerned the hydraulicians, e.g, flow over immersed bodies. The following are two typical examples.(1) Flow over a thin plateFigure 8-3 illustrates the differences between the ideal solutions by the hydrodynamicists and the experimental observations by the hydraulicians for flow over a thin plate. For an ideal-fluid flow (Figure 8-3a), the fluid is inviscid, there is no friction between the fluid and the surface of the thin plate. Therefore, the fluid will maintain its free stream velocity when it flows over the thin plate. However, for a real-fluid flow, the interaction between the viscous fluid with the surface leads to a velocity gradient near the surface of the plate although the fluid far away from the plate still maintains its free stream velocity.(2) Flow over a circular cylinderFigure 8-5 shows the patterns of ideal and real flow over a circular cylinder. In absence of viscous effects, the wall shear stress is zero therefore the streamlines are symmetrical (see Figure 8-6a). The fluid coasts from the front (point A), pasts the top (point C) and then reaches to the rear (point F) of the cylinder.However, the experimental observations by the hydraulicians are very different from the above analysis by the hydrodynamicists, as shown in Figure 8-4b. A real-fluid flow cannot coast along the cylinder surface down to point F. Instead, flow separation occurs from the surface at a point between point C and F, leading to the formation of turbulent wake in the downstream (see Figure 8-4b). The friction between the viscous fluid and the cylinder surface leads to inevitable energy loss so that the flow does not have sufficient kinetic energy to travel along the surface down to the rear of the cylinder.From the above examples, it seems that the hydrodynamicists calculated what can NOT be observed while the hydraulicians observed what can NOT be calculated [2]. By early 20th century, the hydraulicians and hydrodynamicists had completely gone to live in their own worlds. The hydraulicians continued to solve their problems by trial and error based on experiments while the hydrodynamicists kept publishing academic papers based on mathematics with little bearing on engineering problems.(a) Ideal flow over a thin plate(b) Real flow over a thin plateFigure 8-3 Ideal (a) and real (b) flow over a thin plate(a) Ideal flow a cylinder (b) Real turbulent flow over a cylinderFigure 8-4 Ideal (a) and real (b) flow over a cylinder8.3.2 The boundary layer conceptThe revolutionary thinking was finally due in 1904. The two fields of theoretical hydrodynamics and experimental hydraulics were united by a German professor, Ludwig Prandtl (1857-1953). Prandtl proposed the concept of the boundary layer , which has brought the hydrodynamics and hydraulics together and laid the foundation of modern fluid mechanics.F A CTurbulentwakeThe key concept of the boundary layer is to conceptually divide the flow into two regions: •The boundary layer, the region close to solid surfaces, the effects of viscosity are too large to be ignored. Within the boundary layer, ideal-fluid flow is unsatisfactory and a set of boundary layer equations should be used.•Free stream region, the region outside the boundary layer, the effects of viscosity is small and can be neglected. In this region, Ideal-fluid flow is satisfactory.At the edge of boundary layer, the pressures and velocities of the two regions should be matched. Prandtl arbitrarily suggested the boundary layer be considered that region in which the x component of the velocity, v, is less than 0.99 times of the free-stream velocity, V, as shown in Figure 8-5.Figure 8-5 Thickness of the boundary layerThe introduction of the boundary layer concept is revolutionary in seamlessly uniting the fields of theoretical hydrodynamics and experimental hydraulics. The boundary layer concept is commonly accepted as the foundation of modern fluid mechanics, because it has •clarified numerous unexplained phenomena;•provided a much better intellectual basis for discussing complicated flows;•become a standard idea in minds of fluid mechanicians;•brought analogous ideas in heat and mass transfer, generally with useful results. However, it should be noted that•the division of the flow filed by the boundary layer concept does NOT correspond any physically obvious boundary;•the edge of boundary layer does NOT correspond to any sudden change in the flow but rather corresponds to an arbitrary definition;•even with this simplification the calculation is still difficult, and in general only approximate mathematical solutions are possible.Let’s use the boundary layer concept to explain the patterns of flow over a thin plate and flow over a circular cylinder at various Reynolds’ numbers.(1). Flow over a thin plate (Figure 8-6) [1]At a very low Reynolds number, e.g. Re = 0.1 (Figure 8-6a), the viscous force is more important than the inertial force. The viscous effects are therefore strong and the plate affects the flow considerably in a wide range (see the grey area) in all directions. Consequently, there is an extensively wide range around the plate in which the streamlines deflected considerably. The boundary layer is very thick. Outside the boundary layer is the free stream region where viscous effects are no long important so that the ideal-flow solutions is applicable.At a moderate Reynolds number, e.g. Re = 10 (Figure 8-6b), the region in which the viscous effects are important becomes much smaller. The boundary layer is much thinner. The streamlines over the plate only deflected somewhat.At a large Reynolds number, e.g. Re = 107 (Figure 8-6c), the flow is dominated by inertial force. The viscous effects are negligible anywhere except in a thin boundary layer close to the surface of the plate and the wake region. As the boundary layer is very thin, the flow streamlines are largely unaffected except slightly deflected near and within the boundary layer.Figure 8-6 Patterns of flow over a thin plate [1] at (a) a low Reynolds number; (b) a moderate Reynolds number and (c) a large Reynolds numberFigure 8-7 Patterns of flows over a circular cylinder [1] at (a) a low Reynolds number; (b) a moderate Reynolds number and (c) a large Reynolds number2). Flow over a circular cylinder (Figure 8-7) [1]At a low Reynolds number, e.g. Re = 0.1 (Figure 8-7a), flow past a cylinder is dominated by the viscous force. The viscous effects influence a large portion of the flow field, stretching to several diameters in any direction of the cylinder. However, the flow can still coast along the surface of the cylinder slowly. Such flow is sometime called creeping flow, which has streamlines essentially symmetric about the centre of the cylinder.At a moderate Reynolds number, e.g. Re = 50 (Figure 8-7b), the inertial force becomes more important. The region ahead of the cylinder in which the viscous effects are important becomes much smaller. The viscous effects are convected downstream and the flow loses its symmetry. The flow inertia dominates so that it does not coast along the surface down to the rear of the body, resulting in the formation of flow separation bubbles behind the cylinder.At a large Reynolds number, e.g. Re = 105 (Figure 8-6c), the flow is dominated by the inertialforce. The region affected by the viscous forces is forced further downstream, leading to theformation of a very thin boundary layer on the front portion of the cylinder. The boundary lay can be laminar or turbulent, depending on Reynolds number. Due to the strong inertia force, the boundary layer separation occurs from the cylinder, leading to the formation of a turbulent wake region extending far downstream. In the free stream region outside the boundary layer and the wake region, the velocity gradient is zero and the fluid flows as if it were inviscid.8.4 Drag force and streamlined bodies8.4.1 Drag forceIn 1710, Isaac Newton (cited in [2]) dropped hollow spheres from the inside of the dome of St Paul’s Cathedral in London and measured their rate of fall. He calculated that the drag force F D on a sphere and concluded that the following equation holds 242222V D V A F D ρπρ== where A is called projected (or frontal) area – the projected area seen by a person lookingtoward the object from a direction parallel to the upstream (see Figure 8-8).Figure 8-8 Drag force on a free-fall sphereIn other words, Isaac Newton thought that 122=V A F D ρ. However, subsequent experimental investigations by many other researchers found that the above formula must be modified by a coefficient C D in the right-hand side, i.e. D D C V A F =22ρ This is essentially same as the definition of drag coefficient C D in E8-3. Normally, drag coefficient C D is not 1. We can calculate the drag force of the flow on an immersed body as (E8-5)Therefore, when calculate drag force using E8-5, we have accumulated the effects of all rest factors into a single coefficient, C D , i.e. drag coefficient. One can see that the drag coefficient C D in E8-5 plays a similar role of the friction factor f in E6-22. The key difference between E8-5 and E6-22 is that in the case of pipe flow, the geometry of pipes (with different length and diameter) varies while all spheres have the same shape.8.4.2 Drag coefficient chartAccording to E8-1 and the discussion in Section 8-2, the drag coefficient of an object will be a function of Reynolds number, the shape and the surface properties of the object. We haverties)face_prope ,shape,sur Φ(C D Re = (E8-6)Practically, finding the exact function of E8-6 is extremely difficult, if not impossible. Therefore, for engineering applications, what we need is a drag coefficient chart, similar to Moody chart used for determining friction factor in pipe flows. Figure 8-9 shows the dragcoefficient as a function of Reynolds number for a smooth sphere and a smooth cylinder.Figure 8-9 Drag coefficient of a smooth sphere and a smooth circular cylinder [1].EX8-1: An exampleWe caught two breams in two consecutive casts. If we pulled the strings at the same speed, explain why we felt it was much harder to pull the big bream?Solutions:Figure 8-10The projected area of the big bream, A bf , is a much bigger than that of the small bream A sf . As both fishes are bream, we can reasonable assume that the two fishes have similar shape and surface characteristics. As both fishes were caught in consecutive casts in the same water area and we pulled the string at the same speed V , the water flows over the two fishes have same Reynolds numbers. Therefore, the drag coefficients can be taken as same. According to E8-5, the water would have induced much higher drag force on the big bream when we pulled the string.8.4.3 Pressure dragEquation E8-1 in Section 8.2 clearly shows that the drag consists of two components, friction drag and pressure drag. For flow over an immersed circular cylinder, as shown in Figure 8-7c, the fluid friction within the boundary layer certainly leads to the friction drag. In this section, let’s have a detailed analysis on the cause of pressure drag.Let’s start with inviscid flows, as shown in Figure 8-11. In absence of viscosity, the flow will coast along the cylinder surface and the streamlines are symmetrical. Based on theoretical hydrodynamics (further details can be found in Chapter 6 of Reference [1]), the distribution of pressure and velocity along the surface of the cylinder are )sin 41(21220θρ−+=V P P (E8-7) θsin 2V V fs = (E8-8) which are plotted in Figures 8-11b and 8-11c.Figure 8-11c indicates that for an ideal fluid (0=μ and ρ is constant), the fluid velocity along the surface varies from 0=fs V at the very front and rear (stagnation point A and F) of the cylinder to the maximum of V V fs 2= at the bop (point C) and bottom of the cylinder.Figure 8-11 Ideal flow over a circular cylinder [1] (a) streamlines for the ideal flow; (b) pressure distribution of the ideal flow; (c) fluid velocity distribution on the cylinder surfaceFigure 8-12 Real flow over a circular cylinder [1] (a) boundary layer separation; (b)distribution of pressure coefficient.Similarly, as shown in Figure 8-11b, the pressure distribution is also symmetrical about thevertical midplane of the cylinder, varying from a minimum of 2023V P ρ−at the top orbottom of the cylinder to a maximum of 2021V P ρ+. The decrease in pressure in thedirection of flow along the front half of the cylinder is termed as favourable pressure gradientwhile the increase in pressure in the direction of flow along the rear half of the cylinder istermed adverse pressure gradient . In absence of viscous effects, the fluid travelling from thefront to the back of the cylinder coasts down the “pressure hill” (see Figure 8-5b) from°=0θat point A to °=90θat point C and then back up to the hill to °=180θ(from point C topoint F ). Therefore, there is only energy exchange between kinetic energy and pressureenergy without any energy loss.However, the experimental observations are very different from the above theoreticalanalysis, as shown in Figure 8-12. At a large Reynolds number, the flow forms the boundarylayer on the surface of the cylinder and cannot coast along the cylinder surface down to therear stagnation point F. The boundary layer separation occurs at point D on the rear surface, (a)(b)leading to the formation of turbulent wakes in the downstream (see Figure 8-12a). The separation of the boundary layer can be explained by the pressure distribution in Figure 12b. Due to the friction between the viscous fluid and the cylinder surface, energy loss is inevitable so that after pass through point C, the fluid does not have enough kinetic energy to climb the pressure hill up to point F which sits on the top of pressure hill therefore the boundary layer separates at point D in Figure 12a.Figure 8-12b also indicates that the location of separation therefore the width of the turbulent wake and the pressure distribution on the surface depend on the nature of the boundary layer. Compared with a laminar boundary layer, a turbulent boundary layer has more kinetic energy and momentum so that it can flow further around the cylinder, resulting in a narrower wake, less drag, corresponding to a decrease in drag coefficient from point D to E in Figure 8-10. Because of the boundary layer separation, the average pressure on the front half of the cylinder is significantly greater than that on the rear half. This leads to the development of a large pressure drag. Under turbulent conditions, the friction drag is insignificant compared with the pressure drag, as discussed blow.Figure 8-13 Two objects of significant different size that have the same drag force [1]: (a) a circular cylinder - a blunt body, C D = 1.2; (b) a streamlined strut C D = 0.12.Table 8-1 Drag coefficients of various bodies8.4.4 Streamlined bodiesIt is clear now that the drag force developed on an object immersed in turbulent fluid isdominantly pressure drag as a result of boundary layer separation. Therefore, we can optimisethe body shape of the object to minimise the boundary layer separation hence reduce pressuredrag. This requires us to design streamlined bodies .Figure 8-13 shows the significance of body streamlining. The streamlined strut has a sizemuch bigger than the circular cylinder. However, the two bodies have the same drag forces.The boundary layer separation on the streamlined strut has been postponed to the tail of thebody so that pressure drag is minimised compared with that on a circular cylinder, which is ablunt body. It is interesting to revisit the shapes of submarine, fish and aerofoil in Figures 8-1and 8-2, we would appreciate that these bodies are actually all streamlined.8.4.5 Drag coefficient for various objectsThe drag coefficient information for a wide range of objects is available in the literature [1,2].Some of this information is listed in Table 8-1.8.4.6 Drag coefficient at low Reynolds number (Re < 1)At Re < 1, the flow over an immersed body is called creeping flow , dominated by viscouseffects. The drag coefficient gives the 1/Re dependence. Table 8-2 shows the drag coefficientsfor various bodies at Re < 1.Table 8-2 Drag coefficient of various bodies at Re < 1, from Reference [1]8.6 Terminal velocityIf an object in a body of fluid is free to move subject only to gravity, or perhaps centrifugalforces in certain circumstances, then it accelerates to a particular velocity at which the tractiondeveloped and the other forces on the body balance. This velocity is called terminal velocity .Generally, the acceleration is very rapid so that the whole process can be treated as the objecttravelling at the terminal velocity.Figure 8-14a illustrates the concept of terminal velocity of a sphere settling in a fluid. Figure8-14b shows the force analysis of the sphere. When the sphere travels at the terminal velocityV t , the force is balanced. V V V V Re4.20Re6.13Re0.24Re2.22Therefore, as shown in Figure 8-14b, the gravity force F W , drag force F D and buoyancy forceF B are in balance,B D W F F F += (E8-9)We know thatobject object W gV F ρ= (E8-10)object fluid B gV F ρ= (E8-11) projected t fluid D D A V C F 22ρ= (E8-12) where6)2(3433D D V object ππ== (E8-13)42D A projected π=. (E8-14)Assuming Re < 1, for a sphere (see Table 8-2), the drag coefficient is DV C t fluid fluid D ρμ24Re 24==. (E8-15)Substituting E8-15 into E8-12, we have t fluid t fluid t fluid fluid projected t fluid D D DV D V D V A V C F πμπρρμρ342242222===. (E8-16)This is the famous Stock’s law, which is only valid when Re < 1.(a) Concept of terminal velocity (b) Force analysisFigure 8-14 Terminal velocity of a sphereSubstituting E8-11, E8-13 and E8-16 into E8-9, we have fluidfluid object t gD V μρρ18)(2−= (E8-17)Equation E8-17 is not generally given for calculations so that if not available we are requiredto go through the force analysis for its derivation.Once we have calculated the terminal velocity, one final critical step is to double check Re toensure that 0.1Re <=fluid t fluid D V μρ (E8-18)so that our assumption leading to E8-16 is indeed valid.Solutions:We can use a free-body diagram of a mineral particle, as shown in Figure 8-14b. The mineralparticle moves downward with a constant velocity V t (relative to the moving air flow)that isgoverned by a balance between weight of particle, F W , the buoyancy force of the surroundingair, F B , and the drag of air on the particle, F D . Please Note: it is acceptable that thebuoyancy force of the surrounding air, F B , is neglected.(a) We haveB D W F F F += (E8-19)63p p p p W D g gV F πρρ== (E8-20) 63p air p air B D g gV F πρρ== (E8-21)Assuming Re <1, we have the drag coefficient of an mineral particle pt air air D D V C ρμ24Re 24== (E8-22) Therefore the drag force p t air pt air air p t air D p t air D D V D V D V C D V F πμρμπρπρ3244214212222=== (E8-23) Substitute E8-20, E8-21 and E8-23 into E8-19, we have p air p air p p UD D g D g πμπρπρ36633+= Therefore, the terminal velocity of a mineral particle relative to the flowing air is air p air p t gD V μρρ18)(2−= or airp p t gD V μρ182= if buoyancy is neglected,Therefore, we haves m m Ns m s m m kg m kg gD V air p air p t /029.0)/1079.1(18)1020(/8.9)/29.1/2400(18)(25262332=×××××−=−=−−μρρCheck Reynolds number 0.10418.0/1079.11020/029.0/29.1Re 2563<<=××××==−−m Ns m s m m kg D V air p t air μρ Therefore, the assumption to use E8-22 is valid.(b) We can calculate the air travelling velocity in the vertical tube s m m s L m L D Q A Q V tube air /017.0)05.0(14.3)60min 110001min 0.2(44232=××××===π Therefore, the residence time of a mineral particle in the vertical tube is 3.16/)017.0029.0(75.0=+=+=sm m V V L t air t sReferences[1]. Munson BR, Young DF and Okiishi TH, Fundamentals of Fluid Mechanics, 4th Edition,John Wiley & Sons, Brisbane, 2002.[2]. Noel de Nevers, Fluid Mechanics for Chemical Engineers, 3rd Edition, McGraw-Hill’sChemical Engineering Series, Sydney 2005.。
流体力学第八章-39页PPT精品文档

§ 8.3 理想流体的运动微分方程
二、兰姆运动微分方程式(续)
兰姆运动微 分方程式
vtx
fz
1
p z
v2 ()
z 2
x
(
pF
v2 2
)
2(vz y
vy z
)
y
(
pF
v2 2
)
2(vx z
fy
p
f
z
(x,
fx y,
z)
y
o
x
z
§8.3 理想流体的运动微分方程
一、欧拉运动微分方程式(续)
x轴方向的受力
左面中心受力: (pp dx)dydz
x 2
右面中心受力: (pp dx)dydz
x 2
质量力:
fx
p p dx x 2
fy p
fz fx
p p dx x 2
不可压缩流体的定 常或非定常流动:
vvxvyvz 0 x y z
§8.1 微分形式的连续方程
二、其它形式的连续方程(续)
二维可压缩流体 的定常流动:
x(vx)y(vy)0
二维不可压缩流 体的定常或非定 常流动:
vx vy 0 x y
§8.2 流体微团运动的分解 有旋流动和无旋流动
2 z x
v M y v y v y yy 1 2 ( v y z v z y )z 1 2 ( v x y v y x )x 1 2 ( v y z v z y )z 1 2 ( v x y v y x )x
流体力学第8章中文版课件

Chapter 8: External flows
14
8.3 绕淹没体的流动
分离前的湍流边 界层 分离前的层流 边界层
2013-11-25
Chapter 8: External flows
15
8.3 绕淹没体的流动
2013-11-25
Chapter 8: External flows
16
8.3 绕淹没体的流动
W FD
sphere volume CD V 2 A
4 3 1 S water R CD V 2R 2 3 2
1 2
8RS water V 3C D
2013-11-25
1/ 2
8 0.15 1.02 9800 3 1.20 CD
Re
VD
129 0.3 2.42 10 6 1.6 10 5
V 129 m/s
2013-11-25 Chapter 8: External flows 20
8.3 绕淹没体的流动
求解:(b) 对于球在水中的下落情况,则必须考虑施加在球体上的与阻力FD 同方向的浮力 B 的作用:
如果物体形状上有一 个突然的变化,分离 点将出现在形状突然 变化点或其附近。 另外,分离后流 体在某一个位臵 上又会重新附着 在物体上。
2013-11-25
Chapter 8: External flows
10
8.2 分离
在分离点的上游,壁面附 在分离点的下游,壁面附 近的 x方向上的速度分量 近的 x方向上的速度分量在 负 x 方向,因此在正 x 方向,因此 壁面上 壁面上的 的 u/y一定是负的。 u/y是正的。
《流体力学》第八章绕流运动

2
x2
2
y2
2
z2
0
满足拉普拉斯方程的函数称为调和函数。
不可压缩流体势流的速度势函数,是坐标
x,y,z的调和函数。
拉普拉斯方程本身,是不可压缩流体无旋流
动的连续性方程。 H
6
第二节 平面无旋流动
在流场中,某一方向(取作Z轴方向)流速为零,而另两方向的流速与上 述轴向坐标Z无关的流动,称为平面流动。
H
13
第三节 几种简单的平面无旋流动
均匀直线流、源流、汇流、环流 四种简单的平面无旋流动。
¦¨
¦¨
¦¨
H
14
运
速度分量
动
类 别
ux (ur )
uy (u )
均 匀 直 ux a 线 流
uy b
简单平面无旋流动的 与 函数
流函数
势函数
(x,y)
(r,θ)
(x,y)
(r,θ)
ay bx
r(asin bcos )
H
20
管流附面层:附面层的概念对于管流同 样有效。
附面层
¦δΔ ¦δΔ
xE 附面层
入口段的流体运动情况不同于正常的层流
或紊流,在实验室内进行管路阻力试验时,
需避开入口段的影响H 。
21
第十节 曲面附面层的分离现象 和卡门涡街
当流体绕曲面体流动时,沿
附面层外边界上的速度和压
强都不是常数。
u
u P 0
1
第一节 无旋流动
流动场中各点的旋 转角速度等于零的运 动称为无旋流动。在 无旋流动中:
x
1(uz 2 y
uy z
)0
y
1(ux 2 z
流体力学第八章(湍流)

根据定义,平均化运算满足以下法则:
(a)A A A A
(b)A A 平均值再求平均仍然为平均值;
(c) A 0 脉动值求平均为零;
(d)A B (A A)(B B) AB AB AB AB A B AB
(e)A B A B
(
f
)
A t
A t
A s
A s
与流体脉动状态有关。
可见,雷诺应力的实质是湍流脉动所引起的单位时间单 位面积上的动量的统计平均值,也就是脉动运动产生的 附加力。
本章小结
①湍流的基本概念(特征),湍流的判据:临界雷诺数; ②处理湍流运动的平均化方法; ③雷诺应力的理解;
为了平均化运算的方便,进行适当变换,可得:
u (uu) (uv) (uw) 1 p 2u u( u v w )
t x y
z
x
x y z
u (uu) (uv) (uw) 1 p 2u
t x y
z
x
将任意物理量表示为: A A A
速度分量为:
u u u;v v v; w w w; p p p
t x y z x y z
x
将上式展开,利用平均化的连续方程,进行简化,可 以得到:
u u u v u w u 1 p 2 u uu uv uw
t x y z x
x y z
u(u v w ) 0 x y z
这就是 x 方向的平均运动方程(雷诺方程)
同理,可以得到 y ,z 方向的平均运动方程,最终得到形式如
(g) Ads Ads
第二节 湍流平均运动方程和雷诺应力
流体运动: 湍流运动 = 平均运动+脉动运动
湍流运动同样满足连续方程及纳维斯托克斯方程,但由 于湍流运动随时间、空间的剧变性(脉动性),考虑细 致的其真实的运动几乎是不可能的,也是没有意义的。
流体力学课件第8章明渠流动

四、水力计算基本问题
主要可归为四大类
1、验算渠道的输水能力。
已知: b, h, m, n, i
以梯形断面 为例分析
求: Q 验算 v 是否
方法: Q Av Ac Ri K i
合乎要求。
2、计算渠道的粗糙系数。
1.天然河道的横断面 呈不规则形状,分主槽和滩地 枯水期:水流过主槽 丰水期:水流过主槽和滩地
主槽
滩地
2、据渠道过流断面的形状、尺寸是否沿程改变:
(1) 棱柱形渠道 A = f (h) ;
A过流断面面积,h水深 (2)非棱柱形渠道 A = f (h,s) s流程
三、明渠的分类
按断面形状、尺寸是否沿程变化分 棱柱体明渠、非棱柱体明渠
2> 设计渠道时,不但应遵从基本公式,还应考虑水 力最优,但由此设计的渠道却不一定是最经济。
断面面积一定时,流量最大为最佳。 流量一定时,断面面积最小为最佳;
(1)最优断面推导——曼宁公式
Q A R1/6 n
Ri 1 A5/3i1/2
n 2/3
思考:相同面积哪种图形周长最小?
当 n、i、A 一定时, 最小,可使 Q 最大,从理论上分
湿周: d 2
水力半径:
R d 1 sin 4
d
h θ
(1) 当а=1 时, 为满管流动;
(2) 当а< 1 时,为不满管流动。在污水管路 设计中,为通风、防暴及适应污水量的变 化,一般均应设计为不满流。
二、水力特征:
Q AC Ri K i
(1) J= Jp= i ;
(2)水力最优发生在满管之前
流体力学A 8-1

(如图8-1所示)
第八章 不可压缩流体二维边界层
13
§8.1 边界层的基本概念
势流区计算时,假定边界层不存在, 全部流场为势流区,用势流理论来计算绕 流物体表面的速度,并用势流的伯努利方 程求解相应的压强。 边界层计算时,把上述按势流理论求 得的物面速度和压强分布看作为边界层外 边界处的速度和压强,而边界层内边界就 是物体的壁面,在壁面处流速为零,压强 则等于边界层外边界处的压强。
第八章 不可压缩流体二维边界层
14
§8.1 边界层的基本概念
6. 除绕流物体壁面 附近存在边界层 外,工程上还常 常遇到一种管流 边界层。 1) 流体从大容器流入管道,由于粘性在近 壁处形成边界,且厚度沿流动方向增大, 即向管轴扩展。
第八章 不可压缩流体二维边界层
15
§8.1 边界层的基本概念
2)直至在离入口距离为L的c-c断面上,边 界层基本扩展至管轴,距离L称为管道的 起始段长度, c-c断面以后则为充分发 展的管流。 3)当起始段边界层为层流时,起始段长度L 较长,约为L/d=0.058Re。起始段内,除 摩察损失外,还有由于流体动能变化而导 致的附加损失。若附加损失为kv2/2 ,则 起始段内总压强损失为
26
第八章 不可压缩流体二维边界层
§8.2 不可压层流边界层方程
① v 同理 x 1, y x 1,
2 2 v v v v 1 1 x x x x 1, 1, , 2 2 2 x x y y
② v y
(8-5)
4)普朗特边界层方程还可写为
vx vx dU e 2 vx vx vy Ue x y dx y 2
vx v y 0 x y
流体力学习题讲解(修)PPT课件

p1 Hg gh gh1
则
p1
g
Hg
d 2 0.0352
4
4
列等压面1—1的平衡方程
p 油 gh Hg gh
解得Δh为: h p 油 h 15590 0.92 0.70 16.4
Hg g Hg 13600 9.806 13.6
2019/10/28
10
2019/10/28
2019/10/28
13
2019/10/28
14
1-11.如 图 所 示 盛 水U 形 管, 静 止 时, 两 支 管 水 面 距 离 管 口 均 为h, 当U 形 管 绕OZ 轴 以 等 角 速 度ω 旋 转 时, 求 保 持 液 体 不 溢 出 管 口 的 最 大 角 速 度ωmax 。
解:由 液 体 质 量 守 恒 知, 管 液 体 上 升 高 度 与 管 液 体 下 降 高 度 应 相 等,且 两 h 者 液 面 同 在 一 等 压 面 上, 满 足 等 压 面 方
5.59 m s
21
排出水的流量:
q
v
4
D2
v3
4
D2
v
v3
4
D2
5.59 4.43 0.052 0.02 m3 s
4
22
3-2:注 液 瓶 为 了 使 下 部 管 口 的 出 流 量 不 随 时 间 而 变, 在 上 部 瓶 塞 中 插 人 通 气 管, 试 分 析 出 流 量 恒 定 的 原 理 和 调 节。
h hD
hc
JC hc A
流体力学讲义8-2

2 v r v 2 vr vz v 2 2 t r r z r r r r v r v 1 p
t vr v z r v v z r
D 2
v
v v
v
v z
2
c1
v
1
dP
4 dz
r
2
c 1 ln r c 2
根据该问题的物理特性,在管道中的流动速度应处处有界,所以必有: c 1 0 。
0 ,得: 2 c
由管壁边界条件, v
1 dP 4 dz
r
D 2
R
R 。
2
dP dz
P1 P 2
,
L
速度场的解为:
v r
84不可压缩牛顿流体的解析解二两平行平板间流动的速度场1物理问题及简化水平放置的两块无限大平行平板间充满了不可压缩牛顿流体不计质量力平板间的距离为2h如图已知上板以等速度u求平板间速度分布及应力分布平面couette流动示意图84不可压缩牛顿流体的解析解1物理问题及简化流动的几何边界是平行平面流动方向平行于x轴用直角坐标描述该流场最合适
力 矩:因为内柱面上的切应力和旋转方向相反,所以为阻力矩,其大小等于
M
z
0 r
2
r R1
R d
2 1
4 R 1 R 2
2
2
R
2 2
R
2 1
上式也可用作测量流体粘度的公式,只要测定内圆柱上流体作用力矩和转速以及内 外圆柱的半径,就可由该式计算流体动力粘度系数。 压强分布: 可将速度分布公式代入径向动量方程积分求出, 说 明: 压强的定解条件是必须给定流场一点的压强。
许贤良_陈庆光等编著《流体力学》课后详解
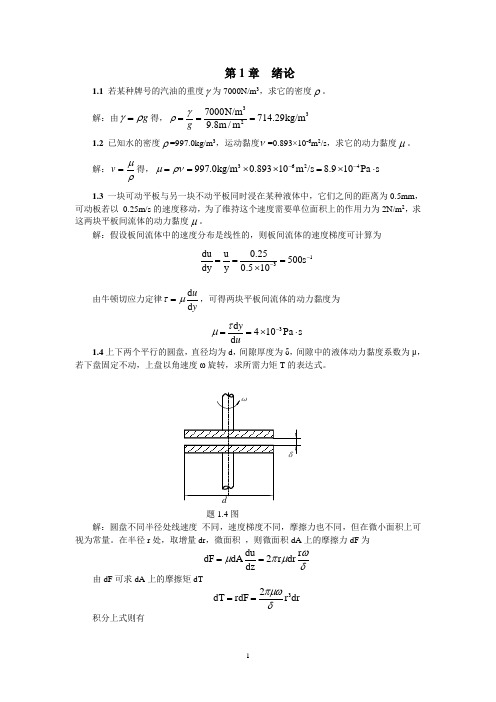
第1章 绪论1.1 若某种牌号的汽油的重度γ为7000N/m 3,求它的密度ρ。
解:由g γρ=得,3327000N/m 714.29kg/m9.8m /m γρ===g1.2 已知水的密度ρ=997.0kg/m 3,运动黏度ν=0.893×10-6m 2/s ,求它的动力黏度μ。
解:ρμ=v 得,3624997.0kg/m 0.89310m /s 8.910Pa s μρν--==⨯⨯=⨯⋅ 1.3 一块可动平板与另一块不动平板同时浸在某种液体中,它们之间的距离为0.5mm ,可动板若以 0.25m/s 的速度移动,为了维持这个速度需要单位面积上的作用力为2N/m 2,求这两块平板间流体的动力黏度μ。
解:假设板间流体中的速度分布是线性的,则板间流体的速度梯度可计算为13du u 0.25500s dy y 0.510--===⨯ 由牛顿切应力定律d d uyτμ=,可得两块平板间流体的动力黏度为 3d 410Pa s d yuτμ-==⨯⋅1.4上下两个平行的圆盘,直径均为d ,间隙厚度为δ,间隙中的液体动力黏度系数为μ,若下盘固定不动,上盘以角速度ω旋转,求所需力矩T 的表达式。
题1.4图解:圆盘不同半径处线速度 不同,速度梯度不同,摩擦力也不同,但在微小面积上可视为常量。
在半径r 处,取增量dr ,微面积 ,则微面积dA 上的摩擦力dF 为du r dF dA2r dr dz ωμπμδ== 由dF 可求dA 上的摩擦矩dT32dT rdF r dr πμωδ==积分上式则有d 43202d T dT r dr 32πμωπμωδδ===⎰⎰1.5 如下图所示,水流在平板上运动,靠近板壁附近的流速呈抛物线形分布,E 点为抛物线端点,E 点处0d d =y u ,水的运动黏度ν=1.0×10-6m 2/s ,试求y =0,2,4cm 处的切应力。
(提示:先设流速分布C By Ay u ++=2,利用给定的条件确定待定常数A 、B 、C )题1.5图解:以D 点为原点建立坐标系,设流速分布C By Ay u ++=2,由已知条件得C=0,A=-625,B=50则2u 625y 50y =-+ 由切应力公式du dy τμ=得du(1250y 50)dyτμρν==-+ y=0cm 时,221510N/m τ-=⨯;y=2cm 时,222 2.510N/m τ-=⨯;y=4cm 时,30τ= 1.6 某流体在圆筒形容器中。
流体力学第八章

习题8-5:解N-S方程求平板间的速度分布
由流动的特性 u 0, w 0, 0, f g
z
t
充分发展流动 二u 维,0、由定连常续性方程 x
v0
u t
u
u x
vu仅uy 是wyuz的函fx数
1
p x
(
2u x2
2u y 2
2u z 2
)
v t
u
v x
v
v y
w v z
fy
1
p y
(
2v x2
y
δ*
物理意义——边界
δ* * x
层流体的动量损失
U 2 ** Uudy u2dy
0
0
8.4 层流边界层流动的基本方程
二、边界层方程
1. 边界层的基本特征
(1) L
y
(2) u u y x
0
L
x
(3)边界层厚度沿着流动方向增加
(4)边界层内粘性力与惯性力同数量级
8.4 层流边界层流动的基本方程
y
0 1
L
外部势流
U
边界层流
x
L u v U ~ v ~ v x y L L U
例:水,L=0.5m,U=0.2m/s,Re=1105,~3mm
8.4 层流边界层流动的基本方程 2. 边界层微分方程 二元不可压缩定常流动边界层方程(不计质量力)
u v 0 x y
u
u x
2. 边界层厚度
y 圆管流与边界外层部流势速流度剖面相似 U
— u=0.99U
x
0
流态判断准则—雷诺数
Re x
Ux
Re
U
Re的物理意义: 惯性力/粘性力 & 流态判断准则
流体力学 第8章
b 2h 1 m
R A
2
(8-5)
水力半径
8.2 明渠均匀流
8.2.3 明渠均匀流的基本公式
均匀流动水头损失计算公式——谢才公式
v C RJ
上式为均匀流的通用公式,既适用于有压管道均匀流, 也适用于明渠均匀流。 对明渠均匀流有 流量
v C Ri
Q Av AC Ri K i
(bhc )3 b 2 hc3 g b
得
hc 3
Q 2
gb
2
3
q 2
g
(8 - 22)
Q 式中,q 称为单宽流量。 b
8.4 明渠流动状态
临界流时的流速是临界流速(vc),由式(8-21)得
Ac vc g Bc
上式与微波速度式相同。
将渠道中的水深 h与临界水深hc相比较,同样可以判 别明渠水流的流动状态,即
8.1 概
述
1 2 i sin l
通常以水平距离lx代替流程长度l,以铅垂断面作为过 流断面,以铅垂深度h作为过流断面的水深,则
1 2 i tan lx
8.1 概
底坡的分类
述
正坡或顺坡:
底线高程沿程降低,i>0
平底坡: 底线高程沿程不变,i=0 反底坡或逆坡:
下游:h → hc < h0,J> i, i-J<0;h→ hc ,Fr
dh 2 →1,1-Fr →0,所以 ds ,水面线与C-C线正交,水
8.6.2 水面曲线分析 实际水深等于正常水深 h=h0时,J=i,分子i-J=0; 实际水深等于临界水深 h=hc时,Fr=1,分母 1-Fr2=0; 分析水面曲线的变化,需 借助h0线(N-N线)和hc线(CC线)将流动空间分区进行。
力学_张汉壮_第八章流体

返回主目录
上一页
下一页
动流体内任意一点的压强
如图 8.2.2-1 所示。对所选取的小三棱体应用牛顿第二定律:
x 方向: Px Sx P S sin max y 方向: Py S y P S cos mg may
1 m [( x y ) z ] , S x 2
3. 帕斯卡原理:对密闭流体,表面所加压强能按它的大小 传递到各处及器壁上。
返回主目录 上一页 下一页
例 8.1.3-1 如例 8.1.3-1 图所示, 一半径为 r 的圆 球悬浮于两种液体的交界面上, 两种液体的密度分 别为 1 和 2 。位于交界面上方的球冠的高度 d 3 r , 液面与交界面的高度差为 h 。求, (1)圆球的质量 M ; (2)试问密度为 1 的液体对圆球的作用力是什么 方向? (3)试不用积分的方法分别求出两种液体对圆球 的作用力 F1 和 F2 。
1
和 F2 ,即,与作用在小球上的压力的合力相同。 上一页 下一页 返回主目录
设小球与两种流体的交界面面积为 S , 则, 在液体 1 和 2 中球 冠的体积分别为:
1 V1 d (3 2 d 2 ) 6 4 1 V2 V V1 r 3 d (3 2 d 2 ) 3 6
动流体描述
动流体内任一压强 理想流体稳定流动 连续性方程
伯努利方程
返回主目录
上一页
下一页
动流体的描述
1. 动流体的描述方法:
将流体分成许多有相互作用的流体元, 并追踪各个流体元, 建立动力学方程, 确定它们各个时刻在空间的位置、速度、加速度,描述流体的这一方法称为 拉格朗日方法。另外一种描述流体的方法称为欧拉法,即,把注意力集中在 空间各点,观察各个流体元流经这些空间点附近时的流动速度和加速度,而 不去判别某一瞬时占据各空间点的是哪些流体元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
?
dT T
?
(k ? 1)M 2 1? M 2
dA A
气流速度与流道断面面积的关系
dA ? (M 2 ? 1) dV
A
V
dp kM 2 dA p ? 1? M 2 A
d? ?
?
M2 1? M 2
p V2 e? ? ? C
?2
V2
V2
?
h?
?C ? 2
CPT ?
2
?C
(4)状态方程
p ? RT
?
§8-3 一维定常流动基本方程
二、一维等熵定常流动基本方程 等熵:可逆绝热过程
?VA ? m ? 常数
1 VdV ? dp ? 0 ?
?
h?
V2 2
?
CPT
?
V2 2
?
常数
(运动方程与能量方程等价)
?广义的理解, 声速是指在可压缩介质中,微弱扰
动的传播速度。
音速计算公式:
绝对坐标系 非定常运动
相对坐标系 定常运动
定常流动连续性方程:
? aA ? (? ? d? )(a ? dv)A ? dv ? a d ?
?
X方向的动量方程:
pA ? ( p ? dp) A
? ? aA[(a ? dv) ? a] ? dp ? ? adv
两方程联立得: a ? dp
d?
小扰动的传播为绝热过程
p
?k
? cokRT
d?
?
音速计算公式: a ? kRT
相对坐标系 定常运动
结论:
a ? dp
d?
a ? kRT
(1)流体中的声速是状态参数的函数 。同一种流体, 温度越高,传播速度越快
(2)声速在一定程度上反映了流体压缩性的大小。 越难压缩的流体传播的速度越快
VdV ? 1 dp ? 0 ?
VdV ? 1 dp ? 0 ?
?u ? u ?u ? v ?u ? ?
?u ?
X?
1 ?p
?
V dV ?
1 dp ? 0 ?
VdV ? 1 dp ? 0
?t ?x ?y ?z
? ?x dx ? dx
?
(3)能量方程
z?
p
V2 ?
?C
? g 2g
p V2 ? ?C
?2
在高速气体的流动过程中,不可逆是因气体的粘性摩擦、 激波的出现以及因温度梯度存在而引起的热传导。
对等熵过程的状态方程为:
p
?K
?
const
.
§5-1 音 速
一、音速(Sonic Velocity)
音速:小(弱)扰动在介质中的传播速度。
?狭义的理解,音速是声音的传播速度,但人耳所能
听到的声音频率范围 约为每秒 20~20000次,是有 限的。
超音速运动的飞行器,激波的出现会引起很大的阻力;在 超音速风洞、进气道和压气机等内流设备,在气流由超音 速变为亚音速出现的激波,会降低风洞和发动机的效率。
§8-3 一维定常流动基本方程
一维、理想、定常、不计重力
不可压缩
可压缩
(1)连续性方程 VA ? Q ? 常数
?VA ? m ? 常数
(2)运动方程
!!气流扰动
M>1,V ? a
扰动只影响马赫锥内流场
不能向上游传 播
马赫锥
马赫角:
sin? ? a ? 1 VM
§5-2 激波
超音速运动的子弹
M1 ? 1
M2 ? 1
p ?,? ?,T ?, V ?
相对坐标系
超音速气流绕物体流动时,在流场中往往出现突跃 的压缩波。气流通过这种压缩波时,压强、密度、温度都 突跃的升高,速度则突跃的下降,这种突跃的压缩波就是 激波。激波是一种强扰动波
状态方程
p ? RT
?
p
?k
?
const.
完全气体 等熵过程
2 两种特定状态参数
滞止状态参数:流动速度为零时的状态参数
? 0 , p0 ,T0 , h0 , a0
滞止状态断面与任意断面的能量方程:
h?
V2 2
?
h0
?
V0 2 2
?
h0
?
C pT0
再联立 a ? kRT
K
CP
?
K
R ?1
M ?V a
0
高压储气罐
p ? RT
?
p
? k ? const.
T0 ? 1 ? k ? 1 M 2
T
2
p0
?
(T )0
k k?1
?
(1?
k
?
1
M
2
k
) k?1
pT
2
?0
?
(T )0
1 k?1
?
(1?
k
?
1
M
2
1
) k?1
?T
2
p0, ?0,T0
V0 ? 0
2
2 0 p ,?,T
二、临界参数:M=1断面上的参数
(3)声速与介质的性质有关。
二、马赫数、马赫波
1 马赫数:流体的流速与音速之比,即
M?V a
气体流动分类:M ? 1 为亚音速流 M =1 为音速流 M ? 1 为超音速流
2 扰动在气流中传播性质:
M=0,V = 0 扰动将传遍全流场 M<1 ,V ? a 扰动将传遍全流场
M=1,V =a 扰动只影响下半流场
? ?, p?,T ?,h?,a?
当M=1,则有:
T0 T*
? 1?
k?1M 2 2
?
k?1 2
p0 p?
?
(
T0 T?
)
k k ?1
?
k?1 k
(
) k?1
2
?0 ??
?
(
T0 T?
1
) k?1
?
k?1 1
(
) k?1
2
对于空气k=1.4,则
T* ? 0.833T0 p? ? 0.528 p0
M ?1
第八章 可压缩气体动力学基础
一、音速 二、激波 三、一维定常气流的基本方程 四、气体在变截面喷管中的流动 五、收缩喷管和缩放喷管
预备知识:运动热力学 基本知识
1 气体的状态方程,完全气体
完全气体的状态方程: p ? RT
?
定压比热
K
CP
?
K
R ?1
定容比热 ,
CV
?
1R K ?1
比热比 K ? C P
CV
空气 K ? 1.4
2 单位质量气体的焓(enthalpy ) h h=e+p/? (内能+压力能)
e ? CVT
K
h?
CPT
?
K
RT ?1
预备知识:运动热力学 基本知识 3 熵s:entropy ds ? dq ? 0
T
ds ? 0 绝热可逆过程——等熵过程
ds ? 0 绝热不可逆过程——熵增过程
p
?k
?
const.
?
dp ? k d ? p?
VdV ? ? dp ? ? dp d ? ? ? a2 d ?
? d? ?
?
?
d? ?
?
VdV ? a2
?
V2 ? a2
dV V
?
?M2
dV V
dA ? (M 2 ? 1) dV
A
V
dp kM 2 dA ? p ? 1? M 2 A
(4)状态方程 p ? ? RT
? ? ? 0.633 ? 0
§5-4 气体在变截面上的流动
一、气体流动参数与截面面积的关系
(1)连续性方程 ?VA ? 常数
? d ? ? dA ? dV ? 0 ? AV
(2)动量方程 dp ? VdV ? 0
?
音速定义
a2 ? dp
d?
d? ?
?
?M2
dV V
?
M2 1? M 2
dA A
(3)等熵过程
