第十四届中环杯中小学生思维能力训练活动五年级决赛试卷及解析
14届中环杯决赛五年级

第十四届野中环杯冶小学生思维能力训练活动五年级决赛得分院注意院每小题前的野阴冶由阅卷人员填写袁考生请勿填写遥一尧填空题院渊每小题 5 分袁共 50 分袁请将答案填写在题中横线处遥 冤1. 计算院11.99伊73+1.09伊297+ 1 伊渊32-12冤=遥22. 420伊814伊1616 除以 13 的余数为遥3. 五年级有甲尧乙两个班袁甲班学生人数是乙班学生人数的 5 袁如果从乙班调 3 人到甲班袁甲班学生人数就是乙班学生 7AE OF人数的 4 遥 甲班原有学生人遥54. 已知 990伊991伊992伊993= 966428A91B40袁则 AB=遥BCD第 5题5. 如 图 袁吟ABC 面 积 为 60袁E尧F分 别 为 AB尧AC 上 的 点袁 满足 AB=3AE袁AC=3A F遥 点 D 是线段 BC 上的动点袁设吟FBD 的面积为 S1袁吟EDC 的面积为 S2袁 则 S1窑S2 的最大值伊2为遥06. 如图袁 在每个方框中填入一个数字袁 使得乘法竖式成1立遥 则这个算式乘积的最大值与最小值之差为遥47. 有 15 位选手参加一个围棋锦标赛袁每两个人之间需要比赛一场遥赢一场得 2 分袁平一场各 1 得分袁输一场得0 分遥如第 6题果一位选手的得分不少于 20 分袁他就能获得一份奖品遥 那么袁最多有位选手能够获得奖品遥中环8. 在一场 1000 米的比赛中袁一个沙漏以相同的速率在漏沙子袁漏出来的沙子都掉入一个杯中渊这个沙漏是在比赛进行了一段时间后才开始漏的冤遥 小明以匀速进行跑动遥 当他跑到好难杯200 米的时候袁第 a 颗沙子正好掉入杯中曰当他跑到 300 米的时候袁第 bc 颗沙子正好掉入杯中曰当他跑到 400 米的时候袁第de 颗沙子正好掉入杯中曰当他跑到 500 米的时候袁第 fg 颗沙子 正好掉入杯中渊a尧b尧c尧d尧e尧f尧g 都是 0~9 的数字袁并且它们的值的真a可以相同冤遥我们发现院渊1冤 a 是 2 的倍数曰渊2冤 bc 是一个质数曰中环渊3冤 de 是 5 的倍数曰渊4冤 fg 是 3 的倍数遥那么袁四位数 debc=渊如果有多个解袁需要将所有解写在横线中冤遥好难杯9. 如图 a袁七个汉字写在图中的七个圆圈内袁要求从某一个圆圈开始袁沿着线段一笔画这个图形渊所有圆圈都要走到袁而且只能走到一次冤袁将这个一笔画路径上的字连成一个字串的真b第 9题渊例如图 b袁从野中冶开始一笔画袁得到的字串为野中环难杯真的好冶冤遥 AB那么袁能够组成的不同字串有个遥10. 如图袁两个正方形 A BEG尧GECD袁点 H 是 GE 中点D袁C DF =1 3遥联结DH尧CH尧A F尧BF袁正方形ABEG的面积为m平方厘米袁阴影G部分的面积为 n 平方厘米遥 已知 m尧n 都是正整数袁且 m 有 9 个约数袁HEJ则正方形 A BEG 的边长为厘米遥I二尧动手动脑题院渊每小题 10 分袁共 50 分袁除第 15 题外袁请给出详细 D FC解题步骤遥 冤第 10 题11. 甲尧 乙两人同时从 A尧B两地出发袁 相向而行袁 甲每小时行12.5 千米袁乙每小时行 10 千米遥甲行 30 分钟后袁到达恒生银行门口袁想起来自己的信用卡没有带袁所以他原速返回 A 地去拿卡遥 到达 A 地后袁甲忘记卡放在哪里了袁花了半小时才找到卡遥 找到卡后袁甲又用原速去往 B 地袁结果当乙到达 A 地时袁甲还需要 15 分钟才能到达 B地遥 那么 A 尧B 间的距离是多少千米钥12. 如果一个数的奇约数的个数有 2m渊m 为自然数冤个袁则我们称这样的数为野中环数冶遥 比如 3 的奇约数有 1尧3袁一共 2=21 个袁所以 3 是一个野中环数冶遥 再比如 21 的奇约数有 1尧3尧7尧21袁一共 4=22 个袁所以 21 也是一个野中环数冶遥 我们希望能找到 n 个连续的野中环数冶遥 求院 n 的最大值遥113. 下左图是一个奇怪的黑箱子袁这个黑箱子有一个输入口袁一个输出口遥 我们在输入口输入 一个数字袁那么在输出口就会产生一个数字结果袁其遵循的规则是院渊1冤 如果输入的数字是奇数 k袁则输出的就是 4k+1曰 渊2冤 如果输入的数字是偶数 k袁则输出的就是衣 k 2遥 比如院输入的是数字 8袁那么输出的就是 8衣2=4曰输入的是数字 3袁那么输出的就是 3伊4+1=13遥 现在袁将三个这样的黑箱子串联在一起渊如下右图冤袁这样第一个黑箱子的输出成为第二个黑箱 子 的输入袁依次类推遥 比如输入数字 16袁经过第一个黑箱子袁得到结果 8袁这个 8 就作为第二个黑箱子 的输入遥 经过第二个黑箱子袁得到结果 4袁这个 4 就作为第三个黑箱子的输入遥 经过第三个黑箱子 袁得到结果 2袁这个 2 结果就是最后的输出了遥 我们可以用 16寅8寅4寅2 来表示这样的过程遥输入输出输入输出现在袁美羊羊尧喜羊羊尧懒羊羊尧羊爸爸在这个串联的黑箱子输入端输入不同的正整数袁其中羊 爸爸输入的数字最大袁得到的 4 个最终输出结果竟然是相同的遥当这个输出结果最小时袁求院羊爸爸 的输入值是多少钥15. 渊1冤 你能将下面的长方形图纸分割成全等的 4 个图形吗渊如参考 图冤钥 请给出不同于参考图的另外三种分割方法遥4030参考图 403040 3040 30渊2冤 画一个封闭的环袁水平或竖直穿过相邻的单元格遥 环不能交叉或重 叠袁下图就是一些不允许出现的情况遥14. 如图袁我们将很多边长为 1 的小正方形放入等腰吟A BC 中袁BC 边上的高为 AH袁AH 和 BC 的长度都是正整数遥 要求所有小正方形都有两条边与 BC 平行渊如图所示冤遥 先放最下面一层袁从两 边往中间放渊最靠边的小正方形的一个顶点正好在三角形的边上冤袁直到中间的空隙放不下一个小 正 方形为止遥然后放倒数第二层袁同样从两边往中间放袁直到中间的空隙放不下一个小正方形为止遥依次 类推袁不断地往上面叠放小正方形袁直到无法再往上叠为止遥我们发现袁每层的中间都没有产生空隙袁 而且 BC 臆8遥 最后袁整个吟ABC 内一共放了 330 个小正方形遥 求院BC 长度的最大值遥AHABCH下图中有数字的单元格不能作为环的一部分袁单元格内的数字表示其 周 围八个相邻的单元格内被环占住的个数袁请在图中画出这个环遥45758474448311332。
第十一届中环杯小学生思维能力训练活动五年级决赛题目

第十一届“中环杯”小学生思维能力训练活动五年级决赛一、填空题:1.计算:201120111949195019502009⨯-⨯=()。
2.将一堆练习本平均分给班上的同学,每人可得到12本;如果只分给男生,则每个男生可以比原来多分到9本。
那么该班男生人数与女生人数的比是()。
3.10个小朋友的平均身高是1.5米,其中有一些低于1.4米的,他们的平均身高是1.2米;另一些高于1.4米的,他们的平均身高是1.6米。
那么最多有()人的身高恰好是1.4米。
4.小明心里想了一个正整数,并且求出了它分别被14和21除后所得的余数,已知这两个余数的和是33,则该整数被42除的余数是()。
5.有一列数:1、3、3、9、7、3从第三个数开始,每个数都是它前面两个数的乘积的个位数字。
在这列数中取连续的2011个数,使得这2011个数的乘积最大,这个最大的乘积的个位数字是()。
6.有61只乒乓球,将它们放在20个盒子里,不允许有空盒子,每个盒子里最多放5只乒乓球,那么最少有()个盒子里的乒乓球数量相同。
7.如图,两个等腰直角三角形重叠在一起,阴影部分为重合部分,阴影部分的面积是()平方厘米。
8.小明有5双袜子,颜色分别是白色、黑色、红色、蓝色、灰色。
有一天,他发现掉了其中的3只袜子,情况可能是:掉了的3只袜子其中有2只颜色一样,于是他还有3双袜子;也有可能是掉了的3只袜子颜色两辆不同,于是他只剩下2双袜子了。
那么后者的可能性是前者的()倍。
二、动手动脑题:1.已知两个正整数的差是21,它们的最大公约数和最小公倍数的和是287,求这两个数的和是多少?2.A、B、C三辆车以相同的速度同时从甲地开往乙地。
出发后1小时,A车出了故障,于是B和C两车继续前进,A车停留半小时后,以原速度的56继续前进。
B、C两车行至距离甲地240千米处时,B车出了故障,于是C车继续前进,B车停留半小时后,也以原速度的56继续前进。
结果,C车比B车早1小时到达乙地,B车比A车早1小时到达乙地。
五年级上册数学试题-思维竞赛试卷 人教版(含答案)

小学五年级上册数学思维竞赛试卷一、填空题(每空 3 分,共 42 分) 1.三个连续自然数的乘积是 4080,这三个数是 、 、 。
2.一个大于 10 的自然数,除以 5 余 3,除以 7 余 1,除以 9 余 8,问满足条件的最小自然数是 。
3.今年妈妈 32 岁,女儿 12 岁, 年前,妈妈的年龄是女儿的 5 倍。
4.弟弟有 17 元钱,哥哥有 25 元钱,哥哥给弟弟 元后,弟弟的钱是哥哥的 2 倍。
5.有 30 枚硬币,由 2 分和 5 分组成,共值 9 角 9 分,有 2 分硬币 枚,5 分硬币枚。
6.右图是一块长方形耕地,它由四个小长方形拼合而成,其中三个小长方形的面积分别为 公顷,其中阴影部分的面积是 公顷。
,那么原来这个三位小数最大是 ,最小是。
8.一个六位数567 能被 99 整除,这个六位数最小是 。
9.某数除以 3 余 1,除以 4 余 2,除以 5 余 3,除以 6 余 4,这个数最小是 。
10.A 、B 、C 、D 四支球队进行循环赛(即每两队赛一场),比赛进行一段时间,A 赛了 3 场, B 赛了 2 场,C 赛了 1 场,D 赛了 场。
二、计算题(每题 4 分,共 16 分)1.(873×477-198)÷(476×874+199)2. 2000×1999-1999×1998+1998×1997-1997×1996+…+2×13.765×213÷27+765×327÷274.999999× 777778+333333 × 666666 1、某班有 40 名学生,其中 15 人参加数学小组,18 人参加航模小组,有 10 人两个小组都参加。
那么有多少人两个小组都不参加?2、有一根长为 180 厘米的绳子,从一端开始每隔 3 厘米作一记号,每隔 4 厘米也作一记号, 然后将标有记号的地方剪断。
初赛14届中环杯五年级试题

1. 计算:(1+1/2)x(1-1/2)x(1+1/3)x(1-1/3)x……x(1+1/10)x(1-1/10)=____2. 最接近2013的质数是______3. 黑箱中有60块大小、形状都相同的木块,每15块涂上相同的颜色,一次至少取出_____块才能保证期中至少有2块木块颜色相同。
4. 一共有52个学生参加游园活动,其中参观植物馆的有12人,参观动物馆的有26人,参观科技馆的有23人,既参观植物馆又参观动物馆的有5人,既参观植物馆又参观科技馆的有2人,既参观动物馆又参观科技馆的有4人,三个馆都参观的有1人,则有____人这三个馆都没有参观。
5. 如图,∠B=30°,∠D=20°,∠A=60°,则∠BCD(图中有圆弧部分的那个角)的度数为______°。
6. 一次考试中,小明需要计算37+31xa的值,结果他计算成了37+31+a。
幸运的是,他仍然得到了正确的结果。
则a=______。
7. 某次射箭比赛,满分是10分,初赛阶段淘汰所有参赛者的50%。
已知进入复赛的选手平均分比全体选手的平均分高2分,且进入复赛选手的平均分是8分。
则被淘汰选手的平均分是______分。
8. 有若干本书和若干本练习本。
如果按每1本书配2本练习本分给一些学生,那么练习本分完时还剩2本书,如果按每3本书配5本练习本分给另一些学生,那么书分完时还剩1本练习本。
那么,书有____本,练习本有____本。
9. 在51个连续奇数1、3、5、……101中选取k个数,使得它们的和为2013,那么k的最大值是_____。
10. 小明和小强玩了一个数字游戏,小明选择了一个数字x(0-9之间),然后说:“我正在考虑一个三位数(百位允许为0),这个三位数的百位为x,十位为3,并且能被11整除,请你找出这个三位数的个位数。
”小强非常开心,因为他知道能被11整除的数的规律。
但是他思考后发现这样的三位数不存在。
第 14 届“中环杯”中小学生思维能力训练活动六年级决赛答案

2 2 n 2 2 1 2 6 2 n n n 1 2 1 n n 1 2n 1 2 2 2 2 2 6 6 n n 1 2n 1 n n 2 n 1 6 6 n n 1 2n 1 n 2 6 2
3. 【答案】 8 【解答】设钱老师买了 x 本数学书, y 本物理书,根据题意,我们有
x y 7 7 6 y x y ,所以我们只要找到最小的 y ,使得 y 与 y 之间包含一个正整数即 y 6 6 x y 13 49 可。简单尝试一下,发现 6 ~ 7 之间没有任何正整数,而 7 ~ 之间含有数字 8 ,所以 x 8 6
n n 1 2
2
所以 12 2 22 32 2 42 52 2 62 2 202
20 212 4410 2
而前面还有一个 4410 x ,所以当 0 x 1 时,可以取到最小值。我们就取 x 0 ,此时
4410 x x 1 2 22 x 2 32 x 3 2 4 2 x 4 2 20 2 x 20 13 2 23 33 2 43 2 203 13 23 33 43 203 23 43 203 1 2 20 23 13 23 103
x 30 y 15
即加热 30 秒后往外倒 15 秒水,最少 45 秒后小明能喝到 30 C 的水 13. 【答案】 670 【解答】设总人数为 x ,每人分到的书的数量为 q ,余下的书的数量为 r ,则 2014 xq r ,由于 x 为三位数,所以 q 2 。如果 q 3 ,则 2014 xq r 3x x 671 ,由于 0 r x ,所以 r 670 ;所以,只要当 q 2 的时候,能够取到大于等于 670 的余数,那么就 不用考虑 q 3 的情况了。显然, 2014 672 2 670 ,此时取到余数 670 ,所以我们只要将 注意力集中在 q 2 的情况即可。 此时 2014 2x r ,由于 0 r x ,从而推出 x 的取值范围为 672 ~ 999 ,随着 x 的增大, r 在 减小,所以当 x 672 时,此时 r 最大,其最大值就是 670 14. 【答案】
2014年中环杯五年级---答案版
例 2、一个三位数是它本身各位数字和的 35 倍,求这个三位数。
例 3、一个四位数是其数字和的 288 倍,求所有满足条件的四位数。
第 4 页 共 5 页
“中环杯”青少年科技报思维训练“中环杯”网站内容精选
例 1、
例 2、
第 5 页 共 5 页
例 3、 如图 3 所示, 两个正三角形 ABC 和 ECF 并排摆放, 联结 DF、 D、 G 是 AB、 CE 的中点, FG、 DG 得到 DFG 。 已知 ECF 的面积为 10,求 DFG 的面积。
第 2 页 共 5 页
“中环杯”青少年科技报思维训练营---五年级
王洪福老师
数学
三角形的等积变形
第 1 页 共 5 页
“中环杯”青少年科技报思维训练营---五年级
王洪福老师
数学
例 2、如图 1 所示,两个等腰三角形 ABC 和 ECD 并排摆放,F、G 是 AB、CE 的中点,联结 F、G 得到 CFG 。 已知 ABC 的直角边长为 6, ECD 的直角边长为 10,求 CFG 的面积。
“中环杯”青少年科技报思维训练营---五年级
王洪福老师
数学
2014 年第十五届“中环杯”青少年科技报思维训练营 五年级
王洪福老师
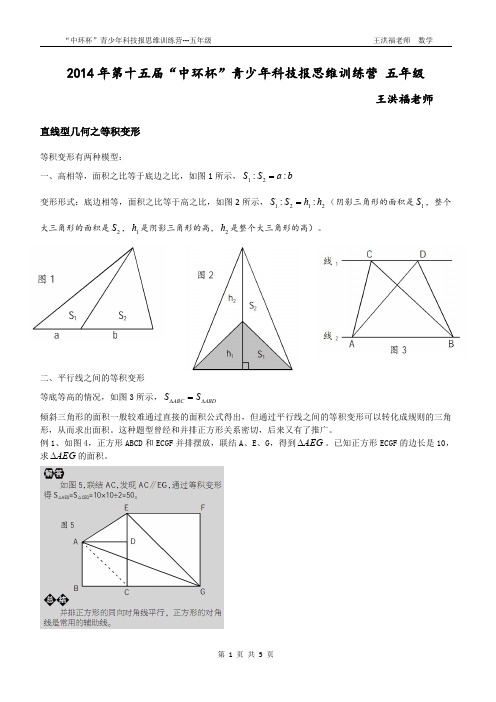
直线型几何之等积变形
等积变形有两种模型: 一、高相等,面积之比等于底边之比,如图 1 所示, S1 : S 2 a : b 变形形式:底边相等,面积之比等于高之比,如图 2 所示, S1 : S 2 h1 : h2 (阴影三角形的面积是 S1 ,整个 大三角形的面积是 S 2 , h1 是阴影三角形的高, h2 是整个大三角形的高)。
2
第 3 页 共 5 页
“中环杯”青少年科技报思维训练营---五年级
第十四届中环杯中小学生思维能力训练活动六年级决赛试卷及解析

12. 【答案】45 【解答】设加热 x 秒,往外倒水 y 秒,小明 x y 秒后可以喝到 30C 的水。
求(注意,要使得 7 | 66666a a 6 ,与题意不符)
7. 【答案】 6
【解答】设小正方形的边长为
x
,则
S1
2
1 2
12
x
12
x
144
x2
,而
S2
x2
,所以
S1
S2
144
。由于
S1
3S2
,所以
S2
1 4
144
36
,从而推出边长为 6
8. 【答案】
3 47 9 36 48 35 7469258 2 76 25 19 1 81 【解答】如图,从大数字开始分配位置,其中安排数字 6 的时候需要分类讨论,其它都是 直接定下来的。
那么袁五人中分数第二高的人的得分是
分遥
10. 4410 x + x -1 +2 伊 22 x -2 +32 x -3 +2 伊42 x -4
小值为
遥
+ 噎 +2 伊202 x - 20
的最
二尧动手动脑题院渊每小题 10 分袁共 50 分袁除第 15 题外袁请给出详细解题步骤遥 冤 11. 解方程院 x-1 + 2x-1 = x-3 遥
A B
2 6
或
A B
6 2
或
A B
3 5
或
A B
5 3
;
(7)当
D
9
时,
A B
1 8
或
A B
8 1
或
A B
2 7
小学五年级数学思维竞赛试题(含答案)

小学五年级数学思维竞赛试题 (全卷共4页,满分100分,时间80分钟) 一、填空题(每空2分,共40分)。
1.下图中阴影部分的大小占整个图形的()()。
2.在685的后面补上三个数字,组成一个同时是2、5、3的倍数的最小六位数,这个六位数是( )。
3.算式4÷11的商的小数部分第100位上的数字是( ),这100位数字的和是( )。
4.已知7070×A=7140×B,其中A 和B 是两个不为0的相邻自然数,A=( ), B=( )。
5.一筐苹果不超过70个,2个2个地数剩1个,5个5个地数剩3个,3个3个地数正好数玩,这框苹果最多( )个。
6.按规律填空:21,43,107,2417,5841,(),()。
7.从算式32+61+91+121+151+181中去掉( )和( )后,剩余分数 的和是1。
8.用完全相同的小正方体搭一个立体图形,从前面、上面和右面看到的图形分别是 、 、 ,搭这个立体图形至少要( )个小正方体。
9.用一块长14厘米,宽9厘米,高3厘米的长方体木料截出一个最大的正方 体,这个正方体的体积是( )厘米³,最多可以截出( )个这样的正方体。
10.一个长方体,如果高减少3㎝,就变成了一个正方体,这时表面积比原来 减少96㎝²,原来长方体的表面积是( )㎝²,体积是( )㎝³。
11.一个分数的分子和分母的差是9,化成小数后是0.85,这个分数是( )。
12.五(1)班学生中会打篮球的有25人,会游泳的有15人,两项运动都会有×××××××××××××密封线内不要答题题×××××××××××××××××学校班级姓名学号10人,两项都不会的有14人,五(1)班有( )名学生。
(全)小学五年级数学思维训练50题(附解析及答案)

(全)小学五年级数学思维训练50题(附解析及答案)小学五年级数学思维训练50题(附解析及答案)1.一副扑克牌共54张,最上面的一张是红桃K。
如果每次把最上面的12张牌移到最下面而不改变它们的顺序及朝向,那么,至少经过多少次移动,红桃K才会又出现在最上面?解:因为[54,12]=108,所以每移动108张牌,又回到原来的状况。
又因为每次移动12张牌,所以至少移动108÷12=9(次)。
2.爷爷对XXX说:“我现在的年龄是你的7倍,过几年是你的6倍,再过若干年就分别是你的5倍、4倍、3倍、2倍。
”你知道爷爷和XXX现在的年龄吗?解:爷爷70岁,XXX10岁。
提示:爷爷和XXX的年龄差是6,5,4,3,2的公倍数,又考虑到年龄的实际情况,取公倍数中最小的。
(60岁)3.某质数加6或减6得到的数仍是质数,在50以内你能找出几个这样的质数?并将它们写出来。
解:11,13,17,23,37,47。
4.在放暑假的8月份,XXX有五天是在姥姥家过的。
这五天的日期除一天是合数外,其它四天的日期都是质数。
这四个质数分别是这个合数减去1,这个合数加上1,这个合数乘上2减去1,这个合数乘上2加上1。
问:XXX是哪几天在姥姥家住的?解:设这个合数为a,则四个质数分别为(a-1),(a +1),(2a-1),(2a+1)。
由于(a-1)与(a+1)是相差2的质数,在1~31中有五组:3,5;5,7;11,13;17,19;21,31。
经试算,只要当a=6时,满足题意,以是这五天是8月5,6,7,11,13日。
5.有两个整数,它们的和恰好是两个数字相同的两位数,它们的乘积恰好是三个数字相同的三位数。
求这两个整数。
解:3,74;18,37。
提示:三个数字相同的三位数必有因数111。
因为111=3×37,所以这两个整数中有一个是37的倍数(只能是37或74),另一个是3的倍数。
6.在一根100厘米长的木棍上,从左至右每隔6厘米染一个红点,同时从右至左每隔5厘米也染一个红点,然后沿红点处将木棍逐段锯开。
五年级上册数学14套新思维训练试题(人教版)

五年级上册数学14套新思维训练试题(人教版)五年级训练(1)学习目标:掌握小数的意义,熟练进行计算、简算。
一、填一填1、求2.4的一半是多少?有算式表示是( ).2、一个正方形的边长是0.65,它的周长是( )米,面积是( )平方米.3、4.25的5倍是( ).0.84的十分之四是( ).4、鄙人面的○里填上“<、>或=”.3.8×0.9○3.8 52.6○52.6×1.0178.5×1.2○7.85×0.12 81.3○81.3×0.8612.5×0○12.5 123×10○1235、一桶油重4.8千克,半桶油重()千克?6、两个因数的积是3.8,如果两个因数的都缩小10倍,积变为( )7、甲数是76.5,乙数比甲数的4倍少63.8,乙数是( ).8、3.7094保留一位小数约是();精确到百分位约是();精确到0.001约是( ).二、列式计算37.6的百分之四是多少? 3.87的6倍是多少?0.375的十分之五是多少? 12个0.7的和是多少?15的十分之八是多少?2.4的百分之二十五是多少?三、用简便方法计算12.5×4.4×8 32.8×2.5×0.47.75×2.8+2.8×2.25 0.65×10.19.7×99 7.63×99+7.630.58×3.2+7.8×0.58-0.58 2.9+6.7×2.9+2.9×2.3四、数学病院,把正确的竖式写在右面。
五.解决问题1一支自动铅笔的售价是3.5元,一支钢笔的售价是自动铅笔的2.4倍,买一支自动铅笔和一支钢笔共需多少元?2食品店运来35瓶鲜牛奶,运来的酸奶瓶数是鲜奶的2.4倍,运来的酸奶比鲜奶多多少瓶?3一个电影院的票价有两种,4.5元一张的有400个座位,3.5元一张的有350个座位。
第十四届“中环杯”小学生思维能力训练活动五年级选拔赛.doc

【分析】表面积比原来正方体的表面积增加了两个长方形
如下图, MJ 12 4 3 5 , MI 12 ,由勾股定理, IJ 13 所以新增的长方形面积为 12 13 156 两部分表面积之和为 6 122 2 156 1176平方厘米。
A
B
I
M
J
E
F
14. 如图是一个除法算式,在空格中填入合适的数字能使这个算式成立。那么被除数是 。
又由勾股定理
AJ 2 ID 2 DA 2 40 HI 2 IK 2 KH 2 117
第一天 9 点时, 整块草地上的杂草被除干净了, 即草量为 0,所以到第二天 8 点 30
分时,草长了 23 小时 30 分钟,即 1410 分钟,共长了 1410 份草 这些草被 10 位工人用 30 分钟除干净了,
所以 1 个工人 1 分钟可除草 1410 10 30 4.7 份
第三天 8 点时,草长了 23 小时 30 分钟,即 1410 分钟,共长了 1410 份草, 8 个工
,既参观动物馆又参观科技馆的有 4人,三个馆都参观的有 1人,则有 ________人这三个馆
都没有参观。
【分析】 共有 12 26 23 5 2 4 1 51人参观了至少一个馆, 所以有 1 个人三个馆都
没参观。
5. 如图, B 30 , A 60 , D 20 ,则 BCD (图中有圆弧部分的那个角)的度数为 ___
_。
【分析】如下图,连接 AI ,延长 CD 交 GH 于 K
易知 KD 4,GK 3 ,所以 GD 5,同理 AH 5 又由 HK 9, DE 3,KD 4 , ID : IK DE : HK ,可知 ID 2 设 IJ a, JA b ,由勾股定理
青少年科技报-五年级(1-9期)解析版

n n 大的约数 ) , 考虑到它一共有 10 个约数, 所以必须为 2 34 或 24 3 , 显然 2 34 3 2 =162 比较大。
【点评】 难度: ☆☆☆ 本题考查整数的约数个数定理:若
an a2 a3 n p1a1 p2 p3 ... pn ,则 n 的约数个数:
d (n) (a1 1)(a2 1)( a3 1)...( a4 1) 。在本题中,由第
b a 2 ,而且 1 号、10 号不能同时选出。 c b 2
b a 2 (b 1) a 1 ,考虑到 c b 2 (c 2) (b 1) 1
3
我们先不考虑 1 号、 10 号的问题。由于
1 a<b<c 10 ,所以 1 a<b-1<c-2 8 ,一共有 C8 =56 (种)选法,其中 1 号、10 号被
2 3
2
3
【点评】 难度: ☆☆☆ 本题是一道排列组合的综合问题,结合了特殊元素、分类分步等方法。位置与气球作为 两个不同维度应分步讨论, 每个维度内再根据特殊要求作分类讨论, 承接上一期分类分步思 想,进一步深化练习。
同时选出的选法有 6 种,所以答案为 56 6 50 (种) 。 【点评】 难度: ☆☆☆ 本题考查环型排列中的不相邻问题。插空法是解决直线型排列中不相邻问题最常用的 方法,本题需先将环型排列转化为直线型排列,即可轻松求出答案。 官方解答中对不等式的应用超越了大多数五年级考生的能力范围, 因此用插空法来解题 可能更易理解,在此提出以下两种解法供大家参考: (1) 插空法: 先将环型排列转化成直线型排列,即将 10 个站台编号为 1、2、…、10,按直线型插空 法来做,再去掉 1 号和 10 号同时被选出的情况。 在 1 10 号中选出三个不相邻的站台,即相当于将选出的三个站台插入另 7 个站台所形 成的 8 个空隙中(不能插入同一个空隙) ,总共有 C8 =56 (种)情况。其中同时选出 1 号跟 10 号的情况里,还需再选出一个站台,只能在 3 案为 56 6 50 (种) 。 (2) 排除法:
五年级下册数学思维训练能力测试题(含答案)

五年级下册数学思维训练能力测试题1.12+14=1-14= 34,12+14+18=1-18= 78,则12+14+18+116+132+164=( - = )。
2.14-18=18,14-18-116=116,14-18-116-132=132,则14-18-116-132-164 =( )。
3. , =( ) 。
4.( )个17 是67 ,29 里面有( )个19 。
5.找规律填数。
①23、69、1827、( 5481 )。
② 12 、24、38、( 416)。
6.在右图中,和a 平行的棱有( 3)条,和a 相交并垂直的棱有( 4 )条。
分成( )份,水中含盐量占( )份。
8.把8米长的绳子平均剪成5段,每段占全长的( 1 ),每段长( 8)米。
9.奇数+奇数=( ),奇数+偶数=( ),偶数+偶数=( )。
10.错误!未找到引用源。
的分子和分母的最大公因数是( ),最小公倍数是( )。
11.10以内质数和是( ),100以内最大的质数是( )。
12.能同时被2、3、5整除的最小三位数是( 120 )。
13.三个连续偶数的乘积是48,这三个数是( 2 )、( 4 )、( )。
14.每个质数都只有( )个因数;一个合数至少有( )个因数。
15.所有分母是8的最简真分数的和是( )。
16.分数310 、56 、728 、2751 、 5436 中,(3 、3 )是最简分数,( 27)能化成有限小数。
17.240有( )个因数。
自然数123456789是( )。
(填质数或合数)18.两个数的最小公倍数是240,最大公约数是12,已知其中一个数60,另一个数是( )。
19.有一些糖果平均分成若干包,每包10粒余9粒,每包12粒余11粒,每15粒余14粒。
这些糖果最少有( )粒。
20.写出3个大于13 而小于12 的分数:(11)、( 10)、(9)。
21.如果把58的分子加上5,要使分数的大小不变,分母应该加上( )。
第十四届中环杯五级决赛详解

第十四届中环杯五年级决赛一、填空题(每题 5 分,共 50 分)1 1. 计算:×× 297+22 2×(3 -1 )=_________【剖析】原式 =11××73+1.09 ×11× 27+4=11 ×× 100+4=1199+4=12032. 420× 814× 1616 除以 13 的余数为 __________【剖析】 420× 814×1616≡ 4× 8× 4≡ 128≡ 11(mod13)3.五年级有甲乙两班,甲班学生人数是乙班学生人数的5/7,假如从乙班调 3 人去甲班,甲班学生人数就是乙班学生人数的4/5,甲班原有学生_________人【剖析】本来人数比为甲:乙=5: 7=15: 21 ,人数调整后代数比为甲:乙=4 : 5=16 : 20 ,前后两次总人数不变,所以将总人数变成[(5+7),(4+5)]=36份,比率调整如上,发现人数调整为1份,所以 1 份为 3 人,所以甲班原有学生15× 3=45 人。
4. 已知 990× 991× 992× 993= 966428 A91B40,则AB =【剖析】因为99 丨 990,所以 99 丨966428 A91B40所以 99 丨 96+64+28+ A9 + 1B +40 → 99 丨AB +247→AB=505.如图,△ ABC 面积为 60,E、F 分别为 AB 和 AC 上的点,知足 AB=3AE ,AC=3AF ,点D 是线段 BC 上的动点,设△ FBD 的面积为 S1, △ EDC 的面积为 S2,则 S1× S2的最大值为__________.【剖析】因为AEAF1,所以 EF ∥ BC AB AC32所以 S EBD = S FBD =S1→ S1+S2=S EBC=S ABC =403和一准时,差越小,积越大,所以当S1 =S2时,即 D 为中点时, S1× S2最大为 20×20=4006.如,在每个方框中填入一个数字,使得乘法式建立,个算式乘的最大和最小的之差 __________.【剖析】易得,乘数中下方数的十位1,因十位数字乘上边的数获得的三位数,百位上的 2 乘上边的数获得的四位数。
中环杯小学生思维能力训练活动

第十五届“中环杯”小学生思维能力训练活动五年级选拔赛填空题:1、已知2468135713572468mn++++++-=++++++,其中m, n 是两个互质的正整数,则10m n +=____【考点】分数计算 【答案】110 分析:20169==162020-原式 ,10m n +=10×9+20=1102、D 老师家里有五个烟囱,这五个烟囱正好从矮到高排成一排,相邻两个烟囱之间的高度差为2厘米,其中最高的烟囱又正好等于最矮的两个烟囱的高度之和,则五个烟囱的高度之和是________厘米 【考点】等差数列,方程 【答案】50分析:设这五个烟囱分别为x-4,x-2,x ,x+2,x+4,则x+4=x-2+x-4,x=10,和为5x=503、已知()()33222014a b c d ⨯+-=,其中a 、b 、c 、d 是四个正整数,请你写出满足条件的一个乘法算式:___________ 【考点】数的拆分,分解质因数 【答案】答案不唯一分析:2014=1×2014=2×1007=19×106=38×53其中一解为2014=()()22335932+⨯-4、一个长方体的长、宽分别为20厘米、15厘米,其体积的数值与表面积的数值相等,则它的高为______厘米(答案写为假分数) 【考点】立体几何,方程 【答案】6023分析:设高为h ,则20×15×h=(20×15+20h+15h )×2,则h=60235、一次中环杯比赛,满分为100分,参赛学生中,最高分为83分,最低分为30分(所有的分数都是整数),一共有8000个学生参加,那么至少有_____个学生的分数相同 【考点】抽屉原理 【答案】149分析:83-30+1=54,800054=1488÷⋅⋅⋅,148+1=149个6、对35个蛋黄月饼进行打包,一共有两种打包规格:大包袋里每包有9个月饼,小包装里每包有4个月饼。
五年级数学思维兴趣班能力展示活动题卷及答案

五年级数学思维兴趣班能力展示活动题卷及答案一、填空题1、2.019×330+20.19×66+201.9×0.1=。
2、定义一种新运算“⊙”:A⊙B=(A+2019)×(B-2019),那么1981⊙2039的值为。
3、如果上一题的正确答案为A,那么A有个因数。
4、已知整数N(N>3)被4、5、6、7除的余数均为3。
则N的最小值为。
5、有一列数,这列数中的第一个数是2,第二个数是3。
从第三个数开始,每个数都是它前面两个数乘积的个位数: 2,3,6,8,8,4,……那么,在这列数中的第2019个数是。
6.如右图所示,大正方形面积为60,小正方形面积为36,小正方形的每个顶点均在大正方形边上,且每个顶点将边分成两部分,长分别为a、b。
则a×b=。
7、如右图所示,建筑工地要砌一个长12分米、宽10分米、高5分米的长方体无盖水池,且底面和四壁均厚1分米。
如果用棱长为1分米的立方体砖块来砌,则共需要块砖。
8、有一个五位数,在它后面写上一个2,能得到一个六位数;在它前面写上一个2,也能得到一个六位数。
如果第一个六位数是第二个六位数的3倍,那么原来这个五位数是。
9、一辆汽车在甲、乙两地间往返行驶,从甲地去乙地时平均速度为60千米/时。
若要使这辆车往返的平均速度为72千米/时,则从乙地回甲地时的平均速度应为千米/时。
10、在1,2,3,4,……,2019中最多可以选出个数,使得选出的数中任意两个的和都不能被9整除。
11、有一根长树枝的左端有8只间隔相等的甲虫,向右爬行;树枝的右端则有6只间隔相等的甲虫,向左爬行。
如果所有甲虫的速度都相同;两只甲虫若迎面相遇就立即同时掉头往回爬;爬出树枝两头的甲虫则会掉下去。
当所有甲虫掉下树枝时,它们一共相遇了次。
12、如果一个自然数中恰好含有两个相邻的数字6,我们把它叫做“大顺数”(例如665、2669、6606都是“大顺数”,但6265或1666不是“大顺数”)。
第十四届“中环杯”小学生思维能力训练活动五年级选拔赛.doc

第十四届“中环杯”小学生思维能力训练活动 五年级选拔赛 一、填空题 1. 计算:11111111111122331010⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+⨯-⨯+⨯-⨯⨯+⨯-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭_____________。
【分析】原式3411129111112310231021020=⨯⨯⨯⨯⨯⨯⨯=⨯=2. 最接近2013的质数是________。
【分析】20113.黑箱中有60块大小、形状都相同的木块,每15块涂上相同的颜色。
一次至少取出_______块才能保证其中至少有2块木块颜色相同。
【分析】共60154÷=种颜色,需要取出415+=块4.一共有52个学生参加游园活动,其中参观植物馆的有12人,参观动物馆的有26人,参观科技馆的有23人,既参观植物馆又参观动物馆的有5人,既参观植物馆又参观科技馆的有2人,既参观动物馆又参观科技馆的有4人,三个馆都参观的有1人,则有________人这三个馆都没有参观。
【分析】共有122623524151++---+=人参观了至少一个馆,所以有1个人三个馆都没参观。
5.如图,30,60,20B A D ∠=︒∠=︒∠=︒,则BCD ∠(图中有圆弧部分的那个角)的度数为________︒。
【分析】四边形内角和为360°,所以优角360302060250BCD ∠=︒-︒-︒-︒=︒6.一次考试中,小明需要计算3731a +⨯的值,结果他计算成了3731a ++。
幸运的是,他仍然得到了正确的结果。
则a =_________。
【分析】由题意313731373130a a a +⨯=++⇒=7.某次射箭比赛,满分是10份,初赛阶段淘汰所有参赛者的50%。
已知进入复赛的选手平均分比全体选手的平均分高2分,且进入复赛选手的平均分是8分。
则被淘汰选手的平均分是_________。
【分析】设共有2n 人,则进入复赛的选手为n 人、被淘汰的选手也为n 人。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
得分院
注意院每小题前的野阴冶由阅卷人员填写袁考生请勿填写遥
一尧填空题院渊每小题 5 分袁共 50 分袁请将答案填写在题中横线处遥 冤
1.
计算院11.99伊73+1.09伊297+
1 2
伊渊32-12冤=
遥 A
2. 420伊814伊1616 除以 13 的余数为
输入
输出
输入
输出
现在袁美羊羊尧喜羊羊尧懒羊羊尧羊爸爸在这个串联的黑箱子输入端输入不同的正整数袁其中羊 爸爸输入的数字最大袁得到的 4 个最终输出结果竟然是相同的遥当这个输出结果最小时袁求院羊爸爸 的输入值是多少钥
15. 渊1冤 你能将下面的长方形图纸分割成全等的 4 个图形吗渊如参考 图冤钥 请给出不同于参考图的另外三种分割方法遥
比赛一场遥 赢一场得 2 分袁平一场各 1 得分袁输一场得 0 分遥 如 果一位选手的得分不少于 20 分袁他就能获得一份奖品遥 那么袁
第6题
最多有
位选手能够获得奖品遥
8. 在一场 1000 米的比赛中袁一个沙漏以相同的速率在漏
中Байду номын сангаас
环
沙子袁漏出来的沙子都掉入一个杯中渊这个沙漏是在比赛进行
了一段时间后才开始漏的冤遥 小明以匀速进行跑动遥 当他跑到 好
40
30
参考图
40
40
40
30
30
30
渊2冤 画一个封闭的环袁水平或竖直穿过相邻的单元格遥 环不能交叉或 重叠袁下图就是一些不允许出现的情况遥
14. 如图袁我们将很多边长为 1 的小正方形放入等腰吟A BC 中袁BC 边上的高为 A H袁A H 和 BC 的长度都是正整数遥 要求所有小正方形都有两条边与 BC 平行渊如图所示冤遥 先放最下面一层袁从两 边往中间放渊最靠边的小正方形的一个顶点正好在三角形的边上冤袁直到中间的空隙放不下一个小
有带袁所以他原速返回 A 地去拿卡遥 到达 A 地后袁甲忘记卡放在哪里了袁花了半小时才找到
卡遥 找到卡后袁甲又用原速去往 B 地袁结果当乙到达 A 地时袁甲还需要 15 分钟才能到达 B
地遥 那么 A 尧B 间的距离是多少千米钥
12. 如果一个数的奇约数的个数有 2m渊m 为自然数冤个袁则我们称这样的数为野中环数冶遥 比如 3 的奇约数有 1尧3袁一共 2=21 个袁所以 3 是一个野中环数冶遥 再比如 21 的奇约数有 1尧3尧 7尧21袁一共 4=22 个袁所以 21 也是一个野中环数冶遥 我们希望能找到 n 个连续的野中环数冶遥 求院 n 的最大值遥
13. 下左图是一个奇怪的黑箱子袁这个黑箱子有一个输入口袁一个输出口遥 我们在输入口输入 一个数字袁那么在输出口就会产生一个数字结果袁其遵循的规则是院
渊1冤 如果输入的数字是奇数 k袁则输出的就是 4k+1曰 渊2冤 如果输入的数字是偶数 k袁则输出的就是 k衣2遥 比如院输入的是数字 8袁那么输出的就是 8衣2=4曰输入的是数字 3袁那么输出的就是 3伊4+1=13遥 现在袁将三个这样的黑箱子串联在一起渊如下右图冤袁这样第一个黑箱子的输出成为第二个黑箱 子的输入袁依次类推遥 比如输入数字 16袁经过第一个黑箱子袁得到结果 8袁这个 8 就作为第二个黑箱 子的输入遥 经过第二个黑箱子袁得到结果 4袁这个 4 就作为第三个黑箱子的输入遥 经过第三个黑箱 子袁得到结果 2袁这个 2 结果就是最后的输出了遥 我们可以用 16寅8寅4寅2 来表示这样的过程遥
的
真
b
第9题
渊例如图 b袁从野中冶开始一笔画袁得到的字串为野中环难杯真的好冶冤遥 A
B
那么袁能够组成的不同字串有
个遥
10.
如图袁两个正方形
A BEG尧GECD袁点 H
是
GE
中点袁
DF DC
=
1 3
遥
联结 DH尧CH尧A F尧BF袁正方形 A BEG
的面积为 m 平方厘米袁阴影
G
H
E
部分的面积为 n 平方厘米遥 已知 m尧n 都是正整数袁且 m 有 9 个约数袁
的
真
a
中
环
渊3冤 de 是 5 的倍数曰渊4冤 fg 是 3 的倍数遥
那么袁四位数 debc = 要将所有解写在横线中冤遥
渊如果有多个解袁需
好
难
杯
9. 如图 a袁七个汉字写在图中的七个圆圈内袁要求从某一
个圆圈开始袁沿着线段一笔画这个图形渊所有圆圈都要走到袁 而且只能走到一次冤袁将这个一笔画路径上的字连成一个字串
遥
3. 五年级有甲尧乙两个班袁甲班学生人数是乙班学生人数
的
5 7
袁如果从乙班调 3 人到甲班袁甲班学生人数就是乙班学生
E O
F
人数的
4 5
遥
甲班原有学生
人遥
4. 已知 990 伊991伊992伊993= 966428A 91B40袁
则 AB=
遥
B
D
C
第5题
5. 如 图 袁 吟A BC 面 积 为 60袁E尧F 分 别 为 A B尧A C 上 的
J
则正方形 A BEG 的边长为
厘米遥
I
二尧动手动脑题院渊每小题 10 分袁共 50 分袁除第 15 题外袁请给出详细 解题步骤遥 冤
DF
C
第 10 题
11. 甲尧 乙两人同时从 A 尧B 两地出发袁 相向而行袁 甲每小时行
12.5 千米袁乙每小时行 10 千米遥 甲行 30 分钟后袁到达恒生银行门口袁想起来自己的信用卡没
难
杯
200 米的时候袁第 a 颗沙子正好掉入杯中曰当他跑到 300 米的
时候袁第 bc 颗沙子正好掉入杯中曰当他跑到 400 米的时候袁第
de 颗沙子正好掉入杯中曰当他跑到 500 米的时候袁第 fg 颗沙子 正好掉入杯中渊a尧b尧c尧d尧e尧f尧g 都是 0~9 的数字袁并且它们的值 可以相同冤遥我们发现院渊1冤 a 是 2 的倍数曰渊2冤 bc 是一个质数曰
点袁 满足 A B=3A E袁A C=3A F遥 点 D 是线段 BC 上的动点袁设
吟FBD 的面积为 S1袁吟EDC 的面积为 S2袁 则 S1窑S2 的最大值
伊
2
为
遥
0
6. 如图袁 在每个方框中填入一个数字袁 使得乘法竖式成
1
立遥 则这个算式乘积的最大值与最小值之差为
遥
4
7. 有 15 位选手参加一个围棋锦标赛袁每两个人之间需要
正方形为止遥然后放倒数第二层袁同样从两边往中间放袁直到中间的空隙放不下一个小正方形为止遥
依次类推袁不断地往上面叠放小正方形袁直到无法再往上叠为止遥我们发现袁每层的中间都没有产生
空隙袁而且
BC AH
臆8遥
最后袁整个吟A BC 内一共放了 330 个小正方形遥
