山东省2019年各市中考真题汇编:综合试题
2019山东济南中考试题及答案

济南市2019年初三年级学业水平考试英语试题本试题分选择题部分和非选择题部分,共10页,满分为150分,考试用时120分钟。
答题前,请考生务必将自己的姓名、座号和准考证号填写在答题卡上,并同时将考点、姓名、准考证号和座号填写在试卷规定的位置。
答题时,选择题部分每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑; 如需改动,用橡皮擦干净后,再选涂其他答案标号。
非选择题部分,用0.5毫米黑色签字笔在答题卡上题号所提示的答题区域作答。
直接在试题上作答无效。
选择题部分(共105分)I. 听力测试(30分)A)听录音,从每组句子中选出一个你所听到的句子如每个句子听一遍。
1. A. Please come here, Amy. B. Let's go to the factory. C. This is my sister Cindy.2. A. I play tennis once a week. B. He never eats junk food. C. She gets up at six o'clock.3. A. Were you late for school? B. Do you have a basketball? C. Did you buy any vegetables?4. A. Tina has long straight hair. B. Lisa had a wonderful idea. C. Anna will be back next year.5. A.What's his phone number? B. What's the matter with her? C. Where is our music teacher?C)在录音中,你将听到一段对话及五个问题。
请根据对话内容及问题选择正确答案。
对话及问题听两遍。
1. A.Food. B. Water. C. Paper.2. A.Four. B. Six. C. Ten.3. A.At about 7:00. B. At about 8:00. C. At about 9:00.4. A.Play chess. B.Have a talk. C. Sing a song.5. A.Cooking. B.Writing. C. Shopping.D)在录音中,你将听到一篇短文及五个问题。
2019年山东省青岛中考地理试卷及答案解析

山东省青岛市2019年初中毕业会考、高级中等学校招生考试地理本试卷满分80分;考试时间90分钟。
第Ⅰ卷(选择题共35分)一、单项选择题(本题35小题,每小题1分,共35分)在每小题给出的四个选项中,只有一项是符合题意要求的。
2019年4月28日,北京世界园艺博览会在长城脚下的延庆开幕。
本届世园会的主题是“绿色生活,美好家园”。
读图1北京世园会的会徽“长城之花”,完成1~2题。
1.符合本届世园会主题理念的是()A.大树移植,快速绿化B.人工造景,征服自然C.顺应自然,保护生态D.远离城市,回归乡村2.下列描述能够体现山东馆特色的是()A.京华京韵B.齐鲁胜境图1C.浙乡映像D.徽派三雕读图2全球部分区域光照图(图中阴影部分表示黑夜),完成3~4题。
3.图中①点的地理坐标是()A.66.5°S,90°EB.66.5°N,90°WC.66.5°N,90°ED.66.5°S,90°W4.下列关于图中①②③三点的叙述,正确的是()A.①点位于中纬度地区B.②点位于东半球C.③点有极夜现象D.②点位于③点的东北方向图2 读图3非洲地形图和马达加斯加岛A、B两地气候资料图,完成5~7题。
图35.有关非洲地形特征的叙述,正确的是()A.地势东南高西北低B.平原面积广大C.海岸线曲折破碎D.平均海拔最高6.与甲河相比,乙河()A.长度长B.水量季节变化小C.水量大D.支流多7.影响A、B两地降水差异的主要因素是()A.纬度位置B.海陆分布C.地形地势D.人类活动读图4美国本土主要城市、工业区分布示意图,完成8~9题。
图48.美国东北部工业区发展工业的主要优势条件有()①气候暖湿,地形平坦②煤、铁、石油资源丰富③五大湖水运便利,沿海多良港④发展历史悠久A.①②B.②③C.①④D.③④9.下列城市与其主要地理事项对应正确的是()A.洛杉矶——大西洋沿岸港口城市B.旧金山——温带海洋性气候C.纽约——美国政治和经济中心D.新奥尔良——密西西比河河口读图5我国传统民居景观图,完成10~11题。
2019年全国中考数学真题分类汇编:正多边形、弧长与扇形面积(含答案)

2019年全国中考数学真题分类汇编:正多边形、弧长与扇形面积一、选择题1.(2019年山东省青岛市)如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=4,∠A=45°,则的长度为()A.πB.2πC.2πD.4π【考点】切线的性质、等腰直角三角形的判定和性质、弧长的计算【解答】解:连接OC、OD,∵AC,BD分别与⊙O相切于点C,D.∴OC⊥AC,OD⊥BD,∵∠A=45°,∴∠AOC=45°,∴AC=OC=4,∵AC=BD=4,OC=OD=4,∴OD=BD,∴∠BOD=45°,∴∠COD=180°﹣45°﹣45°=90°,∴的长度为:=2π,故选:B.2.(2019年山东省枣庄市)如图,在边长为4的正方形ABCD中,以点B为圆心,AB为半径画弧,交对角线BD于点E,则图中阴影部分的面积是(结果保留π)()A .8﹣πB .16﹣2πC .8﹣2πD .8﹣π【考点】正方形的性质、扇形的面积【解答】解:S 阴=S △ABD ﹣S 扇形BAE =×4×4﹣=8﹣2π, 故选:C .3. (2019年云南省)一个圆锥的侧面展开图是半径为8的半圆,则该圆锥的全面积是( )A.48πB.45πC.36πD.32π【考点】圆锥的全面积【解答】设圆锥底面圆的半径为r ,母线长为l ,则底面圆的周长等于半圆的弧长8π,∴ ππ82=r ,∴4=r ,圆锥的全面积等于πππππ4832162=+=+=+r rl S S 底侧, 故选A4. (2019年浙江省温州市)若扇形的圆心角为90°,半径为6,则该扇形的弧长为( )A .πB .2πC .3πD .6π【考点】弧长公式计算.【解答】解:该扇形的弧长==3π. 故选:C .5. (2019年湖北省荆州市)如图,点C 为扇形OAB 的半径OB 上一点,将△OAC 沿AC 折叠,点O 恰好落在上的点D 处,且l :l =1:3(l 表示的长),若将此扇形OAB 围成一个圆锥,则圆锥的底面半径与母线长的比为( )A .1:3B .1:πC .1:4D .2:9【考点】圆锥的侧面积【解答】解:连接OD 交OC 于M .由折叠的知识可得:OM=OA,∠OMA=90°,∴∠OAM=30°,∴∠AOM=60°,∵且:=1:3,∴∠AOB=80°设圆锥的底面半径为r,母线长为l,=2πr,∴r:i=2:9.故选:D.6. (2019年西藏)如图,从一张腰长为90cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面半径为()A.15cm B.12cm C.10cm D.20cm【考点】圆锥的侧面积【解答】解:过O作OE⊥AB于E,∵OA=OB=90cm,∠AOB=120°,∴∠A=∠B=30°,∴OE=OA=45cm,∴弧CD的长==30π,设圆锥的底面圆的半径为r,则2πr=30π,解得r=15.故选:A.二、填空题1.(2019年重庆市)如图,在菱形ABCD中,对角线AC,BD交于点O,∠ABC=60°,AB=2,分别以点A、点C为圆心,以AO的长为半径画弧分别与菱形的边相交,则图中阴影部分的面积为.(结果保留π)【考点】扇形面积公式、菱形的性质【解答】解:∵四边形ABCD是菱形,∴AC⊥BD,∠ABO=∠ABC=30°,∠BAD=∠BCD=120°,∴AO=AB=1,由勾股定理得,OB==,∴AC=2,BD=2,∴阴影部分的面积=×2×2﹣×2=2﹣π,故答案为:2﹣π.2. (2019年山东省滨州市)若正六边形的内切圆半径为2,则其外接圆半径为.【考点】正多边形和圆、等边三角形的判定与性质、三角函数【解答】解:如图,连接OA、OB,作OG⊥AB于G;则OG=2,∵六边形ABCDEF正六边形,∴△OAB是等边三角形,∴∠OAB=60°,∴OA===,∴正六边形的内切圆半径为2,则其外接圆半径为.故答案为:.3. (2019年山东省青岛市)如图,五边形ABCDE是⊙O的内接正五边形,AF是⊙O的直径,则∠BDF的度数是°.【考点】正多边形和圆、圆周角定理【解答】解:连接AD,∵AF是⊙O的直径,∴∠ADF=90°,∵五边形ABCDE是⊙O的内接正五边形,∴∠ABC=∠C=108°,∴∠ABD=72°,∴∠F=∠ABD=72°,∴∠FAD=18°,∴∠CDF=∠DAF=18°,∴∠BDF=36°+18°=54°,故答案为:54.4. (2019年广西贵港市)如图,在扇形OAB中,半径OA与OB的夹角为120°,点A与点B的距离为2,若扇形OAB恰好是一个圆锥的侧面展开图,则该圆锥的底面半径为______.【考点】圆锥面积公式【解答】解:连接AB ,过O 作OM ⊥AB 于M ,∵∠AOB=120°,OA=OB ,∴∠BAO=30°,AM=, ∴OA=2,∵=2πr , ∴r=故答案是:5. (2019年广西贺州市)已知圆锥的底面半径是1,高是,则该圆锥的侧面展开图的圆心角是度.【考点】圆锥面积公式【解答】解:设圆锥的母线为a ,根据勾股定理得,a =4,设圆锥的侧面展开图的圆心角度数为n °,根据题意得2π•1=,解得n =90,即圆锥的侧面展开图的圆心角度数为90°.故答案为:90.6. (2019年江苏省泰州市)如图,分别以正三角形的3个顶点为圆心,边长为半径画弧,三段弧围成的图形称为莱洛三角形.若正三角形边长为6cm ,则该莱洛三角形的周长为 cm .【考点】扇形弧长公式【解答】∵l=180R n π=1806120⨯π=4π, ∴4π×3=12π. 故答案为:12π.7.(2019年江苏省无锡市)已知圆锥的母线成为5cm ,侧面积为15πcm 2,则这个圆锥的底面圆半径为 cm .【考点】圆锥侧面积【解答】圆锥底面圆的半径r=15π÷5π=3.8. (2019年江苏省扬州市)如图,AC 是⊙O 的内接正六边形的一边,点B 在弧AC 上,且BC 是⊙O 的内接正十边形的一边,若AB 是⊙O 的内接正n 边形的一边,则n=__15_。
2019年山东省济南市中考数学试卷(含解析版)

2019年山东省济南市中考数学试卷一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(4分)﹣7的相反数是()A.﹣7B.﹣C.7D.12.(4分)以下给出的几何体中,主视图是矩形,俯视图是圆的是()A.B.C.D.3.(4分)2019年1月3日,“嫦娥四号”探测器成功着陆在月球背面东经177.6度、南纬45.5度附近,实现了人类首次在月球背面软着陆.数字177.6用科学记数法表示为()A.0.1776×103B.1.776×102C.1.776×103D.17.76×102 4.(4分)如图,DE∥BC,BE平分∠ABC,若∠1=70°,则∠CBE的度数为()A.20°B.35°C.55°D.70°5.(4分)实数a、b在数轴上的对应点的位置如图所示,下列关系式不成立的是()A.a﹣5>b﹣5B.6a>6b C.﹣a>﹣b D.a﹣b>06.(4分)下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是()A.赵爽弦图B.笛卡尔心形线C.科克曲线D.斐波那契螺旋线7.(4分)化简+的结果是()A.x﹣2B.C.D.8.(4分)在学校的体育训练中,小杰投掷实心球的7次成绩如统计图所示,则这7次成绩的中位数和平均数分别是()A.9.7m,9.9m B.9.7m,9.8m C.9.8m,9.7m D.9.8m,9.9m 9.(4分)函数y=﹣ax+a与y=(a≠0)在同一坐标系中的图象可能是()A.B.C.D.10.(4分)如图,在菱形ABCD中,点E是BC的中点,以C为圆心、CE为半径作弧,交CD于点F,连接AE、AF.若AB=6,∠B=60°,则阴影部分的面积为()A.9﹣3πB.9﹣2πC.18﹣9πD.18﹣6π11.(4分)某数学社团开展实践性研究,在大明湖南门A测得历下亭C在北偏东37°方向,继续向北走105m后到达游船码头B,测得历下亭C在游船码头B的北偏东53°方向.请计算一下南门A与历下亭C之间的距离约为()(参考数据:tan37°≈,tan53°≈)A.225m B.275m C.300m D.315m12.(4分)关于x的一元二次方程ax2+bx+=0有一个根是﹣1,若二次函数y=ax2+bx+的图象的顶点在第一象限,设t=2a+b,则t的取值范围是()A.<t<B.﹣1<t≤C.﹣≤t<D.﹣1<t<二、填空题:(本大题共6个小题,每小题4分,共24分.)13.(4分)分解因式:m2﹣4m+4=.14.(4分)如图,一个可以自由转动的转盘,被分成了6个相同的扇形,转动转盘,转盘停止时,指针落在红色区域的概率等于.15.(4分)一个n边形的内角和等于720°,则n=.16.(4分)代数式与代数式3﹣2x的和为4,则x=.17.(4分)某市为提倡居民节约用水,自今年1月1日起调整居民用水价格.图中l1、l2分别表示去年、今年水费y(元)与用水量x(m3)之间的关系.小雨家去年用水量为150m3,若今年用水量与去年相同,水费将比去年多元.18.(4分)如图,在矩形纸片ABCD中,将AB沿BM翻折,使点A落在BC上的点N处,BM为折痕,连接MN;再将CD沿CE翻折,使点D恰好落在MN上的点F处,CE为折痕,连接EF并延长交BM于点P,若AD=8,AB=5,则线段PE的长等于.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.)19.(6分)计算:()﹣1+(π+1)0﹣2cos60°+20.(6分)解不等式组,并写出它的所有整数解.21.(6分)如图,在▱ABCD中,E、F分别是AD和BC上的点,∠DAF=∠BCE.求证:BF=DE.22.(8分)为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买A种图书花费了3000元,购买B种图书花费了1600元,A种图书的单价是B种图书的1.5倍,购买A种图书的数量比B种图书多20本.(1)求A和B两种图书的单价;(2)书店在“世界读书日”进行打折促销活动,所有图书都按8折销售学校当天购买了A种图书20本和B种图书25本,共花费多少元?23.(8分)如图,AB、CD是⊙O的两条直径,过点C的⊙O的切线交AB的延长线于点E,连接AC、BD.(1)求证;∠ABD=∠CAB;(2)若B是OE的中点,AC=12,求⊙O的半径.24.(10分)某学校八年级共400名学生,为了解该年级学生的视力情况,从中随机抽取40名学生的视力数据作为样本,数据统计如下:4.2 4.1 4.7 4.1 4.3 4.3 4.4 4.6 4.15.25.2 4.5 5.0 4.5 4.3 4.4 4.8 5.3 4.5 5.24.4 4.2 4.35.3 4.9 5.2 4.9 4.8 4.6 5.14.2 4.4 4.5 4.1 4.55.1 4.4 5.0 5.2 5.3根据数据绘制了如下的表格和统计图:等级视力(x)频数频率A x<4.240.1B 4.2≤x≤4.4120.3C 4.5≤x≤4.7aD 4.8≤x≤5.0bE 5.1≤x≤5.3100.25合计401根据上面提供的信息,回答下列问题:(1)统计表中的a=,b=;(2)请补全条形统计图;(3)根据抽样调查结果,请估计该校八年级学生视力为“E级”的有多少人?(4)该年级学生会宣传部有2名男生和2名女生,现从中随机挑选2名同学参加“防控近视,爱眼护眼”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.25.(10分)如图1,点A(0,8)、点B(2,a)在直线y=﹣2x+b上,反比例函数y=(x >0)的图象经过点B.(1)求a和k的值;(2)将线段AB向右平移m个单位长度(m>0),得到对应线段CD,连接AC、BD.①如图2,当m=3时,过D作DF⊥x轴于点F,交反比例函数图象于点E,求的值;②在线段AB运动过程中,连接BC,若△BCD是以BC为腰的等腰三形,求所有满足条件的m的值.26.(12分)小圆同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.(一)猜测探究在△ABC中,AB=AC,M是平面内任意一点,将线段AM绕点A按顺时针方向旋转与∠BAC相等的角度,得到线段AN,连接NB.(1)如图1,若M是线段BC上的任意一点,请直接写出∠NAB与∠MAC的数量关系是,NB与MC的数量关系是;(2)如图2,点E是AB延长线上点,若M是∠CBE内部射线BD上任意一点,连接MC,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由.(二)拓展应用如图3,在△A1B1C1中,A1B1=8,∠A1B1C1=60°,∠B1A1C1=75°,P是B1C1上的任意点,连接A1P,将A1P绕点A1按顺时针方向旋转75°,得到线段A1Q,连接B1Q.求线段B1Q长度的最小值.27.(12分)如图1,抛物线C:y=ax2+bx经过点A(﹣4,0)、B(﹣1,3)两点,G是其顶点,将抛物线C绕点O旋转180°,得到新的抛物线C′.(1)求抛物线C的函数解析式及顶点G的坐标;(2)如图2,直线l:y=kx﹣经过点A,D是抛物线C上的一点,设D点的横坐标为m(m<﹣2),连接DO并延长,交抛物线C′于点E,交直线l于点M,若DE=2EM,求m的值;(3)如图3,在(2)的条件下,连接AG、AB,在直线DE下方的抛物线C上是否存在点P,使得∠DEP=∠GAB?若存在,求出点P的横坐标;若不存在,请说明理由.2019年山东省济南市中考数学试卷参考答案与试题解析一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(4分)﹣7的相反数是()A.﹣7B.﹣C.7D.1【分析】根据相反数的概念解答即可.【解答】解:﹣7的相反数为7,故选:C.【点评】本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“﹣”号;一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.2.(4分)以下给出的几何体中,主视图是矩形,俯视图是圆的是()A.B.C.D.【分析】根据几何体的正面看得到的图形,可得答案.【解答】解:A、主视图是圆,俯视图是圆,故A不符合题意;B、主视图是矩形,俯视图是矩形,故B不符合题意;C、主视图是三角形,俯视图是圆,故C不符合题意;D、主视图是个矩形,俯视图是圆,故D符合题意;故选:D.【点评】本题考查了简单几何体的三视图,熟记简单几何的三视图是解题关键.3.(4分)2019年1月3日,“嫦娥四号”探测器成功着陆在月球背面东经177.6度、南纬45.5度附近,实现了人类首次在月球背面软着陆.数字177.6用科学记数法表示为()A.0.1776×103B.1.776×102C.1.776×103D.17.76×102【分析】用科学记数法表示较大的数时,一般形式为a×10n,其中1≤|a|<10,n为整数,据此判断即可.【解答】解:177.6=1.776×102.故选:B.【点评】此题主要考查了用科学记数法表示较大的数,一般形式为a×10n,其中1≤|a|<10,确定a与n的值是解题的关键.4.(4分)如图,DE∥BC,BE平分∠ABC,若∠1=70°,则∠CBE的度数为()A.20°B.35°C.55°D.70°【分析】根据平行线的性质可得∠1=∠ABC=70°,再根据角平分线的定义可得答案.【解答】解:∵DE∥BC,∴∠1=∠ABC=70°,∵BE平分∠ABC,∴∠CBE=∠ABC=35°,故选:B.【点评】此题主要考查了平行线的性质,以及角平分线的定义,关键是掌握两直线平行,内错角相等.5.(4分)实数a、b在数轴上的对应点的位置如图所示,下列关系式不成立的是()A.a﹣5>b﹣5B.6a>6b C.﹣a>﹣b D.a﹣b>0【分析】根据数轴判断出a、b的正负情况以及绝对值的大小,然后解答即可.【解答】解:由图可知,b<0<a,且|b|<|a|,∴a﹣5>b﹣5,6a>6b,﹣a<﹣b,a﹣b>0,∴关系式不成立的是选项C.故选:C.【点评】本题考查了实数与数轴,实数的大小比较,利用了两个负数相比较,绝度值大的反而小.6.(4分)下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是()A.赵爽弦图B.笛卡尔心形线C.科克曲线D.斐波那契螺旋线【分析】根据把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心;如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.【解答】解:A、不是轴对称图形,是中心对称图形,故此选项错误;B、是轴对称图形,不是中心对称图形,故此选项错误;C、是轴对称图形,是中心对称图形,故此选项正确;D、不是轴对称图形,不是中心对称图形,故此选项错误;故选:C.【点评】此题主要考查了轴对称图形和中心对称图形,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.7.(4分)化简+的结果是()A.x﹣2B.C.D.【分析】原式通分并利用同分母分式的加法法则计算即可求出值.【解答】解:原式=+==,故选:B.【点评】本题考查分式的加减法;熟练掌握分式的运算法则,正确进行因式分解是解题的关键.8.(4分)在学校的体育训练中,小杰投掷实心球的7次成绩如统计图所示,则这7次成绩的中位数和平均数分别是()A.9.7m,9.9m B.9.7m,9.8m C.9.8m,9.7m D.9.8m,9.9m 【分析】将这7个数据从小到大排序后处在第4位的数是中位数,利用算术平均数的计算公式进行计算即可.【解答】解:把这7个数据从小到大排列处于第4位的数是9.7m,因此中位数是9.7m,平均数为:(9.5+9.6+9.7+9.7+9.8+10.1+10.2)÷7=9.8m,故选:B.【点评】考查中位数、算术平均数的计算方法,将一组数据从小到大排列后处在中间位置的一个数或两个数的平均数就是这组数据的中位数,平均数则是反映一组数据的集中水平.9.(4分)函数y=﹣ax+a与y=(a≠0)在同一坐标系中的图象可能是()A.B.C.D.【分析】根据反比例函数与一次函数的图象特点解答即可.【解答】解:a>0时,﹣a<0,y=﹣ax+a在一、二、四象限,y=在一、三象限,无选项符合.a<0时,﹣a>0,y=﹣ax+a在一、三、四象限,y=(a≠0)在二、四象限,只有D 符合;故选:D.【点评】本题主要考查了反比例函数的图象性质和一次函数的图象性质,关键是由a的取值确定函数所在的象限.10.(4分)如图,在菱形ABCD中,点E是BC的中点,以C为圆心、CE为半径作弧,交CD于点F,连接AE、AF.若AB=6,∠B=60°,则阴影部分的面积为()A.9﹣3πB.9﹣2πC.18﹣9πD.18﹣6π【分析】连接AC,根据菱形的性质求出∠BCD和BC=AB=6,求出AE长,再根据三角形的面积和扇形的面积求出即可.【解答】解:连接AC,∵四边形ABCD是菱形,∴AB=BC=6,∵∠B=60°,E为BC的中点,∴CE=BE=3=CF,△ABC是等边三角形,AB∥CD,∵∠B=60°,∴∠BCD=180°﹣∠B=120°,由勾股定理得:AE==3,∴S△AEB=S△AEC=×6×3×=4.5=S△AFC,∴阴影部分的面积S=S△AEC+S△AFC﹣S扇形CEF=4.5+4.5﹣=9﹣3π,故选:A.【点评】本题考查了等边三角形的性质和判定,菱形的性质,扇形的面积计算等知识点,能求出△AEC、△AFC和扇形ECF的面积是解此题的关键.11.(4分)某数学社团开展实践性研究,在大明湖南门A测得历下亭C在北偏东37°方向,继续向北走105m后到达游船码头B,测得历下亭C在游船码头B的北偏东53°方向.请计算一下南门A与历下亭C之间的距离约为()(参考数据:tan37°≈,tan53°≈)A.225m B.275m C.300m D.315m【分析】如图,作CE⊥BA于E.设EC=xm,BE=ym.构建方程组求出x,y即可解决问题.【解答】解:如图,作CE⊥BA于E.设EC=xm,BE=ym.在Rt△ECB中,tan53°=,即=,在Rt△AEC中,tan37°=,即=,解得x=180,y=135,∴AC===300(m),故选:C.【点评】本题考查解直角三角形的应用﹣方向角等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,学会利用参数构建方程组解决问题,属于中考常考题型.12.(4分)关于x的一元二次方程ax2+bx+=0有一个根是﹣1,若二次函数y=ax2+bx+的图象的顶点在第一象限,设t=2a+b,则t的取值范围是()A.<t<B.﹣1<t≤C.﹣≤t<D.﹣1<t<【分析】二次函数的图象过点(﹣1,0),则a﹣b+=0,而t=2a+b,则a=,b =,二次函数的图象的顶点在第一象限,则﹣>0,﹣>0,即可求解.【解答】解:∵关于x的一元二次方程ax2+bx+=0有一个根是﹣1,∴二次函数y=ax2+bx+的图象过点(﹣1,0),∴a﹣b+=0,∴b=a+,t=2a+b,则a=,b=,∵二次函数y=ax2+bx+的图象的顶点在第一象限,∴﹣>0,﹣>0,将a=,b=代入上式得:>0,解得:﹣1<t<,﹣>0,解得:t或1<t<3,故:﹣1<t<,故选:D.【点评】主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用二、填空题:(本大题共6个小题,每小题4分,共24分.)13.(4分)分解因式:m2﹣4m+4=(m﹣2)2.【分析】原式利用完全平方公式分解即可.【解答】解:原式=(m﹣2)2,故答案为:(m﹣2)2【点评】此题考查了因式分解﹣运用公式法,熟练掌握完全平方公式是解本题的关键.14.(4分)如图,一个可以自由转动的转盘,被分成了6个相同的扇形,转动转盘,转盘停止时,指针落在红色区域的概率等于.【分析】首先确定在图中红色区域的面积在整个面积中占的比例,根据这个比例即可求出指针落在红色区域的概率.【解答】解:由于一个圆平均分成6个相等的扇形,而转动的转盘又是自由停止的,所以指针指向每个扇形的可能性相等,即有8种等可能的结果,在这6种等可能结果中,指针指向红色部分区域的有2种可能结果,所以指针落在红色区域的概率是=;故答案为.【点评】此题考查了概率公式,用到的知识点为:概率=相应的面积与总面积之比.15.(4分)一个n边形的内角和等于720°,则n=6.【分析】多边形的内角和可以表示成(n﹣2)•180°,依此列方程可求解.【解答】解:依题意有:(n﹣2)•180°=720°,解得n=6.故答案为:6.【点评】本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.16.(4分)代数式与代数式3﹣2x的和为4,则x=﹣1.【分析】根据题意列出方程,求出方程的解即可得到x的值.【解答】解:根据题意得:+3﹣2x=4,去分母得:2x﹣1+9﹣6x=12,移项合并得:﹣4x=4,解得:x=﹣1,故答案为:﹣1【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.17.(4分)某市为提倡居民节约用水,自今年1月1日起调整居民用水价格.图中l1、l2分别表示去年、今年水费y(元)与用水量x(m3)之间的关系.小雨家去年用水量为150m3,若今年用水量与去年相同,水费将比去年多210元.【分析】根据函数图象中的数据可以求得x>120时,l2对应的函数解析式,从而可以求得x=150时对应的函数值,由l1的的图象可以求得x=150时对应的函数值,从而可以计算出题目中所求问题的答案,本题得以解决.【解答】解:设当x>120时,l2对应的函数解析式为y=kx+b,,得,即当x>120时,l2对应的函数解析式为y=6x﹣240,当x=150时,y=6×150﹣240=660,由图象可知,去年的水价是480÷160=3(元/m3),故小雨家去年用水量为150m3,需要缴费:150×3=450(元),660﹣450=210(元),即小雨家去年用水量为150m3,若今年用水量与去年相同,水费将比去年多210元,故答案为:210.【点评】本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.18.(4分)如图,在矩形纸片ABCD中,将AB沿BM翻折,使点A落在BC上的点N处,BM为折痕,连接MN;再将CD沿CE翻折,使点D恰好落在MN上的点F处,CE为折痕,连接EF并延长交BM于点P,若AD=8,AB=5,则线段PE的长等于.【分析】根据折叠可得ABNM是正方形,CD=CF=5,∠D=∠CFE=90°,ED=EF,可求出三角形FNC的三边为3,4,5,在Rt△MEF中,由勾股定理可以求出三边的长,通过作辅助线,可证△FNC∽△PGF,三边占比为3:4:5,设未知数,通过PG=HN,列方程求出待定系数,进而求出PF的长,然后求PE的长.【解答】解:过点P作PG⊥FN,PH⊥BN,垂足为G、H,由折叠得:ABNM是正方形,AB=BN=NM=MA=5,CD=CF=5,∠D=∠CFE=90°,ED=EF,∴NC=MD=8﹣5=3,在Rt△FNC中,FN==4,∴MF=5﹣4=1,在Rt△MEF中,设EF=x,则ME=3﹣x,由勾股定理得,12+(3﹣x)2=x2,解得:x=,∵∠CFN+∠PFG=90°,∠PFG+∠FPG=90°,∴△FNC∽△PGF,∴FG:PG:PF=NC:FN:FC=3:4:5,设FG=3m,则PG=4m,PF=5m,∴GN=PH=BH=4﹣3m,HN=5﹣(4﹣3m)=1+3m=PG=4m,解得:m=1,∴PF=5m=5,∴PE=PF+FE=5+=,故答案为:.【点评】考查折叠轴对称的性质,矩形、正方形的性质,直角三角形的性质等知识,知识的综合性较强,是有一定难度的题目.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.)19.(6分)计算:()﹣1+(π+1)0﹣2cos60°+【分析】首先计算乘方、开方,然后计算乘法,最后从左向右依次计算,求出算式的值是多少即可.【解答】解:()﹣1+(π+1)0﹣2cos60°+=2+1﹣2×+3=3﹣1+3=5【点评】此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.20.(6分)解不等式组,并写出它的所有整数解.【分析】先求出不等式的解集,再求出不等式组的解集,即可得出答案.【解答】解:解①得:x≤4;解②得:x>2;∴原不等式组的解集为2<x≤4;∴原不等式组的所有整数解为3、4.【点评】本题考查了解一元一次不等式组,一元一次不等式的应用,解此题的关键是能根据不等式的解集求出不等式组的解集.21.(6分)如图,在▱ABCD中,E、F分别是AD和BC上的点,∠DAF=∠BCE.求证:BF=DE.【分析】由平行四边形的性质得出∠B=∠D,∠BAD=∠BCD,AB=CD,证出∠BAF =∠DCE,证明△ABF≌△CDE(ASA),即可得出BF=DE.【解答】证明:∵四边形ABCD是平行四边形,∴∠B=∠D,∠BAD=∠BCD,AB=CD,∵∠DAF=∠BCE,∴∠BAF=∠DCE,在△ABF和△CDE中,,∴△ABF≌△CDE(ASA),∴BF=DE.【点评】本题考查了平行四边形的性质、全等三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等是解题的关键.22.(8分)为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买A种图书花费了3000元,购买B种图书花费了1600元,A种图书的单价是B种图书的1.5倍,购买A种图书的数量比B种图书多20本.(1)求A和B两种图书的单价;(2)书店在“世界读书日”进行打折促销活动,所有图书都按8折销售学校当天购买了A种图书20本和B种图书25本,共花费多少元?【分析】(1)设B种图书的单价为x元,则A种图书的单价为1.5x元,根据数量=总价÷单价结合花3000元购买的A种图书比花1600元购买的B种图书多20本,即可得出关于x的分式方程,解之经检验后即可得出结论;(2)根据总价=单价×数量,即可求出结论.【解答】解:(1)设B种图书的单价为x元,则A种图书的单价为1.5x元,依题意,得:﹣=20,解得:x=20,经检验,x=20是所列分式方程的解,且符合题意,∴1.5x=30.答:A种图书的单价为30元,B种图书的单价为20元.(2)30×0.8×20+20×0.8×25=880(元).答:共花费880元.【点评】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.23.(8分)如图,AB、CD是⊙O的两条直径,过点C的⊙O的切线交AB的延长线于点E,连接AC、BD.(1)求证;∠ABD=∠CAB;(2)若B是OE的中点,AC=12,求⊙O的半径.【分析】(1)根据半径相等可知∠OAC=∠OCA,∠ODB=∠OBD,再根据对顶角相等和三角形内角和定理证明∠ABD=∠CAB;(2)连接BC.由CE为⊙O的切线,可得∠OCE=90°,因为B是OE的中点,得BC =OB,又OB=OC,可知△OBC为等边三角形,∠ABC=60°,所以BC=AC=4,即⊙O的半径为4.【解答】解:(1)证明:∵AB、CD是⊙O的两条直径,∴OA=OC=OB=OD,∴∠OAC=∠OCA,∠ODB=∠OBD,∵∠AOC=∠BOD,∴∠OAC=∠OCA=∠ODB=∠OBD,即∠ABD=∠CAB;(2)连接BC.∵AB是⊙O的两条直径,∴∠ACB=90°,∵CE为⊙O的切线,∴∠OCE=90°,∵B是OE的中点,∴BC=OB,∵OB=OC,∴△OBC为等边三角形,∴∠ABC=60°,∴∠A=30°,∴BC=AC=4,∴OB=4,即⊙O的半径为4.【点评】本题考查了切线的性质、圆周角定理、含30°角的直角三角形的性质,正确的作出辅助线是解题的关键.24.(10分)某学校八年级共400名学生,为了解该年级学生的视力情况,从中随机抽取40名学生的视力数据作为样本,数据统计如下:4.2 4.1 4.7 4.1 4.3 4.3 4.4 4.6 4.15.25.2 4.5 5.0 4.5 4.3 4.4 4.8 5.3 4.5 5.24.4 4.2 4.35.3 4.9 5.2 4.9 4.8 4.6 5.14.2 4.4 4.5 4.1 4.55.1 4.4 5.0 5.2 5.3根据数据绘制了如下的表格和统计图:等级视力(x)频数频率A x<4.240.1B 4.2≤x≤4.4120.3C 4.5≤x≤4.7aD 4.8≤x≤5.0bE 5.1≤x≤5.3100.25合计401根据上面提供的信息,回答下列问题:(1)统计表中的a=8,b=0.15;(2)请补全条形统计图;(3)根据抽样调查结果,请估计该校八年级学生视力为“E级”的有多少人?(4)该年级学生会宣传部有2名男生和2名女生,现从中随机挑选2名同学参加“防控近视,爱眼护眼”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.【分析】(1)由所列数据得出a的值,继而求出C组对应的频率,再根据频率之和等于1求出b的值;(2)总人数乘以b的值求出D组对应的频数,从而补全图形;(3)利用样本估计总体思想求解可得;(4)列表得出所有等可能的情况数,找出刚好抽到一男一女的情况数,即可求出所求的概率.【解答】解:(1)由题意知C等级的频数a=8,则C组对应的频率为8÷40=0.2,∴b=1﹣(0.1+0.3+0.2+0.25)=0.15,故答案为:8、0.15;(2)D组对应的频数为40×0.15=6,补全图形如下:(3)估计该校八年级学生视力为“E级”的有400×0.25=100(人);(4)列表如下:男男女女男(男,男)(女,男)(女,男)男(男,男)(女,男)(女,男)女(男,女)(男,女)(女,女)女(男,女)(男,女)(女,女)得到所有等可能的情况有12种,其中恰好抽中一男一女的情况有8种,所以恰好选到1名男生和1名女生的概率=.【点评】本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.也考查了统计图.25.(10分)如图1,点A(0,8)、点B(2,a)在直线y=﹣2x+b上,反比例函数y=(x >0)的图象经过点B.(1)求a和k的值;(2)将线段AB向右平移m个单位长度(m>0),得到对应线段CD,连接AC、BD.①如图2,当m=3时,过D作DF⊥x轴于点F,交反比例函数图象于点E,求的值;②在线段AB运动过程中,连接BC,若△BCD是以BC为腰的等腰三形,求所有满足条件的m的值.【分析】(1)先将点A坐标代入直线AB的解析式中,求出a,进而求出点B坐标,再将点B坐标代入反比例函数解析式中即可得出结论;(2)①先确定出点D(5,4),进而求出点E坐标,进而求出DE,EF,即可得出结论;②先表示出点C,D坐标,再分两种情况:Ⅰ、当BC=CD时,判断出点B在AC的垂直平分线上,即可得出结论;Ⅱ、当BC=BD时,先表示出BC,用BC=BD建立方程求解即可得出结论.【解答】解:(1)∵点A(0,8)在直线y=﹣2x+b上,∴﹣2×0+b=8,∴b=8,∴直线AB的解析式为y=﹣2x+8,将点B(2,a)代入直线AB的解析式y=﹣2x+8中,得﹣2×2+8=a,∴a=4,∴B(2,4),将B(2,4)在反比例函数解析式y=(x>0)中,得k=xy=2×4=8;(2)①由(1)知,B(2,4),k=8,∴反比例函数解析式为y=,当m=3时,∴将线段AB向右平移3个单位长度,得到对应线段CD,∴D(2+3,4),即:D(5,4),∵DF⊥x轴于点F,交反比例函数y=的图象于点E,∴E(5,),∴DE=4﹣=,EF=,∴==;②如图,∵将线段AB向右平移m个单位长度(m>0),得到对应线段CD,∴CD=AB,AC=BD=m,∵A(0,8),B(2,4),∴C(m,8),D((m+2,4),∵△BCD是以BC为腰的等腰三形,∴Ⅰ、当BC=CD时,∴BC=AB,∴点B在线段AC的垂直平分线上,∴m=2×2=4,Ⅱ、当BC=BD时,∵B(2,4),C(m,8),∴BC=,∴=m,∴m=5,即:△BCD是以BC为腰的等腰三形,满足条件的m的值为4或5.【点评】此题是反比例函数综合题,主要考查了待定系数法,平移的性质,等腰三角形的性质,线段的垂直平分线的性质,用方程的思想解决问题是解本题的关键.26.(12分)小圆同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.(一)猜测探究在△ABC中,AB=AC,M是平面内任意一点,将线段AM绕点A按顺时针方向旋转与∠BAC相等的角度,得到线段AN,连接NB.(1)如图1,若M是线段BC上的任意一点,请直接写出∠NAB与∠MAC的数量关系是∠NAB=∠MAC,NB与MC的数量关系是NB=CM;(2)如图2,点E是AB延长线上点,若M是∠CBE内部射线BD上任意一点,连接MC,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由.(二)拓展应用如图3,在△A1B1C1中,A1B1=8,∠A1B1C1=60°,∠B1A1C1=75°,P是B1C1上的任意点,连接A1P,将A1P绕点A1按顺时针方向旋转75°,得到线段A1Q,连接B1Q.求线段B1Q长度的最小值.【分析】(一)①结论:∠NAB=∠MAC,BN=MC.根据SAS证明△NAB≌△MAC即可.②①中结论仍然成立.证明方法类似.(二)如图3中,在A1C1上截取A1N=A1Q,连接PN,作NH⊥B1C1于H,作A1M⊥B1C1于M.理由全等三角形的性质证明B1Q=PN,推出当PN的值最小时,QB1的值最小,求出HN的值即可解决问题.【解答】解:(一)(1)结论:∠NAB=∠MAC,BN=MC.理由:如图1中,∵∠MAN=∠CAB,∴∠NAB+∠BAM=∠BAM+∠MAC,∴∠NAB=∠MAC,∵AB=AC,AN=AM,∴△NAB≌△MAC(SAS),∴BN=CM.故答案为∠NAB=∠MAC,BN=CM.(2)如图2中,①中结论仍然成立.理由:∵∠MAN=∠CAB,∴∠NAB+∠BAM=∠BAM+∠MAC,∴∠NAB=∠MAC,∵AB=AC,AN=AM,∴△NAB≌△MAC(SAS),∴BN=CM.(二)如图3中,在A1C1上截取A1N=A1Q,连接PN,作NH⊥B1C1于H,作A1M⊥B1C1于M.∵∠C1A1B1=∠P A1Q,∴∠QA1B1=∠P A1N,∵A1A=A1P,A1B1=AN,∴△QA1B1≌△P A1N(SAS),∴B1Q=PN,∴当PN的值最小时,QB1的值最小,在Rt△A1B1M中,∵∠A1B1M=60°,A1B1=8,∴A1M=A1B1•sin60°=4,∵∠MA1C1=∠B1A1C1﹣∠B1A1M=75°﹣30°=45°,∴A1C1=4,∴NC1=A1C1﹣A1N=4﹣8,在Rt△NHC1,∵∠C1=45°,∴NH=4﹣4,根据垂线段最短可知,当点P与H重合时,PN的值最小,∴QB1的最小值为4﹣4.【点评】本题属于几何变换综合题,考查了全等三角形的判定和性质,等腰三角形的性质,解直角三角形,垂线段最短等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用垂线段最短解决最值问题,属于中考压轴题.27.(12分)如图1,抛物线C:y=ax2+bx经过点A(﹣4,0)、B(﹣1,3)两点,G是其顶点,将抛物线C绕点O旋转180°,得到新的抛物线C′.(1)求抛物线C的函数解析式及顶点G的坐标;(2)如图2,直线l:y=kx﹣经过点A,D是抛物线C上的一点,设D点的横坐标为m(m<﹣2),连接DO并延长,交抛物线C′于点E,交直线l于点M,若DE=2EM,求m的值;(3)如图3,在(2)的条件下,连接AG、AB,在直线DE下方的抛物线C上是否存在点P,使得∠DEP=∠GAB?若存在,求出点P的横坐标;若不存在,请说明理由.【分析】(1)运用待定系数法将A(﹣4,0)、B(﹣1,3)代入y=ax2+bx中,即可求得a和b的值和抛物线C解析式,再利用配方法将抛物线C解析式化为顶点式即可求得顶点G的坐标;(2)根据抛物线C绕点O旋转180°,可求得新抛物线C′的解析式,再将A(﹣4,0)代入y=kx﹣中,即可求得直线l解析式,根据对称性可得点E坐标,过点D作DH ∥y轴交直线l于H,过E作EK∥y轴交直线l于K,由DE=2EM,即可得=,再证明△MEK∽△MDH,即可得DH=3EK,建立方程求解即可;(3)连接BG,易证△ABG是Rt△,∠ABG=90°,可得tan∠DEP=tan∠GAB=,在x轴下方过点O作OH⊥OE,在OH上截取OH=OE=,过点E作ET⊥y轴于T,连接EH交抛物线C于点P,点P即为所求的点;通过建立方程组求解即可.。
2019年山东省青岛市中考试题含答案解析

2019年山东省青岛市中考试题解析(满分150分,考试时间120分钟)一、选择题(本大题共8小题,每小题3分,共24分)1.(2019山东青岛,1,3分)( )A .B .C .D 【答案】D【解析】只有符号不同的两个数互为相反数,D .【知识点】相反数2. (2019山东青岛,2,3分)下列四个图形中,既是轴对称图形,又是中心对称图形的是( )【答案】D【解析】解、是轴对称图形,不是中心对称图形,故选项A 错误; 不是轴对称图形,是中心对称图形,故选项B 错误; 是轴对称图形,不是中心对称图形,故选项C 错误; 既是轴对称图形,又是中心对称图形,故选项D 正确, 故选D .【知识点】轴对称图形;中心对称图形3. (2019山东青岛,3,3分)2019年1月3日,我国“嫦娥四号”月球探测器在月球背面软着陆,实现人类有史以来首次成功登陆月球背面.已知月球与地球之间的平均距离约为384000km ,把384000km 用科学记数法可以表示为( ) A .438.410km ⨯ B .53.8410km ⨯ C .60.38410km ⨯ D .63.8410km ⨯【答案】B【解析】解:科学记数法表示384 5000 3.8410km =⨯,故选B . 【知识点】科学记数法-表示较大的数4. (2019山东青岛,4,3分)计算223(2)(3)m m m m --+gg 的结果是( ) A .58m B .58m - C .68m D .45412m m -+【答案】A【解析】解:原式2342m m =g 58m =,故选A . 【知识点】幂的乘方与积的乘方;同底数幂的乘法5. (2019山东青岛,5,3分)如图,线段AB 经过O e 的圆心,AC ,BD 分别与O e 相切于点C ,D .若4AC BD ==,45A ∠=︒,则¶CD的长度为( )A .πB .2πC .D .4π【答案】B【解析】解:连接OC 、OD ,AC Q ,BD 分别与O e 相切于点C ,D . OC AC ∴⊥,OD BD ⊥, 45A ∠=︒Q , 45AOC ∴∠=︒, 4AC OC ∴==,4AC BD ==Q ,4OC OD ==, OD BD ∴=, 45BOD ∴∠=︒,180454590COD ∴∠=︒-︒-︒=︒, ∴¶CD的长度为:9042180ππ⨯=, 故选B .【知识点】弧长的计算;切线的性质;等腰直角三角形的判定和性质,6.(2019山东青岛,6,3分)如图,将线段AB 先向右平移5个单位,再将所得线段绕原点按顺时针方向旋转90︒,得到线段A B '',则点B 的对应点B '的坐标是( )A .(4,1)-B .(1,2)-C .(4,1)-D .(1,2)-【答案】D【解析】解:将线段AB 先向右平移5个单位,点(2,1)B ,连接OB ,顺时针旋转90︒,则B '对应坐标为(1,2)-,故选D .【知识点】平面直角坐标系;坐标与图形变化7. (2019山东青岛,7,3分)如图,BD 是ABC ∆的角平分线,AE BD ⊥,垂足为F .若35ABC ∠=︒,50C ∠=︒,则CDE ∠的度数为( )A .35︒B .40︒C .45︒D .50︒【答案】A【解析】解:BD Q 是ABC ∆的角平分线,AE BD ⊥,ABD EBD ∴∠=∠,AFB EFB ∠=∠, BF BF =Q ,()ABF EBF ASA ∴∆∆∽,AF EF ∴=,AB BE =, AD DE ∴=,35ABC ∠=︒Q ,50C ∠=︒, 18095BAC ABC C ∴∠=︒-∠-∠=︒, 在DAB ∆与DEB ∆中,AB BE AD DE BD BD =⎧⎪=⎪⎨=⎪⎪⎩,()ABD EAD SSS ∴∆≅∆,95BED BAD ∴∠=∠=︒,360959535145ADE ∴∠=︒-︒-︒-︒=︒, 18035CDE ADE ∴∠=︒-∠=︒, 故选A .【知识点】三角形内角和定理8. (2019山东青岛,8,3分)已知反比例函数aby x=的图象如图所示,则二次函数22y ax x =-和一次函数y bx a =+在同一平面直角坐标系中的图象可能是( )【答案】C【解析】解:Q 当0x =时,220y ax x =-=,即抛物线22y ax x =-经过原点,故A 错误; Q 反比例函数aby x=的图象在第一、三象限, 0ab ∴>,即a 、b 同号,当0a <时,抛物线22y ax x =-的对称轴10x a=<,对称轴在y 轴左边,故D 错误; 当0a >时,0b >,直线y bx a =+经过第一、二、三象限,故B 错误,C 正确. 故选C .【知识点】二次函数的图象;一次函数的图象二、填空题(本大题共6小题,每小题3分,共18分)9.(2019山东青岛,9,3分)0-=_________【答案】1.【解析】0211-=-=,故答案为1.【知识点】零指数幂;二次根式的混合运算10.(2019山东青岛,10,3分)若关于x的一元二次方程220x x m-+=有两个相等的实数根,则m的值为_________【答案】1 8【解析】解:根据题意得:△1420m=-⨯=,整理,得180m-=,解得18m=,【知识点】根的判别式11.(2019山东青岛,11,3分)射击比赛中,某队员10次射击成绩如图所示,则该队员的平均成绩是环.【答案】8.5【解析】解:该队员的平均成绩为1(16172849210)8.510⨯+⨯+⨯+⨯+⨯=(环),故答案为8.5.【知识点】条形统计图;加权平均数12.(2019山东青岛,12,3分)如图,五边形ABCDE是Oe的内接正五边形,AF是Oe的直径,则BDF∠的度数是︒.【答案】54【解析】解:连接AD,AFQ是Oe的直径,90ADF∴∠=︒,Q 五边形ABCDE 是O e 的内接正五边形,108ABC C ∴∠=∠=︒, 72ABD ∴∠=︒, 72F ABD ∴∠=∠=︒, 18FAD ∴∠=︒, 18CDF DAF ∴∠=∠=︒, 361854BDF ∴∠=︒+︒=︒, 故答案为:54.【知识点】正多边形和圆;圆周角定理13. (2019山东青岛,13,3分)如图,在正方形纸片ABCD 中,E 是CD 的中点,将正方形纸片折叠,点B 落在线段AE 上的点G 处,折痕为AF .若4AD cm =,则CF 的长为 cm .【答案】6-【解析】解:设BF x =,则FG x =,4CF x =-.在Rt ADE ∆中,利用勾股定理可得AE =.根据折叠的性质可知4AG AB ==,所以4GE =.在Rt GEF ∆中,利用勾股定理可得2224)EF x =+, 在Rt FCE ∆中,利用勾股定理可得222(4)2EF x =-+,所以22224)(4)2x x +=-+,解得2x =.则46FC x =-=-故答案为6-【知识点】正方形的性质;翻折变换(折叠问题)14.(2019山东青岛,14,3分)如图,一个正方体由27个大小相同的小立方块搭成,现从中取走若干个小立方块,得到一个新的几何体.若新几何体与原正方体的表面积相等,则最多可以取走个小立方块.【答案】4【解析】解:若新几何体与原正方体的表面积相等,则新几何体的三视图与原来的几何体的三视图相同,所以最多可以取走4个小立方块.故答案为:4【知识点】认识立体图形三、解答题(本大题共9小题,满分78分,各小题都必须写出解答过程)15.(2019山东青岛,15,4分)请用直尺、圆规作图,不写作法,但要保留作图痕迹.已知:α∠,直线l及l上两点A,B.求作:Rt ABC∆,使点C在直线l的上方,且90ABC∠=︒,BACα∠=∠.【思路分析】先作DABα∠=,再过B点作BE AB⊥,则AD与BE的交点为C点.【解题过程】解:如图,ABC∆为所作.【知识点】作图题16.(2019山东青岛,16,8分)(1)化简:22(2)m n m nnm m-+÷-;(2)解不等式组16155318x x ⎧-⎪⎨⎪-<⎩„,并写出它的正整数解.【思路分析】(1)按分式的运算顺序和运算法则计算求值; (2)先确定不等式组的解集,再求出满足条件的正整数解.【解题过程】解:(1)原式222m n m n mnm m-+-=÷2()m n mm m n -=⨯- 1m n=-; (2)16155318x x ⎧-⎪⎨⎪-<⎩①②„由①,得1x -…, 由②,得3x <.所以该不等式组的解集为:13x -<„. 所以满足条件的正整数解为:1、2.【知识点】分式的混合运算;一元一次不等式组的整数解17. (2019山东青岛,17,6分)小明和小刚一起做游戏,游戏规则如下:将分别标有数字1,2,3,4的4个小球放入一个不透明的袋子中,这些球除数字外都相同.从中随机摸出一个球记下数字后放回,再从中随机摸出一个球记下数字.若两次数字差的绝对值小于2,则小明获胜,否则小刚获胜.这个游戏对两人公平吗?请说明理由.【思路分析】列表得出所有等可能的情况数,找出两次数字差的绝对值小于2的情况数,分别求出两人获胜的概率,比较即可得到游戏公平与否. 【解题过程】解:这个游戏对双方不公平. 理由:列表如下:所有等可能的情况有16种,其中两次数字差的绝对值小于2的情况有(1,1),(2,1),(1,2),(2,2),(3,2),(2,3),(3,3),(4,3),(3,4),(4,4)共10种,故小明获胜的概率为:105168=,则小刚获胜的概率为:63168=,Q5388≠, ∴这个游戏对两人不公平.【知识点】游戏公平吗18. (2019山东青岛,18,6分)为了解学生每天的睡眠情况,某初中学校从全校800名学生中随机抽取了40名学生,调查了他们平均每天的睡眠时间(单位:)h ,统计结果如下:9,8,10.5,7,9,8,10,9.5,8,9,9.5,7.5,9.5,9,8.5,7.5,10,9.5,8,9,7,9.5,8.5,9,7,9,9,7.5,8.5,8.5,9,8,7.5,9.5,10,9.5,8.5,9,8,9. 在对这些数据整理后,绘制了如下的统计图表: 睡眠时间分组统计表睡眠时间分布情况请根据以上信息,解答下列问题:(1)m = ,n = ,a = ,b = ;(2)抽取的这40名学生平均每天睡眠时间的中位数落在 组(填组别);(3)如果按照学校要求,学生平均每天的睡眠时间应不少于9h ,请估计该校学生中睡眠时间符合要求的人数.【思路分析】(1)根据40名学生平均每天的睡眠时间即可得出结果; (2)由中位数的定义即可得出结论;(3)由学校总人数⨯该校学生中睡眠时间符合要求的人数所占的比例,即可得出结果. 【解题过程】解:(1)78t <„时,频数为7m =;910t <„时,频数为18n =;7100%17.5%40a ∴=⨯=;18100%45%40b =⨯=; 故答案为:7,18,17.5%,45%;(2)由统计表可知,抽取的这40名学生平均每天睡眠时间的中位数为第20个和第21个数据的平均数,∴落在第3组;故答案为:3;(3)该校学生中睡眠时间符合要求的人数为18480044040+⨯=(人); 答:估计该校学生中睡眠时间符合要求的人数为440人.【知识点】算术平均数;频数(率)分布表;用样本估计总体;中位数;扇形统计图19.(2019山东青岛,19,6分)如图,某旅游景区为方便游客,修建了一条东西走向的木栈道AB ,栈道AB 与景区道路CD 平行.在C 处测得栈道一端A 位于北偏西42︒方向,在D 处测得栈道另一端B 位于北偏西32︒方向.已知120CD m =,80BD m =,求木栈道AB 的长度(结果保留整数). (参考数据:17sin3232︒≈,17cos3220︒≈,5tan328︒≈,27sin 4240︒≈,3cos 424︒≈,9tan 42)10︒≈【思路分析】过C 作CE AB ⊥于E ,DF AB ⊥交AB 的延长线于F ,于是得到//CE DF ,推出四边形CDFE 是矩形,得到120EF CD ==,DF CE =,解直角三角形即可得到结论. 【解题过程】解:过C 作CE AB ⊥于E ,DF AB ⊥交AB 的延长线于F , 则//CE DF ,//AB CD Q ,∴四边形CDFE 是矩形,120EF CD ∴==,DF CE =,在Rt BDF ∆中,32BDF ∠=︒Q ,80BD =, 17cos32806820DF BD ∴=︒=⨯≈g ,1785sin3280322BF BD =︒=⨯≈g , 1552BE EF BF ∴=-=, 在Rt ACE ∆中,42ACE ∠=︒Q ,68CE DF ==, 9306tan 4268105AE CE ∴=︒=⨯=g ,155********AB AE BE m ∴=+=+≈, 答:木栈道AB 的长度约为134m .【知识点】解直角三角形的应用-方向角问题20. (2019山东青岛,20,8分)甲、乙两人加工同一种零件,甲每天加工的数量是乙每天加工数量的1.5倍,两人各加工600个这种零件,甲比乙少用5天.(1)求甲、乙两人每天各加工多少个这种零件?(2)已知甲、乙两人加工这种零件每天的加工费分别是150元和120元,现有3000个这种零件的加工任务,甲单独加工一段时间后另有安排,剩余任务由乙单独完成.如果总加工费不超过7800元,那么甲至少加工了多少天?【思路分析】(1)设乙每天加工x 个零件,则甲每天加工1.5x 个零件,根据甲比乙少用5天,列分式方程求解;(2)设甲加工了x 天,乙加工了y 天,根据3000个零件,列方程;根据总加工费不超过7800元,列不等式,方程和不等式综合考虑求解即可.【解题过程】解:(1)设乙每天加工x 个零件,则甲每天加工1.5x 个零件,由题意得:60060051.5x x=+ 化简得600 1.56005 1.5x ⨯=+⨯解得40x = 1.560x ∴=经检验,40x =是分式方程的解且符合实际意义.答:甲每天加工60个零件,乙每天加工,40个零件.(2)设甲加工了x 天,乙加工了y 天,则由题意得604030001501207800x y x y +=⎧⎨+⎩①②„ 由①得75 1.5y x =-③将③代入②得150120(75 1.5)7800x x +-„解得40x …,当40x =时,15y =,符合问题的实际意义.答:甲至少加工了40天.【知识点】一元一次不等式的应用;分式方程的应用21. (2019山东青岛,21,8分)如图,在ABCD Y 中,对角线AC 与BD 相交于点O ,点E ,F 分别为OB ,OD 的中点,延长AE 至G ,使EG AE =,连接CG .(1)求证:ABE CDF ∆≅∆;(2)当AB 与AC 满足什么数量关系时,四边形EGCF 是矩形?请说明理由.【思路分析】(1)由平行四边形的性质得出AB CD =,//AB CD ,OB OD =,OA OC =,由平行线的性质得出ABE CDF ∠=∠,证出BE DF =,由SAS 证明ABE CDF ∆≅∆即可;(2)证出AB OA =,由等腰三角形的性质得出AG OB ⊥,90OEG ∠=︒,同理:CF OD ⊥,得出//EG CF ,由三角形中位线定理得出//OE CG ,//EF CG ,得出四边形EGCF 是平行四边形,即可得出结论.【解题过程】解:(1)证明:Q 四边形ABCD 是平行四边形,AB CD ∴=,//AB CD ,OB OD =,OA OC =,ABE CDF ∴∠=∠,Q 点E ,F 分别为OB ,OD 的中点,12BE OB ∴=,12DF OD =, BE DF ∴=,在ABE ∆和CDF ∆中,AB CD BAE CDFBE DF =⎧⎪∠=∠⎨⎪=⎩,()ABE CDF SAS ∴∆≅∆;(2)解:当2AC AB =时,四边形EGCF 是矩形;理由如下:2AC OA =Q ,2AC AB =,AB OA ∴=,E Q 是OB 的中点,AG OB ∴⊥,90OEG ∴∠=︒,同理:CF OD ⊥,//AG CF ∴,//EG CF ∴,EG AE =Q ,OA OC =,OE ∴是ACG ∆的中位线,//OE CG ∴,//EF CG ∴,∴四边形EGCF 是平行四边形,90OEG ∠=︒Q ,∴四边形EGCF 是矩形.【知识点】全等三角形的判定与性质;平行四边形的性质;矩形的判定;三角形中位线定理22. (2019山东青岛,22,10分)某商店购进一批成本为每件30元的商品,经调查发现,该商品每天的销售量y (件)与销售单价x (元)之间满足一次函数关系,其图象如图所示.(1)求该商品每天的销售量y 与销售单价x 之间的函数关系式;(2)若商店按单价不低于成本价,且不高于50元销售,则销售单价定为多少,才能使销售该商品每天获得的利润w (元)最大?最大利润是多少?(3)若商店要使销售该商品每天获得的利润不低于800元,则每天的销售量最少应为多少件?【思路分析】(1)将点(30,150)、(80,100)代入一次函数表达式,即可求解;(2)由题意得2(30)(2160)2(55)1250w x x x =--+=--+,即可求解;(3)由题意得(30)(2160)800x x --+…,解不等式即可得到结论. 【解题过程】解:(1)设y 与销售单价x 之间的函数关系式为:y kx b =+,将点(30,100)、(45,70)代入一次函数表达式得:100307045k b k b =+⎧⎨=+⎩, 解得:2160k b =-⎧⎨=⎩, 故函数的表达式为:2160y x =-+;(2)由题意得:2(30)(2160)2(55)1250w x x x =--+=--+,20-<Q ,故当55x <时,w 随x 的增大而增大,而3050x 剟, ∴当50x =时,w 由最大值,此时,1200w =,故销售单价定为50元时,该超市每天的利润最大,最大利润1200元;(3)由题意得:(30)(2160)800x x --+…,解得:70x „,∴每天的销售量216020y x =-+…,∴每天的销售量最少应为20件.【知识点】二次函数的应用23. (2019山东青岛,23,10分)问题提出:如图,图①是一张由三个边长为1的小正方形组成的“L ”形纸片,图②是一张a b ⨯的方格纸(a b ⨯的方格纸指边长分别为a ,b 的矩形,被分成a b ⨯个边长为1的小正方形,其中2a …,2b …,且a ,b 为正整数).把图①放置在图②中,使它恰好盖住图②中的三个小正方形,共有多少种不同的放置方法?问题探究:为探究规律,我们采用一般问题特殊化的策略,先从最简单的情形入手,再逐次递进,最后得出一般性的结论. 探究一:把图①放置在22⨯的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图③,对于22⨯的方格纸,要用图①盖住其中的三个小正方形,显然有4种不同的放置方法.探究二:把图①放置在32⨯的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图④,在32⨯的方格纸中,共可以找到2个位置不同的 2 2⨯方格,依据探究一的结论可知,把图①放置在32⨯的方格纸中,使它恰好盖住其中的三个小正方形,共有248⨯=种不同的放置方法.探究三:把图①放置在2a ⨯的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图⑤,在2a ⨯的方格纸中,共可以找到 个位置不同的22⨯方格,依据探究一的结论可知,把图①放置在2a ⨯的方格纸中,使它恰好盖住其中的三个小正方形,共有 种不同的放置方法.探究四:把图①放置在3a ⨯的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图⑥,在3a ⨯的方格纸中,共可以找到 个位置不同的22⨯方格,依据探究一的结论可知,把图①放置在3a ⨯的方格纸中,使它恰好盖住其中的三个小正方形,共有 种不同的放置方法.⋯⋯问题解决:把图①放置在a b ⨯的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?(仿照前面的探究方法,写出解答过程,不需画图.)问题拓展:如图,图⑦是一个由4个棱长为1的小立方体构成的几何体,图⑧是一个长、宽、高分别为a ,b ,(2c a …,2b …,2c …,且a ,b ,c 是正整数)的长方体,被分成了a b c ⨯⨯个棱长为1的小立方体.在图⑧的不同位置共可以找到 个图⑦这样的几何体.【思路分析】对于图形的变化类的规律题,首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.【解题过程】解:探究三:根据探究二,2a ⨯的方格纸中,共可以找到(1)a -个位置不同的22⨯方格,根据探究一结论可知,每个22⨯方格中有4种放置方法,所以在2a ⨯的方格纸中,共可以找到(1)4(44)a a -⨯=-种不同的放置方法;故答案为1a -,44a -;探究四:与探究三相比,本题矩形的宽改变了,可以沿用上一问的思路:边长为a ,有(1)a -条边长为2的线段, 同理,边长为3,则有312-=条边长为2的线段,所以在3a ⨯的方格中,可以找到2(1)(22)a a -=-个位置不同的22⨯方格,根据探究一,在在3a ⨯的方格纸中,使它恰好盖住其中的三个小正方形,共有(22)4(88)a a -⨯=-种不同的放置方法.故答案为22a -,88a -;问题解决:在a b ⨯的方格纸中,共可以找到(1)(1)a b --个位置不同的22⨯方格,依照探究一的结论可知,把图①放置在a b ⨯的方格纸中,使它恰好盖住其中的三个小正方形,共有4(1)(1)a b --种不同的放置方法;问题拓展:发现图⑦示是棱长为2的正方体中的一部分,利用前面的思路,这个长方体的长宽高分别为a 、b 、c ,则分别可以找到(1)a -、(1)b -、(1)c -条边长为2的线段,所以在a b c ⨯⨯的长方体共可以找到(1)(1)(1)a b c ---位置不同的222⨯⨯的正方体,再根据探究一类比发现,每个222⨯⨯的正方体有8种放置方法,所以在a b c ⨯⨯的长方体中共可以找到8(1)(1)(1)a b c ---个图⑦这样的几何体;故答案为8(1)(1)(1)a b c ---.【知识点】规律型24. (2019山东青岛,24,12分)已知:如图,在四边形ABCD 中,//AB CD ,90ACB ∠=︒,10AB cm =,8BC cm =,OD 垂直平分A C .点P 从点B 出发,沿BA 方向匀速运动,速度为1/cm s ;同时,点Q 从点D 出发,沿DC 方向匀速运动,速度为1/cm s ;当一个点停止运动,另一个点也停止运动.过点P 作PE AB ⊥,交BC 于点E ,过点Q 作//QF AC ,分别交AD ,OD 于点F ,G .连接OP ,EG .设运动时间为()(05)t s t <<,解答下列问题:(1)当t 为何值时,点E 在BAC ∠的平分线上?(2)设四边形PEGO 的面积为2()S cm ,求S 与t 的函数关系式;(3)在运动过程中,是否存在某一时刻t ,使四边形PEGO 的面积最大?若存在,求出t 的值;若不存在,请说明理由;(4)连接OE ,OQ ,在运动过程中,是否存在某一时刻t ,使OE OQ ⊥?若存在,求出t 的值;若不存在,请说明理由.【思路分析】(1)当点E 在BAC ∠的平分线上时,因为EP AB ⊥,EC AC ⊥,可得PE EC =,由此构建方程即可解决问题.(2)根据()OEG OPE OEG OPC PCE OEC OPEG S S S S S S S ∆∆∆∆∆∆=+=++-四边形构建函数关系式即可.(3)利用二次函数的性质解决问题即可.(4)证明EOC QOG ∠=∠,可得tan tan EOC QOG ∠=∠,推出EC GQ OC OG=,由此构建方程即可解决问题. 【解题过程】解:(1)在Rt ABC ∆中,90ACB ∠=︒Q ,10AB cm =,8BC cm =,6()AC cm ∴=,OD Q 垂直平分线段AC ,3()OC OA cm ∴==,90DOC ∠=︒,//CD AB Q ,BAC DCO ∴∠=∠,DOC ACB ∠=∠Q ,DOC BCA ∴∆∆∽, ∴AC AB BC OC CD OD ==, ∴61083CD OD==, 5()CD cm ∴=,4()OD cm =,PB t =Q ,PE AB ⊥, 易知:34PE t =,54BE t =, 当点E 在BAC ∠的平分线上时,EP AB ⊥Q ,EC AC ⊥,PE EC ∴=, ∴35844t t =-, 4t ∴=.∴当t 为4秒时,点E 在BAC ∠的平分线上.(2)如图,连接OE ,PC .()OEG OPE OEG OPC PCE OEC OPEG S S S S S S S ∆∆∆∆∆∆=+=++-四边形 141415315(4)3[3(8)(8)3(8)252524524t t t t t =-+-+---g g g g g g g g 281516(05)33t t t =-++<<. (3)存在.28568()(05)323S t t =--+<<Q , 52t ∴=时,四边形OPEG 的面积最大,最大值为683. (4)存在.如图,连接OQ .OE OQ ⊥Q ,90EOC QOC ∴∠+∠=︒,90QOC QOG ∠+∠=︒Q ,EOC QOG ∴∠=∠,tan tan EOC QOG ∴∠=∠,∴EC GQ OC OG=, ∴358544345t t t -=-, 整理得:25661600t t -+=, 解得165t =或10(舍弃) ∴当165t =秒时,OE OQ ⊥.【知识点】相似三角形的判定和性质;锐角三角函数,。
2019年中考数学试题汇编 二元一次方程组解答题部分(解析版)

1.(2019年山东省烟台市)亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?(2)若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?【分析】(1)设计划调配36座新能源客车x辆,该大学共有y名志愿者,则需调配22座新能源客车(x+4)辆,根据志愿者人数=36×调配36座客车的数量+2及志愿者人数=22×调配22座客车的数量﹣2,即可得出关于x,y的二元一次方程组,解之即可得出结论;(2)设需调配36座客车m辆,22座客车n辆,根据志愿者人数=36×调配36座客车的数量+22×调配22座客车的数量,即可得出关于m,n的二元一次方程,结合m,n均为正整数即可求出结论.【解答】解:(1)设计划调配36座新能源客车x辆,该大学共有y名志愿者,则需调配22座新能源客车(x+4)辆,依题意,得:,解得:.答:计划调配36座新能源客车6辆,该大学共有218名志愿者.(2)设需调配36座客车m辆,22座客车n辆,依题意,得:36m+22n=218,∴n=.又∵m,n均为正整数,∴.答:需调配36座客车3辆,22座客车5辆.【点评】本题考查了二元一次方程组的应用以及二元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)找准等量关系,正确列出二元一次方程.2.(2019年福建省)解方程组.【分析】方程组利用加减消元法求出解即可.【解答】解:,①+②得:3x=9,即x=3,把x=3代入①得:y=﹣2,则方程组的解为.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.3.(2019年海南省)时下正是海南百香果丰收的季节,张阿姨到“海南爱心扶贫网”上选购百香果,若购买2千克“红土”百香果和1千克“黄金”百香果需付80元,若购买1千克“红土”百香果和3千克“黄金”百香果需付115元.请问这两种百香果每千克各是多少元?【分析】设“红土”百香果每千克x元,“黄金”百香果每千克y元,由题意列出方程组,解方程组即可.【解答】解:设“红土”百香果每千克x元,“黄金”百香果每千克y元,由题意得:,解得:;答:“红土”百香果每千克25元,“黄金”百香果每千克30元.【点评】本题考查了二元一次方程组的应用以及二元一次方程组的解法;根据题意列出方程组是解题的关键.4.(2019年吉林省)问题解决糖葫芦一般是用竹签串上山楂,再蘸以冰糖制作而成.现将一些山楂分别串在若干根竹签上.如果每根竹签串5个山楂,还剩余4个山楂;如果每根竹签串8个山楂,还剩余7根竹签.这些竹签有多少根?山楂有多少个?反思归纳现有a根竹签,b个山楂.若每根竹签串c个山楂,还剩余d个山楂,则下列等式成立的是(2)(填写序号).(1)bc+d=a;(2)ac+d=b;(3)ac﹣d=b.【分析】问题解决设竹签有x根,山楂有y个,由题意得出方程组:,解方程组即可;反思归纳由每根竹签串c个山楂,还剩余d个山楂,得出ac+d=b即可.【解答】问题解决解:设竹签有x根,山楂有y个,由题意得:,解得:,答:竹签有20根,山楂有104个;反思归纳解:∵每根竹签串c个山楂,还剩余d个山楂,则ac+d=b,故答案为:(2).【点评】本题考查了二元一次方程组的应用以及二元一次方程组的解法;根据题意列出方程组是解题的关键.5.【分析】设每节火车车皮装物资x吨,每辆汽车装物资y吨,根据题意,得,求解即可;【解答】解:设每节火车车皮装物资x吨,每辆汽车装物资y吨,根据题意,得,∴,∴每节火车车皮装物资50吨,每辆汽车装物资6吨;【点评】本题考查二元一次方程组的应用;能够根据题意列出准确的方程组,并用加减消元法解方程组是关键.6.(2019年山西省)解方程组:【分析】(1)先根据二次根式的性质,特殊角的三角函数,0次幂进行计算,再合并同类二次根式;(2)用加减法进行解答便可.【解答】解:(2)①+②得,4x=﹣8,∴x=﹣2,把x=﹣2代入①得,﹣6﹣2y=﹣8,∴y=1,∴.【点评】本题是解答题的基本计算题,主要考查了实数的计算,解二元一次方程组,是基础题,要求100%得分,不能有失误.7.(2019年广西河池市)在某体育用品商店,购买30根跳绳和60个毽子共用720元,购买10根跳绳和50个毽子共用360元.(1)跳绳、毽子的单价各是多少元?(2)该店在“五•四”青年节期间开展促销活动,所有商品按同样的折数打折销售.节日期间购买100根跳绳和100个毽子只需1800元,该店的商品按原价的几折销售?【分析】(1)设跳绳的单价为x元/条,毽子的单件为y元/个,根据:购买30根跳绳和60个毽子共用720元,购买10根跳绳和50个毽子共用360元,列方程组求解即可;(2)设该店的商品按原价的x折销售,根据:购买100根跳绳和100个毽子只需1800元,列出方程求解可得.【解答】解:(1)设跳绳的单价为x元/条,毽子的单件为y元/个,可得:,解得:,答:跳绳的单价为16元/条,毽子的单件为5元/个;(2)设该店的商品按原价的x折销售,可得:(100×16+100×4)×=1800,解得:x=9,答:该店的商品按原价的9折销售.【点评】本题主要考查二元一次方程组及一元一次方程的应用,理解题意找到相等关系是解题关键.8.(2019年广东省广州市)解方程组:.【分析】运用加减消元解答即可.【解答】解:,②﹣①得,4y=2,解得y=2,把y=2代入①得,x﹣2=1,解得x=3,故原方程组的解为.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.9.(2019年湖南省益阳市)为了提高农田利用效益,某地由每年种植双季稻改为先养殖小龙虾再种植一季水稻的“虾•稻”轮作模式.某农户有农田20亩,去年开始实施“虾•稻”轮作,去年出售小龙虾每千克获得的利润为32元(利润=售价﹣成本).由于开发成本下降和市场供求关系变化,今年每千克小龙虾的养殖成本下降25%,售价下降10%,出售小龙虾每千克获得利润为30元.求去年每千克小龙虾的养殖成本与售价;【分析】设今年稻谷的亩产量为z千克,由题意列出不等式,就不等式即可.【解答】解:(1)设去年每千克小龙虾的养殖成本与售价分别为x元、y元,由题意得:,解得:;答:去年每千克小龙虾的养殖成本与售价分别为8元、40元;【点评】本题考查了二元一次方程组的应用;根据题意列出方程组或不等式是解题的关键.10(2019年山东省淄博市)“一带一路”促进了中欧贸易的发展,我市某机电公司生产的A,B两种产品在欧洲市场热销.今年第一季度这两种产品的销售总额为2060万元,总利润为1020万元(利润【分析】设A,B两种产品的销售件数分别为x件、y件;由题意列出方程组,解方程组即可.【解答】解:设A,B两种产品的销售件数分别为x件、y件;由题意得:,解得:;答:A,B两种产品的销售件数分别为160件、180件.【点评】本题考查了二元一次方程组的应用以及二元一次方程组的解法;根据题意列出方程组是解题的关键.11(2019年浙江省丽水市)解方程组【分析】根据二元一次方程组的解法,先将式子①化简,再用加减消元法(或代入消元法)求解;【解答】解:,将①化简得:﹣x+8y=5 ③,②+③,得y=1,将y=1代入②,得x=3,∴;【点评】本题考查二元一次方程组的解法;熟练掌握加减消元法或代入消元法解方程组是解题的关键.12(2019年江苏省盐城市)体育器材室有A、B两种型号的实心球,1只A型球与1只B型球的质量共7千克,3只A型球与1只B型球的质量共13千克.(1)每只A型球、B型球的质量分别是多少千克?(2)现有A型球、B型球的质量共17千克,则A型球、B型球各有多少只?【分析】(1)直接利用1只A型球与1只B型球的质量共7千克,3只A型球与1只B型球的质量共13千克得出方程求出答案;(2)利用分类讨论得出方程的解即可.【解答】解:(1)设每只A型球、B型球的质量分别是x千克、y千克,根据题意可得:,解得:,答:每只A型球的质量是3千克、B型球的质量是4千克;(2)∵现有A型球、B型球的质量共17千克,∴设A型球1个,设B型球a个,则3+4a=17,解得:a=(不合题意舍去),设A型球2个,设B型球b个,则6+4b=17,解得:b=(不合题意舍去),设A型球3个,设B型球c个,则9+4c=17,解得:c=2,设A型球4个,设B型球d个,则12+4d=17,解得:d=(不合题意舍去),设A型球5个,设B型球e个,则15+4e=17,解得:a=(不合题意舍去),综上所述:A型球、B型球各有3只、2只.【点评】此题主要考查了二元一次方程组的应用,正确分类讨论是解题关键.13(2019年湖南省怀化市)解二元一次方组:【分析】直接利用加减消元法进而解方程组即可.【解答】解:,①+②得:2x=8,解得:x=4,则4﹣3y=1,解得:y=1,故方程组的解为:.【点评】此题主要考查了解二元一次方程组,正确掌握解题方法是解题关键.14(2019年山东省潍坊市)己知关于x,y的二元一次方程组的解满足x>y,求k的取值范围.【分析】先用加减法求得x﹣y的值(用含k的式子表示),然后再列不等式求解即可.【解答】解:①﹣②得:x﹣y=5﹣k,∵x>y,∴x﹣y>0.∴5﹣k>0.解得:k<5.【点评】本题主要考查的是二元一次方程组的解,求得x﹣y的值(用含k的式子表示)是解题的关键.15(2019年浙江省温州市)某旅行团32人在景区A游玩,他们由成人、少年和儿童组成.已知儿童10人,成人比少年多12人.(1)求该旅行团中成人与少年分别是多少人?(2)因时间充裕,该团准备让成人和少年(至少各1名)带领10名儿童去另一景区B游玩.景区B的门票价格为100元/张,成人全票,少年8折,儿童6折,一名成人可以免费携带一名儿童.①若由成人8人和少年5人带队,则所需门票的总费用是多少元?②若剩余经费只有1200元可用于购票,在不超额的前提下,最多可以安排成人和少年共多少人带队?求所有满足条件的方案,并指出哪种方案购票费用最少.【分析】(1)根据题意可以列出相应的方程组,本题得以解决;(2)①根据题意可以求得由成人8人和少年5人带队,所需门票的总费用;②利用分类讨论的方法可以求得相应的方案以及花费,再比较花费多少即可解答本题.【解答】解:(1)设成人有x人,少年y人,,解得,,答:该旅行团中成人与少年分别是17人、5人;(2)①由题意可得,由成人8人和少年5人带队,则所需门票的总费用是:100×8+5×100×0.8+(10﹣8)×100×0.6=1320(元),答:由成人8人和少年5人带队,则所需门票的总费用是1320元;②设可以安排成人a人,少年b人带队,则1≤a≤17,1≤b≤5,当10≤a≤17时,若a=10,则费用为100×10+100×b×0.8≤1200,得b≤2.5,∴b的最大值是2,此时a+b=12,费用为1160元;若a=11,则费用为100×11+100×b×0.8≤1200,得b≤,∴b的最大值是1,此时a+b=12,费用为1180元;若a≥12,100a≥1200,即成人门票至少是1200元,不合题意,舍去;当1≤a<10时,若a=9,则费用为100×9+100b×0.8+100×1×0.6≤1200,得b≤3,∴b的最大值是3,a+b=12,费用为1200元;若a=8,则费用为100×8+100b×0.8+100×2×0.6≤1200,得b≤3.5,∴b的最大值是3,a+b=11<12,不合题意,舍去;同理,当a<8时,a+b<12,不合题意,舍去;综上所述,最多安排成人和少年12人带队,有三个方案:成人10人,少年2人;成人11人,少年1人;成人9人,少年3人;其中成人10人,少年2人时购票费用最少.【点评】本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质和分类讨论的数学思想解答.16(2019年甘肃省武威市、陇南市)小甘到文具超市去买文具.请你根据如图中的对话信息,求中性笔和笔记本的单价分别是多少元?【分析】根据对话分别利用总钱数得出等式求出答案.【解答】解:设中性笔和笔记本的单价分别是x元、y元,根据题意可得:,解得:,答:中性笔和笔记本的单价分别是2元、6元.【点评】此题主要考查了二元一次方程组的应用,正确得出等量关系是解题关键.17(2019年山东省枣庄市)对于实数a、b,定义关于“⊗”的一种运算:a⊗b=2a+b,例如3⊗4=2×3+4=10.(1)求4⊗(﹣3)的值;(2)若x⊗(﹣y)=2,(2y)⊗x=﹣1,求x+y的值.【分析】(1)原式利用题中的新定义计算即可求出值;(2)已知等式利用题中的新定义化简,计算即可求出所求.【解答】解:(1)根据题中的新定义得:原式=8﹣3=5;(2)根据题中的新定义化简得:,①+②得:3x+3y=﹣3,则x+y=﹣1.【点评】此题考查了解二元一次方程组,以及实数的运算,熟练掌握运算法则是解本题的关键.。
19年中考英语真题 分类 专题17.4 任务型阅读(综合任务)(第02期)(解析版)

2019年中考真题英语分项汇编专题17 任务型阅读考点4 综合任务Passage 1(2019 •山东省青岛市)Drones are like airplanes, only without a pilot. No one without a pilot’s license should be allowed to have one.Something bad or unexpected can happen when people send up a self-controlled flying machine like a drone without knowing how to really control it. Drones can become flyaways, and can be caught up on a jet stream (喷气流) and blown away. A falling drone can do much damage (损害) to buildings and people.Though drones can be harmful, they can be very helpful. At a sports event, drones can be used to give the spectators (观众) a view from above or help coaches see how their players are doing. They are also becoming a useful tool for firefighters, helping them find and fight wildfires. Drones can watch secretly on populations of animals in the wild, especially endangered ones. In some faraway places in the world, drones are the fastest way to send medicine to people who are in great need of it.Some people think drones can only be used by governments to help when needed. Others think that if rules are obeyed, there should be little risk to people and property (财产). Drone makers say drones are exciting new technology and that the future will be controlled by them.57. 用英语列举drones的两种用途。
2019年山东省菏泽市中考试题含答案解析

2019年山东省菏泽市中考试题解析(满分120分,考试时间120分钟)一、选择题(本大题共8小题,每小题3分,共24分)1.(2019山东菏泽,1,3分)下列各数中,最大的数是( )A .−12B .14C .0D .﹣2【答案】B【解析】解:﹣2<−12<0<14,则最大的数是14,故选B . 【知识点】有理数大小比较2. (2019山东菏泽,2,3分)下列图形中,既是轴对称图形,又是中心对称图形的是( )【答案】C【解析】解:A 、不是轴对称图形,是中心对称图形,故此选项错误;B 、是轴对称图形,不是中心对称图形,故此选项错误;C 、是轴对称图形,也是中心对称图形,故此选项正确;D 、不是轴对称图形,是中心对称图形,故此选项错误,故选C .【知识点】轴对称图形;中心对称图形3. (2019山东菏泽,3,3分)下列运算正确的是( )A .(﹣a 3)2=﹣a 6B .a 2•a 3=a 6C .a 8÷a 2=a 4D .3a 2﹣2a 2=a 2 【答案】D【解析】解:A 、原式=a 6,不符合题意;B 、原式=a 5,不符合题意;C 、原式=a 6,不符合题意;D 、原式=a 2,符合题意,故选D .【知识点】合并同类项;同底数幂的乘法;幂的乘方与积的乘方;同底数幂的除法4. (2019山东菏泽,4,3分)一个几何体的三视图如图所示,则这个几何体的表面积是( )A .5cm 2B .8cm 2C .9cm 2D .10cm 2【答案】D【解析】解:由题意推知几何体是长方体,长、宽、高分别1cm 、1cm 、2cm ,所以其面积为:2×(1×1+1×2+1×2)=10(cm 2),故选D .【知识点】由三视图判断几何体5. (2019山东菏泽,5,3分))已知{x =3y =−2是方程组{ax +by =2bx +ay =−3的解,则a +b 的值是( ) A .﹣1B .1C .﹣5D .5 【答案】A【解析】解:将{x =3y =−2代入{ax +by =2bx +ay =−3, 可得:{3a −2b =23b −2a =−3, 两式相加:a +b =﹣1,故选A .【知识点】二元一次方程组的解6.(2019山东菏泽,6,3分)如图,AB 是⊙O 的直径,C ,D 是⊙O 上的两点,且BC 平分∠ABD ,AD 分别与BC ,OC 相交于点E ,F ,则下列结论不一定成立的是( )A .OC ∥BDB .AD ⊥OC C .△CEF ≌△BED D .AF =FD【答案】C【解析】解:∵AB 是⊙O 的直径,BC 平分∠ABD ,∴∠ADB =90°,∠OBC =∠DBC ,∴AD ⊥BD ,∵OB =OC ,∴∠OCB =∠OBC ,∴∠DBC =∠OCB ,∴OC ∥BD ,选项A 成立;∴AD⊥OC,选项B成立;∴AF=FD,选项D成立;∵△CEF和△BED中,没有相等的边,∴△CEF与△BED不全等,选项C不成立,故选C.【知识点】圆周角定理7.(2019山东菏泽,7,3分)在平面直角坐标系中,一个智能机器人接到的指令是:从原点O出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点A1,第二次移动到点A2……第n次移动到点A n,则点A2019的坐标是()A.(1010,0)B.(1010,1)C.(1009,0)D.(1009,1)【答案】C【解析】解:A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,1),A6(3,1),…,2019÷4=504…3,所以A2019的坐标为(504×2+1,0),则A2019的坐标是(1009,0),故选C.【知识点】点的坐标规律8.(2019山东菏泽,8,3分)如图,正方形ABCD的边长为2cm,动点P,Q同时从点A出发,在正方形的边上,分别按A→D→C,A→B→C的方向,都以1cm/s的速度运动,到达点C运动终止,连接PQ,设运动时间为xs,△APQ的面积为ycm2,则下列图象中能大致表示y与x的函数关系的是()【答案】A【解析】解:①当0≤x ≤2时,∵正方形的边长为2cm ,∴y =S △APQ =12AQ •AP =12x 2;②当2≤x ≤4时,y =S △APQ =S 正方形ABCD ﹣S △CP ′Q ′﹣S △ABQ ′﹣S △AP ′D ,=2×2−12(4﹣x )2−12×2×(x ﹣2)−12×2×(x ﹣2)=−12x 2+2x∴y 与x 之间的函数关系可以用两段二次函数图象表示,纵观各选项,只有A 选项图象符合.故选A .【知识点】动点问题的函数图象二、填空题(本大题共6小题,每小题3分,共18分)9.(2019山东菏泽,9,3分)计算(12)﹣1﹣(﹣3)2的结果是_________ 【答案】﹣7【解析】解:原式=2﹣9=﹣7.【知识点】实数运算;有理数的乘方;有理数的减法;负整数指数幂10. (2019山东菏泽,10,3分)已知x =√6+√2,那么x 2﹣2√2x 的值是_________【答案】4.【解析】解:∵x −√2=√6,∴x 2﹣2√2x +2=6,∴x 2﹣2√2x =4.【知识点】二次根式的化简求值11. (2019山东菏泽,11,3分)如图,AD ∥CE ,∠ABC =100°,则∠2﹣∠1的度数是_________【答案】80° 【解析】解:作BF ∥AD ,∵AD ∥CE ,∴AD ∥BF ∥EC ,∴∠1=∠3,∠4+∠2=180°,∠3+∠4=100°,∴∠1+∠4=100°,∠2+∠4=180°,∴∠2﹣∠1=80°.故答案为:80°.【知识点】平行线的性质12. (2019山东菏泽,12,3分)一组数据4,5,6,x 的众数与中位数相等,则这组数据的方差是_________ 【答案】12【解析】解:若众数为4,则数据为4,4,5,6,此时中位数为4.5,不符合题意;若众数为5,则数据为4,5,5,6,中位数为5,符合题意,此时平均数为4+5+5+64=5,方差为14[(4﹣5)2+(5﹣5)2+(5﹣5)2+(6﹣5)2]=12; 若众数为6,则数据为4,5,6,6,中位数为5.5,不符合题意, 故答案为12. 【知识点】中位数;众数;方差13. (2019山东菏泽,13,3分)如图,E ,F 是正方形ABCD 的对角线AC 上的两点,AC =8,AE =CF =2,则四边形BEDF 的周长是 .【答案】【解析】解:如图,连接BD 交AC 于点O ,∵四边形ABCD 为正方形,∴BD ⊥AC ,OD =OB =OA =OC ,∵AE=CF=2,∴OA﹣AE=OC﹣CF,即OE=OF,∴四边形BEDF为平行四边形,且BD⊥EF,∴四边形BEDF为菱形,∴DE=DF=BE=BF,∵AC=BD=8,OE=OF=8−42=2,由勾股定理得:DE=√OD2+OE2=√42+22=2√5,∴四边形BEDF的周长=4DE=4×2√5=8√5,故答案为:【知识点】全等三角形的判定与性质;正方形的性质14.(2019山东菏泽,14,3分)如图,直线y=−34x﹣3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是.【答案】(−73,0)或P(−173,0).【解析】解:∵直线y=−34x﹣3交x轴于点A,交y轴于点B,∴令x=0,得y=﹣3,令y=0,得x=﹣4,∴A(﹣4,0),B(0.﹣3),∴OA=4,OB=3,∴AB=5,设⊙P与直线AB相切于D,连接PD,则PD⊥AB,PD=1,∵∠ADP=∠AOB=90°,∠P AD=∠BAO,∴△APD∽△ABO,∴PDOB=APAB,∴13=AP 5, ∴AP =53,∴OP =73或OP =173,∴P (−73,0)或P (−173,0), 故答案为:(−73,0)或P (−173,0).【知识点】一次函数的图象;切线的判定与性质; 相似三角形的判定和性质三、解答题(本大题共8小题,满分78分,各小题都必须写出解答过程)15. (2019山东菏泽,15,6分)解不等式组:{x −3(x −2)≥−4,x −1<2x+13. 【思路分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【解题过程】解:解不等式x ﹣3(x ﹣2)≥﹣4,得:x ≤5,解不等式x ﹣1<2x+13,得:x <4, 则不等式组的解集为x <4.【知识点】解一元一次不等式组16.(2019山东菏泽,16,6分)先化简,再求值:1x−y (2y x+y −1)÷1y 2−x 2,其中x =y +2019.【思路分析】根据分式的减法和乘除法可以化简题目中的式子,然后将x =y +2019代入化简后的式子即可解答本题.【解题过程】解:1x−y (2y x+y −1)÷1y 2−x 2 =1x−y ⋅2y−(x+y)x+y⋅(y +x)(y −x) =﹣(2y ﹣x ﹣y )=x ﹣y ,∵x =y +2019,∴原式=y +2019﹣y =2019.【知识点】分式的化简求值17.(2019山东菏泽,17,6分)如图,四边形ABCD是矩形.(1)用尺规作线段AC的垂直平分线,交AB于点E,交CD于点F(不写作法,保留作图痕迹);(2)若BC=4,∠BAC=30°,求BE的长.【思路分析】(1)根据线段的垂直平分线的作图解答即可;(2)利用含30°的直角三角形的性质解答即可.【解题过程】解:(1)如图所示:(2)∵四边形ABCD是矩形,EF是线段AC的垂直平分线,∴AE=EC,∠CAB=∠ACE=30°,∴∠ECB=60°,∴∠ECB=30°,∵BC=4,∴BE=4√3 3.【知识点】矩形的性质;线段垂直平分线的性质;作图18.(2019山东菏泽,18,6分)列方程(组)解应用题:德上高速公路巨野至单县段正在加速建设,预计2019年8月竣工.届时,如果汽车行驶高速公路上的平均速度比在普通公路上的平均速度提高80%,那么行驶81千米的高速公路比行驶同等长度的普通公路所用时间将会缩短36分钟,求该汽车在高速公路上的平均速度.【思路分析】设汽车行驶在普通公路上的平均速度是x千米/分钟,则汽车行驶在高速公路上的平均速度是1.8x 千米/分钟,根据“行驶81千米的高速公路比行驶同等长度的普通公路所用时间将会缩短36分钟”列出方程并解答.【解题过程】解:设汽车行驶在普通公路上的平均速度是x千米/分钟,则汽车行驶在高速公路上的平均速度是1.8x千米/分钟,由题意,得811.8x+36=81x.解得x=1.经检验,x=1是所列方程的根,且符合题意.所以1.8x=1.8(千米/分钟).答:汽车行驶在高速公路上的平均速度是1.8千米/分钟.【知识点】分式方程的应用19.(2019山东菏泽,19,7分)由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达A处时,测得小岛B位于它的北偏东30°方向,且与航母相距80海里再航行一段时间后到达C处,测得小岛B位于它的西北方向,求此时航母与小岛的距离BC的长.【思路分析】过点C作CD⊥AB于点D,根据题意得到∠BAD=60°,∠BCD=45°,AC=80,解直角三角形即可得到结论.【解题过程】解:过点C作CD⊥AB于点D,由题意,得:∠BAD=60°,∠BCD=45°,AC=80,在Rt△ADB中,∠BAD=60°,∴tan60°=BDAD=√3,∴AD=BD √3,在Rt△BCD中,∠BCD=45°,∴tan45°=BDCD=1,∴BD=CD,∴AC=AD+CD=BD3+BD=80,∴BD=120﹣40√3,∴BC=√2BC=120√2−40√6,答:BC的距离是(120√2−40√6)海里.【知识点】解直角三角形的应用﹣方向角问题20. (2019山东菏泽,20,7分)如图,▱ABCD 中,顶点A 的坐标是(0,2),AD ∥x 轴,BC 交y 轴于点E ,顶点C 的纵坐标是﹣4,▱ABCD 的面积是24.反比例函数y =k x的图象经过点B 和D ,求:(1)反比例函数的表达式;(2)AB 所在直线的函数表达式.【思路分析】(1)根据题意得出AE =6,结合平行四边形的面积得出AD =BC =4,继而知点D 坐标,从而得出反比例函数解析式;(2)先根据反比例函数解析式求出点B 的坐标,再利用待定系数法求解可得.【解题过程】解:(1)∵顶点A 的坐标是(0,2),顶点C 的纵坐标是﹣4,∴AE =6,又▱ABCD 的面积是24,∴AD =BC =4,则D (4,2)∴k =4×2=8,∴反比例函数解析式为y =8x ;(2)由题意知B 的纵坐标为﹣4,∴其横坐标为﹣2,则B (﹣2,﹣4),设AB 所在直线解析式为y =kx +b ,将A (0,2)、B (﹣2,﹣4)代入,得:{b =2−2k +b =−4, 解得:{k =3b =2, 所以AB 所在直线解析式为y =3x +2.【知识点】待定系数法求一次函数解析式;反比例函数系数k 的几何意义;平行四边形的性质21.(2019山东菏泽,21,10分)4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”我市某中学响应号召,鼓励师生利用课余时间广泛阅读,该校文学社发起了“读书感悟•分享”比赛活动根据参赛学生的成绩划分为A,B,C,D四个等级,并绘制了下面不完整的统计图表,根据图表中提供的信息解答下列问题;频数频率A4BC a0.3D16b(1)求a,b的值;(2)求B等级对应扇形圆心角的度数;(3)学校要从A等级的学生中随机选取2人参加市级比赛,求A等级中的学生小明被选中参加市级比赛的概率.【思路分析】(1)根据A等级有4人,所占的百分比是10%即可求得总人数,然后求得a和b的值;(2)首先计算出B等级频数,再利用360°乘以对应的百分比即可求得B等级所对应的圆心角度数;(3)利用列举法求得选中A等级的小明的概率.【解题过程】解:(1)总人数:4÷10%=40,a=40×0.3=12,b=1640=0.4;(2)B的频数:40﹣4﹣12﹣16=8,B等级对应扇形圆心角的度数:840×360°=72°;(3)用a表示小明,用b、c、d表示另外三名同学.则选中小明的概率是:612=12.【知识点】扇形统计图;频数(率)分布表;概率22.(2019山东菏泽,22,10分)如图,BC是⊙O的直径,CE是⊙O的弦,过点E作⊙O的切线,交CB的延长线于点G,过点B作BF⊥GE于点F,交CE的延长线于点A.(1)求证:∠ABG=2∠C;(2)若GF=3√3,GB=6,求⊙O的半径.【思路分析】(1)连接OE,根据切线的性质得到OE⊥EG,推出OE∥AB,得到∠A=∠OEC,根据等腰三角形的性质得到∠OEC=∠C,求得∠A=∠C,根据三角形的外角的性质即可得到结论;(2)根据勾股定理得到BF=√BG2−GF2=3,根据相似三角形的性质即可得到结论.【解题过程】解:(1)证明:连接OE,∵EG是⊙O的切线,∴OE⊥EG,∵BF⊥GE,∴OE∥AB,∴∠A=∠OEC,∵OE=OC,∴∠OEC=∠C,∴∠A=∠C,∵∠ABG=∠A+∠C,∴∠ABG=2∠C;(2)解:∵BF⊥GE,∴∠BFG=90°,∵GF=3√3,GB=6,∴BF=√BG2−GF2=3,∵BF∥OE,∴△BGF∽△OGE,∴BFOE=BGOG,∴3OE=66+OE,∴OE=6,∴⊙O的半径为6.【知识点】圆周角定理;切线的性质;相似三角形的判定和性质;等腰三角形的判定和性质23.(2019山东菏泽,23,10分)如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°.(1)如图1,连接BE,CD,BE的廷长线交AC于点F,交CD于点P,求证:BP⊥CD;(2)如图2,把△ADE绕点A顺时针旋转,当点D落在AB上时,连接BE,CD,CD的延长线交BE于点P,若BC=6√2,AD=3,求△PDE的面积.【思路分析】(1)根据等腰直角三角形的性质得到AD=AE,AB=AC,∠BAC﹣∠EAF=∠EAD﹣∠EAF,求得∠BAE=∠DAC,根据全等三角形的性质得到∠ABE=∠ACD,根据余角的性质即可得到结论;(2)根据全等三角形的性质得到∠ABE=∠ACD,BE=CD,求得∠EPD=90°,得到DE=3√2,AB=6,求得BD=6﹣3=3,CD=√AD2+AC2=3√5,根据相似三角形的性质得到PD=√55,PB=6√55根据三角形的面积公式即可得到结论.【解题过程】解:(1)∵△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°.∴AD=AE,AB=AC,∠BAC﹣∠EAF=∠EAD﹣∠EAF,即∠BAE=∠DAC,在△ABE与△ADC中,{AB=AC∠BAE=∠CAD AE=AD,∴△ABE≌△ADC(SAS),∴∠ABE=∠ACD,∵∠ABE+∠AFB=∠ABE+∠CFP=90°,∴∠CPF=90°,∴BP⊥CD;(2)在△ABE与△ACD中,{AE=AD∠EAB=∠CAB=90°AB=AC,∴△ABE≌△ACD(SAS),∴∠ABE=∠ACD,BE=CD,∵∠PDB=∠ADC,∴∠BPD=∠CAB=90°,∴∠EPD=90°,BC=6√2,AD=3,求△PDE的面积.∵BC=6√2,AD=3,∴DE=3√2,AB=6,∴BD=6﹣3=3,CD=√AD2+AC2=3√5,∵△BDP∽△CDA,∴BDCD=PDAD=PBAC,∴3√5=PD3=PB6,∴PD=3√55,PB=6√55∴PE=3√5−6√55=9√55,∴△PDE的面积=12×9√55×3√55=2710.【知识点】全等三角形的判定与性质;等腰直角三角形;旋转的性质;相似三角形的判定和性质;勾股定理24.(2019山东菏泽,24,10分)如图,抛物线与x轴交于A,B两点,与y轴交于点C(0,﹣2),点A的坐标是(2,0),P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E,抛物线的对称轴是直线x=﹣1.(1)求抛物线的函数表达式;(2)若点P 在第二象限内,且PE =14OD ,求△PBE 的面积.(3)在(2)的条件下,若M 为直线BC 上一点,在x 轴的上方,是否存在点M ,使△BDM 是以BD 为腰的等腰三角形?若存在,求出点M 的坐标;若不存在,请说明理由.【思路分析】(1)点A (2,0)、点B (﹣4,0),则函数的表达式为:y =a (x ﹣2)(x +4)=a (x 2+2x ﹣8),即可求解;(2)PE =14OD ,则PE =(14x 2+12x ﹣2−12x +2)=14(﹣x ),求得:点D (﹣5,0),利用S △PBE =12PE ×BD =12(14x 2+12x ﹣2−12x +2)(﹣4﹣x ),即可求解; (3)BD =1=BM ,则y M =﹣BM sin ∠ABC =﹣1×5=−√55,即可求解. 【解题过程】解:(1)点A 的坐标是(2,0),抛物线的对称轴是直线x =﹣1,则点B (﹣4,0), 则函数的表达式为:y =a (x ﹣2)(x +4)=a (x 2+2x ﹣8),即:﹣8a =﹣2,解得:a =14,故抛物线的表达式为:y =14x 2+12x ﹣2;(2)将点B 、C 的坐标代入一次函数表达式:y =mx +n 并解得:直线BC 的表达式为:y =−12x ﹣2,则tan ∠ABC =12,则sin ∠ABC =5, 设点D (x ,0),则点P (x ,14x 2+12x ﹣2),点E (x ,12x ﹣2), ∵PE =14OD ,∴PE =(14x 2+12x ﹣2−12x +2)=14(﹣x ), 解得:x =0或﹣5(舍去x =0),即点D (﹣5,0)S △PBE =12×PE ×BD =12(14x 2+12x ﹣2−12x +2)(﹣4﹣x )=58; (3)由题意得:△BDM 是以BD 为腰的等腰三角形,只存在:BD =BM 的情况,BD=1=BM,则y M=﹣BM sin∠ABC=﹣15=−√55,则x M=−20+2√55,故点M(−20+2√55,−√55).【知识点】二次函数综合题;数形结合;函数思想;二次函数的解析式;。
2019年山东省菏泽市中考试题含答案解析

2019年山东省菏泽市中考试题解析(满分120分,考试时间120分钟)一、选择题(本大题共8小题,每小题3分,共24分)1.(2019山东菏泽,1,3分)下列各数中,最大的数是( )A .−12B .14C .0D .﹣2【答案】B【解析】解:﹣2<−12<0<14,则最大的数是14,故选B . 【知识点】有理数大小比较2. (2019山东菏泽,2,3分)下列图形中,既是轴对称图形,又是中心对称图形的是( )【答案】C【解析】解:A 、不是轴对称图形,是中心对称图形,故此选项错误;B 、是轴对称图形,不是中心对称图形,故此选项错误;C 、是轴对称图形,也是中心对称图形,故此选项正确;D 、不是轴对称图形,是中心对称图形,故此选项错误,故选C .【知识点】轴对称图形;中心对称图形3. (2019山东菏泽,3,3分)下列运算正确的是( )A .(﹣a 3)2=﹣a 6B .a 2•a 3=a 6C .a 8÷a 2=a 4D .3a 2﹣2a 2=a 2 【答案】D【解析】解:A 、原式=a 6,不符合题意;B 、原式=a 5,不符合题意;C 、原式=a 6,不符合题意;D 、原式=a 2,符合题意,故选D .【知识点】合并同类项;同底数幂的乘法;幂的乘方与积的乘方;同底数幂的除法4. (2019山东菏泽,4,3分)一个几何体的三视图如图所示,则这个几何体的表面积是( )A .5cm 2B .8cm 2C .9cm 2D .10cm 2【答案】D【解析】解:由题意推知几何体是长方体,长、宽、高分别1cm 、1cm 、2cm ,所以其面积为:2×(1×1+1×2+1×2)=10(cm 2),故选D .【知识点】由三视图判断几何体5. (2019山东菏泽,5,3分))已知{x =3y =−2是方程组{ax +by =2bx +ay =−3的解,则a +b 的值是( ) A .﹣1B .1C .﹣5D .5 【答案】A【解析】解:将{x =3y =−2代入{ax +by =2bx +ay =−3, 可得:{3a −2b =23b −2a =−3, 两式相加:a +b =﹣1,故选A .【知识点】二元一次方程组的解6.(2019山东菏泽,6,3分)如图,AB 是⊙O 的直径,C ,D 是⊙O 上的两点,且BC 平分∠ABD ,AD 分别与BC ,OC 相交于点E ,F ,则下列结论不一定成立的是( )A .OC ∥BDB .AD ⊥OC C .△CEF ≌△BED D .AF =FD【答案】C【解析】解:∵AB 是⊙O 的直径,BC 平分∠ABD ,∴∠ADB =90°,∠OBC =∠DBC ,∴AD ⊥BD ,∵OB =OC ,∴∠OCB =∠OBC ,∴∠DBC =∠OCB ,∴OC ∥BD ,选项A 成立;∴AD⊥OC,选项B成立;∴AF=FD,选项D成立;∵△CEF和△BED中,没有相等的边,∴△CEF与△BED不全等,选项C不成立,故选C.【知识点】圆周角定理7.(2019山东菏泽,7,3分)在平面直角坐标系中,一个智能机器人接到的指令是:从原点O出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点A1,第二次移动到点A2……第n次移动到点A n,则点A2019的坐标是()A.(1010,0)B.(1010,1)C.(1009,0)D.(1009,1)【答案】C【解析】解:A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,1),A6(3,1),…,2019÷4=504…3,所以A2019的坐标为(504×2+1,0),则A2019的坐标是(1009,0),故选C.【知识点】点的坐标规律8.(2019山东菏泽,8,3分)如图,正方形ABCD的边长为2cm,动点P,Q同时从点A出发,在正方形的边上,分别按A→D→C,A→B→C的方向,都以1cm/s的速度运动,到达点C运动终止,连接PQ,设运动时间为xs,△APQ的面积为ycm2,则下列图象中能大致表示y与x的函数关系的是()【答案】A【解析】解:①当0≤x ≤2时,∵正方形的边长为2cm ,∴y =S △APQ =12AQ •AP =12x 2;②当2≤x ≤4时,y =S △APQ =S 正方形ABCD ﹣S △CP ′Q ′﹣S △ABQ ′﹣S △AP ′D ,=2×2−12(4﹣x )2−12×2×(x ﹣2)−12×2×(x ﹣2)=−12x 2+2x∴y 与x 之间的函数关系可以用两段二次函数图象表示,纵观各选项,只有A 选项图象符合.故选A .【知识点】动点问题的函数图象二、填空题(本大题共6小题,每小题3分,共18分)9.(2019山东菏泽,9,3分)计算(12)﹣1﹣(﹣3)2的结果是_________ 【答案】﹣7【解析】解:原式=2﹣9=﹣7.【知识点】实数运算;有理数的乘方;有理数的减法;负整数指数幂10. (2019山东菏泽,10,3分)已知x =√6+√2,那么x 2﹣2√2x 的值是_________【答案】4.【解析】解:∵x −√2=√6,∴x 2﹣2√2x +2=6,∴x 2﹣2√2x =4.【知识点】二次根式的化简求值11. (2019山东菏泽,11,3分)如图,AD ∥CE ,∠ABC =100°,则∠2﹣∠1的度数是_________【答案】80° 【解析】解:作BF ∥AD ,∵AD ∥CE ,∴AD ∥BF ∥EC ,∴∠1=∠3,∠4+∠2=180°,∠3+∠4=100°,∴∠1+∠4=100°,∠2+∠4=180°,∴∠2﹣∠1=80°.故答案为:80°.【知识点】平行线的性质12. (2019山东菏泽,12,3分)一组数据4,5,6,x 的众数与中位数相等,则这组数据的方差是_________ 【答案】12【解析】解:若众数为4,则数据为4,4,5,6,此时中位数为4.5,不符合题意;若众数为5,则数据为4,5,5,6,中位数为5,符合题意,此时平均数为4+5+5+64=5,方差为14[(4﹣5)2+(5﹣5)2+(5﹣5)2+(6﹣5)2]=12; 若众数为6,则数据为4,5,6,6,中位数为5.5,不符合题意, 故答案为12. 【知识点】中位数;众数;方差13. (2019山东菏泽,13,3分)如图,E ,F 是正方形ABCD 的对角线AC 上的两点,AC =8,AE =CF =2,则四边形BEDF 的周长是 .【答案】【解析】解:如图,连接BD 交AC 于点O ,∵四边形ABCD 为正方形,∴BD ⊥AC ,OD =OB =OA =OC ,∵AE=CF=2,∴OA﹣AE=OC﹣CF,即OE=OF,∴四边形BEDF为平行四边形,且BD⊥EF,∴四边形BEDF为菱形,∴DE=DF=BE=BF,∵AC=BD=8,OE=OF=8−42=2,由勾股定理得:DE=√OD2+OE2=√42+22=2√5,∴四边形BEDF的周长=4DE=4×2√5=8√5,故答案为:【知识点】全等三角形的判定与性质;正方形的性质14.(2019山东菏泽,14,3分)如图,直线y=−34x﹣3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是.【答案】(−73,0)或P(−173,0).【解析】解:∵直线y=−34x﹣3交x轴于点A,交y轴于点B,∴令x=0,得y=﹣3,令y=0,得x=﹣4,∴A(﹣4,0),B(0.﹣3),∴OA=4,OB=3,∴AB=5,设⊙P与直线AB相切于D,连接PD,则PD⊥AB,PD=1,∵∠ADP=∠AOB=90°,∠P AD=∠BAO,∴△APD∽△ABO,∴PDOB=APAB,∴13=AP 5, ∴AP =53,∴OP =73或OP =173,∴P (−73,0)或P (−173,0), 故答案为:(−73,0)或P (−173,0).【知识点】一次函数的图象;切线的判定与性质; 相似三角形的判定和性质三、解答题(本大题共8小题,满分78分,各小题都必须写出解答过程)15. (2019山东菏泽,15,6分)解不等式组:{x −3(x −2)≥−4,x −1<2x+13. 【思路分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【解题过程】解:解不等式x ﹣3(x ﹣2)≥﹣4,得:x ≤5,解不等式x ﹣1<2x+13,得:x <4, 则不等式组的解集为x <4.【知识点】解一元一次不等式组16.(2019山东菏泽,16,6分)先化简,再求值:1x−y (2y x+y −1)÷1y 2−x 2,其中x =y +2019.【思路分析】根据分式的减法和乘除法可以化简题目中的式子,然后将x =y +2019代入化简后的式子即可解答本题.【解题过程】解:1x−y (2y x+y −1)÷1y 2−x 2 =1x−y ⋅2y−(x+y)x+y⋅(y +x)(y −x) =﹣(2y ﹣x ﹣y )=x ﹣y ,∵x =y +2019,∴原式=y +2019﹣y =2019.【知识点】分式的化简求值17.(2019山东菏泽,17,6分)如图,四边形ABCD是矩形.(1)用尺规作线段AC的垂直平分线,交AB于点E,交CD于点F(不写作法,保留作图痕迹);(2)若BC=4,∠BAC=30°,求BE的长.【思路分析】(1)根据线段的垂直平分线的作图解答即可;(2)利用含30°的直角三角形的性质解答即可.【解题过程】解:(1)如图所示:(2)∵四边形ABCD是矩形,EF是线段AC的垂直平分线,∴AE=EC,∠CAB=∠ACE=30°,∴∠ECB=60°,∴∠ECB=30°,∵BC=4,∴BE=4√3 3.【知识点】矩形的性质;线段垂直平分线的性质;作图18.(2019山东菏泽,18,6分)列方程(组)解应用题:德上高速公路巨野至单县段正在加速建设,预计2019年8月竣工.届时,如果汽车行驶高速公路上的平均速度比在普通公路上的平均速度提高80%,那么行驶81千米的高速公路比行驶同等长度的普通公路所用时间将会缩短36分钟,求该汽车在高速公路上的平均速度.【思路分析】设汽车行驶在普通公路上的平均速度是x千米/分钟,则汽车行驶在高速公路上的平均速度是1.8x 千米/分钟,根据“行驶81千米的高速公路比行驶同等长度的普通公路所用时间将会缩短36分钟”列出方程并解答.【解题过程】解:设汽车行驶在普通公路上的平均速度是x千米/分钟,则汽车行驶在高速公路上的平均速度是1.8x千米/分钟,由题意,得811.8x+36=81x.解得x=1.经检验,x=1是所列方程的根,且符合题意.所以1.8x=1.8(千米/分钟).答:汽车行驶在高速公路上的平均速度是1.8千米/分钟.【知识点】分式方程的应用19.(2019山东菏泽,19,7分)由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达A处时,测得小岛B位于它的北偏东30°方向,且与航母相距80海里再航行一段时间后到达C处,测得小岛B位于它的西北方向,求此时航母与小岛的距离BC的长.【思路分析】过点C作CD⊥AB于点D,根据题意得到∠BAD=60°,∠BCD=45°,AC=80,解直角三角形即可得到结论.【解题过程】解:过点C作CD⊥AB于点D,由题意,得:∠BAD=60°,∠BCD=45°,AC=80,在Rt△ADB中,∠BAD=60°,∴tan60°=BDAD=√3,∴AD=BD √3,在Rt△BCD中,∠BCD=45°,∴tan45°=BDCD=1,∴BD=CD,∴AC=AD+CD=BD3+BD=80,∴BD=120﹣40√3,∴BC=√2BC=120√2−40√6,答:BC的距离是(120√2−40√6)海里.【知识点】解直角三角形的应用﹣方向角问题20. (2019山东菏泽,20,7分)如图,▱ABCD 中,顶点A 的坐标是(0,2),AD ∥x 轴,BC 交y 轴于点E ,顶点C 的纵坐标是﹣4,▱ABCD 的面积是24.反比例函数y =k x的图象经过点B 和D ,求:(1)反比例函数的表达式;(2)AB 所在直线的函数表达式.【思路分析】(1)根据题意得出AE =6,结合平行四边形的面积得出AD =BC =4,继而知点D 坐标,从而得出反比例函数解析式;(2)先根据反比例函数解析式求出点B 的坐标,再利用待定系数法求解可得.【解题过程】解:(1)∵顶点A 的坐标是(0,2),顶点C 的纵坐标是﹣4,∴AE =6,又▱ABCD 的面积是24,∴AD =BC =4,则D (4,2)∴k =4×2=8,∴反比例函数解析式为y =8x ;(2)由题意知B 的纵坐标为﹣4,∴其横坐标为﹣2,则B (﹣2,﹣4),设AB 所在直线解析式为y =kx +b ,将A (0,2)、B (﹣2,﹣4)代入,得:{b =2−2k +b =−4, 解得:{k =3b =2, 所以AB 所在直线解析式为y =3x +2.【知识点】待定系数法求一次函数解析式;反比例函数系数k 的几何意义;平行四边形的性质21.(2019山东菏泽,21,10分)4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”我市某中学响应号召,鼓励师生利用课余时间广泛阅读,该校文学社发起了“读书感悟•分享”比赛活动根据参赛学生的成绩划分为A,B,C,D四个等级,并绘制了下面不完整的统计图表,根据图表中提供的信息解答下列问题;频数频率A4BC a0.3D16b(1)求a,b的值;(2)求B等级对应扇形圆心角的度数;(3)学校要从A等级的学生中随机选取2人参加市级比赛,求A等级中的学生小明被选中参加市级比赛的概率.【思路分析】(1)根据A等级有4人,所占的百分比是10%即可求得总人数,然后求得a和b的值;(2)首先计算出B等级频数,再利用360°乘以对应的百分比即可求得B等级所对应的圆心角度数;(3)利用列举法求得选中A等级的小明的概率.【解题过程】解:(1)总人数:4÷10%=40,a=40×0.3=12,b=1640=0.4;(2)B的频数:40﹣4﹣12﹣16=8,B等级对应扇形圆心角的度数:840×360°=72°;(3)用a表示小明,用b、c、d表示另外三名同学.则选中小明的概率是:612=12.【知识点】扇形统计图;频数(率)分布表;概率22.(2019山东菏泽,22,10分)如图,BC是⊙O的直径,CE是⊙O的弦,过点E作⊙O的切线,交CB的延长线于点G,过点B作BF⊥GE于点F,交CE的延长线于点A.(1)求证:∠ABG=2∠C;(2)若GF=3√3,GB=6,求⊙O的半径.【思路分析】(1)连接OE,根据切线的性质得到OE⊥EG,推出OE∥AB,得到∠A=∠OEC,根据等腰三角形的性质得到∠OEC=∠C,求得∠A=∠C,根据三角形的外角的性质即可得到结论;(2)根据勾股定理得到BF=√BG2−GF2=3,根据相似三角形的性质即可得到结论.【解题过程】解:(1)证明:连接OE,∵EG是⊙O的切线,∴OE⊥EG,∵BF⊥GE,∴OE∥AB,∴∠A=∠OEC,∵OE=OC,∴∠OEC=∠C,∴∠A=∠C,∵∠ABG=∠A+∠C,∴∠ABG=2∠C;(2)解:∵BF⊥GE,∴∠BFG=90°,∵GF=3√3,GB=6,∴BF=√BG2−GF2=3,∵BF∥OE,∴△BGF∽△OGE,∴BFOE=BGOG,∴3OE=66+OE,∴OE=6,∴⊙O的半径为6.【知识点】圆周角定理;切线的性质;相似三角形的判定和性质;等腰三角形的判定和性质23.(2019山东菏泽,23,10分)如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°.(1)如图1,连接BE,CD,BE的廷长线交AC于点F,交CD于点P,求证:BP⊥CD;(2)如图2,把△ADE绕点A顺时针旋转,当点D落在AB上时,连接BE,CD,CD的延长线交BE于点P,若BC=6√2,AD=3,求△PDE的面积.【思路分析】(1)根据等腰直角三角形的性质得到AD=AE,AB=AC,∠BAC﹣∠EAF=∠EAD﹣∠EAF,求得∠BAE=∠DAC,根据全等三角形的性质得到∠ABE=∠ACD,根据余角的性质即可得到结论;(2)根据全等三角形的性质得到∠ABE=∠ACD,BE=CD,求得∠EPD=90°,得到DE=3√2,AB=6,求得BD=6﹣3=3,CD=√AD2+AC2=3√5,根据相似三角形的性质得到PD=√55,PB=6√55根据三角形的面积公式即可得到结论.【解题过程】解:(1)∵△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°.∴AD=AE,AB=AC,∠BAC﹣∠EAF=∠EAD﹣∠EAF,即∠BAE=∠DAC,在△ABE与△ADC中,{AB=AC∠BAE=∠CAD AE=AD,∴△ABE≌△ADC(SAS),∴∠ABE=∠ACD,∵∠ABE+∠AFB=∠ABE+∠CFP=90°,∴∠CPF=90°,∴BP⊥CD;(2)在△ABE与△ACD中,{AE=AD∠EAB=∠CAB=90°AB=AC,∴△ABE≌△ACD(SAS),∴∠ABE=∠ACD,BE=CD,∵∠PDB=∠ADC,∴∠BPD=∠CAB=90°,∴∠EPD=90°,BC=6√2,AD=3,求△PDE的面积.∵BC=6√2,AD=3,∴DE=3√2,AB=6,∴BD=6﹣3=3,CD=√AD2+AC2=3√5,∵△BDP∽△CDA,∴BDCD=PDAD=PBAC,∴3√5=PD3=PB6,∴PD=3√55,PB=6√55∴PE=3√5−6√55=9√55,∴△PDE的面积=12×9√55×3√55=2710.【知识点】全等三角形的判定与性质;等腰直角三角形;旋转的性质;相似三角形的判定和性质;勾股定理24.(2019山东菏泽,24,10分)如图,抛物线与x轴交于A,B两点,与y轴交于点C(0,﹣2),点A的坐标是(2,0),P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E,抛物线的对称轴是直线x=﹣1.(1)求抛物线的函数表达式;(2)若点P 在第二象限内,且PE =14OD ,求△PBE 的面积.(3)在(2)的条件下,若M 为直线BC 上一点,在x 轴的上方,是否存在点M ,使△BDM 是以BD 为腰的等腰三角形?若存在,求出点M 的坐标;若不存在,请说明理由.【思路分析】(1)点A (2,0)、点B (﹣4,0),则函数的表达式为:y =a (x ﹣2)(x +4)=a (x 2+2x ﹣8),即可求解;(2)PE =14OD ,则PE =(14x 2+12x ﹣2−12x +2)=14(﹣x ),求得:点D (﹣5,0),利用S △PBE =12PE ×BD =12(14x 2+12x ﹣2−12x +2)(﹣4﹣x ),即可求解; (3)BD =1=BM ,则y M =﹣BM sin ∠ABC =﹣1×5=−√55,即可求解. 【解题过程】解:(1)点A 的坐标是(2,0),抛物线的对称轴是直线x =﹣1,则点B (﹣4,0), 则函数的表达式为:y =a (x ﹣2)(x +4)=a (x 2+2x ﹣8),即:﹣8a =﹣2,解得:a =14,故抛物线的表达式为:y =14x 2+12x ﹣2;(2)将点B 、C 的坐标代入一次函数表达式:y =mx +n 并解得:直线BC 的表达式为:y =−12x ﹣2,则tan ∠ABC =12,则sin ∠ABC =5, 设点D (x ,0),则点P (x ,14x 2+12x ﹣2),点E (x ,12x ﹣2), ∵PE =14OD ,∴PE =(14x 2+12x ﹣2−12x +2)=14(﹣x ), 解得:x =0或﹣5(舍去x =0),即点D (﹣5,0)S △PBE =12×PE ×BD =12(14x 2+12x ﹣2−12x +2)(﹣4﹣x )=58; (3)由题意得:△BDM 是以BD 为腰的等腰三角形,只存在:BD =BM 的情况,BD=1=BM,则y M=﹣BM sin∠ABC=﹣15=−√55,则x M=−20+2√55,故点M(−20+2√55,−√55).【知识点】二次函数综合题;数形结合;函数思想;二次函数的解析式;。
2019年山东省临沂市(初三学业水平考试)中考地理真题试卷含答案

2019年山东省临沂市中考地理试卷一、选择题,共25道题,每题2分,共50分.在每题所列出的四个选项中,只有一项是最符合题目要求的.1.北京和张家口联合举办2022年冬奥会。
据如图“张家口某滑雪场等高线图”,完成第1~2题。
初学者应尽量选择坡度较缓的滑雪道练习。
图中所示四条滑雪道最适合初学者练习的是()A.L1滑雪道B.L2滑雪道C.L3滑雪道D.L4滑雪道2.四位学生绘制的MN段地形剖面示意图,其中正确的是()3.2019年4月10日21时,美国、中国、智利、比利时、丹麦和日本等国同时发布人类首张黑洞照片。
据图“EHT(事件视界望远镜)分布示意图”完成第3~4题。
黑洞照片分别以英语、汉语、西班牙语、丹麦语和日语发布,其中在世界上使用范围最广和使用人数最多的语言分别是()A.西班牙语、日语B.英语、汉语C.英语、西班牙语D.汉语、英语4.黑洞照片是由分布在全球的八座射电望远镜虚拟出一个地球大小的“事件视界望远镜”捕获的。
对图中望远镜的位置,描述错误的是()A.aef所处位置地壳不稳定B.b位于欧洲大陆上C.c所处的纬度位置最高D.d位于大西洋中的岛屿上5.如表为临沂市某一周的天气状况,据此完成第5~6题。
周一周二周三周四周五周六周日﹣3~4℃微风﹣1~9℃微风﹣4~7℃微风﹣3~9℃微风﹣2~7℃微风﹣1~8℃北风4﹣5级﹣5~4℃北风5~6级一周中,临沂市气温日较差最大的一天是()A.周二B.周三C.周四D.周日6.据表,以下天气播报正确的是()A.周二小雪转大雪B.周三晴转多云,气温回升C.周五有雾,不利于户外运动D.周六多云,有沙尘天气7.习近平主席于2019年3月21日至26日对意大利、摩纳哥、法国进行了国事访问。
据图完成第7~8题。
下列关于欧洲西部的叙述错误的是()A.人口稠密,国家众多B.工业密集,发达国家集中C.畜牧业发达,机械化程度高D.农业发达,成为国民经济的支柱8.习近平主席于2019年3月21日至26日对意大利、摩纳哥、法国进行了国事访问。
2019年山东省中考数学真题分类汇编 专题05 四边形 (原卷版)

A.OM=12B.MB=MO((专题05四边形一、选择题1.(2019山东淄博)如图,矩形内有两个相邻的正方形,其面积分别为2和8,则图中阴影部分的面积为()A.2B.2C.22D.62.(2019山东临沂)如图,在平行四边形A BCD中,M、N是BD上两点,BM=DN,连接AM、MC、CN、NA,添加一个条件,使四边形AMCN是矩形,这个条件是()AC C.BD⊥AC D.∠AMB=∠CND3.2019山东枣庄)如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF 的位置.若四边形AECF的面积为20,DE=2,则AE的长为()A.4B.25C.6D.264.(2019山东威海)如图,E是ABCD边AD延长线上一点,连接BE,CE,BD,BE交CD于点F.添加以下条件,不能判定四边形BCED为平行四边形的是()A.∠ABD=∠DCE B.DF=CF C.∠AEB=∠BCD D.∠AEC=∠CBD5.2019山东潍坊)如图,在矩形ABCD中,AB=2,BC=3,动点P沿折线BCD从点B开始运动到点D.设运动的路程为△x,ADP的面积为y,那么y与x之间的函数关系的图象大致是()4四边形NFB =1:8.上述结论中,所有正确结论的序号是A.B.C.D.6.(2019山东菏泽)如图,正方形ABCD的边长为2cm,动点P,Q同时从点A出发,在正方形的边上,分别按A→D→C,A→B→C的方向,都以1cm/s的速度运动,到达点C运动终止,连接PQ,设运动时间为△xs,APQ的面积为ycm2,则下列图象中能大致表示y与x的函数关系的是()A.B.C.D.7.(2019山东泰安)如图,矩形ABCD中,AB=4,AD=2,E为AB的中点,F为EC上一动点,P为DF 中点,连接PB,则PB的最小值是()A.2B.4C.2D.228.(2019山东德州)如图,正方形ABCD,点F在边AB上,且AF:FB=1:2,CE⊥DF,垂足为M,且交AD于点E,AC与DF交于点N,延长CB至G,使BG=12BC,连接CM.有如下结论:①DE=AF;②AN=2AB;③∠ADF=∠GMF;④△SANF:SC()A.①②B.①③C.①②③D.②③④二、填空题9.(2019山东济宁)如图,该硬币边缘镌刻的正九边形每个内角的度数是.10.(2019山东枣庄)用一条宽度相等的足够长的纸条打一个结(如图1所示),然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE.图中,∠BAC=度.11.(2019山东威海)如图,在四边形ABCD中,AB∥DC,过点C作CE⊥BC,交AD于点E,连接BE,∠BEC=∠DEC,若AB=6,则CD=.D CEA B12.(2019山东威海)如图,在四边形ABCD中,AB∥CD,连接AC,BD.若∠ACB=90°,AC=BC,AB =BD,则∠ADC=°.13.(2019山东菏泽)如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是.14.(2019 山东青岛)如图,在正方形纸片 A BCD 中,E 是 CD 的中点,将正方形纸片折叠,点 B 落在线段AE 上的点 G 处,折痕为 AF .若 AD =4cm ,则 CF 的长为cm .15.(2019 山东泰安)如图,矩形 ABCD 中,AB =36 ,BC =12,E 为 AD 中点,F 为 AB 上一点,将△AEF 沿 EF 折叠后,点 A 恰好落到 CF 上的点 G 处,则折痕 EF 的长是 .16.(2019 山东滨州)如图,平行四边形ABCD 的对角线 AC ,BD 交于点 O ,CE 平分∠BCD 交 AB 于点 E ,交 BD 于点 F ,且∠ABC =60°,AB =2BC ,连接 OE .下列结论:①EO ⊥AC ;②S △AOD =4△S OCF ;③AC :BD = 21 :7;④FB 2=OF •DF .其中正确的结论有(填写所有正确结论的序号)DCOFAEB17.(2019 山东潍坊)如图,在矩形 ABCD 中,AD =2.将∠A 向内翻折,点 A 落在 BC 上,记为 A ′,折痕为 DE .若将∠B 沿 EA ′向内翻折,点 B 恰好落在 DE 上,记为 B ′,则 AB = .(18.(2019 山东泰安)在平面直角坐标系中,直线 l :y =x +1 与 y 轴交于点 A 1,如图所示,依次作正方形OA 1B 1C 1,正方形 C 1A 2B 2C 2,正方形 C 2A 3B 3C 3,正方形 C 3A 4B 4C 4,……,点 A 1,A 2,A 3,A 4,……在直线 l 上,点 C 1,C 2,C 3,C 4,……在 x 轴正半轴上,则前 n 个正方形对角线长的和是.三、解答题19.(2019 山东菏泽)如图,四边形 ABCD 是矩形.(1)用尺规作线段 AC 的垂直平分线,交 AB 于点 E ,交 CD 于点 F (不写作法,保留作图痕迹);(2)若 BC =4,∠BAC =30°,求 BE 的长.20.(2019 山东枣庄)如图,BD 是菱形 ABCD 的对角线,∠CBD =75°,(1)请用尺规作图法,作 A B 的垂直平分线 EF ,垂足为 E ,交 AD 于 F ;(不要求写作法,保留作图痕迹)(2)在(1)条件下,连接 BF ,求∠DBF 的度数.21. 2019 山东青岛)如图,在 ABCD 中,对角线 AC 与 BD 相交于点 O ,点 E ,F 分别为 OB ,OD 的中点,延长 AE 至 G ,使 EG =AE ,连接 CG .(△1)求证: ABE ≌△CDF ;(2)当 AB 与 AC 满足什么数量关系时,四边形 EGCF 是矩形?请说明理由.22.(2019山东滨州)如图,矩形A BCD中,点E在边CD上,将△BCE沿BE折叠,点C落在AD边上的点F处,过点F作FG∥CD交BE于点G,连接CG.(1)求证:四边形CEFG是菱形;(2)若AB=6,AD=10,求四边形CEFG的面积.23.(2019山东聊城)在菱形ABCD中,点P是BC边上一点,连接AP,点E,F是AP上的两点,连接DE,BF,使得∠AED=∠ABC,∠ABF=∠BPF.求证:(△1)ABF≌△DAE;(2)DE=BF+EF.24.(2019山东泰安)在矩形ABCD中,AE⊥BD于点E,点P是边AD上一点.(1)若BP平分∠ABD,交AE于点G,PF⊥BD于点F,如图①,证明四边形AGFP是菱形;(2)若PE⊥EC,如图②,求证:AE•AB=DE•AP;(3)在(2)的条件下,若AB=1,BC=2,求AP的长.25.(2019山东泰安)如图,四边形A BCD是正方形,△EFC是等腰直角三角形,点E在AB上,且∠CEF=90°,FG⊥AD,垂足为点C.(1)试判断AG与FG是否相等?并给出证明;(2)若点H为CF的中点,GH与DH垂直吗?若垂直,给出证明;若不垂直,说明理由.26.(2019山东潍坊)如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接DG,过点A作AH ∥DG,交BG于点H.连接HF,AF,其中AF交EC于点M.(△1)求证:AHF为等腰直角三角形.(2)若AB=3,EC=5,求EM的长.27.(2019山东临沂)如图,在正方形ABCD中,E是DC边上一点,(与D、C不重合),连接△AE,将ADE沿AE所在的直线折叠得到△AFE,延长EF交BC于G,连接AG,作GH⊥AG,与AE的延长线交于点H,连接CH.显然AE是∠DAF的平分线,EA是∠DEF的平分线.仔细观察,请逐一找出图中其他的角平分线(仅限于小于180°的角平分线),并说明理由.28.(2019山东威海)如图,在正方形A BCD中,AB=10cm,E为对角线BD上一动点,连接AE,CE,过E点作EF⊥AE,交直线BC于点F.E点从B点出发,沿着BD方向以每秒2cm的速度运动,当点E与点D重合时,运动停止.设△BEF的面积为ycm2,E点的运动时间为x秒.(1)求证:CE=EF;(2)求y与x之间关系的函数表达式,并写出自变量x的取值范围;(△3)求BEF面积的最大值.29.(2019山东潍坊)如图1,菱形ABCD的顶点A,D在直线上,∠BAD=60°,以点A为旋转中心将菱形ABCD顺时针旋转α(0°<α<30°),得到菱形AB′C′D′,B′C′交对角线AC于点M,C′D′交直线l于点N,连接MN.(1)当MN∥B′D′时,求α的大小.(2)如图2,对角线B′D′交AC于点H,交直线l与点G,延长C′B′交AB于点E,连接△EH.当HEB′的周长为2时,求菱形ABCD的周长.30.(2019山东济宁)如图1,在矩形ABCD中,AB=8,AD=10,E是CD边上一点,连接AE,将矩形ABCD沿AE折叠,顶点D恰好落在BC边上点F处,延长AE交BC的延长线于点G.(1)求线段CE的长;(2)如图2,M,N分别是线段AG,DG上的动点(与端点不重合),且∠D MN=∠DAM,设AM=x,DN=y.①写出y关于x的函数解析式,并求出y的最小值;②是否存在这样的点△M,使D MN是等腰三角形?若存在,请求出x的值;若不存在,请说明理由.31.(2019山东德州)(1)如图1,菱形AEGH的顶点E、H在菱形ABCD的边上,且∠BAD=60°,请直接写出HD:GC:EB的结果(不必写计算过程)t ((2)将图 1 中的菱形 AEGH 绕点 A 旋转一定角度,如图 2,求 HD :GC :EB ;(3)把图 2 中的菱形都换成矩形,如图 3,且 AD :AB =AH :AE =1:2,此时 HD :GC :EB 的结果与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程);若无变化,请说明理由.32.(2019 山东淄博)如图 1,正方形 ABDE 和 BCFG 的边 AB ,BC 在同一条直线上,且 AB =2BC ,取EF 的中点 M ,连接 MD ,MG ,MB .(1)试证明 DM ⊥MG ,并求MB的值.MG(2)如图 2,将图 1 中的正方形变为菱形,设∠EAB =2α(0<α<90°),其它条件不变,问(1)中 值有变化吗?若有变化,求出该值(用含 α 的式子表示);若无变化,说明理由.MBMG的33.(2019 山东青岛)已知:如图,在四边形 ABCD 中,AB ∥CD ,∠ACB =90°,AB =10cm ,BC =8cm ,OD 垂直平分 AC .点 P 从点 B 出发,沿 BA 方向匀速运动,速度为 1cm/s ;同时,点 Q 从点 D 出发,沿DC 方向匀速运动,速度为 1cm/s ;当一个点停止运动,另一个点也停止运动.过点P 作 PE ⊥AB ,交 BC于点 E ,过点 Q 作 QF ∥AC ,分别交 AD ,OD 于点 F ,G .连接 OP ,EG .设运动时间为 (s ) 0<t <5),解答下列问题:(1)当 t 为何值时,点 E 在∠BAC 的平分线上?(2)设四边形 PEGO 的面积为 S (cm 2),求 S 与 t 的函数关系式;(3)在运动过程中,是否存在某一时刻 t ,使四边形 PEGO 的面积最大?若存在,求出 t 的值;若不存在,请说明理由;(4)连接 OE ,OQ ,在运动过程中,是否存在某一时刻 t ,使 OE ⊥OQ ?若存在,求出 t 的值;若不存在,请说明理由.。
2019年山东省青岛市中考数学试题(word版,含解析)

2019年山东省青岛市中考数学试卷、选择题(本大题共 8小题,每小题3分,共24分)在每小题给出的四个选项中,只有 一项是符合题目要求的. (3分)-二的相反数是( )B .-返36. ( 3分)如图,将线段 AB 先向右平移5个单位,再将所得线段绕原点按顺时针方向旋转90°,得到线段 A ' B ',则点B 的对应点B '的坐标是( )1. A .-二 3. 4.5. (3分)2019年1月3日,我国“嫦娥四号”月球探测器在月球背面软着陆, 史以来首次成功登陆月球背面•已知月球与地球之间的平均距离约为 384000km 用科学记数法可以表示为( A . 38.4 x 104km B . 3.84 x 105km C . 0.384X 10 6km D . 3.84 x 106km223(3 分)计算(-2m ) ?( - m?m +3m ) 的结果是(A . 8m 5B . - 8m 5C .8m 6(3分)如图,线段 AB 经过O O 的圆心,AC , BD 分别与O O 相切于点实现人类有 384000km ,把45—4m +12m C , D .若 AC=B . 2nC . 2 ':n 2.A .A • (- 4,1)B • (- 1 ,2)C. (4,- 1) D . (1,- 2)7.(3分)如图,BD是厶ABC的角平分线, AE丄BD,垂足为F.若/ ABC = 35°,/ C =50°,则/ CDE的度数为(B .40°)A . 35°C. 45°D. 50°& ( 3分)已知反比例函数y=二的图象如图所示, 则二次函数2y= ax - 2x和一次函数y =bx+a在同一平面直角坐标系中的图象可能是(、填空题(本大题共6小题,每小题3分,共18分)9. (3分)计算:丄——(匚)〜V2210. (3分)若关于x的一元二次方程2x2-x+m= 0有两个相等的实数根,则m的值为__________ .11. ________________________________________________________________________ (3分)射击比赛中,某队员10次射击成绩如图所示,则该队员的平均成绩是_________________ 环.12. (3分)如图,五边形ABCDE是O O的内接正五边形,AF是O O的直径,则/ BDF的度数是___________ ° .13. (3分)如图,在正方形纸片ABCD中,E是CD的中点,将正方形纸片折叠,点B落在线段AE上的点G处,折痕为AF.若AD = 4cm,则CF的长为 _____________ cm .14. (3分)如图,一个正方体由27个大小相同的小立方块搭成,现从中取走若干个小立方块,得到一个新的几何体•若新几何体与原正方体的表面积相等,则最多可以取走三、作图题(本大题满分4分)请用直尺、圆规作图,不写作法,但要保留作图痕迹.15. (4分)请用直尺、圆规作图,不写作法,但要保留作图痕迹.已知:/ a直线I及I上两点A,B.四、解答题(本大题共9小题,共74分)2. 216. (8 分)(1)化简:22!十(——-2n);in n(2)解不等式组* 5 5,并写出它的正整数解.3x-l<8忙■17. (6分)小明和小刚一起做游戏,游戏规则如下:将分别标有数字 1 , 2, 3, 4的4个小球放入一个不透明的袋子中,这些球除数字外都相同.从中随机摸出一个球记下数字后放回,再从中随机摸出一个球记下数字. 若两次数字差的绝对值小于2,则小明获胜,否则小刚获胜•这个游戏对两人公平吗?请说明理由.18. (6分)为了解学生每天的睡眠情况,某初中学校从全校800名学生中随机抽取了40名学生,调查了他们平均每天的睡眠时间(单位:h),统计结果如下:9, 8, 10.5, 7, 9, 8, 10, 9.5, 8, 9, 9.5, 7.5, 9.5, 9, 8.5, 7.5, 10 , 9.5, 8 , 9 , 7 ,9.5 , 8.5 , 9 , 7 , 9 , 9 , 7.5 , 8.5 , 8.5 , 9 , 8 , 7.5 , 9.5 , 10 , 9.5 , 8.5 , 9 , 8 , 9.在对这些数据整理后,绘制了如下的统计图表:睡眠时间分组统计表睡眠时间分布情况(1)m= ______ , n= ________ , a= _________ , b= ________ ;(2)抽取的这40名学生平均每天睡眠时间的中位数落在__________ 组(填组别);(3)如果按照学校要求,学生平均每天的睡眠时间应不少于9h,请估计该校学生中睡眠时间符合要求的人数.睡眠时间分布情况19. (6分)如图,某旅游景区为方便游客,修建了一条东西走向的木栈道AB,栈道AB与景区道路CD平行.在C处测得栈道一端A位于北偏西42°方向,在D处测得栈道另一端B位于北偏西32。
(完整word版)2019年山东省济南市数学中考试题含答案,推荐文档

山东省济南市2019年学业水平考试数学试题一、选择题(本大题共1. (2019 济南,A . 2 1, 4分)B.12小题,每小题4分,共48 分)4的算术平方根是()—2 C . ± 23 .D. ;2)4.2019 济南,3,量子密钥分发,这标志数法表示为(A . 0.76 X 104(2019 济南,4,产,下面瓦当D.4分)2019年1月,墨子号”量子卫星实现了距离达7600千米的洲际墨子号”具备了洲际量子保密通信的能力. 数字7600用科学记标心着)B . 7.6 X 103C . 7.6X 1044分)瓦当”是中国古建筑装饰XX头的附件,”图案中既是轴对称图形又是中心对称图形的是(D . 76 X 102是中国特有的文化艺术遗)C5 .A(2019济南,的度数为(A . 17.55, 4分))B如图,AF是/ BAC的平分线,DF//AC,D若/ 1 = 35 °则/ BAFB .35 °C .55 °D .70 °R6. ( 2019济南,6, 4分)下列运算正确的是( )A . a2+ 2a= 3a3B . (—2a3)2= 4a5C . (a + 2)(a —1) = a2+ a—2D . (a + b)2= a2+ b27. (2019济南,7, 4分)关于x的方程3x—2m = 1的解为正数,则m的取值范围是(1A . m v —2B . m>—1 D . m v12 & ( 2019济南,8, 4分)在反比例函数 y =— x 图象上有三个点C (X 3, y 3),若X 1V O v X 2V X 3,则下列结论正确的是( A . y 3 v y 2v y iB . y i v y 3v y 2C . y 2v y 3v y i9. ( 20i9济南,9, 4分)如图,在平面直角坐标系中,△ABC 的顶点都在方格线的格点上,将△ABC 绕点P 顺时针方向旋转90°得到△AB'C',则点P 的坐标为( )A. (0, 4)B . ( i , i )C . (i , 2)D . (2, i )iO . (20i9济南,iO , 4分)下面的统计图大致反应了我国20i2年至20i7年人均阅读量的情况.根据统计图提供的信息,下列推断不合理的是()A .与20i6年相比,20i7年我国电子书人均阅读量有所降低 B.20i2年至20i7年,我国纸质书的人均阅读量的中位数是4.57C. 从20i4年到20i7年,我国纸质书的人均阅读量逐年增长D.20i3年我国纸质书的人均阅读量比电子书的人均阅读量的 i.8倍还多ii.(20i9济南,ii , 4分)如图,一个扇形纸片的圆心角为 90°半径为6.如图2,将这张扇形纸片折叠,使点 A 与点0恰好重合,折痕为 CD ,图中阴影为重合部分,则阴影 部分的面积为()A (x i , y i )、B (X 2, y 2)、)D . y 3V y i v y 29厂厂9厂9 n A . 6 n—2 3 B . 6n—9 .3 C . i2 n—2 3 D .—12. (2019济南,11, 4分)若平面直角坐标系内的点M 满足横、纵坐标都为整数,则把点M 叫做 整点”例如:P ( 1,0)、Q (2,— 2)都是 整点”抛物线y = mx 2—4mx + 4m —2(m >0)与x 轴交于点A 、B 两点,若该抛物线在 A 、B 之间的部分与线段 AB 所围成 的区域(包括边界)恰有七个整点,贝U m 的取值范围是( )1 1A Y m v 1B . -< m W 1C . 1v m < 2D . 1v m v 222 二、填空题(本大题共6小题,每小题4分,共24分)13. __________________________________________________ (2019 济南,13,4 分)分解因式: m 2— 4= _________________________________________________________ ; 14. (2019济南,14, 4分)在不透明的盒子中装有5个黑色棋子和若于个白色做子,每个1棋子除颜色外都相同,任意摸出一个棋子,摸到黑包棋子的概率是 1,则白色棋子的个数是= _____________ ;15( 2019济南,15,4分)一个正多边形的每个内角等于 108。
2019年山东省枣庄中考地理试卷(含答案与解析)

绝密★启用前山东省枣庄市2019年初中学业水平考试地 理第Ⅰ卷(选择题 共36分)一、选择题。
北京天安门广场上的国旗,每天伴着日出而升起,随着日落而降下。
下表是北京某1.一年之中,造成天安门广场的升旗时间不同的根本原因是( )A .地球自转B .地球公转C .昼夜更替D .四季变化2.四个节日,北京正午太阳高度最大的是( )A .1月1日B .5月1日C .7月1日D .10月1日读亚洲大陆30°N 局部地形剖面图(下图),完成下面小题。
3.苏伊士运河沟通了( )A .黑海和地中海B .大西洋和地中海C .红海和阿拉伯海D .地中海和红海 4.青藏高原最突出的自然特征是( )A .高寒B .干旱C .湿热D .冷湿 5.下列说法错误的是( )A .阿拉伯高原终年炎热干燥B .波斯湾沿岸石油资源丰富C .印度河平原人口稀疏D .喜马拉雅山脉是由板块挤压隆起形成的读新疆及周边地区图(下图),完成下面小题。
6.新疆邻国众多,图中甲国是( )A .蒙古B .印度C .俄罗斯D .哈萨克斯坦 7.以新疆为源地的大型跨区域工程是( )A .青藏铁路B .西电东送 C.南水北调D .西气东输8.下列关于新疆地理特征的叙述,正确的是( )A .是我国跨经度最广的省级行政区B .地形格局可以概括为“三山夹两盆”C .绿洲农业的水源主要来自大气降水D .河流稀少,全部为内流河 读我国某区域示意图,完成下面小题。
9.该区域成为我国最大商品粮基地的主要社会经济条件是( )A .地广人稀B .人多地少C .交通便捷D .开发历史悠久10.该区域水稻种植北界不断北移、种植面积不断扩大的主要自然原因是( )-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效------------毕业学校_____________ 姓名_____________ 准考证号_____________ ____________________________________________________A.夏季高温多雨B.全球气候变暖C.黑土地肥沃D.地势平坦11.大规模农垦引发该区域沼泽面积锐减、水土流失等一系列生态环境问题。
2019年山东省东营中考地理试卷

绝密★启用前山东省东营市2019年初中学业水平考试地 理第Ⅰ卷(选择题 共50分)一、选择题(下列各题给出的四个选项中,只有一个选项是最符合题意的。
每小题2分,共50分)北京时间2018年12月8日凌晨,在四川西昌(102°E ,28°N )卫星发射中心成功发射嫦娥四号探测器,开启了中国月球探测的新旅程。
据此完成下列各题。
1.嫦娥四号探测器发射成功时,东营正处于( )A .春季B .夏季C .秋季D .冬季2.下图四点的位置与西昌最为接近的是( )A .B .C .D .2018年,全球共发生六级以上地震119次,最大地震是8月19日在斐济群岛地区发生的8.1级地震。
读图完成下面小题。
3.有关地震的叙述,正确的是 ( )A .地震集中在板块与板块的交界地带B .现在科技水平下,地震已能够精准预测C .地震主要是人类活动造成的灾害D .地震发生时,要迅速乘坐电梯逃生4.据图可知,斐济群岛所处大洲和濒临的大洋是( )A .亚洲太平洋B .大洋洲印度洋C .亚洲印度洋D .大洋洲太平洋“回南天”一般出现在二、三月份,主要是因为冷空气走后,暖湿气流迅速反攻,气温回暖、湿度回升,形成连日的小雨或大雾。
下图是2019年某次“回南天”形成示意图。
读图完成下面小题。
5.由图可知,本次“回南天”现象发生在( )A .长江流域B .四川盆地C .闽赣地区D .粤桂地区6.“回南天”发生时,当地的天气一般是( )A .B .C .D .7.本次“回南天”现象对当地的主要影响有( )A .多雾,影响交通出行B .多暴雨,发生水灾-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效------------毕业学校_____________ 姓名_____________ 准考证号_____________ ____________________________________________________C.天气干燥,适合晾晒衣物D.气温回升,大量积雪融化下图是我国东部某地等高线地形图,读图完成下面小题。
2019年山东省青岛市中考物理试卷【中考真题】
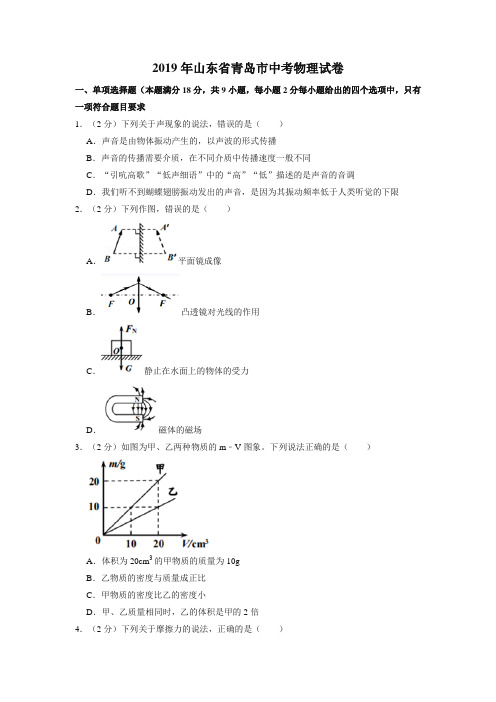
2019年山东省青岛市中考物理试卷一、单项选择题(本题满分18分,共9小题,每小题2分每小题给出的四个选项中,只有一项符合题目要求1.(2分)下列关于声现象的说法,错误的是()A.声音是由物体振动产生的,以声波的形式传播B.声音的传播需要介质,在不同介质中传播速度一般不同C.“引吭高歌”“低声细语”中的“高”“低”描述的是声音的音调D.我们听不到蝴蝶翅膀振动发出的声音,是因为其振动频率低于人类听觉的下限2.(2分)下列作图,错误的是()A.平面镜成像B.凸透镜对光线的作用C.静止在水面上的物体的受力D.磁体的磁场3.(2分)如图为甲、乙两种物质的m﹣V图象。
下列说法正确的是()A.体积为20cm3的甲物质的质量为10gB.乙物质的密度与质量成正比C.甲物质的密度比乙的密度小D.甲、乙质量相同时,乙的体积是甲的2倍4.(2分)下列关于摩擦力的说法,正确的是()A.发生相对运动的两个物体间一定会产生滑动摩擦力B.滑动摩擦力的方向总是与物体的运动方向相反C.一个物体对另一个物体产生摩擦力的作用,同时自身也受到摩擦力D.滚动摩擦一定比滑动摩擦小5.(2分)如图为探究杠杆平衡条件的实验装置,杠杆平衡时,钩码对杠杆的阻力F2=10N,阻力臂l2=20cm,测力计示数F1=25N,则动力臂l1为()A.15cm B.8cm C.50cm D.80cm6.(2分)下列实验与手摇发电机工作原理相同的是()A.电磁铁B.通电线圈在磁场中扭转C.电磁效应D.磁场对电流的作用7.(2分)下列对一些数据的估测,最接近实际的是()A.课桌的高度约为800cmB.青岛夏季的最高气温约为50℃C.中学生100m跑的平均速度约为15m/sD.将20个鸡蛋从一楼提至二楼,对鸡蛋做的功约为30J8.(2分)下列实验,正确运用控制变量方法的是()A.研究液体压强与液体密度的关系,将压强计的探头放入不冋液体的同一深度B.研究动能大小与质量的关系,将质量不同的小球从同一斜面不同高度自由滚下C.研究电阻大小与材料的关系,将长度相同、粗细不同的铜丝和铁丝分别接入同一电路D.研究不同物质的吸热能力,使质量不同的水和食用油升高相同的温度9.(2分)如图为盆景的一个自动供水装置。
2019年山东省东营市中考地理试卷

2019年山东省东营市中考地理试卷一、选择题(下列各题给出的四个选项中,只有一个选项是最符合题意的.每小题4分,共50分)1. 观察“地球仪示意图”,完成(1)~(2)题。
(1)下列现象由地球自转产生的是()A.昼夜现象B.太阳每天东升西落C.四季变化D.一年中正午物体影子的长短变化(2)关于图示区域海陆分布的叙述,正确的是()A.海洋面积小于陆地面积B.甲是一个四面环海的岛国C.乙为非洲,丙为印度洋D.乙、丁所在大洲的分界线是巴拿马运河2. 读某区域经纬网图,完成(1)~(2)题。
(1)图中②地的经纬度是()A.40∘S,20∘WB.40∘S,20∘EC.40∘N,20∘WD.40∘N,20∘E(2)下列关于图中信息的判断,正确的是()A.④地有极昼极夜现象B.③地位于西半球C.①地位于③地的西北方D.⑤地所在纬线比①地所在纬线长3. 2019年4月20日,中国万达•2019黄河口国际马拉松赛在东营举行,比赛设马拉松、半程马拉松、迷你马拉松三个项目。
据此回答(1)~(3)题。
(1)迷你马拉松里程为5km,在比例尺为1:20000的比赛路线图上,该里程的长度为()A.10厘米B.25厘米C.40厘米D.100厘米(2)赛事期间,参赛选手在东营可能看到的景象有()①黄河里大量浮冰顺流而下②文化广场上正在进行吕剧表演③野外提油机正在工作④绿油油的麦苗长势喜人A.①②③B.②③④C.①②④D.①③④(3)“黄蓝交汇”是黄河入海口特有的景观,每年吸引大量游客前来观赏。
这种景观的形成主要是因为黄河下游()A.含沙量大B.水污染严重C.是地上河D.流经地区降水丰富4. 读南非轮廓图,下列关于南非的描述,正确的是()A.好望角属于地中海气候,7月炎热干燥B.大部分位于低纬度、热带地区C.矿产资源丰富,属发达国家D.地形以高原为主,居民多为黑种人5. 读亚洲某区域地图,完成(1)~(2)题。
(1)图中数字与其所代表的地理事物名称,对应正确的是()A.①–昆仑山脉B.②–缅甸C.③–阿拉伯海D.④–恒河(2)7月份,一支科考队从甲地到乙地进行实地考察,沿途见闻可信的有()A.甲地民居多为房顶坡度大的碉房B.乙地此时盛行东北季风C.甲地许多家庭都安装了太阳能热水器D.乙地居民正在忙着收割小麦6. 2018年世界杯足球赛在俄罗斯的莫斯科、圣彼得堡等11个城市举行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山东省2019年各市中考真题汇编综合试题14.(2019·滨州)逻辑推理是化学学习中常用的思维方法,下列推理正确的是()A. 化合物是由不同元素组成的纯净物,所以由不同种元素组成的纯净物一定是化合物B. 中和反应生成盐和水,则生成盐和水的反应一定是中和反应C. 单质中只含有一种元素,所以只含有一种元素的物质一定是单质D. 活泼金属能与稀盐酸反应放出气体,则能与稀盐酸反应放出气体的物质一定是活泼金属【答案】A【解析】A、不同元素组成的纯净物一定是化合物,说法正确,故此选项正确。
B、有盐和水生成的反应不一定是中和反应,例如氧化铜和硫酸反应能生成硫酸铜和水,但是不属于中和反应,故选项错误。
C、单质中只含一种元素,但是只含一种元素的物质不一定是单质,在同素异形体组成的混合物中,仍满足只有一种元素,但该物质不是单质,而是混合物,故此选项错误。
D、活泼金属能与稀盐酸反应放出气体,则能与稀盐酸反应放出气体的物质不一定是活泼金属,错误。
14.(2019·德州)推理是一种重要的思维方法。
下列推理正确的是()A.分子是构成物质的微粒,所以物质都是由分子构成B.氧气由氧元素组成,所以制取氧气的反应物一定含有氧元素C.溶液是均一、稳定的混合物,所以均一、稳定的物质就是溶液D.化合物由多种元素组成,所以由多种元素组成的物质就是化合物【答案】B【解析】分子是构成物质的微粒,物质可以由分子、原子或离子构成;氧气由氧元素组成,所以制取氧气的反应物一定含有氧元素;溶液是均一、稳定的混合物,均一、稳定的物质不一定是溶液,如水是纯净物;化合物由多种元素组成,由多种元素组成的纯净物是化合物。
故选B。
9.(2019·东营)下列观点不正确的是()A.自然界中的物质都是由许许多多的微观粒子按特定方式聚集而成B.物质的性质是决定物质用途的唯一因素,物质的用途反映物质的性质C.常见金属的提炼难易程度和应用的先后顺序与金属活动性顺序有关D.同一反应在相同条件下,反应物的颗粒越小,反应越剧烈解析A.自然界中的物质都是由许许多多的微观粒子按特定方式聚集而成,正确;B.物质的性质决定物质用途,但不是唯一因素,错误;C.对比金属活动性强弱关系与人类利用金属的先后,可以发现人类使用较早的金属,其活动性较弱;结合学习中对金属铁、铝的冶炼的认识,可知:金属活动性越强,金属的冶炼难易程度越难,这也影响了人类对金属的使用,正确;D.同一反应在相同条件下,反应物的颗粒越小,反应物的接触面积越大,反应越剧烈,正确。
故选:B。
8.(2019·菏泽)推理是常用的学习方法。
下列推理正确的是()A. 红磷和木炭都可以在空气中燃烧,所以也可用木炭代替红磷测定空气中O2的含量B. 由一种元素组成的纯净物一定是单质,所以单质一定只含有一种元素C. 中和反应生成盐和水,所以有盐和水生成的反应一定是中和反应D. 化学反应通常伴有能量的变化,所以人类利用的能量都是由化学反应提供的【答案】B【解析】A、红磷和木炭都可以在空气中燃烧,木炭在空气中燃烧生成二氧化碳气体,虽除去氧气,而增加了新的气体,没有形成压强差,不能用木炭代替红磷测定空气中O2的含量,故选项推理错误。
B、由一种元素组成的纯净物一定是单质,则单质一定只含有一种元素,故选项推理正确。
C、中和反应生成盐和水,但生成盐和水的反应不一定是中和反应,如CO2+2NaOH═Na2CO3+H2O,故选项推理错误。
D、化学反应通常伴有能量的变化,但人类利用的能量不一定都是由化学反应提供的,故选项推理错误。
故选:B。
15.(2019·聊城)逻辑推理是一种重要的化学思维方法。
下列推理合理的是()A.在同一化合物中,金属元素显正价,则非金属元素一定显负价B.化学变化伴随着能量的变化,则有能量变化的一定是化学变化C.蜡烛燃烧生成二氧化碳和水,则蜡烛组成中一定含有碳元素和氢元素D.催化剂的质量在反应前后不变,则在反应前后质量不变的物质一定是该反应的催化剂解析A、在同一化合物中,金属元素显正价,非金属元素不一定显负价,例如氢氧化钠中,氢元素化合价是+1,该选项说法不正确;B、有能量变化的不一定是化学变化,例如电灯通电时放热,不是化学变化,该选项说法不正确;C、蜡烛燃烧生成二氧化碳和水,则蜡烛组成中一定含有碳元素和氢元素,该选项说法正确;D、在反应前后质量不变的物质不一定是该反应的催化剂,例如红磷在空气中燃烧时,氮气反应前后质量不变,但是氮气不是催化剂,不正确。
故选C。
12.(2019·聊城)归纳是化学学习过程中常用的方法,下列归纳中不正确的是()A.单质:氩气、液氧、铝粉B.常量元素:钙、碳、氧C.铵态氮肥:尿素、氯化铵、硝酸铵D.新能源:氢能、太阳能,核能解析A.由同种元素组成的纯净物叫单质,氩气、液氧、铝粉都是单质,故A正确;B.钙、碳、氧都是常量元素,故B正确;C.由铵根离子和酸根离子构成的化合物叫铵态氮肥;铵态氮肥要有铵根,而尿素没有铵根,不是铵态氮肥,故C错误;D.氢能、太阳能,核能、风能、地热能、潮汐能都属于新能源,故D正确。
故选:C。
12.(2019·潍坊)逻辑推理是学好化学的重要思维方法。
以下推理正确的是()A.有机物都含有碳元素,所以含有碳元素的化合物一定是有机物B.由同种分子构成的物质是纯净物,所以纯净物一定由同种分子构成C.某物质在空气中燃烧生成水,所以该物质中一定含有氢元素D.溶液具有均一性和稳定性,所以具有均一性和稳定性的液体一定是溶液解析A.我们把含有碳元素的化合物叫有机化合物,但是像二氧化碳、一氧化碳、碳酸钙、碳酸钠等具有无机化合物的特点,因此把它们看作无机化合物,所以A错误;B.分子、原子、离子都可以构成物质,故B错误;C.因为反应前后元素的种类不变,所以某物质在空气中燃烧生成水,该物质中一定含有氢元素,故C正确;D.溶液必须是混合物,具有均一性和稳定性的液体不一定都是混合物,D错误。
选C。
10.(2019·临沂)逻辑推理是一种重要的化学思维方法。
下列推理合理的是()A.因为碱溶液呈碱性,所以显碱性的溶液一定都是碱的溶液B.因为H2O和H2O2的组成元素相同,所以它们的化学性质相同C.置换反应中一定有单质生成,则有单质生成的化学反应一定是置换反应D.单质中只含有一种元素,但是只含有一种元素的物质不一定是单质解析A、碱溶液呈碱性,但显碱性的溶液不一定都是碱的溶液,也可能是碳酸钠等盐溶液,故选项推理错误。
B、H2O和H2O2的组成元素相同,但它们分子的构成不同,它们的化学性质不同,故选项推理错误。
C、置换反应有单质生成,但有单质生成的反应不一定为置换反应,如CO+CuO加热Cu+CO2,故选项推理错误。
D、单质是由同种元素组成的纯净物,单质中只含有一种元素,但由同种元素组成的物质不一定是单质,也可能是混合物,如氧气和臭氧的混合物,故选项推理正确。
故选:D。
7.(2019·东营)对下列事实的解释不正确的是()事实解释A 五月槐花香浓郁,六月荷塘清久远分子是不断运动的;不同分子性质不同B 家中绿植枝叶生长不茂盛,叶色淡黄缺少氮肥C 用洗洁精洗去餐盘上的油渍洗洁精能溶解油渍D 常用醋酸或盐酸除水垢醋酸和盐酸中均含有H+解析A、五月槐花香浓郁,六月荷塘清久远,是由分子在不断运动,才能闻到味,两种分子性质不同,味道不同,故A解释正确;B、氮肥促进叶色浓绿;家中绿植枝叶生长不茂盛,叶色淡黄,缺少氮肥,故B解释正确;C、用洗洁精洗去餐盘上的油渍是利用洗洁精的乳化原理,故C解释错误;D、常用醋酸或盐酸除水垢,是因为醋酸和盐酸中均含有H+,用酸将水垢反应掉,故D解释正确。
故选:C。
8.(2019•烟台)归纳总结是学习化学的重要方法。
下列各组对主题知识的归纳中不完全正确的是()A.化学与能源 B.化学与生活①煤、石油、天然气等化石燃料是不可再生能源②氢氧燃料电池是把电能转变为化学能的装置①鉴别棉织物和毛织物可灼烧闻气味②炒菜时锅中的油不慎着火可用锅盖盖灭C.化学与健康D.化学与材料①碘摄入不足或过量均会引起人体甲状腺肿大②食用甲醛溶液浸泡的水产品对人体有害①涂油漆可防止钢铁材料生锈②生铁、不锈钢和青铜都属于合金解析A、①煤、石油、天然气等化石燃料是不可再生能源,正确;②氢氧燃料电池是把化学能转变为电能的装置,错误;B、①毛织物灼烧有烧焦羽毛的气味,棉织物灼烧是烧纸的气味,故鉴别棉织物和毛织物可灼烧闻气味,正确;②炒菜时锅中的油不慎着火可用锅盖盖灭,能隔绝氧气,正确;C、①碘摄入不足或过量均会引起人体甲状腺肿大,正确;②食用甲醛溶液浸泡的水产品对人体有害,正确;C、①涂油漆可防止钢铁材料生锈,正确;②生铁、不锈钢和青铜都属于合金,正确;故选:A。
12.(2019·临沂)根据你所学的化学知识和生活经验判断,下列做法不科学的是()A.用肥皂水区分硬水和软水B.用钢刷、沙等擦洗铝制炊具C.用燃烧的方法区分羊毛纤维和合成纤维D.用相互刻画来比较黄铜片(铜锌合金)和铜片的硬度解析A、硬水和软水的区别在于所含的钙镁离子的多少,可用肥皂水来区分硬水和软水,加入肥皂水,若产生泡沫较多,则是软水,若产生泡沫较少,则是硬水,可以鉴别,故选项说法正确。
B、铝在空气中能与氧气反应,其表面生成一层致密的氧化铝薄膜,从而阻止铝进一步被氧化,不宜用钢刷、沙等等来擦洗铝制炊具,用钢刷、沙等擦洗,会破坏铝制品表面的氧化膜,故选项说法错误。
C、用燃烧的方法区分羊毛纤维和合成纤维,产生烧焦羽毛气味的是羊毛纤维,产生特殊气味的是合成纤维,故选项说法正确。
D、合金的硬度比组成它的纯金属的硬度大,用相互刻画来比较黄铜片(铜锌合金)和铜片的硬度,故选项说法正确。
故选:B。
7.(2019·聊城)下列有关实验现象描述正确的是()A.电解水时,与正极和负极相连的玻璃管中产生气体的体积比是2:1B.铁丝在氧气中剧烈燃烧,火星四射,生成黑色固体C.CO2气体通入紫色石蕊试液中,试液变成蓝色D.把硫酸铵和氢氧化钙固体混合研磨,释放出有刺激性气味的氨气解析A、电解水时,与正极和负极相连的玻璃管中产生气体的体积比是1:2,故A错误;B、铁丝在氧气中剧烈燃烧,火星四射,生成黑色固体,故B正确;C、CO2气体通入紫色石蕊试液中,由于二氧化碳能与水化合生成了碳酸,碳酸显酸性,试液变成红色,故C错误;D、把硫酸铵和氢氧化钙固体混合研磨,释放出有刺激性气味的气体,生成了氨气是结论不是现象。
故D错误。
故选:B。
15.(2019·泰安)如图是某化学兴趣小组设计的观察铁制品锈蚀的实验装置。
下列相关叙述中正确的是()①一段时间后,铁丝会由下向上出现锈蚀现象②一段时间后,水面处铁丝锈蚀严重③一段时间后,塑料瓶会变膨胀,因为铁生锈要放热④一段时间后,塑料瓶会变瘪,因为铁生锈与空气有关A.①② B.②④ C.②③ D.③④解析在水面处的铁丝与水和氧气充分接触,最先生锈,由于铁生锈需要消耗氧气,导致瓶内的气压减小,故一段时间后塑料瓶会变瘪;故选:B。
