立体几何证明定理及性质总结
高中数学立体几何证明定理及性质总结

高中数学立体几何证明定理及性质总结高中数学立体几何是数学的一个重要分支,主要研究与三维空间中的几何形体相关的性质和定理。
在学习过程中,我们会遇到许多重要的定理和性质,下面是对其中一些重要的定理和性质进行总结的文章,以便于我们更好地掌握该知识点。
一、三角形的五种中线定理:1.三角形的三条中线交于一点,并且该点离三角形三个顶点的距离相等,这个点称为三角形的重心。
2.三角形的三条中线外接圆半径为内接圆半径的两倍。
3.三角形的三条中线构成的小三角形,其面积之和等于三角形面积的三分之一4. 中线长与边长的关系:三角形三边长分别为a、b、c,则三角形的三条中线长分别为m_a = 0.5*sqrt(2*b^2+2*c^2-a^2),m_b =0.5*sqrt(2*a^2+2*c^2-b^2),m_c = 0.5*sqrt(2*a^2+2*b^2-c^2)。
5.中线垂直性质:三角形的三条中线互相垂直,且互相平分。
二、三角形的四种高定理:1.三角形的三条高交于一点,并且该点到三角形三个顶点的距离相等,这个点称为三角形的垂心。
2.高线长与边长的关系:三角形三边长分别为a、b、c,则三角形的三条高线长分别为h_a=2*S/a,h_b=2*S/b,h_c=2*S/c,其中S为三角形的面积。
3.垂心到顶点距离的关系:设山脚底角为A,垂足为D,有AH/HD=BH/HE=CH/HF=2,其中H为垂心,E,F为垂足。
4.垂心角的关系:设山脚底角为A,垂足为D,有∠BHC=2∠A,∠BHC=2∠A,∠CHB=2∠A。
三、三角形的欧拉定理:设O为三角形的外心,G为重心,H为垂心,则有OG=1/3GH。
四、圆的性质:1.垂径定理:直径AB垂直于弧CD,则弦CD的中点E与弦AB的中点F,以及圆心O在一条直线上,且OE=OF=1/2CD。
2.正接定理:一个直角三角形的斜边上的圆的直径与该斜边上的直角边成正切关系。
3.切线定理:从一个点外切于圆的切线恒垂直于该点至圆心的半径。
立体几何所有的定理大总结(绝对全)

⽴体⼏何所有的定理⼤总结(绝对全)(⼆)异⾯直线所成⾓1.定义:不同在任何⼀个平⾯内的两条直线或既不平⾏也不相交的两条直线叫异⾯直线。
2.画法:借助辅助平⾯。
1.定义:对于异⾯直线a 和b ,在空间任取⼀点P ,过P 分别作a 和b 的平⾏线1a 和1b ,我们把1a 和1b 所成的锐⾓或者叫做异⾯直线a 和b 所成的⾓。
2.范围:(0°,90°】(★空间两条直线所成⾓范围:【0°,90°】)(三)线⾯⾓1.定义:当直线l 与平⾯α相交且不垂直时,叫做直线l 与平⾯α斜交,直线l 叫做平⾯α的斜线。
设直线l 与平⾯α斜交与点M ,过l 上任意点A ,做平⾯α的垂线,垂⾜为O ,把点O 叫做点A 在平⾯α上的射影,直线OM 叫做直线l 在平⾯α上的射影。
1.定义:把直线l 与其在平⾯α上的射影所成的锐⾓叫做直线l 和平⾯α所成的⾓。
2.范围【0°,90°】(★斜线与平⾯所成⾓范围:【0°,90°】)(三)⼆⾯⾓1.定义:(1)半平⾯:平⾯内的⼀条直线把这个平⾯分成两个部分,其中每⼀个部分叫做半平⾯。
(3)⼆⾯⾓的棱:这⼀条直线叫做⼆⾯⾓的棱。
(4)⼆⾯⾓的⾯:这两个半平⾯叫做⼆⾯⾓的⾯。
(5)⼆⾯⾓的平⾯⾓:以⼆⾯⾓的棱上任意⼀点为端点,在两个⾯内分别作垂直于棱的两条射线,这两条射线所成的⾓叫做⼆⾯⾓的平⾯⾓。
(6)直⼆⾯⾓:平⾯⾓是直⾓的⼆⾯⾓叫做直⼆⾯⾓。
1.定义:从⼀条直线出发的两个半平⾯所组成的图形叫做⼆⾯⾓。
2.表⽰:如下图,可记作α-AB-β或P-AB-Q3.范围为【0°,180°】(五)六种距离1.点到点的距离:两点之间的线段PQ 的长。
2.点到线的距离:过P 点作1PP ⊥l ,交l 于1P ,线段1PP 的长。
3.点到⾯的距离:过P 点作1PP ⊥α,交α于1P ,线段1PP 的长。
立体几何常考定理总结(八大定理)

立体几何常考定理总结(八大定理)一、线面平行的判定定理:线线平行线面平行文字语言:如果平面外的一条直线与平面内的一条直线平行,则这条直线与平面平行、符号语言:关键点:在平面内找一条与平面外的直线平行的线二、线面平行的性质定理:线面平行线线平行文字语言:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行、符号语言:关键点:需要借助一个经过已知直线的平面,接着找交线。
三、面面平行的判定定理:线面平行面面平行文字语言:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行、符号语言:关键点:在要证明面面平行的其中一个面内找两条相交直线和另一面线面平行。
四、面面平行的性质定理: 面面平行线线平行、面面平行线面平行文字语言:如果两个平行平面同时和第三个平面相交,那么所得的两条交线平行、符号语言:关键点:找第三个平面与已知平面都相交,则交线平行文字语言:如果两个平面平行,那么其中一个平面内的任意一条直线平行于另一个平面、符号语言:关键:只要是其中一个平面内的直线就行五、线面垂直的判定定理:线线垂直线面垂直文字语言:如果一条直线和一个平面内的两条相交直线垂直,那么这条直线垂直于这个平面、符号语言:关键点:在平面内找两条相交直线与所要证的直线垂直六、线面垂直的性质定理:线面垂直线线垂直文字语言:若一条直线垂直于一个平面,则这条直线垂直平面内的任意一条直线、符号语言:关键点:往往线面垂直中的线线垂直需要用这个定理推出七、平面与平面垂直的判定定理:线面垂直面面垂直文字语言:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直、(如果一条直线垂直于一个平面,并且有另一个平面经过这条直线,那么这两个平面垂直)符号表示:关键点:在需要证明的两个平面中找线面垂直八、平面与平面垂直的性质定理:面面垂直线面垂直文字语言:如果两个平面互相垂直,那么在一个平面内垂直于它们的交线的直线垂直于另一个平面、符号语言:关键点:先找交线,再在其中一个面内找与交线垂直的线。
常考定理总结(八大定理)

lmβααba立体几何的八大定理一、线面平行的判定定理:线线平行⇒线面平行文字语言:如果平面外.的一条直线与平面内.的一条直线平行,则这条直线与平面平行. 符号语言://a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α关键点:在平面内找一条与平面外的直线平行的线...................... 二、线面平行的性质定理:线面平行⇒线线平行文字语言:如果一条直线和一个平面平行,经过..这条直线的平面和这个平面相交..,那么这条直线就和交线..平行. 符号语言://l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m关键点:需要借助一个经过已知直线的平面,接着找交线。
.......................... 三、面面平行的判定定理:线面平行⇒ 面面平行文字语言:如果一个平面内.有两.条相交..直线都平行..于另一个平面..,那么这两个平面平行. 符号语言://a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥ 关键点:在要证明面面平行的其中一个面内找两条相交直线和另一面线面平行。
................................... 四、面面平行的性质定理: 面面平行⇒线线平行、面面平行⇒线面平行 文字语言:如果两个平行平面同时..和第三..个.平面相交..,那么所得的两条交线..平行. 符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭关键点:找第三个平面与已知平面都相.................交,则交线平行.......文字语言:如果两个平面平行,那么其中一个平面内的任意..一条直线平行于另一个平面.符号语言://,//a a αβαβ⊂⇒ 关键:只要是其中一个平面内的直线就行..................nmAαaBA l βαaβα五、线面垂直的判定定理:线线垂直⇒线面垂直文字语言:如果一条直线和一个平面内.的两.条相交..直线垂直..,那么这条直线垂直于这个平面. 符号语言:,a ma n a m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭关键点:在平面内找两条相交直线与所要证的直线垂直........................ 六、线面垂直的性质定理:线面垂直⇒线线垂直文字语言:若一条直线垂直于一个平面,则这条直线垂直平面内的任意..一条直线. 符号语言:l l a a αα⊥⎫⇒⊥⎬⊂⎭关键点:往往线面垂直中的线线垂直需要用这个定理推出......................... 七、平面与平面垂直的判定定理:线面垂直⇒面面垂直文字语言:如果一个平面经过..另一个平面的一条垂线,则这两个平面互相垂直. (如果一条直线垂直于一个平面,并且有另一个平面经过这条直线,那么这两个平面垂直)符号表示:a a ααββ⊥⎫⇒⊥⎬⊂⎭关键..点:在需要证明的两个平面中找线面垂直..................八、平面与平面垂直的性质定理:面面垂直⇒线面垂直文字语言:如果两个平面互相垂直,那么在一个平面内垂直..于它们的交线..的直线垂直于另一个平面.符号语言:l AB AB AB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭关键点:先找交线,再在其中一个面内找与交线垂直的线。
立体几何常考定理的总结(八大定理)
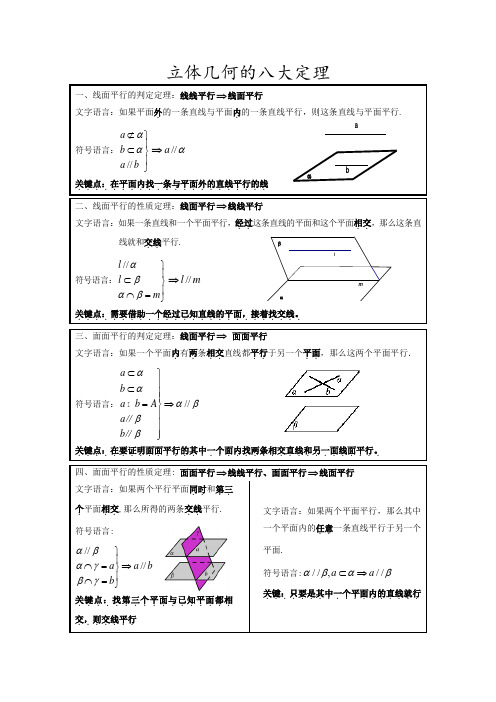
lmβααba立体几何的八大定理一、线面平行的判定定理:线线平行⇒线面平行文字语言:如果平面外.的一条直线与平面内.的一条直线平行,则这条直线与平面平行. 符号语言://a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α关键点:在平面内找一条与平面外的直线平行的线...................... 二、线面平行的性质定理:线面平行⇒线线平行文字语言:如果一条直线和一个平面平行,经过..这条直线的平面和这个平面相交..,那么这条直线就和交线..平行. 符号语言://l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m关键点:需要借助一个经过已知直线的平面,接着找交线。
.......................... 三、面面平行的判定定理:线面平行⇒ 面面平行文字语言:如果一个平面内.有两.条相交..直线都平行..于另一个平面..,那么这两个平面平行. 符号语言://a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥ 关键点:在要证明面面平行的其中一个面内找两条相交直线和另一面线面平行。
................................... 四、面面平行的性质定理: 面面平行⇒线线平行、面面平行⇒线面平行 文字语言:如果两个平行平面同时..和第三..个.平面相交..,那么所得的两条交线..平行. 符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭关键点:找第三个平面与已知平面都相.................交,则交线平行.......文字语言:如果两个平面平行,那么其中一个平面内的任意..一条直线平行于另一个平面.符号语言://,//a a αβαβ⊂⇒ 关键:只要是其中一个平面内的直线就行..................nmAαaBA l βαaβα五、线面垂直的判定定理:线线垂直⇒线面垂直文字语言:如果一条直线和一个平面内.的两.条相交..直线垂直..,那么这条直线垂直于这个平面. 符号语言:,a ma n a m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭关键点:在平面内找两条相交直线与所要证的直线垂直........................ 六、线面垂直的性质定理:线面垂直⇒线线垂直文字语言:若一条直线垂直于一个平面,则这条直线垂直平面内的任意..一条直线. 符号语言:l l a a αα⊥⎫⇒⊥⎬⊂⎭关键点:往往线面垂直中的线线垂直需要用这个定理推出......................... 七、平面与平面垂直的判定定理:线面垂直⇒面面垂直文字语言:如果一个平面经过..另一个平面的一条垂线,则这两个平面互相垂直. (如果一条直线垂直于一个平面,并且有另一个平面经过这条直线,那么这两个平面垂直)符号表示:a a ααββ⊥⎫⇒⊥⎬⊂⎭关键点:....在需要证明的两个平面中找线面垂直................八、平面与平面垂直的性质定理:面面垂直⇒线面垂直文字语言:如果两个平面互相垂直,那么在一个平面内垂直..于它们的交线..的直线垂直于另一个平面.符号语言:l AB AB AB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭关键点:先找交线,再在其中一个面内找与交线垂直的线。
立体几何判定定理与性质定理汇总

文字语言:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行. 符号语言:α⊄a ,α⊂b ,且b a //α//a ⇒.图形语言:定理二(平面与平面平行的判定定理)文字语言:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行. 符号语言:β⊂a ,β⊂b ,P b a = ,α//a ,α//b αβ//⇒.定理三(直线与平面平行的性质定理)文字语言:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行.符号语言:α//a ,β⊂a ,且b =βα b a //⇒.图形语言:证明:因为b =βα ,所以α⊂b .又因为α//a ,所以a 与b 无公共点.又因为β⊂a ,β⊂b ,所以b a //.定理四(平面与平面平行的性质定理)文字语言:如果两个平行平面同时和第三个平面相交,那么它们的交线平行. 符号语言:βα//,a =γα ,b =γβ b a //⇒.图形语言:αb a αa αβa bαγa b αβ文字语言:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直. 符号语言:a c ⊥,b c ⊥,P b a = ,α⊂a ,α⊂b α//c ⇒.图形语言:定理六(平面与平面垂直的判定定理)文字语言:一个平面过另一个平面的垂线,则这两个平面垂直.符号语言:α⊥a ,β⊂a ,αβ⊥⇒.图形语言:定理七(直线与平面垂直的性质定理)文字语言:垂直于同一平面的两条直线平行.符号语言:α⊥a ,α⊥b b a //⇒.图形语言:定理八(平面与平面垂直的性质定理)文字语言:对于两个相互垂直的平面,在一个平面内垂直交线的直线垂直另一平面. 符号语言:βα⊥,m =βα ,β⊂a ,m a ⊥α⊥⇒a .图形语言:αβa αb a βa m α。
高中数学立体几何判定定理及性质
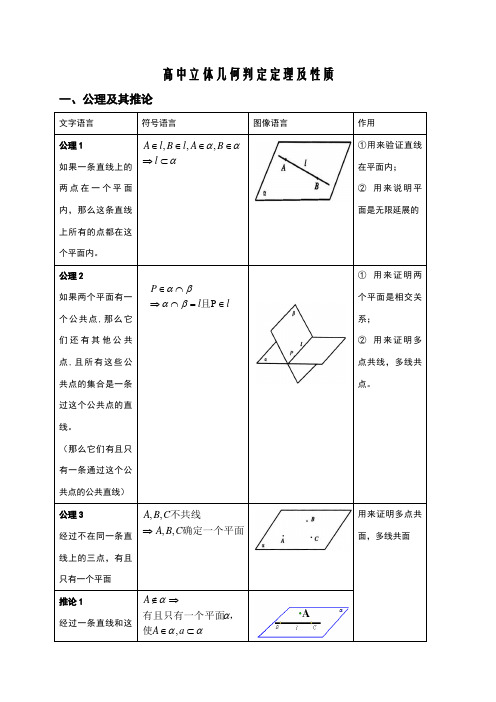
高中立体几何判定定理及性质一、公理及其推论文字语言 符号语言图像语言作用公理1如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内。
ααα⊂⇒∈∈∈∈l B A l B l A ,,,①用来验证直线在平面内; ② 用来说明平面是无限延展的公理2如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线。
(那么它们有且只有一条通过这个公共点的公共直线)ll P ∈=⋂⇒⋂∈P 且βαβα① 用来证明两个平面是相交关系;② 用来证明多点共线,多线共点。
公理3经过不在同一条直线上的三点,有且只有一个平面 确定一个平面不共线C B A C B A ,,,,⇒用来证明多点共面,多线共面推论1经过一条直线和这αααα⊂∈⇒∉a A A ,使,有且只有一个平面条直线外的一点,有且只有一个平面推论2经过两条相交直线,有且只有一个平面ααα⊂⊂⇒=⋂baPba,使,有且只有一个平面推论3经过两条平行直线,有且只有一个平面ααα⊂⊂⇒baba,使,有且只有一个平面∥公理4 (平行公理)平行于同一条直线的两条直线平行cacbba∥∥∥⇒⎭⎬⎫用来证明线线平行二、平行关系文字语言符号语言图像语言作用(1)公理4 (平行公理)平行于同一条直线的两条直线平行cacbba∥∥∥⇒⎭⎬⎫(2)线面平行的判定定理如果平面外一条直线和这个平面内的一条直线平行,那ααα∥∥ababa⇒⎪⎭⎪⎬⎫⊂⊄么这条直线和这个平面平行。
(3)线面平行的性质定理如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
baabb∥∥⇒⎪⎭⎪⎬⎫⊂=⋂ββαβ(4)面面平行的判定定理如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.βαααββ∥∥∥⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫⊂⊂=⋂baObaba(5)面面平行的判定如果两个平面垂直于同一条直线,那么这两个平面平行。
立体几何所有的定理大总结绝对全

(二)异面直线所成角1.定义:不一样在任何一个平面内的两条直线或既不平行也不订交的两条直线叫异面直线。
2.画法:借助协助平面。
1.定义:关于异面直线 a 和 b,在空间任取一点 P,过 P 分别作 a 和 b 的平行线a1和b1,我们把 a1和b1所成的锐角或许叫做异面直线 a 和 b 所成的角。
2.范围: (0 °, 90°】( ★空间两条直线所成角范围:【0°, 90°】 )(三)线面角1. 定义:当直线 l 与平面α订交且不垂直时,叫做直线 l 与平面α斜交,直线 l 叫做平面α的斜线。
设直线 l 与平面α斜交与点 M,过 l 上随意点 A,做平面α的垂线,垂足为O,把点 O叫做点 A 在平面α上的射影,直线 OM叫做直线 l 在平面α上的射影。
1.定义:把直线 l 与其在平面α上的射影所成的锐角叫做直线 l 和平面α所成的角。
2.范围【 0°, 90°】(★斜线与平面所成角范围:【0°, 90°】)(三)二面角1.定义:(1)半平面:平面内的一条直线把这个平面分红两个部分,此中每一个部分叫做半平面。
(3)二面角的棱:这一条直线叫做二面角的棱。
(4)二面角的面:这两个半平面叫做二面角的面。
(5)二面角的平面角:以二面角的棱上随意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。
(6)直二面角:平面角是直角的二面角叫做直二面角。
1.定义:从一条直线出发的两个半平面所构成的图形叫做二面角。
2. 表示:以下列图,可记作 α-AB- β或 P-AB-Q3. 范围为【 0°, 180°】(五)六种距离1. 点到点的距离:两点之间的线段 PQ 的长。
2. 点到线的距离:过 P 点作 PPl ,交 l 于 P ,线段 PP 的长。
1 1 13. 点到面的距离:过 P 点作 PP 1,交 于 P 1 ,线段 PP 1 的长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.直线和平面的三种位置关系:
1.
线面平行 2. 线面相交
l
符号表示:
符号表示:
3. 线在面内
符号表示:
二.平行关系:
1.线线平行:
方法一:用线面平行实现。
方法二:用面面平行
实现。
m
l
m
l
l
//
//
⇒
⎪
⎭
⎪
⎬
⎫
=
⋂
⊂
β
α
β
α
m
l
m
l//
//
⇒
⎪
⎭
⎪
⎬
⎫
=
⋂
=
⋂
β
γ
α
γ
β
α
方法三:用线面垂直实现。
若α
α⊥
⊥m
l,,则m
l//。
2.线面平行:
方法一:用线线平行实现。
α
α
α//
//
l
l
m
m
l
⇒
⎪
⎭
⎪
⎬
⎫
⊄
⊂
方法二:用面面平行实现。
α
β
β
α
//
//
l
l
⇒
⎭
⎬
⎫
⊂
3.面面平行:
方法一:用线线平行实现。
方法二:用线面
平行实现
l
βααβ//',','
//'//⇒⎪⎪
⎭⎪
⎪
⎬
⎫
⊂⊂且相交且相交m l m l m m l l 。
βαβαα//,////⇒⎪⎭
⎪⎬⎫⊂且相交m l m l
三.垂直关系: 1. 线面垂直:
方法一:用线线垂直实现。
方法二:用面面垂直实现。
α
α⊥⇒⎪⎪
⎭⎪⎪⎬⎫
⊂=⋂⊥⊥l AB AC A AB AC AB l AC
l ,
αββαβα⊥⇒⎪⎭⎪
⎬⎫⊂⊥=⋂⊥l l m l m , 2. 面面垂直:
方法一:用线面垂直实现。
方法二:计算所成二面角为直角。
βαβα⊥⇒⎭
⎬⎫
⊂⊥l l
3.
线线垂直:
方法一:用线面垂直实现。
m l m l ⊥⇒⎭
⎬⎫
⊂⊥αα
方法二:三垂线定理及其逆定理。
PO l OA l PA l αα⊥⎫
⎪
⊥⇒⊥⎬⎪⊂⎭。
