中考数学压轴题破解策略专题18《弦图模型》

初中数学勾股定理之“赵爽弦图”模型(解析版)

勾股定理之“赵爽弦图”模型【知识梳理】“赵爽弦图”的面积关系是中考常考的一种题型，一般出现在选择题、填空题中，如果能够记住面积之间的关系，那么做此类题时一定非常高效.【考点剖析】一．选择题(共2小题)1如图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若AC= 6，BC=5，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到如图2所示的“数学风车”，则这个风车的外围周长是()A.76B.72C.68D.52【分析】由题意∠ACB为直角，利用勾股定理求得外围中一条边，又由AC延伸一倍，从而求得风车的一个轮子，进一步求得四个．【解答】解：依题意，设“数学风车”中的四个直角三角形的斜边长为x，则x2=122+52=169所以x=13所以“数学风车”的周长是：(13+6)×4=76．故选：A．【点评】本题是勾股定理在实际情况中应用，并注意隐含的已知条件来解答此类题．2“赵爽弦图”巧妙地利用面积关系证明了勾股定理．在如图所示的“赵爽弦图”中，△ABH，△BCG，△CDF和△DAE是四个全等的直角三角形，四边形ABCD，EFGH都是正方形．若AB=10，EF=2，则AH的长为()A.62B.82C.6D.8【分析】由题意得，设AH=DE=CF=BG=x，则AE=DF=CG=BH=2+x，再根据勾股定理即可求解．【解答】解：∵△ABH，△BCG，△CDF和△DAE是四个全等的直角三角形，四边形ABCD，EFGH都是正方形．AB=10，EF=2，∴设AH=DE=CF=BG=x，则AE=DF=CG=BH=2+x，在Rt△AHB中，AB2=AH2+BH2，即102=x2+(x+2)2，整理得，x2+2x-48=0，解得：x1=6，x2=-8(不符合题意，舍去)，∴AH=6．故选：C．【点评】本题考查了正方形的性质、勾股定理、全等三角形的性质，根据题意得到线段的关系，然后根据勾股定理列出方程并求解是解题关键．二．填空题(共4小题)3“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b，若(a+b)2=107，大正方形的面积为57，则小正方形的边长为　7　．【分析】观察图形可知，小正方形的面积=大正方形的面积-4个直角三角形的面积，利用已知(a+b)2= 107，大正方形的面积为57，可以得出直角三角形的面积，进而求出答案．【解答】解：如图所示：∵(a+b)2=107，∴a2+2ab+b2=107，∵大正方形的面积为57，∴2ab=107-57=50，∴小正方形的面积为57-50=7，故小正方形的边长为7．故答案为：7．【点评】本题考查勾股定理的证明，解题的关键是熟练运用勾股定理以及完全平方公式，本题属于基础题型．4如图，由四个全等的直角三角形拼成“赵爽弦图”．Rt △ABF 中，∠AFB =90°，AF =4，AB =5．四边形EFGH 的面积是1．【分析】四边形EFGH 的面积=四边形ABCD 的面积-四个全等直角三角形的面积．直角三角形的面积需利用勾股定理求出直角边后解答．【解答】解：因为AB =5，所以S 正方形ABCD =5×5=25．Rt △ABF 中，AF =4，AB =5，则BF =52-42=3，所以S Rt △ABF =12×3×4=6，四个直角三角形的面积为：6×4=24，四边形EFGH 的面积是25-24=1．故答案为1【点评】此题主要考查了勾股定理，以及正方形面积、三角形面积，难易程度适中．5如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形E 的边长为7cm ，则图中五个正方形A 、B 、C 、D 、E 的面积和为98cm 2．【分析】根据正方形的面积公式，连续运用勾股定理，发现：四个小正方形的面积和等于最大正方形的面积．【解答】解：设正方形A 、B 、C 、D 的边长分别是a 、b 、c 、d ，则正方形A的面积=a2，正方形B的面积=b2，正方形C的面积=c2，正方形D的面积=d2，又∵a2+b2=x2，c2+d2=y2，∴正方形A、B、C、D、E的面积和=(a2+b2)+(c2+d2)+72=x2+y2+72=72+72=98(cm2)．即正方形A，B，C，D、E的面积的和为98cm2．故答案为：98．【点评】本题考查了勾股定理：直角三角形中，两直角边的平方和等于斜边的平方．熟练运用勾股定理进行面积的转换是解题关键．6图(1)是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．在Rt△ABC中，若直角边AC=6cm，BC=5cm，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到图(2)所示的“数学风车”．则①图中小正方形的面积为1cm2　；②若给这个“数学风车”的外围装饰彩带，则需要彩带的长度至少是76cm．【分析】①表示出小正方形的边长，然后利用正方形的面积公式列式计算即可得解；②利用勾股定理求出外围直角三角形的斜边，然后根据周长公式列式计算即可得解．【解答】解：图①，小正方形的面积=(6-5)2=1cm2；图②，外围直角三角形的斜边=122+52=13cm，周长=4×(13+6)=4×19=76cm，即，需要彩带的长度至少是76cm．故答案为：1cm2，76cm．【点评】本题考查了勾股定理的证明，读懂题目信息并准确识图是解题的关键．三．解答题(共3小题)7如图①，美丽的弦图，蕴含着四个全等的直角三角形．(1)如图①弦图中包含了一大，一小两个正方形，已知每个直角三角形较长的直角边为a．较短的直角边为b，斜边长为c，可以验证勾股定理；(2)如图②，将八个全等的直角三角形紧密地拼接，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1、S2、S3，若S1+S2+S3=16，则S2=　163　．【分析】(1)由图可知，小正方形的面积可直用边长乘边长，为(a -b )2，也可用大正方形的面积减去四个全等的直角三角形的面积，为c 2-4×12ab ，以此即可证明；(2)设正方形MNKT 的面积为x ，八个全等的直角三角形的面积均为y ，可得S 1=8y +x ，S 2=4y +x ，S 3=x ，则S 1+S 2+S 3=12y +3x =16，根据整体思想即可求出S 2=4y +x =163．【解答】(1)证明：S 小正方形=a -b 2=a 2-2ab +b 2，另一方面S 小正方形=c 2-4×12ab =c 2-2ab ，即a 2-2ab +b 2=c 2-2ab ，则a 2+b 2=c 2；(2)解：设正方形MNKT 的面积为x ，八个全等的直角三角形的面积均为y ，∵S 1+S 2+S 3=16，∴S 1=8y +x ，S 2=4y +x ，S 3=x ，∴S 1+S 2+S 3=12y +3x =16，∴4y +x =163，∴S 2=4y +x =163．故答案为：163．【点评】本题主要考查勾股定理的证明，利用数形结合的思想来答题是解题关键．8我们发现，用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题，这种方法称为等面积法，这是一种重要的数学方法．请你用等面积法来探究下列两个问题：(1)如图1是著名的赵爽弦图，由四个全等的直角三角形拼成，请你用它来验证勾股定理；(2)如图2，在Rt △ABC 中，∠ACB =90°，CD 是AB 边上的高，AC =4，BC =3，求CD 的长度．【分析】(1)根据题意，我们可在图中找等量关系，由中间的小正方形的面积等于大正方形的面积减去四个直角三角形的面积，列出等式化简即可得出勾股定理的表达式．(2)先由勾股定理求出AB 的长，再根据三角形的面积求CD 的长即可．【解答】解：(1)∵大正方形面积为c 2，直角三角形面积为12ab ，小正方形面积为：(b -a )2，∴c 2=4×12ab +(a -b )2=2ab +a 2-2ab +b 2即c2=a2+b2．(2)在Rt△ABC中，∵∠ACB=90°，∴由勾股定理，得：AB=AC2+BC2=42+32=5∵CD⊥AB，∴S△ABC=12AC•BC=12AB•CD∴CD=4×35=125．【点评】本题考查了学生对勾股定理的证明和对三角形和正方形面积公式的熟练掌握和运用，属于基本题型．9图甲是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成，面积为74的正方形．在Rt△ABC中，若直角边BC=5，将四个直角三角形中边长为5的直角边分别向外延长一倍，得到图乙所示的“数学风车”．(1)这个风车至少需要绕着中心旋转90°才能和本身重合；(2)求这个风车的外围周长(图乙中的实线)．【分析】(1)根据旋转角及旋转对称图形的定义结合图形特点作答．(2)在直角△ABC中，已知BC，AB，根据勾股定理即可计算AC的长，AC=7，故求得BD即可计算风车的外围周长．【解答】解：(1)：∵360°÷4=90°，∴该图形绕中心至少旋转90度后能和原来的图案互相重合．(2)在直角△BCD中，BD为斜边，已知BC=5，AB=74，由勾股定理得：AC=7，CD=7+5=12，∴BD=52+122=13，∵风车的外围周长为4(BD+AD)=4(13+5)=72．【点评】本题考查了旋转角的定义及勾股定理在直角三角形中的运用，考查了全等三角形对应边相等的性质，本题中正确的计算BD是解题的关键．【过关检测】一．选择题(共10小题)10(2022春•东城区期末)如图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若AC=6，BC=5，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到图2所示的“数学风车”，则这个风车的外围周长是()A.72B.52C.80D.76【分析】由题意∠ACB为直角，利用勾股定理求得外围中一条边，又由AC延伸一倍，从而求得风车的一个轮子，进一步求得四个．【解答】解：依题意，设“数学风车”中的四个直角三角形的斜边长为x，则x2=122+52=169所以x=13所以“数学风车”的周长是：(13+6)×4=76．故选：D．【点评】本题是勾股定理在实际情况中应用，并注意隐含的已知条件来解答此类题．11(2021秋•邳州市期中)公元3世纪切，中国古代书学家赵爽注《周髀算经》时，创造了“赵爽弦图”．如图，勾a=3，弦c=5，则小正方形ABCD的面积为()A.1B.3C.4D.9【分析】根据勾股定理和正方形的面积公式可求解．【解答】解：如图，∵勾a=3，弦c=5，∴股b=52-32=4，∴小正方形的边长=4-3=1，∴小正方形的面积=12=1，故选：A．【点评】本题运用了勾股定理和正方形的面积公式，关键是运用了数形结合的数学思想．12(2021春•长垣市期末)“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形，如图，其直角三角形的两条直角边的长分别是2和4，则小正方形与大正方形的面积比是()A.1：2B.1：4C.1：5D.1：10【分析】根据题意求得小正方形的边长，根据勾股定理求出大正方形的边长，由正方形的面积公式即可得出结果．【解答】解：∵直角三角形的两条直角边的长分别是2和4，∴小正方形的边长为2，根据勾股定理得：大正方形的边长=22+42=25，∴小正方形面积大正方形面积=22252=420=15．故选：C．【点评】本题考查了勾股定理和正方形的面积．本题是用数形结合来证明勾股定理，锻炼了同学们的数形结合的思想方法．13(2022秋•青秀区校级期末)“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b，若(a+b)2=21，小正方形的面积为5，则大正方形的面积为()A.12B.13C.14D.15【分析】由题意可知：中间小正方形的边长为：a-b，根据勾股定理以及题目给出的已知数据即可求出大正方形的边长．【解答】解：由题意可知：中间小正方形的边长为：a-b=5，∵(a+b)2=(a-b)2+4ab=5+4ab=21，∴ab=4，∴大正方形的面积=4×12ab+5=13，故选：B．【点评】本题考查勾股定理的证明，解题的关键是熟练运用勾股定理以及完全平方公式，本题属于基础题型．14(2022秋•南岸区校级期中)我国是最早了解勾股定理的国家之一，根据《周髀算经》的记载，勾股定理的公式与证明是在商代由商高发现的，故又称之为“商高定理”．三国时代的蒋铭祖对《蒋铭祖算经》勾股定理作出了详细注释，并给出了另外一种证明．下面四幅图中，不能证明勾股定理的是()A. B. C. D.【分析】根据基础图形的面积公式表示出各个选项的面积，同时根据割补的思想可以写出另外一种面积表示方法，即可得出一个等式，进而可判断能否证明勾股定理．【解答】解：A 、大正方形的面积为：c 2；也可看作是4个直角三角形和一个小正方形组成，则其面积为：12ab ×4+(b -a )2=a 2+b 2，∴a 2+b 2=c 2，故A 选项能证明勾股定理；B 、大正方形的面积为：(a +b )2；也可看作是4个直角三角形和一个小正方形组成，则其面积为：12ab ×4+c 2=2ab +c 2，∴(a +b )2=2ab +c 2，∴a 2+b 2=c 2，故B 选项能证明勾股定理；C 、梯形的面积为：12(a +b )(a +b )=12(a 2+b 2)+ab ；也可看作是2个直角三角形和一个等腰直角三角形组成，则其面积为：12ab ×2+12c 2=ab +12c 2，∴ab +12c 2=12(a 2+b 2)+ab ，∴a 2+b 2=c 2，故C 选项能证明勾股定理；D 、大正方形的面积为：(a +b )2；也可看作是2个矩形和2个小正方形组成，则其面积为：a 2+b 2+2ab ，∴(a +b )2=a 2+b 2+2ab ，∴D 选项不能证明勾股定理．故选：D ．【点评】本题考查勾股定理的证明方法，熟练掌握内弦图、外弦图是解题关键．15(2022秋•平湖市期末)在认识了勾股定理的赵爽弦图后，一位同学尝试将5个全等的小正方形嵌入长方形ABCD 内部，其中点M ，N ，P ，Q 分别在长方形的边AB ，BC ，CD 和AD 上，若AB =7，BC =8，则小正方形的边长为()A.5B.6C.7D.22【分析】将每个小正方形按照如图所示分成四个全等的直角三角形和一个正方形，设每个直角三角形的较大的直角边为x ，较小的直角边为y ，根据AB =7，BC =8，列出二元一次方程组，求出x 和y ，再求出边长即可．【解答】解：将每个小正方形按照如图所示分成四个全等的直角三角形和一个正方形，设每个直角三角形的较大的直角边为x ，较小的直角边为y ，∵AB =7，BC =8，∴3x+y=73x+2y=8 ，解得x=2 y=1 ，∴小正方形的边长为22+12=5．故选A．【点评】本题考查了勾股定理与二元一次方程组的应用，根据题意运用好赵爽弦图是解题关键．16(2022秋•鄄城县校级月考)如图，阴影部分是两个正方形，图中还有一个直角三角形和一个空白的正方形，阴影部分的面积为25cm2，直角三角形①中较长的直角边长12cm，则直角三角形 ①的面积是()A.16cm2B.25cm2C.30cm2D.169cm2【分析】两个阴影正方形的面积和等于直角三角形另一未知边的平方．利用勾股定理即可求出．【解答】解：∵两个阴影正方形的面积和等于直角三角形另一未知边的平方，∴直角三角形①中较短的直角边长5cm，∵直角三角形①中较长的直角边长12cm，∴直角三角形①的面积=12×5×12=30(cm2)，故选：C．【点评】考查了正方形的面积以及勾股定理的应用．推知“正方形的面积和等于直角三角形另一未知边的平方”是解题的难点．17(2021秋•鹿城区校级期中)如图，Rt△ABC中，∠ACB=90°，∠ABC=30°，分别以AC，BC，AB 为一边在△ABC外面做三个正方形，记三个正方形的面积依次为S1，S2，S3，已知S1=4，则S3为()A.8B.16C.43D.43+4【分析】根据正方形的面积公式结合勾股定理就可发现大正方形的面积是两个小正方形的面积和，即可得出答案．【解答】解：∵S1=AC2=4，∴AC=2，∵Rt△ABC中，∠ACB=90°，∠ABC=30°，∴AB=2AC=4，∴S3=AB2=16，故选：B．【点评】本题考查了勾股定理和正方形面积的应用，注意：分别以直角三角形的边作相同的图形，则两个小图形的面积等于大图形的面积．18(2022秋•温州期末)如图，大正方形ABCD由四个全等的直角三角形和一个小正方形拼接而成．点E为小正方形的顶点，延长CE交AD于点F，连结BF交小正方形的一边于点G，若△BCF为等腰三角形，AG=5，则小正方形的面积为()A.15B.16C.20D.25【分析】由等腰三角形性质可得出BF=CF，利用HL可证得Rt△ABF≌Rt△DCF(HL)，得出AB=AD =2AF，根据余角的性质得出∠BAG=∠ABF，进而推出CF=BF=2AG=10，利用面积法求得BN= 8，再运用勾股定理求得CN=4，即可求得答案．【解答】解：设小正方形为EHMN，如图，∵四边形ABCD和四边形EHMN是正方形，∴AB=AD=CD，∠BAD=90°，CF∥AG，∵△BCF为等腰三角形，且BF>AB=BC，CF>CD=BC，∴BF=CF，在Rt△ABF和Rt△DCF中，AB=CD BF=CF，∴Rt△ABF≌Rt△DCF(HL)，∴∠AFB=∠CFD，AF=DF，∴AB=AD=2AF，∵CF∥AG，∴∠CFD=∠DAG，∴∠AFB=∠DAG，∴AG=FG，∵∠AFB+∠ABF=90°，∠DAG+∠BAG=90°，∴∠BAG=∠ABF，∴AG=BG，∴CF=BF=2AG=10，在Rt△ABF中，AB2+AF2=BF2，∴(2AF)2+AF2=102，∴AF=25，∴AB=BC=45，∵S△BCF=12BC•AB=12CF•BN，∴BN=BC⋅ABCF =45×4510=8，∴CN=BC2-BN2=452-82=4，∵△ABM≌△BCN，∴BM=CN=4，∴MN=BN-BM=8-4=4，∴S正方形EHMN=(MN)2=42=16，故选：B．【点评】本题主要考查了正方形的性质，全等三角形的判定和性质，等腰三角形的判定与性质，平行线的性质，勾股定理，三角形面积等，利用面积法求得BN是解题的关键．19(2022春•南浔区期末)赵爽弦图由四个全等的直角三角形所组成，形成一个大正方形，中间是一个小正方形(如图所示)．某次课后服务拓展学习上，小浔绘制了一幅赵爽弦图，她将EG延长交CD于点I．记小正方形EFGH的面积为S1，大正方形ABCD的面积为S2，若DI=2，CI=1，S2=5S1，则GI的值是()A.105B.9202 C.58D.34【分析】如图，连接DG，先由已知条件分别求得S2=CD2=32=9，S1=95，小正方形边长为355，再由勾股定理得：EG=EH2+HG2=3105，设AE=BF=CG=DH=x，则AF=BG=CH=DE=x+355，由勾股定理得：CD2=DH2+CH2，即9=x2+(x+355)2，进而得AE=BF=CG=DH=x=355=EH，再得CH垂直平分ED，再由三角形的“三线合一”得∠DGH=∠HGE=45°进而得∠DGI=90°最后由勾股定理得：GI=DI2-DG2=22-31052=105，即得选项A．【解答】解：如图，连接DG，∵赵爽弦图由四个全等的直角三角形所组成，形成一个大正方形，中间是一个小正方形，∴AE=BF=CG=DH，AF=BG=CH=DE，CH⊥DE，∵DI=2，CI=1，∴CD=DI+CI=2+1=3，∵大正方形ABCD的面积为S2，∴S2=CD2=32=9，又∵小正方形EFGH的面积为S1，S2=5S1，∴S1=95，∴EF=FG=GH=HE=355，∵将EG延长交CD于点I，∴∠HGE=45°，在Rt△EHG中，由勾股定理得：EG=EH2+HG2=3105，设AE=BF=CG=DH=x，则AF=BG=CH=DE=x+35 5，在Rt△CDH中，由勾股定理得：CD2=DH2+CH2，即9=x2+(x+355)2，解得：x1=355，x2=-655(不合题意，舍去)，即AE=BF=CG=DH=x=355，∴DH=EH=355，∴CH垂直平分ED，∴DG=EG=3105，∴∠DGH=∠HGE=45°，∴∠DGE=45°+45°=90°，∴∠DGI=90°，在Rt△DGI中，由勾股定理得：GI=DI2-DG2=22-31052=105，故选：A．【点评】本题是一道勾股定理的综合题，主要考查了全等三角形的性质，正方形的性质，勾股定理，线段的中垂线判定与性质，等腰三角形的“三线合一”，二次根式计算与化简，关键是巧添辅助线构等腰直角三角形，顺利实现求得答案．二．填空题(共7小题)20(2022秋•锡山区期中)如图，在△ABC中，∠C=90°，AC=5，BC=12．以AB为一边在△ABC 的同侧作正方形ABDE，则图中阴影部分的面积为139．【分析】首先利用勾股定理求得AB边的长度，然后由三角形的面积公式和正方形的面积公式解答．【解答】解：如图，Rt△ABC中，∠ACB=90°，BC=12，AC=5，由勾股定理知，AB=AC2+BC2=13．故S阴影=S正方形ABDE-S△ABC=132-12×5×12=169-30=139．故答案为：139．【点评】本题主要考查了勾股定理，求阴影部分的面积时，采用了“分割法”．21(2022秋•德惠市期末)如图，“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形EFGH拼成的大正方形ABCD．若AE=5，AB=13，则中间小正方形EFGH的面积是49．【分析】根据题意和题目中的数据，可以计算出小正方形的边长，即可得到小正方形的面积．【解答】解：∵AE=5，AB=13，∴BF=AE=5，在Rt△ABF中，AF=AB2+BF2=12，∴小正方形的边长EF=12-5=7，∴小正方形EFGH的面积为7×7=49．故答案为：49．【点评】本题考查了勾股定理的证明，熟练掌握勾股定理是解题的关键．22(2022秋•建邺区校级期中)将四个全等的直角三角形分别拼成正方形(如图1，2)，边长分别为6和2．若以一个直角三角形的两条直角边为边向外作正方形(如图3)，其面积分别为S1，S2．则S1-S2= 12．【分析】首先设四个全等的直角三角形的两条直角边分别为a，b(a>b)，然后根据图1、2列出关于a、b的方程组即可求解．【解答】解：设四个全等的直角三角形的两条直角边分别为a，b(a>b)，根据图1得：a+b=6，根据图2得：a-b=2，联立解得：a=4 b=2，∴S1=16，S2=4，则S1-S2=12．故答案为：12．【点评】此题主要考查了勾股定理证明的应用，解题的关键是正确理解图形中隐含的数量关系．23(2021秋•龙泉驿区校级月考)如图，是由四个全等的直角三角形与中间一个小正方形拼成的一个大正方形，若大正方形的面积是17，小正方形的面积是1，直角三角形的两直角边分别为a ，b ，则(a +b )2的值是33．【分析】先由拼图列出关于面积的方程，再由勾股定理列一个直角三角形三边的方程并整理，最后把值整体代入和平方的展开式(a +b )2=a 2+b 2+2ab 即可得出答案．【解答】解：∵由四个全等的直角三角形与中间一个小正方形拼成的一个大正方形，大正方形的面积是17，小正方形的面积是1，直角三角形的两直角边分别为a ，b ，∴1+4×12ab =17a 2+b 2=172，即2ab =16a 2+b 2=17 ，∴(a +b )2=a 2+b 2+2ab =17+16=33．故答案为：33．【点评】这是一道勾股定理综合题，主要考查了拼图列方程，发现各个图形的面积和a ，b 的关系是解题关键．24(2022秋•金台区校级月考)如图是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若AC =6，BC =5，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到如图所示的“数学风车”，则这个风车的外围周长是76．【分析】通过勾股定理可将“数学风车”的斜边求出，然后可求出风车外围的周长．【解答】解：设将AC 延长到点D ，连接BD ，根据题意，得CD =6×2=12，BC =5．∵∠BCD =90°∴BC 2+CD 2=BD 2，即52+122=BD 2∴BD =13∴AD +BD =6+13=19∴这个风车的外围周长是19×4=76．故答案为：76．【点评】本题考查勾股定理在实际情况中应用，并注意隐含的已知条件来解答此类题．25(2022秋•工业园区校级期中)如图，在弦图中，正方形ABCD 的对角线AC 与正方形EFHI 的对角线EH 交于点K ，对角线AC 交正方形EFHI 于G ，J 两点，记△GKH 面积为S 1，△JIC 面积为S 2，若AE =12，CD =410，则S 1+S 2的值为16．【分析】由题意可得AF =CI ，∠AFG =∠CIJ =90°，FH ∥EI ，即可证明△AFG ≌△CIJ ，FG =IJ ，再根据四边形EFHI 为正方形，得到△GHK ≌△JEK ，从而得到点K 为正方形EFHI 的中心，过点K 作KM ⊥FH 于点M ，由勾股定理得DE =4，FH =8，KM =4，设GH =a ，FG =b ，则a +b =FH =8，最后用a ，b 表示出S 1+S 2=2(a +b )，将a +b 的值代入即可求解．【解答】解：由题意可得，AF =CI ，∠AFG =∠CIJ =90°，FH ∥EI ，∵∠AGF =∠HGK ，∠IJC =∠KJE ，∵FH ∥EI ，∴∠HGK =∠KJE ，∴∠AGF =∠IJC ，在△AFG 和△CIJ 中，∠AGF =∠IJC ∠AFG =∠CIJ =90°AF =CI ，∴△AFG ≌△CIJ (AAS )，∴FG =IJ ，∵四边形EFHI 为正方形，∴EI -IJ =FH -FG ，即HG =EJ ，在△GHK 和△JEK 中，∠HGK =∠KJE ∠GKH =∠JKE HG =EJ，∴△GHK ≌△JEK (AAS )，∴HK =EK ，即点K 为正方形EFHI 的中心，如图，过点K 作KM ⊥FH 于点M ，∵AE=12，CD=410，∴BF=12，AD=410，在Rt△ADE中，由勾股定理得DE=AD2-AE2=4，∴AF=DE=4，EF=AE-AF=12-4=8，则FH=8，KM=4，设GH=a，FG=b，则a+b=FH=8，∴S1=12GH⋅MK=12a×4=2a，S2=S△AFG=12FG⋅AF=12b×4=2b，∴S1+S2=2a+2b=2(a+b)=16．故答案为：16．【点评】本题主要考查全等三角形的判定与性质，勾股定理，三角形的面积，正方形的性质，解题的关键是寻找全等三角形的条件解决问题．26(2022秋•宁德期中)我国古代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”，它是由4个全等的直角三角形与1个小正方形拼成的一个大正方形，如图，若拼成的大正方形为正方形ABCD，面积为9，中间的小正方形为正方形EFGH，面积为2，连接AC，交BG于点P，交DE于点M，①△CGP≌△AEM，②S△AFP-S△CGP=12，③DH+HC=4，④HC=2+22，以上说法正确的是①③④.(填写序号)【分析】由全等三角形的性质，勾股定理，完全平方公式，结合“赵爽弦图”的特点，可以解决问题．【解答】解：∵Rt△BCG≌Rt△DAE，∴CG=AE，∠CGP=∠AEM，∵CH∥AF．∴∠GCP=∠MAE，∴△CGP≌△AEM(ASA)，∴S△CGP=S△AEM，CP=ME，∴S△AFP-S△CGP=S四边形MEFP∵HE=GF，∴HM =PF ，∴S 四边形MEFP =S 四边形MHGP =12S 正方形EFGH=1，∴S △AFP -S △CGP =1，∵DH 2+CH 2=DC 2=9，∴(DH +CH )2=DH 2+CH 2+2DH •CH =9+2DH •CH ，∵CH -DH =HG ，∴(CH -DH )2=HG 2=2，∴CH 2+DH 2-2DH •CH =2，∴2DH •CH =7，∴(DH +CH )2=9+7=16，∴DH +CH =4，∵CH -DH =2，∴HC =4+22=2+22，故答案为：①③④．【点评】本题考查全等三角形的性质和判定，勾股定理，完全平方公式，关键是读懂“赵爽弦图”并灵活应用以上定理和公式．三．解答题(共2小题)27(2021秋•凤翔县期中)如图1是著名的赵爽弦图，由四个全等的直角三角形拼成，用它可以证明勾股定理，思路是：大正方形的面积有两种求法，一种是等于c 2，另一种是等于四个直角三角形与一个小正方形的面积之和，即12ab ×4+b -a 2，从而得到等式c 2=12ab ×4+b -a 2，化简便得结论a 2+b 2=c 2．这里用两种求法来表示同一个量从而得到等式或方程的方法，我们称之为“双求法”．现在，请你用“双求法”解决下面两个问题(1)如图2，在Rt △ABC 中，∠ACB =90°，CD 是AB 边上的高，AC =3，BC =4，求CD 的长度．(2)如图3，在△ABC 中，AD 是BC 边上的高，AB =4，AC =5，BC =6，设BD =x ，求x 的值．【分析】(1)先根据勾股定理先求出AB ，再根据“双求法”求出CD 的长度；(2)运用两个直角三角形根据勾股定理表示出AD ，德关于x 的方程求解．【解答】解：(1)在Rt △ABC 中AB =32+42=5，由面积的两种算法可得：12×3×4=12×5×CD ，解得：CD =125．(2)在Rt △ABD 中AD 2=42-x 2=16-x 2，在Rt △ADC 中AD 2=52-(6-x )2=-11+12x -x 2，所以16-x 2=-11+12x -x 2，解得x=2712=94．【点评】此题考查的知识点是勾股定理的应用，关键是运用勾股定理求解．28(2021春•利辛县期中)如图，小明用4个图1中的矩形组成图2，其中四边形ABCD，EFGH，MNPQ都是正方形，证明：a2+b2=c2．【分析】由题意可得：S正方形ABCD =(a+b)2，S正方形EFGH=c2，S△BEF=12×ab，再根据S正方形ABCD=S正方形EFGH+4S△BEF，即可证得结论．【解答】证明：∵四边形ABCD，EFGH，MNPQ都是正方形，∴S正方形ABCD =(a+b)2，S正方形EFGH=c2，S△BEF=12×ab，∵S正方形ABCD =S正方形EFGH+4S△BEF，∴(a+b)2=c2+4×12×ab，∴a2+2ab+b2=c2+2ab，∴a2+b2=c2．【点评】本题是勾股定理证明题，考查了直角三角形面积，正方形面积，利用图形面积得出结论是解题关键．。

三角形中的重要模型-弦图模型、勾股树模型(学生版+解析版)

三角形中的重要模型-弦图模型、勾股树模型赵爽弦图分为内弦图与外弦图，是中国古代数学家赵爽发现，既可以证明勾股定理，也可以以此命题，相关的题目有一定的难度，但解题方法也常常是不唯一的。

弦图之美，美在简约，然不失深厚，经典而久远，被誉为“中国数学界的图腾”。

弦图蕴含的割补思想，数形结合思想、图形变换思想更是课堂教学中数学思想渗透的绝佳载体。

一个弦图集合了初中平面几何线与形，位置与数量，方法与思想，小身板，大能量，它就是数学教育里的不老神话。

广受数学教师和数学爱好者研究，近年来也成为了各地中考的热点问题。

模型1、弦图模型(1)内弦图模型：如图1，在正方形ABCD中，AE⊥BF于点E，BF⊥CG于点F，CG⊥DH于点G，DH⊥AE于点H，则有结论：△ABE≌△BCF≌△CDG≌△DAH；S正方形ABCD =4S△EAB+S正方形EFGH。

图1图2图3(2)外弦图模型：如图2，在正方形ABCD中，E，F，G，H分别是正方形ABCD各边上的点，且四边形EFGH是正方形，则有结论：△AHE≌△BEF≌△CFG≌△DGH；S正方形ABCD =4S△EAB+S正方形EFGH。

(3)内外组合型弦图模型：如图3，2S正方形EFGH =S正方形ABCD+S正方形PQMN.1(2023秋·湖北·九年级校联考开学考试)如图，2002年8月在北京召开的国际数学家大会会标其原型是我国古代数学家赵爽的《勾股弦图》，它是由四个全等的直角三角形拼接而成如．如果大正方形的面积是16，直角三角形的直角边长分别为a，b，且a2+b2=ab+10，那么图中小正方形的面积是()A.2B.3C.4D.52(2022·安徽安庆·八年级期末)汉代数学家赵爽为了证明勾股定理，构造了一副“弦图”，后人称其为“赵爽弦图”，如图，大正方形ABCD由四个全等的直角三角形和一个小正方形组成，若∠ADE=∠AED，AD =45，则△ADE的面积为()A.24B.6C.25D.2103(2023·山西八年级期末)如图，图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的，若AC=6,BC=5，将四个直角三角形中的边长为6的直角边分别向外延长一倍，得到图2所示的“数学风车”，则这个风车的外围周长是()A.24B.52C.61D.764(2022·杭州九年级月考)我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”．如图是由弦图变化得到，它是用八个全等的直角三角形拼接而成，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3．若S1+S2+S3=12，则下列关于S1、S2、S3的说法正确的是()A.S1=2B.S2=3C.S3=6D.S1+S3=85(2023·广东·九年级专题练习)公元三世纪，我国汉代数学家赵爽在注解《周髀算经》题时给出了“赵爽弦图”．将两个“赵爽弦图”(如图1)中的两个正方形和八个直角三角形按图2方式摆放围成正方形MNPQ，记空隙处正方形ABCD，正方形EFGH的面积分别为S1，S2S1>S2，则下列四个判断：①S1+S2=14S四边形MNPQ②DG=2AF；③若∠EMH=30°，则S1=3S2；④若点A是线段GF的中点，则3S1=4S2，其中正确的序号是模型2. 勾股树模型6(2022·福建·八年级期末)如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，如果正方形A、B、C、D的边长分别为3，4，1，2．则最大的正方形E的面积是．7(2022·浙江·乐清市八年级期中)如图，在四边形ABCD中，∠B=∠D=90°，分别以AB，BC，CD，DA为一边向外作正方形甲、乙、丙、丁，若用S甲，S乙，S丙，S丁来表示它们的面积，那么下列结论正确的是()A.S 甲=S 丁B.S 乙=S 丙C.S 甲-S 乙=S 丁-S 丙D.S 甲+S 乙=S 丙+S 丁8(2022·河南八年级期末)如图，正方形ABCD 的边长为2，其面积标记为S 1，以CD 为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S 2，⋯按照此规律继续下去，则S 9的值为()A.126B.127C.128D.1299(2023春·山东菏泽·八年级校考阶段练习)“勾股树”是以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程所画出来的图形，因为重复数次后的形状好似一棵树而得名．假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树，按照勾股树的作图原理作图，如果第一个正方形面积为1，则第2023代勾股树中所有正方形的面积为．10(2023·浙江八年级期中)如图，以Rt △ABC 的三边为直径，分别向外作半圆，构成的两个月牙形面积分别为S 1、S 2，Rt △ABC 的面积S 3．若S 1=4，S 2=8，则S 3的值为．11(2022春·浙江温州·九年级校考开学考试)如图1，是数学家毕达哥拉斯根据勾股定理所画的“勾股树”．如图2，在Rt △ABC 中，∠BAC =90°，以其三边为边分别向外作正方形，延长EC ，DB 分别交GF ，AH 于点N ，K ，连接KN 交AG 于点M ，若S 1S 2=916，则tan ∠ACB 为()A.12B.23C.34D.51212(2023·贵州遵义·统考二模)如图1，毕达哥拉斯树，也叫“勾股树”，是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的树形图形．在图2中，∠ACB =90°，分别以Rt △ABC 的三条边为边向外作正方形，连接BE ，DG 、BE ，交AC 于点Q ，若∠BAC =30°，BC =2，则四边形EQGD 的面积是．13(2023秋·浙江·八年级专题练习)【背景阅读】勾股定理是人类最伟大的十个科学发现之一，西方国家称之为毕达哥拉斯定理．在我国古书《周髀算经》中就有“若勾三，股四，则弦五”的记载，我国汉代数学家赵爽为了验证勾股定理，创制了一幅“弦图”(如图1)，后人称之为“赵爽弦图”，流传至今．【实践操作】(1)请叙述勾股定理；(2)验证勾股定理，人们已经找到了400多种方法，请从下列几种常见的验证方法中任选一种来验证该定理：(以下图形均满足验证勾股定理所需的条件)【探索发现】(3)如图4、5、6，以直角三角形的三边为边或直径，分别向外部作正方形、半圆、等边三角形，这三个图形中面积关系满足S1+S2=S3的有个；(4)如图7所示，分别以直角三角形三边为直径作半圆，设图中两个月形图案(图中阴影部分)的面积分别为S1、S2，直角三角形面积为S3，请判断S1、S2、S3的关系并说明理由．课后专项训练1(2022·云南九年级一模)如图是按照一定规律“生长”的“勾股树”：经观察可以发现：图(1)中共有3个正方形，图(2)在图(1)的基础上增加了4个正方形，图(3)在图(2)的基础上增加了8个正方形，⋯⋯，照此规律“生长”下去，图(6)应在图(5)的基础上增加的正方形的个数是()A.12B.32C.64D.1282(2022·浙江初三期中)勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载．如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内．若图2中阴影部分的面积为2，且AB+AC=8，则BC的长为()图1图2A.42B.6C.254D.1323(2023·浙江·杭州八年级阶段练习)如图，Rt△ABC中，∠BAC=90°，分别以△ABC的三边为边作正方形ABDE，正方形BCFG，正方形ACHI，AI交CF于点J．三个正方形没有重叠的部分为阴影部分，设四边形BGFJ的面积为S1，四边形CHIJ的面积为S2，若S1-S2=12，S△ABC=4，则正方形BCFG的面积为()A.16B.18C.20D.224(2023春·湖北黄冈·八年级统考期中)“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，设直角三角形较长直角边长为a，较短直角边长为b．若ab=8，大正方形的面积为25，则EF 的长为()A.9B.92C.32D.35(2022·四川成都·模拟预测)勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载．如图1，以直角三角形的各边为边分别向外作正方形，再将较小的两个正方形分别绕直角三角形斜边上的两顶点旋转得到图2．则图2中阴影部分面积等于()A.直角三角形的面积B.最大正方形的面积C.最大正方形与直角三角形的面积和D.较小两个正方形重叠部分的面积6(2023春·广东潮州·九年级校考期末)我国古代数学家赵爽巧妙地用“弦图”证明了勾股定理，标志着中国古代的数学成就．如图所示的“弦图”，是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形．直角三角形的斜边长为13，一条直角边长为12，则小正方形ABCD 的面积的大小为()A.144B.100C.49D.257(2023春·湖北武汉·八年级统考期末)大约公元222年我国汉代数学家赵爽为《周髀算经》一书作序时介绍了“勾股圆方图”，亦称“赵爽弦图”，如图，四个全等的直角三角形拼成大正方形ABCD ，中空的部分是小正方形EFGH ，连接EG ，BD 相交于点O ，BD 与HC 相交于点P ，若GO =GP ，则直角三角形的边CG 与BG 之比是()A.12B.25C.2-1D.3-28(2023春·江苏泰州·七年级统考期末)大约在公元222年，赵爽为《周髀算经》一书作序时，介绍了“勾股圆方图”，亦称“赵爽弦图”(如图1)．某数学兴趣小组类比“赵爽弦图”构造出图2：△ABC 为等边三角形，AD 、BE 、CF 围成的△DEF 也是等边三角形．已知点D 、E 、F 分别是BE 、CF 、AD 的中点，若△ABC 的面积为14，则△DEF 的面积是()A.1B.2C.3D.49(2023·河北石家庄·校考二模)如图1，毕达哥拉斯树，也叫“勾股树”，是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的树形图形．在图2中，∠ACB=90°，分别以Rt△ABC的三条边为边向外作正方形，连接BE，DG，BE交AC于点Q．若∠BAC=30°，BC=2，则四边形EQGD的面积是()B.23C.53+3D.3A.53+3210(2023·江苏扬州·统考中考真题)我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”，后人称之为“赵爽弦图”，它是由4个全等的直角三角形和一个小正方形组成．如图，直角三角形的直角边长为a、b，斜边长为c，若b-a=4，c=20，则每个直角三角形的面积为．11(2022秋·四川成都·八年级校考期中)“勾股图”有着悠久的历史，它曾引起很多人的兴趣．1955年希腊发行了以“勾股图”为背景的邮票(如图1)，欧几里得在《几何原本》中曾对该图做了深入研究．如图2，在△ABC中，∠ACB=90°，分别以△ABC的三条边为边向外作正方形，连接EB,CM,DG,CM分别与AB,BE相交于点P,Q．若∠ABE=30°，则DGQM的值为.12(2022春·安徽合肥·八年级合肥市第四十二中学校考期中)如图①，在Rt△ACB中∠ACB=90°，分别以AC、BC、AB为边，向形外作等边三角形，所得的等边三角形的面积分别为S1、S2、S3，请解答以下问题：(1)S1、S2、S3满足的数量关系是．(2)现将△ABF向上翻折，如图②，若阴影部分的S甲=6、S乙=5、S丙=4，则S△ACB=．13(2023·湖北孝感·统考三模)“勾股树”是以正方形一边为斜边向外作直角三角形，再以直角三角形的两直角边分别向外作正方形，重复这一过程所画出来的图形，因为重复数次后的形状好似一棵树而得名．假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树，按照勾股树的作图原理作图，则第五代勾股树中正方形的个数为．14(2022·山东临沂·统考二模)中国古代的数学家们对于勾股定理的发现和证明，在世界数学史上具有独特的贡献和地位尤其是三国时期的数学家赵爽，不仅最早对勾股定理进行了证明，而且创制了“勾股圆方图”，开创了“以形证数”的思想方法．在图中，小正方形ABCD的面积为1，如果把它的各边分别延长一倍得到正方形A1B1C1D1(如图1)，则正方形的面积为；再把正方形A1B1C1D1的各边分别延长一倍得到正方形A2B2C2D2(如图2)，如此进行下去，得到的正方形A n B n C n D n的面积为(用含n的式子表示，n为正整数)．15(2023·浙江台州·八年级校考期中)如图1，是一个封闭的勾股水箱，其中Ⅰ，Ⅱ，Ⅲ部分是可盛水的正方形，且相互联通，已知∠ACB=90°，AC=6，BC=8，开始时Ⅲ刚好盛满水，而Ⅰ，Ⅱ无水．(1)如图2摆放时，Ⅰ刚好盛满水，而Ⅱ无水，则Ⅲ中有水部分的面积为；(2)如图3摆放时，水面刚好经过Ⅲ的中心O(正方形两条对角线的交点)，则Ⅱ中有水部分的面积为．16(2023·湖北黄冈·统考中考真题)如图，是我国汉代的赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”，它是由四个全等的直角三角形和一个小正方形组成的一个大正方形．设图中AF=a，DF=b，连接AE,BE，若△ADE与△BEH的面积相等，则b2a2+a2b2=．17(2023·江苏徐州·统考二模)如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH．连接AC，若AG平分∠CAD，且正方形EFGH的面积为2，则正方形ABCD的面积为．18(2023·陕西渭南·统考二模)魏朝时期，刘徽利用下图通过“以盈补虚，出入相补”的方法，即“勾自乘为朱方，股自乘为青方，令出入相补，各从其类”证明了勾股定理．如图，四边形ABCD、四边形BFGH和四边形AFMN都是正方形，BF交CD于E，若DE=2，CE=4，则BF的长为．19(2022·宁夏吴忠·统考一模)2002年8月，在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图1)，且大正方形的面积是17，直角三角形的较短直角边为a，较长直角边为b．如果将四个全等的直角三角形按如图2的形式摆放，则图2中最大的正方形的面积为31．试求图1中小正方形的面积是为．20(2023·山东济宁·统考二模)勾股定理是人类最伟大的十个科学发现之一，西方国家称之为毕达哥拉斯定理．在我国古书《周髀算经》中就有“若勾三，股四，则弦五”的记载，我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”(如图1)，后人称之为“赵爽弦图”，流传至今．勾股定理内容为：如果直角三角形的两条直角边分别为a，b，斜边为c，那么a2+b2=c2．(1)如图2、3、4，以直角三角形的三边为边或直径，分别向外部作正方形、半圆、等边三角形，这三个图形中面积关系满足S1+S2=S3的有个；(2)如图5所示，分别以直角三角形三边为直径作半圆，设图中两个月形图案(图中阴影部分)的面积分别为S1，S2，直角三角形面积为S3，请判断S1，S2，S3的关系并证明；(3)如果以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程就可以得到如图6所示的“勾股树”．在如图7所示的“勾股树”的某部分图形中，设大正方形M的边长为定值m，四个小正方形A，B，C，D的边长分别为a，b，c，d，已知∠1=∠2=∠3=∠α，则当∠α变化时，回答下列问题：(结果可用含m的式子表示)①a2+b2+c2+d2=；②b与c的关系为，a与d的关系为．21(2022·湖南·八年级课时练习)如图①，美丽的弦图，蕴含着四个全等的直角三角形．(1)弦图中包含了一大，一小两个正方形，已知每个直角三角形较长的直角边为a，较短的直角边为b，斜边长为c，结合图①，试验证勾股定理．(2)如图②，将这四个直角三角形紧密地拼接，形成飞镖状，已知外围轮廓(粗线)的周长24，OC=3，求该飞镖状图案的面积．(3)如图③，将八个全等的直角三角形紧密地拼接，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1,S2,S3，若S1+S2+S3=40，求S2．22(2023·广东深圳·校联考三模)中华文明源远流长，如图①是汉代数学家赵爽在注解《周髀算经》时给出的图形，人们称之为赵爽弦图，被誉为中国数学界的图腾．2002年北京国际数学家大会依据赵爽弦图制作了会标，该图有4个全等的直角三角形围成几个大正方形和中间一个小正方形，巧妙的证明了勾股定理．问题发现：如图①，若直角三角形的直角边BC=3，斜边AB=5，则中间小正方形的边长CD=，连接BD，△ABD的面积为．知识迁移：如图②，P是正方形ABCD内一点，连接PA，PB，PC，当∠BPC=90°，BP=10时，△PAB的面积为．拓展延伸：如图③，已知∠MBN=90°，以点B为圆心，适当长为半径画弧，交射线BM，BN分别于A，C两点．(1)已知D为线段AB上一个动点，连接CD，过点B作BE⊥CD，垂足为点E；在CE上取一点F，使EF=BE；过点F作GF⊥CD交BC于点G，试判断三条线段BE，DE，GF之间的数量关系，并说明理由．(2)在(1)的条件下，若D为射线BM上一个动点，F为射线EC上一点；当AB=10，CF=2时，直接写出线段DE的长．三角形中的重要模型-弦图模型、勾股树模型赵爽弦图分为内弦图与外弦图，是中国古代数学家赵爽发现，既可以证明勾股定理，也可以以此命题，相关的题目有一定的难度，但解题方法也常常是不唯一的。

中考数学压轴题的两大解题思路图与例题详解，为孩子打印收藏！

中考数学压轴题的两大解题思路图与例题详解，为孩子打印收藏！思路图一：【说明】此思路图主要是利用“点的坐标”建立起“函数”与“图形”之间的关系，通过运用“点的坐标”的代数意义和几何意义，可以将“函数”条件下的问题转化解决有关“图形”的问题；同样，也可以将“图形”条件下的问题转化解决有关“函数”的问题。

压轴题常用的数学知识与方法有：直角三角形勾股定理、三角函数定义、全等与相似三角形的判定与性质、相关特殊平面图形的判定与性质；一元一次方程的解法、一元二次方程的解法、二元一次方程组的解法、待定系数法等。

1、解题方法：若已知函数表达式，先确定有关特殊点的坐标，再转化为相应线段的长度并计算有关线段的长度，最后联系动点坐标、面积公式或特殊图形有关知识解答相关问题。

2、常用技能：1、解题中需要用动点的坐标时应直接设出[如：设动点P （m,n）],先不要考虑动点所在图象的函数表达式。

这样便于分析问题和书写过程，到最后确定关系后再考虑函数表达式进行字母间的转化。

2、解题中需要某点坐标或需要利用某点坐标时，通常过该点向x 轴（或y轴）作垂线，进而把点的坐标问题转化为线段即图形问题（如：涉及图形面积时，通常先过不在坐标轴上的点分别向x轴作垂线，把图形面积分割为直角三角形和直角梯形的面积和差关系）。

3、有关图形计算的常用知识与方法：①把相关条件化入某个直角三角形中，利用直角三角形相关定理和三角函数，计算相关边与角进而解决问题。

这是关于图形计算的核心方法；②判断两个三角形的相似关系（一般情况下确定不变直角三角形与变化直角三角形的相似），利用三角形相似的性质计算相关线段长度或周长进而解决问题。

这是图形计算的疑难之处（若是直角三角形相似两种方法都可以用时，建议选择三角函数比较方便便于理解掌握）。

4、在综合题中，寻找两个三角形相似常用的方法是：通过观察图形若发现有下列三个图形时或存在共锐角的直角三角形，可思考三角形相似解决问题。

弦图与垂直模型-【压轴必刷】中考数学压轴大题之经典模型(全国通用)(解析版)

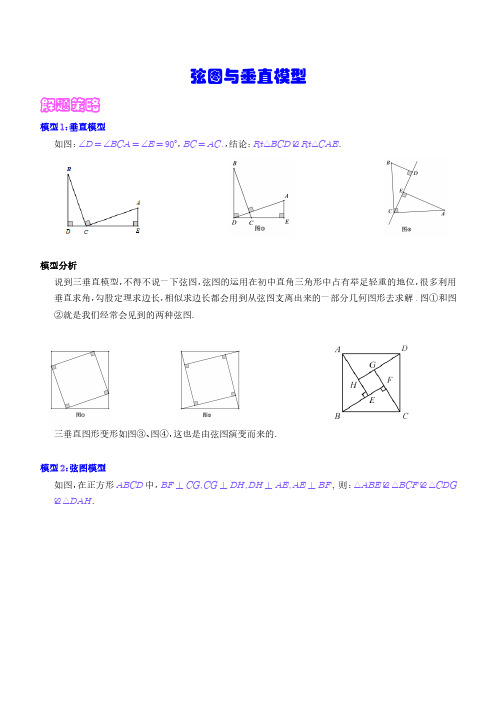
弦图与垂直模型解题策略模型1：垂直模型如图：∠D=∠BCA=∠E=90°，BC=AC.，结论：Rt△BCD≌Rt△CAE.模型分析说到三垂直模型，不得不说一下弦图，弦图的运用在初中直角三角形中占有举足轻重的地位，很多利用垂直求角，勾股定理求边长，相似求边长都会用到从弦图支离出来的一部分几何图形去求解.图①和图②就是我们经常会见到的两种弦图.三垂直图形变形如图③、图④，这也是由弦图演变而来的.模型2：弦图模型如图，在正方形ABCD中，BF⊥CG,CG⊥DH,DH⊥AE,AE⊥BF, 则：△ABE≌△BCF≌△CDG ≌△DAH.经典例题【例1】．(2021·全国·八年级专题练习)如图1，正方形ABCD中，点O是对角线AC的中点，点P是线段AO上(不与点A，O重合)的一个动点，过点P作PE⊥PB且PE交边CD于点E．(1)求证：PE=PB；(2)如图2，若正方形ABCD的边长为2，过点E作EF⊥AC于点F，在点P运动的过程中，PF的长度是否发生变化？若不变，试求出这个不变的值；若变化，请说明理由；(3)用等式表示线段PC，PA，CE之间的数量关系．【答案】(1)见解析；(2)在P点运动的过程中，PF的长度不发生变化．PF的长为定值2；(3)PC=PA+ 2EC．理由见解析．【分析】(1)做辅助线，构建全等三角形，根据ASA证明△BMP≅△PNE即可求解．(2)如图，连接OB，通过证明△OBP≅△FPE，得到PF=OB，则PF为定值是2．(3)根据△AMP和△PCN是等腰直角三角形，得PA=2PM，PC=2NC，整理可得结论．【详解】(1)证明：如图①，过点P作MN∥AD，交AB于点M，交CD于点N．∵PB⊥PE，∴∠BPE=90°，∴∠MPB+∠EPN=90°．∵四边形ABCD是正方形，∴∠BAD=∠D=90°．∵AD∥MN，∴∠BMP=∠BAD=∠PNE=∠D=90，∵∠MPB+∠MB P=90°，∴∠EPN=∠MB P．在Rt△PNC中，∠PCN=45°，∴△PNC是等腰直角三角形，∴PN=CN，∴BM=CN=PN，∴△BMP≌△PNE(ASA)，∴PB=PE．(2)解：在P点运动的过程中，PF的长度不发生变化．理由：如图2，连接OB．∵点O是正方形ABCD对角线AC的中点，∴OB⊥AC，∴∠AOB=90°，∴∠AOB=∠EFP=90°，∴∠OBP+∠BPO=90°．∴∠BPE=90°，∴∠BPO+∠OPE=90°，∴∠OBP=∠OPE．由(1)得PB=PE，∴△OBP≌△FPE(AAS)，∴PF=OB．=2．∵AB=2，△ABO是等腰直角三角形，∴OB=22∴PF的长为定值2．(3)解：PC=PA+2EC．理由：如图1，∵∠BAC=45°，∴△AMP是等腰直角三角形，∴PA=2PM．由(1)知PM=NE，∴PA=2NE．∵△PCN是等腰直角三角形，∴PC=2NC=2(NE+EC)=2NE+2EC=PA+2EC．【点睛】本题主要考查了四边形综合应用，通过对三角形全等的证明找出边之间的关系，准确分析代换求解是解题的关键．【例2】．(2021·黑龙江·哈尔滨市第四十九中学校九年级阶段练习)正方形ABCD中，点E、F在BC、CD 上，且BE=CF，AE与BF交于点G．(1)如图1，求证AE⊥BF；(2)如图2，在GF上截取GM=GB，∠MAD的平分线交CD于点H，交BF于点N，连接CN，求证：AN+CN=2BN；【答案】(1)见解析；(2)见解析；【分析】(1)根据正方形的性质得AB=BC，∠ABC=∠BCD=90°，用SAS证明△ABE≌△BCF，得∠BAE =∠CBF，根据三角形内角和定理和等量代换即可得；(2)过点B作BH⊥BN，交AN于点H，根据正方形的性质和平行线的性质，用SAS证明△A GB≌△AGM，得∠BAG=∠MAG，根据角平分线性质得∠BHA=∠GAN=45°，则△HBN是等腰直角三角形，用SAS证明△ABH≌△CBN，得AH=CN，在Rt△HBN中，根据勾股定理即可得；【详解】解：(1)∵四边形ABCD 是正方形，∴AB=BC，∠ABC=∠BCD=90°，在△ABE和△BCF中，AB=BC∠ABE=∠BCFBE=CF∴△ABE≌△BCF(SAS)，∴∠BAE=∠CBF，∵∠AEB+∠BAE=180°-∠ABC=180°-90°=90°，∴∠AEB+∠CBF=90°，∴∠E GB=180°-(∠AEB+∠CBF)=180°-90°=90°，∴AE⊥BF；(2)如图所示，过点B作BH⊥BN，交AN于点H，∵四边形ABCD是正方形，∴AB=AC，∠ABC=∠HBN=90°，∵∠HBN=∠HBA+∠ABN=90°，∠ABC=∠CBN+∠ABN=90°，∴∠HBA=∠CBN，由(1)得，AE⊥BF，∴∠A GB=∠AGM=90°，∴∠HBG=∠AGM=90°,∴HB⎳AE，∴∠BHA=∠EAN，在△A GB和△AGM中，AG=AG∠A GB=∠AGMGB=GM∴△A GB≌△AGM(SAS)，∴∠BAG=∠MAG，∵AN平分∠DAM，∴∠DAN=∠MAN，∴∠BAG+∠MAG+∠MAN+∠DAN=90°，2∠MAG+2∠MAN=90°，∠MAG+∠MAN=45°，∠GAN=45°，∴∠BHA=∠GAN=45°，∴∠BNH=180°-∠HBN-∠BHA=180°-90°-45°=45°，∴△HBN是等腰直角三角形，∴BH=BN，在△ABH和△CBN中，BH=BN∠HBA=∠CBNAB=CB∴△ABH≌△CBN(SAS)，∴AH=CN，在Rt△HBN中，根据勾股定理HN=BH2+BN2=2BN，∴AN+CN=AN+AH=HN=2BN；【点睛】本题考查了正方形的性质，全等三角形的判定与性质，三角形内角和定理，角平分线，等腰直角三角形的判定与性质，勾股定理和锐角三角函数，解题的关键是掌握并灵活运用这些知识点．【例3】．(2021·云南曲靖·八年级期末)如图1，在正方形ABCD中，E为BC上一点，连接AE，过点B作BG⊥AE于点H，交CD于点G．(1)求证：AE=BG；(2)如图2，连接AG、GE，点M、N、P、Q分别是AB、AG、GE、EB的中点，试判断四边形MNPQ的形状，并说明理由；(3)如图3，点F、R分别在正方形ABCD的边AB、CD上，把正方形沿直线FR翻折，使得BC的对应边B'C'恰好经过点A，过点A作AO⊥FR于点O，若AB'=1，正方形的边长为3，求线段OF的长．【答案】(1)见解析；(2)四边形MNPQ为正方形，理由见解析；(3)10 6【分析】(1)由四边形ABCD为正方形，可得∠ABC=∠BCD=90°，推得∠ABG+∠CBG=90°，由BG⊥AE，可得∠BAE+∠ABG=90°，可证△ABE≅△BCG ASA即可；(2)M、N为AB、AG中点，可得MN为△ABG的中位线，可证MN⎳BG，MN=12BG，由点M、N、P、Q分别是AB、AG、GE、EB的中点，可得PQ是△BEG的中位线，MQ为△ABE的中位线，NP为△AEG的中位线，可证PQ⎳BG，PQ=12BG，MQ⎳AE，MQ=12AE，NP⎳AE，NP=12AE，可证四边形MNPQ为平行四边形．再证四边形MNPQ为菱形，最后证MN⊥MQ即可；(3)延长AO交BC于点S，由对称性可得BF=B'F，AB'=BS=1，AO=SO，由勾股定理可求AS=10，可得AO=12AS=102，设AF=x，在Rt△AB'F中，12+(3-x)2=x2，解得x=53，在Rt△AOF中，可求OF=106．【详解】(1)证明：∵四边形ABCD为正方形，∴∠ABC=∠BCD=90°，∴∠ABG+∠CBG=90°，∵BG⊥AE，∴∠AHB=90°，∴∠BAE+∠ABG=90°，∴∠BAE=∠CBG，在△ABE与△BCG中，∠BAE=∠CBGAB=BC∠ABC=∠BCD，∴△ABE≅△BCG ASA，∴AE=BG．(2)解：四边形MNPQ为正方形，理由如下：∵M、N为AB、AG中点，∴MN为△ABG的中位线，∴MN⎳BG，MN=12BG，∵点M、N、P、Q分别是AB、AG、GE、EB的中点，∴PQ是△BEG的中位线，MQ为△ABE的中位线，NP为△AEG的中位线，，∴PQ⎳BG，PQ=12BG，MQ⎳AE，MQ=12AE，NP⎳AE，NP=12AE，∴MN=PQ，MQ=NP，∴四边形MNPQ为平行四边形．∵AE=BG，∴MN=MQ，∴四边形MNPQ为菱形，∵BG⊥AE，MQ⎳AE，∴MQ⊥BG，∵MN⎳BG，∴MN⊥MQ，∴四边形MNPQ为正方形．(3)解：延长AO交BC于点S，由对称性可知BF=B'F，AB'=BS=1，AO=SO，在Rt△ABS中，AS=AB2+BS2=10，∴AO=12AS=102，设AF=x，则BF=B'F=3-x，在Rt△AB'F中，12+(3-x)2=x2，x=53，∴AF=53，在Rt△AOF中，2=106．OF=AF2-AO2=53 2-102【点睛】本题考查正方形性质与判定，等角的余角性质三角形全等判定与性质，三角形中位线判定与性质，勾股定理，根据勾股定理建构方程，解拓展一元一次方程等知识，掌握以上知识是解题关键．【例4】．(2021·河南商丘·八年级期中)在平面直角坐标系中，点A的坐标为4,0，点B为y轴正半轴上的一个动点，以B为直角顶点，AB为直角边在第一象限作等腰Rt△ABC．(1)如图1，若OB=3，则点C的坐标为______；(2)如图2，若OB=4，点D为OA延长线上一点，以D为直角顶点，BD为直角边在第一象限作等腰Rt△BDE，连接AE，求证：AE⊥AB；(3)如图3，以B为直角顶点，OB为直角边在第三象限作等腰Rt△OBF．连接CF，交y轴于点P，求线段BP的长度．【答案】(1)点C(3，7)；(2)证明见详解过程；(3)2．【分析】(1)如图1，过点C作CH⊥y轴，由“AAS”可证△ABO≌△BCH，可得CH=OB=3，BH=AO=4，可求解；(2)过点E作EF⊥x轴于F，由“AAS”可证△ABO≌△BCH，可得BO=DF=4，OD=EF，由等腰直角三角形的性质可得∠BAO=45°，∠EAF=∠AEF=45°，可得结论；(3)由(1)可知△ABO≌△BCG，可得BO=GC，AO=BG=4，再由“AAS”可证△CPG≌△FPB，可得PB=PG=2．(1)如图1，过点C作CH⊥y轴于H，∴∠CHB=∠ABC=∠AOB=90°，∴∠BCH+∠HBC=90°=∠HBC+∠ABO，∴∠ABO=∠BCH，在△ABO和△BCH中，∠CHB=∠AOB∠BCH=∠ABOBC=AB，∴△ABO≌△BCH(AAS)，∴CH=OB=3，BH=AO=4，∴OH=7，∴点C(3，7)，故答案为：(3，7)；(2)过点E作EF⊥x轴于F，∴∠EFD=∠BDE=∠BOD=90°，∴∠BDO+∠EDF=90°=∠BDO+∠DBO，∴∠DBO=∠EDF，在△BOD和△DFE中，∠BOD=∠EFD∠DBO=∠EDFBD=ED，∴△BOD≌△DFE(AAS)，∴BO=DF=4，OD=EF，∵点A的坐标为(4，0)，∴OA=OB=4，∴∠BAO=45°，∵OA=DF=4，∴OD=AF=EF，∴∠EAF=∠AEF=45°，∴∠BAE=90°，∴BA⊥AE；(3)过点C作CG⊥y轴G，由(1)可知：△ABO≌△BCG，∴BO=GC，AO=BG=4，∵BF=BO，∠OBF=90°，∴BF=GC，∠CGP=∠FBP=90°，又∵∠CPG=∠FPB，∴△CPG≌△FPB(AAS)，∴BP=GP，∴BP=12BG=2．【点睛】本题是三角形综合题，考查了全等三角形的判定和性质，等腰直角三角形的性质等知识，添加恰当辅助线构造直角三角形是本题的关键．【例5】．(2021·黑龙江·哈尔滨市风华中学校九年级阶段练习)如图1，正方形ABCD中，点E是边BC延长线上一点，连接DE，过点B作BF⊥DE，垂足为点F，BF与CD相交于点G．(1)求证：△BCG≌△DCE；(2)如图2，连接BD，若BE=42，DG=22，求tan∠DBG的值．【答案】(1)见解析；(2)1 2【分析】(1)由正方形的性质结合已知条件，利用ASA判定三角形全等即可；(2)过点G作GH⊥BD垂足为H，由全等求得CG=CE，进一步结合图形求得BC和CG的长，然后在RT△BDC中求得GH和BH的长，最后在RT△BHG中，利用tan∠DBG=HGBH，即可求得答案．【详解】(1)证明：∵四边形ABCD是正方形，∴∠BCG=∠DCE=90°，BC=CD，∵BF⊥DE，∴∠DFG=∠BCG=90°，∵∠BGC=∠DGF，∴∠CBG=∠CDE．在△BCG和△DCE中，∠CBG=∠CDE BC=CD∠BCG=∠DCE，∴△BCG≌△DCE，(2)解：过点G作GH⊥BD垂足为H，∵△BCG≌△DCE，∴CG=CE，∵BE=BC+CE=42，DG=CD-CG=22，∴BC=CD=32，CG=CE=2，在RT△BDC中，∵∠BCD=90°，∴BD=CD2+BC2=322+322=6，∵∠DHG=45°，∠DHG=90°，DG=22，∴DHDG=sin45°=2 2，∴DH=2，∴GH=DH=2，∵BH=BD-DH，∴BH=6-2=4，在RT△BHG中，∵∠BHG=90°，∴tan∠DBG=HGBH，∴tan∠DBG=12【点睛】本题考查三角形全等的证明，直角三角形中锐角三角函数的定义等相关知识点，熟练掌握数形结合思想解题是重点．培优训练一、解答题1.(2022·江苏·八年级课时练习)如图1，在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．(1)由图1，证明：DE=AD+BE；(2)当直线MN绕点C旋转到图2的位置时，请猜想出DE，AD，BE的等量关系并说明理由；(3)当直线MN绕点C旋转到图3的位置时，试问DE，AD，BE又具有怎样的等量关系？请直接写出这个等量关系(不必说明理由)．【答案】(1)证明见解析；(2)DE=AD-BE，证明过程见解析；(3)DE=BE-AD，证明过程见解析【分析】(1)先证明△ADC≌△CEB，得到AD=CE，DC=BE，进而得到DE=CE+DC=AD+BE即可；(2)同(1)中思路，证明△ADC≌△CEB，进而得到DE=CE-DC=AD-BE即可；(3)同(1)中思路，证明△ADC≌△CEB，进而得到DE=DC-CE=BE-AD即可．【详解】解：(1)证明：在△ABC中，∵∠ACB=90°，∴∠ACD+∠BCE=90°，∵AD⊥MN，∴∠ACD+∠CAD=90°，∴∠BCE=∠CAD，又∵AC=BC，∠ADC=∠CEB=90∘，∴△ADC≌△CEB(AAS)，∴AD=CE，DC=BE，∵直线MN经过点C，∴DE=CE+DC=AD+BE；(2)DE，AD，BE的等量关系为：DE=AD-BE，理由如下：∵AD⊥MN于D，BE⊥MN于E∴∠ADC=∠BEC=∠ACB=90°，∴∠CAD+∠ACD=90°，∠ACD+∠BCE=90°，∴∠CAD=∠BCE，在△ADC和△CEB中∠CAD=∠BCE∠ADC=∠BEC=90∘AC=CB，∴△ADC≌△CEB AAS∴CE=AD，CD=BE，∴DE=CE-CD=AD-BE；(3)当MN旋转到图3的位置时，DE、AD、BE所满足的等量关系是DE=BE-AD，理由如下：∵AD⊥MN于D，BE⊥MN于E∴∠ADC=∠BEC=∠ACB=90°，∴∠CAD+∠ACD=90°，∠ACD+∠BCE=90°，∴∠CAD=∠BCE，在△ADC和△CEB中∠CAD=∠BCE∠ADC=∠BEC=90∘AC=CB，∴△ADC≌△CEB AAS∴CE=AD，CD=BE，∴DE=CD-CE=BE-AD.【点睛】本题考查了全等三角形的判定方法、等腰直角三角形的性质及等角的余角相等等知识点，熟练掌握三角形全等的判定方法是求解的关键．2.(2022·全国·八年级专题练习)如图所示，△ABC中，AB=AC，∠BAC=90°，点D为AB上一点，过点B作直线CD的垂线，垂足为E，连接AE，过点A作AE的垂线交CE于点F．(1)如图1，求∠AEC的度数；(2)如图2，连接BF，且∠ABF-∠EAB=15°，求证：BF=2CF；(3)如图3，在(2)的条件下，G为DF上一点，连接AG，若∠AGD=∠EBF，AG=2，求CF的长．【答案】(1)45°；(2)见解析；(3)2【分析】(1)先证明∠EAB=∠FAC, ∠AEB=∠AFC,再证明△ABE≅△ACF,再利用全等三角形的性质结合等腰直角三角形的性质可得答案；(2)利用全等三角形的性质先求解∠EBF=60°，证明BE=CF, 再求解∠EFB=30°，从而可得结论；(3)如图，过A作AM⊥EF于M, 交BF于N, 连接EN, 证明△BEN为等边三角形，再证明△AGM≅△ENM，再利用全等三角形的性质可得答案.【详解】解：(1)∵∠BAC=90°，AE⊥AF,∴∠EAB+∠DAF=∠DAF+∠FAC=90°,∠EAF=90°,∴∠EAB=∠FAC,∵BE⊥CE,∴∠BED=90°,∴∠AEB=∠BED+∠AEF=90°+∠AEF=∠AFC, 即∠AEB=∠AFC,∴△ABE≅△ACF，∴AE=AF，∠AEC=45°．(2)∵△ABE≅△ACF，∴∠ABE=∠ACF,BE=CF,∴∠AEB=∠AFC=90°+45°=135°,∴∠EBA+∠EAB=45°,∵∠ABF-∠EAB=15°,∴∠ABF=15°+∠EAB,∴∠EBF=∠EBA+∠ABF=∠EBA+∠EAB+15°=60°,∴∠BFE=90°-60°=30°,∴BF=2BE，∵BE=CF，∴BF=2CF．(3)如图，过A作AM⊥EF于M, 交BF于N, 连接EN,∵AE=AF,AM⊥EF,AE⊥AF,∴EM=MF=AM,NE=NF,∴∠NEF=∠NFE=30°,∴∠ENB=∠NEF+∠NFE=60°,∴∠EBN=∠ENB=60°,∴△BEN为等边三角形，∠ENF=120°,∴BE=BN=12BF=FN=EN，∵∠AGD=∠EBF=60°, AM⊥EF,∴∠ENM=12∠ENF=60°,∵AM=EM,∠AMG=∠EMN=90°,∠AGM=∠ENM=60°,∴△AGM≅△ENM，∴AG=EN=2，∴CF=BE=2．【点睛】本题考查的是全等三角形的判定与性质，等腰三角形的性质，直角三角形斜边上的中线等腰斜边的一半，等边三角形的判定与性质，含30°的直角三角形的性质，熟练的应用以上知识解题的关键.3.(2020·北京市第十三中学九年级期中)已知：Rt△ABC中，∠ACB=90°，AC=BC．(1)如图1，点D是BC边上一点(不与点B，C重合)，连接AD，过点B作BE⊥AD，交AD的延长线于点E，连接CE．①若∠BAD=α，求∠DBE的大小(用含α的式子表示)；②用等式表示线段EA，EB和EC之间的数量关系，并证明．(2)如图2，点D在线段BC的延长线上时，连接AD，过点B作BE⊥AD，垂足E在线段AD上，连接CE．①依题意补全图2；②直接写出线段EA，EB和EC之间的数量关系．【答案】(1)①∠DBE=45°-α；②AE-BE=2EC，证明见解析；(2)①补全图形见解析；②EB-EA= 2EC．【分析】(1)①根据等腰直角三角形的性质得到∠CAB=45°，即可求出∠CAD=45∘-α．根据三角形的内角和即可求出∠DBE=∠CAD=45∘-α；②过点C作CR⊥CE交AE于R，然后证明△ACR≌△BCE，得到AR=BE，CR=CE，即可得到△CER 是等腰直角三角形，ER=2CE，由此即可求解；(2)①根据题目要求作图即可；②过点C作CF⊥CE，交AD的延长线于点F.根据三角形的内角和定理得到∠CAF=∠CBE，证明△ACF ≌△BCE.根据全等三角形的性质有AF=BE，CF=CE．根据等腰直角三角形的性质有EF=2EC．则有 AF-EA=2EC，即可求出线段EA，EB和EC之间的数量关系．【详解】解：(1)①如图1中，∵∠ACB=90°，AC=BC，∴∠CAB=45°，∵∠BAD=α，∴∠CAD=45°-α．∵∠ACB=90°，BE⊥AD，∠ADC=∠BDE，∴∠DBE=∠CAD=45°-α；②结论：AE-BE=2EC．理由：如图，过点C作CR⊥CE交AE于R．∴∠ACB=∠RCE=90°，∴∠ACR=∠BCE，∵∠CAR+∠ADC=90°，∠CBE+∠BDE=90°，∠ADC=∠BDE，∴∠CAR=∠CBE，在△ACR和△BCE中，∠ACR=∠BCECA=CB∠CAR=∠CBE，∴△ACR≌△BCE(ASA)，∴AR=BE，CR=CE，∴△CER是等腰直角三角形，∴ER=2CE，∴AE-BE=AE-AR=ER=2EC．(2)①补全图形，如图2所示：②猜想：当D 在BC 边的延长线上时，EB -EA =2EC ；理由如下：过点C 作CF ⊥CE ，交AD 的延长线于点F ，如图3所示：则∠ECF =90°，∵∠ACB =90°，∴∠ACD =90°，∴∠ECF +∠ACE =∠ACB +∠ACE ，即∠ACF =∠BCE ，∵∠CAF +∠ADB =90°，∠CBE +∠ADB =90°，∴∠CAF =∠CBE ，在△ACF 和△BCE 中，∠ACF =∠BCEAC =BC ∠CAF =∠CBE，∴△ACF ≌△BCE (ASA )，∴AF =BE ，CF =CE ．∵∠ECF =90°，∴△CEF 是等腰直角三角形，∴EF =2EC ，即AF -EA =2EC ．∴EB -EA =2EC ．【点睛】考查等腰直角三角形的性质，三角形的内角和定理，全等三角形的判定与性质等，难度一般，掌握全等三角形的判定定理是解题的关键．4.(2021·四川省成都市七中育才学校七年级期中)已知：△ABC 中，∠ACB =90°，AC =CB ，D 为直线BC 上一动点，连接AD ，在直线AC 右侧作AE ⊥AD ，且AE =AD ．(1)如图1，当点D 在线段BC 上时，过点E 作EH ⊥AC 于H ，连接DE ．求证：EH =AC ；(2)如图2，当点D 在线段BC 的延长线上时，连接BE 交CA 的延长线于点M ．求证：BM =EM ；(3)当点D在直线CB上时，连接BE交直线AC于M，若2AC=5CM，请求出S△ADBS△AEM的值．【答案】(1)见解析；(2)见解析；(3)43或47【分析】(1)由“AAS”可证△AHE≌△DCA，可得EH=AC，即可求证；(2)过点E作EN⊥AC，交CA延长线于N，由“AAS”可证△ANE≌△DCA，可得AC=EN=BC，由“AAS”可证△ENM≌△BCM，可得BM=EM；(3)AC=5a，CM=2a，分三种情况：当点D在线段BC上，点D在线段BC的延长线上，点D在线段CB的延长线上，由全等三角形的性质可求得相应线段的长，再由三角形的面积公式可求解．【详解】证明(1)∵AE⊥AD，∠ACB=90°，∴∠EAH=90°-∠CAD，∠ADC=90°-∠CAD，∴∠EAH=∠ADC，在△AHE与△DCA中∠AHE=∠ACB=90°∠EAH=∠ADCAE=AD，∴△AHE≌△DCA(AAS)，∴EH=AC；(2)如图2，过点E作EN⊥AC，交CA延长线于N，∵AE⊥AD，∠ACB=90°，∴∠EAN=90°-∠CAD，∠ADC=90°-∠CAD，∴∠EAN=∠ADC，在△ANE与△DCA中，∠ANE=∠DCA=90°∠ENA=∠ACDAN=AD∴△ANE≌△DCA(AAS)，∴EN=AC，又∵AC=BC，∴EN=BC，又在△ENM与△BCM中，∠EMN=∠BMC∠N=∠BCA=90°EN=BC∴△ENM≌△BCM(AAS)，则BM=EM；(3)如图，当点D 在线段BC 上时，∵2AC =5CM ，∴可设AC =5a ，CM =2a ，由(1)得：△AHE ≌△DCA ，则AH =CD ，EH =AC =BC =5a ，由∵∠EHM =∠BCM =90° ，∠BMC =∠EMH ，∴△MHE ≌△MCB (AAS )，∴CM =HM ，即HM =CM =2a ，∴AH =AC -CM -HM =5a -2a -2a =a ，∴AM =AH +HM =3a ，CD =AH =a ，EH =AC =5a ， BD =BC -CD =4a ，∴S △ADB S △AEM =12BD ×AC 12AM ×EH =12×4a ×5a 12×3a ×5a =43；如图，点D 在CB 延长线上时，过点E 作EN ⊥AC ，交AC 延长线于N ，∵2AC =5CM ，∴可设AC =5a ，CM =2a ，∵EN ⊥AC ，AE ⊥AD ，∴∠ANE =∠EAD =∠ACB =90° ，∴∠EAN =90°-∠CAD ，∠ADC =90°-∠CAD ，∴∠EAN =∠ADC ，在△ANE 与△DCA 中，∠ANE =∠DCA =90°∠ENA =∠ACDAN =AD∴△ANE ≌△DCA (AAS )，∴EN =AC ，AN =CD ，又∵AC =BC ，∴EN =BC ，又在△ENM 与△BCM 中，∠EMN =∠BMC∠N =∠BCA=90°EN =BC∴△ENM ≌△BCM (AAS )，∴CM =NM =2a ，NE =BC =AC =5a ，∴AN =AC +CM +MN =9a ，AM =AC +CM =7a ，AN =CD =9a ，∴BD =4a ，∴S △ADB S △AEM =12BD ×AC 12AM ×EN =12×4a ×5a 12×7a ×5a =47，点D 在BC 延长线上由图2得：AC <CM ，∴2AC =5CM 不可能，故舍去综上：S △ADB S △AEM的值为43 或47【点睛】本题是三角形综合题，考查了等腰直角三角形的性质，全等三角形的判定和性质，添加恰当辅助线构造全等三角形是本题的关键．5.(2022·江苏·八年级课时练习)在△ABC 中，AB =BC ，∠B =90°，点D 为直线BC 上的一个动点(不与B 、C 重合)，连结AD ，将线段AD 绕点D 按顺时针方向旋转90°，使点A 旋转到点E ，连结EC ．(1)如果点D 在线段BC 上运动，如图1：求证：∠BAD =∠EDC(2)如果点D 在线段BC 上运动，请写出AC 与CE 的位置关系．通过观察、交流，小明形成了以下的解题思路：过点E 作EF ⊥BC 交直线BC 于F ，如图2所示，通过证明△DEF ≌△ABD ，可推证△CEF 等腰直角三角形，从而得出AC 与CE 的位置关系，请你写出证明过程．(3)如果点D 在线段CB 的延长线上运动，利用图3画图分析，(2)中的结论是否仍然成若成立，请证明；若不成立，请说明理由．【答案】(1)见解析；(2)垂直，理由见解析；(3)成立，证明见解析【分析】(1)根据直角三角形的性质证明即可；(2)过点E 作EF ⊥BC 交直线BC 于F ，如图2所示，通过证明△DEF ≌△ABD ，可推证△CEF 等腰直角三角形，从而得出AC 与CE 的位置关系；(3)如图3所示，过点E 作EF ⊥DC 于F ，证明△ABD ≌△DFE ，进一步可证明AC ⊥EC【详解】解：(1)证明：∵∠B =90°∴∠BDA +∠BAD =90°∵∠ADE=90°∴∠BDA+∠EDC=90°∴∠BAD=∠EDC(2)垂直∵EF⊥BC∴∠EFD=90°∵∠B=90°∴∠EFD=∠B在△ABD和△DFE中∠BAD=∠FDE∠B=∠DFEAD=DE∴△ABD≌△DFE AAS∴AB=DF，BD=EF∵AB=BC∴BC=DF，∴BC-DC=DF-DC即BD=CF．∴EF=CF又∵∠EFC=90°∴∠ECF=45°，且∠ACB=45°∴∠ACE=180°-90°=90°即AC⊥CE．(3)(2)中的结论仍然成立如图3所示，过点E作EF⊥DC于F ∵∠ABD=90°∴∠EDF=∠DAB=90°-∠ADB在△ABD和△DFE中∠DAB=∠EDF∠ABD=∠DFEAD=DE∴△ABD≌△DFE AAS∴DB=EF，AB=DF=BC∴BC-BF=DF-BF即FC=DB∴FC=EF∴∠DCE=45°∴∠ACE=∠DCE+∠ACB=90°∴AC⊥EC．【点睛】此题是几何变换综合题，主要考查了旋转的性质，全等三角形的判定和性质，证明△ABD≌△DFE是解本题的关键．6.(2021·黑龙江·哈尔滨市第四十七中学八年级开学考试)如图，已知△ABC中，AB=AC，∠BAC= 90°，分别过B、C向过A的直线作垂线，垂足分别为E、F．(1)如图1，过A的直线与斜边BC不相交时，直接写出线段EF、BE、CF的数量关系是______；(2)如图2，过A的直线与斜边BC相交时，探究线段EF、BE、CF的数量关系并加以证明；(3)在(2)的条件下，如图3，直线FA交BC于点H，延长BE交AC于点G，连接BF、FG、HG，若∠AHB=∠GHC，EF=CF=6，EH=2FH，四边形ABFG的面积是90，求△GHC的面积．【答案】(1)数量关系为：EF=BE+CF；(2)数量关系为：EF=BE-CF．证明见详解；(3)S△GHC=15．【分析】(1)数量关系为：EF=BE+CF．利用一线三直角得到∠BEA=∠AFC=90°，∠EBA=∠FAC，再证△EBA≌△FEC(AAS)可得BE=AF，AE=CF即可；(2)数量关系为：EF=BE-CF．先证∠BEA=∠AFC=90°，∠EBA+∠EAB=90°，∠EAB+∠FAC= =90°，可得∠EBA=∠FAC，再证△EBA≌△FEC(AAS)，可得BE=AF，AE=CF即可；(3)先由(2)结论EF=BE-CF；EF=CF=6，求出BE=AF=12，由EH=2FH，可求FH=2，EH=4，利用对角线垂直的四边形面积可求BG=2×90AF=18012=15，再求EG=3，AH=10，分别求出S△ACF=12AF⋅FC=36，S△HCF=12HF⋅FC=6，S△AGH=12AH⋅EG=15，利用面积差即可求出．【详解】解：(1)数量关系为：EF=BE+CF．∵BE⊥EF，CF⊥EF，∠BAC=90°，∴∠BEA=∠AFC=90°，∠EBA+∠EAB=90°，∠EAB+∠FAC=180°-∠BAC=90°，∴∠EBA=∠FAC，在△EBA和△FEC中，∵∠AEB=∠CFA ∠EBA=∠FAC AB=CA，∴△EBA≌△FAC(AAS)，∴BE =AF ，AE =CF ，∴EF =AF +AE =BE +CF ；(2)数量关系为：EF =BE -CF ．∵BE ⊥AF ，CF ⊥AF ，∠BAC =90°，∴∠BEA =∠AFC =90°，∠EBA +∠EAB =90°，∠EAB +∠FAC ==90°，∴∠EBA =∠FAC ，在△EBA 和△FEC 中，∵∠AEB =∠CFA∠EBA =∠FAC AB =CA，∴△EBA ≌△FAC (AAS )，∴BE =AF ，AE =CF ，∴EF =AF -AE =BE -CF ；(3)∵EF =BE -CF ；EF =CF =6，∴BE =AF =EF +CF =6+6=12，∵EH =2FH ，EH +FH =EF =6，∴2FH +FH =6，解得FH =2，∴EH =2FH =4，S 四边形ABFG =12AF ⋅BG =90，∴BG =2×90AF =18012=15，∴EG =BG -BE =15-12=3，AH =AE +EH =6+4=10，∵S △ACF =12AF ⋅FC =12×12×6=36，S △HCF =12HF ⋅FC =12×2×6=6，S △AGH =12AH ⋅EG =12×10×3=15，∴S △GHC =S △ACF -S △HCF -S △AGH =36-6-15=15．【点睛】本题考查图形变换探究线段和差问题，感知，探究以及应用，三角形全等判定与性质，三角形面积，四边形面积，与三角形高有关的计算，掌握图形变换探究线段和差问题，感知，探究以及应用，三角形全等判定与性质，三角形面积，四边形面积，与三角形高有关的计算是解题关键．7.(2021·江苏泰州·八年级期末)如图，正方形ABCD 边长为4，点G 在边AD 上(不与点A 、D 重合)，BG 的垂直平分线分别交AB 、CD 于E 、F 两点，连接EG ．(1)当AG =1时，求EG 的长；(2)当AG 的值等于时，BE =8-2DF ；(3)过G 点作GM ⊥EG 交CD 于M①求证：GB 平分∠AGM ；②设AG =x ，CM =y ，试说明16xy -4x -4y-1的值为定值．【答案】(1)178；(2)8-43(3)①见解析；②16xy -4x -4y-1=0，理由见解析【分析】(1)根据EF 是线段BG 的垂直平分线，BE =EG ，设EG =EB =x ，则AE =AB -BE =4-x ，再由勾股定理求解即可；(2)过点F 作FH ⊥AB 于H ，连接FB ，FG ，由BE =8-2DF ，CF =CD -DF =4-DF ，得到BE =2CF ，先证明四边形BCFH 是矩形，得到CF =HB ，则BH =EH =FC ，设AG =x ，BE =y ，则AE =4-y ，GD =4-x ，CF =12y ，DF =4-12y 由AE 2+AG 2=EG 2，GD 2+DF 2=GF 2，BC 2+FC 2=BF 2，可以得到4-y 2+x 2=y 2①，4-x 2+4-12y 2=42+12y 2②，联立①②求解即可得到答案；(3)①先证明∠EBG =∠E GB ，然后根据ABG +∠A GB =90°，∠E GB +∠BGM =90°，即可得到∠A GB =∠BGM ；②连接BM ，过点B 作BH ⊥GM ，由角平分线的性质得到BH =AB =4，由S 正方形ABCD =S △ABG +S △MB G +S △BCM +S △CDM =4×4=16，可以得到2x +2GM +2y +124-x 4-y =16，由勾股定理可以得到DM 2+GD 2=GM 即4-x 2+4-y 2=4-xy 4 ，最后解方程即可得到答案．【详解】解：(1)∵EF 是线段BG 的垂直平分线，∴BE =EG ，∵四边形ABCD 是正方形，且边长为4，∴AB =4，∠A =90°，设EG =EB =x ，则AE =AB -BE =4-x ，∵AE 2+AG 2=EG 2，∴4-x 2+12=x 2，解得x =178，∴EG =178；(2)如图所示，过点F 作FH ⊥AB 于H ，连接FB ，FG∵EF 是线段BG 的垂直平分线，∴BF =FG ，∵BE =8-2DF ，CF =CD -DF =4-DF ，∴BE =2CF ，∵四边形ABCD 是正方形，FH ⊥AB ，∴∠HBC =∠C =∠BHF =90°，∴四边形BCFH 是矩形，∴CF =HB ，∴BH =EH =FC ，设AG =x ，BE =y ，则AE =4-y ，GD =4-x ，CF =12y ，DF =4-12y ∵AE 2+AG 2=EG 2，GD 2+DF 2=GF 2，BC 2+FC 2=BF 2，∴4-y 2+x 2=y 2①，4-x 2+4-12y 2=42+12y 2②，联立①②解得x =8-43或x =8+43(舍去)，∴当AG =8-43时，BE =8-2DF ，故答案为：8-43；(3)①∵EF 是线段BG 的垂直平分线，∴EG =BE ，∴∠EBG =∠E GB ，∵四边形ABCD 是正方形，EG ⊥GM ，∴∠A =∠EGM =90°，∴∠ABG +∠A GB =90°，∠E GB +∠BGM =90°，∴∠A GB =∠BGM ，∴BG 平分∠AGM ；②如图，连接BM ，过点B 作BH ⊥GM ，由(3)①得BG 平分∠AGM ，∴BH =AB =4，∵AG =x ，CM =y ，∴DG =4-x ，DM =4-y ，∵S 正方形ABCD =S △ABG +S △MB G +S △BCM +S △CDM =4×4=16，∴12AG ·AB +12GM ·BH +12CM ·BC +12DM ·GD =16，∴2x +2GM +2y +124-x 4-y =16，∴GM =4-xy 4，∵DM 2+GD 2=GM ，∴4-x 2+4-y 2=4-xy 4 ∴16-8x +x 2+16-8y +y 2=16-2xy +x 2y 216∴x +y 2-8x +y +16=x 2y 216，∴x +y -4 2=x 2y 216，∴x +y -4=±xy 4，当x +y -4=xy 4时，则4x +4y -16=xy ，∴y =16-4x 4-x =4(不符合题意)，∴4x +4y -16=-xy∴16xy -4x -4y-1=0．【点睛】本题主要考查了正方形的性质，勾股定理，角平分线的性质，线段垂直平分线的性质，等腰三角形的性质与判定，三角形的面积等等，解题的关键在于能够熟练掌握相关知识进行求解．8.(2021·全国·八年级专题练习)已知，如图，在Rt △ABC 中，∠BAC =90°，∠ABC =45°，点D 为直线BC 上一动点(点D 不与点B ，C 重合)．以AD 为边作正方形ADEF ，连接CF ，当点D 在线段BC 的反向延长线上，且点A ，F 分别在直线BC 的两侧时．(1)求证：△ABD ≌△ACF ；(2)若正方形ADEF 的边长为22，对角线AE ，DF 相交于点O ，连接OC ，求OC 的长度．【答案】(1)证明见解析； (2)OC =2【分析】(1)由题意易得AD =AF ，∠DAF =90°，则有∠DAB =∠FAC ，进而可证AB =AC ，然后问题可证；(2)由(1)可得△ABD ≌△ACF ，则有∠ABD =∠ACF ，进而可得∠ACF =135°，然后根据正方形的性质可求解．【详解】(1)证明：∵四边形ADEF 为正方形，∴AD =AF ，∠DAF =90°，又∵∠BAC =90°，∴∠DAB =∠FAC ，∵∠ABC =45°，∠BAC =90°，∴∠ACB =45°，∴∠ABC=∠ACB，∴AB=AC，∴△ABD≌△ACF(SAS)；(2)解：由(1)知△ABD≌△ACF，∴∠ABD=∠ACF，∵∠ABC=45°，∴∠ABD=135°，∴∠ACF=135°，由(1)知∠ACB=45°，∴∠DCF=90°，∵正方形ADEF边长为22，∴DF=4，∴OC=12DF=12×4=2．【点睛】本题主要考查正方形的性质及等腰直角三角形的性质，熟练掌握正方形的性质及等腰直角三角形的性质是解题的关键．9.(2021·安徽安庆·八年级期末)如图1，点E为正方形ABCD内一点，∠AEB=90°，将Rt△ABE绕点B按顺时针方向旋转90°(即∠EBE'=90°)，得到△CBE′(点A的对应点为点C)延长AE交CE于点F，连接DE．(1)试判断四边形BE′FE的形状，并说明理由．(2)如图2，若DA=DE，请猜想线段CF于FE'的数量关系并加以证明．(3)如图1，若AB=17，CF=3，请直接写出DE的长．【答案】(1)正方形，理由见解析；(2)CF=FE'，证明见解析；(3)5【分析】(1)由旋转的特征可得到∠E′=∠AEB=90°、∠EBE′=90°、BE′=BE，再由∠BEF=180°-∠AEB =90°，可判定四边形BE′FE是正方形；(2)过点D作DG⊥AE于点G，由DA=DE得AG=12AE，再证明△ADG≌△BAE，且由四边形BE′FE是正方形，得到FE′=AG=12CE′，可证得结论；(3)过点D作DG⊥AE于点G，由旋转及四边形BE′FE是正方形可得如下关系：AE=CE′=FE′+CF= FE′+3=BE+3，在Rt△BAE中根据勾股定理求出BE、AE的长，由(1)可知，△ADG≌△BAE，得到DG=BE，AG=BE，再由勾股定理求出DE的长．【详解】解：(1)四边形BE′FE是正方形．理由如下：由旋转得，∠E′=∠AEB=90°，∠EBE′=90°，∵∠BEF=180°-∠AEB=90°，∴四边形BE′FE是矩形，由旋转得，BE′=BE，∴四边形BE′FE是正方形．(2)CF=FE'，证明：如图2，过点D作DG⊥AE于点G，则∠DGA=∠AEB=90°，∵DA=DE，∴AG=12AE，∵四边形ABCD是正方形，∴DA=AB，∠DAB=90°，∴∠BAE+∠DAG=90°，∵∠ADG+∠DAG=90°，∴∠ADG=∠BAE，在△ADG和△BAE中∠ADG=∠BAE∠AGD=∠AEBAD=AB，∴△ADG≌△BAE(AAS)，∴AG=BE；∵四边形BE′FE是正方形，∴BE=FE′，∴AG=FE′，由旋转得，AE=CE′，∴12AE=12CE′，∴FE′=12AE=12CE′，∴CF=FE'．(3)如图3，过点D作DG⊥AE于点G，∵BE=FE′，CF=3，∴AE=CE′=FE′+CF=FE′+3=BE+3，∵AE2+BE2=AB2，且AB=17，∴(BE+3)2+BE2=(17)2，解得，BE=1或BE=-4(不符合题意，舍去)，∴AE=1+3=4，由(2)得，△ADG≌△BAE，∴DG=AE=4，AG=BE=1，∴GE=AE-AG=4-1=3，∵∠DGE=90°，∴DE=DG2+GE2=42+32=5．【点睛】此题考查了正方形的性质与判定、旋转的性质、等腰三角形的性质、全等三角形的判定与性质、勾股定理等知识点，解题的关键是正确地作出解题所需要的辅助线，构造全等三角形．10.(2021·湖北鄂州·八年级期末)如图，四边形ABCD是正方形，点P是线段AB的延长线上一点，点M是线段AB上一点，连接DM，以点M为直角顶点作MN⊥DM交∠CBP的角平分线于N，过点C作CE⎳MN交AD于E，连接EM，CN，DN．(1)求证：DM=MN．(2)求证：EM⎳CN．(3)若AE=1，BN=32，求DN的长．【答案】(1)见解析；(2)见解析；(3)52【分析】(1)在边DA上截取线段DF，使DF=MB连MF，证明△MDF≌△N MB即可求解；(2)由(1)△MDF≌△N MB，证明四边形EMNC为平行四边形即可求解；(3)过N作NQ⊥AP垂足为Q，由(2)知，△EDC≌△MAD；得到AD-DE=AB-AM，AE=MB，BN平分∠CBP所以∠NBQ=45°，可知三角形NBQ是等腰直角三角形，再用勾股定理即可求出和MN和DN．【详解】(1)证明：在边DA上截取线段DF，使DF=MB连MF．∵四边形ABCD是正方形∴AB=BC=CD=AD;∠DAB=∠ABC=∠BCD=∠CDA=90°∴∠CBP=180°-∠ABC=90°∵BN平分∠CBP∴∠CBP=45°∴∠NBM=∠ABC+∠CBN=90°+45°=135°∵DF=MB,AD=AB∴AD-DF=AB-MB∴AF =AM在Rt △FAM 中,AF =AM ,∴∠AFM =∠AMF =45°∴∠MFD =180°-∠AFM =135°∴∠MFD =∠NBM∵∠DMN =90°∴∠N MB +∠DMA =180°-90°=90°∵∠DMA +∠MDF =90°∴∠N MB =∠MDF在△MDF 和△N MB 中∠MFD =∠NBADF =MB∠MDF =∠NMB∴△MDF ≌△N MB (ASA )∴DM =MN ．(2)如图，设DM 与CE 的交点为H ，∵四边形ABCD 是正方形∴AD =DC ,∠DAM =∠CDE =90°∵∠DMN =90°,CE ⎳MN∴∠DHC =90°,∴∠HDC +∠DCH =90°∴∠HDC +∠ADM =90°∴∠DCE =∠ADM ,在△EDC 和△MAD 中，∠CDE =∠DAMAD =DC∠DCE =∠ADM∴△EDC ≌△MAD (ASA )．∴EC =DM 又DM =MN ，∴EC =MN 又EC ⎳MN ．∴四边形EMNC 为平行四边形．∴EM ⎳CN ．(3)解：如图所示，过N 作NQ ⊥AP 垂足为Q ．由(2)知，△EDC ≌△MAD∴DE =MA ，又AD =AB∴AD -DE =AB -AM 即AE =MB =1∵BN平分∠CBP所以∠NBQ=45°，∴三角形NBQ是等腰直角三角形，在Rt△NBQ中，设BQ=x，则NQ=BQ=x，即x2+x2=(32)2，∴x=3．∴NQ=3，MQ=1+3=4，在Rt△MQN中，MN=32+42=5，又∵在Rt△DMN中，MN=5，DM=5，∴DN=52+52=52．【点睛】此题考查的是全等三角形的性质、等腰三角形的性质和判定和判定以及勾股定理的应用，掌握它们的性质和判定是解题的关键．11.(2022·广东·塘厦初中八年级期中)四边形ABCD为正方形，点E为线段AC上一点，连接DE，过点E作EF⊥DE，交射线BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．(1)如图，求证：矩形DEFG是正方形；(2)若AB=4，CE=22，求CG的长度；(3)当线段DE与正方形ABCD的某条边的夹角是40°时，直接写出∠EFC的度数．【答案】(1)见解析；(2)22；(3)∠EFC=130°或40°【分析】(1)作EP⊥CD于P，EQ⊥BC于Q，证明Rt△EQF≌Rt△EPD，得到EF=ED，根据正方形的判定定理证明即可；(2)通过计算发现E是AC中点，点F与C重合，△CDG是等腰直角三角形，由此即可解决问题；(3)分两种情形：①如图3，当DE与AD的夹角为40°时，求得∠DEC=45°+40°=85°，得到∠CEF=5°，根据角的和差得到∠EFC=130°，②如图4，当DE与DC的夹角为40°时，根据三角形的内角和定理即可得到结论．【详解】(1)证明：如图1，作EP⊥CD于P，EQ⊥BC于Q，∵∠DCA=∠BCA，∴EQ=EP，∵∠QEF+∠FEC=45°，∠PED+∠FEC=45°，∴∠QEF =∠PED ，在△EQF 和△EPD 中，∠QEF =∠PEDEQ =EP ∠EOF =∠EPD，∴△EQF ≌△EPD (ASA )，∴EF =ED ，∴矩形DEFG 是正方形；(2)如图2中，在Rt △ABC 中，AC =2AB =42，∵CE =22，∴AE =CE ，∴点F 与C 重合，此时△DCG 是等腰直角三角形，∴四边形DECG 是正方形，∴CG =CE =22；(3)①如图3，当DE 与AD 的夹角为40°时，∠DEC =45°+40°=85°，∵∠DEF =90°，∴∠CEF =5°，∵∠ECF =45°，∴∠EFC =130°，②如图4，当DE 与DC 的夹角为40°时，∵∠DEF =∠DCF =90°，∴∠EFC =∠EDC =40°，综上所述，∠EFC =130°或40°．【点睛】此题考查了正方形的判定以及性质，涉及了全等三角形的证明、等腰直角三角形等性质，熟练掌握相关基本性质是解题的关键．12.(2021·山西·八年级期末)综合与实践：如图1，在正方形ABCD 中，连接对角线AC ，点O 是AC 的中点，点E 是线段OA 上任意一点(不与点A ，O 重合)，连接DE ，BE ．过点E 作EF ⊥DE 交直线BC于点F．。

勾股定理之蚂蚁行程、弦图模型(原卷版)-2023年中考数学重难点解题大招复习讲义-几何模型篇

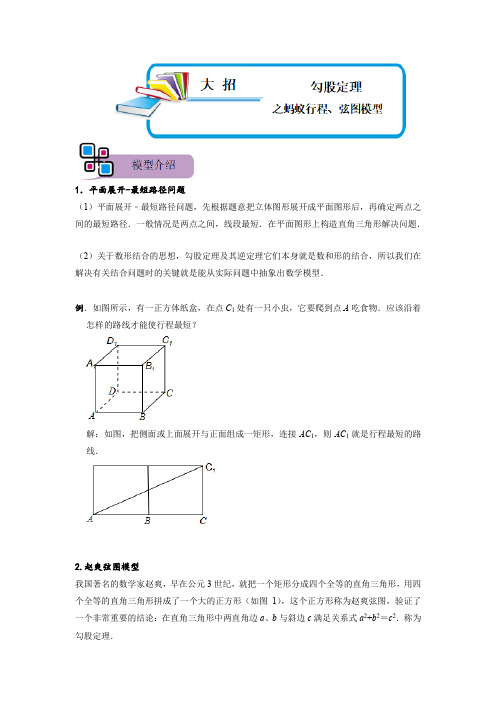
1．平面展开-最短路径问题（1）平面展开﹣最短路径问题，先根据题意把立体图形展开成平面图形后，再确定两点之间的最短路径．一般情况是两点之间，线段最短．在平面图形上构造直角三角形解决问题．（2）关于数形结合的思想，勾股定理及其逆定理它们本身就是数和形的结合，所以我们在解决有关结合问题时的关键就是能从实际问题中抽象出数学模型．例．如图所示，有一正方体纸盒，在点C1处有一只小虫，它要爬到点A吃食物．应该沿着怎样的路线才能使行程最短？解：如图，把侧面或上面展开与正面组成一矩形，连接AC1，则AC1就是行程最短的路线．2.赵爽弦图模型我国著名的数学家赵爽，早在公元3世纪，就把一个矩形分成四个全等的直角三角形，用四个全等的直角三角形拼成了一个大的正方形（如图1），这个正方形称为赵爽弦图，验证了一个非常重要的结论：在直角三角形中两直角边a、b与斜边c满足关系式a2+b2＝c2．称为勾股定理．把这四个全等的直角三角形拼成了另一个大的正方形（如图2），也能验证这个结论证明：由图2得，大正方形面积＝4×＝（a +b ）2，整理得b 2+c 2+2ab ＝2ab +c 2，∴c 2＝a 2+b 2，即直角三角形两直角边的平方和等于斜边的平方．考点一：行程最短问题【例1】．如图，有一个圆柱，它的高等于16cm ，底面半径等于4cm ，在圆柱下底面的A 点有一只蚂蚁，它想吃到上底面上与A 点相对的B 点处的食物，需要爬行的最短路程是 cm ．（π取3）➢变式训练【变式1-1】．如图，圆锥的底面圆的半径为10cm ，母线长为40cm ，C 为母线P A 的中点，一只蚂蚁欲从点B 处沿圆锥的侧面爬到点C处，则它爬行的最短距离是 cm ．例题精讲【变式1-2】．如图，一只蚂蚁从长为7cm、宽为5cm，高是9cm的长方体纸箱的A点沿纸箱爬到B点，那么它所走的最短路线的长是cm．【变式1-3】．如图是一个三级台阶，它的每一级长、宽、高分别是2米、0.3米、0.2米，A，B是这个台阶上两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿台阶面爬行到B点最短路程是米．考点二：弦图模型的应用【例2】．如图，“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形EFGH拼成的大正方形ABCD．若AE＝5，AB＝13，则中间小正方形EFGH的面积是．➢变式训练【变式2-1】．如图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成．若较短的直角边BC＝2.5，将四个直角三角形中较长的直角边分别向外延长一倍，得到图2所示的“数学风车”，若△BCD的周长是15，则这个风车的外围周长是．【变式2-2】．如图，在弦图中，正方形ABCD的对角线AC与正方形EFHI的对角线EH交于点K，对角线AC交正方形EFHI于G，J两点，记△GKH面积为S1，△JIC面积为S2，若AE＝12，CD＝4，则S1+S2的值为．1．如图所示，一只小蚂蚁从棱长为1的正方体的顶点A出发，经过每个面的中心点后，又回到A点，蚂蚁爬行最短程S满足（）A．5＜S≤6B．6＜S≤7C．7＜S≤8D．8＜S≤92．如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”，图中的四个直角三角形是全等的，如果大正方形ABCD的面积是小正方形EFGH面积的13倍，那么tan ∠ADE的值为（）A．B．C．D．3．如图是由“赵爽弦图”变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNPQ的面积分别为S1、S2、S3．若S1+S2+S3＝60，则S2的值是（）A．12B．15C．20D．304．四个全等的直角三角形围成一个大正方形，中间空出的部分是一个小正方形，这样就组成了一个“赵爽弦图”（如图）．如果小正方形面积为4，大正方形面积为74，直角三角形中较小的锐角为θ，那么tanθ的值是（）A．B．C．D．5．赵爽弦图由四个全等的直角三角形所组成，形成一个大正方形，中间是一个小正方形（如图所示）．某次课后服务拓展学习上，小浔绘制了一幅赵爽弦图，她将EG延长交CD于点I．记小正方形EFGH的面积为S1，大正方形ABCD的面积为S2，若DI＝2，CI＝1，S2＝5S1，则GI的值是（）A．B．C．D．6．如图，一只蚂蚁沿着图示的路线从圆柱高AA1的端点A到达A1，若圆柱底面半径为，高为5，则蚂蚁爬行的最短距离为．7．如图，底面半径为1，母线长为4的圆锥，一只小蚂蚁若从A点出发，绕侧面一周又回到A点，它爬行的最短路线长是．8．将四个全等的直角三角形分别拼成正方形（如图1，2），边长分别为6和2．若以一个直角三角形的两条直角边为边向外作正方形（如图3），其面积分别为S1，S2．则S1﹣S2＝．9．如图1，四个全等的直角三角形围成一个大正方形，中间是一个小正方形，这个图形是我国汉代赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”．连接四条线段得到如图2的新的图案，如果图1中的直角三角形的长直角边为5，短直角边为3，图2中阴影部分的面积为S，那么S的值为．10．如图所示一棱长为3cm的正方体，把所有的面均分成3×3个小正方形．其边长都为1cm，假设一只蚂蚁每秒爬行2cm，则它从下底面点A沿表面爬行至侧面的B点，最少要用秒钟．11．如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形E 的边长为7cm，则图中五个正方形A、B、C、D、E的面积和为cm2．12．我国汉代数学家赵爽为了证明勾股定理，创制了一幅弦图，后人称其为赵爽弦图（如图1）．图2为小明同学根据弦图思路设计的，在正方形ABCD中，以点B为圆心，AB为半径作，再以CD为直径作半圆交于点E，若边长AB＝10，则△CDE的面积为．13．图1是一个勾股定理演示教具的正面示意图，当它倒过来时，大正方形中的全部墨水恰能注满两个小正方形．王老师有一个内长为11寸，内宽为9寸的木质盒子（如图2）．现要自制一个这样的教具（由三个正方形和一个直角三角形组成），使得教具恰好摆入这个盒子中，以便保护和携带（如图3所示，A，B，C，D，E五点均紧贴盒子边缘，教具的厚度等于木盒的内高）．此时盒子的空间利用率为．14．我国古代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”，它是由4个全等的直角三角形与1个小正方形拼成的一个大正方形，如图，若拼成的大正方形为正方形ABCD，面积为9，中间的小正方形为正方形EFGH，面积为2，连接AC，交BG于点P，交DE 于点M，①△CGP≌△AEM，②S△AFP﹣S△CGP＝，③DH+HC＝4，④HC＝2+，以上说法正确的是.（填写序号）15．一个长方体盒子，它的长是12dm，宽是4dm，高是3dm，（1）请问：长为12.5dm的铁棒能放进去吗？（1）如果有﹣只蚂蚁要想从D处爬到C处，求爬行的最短路程．16．如图①，美丽的弦图，蕴含着四个全等的直角三角形．（1）如图①弦图中包含了一大，一小两个正方形，已知每个直角三角形较长的直角边为a．较短的直角边为b，斜边长为c，可以验证勾股定理；（2）如图②，将八个全等的直角三角形紧密地拼接，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1、S2、S3，若S1+S2+S3＝16，则S2＝．17．如图1是著名的赵爽弦图，由四个全等的直角三角形拼成，用它可以证明勾股定理，思路是：大正方形的面积有两种求法，一种是等于c2，另一种是等于四个直角三角形与一个小正方形的面积之和，即，从而得到等式c2＝，化简便得结论a2+b2＝c2．这里用两种求法来表示同一个量从而得到等式或方程的方法，我们称之为“双求法”．现在，请你用“双求法”解决下面两个问题（1）如图2，在Rt△ABC中，∠ACB＝90°，CD是AB边上的高，AC＝3，BC＝4，求CD的长度．（2）如图3，在△ABC中，AD是BC边上的高，AB＝4，AC＝5，BC＝6，设BD＝x，求x的值．。

赵爽弦图模型-学生版--中考数学专题专练

赵爽弦图模型模型讲解◎结论1：在正方形ABCD的四边AB，BC，CD，DA上分别取点E，F，G，H，使得BE=CF= GD=AH，则四边形EHGF是正方形.◎结论2：如图所示，在正方形ABCD的四边AB，BC，CD，DA上分别取点E，F，G，H,使得BE=CF=GD=AH,此外EQ∥BC，HP∥CD，GO∥DA，FR∥AB，则四边形ORQP是正方形.◎结论3：如图所示，在正方形ABCD的四边AB，BC，CD，DA上分别取点E，F，G，H，使得BE=CF=GD=AH，此外EQ∥BC，HP∥CD，GO∥DA，FR∥AB，则:(1)S正方形ABCD =4SΔAEH十S正方形EFGH;(2)S正方形EFGH =4SΔHPE十S正方形OPQR;(3)S正方形ABCD -S正方形EFGH=S正方形EFGH-S正方形OPQR.(4)2S正方形EFGH =S正方形ABCD十S正方形OPQR注：常见的勾股数组合①3,4,5； ②5,12,13；③6,8,10；④8,15,17；⑤9,12,15;1(2023春·四川南充·八年级四川省南充高级中学校考阶段练习)如图所示的“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲．该图由四个全等的直角三角形和一个小正方形拼成一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b．若ab=10，大正方形面积为25，则小正方形边长为()A．3B．2C．5D．32(2023春·河北沧州·八年级校考阶段练习)如图，用4个相同的直角三角形与一个小正方形拼成的大正方形，若图中直角三角形较短的直角边长是5，小正方形的边长是7，则大正方形的面积是()A．121B．144C．169D．1963(2022秋·福建三明·八年级统考期末)某大会会标如图所示，它是由相同的直角三角形与中间的小正方形拼成的一个大正方形．若大正方形的面积是13，小正方形的面积是1，直角三角形中较长的直角边为a，较短的直角边为b，则a+b2的值()A．13B．19C．25D．1694(2021秋·贵州六盘水·八年级统考阶段练习)如图，这是“赵爽弦图”，△ABH，△BCG，△CDF，△DAE是四个全等的直角三角形，四边形ABCD和四边形EFGH都是正方形，如果EF=1，AH=3，那么AB等于()A．4B．5C．9D．105(2023春·全国·八年级专题练习)如图是由4个全等的直角三角形与1个小正方形拼成的正方形图案．已知大正方形面积为25，小正方形面积为1，若用a、b表示直角三角形的两直角边(a>b)，则下列说法：①a2+b2=25，②a-b=1，③ab=12，④a+b=7．正确的是()A．①②B．①②③C．①②④D．①②③④6(2023春·全国·八年级专题练习)用四个全等的直角三角形拼成如图①所示的大正方形，中间也是一个正方形，它是美丽的弦图，其中四个直角三角形的直角边长分别为a,b a<b，斜边长为c．(1)结合图①，求证：a2+b2=c2；(2)如图②，将这四个全等的直角三角形无缝隙无重叠地拼接在一起，得到图形ABCDEFGH．若该图形的周长为48，OH=6．求该图形的面积．7(2023秋·河南洛阳·八年级统考期末)八年级课外兴趣小组活动时，老师提出了如下问题：将2a -3ab -4+6b 因式分解．【观察】经过小组合作交流，小明得到了如下的解决方法：解法一：原式=2a -3ab -4-6b =a 2-3b -22-3b =2-3b a -2解法二：原式=2a -4 -3ab -6b =2a -2 -3b a -2 =a -2 2-3b【感悟】对项数较多的多项式无法直接进行因式分解时，我们可以将多项式分为若干组，再利用提公因式法、公式法达到因式分解的目的，这就是因式分解的分组分解法．分组分解法在代数式的化简、求值及方程、函数等学习中起着重要的作用．(温馨提示：因式分解一定要分解到不能再分解为止)【类比】(1)请用分组分解法将x 2-a 2+x +a 因式分解；【应用】(2)“赵爽弦图”是我国古代数学的骄傲，我们利用它验证了勾股定理．如图，“赵爽弦图”是由四个全等的直角三角形围成的一个大正方形，中间是一个小正方形．若直角三角形的两条直角边长分别是a 和b (a >b )，斜边长是3，小正方形的面积是1．根据以上信息，先将a 4-2a 3b +2a 2b 2-2ab 3+b 4因式分解，再求值．8(2023春·全国·八年级专题练习)我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形(如图1)与中间的一个小正方形拼成一个大正方形(如图2)．(1)利用图2正方形面积的等量关系得出直角三角形勾股的定理，该定理的结论用字母表示：；(2)用图1这样的两个直角三角形构造图3的图形，满足AE=BC=a，DE=AC=b，AD=AB=c，∠AED=∠ACB=90°，求证(1)中的定理结论；(3)如图，由四个全等的直角三角形拼成的图形，设CE=m，HG=n，求正方形BDFA的面积．(用m，n表示)9(2020秋·广东佛山·八年级统考期中)我们在探索乘法公式时，设置由图形面积的不同表示方法验证了乘法公式．我国著名的数学家赵爽，早在公元3世纪，就把一个矩形分成四个全等的直角三角形，用四个全等的直角三角形拼成了一个大的正方形(如图①)，这个图形称为赵爽弦图，验证了一个非常重要的结论：在直角三角形中两直角边a，b与斜边c满足关系式a2+b2=c2，称为勾股定理．(1)爱动脑筋的小明把这四个全等的直角三角形拼成了另一个大的正方形(如图②)，也能验证这个结论，请你帮助小明完成验证的过程．(2)如图，在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上．请在图中画出△ABC的高BD，利用上面的结论，求高BD的长．10(2022春·安徽芜湖·八年级统考期中)图①是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．(1)在Rt△ABCC中，AC=a，BC=b，∠ACB=90°，若图①中大正方形的面积为61，小正方形的面积为1，求a+b2；(2)在(1)的条件下，若将图①中的四个直角三角形中较长的直角边分别向外延长一倍，得到图②所示的“数学风车”，求这个风车的外围周长(图中实线部分)．。

专题18《弦图模型》

3．略．【提示】显然四边形 EHBC 为矩形，所以 FH＝BC＝AB，所以△PAB≌△FHE（ ASA）．所以 HF＝AP．
7
则四边形 ABSR 是平行四边形．因为∠ABC＝90°，所以四边形 ABSR 是矩形．所以∠R＝∠S＝90°，RS＝AB＝10，AR＝BS．因为 AM⊥DN．所以由（1）中的结论可得 DN ＝ AR ．
AM AB 设 SC＝x，DS＝y，则 AR＝BS＝5＋x．RD＝10－y ，所以在 Rt△CSD 中，x2＋y2＝25．在 Rt△ARD 中．（5＋x）2＋（10－y）2＝100．
边形 OMND 为矩形，易证△AOM≌△ABN，所以 AM＝BN＝ 2 ，OM＝AN＝ k ，BD＝ k － 2 ，
2
2
OD＝ k ＋ 2 ，所以点 B（ k ＋ 2 ， k － 2 ），根据双曲线表达式，有（ k ＋ 2 ）·（ k
2
2
2
2
2
＋ 2 ）＝k，解得 k＝1＋ 5 ．
2．∠APD＝45°，为固定值．【提示】如图，过点 A 作 AF⊥AB，并截取 AF＝BD，连结 DF，CF．可得 AF∥CE，AF＝CE，所以四边形 AFCE 是平行四边形，所以 FC∥AE，∠APD＝∠FCD．易证△DAF≌△CBD．则∠1 ＝∠2，FD＝DC．从而∠APD＝∠FCD＝45°．
联立方程组
(5
x2 y2 25 x)2 (10 y)2
102
，
x 5
x 3
得
y
0
（舍），或
y
． 4
所以 AR＝5＋x＝8，所以 DN ＝ AR ＝ 8 ＝ 4 ．
AM AB 10 5
进阶训练 1．如图，在平面直角坐标系中，经过点 A 的双曲线，y＝ k （k＞0）同时经过点 B．且 x

第6讲弦图模型(解析版)

中考数学几何模型6：弦图模型名师点睛拨开云雾开门见山弦图模型，包含两种模型：内弦图模型和外弦图模型.（一）内弦图模型：如图，在正方形ABCD中，AE⊥BF于点E，BF⊥CG于点F，CG⊥DH于点G，DH ⊥AE于点H，则有结论：△ABE≌△BCF≌△CDG≌△DAH.注意局部弦图（二）外弦图模型：如图，在正方形ABCD中，E，F，G，H分别是正方形ABCD各边上的点，且四边形EFGH是正方形，则有结论：△AHE≌△BEF≌△CFG≌△DGH.包含“一线三垂直”典题探究启迪思维探究重点例题1. 如图，在△ABC中，∠ABC=90°，分别以AB，AC向外作正方形ABDE，ACFG，连接EG，若AB=12，BC=16，求△AEG的面积.变式练习>>>1．如图，四边形ABCD是边长为4的正方形，点E在边AD上，连接CE，以CE为边作正方形CEFG，点D，F在直线CE的同侧，连接BF，若AE=1，求BF的长.例题2. 如图，以Rt△ABC的斜边BC在△ABC同侧作正方形BCEF，该正方形的中心为点O，连接AO.若AB=4，AO=62，求AC的长.变式练习>>>2．如图，点A，B，C，D，E都在同一条直线上，四边形X，Y，Z都是正方形，若该图形总面积是m，正方形Y的面积是n，则图中阴影部分的面积是___________.例题3. 如图，在△ABC 中，∠BAC=45°，D 为△ABC 外一点，满足∠CBD=90°，BC=BD ，若=4.5ACD S △，求AC 的长.变式练习>>>3．点P 是正方形ABCD 外一点，PB=10cm ，△APB 的面积是60cm 2，△CPB 的面积是30cm 2．求正方形ABCD 的面积.例题4. 在边长为10的正方形ABCD 中，内接有6个大小相同的正方形，P 、Q 、M 、N 是落在大正方形边上的小正方形的顶点，如图所示，求这六个小正方形的面积.变式练习>>>4．如图，在平面直角坐标系中，经过点A的双曲线y＝（x＞0）同时经过点B，且点A在点B的左侧，点A的横坐标为，∠AOB＝∠OBA＝45°，则k的值为1+．【解答】解：在△AOM和△BAN中，，∴△AOM≌△BAN（AAS），∴AM＝BN＝，OM＝AN＝，∴OD＝+，BD＝﹣，∴B（+，﹣），∴双曲线y＝（x＞0）同时经过点A和B，∴（+）•（﹣）＝k，整理得：k2﹣2k﹣4＝0，解得：k＝1±（负值舍去），∴k＝1+；故答案为：1+．例题5. 如图，在等腰Rt △ACB 和等腰Rt △DCE 中，∠AXB=∠DCE=90°，连接AD ，BE ，点I 在AD 上，（1）若IC ⊥BE ，求证：I 为AD 中点；（2）若I 为AD 中点，求证：IC ⊥BE例题6. 在平面直角坐标系中，直线l 的解析式为2y x b =+，其与x 轴交于点A,与y 轴交于点B ，在直线l 移动的过程中，直线y=4上是否存在点P ，使得△PAB 是等腰直角三角形，若存在，请求出满足条件的所有点P 的坐标，如不存在，请说明理由.达标检测领悟提升强化落实1. 如图所示，“赵爽弦图”是由8个全等的直角三角形拼接而成的，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3，已知S1+S2+S3＝10，则S2的值是．【解答】解：将四边形MTKN的面积设为x，将其余八个全等的三角形面积一个设为y，∵正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3，S1+S2+S3＝10，∴得出S1＝8y+x，S2＝4y+x，S3＝x，∴S1+S2+S3＝3x+12y＝10，故3x+12y＝10，x+4y＝，所以S2＝x+4y＝，故答案为：．2. 我国古代数学家赵爽利用弦图证明了勾股定理，这是著名的赵爽弦图（如图1）．它是由四个全等的直角三角形拼成了内、外都是正方形的美丽图案．在弦图中（如图2），已知点O为正方形ABCD的对角线BD的中点，对角线BD分别交AH，CF于点P、Q．在正方形EFGH的EH、FG两边上分别取点M，N，且MN经过点O，若MH＝3ME，BD＝2MN＝4．则△APD的面积为5．【解答】解：如图，连接FH，作EK∥MN，OL⊥DG∵四边形ABCD是正方形，且BD＝2MN＝4∴MN＝2，AB＝2∵四边形EFGH是正方形∴FO＝HO，EH∥FG∴∠HMO＝∠FNO，∠MHO＝∠NFO，且FO＝HO∴△MHO≌△FNO（AAS），∴MH＝FN∵MH＝3ME，∴MH＝FN＝3EM，EH＝EF＝4EM∴EK∥KN，EH∥FG，∴四边形EMNK是平行四边形∴MN＝EK＝2，KN＝EM，∴FK＝2EM∵EF2+FK2＝EK2，∴16EM2+4EM2＝20，∴EM＝1，∴EH＝4，∵AD2＝（AE+4）2+DH2，且AE＝DH∴DH＝AE＝2，∴AH＝6∵PH∥OL，∴，∴PH＝1，∴AP＝5，∴S△APD＝×5×2＝5故答案为53．如图，在△ABC中，∠ACB＝90°，分别以边AB、AC向外作正方形ABDE和正方形ACFG，连接CE，BG，EG．（正方形的各边都相等，各角均为90°）（1）判断CE与BG的关系，并说明理由；（2）若BC＝3，AB＝5，则AEG面积等于6．【解答】解：（1）如图，∵∠EAB＝∠GAC＝90°，∴∠EAC＝∠BAG，在△EAC和△BAG中，，∴△EAC≌△BAG（SAS），∴CE＝BG，∠AEC＝ABG，∵∠AEC+∠APE＝90°，∠APE＝∠BPC，∴∠BPC+∠ABG＝90°，∴CE⊥BG；（2）延长GA，过E作EQ⊥AQ，∵∠EAB＝∠GAC＝90°，∴∠EAG+∠BAC＝180°，∵∠EAG+∠EAQ＝180°，∴∠EAQ＝∠BAC，∴EQ＝AE•sin∠EAQ＝AB•BC＝3，∵BC＝3，AB＝5，∴AC＝＝4，∴AEG面积＝AG•EQ＝×4×3＝6．4．【问题解决】一节数学课上，老师提出了这样一个问题：如图1，点P是正方形ABCD内一点，P A＝1，PB＝2，PC ＝3．你能求出∠APB的度数吗？小明通过观察、分析、思考，形成了如下思路：思路一：将△BPC绕点B逆时针旋转90°，得到△BP′A，连接PP′，求出∠APB的度数；思路二：将△APB绕点B顺时针旋转90°，得到△CP'B，连接PP′，求出∠APB的度数．请参考小明的思路，任选一种写出完整的解答过程．【类比探究】如图2，若点P是正方形ABCD外一点，P A＝3，PB＝1，PC＝，求∠APB的度数．【解答】解：（1）思路一、如图1，将△BPC绕点B逆时针旋转90°，得到△BP′A，连接PP′，∴△ABP'≌△CBP，∴∠PBP'＝90°，BP'＝BP＝2，AP'＝CP＝3，在Rt△PBP'中，BP＝BP'＝2，∴∠BPP'＝45°，根据勾股定理得，PP'＝BP＝2，∵AP＝1，∴AP2+PP'2＝1+8＝9，∵AP'2＝32＝9，∴AP2+PP'2＝AP'2，∴△APP'是直角三角形，且∠APP'＝90°，∴∠APB＝∠APP'+∠BPP'＝90°+45°＝135°；（2）如图2，将△BPC绕点B逆时针旋转90°，得到△BP′A，连接PP′，∴△ABP'≌△CBP，∴∠PBP'＝90°，BP'＝BP＝1，AP'＝CP＝，在Rt△PBP'中，BP＝BP'＝1，∴∠BPP'＝45°，根据勾股定理得，PP'＝BP＝，∵AP＝3，∴AP2+PP'2＝9+2＝11，∵AP'2＝（）2＝11，∴AP2+PP'2＝AP'2，∴△APP'是直角三角形，且∠APP'＝90°，∴∠APB＝∠APP'﹣∠BPP'＝90°﹣45°＝45°．5．如图，已知∠ABC＝90°，D是直线AB上一点，AD＝BC．（1）如图1，过点A作AF⊥AB，并截取AF＝BD，连接DC、DF、CF．①求证：AF+AB＝BC②判断FD与DC的关系并证明；（2）如图2，E是直线BC上一点，且CE＝BD，直线AE、CD相交于点P，∠APD的度数是一个固定的值吗？若是，请求出它的度数；若不是，请说明理由．【解答】（1）证明：①∵AD＝BC，∴AD＝AB+BD，AF＝BD，∴AF+AB＝BC．②∵AF⊥AB，∴∠F AD＝90°，又∵∠DBC＝90°，∴∠F AD＝∠DBC，∵AF＝BD，AD＝BC，∴△F AD≌△DBC（SAS），∴FD＝CD，∠ADF＝∠BCD，∴∠BDC+∠ADF＝∠BDC+∠BCD＝90°，即DF⊥DC；（2）解：作AF⊥AB于A，使AF＝BD，连结DF，CF，如图，∵AF⊥AD，∠ABC＝90°，∴∠F AD＝∠DBC，在△F AD与△DBC中，，∴△F AD≌△DBC（SAS），∴FD＝DC，∴△CDF是等腰三角形，∵△F AD≌△DBC，∴∠FDA＝∠DCB，∵∠BDC+∠DCB＝90°，∴∠BDC+∠FDA＝90°，∴△CDF是等腰直角三角形，∴∠FCD＝45°，∵AF∥CE，且AF＝CE，∴四边形AFCE是平行四边形，∴AE∥CF，∴∠APD＝∠FCD＝45°．6．【探究证明】（1）某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究，提出下列问题，请你给出证明．如图1，矩形ABCD中，EF⊥GH，EF分别交AB，CD于点E，F，GH分别交AD，BC于点G，H，求证：；【结论应用】（2）如图2，在满足（1）的条件下，又AM⊥BN，点M，N分别在边BC，CD上，若，则的值为；（直接写出结果）【联系拓展】（3）如图3，四边形ABCD中，∠ABC＝90°，AB＝AD＝6，BC＝CD＝3，AM⊥DN，点M，N分别在边BC，AB上，求的值．【解答】解：（1）过点A作AP∥EF，交CD于P，过点B作BQ∥GH，交AD于Q，如图1，∵四边形ABCD是矩形，∴AB∥DC，AD∥BC．∴四边形AEFP、四边形BHGQ都是平行四边形，∴AP＝EF，GH＝BQ．又∵GH⊥EF，∴AP⊥BQ，∴∠QAT+∠AQT＝90°．∵四边形ABCD是矩形，∴∠DAB＝∠D＝90°，∴∠DAP+∠DP A＝90°，∴∠AQT＝∠DP A．∴△PDA∽△QAB，∴，∴；（2）如图2，∵EF⊥GH，AM⊥BN，∴由（1）中的结论可得，；∴，故答案为；（3）过点D作平行于AB的直线，交过点A平行于BC的直线于R，交BC的延长线于S，如图3，则四边形ABSR是平行四边形．∵∠ABC＝90°，∴平行四边形ABSR是矩形，∴∠R＝∠S＝90°，RS＝AB＝6，AR＝BS．∵AM⊥DN，∴由（1）中的结论可得．设SC＝x，DS＝y，则AR＝BS＝3+x，RD＝6﹣y，∴在Rt△CSD中，x2+y2＝9①，在Rt△ARD中，（3+x）2+（6﹣y）2＝36②，由②﹣①得x＝2y﹣3③，解方程组，得（舍去），或，∴AR＝3+x＝，∴＝＝．7．如图，直角梯形ABCD中，AD∥BC，∠ADC＝90°，l是AD的垂直平分线，交AD于点M，以腰AB 为边作正方形ABFE，EP⊥l于P．求证：2EP+AD＝2CD．【解答】证明：作AH⊥BC于H，延长EP交AH于G，∵l是AD的垂直平分线，∴AM＝MD＝AD，l∥AH，又∵四边形ABCD是直角梯形，∴四边形AHCD是矩形，∴AH＝CD，∵PE⊥l，∴EG⊥AH，∴四边形AGPM是矩形，∴GP＝AM＝AD，∴∠AHB＝∠AGE＝90°，∴∠1+∠2＝90°，在正方形ABFE中，AB＝AE，∠BAE＝90°，∴∠2+∠3＝90°，∴∠1＝∠3，在△ABH和△EAG中，，∴△ABH≌△EAG（AAS），∴AH＝EG，∴CD＝GP+PE＝AD+PE，即2CD＝AD+2PE．8．提出问题：如图1，在△ABC中，∠ACB＝90°，分别以边AB、AC向外作正方形ABDE和正方形ACFG，连接CE，BG，EG．（1）探索CE与BG的关系；（2）探究△ABC与△AEG面积是否仍然相等？说明理由．（3）如图2，学校教学楼前的一个六边形花圃被分成七个部分，分别种上不同品种的花卉，已知△CDG 是直角三角形，∠CGD＝90°，DG＝3m，CG＝4m，四边形ABCD、CIHG、GFED均为正方形，则这个六边形花圃ABIHFE的面积为74m2．【解答】解（1）CE＝BG，CE⊥BG；理由：∵∠EAB＝∠GAC＝90°，∴∠EAC＝∠BAG，在△EAC和△BAG中，，∴△EAC≌△BAG（SAS），∴CE＝BG，∠AEC＝ABG，∵∠AEC+∠APE＝90°，∠APE＝∠BPC，∴∠BPC+∠ABG＝90°，∴CE⊥BG；即：CE＝BG，CE⊥BG；（2）如图1，过点E作EH⊥AG交GA延长线于H；∴∠EHA＝∠90°＝∠BCA，∵∠EAH+∠BAH＝90°，∠BAC+∠BAH＝90°，∴∠EAH＝∠BAC，在△EHA和△BCA中，，∴△EHA≌△BCA，∴EH＝BC，∵AC＝AG∴S△ABC＝AC×BC＝AC×EH，S△AGE＝AG×EH＝AC×EH，∴S△ABC＝S△AGE，（3）∵在Rt△CDG中，DG＝3m，CG＝4m，∴CD＝5m，∵四边形ABCD，CIHG、GFED均为正方形∴CG＝GH＝4，DG＝FG＝3，同（2）的方法得出S△BCI＝S△CDG，S△ADE＝S△CDG∴S六边形花圃ABIHFE＝S正方形ABCD+S△BCI+S正方形CIHG+S△FGH+S正方形DEFG+S△ADE+S△SDG ＝S正方形ABCD+S△CDG+S正方形CIHG+S△FGH+S正方形DEFG+S△CDG+S△CDG＝S正方形ABCD+S正方形CIHG+S△FGH+S正方形DEFG+3S△CDG＝CD2+CG2+GH×FG+DG2+3×CG×DG＝52+42+×4×3+32+×4×3＝25+16+6+9+18＝74（m2）．故答案为74m2．9．已知：l1∥l2∥l3∥l4，平行线l1与l2、l2与l3、l3与l4之间的距离分别为d1、d2、d3，且d1＝d3＝1，d2＝2．我们把四个顶点分别在l1、l2、l3、l4这四条平行线上的四边形称为“格线四边形”．（1）如图1，正方形ABCD为“格线四边形”，则正方形ABCD的边长为．（2）矩形ABCD为“格线四边形”，其长：宽＝2：1，求矩形ABCD的宽．（3）如图1，EG过正方形ABCD的顶点D且垂直l1于点E，分别交l2，l4于点F，G．将∠AEG绕点A 顺时针旋转30°得到∠AE′D′（如图2），点D′在直线l3上，以AD′为边在E′D′左侧作菱形AB′C′D′，使B′，C′分别在直线l2，l4上，求菱形AB′C′D′的边长．【解答】解：（1）∵l1∥l2∥l3∥l4，∠AED＝90°∴∠DGC＝90°，∵四边形ABCD为正方形∴∠ADC＝90°，AD＝CD，∵∠ADE+∠2＝90°，∴∠1+∠2＝90°，∴∠1＝∠ADE，∵l3∥l4，∴∠1＝∠DCG，∠ADE＝∠DCG，在△AED与△DGC中，，∴△AED≌△GDC（AAS），∴AE＝GD＝1，ED＝GC＝3，∴AD＝＝，故答案为：；（2）如图2过点B作BE⊥L1于点E，反向延长BE交L4于点F，则BE＝1，BF＝3，∵四边形ABCD是矩形，∴∠ABC＝90°，∴∠ABE+∠FBC＝90°，∵∠ABE+∠EAB＝90°，∴∠FBC＝∠EAB，当AB＜BC时，AB＝BC，∴AE＝BF＝，∴AB＝＝；如图3当AB＞BC时，同理可得：BC＝，∴矩形的宽为：，；（3）如图4过点E′作ON垂直于l1分别交l1，l3于点O，N，∵∠OAE′＝30°，则∠E′FN＝60°∵AE′＝AE＝1，故E′O＝，E′N＝，E′D′＝，由勾股定理可知菱形的边长为：＝＝．10．四边形ABCD是边长为4的正方形，点E在边AD所在直线上，连接CE，以CE为边，作正方形CEFG （点D，点F在直线CE的同侧），连接BF．（1）如图1，当点E与点A重合时，请直接写出BF的长；（2）如图2，当点E在线段AD上时，AE＝1；①求点F到AD的距离；②求BF的长；（3）若BF＝3，请直接写出此时AE的长．【解答】解：（1）作FH⊥AB于H，如图1所示：则∠FHE＝90°，∵四边形ABCD和四边形CEFG是正方形，∴AD＝CD＝4，EF＝CE，∠ADC＝∠DAH＝∠BAD＝∠CEF＝90°，∴∠FEH＝∠CED，在△EFH和△CED中，，∴△EFH≌△CED（AAS），∴FH＝CD＝4，AH＝AD＝4，∴BH＝AB+AH＝8，∴BF＝＝＝4；（2）过F作FH⊥AD交AD的延长线于点H，作FM⊥AB于M，如图2所示：则FM＝AH，AM＝FH，①∵AD＝4，AE＝1，∴DE＝3，同（1）得：△EFH≌△CED（AAS），∴FH＝DE＝3，EH＝CD＝4，即点F到AD的距离为3；②∴BM＝AB+AM＝4+3＝7，FM＝AE+EH＝5，∴BF＝＝＝；（3）分三种情况：①当点E在边AD的左侧时，过F作FH⊥AD交AD于点H，交BC延长线于K．如图3所示：同（1）得：△EFH≌△CED，∴FH＝DE＝AE+4，EH＝CD＝4，∴FK＝8+AE，在Rt△BFK中，BK＝AH＝EH﹣AE＝4﹣AE，由勾股定理得：（4﹣AE）2+（8+AE）2＝（3）2，解得：AE＝1或AE＝﹣5（舍去），∴AE＝1；②当点E在边AD的右侧时，过F作FH⊥AD交AD的延长线于点H，交BC延长线于K，如图4所示：同理得：AE＝2+或2﹣（舍去）．③当点E在AD上时，可得：（8﹣AE）2+（4+AE）2＝90，解得AE＝5或﹣1，5＞4不符合题意．综上所述：AE的长为1或2+．。

中考数学几何专项复习题-11弦图模型知识精讲

弦图模型知识精讲1.证法一以a、b为直角边（b＞a），以c为斜边作四个全等的直角三角形，则每个直角三角形的面积等于，如图所示：∵Rt△DAH≌Rt△ABE，∴∠HDA＝∠EAB，∵∠ADH＋∠HAD＝90°，∴∠EAB＋∠HAD＝90°，∴∠DAB＝90°∵AB＝AD，∴四边形ABCD是一个边长为c的正方形，它的面积等于c2，∵EF＝FG＝GH＝HE＝b－a，∠HEF＝90°，∴四边形EFGH是一个边长为(b－a)的正方形，它的面积等于(b－a)2，，∴a2＋b2＝c2.2.证法二以a、b为直角边（b＞a），以c为斜边作四个全等的直角三角形，则每个直角三角形的面积等于，如图所示：∵Rt△HAE≌Rt△EBF，∴∠AHE＝∠BEF，∵∠AEH＋∠AHE＝90°，∴∠AEH＋∠BEF＝90°，∴∠HEF＝180°－90°＝90°，∴四边形EFGH是一个边长为c的正方形.它的面积等于c2，∵Rt△GDH≌Rt△HAE，∴∠HGD＝∠EHA.∵∠HGD＋∠GHD＝90°，∴∠EHA＋∠GHD＝90°，又∵∠GHE＝90°，∴∠DHA＝90°＋90°＝180°，∵四边形EFGH是一个边长为（a＋b）的正方形，它的面积等于（a＋b）2，，∴a2＋b2＝c2.3.证法三以a、b为直角边，以c为斜边作两个全等的直角三角形，则每个直角三角形的面积等于，如图所示：∵Rt△EAD≌Rt△CBE，∴∠ADE＝∠BEC.∵∠AED＋∠ADE＝90°，∴∠AED＋∠BEC＝90°，∴∠DEC＝180°－90°＝90°，∴△DEC是一个等腰直角三角形，它的面积等于又∵∠DAE＝90°，∠EBC＝90°，∴AD∥BC，∴四边形ABCD是一个直角梯形，它的面积等于，a2＋b2＝c2.4.证法四如图所示，分别以a、b为直角边，以c为斜边的四个直角三角形全等，图中3个正方形的边长分别为a、b、c，整个图形的面积为S，则：∵△ABH≌△HEF，∴∠BAH＝∠EHF，∴∠BAH＋∠AHB＝∠EHF＋∠AHB＝90°，∴∠AHF＝90°，∴四边形AHFI是正方形，，∴，∴a2＋b2＝c2.5.证法五分别以a、b为直角边，以c为斜边的四个直角三角形全等，将它们按如图所示拼成一个多边形，并延长AC交DF于点P.∵D、E、F在一条直线上，且Rt△GEF≌Rt△EBD，∴∠EGF＝∠BED，∵∠EGF＋∠GEF＝90°，∴∠BED＋∠GEF＝90°，∴∠BEG＝180°－90°＝90°又∵AB＝BE＝EG＝GA＝c，∴四边形ABEG是一个边长为c的正方形，∴∠ABC＋∠CBE＝90°，∵Rt△ABC≌Rt△EBD，∴∠ABC＝∠EBD.∴∠EBD＋∠CBE＝90°，即∠CBD＝90°，又∵∠BDE＝90°，∠BCP＝90°，BC＝BD＝a，∴四边形BDPC是一个边长为a的正方形，同理，四边形HPFG是一个边长为b的正方形，设多边形GHCBE的面积为S，则，，∴a2＋b2＝c2.。

中考数学压轴题专项汇编专题弦图模型

专题18 弦图模型破解策略1．内弦图ABCDBFCGCGDHDHAEAEBFABEBCFCDGDAH．≌△在正方形⊥中，≌△⊥，，⊥则△，⊥≌△，如图，ABCBFC＝90°＝∠因为∠证明ABEFBCFBCFCB－90°．＝∠所以∠＋∠＋∠ABEFC B．＝∠所以∠ABBABEBCF，．所以△又因为＝≌△C ABEBCFCDGDAH．同理可得△≌△≌△≌△ADGFHECB2．外弦圈ABCDMNPQABCD边上，且，如图，在正方形在正方形中，点，，MUPQQBMMCNNDPPAQ．≌△≌△四边形≌△为正方形，则△BQMNC＝90°，因为∠＝∠＝∠证明BQMQMBQMBNMC＝90°，＋∠＝∠所以∠＋∠BQMNM C．＝∠所以∠QMMNQBMMCN．，所以△又因为＝≌△QHMMCNNDPPAQ．同理可得△≌△≌△≌△PADQNCMB3．括展ABHABHBEAHE．所以⊥）如图，在Rt△中．∠＝90°，于点1 （ABEBHEAH B．≌△≌△△QBMBLKQBBLQMBK，所以＝，⊥Rt△）如图，在（ 2Rt △和中，QBMBLK．△≌△7/ 1AEHBBKBLKQM＝90°，，⊥证明因为∠KQMBKBIKBL十∠所以∠＋∠90°＝∠＝KQMB所以∠，＝∠BLQB＝又因为．BLKQBM≌△所以△．QKELMB例题讲解CEADCEEABCD，以的正方形，点4所在的直线上，连结1 四边形在边是边长为例AEADCECEFGDFBFE，上时，1．为边，作正方形当点（点＝，在线段在直线的同侧），连结BF求的长．FEADGCBHFADADFH交，解如图，过点的延长线于点作⊥KFHBC交．延长的延长线于点CEFGABCD和四边形是正方形，因为四边形CDEHEDADFHECDFEHAE－4＝3，．＝根据“弦图模型”可得△≌△，所以＝＝＝EDDHHKCDHKCDCKEH＝－因为为矩形，所以1＝＝4，＝．＝CKBCBKHKFKFH＝．5＝＋．，所以＝十＝72274BKFK?BF＝所以＝7/ 2FDEAHGKCBACBACBCDCBDS，求．45°，若5如图，△＝为等腰直角三角形，∠＝90°，∠4＝例2ACD△的长．DBCAFDFBFEBDBBEACE⊥如图，过点解．作作⊥交于点，过点的延长线于点CEBBFD由“外弦图模型”可得△，≌△CEBF＝．所以EFAEBEAC，所以易证＝＝，112ACEFSAC，＝4·＝．所以＝5ACD△22AC从而＝3．FDBECA 某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探例3 究，提出下列问题，请你给出证明．BCGHADFEFEFABCDCHABCDF，，）如图（11，在矩形中，于点⊥，，分别交，分别交ADEF HG．求证：于点＝ABGHEF CDBNAMMNBC上，若，点，分别在边122＝（）如图，在满足（）的条件下，又，⊥GHBN11＝．，则AM15DNADABABCABCDCDBCAM，＝10＝＝90°，，在四边形33（）如图中，∠＝，－⊥，57 / 3DN ABMNBC分别在边上，求，点的值．，AM DNDDFFCCMGGMHHBBBNEAAAE3图2图1图AAPEFCDPBBQGHADQ．作作∥．交∥于点于点，过点，交（解 1））如图4．过点ABCD是矩形．因为四边形ABDCADB C．∥∥，所以AEFPBHGQ都是平行四边形，，四边形所以四边形APEFGHBQ．＝＝，所以CHEF．⊥又因为APBQ．所以⊥QATAQT＝90＋∠°．所以∠ABCD是矩形，因为四边形DABD＝90°，所以∠＝∠DAPDPA＝90°，所以∠＋∠AQTDP A．所以∠＝∠PDAQA B．所以△∽△APAD＝所以，BQABADEF＝．所以GHABPFCDGQTHAEBEFGHAMBN．）因为（ 2⊥，⊥7/ 4ADADBNEF＝，所以由（1＝）中的结论可得．AMGHABAB11EFBN．所以＝＝15GHAM BCPBCDABA，交3）如图5．过点的直线于点作平行于且平行于的直线，交过点（S．的延长线于点ABSR是平行四边形．则四边形ABC＝90°，因为∠ABSR是矩形．所以四边形RSRSABARBS．，1090°，＝所以∠＝＝∠＝＝AMDN．因为⊥DNAR＝）中的结论可得．所以由（1AMAB SCxDSyARBSxRDy，－．，＝，则＝＝10＝设5＝＋22yCSDx 25＋．所以在Rt△＝中，22yxARD 100＋＝）＋（10－．在 Rt△）中．（522?25x??y程组，联立方?ARx＝8＋5，所以＝DNAR84＝＝所22210??x)?(10?y)(5?x?35?x???得（舍），或．??y?0y?4??以＝．AMAB105DSRCMBNA进阶训练k kAy＞0）同时经过点B．如图，在平面直角坐标系中，经过点 1的双曲线，＝（．且x7 / 5kABAOBAAOB°，则．点．∠在点＝的左侧，点＝∠__ __＝45的横坐标为2y AB xO BCEABADBDABC上的一点，且上的点，．＝是直线 2．如图，巳知∠＝90°，C是直线APDPAEDCCEB 请求出它的度，，∠相交于点＝的度数是一个固定的值吗？若是，D．直线数；若不是，请说明理由．APBECDABCDPADADBP的垂直平分线分别 3．如图，在正方形上，且不与中，点，在重合．CDABEFQEEHABHEHBPMHF．求证：作⊥与，过点于点．交于点交，于，两点，垂足为AP．＝ECDPQBHAF7/ 6参考答案：型弦图模：专题18．＋1 1．5NAMABAMBDxyBDDM，则四，过点，轴于点【提示】过点轴于点作作⊥交于点，直线⊥kk BDOMANOMNDAOMABNAMBN，＝为矩形，易证△＝≌△＝，所以－＝，＝边形，2222kkkkk BOD （）有（所以点·（＋＋，）－，根据双曲线表达式，＝＋，222222222kk＋，解得．＝）＝＋152y ANMB xO DAPD45．∠°，为固定值．＝ 2CEAFCFAFCEAFAABAFBDDF，【提示】如图，过点．可得作⊥，，并截取∥＝＝，连结，CBDAFAPDFCAFCEFCAE1D所以四边形D是平行四边形，所以∥．易证△，∠≌△＝∠．则∠FCDDAPDFD°．，2＝∠＝＝C．从而∠45＝∠AFPBE12C3D3．略．ASAFHEBCABPABFHEHBC．所≌△）（显然四边形【提示】为矩形，所以＝＝，所以△APHF．以＝7/ 7。

三角形中的重要模型-弦图模型、勾股树模型(学生版)

三角形中的重要模型-弦图模型、勾股树模型赵爽弦图分为内弦图与外弦图，是中国古代数学家赵爽发现，既可以证明勾股定理，也可以以此命题，相关的题目有一定的难度，但解题方法也常常是不唯一的。

弦图之美，美在简约，然不失深厚，经典而久远，被誉为“中国数学界的图腾”。

弦图蕴含的割补思想，数形结合思想、图形变换思想更是课堂教学中数学思想渗透的绝佳载体。

一个弦图集合了初中平面几何线与形，位置与数量，方法与思想，小身板，大能量，它就是数学教育里的不老神话。

广受数学教师和数学爱好者研究，近年来也成为了各地中考的热点问题。

模型1、弦图模型(1)内弦图模型：如图1，在正方形ABCD中，AE⊥BF于点E，BF⊥CG于点F，CG⊥DH于点G，DH⊥AE于点H，则有结论：△ABE≌△BCF≌△CDG≌△DAH；S正方形ABCD =4S△EAB+S正方形EFGH。

图1图2图3(2)外弦图模型：如图2，在正方形ABCD中，E，F，G，H分别是正方形ABCD各边上的点，且四边形EFGH是正方形，则有结论：△AHE≌△BEF≌△CFG≌△DGH；S正方形ABCD =4S△EAB+S正方形EFGH。

(3)内外组合型弦图模型：如图3，2S正方形EFGH =S正方形ABCD+S正方形PQMN.1(2023秋·湖北·九年级校联考开学考试)如图，2002年8月在北京召开的国际数学家大会会标其原型是我国古代数学家赵爽的《勾股弦图》，它是由四个全等的直角三角形拼接而成如．如果大正方形的面积是16，直角三角形的直角边长分别为a，b，且a2+b2=ab+10，那么图中小正方形的面积是()A.2B.3C.4D.52(2022·安徽安庆·八年级期末)汉代数学家赵爽为了证明勾股定理，构造了一副“弦图”，后人称其为“赵爽弦图”，如图，大正方形ABCD由四个全等的直角三角形和一个小正方形组成，若∠ADE=∠AED，AD =45，则△ADE的面积为()A.24B.6C.25D.2103(2023·山西八年级期末)如图，图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的，若AC=6,BC=5，将四个直角三角形中的边长为6的直角边分别向外延长一倍，得到图2所示的“数学风车”，则这个风车的外围周长是()A.24B.52C.61D.764(2022·杭州九年级月考)我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”．如图是由弦图变化得到，它是用八个全等的直角三角形拼接而成，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3．若S1+S2+S3=12，则下列关于S1、S2、S3的说法正确的是()A.S1=2B.S2=3C.S3=6D.S1+S3=85(2023·广东·九年级专题练习)公元三世纪，我国汉代数学家赵爽在注解《周髀算经》题时给出了“赵爽弦图”．将两个“赵爽弦图”(如图1)中的两个正方形和八个直角三角形按图2方式摆放围成正方形MNPQ，记空隙处正方形ABCD，正方形EFGH的面积分别为S1，S2S1>S2，则下列四个判断：①S1+S2=14S四边形MNPQ②DG=2AF；③若∠EMH=30°，则S1=3S2；④若点A是线段GF的中点，则3S1=4S2，其中正确的序号是模型2. 勾股树模型6(2022·福建·八年级期末)如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，如果正方形A、B、C、D的边长分别为3，4，1，2．则最大的正方形E的面积是．7(2022·浙江·乐清市八年级期中)如图，在四边形ABCD中，∠B=∠D=90°，分别以AB，BC，CD，DA为一边向外作正方形甲、乙、丙、丁，若用S甲，S乙，S丙，S丁来表示它们的面积，那么下列结论正确的是()A.S 甲=S 丁B.S 乙=S 丙C.S 甲-S 乙=S 丁-S 丙D.S 甲+S 乙=S 丙+S 丁8(2022·河南八年级期末)如图，正方形ABCD 的边长为2，其面积标记为S 1，以CD 为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S 2，⋯按照此规律继续下去，则S 9的值为()A.126B.127C.128D.1299(2023春·山东菏泽·八年级校考阶段练习)“勾股树”是以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程所画出来的图形，因为重复数次后的形状好似一棵树而得名．假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树，按照勾股树的作图原理作图，如果第一个正方形面积为1，则第2023代勾股树中所有正方形的面积为．10(2023·浙江八年级期中)如图，以Rt △ABC 的三边为直径，分别向外作半圆，构成的两个月牙形面积分别为S 1、S 2，Rt △ABC 的面积S 3．若S 1=4，S 2=8，则S 3的值为．11(2022春·浙江温州·九年级校考开学考试)如图1，是数学家毕达哥拉斯根据勾股定理所画的“勾股树”．如图2，在Rt △ABC 中，∠BAC =90°，以其三边为边分别向外作正方形，延长EC ，DB 分别交GF ，AH 于点N ，K ，连接KN 交AG 于点M ，若S 1S 2=916，则tan ∠ACB 为()A.12B.23C.34D.51212(2023·贵州遵义·统考二模)如图1，毕达哥拉斯树，也叫“勾股树”，是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的树形图形．在图2中，∠ACB =90°，分别以Rt △ABC 的三条边为边向外作正方形，连接BE ，DG 、BE ，交AC 于点Q ，若∠BAC =30°，BC =2，则四边形EQGD 的面积是．13(2023秋·浙江·八年级专题练习)【背景阅读】勾股定理是人类最伟大的十个科学发现之一，西方国家称之为毕达哥拉斯定理．在我国古书《周髀算经》中就有“若勾三，股四，则弦五”的记载，我国汉代数学家赵爽为了验证勾股定理，创制了一幅“弦图”(如图1)，后人称之为“赵爽弦图”，流传至今．【实践操作】(1)请叙述勾股定理；(2)验证勾股定理，人们已经找到了400多种方法，请从下列几种常见的验证方法中任选一种来验证该定理：(以下图形均满足验证勾股定理所需的条件)【探索发现】(3)如图4、5、6，以直角三角形的三边为边或直径，分别向外部作正方形、半圆、等边三角形，这三个图形中面积关系满足S1+S2=S3的有个；(4)如图7所示，分别以直角三角形三边为直径作半圆，设图中两个月形图案(图中阴影部分)的面积分别为S1、S2，直角三角形面积为S3，请判断S1、S2、S3的关系并说明理由．课后专项训练1(2022·云南九年级一模)如图是按照一定规律“生长”的“勾股树”：经观察可以发现：图(1)中共有3个正方形，图(2)在图(1)的基础上增加了4个正方形，图(3)在图(2)的基础上增加了8个正方形，⋯⋯，照此规律“生长”下去，图(6)应在图(5)的基础上增加的正方形的个数是()A.12B.32C.64D.1282(2022·浙江初三期中)勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载．如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内．若图2中阴影部分的面积为2，且AB+AC=8，则BC的长为()图1图2A.42B.6C.254D.1323(2023·浙江·杭州八年级阶段练习)如图，Rt△ABC中，∠BAC=90°，分别以△ABC的三边为边作正方形ABDE，正方形BCFG，正方形ACHI，AI交CF于点J．三个正方形没有重叠的部分为阴影部分，设四边形BGFJ的面积为S1，四边形CHIJ的面积为S2，若S1-S2=12，S△ABC=4，则正方形BCFG的面积为()A.16B.18C.20D.224(2023春·湖北黄冈·八年级统考期中)“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，设直角三角形较长直角边长为a，较短直角边长为b．若ab=8，大正方形的面积为25，则EF 的长为()A.9B.92C.32D.35(2022·四川成都·模拟预测)勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载．如图1，以直角三角形的各边为边分别向外作正方形，再将较小的两个正方形分别绕直角三角形斜边上的两顶点旋转得到图2．则图2中阴影部分面积等于()A.直角三角形的面积B.最大正方形的面积C.最大正方形与直角三角形的面积和D.较小两个正方形重叠部分的面积6(2023春·广东潮州·九年级校考期末)我国古代数学家赵爽巧妙地用“弦图”证明了勾股定理，标志着中国古代的数学成就．如图所示的“弦图”，是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形．直角三角形的斜边长为13，一条直角边长为12，则小正方形ABCD 的面积的大小为()A.144B.100C.49D.257(2023春·湖北武汉·八年级统考期末)大约公元222年我国汉代数学家赵爽为《周髀算经》一书作序时介绍了“勾股圆方图”，亦称“赵爽弦图”，如图，四个全等的直角三角形拼成大正方形ABCD ，中空的部分是小正方形EFGH ，连接EG ，BD 相交于点O ，BD 与HC 相交于点P ，若GO =GP ，则直角三角形的边CG 与BG 之比是()A.12B.25C.2-1D.3-28(2023春·江苏泰州·七年级统考期末)大约在公元222年，赵爽为《周髀算经》一书作序时，介绍了“勾股圆方图”，亦称“赵爽弦图”(如图1)．某数学兴趣小组类比“赵爽弦图”构造出图2：△ABC 为等边三角形，AD 、BE 、CF 围成的△DEF 也是等边三角形．已知点D 、E 、F 分别是BE 、CF 、AD 的中点，若△ABC 的面积为14，则△DEF 的面积是()A.1B.2C.3D.49(2023·河北石家庄·校考二模)如图1，毕达哥拉斯树，也叫“勾股树”，是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的树形图形．在图2中，∠ACB=90°，分别以Rt△ABC的三条边为边向外作正方形，连接BE，DG，BE交AC于点Q．若∠BAC=30°，BC=2，则四边形EQGD的面积是()B.23C.53+3D.3A.53+3210(2023·江苏扬州·统考中考真题)我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”，后人称之为“赵爽弦图”，它是由4个全等的直角三角形和一个小正方形组成．如图，直角三角形的直角边长为a、b，斜边长为c，若b-a=4，c=20，则每个直角三角形的面积为．11(2022秋·四川成都·八年级校考期中)“勾股图”有着悠久的历史，它曾引起很多人的兴趣．1955年希腊发行了以“勾股图”为背景的邮票(如图1)，欧几里得在《几何原本》中曾对该图做了深入研究．如图2，在△ABC中，∠ACB=90°，分别以△ABC的三条边为边向外作正方形，连接EB,CM,DG,CM分别与AB,BE相交于点P,Q．若∠ABE=30°，则DGQM的值为.12(2022春·安徽合肥·八年级合肥市第四十二中学校考期中)如图①，在Rt△ACB中∠ACB=90°，分别以AC、BC、AB为边，向形外作等边三角形，所得的等边三角形的面积分别为S1、S2、S3，请解答以下问题：(1)S1、S2、S3满足的数量关系是．(2)现将△ABF向上翻折，如图②，若阴影部分的S甲=6、S乙=5、S丙=4，则S△ACB=．13(2023·湖北孝感·统考三模)“勾股树”是以正方形一边为斜边向外作直角三角形，再以直角三角形的两直角边分别向外作正方形，重复这一过程所画出来的图形，因为重复数次后的形状好似一棵树而得名．假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树，按照勾股树的作图原理作图，则第五代勾股树中正方形的个数为．14(2022·山东临沂·统考二模)中国古代的数学家们对于勾股定理的发现和证明，在世界数学史上具有独特的贡献和地位尤其是三国时期的数学家赵爽，不仅最早对勾股定理进行了证明，而且创制了“勾股圆方图”，开创了“以形证数”的思想方法．在图中，小正方形ABCD的面积为1，如果把它的各边分别延长一倍得到正方形A1B1C1D1(如图1)，则正方形的面积为；再把正方形A1B1C1D1的各边分别延长一倍得到正方形A2B2C2D2(如图2)，如此进行下去，得到的正方形A n B n C n D n的面积为(用含n的式子表示，n为正整数)．15(2023·浙江台州·八年级校考期中)如图1，是一个封闭的勾股水箱，其中Ⅰ，Ⅱ，Ⅲ部分是可盛水的正方形，且相互联通，已知∠ACB=90°，AC=6，BC=8，开始时Ⅲ刚好盛满水，而Ⅰ，Ⅱ无水．(1)如图2摆放时，Ⅰ刚好盛满水，而Ⅱ无水，则Ⅲ中有水部分的面积为；(2)如图3摆放时，水面刚好经过Ⅲ的中心O(正方形两条对角线的交点)，则Ⅱ中有水部分的面积为．16(2023·湖北黄冈·统考中考真题)如图，是我国汉代的赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”，它是由四个全等的直角三角形和一个小正方形组成的一个大正方形．设图中AF=a，DF=b，连接AE,BE，若△ADE与△BEH的面积相等，则b2a2+a2b2=．17(2023·江苏徐州·统考二模)如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH．连接AC，若AG平分∠CAD，且正方形EFGH的面积为2，则正方形ABCD的面积为．18(2023·陕西渭南·统考二模)魏朝时期，刘徽利用下图通过“以盈补虚，出入相补”的方法，即“勾自乘为朱方，股自乘为青方，令出入相补，各从其类”证明了勾股定理．如图，四边形ABCD、四边形BFGH和四边形AFMN都是正方形，BF交CD于E，若DE=2，CE=4，则BF的长为．19(2022·宁夏吴忠·统考一模)2002年8月，在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图1)，且大正方形的面积是17，直角三角形的较短直角边为a，较长直角边为b．如果将四个全等的直角三角形按如图2的形式摆放，则图2中最大的正方形的面积为31．试求图1中小正方形的面积是为．20(2023·山东济宁·统考二模)勾股定理是人类最伟大的十个科学发现之一，西方国家称之为毕达哥拉斯定理．在我国古书《周髀算经》中就有“若勾三，股四，则弦五”的记载，我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”(如图1)，后人称之为“赵爽弦图”，流传至今．勾股定理内容为：如果直角三角形的两条直角边分别为a，b，斜边为c，那么a2+b2=c2．(1)如图2、3、4，以直角三角形的三边为边或直径，分别向外部作正方形、半圆、等边三角形，这三个图形中面积关系满足S1+S2=S3的有个；(2)如图5所示，分别以直角三角形三边为直径作半圆，设图中两个月形图案(图中阴影部分)的面积分别为S1，S2，直角三角形面积为S3，请判断S1，S2，S3的关系并证明；(3)如果以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程就可以得到如图6所示的“勾股树”．在如图7所示的“勾股树”的某部分图形中，设大正方形M的边长为定值m，四个小正方形A，B，C，D的边长分别为a，b，c，d，已知∠1=∠2=∠3=∠α，则当∠α变化时，回答下列问题：(结果可用含m的式子表示)①a2+b2+c2+d2=；②b与c的关系为，a与d的关系为．21(2022·湖南·八年级课时练习)如图①，美丽的弦图，蕴含着四个全等的直角三角形．(1)弦图中包含了一大，一小两个正方形，已知每个直角三角形较长的直角边为a，较短的直角边为b，斜边长为c，结合图①，试验证勾股定理．(2)如图②，将这四个直角三角形紧密地拼接，形成飞镖状，已知外围轮廓(粗线)的周长24，OC=3，求该飞镖状图案的面积．(3)如图③，将八个全等的直角三角形紧密地拼接，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1,S2,S3，若S1+S2+S3=40，求S2．22(2023·广东深圳·校联考三模)中华文明源远流长，如图①是汉代数学家赵爽在注解《周髀算经》时给出的图形，人们称之为赵爽弦图，被誉为中国数学界的图腾．2002年北京国际数学家大会依据赵爽弦图制作了会标，该图有4个全等的直角三角形围成几个大正方形和中间一个小正方形，巧妙的证明了勾股定理．问题发现：如图①，若直角三角形的直角边BC=3，斜边AB=5，则中间小正方形的边长CD=，连接BD，△ABD的面积为．知识迁移：如图②，P是正方形ABCD内一点，连接PA，PB，PC，当∠BPC=90°，BP=10时，△PAB的面积为．拓展延伸：如图③，已知∠MBN=90°，以点B为圆心，适当长为半径画弧，交射线BM，BN分别于A，C两点．(1)已知D为线段AB上一个动点，连接CD，过点B作BE⊥CD，垂足为点E；在CE上取一点F，使EF=BE；过点F作GF⊥CD交BC于点G，试判断三条线段BE，DE，GF之间的数量关系，并说明理由．(2)在(1)的条件下，若D为射线BM上一个动点，F为射线EC上一点；当AB=10，CF=2时，直接写出线段DE的长．。

2024年中考数学压轴题重难点知识剖析及训练—一线三等角相似、三垂直模型压轴题专题(含解析)

2024年中考数学压轴题重难点知识剖析及训练—一线三等角相似、三垂直模型压轴题专题（含解析）一线三等角概念“一线三等角”是一个常见的相似模型，指的是有三个等角的顶点在同一条直线上构成的相似图形，这个角可以是直角，也可以是锐角或钝角。

不同地区对此有不同的称呼，“K形图”，“三垂直”，“弦图”等，以下称为“一线三等角”。

“一线三等角”的两种基本类型1.三等角都在直线的同侧2.三等角分居直线的两侧3.在初三各学校的考试和中考试题中，一线三等角的相似属于压轴题的热点题型之一，本专题从中考试题和初三各名校的试题中，精选一线三等角相似模型的经典好体，并根据角度区别把一线三等角模型细分为三类题型：三垂直模型、一线三锐角、一线三钝角，适合于初三学生进行压轴题专项突破时使用。

类型一：三垂直模型1.（雅礼）如图，点A 是双曲线()80y x x=<上一动点，连接OA ，作OB OA ⊥，使2OA OB =，当点A 在双曲线()80y x x =<上运动时，点B 在双曲线ky x=上移动，则k 的值为.【解答】解：过A 作AC ⊥y 轴于点C ，过B 作BD ⊥y 轴于点D ，∵点A 是反比例函数y ＝（x ＜0）上的一个动点，点B 在双曲线y ＝上移动，∴S △AOC ＝×|﹣8|＝4，S △BOD ＝|k |，∵OB ⊥OA ，∴∠BOD +∠AOC ＝∠AOC +∠OAC ＝90°，∴∠BOD ＝∠OAC ，且∠BDO ＝∠ACO ，∴△AOC ∽△OBD ，∵OA ＝2OB ，∴＝（）2＝，∴＝，∴|k |＝2．∴k ＜0，∴k ＝﹣2，故答案为：﹣2．2.（青竹湖）如图，︒=∠90AOB ，反比例函数()04<-=x xy 的图象过点()a A ,1-，反比例函数xky =()0,0>>x k 的图象过点B ，且x AB //轴，过点B 作OA MN //，交x 轴于点M ，交y 轴于点N ，交双曲线x ky =于另一点，则OBC ∆的面积为.【解答】解：∵反比例函数的图象过点A （﹣1，a ），∴a ＝﹣＝4，∴A（﹣1，4），过A作AE⊥x轴于E，BF⊥x轴于F，∴AE＝4，OE＝1，∵AB∥x轴，∴BF＝4，∵∠AOB＝90°，∴∠EAO+∠AOE＝∠AOE+∠BOF＝90°，∴∠EAO＝∠BOF，∴△AEO∽△OFB，∴＝，∴OF＝16，∴B（16，4），∴k＝16×4＝64，∵直线OA过A（﹣1，4），∴直线AO的解析式为y＝﹣4x，∵MN∥OA，∴设直线MN的解析式为y＝﹣4x+b，∴4＝﹣4×16+b，∴b＝68，∴直线MN的解析式为y＝﹣4x+68，∵直线MN交x轴于点M，交y轴于点N，∴M（17，0），N（0，68），解得，或，∴C（1，64），﹣S△OCN﹣S△OBM＝﹣﹣＝510，∴△OBC的面积＝S△OMN故答案为510．3．（广益）如图，点A，B在反比例函数y＝（k＞0）的图象上，点A的横坐标为2，点B的纵坐标为1，OA⊥AB，则k的值为．【解答】解：过点A作AM⊥x轴于点M，过点B作BN⊥AM于N，∵∠OAB＝90°，∴∠OAM+∠BAN ＝90°，∵∠AOM+∠OAM＝90°，∴∠BAN＝∠AOM，∴△AOM∽△BAN，∴＝，∵点A，B在反比例函数y＝（k＞0）的图象上，点A的横坐标为2，点B的纵坐标为1，∴A（2，），B（k，1），∴OM＝2，AM＝，AN＝﹣1，BN＝k﹣2，∴＝，解得k1＝2（舍去），k2＝8，∴k的值为8，故答案为：8．4．（长沙中考2020）在矩形ABCD 中，E 为DC 上的一点，把ADE ∆沿AE 翻折，使点D 恰好落在BC 边上的点F ．（1）求证：ABF FCE∆∆:（2）若23,4AB AD ==，求EC 的长；（3）若2AE DE EC -=，记,BAF FAE αβ∠=∠=，求tan tan αβ+的值．【详解】（1）证明：∵四边形ABCD 是矩形，∴∠B=∠C=∠D=90°，∴∠AFB+∠BAF=90°，∵△AFE 是△ADE 翻折得到的，∴∠AFE=∠D=90°，∴∠AFB+∠CFE=90°，∴∠BAF=∠CFE ，∴△ABF ∽△FCE ．（2）解：∵△AFE 是△ADE 翻折得到的，∴AF=AD=4，∴()22224232AF AB --，∴CF=BC-BF=AD-BF=2，由（1）得△ABF ∽△FCE ，∴CE CF BF AB =，∴2223CE =，∴EC=233（3）解：由（1）得△ABF ∽△FCE ，∴∠CEF=∠BAF=α，∴tan α+tan β=BF EF CE EFAB AF CF AF+=+，设CE=1，DE=x ，∵2AE DE EC -=，∴AE=DE+2EC=x+2，AB=CD=x+1，2244AE DE x -=+∵△ABF ∽△FCE ，∴AB CF AF EF =2144x x x x -=+(211121x x x xx ++-+ ，∴112x x +=，∴1x x =-x 2-4x+4=0，解得x=2，∴CE=1，213x -=，EF=x=2，AF=2244AE DE x -=+=23tan α+tan β=CE EF CF AF +33323．5.（广益）矩形ABCD中，8AB=，12AD=，将矩形折叠，使点A落在点P处，折痕为DE．（1）如图1，若点P恰好在边BC上．①求证：△EBP∽△PCD；②求AE的长；（2）如图2，若E是AB的中点，EP的延长线交BC于点F，求BF的长．图1图2【解答】解：（1）①∵四边形ABCD是矩形，∴∠B＝∠C＝∠BAD＝90°，∴∠BPE+∠BEP＝90°，由折叠知，∠DPE＝∠BAD＝90°，∴∠BPE+∠CPD＝90°，∴∠BEP＝∠CPD，∵∠B＝∠C＝90°，∴△EBP∽△PCD；②∵四边形ABCD是矩形，∴∠B＝∠C＝90°，CD＝AB＝8，BC＝AD＝12，由折叠知，PE＝AE，DP＝AD＝12，在Rt△DPC中，CP＝＝4，∴BP＝BC﹣CP＝12﹣4，在Rt△PBE中，PE2﹣BE2＝BP2，∴AE2﹣（8﹣AE）2＝（12﹣4）2，∴AE＝18﹣6；（2）如图，过点P作GH∥BC交AB于G，交CD于H．则四边形AGHD是矩形，设EG＝x，则BG＝4﹣x，∵∠A＝∠EPD＝90°，∠EGP＝∠DHP＝90°，∴∠EPG+∠DPH＝90°，∠DPH+∠PDH＝90°，∴∠EPG＝∠PDH，∴△EGP∽△PHD，∴＝＝＝＝，∴PH＝3EG＝3x，DH＝AG＝4+x，在Rt△PHD中，PH2+DH2＝PD2，∴（3x）2+（4+x）2＝122，解得x＝（负值已经舍弃），∴BG＝4﹣＝，在Rt△EGP中，GP＝＝，∵GH∥BC，∴△EGP∽△EBF，∴＝，∴＝，∴BF＝3．6．（长郡）如图，在平面直角坐标系中，O 为原点，已知点Q 是射线OC 上一点，182OQ =，点P 是x 轴正半轴上一点，tan 1POC ∠=，连接PQ ，A 经过点O 且与QP 相切于点P ，与边OC 相交于另一点D ．(1)若圆心A 在x 轴上，求A 的半径；(2)若圆心A 在x 轴的上方，且圆心A 到x 轴的距离为2，求A 的半径；(3)在（2）的条件下，若10OP <，点M 是经过点O ，D ，P 的抛物线上的一个动点，点F 为x 轴上的一个动点，若满足1tan 2OFM ∠=的点M 共有4个，求点F 的横坐标的取值范围．【解答】解：（1）∵圆心A 在x 轴上，⊙A 经过点O 且与QP 相切于点P ，∴PQ ⊥x 轴，OP 为直径，∵tan ∠POC ＝1，，∴PQ ＝OP ，∵在Rt △OPQ 中，．∴OP ＝18．∴⊙A 的半径为9；（2）如图所示，过点A 作AM ⊥x 轴于点M ，过点Q 作QB ⊥x 轴于B ，连接AP ，∵PQ是⊙A的切线，∴AP⊥PQ，则∠APQ＝90°，∵AM⊥x轴，QB⊥x轴，∴∠AMP＝∠PBC＝90°，∴∠PAM＝90°﹣∠APM＝∠QPB，∴△APM∽△PBQ，∴，∵tan∠POC＝1，QB＝18，∴OB＝QB＝18，∵AM＝2，设MP＝MO＝x，∴PB＝18﹣2x，∴，解得x＝3或x＝6，∴MO＝3或MO＝x，∴A（3，2）或A（6，2），∴AP＝＝或AP＝＝2．∴半径为或2．（3）∵OP＜10，∴BO＝3，P（6，0），∴A（3，2），∵tan∠POC＝1，设D（a，a），∵，∴（3﹣a）2+（2﹣a）2＝13，解得：a＝0或a＝5，∴D（5，5），设抛物线解析式为y＝ax2+bx，将点P（6，0），D（5，5）代入得，，解得：，∴y＝﹣x2+6x，∵点F可能在点O的左边或点P的右边，，则|K FM|＝，设直线MF：或，联立，，得或，当或，解得：或，∴直线MF：或，令y＝0，解得：或，∴或．7.（麓山国际）有一边是另一边的倍的三角形叫做智慧三角形，这两边中较长边称为智慧边，这两边的夹角叫做智慧角．（1）已知Rt△ABC为智慧三角形，且Rt△ABC的一边长为，则该智慧三角形的面积为；（2）如图①，在△ABC中，∠C＝105°，∠B＝30°，求证：△ABC是智慧三角形；（3）如图②，△ABC是智慧三角形，BC为智慧边，∠B为智慧角，A（3，0），点B，C在函数y＝上（x＞0）的图象上，点C在点B的上方，且点B的纵坐标为．当△ABC是直角三角形时，求k的值．＝AC•AB，【解答】解：（1）如图1，设∠A＝90°，AC≤AB，S△ABC①若AC＝，i）AB＝AC＝2，∴S＝，ii）BC＝AC＝2，则AB＝，∴S＝，②若AB＝，i）AB＝AC，即AC＝，∴S＝，ii）BC＝AB＝2，则AC＝∴S＝，③若BC＝，若AB＝AC＝＝1，∴S＝，若AB＝AC，AB＝，，S＝××＝，故答案为：或1或或或．（2）证明：如图2，过点C作CD⊥AB于点D，∴∠ADC＝∠BDC＝90°，在Rt△BCD中，∠B＝30°，∴BC＝2CD，∠BCD＝90°﹣∠B＝60°，∵∠ACB＝105°，∴∠ACD＝∠ACB﹣∠BCD＝45°，∴Rt△ACD中，AD＝CD，∴AC＝，∴，∴△ABC是智慧三角形．（3）∵△ABC是智慧三角形，BC为智慧边，∠B为智慧角，∴BC＝AB，∵△ABC是直角三角形，∴AB不可能为斜边，即∠ACB≠90°∴∠ABC＝90°或∠BAC＝90°①当∠ABC＝90°时，过B作BE⊥x轴于E，过C作CF⊥EB于F，过C作CG⊥x轴于G，如图3，∴∠AEB＝∠F＝∠ABC＝90°，∴∠BCF+∠CBF＝∠ABE+∠CBF＝90°，∴∠BCF＝∠ABE，∴△BCF∽△ABE，∴，设AE＝a，则BF＝AE＝a，∵A（3，0），∴OE＝OA+AE＝3+a，∵B的纵坐标为，即BE＝，∴CF＝BE＝2，CG＝EF＝BE+BF＝，B（3+a，），∴OG＝OE﹣GE＝OE﹣CF＝3+a﹣2＝1+a，∴C（1+a，），∵点B、C在在函数y＝上（x＞0）的图象上，∴（3+a）＝（1+a）（+a）＝k解得：a1＝﹣2（舍去），a2＝1，∴k＝，②当∠BAC＝90°时，过C作CM⊥x轴于M，过B作BN⊥x轴于N，如图4，∴∠CMA＝∠ANB＝∠BAC＝90°，∴∠MCA+∠MAC＝∠MAC+∠NAB＝90°，∴∠MCA＝∠NAB，∴△MCA∽△NAB，∵BC＝，∴2AB2＝BC2＝AB2+AC2，∴AC＝AB，∴△MCA≌△NAB（AAS），∴AM＝BN＝，∴OM＝OA﹣AM＝3﹣，设CM ＝AN ＝b ，则ON ＝OA +AN ＝3+b ，∴C （3﹣，b ），B （3+b ，），∵点B 、C 在在函数y ＝上（x ＞0）的图象上，∴（3﹣）b ＝（3+b ）＝k解得：b ＝，∴k ＝18+15，综上所述，k 的值为或。

人教版八年级下册第18章平行四边形——弦图模型及半角模型专题(PDF版,无答案)

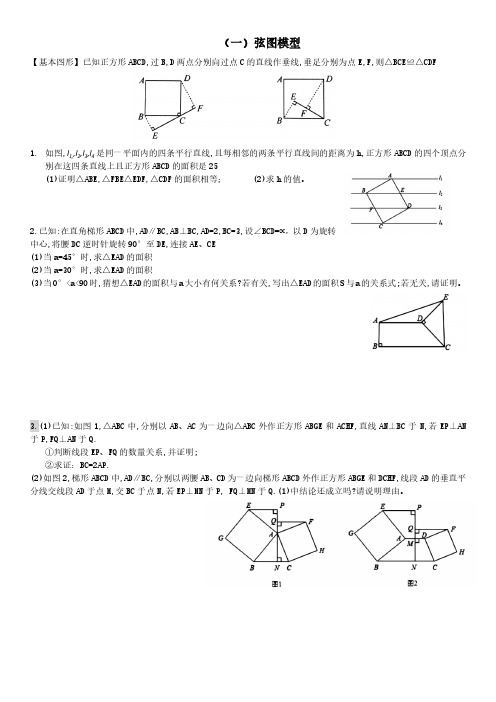
（一）弦图模型【基本图形】已知正方形ABCD,过B,D两点分别向过点C的直线作垂线,垂足分别为点E,F,则△BCE≌△CDF1.如图,l1,,l2,l3,l4是同一平面内的四条平行直线,且每相邻的两条平行直线间的距离为h,正方形ABCD的四个顶点分别在这四条直线上且正方形ABCD的面积是25(1)证明△ABE,△FBE△EDF,△CDF的面积相等； (2)求h的值。

2.已知:在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,设∠BCD=∝，以D为旋转中心,将腰DC逆时针旋转90°至DE,连接AE、CE(1)当a=45°时,求△EAD的面积(2)当a=30°时,求△EAD的面积(3)当0°<a<90时,猜想△EAD的面积与a大小有何关系?若有关,写出△EAD的面积S与a的关系式;若无关,请证明。

3.(1)已知:如图1,△ABC中,分别以AB、AC为一边向△ABC外作正方形ABGE和ACHF,直线AN⊥BC于N,若EP⊥AN 于P,FQ⊥AN于Q.①判断线段EP、FQ的数量关系,并证明;②求证：BC=2AP.(2)如图2,梯形ABCD中,AD∥BC,分别以两腰AB、CD为一边向梯形ABCD外作正方形ABGE和DCHF,线段AD的垂直平分线交线段AD于点M,交BC于点N,若EP⊥MN于P, FQ⊥MN于Q.(1)中结论还成立吗?请说明理由。

【变式训练】如图，分别以ABC ∆的AC 和BC 为一边，在ABC ∆的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．4．如图,直角梯形ABCD 中,AD/BC,∠ADC=90°,是AD 的垂直平分线,交AD 于点M,以腰AB 为边作正方形ABFE ， EP ⊥l 于点P.求证:2EP+AD=2CD（二）半角模型半角模型【用旋转和对称（翻折）的方法解决问题】ABCD 中，若M 、N 分别在边BC 、CD 上移动，且满足MN=BM +DN ，则有以下基本结论（需记忆）：①.∠MAN=45°；②.；③.AM 、AN 分别平分∠BMN 和∠DNM.同样，在正方形ABCD 中,若已知∠MAN=45°，则会有：①.MN=BM +DN; ②;③.AM 、AN 分别平分∠BMN和∠DNM;④若继续作AH ⊥MN 于点H ,则有AH=AB.1.在正方形ABCD 中，已知∠MAN=45°，若M、N 分别在边CB 、DC 的延长线上移动，试探究线段MN 、BM 、DN 之间ABC CMN 2=∆ABC CMN 2=∆P C G F B Q A DE的数量关系.k、m、n为边长的三角形的形状是什么并试着证明你的猜想。

中考数学压轴题分析：赵爽弦图与勾股定理

中考数学压轴题分析：赵爽弦图与勾股定理本文内容选自2021年贵州中考数学压轴题。

以赵爽弦图为背景，考查勾股定理的证明以及应用等，难度不大。

【中考真题】（2021·贵阳）（1）阅读理解我国是最早了解勾股定理的国家之一，它被记载于我国古代的数学著作《周髀算经》中．汉代数学家赵爽为了证明勾股定理，创制了一幅如图①所示的“弦图”，后人称之为“赵爽弦图”．根据“赵爽弦图”写出勾股定理和推理过程；（2）问题解决勾股定理的证明方法有很多，如图②是古代的一种证明方法：过正方形的中心，作，将它分成4份，所分成的四部分和以为边的正方形恰好能拼成以为边的正方形．若，，求的值；（3）拓展探究如图③，以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程就可以得到“勾股树”的部分图形．设大正方形的边长为定值，小正方形，，，的边长分别为，，，．已知，当角变化时，探究与的关系式，并写出该关系式及解答过程与的关系式用含的式子表示）．【分析】（1）勾股定理的证法主要是根据面积等量关系。

先用正方形的面积公式得到正方形的面积为c²，再把正方形分割成5个部分，并把它们的面积加起来，再建立等量关系即可得到结论。

难度不大。

（2）本题主要根据全等的性质，得到对应边的关系，解方程组得到结论。

（3）根据勾股定理与相似（三角）等可以得到b、c与n的等量关系。

【答案】解：（1）（直角三角形两条直角边的平方和等于斜边的平方），证明如下：如图①是由直角边长分别为，的四个全等的直角三角形与中间一个边长为的小正方形拼成的一个边长为的大正方形，的面积正方形的面积正方形的面积，即，整理得：；（2）由题意得：正方形被分成4个全等的四边形，设，，，正方形是由正方形被分成的4个全等的四边形和正方形拼成，，，，，，，解得：，．（3），理由如下：如图③所示：设正方形的边长为，正方形的边长为，，，△△，，，即，，，，在△中，由勾股定理得：，，．。

第6讲弦图模型(原卷版)

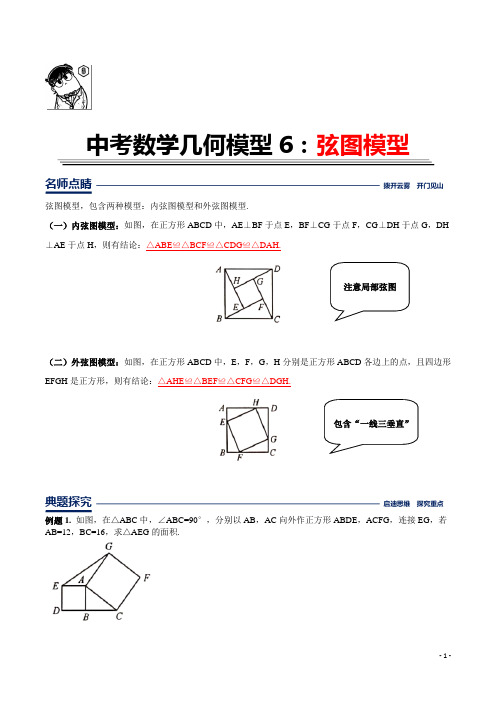
中考数学几何模型6：弦图模型名师点睛拨开云雾开门见山弦图模型，包含两种模型：内弦图模型和外弦图模型.（一）内弦图模型：如图，在正方形ABCD 中，AE ⊥BF 于点E ，BF ⊥CG 于点F ，CG ⊥DH 于点G ，DH ⊥AE 于点H ，则有结论：△ABE ≌△BCF ≌△CDG ≌△DAH.（二）外弦图模型：如图，在正方形ABCD 中，E ，F ，G ，H 分别是正方形ABCD 各边上的点，且四边形EFGH 是正方形，则有结论：△AHE ≌△BEF ≌△CFG ≌△DGH.典题探究启迪思维探究重点例题1. 如图，在△ABC 中，∠ABC=90°，分别以AB ，AC 向外作正方形ABDE ，ACFG ，连接EG ，若AB=12，BC=16，求△AEG 的面积.注意局部弦图包含“一线三垂直”变式练习>>>1．如图，四边形ABCD是边长为4的正方形，点E在边AD上，连接CE，以CE为边作正方形CEFG，点D，F在直线CE的同侧，连接BF，若AE=1，求BF的长.例题2. 如图，以Rt△ABC的斜边BC在△ABC同侧作正方形BCEF，该正方形的中心为点O，连接AO.若AB=4，AO=62，求AC的长.变式练习>>>2．如图，点A，B，C，D，E都在同一条直线上，四边形X，Y，Z都是正方形，若该图形总面积是m，正方形Y的面积是n，则图中阴影部分的面积是___________.例题3. 如图，在△ABC 中，∠BAC=45°，D 为△ABC 外一点，满足∠CBD=90°，BC=BD ，若=4.5ACD S △，求AC 的长.变式练习>>>3．点P 是正方形ABCD 外一点，PB=10cm ，△APB 的面积是60cm 2，△CPB 的面积是30cm 2．求正方形ABCD 的面积.例题4. 在边长为10的正方形ABCD 中，内接有6个大小相同的正方形，P 、Q 、M 、N 是落在大正方形边上的小正方形的顶点，如图所示，求这六个小正方形的面积.变式练习>>>4．如图，在平面直角坐标系中，经过点A的双曲线y＝（x＞0）同时经过点B，且点A在点B的左侧，点A的横坐标为，∠AOB＝∠OBA＝45°，则k的值为．例题5. 如图，在等腰Rt△ACB和等腰Rt△DCE中，∠AXB=∠DCE=90°，连接AD，BE，点I在AD上，（1）若IC⊥BE，求证：I为AD中点；（2）若I为AD中点，求证：IC⊥BE例题6. 在平面直角坐标系中，直线l 的解析式为2y x b =+，其与x 轴交于点A,与y 轴交于点B ，在直线l 移动的过程中，直线y=4上是否存在点P ，使得△PAB 是等腰直角三角形，若存在，请求出满足条件的所有点P 的坐标，如不存在，请说明理由.达标检测领悟提升强化落实1. 如图所示，“赵爽弦图”是由8个全等的直角三角形拼接而成的，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3，已知S1+S2+S3＝10，则S2的值是．2. 我国古代数学家赵爽利用弦图证明了勾股定理，这是著名的赵爽弦图（如图1）．它是由四个全等的直角三角形拼成了内、外都是正方形的美丽图案．在弦图中（如图2），已知点O为正方形ABCD的对角线BD的中点，对角线BD分别交AH，CF于点P、Q．在正方形EFGH的EH、FG两边上分别取点M，N，且MN经过点O，若MH＝3ME，BD＝2MN＝4．则△APD的面积为．3．如图，在△ABC中，∠ACB＝90°，分别以边AB、AC向外作正方形ABDE和正方形ACFG，连接CE，BG，EG．（正方形的各边都相等，各角均为90°）（1）判断CE与BG的关系，并说明理由；（2）若BC＝3，AB＝5，则AEG面积等于．4．【问题解决】一节数学课上，老师提出了这样一个问题：如图1，点P是正方形ABCD内一点，P A＝1，PB＝2，PC ＝3．你能求出∠APB的度数吗？小明通过观察、分析、思考，形成了如下思路：思路一：将△BPC绕点B逆时针旋转90°，得到△BP′A，连接PP′，求出∠APB的度数；思路二：将△APB绕点B顺时针旋转90°，得到△CP'B，连接PP′，求出∠APB的度数．请参考小明的思路，任选一种写出完整的解答过程．【类比探究】如图2，若点P是正方形ABCD外一点，P A＝3，PB＝1，PC＝，求∠APB的度数．5．如图，已知∠ABC＝90°，D是直线AB上一点，AD＝BC．（1）如图1，过点A作AF⊥AB，并截取AF＝BD，连接DC、DF、CF．①求证：AF+AB＝BC②判断FD与DC的关系并证明；（2）如图2，E是直线BC上一点，且CE＝BD，直线AE、CD相交于点P，∠APD的度数是一个固定的值吗？若是，请求出它的度数；若不是，请说明理由．6．【探究证明】（1）某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究，提出下列问题，请你给出证明．如图1，矩形ABCD中，EF⊥GH，EF分别交AB，CD于点E，F，GH分别交AD，BC于点G，H，求证：；【结论应用】（2）如图2，在满足（1）的条件下，又AM⊥BN，点M，N分别在边BC，CD上，若，则的值为；（直接写出结果）【联系拓展】（3）如图3，四边形ABCD中，∠ABC＝90°，AB＝AD＝6，BC＝CD＝3，AM⊥DN，点M，N分别在边BC，AB上，求的值．7．如图，直角梯形ABCD中，AD∥BC，∠ADC＝90°，l是AD的垂直平分线，交AD于点M，以腰AB 为边作正方形ABFE，EP⊥l于P．求证：2EP+AD＝2CD．8．提出问题：如图1，在△ABC中，∠ACB＝90°，分别以边AB、AC向外作正方形ABDE和正方形ACFG，连接CE，BG，EG．（1）探索CE与BG的关系；（2）探究△ABC与△AEG面积是否仍然相等？说明理由．（3）如图2，学校教学楼前的一个六边形花圃被分成七个部分，分别种上不同品种的花卉，已知△CDG 是直角三角形，∠CGD＝90°，DG＝3m，CG＝4m，四边形ABCD、CIHG、GFED均为正方形，则这个六边形花圃ABIHFE的面积为．9．已知：l1∥l2∥l3∥l4，平行线l1与l2、l2与l3、l3与l4之间的距离分别为d1、d2、d3，且d1＝d3＝1，d2＝2．我们把四个顶点分别在l1、l2、l3、l4这四条平行线上的四边形称为“格线四边形”．（1）如图1，正方形ABCD为“格线四边形”，则正方形ABCD的边长为．（2）矩形ABCD为“格线四边形”，其长：宽＝2：1，求矩形ABCD的宽．（3）如图1，EG过正方形ABCD的顶点D且垂直l1于点E，分别交l2，l4于点F，G．将∠AEG绕点A 顺时针旋转30°得到∠AE′D′（如图2），点D′在直线l3上，以AD′为边在E′D′左侧作菱形AB′C′D′，使B′，C′分别在直线l2，l4上，求菱形AB′C′D′的边长．10．四边形ABCD是边长为4的正方形，点E在边AD所在直线上，连接CE，以CE为边，作正方形CEFG （点D，点F在直线CE的同侧），连接BF．（1）如图1，当点E与点A重合时，请直接写出BF的长；（2）如图2，当点E在线段AD上时，AE＝1；①求点F到AD的距离；②求BF的长；（3）若BF＝3，请直接写出此时AE的长．。