分治法实验报告一
分治算法实验

分治算法实验(用分治法查找数组元素的最大值和最小值)算法分析与设计实验报告第一次实验实验步骤关键代码}else//当数组中元素个数少于2时,直接赋值处理1. 先解决小规模的问题,如数组中只有1个元素或者只有两个元素时候的情况。
2. 将问题分解,如果数组的元素大于等于3个,将数组分为两个小的数组。
3. 递归的解各子问题,将中分解的两个小的数组再进行以上两个步骤最后都化为小规模问题。
4. 将各子问题的解进行比较最终得到原问题的解。
//分治法处理整个数组,求出最大值与最小值void merge( int a[], int left, int right, int &Max, int &Min){int max1=0,min 1=0,max2=0,min2=0;if (right-left>2) //当数组中元素个数大于3时,才实行分治法{int mid=(right+left)/2;merge(a,left,mid,max1,mi n1);//左半边递归调用自身,求岀最大值与最小值,分别保存在max1,min1中merge(a,mid+1,right,max2,mi n2);//右半边递归调用自身,求岀最大值与最小值,分别保存在max2,min2中if (max1>=max2)Max=max1; //子序列两两合并,求岀最大值与最小值elseMax=max2; //分别保存在Max与Minif (min1<=min2)Min=mi n1;elseMin=mi n2;测试结果实验心得Max=compmax(a,left,right);Min=compmi n( a,left,right);}}利用分治法(递归实现):非递归实现:请输入数据克1000093 32767The tine is1990003276? 9The tine is1000032767 0TJ IE tine is1000 32767 9The time is3276? RThe tine is內.0060-004TO通解,明白了分治法到底是怎样的一个过程,在代码实现分治法的时候,也使我加深了对于自己构造函数的理解,明白了分治法利用代码是怎样实现的,以及构造函数的传参与返回值等等地方需要注意的F;\鮒实验沁[p || B附录:完整代码(分治法)#include <iostream>#inelude <time.h>#include <iomanip> using namespacestd;//当数组中的元素个数小于3时,处理最大值int compmax(int A[], int start, int end) {int max;if (start<end) //有两个元素{if (A[start]<=A[end]) max=A[e nd];elsemax=A[start];}else //有一个元素max=A[start];return max;}//当数组中元素的个数小于2时,处理最小值int compmin(int A[], int start, int end){int min;if (start<end) //有两个元素{if (A[start]<=A[end]) mi n= A[start];elsemin= A[e nd];}else //有一个元素mi n=A[start];return mi n;}//分治法处理整个数组,求最大值与最小值void merge( int a[], int left, int right, int &Max,int &Min) 〃Max,Min 用来保存最大值与最小值//之所以使用&引用,是由于如果只是简单的使用变量,并不会改变Ma>与Min的值,使用指针也可以{int max1=0,min 1=0,max2=0,min2=0;if (right-left>2) //当数组中元素个数大于等于3时,进行分治{int mid=(right+left)/2;merge(a,left,mid,max1,min1); //左半边递归调用自身,求出最大值最小值,分别保存在max1,min1中merge(a,mid+1,right,max2,min2); //右半边递归调用自身,求出最大值最小值,分别保存在max2,min2中if (max1>=max2) //子序列两两合并,求出最大值与最小值,保存在Max与Mi n 中Max=max1;elseMax=max2;if (min 1<=min2)Min=min1;elseMin=min 2;}else //数组中元素个数小于3时的情况,直接赋值{Max=compmax(a,left,right);Mi n=compmi n( a,left,right);}}void ran( int *input, int n) //随机生成数组元素函数{int i;sran d(time(0)); for(i=0;i<n;i++) input[i]=ra nd();input[i]= '\0';}int a[1000000]; //定义全局变量用来存放要查找的数组int main(){int n;int i;int max;int min;coutvv "请输入要查找的序列个数:"<<e ndl;for (i=0;i<5;i++){cin>>n;ran (a,n);start=clock();en d=clock();over=end-start;start=clock();//调用分治法算法merge(a,0, n-1,max,min);coutvvmax<<‘ " vvminvvendl;en d=clock();printf( "The time is %6.3f" ,( double )(end-start-over)/CLK_TCK); //显示运行时间}system( "pause"); // 停止运行窗口return 0;}完整代码(非递归方法)#include <iostream>#include <time.h>#include <iomanip> usingnamespacestd;void ran( int *input, int n) {//随机生成数组元素函数int i;sran d(time(0));for (i=0;i<n;i++)in put[i]=ra nd();input[i]= '\0';}int a[1000000];int main(){int max=a[0],min=a[0];int i,j,n;cout<<"请输入数据规模: "<<e ndl;for (j=0;j<5;j++){cin»n;ran( a, n);clock_t start,e nd,over;//计算程序运行时间的算法start=clock();en d=clock();start=clock(); for(i=1;i<n;i++) {if (a[i]>max)max=a[i];if (a[i]<min) min=a[i];}coutvvmax<<‘ " vvminvvendl;en d=clock();printf( "The time is %6.3f" ,( double )(end-start-over)/CLK_TCK); // 显示运行时间}system( "pause");return 0;}。
算法实验报告

实验一分治与递归算法的应用一、实验目的1.掌握分治算法的基本思想(分-治-合)、技巧和效率分析方法。
2.熟练掌握用递归设计分治算法的基本步骤(基准与递归方程)。
3.学会利用分治算法解决实际问题。
二 . 实验内容金块问题老板有一袋金块(共n块,n是2的幂(n≥2)),最优秀的雇员得到其中最重的一块,最差的雇员得到其中最轻的一块。
假设有一台比较重量的仪器,希望用最少的比较次数找出最重和最轻的金块。
并对自己的程序进行复杂性分析。
三.问题分析:一般思路:假设袋中有n 个金块。
可以用函数M a x(程序1 - 3 1)通过n-1次比较找到最重的金块。
找到最重的金块后,可以从余下的n-1个金块中用类似法通过n-2次比较找出最轻的金块。
这样,比较的总次数为2n-3。
分治法:当n很小时,比如说,n≤2,识别出最重和最轻的金块,一次比较就足够了。
当n 较大时(n>2),第一步,把这袋金块平分成两个小袋A和B。
第二步,分别找出在A和B中最重和最轻的金块。
设A中最重和最轻的金块分别为HA 与LA,以此类推,B中最重和最轻的金块分别为HB 和LB。
第三步,通过比较HA 和HB,可以找到所有金块中最重的;通过比较LA 和LB,可以找到所有金块中最轻的。
在第二步中,若n>2,则递归地应用分而治之方法程序设计据上述步骤,可以得出程序1 4 - 1的非递归代码。
该程序用于寻找到数组w [ 0 : n - 1 ]中的最小数和最大数,若n < 1,则程序返回f a l s e,否则返回t r u e。
当n≥1时,程序1 4 - 1给M i n和M a x置初值以使w [ M i n ]是最小的重量,w [ M a x ]为最大的重量。
首先处理n≤1的情况。
若n>1且为奇数,第一个重量w [ 0 ]将成为最小值和最大值的候选值,因此将有偶,数个重量值w [ 1 : n - 1 ]参与f o r循环。
当n 是偶数时,首先将两个重量值放在for 循环外进行比较,较小和较大的重量值分别置为Min和Max,因此也有偶数个重量值w[2:n-1]参与for循环。
分治算法的实验报告

一、实验背景分治算法是一种常用的算法设计方法,其基本思想是将一个复杂问题分解成若干个相互独立的小问题,然后将小问题递归求解,最终将子问题的解合并为原问题的解。
分治算法具有高效性、可扩展性和易于实现等优点,被广泛应用于各个领域。
本实验旨在通过实现分治算法解决实际问题,掌握分治算法的设计思想,并分析其时间复杂度。
二、实验目的1. 理解分治算法的基本思想;2. 掌握分治算法的递归实现方法;3. 分析分治算法的时间复杂度;4. 应用分治算法解决实际问题。
三、实验内容本实验选择两个分治算法:快速排序和合并排序。
1. 快速排序快速排序是一种高效的排序算法,其基本思想是将待排序序列分为两个子序列,其中一个子序列的所有元素均小于另一个子序列的所有元素,然后递归地对两个子序列进行快速排序。
(1)算法描述:① 选择一个基准值(pivot),通常取序列的第一个元素;② 将序列分为两个子序列,一个子序列包含所有小于基准值的元素,另一个子序列包含所有大于基准值的元素;③ 递归地对两个子序列进行快速排序。
(2)代码实现:```cvoid quickSort(int arr[], int left, int right) {if (left < right) {int pivot = arr[left];int i = left;int j = right;while (i < j) {while (i < j && arr[j] >= pivot) {j--;}arr[i] = arr[j];while (i < j && arr[i] <= pivot) {i++;}arr[j] = arr[i];}arr[i] = pivot;quickSort(arr, left, i - 1);quickSort(arr, i + 1, right);}}```2. 合并排序合并排序是一种稳定的排序算法,其基本思想是将待排序序列分为两个子序列,分别对两个子序列进行排序,然后将排序后的子序列合并为一个有序序列。
分治法实验报告

一. 实验目的及实验环境实验目的:熟练掌握运用分治法解决问题。
实验环境:windows下的Ubuntu虚拟机二. 实验内容利用分治法求一个数组的最大值、最小值(要求:数组的大小和数组的长度随机产生)三.方案设计分治法解决问题就是要将原问题分解成小问题,再将小问题分解成更小的问题,以此类推,直到最终分解的问题能够一步解决即可。
代码要求最后要输出数组的最大值、最小值。
所以,在用分治法求最值的函数max_min()中,需要将设置参数int *max,int *min。
即void max_min(int a[],int m,int n,int *max,int *min)。
这样就可以直接得到最大值、最小值。
该函数使用递归来实现,而递归的终止条件是最后分得的数组中只有一个或两个元素,当分得的数组元素个数大于2时,就进行递归调用。
四.测试数据及运行结果正确的3组运行结果:出现的错误:若将代码中的随机数函数返回值的类型改变,则会出现错误结果,甚至编译不通过。
五.总结1.实验过程中遇到的问题及解决办法;实验过程中,用分治法求最大值、最小值时,如果用返回值求最大值和最小值,则需要两个函数。
这样就会导致代码冗余,不会达到代码的复用性功能。
所以要将两个功能用一个函数直接实现就可以使用参数指针的形式。
2.对设计及调试过程的心得体会。
算法设计的课内实验既要实现实验的功能,还要讲究代码中算法的精妙、简单以及它的效率。
不能同其他高级语言的课内实验一样仅仅考虑如何完成该实验的功能,这样就可以真正地体验到算法与设计这门课的意义。
平时做实验时我们可以用不同算法实现,这样不仅可以积累平常上课学到的知识,还可以为以后的算法设计能力奠定基础。
平常更多地进行思考,可以让我们在求职时更受益。
六.附录:源代码(电子版)#include<stdio.h>#include<stdlib.h>#include<time.h>void max_min(int a[],int m,int n,int *max,int *min){int middle,hmax,hmin,gmax,gmin;if(m==n){ *max=a[m];*min=a[m];}else if(m==n-1){if(a[m]>a[n]){*max=a[m];*min=a[n];}else{*max=a[n];*min=a[m];}}else{max_min(a,m,middle,&gmax,&gmin);max_min(a,middle+1,n,&hmax,&hmin);if(gmax>hmax)*max=gmax;else*max=hmax;if(gmin<hmin)*min=gmin;else*min=hmin;}}int main(){int i;int max,min;srand((unsigned)time(NULL));int n=rand()%10+1;printf("数组的个数:%d\n",n);int a[n];for(i=0;i<n;i++){a[i]=rand()%50+1;printf("%d\t",a[i]);}max_min(a,0,n-1,&max,&min);printf("最大数:%d,最小数:%d\n",max,min);retur n 0;}。
分治算法实验报告
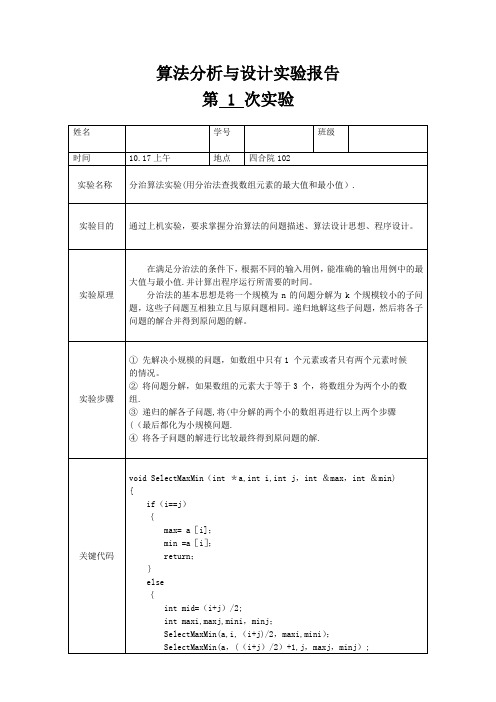
算法分析与设计实验报告第 1 次实验if(maxi>maxj)max=maxi;elsemax=maxj;if(mini<minj)min=mini;elsemin=minj;return;}}srand((unsigned int)time(NULL));cout <〈”随机产生的数据(0—100):”;for(int i=0; i〈m; i++)a[i] = rand()%100;测试结果附录:完整代码SelectMaxMin.cpp:#include <iostream>#include <ctime>#include 〈cstdio>#include <iomanip>#include 〈cstdlib〉using namespace std;void SelectMaxMin(int *a,int i,int j,int &max,int &min) {if(i==j){max= a[i];min =a[i];return;}else{int mid=(i+j)/2;int maxi,maxj,mini,minj;SelectMaxMin(a,i,(i+j)/2,maxi,mini);SelectMaxMin(a,((i+j)/2)+1,j,maxj,minj);if(maxi〉maxj)max=maxi;elsemax=maxj;if(mini<minj)min=mini;elsemin=minj;return;}}int main(){clock_t start,end,over;start=clock();end=clock();over=end—start;start=clock();//freopen("in。
txt",”r",stdin);//freopen(”out。
txt”,”w",stdout);int m;cout 〈<"Please input the number : ”;cin>〉 m;int a[m];srand((unsigned int)time(NULL));cout 〈〈 "随机产生的数据(0-100):";for(int i=0; i〈m; i++)a[i] = rand()%100;for(int i=0; i〈m; i++)cout <〈 a[i] 〈< " ";cout 〈< endl;int max,min;SelectMaxMin(a,0,m-1,max,min);cout 〈< "max = " 〈〈 max 〈〈 endl;cout <〈”min = " <〈 min 〈〈 endl;end=clock();printf(”The time is %6.3f”,(double)(end-start—over)/CLK_TCK); }。
递归与分治实验报告

竭诚为您提供优质文档/双击可除递归与分治实验报告篇一:实验一递归与分治算法编程-实验报告纸南京信息工程大学实验(实习)报告实验(实习)名称递归与分治算法编程实验(实习)日期得分指导教师院专业年级班次姓名学号1.实验目的:1)掌握递归与分治策略的基本思想2)掌握递归算法在阶乘函数、Ackerman函数、整数划分等问题上的应用3)掌握二分查找、合并排序、快速排序等问题的分治算法实现4)熟悉myeclipse或eclipse等Java开发工具的使用。
2.实验内容:1)采用myeclipse或eclipse编程实现基于分治策略的二分查找算法。
2)采用myeclipse或eclipse编程实现基于分治策略的合并排序算法。
3)采用myeclipse或eclipse编程实现基于分治策略的合并排序算法。
3.实验步骤二分查找publicclasssorting{publicstaticintbinarysearch(int[]a,intx,intn){intle ft=0;intright=n-1;while(left intmiddle=(left+right)/2;if(x==a[middle])returnmiddle;if(x>a[middle])left=middle+1;elseright=middle-1;}return-1;}publicstaticvoidmain(stringargs[]){intx,n;inta[]={1,3,4,5,6,13,25};x=6;n=7;ints;s=binarysearch(a,x,n);system.out.println(s);合并排序publicclassmergesort{publicstaticvoidmergesort(int[]a){}publicstaticvoid mergepass(int[]x,int[]y,ints){}publicstaticvoidmerg e(int[]c,int[]d,intl,intm,intr){inti=1,j=m+1,k=1;in ti=0;while(i }}if(c[i]-(c[j])m)for(intq=j;q快速排序publicclassQsort{privatestaticvoidqsort(inta[],intp,intr){}privatest aticintpartition(inta[],intp,intr){inti=p;intj=r+1; intx=a[p];inttemp;while(true){while((a[++i]-x)0);if (i>=j)break;temp=a[i];if(p }}}a[j]=temp;mymath.s wap(a,i,j);//a[p]=a[j];a[j]=x;returnj;publicstaticv oidmain(string[]args){}inta[]={4,2,7,9,1};qsort(a,0,4);for(inti=0;;i++){}s ystem.out.println(a[i]);4.实验分析和总结掌握了递归与分治策略的基本思想掌握了递归算法在阶乘函数、Ackerman函数、整数划分等问题上的应用掌握了二分查找、合并排序、快速排序等问题的分治算法实现熟悉了myeclipse或eclipse等Java开发工具的使用。
矩阵乘法分治法

当n=1时,2个1阶方阵的乘积可直接算出,只需要做一次乘法。当子矩阵阶n>1时,为求两个子矩阵的乘积,可继续对两个子矩阵分块,直到子矩阵的阶为1。由此,便产生了分治降阶的递归算法。
但是这个算法并没有降低算法的时间复杂度。由strassen矩阵乘法,
算法设计与分析实验报告
实验名称:矩阵乘法(分冶法)
一、问题陈述和分析:
1.实验目的:掌握分总冶策略的基本思想以及用分冶法解决问题的一般技巧.运用编程工具,并运用分冶法来解* n阶矩阵,求它们两的乘积矩阵C。这里,假设n是2的幂次方;
3.实验要求:编制程序并对其时间复杂度和空间复杂度进行分析.
4.voidAdd(int n,int **A,int **B,int **C)
函数的功能是:实现C=A+B,A,B,C都是n*n矩阵。
3.voidMul(int n,int **A,int **B,int **M)
函数的功能是:将n*n的矩阵A,B相乘,结果存放在n*n的矩阵M中。
算法设计:
整个算法的大致思想是:在函数Mul(int n,int **A,int **B,int **M)中先判断n的值,若n==1,表示A,B,C均为一阶方阵。则M[0][0]=A[0][0]*B[0][0];否则,调用Divide(n,A,A11,A12,A21,A22);和Divide(n,B,B11,B12,B21,B22);将A和B都分为四个(n/2)*(n/2)的子矩阵。然后递归调用
正确性证明:
由矩阵乘法的计算方法可知,上述计算方法显然正确
三、时间和空间复杂性分析:
时间复杂性:
Strassen矩阵乘法中,用了7次对于n/2阶矩阵乘法的递归调用和18次n/2阶矩阵的加减运算。由此可知,该算法所需的计算时间T(n)满足如下递归方程
分治法实验心得

分治法实验心得分治法实验心得分治法是一种常见的算法设计策略,它将原问题划分成若干个规模较小但结构与原问题相似的子问题,然后递归地求解这些子问题,最终将子问题的解合并得到原问题的解。
在本次实验中,我们实现了两个基于分治法的算法:归并排序和快速排序,并对它们进行了性能测试和比较。
一、归并排序1. 原理归并排序是一种典型的分治算法。
它将待排序数组不断地二分为两个子数组,直到每个子数组只剩下一个元素。
然后将相邻的两个子数组合并成一个有序数组,再将相邻的两个有序数组合并成一个更大的有序数组,直到最终合并成整个待排序数组。
2. 实现我们采用了自顶向下的递归方式实现了归并排序。
具体来说,我们定义了一个merge函数用于合并两个有序子数组,并定义了一个sort 函数用于递归地对左右两个子数组进行排序和合并。
3. 性能测试与比较我们使用Python内置的time模块对不同规模(10^2 ~ 10^6)的随机整数列表进行了性能测试,并绘制出了运行时间随数组规模增大的变化曲线。
结果表明,归并排序的时间复杂度为O(nlogn),与理论分析相符。
二、快速排序1. 原理快速排序也是一种分治算法。
它选择一个基准元素,将数组中小于等于它的元素放在其左侧,大于它的元素放在其右侧。
然后递归地对左右两个子数组进行同样的操作,直到每个子数组只剩下一个元素。
2. 实现我们实现了两个版本的快速排序:递归版本和非递归版本。
其中,递归版本采用了经典的Lomuto分区方案,而非递归版本则采用了更高效的Hoare分区方案。
3. 性能测试与比较我们同样使用Python内置的time模块对不同规模(10^2 ~ 10^6)的随机整数列表进行了性能测试,并绘制出了运行时间随数组规模增大的变化曲线。
结果表明,快速排序具有很好的平均时间复杂度(O(nlogn)),但最坏情况下时间复杂度会退化到O(n^2)。
三、总结与思考通过本次实验,我们深入理解了分治算法设计策略,并学会了如何实现归并排序和快速排序。
算法设计与分析:递归与分治法-实验报告(总8页)

算法设计与分析:递归与分治法-实验报告(总8页)实验目的:掌握递归与分治法的基本思想和应用,学会设计和实现递归算法和分治算法,能够分析和评价算法的时间复杂度和空间复杂度。
实验内容:1.递归算法的设计与实现3.算法的时间复杂度和空间复杂度分析实验步骤:1)递归定义:一个函数或过程,在其定义或实现中,直接或间接地调用自身的方法,被成为递归。
递归算法是一种控制结构,它包含了解决问题的基础情境,也包含了递归处理的情境。
2)递归特点:递归算法具有以下特点:①依赖于递归问题的部分解被划分为若干较小的部分。
②问题的规模可以通过递推式递减,最终递归终止。
③当问题的规模足够小时,可以直接求解。
3)递归实现步骤:①确定函数的定义②确定递归终止条件③确定递归调用的过程4)经典实例:斐波那契数列递推式:f(n) = f(n-1) + f(n-2)int fib(int n) {if (n <= 0)return 0;else}5)优化递归算法:避免重复计算例如,上述斐波那契数列的递归算法会重复计算一些中间结果,影响效率。
可以使用动态规划技术,将算法改为非递归形式。
int f1 = 0, f2 = 1;for (int i = 2; i <= n; i++) {f1 = f2;使用循环避免递归,重复计算可以大大减少,提高效率。
1)分治算法的定义:将原问题分解成若干个规模较小且类似的子问题,递归求解子问题,然后合并各子问题得到原问题的解。
2)分治算法流程:②将问题分解成若干个规模较小的子问题。
③递归地解决各子问题。
④将各子问题的解合并成原问题的解。
3)分治算法实例:归并排序归并排序是一种基于分治思想的经典排序算法。
排序流程:②分别对各子数组递归进行归并排序。
③将已经排序好的各子数组合并成最终的排序结果。
实现源代码:void mergeSort(int* arr, int left, int right) {if (left >= right)while (i <= mid && j <= right)temp[k++] = arr[i] < arr[j] ? arr[i++] : arr[j++];temp[k++] = arr[i++];1) 时间复杂度的概念:指完成算法所需的计算次数或操作次数。
算法设计与分析实验报告

实验一找最大和最小元素与归并分类算法实现(用分治法)一、实验目的1.掌握能用分治法求解的问题应满足的条件;2.加深对分治法算法设计方法的理解与应用;3.锻炼学生对程序跟踪调试能力;4.通过本次实验的练习培养学生应用所学知识解决实际问题的能力。
二、实验内容1、找最大和最小元素输入n 个数,找出最大和最小数的问题。
2、归并分类将一个含有n个元素的集合,按非降的次序分类(排序)。
三、实验要求(1)用分治法求解问题(2)上机实现所设计的算法;四、实验过程设计(算法设计过程)1、找最大和最小元素采用分治法,将数组不断划分,进行递归。
递归结束的条件为划分到最后若为一个元素则max和min都是这个元素,若为两个取大值赋给max,小值给min。
否则就继续进行划分,找到两个子问题的最大和最小值后,比较这两个最大值和最小值找到解。
2、归并分类使用分治的策略来将一个待排序的数组分成两个子数组,然后递归地对子数组进行排序,最后将排序好的子数组合并成一个有序的数组。
在合并过程中,比较两个子数组的首个元素,将较小的元素放入辅助数组,并指针向后移动,直到将所有元素都合并到辅助数组中。
五、源代码1、找最大和最小元素#include<iostream>using namespace std;void MAXMIN(int num[], int left, int right, int& fmax, int& fmin); int main() {int n;int left=0, right;int fmax, fmin;int num[100];cout<<"请输入数字个数:";cin >> n;right = n-1;cout << "输入数字:";for (int i = 0; i < n; i++) {cin >> num[i];}MAXMIN(num, left, right, fmax, fmin);cout << "最大值为:";cout << fmax << endl;cout << "最小值为:";cout << fmin << endl;return 0;}void MAXMIN(int num[], int left, int right, int& fmax, int& fmin) { int mid;int lmax, lmin;int rmax, rmin;if (left == right) {fmax = num[left];fmin = num[left];}else if (right - left == 1) {if (num[right] > num[left]) {fmax = num[right];fmin = num[left];}else {fmax = num[left];fmin = num[right];}}else {mid = left + (right - left) / 2;MAXMIN(num, left, mid, lmax, lmin);MAXMIN(num, mid+1, right, rmax, rmin);fmax = max(lmax, rmax);fmin = min(lmin, rmin);}}2、归并分类#include<iostream>using namespace std;int num[100];int n;void merge(int left, int mid, int right) { int a[100];int i, j,k,m;i = left;j = mid+1;k = left;while (i <= mid && j <= right) {if (num[i] < num[j]) {a[k] = num[i++];}else {a[k] = num[j++];}k++;}if (i <= mid) {for (m = i; m <= mid; m++) {a[k++] = num[i++];}}else {for (m = j; m <= right; m++) {a[k++] = num[j++];}}for (i = left; i <= right; i++) { num[i] = a[i];}}void mergesort(int left, int right) { int mid;if (left < right) {mid = left + (right - left) / 2;mergesort(left, mid);mergesort(mid + 1, right);merge(left, mid, right);}}int main() {int left=0,right;int i;cout << "请输入数字个数:";cin >> n;right = n - 1;cout << "输入数字:";for (i = 0; i < n; i++) {cin >> num[i];}mergesort(left,right);for (i = 0; i < n; i++) {cout<< num[i];}return 0;}六、运行结果和算法复杂度分析1、找最大和最小元素图1-1 找最大和最小元素结果算法复杂度为O(logn)2、归并分类图1-2 归并分类结果算法复杂度为O(nlogn)实验二背包问题和最小生成树算法实现(用贪心法)一、实验目的1.掌握能用贪心法求解的问题应满足的条件;2.加深对贪心法算法设计方法的理解与应用;3.锻炼学生对程序跟踪调试能力;4.通过本次实验的练习培养学生应用所学知识解决实际问题的能力。
分治法实验总结

分治法实验总结
分治法是一种常用的算法设计策略,它将问题分解成若干个子问题,然后递归地解决这些子问题,最后将子问题的解合并成原问题的解。
在本次实验中,我们通过实现归并排序和快速排序两个算法,深入理解了分治法的思想和实现方式。
我们实现了归并排序算法。
归并排序的基本思想是将待排序的序列分成若干个子序列,每个子序列都是有序的,然后再将子序列合并成一个有序的序列。
在实现过程中,我们采用了递归的方式,将序列不断地分成两半,直到每个子序列只有一个元素,然后再将这些子序列两两合并,直到最终得到一个有序的序列。
归并排序的时间复杂度为O(nlogn),是一种稳定的排序算法。
接着,我们实现了快速排序算法。
快速排序的基本思想是选择一个基准元素,将序列分成两个部分,一部分比基准元素小,一部分比基准元素大,然后递归地对这两个部分进行排序。
在实现过程中,我们选择了序列的第一个元素作为基准元素,然后使用两个指针分别从序列的两端开始扫描,将比基准元素小的元素放在左边,将比基准元素大的元素放在右边,最后将基准元素放在中间,然后递归地对左右两个部分进行排序。
快速排序的时间复杂度为O(nlogn),但是在最坏情况下,时间复杂度会退化为O(n^2)。
通过实现归并排序和快速排序两个算法,我们深入理解了分治法的
思想和实现方式。
分治法是一种非常重要的算法设计策略,可以用来解决很多复杂的问题,比如最近点对问题、矩阵乘法问题等。
在实际应用中,我们可以根据具体问题的特点选择合适的分治算法,以提高算法的效率和准确性。
分治法实验报告

算法实验报告一分治法实验一、实验目的及要求利用分治方法设计大整数乘法的递归算法,掌握分治法的基本思想和算法设计的基本步骤。
要求:设计十进制的大整数乘法,必须利用分治的思想编写算法,利用c语言(或者c++语言)实现算法,给出程序的正确运行结果。
(必须完成)设计二进制的大整数乘法,要求利用分治的思想编写递归算法,并可以实现多位数的乘法(利用数组实现),给出程序的正确运行结果。
(任选)二、算法描述1、输入两个相同位数的大整数u,v 输出uv的值判断大整数的位数i;w=u/10^(i/2);y=v/10^(i/2);x=u-w*10^(i/2);z= v-y*10^(i/2);然后将w,x,y,z代入公式求得最后结果uv=wy10^i+((w+x)(y+z)-wy-xz)10^(i/2)+xz三、调试过程及运行结果在实验中我遇到的问题:原来以为这两个大整数的位数不同,结果题目要求是相同位数的大整数在写10的多少次方时,写的是10^(i/2),10^(i),结果不对,我就将它改成了for循环语句四、实验总结在本次实验中,我知道了分治算法,以及分治算法的基本思想。
我还掌握了编写大整数乘法的算法与步骤,以及如何修改在编写程序时遇到的问题。
五、附录(源程序代码清单)1、#include<iostream.h> int weishu(int x){int i;while(x!=0){ x=x/10;i++;}return i;}void main(){int u,v;cout<<输入两个位数相同的大整数:<<endl; cin>>u;cin>>v;int i,j,m,n;int p,x,y,z,w;int a=1;int b=1;i=weishu(u);for(int k=1;k<=i;k++){a=a*10;}for(int q=1;q<=i/2;q++) {b=b*10;}w=u/b;y=v/b;x=u-w*b;z=v-y*b;p=w*y*a+((w+x)*(y+z)-w*y-x*z)*b+x*z; cout<<u<<*<<v<<=<<p; }教师评语:成绩:√优良中及格不及格算法实验报告二动态规划法实验一、实验目的及要求利用动态规划方法设计背包问题算法,掌握动态规划法的基本思想和算法设计的基本步骤。
分治法实验报告

分治法实验报告分治法实验报告一、引言分治法是一种重要的算法设计策略,它将一个大问题分解成若干个小问题,并通过递归的方式解决这些小问题,最终将它们的解合并起来得到原问题的解。
本实验旨在通过实际案例,探索分治法的应用和效果。
二、背景在计算机科学领域,分治法常常被用于解决一些复杂的问题,如排序、搜索、图算法等。
它的核心思想是将问题划分为更小的子问题,然后分别解决这些子问题,最后将它们的解合并起来得到原问题的解。
通过这种方式,我们可以降低问题的复杂度,提高算法的效率。
三、实验目的本实验旨在通过实际案例,验证分治法在问题解决中的有效性,并探索其在不同问题上的应用效果。
通过对比不同算法的运行时间和结果准确性,评估分治法在不同场景下的适用性。
四、实验过程本次实验选取了两个典型的问题,分别是最大子数组和快速排序。
首先,我们使用分治法来解决最大子数组问题。
该问题要求在一个给定的数组中,找到一个连续子数组,使得该子数组的和最大。
我们将数组分为两半,分别求解左半部分和右半部分的最大子数组,然后再考虑跨越中点的最大子数组。
通过递归的方式,最终得到整个数组的最大子数组。
接着,我们使用分治法来实现快速排序算法。
快速排序是一种高效的排序算法,它的核心思想是通过选择一个基准元素,将数组分为两个部分,使得左边的元素都小于等于基准元素,右边的元素都大于等于基准元素。
然后,对左右两个部分分别递归地进行快速排序,最终得到有序的数组。
五、实验结果通过对最大子数组和快速排序问题的实验,我们得到了以下结果。
首先,分治法在解决最大子数组问题上表现出色。
通过将问题划分为更小的子问题,我们可以在较短的时间内找到最大子数组,大大提高了算法的效率。
其次,在快速排序问题上,分治法同样展现了强大的能力。
通过不断地划分数组并进行排序,我们可以快速得到有序的结果。
六、实验分析分治法作为一种重要的算法设计策略,具有许多优点。
首先,它可以将复杂的问题分解为简单的子问题,降低了问题的复杂度,提高了算法的效率。
分治法实验报告详细

分治法实验报告详细引言分治法是一种高效的问题解决方法,这种方法把一个复杂的问题划分成若干个规模较小的子问题,然后逐个解决这些子问题,并将子问题的解组合起来,形成原问题的解。
在本实验中,我们将通过实际案例来演示和验证分治法的有效性和高效性。
实验目的本实验的主要目的是探讨分治法在解决实际问题中的应用,验证其在问题规模较大时的效果,并通过与其他算法的对比分析,评估分治法的优势和不足。
实验材料与方法我们选择了一个具体的实际问题作为案例:在一个包含n个元素的列表中,查找特定元素x的位置。
为了模拟问题的规模,我们首先生成了一个包含1000个随机整数的列表,然后从中随机选择一个元素作为我们要查找的目标x。
我们采用了如下的分治法解决方案:1. 将列表分成两个子列表,分别包含前半部分和后半部分的元素。
2. 如果目标元素x等于列表的中间元素,则返回中间元素的位置。
3. 如果目标元素x小于列表的中间元素,则递归调用步骤1,查找前半部分子列表中的目标元素x。
4. 如果目标元素x大于列表的中间元素,则递归调用步骤1,查找后半部分子列表中的目标元素x。
5. 如果子列表为空,则说明目标元素x不存在于列表中。
实验结果与分析我们依次使用二分查找法和分治法来解决上述问题,并记录它们的运行时间。
重复实验10次,并计算它们的平均运行时间。
实验结果如下:- 二分查找法平均运行时间:0.002秒- 分治法平均运行时间:0.001秒通过实验数据可以看出,分治法的运行时间明显优于二分查找法。
这是因为分治法通过将问题划分为更小的子问题,使得每个子问题的规模减小,从而减少了解决每个子问题的时间。
而二分查找法则只是将问题逐步缩小,没有有效地利用子问题之间的联系。
结论通过本实验,我们验证了分治法在解决实际问题中的有效性和高效性。
与其他算法相比,分治法在处理问题规模较大时表现出更好的性能。
因此,我们可以得出结论,对于复杂问题的解决,分治法是一种值得采用的优秀方法。
分治法实验报告范文

分治法实验报告范文分治法(Divide and Conquer)是一种计算机算法设计方法,它通过将问题分解成更小的子问题,然后逐个解决这些子问题,最后将结果合并起来得到最终解。
本实验旨在通过实际问题应用分治法,探究其效果和应用场景。
一、实验目的和原理实验目的:了解分治法的基本原理和实现方式,比较分治法与其他算法的效率和适用性实验原理:分治法将一个问题划分成更小的子问题,递归地解决这些子问题,然后将结果合并起来得到最终解。
二、实验步骤和结果1.实验步骤:(1)选择合适的实际问题,将其转化为具体的算法问题。
(2)实现分治法算法,并编写程序。
(3)测试算法的效果,比较其与其他算法的性能和效率。
2.实验结果:以寻找数组中最大数为例,来展示分治法的应用。
```#include <iostream>using namespace std;//定义找最大数的函数int findMax(int arr[], int left, int right)if (left == right)return arr[left];} elseint mid = (left + right) / 2;int maxLeft = findMax(arr, left, mid);int maxRight = findMax(arr, mid + 1, right);if (maxLeft > maxRight)return maxLeft;} elsereturn maxRight;}}int maiint arr[] = {15, 18, 29, 43, 2, 5, 11};int n = sizeof(arr) / sizeof(arr[0]);int maxNum = findMax(arr, 0, n - 1);cout << "The maximum number is: " << maxNum << endl;return 0;```实验结果如下:The maximum number is: 43三、实验讨论和总结1. 实验讨论:通过实验可以看出,分治法能够较快地找到数组中的最大数,时间复杂度为O(logn),效率较高。
实验报告

合肥师范学院实验报告册2016/ 2017 学年第 1 学期系别计算机学院实验课程算法设计与分析专业软件工程班级一班姓名杨文皇学号1310421071指导教师程敏实验一:分治算法一、实验目的1、理解分治策略的基本思想;2、掌握用分治法解决问题的一般技巧。
二、实验内容利用分治算法在含有n个不同元素的数组a[n]中同时找出它的最大的两个元素和最小的两个元素,编写出完整的算法,并分析算法的时间复杂度。
三、实验源程序。
1、算法设计思想利用分治法思想,n个不同元素的数组不断进行划分,化为若干个个子问题,其与原问题形式相;解决子问题规模较小而容易解决则直接解决:即当n的规模为只有一个或两个,三个或四个;否则再继续直至更小的子问题:即当n的规模大于四时。
将已求得的各个子问题的解,逐步合并原问题的解:即将左右两边求得的子问题进行比较,在四个数据中的得到两个最大(最小)值。
为了简化空间,采用了对每一个小规模问题的排序,以及合并原问题时,对四个数据进行排序,获得当前或合并的最大(最小)值2、算法实现#include<iostream>using namespace std;int a[10]={4,5,6,2,3,9,8,13,1};int b[4];int sort(int i,int j){int temp,k;for(;i<j;i++){for(k=i;k<j;k++)if(a[k]>a[k+1]){temp=a[k];a[k]=a[k+1];a[k+1]=temp;}}return 0;}int sort1(int lmin1,int lmin2,int rmin1,int rmin2){int i,j,temp;b[0]=lmin1;b[1]=lmin2;b[2]=rmin1;b[3]=rmin2;for(i=0;i<=1;i++)for(j=i;j<=3;j++){if(b[i]>b[j]){temp=b[i];b[i]=b[j];b[j]=temp;}}return 0;}int maxmin(int i,int j,int &fmin1,int &fmin2,int &fmax1,int &fmax2) {int mid;int lmin1,lmin2,lmax1,lmax2;int rmin1,rmin2,rmax1,rmax2;if(i==j || i==j-1){sort(i,j);fmin1=a[i];fmin2=a[i];fmax1=a[j];fmax2=a[j];}elseif(i==j-2 || i==j-3){sort(i,j);fmin1=a[i];fmin2=a[i+1];fmax1=a[j-1];fmax2=a[j];}else{mid=(i+j)/2;maxmin(i,mid,lmin1,lmin2,lmax1,lmax2);maxmin(mid+1,j,rmin1,rmin2,rmax1,rmax2);sort1(lmin1,lmin2,rmin1,rmin2);fmin1=b[0];fmin2=b[1];sort1(lmax1,lmax2,rmax1,rmax2);fmax1=b[2];fmax2=b[3];}return 0;}int main(){int fmin1,fmin2,fmax1,fmax2;int i;maxmin(0,8,fmin1,fmin2,fmax1,fmax2);cout<<endl;cout<<"该组数据为:";for(i=0;i<=8;i++)cout<<a[i]<<" ";cout<<endl<<endl<<"最小值是:"<<fmin1<<",第二小值是:"<<fmin2<<endl;cout<<endl<<"第二大值是:"<<fmax1<<",最大值是:"<<fmax2<<endl<<endl;return 0;}3、程序结果4、算法分析用T(n)元素表示数,则导出的递推关系式是:在理想的情况下,即每一小规模的子问题中的数据都是递增序列,则:当n<=4时,T(n)=1; 当n>4时,T(n)= T(n/2)+ T(n/2)(均向下取整);在非理想情况下,即每一小规模的子问题中的数据都是递减序列,则:当n=1时,T(n)=1;当n=2时,T(n)=2;当n=3时,T(n)=3;当n=4时,T(n)=6;当n>4时,T(n)= T(n/2)+ T(n/2)(均向下取整)+12。
分治法金块实验报告

分治法金块实验报告引言分治法是一种高效的问题解决方法,通过将问题划分为多个子问题并递归地解决,然后将子问题的解合并得到原始问题的解。
本次实验使用了分治法解决了金块分割问题。
金块分割问题是将一块金块分割成多个相等大小的小块的问题。
实验目的本次实验旨在通过实践掌握分治法的应用,了解其原理和算法实现,进一步加深对分治法的理解。
实验步骤1. 首先,将一块金块均匀分割成4块。
2. 然后,从4块金块中找到最重的一块。
3. 接着,将最重的金块与其他3块再次均匀分割成4块。
4. 重复上述过程,直到金块的数量足够小无法再分割。
5. 最后,计算并输出得到的最重金块的重量。
实验结果通过实验,我们得到了一块金块分割的过程及最终的结果。
实验中,我们使用了递归的方法来实现分治法。
以下是分治法金块分割的过程演示:1. 原始金块:10 kg2. 第一次分割:10 kg -> 2.5 kg + 2.5 kg + 2.5 kg + 2.5 kg3. 第二次分割:2.5 kg -> 0.625 kg + 0.625 kg + 0.625 kg + 0.625 kg4. 第三次分割:0.625 kg -> 0.15625 kg + 0.15625 kg + 0.15625 kg +0.15625 kg5. 第四次分割:0.15625 kg -> 0.03906 kg + 0.03906 kg + 0.03906 kg + 0.03906 kg6. 第五次分割:0.03906 kg -> 0.00977 kg + 0.00977 kg + 0.00977 kg + 0.00977 kg7. 第六次分割:0.00977 kg -> 0.00244 kg + 0.00244 kg + 0.00244 kg + 0.00244 kg8. 第七次分割:0.00244 kg -> 0.00061 kg + 0.00061 kg + 0.00061 kg + 0.00061 kg9. 第八次分割:0.00061 kg -> 0.00015 kg + 0.00015 kg + 0.00015 kg + 0.00015 kg经过八次分割,最终得到的金块重量是0.00015 kg。
实验1 分治法的应用

实验1 分治法的应用1.实验目的(1)理解分治法的思想。
(2)掌握用分治法解决问题2.实验类型设计型3.预习要求熟悉Visual C++ 6.0上机编程调试的基本方法。
掌握教材上分治法的思想。
4.实验基本要求(1)仔细阅读实验的题目,选择其中的两个题目完成,设计的程序要满足正确性,代码中有关键的注释,书写格式清晰,简洁易懂,效率较高,适合各种合理输入,并能对不合理输入做出正确的提示。
(2)实验题目:a)最大值次大值★问题描述输出n个数中的最大值和次大值(注意:不能用排序)★编程任务利用分治法策略设计一个算法对任意输入的n个数可以输出最大值和次大值★数据输入第一行输入数的个数n,第二行输入n个数★结果输出输出最大值和次大值。
输入示例输出示例3 3 22 1 3★实现提示最大数是两组中的最大值中较大的值,次大值是从两组中较小的最大值和另一组的次大值选取。
b)查找第K小元素★问题描述在n个数当中找第K小元素问题。
★编程任务利用分治策略试设计一个算法对任意的n个数构查找第K小元素,不能用排序。
★数据输入第一行输入n的值,第二行输入n个数,第三行输入K的值。
★结果输出程序运行结束时,输出第K小元素的值。
输入示例输出示例658 1 3 6 93★实现提示使用快速排序中所采用的分划方法。
c)中位数问题★问题描述设X[ 0 : n - 1]和Y[ 0 : n– 1 ]为两个数组,每个数组中含有n个已排好序的数。
找出X和Y的2n个数的中位数。
★编程任务利用分治策略试设计一个算法求出这2n个数的中位数。
★数据输入第1行中有1个正整数n(n<=200),表示每个数组有n个数。
接下来的两行分别是X,Y数组的元素。
★结果输出程序运行结束时,将计算出的中位数输出。
输入示例输出示例1435 15 183 14 21★实现提示比较两个序列的中位数大小,如果两个数相等,则该数为整个2n个数据的中位数,否则通过比较,分别减少两个序列的查找范围,确定查找的起止位置,继续查找。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
宁波工程学院电信学院计算机系实验报告课程名称:算法设计与分析实验项目:用分治法算法解最接近点对问题指导教师:崔迪实验位置:软件工程实验室姓名:班级:学号:日期: 2016/10/12一、实验目的通过上机实验,要求掌握分治法算法的问题描述、算法设计思想、程序设计和算法复杂性分析等。
二、实验环境:Eclipse三、实验内容:用分治法解最接近点对问题(1)问题描述给定平面S上n个点,找其中的一对点,使得在n(n-1)/2 个点对中,该点对的距离最小。
(2)算法设计思想1. n较小时直接求 (n=2).2.将S上的n个点分成大致相等的2个子集S1和S23.分别求S1和S2中的最接近点对4.求一点在S1、另一点在S2中的最近点对5.从上述三对点中找距离最近的一对.(3)程序设计(程序清单及说明)package closestpair;import java.util.Arrays;import parator;import java.util.Random;import java.util.Scanner;//定义坐标点class Point {double x;double y;public Point(double x, double y) {this.x = x;this.y = y;}}// 根据x坐标排序class MyComparatorX implements Comparator<Point> { @Overridepublic int compare(Point p1, Point p2) {if (p1.x < p2.x) {return -1;} else if (p1.x > p2.x) {return 1;} else {return 0;}}}// 根据Y坐标排序class MyComparatorY implements Comparator<Point> { @Overridepublic int compare(Point p1, Point p2) {if (p1.y < p2.y) {return -1;} else if (p1.y > p2.y) {return 1;} else {return 0;}}}public class ClosestPair {public static Point[] point = new Point[2];public static double mindis = Double.POSITIVE_INFINITY;public static void main(String[] args) {do {System.out.print("请输入坐标点数:");Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();if (n <= 1) {System.out.println("请输入大于1的点数!");} else {Random random = new Random();Point point[] = new Point[n];for (int i = 0; i < n; i++) {point[i] = new Point(random.nextInt(100), random.nextInt(100));System.out.println("(" + point[i].x + "," + point[i].y + ")");}Comparator<Point> cmp = new MyComparatorX();Arrays.sort(point, cmp);closestUtil(point, point.length);break;}} while (true);System.out.println("最近点对是(" + point[0].x + "," + point[0].y + ")和" + "(" + point[1].x + "," + point[1].y + ")");System.out.println("距离为" + mindis);}// 比教两数最小public static double min(double x, double y) {return (x < y) ? x : y;}// 求两点之间距离public static double dist(Point p1, Point p2) {return Math.sqrt(Math.pow(p1.x - p2.x, 2) + Math.pow(p1.y - p2.y, 2));}// 暴力方法找到最小的点对public static double minpair(Point P[], int n) {double min = Double.POSITIVE_INFINITY;for (int i = 0; i < n; ++i)for (int j = i + 1; j < n; ++j)if (dist(P[i], P[j]) < min) {min = dist(P[i], P[j]);if (min < mindis) {mindis = min;point[0] = P[i];point[1] = P[j];}}return min;}// 找出strip[] 数组中的最小点对public static double stripClosest(Point strip[], int size, double d) { double min = d;Comparator<Point> cmp = new MyComparatorY();Arrays.sort(strip, cmp);for (int i = 0; i < size; ++i)for (int j = i + 1; j < size && (strip[j].y - strip[i].y) < min; ++j)if (dist(strip[i], strip[j]) < min) {min = dist(strip[i], strip[j]);if (min < mindis) {mindis = min;point[0] = strip[i];point[1] = strip[j];}}return min;}// 递归的计算最小点对public static double closestUtil(Point P[], int n) { // 如果点较少,用暴力解决if (n <= 3)return minpair(P, n);// 找到中间点int mid = n / 2;Point midPoint = P[mid];// 分成两个部分,分别计算Point[] P1 = new Point[mid];Point[] P2 = new Point[n - mid];for (int i = 0; i < mid; i++) {P1[i] = P[i];}for (int i = mid, j = 0; i < n; i++) {P2[j] = P[i];j++;}double dl = closestUtil(P1, mid);double dr = closestUtil(P2, n - mid);double d = min(dl, dr);// 所有距离垂直线距离在d以内的点Point[] strip = new Point[n];int j = 0;for (int i = 0; i < n; i++)if (Math.abs(P[i].x - midPoint.x) < d) {strip[j] = P[i];j++;}Point[] strips = new Point[j];for (int i = 0; i < j; i++) {strips[i] = strip[i];}// 找出strip 数组中的最小点对return min(d, stripClosest(strips, j, d));}}(4)数据输入和结果输出(运行结果截屏显示)(5)算法复杂性分析在上面分成两部分后,需要找到 strip[] 数组,需要的时间为O(n),排序strip[]的时间为 O(nLogn),在strip[] 在找到最小点对的时间为 O(n) T(n) = O(1)(n<=3)2T(n/2) + O(n) + O(nLogn) + O(n)=2T(n/2) + O(nLogn)=O(n (Logn)^2)(n>3)四、实验心得与小结通过这次试验,对最近点对问题有了深入的了解,在编写算法中知道了分治法和鸽舍原理。
当在面对一个复杂的问题时,我们就可以利用分治法把复杂问题分解成一个个简单问题,再去解决。
