22.3菱形的判定常考题(含有详细的答案解析)

合集下载

菱形的判定(含答案)

菱形的判定一、选择题1．下列四边形中不一定为菱形的是（）A．对角线相等的平行四边形 B．每条对角线平分一组对角的四边形C．对角线互相垂直的平行四边形 D．用两个全等的等边三角形拼成的四边形2．四个点A，B，C，D在同一平面内，从①AB∥CD；②AB=CD；③AC⊥BD；④AD= BC； ⑤AD∥BC．这5个条件中任选三个，能使四边形ABCD是菱形的选法有（）．A．1种 B．2种 C．3种 D．4种3．菱形的周长为32cm，一个内角的度数是60°，则两条对角线的长分别是（）A．8cm和43cm B．4cm和83cm C．8cm和83cm D．4cm和43cm二、填空题4．如图1所示，已知□ABCD，AC，BD相交于点O，•添加一个条件使平行四边形为菱形，添加的条件为________．（只写出符合要求的一个即可）图1 图25．如图2所示，D，E，F分别是△ABC的边BC，CA，AB上的点，且DE∥AB，DF∥CA，要使四边形AFDE 是菱形，则要增加的条件是________．（只写出符合要求的一个即可）6．菱形ABCD的周长为48cm，∠BAD： ∠ABC= 1：•2，•则BD=•_____，•菱形的面积是______．7．在菱形ABCD中，AB=4，AB边上的高DE垂直平分边AB，则BD=_____，AC=_____．四、思考题9．如图，矩形ABCD的对角线相交于点O，PD∥AC，PC∥BD，PD，PC相交于点P，四边形PCOD是菱形吗？试说明理由．]2、如图ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F．求证：四边形AFCE是菱形．3如图所示，四边形ABCD、DEBF都是矩形，AB=BF，AD、BE相交于M，BC、DF交于N，求证：四边形BMDN是菱形．1、用两个边长为a的等边三角形纸片拼成的四边形是___________2、有一组邻边相等的四边形是菱形（）3、对角线互相垂直的四边形是菱形（）4、对角线互相平分垂直的四边形是菱形（）5、如图，△ABC中，AD平分∠BAC，DE∥AC，与AB相交于点E，DF∥AB，与AC相交于点F，试说明四边形AEDF是菱形。

菱形的性质和判定经典试题综合训练(含解析)

菱形的性质和判定经典试题综合训练（含解析）一．选择题（共15小题）1．如图，△ABC中，DE∥BC，EF∥AB，要判定四边形DBFE是菱形，还需要添加的条件是（）A．AB=AC B．AD=BD C．BE⊥AC D．BE平分∠ABC2．求证：菱形的两条对角线互相垂直．已知：如图，四边形ABCD是菱形，对角线AC，BD交于点O．求证：AC⊥BD．以下是排乱的证明过程：①又BO=DO；②∴AO⊥BD，即AC⊥BD；③∵四边形ABCD是菱形；④∴AB=AD．证明步骤正确的顺序是（）A．③→②→①→④B．③→④→①→②C．①→②→④→③D．①→④→③→②3．下列性质中菱形不一定具有的性质是（）A．对角线互相平分B．对角线互相垂直C．对角线相等D．既是轴对称图形又是中心对称图形4．如图，菱形ABCD的对角线AC、BD的长分别是6cm、8cm，AE⊥BC于点E，则AE的长是（）A．cm B．cm C．cm D．5cm5．如图，四边形ABCD中，对角线相交于点O，E、F、G、H分别是AD、BD、BC、AC的中点，要使四边形EFGH是菱形，则四边形ABCD需满足的条件是（）A．AB=AD B．AC=BD C．AD=BC D．AB=CD6．如图，菱形ABCD的周长为16，面积为12，P是对角线BD上一点，分别作P点到直线AB、AD的垂线段PE、PF，则PE+PF等于（）A．6 B．3 C．1.5 D．0.757．若菱形的周长为52cm，面积为120cm2，则它的对角线之和为（）A．14cm B．17cm C．28cm D．34cm8．如图，作菱形ABCD的高AE，E为CD的中点．AE=cm，则菱形ABCD的周长是（）A．4cm B．4cm C．4cm D．8cm9．如图，菱形ABCD中，过A作BD的平行线交CD的延长线于点E，下列结论：（1）∠EAC=90°，（2）DA=DE，（3）∠ABC=2∠E，其中正确的有（）A．0个B．1个C．2个D．3个10．如图，以△ABC的三边为边在BC的同侧分别作三个等边三角形，即△ABD、△BCE、△ACF，当△ABC 满足什么条件时，四边形ADEF是菱形？（）A．AB=AC B．∠BAC=90°C．∠BAC=120°D．∠BAC=150°11．已知菱形的周长为4，两条对角线的和为6，则菱形的面积为（）A．2 B．C．3 D．412．四个点A，B，C，D在同一平面内，从①AB∥CD；②AB=CD；③AC⊥BD；④AD=BC；⑤AD∥BC，这五个条件中任选三个，能使四边形ABCD是菱形的选法有（）A．1种B．2种C．3种D．4种13．已知：如图，在菱形ABCD中，F为边AB的中点，DF与对角线AC交于点G，过G作GE⊥AD于点E，若AB=2，且∠1=∠2，则下列结论不正确的是（）A．DF⊥AB B．CG=2GA C．CG=DF+GE D．S四边形BFGC=﹣114．如图，O是菱形ABCD的对角线AC、BD的交点，E、F分别是OA、OC的中点．下列结论：①S△ADE=S；②四边形BFDE也是菱形；③四边形ABCD的面积为EF×BD；④∠ADE=∠EDO；⑤△DEF是轴对称△EOD图形．其中正确的结论有（）A．5个B．4个C．3个D．2个15．如图，在Rt△ABC中，∠ACB=90°，AC=BC=6cm，动点P从点A出发，沿AB方向以每秒cm的速度向终点B运动；同时，动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动，将△PQC沿BC 翻折，点P的对应点为点P′．设Q点运动的时间为t秒，若四边形QP′CP为菱形，则t的值为（）A．B．2 C． D．3二．填空题（共9小题）16．如图，在∠MON的两边上分别截取OA、OB，使OA=OB；分别以点A、B为圆心，OA长为半径作弧，两弧交于点C；连接AC、BC、AB、OC．若AB=2cm，四边形OACB的面积为4cm2．则OC的长为cm．17．如图，四边形ABCD是轴对称图形，且直线AC是对称轴，AB∥CD，则下列结论：①AC⊥BD；②AD ∥BC；③四边形ABCD是菱形；④△ABD≌△CDB．其中正确的是（只填写序号）18．如图，四边形ABCD中，E，F，G，H分别是边AB、BC、CD、DA的中点．若四边形EFGH为菱形，则对角线AC、BD应满足条件．19．如图，在△ABC中，点D是BC的中点，点E，F分别在线段AD及其延长线上，且DE=DF．给出下列条件：①BE⊥EC；②BF∥CE；③AB=AC；从中选择一个条件使四边形BECF是菱形，你认为这个条件是（只填写序号）．20．如图，菱形ABCD的周长为40，面积为25，P是对角线BD上一点，分别作P点到直线AB、AD的垂线段PE、PF，则PE+PF等于．21．如图，菱形纸片ABCD，∠A=60°，P为AB中点，折叠菱形纸片ABCD，使点C落在DP所在的直线上，得到经过点D的折痕DE，则∠DEC等于度．22．如图，菱形ABCD和菱形ECGF的边长分别为3和4，∠A=120°，则图中阴影部分的面积．23．如图，点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点，当四边形ABCD的边至少满足条件时，四边形EFGH是菱形．24．如图，在Rt△ABC中，∠C=90°，AC=BC=6cm，点P从点B出发，沿BA方向以每秒cm的速度向终点A运动；同时，动点Q从点C出发沿CB方向以每秒1cm的速度向终点B运动，将△BPQ沿BC翻折，点P的对应点为点P′．设Q点运动的时间t秒，若四边形QPBP′为正方形，则t的值为．三．解答题（共9小题）25．如图，AD是△ABC的角平分线，过点D分别作AC和AB的平行线，交AB于E，交AC于F，求证：四边形AEDF是菱形．26．如图所示，已知四边形ABCD，ADEF都是菱形，∠BAD=∠FAD，∠BAD为锐角．（1）求证：AD⊥BF；（2）若BF=BC，求∠ADC的度数．27．如图，△ABC中，AB=AC，∠BAC=40°，将△ABC绕点A按逆时针方向旋转100°．得到△ADE，连接BD，CE交于点F．（1）求证：△ABD≌△ACE；（2）求证：四边形ABFE是菱形．28．如图，AE∥BF，AC平分∠BAE，且交BF于点C，BD平分∠ABF，且交AE于点D，连接CD．（2）若∠ADB=30°，BD=6，求AD的长．29．如图，△ABC是以BC为底的等腰三角形，AD是边BC上的高，点E、F分别是AB、AC的中点．（1）求证：四边形AEDF是菱形；（2）如果四边形AEDF的周长为12，两条对角线的和等于7，求四边形AEDF的面积S．30．如图，在四边形ABCD中，AB=AD，CB=CD，E是CD上一点，BE交AC于F，连接DF．（1）证明：∠BAC=∠DAC，∠AFD=∠CFE；（2）若AB∥CD，试证明四边形ABCD是菱形；（3）在（2）的条件下，若BE⊥CD，试证明∠EFD=∠BCD．31．如图，在△ABC中，∠ACB=90°，点D，E分别是边BC，AB上的中点，连接DE并延长至点F，使EF=2DE，连接CE、AF．（1）证明：AF=CE；（2）当∠B=30°时，试判断四边形ACEF的形状并说明理由．32．如图，在△ABC中，∠ABC=90°，BD为AC的中线，过点C作CE⊥BD于点E，过点A作BD的平行线，交CE的延长线于点F，在AF的延长线上截取FG=BD，连接BG、DF．（2）若AF=8，CF=6，求四边形BDFG的面积．33．如图所示，在菱形ABCD中，AB=4，∠BAD=120°，△AEF为正三角形，点E、F分别在菱形的边BC、CD上滑动，且E、F不与B、C、D重合．（1）证明不论E、F在BC、CD上如何滑动，总有BE=CF；（2）当点E、F在BC、CD上滑动时，分别探讨四边形AECF和△CEF的面积是否发生变化？如果不变，求出这个定值；如果变化，求出最大（或最小）值．菱形的性质和判定经典试题综合训练参考答案与试题解析一．选择题（共15小题）1．如图，△ABC中，DE∥BC，EF∥AB，要判定四边形DBFE是菱形，还需要添加的条件是（）A．AB=AC B．AD=BD C．BE⊥AC D．BE平分∠ABC【分析】当BE平分∠ABC时，四边形DBFE是菱形，可知先证明四边形BDEF是平行四边形，再证明BD=DE 即可解决问题．【解答】解：当BE平分∠ABC时，四边形DBFE是菱形，理由：∵DE∥BC，∴∠DEB=∠EBC，∵∠EBC=∠EBD，∴∠EBD=∠DEB，∴BD=DE，∵DE∥BC，EF∥AB，∴四边形DBEF是平行四边形，∵BD=DE，∴四边形DBEF是菱形．其余选项均无法判断四边形DBEF是菱形，故选D．2．求证：菱形的两条对角线互相垂直．已知：如图，四边形ABCD是菱形，对角线AC，BD交于点O．求证：AC⊥BD．以下是排乱的证明过程：①又BO=DO；②∴AO⊥BD，即AC⊥BD；③∵四边形ABCD是菱形；④∴AB=AD．证明步骤正确的顺序是（）A．③→②→①→④B．③→④→①→②C．①→②→④→③D．①→④→③→②【分析】根据菱形是特殊的平行四边形以及等腰三角形的性质证明即可．【解答】证明：∵四边形ABCD是菱形，∴AB=AD，∵对角线AC，BD交于点O，∴BO=DO，∴AO⊥BD，即AC⊥BD，∴证明步骤正确的顺序是③→④→①→②，故选B．3．下列性质中菱形不一定具有的性质是（）A．对角线互相平分B．对角线互相垂直C．对角线相等D．既是轴对称图形又是中心对称图形【分析】根据菱形的性质解答即可得．【解答】解：A、菱形的对角线互相平分，此选项正确；B、菱形的对角线互相垂直，此选项正确；C、菱形的对角线不一定相等，此选项错误；D、菱形既是轴对称图形又是中心对称图形，此选项正确；故选：C．4．如图，菱形ABCD的对角线AC、BD的长分别是6cm、8cm，AE⊥BC于点E，则AE的长是（）A．cm B．cm C．cm D．5cm【分析】根据菱形的性质得出BO、CO的长，在RT△BOC中求出BC，利用菱形面积等于对角线乘积的一半，也等于BC×AE，可得出AE的长度．【解答】解：∵四边形ABCD是菱形，∴CO=AC=3cm，BO=BD=4cm，AO⊥BO，∴BC==5cm，∴S菱形ABCD==×6×8=24cm2，∵S菱形ABCD=BC×AE，∴BC×AE=24，∴AE=cm．故选：B．5．如图，四边形ABCD中，对角线相交于点O，E、F、G、H分别是AD、BD、BC、AC的中点，要使四边形EFGH是菱形，则四边形ABCD需满足的条件是（）A．AB=AD B．AC=BD C．AD=BC D．AB=CD【分析】由点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点，根据三角形中位线的性质，可得EF=GH=AB，EH=FG=CD，又由当EF=FG=GH=EH时，四边形EFGH是菱形，即可求得答案．【解答】解：∵点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点，∴EF=GH=AB，EH=FG=CD，∵当EF=FG=GH=EH时，四边形EFGH是菱形，∴当AB=CD时，四边形EFGH是菱形．故选：D．6．如图，菱形ABCD的周长为16，面积为12，P是对角线BD上一点，分别作P点到直线AB、AD的垂线段PE、PF，则PE+PF等于（）A．6 B．3 C．1.5 D．0.75【分析】连AP，由菱形ABCD的周长为16，根据了菱形的性质得AB=AD=4，并且S菱形ABCD=2S△ABD，则S△=×12=6，由于S△ABD=S△APB+S△APD，再根据三角形的面积公式得到•PE•AB+•PF•AD=6，即可得到ABDPE+PF的值．【解答】解：连AP，如图，∵菱形ABCD的周长为16，∴AB=AD=4，∴S菱形ABCD=2S△ABD，∴S△ABD=×12=6，而S△ABD=S△APB+S△APD，PE⊥AB，PF⊥AD，∴•PE•AB+•PF•AD=6，∴2PE+2PF=6，∴PE+PF=3．故选B．7．若菱形的周长为52cm，面积为120cm2，则它的对角线之和为（）A．14cm B．17cm C．28cm D．34cm【分析】作出图形，根据菱形的对角线互相垂直平分可得AC⊥BD，AO=CO=AC，BO=DO=BD，然后根据菱形的面积等于对角线乘积的一半列式整理可得AO•BO=60，根据菱形的周长求出AB=13，再利用勾股定理可得AO2+BO2=169，然后利用完全平方公式整理并求出AO+BO，再求解即可．【解答】解：如图，∵四边形ABCD是菱形，∴AC⊥BD，AO=CO=AC，BO=DO=BD，∵菱形的面积为120cm2，∴AC•BD=120，即×2AO•2BO=120，所以，AO•BO=60，∵菱形的周长为52cm，∴AB=13cm，在Rt△AOB中，由勾股定理得，AO2+BO2=AB2=132=169，所以，（AO+BO）2=AO2+2AO•BO+BO2=169+60×2=289，所以，AO+BO=17，所以，AC+BD=2（AO+BO）=2×17=34cm．故选D．8．如图，作菱形ABCD的高AE，E为CD的中点．AE=cm，则菱形ABCD的周长是（）A．4cm B．4cm C．4cm D．8cm【分析】通过解直角三角形ADE得到边AD的长度，然后由菱形的周长公式进行解答．【解答】解：在菱形ABCD中，AD=CD．∵E为CD的中点，AE⊥CD，∴ED=CD=AD，∴∠DAE=30°，∵AE=cm，∴AD===2（cm），∴菱形ABCD的周长=4AD=8cm．故选：D．9．如图，菱形ABCD中，过A作BD的平行线交CD的延长线于点E，下列结论：（1）∠EAC=90°，（2）DA=DE，（3）∠ABC=2∠E，其中正确的有（）A．0个B．1个C．2个D．3个【分析】根据菱形的性质、平行线的性质、平行四边形的判定和性质等知识一一判断即可．【解答】解：∵四边形ABCD是菱形，∴AC⊥BD，AB∥CD，AB=AD，∠ABC=2∠ABD，∵AE∥BD，∴AE⊥AC，∴∠EAC=90°，故①正确，∵AB∥DE，AE∥BD，∴四边形ABDE是平行四边形，∴AB=DE，∠E=∠ABD，∴AD=DE，故②正确，∴∠ABC=2∠E，故③正确，故选D．10．如图，以△ABC的三边为边在BC的同侧分别作三个等边三角形，即△ABD、△BCE、△ACF，当△ABC 满足什么条件时，四边形ADEF是菱形？（）A．AB=AC B．∠BAC=90°C．∠BAC=120°D．∠BAC=150°【分析】根据等边三角形性质得出BD=AB，BE=BC，∠DBA=∠EBC=60°，求出∠DBE，证△DBE≌△ABC，推出DE=AC=AF，同理AD=EF得出平行四边形ADEF，根据菱形的判定判断即可．【解答】解：∵△ABD和△BCE是等边三角形，∴BD=AB，BE=BC，∠DBA=∠EBC=60°，∴∠DBE=∠CBA=60°﹣∠EBA，在△DBE和△ABC中，，∴△DBE≌△ABC（SAS），∴DE=AC，∵△AFC是等边三角形，∴AF=AC，∴AF=DE，同理AD=EF，∴四边形ADEF是平行四边形，当AB=AC时，∵AD=AB，AC=AF，∴AD=AF，∴四边形ADEF是菱形，故选A．11．已知菱形的周长为4，两条对角线的和为6，则菱形的面积为（）A．2 B．C．3 D．4【分析】由菱形的性质和勾股定理得出AO+BO=3，AO2+BO2=AB2，（AO+BO）2=9，求出2AO•BO=4，即可得出答案．【解答】解：如图四边形ABCD是菱形，AC+BD=6，∴AB=，AC⊥BD，AO=AC，BO=BD，∴AO+BO=3，∴AO2+BO2=AB2，（AO+BO）2=9，即AO2+BO2=5，AO2+2AO•BO+BO2=9，∴2AO•BO=4，∴菱形的面积=AC•BD=2AO•BO=4；故选：D．12．四个点A，B，C，D在同一平面内，从①AB∥CD；②AB=CD；③AC⊥BD；④AD=BC；⑤AD∥BC，这五个条件中任选三个，能使四边形ABCD是菱形的选法有（）A．1种B．2种C．3种D．4种【分析】由平行四边形的判定方法和菱形的判定方法得出能使四边形ABCD是菱形的选法有4种，即可得出结论．【解答】解：∵AB∥CD，AB=CD，∴四边形ABCD是平行四边形，∵AC⊥BD，∴四边形ABCD是菱形；∴①②③能使四边形ABCD是菱形；∵AB∥CD，AD∥BC，∴四边形ABCD是平行四边形，∵AC⊥BD，∴四边形ABCD是菱形；∴①③⑤能使四边形ABCD是菱形；∵AD=BC，AD∥BC，∴四边形ABCD是平行四边形，∵AC⊥BD，∴四边形ABCD是菱形；∴③④⑤能使四边形ABCD是菱形；∵AB=CD，AD=BC，∴四边形ABCD是平行四边形，∵AC⊥BD，∴四边形ABCD是菱形；∴②③④能使四边形ABCD是菱形；∴能使四边形ABCD是菱形的选法有4种．故选：D．13．已知：如图，在菱形ABCD中，F为边AB的中点，DF与对角线AC交于点G，过G作GE⊥AD于点E，若AB=2，且∠1=∠2，则下列结论不正确的是（）A．DF⊥AB B．CG=2GA C．CG=DF+GE D．S四边形BFGC=﹣1【分析】A、由四边形ABCD是菱形，得出对角线平分对角，求得∠GAD=∠2，得出AG=GD，AE=ED，由SAS证得△AFG≌△AEG，得出∠AFG=∠AEG=90°，即可得出A正确；B、由DF⊥AB，F为边AB的中点，证得AD=BD，证出△ABD为等边三角形，得出∠BAC=∠1=∠2=30°，由AC=2AB•cos∠BAC，AG=，求出AC，AG，即可得出B正确；C、由勾股定理求出DF=，由GE=tan∠2•ED求出GE，即可得出C正确；D、由S四边形BFGC=S△ABC﹣S△AGF求出数值，即可得出D不正确．【解答】解：∵四边形ABCD是菱形，∴∠FAG=∠EAG，∠1=∠GAD，AB=AD，∵∠1=∠2，∴∠GAD=∠2，∴AG=GD，∵GE⊥AD，∴GE垂直平分AD，∴AE=ED，∵F为边AB的中点，∴AF=AE，在△AFG和△AEG中，，∴△AFG≌△AEG（SAS），∴∠AFG=∠AEG=90°，∴DF⊥AB，∴A正确；∵DF⊥AB，F为边AB的中点，∴AF=AB=1，AD=BD，∵AB=AD，∴AD=BD=AB，∴△ABD为等边三角形，∴∠BAD=∠BCD=60°，∴∠BAC=∠1=∠2=30°，∴AC=2AB•cos∠BAC=2×2×=2，AG===，∴CG=AC﹣AG=2﹣=，∴CG=2GA，∴B正确；∵GE垂直平分AD，∴ED=AD=1，由勾股定理得：DF===，GE=tan∠2•ED=tan30°×1=，∴DF+GE=+==CG，∴C正确；∵∠BAC=∠1=30°，∴△ABC的边AC上的高等于AB的一半，即为1，FG=AG=，S四边形BFGC=S△ABC﹣S△AGF=×2×1﹣×1×=﹣=，∴D不正确；故选：D．14．如图，O是菱形ABCD的对角线AC、BD的交点，E、F分别是OA、OC的中点．下列结论：①S△ADE=S；②四边形BFDE也是菱形；③四边形ABCD的面积为EF×BD；④∠ADE=∠EDO；⑤△DEF是轴对称△EOD图形．其中正确的结论有（）A．5个B．4个C．3个D．2个【分析】①正确，根据三角形的面积公式可得到结论．②根据已知条件利用菱形的判定定理可证得其正确．③正确，根据菱形的面积等于对角线乘积的一半即可求得．④不正确，根据已知可求得∠FDO=∠EDO，而无法求得∠ADE=∠EDO．⑤正确，由已知可证得△DEO≌△DFO，从而可推出结论正确．【解答】解：①正确∵E、F分别是OA、OC的中点．∴AE=OE．∵S△ADE=×AE×OD=×OE×OD=S△EOD∴S△ADE=S△EOD．②正确∵四边形ABCD是菱形，E，F分别是OA，OC的中点．∴EF⊥OD，OE=OF．∵OD=OD．∴DE=DF．同理：BE=BF∴四边形BFDE是菱形．③正确∵菱形ABCD的面积=AC×BD．E、F分别是OA、OC的中点．∴EF=AC．∴菱形ABCD的面积=EF×BD．④不正确，由已知可求得∠FDO=∠EDO，而无法求得∠ADE=∠EDO．⑤正确∵EF⊥OD，OE=OF，OD=OD．∴△DEO≌△DFO．∴△DEF是轴对称图形．∴正确的结论有四个，分别是①②③⑤，故选B．15．如图，在Rt△ABC中，∠ACB=90°，AC=BC=6cm，动点P从点A出发，沿AB方向以每秒cm的速度向终点B运动；同时，动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动，将△PQC沿BC 翻折，点P的对应点为点P′．设Q点运动的时间为t秒，若四边形QP′CP为菱形，则t的值为（）A．B．2 C． D．3【分析】首先连接PP′交BC于O，根据菱形的性质可得PP′⊥CQ，可证出PO∥AC，根据平行线分线段成比例可得=，再表示出AP、AB、CO的长，代入比例式可以算出t的值．【解答】解：连接PP′交BC于O，∵若四边形QPCP′为菱形，∴PP′⊥QC，∴∠POQ=90°，∵∠ACB=90°，∴PO∥AC，∴=，∵设点Q运动的时间为t秒，∴AP=t，QB=t，∴QC=6﹣t，∴CO=3﹣，∵AC=CB=6，∠ACB=90°，∴AB=6，∴=，解得：t=2，故选：B．二．填空题（共9小题）16．如图，在∠MON的两边上分别截取OA、OB，使OA=OB；分别以点A、B为圆心，OA长为半径作弧，两弧交于点C；连接AC、BC、AB、OC．若AB=2cm，四边形OACB的面积为4cm2．则OC的长为4cm．【分析】根据作法判定出四边形OACB是菱形，再根据菱形的面积等于对角线乘积的一半列式计算即可得解．【解答】解：根据作图，AC=BC=OA，∵OA=OB，∴OA=OB=BC=AC，∴四边形OACB是菱形，∵AB=2cm，四边形OACB的面积为4cm2，∴AB•OC=×2×OC=4，解得OC=4cm．故答案为：4．17．如图，四边形ABCD是轴对称图形，且直线AC是对称轴，AB∥CD，则下列结论：①AC⊥BD；②AD ∥BC；③四边形ABCD是菱形；④△ABD≌△CDB．其中正确的是①②③④（只填写序号）【分析】根据轴对称图形的性质，结合菱形的判定方法以及全等三角形的判定方法分析得出答案．【解答】解：因为l是四边形ABCD的对称轴，AB∥CD，则AD=AB，∠1=∠2，∠1=∠4，则∠2=∠4，∴AD=DC，同理可得：AB=AD=BC=DC，所以四边形ABCD是菱形．根据菱形的性质，可以得出以下结论：所以①AC⊥BD，正确；②AD∥BC，正确；③四边形ABCD是菱形，正确；④在△ABD和△CDB中∵∴△ABD≌△CDB（SSS），正确．故答案为：①②③④．18．如图，四边形ABCD中，E，F，G，H分别是边AB、BC、CD、DA的中点．若四边形EFGH为菱形，则对角线AC、BD应满足条件AC=BD．【分析】添加的条件应为：AC=BD，把AC=BD作为已知条件，根据三角形的中位线定理可得，HG平行且等于AC的一半，EF平行且等于AC的一半，根据等量代换和平行于同一条直线的两直线平行，得到HG 和EF平行且相等，所以EFGH为平行四边形，又EH等于BD的一半且AC=BD，所以得到所证四边形的邻边EH与HG相等，所以四边形EFGH为菱形．【解答】解：添加的条件应为：AC=BD．证明：∵E，F，G，H分别是边AB、BC、CD、DA的中点，∴在△ADC中，HG为△ADC的中位线，所以HG∥AC且HG=AC；同理EF∥AC且EF=AC，同理可得EH=BD，则HG∥EF且HG=EF，∴四边形EFGH为平行四边形，又AC=BD，所以EF=EH，∴四边形EFGH为菱形．故答案为：AC=BD19．如图，在△ABC中，点D是BC的中点，点E，F分别在线段AD及其延长线上，且DE=DF．给出下列条件：①BE⊥EC；②BF∥CE；③AB=AC；从中选择一个条件使四边形BECF是菱形，你认为这个条件是③（只填写序号）．【分析】首先利用对角线互相平分的四边形是平行四边形判定该四边形为平行四边形，然后结合菱形的判定得到答案即可．【解答】解：由题意得：BD=CD，ED=FD，∴四边形EBFC是平行四边形，①BE⊥EC，根据这个条件只能得出四边形EBFC是矩形，②BF∥CE，根据EBFC是平行四边形已可以得出BF∥CE，因此不能根据此条件得出菱形，③AB=AC，∵，∴△ADB≌△ADC，∴∠BAD=∠CAD∴△AEB≌△AEC（SAS），∴BE=CE，∴四边形BECF是菱形．故答案为：③．20．如图，菱形ABCD的周长为40，面积为25，P是对角线BD上一点，分别作P点到直线AB、AD的垂线段PE、PF，则PE+PF等于 2.5．【分析】直接利用菱形的性质得出AB=AD=10，S△ABD=12.5，进而利用三角形面积求法得出答案．【解答】解：∵菱形ABCD的周长为40，面积为25，∴AB=AD=10，S△ABD=12.5，∵分别作P点到直线AB、AD的垂线段PE、PF，∴×AB×PE+×PF×AD=12.5，∴×10（PE+PF）=12.5，∴PE+PF=2.5．故答案为：2.5．21．如图，菱形纸片ABCD，∠A=60°，P为AB中点，折叠菱形纸片ABCD，使点C落在DP所在的直线上，得到经过点D的折痕DE，则∠DEC等于75度．【分析】连接BD，由菱形的性质及∠A=60°，得到三角形ABD为等边三角形，P为AB的中点，利用三线合一得到DP为角平分线，得到∠ADP=30°，∠ADC=120°，∠C=60°，进而求出∠PDC=90°，由折叠的性质得到∠CDE=∠PDE=45°，利用三角形的内角和定理即可求出所求角的度数．【解答】解：连接BD，∵四边形ABCD为菱形，∠A=60°，∴△ABD为等边三角形，∠ADC=120°，∠C=60°，∵P为AB的中点，∴DP为∠ADB的平分线，即∠ADP=∠BDP=30°，∴∠PDC=90°，∴由折叠的性质得到∠CDE=∠PDE=45°，在△DEC中，∠DEC=180°﹣（∠CDE+∠C）=75°．故答案为：75．22．如图，菱形ABCD和菱形ECGF的边长分别为3和4，∠A=120°，则图中阴影部分的面积．【分析】作BM⊥FG于M，交EC于N，如图，根据菱形的性质得BC=CD=3，CG=GF=4，AB∥CE∥GF，∠ABC=∠BCD=∠CGF=120°，则∠BCN=∠BGM=60°，再根据含30度的直角三角形三边的关系，在Rt△BCN中可计算出BN=CN=，在Rt△BMG中可计算出BM=GM=，则MN=BM﹣BN=﹣=2，然后根据三角形面积公式和梯形面积公式，利用S阴影部分=S△BCD+S梯形CDFG﹣S△BGF进行计算即可．另一种解法为把阴影部分的面积转化为△BCD的面积进行计算．【解答】解：连接CF，如图，∵四边形ABCD和四边形CGFE为菱形，∠A=120°，∴∠DBC=∠FCG=30°，∴BD∥CF，∴S△FDB=S△CDB=S菱形ABCD=•2••32=．故答案为．23．如图，点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点，当四边形ABCD的边至少满足AB=CD条件时，四边形EFGH是菱形．【分析】首先利用三角形的中位线定理证出EF∥AB，EF=AB，HG∥AB，HG=AB，可得四边形EFGH是平行四边形，再根据邻边相等的平行四边形是菱形，添加条件AB=CD后，证明EF=EH即可．【解答】解：需添加条件AB=CD．∵E，F是AD，DB中点，∴EF∥AB，EF=AB，∵H，G是AC，BC中点，∴HG∥AB，HG=AB，∴EF∥HG，EF=HG，∴四边形EFGH是平行四边形，∵E，H是AD，AC中点，∴EH=CD，∵AB=CD，∴EF=EH，∴四边形EFGH是菱形．故答案为：AB=CD．24．如图，在Rt△ABC中，∠C=90°，AC=BC=6cm，点P从点B出发，沿BA方向以每秒cm的速度向终点A运动；同时，动点Q从点C出发沿CB方向以每秒1cm的速度向终点B运动，将△BPQ沿BC翻折，点P的对应点为点P′．设Q点运动的时间t秒，若四边形QPBP′为正方形，则t的值为2．【分析】根据正方形的判定定理得到BQ=BP时，四边形QPBP′为正方形进行解答即可．【解答】解：由题意得，当△BPQ为等腰直角三角形时，四边形QPBP′为正方形，则BQ=BP，即6﹣t=×t，解得t=2．故答案为：2．三．解答题（共9小题）25．如图，AD是△ABC的角平分线，过点D分别作AC和AB的平行线，交AB于E，交AC于F，求证：四边形AEDF是菱形．【分析】由已知易得四边形AEDF是平行四边形，由角平分线和平行线的定义可得∠FAD=∠FDA，∴AF=DF，∴四边形AEDF是菱形；【解答】证明：∵AD是△ABC的角平分线，∴∠EAD=∠FAD，∵DE∥AC，DF∥AB，∴四边形AEDF是平行四边形，∠EAD=∠ADF，∴∠FAD=∠FDA∴AF=DF，∴四边形AEDF是菱形．26．如图所示，已知四边形ABCD，ADEF都是菱形，∠BAD=∠FAD，∠BAD为锐角．（1）求证：AD⊥BF；（2）若BF=BC，求∠ADC的度数．【分析】（1）连结DB 、DF ．根据菱形四边相等得出AB=AD=FA ，再利用SAS 证明△BAD ≌△FAD ，得出DB=DF ，那么D 在线段BF 的垂直平分线上，又AB=AF ，即A 在线段BF 的垂直平分线上，进而证明AD ⊥BF ；（2）设AD ⊥BF 于H ，作DG ⊥BC 于G ，证明DG=CD ．在直角△CDG 中得出∠C=30°，再根据平行线的性质即可求出∠ADC=180°﹣∠C=150°．【解答】（1）证明：如图，连结DB 、DF ．∵四边形ABCD ，ADEF 都是菱形，∴AB=BC=CD=DA ，AD=DE=EF=FA ．在△BAD 与△FAD 中，，∴△BAD ≌△FAD ，∴DB=DF ，∴D 在线段BF 的垂直平分线上， ∵AB=AF ，∴A 在线段BF 的垂直平分线上，∴AD 是线段BF 的垂直平分线，∴AD ⊥BF ；（2）如图，设AD ⊥BF 于H ，作DG ⊥BC 于G ，则四边形BGDH 是矩形，∴DG=BH=BF ．∵BF=BC ，BC=CD ，∴DG=CD ．在直角△CDG 中，∵∠CGD=90°，DG=CD ，∴∠C=30°，∵BC ∥AD ，∴∠ADC=180°﹣∠C=150°．27．如图，△ABC 中，AB=AC ，∠BAC=40°，将△ABC 绕点A 按逆时针方向旋转100°．得到△ADE ，连接BD ，CE 交于点F ．（1）求证：△ABD ≌△ACE ；（2）求证：四边形ABFE 是菱形．【分析】（1）根据旋转角求出∠BAD=∠CAE ，然后利用“边角边”证明△ABD 和△ACE 全等．（2）根据对角相等的四边形是平行四边形，可证得四边形ABFE 是平行四边形，然后依据邻边相等的平行四边形是菱形，即可证得．【解答】（1）证明：∵ABC绕点A按逆时针方向旋转100°，∴∠BAC=∠DAE=40°，∴∠BAD=∠CAE=100°，又∵AB=AC，∴AB=AC=AD=AE，在△ABD与△ACE中，，∴△ABD≌△ACE（SAS）．（2）证明：∵∠BAD=∠CAE=100°AB=AC=AD=AE，∴∠ABD=∠ADB=∠ACE=∠AEC=40°．∵∠BAE=∠BAD+∠DAE=140°，∴∠BFE=360°﹣∠BAE﹣∠ABD﹣∠AEC=140°，∴∠BAE=∠BFE，∴四边形ABFE是平行四边形，∵AB=AE，∴平行四边形ABFE是菱形．28．如图，AE∥BF，AC平分∠BAE，且交BF于点C，BD平分∠ABF，且交AE于点D，连接CD．（1）求证：四边形ABCD是菱形；（2）若∠ADB=30°，BD=6，求AD的长．【分析】（1）由平行线的性质和角平分线定义得出∠ABD=∠ADB，证出AB=AD，同理：AB=BC，得出AD=BC，证出四边形ABCD是平行四边形，即可得出结论；（2）由菱形的性质得出AC⊥BD，OD=OB=BD=3，再由三角函数即可得出AD的长．【解答】（1）证明：∵AE∥BF，∴∠ADB=∠CBD，又∵BD平分∠ABF，∴∠ABD=∠CBD，∴∠ABD=∠ADB，∴AB=AD，同理：AB=BC，∴AD=BC，∴四边形ABCD是平行四边形，又∵AB=AD，∴四边形ABCD是菱形；（2）解：∵四边形ABCD是菱形，BD=6，∴AC⊥BD，OD=OB=BD=3，∵∠ADB=30°，∴cos∠ADB==，∴AD==2．29．如图，△ABC是以BC为底的等腰三角形，AD是边BC上的高，点E、F分别是AB、AC的中点．（1）求证：四边形AEDF是菱形；（2）如果四边形AEDF的周长为12，两条对角线的和等于7，求四边形AEDF的面积S．【分析】（1）先根据直角三角形斜边上中线的性质，得出DE=AB=AE，DF=AC=AF，再根据AB=AC，点E、F分别是AB、AC的中点，即可得到AE=AF=DE=DF，进而判定四边形AEDF是菱形；（2）设EF=x，AD=y，则x+y=7，进而得到x2+2xy+y2=49，再根据Rt△AOE中，AO2+EO2=AE2，得到x2+y2=36，据此可得xy=，进而得到菱形AEDF的面积S．【解答】解：（1）∵AD⊥BC，点E、F分别是AB、AC的中点，∴Rt△ABD中，DE=AB=AE，Rt△ACD中，DF=AC=AF，又∵AB=AC，点E、F分别是AB、AC的中点，∴AE=AF，∴AE=AF=DE=DF，∴四边形AEDF是菱形；（2）如图，∵菱形AEDF的周长为12，∴AE=3，设EF=x，AD=y，则x+y=7，∴x2+2xy+y2=49，①∵AD⊥EF于O，∴Rt△AOE中，AO2+EO2=AE2，∴（y）2+（x）2=32，即x2+y2=36，②把②代入①，可得2xy=13，∴xy=，∴菱形AEDF的面积S=xy=．30．如图，在四边形ABCD中，AB=AD，CB=CD，E是CD上一点，BE交AC于F，连接DF．（1）证明：∠BAC=∠DAC，∠AFD=∠CFE；（2）若AB∥CD，试证明四边形ABCD是菱形；（3）在（2）的条件下，若BE⊥CD，试证明∠EFD=∠BCD．【分析】（1）先判断出△ABC≌△ADC得到∠BAC=∠DAC，再判断出△ABF≌△ADF得出∠AFB=∠AFD，最后进行简单的推算即可；（2）先由平行得到角相等，用等量代换得出∠DAC=∠ACD，最后判断出四边相等；（3）由（2）得到判断出△BCF≌△DCF，结合BE⊥CD即可．【解答】证明：（1）在△ABC和△ADC中．∴△ABC≌△ADC，∴∠BAC=∠DAC，在△ABF和△ADF中，∴△ABF≌△ADF，∴∠AFB=∠AFD，∵∠CFE=∠AFB，∴∠AFD=∠CFE，∴∠BAC=∠DAC，∠AFD=∠CFE；（2）∵AB∥CD，∴∠BAC=∠ACD，∵∠BAC=∠DAC，∴∠BAC=∠ACD，∴∠DAC=∠ACD，∴AD=CD，∵AB=AD，CB=CD，∴AB=CB=CD=AD，∴四边形ABCD是菱形；（3）∵四边形ABCD是菱形，∴BC=CD，∠BCF=∠DCF，∵CF=CF，∴△BCF≌△DCF，∴∠CBF=∠CDF，∵BE⊥CD，∴∠BEC=∠DEF=90°，∴∠EFD=∠BCD．31．如图，在△ABC中，∠ACB=90°，点D，E分别是边BC，AB上的中点，连接DE并延长至点F，使EF=2DE，连接CE、AF．（1）证明：AF=CE；（2）当∠B=30°时，试判断四边形ACEF的形状并说明理由．【分析】（1）由三角形中位线定理得出DE∥AC，AC=2DE，求出EF∥AC，EF=AC，得出四边形ACEF是平行四边形，即可得出AF=CE；（2）由直角三角形的性质得出∠BAC=60°，AC=AB=AE，证出△AEC是等边三角形，得出AC=CE，即可得出结论．【解答】（1）证明：∵点D，E分别是边BC，AB上的中点，∴DE∥AC，AC=2DE，∵EF=2DE，∴EF∥AC，EF=AC，∴四边形ACEF是平行四边形，∴AF=CE；（2）解：当∠B=30°时，四边形ACEF是菱形；理由如下：∵∠ACB=90°，∠B=30°，∴∠BAC=60°，AC=AB=AE，∴△AEC是等边三角形，∴AC=CE，又∵四边形ACEF是平行四边形，∴四边形ACEF是菱形．32．如图，在△ABC中，∠ABC=90°，BD为AC的中线，过点C作CE⊥BD于点E，过点A作BD的平行线，交CE的延长线于点F，在AF的延长线上截取FG=BD，连接BG、DF．（1）求证：四边形BDFG是菱形；（2）若AF=8，CF=6，求四边形BDFG的面积．【分析】（1）首先可判断四边形BDFG是平行四边形，再由直角三角形斜边中线等于斜边一半，可得BD=FD，则可证明四边形BDFG是菱形；（2）首先过点B作BH⊥AG于点H，由AF=8，CF=6，可利用勾股定理求得AC的长，即可求得DF的长，然后由菱形的性质求得BG=GF=DF=5，再求出EF的长即可解决问题．【解答】证明：（1）∵AG∥BD，BD=FG，∴四边形BGFD是平行四边形，∵CE⊥BD，∴CE⊥AG，又∵BD为AC的中线，∴BD=DF=AC，∴四边形BDFG是菱形，（2）∵AF=8，CF=6，CF⊥AG，∴AC==10，∴DF=AC=5，∵四边形BDFG是菱形，∴BD=GF=DF=5，∵DE∥AG，CD=AD，∴CE=EF=3∴S菱形BDFG=GF•EF=15．33．如图所示，在菱形ABCD中，AB=4，∠BAD=120°，△AEF为正三角形，点E、F分别在菱形的边BC、CD上滑动，且E、F不与B、C、D重合．（1）证明不论E、F在BC、CD上如何滑动，总有BE=CF；（2）当点E、F在BC、CD上滑动时，分别探讨四边形AECF和△CEF的面积是否发生变化？如果不变，求出这个定值；如果变化，求出最大（或最小）值．【分析】（1）先求证AB=AC，进而求证△ABC、△ACD为等边三角形，得∠4=60°，AC=AB进而求证△ABE ≌△ACF，即可求得BE=CF；（2）根据△ABE≌△ACF可得S△ABE=S△ACF，故根据S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC即可解题；当正三角形AEF的边AE与BC垂直时，边AE最短．△AEF的面积会随着AE的变化而变化，且当AE最短时，正三角形AEF的面积会最小，又根据S△CEF=S四边形AECF﹣S△AEF，则△CEF的面积就会最大．【解答】（1）证明：连接AC，如下图所示，∵四边形ABCD为菱形，∠BAD=120°，∠1+∠EAC=60°，∠3+∠EAC=60°，∴∠1=∠3，∵∠BAD=120°，∴∠ABC=60°，∴△ABC和△ACD为等边三角形，∴∠4=60°，AC=AB，∴在△ABE和△ACF中，，∴△ABE≌△ACF（ASA）．∴BE=CF；（2）解：四边形AECF的面积不变，△CEF的面积发生变化．理由：由（1）得△ABE≌△ACF，则S△ABE=S△ACF，故S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC，是定值，作AH⊥BC于H点，则BH=2，S四边形AECF=S△ABC=BC•AH=BC•=4，由“垂线段最短”可知：当正三角形AEF的边AE与BC垂直时，边AE最短．故△AEF的面积会随着AE的变化而变化，且当AE最短时，正三角形AEF的面积会最小，又S△CEF=S四边形AECF﹣S△AEF，则此时△CEF的面积就会最大．∴S△CEF=S四边形AECF﹣S△AEF=4﹣×2×=．答：最大值是．。

菱形的性质与判定复习题含答案

菱形的性质1、菱形具有而一般平行四边形不具有的性质是（）A. 对角相等B. 对边相等C. 对角线互相垂直D. 对角线相等2、菱形的周长为100cm ，一条对角线长为14cm ，它的面积是（） A. 168cm 2B. 336cm 2C. 672cm 2D.84cm 23、下列语句中，错误的是（）A. 菱形是轴对称图形，它有两条对称轴B. 菱形的两组对边可以通过平移而相互得到C. 菱形的两组对边可以通过旋转而相互得到D. 菱形的相邻两边可以通过旋转而相互得到4、菱形的两条对角线分别是6 cm ，8 cm ，则菱形的边长为_____，面积为______．5、四边形ABCD 是菱形，点O 是两条对角线的交点，已知AB ＝5, AO ＝4，求对角线BD 和菱形ABCD 的面积.6、如图，在菱形ABCD 中，∠ADC=120°，则BD ：AC 等于（）．（A ）：2 （B ）：3 （C ）1：2 （D ）：17、菱形ABCD 的周长为20cm ，两条对角线的比为3∶4，求菱形的面积。

8、如左下图，菱形ABCD 的对角线AC 、BD 交于点O ，且AC ＝16cm ，BD ＝12cm ，求菱形ABCD 的高DH 。

3339、如右上图，在菱形ABCD中,∠BAD＝80°，AB的垂直平分线交对角线AC于点F，E为垂足，连接DF，则∠CDF的度数为．10、在菱形ABCD中，∠A与∠B的度数比为1：2，周长是48cm．求：（1）两条对角线的长度；（2）菱形的面积．11、如图所示，在平面直角坐标系中，菱形MNPO的顶点P的坐标是（3，4），则顶点M、N的坐标分别是（）A．M（5，0），N（8，4） B．M（4，0），N（8，4）C．M（5，0），N（7，4） D．M（4，0），N（7，4）12、（2010•襄阳）菱形的周长为8cm，高为1cm，则该菱形两邻角度数比为（）A．3：1 B．4：1 C．5：1 D．6：113、如左下图，菱形ABCD的对角线AC、BD相交于点O，且AC=8，BD=6，过点O作OH丄AB，垂足为H，则点0到边AB的距离OH= _________ ．14、如右上图，菱形ABCD的边长是2cm，E是AB的中点，且DE丄AB，则菱形ABCD的面积为cm2．15、【提高题】如图，在菱形ABCD中，顶点A到边BC、CD的距离AE、AF都为5，EF＝6，那么，菱形ABCD的边长是菱形的判定1、能够判别一个四边形是菱形的条件是（）A. 对角线相等且互相平分B. 对角线互相垂直且相等C. 对角线互相平分D. 一组对角相等且一条对角线平分这组对角2、平行四边形ABCD的两条对角线AC、BD相交于点O, AB=5, AO=2, OB=1. 四边形ABCD 是菱形吗？为什么？3、如左下图，AD是△ABC的角平分线。

22.3菱形的判定常考题(含有详细的答案解析)

菱形的判定2一、选择题1、在平面直角坐标系中，已知点 A (0, 2), B (- 恥,0) , C (0, - 2), D (2方,0),贝U 以这四个点为顶点的四边形ABCD 是( )A 、矩形B 菱形C 正方形D 、梯形2如图，下列条件之一能使平行四边形 ABCD 是菱形的为()① AC 丄 BD ;② / BAD=90°;③ AB=BC ;④ AC=BD .A 、①③B 、②③D 、①②③3、能判定一个四边形是菱形的条件是()A 、对角线相等且互相垂直B 对角线相等且互相平分C 对角线互相垂直D 、对角线互相垂直平分4、四边形的四边长顺次为a 、b 、c 、d ，且a 2+b 2+c 2+d 2=ab+bc+cd+ad ，则此四边形一定是( )A 、平行四边形B 、矩形C 菱形D 、正方形填空2、如图，平行四边形 ABCD 中，AF 、CE 分别是/ BAD 和/BCD 的角平分线，根据现有的图形，请添加一个条件,个即可，图中不能再添加别的点”和线”)3、在四边形 ABCD 中，对角线 AC BD 交于点 0，从(1) AB=CD (2) AB // CD; (3) OA=OC; (4) OB=OD; ( 5)AC 丄BD; (6) AC 平分/ BAD 这六个条件中，选取三个推出四边形 ABCD 是菱形.如(1) (2) ( 5) => ABCD 是菱形, 再写出符合要求的两个： __________________ => ABCD 是菱形； ________________ => ABCD 是菱形C ③④ ABCD 成为一个菱形，需要添加一个条件，那么你添加的条件是使四边形 AECF 为菱形，则添加的一个条件可以(只需写出1、如图，如果要使平行四边形是D 是BC 的中点，连接AD ,在AD 的延长线上取一点E ,连接BE ,(1) 求证：△ ABEBA ACE(2)当AE 与AD 满足什么数量关系时，四边形 ABEC 是菱形？并说明理由.2、如图，在？ABCD 中，E, F 分别为边 AB , CD 的中点，连接 DE 、BF 、BD.(1) 求证：△ ADEBA CBF.(2) 若AD 丄BD ,则四边形BFDE 是什么特殊四边形？请证明你的结论.3、(2007?娄底)如图，已知点 D 在厶ABC 的BC 边上，DE// AC 交AB 于E , DF// AB 交AC于F .(1) 求证：AE=DF ;(2) 若AD 平分/ BAC,试判断四边形 AEDF 的形状，并说明理由.ABCD 中，AB// CD, BC=CD AD 丄 BD , E 为 AB 中点，求证：四边形 BCDE 是5、如图，在 △ ABC 和厶DCB 中，AB=DC AC=DB, AC 与DB 交于点 M .(1) 求证：△ ABCBA DCB;(2) 过点C 作CN// BD,过点B 作BN // AC, CN 与BN 交于点N ,试判断线段BN 与CN 的数量关系，并证明你的结论.A三、解答题(共11小题)菱形.6如图，△ ABC中，AC的垂直平分线MN交AB于点D,交AC于点O, CE// AB交MN于E,连接AE、CD.(1)求证：AD=CE(2)_________________________________________ 填空：四边形ADCE的形状是 .7如图△ ABC与厶CDE都是等边三角形，点E、F分别在AC BC上，且EF// AB(1)求证：四边形EFCD是菱形；(2)设CD=4,求D、F两点间的距离.8 (2007?双柏县)如图，在梯形纸片ABCD中，AD// BC, AD>CD,将纸片沿过点D的直线折叠，使点C落在AD上的点C处，折痕DE 交BC于点E,连接C'.求证：四边形CDC E是菱形.9已知：如图，平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别相交于点E、F. 求证：四边形AFCE是菱形.A E D/A/B F C10、如图，等边△ ABC的边长为2, E是边BC上的动点，EF// AC交边AB于点F,在边AC上取一点P,使PE=EB 连接FP.(1)请直接写出图中与线段EF相等的两条线段；(不再另外添加辅助线)(2)探究：当点E在什么位置时，四边形EFPC是平行四边形？并判断四边形EFPC是什么特殊的平行四边形，请说明理由；(1)11若如图，在四边形ABCD中，点E、F分别是AD BC的中点，G H分别是BDAC的中点，AB CD满足什么条件时，四边形EGFH是菱形？请证明你的结论。

22.3菱形的性质常考题(含详细的解析)

22.3菱形的性质常考题一、选择题（共18小题）1、（2009•长春）菱形OABC在平面直角坐标系中的位置如图所示．∠AOC=45°，OC=，则点B的坐标为（）A、（，1）B、（1，）C、（+1，1）D、（1，+1）2、（2010•盐城）如图：在菱形ABCD中，AC=6，BD=8，则菱形的边长为（）A、5B、10C、6D、83、（2010•南通）如图，在菱形ABCD中，AB=5，∠BCD=120°，则对角线AC等于（）A、20B、15C、10D、54、（2010•北京）菱形的两条对角线的长分别是6和8，则这个菱形的周长是（）A、24B、20C、10D、55、（2009•河池）已知菱形的边长和一条对角线的长均为2cm，则菱形的面积为（）A、3cm2B、4cm2C、cm2D、2cm26、（2009•杭州）如图，在菱形ABCD中，∠A=110°，E，F分别是边AB和BC的中点，EP⊥CD于点P，则∠FPC=（）A、35°B、45°C、50°D、55°7、（2008•台州）如图，在菱形ABCD中，对角线AC、BD相交于点O，E为AB的中点，且OE=a，则菱形ABCD的周长为（）A、16aB、12aC、8aD、4a8、（2008•江汉区）如图，四边形ABCD是菱形，过点A作BD的平行线交CD的延长线于点E，则下列式子不成立的是（）A、DA=DEB、BD=CEC、∠EAC=90°D、∠ABC=2∠E9、（2007•嘉兴）如图，在菱形ABCD中，不一定成立的是（）A、四边形ABCD是平行四边形B、AC⊥BDC、△ABD是等边三角形D、∠CAB=∠CAD10、（2005•扬州）如图是一个利用四边形的不稳定性制作的菱形晾衣架．已知其中每个菱形的边长为20cm，墙上悬挂晾衣架的两个铁钉A、B之间的距离为20cm，则∠1等于（）A、90°B、60°C、45°D、30°11、（2005•济宁）已知菱形的边长为6cm，一个内角为60°，则菱形较短的对角线长是（）A、6cmB、cmC、3cmD、cm12、（2004•重庆）如图，在菱形ABCD中，∠BAD=80°，AB的垂直平分线交对角线AC于点F，点E为垂足，连接DF，则∠CDF为（）A、80°B、70°C、65°D、60°13、在菱形ABCD中，AE⊥BC，AF⊥CD，且E，F分别为BC，CD的中点，那么∠EAF的度数为（）A、75°B、60°C、45°D、30°14、菱形的周长等于高的8倍，则此菱形的较大内角是（）A、60°B、90°C、120°D、150°15、在菱形ABCD中，AC与BD相交于点O，则下列说法不正确的是（）A、AO⊥BOB、∠ABD=∠CBDC、AO=BOD、AD=CD16、菱形的周长为20cm，两邻角的比为1：2，则较长的对角线长为（）A、4.5cmB、4cmC、5cmD、4cm17、已知菱形的两条对角线长分别为4cm和10cm，则菱形的边长为（）A、116cmB、29cmC、cmD、cm18、菱形的周长为20cm，两邻角的比为1：3，则菱形的面积为（）A、25cm2B、16cm2C、cm2D、cm2二、填空题（共12小题）19、（2006•泉州）菱形ABCD的一条对角线长为6，边AB的长是方程x2﹣7x+12=0的一个根，则菱形ABCD的周长为_________．20、（2008•陕西）如图，菱形ABCD的边长为2，∠ABC=45°，则点D的坐标为_________．21、（2009•临沂）如图，在菱形ABCD中，∠ADC=72°，AD的垂直平分线交对角线BD于点P，垂足为E，连接CP，则∠CPB=_________度．22、（2008•肇庆）边长为5cm的菱形，一条对角线长是6cm，则另一条对角线的长是_________cm．23、（2003•盐城）已知菱形ABCD的对角线AC=6cm，BD=8cm，则菱形的边长是_________cm．24、如图，在由12个边长都为1且有一个锐角为60°的小菱形组成的网格中，点P是其中的一个顶点，以点P为直角顶点作格点直角三角形（即顶点均在格点上的三角形），请你写出所有可能的直角三角形斜边的长_________．25、（2011•长沙）已知菱形的两条对角线长分别是6cm和8cm，则周长是_________cm．26、（2009•江西）如图，一活动菱形衣架中，菱形的边长均为16cm，若墙上钉子间的距离AB=BC=16cm，则∠1= _________度．27、（2009•本溪）如图所示，菱形ABCD中，对角线AC，BD相交于点O，H为AD边中点，菱形ABCD的周长为24，则OH的长等于_________．28、（2008•镇江）如图所示，两个全等菱形的边长为1厘米，一只蚂蚁由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动，行走2008厘米后停下，则这只蚂蚁停在_________点．29、（2008•温州）如图，菱形ABCD中，∠A=60°，对角线BD=8，则菱形ABCD的周长等于_________．30、（2008•恩施州）已知菱形的两对角线长分别为6cm和8cm，则菱形的面积为_________cm2．答案与评分标准一、选择题（共18小题）1、（2009•长春）菱形OABC在平面直角坐标系中的位置如图所示．∠AOC=45°，OC=，则点B的坐标为（）A、（，1）B、（1，）C、（+1，1）D、（1，+1）考点：坐标与图形性质；菱形的性质。

菱形的判定配套练习-含答案

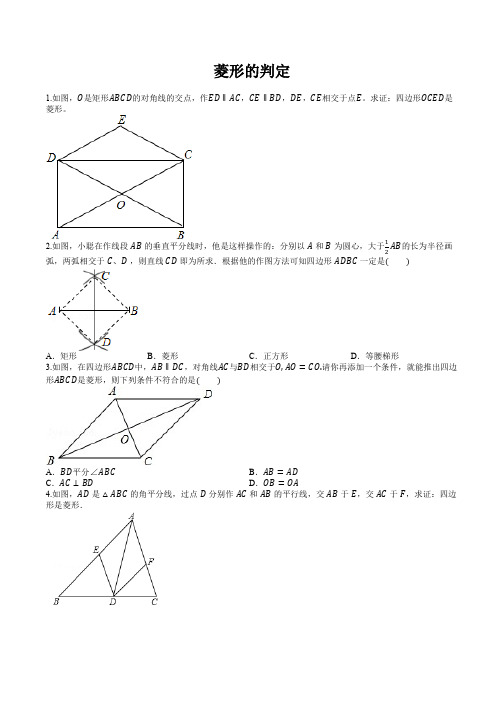
菱形的判定1.如图，O是矩形ABCD的对角线的交点，作ED∥AC，CE∥BD，DE，CE相交于点E。

求证：四边形OCED是菱形。

AB的长为半径画2.如图，小聪在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于12弧，两弧相交于C、D，则直线CD即为所求．根据他的作图方法可知四边形ADBC一定是()A．矩形B．菱形C．正方形D．等腰梯形3.如图，在四边形ABCD中，AB∥DC，对角线AC与BD相交于O,AO=CO.请你再添加一个条件，就能推出四边形ABCD是菱形，则下列条件不符合的是()A．BD平分∠ABC B．AB=ADC．AC⊥BD D．OB=OA4.如图，AD是△ABC的角平分线，过点D分别作AC和AB的平行线，交AB于E，交AC于F，求证：四边形是菱形．5.如图，在▱ABCD中，BD是对角线，且DB⊥BC，E,F分别为边AB、CD的中点．求证：四边形DEBF是菱形．6.如图，在△ABC中，AD是∠BAC的平分线，EF垂直平分AD交AB于E，交AC于F．求证：四边形AEDF是菱形．7.如图，在平行四边形ABCD中，E为BC边上的一点，连结AE，BD，且AE=AB.(1) 求证：∠ABE=∠EAD;(2) 若∠AEB=2∠ADB，求证：四边形ABCD是菱形8.如图，在平行四边形ABCD中，E是AD边上的中点，连接BE，并延长BE交CD的延长线于点F．(1) 求证：△ABE≅△DFE；(2) 连接BD、AF，当BE平分∠ABD时，求证：四边形ABDF是菱形．9.如图，在菱形ABCD中，E、F为对角线BD的三等分点．求证：四边形AFCE是菱形．10.如图，在平行四边形ABCD中，BD的垂直平分线EF与AD交于点E，与BC交于点F，与BD交于点O．(1) 证明：OE=OF．(2) 证明：四边形BEDF是菱形．11.如图，在平行四边形ABCD中，对角线AC，BD交于点O，点E，点F在BD上，且BE=DF，连接AE 并延长，交BC于点G，连接CF并延长，交AD于点H．(1) 求证：△AOE≅△COF；(2) 若AC平分∠HAG，求证：四边形AGCH是菱形．12.如图，在四边形ABCD中，AB=AD，CB=CD，点F是AC上一点，连接BF，DF．(1) 求证：△ABF≅△ADF；(2) 若AB∥CD，求证：四边形ABCD是菱形．13.如图，在△ABC中，AD⊥BC于点D，点D，E，F分别是BC，AB，AC的中点．求证：四边形AEDF是菱形．14.如图，平行四边形ABCD的边CD的垂直平分线与边DA，BC的延长线分别交于点E，F，与边CD交于点O，连接CE，DF．(1) 求证：DE=CF；(2) 请判断四边形ECFD的形状，并证明你的结论．菱形的判定1.【答案】略【解析】∵DE∥AC,CE∥BD，∴四边形OCED是平行四边形，∵四边形ABCD是矩形，∴AC与BD相等且互相平分，∴OD=OC，∴四边形OCED是菱形．2.【答案】B【解析】根据做法可知：AC=CB=BD=AD，故四边形ADBC是菱形3.【答案】D【解析】由已知条件可得△AOB≌△COD，AB=CD，∴四边形ABCD是平行四边形，∴AD=BC，A．∵BD平分∠ABC，∴∠ABO=∠CBO，∴∠CBO=∠CDO，∴CB=CD，∴AB=BC=CD=AD，∴四边形ABCD是菱形；故A正确；B．∵AB=AD，∴AB=BC=CD=AD，∴四边形ABCD是菱形；故B正确；C．AC⊥BD,AO=CO，∴AB=BC，∴AB=BC=CD=AD，∴四边形ABCD是菱形；故C正确；D．OB=OA，能判定四边形是矩形，故D不正确，选D．【备注】菱形的判定4.【答案】略【解析】∵AD是△ABC的角平分线∴∠EAD=∠FAD∵DE // AC，DF // AB∴四边形AEDF是平行四边形，∠EAD=∠ADF∴∠FAD=∠FDA∴AF=DF∴四边形AEDF是菱形5.【答案】略【解析】∵DB⊥BC，F是边CD的中点∴BF=12CD∴BF=DF∵四边形ABCD是平行四边形∴AB // CD∴∠ADB=∠CBD=90∘∵E是边AB的中点∴DE=12AB∴DE=BE∵AB=CD∵BE=DF∴BF=DF=DE=BE∴四边形DEBF是菱形6.【答案】略【解析】∵AD平分∠BAC∴∠BAD=∠CAD又∵EF⊥AD∴∠AOE=∠AOF=90∘∵△AEO与△AFO中{∠EAO=∠FAO AO=AO∠AOE=∠AOF∴△AEO≅△AFO(ASA)∴EO=FO∵EF垂直平分AD∴EF、AD相互平分∴四边形AEDF是平行四边形又EF⊥AD∴平行四边形AEDF为菱形7.(1)【答案】略【解析】在平行四边形ABCD中，AD∥BC,∴∠AEB=∠EAD,∵AE=AB,∴∠ABE=∠AEB,∴∠ABE=∠EAD;(2)【答案】略【解析】∵AD∥BC,∴∠ADB=∠DBE,∵∠ABE=∠AEB,∠AEB=2∠ADB,∴∠ABE=2∠ADB,∴∠ABD=∠ABE−∠DBE=2∠ADB−∠ADB=∠ADB,∴AB =AD,又∵四边形ABCD 是平行四边形，∴四边形ABCD 是菱形．8.(1)【答案】略【解析】∵ 四边形 ABCD 为平行四边形，∴AB ∥CD ．∵ 点 F 在 CD 的延长线上，∴FD ∥AB ．∴∠ABE =∠DFE ．∵E 是 AD 中点，∴AE =DE ．在 △ABE 和 △DFE 中，∵{∠ABE =∠DFE∠BEA =∠DEF AE =DE∴△ABE ≅△DFE ；(2)【答案】略【解析】∵△ABE ≅△DFE ，∴AB =DF ．∵AB ∥DF ，AB =DF ，∴ 四边形 ABDF 是平行四边形．∵BF 平分 ∠ABD ，∴∠ABF =∠DBF ．∵AB ∥DF ，∴∠ABF =∠DFB ，∴∠DBF =∠DFB ．∵DB =DF ．∴ 四边形 ABDF 是菱形．9.【答案】略【解析】如图，连接 AC ，交 BD 于点 O ．∵ 四边形 ABCD 是菱形，∴ AC ⊥BD ，OA =OC ，OD =OB ．又 E ，F 为对角线 DB 的三等分点，∴ DE =BF ．又OE=OD−DE，OF=OB−BF，∴OE=OF．∴四边形AECF为平行四边形．又AC⊥BD，∴四边形AFCE是菱形．10.(1)【答案】略【解析】∵EF是BD的垂直平分线，四边形ABCD是平行四边形，∴OD=OB，AD∥BC，∴∠EDB=∠FBD，又∠EOD=∠FOB，∴△ODE≅△OBF，∴OE=OF．(2)【答案】略【解析】∵EF⊥BD，∴四边形EBFD的对角线垂直互相平分，∴四边形EBFD是菱形．11.(1)【答案】略【解析】如图．在平行四边形ABCD中，对角线AC，BD交于点O，∴AO=CO，BO=DO．∵BE=DF，∴BO−BE=DO−DF．即EO=FO．在△AOE和△COF中，{EO=FO,∠1=∠2, AO=CO.∴△AOE≅△COF．(2)【答案】略【解析】由（1），△AOE≅△COF．∴∠3=∠4．∴AG∥CH．在平行四边形 ABCD 中，AD ∥BC ，即 AH ∥GC ． ∴ 四边形 AGCH 是平行四边形．∵AC 平分 ∠HAG ，∴∠4=∠5．∴∠3=∠5．∴HA =HC ，∴ 四边形 AGCH 是菱形．12.(1)【答案】略【解析】在 △ABC 与 △ADC 中∵ {AB =ADCB =CD AC =AC∴ △ABC ≅△ADC ，∴ ∠BAC =∠DAC ，在 △ABF 与 △ADF 中∵ {AB =AD∠BAF =∠DAF AF =AF∴ △ABF ≅△ADF ．(2)【答案】略【解析】由（1）得 ∠BAC =∠DAC ，∵ AB ∥CD ，∴ ∠BAC =∠DCA ，∴ ∠DAC =∠DCA ，∴ DA =DC ，∵ AB =AD ，CB =CD ，∴ AB =AD =CB =CD ．∴ 四边形 ABCD 是菱形．13.【答案】∵ 点 D ，E ，F 分别是 BC ，AB ，AC 的中点， ∴DE ∥AC ，DF ∥AB ．∴ 四边形 AEDF 是平行四边形．又 AD ⊥BC ，BD =DC ，∴AB =AC ．∴AE =AF ．∴ 平行四边形 AEDF 是菱形．14.(1)【答案】略【解析】 ∵ 四边形 ABCD 是平行四边形，∴AD ∥BC ，∴∠EDO =∠FCO ，∠DEO =∠CFO ，∵EF平分CD，∴DO=CO，∴△EOD≅△FOC，∴DE=CF．(2)【答案】四边形ECFD是菱形．【解析】∵EF是CD的垂直平分线，∴DE=EC，CF=DF，又DE=CF，∴DE=EC=CF=DF，∴四边形ECFD是菱形．。

菱形的判定(含答案)

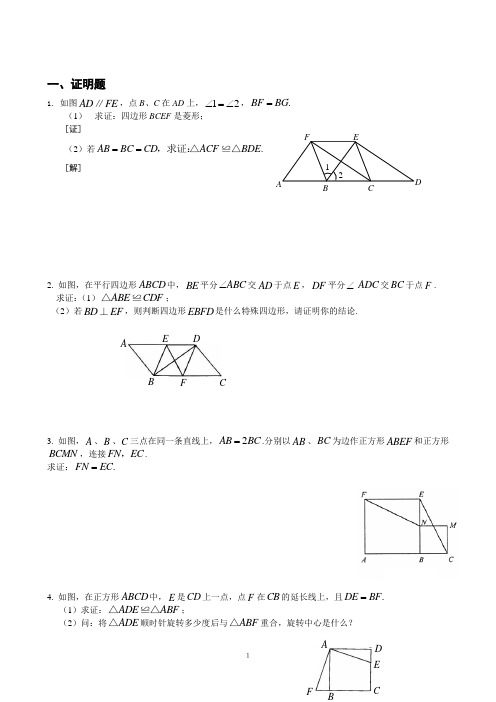
１一、证明题1. 如图AD FE ∥，点B 、C 在AD 上，12∠=∠，.BF BG =（1）求证：四边形BCEF 是菱形； [证]（2）若.AB BC CD ACF BDE ==，求证：△≌△ [解]2. 如图，在平行四边形ABCD 中，BE 平分ABC ∠交AD 于点E ，DF 平分∠ADC 交BC 于点F . 求证：（1）ABE CDF △≌；（2）若BD EF ⊥，则判断四边形EBFD 是什么特殊四边形，请证明你的结论.3. 如图，A 、B 、C 三点在同一条直线上，2AB BC =.分别以AB 、BC 为边作正方形ABEF 和正方形BCMN ，连接FN EC ，. 求证：.FN EC =4. 如图，在正方形ABCD 中，E 是CD 上一点，点F 在CB 的延长线上，且.DE BF = （1）求证：ADE ABF △≌△；（2）问：将ADE △顺时针旋转多少度后与ABF △重合，旋转中心是什么？FEB ACD12FDEC AB ADB CE BBF２5. 如图，在正方形ABCD 中，G 是BC 上的任意一点（G 与B C 、两点不重合），E F 、是AG 上的两点（E F 、与A G 、两点都不重合），若AF BF EF =+，12∠=∠，请判断线段DE 与BF 有怎样的位置关系，并证明你的结论.6. 如图，四边形ABCD 是平行四边形，AC 、BD 交于点O ，∠1 =∠2．（1）求证：四边形ABCD 是矩形；（2）若∠BOC =120°，AB = 4cm ，求四边形ABCD 的面积．2 ABCDEF G 1D３7. 如图，在ABC △中，AB AC ，D 为BC 中点.四边形ABDE 是平行四边形. 求证：四边形ADCE 是矩形.8. 如图，菱形ABCD 的对角线AC 与BD 相交于点O ，点E 、F 分别为边AB 、AD 的中点，连接EF 、OE 、OF .求证：四边形AEOF 是菱形.9. 在正方形ABCD 中，AC 为对角线，E 为AC 上一点，连接EB 、ED ．（1）求证：△BEC ≌△DEC ；（2）延长BE 交AD 于F ，当∠BED =120°时，求∠A F DB E O４CD10. 已知：如图，在正方形ABCD 中，点E 、F 分别在BC 和CD 上，AE = AF ．（1）求证：BE = DF ；（2）连接AC 交EF 于点O ，延长OC 至点M ，使OM = OA ，连接EM 、FM ．判断四边形AEMF 是什么特殊四边形？并证明你的结论．证明：（1）（2）11. 如图，四边形ABCD 是边长为a 的正方形，点G ，E 分别是边AB ，BC 的中点，∠AEF =90o ，且EF 交正方形外角的平分线CF 于点F ．（1）证明：∠BAE =∠FEC ；（2）证明：△AGE ≌△ECF ；（3）求△AEF 的面积．12. 如图，已知四边形ABCD 是菱形， DE ⊥AB ，DF ⊥BC . 求证:△ADE ≌△CDF .A DB E FO C５13. 已知梯形ABCD 中，BC AD //，AD AB = (如图所示)．BAD ∠的平分线AE 交BC 于点E ，联结DE ． (1) 在图中，用尺规作BAD ∠的平分线AE (保留作图痕迹，不写作法)，并证明四边形ABED 是菱形；(2) 若︒=∠60ABC ，BE EC 2=，求证：DC ED ⊥．14. 如图，正方形ABCD 中，E F 、分别是AB BC 、边上的点，且.AE BF =求证.AF DE ⊥15. 如图，将矩形纸片ABCD 沿EF 折叠，使点A 与点C 重合，点D 落在点G 处，EF 为折痕．（1）求证：FGC EBC △≌△；（2）若84AB AD ==，，求四边形ECGF （阴影部分）的面积．A BC D D C F B E A６16. 如图，在△ABC 中，D 是BC 边的中点，E 、F 分别在AD 及其延长线上，CE ∥BF ，连接BE 、CF ．（1）求证：△BDF ≌△CDE ；（2）若AB ＝AC ，求证：四边形BFCE 是菱形．一、证明题1. （1）证：2.AD FE FEB ∴∠=∠∥，12 1.FEB ∠=∠∴∠=∠，..BF BC BC EF BF EF =∴=∴=，∴四边形BCEF 是平行四边形.BF BC =，∴四边形BCEF 是菱形. （5分）（2）证：EF BC AB BC CD AD FE ===，，∥，∴四边形ABEF 、四边形CDEF 均为平行四边形，AF BE FC ED ∴==，.（8分）又2AC BC BD ==，.ACF BDE ∴△≌△ （10分）2. 证明：（1）∵四边形ABCD 是平行四边形，∴A C AB CD ABC ADC ∠=∠=∠=∠，，∵BE 平分ABC ∠，DF 平分ADC ∠，∴ABE CDF ∠=∠ 2′ ∴()ABE CDF ASA △≌△4′ （2）由ABE CDF △≌△，得AE CF =5′在平行四边形ABCD 中，AD BC AD BC =∥，７∴DE BF DE BF =∥，∴四边形EBFD 是平行四边形 6′ 若BD EF ⊥，则四边形EBFD 是菱形 8′3. 证明：在正方形ABEF 和正方形BCMN 中，90AB BE EF BC BN FEN EBC ===∠=∠=，，°. （2分） 2AB BC =， .EN BC ∴=（4分） FEN EBC ∴△≌△. （5分）.FN EC ∴= （6分）4. （1）证明：在正方形ABCD 中， 90D ABC AD AB ∠=∠==°，，（1分） 90ABF D ABF ∴∠=∴∠=∠°，，（3分）又DE BF =，4分）ADE ABF ∴△≌△；5分）（2）将ADE △顺时针旋转90度后与ABF △重合，（7分）旋转中心是A 点．（9分）5. 根据题目条件可判断.DE BF ∥证明如下：∵四边形ABCD 为正方形，∴ 290AB AD BAF ∠+∠==，°． ∵,AF AE EF =+又,AF BF EF =+ ∴AE BF =，∵12,∠=∠∴().ABF DAE SAS △≌△5分∴AFB DEA ∠=∠，BAF ADE ∠=∠. ∴290ADE ∠+∠=°.∴90AED BFA ∠=∠=°. ∴.DE BF ∥ 9分6. （1）∵∠1 =∠2，∴BO=CO 即2 BO=2CO （1分） ∵四边形ABCD 是平行四边形∴ AO=CO ，BO=OD （2分）即AC=2CO ，BD= 2 BO ∴AC= BD （3分）∵四边形ABCD 是平行四边形 ∴四边形ABCD 是矩形（4分）（2）在△BOC 中，∠BOC =120°， ∴ ∠1 =∠2 =（180°—120°）÷2 = 30° （5分） ∴在Rt △ABC 中，AC=2AB=2⨯4=8(cm )，D８∴BC=344822=-(cm ) （6分） ∴四边形ABCD 的面积=24)= （7分）7. 证明：四边形ABDE 是平行四边形， AE BC ∴∥，AB DE =，.AE BD = 2分 D 为BC 中点， ∴.CD BD =3分.CD AE CD AE ∴=∥∴四边形ADCE 是平行四边形.5分AB AC =， ∴.AC DE =∴平行四边形ADCE 是矩形.7分8. 证明：点E F 、分别为AB AD 、的中点，1122AE AB AF AD ∴=，=． 2分又四边形ABCD 是菱形， AB AD ∴=． AE AF ∴=．４分又菱形ABCD 的对角线AC 与BD 相交于点O ， O ∴为BD 的中点.OE OF ∴、是ABD △的中位线. 6分 OE AD OF AB ∴∥，∥．∴四边形AEOF 是菱形. 10分9. （1）证明：∵四边形ABCD 是正方形∴BC ＝CD ，∠ECB ＝∠ECD ＝45°又EC ＝EC …………………………2分 ∴△ABE ≌△ADE ……………………3分（2）∵△ABE ≌△ADE∴∠BEC ＝∠DEC ＝12∠BED …………4分 ∵∠BED ＝120°∴∠BEC ＝60°＝∠AEF ……………5分 ∴∠EFD ＝60°+45°＝105° …………………………6分10. 证明：（1）∵四边形ABCD 是正方形，AF DBEO９∴AB ＝AD ,∠B = ∠D = 90°． ∵AE = AF ，∴Rt Rt ABE ADF △≌△． ∴BE ＝DF ．4分（2）四边形AEMF 是菱形．∵四边形ABCD 是正方形， ∴∠BCA = ∠DCA = 45°，BC = DC ．∵BE ＝DF ，∴BC －BE = DC －DF . 即CE CF =． ∴OE OF =． ∵OM = OA ，∴四边形AEMF 是平行四边形． ∵AE = AF ，∴平行四边形AEMF 是菱形．8分11. （1）证明：∵∠AEF =90°，∴∠FEC +∠AEB =90°．………………………………………1分在Rt △ABE 中，∠AEB +∠BAE =90°，∴∠BAE =∠FEC ；……………………………………………3分（2）证明：∵G ，E 分别是正方形ABCD 的边AB ，BC 的中点，∴AG=GB=BE=EC ，且∠AGE =180°－45°=135°．又∵CF 是∠DCH 的平分线，∴∠ECF =90°+45°=135°．………………………………………4分在△AGE 和△ECF 中，135AG EC AGE ECF GAE FEC =⎧⎪∠=∠=⎨⎪∠=∠⎩，，AD BEF O C１０∴△AGE ≌△ECF ； …………………………………………6分（3）解：由△AGE ≌△ECF ，得AE=EF ．又∵∠AEF =90°，∴△AEF 是等腰直角三角形．………………………………7分由AB=a ，BE =21a ，知AE =25a ， ∴S △AEF =85a 2．…………………………9分12. 证明：在△ADE 和△CDF 中,∵四边形ABCD 是菱形,∴∠A =∠C ，AD =CD .……………………2分又DE ⊥AB ，DF ⊥BC ,∴∠AED =∠CFD =900.……………………4分∴△ADE ≌△CDF . ……………………6分13. (1) 图略（有作图痕迹，且正确）．证明：∵AE 为BAD ∠的平分线，∴DAE BAE ∠=∠．又∵BC AD //，∴AEB DAE ∠=∠．∴AEB BAE ∠=∠．∴BE AB =． ∵AB AD =，∴BE AD =．∵BE AD //，∴四边形ABED 是平行四边形． ∵AB AD =，∴四边形ABED 是菱形．(2)证明：由(1) 知，四边形ABED 是菱形，∴AB DE //，BE DE =． ∴︒=∠=∠60ABC DEC ．(方法一)设线段EC 中点为F ，联结DF ，则FC EF =． ∵BE EC 2=，BE DE =．∴FC EF DE ==． ∵︒=∠60DEF ，∴△DEF 为等边三角形．∴︒=∠=∠60EFD EDF ，FC EF DF ==．∴FCD FDC ∠=∠．∴FDC FCD FDC DFE ∠=∠+∠=∠2．∴︒=∠30FDC ．∴︒=∠+∠=∠90FDC EDF EDC ，即DC DE ⊥．(方法二)作EC DH ⊥，垂足为H ，则︒=∠30EDH ．∴在Rt △DEH 中，ED EH 21=，ED DH 23=． ∵BE DE =，BE EC 2=，∴ED HC 23=．在Rt △DCH 中，3tan ==∠DHHCCDH ．∴︒=∠60CDH ．∴︒=∠+∠=∠90EDH CDH EDC ，即DC DE ⊥．14. 证明：四边形ABCD 为正方形90DA ABDAE ABF ∴=∠=∠=° 又AE BF =DAE ABF ∴△≌△ADE BAF ∴∠=∠（4分）90ADE AED ∠+∠=°90BAF AED ∴∠+∠=°AF DE ∴⊥ （3分）15. （1）证明：四边形ABCD 是矩形， 90A B BCD D AD BC ∴∠=∠=∠=∠==°，． ······························································ 1分将矩形纸片ABCD 沿EF 折叠，点A 与点C 重合，点D 落在点G 处，90G D ∴∠=∠=°，90ECG A CG AD ∠=∠==°，， ·················································· 2分 9090G B CG BC ECG BCD ∴∠=∠==∠=∠=°，，°，90GCF BCE FCE ∴∠=∠=∠°-， ·················································································· 3分 FGC EBC ∴△≌△． ·········································································································· 4分（2）解：由（1）得FGC EBC △≌△，EBCF ECGF AEFD S S S ∴==四边形四边形四边形，2ABCD ECGF AEFD EBCF S S S S ∴=+=矩形四边形四边形四边形，11841222ABCD ECGF S S ∴==⨯⨯=矩形四边形． ······································································· 6分16. （1）证明：∵ D 是BC 的中点，∴BD =CD ．………………………………1分 ∵CE ∥BF ∴∠DBF=∠DCE ． ………………………………………………2分又∵∠BDF=∠CDE ， …………………………………………………………3分 ∴△BDF ≌△CDE ． ……………………………………………………………4分（2）证明：∵△CDE ≌△BDF ，∴DE ＝DF ．………………………………5分 ∵BD ＝CD ，∴四边形BFCE 是平行四边形．…………………………………6分在△ABC 中，∵AB ＝AC ，BD =CD ． ∴AD ⊥BC ，即EF ⊥BC ．……………7分 ∴平行四边形BFCE 是菱形． …………………………………………………8分（另解）∵△CDE ≌△BDF ，∴CE ＝BF ． ……………………………………5分 ∵CE ∥BF ，∴四边形BFCE 是平行四边形．……………………………………6分 ∴BE =CF ．在△ABC 中，∵AB ＝AC ，BD =CD ．∴AD ⊥BC ，即AD 垂直平分BC ，∴BE =CE ．…………………………………7分 ∴平行四边形BFCE 是菱形． ……………………………………………………8分。

菱形的性质与判定复习题

菱形练习题知识点1 菱形的定义菱形的定义：有一组邻边相等的平行四边形叫做菱形;数学语言：如图,在平行四边形ABCD中,如果AB=AD,那么平行四边形ABCD 是菱形;知识点2 菱形的性质（1）菱形的四条边都相等；（2）菱形的两条对角线互相垂直,并且每一条对角线平分一组对角；（3）对称性：既是关于对角线的交点成中心对称图形,又是以对角线所在直线为对称轴的轴对称图形；（4）菱形的面积公式：①菱形的面积=底×高；②菱形的面积=两条对角线乘积的一半巩固练习1．菱形的对角线长分别为6和8,则菱形的边为 ,菱形的面积为 ;2．若菱形周长为52cm,一条对角线长为10cm,则其面积为A．240 cm2 B．120 cm2 C．60 cm2 D．30 cm23．如下图,菱形ABCD中,O是对角线AC BDAO=,则，的交点,5cmAB=,4cmBD=____________cm．4、如上图,菱形ABCD的对角线AC、BD相交于点O,且AC＝8,BD＝6,过点O作OH丄AB,垂足为H,则点O到边AB的距离___________5．一个菱形两条对角线之比为1︰2,一条较短的对角线长为4cm,那么菱形的边长为A ．2cmB ．4cmC ．(225)cm +D ．25cm6．如图,菱形ABCD 的边长为2,45ABC ∠=,则点D 的坐标为．7．如图,将一个长为10cm,宽为8cm 的矩形纸片对折两次后,沿所得矩形两邻边中点的连线虚线剪下,再打开,得到的菱形的面积为A ．210cmB ．220cmC ．240cmD ．280cm8.如图所示,菱形ABCD 中,对角线AC BD 、相交于点O ,H 为AD 边中点,菱形ABCD 的周长为24,则OH 的长等于． 9．菱形ABCD 中,AE 垂直平分BC ,垂足为E ,AB ＝4cm ．那么,菱形ABCD 的面积是 ,对角线BD 的长是． 10．如图,点E ,F 分别是菱形ABCD 中BC ,CD 边上的点E ,F 不与B ,C ,D 重合在不连辅助线的情况下请添加一个条件,说明AE ＝AF ．11、如图,在菱形ABCD 中,AE⊥BC,E 为垂足.且BE=CE,AB=2.求：1∠BAD 的度数；2对角线AC 的长及菱形ABCD 的周长.AD CE BO B AD x yC B AHD CO12．如图,在菱形ABCD 中,E 是AB 的中点,且DE ⊥AB ,AB ＝4．求：1∠ABC 的度数；2菱形ABCD 的面积． 13.在菱形ABCD 中,对角线AC 与BD 相交于点O,AB=5,AC=6.过点D 作DE∥AC 交BC 的延长线于点E.1求△BDE 的周长； 2点P 为线段BC 上的点,连接PO 并延长交AD 于点Q,求证：BP=DQ. 14．如图,四边形ABCD 是菱形,DE ⊥AB 交BA 的延长线于E ,DF ⊥BC ,交BC 的延长线于F ;请你猜想DE 与DF 的大小有什么关系并证明你的猜想．有一个角为60°的特殊菱形1．若菱形的边长为1cm,其中一内角为60°,则它的面积为A ．23cm 2B ．23cmC ．22cmD ．223cm 2．已知菱形的周长为96㎝,两个邻角的比是1︰2,则较短对角线的长是A ．21㎝B ．22㎝C ．23㎝D ．24㎝3．如图,在菱形ABCD 中,60A ∠=°,E 、F 分别是AB 、AD 的中点,若2EF =,则菱形ABCD 的边长是_____________．4．如图,菱形ABCD 中,∠B ＝60°,AB ＝2,E 、F 分别是B C ．CD 的中点,连接AE 、EF 、AF ,则△AEF 的周长为A ． 32B ． 33C ． 34D ． 3提高题1．如图,菱形111AB C D 的边长为1,160B ∠=；作211AD B C ⊥于点2D ,以2AD 为一边,做第二个菱形222AB C D ,使260B ∠=；作322AD B C ⊥于点3D ,以3AD 为一边做第三个菱形333AB C D ,使360B ∠=；依此类推,这样做的第n 个菱形n n n AB C D 的边n AD 的长是． A D FC E B2．如图,在菱形ABCD 中,∠A ＝110°,E ,F 分别是边AB 和BC 的中点,EP ⊥CD 于点P ,则∠FPC ＝A ．35° B．45° C．50° D．55°知识点3 菱形的判定方法（1）有一组邻边相等的平行四边形是菱形；（2）对角线互相垂直的平行四边形是菱形；（3）四条边都相等的四边形是菱形.1．把菱形ABCD 沿对角线AC 的方向平移到菱形A′B′C′D′的位置,它们重叠部分的四边形A′FCE 是A ．正方形B ．矩形C ．菱形D ．不确定2．如图,下列条件之一能使平行四边形ABCD 是菱形的为①AC BD ⊥ ②90BAD ∠= ③AB BC = ④AC BD =A ．①③B ．②③C ．③④D ．①②③ 3．如图,□ABCD 中,AE 、CF 分别是∠BAD 和∠BCD 的角平分线,根据现有的图形,请添加一个条件,使四边形AECF 为菱形,则添加的一个条件可以是只需写出一个即可,图中不能再添加别的“点”和“线”.4．如图,在三角形ABC 中,AB ＞AC ,D 、E 分别是AB 、AC 上的点,△ADE 沿线段DE 翻折,使点A 落在边BC 上,记为A '．若四边形ADA E '是菱形,则下列说法正确的是1D B A C BCDB DC ABC DA．DE是△ABC的中位线 B．AA'是BC边上的中线C．AA'是BC边上的高 D．AA'是△ABC的角平分线5．四个点A,B,C,D在同一平面内,从①AB∥CD；②AB=CD；③AC⊥BD；④AD= BC；⑤AD∥BC．这5个条件中任选三个,能使四边形ABCD是菱形的选法有．A．1种 B．2种 C．3种 D．4种证明题1.如图,在△ABC中,AB=AC,点D、E、F分别是AB、BC、AC的中点,求证：四边形ADEF是菱形2．两个完全相同的矩形纸片ABCD、BFDE如图放置,AB＝BF．求证：四边形BNDM为菱形．3、如图,将两张等宽的长方形纸条交叉叠放,重叠部分是一个四边形ABCD,若AD=6cm,∠ABC=60°,则四边形ABCD的面积等于__________cm2．4、如图,在平行四边形ABCD中,∠DAB＝60°,AB＝2AD,点 E、F分别是CD的中点,过点A 作AG∥BD,交CB的延长线于点G;求证：四边形DEBF是菱形;5、如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,且AF=CE=AE．1说明四边形ACEF是平行四边形；2当∠B满足什么条件时,四边形ACEF是菱形,并说明理由;6．在矩形ABCD中,AB＝6cm, BC＝8cm,若将矩形对角线BD对折,使B点与D 点重合,折痕为EF,问：四边形EBFD是菱形吗请说明理由,并求这个菱形的边长．7．如图,□ABCD中,AB⊥AC,AB＝1,BC＝5．对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F．1证明：当旋转角为90°时,四边形ABEF是平行四边形；2试说明在旋转过程中,线段AF与EC总保持相等；3在旋转过程中,四边形BEDF可能是菱形吗如果不能,请说明理由；如果能,画出图形并写出此时AC绕点O顺时针旋转的度数．8．如图,ABC△中,点O是边AC上一个动点,过O作直线MN BC∥,设MN交BCA∠的平分线于点E,交BCA∠的外角平分线于点F．1探究：线段OE与OF的数量关系并加以证明；2当点O在边AC上运动时,四边形BCFE有可能是菱形吗若是,请证明,若不是,则说明理由AF NDCBM E O。

菱形地判定专项练习30题

实用标准
菱形的判定专项练习 30 题（有答案）
1．如图，梯形 ABCD中， AD∥BC， BA=AD=DC=BC，点 E 为 BC的中点．（ 1）求证：四边形 ABED是菱形；（ 2）过 A 点作 AF⊥BC于点 F，若 BD=4cm，求 AF的长．
2．如图，四边形 ABCD中，对角线 AC、BD相交于点 O，且 AC⊥ BD．点 M，N 分别在 BD、AC上，且 AO=ON=N，CBM=MO=O．D 求证： BC=2DN．
3．如图，在△ ABC中， AB=AC， D， E， F 分别是 BC， AB，AC的中点．（ 1）求证：四边形 AEDF是菱形；（ 2）若 AB=12cm，求菱形 AEDF的周长．
4．如图，在 ? ABCD中， EF∥BD，分别交 BC， CD于点 P，Q，交 AB， AD的延长线于点求证：（ 1）∠ E=∠ F；（ 2） ? ABCD是菱形．
22．如图所示，在 ? ABCD中，点 E 在 BC上， AE平分∠ BAF，过点 E 作 EF∥AB．求证：四边形 ABEF为菱形．
23．已知，如图，矩形 ABCD中， AB=4cm， AD=8cm，作∠ CAE=∠ ACE交 BC于 E，作∠ ACF=∠ CAF交 AD于 F．（ 1）求证： AECF是菱形；（2）求四边形 AECF的面积．
精彩文档
实用标准
11．如图，在△ ABC中， AB=AC，点 D、E、 F 分别是△ ABC三边的中点．求证：四边形 ADEF是菱形．
12．如图，在四边形 ABCD中， AB=CD，M、 N、 E、 F 分别为 AD、 BC、BD、 AC的中点，求证：四边形 MENF为菱形．
13．已知：如图，在梯形 ABCD中， AD∥ BC，AB=AD，∠ BAD的平分线 AE交 BC于点 E，连接 DE．求证：四边形 ABED 是菱形．

菱形的判定专项练习题

菱形的判定专项练习30题（有答案）1．如图，梯形ABCD中，AD∥BC，BA=AD=DC=BC，点E为BC的中点．（1）求证：四边形ABED是菱形；（2）过A点作AF⊥BC于点F，若BD=4cm，求AF的长．2．如图，四边形ABCD中，对角线AC、BD相交于点O，且AC⊥BD．点M，N分别在BD、AC上，且AO=ON=NC，BM=MO=OD．求证：BC=2DN．3．如图，在△ABC中，AB=AC，D，E，F分别是BC，AB，AC的中点．（1）求证：四边形AEDF是菱形；（2）若AB=12cm，求菱形AEDF的周长．4．如图，在▱ABCD中，EF∥BD，分别交BC，CD于点P，Q，交AB，AD的延长线于点E，F．已知BE=BP．求证：（1）∠E=∠F；（2）▱ABCD是菱形．5．如图，在△ABC中，D是BC的中点，E是AD的中点，过点A作AF∥BC，AF与CE的延长线相交于点F，连接BF．（1）求证：AF=DC；（2）若∠BAC=90°，求证：四边形AFBD是菱形．6．已知平行四边形ABCD中，对角线BD平分∠ABC，求证：四边形ABCD是菱形．7．如图，在一个含30°的三角板ABC中，将三角板沿着AB所在直线翻转180°得到△ABF，再将三角板绕点C顺时针方向旋转60°得到△DEC，点F在AC上，连接AE．（1）求证：四边形ADCE是菱形．（2）连接BF并延长交AE于G，连接CG．请问：四边形ABCG是什么特殊平行四边形？为什么？8．如图，已知四边形ABCD是平行四边形，DE⊥AB，DF⊥BC，垂足分别是为E F，并且DE=DF．求证：四边形ABCD是菱形．9．如图，在△ABC中，DE∥BC，分别交AB，AC于点D，E，以AD，AE为边作▱ADFE交BC于点G，H，且EH=EC．求证：（1）∠B=∠C；（2）▱ADFE是菱形．10．如图，在△ABC中，∠ACB=90°，CD是AB边上的高，∠BAC的平分线AE交CD于F，EG⊥AB于G．（1）求证：△AEG≌△AEC；（2）△CEF是否为等腰三角形，请证明你的结论；（3）四边形GECF是否为菱形，请证明你的结论．11．如图，在△ABC中，AB=AC，点D、E、F分别是△ABC三边的中点．求证：四边形ADEF是菱形．12．如图，在四边形ABCD中，AB=CD，M、N、E、F分别为AD、BC、BD、AC的中点，求证：四边形MENF 为菱形．13．已知：如图，在梯形ABCD中，AD∥BC，AB=AD，∠BAD的平分线AE交BC于点E，连接DE．求证：四边形ABED是菱形．14．如图，在△ABC中，AB=AC，M、O、N分别是AB、BC、CA的中点．求证：四边形AMON是菱形．15．如图：在△ABC中，∠BAC=90°，AD⊥BC于D，CE平分∠ACB，交AD于G，交AB于E，EF⊥BC于F．求证：四边形AEFG是菱形．16．如图，矩形ABCD绕其对角线交点旋转后得矩形AECF，AB交EC于点N，CD交AF于点M．求证：四边形ANCM是菱形．17．如图，四边形ABCD、DEBF都是矩形，AB=BF，AD、BE交于M，BC、DF交于N，那么四边形BMDN是菱形吗？如果是，请写出证明过程；如果不是，说明理由．18．已知如图所示，AD是△ABC的角平分线，DE∥AC交AB于E，DF∥AB交AC于F，四边形AEDF是菱形吗？说明理由．19．已知：如图所示，BD是△ABC的角平分线，EF是BD的垂直平分线，且交AB于E，交BC于点F．求证：四边形BFDE是菱形．20．如图，在平行四边形ABCD中，O是对角线AC的中点，过点O作AC的垂线与边AD、BC分别交于E、F．求证：四边形AFCE是菱形．21．如图，在矩形ABCD中，EF垂直平分BD．（1）判断四边形BEDF的形状，并说明理由．（2）已知BD=20，EF=15，求矩形ABCD的周长．22．如图所示，在▱ABCD中，点E在BC上，AE平分∠BAF，过点E作EF∥AB．求证：四边形ABEF为菱形．23．已知，如图，矩形ABCD中，AB=4cm，AD=8cm，作∠CAE=∠ACE交BC于E，作∠ACF=∠CAF交AD于F．（1）求证：AECF是菱形；（2）求四边形AECF的面积．24．如图，平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F．问四边形AFCE是菱形吗？请说明理由．25．如图：在平行四边形ABCD中，E、F分别是边AB、CD的延长线上一点，且BE=DF，连接EF交AC于O．（1）AC与EF互相平分吗？为什么？（2）连接CE、AF，再添加一个什么条件，四边形AECF是菱形？为什么？26．已知：如图，△ABC和△DBC的顶点在BC边的同侧，AB=DC，AC=BD交于E，∠BEC的平分线交BC于O，延长EO到F，使EO=OF．求证：四边形BFCE是菱形．27．如图，在△ABC中，D是BC边的中点，F，E分别是AD及其延长线上的点，CF∥BE．（1）求证：△BDE≌△CDF；（2）请连接BF，CE，试判断四边形BECF是何种特殊四边形，并说明理由；（3）在（2）下要使BECF是菱形，则△ABC应满足何条件？并说明理由．28．如图，在△ABC中，∠ACB=90°，BC的垂直平分线DE交BC于D，交AB于E，F在DE上，并且AF=CE．（1）求证：四边形ACEF是平行四边形；（2）当∠B的大小满足什么条件时，四边形ACEF是菱形？请回答并证明你的结论．29．如图，在△ABC中，AD是∠BAC的平分线，EF垂直平分AD交AB于E，交AC于F．求证：四边形AEDF是菱形．30．如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA 的外角平分线于点F．（1）探究：线段OE与OF的数量关系并加以证明；（2）当点O运动到何处，且△ABC满足什么条件时，四边形AECF是正方形？（3）当点O在边AC上运动时，四边形BCFE会是菱形吗？若是，请证明，若不是，则说明理由．矩形的判定专项练习30题参考答案：1．1）证明：∵点E为BC的中点，∴BE=CE=BC，∵BA=AD=DC=BC，∴AB=BE=ED=AD，∴四边形ABED是菱形；（2）解：过点D作DH⊥BC，垂足为H，∵CD=DE=CE，∴∠DEC=60°，∴∠DBE=30°，在Rt△BDH中，BD=4cm，∴DH=2cm，∵AF=DH，∴AF=2cm．2．∵AO=ON，BM=MO，∴四边形AMND是平行四边形，∵AC⊥BD，∴平行四边形AMND是菱形，∴MN=DN，∵ON=NC，BM=MO，∴MN=BC，∴BC=2DN 3．（1）∵D，E分别是BC，AB的中点，∴DE∥AC且DE=AF=AC．同理DF∥AB且DF=AE=AB．又∵AB=AC，∴DE=DF=AF=AE，∴四边形AEDF是菱形．（2）∵E是AB中点，∴AE=AB=6cm，因此菱形AEDF的周长为4×6=24cm．4．（1）∵BE=BP，∴∠E=∠BPE，∵BC∥AF，∴∠BPE=∠F，∴∠E=∠F．（2）∵EF∥BD，∴∠E=∠ABD，∠F=∠ADB，∴∠ABD=∠ADB，∴AB=AD，∵四边形ABCD是平行四边形，∴□ABCD是菱形．5．1）证明：∵E是AD的中点，∴∠1=∠2，在△AEF和△DEC 中，∴△AFE≌△DCE（AAS），∴AF=DC；（2）证明：∵D是BC的中点，∴DB=CD=BC，∵AF=CD，∴AF=DB，∵AF∥BD，∴四边形AFBD是平行四边形，∵∠BAC=90°，D为BC中点，∴AD=CB=DB，∴四边形AFBD是菱形．6．∵对角线BD平分∠ABC，∴∠1=∠2，∵四边形ABCD是平行四边形，∴AB∥DC，∴∠3=∠1，∴∠3=∠2，∴DC=BC，又∵四边形ABCD是平行四边形，∴四边形ABCD是菱形．7．（1）∵三角板ABC中，将三角板沿着AB所在直线翻转180°得到△ABF，∴△ABC≌△ABF，且∠BAC=∠BAF=30°，∴∠FAC=60°，∴AD=DC=AC，又∵△ABC≌△EFC，∴CA=CE，又∵∠ECF=60°，∴AC=EC=AE，∴AD=DC=CE=AE，（2）证明：由（1）可知：△ACD，△AFC是等边三角形，△ACB≌△AFB，∴∠EDC=∠BAC=∠FAC=30°，且△ABC为直角三角形，∴BC=AC，∵EC=CB，∴EC=AC，∴E为AC中点，∴DE⊥AC，∴AE=EC，∵AG∥BC，∴∠EAG=∠ECB，∠AGE=∠EBC，∴△AEG≌△CEB，∴AG=BC，（7分）∴四边形ABCG是平行四边形，∵∠ABC=90°，∴四边形ABCG是矩形8．在△ADE和△CDF中，∵四边形ABCD是平行四边形，∴∠A=∠C，∵DE⊥AB，DF⊥BC，∴∠AED=∠CFD=90°．又∵DE=DF，∴△ADE≌△CDF（AAS）∴DA=DC，∴平行四边形ABCD是菱形9．（1）∵在▱ADFE中，AD∥EF，∴∠EHC=∠B（两直线平行，同位角相等）．∵EH=EC（已知），∴∠EHC=∠C（等边对等角），∴∠B=∠C（等量代换）；（2）∵DE∥BC（已知），∴∠AED=∠C，∠ADE=∠B．∵∠B=∠C，∴∠AED=∠ADE，∴AD=AE，∴▱ADFE是菱形．10．1）证明：∵∠ACB=90°，∴AC⊥EC．在Rt△AEG与Rt△AEC中，，∴Rt△AEG≌Rt△AEC（HL）；（2）解：△CEF是等腰三角形．理由如下：∵CD是AB边上的高，∴CD⊥AB．又∵EG⊥AB，∴EG∥CD，∴∠CFE=∠GEA．又由（1）知，Rt△AEG≌Rt△AEC，∴∠GEA=∠CEA，∴∠CEA=∠CFE，即∠CEF=∠CFE，∴CE=CF，即△CEF是等腰三角形；（3）解：四边形GECF是菱形．理由如下：∵由（1）知，Rt△AEG≌Rt△AEC，则GE=EC；由（2）知，CE=CF，∴GE=EC=FC．又∵EG∥CD，即GE∥FC，∴四边形GECFR是菱形．11．∵D、E、F分别是△ABC三边的中点，∴DE AC，EF AB，∴四边形ADEF为平行四边形．又∵AC=AB，∴DE=EF．∴四边形ADEF为菱形．12．∵M、E、分别为AD、BD、的中点，∴ME∥AB，ME=AB，同理：FH∥AB，FH=AB，∴四边形MENF是平行四边形，∵M．F是AD，AC中点，∴MF=DC，∵AB=CD，∴MF=ME，∴四边形MENF为菱形13．∵AE平分∠BAD，∵，∴△BAE≌△DAE（SAS）…（2分）∴BE=DE，…（3分）∵AD∥BC，∴∠DAE=∠AEB，…（4分）∴∠BAE=∠AEB，∴AB=BE，…（5分）∴AB=BE=DE=AD，…（6分）∴四边形ABED是菱形．14．∵AB=AC，M、O、N分别是AB、BC、CA的中点，∴AM=AB=AC=AN，M0∥AC，NO∥AB，且MO=AC=AN，NO=AB=AM（三角形中位线定理），∴AM=MO=AN=NO，∴四边形AMON是菱形（四条边都相等的四边形是菱形）15．证法一：∵AD⊥BC，∴∠ADB=90°，∵∠BAC=90°，∴∠B+∠BAD=90°，∠BAD+∠CAD=90°，∴∠B=∠CAD，∵CE平分∠ACB，EF⊥BC，∠BAC=90°（EA⊥CA），∴AE=EF（角平分线上的点到角两边的距离相等），∵CE=CE，∴由勾股定理得：AC=CF，∵△ACG和△FCG中，∴△ACG≌△FCG，∴∠CAD=∠CFG，∵∠B=∠CAD，∴∠B=∠CFG，∴GF∥AB，∵AD⊥BC，EF⊥BC，∴AD∥EF，即AG∥EF，AE∥GF，∴平行四边形AEFG是菱形．证法二：∵AD⊥BC，∠CAB=90°，EF⊥BC，CE平分∠ACB，∴AD∥EF，∠4=∠5，AE=EF，∵∠1=180°﹣90°﹣∠4，∠2=180°﹣90°﹣∠5，∴∠1=∠2，∵AD∥EF，∴∠2=∠3，∴∠1=∠3，∴AG=AE，∵AE=EF，∴AG=EF，∵AG∥EF，∴四边形AGFE是平行四边形，∵AE=EF，∴平行四边形AGFE是菱形．16．∵CD∥AB，∴∠FMC=∠FAN，∴∠NAE=∠MCF（等角的余角相等），在△CFM和△AEN中，，∴△CFM≌△AEN（ASA），∴CM=AN，∴四边形ANCM为平行四边形，在△ADM和△CFM中，，∴△ADM≌△CFM（AAS），∴AM=CF，∴四边形ANCM是菱形17．四边形BMDN是菱形．∵AM∥BC，∴∠AMB=∠MBN，∵BM∥FN∴∠MBN=∠BNF，∴∠AMB=∠BNF，又∵∠A=∠F=90°，AB=BF，∴△ABM≌△BFN，∴DM=DN，∵ED=BF=AB，∠E=∠A=90°，∠AMB=∠EMD，∴△ABM≌△EDM，∴BM=DM，∴MB=MD=DN=BN，∴四边形BMDN是菱形18．如图，由于DE∥AC，DF∥AB，所以四边形AEDF 为平行四边形．∵DE∥AC，∴∠3=∠2，又∠1=∠2，∴∠1=∠3，∴AE=DE，∴平行四边形AEDF为菱形．19．∵EF是BD的垂直平分线，∴EB=ED，∴∠EBD=∠EDB．∵BD是△ABC的角平分线，∴∠EBD=∠FBD．∴∠FBD=∠EDB，∴ED∥BF．同理，DF∥BE，∴四边形BFDE是平行四边形．又∵EB=ED，∴四边形BFDE是菱形．20．方法一：∵AE∥FC．∴∠EAC=∠FCA．（2分）又∵∠AOE=∠COF，AO=CO，∴△AOE≌△COF．（5分）∴EO=FO．又EF⊥AC，∴AC是EF的垂直平分线．（8分）∴AF=AE，CF=CE，又∵EA=EC，∴AF=AE=CE=CF．∴四边形AFCE为菱形．（10分）方法二：同方法一，证得△AOE≌△COF．（5分）∴AE=CF．∴四边形AFCE是平行四边形．（8分）又∵EF是AC的垂直平分线，方法三：同方法二，证得四边形AFCE是平行四边形．（8分）又EF⊥AC，（9分）∴四边形AFCE为菱形21．（1）四边形BEDF是菱形．在△DOF和△BOE中，∠FDO=∠EBO，OD=OB，∠DOF=∠BOE=90°，所以△DOF≌△BOE，所以OE=OF．又因为EF⊥BD，OD=OB，所以四边形BEDF为菱形．（5分）（2）如图，在菱形EBFD中，BD=20，EF=15，则DO=10，EO=7.5．由勾股定理得DE=EB=BF=FD=12.5．S菱形EBFD =EF•BD=BE•AD，即所以得AD=12．根据勾股定理可得AE=3.5，有AB=AE+EB=16．由2（AB+AD）=2（16+12）=56，故矩形ABCD的周长为5622．∵四边形ABCD是平行四边形，∴AF∥BE，又∵EF∥AB，∴四边形ABEF为平行四边形，∵AE平分∠BAF，∴∠BAE=∠FAE，∵∠FAE=∠BEA，∴∠BAE=∠BEA，∴BA=BE，∴平行四边形ABEF为菱形23．（1）证明：在矩形ABCD中，∵AB∥CD，∴∠BAC=∠DCA，又∠CAE=∠ACE，∠ACF=∠CAF，∴∠EAC=∠FCA．∴AE∥CF．∴四边形AECF为平行四边形，又∠CAE=∠ACE，∴AE=EC．∴▱AECF为菱形．（2）设BE=x，则EC=AE=8﹣x，在Rt△ABE中，AB2+BE2=AE2，所以EC=5，即S菱形AECF=EC×AB=5×4=20．24．四边形AFCE是菱形，理由是：∵四边形ABCD是平行四边形，∴AD∥BC，∴=，∵AO=OC，∴OE=OF，∴四边形AFCE是平行四边形，∵EF⊥AC，∴平行四边形AFCE是菱形25．（1）AC与EF互相平分，连接CE，AF，∵平行四边形ABCD，∴AB∥CD，AB=CD，又∵BE=DF，∴AB+BE=CD+DF，∴AE=CF，∴AE∥CF，AE=CF，∴四边形AECF是平行四边形，∴AC与EF互相平分；（2）条件：EF⊥AC，∵EF⊥AC，又∵四边形AECF是平行四边形，∴平行四边形AECF是菱形．26．∵AB=DC AC=BD BC=CB，∴△ABC≌△DCB，∴∠DBC=∠ACB，∴BE=CE，又∵∠BEC的平分线是EF，∴EO是中线（三线合一），∴BO=CO，∴四边形BFCE是平行四边形（对角线互相平分），又∵BE=CE，∴四边形BFCE是菱形．27．（1）证明：∵CF∥BE，∴∠EBD=∠FCD，D是BC边的中点，则BD=CD，∠BDE=∠CDF，∴△BDE≌△CDF．（2）如图所示，由（1）可得CF=BE，又CF∥BE，所以四边形BECF是平行四边形；（3）△ABC是等腰三角形，即AB=AC，理由：当AB=AC 时，则有AD⊥BC，又（2）中四边形为平行四边形，所以可判定其为菱形．28．（1）∵DE为BC的垂直平分线，∴∠EDB=90°，BD=DC，又∵∠ACB=90°，∴DE∥AC，∴E为AB的中点，∴在Rt△ABC中，CE=AE=BE，∴∠AEF=∠AFE，且∠BED=∠AEF，∠DEC=∠DFA，∴AF∥CE，又∵AF=CE，∴四边形ACEF为平行四边形；（2）要使得平行四边形ACEF为菱形，则AC=CE即可，∵DE∥AC，∴∠BED=∠BAC，∠DEC=∠ECA，又∵∠BED=∠DEC，∴∠EAC=∠ECA，∴AE=EC，又EB=EC，∴AE=EC=EB，∵CE=AB，∴AC=AB即可，在Rt△ABC中，∠ACB=90°，∴当∠B=30°时，AB=2AC，故∠B=30°时，四边形ACEF为菱形．29．∵AD平分∠BAC∴∠BAD=∠CAD又∵EF⊥AD，∴∠AOE=∠AOF=90°∵在△AEO和△AFO中，∴△AEO≌△AFO（ASA），∴EO=FO即EF、AD相互平分，∴四边形AEDF是平行四边形又EF⊥AD，∴平行四边形AEDF为菱形30．1）解：OE=OF．理由如下：∵CE是∠ACB的角平分线，∴∠ACE=∠BCE，又∵MN∥BC，∴∠NEC=∠ECB，∴∠NEC=∠ACE，∴OE=OC，∵OF是∠BCA的外角平分线，∴∠OCF=∠FCD，又∵MN∥BC，∴∠OFC=∠ECD，∴∠OFC=∠COF，∴OF=OC，∴OE=OF；（2）解：当∠ACB=90°，点O在AC的中点时，∵OE=OF，∴四边形AECF是正方形；（3）答：不可能．解：如图所示，∵CE平分∠ACB，CF平分∠ACD，∴∠ECF=∠ACB+∠ACD=（∠ACB+∠ACD）=90°，若四边形BCFE是菱形，则BF⊥EC，但在△GFC中，不可能存在两个角为90°，所以不存在其为菱形．。

菱形的判定练习题

菱形的判定练习题1 、菱形的一边与两条对角线构成的角的差为30°，则菱形的各角度数为多少？分析：根据菱形的性质，对角线互相垂直且平分每一组对角，可知菱形的两条对角线分菱形为四个全等的直角三角形．解：因为菱形的对角线互相垂直且平分每一组对角，所以可知两邻角一半的和为90°，又因为它们的差是30°，所以可得，每一组邻角的对角相等，所以菱形的各角为60°，120°，60°，120°．2 、如图，菱形ABCD，E、F分别为BC、CD上的点，且∠B=∠EAF=60°，若∠BAE=20°，求∠CEF的度数．分析：连结AC，由菱形的性质与已知条件可得△ABC为等边三角形，所以∠BAC=∠ACD=60°，由∠EAF=60°，可得∠BAE=∠CAF，进而可得△ABE≌△ACF，∴AE=AF得△AEF为等边三角形，从而求出∠CEF．解：连结AC，∵菱形ABCD∴AB=BC，∠ACB=∠ACD(菱形的四条边相等，每一条对角线平分一组对角)∵∠B=60°∴△ABC为等边三角形∴∠BAC＝∠ACB＝∠ACD=60°∴AB=AC∵∠EAF=60°∴∠BAE＋∠EAC=∠EAC＋∠CAF=60°∴∠BAE=∠CAF∴△ABE≌△ACF(ASA)∴AE=AF∴△AEF是等边三角形∴∠AEF=60°∵∠AEC=∠AEF＋∠CEF=∠B＋∠BAE(三角形的外角定理)∴∠CEF＝∠BAE＝20°说明：菱形是特殊的平行四边形，除具有平行四边形的性质外，还有特性：(1)菱形的四条边相等．(2)菱形的对角线互相垂直平分，并且每一条对角线平分一组对角．3、如图，AD是△ABC的角平分线，AD的垂直平分线交AB于E，交AC于F，求证：四边形AEDF是菱形．分析：只需判定四边形AEDF是平行四边形即可．证明：∵EF是AD的垂直平分线∴AE=DE．∴∠1=∠3∴AD平分∠BAC ∴∠1=∠2∴∠2=∠3∴AC∥DE(内错角相等，两直线平行)同理AB∥DF四边形AEDF是平行四边形(两组对边分别平行的四边形是平行四边形) ∵AD⊥EF∴AEDF是菱形(对角线互相垂直的平行四边形是菱形)说明：菱形常用的判定方法有：。

菱形的性质和判定(含解析)

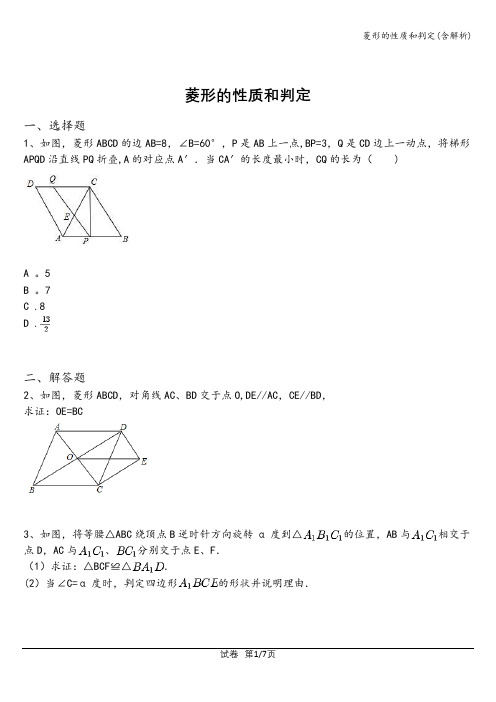
菱形的性质和判定一、选择题1、如图，菱形ABCD的边AB=8，∠B=60°，P是AB上一点,BP=3，Q是CD边上一动点，将梯形APQD沿直线PQ折叠,A的对应点A′．当CA′的长度最小时，CQ的长为（ )A 。

5B 。

7C .8D .二、解答题2、如图，菱形ABCD，对角线AC、BD交于点O,DE//AC，CE//BD，求证：OE=BC3、如图，将等腰△ABC绕顶点B逆时针方向旋转α度到△的位置，AB与相交于点D，AC与、分别交于点E、F．（1）求证：△BCF≌△．(2）当∠C=α度时，判定四边形的形状并说明理由．4、如图,矩形ABCD 中,对角线AC 的垂直平分线交AD 、BC 于点E 、F,AC 与EF 交于点O ，连结AF 、CE ．（1）求证：四边形AFCE 是菱形；（2）若AB=3,AD=4，求菱形AFCE 的边长。

5、如图，CD 是△ABC 的中线，点E 是AF 的中点，CF∥AB．（1)求证：CF=AD ；（2）若∠ACB=90°,试判断四边形BFCD 的形状，并说明理由．6、如图,将矩形A 1B 1C 1D 1沿EF 折叠,使B 1点落在A 1D 1边上的B 点处；再将矩形A 1B 1C 1D 1沿BG 折叠，使D 1点落在D 点处且BD 过F 点．（1)求证：四边形BEFG 是平行四边形；(2）当∠B 1FE 是多少度时,四边形BEFG 为菱形？试说明理由．菱形的性质和判定的答案和解析一、选择题1、答案：B试题分析：作CH⊥AB于H，如图，根据菱形的性质可判断△ABC为等边三角形,则CH=AB=4，AH=BH=4，再利用勾股定理计算出CP=7，再根据折叠的性质得点A′在以P点为圆心，PA为半径的弧上，利用点与圆的位置关系得到当点A′在PC上时，CA′的值最小，然后证明CQ=CP即可。

解：作CH⊥AB于H，如图，∵菱形ABCD的边AB=8,∠B=60°,∴△ABC为等边三角形，∴CH=AB=4，AH=BH=4，∵PB=3,∴HP=1，在Rt△CHP中，CP= =7，∵梯形APQD沿直线PQ折叠,A的对应点A′，∴点A′在以P点为圆心，PA为半径的弧上，∴当点A′在PC上时,CA′的值最小，∴∠APQ=∠CPQ，而CD∥AB，∴∠APQ=∠CQP，∴∠CQP=∠CPQ，∴CQ=CP=7．故选：B．二、解答题2、答案：证明见解析试题分析：先求出四边形OCED是平行四边形，再根据菱形的对角线互相垂直求出∠COD=90°，证明OCED 是矩形，利用勾股定理即可求出BC=OE．证明：∵DE∥AC，CE∥BD,∴四边形OCED是平行四边形，∵四边形ABCD是菱形,∴∠COD=90°，∴四边形OCED是矩形，∴DE=OC，∵OB=OD，∠BOC=∠ODE=90°，∴BC===OE3、答案：（1)见解答过程(2)见解答过程试题分析:（1）根据等腰三角形的性质得到AB=BC，∠A=∠C，由旋转的性质得到=AB=BC，∠A=∠=∠C，∠BD=∠，根据全等三角形的判定定理得到△BCF≌△（2)由旋转的性质得到∠=∠A,根据平角的定义得到∠DEC=180°-α，根据四边形的内角和得到∠ABC=360°—∠—∠C—∠=180°-α，证的四边形是平行四边形，由于=BC，即可得到四边形是菱形。

菱形的判定(5种题型)(解析版)

菱形的判定（5种题型）【知识梳理】一、菱形的判定：①菱形定义：一组邻边相等的平行四边形是菱形（平行四边形+一组邻边相等＝菱形）；②四条边都相等的四边形是菱形．几何语言：∵AB＝BC＝CD＝DA∴四边形ABCD是菱形；③对角线互相垂直的平行四边形是菱形（或“对角线互相垂直平分的四边形是菱形”）．几何语言：∵AC⊥BD，四边形ABCD是平行四边形∴平行四边形ABCD是菱形要点诠释：前一种方法是在四边形的基础上加上四条边相等.后两种方法都是在平行四边形的基础上外加一个条件来判定菱形。

二．菱形的判定与性质（1）依次连接四边形各边中点所得的四边形称为中点四边形．不管原四边形的形状怎样改变，中点四边形的形状始终是平行四边形．（2）菱形的中点四边形是矩形（对角线互相垂直的四边形的中点四边形定为矩形，对角线相等的四边形的中点四边形定为菱形．）（3）菱形是在平行四边形的前提下定义的，首先它是平行四边形，但它是特殊的平行四边形，特殊之处就是“有一组邻边相等”，因而就增加了一些特殊的性质和不同于平行四边形的判定方法．（4）正方形是特殊的菱形，菱形不一定是正方形，所以，在同一平面上四边相等的图形不只是正方形．【考点剖析】题型一：添加一个条件使四边形为菱形∥，例1．（2023·安徽·校联考一模）如图，四边形ABCD的对角线AC，BD相交于点O，若AB CD =，想要判断四边形ABCD是菱形，则可以添加一个条件是_____________．AO CO【答案】AB AD =（答案不唯一）【分析】根据菱形的判定方法进行解答即可．【详解】解：∵AB CD ∥，∴OAB OCD ∠=∠，OBA ODC ∠=∠，∵AO CO =，∴△≌△AO B C O D ， ∴AB CD =，∵AB CD ∥，∴四边形ABCD 为平行四边形，如果添加AB AD =，可以通过有一组邻边相等的平行四边形是菱形，判断四边形ABCD 为菱形；故答案为：AB AD =．【点睛】本题主要考查了三角形全等的判定和性质，平行四边形的判定，平行线的性质，菱形的判定，解题的关键是熟练掌握菱形的判定方法．【变式】如图，▱ABCD 的对角线AC ，BD 相交于点O ，请添加一个条件：，使▱ABCD 是菱形．【分析】根据菱形的定义得出答案即可．【解答】解：∵邻边相等的平行四边形是菱形，∴当AD ＝DC ，▱ABCD 为菱形；故答案为：AD ＝DC （答案不唯一）．【点评】此题主要考查了菱形的判定以及平行四边形的性质，根据菱形的定义得出是解题关键．题型二：证明四边形为菱形例2.如图，在△ABC中，AC＝BC，点D，E，F分别是AB，AC，BC的中点，连接DE，DF．求证：四边形DFCE 是菱形．【分析】根据三角形的中位线的性质和菱形的判定定理即可得到结论；【解答】证明：∵点D，E，F分别是AB，AC，BC的中点，∴DE∥CF，DE＝BC，DF∥CE，DF＝AC，∴四边形DECF是平行四边形，∵AC＝BC，∴DE＝DF，∴四边形DFCE是菱形；【点评】本题考查了菱形的判定和性质，等腰三角形的性质，三角形的中位线的性质，熟练掌握菱形的判定定理是解题的关键．例3.如图，四边形ABCD为平行四边形，EF∥BD，分别交BC，CD于点P，Q，交AB，AD的延长线于E，F，且BE＝BP，求证：（1）∠E＝∠F；（2）四边形ABCD是菱形．【分析】（1）首先判定四边形BPFD是平行四边形，所以BP∥DF，利用平行线的性质可得∠F＝∠BPE，又因为BE＝BP，可得∠E＝∠F；（2）利用平行线的性质以及菱形的判定方法进而得出即可．【解答】证明：（1）∵四边形ABCD是平行四边形，∴BP∥DF，∵EF∥BD，∴四边形BPFD是平行四边形，∴BP∥DF，∴∠F＝∠BPE，∵BE＝BP，∴∠E＝∠BPE，∴∠E＝∠F；（2）∵EF∥BD，∴∠E＝∠ABD，∠F＝∠ADB∴∠ABD＝∠ADB，又∵四边形ABCD为平行四边形，∴四边形ABCD是菱形．【点评】本题考查了平行四边形的性质和判定、菱形的判定等知识，得出四边形BPFD是平行四边形是解题关键．【变式】如图，已知平行四边形ABCD，点E在AC的延长线上，连接BE、DE，过点D作DF∥EB交CA的延长线于点F，连接FB（1）求证：△DAF≌△BCE；（2）如果四边形ABCD是菱形，求证：四边形BEDF是菱形．【分析】（1）由平行四边形的性质得出AD＝CB，AD∥CB，证出∠DAF＝∠BCE，∠DFA＝∠BEC，由AAS证明△DAF≌△BCE即可；（2）先证明四边形BEDF是平行四边形，再由菱形的性质得出AC⊥BD，即可得出四边形BEDF是菱形．【解答】（1）证明：∵四边形ABCD是平行四边形，∴AD＝CB，AD∥CB，∴∠DAC＝∠BCA，∴∠DAF＝∠BCE，∵DF∥EB，∴∠DFA＝∠BEC，在△DAF和△BCE中，，∴△DAF≌△BCE（AAS）；（2）证明：连接BD，如图所示：由（1）得：△DAF≌△BCE，∴DF＝BE，又∵DF∥BE，∴四边形BEDF是平行四边形，∵四边形ABCD是菱形，∴AC⊥BD，即EF⊥BD，∴四边形BEDF是菱形．【点评】本题考查了菱形的判定与性质、平行四边形的性质、全等三角形的判定与性质；熟练掌握平行四边形的性质，并能进行推理论证是解决问题的关键．题型三：根据菱形的判定与性质求角度例4．（2023春·福建福州·九年级统考期中）如图，在ABC 中，30ACB ∠=︒，将ABC 绕点C 顺时针旋转60︒得到DEC ，连接AE ．(1)求证：AB AE =；(2)若A ABC CB =∠∠，证明：直线AE 与BC 互相垂直．【分析】（1）由ABC 绕点C 顺时针旋转60︒得到DEC ，可得60BCE ∠=︒，BC EC =，而30ACB ∠=︒，即得30ACE ACB ∠=︒=∠，可证()SAS ACB ACE △≌△，故AB AE =；（2）根据ABC 绕点C 顺时针旋转得到DEC ，AB AC =，可得AC DC DE AE ===，证明四边形ACDE 是菱形，得到DA CD ∥；又306090BCD ∠=︒+︒=︒，进而推导出AE BC ⊥．【详解】（1）证明：ABC 绕点C 顺时针旋转60︒得到DEC ，60BCE ∴∠=︒，BC EC =，30ACB ∠=︒，30ACE ACB ∴∠=︒=∠，AC AC =，()SAS ACB ACE ∴≌，AB AE =∴；（2）解：ABC 绕点C 顺时针旋转得到DEC ，AC DC ∴=，AB DE =，由（1）可知AB AE =，AE DE ∴=，若AB AC =，则AC AE =，AC DC DE AE ∴===，∴四边形ACDE 是菱形，AE CD ∴∥；30ACB ∠=︒，将ABC 绕点C 顺时针旋转60︒得到DEC ，306090BCD ∴∠=︒+︒=︒，即CD BC ⊥，AE BC ∴⊥，即直线AE 与BC 互相垂直．【点睛】本题考查三角形的旋转问题，涉及菱形的判定及全等三角形的判定与性质，解题的关键是掌握旋转的性质，证明ACB ACE △≌△．模拟预测）如图，在正方形网格中，ABC 的顶点在格点上，请仅用无刻度的直尺 (1)在图1中，作45CAE ∠=︒．(2)在图2中，作ABC 的角平分线CF ．【分析】（1）如图，取格点E ，连接AE ，则CAE ∠即为所作；（2）如图，取格点F ，作射线CF ，则射线CF 即为所作；【详解】（1）解：如图，CAE ∠即为所作，由图可得：2AN CM ==，1CN EM ==，90ANC CME ∠=∠=︒，∴()SAS ANC CME ≌，∴CAN ECM ∠=∠，AC CE =，∵90CAN ACN ∠+∠=︒，∴90ECM ACN ∠∠=︒，∴90ACE ∠=︒，∵AC CE =，∴45CAE CEA ∠=∠=︒；（2）解：如图，射线CF 即为所作，由图可得：AC CG GF AF ===∴四边形ACGF 为菱形，∴CF 平分ACG ∠，即CF 是ABC 的角平分线【点睛】本题考查网格作图，全等三角形判定与性质，等腰直角三角形，菱形的判定与性质，熟练掌握菱形的判定与性质是解题的关键．题型四：根据菱形的判定与性质求线段长例5.（2023·山西长治·校联考二模）如图，在ABCD Y 中，对角线AC ，BD 相交于点O ，E 为OD 的中点，连接AE ，CE ．(1)实践与操作：利用尺规在线段OB 上作出点F ，使得四边形AFCE 为平行四边形，连接AF ，CF ；（要求：尺规作图并保留作图痕迹，不写作法，标明字母）(2)应用与求解：若4,60AB BC ABC ==∠=︒，求EF 的长．【答案】(1)见解析(2)【分析】（1）利用圆规在OB 上作OF OE =，根据对角线互相平分的四边形是平行四边形可得四边形AFCE 为平行四边形；（2）先根据平行四边形的性质和已知条件证明EF OB =，再证ABC 是等边三角形，求出4AC =，再证四边形ABCD 是菱形，推出BO AC ⊥，最后根据勾股定理求出OB 即可．【详解】（1）解：如图所示：以点O 为圆心，OE 长为半径作弧，与线段OB 的交点即为点F ，连接AF ，CF ．（2）解：由（1）知OF OE =，ABCD Y 中，E 为OD 的中点，∴1122OE OD OB ==， ∴12OF OE OB ==，∴EF OB =，4,60AB BC ABC ==∠=︒，∴ABC 是等边三角形，∴4AC =，ABCD Y 中，AB BC =，∴四边形ABCD 是菱形，∴BD AC ⊥，即BO AC ⊥， ∴122AO AC ==，∴OB ==∴EF =【点睛】本题考查尺规作图，平行四边形的判定与性质，菱形的判定与性质，等边三角形的判定与性质，勾股定理等，解题的关键是掌握菱形、平行四边形、等腰三角形的性质．【变式】如图，四边形ABCD 中，BD 垂直平分AC ，垂足为点E ，点F 为四边形ABCD 外一点，DA 平分∠BDF ，∠ADF ＝∠BAD ，且AF ⊥AC ．（1）求证：四边形ABDF 是菱形；（2）若AB ＝5，求AC 的长．【分析】（1）首先证明四边形ABDF 是平行四边形，再证明邻边相等即可证明．（2）在Rt △AFC 中，利用勾股定理求解即可．【解答】（1）证明：∵∠ADF ＝∠BAD ，∴AB ∥DF ，∵AF ⊥AC ，BD ⊥AC ，∴AF ∥BD ，∴四边形ABDF 是平行四边形；∵DA 平分∠BDF ，∴∠ADF ＝∠BDA ，∴∠BAD ＝∠BDA ，∴BD ＝AB ，∴四边形ABDF 是菱形．（2）解：∵DA 平分∠BDF ，∴∠ADF ＝∠BDA ，∵BD垂直平分线段AC，∴DA＝DC，∴∠ADB＝∠BDC＝∠ADF，∵DA＝DF＝DC，∴∠DAF＝∠F，∠DAC＝∠DCA，∴∠ADC＝180°﹣2∠DAC，∠ADF＝180°﹣2∠DAF，∵∠DAF+∠DAC＝90°，∴∠ADF+∠ADC＝360°﹣2（∠DAC+∠DAF）＝180°，∴C，D，F三点共线，∴∠ADB＝∠BDC＝∠ADF＝60°，∵FA＝FD，∴△ADF是等边三角形，∴AF＝DF＝CD＝5，∵∠FAC＝90°，∴AC＝＝5．【点评】本题考查了平行四边形的判定和性质、菱形的判定、角平分线的性质，勾股定理的应用，解题的关键是利用勾股定理列方程，属于中考常考题型．题型五：根据菱形的判定与性质求面积例6.已知，如图，在▱ABCD中，BF平分∠ABC交AD于点F，AE⊥BF于点O，交BC于点E，连接EF．（1）求证：四边形ABEF是菱形；（2）若AE＝6，BF＝8，CE＝3，求四边形ABCD的面积．【分析】（1）先证明四边形ABEF是平行四边形，再证明邻边相等即可证明．（2）作FG⊥BC于G，根据S菱形ABEF＝•AE•BF＝BE•FG，先求出FG即可解决问题．【解答】（1）证明：∵四边形ABCD是平行四边形∴AD∥BC，∴∠EBF＝∠AFB，∵BF平分∠ABC，∴∠ABF＝∠CBF，∴∠ABF＝∠AFB，∴AB＝AF，∵BO⊥AE，∴∠AOB＝∠EOB＝90°，∵BO＝BO，∴△BOA≌△BOE（ASA），∴AB＝BE，∴BE＝AF，BE∥AF，∴四边形ABEF是平行四边形，∵AB＝AF．∴四边形ABEF是菱形．（2）解：作FG⊥BC于G，∵四边形ABEF是菱形，AE＝6，BF＝8，∴AE⊥BF，OE＝AE＝3，OB＝BF＝4，∴BE＝＝5，∵S菱形ABEF＝•AE•BF＝BE•FG，∴GF＝，∴S平行四边形ABCD＝BC•FG＝．【点评】本题考查平行四边形的性质、菱形的判定和性质、勾股定理等知识，解题的关键是利用面积法求出高FG，记住菱形的三种判定方法，属于中考常考题型．【变式】如图，在△ABC中，D、E分别是AB、AC的中点，BE＝2DE，延长DE到F，使EF＝BE，连接CF．（1）求证：四边形BCFE为菱形；（2）若CE＝8，∠CFE＝60°，求四边形BCFE的面积．【分析】（1）证明DE是△ABC的中位线，由三角形中位线定理得出DE∥BC，BC＝2DE，由已知条件得出EF ＝BC，证出四边形BCFE是平行四边形，再由EF＝BE，即可得出结论；（2）作CM⊥DF于M，由菱形的性质得出EF＝CF，证出△CEF是等边三角形，得出CF＝CE＝8，由三角函数求出CM，即可得出四边形BCFE的面积．【解答】（1）证明：∵D、E分别是AB、AC的中点，∴DE是△ABC的中位线，∴DE∥BC，BC＝2DE，∴EF∥BC，∵BE＝2DE，∴BC＝BE，∵EF＝BE，∴EF ＝BC ，∴四边形BCFE 是平行四边形，又∵EF ＝BE ，∴四边形BCFE 为菱形；（2）解：作CM ⊥DF 于M ，如图所示：由（1）得：四边形BCFE 为菱形，∴EF ＝CF ，∵∠CFE ＝60°，∴△CEF 是等边三角形，∴CF ＝CE ＝8，∴CM ＝CF •sin60°＝8×＝4，∴四边形BCFE 的面积＝EF •CM ＝8×4＝32．【点评】三角形中位线定理、等边三角形的判定与性质；熟练掌握菱形的判定与性质，证明△CEF 是等边三角形是解决问题（2）的突破口．【过关检测】一、单选题 1．（2023·陕西西安·校考二模）在下列条件中，能判定平行四边形ABCD 为菱形的是（）A ．AB BC ⊥B ．AC BD = C ．AB BC = D ．AB AC =【答案】C【分析】根据菱形的判定定理，即可进行解答．【详解】解：A 、若AB BC ⊥，则平行四边形ABCD 为矩形；不符合题意；B 、若AC BD =，则平行四边形ABCD 为正方形；不符合题意； C 、若AB BC =，则平行四边形ABCD 为菱形；符合题意；D 、若AB BC =，则平行四边形不是特殊的平行四边形；不符合题意；故选：C ．【点睛】本题主要考查了菱形的判定，解题的关键是掌握有一组另邻边相等的平行四边形是菱形，对角线互相垂直的平行四边形是菱形． A ．点O 为ABCD Y 的对称中心C ．::ABE BDF S S AE ED =△△【答案】B 【分析】由作图知，EF 是线段BD 的垂直平分线，利用平行四边形的性质可判断选项A ；根据菱形的判定定理可判断选项C ；根据菱形的性质得到BDF BDE S S =△△，可判断选项D ；BE 不一定平分ABD ∠，选项B 不正确．【详解】解：由作图知，EF 是线段BD 的垂直平分线，即点O 为ABCD Y 的对称中心，故选项A 正确，不符合题意；∵四边形ABCD 是平行四边形，∴DE BF ∥，∴DEF BFE ∠=∠，∵EF 是线段BD 的垂直平分线，∴BE ED =，BF FD =，BFE EFD ∠=∠，∴DEF EFD ∠=∠，∴DE DF =，∴DE DF BE BF ===，∴四边形BEDF 为菱形，故选项D 正确，不符合题意；∴BDF BDE S S =△△，∴:::ABE BDF ABE BDE S S S S AE ED ==△△△△，故选项C 正确，不符合题意；BE 不一定平分ABD ∠，故选项B 不正确，符合题意；故选：B ．【点睛】本题考查平行四边形的性质，菱形的判定等知识，解题的关键是熟练掌握基本知识，属于中考常考题型． 3．（2023·陕西西安·校考一模）在平行四边形ABCD 中，添加下列条件，能判定平行四边形ABCD 是菱形的是( )A ．AB AD =B ．AC BD = C ．90ABC ∠= D ．AB CD =【答案】A【分析】根据一组邻边相等的平行四边形是菱形即可求得答案．【详解】解：∵四边形ABCD 是平行四边形，又AB AD =， ∴平行四边形ABCD 是菱形，故选：A ．【点睛】本题考查菱形的判定，熟记菱形的判定是解题的关键． 4．（2023·河北衡水·校联考模拟预测）春节期间，某广场布置了一个菱形花坛，两条对角线长分别为2310m ⨯和2410m ⨯，其面积用科学记数法表示为( )A ．42610m ⨯B ．421.210m ⨯C ．521.210m ⨯D ．22610m ⨯【答案】A 【分析】利用菱形的面积等于对角线乘积的一半进行计算，或者利用菱形对角线垂直的性质进行面积求解，最后化为科学记数法的形式即可．【详解】菱形的对角线相互垂直()2222ABD CBD ABCD BD AO OC BD AO BD CO BD AC S S S ⨯+⨯⨯⨯=+=+==四边形∴菱形的面积=对角线成绩的一半=224131********⨯⨯⨯⨯=⨯2m 【点睛】本题考查用对角线计算菱形的面积及科学记数法，也可以利用对角线垂直的性质进行面积的计算，注意所有对角线垂直的四边形面积均等于对角线乘积的一半．正确的使用公式和理解科学记数法的写法是解题的关键． 5．（2023·陕西西安·西安市铁一中学校考模拟预测）在下列条件中，能够判定ABCD Y 为菱形的是（）A ．AB AC =B ．AC BD ⊥ C ．90A ∠=︒ D ．AC BD = 【答案】B【分析】由菱形的判定和矩形的判定分别对各个选项进行判断即可．【详解】解：A 、由AB AC =，不能判定ABCD Y 为菱形，故选项不符合题意；B 、由AC BD ⊥，能判定ABCD Y 为菱形，故选项符合题意；C 、由90A ∠=︒，不能判定ABCD Y 为菱形，故选项不符合题意；D 、由AC BD =，能判定ABCD Y 为矩形，不能判定ABCD Y 为菱形，故选项不符合题意；故选：B ．【点睛】本题考查了菱形的判定，熟练掌握菱形的判定定理是解题的关键．二、填空题【答案】2【分析】由菱形的性质可得OA OD 、的长，则可求得AD 的长，再由三角形中位线定理即可求得结果．【详解】解：在菱形ABCD 中，114322OA AC OD OB BD =====、，AC BD ⊥，由勾股定理得：5AD ，∵H是AB的中点，∴OH是ABD△的中位线，∴1522 OH AD==，故答案为：5 2．【点睛】本题考查了菱形的性质，勾股定理，三角形中位线定理，熟悉这些性质与定理是解题的关键．7．（2023·宁夏石嘴山·统考一模）如图，是小明作线段AB的垂直平分线的作法及作图痕迹，则四边形ADBC一定是______________．【答案】菱形【分析】根据作图方法可知AC BC AD BD===，再根据四条边相等的四边形是菱形即可得到答案．【详解】解：由作图方法可知，AC BC AD BD===，∴四边形ABCD是菱形，故答案为：菱形．【点睛】本题主要考查了菱形的判定，线段垂直平分线的尺规作图，熟知菱形的判定条件是解题的关键．8．（2023·广东广州·广州市育才中学校考一模）菱形的两个内角的度数比是1：3，一边上的高长是4，则菱形的面积是__________．【答案】【分析】根据菱形相邻的两个角度之比求出对应的角度，利用等腰直角三角形的性质求出菱形的边长，然后用菱形面积公式计算即可．【详解】如左图所示，∵菱形对角相等，互补，且两个内角的度数比是1：3，118045,1804513513A C B D ∴∠=∠=⨯︒=︒∠=∠=︒−︒=︒+，如图1所示，过点D 作BC 边上的高交BC 于点H ，则4DH =，90DHC ∠=︒，45C ∠=︒，∴△CDH 是等腰直角三角形，4CH DH ∴==，CD ∴=∵菱形四条边都相等，BC CD ∴==4ABCD S BC DH =⋅==菱如图2，当过点A 作CD 边上的高交CD 于点H ，同理可证△ADH 为等腰直角三角形，可求得CD AD ==4ABCD S CD AH =⋅==菱故答案为：【点睛】本题考查了菱形的性质，等腰直角三角形的性质，解题的关键在于求出菱形的边长． 9．（2023春·四川成都·九年级成都嘉祥外国语学校校考阶段练习）如图，在ABCD Y 中，尺规作图：以点A 为圆心，AB 的长为半径画弧交AD 于点F ，分别以点B ，F 为圆心，以大于BF 的长为半径画弧交于点P ，作射线AP 交BC 与点E ，若12BF =，10AB =，则AE AB +的值为________．【答案】26【分析】证明四边形ABEF 是菱形，利用勾股定理求出OA 即可解决问题．【详解】解：由题意可知：AB AF =，AE BF ⊥，OB OF ∴=，BAE EAF ∠=∠，四边形ABCD 是平行四边形，AD BC ∴∥，EAF AEB ∴∠=∠，BAE AEB ∴∠=∠，AB BE AF \==，AF BE ∥，∴四边形ABEF 是平行四边形，AB AF =，∴四边形ABEF 是菱形，OA OE ∴=，162OB OF BF ===，在Rt AOB △中，8OA ，216AE OA ∴==，26AE AB ∴+=．故答案为：26．【点睛】本题考查了平行四边形的性质、菱形的判定和性质、勾股定理等知识，解题的关键是判定四边形ABEF 是菱形．【答案】8【分析】如图所示，连接EF ，设AE BF 、交于O ，由作图方法可知，AE 是线段BF 的垂直平分线，则BE FE =，OB OF =，证明OAF OEB △≌△，得到AF BE =，进而证明四边形ABEF 是菱形，则13902OB BF AE OA AOB ====︒，，∠ ，由勾股定理得4OA ==，则28AE OA ==．【详解】解：如图所示，连接EF ，设AE BF 、交于O ，由作图方法可知，AE 是线段BF 的垂直平分线，∴BE FE =，OB OF =，∵四边形ABCD 是平行四边形，∴AD BC ∥，∴OAF OEB OFA OBE ==∠∠，∠∠，∴()AAS OAF OEB △≌△，∴AF BE =，∴AF AB EF BE ===，∴四边形ABEF 是菱形，∴13902OB BF AE OA AOB ====︒，，∠ ，在Rt ABO △中，由勾股定理得4OA ==，∴28AE OA ==，故答案为：8．【点睛】本题主要考查了菱形的性质与判定，平行四边形的性质，勾股定理，线段垂直平分线的性质和尺规作图，证明四边形ABEF 是菱形是解题的关键． 11．（2023春·四川成都·九年级专题练习）如图，在ABC 中，AB AC =，分别以C 、B 为圆心，取AB 的长为半径作弧，两弧交于点D ．连接BD 、AD ．若130ABD ∠=︒，则CAD ∠=__________．【答案】25︒/25度【分析】由题意和作法可知：AB AC BD CD ===，可得四边形ABDC 是菱形，再根据菱形及等腰三角形的性质，即可求解．【详解】解：如图：连接CD ，由题意和作法可知：AB AC BD CD ===，∴四边形ABDC 是菱形，)()11180180130252BAD ABD ∠︒−∠=︒−︒=︒，25CAD BAD ∴∠=∠=︒，故答案为：25︒．【点睛】本题考查了菱形的判定与性质，等腰三角形的性质，证得四边形ABDC 是菱形是解决本题的关键．12．（2023·甘肃陇南·校考一模）如图，在平行四边形ABCD 中，2AB BC ==，60BAD ∠=︒，点M 为CD 的中点，连接AM BE AM ⊥，于点E ，则BE 的长为 ___________．【答案】【分析】连接BD BM ，，由题意可得△BCD 是等边三角形，BM CD ⊥，利用勾股定理分别求出BM AM 、，再由等积法求BE 的长即可．【详解】解：连接BD BM ，，∵四边形ABCD 是平行四边形，2AB BC ==，∴四边形ABCD 是菱形，∴2AB BC CD DA ====，CD AB ∥∵60BAD ∠=︒，∴60C ∠=︒，∴BCD △是等边三角形，∵M 是CD 的中点，∴BM CD ⊥， ∴112CM DM CD ===，AB BM ⊥，∵21BC CM ==，，∴BM =在Rt ABM 中，AM ===∵BE AM ⊥，∴AB BM BE AM ⋅==，故答案为：．【点睛】本题考查平行四边形的性质，菱形的判定及性质，等边三角形的判定与性质，熟练掌握菱形的判定及性质，等边三角形的性质，勾股定理，等积法是解题的关键． 13．（2023·湖北襄阳·校考一模）如图，▱ABCD 中，AB AD =，点E 是AB 上一点，连接CE 、DE ，且BC CE =，若40BCE ∠=︒，则ADE ∠=______．【答案】15︒/15度【分析】首先证明四边形ABCD 是菱形，然后根据等腰三角形的性质可得()118040702CEB B ∠=∠=︒−︒=︒，利用三角形内角和定理即可解决问题．【详解】解：在▱ABCD 中，AB AD =， ∴四边形ABCD 是菱形，AB AD BC CD ∴===，//AB CD ，BC CE =，CD CE ∴=，CED CDE ∴∠=∠，40BCE ∠=︒，()118040702CEB B ∴∠=∠=︒−︒=︒，70ADC B ∴∠=∠=︒，70ECD BEC ∠=∠=︒，()118070552CDE CED ∴∠=∠=︒−︒=︒，705515ADE ∴∠=︒−︒=︒．故答案为：15︒．【点睛】本题考查了平行四边形的性质，菱形的判定与性质，等腰三角形的性质，解决本题的关键是掌握菱形的判定与性质．三、解答题 14．（2023·陕西榆林·统考二模）如图，在ABC 中，BAC ∠的平分线AD 交BC 于点D ．请利用尺规分别在AB 、AC 上求作点E 、F ，使得四边形AEDF 是菱形．（保留作图痕迹，不写作法）【答案】见解析【分析】作AD 的垂直平分线交,AC AB 于点,E F ，则点,E F 即为所求．【详解】解：如图所示，作AD 的垂直平分线交,AC AB 于点,E F ，则点,E F 即为所求理由如下，∵EF 是AD 的垂直平分线，∴,==EA ED FA FD ，∴EAD EDA ∠=∠，∵BAC ∠的平分线AD 交BC 于点D ，∴∠∠E A D F A D =，∴EDA FAD ∠=∠，∴AF DE ∥，同理可得AE DF ∥，∴四边形AEDF 是平行四边形，∵EA ED =，∴四边形AEDF 是菱形．【点睛】本题考查了作垂直平分线，角平分线的定义，菱形的判定，熟练掌握基本作图是解题的关键． (1)求证：ABC ADC ≅．(2)若EO CO =，试判断四边形【答案】(1)见解析(2)四边形BCDE 是菱形，理由见解析【分析】(1)根据SSS 定理推出即可；(2)先判断AC 为BD 的垂直平分线得到AC BD OB OD ⊥=，，再由EO CO =，可判断四边形BCDE 为平行四边形，然后利用AC BD ⊥可判断四边形BCDE 是菱形．【详解】（1）在ABC 与ADC △中，AB AD BC DCAC AC =⎧⎪=⎨⎪=⎩，∴()ΑSSS BC ADC ≅．（2）四边形BCDE 是菱形，理由如下：∵AB AD CB CD ==，，∴AC 垂直平分BD ，即AC BD ⊥且BO DO =．∵EO CO =，∴四边形BCDE 是平行四边形．∵AC BD ⊥，∴四边形BCDE 是菱形．【点睛】本题考查了全等三角形的判定，线段的垂直平分线的判定和性质及菱形的判定，解题的关键是了解菱形的判定方法，难度不大．九年级专题练习）如图，在ABC 中，上的中点，将ABC 绕着点【答案】(1)见解析(2)【分析】（1）根据旋转的性质可得,AC BD AD BC ==，从而得到AC BD AD BC ===，即可求证；（2）过点A 作AE BC ⊥于点E ，先证明ABC 是等边三角形，可得112BE BC ==，2AB BC ==，再由勾股定理可得AE【详解】（1）证明：∵将ABC 绕着点O 旋转180︒得ABD △，∴,AC BD AD BC ==，∵AC BC =，∴AC BD AD BC ===，∴四边形AECD 是菱形；（2）解：如图，过点A 作AE BC ⊥于点E ，∵60,2B BC AC ∠=︒==，∴ABC 是等边三角形， ∴112BE BC ==，2AB BC ==，∴AE∴菱形AECD 的面积为AE BC ⨯=【点睛】等边三角形的判定和性质，勾股定理，熟练掌握菱形的判定和性质，等边三角形的判定和性质，勾股定理是解题的关键． 17．（2023·黑龙江哈尔滨·统考一模）如图，方格纸中每个小正方形的边长均为1，ABC 的顶点和点O 均在小正方形的顶点上．(1)在方格纸中画出DEF ，使DEF 和ABC 关于点O 对称（点A 、B 、C 的关于点O 的对称点分别为点D 、E 、F ）；(2)在方格纸中画出以线段EF 为一边的菱形EFMN ，且菱形EFMN 的面积为3，连接CN ．请直接写出线段CN 的长．【答案】(1)见解析(2)图见解析；CN =【分析】（1）作出点A 、B 、C 关于点O 的对称点D 、E 、F ，顺次连接即可得出DEF ；（2）找出格点M 、N ，连接MF 、MN 、NE ，即可得出菱形EFMN ，求出线段CN 的长即可．【详解】（1）解：如图，作出点A 、B 、C 关于点O 的对称点D 、E 、F ，顺次连接，则DEF 即为所求．（2）解：如图，找出格点M 、N ，连接MF 、MN 、NE 、CN ，则菱形EFMN 即为所求作的菱形；根据格点特点可知，EF MF MN EN ===，∴四边形EFMN 为菱形，1334211132EFMN S =⨯−⨯⨯⨯−−=菱形，CN【点睛】本题主要考查了作中心对称图形，菱形的判断，勾股定理，解题的关键是数形结合，熟练掌握方格纸的特点．【答案】见解析【分析】先利用ABD BDC ∠=∠，证明AB DC ，进而证明四边形ABCD 为平行四边形，再有勾股定理逆定理证明AOB 为直角三角形，得到AC BD ⊥，则问题可证．【详解】证明：∵ABD BDC ∠=∠，∴AB DC ，∵AB CD =∴四边形ABCD 为平行四边形，∵AB CD =2OA =，1OB =，∴22222221OA OB AB +=+==，∴AOB 为直角三角形，即AC BD ⊥，∴四边形ABCD 是菱形．【点睛】本题考查了菱形的判定和勾股定理逆定理，解答关键是熟练掌握菱形的判定方法． (1)求证：四边形AECF 是菱形；(2)若1BE =，4EC =，求EF 【答案】(1)见解析(2)EF 的长为【分析】（1）由D 是AC 的中点，可得AD CD =，由DF DE =，可证四边形AECF 是平行四边形，由DE AC ⊥，可证平行四边形AECF 是菱形；（2）由题意知4AE CE ==，在Rt ABE △中，由勾股定理，得AB =，计算求AB 的值，在Rt ABC△中，由勾股定理，得AC =AC 的值，根据12AECF S EF AC AB EC =⋅=⋅菱形，计算求解即可．【详解】（1）证明：∵D 是AC 的中点，∴AD CD =，∵DF DE =，∴四边形AECF 是平行四边形，又∵DE AC ⊥，∴平行四边形AECF 是菱形；（2）解：∵1BE =，4EC =，四边形AECF 是菱形，∴4AE CE ==，∴在Rt ABE △中，由勾股定理，得AB =∴在Rt ABC △中，由勾股定理，得AC = ∵12AECF S EF AC AB EC =⋅=⋅菱形，∴EF =∴EF 的长为【点睛】本题考查了菱形的判定与性质，勾股定理．解题的关键在于对知识的熟练掌握与灵活运用． 20．（2023春·辽宁本溪·九年级统考开学考试）如图，ABCD Y 的对角线AC ，BD 相交于点O ，点O 作AC 的垂线，与AD ，BC 分别相文于点E ，F ，连接EC ，AF ．(1)求证：四边形AECF 是菱形；(2)若4=EC ED ，DOE 的面积是2，求ABCD Y 的面积．【答案】(1)见解析(2)40【分析】（1）由平行四边形的性质得到OA OC =，AD BC ∥，进一步证明()AAS AOE COF △≌△，则AE CF =，即可证明四边形AECF 是平行四边形，由EF AC ⊥即可得到结论；（2）由菱形的性质得到AE CE =，进一步得到4AE EC ED ==，则48==AOE DOE S S △△，即可得到10=+=AOD AOE DOE S S S △△△，由平行四边形的性质即可得到ABCD Y 的面积．【详解】（1）证明：∵四边形ABCD 为平行四边形，∴OA OC =，AD BC ∥，∴DAC ACF ∠=∠，AEF EFC ∠=∠，∴()AAS AOE COF △≌△，∴AE CF =，∵AE CF ∥，∴四边形AECF 是平行四边形，∵EF AC ⊥，∴四边形AECF 是菱形；（2）解：∵四边形AECF 是菱形，∴AE CE =，∵4=EC ED ，∴4AE EC ED ==，∴48==AOE DOE S S △△，∴10=+=AOD AOE DOE S S S △△△，∵四边形ABCD 是平行四边形，∴AC 与BD 互相平分，∴AOD COD BOC AOB S S S S ===△△△△， ∴4=ABCD AOD S S △， ∴40=ABCDS 答：ABCD Y 的面积为40．【点睛】此题考查了平行四边形的判定和性质、菱形的判定和性质、全等三角形的判定和性质等，熟练掌握相关判定和性质是关键． 21．（2023·陕西宝鸡·统考二模）如图，在四边形ABCD 中，AB CD =，过A 作AE BD ⊥交BD 于点E ，过C 作CF BD ⊥交BD 于F ，且AE CF =．请你在不添加辅助线的情况下，添一个条件______，使得四边形ABCD 是菱形，并说明理由．【答案】答案不唯一，见解析【分析】添加条件AB AD =，根据HL 证明Rt Rt ABE CDF ≌△△，从而得到ABE CDF ∠=∠，再根据平等线的判断得到AB CD =，从而得到结论．【详解】解：AB AD =．理由：∵AE BD ⊥，CF BD ⊥，∴90AEB CFD ∠=∠=︒，在Rt ABE △和Rt CDF △中，AB CD AE CF =⎧⎨=⎩，∴()Rt Rt HL ABE CDF ≌△△，∴ABE CDF ∠=∠，∴AB CD ∥，∵AB CD =，∴四边形ABCD 是平行四边形．∵AB AD =，∴四边形ABCD 是菱形．（注：答案不唯一）【点睛】本题考查了菱形的判定，熟练掌握全等三角形的性质与判定，平行线的性质与判定和菱形的判定是解题的关键．的交点．若将BED 沿直线 (1)求证：四边形BEDF 是菱形；(2)若::1:3:22AE DE AB =【答案】(1)证明见解析(2)【分析】（1）由平行四边形的性质可得DE BF ∥，则EDB FBD ∠=∠，由折叠的性质可得DE DF =，EDB FDB ∠=∠，则FBD FDB ∠=∠，BF DF DE ==，进而结论得证；（2）设AE a =，则3DE a =，AB =，3BE a =，4AD a =，由()()222293a a a +==，即222AE AB BE +=，可得ABE 是直角三角形，且90BAE ∠=︒，则四边形ABCD 是矩形，由平行四边形ABCD的面积为可得AD AB ⨯=即4a ⨯=解得22a =，根据2BEDF BD EF S DE AB ⋅=⋅=菱形，计算求解即可得EF BD ⋅的值．【详解】（1）证明：∵四边形ABCD 是平行四边形，∴DE BF ∥，∴EDB FBD ∠=∠，。

(完整版)菱形知识点及经典题-推荐文档

菱形【知识梳理】1.定义: 有一组邻边相等的平行四边形叫做菱形（菱形是平行四边形: 一组邻边相等）2.性质: （1）边: 四条边都相等；（2）角: 对角相等、邻角互补；（3）对角线: 对角线互相垂直平分且每条对角线平分每组对角；（4）对称性：既是轴对称图形又是中心对称图形.3.菱形的判定方法:一组邻边相等的平行四边形是菱形对角线互相垂直平分的平行四边形是菱形对角线互相垂直平分的四边形是菱形四条边都相等的四边形是菱形4.识别菱形的常用方法（1）先说明四边形ABCD为平行四边形, 再说明平行四边形ABCD的任一组邻边相等.（2）先说明四边形ABCD为平行四边形, 再说明对角线互相垂直．（3）说明四边形ABCD的四条相等.5、面积:设菱形ABCD的一边长为a, 高为h, 则S菱形=ah；若菱形的两对角线的长分别为a,b, 则S菱形=ab【经典题】一、选择题1.(201.广东省珠海市.边长为3 cm的菱形的周长是.. )A.6 cmB.9 cmC.12 cmD.15 cm3.(201.贵州省毕节地区.如图所示, 菱形ABCD 中, 对角线AC.BD 相交于点O, H 为AD 边的中点, 菱形ABCD 的周长为28, 则OH 的长等于. ）A.3.5B.4C.7D.14B C（第8题图）4.(201.湖南省长沙市.如图, 已知菱形ABCD 的边长等于2, ∠DAB=60°,则对角线BD 的长....)A. 1B.C. 2D. 25.(201.江苏省徐州市.若顺次连接四边形的各边中点所得的四边形是菱形, 则该四边形一定是矩形 B.等腰梯形C.对角线相等的四边形D.对角线互相垂直的四边形6.(201.山东省枣庄市.如图, 菱形ABCD的边长为4, 过点A.C作对角线AC的垂线, 分别交CB和AD的延长线于点E, F,AE=3, 则四边形AECF的周长为.. ）A. 22B. 18C. 14D. 117.(201.浙江省宁波市.菱形的两条对角线长分别是6和8, 则此菱形的边长...... .. ）A.1.......B........C.......D.58.(201.黑龙江省农垦牡丹江管理局.如图, 在菱形ABCD中, E是AB边上一点, 且∠A=∠EDF=60°, 有下列结论: ①AE=BF；②△DEF是等边三角形；③△BEF是等腰三角形；④∠ADE=∠BEF, 其中结论正确的个数是（）A. 3B. 4C. 1D. 29.(201.上海市.如图, 已知AC.BD是菱形ABCD的对角线, 那么下列结论一定正确的是.. ）.(A)△ABD与△ABC的周长相等；(B)△ABD与△ABC的周长相等；(C)菱形的周长等于两条对角线之和的两倍；(D)菱形的面积等于两条对角线之积的两倍.10.(201.浙江省台州市.如图, 菱形ABCD的对角线AC=4cm, 把它沿着对角线AC方向平移1cm得到菱形EFGH, 则图中阴影部分图形的面积与四边形EMCN的面积之比为（）A．4：3 B．3：2 C．14: 9 D．17: 9二、填空题11.(201.吉林省长春市.如图, 在边长为3的菱形ABCD中, 点E在边CD上, 点F为BE延长线与AD延长线的交点. 若DE=1, 则DF的长为.. .12.(201.福建省莆田市.如图, 菱形ABCD的边长为4, ∠BAD=120°, 点E是AB的中点, 点F是AC上的一动点, 则EF+BF的最小值是2 ．13.(201.甘肃省陇南市.如图, 四边形ABCD是菱形, O是两条对角线的交点, 过O点的三条直线将菱形分成阴影和空白部分. 当菱形的两条对角线的长分别为6和8时, 则阴影部分的面积为12.14.(201.甘肃省兰州市.如果菱形的两条对角线的长为a 和b, 且a, b 满足（a ﹣1）2+=0, 那么菱形的面积等于 _________ .15.(201.湖北省十堰市.如图, 在△ABC 中, 点D 是BC 的中点, 点E 、F 分别在线段AD 及其延长线上, 且DE=DF, 给出下列条件: ①BE ⊥EC ；②BF ∥CE ；③AB=AC ；从中选择一个条件使四边形BECF 是菱形, 你认为这个条件.... （只填写序号）DAB C F E16.(201.江苏省宿迁市.如图, 在平面直角坐标系xOy 中, 若菱形ABCD 的顶点A, B 的坐标分别为(－3, 0), (2,0), 点D 在y 轴上, 则点C 的坐标......17.(201.辽宁省大连市.如图, 菱形ABCD 中, AC.BD 相交于点O, 若∠BCO=55°, 则∠ADO=. .18.(201.四川省宜宾市.菱形的周长为20cm, 两个相邻的内角的度数之比为l ∶2, 则较长的对角线长度是cm.19.(201.四川省凉山州.顺次连接矩形四边中点所形成的四边形... , 学校的一块菱形花圃两对角线的长分别是6m 和8m, 则这个花圃的面积......20.(201.四川省泸州市.一个平行四边形的一条边长为3, 两条对角线的长分别为4和, 则它的面积...... .21.(201.福建省漳州市.若菱形的周长为20cm, 则它的边长是 cm ．22.(201.重庆市A 卷.如图, 菱形ABCD 中, ∠A=60°, BD=7, 则菱形ABCD 的周长为________.CAB23.(201.辽宁省锦州市.菱形ABCD 的边长为2, ,E 是AD 边中点, 点P 是对角线BD 上的动点, 当AP+PE 的值最小时, PC 的长是__________.24.(201.山东省淄博市.已知□ABCD, 对角线AC, BD 相交于点O, 请你添加一个适当的条件, 使□ABCD 成为一个菱形. 你添加的条件........三、证明题25.(201.福建省厦门市.如图6, 在四边形ABCD.., AD ∥BC, AM ⊥BC, 垂足为M, AN ⊥DC, 垂足为N. 若∠BAD ＝∠BCD, AM ＝AN, 求证四边形ABCD 是菱形.B D(第15题图)图626.(201.贵州省贵阳市.如图, 在Rt △ABC 中, ∠ACB=90°, D.E 分别为AB, AC 边上的中点, 连接DE, 将△ADE 绕点E 旋转180°得到△CFE, 连接AF, CD.（1）求证: 四边形ADCF 是菱形；（5分）（2）若BC =8, AC =6, 求四边形ABCF 的周长．（5分）27.(201.江苏省淮安市.如图, 在三角形ABC 中, AD 平分∠BAC, 将△ABC 折叠, 使点A 与点D 重合, 展开后折痕分别交AB.AC 于点E 、F, 连接DE 、DF.求证: 四边形AEDF 是菱形.28.(201.四川省乐山市.如图, 在△ABC 中, AB=AC, 四边形ADEF 是菱形, 求证: BE=CE.29.(201.湖南省张家界市.如图, 在四边形ABCD 中, AB ＝AD, CB ＝CD, AC 与BD 相交于O 点, OC=OA, 若E 是CD 上任意一点, 连结BE 交AC 于点F, 连结DF.（1）证明: △CBF ≌△CDF ；（2）若AC=2, BD=2,求四边形ABCD 的周长；（3）请你添加一个条件, 使得∠EFD ＝∠BAD, 并予以证明.第18题图 E D C A四、猜想、探究题30.(201.四川省攀枝花市.如图, 两个连接在一起的菱形的边长都是1cm, 一只电子甲虫, 从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行, 当电子甲虫爬行2014cm时停下, 则它停的位置是（）A．点F B．点E C．点A D．点C。

菱形的判定练习题

菱形的判定练习题菱形的判定练习题菱形，作为一种几何形状，常常出现在我们的生活中。

无论是在建筑设计中的窗户，还是在珠宝设计中的吊坠，菱形都给人一种独特而美妙的感觉。

然而，要判断一个图形是否为菱形并不是一件简单的事情。

在这篇文章中，我们将通过一些练习题来帮助读者更好地理解和掌握菱形的判定方法。

练习题一：给定一个图形，边长分别为a、b、c和d，判断该图形是否为菱形。

解答提示：要判断一个图形是否为菱形，我们需要满足两个条件：首先，该图形必须是四边形；其次，该四边形的四条边必须相等。

因此，我们可以通过比较四条边的长度来判断该图形是否为菱形。

练习题二：给定一个图形，顶点坐标分别为A(x1, y1)、B(x2, y2)、C(x3, y3)和D(x4, y4)，判断该图形是否为菱形。

解答提示：要判断一个图形是否为菱形，我们可以利用菱形的性质：菱形的对角线互相垂直且长度相等。

因此，我们可以计算出该四边形的对角线长度，然后比较它们的长度和垂直关系来判断该图形是否为菱形。

练习题三：给定一个图形，已知其内角的度数分别为α、β、γ和δ，判断该图形是否为菱形。

解答提示：要判断一个图形是否为菱形，我们可以利用菱形的性质：菱形的内角都是直角。

因此，我们可以计算出该四边形的内角度数，然后判断它们是否都等于90度来判断该图形是否为菱形。

练习题四：给定一个图形，已知其外角的度数分别为α、β、γ和δ，判断该图形是否为菱形。

解答提示：要判断一个图形是否为菱形，我们可以利用菱形的性质：菱形的外角都是锐角。

因此，我们可以计算出该四边形的外角度数，然后判断它们是否都小于90度来判断该图形是否为菱形。

练习题五：给定一个图形，已知其对边的夹角分别为α、β、γ和δ，判断该图形是否为菱形。

解答提示：要判断一个图形是否为菱形，我们可以利用菱形的性质：菱形的对边夹角相等。

因此，我们可以计算出该四边形的对边夹角，然后判断它们是否都相等来判断该图形是否为菱形。

菱形的判定专项练习30题

菱形的判定专项练习30题(有答案)ok

菱形的判定专项练习30题(有答案)ok菱形的判定专项练习30题（有答案）1．如图，梯形ABCD中，AD∥BC，BA=AD=DC=BC，点E为BC的中点．（1）求证：四边形ABED是菱形；（2）过A点作AF⊥BC于点F，若BD=4cm，求AF的长．2．如图，四边形ABCD中，对角线AC、BD相交于点O，且AC⊥BD．点M，N分别在BD、AC上，且AO=ON=NC，BM=MO=OD．求证：BC=2DN．3．如图，在△ABC中，AB=AC，D，E，F分别是BC，AB，AC的中点．（1）求证：四边形AEDF是菱形；（2）若AB=12cm，求菱形AEDF的周长．4．如图，在▱ABCD中，EF∥BD，分别交BC，CD于点P，Q，交AB，AD的延长线于点E，F．已知BE=BP．求证：（1）∠E=∠F；（2）▱ABCD是菱形．5．如图，在△ABC中，D是BC的中点，E是AD的中点，过点A作AF∥BC，AF与CE的延长线相交于点F，连接BF．（1）求证：AF=DC；（2）若∠BAC=90°，求证：四边形AFBD是菱形．6．已知平行四边形ABCD中，对角线BD平分∠ABC，求证：四边形ABCD是菱形．7．如图，在一个含30°的三角板ABC中，将三角板沿着AB所在直线翻转180°得到△ABF，再将三角板绕点C顺时针方向旋转60°得到△DEC，点F在AC上，连接AE．（1）求证：四边形ADCE是菱形．（2）连接BF并延长交AE于G，连接CG．请问：四边形ABCG是什么特殊平行四边形？为什么？8．如图，已知四边形ABCD是平行四边形，DE⊥AB，DF⊥BC，垂足分别是为E F，并且DE=DF．求证：四边形ABCD是菱形．9．如图，在△ABC中，DE∥BC，分别交AB，AC于点D，E，以AD，AE为边作▱ADFE交BC于点G，H，且EH=EC．求证：（1）∠B=∠C；（2）▱ADFE是菱形．10．如图，在△ABC中，∠ACB=90°，CD是AB边上的高，∠BAC的平分线AE交CD于F，EG⊥AB于G．（1）求证：△AEG≌△AEC；（2）△CEF是否为等腰三角形，请证明你的结论；（3）四边形GECF是否为菱形，请证明你的结论．11．如图，在△ABC中，AB=AC，点D、E、F分别是△ABC三边的中点．求证：四边形ADEF是菱形．12．如图，在四边形ABCD中，AB=CD，M、N、E、F分别为AD、BC、BD、AC的中点，求证：四边形MENF 为菱形．13．已知：如图，在梯形ABCD中，AD∥BC，AB=AD，∠BAD的平分线AE交BC于点E，连接DE．求证：四边形ABED是菱形．14．如图，在△ABC中，AB=AC，M、O、N分别是AB、BC、CA的中点．求证：四边形AMON是菱形．15．如图：在△ABC中，∠BAC=90°，AD⊥BC于D，CE平分∠ACB，交AD于G，交AB于E，EF⊥BC于F．求证：四边形AEFG是菱形．16．如图，矩形ABCD绕其对角线交点旋转后得矩形AECF，AB交EC于点N，CD交AF于点M．求证：四边形ANCM是菱形．17．如图，四边形ABCD、DEBF都是矩形，AB=BF，AD、BE交于M，BC、DF交于N，那么四边形BMDN是菱形吗？如果是，请写出证明过程；如果不是，说明理由．18．已知如图所示，AD是△ABC的角平分线，DE∥AC交AB于E，DF∥AB交AC于F，四边形AEDF是菱形吗？说明理由．19．已知：如图所示，BD是△ABC的角平分线，EF是BD的垂直平分线，且交AB于E，交BC于点F．求证：四边形BFDE是菱形．20．如图，在平行四边形ABCD中，O是对角线AC的中点，过点O作AC的垂线与边AD、BC分别交于E、F．求证：四边形AFCE是菱形．21．如图，在矩形ABCD中，EF垂直平分BD．（1）判断四边形BEDF的形状，并说明理由．（2）已知BD=20，EF=15，求矩形ABCD的周长．22．如图所示，在▱ABCD中，点E在BC上，AE平分∠BAF，过点E作EF∥AB．求证：四边形ABEF为菱形．23．已知，如图，矩形ABCD中，AB=4cm，AD=8cm，作∠CAE=∠ACE交BC于E，作∠ACF=∠CAF交AD于F．（1）求证：AECF是菱形；（2）求四边形AECF的面积．24．如图，平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F．问四边形AFCE是菱形吗？请说明理由．25．如图：在平行四边形ABCD中，E、F分别是边AB、CD的延长线上一点，且BE=DF，连接EF交AC于O．（1）AC与EF互相平分吗？为什么？（2）连接CE、AF，再添加一个什么条件，四边形AECF是菱形？为什么？26．已知：如图，△ABC和△DBC的顶点在BC边的同侧，AB=DC，AC=BD交于E，∠BEC的平分线交BC于O，延长EO到F，使EO=OF．求证：四边形BFCE是菱形．27．如图，在△ABC中，D是BC边的中点，F，E分别是AD及其延长线上的点，CF∥BE．（1）求证：△BDE≌△CDF；（2）请连接BF，CE，试判断四边形BECF是何种特殊四边形，并说明理由；（3）在（2）下要使BECF是菱形，则△ABC应满足何条件？并说明理由．28．如图，在△ABC中，∠ACB=90°，BC的垂直平分线DE交BC于D，交AB于E，F在DE上，并且AF=CE．（1）求证：四边形ACEF是平行四边形；（2）当∠B的大小满足什么条件时，四边形ACEF是菱形？请回答并证明你的结论．29．如图，在△ABC中，AD是∠BAC的平分线，EF垂直平分AD交AB于E，交AC于F．求证：四边形AEDF是菱形．30．如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA 的外角平分线于点F．（1）探究：线段OE与OF的数量关系并加以证明；（2）当点O运动到何处，且△ABC满足什么条件时，四边形AECF是正方形？（3）当点O在边AC上运动时，四边形BCFE会是菱形吗？若是，请证明，若不是，则说明理由．参考答案：1．1）证明：∵点E为BC的中点，∴BE=CE=BC，∵BA=AD=DC=BC，∴AB=BE=ED=AD，∴四边形ABED是菱形；（2）解：过点D作DH⊥BC，垂足为H，∵CD=DE=CE，∴∠DEC=60°，∴∠DBE=30°，在Rt△BDH中，BD=4cm，∴DH=2cm，∵AF=DH，∴AF=2cm．2．∵AO=ON，BM=MO，∴四边形AMND是平行四边形，∵AC⊥BD，∴平行四边形AMND是菱形，∴MN=DN，∵ON=NC，BM=MO，∴MN=BC，∴BC=2DN 3．（1）∵D，E分别是BC，AB的中点，∴DE∥AC且DE=AF=AC．同理DF∥AB且DF=AE=AB．又∵AB=AC，∴DE=DF=AF=AE，∴四边形AEDF是菱形．（2）∵E是AB中点，∴AE=AB=6cm，因此菱形AEDF的周长为4×6=24cm．4．（1）∵BE=BP，∴∠E=∠BPE，∵BC∥AF，∴∠BPE=∠F，∴∠E=∠F．（2）∵EF∥BD，∴∠E=∠ABD，∠F=∠ADB，∴∠ABD=∠ADB，∴AB=AD，∵四边形ABCD是平行四边形，∴□ABCD是菱形．5．1）证明：∵E是AD的中点，∴∠1=∠2，在△AEF和△DEC 中，∴△AFE≌△DCE（AAS），∴AF=DC；（2）证明：∵D是BC的中点，∴DB=CD=BC，∵AF=CD，∴AF=DB，∵AF∥BD，∴四边形AFBD是平行四边形，∵∠BAC=90°，D为BC中点，∴AD=CB=DB，∴四边形AFBD是菱形．6．∵对角线BD平分∠ABC，∴∠1=∠2，∵四边形ABCD是平行四边形，∴AB∥DC，∴∠3=∠1，∴∠3=∠2，∴DC=BC，又∵四边形ABCD是平行四边形，∴四边形ABCD是菱形．7．（1）∵三角板ABC中，将三角板沿着AB所在直线翻转180°得到△ABF，∴△ABC≌△ABF，且∠BAC=∠BAF=30°，∴∠FAC=60°，∴AD=DC=AC，又∵△ABC≌△EFC，∴CA=CE，又∵∠ECF=60°，∴AC=EC=AE，∴AD=DC=CE=AE，（2）证明：由（1）可知：△ACD，△AFC是等边三角形，△ACB≌△AFB，∴∠EDC=∠BAC=∠FAC=30°，且△ABC为直角三角形，∴BC=AC，∵EC=CB，∴EC=AC，∴E为AC中点，∴DE⊥AC，∴AE=EC，∵AG∥BC，∴∠EAG=∠ECB，∠AGE=∠EBC，∴△AEG≌△CEB，∴AG=BC，（7分）∴四边形ABCG是平行四边形，∵∠ABC=90°，∴四边形ABCG是矩形8．在△ADE和△CDF中，∵四边形ABCD是平行四边形，∴∠A=∠C，∵DE⊥AB，DF⊥BC，∴∠AED=∠CFD=90°．又∵DE=DF，∴△ADE≌△CDF（AAS）∴DA=DC，∴平行四边形ABCD是菱形9．（1）∵在▱ADFE中，AD∥EF，∴∠EHC=∠B（两直线平行，同位角相等）．∵EH=EC（已知），∴∠EHC=∠C（等边对等角），∴∠B=∠C（等量代换）；（2）∵DE∥BC（已知），∴∠AED=∠C，∠ADE=∠B．∵∠B=∠C，∴∠AED=∠ADE，∴AD=AE，∴▱ADFE是菱形．10．1）证明：∵∠ACB=90°，∴AC⊥EC．在Rt△AEG与Rt△AEC中，，∴Rt△AEG≌Rt△AEC（HL）；（2）解：△CEF是等腰三角形．理由如下：∵CD是AB边上的高，∴CD⊥AB．又∵EG⊥AB，∴EG∥CD，∴∠CFE=∠GEA．又由（1）知，Rt△AEG≌Rt△AEC，∴∠GEA=∠CEA，∴∠CEA=∠CFE，即∠CEF=∠CFE，∴CE=CF，即△CEF是等腰三角形；（3）解：四边形GECF是菱形．理由如下：∵由（1）知，Rt△AEG≌Rt△AEC，则GE=EC；由（2）知，CE=CF，∴GE=EC=FC．又∵EG∥CD，即GE∥FC，∴四边形GECFR是菱形．11．∵D、E、F分别是△ABC三边的中点，∴DE AC，EF AB，∴四边形ADEF为平行四边形．又∵AC=AB，∴DE=EF．∴四边形ADEF为菱形．12．∵M、E、分别为AD、BD、的中点，∴ME∥AB，ME=AB，同理：FH∥AB，FH=AB，∴四边形MENF是平行四边形，∵M．F是AD，AC中点，∴MF=DC，∵AB=CD，∴MF=ME，∴四边形MENF为菱形13．∵AE平分∠BAD，∵，∴△BAE≌△DAE（SAS）…（2分）∴BE=DE，…（3分）∵AD∥BC，∴∠DAE=∠AEB，…（4分）∴∠BAE=∠AEB，∴AB=BE，…（5分）∴AB=BE=DE=AD，…（6分）∴四边形ABED是菱形．14．∵AB=AC，M、O、N分别是AB、BC、CA的中点，∴AM=AB=AC=AN，M0∥AC，NO∥AB，且MO=AC=AN，NO=AB=AM（三角形中位线定理），∴AM=MO=AN=NO，∴四边形AMON是菱形（四条边都相等的四边形是菱形）15．证法一：∵AD⊥BC，∴∠ADB=90°，∵∠BAC=90°，∴∠B+∠BAD=90°，∠BAD+∠CAD=90°，∴∠B=∠CAD，∵CE平分∠ACB，EF⊥BC，∠BAC=90°（EA⊥CA），∴AE=EF（角平分线上的点到角两边的距离相等），∵CE=CE，∴由勾股定理得：AC=CF，∵△ACG和△FCG中，∴△ACG≌△FCG，∴∠CAD=∠CFG，∵∠B=∠CAD，∴∠B=∠CFG，∴GF∥AB，∵AD⊥BC，EF⊥BC，∴AD∥EF，即AG∥EF，AE∥GF，∴平行四边形AEFG是菱形．证法二：∵AD⊥BC，∠CAB=90°，EF⊥BC，CE平分∠ACB，∴AD∥EF，∠4=∠5，AE=EF，∵∠1=180°﹣90°﹣∠4，∠2=180°﹣90°﹣∠5，∴∠1=∠2，∵AD∥EF，∴∠2=∠3，∴∠1=∠3，∴AG=AE，∵AE=EF，∴AG=EF，∵AG∥EF，∴四边形AGFE是平行四边形，∵AE=EF，∴平行四边形AGFE是菱形．16．∵CD∥AB，∴∠FMC=∠FAN，∴∠NAE=∠MCF（等角的余角相等），在△CFM和△AEN中，，∴△CFM≌△AEN（ASA），∴CM=AN，∴四边形ANCM为平行四边形，在△ADM和△CFM中，，∴△ADM≌△CFM（AAS），∴AM=CF，∴四边形ANCM是菱形17．四边形BMDN是菱形．∵AM∥BC，∴∠AMB=∠MBN，∵BM∥FN∴∠MBN=∠BNF，∴∠AMB=∠BNF，又∵∠A=∠F=90°，AB=BF，∴△ABM≌△BFN，∴DM=DN，∵ED=BF=AB，∠E=∠A=90°，∠AMB=∠EMD，∴△ABM≌△EDM，∴BM=DM，∴MB=MD=DN=BN，∴四边形BMDN是菱形18．如图，由于DE∥AC，DF∥AB，所以四边形AEDF 为平行四边形．∵DE∥AC，∴∠3=∠2，又∠1=∠2，∴∠1=∠3，∴AE=DE，∴平行四边形AEDF为菱形．19．∵EF是BD的垂直平分线，∴EB=ED，∴∠EBD=∠EDB．∵BD是△ABC的角平分线，∴∠EBD=∠FBD．∴∠FBD=∠EDB，∴ED∥BF．同理，DF∥BE，∴四边形BFDE是平行四边形．又∵EB=ED，∴四边形BFDE是菱形．20．方法一：∵AE∥FC．∴∠EAC=∠FCA．（2分）又∵∠AOE=∠COF，AO=CO，∴△AOE≌△COF．（5分）∴EO=FO．又EF⊥AC，∴AC是EF的垂直平分线．（8分）∴AF=AE，CF=CE，又∵EA=EC，∴AF=AE=CE=CF．∴四边形AFCE为菱形．（10分）方法二：同方法一，证得△AOE≌△COF．（5分）∴AE=CF．∴四边形AFCE是平行四边形．（8分）又∵EF是AC的垂直平分线，方法三：同方法二，证得四边形AFCE是平行四边形．（8分）又EF⊥AC，（9分）∴四边形AFCE为菱形21．（1）四边形BEDF是菱形．在△DOF和△BOE中，∠FDO=∠EBO，OD=OB，∠DOF=∠BOE=90°，所以△DOF≌△BOE，所以OE=OF．又因为EF⊥BD，OD=OB，所以四边形BEDF为菱形．（5分）（2）如图，在菱形EBFD中，BD=20，EF=15，则DO=10，EO=7.5．由勾股定理得DE=EB=BF=FD=12.5．S菱形EBFD =EF•BD=BE•AD，即所以得AD=12．根据勾股定理可得AE=3.5，有AB=AE+EB=16．由2（AB+AD）=2（16+12）=56，故矩形ABCD的周长为5622．∵四边形ABCD是平行四边形，∴AF∥BE，又∵EF∥AB，∴四边形ABEF为平行四边形，∵AE平分∠BAF，∴∠BAE=∠FAE，∵∠FAE=∠BEA，∴∠BAE=∠BEA，∴BA=BE，∴平行四边形ABEF为菱形23．（1）证明：在矩形ABCD中，∵AB∥CD，∴∠BAC=∠DCA，又∠CAE=∠ACE，∠ACF=∠CAF，∴∠EAC=∠FCA．∴AE∥CF．∴四边形AECF为平行四边形，又∠CAE=∠ACE，∴AE=EC．∴▱AECF为菱形．（2）设BE=x，则EC=AE=8﹣x，在Rt△ABE中，AB2+BE2=AE2，所以EC=5，即S菱形AECF=EC×AB=5×4=20．24．四边形AFCE是菱形，理由是：∵四边形ABCD是平行四边形，∴AD∥BC，∴=，∵AO=OC，∴OE=OF，∴四边形AFCE是平行四边形，∵EF⊥AC，∴平行四边形AFCE是菱形25．（1）AC与EF互相平分，连接CE，AF，∵平行四边形ABCD，∴AB∥CD，AB=CD，又∵BE=DF，∴AB+BE=CD+DF，∴AE=CF，∴AE∥CF，AE=CF，∴四边形AECF是平行四边形，∴AC与EF互相平分；（2）条件：EF⊥AC，∵EF⊥AC，又∵四边形AECF是平行四边形，∴平行四边形AECF是菱形．26．∵AB=DC AC=BD BC=CB，∴△ABC≌△DCB，∴∠DBC=∠ACB，∴BE=CE，又∵∠BEC的平分线是EF，∴EO是中线（三线合一），∴BO=CO，∴四边形BFCE是平行四边形（对角线互相平分），又∵BE=CE，∴四边形BFCE是菱形．27．（1）证明：∵CF∥BE，∴∠EBD=∠FCD，D是BC边的中点，则BD=CD，∠BDE=∠CDF，∴△BDE≌△CDF．（2）如图所示，由（1）可得CF=BE，又CF∥BE，所以四边形BECF是平行四边形；（3）△ABC是等腰三角形，即AB=AC，理由：当AB=AC 时，则有AD⊥BC，又（2）中四边形为平行四边形，所以可判定其为菱形．28．（1）∵DE为BC的垂直平分线，∴∠EDB=90°，BD=DC，又∵∠ACB=90°，∴DE∥AC，∴E为AB的中点，∴在Rt△ABC中，CE=AE=BE，∴∠AEF=∠AFE，且∠BED=∠AEF，∠DEC=∠DFA，∴AF∥CE，又∵AF=CE，∴四边形ACEF为平行四边形；（2）要使得平行四边形ACEF为菱形，则AC=CE即可，∵DE∥AC，∴∠BED=∠BAC，∠DEC=∠ECA，又∵∠BED=∠DEC，∴∠EAC=∠ECA，∴AE=EC，又EB=EC，∴AE=EC=EB，∵CE=AB，∴AC=AB即可，在Rt△ABC中，∠ACB=90°，∴当∠B=30°时，AB=2AC，故∠B=30°时，四边形ACEF为菱形．29．∵AD平分∠BAC∴∠BAD=∠CAD又∵EF⊥AD，∴∠AOE=∠AOF=90°∵在△AEO和△AFO中，∴△AEO≌△AFO（ASA），∴EO=FO即EF、AD相互平分，∴四边形AEDF是平行四边形又EF⊥AD，∴平行四边形AEDF为菱形30．1）解：OE=OF．理由如下：∵CE是∠ACB的角平分线，∴∠ACE=∠BCE，又∵MN∥BC，∴∠NEC=∠ECB，∴∠NEC=∠ACE，∴OE=OC，∵OF是∠BCA的外角平分线，∴∠OCF=∠FCD，又∵MN∥BC，∴∠OFC=∠ECD，∴∠OFC=∠COF，∴OF=OC，∴OE=OF；（2）解：当∠ACB=90°，点O在AC的中点时，∵OE=OF，∴四边形AECF是正方形；（3）答：不可能．解：如图所示，∵CE平分∠ACB，CF平分∠ACD，∴∠ECF=∠ACB+∠ACD=（∠ACB+∠ACD）=90°，若四边形BCFE是菱形，则BF⊥EC，但在△GFC中，不可能存在两个角为90°，所以不存在其为菱形．。

菱形的判定专项练习30题

菱形的判断专项练习30 题（有答案）1．如图，梯形ABCD中， AD∥BC， BA=AD=DC=BC，点 E 为 BC的中点．（1）求证：四边形 ABED是菱形；（2）过 A 点作 AF⊥BC 于点 F，若 BD=4cm，求 AF的长．2．如图，四边形 ABCD中，对角线 AC、BD订交于点 O，且 AC⊥BD．点 M，N 分别在 BD、AC上，且 AO=ON=NC，BM=MO=OD．求证： BC=2DN．3．如图，在△ ABC 中， AB=AC， D， E， F 分别是 BC， AB，AC的中点．（1）求证：四边形 AEDF是菱形；（2）若 AB=12cm，求菱形 AEDF的周长．4．如图，在 ? ABCD中， EF∥BD，分别交 BC， CD于点 P，Q，交 AB， AD的延伸线于点 E， F．已知BE=BP．求证：（ 1）∠ E=∠F；（2） ? ABCD是菱形．5．如图，在△ ABC 中， D 是 BC的中点， E 是 AD的中点，过点 A 作 AF∥BC， AF与 CE的延伸线订交于点F，连结 BF．（1）求证： AF=DC；（ 2）若∠ BAC=90°，求证：四边形AFBD是菱形．6．已知平行四边形ABCD中，对角线BD均分∠ ABC，求证：四边形ABCD是菱形．AB所在直线翻转180°获得△ ABF，再将三角板绕点 C 顺7．如图，在一个含30°的三角板ABC中，将三角板沿着时针方向旋转60°获得△ DEC，点 F 在 AC上，连结AE．（1）求证：四边形 ADCE是菱形．（2）连结 BF 并延伸交 AE 于 G，连结 CG．请问：四边形 ABCG是什么特别平行四边形？为何？8．如图，已知四边形 ABCD是平行四边形， DE⊥AB，DF⊥BC，垂足分别是为 E F ，而且 DE=DF．求证：四边形 ABCD 是菱形．9．如图，在△ ABC 中， DE∥B C，分别交 AB， AC于点 D，E，以 AD，AE为边作 ? ADFE交 BC于点 G， H，且EH=EC．求证：（ 1）∠ B=∠C；（2） ? ADFE是菱形．10．如图，在△ ABC 中，∠ ACB=90°， CD是 AB 边上的高，∠ BAC 的均分线AE交 CD于 F，EG⊥AB 于 G．（1）求证：△ AEG≌△ AEC；（2）△ CEF能否为等腰三角形，请证明你的结论；（3）四边形 GECF能否为菱形，请证明你的结论．11．如图，在△ ABC 中， AB=AC，点 D、E、 F 分别是△ ABC 三边的中点．求证：四边形ADEF是菱形．12．如图，在四边形ABCD中， AB=CD，M、 N、 E、 F 分别为 AD、 BC、BD、 AC的中点，求证：四边形MENF为菱形．13．已知：如图，在梯形 ABCD中， AD∥BC， AB=AD，∠ BAD的均分线 AE交 BC于点 E，连结 DE．求证：四边形 ABED 是菱形．14．如图，在△ ABC 中， AB=AC， M、 O、N 分别是 AB、 BC、CA的中点．求证：四边形AMON是菱形．15．如图：在△ ABC 中，∠ BAC=90°， AD⊥BC 于 D， CE均分∠ ACB，交AD于 G，交 AB于 E，EF⊥BC 于 F．求证：四边形AEFG是菱形．16．如图，矩形ABCD绕其对角线交点旋转后得矩形AECF， AB交 EC于点 N， CD交 AF 于点 M．求证：四边形ANCM是菱形．17．如图，四边形 ABCD、 DEBF都是矩形， AB=BF， AD、 BE交于 M，BC、 DF交于 N，那么四边形 BMDN是菱形吗？假如是，请写出证明过程；假如不是，说明原因．18．已知以下图， AD是△ ABC的角均分线， DE∥AC 交 AB 于 E，DF∥AB 交 AC于 F，四边形 AEDF是菱形吗？说明原因．19．已知：以下图， BD是△ ABC的角均分线， EF 是 BD的垂直均分线，且交 AB 于 E，交 BC于点 F．求证：四边形BFDE是菱形．20．如图，在平行四边形ABCD中， O是对角线 AC的中点，过点O作 AC的垂线与边AD、 BC分别交于E、 F．求证：四边形AFCE是菱形．21．如图，在矩形ABCD中， EF 垂直均分BD．（1）判断四边形 BEDF的形状，并说明原因．（2）已知 BD=20， EF=15，求矩形 ABCD的周长．22．以下图，在? ABCD中，点 E 在 BC上， AE均分∠ BAF，过点 E 作 EF∥AB．求证：四边形ABEF为菱形．23．已知，如图，矩形ABCD中， AB=4cm， AD=8cm，作∠ CAE=∠ACE 交 BC于 E，作∠ ACF=∠CAF 交 AD于 F．（ 1）求证： AECF是菱形；（2）求四边形AECF的面积．24．如图，平行四边形 ABCD的对角线 AC的垂直均分线与边 AD、 BC分别交于 E、F．问四边形 AFCE是菱形吗？请说明原因．25．如图：在平行四边形ABCD中， E、F 分别是边 AB、 CD的延伸线上一点，且BE=DF，连结 EF交 AC于 O．（1） AC与 EF 相互均分吗？为何？（2）连结 CE、 AF，再增添一个什么条件，四边形AECF是菱形？为何？26．已知：如图，△ ABC 和△ DBC的极点在 BC边的同侧， AB=DC，AC=BD交于 E，∠ BEC的均分线交 BC于 O，延伸EO 到 F，使 EO=OF．求证：四边形 BFCE是菱形．27．如图，在△ ABC 中， D 是 BC边的中点， F，E 分别是 AD及其延伸线上的点， CF∥BE．（1）求证：△ BDE≌△ CDF；（2）请连结 BF， CE，试判断四边形 BECF是何种特别四边形，并说明原因；（3）在（ 2）下要使 BECF是菱形，则△ ABC 应知足何条件？并说明原因．28．如图，在△ ABC 中，∠ ACB=90°， BC的垂直均分线 DE交 BC于 D，交 AB于 E， F 在 DE上，而且AF=CE．（1）求证：四边形 ACEF是平行四边形；（2）当∠B 的大小知足什么条件时，四边形ACEF是菱形？请回答并证明你的结论．29．如图，在△ ABC 中， AD是∠ BAC的均分线， EF 垂直均分 AD交 AB 于 E，交 AC于 F．求证：四边形AEDF是菱形．30．如图，△ ABC中，点 O是边 AC上一个动点，过O作直线 MN∥BC，设 MN交∠ BCA的均分线于点E，交∠BCA的外角均分线于点F．（ 1）研究：线段OE与 OF的数目关系并加以证明；（ 2）当点 O运动到哪处，且△ ABC 知足什么条件时，四边形AECF是正方形？（ 3）当点 O在边 AC上运动时，四边形BCFE会是菱形吗？假如，请证明，若不是，则说明原因．矩形的判断专项练习30 题参照答案：1． 1）证明：∵点 E 为 BC的中点，∴BE=CE= BC，在△ AEF 和△ DEC中，∵BA=AD=DC=BC，∴△ AFE≌△ DCE（ AAS），∴AF=DC；∴AB=BE=ED=AD，∴四边形 ABED是菱形；（ 2）证明：∵D 是 BC的中点，（ 2）解：过点 D 作 DH⊥BC，垂足为∴DB=CD= BC，H，∵CD=DE=CE，∵AF=CD，∴∠ DEC=60°，∴AF=DB，∴∠ DBE=30°，∵AF∥BD，在 Rt△BDH中， BD=4cm，∴四边形 AFBD是平行四边形，∴DH=2cm，∵∠ BAC=90°， D 为 BC中点，∵AF=DH，∴AD= CB=DB，∴AF=2cm．∴四边形AFBD是菱形．2．∵ AO=ON， BM=MO，∴四边形 AMND是平行四边形，∵AC⊥BD，∴平行四边形 AMND是菱形，∴ MN=DN，6．∵对角线 BD均分∠ ABC，∵ON=NC， BM=MO，∴ MN= BC，∴ BC=2DN∴∠ 1=∠2，∵四边形 ABCD是平行四边形，3．（ 1）∵ D， E 分别是 BC， AB的中点，∴AB∥DC，∴DE∥AC 且 DE=AF= AC．∴∠ 3=∠1，∴∠ 3=∠2，同理 DF∥AB 且 DF=AE= AB．∴DC=BC，又∵四边形 ABCD是平行四边形，又∵ AB=AC，∴ DE=DF=AF=AE，∴四边形 ABCD是菱形．∴四边形 AEDF是菱形．（2）∵E是 AB中点，∴ AE= AB=6cm，所以菱形 AEDF的周长为 4×6=24cm．4．（ 1）∵ BE=BP，∴∠ E=∠BPE，7．（ 1）∵三角板 ABC中，将三角板沿着AB 所在直线翻∵BC∥AF，转 180°获得△ ABF，∴∠ BPE=∠F，∴∠ E=∠F．∴△ ABC≌△ ABF，且∠ BAC=∠BAF=30°，（ 2）∵ EF∥BD，∴∠ FAC=60°，∴∠ E=∠ABD，∠ F=∠ADB，∴AD=DC=AC，∴∠ ABD=∠ADB，又∵△ ABC≌△ EFC，∴AB=AD，∴CA=CE，∵四边形 ABCD是平行四边形，又∵∠ ECF=60°，∴□ ABCD是菱形．∴AC=EC=AE，5． 1）证明：∵E 是 AD的中点，∴AD=DC=CE=AE，∴AE=DE，∴四边形 ADCE是菱形；∵AF∥BC，∴∠ 1=∠2，（ 2）证明：由（ 1）可知：△ ACD，△ AFC 是等边三角形，△ACB≌△ AFB，∴∠ EDC=∠BAC= ∠FAC=30°，且△ ABC 直角三角形，∴B C= AC，∵EC=CB，∴E C= AC，∴E AC中点，∴DE⊥AC，∴AE=EC，∵AG∥BC，∴∠ EAG=∠ECB，∠ AGE=∠EBC，∴△ AEG≌△ CEB，∴A G=BC，（7 分）∴四形 ABCG是平行四形，∵∠ ABC=90°，∴四形 ABCG是矩形8．在△ ADE和△ CDF中，∵四形ABCD是平行四形，∴∠ A=∠C，∵DE⊥AB，DF⊥BC，∴∠ AED=∠CFD=90°．又∵ DE=DF，∴△ ADE≌△ CDF（ AAS）∴DA=DC，∴平行四形ABCD是菱形9．（ 1）∵在 ? ADFE中， AD∥EF，∴∠ EHC=∠B（两直平行，同位角相等）．∵EH=EC（已知），∴∠ EHC=∠C（等等角），∴∠ B=∠C（等量代）；（2）∵ DE∥BC（已知），∴∠AED=∠C，∠ ADE=∠B．∵∠ B=∠C，∴∠ AED=∠ADE，∴AD=AE，∴ ? ADFE是菱形．10． 1）明：∵∠ ACB=90°，∴AC⊥EC．又∵ EG⊥AB， AE 是∠ BAC的均分，∴GE=CE．在 Rt△AEG与 Rt△AEC中，，（2）解：△ CEF 是等腰三角形．原因以下：∵CD是 AB 上的高，∴CD⊥AB．又∵ EG⊥AB，∴EG∥CD，∴∠ CFE=∠GEA．又由（ 1）知， Rt△AEG≌Rt△AEC，∴∠ GEA=∠CEA，∴∠ CEA=∠CFE，即∠ CEF=∠CFE，∴CE=CF，即△ CEF 是等腰三角形；（ 3）解：四形GECF是菱形．原因以下：∵由（ 1）知， Rt△AEG≌Rt△AEC，GE=EC；由（ 2）知， CE=CF，∴GE=EC=FC．又∵ EG∥CD，即GE∥FC，∴四形GECFR是菱形．11．∵ D、 E、 F 分是△ ABC 三的中点，∴DE AC，EF AB，∴四形ADEF平行四形．又∵ AC=AB，∴D E=EF．∴四形ADEF菱形．12．∵ M、 E、分AD、 BD、的中点，∴ME∥AB， ME= AB，同理： FH∥AB， FH= AB，∴四形MENF是平行四形，∵M． F 是 AD， AC中点，∴MF= DC，∵AB=CD，∴MF=ME，∴四形MENF菱形13．∵ AE 均分∠ BAD，∴∠ BAE=∠DAE，⋯（ 1 分）在△ BAE和△ DAE中，∵，∴Rt△AEG≌Rt△AEC（ HL）；∴△ BAE≌△ DAE（SAS）⋯（2分）∴BE=DE，⋯（ 3 分）∵AD∥EF，∵AD∥BC，∴∠ 2=∠3，∴∠ DAE=∠AEB，⋯（ 4 分）∴∠ 1=∠3，∴∠ BAE=∠AEB，∴AG=AE，∴AB=BE，⋯（ 5 分）∵AE=EF，∴AB=BE=DE=AD，⋯（ 6 分）∴AG=EF，∴四形 ABED是菱形．∵AG∥EF，∴四形 AGFE是平行四形，∵AE=EF，∴平行四形 AGFE是菱形．14．∵ AB=AC， M、 O、 N 分是 AB、 BC、 CA的中点，∴AM= AB= AC=AN，M0∥AC，NO∥AB，且MO= AC=AN，16．∵ CD∥AB，NO= AB=AM（三角形中位定理），∴∠ FMC=∠FAN，∴∠ NAE=∠MCF（等角的余角相等），∴AM=MO=AN=NO，在△ CFM和△ AEN中，∴四形 AMON是菱形（四条都相等的四形是菱形）15．法一：∵ AD⊥BC，，∴∠ ADB=90°，∵∠ BAC=90°，∴△ CFM≌△ AEN（ ASA），∴∠ B+∠BAD=90°，∠ BAD+∠CAD=90°，∴CM=AN，∴∠ B=∠CAD，∴四形 ANCM平行四形，∵CE均分∠ ACB，EF⊥BC，∠ BAC=90°（ EA⊥CA），在△ ADM和△ CFM中，∴AE=EF（角均分上的点到角两的距离相等），∵CE=CE，，∴由勾股定理得： AC=CF，∵△ ACG和△ FCG中∴△ ADM≌△ CFM（ AAS），∴AM=CF，，∴四形 ANCM是菱形17．四形 BMDN是菱形．∴△ ACG≌△ FCG，∵AM∥BC，∴∠ CAD=∠CFG，∴∠ AMB=∠MBN，∵∠ B=∠CAD，∵BM∥FN∴∠ B=∠CFG，∴∠ MBN=∠BNF，∴GF∥AB，∴∠ AMB=∠BNF，∵AD⊥BC，EF⊥BC，又∵∠ A=∠F=90°， AB=BF，∴AD∥EF，∴△ ABM≌△ BFN，即 AG∥EF，AE∥GF，∴BM=BN，∴四形 AEFG是平行四形，同理，△ EMD≌△ CND，∵AE=EF，∴DM=DN，∴平行四形 AEFG是菱形．∵ED=BF=AB，∠ E=∠A=90°，∠ AMB=∠EMD，∴△ ABM≌△ EDM，法二：∵AD⊥BC，∠CAB=90°，EF⊥BC，CE均分∠ ACB，∴BM=DM，∴AD∥EF，∠ 4=∠5， AE=EF，∴MB=MD=DN=BN，∵∠ 1=180° 90° ∠ 4，∠ 2=180° 90° ∠ 5，∴四形 BMDN是菱形∴∠ 1=∠2，18．如图，因为 DE∥AC，DF∥AB，所以四边形AEDF为∠FDO=∠EBO， OD=OB，∠ DOF=∠BOE=90°，平行四边形．所以△ DOF≌△ BOE，∵DE∥AC，∴∠ 3=∠2，所以 OE=OF．又∠ 1=∠2，∴∠ 1=∠3，又因为 EF⊥BD， OD=OB，∴AE=DE，∴平行四边形 AEDF为菱形．所以四边形 BEDF为菱形．（5 分）（ 2）如图，在菱形 EBFD中， BD=20， EF=15，则 DO=10， EO=．由勾股定理得 DE=EB=BF=FD=．19．∵ EF 是 BD的垂直均分线，S 菱形EBFD=EF? BD=BE? AD，∴EB=ED，∴∠ EBD=∠EDB．即∵BD是△ ABC的角均分线，∴∠ EBD=∠FBD．所以得 AD=12．∴∠ FBD=∠EDB，依据勾股定理可得 AE=，有 AB=AE+EB=16．∴ED∥BF．由 2（AB+AD） =2（ 16+12） =56，同理， DF∥BE，故矩形 ABCD的周长为 56∴四边形 BFDE是平行四边形．22．∵四边形 ABCD是平行四边形，又∵ EB=ED，∴AF∥BE，∴四边形 BFDE是菱形．又∵ EF∥AB，∴四边形 ABEF为平行四边形，∵AE 均分∠ BAF，∴∠ BAE=∠FAE，∵∠ FAE=∠BEA，∴∠ BAE=∠BEA，20．方法一：∵ AE∥FC．∴BA=BE，∴∠ EAC=∠FCA．（ 2 分）∴平行四边形 ABEF为菱形又∵∠ AOE=∠COF， AO=CO，23．（ 1）证明：在矩形 ABCD中，∴△ AOE≌△ COF．（5 分）∵AB∥CD，∴EO=FO．∴∠ BAC=∠DCA，又 EF⊥AC，又∠ CAE=∠ACE，∠ ACF=∠CAF，∴AC是 EF 的垂直均分线．（8 分）∴∠ EAC=∠FCA．∴AF=AE， CF=CE，∴AE∥CF．又∵ EA=EC，∴四边形 AECF为平行四边形，∴AF=AE=CE=CF．又∠ CAE=∠ACE，∴四边形 AFCE为菱形．（ 10 分）∴AE=EC．方法二：同方法一，证得△ AOE≌△ COF．（ 5 分）∴ ? AECF为菱形．∴AE=CF．（ 2）设 BE=x，则 EC=AE=8﹣ x，∴四边形 AFCE是平行四边形．（ 8 分）在 Rt△ABE中，又∵ EF 是 AC的垂直均分线，222 AB +BE =AE，∴EA=EC，222即 4 +x =（ 8﹣ x）．∴四边形 AFCE是菱形．（ 10 分）解之得 x=3，方法三：同方法二，证得四边形 AFCE是平行四边形．（8所以 EC=5，分）即 S=EC×AB=5×4=20．菱形 AECF又 EF⊥AC，（ 9 分）24．四边形 AFCE是菱形，原因是：∴四边形 AFCE为菱形∵四边形 ABCD是平行四边形，21．（ 1）四边形 BEDF是菱形．∴AD∥BC，在△ DOF和△ BOE中，∴= ，∵AO=OC，∴OE=OF，∴四边形AFCE是平行四边形，∵E F⊥AC，∴平行四边形AFCE是菱形25．（ 1） AC与 EF 相互均分，连结CE， AF，∵平行四边形ABCD，∴AB∥CD， AB=CD，又∵ BE=DF，∴A B+BE=CD+DF，∴A E=CF，∴AE∥CF， AE=CF，∴四边形AECF是平行四边形，∴AC与 EF 相互均分；（2）条件： EF⊥AC，∵EF⊥AC，又∵四边形 AECF是平行四边形，∴平行四边形 AECF是菱形．26．∵ AB=DC AC=BD BC=CB，∴△ ABC≌△ DCB，∴∠ DBC=∠ACB，∴B E=CE，又∵∠ BEC的均分线是EF，∴EO是中线（三线合一），∴BO=CO，∴四边形 BFCE是平行四边形（对角线相互均分），又∵ BE=CE，∴四边形BFCE是菱形．27．（ 1）证明：∵ CF∥BE，∴∠ EBD=∠FCD，D是BC边的中点，则BD=CD，∠BDE=∠CDF，∴△ BDE≌△ CDF．（2）以下图，由（ 1）可得 CF=BE，又 CF∥BE，所以四边形 BECF是平行四边形；（3）△ ABC是等腰三角形，即 AB=AC，原因：当 AB=AC 时，则有 AD⊥BC，又（ 2）中四边形为平行四边形，所以可判断其为菱形．28．（ 1）∵ DE 为 BC的垂直均分线，∴∠ EDB=90°， BD=DC，又∵∠ ACB=90°，∴DE∥AC，∴E为 AB的中点，∴在 Rt△ABC中， CE=AE=BE，∴∠ AEF=∠AFE，且∠BED=∠AEF，∠DEC=∠DFA，∴AF∥CE，又∵ AF=CE，∴四边形 ACEF为平行四边形；（2）要使得平行四边形 ACEF为菱形，则 AC=CE即可，∵DE∥AC，∴∠ BED=∠BAC，∠ DEC=∠ECA，又∵∠ BED=∠DEC，∴∠ EAC=∠ECA，∴AE=EC，又 EB=EC，∴AE=EC=EB，∵C E= AB，∴A C= AB即可，在 Rt△ABC中，∠ ACB=90°，∴当∠ B=30°时， AB=2AC，故∠ B=30°时，四边形 ACEF为菱形．29．∵ AD 均分∠ BAC∴∠ BAD=∠CAD又∵ EF⊥AD，∴∠ AOE=∠AOF=90°∵在△ AEO和△ AFO中，∴△ AEO≌△ AFO（ ASA），∴EO=FO即 EF、 AD相互均分，∴四边形 AEDF是平行四边形又EF⊥AD，∴平行四边形 AEDF为菱形30． 1）解： OE=OF．原因以下：∵CE是∠ ACB的角均分线，∴∠ ACE=∠BCE，又∵ MN∥BC，∴∠ NEC=∠ECB，∴∠ NEC=∠ACE，∴OE=OC，∵OF是∠ BCA的外角均分线，∴∠ OCF=∠FCD，又∵ MN∥BC，∴∠ OFC=∠ECD，∴∠ OFC=∠COF，若四边形BCFE是菱形，则BF⊥EC，但在△ GFC中，不行能存在两个角为其为菱形．90°，所以不存在∴OF=OC，∴OE=OF；（ 2）解：当∠ ACB=90°，点∵OE=OF，∴四边形AECF是正方形；O在AC的中点时，（ 3）答：不行能．解：以下图，∵CE均分∠ ACB， CF均分∠ ACD，∴∠ ECF= ∠ACB+ ∠ACD= （∠ ACB+∠ACD）=90°，。

菱形性质及判定练习题

菱形性质及判定练习题
菱形是一种特殊的四边形，具有一些独特的性质。

本文将介绍
关于菱形性质的一些基本概念，并提供一些判定练题，以帮助大家
加深对菱形的理解。

菱形的定义和性质
菱形是一个有四条边的四边形，其特点是所有四条边的长度相等。

以下是一些关于菱形的基本性质：
1. 菱形的对边平行：菱形的对边是平行的。

这意味着连接菱形
对角线的线段也是平行的。

2. 菱形的对角线相等：菱形的两条对角线相等的长度。

3. 菱形的角度性质：菱形的内角都是直角，即90度。

此外，
菱形的两个邻边的夹角也是相等的。

这意味着，如果一个角是直角，则菱形的其他三个角也都是直角。

菱形的判定练题
下面是一些菱形的判定练题，用以考察你对菱形性质的理解。

1. 若一个四边形的边长都相等，且对角线相等，是否可以判定该四边形是菱形？
2. 若一个四边形的对边平行，且对角线相等，是否可以判定该四边形是菱形？
3. 若一个四边形的内角都是直角，对角线相等，是否可以判定该四边形是菱形？
4. 若一个四边形的两个邻边的夹角相等，对角线相等，是否可以判定该四边形是菱形？
请你在思考后回答以上问题，并确切判断其是否是菱形。

这些练题将帮助你加深对菱形性质的认识和理解。

---
菱形是一种有四条边的特殊四边形，其所有边长相等。

菱形的
对边平行，对角线相等，内角都是直角，且邻边的夹角相等。

通过
判定四边形的边长、对边平行、内角直角以及邻边夹角相等的条件，我们可以推断出一个四边形是否是菱形。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

A、等腰梯形B、正方形形的性质。
分析：由于两个等边三角形的边长都相等，则得到的四边形的四条边也相等，即是菱形．
解答：解：由题意可得：得到的四边形的四条边相等，即是菱形．
故选D．
点评：本题利用了菱形的概念：四边相等的四边形是菱形．
7、汶川地震后，吉林电视台法制频道在端午节组织发起“绿丝带行动”，号召市民为四川受灾的人们祈福．人们将绿丝带剪成小段，并用别针将折叠好的绿丝带别在胸前，如图所示，绿丝带重叠部分形成的图形是（）
故选C．
点评：本题综合考查了垂径定理和菱形的判定方法．
二、填空题（共8小题）
11、（2009•青海）如图，四边形ABCD的对角线互相平分，要使它变为菱形，需要添加的条件是AC⊥BD或AB=BC或BC=CD或AB=AD（只填一个你认为正确的即可）．
考点：菱形的判定。
专题：开放型。
分析：根据平行四边形的性质和菱形的性质，可添加：AC⊥BD或AB=BC，或BC=CD，或CD=DA，或AB=AD．
（1）说明四边形ACEF是平行四边形；
（2）当∠B满足什么条件时，四边形ACEF是菱形，并说明理由。
答案与评分标准
一、选择题（共10小题）
1、（2008•天津）在平面直角坐标系中，已知点A（0，2），B（﹣2 ，0），C（0，﹣2），D（2 ，0），则以这四个点为顶点的四边形ABCD是（）
A、矩形B、菱形
3、在四边形ABCD中，对角线AC、BD交于点O，从（1）AB=CD；（2）AB∥CD；（3）OA=OC；（4）OB=OD；（5）AC⊥BD；（6）AC平分∠BAD这六个条件中，选取三个推出四边形ABCD是菱形．如（1）（2）（5）=＞ABCD是菱形，再写出符合要求的两个：_________=＞ABCD是菱形；_________=＞ABCD是菱形
2（a2+b2+c2+d2）=2（ab+bc+cd+ad），）
∴（a﹣b）2+（b﹣c）2+（c﹣d）2+（a﹣d）2=0，
由非负数的性质可知：（a﹣b）=0，（b﹣c）=0，（c﹣d）=0，（a﹣d）=0，
∴a=b=c=d，
∴四边形一定是菱形，
故选C．
点评：此题主要考查了菱形的判定，关键是整理配方式子，还利用了非负数的性质．
填空
1、如图，如果要使平行四边形ABCD成为一个菱形，需要添加一个条件，那么你添加的条件是_________．
2、如图，平行四边形ABCD中，AF、CE分别是∠BAD和∠BCD的角平分线，根据现有的图形，请添加一个条件，使四边形AECF为菱形，则添加的一个条件可以是_________．（只需写出一个即可，图中不能再添加别的“点”和“线”）
（1）求证：AD=CE；
（2）填空：四边形ADCE的形状是_________．
7如图△ABC与△CDE都是等边三角形，点E、F分别在AC、BC上，且EF∥AB
（1）求证：四边形EFCD是菱形；
（2）设CD=4，求D、F两点间的距离．
8（2007•双柏县）如图，在梯形纸片ABCD中，AD∥BC，AD＞CD，将纸片沿过点D的直线折叠，使点C落在AD上的点C处，折痕DE交BC于点E，连接C′E．
A、①③B、②③
C、③④D、①②③
3、能判定一个四边形是菱形的条件是（）
A、对角线相等且互相垂直B、对角线相等且互相平分
C、对角线互相垂直D、对角线互相垂直平分
4、四边形的四边长顺次为a、b、c、d，且a2+b2+c2+d2=ab+bc+cd+ad，则此四边形一定是（）
A、平行四边形B、矩形
C、菱形D、正方形
（2）探究：当点E在什么位置时，四边形EFPC是平行四边形？并判断四边形EFPC是什么特殊的平行四边形，请说明理由；
（1）
11若如图，在四边形ABCD中，点E、F分别是AD、BC的中点，G、H分别是BD、AC的中点，AB、CD满足什么条件时，四边形EGFH是菱形？请证明你的结论。
图，在△ABC中，∠ACB=90°，BC的垂直平分线DE交BC于D，交AB于E，F在DE上，且AF=CE=AE．
A、正方形B、等腰梯形
C、菱形D、矩形
考点：菱形的判定。
专题：应用题。
分析：首先可判断重叠部分为平行四边形，且两条彩带宽度相同；再由平行四边形的面积可得邻边相等，则重叠部分为菱形．
解答：解：过点A作AE⊥BC于E，AF⊥CD于F，因为两条彩带宽度相同，
所以AB∥CD，AD∥BC，AE=AF．
∴四边形ABCD是平行四边形．
∵S▱ABCD=BC•AE=CD•AF．又AE=AF．
∴BC=CD，
∴四边形ABCD是菱形．
故选C．
点评：本题利用了平行四边形的判定和平行四边形的面积公式、一组邻边相等的平行四边形是菱形．
5、（2007•泸州）在同一平面内，用两个边长为a的等边三角形纸片（纸片不能裁剪）可以拼成的四边形是（）
A、矩形B、菱形
菱形的判定2
一、选择题
1、在平面直角坐标系中，已知点A（0，2），B（﹣2 ，0），C（0，﹣2），D（2 ，0），则以这四个点为顶点的四边形ABCD是（）
A、矩形B、菱形
C、正方形D、梯形
2如图，下列条件之一能使平行四边形ABCD是菱形的为（）
①AC⊥BD；②∠BAD=90°；③AB=BC；④AC=BD．
12、（2007•成都）如图，如果要使平行四边形ABCD成为一个菱形，需要添加一个条件，那么你添加的条件是AB=AD或AC⊥BD．
考点：菱形的判定；平行四边形的性质。
专题：开放型。
分析：菱形的判定方法有三种：
①定义：一组邻边相等的平行四边形是菱形；
②四边相等；
③对角线互相垂直平分的四边形是菱形．
∴可添加：AB=AD或AC⊥BD．
∵S▱ABCD=BC•AE=CD•AF．又AE=AF．
∴BC=CD，
∴四边形ABCD是菱形．
故选C．
点评：本题利用了平行四边形的判定和平行四边形的面积公式、一组邻边相等的平行四边形是菱形．
8、能判定一个四边形是菱形的条件是（）
A、对角线相等且互相垂直B、对角线相等且互相平分
C、对角线互相垂直D、对角线互相垂直平分
（1）求证：△ADE≌△CBF．
（2）若AD⊥BD，则四边形BFDE是什么特殊四边形？请证明你的结论．
3、（2007•娄底）如图，已知点D在△ABC的BC边上，DE∥AC交AB于E，DF∥AB交AC于F．
（1）求证：AE=DF；
（2）若AD平分∠BAC，试判断四边形AEDF的形状，并说明理由．
4、（2011•常州）已知：如图，在梯形ABCD中，AB∥CD，BC=CD，AD⊥BD，E为AB中点，求证：四边形BCDE是菱形．
5、如图，在△ABC和△DCB中，AB=DC，AC=DB，AC与DB交于点M．
（1）求证：△ABC≌△DCB；
（2）过点C作CN∥BD，过点B作BN∥AC，CN与BN交于点N，试判断线段BN与CN的数量关系，并证明你的结论．
6如图，△ABC中，AC的垂直平分线MN交AB于点D，交AC于点O，CE∥AB交MN于E，连接AE、CD．
10、（2008•梅州）如图所示，圆O的弦AB垂直平分半径OC，则四边形OACB（）
A、是正方形B、是长方形
C、是菱形D、以上答案都不对
考点：垂径定理；菱形的判定。
分析：根据垂径定理和特殊四边形的判定方法求解．
解答：解：由垂径定理知，OC垂直平分AB，即OC与AB互相垂直平分，所以四边形OACB是菱形．
求证：四边形CDC′E是菱形．
9已知：如图，平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别相交于点E、F．
求证：四边形AFCE是菱形．
10、如图，等边△ABC的边长为2，E是边BC上的动点，EF∥AC交边AB于点F，在边AC上取一点P，使PE=EB，连接FP．
（1）请直接写出图中与线段EF相等的两条线段；（不再另外添加辅助线）
三、解答题（共11小题）
1、如图，在△ABC中，AB=AC，D是BC的中点，连接AD，在AD的延长线上取一点E，连接BE， CE．
（1）求证：△ABE≌△ACE；
（2）当AE与AD满足什么数量关系时，四边形ABEC是菱形？并说明理由．
2、如图，在▱ABCD中，E，F分别为边AB，CD的中点，连接DE、BF、BD．
A、平行四边形B、矩形
C、菱形D、正方形
考点：菱形的判定；非负数的性质：偶次方。
分析：本题可通过整理配方式子a2+b2+c2+d2=ab+bc+cd+ad得到（a﹣b）2+（b﹣c）2+（c﹣d）2+（a﹣d）2=0，从而得出a=b=c=d，∴四边形一定是菱形．
解答：解：整理配方式子a2+b2+c2+d2=ab+bc+cd+ad，
解答：解：根据菱形的判定：对角线互相垂直的平行四边形是菱形，有一组邻边相等的平行四边形是菱形可知：①，③正确．
故选A．
点评：本题考查菱形的判定，即对角线互相垂直的平行四边形是菱形，有一组邻边相等的平行四边形是菱形．
4、（2007•衢州）红丝带是关注艾滋病防治问题的国际性标志，人们将红丝带剪成小段，并用别针将折叠好的红丝带别在胸前，如图所示．红丝带重叠部分形成的图形是（）
解答：解：四边形ABCD的对角线互相平分，则四边形ABCD为平行四边形，
再依据：一组邻边相等的平行四边形是菱形；对角线互相垂直的平行四边形是菱形，
可添加：AC⊥BD或AB=BC，或BC=CD，或CD=DA，或AB=AD（答案不唯一）
点评：本题考查平行四边形及菱形的判定．菱形的判定方法有三种：①定义：一组邻边相等的平行四边形是菱形；②四边相等；③对角线互相垂直平分的四边形是菱形．