delphi kmp字符串匹配率算法
KMP字符串匹配算法

KMP是一种著名的字符串模式匹配算法,它的名称来自三个发明人的名字。
这个算法的一个特点就是,在匹配时,主串的指针不用回溯,整个匹配过程中,只需要对主串扫描一遍就可以了。
因此适合对大字符串进行匹配。
搜了网上很多KMP的代码下来调试,发现不是下标越界,就是死循环的,相当诡异...最后重新拿起严老师那本《数据结构》来翻,各种费解,有个地方用下标值和字符串下标0的元素做判断,更是诡异了...过了一天,忽然觉悟了。
网上这些代码都是来自《数据结构》或者和他同源的版本的,而它使用的是以下标1为起始的字符串!对这种字符串组织格式,下标0存放的是字符串的长度。
可是如今主流的语言,几乎都是用的下标0作为起始,书本上的代码显然没法用,那就自己重写一个吧。
算法的原理字符串匹配嘛,无非就是两个指针,分别指向主串和模式串,然后依次往后移,检查是否一致。
在遇到不能匹配的情况时(简称“失配”),一般的方法,就是让两个指针回溯,主串指针往后再移动一位,从头开始匹配。
这其中做了很多重复劳动,我们可以分析一下:可以看到模式串在匹配到下标5时失配了。
我们抓出模式串和主串在前方匹配的5个字符,并在模式串部分的前端和主串部分的后端找到了一对最长的相等的字串(不等于原来的串),用阴影标记一下,后面有用。
接着移动模式串,继续匹配:看出什么规律了么?每次比较,其实都是“abaab”的前端和后端的字串进行比较:第一回是"abaa"vs"baab"第二回是"aba"vs"aab"第三回是"ab"vs"ab"可见,只有在模式串部分的前端和主串部分的后端重合的时候,才可能继续匹配。
是这样么?当然是的,因为我们之前找出的是最长的,相等的字串!这样就能把中间无效的对比步骤省略,主串的指针不变,模式串的指针直接跳到下标2继续匹配。
这里的下标2就等于最长相等字串的长度。
kmp 字符串匹配算法

kmp 字符串匹配算法KMP字符串匹配算法KMP算法,全称为Knuth-Morris-Pratt算法,是一种用于字符串匹配的高效算法。
它的核心思想是通过预处理模式串,根据模式串的前缀和后缀的特性来确定匹配失败时的下一步跳转位置,从而避免不必要的比较操作,提高匹配效率。
KMP算法的应用非常广泛,例如在文本编辑器中搜索关键字、DNA序列比对、音频和视频处理等领域都有广泛的应用。
1. KMP算法的基本原理KMP算法的基本原理是利用模式串的前缀和后缀的特性来确定匹配失败时的下一步跳转位置,从而避免不必要的比较操作,提高匹配效率。
具体来说,KMP算法通过预处理模式串,构建一个跳转表,用于确定匹配失败时的下一步跳转位置。
跳转表的构建过程是通过遍历模式串,计算每个位置的最长相同前缀后缀长度。
2. KMP算法的步骤KMP算法的步骤可以分为两个阶段:预处理和匹配。
2.1 预处理阶段在预处理阶段,首先需要计算模式串的最长相同前缀后缀长度。
具体步骤如下:- 定义两个指针i和j,分别指向模式串的第一个字符和第二个字符;- 如果i和j指向的字符相同,则将i和j都向后移动一位,并将j位置的最长相同前缀后缀长度记录在跳转表中;- 如果i和j指向的字符不同,则根据跳转表中记录的最长相同前缀后缀长度,更新j的位置。
2.2 匹配阶段在匹配阶段,根据跳转表进行匹配操作。
具体步骤如下:- 定义两个指针i和j,分别指向文本串和模式串的第一个字符;- 如果i和j指向的字符相同,则将i和j都向后移动一位;- 如果i和j指向的字符不同,则根据跳转表中记录的最长相同前缀后缀长度,更新j的位置。
3. KMP算法的优势相比于朴素的字符串匹配算法,KMP算法具有以下优势:- 避免了不必要的比较操作,减少了时间复杂度;- 预处理过程只需要对模式串进行一次,之后的匹配过程可以复用跳转表,减少了空间复杂度;- 适用于大规模的字符串匹配问题,可以高效地处理大文本串和大模式串。
KMP字符串模式匹配算法解释

个人觉得这篇文章是网上的介绍有关KMP算法更让人容易理解的文章了,确实说得很“详细”,耐心地把它看完肯定会有所收获的~~,另外有关模式函数值next[i]确实有很多版本啊,在另外一些面向对象的算法描述书中也有失效函数f(j)的说法,其实是一个意思,即next[j]=f(j-1)+1,不过还是next[j]这种表示法好理解啊:KMP字符串模式匹配详解KMP字符串模式匹配通俗点说就是一种在一个字符串中定位另一个串的高效算法。
简单匹配算法的时间复杂度为O(m*n);KMP匹配算法。
可以证明它的时间复杂度为O(m+n).。
一.简单匹配算法先来看一个简单匹配算法的函数:int Index_BF ( char S [ ], char T [ ], int pos ){/* 若串S 中从第pos(S 的下标0≤pos<StrLength(S))个字符起存在和串T 相同的子串,则称匹配成功,返回第一个这样的子串在串S 中的下标,否则返回-1 */int i = pos, j = 0;while ( S[i+j] != '\0'&& T[j] != '\0')if ( S[i+j] == T[j] )j ++; // 继续比较后一字符else{i ++; j = 0; // 重新开始新的一轮匹配}if ( T[j] == '\0')return i; // 匹配成功返回下标elsereturn -1; // 串S中(第pos个字符起)不存在和串T相同的子串} // Index_BF此算法的思想是直截了当的:将主串S中某个位置i起始的子串和模式串T相比较。
即从j=0 起比较S[i+j] 与T[j],若相等,则在主串S 中存在以i 为起始位置匹配成功的可能性,继续往后比较( j逐步增1 ),直至与T串中最后一个字符相等为止,否则改从S串的下一个字符起重新开始进行下一轮的"匹配",即将串T向后滑动一位,即i 增1,而j 退回至0,重新开始新一轮的匹配。
kmp,字符串匹配算法

m:\汇总\1\kmp\kmp\kmp.cpp // kmp.cpp : Defines the entry point for the console application. // #include "stdafx.h" int _tmain(int argc, _TCHAR* argv[]) { return 0; } #include <iostream> #include <string.h> using namespace std; void get_nextval(const char *T, int next[]) { //求模式串T的next函数值并存入数组next。 int j = 0, k = -1; next[0] = -1; while ( T[j] != '\0' ) { if (k == -1 || T[j] == T[k]) { ++j; ++k; if (T[j]!=T[k]) next[j] = k; else next[j] = next[k]; } else k = next[k]; } } int KMP(const char *Text,const char* Pattern) //const表示函数内部不会改变这个参数的值。 { if( !Text||!Pattern|| Pattern[0]=='\0' || Text[0]=='\0' )// return -1;//空指针或空串,返回-1。 int len=0; const char * c=Pattern; while(*c++!='\0')//移动指针比移动下标快。 { ++len;//字符串长度。 } int *next=new int[len+1]; get_nextval(Pattern,next);//求Pattern的next函数值 int index=0,i=0,j=0; while(Text[i]!='\0' && Pattern[j]!='\0' ) { if(Text[i]== Pattern[j]) { ++i;//继续比较后继字符 ++j; } else { index += j-next[j]; if(next[j]!=-1) j=next[j];//模式串向右移动 else { j=0; ++i; } } } delete []next;
KMP模式匹配算法

KMP模式匹配算法KMP算法是一种字符串匹配算法,用于在一个主串中查找一个模式串的出现位置。
该算法的核心思想是通过预处理模式串,构建一个部分匹配表,从而在匹配过程中尽量减少不必要的比较。
KMP算法的实现步骤如下:1.构建部分匹配表部分匹配表是一个数组,记录了模式串中每个位置的最长相等前后缀长度。
从模式串的第二个字符开始,依次计算每个位置的最长相等前后缀长度。
具体算法如下:-初始化部分匹配表的第一个位置为0,第二个位置为1- 从第三个位置开始,假设当前位置为i,则先找到i - 1位置的最长相等前后缀长度记为len,然后比较模式串中i位置的字符和模式串中len位置的字符是否相等。
- 如果相等,则i位置的最长相等前后缀长度为len + 1- 如果不相等,则继续判断len的最长相等前后缀长度,直到len为0或者找到相等的字符为止。
2.开始匹配在主串中从前往后依次查找模式串的出现位置。
设置两个指针i和j,分别指向主串和模式串的当前位置。
具体算法如下:-当主串和模式串的当前字符相等时,继续比较下一个字符,即i和j分别向后移动一个位置。
-当主串和模式串的当前字符不相等时,根据部分匹配表确定模式串指针j的下一个位置,即找到模式串中与主串当前字符相等的位置。
如果找到了相等的位置,则将j移动到相等位置的下一个位置,即j=部分匹配表[j];如果没有找到相等的位置,则将i移动到下一个位置,即i=i+13.检查匹配结果如果模式串指针j移动到了模式串的末尾,则说明匹配成功,返回主串中模式串的起始位置;如果主串指针i移动到了主串的末尾,则说明匹配失败,没有找到模式串。
KMP算法的时间复杂度为O(m+n),其中m为主串的长度,n为模式串的长度。
通过预处理模式串,KMP算法避免了在匹配过程中重复比较已经匹配过的字符,提高了匹配的效率。
总结:KMP算法通过构建部分匹配表,实现了在字符串匹配过程中快速定位模式串的位置,减少了不必要的比较操作。
字符串匹配kmp算法

字符串匹配kmp算法字符串匹配是计算机科学中的一个基本问题,它涉及在一个文本串中寻找一个模式串的出现位置。
其中,KMP算法是一种更加高效的算法,它不需要回溯匹配过的字符,在匹配失败的时候,根据已经匹配的字符和模式串前缀的匹配关系直接跳跃到下一次匹配的起点。
下面,我将详细介绍KMP算法原理及其实现。
1. KMP算法原理KMP算法的核心思想是:当模式串中的某个字符与文本串中的某个字符不相同时,根据已经匹配的字符和模式串前缀的匹配关系,跳过已经比较过的字符,从未匹配的字符开始重新匹配。
这个过程可以通过计算模式串的前缀函数(即next数组)来实现。
具体地,假设现在文本串为T,模式串为P,它们的长度分别为n和m。
当对于文本串T的第i个字符和模式串P的第j个字符(i和j都是从0开始计数的)进行匹配时:如果T[i]和P[j]相同,则i和j都加1,继续比较下一个字符;如果T[i]和P[j]不同,则j回溯到next[j](next[j]是P[0]到P[j-1]的一个子串中的最长的既是自身的前缀又是后缀的子串的长度),而i不会回溯,继续和P[next[j]]比较。
如果匹配成功,则返回i-j作为P在T中的起始位置;如果匹配失败,则继续执行上述过程,直到文本串T被遍历完或匹配成功为止。
2. KMP算法步骤(1)计算模式串的前缀函数next[j]。
next[j]表示P[0]到P[j-1]的一个子串中的最长的既是自身的前缀又是后缀的子串的长度。
具体计算方式如下:先令next[0]=-1,k=-1(其中k表示相等前缀的长度,初始化为-1),j=0。
从j=1向后遍历整个模式串P:如果k=-1或者P[j]=P[k],则next[j+1]=k+1,k=j,j+1;否则,令k=next[k],再次执行步骤2。
(2)使用next数组进行匹配。
从文本串T的第0个字符开始,从模式串P的第0个字符开始匹配,如果匹配失败,根据next数组进行回溯。
delphi kmp字符串匹配率算法

delphi kmp字符串匹配率算法【原创版】目录一、引言二、KMP 算法的原理三、KMP 算法的实现四、KMP 算法的应用示例五、总结正文一、引言在计算机科学领域,字符串匹配问题是一个常见且重要的问题。
如何快速地在一个文本字符串中查找一个模式字符串,是字符串匹配问题的核心。
KMP 算法,全称为 Knuth-Morris-Pratt 算法,是一种高效的字符串匹配算法,可以在 O(nm) 的时间复杂度内完成匹配,其中 n 是文本字符串的长度,m 是模式字符串的长度。
二、KMP 算法的原理KMP 算法的核心思想是利用已经匹配过的字符串信息来避免不必要的字符比较。
当某个字符匹配失败时,可以根据已经匹配成功的字符串的末尾字符来跳过已经匹配过的部分,从而减少重复比较。
为了实现这个思想,KMP 算法需要预处理模式字符串,计算出每个字符的 next 数组,用于存储当前字符匹配失败后需要跳过的字符个数。
三、KMP 算法的实现KMP 算法的实现主要包括两个步骤:预处理和匹配。
预处理阶段,需要计算出模式字符串的 next 数组。
匹配阶段,使用 next 数组来引导模式字符串在文本字符串中的匹配过程。
具体来说,从左到右逐个字符地比较模式字符串和文本字符串。
当发现不匹配的字符时,利用 next 数组跳过已经匹配过的部分,继续匹配。
如果模式字符串匹配完文本字符串,则匹配成功;否则,匹配失败。
四、KMP 算法的应用示例假设有一个文本字符串"ABCABCDDDEABCDABHJJEEIDAEAENN",和一个模式字符串"ABCDABC",使用 KMP 算法进行匹配。
首先预处理模式字符串,得到 next 数组:-1, 0, 0, 0, 0, 1, 2, 3。
然后进行匹配,得到匹配结果为:i=3, j=3。
由于 j 等于模式字符串的长度,所以匹配成功。
五、总结KMP 算法是一种高效的字符串匹配算法,利用预处理和 next 数组来避免重复比较,从而提高匹配速度。
KMP算法解决字符串匹配问题

KMP算法解决字符串匹配问题作者:原⽂地址:要解决的问题假设字符串str长度为N,字符串match长度为M,M <= N, 想确定str中是否有某个⼦串是等于match的。
返回和match匹配的字符串的⾸字母在str的位置,如果不匹配,则返回-1OJ可参考:暴⼒⽅法从str串中每个位置开始匹配match串,时间复杂度O(M*N)KMP算法KMP算法可以⽤O(N)时间复杂度解决上述问题。
流程我们规定数组中每个位置的⼀个指标,这个指标定义为这个位置之前的字符前缀和后缀的匹配长度,不要取得整体。
例如: ababk 这个字符串,k之前位置的字符串为abab,前缀ab 等于后缀ab,长度为2,所以k位置的指标为2,下标为3的b之前的字符串aba ,前缀a 等于后缀a, 长度为1,所以下标为3的b的指标为1,⼈为规定:下标为0的字符的指标是-1,下标为1的字符的指标0假设match串中每个位置我们都已经求得了这个指标值,放在了⼀个next数组中,这个next数组有助于我们加速整个匹配过程。
假设在某个时刻,匹配的到的字符如下其中str的i..j⼀直可以匹配上match串的0...m, str中的x位置和match串中的y位置第⼀次匹配不上。
如果使⽤暴⼒⽅法,此时我们需要从str的i+1位置重新开始匹配match串的0位置,这样算法的复杂度⽐较⾼。
⽽使⽤KMP算法,利⽤next数组,可以加速这⼀匹配过程,具体流程是,我们可以先得到y位置的next数组信息,假设y的next数组信息是2,如下图那么0...k 这⼀段完全等于f...m这⼀段,所以对于match来说,当y位置匹配不上x位置以后, ⽆需从i+1开始匹配0位置的值,⽽是可以直接让x位置匹配位置p上的值,如下图其中p的位置由y位置的next数组确定,因为y的next数组值为2(即p位置)。
如果匹配上了,则x来到下⼀个位置(即x+1位置),p来到下⼀个位置(即f位置)继续匹配,如果再次匹配不上,假设p位置的next数组值为0, 则继续⽤x匹配0位置上的值,如下图如果x位置的值依旧不等于0位置的值,则宣告本次匹配失败,str串来到x下⼀个位置,match串从0位置开始继续匹配。
字符串匹配算法掌握常用的字符串匹配算法及其时间复杂度

字符串匹配算法掌握常用的字符串匹配算法及其时间复杂度字符串匹配算法是计算机科学中重要的一部分,广泛应用于文本编辑、搜索引擎、数据挖掘等领域。
在字符串匹配过程中,我们需要找到一个模式字符串在给定文本字符串中的出现位置。
为了解决这个问题,人们提出了各种各样的字符串匹配算法。
1. 暴力匹配算法(Brute Force)暴力匹配算法是最简单直接的字符串匹配算法。
它的思想是逐个比较模式字符串中的字符和文本字符串中的字符,如果不匹配,则将模式字符串向后移动一个位置再继续比较。
时间复杂度为O(m*n),其中m为模式字符串的长度,n为文本字符串的长度。
2. KMP算法KMP算法是一种高效的字符串匹配算法,它利用已经匹配过的信息来避免无效的比较。
首先,通过计算模式字符串的最长公共前后缀数组,确定每次匹配失败时模式字符串应该移动的位置。
然后,在匹配过程中根据最长公共前后缀数组来进行移动。
KMP算法的时间复杂度为O(m+n)。
3. Boyer-Moore算法Boyer-Moore算法是一种高效的字符串匹配算法,它利用了不匹配字符的信息来进行跳跃式的比较。
首先,通过计算模式字符串中每个字符最后出现的位置,确定每次匹配失败时模式字符串应该向后移动的位置。
然后,在匹配过程中根据不匹配字符的信息来进行移动。
Boyer-Moore算法的时间复杂度为O(m+n)。
4. Rabin-Karp算法Rabin-Karp算法利用哈希函数对模式字符串和文本字符串进行哈希计算,然后逐个比较哈希值。
如果哈希值相同,再逐个比较字符。
这样可以减少字符比较的次数,从而提高匹配效率。
Rabin-Karp算法的时间复杂度为O(m+n)。
综上所述,字符串匹配算法包括暴力匹配算法、KMP算法、Boyer-Moore算法和Rabin-Karp算法等。
它们针对不同的情况和要求,具有不同的特点和适用范围。
在实际应用中,我们可以根据具体的需求选择合适的算法来进行字符串匹配,以达到更高的效率和准确性。
delphi kmp字符串匹配率算法

delphi kmp字符串匹配率算法KMP算法(Knuth–Morris–Pratt算法)是一种用来解决字符串匹配问题的有效算法。
其核心思想是通过预处理模式串,构建一个跳转表,以避免不必要的比较。
下面是使用Delphi实现KMP字符串匹配算法的示例:```delphifunction KMPSearch(const text, pattern: string): Single;varm, n, i, j: Integer;lps: array of Integer;beginm := Length(pattern);n := Length(text);// 构建跳转表SetLength(lps, m);i := 1;j := 0;while i < m dobeginif pattern[i] = pattern[j] thenbeginInc(j);lps[i] := j;Inc(i);endelsebeginif j <> 0 thenj := lps[j - 1]elsebeginlps[i] := 0;Inc(i);end;end;end;// 在文本中搜索模式串i := 0;j := 0;while i < n dobeginif pattern[j] = text[i] thenbeginInc(i);Inc(j);if j = m thenbeginResult := 1.0 - (m / n); // 匹配率为1.0减去模式串在文本中的占比Exit;end;endelsebeginif j <> 0 thenj := lps[j - 1]elseInc(i);end;end;Result := 0.0; // 未找到匹配的模式串,匹配率为0end;```使用示例:```delphivartext, pattern: string;matchRate: Single;begintext := 'ABABCABABDABABABCABAB';pattern := 'ABABCABAB';matchRate := KMPSearch(text, pattern);WriteLn('匹配率:', matchRate * 100, '%');end;```这个示例中,我们在`ABABCABABDABABABCABAB`字符串中搜索`ABABCABAB`模式串的匹配率。
字符串kmp模式匹配算法

字符串kmp模式匹配算法【字符串kmp模式匹配算法】引言:字符串是计算机科学中非常常见的数据类型,而字符串的模式匹配是一个重要的问题。
模式匹配是指在一个长字符串中寻找一个给定的模式,以确定该模式是否存在于字符串中。
其中,kmp模式匹配算法是一种高效的字符串匹配算法,它在时间复杂度上优于暴力匹配算法,并且在实际应用中有着广泛的应用。
本文将一步一步回答有关kmp模式匹配算法的问题,对其原理、实现细节和应用进行详细阐述。
第一部分:kmp模式匹配算法的原理1. 什么是kmp模式匹配算法?kmp模式匹配算法是一种用于在字符串中寻找给定模式的高效算法。
不同于暴力匹配算法,kmp算法通过预处理匹配字符串的信息,从而在匹配过程中可以跳过一些不必要的字符比较操作,从而提高了匹配效率。
2. kmp模式匹配算法的原理是什么?kmp模式匹配算法的核心是建立一个跳转表,该表存储着模式字符串的任意位置字符不匹配时,下一步应该跳到哪个位置继续匹配。
通过将匹配失败时的跳转表与模式字符串构造出来,可以在匹配过程中根据模式字符串的内容直接跳到有效位置,从而避免了无效的字符比较。
3. 如何构造kmp算法中的跳转表?构造kmp算法中的跳转表需要对模式字符串进行预处理。
预处理过程中,首先计算出每个位置之前最长的相同前缀后缀长度,并将其存储在数组next[]中。
然后,根据next[]数组的内容,构造跳转表。
第二部分:kmp模式匹配算法的具体实现4. kmp算法的具体实现过程是什么?kmp算法的实现过程可以分为两个阶段:预处理阶段和匹配阶段。
预处理阶段用于计算next[]数组,匹配阶段用于根据next[]数组执行匹配。
5. 预处理阶段的具体步骤是什么?a) 首先,根据模式字符串计算next[]数组。
next[i]表示模式字符串中第i个字符之前的子串中最长的相同前缀后缀长度。
b) 初始化计数器i和j为0,然后逐个计算next[i]的值。
如果模式字符串的第i个字符与模式字符串的第j个字符相等,则令next[i] = j+1,并同时递增i和j。
「算法」面试题:KMP字符串匹配算法

「算法」面试题:KMP字符串匹配算法原创:苍茗KMP 算法是一个高效的字符串匹配算法,由Knuth、Morris、Pratt三人提出,并使用三人名字的首字母命名。
在KMP之前,字符串匹配算法往往是遍历字符串的每一个字符进行比对,算法复杂度是O(mn)。
而KMP算法通过预处理能够把复杂度降低到O(m+n)。
KMP算法假设给定一个字符串1 ABCABCABDEF,现在需要搜索字符串2 ABCABD 在字符串 1 中出现的位置。
从 0 位置开始比对,到位置 5 时发现字符不相同,字符串 1 的字符为 C,字符串 2 的字符为 D。
接下来如何继续比对呢?KMP 算法的核心就在于这里。
考虑到字符串 2 中有两个 AB 重复出现,因此可以把第一个 AB 移动到第二个 AB 处继续比对。
这个移动过程就是利用了已经匹配的字符信息,直接将字符串前移 3 位提高了比对效率。
假设给定一个长度为 n 的字符串 O ,查找长度为 m 的字符串 f 在O中出现的位置,如下图所示(图片来自网络)。
当比对到第 i 个字符不相等时,需要把字符串 f 向前移动继续比对,KMP算法通过计算最大公共长度来移动。
当满足如下条件时,f 可以前移 k 位继续比对。
•字符串 A 是 f 的一个前缀;•字符串 B 是 f 的一个后缀;•字符串 A 和字符串 B 相等。
KMP 算法的核心即在于求解 f 中每一个位置之前的字符串的前缀和后缀的最大公共长度。
注意,这个最大长度不包括字符串本身。
当比较到第 i 位置时,如果不相同,而此时最大公共长度为 j,则 f 前移的距离为 k = i – j 。
最大公共长度的计算前缀是除了最后一个字符的子字符串,后缀是指除了第一个字符的子字符串。
对于字符串ABCA,前缀有A、AB、ABC,后缀有A、CA、BCA,相同的前缀后缀只有A。
最大公共长度是指当前位置前面的字符串相同前缀后缀的最大长度,使用 next 数组表示。
KMP算法数据结构中的字符串匹配算法

KMP算法数据结构中的字符串匹配算法KMP算法是一种高效的字符串匹配算法,它在数据结构中被广泛应用于解决字符串匹配问题。
KMP算法的核心思想是利用已经匹配过的信息,尽可能减少回溯的次数,从而提高匹配的效率。
本文将介绍KMP算法的原理、实现步骤以及应用场景,帮助读者更好地理解和运用这一经典的算法。
### 1. KMP算法原理KMP算法的原理基于两个重要概念:最长公共前缀和部分匹配值。
最长公共前缀是指一个字符串的前缀(不包括整个字符串本身)与该字符串的另一个后缀相同的最大长度;部分匹配值是指字符串的前缀与后缀的最长公共部分的长度。
KMP算法通过预处理模式串,构建部分匹配表,实现在匹配过程中的高效跳转,从而减少不必要的比较次数。
### 2. KMP算法实现步骤KMP算法的实现步骤主要包括以下几个关键步骤:#### 2.1 构建部分匹配表首先,需要对模式串进行预处理,计算出每个位置的部分匹配值。
这一步是KMP算法的关键,也是提高匹配效率的核心。
通过部分匹配表,可以在匹配过程中实现快速跳转,避免不必要的回溯。
#### 2.2 匹配过程在匹配过程中,利用部分匹配表中的信息,实现模式串相对于文本串的高效移动。
通过比较文本串和模式串中对应位置的字符,根据部分匹配表中的数值进行跳转,从而快速定位匹配位置。
#### 2.3 匹配成功或失败处理如果匹配成功,返回匹配的起始位置;如果匹配失败,根据部分匹配表中的信息,调整模式串的位置,继续匹配直至完成整个文本串的匹配。
### 3. KMP算法应用场景KMP算法在实际应用中具有广泛的应用场景,特别适用于需要频繁进行字符串匹配的情况。
以下是一些常见的应用场景:- 字符串匹配:在文本编辑器、搜索引擎等软件中,用于查找指定字符串在文本中的位置。
- 数据压缩:在数据压缩算法中,用于查找重复出现的子串,实现数据的高效压缩。
- DNA序列比对:在生物信息学中,用于比对DNA序列,寻找相似性或重复出现的基因片段。
Kmp字符串模式匹配算法

Kmp中查找一个字符串中是否包含另外一个字符串#include〈stdio.h>2 #include<string。
h〉3 void makeNext(const char P[],int next[])4 {5 int q,k;6 int m = strlen(P);7 next[0] = 0;8 for (q = 1,k = 0; q 〈m;++q)9 {10 while(k 〉0 &&P[q]!= P[k])11 k = next[k—1];12 if (P[q] == P[k])13 {14 k++;15 }16 next[q] = k;17 }18 }1920 int kmp(const char T[],const char P[],int next[])21 {22 int n,m;23 int i,q;24 n = strlen(T);25 m = strlen(P);26 makeNext(P,next);27 for (i = 0,q = 0; i 〈n;++i)28 {29 while(q > 0 &&P[q]!= T[i])30 q = next[q—1];31 if (P[q]== T[i])32 {33 q++;34 }35 if (q == m)36 {37 printf("Pattern occurs with shift:%d\n”,(i-m+1));38 }39 }40 }4142 int main()43 {44 int i;45 int next[20]={0};46 char T[] = ”ababxbababcadfdsss”;47 char P[] = "abcdabd”;48 printf(”%s\n”,T);49 printf("%s\n",P );50 // makeNext(P,next);51 kmp(T,P,next);52 for (i = 0; i 〈strlen(P);++i)53 {54 printf(”%d ”,next[i]);55 }56 printf(”\n”);5758 return 0;59 }1.已知前一步计算时最大相同的前后缀长度为k(k>0),即P[0]···P[k—1];2.此时比较第k项P[k]与P[q],如图1所示3.如果P[K]等于P[q],那么很简单跳出while循环;4.关键!关键有木有!关键如果不等呢???那么我们应该利用已经得到的next[0]···next[k-1]来求P[0]···P[k—1]这个子串中最大相同前后缀,可能有同学要问了——为什么要求P[0]···P[k—1]的最大相同前后缀呢???是啊!为什么呢?原因在于P[k]已经和P[q]失配了,而且P[q—k]··· P[q—1]又与P[0]···P[k-1]相同,看来P[0]···P[k-1]这么长的子串是用不了了,那么我要找个同样也是P[0]打头、P[k—1]结尾的子串即P[0]···P[j—1](j==next[k-1]),看看它的下一项P[j]是否能和P[q]匹配。
KMP字符串匹配算法
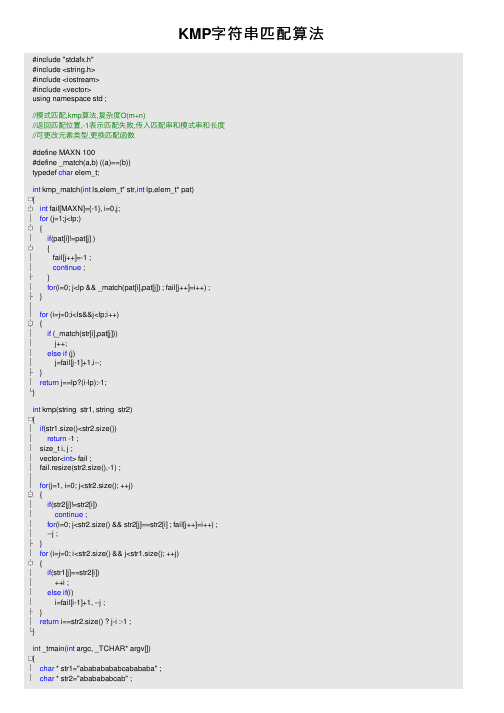
KMP字符串匹配算法#include "stdafx.h"#include <string.h>#include <iostream>#include <vector>using namespace std ;//模式匹配,kmp算法,复杂度O(m+n)//返回匹配位置,-1表⽰匹配失败,传⼊匹配串和模式串和长度//可更改元素类型,更换匹配函数#define MAXN 100#define _match(a,b) ((a)==(b))typedef char elem_t;int kmp_match(int ls,elem_t* str,int lp,elem_t* pat){int fail[MAXN]={-1}, i=0,j;for (j=1;j<lp;){if(pat[i]!=pat[j] ){fail[j++]=-1 ;continue ;}for(i=0; j<lp && _match(pat[i],pat[j]) ; fail[j++]=i++) ;}for (i=j=0;i<ls&&j<lp;i++){if (_match(str[i],pat[j]))j++;else if (j)j=fail[j-1]+1,i--;}return j==lp?(i-lp):-1;}int kmp(string str1, string str2){if(str1.size()<str2.size())return -1 ;size_t i, j ;vector<int> fail ;fail.resize(str2.size(),-1) ;for(j=1, i=0; j<str2.size(); ++j){if(str2[j]!=str2[i])continue ;for(i=0; j<str2.size() && str2[j]==str2[i] ; fail[j++]=i++) ;--j ;}for (i=j=0; i<str2.size() && j<str1.size(); ++j){if(str1[j]==str2[i])++i ;else if(i)i=fail[i-1]+1, --j ;}return i==str2.size() ? j-i :-1 ;}int _tmain(int argc, _TCHAR* argv[]){char * str1="abababababcabababa" ;char * str2="ababababcab" ;int i=kmp_match(strlen(str1),str1,strlen(str2),str2) ;cout<<i<<endl ;i=kmp(str1,str2) ;cout<<i<<endl ;getchar() ;return 0;}。
KMP算法(字符串匹配)

KMP算法(字符串匹配)遇到字符串匹配问题,⼀般我就只能想到O(nm)的朴素算法...今天有这样⼀种算法,使得复杂度变为O(n),这就是KMP(烤馍⽚)算法粘⼀个模板题先:给出两个字符串s1和s2,其中s2为s1的⼦串,求出s2在s1中所有出现的位置。
然后本题还要求输出所有s2中字符的前缀数组,现在留下⼀个疑点,前缀数组(这是啥?),先往后看⾸先确定⼀点,就是在进⾏字符串匹配时,会是拿⼀个字符串与另⼀个字符串的⼀部分进⾏⽐较,那么我们有以下称呼(拿本题进⾏举例):s2叫做模式串,s1叫做母串我们先分析朴素算法的原理与弊端:朴素算法是将每⼀个母串字符拿出⽐较,⼀旦不符合就会放弃前⾯匹配的所有信息,重头再来,然⽽KMP不然,KMP就是⼀种"失败为成功之母"的算法,每次在匹配失败时利⽤前⾯信息进⾏更⾼效的匹配,具体的思想需要⽤到这个"前缀数组"那么这是啥呢?先考虑⼀个问题:如何利⽤失败信息,如果匹配失败,我们会放弃当前匹配,然⽽这起码证明前⾯的匹配都是成功的,也就是说,只要我找到模式串前⾯的能与⾃⼰(当前匹配失败之前的⼀个位置)匹配上的⼦串,那么⼀定也能与前⾯匹配,进⾏再次查找,⽽不⽤进⾏朴素算法暴⼒枚举,前缀数组就是保存这样的指针的数组,预处理⼤概是这样的:inline void init(){p[1]=0;int j=0;for(int i=1;i<m;i++){while(j>0&&b[j+1]!=b[i+1]) j=p[j];if(b[j+1]==b[i+1]) j++;p[i+1]=j;}}总体代码是这样的:#include<cstdio>#include<cstring>#include<string>using namespace std;char a[1000005];char b[1000005];int p[1000005];int n,m;inline void init(){p[1]=0;int j=0;for(int i=1;i<m;i++){while(j>0&&b[j+1]!=b[i+1]) j=p[j];if(b[j+1]==b[i+1]) j++;p[i+1]=j;}}inline void find(){int j=0;for(int i=0;i<n;i++){while(j>0&&a[i+1]!=b[j+1]) j=p[j];if(b[j+1]==a[i+1]) j++;if(j==m){printf("%d\n",i-m+2);j=p[j];}}}int main(){scanf("%s%s",a+1,b+1);n=strlen(a+1);m=strlen(b+1);init();find();for(int i=1;i<=m;i++)printf("%d ",p[i]);return 0;}为什么KMP主体与预处理这么像呢?因为预处理本⾝就是我\ \ \ \ 匹配\ \ \ \ \ 我⾃⼰最后就是输出前缀数组了Processing math: 100%。
字符串的模式匹配算法——KMP模式匹配算法

字符串的模式匹配算法——KMP模式匹配算法朴素的模式匹配算法(C++)朴素的模式匹配算法,暴⼒,容易理解#include<iostream>using namespace std;int main(){string mainStr, str;cin >> mainStr >> str;int i, j, pos = -1, count = 0;for(i = 0; i < mainStr.length(); i++){for(j = 0; j < str.length(); j++, i++){if(mainStr[i] != str[j]){break;}if(j == str.length() - 1){if(count == 0){pos = i - j; //记录第⼀个与str相等的字符串在主串mainStr中的第⼀个字母的下标}count++; //记录与str相等的字符串的数量}}i = i - j; //对i值(主串指针)进⾏回溯操作}cout << "pos=" << pos << ",count=" << count << endl;return 0;}KMP模式匹配算法(C++)KMP模式匹配算法相⽐较朴素的模式匹配算法,减少了主串指针回溯的操作#include<iostream>using namespace std;int main(){string mainStr, str;cin >> mainStr >> str;int i, j, pos = -1, count = 0;int next[256];//计算next数组的数值i = 0;j = -1;next[0] = -1;while(i < str.length()){if(j == -1 || str[i] == str[j]){i++;j++;next[i] = j;}else{j = next[j];}}//查找⼦串的位置和数量i = 0;j = 0;while(i < mainStr.length()){if(mainStr[i] != str[j]){j = next[j];}else{if(j == str.length() - 1){if(count == 0){pos = i - j; //记录⼦串第⼀次的第⼀个字母出现在主串中的位置}count++; //记录在主串中含有⼦串的数量}}i++;j++;}cout << "pos=" << pos << ",count=" << count << endl;return 0;}KMP模式匹配算法改进(C++)改进操作在于计算next数组数值的时候考虑了特殊情况 —— ⼦串形如abcabcabx #include<iostream>using namespace std;int main(){string mainStr, str;cin >> mainStr >> str;int i, j, pos = -1, count = 0;int next[256];//计算next数组的数值i = 0;j = -1;next[0] = -1;while(i < str.length()){if(j == -1 || str[i] == str[j]){i++;j++;if(str[j] == str[i]){next[i] = next[j];}else{next[i] = j;}}else{j = next[j];}}//查找⼦串的位置和数量i = 0;j = 0;while(i < mainStr.length()){if(mainStr[i] != str[j]){j = next[j];}else{if(j == str.length() - 1){if(count == 0){pos = i - j; //记录⼦串第⼀次的第⼀个字母出现在主串中的位置}count++; //记录在主串中含有⼦串的数量}}i++;j++;}cout << "pos=" << pos << ",count=" << count << endl; return 0;}。
KMP字符串匹配算法

KMP字符串匹配算法去年冬天就接触KMP算法了,但是听的不明不⽩,遇到字符串匹配的题我⼤都直接使⽤string中的find解决了,但今天数据结构课⼜讲了⼀下,我觉得有必要再来回顾⼀下。
之前看过很多关于KMP的博客,有很多虽然很好,但是要么太专业,要么很难想象,这篇博客⽤了⼤量的图⽰例⼦来说明,主要在于启发,后⾯给出代码说明。
K M P算法引⼊:KMP是三位⼤⽜:D.E.Knuth、J.H.Morris和V.R.Pratt同时发现的。
KMP算法要解决的问题就是在字符串(也叫主串)中的模式(pattern)定位问题。
说简单点就是我们平时常说的关键字搜索。
模式串就是关键字(接下来称它为P),如果它在⼀个主串(接下来称为T)中出现,就返回它的具体位置,否则返回-1(常⽤⼿段)。
⾸先,对于这个问题有⼀个很单纯的想法:从左到右⼀个个匹配,如果这个过程中有某个字符不匹配,就跳回去,将模式串向右移动⼀位。
这有什么难的?我们可以这样初始化:之后我们只需要⽐较i指针指向的字符和j指针指向的字符是否⼀致。
如果⼀致就都向后移动,如果不⼀致,如下图:A和E不相等,那就把i指针移回第1位(假设下标从0开始),j移动到模式串的第0位,然后⼜重新开始这个步骤:基于这个想法我们可以得到以下的程序:1public static int bf(String ts, String ps)2{3int i = 0; //主串的位置4int j = 0; //⼦串的位置5while(i < t.length && j <p.length)6{7if(t[i] == p[j])///当两个字符相同,就⽐较下⼀个8{9i++;10j++;11}12else13{14i = i - j + 1;///⼀旦不匹配,i后退15j = 0; ///j归016}1718}19if(j ==p.length)20{21return i - j;///匹配成功返回⼦串在母串最先出现的位置22}23else24{25return-1;///不成功返回-126}2728}然⽽这并不是⼀种优秀的算法,因为会出现指针的回退,⼀旦匹配不成功就要退回⼦串的其实位置,⽽之前完成的部分匹配也将作废,时间复杂度为O(n*m)。
字符串的两种模式匹配算法--暴力法与KMP算法
字符串的两种模式匹配算法--暴⼒法与KMP 算法对于字符串⽽⾔,最常见的基本操作莫过于查找某⼀字符串(模式串)在另⼀字符串(主串)中的位置,这⼀操作过程叫做字符串的模式匹配,常见的模式匹配算法有朴素模式匹配算法和KMP模式匹配算法,下⾯结合代码对这两种模式匹配算法的思想做个总结。
1.朴素模式匹配算法(暴⼒法)朴素模式匹配算法的思想就是,把主串中的每⼀个字符作为⼦串开头,与要匹配的字符串进⾏逐字符匹配,直到所有字符匹配成功或全部遍历完成为⽌。
2.KMP 模式匹配算法KMP算法相⽐朴素模式匹配算法效率提升了很多,因为它避免很多不必要的⽐较操作,KMP算法过程只更新j,⽽不回退i,前提是先计算出表⽰模式串下标j的变化数组next,next 数组各值的含义:代表当前字符之前的字符串(下标为0,1,…,j-1)中,有多⼤长度的相同前缀后缀,例如如果next [j] = k,代表j 之前的字符串中有最⼤长度为k 的相同前缀后缀。
#include <iostream>using namespace std ;/* 返回模式串P在主串S 中的位置,若不存在,则函数返回值为-1 */int index (const char * s , const char * p ){int sLen = strlen (s );int pLen = strlen (p );int i = 0; // i ⽤于主串s 中当前位置的下标int j = 0; // j ⽤于模式串p 中当前位置的下标while (i < sLen && j < pLen ){if (s [i ] == p [j ]) // 两字符相等,则递增i 和j ,⽐较下⼀位置字符{i ++;j ++;}else // 两字符不等{i = i - j + 1; // 回退i ,回到上次匹配开始的⾸位的下⼀位/* 此时T[j]与S[i]匹配失败,⽽j 是从0开始递增的,表明前j 个字符匹配都是成功的,由此可得到i 是从(i-j )开始递增的,则下次匹配从(i-j+1)开始。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
delphi kmp字符串匹配率算法
摘要:
一、算法背景
1.Delphi KMP算法介绍
2.字符串匹配问题的重要性
二、KMP算法原理
1.预处理子字符串
2.利用部分匹配表避免无效匹配
3.计算最长前缀后缀长度
三、Delphi实现KMP算法
1.创建KMP函数
2.实现预处理子字符串
3.实现部分匹配查找
四、KMP算法的应用
1.文本搜索
2.模式识别
正文:
一、算法背景
在计算机科学中,字符串匹配问题是一个重要且常见的问题。
它涉及到在文本中查找特定模式或关键字,例如在文本编辑器中查找并替换文本,或在搜索引擎中根据关键词匹配网页。
为了解决这个问题,许多高效的算法被提出,
其中就包括Delphi KMP算法。
二、KMP算法原理
KMP(Knuth-Morris-Pratt)算法是一种高效的字符串匹配算法,其关键在于通过预处理子字符串,避免无效的匹配。
具体来说,KMP算法分为以下三个步骤:
1.预处理子字符串:根据子字符串的前缀与后缀信息,构建一个最长前缀后缀长度表。
2.利用部分匹配表避免无效匹配:在匹配过程中,如果某个字符匹配失败,可以根据最长前缀后缀长度表,将模式串向右移动若干个字符,而不是从头开始重新匹配。
3.计算最长前缀后缀长度:通过计算子字符串的最长前缀后缀长度,可以更快地找到匹配的位置。
三、Delphi实现KMP算法
在Delphi中,我们可以通过以下步骤实现KMP算法:
1.创建KMP函数:定义一个函数,接收两个字符串参数,分别为文本和模式串。
2.实现预处理子字符串:在函数内部,首先计算模式串的最长前缀后缀长度,并构建部分匹配表。
3.实现部分匹配查找:在主匹配过程中,根据部分匹配表避免无效匹配,从而提高匹配效率。
四、KMP算法的应用
KMP算法在许多领域都有广泛应用,例如:
1.文本搜索:在文本编辑器或搜索引擎中,根据关键词快速查找并匹配相关文本。
2.模式识别:在图像处理、音频分析等领域,根据预处理的数据,识别特定的模式或信号。
