神经网络基于BP网络的多层感知器实验报告
神经网络 实验报告

神经网络实验报告神经网络实验报告引言:神经网络是一种模仿人脑神经元网络结构和功能的计算模型,它通过学习和训练来实现模式识别、分类和预测等任务。
本次实验旨在探索神经网络的基本原理和应用,并通过实践验证其效果。
一、神经网络的基本原理1.1 神经元模型神经元是神经网络的基本单元,它接收来自其他神经元的输入信号,并通过激活函数进行处理后输出。
我们采用的是Sigmoid函数作为激活函数,它能够将输入信号映射到0到1之间的值。
1.2 神经网络结构神经网络由输入层、隐藏层和输出层组成。
输入层接收外部输入的数据,隐藏层用于处理和提取特征,输出层给出最终的预测结果。
隐藏层的数量和每层神经元的数量是根据具体问题而定的。
1.3 反向传播算法反向传播算法是神经网络中最常用的训练算法,它通过计算误差和调整权重来不断优化网络的预测能力。
具体而言,它首先进行前向传播计算得到预测结果,然后计算误差,并通过链式法则将误差反向传播到每个神经元,最后根据误差调整权重。
二、实验设计2.1 数据集选择本次实验选择了一个手写数字识别的数据集,其中包含了大量的手写数字图片和对应的标签。
这个数据集是一个经典的机器学习数据集,可以用来评估神经网络的分类能力。
2.2 神经网络参数设置为了探究神经网络的性能和泛化能力,我们设置了不同的参数组合进行实验。
主要包括隐藏层数量、每层神经元数量、学习率和训练轮数等。
2.3 实验步骤首先,我们将数据集进行预处理,包括数据归一化和标签编码等。
然后,将数据集划分为训练集和测试集,用于训练和评估网络的性能。
接下来,根据不同的参数组合构建神经网络,并使用反向传播算法进行训练。
最后,通过测试集评估网络的分类准确率和损失函数值。
三、实验结果与分析3.1 参数优化我们通过对不同参数组合的实验进行比较,找到了在手写数字识别任务上表现最好的参数组合。
具体而言,我们发现增加隐藏层数量和神经元数量可以提高网络的分类准确率,但同时也会增加训练时间。
BP神经网络实验报告

BP神经网络实验报告一、引言BP神经网络是一种常见的人工神经网络模型,其基本原理是通过将输入数据通过多层神经元进行加权计算并经过非线性激活函数的作用,输出结果达到预测或分类的目标。
本实验旨在探究BP神经网络的基本原理和应用,以及对其进行实验验证。
二、实验方法1.数据集准备本次实验选取了一个包含1000个样本的分类数据集,每个样本有12个特征。
将数据集进行标准化处理,以提高神经网络的收敛速度和精度。
2.神经网络的搭建3.参数的初始化对神经网络的权重和偏置进行初始化,常用的初始化方法有随机初始化和Xavier初始化。
本实验采用Xavier初始化方法。
4.前向传播将标准化后的数据输入到神经网络中,在神经网络的每一层进行加权计算和激活函数的作用,传递给下一层进行计算。
5.反向传播根据预测结果与实际结果的差异,通过计算损失函数对神经网络的权重和偏置进行调整。
使用梯度下降算法对参数进行优化,减小损失函数的值。
6.模型评估与验证将训练好的模型应用于测试集,计算准确率、精确率、召回率和F1-score等指标进行模型评估。
三、实验结果与分析将数据集按照7:3的比例划分为训练集和测试集,分别进行模型训练和验证。
经过10次训练迭代后,模型在测试集上的准确率稳定在90%以上,证明了BP神经网络在本实验中的有效性和鲁棒性。
通过调整隐藏层结点个数和迭代次数进行模型性能优化实验,可以发现隐藏层结点个数对模型性能的影响较大。
随着隐藏层结点个数的增加,模型在训练集上的拟合效果逐渐提升,但过多的结点数会导致模型的复杂度过高,容易出现过拟合现象。
因此,选择合适的隐藏层结点个数是模型性能优化的关键。
此外,迭代次数对模型性能也有影响。
随着迭代次数的增加,模型在训练集上的拟合效果逐渐提高,但过多的迭代次数也会导致模型过度拟合。
因此,需要选择合适的迭代次数,使模型在训练集上有好的拟合效果的同时,避免过度拟合。
四、实验总结本实验通过搭建BP神经网络模型,对分类数据集进行预测和分类。
实训神经网络实验报告

一、实验背景随着人工智能技术的飞速发展,神经网络作为一种强大的机器学习模型,在各个领域得到了广泛应用。
为了更好地理解神经网络的原理和应用,我们进行了一系列的实训实验。
本报告将详细记录实验过程、结果和分析。
二、实验目的1. 理解神经网络的原理和结构。
2. 掌握神经网络的训练和测试方法。
3. 分析不同神经网络模型在特定任务上的性能差异。
三、实验内容1. 实验一:BP神经网络(1)实验目的:掌握BP神经网络的原理和实现方法,并在手写数字识别任务上应用。
(2)实验内容:- 使用Python编程实现BP神经网络。
- 使用MNIST数据集进行手写数字识别。
- 分析不同学习率、隐层神经元个数对网络性能的影响。
(3)实验结果:- 在MNIST数据集上,网络在训练集上的准确率达到98%以上。
- 通过调整学习率和隐层神经元个数,可以进一步提高网络性能。
2. 实验二:卷积神经网络(CNN)(1)实验目的:掌握CNN的原理和实现方法,并在图像分类任务上应用。
(2)实验内容:- 使用Python编程实现CNN。
- 使用CIFAR-10数据集进行图像分类。
- 分析不同卷积核大小、池化层大小对网络性能的影响。
(3)实验结果:- 在CIFAR-10数据集上,网络在训练集上的准确率达到80%以上。
- 通过调整卷积核大小和池化层大小,可以进一步提高网络性能。
3. 实验三:循环神经网络(RNN)(1)实验目的:掌握RNN的原理和实现方法,并在时间序列预测任务上应用。
(2)实验内容:- 使用Python编程实现RNN。
- 使用Stock数据集进行时间序列预测。
- 分析不同隐层神经元个数、学习率对网络性能的影响。
(3)实验结果:- 在Stock数据集上,网络在训练集上的预测准确率达到80%以上。
- 通过调整隐层神经元个数和学习率,可以进一步提高网络性能。
四、实验分析1. BP神经网络:BP神经网络是一种前向传播和反向传播相结合的神经网络,适用于回归和分类问题。
多层感知器学习算法研究

多层感知器学习算法研究中文摘要多层感知器学习算法研究中文摘要多层感知器是一种单向传播的多层前馈网络模型,由于具有高度的非线性映射能力,是目前神经网络研究与应用中最基本的网络模型之一,广泛应用于模式识别、图像处理、函数逼近、优化计算、最优预测和自适应控制等领域。
而多层感知器采用的是BP算法。
BP算法的收敛速度慢是个固有的缺点,因为它是建立在基于只具有局部搜索能力的梯度法之上的,是只具有局部搜索能力的方法,若用于多个极小点的目标函数时,是无法避免陷入局部极小和速度慢的缺点的。
因此,对BP算法的研究一直以来都是非常重要的课题。
毕业设计课题旨在对多层感知器的学习算法进行研究,并提出一种新的学习算法。
由于BPWE (权值外推BP)算法和TBP (三项BP)算法都是基于权值调整的改进算法,而考虑将TBP算法中的均衡因子融入到BPWE算法中,从而使后者对权值的调整由原来的两项增加为三项,从而提出一种新的学习算法---TWEBP算法。
为了验证本算法的优点,采用了三个例子,分别对异或问题、三分类问题和函数逼近问题进行了实验,发现其收敛速度和逃离局部极小点的能力都优于传统算法。
关键词:多层感知器学习算法趋势外推均衡因子TWEBP作者:王之仓指导教师:邓伟Research on Multilayer Perceptron Learning AlgorithmABSTRACTMultilayer Perceptron is a sort of multilayer feed-forward single direct propagation network model. Because of its good nonlinear mapping ability, it is one of the basic models in the research and application of neural network at present, which has been widely applied to pattern recognition, image processing, function approximation, optimization computation, optional prediction, adaptation control and so on. Multilayer Perception trained with BP algorithm often has a low convergence speed as a natural drawback,because it is based on gradient descent method which is only local searching. When applied to an object function with many local minimums, it is not possible for BP algorithm toAbstract Research on Multilayer Perceptron Learning Algorithm avoid being trapped in local minimum and to have a low converges speed. In a word, the research on BP algorithm has become very important for a long time.The purpose of this design task is to study the algorithms of Multilayer Perceptron, and a new BP algorithm is presented. Both BPWE algorithm (back-propagation by weight extrapolation) and TBP algorithm (a three-term back propagation algorithm) are based on weight value adjusted. Considered to add the proportional factor of the TBP algorithm into BPWE algorithm, it made the latter can adjust weight value by three terms too. A new BP algorithm,named TWEBP (the three-term weight extrapolation back propagation algorithm), is presented based on the two algorithm proposed just now. This new TWEBP algorithm is tested on three examples and the convergence behavior of the TWEBP and BP algorithm are compared. The results show that the proposed algorithm generally out-perfoims the conventional algorithm in terms of convergence speed and the ability to escape from local minima. Keywords:Multilayer Perceptron, learning algorithm, extrapolation, proportional factor, TWEBP目录攸顺 ......................................... ............. .. (I)ABSTRACT .................... (II)第一章绪论 (1)1.1基本概念 (1)1.2神经网络的发展过程 (2)1.2.1产生背景 (2)1.2.2发展历史 (2)1.2.3现状 (4)1.3多层感知器 (5)1.3.1基本概念 (5)1.3.2多层感知器学习算法存在的问题 (6)1.3.3多层感知器学习算法的研究成果 (7)1.4毕业设计工作及论文结构 (8)1.4.1毕业设计工作 (8)1.4.2论文结构 .......................................................... . (8)第二章反向传播算法 (9)2.1反向传播算法 (9)2.1.1学习规则 (9)2.1.2学习过程 (9)2.1.3反向传播算法的步骤 (11)2.2反向传播算法的贡献和局限性 (12)2.2.1反向传播算法的贡献 (12)2.2.2反向传播算法的局限性 (12)2.3对反向传播算法的进一步讨论 (13)2.3.1激活函数 (13).2.3.2 ............................... ...................................................................................... ;162.3.3云力量项 (16)2.3.4学习速率 (17)2.3.5误差函数.................. . (19)2.4小结 (20)第三章性能优化 (21)3.1性能优化的理论基础 (21)3.2最速下降法 (23)3.3牛顿法 (24)3.4共轭梯度法 (25)3.5小结 (27)第四章TWEBP算法 (29)4.1趋势外推思想 (29)4.1.1趋势外推 (29)4.1,2 BPWE 算法 (30)4.2TBP 算法 (32)4.3TWEBP 算法 (32)4.4计算机仿真 (33)4.4.1 XOR 问题 (33)4.4.2三分类问题 (37)4.4.3函数逼近问题 (42)4.5 4^ (46)第五章总结与展望 (47)#%娜.......... .. (48)攻读学位期间公幵发表的论文 (50)® (51)第一章绪论一个神经元有两种状态,即兴奋和抑制,平时处于抑制状态的神经元,其树突和胞体接收其他神经元经由突触传来的兴奋电位,多个输入在神经元中以代数和的方式叠加;如果输多层感知器学习算法研究第一韋绪论入兴奋总量超过某个阈值,神经元就会被激发进入兴奋状态,发出输出脉冲,并由轴突的突触传递给其他神经元。
神经网络的BP算法实验报告

计算智能基础实验报告实验名称:BP神经网络算法实验班级名称:341521班专业:探测制导与控制技术姓名:***学号:********一、 实验目的1)编程实现BP 神经网络算法;2)探究BP 算法中学习因子算法收敛趋势、收敛速度之间的关系;3)修改训练后BP 神经网络部分连接权值,分析连接权值修改前和修改后对相同测试样本测试结果,理解神经网络分布存储等特点。
二、 实验要求按照下面的要求操作,然后分析不同操作后网络输出结果。
1)可修改学习因子2)可任意指定隐单元层数3)可任意指定输入层、隐含层、输出层的单元数4)可指定最大允许误差ε5)可输入学习样本(增加样本)6)可存储训练后的网络各神经元之间的连接权值矩阵;7)修改训练后的BP 神经网络部分连接权值,分析连接权值修改前和修改后对相同测试样本测试结果 。
三、 实验原理1BP 神经网络算法的基本思想误差逆传播(back propagation, BP)算法是一种计算单个权值变化引起网络性能变化的较为简单的方法。
由于BP 算法过程包含从输出节点开始,反向地向第一隐含层(即最接近输入层的隐含层)传播由总误差引起的权值修正,所以称为“反向传播”。
BP 神经网络是有教师指导训练方式的多层前馈网络,其基本思想是:从网络输入节点输入的样本信号向前传播,经隐含层节点和输出层节点处的非线性函数作用后,从输出节点获得输出。
若在输出节点得不到样本的期望输出,则建立样本的网络输出与其期望输出的误差信号,并将此误差信号沿原连接路径逆向传播,去逐层修改网络的权值和节点处阈值,这种信号正向传播与误差信号逆向传播修改权值和阈值的过程反复进行,直训练样本集的网络输出误差满足一定精度要求为止。
2 BP 神经网络算法步骤和流程BP 神经网络步骤和流程如下:1) 初始化,给各连接权{},{}ij jt W V 及阈值{},{}j t θγ赋予(-1,1)间的随机值;2) 随机选取一学习模式对1212(,),(,,)k k k k k k k n k n A a a a Y y y y ==提供给网络;3) 计算隐含层各单元的输入、输出;1n j ij i j i s w a θ==⋅-∑,()1,2,,j j b f s j p ==4) 计算输出层各单元的输入、输出;1t t jt j t j l V b γ==⋅-∑,()1,2,,t t c f l t q ==5) 计算输出层各单元的一般化误差;()(1)1,2,,k k t t tt t t d y c c c t q =-⋅-=6) 计算中间层各单元的一般化误差;1[](1)1,2,,q kk jt jt j j t e d V b b j p ==⋅⋅-=∑7) 修正中间层至输出层连接权值和输出层各单元阈值;(1)()k jt jt t j V iter V iter d b α+=+⋅⋅(1)()k t t t iter iter d γγα+=+⋅8) 修正输入层至中间层连接权值和中间层各单元阈值;(1)()kk ij ij j i W iter W iter e a β+=+⋅⋅(1)()kj j j iter iter e θθβ+=+⋅9) 随机选取下一个学习模式对提供给网络,返回步骤3),直至全部m 个模式训练完毕;10) 重新从m 个学习模式对中随机选取一个模式对,返回步骤3),直至网络全局误差函数E 小于预先设定的一个极小值,即网络收敛;或者,当训练次数大于预先设定值,强制网络停止学习(网络可能无法收敛)。
bp实验报告
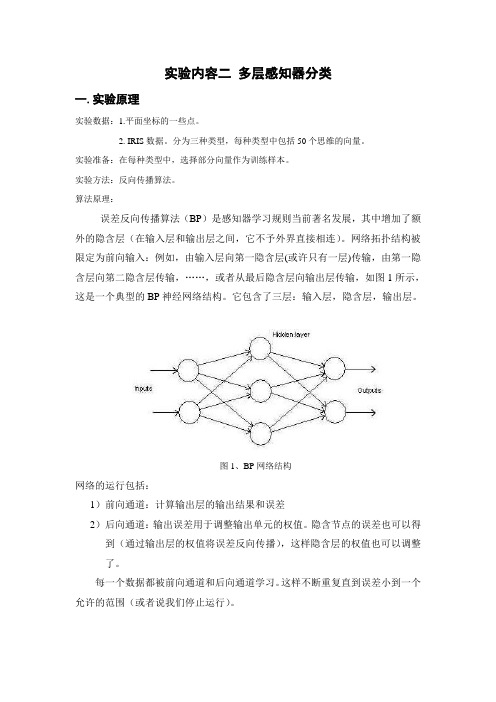
实验内容二多层感知器分类一.实验原理实验数据:1.平面坐标的一些点。
2. IRIS数据。
分为三种类型,每种类型中包括50个思维的向量。
实验准备:在每种类型中,选择部分向量作为训练样本。
实验方法:反向传播算法。
算法原理:误差反向传播算法(BP)是感知器学习规则当前著名发展,其中增加了额外的隐含层(在输入层和输出层之间,它不予外界直接相连)。
网络拓扑结构被限定为前向输入:例如,由输入层向第一隐含层(或许只有一层)传输,由第一隐含层向第二隐含层传输,……,或者从最后隐含层向输出层传输,如图1所示,这是一个典型的BP神经网络结构。
它包含了三层:输入层,隐含层,输出层。
图1、BP网络结构网络的运行包括:1)前向通道:计算输出层的输出结果和误差2)后向通道:输出误差用于调整输出单元的权值。
隐含节点的误差也可以得到(通过输出层的权值将误差反向传播),这样隐含层的权值也可以调整了。
每一个数据都被前向通道和后向通道学习。
这样不断重复直到误差小到一个允许的范围(或者说我们停止运行)。
BP 网络最常用的工作形式是这样的: 1)权值和阈值随机取为很小的数据2)输入训练采样,按下面3)—5)步运行每一采样值 3)计算网络中每一层的输出()()()(1)()()()l l l l l x f s f w x θ-==+ (i ) 4)计算训练误差()()'(()()l l l j q j j j d x f s ∂=-,输出层误差 (ii ) 1()'()(1)(1)1()l n l l l l jjkj k f s w +++=∂=∂∑,隐含层和输入层误差(iii ) 5)修正权值和阈值(1)()()(1)()()[1][]([][1])l l l l l l j i j i j i j i j i w k w k x w k w k μη+-+=+∂+-- (iv ) (1)()()()()[1][]([][1])l l l l l jj j j j k k k k θθμηθθ++=+∂+-- (v ) 6)所有采样值都完成了3)—5)步后,一次训练周期结束。
BP神经网络原理与应用实习论文

学年论文(本科)学院数学与信息科学学院专业信息与计算科学专业年级10级4班姓名徐玉琳于正平马孝慧李运凤郭双双任培培论文题目BP神经网络原理与应用指导教师冯志敏成绩2013年 9月 24日BP神经网络的原理与应用1.BP神经网络的原理1.1 BP神经网络的结构BP神经网络模型是一个三层网络,它的拓扑结构可被划分为:输入层(InputLayer )、输出层(Outp ut Layer ) ,隐含层(Hide Layer ).其中,输入层与输出层具有更重要的意义,因此也可以为两层网络结构(把隐含层划入输入层,或者把隐含层去掉)每层都有许多简单的能够执行并行运算的神经元组成,这些神经元与生物系统中的那些神经元非常类似,但其并行性并没有生物神经元的并行性高.BP神经网络的特点:1)网络由多层构成,层与层之间全连接,同一层之间的神经元无连接.2)BP网络的传递函数必须可微.因此,感知器的传递函数-——二值函数在这里没有用武之地.BP网络一般使用Sigmoid函数或线性函数作为传递函数.3)采用误差反向传播算法(Back-Propagation Algorithm)进行学习.在BP 网络中,数据从输入层隐含层逐层向后传播,训练网络权值时,则沿着减少误差的方向,从输出层经过中间各层逐层向前修正网络的连接权值.随着学习的不断进行,最终的误差越来越来小.BP神经网络的学习过程BP神经网络的学习算法实际上就是对误差函数求极小值的算法,它采用的算法是最速下降法,使它对多个样本进行反复的学习训练并通过误差的反向传播来修改连接权系数,它是沿着输出误差函数的负梯度方向对其进行改变的,并且到最后使误差函数收敛于该函数的最小点.1.3 BP网络的学习算法BP网络的学习属于有监督学习,需要一组已知目标输出的学习样本集.训练时先使用随机值作为权值,修改权值有不同的规则.标准的BP神经网络沿着误差性能函数梯度的反向修改权值,原理与LMS算法比较类似,属于最速下降法.拟牛顿算法牛顿法是一种基于二阶泰勒级数的快速优化算法.其基本方法是1(1)()()()x k x k A k g k -+=-式中 ()A k ----误差性能函数在当前权值和阀值下的Hessian 矩阵(二阶导数),即2()()()x x k A k F x ==∇牛顿法通常比较梯度法的收敛速度快,但对于前向型神经网络计算Hessian 矩阵是很复杂的,付出的代价也很大.有一类基于牛顿法的算法不需要二阶导数,此类方法称为拟牛顿法(或正切法),在算法中的Hessian 矩阵用其近似值进行修正,修正值被看成梯度的函数. 1)BFGS 算法在公开发表的研究成果中,你牛顿法应用最为成功得有Boryden,Fletcher,Goldfard 和Shanno 修正算法,合称为BFG 算法. 该算法虽然收敛所需的步长通常较少,但在每次迭代过程所需要的计算量和存储空间比变梯度算法都要大,对近似Hessian 矩阵必须进行存储,其大小为n n ⨯,这里n 网络的链接权和阀值的数量.所以对于规模很大的网络用RPROP 算法或任何一种梯度算法可能好些;而对于规模较小的网络则用BFGS 算法可能更有效. 2)OSS 算法 由于BFGS 算法在每次迭代时比变梯度算法需要更多的存储空间和计算量,所以对于正切近似法减少其存储量和计算量是必要的.OSS 算法试图解决变梯度法和拟牛顿(正切)法之间的矛盾,该算法不必存储全部Hessian 矩阵,它假设每一次迭代时与前一次迭代的Hessian 矩阵具有一致性,这样做的一个有点是,在新的搜索方向进行计算时不必计算矩阵的逆.该算法每次迭代所需要的存储量和计算量介于梯度算法和完全拟牛顿算法之间. 最速下降BP 法最速下降BP 算法的BP 神经网络,设k 为迭代次数,则每一层权值和阀值的修正按下式进行(1)()()x k x k g k α+=-式中()x k —第k 次迭代各层之间的连接权向量或阀值向量;()g k =()()E k x k ∂∂—第k 次迭代的神经网络输出误差对各权值或阀值的梯度向量.负号表示梯度的反方向,即梯度的最速下降方向;α—学习效率,在训练时是一常数.在MATLAB 神经网络工具箱中,,可以通过改变训练参数进行设置;()E K —第k 次迭代的网络输出的总误差性能函数,在MATLAB 神经网络工具箱中BP 网络误差性能函数默认值为均方误差MSE,以二层BP 网络为例,只有一个输入样本时,有2()()E K E e k ⎡⎤=⎣⎦21S≈22221()S i i i t a k =⎡⎤-⎣⎦∑ 222212,1()()()()s ii j i i j a k f w k a k b k =⎧⎫⎪⎪⎡⎤=-⎨⎬⎣⎦⎪⎪⎩⎭∑21221112,,11()(()())()s s i j i j i i i j j f w k f iw k p ib k b k ==⎧⎫⎡⎤⎛⎫⎪⎪=++⎢⎥ ⎪⎨⎬⎢⎥⎝⎭⎪⎪⎣⎦⎩⎭∑∑若有n 个输入样本2()()E K E e k ⎡⎤=⎣⎦21nS ≈22221()S ii i ta k =⎡⎤-⎣⎦∑根据公式和各层的传输函数,可以求出第k 次迭代总误差曲面的梯度()g k =()()E k x k ∂∂,分别代入式子便可以逐次修正其权值和阀值,并是总的误差向减小的方向变化,直到达到所需要的误差性能为止. 1.4 BP 算法的改进BP 算法理论具有依据可靠、推导过程严谨、精度较高、通用性较好等优点,但标准BP 算法存在以下缺点:收敛速度缓慢;容易陷入局部极小值;难以确定隐层数和隐层节点个数.在实际应用中,BP 算法很难胜任,因此出现了很多改进算.利用动量法改进BP 算法标准BP 算法实质上是一种简单的最速下降静态寻优方法,在修正W(K)时,只按照第K 步的负梯度方向进行修正,而没有考虑到以前积累的经验,即以前时刻的梯度方向,从而常常使学习过程发生振荡,收敛缓慢.动量法权值调整算法的具体做法是:将上一次权值调整量的一部分迭加到按本次误差计算所得的权值调整量上,作为本次的实际权值调整量,即:其中:α为动量系数,通常0<α<0.9;η—学习率,范围在0.001~10之间.这种方法所加的动量因子实际上相当于阻尼项,它减小了学习过程中的振荡趋势,从而改善了收敛性.动量法降低了网络对于误差曲面局部细节的敏感性,有效的抑制了网络陷入局部极小.自适应调整学习速率标准BP算法收敛速度缓慢的一个重要原因是学习率选择不当,学习率选得太小,收敛太慢;学习率选得太大,则有可能修正过头,导致振荡甚至发散.可采用图所示的自适应方法调整学习率.调整的基本指导思想是:在学习收敛的情况下,增大η,以缩短学习时间;当η偏大致使不能收敛时,要及时减小η,直到收敛为止.动量-自适应学习速率调整算法采用动量法时,BP算法可以找到更优的解;采用自适应学习速率法时,BP算法可以缩短训练时间.将以上两种方法结合起来,就得到动量-自适应学习速率调整算法.1. L-M学习规则L-M(Levenberg-Marquardt)算法比前述几种使用梯度下降法的BP算法要快得多,但对于复杂问题,这种方法需要相当大的存储空间L-M(Levenberg-Marquardt)优化方法的权值调整率选为:其中:e —误差向量;J —网络误差对权值导数的雅可比(Jacobian )矩阵;μ—标量,当μ很大时上式接近于梯度法,当μ很小时上式变成了Gauss-Newton 法,在这种方法中,μ也是自适应调整的. 1.5 BP 神经网络的设计 网络的层数输入层节点数取决于输入向量的维数.应用神经网络解决实际问题时,首先应从问题中提炼出一个抽象模型,形成输入空间和输出空间.因此,数据的表达方式会影响输入向量的维数大小.例如,如果输入的是64*64的图像,则输入的向量应为图像中所有的像素形成的4096维向量.如果待解决的问题是二元函数拟合,则输入向量应为二维向量.理论上已证明:具有偏差和至少一个S 型隐含层加上一个线性输出层的网络,能够逼近任何有理数.增加层数可以更进一步的降低误差,提高精度,但同时也使网络复杂化,从而增加了网络权值的训练时间.而误差精度的提高实际上也可以通过增加神经元数目来获得,其训练效果也比增加层数更容易观察和调整.所以一般情况下,应优先考虑增加隐含层中的神经元数. 隐含层的神经元数网络训练精度的提高,可以通过采用一个隐含层,而增加神经元数了的方法来获得.这在结构实现上,要比增加隐含层数要简单得多.那么究竟选取多少隐含层节点才合适?这在理论上并没有一个明确的规定.在具体设计时,比较实际的做法是通过对不同神经元数进行训练对比,然后适当地加上一点余量.1)0niMi C k =>∑,k 为样本数,M 为隐含层神经元个数,n 为输入层神经元个数.如i>M,规定C i M =0.2)和n 分别是输出层和输入层的神经元数,a 是[0.10]之间的常量.3)M=2log n ,n 为输入层神经元个数.初始权值的选取由于系统是非线性的,初始值对于学习是否达到局部最小、是否能够收敛及训练时间的长短关系很大.如果初始值太大,使得加权后的输入和n落在了S型激活函数的饱和区,从而导致其导数f (n)非常小,从而使得调节过程几乎停顿下来.所以一般总是希望经过初始加权后的每个神经元的输出值都接近于零,这样可以保证每个神经元的权值都能够在它们的S型激活函数变化最大之处进行调节.所以,一般取初始权值在(-1,1)之间的随机数.学习速率学习速率决定每一次循环训练中所产生的权值变化量.大的学习速率可能导致系统的不稳定;但小的学习速率导致较长的训练时间,可能收敛很慢,不过能保证网络的误差值不跳出误差表面的低谷而最终趋于最小误差值.所以在一般情况下,倾向于选取较小的学习速率以保证系统的稳定性.学习速率的选取范围在0.01-0.8之间.1.6BP神经网络局限性需要参数多且参数选择没有有效的方法对于一些复杂问题 ,BP 算法可能要进行几小时甚至更长的时间训练,这主要是由于学习速率太小所造成的.标准BP 网络学习过程缓慢,易出现平台,这与学习参数率l r的选取有很大关系.当l r较时,权值修改量大,学习速率也快,但可能产生振荡;当l r较小时,虽然学习比较平稳,但速度十分缓慢.容易陷入局部最优BP网络易陷入局部最小, 使 BP网络不能以高精度逼近实际系统.目前对于这一问题的解决有加入动量项以及其它一些方法.BP 算法本质上是以误差平方和为目标函数 , 用梯度法求其最小值的算法.于是除非误差平方和函数是正定的, 否则必然产生局部极小点, 当局部极小点产生时 , BP算法所求的就不是解.1.6.3 样本依赖性这主要表现在网络出现的麻痹现象上.在网络的训练过程中,如其权值调的过大,可能使得所有的或大部分神经元的加权值偏大,这使得激活函数的输入工作在S型转移函数的饱和区,从而导致其导函数非常小,使得对网络权值的调节过程几乎停顿下来.通常为避免这种现象的发生,一是选取较小的初始权值,二是采用较小的学习速率,但又要增加时间训练.初始权敏感对于一些复杂的问题,BP算法可能要进行几个小时甚至更长时间的训练.这主要是由于学习速率太小造成的.可采用变化的学习速率或自适应的学习速率来加以改进.2.BP神经网络应用2.1 手算实现二值逻辑—异或这个例子中,采用手算实现基于BP网络的异或逻辑.训练时采用批量训练的方法,训练算法使用带动量因子的最速下降法.在MATLAB中新建脚本文件main_xor.m,输入代码如下:%脚本%批量训练方式.BP网络实现异或逻辑%%清理clear allclcrand('seed',2)eb = 0.01; %误差容限eta = 0.6; %学习率mc = 0.8; %动量因子maxiter = 1000; %最大迭代次数%% 初始化网络nSampNum = 4;nSampDim = 2;nHidden = 3;nOut = 1;w = 2*(rand(nHidden,nSampDim)-1/2);b = 2*(rand(nHidden,1)-1/2);wex = [w,b];W = 2*(rand(nOut,nHidden)-1/2);B = 2*(rand(nOut,1)-1/2);WEX = [W,B];%%数据SampIn=[0,0,1,1;...0,1,0,1;…1,1,1,1];expected = [0,1,1,0];%%训练iteration = 0;errRec = [];outRec =[];for i = 1:maxiter% 工作信号正向传播hp = wex*SampIn;tau = logsig(hp);tauex = [tau',1*ones(nSampNum,1)]';HM = WEX*tauex;out = logsig(HM);outRec = [outRec,out'];err = expected - out;sse = sumsqr(err);errRec = [errRec,sse];fprintf('第%d 次迭代,误差:%f \n',i,sse);% 判断是否收敛iteration = iteration + 1;if sse <= ebbreak;end% 误差信号反向传播% DELTA 和delta 为局部梯度DELTA = err.*dlogsig(HM,out);delta = W' * DELTA.*dlogsig(hp,tau);dWEX = DELTA*tauex';dwex = delta*SampIn';% 更新权值if i == 1WEX = WEX + eta*dWEX;wex = wex + eta*dwex;elseWEX = WEX + (1-mc)*eta*dWEX + mc*dWEXold;wex = wex + (1-mc)*eta*dwex+mc*dwexold;enddWEXold = dWEX;dwexold = dwex;W = WEX(:,1:nHidden);end%%显示figure(1)grid[nRow,nCol]=size(errRec);semilogy(1:nCol,errRec,'LineWidth',1.5);title('误差曲线');xlabel('迭代次数');x=-0.2:.05:1.2;[xx,yy] = meshgrid(x);for i=1:length(xx)for j=1:length(yy)xi=[xx(i,j),yy(i,j),1];hp = wex*xi';tau = logsig(hp);tauex = [tau',1]';HM = WEX*tauex;out = logsig(HM);z (i,j) =out;endendfigure(2)mesh(x,x,z);figure(3)plot([0,1],[0,1],'*','LineWidth',2);hold onplot([0,1],[1,0],'O','LineWidth',2);[c,h]=contour(x,x,z,0.5,'b');clabel(c,h);legend('0','1','分类面');title('分类面')2.2 误差下降曲线如下图所示:Finger 1010*******400500600700800900100010-210-110误差曲线迭代次数网格上的点在BP 网络映射下的输出如下图:Finger 2异或本质上是一个分类问题,,分类面如图:Finger 3分类面-0.200.20.40.60.81 1.2本文介绍了神经网络的研究背景和现状,分析了目前神经网络研究中存在的问题.然后描述了BP神经网络算法的实现以及BP神经网络的工作原理,给出了BP网络的局限性.本文虽然总结分析了BP神经网络算法的实现,给出了实例分析,但是还有很多的不足.所总结的BP神经网络和目前研究的现状都还不够全面,经过程序调试的图形有可能都还存在很多细节上的问题,而图形曲线所实现效果都还不够好,以及结果分析不够全面、正确、缺乏科学性等,这些都还是需加强提高的.近几年的不断发展,神经网络更是取得了非常广泛的应用,和令人瞩目的发展.在很多方面都发挥了其独特的作用,特别是在人工智能、自动控制、计算机科学、信息处理、机器人、模式识别等众多方面的应用实例,给人们带来了很多应用上到思考,和解决方法的研究.但是神经网络的研究最近几年还没有达到非常热门的阶段,这还需有很多热爱神经网络和研究神经网络人员的不断研究和创新,在科技高度发达的现在,我们有理由期待,也有理由相信.我想在不久的将来神经网络会应用到更多更广的方面,人们的生活会更加便捷.学年论文成绩评定表。
基于BP神经网络的人体活动识别方法

物联网技术 2021年 / 第12期400 引 言随着微电子机械系统(MEMS )、机器学习等技术的快速发展,同时人们对健康状况的关注和对更高生活品质的追求,使得基于惯性传感器的人体活动识别成为当下热门的研究课题。
基于惯性传感器的人体活动识别技术在辅助老年人生活、医疗保健、体育运动和人机交互等方面[1]发挥着重要作用。
用于人体活动数据采集的惯性传感器主要由加速度计、陀螺仪和磁力计等构成,能够准确采集人体活动时产生的加速度信号、角速度信号和磁场[2]。
传感器器件的发展促使惯性传感器朝着小体积、低成本、低功耗、高灵敏度的方向不断进步,使其被集成在智能手环、智能手机和可穿戴设备上成为可能,相信在未来,其在人体活动识别领域的应用也将越来越广泛。
人体活动识别中常见的机器学习算法模型有决策树、朴素贝叶斯、人工神经网络、支持向量机、K 最近邻和隐马尔科夫模型等[3]。
文献[4]提出了一种基于多传感器的分布式人体定位方法,该多传感器系统采用决策树分类器(DT )、均值和方差特征,整体识别准确率达96.4%。
文献[5]提出了一种基于朴素贝叶斯分类器(NB )的早期手势识别方法,实验结果表明,所提出的新方法优于许多专门为早期手势识别而设计的更复杂的方法。
文献[6]建立了支持向量机(SVM )分类模型,用于体操动作的识别,该模型对6种体操动作的平均识别率超97%。
文献[7]采用K 最近邻分类器(KNN )进行人体活动识别,采用粒子群优化算法(PSO-KNN )搜索KNN 分类器中k 参数的最优值。
实验结果表明,优化后的算法提高了对人体动作的识别精度。
本文提出了基于BP 神经网络的人体活动识别方法,并在公开的DaLiAc (DailyLife Activities, DaLiAc )数据集上验证了我们所提分类模型用于人体活动识别的有效性。
1 人体活动识别模型1.1 BP 神经网络模型多层网络的学习能力较单层感知器增强很多,但要训练多层网络,则需要更强大的学习算法。
BP神经网络实验报告

BP神经网络实验报告BP神经网络实验报告一、实验目的本实验的目的是熟悉MATLAB中神经网络工具箱的使用方法,同时通过编程实现BP网络逼近标准正弦函数,来加深对BP网络的了解和认识,理解信号的正向传播和误差的反向传递过程。
二、实验原理传统的感知器和线性神经网络无法解决线性不可分问题,因此在实际应用过程中受到了限制。
而BP网络却拥有良好的繁泛化能力、容错能力以及非线性映射能力,因此成为应用最为广泛的一种神经网络。
BP算法将研究过程分为两个阶段:第一阶段是信号的正向传播过程,输入信息通过输入层、隐层逐层处理并计算每个单元的实际输出值;第二阶段是误差的反向传递过程,若在输入层未能得到期望的输出值,则逐层递归的计算实际输出和期望输出的差值(即误差),以便根据此差值调节权值。
这种过程不断迭代,最后使得信号误差达到允许或规定的范围之内。
基于BP算法的多层前馈型网络模型的拓扑结构如下图所示:BP算法的数学描述:三层BP前馈网络的数学模型如下图所示。
三层前馈网中,输入向量为X=(x1,x2.xi。
xn)T;隐层输入向量为Y=(y1,y2.___。
y_m)T;输出层输出向量为O=(o1,o2.ok。
ol)T;期望输出向量为d=(d1,d2.dk。
dl)T。
输入层到隐层之间的权值矩阵用V表示,V=(v1,v2.其中列向量vj 为隐层第j个神经元对应的权向量;v_j。
v_m)Y,隐层到输出层之间的权值矩阵用W表示,W=(w1,w2.wk。
wl),其中列向量wk为输出层第k个神经元对应的权向量。
下面分析各层信号之间的数学关系。
对于输出层,有:yj=f(netj)。
j=1,2.mnetj=∑vijxi。
j=1,2.m对于隐层,有:Ok=f(netk)。
k=1,2.l___∑wjk*yi。
k=1,2.lj=1其中转移函数f(x)均为单极性Sigmoid函数:f(x)=1/(1+e^-x),具有连续、可导的特点,且f'(x)=f(x)[1-f(x)]。
BP人工神经网络试验报告一

BP⼈⼯神经⽹络试验报告⼀学号:北京⼯商⼤学⼈⼯神经⽹络实验报告实验⼀基于BP算法的XX及Matlab实现院(系)专业学⽣姓名成绩指导教师2011年10⽉⼀、实验⽬的:1、熟悉MATLAB 中神经⽹络⼯具箱的使⽤⽅法;2、了解BP 神经⽹络各种优化算法的原理;3、掌握BP 神经⽹络各种优化算法的特点;4、掌握使⽤BP 神经⽹络各种优化算法解决实际问题的⽅法。
⼆、实验内容:1 案例背景1.1 BP 神经⽹络概述BP 神经⽹络是⼀种多层前馈神经⽹络,该⽹络的主要特点是信号前向传递,误差反向传播。
在前向传递中,输⼊信号从输⼊层经隐含层逐层处理,直⾄输出层。
每⼀层的神经元状态只影响下⼀层神经元状态。
如果输出层得不到期望输出,则转⼊反向传播,根据预测误差调整⽹络权值和阈值,从⽽使BP 神经⽹络预测输出不断逼近期望输出。
BP 神经⽹络的拓扑结构如图1.1所⽰。
图1.1 BP 神经⽹络拓扑结构图图1.1中1x ,2x , ……n x 是BP 神经⽹络的输⼊值1y ,2y , ……n y 是BP 神经的预测值,ij ω和jk ω为BP 神经⽹络权值。
从图1.1可以看出,BP 神经⽹络可以看成⼀个⾮线性函数,⽹络输⼊值和预测值分别为该函数的⾃变量和因变量。
当输⼊节点数为n ,输出节点数为m 时,BP 神经⽹络就表达了从n 个⾃变量到m 个因变量的函数映射关系。
BP 神经⽹络预测前⾸先要训练⽹络,通过训练使⽹络具有联想记忆和预测能⼒。
BP 神经⽹络的训练过程包括以下⼏个步骤。
步骤1:⽹络初始化。
根据系统输⼊输出序列()y x ,确定⽹络输⼊层节点数n 、隐含层节点数l ,输出层节点数m ,初始化输⼊层、隐含层和输出层神经元之间的连接权值ij ω和式中, l 为隐含层节点数; f 为隐含层激励函数,该函数有多种表达形式,本章所选函数为:步骤3:输出层输出计算。
根据隐含层输出H ,连接权值jk ω和阈值b ,计算BP 神经⽹络预测输出O 。
神经网络实验报告

一、实验目的本次实验旨在了解神经网络的基本原理,掌握神经网络的构建、训练和测试方法,并通过实验验证神经网络在实际问题中的应用效果。
二、实验内容1. 神经网络基本原理(1)神经元模型:神经元是神经网络的基本单元,它通过接收输入信号、计算加权求和、应用激活函数等方式输出信号。
(2)前向传播:在神经网络中,输入信号通过神经元逐层传递,每层神经元将前一层输出的信号作为输入,并计算输出。
(3)反向传播:在训练过程中,神经网络通过反向传播算法不断调整各层神经元的权重和偏置,以最小化预测值与真实值之间的误差。
2. 神经网络构建(1)确定网络结构:根据实际问题选择合适的网络结构,包括输入层、隐含层和输出层的神经元个数。
(2)初始化参数:随机初始化各层神经元的权重和偏置。
3. 神经网络训练(1)选择损失函数:常用的损失函数有均方误差(MSE)和交叉熵(CE)等。
(2)选择优化算法:常用的优化算法有梯度下降、Adam、SGD等。
(3)训练过程:将训练数据分为训练集和验证集,通过反向传播算法不断调整网络参数,使预测值与真实值之间的误差最小化。
4. 神经网络测试(1)选择测试集:从未参与训练的数据中选取一部分作为测试集。
(2)测试过程:将测试数据输入网络,计算预测值与真实值之间的误差,评估网络性能。
三、实验步骤1. 数据准备:收集实验所需数据,并进行预处理。
2. 神经网络构建:根据实际问题确定网络结构,初始化参数。
3. 神经网络训练:选择损失函数和优化算法,对网络进行训练。
4. 神经网络测试:将测试数据输入网络,计算预测值与真实值之间的误差,评估网络性能。
四、实验结果与分析1. 实验结果(1)损失函数曲线:观察损失函数随训练轮数的变化趋势,分析网络训练效果。
(2)测试集误差:计算测试集的预测误差,评估网络性能。
2. 结果分析(1)损失函数曲线:从损失函数曲线可以看出,随着训练轮数的增加,损失函数逐渐减小,说明网络训练效果较好。
BP神经网络算法实验报告

计算各层的输入和输出
es
计算输出层误差 E(q)
E(q)<ε
修正权值和阈值
结
束
图 2-2 BP 算法程序流程图
3、实验结果
任课教师: 何勇强
日期: 2010 年 12 月 24 日
中国地质大学(北京) 课程名称:数据仓库与数据挖掘 班号:131081 学号:13108117 姓名:韩垚 成绩:
任课教师: 何勇强
(2-7)
wki
输出层阈值调整公式:
(2-8)
ak
任课教师: 何勇强
E E netk E ok netk ak netk ak ok netk ak
(2-9)
日期: 2010 年 12 月 24 日
中国地质大学(北京) 课程名称:数据仓库与数据挖掘 隐含层权值调整公式: 班号:131081 学号:13108117 姓名:韩垚 成绩:
Ep
系统对 P 个训练样本的总误差准则函数为:
1 L (Tk ok ) 2 2 k 1
(2-5)
E
1 P L (Tkp okp )2 2 p 1 k 1
(2-6)
根据误差梯度下降法依次修正输出层权值的修正量 Δwki,输出层阈值的修正量 Δak,隐含层权 值的修正量 Δwij,隐含层阈值的修正量
日期: 2010 年 12 月 24 日
隐含层第 i 个节点的输出 yi:
M
yi (neti ) ( wij x j i )
j 1
(2-2)
输出层第 k 个节点的输入 netk:
q q M j 1
netk wki yi ak wki ( wij x j i ) ak
实验七:基于神经网络的模式识别实验

实验七:基于神经网络的模式识别实验一、实验目的理解BP神经网络和离散Hopfield神经网络的结构和原理,掌握反向传播学习算法对神经元的训练过程,了解反向传播公式。
通过构建BP网络和离散Hopfield网络模式识别实例,熟悉前馈网络和反馈网络的原理及结构。
综合掌握模式识别的原理,了解识别过程的程序设计方法。
二、实验内容熟悉模式识别的理论方法,用选择一种合适的识别方法,对图像中的字符(英文字母)进行识别,能够区分出不同的形态的26个字母。
在Matlab中,采用BP神经网络,对读取的数据进行训练,进而识别。
1. 程序设计(1)程序各流程图实验中主程序流程图如图4-1所示:图4-1主程序流程图其中图像预处理的流程如图4-2 所示:图4-2图像预处理的流程神经网络训练的具体流程如图4-3所示:图4-3 神经网络训练流程(2)程序清单%形成用户界面clear all;%添加图形窗口H=figure('Color',[0.85 0.85 0.85],...'position',[400 300 500 400],...'Name','基于BP神经网络的英文字母识别',...'NumberTitle','off',...'MenuBar','none');%画坐标轴对象,显示原始图像h0=axes('position',[0.1 0.6 0.3 0.3]);%添加图像打开按钮h1=uicontrol(H,'Style','push',...'Position',[40 100 80 60],...'String','选择图片',...'FontSize',10,...'Call','op');%画坐标轴对象,显示经过预处理之后的图像h2=axes('position',[0.5 0.6 0.3 0.3]);%添加预处理按钮h3=uicontrol(H,'Style','push',...'Position',[140 100 80 60],...'String','二值化',...'FontSize',10,...'Call','preprocess');%添加识别按钮h4=uicontrol(H,'Style','push',...'Position',[240 100 80 60],...'String','字母识别',...'FontSize',10,...'Call','recognize');%添加显示识别结果的文本框%添加训练神经网络按钮h6=uicontrol(H,'Style','push',...'Position',[340 100 80 60],...'String','网络训练',...'FontSize',10,...'Call','Example1Tr');%预处理%preprocessp1=ones(16,16);bw=im2bw(X,0.5);%转换成二值图像%用矩形框截取图像[i,j]=find(bw==0);imin=min(i);imax=max(i);jmin=min(j);jmax=max(j);bw1=bw(imin:imax,jmin:jmax);%调整比例,变换成16*16图像rate=16/max(size(bw1));bw1=imresize(bw1,rate);[i,j]=size(bw1);i1=round((16-i)/2);j1=round((16-j)/2);p1(i1+1:i1+i,j1+1:j1+j)=bw1;p1=-1.*p1+ones(16,16);%显示预处理的结果axes(h2);imshow(p1);%Example1Tr,训练网络M=1;%人数N=26*M;%样本数%获取26个大写字母图像的数据for kk=0:N-1p1=ones(16,16);%初始化16*16的二值图像(全白)m=strcat(int2str(kk),'.bmp');%形成文件名x=imread(m,'bmp');%读取图像bw=im2bw(x,0.5);%转换成二值图像数据%用矩形框截取[i,j]=find(bw==0);%查找像素为黑的坐标%取边界坐标imin=min(i);imax=max(i);jmin=min(j);jmax=max(j);bw1=bw(imin:imax,jmin:jmax);%截取%调整比例,缩放成16*16的图像rate=16/max(size(bw1));bw1=imresize(bw1,rate);%会存在转换误差%将bw1转换成标准的16*16图像p1[i,j]=size(bw1);i1=round((16-i)/2);j1=round((16-j)/2);p1(i1+1:i1+i,j1+1:j1+j)=bw1;p1=-1.*p1+ones(16,16);%将p1转换成输入向量for m=0:15p(m*16+1:(m+1)*16,kk+1)=p1(1:16,m+1);endend%形成目标向量for kk=0:M-1for ii=0:25t(kk+ii+1)=ii;endend%设置输入向量范围pr(1:256,1)=0;pr(1:256,2)=1;%创建两层BP神经网络,隐层有25个节点net=newff(pr,[25 1],{'logsig' 'purelin'},'traingdx','learngdm'); net.trainParam.epochs=2500;net.trainParam.goal=0.001;net.trainParam.show=10;net.trainParam.lr=0.05;%训练神经网络net=train(net,p,t);%存储训练好的神经网络%recognize,字符识别%生成向量形式M=figure('Color',[0.75 0.75 0.75],...'position',[200 200 400 200],...'Name','基于BP神经网络的英文字母识别结果',...'NumberTitle','off',...'MenuBar','none');M0=uicontrol(M,'Style','push',...'Position',[150 80 130 40],...'String','请先训练网络',...'FontSize',12,...'call','delete(M(1)) ' );for m=0:15q(m*16+1:(m+1)*16,1)=p1(1:16,m+1);end%识别[a,Pf,Af]=sim(net,q);a=round(a);switch acase 0,M0=uicontrol(M,'Style','push',...'Position',[150 80 130 40],...'String','这个字母是A',...'FontSize',12,...'call',...'delete(M(1))');case 1,M0=uicontrol(M,'Style','push',...'Position',[150 80 130 40],...'String','这个字母是B',...'FontSize',12,...'call',...'delete(M(1))');case 2,M0=uicontrol(M,'Style','push',...'Position',[150 80 130 40],...'String','这个字母是C',...'FontSize',12,...'call',...'delete(M(1))');case 3,M0=uicontrol(M,'Style','push',...'Position',[150 80 130 40],...'String','这个字母是D',...'FontSize',12,...'call',...'delete(M(1))');case 4,M0=uicontrol(M,'Style','push',... 'Position',[150 80 130 40],...'String','这个字母是E',...'FontSize',12,...'call',...'delete(M(1))');case 5,M0=uicontrol(M,'Style','push',... 'Position',[150 80 130 40],...'String','这个字母是F',...'FontSize',12,...'call',...'delete(M(1))');case 6,M0=uicontrol(M,'Style','push',... 'Position',[150 80 130 40],...'String','这个字母是G',...'FontSize',12,...'call',...'delete(M(1))');case 7,M0=uicontrol(M,'Style','push',... 'Position',[150 80 130 40],...'String','这个字母是H',...'FontSize',12,...'call',...'delete(M(1))');case 8,M0=uicontrol(M,'Style','push',... 'Position',[150 80 130 40],...'String','这个字母是I',...'FontSize',12,...'call',...'delete(M(1))');case 9,M0=uicontrol(M,'Style','push',... 'Position',[150 80 130 40],...'String','这个字母是J',...'FontSize',12,...'call',...'delete(M(1))');case 10,M0=uicontrol(M,'Style','push',... 'Position',[150 80 130 40],...'String','这个字母是K',...'FontSize',12,...'call',...'delete(M(1))');case 11,M0=uicontrol(M,'Style','push',... 'Position',[150 80 130 40],...'String','这个字母是L',...'FontSize',12,...'call',...'delete(M(1))');case 12,M0=uicontrol(M,'Style','push',... 'Position',[150 80 130 40],...'String','这个字母是M',...'FontSize',12,...'call',...'delete(M(1))');case 13,M0=uicontrol(M,'Style','push',... 'Position',[150 80 130 40],...'String','这个字母是N',...'FontSize',12,...'call',...'delete(M(1))');case 14,M0=uicontrol(M,'Style','push',...'Position',[150 80 130 40],...'String','这个字母是O',...'FontSize',12,...'call',...'delete(M(1))');case 15,M0=uicontrol(M,'Style','push',... 'Position',[150 80 130 40],...'String','这个字母是P',...'FontSize',12,...'call',...'delete(M(1))');case 16,M0=uicontrol(M,'Style','push',... 'Position',[150 80 130 40],...'String','这个字母是Q',...'FontSize',12,...'call',...'delete(M(1))');case 17,M0=uicontrol(M,'Style','push',... 'Position',[150 80 130 40],...'String','这个字母是R',...'FontSize',12,...'call',...'delete(M(1))');case 18,M0=uicontrol(M,'Style','push',... 'Position',[150 80 130 40],...'String','这个字母是S',...'FontSize',12,...'call',...'delete(M(1))');case 19,M0=uicontrol(M,'Style','push',... 'Position',[150 80 130 40],...'String','这个字母是T',...'FontSize',12,...'call',...'delete(M(1))');case 20,M0=uicontrol(M,'Style','push',... 'Position',[150 80 130 40],...'String','这个字母是U',...'FontSize',12,...'call',...'delete(M(1))');case 21,M0=uicontrol(M,'Style','push',... 'Position',[150 80 130 40],...'String','这个字母是V',...'FontSize',12,...'call',...'delete(M(1))');case 22,M0=uicontrol(M,'Style','push',... 'Position',[150 80 130 40],...'String','这个字母是W',...'FontSize',12,...'call',...'delete(M(1))');case 23,M0=uicontrol(M,'Style','push',... 'Position',[150 80 130 40],...'String','这个字母是X',...'FontSize',12,...'call',...'delete(M(1))');case 24,M0=uicontrol(M,'Style','push',... 'Position',[150 80 130 40],...'String','这个字母是Y',...'FontSize',12,...'call',...'delete(M(1))');case 25,M0=uicontrol(M,'Style','push',...'Position',[150 80 130 40],...'String','这个字母是Z',...'FontSize',12,...'call',...'delete(M(1))');End%op%读取图像文件[filename,pathname]=uigetfile({'*.bmp';'*.jpg';...'*.gif';'*.*'},...'Pick an Image File');X=imread([pathname,filename]);%显示图像axes(h0);%将h0设置为当前坐标轴句柄imshow(X);%在h0上显示原始图像2. 实验结果图5-1为实验的主窗口,用于选择图片,进行二值化,网络训练和字符识别。
阐述bp神经网络的原理

阐述bp神经网络的原理
BP神经网络全称为反向传播神经网络,是一种常用的人工神经网络模型。
其原理基于两个基本思想:前向传播和反向误差传播。
前向传播:BP神经网络是一个多层感知器,由输入层、隐藏层和输出层组成。
输入层接收外部输入的数据,隐藏层负责处理输入,并传递给输出层,输出层根据处理结果生成输出。
隐藏层和输出层的每个神经元都有一个权重向量,用于对输入数据进行线性组合。
然后,通过激活函数对线性组合结果进行非线性变换,得到该神经元的输出。
隐藏层和输出层的每个神经元的输出都会作为下一层神经元的输入。
反向误差传播:当神经网络的输出与期望输出之间存在差异时,需要通过反向传播算法来调整权重,以减小这个误差。
算法的基本思想是将误差从输出层向隐藏层逐层传递,通过调整每个神经元的权重,最终使得网络的输出与期望输出尽可能接近。
具体实现时,首先计算输出层的误差,然后根据误差调整输出层的权重。
接下来,将误差反向传播到隐藏层,再根据误差调整隐藏层的权重。
这个过程会不断迭代,直到网络的输出与期望输出的误差足够小。
通过反向误差传播算法,BP神经网络可以学习到输入-输出的映射关系,从而能
够对未知输入进行预测或分类。
然而,BP神经网络也存在一些问题,例如容易陷入局部极小值、对初始权重较敏感等,因此在实际应用中需要进行一定的调优和训练策略。
神经网络中的感知器与多层感知器

神经网络中的感知器与多层感知器神经网络是一种模仿人类神经系统的信息处理系统,能够通过学习和自我适应来完成任务。
神经网络在图像识别、语音识别、自然语言处理等领域有着广泛的应用。
其中,感知器和多层感知器是神经网络中最基本的结构,本文将分别介绍它们的原理、应用和局限性。
一、感知器(Perceptron)感知器是神经网络的最基本单元,它基于线性分类模型,能够将输入数据进行分类。
感知器的构成由输入层、权值、偏移量、激活函数和输出层组成。
1、输入层:输入层是感知器的数据源,同时也是神经元的接收器,输入层的节点数决定了输入数据的维度。
2、权值:输入信号与感知器之间的连接是用权值来表示的,权值决定了输入节点的重要程度。
权值的调整也是感知器训练的核心。
3、偏移量:偏移量是一个常数,它与权值结合起来作为阈值判断的依据。
4、激活函数:激活函数是连接多个神经元之间的唯一方式,也是用于处理输入数据的函数,它将输入的信号进行处理后输出到输出层。
5、输出层:输出层的节点数决定了对数据进行分类的结果。
可以是二分类或多分类。
感知器的训练过程就是通过上面的结构来不停地调整每个输入节点的权值,从而不停地改进分类结果。
感知器的应用:感知器广泛应用于二元分类的问题中,例如数字识别和人脸识别。
感知器的局限性:但是,感知器有很大的局限性,例如无法处理非线性分类问题,只能进行两类问题的分类。
因此,需要使用多层感知器来解决这些问题。
二、多层感知器(Multi-Layer Perceptron, MLP)多层感知器是感知器的扩展,通过添加多个隐藏层使其可以处理非线性分类问题。
隐藏层的加入使得神经网络学习到了更加复杂的特征,并且可以解决分类问题。
多层感知器的结构与感知器相似,只是中间加入了隐藏层,隐藏层将原数据进行转换和处理,以得到更好的输入数据。
隐层和输出之间的连接仍然可以使用任何激活函数,例如Sigmoid函数。
多层感知器的训练过程和感知器类似,也是不断地调整权重来训练,但多层感知器的训练相较于单层感知器显得更加复杂,因为它需要在每个隐藏层之间做权值传导和梯度求导。
基于BP算法的多层感知器设计

01
02
多层感知器 是一 种单 向按误 差传播 的多层前馈 网络模 型 , 为 目前应用 最广泛 、 究最基 本 的网络模 型之一 , 作 研 多 层感知器具有非 线性映射能力 高的突 出特点 , 在处 理图像 、
0
识别模式 和优化测算 、函数逼 近以及 自适应 控制等方 面都
发挥 了重要 的作用 。
对 于 一 些 复 杂 的 问题 , 况 也 同 样 如 此 , 就 导 致 了 网络 收 情 这
及论证 , 于梯度法进行相关计算 。 基
多层感 知器 是 B P网络 的实质 ,P网络 实际 上是一 种 B 以B P算法为基础 的多层前 向网络 , 以很好地解决 非线 性 可 可分 问题 , 弥补 了单层感 知器 的缺憾 , 并且 具有操 作 简单 、 可行性高 、 运行稳定等优 势 , 渐成为十 分常用 的神经 网络 逐
2 全 局 优 化 性 不 高 )
B P算法本身是根据梯度下 降法来进 行计算 的 ,其算法 的规则还不够完善 , 于贪 婪的计算方 法 , 属 可以使权重值集 中于某个点 , 这样 的计算结 果通常可能 产生局部 的极 小值 , 但 不能保证该结果为误差的全局最优化。针对这一 问题 , 附 加动量法可以有效地解决。
国内在研究概念图的过程中 , 注重借鉴国外 的研究成果 。 很
的过程才能更好 地发挥 , 而这方面 的涉及 面较广 , 如教育 改 革、 政策 中对概念 图制作 的要求 、 念图 软件 的推广 、 生 概 师 对其制作技术的重视程度等 。另外 , 在教学过程中对 概念 图 绘制 的时间及效果的控制需要一 定的经验 和技 巧 ,这些也 许是桎梏概念图迅猛发展 的决定性 因素 。 () 3 概念 图不 是万 能的。并不是所有的教学采用 概念 图 都会产生 比传统教学更好 的效果 。另外 , 对于程序性 知识 的 效果要优于理论性知识的效果 。因此 , 选择适合概念图特点 和 功 能 的教 学 内容 , 促 进 教 学 效果 。 会 () 4 缺乏 以人 为本 的思想 。概念图能检验并完善学 习者 的认知结构 , 激发学生 的创 造性思维 , 但是 国内大量研究 只 是在 概念 图与课程整合 的过 程 中概 述 了对学 习者的影 响 , 并没有 真正站在学生的角度分析 如何设计 概念图才能对学
多层感知器实验报告总结

一、实验背景随着人工智能和机器学习技术的不断发展,多层感知器(Multilayer Perceptron,MLP)作为一种重要的前向神经网络模型,在图像识别、自然语言处理等领域得到了广泛应用。
本次实验旨在通过实现一个简单的多层感知器模型,加深对MLP的理解,并验证其在实际应用中的效果。
二、实验目的1. 理解多层感知器的基本原理和结构;2. 掌握多层感知器的实现方法;3. 通过实验验证多层感知器在非线性分类问题上的应用效果。
三、实验环境1. 操作系统:Windows 102. 编程语言:Python3. 库:NumPy、TensorFlow四、实验内容1. 多层感知器模型搭建(1)输入层:根据实际问题,确定输入层的节点数。
例如,在图像识别问题中,输入层节点数等于图像像素数。
(2)隐藏层:确定隐藏层的层数和每层的节点数。
通常情况下,随着层数的增加,模型的性能会提高,但过深的网络可能导致过拟合。
(3)输出层:根据实际问题,确定输出层的节点数。
例如,在二分类问题中,输出层节点数为1。
(4)激活函数:选择合适的激活函数,如Sigmoid、ReLU等。
2. 损失函数和优化算法(1)损失函数:常用的损失函数有均方误差(MSE)和交叉熵(Cross-Entropy)等。
(2)优化算法:常用的优化算法有梯度下降(Gradient Descent)、Adam等。
3. 模型训练(1)将数据集划分为训练集和测试集。
(2)使用训练集对模型进行训练,并不断调整参数。
(3)使用测试集对模型进行评估,以验证模型的性能。
4. 模型评估(1)计算模型的准确率、召回率、F1值等指标。
(2)可视化模型预测结果,分析模型的性能。
五、实验结果与分析1. 实验数据本次实验以MNIST数据集为例,MNIST数据集包含0-9数字的手写图像,共有60000个训练样本和10000个测试样本。
2. 实验结果(1)模型准确率:在训练集和测试集上,多层感知器的准确率分别为98.5%和96.2%。
人工智能实验报告-BP神经网络算法的简单实现

⼈⼯智能实验报告-BP神经⽹络算法的简单实现⼈⼯神经⽹络是⼀种模仿⼈脑结构及其功能的信息处理系统,能提⾼⼈们对信息处理的智能化⽔平。
它是⼀门新兴的边缘和交叉学科,它在理论、模型、算法等⽅⾯⽐起以前有了较⼤的发展,但⾄今⽆根本性的突破,还有很多空⽩点需要努⼒探索和研究。
1⼈⼯神经⽹络研究背景神经⽹络的研究包括神经⽹络基本理论、⽹络学习算法、⽹络模型以及⽹络应⽤等⽅⾯。
其中⽐较热门的⼀个课题就是神经⽹络学习算法的研究。
近年来⼰研究出许多与神经⽹络模型相对应的神经⽹络学习算法,这些算法⼤致可以分为三类:有监督学习、⽆监督学习和增强学习。
在理论上和实际应⽤中都⽐较成熟的算法有以下三种:(1) 误差反向传播算法(Back Propagation,简称BP 算法);(2) 模拟退⽕算法;(3) 竞争学习算法。
⽬前为⽌,在训练多层前向神经⽹络的算法中,BP 算法是最有影响的算法之⼀。
但这种算法存在不少缺点,诸如收敛速度⽐较慢,或者只求得了局部极⼩点等等。
因此,近年来,国外许多专家对⽹络算法进⾏深⼊研究,提出了许多改进的⽅法。
主要有:(1) 增加动量法:在⽹络权值的调整公式中增加⼀动量项,该动量项对某⼀时刻的调整起阻尼作⽤。
它可以在误差曲⾯出现骤然起伏时,减⼩振荡的趋势,提⾼⽹络训练速度;(2) ⾃适应调节学习率:在训练中⾃适应地改变学习率,使其该⼤时增⼤,该⼩时减⼩。
使⽤动态学习率,从⽽加快算法的收敛速度;(3) 引⼊陡度因⼦:为了提⾼BP 算法的收敛速度,在权值调整进⼊误差曲⾯的平坦区时,引⼊陡度因⼦,设法压缩神经元的净输⼊,使权值调整脱离平坦区。
此外,很多国内的学者也做了不少有关⽹络算法改进⽅⾯的研究,并把改进的算法运⽤到实际中,取得了⼀定的成果:(1) 王晓敏等提出了⼀种基于改进的差分进化算法,利⽤差分进化算法的全局寻优能⼒,能够快速地得到BP 神经⽹络的权值,提⾼算法的速度;(2) 董国君等提出了⼀种基于随机退⽕机制的竞争层神经⽹络学习算法,该算法将竞争层神经⽹络的串⾏迭代模式改为随机优化模式,通过采⽤退⽕技术避免⽹络收敛到能量函数的局部极⼩点,从⽽得到全局最优值;(3) 赵青提出⼀种分层遗传算法与BP 算法相结合的前馈神经⽹络学习算法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
神经网络基于BP网络的多层感知器实验报告二、基于BP网络的多层感知器一:实验目的:1、理解多层感知器的工作原理2、通过调节算法参数了解参数的变化对于感知器训练的影响3、了解多层感知器局限性二:实验原理:BP的基本思想:信号的正向传播误差的反向传播–信号的正向传播:输入样本从输入层传入,经各隐层逐层处理后,传向输出层。
–误差的反向传播:将输入误差以某种形式通过隐层向输入层逐层反传,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号来作为修正各单元权值的依据。
1、基本BP算法的多层感知器模型:2、BP学习算法的推导:当网络输出与期望输出不等时,存在输出误差E将上面的误差定义式展开至隐层,有进一步展开至输入层,有调整权值的原则是使误差不断地减小,因此应使权值的调整量与误差的梯度下降成正比,即η∈(0,1)表示比例系数,在训练中反应学习速率 BP算法属于δ学习规则类,这类算法被称为误差的梯度下降(Gradient Descent)算法。
<实验步骤>1、用Matlab编程,实现解决该问题的单样本训练BP网络,设置一个停止迭代的误差Emin和最大迭代次数。
在调试过程中,通过不断调整隐层节点数,学习率η,找到收敛速度快且误差小的一组参数。
产生均匀分布在区间[-4,4]的测试样本,输入建立的模型得到输出,与Hermit多项式的期望输出进行比较计算总误差(运行5次,取平均值),并记录下每次迭代结束时的迭代次数。
(要求误差计算使用RME,Emin 设置为0、1)程序如下:function dyb %单样本程序 clc; close all; clear; x0=[1:;-4:0、08:4];%样本个 x0(1,:)=-1; x=x0'; yuzhi=0、1;%阈值j=input('请输入隐层节点数 j = ');%隐层节点数 n=input('请输入学习效率 n = ');%学习效率 w=rand(1,j); w=[yuzhi,w]; %输出层阈值 v=rand(2,j); v(1,:)=yuzhi;%隐层阈值err=zeros(1,); wucha=0; zhaosheng=0、01*randn(1,);%噪声erro=[]; ERRO=[];%误差,为画收敛曲线准备 Emin=0、1;d=zeros(1,); for m=1: d(m)=hermit(x(m,2));%期望 end;o=zeros(1,); j=zeros(1,j); =zeros(1,j); p=1; q=1; azc=0; acs=0; for z=1:5 while q<30000 Erme=0; for p=1:y=zeros(1,j); for i=1:j j(1,i)=x(p,:)*v(:,i);y(1,i)=1/(1+exp(-j(1,i))); end; y=[-1 y];o(p)=w*y'+zhaosheng(p);%噪声 wucha = d(p)-o(p);err(1,p)=1/2*wucha^2; erro=[erro,wucha]; for m=1:j+1w(1,m)=w(1,m)+n*wucha*y(1,m); end; for m=1:jv(:,m)=v(:,m)+n*wucha*w(1,m)*y(1,m)*(1-y(1,m))*x(p,:)'; end q=q+1; end; for t=1:; Erme=Erme+err(1,t); end;err=zeros(1,); Erme=sqrt(Erme/); ERRO=[ERRO,Erme]; ifErme<Emin break; end; end; azc=azc+Erme; acs=acs+q; end disp('最终误差:'); pinjunwucha=1/5*azc figure(1);plot(x(:,2),d,'--r'); hold on; plot(x(:,2),o,'--b'); disp('次数:'); pjcx=1/5*acs figure(2); plot(ERRO); figure(3); plot(x(:,2),d,'--rp');endfunction F =hermit(x)%hermit子函数 F =1、1*(1-x+2*x^2)*exp(-x^2/2);end运行结果如下:表格1、单样本BP算法平均最小误差学习率结点数0、050、070、10、120、150、1880、09650、08590、019530、09450、08740、0925100、09680、09440、09830、09200、08210、0982120、08860、08560、08850、09460、08340、0928150、09150、09270、08780、09240、07380、08442、实现解决该问题的批处理训练BP网络,调整参数如上。
产生均匀分布在区间[-4,4]的测试样本,输入建立的模型得到输出,与Hermit多项式的期望输出进行比较计算总误差(运行5次,取平均值),并记录下每次迭代结束时的迭代次数。
程序如下:function pcl %批处理 close all; clc; x=[-4:0、08:4];%样本个 j=input('请输入隐层节点数 j = ');%隐层节点数n=input('请输入学习效率 n = ');%学习效率 a=0、1;%动量系数w=rand(1,j); v=rand(1,j); err=zeros(1,); wucha=0;zhaosheng=0、01*randn(1,);%噪声 erro=[]; ERRO=[];%误差,为画收敛曲线准备 Emin=0、1; d=zeros(1,); for m=1:d(1,m)=hermit(x(m));%期望 end; o=zeros(1,); j=zeros(1,j); =zeros(1,j); y=zeros(1,j); p=1; q=1; azc=0; acs=0; forz=1:5 while q<30000 Erro=0; Erme=0; for p=1: for i=1:jj(1,i)=v(1,i)*x(1,p); y(1,i)=1/(1+exp(-j(1,i))); end;o(1,p)=w*y'+zhaosheng(p);%噪声 wucha=d(1,p)-o(1,p);%误差err(1,p)=1/2*wucha^2; erro=[erro,wucha]; q=q+1; end; fort=1:; Erro=Erro+erro(t); Erme=Erme+err(1,t); end; erro=[]; for m=1:j; w(1,m)=w(1,m)+n*Erro*y(1,m);v(1,m)=v(1,m)+n*Erro*w(1,m)*y(1,m)*(1-y(1,m))*x(1,p); end; Erme=sqrt(Erme/); ERRO=[ERRO,Erme]; if Erme<Emin break; end; end; azc=azc+Erme; acs=acs+q; end disp('平均误差:'); pjwc=1/5*azc figure(1); plot(x,d,'--r'); hold on;plot(x,o,'--b'); disp('平均次数:'); pjcs=1/5*acsfigure(2); plot(ERRO); figure(3); plot(x,d);endfunction F = hermit(x)%hermit子函数 F =1、1*(1-x+2*x^2)*exp(-x^2/2);end运行结果如下:表格2、批处理BP算法平均最小误差学习率结点数0、050、070、20、1 50、17 50、096 60、097 30、097 40、098 60、099 30、0913 80、097 20、093 30、091 30、097 60、092 20、0915 100、094 50、095 70、093 70、094 80、095 70、08171 20、09250、09110、09520、09370、09153、对批处理训练BP算法增加动量项调整参数如上,记录结果,并与没有带动量项的批处理训练BP算法的结果相比较程序如下:function jdlx %加动量项 close all; clc; x=[-4:0、08:4];%样本个 j=input('请输入隐层节点数 j = ');%隐层节点数 n=input('请输入学习效率 n = ');%学习效率 a=0、1;%动量系数 w=rand(1,j); v=rand(1,j); err=zeros(1,); wucha=0; zhaosheng=0、01*randn(1,);%噪声 erro=[]; ERRO=[];%误差,为画收敛曲线准备 Emin=0、1; d=zeros(1,); for m=1:d(1,m)=hermit(x(m));%期望 end; o=zeros(1,); j=zeros(1,j); =zeros(1,j); y=zeros(1,j); p=1; q=1; azc=0; acs=0; forz=1:5 while q<30000 Erro=0; Erme=0; for p=1: for i=1:jj(1,i)=v(1,i)*x(1,p); y(1,i)=1/(1+exp(-j(1,i))); end;o(1,p)=w*y'+zhaosheng(p);%噪声 wucha=d(1,p)-o(1,p);%误差err(1,p)=1/2*wucha^2; erro=[erro,wucha]; q=q+1; end; fort=1:; Erro=Erro+erro(t); Erme=Erme+err(1,t); end; erro=[]; for m=1:j; if m==1 w(1,m)=w(1,m)+n*Erro*y(1,m); elsew(1,m)=w(1,m)+n*Erro*y(1,m)+a*w(1,m-1); endv(1,m)=v(1,m)+n*Erro*w(1,m)*y(1,m)*(1-y(1,m))*x(1,p); end; Erme=sqrt(Erme/); ERRO=[ERRO,Erme]; if Erme<Emin break; end; end; azc=azc+Erme; acs=acs+q; end disp('平均误差:'); pjwc=1/5*azc figure(1); plot(x,d,'--r'); hold on;plot(x,o,'--b'); disp('平均次数:'); pjcs=1/5*acsfigure(2); plot(ERRO); figure(3); plot(x,d);endfunction F = hermit(x)%hermit子函数 F =1、1*(1-x+2*x^2)*exp(-x^2/2);end运行结果如下:4、对批处理BP算法改变参数:学习率η、迭代次数、隐层节点数,观察算法的收敛发散,以及测试误差的变化(对每个参数取几个不同参数,分别运行5次,结果取平均值)。
