集合与函数练习题(附答案)

合集下载

高中数学必修1第一章集合与函数概念专项练习题(附答案)

高中数学必修1第一章集合与函数概念专项练习题一、单选题1.若函数f(x)＝ |x +2| 的单调递增区间是（）A. (0,+∞)B. (−∞,+∞)C. [2,+∞)D. [−2,+∞)2.设全集 U ={-2,-1,0,1,2} ， A ={−2,−1,0} ， B ={0,1,2} ，则图中阴影部分所表示的集合为（）A. {0}B. {−2,−1}C. {1,2}D. {0,1,2} 3.函数 f(x)=2xe x +e −x 的大致图像是（）A. B. C. D.4.已知集合A={x|y= √(1−x)(x +3) }，B={x|log 2x≤1}，则A∩B=（） A. {x|﹣3≤x≤1} B. {x|0＜x≤1} C. {x|﹣3≤x≤2} D. {x|x≤2}5.设函数 f(x)={|x +1|,x ≤0,|log 4x|,x〉0, 若关于 x 的方程 f(x)=a 有四个不同的解 x 1,x 2,x 3,x 4, 且 x 1<x 2<x 3<x 4, 则 x 3(x 1+x 2)+1x32x 4 的取值范围是（）A. (−1,72] B. (−1,72) C. (−1,+∞) D. (−∞,72]6.已知全集U=N ，集合P ={1,2,3,4,6},P ={1,2,3,5,9}则P ∩(C U Q )=( )A. {1,2,3}B. {5,9}C. {4,6}D. {1,2,3,4,6} 7.函数 y =√−x 2−3x+4的定义域为（）A. (−4，−1)B. (−4，1)C. (−1，1)D. (−1，1]8.已知实数 a >0 ， a ≠1 ，函数 f(x)=log a |x| 在 (−∞,0) 上是减函数，又 g(x)=a x +1a x ，则下列选项正确的是( )A. g(−2)<g(1)<g(3)B. g(1)<g(−2)<g(3)C. g(3)<g(−2)<g(1)D. g(−2)<g(3)<g(1)9.已知奇函数 y =f(x) 在 (−∞,0) 上单调递减，且 f(1)=0 ，若 a =f(log 318) ， b =f(log 214) ， c =f(log 23) ，则 a,b,c 的大小关系是（）A. c <b <aB. a <b <cC. a <c <bD. c <a <b10.设a=√2+√3 ， M={x|x≤√10}，给出下列关系：①a ⊂M ； ②M ⊇{a}； ③{a}∈M ； ④{Ф}⊆{a}； ⑤2a ∉M ；其中正确的关系式共有（）A. 2个B. 3个C. 4个D. 5个 11.集合 A ={−1,0,1,2,3} , B ={x|log 2(x +1)<2} ，则 A ∩B 等于（）A. {−1,0,1,2}B. {0,1,2}C. {−1,0,1,2,3}D. {0,1,2,3} 12.函数 y =xe cosx (−π≤x ≤π) 的大致图象为( )A. B. C. D.13.若定义在R 上的偶函数f （x ）在[0，+∞）上是减函数，则有（）A. f （3）＜f （﹣2）＜f （1）B. f （1）＜f （﹣2）＜f （3）C. f （﹣2）＜f （1）＜f （3）D. f （3）＜f （1）＜f （﹣2） 14.设f (x )的定义域为D ，若f (x )满足下面两个条件，则称f (x )为闭函数.①f (x )在D 内是单调函数；②存在[a,b ]⊆D ，使f (x )在[a,b ]上的值域为[a,b ] ，如果f (x )=√2x +1+k 为闭函数，那么k 的取值范围是（）A. −1<k ≤−12 B. 12≤k <1 C. k >−1 D. k ＜1 15.如果若干个函数的图象经过平移后能够重合，则称这些函数为“同簇函数”．给出下列函数：①f （x ）=sinxcosx ； ②f （x ）=2sin （x+π4）；③f （x ）=sinx+√3cosx ； ④f （x ）=√2sin2x+1．其中“同簇函数”的是（）A. ①②B. ①④C. ②③D. ③④ 16.下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是（）A. y =−x 2+1B. y =lg |x |C. y =1x D. y =e −x 17.下列函数中，是偶函数且在区间 (0,+∞) 上为增函数的是（） A. y =2ln x B. y =|x 3| C. y =x −1x D. y =cosx18.已知 f(12x −1)=2x +3，f(m)=6 ,则 m 等于（） A. −14 B. 14 C. 32 D. −32 19.若函数y=x 2﹣3x ﹣4的定义域为[0，m]，值域为 [−254,−4] ，则m 的取值范围是（）A. （0，4]B. [−254,−4] C. [32,3] D. [32,+∞)20.下列函数中，既是偶函数又存在零点的是（）A. y=x 2+1B. y=|lgx|C. y=cosxD. y=e x ﹣1二、填空题21.已知集合A={1，m+2，m 2+4}，且5∈A ，则m=________．22.已知函数 f(x)={x +1,x ≤1f(log 2x),x >1 ，则 f(4)= ________； f(x) 的零点为________.23.函数f （x ）=lg （2sinx ﹣1）的定义域为________．24.已知函数 f(x) 是定义在R 上的奇函数，当 x ≥0 时， f(x)=2x −c ，则 f(−2)= ________ 25.已知集合 A ={x|x 2−3x +2=0,x ∈R},B ={x|0<x <5,x ∈N} ,则满足条件 A ⊆C ⊆B 的集合 C 的个数为________．26.若函数 f(x)=lnx −kx 在区间 [1,+∞) 上单调递减，则实数 k 的取值范围是________ 27.设集合A={x|x 2﹣2ax+a=0，x ∈R}，B={x|x 2﹣4x+a+5=0，x ∈R}，若A 和B 中有且仅有一个是∅，则实数a 的取值范围是________．28.已知函数f （x ）满足f （x ﹣1）=x 2﹣x+1，则f （3）=________． 29.函数 f(x)=lg(x −3)+(x−2)0x+1的定义域是________30.函数 y =√5+4x −x 2 的值域是________．31.已知函数f （x ）= {log 2(1−x),x ≤0f(x −1)−f(x −2),x >0，则f （2016）=________32.已知定义在R 上的奇函数f （x ），当x≥0时，f （x ）=x 2﹣3x ．则关于x 的方程f （x ）=x+3的解集为________． 33.如果对定义在R 上的函数f （x ），对任意两个不相等的实数x 1 ， x 2 ，都有x 1f （x 1）+x 2f （x 2）＞x 1f （x 2）+x 2f （x 1），则称函数f （x ）为“H 函数”．给出下列函数①y=x 2；②y=e x +1；③y=2x ﹣sinx ；④f (x )={ln |x |,x ≠00,x =0．以上函数是“H 函数”的所有序号为 ________． 34.已知函数f （x ）= {(2−a)x +1(x <1)a x (x ≥1) 在（﹣∞，+∞）上单调递增，则实数a 的取值范围是________．35.函数 y =√3−xlog2(x+1)的定义域是________ .三、解答题36.设f （x ）=x 2﹣2|x|+3（﹣3≤x≤3）（1）证明f （x ）是偶函数；（2）指出函数f （x ）的单调增区间；（3）求函数f （x ）的值域．37.已知函数f(x)=(x+1)(x+a)x为奇函数. （1）求实数a的值；（2）当x∈[1m ,1n](m>0,n>0)时，若函数f(x)的值域为[3−3m,3−3n]，求m，n的值.38.某租赁公司拥有汽车100辆．当每辆车的月租金为3000元时，可全部租出．当每辆车的月租金每增加50元时，未租出的车将会增加一辆．租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元．（Ⅰ）当每辆车的月租金定为3600元时，能租出多少辆车？（Ⅱ）当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？39.设函数f(x)=x2−2|x−a|+3,x∈R.（1）王鹏同学认为，无论a取何值，f(x)都不可能是奇函数，你同意他的观点吗？请说明你的理由；（2）若f(x)是偶函数，求a的值；（3）在（2）的情况下，画出y=f(x)的图象并指出其单独递增区间.40.已知集合A={a,b,2}，B={2,b2,2a}，若A=B，求实数a，b的值.41.设f(x)=14x+2，先分别求f（0）+f（1），f（﹣1）+f（2），f（﹣2）+f（3），然后归纳猜想一般性结论，并给出证明．42.已知函数f(x)=log a(x+1)，g(x)=log a(4−2x)（a>0，且a≠1），设F(x)=f(x)−g(x)．（1）求函数F(x)的定义域；（2）求使函数F(x)的值为正数的x的取值范围．43.求函数y=2x﹣3+ √13−4x的值域．44.某通讯公司需要在三角形地带OAC 区域内建造甲、乙两种通信信号加强中转站，甲中转站建在区域BOC 内，乙中转站建在区域AOB 内．分界线OB 固定，且OB=（1+ √3 ）百米，边界线AC 始终过点B ，边界线OA 、OC 满足∠AOC=75°，∠AOB=30°，∠BOC=45°．设OA=x （3≤x≤6）百米，OC=y 百米．（1）试将y 表示成x 的函数，并求出函数y 的解析式；（2）当x 取何值时？整个中转站的占地面积S △OAC 最小，并求出其面积的最小值．45.已知由方程kx 2－8x ＋16＝0的根组成的集合A 只有一个元素，试求实数k 的值．46.已知 y =f(x) 为二次函数，其图象顶点为 (1,−3) ，且过坐标原点. （1）求 y =f(x) 的解析式；（2）求 y =f(x) 在区间 [0,m] 上的最大值.47.设全集U=R ，集合A={x|﹣2＜x ＜2}，集合B={x|x 2﹣4x+3＞0} 求A∩B ，A ∪B ，A∩∁U B ．48.已知函数 f(x)=√x ， g(x)=|x −2| . （1）求方程 f(x)=g(x) 的解集；（2）定义： max{a,b}={a,a ≥bb,a <b .已知定义在 [0,+∞) 上的函数 ℎ(x)=max{f(x),g(x)} . ①求 ℎ(x) 的单调区间；②若关于 x 的方程 ℎ(x)=m 有两个实数解，求 m 的取值范围.49.已知函数f（x）是定义在R上的偶函数，且当x≤0时，f（x）=x2+2x．（1）现已画出函数f（x）在y轴左侧的图象，如图所示，请补全函数f（x）的图象，并根据图象写出函数f（x）（x∈R）的递增区间；（2）写出函数f（x）（x∈R）的值域；（3）写出函数f（x）（x∈R）的解析式．50.已知函数f(x)=|x+1|−|x|.（1）解关于x的不等式f(x)+f(x−1)<1；（2）若关于x的不等式f(x)−f(x−1)<m−2|x|有解，求m的取值范围.答案解析部分一、单选题1.【答案】D2.【答案】C3.【答案】D4.【答案】B5.【答案】A6.【答案】C7.【答案】C8.【答案】B9.【答案】D10.【答案】A11.【答案】B12.【答案】A13.【答案】A14.【答案】A15.【答案】C16.【答案】A17.【答案】B18.【答案】A19.【答案】C20.【答案】C二、填空题21.【答案】3或122.【答案】2；-123.【答案】（π6+2kπ，5π6+2kπ），k∈Z24.【答案】25.【答案】426.【答案】[1,+∞)27.【答案】（﹣1，0]∪[1，+∞）28.【答案】1329.【答案】(3,+∞)30.【答案】[0，3]31.【答案】032.【答案】{2+ √7，﹣1，﹣3}33.【答案】②③34.【答案】 [ 32 ，2） 35.【答案】 (−1,0)∪(0,3] 三、解答题36.【答案】（1）证明：f （x ）的定义域为{x|﹣3≤x≤3}，关于原点对称又f （﹣x ）=（﹣x ）2﹣2|﹣x|+3=x 2﹣2|x|+3=f （x ），∴f （x ）是偶函数；（2）解： f(x)={x 2+2x +3=(x +1)2+2(−3≤x ≤0)x 2−2x +3=(x −1)2+2(0<x ≤3) 作出函数的图象，如图，可知：f （x ）的单调增区间为[﹣1，0]和[1，3]（3）解：由（2）知，x=±1时，函数取得最小值；x=±3时，函数取得最大值 ∴函数f （x ）的值域为[2，6]．37.【答案】（1）解：函数f （x ）的定义域为： {x ∈R|x ≠0} ， f(x)=(x+1)(x+a)x=x +ax+1+a ，∴ f(−x)+f(x)=−x −ax +1+a +x +ax +1+a =0 ， ∴ a =−1 ；（2）解：由（1）可知： f(x)=x −1x ，显然 f(x)=x −1x 在 [1m ,1n ] 上单调递增，∴{1m −m =3−3m 1n−n =3−3n，∴ m ， n 是方程 2x 2−3x +1=0 的两个实根，且 m >n ， ∴ m =1,n =12 .38.【答案】解：（Ⅰ）当每辆车的月租金定为3600元时，未租出的车辆数为，所以这时租出了88辆车．（Ⅱ）设每辆车的月租金定为x 元，则租赁公司的月收益为，整理得．所以，当x=4050时，f （x ）最大，最大值为f （4050）=307050，即当每辆车的月租金定为4050元时，租赁公司的月收益最大，最大月收益为307050元 39.【答案】（1）解：我同意王鹏同学的看法，理由如下： f(a)=a 2+3,f(−a)=a 2−4|a|+3若 f(x) 为奇函数，则有 f(a)+f(−a)=0 ， ∴a 2−2|a|+3=0显然 a 2−2|a|+3=0 无解，所以 f(x) 不可能是奇函数（2）解：若 f(x) 为偶函数，则有 f(x)=f(−x) ∴2|a|=0 , 解得 a =0 ，此时 f(x)=x 2−2|x|+3 ，是偶函数.（3）解：由（2）知 f(x)=x 2−2|x|+3 ，其图象如图所示其单调递增区间是 (−1,0) 和 (1,+∞) .40.【答案】解：由已知 A =B ，得 {a =2a b =b 2 （1）或 {a =b 2b =2a .（2）解（1）得 {a =0b =0 或 {a =0b =1 ，解（2）得 {a =0b =0 或 {a =14b =12，又由集合中元素的互异性得 {a =0b =1 或 {a =14b =12 . 41.【答案】解：f （0）+f （1）= ，同理可得：f （﹣1）+f （2）= ，f （﹣2）+f （3）=．一般性结论：或写成“若x 1+x 2=1，则f （x 1）+f （x 2）=．”证明： ==42.【答案】（1）解：∵函数 f(x)=log a (x +1) ， g(x)=log a (4−2x) ∴ F(x)=f(x)−g(x)=log a (x +1)−log a (4−2x) ∴其定义域满足： {x +1>04−2x >0 ，解得 −1<x <2∴函数 F(x) 的定义域为 (−1,2)（2）解：要使函数 F(x) 的值为正数，等价于 f(x)>g(x) ，即 log a (x +1)>log a (4−2x) . ①当 a >1 时，可得 x +1>4−2x ，解得 x >1 . ∵定义域为 (−1,2)∴实数 x 的取值范围是 (1,2)②当 0<a <1 时，可得 x +1<4−2x ，解得 x <1 . ∵定义域为 (−1,2)∴实数 x 的取值范围是 (−1,1)综上，当 a >1 时，解集为 (1,2) ；当 0<a <1 ，解集为 (−1,1) 43.【答案】解：令则，t≥0 ∴y=﹣3+t=﹣t 2+t+=﹣ （t ﹣1）2+4（t≥0）根据二次函数的性质可知，当t=1即x=3时，函数有最大值4 故答案为：（﹣∞，4]44.【答案】（1）解：结合图形可知，S △BOC +S △AOB =S △AOC ．于是， 12 x （1+ √3 ）sin30°+ 12 y （1+ √3 ）sin45°= 12 xysin75°，解得：y= √2xx−2 ，（其中3≤x≤6）（2）解：由（1）知，y= √2x x−2 （3≤x≤6），因此，S △AOC = 12 xysin75°= 1+√34 • x 2x−2= 1+√34[（x ﹣2）+ 4x−2 +4] ≥2+2 √3 （当且仅当x ﹣2= 4x−2 ，即x=4时，等号成立）．∴当x=400米时，整个中转站的占地面积S △OAC 最小，最小面积是（2+2 √3 ）×104平方米． 45.【答案】解：当k ＝0时，原方程变为－8x ＋16＝0，所以x ＝2，此时集合A 中只有一个元素2.当k≠0时，要使一元二次方程kx 2－8x ＋16＝0有一个实根，需Δ＝64－64k ＝0，即k ＝1.此时方程的解为x 1＝x 2＝4，集合A 中只有一个元素4.综上可知k ＝0或146.【答案】（1）解：设 f(x) 解析式为： f(x)=a(x −1)2−3 ∵f(x) 过坐标原点 ∴f(0)=a −3=0 ，解得： a =3∴f(x)=3(x −1)2−3=3x 2−6x（2）解：由（1）知： f(x) 为开口方向向上，对称轴为 x =1 的二次函数 ①当 0<m <2 时， f(x)max =f(0)=0 ，当 m =2 时， f(x)max =f(0)=f(m)=0 ， ②当 m >2 时， f(x)max =f(m)=3m 2−6m47.【答案】解：全集U=R ，集合A={x|﹣2＜x ＜2}，集合B={x|x 2﹣4x+3＞0}={x|x ＜1或x ＞3}，所以A∩B={x|﹣2＜x ＜1}，A ∪B={x|x ＜2或x ＞3}，∁U B={x|1≤x≤3}，所以A∩∁U B={x|1≤x ＜2}48.【答案】（1）解：当 x ≥2 时，方程 f(x)=g(x) 为 √x =x −2 ，即 (√x −2)(√x +1)=0 ，解得 x =4 ，当 0≤x <2 时，方程 f(x)=g(x) 为 √x =2−x ，即 (√x +2)(√x −1)=0 ，解得 x =1 ，综上，方程 f(x)=g(x) 的解集为 {1,4} .（2）解：① f(x)≥g(x)⇒1≤x ≤4 ， f(x)<g(x)⇒0≤x <1 或 x >4所以 ℎ(x)=max{f(x),g(x)}={2−x,0≤x <1√x,1≤x ≤4x −2,x >4 ，所以， ℎ(x) 的单调递增区间为 [1,+∞) ，单调递减区间为 [0,1) .②由①知 ℎ(x)min =ℎ(1)=1 ， ℎ(0)=2 ，当 1<m ≤2 时，方程 ℎ(x)=m 有两个实数解，综上，实数 m 的取值范围为 (1,2] .49.【答案】（1）解：根据偶函数的图象关于y 轴对称，作出函数在R 上的图象，结合图象可得函数的增区间为（﹣1，0）、减区间为（1，+∞）（2）解：结合函数的图象可得，当x=1，或 x=﹣1时，函数取得最小值为﹣1，函数没有最大值，故函数的值域为[﹣1，+∞）（3）解：当x ＞0时，﹣x ＜0，再根据x≤0时，f （x ）=x 2+2x ，可得f （﹣x ）=（﹣x ）2+2（﹣x ）=x 2﹣2x ．再根据函数f （x ）为偶函数，可得f （x ）=x 2﹣2x ．综上可得，f （x ）= {x 2+2x,x ≤0x 2−2x,x ＞050.【答案】（1）解： f(x)+f(x −1)<1⇔|x +1|−|x −1|<1⇔{x ⩽−1−x −1−1+x <1 或 {−1<x <1x +1−1+x <1 或 {x ⩾1x +1−x +1<1⇔x ⩽−1 或 −1<x <12⇔x <12所以，原不等式的解集为 (−∞,12)（2）解： f(x)−f(x −1)<m −2|x| 有解即 |x +1|+|x −1|<m 有解则 m >(|x +1|+|x −1|)min 即可.由于 |x +1|+|x −1|⩾|(x +1)−(x −1)|=2 ，当且仅当 (x +1)(x −1)≤0 ，即当 −1≤x ≤1 时等号成立，故 m >2 . 所以， m 的取值范围是 (2,+∞) .。

集合与函数测试题(附答案)

已知集合M ＝{－1,0,1}，N ＝{x |x ＝ab ，a ，b ∈M 且a ≠b }，则集合M 与集合N 的关系是( C )A ．M ＝NB ．M NC ．N MD ．M ∩N ＝∅2．已知全集U ＝R ，集合A ＝{x |x 2－2x －3>0}，B ＝{x |2<x <4}，则(∁U A )∩B ＝( C ) A ．{x |－1≤x ≤4} B ．{x |2<x ≤3} C ．{x |2≤x <3}D ．{x |－1<x <4}已知全集U ＝R ，集合A ＝{x |lg x ≤0}，B ＝{x |2x ≤1}，则∁U (A ∪B )＝( B ) A ．(－∞，1) B ．(1，＋∞) C ．(－∞，1]D ．[1，＋∞)函数f (x )＝log 2x －1x 的一个零点落在下列哪个区间( B )A ．(0,1)B ．(1,2)C ．(2,3)D ．(3,4)已知a 是函数f (x )＝2x －log 12x 的零点，若0<x 0<a ，则f (x 0)的值满足( B )A ．f (x 0)＝0B ．f (x 0)<0C ．f (x 0)>0D ．f (x 0)的符号不确定函数f (x )＝⎩⎪⎨⎪⎧－x ＋3a ， x <0a x ， x ≥0(a >0且a ≠1)是R 上的减函数，则a 的取值范围是( B )A ．(0,1)B ．[13，1)C ．(0，13]D ．(0，23]若函数f (x )＝|x |(x －b )在[0,2]上是减函数，则实数b 的取值范围是( D ) A ．(－∞，4] B ．(－∞，2] C ．[2，＋∞)D ．[4，＋∞)函数f (x )＝log 2(3x ＋1)的值域为( A ) A ．(0，＋∞) B ．[0，＋∞) C ．(1，＋∞)D ．[1，＋∞)函数y ＝16－4x 的值域是( C ) A ．[0，＋∞) B ．[0,4] C ．[0,4) D ．(0,4)若关于x 的方程log 12x ＝m1－m 在区间(0,1)上有解，则实数m 的取值范围是( A )A ．(0,1)B ．(1,2)C ．(－∞，1)∪(2，＋∞)D ．(－∞，0)∪(1，＋∞)设a ＝log 132，b ＝log 1213，c ＝⎝⎛⎭⎫120.3，则( B ) A ．a ＜b ＜c B ．a ＜c ＜b C ．b ＜c ＜aD ．b ＜a ＜c已知曲线f (x )＝x n ＋1(n ∈N *)与直线x ＝1交于点P ，若设曲线y ＝f (x )在点P 处的切线与x 轴交点的横坐标为x n ，则log 2011x 1＋log 2011x 2＋…＋log 2011x 2010的值为( B )A ．－log 20112010－2B ．－1C ．log 20112010－1D ．1设函数f (x )定义在实数集上，它的图象关于直线x ＝1对称，且当x ≥1时，f (x )＝3x －1，则有( B )A ．f ⎝⎛⎭⎫13<f ⎝⎛⎭⎫32<f ⎝⎛⎭⎫23B ．f ⎝⎛⎭⎫23<f ⎝⎛⎭⎫32<f ⎝⎛⎭⎫13 C ．f ⎝⎛⎭⎫23<f ⎝⎛⎭⎫13<f ⎝⎛⎭⎫32D ．f ⎝⎛⎭⎫32<f ⎝⎛⎭⎫23<f ⎝⎛⎭⎫13定义某种运算S ＝a ⊗b ，运算原理如框图所示，则式子2⊗ln e ＋2⊗⎝⎛⎭⎫13－1的值为( A )A ．13B ．11C ．8D ．4设偶函数f (x )在(0，＋∞)上为减函数，且f (2)＝0，则不等式f (x )＋f (－x )x >0的解集为( B )A ．(－2,0)∪(2，＋∞)B ．(－∞，－2)∪(0,2)C ．(－∞，－2)∪(2，＋∞)D ．(－2,0)∪(0,2)已知函数f (x )＝log a (x ＋b )的大致图象如图，其中a 、b 为常数，则函数g (x )＝a x ＋b 的大致图象是( B )若指数函数f (x )＝a x (a >0，a ≠1)图象上的任意一点P (x 0，y 0)处的导数都大于零，则函数y ＝xa x|x |的图象的大致形状是( C )若函数f (x )＝ka x －a －x (a >0且a ≠1)在(－∞，＋∞)上是单调递增的奇函数，则g (x )＝log a (x＋k )的图象是( C )已知函数f (x )＝x 2－4x ＋3，集合M ＝{(x ，y )|f (x )＋f (y )≤0}，集合N ＝{(x ，y )|f (x )－f (y )≥0}，则集合M ∩N 的面积是( C )A.π4 B.π2 C ．π D ．2π13．已知函数f (x )对任意实数x 都有f (x ＋3)＝－f (x )，又f (4)＝－2，则f (2011)＝____2____. 已知f (x )＝log a x ，(a >0且a ≠1)满足f (9)＝2，则f (3a )＝_____3___.函数y ＝a x －1(a >0，且a ≠1)的图象恒过定点A ，若点A 在一次函数y ＝mx ＋n 的图象上，其中m ，n >0，则1m ＋1n的最小值为____4____．定义：F (x ，y )＝y x (x >0，y >0)，已知数列{a n }满足：a n ＝F (n ，2)F (2，n )(n ∈N *)，若对任意正整数n ，都有a n ≥a k (k ∈N *，k 为常数)成立，则a k 的值为____89____．用二分法求方程x 3－2x －5＝0在区间[2,3]上的近似解，取区间中点x 0＝2.5，那么下一个有解区间为____[2,2.5]____．设函数f (x )＝|x |x ＋bx ＋c ，给出下列4个命题： ①b ＝0，c >0时，方程f (x )＝0只有一个实数根； ②c ＝0时，y ＝f (x )是奇函数； ③y ＝f (x )的图象关于点(0，c )对称； ④函数f (x )至多有2个零点．上述命题中的所有正确命题的序号是____①②③____．已知集合A ＝{x |x 2－2x －3≤0，x ∈R }，B ＝{x |x 2－2mx ＋m 2－4≤0，x ∈R ，m ∈R }． (1)若A ∩B ＝[0,3]，求实数m 的值； (2)若A ⊆∁R B ，求实数m 的取值范围． A ＝{x |－1≤x ≤3} B ＝{x |m －2≤x ≤m ＋2}． (1)∵A ∩B ＝[0,3]，∴⎩⎪⎨⎪⎧ m －2＝0m ＋2≥3，⎩⎪⎨⎪⎧m ＝2m ≥1，∴m ＝2. (2)∁R B ＝{x |x <m －2或x >m ＋2} A ⊆∁R B ，∴m －2>3或m ＋2<－1. ∴m >5或m <－3.已知全集U ＝R ，非空集合A ＝{x |x －2x －(3a ＋1)<0}，B ＝{x |x －a 2－2x －a <0}．(1)当a ＝12时，求(∁U B )∩A ；(2)命题p ：x ∈A ，命题q ：x ∈B ，若q 是p 的必要条件，求实数a 的取值范围．(1)当a ＝12时，A ＝{x |x －2x －52<0}＝{x |2<x <52}，B ＝{x |x －94x －12<0}＝{x |12<x <94}．∴(∁U B )∩A ＝{x |x ≤12或x ≥94}∩{x |2<x <52}＝{x |94≤x <52}．(2)若q 是p 的必要条件，即p ⇒q ，可知A ⊆B ，由a 2＋2>a ，得B ＝{x |a <x <a 2＋2}，当3a ＋1>2，即a >13时，A ＝{x |2<x <3a ＋1}，⎩⎪⎨⎪⎧a ≤2a 2＋2≥3a ＋1，解得13<a ≤3－52；当3a ＋1＝2，即a ＝13时，A ＝∅，符合题意；当3a ＋1<2，即a <13时，A ＝{x |3a ＋1<x <2}．⎩⎪⎨⎪⎧a ≤3a ＋1a 2＋2≥2，解得a ≥－12，∴－12≤a <13；综上，a ∈[－12，3－52]．已知函数f (x )＝e x －k －x ，(x ∈R )(1)当k ＝0时，若函数g (x )＝1f (x )＋m的定义域是R ，求实数m 的取值范围；(2)试判断当k >1时，函数f (x )在(k,2k )内是否存在零点． (1)当k ＝0时，f (x )＝e x －x ，f ′(x )＝e x －1，令f ′(x )＝0得，x ＝0，当x <0时f ′(x )<0，当x >0时，f ′(x )>0， ∴f (x )在(－∞，0)上单调减，在[0，＋∞)上单调增． ∴f (x )min ＝f (0)＝1，∵对∀x ∈R ，f (x )≥1，∴f (x )－1≥0恒成立， ∴欲使g (x )定义域为R ，应有m >－1.(2)当k >1时，f (x )＝e x －k －x ，f ′(x )＝e x －k －1>0在(k,2k )上恒成立．∴f (x )在(k,2k )上单调增．又f (k )＝e k －k －k ＝1－k <0，f (2k )＝e 2k －k －2k ＝e k －2k ，令h (k )＝e k －2k ，∵h ′(k )＝e k －2>0，∴h (k )在k >1时单调增， ∴h (k )>e －2>0，即f (2k )>0，∴由零点存在定理知，函数f (x )在(k,2k )内存在零点．已知f (x )＝ln x ＋x 2－bx .(1)若函数f (x )在其定义域内是增函数，求b 的取值范围；(2)当b ＝－1时，设g (x )＝f (x )－2x 2，求证函数g (x )只有一个零点． (1)∵f (x )在(0，＋∞)上递增，∴f ′(x )＝1x ＋2x －b ≥0，对x ∈(0，＋∞)恒成立，即b ≤1x ＋2x 对x ∈(0，＋∞)恒成立，∴只需b ≤⎝⎛⎭⎫1x ＋2x min ， ∵x >0，∴1x ＋2x ≥22，当且仅当x ＝22时取“＝”，∴b ≤22，∴b 的取值范围为(－∞，22]．(2)当b ＝－1时，g (x )＝f (x )－2x 2＝ln x －x 2＋x ，其定义域是(0，＋∞)， ∴g ′(x )＝1x－2x ＋1＝－2x 2－x －1x ＝－(x －1)(2x ＋1)x ，令g ′(x )＝0，即－(2x ＋1)(x －1)x ＝0，∵x >0，∴x ＝1，当0<x <1时，g ′(x )>0；当x >1时，g ′(x )<0，∴函数g (x )在区间(0,1)上单调递增，在区间(1，＋∞)上单调递减， ∴当x ≠1时，g (x )<g (1)，即g (x )<0，当x ＝1时，g (x )＝0. ∴函数g (x )只有一个零点．已知关于x 的二次函数f (x )＝ax 2－4bx ＋1.(1)已知集合P ＝{－1,1,2,3,4,5}，Q ＝{－2，－1,1,2,3,4}，分别从集合P 和Q 中随机取一个数作为a 和b ，求函数y ＝f (x )在区间[1，＋∞)上是增函数的概率；(2)在区域⎩⎪⎨⎪⎧x ＋y －8≤0x >0y >0内随机任取一点(a ，b )．求函数y ＝f (x )在区间[1，＋∞)上是增函数的概率．(1)∵a ∈P ，∴a ≠0.∴函数f (x )＝ax 2－4bx ＋1的图象的对称轴为x ＝2ba ，要使f (x )＝ax 2－4bx ＋1在区间[1，＋∞)上为增函数，当且仅当a >0且2ba ≤1，即2b ≤a .若a ＝1，则b ＝－2，－1；若a ＝2，则b ＝－2，－1,1；若a ＝3，则b ＝－2，－1,1；若a ＝4，则b ＝－2，－1,1,2；若a ＝5，则b ＝－2，－1,1,2.所求事件包含基本事件的个数是2＋3＋3＋4＋4＝16. ∴所求事件的概率为1636＝49.(2)由条件知a >0，∴同(1)可知当且仅当2b ≤a 且a >0时，函数f (x )＝ax 2－4bx ＋1在区间[1，＋∞)上为增函数，依条件可知试验的全部结果所构成的区域⎩⎨⎧⎭⎬⎫(a ，b )|⎩⎪⎨⎪⎧a ＋b －8≤0a >0b >0，为△OAB ，所求事件构成区域为如图阴影部分．由⎩⎪⎨⎪⎧a ＋b －8＝0a －2b ＝0.得交点D ⎝⎛⎭⎫163，83， ∴所求事件的概率为P ＝12×8×8312×8×8＝13.“5·12”汶川大地震是华人心中永远的痛！在灾后重建中拟在矩形区域ABCD 内建一矩形(与原方位一样)的汶川人民纪念广场(如图)，另外△AEF 内部有一废墟作为文物保护区不能占用，经测量AB ＝100m ，BC ＝80m ，AE ＝30m ，AF ＝20m ，如何设计才能使广场面积最大？建立如图所示的直角坐标系，则E (30,0)，F (0,20)，∴线段EF的方程是x 30＋y20＝1(0≤x ≤30)在线段EF 上取点P (m ，n )，作PQ ⊥BC 于点Q ，PR ⊥CD 于点R ，设矩形PQCR 的面积为S ，则S ＝|PQ |·|PR |＝(100－m )(80－n )又∵m 30＋n20＝1(0≤m ≤30)，∴n ＝20⎝⎛⎭⎫1－m 30， ∴S ＝(100－m )⎝⎛⎭⎫80－20＋2m3 ＝－23(m －5)2＋180503(0≤m ≤30)∴当m ＝5m 时，S 有最大值，此时|EP ||PF |＝30－55＝51.故当矩形广场的两边在BC 、CD 上，一个顶点在线段EF 上，且这个顶点分EF 成时，广场的面积最大．。

高中数学必修一第一章《集合与函数概念》单元测试题(含答案)

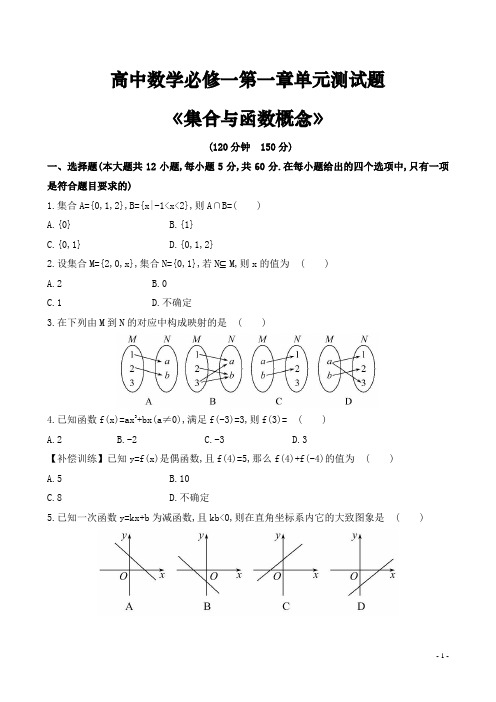
高中数学必修一第一章单元测试题《集合与函数概念》(120分钟150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.集合A={0,1,2},B={x|-1<x<2},则A∩B=( )A.{0}B.{1}C.{0,1}D.{0,1,2}2.设集合M={2,0,x},集合N={0,1},若N⊆M,则x的值为( )A.2B.0C.1D.不确定3.在下列由M到N的对应中构成映射的是( )4.已知函数f(x)=ax3+bx(a≠0),满足f(-3)=3,则f(3)= ( )A.2B.-2C.-3D.3【补偿训练】已知y=f(x)是偶函数,且f(4)=5,那么f(4)+f(-4)的值为( )A.5B.10C.8D.不确定5.已知一次函数y=kx+b为减函数,且kb<0,则在直角坐标系内它的大致图象是( )6.若f(x)=则f的值为( )A.-B.C.D.7.若f(g(x))=6x+3,且g(x)=2x+1,则f(x)= ( )A.3B.3xC.6x+3D.6x+18.下列四个图形中,不是以x为自变量的函数的图象是( )9.已知集合A={x|x2+x+1=0},若A∩R=∅,则实数m的取值范围是( )A.m<4B.m>4C.0<m<4D.0≤m<410.函数f(x)=|x|和g(x)=x(2-x)的单调递增区间分别是( )A.(-∞,0]和(-∞,1]B.(-∞,0]和[1,+∞)C.[0,+∞)和(-∞,1]D.[0,+∞)和[1,+∞)11.对于任意两个正整数m,n,定义某种运算“※”如下:当m,n都为正偶数或正奇数时,m※n=m+n;当m,n中一个为正偶数,另一个为正奇数时,m※n=mn.则在此定义下,集合M={(a,b)|a ※b=12,a∈N*,b∈N*}中的元素个数是( )A.10个B.15个C.16个D.18个12.设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则使<0的x的取值范围为( )A.(-1,0)∪(1,+∞)B.(-∞,-1)∪(0,1)C.(-∞,-1)∪(1,+∞)D.(-1,0)∪(0,1)二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13.已知集合A={x|1≤x<2},B={x|x<a},若A∩B=A,则实数a的取值范围是.14.已知a是实数,若集合{x|ax=1}是任何集合的子集,则a的值是.15.已知f(x)为偶函数,则f(x)=x1,1x0, ______,0x 1.+-⎧⎨⎩≤≤≤≤16.定义在R上的奇函数f(x)为减函数,若a+b≤0,给出下列不等式:①f(a)f(b)≤0;②f(a)+f(b)≤f(-a)+f(-b);③f(b)f(-b)≤0;④f(a)+f(b)≥f(-a)+f(-b).其中正确的是.(把你认为正确的不等式的序号全写上).三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)设全集为R,集合A={x|3≤x<6},B={x|2<x<9}.(1)分别求A∩B,(B)∪A.R(2)已知C={x|a<x<a+1},若C⊆B,求实数a取值构成的集合.18.(12分)已知函数f(x)=.(1)判断点(3,14)是否在f(x)的图象上.(2)当x=4时,求f(x)的值.(3)当f(x)=2时,求x的值.19.(12分)若函数f(x)=x2+4x+a的定义域和值域均为[-2,b](b>-2),求实数a,b的值.20.(12分)已知函数f(x)=ax+b,且f(1)=2,f(2)=-1.(1)求f(m+1)的值.(2)判断函数f(x)的单调性,并用定义证明.21.(12分)(2015·葫芦岛高一检测)已知函数f(x)对任意实数x,y恒有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,又f(1)=-2.(1)判断f(x)的奇偶性.(2)求证:f(x)为R上的减函数.(3)求f(x)在区间[-3,3]上的值域.22.(12分)定义在(-1,1)上的函数f(x)满足:①对任意x,y∈(-1,1),都有f(x)+f(y)=f;②f(x)在(-1,1)上是单调递减函数,f=-1.(1)求f(0)的值.(2)求证:f(x)为奇函数.(3)解不等式f(2x-1)<1.高中数学必修一第一章单元测试题《集合与函数概念》参考答案(120分钟150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.集合A={0,1,2},B={x|-1<x<2},则A∩B=( )A.{0}B.{1}C.{0,1}D.{0,1,2}【解析】选C.因为A={0,1,2},B={x|-1<x<2},所以A∩B={0,1}.2.(2015·天津高一检测)设集合M={2,0,x},集合N={0,1},若N⊆M,则x的值为( ) A.2 B.0C.1D.不确定【解析】选C.因为N⊆M,所以集合N中元素均在集合M中,所以x=1.3.在下列由M到N的对应中构成映射的是( )【解析】选C.选项A中,集合M中的数3在集合N中没有数与之对应,不满足映射的定义;选项B中,集合M中的数3在集合N中有两个数a,b与之对应;选项D中,集合M中的数a在集合N中有两个数1,3与之对应,不满足映射的定义.4.已知函数f(x)=ax3+bx(a≠0),满足f(-3)=3,则f(3)= ( )A.2B.-2C.-3D.3【解析】选 C.方法一:f(-3)=a(-3)3+b(-3)=-33a-3b=-(33a+3b)=3,所以33a+3b=-3.f(3)=33a+3b=-3.方法二:显然函数f(x)=ax3+bx为奇函数,故f(3)=-f(-3)=-3.【补偿训练】已知y=f(x)是偶函数,且f(4)=5,那么f(4)+f(-4)的值为( )A.5B.10C.8D.不确定【解析】选B.因为f(x)是偶函数,所以f(-4)=f(4)=5,所以f(4)+f(-4)=10.5.已知一次函数y=kx+b为减函数,且kb<0,则在直角坐标系内它的大致图象是( )【解析】选A.选项A图象为减函数,k<0,且在y轴上的截距为正,故b>0,满足条件,而B,C,D 均不满足条件.6.若f(x)=则f的值为( )A.-B.C.D.【解析】选C.因为<1,所以应代入f(x)=1-x2,即f=1-=.7.若f(g(x))=6x+3,且g(x)=2x+1,则f(x)= ( )A.3B.3xC.6x+3D.6x+1【解析】选B.由f(g(x))=f(2x+1)=6x+3=3(2x+1),知f(x)=3x.8.(2015·西城区高一检测)下列四个图形中,不是以x为自变量的函数的图象是( )【解析】选C.由函数定义知,定义域内的每一个x都有唯一函数值与之对应,A,B,D选项中的图象都符合;C项中对于大于零的x而言,有两个不同的值与之对应,不符合函数定义.9.已知集合A={x|x2+x+1=0},若A∩R=∅,则实数m的取值范围是( )A.m<4B.m>4C.0<m<4D.0≤m<4【解析】选D.因为A∩R=∅,所以A=∅,即方程x2+x+1=0无解,所以Δ=()2-4<0,所以m<4.又因为m≥0,所以0≤m<4.10.(2015·赣州高一检测)函数f(x)=|x|和g(x)=x(2-x)的单调递增区间分别是( ) A.(-∞,0]和(-∞,1] B.(-∞,0]和[1,+∞)C.[0,+∞)和(-∞,1]D.[0,+∞)和[1,+∞)【解析】选C.函数f(x)=|x|的单调递增区间为[0,+∞),函数g(x)=x(2-x)=-(x-1)2+1的单调递增区间为(-∞,1].11.对于任意两个正整数m,n,定义某种运算“※”如下:当m,n都为正偶数或正奇数时,m※n=m+n;当m,n中一个为正偶数,另一个为正奇数时,m※n=mn.则在此定义下,集合M={(a,b)|a ※b=12,a∈N*,b∈N*}中的元素个数是( )A.10个B.15个C.16个D.18个【解析】选B.若a,b同奇偶,有12=1+11=2+10=3+9=4+8=5+7=6+6,前面的每种可以交换位置,最后一种只有1个点(6,6),这时有2×5+1=11;若a,b一奇一偶,有12=1×12=3×4,每种可以交换位置,这时有2×2=4,所以共有11+4=15个.12.(2015·西安高一检测)设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则使<0的x的取值范围为( )A.(-1,0)∪(1,+∞)B.(-∞,-1)∪(0,1)C.(-∞,-1)∪(1,+∞)D.(-1,0)∪(0,1)【解析】选D.由f(x)为奇函数,可知=<0.而f(1)=0,则f(-1)=-f(1)=0.又f(x)在(0,+∞)上为增函数,所以当0<x<1时,f(x)<0=f(1),此时<0;又因为f(x)为奇函数,所以f(x)在(-∞,0)上为增函数,所以当-1<x<0时,f(x)>0=f(-1),此时<0,即所求x的取值范围为(-1,0)∪(0,1).二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13.(2015·开封高一检测)已知集合A={x|1≤x<2},B={x|x<a},若A∩B=A,则实数a的取值范围是.【解析】因为A∩B=A,所以A B,所以a≥2.答案:a≥214.已知a是实数,若集合{x|ax=1}是任何集合的子集,则a的值是.【解析】若集合{x|ax=1}是任何集合的子集,则它是空集,即方程ax=1无解,所以a=0.答案:015.已知f(x)为偶函数,则f(x)=x1,1x0, ______,0x 1.+-⎧⎨⎩≤≤≤≤【解析】当x∈[0,1]时,-x∈[-1,0],f(-x)=-x+1,又因为f(x)为偶函数,所以f(x)=f(-x)=1-x.答案:1-x16.定义在R上的奇函数f(x)为减函数,若a+b≤0,给出下列不等式:①f(a)f(b)≤0;②f(a)+f(b)≤f(-a)+f(-b);③f(b)f(-b)≤0;④f(a)+f(b)≥f(-a)+f(-b).其中正确的是.(把你认为正确的不等式的序号全写上).【解析】若a+b≤0,则a≤-b,b≤-a,又因为f(x)为R上递减的奇函数,所以f(a)≥f(-b),f(b)≥f(-a),所以f(a)+f(b)≥f(-a)+ f(-b),④正确;又因为f(-b)=-f(b),所以f(b)f(-b)=-f(b)f(b)≤0,③正确.其余错误.答案:③④三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)设全集为R,集合A={x|3≤x<6},B={x|2<x<9}.B)∪A.(1)分别求A∩B,(R(2)已知C={x|a<x<a+1},若C⊆B,求实数a取值构成的集合.【解析】(1)A∩B={x|3≤x<6}.因为B={x|x≤2或x≥9},RB)∪A={x|x≤2或3≤x<6或x≥9}.所以(R(2)因为C⊆B,如图所示:所以解得2≤a≤8,所以所求集合为{a|2≤a≤8}.18.(12分)已知函数f(x)=.(1)判断点(3,14)是否在f(x)的图象上.(2)当x=4时,求f(x)的值.(3)当f(x)=2时,求x的值.【解析】(1)因为f(x)=,所以f(3)==-,所以点(3,14)不在f(x)的图象上.(2)f(4)==-3.(3)令=2,即x+2=2x-12,解得x=14.19.(12分)若函数f(x)=x2+4x+a的定义域和值域均为[-2,b](b>-2),求实数a,b的值.【解析】因为函数f(x)的对称轴方程为x=-2,所以函数f(x)在定义域[-2,b](b>-2)上单调递增,所以函数f(x)的最小值为f(-2)=a-4=-2,所以a=2.函数f(x)的最大值为f(b)=b2+4b+2=b.所以b2+3b+2=0,解得b=-1或b=-2(舍去),所以b=-1.20.(12分)(2015·烟台高一检测)已知函数f(x)=ax+b,且f(1)=2,f(2)=-1.(1)求f(m+1)的值.(2)判断函数f(x)的单调性,并用定义证明.【解析】(1)由f(1)=2,f(2)=-1,得a+b=2,2a+b=-1,即a=-3,b=5,故f(x)=-3x+5,f(m+1)=-3(m+1)+5=-3m+2.(2)函数f(x)在R上单调递减,证明如下:任取x1<x2(x1,x2∈R),则f(x2)-f(x1)=(-3x2+5)-(-3x1+5)=3x1-3x2=3(x1-x2),因为x1<x2,所以f(x2)-f(x1)<0,即f(x2)<f(x1),所以函数f(x)在R上单调递减.【拓展延伸】定义法证明函数单调性时常用变形技巧(1)因式分解:当原函数是多项式函数时,作差后的变形通常进行因式分解.(2)通分:当原函数是分式函数时,作差后往往进行通分,然后对分子进行因式分解.(3)配方:当原函数是二次函数时,作差后可考虑配方,便于判断符号.21.(12分)(2015·葫芦岛高一检测)已知函数f(x)对任意实数x,y恒有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,又f(1)=-2.(1)判断f(x)的奇偶性.(2)求证:f(x)为R上的减函数.(3)求f(x)在区间[-3,3]上的值域.【解析】(1)取x=y=0,则f(0+0)=2f(0),所以f(0)=0.取y=-x,则f(x-x)=f(x)+f(-x),所以f(-x)=-f(x)对任意x∈R恒成立,所以f(x)为奇函数.(2)任取x1,x2∈(-∞,+∞),且x1<x2,则x2-x1>0,f(x2)+f(-x1)=f(x2-x1)<0,所以f(x2)<-f(-x1),又f(x)为奇函数,所以f(x1)>f(x2),所以f(x)是R上的减函数.(3)由(2)知f(x)在R上为减函数,所以对任意x∈[-3,3],恒有f(3)≤f(x)≤f(-3),因为f(3)=f(2)+f(1)=f(1)+f(1)+f(1)=-2×3=-6,所以f(-3)=-f(3)=6,所以f(x)在[-3,3]上的值域为[-6,6].22.(12分)定义在(-1,1)上的函数f(x)满足:①对任意x,y∈(-1,1),都有f(x)+f(y)=f;②f(x)在(-1,1)上是单调递减函数,f=-1.(1)求f(0)的值.(2)求证:f(x)为奇函数.(3)解不等式f(2x-1)<1.【解题指南】(1)结合已知等式利用赋值法求解.(2)利用赋值法并结合奇偶性定义判断.(3)结合(2)的结论及已知条件得f=1,再利用奇偶性和单调性脱去符号“f”,转化为一次不等式求解.【解析】(1)令x=y=0,得2f(0)=f(0),所以f(0)=0.(2)令y=-x,得f(x)+f(-x)=f(0)=0,即f(x)=-f(-x),所以f(x)为奇函数.(3)因为f=-1,f(x)为奇函数,所以f=1,所以不等式f(2x-1)<1等价于f(2x-1)<f,又因为f(x)在(-1,1)上是减函数,所以2x-1>-,-1<2x-1<1,解得<x<1.所以不等式的解集为.【误区警示】解答本题(3)时易忽视函数定义域而得出解集为的错误.。

高一数学必修1《集合与函数概念》测试卷(含答案)

高一数学必修1《集合与函数概念》测试卷(含答案)第一章（一）《集合与函数概念》测试卷考试时间：120分钟满分：150分一.选择题（本大题共12小题，每小题5分，共60分）1.下列叙述正确的是（）A.函数的值域就是其定义中的数集BB.函数y=f(x)的图像与直线x=m至少有一个交点C.函数是一种特殊的映射D.映射是一种特殊的函数2.如果A={x|x>-1}，则下列结论正确的是（）A.XXXB.{}⊆AC.{}∈AD.∅∈A3.设f(x)=(2a-1)x+b在R上是减函数，则有（）A.a≥1/2B.a≤1/2C.a>1/2D.a<1/24.定义在R上的偶函数f(x)，对任意x1,x2∈[0,+∞)(x1≠x2)，有|x1-x2|<π/2，则有（）A.f(3)<f(-2)<f(1)B.f(1)<f(-2)<f(3)C.f(-2)<f(1)<f(3)D.f(3)<f(1)<f(-2)5.若奇函数f(x)在区间[1,3]上为增函数，且有最小值，则它在区间[-3,-1]上（）A.是减函数，有最小值0B.是增函数，有最小值0C.是减函数，有最大值0D.是增函数，有最大值06.设f:x→x是集合A到集合B的映射，若A={-2,0,2}，则AB等于（）A.{}B.{2}C.{0,2}D.{-2,0}7.定义两种运算：a⊕b=ab，a⊗b=a²+b²，则函数f(x⊗3-3)为（）A.奇函数B.偶函数C.既不是奇函数又不是偶函数D.既是奇函数又是偶函数8.若函数f(x)是定义域在R上的偶函数，在(-∞,0)上是减函数，且f(-2)=1/4，则使f(x)<1/4的x的取值范围为（）A.(-2,2)B.(-2,0)∪(0,2)C.(-∞,-2)∪(2,+∞)D.(-∞,-2]∪[2,+∞)9.函数f(x)=x+(x|x|)的图像是（）10.设f(x)是定义域在R上的奇函数，f(x+2)=-f(x)，当|x|<1时，f(x)=x，则f(7.5)的值为（）A.-0.5B.0.5C.-5.5D.7.511.已知f(-2x+1)=x²+1，且-1/2≤x≤1/2，则f(x)的值域为（）A.[1,5/4]B.[1/4,5/4]C.[0,5/4]D.[1/4,2]12.设f(x)是定义在R上的奇函数，且f(x)在[-2,2]上单调递增，则f(x)在(-∞,-2)∪(2,+∞)上（）A.单调递减B.单调不增也不减C.单调递增D.无法确定第一章（一）《集合与函数概念》测试卷考试时间：120分钟满分：150分一、选择题（本大题共12小题，每小题5分，共60分）1.下列叙述正确的是（）A。

(word版)高中数学(必修1)集合与函数试题及答案,文档

集合根底训练A组一、选择题:1．以下各项中，不可以组成集合的是〔C〕A．所有的正数B．等于2的数C．接近于0的数D．不等于0的偶数2．以下四个集合中，是空集的是〔D〕A．{x|x33}B．{(x,y)|y2x2,x,yR}C．{x|x20}D．{x|x2x10,xR}3．以下表示图形中的阴影局部的是〔A〕A．(AUC)I(BUC)A B B．(AUB)I(AUC)C．(AUB)I(BUC)D．(AUB)I C C 4．下面有四个命题：〔1〕集合N中最小的数是1；〔2〕假设a不属于N，那么a属于N；〔3〕假设a N,b N,那么ab的最小值为2；〔4〕x212x的解可表示为1,1其中正确命题的个数为〔A〕A．0个B．1个C．2个D．3个5．假设集合M a,b,c中的元素是△ABC的三边长，那么△ABC一定不是〔D〕A．锐角三角形B．直角三角形C．钝角三角形D．等腰三角形二、填空题:1．假设集合2．设集合A x|3 x 7，B x|2 x 10，那么AUBx|2 x10 A {x 3 x 2},B {x2k 1 x 2k 1},且A B，那么实数k的取值范围是k|1k 1 23．Ayy x22x1,B yy2x1，那么AI B y|y0三、解答题:1．集合A8N，试用列举法表示集合A xN|6x解：由题意可知6x是8的正约数，当6x1,x5；当6x2,x4；当6x4,x2；当6x8,x2；而x0，∴x2,4,5，即A2,4,512A{x2x5}， B{xm1x2m1}，BA ,m 的取值范围．求解：当m 1 2m1，即m 2时，B ,满足BA ，即m 2；当m12m1，即m2时，B3,满足BA ，即m2；当m12m 1，即m2时，由Bm 1 2即2m 3；A ，得1 52mm33A a,a1, 3,Ba 3,2a 1,a 1 ，假设AI B3，求实数a 的值．集合22解：∵AI B3 ，∴ 3 B ，而a 2 1 3，∴当a3 3,a 0,A0,1, 3,B3,1,1，这与AI B3 矛盾；当2a 1 3,a 1,符合AI B3∴a14．设全集，2有实数根，2有实数根,求CMINUR Mm|mxx10Nn|xxn0 U解：当m0时，x1，即0 M ；当m 0时， 14m0,即m 1 0，且m4∴m1 ，∴C U Mm|m1 , 而对于N ， 14n0,即n1 ，∴Nn|n14444∴(C U M)I Nx|x14综合训练B 组一、选择题1．以下命题正确的有〔A 〕〔1〕很小的实数可以构成集合；〔2〕集合 y|yx 2 1与集合 x,y|yx 2 1是同一个集合；3 61 5个元素；〔3〕1,,,这些数组成的集合有2 42〔4〕集合 x,y|xy0,x,yR 是指第二和第四象限内的点集。

集合与函数概念试题及答案`

集合与函数概念试题卷一、选择题（本大题10小题，每小题5分，满分50分） 1．用列举法表示集合|{R x M ∈=}0442=+-x x 为（） A ．}2,2{B ．}2{C ．}2{=xD ．}044{2=+-x x2．已知集合A=}24|{<<-x x ，B=}12|{<<-x x ，则（） A ．A>B B ．A ⊆BC ．A BD ．A ⊇B3．{|2}M x R x =∈≥，a π=，则下列四个式子○1M a ∈；○2}{a M ； ○3a ⊆M ；○4{}a M π=，其中正确的是（）A ．○1○2 B ．○1 ○4 C ．○2○3 D ．○1○2○4 4．已知集合M 和P 如图所示，其中阴影部分表示为（） A ．P MB ．P MC ．P)(M C PD ．P)(M C M5．已知全集U={1,2,3,4,5,6,7,8}，A={2,5,8}，B={1,3,5,7}，那么(C U A)∩B =（）A ．{5}B ．{1, 3,4,5,6,7,8}C ．{2,8}D ．{1,3,7}6．如图，以下4个对应不是从A 到B 的映射的是（）7．若)(x f 的定义域为[0，1]，则)2(+x f 的定义域为（） A ．[0，1]B ．[2，3]C ．[－2，－1]D ．无法确定 8．已知函数32)1(+=+x x f 则)(x f 等于（） A ．32+x B ．22+xC ．12+xD ．12-x9．拟定从甲地到乙地通话m 分钟的电话费由() 1.06(f m ==0.5[]1)m +（元）决定，其中0>m , ][m 是大于或等于m 的最小整数，（如[3]=3，[3.8]=4，[3.1]=4），则从甲地到乙地通话时间为5.5分钟的电话费为（） A ．3.71元B ．3.97元C ．4.24元D ．4.77元10．如图，矩形ABCD 中，AB ＝1，AD ＝2，M 是CD 的中点，点P 在矩形的边上沿A →B →C →M 运动，则△APM的面积y 与点P 经过的路程x 之间的函数关系用图象表示大致是下图中的（）9 4 13 -3 2 -2 1 -1300 450 6009001 -12 -23 31 4 91 2 31 2 3 4 5 62122231A ．B ．C ．D ．开平方求正弦求平方乘以2M PM P二、填空题（本大题共5小题，每小题4分，满分20分） 11．已知集合A=},21{，请写出集合A 的所有子集 . 12．已知函数1)(2++=x x x f ，则)2(f = _________； =))2((f f _________；=-)(b a f _________.13．函数32)(2++-=x x x f 在区间[-1,5]上的最大值为，最小值为 .14．已知函数)(x f 的定义域为[2,5]且为减函数，有)()32(a f a f >+，则a 的取值范围是_________.15. 已知函数3)(24+-=ax x x f ，20)2010(=f ，则=-)2010(f . 三、解答题（本大题共6小题，共80分）、16．求下列函数的定义域：（本题12分）①23212---=x x x x f ）（ ②xx x f 11)(+-=17．求下列函数的值域：（本题12分）①2322--=x x y ]5,3[-∈x ②12+=x xy18．判断函数3y x x =+的单调性和奇偶性,并证明你的结论 3322(()())a b a b a ab b -=-++．（本题12分）19．已知103a <≤，若2()21f x ax x =-+在区间[1，3]上的最大值为()M a ，最小值为()N a ，令()()()g a M a N a =-。

集合与函数测试题(含答案)

集合与函数测试题一、选择题：（本大题共12个小题，每小题5分，共60分。

）1.设集合{}12A x x =-<≤，{}B x x a =<，若A B ≠∅ ，则a 的取值范围是（） A.2a < B.2a >- C.1a >- D.12a -<≤ 2.给出下列函数：①1y ax =+；②1y x=；③()21y a x =+.在其定义域上是增函数的个数为（）A.0B.1C.2D.33.已知函数()2211x f x x+=-，则（）有 A.()f x 是奇函数，且()()1ff x x =- B.()f x 是奇函数，且()()1f f x x = C.()f x 是偶函数，且()()1f f x x =- D.()f x 是偶函数，且()()1f f x x=4.对任意的,x y ∈R ，函数()f x 都满足()()()2f x y f x f y +=++恒成立，则()()55f f +-等于（）A.0B.4-C.2-D.2 5.设函数()3f x ax cx d =++则()()11f f -+的值（） A.大于0 B.小于0C.等于0D.以上结论都不对6.设f x x →∶是集合A 到集合B 的映射，若{}2,0,2A =-，则A B = （） A.{}0 B.{}2 C.{}0,2 D.{}2,0- 7.定义两种运算：a b ab ⊕=，22a b a b ⊗=+，则函数()222xf x x ⊕=⊗-为（）A.奇函数B.偶函数C.既不是奇函数又不是偶函数D.既是奇函数又是偶函数 8.若函数()k xf x x-=在(),0-∞上是减函数，则实数k 的取值范围是（） A.0k = B.0k > C.0k < D.0k ≥密封线姓名：班级：学号：9.函数()1y x x =-在区间A 上是增函数，那么区间A 最大为( )A.(),0-∞B.10,2⎡⎤⎣⎦C.[)0,+∞D.()1,2+∞10.若函数()f x 和()g x 都是奇函数，且()()()2F x af x bf x =++在区间()0,+∞上有最大值5，则()F x 在区间(),0-∞上（）A.有最小值5-B.有最大值5-C.有最小值1-D.有最大值3- 11.若()f x 满足()()f x f x -=，在区间(],1-∞-上是增函数，则（）A.()()()3122f f f -<-< B.()()()3122f f f -<-< C.()()()3212f f f <-<- D.()()()3212f f f <-<-12.设奇函数()f x 在[]1,1-上是增函数，且()11f -=-.若对所有的[]1,1x ∈-及任意的[]1,1a ∈-都满足()221f x t at -+≤，则t 的取值范围是（）A.22t -≤≤B.1122t -≤≤ C.2t ≥或2t -≤或0t = D.12t ≥或12t -≤或0t =二、填空题：（本大题共4个小题，每小题4分，共16分。

集合与函数概念(含答案)

集合与函数概念一、选择题1．设全集U ＝{(x ，y )| x ∈R ，y ∈R }，集合M ＝⎭⎬⎫⎩⎨⎧1＝2－3－|),(x y y x ， P ＝{(x ，y )| y ≠x ＋1}，那么C U (M ∪P )等于( )． A ．∅B ．{(2，3)}C ．(2，3)D ．{(x ，y )| y ＝x ＋1}2．假设A ＝{a ，b }，B ⊆A ，则集合B 中元素的个数是( )． A ．0B ．1C ．2D ．0或1或23．函数y ＝f (x )的图象与直线x ＝1的公共点数目是( )． A ．1B ．0C ．0或1D ．1或24．设函数f (x )＝2x ＋3，g (x ＋2)＝f (x )，则g (x )的表达式是( )． A ．2x ＋1B ．2x －1C ．2x －3D ．2x ＋75. 已知函数f (x )＝ax 3＋bx 2＋cx ＋d 的图象如下图，则( )． A ．b ∈(－∞，0) B ．b ∈(0，1) C ．b ∈(1，2)D ．b ∈(2，＋∞)6．设函数f (x )＝⎩⎨⎧00＋＋2 x c x c bx x ，，≤，假设f (－4)＝f (0)，f (－2)＝－2，则关于x 的方程f (x )＝x 的解的个数为( )．A ．1B ．2C ．3D ．47．设集合A ＝{x | 0≤x ≤6}，B ＝{y | 0≤y ≤2}，以下从A 到B 的对应法则f 不是映射的是( )．A ．f :x →y ＝21x B ．f :x →y ＝31xC ．f :x →y ＝41x D ．f :x →y ＝61x 8．有下面四个命题：①偶函数的图象一定与y 轴相交； ②奇函数的图象一定通过原点； ③偶函数的图象关于y 轴对称；④既是奇函数，又是偶函数的函数一定是f (x )＝0(x ∈R )．其中正确命题的个数是( )． A ．1B ．2C ．3D ．4(第5题) ＞9．函数y＝x2－6x＋10在区间(2，4)上是()．A．递减函数B．递增函数C．先递减再递增D．先递增再递减10．二次函数y＝x2＋bx＋c的图象的对称轴是x＝2，则有()．A．f(1)＜f(2)＜f(4)B．f(2)＜f(1)＜f(4)C．f(2)＜f(4)＜f(1)D．f(4)＜f(2)＜f(1)二、填空题11．集合{3，x，x2－2x}中，x应满足的条件是．12．假设集合A＝{x | x2＋(a－1)x＋b＝0}中，仅有一个元素a，则a＝___，b＝___．13．建造一个容积为8 m3，深为2 m的长方体无盖水池，如果池底和池壁的造价每平方米分别为120元和80元，那么水池的最低总造价为元．14．已知f(x＋1)＝x2－2x，则f(x)＝；f(x－2)＝．15．y＝(2a－1)x＋5是减函数，求a的取值范围．16．设f(x)是R上的奇函数，且当x∈［0，＋∞)时，f(x)＝x(1＋x3)，那么当x∈(－∞，0］时，f(x)＝．三、解答题17．已知集合A＝{x∈R| ax2－3x＋2＝0}，其中a为常数，且a∈R．①假设A是空集，求a的范围；②假设A中只有一个元素，求a的值；③假设A中至多只有一个元素，求a的范围．18．已知M＝{2，a，b}，N＝{2a，2，b2}，且M＝N，求a，b的值．19．证明f(x)＝x3在R上是增函数．20．判断以下函数的奇偶性： (1)f (x )＝3x 4＋21x ；(2)f (x )＝(x －1)xx－＋11； (3)f (x )＝1－x ＋x －1；(4)f (x )＝12－x ＋21x －第一章集合与函数概念参考答案一、选择题1．B 2．D 3．C 4．B 5．A 6．C 7．A 8．A 9．C 10．B ．二、填空题11．x ≠3且x ≠0且x ≠－1．12．a ＝31，b ＝91．13．1 760元．14．f (x )＝x 2－4x ＋3，f (x －2)＝x 2－8x ＋15． 15．(－∞，21)． 16．x (1－x 3)．三、解答题17．解：①∵A 是空集， ∴方程ax 2－3x ＋2＝0无实数根．∴⎩⎨⎧∆，a a 08－9＝,0 解得a ＞89．②∵A 中只有一个元素，∴方程ax 2－3x ＋2＝0只有一个实数根．当a ＝0时，方程化为－3x ＋2＝0，只有一个实数根x ＝32；当a ≠0时，令Δ＝9－8a ＝0，得a ＝89，这时一元二次方程ax 2－3x ＋2＝0有两个相等的实数根，即A 中只有一个元素．由以上可知a ＝0，或a ＝89时，A 中只有一个元素． ③假设A 中至多只有一个元素，则包括两种情形：A 中有且仅有一个元素；A 是空集．由①②的结果可得a ＝0，或a ≥89．18．解：根据集合中元素的互异性，有≠ ＜⎩⎨⎧==⎩⎨⎧==ab b a b b a a 2222或解得或或再根据集合中元素的互异性，得或19．证明：设x 1，x 2∈R 且x 1＜x 2，则f (x 1)－f (x 2)＝31x －32x ＝(x 1－x 2)(21x ＋x 1x 2＋22x )．又21x ＋x 1x 2＋22x ＝(x 1＋21x 2)2＋4322x ．由x 1＜x 2得x 1－x 2＜0，且x 1＋21x 2与x 2不会同时为0，否则x 1＝x 2＝0与x 1＜x 2矛盾，所以 21x ＋x 1x 2＋22x ＞0．因此f (x 1)－ f (x 2)＜0，即f (x 1)＜f (x 2)， f (x )＝x 3 在 R 上是增函数．20．解：(1)∵ 函数定义域为{x | x ∈R ，且x ≠0}， f (－x )＝3(－x )4＋21）（－x ＝3x 4＋21x ＝f (x )，∴f (x )＝3x 4＋21x 是偶函数． (2)由xx－＋11≥0⇔⎩⎨⎧≠01－－1＋1x x x ))(( 解得－1≤x ＜1． ∴ 函数定义域为x ∈［－1，1)，不关于原点对称，∴f (x )＝(x －1)xx－11＋为非奇非偶函数．(3)f (x )＝1－x ＋x －1定义域为x ＝1，∴ 函数为f (x )＝0(x ＝1)，定义域不关于原点对称， ∴f (x )＝1－x ＋x －1为非奇非偶函数． (4)f (x )＝1－2x ＋2－1x 定义域为≥ －10≥1－22x x ⇒ x ∈{±1}，∴函数变形为f (x )＝0 (x ＝±1)，∴f (x )=1－2x ＋2－1x 既是奇函数又是偶函数．a ＝0b ＝1 a ＝0b ＝0a ＝41b ＝21 a ＝0b ＝1 a ＝41 b ＝21 ≥0。

函数与集合专题测试题及答案

实用文档集合与函数专题测试题一．选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{0,1,2},{31|}M N a a M ==-∈,则 M N ⋂=( )A ．{0,1} B. {0,1,2} C. {2} D. φ2.函数2lg(2)y x x =--的定义域是（）A ．[2,1)-- B. [1,2] C. (1,2] D. [2,1]--3.“1a =”是“函数()f x x a =-在区间[1,)+∞上为增函数”的（）A ．充分不必要条件B 必要不充分条件C 充要条件D 既不充分也不必要条件4．为了得到3lg10x y +=的图像，只需把lg y x =的图像上所有的点 ( )A 向左平移3个单位长度，再向上平移1个单位长度；实用文档B 向右平移3个单位长度，再向上平移1个单位长度；C 向左平移3个单位长度，再向下平移1个单位长度；D 向右平移3个单位长度，再向下平移1个单位长度.5对于集合M 、N ，定义{}M N x x M x N -=∈∉且，()()M N M N N M ⊕=--，设{}23,A y y x x x R ==-∈，{}2,x B y y x R ==-∈，则A B ⊕= （） A.9(,0]4- B. 9[,0)4- C. 9(,)[0,)4-∞-+∞ D. 9(,)(0,)4-∞-+∞ 6.函数)1y x =<-的反函数是( )A.)0y x =>B.)0y x =>C.)1y x =<-D.)1y x =<-7. 32()32f x x x =-+在区间[1,1]-上的最大值是（）A. 2-B. 0C. 2D. 48.函数1(0,1)x y a b a a =+->≠且的图象经过第二、三、四象限，则一定有（）A.01a <<且0b >B.1a >且0b >C.01a <<且0b <D.1a >且0b <实用文档 9.已知()f x 是定义在(,0)(0,)-∞+∞上的奇函数，当0x >时， ()f x 的图象如图所示，则不等式[()()]0x f x f x ⋅--<的解集为（）A (3,0)(0,3)-B (,3)(0,3)-∞-C (,3)(3,)-∞-+∞D (3,0)(3,)-+∞10.定义域为R 的函数1(2)()|2|1(2)x f x x x ⎧≠⎪=-⎨⎪=⎩，若关于x 的方程2()()0f x bf x c ++=恰有5个不同的实数解 12345,,,,x x x x x ，则12345()f x x x x x ++++等于（）A. 14B. 18C. 112D. 11611.已知()f x 是R 上的增函数，点A (1,2)、(1,1)B -在它的图象上，1()f x -为它的反函数，则不等式13(log )1f x -<的解集是（）A. (1,2)B. (1,1)-C. (3,9)D. 1(,3)312.若函数2()log (2)(01)a f x x x a a =+>≠且在区间1(0,)2上恒有()0f x >，则()f x 的单调增区间是实用文档（） A.1(,)4-∞- B. 1(,)4-+∞ C. (0,)+∞ D. 1(,)2-∞- 二．填空题：本大题共4小题，每小题5分，共20分.把答案填在题中横线上.13.设函数221,1()2,1x x f x x x x ⎧-≤=⎨-+>⎩，则1()(2)f f 的值为_______________. 14.不等式20ax bx c ++>，解集区间为1(,2)2-，对于系数,,,a b c 有如下结论： ①0a >；②0b >；③ 0c >；④0a b c ++>；⑤0a b c -+>其中正确结论的序号是___________ .15.定义在(1,1)-上的函数()f x 满足：()()0f x f x -+=，当(1,1)x ∈-时，函数()f x 的导函数'()0f x <恒成立.如果2(1)(1)0f a f a -+->，则实数a 的取值范围是________________；16.已知函数()f x ()x R ∈满足(1)(1)f x f x +=-，且[1,1]x ∈-时，2()f x x =，则()y f x =与5log y x =的图像的交点个数为_______________ .三．解答题：本大题共4小题，共70分.解答应写出文字说明，证明过程或演算步骤.17.（本小题满分10分）实用文档已知函数()f x =A, []()lg (1)(2)(1)g x x a a x a =---<的定义域为B .(1)求A(2)若B A ⊆，求实数A 的取值范围.18.（本小题满分12分）已知函数1()21x f x a =+-是奇函数.（Ⅰ）求常数a 的值；（Ⅱ）求函数()f x 的反函数.19.（本小题满分12分）已知函数()f x 满足1(1)()f x f x +=，且()f x 是偶函数，当[3,4]x ∈时，3()log f x x =，求当[1,1]x ∈-时，()f x 的解析式.20.（本小题满分12分）设2()32f x ax bx c =++，若0a b c ++=，(0)(1)0f f >，求证：（1）方程()0f x =有实根; (2) 21ba -<<-;实用文档(3) 设12,x x 是方程()0f x =1223x x ≤-<. 21.（本小题满分12分）已知定义在R 上的函数()f x 满足：① 值域为(1,1)-，且当0x >时，1()0f x -<<；② 对于定义域内任意实数,x y ，均有()()()1()()f x f y f x y f x f y ++=+. （1）求(0)f 的值；（2）判断函数()f x 的单调性，并给出证明；（3）若函数()f x 存在反函数()g x ，求证：*21111()()()()()511312g g g g n N n n +++>∈++ 22.（本小题满分12分）已知函数432()41f x x x ax =-+-在区间(]0,1上单调递增，在区间[)1,2上单调递减.（1）求a 的值；（2）若点A 00(,())x f x 在函数()f x 的图象上，求证：点A 关于直线1x =的对称点B 也在函数()f x 的图象上；（3）是否存在实数b，使得函数42g x x bx=++（其中b<4）的图像与()()1f x的图像恰有3个交点？若有，求出实数b的范围；若不存在，说明理由.集合与函数专题模拟参考答案一、选择题1.提示：集合为中学数学提供了大量的符号，所以高考在几何方面的考查，主要看对集合符号的认识.本题的关键在于弄清集合N中的元素是什么，由题得M N⋂=N=-，所以，{2}{1,2,5}答案： C实用文档实用文档2.提示：由题意可得220120x x x x +⎧≥⎪-⎨⎪-->⎩，即可直接解，也可带值检验.答案：A3.提示：函数()f x x a =-的对称轴为x a =结合图象解之，其增区间为[),a +∞.区间[1,)+∞⊆[),a +∞.答案：A4. 提示：先将3lg10x y +=变形为lg(3)1y x =+-，然后利用平移公式求解. 答案：C5.提示：这是考查学生学习潜能的一道题，关键在于读懂题中的定义，集合A 、B 表示的是函数值域，然后将9[,),(,0)4A B =-+∞=-∞代入即可. 答案：C6. 提示：本题为反函数的基本题目，反函数在新课程中没有要求，在大纲版却是一个必考内容，基本上以客观题的形式出现，难度中等.反函数问题的解法有两种，一是间接法，就是利用原函数与反函数的定义域、值域的关系来解；也可以利用原函数经过点（a,b ），其反函数经过点（b,a ）来解，这时候取点验证就可以.本题略解：解法1：原函数的值域(0,)+∞，即为反函数定义域.解法2：在实用文档原函数经过点()，反函数必过点(1,，验证即可.答案：A7. 提示：直接利用导数求定区间[-1,1]下的最大值.答案：C8. 提示：分0a >和01a <<两类讨论来解.答案：C9. 提示：数形结合思想的考查是两个方面，客观题一般由“数”到“形”，命题主要围绕函数性质；主观题一般由“形”到“数”.由“数”到“形”需要意识，这种意识主要是函数性质的应用意识，比如函数的奇偶性，其主要作用是画图.本题由()f x 为奇函数得[()()]0x f x f x ⋅--<即为2()0x f x <，由图得0()0x f x >⎧⎨<⎩解得03x <<，再由奇函数图象关于原点对称得0()0x f x <⎧⎨>⎩，得30x -<<.答案：A10. 提示：由已知，方程2()()0f x bf x c ++=恰有5个不同的实数解，则其解必满足()1f x =或()(1)f x m m =≠.由()1f x =知，1231,3,2x x x ===；由()f x m =得，实用文档 45112,2x x m m =+=-，1234510x x x x x ∴++++=，所以 123451()(10)8f x x x x x f ++++== 答案：B11. 提示：由已知得11(2,1),(1,1)A B -在1()f x -的图象上，且1()f x -在(,)-∞+∞上递增，这样，不等式13(log )1f x -< 等价于31log 2x <<，解得，39x <<. 答案：C12. 提示：先由已知得01a <<，再由复合函数单调性解之.答案：D二、填空题13. 提示：先求(2)4f =，再计算，1115()()(2)416f f f ==. 答案：1516 14. 提示：二次函数问题在高考中常考常新，常考不衰，主要因为二次函数在中学阶段研究的最全面，应用的最广泛，几乎所有的问题都要用二次函数类解决，所以二次函数的学习要引起足够的重视.本题有效的考查二次函数根与系数的关系.由已知得0a <，12-、2是对应的二次方程的两个根，对称轴实用文档是它们的中点；0，1都在解集范围内，代入判断知②③④正确.答案：②③④15. 提示：由题知，()f x 为奇函数，且在(1,1)-上递减，所以2(1)(1)0f a f a -+->等价于2211111111a a a a -<-<⎧⎪-<-<⎨⎪-<-⎩，解得1a <<.答案：1a <<16. 提示：由(1)(1)f x f x +=-得，函数()f x 的周期为T=2，结合图像即可求出交点个数.答案：4三、解答题17.解：⑴ 3201x x +-≥+,101x x -∴≥+,1x ∴<-或1x ≥，即(,1)[1,)A =-∞-+∞； ⑵(1)(2)0x a a x --->，(1)(2)0x a x a ∴---<，1a <，21a a ∴<+， ∴不等式的解为21a x a <<+，即(2,1)B a a =+.B A ⊆，11a +≤-或21a ≥， ∴2a ≤-或12a ≥. 18.解：⑴解法1：函数1()21x f x a =+-是奇函数，()()f x f x ∴-=-，实用文档即112121x x a a -+=----，即211221x x x a a +=----，即1221212x x x a =---，即121,2a a =∴=. 解法2：由题意知函数的定义域为(,0)(0,)-∞+∞，又知函数为奇函数，所以有(1)(1)f f ∴-=-，解得12a =. ⑵11()212x y f x ==+-，12112x y ∴=+-，12212x y y +∴=-，20x >，12012y y +∴>- 12y ∴<-或12y >，又212log 12y x y +=-， ∴函数()f x 的反函数为121112()log ()1222x f x x x x -+=<->-或. 19.解：由1(1)()f x f x +=，得1(2)()(1)f x f x f x +==+，2T ∴=.当[1,0]x ∈-时，4[3,4]x +∈，3(4)log (4)f x x ∴+=+，而(4)()f x f x +=，3()log (4)f x x =+. 当(0,1]x ∈时，[1,0)x -∈-，3()log (4)f x x -=-+，而()f x 是偶函数，()()f x f x -=，即3()log (4)f x x =-+∴33log (4),10()log (4),01x x f x x x +-≤≤⎧=⎨-+<≤⎩实用文档20解：⑴若0a =，则b c =-，2(0)(1)(32)0f f c a b c c ⋅-=++=-≤，与已知矛盾，0a ∴≠.方程2320ax bx c ++=的判别式24(3)b ac ∆=-，由条件0a b c ++=，消去b ，得2222134()4[()]024a c ac a c c ∆=+-=-+>，故方程()0f x =有实根. ⑵(0)(1)0f f ⋅>，(0)(1)0f f ⋅>，由条件0abc ++=，消去c ，故()(2)0a b a b ++<.(1)(2)0b b a a a ∴++<，故21b a-<<-. ⑶由条件知1223b x x a +=-，1233c a b x x a a +⋅==-，2212431()()923b x x a -=++，21b a -<<-，21214()39x x ∴≤-<，故12233x x ≤-<. 21.解：（1）在()()()1()()f x f y f x y f x f y ++=+中，令0,0x y >=，则有()(0)(),1()(0)f x f f x f x f +=+ 整理得2(0)[()1]0f f x -≠，因此有(0)0f =.（2）函数()f x 在R 上单调递减.证明如下：在()()()1()()f x f y f x y f x f y ++=+中，令,y x =-注意到(0)0f =，得()()0f x f x +-=，所以函数()f x 为奇函数.因此有()()()1()()f x f y f x y f x f y --=-，即()()()[1()()]f x f y f x y f x f y -=-- 设x y -∞<<<+∞，则0y x ->，故()0f y x -<实用文档又由于函数()f x 的值域为(1,1)-，所以1()()1,1()()0f x f y f x f y -<<-> 即()()()[1()()]0f x f y f y x f x f y -=--->所以，函数()f x 在R 上单调递减.（3）由反函数定义，得 ()()[]1()()f x f y x yg f x f y --=-，令(),()f x s f y t ==，则 (),()x g s y g t ==，因此，又有()()()1s t g s g t g st--=-，可以验证，此式对任意的,(1,1)s t ∈-都成立. 由于211111(1)(2)1211131(1)(2)111(1)(2)12n n n n n n n n n n n n -++++===++++----++++，所以2111()()()3112g g g n n n n =-++++. 由此可得， 2111()()()51131g g g n n +++++111111[()()][()()][()()]111221*********()()()()()112222g g g g g g n n g g g g g n n =-+-++-++++++=-=+->+++ 点评：抽象函数单调性问题一般离不开定义，即做差()()f x f y -，于是证明函数的奇偶性是解题的第一关键；根据函数单调性与奇偶性的关系有效的利用11()()22g g n n -=-++进行变形是解题的第二关键；由原函数与其反函数的定义实用文档域与值域的关系利用当10x -<<时，()0g x >，即1110,()022g n n -<-<->++成为圆满解决问题的第三关键.本题完成这些步骤都是在抽象式中进行的，题解到“山穷水尽”时，巧妙的利用了特殊与一般，联想与类比使得问题变得“柳暗花明”.22.提示：（1）由题知1x =处()f x 取得极大值，即'(1)0f =于是求得a 值；（2）这一问的关键在于“关于直线1x =的对称”的点的表示；（3）将“函数()g x 与()f x 的图像恰有3个交点”转化为“方程324(4)20x b x +-+=有3个根”进而利用导数求解.解：（1）由条件知1x =是()f x 的极大值点，所以'(1)0f =.又'32()4122f x x x ax =-+ 所以'(1)41220f a =-+=，即 4a =.（2）43222()441(2)1f x x x x x x =-+-=--，设A 00(,())x f x 在函数()f x 的图像上，即22000()(2)1f x x x =--则A 关于直线1x =的对称点为B 00(2,())x f x -.因为2222000000(2)(2)(22)1(2)1()f x x x x x f x -=----=--=所以点B 也在()f x 图像上.实用文档（3）函数()g x 与()f x 的图像恰有3个交点，即方程()()g x f x =有3个根，即421x bx ++432441x x x =-+-有3个根，即方程324(4)20x b x +-+=有3个根. 令()h x 324(4)2x b x =+-+. 则/()h x 2122(4)x b x =+- /1()00h x x =⇒=或2406b x -=>，所以 ()h x 在0x =处有极大值，在46b x -=处有极小值. (0)20h =>，∴三次函数()0h x =有三个根的条件为4()06b h -<，从而 32444()(4)()20266b b b b --+-+<⇒<-.。

集合与函数概念单元测试题经典(含答案)

Equation Chapter 1 Section 1 【2 】第一章聚集与函数概念测试题一：选择题 1.下列聚集中与聚集{21,}x x k k N +=+∈不相等的是（）A ．{23,}x x k k N =+∈B ．{41,}x x k k N +=±∈C ．{21,}x x k k N =+∈D ．{23,3,}x x k k k Z =-≥∈2.图中暗影部分所表示的聚集是（）A.B∩［CU(A ∪C)］B.(A ∪B) ∪(B ∪C)C.(A ∪C)∩(CUB)D.［CU(A∩C)］∪B3.已知聚集2{1}A y y x ==+,聚集2{26}B x y x ==-+,则A B =（）A ．{(,)1,2}x y x y ==B ．{13}x x ≤≤C ．{13}x x -≤≤D ．∅4.已知聚集2{40}A x x =-=,聚集{1}B x ax ==,若B A ⊆,则实数a 的值是（）A ．0B ．12±C ．0或12±D ．0或125.已知聚集{1,2,3,}A a =,2{3,}B a =,则使得Φ=B A C U )(成立的a 的值的个数为（）A ．2B ．3C ．4D ．56.设A .B 为两个非空聚集,界说{(,),}A B a b a A b B ⊕=∈∈,若{1,2,3}A =,{2,3,4}B =,则A B ⊕中的元素个数为（）A ．3B ．7C ．9D ．127.已知A.B 两地相距150千米,或人开汽车以60千米/小时的速度从A 地到达B 地,在B 地逗留1小时后再以50千米/小时的速度返回A 地,把汽车分开A 地的距离x 表示为时光t （小时）的函数表达式是（）A ．x=60tB ．x=60t+50C ．x=⎩⎨⎧>-≤≤)5.3(,50150)5.20(,60t t t tD ．x=⎪⎩⎪⎨⎧≤<--≤<≤≤)5.65.3(),5.3(50150)5.35.2(,150)5.20(,60t t t t t 8.已知g(x)=1-2x,f[g(x)]=)0(122≠-x x x ,则f(21)等于（）A ．1B ．3C ．15D ．309.函数y=xx ++-1912是（） A ．奇函数 B ．偶函数 C ．既是奇函数又是偶函数 D ．非奇非偶数10.设函数f (x)是（－∞,+∞）上的减函数,又若a ∈R,则（）A ．f(a)>f(2a)B ．f(a2)<f(a)C ．f(a2+a)<f(a)D ．f(a2+1)<f(a)二.填空题11.设聚集A={23≤≤-x x },B={x 1122-≤≤-k x k },且A ⊇B,则实数k 的取值规模是.12.已知x ∈[0,1],则函数y=x x --+12的值域是. 13.设函数x y 111+=的界说域为___________________;值域为_____________________________.14.设f(x)是界说在R 上的偶函数,在区间（－∞,0）上单调递增,且知足, 22(25)(21)f a a f a a -+-<++求实数a 的取值规模_______________.15.设f(x)是界说在R 上的奇函数,且y=f (x)的图象关于直线21=x 对称,则f (1)+ f (2)+ f (3)+ f (4)+ f (5)=_________. 16、若函数()xp x x f -=在()+∞,1上是增函数,则实数p 的取值规模是_______________．三.解答题 17.聚集A={（x,y ）022=+-+y mx x },聚集B={（x,y ）01=+-y x ,且02≤≤x },又A φ≠⋂B ,求实数m 的取值规模.18.如图,用长为1的铁丝弯成下部为矩形,上部为半圆形的框架,若半圆半径为x,求此框架围成的面积y 与x 的函数式y=f(x),并写出它的界说域.19.函数22()2f x x mx m m =-+-,22()(41)4g x x m x m m =-+++, 22()4(124)9812h x x m x m m =-++++,令聚集{()()()0}M x f x g x h x =⋅⋅=,且M 为非空聚集,求实数m 的取值规模. 20.已知函数y=f (x)是界说在R 上的周期函数,周期T=5,函数y=f(x)(－1≤x ≤1)是奇函数,又知y=f (x)在［0,1］上是一次函数,在［1,4］上是二次函数,且在x=2时函数取得最小值,最小值为－5.（1）证实：f (1)+f (4)=0;（2）试求y=f(x)在［1,4］上的解析式;（3）试求y=f(x)在［4,9］上的解析式.21.已知()f x 是界说在[-1,1]上的奇函数,当,[1,1]a b ∈-,且0a b +≠时有()()0f a f b a b +>+. （1）断定函数()f x 的单调性,并赐与证实;（2）若2(1)1,()21f f x m bm =≤-+对所有[1,1],[1,1]x b ∈-∈-恒成立,求实数m 的取值规模.第一章聚集与函数概念测试题一：选择题1.下列聚集中与聚集{21,}x x k k N +=+∈不相等的是（ C ）A ．{23,}x x k k N =+∈B ．{41,}x x k k N +=±∈C ．{21,}x x k k N =+∈D ．{23,3,}x x k k k Z =-≥∈2.图中暗影部分所表示的聚集是（A ）A.B∩［CU(A ∪C)］B.(A ∪B) ∪(B ∪C)C.(A ∪C)∩(CUB)D.［CU(A∩C)］∪B3.已知聚集2{1}A y y x ==+,聚集2{26}B x y x ==-+,则A B =（ B ）A ．{(,)1,2}x y x y ==B ．{13}x x ≤≤C ．{13}x x -≤≤D ．∅4.已知聚集2{40}A x x =-=,聚集{1}B x ax ==,若B A ⊆,则实数a 的值是（ C ）A ．0B ．12±C ．0或12±D ．0或125.已知聚集{1,2,3,}A a =,2{3,}B a =,则使得()R A B =∅成立的a 的值的个数为（ C ）A ．2B ．3C ．4D ．56.设A .B 为两个非空聚集,界说{(,),}A B a b a A b B ⊕=∈∈,若{1,2,3}A =,{2,3,4}B =,则A B ⊕中的元素个数为（ A ）A ．3B ．7C ．9D ．127.已知A.B 两地相距150千米,或人开汽车以60千米/小时的速度从A 地到达B 地,在B 地逗留1小时后再以50千米/小时的速度返回A 地,把汽车分开A 地的距离x 表示为时光t （小时）的函数表达式是（ D ）A ．x=60tB ．x=60t+50C ．x=⎩⎨⎧>-≤≤)5.3(,50150)5.20(,60t t t tD ．x=⎪⎩⎪⎨⎧≤<--≤<≤≤)5.65.3(),5.3(50150)5.35.2(,150)5.20(,60t t t t t 8.已知g(x)=1-2x,f[g(x)]=)0(122≠-x x x ,则f(21)等于（ C ） A ．1B ．3C ．15D ．309.函数y=xx ++-1912是（ B ） A ．奇函数 B ．偶函数 C ．既是奇函数又是偶函数 D ．非奇非偶数10.设函数f (x)是（－∞,+∞）上的减函数,又若a ∈R,则（ D ）A ．f(a)>f(2a)B ．f(a2)<f(a)C ．f(a2+a)<f(a)D ．f(a2+1)<f(a)二.填空题11.设聚集A={23≤≤-x x },B={x 1122-≤≤-k x k },且A ⊇B,则实数k 的取值规模是{21<≤-k k };.12.已知x ∈[0,1],则函数y=x x --+12的值域是[3,12-]. 13.设函数x y 111+=的界说域为_｛x ｜x ＜0且x≠－1,或x ＞0};值域为_{y ｜y ＜0,或0＜y ＜1,或y ＞1}14、设f(x)是界说在R 上的偶函数,在区间（－∞,0）上单调递增,且知足, 22(25)(21)f a a f a a -+-<++求实数a 的取值规模_______________.（－4,1）15.设f(x)是界说在R 上的奇函数,且y=f (x)的图象关于直线21=x 对称,则f (1)+ f (2)+ f (3)+ f (4)+ f(5)=_________.0 16、若函数()xp x x f -=在()+∞,1上是增函数,则实数p 的取值规模是_______________．三.解答题15.聚集A={（x,y ）022=+-+y mx x },聚集B={（x,y ）01=+-y x ,且02≤≤x },又A φ≠⋂B ,求实数m 的取值规模.16．解：由A ⋂B φ≠知方程组,,2001202y x y x y mx x 消去内有解在≤≤⎩⎨⎧=+-+-+122+-≤m16.如图,用长为1的铁丝弯成下部为矩形,上部为半圆形的框架,若半圆半径为x,求此框架围成的面积y 与x 的函数式y=f(x),并写出它的界说域.18．解：AB=2x, CD =πx,于是AD=221x x π--, 是以,y=2x·221x x π--+22x π, 即y=-lx x ++224π.由⎪⎩⎪⎨⎧>-->022102x x x π,得0<x<,21+π 函数的界说域为（0,21+π）. 18.已知聚集2{10,,}A x ax bx a R b R =++=∈∈,求（1）当2b =时,A 中至多只有一个元素,求a 的取值规模; （4分）（2）当2b =-时,A 中至少有一个元素,求a 的取值规模; （4分）（3）当a .b 知足什么前提时,聚集A 为非空聚集. （6分）18.（1）1a ≥或0a =个中：当0a =时,1{}2A =-,当1a =时,{1}A =-,当1a >时,A =∅（2）1a ≤或0a =,即1a ≤个中：当0a =时,1{}2A =-,当1a =时,{1}A =-,当1a <时,0∆>（3）当0a =时,0b ≠,当0a ≠时,240b a -≥ 一、选做题（此题做对可加15分,但总分不超过120分,做错不扣分）19.已知函数22()2f x x mx m m =-+-,22()(41)4g x x m x m m =-+++, 22()4(124)9812h x x m x m m =-++++,令聚集{()()()0}M x f x g x h x =⋅⋅=,且M 为非空聚集,求实数m 的取值规模. 19.12m ≤-或14m ≥- 个中：令m 可能取的值构成的聚集为A ,求R A .22222244()0(41)4(4)0(124)44(982)0m m m m m m m m m ⎧--<⎪+-+<⎨⎪+-⋅++<⎩解得：1124R A m m ⎧⎫=-<<-⎨⎬⎩⎭ 19．已知函数y=f (x)是界说在R 上的周期函数,周期T=5,函数y=f(x)(－1≤x ≤1)是奇函数,又知y=f (x)在［0,1］上是一次函数,在［1,4］上是二次函数,且在x=2时函数取得最小值,最小值为－5.（1）证实：f (1)+f (4)=0;（2）试求y=f(x)在［1,4］上的解析式;（3）试求y=f(x)在［4,9］上的解析式.19．(1)证实：略. (2)解：f (x)=2(x －2)2－5(1≤x≤4);(3)解：f (x)=⎩⎨⎧≤<--≤≤+-96 ,5)7(264 ,1532x x x x 27.已知()f x 是界说在[-1,1]上的奇函数,当,[1,1]a b ∈-,且0a b +≠时有()()0f a f b a b+>+. （1）断定函数()f x 的单调性,并赐与证实;（2）若2(1)1,()21f f x m bm =≤-+对所有[1,1],[1,1]x b ∈-∈-恒成立,求实数m 的取值规模.27.(1)证实：令－1≤x1<x2≤1,且a= x1,b=－x2则0)()(2121>--+x x x f x f ∵x1－ x2<0,f(x)是奇函数 ∴f(x1)－f(x2)<0即f(x1)<f(x2) ∵x1<x2 ∴f(x)是增函数(2)解：∵f(x)是增函数,且f(x)≤m2－2bm+1对所有x ∈[－1,2]恒成立∴[f(x)]max≤m2－2bm+1 [f(x)]max=f(1)=1∴m2－2bm+1≥1即m2－2bm≥0在b ∈[－1,1]恒成立∴y= －2mb+m2在b ∈[－1,1]恒大于等于0∴⎪⎩⎪⎨⎧≥+⨯-≥+-⨯-0120)1(222m m m m ,∴⎩⎨⎧≥≤-≤≥2020m m m m 或或 ∴m 的取值规模是)2[}0{]2-(∞+-∞，，。

【必刷题】2024高一数学上册集合与函数专项专题训练(含答案)

【必刷题】2024高一数学上册集合与函数专项专题训练（含答案）试题部分一、选择题：1. 设集合A={x|x²3x+2=0}，则A中元素的个数为（）A. 0个B. 1个C. 2个D. 3个2. 若集合M={1，2，3}，N={x|x²4x+3=0}，则M∩N的结果是（）A. {1}B. {2}C. {3}D. {1，2}3. 已知函数f(x)=2x+1，那么f(2)的值为（）A. 5B. 6C. 7D. 84. 下列函数中，哪一个是一对一函数？（）A. f(x)=x²B. f(x)=2xC. f(x)=|x|D. f(x)=x³5. 若函数g(x)=3x2，那么g(1)的值为（）A. 5B. 4C. 3D. 26. 设函数h(x)=x²2x，那么h(x)的最小值是（）A. 1B. 0C. 1D. 27. 若函数f(x)=kx²+2x+1（k≠0），且f(x)是单调递增函数，则k的取值范围是（）A. k>0B. k<0C. k=0D. k≠08. 已知集合P={x|1≤x≤4}，那么不属于P的数是（）A. 0B. 2C. 3D. 59. 若函数f(x)=x²+2x+1，那么f(x)的图像是（）A. 向上开口的抛物线B. 向下开口的抛物线C. 经过原点的直线D. 水平直线10. 已知函数g(x)=|x1|，那么g(x)在x=1处的导数是（）A. 0B. 1C. 1D. 不存在二、判断题：1. 集合{1，2，3}和{3，2，1}是同一个集合。

（）2. 函数f(x)=x²和g(x)=|x|在定义域内都是单调递增的。

（）3. 若函数h(x)=kx²+bx+c（k≠0），则h(x)的图像一定是一个抛物线。

（）4. 对于任意实数x，都有|x|²=x²。

（）5. 函数f(x)=2x+3和g(x)=2x3的图像关于y轴对称。

高一数学必修1《集合与函数概念》测试卷(含答案)

第一章《集合与函数概念》测试卷考试时间：120分钟满分：150分一.选择题.(本大题共12小题，每小题5分，共60分) 1.下列叙述正确的是（）A.函数的值域就是其定义中的数集BB.函数()y f x =的图像与直线x m =至少有一个交点C.函数是一种特殊的映射D.映射是一种特殊的函数2.如果{}1A x x =>-，则下列结论正确的是（） A.0A ⊆ B.{}0A ⊆ C.{}0A ∈ D.A ∅∈3.设()(21)f x a x b =-+在R 上是减函数，则有（）A.12a ≥B.12a ≤C.12a >D.12a <4.定义在R 上的偶函数()f x ，对任意1x ，2x ∈[)0,+∞12()x x ≠，有1212()()0f x f x x x -<-，则有（）A.(3)(2)(1)f f f <-<B.(1)(2)(3)f f f <-<C.(2)(1)(3)f f f -<<D.(3)(1)(2)f f f <<-5.若奇函数()f x 在区间[]1,3上为增函数，且有最小值0，则它在区间[]3,1--上（） A.是减函数，有最小值0 B. 是增函数，有最小值0C.是减函数，有最大值0D. 是增函数，有最大值06.设:f x x →是集合A 到集合B 的映射，若{}2,0,2A =-，则A B 等于（） A.{}0 B.{}2 C.{}0,2 D.{}2,0-7.定义两种运算：a b ab ⊕=，22a b a b ⊗=+，则函数3()33xf x x ⊕=⊗-为（）A.奇函数B.偶函数C.既不是奇函数又不是偶函数D.既是奇函数又是偶函数8.若函数()f x 是定义域在R 上的偶函数，在(),0-∞上是减函数，且(2)0f -=，则使()0f x <的x 的取值范围为（）A.()2,2-B.()()2,00,2-C.()(),22,-∞-+∞D. (][),22,-∞-+∞9.函数()xf x x x=+的图像是（）10.设()f x 是定义域在R 上的奇函数，(2)()f x f x +=-，当01x <≤时，()f x x =，则(7.5)f 的值为（）A. -0.5B. 0.5C. -5.5D. 7.511.已知2(21)1f x x -+=+，且(21)f x -+的定义域为[)2,1-，则()f x 的解析式为（） A.)51(,452141)(2≤<--+=x x x x f B. )51(,452141)(2≤<-+-=x x x x f C.21153()(0)4242f x x x x =+-<≤，D.21153()(0)4242f x x x x =-+<≤， 12.已知函数()f x 是定义在R 上的不恒为零的偶函数，且对任意实数x 都有(1)(1)(x f x x f x +=+，则5(())2f f 的值是（） A.0 B.12 C.1 D.52二．填空题.（本大题共4小题，每小题5分，共20分）13.已知21()32x f x x x +=-+，则()f x 的定义域为 . 14.设函数(1)()()x x a f x x++=为奇函数，则a 的值为 .15.设22,1(),12x x f x x x +≤-⎧=⎨-<<⎩，若()f x =3，则x 的值为 .16.关于函数()()1(),,00,f x x x x=-∈-∞+∞，有下列四个结论：○1()f x 的值域为R ； ○2()f x 是定义域上的增函数； ○3对任意的()(),00,x ∈-∞+∞，都有()()0f x f x -+=成立； ○4()f x 与20()x x g x x x=-表示同一个函数. 把你认为正确的结论的序号填写到横线上 .三．解答题.（本大题共6小题，其中17题10分，其余5个小题每题12分，共70分）17.设函数()f x 是定义域在R 上的奇函数，当0x >时，2()331f x x x =-+-，求()f x 在R 上的解析式.18.已知集合{}{}13,22A x x B x m x m -≤≤=-≤≤+=. （1）若{}03A B x x =≤≤，求实数m 的值（2）若R A C B ⊆，求实数m 的取值范围.19.二次函数()f x 的最小值为1，且(0)(2)3f f ==. （1）求()f x 的解析式；（2）若()f x 在区间[]2,1a a +上不单调，求a 的取值范围.20.某商场国庆节期间搞促销活动，规定：顾客购物总金额不超过800元，不享受任何折扣；如果顾客购物总金额超过800元，则超过的部分享受一定的折扣优惠，按下表折扣分别累计计算：可以享受折扣优惠的金额折扣率不超过500元的部分 5% 超过500元的部分10%若某人在此商场购物总金额为x 元，则可以获得的折扣金额为y 元.（1）试写出y x 关于的函数解析式；（2）若30y =，求此人购物实际所付金额.21.已知函数2()2(1)f x x a x a =+-+.（1）当1a =-时，求()f x 在[]3,3-上的值域; （2）求()f x 在区间[]3,3-上的最小值.22.已知2()1ax b f x x +=+是定义域在()1,1-上的奇函数，且12()25f =. （1）求()f x 的解析式；（2）判断()f x 的单调性，并证明你的结论；（3）解不等式(22)()0f t f t -+<.第一章《集合与函数概念》答案解析一.选择题.(本大题共12小题，每小题5分，共60分)CBDAD CAADA BA二.填空题.（本大题共4小题，每小题5分，共20分）13.[)()()1,11,22,-+∞或者{}11,2x x x x ≥-≠≠且14. -1 15.3 16.①③三.解答题.（本大题共6小题，其中17题10分，其余5个小题每题12分，共70分）2222217.0,0()3()3()1331()()()331()(0)0331,0()0,0331,0x x f x x x x x f x f x f x x x f x R f x x x f x x x x x <->∴-=--+--=---∴=--=++∴=⎧++<⎪∴==⎨⎪-+->⎩解：设则是奇函数又是上的奇函数{}()()2018.(1)2232.(2),2,2232153,35,U U m m m m B C B x x m x m A C Bm m m m m -=⎧⇒=⎨+≥⎩∴≠∅=<->+⊆∴->+<-><-∴-∞-+∞解：由题意得: 的值为由题意知:则或或得到或的取值范围为22219.(1)(0)(2)3()1()1()(1)1(0)(0)132()2(1)1,()243211(2)02112f f f x x f x f x a x a f a a f x x f x x x a a a a a a ==∴=∴=-+>=+==∴=-+=-+<+⎧⇒<<⎨<<+⎩∴解：二次函数的对称轴为又有最小值设由得即由题意得: 的取值范围102⎛⎫⎪⎝⎭为，0,080020.(1):(800)5%,800130025(1300)10%,1300(2)305005%2525(1300)10%30,135013503013201320x y x x x x x x ≤≤⎧⎪=-⨯<≤⎨⎪+-⨯>⎩>⨯=∴+-⨯==∴-=∴解：由题意得解得此人购物实际所付金额为元.[](][][]2min 21.(1)1()41()2()-3,22,3()=(2)5(3)20,(3)4()3,3-5,20(2)()113,4a f x x x f x x f x f x f f f f x f x x a a a =-=--∴=∴∴=--==-∴-=--<->解：当时, 的对称轴为在上单调递减,在上单调递增／又在上的值域为的对称轴为 ①当即时 [][](][]min 2min()-33()=(3)155313,24()-3,11,3()=(1)3113,2()-33f x f x f a a a f x a a f x f a a a a a f x f ∴-=--≤-≤-≤≤--∴-=-+--><-∴ 在，上单调递增／ ②当即时在上单调递减,在上单调递增／ ③当即时在，上单调递减 min 2min ()=(3)7+37+3,2()=31,24155,4x f a a a f x a a a a a =<-⎧⎪-+--≤≤⎨⎪->⎩／综上所述，／()()22212121222.(1)()1,1(0)0()112()2522,115()12()1(2)()-1,1,(1,1),,()()f x f baxf x x f aa xf x x f x x x x x x f x f x -∴==∴=+=∴==+∴=+∈-<-=解：是上的奇函数又解得在上单调递增. 证明:任意取且则()1212122222121212221212121212()(1)11(1)(1)110,10,10,10()()0,()()()-1,1(3)(22)()0x x x x x x x x x x x x x x x x x f x f x f x f x f x f t f t ---=++++-<<<∴-<->+>+>∴-<<∴-+<∴即在上单调递增. ()()(22)()()1,1()()(22)()(2)()1,122121221,231112.23f t f t f x f t f t f t f t f x t tt t t -<--∴-=-∴-<---<-⎧⎪∴-<-<<<⎨⎪-<-<⎩⎛⎫∴ ⎪⎝⎭易知是上的奇函数又由知是上的增函数解得不等式的解集为，。

人教版高中数学必修一第一章《集合与函数》精选习题(含答案解析)

人教版高中数学必修一第一章《集合与函数》单元检测精选（含答案解析）(时间：120分钟满分：150分) 第Ⅰ卷 (选择题共60分)一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．集合A ＝{0,2，a }，B ＝{1，a 2}，若A ∪B ＝{0,1,2,4,16}，则a 的值为( ) A ．0 B ．1 C ．2D ．42．设函数f (x )＝，则f (f(31)的值为( )A.128127B ．－128127C.81D.1613．若函数y ＝f (x )的定义域是[0,2]，则函数g (x )＝x －1f(2x的定义域是( ) A ．[0,1]B ．[0,1)C ．[0,1)∪(1,4]D ．(0,1)4．已知f (x )＝(m －1)x 2＋3mx ＋3为偶函数，则f (x )在区间(－4,2)上为( ) A ．增函数B ．减函数C ．先递增再递减D ．先递减再递增5．三个数a ＝0.32，b ＝log 20.3，c ＝20.3之间的大小关系是( ) A ．a <c <b B ．a <b <c C ．b <a <cD ．b <c <a6．若函数f (x )唯一的一个零点同时在区间(0,16)、(0,8)、(0,4)、(0,2)内，那么下列命题中正确的是( )A ．函数f (x )在区间(0,1)内有零点B ．函数f (x )在区间(0,1)或(1,2)内有零点C ．函数f (x )在区间[2,16)内无零点D ．函数f (x )在区间(1,16)内无零点7．已知0<a <1，则方程a |x |＝|log a x |的实根个数是( ) A ．2 B ．3C ．4D ．与a 值有关8．函数y ＝1＋ln(x －1)(x >1)的反函数是( ) A ．y ＝e x ＋1－1(x >0)B ．y ＝e x －1＋1(x >0)C ．y ＝e x ＋1－1(x ∈R )D ．y ＝e x －1＋1(x ∈R )9．函数f (x )＝x 2－2ax ＋1有两个零点，且分别在(0,1)与(1,2)内，则实数a 的取值范围是( )A ．－1<a <1B ．a <－1或a >1C ．1<a <45D ．－45<a <－110．若一系列函数的解析式和值域相同，但其定义域不同，则称这些函数为“同族函数”，例如函数y ＝x 2，x ∈[1,2]与函数y ＝x 2，x ∈[－2，－1]即为“同族函数”．请你找出下面函数解析式中能够被用来构造“同族函数”的是( )A ．y ＝xB ．y ＝|x －3|C ．y ＝2xD ．y ＝11．下列4个函数中： ①y ＝2008x －1；②y ＝log a 2 009＋x 2 009－x(a >0且a ≠1)； ③y ＝x ＋1x2 009＋x2 008；④y ＝x (a －x －11＋21)(a >0且a ≠1)．其中既不是奇函数，又不是偶函数的是( ) A ．①B ．②③C ．①③D ．①④12．设函数的集合P ＝{f (x )＝log 2(x ＋a )＋b |a ＝－21，0，21，1；b ＝－1,0,1}，平面上点的集合Q ＝{(x ，y )|x ＝－21，0，21，1；y ＝－1,0,1}，则在同一直角坐标系中，P 中函数f (x )的图象恰好经过Q 中两个点的函数的个数是( )A ．4B ．6C ．8D ．10第Ⅱ卷 (非选择题共90分)二、填空题(本大题共4个小题，每小题5分，共20分，请把正确答案填在题中横线上)13．已知函数f (x )，g (x )分别由下表给出：x 1 2 3 f (x )131x 1 2 3 g (x )321则不等式f [g (x )]>g [f (x )]的解为________． 14．已知log a 21>0，若≤a 1，则实数x 的取值范围为______________．15．直线y ＝1与曲线y ＝x 2－＋a 有四个交点，则a 的取值范围为________________．16．已知下表中的对数值有且只有一个是错误的.三、解答题(本大题共6个小题，共70分，解答时应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分10分)设全集为R，A＝{x|3≤x<7}，B＝{x|2<x<10}．求：A∪B，∁R(A∩B)，(∁R A)∩B.18．(本小题满分12分)(1)已知全集U＝R，集合M＝{x|≤0}，N＝{x|x2＝x＋12}，求(∁U M)∩N；(2)已知全集U＝R，集合A＝{x|x<－1或x>1}，B＝{x|－1≤x<0}，求A∪(∁U B)．19．(本小题满分12分)已知集合A＝{x|－2＜x＜－1或x＞1}，B＝{x|a≤x＜b}，A∪B＝{x|x＞－2}，A ∩B＝{x|1＜x＜3}，求实数a，b的值．20．(本小题满分12分)已知集合A＝{x|x≤a＋3}，B＝{x|x<－1或x>5}．(1)若a＝－2，求A∩∁R B；(2)若A⊆B，求a的取值范围．21．(本小题满分12分)设集合A＝{x|x2－8x＋15＝0}，B＝{x|ax－1＝0}．(1)若a＝51，判断集合A与B的关系；(2)若A∩B＝B，求实数a组成的集合C.22．(本小题满分12分)已知集合A＝{x|(a－1)x2＋3x－2＝0}，B＝{x|x2－3x＋2＝0}．(1)若A≠∅，求实数a的取值范围；(2)若A∩B＝A，求实数a的取值范围．参考答案与解析1．D [∵A ∪B ＝{0,1,2，a ，a 2}，又∵A ∪B ＝{0,1,2,4,16}， ∴a2＝16，a ＝4，即a ＝4. 否则有a2＝4a ＝16矛盾．]2．A [∵f (3)＝32＋3×3－2＝16， ∴f(31＝161，∴f (f(31)＝f (161)＝1－2×(161)2＝1－2562＝128127.] 3．B [由题意得：x ≠10≤2x ≤2，∴0≤x <1.] 4．C [∵f (x )＝(m －1)x 2＋3mx ＋3是偶函数，∴m ＝0，f (x )＝－x 2＋3，函数图象是开口向下的抛物线，顶点坐标为(0,3)，f (x )在(－4,2)上先增后减．]5．C [20.3>20＝1＝0.30>0.32>0＝log 21>log 20.3.]6．C [函数f (x )唯一的一个零点在区间(0,2)内，故函数f (x )在区间[2,16)内无零点．] 7．A [分别画出函数y ＝a |x |与y ＝|log a x |的图象，通过数形结合法，可知交点个数为2.]8．D [∵函数y ＝1＋ln(x －1)(x >1)，∴ln(x －1)＝y －1，x －1＝e y －1，y ＝e x －1＋1(x ∈R )．] 9．C [∵f (x )＝x 2－2ax ＋1， ∴f (x )的图象是开口向上的抛物线．由题意得：f(2>0.f(1<0，即4－4a ＋1>0，1－2a ＋1<0，解得1<a <45.] 10．B11．C [其中①不过原点，则不可能为奇函数，而且也不可能为偶函数；③中定义域不关于原点对称，则既不是奇函数，又不是偶函数．] 12．B [当a ＝－21，f (x )＝log 2(x －21)＋b ， ∵x >21，∴此时至多经过Q 中的一个点；当a ＝0时，f (x )＝log 2x 经过(21，－1)，(1,0)， f (x )＝log 2x ＋1经过(21，0)，(1,1)；当a ＝1时，f (x )＝log 2(x ＋1)＋1经过(－21，0)，(0,1)， f (x )＝log 2(x ＋1)－1经过(0，－1)，(1,0)；当a ＝21时，f (x )＝log 2(x ＋21)经过(0，－1)，(21，0) f (x )＝log 2(x ＋21)＋1经过(0,0)，(21，1)．]13．x ＝2解析 ∵f (x )、g (x )的定义域都是{1,2,3}，∴当x ＝1时，f [g (1)]＝f (3)＝1，g [f (1)]＝g (1)＝3，不等式不成立；当x ＝2时，f [g (2)]＝f (2)＝3，g [f (2)]＝g (3)＝1，此时不等式成立；当x ＝3时，f [g (3)]＝f (1)＝1，g [f (3)]＝g (1)＝3，此时，不等式不成立．因此不等式的解为x ＝2. 14．(－∞，－3]∪[1，＋∞) 解析由log a 21>0得0<a <1. 由≤a 1得≤a －1，∴x 2＋2x －4≥－1，解得x ≤－3或x ≥1. 15．1＜a ＜45解析 y ＝x2＋x ＋a ，x ＜0，x2－x ＋a ，x ≥0，作出图象，如图所示．此曲线与y 轴交于(0，a )点，最小值为a －41，要使y ＝1与其有四个交点，只需a －41＜1＜a ，∴1＜a ＜45. 16．lg1.5解析 ∵lg9＝2lg3，适合，故二者不可能错误，同理：lg8＝3lg2＝3(1－lg5)，∴lg8，lg5正确．lg6＝lg2＋lg3＝(1－lg5)＋lg3＝1－(a ＋c )＋(2a －b )＝1＋a －b －c ，故lg6也正确．17．解：∵全集为R ，A ＝{x |3≤x <7}，B ＝{x |2<x <10}， ∴A ∪B ＝{x |2<x <10}，A ∩B ＝{x |3≤x <7}， ∴∁R (A ∩B )＝{x |x ≥7或x <3}． ∵∁R A ＝{x |x ≥7或x <3}，∴(∁R A )∩B ＝{x |2<x <3或7≤x <10}．18．解：(1)M ＝{x |x ＋3＝0}＝{－3}，N ＝{x |x 2＝x ＋12}＝{－3,4}， ∴(∁U M )∩N ＝{4}．(2)∵A ＝{x |x <－1或x >1}，B ＝{x |－1≤x <0}， ∴∁U B ＝{x |x <－1或x ≥0}． ∴A ∪(∁U B )＝{x |x <－1或x ≥0}． 19．解：∵A ∩B ＝{x |1＜x ＜3}，∴b ＝3，又A∪B＝{x|x＞－2}，∴－2＜a≤－1，又A∩B＝{x|1＜x＜3}，∴－1≤a＜1，∴a＝－1.20．解：(1)当a＝－2时，集合A＝{x|x≤1}，∁R B＝{x|－1≤x≤5}，∴A∩∁R B＝{x|－1≤x≤1}．(2)∵A＝{x|x≤a＋3}，B＝{x|x<－1或x>5}，A⊆B，∴a＋3<－1，∴a<－4.解题技巧：本题主要考查了描述法表示的集合的运算，集合间的关系，解决本题的关键是借助于数轴求出符合题意的值．在解决(2)时，特别注意参数a是否取到不等式的端点值．21．解：A＝{x|x2－8x＋15＝0}＝{3,5}．(1)若a＝51，则B＝{5}，所以B A.(2)若A∩B＝B，则B⊆A.当a＝0时，B＝∅，满足B⊆A；当a≠0时，B＝a1，因为B⊆A，所以a1＝3或a1＝5，即a＝31或a＝51；综上所述，实数a组成的集合C为51.22．解：(1)①当a＝1时，A＝32≠∅；②当a≠1时，Δ≥0，即a≥－81且a≠1，综上，a≥－81；(2)∵B＝{1,2}，A∩B＝A，∴A＝∅或{1}或{2}或{1,2}．①A＝∅，Δ<0，即a<－81；②当A＝{1}或{2}时，Δ＝0，即a＝0且a＝－81，不存在这样的实数；③当A＝{1,2}，Δ>0，即a>－81且a≠1，解得a＝0.综上，a<－81或a＝0.11。

必修一第一章集合与函数概念同步练习(含答案)

第一章集合与函数概念同步练习1.1.1 集合的含义与表示一. 选择题：1.下列对象不能组成集合的是（）A.小于100的自然数B.大熊猫自然保护区C.立方体内若干点的全体D.抛物线2x y =上所有的点 2.下列关系正确的是（）A.N 与+Z 里的元素都一样B.},,{},,{c a b c b a 与为两个不同的集合C.由方程0)1(2=-x x 的根构成的集合为}1,1,0{D.数集Q 为无限集 3.下列说法不正确的是（）A.*0N ∈B.Z ∉1.0C.N ∈0D.Q ∈24.方程⎩⎨⎧-=-=+3212y x y x 的解集是（）A.}1,1{-B.)1,1(-C.)}1,1{(-D.1,1-二.填空题：5.不大于6的自然数组成的集合用列举法表示______________.6.试用适当的方式表示被3除余2的自然数的集合____________.7.已知集合}7,3,2,0{=M ，由M 中任取两个元素相乘得到的积组成的集合为 ________. 8.已知集合}012{2=++∈=x ax R x M 只含有一个元素，则实数=a ______,若M 为空集,可a 的取值范围为_________.三.解答题：9.代数式}{)8(2x x x ∈-- ，求实数x 的值。

10.设集合A=},,2),{(N y x x y y x ∈+-=，试用列举法表示该集合。

11.已知}33,2{12+++∈x x x 试求实数x 的值。

1.1.2 集合的含义与表示一. 选择题：1.集合Φ与}0{的关系，下列表达正确的是（） A.φ=}0{ B.φ⊆}0{ C.}0{∈φ D.φ}0{⊇2.已知集合A=}3,2,1{，则下列可以作为A 的子集的是（）A.}4,1{B.}3,2{C.}4,2{D.}4,3,1{ 3.集合},,{c b a 的非空真子集个数是（）A.5B.6C.7D.8 4.已知集合M={正方形}，N={菱形}，则（）A.N M =B.N M ∈C.M ≠⊂ND.N ≠⊂M二.填空题5.用适当的符号填空①},2_____{0Z n n x x ∈=②}_____{1质数③},,_____{}{c b a a ④}0))((_____{},{=--b x a x x b a ⑤},12______{},14{++∈+=∈+=N k k x x N k k x x 6.写出集合}1{2=x x 的所有子集_______________________7.设集合}{},63{a x x B x x A <=≤<-=，且满足A ≠⊂,B 则实数a 的取值范围是_________三.解答题8.已知集合B 满足}2,1{≠⊂B ⊆}5,4,3,2,1{，试写出所有这样的集合 9.已知}5{>=x x A ，}3{x x B <=，试判断A 与B 的关系 10.已知A=}3,4,1{},2,1{a B a =+，且B A ⊆，求a 的值1.1.3集合的基本运算（一）一.选择题1.已知集合A=}4,3,2,1{，}6,4,1{=B ，则=B A I （） A.}4,2,1{ B.}6,4,3,2,1{ C.}4,1{ D.}4,3,1{2.设A=}2{->x x ，}21{<<-=x x B ，则=B A Y （） A.R B.}2{<x x C.}1{->x x D.}2{->x x3.设{=A 等腰三角形} ，B={等边三角形}，C={直角三角形}，=C B A I Y )(（） A.{等腰三角形} B.{直角三角形} C.φ D.{等腰直角三角形}4.已知集合}90{<<∈=x Z x M ，},2{+∈==N n n x x N ，则=N M I （）A.{}6,4,2B.{}8,6,4,2C.{}7,6,5,4,3,2D.{}8,7,6,5,4,3,2,1 二.填空题5.{偶数}I {奇数}=__________.6.已知集合}31{<≤-=x x A ，}13{≤<-=x x B ，则=B A I __________.7.若集合A B A =I ，则=B A Y ___________.8.已知集合}33{<≤-=x x A ，}2{≤=x x B ，则=B A Y ___________.三.解答题9.集合},,523),{(R y x y x y x A ∈=-=},,132),{(R y x y x y x B ∈-=+=，求 B A I 10.已知集合},3,1{a A =，}1,1{2+-=a a B ，且A B A =Y ，求a 的值 11.已知集合},02{2=+-∈=b ax x R x A }05)2(6{2=++++∈=b x a x R x B且}21{=B A I ，求B A Y1.1.3集合的基本运算（二）一.选择题1.已知全集R U =，集合}1{<=x x M ，则M C u 为（） A.}1{≥x x B.}1{>x x C.}1{<x x D.}1{≤x x2.设全集}4,3,2{=U ，}2,3{-=a A ，}3{=A C u ，则a 的值是（） A.7 B.1- C.17-或 D.71-或3.已知全集R U =，集合}32{<≤-=x x A ，则A C u =（）A.}32{≥-≤x x x 或B.}32{>-≤x x x 或C.}32{>-<x x x 或D.}32{≥-<x x x 或 4.已知全集}8,7,6,5,4,3,2,1{=U ，集合}5,4,3{=A ，}6,3,1{=B ，那么集合 C={2，7，8}可以表示为（）A.B C uB.B A IC.B C A C u u ID.B C A C u u Y二.填空题5.设全集R U =，}62{<≤=x x A ，}4{≤=x x B ，则B A I =__，__=B C A u I ,__=B A C u I .6.全集=U {三角形}，=A {直角三角形}，则A C u =____________.7.设全集}4,3,2,1,0{=U }3,2,1,0{=A ，}4,3,2{=B ，则=B A C u I ____8.已知全集},2,1,0{=U 且}2{=A C u ，则A 的真子集共有___个.三.解答题9.设全集R U =，集合},43{R x x x M ∈<≤-=，},51{R x x x N ∈≤<-=,求①N M Y ②N C M C u u I10.设全集=U {1，2，3，4，5，6，7，8，9}，集合}2{=B A I ，}9,1{=B C A C u u I ，}8,6,4{=B A C u I ，求B A ,11.已知}1,4,2{2+-=x x U ，}1,2{+=x B ，}7{=B C u ，求x 的值1.2.1函数的概念（一）一.选择题1.函数13)(+=x x f 的定义域为（）A.)31,(--∞B.),31(+∞- C.),31[+∞- D.]31,(--∞2.已知函数q px x x f ++=2)(满足0)2()1(==f f ，则)1(-f 的值为（） A.5 B.5- C.6 D.6-3.下列函数中)()(x g x f 与表示同一函数的是（）A.1)()(0==x g x x f 与 B.xx x g x x f 2)()(==与C.22)1()()(+==x x g x x f 与D.33)()(x x g x x f ==与 4.下列各图象中，哪一个不可能为)(x f y =的图象（）二.填空题5.已知x x x f 2)(2-=，则=)2(f ______________.6.已知12)1(2+=+x x f ,则=)(x f ______________.7.已知)(x f 的定义域为],4,2[则)23(-x f 的定义域为_______________. 8.函数11)(22---=x x x f 的定义域为______________.三.解答题9.设⎩⎨⎧≥+<-=)0(22)0(12)(2x x x x x f ，求)2(-f 和)3(f10.求下列函数的定义域（1）321)(+=x x f （2）x x x g -++=1)10()(011.已知)(x f 为一次函数，且34)]([+=x x f f ，求)(x fx(D)(B)(C) (A)x1.2.1函数的概念（二）一、选择题1.函数x x y 22-=的定义域为}3,2,1,0{，其值域为（） A.}3,0,1{- B.}3,2,1,0{ C.}31{≤≤-y y D.}30{≤≤y y2.函数)(11)(2R x xx f ∈+=的值域是（） A.)1,0( B.]1,0( C.)1,0[ D.]1,0[ 3.下列命题正确的有（） ①函数是从其定义域到值域的映射②x x x f -+-=23)(是函数③函数)(2N x x y ∈=的图象是一条直线④x x g xx x f ==)()(2与是同一函数 A.1个 B.2个 C.3个 D.4个 4.函数xx x y -+=)32(的定义域为（）A.⎭⎬⎫⎩⎨⎧-≠<230x x x 且B.{}0<x xC.{}0>x xD.⎭⎬⎫⎩⎨⎧-≠≠∈230x x R x 且二.填空题5.已知函数⎪⎩⎪⎨⎧≥<<--≤+=2,221,1,2)(2x x x x x x x f ，若3)(=x f ，则x 的值为__________.6.设函数33)(2+-=x x x f ，则)()(a f a f --等于____________.7.设函数x x x f --=1)(，则=)]1([f f ____________.8.函数[]3,1,322∈+-=x x x y 的值域是________________.三.解答题9.求函数242x x y --=的值域10.已知函数1122---=x x y ，求20072008y x +的值 11.已知函数bax xx f +=)(（a .0≠a ，b 且为常数）满足1)2(=f ，x x f =)(有唯一解，求函数)(x f y =的解析式和)]3([-f f 的值.1.2.2 函数表示法（一）一、选择题1.设集合{}c b a A ,,=，集合B=R ，以下对应关系中，一定能成建立A 到B 的映射的是（）A.对A 中的数开B.对A 中的数取倒数C.对A 中的数取算术平方D.对A 中的数开立方2.某人从甲村去乙村，一开始沿公路乘车，后来沿小路步行，图中横轴表示走的时间，纵轴表示某人与乙村的距离，则较符合该人走法的图是（）3.已知函数23)12(+=+x x f ，且2)(=a f ，则a 的值等于（）A.8B.1C.5D.1-4.若x xx f -=1)1(，则当10≠≠x x 且时，)(x f 等于（）A.x 1B.11-xC.x -11D.11-x二.填空题5.若[]36)(+=x x g f ，且12)(+=x x g ，则=)(x f ______________.6.二次函数的图象如图所示，则此函数的解析式为___________.ttt ABDC7.已知函数⎩⎨⎧<≥=0,0,)(2x x x x x f 则=-)2(f ________,)4(f =_______8.集合}5,3,1{-=B ，12)(-=x x f 是A 到B 的函数，则集合 A 可以表示为____________________三.解答题9.已知函数)(x f 是一次函数，且14)]([-=x x f f ，求)(x f 的解析式10.等腰三角形的周长为24，试写出底边长y 关于腰长x 的函数关系式，并画出它的图象 11.作出函数31--+=x x y 的图象，并求出相应的函数值域1.2.2 函数表示法（二）一、选择题1.已知集合{}{}20,40≤≤=≤≤=y y B x x A ，按对应关系f ，不能成为从A 至B 的映射的一个是（） A.x y x f 21:=→ B.2:-=→x y x f C.x y x f =→: D.2:-=→x y x f2.如图，函数1+=x y 的图象是（）y3.设}8,6,2,1,0,21{},4,2,1,0{==B A ，下列对应关系能构成A 到B 的映射的是（）A.1:3-→x x fB.2)1(:-→x x fC.12:-→x x fD.x x f 2:→4.已知函数⎩⎨⎧>+-≤+=1,31,1)(x x x x x f ，则⎥⎦⎤⎢⎣⎡)25(f f =（） A.21 B.23 C.25 D.29 二.填空题5.设函数⎪⎪⎩⎪⎪⎨⎧≥<≤-<≤-+=2,320,2101,22)(x x x x x x f ，则)43(-f 的值为______, )(x f 的定义域为_____.6.)(x f 的图象如图，则)(x f =____________.7.对于任意R x ∈都有)(2)1(x f x f =+，当10≤≤x 时，)5.1-的值是____________.8.23)1(+=+x x f ，且2)(=a f ，则a 的值等于____________.三.解答题9.作出下列函数的图象（1）x y -=1,)2(≤∈x Z x 且（2）3422--=x x y ,)30(<≤xA B CD10.已知函数⎩⎨⎧<+≥-=4),3(4,4)(x x f x x x f ，求)1(-f 的值11.求下列函数的解析式（1）已知)(x f 是二次函数，且1)()1(,2)0(-=-+=x x f x f f ，求)(x f （2）已知x x f x f 5)()(3=-+，求)(x f1.3.1 函数单调性与最大（小）值（一）一.选择题1.若),(b a 是函数)(x f y =的单调递增区间，()b a x x ,,21∈，且21x x <，（） A.)()(21x f x f < B.)()(21x f x f = C.)()(21x f x f > D.以上都不正确2.下列结论正确的是（）A.函数x y -=在R 上是增函数B.函数2x y =在R 上是增函数C.x y =在定义域内为减函数D.xy 1=在)0,(-∞上为减函数 3.函数111--=x y （） A.在),1(+∞-内单调递增 B.在),1(+∞-内单调递减 C.在),1(+∞内单调递增 D.在),1(+∞内单调递减 4.下列函数在区间),0(+∞上为单调增函数的是（） A.x y 21-= B.x x y 22+= C.2x y -= D.xy 2=二.填空题5.已知函数)(x f 在),0(+∞上为减函数，那么)1(2+-a a f 与)43(f 的大小关系是________.6.函数)(x f y =7.已知13)(22-+-=a ax ax x f )0(<a ，则3(f ______.8.函数342+--=x x y 的单调递增区间为_______,当=x _______时,y 有最______值为____.三.解答题9.已知)(x f y =在定义域)1,1(-上为减函数，且)1()1(2-<-a f a f 求a 的取值范围。

高一数学人教版必修一第一章《集合与函数概念》综合测试题(含答案)

第一章集合与函数概念综合测试题、选择题1函数讨二2x -1的定义域是（）2•已知集合 A 到B 的映射f:x T y=2x+1，那么集合A 中元素2在B 中对应的元素是（）A • 2B • 6C • 5D • 83•设集合 A 二{x|1 ：：： x ：：： 2}, B 二{x|x ：：： a}.若 A B,则 a 的范围是（）A • a_2B • a < 1C • a - 1D . a 乞 24•函数y =（k • 2）x • 1在实数集上是减函数，则 k 的范围是（）A • k l ：—2B • k z ；—2C • k ^ -2D • k-25•全集 U ={ 0,1,3,5,6,8},集合 A = { 1 , 5, 8 }, B ={2},则（6 A ） B =（）A （2，；）B.[]；）2 2—1 C.（「2） -1D.（ =，2]B • { 0,3,6} {2,1,5,8} D • {0,2,3,6}F列各组函数中，表示同一函数的是（0 x y =x ,y =A •xB y = .x -1 . x 1, y = . x2 -1—2Dy=|x|,y = （、x）F列函数是奇函数的是（1A • y =x2B • y =2x2 3 （一“）若奇函数f x在1,3】上为增函数，且有最小值0,则它在1-3,-1】上A •是减函数，有最小值C •是减函数，有最大值设集合M = X - 2乞x -2 :f,B •是增函数,D •是增函数,N 二：y0 -有最小值有最大值y乞2：,给出下列四个图形，其中能表示集合M为定义域，N为值域的函数关系的是（）x2 x 010. 已知f (x) X=0，则 f [ f (-3)]等于( )0 x cO2A . 0 B. n C. n D. 9二. 填空题r X +5(XA 1) nt211. 已知f(x—1)=x2，贝y f(x)= .14.已知f (x) = 2 ，则2x +1(x 兰1)f[f(1)> _______________________ .212. 函数y = x -6x的减区间是_____________ .13•设偶函数f (x)的定义域为R，当x・[0, •：：)时f(x)是增函数，则f (2), f (二)，f (-3)的大小关系是_________________________三、解答题14.设U =R, A x _1[ B J x 0 ：： x ：： 5?,求C u 切B 和A C U B .15. 求下列函数的定义域(4)f(X)x —22(2) f(x)|x| -216.集合A = 'xx2• 4x = 0； B -汉x2• 2 a T x • a2-1 = 0若A B = B求a 的取值范围。

集合与函数综合试题多套含答案

集合与函数综合训练含答案第一套：集合概念·基础练习第二套：子集、全集、补集·基础练习第三套：交集、并集·基础练习第四套：集合与函数结合规律试题第五套：集合与函数综合试题一第六套：集合与函数综合试题二第七套：提升训练试题集合·基础练习(一)选择题1．下列命题正确的是[ ]A ．1是集合N 中最小的数．B ．x 2－4x ＋4=0的解集为{2，2}C ．{0}不是空集D ．太湖中的鱼所组成的集合是无限集 2．下列各条件(1)大于5小于20且既能被3整除也能被2整除的数的全体； (2)方程x 2＋2x ＋7=0的解的全体； (3)某学校校园内部的柳树的全体； (4)大于50的无理数的全体；其中能确定一个集合的有________个．A ．1个B ．2个C ．3个D ．4个3．已知集合A={y|y=－x 2＋5x －4，x ∈R}，则有[ ]A ．1∈A ，且4∈A(二)填空题1．已知集合A={x ∈R|ax 2＋2x ＋1=0，a ∈R}，若A 中元素至多只有一个，则a 的取值范围是________．2．实数集{3，x ，x 2－2x}中的元素x 应满足的条件为________． 3．已知x 、y 、z ∈R ，且x 、y 、z 都不为0，则M=5．设A={x|x=2k ，k ∈Z}，B={x|x=2k ＋1，k ∈Z}，C={x|x=4k ＋1，k ∈Z}，又若a ∈A ，b ∈B ，则a ＋b ∈________(填A 、B 、C 之一)．B 1A 4AC 1A 4AD 1A 4A．∈，但．，但∈．，且∉∉∉∉m|m =x |x|＋＋＋中元素的个数为．y y z z xyz xyz ||||||⎧⎨⎩⎫⎬⎭4(x y)x y =52x 4y =8．集合，＋－－用列举法表示为．⎧⎨⎩⎫⎬⎭⎧⎨⎪⎩⎪1．用两种方式写出下列各题解的集合．2．设f(x)=x 2＋ax ＋b ，A={x|f(x)=x}={a}，求a 、b 的值．3．已知小于或等于x 的最大整数与大于或等于x 的最小整数之和是7，求x 的集合．ab ∈A ．参考答案(一)选择题1．C((A)中N 包含元素0．(B)不满足集合元素互异性．(D)太湖中鱼是有限的而不是无穷多的)2．D(注意(B)中x 2＋2x ＋7=0的解集是空集，(C)学校校园内部的树是确定的．)3．B(集合A 是二次函数y=－x 2＋5x －4中，y 的取值范围，而不是一元二次方程－x 2＋5x －4=0的解集，而y=－x 2＋5x －4=－(x(二)填空题1．a ≥1或a=0 ①当ax 2＋2x ＋1=0是一元二次方程时，即a ≠0时，Δ=4－4a ≤0，∴ a ≥1②当a=0时，ax 2＋2x ＋1=0是一元一次方程2x ＋1=0也有一个根，因此也满足条件．2．x ≠－1且x ≠0且x ≠3(由集合元素的互异性知，3．3个 ①当x ，y ，z 都是正数时m=4 ②当x ，y ，z 都是负数时m=－4 ③当x ，y ，z 有两个正数一个负数或两个负数一个正数时m=0)①＋＋②－③－④＋＜x =32y 5x y =4x 1=0 (x 1)=0 (x 1)0222⎧⎨⎩*4A ={x|x =n2m N n N}a A b A m．已知，∈，∈，若∈，∈，求证：－≤，故∈，但．52942)+941A 4A ∉x 3x 2x 3x 2x x x 3x 3x 1x 0x 3x 1x 0x 3)22≠－≠－≠≠≠且≠－≠且≠≠－且≠且≠⎧⎨⎪⎩⎪⇒⎧⎨⎪⎩⎪⇒5．B(A={x|x=2k ，k ∈z}={偶数} B={奇数} C 集合为所有被4整除余1的数，∵ a 为偶数，b 为奇数，∴ a ＋b 为奇数故a ＋b ∈B)(三)解答题②{x|x 2－1=0}={1，－1} ③{x|(x －1)2=0}={1}b=0，∵ A={a}∴ 方程x 2＋(a －1)x ＋b=0有两个相等实根为a ，∴ 将a 代入方程得：a 2＋a(a －1)＋b=0①又由Δ=0得(a －1)2－4b=0② 解3．{x ∈R|3＜x ＜4} ①当x 是整数时：x ＋x=7 x=3.5∈Z ，舍去．②当x不是整数时，设n ＜x ＜n ＋1，n ∈Z ，∴ n ＋(n ＋1)=7，∴ n=3 ∴ 3＜x ＜4，∴ {x ∈R|3＜x ＜4})∴ ab ∈A1{(x y)|x =32y 5x y =4={(11)}．①，＋＋，－⎧⎨⎩⎫⎬⎭④＋＜{x|(x 1)0}=2∅2a =13b =19(f(x)=x x ax b =x x (a 1)x 22．，．由得＋＋，即＋－＋①②得，．a =13b =19)4 a b A a =n 2b =n 2m m n n N(m m ) ab =n m m N n n N 1m 2m 1212211121212．证明：∵，∈∴设，．，，，∈＞∴∵＋∈，∈．n m m 2212+子集、全集、补集·基础练习(一)选择题[ ]A ．1个B ．2个C ．3个D ．4个[ ]是[ ]A ．8B ．7C ．6D ．5[ ](二)填空题1．设I={0，1，2，3，4，5}，A={0，1，3，5}，B={0，①0________A ②{0}________B ③C I A________C I B1{0}{012}{0}{01．在以下五个写法中：①∈，，②③，，≠∅⊂2}{120} 01{x|x {12}}⊆∅⊆，，④∈⑤∈，写法正确的个数有2A ={(x y)|yx=1}B ={(x y)|y =x}．集合，与，的关系是A A =B B A B C A BD A B ．．．．≠≠⊂⊇⊃3{01}M {01234}．满足条件，，，，，的不同集合的个数≠⊂⊆M 4I =R A ={x|x 32}a =123．全集，＞，则-A a C A B a C A C {a}C AD {a}A I I I ．．．．∈≠⊆/⊆⊂1}从“∈、、、”中选择适当的符号填空．∉⊆⊇④⑤⑥1C B C A AB I I ∅2M ={x|x 1=0}N ={x|ax 1=0}N M a 2．设－，－，若，则的值为⊆3．已知A={x|x=(2n ＋1)π， n ∈Z}，B={y|y=(4k ±1)π，k ∈Z}，那么A 与B 的关系为________．________，n=________．的取值范围是________． (三)解答题a 的值．2．已知集合A={x ∈R|x 2＋3x ＋3=0}，B={y ∈B|y 2－5y ＋6=0}，3．已知集合A={x|x=a 2＋1，a ∈N}，B={x|x=b 2－4b ＋5，b ∈N}，求证：A=B ．参考答案(一)选择题和③是正确的)有意义，故A 中少一个点(0，0)，因此A B)3．C(M 中必须含有0、1，另外再在2、3、4中任取1个、2个或3个，这样集合M 的个数为3＋3＋1=7个)注：此题也可以理解为求{2，3，4}集合的非空子集个数为23－1=7个(二)填空题2． ±1或0(忽略空集是学生常犯的错误，本题应考虑两方面：①4M ={(x y)|mx ny =4}{(21)(25)}M ．设，＋且，，－，，则⊆=m 5A ={x|4x p 0}B ={x|x 1x 2}A B ．设＋＜，＜－或＞，若使，则⊆P 1A ={13a}B ={1a a 1}A B 2．已知集合，，，，－＋且，求⊇A P B P ⊆⊂≠，求满足条件的集合． B(=)A B 1．①集合与集合之间应用，或而不是属于关系．②空集是任何非空集合的真子集．③两集合相等时也可以写成的形式．④中不含任何元素．⑤此集合的元素是集合而不是数字．故②⊆⊇⊆∅210．注意与这两个式子是不同的，前者只有≠时才B(yx=y=xx 1 ．①∈②③④⑤⑥⊆⊆∉⊆⊇N a =1N =a =0)≠时，±，②时∅∅3．A=B(此题应注意两点：①{2n ＋1|n ∈Z}与{4k ±1|k ∈Z}都表示奇数集 ②A 与B 的代表元素虽然字母不同但含义相同，因此A 与B 是两个相等集合)(三)解答题－2=0 ∴ a=2或a=－1 ②当a 2－a ＋1=a 时，a=1，代入A 中不满足A 中元素互异性，舍去 ∴ a=2或a=－1．)3．(提示：任取x ∈B ，x=b 2－4b ＋5=(b －2)2＋1，b ∈N4((21)(25)mx ny =4．，由已知得：，和－，是方程＋的两组4343解，将，和－，代入方程得：＋－＋解得．x =2y =1x =2y =52m n =42m 5n =4 m =43n =43⎧⎨⎩⎧⎨⎪⎪⎩⎪⎪)1a =2a =1( B A a a 1=3a a 22．或－∵∴①当－＋时，－⊆2{2}{3}(A =B ={23}B {2}{3} P {2}{3})．或或由已知，，，的真子集为：，，又∵是任何集合的子集，∴可以是，，∅∅∅∅∅交集、并集·基础练习(一)选择题1．已知I={x ∈N|x ≤7}，集合A={3，5，7}，集合B={2，3，4，5}，则[ ] A ．C I A={1，2，4，6}B ．(C I A)∩(C I B)={1，2，3，4，6}D ．B ∩C I A={2，4}2．两个非空集合A 、B 满足A ∩B=A 且A ∪B=A ，那么A 、B 的关系是[ ]C ．A=BD ．以上说法都不对3．若4∩B={a ，b}，A ∪B={a ，b ，c ，d}，则符合条件的不同的集合A 、B 有[ ]A ．16对B ． 8对C ． 4对D ． 3对4．已知集合A ∪B={a ，b ，c ，d}，A={a ，b}则集合B 的子集最多可能有[ ]A ．8个B ．16个C ．4个D ．2个5．已知集合A 为全集I 的任一子集，则下列关系正确的是[ ](二)填空题(1)A ∩C I A=________ (2)A ∪C I A=________C A C B =I ．∩∅A A B B B A．．≠⊂⊇A C A I B (A C A)C (A C A)ID C AI I I I ．．∩．∪．≠≠≠⊂⊆∅⊂∅⊂1I A I B I A B ．已知是全集，，，，则≠≠≠⊂⊂⊂(3)A ∩C I B=________ (4)B ∪C I A=________ (5)C I I=________(7)C I (C I (A ∩B))=________(8)A ∩I=________ (9)B ∪I=________2．集合A={有外接圆的平行四边形}，B={有内切圆的平行四边形}，则A ∩B=________．3．设集合A={(x ，y)|a 1x ＋b 1y ＋c 1=0}，B={(x ，y)|a 2x ＋b 2y ＋b 1y ＋c 1)(a 2x ＋b 2y ＋c 2)=0的解集是________．4．集合A={x|x ＜－2，或x ＞2}，B={x|x ＜1，或x ＞4}，则A ∩B=________；A ∪B=________．实数a 的取值范围是________． (三)解答题1．A={(x ，y)|ax －y 2＋b=0}，B={(x ，y)|x 2－ay －b=0}，已知2．已知 A={x|a ≤x ≤a ＋3}，B={x|x ＜－1或x ＞5}，(2)若A ∪B=B ，求 a 的取值范围．3．设方程2x 2＋x ＋p=0的解集为A ，方程2x 2＋qx ＋2=0的解4．以实数为元素的两个集合A={2，4，a 3－2a 2－a ＋7}，B={－4，a ＋3，(6)C =I ∅c =0}a x b y c =0a xb yc =02111222，则方程组＋＋＋＋的解集是；方程＋⎧⎨⎩(a x 15A ={1a}B ={1|a|}A B =．已知集合－，，集合，，若∩，则：∅A B {(12)}a b ∩，，求、．⊇(1)A B =a 若∩，求的取值范围．∅集为，∩，求∪．B A B =12A B ⎧⎨⎩⎫⎬⎭a 2－2a ＋2，a 3＋a 2＋3a ＋7}，已知A ∩B={2，5}，求：a ．5．某中学高中一年级学生参加数学小组的有45人，参加物理小组的有37人，其中同时参加数学小组和物理小组的有15人，数学小组和物理小组都没有参加的有127人，问该校高中一年级共有多少学生？参考答案(一)选择题1．D(N={0，1，2，3，…}，而集合N 中含有0是容易忽略的，故(A)C I A={0，1，2，4，6}．(B)中(C I A)∩(C I B)=C I (A ∪B)={0，1，6} (C)A ∩C I B 只要找出在A 中且不在B 中的元素即可为{7})2．C(根据集合运算的结果确定集合之间的关系是常用知识，由A3．C(由韦恩图可推断如下：4．B(B 的元素个数n 最多时子集个数最多，而集合B 最多有4个元素为a 、b 、c 、d ，因此共有24=16个子集．)5．B(注意A 为全集I 的任一子集意味着A 有可能是空集也有可能(二)填空题2．{正方形}(有外接圆的平行四边形可证明是长方形，有内切圆的平行四边形可证明是菱形)3．A ∩B ；A ∪B(注意“{”联立起来的方程组表示两个条件必须同时满足是“并且”的意思，而方程(a 1x ＋b 1y ＋c 1)(a 2x ＋b 2y ＋c 2)=0是a 1x ＋b 1y ＋c 1=0或a 2x ＋b 2y ＋c 2=0．)4．(－∞，－2)∪(4，＋∞)；(－∞，1)∪(2，＋∞) (A ∩B ：A ∪B ：)∩得，由∪得，故此题B =A A B A B =A B A A =B)⊆⊆是全集，而只有中∩是正确的(B)A C A =I ∅⊆∅)1(1) (2)I (3) (4)I (5) (6)I (7)A (8)A (9)I ．∅∅∅(三)解答题2．(1)解：∴ a ＋3＜－1或a ＞5 ∴ a ＜－4或a ＞54．解：∵ A ∩B={2，5} ∴ 5∈A 代入得a 3－2a 2－a ＋7=5∴ a=2或a=±11)当a=2时，B={－4，5，2，25} A={2，4，5}2)当a=1时，B={－4，4，1，12}，与A ∩B={2，5}矛盾，舍去 3)当a=－1时，同理舍去 ∴ a=2 5．解：30＋15＋22＋127=194(人)答：该校高一年级学生共194人5a 0a 1(|a|1|a|1|a|a a 0a 1)．＜且≠－由互异性及题意可知：≠≠≠＜≠－⎧⎨⎪⎩⎪⇒⎧⎨⎩11212012401203722．解：由∩，知，满足方程组－＋－－将，代入得－＋－－∴－A B {()}x=y=ax y b=x ay b=x=y=a b=a b= a=b=⊇⎧⎨⎪⎩⎪⎧⎨⎩⎧⎨⎩依题意得≥－＋≤∴－≤≤解：由∪知a 1a 351a 2(2)A B =B A B⎧⎨⎩⊆3A B =12p =1q =5A B ={12}．解：由∩知为两方程的公共根，代入方程得－－再代入原方程，得∪－，，1212⎧⎨⎩强化训练·规律篇（一）选择题1．点M（-3t，4t）（t≠0）是角α终边上一点，则有 [ ][ ]A．在一、二象限取正，三、四象限取负B．在一、四象限取正，二、三象限取负C．在一、三象限取正，二、四象限取负D．仅在一象限取正[ ]A．第一象限B．第三象限C．第一或第三象限D．第二或第四象限[ ]D．1[ ] A．2πB．π[ ]C．[0，2）D．[0，2]（ω1≠0，ω2≠0），它们的最小正周期分别是T1，T2，那么“这两个函数的图像重合或通过平移使它们重合”是“T1=T2”的[ ]A．充分但不必要条件B．必要但不充分条件C．充要条件D．既不充分也不必要条件图像[ ]sin（-3x）的图像，这种变动可以是[ ]的图像[ ]A．与g（x）的图像相同B．与g（x）的图像关于y轴对称12．函数f（x）=3sin（2x+5θ）的图像关于y轴对称的充要条件是 [ ]13．若A为△ABC的内角，则sinA＋cosA的取值范围是 [ ][ ]15．方程2sinx=x的实根的个数是[ ]A．0个B．1个C．2个D．3个（二）填空题16．若θ∈（0，2π），则使sinθ＜cosθ＜tgθ成立的θ的取值范围是______。

集合与函数测试题高考综合(含答案)

集合与函数测试题一．选择题1已知命题“012,2<++∈ax x x R 存在”是真命题，则实数a 的取值范围是（ )A ．)1,(--∞B ．),1(+∞C ．),1()1,(+∞--∞D ．（—1，1）2、若{}8222<≤∈=-x Z x A {}1log R <∈=x x B x ，则)(C R B A ⋂的元素个数为（） A.0B.1C.2D.33、设1a >，函数()log a f x x =在区间[,2]a a 上的最大值与最小值之差为12，则a =（） A ．2 B ．4 C ．22 D ．24、在R 上定义的函数()x f 是偶函数，且()()x f x f -=2，若()x f 在区间[]2,1是减函数，则函数 ()x f （）A.在区间[]1,2--上是减函数，区间[]4,3上是增函数B.在区间[]1,2--上是减函数，区间[]4,3上是减函数C.在区间[]1,2--上是增函数，区间[]4,3上是增函数D.在区间[]1,2--上是增函数，区间[]4,3上是减函数 5 .设⎭⎬⎫⎩⎨⎧-∈3,21,1,1α，则使函数αx y =的定义域为R 且为奇函数的所有α的值为（） A. -1,3 B.-1,1 C. 1,3 D.-1,1,3 6．已知(31)4,1()log ,1a a x a x f x x x -+<⎧=⎨>⎩是(,)-∞+∞上的减函数，那么a 的取值范围是 A.(0,1) B.1(0,)3C.1[,1)7D.11[,)737．若函数2)1(log )(223++++=x x b ax x f 在)0,(-∞上有最小值－5，（a ，b 为常数），则函数)(x f 在),0(+∞上（）A ．有最大值9B ．有最小值5C ．有最大值3D ．有最大值58．函数|3||4|92-++-=x x x y 的图象关于（）A ．x 轴对称B ．y 轴对称C ．原点对称D ．直线0=-y x 对称9．若函数21(1)()lg (1)x x f x x x ⎧+≤=⎨>⎩,则f(f(10)=（）A ．lg101B ．2C ．1D ．010．设函数)(x f 是定义在R 上的奇函数，且对任意R ∈x 都有)4()(+=x f x f ，当 )02(，-∈x 时， x x f 2)(=，则)2011()2012(f f -的值为（） A.21-B.21C. 2D.2-11．已知函数f (x )＝x 2＋ax ＋b －3(x ∈R )图象恒过点(2,0)，则a 2＋b 2的最小值为( ) A ．5 B.15 C ．4 D.1412. 设函数()f x =cx bax ++2的图象如下图所示，则a 、b 、c 的大小关系是11-1-1OxyA.a ＞b ＞cB.a ＞c ＞bC.b ＞a ＞cD.c ＞a ＞b二、填空题13、函数x x f 6log 21)(-=的定义域为__ 14、若24log 3,(22)x x x -=-=则＿＿＿15. 已知函数)(x f 是定义在),(∞+∞-上的偶函数. 当)0,(∞-∈x 时，4)(x x x f -=，则当 ),0(∞+∈x 时，=)(x f16. .函数()y f x =是R 上的偶函数，且在(,0]-∞上是增函数，若()(2)f a f ≤,则实数a 的取值范围是______三、解答题17．(本小题满分10分) 计算：（1）0021)51(1212)4(2---+-+- （2）91log 161log 25log 532∙∙18．（本小题满分12分）已知函数()f x 在定义域()0,+∞上为增函数，且满足()()()(),31f xy f x f y f =+=(1)求()()9,27f f 的值 (2)解不等式()()82f x f x +-<19. （12分）已知函数2()(8),f x ax b x a ab =+---的零点是－3和2.（Ⅰ）求函数()f x 的解析式；（Ⅱ）当函数f （x ）的定义域是[0，1]时，求函数()f x 的值域.20. （本小题满分12分）某地区预计明年从年初开始的前x 个月内，对某种商品的需求总量．．．．()f x （万件）与月份x 的近似关系为1()(1)(352)(12)150f x x x x x N x =+-∈≤且．（1）写出明年第x 个月的需求量()g x （万件）与月份x 的函数关系式，并求出哪个月份的需求量超过1.4万件；（2）如果将该商品每月都投放市场p 万件，要保持每月都满足市场需求，则p 至少为多少万件．21.．(本小题满分12分) 定义在非零实数集上的函数()f x 满足()()(),f xy f x f y =+且()f x 是区间()0,+∞上的增函数()1求(1),(1)f f -的值； ()2求证：()()f x f x -=； ()3解不等式1(2)()02f f x +-≤.22．（本小题满分14分）设二次函数2()(,,)f x ax bx c a b c R =++∈满足下列条件：①当x ∈R 时，()f x 的最小值为0，且f (x －1)=f (－x －1)成立； ②当x ∈(0,5)时，x ≤()f x ≤21x -+1恒成立。