超静定结构的概念和超静定结构次数的确定
超静定结构的计算

单元10 超静定结构的计算【学习目标】1、掌握力法、位移法的基本原理,能用这些方法计算常用的简单超静定结构的内力;2、熟练应用力矩分配法计算连续梁和无侧位移刚架;了解超静定结构的特征。
【知识点】1、超静定结构的概念、超静定次数及确定;力法的基本原理、基本结构;典型方程;用力法计算简单的超静定梁和刚架;支座移动时单跨超静定梁的内力。
2、力矩分配法的基本原理;转动刚度、分配系数、传递系数、分配弯矩、传递弯矩;用力矩分配法计算连续梁和无侧移刚架。
【工作任务】任务1 用力法计算超静定结构任务2 用力矩分配法计算超静定结构【教学设计】通过对力法和力矩分配法的学习让学生理解这两种方法在解决超静定结构各有何特点,通过例题的讲解能使学生能更好地理解两种方法在解超静定结构的特点。
10.1 用力法计算超静定结构10.1.1 超静定次数的确定我们知道,超静定结构由于有多余约束存在,约束反力未知量的数目多于平衡方程数目,仅靠平衡方程不能确定结构的支座反力。
从几何组成方面来说,结构的超静定次数就是多余约束的个数;从静力平衡看,超静定次数就是运用平衡方程分析计算结构未知力时所缺少的方程个数,即多余未知力的个数。
所以,要确定超静定次数,可以把原结构中的多余约束去掉,使之变成几何不变的静定结构,而去掉的约束个数就是结构的超静定次数。
超静定结构去掉多余约束有以下几种方法:(1)去掉支座处的一根链杆或者切断一根链杆,相当于去掉一个约束。
图10-1(2)去掉一个铰支座或者去掉一个单铰,相当于去掉两个约束。
图10-2图10-1图10-2(3)去掉一个固定端支座或者切断一根梁式杆,相当于去掉三个约束。
图10-3(4)将一个固定端支座改为铰支座或者将一刚性连接改为单铰连接,相当于去掉一个约束。
图图10-4用去掉多余约束的方法可以确定任何超静定结构的次数,去掉多余约束后的静定结构,称为原超静定结构的基本结构。
对于同一个超静定结构来说,去掉多余约束可以有多种方法,所以基本结构也有多种形式。
超静定结构的受力分析及特性

超静定结构的受力分析及特性一、超静定结构的特征及超静定次数超静定结构的静力特征是仅由静力平衡条件不能唯一地确定全部未知反力和内力。
结构的多余约束数或用静力平衡条件计算全部未知反力和内力时所缺少的方程数称为结构的超静定次数。
通常采用去除多余约束的方法来确定结构的超静定次数。
即去除结构的全部多余约束,使之成为无多余约束的几何不变体系,这时所去除的约束数就是结构的超静定次数。
去除约束的方法有以下几种:(一)切断一根两端铰接的直杆(或支座链杆),相当于去除一个约束。
(二)切断一根两端刚接的杆件,相当于去除三个约束。
(三)切断——个单铰(或支座固定铰),相当于去除二个约束;切断一个复铰(连接n根杆件的铰),相当于去除2(n—1)个约束。
(四)将单刚结点改为单铰节点,相当于去除一个约束;将连接n个杆件的复刚节点改为复铰节点,相当于去除n—1个约束。
去除一个超静定结构多余约束的方法可能有几种,但不管采用哪种方法,所得超静定次数一定相同。
去除图4—1a所示超静定结构的多余约束的方法之一如图4—1b所示,去除六个多余约束后,就成为静定结构,故为超静定六次。
再用其他去除多余约束的方案确定其超静定次数,结果是相同的。
二、力法的基本原理(一)力法基本结构和基本体系去除超静定结构的多余约束,代以相应的未知力Xi (i=1、2、…、n),Xi 称为多余未知力或基本未知力,其方向可以任意假定。
去除多余约束后的结构称为力法基本结构。
力法基本结构在各多余未知力、外荷载(有时还有温度变化、支座位移等)共同作用下的体系称为力法基本体系,它是用力法计算超静定结构的基础。
选取力法基本结构应注意下面两点:1.基本结构一般为静定结构,即无多余约束的几何不变体系。
有时当简单超静定结构的解为已知时,也可以将它作为复杂超静定结构的基本结构,以简化计算。
2.选取的基本结构应使力法典型方程中的系数和自由项的计算尽可能简便,并尽量使较多的副系数和自由项等于零。
超静定次数的确定

将复铰结点A 拆开,在刚结点B 处插入一个单铰并切断 一个链杆,复铰A相当于两个单铰的作用,共去除六个约 束,即n = 6。
结构力学电子教案
第八章
力法
第11页
对于框架,可采用下式计算超静定次数
n= 3 c−h
式中 c 为框格数,h 为单铰数 先将结构中每个框格都看作是无铰的,每个单铰的存 在就减少1次超静定。
结构力学电子教案
第八章
力法
第1页
§8-1 超静定结构的概述和超静定次数的确定 一.超静定结构的一般概念
超静定结构的两个特征: 1. 几何特征: 超静定结构是具有多余约束 的几何不变体系。
结构力学电子教案
第八章
力法
第2页
P
必要约束: 多余约束:
X1
多余约束力
X1
结构力学电子教案
第八章
力法Biblioteka 第3页思考:结构力学电子教案
第八章
力法
第12页
例1:
(a) (b)
框格数c = 2
单铰数h = 2
框格数c = 4 单铰数h = 6
n = 3×2-2 = 4
n = 3×4-6 = 6
结构力学电子教案
第八章
力法
第13页
例2:
n=2
X1 X2
X1 X2
X3
X4
n=4
结构力学电子教案
第八章
力法
第14页
n=3
X1 X3 X2
X1 X2
X3 X4
n = 4+6-2=8
结构力学电子教案
第八章
力法
第8页
(2)撤去两杆间的一个单铰或撤去一个铰支座,等于去 除两个约束。
《建筑力学》期末复习指导

11秋建筑施工与管理专科《建筑力学》期末复习指导一、课程说明《建筑力学》是广播电视大学土木工程专业(本科)和水利水电工程专业(本科)的补修课。
本课程的教材:《建筑力学》,作者:吴国平,中央广播电视大学出版社出版。
二、考试说明1、考核方式闭卷考试,考试时间为90分钟。
2、试题类型试题类型分为两类:第一类判断题与选择题,占30%;第二类计算题,占70%。
计算题共4题,主要类型有:求静定结构支座反力并画内力图,梁的正应力强度计算,图乘法求位移,力法计算超静定结构,力矩分配法计算超静定结构。
三、复习要点第一章静力学基本知识一、约束与约束反力1.柔索约束:由软绳构成的约束。
约束反力是拉力;2.光滑面约束:由两个物体光滑接触构成的约束。
约束反力是压力;3.滚动铰支座:将杆件用铰链约束连接在支座上,支座用滚轴支持在光滑面上,这样的支座称为滚动铰支座。
约束反力垂直光滑面;4.链杆约束:链杆是两端用光滑铰链与其它物体连接,不计自重且中间不受力作用的杆件。
约束反力作用线与两端铰链的连线重合。
5.固定铰支座:将铰链约束与地面相连接的支座。
约束反力是一对相互垂直的力6.固定端:使杆件既不能发生移动也不能发生转动的约束。
约束反力是一对相互垂直的力和一个力偶。
二、力矩与力偶1.力偶不等效一个力,也不能与一个力平衡。
2.力偶的转动效果由力偶矩确定,与矩心无关。
3.力对点之矩一般与矩心位置有关,对不同的矩心转动效果不同4.力偶与矩心位置无关,对不同点的转动效果相同。
三、主矢和主矩1.主矢与简化中心位置无关,主矩与简化中心位置有关。
2.平面任意力系向一点简化的结果a)主矢不为零,主矩为零:一个合力;b)主矢不为零,主矩不为零:一个合力、一个合力偶;c)主矢为零,主矩不为零——一个合力偶;d)主矢为零,主矩为零——平衡力系。
四、平面力系1.平面任意力系的主矢和主矩同时为零,即,是平面任意力系的平衡的必要与充分条件。
2.平面一般力系有三个独立方程可求解三个未知数,平面平行力系有二个独立方程可求解二个未知数。
超静定结构的超静定次数

超静定结构的超静定次数超静定结构是指在受力平衡条件下,由于约束条件数量大于自由度数量,使得结构不具有唯一的平衡位置。
超静定结构的超静定次数是指约束条件数量与自由度数量之差。
一、超静定结构的特点超静定结构具有以下特点:1. 约束条件数量大于自由度数量:超静定结构的约束条件数量大于自由度数量,使得结构不具有唯一的平衡位置。
这导致了结构的设计和分析变得更加困难。
2. 结构具有较高的刚度:由于超静定结构的约束条件数量较多,结构具有较高的刚度。
这使得超静定结构在承受荷载时能够更好地保持形状稳定性。
3. 结构能够承受更大的荷载:超静定结构由于具有较高的刚度,能够承受更大的荷载。
这使得超静定结构在工程实践中得到广泛应用。
二、超静定结构的应用超静定结构在工程实践中有着广泛的应用,主要包括以下几个方面:1. 桥梁工程:超静定结构在桥梁工程中得到了广泛应用。
由于桥梁需要承受大量的荷载,超静定结构能够提供更高的刚度和稳定性,保证桥梁在使用过程中不发生塌陷或变形。
2. 建筑结构:超静定结构在建筑结构中也有重要的应用。
例如,高层建筑的框架结构通常采用超静定结构设计,以提高结构的稳定性和抗震性能。
3. 机械设备:超静定结构在机械设备中也有广泛的应用。
例如,汽车的悬挂系统和起重机的支撑结构都是超静定结构,能够提供更高的稳定性和承载能力。
三、超静定结构的分析方法超静定结构的分析方法主要包括以下几个步骤:1. 定义自由度和约束条件:首先确定结构的自由度和约束条件。
自由度是指结构中可以独立变形的数量,约束条件是指结构中限制自由度的条件。
2. 建立平衡方程:根据结构的受力平衡条件,建立结构的平衡方程。
平衡方程是超静定结构分析的基础,通过平衡方程可以求解结构的受力状态。
3. 引入支座反力:由于超静定结构的约束条件数量大于自由度数量,结构中存在未知的支座反力。
通过引入支座反力,可以将超静定结构转化为静定结构进行分析。
4. 求解支座反力:利用平衡方程和约束条件,求解支座反力。
超静定结构及力学原理和方程重难点分析
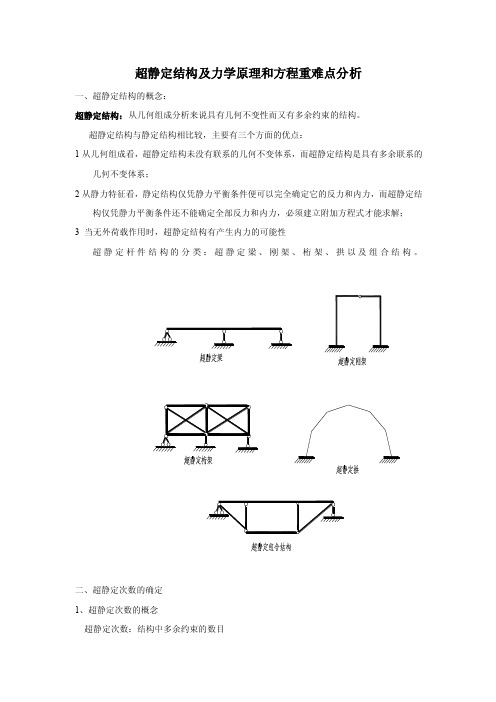
超静定结构及力学原理和方程重难点分析一、超静定结构的概念:超静定结构:从几何组成分析来说具有几何不变性而又有多余约束的结构。
超静定结构与静定结构相比较,主要有三个方面的优点:1从几何组成看,超静定结构未没有联系的几何不变体系,而超静定结构是具有多余联系的几何不变体系;2从静力特征看,静定结构仅凭静力平衡条件便可以完全确定它的反力和内力,而超静定结构仅凭静力平衡条件还不能确定全部反力和内力,必须建立附加方程式才能求解;3 当无外荷载作用时,超静定结构有产生内力的可能性超静定杆件结构的分类:超静定梁、刚架、桁架、拱以及组合结构。
二、超静定次数的确定1、超静定次数的概念超静定次数:结构中多余约束的数目2、方法去掉多余联系的常用方法如下:(1)去掉一根支杆或切断一根链杆,相当于去掉一个联系; (2)去掉一个单铰,相当于去掉二个约束;(3)切断一根弯杆或去掉一个固定支座,相当于去掉三个联系(4)将固定支座改成不动铰支座或将受弯杆切断改铰结,各相当去掉一个联系 3、举例例如图1所示的单跨静定梁,若去掉B 支座的支杆,代以多未知力B X ,则原梁变为静定的简支梁(即为基本结构),如图1(b )所示;若将固定端A 支座加一个单铰,代以多余未知力A X ,则原梁变为静定的简支梁(即为基本结构),如图1(c )所示,所有原结构一次超静定结构.同理,如图2所示的刚架,可将A 、B 两固定改成铰支座,代以多余力A X 、B X ,则得如图2(b )所示的静定三铰刚架;或者去掉铰C ,代以多余力1X 、2X ,则得如图2(c )所示的两各静定悬臂刚架;或者去掉铰C ,故原结构为二次超静定结构。
三、力法原理和力法方程1.力法的基本原理:将超静定结构转化为含多余力的静定结构 (一)一次超静定结构 (1)确定超静定次数:n=1次 (2)选基本结构⎩⎨⎧)几何不变体系(静定结构b a )((3)位移条件: 01=∆ (a) 根据叠加原理 :p1111∆+∆=∆ (b )11111x δ=∆ (c)(4)力法方程(一次):将(c )代入(b )式得:01111=∆+px δ…………(6-1)式中:--11δ系数(单位多余力1=X 作用时,B 点沿1x 方向的位移)--∆p1自由项(荷载单独作用时B 点沿1x 方向的位移)1x --基本未知量(多余未知力或多余力)系数(11δ) 和自由项(p1∆)都是基本结构(静定结构)在已知外力作用下的位移,可用上一章讲的单位荷载法或图乘法求得,代入(6-1)式后可求出多余未知力1x ,求得1x 之后其余的计算(支座反力和内力)同静定结构。
超静定结构的概述

(a)
(b)
图 11-3
除上述主要特征外,超静定结构还具有整体性强、变形小、受力较为 均匀等特点,因而这种结构在实际工程中被广泛采用。例如,图11-4a 所 示的两跨连续梁较图11-4b 所示的两跨简支梁,在力 F 作用点处的弯矩和 挠度均为小。
(a) 静定结构
(b) 超静定结构
(c) 静定结构受力图
算上来说,静定结构的静力特征是用静力平衡条件就能求得全 部反力和内力;而超静定结构的静力特征是仅用静力平衡条件不能求得 全部反力和内力。例如,对图11-1a 所示的静定梁,其受力图如图11-1c 所示,梁的反力(FAx、FAy、FB)和内力(FN、FQ、M)分别由三个静 力平衡方程求得。 而对图 11-lb 所示的连续梁,其受力图如图 11-ld 所示, 梁的反力共有四个(FAx、FAy、Fx1、FB),其中Fx1称为多余约束所对应 的多余未知力,用三个静力平衡方程不可能将此四个反力全部求得,只 要有一个反力尚未确定,梁的内力就不能确定。因此,还须补充其他条 件,才能求解。
【例11-3】确定图11-13a 所示结构的超静定次数。
解:图11-13a 所示刚架,具有一个多余约束。若将横梁某处改为铰接, 即相当于去掉一个约束,得到如图11-13b 所示的静定结构,故原结构 n = l。
若去掉支座 B 处的水平支杆,则得图11-13c 所示的静定结构。 但是,若去掉支座 B 或支座 A 的竖向支杆,即成可变体系如图11-13d 所 示,显然这是不允许的,所以此刚架支座处的竖向支杆不能作为多余约束。
图 11-6
② 去掉一个单铰,相当于去掉两个约束 。 如图11-7a 所示的结构,去掉一个单铰而变成静定结构,如图11-7b 所示。 因 n = 2,故该结构为两次超静定 。
超静定结构的概念及超静定次数的确定(PPT)

04 超静定结构的实际应用
桥梁工程
桥梁工程中,超静定结构的应用可以增加结构的稳定性和安全性,提高桥梁的承 载能力。例如,连续梁桥采用超静定结构形式,可以减小梁体的振动和变形,提 高行车舒适性和安全性。
此外,超静定结构在桥梁工程中还可以用于抵抗风、地震等自然灾害的影响,提 高桥梁的抗震性能和抗风能力。
ቤተ መጻሕፍቲ ባይዱ
渐进法
总结词
通过逐步逼近的方法求解超静定结构的位移和内力的方法。
详细描述
渐进法是一种基于迭代思想的求解方法,通过逐步逼近的方法求解超静定结构的位移和内力。该方法首先假设一 组初始解,然后逐步修正解的近似值,直到满足精度要求或达到预设的迭代次数为止。渐进法可以处理复杂的超 静定结构问题,具有较高的计算效率和精度。
建筑工程
在建筑工程中,超静定结构的应用可以提高结构的稳定性和 刚度,增强建筑物的承载能力和抗震性能。例如,高层建筑 采用超静定结构形式,可以减小风力、地震等外部荷载对建 筑物的影响,保证建筑物的安全性和稳定性。
此外,超静定结构在建筑工程中还可以用于优化建筑物的空 间布局和结构形式,提高建筑物的美观性和实用性。
超静定结构
在任何一组确定的平衡力系作用 下,需要用多余的约束条件才能 确定结构的平衡状态的体系。
超静定结构的特性
具有多余的约束
超静定结构有多余的约束,这些 多余的约束可以提供额外的稳定 性,使结构在受到外力作用时具
有更好的抵抗变形的能力。
存在内力
由于超静定结构的约束多余,当 受到外力作用时,会在结构内部 产生内力,这些内力有助于抵抗
判别准则二
如果一个结构的支座反力数目小于其约束数目, 则该结构为超静定结构。
判别准则三
如果一个结构的受力状态不能由静力平衡方程完 全确定,则该结构为超静定结构。
超静定结构的超静定次数

超静定结构的超静定次数超静定结构是指在外力作用下,结构内部的约束力大于外力的个数,从而使得结构处于静定状态的一种结构形式。
即结构内部的约束力可以完全抵消外力的作用,使得结构保持平衡。
超静定结构的超静定次数是指结构内部的约束力多于外力的个数。
超静定次数越高,结构的稳定性越好。
超静定结构的超静定次数取决于结构的约束性质和约束方式。
常见的超静定结构有悬挑梁、连续梁和桁架等。
这些结构的超静定次数可以通过力平衡方程和几何关系进行计算。
在设计超静定结构时,需要合理选择约束方式和约束点的位置,以提高结构的稳定性和承载能力。
悬挑梁是一种常见的超静定结构。
它由一根悬挑在空中的梁组成,一端固定在墙上,另一端悬空。
在外力作用下,悬挑梁的约束力可以完全抵消外力的作用,使得梁保持平衡。
悬挑梁的超静定次数为1,即悬挑梁有一个多余的约束力。
连续梁是另一种常见的超静定结构。
它由多个梁段组成,梁段之间通过铰接连接。
在外力作用下,连续梁的约束力可以完全抵消外力的作用,使得梁保持平衡。
连续梁的超静定次数为2,即连续梁有两个多余的约束力。
桁架是一种由杆件和节点组成的超静定结构。
杆件之间通过节点连接,形成一个刚性的空间网格结构。
在外力作用下,桁架的约束力可以完全抵消外力的作用,使得结构保持平衡。
桁架的超静定次数取决于节点的个数和杆件的个数。
一般情况下,桁架的超静定次数为3,即桁架有三个多余的约束力。
超静定结构的超静定次数越高,结构的稳定性越好。
在实际工程中,超静定结构常用于悬挑梁、连续梁和桁架等场合。
例如,在大跨度桥梁的设计中,常采用连续梁结构,以提高桥梁的稳定性和承载能力。
此外,在高层建筑的设计中,常采用悬挑梁结构,以增加建筑物的空间利用率。
超静定结构的设计需要考虑结构的约束性质和约束方式。
合理选择约束方式和约束点的位置,可以提高结构的稳定性和承载能力。
同时,超静定结构的设计还需要考虑结构的材料性质和施工工艺。
选择合适的材料和采用适当的施工方法,可以确保结构的安全性和经济性。
结构力学五

五.力法一.超静定结构概念和超静定次数的确定1.超静定结构的概念:有多余约束存在,支座反力和内力不能仅靠静力平衡方程确定的几何不变体系;2.超静定结构的性质:(1)多余约束反力的确定,除使用静力平衡条件外,还需考虑变形;(2)受力情况与材料的物理性质、截面几何性质有关系;(刚度)(3)去掉一些约束后,体系仍可以保持几何不变;(4)制造误差、支座移动、温度等原因能使结构产生内力;2.超静定次数的确定:(1)超静定次数=未知力个数-平衡方程的个数=多余未知力的个数=多余约束的个数=把结构变成静定结构时所需撤除的约束个数(2)将超静定结构变成静定结构的几种基本方法:A.去掉支座的一根链杆或切断一根链杆,相当于去掉一个约束;B.去掉一个单铰,相当于去掉两个约束;C.将刚性连接改成单铰连接,相当于去掉一个约束;D.刚性连接处切断,相当于去掉三个约束;(3)需要注意的几个问题:A去掉的约束必须是保证体系几何不变的多余约束;B.多余约束必须都拆除;C.去多余约束的办法不仅只有一种,只是要保证去掉约束后保证其几何不变性;D.去掉多余约束后的静定结构称该超静定结构的基本结构,由上知基本结构不唯一;二.计算超静定结构的基本方法(1)计算超静定结构的方法很多,但基本方法只有两种:力法、位移法;(2)力法:多余约束力为基本未知量,位移谐调建立平衡方程(3)位移法:位移为基本未知量,节点受力平衡建立平衡方程(4)力法位移法基本思路:把不会算的结构通过未知量转换成会算的结构即基本结构(5)力法与位移法计算步骤:A.选取基本结构、基本未知量;B.用关于力的或位移的代数方程组求解未知量;三.力法思想(1)取图b为基本结构,则相应的基本体系为图e,这种情况下,图a中C处可动铰支座被视为多余约束,X1为基本未知量;(2)图a为一次超静定;(3)力法方程的概念(以图b所示的基本结构为例):图a中,在F P作用下,体系将产生变形,但支座C处竖向位移为零(约束边界条件决定),想要静力等效,在基本体系1中(图e),基本结构在F P和基本未知量X1的作用下,C点的竖向位移为零;力法中,体系必须为线性体系,内力和位移才可以使用叠加原理,在图e 中,使用叠加原理保证C点的竖向位移为零是力法的基本思想;在F P作用下,基本结构C 点将发生竖向的位移分量Δ1P,同样,在基本未知量X1作用下,C点将产生竖向位移分量Δ11,Δ1P和Δ11必须保证C点竖向位移分量为零,则有Δ1P+Δ11=0由图乘法可以求得Δ1P和Δ11(X1的函数),然后通过C点位移为零建立方程,最终求得X1;(4)力法典型方程:⎪⎭⎪⎬⎫=∆+++=∆=∆+++=∆=∆+++=∆0X X X 0X X X 0X X X P 33332321313P 23232221212P 131********δδδδδδδδδ相同道理,如果是n 次超静定,力法方程可表示成为⎪⎪⎭⎪⎪⎬⎫=∆++++=∆++++=∆++++0X X X 0X X X 0X X X nF n nn 22n 11n F 2n n 2222121F 1n n 1212111δδδδδδδδδ矩阵表达式:0X X X nF F2F 1n 21nn 1n 1n n 22121n 11211=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∆∆∆+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡δδδδδδδδδ 柔度系数:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡nn 22n1n22212n 11211δδδδδδδδδ自由项:{}iF ∆根据位移互等定理,柔度矩阵是一个对称矩阵,主对角线元素ii δ称为主系数,主系数均为正值且不等于零。
静定结构与超静定结构的概念

静定结构与超静定结构的概念
静定结构是指由力学平衡条件完全确定的结构体系。
这种结构体系的节点数和支座数
均为定值,因此问题可以被简化为一组线性方程组,能够通过矩阵运算得到完整的结构位
移和内力。
因此,静定结构具有稳定可靠、计算简单等优点。
常见的静定结构有梁、柱、
桁架等。
超静定结构则是指节点数和支座数不足以完全确定结构体系的构件,在此基础上另外
增设一定数目的约束,即超数约束,从而使结构体系的DOF(自由度)等于零或小于零,可以通过高斯消元、截可省略算法等方法进行求解。
常见的超静定结构有悬链、钢框架、高
层建筑等。
超静定结构相对于静定结构具有以下特点:
1.灵活编排:在设计中,超静定结构通过增加适量的支承约束,可以根据实际情况安
排构件的位置,达到灵活编排的目的。
2.承载能力大:超静定结构的约束力较大,因此在承载能力方面比静定结构更有优势,能够承受更大的荷载。
3.变形小:超静定结构的约束力较大,因此在荷载下变形较小,对结构的稳定性和耐
久性都有良好的保证。
4.抗剪承载能力强:由于超静定结构的超数约束,使得其具有很好的抗剪承载能力,
因此比较适合用于高层、大跨度等大型结构的设计中。
需要注意的是,在设计超静定结构时,要考虑结构的稳定性,避免出现过度约束、约
束不当等问题,以免影响结构的受力性能和使用寿命。
同时,在考虑承重能力的同时,也
要注重结构的变形控制,以达到有效的结构控制和优化设计的目的。
材料力学 第11章 超静定结构

心有所信,方能行远。
本课件部分图片来源网络,仅供教学使用
材料力学
11.3 对称及对称性质的应用
一、对称结构的对称变形与反对称变形 结构几何尺寸、形状,构件材料及约束条件均对称于某一
轴,则称此结构为对称结构。 若外力对称于结构对称轴, 结构将产生对称变形。 若外力反对称于结构对称轴,结构将产生反对称变形。
X
2
8EI
0
⑥求其它支反力
由平衡方程得其它支反力, 全部表示于图中。
X
1
1 qa() 28
X
2
3 7
qa()
A
q B
冯康 (1920-1993)
【人物介绍】
冯康,浙江绍兴人 ,出生于 江苏省南京市,数学家、中国有限 元法创始人、计算数学研究的奠基 人和开拓者。
1965年发表名为《基于变分 原理的差分格式》的论文,这篇论 文被国际学术界视为中国独立发展 “有限元法”的重要里程碑 。
3. 在结构外部和内部均存在多余约束,即支反力和内 力都是超静定的。
四. 超静定结构的分析方法 1.力法:以未知力为基本未知量的求解方法。
2.位移法:以未知位移为基本未知量的求解方法。
材料力学
外力超静定
内力超静定 外力和内力超静定
材料力学
11.2 用力法解超静定结构
一、力法的基本思路(举例说明)
a A
a
②选取并去除多余约束,代以多 q 余约束反力。
③建立力法正则方程
B q
A X1 X2
④计算系数dij和自由项DiP
B
用莫尔定理求得
材料力学
A x1 q
x2
B
A
x2
x1 1
建筑工程技术专业《15-1超静定结构的概念及超静定次数的判断》

①去掉一根链杆,相当于去掉一个约束;
②撤除一个单铰,相当于去掉两个约束;
③截断一根连续杆件,相当于去掉三个约束
④将连续变为单铰,相当于去掉一个约束。
老师原声
6
PPT6
在去除约束判断超静定次数时,要注意以下事项:
①同一结构,超静定次数是确定的,但去多余约束的方式有多种。如下图结构,我们可以去掉中间的两个支座,使其变成简支梁,也可以去掉右边两个支座,使其变成外伸梁。
15-1超静定结构的概念及超静定次数的判断脚本
序号
画 面
解 说
配音
背景音乐
字幕
1
片头:微课标题
超静定结构的概念及超静定次数的判断
老师原声
动感纯音乐
2
PPT2
大家好!这次课,我们来学习超静定结构的概念及超静定次数的判断。我们将认识超静定结构的概念及特点,熟悉常见的超静定结构,学会判断超静定次数的方法。
②必须去掉所有多余约束,使体系成为几何不变体系,但也不能多去,使体系几何可变。
③要确保去掉的是多余约束,不能去掉必要约束,不能将原超静定结构变为瞬变体系。例如这个超静定拱,可以去掉任一个水平支座链杆,但不能去掉任一个竖向支座链杆。
7
PPT7
超静定结构的概念,及超静定次数的判断,就给大家介绍到这里,这次课到此结束,谢谢大家观看,下次课再见!
老师原声
4
ppt4
常见超静定结构包括超静定梁,超静定刚架、超静定桁架、超静定拱、超静定组合结构和超静定铰接排架等。这些结构,计算自由度都是小于0的,也就是约束有多余。需要说明的是,这里所谓的多余,并不是真正的多余,仅仅只是从几何构造性上来说,这些约束是多余的。在承载方面,它们不但不多余,而且还发挥着非常重要的作用。这些多余约束上的约束反力,与结构变形有关,仅靠平衡方程是无法求解的。所以超静定结构的力学计算,比静定结构复杂的多。但由于超静定结构刚度大,整体性好,承载能力强,因此,在工程中应用较多。
超静定结构的概念和超静定结构次数的确定

超静定构造旳概念和超静定构造次数旳拟定1.超静定构造旳概念
从几何构成分析旳角度来看,构造可以分为
静定构造:几何不变,无多余约束。
超静定构造:几何不变,有多余约束。
例:如图1所示,有一种多余约束:可去掉任一根支座链杆。
图1
支座反力和内力仅由静力平衡条件无法所有唯一拟定旳、几何不变但有多余约束旳体系,就是超静定构造
多余约束
多余约束旳选用方案并不一定是唯一旳,但是总数目是不变旳。
多余未知力(多余力)
多余约束中产生旳约束力是多余力,多余力旳大小不能由静力平衡条件拟定。
2.超静定次数旳拟定
多余约束旳数目就是超静定次数
判断措施:去掉多余约束使原构造变成静定构造旳措施。
●去掉一根支座链杆或切断一根链杆:去掉一种约束。
●去掉一种铰支座或联结两钢片旳单铰:去掉两个约束。
如图2所
示。
图
●将固定端改成铰支座或将持续杆件上旳刚性联结改成单铰联结:
去掉一种约束。
如
图3中旳固定端改为图4中旳铰支座;图5中旳刚性结点改为图6中旳铰结点。
图图
图图
图8 (c)
这部分是背面力法旳基础。
大伙要纯熟掌握。
如果给出一种超静定构造,要会判断构造旳超静定次数。
超静定结构的概念及超静定次数的确定ppt课件

➢力法基本未知量数目(超静定次数)是唯一的,而基本结构不唯一。
简支梁作为基本结构
原结构
X2
X1
还可以选择哪些 基本结构?
Strucural Analysis
.
School of Civil Engineering, Tongji8Univ.
➢土木工程专业的力学可分为两大类,即“结构力学类”和“弹性力学 类”。
“结构力学类”包括理论力学、材料力学和结构力学,其分析方法具有 强烈的工程特征,简化模型是有骨架的体系(质点、杆件或杆系), 其力法基本未知量一般是“力”,方程形式一般是线性方程。
“弹性力学类”包括弹塑性力学和岩土力学,其思维方式类似于高等数
§9-1 超静定结构的概念
❖ “力法”的发展
➢法国的纳维于1829年提出了求解超静定结构问题的一般方法(基本方 程)。
➢19世纪30年代,由于桥梁跨度的增长,出现了金属桁架结构。从1847 年开始的数十年间,学者们应用图解法、解析法等研究静定桁架的受 力,这奠定了桁架理论的基础。1894年英国的麦克斯韦创立了单位荷 载法和位移互等定理,并用单位荷载法求出桁架的位移,由此学者们 终于得到了求解超静定问题的方法——力法。
(√)
X2
多体悬臂刚 架作为基本
结构
(√)
瞬变体系不 能作为基本
结构
(×)
一个超静定结构可能有多种形式的基本结构,不同基本结构带来不同的计算工作量。
Strucural Analysis
.
School of Civil Engineering, Tong1ji3Univ.
§9-1 超静定次数和力法基本结构
结构力学 力法 超静定次数的确定

1 0
变形条件
在变形条件成立条件下,基本体系的内力和 位移与原结构等价.
湖南交职院
退出
返回
00:19
§7-3 力法的基本概念
A B
结构力学
基本结构(悬臂梁)
超静定结构计算
基本结构
静定结构计算
对静定结构进行内力、位移计算,已经很掌握。
A
q
△ 11
B
△1P
A
B
X1
湖南交职院
退出
返回
00:19
§7-3 力法的基本概念
湖南交职院
退出
返回
00:19
§7-1 超静定结构概述
思考:多余约束是多余的吗?
结构力学
从几何角度与结构的受力特性和使用要求两方面讨论。
q q B l
A
q 8 l2
A
A C
0.5l 0.5l
2
B
B
A
ql
2
ql 32
C
B
ql
2
64
64
超静定结构的优点为: 1. 内力分布均匀 2. 抵抗破坏的能力强
退出 返回
结构力学
在荷载作用下B 点产生向下的位移为⊿1P, 未知力 的作用将使B点产生的向上的位移为⊿1X 。 要使体系的受力情况与原结构一样, 则必须B 的 位移也与原结构一样,要求: 位移协调条件Δ1=Δ1X+Δ1P=0 (a)
静定悬臂刚架
静定三铰刚架
(5)去掉一个连接n个杆件的铰结点,等于拆掉2(n-1) 个约束。 (6)去掉一个连接n个杆件的刚结点,等于拆掉3(n-1) 个约束。
湖南交职院
退出
返回
00:19
超静定结构的概念和超静定次数的确定

第5章力法超静定结构的概念和超静定次数的确定1. 超静定结构的概念前面讨论的是静定结构,从本章开始我们讨论超静定结构的受力情况。
关于结构的静定性可以从两个方面来定义从几何组成的角度来定义静定结构就是没有多余联系的几何不变体系;从受力的角度来定义,静定结构就是只用静力平衡方程就能求出全部反力和内力的结构。
现在,我们要讨论的是超静定结构。
它同样可以从以上两个方面来定义,从几何组成的角度来定义,超静定结构就是具有多余联系的几何不变体系;从受力的角度来定义,超静定结构就是只用静力平衡方程不能求出全部的反力或内力的结构。
如图(a)所示的简支梁是静定的,当跨度增加时,其内力和变形都将迅速增加。
为减少梁的内力和变形,在梁的中部增加一个支座,如图(b)所示,从几何组成的角度分析,它就变成具有一个多余联系的结构。
也正是由于这个多余联系的存在,使我们只用静力平衡方程就不能求出全部4个约束反力F ax、F ay、F by、F cy和全部内力。
具有多余约束、仅用静力平衡条件不能求出全部支座反力或内力的结构称为超静定结构。
图(b)和图所示的连续梁和刚架都是超静定结构。
图给出了工程中常见的几种超静定梁、刚架、桁架、拱、组合结构和排架。
本章讨论如何用力法计算这种类型的结构。
图图图2. 超静定次数的确定力法是解超静定结构最基本的方法。
用力法求解时,首先要确定结构的超静定次数。
通常将多余联系的数目或多余未知力的数目称为超静定结构的超静定次数。
如果一个超静定结构在去掉n个联系后变成静定结构,那么,这个结构就是n次超静定。
显然,我们可用去掉多余联系使原来的超静定结构(以后称原结构)变成静定结构的方法来确定结构的超静定次数。
去掉多余联系的方式,通常有以下几种:(1) 去掉支座处的一根支杆或切断一根链杆,相当于去掉一个联系。
如图所示结构就是一次超静定结构。
图中原结构的多余联系去掉后用未知力x1代替。
图(2) 去掉一个单铰,相当于去掉两个联系(图图(3) 把刚性联结改成单铰联结,相当于去掉一个联系(图。
力法的基本概念

一、超静定结构和超静定次数1超静定结构的概念①几何构造方面:有多余约束的几何不变体系。
②力学解答方面:方程的个数少于未知力的个数。
2.超静定次数的确定去掉多余约束使超静定结构成为静定结构,所去掉的多余约束数目,就是超静定次数。
一般地,*切断链杆(或支杆)是去掉了一个约束,相应一个约束力;*拆开一个铰(或固定铰支座)是去掉了两个约束,相应两个约束力;*切端刚结点(或固定支座)是去掉了三个约束,相应三个约束力;*刚结点变为铰结点,是去掉了一个约束,相应一个约束力;②③?11d练习:按上述去掉约束的办法,判定下列结构的超静定次数。
二、力法的基本结构和多余未知力1.超静定结构经过去掉多余约束后,变为静定结构,这个静定结构称为力法的基本结构。
去掉的多余约束所对应的约束力,称为力法的多余约束力。
基本结构、荷载与多余未知力合称基本体系。
2.基本结构的形式不唯一。
一般地,基本结构和多余未知力同时产生。
选取时,应使计算简单为前提。
前例题与练习中,给出了每个结构的部分基本结构和相应的多余未知力。
三、力法原理1.基本假设:弹性小变形2.确定超静定次数,选取恰当的基本体系3.位移协调条件的确定(即,补充方程的建立)4.计算柔度系数(单位未知力产生的位移),建立力法方程5.结构内力的叠加公式6.作内力图示例1P ~* A ElElP *LX■Ck丁L nZf———r基本体系解:1)一次超静定结构,取基本体系如图所示。
2)基本思路超静定结构用平面三个平衡方程是不够的。
注意到原结构在荷载作用下的内力和变形是唯一确定的,特别地,支座反力也是确定的。
因此,如果设X是支座反力,则原结构的内力与变形就与基本体系(其结构是静定的)在荷载P和支座反力X共同作用下的内力与变形等价。
这样,原超静定结构的计算就转化为静定结构的计算。
问题是,X是未知的。
需要考虑位移协调条件,即,补充方程。
显然,基本体系中,B端是自由端;而原超静定结构中却是有支座的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
支座反力与内力仅由静力平衡条件无法全部唯一确定的、几何不变但有多余约束的体系,就就是超静定结构
多余约束
多余约束的选取方案并不一定就是唯一的,但就是总数目就是不变的。
多余未知力(多余力)
多余约束中产生的约束力就是多余力,多余力的大小不能由静力平衡条件确定。
2、超静定次数的确定
多余约束的数目就就是超静定次数
判断方法:去掉多余约束使原结构变成静定结构的方法。
● 去掉一根支座链杆或切断一根链杆:去掉一个约束。
● 去掉一个铰支座或联结两钢片的单铰:去掉两个约束。
如图2所示。
● 将固定端改成铰支座或将连续杆件上的刚
性联结改成单铰联结:去掉一个约束。
如
图3中的固定端改为图4中的铰支座;图5中
的刚性结点改为图6中的铰结点。
● 去掉一个固定端或将刚性联
结切断如图7所示:去掉三个
约束。
在确定超静定次数时,还应注意以下两点:
(1)不要把原结构拆成一个几何可
变体系。
所以要特别注意非多余约束不能去掉,比如 (a)中的水平链杆支座不能去掉。
(2) 要把所有多余约束全部去掉。
如 图8(a)所示结构,如果只去掉一根水平链杆支座得到如图8 (b)所示结构,则其中的闭合框仍具有三个多余约束,必须把闭合框再切开一个截面,
图1
图2
图3 图4
图5 图6 图7。
