平行四边形基本知识点
《平行四边形》基本知识点总结

《平行四边形》基本知识点总结一.平行四边形:1:定义:两组对边分别平行的四边形是平行四边形.2.性质(1)边:平行四边形两组对边分别平行且相等;(2)角:平行四边形的邻角互补,对角相等;(3)对角线:平行四边形的对角线互相平分;(4)两条平行线间的平行线段相等,平行线间的距离处处相等。
(5)过平行四边形两对角线的交点的直线将平行四边形的面积二等分。
3.判定:(1)边:①(定义法):两组对边分别平行的四边形是平行四边形②两组对边分别相等的四边形是平行四边形③一组平行且相等的四边形是平行四边形(2)角:两组对角分别相等的四边形是平行四边形(3)对角线:对角线互相平分的四边形是平行四边形4:有关面积:(1)如图1:S = AB·CF = AD·CE(2)如图2: S△AOB =S△COB=S△COD= S△AOD(依据:等底等高的两三角形面积相等)(3)如图3:S△ABC =S△CBD,S△AOD= S△COD(依据:等底等高的两三角形面积相等)S△AOB :S△AOD=BO:OD,S△AOD:S△COD=AO:OC,(依据:等高不等底的两三角形面积之比等于对应底之比)5:三角形中位线(1)定义:连接三角形两边中点的线段是三角形的中位线(2)定理:三角形的中位线平行于第三边,并且等于第三边的一半(3)中点四边形:顺次连结四边形各边中点所得的四边形叫中点四边形,它是平行四边形二、矩形:1:定义:有一个角是直角的平行四边形是矩形,2:性质:(1)矩形具备平行四边形的所有性质(2)矩形的四个角都是直角(3)对角线相等;3:判定:(1)(定义法):有一个角是直角的平行四边形是矩形,(2)有三个角是直角的四边形是矩形(3)对角线互相平分且相等的四边形是矩形(4)对角线相等的平行四边形是矩形4:直角三角形两重要性质:(1)在直角三角形中,30°的角所对直角边等于斜边的一半。
(2)直角三角形斜边上的中线等于斜边的一半。
(完整版)平行四边形基本知识点总结

(完整版)平行四边形基本知识点总结平行四边形基本知识点总结
平行四边形是一种特殊的四边形,它具有一些独特的性质和特点。
以下是平行四边形的基本知识点总结:
定义
平行四边形是指具有两组对边分别平行的四边形。
性质
1. 对边平行性质:平行四边形的两组对边分别平行。
2. 对角线性质:平行四边形的对角线互相平分,并且长度相等。
3. 内角和性质:平行四边形的内角的和为180度。
4. 外角性质:平行四边形的外角的和为360度。
5. 对边长度性质:平行四边形的对边长度相等。
6. 同底角性质:与平行四边形的一条边相邻,另一条边平行的两个内角相等。
7. 同旁内角性质:与平行四边形的两条边相邻,另一条边平行的两个内角互补。
判定方法
1. 对边平行判定:如果一个四边形中有两组对边分别平行,则它是一个平行四边形。
2. 对角线平分判定:如果一个四边形的对角线互相平分,并且长度相等,则它是一个平行四边形。
特殊类型
1. 矩形:具有四个内角都为90度的平行四边形。
2. 正方形:具有四个内角都为90度,且四条边长度相等的平
行四边形。
相关公式
1. 平行四边形的面积公式:面积 = 底边长度 ×高度。
2. 平行四边形的周长公式:周长= 2 ×(底边长度+ 侧边长度)。
以上是关于平行四边形的基本知识点总结。
通过了解这些性质
和定理,可以更好地理解和解决相关的数学问题。
数学平行四边形重要知识点

数学平行四边形重要知识点
平行四边形(Parallelogram),是在同一个二维平面内,由两组平行线段组成的闭合图形。
下面是店铺整理的数学平行四边形重要知识点,欢迎阅览。
1、平行四边形的概念
两组对边分别平行的四边形叫做平行四边形。
平行四边形用符号“□ABCD”表示,如平行四边形ABCD记作“□ABCD”,读作“平行四边形ABCD”。
2、平行四边形的性质
(1)平行四边形的邻角互补,对角相等。
(2)平行四边形的对边平行且相等。
推论:夹在两条平行线间的平行线段相等。
(3)平行四边形的对角线互相平分。
(4)若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的'交点为中点,并且这两条直线二等分此平行四边形的面积。
3、平行四边形的判定
(1)定义:两组对边分别平行的四边形是平行四边形
(2)定理1:两组对角分别相等的四边形是平行四边形
(3)定理2:两组对边分别相等的四边形是平行四边形
(4)定理3:对角线互相平分的四边形是平行四边形
(5)定理4:一组对边平行且相等的四边形是平行四边形
4、两条平行线的距离
两条平行线中,一条直线上的任意一点到另一条直线的距离,叫做这两条平行线的距离。
平行线间的距离处处相等。
5、平行四边形的面积
S平行四边形=底边长×高=ah
【数学平行四边形重要知识点】。
平行四边形基础知识点

A BCDADCCB平行四边形知识点总结1、平行四边形(1)定义:两组对边分别平行的四边形叫做平行四边形。
记作ABCD。
(如右图:AB∥CD,AD∥BC)(2)性质:①对边相等②对角相等,邻角互补③对角线互相平分(3)判定:定义:两组对边分别平行的四边形叫做平行四边形。
两组对边分别相等的四边形是平行四边形。
两组对角分别相等的四边形是平行四边形。
对角线互相平分的四边形是平行四边形。
一组对边平行且相等的四边形是平行四边形。
(4)面积 = 底×高(5)平行四边形是中心对称图形,但不是轴对称图形,平行四边形的对角线的交点是平行四边形的对称中心。
2、矩形(特殊的平行四边形)(1)定义:有一个角是直角的平行四边形叫做矩形。
(2)性质:①四个角都是直角②对角线相等(3)判定:对角线相等的平行四边形是矩形。
有三个角是直角的四边形是矩形。
(4)面积= 长X宽(5)矩形既是轴对称图形又是中心对称图形。
矩形的对称中心是矩形对角线的交点;矩形有两条对称轴,矩形的对称轴是过矩形对边中点的直线;矩形的对称轴过矩形的对称中心。
3、菱形(特殊的平行四边形)(1)定义:有一组邻边相等的平行四边形叫做菱形。
(2)性质:①四条边都想等②两条对角线互相垂直,且每条对角线平分一组对角(3)判定:对角线互相垂直的平行四边形是菱形。
四条边相等的四边形是菱形。
(4)菱形ABCD的对角线是AC、BD,则菱形的面积公式是:S=底×高,S=12AC BD⨯⨯(5)菱形既是中心对称图形又是轴对称图形,菱形的对称中心是菱形对角线的交点,菱形的对称轴是菱形对角线所在的直线,菱形的对称轴过菱形的对称中心。
4、两条平行线之间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离。
5、三角形的中位线定理:平行于三角形的第三边,且等于第三边的一半。
6、直角三角形性质:直角三角形斜边上的中线等于斜边的一半。
1.(2016•徐州)如图,在△ABC中,∠ABC=90°,∠BAC=60°,△ACD是等边三角形,E 是AC的中点,连接BE并延长,交DC于点F,求证:(1)△ABE≌△CFE;(2)四边形ABFD是平行四边形.2.(2016•梅州)如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD 上的点,且BE=DF,连接EF交BD于O.(1)求证:BO=DO;[来源:学+科+网](2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AE的长.3.(2015•扬州)如图,将▱ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.(1)求证:四边形BCED′是平行四边形;(2)若BE平分∠ABC,求证:AB2=AE2+BE2.4.(2016•青岛)已知:如图,在▱ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点0.(1)求证:△ABE≌△CDF;(2)连接DG,若DG=BG,则四边形BEDF是什幺特殊四边形?请说明理由.。
平行四边形知识点归纳和题型归类

平行四边形知识点归纳和题型归类平行四边形知识点归纳和题型归类要点梳理】要点一、平行四边形1.定义:有两组对边分别平行的四边形叫做平行四边形。
2.性质:(1)对边相等;(2)同位角相等;(3)相邻角互补;(4)是中心对称图形。
3.面积:S = 底 ×高。
4.判定:边:(1)有两组对边分别平行的四边形是平行四边形;(2)对边相等的四边形是平行四边形;(3)对角线互相平分的四边形是平行四边形。
角:(4)有一组对边平行,且同位角相等的四边形是平行四边形。
对角线:有一组对边相等,且互相平分的四边形是平行四边形。
要点诠释:平行线的性质:(1)平行线间的距离相等;(2)等底等高的平行四边形面积相等。
要点二、矩形1.定义:有四个角都是直角的平行四边形叫做矩形。
2.性质:(1)对边相等;(2)相邻角互补;(3)对角线相等;(4)是中心对称图形,也是轴对称图形。
3.面积:S = 长 ×宽。
4.判定:有四个角都是直角的平行四边形是矩形。
要点诠释:由矩形得直角三角形的性质:(1)直角三角形斜边上的中线等于斜边的一半;(2)直角三角形中,30度角所对应的直角边等于斜边的一半。
要点三、菱形1.定义:有四个边都相等的平行四边形叫做菱形。
2.性质:(1)对边相等;(2)相邻角互补;(3)对角线相等;(4)是中心对称图形,也是轴对称图形。
3.面积:S = 对角线之积的一半。
4.判定:有一组对边平行且相等的四边形是菱形。
要点四、正方形1.定义:四条边都相等,四个角都是直角的平行四边形叫做正方形。
2.性质:(1)对边相等;(2)相邻角互补;(3)对角线相等;(4)是中心对称图形,也是轴对称图形;(5)两条对角线把正方形分成四个全等的等腰直角三角形。
3.面积:S = 边长的平方,也可以用对角线的平方的一半求解。
4.判定:(1)有一组对边平行且相等的菱形是正方形;(2)有四个角都是直角的矩形是正方形;(3)对角线互相垂直平分且相等的四边形是正方形;(4)四条边都相等,四个角都是直角的四边形是正方形。
平行四边形初中知识点

平行四边形初中知识点
一、平行四边形的定义。
1. 两组对边分别平行的四边形叫做平行四边形。
- 用符号“▱”表示平行四边形,例如平行四边形ABCD记作“▱ABCD”。
二、平行四边形的性质。
1. 边的性质。
- 平行四边形的对边平行且相等。
- 即若▱ABCD,则AB = CD,AD = BC;AB∥CD,AD∥BC。
2. 角的性质。
- 平行四边形的对角相等,邻角互补。
- 在▱ABCD中,∠A = ∠C,∠B = ∠D;∠A+∠B = 180°,∠B + ∠C=180°等。
3. 对角线的性质。
- 平行四边形的对角线互相平分。
- 若▱ABCD,对角线AC、BD相交于点O,则AO = CO,BO = DO。
三、平行四边形的判定。
1. 边的判定。
- 两组对边分别平行的四边形是平行四边形(定义判定)。
- 两组对边分别相等的四边形是平行四边形。
- 一组对边平行且相等的四边形是平行四边形。
2. 角的判定。
- 两组对角分别相等的四边形是平行四边形。
3. 对角线的判定。
- 对角线互相平分的四边形是平行四边形。
四、平行四边形的面积。
1. 平行四边形的面积等于底乘以高。
- 若平行四边形的底为a,这条底边上的高为h,则面积S = ah。
- 同底(等底)等高的平行四边形面积相等。
平行四边形知识点
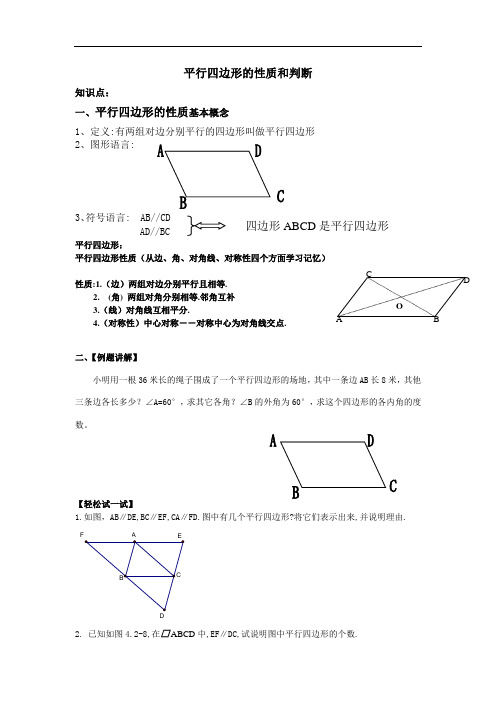
A BC DO 平行四边形的性质和判断知识点:一、平行四边形的性质基本概念1、定义:有两组对边分别平行的四边形叫做平行四边形2、图形语言:3、符号语言平行四边形:平行四边形性质(从边、角、对角线、对称性四个方面学习记忆) 性质:1.(边)两组对边分别平行且相等.2. (角) 两组对角分别相等.邻角互补3.(线)对角线互相平分.4.(对称性)中心对称--对称中心为对角线交点.二、【例题讲解】小明用一根36米长的绳子围成了一个平行四边形的场地,其中一条边AB 长8米,其他三条边各长多少?∠A=60°,求其它各角?∠B 的外角为60°,求这个四边形的各内角的度数。
【轻松试一试】1.如图,AB ∥DE,BC ∥EF,CA ∥FD.图中有几个平行四边形?将它们表示出来,并说明理由.AFD2. 已知如图4.2-8,中,EF ∥DC,试说明图中平行四边形的个数.NMH G F E D CBA图4.2-8角的计算:1、中, BC=2AB, CA ⊥AB,则∠B=______度,∠CAD=______度.DCB A2中,∠A : ∠B=3:2,则∠C=___ 度,∠D=______度.边及周长的计算1、如图,平行四边形的对角线相交于点O ,BC=7㎝,BD=10㎝,AC=6㎝。
求△AOD 的周长。
2平行四边形的周长是100cm, AB:BC=4:1,则AB 的长是_______。
3.已知平行四边形的面积是144,相邻两边上的高分别为8和9,则它的周长是______________.4.用20米长的一铁丝围成一个平行四边形,使长边与短边的比为3:2,则它的边长为________短边长为__________.平行四边形的判断平行四边形的四个(或五个)判定方法,这些判定的方法是: 从边看: ①两组对边分别平行的四边形是平行四边形; ②两组对边分别相等的四边形是平行四边形; ③一组对边平行且相等的四边形是平行四边形.从对角线看:对角线互相平分的四边形是平行四边形.(从角看:两组对角分别相等的四边形是平行四边形.)【例题讲解】已知:如图,ABCD 中,E 、F 分别是AD 、BC 的中点,求证:BE=DF .分析:证明BE=DF ,可以证明两个三角形全等,也可以证明四边形BEDF 是平行四边形,比较方法,可以看出第二种方法简单. 证明:∵ 四边形ABCD 是平行四边形, ∴ AD ∥CB ,AD=CD . ∵ E 、F 分别是AD 、BC 的中点, ∴ DE ∥BF ,且DE=21AD ,BF=21BC .∴ DE=BF .∴ 四边形BEDF 是平行四边形(一组对边平行且相等的四边形平行四边形). ∴ BE=DF .例2、已知:如图,ABCD 中,E 、F 分别是AC 上两点,且BE ⊥AC 于E ,DF ⊥AC 于F .求证:四边形BEDF 是平行四边形.分析:因为BE ⊥AC 于E ,DF ⊥AC 于F ,所以BE ∥DF .需再证明BE=DF ,这需要证明△ABE 与△CDF 全等,由角角边即可.证明:∵ 四边形ABCD 是平行四边形, ∴ AB=CD ,且AB ∥CD . ∴ ∠BAE=∠DCF .∵ BE ⊥AC 于E ,DF ⊥AC 于F ,∴ BE ∥DF ,且∠BEA=∠DFC=90°. ∴ △ABE ≌△CDF (AAS ). ∴ BE=DF .∴ 四边形BEDF 是平行四边形(一组对边平行且相等的四边形平行四边形)例3、 已知:如图3,E 、F 是平行四边形ABCD 对角线AC 上两点,且AE =CF 。
5第五讲平行四边形初步

第五讲平行四边形初步第一部分知识梳理一、平行四边形的性质1.两组对边分别_____ 的四边形叫做平行四边形.它用符号“口“表示,平行四边形ABCD 记作__________ 。
2.平行四边形的两组对边分别_______ 且_____ ;平行四边形的两组对角分别______ : 两邻角______ :平行四边形的对角线_______ :平行四边形的面积=底边长x _________ .3.在L UBCD中,若ZA-Z5=40°,贝lJZA= _________ , ZB= _________ .4.若平行四边形周长为54cm,两邻边之差为5cm,则这两边的长度分别为 ____________ .5.若L UBCD的对角线AC平分ZDAB,则对角线AC与BD的位置关系是_________ ・6.如图,LL坊CD中,CE丄AB,垂足为£,如果ZA = 115°,则ZBCE= ____________ .7. _______________________________________________________________ 如图,在LL拐CD 中,DB=DC、ZA=65。
,CE丄BD 于E,则ZBCE= _____________________二、平行四边形的判定1.平行四边形的判左方法有:从边的条件有:①两组对边__________ 的四边形是平行四边形;②两组对边________ 的四边形是平行四边形;③一组对边_________ 的四边形是平行四边形.从对角线的条件有:④两条对角线__________ 的四边形是平行四边形.从角的条件有:⑤两组对角______ 的四边形是平行四边形.注意:一组对边平行另一组对边相等的四边形_____ 是平行四边形.(填“一左"或“不一泄”)第二部分例题与解题思路方法归纳知识点一平行四边形的性质【例题1】如图,在平行四边形ABCD中,E为BC中点,AE的延长线与DC的延长线相交于点F.(1)证明:ZDFA=ZFAB;(2)证明:A ABE^AFCE・K选题意图》此题主要考查平行四边形的性质和判左以及全等三角形的证明,使学生能够灵活运用平行四边形知识解决有关问题.K解题思路3(1)利用平行四边形的两组对边分别平行即可得到两角相等:(2)利用上题证得的结论及平行四边形对边相等即可证明两三角形全等.K参考答案》证明:(1)•••在平行四边形ABCD中,•••DF〃AB,AZDFA=ZFAB;(2) TE为BC中点,•••EC=EB・Z.DFA =乙FABAlztAABE 与A FCE中,厶CEF = Z-BEAfEB = ECAAABE^AFCE.【课堂训练题】1.如图,在口ABCD中,E为BC的中点,连接DE.延长DE交AB的延长线于点F・求证:K参考答案』解:由ABCD是平行四边形得AB〃CD,AZCDE=ZF, ZC=ZEBF・又TE为BC的中点,AADEC^AFEB,:.DC=FB ・又TAB二CD,AAB=BF ・2.如图,在平行四边形ABCD中,ZBAD=32°.分别以BC、CD为边向外作A BCE和A DCF,使BE=BC, DF=DC, ZEBC=ZCDF,延长AB交边EC于点G,点G在E、C两点之间, 连接AE、AF.(1)求证:A ABE^AFDA:K参考答案月证明:(I)在平行四边形ABCD中,AB二DC, 又VDF=DC>A AB=D F・同理EB=AD.在平行四边形ABCD中,ZABC=ZADC,又TZEBOZCDF,AZABE=ZADF.AAABE^AFDA ・(2)VAABE^AFDA, AZAEB=ZDAF ・VZEBG=ZEAB+ZAEB, AZEBG=ZDAF+ZEAB, VAE 丄AF,••• ZEAF=90°.VZBAD=32°,••• ZDAF+ZEAB=90° - 32°=58°.AZEBG=58°.知识点二平行四边形的面积相关【例题2】阅读下而操作过程,回答后而问题:在一次数学实践探究活动中,小强过A、C 两点画直线AC把平行四边形ABCD分割成两个部分(如图(a)),小刚过AB、AC的中点画直线EF,把平行四边形ABCD也分割成两个部分(如图(b));(1) __________________________________________ 这两种分割方法中而积之间的关系为:Si S2, S3 _____________________________________ S4;(2)根据这两位同学的分割方法,你认为把平行四边形分割成满足以上而积关系的直线有条,请在图(c)的平行四边形中画岀一种:(3)由上述实验操作过程,你发现了什么规律?[[选题意图》平行四边形的两条对角线交于一点,这个点是平行四边形的中心,也是两条对角线的中点,经过中心的任意一条直线可将平行四边形分成完全重合的两个图形.&解题思路3(1)都是相等关系,因为AC, EF都经过平行四边形的对称中心,故分得的两部分的而积相等;(2)有无数条,因为经过对称中心的直线有无数条:(3)经过平行四边形对称中心的宜线把平行四边形的而积分成相等的两份.g参考答案》解:(1) Si=S2, S3=S4:(2)无数,如图,所以直线过0即可;(3)经过平行四边形对称中心的任意直线,都可以把平行四边形分成满足条件的图形.【课堂训练题】1 •已知平行四边形ABCD的周长为36cm,过D作AB,BC边上的髙DE、DF,且DE = 4齿cm,DF = 5嶺cm、求平行四边形ABCD的面积・K参考答案》解:设AB=x,则BC=18-x,由AB・DE=BC・DF代入数值得:4\/3x = 5\/3 (18・x),解之x=10,所以平行四边形ABCD的面积为40^3.2.如图,在平行四边形ABCD中.EF〃BC, GH〃AB, EF、GH的交点P在BD上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
判定 : 对角线相等的平行四边形是矩形;有三个角是直角的四边形是矩形. 3、菱形 : 有一组邻边相等的平行四边形叫做菱形.
菱形具有平行四边形的所有性质; 并且四条边都相等, 对角线互相垂直平分 , 每一条对角线平分一组对角.
判定 : 对角线 互相垂直的平行四边形 是菱形;对角线 互相垂直平分的四边形 是菱形;四条边相等的 四边形 是菱形.
正方形 既是矩形又是菱形. 只有一组对边平行的四边形叫做 梯形 ;不平行的一组对边相等的梯形 等腰梯 形.
平行四边形基本知识点
1、平行四边形:两组对边分别平行的四边形叫做平行四边形.
性质及判定:
平行四边形
对边平行 对边相等 对角相等 对角线互相平分
两组对边平行的四边形 两组对边相等的四边形 两组对角相等的四边形 对角线互相平分的四边形 一组对边平行且相等的四边形
平行四边形
三角形的 中位线 平行于三角形的第三边,且等于第三边的一半. 2、矩形Байду номын сангаас: 有一个角是直角的平行四边形叫做矩形 ( 长方形 ) .
