考研高等数学知识点整理(附思维导图)
考研数学 知识结构思维导图(数二)
1.分离变量,物以类聚人以群分 2.y'在等式左侧,右侧应写成乘积形式
一阶微分方程的求解
齐次型
y'=f(y/x)
对x求导
1/y'=f(x/y)
对y求导
换元后分离变量,交换x和y的地位
一阶线性型(或可换元为它)
y'+p(x)y=q(x) 伯努利方程
y'+p(x)y=q(x)的特殊形式
伯努利方程可理解为一 阶线性方程的普遍形式
符号函数 抽象函数
复合函数
偏导函数
换元法
一元函数积分换元法 二元函数积分换元法
应用
面积
1.积分变化口诀:后积先定限,限内画直 线,先交先下限,后交写上限;
2.注意对称性得0的应用可以极大地化简计 算
微分方程
可分离变量
y'=f(x).g(y)
分离变量
y'=f(ax+by+c)
换元后再分离变量
一般一层积分不易处理,化成两层积分,在交换 积分次序
分部积分法
换序型
反常积分的计算
研究对象
常规题型取绝对值时取值范围
曲线平移时相关符号不同取值范围所对应的面积
切线综合
函数列综合
题型总结
在平面极坐标系中,如果极径ρ随极角θ的 增加而成比例增加(或减少),这样的动
点所形成的轨迹叫做螺线。
阿基米德螺旋线
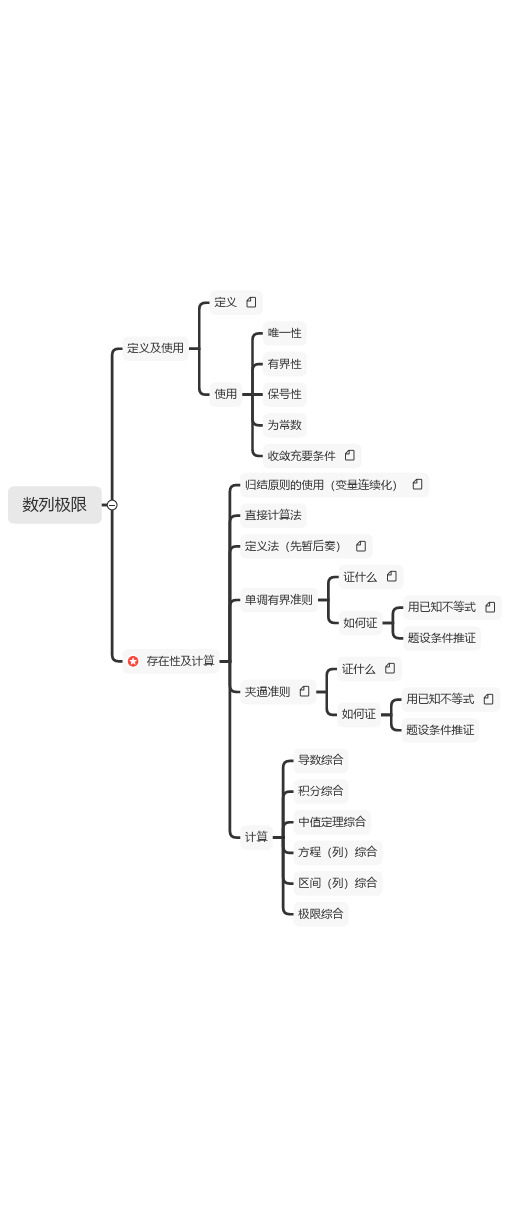
数列极限
定义
定义及使用
唯一性 有界性
使用
保号性
为常数
收敛充要条件
归结原则的使用(变量连续化)
直接计算法
定义法(先暂后奏)
(完整word版)考研高等数学知识点总结

高等数学知识点总结导数公式:基本积分表:三角函数的有理式积分:222212211cos 12sin u dudx x tg u u u x u u x +==+-=+=, , , ax x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22='='⋅-='⋅='-='='222211)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx ctgxdx x C x dx tgx x Cctgx xdx x dx C tgx xdx x dx xx)ln(ln csc csc sec sec csc sin sec cos 22222222C axx a dx C x a xa a x a dx C a x ax a a x dx C a xarctg a x a dx Cctgx x xdx C tgx x xdx Cx ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ一些初等函数: 两个重要极限:三角函数公式: ·诱导公式:·和差角公式: ·和差化积公式:2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβαβαβαβαβα-+=--+=+-+=--+=+αββαβαβαβαβαβαβαβαβαβαβαctg ctg ctg ctg ctg tg tg tg tg tg ±⋅=±⋅±=±=±±=±1)(1)(sin sin cos cos )cos(sin cos cos sin )sin(μμμxxarthx x x archx x x arshx e e e e chx shx thx e e chx e e shx x x xx xx xx -+=-+±=++=+-==+=-=----11ln21)1ln(1ln(:2:2:22)双曲正切双曲余弦双曲正弦...590457182818284.2)11(lim 1sin lim 0==+=∞→→e xxx x x x·倍角公式:·半角公式:ααααααααααααααααααcos 1sin sin cos 1cos 1cos 12cos 1sin sin cos 1cos 1cos 122cos 12cos 2cos 12sin -=+=-+±=+=-=+-±=+±=-±=ctg tg·正弦定理:R CcB b A a 2sin sin sin === ·余弦定理:C ab b a c cos 2222-+=·反三角函数性质:arcctgx arctgx x x -=-=2arccos 2arcsin ππ高阶导数公式——莱布尼兹(Leibniz )公式:)()()()2()1()(0)()()(!)1()1(!2)1()(n k k n n n n nk k k n k n n uv v u k k n n n v u n n v nu v u v u C uv +++--++''-+'+==---=-∑ΛΛΛ中值定理与导数应用:拉格朗日中值定理。
(完整版)考研高等数学知识点总结(最新整理)

du u dx u dy u dz x y z
全微分的近似计算:z dz f x (x, y)x f y (x, y)y 多元复合函数的求导法:
z f [u(t),v(t)]
dz z u z v dt u t v t
z f [u(x, y),v(x, y)]
z z u z v x u x v x
x2 a2 dx x x2 a2 a2 ln x x2 a2 C
2
2
a2 x2 dx x a2 x2 a2 arcsin x C
2
2
a
sin
x
2u 1u
2
, cos
x
1 1
u u
2 2
, u
tg
x , dx 2
2du 1 u2
1 / 13
一些初等函数:
两个重要极限:
双曲正弦 : shx ex ex 2
当u u(x, y),v v(x, y)时,
du u dx u dy x y
dv v dx v dy x y
隐函数的求导公式:
隐函数F (x,
y)
0, dy dx
Fx Fy
, d 2 y dx 2
x
(
Fx Fy
)+
y
(
Fx Fy
)
dy dx
隐函数F (x, y, z) 0, z Fx , z Fy
x
x
三角函数公式: ·诱导公式:
函数 角A -α 90°-α 90°+α 180°-α 180°+α 270°-α 270°+α 360°-α 360°+α
sin cos tg ctg
-sinα cosα cosα sinα -sinα -cosα -cosα -sinα sinα
高等数学考研知识点总结

高等数学考研知识点总结
嘿,宝子们!今天咱就来唠唠高等数学考研那些知识点哈!
先来说说函数极限吧!就好比你跑步,你能跑的最远距离就是那个极限呀!比如说,给你个函数 f(x) = (x - 1)/(x - 1),当 x 趋近于 1 的时候,这极限不就等于 1 嘛,这多明显呀!
然后呢,还有导数!导数就像是汽车的速度表,能告诉你函数变化的快慢。
就像曲线y = x²,它的导数就是 2x 呀,这就是告诉你在每个点上变化得有多快!“哎呀,这导数可太重要啦!”
再说说积分呀!积分就像把无数个小碎片拼成一个完整的东西。
比如你要计算一个图形的面积,用积分不就能搞定嘛!“哇塞,积分真的好神奇呀!”
高等数学里还有无穷级数呢!这就好像是一串无穷无尽的糖果,你得好好研究怎么去数清楚呀!像幂级数,那可真是考研的重点呀!
高等数学可不简单,但咱别怕呀!只要咱认真学,肯定能搞定它。
就像爬山一样,虽然过程累,但爬到山顶那一刻,哇,那感觉超棒的!宝子们,
加油呀!咱一定能在高等数学考研的道路上取得胜利!我相信你们都可以的!这就是我的观点,高等数学难,但我们能战胜它!。
考研数学思维导图高等数学篇

= o(α )
如果lim β = ∞,那么就说β是比α低阶的无穷小 α
如果lim β = c ≠ 0,那么就说β与α是同阶无穷小 α
如果
lim
β αk
= c ≠ 0, k
> 0,那么就说β是关于α的k阶无穷小
如果lim β = 1,那么就说β与α是等价无穷小,记作α ~ β α
⑨
sin x =
x
−
1 6
(x) − kx] = lim[ f x→-∞
(x) − kx] = b,则y
=
kx + b是曲线y
=
f
( x)的一条斜渐近线
2/31
数列极限的定义
lim
n→∞
xn =A
⇔
∀ε
>
0, ∃N
>
0,当n
>
N 时, 有
xn
−
A
<
ε
极限性质
是常数 唯一性 有界性 保号性
设数列{xn}收敛,则( )
(A)当 lim sin n→∞
中值定理证明方法(上) .................................................... 10
第十章 重积分...............................................................................25
② 设函数f (x)在闭区间[a,b]上连续,且f (a)与f (b)异号(即f (a) • f (b) < 0),
则在开区间(a,b)内至少有一点 ξ,使f (ξ ) = 0.
③ 设函数f (x)在闭区间[a,b]上连续,且在这区间的端点取不同的函数值,f (a) = A, f (b) = B,
高等数学a1思维导图第一章

高等数学a1思维导图第一章
高等数学a1的第一章主要讲的是集合的概念。
集合是一组有相
同特点或共同性质的事物的统称,它是数学研究中非常重要的知识点。
集合由不同元素构成,它们构成了某些特定的结构。
集合几何定义,是指将一组有共同特点的元素看作一个整体,形
成一个集合。
例如,将一组字符看作一个字符串。
集合的概念在其他
学科中也有用,比如组合,统计,数论等等,它们可以分为有序集合、无序集合和有穷集合。
图论研究中也有另一种称为子集的概念。
子集是指集合A中包含
在集合B中的所有元素,它们具有集合A特定的性质,是集合A的一
个子集。
必要性原理也常常用在集合论中,它指出集合A和集合B之间可
能存在一定的依赖关系,如果集合A包含某个元素,则集合B也必定
包含该元素。
本章的内容为我们提供了更深刻的理解集合的概念,帮助我们更
好地应用这种思维方式,更有效地解决问题,从而更好地推动数学的
发展。
考研数学一章节知识结构图
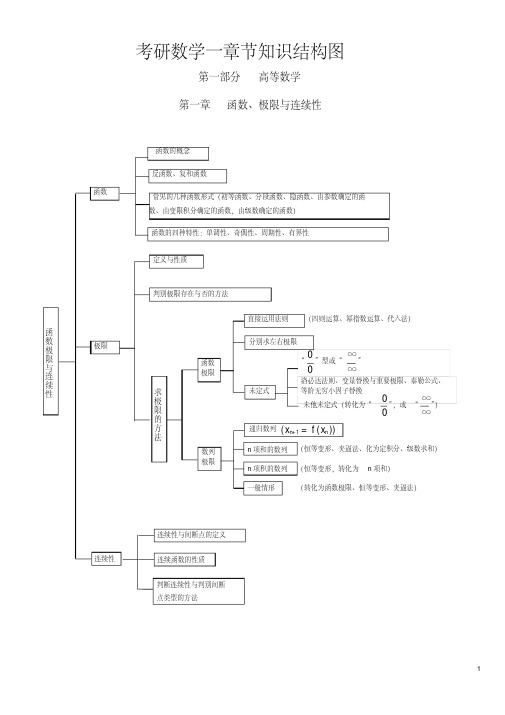
重积分
计算公式 二重积分的极坐标变换面积微元 重积分变量替换 三重积分柱坐标变换,体积微元
d σ= rdrd θ dV = rdrd θ dz
三重积分球坐标变换、体积微元
几何应用 应用 物理应用 多元函数积 分学 平面图形面积、体积 质量、质心、转动惯量
dV = ρ sin ? dρ d? dθ
2
基本概念、性质
8
第九章
常微分方程
基本概念 一阶微分方程 基本类型 变量可分离方程 一阶线性方程 全微分方程 伯努力方程 可化为基本类型 齐次方程 用某些简单的变量代换求解某些微分方程
常 微 分 方 程
解的叠加原理 性质 通解的结构 可降阶的 高 阶微分方程 基本概念 可降阶的类型 二阶,高阶微分方程
基本概念 二阶线性常系数方程 高阶线 性微 分方程 二阶微分方程(含 某些高阶情形) 特殊的二阶线性变系数方程 可化为求解微分方程的情形(含变限积分的方程)
奇偶性与周期函数的导数性质 隐函数与反函数求导法 分阶函数求导法 基本求导法则 含参数方程所确定的函数的求导 对数求导法及幂指数求导法 导 数的 计 算与 高 阶导数 高阶导数
导 数 与 微 分
高阶导数的定义
极大值、极小值
微分 中值 定理 与 导数的应用
几种微分中值定理
( 费马定理、罗尔定理、拉格朗日中值定理、泰勒公定、柯西定理)
17
第三章
多维随机变量及其概率分布
基本概念
多维,二维随机变量 离散型
考研数学一章节知识结构图
第一部分 第一章 高等数学 函数、极限与连续性
函数的概念 反函数、复和函数 函数 常见的几种函数形式(初等函数、分段函数、隐函数、由参数确定的函 数、由变限积分确定的函数,由级数确定的函数) 函数的四种特性:单调性、奇偶性、周期性、有界性
高数基础知识总结与重点概念整理

高数基础知识总结与重点概念整理
一、导数与微分
导数:描述函数在某一点附近的变化率,是函数值的极限。
可导性:函数在某点可导,当且仅当该点附近存在一个定义恰当的导数。
微分:一个近似值,表示函数在某点附近的小变化所引起的函数值的大致变化。
二、积分
不定积分:求一个函数的原函数(或反导数),即求函数的不定积分。
定积分:对一个区间上函数的值的总和的量度,即求函数的定积分。
微积分基本定理:定积分可化为不定积分的计算。
三、级数
数列:一个数字序列。
无穷级数:无穷多个数的和,即数列的和。
收敛性:无穷级数趋于一个有限的和的性质称为收敛性。
发散性:无穷级数不收敛的性质称为发散性。
四、多元函数
多元函数:定义在多个变量上的函数。
偏导数:多元函数对一个变量的导数。
方向导数:描述函数在某点处沿某一方向的变化率。
梯度:方向导数的最大值,表示函数在某点处沿梯度方向的增长最快的方向。
五、微分方程
微分方程:包含未知函数的导数或微分的方程。
初值问题:给定初始条件的微分方程问题。
通解与特解:满足微分方程的解称为通解,满足特定初始条件的解称为特解。
2023年考研数学高数知识点终极梳理

2023年考研数学高数知识点终极梳理2023年考研数学高数知识点终极梳理作为考生来说,复习肯定要扎扎实实的,押题的话,我们正好改成重点,尤其是到了冲刺阶段,有所侧重的做题型复习也是有必要的,我们经常说要“抓重点”,抓住重点就可以进步复习的效率,要是侧重掌握某些题型、加深印象,这与全面复习掌握根底是不矛盾的。
我们认为押题和有所侧重是在打好根底的情况下侧重,这样才不会走偏,假如一个考生就想押题,让教师告诉你几道题就得高分,这样是不正确的,往往不会成功。
第一章函数、极限与连续1、函数的有界性2、极限的定义〔数列、函数〕3、极限的性质〔有界性、保号性〕4、极限的计算〔重点〕〔四那么运算、等价无穷小交换、洛必达法那么、泰勒公式、重要极限、单侧极限、夹逼定理及定积分定义、单调有界必有极限定理〕5、函数的连续性6、连续点的类型7、渐近线的'计算第二章导数与微分1、导数与微分的定义〔函数可导性、用定义求导数〕2、导数的计算〔“三个法那么一个表”:四那么运算、复合函数、反函数,根本初等函数导数表:“三种类型”:幂指型、隐函数、参数方程;高阶导数〕3、导数的应用〔切线与法线、单调性〔重点〕与极值点、利用单调性证明函数不等式、凹凸性与拐点、方程的根与函数的零点、曲率〔数一、二〕〕第三章中值定理1、闭区间上连续函数的性质〔最值定理、介值定理、零点存在定理〕2、三大微分中值定理〔重点〕〔罗尔、拉格朗日、柯西〕3、积分中值定理4、泰勒中值定理5、费马引理第四章一元函数积分学1、原函数与不定积分的定义2、不定积分的计算〔变量代换、分部积分〕3、定积分的定义〔几何意义、微元法思想〔数一、二〕〕4、定积分性质〔奇偶函数与周期函数的积分性质、比拟定理〕5、定积分的计算6、定积分的应用〔几何应用:面积、体积、曲线弧长和旋转面的面积〔数一、二〕,物理应用:变力做功、形心质心、液体静压力〕7、变限积分〔求导〕8、广义积分〔收敛性的判断、计算〕第五章空间解析几何〔数一〕1、向量的运算〔加减、数乘、数量积、向量积〕2、直线与平面的方程及其关系3、各种曲面方程〔旋转曲面、柱面、投影曲面、二次曲面〕的求法第六章多元函数微分学1、二重极限和二元函数连续、偏导数、可微及全微分的定义2、二元函数偏导数存在、可微、偏导函数连续之间的关系3、多元函数偏导数的计算〔重点〕4、方向导数与梯度5、多元函数的极值〔无条件极值和条件极值〕6、空间曲线的切线与法平面、曲面的切平面与法线第七章多元函数积分学〔除二重积分外,数一〕1、二重积分的计算〔对称性〔奇偶、轮换〕、极坐标、积分次序的选择〕2、三重积分的计算〔“先一后二”、“先二后一”、球坐标〕3、第一、二类曲线积分、第一、二类曲面积分的计算及对称性〔主要关注不带方向的积分〕4、格林公式〔重点〕〔直接用〔不满足条件时的处理:“补线”、“挖洞”〕,积分与途径无关,二元函数的全微分〕5、高斯公式〔重点〕〔不满足条件时的处理〔类似格林公式〕〕6、斯托克斯公式〔要求低;何时用:计算第二类曲线积分,曲线不易参数化,常表示为两曲面的交线〕7、场论初步〔散度、旋度〕第八章微分方程1、各类微分方程〔可别离变量方程、齐次方程、一阶线性微分方程、伯努利方程〔数一、二〕、全微分方程〔数一〕、可降阶的高阶微分方程〔数一、二〕、高阶线性微分方程、欧拉方程〔数一〕、差分方程〔数三〕〕的求解2、线性微分方程解的性质〔叠加原理、解的构造〕3、应用〔由几何及物理背景列方程〕第九章级数〔数一、数三〕1、收敛级数的性质〔必要条件、线性运算、“加括号”、“有限项”〕2、正项级数的判别法〔比拟、比值、根值,p级数与推广的p级数〕3、交织级数的莱布尼兹判别法4、绝对收敛与条件收敛5、幂级数的收敛半径与收敛域6、幂级数的求和与展开7、傅里叶级数〔函数展开成傅里叶级数,狄利克雷定理〕。
23考研高数命题点思维导图
3 2
(y ′′ ≠ 0 )
曲率圆表达式
定积分
定积分
实际意义
曲边梯形的面积 变速直线运动的路程
精确定义
b a
f (x)dx
=
lim
n→∞
n i =1
f a +
b
− n
a
i
b
− n
a
定积分的存在性(一元函数的可积性)
存在的充分条件 存在的必要条件
性质
区间长度、线性性、可加性、保号性
可积函数必有界
有理函数的积分: QPnm((xx))dx (n < m ), Pn (x)、Qm (x)分别是 x的n次多项式和 m次多项式
1)将
Qm
(
x
)因式分解;2
)把
Pn (x) Qm (x)
拆成若干最简有理分式
之和
定积分的应用
定积分在几何学上的应用
平面图形的面积
直角坐标 极坐标
旋转体的体积 绕x轴转
体积
有限个无穷小之和是无穷小
无穷小
有界函数与无穷小的乘积是无穷小
运算
运算步骤
无穷小的比较
①化简先行:等价替换(常用的有sinx~x,ln(1+x)~x,1-cosx~1/2x^2 ,e^x-1~x,tanx~x,(1+x)^α-1~αx等)、恒等变形、抓大头)
①有分母,通分;没有分母,创造分母
∞-∞
导数的应用
函数的单调性 曲线的凹凸性 曲线的拐点 函数的极值与最值 曲率(数学三不考)
单调增加 单调减少
f ′(x) > 0 f ′(x) < 0
定义
图形是凹的 图形是凸的
考研必看考研数学基础知识点梳理(高数篇)

考研数学基础知识点梳理(高数篇) 第一章函数、极限与连续1、函数的有界性2、极限的定义(数列、函数)3、极限的性质(有界性、保号性)4、极限的计算(重点)(四则运算、等价无穷小替换、洛必达法则、泰勒公式、重要极限、单侧极限、夹逼定理及定积分定义、单调有界必有极限定理)5、函数的连续性6、间断点的类型7、渐近线的计算第二章导数与微分1、导数与微分的定义(函数可导性、用定义求导数)2、导数的计算(“三个法则一个表”:四则运算、复合函数、反函数,基本初等函数导数表;“三种类型”:幂指型、隐函数、参数方程;高阶导数)3、导数的应用(切线与法线、单调性(重点)与极值点、利用单调性证明函数不等式、凹凸性与拐点、方程的根与函数的零点、曲率(数一、二)) 第三章中值定理1、闭区间上连续函数的性质(最值定理、介值定理、零点存在定理)2、三大微分中值定理(重点)(罗尔、拉格朗日、柯西)3、积分中值定理4、泰勒中值定理5、费马引理第四章一元函数积分学1、原函数与不定积分的定义2、不定积分的计算(变量代换、分部积分)3、定积分的定义(几何意义、微元法思想(数一、二))4、定积分性质(奇偶函数与周期函数的积分性质、比较定理)5、定积分的计算6、定积分的应用(几何应用:面积、体积、曲线弧长和旋转面的面积(数一、二),物理应用:变力做功、形心质心、液体静压力)7、变限积分(求导)8、广义积分(收敛性的判断、计算)第五章空间解析几何(数一)1、向量的运算(加减、数乘、数量积、向量积)2、直线与平面的方程及其关系3、各种曲面方程(旋转曲面、柱面、投影曲面、二次曲面)的求法第六章多元函数微分学1、二重极限和二元函数连续、偏导数、可微及全微分的定义2、二元函数偏导数存在、可微、偏导函数连续之间的关系3、多元函数偏导数的计算(重点)4、方向导数与梯度5、多元函数的极值(无条件极值和条件极值)6、空间曲线的切线与法平面、曲面的切平面与法线第七章多元函数积分学(除二重积分外,数一)1、二重积分的计算(对称性(奇偶、轮换)、极坐标、积分次序的选择)2、三重积分的计算(“先一后二”、“先二后一”、球坐标)3、第一、二类曲线积分、第一、二类曲面积分的计算及对称性(主要关注不带方向的积分)4、格林公式(重点)(直接用(不满足条件时的处理:“补线”、“挖洞”),积分与路径无关,二元函数的全微分)5、高斯公式(重点)(不满足条件时的处理(类似格林公式))6、斯托克斯公式(要求低;何时用:计算第二类曲线积分,曲线不易参数化,常表示为两曲面的交线)7、场论初步(散度、旋度)第八章微分方程1、各类微分方程(可分离变量方程、齐次方程、一阶线性微分方程、伯努利方程(数一、二)、全微分方程(数一)、可降阶的高阶微分方程(数一、二)、高阶线性微分方程、欧拉方程(数一)、差分方程(数三))的求解2、线性微分方程解的性质(叠加原理、解的结构)3、应用(由几何及物理背景列方程)第九章级数(数一、数三)1、收敛级数的性质(必要条件、线性运算、“加括号”、“有限项”)2、正项级数的判别法(比较、比值、根值,p级数与推广的p级数)3、交错级数的莱布尼兹判别法4、绝对收敛与条件收敛5、幂级数的收敛半径与收敛域6、幂级数的求和与展开7、傅里叶级数(函数展开成傅里叶级数,狄利克雷定理)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考研高等数学知识点整理(附思
维导图)
被考研高数折磨过的小伙伴一定都知道那种痛苦:
泰勒展开、麦克劳林展开、夹逼定理、定积分不定积分、微分多元微分......
作为成功登陆的一员,我觉得有义务帮对岸的朋友考研一把。
下面这张考研高数知识图我之前用过,希望能给你带来好运。
我不多说了。
一、函数
先明确一些基本概念,比如函数的定义,函数的性质,什么是复合函数,反函数,隐函数。
理解概念很重要!理解概念很重要!理解概念很重要!重要的事情说三遍~
很多问题我们不会做。
其实不是我们解决问题的能力不好,而是我们连基本概念都没搞清楚,自然无从下手,或者说解决问题的方向是偏了!这是我十几年应试的血泪教训!
熟悉基本初等函数,包括幂函数、指数函数、对称函数、三角函数、反三角函数,要把公式和参数适用范围记住;
常用的函数有绝对值函数、符号函数、整数函数、狄利克雷函数、极大值函数、可变积分上限函数(我认为是最变态的)和双曲函数。
二、极限
同样的,先厘清极限的定义
了解数列极限的基本性质:极限的唯一性,收敛数列的有界性和保号性,收敛数列与子数列间的关系
了解函数极限(区别于数列极限)的基本性质:
极限的唯一性,局部有界性和局部保号性(这是和数列极限很大的不同)
无穷小量和无穷大量
极限的四则运算
极限存在的判别方法:单调有界定律和夹迫定律(也有叫夹逼定理的,说的都是一个意思),这两个定律很常见,注意熟练使用
三、函数的连续性
四、导数与微分
基本初等函数的导数公式都得背下来
五、中值定理
这部分很难(可能只是对我来说,我是个坏学生),也是常规考试的重点。
六、函数单调性与凹凸性
这部分也是重点。
七、渐近线与曲率
八、不定积分
和微分一样,基本积分公式也得去记
九、定积分
重点理解定积分的定义和性质(再次强调)
然后去记重要的定理、公式和关系
十、无穷级数
功能扩展很烦人,但是很重要。
大家可能都看过这些表情包。
十一、常微分方程与差分方程
要记公式
十二、空间解析几何与向量代数
理解向量运算,后面的平面方程也就很容易理解了
十三、多元函数微分学
条件极值经常考
十四、重积分
这部分主要注意一点:从里层到外层展开的过程要细心,不然展开到最后发现错了又得重新开始
十五、曲线积分与曲面积分
我当年没考这个,没什么发言权。
图片模糊的话,点击图片“查看原图”,或者你们直接下载源文件,开头的时候已经放过一次了,担心你们忘了,最后再附上源文件↓↓↓
以上知识整理图来源MindMaster思维导图社区,里面也有政治、英语等公共课的考研复习资料,大家也可以自行去搜索↓↓↓
>>>思维导图社区-考研复习资料在线使用。
