四年级奥数巧用变化规律教案
四年级奥数:第10讲 变化规律(二)

第10講變化規律(二)一、知識要點乘、除變化規律見下表(m≠0)我們學習了和、差、積、商的變化規律,這一周,我們利用這些規律來解決一些較簡單的問題。
二、精講精練【例題1】兩數相減,被減數減少8,要使差減少12.減數應有什麼變化?練習1:1.兩數相減,如果被減數增加6,要使差增加15,減數應有什麼變化?2.兩數相減,如果被減數增加20,要使差減少12.減數應有什麼變化?【例題2】兩個數相除,商是8,餘數是20,如果被除數和除數同時擴大10倍,商是多少?餘數是多少?練習2:1.兩數相除,商是6,餘數是30,如果被除數和除數同時擴大10倍,商是多少?餘數是多少?2.兩個數相除,商是9,餘數是3。
如果被除數和除數同時擴大120倍,商是多少?餘數是多少?【例題3】兩數相乘,積是48。
如果一個因數擴大2倍,另一個因數縮小3倍,那麼積是多少?練習3:1.兩數相乘,積是20。
如果一個因數擴大3倍,另一個因數縮小4倍,那麼積是多少?2.兩數相除,商是19。
如果被除數擴大20倍,除數縮小4倍,那麼商是多少?【例題4】小華在計算兩個數相加時,把一個加數個位上的1錯誤地寫成7,把另一個加數十位上的3錯誤地寫成8,所得的和是1996。
原來兩個數相加的正確答案是多少?練習4:1.小明在計算加法時,把一個加數十位上的0錯寫成8,把另一個加數個位上的6錯寫成9,所得的和是532。
正確的和是多少?2.小強在計算加法時,把一個加數十位上的7錯寫成1.把個位上的8錯寫成0,所得的和是285。
正確的和是多少?【例題5】王霞在計算題時,由於粗心大意,把被減數個位上的3錯寫成5,把十位上的6錯寫成0,這樣算得差是189。
正確的差是多少?練習5:1.小軍在做題時,把被減數個位上的3錯寫成8,把十位上的0錯寫成6,這樣算得的差是198。
正確的差是多少?2.小剛在做題時,把減數個位上的9錯寫成6,把十位上的3錯寫成8,這樣算得的差是268。
正確的差是多少?三、課後作業1.兩數相減,減數減少9,要使差增加16,被減數應有什麼變化?2.兩個數相除,商是8,餘數是600。
和差的变化规律 《举一反三》四年级奥数教案

《举一反三》四年级奥数教案一、教学内容:举一反三P44--P47二、教学目标:1、两个加数同时变化时,和的变化规律。
2、被减数和减数同时变化时,差的变化规律。
三、教学难点:理解两数同时变化时,和、差的变化过程。
四、教学设计:1、复习上周所学内容,讲解作业。
作业1:计算9+18+27+36+...+261+270.[分析]:这个数列后项和前项的差是9,都相等,所以这个数列是等差数列,我们可以用求和公式计算。
要求这一数列的和,首先要求出项数是多少,用项数公式。
项数=(末项-首项)÷公差+1=(270-9)÷9+1=30;首项=9,末项=270,项数=30,则由求和公式可得,和=(首项+末项)×项数÷2=﹙9+270﹚×30÷2=4185。
作业2:1+2-3+4+5-6+7+8-9+...+58+59-60[分析]:原式=(1+2+3+...+59+60)-2×(3+6+9+ (60)=(1+60)×60÷2-2×[(3+60)×20÷2] = 570。
2、新课内容I、我们知道两个数的和的最基本的变化规律是:一个加数不变,和随另一个加数的增加(减少)而增加(减少);和与加数增加或减少的数量都是相等的。
下面我们要讲的和的变化规律都是以此为基础演变的。
【例题1】:两个数相加,一个加数减少10,另一个加数增加10,和是否会起变化?【分析】:一个加数+另一个加数=和+10 - -10- +10 +10和先增加10,后减少10,所以和不变。
练习:疯狂操练1(1)、(2)、(3)总结:两个加数同时变化时,和的变化规律有两种。
两个加数同时增加(或减少),和增加(或减少)的数量等于两个加数增加(或减少)的数量之和;两个加数中,一个加数增加,另一个加数减少,和的变化量就是较大变化量与较小变化量的差。
【例题2】:两个数相加,如果一个加数减少8,要使和增加8,另一个加数应有什么变化?【分析】:一个加数+另一个加数=和-8 - -8-8 → 不变 → +8和先增加8,后增加8,所以和增加16。
四年级奥数数字变换与规律的奥妙探索与应用

四年级奥数数字变换与规律的奥妙探索与应用数字变换与规律是奥数中一个重要的题型,通过探索数字的规律并应用到实际问题中,可以培养学生的逻辑思维和分析能力。
本文将从四年级的角度出发,对数字变换与规律的奥妙进行探索和应用。
一、数字的顺序变换在数字的顺序变换中,学生需要观察一组数字的排列顺序,找出其中的规律,并根据规律将数字进行变换。
以简单的例子来说明如何进行顺序变换。
例1:给定一组数字:2,4,6,8,10,...观察这组数字,我们可以发现每个数字都是前一个数字加上2,因此可以将规律表示为“每个数字是前一个数字加2”。
根据这个规律,我们可以继续写下去:12,14,16,18,20,...同样的方法可以应用到其他的数字序列中,通过发现规律,我们可以进行数字的顺序变换。
二、数字的排列组合在数字的排列组合中,学生需要观察给定的数字,并找出它们之间的关系,然后进行排列组合。
以下是一个例子来说明该过程。
例2:给定一组数字:1,2,3,4观察这组数字,我们可以发现每个数字都能和其他数字进行组合,而且每个数字只能出现一次。
因此我们可以列出所有的排列组合:1,2,3,41,2,4,31,3,2,41,3,4,21,4,2,31,4,3,22,1,3,42,1,4,32,3,1,42,3,4,12,4,1,32,4,3,13,1,2,43,1,4,23,2,1,43,2,4,13,4,1,23,4,2,14,1,2,34,1,3,24,2,1,34,2,3,14,3,1,24,3,2,1通过数字排列组合的训练,可以培养学生的思维灵活性和观察能力。
三、数字的奇偶变换数字的奇偶变换是另一类常见的数字变换题型。
学生需要观察给定的数字,然后按照一定的规则进行奇偶变换。
以下是一个例子。
例3:给定一组数字:1,2,3,4,5,6,7,8,9,10观察这组数字,我们可以发现规律:奇数变换为偶数,偶数变换为奇数。
根据这个规律,我们可以进行奇偶变换:1(奇)变为2(偶)2(偶)变为1(奇)3(奇)变为4(偶)4(偶)变为3(奇)5(奇)变为6(偶)6(偶)变为5(奇)7(奇)变为8(偶)8(偶)变为7(奇)9(奇)变为10(偶)10(偶)变为9(奇)通过这样的训练,学生可以培养对数字奇偶关系的敏感度,并能够准确地进行奇偶变换。
小学四年级奥数竞赛:变化规律
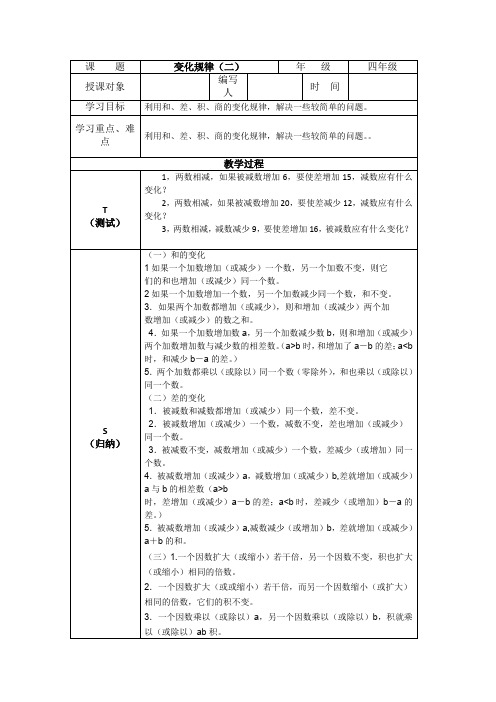
课题变化规律(二)年级四年级授课对象编写人时间学习目标利用和、差、积、商的变化规律,解决一些较简单的问题。
学习重点、难点利用和、差、积、商的变化规律,解决一些较简单的问题。
教学过程T (测试)1,两数相减,如果被减数增加6,要使差增加15,减数应有什么变化?2,两数相减,如果被减数增加20,要使差减少12,减数应有什么变化?3,两数相减,减数减少9,要使差增加16,被减数应有什么变化?S (归纳)(一)和的变化1如果一个加数增加(或减少)一个数,另一个加数不变,则它们的和也增加(或减少)同一个数。
2如果一个加数增加一个数,另一个加数减少同一个数,和不变。
3.如果两个加数都增加(或减少),则和增加(或减少)两个加数增加(或减少)的数之和。
4.如果一个加数增加数a,另一个加数减少数b,则和增加(或减少)两个加数增加数与减少数的相差数。
(a>b时,和增加了a-b的差;a<b 时,和减少b-a的差。
)5.两个加数都乘以(或除以)同一个数(零除外),和也乘以(或除以)同一个数。
(二)差的变化1.被减数和减数都增加(或减少)同一个数,差不变。
2.被减数增加(或减少)一个数,减数不变,差也增加(或减少)同一个数。
3.被减数不变,减数增加(或减少)一个数,差减少(或增加)同一个数。
4.被减数增加(或减少)a,减数增加(或减少)b,差就增加(或减少)a与b的相差数(a>b时,差增加(或减少)a-b的差;a<b时,差减少(或增加)b-a的差。
)5.被减数增加(或减少)a,减数减少(或增加)b,差就增加(或减少)a+b的和。
(三)1.一个因数扩大(或缩小)若干倍,另一个因数不变,积也扩大(或缩小)相同的倍数。
2.一个因数扩大(或或缩小)若干倍,而另一个因数缩小(或扩大)相同的倍数,它们的积不变。
3.一个因数乘以(或除以)a,另一个因数乘以(或除以)b,积就乘以(或除以)ab积。
(四)商的变化1.被除数扩大(或缩小)若干倍,除数不变,商也扩大(或缩小)同样的倍数。
【小学四年级奥数讲义】变化规律(二)

【小学四年级奥数讲义】变化规律(二)一、知识重点乘、除变化规律见下表(m≠0)被乘数( a)乘数(b)积(c)×÷ m不变×÷ m不变×÷ m×÷ m×÷ m÷× m不变被除数( a)除数(b)商(c)×÷ m不变×÷ m不变×÷ m÷× m×÷ m×÷ m不变我们学习了和、差、积、商的变化规律,这一周,我们利用这些规律来解决一些较简单的问题。
二、精讲精练【例题 1】两数相减,被减数减少8,要使差减少12.减数应有什么变化?练习 1:1. 两数相减,假如被减数增添6,要使差增添 15,减数应有什么变化?2.两数相减,假如被减数增添 20,要使差减少 12. 减数应有什么变化?【例题 2】两个数相除,商是8,余数是 20,假如被除数和除数同时扩大10倍,商是多少?余数是多少?练习 2:1.两数相除,商是 6,余数是 30,假如被除数和除数同时扩大 10 倍,商是多少?余数是多少?2.两个数相除,商是 9,余数是 3。
假如被除数和除数同时扩大 120 倍,商是多少?余数是多少?【例题 3】两数相乘,积是 48。
假如一个因数扩大 2 倍,另一个因数减小 3 倍,那么积是多少?练习 3:1.两数相乘,积是 20。
假如一个因数扩大 3 倍,另一个因数减小 4 倍,那么积是多少?2. 两数相除,商是 19。
假如被除数扩大 20 倍,除数减小 4 倍,那么商是多少?【例题 4】小华在计算两个数相加时,把一个加数个位上的 1 错误地写成 7,把另一个加数十位上的 3 错误地写成 8,所得的和是 1996。
本来两个数相加的正确答案是多少?练习 4:1.小明在计算加法时,把一个加数十位上的 0 错写成 8,把另一个加数个位上的 6 错写成 9,所得的和是 532。
四年级奥数教程第5讲:在变化中找规律

四年级奥数教程第5讲:在变化中找规律四年级奥数教程第5讲:在变化中找规律事物的发展变化都是有规律的,那么怎样才能找到规律呢?这就要求我们认真观察事物,只有这样我们才能更好地了解和掌握它。
从⽽找到解决问题的⽅法和途径。
在数学竞赛中,常常会出现⼀些数或者图形,它们的计算或者排列往往有⼀定的规律,我们要通过观察、思考去发现这些规律,也就是发现和总结数与数、图形与图形的内在联系和变化规律,然后就能分析和解决问题了。
例11×5+4=9=3×3;2×6+4=16=4×4;3×7+4=25=5×5;4×8+4=36=6×6;P29页:练习题……10××12102;102×102例 2 请先计算下⾯⼀组算式的前三题,然后找出其中的规律,并根据规律直接写出后六道题的得数。
1×8+1= ;912×8+2= ;98123×8+3= ;9871234×8+4= ;987612345×8+5= ;98765123456×8+6= ;9876541234567×8+7= ;987654312345678×8+8= ;98765432123456789×8+9= . 987654321随堂练习11)找规律,在□⾥填上适当的数。
12 43 6 94 8 12 165 □□□□6 12 □□□□2)找规律,填得数。
12 345 679×9=111 111 111;12 345 679×18= ;18=9×2;222 222 22212 345 679×27= ;27=9×3;333 333 33312 345 679×36= ;444 444 44412 345 679×54= ;666 666 66612 345 679×45= ;555 555 55512 345 679×81= ;999 999 99912 345 679×72= ;888 888 88812 345 679×63= ;777 777 777例3 根据下列⽅框或等式中出现的数的规律,在括号内填上适当的数。
四年级上册奥数(教案)第2讲:数的变化规律

4×2=8
答:另一个乘数应该缩小8倍。
(二)例题2:(13分)
两数相乘,如果一个乘数扩大6倍,另一个乘数缩小3倍,积将有什么变化?
师:如果让我们直接去想一个乘数扩大6倍,另一个乘数缩小3倍,积有什么变化?我们肯定无法直接了解。所以我们先假设出一个乘法算式出来,然后代入条件,再去解决。
师:大家可以想一个乘法算式出来。
6×2=12(元)
6×40=240(元)
6×200=1200(元)
师:仔细观察、比较这组算式,你能发现什么?
生1:有一个乘数都是6。
生2:对,一个乘数相同,另一个乘数不同,积也不同。
师:观察得真仔细!一个乘数相同可以说一个乘数不变,那另一个乘数呢?
生3:另一个乘数变了,积也变了。
生4:我看到一个乘数不变,另一个乘数越变越大,积也越变越大。
二、教学重点:
使学生经历积的变化规律的发现过程,初步获得探索和发现数学规律的基本方法和经验。
三、教学难点:
发现规律,掌握规律。
四、教学准备:
PPT
五、教学过程:
第一课时(50分钟)
一、导入(5分)
阿派最近喜欢上了吃橙子,请你们帮忙算一算,一千克橙子6元,买2千克花掉多少钱?40千克呢?200千克呢?(学生回答)
板书:
20×2=40
20÷4=5
答:如果被除数扩大2倍,除数不变,则商是40。如果被除数缩小4倍,除数不变,则商是5。”
小结:商的变化规律:除数不变,被除数扩大或缩小多少倍(0除外),商也会随着扩大或缩小相同的倍数;
练习3:(7分)
两数相除,商是100,如果被除数不变,除数扩大2倍,商是多少?如果被除数不变,除数缩小5倍,商又是多少呢?
小学四年级奥数教案

小学四年级奥数教案【篇一:四年级全集奥数教案】找规律(一)一、知识讲解观察是解决问题的根据。
通过观察,得以揭示出事物的发展和变化规律,在一般情况下,我们可以从以下几个方面来找规律:1.根据每组相邻两个数之间的关系,找出规律,推断出所要填的数;2.根据相隔的每两个数的关系,找出规律,推断出所要填的数;3.要善于从整体上把握数据之间的联系,从而很快找出规律;4.数之间的联系往往可以从不同的角度来理解,只要言之有理,所得出的规律都可以认为是正确的。
二、结合例子精讲【例题1】先找出下列数排列的规律,并根据规律在括号里填上适当的数。
1,4,7,10,(),16,19【思路导航】在这列数中,相邻的两个数的差都是3,即每一个数加上3都等于后面的数。
根据这一规律,括号里应填的数为:10+3=13或16-3=13.像上面依照肯定的按次排列的一串数叫做数列。
练1:先找出下列各列数的排列规律,然后在括号里填上适当的数。
(1)2,6,10,14,(),22,26(2)3,6,9,12,(),18,21(3)33,28,23,(),13,(),3(4)55,49,43,(),31,(),19(5)3,6,12,(),48,(),192(6)2,6,18,(),162,()(7)128,64,32,(),8,(),2(8)19,3,17,3,15,3,(),(),11,3.【例题2】先找出下列数排列的规律,然后在括号里填上适当的数。
1,2,4,7,(),16,22【思路导航】在这列数中,前4个数每相邻的两个数的差依次是1,2,3.由此可以推算7比括号里的数少4,括号里应填:7+4=11.经验证,所填的数是正确的。
应填的数为:7+4=11或16-5=11.练2:先找出下列数排列的规律,然后在括号里填上适当的数。
(1)10,11,13,16,20,(),31(2)1,4,9,16,25,(),49,64(3)3,2,5,2,7,2,(),(),11,2(4)53,44,36,29,(),18,(),11,9,8(5)81,64,49,36,(),16,(),4,1。
小学奥数:第1讲四年级数学速算与巧算教案

一、导入速算与巧算是计算中的一个重要组成部分,掌握一些速算与巧算的方法,有助于提高我们的计算能力和思维能力。
这一周我们学习加、减法的巧算方法,这些方法主要根据加、减法的运算定律和运算性质,通过对算式适当变形从而使计算简便。
在巧算方法里,蕴含着一种重要的解决问题的策略。
转化问题法即把所给的算式,根据运算定律和运算性质,或改变它的运算顺序,或减整从而变成一个易于算出结果的算式。
二、同步题型分析题型1:两数相加,和凑整;同尾两数直接相减,差凑整例1:计算9+99+999+9999分析与解答:这四个加数分别接近10、100、1000、10000。
在计算这类题目时,常使用减整法,例如将99转化为100-1。
这是小学数学计算中常用的一种技巧。
9+99+999+9999=(10-1)+(100-1)+(1000-1)+(10000-1)=10+100+1000+10000-4=11106例2:计算489+487+483+485+484+486+488分析与解答:认真观察每个加数,发现它们都和整数490接近,所以选490为基准数。
489+487+483+485+484+486+488=490×7-1-3-7-5-6-4-2=3430-28=3402想一想:如果选480为基准数,可以怎样计算?例3:计算453+598+147-198【分析】观察数字的特点,不难发现453与147两数相加可以等到整百数,598与198两数的尾数相同,相减的差也是整百数,这样计算起来比较简便。
453+598+147-198=(453+147)+(598-198)=600+400=1000题型2:带符号搬家,减法性质的应用例1:计算下面各题。
174-(41+74)527-114+14 145+387-187答案:59 427 34531.34-(7.34+2.25) -7.75 63×15÷7 ×60答案:14 、81002.巧算下列各题:(1)72+(14+28)(2)145+387-187(3)132-(27+32)(4)527-114+14114, 345,73,427799+405 (15+14)+(185+186) 217+263+18376+(282+424+218) 579-221-31-8 157-(57+25)1204;400;663;1000;319;75专题简析:乘、除法的巧算方法主要是利用乘、除法的运算定律和运算性质以及积、商的变化规律,通过对算式适当变形,将其中的数转化成整十、整百、整千…的数,或者使这道题计算中的一些数变得易于口算,从而使计算简便。
小学四年级奥数课件:变化规律

3,两数相减,减数减少9,要使差增加16,被减数应有 什么变化?
例5:被减数、减数、差相加得2076,差是减 数的一半。如果被减数不变,差增加42,减 数应变为多少?
思路导航: 减数与差的和即是被减数。2076里有2个被减数,被减 数等于2076÷2=1038.差是减数的一半,也就是说减 数是差的2倍,差应为1038÷(2+1)=346,减数为 346×2=692。被减数不变,差增加42,减数应减少42, 所以减数应变为692-42加数 另一个加 (a) 数 (b)
±m
不变
不变
±m
和(c)
±m ±m
±m
-
不变
+m
被减数(a) 减数(b) 差(c)
±m
不变
±m
不变
±m ±m
±m - +m
不变
例1:两个数相加,一个加数增加9,另一个 加数减少9,和是否发生变化?
• 分析与解答:一个加数增加9,假如另一个加数不变,和 就增加9;假如一个加数不变,另一个加数减少9,和就 减少9;和先增加9,接着又减少9,所以不发生变化。
练习五
1、在一个减法算式里,被减数、减数与差的和是 120,而差是减数的3倍。如果差不变,被减数减 少5,减数应变为多少?
2、在一个减法算式里,被减数、减数与差的和是 90,而差是减数的2倍。如果被减数不变,差增加 7,减数应变为多少?
3、在一个减法算式里,被减数、减数与差的和是 180,而差比减数少8。如果被减数不变,减数减 少16,差应变为多少?
例4:两数相减,被减数减少8,要使 差减少12,减数应有什么变化?
• 分析与解答:被减数减少8,假如减数不变,差也减 少8;现在要使差减少12,减数应增加12-8=4。
变化规律探究教案

变化规律探究教案一、教案背景数学是一门让人神往的学科,它有着无穷无尽的奇妙与乐趣。
而在数学中,变化规律是一个重要的概念,对于其深刻的理解与掌握,不仅能够增强学生的数学思维能力,还能培养学生的逻辑推理能力,提高学生成绩。
本教案就是基于此,旨在通过把变化规律教学紧密结合实际生活,让学生充分掌握变化规律,从而进一步提升他们的数学素养以及生活能力。
二、教案目标通过本次教案学习,学生应当掌握如下内容:1.掌握变化规律的概念,并能够将其应用到实际生活中;2.学习掌握变化规律的一些常用方法,如找规律、归纳法等;3.培养学生的数学思维能力以及逻辑推理能力;4.激发学生的数学兴趣,提高学生成绩。
三、教学内容1.变化规律的概念变化规律,指的是各种事物或现象随着时间或其他因素的推移而发生的规律性变化。
例如,一件商品的售价在促销期间随着时间推移而下降,学生的成绩也随着时间的推移,被改进的技术与产品也会随时间的推移得到不断的完善和提高。
这些都是实际生活中变化规律的体现。
2.变化规律的常用方法(1)找规律法找规律法是最常见的一种方法,它是指在大量的数据中寻找特定的规律,并应用到实际生活中。
例如,在研究某商品的售价变化规律时,我们可以通过收集、整理、分析大量的数据,找出其售价下降的时间节点以及下降数量的规律,从而得出具有可预测性的变化规律。
(2)归纳法归纳法是另一种常用的变化规律寻找方法,它是通过观察总结、归纳低阶次数的规律,推导出高阶次数的规律。
例如,探究互联网发展趋势时,我们可以通过查阅前几年的数据资料,发现互联网用户的增长速度开始逐渐放缓,越来越多的用户开始深度使用互联网,从而推测出未来的互联网发展趋势。
3.变化规律和实际生活的联系变化规律在实际生活中的应用是无处不在的。
我们可以在商品的促销、股票的投资分析、自然资源的开发利用等众多方面找到变化规律的应用。
例如,在商品促销时,往往选择在节假日等特定时间段进行,这就是利用商品售价的变化规律来增加商品销量。
四年级奥数专题第二讲 变化规律

四年级奥数专题第二讲变化规律【一】两个数相加,一个加数增加2,另一个加数减少2,和是否会起变化?练习1、两个数相加,一个加数增加3,另一个加数减少3,和是否会起变化?2、两个数相加,一个加数减少5,另一个加数增加3,和是否会起变化?【二】如果a+b=20,那么a+(b-2)=20-()练习1、如果a-b=6,那么(a+2)-b=6+()。
2、如果a-b=8,那么(a-2)-b=8-()。
【三】两个数相加,一个加数减少8,另一个加数也减少8,和是否会起变化?练习1、两个数相加,一个加数增加10,另一个加数减少6,和是否会起变化?2、两个数相加,一个加数增加7,另一个加数也增加7,和是否会起变化?【四】两个数相加,如果一个加数减少5,要使和增加5,另一个加数应有什么变化?练习1、两个数相加,如果一个加数增加3,要使和减少18,另一个加数应有什么变化?2、两个数相加,如果一个加数减少10,要使和增加10,另一个加数应有什么变化?【五】两数相减,如果被减数减少6,减数也减少6,差是否会起变化?练习1、两数相减,如果被减数增加20,减数也增加20,差是否会起变化?2、两数相减,如果被减数增加16,减数减少16,差是否会起变化?【六】两数相减,如果被减数增加10,要使差减少12,减数应有什么变化?练习1、两数相减,被减数减少30,要使差增加28,减数应有什么变化?2、两数相减,被减数减少50,要使差减少80,减数应有什么变化?【七】被减数、减数、差相加得144,差是减数的一半。
如果被减数不变,差增加8,减数应变为多少?练习1、在一个减法算式里,被减数、减数与差的和是160,而差是减数的4倍。
如果差不变,被减数减少5,减数应为多少?2、在一个减法算式里,被减数、减数与差的和是60,而差是减数的2倍。
如果被减数不变,差增加3,减数应变为多少?课外作业1、a和b相加,a减少3,b也减少3,和会起什么变化?2、如果a-b=48,那么a-(b+6)=48-()。
四年级奥数变化规律电子教案

四年级奥数变化规律第9讲变化规律(一)一、知识要点和、差的规律二、精讲精练【例题1】两个数相加,一个加数增加9,另一个加数减少9,和是否发生变化?练习1:1.两个数相加,一个数减8,另一个数加8,和是否变化?2.两个数相加,一个数加3.另一个数也加3.和起什么变化?3.两个数相加,一个数减6,另一个数减2.和起什么变化?【例题2】两个数相加,如果一个加数增加10,要使和增加6,那么另一个加数应有什么变化?练习2:1.两个数相加,如果一个加数增加8,要使和增加15,另一个加数应有什么变化?2.两个数相加,如果一个加数增加8,要使和减少15,另一个加数应有什么变化?3.两个数相加,如果一个加数减少8,要使和减少8,另一个加数应有什么变化?【例题3】两数相减,如果被减数增加8,减数也增加8,差是否起变化?练习3:1.两数相减,被减数减少6,减数也减少6,差是否起变化?2.两数相减,被减数增加12.减数减少12.差起什么变化?收集于网络,如有侵权请联系管理员删除3.两数相减,被减数减少10,减数增加10,差起什么变化?【例题4】两数相乘,如果一个因数扩大8倍,另一个因数缩小2倍,积将有什么变化?练习4:1.两数相乘,如果一个因数缩小4倍,另一个因数扩大4倍,和是否起变化?2.两数相乘,如果一个因数扩大3倍,另一个因数缩小12倍,积将有什么变化?3.两数相乘,如果一个因数扩大3倍,另一个因数扩大6倍,积将有什么变化?【例题5】两数相除,如果被除数扩大4倍,除数缩小2倍,商将怎样变化?练习5:1.两数相除,被除数扩大30倍,除数缩小5倍,商将怎样变化?2.两数相除,被除数缩小12倍,除数缩小2倍,商将怎样变化?3.两数相除,除数扩大6倍,要使商扩大3倍,被除数应怎样变化?第10讲变化规律(二)一、知识要点我们学习了和、差、积、商的变化规律,这一周,我们利用这些规律来解决一些较简单的问题。
二、精讲精练【例题1】两数相减,被减数减少8,要使差减少12.减数应有什么变化?收集于网络,如有侵权请联系管理员删除练习1:1.两数相减,如果被减数增加6,要使差增加15,减数应有什么变化?2.两数相减,如果被减数增加20,要使差减少12.减数应有什么变化?3.两数相减,减数减少9,要使差增加16,被减数应有什么变化?【例题2】两个数相除,商是8,余数是20,如果被除数和除数同时扩大10倍,商是多少?余数是多少?练习2:1.两数相除,商是6,余数是30,如果被除数和除数同时扩大10倍,商是多少?余数是多少?2.两个数相除,商是9,余数是3。
积商的变化规律 《举一反三》四年级奥数教案

《举一反三》四年级奥数教案一、教学内容:举一反三P48--P51二、教学目标:1 、两个因数同时变化时,积的变化规律。
2 、被除数和除数同时变化时,商的变化规律。
三、教学难点:理解两数同时变化时,积、商的变化过程。
四、教学设计:1、复习上周所学内容,讲解作业(疯狂操练5(2))。
【分析】:被减数+减数+差=90,被减数=减数+差所以被减数=90÷2=45。
被减数=减数+差=减数+2×减数=(1+2)×差=45减数=45÷(1+2)=15,差=2×减数=2×15=30。
当被减数不变,差增加7,则减数减少7,所以减数应变为30-7=23。
2、新课内容I、我们知道两数相乘,积的最基本的变化规律是:一个因数不变,积随另一个因数的扩大(缩小)而扩大(缩小);积与因数的扩大或缩小的数量都是相等的。
下面我们要讲的积的变化规律都是以此为基础演变的。
【例题1】:两个数相乘,一个因数扩大3倍,要是积扩大9倍,另因数应该怎么变化?【分析】:一个因数×另一个因数=积↑3倍-↑3倍积:↑3倍→↑9倍积先扩大3倍,要使积扩大9倍,只要积再扩大3倍。
积扩大3倍,所以另一个因数也扩大3倍。
练习:疯狂操练1(1)、(2)、(3)总结:【例题2】:两数相乘,积是96。
如果一个因数缩小4倍,另一个因数扩大3倍,那么积是多少?【分析】:一个因数×另一个因数=96↓4倍-↓4倍(96÷4=24)-↑3倍↑3倍(24×3=72)积先缩小4倍(96÷4=24),后扩大3倍(24×3=72),积是72。
方法二:见书P49 (例题2【思路导航】)练习:疯狂操练2(1)、(2)总结:II、学习了积的变化规律,下面我们来看看商的变化规律。
我们知道商最基本的变化规律是:如果被除数不变,商随除数的扩大(缩小)而缩小(扩大);如果除数不变,商随被除数的扩大(缩小)而扩大(缩小);差与除数、被倍数扩大或缩小的倍数相等。
四年级数学(人教版)-变化规律-1教案

第四单元第7课时:变化规律年级:四年级教材版本:北京版授课教师单位及姓名:指导教师单位及姓名:一、教学背景简述《小数点移动引起小数大小变化的规律》一课是北京版教材小学数学四年级下册“小数”单元中的学习内容,核心内容是小数点位置的移动引起小数大小变化的规律。
这部分知识是在学生认识了小数的意义、小数的性质等内容基础上进行的学习,是小数乘法和除法计算的依据。
对学生来说,形式化地记住规律并不困难,但要自己探索发现并真正理解规律却不容易。
“小数点位置移动引起小数大小的变化”中,小数点向右移动一位,相当于原数乘10;小数点向右移动两位,相当于原数乘100;小数点向右移动三位,相当于原数乘1000……;小数点向左移动一位,相当于原数除以10……。
引导学生理解小数点位置移动引起小数大小变化的规律是本节课的一个深度学习点,怎样才算实现了规律的意义理解呢?首先,学生能够调动自己已有的知识和生活经验,充分解释“0.1相当于0.01×10,0.01相当于0.1÷10”等。
例如学生能用“元、角、分”和“米、厘米”等模型解释,0.1元是1角,也就是10分,0.01元是1分,10分等于1分乘10,1分等于10分除以10。
其次,还能根据《小数的意义》一课中的直观模型图、画线段图等方法解释小数点位置移动前后两个数之间的关系。
最后,学生还能够结合位值制、十进制等已有知识,体会并尝试解释规律的本质,沟通和建立知识之间的联系。
经历这个过程才能改变学生对小数点移动引起小数大小变化规律的表面现象的原有认识,从更深层次,依托数位顺序表结合“十进制”“位值制”明白小数大小变化的根本原因,沟通“规律”与“小数意义”“计数单位”“十进制”等知识间的联系。
小数点移动背后的本质是,计数单位变了,而计数单位的个数没有变。
二、学习目标1.经历观察、比较、猜测、验证的过程,探索小数点向右移动引起小数大小变化的规律,多角度理解小数点向右移动引起小数大小变化的道理。
四年级数学(人教版)-变化规律应用-教案

教学内容:第四单元第八课时变化规律的应用年级:四年级 教材版本:人教版一、教学背景简述《变化规律的应用》是人教版教材四年级下册第四单元《小数的意义和性质》的学习内容,本节内容的学习是基于学生对小数有了深刻的认识之后进行的。
因为小数是十进分数,所以小数点移动会引起小数大小发生变化。
把小数点向右移动一位、两位、三位......n 位,小数的值分别扩大到原来数的10倍、100倍、1000倍......10n 倍。
如果小数点分别向左移动一位、两位、三位......n 位,则小数的值分别缩小到原数的110、1100、11000 (1)10n 。
人教版的规律呈现方式是:小数点向右移动一位,相当于原数乘10,小数就扩大到原数的10倍;小数点向右移动两位,相当于原数乘100,小数就扩大到原数的100倍;小数点向右移动三位,相当于原数乘1000,小数就扩大到原数的1000倍;小数点向左移动一位,相当于原数除以10,小数就缩小到原数的110;小数点向左移动两位,相当于原数除以100,小数就缩小到原数的1100;小数点向左移动三位,相当于原数除以1000,小数就缩小到原数的11000。
学生经过上节课《变化规律》的学习,已经探究出了小数点移动引起小数大小变化的规律,本课的重点在于学生依据已有的经验,应用小数点移动引起小数大小变化的规律,发展学生的迁移与推理能力。
在掌握规律的过程中,学生对于小数点移动引起小数大小变化的规律不容易应用,尤其是利用小数点移动引起小数大小变化的规律解决问题,涉及把小数扩大(缩小)到原来的多少倍(几分之一)与小数点移动建立联系,这是学生思维的难点,所以需要帮助学生进一步认识规律,理解规律,最后掌握规律,并应用规律解决问题。
二、学习目标1.经历观察、比较、猜想、验证的过程,探索并理解小数点向左移动引起小数大小变化的规律。
2.体会数位之间的关系,基于学习小数点向右移动引起小数大小变化规律的经验,发展迁移和推理能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
另一个加数(b)
和(c)
±m
不变
±m
不变
±m
±m
±m
m
不变
被减数(a)
减数(b)
差(c)
±m
不变
±m
不变
±m
m
±m
±m
不变
知识点二:积与商变化规律
乘、除变化规律见下表(m≠0)
被乘数(a)
乘数(b)
积(c)
×÷m
不变
×÷m
不变
×÷m
×÷m
×÷m
÷×m
不变
被除数(a)
除数(b)
商(c)
×÷m
2.两数相减,被减数增加12,减数减少12,差起什么变化?
3.两数相减,被减数减少10,减数增加10,差起什么变化?
例4:两数相乘,如果一个因数扩大8倍,另一个因数缩小2倍,积将有什么变化?
分析与解答:如果一个因数扩大8倍,另一个因数不变,积将扩大8倍;如果一个因数不变,另一个因数缩小2倍,积将缩小2倍。积先扩大8倍又缩小2倍,因此,积扩大了8÷2=4倍。
分析与解答:一个加数增加9,假如另一个加数不变,和就增加9;假如一个加数不变,另一个加数减少9,和就减少9;和先增加9,接着又减少9,所以不发生变化。
过五关之一
1.两个数相加,一个数减8,另一个数加8,和是否变化?
2.两个数相加,一个数加3,另一个数也加3,和起什么变化?
3.两个数相加,一个数减6,另一个数减2,和起什么变化?
2.解题:
⑴音乐老师到琴行买了2支长笛和两把小号,共付57元,若买三支长笛和两把小号需付63元,那么买一支长笛和一把小号各应付多少元?
⑵甲、乙两数和是70,乙、丙两数和是140,甲、丙两数和是90,求甲、乙、丙三数个是多少?
二.探索新知
例1:两个数相加,一个加数增加9,另一个加数减少9,和是否发生变化?
例2:两个数相加,如果一个加数增加10,要使和增加6,那么另一个加数应有什么变化?
分析与解答:一个加数增加10,假如另一个加数不变,和就增加10。现在要使和增加6,那么另一个加数应减少10-6=4。
过五关之二
1.两个数相加,如果一个加数增加8,要使和增加15,另一个加数应有什么变化?
2.两个数相加,如果一个加数增加8,要使和减少15,另一个加数应有什么变化?
(1)加减消去法
应用加减的运算,在两个加减相等的算式中消去一个要求的数量
(2)带入消去法
应用加减乘除运算,变换一个已知条件,先用一个数量代换另一个数量,再将变换后的一个要求的数带入另一个等式里,从而消去一个要求的数量。
▲解题关键
用消去法解题的关键是设法使问题中要求的两个未知数量先变成一个,求出这个未知量后方能进一步求出另一个。
不变
×÷m
不变
×÷m
÷×m
×÷m
×÷m
不变
全课总结。
作业:
学生:教师:
请听老师说:
课题:巧用变化规律
学生:年级:四年级升五年级授课日期:2013-7-29
时间段:10:00-12:00第3次课
教学重难点:
1、两个加数同时变化时,和的变化规律。
2、被减数和减数同时变化时,差的变化规律。
3.两个因数同时变化时,积的变化规律。
4.被除数和除数同时变化时,商的变化规律。
教学难点:理解两数同时变化时,和、差、积、商的变化过程。
3.两数相除,除数扩大6倍,要使商扩大3倍,被除数应怎样变化?
19、细胞也是生物最基本的功能单位,生物的呼吸、消化、排泄、生长、发育、繁殖、遗传等生命活动都是通过细胞进行的。
5、在咀嚼米饭过程中,米饭出现了甜味,说明了什么?
知识点一:和与差变化规律
9、在17世纪,人们发现把两个凸透镜组合起来明显提高了放大能力,这就是早期的显微镜。和、差的规律见下表(m≠0)
过五关之四
1.两数相乘,如果一个因数缩小4倍,另一个因数扩大4倍,和是否起变化?
2.两数相乘,如果一个因数扩大3倍,另一个因数缩小12倍,积将有什么变化?
一、填空:
6、化学变化伴随的现象有改变颜色、发光发热、产生气体、产生沉淀物。
3.两数相乘,如果一个因数扩大3倍,另一个因数扩大6倍,积将有什么变化?
一、填空:
例5:两数相除,如果被除数扩大4倍,除数缩小2倍,商将怎样变化?
9、淡水是我们人类和其他生物生存的必需品,但是地球上的淡水资源十分有限,地球上的多数地区缺水。分析与解答:如果被除数扩大4倍,除数不变,商就扩大4倍;如果被除数不变,除数缩小2倍,商就扩大2倍。商先扩大4倍,接着又扩大2倍,商将扩大4×2=8倍。
3.两个数相加,如果一个加数减少8,要使和减少8,另一个加数应有什么变化?
例3:两数相减,如果被减数增加8,减数也增加8,差是否起变化?
分析与解答:被减数增加8,假如减数不变,差就增加8;假如被减数不变,减数增加8,差就减少8。两个数的差先增加8,接着又减少8,所以不起什么变化。
过五关之三
1.两数相减,被减数减少6,减数也减少6,差是否起变化?
过五关之五
1.两数相除,被除数扩大30倍,除数缩小5倍,商将怎样变化?
8、铁生锈的原因是什么?人们怎样防止铁生锈?
12、淡水在自来水厂中除了沉淀和过滤之外,还要加入药物进行灭菌处理,这样才能符合我们使用的标准。2.两数相除,被除数缩小12倍,除数缩小2倍,商将怎样变化?
7、我们每个人应该怎样保护身边的环境?
授课内容:
一、复习:消去法解题
1.用自己的话说一说什么是消去法?
2.消去法
有的应用题含有含有两种未知的相关联的数量关系,包含有两个要求的不同数量,解答这类问题,应该设法消去一个要求的数量,从而求出另一个要求的数量,然后再求出消去的要求的那个数量,这种方法叫消去法。
★基本方法
解答这类问题Байду номын сангаас由于方法不同可分为加减消去法,带入消去法。
