软考高级-运筹PPT讲解
合集下载
《运筹学图解法》课件

提高建模能力
提高模型解释和应用能力
提高求解效率的策略与技巧
选择合适的图解 法:根据问题类 型选择合适的图 解法,如最短路 径问题、最大流 问题等。
优化算法:对图 解法进行优化, 如使用动态规划、 贪心算法等。
并行计算:利用 多核处理器进行 并行计算,提高 求解速度。
利用软件工具: 使用专业的图解 法软件,如 Matlab、 Python等,提 高求解效率。
缺点:需要一定 的数学基础,不 适合初学者使用
运筹学图解法的基本步骤
确定问题目标
明确问题的性质 和类型
确定问题的目标 和约束条件
分析问题的关键 因素和影响因素
确定问题的求解 方法和步骤
建立模型
确定问题:明确需要解决的问题
建立模型:根据数据建立数学模 型
添加标题
添加标题
添加标题
添加标题
收集数据:收集与问题相关的数 据
模型验证与优化的方法与技巧
模型验证:通过实际数据验证模型的准确性和可靠性
模型优化:根据实际需求对模型进行优化,提高模型的效 率和效果
模型选择:根据实际问题选择合适的模型,提高模型的适 用性和准确性
模型调整:根据实际数据对模型进行调整,提高模型的适 应性和准确性
模型评估:对模型进行评估,了解模型的优缺点和改进方 向
软件工具的使用:熟悉软件工具 的界面和功能,掌握基本的操作 方法
软件工具的优化与调整:根据问 题特点和需求,对软件工具进行 优化和调整,提高求解效率和准 确性
软件工具的常见问题与解决方 案:了解软件工具的常见问题, 掌握相应的解决方案,提高求 解效率和准确性
软件工具的学习与提高:不断学 习和实践,提高软件工具的使用 水平和求解能力
《运筹学总复习》课件

应用领域:物流、供应链管理、路径规划等。
难点:计算复杂度高,难以找到最优解。
生产与存储问题
问题描述:生产与存储问题是指在给定时间内,如何安排生产计划和存储策略,以最小化生产成本和存 储成本。 经典模型:经济批量模型(EOQ)、生产存储模型(P-S模型)、生产存储模型(P-S模型)等。
求解方法:动态规划、线性规划、整数规划等。
非线性规划的求解方法:非线性规划的求解方法包括梯度下降法、牛顿法、遗传算法等。
整数规划
定义:整数规划是一种特殊的线性规划,其中所有变量都必须是整数
目标函数:整数规划的目标函数通常是线性的,表示为决策变量的 线性组合 约束条件:整数规划的约束条件通常是线性的,表示为决策变量的线 性不等式或不等式 求解方法:整数规划的求解方法包括分支定界法、割平面法、遗传 算法等
MATL AB在运筹学中的应 用包括优化问题、决策问题、
排队论等
Python在运筹学中的应用
Python语言简介:一种广泛应用于科学计算、数据分析和机器学习等领域的编程语言 Python在运筹学中的应用:可以用于求解线性规划、整数规划、非线性规划等运筹学问题 Python库介绍:如scipy、numpy、pandas等,可以用于进行运筹学计算和可视化 Python代码示例:展示如何使用Python编写运筹学问题的求解代码
Gurobi优化器介绍与使用
Gurobi优化器是一款功能强大的优化工具,广泛应用于运筹学、数学规划等领域。
Gurobi优化器支持多种编程语言,如Python、C++、Java等,方便用户进行编程实 现。
Gurobi优化器提供了丰富的优化算法,如线性规划、非线性规划、整数规划等,满足 不同问题的求解需求。
难点:计算复杂度高,难以找到最优解。
生产与存储问题
问题描述:生产与存储问题是指在给定时间内,如何安排生产计划和存储策略,以最小化生产成本和存 储成本。 经典模型:经济批量模型(EOQ)、生产存储模型(P-S模型)、生产存储模型(P-S模型)等。
求解方法:动态规划、线性规划、整数规划等。
非线性规划的求解方法:非线性规划的求解方法包括梯度下降法、牛顿法、遗传算法等。
整数规划
定义:整数规划是一种特殊的线性规划,其中所有变量都必须是整数
目标函数:整数规划的目标函数通常是线性的,表示为决策变量的 线性组合 约束条件:整数规划的约束条件通常是线性的,表示为决策变量的线 性不等式或不等式 求解方法:整数规划的求解方法包括分支定界法、割平面法、遗传 算法等
MATL AB在运筹学中的应 用包括优化问题、决策问题、
排队论等
Python在运筹学中的应用
Python语言简介:一种广泛应用于科学计算、数据分析和机器学习等领域的编程语言 Python在运筹学中的应用:可以用于求解线性规划、整数规划、非线性规划等运筹学问题 Python库介绍:如scipy、numpy、pandas等,可以用于进行运筹学计算和可视化 Python代码示例:展示如何使用Python编写运筹学问题的求解代码
Gurobi优化器介绍与使用
Gurobi优化器是一款功能强大的优化工具,广泛应用于运筹学、数学规划等领域。
Gurobi优化器支持多种编程语言,如Python、C++、Java等,方便用户进行编程实 现。
Gurobi优化器提供了丰富的优化算法,如线性规划、非线性规划、整数规划等,满足 不同问题的求解需求。
运筹学PPT完整版

线性规划通常解决下列两类问题:
(1)当任务或目标确定后,如何统筹兼顾,合理安排,用 最少的资源 (如资金、设备、原标材料、人工、时间等) 去完成确定的任务或目标 (2)在一定的资源条件限制下,如何组织安排生产获得最 好的经济效益(如产品量最多 、利润最大.)
线性规划问题的数学模型
例1.1 如图所示,如何截取x使铁皮所围成的容积最 大?
(2)
x j 0, j 1,2,, n (3)
求解线性规划问题,就是从满足约束条件(2)、(3)的方程组 中找出一个解,使目标函数(1)达到最大值。
线性规划问题的数学模型
Page 27
可行解:满足约束条件②、③的解为可行解。所有可行解 的集合为可行域。
最优解:使目标函数达到最大值的可行解。
绪论
本章主要内容: (1)运筹学简述 (2)运筹学的主要内容 (3)本课程的教材及参考书 (4)本课程的特点和要求 (5)本课程授课方式与考核 (6)运筹学在工商管理中的应用
运筹学简述
Page 2
运筹学(Operations Research) 系统工程的最重要的理论基础之一,在美国有人把运筹
学称之为管理科学(Management Science)。运筹学所研究的 问题,可简单地归结为一句话: “依照给定条件和目标,从众多方案中选择最佳方案” 故有人称之为最优化技术。
Page 3
运筹学的主要内容
Page 4
数学规划(线性规划、整数规划、目标规划、动态 规划等) 图论 存储论 排队论 对策论 排序与统筹方法 决策分析
本课程的教材及参考书
Page 5
❖选用教材 ➢ 《运筹学基础及应用》胡运权主编 哈工大出版社
❖参考教材 ➢ 《运筹学教程》胡运权主编 (第2版)清华出版社 ➢ 《管理运筹学》韩伯棠主编 (第2版)高等教育出版社 ➢ 《运筹学》(修订版) 钱颂迪主编 清华出版社
(1)当任务或目标确定后,如何统筹兼顾,合理安排,用 最少的资源 (如资金、设备、原标材料、人工、时间等) 去完成确定的任务或目标 (2)在一定的资源条件限制下,如何组织安排生产获得最 好的经济效益(如产品量最多 、利润最大.)
线性规划问题的数学模型
例1.1 如图所示,如何截取x使铁皮所围成的容积最 大?
(2)
x j 0, j 1,2,, n (3)
求解线性规划问题,就是从满足约束条件(2)、(3)的方程组 中找出一个解,使目标函数(1)达到最大值。
线性规划问题的数学模型
Page 27
可行解:满足约束条件②、③的解为可行解。所有可行解 的集合为可行域。
最优解:使目标函数达到最大值的可行解。
绪论
本章主要内容: (1)运筹学简述 (2)运筹学的主要内容 (3)本课程的教材及参考书 (4)本课程的特点和要求 (5)本课程授课方式与考核 (6)运筹学在工商管理中的应用
运筹学简述
Page 2
运筹学(Operations Research) 系统工程的最重要的理论基础之一,在美国有人把运筹
学称之为管理科学(Management Science)。运筹学所研究的 问题,可简单地归结为一句话: “依照给定条件和目标,从众多方案中选择最佳方案” 故有人称之为最优化技术。
Page 3
运筹学的主要内容
Page 4
数学规划(线性规划、整数规划、目标规划、动态 规划等) 图论 存储论 排队论 对策论 排序与统筹方法 决策分析
本课程的教材及参考书
Page 5
❖选用教材 ➢ 《运筹学基础及应用》胡运权主编 哈工大出版社
❖参考教材 ➢ 《运筹学教程》胡运权主编 (第2版)清华出版社 ➢ 《管理运筹学》韩伯棠主编 (第2版)高等教育出版社 ➢ 《运筹学》(修订版) 钱颂迪主编 清华出版社
运筹学课件PPT课件

整数规划的解法
总结词
整数规划的解法可以分为精确解法和近似解法两大类。
详细描述
整数规划的解法可以分为两大类,一类是精确解法,另一类是近似解法。精确解法包括割平面法、分支定界法等, 这些方法可以找到整数规划的精确最优解。而近似解法包括启发式算法、元启发式算法等,这些方法可以找到整 数规划的近似最优解,但不一定能保证找到最优解。
模拟退火算法采用Metropolis准则来 判断是否接受一个较差解,即如果新 解的能量比当前解的能量低,或者新 解的能量虽然较高但接受的概率足够 小,则接受新解。
模拟退火算法的应用
01
模拟退火算法在旅行商问题中得到了广泛应用。通过模拟退火算 法,可以求解旅行商问题的最优解,即在给定一组城市和每对城 市之间的距离后,求解访问每个城市恰好一次并返回出发城市的 最短路径。
动态规划的解法
确定问题的阶段和状态
首先需要确定问题的阶段和状态,以便将问 题分解为子问题。
建立状态转移方程
根据问题的特性,建立状态转移方程,描述 状态之间的转移关系。
求解子问题
求解每个子问题,并存储其解以供将来使用。
递推求解
从最后一个阶段开始,通过递推方式向前求 解每个阶段的最优解。
动态规划的应用
线性规划的解法
单纯形法
01
单纯形法是求解线性规划问题的经典方法,通过迭代过程逐步
找到最优解。
对偶理论
02
对偶理论是线性规划的一个重要概念,它通过引入对偶问题来
简化求解过程。
分解算法
03
分解算法是将大规模线性规划问题分解为若干个小问题,分别
求解后再综合得到最优解。
线性规划的应用
生产计划
线性规划可以用于生产计划问题, 通过优化资源配置和生产流程, 提高生产效率和利润。
运筹课件PPT课件

它涉及到的问题包括最短路径、 最小生成树、最大流等。
图论与网络优化在计算机科学、 交通运输、通信网络等领域有 广泛应用,如路由算法、网络 设计等。
03 运筹学在现实生活中的应 用
生产与库存管理
01
02
03
生产计划
运筹学通过数学模型和算 法,帮助企业制定生产计 划,优化资源配置,提高 生产效率。
库存控制
Excel Solver的特点
Excel Solver易于使用
它提供了一个直观的用户界面,用户可以通过简单的拖放操作来定义问题。
Excel Solver具有广泛的适用性
它可以处理各种类型的优化问题,包括线性规划、整数规划、目标规划、非线性规划等。
Excel Solver具有高效性
它使用了多种优化算法,可以快速求解大规模问题。
它使用了高效的算法和优化的数据结构,可以快速地处理大规模数据和计算任务。
05 案例分析与实践
生产计划优化案例
总结词
生产计划是企业管理中的重要环节,通过优化生产计划可以提高企业的生产效率 和资源利用率。
详细描述
生产计划优化案例主要涉及如何根据市场需求、产品特性、生产能力等因素制定 合理的生产计划,以实现生产效益的最大化。具体包括对生产计划的制定、执行 、调整等环节进行优化,提高生产计划的准确性和灵活性。
运筹学的重要性
01
提高效率
降低成本
02
03
增强决策科学性
运筹学能够通过优化资源配置和 流程,提高系统的效率和生产力。
通过合理的资源配置和计划安排, 运筹学可以帮助企业降低成本和 资源消耗。
运筹学提供的数据分析和模型预 测等方法,有助于增强决策的科 学性和准确性。
运筹学课件第二节图解法.ppt

运筹学教程
基:设A 为约束方程组的m×n阶系数矩阵 (n>m),R(A)=m,B是矩阵A中的一个m×m阶满秩子 矩阵,称B是线性规划问题的一个基,设 P1 P2…Pj…Pm
列向量Pj(j=1,2,…m) 为基向量,Pj 所对应的变量xj 基变量,其余变量为非基变量. 秩:设在矩阵A中存在一个不等于零的r阶子式D,且所有的r+1阶
0
1〡 2〡 3A 4〡 5〡 6〡 7〡 8〡 9〡C
(1/3) x1 +(1/3)x2 =1
两个约束条件 及非负条件x1,x2 0所代表的公共部分 --图中阴影区,就是满足所有约束条件和非 负条件的点的集合,即可行域。在这个区域中 的每一个点都对应着一个可行的生产方案。
运筹学教程
令 Z=2x1+3x2=c,其中c为任选的一个常数,在图中画出直线 2x1+3x2=c, 这条直线上的点即对应着一个可行的生产方案,即使两种产品的总利润达 到c。 这样的直线有无数条,而且相互平行,称这样的直线为目标函数等值线。 只要画出两条目标函数等值线,比如令c=0和c=6,就能看出 目标函数值递增的方向, 用箭头标出这个方向。 图中两条虚线 l1和l2就 分别代表 目标函数等值线
a11 . B . am1
. . a1m . . . ( P , P ,......,P ) 1 2 m . . . . . amm
子式全等于零,那么D为A的最高阶非零子式,数r称为A的秩.
运筹学教程
基解:在约束方程组中,令所有的非基变量 xm1 xm2 ...... xn 0 ,有因为有 B 0 根据克莱姆法则,有m个约束方程可解出m 个变量的唯一解, X B ( x1, x2 ,......,xm )T 将此解加上非基变量取0的值有
第2章 运筹学课件图解法

4x2 12
x2
A
可行域
B
max z 2 x1 3x2 s.t x1 2 x2 8 x1 16 4 x 12 2 x , x 0 1 2
最优解(4,2)
x1
x1 16
x1 2x2 8
结论: 可行域一定是凸集 若最优解存在,则最优解一定 在凸集的顶点达到
上例中求得 问题的解是唯一的, 但对一般线性规划问题,求解结果还 可能出现以下几种情况: 1、无穷多最优解(多重解)
若将上例中的目标函数 max z 2x1 4x2 改为则表示目标函数中以参数的等值线 与约束条件的边界平行,当值由小变大 时,将与此边界重合,线段AB上的所有 点都是最优解。
向量Pj 对应的决策变量是x j
T
用矩阵表述:
max z CX ( LP4 ) s.t AX b X 0
其中
A (aij )mn ( p1, p2 pn )
0 (0,0,0)
T
max z CX s.t AX b X 0
自从1947年G. B. Dantzig 提出求解线
性规划的单纯形方法以来,线性规划在理论
上趋向成熟,在实用中日益广泛与深入。特 别是在计算机能处理成千上万个约束条件和 决策变量的线性规划问题之后,线性规划的 适用领域更为广泛了,已成为现代管理中经 常采用的基本方法之一。
§2.1 问题的提出 §2.2 线性规划的图解法 §2.3 图解法的灵敏度分析
2. 存在一定的约束条件,这些约束都可 以用一组线性等式或线性不等式表示。
3. 都有一个要达到的目标,它可以用决 策变量的线性函数来表示。按问题的 不同要求,目标函数实现最大化或最
运筹学PPT完整版

优化炼油程序及产品供应、配送和营销
每年节约成本600万美元 每年节约成本7000万
优化商业用户的电话销售中心选址
控制成本库存(制定最优再定购点和定购 量确保安全库存) 制定最优铁路时刻表并调整铁路日运营量
优化员工安排,以最低成本服务客户
每年节约成本4.06亿美元,销 售额大幅增加 每年节约成本380万美元
s.t
n j1
aij
xj
bi
(i 1,2,,m)
(2)
xj 0, j 1,2,,n (3)
求解线性规划问题,就是从满足约束条件(2)、(3)的方程组 中找出一个解,使目标函数(1)达到最大值。
线性规划问题的数学模型
Page 28
可行解:满足约束条件②、③的解为可行解。所有可行解 的集合为可行域。
(5) 目标函数是最小值,为了化为求最大值,令z′=-z,得到max z′=-z,即当z达到最小值时z′达到最大值,反之亦然;
线性规划问题的数学模型
标准形式如下:
maxZ 2x1 x2 3(x3 x3)0x4 0x5
5x1 x2 (x3 x3) x4 7
1 2
1 0
0 1
r(A)=2,2阶子矩阵有10个,其中基矩阵只有9个,即
5 1
1 1 5 0 1 1
B 1 106 B 2 6 2 B 3 101 B 4 6 0
5 1 1 0
1 1 1 0
1 0
B 5 100 B 6 2 1 B 7 2 0 B 8 6 1 B 9 0 1
线性规划问题的数学模型
Page 17
2. 线性规划的数学模型由三个要素构成 决策变量 Decision variables 目标函数 Objective function 约束条件 Constraints
每年节约成本600万美元 每年节约成本7000万
优化商业用户的电话销售中心选址
控制成本库存(制定最优再定购点和定购 量确保安全库存) 制定最优铁路时刻表并调整铁路日运营量
优化员工安排,以最低成本服务客户
每年节约成本4.06亿美元,销 售额大幅增加 每年节约成本380万美元
s.t
n j1
aij
xj
bi
(i 1,2,,m)
(2)
xj 0, j 1,2,,n (3)
求解线性规划问题,就是从满足约束条件(2)、(3)的方程组 中找出一个解,使目标函数(1)达到最大值。
线性规划问题的数学模型
Page 28
可行解:满足约束条件②、③的解为可行解。所有可行解 的集合为可行域。
(5) 目标函数是最小值,为了化为求最大值,令z′=-z,得到max z′=-z,即当z达到最小值时z′达到最大值,反之亦然;
线性规划问题的数学模型
标准形式如下:
maxZ 2x1 x2 3(x3 x3)0x4 0x5
5x1 x2 (x3 x3) x4 7
1 2
1 0
0 1
r(A)=2,2阶子矩阵有10个,其中基矩阵只有9个,即
5 1
1 1 5 0 1 1
B 1 106 B 2 6 2 B 3 101 B 4 6 0
5 1 1 0
1 1 1 0
1 0
B 5 100 B 6 2 1 B 7 2 0 B 8 6 1 B 9 0 1
线性规划问题的数学模型
Page 17
2. 线性规划的数学模型由三个要素构成 决策变量 Decision variables 目标函数 Objective function 约束条件 Constraints
《高级运筹学》约束非线性规划

i*gi (x1*, x2* , x3* ) 0, i 1, 2
(6) (7)
从几何上看,(5)式的f(x*)和 g1(x*)都通过x*且应共线。 实际上,由于x*是(4)的最优解,所以,当动点x由x*出发 沿着g1(x)=0上的各个方向移动时,目标函数值f(x)均增加, 不仅如此,而且 x由x*出发往g1(x)0的内部移动时(即下 图所示箭头方向),f(x)也应增加。
x*
g1(x) 0
g2(x) 0
由于梯度指向函数值的增加方向,因此,f(x*)和g1(x*) 不仅共线,而且应该是同方向的。即(6)中的
* 1
0,
* 2
0
(8)
总之,(4)的最优解x*应满足条件 (6)(7)(8)
x* g1(x*) g1(x) 0
f (x*) g2(x) 0
f (x*) 1*g1(x*) 2*g2 (x*) 0
s.t. gi (x) 0 hj (x) 0
i 1,..., m j 1,...,l
(9)
构造拉格朗日函数
m
l
L(x,, ) f (x) i gi (x) jhj (x)
i 1
j 1
(10)
min f (x)
xRn
s.t. gi (x) 0 hj (x) 0
i 1,..., m j 1,...,l
求解一般约束非线性规划问题,比无约束问题和线性规 划问题都要复杂得多。
考虑问题
min f (x) x12 x22
s.t. x1 x2 1 0
1 x1 0
1 x2 0
x2
可行域是一个 三角形及其内 部,目标函数 等值线是以原 点为圆心的同 心圆。
1
x*
(6) (7)
从几何上看,(5)式的f(x*)和 g1(x*)都通过x*且应共线。 实际上,由于x*是(4)的最优解,所以,当动点x由x*出发 沿着g1(x)=0上的各个方向移动时,目标函数值f(x)均增加, 不仅如此,而且 x由x*出发往g1(x)0的内部移动时(即下 图所示箭头方向),f(x)也应增加。
x*
g1(x) 0
g2(x) 0
由于梯度指向函数值的增加方向,因此,f(x*)和g1(x*) 不仅共线,而且应该是同方向的。即(6)中的
* 1
0,
* 2
0
(8)
总之,(4)的最优解x*应满足条件 (6)(7)(8)
x* g1(x*) g1(x) 0
f (x*) g2(x) 0
f (x*) 1*g1(x*) 2*g2 (x*) 0
s.t. gi (x) 0 hj (x) 0
i 1,..., m j 1,...,l
(9)
构造拉格朗日函数
m
l
L(x,, ) f (x) i gi (x) jhj (x)
i 1
j 1
(10)
min f (x)
xRn
s.t. gi (x) 0 hj (x) 0
i 1,..., m j 1,...,l
求解一般约束非线性规划问题,比无约束问题和线性规 划问题都要复杂得多。
考虑问题
min f (x) x12 x22
s.t. x1 x2 1 0
1 x1 0
1 x2 0
x2
可行域是一个 三角形及其内 部,目标函数 等值线是以原 点为圆心的同 心圆。
1
x*
运筹学PPT完整版

C 变量:决策变量和非决策变量
B 约束条件:线性等式或不等式
A 目标函数:求最大值或最小值
非线性规划
目标函数:非线性函数
约束条件:非线性不等式
求解方法:梯度下降法、 牛顿法、拟牛顿法等
应用领域:生产计划、资 源分配、投资决策等
动态规划
基本概念:将复杂问题分解为若干子 0 1 问题,通过求解子问题来解决原问题
运筹学广泛应用于生产、运输、库存、销售、人力 资源等各个领域。
运筹学通过建立数学模型,求解最优解,以实现资 源的合理配置和高效利用。
运筹学的应用领域
生产与运营管理 项目管理 交通与运输规划
供应链管理 财务管理 资源分配与调度
运筹学的发展历程
起源:二战期间, 军事需求推动运 筹学的发展
20世纪50年代: 运筹学逐渐应用 于工业、经济等 领域
适用范围:解决资源分配、路径规划、 02 生产调度等问题
主要步骤:划分阶段、确定状态、建 0 3 立状态转移方程、求解最优解
特点:具有最优子结构性质,能够高 04 效地求解复杂问题
运筹学的实际应 用
生产计划与调度
生产计划:根据市场需求和生产能力制定生产计划, 包括生产数量、生产时间、生产地点等
生产调度:根据生产计划,合理分配生产资源,包 括人员、设备、原材料等
场趋势
运筹学在生物学中 的应用:分析生物 种群数量变化,预
测生物进化趋势
运筹学在工程学中 的应用:优化工程 设计,提高工程效
率
THANK YOU
汇报人:稻小壳
运筹学与人工智 能的结合,拓展
2 了运筹学的应用
领域
3 运筹学与人工智
能的结合,推动 了运筹学的理论 研究和实践应用
运筹学PPT
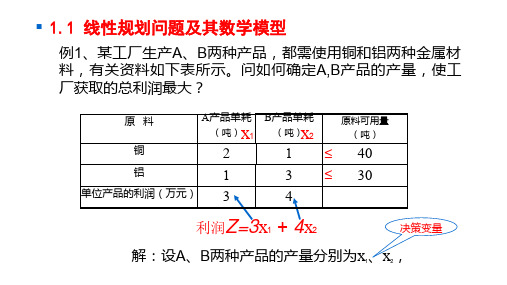
特征:
目标取极大(MaxZ) 约束条件取等式(=) 变量取非负(0),并约定:bi0
缩写形式
n
maxZ c j x j
j 1
n
s.t. j 1 aij x j
bi
(i 1,2,, m)
x
j
0
( j 1,2,, n)
向量形式
maxZ CX
模型的共同特征
1每一问题都可以用一组变量(x1, x2, …, xn )表示某一方案,一 般
情形下,变量的取值是非负的;
2 约束条件用线性等式或线性不等式表示;
3都有一个目标函数,且这个目标函数可表示为一组变量的线性 函 数; 4要求求出一组或多组方案,使目标函数实现最大化(Max)或 者 最小化(Min)。
可行解:满足LP问题所有约束条件的解 最优解:满足目标函数的可行解
MaxZ CX AX b X 0
基、基变量、非基变量:
X x1 x2 xm xm1 xn
a11 a12 a1m a1m1 a1n
A
am1 am2 amm amm1 amn
1.1 线性规划问题及其数学模型
例1、某工厂生产A、B两种产品,都需使用铜和铝两种金属材 料,有关资料如下表所示。问如何确定A,B产品的产量,使工 厂获取的总利润最大?
原料
A产品单耗 B产品单耗
x x (吨) 1 (吨) 2
原料可用量 (吨)
铜
2
1 ≤ 40
铝
1
3 ≤ 30
单位产品的利润(万元) 3
基本可行解:满足非负约束条件的基本解。 即:xj 0, j 1,2,m
高项运筹学 PPT课件

第27章 高项运筹学
2020/3/31
全国计算机技术与软件专业技术资格(水平)考试培训
1
基本介绍
运筹学是一门专门的学科,博大精深。在信息系统项目 管理师考试中通常会考察3分左右,且计算量很大,但是只要 把一些常见的思想、常见的解题方法掌握了,再把历年的真 题搞清楚,基本就OK了。
2020/3/31
2020/3/31
全国计算机技术与软件专业技术资格(水平)考试培训
13
历年试题解析
2020/3/31
全国计算机技术与软件专业技术资格(水平)考试培训
14
历年试题解析
所谓决策,是指为确定未来某个行动的目标,根据自 己的经验,在占有一定信息的基础上,借助于科学的方法 和工具,对需要决定的问题的各个因素进行分析、计算和 评价,并从两个以上的可行方案中,选择一个最优方案的 分析判断过程。
7
常见题型和解题思路
状态转移矩阵 状态转移矩阵是俄国数学家马尔科夫提出的,他
在20世纪初发现,一个系统的某些因素在转移中,第 n次结果只受第n-1的结果影响,即只与当前所处状态 有关,而与过去状态无关。在马尔科夫分析中,引入 状态转移这个概念。
所谓状态是指客观事物可能出现或存在的状态; 状态转移是指客观事物由一种状态转移到另一种状态 的概率。
全国计算机技术与软件专业技术资格(水平)考试培训
பைடு நூலகம்
12
常见题型和解题思路
图论 图论(Graph Theory)是数学的一个分支。它
以图为研究对象。图论中的图是由若干给定的点及连 接两点的线所构成的图形,这种图形通常用来描述某 些事物之间的某种特定关系,用点代表事物,用连接 两点的线表示相应两个事物间具有这种关系。
2020/3/31
全国计算机技术与软件专业技术资格(水平)考试培训
1
基本介绍
运筹学是一门专门的学科,博大精深。在信息系统项目 管理师考试中通常会考察3分左右,且计算量很大,但是只要 把一些常见的思想、常见的解题方法掌握了,再把历年的真 题搞清楚,基本就OK了。
2020/3/31
2020/3/31
全国计算机技术与软件专业技术资格(水平)考试培训
13
历年试题解析
2020/3/31
全国计算机技术与软件专业技术资格(水平)考试培训
14
历年试题解析
所谓决策,是指为确定未来某个行动的目标,根据自 己的经验,在占有一定信息的基础上,借助于科学的方法 和工具,对需要决定的问题的各个因素进行分析、计算和 评价,并从两个以上的可行方案中,选择一个最优方案的 分析判断过程。
7
常见题型和解题思路
状态转移矩阵 状态转移矩阵是俄国数学家马尔科夫提出的,他
在20世纪初发现,一个系统的某些因素在转移中,第 n次结果只受第n-1的结果影响,即只与当前所处状态 有关,而与过去状态无关。在马尔科夫分析中,引入 状态转移这个概念。
所谓状态是指客观事物可能出现或存在的状态; 状态转移是指客观事物由一种状态转移到另一种状态 的概率。
全国计算机技术与软件专业技术资格(水平)考试培训
பைடு நூலகம்
12
常见题型和解题思路
图论 图论(Graph Theory)是数学的一个分支。它
以图为研究对象。图论中的图是由若干给定的点及连 接两点的线所构成的图形,这种图形通常用来描述某 些事物之间的某种特定关系,用点代表事物,用连接 两点的线表示相应两个事物间具有这种关系。
(精品) 运筹(618页PPT课件)

-10-
Dantzig的故事II
在Dantzig刚刚给出了线性规划的单纯法不久,他参加了一 次学术会议。在会上他讲解了他的方法,…
当我讲完以后, 会议主席征询意见和评论。 死一般的寂静 持续了一会儿后,一只手举了起来,那是Hotelling。
我需要解释以下,Hotelling非常胖。他喜欢在海里游泳。 据说,当他在海里游泳时,能见到海平面明显升高。这个巨鲸 似的人站在屋子的后面,他富有表情的胖脸上流露出我们所熟 悉的那种无所不知的微笑。他说道:“但是我们都知道这个世 界是非线性的。”
• Improved truck dispatching at Reynolds Metals improves on-time delivery and reduces freight cost by $7 million/yr.
• GTE local capacity expansion ne blending at Texaco results in saving of over $30 million/yr.
-17-
Summary
• Answered the question: What is Operations Research & Management Science? and provided some historical perspective.
-15-
Other Success Stories (cont.)
• Optimizing global supply chains saves Digital Equipment over $300 million.
• Restructuring North America Operations, Proctor and Gamble reduces plants by 20%, saving $200 million/yr.
Dantzig的故事II
在Dantzig刚刚给出了线性规划的单纯法不久,他参加了一 次学术会议。在会上他讲解了他的方法,…
当我讲完以后, 会议主席征询意见和评论。 死一般的寂静 持续了一会儿后,一只手举了起来,那是Hotelling。
我需要解释以下,Hotelling非常胖。他喜欢在海里游泳。 据说,当他在海里游泳时,能见到海平面明显升高。这个巨鲸 似的人站在屋子的后面,他富有表情的胖脸上流露出我们所熟 悉的那种无所不知的微笑。他说道:“但是我们都知道这个世 界是非线性的。”
• Improved truck dispatching at Reynolds Metals improves on-time delivery and reduces freight cost by $7 million/yr.
• GTE local capacity expansion ne blending at Texaco results in saving of over $30 million/yr.
-17-
Summary
• Answered the question: What is Operations Research & Management Science? and provided some historical perspective.
-15-
Other Success Stories (cont.)
• Optimizing global supply chains saves Digital Equipment over $300 million.
• Restructuring North America Operations, Proctor and Gamble reduces plants by 20%, saving $200 million/yr.
运筹演示2
• • • • • • •
二、表上作业法的基本步骤 1.编制初始方案,确定初始可行解。 使用方法:最小元素法、伏格尔法。 2.最优性检验 使用方法:闭回路法、位势法。 3.方案的调整 使用方法:闭回路法
• 例:某公司经销甲产品,该产品有三个加 工厂,产量分别为7、4、9吨,该产品有四 个销售地点,销售量为3、6、5、6吨,已 知单位定价,问如何在满足各销售点的需 求量的前提下,使花费最小?
2
3 4
3
7 6
8
7 4
9
3 2
5
7 6
6
4 5
2
4 8
14
11 15
单位售价
20
24
18
22
16
20
• 运输问题应用: • 一、生产计划问题 • 某拖拉机厂与某单位签订了生产70台某种型号拖拉机的合 同,按合同规定明年每个季度末分别提供10、15、25、 20台拖拉机,已知该厂各季度的生产能力及生产每台拖拉 机的成本如表所示,如生产出来的拖拉机当季度不交货, 每台每积压一个季度需要储存维护费用0.15万元,问该厂 怎样安排各季度生产计划,既完成合同又使得总费用最少。
原料 工时 利润
Ⅰ型
Ⅱ型 资源限制
2
3 100
4
2 120
6
4
求解线性规划的方法: 1.图解法 2.单纯形法 3.大M法 4.对偶单纯形法 例2. minZ=15x1+24x2 +5x3 6x2+x3 ≥2 5x1+2x2+x3 ≥ 1 x1, x2 ,x3≥ 0
• • • •
第三章 运输问题 第一节 平衡运输问题的数学模型 运输问题的提出 例:某公司经销甲产品,该产品有三个加工厂,产量分别 为7、4、9吨,该产品有四个销售地点,销售量为3、6、 5、6吨,已知单位定价,问如何在满足各销售点的需求量 的前提下,使花费最小?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
创新 专业 高效 进取 共赢
三步: 1、计算期望时间:μ=(6+4*21+36)/6=21(天) 2、计算标准差:σ=(36-6)/6=5(天) 3、在正态分布图上标注时间参数,确定时间段区间概率
创新 专业 高效 进取 共赢
某机构拟进行办公自动化系统的建设,有四种方式可以选择,项目经理提供了如下表所
A、1/4
B、3/8
C、1/2
D、1/3
创新 专业 高效 进取 共赢
请重建你对数学的
自信!
创新 专业 高效 进取 共赢
数量、单位产品可获得利润以及企业现有原材料数如表所示:
则公司可以获得的最大利润是(1)万元。取得最大利润时,原材料(2)尚有剩余。
(1) A、21
B、34
C、39
D、48
(2) A、甲
B、乙
C、丙
D、乙和丙
创新 专业 高效 进取 共赢
创新 专业 高效 进取 共赢
某工厂计划生产甲、乙两种产品,生产每套产品所需的设备台时、A、B两种原材料和可
现值,指的是n年之后的钱,折合到现在的价值。
如果n年之后的钱y,其现值为x,那么x一定小于y。把y折合到现在变成x,有时简称 “折现”,这个过程就是计算y的现值的过程。折现公式为: x=y/(1+r)n,其中,n为年份数,r为贴现率(考试题中,y、n、r一般是已知信息)。
创新 专业 高效 进取 共赢
软考直播-运筹学 20200315
创新 专业 高效 进取 共赢
高级 特点 策略 用时
第1~30题
第31~65题
技术类,1/3悲剧题 管理类,没有悲剧题
控制情绪
大量拿分
90分钟
第66~70题 运筹学
千万别急 50分钟
第71~75题 英语题 …… 10分钟
创新 专业 高效 进取 共赢
完成某信息系统集成项目中的一个最基本的工作单元A所需的时间,乐观的估计需8天,
悲观的估计需38天,最可能的估计需20天,按照PERT方法进行估算,项目的工期应该
为(1),在26天以后完成的概率大致为(2)。
(1) A、20
B、21
C、22
D、23
(2) A、8.9%
B、15.9%
C、22.2%
D、28.6%
创新 专业 高效 进取 共赢
三步: 1、计算期望时间:μ=(tO+4tM+tP)/6 2、计算标准差:σ=( tP -tO)/6 3、在正态分布图上标注时间参数(μ、σ),确定时间段区间概率
创新 专业 高效 进取 共赢
创新 专业 高效 进取 共赢
有一辆货车每天沿着公路给4个零售店运送6箱货物,如果各零售店出售该货物所得利润
如下表所示,适当规划在各零售店卸下的货物的箱数,可获得最大利润()万元。
A. 15
B. 17
C. 19
D. 21
创新 专业 高效 进取 共赢
创新 专业 高效 进取 共赢
有关费用,从甲线到乙线的最小费用路线是(1)条,最小费用为(2)
(1)A、1
B、2
C、3
D、4
(2)A、15
B、16
C、17
D、18
创新 专业 高效 进取 共赢
创新 专业 高效 进取 共赢
有一种游戏为掷两颗骰子,其规则为;当点数和为2时,游戏者输9元;点数和为7或者
11时,游戏者赢X元;其他点数时均输1元。依据EMV准侧,当X超过()元时游戏才对
游戏者有利。
A、3.5
B、4
C、4.5
D、5
创新 专业 高效 进取 共赢
袋子里有50个乒乓球,其中20个黄球,30个白球。现在两个人依次不放回地从袋子中
取出一个球,第二个人取出黄球的概率是()
A、1/5
B、3/5
C、2/5
D、4/5
创新 专业 高效 进取 共赢
同时抛掷3枚均匀的硬币,恰好有两枚正面向上的概率为()。
示的决策树。其中在复用的情况下,如果变化大则存在两种可能,简单构造的概率为0.2,
成本约31万元;复杂构造的概率为0.8,成本约49万元。据此表,管理者选择建设方式
的最佳决策是()。
A、企业自行从头开发
B、复用已有的构件
C、外购现成的软件产品
D、承包给专业公司开发
创新 专业 高效 进取 共赢
创新 专业 高效 进取 共赢
某企业要投产一种新产品,生产方案有四个:A新建全自动生产线;B新建半自动生产线;
C购置旧生产设备;D外包加工生产。未来该产品的销售前景估计为较好、一般和较差三
种,不同情况下该产品的收益值如下表:(单位:百万元)
依后悔值(在同样的条件下,选错方案所产生的收益损失值)的方法决策应该选()方
案
A、新建全自动生产线
投资回收期,就是“回本时间”。
软考的选择题考试中,一般投资回收期的单位为年。 静态投资回收期不考虑资金的时间价值,其计算方法为:
静态投资回收期=回本年的年份数-1+(回本年上年累计净利润的绝对值/回本年净现金 流量),其中,回本年为累计净利润开始出现正值的年份。
创新 专业 高效 进取 共赢
创新 专业 高效 进取 共赢
A、64 B、74 C、76
D、68
创新 专业 高效 进取 共赢
创新 专业 高效 进取 共赢
下图中,从A到E的最短长度是()(图中每边旁的数字为该条边的长度)。
A. 17
B. 18
C. 19
D. 20
创新 专业 高效 进取 共赢
已知网络图各段路线所需费用如下图所示,图中甲线和乙线上的数字分别是对相应点的
获取利润以及可利用资源数量如下表所示。则应按()方案来安排计划以使该工厂获利
最多。
A、生产甲2套,乙3套
B、生产甲1套,乙4套
C、生产甲3套,乙4套
D、生产甲4套,乙2套
创新 专业 高效 进取 共赢
某公司现有400万元用于投资甲乙丙三个项目,投资额以百万元为单位,已知甲乙丙三 项投资的可能方案及相应获得的收益如下表所示: 则该公司能够获得的最大收益是()百万元 A、17 B、18 C、20 D、21
动态投资回收期考虑资金的时间价值,其计算方法为: 动态投资回收期=回本年的年份数-1+(回本年上年累计净现值的绝对值/回本年净现 值),其中,回本年为累计净现值开始出现正值的年份。
创新 专业 高效 进取 共赢
创新 专业 高效 进取 共赢
某企业需要采用甲、乙、丙三种原材料生产Ⅰ、Ⅱ两种产品。生产两种产品所需原材料
B、新建半自动生产线
C、购置旧生产设备
D、外包加工生产
创新 专业 高效 进取 共赢
创新 专业 高效 进取 共赢
某公司从甲地向丁地运送物质,运输过程中先后需经过乙、丙两个中转站,其中乙中转
站可以选择乙1和乙2两个可选地点,丙中转站可以选择丙1、丙2、丙3三个可选地点,
各相邻两地之间的距离如表所示,则甲地到丁地之间的最短距离是()
某软件企业2006 年初计划投资2000 万人民币开发某产品,预计从2007 年开始盈利,
各年产品销售额如表所示。根据表中的数据,该产品的静态投资回收期是(1)年,动
态投资回收期是(2)年。(设贴现率为0.1)
(1)A、1.8
B、1.9
C、2
D、2ቤተ መጻሕፍቲ ባይዱ2
(2)A、2
B、2.1
C、2.2
D、3
创新 专业 高效 进取 共赢
三步: 1、计算期望时间:μ=(6+4*21+36)/6=21(天) 2、计算标准差:σ=(36-6)/6=5(天) 3、在正态分布图上标注时间参数,确定时间段区间概率
创新 专业 高效 进取 共赢
某机构拟进行办公自动化系统的建设,有四种方式可以选择,项目经理提供了如下表所
A、1/4
B、3/8
C、1/2
D、1/3
创新 专业 高效 进取 共赢
请重建你对数学的
自信!
创新 专业 高效 进取 共赢
数量、单位产品可获得利润以及企业现有原材料数如表所示:
则公司可以获得的最大利润是(1)万元。取得最大利润时,原材料(2)尚有剩余。
(1) A、21
B、34
C、39
D、48
(2) A、甲
B、乙
C、丙
D、乙和丙
创新 专业 高效 进取 共赢
创新 专业 高效 进取 共赢
某工厂计划生产甲、乙两种产品,生产每套产品所需的设备台时、A、B两种原材料和可
现值,指的是n年之后的钱,折合到现在的价值。
如果n年之后的钱y,其现值为x,那么x一定小于y。把y折合到现在变成x,有时简称 “折现”,这个过程就是计算y的现值的过程。折现公式为: x=y/(1+r)n,其中,n为年份数,r为贴现率(考试题中,y、n、r一般是已知信息)。
创新 专业 高效 进取 共赢
软考直播-运筹学 20200315
创新 专业 高效 进取 共赢
高级 特点 策略 用时
第1~30题
第31~65题
技术类,1/3悲剧题 管理类,没有悲剧题
控制情绪
大量拿分
90分钟
第66~70题 运筹学
千万别急 50分钟
第71~75题 英语题 …… 10分钟
创新 专业 高效 进取 共赢
完成某信息系统集成项目中的一个最基本的工作单元A所需的时间,乐观的估计需8天,
悲观的估计需38天,最可能的估计需20天,按照PERT方法进行估算,项目的工期应该
为(1),在26天以后完成的概率大致为(2)。
(1) A、20
B、21
C、22
D、23
(2) A、8.9%
B、15.9%
C、22.2%
D、28.6%
创新 专业 高效 进取 共赢
三步: 1、计算期望时间:μ=(tO+4tM+tP)/6 2、计算标准差:σ=( tP -tO)/6 3、在正态分布图上标注时间参数(μ、σ),确定时间段区间概率
创新 专业 高效 进取 共赢
创新 专业 高效 进取 共赢
有一辆货车每天沿着公路给4个零售店运送6箱货物,如果各零售店出售该货物所得利润
如下表所示,适当规划在各零售店卸下的货物的箱数,可获得最大利润()万元。
A. 15
B. 17
C. 19
D. 21
创新 专业 高效 进取 共赢
创新 专业 高效 进取 共赢
有关费用,从甲线到乙线的最小费用路线是(1)条,最小费用为(2)
(1)A、1
B、2
C、3
D、4
(2)A、15
B、16
C、17
D、18
创新 专业 高效 进取 共赢
创新 专业 高效 进取 共赢
有一种游戏为掷两颗骰子,其规则为;当点数和为2时,游戏者输9元;点数和为7或者
11时,游戏者赢X元;其他点数时均输1元。依据EMV准侧,当X超过()元时游戏才对
游戏者有利。
A、3.5
B、4
C、4.5
D、5
创新 专业 高效 进取 共赢
袋子里有50个乒乓球,其中20个黄球,30个白球。现在两个人依次不放回地从袋子中
取出一个球,第二个人取出黄球的概率是()
A、1/5
B、3/5
C、2/5
D、4/5
创新 专业 高效 进取 共赢
同时抛掷3枚均匀的硬币,恰好有两枚正面向上的概率为()。
示的决策树。其中在复用的情况下,如果变化大则存在两种可能,简单构造的概率为0.2,
成本约31万元;复杂构造的概率为0.8,成本约49万元。据此表,管理者选择建设方式
的最佳决策是()。
A、企业自行从头开发
B、复用已有的构件
C、外购现成的软件产品
D、承包给专业公司开发
创新 专业 高效 进取 共赢
创新 专业 高效 进取 共赢
某企业要投产一种新产品,生产方案有四个:A新建全自动生产线;B新建半自动生产线;
C购置旧生产设备;D外包加工生产。未来该产品的销售前景估计为较好、一般和较差三
种,不同情况下该产品的收益值如下表:(单位:百万元)
依后悔值(在同样的条件下,选错方案所产生的收益损失值)的方法决策应该选()方
案
A、新建全自动生产线
投资回收期,就是“回本时间”。
软考的选择题考试中,一般投资回收期的单位为年。 静态投资回收期不考虑资金的时间价值,其计算方法为:
静态投资回收期=回本年的年份数-1+(回本年上年累计净利润的绝对值/回本年净现金 流量),其中,回本年为累计净利润开始出现正值的年份。
创新 专业 高效 进取 共赢
创新 专业 高效 进取 共赢
A、64 B、74 C、76
D、68
创新 专业 高效 进取 共赢
创新 专业 高效 进取 共赢
下图中,从A到E的最短长度是()(图中每边旁的数字为该条边的长度)。
A. 17
B. 18
C. 19
D. 20
创新 专业 高效 进取 共赢
已知网络图各段路线所需费用如下图所示,图中甲线和乙线上的数字分别是对相应点的
获取利润以及可利用资源数量如下表所示。则应按()方案来安排计划以使该工厂获利
最多。
A、生产甲2套,乙3套
B、生产甲1套,乙4套
C、生产甲3套,乙4套
D、生产甲4套,乙2套
创新 专业 高效 进取 共赢
某公司现有400万元用于投资甲乙丙三个项目,投资额以百万元为单位,已知甲乙丙三 项投资的可能方案及相应获得的收益如下表所示: 则该公司能够获得的最大收益是()百万元 A、17 B、18 C、20 D、21
动态投资回收期考虑资金的时间价值,其计算方法为: 动态投资回收期=回本年的年份数-1+(回本年上年累计净现值的绝对值/回本年净现 值),其中,回本年为累计净现值开始出现正值的年份。
创新 专业 高效 进取 共赢
创新 专业 高效 进取 共赢
某企业需要采用甲、乙、丙三种原材料生产Ⅰ、Ⅱ两种产品。生产两种产品所需原材料
B、新建半自动生产线
C、购置旧生产设备
D、外包加工生产
创新 专业 高效 进取 共赢
创新 专业 高效 进取 共赢
某公司从甲地向丁地运送物质,运输过程中先后需经过乙、丙两个中转站,其中乙中转
站可以选择乙1和乙2两个可选地点,丙中转站可以选择丙1、丙2、丙3三个可选地点,
各相邻两地之间的距离如表所示,则甲地到丁地之间的最短距离是()
某软件企业2006 年初计划投资2000 万人民币开发某产品,预计从2007 年开始盈利,
各年产品销售额如表所示。根据表中的数据,该产品的静态投资回收期是(1)年,动
态投资回收期是(2)年。(设贴现率为0.1)
(1)A、1.8
B、1.9
C、2
D、2ቤተ መጻሕፍቲ ባይዱ2
(2)A、2
B、2.1
C、2.2
D、3
创新 专业 高效 进取 共赢
