行列式的性质
行列式的认识

行列式的认识在线性代数中,行列式是一种非常重要的概念,它是一个方阵的一个标量量度。
它在许多领域中都有着广泛的应用,包括物理,工程学,统计学和计算机图形学等。
1. 行列式的定义行列式通常表示为$det(A)$或$|A|$。
它是一个方阵的数字值,如果它是正的,则表示该矩阵是“正定”的,否则表示它是“负定”的。
一个矩阵的行列式的计算方式如下:$$ det(A)=\sum_{\sigma\in S_{n}}(-1)^{\tau(\sigma)}\prod_{i=1}^{n}a_{i,\sigma_i},$$其中,$n$是矩阵的阶数,$a_{i,j}$是矩阵$A$中第$i$行第$j$列的元素,$S_n$是$n$个元素的置换群,$\sigma$是$S_n$中一个置换。
$\tau(\sigma)$表示置换$\sigma$的逆序数,即该置换可以通过多少次交换相邻的元素变为单位置换。
$(-1)^{\tau(\sigma)}$表示符号,当逆序数是偶数时取值为正,当逆序数是奇数时取值为负。
因此,行列式的值可以通过先列出所有可能的$n!$种置换,然后计算每个置换的贡献来得到。
2. 行列式的性质行列式有许多令人惊讶的性质。
以下是一些重要性质的概述:2.1 行列式的性质1:任意交换矩阵的两行或两列,行列式的值会发生反转。
根据上述公式,当交换两行时,置换的符号改变了,因为逆序数的奇偶性改变了。
当交换两列时,置换的奇偶性也改变了,因此结果符号仍然改变。
例如,对于一个3x3的矩阵A,如果我们交换第1行和第2行,那么行列式的值将由$det(A)$变为$-det(A)$。
2.2 行列式的性质2:如果矩阵的两行或两列成比例,那么该行列式的值为零。
如果两行成比例,那么矩阵的行列式为零,因为对于任何置换$\sigma$,这两行的元素始终被映射到了同一列。
结果是,对于每个乘积$a_{i,\sigma_i}$,该乘积乘以一个相同的因子$a_{j,\sigma_j}=ka_{i,\sigma_j}$,其中$k$是一个常数。
1.2行列式性质

a13 a23 12 a33
a23 a33 3 a21 a33 a31
1
0 2
0 1 2
100 298
100 0 200 1 300 2
例2
计算行列式 2 1 199
3
1 2 3 0 1 2 100 1 199 2 298 3
解
1 2 3
0 1 2
100 1 200 2 300 3
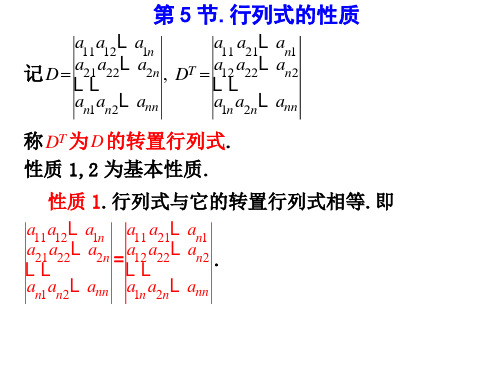
D T 称为D的转置行列式。从而有 D D T
这条性质说明行列式的行和列的地位是相同的。也就 是说,对“行”成立的性质,对于“列”成立的
性质2 互换行列式的两行(列),行列式反号。即
r r i j
D
c c i j
D,
则D D
推论 如果行列式有两行(列)完全相同,则此行列式等 于零。 性质3 行列式D的某一行(列)的所有元素都乘以数k 得到行列式D1,等于数k乘以此行列式。即
0 an
例6 设
a11 11 ak 1 k1 c11 c n1
这是用两条线将行列式分成四 块了,其中一块为0,与0不在 同一对角线上的两块必须方块
D
a1 k akk kk c1 k c nk
0
c11 c n1 b11 11 bn1 bn1
0
解
b a Dn a a
a b a a
a a a a a b a a
a b a a
a a a b
a a a a
c1 c2 cn
b (n 1)a a a a a b (n 1)a b a a a b (n 1)a a a b a b (n 1)a a a a b
行列式的性质有什么技巧吗

行列式的性质有什么技巧吗行列式是矩阵的一个重要性质,对于解方程组、求逆矩阵以及矩阵的特征值等计算都有着重要作用。
在计算行列式的过程中,可以根据行列式的性质来简化计算,提高计算效率。
下面将介绍一些常用的行列式的性质和计算技巧。
1. 行列互换性质:行列式的值不变,当交换行列式中任意两行(或两列)的位置。
例如,对于一个3阶行列式A,若交换第一行和第二行的位置,行列式值不变。
2. 行列式的取公因子性质:行列式的值等于公因子与剩余元素构成的行列式的值的乘积。
例如,对于一个3阶行列式A,如果第一行的元素可以取公因子k,那么行列式A的值等于第一行元素乘以公因子k的行列式B的值,即A = k * B。
3. 行列式的倍性性质:行列式的某一行(或列)的元素乘以一个常数k,与行列式的值的乘积相等。
例如,对于一个3阶行列式A,如果将第一行的元素都乘以常数k,那么行列式A的值等于第一行元素乘以常数k的行列式B的值,即A = k * B。
4. 行列式对行的线性关系:如果行列式中两行成比例,那么这个行列式的值为0。
例如,如果行列式的第一行的元素都等于第二行元素的两倍,那么这个行列式的值为0。
5. 行列式的行列式和斜交性质:行列式中有两行(或两列)完全相同,那么这个行列式的值为0。
例如,如果行列式的第一行跟第二行完全相同,那么这个行列式的值为0。
6. 行列式的二次行列和二次展开定理:对于一个n阶的行列式,可以通过二次行列和二次展开定理来计算行列式的值。
即将行列式按矩阵中的某一行(或列)展开,然后将展开后的行列式分割成若干个小行列式,这些小行列式的值与对应元素的代数余子式成正负关系。
通过递归地计算这些小行列式的值,最终可以得到行列式的值。
7. 行列式的上三角行列的性质:一个上三角阵的行列式,等于对角线上的元素的乘积。
即对于一个n阶的上三角阵A,它的行列式的值等于A的对角线上的元素的乘积。
这个性质在求解方程组的过程中特别有用。
8. 行列式的性质与矩阵求逆的关系:如果一个矩阵A可逆,那么它的行列式不等于0;反之,如果一个矩阵的行列式不等于0,那么它可逆。
行列式的性质与计算方法

行列式的性质与计算方法行列式是线性代数中非常重要的概念,是矩阵的一个标量。
它可以用来描述线性方程组的解的情况,也可以用来判断矩阵是否可逆等。
在本文中,我们将探讨行列式的性质和计算方法。
一、行列式的性质1. 行列式与转置矩阵矩阵的转置是指将矩阵的行和列调换,得到的新矩阵称为原矩阵的转置矩阵。
如果行列式的元素都是实数,那么它的值不会受转置操作的影响,即$\left|A\right|=\left|A^{T}\right|$2. 行列式的行列互换行列式的行列互换是指将行列式的任意两行或两列互换位置,得到的新行列式称为原行列式的行列互换。
行列互换会改变行列式的符号,即$\left|A\right|=-\left|A_{i j}\right| \text { , } i \neq j$其中$A_{i j}$表示将矩阵$A$的第$i$行和第$j$列删除后得到的$(n-1)\times(n-1)$矩阵的行列式。
3. 行列式的元素线性组合如果一个行列式的某一列(或某一行)减去另一列(或行)的$k$倍,得到的新行列式的值等于原行列式的值乘以$k$,即$\left|\begin{array}{cccc}{a_{1}} & {a_{2}} & {\cdots} & {a_{n}} \\ {\vdots} & {} & {\vdots} & {\vdots} \\ {a_{i}} & {a_{i}} & {\cdots} & {a_{i}}+k a_{j} \\ {\vdots} & {} & {\vdots} & {\vdots} \\ {a_{j}}& {a_{j}} & {\cdots} &{a_{j}}\end{array}\right|=\left|\begin{array}{cccc}{a_{1}} & {a_{2}} & {\cdots} & {a_{n}} \\ {\vdots} & {} & {\vdots} & {\vdots} \\ {a_{i}} & {a_{i}} & {\cdots} & {a_{i}} \\ {\vdots} & {} & {\vdots} & {\vdots} \\ {a_{j}} & {a_{j}} & {\cdots} &{a_{j}}\end{array}\right|+k\left|\begin{array}{cccc}{a_{1}} &{a_{2}} & {\cdots} & {a_{n}} \\ {\vdots} & {} & {\vdots} & {\vdots} \\ {a_{i}} & {a_{i}} & {\cdots} & {a_{j}} \\ {\vdots} & {} & {\vdots}& {\vdots} \\ {a_{j}} & {a_{j}} & {\cdots} &{a_{j}}\end{array}\right|$4. 行列式的行列成比例如果一个行列式的某两行或某两列成比例,那么该行列式的值为$0$,即$\left|\begin{array}{cccc}{a_{1}} & {a_{2}} & {\cdots} & {a_{n}} \\ {\vdots} & {} & {\vdots} & {\vdots} \\ {k a_{i 1}} & {k a_{i 2}} & {\cdots} & {k a_{i n}} \\ {\vdots} & {} & {\vdots} & {\vdots} \\{a_{j}} & {a_{j}} & {\cdots} & {a_{j}}\end{array}\right|=0$其中$\left(a_{i 1}, a_{i 2}, \cdots, a_{i n}\right)$和$\left(a_{j 1},a_{j 2}, \cdots, a_{j n}\right)$是比例行列式的两行,$k$是一个非零实数。
行列式的性质及求解方法

行列式的性质及求解方法行列式是线性代数中的一个重要概念,具有广泛的应用领域,例如矩阵求逆、线性方程组的解法、空间向量的叉积等。
在本文中,我们将探讨行列式的性质及其求解方法。
一、行列式的定义及性质1.1 行列式的定义对于一个$n$阶方阵$A=[a_{ij}]$,定义它的行列式为:$$\begin{vmatrix}a_{11} & a_{12} & \cdots & a_{1n} \\a_{21} & a_{22} & \cdots & a_{2n} \\\vdots & \vdots & \ddots & \vdots \\a_{n1} & a_{n2} & \cdots & a_{nn}\\\end{vmatrix}=\sum_{\sigma \in S_n}(-1)^{\mathrm{sgn}(\sigma)}a_{1\sigma(1)}a_{2\sigma(2)}\cdotsa_{n\sigma(n)}$$其中,$\sigma$是$n$个元素的全排列,$S_n$表示$n$个元素的置换群,$\mathrm{sgn}(\sigma)$表示$\sigma$的符号,即$(-1)^k$,其中$k$为$\sigma$的逆序数。
1.2 行列式的性质- 行列式的值不变性行列式的值只与矩阵的元素有关,而与矩阵的行列变换或线性组合无关。
- 互换矩阵的两行或两列,行列式变号将矩阵的两行(列)互换,则该行列式的值取相反数。
- 矩阵的某一行(列)乘以一个数$k$,行列式的值乘以$k$将矩阵的某一行(列)乘以一个数$k$,则该行列式的值乘以$k$。
- 矩阵的某一行(列)加上另一行(列)的k倍,行列式不变将矩阵的某一行(列)加上另一行(列)的k倍,行列式的值不变。
- 方阵的行列式等于其转置矩阵的行列式$$\begin{vmatrix}a_{11} & a_{12} & \cdots & a_{1n} \\a_{21} & a_{22} & \cdots & a_{2n} \\\vdots & \vdots & \ddots & \vdots \\a_{n1} & a_{n2} & \cdots & a_{nn}\\\end{vmatrix}=\begin{vmatrix}a_{11} & a_{21} & \cdots & a_{n1} \\a_{12} & a_{22} & \cdots & a_{n2} \\\vdots & \vdots & \ddots & \vdots \\a_{1n} & a_{2n} & \cdots & a_{nn}\\\end{vmatrix}$$二、行列式的求解方法2.1 按定义计算法按照上述定义,计算行列式涉及到全排列的遍历与逆序数的计算,这种方法虽然理论上可行,但计算量较大,不适用于较大的矩阵。
线性代数 第三节 行列式的性质

第三节 行列式的性质分布图示★ 引言★ 性质1 ★ 例1 ★ 性质2 ★ 例2 ★ 例3 ★ 性质3 ★ 例4 ★ 例5 ★ 例6★ 性质4 ★ 例7 ★ 例8★ 性质5 ★ 例9 ★ 利用“三角化”计算行列式 ★ 例10 ★ 例11 ★ 例12 ★ 例13★ 例14 ★ 例15 ★ 例16★ 内容小结 ★ 课堂练习 ★ 习题1-3内容要点一、行列式的性质将行列式D 的行与列互换后得到的行列式,称为D 的转置行列式,记为T D 或'D ,即若,212222111211nn n n n n a a a a a a a a a D = 则 nnnnn n T a a a a a aa a a D212221212111=. 性质1 行列式与它的转置行列式相等, 即.T D D =注 由性质1知道,行列式中的行与列具有相同的地位,行列式的行具有的性质,它的列也同样具有.性质2 交换行列式的两行(列),行列式变号.推论 若行列式中有两行(列)的对应元素相同,则此行列式为零. 性质3 用数k 乘行列式的某一行(列), 等于用数k 乘此行列式, 即.2121112112121112111kD a a a a a a a a a k a a a ka ka ka a a a D nnn n in i i n nn n n in i i n ===第i 行(列)乘以k ,记为k i ⨯γ(或k C i ⨯).推论1 行列式的某一行(列)中所有元素的公因子可以提到行列式符号的外面. 推论2 行列式中若有两行(列)元素成比例,则此行列式为零. 性质4 若行列式的某一行(列)的元素都是两数之和, 例如,nnn n in in i i i i na a a cbc b c b a a a D 21221111211+++=. 则21212111211212111211D D a a a c c c a a a a a a b b b a a a D nnn n in i i n nn n n in i i n +=+=. 性质5 将行列式的某一行(列)的所有元素都乘以数k 后加到另一行(列)对应位置的元素上, 行列式不变.注: 以数k 乘第j 行加到第i 行上,记作j i kr r +; 以数k 乘第j 列加到第i 列上,记作j i kc c +.二、行列式的计算计算行列式时,常用行列式的性质,把它化为三角形行列式来计算. 例如化为上三角形行列式的步骤是:如果第一列第一个元素为0, 先将第一行与其它行交换使得第一列第一个元素不为0; 然后把第一行分别乘以适当的数加到其它各行,使得第一列除第一个元素外其余元素全为0;再用同样的方法处理除去第一行和第一列后余下的低一阶行列式,如此继续下去,直至使它成为上三角形行列式,这时主对角线上元素的乘积就是所求行列式的值.例题选讲例1若210101321-=D , 则.213102011D D T =-=例2(1)01212111012110121---=--(第一、二行互换).(2)102110211012110121---=--(第二、三列(3)072501111=(第一、二两行相等) (4)0337224112=---(第二、三列相等)例3(1)02222510211=--因为第三行是第一行的2倍. (2)07541410053820141=---因为第一列与第二列成比例,即第二列是第一列的4倍.例4 若121013201--=D , 则D 212101321)2(12101342-=---=----又 D 41210132141240112204=--=--.例5 (E01) 设,1333231232221131211=a a a a a a a a a 求.53531026333231232221131211a a a a a a a a a ---- 解 利用行列式性质,有33323123222113121153531026a a a a a a a a a ----=3332312322211312115353522a a a a a a a a a ---5)3(2⋅-⋅-=333231232221131211a a a a a a a a a15)3(2⋅⋅-⋅-=.30=例6 证明奇数阶反对称行列式的值为零. 证 设反对称行列式D 0000321323132231211312 nn n n n n a a a a a a a a a a a a ------= 其中),(时j i a a ji ij ≠-=).(0时j i a ij == 利用行列式性质1及性质3的推论1,有D T D =0000)1(321323132231211312 nnnn nn n a a a a a a a a a a a a -------=,)1(D n -= 当n 为奇数时有,D D -=即.0=D例7(1).110111311103111132+=++= (2)()1)2(1272305)2(11121272305211--+--++=----+122720521112730511---+--=.例8 因为,12310403212213==++--+而15)40()29(02213123=+++=-+-.因此221312303212213-+-≠++--+. 注: 一般来说下式是不成立的22211211222112112222212112121111b b b b a a a a b a b a b a b a +≠++++.例9(1)13201013113214113112----r r ,上式表示第一行乘以-1后加第二行上去, 其值不变.(2)33204103113214113113c c +--,上式表示第一列乘以1后加到第三列上去, 其值不变.例10计算行列式2150321263-=D .解 先将第一行的公因子3提出来:,21503242132150321263-=- 再计算.162354100430201541104702215421087042127189087042132150324213=⨯====----=-=D例11 (E02) 计算.3351110243152113------=D 解 21c c D→3315112043512131------- 14125r r r r +-72160112064802131------32r r ↔ 72160648011202131----- 242384r r r r -+ 1510001080011202131----3445r r +.40250001080011202131=---例12 (E03) 计算.3111131111311113=D 解 注意到行列式的各列4个数之和都是6.故把第2,3,4行同时加到第1行,可提出公因子6,再由各行减去第一行化为上三角形行列式.D4321r r r r +++311113111131111163111131111316666= 141312r r r r r r --- .4820000200002011116=例13 (E04) 计算.1111000000332211a a a a a a --- 解 根据行列式的特点,可将第1列加至第2列,然后将第2列加至第3列,再将第3列加至第4列,目的是使4D 中的零元素增多.4D12c c +112100000033221a a a a a -- 23c c + 1321000000003321a a a a -34c c +.44321000000000321321a a a a a a =例14 (E05) 计算.3610363234232dc b a c b a b a ad c b a c b a b a a dc b a c b a b a ad c b a D ++++++++++++++++++=解 从第4行开始,后一行减前一行:D r r r r r r ---33412.363023200c b a b a a c b a b a a cb a b a a dc b a +++++++++3423r r r r -- .20200ba a ab a a a cb a b a a dc b a +++++34r r -..0002004a ab a a cb a b a a dc b a=++++例15 设nnn nkn n k kk k kb bc c b b c c a a a a D111111111111000=,,)det(,)det(1111211111nnn nij kk k kij b b b b b D a a a a a D ====证明 .21D D D =证 对1D 作运算,j i kr r +对2D 作运算,j i kc c +可分别把1D 和2D 化为下三角形行列式.1D =kk k p p p1110;11kk p p =2D =nnn q q q 1110.11nn q q = 对D 的前k 行作与对1D 相同的运算,j i kr r +再对后n 列作与对2D 相同的运算,j i kc c +即把D 化为下三角形行列式,且D nn kk q q p p 1111⋅=.21D D = 证毕.例16 (E06) 解方程.0113211232113221132111321=-+-+-+-+-------xa a a a a a a x a a a a a a a x a a a a a a a x a a a a a a a a n n n n n n nn n n n n解 从第二行开始每一行都减去第一行得),)(())((00000000000001221112211321x a a x a x a a xa xa x a x a a a a a a n n n n n n ----=---------由,0))(())((12211=------x a a x a x a a n n 解得方程的1-n 个根:.,,,,11222211----====n n n n a x a x a x a x课堂练习1. 计算行列式.0112012120112110-----=D 2. 计算n 阶行列式 ab b b bb a b b b b a。
第五节行列式的性质

1 2
0 0 0 1 0
0 0 0 2 6
1 1 2 3 1
r5 + 2r4
0 0
2 0
0 1
4 0
1 2 12
0 0 0 1 0
0 0 0 0 6
例2: 计算 n 阶行列式
a b b b
b a b b
D b b a b .
b b b a
解: 将第2, 3, ···, n 列都加到第一列得:
行列式:
p11
0
D1
p11 pkk ;
pk1 pkk
对D2作列运算 ci+kcj , 把D2化为下三角形行列式:
q11
0
D2
q11 qnn .
qn1 pnk
先对D的前k行作行运算 ri+trj , 然后对D的后n列 作列运算 ci+kcj , 把D化为下三角形行列式:
p11
0
D
35 8
538
推论: 如果行列式有两行(列)完全相同, 则此行列 式为零.
证明: 互换相同的两行, 则有D = – D, 所以D = 0. 性质3: 行列式的某一行(列)中所有的元素都乘以
同一数k, 等于用数k乘此行列式.
即 a11 a12 a1n
a11 a12 a1n
kai1 kai2 kain k ai1 ai2 ain
a21 (a2i ka2 j ) a2 j a2n
an1 (ani kanj ) anj ann
引入记号: 用 ri 表示第 i 行, ci 表示第 i 列. 在计算行列式时, 我们经常利用性质2,3,6对行列
式进行变换.
利用性质2交换行列式的第 i, j 两行(列), 记作
1.4 行列式的性质

a 1n
则
D b1 a n1
bn c1 ann a n1
一、行列式的性质
注: 性质5可以推广到某一行(列)的元素为几组 数的和的情形. 性质6 把行列式的某一行(列)的各元素乘以同一
个倍数然后加到另一行(列)对应的元素上去,行
列式的值不变.
注:以数 k 乘第 j 行(列)加到第 i 行(列)上,记作
例5 设 D
ak1 c 11 c n1
a b 11 a 1 k 11 b 1 n D a ,D b , 1 det( ij) 2 det( ij) a b k 1 a kk n 1 b nn
D D . 证明 D 1 2
二、行列式性质的应用
1 1 3 1
1 1 1 3
二、行列式性质的应用
r2 ( 1 ) r1 r3 ( 1 ) r1 r4 ( 1 ) r1
1 0 6 0 0
1 2 0 0
1 0 2 0
1 0 6 8 48. 0 2
二、行列式性质的应用
例4 计算行列式
a b c d a ab abc abcd D . a 2a b 3a 2b c 4a 3b 2c d a 3a b 6a 3b c 10a 6b 3c d
D 4 1
r1 r2
6 1
0 2
0 1
4 1 1
二、行列式性质的应用
6 0 0 4 1 1 1 2 1
c3 c2
6
0
0
4 1 0 18. 1 2 3
1
(方法二)
2 D 1 4 1 1 200+1 100+2 100+1
§5 行列式的性质

(2) 利用性质把行列式化为上三角形行列式,从 而算得行列式的值.
1 2 3
例如 0 0 0 0 0 0 0 3 1 2 3 1 2
性质5 (拆分) 若行列式的某一列(行)的元素 都是两数之和. a11 a12 (a1i a1i ) a1n a 21 a 22 (a 2 i a i ) a 2 n 例如 2 D a n1 a n 2 (a ni a ) a nn ni
证明
D D1 D2 .
1 2
0
0
3 4 0 0 如D = ? 0 0 -1 3 0 0 5 1
a 0 0 b 0 a b 0 例5 D = 0 c d 0 c 0 0 d
看P15例11
三、小结
行列式的6个性质
同样成立). 计算行列式常用方法 (1) 利用定义;
(行列式中行与列具有同
等的地位,行列式的性质凡是对行成立的对列也
= a4
看P13例9
例4
a11 a1k 0 b11 b1n bn1 bnn a k 1 a kk 设D c11 c1k c n1 c nk
b11 b1n a11 a1k , D1 det(a ij ) , D2 det(bij ) bn1 bnn a k 1 a kk
a11
n
a12 a22
a1n a2 n
a21 an1
an 2 ann
性质4 行列式中如果有两行(列)元素成比 例,则此行列式为零;行列式的某一行(列) 元素全为零,则行列式为零.
1 2 3 例如 4 5 6 2 4 6 1 2 3
1 24 1
2 5 2
第五节--行列式的性质

第 2n 列依次与第 2n – 1 列、···、第 2 列对调,得
ab0
0
cd0
0
00a
b
D2n
,
ab
cd
00c
d
本若请本若请本若请本若请本本若若请请本若节想请单节想本单若节想请单节想本单若节节想想请单单节想内结本单若击内请结节击想内结本单若击内请结节击想内 内结 结本单若击击内请结容束节击想返本容单若束内请返结容束节击想返本容单若束内请返结容 容束 束节击想返返本容单若束已本内请返结回节已击想本本容单若回束已本内请返结回节已击想本本容单若回束已 已本 本内请返结回回节已击想本结本堂容单若回束按内结请返结本堂若节已击想按本结请本 本堂容单若 若回束按内结请 请返结本堂若节已击想按本结 结请本堂 堂容单若回束按按内结请返结堂束节课已击想按本钮容束单回束节课想内结返结钮堂束单节 节课已击想 想按本钮容束单单回束节课想内结返结钮堂束 束单节课 课已击想按本钮钮容束单回束课内,结返结钮堂.已击按本内,!结容束回束课.击内 内,结!返结 结钮堂.已击击按本内,!结容束回束课.击内,,结!返结钮堂..已击按本,!!容束回束课.结!返钮堂容束已按本,返容 容束回束 束课.结!返返钮堂容束已按本,返容束回束课.结!返钮堂已按本,束回课.已本结!钮堂回已 已按本 本,束回回课.已本结!钮堂回已按本,束回课.结!钮堂按,结堂束课.按结 结!钮堂堂按按,结堂束课.按结!钮堂按,束课.!钮束课,钮束束课课.!钮钮束课,钮束课.!钮,.,!.,,!..,!!.,!.!
性质2 互换行列式旳两行,行列式变号.
性质2 互换行列式的两行,行列式变号. 证明 设行列式
b11 b12 b1n
D1
b21
b22
矩阵论基础1.4行列式的性质

矩阵论基础1.4⾏列式的性质第四节⾏列式的性质⾏列式有如下7条性质n阶⾏列式:,若把D的⾏变为列得到新⾏列式如下,⾏列式D T (或D′)称为⾏列式D的转置⾏列式.注意:转置⾏列式也可以看作以主对⾓线为轴,⾏列式翻转180°的结果.性质1 ⾏列式D=D T证明: ,应⽤数学归纳法,当n=2时,结论显然成⽴,即假设n-1时结论成⽴,即n-1阶⾏列式与它的转置⾏列式相等,将n阶⾏列式D按第⼀⾏展开,有将n阶⾏列式D T按第⼀列展开,有所以n阶⾏列式D=D T由⾏列式的性质1可以看出,⾏列式的⾏和列的地位相同,⾏所具有的性质对于列也成⽴,反之亦然.性质2 若⾏列式中有某⼀⾏(或列)为零,则这个⾏列式的值等于零.说明:把⾏列式按此⾏(或列)展开即可.性质3 ⾏列式中任何两⾏(或两列)互换位置, ⾏列式的值变号.证明: ,第⼀⾏与第三⾏互换位置后,⾏列式变为将D按第⼀⾏展开,得将D1按第三⾏展开,得此性质对于n阶⾏列式也成⽴.推论: 如果⾏列式有两⾏(列)完全相同, 则此⾏列式等于零.说明:交换这两⾏(列)⾏列式D化为D1,由性质2知,-D=D1,由于交换的两⾏(列)相同,故D=D1,因此,-D=D,D=0性质4 ⾏列式的某⼀⾏(列)中所有的元素都乘以同⼀数λ, 等于⽤数λ乘此⾏列式.反之, ⾏列式的某⼀⾏(列)中所有的元素有公因数,则可以把这个公因数从⾏列式中提出来,即说明:上⾯两个⾏列式若按第i⾏展开,结果是相同的.推论:⾏列式中如果有两⾏(列)元素对应成⽐例, 则此⾏列式等于零.性质5 若⾏列式的某⼀⾏(列)的每个元素都是两个数之和, 例如第i⾏的元素都是两数之和: 即,则D等于下列两个⾏列式之和:.说明:记三个⾏列式为D,D1,D2,则性质6 把⾏列式的某⼀⾏(列)的各元素乘以同⼀数然后加到另⼀⾏(列)对应的元素上去, ⾏列式不变. 即.说明:性质5和性质4可得性质6,这个性质在⾏列式的计算中⾮常重要.性质7 ⾏列式每⼀⾏(或列)的每个元素与另⼀⾏(或列)对应元素的代数余⼦式的乘积的和等于零,即说明: n阶⾏列式按第j⾏展开,于是得下⾯结论 , 或在处理和计算⾏列式时,常⽤上述7条性质,为了表达简洁,引⼊下列记号(1)(2)(3)(4)(5)(6)(7)(8)例如,例9 计算⾏列式解:利⽤⾏列式的性质,把D化为相等的上(下)三⾓⾏列式,再写出结果,这是计算⾏列式的常⽤⽅法.说明:(1)利⽤性质6,先把a11下⾯的所有元素化为零;(2) 再把a22下⾯的所有元素化为零;(3)重复操作,直到化为三⾓⾏列式为⽌;(4)对于列也可以采⽤同样的处理⽅法,化为其它类型的三⾓⾏列式,再求值.求⾏列式的值时,常⽤的⽅法还有按某⾏(列)展开,达到降阶的⽬的,从⽽化简⾏列式,直到求出结果为⽌.例10 计算⾏列式解:要善于⽤两种⽅法求⾏列式的值:1.化为三⾓⾏列式(四种结果)2.按某⼀⾏(列)展开(选零较多的⾏(列)).例11 计算⾏列式解:因第⼀列与第三列对应元素成⽐例,所以D=0.例12 计算⾏列式解:例13 计算⾏列式解:D1中每⾏提出公因⼦(-1),得所以D1=0D2按第⼀⾏展开,得例14 计算⾏列式解:同理可得例15 计算三阶Vandermonde⾏列式解:同理可得n阶Vandermonde⾏列式例16 计算(m+n)阶零块⾏列式解:记,对|A|作若⼲次r i+λr j操作,化为下三⾓⾏列式,设为对|B|作若⼲次c i+λc j操作,化为下三⾓⾏列式,设为把对|A|的操作全部施于D的前n⾏,再把对|B|的操作全部施于D的后m列,得同理可知以下三个零块⾏列式的值(1)(2)注:(3)说明:1.(2)中⾏列式D可化为下三⾓⾏列式,利⽤前⾯的结论,可推得2. 四种结果要牢记.。
1章3节 行列式的性质

a13 a23 =1 a33 10a13 5a23 5a33
-3 c1 5 c3
6a11 求 3a21 3a31
2a12 a22 a32
2a11
10a13 5a23 。 5a33
2a12 a22 a32 2a13 a23 a33
a31 6a11
解 3a21 3a31
2a12 a22 a32
a11
kc j
a12 kai 2 an 2
ka1 j kaij kanj
a1, n1 kai ,n1 an,n 1
a1n ain ann
a1n kain ann
即 k ai1 ai 2
an1 an 2
a11 k ai1 an1 a1 j aij anj
an,n1 ann
a1n ain ann
a12 0 a23 L a2 n
a13 a23 0 L
L L L L
a1n a2 n a3n L 0
转置值不变
a3n L
则有 D DT
0 a12 a13 L a1n a12 0 a23 L a2 n a13 L a23 L 0 L L a3n L L a1n a2 n a3n L 0
25 12
例
3
25 1 12 1 3
75 36 2 25 3 12 3 2 50 24 3 25 2 12 2 3
25 c1 12 c 2
c1 = c 2
1 1 3 25 12 3 3 2 2 2 3
25 12 0
=0
6、两行(列)成比例,值为零。
推论2
a b d e g h
c f i
c f i
d
行列式的性质与计算

行列式的性质与计算行列式是线性代数中的基本概念之一,它是一个非常重要的工具,在数学和许多其他领域中都有广泛的应用。
行列式的性质和计算是学习线性代数的基础之一。
一、行列式的定义行列式是由n个数字aij(i=1,2,n;j=1,2,n)组成的矩形表格,通常用大写字母D表示。
这些数字按照一定的规则排列,形成一个n阶方阵。
行列式D的值是一个与方阵有关的唯一的数,它反映了方阵线性变换的性质。
二、行列式的性质1.行列式的行和列具有相同的地位,因此行列式的性质可以按照行或列来描述。
2.交换两行或两列的位置,行列式的值不变。
即,如果i≠j,那么Dij=Dji。
3.行列式的某一行或某一列中所有元素的公因子可以提取出来,提取后剩余的元素按照原来的相对位置排列组成的行列式与原来的行列式相等。
即,如果k为常数,那么Dk=kD。
4.行列式中两行或两列对应元素相同,行列式的值为零。
即,如果i=j,那么Dij=0。
5.行列式可以按照某一行或某一列展开,展开后得到的行列式与原来的行列式相等。
6.行列式可以按照主对角线进行展开,展开后得到的行列式与原来的行列式相等。
7.行列式可以按照某一行或某一列进行递推展开,展开后得到的行列式与原来的行列式相等。
8.行列式可以按照某一行或某一列进行递归展开,展开后得到的行列式与原来的行列式相等。
三、行列式的计算行列式的计算是线性代数中的基本技能之一,也是解决许多问题的关键步骤。
下面介绍几种常见的计算方法:1.利用定义计算根据行列式的定义,我们可以直接计算行列式的值。
对于n阶方阵A,其行列式的定义为D=a11A11+a12A12+.+anAn,其中Aii是元素aij的代数余子式。
利用这个公式,我们可以直接计算任意一个n阶方阵的行列式。
2.利用性质计算利用行列式的性质,我们可以简化行列式的计算。
例如,根据行列式的交换律,我们可以将两行或两列交换位置;根据行列式的倍数律,我们可以将一行或一列乘以一个常数;根据行列式的零律,我们可以将一行或一列中所有元素设置为零;根据行列式的展开律,我们可以将行列式按照某一行或某一列展开等等。
行列式的性质及其运用

1111
解: D 1
3
1
1 r1 r2 r3 r4
1
3
1
11 6
3
1
r2 r1
1 6 0 r3 r1
2
0
0
1131
1131
1 1 3 1 r4 r1 0 0 2 0
1113
1 1 1 3 1113
0002
6 23 48 .
1.2 行列式性质的运用
例题
ab
c
d
例 5 计算行列式 D a a b a b c
0 0 a 2a b
0 0 3a 7a 3b
00 0
a
1.2 行列式性质的运用
例题
方法二:
ab
c
a ab abc D
a 2a b 3a 2b c
d abcd 4a 3b 2c d
ab c
d
0 a r4 r3
r3 r2
ab
abc
r2 r1 0 a 2a b 3a 2b c
a 3a b 6a 3b c 10a 6b 3c d
a11 a12
a1n
a11
a12
a1n
ai1 ai2 D
a j1 a j2
ain
ai1 ka j1 ai2 ka j2
ri krj
a jn
a j1
aj2
ain ka jn a jn
an1 an2
ann
an1
an2
ann
1.1 行列式的性质
性质
性质 2、性质 3 和性质 5 常用来计算行列式,它们的标记如下. ① 互换 i,j 两行(列): ri rj (ci c j ) . ② 第 i 行(列)乘以某非零常数 k: kri (kci ) . ③ 将第 j 行(列)的 k 倍加到第 i 行(列)上: ri krj (ci kcj ) .
第5节行列式的性质
2 1 1 2 例 7.计算 D 1 1 2 2 . 2 0 1 1 1 3 2 2
2 1 1 2 1 2 1 2 r2r1 1 c1c2 r4 3r1 1 1 2 2 1 1 2 2 解: 0 2 0 1 1 0 2 1 1 0 1 3 2 2 3 1 2 2 0 1 =0 0 0 1 0 0 0 1 2 2 1 r3 3 3 4 r2 0 1 2 1 0 1 7 4 0 1 1 0 0 2 2 9 0 2 1 18 . 1 2 1 2 2 r33r2 1 r2 1 2 1 r4 0 3 3 4 0 1 7 4 0 2 1 2 c3 3 3 4 c2 2 1 1 7 1 4 1 1 0 0 2 2 r3 2 1 r4 9 1 9 3
b c d r4 r3 r3r2 0 a a b a b c 解: D 0 a 2a b 3a 2b c 0 a 3a b 6a 3b c
a 0 0 0 b c d a r3 a a b a b c r4 0 0 a 2a b 0 0 0 a 3a b b c d a a b a b c a4 0 a 2a b 0 0 a
a11 ak1 例 10.设 D c11 cn1 a1k 0 akk 0 c1k b11 cnk bn1 0 0 b1n bnn
D1
a11 ak1
a1k akk
,
ቤተ መጻሕፍቲ ባይዱ
D2
b11 bn1
b1n bnn
证明: D D1D2 .
注:此题为 a 0 ab 的推广.
c b
证:对 D1 作运算 ri kr j 化为: D1
1 1 0 0
初数数学中的行列式公式详解

初数数学中的行列式公式详解行列式是初等数学中非常重要的概念之一,它在线性代数、线性方程组以及向量空间等领域具有广泛的应用。
本文将详细解析行列式的定义、性质和相关公式,帮助读者更好地理解和应用行列式。
一、行列式的定义行列式是一个方阵的标量量,它的值为一个数。
对于一个n阶方阵A=[a[i,j]],它的行列式记为|A|或det(A)。
行列式的计算需要按照一定的规则进行,下面将介绍常用的行列式计算方法。
二、行列式的计算方法1. 一阶行列式对于一个1×1的行列式,例如A=[a],它的值就是a。
2. 二阶行列式对于一个2×2的行列式,例如A=[a11,a12;a21,a22],它的值可以通过交叉相乘再相减的方法进行计算:|A|=a11·a22-a12·a21。
3. 三阶及以上的行列式对于三阶及以上的方阵,可以使用拉普拉斯展开或三角形法则进行计算。
拉普拉斯展开的思想是:把一个n阶行列式按照某一行(或列)的元素展开,然后递归地计算这些元素的(n-1)阶行列式,直到计算到二阶行列式为止。
三、行列式的性质行列式具有多种重要的性质,下面将介绍几条常用的性质。
1. 行列互换性质行列式的值不变,当互换它的任意两行(或两列)时。
2. 行列式倍乘性质行列式中的一行(或一列)的每个元素都乘上同一个数k,行列式的值也同样乘以k。
3. 行列式的展开性质行列式可以按任意一行(或一列)展开,得到的结果相同。
4. 行列式的转置性质一个方阵与其转置阵的行列式相等。
5. 行列式的相似性质相似矩阵的行列式相等。
四、常见的行列式公式1. 三阶行列式的展开式对于一个三阶行列式A=[a[i,j]],可以使用拉普拉斯展开进行计算:|A|=a11·a22·a33+a12·a23·a31+a13·a21·a32-a13·a22·a31-a12·a21·a33-a11·a23·a32。
§4行列式的性质

§1.4 行列式的性质性质1 设nnn n a a a a D1111 , nnnn a a a a D1111Τ , 则D D Τ. 证 令),,2,1,(n j i a b ji ij , 则nnn n b b b b D1111Τ n n np p p p p p b b b 212121)()1( )(21n p p pD a a an p p p p p p n n21)(2121)1( (根据Th2)性质2 设jn j in i a a a a D j i 11, ,in i jnj a a a a D 111 , 则D D 1. 证 ),,2,1(,n k a b a b ik jk jk ik ),,2,1(:,n k a b j i l lk lk)()1(111j i jp ip jn j ini b b b b b b D )( j i p p ))(1()1( i j ip jp t b b )( i j p p t )()1()1( i j jp ip t a all i j j i p q j i l p q p q :,,)()1()1( j i jq iq t a a D )( j i q q t 推论1 D 对调两列得2D D D 2.证 因为D 对调两列得2D , 相当于T D 对调两行得T2D所以D D D D T T22 推论2 D 中某两行(列)元素对应相等0 D . 证 因为对调此两行(列)后,D 的形式不变 所以0 D D D例如, 对于任意的c b a ,,, 都有0321321 c b a .性质3 kD a a ka ka a a nnn in i n11111, kD a ka a a ka a nnnjn nj11111 证(1) 左端])([)1(11n i np ip p a ka a )(1n i p p p kD a a a k n i np ip p )()1(11 推论1 D 中某行(列)元素全为00 D . 推论2 D 中某两行(列)元素成比例0 D . 性质4 若对某个i , 有),,2,1(n j c b a ij ij ij , 则nn n in i n a a a a a a11111nn n in i n a a b b a a11111 nnn in i n a a c c a a11111 证 左端)()1(11n i np ip p a a a )(1n i p p p )()1(11n i np ip p a b a )()1(11n i np ip p a c a 右端(1)+ 右端(2) [注] 性质4对于列的情形也成立.性质5jn j in i a a a a 11)(111j i a a a a a a jn j jnin j i kr r ji[注] 性质5对于列的情形也成立.例5 计算1314211311023351D .解 119211110160551003351D 1113200112033515112320011103351)5(1300320011103351)5( 211000320011103351)5( 55 例6 计算x a a a x aa a x D n. 解 x a a a x aa n x D n r r r n111])1([)(21 ax a x a n x00111])1([1)]()1([ n a x a n x例7 计算10001030012321n n D n . 解 )2(11000010000103222,,21n ntD j jc c nj n§1.5 行列式按行(列)展开余子式:在n 阶行列式中,将元素ij a 所在的行与列上的元素划去,其余 元素按照原来的相对位置构成的1 n 阶行列式,称为元素ij a 的 余子式,记作ij M .代数余子式:元素ij a 的代数余子式ij j i ij M A )1(.定理3 nnn n nn a a a a a a a a a D212222111211in in i i i i A a A a A a 2211 ),,2,1(n i nj nj j j j j A a A a A a 2211 ),,2,1(n j 证 证明第一式, 分以下3步. 第1步:1,11,11,111 n n n n nna a a a M1111,11)()1( n n p n p p p a a )11( n p innn n n n n n n a a a a a a a 0,11,11,111,111n n n n p n p n p p p p a a a ,,11)(1111)1(n n n n n p n p n p np p p p a a a ,,11)(1111)1(+n n n n n p n p n p np p p p a a a ,,11)(1111)1(1111,11)()1( n n p n p n p p nn a a a )()(1111 n n p p n p p nn nn nn n n nn nn nn A a M a M a )1(第2步: njj i ijj i ja D D a a a D D a j i D 43,1,12110000),(ijnjj i j i j j n i n a a D D a a D D a 0000)1(43,1,1211)()(ij ij ij ij j i A a M a )()1( 第3步:),()2,()1,(n i D i D i D D in in i i i i A a A a A a 2211例8 计算1314211311023351D .解 34012113110272016D 3411127216)1(23 5517520)1)(1(1071125020)1(22 例9 计算dcdcd c b a b a b a D n2.解 )12()1(21120000)1( n n n dD aD)12()1(2210000)1( n n n c D b)1(21)12()1(2)12()12()1)(1()1( n n n n n D bc D ad 21)1(2)()(D bc ad D bc ad n n bc ad dc b a D2n n bc ad D )(2例10 计算n n n D n 000111001330122111.解 )!1()1(11 n nD D n n n)!1()1()!11()1()1(11)1(2 n n D n n n n n nn n n D n n n n n !)1(1!)1()1(12nn n n n D n n n n !)1(1!)1(3!)1(3)1(142 1)1(2)1(122111322Dn n D n n 1432)1(3)1(2)1(1)1()!(课后作业:习题一 4 (1) (2) 5 (1) (2) (3) 7 (1) (2)。
第2讲 行列式性质

… ………
… ………
an1 an2 … ann
an1 an2 … ann
性质4 如果行列式有两行(列)的对应元素成
比例,则此行列式的值为零
15 6
例1 D= 2 3 8 =0
4 6 16
例2 设
a11 a12 a13
6a11 2a12 10a13
a21 a22 a23 =1,求 3a21 a22 5a23 。
123
例2 计算行列式的值 D= ○3 1 2 ○2 ○3 1
化成上三角式
解
123
123
D= 0 5 7 =- 0 1 5 =-
123
0 1 5
=18
0 1 5
0 5 7
0 0 18
r2 3r1 r3 2r1
r2 r3
120 1 例3 计算行列式的值 D= 1 3 5 0
r2 r1 r4 r1
a31 a32 a33
3a31 a32 5a33
解:
6a11 2a12 10a13 3a21 a22 5a23 3a31 a32 5a33
3a11 a12 5a13 2 3a21 a22 5a23
3a31 a32 5a33
a11 a12 a13 2(3)5 a21 a22 a23
a31 a32 a33
第二讲 行列式的性质
一 行列式的性质(6条) 二 一些特殊的行列式
行列式的转置:
第1行变为第1列, 第2行变为第2列,
… 第n行变为第n列
将行列式D的同号数的行换为同号数的列得到
的行列式称为D的转置行列式,记为DT或D
a11 a12 … a1n
D=
a21 …
a22 …
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
性质4:行列式某一行元素加上另一 行 对应元素的k倍,行列式的值不变 。
a j1
ajn
an1
ann
a11 a1n
a11 a1n
ai1 ain kaj1 kajn
aj1 ajn
aj1 ajn
an1 ann
an1 ann
问题
a11
a1n
ai1 b1 ain bn ?
an1
ann
a a
11
1n
a11 a 1n
a11
a22 a
32
a23 a33
a12
a21 a31
a23 a33
a13
a21 a31
a22 . a32
a21 D1 a11
a31
a22 a12 a32
a23 a13 a33
a12a21a33 a13a22a31 a11a23a32 a11a22a33 a13a21a32 a12a23a31
a a b b
i1
in
1
n
a a
n1
nn
a a
n1
nn
性质5:若行列式某一行的元素是两数 之 和,则行列式可拆成两个行列式的 和。
推论:若行列式某一行的元素都是m 个元素的和,则行列式可以写成m个 行列式的和。
练习 写出行列式的性质。
证明你写出的行列式的性质。
性质2:互换两行,行列式变号 。
怎么证明呢?
a11
ai1
ai1
an1
我们考虑下面的行列式
a1n
两行相同行列式的值为0.
a i n 将行列式按第j行展开.
ain
ann
a j1 Ai1
a
j
2
A i2
a A jn in
D,
0,
(i j). (i j).
a1 j A1i
a2
j
A 2i
aA nj ni
D,
Hale Waihona Puke 0,(i j). (i j).
性质2:互换两行,行列式变号。即
a11
ai1
a j1
an1
a1n
ain
a jn
ann
a11
a j1
ai1
a n1
a1n
a jn
ain
ann
a11 D a21
a31
a12 a22 a32
a13 a23 a33
a11a22a33 a12a23a31 a13a21a32 a13a22a31 a11a23a32 a12a21a33
a11
设D
a21
an1
行列式的性质
a12 a1n
a22
a2n
则转置行列式为
an2 ann
a11 a21 an1
DT
a12
a22 an2
a1n a2n ann
性质1:D DT
由行列式的定义即可证明这条性质。
在行列式中,行和列的位置是对称的, 对行成立的,对列也成立。
因此下面只介绍关于行列式的行的性质。
a11
a22 a
32
a23 a33
a12
a21 a31
a23 a33
a13
a21 a31
a22 . a32
推论:若行列式中有两行元素完全相同 则行列式为零。
设Aij为元素aij的代数余子式,则有
aj1 Ai1 aj 2 Ai2 ajn Ain 0 (i j) a1j A1i a2 j A2i anj Ani 0 (i j)
2 2 3 4 1 1 1
8 2 7
性质4:行列式某一行元素加上另 一行对应元素的k倍,行列式的值 不变。即:
a11
a1n
a11 a1n
ai1 ka j1 ain kajn
ai1 ain
.
a j1
ajn
aj1 ajn
an1
ann
an1 ann
a11
a1n
ai1 ka j1 ain kajn
这是非常有用的两个公式,应该记住。
性质3:用数k乘行列式某一行中所有元 素,等于用k乘此行列式。即
a a
11
1n
a a
11
1n
ka ka k a a
i1
in
i1
in
a a
n1
nn
a a
n1
nn
推论:某一行的所有元素的公因子可以 提到行列式符号的外面。
8 4 6 4 2 3 2 1 1 2 2 1 1 16 2 7 16 2 7
