双三次插值bicubicinterpolation原理及MATLAB源码实现

合集下载

样条曲面插值

样条曲面插值
样条曲面插值是一种数学方法，用于从离散的点集构建平滑的曲面。

这些点通常表示在二维或三维空间中的位置，而样条曲面则用于近似这些点并创建一个连续的曲面。

插值是指根据已知的离散数据点来推断出其他位置上的数值。

样条曲面插值的目标是通过一个连续且光滑的曲面，最好地逼近这些离散数据点。

常见的样条曲面插值方法包括：
1. 双三次插值样条曲面（Bicubic Interpolation）：这种方法使用双三次样条插值来创建一个连续的曲面，它在每个方向上都使用三次多项式来逼近数据点。

2. Bezier曲面：Bezier曲面是由Bezier曲线推广而来的，它利用多个Bezier曲线的控制点来构建曲面。

3. B样条曲面（B-spline Surface）：B样条曲面使用多个B样条来构建曲面，这些B样条由节点序列和控制点确定。

4. 样条插值基础上的曲面拟合：在这种方法中，通过使用已知数据点，先进行样条插值以获得一个曲面网络，然后利用这个网络进行曲面拟合。

这些方法都有其独特的优势和适用场景，但都旨在从离散的点集构建出平滑、连续的曲面，使得对数据的预测和分析更加准确和可靠。

计算机视觉（五）双三次插值（Bi...

计算机视觉（五）双三次插值（Bi...超分辨率基础_插值算法简介1.插值算法数学的数值分析领域中，内插或称插值（英语：interpolation)是一种通过已知的、离散的数据点，在范围内推求新数据点的过程或方法。

常见的三种插值算法为最近邻插值、双线性插值和双三次插值。

一组离散数据点在一个外延的插值。

曲线中实际已知数据点是红色的；连接它们的蓝色曲线即为插值。

2.最近邻插值算法最邻插值算法(Nearest Neighborinterpolation)是最简单的一种插值算法，当图片放大时，缺少的像素通过直接使用与之最近原有像素生成，原理就是选取距离插入的像素点（x+u, y+v)【注：x,y为整数，u，v为小数】最近的一个像素点，用它的像素点的灰度值代替插入的像素点。

i+u, j+v为待求像素坐标，如果 i+u, j+v落在A区，即 u<0.5,v<0.5，则将左上角像素的灰度值赋给待求像素，同理落在B区则赋予右上角的像素灰度值，落在C区则赋予左下角像素的灰度值，落在D区则赋予右下角像素的灰度值。

最近邻插值法计算量较小，但可能会造成生的图像灰度上的不连续，在变化地方可能出现明显锯齿状。

3.双线性插值算法在数学上，双线性插值是有两个变量的插值函数的线形插值扩展，其核心思想是在两个方向分别进行一次线性插值。

以上是一维的，接下来看看二维中的双线性插值首先在x方向上面线性插值，得到R2、R1然后以R2,R1在y方向上面再次线性插值如果选择一个坐标系统使得 f 的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1)，那么插值公式就可以化简为用矩阵表示双线性内插法的计算比最邻近点法复杂，计算量较大但没有灰度不连续的缺点，结果基本令人满意。

它具有低通滤波性质，使高频分量受损，图像轮廓可能会有一点模糊。

4.双三次插值算法(bicubic interpolation)在数值分析这个数学分支中，双三次插值（英语：Bicubic interpolation）是二维空间中最常用的插值方法。

matlab三次样条插值例题解析

文章标题：深度解析Matlab三次样条插值1. 前言在数学和工程领域中，插值是一种常见的数值分析技术，它可以用来估计不连续数据点之间的值。

而三次样条插值作为一种常用的插值方法，在Matlab中有着广泛的应用。

本文将从简单到复杂，由浅入深地解析Matlab中的三次样条插值方法，以便读者更深入地理解这一技术。

2. 三次样条插值概述三次样条插值是一种利用分段三次多项式对数据点进行插值的方法。

在Matlab中，可以使用spline函数来进行三次样条插值。

该函数需要输入数据点的x和y坐标，然后可以根据需要进行插值操作。

3. 三次样条插值的基本原理在进行三次样条插值时，首先需要对数据点进行分段处理，然后在每个分段上构造出一个三次多项式函数。

这些多项式函数需要满足一定的插值条件，如在数据点处函数值相等、一阶导数相等等。

通过这些条件，可以得到一个关于数据点的插值函数。

4. Matlab中的三次样条插值实现在Matlab中，可以使用spline函数来进行三次样条插值。

通过传入数据点的x和y坐标，可以得到一个关于x的插值函数。

spline函数也支持在已知插值函数上进行插值点的求值，这为用户提供了极大的灵活性。

5. 三次样条插值的适用范围和局限性虽然三次样条插值在许多情况下都能够得到较好的插值效果，但也存在一些局限性。

在数据点分布不均匀或有较大噪音的情况下，三次样条插值可能会出现较大的误差。

在实际应用中，需要根据具体情况选择合适的插值方法。

6. 个人观点和总结通过对Matlab中三次样条插值的深度解析，我深刻地理解了这一插值方法的原理和实现方式。

在实际工程应用中，我会根据数据点的情况选择合适的插值方法，以确保得到准确且可靠的结果。

我也意识到插值方法的局限性，这为我在实际工作中的决策提供了重要的参考。

通过以上深度解析，相信读者已经对Matlab中的三次样条插值有了更加全面、深刻和灵活的理解。

在实际应用中，希望读者能够根据具体情况选择合适的插值方法，以提高工作效率和准确性。

三次样条插值函数MATLAB编程实现

三次样条插值函数为()()[)()[]1011,,,,n n n S x x x x S x S x x x x-⎧∈⎪=⎨⎪∈⎩ 利用三次埃尔米特插值函数表示三次样条插值函数，即()()()()())111111,,j j j j j j j j j j j S x y x y x m x m x x x x ααββ++++++⎡=+++∈⎣（0,1,,1j n =-）基函数满足()()()()()()21112111121121111212jj j j j j j j j j j j j j j j j j j jj j j j x x x x x x x x xx xx x x x x x xx xx x x x xx x x x x x xααββ++++++++++++⎛⎫⎛⎫--=+ ⎪⎪ ⎪⎪--⎝⎭⎝⎭⎛⎫⎛⎫--=+ ⎪⎪ ⎪⎪--⎝⎭⎝⎭⎛⎫-=-⎪ ⎪-⎝⎭⎛⎫-=-⎪ ⎪-⎝⎭由上式易得()()()()()()()()()()()()()()1331111331112211112211612612246246j j j j j j j j j j j j j j j j j j j j j j jj j j j j x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x xx ααββ+++++++++++++++''=---+''=-+--+''=---+''=---则有()()()()()()()()()()()111111113333111111122221111661212242466j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j S x y x y x m x m x x x x x y x y x x x x x x x x x x x x x m x m x x x x x x x x x ααββ+++++++++++++++++++''''''''''=+++⎡⎤⎡⎤++⎢⎥⎢⎥=-+-+⎢⎥⎢⎥----⎣⎦⎣⎦⎡⎤++⎢⎥+-+-⎢⎥----⎣⎦)1,j j x x x +⎡⎤⎢⎥⎡∈⎣⎢⎥⎣⎦（0,1,,1j n =-）同理有()()()()()()()()()()()()()()()11111113333111111122221111661212242466j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j S x y x y x m x m x x x x x y x y x x x x x x x x x x x x x m x m x x x x x x x x x ααββ------------------''''''''''=+++⎡⎤⎡⎤++⎢⎥⎢⎥=-+-+⎢⎥⎢⎥----⎣⎦⎣⎦⎡⎤⎡++⎢⎥+-+-⎢⎥----⎣⎦⎣)1,j j x x x -⎤⎢⎥⎡∈⎣⎢⎥⎦（1,,j n =）根据样条函数二阶导数连续性，即()()100j j j j S x S x +''''+=-（1,,1j n =-）即()()()()()()()()()()()()()()()()111111332211111111113322111166426624j j jj j j j j j j jj j jj j j j j j jj j j j jj j j j j jjj jj jj jj x x y x x y x x x x m m x x xx xx xx x x y x x y x x x x m m x x xx xx xx ++++++++++--------------+++--------=+++----（1,,1j n =-）化简得()()()()()111111111111233j j j j j j j j j j j j j j j j j j jj j xx m x x m x x m x x x x y y y y x x x x +-+--+-++-+--+-+---=-+---（1,,1j n =-）可得线性方程组()()()()()()()()()()0121201023231213121221111110212110211032213221322122233333n n n n n n n n n n n n m m x x x x x x m x x x x x x m x x x x x x m m m x x x x y y y y x x x x x x x x y y y y x x x x y ------⨯+-+⨯⎛⎫ ⎪ ⎪ ⎪---⎛⎫⎪ ⎪--- ⎪ ⎪⎪ ⎪⎪ ⎪ ⎪--- ⎪⎝⎭ ⎪ ⎪ ⎪⎝⎭---+------+---=()()()121112112113n n n n n n n n n n n n n x x x x y y y x x x x ----------⨯⎛⎫⎪ ⎪ ⎪ ⎪⎪⎪ ⎪-- ⎪-+- ⎪--⎝⎭为了使样条插值问题有惟一解，我们在原有方程基础上增加两个边界条件。

双三次插值原理

双三次插值原理
双三次插值原理是一种数字图像处理技术，常用于图像放大或缩小的过程中。

其基本原理是根据已有的像素点，通过一个三次函数来近似估算出缺失的像素点的取值。

这个三次函数由16个系数决定，这些系数要根据已知的像素点进行插值计算。

双三次插值的优点是可以获得较为平滑的插值效果，同时保留了原图像的细节和清晰度。

但是，它也有一些缺点，比如处理速度较慢，需要占用大量的计算资源。

在实际应用中，双三次插值常常与其他图像处理技术结合使用，以达到更好的效果。

比如，可以先进行图像去噪处理，再进行双三次插值，以获得更好的放大效果。

- 1 -。

matlab三次样条插值的方法

matlab三次样条插值的方法Cubic spline interpolation is a common method used in MATLAB to approximate values between specified data points. This technique involves fitting a piecewise cubic polynomial to the data points, ensuring that the function is smooth and continuous at the knots. Through this process, the spline curve can accurately represent the overall trend of the data, making it particularly useful in various scientific and engineering applications.三次样条插值是MATLAB中常用的一种方法，用于在指定数据点之间近似数值。

这种技术涉及将分段三次多项式拟合到数据点，确保在节点处函数平滑连续。

通过这个过程，样条曲线可以准确地表示数据的总体趋势，使其特别适用于各种科学和工程应用。

One advantage of cubic spline interpolation is its ability to capture the local behavior of the data while maintaining global smoothness. This is achieved by constructing individual cubic polynomials between adjacent data points, ensuring that the interpolated curve passes through each data point without introducing significant oscillations or deviations. As a result, cubic splines provide a reliableand visually appealing way to interpolate data that may exhibit complex patterns or fluctuations.三次样条插值的一个优点是能够捕捉数据的局部行为，同时保持全局的平滑性。

基于DSPBuilder的双三次插值算法FPGA实现的研究

云南大学学报(自然科学版),2009,31(S2):85～89CN53-1045/N　ISSN0258-7971 Journal of Yunnan U niversityΞ基于DSP Builder的双三次插值算法FPGA实现的研究谢　然1,李玉惠1,沈　慧2,李　勃1,陈海飞1(11昆明理工大学信息工程与自动化学院,云南昆明　650051;21云南省电子工业研究所,云南昆明　650031)摘要:研究利用DSP Builder来完成DSP算法在FPG A上实现的方法.与传统的DSP技术相比,FPG A在实现DSP功能上其并行设计的灵活性和高效性更具优势.研究的设计方法解决了在FPG A上通过编写硬件描述语言(HDL)实现DSP算法的设计难度大、开发周期长2个问题.在此以双三次插值算法为例,研究了这种方法的可行性.关键词:FPG A;Matlab/Simulink;DSP Builder;双三次插值中图分类号:TP312 文献标识码:A 文章编号:0258-7971(2009)S2-0085-05当今的数字信号处理(DSP)技术主要由DSP处理器来构成.尽管DSP处理器具有通过软件设计能实现不同功能的灵活性,但其硬件结构的不可变性导致了其总线的不可变性以及其循序执行的CPU结构,使其在结构化设计和数据处理的速度上发展受到很大限制[1].随着现场可编程门阵列(FP G A)器件工艺技术的发展、集成度的提高和价格成本的下降,设计人员有了新的选择.FP G A中具有丰富的内部逻辑单元阵列和连线资源,这种器件内部一般都内嵌有可配置的高速RAM、PLL、LVDS、LV TTL以及硬件乘法累加器等,有的还直接内嵌DSP功能模块,这些特性使FP G A可以方便地构成各种数字信号处理器.用FP G A来实现数字信号处理可以很好地解决并行性和速度的问题,克服了使用DSP处理器实现时的不足,而且其灵活的现场可配置特性,使得FP G A构成的数字信号处理系统非常易于修改、测试及硬件升级.传统的在FP G A进行DSP算法实现的方法是首先用软件编程语言(C,C++,M语言等)在系统仿真工具中完成系统算法的设计及仿真,再在FP G A中用硬件描述语言将其描述出来,这种方法是非常费时费力的.本文研究一种利用Matlab/Simulink下的DSP Builder工具来实现双三次插值算法建模,并在FP2 G A中实现此算法的快捷有效设计方法.1　双三次插值算法近年来,数字图像处理技术在电子通信领域与信息处理领域得到了广泛的应用.图像插值是数字图像处理中的基本操作,从简单的图像缩放、旋转等操作,到图像配准、三维图像重建等复杂的处理都需要使用到图像插值[2].插值算法的精度会影响图像处理的最终结果,在使用插值算法对图像进行缩放时,插值算法的好坏直接影响图像的失真程度.常用的插值算法包括最近邻域插值、双线性插值和双三次插值等.其中,最近邻域插值是最简单的插值,处理速度快,实现简单,但是它只是把原始像素简单的复制到其邻域内,随着放大倍数的增加,放大图像就会出现明显的方块或锯齿,不能很好地保留原始图像的边缘信息[3].双线性插值虽然能改善这些问题,但是效果并不明显.使用双三次插值算法能够更好地消除锯齿,保留原始图像的边缘信息,放大后的图像较平滑,有较好的视觉效果,但计算量也是很大的.领域为4×4的双三次插值的插值基函数为[4]:Ξ收稿日期:2009-06-04作者简介:谢　然(1982-　),男,北京人,硕士生,主要从事FPGA嵌入式技术应用方面的研分;E-mail:wingxieran@1631com 通讯作者:李玉惠(1964-　),女,云南人,教授,博士,主要从事片上可编程系统(SOPC)方面的研究;E-mail:lbly9177@1631comφ(u )=32|u |3-52|u |5+1, 0≤|u |<1,-12|u |3+52|u |2-4|u |+2, 1≤|u |<2,0. 其它(1)双三次插值算法的领域示意图如图1所示,为计算R 点的像素值,需要利用原始图像中的A 到P 共16个相邻像素.设x 和y 分别是A 到R 点在水平和垂直方向上的距离,则:R =(t 1A +t 2B +t 3C +t 4D )t 5+(t 1E +t 2F +t 3G +t 4H )t 6+(t 1I +t 2J +t 3K +t 4L )t 7+(t 1M +t 2N +t 3O +t 4P )t 8.(2)其中t 1,t 2,t 3和t 4是将各点与R 点在水平方向上的距离代入(1)式计算得到的系数,而t 5,t 6,t 7和t 8是将各点与R 点在垂直方向上的距离代入(1)式计算得到的系数.图1　双三次插值领域示意图Fig 11　Bi -cubic interpoliation neighborhood 2　实现流程211　DSP Builder 设计流程　DSP Builder 是一个系统级(或算法级)设计工具,它构架在多个软件工具之上,实现了Simulink 系统级(算法仿真建模)和R TL 级(硬件实现)2个不同设计领域之间的无缝链接.DSP builder 在Simulink 中以Blockset 形式出现,其中包含多个适用于DSP 开发的库,如算数库、复数信息库、总线控制库等,在每个库中又含有多个子模块,如乘法累加模块、加减模块、乘积模块等.设计人员首先在Simulink 中进行DSP 系统(算法)的建模、系统级仿真然后通过DSP Builder 中的SignalCompiler 模块生成相应的硬件描述语言代码,以及用于控制综合和编译的tcl 脚本文件,最后在QuartusII 中完成逻辑综合、编译适配及以后等相关设计工作.由于在FP G A 上的设计存在:①算法模型的复杂性;②设计应用目标的多样性;③涉及第三方EDA 软件的不同等问题,DSP Builder 提供了2套设计流程[5],即:①手工打开所使用的综合器、适配器(QuartusII 等)对生成的代码进行综合和适配的手动流程;②在Simulink 集成环境中直接调用特定的综合器和适配器执行自动生成的相应脚本,在后台进行综合和适配的自动流程.这2种设计流程如图2所示.图2　DSP Builder 设计流程图Fig 12　DSP Builder design flow chart68云南大学学报(自然科学版) 第31卷图3　Fir4SubsystemFig 13　Fir4subsystem 212　双三次插值的DSP Builder 实现21211　在Simulink 中的建模　FIR (Finite Impulse Response ,有限冲激响应)滤波器大量应用在数字信号处理领域中的内插值计算当中,根据前文所述的双三次插值算法的原理,双三次插值算法的系统级建模可以理解为一个16阶与一个4阶FIR滤波器级联叠加的二维FIR 滤波器(只是插值基函数的抽头系数与滤波器的系数不同).按照这个思路,我们在Simulink 中建立一个mdl 模型文件,用DSP Builder 的层次设计方法,首先设计一个4阶FIR 滤波器子系统,再以此为基础完成整个算法系统建模.4阶FIR 滤波器子系统fir4Subsystem 如图3所示,其内部结构如图4所示.图4　Fir4Subsystem 内部结构图Fig 14　Fir4Subsystem internal structure image然后组成双三次插值算法模型.16阶FIR 滤波器由4个fir4SubSystem 构成,再把4个fir4tap 子系统的输出端分别与一个4阶FIR 滤波器的4个乘法器的输入端连接组成一个二维的FIR 滤波器,第一级16阶FIR 滤波器进行的是沿水平方向4行的插值计算,第二级的4阶FIR 滤波器是对计算出的4个新像素点进行垂直方向的插值计算,最后生成新的像素点R 的值.不难发现这是一种流水线的结构,这种结构有利于硬件系统的并行高速运行.最后在模型中加入仿真信号模块和仿真显示模块,这样就完成了双三次插值算法模型的搭建.需要注意的是,在设计好fir4SubSystem 后需要修改其Mask 参数Mask Type 为“SubSystemAlteraBlockSet ”,才能使后面调用此子系统的更高级系统进行Signal Compile 分析.双三次插值算法模型如图5所示.图5中Chip Signal 模块为线性调频信号发生模块,生成一个线性调频信号011～1Hz ,作为系统仿真的信号源.Scope 模块是波形观察模块,Scope 用于观察插值前和插值后2种波形,Scope1用于观察水平方向一行插值计算后的波形,Scope2用于观察邻域内水平方向插值计算后的波形.t 1,t 2,t 3,t 4和t 5,t 6,t 7,t 8两组系数分别为领域内各点在水平方向和垂直方向到插值点的距离代入插值函数得到的系数,而4个fir4SubSystem 的输入端为每一行的像素点的值,因为这里仅是算法实现的研究,不涉及具体工程,所以fir4t SubSystem 的输入用Chip signal 产生的信号代替,各抽头系数用已知的FIR 滤波器系数代替,图6为78第S2期谢　然等:基于DSP Builder 的双三次插值算法FPG A 实现的研究scope1的波形.由图6可以看出系统的高频部分的幅度被有效衰减,这样可以有效地边缘阶梯失真,但是由于对于低频部分的幅度也有缺损,有些甚至直接为0,所以边缘模糊效应是比较明显的.图5　双三次插值算法模型Fig 15　Bi -cubic interpolation algorithm mode21212　利用Signal Compiler 模块自动生成代码　用鼠标双击模型窗口中的“Signal Compiler ”模块图标即出现图7所示的Signal Compiler 模块的界面.在Family 中选择相应的FP G A 芯片系列号,再点击Compile 按钮即可对模型进行分析,并调用后台的综合器(QuartusII )进行综合生成网表文件,并自动生成Quar 2图6　Scop1的波形Fig 16　Scope1waveform tusII 可直接调用的工程,在QuartusII 中进行编译适配过程,生成编程文件1pof 和1sof 文件.选择好J tag 接口后,点击Program 即可直接用编程文件对FP G A 硬件进行配置下载.选择Export 标签,选择好输出目录,即可以直接输出V HDL 代码,Export 标签界面如图8所示,生成的部分V HDL 代码如下:　……entity alt-dspbuilder-constant-GN6UDURW4Vis generic (　HDL T YPE :string :=“STD-LO GIC -V ECTOR ”;　Bit Pattern :string :=“000111111”;　width :natural :=9);Port (output :out std-logic-vector (8downto 0));end entity ;　……另外,Simulink 中对模型文件1mdl 的仿真只是系统验证级的仿真,并没有对生成的HDL 代码文件进行仿真.HDL 代码的仿真是R TL 级的,与Simulink 中的模型仿真可能存在一些的差异,因此需要对HDL 代码进行功能仿真.Signal Compiler 会自动在工程目录下生成一个仿真所需要的tcl 脚本文件,用Model 2sim 打开tcl 文件其会自动开始进行仿真并自动显示仿真结果,设置好相应参数后,我们根据Simulink 中的波形是否与Modelsim 中的波形一致来验证设计的正确性.88云南大学学报(自然科学版) 第31卷图7　Signal Compiler 窗口Fig 17　Signal Compilerwindow 图8　Export H DL 窗口Fig 18　Export HDL window下面的工作就是针对FP G A 器件的设计,打开QuartusII 环境,定位到相应Simulink 模型所在的目录,打开DSP Builder 建立的QuartusII 的1qpf 项目文件,在QuartusII 中进行相应的时序仿真,并制定器件的管脚、编译适配、对FP G A 进行配置等,以此来完成整个工程的设计工作.3　结　语本文以双三次插值算法为例,对利用DSP Builder 实现从系统级建模到硬件设计代码转换这一设计方法进行了初步的研究.在Matlab/Simulink 环境下利用DSP Builder 可快速进行数字信号处理系统的设计,甚至在设计人员不十分了解FP G A 本身和HDL 语言的时候,先行进行系统级的设计再根据相应要求进行针对性设计.不足的是,这里的研究没有涉及具体的工程应用.笔者要以此为基础,在深入了解DSP Builder 的同时,致力于把其应用在具体的工程项目上.利用DSP Builder 从Simulink 模型自动生成FP G A 实现代码的设计流程,有利于在设计早期及早发现错误和应对硬件设计结构化的趋势.用此方法进行的DSP 系统的FP G A 开发,能得到比独立的DSP 处理器更好的性能,提高了集成度和可靠性,降低了成本,节省了工程时间.这样的设计流程使DSP 功能模块称为FP G A 电路系统中的一个组成部分,是当前FP G A 设计方法的一个新的发展方向.参考文献:[1]　唐俊英.基于DSP Builder 的数字信号处理器的设计[J ].邢台职业技术学院学报,2005(6):48249.[2]　张辉.基于二维卷积的图像插值实时硬件实现[J ].清华大学学报:自然科学版,2007(47):8852888.[3]　王岳环.基于FPG A 的数字图像实时放大设计[J ].计算机工程与应用,2005(8):1082110.[4]　张辉.基于FPG A 的实现X 线医学图像处理系统[J ].中国生物医学工程学报,2008(2):39244.[5]　潘松.现代DSP 技术[M ].西安:西安电子科技大学出版社,2003.(下转第94页)98第S2期谢　然等:基于DSP Builder 的双三次插值算法FPG A 实现的研究The analysis and treatment on the fault ofthe waste heat boiler feedwater pumpZHAN G Jian 2jun ,Q IAN Qiang ,O YAN G Xiao 2hui(Smelting metal and fabrication main plant of Yunnan Copper Co.Ltd ,Kunming 650102,China )Abstract :This article focuses on the causes for motor frequent bearing burning out ,Balance disc and bal 2ance drum damage of ISA waste heat boiler HGM feedwater pump ,and drawing up the handling measures ac 2cording to the results of analysis.Finally ,the handling process and effectiveness are presented.K ey w ords :waste heat boiler ;multi -stage feedwater pump ;throttle bush ;journal bearing ;suspended working333333333333333333333333333333333333333333(上接第89页)A study on FP GA implementation ofbi -cubic interpolation algorithm based on DSP builderXIE Ran 1,L I Yu 2hui 1,SHEN G Hui 2,L I Bo 1,CHEN Hai 2fei 1(11Faculty of Information Engineering and Automation ,Kunming University of Science and Technology ,Kunming 650051,China ;21Yunnan Research Institute of Electronics Industry ,Kunming 650031,China )Abstract :An implementation method of bi -cubic interpolation by using DSP Builder in FP G A was stud paring with traditional DSP technology ,FP G A have certain advantages in implying of DSP functions for its flexibility and efficiency of Concurrent Design.This design method studied in this paper avoids high de 2sign difficulty and long development period by programming hardware description language (HDL )in FP G A to realize DSP algorithms.With the example of bi -cubic interpolation algorithm ,this paper discussed the feasibility of the proposed method.K ey w ords :FP G A ;matlab/Simulink ;DSP builder ;bi -cubic interpolation 49云南大学学报(自然科学版) 第31卷。

双三次插值原理及MATLAB源码实现

%双三次插值具体实现;('E:\\\\图片\');= 2()转化为灰度图像[](); %将图像隔行隔列抽取元素，得到缩小的图像f22;f = ();11f()(2*i,2*j);5; %设置放大倍数1 = (,'')双线性插值结果比较= 8(1);(1,:)(m,:); %将待插值图像矩阵前后各扩展两行两列,共扩展四行四列[f(1,1)(1,1)(:,1)'(m,1)(m,1)][f(1)(1)()'()()];a1=[];b1=[1'];1'1();g1 = (k**n);1*m %利用双三次插值公式对新图象所有像素赋值(); i1()+2;[(1) (u) (1) (2)];1*n()1()+2;[(1)(v)(1)(2)];[f1(i1-11-1) f1(i1-11) f1(i1-11+1) f1(i1-11+2)f1(i11-1) f1(i11) f1(i11+1) f1(i11+2)f1(i1+11-1) f1(i1+11) f1(i1+11+1) f1(i1+11+2)f1(i1+21-1) f1(i1+21) f1(i1+21+1) f1(i1+21+2)];g1()=(A*B*C);8(g1);(8(f)); ('缩小的图像'); %显示缩小的图像()('原图'); %显示原图像(g)('双三次插值放大的图像'); %显示插值后的图像()('双线性插值放大结果'); %显示插值后的图像0()(g);2(2()); %计算原图像和插值图像的傅立叶幅度谱g2(2(g));(1,2,1)(((2)),[8,10])('原图像的傅立叶幅度谱');(1,2,2)(((g2)),[8,10])('双三次插值图像的傅立叶幅度谱');基函数代码：(w1)(w1);w<1>=01-2*w^2^3;w>=1<24-8*5*w^2^3;0;算法原理双三次插值又称立方卷积插值。

matlab双三次插值函数

matlab双三次插值函数在MATLAB中，双三次插值函数可以通过使用`interp2`函数来实现。

`interp2`函数可以在二维网格上对数据进行插值，其中包括双三次插值。

下面我将详细介绍如何使用`interp2`函数进行双三次插值。

首先，`interp2`函数的基本语法如下：Vq = interp2(X, Y, V, Xq, Yq, 'spline');其中，`X`和`Y`是原始数据的网格坐标，`V`是原始数据的值，`Xq`和`Yq`是要进行插值的点的坐标，`Vq`是插值得到的值。

在这里，我们使用`spline`选项来指定双三次插值。

接下来，我将通过一个简单的示例来说明如何使用`interp2`函数进行双三次插值。

假设我们有一组原始数据`X`，`Y`和`V`，我们想要在新的坐标点`Xq`和`Yq`上进行双三次插值。

matlab.% 创建原始数据。

[X, Y] = meshgrid(1:5, 1:5);V = peaks(5); % 以peaks函数生成一个简单的二维数据作为示例。

% 创建新的坐标点。

[Xq, Yq] = meshgrid(1:0.1:5, 1:0.1:5); % 创建更密集的坐标点用于插值。

% 进行双三次插值。

Vq = interp2(X, Y, V, Xq, Yq, 'spline');% 可视化插值结果。

surf(Xq, Yq, Vq);在这个示例中，我们首先创建了原始数据`X`，`Y`和`V`，然后创建了新的坐标点`Xq`和`Yq`，并使用`interp2`函数进行双三次插值。

最后，我们通过绘制三维曲面来可视化插值结果。

需要注意的是，`interp2`函数还有其他选项可以用来指定不同的插值方法，比如线性插值、最近邻插值等。

另外，对于不规则的数据点，还可以使用`griddata`函数进行插值操作。

希望这个例子能够帮助你理解在MATLAB中如何使用双三次插值函数。

插值算法与matlab代码

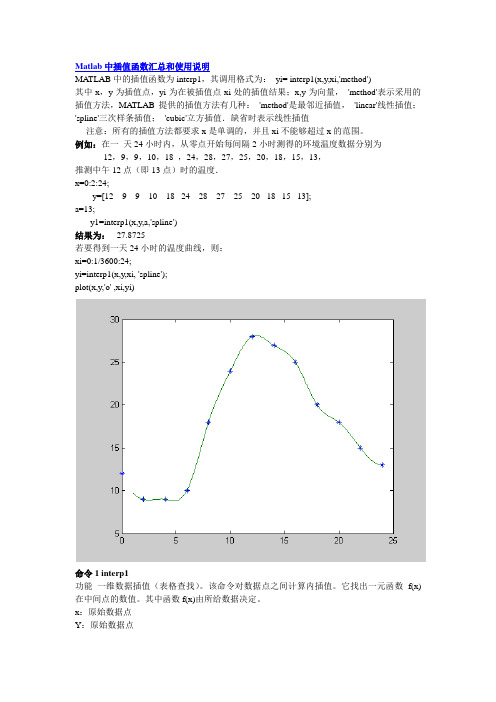
Matlab中插值函数汇总和使用说明MATLAB中的插值函数为interp1，其调用格式为： yi= interp1(x,y,xi,'method')其中x，y为插值点，yi为在被插值点xi处的插值结果；x,y为向量，'method'表示采用的插值方法，MA TLAB提供的插值方法有几种：'method'是最邻近插值，'linear'线性插值；'spline'三次样条插值；'cubic'立方插值．缺省时表示线性插值注意：所有的插值方法都要求x是单调的，并且xi不能够超过x的范围。

例如：在一天24小时内，从零点开始每间隔2小时测得的环境温度数据分别为12，9，9，10，18 ，24，28，27，25，20，18，15，13，推测中午12点（即13点）时的温度．x=0:2:24;y=[12 9 9 10 18 24 28 27 25 20 18 15 13];a=13;y1=interp1(x,y,a,'spline')结果为：27.8725若要得到一天24小时的温度曲线，则：xi=0:1/3600:24;yi=interp1(x,y,xi, 'spline');plot(x,y,'o' ,xi,yi)命令1 interp1功能一维数据插值（表格查找）。

该命令对数据点之间计算内插值。

它找出一元函数f(x)在中间点的数值。

其中函数f(x)由所给数据决定。

x：原始数据点Y：原始数据点xi：插值点Yi：插值点格式(1)yi = interp1(x,Y,xi)返回插值向量yi，每一元素对应于参量xi，同时由向量x 与Y 的内插值决定。

参量x 指定数据Y 的点。

若Y 为一矩阵，则按Y 的每列计算。

yi 是阶数为length(xi)*size(Y,2)的输出矩阵。

(2)yi = interp1(Y,xi)假定x=1:N，其中N 为向量Y 的长度，或者为矩阵Y 的行数。

双三次插值法去除马赛克的原理及matlab代码实现

双三次插值法去除马赛克的原理及matlab代码实现双三次插值法（Bicubic Interpolation）是一种在图像处理中常用的图像重采样方法。

它比双线性插值法（Bilinear Interpolation）更复杂，但可以提供更好的图像质量。

双三次插值法的原理是：在原始图像中，以目标像素为中心，取其周围16个像素的灰度值，根据双三次多项式函数进行拟合，计算出目标像素的灰度值，以实现图像的放大或缩小。

由于其采用更高阶的多项式拟合，因此可以得到比双线性插值法更平滑的图像。

在去除马赛克方面，双三次插值法可以用于对马赛克区域进行插值，以恢复原始图像的细节。

具体实现步骤如下：1. 确定马赛克区域：首先需要确定图像中哪些区域是马赛克区域，这可以通过阈值分割、边缘检测等方法实现。

2. 对马赛克区域进行双三次插值：对于每个马赛克区域，以目标像素为中心，取其周围16个像素的灰度值，根据双三次多项式函数进行拟合，计算出目标像素的灰度值。

3. 合成图像：将插值后的马赛克区域与原始图像中的非马赛克区域进行合成，得到最终的图像。

下面是一个简单的Matlab代码实现：```matlabfunction output = bicubic_interpolation(input, scale) % 输入：原始图像 input，缩放比例 scale% 输出：经过双三次插值后的输出图像 output% 获取输入图像的大小[input_rows, input_cols, channels] = size(input);% 计算输出图像的大小output_rows = input_rows scale;output_cols = input_cols scale;% 对每个像素进行双三次插值output = zeros(output_rows, output_cols, channels); for i = 1:output_rowsfor j = 1:output_cols% 计算当前像素在输入图像中的位置x = (i - 1) / scale + 1;y = (j - 1) / scale + 1;% 对每个通道进行插值for c = 1:channels% 获取周围16个像素的灰度值window = input(round(x-1):round(x+1), round(y-1):round(y+1), c);% 对灰度值进行双三次插值output(i, j, c) = bicubic_interpolation_single(window);endendendendfunction output = bicubic_interpolation_single(input)% 输入：16个像素的灰度值 input（按行优先顺序排列）% 输出：目标像素的灰度值 output% 计算系数矩阵 A 和常数矩阵 BA = [1 -2 1 0 -2 4 -2 1; 4 -8 4 0 -8 24 -8 4; 1 -2 1 0 -2 4 -2 1];B = [-192 48 -32 -64 -32 8; -96 24 -16 -32 -16 4; -96 24 -16 -32 -16 4];% 解线性方程组 Ax=B，得到目标像素的灰度值 outputoutput = A \ B;end```该代码实现了对单通道灰度图像的双三次插值，如果需要处理彩色图像，需要对每个通道分别进行插值。

三次样条插值matlab代码实现

三次样条插值matlab代码实现三次样条插值是一种常用的插值方法，可以用于曲线拟合和数据逼近。

在Matlab中，可以使用内置函数`interp1`来实现三次样条插值。

下面是一个简单的示例代码，演示了如何在Matlab中实现三次样条插值：matlab.% 创建一些示例数据。

x = 1:5;y = [3 6 5 8 2];% 生成更密集的x值，用于插值。

xi = 1:0.1:5;% 使用interp1进行三次样条插值。

yi = interp1(x, y, xi, 'spline');% 绘制原始数据和插值结果。

plot(x, y, 'o', xi, yi, '-');legend('原始数据', '三次样条插值');在这个示例中，我们首先创建了一些示例数据`x`和`y`，然后生成了更密集的`xi`值，用于插值。

接下来，我们使用`interp1`函数进行三次样条插值，并将结果存储在`yi`中。

最后，我们使用`plot`函数将原始数据和插值结果可视化出来。

需要注意的是，`interp1`函数中的第四个参数'spline'表示我们使用三次样条插值方法。

除了'spline'外，还可以选择'linear'（线性插值）或'pchip'（分段立方插值）等方法，具体选择取决于实际情况和数据特点。

以上就是在Matlab中实现三次样条插值的简单示例代码。

当然，实际应用中可能涉及到更复杂的数据和情况，需要根据具体问题进行相应的调整和处理。

希望这个示例能够帮助到你理解如何在Matlab中实现三次样条插值。

bicubic插值

bicubic插值bicubic插值算法，也被称为双三次插值算法，从纯数学的数值分析的角度，属于三次插值（可以理解为导数平滑的插值算法），类比于bilinear插值，值域平滑的插值算法，其保边能力更强；从信号与系统的角度，属于sa信号重建函数，在频域的理想低通滤波器。

从信号与系统的角度理解，bicubic更像一个理想低通滤波器，而bilinear更像一个高斯低通滤波器。

这里主要从信号与系统的角度，去解释bicubic算法，也就是sa函数。

离散信号重建，会涉及到单位冲激、冲激串函数，单位冲激、冲激串函数的傅里叶变换，卷积和乘积的傅里叶变换对，采样定理，混叠以及采样后的信号重建函数。

其实一个看似简单且经典的插值算法，实则背后有着强大的理论支撑。

1、单位冲激、冲激串函数冲激函数与冲激串函数冲激函数是一个奇异函数，在物理层面上，将t解释为时间，那么冲激可视为幅度无穷大、持续时间为0、具有单位面积的尖峰信号。

犹如一道闪电一般，能量极高，但持续时间极短。

从物理的角度，主要用途就是信号取样。

从数学的角度，通常基于泛函（函数的函数）去定义冲激函数，对于一个任意连续函数簇，通过冲激函数的乘积作用后的积分，可以获取原函数取样点（这个函数域到值域的映射关系，定义了冲激泛函）。

2、冲激串的傅里叶变换盒子函数傅里叶变换首先是盒状函数的傅里叶变换，盒状函数本质上是单位脉冲信号，也是单位冲激信号的泛化形式（当A趋于无穷大，W趋于无穷小时）。

盒状函数的傅里叶变换是一个sa函数，值得注意的是，傅里叶变换后的sa函数，其一，幅值是AW（时域盒状函数幅值和时域宽度的乘积）；其二，sa函数的零点距离为1/W，盒状函数的零点距离维W，两者互为倒数。

当盒状函数，W趋于无穷大时，sa函数即趋于冲激函数；故此可知，常数的傅里叶变换是冲激函数。

（常数与零点冲激函数是一对傅里叶变换对）其次是单位冲激函数的傅里叶变换，这个则很简单，由于冲激函数的取样特性，容易知道，傅里叶变换最终结果为常数。

三次样条插值（CubicSplineInterpolation）

三次样条插值（CubicSplineInterpolation）样条插值是⼀种⼯业设计中常⽤的、得到平滑曲线的⼀种插值⽅法，三次样条⼜是其中⽤的较为⼴泛的⼀种。

本篇介绍⼒求⽤容易理解的⽅式，介绍⼀下三次样条插值的原理，并附C语⾔的实现代码。

1. 三次样条曲线原理假设有以下节点1.1 定义样条曲线是⼀个分段定义的公式。

给定n+1个数据点，共有n个区间，三次样条⽅程满⾜以下条件：a. 在每个分段区间（i = 0, 1, …, n-1，x递增），都是⼀个三次多项式。

b. 满⾜（i = 0, 1, …, n ）c. ，导数，⼆阶导数在[a, b]区间都是连续的，即曲线是光滑的。

所以n个三次多项式分段可以写作：，i = 0, 1, …, n-1其中ai, bi, ci, di代表4n个未知系数。

1.2 求解已知:a. n+1个数据点[xi, yi], i = 0, 1, …, nb. 每⼀分段都是三次多项式函数曲线c. 节点达到⼆阶连续d. 左右两端点处特性（⾃然边界，固定边界，⾮节点边界）根据定点，求出每段样条曲线⽅程中的系数，即可得到每段曲线的具体表达式。

插值和连续性：, 其中 i = 0, 1, …, n-1微分连续性：, 其中 i = 0, 1, …, n-2样条曲线的微分式：将步长带⼊样条曲线的条件：a. 由 (i = 0, 1, …, n-1)推出b. 由 (i = 0, 1, …, n-1)推出c. 由 (i = 0, 1, …, n-2)推出d. 由 (i = 0, 1, …, n-2)推出设，则a. 可写为：，推出b. 将ci, di带⼊可得：c. 将bi, ci, di带⼊ (i = 0, 1, …, n-2)可得：端点条件由i的取值范围可知，共有n-1个公式，但却有n+1个未知量m 。

要想求解该⽅程组，还需另外两个式⼦。

所以需要对两端点x0和xn的微分加些限制。

选择不是唯⼀的，3种⽐较常⽤的限制如下。

三次样条插值法matlab程序

三次样条插值法引言在数学和计算机科学领域中，插值是一种常见的技术，用于通过已知数据点的值来估计在这些数据点之间的未知数据点的值。

三次样条插值法是一种广泛应用的插值方法，它通过使用三次多项式来逼近原始数据，从而实现对未知数据点的估计。

本文将介绍三次样条插值法的原理、实现和应用。

原理三次样条插值法的基本原理是通过在每个相邻数据点之间使用三次多项式来逼近原始数据。

这些多项式在每个数据点处具有相同的值和导数，从而保证了插值函数的平滑性。

具体而言，对于给定的数据点集合{ (x0, y0), (x1, y1), …, (xn, yn) }，三次样条插值法将在每个相邻数据点之间构造一个三次多项式，即S(x) = a_i(x - x_i)^3 + b_i(x - x_i)^2 + c_i(x - x_i) + d_i其中，i 表示数据点的索引。

为了确定这些多项式的系数 a_i, b_i, c_i 和 d_i，需要满足以下条件：1.在每个数据点处，插值函数的值与原始数据点的值相等：S(x_i) = y_i2.在每个相邻数据点之间，插值函数的一阶导数连续：S’(x_i) = S’(x_i+1)3.在每个相邻数据点之间，插值函数的二阶导数连续：S’‘(x_i) =S’’(x_i+1)通过求解这些条件，可以得到一个线性方程组，并确定三次样条插值法的插值函数。

实现三次样条插值法的实现可以通过以下步骤完成：1.根据给定的数据点集合，计算相邻数据点之间的差值：h_i = x_i+1 - x_i2.构建一个三对角矩阵 A，其中主对角线元素为 2(h_i + h_i+1)，上下对角线元素为 h_i 和 h_i+13.构建一个向量 B，其中元素为 6 * ((y_i+1 - y_i)/h_i+1 - (y_i - y_i-1)/h_i)，其中 y_i 为原始数据点的值4.解线性方程组 A * C = B，其中 C 为包含S’’(x_i) 的向量5.根据 C 的值计算 a_i, b_i 和 d_i 的值6.根据 a_i, b_i, c_i 和 d_i 的值，构建插值函数 S(x)应用三次样条插值法在实际应用中具有广泛的用途，特别是在曲线拟合、数据平滑和函数逼近方面。

双三次插值bicubicinterpolation原理及MATLAB源码实现

%双三次插值具体实现clc,clear;fff=imread('E:\Documents\BUPT\DIP\图片\lena.bmp');ff = rgb2gray(fff);%转化为灰度图像[mm,nn]=size(ff); %将图像隔行隔列抽取元素，得到缩小的图像fm=mm/2;n=nn/2;f = zeros(m,n);for i=1:mfor j=1:nf(i,j)=ff(2*i,2*j);endendk=5; %设置放大倍数bijiao1 = imresize(f,k,'bilinear');%双线性插值结果比较bijiao = uint8(bijiao1);a=f(1,:);c=f(m,:); %将待插值图像矩阵前后各扩展两行两列,共扩展四行四列b=[f(1,1),f(1,1),f(:,1)',f(m,1),f(m,1)];d=[f(1,n),f(1,n),f(:,n)',f(m,n),f(m,n)]; a1=[a;a;f;c;c];b1=[b;b;a1';d;d];ffff=b1';f1=double(ffff);g1 = zeros(k*m,k*n);for i=1:k*m %利用双三次插值公式对新图象所有像素赋值u=rem(i,k)/k; i1=floor(i/k)+2;A=[sw(1+u) sw(u) sw(1-u) sw(2-u)];for j=1:k*nv=rem(j,k)/k;j1=floor(j/k)+2;C=[sw(1+v);sw(v);sw(1-v);sw(2-v)];B=[f1(i1-1,j1-1) f1(i1-1,j1) f1(i1-1,j1+1) f1(i1-1,j1+2)f1(i1,j1-1) f1(i1,j1) f1(i1,j1+1) f1(i1,j1+2)f1(i1+1,j1-1) f1(i1+1,j1) f1(i1+1,j1+1) f1(i1+1,j1+2)f1(i1+2,j1-1) f1(i1+2,j1) f1(i1+2,j1+1) f1(i1+2,j1+2)];g1(i,j)=(A*B*C);endendg=uint8(g1);imshow(uint8(f)); title('缩小的图像'); %显示缩小的图像figure,imshow(ff);title('原图'); %显示原图像figure,imshow(g);title('双三次插值放大的图像'); %显示插值后的图像figure,imshow(bijiao);title('双线性插值放大结果'); %显示插值后的图像mse=0;ff=double(ff);g=double(g);ff2=fftshift(fft2(ff)); %计算原图像和插值图像的傅立叶幅度谱g2=fftshift(fft2(g));figure,subplot(1,2,1),imshow(log(abs(ff2)),[8,10]);title('原图像的傅立叶幅度谱'); subplot(1,2,2),imshow(log(abs(g2)),[8,10]);title('双三次插值图像的傅立叶幅度谱');基函数代码：function A=sw(w1)w=abs(w1);if w<1&&w>=0A=1-2*w^2+w^3;elseif w>=1&&w<2A=4-8*w+5*w^2-w^3;elseA=0;end算法原理双三次插值又称立方卷积插值。

用matlab实现三次 NURBS插值曲线

用matlab 实现三次 NURBS 插值曲线作者:大漠孤狼发表于matlab 乐园()作者:这是我在大学时做大学生研究计划时写的,当时刚学会matlab ,编写了这个程序,用了很多循环,效率不高.当时我并不清楚循环是matlab 的弱点,等明白了,也不做这方面的工作了,也就懒的去改写了.如果谁需要用,就自己改吧.算法也有一些问题,我就不多说了,自己看吧一、三次NURBS 插值算法给定平面控制顶点d i (i=1,2,…n)及对应的权因子i ω (i=1,2,…n)，可定义一条三次NURBS 曲线。

先对控制顶点进行参数化，得一矢量：U=[u 0,u 1,u 2…,u n+4]则三次NURBS 曲线的分段方程形式为： ∑∑+====33,33,1)()()(k k i i i k k i i i k u N u N d u P ωω u ∈[u k+3,u k+4] k=0,1,2,…,n-3 (1) 首先证明一条性质：若三点d k ,d k+1,d k+2共线，且满足 )()()()(33,2333,233,2333,1++++++++++++=k k k k k k k k k k k k k k k u N u N d u N d u N d ωωωω则三次NURBS 曲线插值点d k+1.证明：由（1）式可得：)()()()()()()(33,2233,1133,233,22133,1133,3+++++++++++++++++++++=k k k k k k k k k k k k k k k k k k k k k k k u N u N u N d u N d u N d u N u P ωωωωωω )()()()()()()(43,3343,2243,11343,23243,22143,114++++++++++++++++++++++++++=k k k k k k k k k k k k k k k k k k k k k k k u N u N u N d u N d u N d u N u P ωωωωωω 由以知可得)()()()()()(33,2233,1133,233,22133,1133,1+++++++++++++++++++++=k k k k k k k k k k k k k k k k k k k k k k u N u N u N d u N d u N d u N d ωωωωωω 故性质得证。

双三次插值代码

双三次插值代码以下是一个示例的双三次插值代码：```pythonimport numpy as npfrom PIL import Imagedef bicubic_interpolation(img, scale):# 获取输入图像的宽度和高度width, height = img.size# 计算插值后的图像的宽度和高度new_width = int(width * scale)new_height = int(height * scale)# 创建一个新的图像对象，用于存储插值后的图像new_img = Image.new("RGB", (new_width, new_height))# 原始图像的像素矩阵pixels = np.array(img)# 遍历新图像的每个像素点for i in range(new_height):for j in range(new_width):# 计算当前像素点在原始图像中的位置x = j / scaley = i / scale# 计算当前像素点在原始图像中的四个邻近像素的位置x1 = int(x) - 1y1 = int(y) - 1x2 = x1 + 1y2 = y1 + 1# 判断是否越界if x1 < 0 or y1 < 0 or x2 >= width or y2 >= height:continue# 计算当前像素点的灰度值gray = cubic_interpolation(pixels, x, y, x1, y1, x2, y2)# 在新图像的相应位置赋值new_img.putpixel((j, i), tuple(gray))return new_imgdef cubic_interpolation(pixels, x, y, x1, y1, x2, y2):# 获取四个邻近像素的灰度值p11, p12, p21, p22 = pixels[y1, x1], pixels[y1, x2], pixels[y2, x1], pixels[y2, x2]# 计算水平方向上的插值hx1 = cubic_interpolation1D(p11[0], p12[0], pixels[y1, int(x)], pixels[y1, int(x) + 1])hx2 = cubic_interpolation1D(p21[0], p22[0], pixels[y2, int(x)], pixels[y2, int(x) + 1])# 计算垂直方向上的插值hy = cubic_interpolation1D(hx1, hx2, y - int(y), y - int(y) + 1)# 计算相应的RGB通道的插值r = cubic_interpolation1D(p11[0], p21[0], hy, hy + 1)g = cubic_interpolation1D(p11[1], p21[1], hy, hy + 1)b = cubic_interpolation1D(p11[2], p21[2], hy, hy + 1)return [int(r), int(g), int(b)]def cubic_interpolation1D(p0, p1, p2, p3, t=0.5):a0 = p3 - p2 - p0 + p1a1 = p0 - p1 - a0a2 = p2 - p0a3 = p1return (a0 * t ** 3 + a1 * t ** 2 + a2 * t + a3)# 读取原始图像original_img = Image.open("original.jpg")# 调用双三次插值函数scaled_img = bicubic_interpolation(original_img, 2)# 保存插值后的图像scaled_img.save("scaled.jpg")```请注意，这只是一个示例代码，并且在实际使用中可能需要根据具体情况进行适当的修改。

matlab旋转实现(最近邻值-双线性-三次卷积插值实现插值)

对图像进行旋转，使用最近邻插值法，双线性插值，三次卷积插值三种方法进行插值。

源码：clc;clear all;close all;Img=imread('test1.bmp');Img=double(Img);[h w]=size(Img);alpha=pi/6; %逆时针旋转的角度wnew=w*cos(alpha)+h*sin(alpha); %新图像的宽widthhnew=w*sin(alpha)+h*cos(alpha); %新图像的高heighthwnew=ceil(wnew); %取整hnew=ceil(hnew);u0=w*sin(alpha); %平移量T=[cos(alpha),sin(alpha);-sin(alpha),cos(alpha)]; %变换矩阵Imgnew1=zeros(hnew,wnew);Imgnew2=zeros(hnew,wnew);Imgnew3=zeros(hnew,wnew);for u=1:hnew %u和v是新图像坐标，变换到原图像坐标x和y中。

for v=1:wnewtem=T*([u;v]-[u0;0]);x=tem(1);y=tem(2);if x>=1 & x<=h & y>=1 & y<=w %若变换出的x和y在原图像范围内x_low=floor(x);x_up=ceil(x);y_low=floor(y);y_up=ceil(y);if (x-x_low)<=(x_up-x) %采用最近点法，选取距离最近点的像素赋给新图像 x=x_low;elsex=x_up;endif (y-y_low)<=(y_up-y)y=y_low;elsey=y_up;endp1=Img(x_low,y_low); %双线性插值，p1到p4是（x,y）周围的四个点 p2=Img(x_up,y_low);p3=Img(x_low,y_low);p4=Img(x_up,y_up);s=x-x_low;t=y-y_low;Imgnew1(u,v)=Img(x,y);Imgnew2(u,v)=(1-s)*(1-t)*p1+(1-s)*t*p3+(1-t)*s*p2+s*t*p4;endif x>=2 & x<=h-2 & y>=2 & y<=w-2 %若变换出的x和y在原图像范围内x_1=floor(x)-1;x_2=floor(x);x_3=floor(x)+1;x_4=floor(x)+2;y_1=floor(y)-1;y_2=floor(y);y_3=floor(y)+1;y_4=floor(y)+2;A=[sw(1+x-x_2),sw(x-x_2),sw(1-(x-x_2)),sw(2-(x-x_2))];C=[sw(1+y-y_2),sw(y-y_2),sw(1-(y-y_2)),sw(2-(y-y_2))];B=[ Img(x_1,y_1),Img(x_1,y_2),Img(x_1,y_3),Img(x_1,y_4);Img(x_2,y_1),Img(x_2,y_2),Img(x_2,y_3),Img(x_2,y_4);Img(x_3,y_1),Img(x_3,y_2),Img(x_3,y_3),Img(x_3,y_4);Img(x_4,y_1),Img(x_4,y_2),Img(x_4,y_3),Img(x_4,y_4)]; Imgnew3(u,v)=A*B*C';endendendsubplot(2,2,1),imshow(Img,[]),title('原图');subplot(2,2,2),imshow(Imgnew1,[]),title('最近邻插值法'); subplot(2,2,3),imshow(Imgnew2,[]),title('双线性插值法'); subplot(2,2,4),imshow(Imgnew3,[]),title('三次卷积插值法');欢迎您的下载，资料仅供参考！致力为企业和个人提供合同协议，策划案计划书，学习资料等等打造全网一站式需求。

三次样条插值的MATLAB实现

MATLAB 程序设计期中考查在许多问题中，通常根据实验、观测或经验得到的函数表或离散点上的信息，去研究分析函数的有关特性。

其中插值法是一种最基本的方法，以下给出最基本的插值问题——三次样条插值的基本提法：对插值区间[]b a ,进行划分：b x x x a n ≤<⋯⋯<<≤10，函数()x f y =在节点i x 上的值()()n i x f y i i ⋯⋯==,2,1,0，并且如果函数()x S 在每个小区间[]1,+i i x x 上是三次多项式，于[]b a ,上有二阶连续导数，则称()x S 是[]b a ,上的三次样条函数，如果()x S 在节点i x 上还满足条件()()n i y x S i i ⋯⋯==,1,0则称()x S 为三次样条插值函数。

三次样条插值问题提法：对[]b a ,上给定的数表如下.求一个分段三次多项式函数()x S 满足插值条件()()n i y x S i i ⋯⋯==,1,0 式，并在插值区间[]b a ,上有二阶连续导数。

这就需要推导三次样条插值公式：记()x f '在节点i x 处的值为()i i m x f ='(n i ⋯⋯=,1,0)(这不是给定插值问题数表中的已知值)。

在每个小区间[]1,+i i x x 利用三次Hermite 插值公式，得三次插值公式：()()()()1111+++++++=i i i i i i i i i m m x y x y x x S ββαα，[]1,+∈i i x x x 。

为了得到这个公式需要n 4个条件：(1).非端点处的界点有n 2个；(2).一阶导数连续有1-n 个条件；(3).二阶导数连续有1-n 个条件，其中边界条件：○1()()nn m x S m x S ='=' 00○2()()αα=''=''nx S x S 00 ○3()()()()16500403βααβαα=''+'=''+'n n x S x S x S x S ○4n y y =0 ()()()()000000-''=+''-'=+'nn x S x S x S x S 其中：()⎩⎨⎧=≠=j i j i x j i,1,0α ()0='j i x α ()0=j i x β 且(1,0,=j i )。