分数加减法速算与巧算教师版
六年级奥数-第一讲.分数的速算与巧算.教师版

第一讲分数的速算与巧算教学目标本讲知识点属于计算大板块内容,分为三个方面系统复习和学习小升初常考计算题型.1、 裂项:是计算中需要发现规律、利用公式的过程,裂项与通项归纳是密不可分的,本讲要求学生掌握裂项技巧及寻找通项进行解题的能力2、 换元:让学生能够掌握等量代换的概念,通过等量代换讲复杂算式变成简单算式。
3、 循环小数与分数拆分:掌握循环小数与分数的互化,循环小数之间简单的加、减运算,涉及循环小数与分数的主要利用运算定律进行简算的问题. 4、通项归纳法通项归纳法也要借助于代数,将算式化简,但换元法只是将“形同”的算式用字母代替并参与计算,使计算过程更加简便,而通项归纳法能将“形似”的复杂算式,用字母表示后化简为常见的一般形式. 知识点拨一、裂项综合 (一)、“裂差”型运算 (1)对于分母可以写作两个因数乘积的分数,即1a b⨯形式的,这里我们把较小的数写在前面,即a b <,那么有1111()a b b a a b=-⨯- (2)对于分母上为3个或4个连续自然数乘积形式的分数,即:1(1)(2)n n n ⨯+⨯+,1(1)(2)(3)n n n n ⨯+⨯+⨯+形式的,我们有:1111[](1)(2)2(1)(1)(2)n n n n n n n =-⨯+⨯+⨯+++1111[](1)(2)(3)3(1)(2)(1)(2)(3)n n n n n n n n n n =-⨯+⨯+⨯+⨯+⨯++⨯+⨯+裂差型裂项的三大关键特征:(1)分子全部相同,最简单形式为都是1的,复杂形式可为都是x(x 为任意自然数)的,但是只要将x 提取出来即可转化为分子都是1的运算。
(2)分母上均为几个自然数的乘积形式,并且满足相邻2个分母上的因数“首尾相接” (3)分母上几个因数间的差是一个定值。
(二)、“裂和”型运算:常见的裂和型运算主要有以下两种形式:(1)11a b a b a b a b a b b a+=+=+⨯⨯⨯ (2)2222a b a b a b a b a b a b b a +=+=+⨯⨯⨯ 裂和型运算与裂差型运算的对比:裂差型运算的核心环节是“两两抵消达到简化的目的”,裂和型运算的题目不仅有“两两抵消”型的,同时还有转化为“分数凑整”型的,以达到简化目的。
巧算分数加减法2(详细教案)
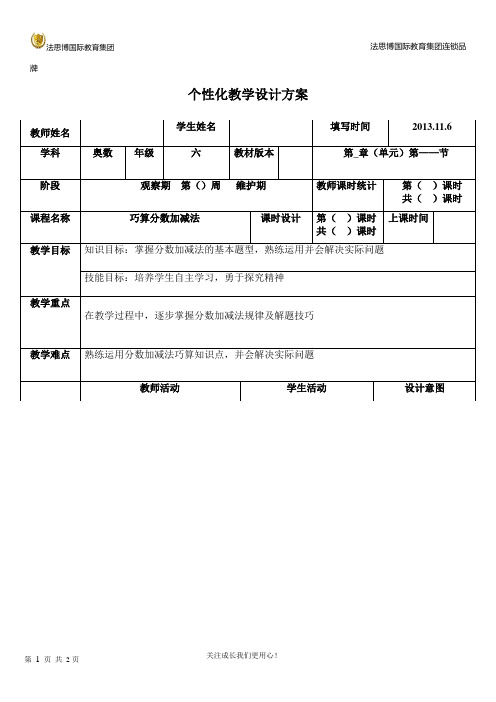
个性化教学设计方案学生姓名填写时间2013.11.6 教师姓名学科奥数年级六教材版本第_章(单元)第——节阶段观察期第()周维护期教师课时统计第()课时共()课时上课时间课程名称巧算分数加减法课时设计第()课时共()课时教学目标知识目标:掌握分数加减法的基本题型,熟练运用并会解决实际问题技能目标:培养学生自主学习,勇于探究精神教学重点在教学过程中,逐步掌握分数加减法规律及解题技巧教学难点熟练运用分数加减法巧算知识点,并会解决实际问题教师活动学生活动设计意图教学过程一、导入一)知识体系在分数的加减运算过程中,虽然掌握运算法则是关键,但是由于习题的类型较多,特点不一,因此在解题时,还要通过观察和分析,找出题目中数的特点,合理、有效地进行计算。
二)解题技巧常用的方法有:拆项相加法、凑整、倒序求和法、错位相减法和分组法等。
三)观察方法二、新授例1.计算:1994+12-113+212-313+412-513+…+199212-199313(拆相相加法)例2.计算:12+14+18+116+132+164+1128解并掌握相关知识要点、解题技巧等。
以及细心观察的重要性。
观察方法:(1)观察数字独有的特点(2)观察数字间的区别与联系(3)观察运算符号拆相相加法的技巧的熟练运用及巩固,回顾上节课内容,得到一个良好的复习效果。
教学过程教师活动学生活动设计意图例3.计算:155+255+355+…+1055-11155-12155-…-20155三、练习及巩固通过练习发现问题,解决问题。
见讲义。
四、本课小结等差数列公式的运用公式回顾:练习中出现倒序数。
回顾倒序数的概念及解题技巧。
倒序数概念:课堂练习课后作业本节课教学计划完成情况:□照常完成□提前完成□延后完成,原因课后记学生的接受程度:□完全能接受□部分能接受□不能接受,原因学生的课堂表现:□很积极□比较积极□一般□不积极,原因学生上次作业完成情况:完成数量% 已完成部分的质量分(5分制)存在问题配合需求:家长学管师备注提交时间教研组长审批教研主任审批注:此表用作每次课的教学设计方案。
分数加减法简便运算ppt课件讲义

分数加减法简便运算ppt课件讲义•分数加减法基本概念•简便运算方法与技巧•典型例题分析与解答•学生常见错误及纠正措施目录•练习题设计与解题思路指导•总结回顾与课堂延伸分数加减法基本概念01分数定义及性质分数定义分数表示整数部分以外的数,形如a/b(b≠0),其中a为分子,b为分母。
分数性质分数的分子与分母同时乘以或除以同一个不为零的数,分数的值不变。
同分母分数相加分母不变,分子相加。
异分母分数相加先通分,将异分母分数转化为同分母分数,再按照同分母分数相加的方法进行运算。
同分母分数相减分母不变,分子相减。
异分母分数相减先通分,将异分母分数转化为同分母分数,再按照同分母分数相减的方法进行运算。
1减去一个分数将1转化为与减数同分母的分数,再进行减法运算。
简便运算方法与技巧02通分与约分方法通分将异分母分数转化为同分母分数,便于进行加减法运算。
通分时,需找到两个分数的最小公倍数作为通分母。
约分在运算过程中或结果中,将分子与分母同时除以它们的最大公约数,以简化分数。
示例2/3 + 5/6 = 4/6 + 5/6 = 9/6 = 3/2,通过通分和约分得到最终结果。
拆分法求解复杂问题拆分法将复杂问题拆分为多个简单问题,分别求解后再合并结果。
在分数加减法中,可将一个分数拆分为两个或多个分数之和或差,以简化运算。
示例7/12 -5/18 = 21/36 -10/36 =11/36,将7/12拆分为21/36,与5/18具有相同分母,方便计算。
凑整法提高计算效率凑整法在运算过程中,通过凑成整数或简单分数来提高计算效率。
例如,可以将某些分数凑成1/2、1/3等常见简单分数,从而简化运算。
示例5/6 -7/9 = 15/18 -14/18 = 1/18,通过凑整法将两个分数转化为具有相同分母的分数,便于计算。
典型例题分析与解答03$frac{2}{5} + frac{1}{5} =$例题两个分数分母相同,分子直接相加。
三年级数学《简单分数的加减法》教案

三年级数学《简单分数的加减法》教案
苏教版三年级数学《简单分数的加减法》教案
教学目标:
1、使学生通过观察,从分数的意义上理解分数加法的算理。
2、使学生会计算分母不超过10、结果不需要约分的同分母分数加法
3、使学生初步知道一个分数的分子、分母相同时,这个分数就是1,从而加深对分数的认识。
教学重点:
理解分数加法的算理、会计算简单的分数加法。
教学难点:
从理解分数意义入手,理解分数加法的算理。
课型课时:
要素组合方式,标准课
教学过程:
一、问题导入
看+想+做
1.口算并说明是怎样计算的。
46-5120+1350-20
2.老师把一张长方形纸平均分成5份,提问
① 这张纸平均分成5份,如果5份都取了,应该用什么数表示?
② 分母相同的分数相加,应该怎么计算呢?
二、自主探究
出示例1:张纸的`几分之几?
①用什么方法计算?
②从图上看结果是多少?
(多找几位同学说一说、同桌同学互相说……采取多种形式加深算理的理解。
)
提问:计算前后分母变了吗?分母为什么不变?
三、巩固拓展
观察讨论
①把长方形平均分成了几份?每份是它的几分之几?
②阴影部分各占几份?分别用什么分数表示?
③怎样计算?为什么?
四、梳理整合
1、完成“做一做”第1题。
2、完成练习二十三的第1-4题。
07-17
02-11
12-23
02-07
07-18
07-18
07-17
07-17
10-14
07-17。
(完整版)分数的加减法和简便运算

分数的加减法一、同分母的分数加减法知识点:在计算同分母的分数加减法中,分母不变,直接用分子相加减.注意:在计算同分母的分数加减法中,得数如果不是最简分数,我们必须将得数约分,使它成为最简分数。
例题一5654+=510564=+=2 注意:因为510不是最简分数,所以得约分,10和5的最大公因数是5,所以分子和分母同时除以5,最后得数是2. 例题二1059105109=-=-注意:因为10不是最简分数,必须约分,因为4和10的最大公因数是2,所以分子和分母同时除以2,最后的数是52知识点回顾:如何将一个不是最简的分数化为最简?(将一个非最简分数化为最简,我们就是将这个分数进行约分,一直约到分子和分母互质为止。
所以要将一个分数进行约分,我们必须找到分子和分母的最大公因数,然后用分子和分母同时除以他们的最大公因数.)专项练习一:同分母的分数加减法的专项练习一、计算错误!- 错误! 错误!— 错误! 1 - 错误! 错误!— 错误!错误!+ 错误! 错误!+ 错误! 错误!+错误! 错误!+ 错误!二、连线19 + 错误! 2 7377+1错误!+错误! 18987+ 错误!+ 错误! 1错误! 11511141+错误!+错误! 2错误!9392+2错误!+错误! 错误! 2121+三、判断对错,并改正(1)错误!+错误!= 错误! (2)6 — 错误!- 错误!=5错误!—错误!—错误! =5错误!-错误!=517四、应用题(1)一根铁丝长错误!米,比另一根铁丝长错误!米,了;另一根铁丝长多少米?(2)3天修一条路,第一天修了全长的错误! ,第二天修了全长的错误!错误!,第三天修了全长的几分之几?二、异分母的分数加减法。
在异分母的分数加减法中,可分为三种情况。
分别是分母是互质关系、分母是倍数关系、分母是一般关系(即非互质也非倍数) 例:A 代表一个分数的分母,B 代表另一个分数的分母ABA B AB B A B A ±±=±或11,分母是倍数关系)(即分子都为的倍数)是或的倍数)是(、,分母互质)即分子都为或、1(1111)2(1(11)1(AB A B AB A B A B B A ABA B AB B A B A ±±=±±±=±)3(、A 和B 是一般关系,就找到A 和B 的最小公倍数,进行通分,再加减。
分数加减法简便计算精品课件

方米?
① 4+ 3 + 1+ 7
5 10 5 10
② (4 + 1)+ ( 3 + 7 )
5 5 10 10
(2)李林喝了一杯牛奶的 1 ,然后加满水,
1
6
又喝了一杯的 ,再倒满水后又喝了半杯,又
3
加满了水,最后把一杯都喝了。李林喝的牛奶
多,还是水多?
1 6
1
1
12
20
=
1-
1 2
+1-1+ 23
分数加减法的 简便运算
PPT教学课件
填空 分数加减混合运算的运算顺序和 整数加减
混合运算的运算顺序 相同.没有括号的分数加 减混合运算顺序是 从左往右依次计算;有括号 的分数加减混合运算的运算顺序是先算 括号 里面的 ,后算 括号外面的 .
1、整数加减法有哪些运算律? 用字母怎样表示?
交换律: a+b = b+a 加法
)
5 8
-
7 12
+
3 8
5 6
+
1 3
+
2 3
+
1 6
2、用简便方法计算下列各题。
1 6
7 49 7
+871----17516(118+85783+-+73+751+9657+4118725)
1+
9 16
+
7 16
4、怎样算简便就怎样算。
3 + 3+ 7 10 4 10
5+ 2+ 1+ 3 6565
④5.43-(3.43+1.2)
(= 0.9+0.1)+(0.75+0.25) =5.43-3.43-1.2)
=1+1=Βιβλιοθήκη -1.2=2=0.8
分数加减法简便运算速算技巧

分数加减法简便运算速算技巧嘿,咱来说说分数加减法简便运算速算技巧!这可是数学学习中的超棒法宝呢。
先看同分母分数相加减,那简直不要太容易!就像好兄弟手牵手,紧紧靠在一起。
比如三分之二加三分之一,嘿,那不就是三分之三嘛,也就是一。
这多简单直接呀!同分母分数相加减,分母不变,分子相加减就搞定。
就好像一群小伙伴穿着同样的衣服,要数清楚他们的总数,只需要把他们头上戴的帽子数量加起来或者减一减就行啦。
再来说说异分母分数相加减。
这就有点像不同部落的人要聚在一起做事。
那得先找到一个共同的“语言”,也就是通分。
通分就像是给不同部落的人找一个大家都能理解的交流方式。
比如二分之一加三分之一,咱就得先把它们通分,变成六分之三加六分之二,结果就是六分之五。
这过程虽然稍微有点麻烦,但只要掌握了方法,那也是小菜一碟。
还有啊,遇到能约分的情况可别放过。
这就好比在一堆宝石里发现了可以打磨得更漂亮的宝贝。
比如四分之三加八分之二,八分之二约分后是四分之一,那就是四分之三加四分之一,结果是一。
多爽啊!约分能让计算变得更简洁,更快得出结果。
有时候呢,会遇到一些连加或者连减的情况。
这时候可以找找有没有可以凑整的分数组合。
就像玩拼图游戏,找到合适的碎片就能快速拼出完整的画面。
比如三分之一加四分之一加三分之二,这里三分之一和三分之二可以先加起来,得到一,再加上四分之一,就是一又四分之一。
另外,对于一些带分数的加减法,咱可以先把带分数拆分成整数部分和分数部分分别计算。
这就像是把一个大礼包拆开来,看看里面都有啥好东西。
比如二又三分之一加三又四分之一,可以先算整数部分二加三等于五,再算分数部分三分之一加四分之一,通分后是十二分之四加十二分之三等于十二分之七,最后结果就是五又十二分之七。
在做分数加减法的时候,一定要仔细观察题目,就像侦探在寻找线索一样。
说不定一个小细节就能让你找到简便的方法呢。
比如有的题目中会出现一些相同的分数,或者分子分母有特殊关系的分数,这都是给你的小提示哦。
分数的加减运算教授学生进行分数的加减运算的方法和技巧

分数的加减运算教授学生进行分数的加减运算的方法和技巧分数是数学中基本的概念之一,是我们在日常生活和学习中经常遇到的。
分数的加减运算是分数运算的基础,掌握了这些方法和技巧,能够帮助学生更好地理解和解决分数运算问题。
下面我们将详细介绍分数的加减运算的方法和技巧。
一、分数的加法运算1. 相同分母的分数相加当两个分数的分母相同时,只需将分子相加即可,分母保持不变。
例如:1/3 + 2/3 = 3/3 = 1。
2. 不同分母的分数相加当两个分数的分母不同时,需要找到两个分数的最小公倍数作为通分的分母,然后将分子按照最小公倍数分别乘以对应的倍数,转化为相同分母的分数。
接着,再按照相同分母的分数相加的方法进行运算。
例如:1/4 + 3/5 = 5/20 + 12/20 = 17/20。
二、分数的减法运算1. 相同分母的分数相减当两个分数的分母相同时,只需将分子相减即可,分母保持不变。
例如:2/5 - 1/5 = 1/5。
2. 不同分母的分数相减方法与相同分母的分数相加类似,需要先找到两个分数的最小公倍数,并按照最小公倍数进行通分。
然后,再按照相同分母的分数相减的方法进行运算。
例如:3/4 - 1/3 = 9/12 - 4/12 = 5/12。
三、分数的加减混合运算对于分数的加减混合运算,需要先按照运算的优先级进行括号内的运算,再进行加减运算。
例如:2/3 + 1/4 - 1/6 = (8/12) + (3/12) - (2/12) = 9/12 = 3/4。
四、分数的化简在运算过程中,我们经常需要将分数化简为最简形式,即分子和分母没有公约数。
分数化简有助于更好地理解和比较分数。
例如:4/8 可以化简为 1/2。
五、注意事项1. 当分数的分母为0时,是不合法的,因为分母不能为0。
在运算中,要注意避免出现分母为0的情况。
2. 在通分的过程中,要确保计算过程准确无误,特别是最小公倍数的计算。
3. 运算过程中要注意细节,例如:正负号的运用、运算符的使用等,以避免因为粗心导致的错误。
人教版五年级数学下册 《分数加减简便运算》分数的加法和减法PPT

16 84 25
125
4.2 3.6 6.4
14.2
加法交换律: a+b=b+a
加法结合律: (a+b)+c=a+(b+c)
第三页,共十七页。
知识点 分数加法的简算
2 下面每组算式的左右两边有什么样的关系?
第四页,共十七页。
位置换了
=
位置换了 两边的加数相同,只是交换了位置,它们的结 果是相等的,说明整数加法的交换律对分数加法同 样适用。
人教版五年级数学下册 《分数加减简便运算》分数的加法和减法PPT
科 目:数学 适用版本:人教版 适用范围:【教师教学】
分数加减简便运算
第一页,共十七页。
1.理解整数加法的运算定律对分数加法同样适用,
掌握分数加、减法的简便计算方法。 (重点)
2.能利用运算定律进行分数的简便计算。 (难点)
第二页,共十七页。
第五页,共十七页。
=
①
②
① ②
运算顺序发生了改变,结果是相等的, 说明整数 加法的结合律对分数加法同样适用。
第六页,共十七页。
利用加法的运算定律计算。
运用了加法结合律
第七页,共十七页。
同时运用了加法交换律 和加法结合律
第八页,共十七页。
知识提炼
整数加法的交换律、结合律在分数加法中同样适 用。
4.便民商店四月份计划销售 7 万元的商品,结果
上半月就销售了
3
8 万元,下半月销售了
3 万元。
8
5
超过计划多少万元?
3 8
+
3 5
-
7 8
= 1(万元) 10
答:超过计划 1 万元。 10
第十五页,共十七页。
这节课你们都学会了哪些知识?
分数加减运算、快捷运算

分数加减运算、快捷运算1. 分数加减运算分数加减运算是数学中常见的计算方式之一。
在进行分数加减运算时,我们需要考虑分子、分母以及符号的变化。
加法运算要计算两个分数的和,你需要按照以下步骤进行:1. 确保分母相同,如果分母不同,则需要进行通分操作。
2. 将分子相加。
3. 保持分母不变,将分子化简至最简形式。
举例来说,假设我们要计算 1/2 + 1/4:1. 由于分母相同,我们直接将分子相加,得到 1 + 1 = 2。
2. 保持分母不变,即为 2/4。
3. 化简 2/4,得到最简形式 1/2。
减法运算要计算两个分数的差,你需要按照以下步骤进行:1. 确保分母相同,如果分母不同,则需要进行通分操作。
2. 将第二个分数的分子取反。
3. 将两个分数的分子相加。
4. 保持分母不变,将分子化简至最简形式。
举例来说,假设我们要计算 3/4 - 1/4:1. 由于分母相同,我们直接将分子相减,得到 3 - 1 = 2。
2. 保持分母不变,即为 2/4。
3. 化简 2/4,得到最简形式 1/2。
2. 快捷运算在进行分数运算时,我们可以使用快捷方式来简化计算过程。
以下是一些常用的快捷运算规则:- 如果分子为 0,则整个分数为 0。
- 如果分子和分母能够被同一个数整除,则可以简化为最简形式。
- 如果分子大于分母,则可以将分数转化为整数和真分数的形式进行计算。
这些快捷规则可以简化分数运算的过程,提高计算效率。
以上是关于分数加减运算和快捷运算的介绍,希望对你有帮助!如有其他问题,请随时向我提问。
小学奥数全解 之 分数加减法速算与巧算

分数加减法速算与巧算知识点拨一、基本运算律及公式一、加法加法交换律:两个数相加,交换加数的位置,他们的和不变。
即:a+b=b+a其中a,b各表示任意一数.例如,7+8=8+7=15.总结:多个数相加,任意交换相加的次序,其和不变.加法结合律:三个数相加,先把前两个数相加,再加上第三个数;或者先把后两个数相加,再与第一个数相加,他们的和不变。
即:a+b+c=(a+b)+c=a+(b+c)其中a,b,c各表示任意一数.例如,5+6+8=(5+6)+8=5+(6+8).总结:多个数相加,也可以把其中的任意两个数或者多个数相加,其和不变。
二、减法在连减或者加减混合运算中,如果算式中没有括号,那么计算时要带数字前面的运算符号“搬家”.例如:a-b-c=a-c-b,a-b+c=a+c-b,其中a,b,c各表示一个数.在加减法混合运算中,去括号时:如果括号前面是“+”号,那么去掉括号后,括号内的数的运算符号不变;如果括号前面是“-”号,那么去掉括号后,括号内的数的运算符号“+”变为“-”,“-”变为“+”.如:a+(b-c)=a+b-ca-(b+c)=a-b-ca-(b-c)=a-b+c在加、减法混合运算中,添括号时:如果添加的括号前面是“+”,那么括号内的数的原运算符号不变;如果添加的括号前面是“-”,那么括号内的数的原运算符号“+”变为“-”,“-”变为“+”。
如:a+b-c=a+(b-c)a-b+c=a-(b-c)a-b-c=a-(b+c)二、加减法中的速算与巧算速算巧算的核心思想和本质:凑整常用的思想方法:1、分组凑整法.把几个互为“补数”的减数先加起来,再从被减数中减去,或先减去那些与被减数有相同尾数的减数.“补数”就是两个数相加,如果恰好凑成整十、整百、整千……,就把其中的一个数叫做另一个数的“补数”.2、加补凑整法.有些算式中直接凑整不明显,这时可“借数”或“拆数”凑整.3、数值原理法.先把加在一起为整十、整百、整千……的数相加,然后再与其它的数相加.4、“基准数”法,基准当几个数比较接近于某一整数的数相加时,选这个整数为“基准数”(要注意把多加的数减去,把少加的数加上)【例 1】 如果111207265009A +=,则A =________(4级) 【考点】分数约分 【难度】2星 【题型】计算 【关键词】希望杯,六年级,一试 【解析】 111112591207265009873773725125920082008+=+=⨯=⨯⨯⨯⨯,所以A =2008. 【答案】2008【例 2】 11410410042282082008+++=_____ 【考点】分数约分 【难度】1星 【题型】计算【关键词】希望杯,五年级,一试【解析】 原式=1111=22222+++ 【答案】2模块一:分组凑整思想【例 3】 1111222233318181923420345204520192020⎛⎫⎛⎫⎛⎫⎛⎫+++++++++++++++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ 【考点】分组凑整 【难度】3星 【题型】计算 【解析】 观察可知分母是2分子和为1分母是3分子和为12+;分母是4分子和为123++;……依次类推;分母是20子和为12319++++. 原式()1111(12)(123)1231923420=+⨯++⨯++++⨯++++ ()1111(12)22(13)3211919223420=+⨯+⨯÷+⨯+⨯÷++⨯+⨯÷ 12319952222=++++=【例 4】 11211232112199511222333331995199519951995+++++++++++++++ 【考点】分组凑整 【难度】3星 【题型】计算 【解析】 观察可知分母是1的和为1;分母是2的和为2;分母是3的和为3;……依次类推;分母是1995的和为1995.这样,此题简化成求1231995++++的和.11211232112199511222333331995199519951995+++++++++++++++ 12341995119951995299819951991010=+++++=+⨯÷=⨯=() 【答案】1991010例题精讲【考点】分组凑整 【难度】2星 【题型】计算【解析】 因为1996=2×2×499。
1-1-3-1_分数加减法速算与巧算.教师版

1-1-3-1_分数加减法速算与巧算.教师版 work Information Technology Company.2020YEAR分数加减法速算与巧算教学目标本讲知识点属于计算板块的部分,难度并不大。
要求学生熟记加减法运算规则和运算律,并在计算中运用凑整的技巧。
知识点拨一、基本运算律及公式一、加法加法交换律:两个数相加,交换加数的位置,他们的和不变。
即:a+b=b+a其中a,b各表示任意一数.例如,7+8=8+7=15.总结:多个数相加,任意交换相加的次序,其和不变.加法结合律:三个数相加,先把前两个数相加,再加上第三个数;或者先把后两个数相加,再与第一个数相加,他们的和不变。
即:a+b+c=(a+b)+c=a+(b+c)其中a,b,c各表示任意一数.例如,5+6+8=(5+6)+8=5+(6+8).总结:多个数相加,也可以把其中的任意两个数或者多个数相加,其和不变。
二、减法在连减或者加减混合运算中,如果算式中没有括号,那么计算时要带数字前面的运算符号“搬家”.例如:a-b-c=a-c-b,a-b+c=a+c-b,其中a,b,c各表示一个数.在加减法混合运算中,去括号时:如果括号前面是“+”号,那么去掉括号后,括号内的数的运算符号不变;如果括号前面是“-”号,那么去掉括号后,括号内的数的运算符号“+”变为“-”,“-”变为“+”.如:a+(b-c)=a+b-ca-(b+c)=a-b-ca-(b-c)=a-b+c在加、减法混合运算中,添括号时:如果添加的括号前面是“+”,那么括号内的数的原运算符号不变;如果添加的括号前面是“-”,那么括号内的数的原运算符号“+”变为“-”,“-”变为“+”。
如:a+b-c=a+(b-c)a-b+c=a-(b-c)a-b-c=a-(b+c)二、加减法中的速算与巧算速算巧算的核心思想和本质:凑整常用的思想方法:1、分组凑整法.把几个互为“补数”的减数先加起来,再从被减数中减去,或先减去那些与被减数有相同尾数的减数.“补数”就是两个数相加,如果恰好凑成整十、整百、整千……,就把其中的一个数叫做另一个数的“补数”.2、加补凑整法.有些算式中直接凑整不明显,这时可“借数”或“拆数”凑整.3、数值原理法.先把加在一起为整十、整百、整千……的数相加,然后再与其它的数相加.4、“基准数”法,基准当几个数比较接近于某一整数的数相加时,选这个整数为“基准数”(要注意把多加的数减去,把少加的数加上)【例 1】 11410410042282082008+++=_____ 【考点】分数约分 【难度】1星 【题型】计算【关键词】2008年,希望杯,第六届,五年级,一试【解析】 原式=1111=22222+++ 【答案】2【例 2】 如果111207265009A+=,则A =________(4级) 【考点】分数约分 【难度】2星 【题型】计算【关键词】2008年,希望杯,第六届,六年级,一试【解析】 111112591207265009873773725125920082008+=+=⨯=⨯⨯⨯⨯,所以A =2008. 【答案】2008模块一:分组凑整思想【例 3】 11211232112199511222333331995199519951995+++++++++++++++ 【考点】分组凑整 【难度】3星 【题型】计算【解析】 观察可知分母是1的和为1;分母是2的和为2;分母是3的和为3;……依次类推;分母是1995的和为1995.这样,此题简化成求1231995++++的和. 11211232112199511222333331995199519951995+++++++++++++++ 12341995119951995299819951991010=+++++=+⨯÷=⨯=() 【答案】1991010【例 4】 1111222233318181923420345204520192020⎛⎫⎛⎫⎛⎫⎛⎫+++++++++++++++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ 【考点】分组凑整 【难度】3星 【题型】计算【解析】 观察可知分母是2分子和为1分母是3分子和为12+;分母是4分子和为123++;……依次类推;分母是20子和为12319++++.原式()1111(12)(123)1231923420=+⨯++⨯++++⨯++++例题精讲()1111(12)22(13)3211919223420=+⨯+⨯÷+⨯+⨯÷++⨯+⨯÷ 12319952222=++++=【例 5】 分母为1996的所有最简分数之和是_________ 【考点】分组凑整 【难度】2星 【题型】计算【解析】 因为1996=2×2×499。
分数的巧算和速算

分数的速算与巧算【专题解析】在分数的简便计算中,掌握一些常用的简算方法,可以提高我们的计算能力,达到速算、巧算的目的。
(1)约分法:在分数乘除法运算中,如果先约分再计算,可以使计算过程更简便。
两个整数相除(后一个不为0)可以直接写成分数的形式。
两个分数相除,可以根据分数的运算性质,将其写成一个分数乘另一个分数的倒数的形式。
(2)错位相减法:根据算式的特点,将原算式扩大一个整数倍(0除外),用扩大后的算式同原算式相减,可以使复杂的计算变得简便。
【典型例题】例1. 计算:(1)5698÷8 (2)166201÷41分析与解:(1)直接把5698拆写成(56+98),除以一个数变成乘以这个数的倒数,再利用乘法分配率计算。
(2)把题中的166201分成41的倍数与另一个较小的数相加的形式,再利用除法的运算性质使计算简便。
(1)5698÷8=(56+98)÷8=(56+98)×81=56×81+98×81=7+91=791(2)166201÷41 = (164 +2041)×411= 164×411+2041×411= 4201 【举一反三】计算:(1)64178÷8 (2)14575÷12 (3)5452÷17(4)170121÷13例2. 计算:200412004200420052006÷+分析与解:数太大了,不妨用常规方法计算一下,先把带分数化成假分数。
分母200420052004⨯÷,这算式可以运用乘法分配律等于20042006⨯,又可以约分。
聪明的同学们,如果你的数感很强的话,不难看出÷2004200420052005的被除数与除数都含有2004,把他们同时除于2004得到11÷12005也是很好算的,这一方法就留给你们吧!12006⨯÷+20042006原式=20042005 1200620051200620061⨯+⨯=+=2005=200420042006 【举一反三】计算:(5)2000÷200020012000+20021(6)238÷238239238+2401例3. 计算:199419921993119941993⨯+-⨯分析与解:仔细观察分子和分母中各数的特点,可以考虑将分子变形。
分数的巧算和速算

分数的巧算和速算 Prepared on 22 November 2020分数的速算与巧算【专题解析】在分数的简便计算中,掌握一些常用的简算方法,可以提高我们的计算能力,达到速算、巧算的目的。
(1)约分法:在分数乘除法运算中,如果先约分再计算,可以使计算过程更简便。
两个整数相除(后一个不为0)可以直接写成分数的形式。
两个分数相除,可以根据分数的运算性质,将其写成一个分数乘另一个分数的倒数的形式。
(2)错位相减法:根据算式的特点,将原算式扩大一个整数倍(0除外),用扩大后的算式同原算式相减,可以使复杂的计算变得简便。
【典型例题】例1. 计算:(1)5698÷8 (2)166201÷41分析与解:(1)直接把5698拆写成(56+98),除以一个数变成乘以这个数的倒数,再利用乘法分配率计算。
(2)把题中的166201分成41的倍数与另一个较小的数相加的形式,再利用除法的运算性质使计算简便。
(1)5698÷8=(56+98)÷8=(56+98)×81=56×81+98×81=7+91=791 (2)166201÷41 = (164 +2041)×411= 164×411+2041×411= 4201【举一反三】计算:(1)64178÷8 (2)14575÷12 (3)5452÷17 (4)170121÷13例2. 计算:200412004200420052006÷+分析与解:数太大了,不妨用常规方法计算一下,先把带分数化成假分数。
分母200420052004⨯÷,这算式可以运用乘法分配律等于20042006⨯,又可以约分。
聪明的同学们,如果你的数感很强的话,不难看出÷2004200420052005的被除数与除数都含有2004,把他们同时除于2004得到11÷12005也是很好算的,这一方法就留给你们吧!12006⨯÷+20042006原式=20042005 1200620051200620061⨯+⨯=+=2005=200420042006 【举一反三】计算:(5)2000÷200020012000+20021(6)238÷238239238+2401例3. 计算:199419921993119941993⨯+-⨯分析与解:仔细观察分子和分母中各数的特点,可以考虑将分子变形。
分数加减法速算与巧算1

分数加减法速算与巧算1引言本文档将介绍分数加减法的速算技巧和巧算方法,旨在帮助学生提高解题效率和准确性。
速算技巧速算整数和带分数的加法- 当两个分数的分母相同,直接将分子相加,分母保持不变。
- 当两个分数的分母不同,需要找到它们的最小公倍数,然后按照最小公倍数分别进行乘法,再将结果相加。
速算整数和带分数的减法- 当两个分数的分母相同,直接将分子相减,分母保持不变。
- 当两个分数的分母不同,需要找到它们的最小公倍数,然后按照最小公倍数分别进行乘法,再将结果相减。
速算带分数的加减法- 首先将带分数转化为假分数,即分子大于分母的分数形式。
- 采用速算整数和带分数的加减法计算。
- 若最终结果为假分数,可以将其化简为带分数形式。
巧算方法近似计算- 对于掌握了速算技巧的学生,可以使用近似计算法简化问题。
- 先用速算方法得到近似的结果,然后对结果进行调整,使其更接近准确答案。
利用简化法则- 对于分数加减法,可以尝试将分子约分或分母约分,以简化计算过程。
- 若分子和分母有公因数,可以先约分,再进行计算。
利用数学性质- 利用分数的性质,如倒数、相反数、相等关系等,可以在计算过程中得到更简化的结果。
结论通过掌握分数加减法的速算技巧和巧算方法,学生可以提高解题效率和准确性。
同时,应该确保自己的计算结果无误,并在必要时进行核对和验证。
> 注意:本文档提供的加减法速算与巧算方法仅供参考,并不适用于复杂的分数问题。
在应用这些方法时,请保持独立思考,并避免引用无法确认的内容。
(小学奥数)分数加减法速算与巧算

分數加減法速算與巧算教學目標本講知識點屬於計算板塊的部分,難度並不大。
要求學生熟記加減法運算規則和運算律,並在計算中運用湊整的技巧。
知識點撥一、基本運算律及公式一、加法加法交換律:兩個數相加,交換加數的位置,他們的和不變。
即:a+b=b +a其中a,b各表示任意一數.例如,7+8=8+7=15.總結:多個數相加,任意交換相加的次序,其和不變.加法結合律:三個數相加,先把前兩個數相加,再加上第三個數;或者先把後兩個數相加,再與第一個數相加,他們的和不變。
即:a+b+c=(a+b)+c=a+(b+c)其中a,b,c各表示任意一數.例如,5+6+8=(5+6)+8=5+(6+8).總結:多個數相加,也可以把其中的任意兩個數或者多個數相加,其和不變。
二、減法在連減或者加減混合運算中,如果算式中沒有括弧,那麼計算時要帶數字前面的運算符號“搬家”.例如:a-b-c=a-c-b,a-b+c=a+c-b,其中a,b,c各表示一個數.在加減法混合運算中,去括弧時:如果括弧前面是“+”號,那麼去掉括弧後,括弧內的數的運算符號不變;如果括弧前面是“-”號,那麼去掉括弧後,括弧內的數的運算符號“+”變為“-”,“-”變為“+”.如:a+(b-c)=a+b-ca-(b+c)=a-b-ca-(b-c)=a-b+c在加、減法混合運算中,添括弧時:如果添加的括弧前面是“+”,那麼括弧內的數的原運算符號不變;如果添加的括弧前面是“-”,那麼括弧內的數的原運算符號“+”變為“-”,“-”變為“+”。
如:a+b-c=a+(b-c)a-b+c=a-(b-c)a-b-c=a-(b+c)二、加減法中的速算與巧算速算巧算的核心思想和本質:湊整常用的思想方法:1、分組湊整法.把幾個互為“補數”的減數先加起來,再從被減數中減去,或先減去那些與被減數有相同尾數的減數.“補數”就是兩個數相加,如果恰好湊成整十、整百、整千……,就把其中的一個數叫做另一個數的“補數”.2、加補湊整法.有些算式中直接湊整不明顯,這時可“借數”或“拆數”湊整.3、數值原理法.先把加在一起為整十、整百、整千……的數相加,然後再與其它的數相加.4、“基準數”法,基準當幾個數比較接近於某一整數的數相加時,選這個整數為“基準數”(要注意把多加的數減去,把少加的數加上)【例 1】1141041004 2282082008+++=_____【例 2】如果111207265009A+=,則A=________(4級)模組一:分組湊整思想【例 3】1121123211219951 1222333331995199519951995 +++++++++++++++【例 4】11112222333181819 23420345204520192020⎛⎫⎛⎫⎛⎫⎛⎫+++++++++++++++++⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭例題精講【例 1】分母為1996的所有最簡分數之和是_________【巩固】所有分母小於30並且分母是質數的真分數相加,和是__________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分数加减法速算与巧算
教学目标
本讲知识点属于计算板块的部分,难度并不大。
要求学生熟记加减法运算规则和运算律,并在计算中运用凑整的技巧。
知识点拨
一、基本运算律及公式
一、加法
加法交换律:两个数相加,交换加数的位置,他们的和不变。
即:a+b=b +a
其中a,b各表示任意一数.例如,7+8=8+7=15.
总结:多个数相加,任意交换相加的次序,其和不变.
加法结合律:三个数相加,先把前两个数相加,再加上第三个数;或者先把后两个数相加,再与第一个数相加,他们的和不变。
即:a+b+c=(a+b)+c=a+(b+c)
其中a,b,c各表示任意一数.例如,5+6+8=(5+6)+8=5+(6+8).
总结:多个数相加,也可以把其中的任意两个数或者多个数相加,其和不变。
二、减法
在连减或者加减混合运算中,如果算式中没有括号,那么计算时要带数字前面的运算符号“搬家”.例如:a-b-c=a-c-b,a-b+c=a+c-b,其中a,b,c各表示一个数.
在加减法混合运算中,去括号时:如果括号前面是“+”号,那么去掉括号后,括号内的数的运算符号不变;如果括号前面是“-”号,那么去掉括号后,括号内的数的运算符号“+”变为“-”,“-”变为“+”.如:a+(b-c)=a+b-c
a-(b+c)=a-b-c
a-(b-c)=a-b+c
在加、减法混合运算中,添括号时:如果添加的括号前面是“+”,那么括号内的数的原运算符号不变;如果添加的括号前面是“-”,那么括号内的数的原运算符号“+”变为“-”,“-”变为“+”。
如:a+b-c=a+(b-c)
a-b+c=a-(b-c)
a-b-c=a-(b+c)
二、加减法中的速算与巧算
速算巧算的核心思想和本质:凑整
常用的思想方法:
1、分组凑整法.把几个互为“补数”的减数先加起来,再从被减数中减
去,或先减去那些与被减数有相同尾数的减数.“补数”就是两个数相加,如果恰好凑成整十、整百、整千……,就把其中的一个数叫做另一个数的“补数”.
2、加补凑整法.有些算式中直接凑整不明显,这时可“借数”或“拆数”凑整.
3、数值原理法.先把加在一起为整十、整百、整千……的数相加,然后再与其它的数相加.
4、“基准数”法,基准当几个数比较接近于某一整数的数相加时,选这个
整数为“基准数”(要注意把多加的数减去,把少加的数加上)
【例 1】
11410410042282082008+++=_____ 【考点】分数约分 【难度】1星 【题型】计算
【关键词】2008年,希望杯,第六届,五年级,一试
【解析】 原式=1111=22222
+++ 【答案】2
【例 2】 如果111207265009A +=,则A =________(4级)
【考点】分数约分 【难度】2星 【题型】计算
【关键词】2008年,希望杯,第六届,六年级,一试
【解析】 111112591207265009873773725125920082008+=+=⨯=⨯⨯⨯⨯,所以A =2008.
【答案】2008
模块一:分组凑整思想
【例 3】 11211232112199511222333331995199519951995
+++++++++++++++L L L L L L 【考点】分组凑整 【难度】3星 【题型】计算
【解析】 观察可知分母是1的和为1;分母是2的和为2;分母是3的和为3;……
依次类推;分母是1995的和为1995.这样,此题简化成求1231995++++L L
的和.
【答案】1991010
【例 4】 1111222233318181923420345204520192020⎛⎫⎛⎫⎛⎫⎛⎫+++++++++++++++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭L L L L
【考点】分组凑整 【难度】3星 【题型】计算
【解析】 观察可知分母是2分子和为1分母是3分子和为12+;分母是4分子和为
123++;……依次类推;分母是
20子和为12319++++L . 原式()1111(12)(123)12319234
20=+⨯++⨯++++⨯++++L L 【例 5】 分母为1996的所有最简分数之和是_________
【考点】分组凑整 【难度】2星 【题型】计算
【解析】 因为1996=2×2×499。
所以分母为1996的最简分数,分子不能是偶数,
也不能是499的倍数,499与3×499。
因此,分母为1996的所有最简真分数之和是
例题精讲
【答案】498
【巩固】 所有分母小于30并且分母是质数的真分数相加,和是__________。
【考点】分组凑整 【难度】2星 【题型】计算
【解析】 小于30的质数有2、3、5、7、11、13、17、19、23、29共十个,分母
为17的真分数相加,和等于
11621531489()()()()81717171717171717++++++++==L L 1712
-。
类似地,可以求出其它分母为质数的分数的和。
因此,所求的和是 【答案】1592
模块二、加补凑整思想
模块三、位值原理
【例 6】 4444499999999999999955555
++++ 【考点】位值原理 【难度】2星 【题型】计算
【解析】 原式
【答案】111109
【例 7】 1111123102612110
++++=L . 【考点】位值原理 【难度】3星 【题型】计算
【解析】 原式()1111123102612110⎛⎫=+++++++++ ⎪⎝⎭
L L 【答案】105511
【巩固】 11111119931992199119901232323
-+-++-L 【考点】位值原理 【难度】3星 【题型】计算
【解析】 本题需要先拆分在分组,然后在做简单的等差数列求和 【答案】111636
【巩固】 111112342346
+-+=_______ 【考点】位值原理 【难度】3星 【题型】计算
【关键词】2008年,第六届,走美杯,五年级,初赛
【解析】 原式111112342364
=+-++++- 【答案】144
模块四、基准数思想。
