(Fortran编程)数值分析之Newton法求解非线性方程组
matlab实验一:非线性方程求解-牛顿法

matlab实验一:非线性方程求解-牛顿法实验一:非线性方程求解程序1:二分法:syms f x;f=input('请输入f(x)=');A=input(’请输入根的估计范围[a,b]=’);e=input('请输入根的误差限e=’);while (A(2)—A(1))>ec=(A(1)+A(2))/2;x=A(1);f1=eval(f);x=c;f2=eval(f);if (f1*f2)〉0A(1)=c;elseA(2)=c;endendc=(A(1)+A(2))/2;fprintf(’c=%。
6f\na=%.6f\nb=%.6f\n',c,A)用二分法计算方程:1.请输入f(x)=sin(x)—x^2/2请输入根的估计范围[a,b]=[1,2]请输入根的误差限e=0。
5e-005c=1.404413a=1。
404411b=1.4044152.请输入f(x)=x^3—x-1请输入根的估计范围[a,b]=[1,1.5]请输入根的误差限e=0.5e-005c=1。
324717a=1。
324715b=1。
324718程序2:newton法:syms f x;f=input(’请输入f(x)=');df=diff(f);x0=input('请输入迭代初值x0=’);e1=input('请输入奇异判断e1=’);e2=input('请输入根的误差限e2=');N=input('请输入迭代次数限N=’);k=1;while (k〈N)x=x0;if abs(eval(f))〈e1 fprintf(’奇异!\nx=%。
6f\n迭代次数为:%d\n’,x0,k)breakelsex1=x0—eval(f)/eval(df);if abs(x1-x0)<e2fprintf('x=%。
6f\n迭代次数为:%d\n’,x1,k)breakelsex0=x1;k=k+1;endendendif k〉=Nfprintf('失败\n')end用newton法计算方程:1.请输入f(x)=x*exp(x)—1请输入迭代初值x0=0。
牛顿法非线性方程求解

《MATLAB 程序设计实践》课程考核1. 编程实现以下科学计算算法,并举一例应用之。
(参考书籍《精通MAT LAB科学计算》,王正林等著,电子工业出版社,2009 年)“牛顿法非线性方程求解”解:弦截法本质是一种割线法,它从两端向中间逐渐逼近方程的根;牛顿法本质上是一种切线法,它从一端向一个方向逼近方程的根,其递推公式为:-=+n n x x 1)()('n n x f x f初始值可以取)('a f 和)('b f 的较大者,这样可以加快收敛速度。
和牛顿法有关的还有简化牛顿法和牛顿下山法。
在MA TLAB 中编程实现的牛顿法的函数为:NewtonRoot 。
功能:用牛顿法求函数在某个区间上的一个零点。
调用格式:root=NewtonRoot )(```eps b a f 其中,f 为函数名; a 为区间左端点; b 为区间右端点 eps 为根的精度;root 为求出的函数零点。
,牛顿法的matlab程序代码如下:function root=NewtonRoot(f,a,b,eps)%牛顿法求函数f在区间[a,b]上的一个零点%函数名:f%区间左端点:a%区间右端点:b%根的精度:eps%求出的函数零点:rootif(nargin==3)eps=1.0e-4;endf1=subs(sym(f),findsym(sym(f)),a);f2=subs(sym(f),findsym(sym(f)),b);if (f1==0)root=a;endif (f2==0)root=b;endif (f1*f2>0)disp('两端点函数值乘积大于0 !');return;elsetol=1;fun=diff(sym(f)); %求导数fa=subs(sym(f),findsym(sym(f)),a);fb=subs(sym(f),findsym(sym(f)),b);dfa=subs(sym(fun),findsym(sym(fun)),a);dfb=subs(sym(fun),findsym(sym(fun)),b);if(dfa>dfb) %初始值取两端点导数较大者root=a-fa/dfa;elseroot=b-fb/dfb;endwhile(tol>eps)r1=root;fx=subs(sym(f),findsym(sym(f)),r1);dfx=subs(sym(fun),findsym(sym(fun)),r1); %求该点的导数值 root=r1-fx/dfx; %迭代的核心公式tol=abs(root-r1);endend例:求方程3x^2-exp(x)=0的一根解:在MATLAB命令窗口输入:>> r=NewtonRoot('3*x^2-exp(x)',3,4)输出结果:X=3.7331流程图:2、编程解决以下科学计算问题1)二自由度可解耦系统的振动模态分析。
matlab牛顿迭代法求方程

一、引言在数值计算中,求解非线性方程是一项常见的任务。
牛顿迭代法是一种常用且有效的方法,它通过不断逼近函数的零点来求解方程。
而在MATLAB中,我们可以利用其强大的数值计算功能来实现牛顿迭代法,快速求解各种非线性方程。
二、牛顿迭代法原理与公式推导1. 牛顿迭代法原理牛顿迭代法是一种利用函数的导数信息不断逼近零点的方法。
其核心思想是利用当前点的切线与x轴的交点来更新下一次迭代的值,直至逼近方程的根。
2. 公式推导与迭代过程假设要求解方程f(x)=0,在初始值x0附近进行迭代。
根据泰勒展开,对f(x)进行一阶泰勒展开可得:f(x) ≈ f(x0) + f'(x0)(x - x0)令f(x)≈0,则有:x = x0 - f(x0)/f'(x0)将x带入f(x)的表达式中,即得到下一次迭代的值x1:x1 = x0 - f(x0)/f'(x0)重复以上过程,直至达到精度要求或者迭代次数上限。
三、MATLAB中的牛顿迭代法实现1. 编写函数在MATLAB中,我们可以编写一个函数来实现牛顿迭代法。
需要定义原方程f(x)的表达式,然后计算其一阶导数f'(x)的表达式。
按照上述推导的迭代公式,编写循环语句进行迭代计算,直至满足精度要求或者达到最大迭代次数。
2. 调用函数求解方程在编写好牛顿迭代法的函数之后,可以通过在MATLAB命令窗口中调用该函数来求解具体的方程。
传入初始值、精度要求和最大迭代次数等参数,即可得到方程的近似根。
四、牛顿迭代法在工程实践中的应用1. 求解非线性方程在工程领域,很多问题都可以转化为非线性方程的求解问题,比如电路分析、控制系统设计等。
利用牛顿迭代法可以高效地求解这些复杂方程,为工程实践提供了重要的数值计算手段。
2. 优化问题的求解除了求解非线性方程外,牛顿迭代法还可以应用于优化问题的求解。
通过求解目标函数的导数等于0的方程,可以找到函数的极值点,从而解决各种优化问题。
数值分析8牛顿迭代法解非线性方程组

) (x x
) (x x
(0)
)
f1 x
f2 x
(y y
(y y
(0)
)
f1 y
f2 y
0
0
f2( x
(0)
,y
(0)
(0)
)
(0)
)
G X
f1 x G f 2 x f1 y f 2 y
u 11 u 12 u 22
1 m 21 A m n1
1 m n ,n 1
1
u 11
u 12 u 22
u1 n u n 1,n u nn
1
d2
dn
1
l 21 1
l n1 ln2 1
a1n a 2n a nn
d2 ln2d 2
dn
l 21 1
yj x 0
2
j
( j = 1,2,··· ) ··,n ··
2
三对角方程组
2 h2 1 1 2h
2
y j1 ( 2 h ) y j y j1 x j h
1 2 2h y1 x1 y2 x2 h 2 y n1 x n1 y x n n
a kk a nk
工作量: n(n – 1)(n + 4)/3
12/18
例 . LDLT分解
1 A 2 1
非线性方程组求解的牛顿迭代法用MATLAB实现

****1. 二元函数的newton 迭代法理论分析设),(y x f z =在点),(00y x 的某一邻域内连续且有直到2阶的连续偏导数,),(00h y h x ++为该邻域内任意一点,则有⎥⎦⎤⎢⎣⎡∂∂+∂∂+≈++==00),(),(),(),(0000y y x x y x f y k y x f xh y x f k y h x f 其中 0x x h -=,0y -=y k 于是方程0),(=y x f 可近似表示为0),(),(),(k =⎥⎦⎤⎢⎣⎡∂∂+∂∂+==k k y y x x k y x f y k y x f x h y x f 即 0),()(),()(),(y k =-+-+k k k k k x k k y x f y y y x f x x y x f同理,设y)g(x,z =在点),(00y x 的某一邻域内连续且有直到2阶的连续偏导数,),(00h y h x ++为该邻域内任意一点,亦有⎥⎦⎤⎢⎣⎡∂∂+∂∂+≈++==00),(),(),(),(0000y y x x y x g y k y x g x h y x g k y h x g其中0x x h -=,0y -=y k 于是方程0),(g =y x 可近似表示为0),(),(),(k =⎥⎦⎤⎢⎣⎡∂∂+∂∂+==k k y y x x k y x g y k y x g x h y x g 即 0),(g )(),()(),(y k =-+-+k k k k k x k k y x y y y x g x x y x g于是得到方程组⎩⎨⎧=-+-+=-+-+0),(g )(),()(),(0),()(),()(),(y k y k k k k k k x k k k k k k k x k k y x y y y x g x x y x g y x f y y y x f x x y x f****求解这个方程组,当0),(),(),(),(≠-k k y k k x k k y k k x y x g y x f y x f y x g 时),(),(),(),(),(),(),(),(k k y k k x k k y k k x k k y k k k k y k k k y x g y x f y x f y x g y x f y x g y x g y x f x x --+=),(),(),(),(),(),(),(),(y k k y k k x k k y k k x k k x k k k k x k k k y x g y x f y x f y x g y x g y x f y x f y x g y --+=从而⎪⎪⎩⎪⎪⎨⎧--+=--+=),(),(),(),(),(),(),(),(y ),(),(),(),(),(),(),(),(k k y k k x k k y k k x k k x k k k k x k k k k k y k k x k k y k k x k k y k k k k y k k k y x g y x f y x f y x g y x g y x f y x f y x g y y x g y x f y x f y x g y x f y x g y x g y x f x x (1) 记符号),(),(),(),(g ),(k k x k k k k x k k y x x x y x g y x f y x f y x g fg f k k -=- ),(),(),(),(),(k k y k k k k y k k y x yy y x f y x g y x g y x f gf fg k k -=-),(),(),(),(),(k k y k k x k k y k k x y x y x y x y x g y x f y x f y x g g f f g k k -=-于是(1)式可改写为⎪⎪⎩⎪⎪⎨⎧--+=--+=),(),(),(),(g k k k k k k k k y x y x y x y x x x k y x y x y x y x y y k g f f g fg f y y g f f g gf fg x x (2)迭代公式为:⎪⎪⎩⎪⎪⎨⎧--+=--+=++),(),(1),(),(1k g k k k k k k k k y x y x y x y x x x k k y x y x y x y x y y k gf fg fg f y yg f f g gf fg x x (3) 通过迭代公式(3)可以迭代出当 ,2,1=k 时,),(k k y x 的值,当δ≤++)1,1(yk xk (0>δ为给定的误差控制项)时,原方程组的根即为),(k k y x 。
牛顿法解非线性方程(MATLAB和C++)

41 end
42 time = toc;
43
44 fprintf('\nIterated times is %g.\n', times);
45 fprintf('Elapsed time is %g seconds.\n', time);
46
47 root = x_iter;
48
49 % subfunction
5
6 // 功能描述:求解非线性方程根,并输出最终解 7 // 迭代式:x(k+1) = x(k) - f(x(k))/df(x(k)). 8 // 使用:修改标出的“修改”部分即可自定义参数
9
10 // 输入:函数 fun,函数导数 dfun,初值 x0,
4
11 // 最大迭代次数 maxiter,停止精度 tol 12 // 输出:迭代数值解 x_iter2
2
Listing 1: MATLAB EXAMPLE 1 % 2013/11/20 15:14:38
2
3 f = @(x)x^2 − 2; 4 df = @(x)2*x; 5 x0 = 3; 6 root = newton(f, df, x0);
C++ 以 C++ 实现的方法并未编写成为一般可调用的方法,而作为一个独立的 文件(包含一个实例),修改部分即可求解对应的方程。具体参照 cpp 文件内 注释。
A 附录
A.1 MATLAB
Listing 2: MATLAB CODE 1 function root = newton(f, df, x0, maxiter, tol) 2 %NEWTON Newton's method for nonlinear equations. 3% 4 % NEWTON's method: x(k+1) = x(k) - f(x(k))/f'(x(k)). 5% 6 % Inputs 7 % f - nonlinear equation. 8 % df - derivative of f(x). 9 % x0 - initial value. 10 % maxiter - maximum iterated times. 11 % tol - precision. 12 % 13 % Outputs 14 % root - root of f(x) = 0.
Newton 法解非线性方程组

Newton法解非线性方程组一.题目重述:编程实现非线性方程组的牛顿解法,并求解如下方程组。
3x1−cos x2x3−0.5=0x12−81x2+0.12+sin x3+1.06=0e−x1x2+20x3+10π−33=0二.算法:非线性方程组的牛顿法为:给定初始解向量x(0),对于k≥1生成x(k)=x(k−1)−J x k−1−1F(x(k−1)).三.编程实现:这里用MATLAB程序实现,建立三个文件如下:1.函数F(X)文件function F =F( X)F(1,1)=3*X(1)-cos(X(2)*X(3))-0.5;F(2,1)=X(1)^2-81*(X(2)+0.1)^2+sin(X(3))+1.06;F(3,1)=exp(-X(1)*X(2))+20*X(3)+(10*pi-3)/3;end2.J(X) 函数(即Jacobian矩阵)文件function F1= F1(X )F1(1,:)=[3,sin(X(1)*X(2))*X(3),sin(X(1)*X(2))*X(2)];F1(2,:)=[2*X(1),-162*(X(2)+0.1),cos(X(3))];F1(3,:)=[exp(-X(1)*X(2))*(-X(2)),exp(-X(1)*X(2))*(-X(1)),20];end3.解题脚本文件文件名zu%% 牛顿法解非线性方程组clear;X0=[0.1;0.1;-0.1];for i=1:200X=X0-F1(X0)\F(X0); %这里采用MATLAB的左除方法,避免算逆矩阵X0=X;endXabs(0-F(X)) % 计算误差四.编程实现结果:在MATLAB中调用上述解题脚本文件(迭代200次),下图中的zu即为上述解题脚本文件名,而format long 是将MATLAB的显示结果调整为15位数字的形式,结果为即解为:x1=0.5,x2=0,x3=−0.5236.(上面出现-0.00000000…的原因是由于MATLAB太过于精确,求得x2是一个绝对值非常小的负数,这里可取x2=0).且误差为:10^-14*(0,0.0222,0.1776),即已达到了10^-14的精度。
科学计算与数学建模实验报告牛顿法求解非线性方程

科学计算与数学建模实验报告牛顿法求解非线性方程一、引言非线性方程是数学中的一个重要研究内容,其求解方法有很多,其中之一就是牛顿法。
牛顿法是一种迭代方法,通过不断逼近函数的零点来求解非线性方程。
在本实验中,我们将使用牛顿法来求解给定的非线性方程,并验证其有效性。
二、实验方法1.确定问题:给定非线性方程f(x)=0,需要求解方程的根。
2.初始化:选择一个初始解x_0,并给定停止准则,如迭代次数、函数误差等。
3.迭代计算:a)计算函数f(x)在x_i处的导数f'(x_i)。
b)利用牛顿迭代公式进行迭代计算:x_{i+1}=x_i-f(x_i)/f'(x_i)。
c)检查迭代终止条件,若满足条件则停止迭代,否则返回步骤a)继续迭代。
4.输出结果:输出迭代过程中的迭代次数和解x。
三、实验结果我们选择一个较为简单的非线性方程f(x)=x^2-2来进行牛顿法求解。
初始解选取为x_0=1,停止准则为函数误差小于等于0.0001根据上述计算方法,我们进行迭代计算,并记录迭代次数和解x的变化情况。
具体结果如下表所示:迭代次数解x-----------------11.521.416731.414241.4142(收敛)从表中可以看出,当迭代4次时,解x已经收敛于1.4142,符合停止准则,因此我们可以认为此时已经找到了方程的根。
四、实验讨论通过上述实验可以发现,牛顿法是一种有效的求解非线性方程的方法。
它利用了函数在特定点处的导数的信息来逼近函数的零点,从而实现了迭代计算。
同时,牛顿法的收敛速度比较快,迭代次数较少,可以在较短的时间内找到方程的根。
然而,牛顿法也存在一些不足之处。
首先,它对初始解的选择较为敏感,不同的初始解可能导致迭代结果的差异。
其次,牛顿法可能出现发散现象,即迭代过程无法收敛到方程的根。
因此,对于一些复杂的非线性方程,我们需要选择合适的方法来求解。
五、总结通过本次实验,我们了解了牛顿法求解非线性方程的基本过程,并验证了其有效性。
非线性方程(组)的数值解法——牛顿法、弦切法

(3) 用 Newton 法解 (x) = 0
x ( x 2 2) 3 ( x) x x2 2
ex76.m
14
弦截法与抛物线法
弦截法与抛物线法
目的:避免计算 Newton 法中的导数,且具有较 高的收敛性(超线性收敛) 弦截法(割线法):用差商代替微商 抛物线法:用二次多项式近似 f(x)
2
x
k
C
2
2
xk 1 C xk C xk 1 C xk C 2k xk C x0 C xk C x0 C k q2 xk C 2 C 2k 1 q
q
2k
对任意 x0>0, 总有 |q|<1, 即牛顿法收敛
8
牛顿法
牛顿的优点
至少二阶局部收敛,收敛速度较快,特别是当迭代点 充分靠近精确解时。
牛顿法是目前求解非线性方程 (组) 的主要方法 牛顿的缺点
对重根收敛Βιβλιοθήκη 度较慢(线性收敛) 对初值的选取很敏感,要求初值相当接近真解 先用其它算法获取一个近似解,然后使用牛顿法
需要求导数!
9
简化的Newton法
f ( xk ) f '( xk ) 迭代格式: xk 1 xk [ f '( xk )]2 f ( xk ) f ''( xk )
13
举例
例:求 x4 - 4x2 + 4=0 的二重根 x* 2 (1) 普通 Newton 法
x2 2 1 ( x ) x 4x
(2) 改进的 Newton 法 x2 2 2 ( x) x
简化的 Newton 法
数值分析 数值分析 Newton迭代法求解非线性方程实验

}//计算出u[i][j]并输出.
第二部分 for(i=k+1;i<n;i++)
{s=0.0;
for(r=0;r<k-1;r++)
{s=s+l[k][r]*u[r][k];}
l[i][k]=(a[i][k]-s)/u[k][k];
printf("%Lf\n",l[i][k]);
{s=0.0;
for(r=0;r<k-1;r++)
{s=s+l[k][r]*u[r][k];}
l[i][k]=(a[i][k]-s)/u[k][k];
printf("l[%d][%d]%Lf\n",i,k,l[i][k]);}
}
}
六、实验结果
七、上机实验体会
在这个试验中同样叶出现了很多问题,对L,U的求解输出中,输出的位置的不同,结果也就会出差错.经过多次调整,结果总算输出了.
通过此次试验,我理解了多重循环的运用,并了解了古人的聪明智慧,]讲将复杂问题简单化,现在的大学生们,应该学习他们的创新及钻研精神。
for(k=0;k<n;k++)
{for(j=k;j<n;j++)
{s=0.0;
for (r=0;r<k-1;r++)
{s=s+l[k][r]*u[r][j];}
u[k][j]=a[k][j]-s;
printf("u[%d][%d]=%Lf\n",k,j,u[k][j]); }
for(i=k+1;i<n;i++)
Newton迭代法求解非线性方程

Newton迭代法求解非线性方程Newton迭代法求解非线性方程一、 Newton 迭代法概述构造迭代函数的一条重要途径是用近似方程来代替原方程去求根。
因此,如果能将非线性方程f (x )=0用线性方程去代替,那么,求近似根问题就很容易解决,而且十分方便。
牛顿(Newton)法就是一种将非线性方程线化的一种方法。
设k x 是方程f (x )=0的一个近似根,把如果)(x f 在k x 处作一阶Taylor 展开,即:)x x )(x ('f )x (f )x (f k k k -+≈ (1-1)于是我们得到如下近似方程:0)x x )(x ('f )x (f k k k =-+ (1-2)设0)('≠k x f ,则方程的解为:x ?=x k +f (x k )f (x k )?(1-3)取x ~作为原方程的新近似根1+k x ,即令: )x ('f )x (f x x k k k 1k -=+, k=0,1,2,…(1-4)上式称为牛顿迭代格式。
用牛顿迭代格式求方程的根的方法就称为牛顿迭代法,简称牛顿法。
牛顿法具有明显的几何意义。
方程:)x x )(x ('f )x (f y k k k -+= (1-5)是曲线)x (f y =上点))x (f ,x (k k 处的切线方程。
迭代格式(1-4)就是用切线式(1-5)的零点来代替曲线的零点。
正因为如此,牛顿法也称为切线法。
牛顿迭代法对单根至少是二阶局部收敛的,而对于重根是一阶局部收敛的。
一般来说,牛顿法对初值0x 的要求较高,初值足够靠近*x时才能保证收敛。
若要保证初值在较大范围内收敛,则需对)x (f 加一些条件。
如果所加的条件不满足,而导致牛顿法不收敛时,则需对牛顿法作一些改时,即可以采用下面的迭代格式:)x ('f )x (f x x k k k 1k λ-=+,=,2,1,0k (1-6)上式中,10<λ<,称为下山因子。
newton法解非线性方程组

newton法解非线性方程组求解非线性方程组是数值计算中的经典问题之一,其中Newton法是一种常用的求解非线性方程组的方法。
本文将介绍Newton法的原理、步骤以及一些注意事项,并通过一个具体的例子来演示其求解过程。
一、Newton法的原理Newton法是基于Taylor级数展开的思想,通过不断迭代求解线性方程组来逼近非线性方程组的解。
我们假设有一个非线性方程组F(x)=0,其中x=(x1,x2,...,xn)为未知数向量,F=(f1(x),f2(x),...,fn(x))为非线性函数向量。
根据Taylor级数展开,可以将非线性方程组F(x)=0近似表示为:F(x+△x)≈F(x)+J(x)△x=0其中△x为近似解与真解之差,J(x)为F(x)的Jacobi矩阵。
通过近似解与真解之差△x来逼近真解,可以将非线性方程组转化为一个线性方程组J(x)△x=-F(x)。
我们可以通过迭代的方式求解这个线性方程组,不断更新近似解x,直到满足精度要求。
二、Newton法的步骤1.初始化迭代初始值x(0)2.计算非线性函数向量F(x)3. 计算Jacobi矩阵J(x)4.解线性方程组J(x)△x=-F(x),得到△x5.更新近似解x=x+△x6.判断是否满足终止条件,如果满足则结束迭代,否则返回步骤2继续迭代在具体实现时,需要注意以下几个问题:1. 初始迭代值的选择:初试迭代值对Newton法的收敛性有一定影响,通常需要根据具体问题的特点进行选择,可以是经验值,也可以采用其他方法得到。
2. Jacobi矩阵的计算:Jacobi矩阵的计算比较复杂,一般采用数值方法来近似求解,比如中心差分法。
3. 线性方程组的求解:线性方程组的求解可以使用一些高效的方法,比如LU分解、Cholesky分解等。
三、例子演示现在我们通过一个简单的例子来演示Newton法的求解过程。
假设我们要求解方程组:f1(x1,x2)=x1^2+x2^2-1=0f2(x1,x2)=x1+x2-1=0首先,我们需要定义非线性函数向量F(x)和Jacobi矩阵J(x):F(x)=[f1(x1,x2),f2(x1,x2)]^TJ(x)=([∂f1/∂x1∂f1/∂x2],[∂f2/∂x1∂f2/∂x2])然后,我们可以进行迭代求解,具体步骤如下:1.初始化迭代初始值x(0)=(0,0)2.计算非线性函数向量F(x):f1(x)=x1^2+x2^2-1f2(x)=x1+x2-13. 计算Jacobi矩阵J(x):J(x)=([2x12x2],[11])4.解线性方程组J(x)△x=-F(x):J(x)△x=-F(x)的解为:△x=[(x1^2+x2^2-1)/(2x1+2x2),(x1+x2-1)/(2x1+2x2)]^T5.更新近似解x=x+△x:x=(x1+△x1,x2+△x2)6.判断是否满足终止条件,如果满足则结束迭代,否则返回步骤2继续迭代。
牛顿法求解非线性方程组matlab源程序

牛顿法求解非线性方程组matlab源程序Newton-Raphson 求解非线性方程组matlab源程序matlab程序如下:function hom[P,iter,err]=newton('f','JF',[7.8e-001;4.9e-001; 3.7e-001],0.01,0.001,1000); disp(P);disp(iter);disp(err);function Y=f(x,y,z)Y=[x^2+y^2+z^2-1;2*x^2+y^2-4*z;3*x^2-4*y+z^2];function y=JF(x,y,z)f1='x^2+y^2+z^2-1';f2='2*x^2+y^2-4*z';f3='3*x^2-4*y+z^2';df1x=diff(sym(f1),'x');df1y=diff(sym(f1),'y');df1z=diff(sym(f1),'z');df2x=diff(sym(f2),'x');df2y=diff(sym(f2),'y');df2z=diff(sym(f2),'z');df3x=diff(sym(f3),'x');df3y=diff(sym(f3),'y');df3z=diff(sym(f3),'z');j=[df1x,df1y,df1z;df2x,df2y,df2z;df3x,df3y,df3z];y=(j);function [P,iter,err]=newton(F,JF,P,tolp,tolfp,max)%输入P为初始猜测值,输出P则为近似解%JF为相应的Jacobian矩阵%tolp为P的允许误差%tolfp为f(P)的允许误差%max:循环次数Y=f(F,P(1),P(2),P(3));for k=1:maxJ=f(JF,P(1),P(2),P(3));Q=P-inv(J)*Y;Z=f(F,Q(1),Q(2),Q(3));err=norm(Q-P);P=Q;Y=Z;iter=k;if (err<tolp)||(abs(Y)<tolfp||abs(Y)<0.0001)breakendend<pre lang="matlab" line="1" file="test.m">function homework4[P,iter,err]=newton('f','JF',[7.8e-001;4.9e-001; 3.7e-001],0.01,0.001,1000); disp(P);disp(iter);disp(err);function Y=f(x,y,z)Y=[x^2+y^2+z^2-1;2*x^2+y^2-4*z;3*x^2-4*y+z^2];function y=JF(x,y,z)f1='x^2+y^2+z^2-1';f2='2*x^2+y^2-4*z';f3='3*x^2-4*y+z^2';df1x=diff(sym(f1),'x');df1y=diff(sym(f1),'y');df1z=diff(sym(f1),'z');df2x=diff(sym(f2),'x');df2y=diff(sym(f2),'y');df2z=diff(sym(f2),'z');df3x=diff(sym(f3),'x');df3y=diff(sym(f3),'y');df3z=diff(sym(f3),'z');j=[df1x,df1y,df1z;df2x,df2y,df2z;df3x,df3y,df3z];y=(j);function [P,iter,err]=newton(F,JF,P,tolp,tolfp,max)%输入P为初始猜测值,输出P则为近似解%JF为相应的Jacobian矩阵%tolp为P的允许误差%tolfp为f(P)的允许误差%max:循环次数Y=f(F,P(1),P(2),P(3));for k=1:maxJ=f(JF,P(1),P(2),P(3));Q=P-inv(J)*Y;Z=f(F,Q(1),Q(2),Q(3));err=norm(Q-P);P=Q;Y=Z;iter=k;if (err<tolp)||(abs(Y)<tolfp||abs(Y)<0.0001)breakend。
牛顿拉夫逊迭代法,fortran

牛顿拉夫逊迭代法,fortran一、牛顿拉夫逊迭代法简介牛顿拉夫逊迭代法(Newton-Raphson method)是一种求解非线性方程或方程组的高效数值方法。
它的基本思想是通过迭代使得函数值逐步逼近零,从而得到方程的根。
该方法以其简单的迭代公式和较快的收敛速度而受到广泛关注。
二、牛顿拉夫逊迭代法的应用牛顿拉夫逊迭代法广泛应用于数学、物理、工程等领域,如求解非线性方程、非线性方程组、微分方程、线性方程组等。
在实际问题中,通常先设定一个初始值,然后通过迭代公式不断更新,直到结果满足精度要求。
三、FORTRAN编程实现牛顿拉夫逊迭代法FORTRAN(Formula Translation)是一种高级编程语言,主要用于数值计算和科学计算。
以下将以一个简单的非线性方程为例,介绍如何用FORTRAN实现牛顿拉夫逊迭代法。
设非线性方程为:f(x) = x^3 - 2x + 1,求解该方程的根。
四、代码实例与分析以下是用FORTRAN实现的牛顿拉夫逊迭代法求解该非线性方程的代码:```fortranprogram newton_raphsonimplicit noneinteger :: i, max_iterreal(8) :: x, x_new, f_old, f_new, tolreal(8), dimension(100) :: x_historymax_iter = 100tol = 1.0e-6x = 1.0x_history(1) = xdo i = 1, max_iterf_old = f(x)x_new = x - f_old / f"(x)f_new = f(x_new)if (abs(f_new) < tol) exitx = x_newx_history(i+1) = xend doprint *, "Root found at:", xdo i = 1, size(x_history)print *, "Iteration", i, ":", x_history(i)end doend program newton_raphson```分析:1.定义变量和参数:设置迭代次数最大值为100,误差容忍度为1.0e-6。
解非线性方程组的一种带参数的newton方法

解非线性方程组的一种带参数的newton方法参数化Newton方法是用于解决非线性方程组的一种数值方法,它将非线性方程组转换为可解决的易于处理的线性方程组。
一、参数化Newton方法的基本概念1. 概念:参数化Newton方法是一种用于解决非线性方程组的数值方法,它将非线性方程组重新表示为可解决的线性方程组,利用一组局部参数来解决复杂的非线性问题。
2. 基本原理:参数化Newton方法的基本原理是将非线性方程组转化为可求解的线性方程组,并取一组有限的局部参数来求解系统的非线性方程,由此得出解的近似值。
3. 优点:使用参数化Newton方法可以很容易地计算出高维空间中复杂系统的参数化空间,并可以更快地求解出系统的解,而且不会出现不可避免的浮点数舍入误差以及计算精度的下降。
二、参数化Newton方法的具体步骤1. 预处理步骤:首先写出给定的非线性方程组,然后用初始值分别给每个未知参数赋值,最后将原非线性方程组升幂转换为多项式结构。
2. 求解步骤:使用参数化Newton方法,计算出非线性方程组的雅可比矩阵并采用局部参数来求解非线性方程,找出该方程组的局部解。
3. 验证步骤:将求得的局部解代入原非线性方程组,计算解的变化量,用来判断该方程组的局部解是否收敛。
如果最终的解比给定的初始值变化量要小,则称为收敛解。
4. 迭代步骤:若迭代解收敛,则接下来可以通过对参数做一些适当的调整,再次求解非线性方程组,直到得到最终解为止。
三、参数化Newton方法的应用1. 工程计算:在工程中,参数化Newton方法可以求解复杂的非线性方程组,在优化设计、动力学处理以及控制系统中具有重要的应用。
2. 统计学习:统计学习中也经常使用参数化Newton方法,如对于最大似然估计、支持向量机模型以及结构风险最小化等模型都可以使用参数化Newton方法来求解。
3. 其他应用:参数化Newton方法也可以用于求解微分方程组、偏微分方程以及李代数模型等,广泛运用于科学计算中。
非线性方程组的Newton法与拟Newton法
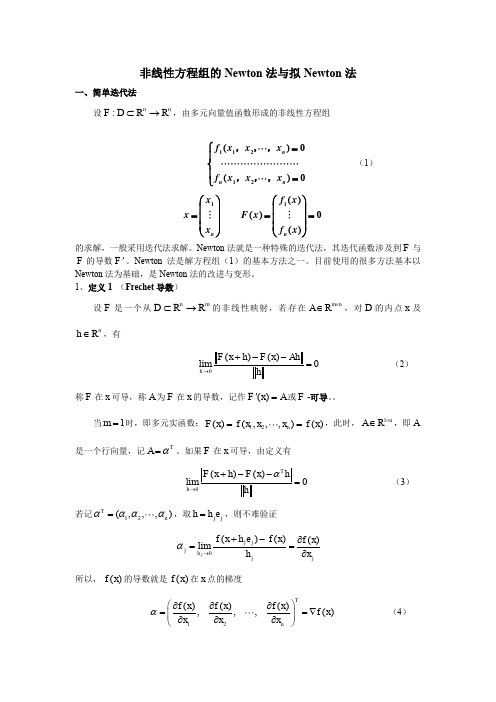
非线性方程组的Newton 法与拟Newton 法一、简单迭代法设:nnF D R R ⊂→,由多元向量值函数形成的非线性方程组11212()0()0n n n f x x x f x x x ⎧=⎪⎨⎪=⎩,,,,,, (1) 11()()0()n n x f x x F x x f x ⎛⎫⎛⎫ ⎪ ⎪=== ⎪⎪ ⎪ ⎪⎝⎭⎝⎭的求解,一般采用迭代法求解。
Newton 法就是一种特殊的迭代法,其迭代函数涉及到F 与F 的导数F '。
Newton 法是解方程组(1)的基本方法之一。
目前使用的很多方法基本以Newton 法为基础,是Newton 法的改进与变形。
1、定义1 (Frechet 导数)设F 是一个从nmD R R ⊂→的非线性映射,若存在m nA R⨯∈,对D 的内点x 及n h R ∈,有()()lim0h F x h F x Ahh→+--= (2)称F 在x 可导,称A 为F 在x 的导数,记作()F x A '=或F -可导。
当1m =时,即多元实函数:12()(,,,)()n F x f x x x f x ==,此时,1n A R ⨯∈,即A是一个行向量,记TA α=。
如果F 在x 可导,由定义有()()lim0T h F x h F x hhα→+--= (3)若记12(,,,)Tn αααα=,取j j h h e =,则不难验证()()()limj j j j h jjf x h e f x f x h x α→+-∂==∂ 所以,()f x 的导数就是()f x 在x 点的梯度12()()(),,,()Tn f x f x f x f x x x x α⎛⎫∂∂∂==∇ ⎪∂∂∂⎝⎭(4)对于一般情形,F :n m D R R ⊂→,记A 的第i 行为Ti α,导数的定义可以写成等价形式0()()lim 0T i i i h f x h f x h hα→+--=,1,2,,i m =所以,可以得到()i i f x α=∇,1,2,,i m = (5)因此,得到多元向量值函数()F x 的导数'F x (),:nnF D R R ⊂→,有111122221212()()()()()()'()()()n n n n n n n n f x f x f x xx x f x f x f x x x x F x DF x R f x f x f x x x x ⨯∂∂∂⎡⎤⎢⎥∂∂∂⎢⎥∂∂∂⎢⎥⎢⎥∂∂∂∈⎢⎥⎢⎥⎢⎥∂∂∂⎢⎥⎢⎥∂∂∂⎣⎦()=()= (6)称()DF x 为()F x 在点x 的Jacobi (雅克比)矩阵。
求非线性方程组所有根的Newton场线法

求非线性方程组所有根的Newton场线法李夏云;陈传淼【摘要】为求解非线性方程组F(x)=0,提出Newton场线微分方程x_t(t)=-(DF(x))~(-1)F(x),x(0)=x~0.在m重根x~*的中心场域中任取初始点x~0,证明了用前向Euler格式得到的解序列x~n一定收敛到此根,故场线法大范围收敛.由此提出求非线性方程组所有根的场线算法,其有效性为数值试验所证实.【期刊名称】《湖南师范大学自然科学学报》【年(卷),期】2009(032)004【总页数】4页(P10-13)【关键词】Newton场线微分方程;场线法;非线性方程组;求所有根【作者】李夏云;陈传淼【作者单位】湖南城市学院数学与计算机科学系,中国益阳 413000;湖南师范大学数学与计算机科学学院,中国长沙 410381【正文语种】中文【中图分类】O241.7;O241.81;O242.23考虑n阶非线性方程组F(x)≡(f1,f2,…,fN)T=0, x=(x1,x2,…,xN)T∈RN,(1)这里F(x)是从N维区域Ω⊂RN到RN的连续且分片光滑的映射.对任意的函数F(x)而言,其结构非常复杂,寻求它的所有根是计算科学的重要问题之一.求解非线性方程组(1)已有许多有效算法和丰富的成果[1-3],经典的Newton法至今都是基本的,重要的.设给定一个初值x0,用Newton公式xk+1-xk=V(xk)≡-(DF(xk))-1F(xk),k=0,1,2,…(2)可得到一近似序列{xk}.其初始点方向V(x0)就是该点的Newton方向,这是最佳的选择.虽然Newton法在根x*附近有二次收敛性,但初值x0在x*的附近才收敛.由于零点事先不知道,实际上寻求一个较好的初值本身就是相当困难的. 以后出现了许多改进和变体,都没有从本质上改变这个限制. 正如蔡大任和白峰杉在文献[1]中所说:“克服Newton法的局部收敛性,寻找大范围收敛的算法可以说是几代人的梦想”.上世纪中叶haye将拓扑学中的Homotopy(同伦)思想用于求解方程(1934)和方程组(1948).设已给函数G(x),G(x0)=0,可作连接x0与根x*的同伦曲线x(t)满足H(t,x(t))=tF(x)+(1-t)G(x)=0,0≤t≤1,x(0)=x0,(3)显然x(0)=x0是H(0,x)=0的根.当t从0连续地改变到1时,我们能设想(有时未必如愿),此延拓曲线x(t)的终点x(1)=x*是H(1,x)=F(x)=0的根.由此发展了相应的数值方法.另一种思路是微分上式,D.V.Devidenko(1953)将它化为微分方程的初值问题xt(t)=-(Hx(t,x))-1Ht(t,x),0≤t≤1,x(0)=x0.(4)它有更多有效的数值方法.同伦算法有大范围的收敛性,在上世纪70年代以来得到迅速发展,并扩展到了许多领域,文献[6]作了总结.目前同伦法也是求非线性方程所有根的最有效的算法之一[1,4-8].但用它解某些复杂问题时有时仍发散,其原因是它仍依赖于函数G(x)及初值x0的选取,它们能使延拓曲线严重地偏离“正确轨道”所致.我们研究非线性微分方程多解计算[9-10],提出了多启动延拓法,它适当扩大了求解范围.逐渐认识到问题的本质:求根的大范围算法应沿着Newton方向.1 Newton方向场和场线微分方程分析Newton法和同伦法的优缺点可知,一种理想的算法应该是沿着Newton方向V(x)前进.取起始点x0,在Davidenko方程(5)中令t=0得起始方向W(x0)=-DG(x0)-1F(x0).对不同的G(x),W(x0)是不同的.若取D-型G(x)=DF(x0)(x-x0)或F-型G(x)=F(x)-F(x0),则其起始方向是Newton方向W(x0)=V(x0).进一步,将起始值x0也看作是一个逐渐变化的过程,得到Newton场线微分方程(5)即曲线x(t)在每点的方向都是Newton方向,它本身准确地描述了一条从x0出发的场线.从场论观点看,对区域Ω上的单值多变量函数F(x),若梯度DF(x)≠0,则过每点x有一个且只有一个梯度方向DF(它为F(x) 增加最快的方向),它们形成一个梯度场. 我们将这种思想用到Newton方向V(x)(它与梯度方向DF(x)完全不同).图1 F=(x3-y,x-y3)T的中心场V(x,y)若DF≠0且F(x)≠0时,V(x)≠0,Ω中无根;若DF≠0,但有某x*∈Ω使F(x*)=0,则x*是单根.这时记K(x*,ρ)⊂Ω为以x*中心,ρ为半径的小球,则V(x)在Ω/K(x*,ρ)中仍是Newton方向场,是所有场线都向x*汇集的中心场(见图1).定义1 以x*为中心所形成的最大中心场区域称为此根的中心场域G(x*).考察许多例子发现,每个根x*附近都存在这样的Newton中心场域.图1显示了F=(x3-y,x-y3)T的方向场V(x),显然原点O是F(x)=0的根,还有两个根(±1,±1).在O点周围形成一个中心场域G,其中任意一点出发的场线都直通原点.注意F的奇线xy=±1/3是4条抛物线,它们将有根的区域分开了.2 场线法及大范围收敛性求解常微分方程组(6)有许多有效的数值方法,我们使用简单的前向Euler法xn+1=xn+hV(xn),x0=x(0),‖xn+1-x(tn)‖≤Ctnh,tn=nh,(6)它是一阶精度的显格式,可自开始和变步长.虽然此格式精度较低(注意,场线法并不要求精确计算场线),但计算简单,能快速接近根.当计算接近根时,F(xn)变小,方向数V(xn)也变小,而xn的变化很小.可以采用较大步长,甚至取h=1(Newton 迭代),以加速收敛.定理1 设在闭区域G上多元函数F(x)适当光滑,梯度DF(x)≠0,且F(x)有一个零点x*,则以G中任意一点x0为起始点,用k≥1阶数值方法所确定的近似解序列xn 一定收敛于此零点x*.适当多步n≥m后进入某邻域‖xn-x*‖≤ρ,并有指数衰减估计‖xn-x*‖≤Cρe-K(tn-tm)→0,n-m→∞,0<K≤1.(7)证前面数值计算产生的点列{xj}有误差估计(6),因此‖xm-x*‖≤‖xm-x(tm)‖+‖x(tm)-x*‖≤Ctmhk+ρ/2≤ρ.即若选h很小,使Ctmhk≤ρ/2.但实际计算表明,要求h很小并非必要.因此适当多步n≥m后,xn进入了x*的邻域K(x*,ρ).在邻域K(x*,ρ)中,r=‖x-x*‖≤ρ,展开因在K中DF(x)≠0,于是V(x)=-(DF(x))-1DF(x)(x-x*)+O(r)(x-x*)=-(x-x*)(1+O(r)),(8)若取x*为球心建立N维球坐标系,用S(θ)表示单位球坐标,则可知V(x)=-S(θ)r(1+O(r))是一个朝x*汇集的中心场.对前向(显式)Euler法(6),简记yn=xn-x*,利用表示(8)有zn=xn+1-xn=-(xn-x*)(1+O(r))h=-yn(1-O(r))h.(9)考虑原函数作差分其中,由不等式ln(1+y)≤y,y>-1,得f(xn+1)-f(xn)≤(ynz+‖z‖2/2)/‖yn‖2=-(1-O(r))h+C(1-O(r))2h2/2.对n求和,对适当小ρ,有及单调下降估计‖F(xn)‖≤‖F(xm)‖e-K(tn-tm).特别地,利用‖F(xn)‖≥c‖xn-x*‖,c>0,可得估计(8).定理得证.注从证明看到,场线法是沿场线单调地逼近零点,因此对求重根仍有效,但可能需要更多的计算步数.场线法对复数根也有效,证明只要将点积换为共轭复数的乘积即可.3 求所有零点的场线算法(FLA)基于定理1可提出求非线性方程组所有根的场线算法(Field-line Algorithm, FLA).设所有根含于某长方体Q中,可设想Q将被F的奇面(可包括DF=0及F=∞的点及场线方向不规则的点等)分割为若干个正则子域,其中有些含一个零点,可用场线法得到;有些没有零点,场线法不收敛,接近奇异面产生振荡或越出此子域等等.由于对这些区域及根的特性不可能有清楚的了解,解决此矛盾的办法是将Q剖分为LN个长方体单元,若单元较小,可期望每个根至少落在某个单元中,因此可得到所有根.采用剖分方法可避免所取初始点离根很远.此种算法也是可并行的.应考虑计算规模,每方向的节点数过少可能漏掉某些根,太大对高维计算工作量巨大.取初始步长应适当小些,如h=0.1,0.2,当接近根时取较大步长,最后为h=1.在循环计算中应设定几个控制参数,其中有(以下数值仅作参考):(1)避免在奇点中断,要求‖DF(x)‖>10-10;(2)避免向无穷发散,控制‖xn-x0‖≤2h1不越出两个单元;(3)避免卷入死循环或不必要的计算,控制最大迭代次数,如K=50,100;(4)还必须控制允许精度,如‖F(xn)‖≤10-6.将根记入数组U.第一个根必存,以后所得的根应与U中已存的根比较.若都不同,例如|x*-U|≥10-4,则是新根,应存入U,否则弃去.计算结束时U中已存所有不同的根.4 高维问题的数值试验考虑4元方程组其Jacobi矩阵DF的奇面方程为x1x2x3x4=a4,a=(3/32)1/12=0.821 0,坐标平面是渐近曲面.此奇面的结构并不复杂.每个一维区间(-2,2)上,只取剖分节点L=2(共24=16个起始点),h=0.2,可求得它的8个根(下表中最后一行是在近似零点上函数的模).若取更多的网格,仍只得此8个实根.表1 8个不同的实根kx1x2x3x4‖F(x)‖1-1.769 7-1.808 2-1.845 2-1.864 31.657 9e-82-1.577 51.807 9-1.841 6-1.833 92.510 6e-83-1.748 6-1.348 91.844 8-1.861 03.340 5e-84-1.605 91.349 41.842 1-1.838 43.490 3e-85-1.765 4-1.712 5-0.799 81.863 62.801 2e-76-1.583 31.716 4-0.839 01.834 82.181 4e-77-1.595 51.519 20.836 71.836 81.8027e-88-1.756 7-1.524 20.801 81.862 32.5964e-8这里没有x1>0的根,加密剖分计算也没有找到.为此取X0=(2,2,2,2)作50次迭代,第15次迭代函数模达到最小1.51,但第16次迭代突然猛增为‖F‖=1.78e+12,以后振荡,因为迭代点X已经接近坐标平面(接近奇异面),根本不收敛.还考虑8维问题取剖分节点L=2,可求出28个不同的实根,CPU时间不到1 s. 参考文献:[1] 蔡大用,白峰衫. 现代科学计算[M].北京:科学出版社,2000.[2] 李庆扬,关治.数值计算原理[M].北京:清华大学出版社,2000.[3] 李庆扬,莫孜中,祁力群.非线性方程组的数值解[M].北京:科学出版社,1987.[4] ALLGOWER E L, GEORG K. Introduction to numerical continuation methods[M].Berlin: Springer-verlag, SIAM, 1990.[5] CHIN-HONG P,HOMH-TAE S.What is the homotopy for a system of nonlinear equations(survery)?[J]J Appl Math Computing,2005,(17):689-700.[6] BRANIN F. Widely convergent method for finding multiple solution of simultaneous nonlinear equations[J].IBM J Res Develop,1972,(16):504-522.[7] ZULEHNER W. A simple homotopy method for determining all isolated solutions to polynomial systems[J]. Math Comp, 1988,(50):167-177.[8] LI T Y, SAUER T. Regularity results for solving systems of polynomials by homotopy method[J]. Numer Math, 1987,(30):283-289.[9] 陈传淼. 科学计算概论[M].北京:科学出版社,2007.[10] 陈传淼,谢资清.非线性微分方程多解计算的搜索延拓法[M].北京:科学出版社,2005.。
Newton迭代法-数值分析非线性方程组数值解法

实验七、Newton 迭代法一、实验目的了解非线性方程与方程组的数值解法;深入理解Newton 迭代法,并用C++实现计算结果。
二、计算公式()())2(),1,0(1 ='-=+n x f x f x x n n n n它对应的迭代方程为显然是f(x)=0的同解方程,故其迭代函数为在 f(x)=0的根x*的某个邻域内,在x*的邻域R 内,对任意初值,应用公式(2)来解方程三、程序代码#include<stdio.h>#include<math.h>#include<conio.h>double f(double x);doubleft(double x);main(){double X0,X1,tol;int n;int count=0;printf("请输入初始值:\n");将f(x)在点x n 作Taylor 展开:)()(')()()(!2)()()(')()(2n n n n n n n n x x x f x f x f x x x f x x x f x f x f -+≈+-''+-+= ——Taylor 展开线性化f(x)=0近似于f(x n )+ f ′(x n )(x-x n )=0 (1)从(1)解出x,记为x n+1 ,则 )()(x f x f x x '-=)()()(x f x f x x '-=ϕ)0)((≠'x f )(δα≤-x R 0)(≈x f 1)()()()(2<≤'∙''=ϕ'L x f x f x f x 0xscanf("%lf",&X0);printf("请输入精度:\n");scanf("%lf",&tol);printf("请输入最大循环次数\n");scanf("%d",&n);X1=X0-f(X0)/ft(X0);while(fabs(X1-X0)>=tol)/*在没有达到精度要求情况下就循环*/ {X0=X1;X1=X0-f(X0)/ft(X0);count++;/*循环次数计数*//*如果循环次数到用户输入的最大循环次数就退出,可以适当修改*/ if(count==n){break;}}printf("方程的根为:%f\n",X1);getch();}/*************************函数功能:用于求f(x)的值**************************/double f(double x){double y;y=x*x*x+2*x*x+10*x-20;return y;}/*************************函数功能:用于求f(x)的导数值**************************/doubleft(double x){double y;y=3*x*x+4*x+10;return y;}四、例题用Newton 迭代法求下面方程的一个正根,计算结果精确到7位小数.02010223=-++x x x []得取初值,2,020∈=x。
用Newton切线法求解非线性方程f_x_0

立时的 x 值, 它可以用前述 Newton 算法来实现求解。 取 x0= 1 作为迭代初值, 根据 (3.1 ) 式迭代公式, 其迭代结果如表 3 2 中: 表 3 取 x0= 1 ,ε=0.00001 2 K=0 0.50000 1 0.44487 2 0.42777
- 2x
3 0.42631
4 0.42630
图 1 Newton 切线法 Newton 切线算法 Step 1 给定初始点 t0, 允许误差 ε>0,置 k=0。 Step 2 检查 φ'(tk) <ε?是, 输出 tk, 停止计算: 否, 转 step 3。 Step 3 计算点 tk+1=tk- φ'(tk) φ''(tk) 置 k:=k+1,转 step 2。 下述定理表明 Newton 法具有局部二阶收敛速度。 t 满足 定理 2.1 设 φ(t)存在三阶连续导数, φ'(t )=0, φ''(t )≠0 则当初始点 t0 充分接近 t 时, Newton 法迭代产生的点列 {tk}至少二 阶收敛于t 。
3 k 2xk 2 2xk
图 2 给出上例中函数 φ(t)的图形
(3.1 )
图 2 例中函数 φ(t)的图形 由于牛顿迭代法的局部收敛性, 它对初值要求较高, 只有初值充分 靠近t , 才能保证序列收敛, 为保证非局部收敛, 我们增加下列条件。 定理 2.2 设 φ(t)在有限区间[a, b]上二阶导数存在, 且满足 (1 ) φ(a)φ(b)<0; (2 ) φ'(x)≠0,x∈[a,b]; (3 ) φ''(x)不变号, x∈[a,b]; (4 ) 初值 x0∈[a,b], 使 φ''(x0)φ(x0)>0。 则牛顿迭代序列{xk}收敛于 φ(x)=0 在[a, b]上的唯一根[2]。 3.问题的求解 设已知非线性方程 f(x)=0, 求其方程的解。 解: 设非线性方程 f(x)=0 有根, 其根为 x0, 则 f(x0)=0, 那么在 x0 点附 f(x)≈min f(x) 近, 有: 又{{x min f(x) =0}圳{x minf2(x)}} 因此, 求解非线性方程 f(x)=0, 可转为求 minf2(x)成立时 x 的值。 Newton 法算法[3] Step 1 给定初始点 x0, 允许误差 ε>0,置 k=0。 Step 2 检查 [f2(xk)]' = 2f(xk)f'(xk) <ε?是, 输出 xk, 停止计算: 否, 转 step 3。 Step 3 计算点 2 f(xk)f'(xk) xk+1=xk- [f2 (xk)]' =xk[f (xk)]'' [f'(xk)]2+f(xk)f''(xk) 置 k:=k+1,转 step 2。 算例 用迭代公式求方程 e- 2x=x 的根的一个近似值。 解: 首先将方程 e- 2x=x 改写为: (上接第 93 页 ) 进一步降低火灾爆炸发生的可能性。 2.3 光电传感器 在粉尘浓度比较高的环境中, 除了增设良好的通风系统, 还要加设 光电传感器, 以便及时发现检测粉尘的浓度, 避免粉尘浓度达到爆炸极 限, 造成严重的事故。 2.4 噪声检测 对现场工作岗位进行噪声检测,按国家和行业要求发放个人防护 噪声和有毒有害物质的员工, 按国家有关法规要求, 用品, 对接触粉尘、 确定需进行职业性体检的岗位及员工, 编制 《职业性体检计划》 , 选择有 资质的医疗机构, 组织员工定期进行职业体检, 建立员工职业性体检档 案。 2.5 根据火灾特点选用的传感器 纺织行业建筑中火灾自动报警系统的设计要点是:根据被保护对 象发生火灾时燃烧的特点确定火灾类型; 根据所需防护面积部位; 按照 火灾探测器的总数和其他报警装置 (如手报 ) 数量确定火灾报警控制器 的总容量; 按划分的报警区域设置区域报警控制器; 根据消防设备确定 联动控制方式; 按防火灭火要求确定报警和联动的逻辑关系; 最后还要 考虑火灾自动报警系统与纺织行业建筑 “3AS” (建设设备自动化系统、 通 信自动化系统、 办公自动化系统 ) 的适应性。 纺织行业建筑中应以感烟火灾探测器选用为主,个别不宜选用感
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
!调用上三角方程组的回代方法
call UP_TRI(AUP,BUP,X,N)
end subroutine LINEQ
subroutine UP_TRI(A,B,X,N)
!上三角方程组的回代方法
imp阵
open(unit=11,file="jieguo.txt")
write(11,100)
100 format(/,T6,"Newton法计算非线性方程组迭代序列:",/)
X=(/1.6,1.2/)
TOL=1D-9
do I=1,ITMAX
ELMAX=DABS(AB(K,K))
ID_MAX=K
!这段程序不是为了赋值最大元素给ELMAX,而是为了找出最大元素对应的标号
do I=K+1,N
if(dabs(AB(I,K))>ELMAX) then
ELMAX=AB(I,K)
module M_GAUSS
!高斯列主元消去法模块
contains
subroutine LINEQ(A,B,X,N)
!高斯列主元消去法
implicit real*8(A-Z)
integer::I,K,N
integer::ID_MAX !主元素标号
real*8::A(N,N),B(N),X(N)
!调用Newton法中的函数
call SOLVE()
end program newton
end do
X(I)=X(I)/A(I,I)
end do
end subroutine UP_TRI
end module M_GAUSS
module M_NEWTON
!关于方程的模块
contains
subroutine SOLVE()
!计算非线性方程组
integer::I,J,N
real*8::A(N,N),B(N),X(N)
X(N)=B(N)/A(N,N)
!回代部分
do I=N-1,1,-1
X(I)=B(I)
do J=I+1,N
X(I)=X(I)-A(I,J)*X(J)
DX2=DSQRT(DX(1)**2+DX(2)**2)
if(DX2<TOL) exit
end do
end subroutine SOLVE
subroutine FUNC(F,X)
!方程函数
implicit real*8(A-Z)
real*8::X(2),F(2)
real*8::AUP(N,N),BUP(N)
!A,B为增广矩阵
real*8::AB(N,N+1)
real*8::VTEMP1(N+1),VTEMP2(N+1)
AB(1:N,1:N)=A
AB(:,N+1)=B
!列主元消去法的核心部分
do K=1,N-1
ID_MAX=I
end if
end do
!交换两行元素,其他不变
VTEMP1=AB(K,:)
VTEMP2=AB(ID_MAX,:)
AB(K,:)=VTEMP2
AB(ID_MAX,:)=VTEMP1
use M_GAUSS
implicit real*8(A-Z)
integer::I,ITMAX=50
integer::N=2
real*8::X(2),F(2),DX(2)
real*8::DF(2,2)
!ITMAX为最大允许迭代次数
!N为方程组维数
DF(1,1) = 2*X(1)
DF(1,2) = 2*X(2)
DF(2,1) = 2*X(1)
DF(2,2 )= -2*X(2)
end subroutine JAC
end module M_NEWTON
program newton
use M_NEWTON
call FUNC(F,X)
call JAC(DF,X)
call LINEQ(DF,-F,DX,N)
X=X+DX
write(11,200)I,X
200 format(I5,2F16.10)
!判断计算精度,满足误差要求时推出循环
!以上交换两行元素,然后开始消元
do I=K+1,N
TEMP=AB(I,K)/AB(K,K)
AB(I,:)=AB(I,:)-TEMP*AB(K,:)
end do
end do
AUP(:,:)=AB(1:N,1:N)
F(1) = X(1)**2 + X(2)**2 - 4
F(2) = X(1)**2 - X(2)**2 - 1
end subroutine FUNC
subroutine JAC(DF,X)
!偏导数矩阵
implicit real*8(A-Z)
real*8::X(2),DF(2,2)
