苏教版高中数学高一必修一第28课时 幂函数2 同步练习
2019—2020年苏教版高中数学必修一《幂函数》课时练习及解析.docx

(新课标)2018-2019学年度苏教版高中数学必修一§3.3 幂函数课时目标 1.通过具体问题,了解幂函数的概念.2.从描点作图入手,画出y=x,y=x2,y=x3,y=12x,y=x-1的图象,总结出幂函数的共性,巩固并会加以应用.1.一般地,把形如________的函数叫做幂函数,其中x是自变量,α是常数.2.在同一平面直角坐标系中,画出幂函数y=x,y=x2,y=x3,y=12x,y=x-1的图象.3.结合2中图象,填空.(1)所有的幂函数图象都过点__________,在(0,+∞)上都有定义.(2)若α>0时,幂函数图象过点________________,且在第一象限内______;当0<α<1时,图象上凸,当α>1时,图象______.(3)若α<0,则幂函数图象过点________,并且在第一象限内单调______,在第一象限内,当x从+∞趋向于原点时,函数在y轴右方无限地逼近于y轴,当x趋于+∞时,图象在x轴上方无限逼近x轴.(4)当α为奇数时,幂函数图象关于______对称;当α为偶数时,幂函数图象关于______对称.(5)幂函数在第____象限无图象.一、填空题1.下列函数是幂函数的是________.(填序号) ①y =x ;②y =x 3;③y =2x ;④y =x -1.2.幂函数f(x)的图象过点(4,12),那么f(8)的值为________.3.下列是y =23x 的图象的是________.(填序号)4.图中曲线是幂函数y =x n 在第一象限的图象,已知n 取±2,±12四个值,则相应于曲线C 1,C 2,C 3,C 4的n 依次为________.5.设a =2535⎛⎫ ⎪⎝⎭,b =3525⎛⎫⎪⎝⎭,c =2525⎛⎫⎪⎝⎭,则a ,b ,c 的大小关系是________. 6.函数f(x)=x α,x ∈(-1,0)∪(0,1),若不等式f(x)>|x|成立,则在α∈{-2,-1,0,1,2}的条件下,α可以取值的个数是________.7.给出以下结论:①当α=0时,函数y=xα的图象是一条直线;②幂函数的图象都经过(0,0),(1,1)两点;③若幂函数y=xα的图象关于原点对称,则y=xα在定义域内y随x的增大而增大;④幂函数的图象不可能在第四象限,但可能在第二象限.则正确结论的序号为________.8.函数y=12x+x-1的定义域是________.9.已知函数y=x-2m-3的图象过原点,则实数m的取值范围是____________________.二、解答题10.比较121.1、121.4、131.1的大小,并说明理由.11.如图,幂函数y =x 3m -7(m ∈N)的图象关于y 轴对称,且与x 轴、y 轴均无交点,求此函数的解析式.能力提升12.已知函数f(x)=(m 2+2m)·21m m x+-,m 为何值时,函数f(x)是:(1)正比例函数;(2)反比例函数;(3)二次函数;(4)幂函数.13.点(2,2)在幂函数f(x)的图象上,点(-2,14)在幂函数g(x)的图象上,问当x 为何值时,有:(1)f(x)>g(x);(2)f(x)=g(x);(3)f(x)<g(x).1.幂函数在第一象限内指数变化规律:在第一象限内直线x =1的右侧,图象从上到下,相应的指数由大变小;在直线x =1的左侧,图象从下到上,相应的指数由大变小.2.求幂函数的定义域时要看指数的正负和指数nm中的m 是否为偶数;判断幂函数的奇偶性时要看指数nm 中的m 、n是奇数还是偶数.y =x α,当α=nm(m 、n ∈N *,m 、 n 互质)时,有:n m y =n mx 的奇偶性 定义域 奇数 偶数 非奇非偶函数 [0,+∞) 偶数 奇数 偶函数 (-∞,+∞) 奇数奇数奇函数(-∞,+∞)3.幂函数y =n mx 的单调性,在(0,+∞)上,nm >0时为增函数,nm <0时为减函数.§2.4 幂函数知识梳理1.y =x α 3.(1)(1,1) (2)(0,0),(1,1) 递增 下凸 (3)(1,1) 递减 (4)原点 y 轴 (5)四 作业设计 1.①②④解析 根据幂函数的定义:形如y =x α的函数称为幂函数,③中自变量x 的系数是2,不符合幂函数的定义,所以③不是幂函数.2.24解析 设幂函数为y =x α,依题意,12=4α,即22α=2-1,∴α=-12.∴幂函数为y =12x-,∴f(8)=128-=18=122=24.3.②解析 y =23x =3x 2,∴x ∈R ,y ≥0,f(-x)=3(-x )2=3x 2=f(x),即y =23x 是偶函数,又∵23<1,∴图象上凸.4.2,12,-12,-2解析 作直线x =t(t>1)与各个图象相交,则交点自上而下的排列顺序恰好是按幂指数的降幂排列的. 5.a>c>b解析 根据幂函数与指数函数的单调性直接可以判断出来,y =25x 在x>0时是增函数,所以a>c ,y =(25)x 在x>0时是减函数,所以c>b.6.2解析 因为x ∈(-1,0)∪(0,1), 所以0<|x|<1.要使f(x)=x α>|x|,x α在(-1,0)∪(0,1)上应大于0, 所以α=-1,1显然是不成立的. 当α=0时,f(x)=1>|x|; 当α=2时,f(x)=x 2=|x|2<|x|; 当α=-2时,f(x)=x -2=|x|-2>1>|x|. 综上,α的可能取值为0或-2,共2个. 7.④解析 当α=0时,函数y =x α的定义域为{x|x ≠0,x ∈R},故①不正确;当α<0时,函数y =x α的图象不过(0,0)点,故②不正确;幂函数y =x -1的图象关于原点对称,但其在定义域内不是增函数,故③不正确.④正确. 8.(0,+∞)解析 y =12x 的定义域是[0,+∞),y =x -1的定义域是(-∞,0)∪(0,+∞),再取交集. 9.m<-32解析 由幂函数的性质知-2m -3>0, 故m<-32.10.解 考查函数y =1.1x ,∵1.1>1, ∴它在(0,+∞)上是增函数.又∵12>13,∴121.1>131.1.再考查函数y =12x ,∵12>0,∴它在(0,+∞)上是增函数. 又∵1.4>1.1,∴121.4>121.1, ∴121.4>121.1>131.1.11.解 由题意,得3m -7<0. ∴m<73.∵m ∈N ,∴m =0,1或2, ∵幂函数的图象关于y 轴对称, ∴3m -7为偶数. ∵m =0时,3m -7=-7, m =1时,3m -7=-4, m =2时,3m -7=-1.故当m =1时,y =x -4符合题意.即y =x -4.12.解 (1)若f(x)为正比例函数,则⎩⎪⎨⎪⎧m 2+m -1=1,m 2+2m ≠0⇒m =1.(2)若f(x)为反比例函数,则⎩⎪⎨⎪⎧m 2+m -1=-1,m 2+2m ≠0⇒m =-1.(3)若f(x)为二次函数,则⎩⎪⎨⎪⎧m 2+m -1=2,m 2+2m ≠0⇒m =-1±132. (4)若f(x)为幂函数,则m 2+2m =1, ∴m =-1±2.13.解 设f(x)=x α,则由题意,得 2=(2)α,∴α=2,即f(x)=x 2.设g(x)=x β,由题意,得14=(-2)β,∴β=-2,即g(x)=x -2.在同一平面直角坐标系中作出f(x)与g(x)的图象,如图所示. 由图象可知:(1)当x>1或x<-1时, f(x)>g(x);(2)当x =±1时,f(x)=g(x); (3)当-1<x<1且x ≠0时, f(x)<g(x).。
苏教版数学高一- 数学苏教必修一练习幂函数的性质

双基达标(限时15分钟)2.给出下列函数,在区间(0,2)上是单调增函数的序号是________.解析逐一判断.(1)(3)(4)在区间(0,2)上都是单调减函数,只有(2)在区间(0,2)上是单调增函数.答案(2)3.比较大小:(-1.2)3,(-1.25)3从大到小的顺序为________.解析∵y=x3在R上是增函数,-1.2>-1.25,∴(-1.2)3>(-1.25)3.答案(-1.2)3>(-1.25)3答案①④④6.求函数y=的定义域、值域和单调区间.解要使函数y=有意义,即要x+2≠0,即x≠-2,∴定义域为(-∞,-2)∪(-2,+∞);值域为(0,+∞);在(-∞,-2)上递增,在(-2,+∞)上递减.综合提高(限时30分钟)8.若幂函数y=(m2+3m-17)·x4m-m2的图象不过原点,则m的值为______.解析由m2+3m-17=1得m2+3m-18=0,∴m=3或m=-6.又当m=3时,指数4m-m2>0,不合题意,当m=-6时,4m-m2<0,符合题意,∴m=-6.答案-610.若x2<,则x的取值范围是________.解析 在同一坐标系中作出幂函数y =x 2和y =的图象如图,由图象可得x 的取值范围为(0,1).答案 (0,1)11.讨论下列函数的定义域、值域,奇偶性与单调性:12.求函数f (x )=x 2+2x +2x 2+2x +1的单调区间.解 f (x )=1+(x +1)-2,其图象是由幂函数y =x -2的图象向左平移1个单位,再向上平移1个单位得到,∵幂函数y =x -2在(-∞,0)上递增,在(0,+∞)上递减,∴函数f (x )在(-∞,-1)上递增,在(-1,+∞)上递减.13.(创新拓展)已知函数y =a x 2-3x +3(a >0且a ≠1),当x ∈[1,3]时有最小值18,求a 的值.解 令t =x 2-3x +3=(x -32)2+34, 当x ∈[1,3]时,t ∈[34,3], ①若a >1,则y min ==18, 解得a =116,与a >1矛盾. ②若0<a <1,则y min =a 3=18, 解得a =12,满足题意.1综合①、②知a=2.。
高一数学 第2章第28课时 幂函数2配套练习 苏教版必修1

高一数学 第2章第28课时 幂函数2配套练习 苏教版必修1分层训练1.函数25y x =的单调减区间为 ( )A .(,1)-∞B .(,0)-∞C .[0,)+∞D .(,)-∞+∞2.幂函数34y x =,13y x =,43y x -=的定义域分别为M 、N 、P ,则 ( )()A M N P ⊂⊂≠≠ ()B N M P ⊂⊂≠≠()C M P N ⊂⊂≠≠ ()D ,,A B C 都不对3.设121.1a -=,120.9b -=,12c x -=,且a c b <<,则对于整数c 的值,下列判断正确的是( )()A 1c > ()B 1c < ()C 1c =()D c 与1的大小关系不能确定4.221333123111(),(),()252T T T ===,则下列关系式正确的是 ( ) A .123T T T << B .312T T T <<C .231T T T <<D .213T T T <<5.函数()a y x a R =∈的图象,当01x <<时,在直线y x =的上方;当1x >时,在直线y x=的下方,则a 的取值范围是 ;6.用“<”、“>”或“=”号填空:(1)若54a a -<-,则a ______0;(2)若0.390.38b b <,则b ______0;(3)若11()()23n n->-(n Z ∈),则当n 为偶数时,n 0; 当n 为奇数时,n 0.7.比较下列各题中两个值的大小:(1)25( 1.5)-与25( 1.7)-;(2)233.14-与23π- (3)13(5)--与13(6)--; (4)143与2128.若1133(1)(32)a a --+<-,求a 的取值范围.拓展延伸9.已知幂函数f (x )=23221++-p p x (p ∈Z )在(0,+∞)上是增函数,且在其定义域内是偶函数,求p 的值,并写出相应的函数f (x ).10.m 为怎样的值时,函数32204()(42)(1)f x mx x m x mx -=++++-+的定义域是R ?本节学习疑点:学生质疑教师释疑。
2.4幂函数试题(苏教版必修1)

新课标高一数学同步测试—2.4幂函数一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分). 1.下列函数中既是偶函数又是(,)-∞0上是增函数的是 ( )A .y x =43B .y x =32C .y x =-2D .y x =-142.函数2-=x y 在区间]2,21[上的最大值是 ( )A .41 B .1- C .4 D .4- 3.下列所给出的函数中,是幂函数的是( )A .3x y -=B .3-=x yC .32x y =D .13-=x y 4.函数34x y =的图象是( )A .B .C .D .5.下列命题中正确的是( )A .当0=α时函数αx y =的图象是一条直线B .幂函数的图象都经过(0,0)和(1,1)点C .若幂函数αx y =是奇函数,则αx y =是定义域上的增函数 D .幂函数的图象不可能出现在第四象限6.函数3x y =和31x y =图象满足( )A .关于原点对称B .关于x 轴对称C .关于y 轴对称D .关于直线x y =对称 7. 函数R x x x y ∈=|,|,满足( )A .是奇函数又是减函数B .是偶函数又是增函数C .是奇函数又是增函数D .是偶函数又是减函数8.函数2422-+=x x y 的单调递减区间是( )A .]6,(--∞B .),6[+∞-C .]1,(--∞D .),1[+∞-9. 如图1—9所示,幂函数αx y =在第一象限的图象,比较1,,,,,04321αααα的大小( ) A .102431<<<<<αααα B .104321<<<<<αααα C .134210αααα<<<<< D .142310αααα<<<<<10. 对于幂函数54)(x x f =,若210x x <<,则)2(21x x f +,2)()(21x f x f +大小关系是( ) A .)2(21x x f +>2)()(21x f x f + B . )2(21x x f +<2)()(21x f x f + C . )2(21x x f +=2)()(21x f x f +D . 无法确定二、填空题:请把答案填在题中横线上(每小题6分,共24分). 11.函数y x =-32的定义域是 .12.幂函数的图象过点(,则f x fx (),)()32741-的解析式是.13.942--=a ax y 是偶函数,且在),0(+∞是减函数,则整数a 的值是 .14.幂函数),*,,,()1(互质n m N k n m x y mn k∈=-图象在一、二象限,不过原点,则n m k ,,的奇偶性为 .三、解答题:解答应写出文字说明.证明过程或演算步骤(共76分) . 15.(12分)比较下列各组中两个值大小(1)060720880896116115353..(.)(.).与;()与--16.(12分)已知幂函数f x xm Z x y y m m ()()=∈--223的图象与轴,轴都无交点,且关于1α3α4α2α轴对称,试确定f x ()的解析式.17.(12分)求证:函数3x y =在R 上为奇函数且为增函数.18.(12分)下面六个幂函数的图象如图所示,试建立函数与图象之间的对应关系..6543212132323123---======x y x y x y x y x y x y );();()(;);();()((A ) (B ) (C ) (D ) (E ) (F )19.(14分)由于对某种商品开始收税,使其定价比原定价上涨x 成(即上涨率为10x),涨价后,商品卖出个数减少bx 成,税率是新定价的a 成,这里a,b 均为正常数,且a <10,设售货款扣除税款后,剩余y元,要使y最大,求x的值. 20.(14分)利用幂函数图象,画出下列函数的图象(写清步骤).(1)yx xx xy x=++++=---22532221221()().参考答案(8)一、CCBAD DCADA 二、11.(,)0+∞; 12.)0()(34≥=x x x f ; 13.5; 14.k m ,为奇数,n 是偶数;三、15. 解:(1)+∞<<<+∞=7.06.00),0(116上是增函数且在函数x y1161167.06.0<∴ (2)函数),0(35+∞=在x y 上增函数且89.088.00<<.)89.0()88.0(,89.088.089.088.0353535353535-<-∴->-∴<∴即16. 解:由.3,1,13203222⎪⎩⎪⎨⎧∈-=--≤--Z m m m m m m 得是偶数.)(1,)(3140-===-=x x f m x x f m 时解析式为时解析式为和17.解: 显然)()()(33x f x x x f -=-=-=-,奇函数;令21x x <,则))(()()(22212121323121x x x x x x x x x f x f ++-=-=-,其中,显然021<-x x ,222121x x x x ++=2222143)21(x x x ++,由于0)21(221≥+x x ,04322≥x ,且不能同时为0,否则021==x x ,故043)21(22221>++x x x .从而0)()(21<-x f x f . 所以该函数为增函数. 18.解:六个幂函数的定义域,奇偶性,单调性如下:(1)323x x y ==定义域[0,+∞),既不是奇函数也不是偶函数,在[0,+∞)是增函数;.),0(16),0(15),0(14),0[3),0[22133223232331上减函数函数,在既不是奇函数也不是偶定义域为)(是减函数;是奇函数,在定义域)(是减函数;是偶函数,在定义域)(是增函数;,是偶函数,在定义域为)(是增函数;,是奇函数,在定义域为)(+∞==+∞==+∞==+∞==+∞==+--+--+-R xx y UR R x x y UR R x x y R x x y R x x y通过上面分析,可以得出(1)↔(A ),(2)↔(F ),(3)↔(E ),(4)↔(C ),(5)↔(D ),(6)↔(B ).19.解:设原定价A 元,卖出B 个,则现在定价为A (1+10x ),现在卖出个数为B (1-10bx),现在售货金额为A (1+10x ) B(1-10bx )=AB(1+10x )(1-10bx ),应交税款为AB(1+10x )(1-10bx)·10a, 剩余款为y = AB(1+10x)(1-10bx ))101(a -= AB )1101100)(101(2+-+--x b x b a , 所以bb x )1(5-=时y 最大 要使y 最大,x 的值为bb x )1(5-=.20.解:(1)1)1(1112112222222++=+++=++++=x x x x x x x y 把函数21,x y =的图象向左平移1个单位, 再向上平移1个单位可以得到函数122222++++=x x x x y 的图象.(2)1)2(35--=-x y 的图象可以由35-=xy 图象向右平移2个单位,再向下平移1个单位而得到.图象略。
高一数学苏教必修同步练习: 幂函数 含答案

3.3 幂函数1、已知函数()()1221a f x a a x-=--为幂函数,则实数α的值为( )A.-1或2B.-2或1C.-1D.1 2、设3412a ⎛⎫=⎪⎝⎭,3415b ⎛⎫= ⎪⎝⎭,1212c ⎛⎫= ⎪⎝⎭,则( ) A. a b c << B. c a b << C. b c a << D. b a c <<3、下列函数中,在(),0-∞上是增函数的是( ) A. 3y x = B. 2y x = C. 1y x=D. 32y x =4、幂函数()22231m m y m m x --=--,当()0,x ∈+∞时为减函数,则实数m 的值是( )A. 2m =B. 1m =-C. 1m =-或2D. m ≠5、下列函数中,是幂函数的是( ) A. 1y = B. 32y x = C. y=D. 2xy =6、幂函数()y f x =的图像经过点()3,3,则()f x ( ) A.是偶函数且在()0,+∞上是增函数 B.是偶函数且在()0,+∞上是减函数 C.是奇函数且在()0,+∞上是减函数D.既不是奇函数,也不是偶函数,且在()0,+∞上是减函数7、已知幂函数()y f x =的图像过点12,22⎛⎫⎪ ⎪⎝⎭,则()2log 2f 的值为( )A. 12 B. 12-C. 2D. 2-8、如图,曲线是幂函数ny x =在第一象限的图像,已知n 取12,2±±四个值,则相应于曲线1234,,,C C C C 的n 值依次为( )A. 112,,,222--B. 112,,,222--C. 11,2,2,22-- D. 112,,2,22--9、幂函数()23f x x =的大致图像为( )A.B.C.D.10、对于幂函数()45f x x=,若120x x <<,则()()1212,22f x f x x x f ++⎛⎫ ⎪⎝⎭的大小关系是( ) A. ()()121222f x f x x x f ++⎛⎫>⎪⎝⎭ B. ()()121222f x f x x x f ++⎛⎫<⎪⎝⎭C. ()()121222f x f x x x f ++⎛⎫=⎪⎝⎭D.无法确定 11、已知幂函数()223mm f x x -++=()Z m ∈为偶函数,且在区间()0,+∞上是增函数,则函数()f x 的解析式为_______12、设11,,1,32α⎧⎫∈-⎨⎬⎩⎭,则使()f x x α=为奇函数且在()0,+∞上单调递减的α的值是__________.13、关于x 的函数()1ay x =- (其中a 的取值可以是11,2,3,1,2-)的图象恒过定点__________.14、已知幂函数的图象经过点(2,则这个函数的解析式为__________. 15、已知幂函数()3m f x x -=()N m *∈的图像关于y 轴对称,且在()0,+∞上是减函数,求满足13233m m f a f a ⎛⎫⎛⎫+-<-- ⎪ ⎪⎝⎭⎝⎭的实数a 的取值范围答案以及解析1答案及解析: 答案:C解析:因为()()1221a f x a a x-=--为幂函数,所以211a a --=,即2a =或1-.又20a -≠,所以1a =-.2答案及解析: 答案:D解析:构造幂函数()()340,y xx =∈+∞,由该函数在定义域内单调递增,知a b >;构造指数函数12xy ⎛⎫= ⎪⎝⎭,由该函数在定义域内单调递减,所以a c <,故c a b >>.3答案及解析: 答案:A 解析:4答案及解析: 答案:A 解析:5答案及解析: 答案:C 解析:6答案及解析: 答案:D解析:由题意设(),nf x x =因为函数()f x 的图像经过点(,3n=解得12n =, 即()f x 既不是奇函数,也不是偶函数,且在()0,+∞上是增函数,故先D7答案及解析: 答案:A解析:设幂函数为()af x x =,由题意,得11=222aa ⎛⎫⇒= ⎪⎝⎭所以()12221log 2log 2=2f =,故选A8答案及解析: 答案:B 解析:函数112222,,,y x y x y x y x --====中,令4x =得到的函数值依次为11,16,,2162,函数值由大到小对应的解析式为112222,,,y x y x y x y x --====因此相应于曲线1234,,,C C C C 的n 值依次为112,,,222--,故选B9答案及解析: 答案:B解析:由于()00f =所以排除C,D 选项,而()()()2233=f x x x f x -=-===,且()f x 的定义域为R,所以()f x 是偶函数,图像关于y 轴对称,故选B.10答案及解析: 答案:A解析:幂函数()45f x x =在()0,+∞上是增函数,大致图像如图所示,设()()12,0,,0A x C x ,其中120x x <<,则AC 的中点E 的坐标为()()121212,0,,,22x x x x AB f x CD f x EF f ++⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭∵()12EF AB CD >+∴()()121222f x f x x x f ++⎛⎫> ⎪⎝⎭故选A11答案及解析: 答案:()4f x x =解析:因为幂函数()223mm f x x -++=()m Z ∈为偶函数,所以223mm -++为偶数.又()f x 在区间()0,+∞上是增函数,所以223m m -++,0∆>, 所以13m -<<,又Z m ∈,223m m -++为偶数, 所以1m =,故所求解析式为()4f x x =12答案及解析: 答案:-1解析:因为()f x x α=为奇函数,所以1,1,3α=-.又因为()f x 在()0,+∞上为减函数,所以1α=-.13答案及解析: 答案:()2,1 解析:14答案及解析: 答案:12y x = 解析:15答案及解析:答案:因为函数()f x 在()0,+∞上单调递减 所以30m -<解得3m < 因为N m *∈,所以1m =或2又函数()f x 的图像关于y 对称,所以3m -是偶数 而231-=-为奇数, 132-=-为偶数,所以1m =故()()2,f x x f x -=在(),0-∞上为增函数,在()0,+∞上为减函数所以1113233f a f a ⎛⎫⎛⎫+-<-- ⎪ ⎪⎝⎭⎝⎭等价于28233a a +>-且 8203a -≠,解得21033a <<且43a ≠ 故实数a 的取值范围为21033a a ⎧<<⎨⎩且43a ⎫≠⎬⎭解析:。
苏教版必修1高中数学幂函数 同步练习

幂函数 同步练习重难点:掌握常见幂函数的概念、图象和性质,能利用幂函数的单调性比较两个幂值的大小.考纲要求:①了解幂函数的概念;②结合函数12321,,,,y x y x y x y y x x=====的图像,了解他们的变化情况.经典例题:比较下列各组数的大小:(1)1.531,1.731,1; (2)(-2)32-,(-107)32,1.134-;(3)3.832-,3.952,(-1.8)53; (4)31.4,51.5.当堂练习:1.函数y =(x 2-2x)21-的定义域是( )A .{x |x ≠0或x ≠2}B .(-∞,0)(2,+∞)C .(-∞,0)[2,+∞ )D .(0,2)3.函数y =52x 的单调递减区间为( )A .(-∞,1)B .(-∞,0)C .[0,+∞ ∞,+∞)3.如图,曲线c 1, c 2分别是函数y =x m 和y =x n 那么一定有( )A .n<m<0B .m<n<0C .m>n>0 4.下列命题中正确的是( )A .当0α=时,函数y x α=的图象是一条直线B .幂函数的图象都经过(0,0),(1,1)两点C .幂函数的y x α= 图象不可能在第四象限内D .若幂函数y x α=为奇函数,则在定义域内是增函数5.下列命题正确的是( )A .幂函数中不存在既不是奇函数又不是偶函数的函数B .图象不经过(—1,1)为点的幂函数一定不是偶函数C .如果两个幂函数的图象具有三个公共点,那么这两个幂函数相同D .如果一个幂函数有反函数,那么一定是奇函数6.用“<”或”>”连结下列各式:0.60.32 0.50.32 0.50.34, 0.40.8- 0.40.6-.7.函数y =221m mx--在第二象限内单调递增,则m 的最大负整数是_______ _.8.幂函数的图象过点(2,14), 则它的单调递增区间是 .9.设x ∈(0, 1),幂函数y =a x 的图象在y =x 的上方,则a 的取值范围是 .10.函数y =34x -在区间上 是减函数.11.试比较530.75380.16,1.5,6.25的大小.12.讨论函数y =x 54的定义域、值域、奇偶性、单调性。
(苏教版)高一数学必修一配套练习:2.4.2幂函数(2)

苏教版高中数学必修一第二章学生同步练习第课时指数函数、对数函数、幂函数

让学生学会学习第29课 指数函数、对数函数、幂函数分层训练:1、设f(log 2x)=2x (x>0),则f(3)的值是( ) A.128 B.256 C.512 D.82、若0<b<1,且log a b<1,则( ) A.0<a<b B.0<b<a C.0<b<a<1 D.0<a<b 或a>13、某工厂去年总产值为a ,计划今后5年内每年比前一年增长10%,则这5年的最后一年该厂的总产值是( ) A.1.14a B.1.15a C.1.16a D.(1+1.15)a此数据满足的规律,其中最接近的一个( ) A.v=log 2tB.v=t 21logC.v=212-tD.v=2t -25、已知函数y=log a (3-ax)在[0,1]上是减函数,则a 报值范围是( ) A.(0,1) B.(1,3) C.(0,3) D.[3,+∞)6、下列结论正确的是( ) A.y=x-3的定义域为RB.y=31x 的定义域为{x|x ∈R ,且x ≠0} C.y=21x 的定义域为(0,+∞)D.y=21-x的定义域为(0,+∞)7、函数f(x)=*)(112N m x m m ∈++的奇偶性为_____________.8、已知f(x)=(m 2+m)122--m m x,当m 取什么值时,(1)f(x)为正比例函数;(2)f(x)为反比例函数;拓展延伸:9、已知f(x)=|lgx|,若当0<a<b<c 时,f(a)>f(c)>f(b),试证:0<ac<1。
幂函数-高中数学必修第一册同步练习

启迪思维 点拨方法 开发潜能 直线提分3.3幂函数同步练习一、单选题1.若函数21()(22)m f x m m x -=--是幂函数,且()y f x =在(0,)+∞上单调递增,则f (2)(=) A .14B .12C .2D .42.若幂函数223()(265)m f x m m x -=-+没有零点,则()f x 的图象关于( )对称 A .原点B .x 轴C .y 轴D .没有3.设232()3a =,231()3b =,131()3c =,则a ,b ,c 的大小关系是( )A .a b c >>B .a c b >>C .c a b >>D .b c a >>4.幂函数的图象经过点1(,2)2,若01a b <<<,则下列各式正确的是( )A .11()()()()f a f b f f b a <<<B .11()()()()f f f b f a a b <<<C .11()()()()f a f b f f a b<<<D .11()()()()f f a f f b a b<<<5.幂函数223()mm y x m Z --=∈的图象如图所示,则m 的值为( )A .13m -<<B .0C .1D .26.已知函数()1(0,1)x f x a a a =+>≠的图象经过定点P ,且点P 在幂函数()h x 的图象上,则()h x 的表达式为( ) A .2()h x x =B .1()h x x -=C .2()h x x -=D .3()h x x =7.有四个幂函数:①2()f x x -=;②1()f x x -=; ③3()f x x =;④13()f x x =.某同学研究了其中的一个函数,他给出这个函数的三个性质:(1)偶函数;(2)值域是{|y y R ∈,且0}y ≠;(3)在(,0)-∞上是增函数.如果他给出的三个性质中,有两个正确,一个错误,则他研究的函数是( ) A .④B .③C .②D .①8.已知幂函数2242()(1)m m f x m x -+=-在(0,)+∞上单调递增,函数()2x g x t =-,对于任意1[1x ∈,5)时,总存在2[1x ∈,5)使得12()()f x g x =,则t 的取值范围是( )A .∅B .7t 或1tC .7t >或1t <D .17t二、多选题9.设11,,1,32α⎧⎫∈-⎨⎬⎩⎭,则使函数y x α=的定义域是R ,且为奇函数的α值可以是( )A .1-B .12C .1D .310.已知幂函数()y x R αα=∈的图象过点(2,8),下列说法正确的是( )A .函数y x α=的图象过原点B .函数y x α=是偶函数C .函数y x α=是单调减函数D .函数y x α=的值域为R11.下列关于幂函数y x α=的性质,描述正确的有( ) A .当1α=-时函数在其定义域上是减函数B .当0α=时函数图象是一条直线C .当2α=时函数是偶函数D .当3α=时函数有一个零点0 12.下列幂函数中满足条件121212()()()(0)22x x f x f x f x x ++<<<的函数是( )A .()f x x =B .2()f x x =C .()f x =D .1()f x x=三、填空题13.已知幂函数()y f x =的图象经过(8,2),则1()8f = .14.已知幂函数221(55)m y m m x +=--在(0,)+∞上为增函数,则实数m = .15.已知幂函数12()f x x =,若(1)(102)f a f a +<-,则a 的取值范围是16. 若1133(1)(32)a a --+<-,则a 的取值范围 .四、解答题17.已知幂函数21()*()()mm f x x m N -+=∈,经过点,试确定m 的值,并求满足条件(2)(1)f a f a ->-的实数a 的取值范围.18.已知m 是整数,幂函数22()m m f x x -++=在[0,)+∞上是单调递增函数.(1)求幂函数()f x 的解析式;(2)作出函数()|()1|g x f x =-的大致图象;(3)写出()g x 的单调区间,并用定义法证明()g x 在区间[1,)+∞上的单调性.19.已知幂函数221()(1)m f x m m x --=--在(0,)+∞上单调递增,又函数()22x xm g x =+. (1)求实数m 的值,并说明函数()g x 的单调性;(2)若不等式(13)(1)0g t g t -++恒成立,求实数t 的取值范围. 20.已知幂函数221()(1)m f x m m x --=--在(0,)+∞上单调递增. (1)求实数m 的值;(2)若(1)(32)m m k k +<-,求实数k 的取值范围.3.3幂函数同步练习答案1.解:因为函数21()(22)m f x m m x -=--是幂函数, 所以2221m m --=,解得1m =-或3m =.又因为()y f x =在(0,)+∞上单调递增,所以10m -,所以3m =,2()f x x =,从而f (2)224==, 故选:D .2.解:幂函数223()(265)m f x m m x -=-+中, 令22651m m -+=,化简得2320m m -+=,解得1m =或2m =;当1m =时,1()f x x -=没有零点,且()f x 的图象关于原点对称; 当2m =时,()f x x =有零点,不满足题意. 故选:A .3.解:由于函数23y x = 是R 上的增函数,2133>,223321()()33∴>,即a b >.由于函数1()3x 是R 上的减函数,2133>,213311()()33∴<,即b c <,又232()3a ==c =a c ∴>,固有a c b >>, 故选:B .4.解:设幂函数解析式为:y x α= (α为常数), 幂函数的图象经过点1(,2)2,∴1()22α=,解得1α=-,∴幂函数解析式为:11y x x-==, ∴幂函数1y x=在(0,)+∞上单调递减, 01a b <<<,1101a b b a∴<<<<<, 又幂函数1y x=在(0,)+∞上单调递减, f ∴(a )f >(b )11()()f f b a>>,故选:B .5.解:根据幂函数的图象可知函数在第一象限内单调递减,且为偶函数. 则2230m m --<, 即13m -<<, m Z ∈,0m ∴=,或1m =,或2m =.若0m =,则331y x x -==为奇函数,不满足条件. 若1m =,则441y x x -==为偶函数,满足条件. 若2m =.则331y x x -==为奇函数,不满足条件. 1m ∴=.故选:C .6.解:函数()1x f x a =+中,令0x ,解得x此时11y f ==+=所以函数()f x 的图象过定点P .设幂函数()y h x x α==.则α=3α=,所以3()h x x =. 故选:D .7.解:对于①,2()f x x -=,是定义域(-∞,0)(0⋃,)+∞上的偶函数,值域是{|0}y y >,且在(,0)-∞上是单调增函数,满足条件;对于②,1()f x x -=,是定义域(-∞,0)(0⋃,)+∞上的奇函数,值域是{|y y R ∈,且0}y ≠,且在(,0)-∞上是单调减函数,不满足条件;对于③,3()f x x =,是定义域R 上的奇函数,值域是R ,且在(,0)-∞上是单调增函数,不满足条件;对于④,13()f x x =,是定义域R 上的奇函数,值域是R ,且在(,0)-∞上是单调增函数,不满足条件. 故选:D .8.解:幂函数2242()(1)mm f x m x -+=-在(0,)+∞上单调递增,∴22(1)1420m m m ⎧-=⎨-+>⎩,解得0m =,2()f x x ∴=,当1[1x ∈,5)时,1()[1f x ∈,25),设集合[1A =,25),又当2[1x ∈,5)时,2()[2g x t ∈-,32)t -,设集合[2B t =-,32)t -, 由题意得:A B ⊆,∴213225t t -⎧⎨-⎩,解得:17t ,故选:D .9.解:对于A ,1α=-时,1y x -=,定义域为(-∞,0)(0⋃,)+∞,不满足题意; 对于B ,12α=时,12y x =,定义域为[0,)+∞,不满足题意;对于C ,1α=时,y x =,定义域为R ,且为奇函数,满足题意;对于D ,3α=时,3y x =,定义域为R ,且为奇函数,满足题意. 故选:CD .10.解:幂函数y x α=的图象过点(2,8), 所以28α=,解得3α=, 所以幂函数为3y x =;所以所以幂函数3y x =的图象过原点,A 正确;且幂函数3y x =是定义域R 上的奇函数,B 错误;幂函数3y x =是定义域R 上的增函数,C 错误;幂函数3y x =的值域是R ,所以D 正确. 故选:AD .11.解:对于A ,1α=-时幂函数1y x -=在(,0)-∞和(0,)+∞是减函数,在其定义域上不是减函数,A 错误;对于B ,0α=时幂函数01(0)y x x ==≠,其图象是一条直线,去掉点(0,1),B 错误;对于C ,2α=时幂函数2y x =在定义域R 上是偶函数,C 正确;对于D ,3α=时幂函数3y x =在R 上的奇函数,且是增函数,有唯一零点是0,D 正确. 故选:CD .12.解:由题意知,当0x >时,()f x 的图象是凹形曲线; 对于A ,函数()f x x =的图象是一条直线,则当210x x >>时,有1212()()()22x x f x f x f ++=,不满足题意;对于B ,函数2()f x x =的图象是凹形曲线,则当210x x >>时,有1212()()()22x x f x f x f ++<,满足题意;对于C ,函数()f x =则当210x x >>时,有1212()()()22x x f x f x f ++>,不满足题意;对于D ,在第一象限内,函数1()f x x=的图象是一条凹形曲线,则当210x x >>时,有1212()()()22x x f x f x f ++<,满足题意. 故选:BD .13.解:设幂函数()(f x x αα=为常数),幂函数()y f x =的图象经过(8,2),82α∴=,解得13α=, ∴幂函数13()f x x =,13111()()882f ∴==,故答案为:12.14.解:由221(55)m y m m x +=--是幂函数,得2551m m --=, 化简得2560m m --=, 解得6m =或1m =-;当6m =时,13y x =,是(0,)+∞上的增函数,满足题意;当1m =-时,1y x -=,不是(0,)+∞上的增函数,舍去. 综上知,实数6m =. 故答案为:6.15.解:幂函数12()f x x =,其定义域为[0,)+∞,且在定义域上是单调增函数; 所以不等式(1)(102)f a f a +<-,等价于1010201102a a a a +⎧⎪-⎨⎪+<-⎩,解得13a -<,所以a 的取值范围是[1-,3). 故答案为:[1-,3).16.解:幂函数13y x -=有两个单调区间,∴根据1a +和32a -的正、负情况,有以下关系10320132a a a a +>⎧⎪->⎨⎪+>-⎩①或10320132a a a a+<⎧⎪-<⎨⎪+>-⎩②或10320a a +<⎧⎨->⎩③; 解三个不等式组:①得2332a <<,②无解,③得1a <-; a ∴的取值范围是(-∞,21)(3-⋃,3)217.解:幂函数()f x经过点,∴21()2mm -+,即211()222mm -+=22m m ∴+=.解得1m =或2m =-.又*m N ∈,1m ∴=.12()f x x ∴=,则函数的定义域为[0,)+∞,并且在定义域上为增函数. 由(2)(1)f a f a ->-得201021a a a a -⎧⎪-⎨⎪->-⎩解得312a <.a ∴的取值范围为[1,3)2. 18.解:(1)由()f x 在[0,)+∞上单调递增可得:220m m -++>,12m ∴-<<, 又m Z ∈,0m ∴=或1m =,2()f x x ∴=;(2)由于2()f x x =,所以2()|1|g x x =-.如图所示:(3)根据函数的图象:函数的单调减区间为:[-∞,1]-和[0,1]. 函数的单调增区间为[1-,0]和[1,)+∞.证明:设121x x <,所以221210,10x x -->.所以212121()()()()0g x g x x x x x -=-+>.所以函数在区间[1,)+∞上为增函数.19.解:(1)因为()f x 是幂函数,所以211m m --=,解得1m =-或2m =,又因为()f x 在(0,)+∞上单调递增,所以210m -->,即12m <-,即1m =-,则1()22x x g x =-, 因为2x y =与12xy =-均在R 上单调递增, 所以函数()g x 在R 上单调递增.(2)因为11()2(2)()22x x x x g x g x ---=-=--=-, 所以()g x 是奇函数,所以不等式(13)(1)0g t g t -++可变为(13)(1)(1)g t g t g t --+=--,由(1)知()g x 在R 上单调递增,所以131t t ---,解得1t .故实数t 的取值范围是(-∞,1]. 20.解:(1)因为()f x 是幂函数,所以211m m --=,解得1m =-,或2m =, 又因为()f x 在(0,)+∞上单调递增.所以210m -->,即12m <-, 所以1m =-.(2)由于1y x=在区间(,0)-∞,(0,)∞上都是减函数,且11(1)(32)k k --+<-. 分三种情况讨论:①当1032k k +<<-,即1k <-时,原不等式成立;②当10k +<,且320k -<时,有132k k +>-,即13223k k k ⎧⎪<-⎪⎪>⎨⎪⎪>⎪⎩,解集为空集. ③当10k +>,且320k ->时,有132k k +>-,解得2332k <<.综上所述:k 的取值范围是(-∞,20)(3⋃,3)2.。
苏教版高中数学必修一幂函数同步练习(5)

幂函数[基础训练A 组]一、选择题1 若)1(,,)1(,1,4,)21(,2522>==-=+====a a y x y x y x y x y y x y xx上述函数是幂函数的个数是( )A 0个B 1个C 2个D 3个2 已知)(x f 唯一的零点在区间(1,3)、(1,4)、(1,5)内,那么下面命题错误的( ) A 函数)(x f 在(1,2)或[)2,3内有零点 B 函数)(x f 在(3,5)内无零点 C 函数)(x f 在(2,5)内有零点 D 函数)(x f 在(2,4)内不一定有零点3 若0,0,1a b ab >>>,12log ln 2a =,则log a b 与a 21log 的关系是( )A 12log log a b a < B 12log log a b a =C 12log log a b a > D 12log log a b a ≤4 求函数132)(3+-=x x x f 零点的个数为 ( ) A 1 B 2 C 3 D 45 已知函数)(x f y =有反函数,则方程0)(=x f ( ) A 有且仅有一个根 B 至多有一个根 C 至少有一个根 D 以上结论都不对6 如果二次函数)3(2+++=m mx x y 有两个不同的零点,则m 的取值范围是( ) A ()6,2- B []6,2- C {}6,2- D ()(),26,-∞-+∞U7 某林场计划第一年造林10000亩,以后每年比前一年多造林20%,则第四年造林( ) A 14400亩 B 172800亩 C 17280亩 D 20736亩二、填空题1 若函数()x f 既是幂函数又是反比例函数,则这个函数是()x f =2 幂函数()f x 的图象过点(,则()f x 的解析式是_____________ 3 用“二分法”求方程0523=--x x 在区间[2,3]内的实根,取区间中点为5.20=x ,那么下一个有根的区间是 4 函数()ln 2f x x x =-+的零点个数为5 设函数)(x f y =的图象在[],a b 上连续,若满足 ,方程0)(=x f在[],a b 上有实根三、解答题1 用定义证明:函数1()f x x x=+在[)1,x ∈+∞上是增函数2 设1x 与2x 分别是实系数方程20ax bx c ++=和20ax bx c -++=的一个根,且1212,0,0x x x x ≠≠≠ ,求证:方程202a x bx c ++=有仅有一根介于1x 和2x 之间3 函数2()21f x x ax a =-++-在区间[]0,1上有最大值2,求实数a 的值4 某商品进货单价为40元,若销售价为50元,可卖出50个,如果销售单价每涨1元, 销售量就减少1个,为了获得最大利润,则此商品的最佳售价应为多少?参考答案一、选择题1 C 2,y x y x ==是幂函数2 C 唯一的零点必须在区间(1,3),而不在[)3,53 A 12log ln 20,01,1a a b =><<>得,12log 0,log 0a b a <>4 C 332()2312212(1)(1)f x x x x x x x x x =-+=--+=---2(1)(221)x x x =-+-,22210x x +-=显然有两个实数根,共三个;5 B 可以有一个实数根,例如1y x =-,也可以没有实数根,例如2xy =6 D 24(3)0,6m m m ∆=-+>>或2m <-7 C 310000(10.2)17280+=二、填空题 11x设(),f x x α=则1α=- 2()f x = (),f x x α=图象过点(,34333,4αα===3 [2,2.5) 令33()25,(2)10,(2.5) 2.5100f x x x f f =--=-<=-> 4 2 分别作出()ln ,()2f x x g x x ==-的图象; 5 ()()0f a f b ≤ 见课本的定理内容 三、解答题1 证明:设1212121211,()()()(1)0x x f x f x x x x x ≤<-=--< 即12()()f x f x <,∴函数1()f x x x=+在[)1,x ∈+∞上是增函数2 解:令2(),2a f x x bx c =++由题意可知2211220,0ax bx c ax bx c ++=-++= 221122,,bx c ax bx c ax +=-+=2222111111(),222a a af x x bx c x ax x =++=-=-22222222223(),222a a a f x x bx c x ax x =++=+=因为120,0,0a x x ≠≠≠∴12()()0f x f x <,即方程202a x bx c ++=有仅有一根介于1x 和2x 之间3 解:对称轴x a =,当[]0,0,1a <是()f x 的递减区间,max ()(0)121f x f a a ==-=⇒=-; 当[]1,0,1a >是()f x 的递增区间,max ()(1)22f x f a a ===⇒=;当01a ≤≤时2max 1()()12,2f x f a a a a ==-+==与01a ≤≤矛盾; 所以1a =-或24 解:设最佳售价为(50)x +元,最大利润为y 元, (50)(50)(50)40y x x x =+---⨯ 240500x x =-++当20x =时,y 取得最大值,所以应定价为70元。
苏教版高中数学必修一幂函数同步练习(1)

幂函数复习重难点:掌握常见幂函数的概念、图象和性质,能利用幂函数的单调性比较两个幂值的大小. 考纲要求:①了解幂函数的概念;②结合函数12321,,,,y x y x y x y y x x=====的图像,了解他们的变化情况.知识梳理:1. 幂函数的基本形式是y x α=,其中x 是自变量,α是常数.要求掌握y x =,2y x =,3y x =,1/2y x =,1y x -=这五个常 用幂函数的图象.2. 观察出幂函数的共性,总结如下:(1)当0α>时,图象过定点 ;在(0,)+∞上 是 函数.(2)当0α<时,图象过定点 ;在(0,)+∞上 是 函数;在第一象限内,图象向上及向右都与坐标轴无限趋近.3. 幂函数y x α=的图象,在第一象限内,直线1x =的右侧,图象由下至上,指数 . y 轴和直线1x =之间,图象由上至下,指数α . 诊断练习:1. 如果幂函数()f x x α=的图象经过点2(2,)2,则(4)f 的值等于 2.函数y =(x 2-2x )21-的定义域是3.函数y =52x 的单调递减区间为 4.函数y =221m mx --在第二象限内单调递增,则m 的最大负整数是_______ _.范例分析:例1比较下列各组数的大小:(1)1.531,1.731,1; (2)(-22)32-,(-107)32,1.134-;(3)3.832-,3.952,(-1.8)53; (4)31.4,51.5.例2已知幂函数6()m y x m Z -=∈与2()m y x m Z -=∈的图象都与x 、y 轴都没有公共点,且 2()m y x m Z -=∈的图象关于y 轴对称,求m 的值.例3幂函数273235()(1)t tf x t t x+-=-+是偶函数,且在(0,)+∞上为增函数,求函数解析式.反馈练习:1.幂函数()y f x=的图象过点1(4,)2,则(8)f的值为 .2.比较下列各组数的大小:32(2)a+32a;223(5)a-+235-;0.50.40.40.5.3.幂函数的图象过点(2,14), 则它的单调递增区间是.4.设x∈(0, 1),幂函数y=a x的图象在y=x的上方,则a的取值范围是.5.函数y=34x-在区间上是减函数.6.一个幂函数y=f(x)的图象过点(3, 427),另一个幂函数y=g(x)的图象过点(-8, -2),(1)求这两个幂函数的解析式;(2)判断这两个函数的奇偶性;(3)作出这两个函数的图象,观察得f (x)< g(x)的解集.巩固练习1.用“<”或”>”连结下列各式:0.60.320.50.320.50.34,0.40.8-0.40.6-.2.函数1322(1)(4)y x x --=-+-的定义域是3.942--=a a x y 是偶函数,且在),0(+∞是减函数,则整数a 的值是 . 4.已知3532x x >,x 的取值范围为5.若幂函数ay x =的图象在0<x<1时位于直线y=x 的下方,则实数a 的取值范围是6.若幂函数()f x 与函数g(x)的图像关于直线y=x 对称,且函数g(x)的图象经过,则()f x 的表达式为7. 函数2()3x f x x +=+的对称中心是 ,在区间 是 函数(填“增、减”)8.比较下列各组中两个值的大小33221.3 1.30.30.35533(1)1.5 1.6(2)0.60.7(3)3.5 5.3(4)0.18.15----与与与与09.若3131)23()2(---<+a a ,求a 的取值范围。
高中数学 3.3幂函数配套训练 苏教版必修1
高中数学 3.3幂函数配套训练 苏教版必修1一、基础过关1.下列结论错误的个数为________.①幂函数图象一定过原点;②当α<0时,幂函数y =x α是减函数;③当α>1时,幂函数y =x α是增函数;④函数y =x 2既是二次函数,也是幂函数.2.在函数y =1x 2,y =2x 2,y =x 2+x ,y =1中,幂函数的个数为________.3.函数y =x 12-1的图象关于x 轴对称的图象大致是______.(填图象编号)4.下列表示y =x 23的图象的是________.(填图象编号)5.给出以下结论:①当α=0时,函数y =x α的图象是一条直线;②幂函数的图象都经过(0,0),(1,1)两点;③若幂函数y =x α的图象关于原点对称,则y =x α在定义域内y 随x 的增大而增大;④幂函数的图象不可能在第四象限,但可能在第二象限.则正确结论的个数为________.6.函数y =x 12+x -1的定义域是________. 7.已知函数f (x )=(m 2+2m )·xm 2+m -1,m 为何值时,函数f (x )是:(1)正比例函数;(2)反比例函数;(3)二次函数;(4)幂函数.8.已知幂函数f (x )=xm 2-m -3为奇函数,且在区间(0,+∞)上是减函数(m ∈N *,且m ≥2).(1)求f (x );(2)比较f (-2 008)与f (-2)的大小.二、能力提升9.设a =5253⎪⎭⎫ ⎝⎛,b =5352⎪⎭⎫ ⎝⎛,c =5252⎪⎭⎫ ⎝⎛,则a ,b ,c 的大小关系为________. 10.函数f (x )=x α,x ∈(-1,0)∪(0,1),若不等式f (x )>|x |成立,则在α∈{-2,-1,0,1,2}的条件下,α可以取值的个数是________. 11.已知幂函数f (x )的图象过点(2,2),幂函数g (x )的图象过点⎝ ⎛⎭⎪⎫2,14. (1)求f (x ),g (x )的解析式;(2)当x 为何值时,①f (x )>g (x );②f (x )=g (x );③f (x )<g (x ).三、探究与拓展12.已知幂函数f (x )=xm 2-2m -3(m ∈N *)的图象关于y 轴对称,且在(0,+∞)上是减函数,求满足(a +1)-m 3<(3-2a )-m 3的a 的取值范围.答案1.32.13.②4.②5.16.(0,+∞)7.解 (1)若f (x )为正比例函数,则⎩⎪⎨⎪⎧ m 2+m -1=1,m 2+2m ≠0⇒m =1.(2)若f (x )为反比例函数,则⎩⎪⎨⎪⎧ m 2+m -1=-1,m 2+2m ≠0⇒m =-1.(3)若f (x )为二次函数,则⎩⎪⎨⎪⎧ m 2+m -1=2,m 2+2m ≠0⇒m =-1±132.(4)若f (x )为幂函数,则m 2+2m =1,∴m =-1± 2.8.解 (1)因为幂函数f (x )=xm 2-m -3为奇函数,且m ∈N *,所以m 2-m -3为奇数.因为f (x )在区间(0,+∞)上是减函数,所以m 2-m -3<0,又m ∈N *,且m ≥2,当m =2时,m 2-m -3=4-2-3=-1,当m =3时,m 2-m -3=3>0,即m >3时,m 2-m -3>0.所以f (x )=x -1.(2)由(1)知f (x )=1x -,所以f (-2 008)=()12008--=-12 008,f (-2)=()12--=-12.因为-12 008>-12, 所以f (-2 008)>f (-2).9.a >c >b10.211.解 (1)设f (x )=x α,∵其图象过点(2,2),故2=(2)α,解得α=2,∴f (x )=x 2.设g (x )=x β,∵其图象过点⎝ ⎛⎭⎪⎫2,14,∴14=2β, 解得β=-2,∴g (x )=x -2.(2)在同一坐标系下作出f (x )=x 2与g (x )=x -2的图象,如图所示.由图象可知:f (x ),g (x )的图象均过点(-1,1)与(1,1).∴①当x >1或x <-1时,f (x )>g (x );②当x =1或x =-1时,f (x )=g (x );③当-1<x <1且x ≠0时,f (x )<g (x ).12.解 ∵函数在(0,+∞)上递减,∴m 2-2m -3<0,解得-1<m <3.∵m ∈N *,∴m =1,2.又函数的图象关于y 轴对称,∴m 2-2m -3是偶数,而22-2×2-3=-3为奇数,12-2×1-3=-4为偶数,∴m =1.而f (x )=x -13在(-∞,0),(0,+∞)上均为减函数, ∴(a +1)-13<(3-2a )-13等价于a +1>3-2a >0或0>a +1>3-2a 或a +1<0<3-2a . 解得a <-1或23<a <32. 故a 的取值范围为⎩⎨⎧⎭⎬⎫a |a <-1或23<a <32.。
高中数学幂函数同步练习 苏教版 必修1

高中数学幂函数同步练习 苏教版 必修1一.选择题1.函数y =x 32图象的大致形状是( )。
(A ) (B ) (C ) (D ) 2.若a ∈(-1, 0),则下列不等式成立的是( )。
(A )(0.2)a<2-a (B )(0.2)a>2-a (C )2-a>2a (D )2a>2-a3.如图,曲线c 1, c 2分别是函数y =x m 和y =x n 在第一象限的图象,那么一定有( )。
(A )n<m<0 (B )m<n<0 (C )m>n>0 (D )n>m>0 4、下列命题中正确的是( )A 、当α=0时,函数αx y =的图象是一条直线 B 、幂函数的图象都经过(0,0),(1,1)两点 C 、幂函数的αx y = 图象不可能在第四象限内 D 、若幂函数αx y =为奇函数,则αx y =是定义域内的增函数5、下列命题正确的是( )(A ) 幂函数中不存在既不是奇函数又不是偶函数的函数 (B )图象不经过(—1,1)为点的幂函数一定不是偶函数 (C )如果两个幂函数的图象具有三个公共点,那么这两个幂函数相同 (D )如果一个幂函数有反函数,那么一定是奇函数 二.填空题6.用“<”或”>”连结下列各式:6.032.0 5.034.0,528.0-526.0-7.已知函数3)(x x f =,则它的反函数)(1x f -= . 8.幂函数的图象过点(2,41), 则它的单调递增区间是 9.设x ∈(0, 1),幂函数y =xa 的图象在y =x 的上方,则a 的取值范围是10.函数y =43-x在区间上 是减函数。
三.解答题11.在下列的各幂函数与各图象之间建立能符合实际情况的一一映射 (1)y =x (2)y =x -2 (3)y =x (4)y =x -1 (5)y =xy x 0c1c2x yoxy oxy oxyo(6)y =x (7)y =x (8)y =x- (9)y =x①②③④⑤⑥⑦⑧⑨12.试比较8375.03525.6,5.1,16.0的大小。
高中数学 2.4幂函数课时作业 苏教版必修1

高中数学 2.4幂函数课时作业苏教版必修1课时目标1.通过具体问题,了解幂函数的概念.2.从描点作图入手,画出y=x,y=x2,y=x3,y=12x,y=x-1的图象,总结出幂函数的共性,巩固并会加以应用.1.一般地,把形如________的函数叫做幂函数,其中x是自变量,α是常数.2.在同一平面直角坐标系中,画出幂函数y=x,y=x2,y=x3,y=12x,y=x-1的图象.3.结合2中图象,填空.(1)所有的幂函数图象都过点__________,在(0,+∞)上都有定义.(2)若α>0时,幂函数图象过点________________,且在第一象限内______;当0<α<1时,图象上凸,当α>1时,图象______.(3)若α<0,则幂函数图象过点________,并且在第一象限内单调______,在第一象限内,当x从+∞趋向于原点时,函数在y轴右方无限地逼近于y轴,当x趋于+∞时,图象在x轴上方无限逼近x轴.(4)当α为奇数时,幂函数图象关于______对称;当α为偶数时,幂函数图象关于______对称.(5)幂函数在第____象限无图象.一、填空题1.下列函数是幂函数的是________.(填序号)①y =x ;②y =x 3;③y =2x ;④y =x -1.2.幂函数f (x )的图象过点(4,12),那么f (8)的值为________.3.下列是y =23x 的图象的是________.(填序号)4.图中曲线是幂函数y =x n在第一象限的图象,已知n 取±2,±12四个值,则相应于曲线C 1,C 2,C 3,C 4的n 依次为________. 5.设a =2535⎛⎫ ⎪⎝⎭,b =3525⎛⎫⎪⎝⎭,c =2525⎛⎫⎪⎝⎭,则a ,b ,c 的大小关系是________. 6.函数f (x )=x α,x ∈(-1,0)∪(0,1),若不等式f (x )>|x |成立,则在α∈{-2,-1,0,1,2}的条件下,α可以取值的个数是________. 7.给出以下结论:①当α=0时,函数y =x α的图象是一条直线; ②幂函数的图象都经过(0,0),(1,1)两点;③若幂函数y =x α的图象关于原点对称,则y =x α在定义域内y 随x 的增大而增大; ④幂函数的图象不可能在第四象限,但可能在第二象限. 则正确结论的序号为________.8.函数y =12x +x -1的定义域是________.9.已知函数y =x -2m -3的图象过原点,则实数m 的取值范围是____________________. 二、解答题10.比较121.1、121.4、131.1的大小,并说明理由.11.如图,幂函数y=x3m-7(m∈N)的图象关于y轴对称,且与x轴、y轴均无交点,求此函数的解析式.能力提升12.已知函数f (x )=(m 2+2m )·21m m x +-,m 为何值时,函数f (x )是:(1)正比例函数; (2)反比例函数;(3)二次函数;(4)幂函数.13.点(2,2)在幂函数f (x )的图象上,点(-2,14)在幂函数g (x )的图象上,问当x为何值时,有:(1)f (x )>g (x );(2)f (x )=g (x );(3)f (x )<g (x ).§2.4幂函数知识梳理。
高中数学《幂函数》同步练习2 湘教版必修1

幂函数诊断练习:1. 如果幂函数()f x x α=的图象经过点,则(4)f 的值等于 2.函数y =(x 2-2x )21-的定义域是3.函数y =52x 的单调递减区间为 4.函数y =221m mx --在第二象限内单调递增,则m 的最大负整数是_______ _.范例分析:例1比较下列各组数的大小:(1)1.531,1.731,1; (2)(-2)32-,(-107)32,1.134-;(3)3.832-,3.952,(-1.8)53; (4)31.4,51.5.例2已知幂函数6()m y x m Z -=∈与2()m y x m Z -=∈的图象都与x 、y 轴都没有公共点,且 2()m y x m Z -=∈的图象关于y 轴对称,求m 的值.例3幂函数273235()(1)t t f x t t x+-=-+是偶函数,且在(0,)+∞上为增函数,求函数解析式.反馈练习:1.幂函数()y f x =的图象过点1(4,)2,则(8)f 的值为 .2.比较下列各组数的大小: 32(2)a + 32a ; 223(5)a -+ 235-; 0.50.4 0.40.5.3.幂函数的图象过点(2,14), 则它的单调递增区间是 .4.设x ∈(0, 1),幂函数y =ax 的图象在y =x 的上方,则a 的取值范围是 .5.函数y =34x -在区间上 是减函数.6.一个幂函数y =f (x )的图象过点(3, 427),另一个幂函数y =g (x )的图象过点(-8, -2),(1)求这两个幂函数的解析式; (2)判断这两个函数的奇偶性; (3)作出这两个函数的图象,观察得f (x )< g (x )的解集.巩固练习1.用“<”或”>”连结下列各式:0.60.32 0.50.32 0.50.34, 0.40.8- 0.40.6-. 2.函数1322(1)(4)y x x --=-+-的定义域是3.942--=a a x y 是偶函数,且在),0(+∞是减函数,则整数a 的值是 . 4.已知3532x x >,x 的取值范围为5.若幂函数ay x =的图象在0<x<1时位于直线y=x 的下方,则实数a 的取值范围是6.若幂函数()f x 与函数g(x)的图像关于直线y=x 对称,且函数g(x)的图象经过,则()f x 的表达式为 7. 函数2()3x f x x +=+的对称中心是 ,在区间 是 函数(填“增、减”)8.比较下列各组中两个值的大小33221.3 1.30.30.35533(1)1.5 1.6(2)0.60.7(3)3.5 5.3(4)0.18.15----与与与与09.若3131)23()2(---<+a a ,求a 的取值范围。
苏教版数学高一苏教版必修1同步训练3.3幂函数
2.4 幂函数1.下列四图中是函数y =x 12的图象的序号是__________.2.若幂函数y =f(x)的图象经过点(9,13),则f(25)的值是__________.3.在下列函数y =1x 2,y =2x 2,y =x 2+x ,y =x +1,y =1中,是幂函数的个数为__________.4.幂函数f(x)的图象过点(4,12),若f(a)=2,则a =__________.5.幂函数f(x)的图象过点(3,427),则f(x)的解析式为__________.6.设a ∈{-1,1,12,3},则使函数y =x a 的定义域为R 且为奇函数的所有a 值为__________.7.在下列函数中,定义域和值域相同的函数的个数为__________.①y =x 2 ②y =x 12 ③y =x 13 ④y =x 53⑤y =x 238.图中曲线是幂函数y =x n 在第一象限的图象,已知n 取±2,±12四个值,则相应于曲线C 1,C 2,C 3,C 4的n 依次为__________.9.设a =0.20.3,b =0.30.3,c =0.30.2,则a 、b 、c 的大小关系是__________. 10.下列四个命题:①y =x-4是偶函数,在(0,+∞)上是单调减函数;②y =x 32是奇函数,在(0,+∞)上是单调增函数;③y =x -12是偶函数,在(0,+∞)上是单调减函数;④y=x -45是偶函数,在(0,+∞)上是单调减函数.其中正确的序号是__________.11.比较下列各题中两个值的大小:(1)1.535,1.735;(2)2.2-23,1.8-23.12.已知幂函数y =f(x)过点(2,22),试求出此函数的解析式,并作出图象,判断奇偶性、单调性.13.已知偶函数f(x)=xm 2-2m -3(m ∈Z )在(0,+∞)上单调递减. (1)求函数f(x)的解析式;(2)若f(2a +1)=f(a),求实数a 的值.14.下列命题正确的个数是__________. ①当α=0时,函数y =x α的图象是一条直线 ②幂函数的图象都经过(0,0)、(1,1)两点③若幂函数y =x α的图象关于原点对称,则y =x α在定义域内y 随x 的增大而增大 ④幂函数的图象不可能在第四象限⑤图象不经过点(-1,1)的幂函数一定不是偶函数15.幂函数的图象过点(2,14),则它的单调增区间是__________.16.设α∈{-2,-1,0,1,2},则使函数y =x α的定义域为R 且为偶函数的α的值为__________.17.已知幂函数f(x)=x 2,g(x)=x 3,则使f(x)>g(x)成立的x 的取值范围是__________.18.已知幂函数f(x)=(2n 2-n)x n +1,若在其定义域上为单调增函数,则n =__________.19.已知函数f(x)=x n 的图象经过点(3,13),则f(x)在区间[14,4]上的最小值为__________.20.若函数f(x)=⎩⎪⎨⎪⎧x -12,x>0,-2,x =0,(x +3)13,x<0,则f(f(f(0)))=__________.21.设α∈{-2,-1,-12,13,12,1,2,3},则使f(x)=x α为奇函数且在(0,+∞)上是单调增函数的α的值的个数是__________.22.两个数(45)12和(910)13的大小关系是__________.23.已知函数f(x)=x α+m 的图象经过点(1,3),又其反函数图象经过点(10,2),则f(x)的解析式为__________.24.(易错题)若(a +1)-13<(3-2a)-13,试求a 的取值范围.25.试探讨下列问题:(1)在幂函数y =x α中,如果α是正偶数,如α=2,4,6,…,这一类函数具有哪些重要性质?(2)在幂函数y =x α中,如果α是正奇数,如α=1,3,5,…,这一类函数具有哪些重要性质?26.已知点(2,2)在幂函数f(x)的图象上,点(-2,14)在幂函数g(x)的图象上,问当x为何值时,(1)f(x)>g(x);(2)f(x)=g(x);(3)f(x)<g(x)?答案与解析基础巩固1.(3) 函数y =x 12的定义域为[0,+∞),且过点(0,0),(1,1),∴不是(2)(4);∵12<1,∴当x>1时函数增得慢,不是(1).∴(3)正确. 2.15 设f(x)=x α,由f(9)=13,即9α=13,32α=3-1, ∴α=-12.∴f(x)=x -12.∴f(25)=25-12=15.3.1 y =1x2=x -2为幂函数.4.14 设f(x)=x α,则f(4)=4α=12,解得α=-12,∴f(x)=x -12. ∴f(a)=a -12=2,得a =14.5.x 34 设f(x)=x α,则427=3α.又427=334,∴α=34.6.1、3 当a =-1或12时,所得幂函数定义域不是R ;当a =1和a =3时,满足题中条件.7.3 ①⑤中函数定义域为R ,值域为[0,+∞),②中函数的定义域与值域都是[0,+∞),③④中两函数的定义域与值域都是R ,∴②③④符合.8.2,12,-12,-2 由题图,知C 1、C 2表示的幂函数在(0,+∞)上都是单调增函数,对应的n 值为正;C 3、C 4表示的幂函数在(0,+∞)上都是单调减函数,相应的n 值为负,又当x =4时,x 2=16,x 12=2,x -12=12,x -2=116,∴相应于C 1,C 2,C 3,C 4的n 依次为2,12,-12,-2.9.a<b<c ∵幂函数y =x 0.3在(0,+∞)上为单调增函数,且0.2<0.3,∴0.20.3<0.30.3,即a<b.又指数函数y =0.3x 为单调减函数,且0.3>0.2, ∴0.30.3<0.30.2,即b<c. ∴a<b<c.10.①④ ①∵y =x -4是偶函数且在第一象限是单调减函数,∴①正确;∵y =x 32=x 3定义域为[0,+∞),不是奇函数,∴②错;∵y =x -12=1x,定义域为(0,+∞),∴不是偶函数,③错; ∵y =x -45是偶函数且在第一象限为单调减函数,∴④正确.11.解:(1)1.535,1.735是幂函数y =x 35的两个函数值,考察函数y =x 35在(0,+∞)上是单调增函数,∵1.5<1.7,∴1.535<1.735.(2)∵函数y =x -23在第一象限内是单调减函数,且2.2>1.8,∴2.2-23<1.8-23.12.解:设幂函数为y =x α,又过点(2,22),得22=2α,∴α=-12.∴函数解析式为y =x -12,定义域为(0,+∞).∴f(x)是非奇非偶函数,且f(x)在(0,+∞)上为减函数,图象为13.解:(1)由m 2-2m -3<0,得-1<m<3. 又m ∈Z ,∴m =0或1或2.而m 2-2m -3为偶数,∴m =1时,m 2-2m -3=-4.∴f(x)=x -4.(2)|2a +1|=|a|,2a +1=a 或2a +1=-a ,∴a =-1或a =-13.能力提升14.2 当α=0时,函数y =x α的定义域为{x|x ≠0,x ∈R },其图象为一条断直线,∴①不正确;当α<0时,函数y =x α的图象不过(0,0)点,∴②不正确;幂函数y =x -1的图象关于原点对称,但其在定义域内不是单调增函数,∴③不正确;幂函数的图象都不在第四象限,故④正确;∵当α∈R 时,幂函数y =x α一定过(1,1)点,∴若幂函数为偶函数,由对称性知它一定过(-1,1)点,∴不过(-1,1)点的幂函数一定不是偶函数,即⑤正确.15.(-∞,0) 设f(x)=x α,由图象过点(2,14),知2α=14,∴α=-2.∴f(x)=x -2,其单调增区间为(-∞,0). 16.217.(-∞,0)∪(0,1) f(x)>g(x),即x 2>x 3, ∴x 2-x 3=x 2(1-x)>0. ∴x 2(x -1)<0. ∴x<1且x ≠0.∴x 的取值范围是(-∞,0)∪(0,1)(也可画出图象观察易得答案).18.-12 由题意2n 2-n =1,解得n =-12或n =1.当n =-12时,f(x)=x ,符合题意;当n =1时,f(x)=x 2在定义域R 上不单调,舍去. ∴n =-12.19.14 ∵f(x)的图象过点(3,13), ∴3n =13.∴n =-1.∴f(x)=x-1在区间[14,4]上为减函数.∴f(x)min =f(4)=4-1=14.20.1 由已知得f(0)=-2,-2<0,∴f(-2)=(-2+3)13=1.1>0.∴f(1)=1-12=1.∴f(f(f(0)))=f(f(-2))=f(1)=1.21.3 y =x 13,y =x ,y =x 3均适合题意.22.(45)12<(910)13 ∵45<910,12>0,∴根据幂函数的单调性,有(45)12<(910)12.又0<910<1,12>13,∴根据指数函数的单调性,有(910)12<(910)13.综上可知,(45)12<(910)13.23.f(x)=x 3+2 由互为反函数的两函数图象之间的关系知,反函数图象过点(10,2), 则(2,10)必在原函数图象上. ∴2α+m =10.① 又f(x)经过点(1,3), ∴1α+m =3.②由②得m =2,代入①,得α=3. ∴f(x)的解析式为f(x)=x 3+2.24.解:由题意,若a +1与3-2a 在同一单调区间内,则有(1)a +1与3-2a 都在(-∞,0)内,且y =x -13在其定义域内是单调减函数,∴有⎩⎪⎨⎪⎧a +1>3-2a ,a +1<0,3-2a<0,解得a ∈;(2)a +1与3-2a 都在(0,+∞)内,且y =x -13为单调减函数,原不等式成立,则必有⎩⎪⎨⎪⎧a +1>3-2a ,a +1>0,3-2a>0,解得23<a<32.若a +1与3-2a 不在同一单调区间内,要使原不等式成立,则有⎩⎪⎨⎪⎧a +1<0,3-2a>0,解得a<-1.综上,可知a 的取值范围是(-∞,-1)∪(23,32).点评:本题主要考查幂函数y =x -13.因为它在(-∞,0)和(0,+∞)上都是单调减函数,且其图象在第三和第一象限内,所以应对a +1与3-2a 所在的单调区间相同与不同分别进行讨论;注重分类讨论思想的应用.借助于函数的图象,将问题考虑全面,谨防考虑不周导致漏解或错解.25.解:(1)具备α>0时幂函数的性质,同时又具备图象关于y 轴对称(即偶函数)这一重要性质.(2)具备α>0时幂函数的性质,同时又具备图象关于原点对称(即为奇函数)这一重要性质.拓展探究26.解:设f(x)=x α,由题意,得2=(2)αα=2, ∴f(x)=x 2.同理可求:g(x)=x -2,在同一坐标系内作出y =f(x)与y =g(x)的图象,如图.由图象可知:(1)当x>1或x<-1时,f(x)>g(x); (2)当x =±1时,f(x)=g(x);(3)当-1<x<0或0<x<1时,f(x)<g(x).。
苏教版高中数学必修一第二章学生同步练习第课时幂函数

第28课 幂函数(2)分层训练1.函数25y x =的单调减区间为 ( ) A .(,1)-∞B .(,0)-∞C .[0,)+∞D .(,)-∞+∞ 2.幂函数34y x =,13y x =,43y x-=的定义域分别为M 、N 、P ,则 ( )()A M N P ⊂⊂≠≠ ()B N M P ⊂⊂≠≠ ()C M P N ⊂⊂≠≠ ()D ,,A B C 都不对3.设121.1a -=,120.9b -=,12c x -=,且a cb <<,则对于整数c 的值,下列判断正确的是 ( ) ()A 1c > ()B 1c < ()C 1c =()D c 与1的大小关系不能确定4.221333123111(),(),()252T T T ===,则下列关系式正确的是 ( )A .123T T T <<B .312T T T <<C .231T T T <<D .213T T T <<5.函数()ay x a R =∈的图象,当01x <<时,在直线y x =的上方;当1x >时,在直线y x =的下方,则a 的取值范围是 ; 6.用“<”、“>”或“=”号填空: (1)若54aa -<-,则a ______0; (2)若0.390.38bb<,则b ______0; (3)若11()()23nn->-(n Z ∈),则当n 为偶数时,n 0; 当n 为奇数时,n 0. 7.比较下列各题中两个值的大小:(1)25( 1.5)-与25( 1.7)-;(2)233.14-与23π-(3)13(5)--与13(6)--; (4)143与2128.若1133(1)(32)a a --+<-,求a 的取值范围.拓展延伸9.已知幂函数f (x )=23221++-p p x (p ∈Z )在(0,+∞)上是增函数,且在其定义域内是偶函数,求p 的值,并写出相应的函数f (x ).10.m为怎样的值时,函数32204()(42)(1)f x mx x m x mx -=++++-+的定义域是R ?本节学习疑点:。
高一数学幂函数同步练习题
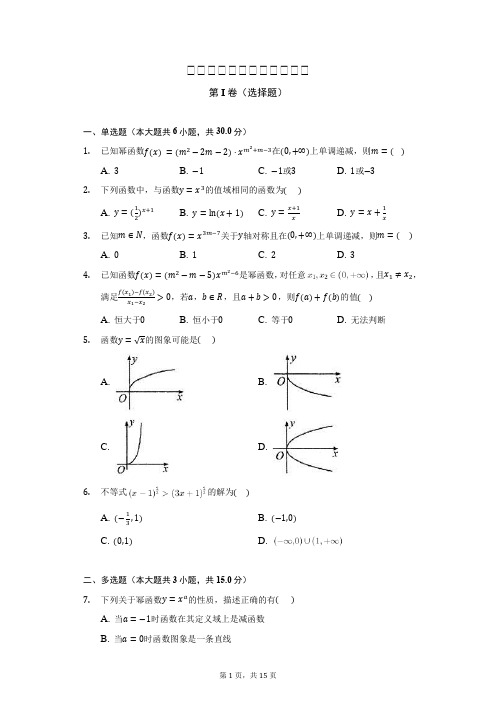
高高高高高高高高高高高高第I 卷(选择题)一、单选题(本大题共6小题,共30.0分) 1. 已知幂函数f(x) =(m 2−2m −2)·x m2+m−3在(0,+∞)上单调递减,则m =( )A. 3B. −1C. −1或3D. 1或−32. 下列函数中,与函数y =x 3的值域相同的函数为( )A. y =(12)x+1B. y =ln(x +1)C. y =x+1xD. y =x +1x3. 已知m ∈N ,函数f(x)=x 3m−7关于y 轴对称且在(0,+∞)上单调递减,则m =( )A. 0B. 1C. 2D. 34. 已知函数f(x)=(m 2−m −5)x m2−6是幂函数,对任意,且x 1≠x 2,满足f(x 1)−f(x 2)x 1−x 2>0,若a ,b ∈R ,且a +b >0,则f(a)+f(b)的值( )A. 恒大于0B. 恒小于0C. 等于0D. 无法判断5. 函数y =√x 的图象可能是( )A.B.C.D.6. 不等式的解为( )A. (−13,1) B. (−1,0) C. (0,1)D.二、多选题(本大题共3小题,共15.0分)7. 下列关于幂函数y =x a 的性质,描述正确的有( )A. 当a =−1时函数在其定义域上是减函数B. 当a =0时函数图象是一条直线C. 当a =2时函数是偶函数D. 当a =3时函数有一个零点08. 若a >b >0,0<c <1,则( )A. log c a <log c bB. c a >c bC. a c >b cD. log c (a +b )>09. 下列式子不正确的是( )A. 1.52.5>1.53.4 B. 1.70.3<0.92.3C. (15)23<(12)23D. 0.80.5<0.90.4第II 卷(非选择题)三、单空题(本大题共5小题,共25.0分)10. 已知幂函数y =f(x)的图象过点(2,2√2),则f(9)= . 11. 已知幂函数f(x)=(m 2−3m +1)x m2−4m+1的图象不过原点,则实数m 的值为 .12. 已知幂函数f(x)过定点(8,12),且满足f(a 2+1)+f(−5)>0,则a 的范围为 . 13. 若幂函数f (x )=(m 2−5m +7)x m 在R 上为增函数,则log m √27+2lg5+lg4+m log m 12= .14. 已知幂函数f(x)=x 2m+1过点(3,27),若f(k 2+3)+f(9−8k)<0,则实数k 的取值范围是 .四、解答题(本大题共5小题,共60.0分) 15. 已知幂函数f(x)=(m 2−2m +2)x 1−3m(1)求函数f(x)的解析式; (2)判断f(x)的奇偶性16. 若点(√2,2)在幂函数f(x)的图像上,点(2,12)在幂函数g(x)的图像上.(1)求f(x)和g(x)的解析式;(2)定义ℎ(x)={f(x),f(x)⩽g(x)g(x),f(x)>g(x),求函数ℎ(x)的最大值和单调区间.17. 已知幂函数f(x)=(−2m 2+m +2)x m+1为偶函数.(1)求函数f(x)的解析式;(2)若函数y =f(x)−2(a −1)x +1在区间(2,3)上为单调函数,求实数a 的取值范围.18. 已知幂函数f(x)=x −3m+5(m ∈N)为偶函数,且在区间(0,+∞)上单调递增.(Ⅰ)求函数f(x)的解析式;(Ⅱ)设函数g(x)=f(x)+2λx −1,若g(x)<0对任意x ∈[1,2]恒成立,求实数λ的取值范围.19.已知幂函数y=f(x)的图象过点(2,√2).2(1)求此函数的解析式;(2)证明:函数f(x)在(0,+∞)上是单调递减函数;(3)判断函数f(x)的奇偶性,并加以证明.答案和解析1.【答案】B【解析】 【分析】本题考查了幂函数的定义与性质的应用问题,是中档题.根据幂函数的定义与性质,列方程求出m 的值,再判断m 是否满足条件. 【解答】解:幂函数y =(m 2−2m −2)x m 2+m−3在(0,+∞)单调递减,∴m 2−2m −2=1, 解得m =3或m =−1; 又m 2+m −3<0,即 ∴m =−1时满足条件, 则实数m 的值为−1. 故选:B .2.【答案】B【解析】 【分析】本题考查函数的值域,属基础题.首先求出y =x 3的值域,根据条件逐项判断即可, 【解答】解:函数y =x 3的值域为R ,而y =(12)x+1>0;y =x+1x=1+1x ≠1;y =x +1x ∈(−∞,−2]∪[2,+∞).只有y=ln(x+1)∈R.故选B.3.【答案】B【解析】【分析】本题考查幂函数的性质,突出考查函数的奇偶性与单调性.依题意,函数f(x)=x3m−7为偶函数,f(x)在(0,+∞)上单调递减,可知3m−7<0且为偶数,结合m∈N,可求得m的值.【解答】解:∵函数f(x)=x3m−7关于y轴对称且在(0,+∞)上单调递减,∴3m−7<0且为偶数,∴m<7,又m∈N,3∴m=0,1或2,又3m−7为偶数,∴m=1.故选:B.4.【答案】A【解析】【分析】本题考查函数的性质,单调性,幂函数的定义,属于拔高题.由题意,判断出函数的单调性及奇偶性,再根据幂函数的性质求解.【解答】>0,得函数单调递增.解:对任意x1,x2∈(0,+∞),且x1≠x2,满足f(x1)−f(x2)x1−x2函数f(x)=(m2−m−5)x m2−6是幂函数,则m2−m−5=1⇒m=3或m=−2.又函数单调递增,故m=3,f(x)=x3,所以f(−x)=−x3=−f(x),a,b∈R,且a+b>0,a>−b,所以f(a)>f(−b)=−f(b)⇒f(a)+f(b)>0.故选:A.5.【答案】A【解析】【分析】本题考查了函数图象的应用,考查了幂函数图象,属于容易题.由函数的定义域和值域排除BD,由特殊值排除C,可得结果.【解答】解:已知函数y=√x=x12,函数的定义域为[0,+∞),值域为[0,+∞),故排除B,D;当x=4时,y=2,故排除C;故选A.6.【答案】B【解析】【分析】本题考查了幂函数的性质,利用幂函数的单调性和奇偶性解不等式.由幂函数f(x)=x23在(0,+∞)上单调递增且为R上的偶函数,可得|x−1|>|3x+1|,从而解得.【解答】解:∵幂函数f(x)=x23在(0,+∞)上单调递增且为R上的偶函数,又∵f(x−1)>f(3x+1),∴|x−1|>|3x+1|整理得x2+x<0,解得−1<x<0,即原不等式的解集为(−1,0).故选B.7.【答案】CD【解析】【分析】本题考查了幂函数的图象与性质的应用问题,属于基础题。
2019—2020年苏教版高中数学必修一3.3幂函数课堂同步练习题.docx

(新课标)2018-2019学年度苏教版高中数学必修一幂函数1.设1{1,1,,3}2a∈-,则使函数y=xα的定义域为R且为奇函数的所有α值为________.2.在下列函数中,定义域和值域相同的函数的个数为______________.①y=x2②12y x=③13y x=④53y x=⑤23y x=3.图中曲线是幂函数y=x n在第一象限的图象,已知n取±2,12±四个值,则对应于曲线C1,C2,C3,C4的n依次为________.4.已知幂函数f(x)=(2n2-n)x n+1,若在其定义域上为单调增函数,则f(x)在区间1[,4]4上的最小值为________.5.已知函数f(x)=xα+m的图象经过点(1,3),又其反函数图象经过点(10,2),则f(f(1))=________.6.(2010安徽高考,文7改编)设253()5a=,352()5a=,252()5a=,则a,b,c的大小关系是________.7.已知幂函数y=f(x)过点2(2,)2,试求出此函数的解析式,并作出图象,判断奇偶性、单调性.8.已知幂函数y =(m 2+2m -2)x m +2在(0,+∞)上是单调增函数,求满足33(1)(32)mm a a --+<-的实数a 的取值范围.参考答案1.1,3 解析:当α=-1或12时,所得幂函数定义域不是R;当α=1或α=3时满足题中条件.2.3 解析:①⑤中函数定义域为R,值域为[0,+∞),②中函数的定义域与值域都是[0,+∞),③④中两函数的定义域与值域都是R,∴②③④符合.3.2,12,12-,-2 解析:由题图,知C1、C2表示的幂函数在(0,+∞)上都是单调增函数,对应n值为正;C3、C4表示的幂函数在(0,+∞)上都是单调减函数,对应的n值为负,又当x=4时,x2=16,122x=,1212x-=,2116x-=,∴对应于C1,C2,C3,C4的n依次为2,12,12-,-2.4.12解析:∵f(x)为幂函数,∴2n2-n=1,解得12n=-或n=1,当12n=-时,()f x x=符合题意;当n=1时,f(x)=x2在定义域上不具有单调性,舍去,∴12n=-,()f x x=.f(x)在[0,+∞)上是单调增函数,∴在1[,4]4上也为单调增函数.∴()min111442f x f⎛⎫===⎪⎝⎭5.29 解析:由互为反函数的两个函数图象之间的关系知,反函数过点(10,2),则(2,10)必在原函数f(x)的图象上,∴2α+m=10,①又f(x)过点(1,3),∴1α+m=3,②由②得m=2,代入①得α=3,∴f(x)=x3+2.∴f(1)=3,f(f(1))=f(3)=33+2=29.6.a>c>b 解析:构造幂函数25y x=,∵该函数在(0,+∞)上是单调增函数.∴22553255⎛⎫⎛⎫>⎪ ⎪⎝⎭⎝⎭,即a>c;构造指数函数25xy⎛⎫= ⎪⎝⎭,∵该函数在R上是单调减函数,∴22552255⎛⎫⎛⎫>⎪ ⎪⎝⎭⎝⎭,即b<c,∴a>c>b.7.解:设幂函数为y =x α,又过点22,2⎛⎫ ⎪ ⎪⎝⎭,得222α=,∴12α=-.∴函数解析式为12y x -=,定义域为(0,+∞).∴f(x)是非奇非偶函数,且f(x)在(0,+∞)上为单调减函数,图象为8.解:由幂函数的定义知,m 2+2m -2=1,即m 2+2m -3=0.解得m =1或m =-3,当m =1时,y =x 3在(0,+∞)上单调增函数.符合题意,当m =-3时,y =x -1在(0,+∞)上是单调减函数,不合题意(舍).∴m =1. ∵13y x -=在(-∞,0)和(0,+∞)上为单调减函数.∴由()()1133132a a --+<-,可得a +1>3-2a >0,或3-2a <a +1<0,或a +1<0<3-2a , ∴a <-1或2332a <<. ∴a 的取值范围是()23,1,32⎛⎫-∞- ⎪⎝⎭.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
幂函数(2)
分层训练
1.函数25y x =的单调减区间为 ( )
A .(,1)-∞
B .(,0)-∞
C .[0,)+∞
D .(,)-∞+∞
2.幂函数3
4y x =,13y x =,4
3y x -=的定义域分别为M 、N 、P ,则 ( )
()A M N P ⊂⊂≠≠ ()B N M P ⊂⊂≠≠
()C M P N ⊂⊂≠≠ ()D ,,A B C 都不对
3.设121.1a -=,120.9b -=,12
c x -=,且a c b <<,则对于整数c 的值,下列判断正确的是 ( )
()A 1c > ()B 1c < ()C 1c = ()D c 与1的大小关系不能确定
4.221
333123111(),(),()252
T T T ===,则下列关系式正确的是 ( ) A .123T T T << B .312T T T <<
C .231T T T <<
D .213T T T <<
5.函数()a y x a R =∈的图象,当01x <<时,在直线y x =的上方;当1x >时,在直线y x =的下方,则a 的取值范围是 ;
6.用“<”、“>”或“=”号填空:
(1)若54a a -<-,则a ______0;
(2)若0.390.38b b <,则b ______0;
(3)若1
1
()()23n n
->-(n Z ∈),则当n 为偶数时,n 0; 当n 为奇数时,n 0.
7.比较下列各题中两个值的大小:
(1)25( 1.5)-与25( 1.7)-;(2)233.14
-与23π- (3)13(5)
--与13(6)--; (4)143与212
8.若1
133
(1)(32)a a --+<-,求a 的取值范围.
拓展延伸
9.已知幂函数f (x )=23221++-p p x (p ∈Z )在(0,+∞)上是增函数,且在其定义域内是偶函数,求p 的值,并写出相应的函数f (x ).
10.m 为怎样的值时,函数32204()(42)
(1)f x mx x m x mx -=++++-+的定义域是R ?。
