海伦公式

合集下载

海伦公式坐标求三角形面积

海伦公式坐标求三角形面积
海伦公式是求三角形面积的一种常用方法。

其公式为：S=√
[p(p-a)(p-b)(p-c)]，其中S表示三角形的面积，a、b、c分别表示三角形的三边长度，p表示半周长，即p=(a+b+c)/2。

要使用海伦公式求三角形面积，需要先确定三角形的三个顶点的坐标。

假设三个顶点的坐标分别为A(x1,y1)、B(x2,y2)、C(x3,y3)，则可以按照以下步骤进行计算：
1. 计算三边长度a、b、c。

可以使用勾股定理或距离公式求出。

2. 计算半周长p=(a+b+c)/2。

3. 根据海伦公式，计算三角形面积S=√[p(p-a)(p-b)(p-c)]。

4. 输出结果。

使用海伦公式求三角形面积时，需要注意的是，三个顶点的坐标必须按照同一方向排列，否则会得到负面积。

此外，如果三条边的长度无法构成一个三角形，计算结果将为0。

- 1 -。

海伦公式的应用

海伦公式的应用海伦公式是解决三角形面积的一种常用方法，可以用于计算任意形状的三角形的面积。

该公式由古希腊数学家海伦提出，被广泛应用于数学、物理、工程等领域。

本文将介绍海伦公式的具体应用及其在实际问题中的重要性。

海伦公式的表达式如下：s = (a + b + c) / 2其中，s为三角形三边长a、b、c的半周长。

利用海伦公式，可以计算任意三角形的面积，表达式如下：面积= √(s × (s-a) × (s-b) × (s-c))这个公式可以非常方便地应用于各种三角形问题。

下面将介绍一些实际问题中海伦公式的应用。

1. 计算三角形的面积最直接的应用就是计算三角形的面积。

通过已知的三边长，可以先计算出半周长s，然后利用海伦公式求得面积。

这在建筑设计、地理测量等领域特别常见。

例如，在一块地块的测量中，需要知道一块不规则地块的面积，可以通过分割成多个三角形，分别计算每个三角形的面积，然后相加，最终得到整个地块的面积。

2. 判断三角形的形状海伦公式还可以用于判断三角形的形状。

根据公式，如果一个三角形的面积为0，则表示该三角形是一条直线，也就是三点共线。

如果面积为正数，则表示该三角形是一个普通的三角形。

如果面积为负数，则表示该三角形是一个内部有缺口的三角形。

利用这一特点，可以通过海伦公式来判断三个点是否共线、是否构成一个三角形。

3. 设计图片处理算法在计算机图形学中，海伦公式经常被用于设计图片处理算法。

例如，计算机生成的三角形构成的立体模型，可以通过海伦公式来计算其表面积，从而进行贴图、光照等处理操作。

海伦公式的高效性和灵活性使得它成为计算机图形学中的重要工具。

4. 优化传感器网络布局在无线传感器网络中，传感器的部署位置对网络的性能具有重要影响。

利用海伦公式，可以计算传感器之间的距离，进而确定最优的传感器布局，以最大限度地覆盖目标区域，并减少能量消耗。

这在动态目标跟踪、环境监测等应用中非常实用。

海伦公式求内切圆半径

海伦公式求内切圆半径
海伦公式是一种通过三角形的三边长度来求解其面积的公式，其
具体公式如下：
$$S = \sqrt{p(p-a)(p-b)(p-c)}$$
其中，$a,b,c$ 为三角形的三边长度，$p$ 为三角形的半周长，
即 $p = \dfrac{a+b+c}{2}$。

对于一个内切圆来说，其半径可以通过三角形的三边长度来求解。

首先我们需要知道以下性质：
内切圆的半径 $r$ 等于三角形面积 $S$ 与半周长 $p$ 的比值，
即 $r = \dfrac{S}{p}$。

因此，我们可以将海伦公式中求得的三角形面积代入，得到内切
圆半径 $r$ 的公式如下：
$$r = \dfrac{\sqrt{p(p-a)(p-b)(p-c)}}{p} =
\dfrac{\sqrt{(p-a)(p-b)(p-c)}}{p}$$
其中，$a,b,c$ 是三角形的三边长度，$p$ 是半周长，$r$ 是内
切圆半径。

需要注意的是，该公式只适用于三角形存在内切圆的情况，即三
条边能够完全包围内切圆。

如果三角形不存在内切圆，则此公式无法
求解。

海伦公式

出为三角形和多边形的面积计算提供了新的方法和思路，在知道三角形三边的长而不知道高的情况下使用海伦公式可以更快更简便的求出面积，比如说在测量土地的面积的时候，不用测三角形的高，只需测两点间的距离，就可以方便地导出答案。
海伦公式
• 海伦公式： [1] S=√p(p-a)(p-b)(p-c) • 假设在平面内，有一个三角形，边长分别为a、b、c，三角形的面积S可由以下公式求得： • S=√p(p-a)(p-b)(p-c)
证明过程
公式简史
• 古希腊的数学发 • 阿基米德 • 展到亚历山大里亚时期，数学的应用得到了很大的发展，其突出的一点就是三角术的发展，在解三角形的过程中，其中一个比较难的问题是如何利用三角形的三边直接求出三角形面积。 • 这个公式是由古希腊数学家阿基米德得出的，但人们常常以古希腊的数学家海伦命名这个公式，称此公式为海伦公式，因为这个公式最早出现在海里的著作《测地术》中，并在海伦的著作《测量仪器》和《度量数》中给出证明。 [1] [5] • 中国宋代的数学家秦九韶在1247年独立提出了“三斜求积术”，虽然它与海伦公式形式上有所不同，但它完全与海伦公式等价，它填补了中国数学史中的一个空白，从中可以看出中国古代已经具有很高的数学水平。

三角形海伦面积公式证明

三角形海伦面积公式证明海伦公式是用来计算任意三角形面积的公式，它得名于古希腊数学家海伦（Heron）。

公式的完整表达式为：海伦公式：设三角形的三边长度分别为a、b、c，则其面积S可通过以下公式计算：S = √[s(s-a)(s-b)(s-c)]其中，s是半周长，定义为s=(a+b+c)/2。

为了证明这个公式，我们可以运用三角形面积公式和勾股定理。

下面是证明的过程：证明：设三角形的三边长度分别为a、b、c，将其对应的顶点标记为A、B、C。

首先，我们假设三角形是一个锐角三角形（对于直角和钝角三角形的证明过程类似）。

根据三角形面积公式，可以用三角形的底边和高表示面积。

我们可以假设底边是边a，那么将底边上的点记为P，垂直于底边的高记为h。

因此，三角形的面积可以表示为：S = （1/2）*a*h。

根据勾股定理，我们可以得到以下关系：b² = (a-h)² + c²c² = (a-h)² + b²将上面两个式子联立，并合并整理得到：b² + c² = 2a² - 2ah + h² ➡️ 2ah = 2a² - b² - c² + h²然后，我们将右边的式子代入到面积公式中：S = (1/2) * a * h= (1/4) * a * (2a² - b² - c² + h²)= (1/4) * (2a³ - ab² - ac² + ah²)根据勾股定理中的关系式b² + c² = 2a² - 2ah + h²，我们得到h² = 2a² - b² - c²，代入上面的式子中可以继续简化得到：S = (1/4) * (2a³ - ab² - ac² + ah²)= (1/4) * (2a³ - ab² - ac² + a(2a² - b² - c²))= (1/4) * (2a³ - ab² - ac² + 2a³ - ab² - ac²)= (1/4) * (4a³ - 2ab² - 2ac²)= (1/4) * 2a (a² - b² - c² + 2ab + 2ac)= 1/2 * a (a + b)(a + c) - a²(b + c) + 1/4 * a(b + c)(b + c - a)= 1/4 * (a + b + c)(a + b - c)(a - b + c)(-a + b + c)由于三角形是个锐角三角形，所以(a + b + c) > 2c，(a + b - c) > 0，(a - b + c) > 0，(-a + b + c) > 0。

用海伦公式计算三角形面积

计算三角形面积的海伦公式
海伦公式：s=sqrt(p*(p-a)(p-b)(p-c))
假设在平面内，有一个三角形，边长分别为a、b、c，三角形的面积S可由以下公式求得：s=sqrt(p*(p-a)(p-b)(p-c))
而公式里的p为半周长（周长的一半）：p=1/2(a+b+c)
扩展资料：
一般来讲仅用四边长无法表达某个四边形面积（某些特例除外），必须添加某些条件，比如角、对角线等。

海伦公式的提出为三角形和多边形的面积计算提供了新的方法和思路，在知道三角形三边的长而不知道高的情况下使用海伦公式可以更快更简便的求出面积。

比如说在测量土地的面积的时候，不用测三角形的高，只需测两点间的距离，就可以方便地导出答案。

三角形求面积公式之海伦公式

三角形求面积公式之海伦公式在咱们学习数学的旅程中，三角形求面积可是个重要的“关卡”。

今天咱就来好好唠唠三角形求面积公式中的海伦公式。

先来说说啥是海伦公式。

海伦公式是：假设在一个三角形中，三条边的长度分别为 a、b、c，半周长 p = (a + b + c) / 2 ，那么这个三角形的面积S = √[p(p - a)(p - b)(p - c)] 。

我记得之前给学生们讲这个公式的时候，那可真是状况百出。

有个小同学瞪着大眼睛问我：“老师，这公式咋这么复杂呀，能好用吗？”我笑着告诉他：“别着急，等你会用了你就知道它的妙处啦！”咱们来实际操作一下，比如说有一个三角形，三条边分别是 3、4、5 。

那咱们先算半周长 p = (3 + 4 + 5) / 2 =6 。

接下来，S = √[6×(6 -3)×(6 - 4)×(6 - 5)] = √[6×3×2×1] = √36 = 6 。

你看，这不就轻松算出面积了嘛！海伦公式在实际生活中也大有用处呢。

就说那次我和朋友出去郊游，看到一块三角形的草地。

我们好奇这块草地的面积有多大。

朋友说：“这可不好算呀！”我灵机一动，拿出尺子大致量了量三条边的长度，然后运用海伦公式，很快就算出了草地的面积。

朋友惊讶地说：“哇，这公式还真厉害！”再深入想想，海伦公式其实体现了数学的一种美妙的和谐。

它把三角形的三条边巧妙地结合在了一起，通过一个简洁的式子就能求出面积。

这就好像是数学世界里的一把神奇钥匙，能打开三角形面积计算的神秘大门。

不过，同学们在使用海伦公式的时候也要小心哦，可别把边的长度给弄错了，不然算出来的结果可就差之千里啦。

总之，海伦公式虽然看起来有点复杂，但只要咱们多练习、多运用，就能熟练掌握，让它成为我们解决三角形面积问题的得力助手。

相信大家在数学的海洋里，凭借着这个公式能更加游刃有余，发现更多的数学之美！。

三角形求面积海伦公式

三角形求面积海伦公式三角形的面积可以通过海伦公式来计算。

海伦公式是由古希腊数学家海伦提出的，用于计算任意三角形的面积。

这个公式可以通过三角形的三条边的长度来求解，具体的公式如下所示：S = √(p * (p - a) * (p - b) * (p - c))其中S表示三角形的面积，a、b、c分别表示三角形的三条边的长度，p表示三角形的半周长，即p = (a + b + c) / 2。

海伦公式的推导过程相对复杂，但是使用起来非常简便。

下面我们将通过一个实例来演示如何使用海伦公式求解三角形的面积。

假设有一个三角形ABC，已知它的三条边的长度分别为a = 5、b = 12、c = 13，我们要求解这个三角形的面积。

我们可以计算出这个三角形的半周长p：p = (a + b + c) / 2 = (5 + 12 + 13) / 2 = 30 / 2 = 15接下来，我们带入海伦公式，计算出三角形的面积S：S = √(p * (p - a) * (p - b) * (p - c)) = √(15 * (15 - 5) * (15 - 12) * (15 - 13)) = √(15 * 10 * 3 * 2) = √(900) = 30所以，三角形ABC的面积为30平方单位。

海伦公式的优点是适用于任意形状的三角形，不需要知道顶点的高度或角度，只需要知道三条边的长度即可。

这使得海伦公式在实际应用中非常方便。

除了使用海伦公式之外，我们还可以通过其他方法来计算三角形的面积。

例如，对于已知顶点坐标的三角形，可以使用向量叉积的方法来计算面积。

此外，如果已知三角形的底边和高，也可以直接使用底边乘以高的一半来计算面积。

总结起来，海伦公式是一种非常实用的方法，可以用来计算任意三角形的面积。

通过海伦公式，我们无需知道三角形的高度或角度，只需要知道三条边的长度即可。

这种简便性使得海伦公式在数学和实际应用中得到广泛的应用。

无论是在建筑设计、地理测量还是其他领域，海伦公式都是一个非常重要的工具。

三角形体积海伦公式

三角形体积海伦公式
三角形的面积可以通过海伦公式来计算。

海伦公式是根据三角形的三条边的长度来计算其面积的公式。

公式如下：
面积= √(s(s-a)(s-b)(s-c))
其中，s是半周长，即s = (a + b + c) / 2，a、b、c分别是三角形的三条边的长度。

海伦公式可以应用于任意形状的三角形，无论是等边三角形、等腰三角形还是一般三角形，都适用。

通过海伦公式，我们可以计算出三角形的面积，从而了解其体积。

然而，需要注意的是，体积是三维空间中的概念，而三角形是二维图形，没有体积这一概念。

所以，海伦公式通常用于计算三角形的面积，而不是体积。

三角形的海伦公式

三角形的海伦公式三角形是几何学中最基本的图形之一，由三条边所围成。

求解三角形的面积是几何学的重要问题之一，而海伦公式就是一种常用的方法。

海伦公式是由古希腊数学家海伦提出的，用于求解已知三角形三边长度的情况下的面积。

该公式的形式可表示为：S = √[s(s - a)(s - b)(s - c)]其中，S代表三角形的面积，a、b、c分别代表三角形的三边长度，s为半周长，即s = (a + b + c)/2。

海伦公式的用途非常广泛，不仅可以用于求解普通三角形的面积，还可以应用于特殊情况的计算，例如等边三角形和直角三角形。

下面通过几个例子来说明海伦公式的使用方法。

例一：已知一个三角形的边长分别为a = 3 cm，b = 4 cm，c = 5 cm，求其面积S。

首先计算半周长s：s = (a + b + c)/2 = (3 + 4 + 5)/2 = 12/2 = 6 cm然后代入海伦公式进行计算：S = √[6(6 - 3)(6 - 4)(6 - 5)] = √[6 * 3 * 2 * 1] = √[36] = 6 cm²所以，该三角形的面积为6平方厘米。

例二：已知一个等边三角形的边长为a = 6 cm，求其面积S。

由于等边三角形的三边长度相等，可以省略半周长的计算，直接代入海伦公式进行计算：S = √[s(s - a)(s - a)(s - a)] = √[3(3 - 6)(3 - 6)(3 - 6)] = √[3 * (-3) * (-3) * (-3)] = √[27] = 3√3 cm²所以，该等边三角形的面积为3√3平方厘米。

例三：已知一个直角三角形的两条直角边长度分别为a = 3 cm，b = 4 cm，求其面积S。

同样进行半周长的计算：s = (a + b + c)/2 = (3 + 4 + 5)/2 = 12/2 = 6 cm代入海伦公式进行计算：S = √[6(6 - 3)(6 - 4)(6 - 5)] = √[6 * 3 * 2 * 1] = √[36] = 6 cm²所以，该直角三角形的面积为6平方厘米。

海伦公式多边形面积

海伦公式多边形面积
海伦公式（Heron's formula）通常用于计算三角形的面积，而不是多边形的面积。

海伦公式基于三角形的三边长度来计算面积，公式如下：
如果三角形的三边长度分别为 a, b, c，且 s 是半周长（即 (a + b + c) / 2），则三角形的面积 A 可以通过以下公式计算：
A = √(s * (s - a) * (s - b) * (s - c))
对于多边形，通常使用其他方法来计算面积。

例如，对于简单多边形（即顶点不交叉的多边形），可以通过将多边形划分为多个三角形，然后计算每个三角形的面积，并将这些面积相加来得到多边形的总面积。

对于复杂多边形（如自相交多边形），计算面积可能需要更复杂的算法，如基于向量或几何变换的方法。

海伦公式推导

海伦公式推导
海伦公式，也称三角形海伦公式，是一个由海伦·普拉特（Hellen Pritchet）于公元前三世纪发现的数学定理。

它把三角形周长S与三角形三边长a， b， c
按比例关联起来：S=a+b+c。

公式可以用来求知三角形的三边长，当知道周长S和
其中两边长时，就能够确定第三边长。

海伦公式可以拓展到几何学中的多边形，海伦公式在三角形以及其他多边形中
都有应用，其中的形变量和积量的变化理论也是几何学的一个基本内容。

海伦公式也用在笛卡尔三元空间中，用来表示任意三个点的几何位置之间的距离关系。

除了几何学上的应用外，海伦公式也有许多其他应用。

例如，在建筑工程计算
中海伦公式被用于确定墙体的尺寸，以满足一定的承重要求。

它还能用于测算三个航行点间的航路距离，测算游泳池的面积，以及在视觉计算、安防监控等以三角形计向量机制的应用中。

总的来说，海伦公式的广泛应用表明，它在几何学中的数学概念与实际应用是
十分紧密的，它在许多领域一直发挥着不可替代的作用。

面积问题海伦公式

面积问题海伦公式在我们学习数学的旅程中，面积问题可是个常客。

今天咱们就来聊聊面积问题中的一个神奇公式——海伦公式。

说起面积，大家最先想到的可能是长方形、正方形这些规则图形的面积计算，那简单得很，长乘宽、边长乘边长就能搞定。

可要是碰到三角形，特别是那些不规则的三角形，计算面积可就没那么容易了。

这时候，海伦公式就像一位超级英雄，闪亮登场啦！海伦公式是这样的：假设三角形的三条边长分别为 a、b、c，半周长 p = （a + b + c）/ 2 ，那么三角形的面积S = √[p(p - a)(p - b)(p - c)] 。

我记得有一次给学生们讲这个公式的时候，发生了一件特别有趣的事儿。

当时我在黑板上画了一个看起来奇奇怪怪的三角形，然后问同学们：“你们谁能算出这个三角形的面积呀？”同学们都皱着眉头，拿着笔在纸上写写画画，嘴里还嘟囔着：“这可怎么算呀？” 我看着他们那苦恼的样子，心里偷笑，然后慢慢地引出了海伦公式。

一开始，大家看到这个公式都有点懵，觉得太复杂了。

我就一步一步地带着他们推导，告诉他们这个公式背后的原理。

慢慢地，有些聪明的孩子眼睛亮了起来，好像发现了新大陆一样。

咱们再回到这个公式，它虽然看起来有点复杂，但是只要掌握了方法，用起来可顺手了。

比如说，有一个三角形，三条边分别是 5、6、7，那咱们先算半周长 p = （5 + 6 + 7）/ 2 = 9 。

然后呢，面积S = √[9×(9 - 5)×(9 - 6)×(9 - 7)] = √[9×4×3×2] = √216 = 6√6 。

海伦公式在实际生活中也有很多用处呢。

想象一下，建筑师在设计一个三角形的屋顶时，需要知道它的面积来计算材料的用量；或者测量人员在测量一块三角形的土地面积时，海伦公式就能大显身手啦。

而且呀，通过学习海伦公式，咱们还能锻炼自己的逻辑思维和数学运算能力。

别小看这一个公式，它可是数学世界里的一颗璀璨明珠呢！在学习数学的道路上，像海伦公式这样的宝藏还有很多很多。

海伦公式-

海伦公式-
海伦公式是一个三角形面积的计算公式。

它是由古希腊数学家海伦（Haelen）在公元前三世纪提出的。

海伦公式可以通过一个三角形三边长度来计算其面积。

公式如下：
S = √(p(p-a)(p-b)(p-c))
其中，S是三角形面积，a,b,c是三角形三边长度，p是三角形半周长，即p = (a + b + c) / 2。

海伦公式是通过三角形半周长来计算面积的，因此称之为海伦公式。

请注意，使用海伦公式前，需要确保输入的三边长度是符合三角形不等式的，即a + b > c, b + c > a, c + a > b.
海伦公式是通过三角形三边长度来计算三角形面积的，因此它可以用来计算任意三角形的面积。

在使用海伦公式时，需要注意的是三角形三边长度都必须是大于零的实数，并且要符合三角形不等式的要求，即a + b > c, b + c > a, c + a > b.
此外，海伦公式的计算过程中需要使用平方根运算，如果使用计算器进行计算，请确保计算器具有平方根运算功能。

总之,海伦公式是一个简单而有效的三角形面积计算
公式，可以被广泛应用于数学、几何、工程等领域。

海伦公式

海伦公式海伦公式又译作希伦公式、海龙公式、希罗公式、海伦－秦九韶公式，传说是古代的叙拉古国王希伦（Heron,也称海龙）二世发现的公式，利用三角形的三条边长来求取三角形面积。

但根据MorrisKline在1908年出版的著作考证，这条公式其实是阿基米德所发现，以托希伦二世的名发表（未查证）。

我国宋代的数学家秦九韶也提出了“三斜求积术”，它与海伦公式基本一样。

假设有一个三角形，边长分别为a、b、c，三角形的面积S可由以下公式求得：S=√[p(p-a)(p-b)(p-c)]而公式里的p为半周长：p=(a+b+c)/2 ——————————————————————————————————————————————注："Metrica"(《度量论》)手抄本中用s作为半周长，所以S=√[p(p-a)(p-b)(p-c)] 和S=√[s(s-a)(s-b)(s-c)]两种写法都是可以的，但多用p作为半周长。

——————————————————————————————————————————————由于任何n边的多边形都可以分割成n-2个三角形，所以海伦公式可以用作求多边形面积的公式。

比如说测量土地的面积的时候，不用测三角形的高，只需测两点间的距离，就可以方便地导出答案。

证明（1）：与海伦在他的著作"Metrica"(《度量论》)中的原始证明不同，在此我们用三角公式和公式变形来证明。

设三角形的三边a、b、c的对角分别为A、B、C，则余弦定理为cosC = (a^2+b^2-c^2)/2abS=1/2*ab*sinC=1/2*ab*√(1-cos^2 C)=1/2*ab*√[1-(a^2+b^2-c^2)^2/4a^2*b^2]=1/4*√[4a^2*b^2-(a^2+b^2-c^2)^2]=1/4*√[(2ab+a^2+b^2-c^2)(2ab-a^2-b^2+c^2)]=1/4*√[(a+b)^2-c^2][c^2-(a-b)^2]=1/4*√[(a+b+c)(a+b-c)(a-b+c)(-a+b+c)]设p=(a+b+c)/2则p=(a+b+c)/2, p-a=(-a+b+c)/2, p-b=(a-b+c)/2,p-c=(a+b-c)/2,上式=√[(a+b+c)(a+b-c)(a-b+c)(-a+b+c)/16]=√[p(p-a)(p-b)(p-c)]所以，三角型ABC面积S=√[p(p-a)(p-b)(p-c)]证明（2）：我国宋代的数学家秦九韶也提出了“三斜求积术”。

海伦公式

海伦公式用已知三边求三角形面积如果已知三角形三边的长度，便可以用有二千年历史的公式来求三角形的面积。

这个公式叫"海伦公式"，由亚历山大里亚的希罗发现（如下）只需要两步：一、求"s"（周长的一半）：二、求面积：例子：每边长度为5 的三角形的面积是多大？一、s = (5+5+5)/2 = 7.5二、A = √(7.5 × 2.5 × 2.5 × 2.5) = √(117.1875) =10.825……海伦公式（Heron's formula或Hero's formula），又译希罗公式[1]、希伦公式、海龙公式，亦称“海伦-秦九韶公式”。

此公式是亚历山大港的海伦发现的，并可在其于公元60年的《Metrica》中找到其证明，利用三角形的三条边长来求取三角形面积。

亦有认为早于阿基米德已经懂得这条公式，而由于《Metrica》是一部古代数学知识的结集，该公式的发现时期很有可能先于海伦的著作。

[2]假设有一个三角形，边长分别为，三角形的面积可由以下公式求得：中国南宋末年数学家秦九韶发现或知道等价的公式，其著作《数书九章》卷五第二题即三斜求积。

“问沙田一段，有三斜，其小斜一十三里，中斜一十四里，大斜一十五里，里法三百步，欲知为田几何？”答曰：“三百十五顷．”其术文是：“以小斜幂并大斜幂，减中斜幂，余半之，自乘于上；以小斜幂乘大斜幂，减上，余四约之为实，……开平方得积。

”若以大斜记为a，中斜记为b，小斜记为c，秦九韶的方法相当于下面的一般公式：像中国古代的数学家一样，他的方法没有证明。

根据现代数学家吴文俊的研究，秦九韶公式可由出入相补原理得出。

一些中国学者将这个公式称为秦九韶公式。

由于任何n边的多边形都可以分区成n-2个三角形，所以海伦公式可以用作求多边形面积的公式。

比如说测量土地的面积的时候，不用测三角形的高，只需测两点间的距离，就可以方便地导出答案。

海伦公式在中考中的运用

海伦公式在中考中的运用
海伦公式是用来计算三角形面积的公式，它可以在中考中被用来
求解各种求面积的问题。

海伦公式的表达式为：S=√[p(p-a)(p-b)(p-c)]，其中S表示三角形的面积，a、b、c分别表示三角形的三条边，p 表示三角形的半周长，即p=(a+b+c)/2。

在中考中，海伦公式可以被应用于各种求三角形面积的题目，如
计算等腰三角形、直角三角形、等边三角形、不规则三角形等的面积。

学生可以通过海伦公式来快速准确地计算三角形的面积，从而解决各
种相关问题。

除了在中考中用来计算三角形的面积外，海伦公式还可以被应用
于其他一些有关三角形的问题，如判断三角形的形状、性质，以及解
决与三角形相关的实际问题等。

总之，海伦公式在中考中的运用范围广泛，对于解决各种三角形
面积相关的问题起着重要的作用。

因此，在复习数学时，学生需要充
分理解和掌握海伦公式的运用方法，以便顺利解决相关问题。

海伦公式及婆罗摩笈多公式

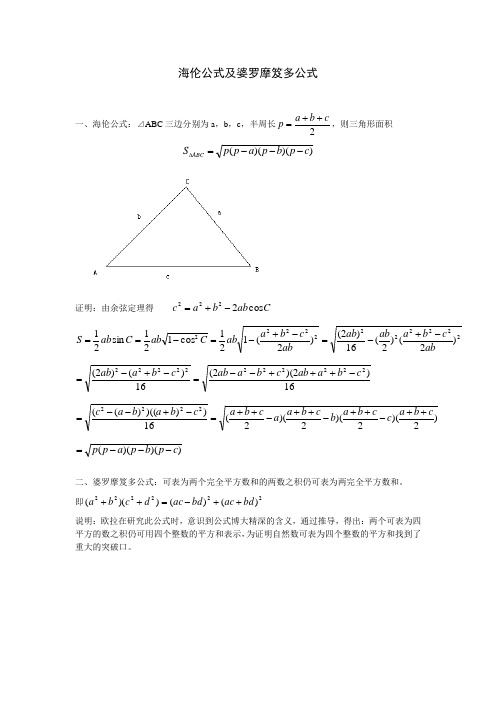
海伦公式及婆罗摩笈多公式一、海伦公式：⊿ABC 三边分别为a ，b ，c ，半周长2c b a p ++=，则三角形面积 ))()((c p b p a p p S ABC ---=∆证明：由余弦定理得 C ab b a c cos 2222-+= 22222222222)2()2(16)2()2(121cos 121sin 21abc b a ab ab ab c b a ab C ab C ab S -+-=-+-=-==16)2)(2(16)()2(22222222222c b a ab c b a ab c b a ab -+++--=-+-= )2)(2)(2)(2(16)))(()((2222c b a c c b a b c b a a c b a c b a b a c ++-++-++-++=-+--=))()((c p b p a p p ---=二、婆罗摩笈多公式：可表为两个完全平方数和的两数之积仍可表为两完全平方数和。

即222222)()())((bd ac bd ac d c b a ++-=++说明：欧拉在研究此公式时，意识到公式博大精深的含义，通过推导，得出：两个可表为四平方的数之积仍可用四个整数的平方和表示，为证明自然数可表为四个整数的平方和找到了重大的突破口。

三、婆罗摩笈多公式：圆内接四边形ABCD 的边分别为a ，b ，c ，d ，半周长2d c b a p +++=,则四边形面积))()()((d p c p b p a p S ABCD ----=证明：内接四边形ABCD 知A+C=180oC cd ab A cd C ab S S S ABD BCD ABCD sin )(21sin 21sin 21+=+=+=∆∆ 由余弦定理得 C ab b a BD cos 2222-+=A cd d c BD cos 2222-+==C cd d c cos 222++C ab b a cos 222-+=C cd d c cos 222++)(2cos 2222cd ab d c b a C +--+= 222222))(2(1)(21cos 1)(21sin )(21cd ab d c b a cd ab C cd ab C cd ab S ABCD +--+-+=-+=+=16)()22())(2()2()422(2222222222222d c b a cd ab cd ab d c b a cd ab cd ab --+-+=+--++-+=))()()((d p c p b p a p ----=。

海伦公式的适用范围

海伦公式的适用范围
哇塞，咱来说说海伦公式呀！海伦公式主要就是用来求三角形面积的哟！它的公式呢就是S=√[p(p-a)(p-b)(p-c)]，这里面的 p 可是很关键的，等于
半周长，也就是（a+b+c）÷2。

比如说有个三角形，三边分别是 3、4、5，那咱就算算哈。

先算出
p=(3+4+5)÷2=6，然后就能用海伦公式算面积啦，就是√[6×(6-3)×(6-
4)×(6-5)]=√(6×3×2×1)=6 呀！厉害吧！
海伦公式在很多地方都超有用的呢！不管是数学题目里呀，还是实际生活中要算个三角形的面积啥的。

它就像一把神奇的钥匙，能打开三角形面积计算的大门呢！你想想看，要是没有它，咱得费多大劲去想别的办法呀！所以呀，海伦公式可真是个宝呀，咱可得好好把它记住，好好用它！你说是不是呀？。