《认识无理数》公开课教学PPT课件【北师大版八年级数学上册】
合集下载
北师大版八年级上册数学课件:2.1 认识无理数(共20张PPT)

(一)
把两个边长为1的小正方形通过 剪、拼,设法得到一个大正方形
1 1
1
1
1
1 1
1
1 2 1 2 1 2
1
1 2
1
1 1
1
1
1
1
1
1
1
1
1
1
1
1
a 2
2
a
.
a 2
2
a
a a a a
小组讨论:
a可能是整数吗? a可能是分数吗?
数怎么又不够用了!
a 2
2
a2=2,1<a2<4 ,得到1<a <2,
一个与该问题的实质内容有着本质联系的较大范围开
始进行解决,再逐步缩小范围,逐步逼近,以致最后 达到问题所要求的解.在解决比较困难的数学问题时,
“逐次逼近法”可以起到化难为易、化繁为简的作
用.
献身科学,执着追求
公元前500年,古希腊的毕达哥 拉斯( Pythagoras) 学派认为“宇宙间 的一切现象都能归结为整数或整数之 比,即都可用有理数来描述。 这学派的成员希伯索斯(Hippasus) 发现边长为1的正方形的对角线的长不 能有理数来表示,这就动摇了毕达哥 拉斯学派的信条,引起了信徒们的恐 慌,他在逃回家的路上,遭到毕氏成 员的追捕,被投入大海。
所以3<x<4,所以x的整数部分为3. (3)由3.12=9.61<10,3.22=10.24>10,所以3.1<x<3.2. 又因为3.162=9.9856<10,3.172=10.0489>10, 所以3.16<x<3.17, 所以精确到十分位为x≈3.2.
[归纳总结] 无理数的估算方法——逐次逼近法. 用“逐次逼近法”来解决一个数学问题时,首先从
把两个边长为1的小正方形通过 剪、拼,设法得到一个大正方形
1 1
1
1
1
1 1
1
1 2 1 2 1 2
1
1 2
1
1 1
1
1
1
1
1
1
1
1
1
1
1
1
a 2
2
a
.
a 2
2
a
a a a a
小组讨论:
a可能是整数吗? a可能是分数吗?
数怎么又不够用了!
a 2
2
a2=2,1<a2<4 ,得到1<a <2,
一个与该问题的实质内容有着本质联系的较大范围开
始进行解决,再逐步缩小范围,逐步逼近,以致最后 达到问题所要求的解.在解决比较困难的数学问题时,
“逐次逼近法”可以起到化难为易、化繁为简的作
用.
献身科学,执着追求
公元前500年,古希腊的毕达哥 拉斯( Pythagoras) 学派认为“宇宙间 的一切现象都能归结为整数或整数之 比,即都可用有理数来描述。 这学派的成员希伯索斯(Hippasus) 发现边长为1的正方形的对角线的长不 能有理数来表示,这就动摇了毕达哥 拉斯学派的信条,引起了信徒们的恐 慌,他在逃回家的路上,遭到毕氏成 员的追捕,被投入大海。
所以3<x<4,所以x的整数部分为3. (3)由3.12=9.61<10,3.22=10.24>10,所以3.1<x<3.2. 又因为3.162=9.9856<10,3.172=10.0489>10, 所以3.16<x<3.17, 所以精确到十分位为x≈3.2.
[归纳总结] 无理数的估算方法——逐次逼近法. 用“逐次逼近法”来解决一个数学问题时,首先从
北师大版数学八年级上册课件:2.1 认识无理数(共13张PPT)

综合能力提升练
13.( 教材母题变式 )如图是16个边长为1的小正方形拼成的大正方形,其中CA,CB,CD,CE中 长度既不是整数,也不是分数的有 3 条.
14.( 改编 )把下列各数填入表示它所在的数集的大括号内: -2,-12,3.020020002…( 每两个 2 之间多 1 个 0 ),272,-π3,-( -3 ),0.333,0,34,-17,3.1·5·,0.12345678910111213…( 小数部分由相继的正整数组 成 ),-1.202020202…( 每两个 2 之间有 1 个 0 ).
( 4 )无理数集合: 3.020020002…( 每两个 2 之间多 1 个 0 ),-
π 3
,0.12345678910111213…(
小数部分由相继的正整数组成
)…
.
综合能力提升练
15.请你在方格纸上按照如下要求设计图形,每个单元格的边长为1.( 所设计图形顶点在格 点上 ) ( 1 )请在图1中设计一个直角三角形,使它三边中有两边边长不是有理数. ( 2 )请在图2中设计一个直角三角形,使它的三边边长都不是有理数.
综合能力提升练
( 1 )整数集合:{-2,-(-3 ),0,-17…}; ( 2 )分数集合: -12 , 272,0.333,-34,3.1·5·,-1.202020202…( 每两个 2 之间 有 1 个 0 )… ; ( 3 )负有理数集合: -2,-12,-34,-17,-1.202020202…( 每两个 2 之间有 1 个 0 )… ;
拓展探究突破练
17.无限循环小数如何化为分数呢?请你仔细阅读下列资料:由于小数部分位数是无限的,所 以不可能写成十分之几、百分之几、千分之几等等的数.转化时需要先去掉无限循环小数 的“无限小数部分”.一般是用扩倍的方法,把无限循环小数扩大十倍、一百倍或一千倍…… 使扩大后的无限循环小数与原无限循环小数的“无限小数部分”完全相同,然后这两个数相
认识无理数.PPT课件(北师大版)

A、面积为3的正方形的边长 B、体积是8的正方体的棱长 C、两直角边分别为2和3的直角三角形的斜边长 2.面积为3的正方形的边长_不__是___有理数;面积为4 的正方形的边长__是___有理数.(填“是”或“不是”)
级:快乐提升 ——练能力: 3.加固一个高2米、宽1米的大门,需 要在对角线位置加固一条木板,设木板 长为a米,则 a的值大约是多少?这个值 可能是分数吗?
必做题:如图,在△ABC中,
CD⊥AB,垂足为D,AC=6,AD=5,
问:CD可能是整数吗?可能是分
数吗?可能是有理数吗?
选做题: B,C是一个生活小区的两个路口,
BC长为2千米,A处是一个花园,从A到B,C两路口 的距离都是2千米,现要从花园到生活小区修一条 最短的路,这条路的长可能是整数吗?可能是分 数吗?说明理由.
视察下图后回答下面问题, (1)如图:以直角三角形的斜边为边的正 方形的面积是多少?
(2)设该正方形的边长为b,b满足什么条 件?
(3)b是有理数吗?
活动五:了解数学史,体会数学文化
请阅读下面材料,并说出自己的感受:
公元前500年,古希腊的毕达哥拉斯( Pythagoras) 学派认为“宇宙间的一切现象都能归结为整数或整 数之比,即都可用有理数来描述。
(一)知识上的总结:
教师提问:本节课你学到了什么知识? (二)数学方法上的总结
教师提问:在讨论大正方形的边长是否为有理数 时,我们是怎样讨论的 ?
总结: “分类讨论”的数学说理方法 教师提问:在研究大正方形的边长是否为分数时,
我们从哪里开始研究的?
总结: “特殊到一般”的研究方法
级:轻松过关 ——打基础: 1.下列各数中,是有理数的是( B )
义务教育教科书(北师大版)数学 八年级上册
级:快乐提升 ——练能力: 3.加固一个高2米、宽1米的大门,需 要在对角线位置加固一条木板,设木板 长为a米,则 a的值大约是多少?这个值 可能是分数吗?
必做题:如图,在△ABC中,
CD⊥AB,垂足为D,AC=6,AD=5,
问:CD可能是整数吗?可能是分
数吗?可能是有理数吗?
选做题: B,C是一个生活小区的两个路口,
BC长为2千米,A处是一个花园,从A到B,C两路口 的距离都是2千米,现要从花园到生活小区修一条 最短的路,这条路的长可能是整数吗?可能是分 数吗?说明理由.
视察下图后回答下面问题, (1)如图:以直角三角形的斜边为边的正 方形的面积是多少?
(2)设该正方形的边长为b,b满足什么条 件?
(3)b是有理数吗?
活动五:了解数学史,体会数学文化
请阅读下面材料,并说出自己的感受:
公元前500年,古希腊的毕达哥拉斯( Pythagoras) 学派认为“宇宙间的一切现象都能归结为整数或整 数之比,即都可用有理数来描述。
(一)知识上的总结:
教师提问:本节课你学到了什么知识? (二)数学方法上的总结
教师提问:在讨论大正方形的边长是否为有理数 时,我们是怎样讨论的 ?
总结: “分类讨论”的数学说理方法 教师提问:在研究大正方形的边长是否为分数时,
我们从哪里开始研究的?
总结: “特殊到一般”的研究方法
级:轻松过关 ——打基础: 1.下列各数中,是有理数的是( B )
义务教育教科书(北师大版)数学 八年级上册
北师大版八年级数学上册课件 第2章 第1节 认识无理数(共32张PPT)

算一算
1
x
x2 ?
2
问:x是整数(或分数)吗?
剪一剪
把两个边长为1的小正方形通过剪、 拼,设法得到一个大正方形,你会吗?
1 1
1 1
拼一拼
•9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。2021/9/82021/9/8Wednesday, September 08, 2021 •10、阅读一切好书如同和过去最杰出的人谈话。2021/9/82021/9/82021/9/89/8/2021 11:00:52 AM •11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。2021/9/82021/9/82021/9/8Sep-218-Sep-21 •12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/9/82021/9/82021/9/8Wednesday, September 08, 2021
(2)无限小数都是无理数; ( ╳ )
(3)无理数都是无限小数; ( √ )
(4)有理数是有限小数. ( ╳ )
强调
无理数是无限不循环小数, 有理数是有限小数或无限循环小数.
c 例3 以下各正方形的边长是无理数的是( )
A.面积为25的正方形;
B.面积为 4 的正方形; 25
C.面积为8的正方形;
13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成。2021/9/82021/9/82021/9/82021/9/89/8/2021 •14、谁要是自己还没有发展培养和教育好,他就不能发展培养和教育别人。2021年9月8日星期三2021/9/82021/9/82021/9/8 •15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年9月2021/9/82021/9/82021/9/89/8/2021 •16、教学的目的是培养学生自己学习,自己研究,用自己的头脑来想,用自己的眼睛看,用自己的手来做这种精神。2021/9/82021/9/8September 8, 2021 •17、儿童是中心,教育的措施便围绕他们而组织起来。2021/9/82021/9/82021/9/82021/9/8
北师大八年级数学上册《认识无理数》课件(共7张PPT)

谢谢观赏
You made my day!
我们,还在路上……
12334567891011…(由相继的正整数组成).
有理数集合:{
…}
无理数集合:{
…}
例2 判断题
(1)有限小数是有理数; ( √ ) (2)无限小数都是无理数; ( × ) (3)无理数都是无限小数; ( √ ) (4)有理数是有限小数. ( × )
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年4月21日星期四2022/4/212022/4/212022/4/21 •2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于独 立思考的人,给那些具有锲而不舍的人。2022年4月2022/4/212022/4/212022/4/214/21/2022 •3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/4/212022/4/21April 21, 2022
北师大版八年级数学上册第二章第一节
认识无理数
把下列各数表示成小数,你发现了什么?
3, 4, 5, 8 , 2 5 9 4511
想一想:
分数化成小数,这些小数有什么特点?
结论:有理数都能化成有限小数或无限循环小数.
即任何有限小数或无限循环小数都是有理数.
像0.585885888588885…,1.41421356…, -2.2360679…等这些数的小数位数都是无限的, 但又不是循环的,而是无限不循环小数.
无限不循环小数叫无理数.(圆周率π也是 一个无限不循环小数,故π是无理数)
பைடு நூலகம்
议一议:
到目前为止所学过的数可以分为几类?
You made my day!
我们,还在路上……
12334567891011…(由相继的正整数组成).
有理数集合:{
…}
无理数集合:{
…}
例2 判断题
(1)有限小数是有理数; ( √ ) (2)无限小数都是无理数; ( × ) (3)无理数都是无限小数; ( √ ) (4)有理数是有限小数. ( × )
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年4月21日星期四2022/4/212022/4/212022/4/21 •2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于独 立思考的人,给那些具有锲而不舍的人。2022年4月2022/4/212022/4/212022/4/214/21/2022 •3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/4/212022/4/21April 21, 2022
北师大版八年级数学上册第二章第一节
认识无理数
把下列各数表示成小数,你发现了什么?
3, 4, 5, 8 , 2 5 9 4511
想一想:
分数化成小数,这些小数有什么特点?
结论:有理数都能化成有限小数或无限循环小数.
即任何有限小数或无限循环小数都是有理数.
像0.585885888588885…,1.41421356…, -2.2360679…等这些数的小数位数都是无限的, 但又不是循环的,而是无限不循环小数.
无限不循环小数叫无理数.(圆周率π也是 一个无限不循环小数,故π是无理数)
பைடு நூலகம்
议一议:
到目前为止所学过的数可以分为几类?
北师大版八年级数学上册教学课件《认识无理数》

a=1.414 213 56…, 它是一个无限不循环小数。
做一做 估计面积为5的正方形的边长b的值,结果精确到百分位。 b=2.236067978…,它也是一个无限不循环小数。
问题3:使用计算器计算,把下列有理数写成小数的形式,你有什么发
现?
3, 3 , 47 , 9 , 11 , 5
5 8 11 90 9
因为 a2=2, 而12=1, 22=4 , 所以 12<a2<22 , 所以 1< a< 2,a不是整数。
从“形”的角度:
取出一个三角形
A C
B
在三角形ABC中,AC=1,BC=1,AB=a; 根据三角形的三边关系:
AC-BC< a<AC+BC 所以0<a<2,且 a≠1,所以a不是整数。
追问2:a可能是分数吗? ① a是分母为2的分数吗? ② a是分母为3的分数吗?
3 3.0, 3 0.6, 5
47 5.875, 8
9
11
5
0.81,
0.12,
0.5
11
90
9
事实上,任何一个有理数都可以写成有限小数或无限循环小数.反过
来,任何有限小数或无限循环小数也都是有理数。
要点归纳
无限不循环小数为无理数. 如π=3.14159265…,
活动:把两个边长为1的小正方形通过剪、拼,设法得到 一个大正方形,你会吗?
1
1
还有好多方法哦!课余时间再动手试一试,比比谁找的多!
1
1
1
1
1
1
1
1
1
1
2
2
1
1
做一做 估计面积为5的正方形的边长b的值,结果精确到百分位。 b=2.236067978…,它也是一个无限不循环小数。
问题3:使用计算器计算,把下列有理数写成小数的形式,你有什么发
现?
3, 3 , 47 , 9 , 11 , 5
5 8 11 90 9
因为 a2=2, 而12=1, 22=4 , 所以 12<a2<22 , 所以 1< a< 2,a不是整数。
从“形”的角度:
取出一个三角形
A C
B
在三角形ABC中,AC=1,BC=1,AB=a; 根据三角形的三边关系:
AC-BC< a<AC+BC 所以0<a<2,且 a≠1,所以a不是整数。
追问2:a可能是分数吗? ① a是分母为2的分数吗? ② a是分母为3的分数吗?
3 3.0, 3 0.6, 5
47 5.875, 8
9
11
5
0.81,
0.12,
0.5
11
90
9
事实上,任何一个有理数都可以写成有限小数或无限循环小数.反过
来,任何有限小数或无限循环小数也都是有理数。
要点归纳
无限不循环小数为无理数. 如π=3.14159265…,
活动:把两个边长为1的小正方形通过剪、拼,设法得到 一个大正方形,你会吗?
1
1
还有好多方法哦!课余时间再动手试一试,比比谁找的多!
1
1
1
1
1
1
1
1
1
1
2
2
1
1
《认识无理数》PPT课件 (公开课)2022年北师大版 (8)

① 3x2 5x3
② (5a2b)(2a2)
③ (5an1b)(2a.) ④ (2x)3(2x2y)
⑤ (x2 yz3)2(x2y)3
收获感悟:
本节课你学到了什么? 发现了什么? 有什么收获? 还存在什么没有解决的问题?
课后作业:
1. 习题 2. 拓展探究:
, 若 (am1bn2)(a2n1b)a5b3 求 mn的值 。
2.客观世界中,的确存在不是有理 数的数,你能列举几个吗?
3.除了本课所认识的非有理数的数 以外,你还能找到吗?
读一读
无理数的发现(教材第23页)
作业布置 习题2.2 1,3
赛一赛
下图是由五个单位正方形组成的纸片, 请你把它剪成三块,然后拼成一个正 方形,你会吗?试试看!
第一章 整式的乘除
4 整式的乘法(第1课时)
3、在你探索单项式乘法运算法则的过 程中,运用了哪些运算律和运算法则?
探索规律:
单项式乘法的法则: 单项式与单项式相乘,把它们的系
数、相同字母的幂分别相乘,其余字母 连同它的指数不变,作为积的因式。
例题解析:
例1 计算:
(1)2 xy 2 ( 1 xy ) 3
(2) 2a2b3 (3a)
(3)7xy2z(2xyz)2
(4)单项式乘以单项式,结果仍为单项式。
完成课本15页:随堂练习
延伸拓展:
一家住房的结构如图
y
2y
示,房子的主人打算把 卧室以外的部分全都铺
卫生间
卧室
上地砖,至少需要多少
x
厨房
4x
平方米的地砖?如果某
种地砖的价格是a元/平 2x
客厅
方米,那么购买所需地
认识无理数(第2课时)北师大数学八年级上册PPT课件
C
CD,EF
解析:设小正方形的边长为x,则x2=2.因为AB2=x2+(3x)2=10x2=20,所以AB的长不是有理数.因为CD2=(2x)2+(2x)2=8x2=16,CD=4,即CD的长是有理数.因为EF2=x2+x2=2x2=4,EF=2,即EF的长是有理数.因为GH2=x2+(2x)2=5x2=10,所以GH的长不是有理数.
2.1 认识无理数(第2课时)
北师大版 数学 八年级 上册
思考导入
1.有理数如何分类?
有理数
整数(如-1,0,2,3,… ):都可看成有限小数
分数(如-,,… ):如何化成小数?可不可能都化成有限小数或无限循环小数?
2.上节课了解到一些数,如a2=2,b2=5中的a,b既不是整数,也不是分数,那么它们究竟是什么数呢?
无理数的概念
提示 有理数与无理数的区别:①有理数是有限小数或无限循环小数,而无理数是无限不循环小数;②所有的有理数都能化成分数(整数可以看成是分母为1的分数),而无理数不能化成分数.注意:形似分数,但它不是分数,是无理数.
概念
无限不循环小数
分类
正无理数和负无理数
三Hale Waihona Puke 常见类型根号型:含有根号,开方开不尽,例如:,(以后学习)
1.借助计算器探索无理数是无限不循环小数.
2.会判断一个数是有理数还是无理数.
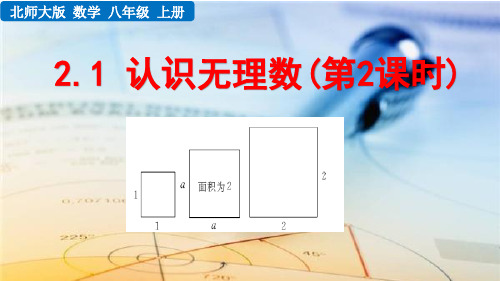
讨论一 面积为2的正方形的边长a究竟是多少呢? (1)如图所示,三个正方形的边长之间有怎样的大小关系?说说你的理由.
无理数的概念
(2)边长a的整数部分是几?十分位是几?百分位呢?千分位呢?……借助计算器进行探索. (3)小明将他的探索过程整理如下,你的结果呢?
CD,EF
解析:设小正方形的边长为x,则x2=2.因为AB2=x2+(3x)2=10x2=20,所以AB的长不是有理数.因为CD2=(2x)2+(2x)2=8x2=16,CD=4,即CD的长是有理数.因为EF2=x2+x2=2x2=4,EF=2,即EF的长是有理数.因为GH2=x2+(2x)2=5x2=10,所以GH的长不是有理数.
2.1 认识无理数(第2课时)
北师大版 数学 八年级 上册
思考导入
1.有理数如何分类?
有理数
整数(如-1,0,2,3,… ):都可看成有限小数
分数(如-,,… ):如何化成小数?可不可能都化成有限小数或无限循环小数?
2.上节课了解到一些数,如a2=2,b2=5中的a,b既不是整数,也不是分数,那么它们究竟是什么数呢?
无理数的概念
提示 有理数与无理数的区别:①有理数是有限小数或无限循环小数,而无理数是无限不循环小数;②所有的有理数都能化成分数(整数可以看成是分母为1的分数),而无理数不能化成分数.注意:形似分数,但它不是分数,是无理数.
概念
无限不循环小数
分类
正无理数和负无理数
三Hale Waihona Puke 常见类型根号型:含有根号,开方开不尽,例如:,(以后学习)
1.借助计算器探索无理数是无限不循环小数.
2.会判断一个数是有理数还是无理数.
讨论一 面积为2的正方形的边长a究竟是多少呢? (1)如图所示,三个正方形的边长之间有怎样的大小关系?说说你的理由.
无理数的概念
(2)边长a的整数部分是几?十分位是几?百分位呢?千分位呢?……借助计算器进行探索. (3)小明将他的探索过程整理如下,你的结果呢?
北师大版八年级上册《认识无理数》【课件】共22页

23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
25、学习是劳动,是充满思想的劳动。——乌申斯基
谢谢!
北师大版八年级上册 《认识无理数》【课件】
6、纪律是自由的第一条件。——黑格 尔 7、纪律是集体的面貌,集体的声音, 集体的 动作, 集体的 表情, 集体的 信念。 ——马 卡连柯
8、我们现在必须完全保持党的纪律, 否则一 切都会 陷入污 泥中。 ——马 克思 9、学校没有纪律便如磨坊没有水。— —夸美 纽斯
10、一个人应该:活泼而守纪律,天 真而不 幼稚, 勇敢而 鲁莽, 倔强而 有原则 ,热情 而不冲 动,乐 夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
25、学习是劳动,是充满思想的劳动。——乌申斯基
谢谢!
北师大版八年级上册 《认识无理数》【课件】
6、纪律是自由的第一条件。——黑格 尔 7、纪律是集体的面貌,集体的声音, 集体的 动作, 集体的 表情, 集体的 信念。 ——马 卡连柯
8、我们现在必须完全保持党的纪律, 否则一 切都会 陷入污 泥中。 ——马 克思 9、学校没有纪律便如磨坊没有水。— —夸美 纽斯
10、一个人应该:活泼而守纪律,天 真而不 幼稚, 勇敢而 鲁莽, 倔强而 有原则 ,热情 而不冲 动,乐 夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数.反过来,任何有限小数或无限循环小数也都是有理数.
要点归纳
二、合作交流,探究新知
无限不循环小数为无理数. 如π=3.14159265…, 0.101 001 000 1…(两个1之间依次多1个0)
三、巩固新知
判断题 (1)有限小数是有理数; ( ) (2)无限小数都是无理数; ( ) (3)无理数都是无限小数; ( ) (4)有理数是有限小数.( )
第二章 实数
2.1 认识无理数
一、创设情境,引入新知
小红是刚升入八年级的新生,一个周末的上午,当工程 师的爸爸给小红出了一道数学题:一个边长为 6 cm的正方形 木板,按如图的痕迹锯掉四个一样的直角三角形.请计算剩下 的正方形木板的面积是多少?剩下的正方形木板的边长又是 多少厘米呢?见过这个数吗?你能帮小红解决这个问题吗?
AC-BC< a<AC+BC 所以0< a <2,且 a ≠ 1,所以 a 不是整数.
二、合作交流,探究新知
追问2:a可能是分数吗? ① a 是分母为 2 的分数吗? ② a 是分母为 3 的分数吗?
(1)2 1
2
4
( 3 )2 9
2
4
(1)2 1 39
( 2 )2 4 ( 4 )2 16 ( 5)2 25
二、合作交流,探究新知
问题3:使用计算器计算,把下列有理数写成小数的形式,你有什么
发现?
3, 3 , 47 , 9 , 11 , 5 5 8 11 90 9
3 3.0, 3 0.6, 47 5.875,
5
8
9
••
0.81,
11
•
0.12,
5
•
0.5
11
90
9
事实上,任何一个有理数都可以写成有限小数或无限循环小
二、合作交流,探究新知
请同学们借助计算器进行探索.
边长 a 1<a<2 1.4<a<1.5 1.41<a<1.42 1.414<a<1.415 1.414 2<a<1.414 3
面积 S 1<S<4 1.96<S<2.25 1.988 1<S<2.016 4 1.999 396<S<2.002 225 1.999 961 64<S<2.000 244 49
二、合作交流,探究新知
想一想 (1)边长 a 会不会算到某一位时,它的平方恰好等于 2 呢?为什么? (2) a 可能是有限小数吗?它会是一个怎样的数呢?
a=1.414 213 56…, 它是一个无限不循环小数.
做一做 估计面积为 5 的正方形的边长 b 的值,结果精确到百分位. b=2.236067978…,它也是一个无限不循环小数.
追问1:a 是一个什么样的数?a 可能是整数吗? 从“数”的角度:
因为 a2=2, 而12=1, 22=4 , 所以 12<a2<22 , 所以 1< a< 2,a不是整数.
二、合作交流,探究新知
从“形”的角度: A
取出一个三角形
C
B 在三角形 ABC 中, AC =1,BC=1,AB=a; 根据三角形的三边关系:
四、归纳小结
无理数的概念及认识 认识无理数
借助计算器求无理数的近似值
再见
3 93
9
3
9
③ a 是分母为 4 的分数吗? ④ a 是分母为多少的分数?
( 5 )2 25 ( 7 )2 49 4 16 4 16
归纳:a 既不是整数,也不是分数,所以 a 不是有理数.
二、合作交流,探究新知
问题2:a 究竟是多少?
面积为2 1
a 2
(1)如图,三个正方形的边长之间有怎样的大小关系? (2)a 的整数部分是几?十分位是几?百分位呢?千分位呢?…… 完成下列表格.
二、合作交流,探究新知
活动:把两个边长为 1 的小正方形通过剪、拼,设法得到一个 大正方形,你会吗?
1
1ቤተ መጻሕፍቲ ባይዱ
二、合作交流,探究新知
还有好多方法哦!课余时间再动手试一试,比比谁找的多!
11 11
1
1
1
1
1
1
2
2
1
1
2
2
11
11
11
11
11
11
二、合作交流,探究新知
问题1:设大正方形的边长为a,则 a 满足什么条件? 因为S大正方形=2,所以a2=2.
