傅里叶变换全部形式推导手写版
傅里叶变换原理

傅里叶变换原理
傅里叶变换是一种数学工具,用于将一个函数(通常是时域上的函数)转换为另一个函数(通常是频域上的函数)。
傅里叶变换的原理包括两个核心思想:信号可以表示为不同频率的正弦波的叠加,以及通过计算信号与不同频率正弦波之间的相关性来获得频谱信息。
一维连续时域信号在傅立叶域的变换公式可以表示为:
F(w) = ∫[从-∞到+∞] f(t) * e^(-j*w*t) dt
其中,F(w)表示频域信号,f(t)表示时域信号,e^(-j*w*t)表示
复指数函数,w表示角频率。
傅里叶变换的逆变换公式可以表示为:
f(t) = 1/2π ∫[从-∞到+∞] F(w) * e^(j*w*t) dw
其中,f(t)表示时域信号,F(w)表示频域信号,e^(j*w*t)表示
复指数函数,w表示角频率。
傅里叶变换在信号处理、图像处理、通信系统等领域广泛应用。
通过将信号从时域转换到频域,可以分析信号的频率成分、滤波、降噪等。
同时,傅里叶变换也可以通过逆变换将频域信号转换回时域,实现信号的还原和复原。
除了一维傅里叶变换,还存在二维和多维傅里叶变换,用于处理二维图像和多维信号。
二维傅里叶变换可以将二维图像转换到频域进行图像增强、滤波等处理,多维傅里叶变换可以对多
维信号进行频域分析。
总之,傅里叶变换是一种重要的数学工具,能够将时域信号转换到频域,通过分析频域信号可以获得信号的频率成分和特征,广泛应用于信号处理和图像处理领域。
傅里叶级数的推导

傅里叶级数的推导傅里叶级数的推导2016年12月14日09:27:47傅里叶级数的数学推导首先,隆重推出傅里叶级数的公式,不过这个东西属于“文物”级别的,诞生于19世纪初,因为傅里叶他老人家生于1768年,死于1830年。
但傅里叶级数在数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学等领域都有着广泛的应用,这不由得让人肃然起敬。
一打开《信号与系统》、《锁相环原理》等书籍,动不动就跳出一个“傅里叶级数”或“傅里叶变换”,弄一长串公式,让人云山雾罩。
如下就是傅里叶级数的公式:不客气地说,这个公式可以说是像“臭婆娘的裹脚布——又臭又长”,而且来历相当蹊跷,不知那个傅里叶什么时候灵光乍现,把一个周期函数f(t)硬生生地写成这么一大堆东西。
单看那个①式,就是把周期函数f(t)描述成一个常数系数a0、及1倍ω的sin和cos函数、2倍ω的sin和cos函数等、到n倍ω的sin和cos函数等一系列式子的和,且每项都有不同的系数,即An和Bn,至于这些系数,需要用积分来解得,即②③④式,不过为了积分方便,积分区间一般设为[-π, π],也相当一个周期T的宽度。
能否从数学的角度推导出此公式,以使傅里叶级数来得明白些,让我等能了解它的前世今生呢?下面来详细解释一下此公式的得出过程:1、把一个周期函数表示成三角级数:首先,周期函数是客观世界中周期运动的数学表述,如物体挂在弹簧上作简谐振动、单摆振动、无线电电子振荡器的电子振荡等,大多可以表述为:f(x)=A sin(ωt+ψ)这里t表示时间,A表示振幅,ω为角频率,ψ为初相(与考察时设置原点位置有关)。
然而,世界上许多周期信号并非正弦函数那么简单,如方波、三角波等。
傅叶里就想,能否用一系列的三角函数An sin(nωt+ψ)之和来表示那个较复杂的周期函数f(t)呢?因为正弦函数sin可以说是最简单的周期函数了。
于是,傅里叶写出下式:(关于傅里叶推导纯属猜想)这里,t是变量,其他都是常数。
傅里叶变换数学推导

傅里叶变换数学推导傅里叶变换是一种重要的数学工具,广泛应用于信号处理、图像处理、通信等领域。
它可以将一个函数表示成频域上的复指数函数的线性组合,从而方便进行频域分析。
本文将从数学推导的角度,介绍傅里叶变换的基本概念和推导过程。
傅里叶变换基本概念傅里叶变换的基本概念是将一个信号函数表示成频域上的复指数函数的线性组合。
假设一个连续函数f(t)的时域表示为:f(t) = A*cos(ωt + φ)其中,A表示信号的幅度,ω表示信号的角频率,φ表示信号的相位。
根据欧拉公式,可以将cos函数表示为复指数函数的形式:f(t) = Re{A*e^(j(ωt + φ))}其中,e^(jx)表示复指数函数cos(x) + jsin(x)。
通过将函数f(t)表示成复指数函数的线性组合,可以方便地进行频域分析。
傅里叶变换的定义对于一个连续函数f(t),其傅里叶变换F(ω)定义为:F(ω) = ∫[f(t)*e^(-jωt)] dt其中,∫表示积分运算,e^(-jωt)表示复指数函数。
傅里叶变换F(ω)表示了函数f(t)对于不同频率的分量的贡献。
傅里叶变换的逆变换傅里叶变换的逆变换表示了频域上的复指数函数的线性组合如何反变换到时域上的函数。
对于一个频域上的复指数函数F(ω),其逆变换f(t)定义为:f(t) = (1/2π) * ∫[F(ω)*e^(jωt)] dω其中,(1/2π)是归一化系数,确保了逆变换的结果在时域上的幅度与原始函数一致。
傅里叶变换的性质傅里叶变换具有多种重要的性质,包括线性性、位移性、尺度性、卷积性等。
这些性质使得傅里叶变换成为分析和处理信号的有力工具。
线性性是指傅里叶变换对线性运算的保持。
例如,对两个函数的线性组合进行傅里叶变换,等于对每个函数分别进行傅里叶变换,并且将结果线性组合。
位移性是指傅里叶变换对信号的时移不变性。
即,对于一个函数f(t)进行傅里叶变换后得到F(ω),若将函数f(t)进行时间位移,即变为f(t - θ),则其傅里叶变换结果为e^(-jωθ)*F(ω)。
傅里叶级数的推导

傅里叶级数的推导2016年12月14日09:27:47傅里叶级数的数学推导首先,隆重推出傅里叶级数的公式,不过这个东西属于“文物”级别的,诞生于19世纪初,因为傅里叶他老人家生于1768年,死于1830年。
但傅里叶级数在数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学等领域都有着广泛的应用,这不由得让人肃然起敬。
一打开《信号与系统》、《锁相环原理》等书籍,动不动就跳出一个“傅里叶级数”或“傅里叶变换”,弄一长串公式,让人云山雾罩。
如下就是傅里叶级数的公式:不客气地说,这个公式可以说是像“臭婆娘的裹脚布——又臭又长”,而且来历相当蹊跷,不知那个傅里叶什么时候灵光乍现,把一个周期函数f(t)硬生生地写成这么一大堆东西。
单看那个①式,就是把周期函数f(t)描述成一个常数系数a0、及1倍ω的sin和cos函数、2倍ω的sin和cos函数等、到n倍ω的sin和cos函数等一系列式子的和,且每项都有不同的系数,即An和Bn,至于这些系数,需要用积分来解得,即②③④式,不过为了积分方便,积分区间一般设为[-π, π],也相当一个周期T的宽度。
能否从数学的角度推导出此公式,以使傅里叶级数来得明白些,让我等能了解它的前世今生呢?下面来详细解释一下此公式的得出过程:1、把一个周期函数表示成三角级数:首先,周期函数是客观世界中周期运动的数学表述,如物体挂在弹簧上作简谐振动、单摆振动、无线电电子振荡器的电子振荡等,大多可以表述为:f(x)=A sin(ωt+ψ)这里t表示时间,A表示振幅,ω为角频率,ψ为初相(与考察时设置原点位置有关)。
然而,世界上许多周期信号并非正弦函数那么简单,如方波、三角波等。
傅叶里就想,能否用一系列的三角函数An sin(nωt+ψ)之和来表示那个较复杂的周期函数f(t)呢?因为正弦函数sin可以说是最简单的周期函数了。
于是,傅里叶写出下式:(关于傅里叶推导纯属猜想)这里,t是变量,其他都是常数。
傅里叶级数到傅里叶变换的推导过程

傅里叶级数到傅里叶变换的推导过程1傅里叶级数和傅里叶变换的概念傅里叶级数和傅里叶变换都是描述信号的频域特性的数学工具。
在介绍它们两个之间的关系之前,先介绍一下它们各自的概念。
傅里叶级数是指把一个周期信号表示为一系列不同频率的正弦波的叠加。
具体的说,如果一个周期为T的信号x(t)可以表示为如下的级数:$$x(t)=a_0+\sum_{n=1}^{\infty}\left[a_n\cos\left(\frac{2\pi n}{T}t\right)+b_n\sin\left(\frac{2\pi n}{T}t\right)\right]$$其中,$a_0$是信号的平均值,$a_n$和$b_n$分别是信号在频率为$n/T$和$-n/T$处的振幅和相位。
傅里叶级数中出现的每一个正弦波都被称为信号的一个频率分量或者傅里叶系数。
傅里叶变换是一种将信号转换到频域的方法。
它的基本思想是把一个非周期信号表示为无数个不同频率的正弦波的叠加。
具体的说,如果一个信号x(t)的傅里叶变换为$X(j\omega)$,则:$$X(j\omega)=\int_{-\infty}^{\infty}x(t)e^{-j\omega t}dt$$其中,$j$是虚数单位,$\omega$是频率。
傅里叶变换中的$X(j\omega)$表示信号在频率为$\omega$处的振幅和相位,也被称为信号的频谱。
2傅里叶级数和傅里叶变换的关系傅里叶级数和傅里叶变换的关系可以用极限的概念来描述。
具体的说,傅里叶变换可以看作是傅里叶级数在频率连续、周期趋于无穷的情况下的一种极限表达形式。
为了更好地理解这个关系,我们可以先从傅里叶级数开始推导。
假设一个周期为T的信号x(t)的傅里叶系数为$a_n$和$b_n$,则有:$$a_n=\frac{1}{T}\int_{0}^{T}x(t)\cos\left(\frac{2\pi n}{T}t\right)dt,\quad b_n=\frac{1}{T}\int_{0}^{T}x(t)\sin\left(\frac{2\pin}{T}t\right)dt$$将傅里叶级数中的$a_n$和$b_n$代入,可以得到:$$x(t)=\lim_{N\rightarrow\infty}\sum_{n=-N}^{N}\left[\frac{1}{T}\int_{0}^{T}x(\tau)e^{-j\frac{2\pin}{T}\tau}d\tau\right]e^{j\frac{2\pi n}{T}t}$$这个式子就是傅里叶级数的频域表达形式,其中的求和符号表示对所有不同的$n$值求和,而求和的范围在$-N$到$N$之间。
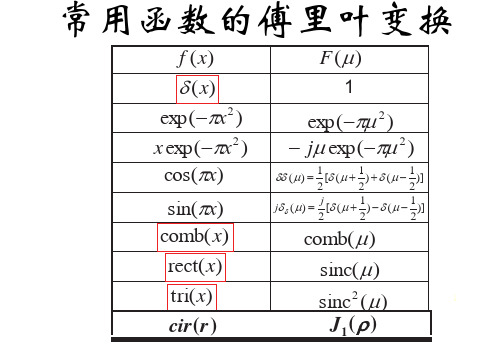
常用傅里叶变换+定理+各种变换规律(推荐)
√
√
f
(t )
=
⎪⎧1 ⎨
−
t
⎪⎩
τ, t 0, t
<τ >τ
τSa 2
ωτ (
)
2
W Sa2 (Wt )
2π
2
F
(ω
)
=
⎪⎧1 ⎨
−
ω
⎪⎩
W,ω <W 0, ω > W
√ e−atu(t), Re{a} > 0
e −a t , Re{a} > 0 √
e−at cosω0tu(t), Re{a} > 0 √
)
√
时域微 分性质 时域积 分性质
√ 时域卷
积性质
√ 对称性
d f (t) dt
∫t f (τ )dτ −∞
f (t) * h(t)
f (−t) f * (t)
f * (−t)
jωF (ω)
F(ω) + πF (0)δ (ω) jω F (ω)H (ω)
F (−ω) F * (−ω ) F * (ω )
−∞ 1/ 2
= ∫ exp(− j2πux)dx
rect
x a
=
1, 0,
−1/ 2
=1
1/2
exp(− j2πux)
− j2πu
-1/2
= sin(πu) πu
结论:
x ≤a 2
其它
= sinc(u) rect(x) F.T. sinc(u)
5
普遍型
F
rect
x a
= a sin(πau) πau
2
2
2
+∞
2π ∑ Fkδ (ω − kω0 ) k =−∞
常用的傅里叶变换拉普拉斯变换Z变换及其性质

Y (e jw ) = X (e jw ) H (e jw )
π
−π
X (e jθ ) H (e j ( ω−θ) )dθ
2
n=−∞
x ( n)
∞
2
=
1 2π
π
−π
X (e jω ) dω
周期信号 f (t ) 的傅里叶变换是由一些冲激函数组成的,这些冲激位于信号的谐频
f (t)为实函数, 若f (t), 则 6)能量积分 [f(t)] dt = 1 2π
F (ω)F (ω)dω =
|F(ω)| dω =
1 2π
S(ω)dω
S(ω) = |F(ω)| 称为能量密度函数(或能量密度) 7.卷积 1)定义 f (τ)f (t − τ)dτ称为f (t),f (t)的卷积,记为f (t) ∗ f (t) 2)定理 f (t) ∗ f (t) = f (t) ∗ f (t) |f (t) ∗ f (t)|≤ |f (t)| ∗ |f (t)| f (t) ∗ [f (t) + f (t) = f (t) ∗ f (t) + f (t) ∗ f (t) ℱ [F(ω)] ℱ[f (t) ∗ f (t)] = F (ω) · F (ω) ℱ[f (t) · f (t)] = 1 F (ω) ∗ F (ω) 2π ℱ[f (t) ∗ f (t) ∗···∗ f (t)] = F (ω) · F (ω) ··· F (ω) 1 2π F (ω) ∗ F (ω) ∗···∗ F (ω)
L[ f (t )dt ] =
一般形式 3 积分定理
L[ f (t )(dt ) 2 ] =
详解傅里叶变换公式

详解傅里叶变换公式傅里叶变换(Fourier Transform)是一种将时域信号转换到频域信号的数学方法。
它可以将一个信号分解为不同频率的正弦波之和,从而揭示信号的频率结构。
傅里叶变换在信号处理、图像处理、通信、物理学等领域具有广泛的应用。
首先,我们要理解时域(Time Domain)和频域(Frequency Domain)的概念。
1. 时域:在时域中,信号表示为时间轴上的函数,例如:```f(t) = A * cos(2 * π* t) + B * sin(2 * π* t)```在这个例子中,f(t) 是一个正弦波函数,t 是时间。
2. 频域:在频域中,信号表示为频率轴上的函数,例如:```F(ω) = A * cos(2 * π* ω) + B * sin(2 * π* ω)```在这个例子中,F(ω) 是一个正弦波函数,ω是频率。
傅里叶变换可以将时域信号转换为频域信号,公式如下:```F(ω) = ∫_{-∞}^{∞} f(t) e^(-jωt) dt```其中,F(ω) 是频域信号,ω是频率,t 是时间,j 是虚数单位,e 是自然对数的底数。
傅里叶变换的逆变换公式如下:```f(t) = ∫_{-∞}^{∞} F(ω) e^(jωt) dω```现在,我们来通过一个简单的例子来说明傅里叶变换。
假设我们有一个正弦波信号,如下所示:f(t) = A * sin(2 * π* t) + B * sin(2 * π* t + π/4)```我们可以使用傅里叶变换将其转换为频域信号,如下所示:```F(ω) = A * cos(2 * π* ω) + B * cos(2 * π* ω+ π/2)```通过傅里叶变换,我们可以看到信号中包含的主要频率成分。
例如,在这个例子中,我们可以看到信号主要包含两个频率成分:一个是A = 1,ω= π/2 的正弦波,另一个是B = 1,ω= π/4 的正弦波。
傅立叶变换的推导

f0t)
1 2
(e
j 2
f0t
e
j 2
f0t )
F( f
)
1 2
[
(
f
f0) ( f
f0)]
8,矩形窗函数 文档仅供参考,如有不当之处,请联系改正。
f (t) GT (t)
A 0
T 2
t
T 2
other
F(
f
)
f
(t)e j2
ftdt
T
2
T 2
Ae j2
ftdt
A
j2
f
(e
j 2
f
T 2
1 T
T
2
T 2
f (t)e jn1tdt
T
两边同乘T,得:T F
(n1)
2
T 2
f (t)e jn1tdt ,其中
T
2
当 T
时,1
2
T
0
n1
∴
2 1
F (n1)
f (t)e jtdt
令 F()
2 1
F(n,1) 则
F (
)
f
(t)e jtdt
f
(t)
n
F (n1) 1
e
j
n1t 1
6,傅里叶变换旳推导 文档仅供参考,如有不当之处,请联系改正。
a0 an (e jn1t e jn1t ) bn (e jn1t e jn1t )
2 n1 2
2j
a0 2
(
an
n1
jbn )e jn1t 2
( an
jbn 2
)e jn1t
令 F(n1)
傅里叶变换基本公式

傅立叶变换是一种数学工具,用于将函数分解为其组成频率。
它是信号处理中的一个基本概念,具有广泛的应用,包括图像处理、数据压缩和通信系统。
傅里叶变换的基本公式由下式给出:
F(w) = ∫f(t)e^(-iwt)dt
在这个公式中,F(w) 是函数f(t) 的傅里叶变换,w 是频率。
符号∫表示积分,符号e^(-iwt)是复指数函数。
用于从其频率分量重建原始函数的逆傅里叶变换由下式给出:
f(t) = (1/2π) ∫F(w)e^(iwt)dw
式中,f(t)为原函数,F(w)为函数的傅里叶变换。
符号∫表示积分,符号e^(iwt)是复指数函数。
傅立叶变换具有许多重要的性质,例如线性、移位不变性和卷积定理,这使其成为分析和处理信号的强大工具。
它是许多领域广泛使用的技术,包括工程、物理和数学。
傅里叶变换简表

傅里叶变换简表
傅里叶变换(Fourier Transform)是一种将信号从时域(时间域)转换到频域(频率域)的数学方法。
傅里叶变换在信号处理、图像处理、通信等领域都有广泛的应用。
下面是傅里叶变换的简表:
傅里叶变换函数:
傅里叶变换F(k) = ∫[f(x) * e^(-2πikx)] dx
反变换函数:
反傅里叶变换f(x) = ∫[F(k) * e^(2πikx)] dk
常见信号的傅里叶变换:
1. 矩形函数(方波)的傅里叶变换:
F(k) = T * sin(πkT) / (πk)
2. 三角波的傅里叶变换:
F(k) = 2AT * sinc(2πATk)
3. 周期函数的傅里叶级数展开:
f(x) = a0 + Σ(an * cos(nωt) + bn * sin(nωt))
4. 高斯函数的傅里叶变换:
F(k) = σ * sqrt(2π) * e^(-π^2σ^2k^2)
5. 常见频率域运算的傅里叶变换:
a. 时移:f(x - x0) 的傅里叶变换F(k) * e^(2πikx0)
b. 频移:e^(2πik0x) 的傅里叶变换 F(k - k0)
c. 放大:f(ax) 的傅里叶变换 F(k/a) / a
d. 缩小:f(bx) 的傅里叶变换 F(k/b) * b
这只是一些傅里叶变换的简单例子,实际上傅里叶变换的应用十分广泛,还有很多复杂的数学关系和公式。
需要根据具体的问题和需求来进行深入研究和学习。
快速傅里叶变换(FFT)的原理及公式
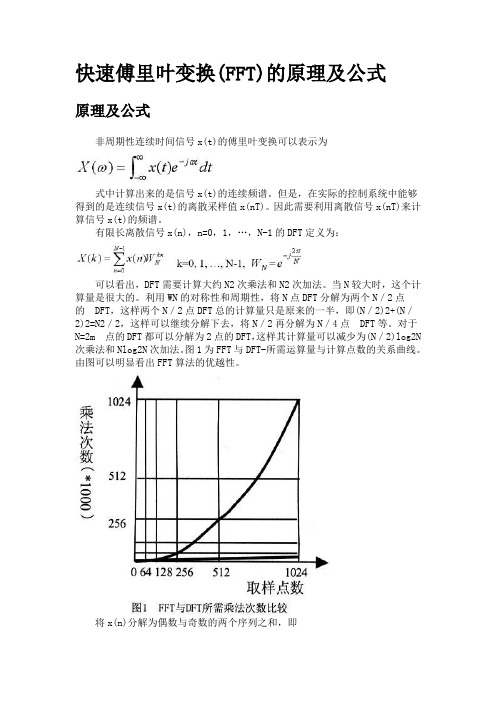
快速傅里叶变换(FFT)的原理及公式原理及公式非周期性连续时间信号x(t)的傅里叶变换可以表示为式中计算出来的是信号x(t)的连续频谱。
但是,在实际的控制系统中能够得到的是连续信号x(t)的离散采样值x(nT)。
因此需要利用离散信号x(nT)来计算信号x(t)的频谱。
有限长离散信号x(n),n=0,1,…,N-1的DFT定义为:可以看出,DFT需要计算大约N2次乘法和N2次加法。
当N较大时,这个计算量是很大的。
利用WN的对称性和周期性,将N点DFT分解为两个N/2点的DFT,这样两个N/2点DFT总的计算量只是原来的一半,即(N/2)2+(N/2)2=N2/2,这样可以继续分解下去,将N/2再分解为N/4点DFT等。
对于N=2m点的DFT都可以分解为2点的DFT,这样其计算量可以减少为(N/2)log2N 次乘法和Nlog2N次加法。
图1为FFT与DFT-所需运算量与计算点数的关系曲线。
由图可以明显看出FFT算法的优越性。
将x(n)分解为偶数与奇数的两个序列之和,即x1(n)和x2(n)的长度都是N/2,x1(n)是偶数序列,x2(n)是奇数序列,则其中X1(k)和X2(k)分别为x1(n)和x2(n)的N/2点DFT。
由于X1(k)和X2(k)均以N/2为周期,且WN k+N/2=-WN k,所以X(k)又可表示为:上式的运算可以用图2表示,根据其形状称之为蝶形运算。
依此类推,经过m-1次分解,最后将N点DFT分解为N/2个两点DFT。
图3为8点FFT的分解流程。
FFT算法的原理是通过许多小的更加容易进行的变换去实现大规模的变换,降低了运算要求,提高了与运算速度。
FFT不是DFT的近似运算,它们完全是等效的。
关于FFT精度的说明:因为这个变换采用了浮点运算,因此需要足够的精度,以使在出现舍入误差时,结果中的每个组成部分的准确整数值仍是可辨认的。
为了FFT的舍入误差,应该允许增加几倍log2(log2N)位的二进制。
傅里叶变换超详细总结

“周期信号都可表示为谐波关系的正弦信号的加权”——傅里叶的第一个主要论点——“非周期信号都可用正弦信号的加权积分表示”——傅里叶的第二个主要论点——频域分析:傅里叶变换,自变量为 j Ω复频域分析:拉氏变换,自变量为 S = σ +j ΩZ域分析:Z 变换,自变量为z傅立叶级数是一种三角级数,它的一般形式是)sin cos (10t n b t n a A n n n ωω++∑∞=将周期性的(非正弦的)波,用一系列的正弦波的迭加来表示,然后对每一项正弦波进行分析,因此提出了把周期函数 f(x) 展开成三角级数01()sin()n n n f t A A n t ωϕ∞==++∑01(cos sin )n n n A a n t b n t ωω∞==++∑为了讨论如何把周期函数展开成三角级数,首先考虑三角函数系的正交性。
{}1,cos ,sin ,cos 2,sin 2,,cos ,sin ,t t t t n t n t ωωωωωω⋯⋯正交性:不同的基本单位向量的点积(内积)等于零,而相同的基本单位向量不等于零傅里叶变换•周期信号的傅里叶级数分析(FS)•非周期信号的傅里叶变换(FT)•周期序列的傅里叶级数(DFS)•非周期的离散时间信号的傅里叶变换(DTFT)•离散傅里叶变换(DFT)1 周期信号的傅里叶级数分析(FS)三角函数集是最重要的基本正交函数集,正、余弦函数都属是三角函数集。
优点:(1)三角函数是基本函数;(2)用三角函数表示信号,建立了时间与频率两个基本物理量之目的联系;(3)单频三角函数是简谐信号,简谐信号容易产生、传输、处理;(4)三角函数信号通过线性时不变系统后,仍为同频三角函数信号,仅幅度和相位有变化,计算方便。
由于三角函数的上述优点,周期信号通常被表示(分解)为无穷多个正弦信号之和。
利用欧拉公式还可以将三角函数表示为复指数函数,所以周期函数还可以展开成无穷多个复指数函数的之和,其优点是与三角函数级数相同。
信号公式汇总之傅里叶变换

信号公式汇总之傅⾥叶变换傅⾥叶级数其中: 合并同频项:其中:指数形式:其中:帕塞⽡尔定理:傅⾥叶变换正变换:逆变换:基本信号的傅⾥叶变换:信号类型傅⾥叶变换单边指数: 双边指数: 门信号: 符号函数: 冲激函数: 常数1: 冲激偶:阶跃函数:性质:f (t )=a +0[a cos (n ωt )+b sin (n ωt )]n =1∑∞n 1n 1a =0f (t )dtT 11∫t 0t +T 01a =n f (t )⋅T 12∫t 0t +T 01cos (n ωt )dt1b =n f (t )⋅T 12∫t 0t +T 01sin (n ωt )dt1f (t )=A +0A sin (n ωt +φ)∑n =1∞n 1n A =0a ,A =0n ,φ=a +b n 2n 2n arctan b na nf (t )=F ⋅e ∑n =−∞∞njn ωt1F =n f (t )e dt =T 11∫t 0t +T 01−jn ωt 1(a −21n jb )=n e ,φ=21a +b n 2n 2j φn n arctan (−)a n b nP =∣F ∣∑n =−∞∞n 2F (j ω)=F [f (t )]=f (t )e dt ∫−∞∞−j ωt f (t )=F [F (j ω)]=−1F (j ω)e d ω2π1∫−∞∞j ωt eε(t )←−αt→α+j ω1e −αt (绝对值)←→α+ω222αg (t )τ←→τSa ()2ωτsgn (t )←→j ω2δ(t )←→11←→2πδ(ω)δ′(t )←→j ωε(t )←→πδ(ω)+j ω1线性: 对称性: 尺度变换: 虚实特性: 位移:时移: 频移: ==>==>推导:傅⾥叶变换:=由冲激函数性质 =卷积:时域卷积: 频域卷积:微积分:时域: 频域:欧拉公式:a f (t )+11a f (t )22←→a F (ω)+11a F (ω)22F (t )←→2πf (−ω)f (at )←→F (j )∣a ∣1a ωF (ω)=R (ω)+jX (ω),R (ω)偶,X (ω)奇f (t )实偶,F (ω)实偶;f (t )实奇,F (ω)虚奇f (t −t )0←→F (j ω)e =−j ωt 0>δ(t −t )0←→e −j ωt 0f (t )e j ωt 0←→F [j (ω−ω)]=0>e j ωt 0←→2πδ(ω−ω)0={cos ωt =(e +e )021j ωt −j ωt sin ωt =(e −e )02j 1j ωt j ωt>{f (t )cos (ωt )←→[F (ω−ω)+F (ω+ω)]02100f (t )sin (ωt )←→[F (ω−ω)+F (ω+ω)]02j 100{cos ωt ←→π[δ(ω−ω)+δ(ω+ω))]000sin ωt ←→[δ(ω−ω)−δ(ω+ω))]0j π00调制定理:若信号f (t )乘以cos ωt 或sin ωt ,等效于f (t )的频谱⼀分为⼆,沿数轴向左或向右各平移ω000f (t )⋅Cos (ωt )0F (j ω)∗2π1π[δ(ω+ω)+0δ(ω−ω))]0F (j ω)∗21δ(ω+ω)+0F (j ω)∗21δ(ω−ω)0f (t )∗δ(t −t )=0f (t −t )0F (j (ω+21ω))+0F (j (ω−21ω)0f (t )∗1f (t )←2→F (ω)⋅1F (ω)2f (t )⋅1f (t )←2→F (ω)∗2π11F (ω)2{微分:←→j ωF (j ω)dt df (t )积分:f (τ)d τ←→F (j ω)+πF (0)δ(ik ω)∫−∞t j ω1{微分:−jtf (t )←→d ωdF (j ω)积分:←→F (x )dx−jt f (t )∫−∞ωe =j θcos θ+jsin θ==>{e =cos ωt +jsin ωt j ωt e=cos ωt −jsin ωt−j ωt ==>{cos (n ωt )=2e +e jn ωt −jn ωtsin (n ωt )=2je −e jn ωt −jn ωt阶跃信号和冲激信号:冲激函数:加权特性: 抽样特性: 尺度变换:冲激偶:抽样特性: 加权特性: 卷积运算:性质:微分: 积分: 微积分: =======> 交换律: 分配律: 结合律: 与冲激函数、冲激偶、阶跃函数 冲激函数: 冲激偶: 阶跃函数: (与阶跃函数卷积就是变上限积分,阶跃函数是个理想的积分器)时移特性:f (t )δ(t )=f (0)δ(t ),f (t )δ(t −t )=0f (t )δ(t −0t )0f (t )δ(t )dt =∫−∞∞f (0)δ(t )dt =∫−∞∞f (0)f (t )δ(t −∫−∞∞t )dt =0f (t )0δ(at )=δ(t ),δ(at −∣a ∣1t )=0δ(t −∣a ∣1)a t 0f (t )δ′(t )dt=∫−∞∞f (t )δ(t )−∣−∞∞δ(t )f ′(t )dt =∫−∞∞−δ(t )f ′(0)dt=∫−∞∞−f ′(0)f (t )δ′(t )=f (0)δ′(t )−f ′(0)δ(t )f (t )δ′(t −t )=0f (t )δ′(t −0t )−0f ′(t )δ(t −0t )0f (t )=f (t )∗1f (t )=2f (τ)f (t −∫−∞∞12τ)d τf (t )=f ′(t )∗1f (t )=2f (t )∗1f ′(t )2f (t )=−1f (t )∗1−1f (t )=2f (t )∗1f (t )2−1f (t )=f (t )∗1−1f ′(t )=2f (t )∗1f (t )2f (t )=(i )f (t )∗1(j )f (t )2(i −j )f (t )∗1f (t )=2f (t )∗2f (t )1f (t )∗1[f (t )+2f (t )]=3f (t )∗1f (t )+2f (t )∗1f (t )3==>并联系统h (t )=h (t )+1h (t )2[f (t )∗1f (t )]∗2f (t )=3f (t )∗1[f (t )∗2f (t )]3==>串联系统h (t )=h (t )∗1h (t )2δ(t )f (t )∗δ(t )=f (t )f (t )∗δ(t −t )=0f (t −t )0f (t −t )∗1δ(t −t )=2f (t −t )∗2δ(t −t )=1f (t −t −1t )2δ′(t )f (t )∗δ′(t )=f ′(t )∗δ(t )=f ′(t )f (t )∗δ′′(t )=f ′′(t )∗δ(t )=f ′′(t )ε(t )f (t )∗ε(t )=f (t )∗δ(t )=−1f (t )=−1f (τ)d τ∫−∞tf (t )∗ε(t −t )=0f (τ−∫−∞tτ)d τ=0f (τ)d τ∫−∞t −t 0f (t −1t )∗1f (t −2t )=2f (t −t −1t )2。
傅里叶变换

则X (t )的频谱函数形状与 x t 形状相同, t f .
尺度改变: F[ x(kt )] X , F x X (kf ) k k k k
1 f
1
t
证明: F[ x(kt )] x(kt )e j2πft dt
2 bn T
T 2 T 2
x sin n1tdt
傅里叶级数表达法——复指数形式:
1 jn1t cos n1t (e e jn1t ) 2
1 jn1t jn1t sin n1t (e e ) 2j
x(t )
n
X n e jn1t
1 T X n 2T x(t )e jn1t dt T 2
双边指数信号幅度和相位:
X ( ) 2 2 a 0 2a
f t
矩形信号: E t / 2 x(t ) 0 t / 2
E——脉高:即矩形脉冲的高度
E
2 O
2
t
τ ——脉宽:即矩形脉冲的宽度(非零区间的宽度) 傅里叶变换为:
x(t )e jt dt e jt d x(t )e j2 ft dt e j2 ft d(2 f )
x(t )e j2 ft dt e j2 ft df
正变换: X ( f ) F[ x(t )] 逆变换: x(t ) F 1[ X ( f )]
0 t t 0 (t t0 ) t t 0
傅里叶变换公式及知识点笔记

傅里叶变换公式及知识点笔记
●时移时域的部分少,复指数符号和时移部分相同
●频移频域部分少,指数符号和频域移动的符号不同,注意就是w前面的系数,别搞错了
●一个域的共轭对应于一个域的翻转后共轭,所以实信号x(t)=x*(t)可以推出x(jw)=x*(-jw);实偶信号是x(t)=x*(t)=x(-t)它的傅里叶变换也是实偶对称函数,实奇函数
x(t)=x*(t)=-x(-t),傅里叶变换是纯虚奇函数
●可以联想一下S域和Z域,积分器和微分器那一部分
●
●tj导时域乘以t频域乘以j然后就是频域的微分
●
●
●可以用来进行们函数推导出Sa(t)函数,
●
●时域相乘频域卷积,不要遗漏2Π
●不要遗漏2Π。
