【精品】高考三视图强化训练30题
高考三视图(含解析)理试题汇总(精编文档).doc

【最新整理,下载后即可编辑】专题21 三视图1.某几何体的三视图如图所示,则其表面积为()A.2π B.3π C.4π D.5π【答案】B点睛:1、首先看俯视图,根据俯视图画出几何体地面的直观图;2、观察正视图和侧视图找到几何体前、后、左、右的高度;3、画出整体,然后再根据三视图进行调整.2.已知三棱锥的正视图与俯视图如图所示,俯视图是边长为2的正三角形,则该三棱锥的侧视图可能为( )A.B.C.D.【答案】B【解析】由正视图和俯视图还原几何体如图所示,由正视图和俯视图对应线段可得2⊥平面时,BC=2,===,当BC ABDAB BD AD∆的边AB上的高为3,只有B选项符合,当BC不垂直平面ABD ABD时,没有符合条件的选项,故选B.点睛:1.解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图.2.三视图中“正侧一样高、正俯一样长、俯侧一样宽”,因此,可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据3.某个长方体被一个平面所截,得到几何体的三视图如图所示,则这个几何体的体积为( )A . 4B . 22C .203 D . 8【答案】D4.如图,正三棱柱111ABC A B C 的主视图是边长为4的正方形,则此正三棱柱的左视图的面积为( )A . 16B . 23C . 43D . 83【答案】D点睛:三视图问题的常见类型及解题策略(1)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示.(2)由几何体的部分视图画出剩余的部分视图.先根据已知的一部分三视图,还原、推测直观图的可能形式,然后再找其剩下部分三视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合. (3)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.5.某几何体的三视图如图所示,则该几何体的体积为 ( )(A) 168π+ (B) 88π+ (C) 1616π+(D) 816π+【答案】A【解析】将三视图还原为原来的几何体,再利用体积公式求解.原几何体为组合体;上面是长方体,下面是圆柱的一半(如图所示), 其体积为21422241682V ππ=⨯⨯+⨯⨯=+.故选A;6.如图5,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的几条棱中,最长的棱的长度为( )(A) 62 (B) 42 (C) 6 (D)4【答案】C【解析】如图所示点睛:对于小方格中的三视图,可以放到长方体,或者正方体里面去找到原图,这样比较好找;7.某几何体的三视图如图所示,则该几何体的表面积为( )A.24π-B.24π+C.20π-D.20π+【答案】A8.已知某空间几何体的三视图如图所示,则该几何体的表面积是()A.B.C.D.【答案】A【解析】由三视图知:几何体为四棱锥,且四棱锥的一条侧棱与底面垂直,如图,平面,,,,,经计算,,,,∴,∴, ,,,∴,故选A .9.一个几何体由多面体和旋转体的整体或一部分组合而成,其三视图如图所示,则该几何体的体积是( )A .1π+B .2π+C .21π+D .3522π++【答案】A【解析】考点:由三视图求体积.10.如图是一个由两个半圆锥与一个长方体组合而成的几何体的三视图,则该几何体的体积为( )A .263π+B .83π+ C .243π+ D .43π+ 【答案】C【解析】试题分析:相当于一个圆锥和一个长方体,故体积为122221433ππ⋅+⋅⋅=+.考点:三视图.11.一个几何体的三视图如图所示,则该几何体的体积为( )A . 143B . 5C . 163D .6【答案】A【解析】考点:三视图.12.一个几何体的三视图如图所示,则该几何体的体积为____.【答案】13【解析】本题考查三视图、四棱锥的体积计算等知识,难度中等.由三视图可知该几何体是底面为长和高均为1的平行四边形,高为1的四棱锥,故其体积为11111V=⨯⨯⨯=.33。
高三专项训练:三视图练习题(一)
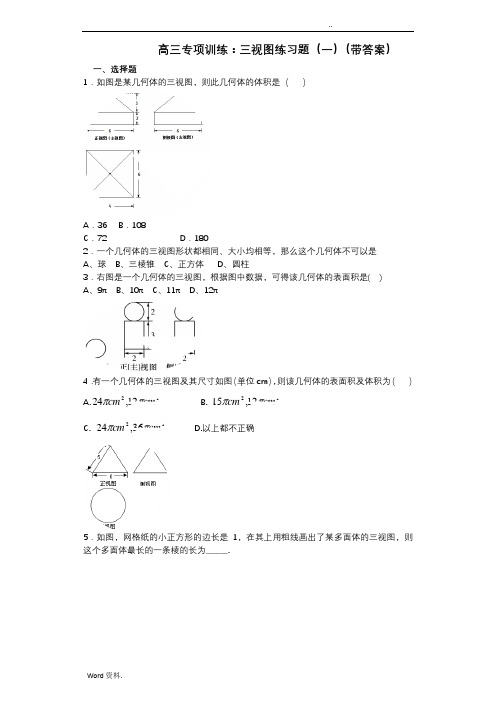
高三专项训练:三视图练习题(一)(带答案)一、选择题1.如图是某几何体的三视图,则此几何体的体积是( )A .36B .108C .72D .1802.一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是A 、球B 、三棱锥C 、正方体D 、圆柱3.右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )A 、9πB 、10πC 、11πD 、12π4.有一个几何体的三视图及其尺寸如图(单位cm ),则该几何体的表面积及体积为( )A.3212,24cm cm ππB. 3212,15cm cm ππC. 3236,24cm cm ππD.以上都不正确5.如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.A. B. CD .36.一空间几何体的三视图如图所示,则该几何体的体积为.A. B. C D. [7. 若某空间几何体的三视图如图所示,则该几何体的体积是A .13 B .23C .1D .28.右图是某几何体的三视图,则该几何体的体积为( )A . B.C. D.1362942π+3618π+9122π+9182π+正视图俯视图9.已知一个几何体的三视图如图所示,则该几何体外接球的表面积为( )A .43π B . 163π C .1912π D . 193π 10.某几何体的正视图如图所示,则该几何体的俯视图不可能的是11.已知某个几何体的三视图如图(主视图中的弧线是半圆),根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )cm 3.A .π+8B .328π+C .π+12D .3212π+侧视图主视俯视第8题图俯视图侧视图 正视图12.已知正六棱柱的底面边长和侧棱长均为2cm ,其三视图中的俯视图如图所示,则其左视图的面积是( )(A )243cm (B )223cm (C )28cm (D )24cm13.下图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )A .6πB .7πC .8πD .9π14.如右图所示,一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的表面积为 ( )A .π3B .π2C .π23 D .π4 15.如图是一个几何体的三视图,若它的体积是33,则图中正视图所标a=( )A .1B 3C 3D .316.已知某几何体的三视图如图所示(单位:cm ),其中正视图、侧视图都是等腰直角三角形,则这个几何体的体积是( )A .338cmB .3316cm C .33216cm D . 3332cm17.一个几何体的三视图如右图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积为A .B .C .D .18.若某空间几何体的三视图如图所示,则该几何体的体积是 ( )A.13 B. 23C. 1D. 2 俯视图侧视图正视图22119.某物体是空心的几何体,其三视图均为右图,则其体积为( )A 、8B 、43π C 、483π+ D 、483π- π12π34π3π312正视图 侧视图俯视图 正视第9题22 4 2侧视图 22俯视20.如图,水平放置的三棱柱ABC-A 1B 1C 1中,侧棱AA 1⊥平面A 1B 1C 1,其正视图是边长为a 的正方形.俯视图是边长为a 的正三角形,则该三棱柱的侧视图的面积为A .a 2B .a 2C a 2D 221.右图是一个几何体的三视图(侧视图中的弧线是半圆),则该几何体的表面积是( )A .20+3π B .24+3π C .20+4π D .24+4π22.一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积为A .12πB .π34C .3πD .π312.23.如右图为一个几何体的三视图,其中俯视图为正三角形,A 1B 1=2,AA 1=4,则该几何体的表面积为( )12正视图 侧视图 俯视图 AC A 11正视图 侧视图俯视图24.图1是设某几何体的三视图,则该几何体的体积为()A.942π+B.3618π+C.9122π+D.9182π+、25.已知某几何体的三视图如图所示,根据图中标注的尺寸(单位cm)可得该几何体的体积是()A.313cm B.323cmC.343cm D.383cm26.小红拿着一物体的三视图(如图所示)给小明看,并让小明猜想这个物件的形状是A. 长方形 B. 圆柱 C. 立方体 D. 圆锥27.一个几何体的三视图如图所示,则这个几何体的体积为()正视图侧视图俯视图332正视图俯视图图1AB .12C .32 D1+28.一个空间几何体的三视图如图(1)所示,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,则该几何体的体积和表面积分别为 ( )A 、64,48+B 、32,48+ C 、643,32+D 、332,48+29.若某多面体的三视图(单位: cm )如图所示,则此多面体的体积是( ) A .21cm 3 B .32cm 3 C .65cm 3 D .87cm 3正视图俯视图图(1)侧(左)视图 1111130.一个空间几何体的正视图、侧视图均是长为2、高为3的矩形,俯视图是直径为2的圆(如右图),则这个几何体的表面积为A .12π+B .7πC . π8D .π2031.(一空间几何体的三视图如图所示,则该几何体的体积为( ).A. B.C.D. 32.已知几何体其三视图(如图),若图中圆半径为1,等腰三角形腰为3,则该几何体表面积为 ( ) A .6π B .5π C.4π D.3π2π+4π+2π4π+正视侧视俯视俯视..A .2,23B .22,2D .2,434.如图,有一个几何体的正视图与侧视图都是底为6cm ,腰为5cm 的等腰三角形,俯视图是直径为6cm 的圆,则该几何体的体积为 ( )A .12πcm 3B .24πcm 3C .36πcm 3D .48πcm 335 (A )348cm (B )324cm (C )332cm (D )328cm36. 如图,直三棱柱的侧棱长和底面边长均为2,正视图和俯视图如图所示,则其侧视图的面积为 ( )A .4B .3C .32D .237.某四面体的三视图如下图所示,则该四面体的四个面中,直角三角形的面积和是_______.二、填空题 正视图 左视图俯视图正视图侧视图 俯视图 第6题 ·38.一个几何体的三视图如右图所示,主视图与俯视图都是一边长为3cm 的矩形,左视图是一个边长为2cm 的等边三角形,则这个几何体的体积为________.39.如图所示是一个几何体的三视图(单位:cm ),主视图和左视图是底边长为4cm ,腰长为22的等腰三角形,俯视图是边长为4的正方形,则这个几何体的表面积是-__________40.某几何体的三视图如图所示,则该几何体的体积的最大值为 .41.一正多面体其三视图如图所示,该正多面体的体积为___________.主视图 左视图俯视图3主视图 俯视图 侧视图42.若某几何体的三视图(单位:cm )如右图所示,则该几何体的体积为 cm 2.43.已知某几何体的三视图如图所示,其中侧视图是等腰直角三角形,正视图是直角三角形,俯视图ABCD 是直角梯形,则此几何体的体积为 ;44.某四面体的三视图如上图所示,该四面体四个面的面积中最大的是1正视图俯视图左视图45.一个几何体的三视图如右图所示(单位:),则该几何体的体积为__________46.一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则球的表面积是_____.47.如图,一个简单空间几何体的三视图其主视图与左视图都是边长为的正三角形,其俯视图轮廓为正方形,则其体积是_________.48. 某几何体的三视图如图所示,则它的体积是___________俯视图m 3m 249.设某几何体的三视图如图所示,则该几何体表面积是50.一个几何体的三视图如右图所示,正视图是一个边长为2的正三角形,侧视图是一个等腰直角三角形,则该几何体的体积为.三视图练习题(一)参考答案1.B【解析】此几何体是一个组合体,下面是一个正四棱柱上面是一个四棱锥.其体积为166********V =⨯⨯+⨯⨯⨯=.2.D【解析】圆的正视图(主视图)、侧视图(左视图)和俯视图均为圆; 三棱锥的正视图(主视图)、侧视图(左视图)和俯视图可以为全等的三角形; 正方体的正视图(主视图)、侧视图(左视图)和俯视图均为正方形; 圆柱的正视图(主视图)、侧视图(左视图)为矩形,俯视图为圆。
三视图练习题及答案

三视图练习题及答案三视图是工程设计、制图等领域中常用的表达方式之一,它能够以三个不同的视角展示一个物体的外观和内部结构,帮助人们更好地理解和分析物体的形状和构造。
为了提高对三视图的理解和应用能力,下面将给出一些三视图练习题及答案,希望对读者有所帮助。
1. 请根据给出的三视图,画出物体的立体图。
答案:根据三视图,我们可以确定物体的形状和尺寸,然后利用透视法将其转化为立体图。
在绘制过程中,需要注意比例和透视关系,以保证立体图的准确性。
2. 给出一个物体的立体图,请根据立体图绘制出相应的三视图。
答案:在绘制三视图时,我们需要观察立体图中的各个面,然后根据其相对位置和大小来绘制对应的正视图、俯视图和侧视图。
在绘制过程中,需要注意比例和尺寸的准确性,以确保三视图能够准确地表达立体图的形状和结构。
3. 请根据给出的三视图,判断物体的形状是什么?答案:通过观察三视图中的线条和面,我们可以判断物体的形状。
例如,如果正视图中的线条是直的,侧视图中的线条是弯曲的,那么物体可能是一个圆柱体。
通过观察三视图中的特征,我们可以逐步推断出物体的形状。
4. 给出一个物体的形状,请根据形状绘制出相应的三视图。
答案:在绘制三视图时,我们需要观察物体的形状和结构,然后根据其特征来绘制对应的正视图、俯视图和侧视图。
在绘制过程中,需要注意线条的粗细和长度,以确保三视图能够准确地表达物体的形状和结构。
通过以上的练习题和答案,我们可以提高对三视图的理解和应用能力。
练习三视图不仅可以帮助我们更好地理解和分析物体的形状和结构,还可以提高我们的制图能力和空间想象力。
在实际工程设计和制图中,三视图是非常重要的表达方式,掌握好三视图的绘制和解读技巧对于工程师和设计师来说是非常必要的。
总之,通过不断地练习和应用,我们可以提高对三视图的掌握程度,为工程设计和制图提供更准确、更有效的表达方式。
希望以上的练习题和答案能够对读者有所帮助,进一步提高对三视图的理解和应用能力。
三视图练习题含答案

23正视图侧视图2俯视图2第3题三视图练习题1.某几何体的三视图如图所示,则它的体积是( ) A.283π-B.83π-C.π28-D.23π2.某四棱锥的三视图如图所示,该四棱锥的表面积是( )A .32 B.16+162 C.48 D.16322+3.如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等边三角形,等腰三角形和菱形,则该几何体的体积为( ) A .43 B .4C .23 D .24.如图是某几何体的三视图,则该几何体的体积为( )A .942π+ B.3618π+C.9122π+D.9182π+ 5.一个空间几何体的三视图如图所示,则该几何体的表面积为( ) A. 48 B.32+817C.48+817D.806.若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是( ) A.35233cm B.32033cm C.22433cm D.16033cm3 32正视图侧视图俯视图第4题第5题第1题 第2题第6 题7.若某空间几何体的三视图如图所示,则该几何体的体积是( ) A.2B.1C.23D.138.某几何体的三视图如图所示,则该几何体的体积为( ) A.π816+ B.π88+ C.π1616+ D.π168+9. 某四棱台的三视图如图所示,则该四棱台的体积是( ) A.4 B.314 C.316D.610. 某三棱锥的三视图如图所示,已知该三视图中正视图和俯视图均为边长为2的正三角形,侧视图为如图所示的直角三角形,则该三棱锥的体积为( ) A .1B .3C .4D .511. 一个几何体的三视图如图所示,则这个几何体的体积为( )A .(8)36π+B .(82)36π+C .(6)36π+D .(92)36π+ 12.某几何体的底面为正方形,其三视图如图所示,则该几何体的体积等于( )A .1B .2C .3D .4第7题第8题第9题第10题3122第11题 211俯视图正视图13第12题13.某几何体的三视图如图所示,则其体积为______.14.若某几何体的三视图(单位:cm )如图所示,则此几何体的体积等于______3cm . 15.某几何体的三视图如图所示,则该几何体的体积是______.16.已知某三棱锥的三视图(单位:cm )如图所示,则该三棱锥的体积是 17.一个空间几何体的三视图如图所示,则这个空间几何体的体积是.18.如图所示,一个三棱锥的三视图是三个直角三角形,则该三棱锥外接球的表面积为19.若某空间几何体的三视图如下图所示,则该几何体的表面积是_______________.20.一个正方体的内切球与它的外接球的体积比是( ).A .1∶33B .1∶22C .1∶383 D .1∶4221.已知球面上A 、B 、C 三点的截面和球心的距离都是球半径的一半,且AB =BC =CA =2,则球表面积是( )A.π964 B. π38C. π4D. π916第17题 24 3正视图 侧视图 俯视图第18题 第15题第14题第13题第16题 第19题22. P 、A 、B 、C 是球O 面上的四点,且PA 、PB 、PC 的两两垂直,PA=PB=PC=9,则球心O 到截面ABC 的距离为23.半径为5的球被一个平面所截,截面面积为16π,则球心到截面的距离为 ( ) A.4 B.3 C.2.5 D.224.表面积为3π的圆锥,它的侧面展开图是一个半圆,则该圆锥的底面直径为________. 25.答案1.A2.B3.C4.D5.C6.B7.B8.A9.B 10.A 11.A 12.A 13.3π 14.24 15.1616-π 16.1 17.67π 18.29π 19. 20+8220.A 21.A 22.233 23.B 24. 2 25.︒9026.3500π 27.π628.π29 29.72 30. 3629+3226-31.2500π 32.π1200。
三视图高考试题集锦

三视图高考试题集锦work Information Technology Company.2020YEAR2立体几何——三视图高考试题集锦1.(14福建卷)某空间几何体的正视图是三角形,则该几何体不可能是 ( A )A .圆柱 B.圆锥 C.四面体 D.三棱柱2.(10年海南卷)正视图是一个三角形的几何体可以是_______(写出三种) 3(11山东卷)右图是长和宽分别相等的两个矩形,给定下列三个命题: ①存在三棱柱,其正(主)视图、俯视图如右图;②存在四棱柱,其正(主)视图、俯视图如右图;③存在圆柱,其正(主)视图、俯视图如右图。
其中真命题的个数是 (A) 3 (B) 2 (C) 1 (D) 04.(14辽宁)7.某几何体三视图如图所示,则该几何体的体积 为( )A .82π- B .8π- C .82π-D .84π-5.(12海南卷)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )()A 6 ()B 9 ()C 12 ()D 186.(14天津卷)已知一个几何体的三视图如图所示(单位:m ),则该几何体的体积为____3m .244242俯视图侧视图正视图俯视图正(主)视图(第4题)(第5题)(第6题)7.(13海南卷)一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到正视图可以为()(A) (B) (C) (D)8.(14湖北卷)在如图所示的空间直角坐标系xyzO 中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为()A.①和②B.③和①C. ④和③D.④和②9.(2014•浙江)某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是()A.90cm2B.129cm2C.132cm2D.138cm23410.(07海南文理)已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是( )A .334000cmB .338000cm C .20003cm D .40003cm(第9题) (第10题)11.(07山东文理)下列几何体各自的三视图中,有且仅有两个视图相同的是 ( )A .①②B .①③C .①④D .②④12.(08海南理)某几何体的一条棱长为7,在该几何体的正视图中,这条棱的投影是长为6的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a 的b 的线段,则b a 的最大值为( ) A .22 B .32 C .4 D .52201010202020正视图侧视图俯视图513.(09海南文理)一个棱锥的三视图如图,则该棱锥的全面积(单位:2cm )为( )A .21248+ B.22448+ C .21236+D .22436+14.(09山东文理)一空间几何体的三视图如图所示,则该几何体的体积为( )A .223π+B .423π+C .232π+D .234π+(第13题) (第14题)15.(11海南文理)在一个几何体的三视图中,正视图和俯视图如右图所示,则相应的侧视图可以为( )15.(10安徽文理)一个几个何体的三视图如图,该几何体的表面积为( )A.280 B.292 C.360 D.37216.(11湖南文理)如图是某几何体的三视图,则该几何体的体积为()A.912 2π+B.9182π+ C.942π+ D.3618π+(第15题)(第16题)20.(09辽宁文理)设某几何体的三视图如下(尺寸的长度单位为m)。
高中三视图练习(含答案97740

俯视侧(左)视24主(正)视图三视图专题练习:1.一个几何体的三视图如图所示,其中俯视图为正三角形,则该几何体的表面积为___________.2.一个几何体的三视图如下图所示, 则该几何体的表面积为______.3.如右图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的表面积为( ) A . π3 B . π2 C . π23 D . π44.右图是一个几何体的三视图,则该几何体 的体积为 ( ) A .6 B .8 C .16D .24正视图侧视图俯视图1223112231第3题图主视图俯视图左视图5.一空间几何体的三视图如图所示,则该几何体的体积为( ).A.223π+ B. 423π+ C. 323π+ D.2343π+6.一个棱锥的三视图如图,则该棱锥的全面积(单位:c2m)为(A)2(B)2(C)2(D)27.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是3cm.222正(主)视图22侧(左)视图俯视图8.设某几何体的三视图如下(尺寸的长度单位为m)。
则该几何体的体积为3m 9.如图是一个几何体的三视图,若它的体积是33,则a_______10.如右图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为12。
则该集合体的俯视图可以是11.右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是(A)9π (B )10π (C)11π (D)12π答案:1. 24+ 2. 2412π+ 3.A. 4.B 5.C. 6.A. 7.18. 8.4. 9.10.C 11.D注意第6题二项分布与超几何分布辨析山东 韩文文二项分布与超几何分布是两个非常重要的、应用广泛的概率模型,实际中的许多问题都可以利用这两个概率模型来解决.在实际应用中,理解并区分两个概率模型是至关重要的.下面举例进行对比辨析.例 袋中有8个白球、2个黑球,从中随机地连续抽取3次,每次取1个球.求: (1)有放回抽样时,取到黑球的个数X的分布列; (2)不放回抽样时,取到黑球的个数Y的分布列. 解:(1)有放回抽样时,取到的黑球数X可能的取值为0,1,2,3.又由于每次取到黑球的概率均为,3次取球可以看成3次独立重复试验,则1~35X B ⎛⎫⎪⎝⎭,.3031464(0)55125P X C ⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭∴;12131448(1)55125P X C ⎛⎫⎛⎫==⨯=⎪ ⎪⎝⎭⎝⎭; 21231412(2)55125P X C ⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭;333141(3)55125P X C ⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭.因此,X 的分布列为2.不放回抽样时,取到的黑球数Y可能的取值为0,1,2,且有:03283107(0)15C C P Y C ===;12283107(1)15C C P Y C ===;21283101(2)15C CP Y C ===.因此,Y 的分布列为辨析:通过此例可以看出:有放回抽样时,每次抽取时的总体没有改变,因而每次抽到某物的概率都是相同的,可以看成是独立重复试验,此种抽样是二项分布模型.而不放回抽样时,取出一个则总体中就少一个,因此每次取到某物的概率是不同的,此种抽样为超几何分布模型.因此,二项分布模型和超几何分布模型最主要的区别在于是有放回抽样还是不放回抽样.所以,在解有关二项分布和超几何分布问题时,仔细阅读、辨析题目条件是非常重要的.超几何分布和二项分布都是离散型分布 超几何分布和二项分布的区别:超几何分布需要知道总体的容量,而二项分布不需要; 超几何分布是不放回抽取,而二项分布是放回抽取(独立重复)当总体的容量非常大时,超几何分布近似于二项分布.........。
三视图练习题

三视图练习题一、基本概念题1. 请简述三视图的概念及其作用。
2. 三视图包括哪三个视图?分别表示物体的哪些信息?3. 在三视图中,主视图、俯视图和左视图之间的位置关系是怎样的?二、识图题(1)正方体(2)长方体(3)圆柱体(1)球体(2)圆锥体(3)圆环体(1)三棱柱(2)四棱锥(3)六棱柱三、绘图题(1)一个长方体,长、宽、高分别为10cm、6cm、4cm。
(2)一个圆柱体,底面直径为8cm,高为10cm。
(3)一个圆锥体,底面直径为6cm,高为8cm。
(1)一把直尺(2)一个手机(3)一个茶壶四、分析题(1)主视图为矩形,俯视图为圆形,左视图为矩形。
(2)主视图为三角形,俯视图为矩形,左视图为三角形。
(1)主视图、俯视图和左视图均为正方形。
(2)主视图、俯视图和左视图均为圆形。
五、应用题(1)主视图为长方形,长、宽、高分别为10cm、6cm、4cm。
(2)主视图为圆形,直径为8cm,高为10cm。
(1)一个长方体木箱,长、宽、高分别为60cm、40cm、20cm。
(2)一个圆柱形水桶,底面直径为40cm,高为50cm。
六、综合题(1)一个长方体上放置一个正方体。
(2)一个圆柱体和一个圆锥体组合在一起。
(1)一个长方体挖去一个圆柱体形成的组合体,长方体的长、宽、高分别为20cm、10cm、5cm,圆柱体直径为5cm,高为10cm。
(2)一个正方体和一个四棱锥组合在一起,正方体边长为8cm,四棱锥底面边长为6cm,高为4cm。
七、判断题1. 三视图中,主视图和俯视图的长度方向一定相同。
()2. 在三视图中,左视图的宽度方向与主视图的高度方向一致。
()3. 任何物体的三视图都可以通过旋转和翻转得到。
()八、选择题A. 主视图B. 俯视图C. 正视图D. 左视图A. 主视图B. 俯视图C. 左视图D. 所有视图A. 主视图反映了物体的长度和高度B. 俯视图反映了物体的长度和宽度C. 左视图反映了物体的宽度和高度D. 三视图中的每个视图都包含了物体的所有尺寸信息九、填空题1. 三视图是用于表达物体______、______和______三个方向尺寸的图样。
三视图高考题学生专用

三视图高考题(3)一、选择题1.以下关于几何体的三视图的论述中,正确的是( ).A.球的三视图总是三个全等的圆 B.正方体的三视图总是三个全等的正方形C.水平放置的正四面体的三视图都是正三角形 D.水平放置的圆台的俯视图是一个圆2. 设四面体的六条棱的长分别为1,1,1,1和a且长为a的棱异面,则a的取值范围是()(A)(B)(C)(D)3. 下列四个几何体中,几何体只有正视图和侧视图相同的是( )A.①② B.①③ C.①④ D.②④4.一个平面四边形的斜二测画法的直观图是一个边长为a的正方形,则原平面四边形的面积等于( ).A.24a2 B.22a2 C.22a2 D.223a25.将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图为( ).6.如下图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为12,则该几何体的俯视图可能是( ).7. 若某几何体的三视图如图所示,则这个几何体的直观图可以是( )9.一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如图所示,则该几何体的俯视图为________.10. 用单位正方体块搭一个几何体,使它的正视图和俯视图如图所示,则它的体积的最大值为________,最小值为________.11.如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为________.12.如果一个几何体的三视图如图所示,其中正视图中△ABC是边长为2的正三角形,俯视图为正六边形,那么该几何体的侧视图的面积为________.13.(2013山东文)一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如右图所示,则该四棱锥侧面积和体积分别是()A .45,8B .45,83C .4(5+1),83D .8,814.(2013四川理) 一个几何体的三视图如图所示,则该几何体的直观图可以是( )15.(2013四川文) 一个几何体的三视图如图所示,则该几何体可以是( )A .棱柱B .棱台C .圆柱D .圆台16.(2012新标) 如图,网格上小正方形的边长为1,粗线画出的是某几何体的三视图,则几何体的体积为A .6B .9C .12D .1817.(2013新标1) 某几何体的三视图如图所示,则该几何体的体积为A .168π+B .88π+C .1616π+D .816π+18.(2013新标2) 一个四面体的顶点在空间直角坐标系O -xyz 中的坐标分别是(1,1,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到正视图可以为( )19.(2012浙江文) 已知某三棱锥的三视图(单位:cm )如图所示,则该三棱锥的体积是A.1cm3B.2cm 3C.3cm 3D.6cm 320.(2014浙江) 某几何体的三视图(单位:cm )如图所示,则该几何体的体积是( )A. 372cm B. 390cm C. 3108cm D. 3138cm 21.(2012北京)某三棱锥的三视图如图所示,该三梭锥的表面积是( )A. 28+65B. 30+65C. 56+ 125D. 60+125 22.(2012湖北理) 已知某几何体的三视图如图所示,则该几何体的体积为A .8π3B .3πC .10π3D .6π23.(2013湖南理)已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能...等于A .1B .2 D .224.(2013湖南文)已知正方体的棱长为1,其俯视图是一个面积为1的矩形,则该正方体的正视图的面积等于____ ___A .B.1C.1225.(2014湖南)一块石材表示的几何何的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于A .1B .2C .3D .426.(2014辽宁)某几何体三视图如图所示,则该几何体的体积为( ) A .82π- B .8π- C .82π-D .84π-27.(2014四川文) 某三棱锥的侧视图、俯视图如图所示,则该三棱锥的体积是( )侧视图俯视图11222211A 、3B 、2 CD 、128.(2014新标2) 如图,网格纸上正方形小格的边长为1(表示1cm ),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm ,高为6cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )A. 1727B. 59C. 1027D. 1329.(2013浙江文) 已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是()A .108 cm 3B .100 cm 3C .92 cm 3D .84 cm 330.(2014江西理)一几何体的直观图如右图,下列给出的四个俯视图中正确的是( )。
三视图练习题

三视图练习题编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(三视图练习题)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为三视图练习题的全部内容。
29.2 三视图一、选择题(共15小题;共75分)1. 下列物体的主视图、俯视图和左视图不全是圆的是()A。
橄榄球B。
兵乓球C。
篮球D。
排球2. 如图,几何体的俯视图是A。
B。
C. D.3。
长方体的主视图与左视图如图所示(单位:),则其俯视图的面积是A。
B。
C. D.4. 如图所示,几何体的俯视图是A. B.C. D.5。
如图是有几个相同的小正方体组成的一个几何体.它的左视图是A. B.C。
D.6。
如图是由八个相同小正方体组成的几何体,则其主视图是A. B。
C。
D。
7. 桌面上放着个长方体和个圆柱体,按下图所示的方式摆放在一起,其左视图是A。
B。
与原题图不一样C. D.8. 下列几何体中,有一个几何体的俯视图的形状与其它三个不一样,这个几何体是( )A. B.C。
D。
9. 图中三视图所对应的直观图是A。
B.C。
D。
10. 如图是常用的一种圆顶螺杆,它的俯视图正确的是A。
B。
C。
D. 11. 如图的几何体的三视图是A。
B.C. D。
12。
如图是由一些相同的小正方体搭成的几何体的三视图,则构成这个几何体的小正方体的个数为A. 个B. 个C. 个D。
个13. 一个几何体由大小相同的小方块搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则从正面看到几何体的形状图是A。
B。
C. D.14。
一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面积为.A. B. C. D.15. 如图所示是某几何体的三视图,根据图中数据,求得该几何体的体积为A. B. C。
高中三视图试题及答案

高中三视图试题及答案一、选择题(每题2分,共10分)1. 在三视图中,主视图、左视图和俯视图分别表示物体的哪个面?A. 正面、侧面、上面B. 侧面、正面、上面C. 正面、上面、侧面D. 上面、侧面、正面2. 以下哪个选项不是三视图的组成部分?A. 主视图B. 左视图C. 右视图D. 俯视图3. 根据三视图的规则,物体的长、宽、高分别在哪个视图中表示?A. 主视图、俯视图、左视图B. 俯视图、主视图、左视图C. 左视图、主视图、俯视图D. 主视图、左视图、俯视图4. 如果一个物体的主视图和俯视图都是圆形,那么这个物体可能是:A. 圆柱体B. 圆锥体C. 球体D. 立方体5. 在绘制三视图时,如果一个物体的左视图和主视图相同,那么这个物体可能是:A. 正方体B. 长方体C. 圆柱体D. 圆锥体二、填空题(每空1分,共10分)6. 三视图包括______、______和______。
7. 物体的三视图应该按照______、______、______的顺序排列。
8. 在三视图中,______视图可以反映物体的高度和长度。
9. 如果一个物体的主视图是一个矩形,左视图是一个圆形,那么这个物体可能是______。
10. 在绘制三视图时,需要考虑物体的______、______和______。
三、简答题(每题5分,共10分)11. 简述三视图的定义及其重要性。
12. 描述如何根据一个物体的主视图和俯视图推断其形状。
四、绘图题(每题5分,共10分)13. 根据以下描述绘制一个物体的三视图:- 主视图:一个正方形- 左视图:一个矩形,宽度为正方形的边长的一半- 俯视图:一个圆形,直径等于正方形的边长14. 根据以下三视图,描述物体的形状:- 主视图:一个圆形- 左视图:一个矩形- 俯视图:一个圆形答案:一、选择题1. A2. C3. D4. C5. A二、填空题6. 主视图、左视图、俯视图7. 主视图、左视图、俯视图8. 左视图9. 圆柱体10. 长度、宽度、高度三、简答题11. 三视图是工程图学中用来描述物体形状的三个基本视图,包括主视图、左视图和俯视图。
三视图高考试题集锦

立体几何——三视图高考真题集锦1.〔14X 卷〕某空间几何体的正视图是三角形,则该几何体不可能是 〔 A 〕 A .圆柱 B.圆锥 C.四面体 D.三棱柱2.〔10年X 卷〕正视图是一个三角形的几何体可以是_______〔写出三种〕 3〔11X 卷〕右图是长和宽分别相等的两个矩形,给定以下三个命题: ①存在三棱柱,其正〔主〕视图、俯视图如右图; ②存在四棱柱,其正〔主〕视图、俯视图如右图;③存在圆柱,其正〔主〕视图、俯视图如右图。
其中真命题的个数是 (A) 3 (B) 2 (C) 1 (D) 0 4.(14X)7.某几何体三视图如下图,则该几何体的体积 为〔 〕A .82π- B .8π- C .82π-D .84π-5.〔12X 卷〕如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为〔 〕()A 6 ()B 9 ()C 12 ()D 186.〔14X 卷〕已知一个几何体的三视图如下图〔单位:m 〕,则该几何体的体积为____3m .〔第4题〕 〔第5题〕 〔第6题〕7.〔13X 卷〕一个四面体的顶点在空间直角坐标系O-xyz 中的坐标分 别是〔1,0,1〕,〔1,1,0〕,〔0,1,1〕,〔0,0,0〕,画该四 面体三视图中的正视图时,以zOx 平面为投影面,则得到正视 图可以为〔 〕244242俯视图侧视图正视图俯视图正〔主〕视图(A) (B)(C)(D)8.〔14X 卷〕在如下图的空间直角坐标系xyz O 中,一个四面体的顶点坐标分别是〔0,0,2〕,〔2,2,0〕,〔1,2,1〕,〔2,2,2〕,给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为〔 〕A.①和②B.③和①C. ④和③D.④和②9.〔202X •X 〕某几何体的三视图〔单位:cm 〕如下图,则此几何体的外表积是〔 〕 A . 90cm 2 B . 129cm 2 C . 132cm 2 D . 138cm 2 10.〔07X 文理〕已知某个几何体的三视图如下图,依据图中标出的尺寸〔单位:cm 〕,可得这个几何体的体积是〔 〕A .334000cmB .338000cm C .202X 3cm D .40003cm〔第9题〕 〔第10题〕201010202020正视图侧视图俯视图11.〔07X 文理〕以下几何体各自的三视图中,有且仅有两个视图相同的是 〔 〕A .①②B .①③C .①④D .②④12.〔08X 理〕某几何体的一条棱长为7,在该几何体的正视图中,这条棱的投影是长为6的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a 的b 的线段,则b a +的最大值为〔 〕A .22B .32C .4D .5213.〔09X 文理〕一个棱锥的三视图如图,则该棱锥的全面积〔单位:2cm 〕为〔 〕A .21248+ B .22448+ C .21236+ D .22436+ 14.〔09X 文理〕一空间几何体的三视图如下图,则该几何体的体积为〔 〕 A .223π+ B .423π+ C .2323π+ D .2343π+〔第13题〕 〔第14题〕15.〔11X 文理〕在一个几何体的三视图中,正视图和俯视图如右图所示,则相应的侧视图可以为〔 〕15.〔10X 文理〕一个几个何体的三视图如图,该几何体的外表积为〔 〕A .280B .292C .360D .372 16.〔11X 文理〕如图是某几何体的三视图,则该几何体的体积为〔 〕A .9122π+B .9182π+ C .942π+ D .3618π+〔第15题〕 〔第16题〕 20.〔09X 文理〕设某几何体的三视图如下〔尺寸的长度单位为m 〕。
三视图专练40题

2017届高三三视图专练例1. 一个四面体的顶点都在球面上,它们的正视图、侧视图、俯视图都是右图.图中圆内有一个以圆心为中心边长为1的正方形.则这个四面体的外接球的表面积是()A.π B.3πC.4πD.6π【分析】由三视图可知:该四面体是正方体的一个内接正四面体.此四面体的外接球的半径为正方体的对角线长为.利用球的表面积计算公式即可得出.解:由三视图可知:该四面体是正方体的一个内接正四面体.∴此四面体的外接球的直径为正方体的对角线长为.∴此四面体的外接球的表面积为表面积为=3π.故选:B.例2. 如图是某几何体的三视图,则该几何体的体积为()A .6B .9C .12D .18【分析】根据几何体的三视图知该几何体是长方体和三棱柱的组合体,结合图中数据求出它的体积即可.解:根据几何体的三视图知,该几何体是上部为长方体,下部为三棱柱的组合体,画出几何体的直观图如图所示,根据图中数据,计算其体积为V 组合体=V 三棱柱+V 长方体=. 选C . 例3. 如图为某几何体的三视图,则该几何体的外接球的表面积为A .B .C .D 272π27π【点睛拨窍】空间几何体与球接、切问题的求解方法(1)求解球与棱柱、棱锥的接、切问题时,一般过球心及接、切点作截面,把空间问题转化为平面图形与圆的接、切问题,再利用平面几何知识寻找几何中元素间的关系求解.(2)若球面上四点P,A,B,C构成的三条线段PA,PB,PC两两互相垂直,且PA=a,PB=b,PC=c,一般把有关元素“补形”成为一个球内接长方体,利用4R2=a2+b2+c2求解.例4. 一个几何体的三视图如图,则该几何体的体积为A.π B.C.D.【分析】由已知的三视图可得:该几何体是一个以俯视图为底面的半圆锥,代入锥体体积公式,可得答案.解:由已知的三视图可得:该几何体是一个以俯视图为底面的半圆锥,其底面面积S==,高h=1,故半圆锥的体积V= =,故选:D【点评】本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.例5. 如图所示,网格纸上小正方形的边长为1,粗线画出的是某一无上盖几何体的三视图,则该几何体的表面积等于()A.39πB.48πC.57πD.63π【分析】由已知中的三视图可得:该几何体为圆柱中挖去一个圆锥,画出直观图,数形结合可得答案.解:该几何体直观图为圆柱中挖去一个圆锥,如图所示,∴该几何体的表面积为S==48π,故选B.【点评】本题考查的知识点是圆柱的体积和表面积,圆锥的体积和表面积,简单几何体的三视图,难度中档.例6. 某几何体的三视图如图所示,则该几何体的体积是()A.B.C.D.【分析】几何体为半球与半圆柱的组合体.解:几何体半球与半圆柱的组合体,半球的半径为1,半圆柱的底面半径为1,高为2,∴几何体的体积V=+=.故选B.例7. 若一个底面是正三角形的三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为()A.B.C.D.【分析】根据由已知底面是正三角形的三棱柱的正视图,我们可得该三棱柱的底面棱长为2,高为1,进而求出底面外接圆半径r,球心到底面的球心距d,球半径R,代入球的表面积公式.即可求出球的表面积.解:由已知底面是正三角形的三棱柱的正视图可得该三棱柱的底面棱长为2,高为1,则底面外接圆半径r=,球心到底面的球心距d=,则球半径R2==,则该球的表面积S=4πR2=。
高考数学三视图练习题
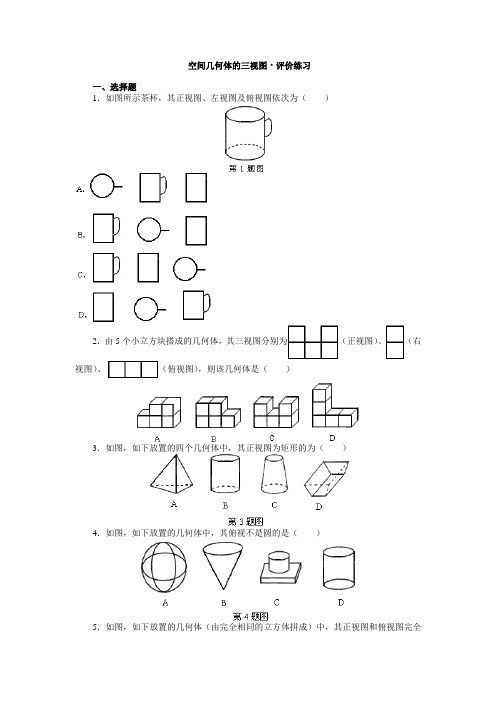
空间几何体的三视图·评价练习一、选择题1.如图所示茶杯,其正视图、左视图及俯视图依次为()2.由5个小立方块搭成的几何体,其三视图分别为(正视图)、(右视图)、(俯视图),则该几何体是()3.如图,如下放置的四个几何体中,其正视图为矩形的为()4.如图,如下放置的几何体中,其俯视不是圆的是()5.如图,如下放置的几何体(由完全相同的立方体拼成)中,其正视图和俯视图完全一样的是()6.如图,下面几何体正视图和左视图类似的是()7.如图,下列选项不是几何体的三种视图为()8.将两个圆盘、一个茶叶桶、一个皮球和一个蒙古包模型按如图所示方式摆放在一起,其正视图是()9.如图,是由一些相同的小正方体构成的几何体的三视图,这些相同的小正体的个数是()A.4 B.5 C.6 D.710.如下图物体的三视图的是()二、填空题11.一个几何体,无论我们从哪个方向看,看到的结果都是一样的,则该几何体必定为______.12.如图所示,桌上放着一个半球,则在它的三视图及从右面看到的图中,有三个图相同,一个不同,这个不同的图应该是_________.13.如图所示的积木是由16块棱长为1cm的正方体堆积而成的,则它表面积为________.14.一个立体图形的三视图一般包括______图、_______图和_______图.15.由小正方体木块搭成的几何体的三视图如下图,则该几何体由_________块小正方体木块搭成.16.如图(1),E、F分别是正方体的面ADD l A l,面BCC l B1的中心,则四边形BFD l E 正在该正方体的面上的射影(即本节所指的正投影)可能是图(2)中的_________(把可能的序号都填上).三、简答题17.试作出下面几何体的三视图18.找出与下列几何体对应的三视图,在三视图的横线上填上对应的序号.19.添线补全下列三视图20.画出如下所示物体的三视图.21.如下图是由小立方块搭成的几何体俯视图,小正方形中的数字表示在该位置的小立方块的个数,请画出它的正视图和左视图.参考答案一、选择题1.C 2.C 3.B 4.C 5.C 6.C 7.A 8.D 9.B 10.C二、填空题11.球12.俯视图13.48cm214.正视图,左视图,俯视图15.7 16.②③三、解答题17.解:18.解:(3),(4),(6),(1),(8),(5),(2),(7).19.解:略20.解:21.解:。
(完整word版)高考三视图强化训练30题
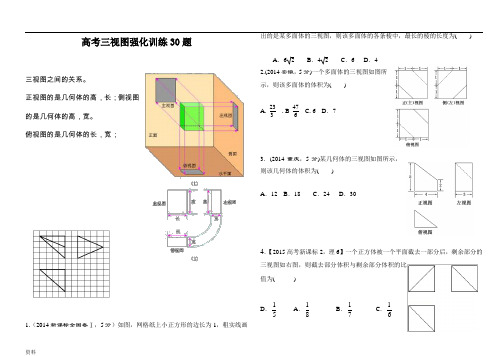
高考三视图强化训练30题三视图之间的关系。
正视图的是几何体的高,长;侧视图的是几何体的高,宽。
俯视图的是几何体的长,宽;1.(2014新课标全国卷Ⅰ,5分)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为()A.6 2 B.4 2 C.6 D.42.(2014安徽,5分)一个多面体的三视图如图所示,则该多面体的体积为()A.233 . B476 C. 6 D.73.(2014重庆,5分)某几何体的三视图如图所示,则该几何体的体积为()A.12 B.18 C.24 D.304.【2015高考新课标2,理6】一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的比值为( )D.51A.81B.71C.615.(2014重庆,5分)某几何体的三视图如图所示,则该几何体的表面积为( )A .54B .60C .66D .726.(2014辽宁,5分)某几何体三视图如图所示,则该几何体的体积为( )A .8-π4B .8-π2C .8-πD .8-2π7.(2014四川,5分)某三棱锥的侧视图、俯视图如图所示,则该三棱锥的体积是 ( )A .3B .2 C. 3 D .18.(2014浙江,5分)某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )A .90 cm 2B .129 cm 2C .132 cm 2D .138 cm 29.(2013浙江,5分)已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )A .108 cm 3B .100 cm 3C .92 cm 3D .84 cm 310.(2013新课标全国Ⅰ,5分)某几何体的三视图如图所示,则该几何体的体积为( )A .16+8πB .8+8πC .16+16πD .8+16π11.【2015高考新课标1,文理11】圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,若该几何体的表面积为1620π+,则r=( )(A)1(B)2(C)4(D)812.【2015高考新课标2,理9】已知A,B是球O的球面上两点,∠AOB=90,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的表面积为( )A.36π B.64π C.144π D.256π13.(2015•北京)某三棱锥的三视图如图所示,则该三棱锥的表面积是()A .2+B.4+C.2+2D.5 14.(2015•重庆)某几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.15.(2015•北京)某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为()A.1 B.C.D.216.(2015•安徽)一个四面体的三视图如图所示,则该四面体的表面积是()A.1+B.1+2C.2+D.217.(2015•重庆)某几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.18.(2015•泉州模拟)若某几何体的三视图(单位:cm)如图所示,则该几何体的体积等于()A.10cm3B.20cm3C.30cm3D.40cm319.(2015•衢州一模)如图是某几何体的三视图,则该几何体的体积为()A.1 B.C.D.20.(2015•西宁校级模拟)某几何体的三视图如图所示,且该几何体的体积是,则正视图中的x 的值是()A.2 B.C.D.321.(2015•金华一模)某三棱锥的三视图如图所示,该三棱锥的体积为()A .80 B.40 C.D.22.(201 1(2016文理).某几何体的三视图如图所示(单位:cm),则该几何体的表面积是cm2,体积是cm3.23.(2016年北京高考)某三棱锥的三视图如图所示,则该三棱锥的体积为()A.16B.13C.12D.124.(2016年山东高考)有一个半球和四棱锥组成的几何体,其三视图如右图所示,则该几何体的体积为(A)π32+31(B)π32+31(C)π62+31(D)π62+125.(2016年四川高考)已知三棱锥的四个面都是腰长为2的等腰三角形,该三棱锥的正视图如图所示,则该三棱锥的体积是__________.26.(2016年天津高考)已知一个四棱锥的底面是平行四边形,该四棱锥的三视图如图所示(单位:m),则该四棱锥的体积为_______m3.27.(2016年全国II 高考)右图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(A )20π (B )24π (C )28π (D )32π28..(2016年全国III 高考)如图,网格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图,则该多面体的表面积为(A )185+(B )545+(C )90 (D )8129.[2014·湖北卷] 在如图1-1所示的空间直角坐标系O xyz 中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2).给出编号为①,②,③,④的四个图,则该四面体的正视图和俯视图分别为( )1A .①和②B .①和③C .③和②D .④和②30.沿一个正方体三个面的对角线截得的几何体如图所示, 则该几何体的左视图为( )(A ) (B ) (C ) (D )单纯的课本内容,并不能满足学生的需要,通过补充,达到内容的完善教育之通病是教用脑的人不用手,不教用手的人用脑,所以一无所能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D . 8- 2π
7. (2014 四川 ,5 分 )某三棱锥的侧视图、俯视图如图所示,则该三棱锥的体积是 ()
A.3 C. 3 D.1
B.2
8.( 2014 浙江 ,5 分)某几何体的三视图 (单位:
cm) 如图所示,则此几何体的表面积是 ( )
A . 90 cm2 C. 132 cm2
B. 129 cm2 D. 138 cm2
( A )20π (B ) 24π ( C) 28π (D ) 32π
26.( 2016 年天津高考)已知一个四棱锥的底面是平行四边形,该四棱锥的三视图 如图所示(单位: m),则该四棱锥的体积为 _______m3.
28..( 2016 年全国 III 高考)如图,网格纸上小正方形的边长为 是某多面体的三视图,则该多面体的表面积为
)
14.( 2015?重庆)某几何体的三视图如图所示,则该几何体的体积为(
)
A.
B.
A.
B.
C.
D.
18.( 2015?泉州模拟)若某几何体的三视图(单位:
的体积等于(
)
cm)如图所示,则该几何体
3
3
3
3
3
A . 10cm B .20cm C. 30cm D. 40cm
19.( 2015?衢州一模)如图是某几何体的三视图,则该几何体的体积为(
1,粗实现画出的
5
30. 沿一个正方体三个面的对角线截得的几何体如图所示, 则该几何体的左视图为( )
( A) 18 36 5
( B) 54 18 5
( C) 90
(D) 81
( A)
(B)
( C)
( D)
29.[2014 湖·北卷 ] 在如图 1-1 所示的空间直角坐标系 O - xyz 中,一个四面体的顶 点坐标分别是 (0, 0,2) ,(2, 2, 0), (1, 2,1), (2, 2, 2).给出编号为①,②,
值为 (
)
1
D.
5
1
A.
8
1
B.
7
1
C.
6
5.( 2014 重庆 , 5 分 )某几何体的三视图如图所示, 则该几何体的表面积为 ( )
1
A . 54 C . 66
B.60 D. 72
6. (2014 辽宁 , 5 分 )某几何体三视图如图所示,则该几何体的体积为
()
π A. 8-4
π B. 8- 2 C.8- π
C.16+ 16π D .8+ 16π
11.【 2015 高考新课标 1,文理 11】圆柱被一个平面
截去一部分后与半球 (半径为 r )组成一个几何体,
该几何体的三视图中的正视图和俯视图如图所示,
若该几何体的表面积为 16 20 ,则 r ( )
(A)1 (C) 4
(B) 2 (D) 8
2
C.
D.
A . 80 B . 40 C.
D.
22.( 201 1( 2016 文理) .某几何体的三视图如图所示
)
(单位: cm),则该几何体的表面积是
2
cm
,体积是
cm 3.
A .1 B. C.
D.
20.( 2015?西宁校级模拟)某几何体的三视图如图所示,且该几何体的体积是
, 23.( 2016 年北京高考)某三棱锥的三视图如图所示,则该三棱锥的体积为(
33
1 ( C) +
2π
36
( D) 1+ 2 π 6
27. (2016 年全国 II 高考) 右图是由圆柱与圆锥组合而成的几何体的三视图, 几何体的表面积为
则该
25.( 2016年四川高考)已知三棱锥的四个面都是腰长为 2的等腰三角形,该三棱锥 的正视图如图所示,则该三棱锥的体积是 __________ .
9.( 2013 浙江 , 5 分)已知某几何体的三视图
图所示,则该几何体的体积是 ( )
3
3
A . 108 cm B. 100 cm
(单位: cm)如
C. 92 cm3
D. 84 cm3
10.( 2013 新课标全国 Ⅰ ,5 分)某几何体的三视图如图所示, 则该几何体的体积为 ( )
A . 16+ 8π B . 8+ 8π
高考三视图强化训练 30 题
三视图之间的关系。 正视图的是几何体的高,长;侧视图 的是几何体的高,宽。 俯视图的是几何体的长,宽;
1.( 2014 新课标全国卷Ⅰ ,5 分 )如图,网格 纸上小正方形的边长为 1,粗实线画出的是某 多面体的三视图,则该多面体的各条棱中,最 长的棱的长度为 ( )
A . 6 2 B. 4 2 C. 6 D . 4 2.(2014 安徽 , 5 分 )一个多面体的三视图如图所示,则该多面体的体积为
15.( 2015?北京)某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为(
)
A .1 B.
C.
D.2
12.【 2015 高考新课标 2,理 9】已知 A,B 是球 O 的球面上两点,∠ AOB=90,C 为
该球面上的动点,若三棱锥 O-ABC 体积的最大值为 36,则球 O 的表面积为
(
)
A .36π B.64 π C.144 π D.256 π
)
则正视图中的 x 的值是(
)
A.2 B.
C.
D.3
21.( 2015?金华一模)某三棱锥的三视图如图所示,该三棱锥的体积为(
)
41ຫໍສະໝຸດ 1A.B.
6
3
1
C.
D. 1
2
24.( 2016 年山东高考)有一个半球和四棱锥组成的几何体,其三 视图如右图所示,则该几何体的体积为
12 ( A) + π
33
12 ( B) + π
16.( 2015?安徽)一个四面体的三视图如图所示,则该四面体的表面积是(
)
13.( 2015?北京)某三棱锥的三视图如图所
示,则该三棱锥的表面积是(
)
A . 2+ C. 2+2
B .4+ D.5
A . 1+ C. 2+
B. 1+2 D. 2
17.( 2015?重庆)某几何体的三视图如图所示,则该几何体的体积为(
()
23
47
A. 3 . B 6 C. 6 D .7
3. (2014 重庆 , 5 分 )某几何体的三视图如图所示, 则该几何体的体积为 ( )
A . 12 B .18 C. 24 D .30
4.【 2015 高考新课标 2,理 6】一个正方体被一个平面截去一部分后,剩余部分的
三视图如右图,则截去部分体积与剩余部分体积的比
③,④的四个图,则该四面体的正视图和俯视图分别为
()
图 1-1 A .①和② B .①和③ C.③和② D.④和②
6
