三视图高考试题集锦word版本
高考三视图(含解析)理试题(卷)汇总
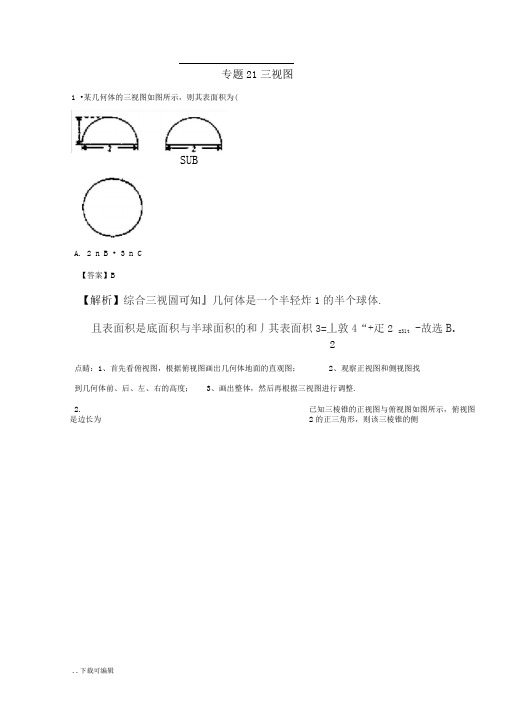
专题21三视图SUBA. 2 n B • 3 n C【答案】B【解析】综合三视圄可知』几何体是一个半轻炸1的半个球体.且表面积是底面积与半球面积的和丿其表面枳3=丄敦4“+疋2=31t-故选B.2点睛:1、首先看俯视图,根据俯视图画出几何体地面的直观图;2、观察正视图和侧视图找到几何体前、后、左、右的高度;3、画出整体,然后再根据三视图进行调整.2.已知三棱锥的正视图与俯视图如图所示,俯视图是边长为2的正三角形,则该三棱锥的侧1 •某几何体的三视图如图所示,则其表面积为(【解析】由正视图和俯视图还原几何体如图所示,由正视图和俯视图对应线段可得AB BD AD 2,当BC 平面ABD时,BC=2,ABD的边AB上的高为、3,只有B选项符合,当BC不垂直平面ABD时,没有符合条件的选项,故选 B.点睛:1.解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图. 2•三视图中“正侧一样高、正俯一样长、俯侧一样宽”,因此,可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据3.某个长方体被一个平面所截,得到几何体的三视图如图所示,则这个几何体的体积为()B【答案】BA. 4 B . 2.2 C . 20 D . 83【答案】D【解析】由三视图可知,该几何体如图所示,其底面为正方形』正方形的边长为2. 口D=3,BF=1,将相同的两个几何体拼在V』构成一个高为斗的长方饥所臥该几何体的体积為煜x仁仪4.如图,正三棱柱ABC ABG的主视图是边长为4的正方形,则此正三棱柱的左视图的面积为()【答案】D【解析】依题意知,此正三棱拄底面定边长为4的正三角形,接柱高为也其侧视囹为矩形,其一边长为2語,一启一边长訶4,故其面积2斗><2曲=8曲;故选D点睛:三视图问题的常见类型及解题策略⑴由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示.(2)由几何体的部分视图画出剩余的部分视图•先根据已知的一部分三视图,还原、推测直观图的可能形式,然后再找其剩下部分三视图的可能形式•当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合.(3)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.原几何体为组合体;上面是长方体,下面是圆柱的一半(如图所示),A. 16 B 2 3 C . 4 3 D . 8,35.某几何体的三视图如图所示,则该几何体的体积为( )8 8 (C) 16 16 (D) 8 16将三视图还原为原来的几何体,再利用体积公式求解.其体积为V 4 2 2122 4 16 8 .故选A; 26•如图5,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的几条棱中,最长的棱的长度为( )(A) 6,2 (B) 4、2 (C) 6 (D)4【答案】C原几何体为三機锥D-A^C, M 中Aff^BC=i r AC=^D^ = DC=2^ ?QN二旳*叭庁)+4 = 6,故最长的棱的长度为= 选C点睛:对于小方格中的三视图,可以放到长方体,或者正方体里面去找到原图,这样比较好找;7.某几何体的三视图如图所示,则该几何体的表面积为()24 2【解析】如图所示A【解析】由已知三视图得到几何体是一个正方怀割去半轻为2的丄个球」所以表面积为S3 12试4&一亦於+ —><4亦囚・24巧故选:A4S&已知某空间几何体的三视图如图所示,则该几何体的表面积是()iEttffl 博视图A. 12十2&+2后B . 12+ 也+2 后C . 12 + 2辽十曲D . |12 +V2 + .J【答案】A【解析】由三视图知:几何体为四棱锥,且四棱锥的一条侧棱与底面垂直,1=-5< 2*2 = 221 =-X2M4=421S ABCD =~X(2+4)X2=69.一个几何体由多面体和旋转体的整体或一部分组合而成,其三视图如图所示,则该几何体如图,P A丄平面ABCD , 朋=2 , AD = 4,医=2 ,经计算,PD = 2石,P匚=«亍,Dt = 2調,•••可••.,故选A.3D. 35 2.2【答案】A 【解析】试題分析;扌艮据三视图可知几何体是组合体;左边罡直三棱柱、右边是半个圆柱,直三棱柱的底面是等腰 亶角三角形,直角边是1,侧犧长是茶圆柱的底面半径是1,母线长是2,二该几何体的体积V =ixlxlx2十丄芝二臥十1・故选;乩2 2考点:由三视图求体积.10•如图是一个由两个半圆锥与一个长方体组合而成的几何体的三视图,则该几何体的体积【答案】C 【解析】A.1 B2C. 2 1的体积是(为(3D. 41 2 体积为—2 2 2 1 4 —3 3试题分析:相当于一个圆锥和一个长方体,故考点:三视图.11. 一个几何体的三视图如图所示,则该几何体的体积为(【解析】试题分析:该几何休的直观團如园所示,连接妙,则该几何体由直三棱柱血D-和四棱锥一吨组合而成,其和易22 +扌心后专詈故应选扎12. 一个几何体的三视图如图所示 ,则该几何体的体积为A.14~316~3D. 6【答案】A考点:三视图.1【答案】-3【解析】本题考查三视图、四棱锥的体积计算等知识,难度中等•由三视图可知该几何体是底1 1面为长和高均为1的平行四边形,高为1的四棱锥,故其体积为V - 1 1 1 - •3 3。
高考三视图(含解析)理试题汇总(精编文档).doc

【最新整理,下载后即可编辑】专题21 三视图1.某几何体的三视图如图所示,则其表面积为()A.2π B.3π C.4π D.5π【答案】B点睛:1、首先看俯视图,根据俯视图画出几何体地面的直观图;2、观察正视图和侧视图找到几何体前、后、左、右的高度;3、画出整体,然后再根据三视图进行调整.2.已知三棱锥的正视图与俯视图如图所示,俯视图是边长为2的正三角形,则该三棱锥的侧视图可能为( )A.B.C.D.【答案】B【解析】由正视图和俯视图还原几何体如图所示,由正视图和俯视图对应线段可得2⊥平面时,BC=2,===,当BC ABDAB BD AD∆的边AB上的高为3,只有B选项符合,当BC不垂直平面ABD ABD时,没有符合条件的选项,故选B.点睛:1.解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图.2.三视图中“正侧一样高、正俯一样长、俯侧一样宽”,因此,可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据3.某个长方体被一个平面所截,得到几何体的三视图如图所示,则这个几何体的体积为( )A . 4B . 22C .203 D . 8【答案】D4.如图,正三棱柱111ABC A B C 的主视图是边长为4的正方形,则此正三棱柱的左视图的面积为( )A . 16B . 23C . 43D . 83【答案】D点睛:三视图问题的常见类型及解题策略(1)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示.(2)由几何体的部分视图画出剩余的部分视图.先根据已知的一部分三视图,还原、推测直观图的可能形式,然后再找其剩下部分三视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合. (3)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.5.某几何体的三视图如图所示,则该几何体的体积为 ( )(A) 168π+ (B) 88π+ (C) 1616π+(D) 816π+【答案】A【解析】将三视图还原为原来的几何体,再利用体积公式求解.原几何体为组合体;上面是长方体,下面是圆柱的一半(如图所示), 其体积为21422241682V ππ=⨯⨯+⨯⨯=+.故选A;6.如图5,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的几条棱中,最长的棱的长度为( )(A) 62 (B) 42 (C) 6 (D)4【答案】C【解析】如图所示点睛:对于小方格中的三视图,可以放到长方体,或者正方体里面去找到原图,这样比较好找;7.某几何体的三视图如图所示,则该几何体的表面积为( )A.24π-B.24π+C.20π-D.20π+【答案】A8.已知某空间几何体的三视图如图所示,则该几何体的表面积是()A.B.C.D.【答案】A【解析】由三视图知:几何体为四棱锥,且四棱锥的一条侧棱与底面垂直,如图,平面,,,,,经计算,,,,∴,∴, ,,,∴,故选A .9.一个几何体由多面体和旋转体的整体或一部分组合而成,其三视图如图所示,则该几何体的体积是( )A .1π+B .2π+C .21π+D .3522π++【答案】A【解析】考点:由三视图求体积.10.如图是一个由两个半圆锥与一个长方体组合而成的几何体的三视图,则该几何体的体积为( )A .263π+B .83π+ C .243π+ D .43π+ 【答案】C【解析】试题分析:相当于一个圆锥和一个长方体,故体积为122221433ππ⋅+⋅⋅=+.考点:三视图.11.一个几何体的三视图如图所示,则该几何体的体积为( )A . 143B . 5C . 163D .6【答案】A【解析】考点:三视图.12.一个几何体的三视图如图所示,则该几何体的体积为____.【答案】13【解析】本题考查三视图、四棱锥的体积计算等知识,难度中等.由三视图可知该几何体是底面为长和高均为1的平行四边形,高为1的四棱锥,故其体积为11111V=⨯⨯⨯=.33。
三视图(20个含答案)
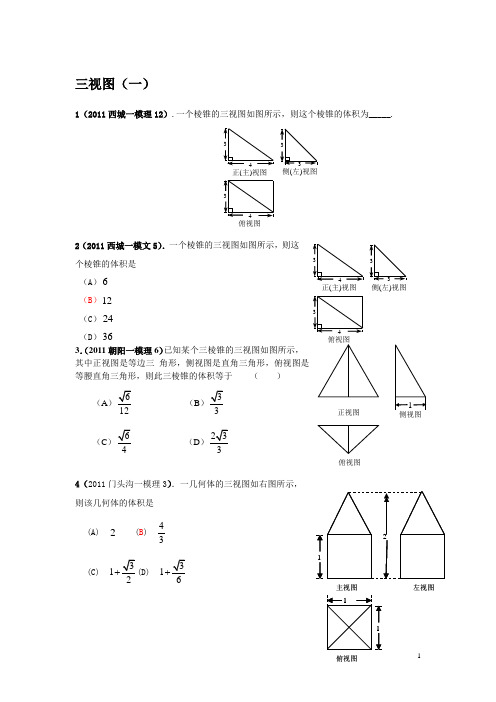
三视图(一)1(2011西城一模理12).一个棱锥的三视图如图所示,则这个棱锥的体积为_____.2(2011西城一模文5).一个棱锥的三视图如图所示,则这个棱锥的体积是(A)6(B)12(C)24(D)363.(2011朝阳一模理6)已知某个三棱锥的三视图如图所示,其中正视图是等边三角形,侧视图是直角三角形,俯视图是等腰直角三角形,则此三棱锥的体积等于()(A )612(B )33(C )64(D )2334(2011门头沟一模理3).一几何体的三视图如右图所示,则该几何体的体积是(A) 2 (B) 4 3(C)312+(D)316+正(主)视图俯视图侧(左)视图3443 33正(主)视图俯视图侧(左)视图3443 33侧视图正视图1俯视图2主视图左视图111ABC DO EA 1B 1C 1D 1 5(2011石景山一模理4).一个空间几何体的三视图及部分数据如图所示(单位:cm ),则这个几何体的体积是( ) A . 33cm B .352cm C . 32cm D .332cm6(2011朝阳一模文6.)已知三棱锥的三视图如图所示,其中侧视图为直角三角形,俯视图为等腰直角三角形,则此三棱锥的体积等于()(A )23(B )33(C )223 (D )2337(2011丰台文5).如图所示,O 是正方体ABCD -A 1B 1C 1D 1对角线A 1C 与AC 1的交点,E 为棱BB 1的中点,则空间四边形OEC 1D 1在正方体各面上的正投影不可能...是( )8(2011海淀一模文11). 如图,在正方体1111ABCD A B C D -中,点P 是上底面1111A B C D 内一动点,则三棱锥P ABC -的主视图与左视图的面积的比值为_____.(A) (B) (C) (D)正视图俯视图侧视图13PDCBA1A 1D 1B 1C 左视主视9(2011门头沟一模文10).一几何体的三视图如左下图所示,则该几何体的体积是10(2011石景山一模文4).一个空间几何体的三视图及部分数据如图所示 (单位:cm ),则这个几何体的表面积是( ) A .29πcm B .212πcm C .215πcm D .224πcm参考答案:1.122.B3.B4.B5.D6.B7.A _8._1__9. 3710.D俯视23主视左视11(第10题(二)1(10。
高考三视图强化训练题.doc

高考三视图强化训练30 题三视图之间的关系。
正视图的是几何体的高,长;侧视图的是几何体的高,宽。
俯视图的是几何体的长,宽;23 47A. 3 . B 6 C.6D.73. (2014 重庆, 5 分) 某几何体的三视图如图所示,则该几何体的体积为() A.12 B .18 C.24 D . 304.【2015高考新课标2,理 6】一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的比值为()D.1A .1B.1C.15 8 7 65.( 2014 重庆, 5 分)某几何体的三视图如图所示,则该几何体的表面积为()1. ( 2014 新课标全国卷Ⅰ, 5 分)如图,网格纸上小正方形的边长为1,粗实线画A. 54 B. 6 0出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为() C. 66 D. 7 2A.6 2 B.4 2 C.6D.42.(2014安徽,5分)一个多面体的三视图如图所示,则该多面体的体积为()6. (2014 辽宁, 5 分) 某几何体三视图如图所示,则该几何体的体积为()A. 8-πB .8-πC . 8-πD . 8-2π4 27. (2014 四川, 5 分 ) 某三棱锥的侧视图、俯视图如图所示,则该三棱锥的体积是()A.3 B .2D . 18.( 2014 浙江, 5 分)某几何体的三视图( 单位: cm)如图所示,则此几何体的表面积是()A. 90 cm 2 B.129 cm 2C. 132 cm 2 D . 138 cm29.( 2013 浙江, 5 分)已知某几何体的三视图( 单位: cm)如图所示,则该几何体的体积是 ()3 3A. 108 cm B . 100 cmC. 92 cm3D.84 cm 310.( 2013 新课标全国Ⅰ ,5分)某几何体的三视图如图所示,则该几何体的体积为 ()A. 16+8πB . 8+8πC . 16+16πD . 8+16π11.【 2015 高考新课标 1,文理 11】圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,若该几何体的表面积为16 20 ,则 r ( )(A)1 (B)2(C)4 (D)812.【 2015 高考新课标 2,理 9】已知 A,B 是球 O的球面上两点,∠ AOB=90,C 为该球面上的动点,若三棱锥 O-ABC体积的最大值为 36,则球 O的表面积为 ( )A.36ππππ13.( 2015? 北京)某三棱锥的三视图如图所示,则该三棱锥的表面积是()A. 2+B. 4+C. 2+2 D. 514.( 2015? 重庆)某几何体的三视图如图所示,则该几何体的体积为()A.1B.C.D.A. B .20.( 2015? 西宁校级模拟)某几何体的三视图如图所示,且该几何体的体积是,C.D.则正视图中的x 的值是()A.2B. C . D.315.( 2015? 北京)某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为()A. 1B. C . D. 221.( 2015? 金华一模)某三棱锥的三视图如图所示,该三棱锥的体积为()16.( 2015? 安徽)一个四面体的三视图如图所示,则该四面体的表面积是()A.80B.40C. D.A.1+ B . 1+2C.2+ D .222. ( 201 1 ( 2016 文理) . 某几何体的三视图如图所示(单位:cm),则该几何体的表面积是2,体积是3.cm cm17.( 2015? 重庆)某几何体的三视图如图所示,则该几何体的体积为()A. B. C. D.23. ( 2016 年北京高考)某三棱锥的三视图如图所示,则该三棱锥的体积为()18.( 2015? 泉州模拟)若某几何体的三视图(单位:cm)如图所示,则该几何体的体积等于() A. B.3 3 3 3C. D.A. 10cmB. 20cm C. 30cm D. 40cm19.( 2015? 衢州一模)如图是某几何体的三视图,则该几何体的体积为()24.( 2016 年山东高考)有一个半球和四棱锥组成的几何体,其三视图如右图所示,则该几何体的体积为( A)1+2π(B)1+ 2 π3 3 3 3(C)1+ 2 π(D)1+ 2 π3 6 625.( 2016年四川高考)已知三棱锥的四个面都是腰长为2的等腰三角形,该三棱锥的正视图如图所示,则该三棱锥的体积是__________ .26.(2016 年天津高考)已知一个四棱锥的底面是平行四边形,该四棱锥的三视图如图所示(单位: m),则该四棱锥的体积为 _______m3.27.( 2016 年全国 II 高考)右图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(A)20π( B)24π( C)28π( D)32π28.. ( 2016 年全国III高考)如图,网格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图,则该多面体的表面积为29.[ 2014·湖北卷 ]在如图1- 1 所示的空间直角坐标系O -xyz 中,一个四面体的顶点坐标分别是(0 ,0, 2) ,(2 ,2,0) ,(1, 2,1) ,(2 ,2,2) .给出编号为①,②,③,④的四个图,则该四面体的正视图和俯视图分别为()图1- 1A.①和② B .①和③ C .③和② D .④和②30.沿一个正方体三个面的对角线截得的几何体如图所示,则该几何体的左视图为()(A)(B)(C)(D)( A)(B)(C)90(D)81。
(完整word版)高考数学三视图题型总结,推荐文档

1 .某几何体的三视图如图所示,则该几何体的体积为( )A .168π+B .88π+C .1616π+D .816π+ 【答案】A 2 .一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为1V ,2V ,3V ,4V ,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有( )A .1243V V V V <<<B .1324V V V V <<<C .2134V V V V <<<D .2314V V V V <<<【答案】C3 .某四棱台的三视图如图所示,则该四棱台的体积是()A.4B.14 3C.163D.6【答案】B4.某几何体的三视图如题()5图所示,则该几何体的体积为()A.5603B.5803C.200D.240【答案】C5.一个四面体的顶点在空间直角坐标系O xyz-中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到正视图可以为()A.B.C.D.【答案】A6.某几何体的三视图如图所示, 则其体积为___3π_____.12211正视图俯视图侧视图第5题图1121【答案】3π 7.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积等于________2cm .【答案】248.某几何体的三视图如图所示,则该几何体的体积是____________.【答案】1616π-9.已知某一多面体内接于一个简单组合体,如果该组合体的正视图.测试图.俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是_______________43 233正视图侧视图俯视图(第12题图)【答案】12π2 .已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积是()A.1cm3 B.2cm3C.3cm3D.6cm35 .将正方形(如图1所示)截去两个三棱锥,得到图2所示的几何体,则该几何体的左视图为7 .如图,网格上小正方形的边长为1,粗线画出的是某几何体的三视图,则几何体的体积为A.6B.9C.12D.1813.某三棱锥的三视图如图所示,该三棱锥的表面积是()+A.2865+B.3065+C.56125D.60125+15.某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是DCBA正、侧视图18. (立体几何)某几何体的三视图如图1所示,它的体积为()A.12πB.45πC.57πD.81π22.一个几何体的三视图如图所示(单位:m),则该几何体的体积________3m.36.一个几何体的三视图如图所示,则该几何体的表面积为______________.第7题图。
三视图高考试题集锦

三视图高考试题集锦work Information Technology Company.2020YEAR2立体几何——三视图高考试题集锦1.(14福建卷)某空间几何体的正视图是三角形,则该几何体不可能是 ( A )A .圆柱 B.圆锥 C.四面体 D.三棱柱2.(10年海南卷)正视图是一个三角形的几何体可以是_______(写出三种) 3(11山东卷)右图是长和宽分别相等的两个矩形,给定下列三个命题: ①存在三棱柱,其正(主)视图、俯视图如右图;②存在四棱柱,其正(主)视图、俯视图如右图;③存在圆柱,其正(主)视图、俯视图如右图。
其中真命题的个数是 (A) 3 (B) 2 (C) 1 (D) 04.(14辽宁)7.某几何体三视图如图所示,则该几何体的体积 为( )A .82π- B .8π- C .82π-D .84π-5.(12海南卷)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )()A 6 ()B 9 ()C 12 ()D 186.(14天津卷)已知一个几何体的三视图如图所示(单位:m ),则该几何体的体积为____3m .244242俯视图侧视图正视图俯视图正(主)视图(第4题)(第5题)(第6题)7.(13海南卷)一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到正视图可以为()(A) (B) (C) (D)8.(14湖北卷)在如图所示的空间直角坐标系xyzO 中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为()A.①和②B.③和①C. ④和③D.④和②9.(2014•浙江)某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是()A.90cm2B.129cm2C.132cm2D.138cm23410.(07海南文理)已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是( )A .334000cmB .338000cm C .20003cm D .40003cm(第9题) (第10题)11.(07山东文理)下列几何体各自的三视图中,有且仅有两个视图相同的是 ( )A .①②B .①③C .①④D .②④12.(08海南理)某几何体的一条棱长为7,在该几何体的正视图中,这条棱的投影是长为6的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a 的b 的线段,则b a 的最大值为( ) A .22 B .32 C .4 D .52201010202020正视图侧视图俯视图513.(09海南文理)一个棱锥的三视图如图,则该棱锥的全面积(单位:2cm )为( )A .21248+ B.22448+ C .21236+D .22436+14.(09山东文理)一空间几何体的三视图如图所示,则该几何体的体积为( )A .223π+B .423π+C .232π+D .234π+(第13题) (第14题)15.(11海南文理)在一个几何体的三视图中,正视图和俯视图如右图所示,则相应的侧视图可以为( )15.(10安徽文理)一个几个何体的三视图如图,该几何体的表面积为( )A.280 B.292 C.360 D.37216.(11湖南文理)如图是某几何体的三视图,则该几何体的体积为()A.912 2π+B.9182π+ C.942π+ D.3618π+(第15题)(第16题)20.(09辽宁文理)设某几何体的三视图如下(尺寸的长度单位为m)。
(完整word版)三视图练习 (2)

三视图练习1.一个几何体的三视图如右图所示,它的正视图和侧视图均为半圆,俯视图为圆,则这个空间几何体的体积是( ) A .32π B .34π C .π4 D .π32.有一个几何体的三视图及其尺寸如下图(单位:cm),则该几何体的表面积为( )A .12πcm 2B .15πcm 2C .24πcm 2D .36πcm 23.某几何体的三视图如图所示,根据图中标出的数据.可得这个几何体的表面积为( )A.错误!未找到引用源。
B.错误!未找到引用源。
C.错误!未找到引用源。
D.124.如图,网格纸上小正方形边长为1,粗线是一个棱锥的三视图,则此棱锥的体积为( ). (A )38 (B )34(C )34 (D)325.一个简单几何体的三视图如图所示,其正视图和俯视图均为正三角形,侧视图为腰长是2的等腰直角三角形则该几何体的体积为( )A .B .1C .D .36.某几何体的三视图如图所示(单位:cm ),则该几何体的侧面PAB 的面积是( ) A .7B .2C .1D .37.说出下列三视图(依次为主视图、左视图、俯视图)表示的几何体是( )A .六棱柱B .六棱锥C .六棱台D .六边形8.一个空间几何体的三视图如图所示,则该几何体的体积为( )A .56πcm 3 B .3πcm 3 B .C .32πcm 3 D .37πcm 3 9.右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( ) (A)9π (B )10π (C)11π (D)12π10.用若干单位正方体搭一个几何体,使它的正视图和俯视图如图所示,则它的体积的最大值和最小值分别为( )A. 9,14B.7,13C. 8,14D. 9,13 11.已知某几何体的三视图如上图所示,其中正视图,侧视图均是由三角形与半圆构成,视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为( ) (A)2132π+(B)4136π+ (C)132+(D) 166+12.一个几何体的三视图如图所示,则该几何体的体积为( )(A)92 (B)72(C)3 (D)4 13.右图是一个几何体的三视图,根据图中数据,可得该几何体的体积是( )(A) 9π (B)1333π- (C )103π (D)133π 14.一个几何体的三视图如图所示,则该几何体的体积是( ) (A )64 (B )72 (C )80(D )11215.一个几何体的三视图如图所示,则该几何体的体积是( )A .64B .72C .80D .11216.已知一个几何体的三视图如下图所示(单位:cm),其中正视图是直角梯形,侧视图和俯视图都是矩形,则这个几何体的体积是________cm 3.17.如图为一个几何体的三视图,其中俯视为正三角形,A 1B 1=2,AA 1=4,则该几何体的表面积为_______。
三视图高考真题-普通用卷
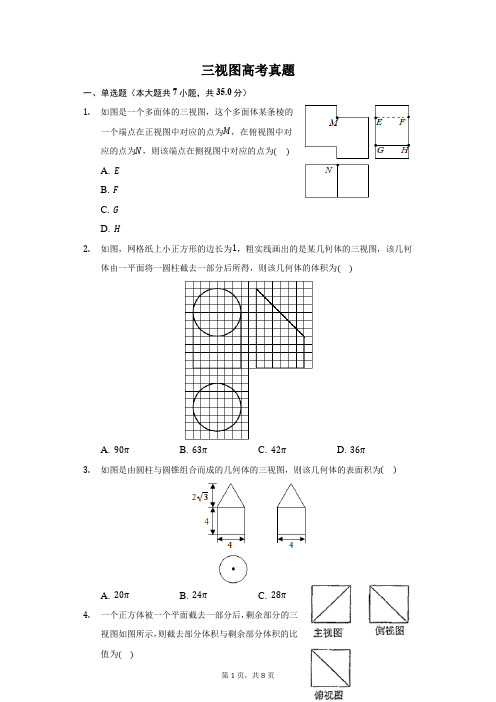
三视图高考真题一、单选题(本大题共7小题,共35.0分)1.如图是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对应的点为M,在俯视图中对应的点为N,则该端点在侧视图中对应的点为()A. EB. FC. GD. H2.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为()A. 90πB. 63πC. 42πD. 36π3.如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为()A. 20πB. 24πC. 28πD. 32π4.一个正方体被一个平面截去一部分后,剩余部分的三视图如图所示,则截去部分体积与剩余部分体积的比A. 18B. 17C. 16D. 155.如图为某几何体的三视图,则该几何体的表面积是()A. 6+4√2B. 4+4√2C. 6+2√3D. 4+2√36.中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是()A. B.C. D.7.某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为()A. 2√17B. 2√5C. 3D. 2二、单空题(本大题共3小题,共15.0分)8.以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为______ (写出符合要求的一组答案即可).9.已知圆锥的顶点为S,母线SA,SB所成角的余弦值为7,SA与圆锥底面所成角为45°,8若△SAB的面积为5√15,则该圆锥的侧面积为.10.中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有______个面,其棱长为______.答案和解析1.【答案】A【解析】解:根据几何体的三视图转换为直观图:根据三视图和几何体的的对应关系的应用,这个多面体某条棱的一个端点在正视图中对应的点为M,在俯视图中对应的点为N,所以在侧视图中与点E对应.故选:A.首先把三视图转换为直观图,进一步求出图形中的对应点.本题考查的知识要点:三视图和几何体的直观图之间的转换、主要考查学生的运算能力和转换能力及思维能力,属于基础题型.2.【答案】B【解析】【分析】本题考查了体积计算公式,考查了空间想象能力,属于基础题.由三视图可得,直观图为一个完整的圆柱减去一个高为6的圆柱的一半,即可求出几何体的体积.【解答】解:由三视图可得,直观图为一个完整的圆柱减去一个高为6的圆柱的一半,圆柱的半径为3,×π×32×6=63π,V=π×32×10−12故选:B.3.【答案】C【解析】【分析】本题考查由三视图求表面积,空间立体几何三视图,属于基础题.空间几何体是一个组合体,上面是一个圆锥,圆锥的底面直径是4,圆锥的高是2√3,在轴截面中圆锥的母线长使用勾股定理求出,写出表面积,下面是一个圆柱,圆柱的底面直径是4,圆柱的高是4,求出圆柱的表面积,注意不包括重合的平面.【解答】解:由三视图知,空间几何体是一个组合体,上面是一个圆锥,圆锥的底面直径是4,圆锥的高是2√3,∴在轴截面中圆锥的母线长是√12+4=4,∴圆锥的侧面积是π×2×4=8π,下面是一个圆柱,圆柱的底面直径是4,圆柱的高是4,∴圆柱表现出来的表面积是π×22+2π×2×4=20π.∴空间组合体的表面积是.故选C.4.【答案】D【解析】解:设正方体的棱长为1,由三视图判断,正方体被切掉的部分为三棱锥,如图所示,∴正方体切掉部分的体积为13×12×1×1×1=16,∴剩余部分体积为1−16=56,∴截去部分体积与剩余部分体积的比值为15.故选:D.由三视图判断,正方体被切掉的部分为三棱锥,把相关数据代入棱锥的体积公式计算即本题考查了由三视图判断几何体的形状,求几何体的体积.5.【答案】C【解析】解:由三视图可知几何体的直观图如图:几何体是正方体的一个角,PA=AB=AC=2,PA、AB、AC两两垂直,故PB=BC=PC=2√2,几何体的表面积为:3×12×2×2+√34×(2√2)2=6+2√3故选:C.先由三视图画出几何体的直观图,利用三视图的数据,利用三棱锥的表面积公式计算即可.本题考查多面体的表面积的求法,几何体的三视图与直观图的应用,考查空间想象能力,计算能力.6.【答案】A【解析】【分析】本题看出简单几何体的三视图的画法,是基本知识的考查.属于基础题.直接利用空间几何体的三视图的画法,判断选项的正误即可.【解答】解:由题意可知,如图摆放的木构件与某一带卯眼的木构件咬合成长方体,小的长方体,是榫头,从图形看出,轮廓是长方形,内含一个长方形,并且一条边重合,另外3边是虚线,所以木构件的俯视图是A.故选:A.7.【答案】B【分析】本题考查空间几何体的三视图,考查计算能力,属于中档题.根据题意,利用侧面展开图,转化求解即可.【解答】解:由题意可知,该几何体是圆柱,底面周长16,高为2,直观图以及侧面展开图如图:圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度:√22+42=2√5.故选B.8.【答案】②⑤或③④【解析】解:观察正视图,推出正视图的长为2和高1,②③图形的高也为1,即可能为该三棱锥的侧视图,④⑤图形的长为2,即可能为该三棱锥的俯视图,当②为侧视图时,结合侧视图中的直线,可以确定该三棱锥的俯视图为⑤,当③为侧视图时,结合侧视图虚线,虚线所在的位置有立体图形的轮廓线,可以确定该三棱锥的俯视图为④.故答案为:②⑤或③④.通过观察已知条件正视图,确定该正视图的长和高,结合长、高、以及侧视图视图中的实线、虚线来确定俯视图图形.该题考查了三棱锥的三视图,需要学生掌握三视图中各个图形边长的等量关系,以及对于三视图中特殊线条能够还原到原立体图形中,需要较强空间想象,属于中等题.9.【答案】40√2π【解析】本题考查圆锥的结构特征,母线与底面所成角,圆锥的侧面面积的求法,考查空间想象能力以及计算能力.利用已知条件求出圆锥的母线长,利用母线与平面所成角求解底面半径,然后求解圆锥的侧面积.【解答】解:圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为78,可得sin∠ASB =√1−(78)2=√158. 由△SAB 的面积为5√15,可得12SA 2sin∠ASB =5√15,即12SA 2×√158=5√15,即SA =4√5. SA 与圆锥底面所成角为45°,可得圆锥的底面半径为:√22×4√5=2√10. 则该圆锥的侧面积:2√10×4√5π=40√2π.故答案为:40√2π.10.【答案】26 ,√2−1【解析】【分析】中间层是一个正八棱柱,有8个侧面,上层是有8+1个面,下层也有8+1个面,故共有26个面;由中间层正八棱柱的棱长加上两个棱长的倍. 【解答】解:该半正多面体共有8+8+8+2=26个面,设其棱长为x ,则x +√22x +√22x =1,解得x =√2−1.故答案为:26,√2−1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何——三视图高考试题集锦
1.(14福建卷)某空间几何体的正视图是三角形,则该几何体不可能是 ( A ) A .圆柱 B.圆锥 C.四面体 D.三棱柱
2.(10年海南卷)正视图是一个三角形的几何体可以是_______(写出三种) 3(11山东卷)右图是长和宽分别相等的两个矩形,给定下列三个命题: ①存在三棱柱,其正(主)视图、俯视图如右图; ②存在四棱柱,其正(主)视图、俯视图如右图;
③存在圆柱,其正(主)视图、俯视图如右图。
其中真命题的个数是 (A) 3 (B) 2 (C) 1 (D) 0 4.(14辽宁)7.某几何体三视图如图所示,则该几何体的体积 为( )A .82π- B .8π- C .82
π
-
D .84
π
-
5.(12海南卷)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )
()A 6 ()B 9 ()C 12 ()D 18
6.(14天津卷)已知一个几何体的三视图如图所示(单位:m ),则该几何体的体积为____3
m .
(第4题) (第5题) (第6题)
7.(13海南卷)一个四面体的顶点在空间直角坐标系O-xyz 中的坐标分 别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四 面体三视图中的正视图时,以zOx 平面为投影面,则得到正视 图可以为( )
2
4
4
24
2
俯视图
侧视图
正视图俯视图
正(主)视图
(A) (B)
(C)
(D)
8.(14湖北卷)在如图所示的空间直角坐标系xyz O 中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为( )
A.①和②
B.③和①
C. ④和③
D.④和②
9.(2014•浙江)某几何体的三视图(单位:cm )如图所示,则此几何体的表面积是( ) A . 90cm 2 B . 129cm 2 C . 132cm 2 D . 138cm 2 10.(07海南文理)已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是( )
A .334000cm
B .3
3
8000cm C .20003cm D .40003cm
(第9题) (第10题)
2010
10
20
20
20正视图
侧视图
俯视图
11.(07山东文理)下列几何体各自的三视图中,有且仅有两个视图相同的是 ( )
A .①②
B .①③
C .①④
D .②④
12.(08海南理)某几何体的一条棱长为7,在该几何体的正视图中,这条棱的投影是长为6的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a 的b 的线段,则b a +的最大值为( )
A .22
B .32
C .4
D .52
13.(09海南文理)一个棱锥的三视图如图,则该棱锥的全面积(单位:2
cm )为( )A .21248+ B .22448+ C .21236+ D .22436+
14.(09山东文理)一空间几何体的三视图如图所示,则该几何体的体积为( ) A .223π+ B .423π+ C .232π+ D .23
4π+
(第13题) (第14题)
15.(11海南文理)在一个几何体的三视图中,正视图和俯视图如右图所示,则相应的侧视图可以为( )
15.(10安徽文理)一个几个何体的三视图如图,该几何体的表面积为()A.280 B.292 C.360 D.372
16.(11湖南文理)如图是某几何体的三视图,则该几何体的体积为()
A.9
12 2
π
+
B.
9
18
2
π+C.942
π+D.3618
π+
(第15题)(第16题)
20.(09辽宁文理)设某几何体的三视图如下(尺寸的长度单位为m)。
则该几何体的体积为3
m
18.(本小题满分12分)三棱锥A BCD
-及其侧视图、俯视图如图所示。
设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN NP
⊥。
⑴证明:P为线段BC的中点;⑵求二面角A NP M
--的余弦值。
侧视图俯视图
11
22
2
2
1
1
M
N
P
D
B
C
A。
