9.6立体几何大题1(教师版)
立体几何经典大题(各个类型的典型题目)

1.如图,已知△ABC 是正三角形,EA ,CD 都垂直于平面ABC ,且EA =AB =2a ,DC =a ,F 是BE 的中点.(1)FD ∥平面ABC ;(2)AF ⊥平面EDB .2.已知线段PA ⊥矩形ABCD 所在平面,M 、N 分别是AB 、PC 的中点。
(1)求证:MN //平面PAD ; (2)当∠PDA =45°时,求证:MN ⊥平面PCD ;F CBAEDA B C D EF 3.如图,在四面体ABCD 中,CB=CD,BD AD ⊥,点E ,F 分别是AB,BD 的中点.求证: (1)直线EF// 面ACD ; (2)平面⊥EFC 面BCD .4.在斜三棱柱A 1B 1C 1—ABC 中,底面是等腰三角形,AB =AC ,侧面BB 1C 1C ⊥底面ABC (1)若D 是BC 的中点,求证 AD ⊥CC 1;(2)过侧面BB 1C 1C 的对角线BC 1的平面交侧棱于M ,若AM =MA 1, 求证 截面MBC 1⊥侧面BB 1C 1C ;(3)AM =MA 1是截面MBC 1⊥平面BB 1C 1C 的充要条件吗?请你叙述判断理由]立体几何大题训练(3)C15. 如图,在正方体ABCD —A 1B 1C 1D 1中,M 、N 、G 分别是A 1A ,D 1C ,AD 的中点. 求证:(1)MN//平面ABCD ; (2)MN ⊥平面B 1BG .6. 如图,在正方体ABCD -A 1B 1C 1D 1中,E 、F 为棱AD 、AB 的中点. (1)求证:EF ∥平面CB 1D 1;(2)求证:平面CAA 1C 1⊥平面CB 1D 1.立体几何大题训练(4)7、如图,在直四棱柱ABCD-A 1B 1C 1D 1中,底面ABCD 为等腰梯形,AB ∥CD ,AB=4,BC=CD=2,AA 1=2,_ G_ M _ D_1_ C_1_ B_1_ A_1_ N_ D _ C_ B _ ABA 1FE、E1分别是棱AD、AA1的中点(1)设F是棱AB的中点,证明:直线EE1∥面FCC1;(2)证明:平面D1AC⊥面BB1C1C。
数学立体几何多选题(讲义及答案)含答案

数学立体几何多选题(讲义及答案)含答案一、立体几何多选题1.如图,正方体1111ABCD A B C D -中的正四面体11A BDC -的棱长为2,则下列说法正确的是( )A .异面直线1AB 与1AD 所成的角是3πB .1BD ⊥平面11AC DC .平面1ACB 截正四面体11A BDC -所得截面面积为3D .正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23【答案】ABD 【分析】选项A ,利用正方体的结构特征找到异面直线所成的角;选项B ,根据正方体和正四面体的结构特征以及线面垂直的判定定理容易得证;选项C ,由图得平面1ACB 截正四面体11A BDC -所得截面面积为1ACB 面积的四分之一;选项D ,分别求出正方体的体对角线长和正四面体11A BDC -的高,然后判断数量关系即可得解. 【详解】A :正方体1111ABCD ABCD -中,易知11//AD BC ,异面直线1A B 与1AD 所成的角即直线1A B 与1BC 所成的角,即11A BC ∠,11A BC 为等边三角形,113A BC π∠=,正确;B :连接11B D ,1B B ⊥平面1111DC B A ,11A C ⊂平面1111D C B A ,即111AC B B ⊥,又1111AC B D ⊥,1111B B B D B ⋂=,有11A C ⊥平面11BDD B ,1BD ⊂平面11BDD B ,所以111BD AC ⊥,同理可证:11BD A D ⊥,1111AC A D A ⋂=,所以1BD ⊥平面11AC D ,正确;C :易知平面1ACB 截正四面体11A BDC -所得截面面积为134ACB S=,错误;D :易得正方体1111ABCD A B C D -()()()2222226++=2的正四面体11A BDC -,故正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23,正确. 故选:ABD. 【点睛】关键点点睛:利用正方体的性质,找异面直线所成角的平面角求其大小,根据线面垂直的判定证明1BD ⊥平面11AC D ,由正四面体的性质,结合几何图形确定截面的面积,并求高,即可判断C 、D 的正误.2.已知三棱锥A BCD -的三条侧棱AB ,AC ,AD 两两垂直,其长度分别为a ,b ,c .点A 在底面BCD 内的射影为O ,点A ,B ,C ,D 所对面的面积分别为A S ,B S ,C S ,D S .在下列所给的命题中,正确的有( ) A .2A BCO D S SS ⋅=; B .3333A B C D S S S S <++;C .若三条侧棱与底面所成的角分别为1α,1β,1γ,则222111sin sin sin 1αβγ++=;D .若点M 是面BCD 内一个动点,且AM 与三条侧棱所成的角分别为2α,2β,2γ,则22cos α+2222cos cos 1βγ+=.【答案】ACD 【分析】由Rt O OA '与Rt O AD '相似,得边长关系,进而判断A 正确;当M 与O 重合时,注意线面角与线线角的关系,即可得C 正确;构造长方体,建立直角坐标系,代入夹角公式计算可得D 正确;代入特殊值,可得B 错误. 【详解】由三棱锥A BCD -的三条侧棱AB ,AC ,AD 两两垂直,则将三棱锥A BCD -补成长方体ABFC DGHE -,连接DO 并延长交BC 于O ', 则AO BC ⊥.对A :由Rt O OA '与Rt O AD '相似,则2O A O O O D '''=⨯ 又12A S BC O D '=⋅,12BCOS BC O O '=⋅, 22221124D S BC O A BC O A ⎛⎫''=⋅=⋅ ⎪⎝⎭所以2A BCOD S SS ⋅=,故A 正确.对B :当1a b c ===时,33318B C D S S S ===,则33338B C D S S S ++=,而332333328A S ⎛⎫=⨯⨯=> ⎪ ⎪⎝⎭,此时3333A B C D S S S S >++,故B 不正确. 对D :分别以AB ,AC ,AD 为x ,y ,z 轴,建立空间直角坐标系. 设(),,M x y z ,则(),,AM x y z =,222AM x y z =++,(),0,0AB a =,()0,,0AC b =,()0,0,AD c =所以222222222cos cos cos AM AB AM AC AM AD AM ABAM ACAM ADαβγ⎛⎫⎛⎫⎛⎫⋅⋅⋅++=++ ⎪ ⎪ ⎪ ⎪⎪⎪⋅⋅⋅⎝⎭⎝⎭⎝⎭2222221x y z AMAMAM=++=,所以D 正确.对C :当M 与O 重合时,AO ⊥面BCD ,由D 有222222cos cos cos 1αβγ++=,由各侧棱与底面所成角与侧棱与所AO 成角互为余角,可得C 正确. 故选:ACD.【点睛】关键点睛:本题考查空间线面角、线线角、面积关系的问题,计算角的问题关键是建立空间直角坐标系,写出点的坐标,利用数量积的公式代入计算,解决这道题目还要结合线面角与线线角的关系判断.3.在直角梯形ABCD 中,2ABC BCD π∠=∠=,1AB BC ==,2DC =,E 为DC 中点,现将ADE 沿AE 折起,得到一个四棱锥D ABCE -,则下列命题正确的有( )A .在ADE 沿AE 折起的过程中,四棱锥D ABCE -体积的最大值为13B .在ADE 沿AE 折起的过程中,异面直线AD 与BC 所成的角恒为4π C .在ADE 沿AE 折起的过程中,二面角A EC D --的大小为45︒D .在四棱锥D ABCE -中,当D 在EC 上的射影恰好为EC 的中点F 时,DB 与平面ABCE 所成的角的正切为15 【答案】ABD 【分析】对于A ,四棱锥D ABCE -的底面面积是固定值,要使得体积最大,需要平面DAE ⊥平面ABCE ,此时DE CE ⊥,可求得1133D ABCE ABCE V S DE -=⋅=可判断A ;对于B ,在ADE 沿AE 折起的过程中,//AE BC ,所以异面直线AD 与AE 所成的角即为AD 与BC所成角,由翻折前可知4DAE π∠=可判断B ;对于C ,利用线面垂直的判定定理,结合翻折前可知AE ⊥平面DEC ,又AE ⊂平面ABCE ,所以平面DEC ⊥平面ABCE ,即二面角A EC D --的在大小为2π判断C ;对于D ,利用线面垂直的判定定理可知DF ⊥平面ABCE ,所以DBF ∠为直线DB 与平面ABCE 所成的角,在直角DFB △中,15tan 5DF DBF BF ∠==,可判断D 正确;【详解】对于A ,ADE 沿AE 折起得到四棱锥D ABCE -,由四棱锥底面面积是固定值,要使得体积最大,需要四棱锥的高最大,即平面DAE ⊥平面ABCE ,此时DE CE ⊥,由已知得1DE =,则111111333D ABCE ABCE V S DE -=⋅=⨯⨯⨯=,故A 正确; 对于B ,在ADE 沿AE 折起的过程中,//AE BC ,所以异面直线AD 与AE 所成的角即为AD 与BC 所成角,又1AB BC ==,2DC =,E 为DC 中点,可知4DAE π∠=,即异面直线AD 与BC 所成的角恒为4π,故B 正确; 对于C ,由翻折前知,,AE EC AE ED ⊥⊥,且ECED E =,则AE ⊥平面DEC ,又AE ⊂平面ABCE ,所以平面DEC ⊥平面ABCE ,即二面角A EC D --的大小为2π,故C 错误; 对于D ,如图连接,DF BF ,由C 选项知,AE ⊥平面DEC ,又DF ⊂平面DEC ,则AE DF ⊥,又由已知得EC DF ⊥,且EC AE E ⋂=,则DF ⊥平面ABCE ,所以DBF ∠为直线DB 与平面ABCE 所成的角,在直角DFB △中,tan 5DFDBF BF∠=====,所以DB 与平面ABCED 正确; 故选:ABD 【点睛】关键点睛:本题考查立体几何综合问题,求体积,求线线角,线面角,面面角,解题的关键要熟悉几种角的定义,通过平移法找到线线角,通过证垂直找到线面角和面面角,再结合三角形求出角,考查了学生的逻辑推理能力,转化能力与运算求解能力,属于难题.4.已知正方体1111ABCD A B C D -的棱长为2,点O 为11A D 的中点,若以O为半径的球面与正方体1111ABCD A B C D -的棱有四个交点E ,F ,G ,H ,则下列结论正确的是( )A .11//A D 平面EFGHB .1AC ⊥平面EFGHC .11A B 与平面EFGH 所成的角的大小为45°D .平面EFGH 将正方体1111ABCD A B C D -分成两部分的体积的比为1:7 【答案】ACD 【分析】如图,计算可得,,,E F G H 分别为所在棱的中点,利用空间中点线面的位置关系的判断方法可判断A 、B 的正确与否,计算出直线AB 与平面EFGH 所成的角为45︒后可得C 正确,而几何体BHE CGF -为三棱柱,利用公式可求其体积,从而可判断D 正确与否. 【详解】如图,连接OA ,则2115OA AA =+=,故棱1111,,,A A A D D D AD 与球面没有交点.同理,棱111111,,A B B C C D 与球面没有交点. 因为棱11A D 与棱BC 之间的距离为26>BC 与球面没有交点.因为正方体的棱长为2,而26<球面与正方体1111ABCD A B C D -的棱有四个交点E ,F ,G ,H , 所以棱11,,,AB CD C C B B 与球面各有一个交点, 如图各记为,,,E F G H .因为OAE △为直角三角形,故22651AE OE OA -=-=,故E 为棱AB 的中点. 同理,,F G H 分别为棱11,,CD C C B B 的中点.由正方形ABCD 、,E F 为所在棱的中点可得//EF BC , 同理//GH BC ,故//EF GH ,故,,,E F G H 共面. 由正方体1111ABCD A B C D -可得11//A D BC ,故11//A D EF因为11A D ⊄平面EFGH ,EF ⊂平面EFGH ,故11//A D 平面EFGH ,故A 正确. 因为在直角三角1BA C 中,122A B =2BC = ,190A BC ∠=︒, 1A C 与BC 不垂直,故1A C 与GH 不垂直,故1A C ⊥平面EFGH 不成立,故B 错误.由正方体1111ABCD A B C D -可得BC ⊥平面11AA B B ,而1A B ⊂平面11AA B B , 所以1BC A B ⊥,所以1EF A B ⊥在正方形11AA B B 中,因为,E H 分别为1,AB BB 的中点,故1EH A B ⊥, 因为EFEH E =,故1A B ⊥平面EFGH ,所以BEH ∠为直线AB 与平面EFGH 所成的角,而45BEH ∠=︒, 故直线AB 与平面EFGH 所成的角为45︒,因为11//AB A B ,故11A B 与平面EFGH 所成的角的大小为45°.故C 正确. 因为,,,E F G H 分别为所在棱的中点,故几何体BHE CGF -为三棱柱, 其体积为111212⨯⨯⨯=,而正方体的体积为8,故平面EFGH 将正方体1111ABCD A B C D -分成两部分的体积的比为1:7,故D 正确. 故选:ACD. 【点睛】本题考查空间中线面位置的判断、空间角的计算和体积的计算,注意根据球的半径确定哪些棱与球面有交点,本题属于中档题.5.如图,矩形ABCD 中, 22AB AD ==,E 为边AB 的中点.将ADE 沿直线DE 翻折成1A DE △(点1A 不落在底面BCDE 内),若M 在线段1A C 上(点M 与1A ,C 不重合),则在ADE 翻转过程中,以下命题正确的是( )A .存在某个位置,使1DE A C ⊥B .存在点M ,使得BM ⊥平面1A DC 成立 C .存在点M ,使得//MB 平面1A DE 成立D .四棱锥1A BCDE -体积最大值为24【答案】CD 【分析】利用反证法可得A 、B 错误,取M 为1A C 的中点,取1A D 的中点为I ,连接,MI IE ,可证明//MB 平面1A DE ,当平面1A DE ⊥平面BCDE 时,四棱锥1A BCDE -体积最大2. 【详解】如图(1),取DE 的中点为F ,连接1,A F CF , 则45CDF ∠=︒,22DF =,故212254222222CF =+-⨯⨯=, 故222DC DF CF ≠+即2CFD π∠≠.若1CA DE ⊥,因为11,A D A E DF FE ==,故1A F DE ⊥,而111A F A C A ⋂=, 故DE ⊥平面1A FC ,因为CF ⊂平面1A FC ,故DE CF ⊥,矛盾,故A 错. 若BM ⊥平面1A DC ,因为DC ⊂平面1A DC ,故BM DC ⊥, 因为DC CB ⊥,BM CB B ⋂=,故CD ⊥平面1A CB ,因为1AC ⊂平面1A CB ,故1CD A C ⊥,但1A D CD <,矛盾,故B 错. 当平面1A DE ⊥平面BCDE 时,四棱锥1A BCDE -体积最大值, 由前述证明可知1A F DE ⊥,而平面1A DE平面BCDE DE =,1A F ⊂平面1A DE ,故1A F ⊥平面BCDE ,因为1A DE △为等腰直角三角形,111A D A E ==,故122A F =, 又四边形BCDE 的面积为13211122⨯-⨯⨯=, 故此时体积为13223224⨯⨯=D 正确. 对于C ,如图(2),取M 为1A C 的中点,取1A D 的中点为I ,连接,MI IE ,则1//,2IM CD IM CD =,而1//,2BE CD BE CD =, 故//,IM BE IM BE =即四边形IEBM 为平行四边形,故//IE BM ,因为IE ⊂平面1A DE ,BM ⊄平面1A DE ,故//MB 平面1A DE , 故C 正确.故选:CD.【点睛】本题考查立体几何中的折叠问题,注意对于折叠后点线面的位置的判断,若命题的不成立,往往需要利用反证法来处理,本题属于难题.6.已知直三棱柱111ABC A B C -中,AB BC ⊥,1AB BC BB ==,D 是AC 的中点,O 为1A C 的中点.点P 是1BC 上的动点,则下列说法正确的是( )A .当点P 运动到1BC 中点时,直线1A P 与平面111ABC 5 B .无论点P 在1BC 上怎么运动,都有11A P OB ⊥C .当点P 运动到1BC 中点时,才有1A P 与1OB 相交于一点,记为Q ,且113PQ QA = D .无论点P 在1BC 上怎么运动,直线1A P 与AB 所成角都不可能是30° 【答案】ABD 【分析】构造线面角1PA E ∠,由已知线段的等量关系求1tan EPPA E AE∠=的值即可判断A 的正误;利用线面垂直的性质,可证明11A P OB ⊥即可知B 的正误;由中位线的性质有112PQ QA =可知C 的正误;由直线的平行关系构造线线角为11B A P ∠,结合动点P 分析角度范围即可知D 的正误 【详解】直三棱柱111ABC A B C -中,AB BC ⊥,1AB BC BB ==选项A 中,当点P 运动到1BC 中点时,有E 为11B C 的中点,连接1A E 、EP ,如下图示即有EP ⊥面111A B C∴直线1A P 与平面111A B C 所成的角的正切值:1tan EPPA E AE∠= ∵112EP BB =,22111152AE A B B E BB =+= ∴15tan PA E ∠=,故A 正确选项B 中,连接1B C ,与1BC 交于E ,并连接1A B ,如下图示由题意知,11B BCC 为正方形,即有11B C BC ⊥而AB BC ⊥且111ABC A B C -为直三棱柱,有11A B ⊥面11B BCC ,1BC ⊂面11B BCC ∴111A B BC ⊥,又1111A B B C B =∴1BC ⊥面11A B C ,1OB ⊂面11A B C ,故11BC OB ⊥ 同理可证:11A B OB ⊥,又11A B BC B ⋂=∴1OB ⊥面11A BC ,又1A P ⊂面11A BC ,即有11A P OB ⊥,故B 正确选项C 中,点P 运动到1BC 中点时,即在△11A B C 中1A P 、1OB 均为中位线∴Q 为中位线的交点∴根据中位线的性质有:112PQ QA =,故C 错误选项D 中,由于11//A B AB ,直线1A P 与AB 所成角即为11A B 与1A P 所成角:11B A P ∠ 结合下图分析知:点P 在1BC 上运动时当P 在B 或1C 上时,11B A P ∠最大为45° 当P 在1BC 中点上时,11B A P ∠最小为23arctan 30>=︒ ∴11B A P ∠不可能是30°,故D 正确 故选:ABD 【点睛】本题考查了利用射影定理构造线面角,并计算其正弦值;利用线面垂直证明线线垂直;中位线的性质:中位线交点分中位线为1:2的数量关系;由动点分析线线角的大小7.如图所示,在长方体1111ABCD A B C D -中,11,2,AB BC AA P ===是1A B 上的一动点,则下列选项正确的是( )A .DP 的最小值为35B .DP 的最小值为5C .1AP PC +的最小值为6D .1AP PC +的最小值为1705【答案】AD 【分析】DP 的最小值,即求1DA B △底边1A B 上的高即可;旋转11A BC 所在平面到平面11ABB A ,1AP PC +的最小值转化为求AC '即可.【详解】求DP 的最小值,即求1DA B △底边1A B 上的高,易知115,2A B A D BD ===,所以1A B 边上的高为355h =,连接111,AC BC ,得11A BC ,以1A B 所在直线为轴,将11A BC 所在平面旋转到平面11ABB A ,设点1C 的新位置为C ',连接AC ',则AC '即为所求的最小值,易知11122,2,cos 10AA AC AAC ''==∠=-, 所以217042222()105AC '=+-⨯⨯⨯-=. 故选:AD. 【点睛】本题考查利用旋转求解线段最小值问题.求解翻折、旋转问题的关键是弄清原有的性质变化与否, (1)点的变化,点与点的重合及点的位置变化;(2)线的变化,翻折、旋转前后应注意其位置关系的变化;(3)长度、角度等几何度量的变化.8.在正方体1111ABCD A B C D -中,如图,,M N 分别是正方形ABCD ,11BCC B 的中心.则下列结论正确的是( )A .平面1D MN 与11BC 的交点是11B C 的中点B .平面1D MN 与BC 的交点是BC 的三点分点 C .平面1D MN 与AD 的交点是AD 的三等分点 D .平面1D MN 将正方体分成两部分的体积比为1∶1 【答案】BC 【分析】取BC 的中点E ,延长DE ,1D N ,并交于点F ,连FM 并延长分别交,BC AD 于,P Q ,连1,D Q PN 并延长交11B C 与H ,平面四边形1D HPQ 为所求的截面,进而求出,,P Q H 在各边的位置,利用割补法求出多面体11QPHD C CD 的体积,即可求出结论.【详解】如图,取BC 的中点E ,延长DE ,1D N ,并交于点F , 连接FM 并延长,设FM BC P ⋂=,FM AD Q ⋂=, 连接PN 并延长交11B C 于点H .连接1D Q ,1D H ,则平面四边形1D HPQ 就是平面1D MN 与正方体的截面,如图所示.111111////,22NE CC DD NE CC DD ==,NE ∴为1DD F ∆的中位线,E ∴为DF 中点,连BF , ,,90DCE FBE BF DC AB FBE DCE ∴∆≅∆==∠=∠=︒, ,,A B F ∴三点共线,取AB 中点S ,连MS ,则12//,,23BP FB MS BP MS BC MS FS =∴==, 22111,33236BP MS BC BC PE BC ∴==⨯=∴=, E 为DF 中点,11//,233PE DQ DQ PE BC AD ∴===N 分别是正方形11BCC B 的中心,11113C H BP C B ∴==所以点P 是线段BC 靠近点B 的三等分点, 点Q 是线段AD 靠近点D 的三等分点,点H 是线段11B C 靠近点1C 的三等分点. 做出线段BC 的另一个三等分点P ', 做出线段11A D 靠近1D 的三等分点G ,连接QP ',HP ',QG ,GH ,1H QPP Q GHD V V '--=, 所以111113QPHD C CD QPHQ DCC D V V V -==多面体长方体正方体 从而平面1D MN 将正方体分成两部分体积比为2∶1. 故选:BC.【点睛】本题考查直线与平面的交点及多面体的体积,确定出平面与正方体的交线是解题的关键,考查直观想象、逻辑推理能力,属于较难题.9.已知正四棱柱1111ABCD A B C D -的底面边长为2,侧棱11AA =,P 为上底面1111D C B A 上的动点,给出下列四个结论中正确结论为( )A .若3PD =,则满足条件的P 点有且只有一个B .若3PD =,则点P 的轨迹是一段圆弧C .若PD ∥平面1ACB ,则DP 长的最小值为2D .若PD ∥平面1ACB ,且3PD =,则平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形的面积为94π 【答案】ABD 【分析】若3PD =,由于P 与1B 重合时3PD =,此时P 点唯一;()313PD =,,则12PD =P 的轨迹是一段圆弧;当P 为11A C 中点时,DP 有最小值为3=断C ;平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形为外接球的大圆,其半径为32=,可得D . 【详解】 如图:∵正四棱柱1111ABCD A B C D -的底面边长为2, ∴1122B D =,又侧棱11AA =, ∴()2212213DB =+=,则P 与1B 重合时3PD =,此时P 点唯一,故A 正确;∵()313PD =∈,,11DD =,则12PD =,即点P 的轨迹是一段圆弧,故B 正确; 连接1DA ,1DC ,可得平面11//A DC 平面1ACB ,则当P 为11A C 中点时,DP 有最小值为()22213+=,故C 错误;由C 知,平面BDP 即为平面11BDD B ,平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形为外接球的大圆,其半径为2221322122++=,面积为94π,故D 正确. 故选:ABD . 【点睛】本题考查了立体几何综合,考查了学生空间想象,逻辑推理,转化划归,数学运算的能力,属于较难题.10.如图,在正方体ABCD ﹣A 1B 1C 1D 1中,点P 在线段B 1C 上运动,则( )A .直线BD 1⊥平面A 1C 1DB .三棱锥P ﹣A 1C 1D 的体积为定值C .异面直线AP 与A 1D 所成角的取值范用是[45°,90°]D .直线C 1P 与平面A 1C 1D所成角的正弦值的最大值为3【答案】ABD 【分析】在A 中,推导出A 1C 1⊥BD 1,DC 1⊥BD 1,从而直线BD 1⊥平面A 1C 1D ;在B 中,由B 1C ∥平面 A 1C 1D ,得到P 到平面A 1C 1D 的距离为定值,再由△A 1C 1D 的面积是定值,从而三棱锥P ﹣A 1C 1D 的体积为定值;在C 中,异面直线AP 与A 1D 所成角的取值范用是[60°,90°];在D 中,以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系,利用向量法能求出直线C 1P 与平面A 1C 1D. 【详解】解:在A 中,∵A 1C 1⊥B 1D 1,A 1C 1⊥BB 1,B 1D 1∩BB 1=B 1, ∴A 1C 1⊥平面BB 1D 1,∴A 1C 1⊥BD 1,同理,DC 1⊥BD 1, ∵A 1C 1∩DC 1=C 1,∴直线BD 1⊥平面A 1C 1D ,故A 正确; 在B 中,∵A 1D ∥B 1C ,A 1D ⊂平面A 1C 1D ,B 1C ⊄平面A 1C 1D , ∴B 1C ∥平面 A 1C 1D ,∵点P 在线段B 1C 上运动,∴P 到平面A 1C 1D 的距离为定值,又△A 1C 1D 的面积是定值,∴三棱锥P ﹣A 1C 1D 的体积为定值,故B 正确; 在C 中,异面直线AP 与A 1D 所成角的取值范用是[60°,90°],故C 错误;在D 中,以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系, 设正方体ABCD ﹣A 1B 1C 1D 1中棱长为1,P (a ,1,a ),则D (0,0,0),A 1(1,0,1),C 1(0,1,1),1DA =(1,0,1),1DC =(0,1,1),1C P =(a ,0,a ﹣1), 设平面A 1C 1D 的法向量(),,n x y z =,则1100n DA x z n DC y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩,取x =1,得1,1,1n,∴直线C 1P 与平面A 1C 1D 所成角的正弦值为:11||||||C P n C Pn ⋅⋅=∴当a =12时,直线C 1P 与平面A 1C 1D ,故D 正确. 故选:ABD .【点睛】求直线与平面所成的角的一般步骤:(1)、①找直线与平面所成的角,即通过找直线在平面上的射影来完成;②计算,要把直线与平面所成的角转化到一个三角形中求解;(2)、用空间向量坐标公式求解.。
立体几何基础题题库1(有详细答案)

立体几何基础题题库1(有详细答案)立体几何基础题题库一(有详细答案)1、二面角βα--l 是直二面角,βα∈∈B A ,,设直线AB 与βα、所成的角分别为∠1和∠2,则(A )∠1+∠2=900 (B )∠1+∠2≥900 (C )∠1+∠2≤900 (D )∠1+∠2<900 解析:C1和∠2分别为直线AB与平面,αβ所成的角。
根据最小角定理:斜线和平面所成的角,是这条斜线和平面内经过斜足的直线所成的一切角中最小的角2ABO ∴∠>∠1902190ABO ∠+∠=∴∠+∠≤2. 下列各图是正方体或正四面体,P ,Q ,R ,S 分别是所在棱的中点,这四个点中不共面...的一个图是PPQQRSSPPPQ Q RR R SS SPP P QQQ R RSSSPP Q Q R RRSS(A )(B )(C )(D ) D解析: A 项:PS 底面对应的中线,中线平行QS ,PQRS 是个梯形B 项:如图C 项:是个平行四边形D 项:是异面直线。
3. 有三个平面α,β,γ,下列命题中正确的是ααα (C )若α⊥γ,β∩α=a ,β∩γ=b ,则a ⊥b (D )若α∥β,β∩γ=?,则α∩γ=? D解析:A 项:如正方体的一个角,三个平面相交,只有一条交线。
B 项:如正方体的一个角,三个平面互相垂直,却两两相交。
C 项:如图4. 如图所示,在正方体ABCD -A 1B 1C 1D 1的侧面AB 1内有一动点P 到直线AB 与直线B 1C 1的距离相等,则动点P 所在曲线的形状为11111C解析:11B C ⊥平面AB 111,B C PB ∴⊥,如图:P 点到定点B 的距离与到定直线AB 的距离相等,建立坐标系画图时可以以点B 1B 的中点为原点建立坐标系。
5. 在正方体ABCD -A 1B 1C 1D 1中与AD 1成600角的面对角线的条数是(A )4条(B )6条(C )8条(D )10条 C解析:如图这样的直线有4条,另外,这样的直线也有4条,共8条。
立体几何大题中有关体积、面积和距离的求法(教师版)

立体几何大题中有关体积、面积和距离的求法(教师版)立体几何大题中有关体积、面积和距离的求法知识点梳理1.柱、锥、台和球的侧面积和体积圆柱:侧面积为$S_\text{侧}=2\pi rh$,体积为$V=\pir^2h$圆锥:侧面积为$S_\text{侧}=\pi rl$,体积为$V=\frac{1}{3}\pi r^2h$圆台:侧面积为$S_\text{侧}=\pi(r_1+r_2)l$,体积为$V=\frac{1}{3}\pi h(r_1^2+r_2^2+r_1r_2)$直棱柱、正棱锥、正棱台、球的表面积和体积公式不再赘述。
2.几何体的表面积直棱柱、棱锥、棱台的表面积就是各面面积之和。
圆柱、圆锥、圆台的侧面展开图分别是矩形、扇形、扇环形;它们的表面积等于侧面积与底面面积之和。
一公式法例1.正三棱柱的侧面展开图是边长分别为2和4的矩形,则它的体积为。
解:因为正三棱柱的侧面展开图是边长分别为2和4的矩形,所以有以下两种情况:①:2是下底面的周长,4是三棱柱的高,此时下底面的边长为$\frac{2}{\sqrt{3}}$,所以体积为$V=\frac{4}{3}\sqrt{3}$,面积为$S=2\sqrt{3}$。
②:4是下底面的周长,2是三棱柱的高,此时下底面的边长为$\sqrt{3}$,所以体积为$V=\frac{4}{3}\sqrt{3}$,面积为$S=2\sqrt{3}$。
所以正三棱柱的体积为$\frac{4}{3}\sqrt{3}$。
例2.如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等边三角形,等腰三角形和菱形,则该几何体的体积为()。
解:由题意可知此几何体是一个四棱锥,由图可知底面两条对角线的长分别为2和3,底面边长为2,所以底面菱形的面积为$S=\frac{3}{2}$,侧棱为$\sqrt{2^2+3^2}= \sqrt{13}$,则棱锥的高$h=\sqrt{3^2-(\frac{\sqrt{13}}{2})^2}=\frac{\sqrt{35}}{2}$。
(完整版)立体几何坐标法教师版

立体几何坐标法:一:一般的公式:1、空间角(1)(线线)设异面直线l 1,l 2的方向向量分别为m 1,m 2,则l 1与l 2的夹角θ满足cos θ=|cos 〈m 1,m 2〉|.(2)(线面)设直线l 的方向向量和平面α的法向量分别为m ,n ,则直线l 与平面α的夹角θ满足sin θ=|cos 〈m ,n 〉|. (3)(面面)求二面角的大小(ⅰ)如图①,AB 、CD 是二面角α-l -β的两个面内与棱l 垂直的直线,则二面角的大小θ=〈AB →,CD →〉.(ⅱ)如图②③,n 1,n 2分别是二面角α-l -β的两个半平面α,β的法向量,则二面角的大小θ满足cos θ=cos 〈n 1,n 2〉或-cos 〈n 1,n 2〉.2、距离(1)点面距的求法:设AB 为平面α的一条斜线段,n 为平面α的法向量,则B 到平面α的距离d =|AB →·n ||n |.(2)线面距、面面距均可转化为点面距(3)两异面直线的距离求法:d =|AB →·n ||n |.(AB 是异面直线上任意两点)二:如何选择建系:8、在如图所示的几何体中,EA ⊥平面ABC ,DB ⊥平面ABC ,AC BC ⊥,且2AC BC BD AE ===,M 是AB 的中点. (Ⅰ)求证:CM EM ⊥;(Ⅱ)求CM 与平面CDE 所成的角.11年重庆 19.(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分.)如题(19)图,在四面体ABCD 中,平面ABC ⊥平面ACD ,AB BC ⊥,AD CD =,CAD ∠=30︒.(Ⅰ)若AD =2,AB BC =2,求四面体ABCD 的体积;(Ⅱ)若二面角C AB D --为60︒,求异面直线AD 与BC 所成角的余弦值.28.【2012高考四川文19】(本小题满分12分)如图,在三棱锥P ABC -中,90APB ∠=,60PAB ∠=,AB BC CA ==,点PEDCM AB在平面ABC 内的射影O 在AB 上。
立体几何共线、共点、共面问题(教师版)

立体几何中的共点、共线、共面问题一、共线问题例1. 若ΔABC 所在的平面和ΔA 1B 1C 1所在平面相交,并且直线AA 1、BB 1、CC 1相交于一点O ,求证:(1)AB 和A 1B 1、BC 和B 1C 1、AC 和A 1C 1分别在同一平面内;(2)如果AB 和A 1B 1、BC 和B 1C 1、AC 和A 1C 1分别相交,那么交点在同一直线上(如图).例2. 点P 、Q 、R 分别在三棱锥A-BCD 的三条侧棱上,且PQ ∩BC =X,QR ∩CD =Z,PR ∩BD =Y.求证:X 、Y 、Z 三点共线.例3. 已知△ABC 三边所在直线分别与平面α交于P 、Q 、R 三点,求证:P 、Q 、R 三点共线。
1.如图1,正方体1111ABCD A BC D -中,1AC 与截面1DBC 交O 点,AC BD ,交M 点,求证:1C O M ,,三点共线. 证明:连结11AC ,1C ∈平面11A ACC ,且1C ∈平面1DBC ,1C ∴是平面11A ACC 与平面1DBC 的公共点.又M AC M ∈∴∈,平面11A ACC . M BD M ∈∴∈,平面1DBC .M ∴也是平面11A ACC 与平面1DBC 的公共点.1C M ∴是平面11A ACC 与平面1DBC 的交线.O 为1AC 与截面1DBC 的交点,O ∴∈平面11A ACC O ∈,平面1DBC ,即O 也是两平面的公共点. 1O C M ∈∴,即1C M O ,,三点共线.2.如图,在四边形ABCD 中,已知AB∥CD,直线AB ,BC ,AD ,DC 分别与平面α相交于点E ,G ,H ,F .求证:E ,F ,G ,H 四点必定共线(在同一条直线上).分析:先确定一个平面,然后证明相关直线在这个平面内,最后证明四点共线.证明 ∵ AB//CD, AB ,CD 确定一个平面β. 又∵AB ∩α=E ,AB β,∴ E ∈α,E ∈β, 即 E 为平面α与β的一个公共点.同理可证F ,G ,H 均为平面α与β的公共点.∵ 两个平面有公共点,它们有且只有一条通过公共点的公共直线,∴ E,F ,G ,H 四点必定共线.点 评:在立体几何的问题中,证明若干点共线时,先证明这些点都是某两平面的公共点,而后得出这些点都在二平面的交线上的结论.二、共面问题1.如图3,设P Q R S M N ,,,,,分别为正方体1111ABCD A BC D - 的棱111111AB BC CC C D A D A A ,,,,,的中点, 求证:P Q R S M N ,,,,,共面.证明:如图3,连结1A B MQ NR ,,.P N ,分别为1AB A A ,的中点,1A B PN ∴∥.111A D BC A M BQ ∴,∥∥.M Q ,分别为11A D BC ,的中点,1AM BQ ∴=. ∴四边形1A BQM 为平行四边形. 1A B MQ ∴∥.PN MQ ∴∥. 因此,直线PN MQ ,可确定一个平面α.同理,由PQ NR ∥可知,直线PQ NR ,确定一个平面β.过两条相交直线PN PQ ,有且只有一个平面,α∴与β重合,即R α∈.同理可证S α∈. 因此,P Q R S M N ,,,,,共面.例4. 直线m 、n 分别和平行直线a 、b 、c 都相交,交点为A 、B 、C 、D 、E 、F ,如图,求证:直线a 、b 、c 、m 、n 共面.例5. 证明两两相交而不共点的四条直线在同一平面内.已知:如图,直线l 1,l 2,l 3,l 4两两相交,且不共点. 求证:直线l 1,l 2,l 3,l 4在同一平面内例6. 已知:A 1、B 1、C 1和A 2、B 2、C 2分别是两条异面直线l 1和l 2上的任意三点,M 、N 、R 、T 分别是A 1A 2、B 1A 2、B 1B 2、C 1C 2的中点.求证:M 、N 、R 、T 四点共面.例7. 在空间四边形ABCD 中,M 、N 、P 、Q 分别是四边上的点,且满足MB AM =NB CN =QDAQ=PD CP =k. (1)求证:M 、N 、P 、Q 共面.(2)当对角线AC =a,BD =b ,且MNPQ 是正方形时,求AC 、BD 所成的角及k 的值(用a,b 表示)三、共点问题例8. 三个平面两两相交得三条直线,求证:这三条直线相交于同一点或两两平行.1.如图2,已知空间四边形ABCD E F ,,分别是 AB AD ,的中点,G H ,分别是BC CD ,上的点, 且2BG DHGC HC==,求证:EG FH AC ,,相交于同一点P . 错解:证明:E 、F 分别是AB,AD 的中点, EF ∴∥BD,EF=21BD,又2==HC DHGC BG ,∴ GH∥BD,GH=31BD,∴四边形EFGH 是梯形,设两腰EG,FH 相交于一点T,2=HCDH ,F 分别是AD.∴AC 与FH 交于一点.∴直线EG,FH,AC 相交于一点正解:证明:E F ,分别是AB AD ,的中点,EF BD ∴∥,且12EF BD =.又2BG DH GC HC ==, GH BD ∴∥,且13GH BD =. EF GH ∴∥,且EF GH >.∴四边形EFHG 是梯形,其两腰必相交,设两腰EG FH ,相交于一点P ,EG ⊂∵平面ABC FH ⊂,平面ACD ,P ∴∈平面ABC P ∈,平面ACD ,又平面ABC 平面ACD AC P AC =∴∈,. 故EG FH AC ,,相交于同一点P .2. 如图,已知平面α,β,且α∩β=l .设梯形ABCD 中,AD∥BC,且AB α,CD β,求证:AB ,CD ,l 共点(相交于一点).分析:AB ,CD 是梯形ABCD 的两条腰,必定相交于一点M ,只要证明M 在l 上,而l 是两个平面α,β的交线,因此,只要证明M∈α,且M∈β即可. 证明: ∵ 梯形ABCD 中,AD∥BC, ∴AB,CD 是梯形ABCD 的两条腰. ∴ AB,CD 必定相交于一点,设 AB ∩CD=M .又∵ AB α,CD β,∴ M∈α,且M∈β. ∴ M∈α∩β.又∵ α∩β=l ,∴ M∈l , 即 AB ,CD ,l 共点.点 评:证明多条直线共点时,与证明多点共线是一样的. 1、(1)证明:∵AA 1∩BB 1=O, ∴AA 1、BB 1确定平面BAO ,∵A 、A 1、B 、B 1都在平面ABO 内, ∴AB ⊂平面ABO ;A 1B 1⊂平面ABO.同理可证,BC 和B 1C 1、AC 和A 1C 1分别在同一平面内.(2)分析:欲证两直线的交点在一条直线上,可根据公理2,证明这两条直线分别在两个相交平面内,那么,它们的交点就在这两个平面的交线上.2证明:如图,设AB ∩A 1B 1=P ; AC ∩A 1C 1=R ;∴ 面ABC ∩面A 1B 1C 1=PR.∵ BC ⊂面ABC ;B 1C 1⊂面A 1B 1C 1, 且 BC ∩B 1C 1=Q ∴ Q ∈PR, 即 P 、R 、Q 在同一直线上.3解析:∵A 、B 、C 是不在同一直线上的三点 ∴过A 、B 、C 有一个平面β 又βα⊂=⋂AB P AB 且,.,,l p l P ∈=⋂∴则设内内又在既在点βααβ.,,,:三点共线同理可证R Q P l R l Q ∴∈∈4解析: 证明若干条直线共面的方法有两类:一是先确定一个平面,证明其余的直线在这个平面里;二是分别确定几个平面,然后证明这些平面重合.证明∵a ∥b,∴过a 、b 可以确定一个平面α.∵A ∈a,a ⊂α,∴A ∈α,同理B ∈a.又∵A ∈m ,B ∈m,∴m ⊂α.同理可证n ⊂α.∵b ∥c,∴过b,c 可以确定平面β,同理可证m ⊂β. ∵平面α、β都经过相交直线b 、m,∴平面α和平面β重合,即直线a 、b 、c 、m 、n 共面.5、解析:证明几条直线共面的依据是公理3及推论和公理1.先证某两线确定平面α,然后证其它直线也在α内. 证明:图①中,l 1∩l 2=P , ∴ l 1,l 2确定平面α.又 l 1∩l 3=A,l 2∩l 3=C,∴ C,A ∈α. 故 l 3⊂α. 同理 l 4⊂α.∴ l 1,l 2,l 3,l 4共面.图②中,l 1,l 2,l 3,l 4的位置关系,同理可证l 1,l 2,l 3,l 4共面. 所以结论成立.6、证明 如图,连结MN 、NR ,则MN ∥l 1,NR ∥l 2,且M 、N 、R 不在同一直线上(否则,根据三线平行公理,知l 1∥l 2与条件矛盾).∴ MN 、NR 可确定平面β,连结B 1C 2,取其中点S.连RS 、ST ,则RS ∥l 2,又RN ∥l 2,∴ N 、R 、S 三点共线.即有S ∈β,又ST ∥l 1,MN ∥l 1,∴MN ∥ST ,又S ∈β,∴ ST ⊂β. ∴ M 、N 、R 、T 四点共面. 7解析:(1)∵MB AM =QD AQ=k ∴ MQ ∥BD ,且MB AM AM +=1+k k∴BD MQ =AB AM =1+k k∴ MQ =1+k kBD又NB CN =PDCP=k ∴ PN ∥BD ,且NB CN CN +=1+k k∴BD NP =CB CN =1+k k 从而NP =1+k kBD∴ MQ ∥NP ,MQ ,NP 共面,从而M 、N 、P 、Q 四点共面. (2)∵MA BM =k 1,NC BN =k1∴MA BM =NC BN =k 1,MABM BM +=11+k∴ MN ∥AC ,又NP ∥BD.∴ MN 与NP 所成的角等于AC 与BD 所成的角. ∵ MNPQ 是正方形,∴∠MNP =90° ∴ AC 与BD 所成的角为90°, 又AC =a ,BD =b ,AC MN =BA BM =11+k ∴ MN =11+k a 又 MQ =11+k b,且MQ =MN , 1+k k b =11+k a ,即k =ba.说明:公理4是证明空间两直线平行的基本出发点.已知:平面α∩平面β=a,平面β∩平面γ=b,平面γ∩平面α=c.求证:a、b、c相交于同一点,或a∥b∥c.证明:∵α∩β=a,β∩γ=b∴a、b⊂β∴a、b相交或a∥b.(1)a、b相交时,不妨设a∩b=P,即P∈a,P∈b而a、b⊂β,a⊂α∴P∈β,P∈α,故P为α和β的公共点又∵α∩γ=c由公理2知P∈c∴a、b、c都经过点P,即a、b、c三线共点.(2)当a∥b时∵α∩γ=c且a⊂α,a⊄γ∴a∥c且a∥b∴a∥b∥c故a、b、c两两平行.由此可知a、b、c相交于一点或两两平行.A 1题2.S 是正三角形ABC 所在平面外的一点,如图SA =SB =SC ,且∠ASB =∠BSC =∠CSA =2π,M 、N 分别是AB 和SC 的中点.求异面直线SM 与BN 所成的角的余弦值.证明:连结CM ,设Q 为CM 的中点,连结QN 则QN∥SM∴∠QNB 是SM 与BN 所成的角或其补角 连结BQ ,设SC =a ,在△BQN 中BN =a 25 NQ =21SM =42a BQ =a 414∴COS∠QNB=5102222=⋅-+NQ BN BQ NQ BN题3.正∆ABC 的边长为a ,S 为∆ABC 所在平面外的一点,SA =SB =SC =a ,E ,F 分别是SC 和AB 的中点.求异面直线SA 和EF 所成角.答案:45°题4.如图,在直三棱柱ABC -A 1B 1C 1中,∠BCA=90°,M 、N 分别是A 1B 1和A 1C 1的中点, 若BC =CA =CC 1,求NM 与AN 所成的角.解:连接MN ,作NG∥BM 交BC 于G ,连接AG , 易证∠GNA 就是BM 与AN 所成的角.设:BC =CA =CC 1=2,则AG =AN =5,GN =B 1M =6,cos∠GNA=1030562556=⨯⨯-+。
数学立体几何多选题(讲义及答案)附解析

数学立体几何多选题(讲义及答案)附解析一、立体几何多选题1.如图,直三棱柱11,ABC A B C -,ABC 为等腰直角三角形,AB BC ⊥,且12AC AA ==,E ,F 分别是AC ,11A C 的中点,D ,M 分别是1AA ,1BB 上的两个动点,则( )A .FM 与BD 一定是异面直线B .三棱锥D MEF -的体积为定值14C .直线11B C 与BD 所成角为2π D .若D 为1AA 中点,则四棱锥1D BB FE -55【答案】CD 【分析】A 当特殊情况M 与B 重合有FM 与BD 相交且共面;B 根据线面垂直、面面垂直判定可证面1BEFB ⊥面11ACC A ,可知EMFS、D 到面1BEFB 的距离,可求D EMF V -;C 根据线面垂直的判定及性质即可确定11B C 与BD 所成角;D 由面面垂直、勾股、矩形性质等确定外接球半径,进而求体积,即可判断各项的正误. 【详解】A :当M 与B 重合时,FM 与BD 相交且共面,错误; B :由题意知:BE AC ⊥,AC EF ⊥且BEEF E =,则AC ⊥面1BEFB ,又AC ⊂面11ACC A ,面1BEFB ⋂面11ACC A EF =,所以面1BEFB ⊥面11ACC A ,又1121122EMFSEF BE =⋅⋅=⨯⨯=,D 到面1BEFB 的距离为1h =,所以1133D EMF EMFV h S-=⋅⋅=,错误; C :由AB BC ⊥,1BC B B ⊥,1B BAB B =,所以BC ⊥面11ABB A ,又11//BC B C ,即11B C ⊥面11ABB A ,而BD ⊂面11ABB A ,则11BD B C ⊥,正确;D :由B 中,面1BEFB ⊥面11ACC A ,即面DEF ⊥面1BEFB ,则D 到面1BEFB 的距离为1h =,又D 为1AA 中点,若1,BF EB 交点为O ,G 为EF 中点,连接,,OG GD OD ,则OG GD ⊥,故2252OD OG GD =+=,由矩形的性质知:152OB OE OF OB ====,令四棱锥1D BB FE -的外接球半径为R ,则5R =,所以四棱锥1D BB FE -的外接球体积为35435V R ππ==,正确. 故选:CD. 【点睛】关键点点睛:利用线面、面面关系确定几何体的高,结合棱锥体积公式求体积,根据线面垂直、勾股定理及矩形性质确定外接球半径,结合球体体积公式求体积.2.如图,已知正方体1ABCD ABC D -的棱长为a ,E 是棱CD 上的动点.则下列结论中正确的有( )A .11EB AD ⊥B .二面角11E A B A --的大小为4πC .三棱锥11A BDE -体积的最小值为313a D .1//D E 平面11A B BA【答案】ABD 【分析】连接1A D 、1B C ,则易证1AD ⊥平面11A DCB ,1EB ⊂平面11A DCB ,则由线面垂直的性质定理可以判断选项A 正确;二面角11E A B A --的平面角为1DA A ∠,易知14DA A π∠=,则可判断选项B 正确;用等体积法,将求三棱锥11A B D E -的体积转化为求三棱锥11E AB D -的体积,当点E 与D 重合时,三棱锥11E AB D -的体积最小,此时的值为316a ,则选项C 错误;易知平面11//D DCC 平面11A B BA ,而1D E ⊂平面11D DCC ,则根据面面平行的性质定理可得1//D E 平面11A B BA ,可判断选项D 正确. 【详解】选项A ,连接1A D 、1B C ,则由正方体1ABCD ABC D -可知,11A D AD ⊥,111A B AD ⊥,1111A DA B A =,则1AD ⊥平面11A DCB ,又因为1EB ⊂平面11A DCB ,所以11EB AD ⊥,选项A 正确; 选项B ,因为11//DE A B ,则二面角11E A B A --即为二面角11D A B A --, 由正方体1ABCD ABC D -可知,11A B ⊥平面1DA A , 则1DA A ∠为二面角11D A B A --的平面角,且14DA A π∠=,所以选项B 正确;选项C ,设点E 到平面11AB D 的距离为d , 则11111113A B D E E AB D AB D V V S d --==⋅,连接1C D 、1C B ,易证平面1//BDC 平面11AB D ,则在棱CD 上,点D 到平面11AB D 的距离最短, 即点E 与D 重合时,三棱锥11A B D E -的体积最小, 由正方体1ABCD ABC D -知11A B ⊥平面1ADD , 所以1111123111113326D AB D B ADDADD a V V S A B a a --==⋅=⋅⋅=, 则选项C 错误;选项D ,由正方体1ABCD ABC D -知,平面11//CC D D 平面11A B BA ,且1D E ⊂平面11CC D D , 则由面面平行的性质定理可知1//D E 平面11A B BA ,则选项D 正确. 故选:ABD. 【点睛】关键点点睛:本题对于选项C 的判断中,利用等体积法求三棱锥的体积是解题的关键.3.已知四面体ABCD 的所有棱长均为2,则下列结论正确的是( ) A .异面直线AC 与BD 所成角为60︒B .点A 到平面BCDC .四面体ABCDD .动点P 在平面BCD 上,且AP 与AC 所成角为60︒,则点P 的轨迹是椭圆 【答案】BC 【分析】在正四面体中通过线面垂直可证得AC ⊥BD ,通过计算可验证BC,通过轨迹法可求得P 的轨迹为双曲线方程即可得D 错误. 【详解】取BD 中点E ,连接,AE CE ,可得BD ⊥面ACE ,则AC ⊥BD ,故A 错误;在四面体ABCD 中,过点A 作AF ⊥面BCD 于点F ,则F 为为底面正三角形BCD 的重心,因为所有棱长均为2,AF ==即点A 到平面BCD 的距离为3,故B 正确;设O 为正四面体的中心则OF 为内切球的半径,OA 我外接球的半径, 因为11433A BCD BCD BCD V S AF S OF -=⋅=⨯⋅△△,所以4AF OF =,即2=6OF AO =,所以四面体ABCD 的外接球体积334433V R OA ππ===,故C 正确;建系如图:26230,0,,0,,0A C ⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,设(,,0)P x y ,则262326,,0,,333AP x y AC →→⎛⎫⎛⎫=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,因为cos 60AP AC AP AC →→→→⋅=,所以22232481224193972y x y +=++⨯+⨯, 即222388=33y x y +++,平方化简可得:2232340039y x y ----,可知点P 的轨迹为双曲线,故D 错误. 故选:BC .【点睛】方法点睛:立体几何中动点轨迹的求解问题,解决此类问题可采用空间向量法,利用空间向量法表示出已知的角度或距离的等量关系,从而得到轨迹方程.4.正方体1111ABCD A B C D -中,E 是棱1DD 的中点,F 在侧面11CDD C 上运动,且满足1//B F 平面1A BE .以下命题正确的有( )A .侧面11CDD C 上存在点F ,使得11B F CD ⊥B .直线1B F 与直线BC 所成角可能为30︒C .平面1A BE 与平面11CDD C 所成锐二面角的正切值为22D .设正方体棱长为1,则过点E ,F ,A 的平面截正方体所得的截面面积最大为5 【答案】AC 【分析】取11C D 中点M ,1CC 中点N ,连接11,,B M B N MN ,易证得平面1//B MN 平面1A BE ,可得点F 的运动轨迹为线段MN .取MN 的中点F ,根据等腰三角形的性质得1B F MN ⊥,即有11B F CD ⊥,A 正确;当点F 与点M 或点N 重合时,直线1B F 与直线BC 所成角最大,可判断B 错误;根据平面1//B MN 平面1A BE ,11B FC ∠即为平面1B MN 与平面11CDD C 所成的锐二面角,计算可知C 正确;【详解】取11C D 中点M ,1CC 中点N ,连接11,,B M B N MN ,则易证得11//B N A E ,1//MN A B ,从而平面1//B MN 平面1A BE ,所以点F 的运动轨迹为线段MN .取MN 的中点F ,因为1B MN △是等腰三角形,所以1B F MN ⊥,又因为1//MN CD ,所以11B F CD ⊥,故A 正确;设正方体的棱长为a ,当点F 与点M 或点N 重合时,直线1B F 与直线BC 所成角最大,此时11tan C B F ∠=1tan 3023︒<=,所以B 错误; 平面1//B MN 平面1A BE ,取F 为MN 的中点,则1MN C F ⊥,1MN B F ⊥,∴11B FC ∠即为平面1B MN 与平面11CDD C 所成的锐二面角,11111tan B C B FC C F∠==22,所以C 正确;因为当F 为1C E 与MN 的交点时,截面为菱形1AGC E (G 为1BB 的交点),面积为62,故D 错误. 故选:AC.【点睛】本题主要考查线面角,二面角,截面面积的求解,空间几何中的轨迹问题,意在考查学生的直观想象能力和数学运算能力,综合性较强,属于较难题.5.如图,点E 为正方形ABCD 边CD 上异于点C ,D 的动点,将ADE 沿AE 翻折成SAE △,在翻折过程中,下列说法正确的是( )A .存在点E 和某一翻折位置,使得SB SE ⊥ B .存在点E 和某一翻折位置,使得//AE 平面SBCC .存在点E 和某一翻折位置,使得直线SB 与平面ABC 所成的角为45°D .存在点E 和某一翻折位置,使得二面角S AB C --的大小为60° 【答案】ACD 【分析】依次判断每个选项:当SE CE ⊥时,⊥SE SB ,A 正确,//AE 平面SBC ,则//AE CB ,这与已知矛盾,故B 错误,取二面角D AE B --的平面角为α,取4=AD ,计算得到2cos 3α=,C 正确,取二面角D AE B --的平面角为60︒,计算得到5tan θ=,故D 正确,得到答案. 【详解】当SE CE ⊥时,SE AB ⊥,SE SA ⊥,故SE ⊥平面SAB ,故⊥SE SB ,A 正确;若//AE 平面SBC ,因AE ⊂平面ABC ,平面ABC 平面SBC BC =,则//AE CB ,这与已知矛盾,故B 错误;如图所示:DF AE ⊥交BC 于F ,交AE 于G ,S 在平面ABCE 的投影O 在GF 上, 连接BO ,故SBO ∠为直线SB 与平面ABC 所成的角,取二面角D AE B --的平面角为α,取4=AD ,3DE =,故5AE DF ==,1CE BF ==,125DG =,12cos 5OG α=,故只需满足12sin 5SO OB α==, 在OFB △中,根据余弦定理:2221213121312sin 1cos 2cos cos 55555OFB ααα⎛⎫⎛⎫⎛⎫=+---∠ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,解得2cos 3α=,故C 正确; 过O 作OMAB ⊥交AB 于M ,则SMO ∠为二面角S AB C --的平面角,取二面角D AE B --的平面角为60︒,故只需满足22DG GO OM ==,设OAG OAM θ∠=∠=,84ππθ<<,则22DAG πθ∠=-,tan tan 22DG OGAG πθθ==⎛⎫- ⎪⎝⎭,化简得到2tan tan 21θθ=,解得5tan θ=,验证满足,故D 正确; 故选:ACD .【点睛】本题考查了线线垂直,线面平行,线面夹角,二面角,意在考查学生的计算能力,推断能力和空间想象能力.6.在长方体1111ABCD A B C D -中,23AB =12AD AA ==,,,P Q R 分别是11,,AB BB AC 上的动点,下列结论正确的是( ) A .对于任意给定的点P ,存在点Q 使得1D P CQ ⊥ B .对于任意给定的点Q ,存在点R 使得1D R CQ ⊥ C .当1AR A C ⊥时,1AR D R ⊥D .当113AC A R =时,1//D R 平面1BDC 【答案】ABD 【分析】如图所示建立空间直角坐标系,计算142D P CQ b ⋅=-,()12222D R CQ b λλ⋅=--,134AR D R ⋅=-,10D R n ⋅=,得到答案.【详解】如图所示,建立空间直角坐标系,设()2,,0P a ,0,23a ⎡∈⎣,()2,23,Q b ,[]0,2b ∈,设11A R AC λ=,得到()22,23,22R λλλ--,[]0,1λ∈. ()12,,2P a D -=,()2,0,CQ b =,142D P CQ b ⋅=-,当2b =时,1D P CQ ⊥,A 正确;()122,23,2D R λλλ=--,()12222D R CQ b λλ⋅=--,取22bλ=+时,1D R CQ ⊥,B 正确; 1AR A C ⊥,则()()12,23,222,23,2212440AR AC λλλλλλ⋅=--⋅--=-+-+=, 14λ=,此时11333313,,,,022224AR D R ⎛⎫⎛⎫⋅=-⋅-=-≠ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,C 错误; 113AC A R =,则4234,,33R ⎛⎫ ⎪ ⎪⎝⎭,14232,,33D R ⎛⎫=- ⎪ ⎪⎝⎭,设平面1BDC 的法向量为(),,n x y z =,则100n BD n DC ⎧⋅=⎪⎨⋅=⎪⎩,解得()3,1,3n =-,故10D R n ⋅=,故1//D R 平面1BDC ,D 正确. 故选:ABD .【点睛】本题考查了空间中的线线垂直,线面平行,意在考查学生的计算能力和空间想象能力,推断能力.7.M ,N 分别为菱形ABCD 的边BC ,CD 的中点,将菱形沿对角线AC 折起,使点D 不在平面ABC 内,则在翻折过程中,下列结论正确的有( )A .MN ∥平面ABDB .异面直线AC 与MN 所成的角为定值C .在二面角D AC B --逐渐变小的过程中,三棱锥D ABC -外接球的半径先变小后变大D .若存在某个位置,使得直线AD 与直线BC 垂直,则ABC ∠的取值范围是0,2π⎛⎫⎪⎝⎭【答案】ABD 【分析】利用线面平行的判定即可判断选项A ;利用线面垂直的判定求出异面直线AC 与MN 所成的角即可判断选项B ;借助极限状态,当平面DAC 与平面ABC 重合时,三棱锥D ABC -外接球即是以ABC ∆外接圆圆心为球心,外接圆的半径为球的半径,当二面角D AC B --逐渐变大时,利用空间想象能力进行分析即可判断选项C;过A 作AH BC ⊥,垂足为H ,分ABC ∠为锐角、直角、钝角三种情况分别进行分析判断即可判断选项D. 【详解】对于选项A:因为M ,N 分别为菱形ABCD 的边BC ,CD 的中点,所以MN 为BCD ∆的中位线,所以//MN BD ,因为MN ⊄平面ABD ,BD ⊂平面ABD ,所以MN ∥平面ABD ,故选项A 正确;对于选项B :取AC 的中点O ,连接,DO BO ,作图如下:则,AC DO AC BO ⊥⊥,BO DO O =,由线面垂直的判定知,AC ⊥平面BOD ,所以AC BD ⊥,因为//MN BD ,所以AC MN ⊥,即异面直线AC 与MN 所成的角为定值90,故选项B 正确;对于选项C:借助极限状态,当平面DAC 与平面ABC 重合时,三棱锥D ABC -外接球即是以ABC ∆外接圆圆心为球心,外接圆的半径为球的半径,当二面角D AC B --逐渐变大时,球心离开平面ABC ,但是球心在底面的投影仍然是ABC ∆外接圆圆心,故二面角D AC B --逐渐变小的过程中,三棱锥D ABC -外接球的半径不可能先变小后变大, 故选项C 错误;对于选项D:过A 作AH BC ⊥,垂足为H ,若ABC ∠为锐角,H 在线段BC 上;若ABC ∠为直角,H 与B 重合;若ABC ∠为钝角,H 在线段BC 的延长线上;若存在某个位置,使得直线AD 与直线BC 垂直,因为AH BC ⊥,所以CB ⊥平面AHD ,由线面垂直的性质知,CB HD ⊥,若ABC ∠为直角,H 与B 重合,所以CB BD ⊥,在CBD ∆中,因为CB CD =, 所以CB BD ⊥不可能成立,即ABC ∠为直角不可能成立;若ABC ∠为钝角,H 在线段BC 的延长线上,则在原平面图菱形ABCD 中,DCB ∠为锐角,由于立体图中DB DO OB <+,所以立体图中DCB ∠一定比原平面图中更小,,所以DCB ∠为锐角,CB HD ⊥,故点H 在线段BC 与H 在线段BC 的延长线上矛盾,因此ABC ∠不可能为钝角;综上可知,ABC ∠的取值范围是0,2π⎛⎫⎪⎝⎭.故选项D 正确;故选:ABD 【点睛】本题考查异面垂直、线面平行与线面垂直的判定、多面体的外接球问题;考查空间想象能力和逻辑推理能力;借助极限状态和反证法思想的运用是求解本题的关键;属于综合型强、难度大型试题.8.如图,正三棱柱11ABC A B C -中,11BC AB ⊥、点D 为AC 中点,点E 为四边形11BCC B 内(包含边界)的动点则以下结论正确的是( )A .()1112DA A A B A BC =-+ B .若//DE 平面11ABB A ,则动点E 的轨迹的长度等于22AC C .异面直线AD 与1BC 6D .若点E 到平面11ACC A的距离等于2EB ,则动点E 的轨迹为抛物线的一部分 【答案】BCD 【分析】根据空间向量的加减法运算以及通过建立空间直角坐标系求解,逐项判断,进而可得到本题答案. 【详解】解析:对于选项A ,()1112AD A A B A BC =-+,选项A 错误; 对于选项B ,过点D 作1AA 的平行线交11A C 于点1D .以D 为坐标原点,1DA DB DD ,,分别为,,x y z 轴的正方向建立空间直角坐标系Oxyz .设棱柱底面边长为a ,侧棱长为b ,则002aA ⎛⎫ ⎪⎝⎭,,,002B a ⎛⎫ ⎪ ⎪⎝⎭,,,102B a b ⎛⎫ ⎪ ⎪⎝⎭,,,102a C b ⎛⎫- ⎪⎝⎭,,,所以122a BC a b ⎛⎫=-- ⎪ ⎪⎝⎭,,,122a AB a b ⎛⎫=- ⎪ ⎪⎝⎭,,. ∵11BC AB ⊥,∴110BC AB ⋅=,即22202a b ⎫⎛⎫--+=⎪ ⎪⎪⎝⎭⎝⎭,解得2b a =. 因为//DE 平面11ABB A ,则动点E的轨迹的长度等于1BB =.选项B 正确. 对于选项C ,在选项A 的基础上,002a A ⎛⎫⎪⎝⎭,,,002B a ⎛⎫ ⎪ ⎪⎝⎭,,,()0,0,0D ,1022a C a ⎛⎫- ⎪ ⎪⎝⎭,,,所以002a DA ⎛⎫= ⎪⎝⎭,,,122a BC a ⎛⎫=- ⎪ ⎪⎝⎭,,因为2111cos ,6||||aBC DA BC DA BC DA a ⎛⎫- ⎪⋅<>===-,所以异面直线1,BC DA 所成角C 正确. 对于选项D,设点E 在底面ABC 的射影为1E ,作1E F 垂直于AC ,垂足为F ,若点E 到平面11ACC A EB ,即有1E F EB =,又因为在1CE F ∆中,3112E F E C =,得1EB E C =,其中1E C 等于点E 到直线1CC 的距离,故点E 满足抛物线的定义,另外点E 为四边形11BCC B 内(包含边界)的动点,所以动点E 的轨迹为抛物线的一部分,故D 正确.故选:BCD 【点睛】本题主要考查立体几何与空间向量的综合应用问题,其中涉及到抛物线定义的应用.9.如图所示,在棱长为1的正方体1111ABCD A B C D -中,过对角线1BD 的一个平面交棱1AA 于点E ,交棱1CC 于点F ,得四边形1BFD E ,在以下结论中,正确的是( )A .四边形1BFD E 有可能是梯形B .四边形1BFD E 在底面ABCD 内的投影一定是正方形C .四边形1BFDE 有可能垂直于平面11BB D D D .四边形1BFD E 6【答案】BCD 【分析】四边形1BFD E 有两组对边分别平行知是一个平行四边形四边形;1BFD E 在底面ABCD 内的投影是四边形ABCD ;当与两条棱上的交点是中点时,四边形1BFD E 垂直于面11BB D D ;当E ,F 分别是两条棱的中点时,四边形1BFD E 的面积最小为6.【详解】过1BD 作平面与正方体1111ABCD A B C D -的截面为四边形1BFD E , 如图所示,因为平面11//ABB A 平面11DCC D ,且平面1BFD E 平面11ABB A BE =.平面1BFD E平面1111,//DCC D D F BE D F =,因此,同理1//D E BF ,故四边形1BFD E 为平行四边形,因此A 错误;对于选项B ,四边形1BFD E 在底面ABCD 内的投影一定是正方形ABCD ,因此B 正确; 对于选项C ,当点E F 、分别为11,AA CC 的中点时,EF ⊥平面11BB D D ,又EF ⊂平面1BFD E ,则平面1BFD E ⊥平面11BB D D ,因此C 正确;对于选项D ,当F 点到线段1BD 的距离最小时,此时平行四边形1BFD E 的面积最小,此时点E F 、分别为11,AA CC 的中点,此时最小值为16232⨯⨯=,因此D 正确. 故选:BCD【点睛】关键点睛:解题的关键是理解想象出要画的平面是怎么样的平面,有哪些特殊的性质,考虑全面即可正确解题.10.半正多面体(semiregularsolid )亦称“阿基米德多面体”,是由边数不全相同的正多边形围成的多面体,体现了数学的对称美.二十四等边体就是一种半正多面体,是由正方体切截而成的,它由八个正三角形和六个正方形构成(如图所示),若它的所有棱长都为2 )A .BF ⊥平面EABB .该二十四等边体的体积为203C .该二十四等边体外接球的表面积为8πD .PN 与平面EBFN 2 【答案】BCD 【分析】A 用反证法判断;B 先补齐八个角成正方体,再计算体积判断;C 先找到球心与半径,再计算表面积判断;D 先找到直线与平面所成角,再求正弦值判断. 【详解】解:对于A ,假设A 对,即BF ⊥平面EAB ,于是BF AB ⊥,90ABF ∠=︒,但六边形ABFPQH 为正六边形,120ABF ∠=︒,矛盾, 所以A 错;对于B ,补齐八个角构成棱长为2的正方体,则该二十四等边体的体积为3112028111323-⋅⋅⋅⋅⋅=,所以B 对;对于C ,取正方形ACPM 对角线交点O , 即为该二十四等边体外接球的球心, 其半径为2R =248R ππ=,所以C 对;对于D ,因为PN 在平面EBFN 内射影为NS , 所以PN 与平面EBFN 所成角即为PNS ∠, 其正弦值为22PS PN =,所以D 对. 故选:BCD .【点睛】本题考查了正方体的性质,考查了直线与平面所成角问题,考查了球的体积与表面积计算问题.。
立体几何(1)教师版

立体几何(1)一.基础训练1.下列命题中,正确序号是①经过不同的三点有且只有一个平面②分别在两个平面内的两条直线一定是异面直线 ③垂直于同一个平面的两条直线是平行直线④垂直于同一个平面的两个平面平行2. 如图所示的等腰直角三角形表示一个水平放置的平面图形的直观图,则这个平面图形的3. 设棱长为1的正方体ABCD-A /B /C /D /中,M 为AA /的中点,则直线CM 和D /D 所成的角的余弦值为 .4. 对于直线m 、 n 和平面 α、β、γ,有如下四个命题:其中正确的命题的个数是5. 如图BC 是R t ⊿ABC 的斜边,过A 作⊿ABC 所在 平面α垂线AP ,连PB 、PC ,过A 作AD ⊥BC 于D , 连PD ,那么图中直角三角形的个数 个6. OX ,OY ,OZ 是空间交于同一点O 的互相垂直的三条直线,点P 到这三条直线的距离分别为3,4,7,则OP 长为_______. 二.典型例题例1. 已知正方体1111ABCD A B C D -,O 是底ABCD 对角线的交点. 求证:(1)C 1O ∥面11AB D ;(2 )1A C ⊥面11AB D .βαβαγαβγβααααα⊥⊂⊥⊥⊥⊥⊥⊥⊥则若则若则若则若,,)4(,//,,)3(//,,)2(,,,//)1(m m n n m m n n m m αPBA CDx′D 1ODBC 1B 1A 1CD 图乙DB C E 例2. 如图,正三棱柱ABC--111C B A 中(地面是正三角形,侧棱垂直于地面),D 是BC 的中点,AB = a .(1) 求证:111C B D A(2) 判断A 1B 与平面ADC 1的位置关系,并证明你的结论例3. 如图甲,在直角梯形PBCD 中,PB ∥CD ,CD ⊥BC ,BC =PB =2CD ,A 是PB 的中点.现沿AD 把平面PAD 折起,使得PA ⊥AB (如图乙所示),E 、F 分别为BC 、AB 边的中点.(Ⅰ)求证:PA ⊥平面ABCD ; (Ⅱ)求证:平面PAE ⊥平面PDE ; (Ⅲ)在PA 上找一点G ,使得FG ∥平面PDE.ABC C 1B 1A 1D例4.如图,在棱长均为4的三棱柱111ABC A B C -中,D 、1D 分别是BC 和11B C 的中点. (1)求证:11A D ∥平面1AB D ;(2)若平面ABC ⊥平面11BCC B ,160O B BC ∠=,求三棱锥 1B ABC -的体积.三 .课后作业 (一).填空题1.给出四个命题:①线段AB 在平面α内,则直线AB 不在α内;②两平面有一个公共点,则一定有无数个公共点;③三条平行直线共面;④有三个公共点的两平面重合. 其中正确命题的个数为2. 直线AB 、AD ⊂α,直线CB 、CD ⊂β,点E ∈AB ,点F ∈BC ,点G ∈CD ,点H ∈DA ,若直线EH∩直线FG=M ,则点M 在 上3. 已知1111A B C D A B C D -是棱长为a 的正方体,求:(1)异面直线1A A 与B C 所成的角为( ) (2)求异面直线1B C 与A C 所成的角( )4. 点p 在平面ABC 上的射影为O ,且PA 、PB 、PC 两两垂直,那么O 是△ABC 的 心5. 如果O A ‖11O A , O B ‖11O B ,那么A O B ∠与111A O B ∠( )6. α、β是两个不同的平面,m 、n 是平面α及β之外的两条不同直线,给出四个论断:①m ⊥n②α⊥β③n ⊥β④m ⊥α以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个..命题: _________________________.B 1D 1AB CD A 1C 1CAD(二) 解答题1. 如图,在多面体ABCDE 中,⊥AE 面ABC ,BD ∥AE ,且BD BC AB AC ===2=,1=AE ,F 为CD 中点. (1)求证:EF// 平面ABC ;(2)求证:⊥EF 平面BCD2. 如图, P A ⊥矩形A B C D 所在平面, ,M N 分别是A B 和P C 的中点.(1)求证: //M N 平面;P A D (2)求证:;M N C D ⊥ (3)若45P D A ∠=, 求证:M N ⊥平面.P C D3. 如图,在四面体ABCD 中,CB =CD , AD ⊥BD ,点E , F 分别是AB , BD 的中点.求证:(Ⅰ)直线EF ∥平面ACD ; (Ⅱ)平面EFC ⊥平面BCD.4. 四棱锥P-ABCD 中,底面ABCD 为直角梯形,90B A D ∠=,AD ∥BC, AB=BC=2, AD=4,PA ⊥底面ABCD ,PD 与底面ABCD 成30角,E 是PD 的中点.(1) 点H 在AC 上且EH ⊥AC ,求E H的坐标;(2) 求AE 与平面PCD 所成角的余弦值;A B C E D F AB C DMNPE BC答案 基础训练1. ③2. 23. 1/34. 1个5. 8个6.37 典型例题例1. 提示:连接A 1C 1交B 1D 1与点O 1。
立体几何考察试题及答案

立体几何考察试题及答案一、选择题1. 若直线l与平面α垂直,则直线l与平面α内任意直线的关系是()。
A. 相交B. 平行C. 异面D. 垂直答案:D2. 已知一个正四面体的棱长为a,求其体积。
A. \( \frac{a^3 \sqrt{2}}{12} \)B. \( \frac{a^3 \sqrt{2}}{6} \)C. \( \frac{a^3 \sqrt{3}}{12} \)D. \( \frac{a^3 \sqrt{3}}{6} \)答案:C二、填空题1. 已知一个长方体的长、宽、高分别为a、b、c,则其对角线的长度为 \( \sqrt{a^2 + b^2 + c^2} \)。
2. 一个球的半径为r,则其表面积为 \( 4\pi r^2 \)。
三、解答题1. 已知一个圆锥的底面半径为r,高为h,求其体积。
解:圆锥的体积公式为 \( V = \frac{1}{3}\pi r^2 h \)。
答:圆锥的体积为 \( \frac{1}{3}\pi r^2 h \)。
2. 已知一个圆柱的底面半径为r,高为h,求其侧面积。
解:圆柱的侧面积公式为 \( A = 2\pi rh \)。
答:圆柱的侧面积为 \( 2\pi rh \)。
四、证明题1. 证明:若直线l与平面α内的两条直线m和n都垂直,则直线l与平面α垂直。
证明:设直线m和n在平面α内的交点为O,由于直线l与m、n都垂直,根据直线与平面垂直的判定定理,直线l与平面α垂直。
答:直线l与平面α垂直。
2. 证明:若两个平面α和β的交线为l,直线m在平面α内且与l平行,直线n在平面β内且与l平行,则直线m与直线n平行。
证明:设直线m与直线n的交点为P,由于m在平面α内且与l平行,n在平面β内且与l平行,根据平面与平面平行的性质,直线m与直线n平行。
答:直线m与直线n平行。
浙江高考历年真题之立体几何大题(文科)

A浙江高考历年真题之立体几何大题(教师版)1、(2005年)如图,在三棱锥P -ABC 中,AB ⊥BC ,AB =BC =12PA ,点O 、D 分别是AC 、PC 的中点,OP ⊥底面ABC . (Ⅰ)求证OD ∥平面PAB(Ⅱ) 求直线OD 与平面PBC 所成角的大小;解析: 方法一:(Ⅰ) ∵O 、D 分别为AC 、PC 中点,O D P A ∴ ∥PA PAB ⊂又平面,OD PAB ∴ 平面∥(Ⅱ)A B B C O A O C ⊥= ,,O A O B O C ∴== ,O P ABC ⊥ 又 平面,.PA PB PC ∴== E PE BC PO E ⊥取BC 中点,连结,则平面OF PE F DF OF PBC ⊥⊥作于,连结,则平面 ODF OD PBC ∴∠ 是与平面所成的角.sin 30O F R t O D F O D F O D∆∠==在中, arcsin30O D P B C ∴ 与平面所成的角为方法二:O P ABC O A O C AB BC ⊥== 平面,,,.O A O B O A O P O B O P ∴⊥⊥⊥ ,,()O O Pz O xyz -以为原点,射线为非负轴,建立空间直角坐标系如图,,0,0,,0,,0,0222AB a A B C⎫⎛⎫⎛⎫=-⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭设,则 ()0,0,.OP h P h =设,则()D PC 为的中点,Ⅰ1,0,,,0,422O D h PA ⎛⎫⎛∴=-=- ⎪ ⎪ ⎝⎭⎝ 又1 (2)O D PA O D PA O D PAB ∴=-∴∴平面∥∥()2,PA a = Ⅱ,h ∴=,,44O D ⎛⎫∴=-⎪⎪⎝⎭,PBC n ⎛=- ⎝ 可求得平面的法向量cos ,30OD nOD n OD n⋅∴〈〉==⋅OD PBC θ设与平面所成的角为,sin cos ,30O D n θ=〈〉=则arcsin30O D P B C ∴ 与平面所成的角为2、(2006年)如图,在四棱锥P-ABCD 中,底面为直角梯形,AD ∥BC,∠BAD=90° ,PA ⊥底面ABCD ,且PA =AD=AB=2BC,M 、N 分别为PC 、PB 的中点. (Ⅰ)求证:PB ⊥DM;(Ⅱ)求BD 与平面ADMN 所成的角。
立体几何大题训练题(含答案)

立体几何大题训练题一、解答题(共17题;共150分)1.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,在四边形ABCD中,∠ABC= ,AB=4,BC=3,CD= ,AD=2 ,PA=4.(1)证明:CD⊥平面PAD;(2)求二面角B-PC-D的余弦值..2.如图,在四棱锥中,平面,在四边形中,,,,,,.(1)证明:平面;(2)求B点到平面的距离3.如图,在四棱锥中,底面为长方形,底面,,,为的中点,F 为线段上靠近B 点的三等分点.(1)求证:平面;(2)求平面与平面所成二面角的正弦值.4.如图,四边形为正方形,分别为的中点,以为折痕把折起,使点到达点的位置,且.(1)证明:平面平面;(2)求与平面所成角的正弦值.5.如图,在三角锥中,, , 为的中点.(1)证明:平面;(2)若点在棱上,且MC=2MB,求点C到平面POM的距离.6.如图,在三角锥中,, , 为的中点.(1)证明:平面;(2)若点在棱上,且二面角为,求与平面所成角的正弦值. 7.如图,在四棱锥P﹣ABCD中,AB∥CD,且∠BAP=∠CDP=90°.(12分)(1)证明:平面PAB⊥平面PAD;(2)若PA=PD=AB=DC,∠APD=90°,求二面角A﹣PB﹣C的余弦值.8.如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.(1)证明:BE⊥平面EB1C1;(2)若AE=A1E,求二面角B–EC–C1的正弦值.9.如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,BAD=60°,E,M,N分别是BC,BB1,A1D的中点(1)证明:MN∥平面C1DE;(2)求二面角A-MA1-N的正弦值。
10.已知三棱柱,底面三角形为正三角形,侧棱底面,,为的中点,为中点.(1)求证:直线平面;(2)求平面和平面所成的锐二面角的余弦值.11.如图,已知三棱柱ABC-A1B1C1,平面A1AC1C⊥平面ABC,∠ABC=90°.∠BAC=30°,A1A=A1C=AC,E,F 分别是AC,A1B1的中点(1)证明:EF⊥BC(2)求直线EF与平面A1BC所成角的余弦值.12.如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.(Ⅰ)证明:平面ACD⊥平面ABC;(Ⅱ)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D﹣AE﹣C 的余弦值.13.如图,四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= AD,∠BAD=∠ABC=90°,E是PD的中点.(Ⅰ)证明:直线CE∥平面PAB;(Ⅱ)点M在棱PC 上,且直线BM与底面ABCD所成角为45°,求二面角M﹣AB﹣D的余弦值.14.如图,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.(Ⅰ)证明:AB1⊥平面A1B1C1;(Ⅱ)求直线AC1与平面ABB1所成的角的正弦值.15.如图所示多面体中,AD⊥平面PDC,四边形ABCD为平行四边形,点E,F分别为AD,BP的中点,AD =3,AP=3 ,PC .(1)求证:EF//平面PDC;(2)若∠CDP=120°,求二面角E﹣CP﹣D的平面角的余弦值.16.如图,四棱锥中,侧棱垂直于底面,,,为的中点,平行于,平行于面,.(1)求的长;(2)求二面角的余弦值.17.如图,在斜三棱柱中,侧面,,,,.(Ⅰ)求证:平面平面;(Ⅱ)若为中点,求二面角的正切值.答案解析部分一、解答题1.【答案】(1)解:连接,由∠ABC= ,AB=4,BC=3,则,又因为CD= ,AD=2 ,所以,即,因为PA⊥平面ABCD,平面ABCD,所以,因为,所以CD⊥平面PAD;(2)解:以点D为坐标原点,的延长线为x,为y轴,过点D与平行线为z轴,建立空间直角坐标系,如图:作交与点G,,即,所以,,所以,所以,,,,则,,,设平面的一个法向量为,则,即,令,则,,即,设平面的一个法向量为,则,即,令,则,,即,由,所以二面角B-PC-D的余弦值为.【解析】【分析】(1)连接,证出,利用线面垂直的性质定理可得,再利用线面垂直的判定定理即可证出.(2)以点D为坐标原点,的延长线为x,为y轴,过点D与平行线为轴,建立空间直角坐标系,分别求出平面的一个法向量与平面的一个法向量,利用向量的数量积即可求解.2.【答案】(1)解:在平面中,,,,则,又,∴,即,又平面,则,又,∴平面.(2)解:在平面中,过A作BC的平行线交CD的延长线于M,因为,,,则,又因为,,所以.所以又,则,所以,在中,.因为,则面,所以由可知:,,所以,则,因此P点到平面的距离为.【解析】【分析】(1)在三角形中,由勾股定理可证得,由平面,可得,根据线面垂直的判定定理即可证得结论;(2) 在平面中,过A作BC的平行线交CD 的延长线于M,因为利用等体积转换即可求得距离.3.【答案】(1)证明:,为线段中点,.平面,平面,.又底面是长方形,.又,平面.平面,. 又,平面.(2)解:由题意,以为轴建立空间直角坐标系,则,,,,,.所以, ,,,设平面的法向量,则,即,令,则,,,同理可求平面的法向量,,,即平面与平面所成角的正弦值为.【解析】【分析】(1)通过,可证明平面,进而可得,结合证明线面垂直.(2)以为轴建立空间直角坐标系,可求出平面的法向量,平面的法向量,则可求出两向量夹角的余弦值,从而可求二面角的正弦值.4.【答案】(1)解:由已知可得,BF⊥PF,BF⊥EF,又,∴BF⊥平面PEF.∴又平面ABFD,平面PEF⊥平面ABFD.(2)解:作PH⊥EF,垂足为H.由(1)得,PH⊥平面ABFD.以H为坐标原点,的方向为y轴正方向,为单位长,建立如图所示的空间直角坐标系H−xyz.由(1)可得,DE⊥PE.又DP=2,DE=1,所以PE= .又PF=1,EF=2,故PE⊥PF.可得.则为平面ABFD的法向量. 设DP与平面ABFD所成角为,则.∴DP与平面ABFD所成角的正弦值为.【解析】【分析】(1)在翻折过程中,作于H,由得到,从而得到面面垂直;(2)DP与平面所成的角就是,在三角形中求其正弦值.5.【答案】(1)∵PA=PC=AC=4 且O是AC的中点∴PO⊥AC∵AB=BC=2 ,AC=4,∴∴∠ABC=90°连接BO则OB=OC∴PO2+BO2=PB2PO⊥OB,PO⊥OCOB∩OC=O∴PO⊥平面ABC(2)过点C作CH⊥OM交OM于点H又∵PO⊥平面ABC∴∴CH的长度为点C到平面POM的距离在△COM中,CM= ,OC=2,∠OCM=45°∴∴OM=∴【解析】【分析】(1)由线面垂直的判定定理易得;(2)由线面垂直可得面面垂直,易找点面距,可求.6.【答案】(1)PA=PC=AC=4 且O是AC的中点PO⊥AC∵AB=BC=2 ,AC=4,∴∴∠ABC=90°连接BO则OB=OC∴PO2+BO2=PB2PO⊥OB,PO⊥OCOB∩OC=O∴PO⊥平面ABC(2)∵PO⊥平面ABC,∴PO⊥OB∴AB=BC=2 O是AC的中点∴OB⊥AC OB⊥平面PAC如图所示以O为坐标原点,为x轴正方向建立如图所示的直角坐标系O-xyz则P(0,0,)A(,0,-2,0),C(0,2,0),B(2,0,0)平面PAC法向量为=(1,0,0)设M(x,2-x,0)平面PAC法向量为=(1,λ,μ),=(0,2,), = (x,4-x,0)则即即得到,∴x=-4(舍),x=即M∴PAM的法向量记PC与平面PAM所成的角为θ∴即PC与平面PAM所成的角为的正弦值为.【解析】【分析】(1)由线面垂直的判定定理易得;(2)先由条件建系,找到点M的位置,再用公式求线面角.7.【答案】(1)证明:∵∠BAP=∠CDP=90°,∴PA⊥AB,PD⊥CD,∵AB∥CD,∴AB⊥PD,又∵PA∩PD=P,且PA⊂平面PAD,PD⊂平面PAD,∴AB⊥平面PAD,又AB⊂平面PAB,∴平面PAB⊥平面PAD;(2)解:∵AB∥CD,AB=CD,∴四边形ABCD为平行四边形,由(1)知AB⊥平面PAD,∴AB⊥AD,则四边形ABCD为矩形,在△APD中,由PA=PD,∠APD=90°,可得△PAD为等腰直角三角形,设PA=AB=2a,则AD= .取AD中点O,BC中点E,连接PO、OE,以O为坐标原点,分别以OA、OE、OP所在直线为x、y、z轴建立空间直角坐标系,则:D(),B(),P(0,0,),C().,,.设平面PBC的一个法向量为,由,得,取y=1,得.∵AB⊥平面PAD,AD⊂平面PAD,∴AB⊥AD,又PD⊥PA,PA∩AB=A,∴PD⊥平面PAB,则为平面PAB的一个法向量,.∴cos<>= = .由图可知,二面角A﹣PB﹣C为钝角,∴二面角A﹣PB﹣C的余弦值为.【解析】【分析】(1.)由已知可得PA⊥AB,PD⊥CD,再由AB∥CD,得AB⊥PD,利用线面垂直的判定可得AB⊥平面PAD,进一步得到平面PAB⊥平面PAD;(2.)由已知可得四边形ABCD为平行四边形,由(1)知AB⊥平面PAD,得到AB⊥AD,则四边形ABCD 为矩形,设PA=AB=2a,则AD= .取AD中点O,BC中点E,连接PO、OE,以O为坐标原点,分别以OA、OE、OP所在直线为x、y、z轴建立空间直角坐标系,求出平面PBC的一个法向量,再证明PD⊥平面PAB,得为平面PAB的一个法向量,由两法向量所成角的余弦值可得二面角A﹣PB﹣C的余弦值.8.【答案】(1)解:由已知得,平面,平面,故.又,所以平面.(2)由(1)知.由题设知,所以,故,.以为坐标原点,的方向为x轴正方向,为单位长,建立如图所示的空间直角坐标系D-xyz,则C(0,1,0),B(1,1,0),(0,1,2),E(1,0,1),,.设平面EBC的法向量为=(x,y,x),则即所以可取= .设平面的法向量为=(x,y,z),则即所以可取=(1,1,0).于是.所以,二面角的正弦值为.【解析】【分析】(1)根据题意由线面垂直的性质得出线线垂直,再由线线垂直的判定定理出线面垂直。
2022学年高三上(编号1-25)立体几何大题汇编(教师版)

,即
令 ,则
面 法向量为
平面 与平面 夹角的余弦值为
,即
, (舍)
4:(2023届广东梅州中学高三上阶段性考试解析第20题)
4:如图,在四棱锥 中,四边形 为直角梯形, , ,平面 平面 , , , .
(1)证明: ;
(2)若四棱锥 的体积为 ,
求平面 与平面 所成的锐二面角的余弦值.
方法提供与解析:(浙江绍兴+谢柏军)
方法提供与解析:(浙江绍兴+谢柏军)
(1)解析: 是正方形
,
直三棱柱
, , 、 面 ,
面
面
面 面
(2)解析: 面
、 分别为 、 中点
以 为原点, 为 轴, 为 轴, 为 轴建立坐标系
, , ,
设面 的法向量为
,即
令 ,则 ,
面
面 的法向量为
平面 与平面 夹角的余弦值为
10:(2023届重庆市巴蜀中学月考卷(一)解析第19题)
方法提供与解析:(衢州张小臣)
解析:(1)证明:取 的中点 ,连接 .
因为 是等边 的中线,所以 .
因为 是棱 的中点, 为 的中点,
所以 ,且 .
因为 ,所以 ,且 ,
所以四边形 是平行四边形,所以 .
因为 , 为 的中点,所以 ,从而 .
立体几何证明题专题(教师版)

立体几何证明题考点1:点线面的位置关系及平面的性质例1.下列命题:①空间不同三点确定一个平面;②有三个公共点的两个平面必重合;③空间两两相交的三条直线确定一个平面;④三角形是平面图形;⑤平行四边形、梯形、四边形都是平面图形;⑥垂直于同一直线的两直线平行;⑦一条直线和两平行线中的一条相交,也必和另一条相交;⑧两组对边相等的四边形是平行四边形.其中正确的命题是________.【解析】由公理3知,不共线的三点才能确定一个平面,所以知命题①错,②中有可能出现两平面只有一条公共线(当这三个公共点共线时),②错.③空间两两相交的三条直线有三个交点或一个交点,若为三个交点,则这三线共面,若只有一个交点,则可能确定一个平面或三个平面.⑤中平行四边形及梯形由公理2可得必为平面图形,而四边形有可能是空间四边形,如图(1)所示.在正方体ABCD—A′B′C′D′中,直线BB′⊥AB,BB′⊥CB,但AB与CB不平行,∴⑥错.AB∥CD,BB′∩AB=B,但BB′与CD不相交,∴⑦错.如图(2)所示,AB=CD,BC=AD,四边形ABCD不是平行四边形,故⑧也错.【答案】④2.若P是两条异面直线l、m外的任意一点,则()A.过点P有且仅有一条直线与l、m都平行B.过点P有且仅有一条直线与l、m都垂直C.过点P有且仅有一条直线与l、m都相交D.过点P有且仅有一条直线与l、m都异面答案B解析对于选项A,若过点P有直线n与l,m都平行,则l∥m,这与l,m异面矛盾.对于选项B,过点P与l、m都垂直的直线,即过P且与l、m的公垂线段平行的那一条直线.对于选项C,过点P与l、m都相交的直线有一条或零条.对于选项D,过点P与l、m都异面的直线可能有无数条.3.已知异面直线a,b分别在平面α,β内,且α∩β=c,那么直线c一定A.与a,b都相交B.只能与a,b中的一条相交C.至少与a,b中的一条相交D.与a,b都平行答案C解析若c与a,b都不相交,则c与a,b都平行,根据公理4,则a∥b,与a,b异面矛盾.考点2:共点、共线、共面问题例1.下列各图是正方体和正四面体,P、Q、R、S分别是所在棱的中点,这四个点不共面的图形是【解析】①在A中易证PS∥QR,∴P、Q、R、S四点共面.②在C中易证PQ∥SR,∴P、Q、R、S四点共面.③在D中,∵QR⊂平面ABC,PS∩面ABC=P且P∉QR,∴直线PS与QR为异面直线.∴P、Q、R、S四点不共面.④在B中P、Q、R、S四点共面,证明如下:取BC中点N,可证PS、NR交于直线B1C1上一点,∴P、N、R、S四点共面,设为α.可证PS∥QN,∴P、Q、N、S四点共面,设为β.∵α、β都经过P、N、S三点,∴α与β重合,∴P、Q、R、S四点共面.【答案】D2.空间四点中,三点共线是这四点共面的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件答案A3.下面三条直线一定共面的是()A .a 、b 、c 两两平行B .a 、b 、c 两两相交C .a ∥b ,c 与a 、b 均相交D .a 、b 、c 两两垂直 答案 C4.已知三个平面两两相交且有三条交线,试证三条交线互相平行或者相交于一点. 【解析】 设α∩β=a ,β∩γ=b ,γ∩α=c ,由a ⊂β,b ⊂β,则a ∩b =O ,如图(1), 或a ∥b ,如图(2),若a ∩b =O ,O ∈a ,a ⊂α,则O ∈α,O ∈b ,b ⊂γ,则O ∈γ, 又γ∩α=c ,因此O ∈c ;若a ∥b ,a ⊄γ,b ⊂γ,则a ∥γ,又a ⊂α,α∩γ=c ,则a ∥c . 因此三条交线相交于一点或互相平行.5.如图所示,已知空间四边形ABCD 中,E 、H 分别是边AB ,AD 的中点,F ,G 分别是边BC ,CD 上的点,且CF CB =CG CD =23.(1)求证:三条直线EF ,GH ,AC 交于一点.(2)若在本题中,AE EB =CF FB =2,AH HD =CGGD =3,其他条件不变.求证:EH 、FG 、BD 三线共点.【解析】 (1)∵E ,H 分别是AB ,AD 的中点, ∴由中位线定理可知,EH 綊12BD . 又∵CF CB =CG CD =23,∴在△CBD 中,FG ∥BD ,且FG =23BD . ∴由公理4知,EH ∥FG ,且EH <FG .∴四边形EFGH 是梯形,EH 、FG 为上、下两底. ∴两腰EF 、GH 所在直线必相交于一点P . ∵P ∈直线EF ,EF ⊂平面ABC , ∴P ∈平面ABC .同理可得P ∈平面ADC . ∴P 在平面ABC 和平面ADC 的交线上.又∵面ABC ∩面ADC =AC , ∴P ∈直线AC .故EF 、GH 、AC 三直线交于一点. (2)∵AE EB =CFFB =2, ∴EF ∥AC .又AH HD =CGGD =3,∴HG ∥AC ,∴EF ∥HG ,且EF >HG . ∴四边形EFGH 为梯形. 设EH 与FG 交于点P , 则P ∈平面ABD ,P ∈平面BCD . ∴P 在两平面的交线BD 上. ∴EH 、FG 、BD 三线共点.考点3:异面直线的夹角1.在正方体ABCD -A 1B 1C 1D 1中,E 为AB 的中点.求BD 1与CE 所成角的余弦值.【解析】 连接AD 1,A 1D 交点为M ,连接ME ,MC ,则∠MEC (或其补角)即为异面直线BD 1与CE 所成的角,设AB =1,CE =52,ME =12BD 1=32,CM 2=CD 2+DM 2=32.在△MEC 中,cos ∠MEC=CE 2+ME 2-CM 22CE ·ME=1515,因此异面直线BD 1与CE 所成角的余弦值为1515.2.如图,若正四棱柱ABCD -A 1B 1C 1D 1的底面边长为2,高为4,则异面直线BD 1与AD 所成角的正切值是______.答案 53.已知正四棱柱ABCD -A 1B 1C 1D 1中,AA 1=2AB ,E 为AA 1中点,则异面直线BE 与CD 1所成角的余弦值为()答案C解析连接BA1,则CD1∥BA1,于是∠A1BE就是异面直线BE与CD1所成的角(或补角),设AB=1,则BE=2,BA1=5,A1E=1,在△A1BE中,cos∠A1BE=5+2-125·2=31010,选C.4.已知正方体ABCD-A1B1C1D1中,E为C1D1的中点,则异面直线AE与BC所成角的余弦值为________.【解析】取A1B1的中点F,连接EF,FA,则有EF∥B1C1∥BC,∠AEF即是直线AE与BC所成的角或其补角.设正方体ABCD—A1B1C1D1的棱长为2a,则有EF=2a,AF=2a2+a2=5a,AE=2a2+2a2+a2=3a.在△AEF中,cos∠AEF=AE2+EF2-AF22AE·EF=9a2+4a2-5a22×3a×2a=23.因此,异面直线AE与BC所成的角的余弦值是23.【答案】2 3考点4:直线与平面平行的判定与性质1.下列命题中正确的是________.①若直线a不在α内,则a∥α;②若直线l上有无数个点不在平面α内,则l∥α;③若直线l与平面α平行,则l与α内的任意一条直线都平行;④如果两条平行线中的一条与一个平面平行,那么另一条也与这个平面平行;⑤若l与平面α平行,则l与α内任何一条直线都没有公共点;⑥平行于同一平面的两直线可以相交.答案⑤⑥解析a∩α=A时,a不在α内,∴①错;直线l与α相交时,l上有无数个点不在α内,故②错;l ∥α时,α内的直线与l平行或异面,故③错;a∥b,b∥α时,a∥α或a⊂α,故④错;l∥α,则l与α无公共点,∴l与α内任何一条直线都无公共点,⑤正确;如图,长方体中,A1C1与B1D1都与平面ABCD 平行,∴⑥正确.2.给出下列四个命题:①若一条直线与一个平面内的一条直线平行,则这条直线与这个平面平行;②若一条直线与一个平面内的两条直线平行,则这条直线与这个平面平行;③若平面外的一条直线和这个平面内的一条直线平行,则这条直线和这个平面平行;④若两条平行直线中的一条与一个平面平行,则另一条也与这个平面平行. 其中正确命题的个数是________个. 答案 1解析 命题①错,需说明这条直线在平面外. 命题②错,需说明这条直线在平面外. 命题③正确,由线面平行的判定定理可知. 命题④错,需说明另一条直线在平面外. 3.已知不重合的直线a ,b 和平面α, ①若a ∥α,b ⊂α,则a ∥b ; ②若a ∥α,b ∥α,则a ∥b ; ③若a ∥b ,b ⊂α,则a ∥α; ④若a ∥b ,a ⊂α,则b ∥α或b ⊂α, 上面命题中正确的是________(填序号). 答案 ④解析 ①若a ∥α,b ⊂α,则a ,b 平行或异面;②若a ∥α,b ∥α,则a ,b平行、相交、异面都有可能;③若a ∥b ,b ⊂α,a ∥α或a ⊂α.4.正方形ABCD 与正方形ABEF 所在平面相交于AB ,在AE 、BD 上各有一点P 、Q ,且AP =DQ .求证:PQ ∥平面BCE .【证明】 方法一 如图所示. 作PM ∥AB 交BE 于M , 作QN ∥AB 交BC 于N , 连接MN .∵正方形ABCD 和正方形ABEF 有公共边AB ,∴AE =BD . 又AP =DQ ,∴PE =QB .又PM ∥AB ∥QN ,∴PM AB =PE AE =QB BD ,QN DC =BQ BD . ∴PM AB =QN DC .∴PM 綊QN ,即四边形PMNQ 为平行四边形. ∴PQ ∥MN .又MN ⊂平面BCE ,PQ ⊄平面BCE , ∴PQ ∥平面BCE .方法二 如图,连接AQ ,并延长交BC 延长线于K ,连接EK . ∵AE =BD ,AP =DQ , ∴PE =BQ ,∴AP PE =DQBQ .又AD ∥BK ,∴DQ BQ =AQ QK ,∴AP PE =AQQK ,∴PQ ∥EK . 又PQ ⊄平面BCE ,EK ⊂平面BCE , ∴PQ ∥平面BCE .方法三 如图,在平面ABEF 内,过点P 作PM ∥BE ,交AB 于点M ,连接QM .∴PM ∥平面BCE .又∵平面ABEF ∩平面BCE =BE , ∴PM ∥BE ,∴AP PE =AMMB .又AE =BD ,AP =DQ ,∴PE =BQ . ∴AP PE =DQ BQ ,∴AM MB =DQ QB . ∴MQ ∥AD .又AD ∥BC ,∴MQ ∥BC ,∴MQ ∥平面BCE .又PM ∩MQ =M , ∴平面PMQ ∥平面BCE .又PQ ⊂平面PMQ , ∴PQ ∥平面BCE .5.一个多面体的直观图和三视图如图所示(其中M ,N 分别是AF ,BC 中点).<1>求证:MN ∥平面CDEF ; <2>求多面体A —CDEF 的体积.解析 (1)证明 由三视图知,该多面体是底面为直角三角形的直三棱柱,且AB =BC =BF =2, DE =CF =22,∴∠CBF =90°.取BF 中点G ,连接MG ,NG ,由M ,N 分别是AF ,BC 中点,可知:NG ∥CF ,MG ∥EF .又MG ∩NG =G ,CF ∩EF =F ,∴平面MNG ∥平面CDEF ,∴MN ∥平面CDEF .(2)作AH ⊥DE 于H ,由于三棱柱ADE —BCF 为直三棱柱,∴AH ⊥平面CDEF ,且AH =2.∴V A -CDEF =13S 四边形CDEF ·AH =13×2×22×2=83.6.若P 为异面直线a ,b 外一点,则过P 且与a ,b 均平行的平面A.不存在B.有且只有一个C.可以有两个D.有无数多个答案B7.如图,在正方体ABCD—A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN,求证:MN∥平面AA1B1B.【证明】方法一如右图,作ME∥BC,交BB1于E;作NF∥AD,交AB于F,连接EF,则EF⊂平面AA1B1B.∵BD=B1C,DN=CM,∴B1M=BN.∵MEBC=B1MB1C,NFAD=BNBD,∴MEBC=BNBD=NFAD,∴ME=NF.又ME∥BC∥AD∥NF,∴MEFN为平行四边形.∴NM∥EF.又∵MN⊄面AA1B1B,∴MN∥平面AA1B1B.方法二如图,连接CN并延长交BA的延长线于点P,连接B1P,则B1P⊂平面AA1B1B.∵△NDC∽△NBP,∴DNNB=CNNP.又CM=DN,B1C=BD,CMMB1=DNNB=CNNP,∴MN∥B1P.∵B1P⊂平面AA1B1B,∴MN∥平面AA1B1B.方法三如右图,作MP∥BB1,交BC于点P,连接NP.∵MP∥BB1,∴CMMB1=CPPB.∵BD=B1C,DN=CM,∴B1M=BN.∵CMMB1=DNNB,∴CPPB=DNNB,∴NP∥DC∥AB.∴平面MNP∥平面AA1B1B.∴MN∥平面AA1B1B.8.如图所示,四棱锥P—ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别为PC、PD、BC的中点.(1)求证:PA∥平面EFG;(2)求三棱锥P—EFG的体积.解析(1)证明如图,取AD的中点H,连接GH,FH.∵E,F分别为PC,PD的中点,∴EF∥CD.∵G,H分别是BC,AD的中点,∴GH∥CD.∴EF∥GH,∴E,F,H,G四点共面.∵F,H分别为DP,DA的中点,∴PA∥FH.∵PA⊄平面EFG,FH⊂平面EFG,∴PA∥平面EFG.(2)∵PD⊥平面ABCD,CG⊂平面ABCD,∴PD⊥CG.又∵CG⊥CD,CD∩PD=D,∴GC⊥平面PCD.∵PF =12PD =1,EF =12CD =1,∴S △PEF =12EF ·PF =12. 又GC =12BC =1,∴V P —EFG =V G —PEF =13×12×1=16.9.如图所示,a ,b 是异面直线,A 、C 与B 、D 分别是a ,b 上的两点,直线a ∥平面α,直线b ∥平面α,AB ∩α=M ,CD ∩α=N ,求证:若AM =BM ,则CN =DN .【证明】 连接AD 交平面α于E 点,并连接ME ,NE . ∵b ∥α,ME ⊂平面ABD ,平面α∩面ABD =ME , ∴ME ∥BD .又在△ABD 中AM =MB , ∴AE =ED .即E 是AD 的中点.又a ∥α,EN ⊂平面ACD ,平面α∩面ADC =EN , ∴EN ∥AC ,而E 是AD 的中点. ∴N 必是CD 的中点,∴CN =DN .10.如图,在三棱柱ABC -A 1B 1C 1中,E 为AC 上一点,若AB 1∥平面C 1EB ,求:AE ∶EC .【解析】 连接B 1C 交BC 1于点F , 则F 为B 1C 中点. ∵AB 1∥平面C 1EB ,AB 1⊂平面AB 1C ,且平面C 1EB ∩平面AB 1C =EF . ∴AB 1∥EF ,∴E 为AC 中点. ∴AE ∶EC =1∶1. 【答案】 1∶1考点5:面面平行的判定及性质1.设m ,n 是平面α内的两条不同直线;l 1,l 2是平面β内的两条相交直线,则α∥β的一个充分而不必要条件是( )A .m ∥β且l 1∥αB .m ∥l 1且n ∥l 2C .m ∥β且n ∥β 答案 B解析 因m ⊂α,l 1⊂β,若α∥β,则有m ∥β且l 1∥α,故α∥β的一个必要条件是m ∥β且l 1∥α,排除A.因m ,n ⊂α,l 1,l 2⊂β且l 1与l 2相交,若m ∥l 1且n ∥l 2,因l 1与l 2相交,故m 与n 也相交,∴α∥β;若α∥β,则直线m 与直线l 1可能为异面直线,故α∥β的一个充分而不必要条件是m ∥l 1且n ∥l 2,应选B.2.棱长为1的正方体ABCD —A 1B 1C 1D 1中,点P ,Q ,R 分别是面A 1B 1C 1D 1,BCC 1B 1,ABB 1A 1的中心,给出下列结论:①PR 与BQ 是异面直线;②RQ ⊥平面BCC 1B 1;③平面PQR ∥平面D 1AC ;④过P ,Q ,R 的平面截该正方体所得截面是边长为2的等边三角形. 以上结论正确的是________.(写出所有正确结论的序号)答案 ③④解析 由于PR 是△A 1BC 1的中位线,所以PR ∥BQ ,故①不正确;由于RQ ∥A 1C 1,而A 1C 1不垂直于面BCC 1B 1,所以②不正确;由于PR ∥BC 1∥D 1A ,PQ ∥A 1B ∥D 1C ,所以③正确;由于△A 1BC 1是边长为2的正三角形,所以④正确.故填③④.3.已知P 为△ABC 所在平面外一点,G 1、G 2、G 3分别是△PAB 、△PCB 、△PAC的重心.<1>求证:平面G 1G 2G 3∥平面ABC ;<2>求S △G 1G 2G 3∶S △ABC .【解析】 (1)如图,连接PG 1、PG 2、PG 3并延长分别与边AB 、BC 、AC 交于点D 、E 、F .连接DE 、EF 、FD .则有PG 1∶PD =2∶3,PG 2∶PE =2∶3.∴G 1G 2∥DE .又G 1G 2不在平面ABC 内,∴G 1G 2∥平面ABC .同理G 2G 3∥平面ABC .又因为G 1G 2∩G 2G 3=G 2,∴平面G 1G 2G 3∥平面ABC .(2)由(1)知PG 1PD =PG 2PE =23,∴G 1G 2=23DE .又DE =12AC ,∴G 1G 2=13AC .同理G 2G 3=13AB ,G 1G 3=13BC .∴△G 1G 2G 3∽△CAB ,其相似比为1∶3.∴S △G 1G 2G 3∶S △ABC =1∶9.4.给出下列关于互不相同的直线l 、m 、n 和平面α、β、γ的三个命题:①若l 与m 为异面直线,l ⊂α,m ⊂β,则α∥β;②若α∥β,l ⊂α,m ⊂β,则l ∥m ;③若α∩β=l ,β∩γ=m ,γ∩α=n ,l ∥γ,则m ∥n .其中真命题为________.答案 ③解析 ①中当α与β不平行时,也能存在符合题意的l 、m .②中l 与m 也可能异面.③中⎭⎪⎬⎪⎫l ∥γl ⊂ββ∩γ=m ⇒l ∥m , 同理l ∥n ,则m ∥n ,正确.5.如图所示,正方体ABCD —A 1B 1C 1D 1中,M 、N 、E 、F 分别是棱A 1B 1,A 1D 1,B 1C 1,C 1D 1的中点.求证:平面AMN ∥平面EFDB .【证明】 连接MF ,∵M 、F 是A 1B 1、C 1D 1的中点,四边形A 1B 1C 1D 1为正方形,∴MF A 1D 1.又A 1D 1 AD ,∴MF AD .∴四边形AMFD 是平行四边形.∴AM ∥DF .∵DF ⊂平面EFDB ,AM ⊄平面EFDB ,∴AM ∥平面EFDB ,同理AN ∥平面EFDB .又AM 、AN ⊂平面ANM ,AM ∩AN =A ,∴平面AMN ∥平面EFDB .6.在正方体ABCD -A 1B 1C 1D 1中,M ,N ,P 分别是C 1C ,B 1C 1,C 1D 1的中点,求证:平面MNP ∥平面A 1BD . 证明 方法一如图(1)所示,连接B 1D 1.∵P ,N 分别是D 1C 1,B 1C 1的中点,∴PN ∥B 1D 1.又B1D1∥BD,∴PN∥BD.又PN⊄平面A1BD,∴PN∥平面A1BD.同理:MN∥平面A1BD.又PN∩MN=N,∴平面PMN∥平面A1BD.方法二如图(2)所示,连接AC1,AC,∵ABCD-A1B1C1D1为正方体,∴AC⊥BD.又CC1⊥平面ABCD,∴AC为AC1在平面ABCD上的射影,∴AC1⊥BD.同理可证AC1⊥A1B,∴AC1⊥平面A1BD.同理可证AC1⊥平面PMN.∴平面PMN∥平面A1BD.7.如图所示,平面α∥平面β,点A∈α,C∈α,点B∈β,D∈β,点E、F分别在线段AB,CD上,且AE∶EB=CF∶FD.求证:EF∥β.【证明】①当AB,CD在同一平面内时,由α∥β,α∩平面ABDC=AC,β∩平面ABDC=BD,∴AC∥BD.∵AE∶EB=CF∶FD,∴EF∥BD.又EF⊄β,BD⊂β,∴EF∥β.②当AB与CD异面时,设平面ACD∩β=DH,且DH=AC,∵α∥β,α∩平面ACDH=AC,∴AC∥DH.∴四边形ACDH是平行四边形.在AH上取一点G,使AG∶GH=CF∶FD,又∵AE∶EB=CF∶FD,∴GF∥HD,EG∥BH.又EG ∩GF =G ,∴平面EFG ∥平面β.∵EF ⊂平面EFG ,∴EF ∥β.综上,EF ∥β.8.已知:如图,斜三棱柱ABC —A 1B 1C 1中,点D 、D 1分别为AC 、A 1C 1上的点.(1)当A 1D 1D 1C 1的值等于何值时,BC 1∥平面AB 1D 1; (2)若平面BC 1D ∥平面AB 1D 1,求AD DC 的值.【解析】 (1)如图,取D 1为线段A 1C 1的中点,此时A 1D 1D 1C 1=1,连接A 1B 交AB 1于点O ,连接OD 1.由棱柱的性质,知四边形A 1ABB 1为平行四边形,所以点O 为A 1B的中点.在△A 1BC 1中,点O 、D 1分别为A 1B 、A 1C 1的中点,∴OD 1∥BC 1.又∵OD 1⊂平面AB 1D 1,BC 1⊄平面AB 1D 1,∴BC 1∥平面AB 1D 1.∴A 1D 1D 1C 1=1时,BC 1∥平面AB 1D 1. (2)由已知,平面BC 1D ∥平面AB 1D 1,且平面A 1BC 1∩平面BDC 1=BC 1,平面A 1BC 1∩平面AB 1D 1=D 1O ,因此BC 1∥D 1O ,同理AD 1∥DC 1.∴A 1D 1D 1C 1=A 1O OB ,A 1D 1D 1C 1=DC AD . 又∵A 1O OB =1,∴DC AD =1,即AD DC =1.考点6:线线、线面垂直1.设α、β是两个不同的平面,a 、b 是两条不同的直线,给出下列四个命题,其中真命题是A .若a ∥α,b ∥α,则a ∥bB .若a ∥α,b ∥β,a ∥b ,则α∥βC .若a ⊥α,b ⊥β,a ⊥b ,则α⊥βD .若a 、b 在平面α内的射影互相垂直,则a ⊥b答案 C解析 与同一平面平行的两条直线不一定平行,所以A 错误;与两条平行直线分别平行的两个平面未必平行,所以B 错误;如图(1),设OA ∥a ,OB ∥b ,直线OA 、OB 确定的平面分别交α、β于AC 、BC ,则OA ⊥AC ,OB ⊥BC ,所以四边形OACB 为矩形,∠ACB 为二面角α-l -β的平面角,所以α⊥β,C 正确;如图(2),直线a 、b 在平面α内的射影分别为m 、n ,显然m ⊥n ,但a 、b 不垂直,所以D 错误,故选C.2.“直线l 垂直于平面α内的无数条直线”是“l ⊥α”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件答案 B3.若m ,n 表示直线,α表示平面,则下列命题中,正确命题的个数为① ⎭⎪⎬⎪⎫m ∥n m ⊥α⇒n ⊥α ② ⎭⎪⎬⎪⎫n ⊥αm ⊥α⇒m ∥n③ ⎭⎪⎬⎪⎫m ⊥αn ∥α⇒m ⊥n ④ ⎭⎪⎬⎪⎫m ∥αm ⊥n ⇒n ⊥αA .1B .2C .3D .4答案 C解析 ①②③正确,④错误.4.如图,四棱锥P -ABCD 中,PA ⊥底面ABCD ,AB ⊥AD ,AC ⊥CD ,∠ABC=60°,PA =AB =BC ,E 是PC 的中点.求证:(1)CD ⊥AE ;(2)PD ⊥平面ABE .【证明】 (1)∵PA ⊥底面ABCD ,∴CD ⊥PA .又CD ⊥AC ,PA ∩AC =A ,故CD ⊥平面PAC ,AE ⊂平面PAC .故CD ⊥AE .(2)∵PA =AB =BC ,∠ABC =60°,故PA =AC .∵E 是PC 的中点,故AE ⊥PC .由(1)知CD ⊥AE ,从而AE ⊥平面PCD ,故AE ⊥PD .易知BA ⊥PD ,故PD ⊥平面ABE .5.设l 是直线,α,β是两个不同的平面( )A.若l∥α,l∥β,则α∥βB.若l∥α,l⊥β,则α⊥βC.若l⊥α,α⊥β,则l⊥βD.若α⊥β,l∥α,则l⊥β答案B解析A项中由l∥α,l∥β不能确定α与β的位置关系,C项中由α⊥β,l⊥α可推出l∥β或l⊂β,D项由α⊥β,l∥α不能确定l与β的位置关系.6.设b,c表示两条直线,α,β表示两个平面,下列命题中真命题是A.若b⊂α,c∥α,则b∥cB.若b⊂α,b∥c,则c∥αC.若c∥α,c⊥β,则α⊥βD.若c∥α,α⊥β,则c⊥β答案C解析如果一条直线平行于一个平面,它不是与平面内的所有直线平行,只有部分平行,故A错;若一条直线与平面内的直线平行,该直线不一定与该平面平行,该直线可能是该平面内的直线,故B 错;如果一个平面与另一个平面的一条垂线平行,那么这两个平面垂直,这是一个真命题,故C对;对D来讲若c∥α,α⊥β,则c与β的位置关系不定,故选C.7. 在三棱柱ABC—A1B1C1中,AA1⊥平面ABC,AC=BC=AA1=2,∠ACB=90°,E为BB1的中点,∠A1DE=90°,求证:CD⊥平面A1ABB1.证明连接A1E,EC,∵AC=BC=2,∠ACB=90°,∴AB=2 2.设AD=x,则BD=22-x.∴A1D2=4+x2,DE2=1+(22-x)2,A1E2=(22)2+1.∵∠A1DE=90°,∴A1D2+DE2=A1E2.∴x= 2.∴D为AB的中点.∴CD⊥AB.又AA1⊥CD,且AA1∩AB=A,∴CD⊥平面A1ABB1.8.如图,长方体ABCD—A1B1C1D1中,底面A1B1C1D1是正方形,O是BD的中点,E是棱AA1上任意一点.<1>证明:BD⊥EC1;<2>如果AB=2,AE=2,OE⊥EC1,求AA1的长.【解析】 (1)如图,连接AC ,A 1C 1,AC 与BD 相交于点O .由底面是正方形知,BD ⊥AC .因为AA 1⊥平面ABCD ,BD ⊂平面ABCD ,所以AA 1⊥BD .又由AA 1∩AC =A ,所以BD ⊥平面AA 1C 1C .再由EC 1⊂平面AA 1C 1C 知,BD ⊥EC 1.(2)设AA 1的长为h ,连接OC 1.在Rt △OAE 中,AE =2,AO =2, 故OE 2=(2)2+(2)2=4.在Rt △EA 1C 1中,A 1E =h -2,A 1C 1=2 2.故EC 21=(h -2)2+(22)2.在Rt △OCC 1中,OC =2,CC 1=h ,OC 21=h 2+(2)2.因为OE ⊥EC 1,所以OE 2+EC 21=OC 21.即4+(h -2)2+(22)2=h 2+(2)2,解得h =3 2.所以AA 1的长为3 2.考点7:面面垂直1.△ABC 为正三角形,EC ⊥平面ABC ,BD ∥CE ,且CE =CA =2BD ,M 是EA 的中点,求证: ①DE =DA ;②平面BDM ⊥平面ECA ;③平面DEA ⊥平面ECA .【证明】 ①取EC 的中点F ,连接DF .∵BD ∥CE ,∴DB ⊥BA .又EC ⊥BC ,在Rt △EFD 和Rt △DBA 中,∵EF =12EC =BD ,FD =BC =AB ,∴Rt △EFD ≌Rt △DBA ,∴DE =DA .②取CA 的中点N ,连接MN 、BN ,则MN 綊12EC .∴MN ∥BD ,∴N 点在平面BDM 内.∵EC ⊥平面ABC ,∴EC ⊥BN .又CA ⊥BN ,∴BN ⊥平面ECA .∵BN ⊂平面BDM ,∴平面BDM ⊥平面ECA .③∵DM ∥BN ,BN ⊥平面ECA ,∴DM ⊥平面ECA ,又DM ⊂平面DEA ,∴平面DEA ⊥平面ECA .2.已知平面PAB ⊥平面ABC ,平面PAC ⊥平面⊥平面PBC ,E 为垂足.①求证:PA ⊥平面ABC ;②当E 为△PBC 的垂心时,求证:△ABC 是直角三角形.【证明】 ①在平面ABC 内取一点D ,作DF ⊥AC 于F .平面PAC ⊥平面ABC ,且交线为AC ,∴DF ⊥平面PAC .又PA ⊂平面PAC ,∴DF ⊥PA .作DG ⊥AB 于G ,同理可证:DG ⊥PA .DG 、DF 都在平面ABC 内,∴PA ⊥平面ABC .②连接BE 并延长交PC 于H ,∵E 是△PBC 的垂心,∴PC ⊥BH .又已知AE 是平面PBC 的垂线,PC ⊂平面PBC ,∴PC ⊥AE .又BH ∩AE =E ,∴PC ⊥平面ABE .又AB ⊂平面ABE ,∴PC ⊥AB .∵PA ⊥平面ABC ,∴PA ⊥AB .又PC ∩PA =P ,∴AB ⊥平面PAC .又AC ⊂平面PAC ,∴AB ⊥AC .即△ABC 是直角三角形.3.如图所示,在斜三棱柱A 1B 1C 1-ABC 中,底面是等腰三角形,AB =AC ,侧面BB 1C 1C ⊥底面ABC .(1)若D 是BC 的中点,求证:AD ⊥CC 1;(2)过侧面BB 1C 1C 的对角线BC 1的平面交侧棱于M ,若AM =MA 1,求证:截面MBC 1⊥侧面BB 1C 1C ;(3)AM =MA 1是截面MBC 1⊥侧面BB 1C 1C 的充要条件吗请你叙述判断理由.【证明】 (1)∵AB =AC ,D 是BC 的中点,∴AD ⊥BC .∵底面ABC ⊥侧面BB 1C 1C ,且交线为BC ,∴由面面垂直的性质定理可知AD ⊥侧面BB 1C 1C .又∵CC 1⊂侧面BB 1C 1C ,∴AD ⊥CC 1.(2)方法一 取BC 1的中点E ,连接DE 、ME .在△BCC 1中,D 、E 分别是BC 、BC 1的中点.∴DE 綊12CC 1.又AA 1綊CC 1,∴DE 綊12AA 1.∵M 是AA 1的中点(由AM =MA 1知),∴DE 綊AM .∴AMED 是平行四边形,∴AD 綊ME .由(1)知AD ⊥面BB 1C 1C ,∴ME ⊥侧面BB 1C 1C .又∵ME ⊂面BMC 1,∴面BMC 1⊥侧面BB 1C 1C .方法二 延长B 1A 1与BM 交于N (在侧面AA 1B 1B 中),连接C 1N .∵AM =MA 1,∴NA 1=A 1B 1.又∵AB =AC ,由棱柱定义知△ABC ≌△A 1B 1C 1.∴AB =A 1B 1,AC =A 1C 1.∴A 1C 1=A 1N =A 1B 1.在△B 1C 1N 中,由平面几何定理知:∠NC 1B 1=90°,即C 1N ⊥B 1C 1.又∵侧面BB 1C 1C ⊥底面A 1B 1C 1,交线为B 1C 1,∴NC 1⊥侧面BB 1C 1C .又∵NC 1⊂面BNC 1,∴截面C 1NB ⊥侧面BB 1C 1C ,即截面MBC 1⊥侧面BB 1C 1C .(3)结论是肯定的,充分性已由(2)证明.下面仅证明必要性(即由截面BMC 1⊥侧面BB 1C 1C 推出AM =MA 1,实质是证明M 是AA 1的中点), 过M 作ME 1⊥BC 1于E 1.∵截面MBC 1⊥侧面BB 1C 1C ,交线为BC 1.∴ME 1⊥面BB 1C 1C .又由(1)知AD ⊥侧面BB 1C 1C ,∵垂直于同一个平面的两条直线平行,∴AD ∥ME 1,∴M 、E 1、D 、A 四点共面.又∵AM ∥侧面BB 1C 1C ,面AME 1D ∩面BB 1C 1C =DE 1,∴由线面平行的性质定理可知AM ∥DE 1.又AD ∥ME 1,∴四边形AME 1D 是平行四边形.∴AD =ME 1,DE 1綊AM .又∵AM ∥CC 1,∴DE 1∥CC 1.又∵D 是BC 的中点,∴E 1是BC 1的中点.∴DE 1=12CC 1=12AA 1.∴AM =12AA 1,∴MA =MA 1.∴AM =MA 1是截面MBC 1⊥侧面BB 1CC 1的充要条件.考点8:平行与垂直的综合问题1.如图所示,在直角梯形ABEF 中,将DCEF 沿CD 折起使∠FDA =60°,得到一个空间几何体.(1)求证:BE ∥平面ADF ;(2)求证:AF ⊥平面ABCD ;(3)求三棱锥E —BCD 的体积.【解析】 (1)由已知条件,可知BC ∥AD ,CE ∥DF ,折叠之后平行关系不变.又因为BC ⊄平面ADF ,AD ⊂平面ADF ,所以BC ∥平面ADF .同理CE ∥平面ADF .又因为BC ∩CE =C ,BC ,CE ⊂平面BCE ,所以平面BCE ∥平面ADF .所以BE ∥平面ADF .(2)由于∠FDA =60°,FD =2,AD =1,所以AF 2=FD 2+AD 2-2×FD ×AD ×cos FDA =4+1-2×2×1×12=3.即AF = 3.所以AF 2+AD 2=FD 2.所以AF ⊥AD .又因为DC ⊥FD ,DC ⊥AD ,AD ∩FD =D ,所以DC ⊥平面ADF .又因为AF ⊂平面ADF ,所以DC ⊥AF .因为AD ∩DC =D ,AD ,DC ⊂平面ABCD ,所以AF ⊥平面ABCD .(3)因为DC ⊥EC ,DC ⊥BC ,EC ,BC ⊂平面EBC ,EC ∩BC =C ,所以DC ⊥平面EBC .又因为DF ∥EC ,AD ∥BC ,∠FDA =60°,所以∠ECB =60°.又因为EC =1,BC =1,所以S △ECB =12×1×1×32=34.所以V E -BCD =V D -EBC =13×DC ×S △ECB =13×1×34=312.2.如图1,在Rt △ABC 中,∠C =90°,D ,E 分别为AC ,AB 的中点,点F 为线段CD 上的一点.将△ADE 沿DE 折起到△A 1DE 的位置,使A 1F ⊥CD ,如图2.<1>求证:DE ∥平面A 1CB ;<2>求证:A 1F ⊥BE ;<3>线段A 1B 上是否存在点Q ,使A 1C ⊥平面DEQ 说明理由.【解析】 (1)因为D ,E 分别为AC ,AB 的中点,所以DE ∥BC .又因为DE ⊄平面A 1CB ,所以DE ∥平面A 1CB .(2)由已知得AC ⊥BC 且DE ∥BC ,所以DE ⊥AC .所以DE ⊥A 1D ,DE ⊥CD ,所以DE ⊥平面A 1DC .而A 1F ⊂平面A 1DC ,所以DE ⊥A 1F .又因为A 1F ⊥CD ,所以A 1F ⊥平面BCDE .所以A 1F ⊥BE .(3)线段A 1B 上存在点Q ,使A 1C ⊥平面DEQ .理由如下:如图,分别取A 1C ,A 1B 的中点P ,Q ,连接PQ ,QE ,PD ,则PQ ∥BC .因为DE ∥BC ,所以DE ∥PQ .所以平面DEQ 即为平面DEP .由(2)知,DE ⊥平面A 1DC ,所以DE ⊥A 1C .又因为P 是等腰三角形DA 1C 底边A 1C 的中点,所以A 1C ⊥DP .所以A 1C ⊥平面DEP .从而A 1C ⊥平面DEQ .故线段A 1B 上存在点Q ,使得A 1C ⊥平面DEQ .3.如图,四棱锥P -ABCD 中,四边形ABCD 为矩形,△PAD 为等腰三角形,∠APD =90°,平面PAD ⊥平面ABCD ,且AB =1,AD =2,E 、F 分别为PC 、BD 的中点.<1>证明:EF ∥平面PAD ;<2>证明:平面PDC ⊥平面PAD ;<3>求四棱锥P —ABCD 的体积.解析 (1)证明:如图,连接AC .∵四边形ABCD 为矩形且F 是BD 的中点,∴F 也是AC 的中点.又E 是PC 的中点,EF ∥AP ,∵EF ⊄平面PAD ,PA ⊂平面PAD ,∴EF ∥平面PAD .(2)证明:∵面PAD ⊥平面ABCD ,CD ⊥AD ,平面PAD ∩平面ABCD =AD ,∴CD ⊥平面PAD .∵CD ⊂平面PDC ,∴平面PDC ⊥平面PAD .(3)取AD 的中点为O .连接PO .∵平面PAD ⊥平面ABCD ,△PAD 为等腰直角三角形,∴PO ⊥平面ABCD ,即PO 为四棱锥P —ABCD 的高.∵AD =2,∴PO =1.又AB =1,∴四棱锥P —ABCD 的体积V =13PO ·AB ·AD =23.。
第一章立体几何初步章末检测教师版

章末检测一、选择题1. 如图所示的长方体,将其左侧面作为上底面,右侧面作为下底面,水平放置,所得的几何体是 ( )A .棱柱B .棱台C .棱柱与棱锥组合体D .无法确定2. 圆柱的轴截面是正方形,面积是S ,则它的侧面积是 ( )A. 1πS B . π S C . 2πS D . 4πS3. 具有如图所示直观图的平面图形ABCD 是 ( )A .等腰梯形B .直角梯形C .任意四边形D .平行四边形4.下列命题正确的是 ( )A .若两条直线和同一个平面所成的角相等,则这两条直线平行B .若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C .若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D .若两个平面都垂直于第三个平面,则这两个平面平行5. 在空间四边形ABCD 的边AB ,BC ,CD ,DA 上分别取E 、F 、G 、H 四点,如果EF ,GH 交于一点P ,则 ( )A .P 一定在直线BD 上B .P 一定在直线AC 上C .P 一定在直线AC 或BD 上 D .P 既不在直线AC 上,也不在直线BD 上6. 平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为( )A. 6π B .43π C .46π D .63π7. 如图所示,则这个几何体的体积等于 ( )A .4B .6C .8D .128. 如图所示,在正方体ABCD —A 1B 1C 1D 1中,若E 是A 1C 1的中点,则直线CE 垂直于 ( )A .ACB .BDC .A 1D D .A 1D 19. 已知平面α⊥平面β,α∩β=l ,点A ∈α,A ∉l ,直线AB ∥l ,直线AC ⊥l ,直线m ∥α,m ∥β,则下列四种位置关系中,不一定成立的是 ( )A .AB ∥m B .AC ⊥m C .AB ∥βD .AC ⊥β10.如图(1)所示,在正方形SG 1G 2G 3中,E ,F 分别是G 1G 2及G 2G 3的中点,D 是EF 的中点,现在沿SE ,SF 及EF 把这个正方形折成一个四面体,使G 1,G 2,G 3三点重合,重合后的点记为G ,如图(2)所示,那么,在四面体S -EFG 中必有( )A .SG ⊥△EFG 所在平面B .SD ⊥△EFG 所在平面C .GF ⊥△SEF 所在平面D .GD ⊥△SEF 所在平面11.如图,ABCD -A 1B 1C 1D 1为正方体,下面结论错误的是 ( )A .BD ∥平面CB 1D 1 B .AC 1⊥BDC .AC 1⊥平面CB 1D 1 D .异面直线AD 与CB 1所成的角为60°12.如图所示,正方体ABCD -A 1B 1C 1D 1中,点P 在侧面BCC 1B 1及其边界上运动,并且总是保持AP ⊥BD 1,则动点P 的轨迹是( )A .线段B 1C B .线段BC 1C .BB 1的中点与CC 1的中点连成的线段D .BC 的中点与B 1C 1的中点连成的线段二、填空题13.设平面α∥平面β,A 、C ∈α,B 、D ∈β,直线AB 与CD 交于点S ,且点S 位于平面α,β之间,AS =8,BS =6,CS =12,则SD =________.14.如图,一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径相等,这时圆柱、圆锥、球的体积之比为______________.15.一个水平放置的圆柱形储油桶(如图所示),桶内有油部分所在圆弧占底面圆周长的14,则油桶直立时,油的高度与桶的高度的比值是_______. 16.已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积等于______ cm 3.三、解答题17.如图所示,长方体ABCD -A 1B 1C 1D 1中,M 、N 分别为AB 、A 1D 1的中点,判断MN 与平面A 1BC 1的位置关系,为什么?18.如图,在四面体ABCD中,CB=CD,AD⊥BD,且E、F分别是AB、BD的中点.求证:(1)EF∥面ACD;(2)面EFC⊥面BCD.19.沿着圆柱的一条母线将圆柱剪开,可将侧面展开到一个平面上,所得的矩形称为圆柱的侧面展开图,其中矩形长与宽分别是圆柱的底面圆周长和高(母线长),所以圆柱的侧面积S=2πrl,其中r为圆柱底面圆半径,l为母线长.现已知一个圆锥的底面半径为R,高为H,在其中有一个高为x的内接圆柱.(1)求圆柱的侧面积;(2)x为何值时,圆柱的侧面积最大?20.ABCD与ABEF是两个全等正方形,AM=FN,其中M∈AC,N∈BF.求证:MN∥平面BCE.21.如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点.已知AB=2,AD=22,PA=2.求:(1)三角形PCD的面积;(2)异面直线BC与AE所成的角的大小.22.如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°,AB=2,AD=1.(1)求证:MN∥平面PAD;(2)求证:平面PMC⊥平面PCD;(3)求三棱锥M—PCD的体积.答案1.A 2.B 3.B 4.C 5.B 6.B 7.A 8.B 9.D 10.A11.D 12.A13.914.3∶1∶215.14-12π16.117.解 直线MN ∥平面A 1BC 1,M 为AB 的中点,证明如下:∵MD/∈平面A 1BC 1,ND/∈平面A 1BC 1.∴MN ⊄平面A 1BC 1.如图,取A 1C 1的中点O 1,连接NO 1、BO 1.∵NO 1綊12D 1C 1, MB 綊12D 1C 1,∴NO 1綊MB. ∴四边形NO 1BM 为平行四边形.∴MN ∥BO 1.又∵BO 1⊂平面A 1BC 1,∴MN ∥平面A 1BC 1.18.证明 (1)∵E ,F 分别是AB ,BD 的中点,∴EF 是△ABD 的中位线,∴EF ∥AD ,∵EF ⊄面ACD ,AD ⊂面ACD ,∴EF ∥面ACD.(2)∵AD ⊥BD ,EF ∥AD ,∴EF ⊥BD.∵CB =CD ,F 是BD 的中点,∴CF ⊥BD.又EF∩CF =F ,∴BD ⊥面EFC.∵BD ⊂面BCD ,∴面EFC ⊥面BCD.19.解 (1)画圆锥及内接圆柱的轴截面(如图所示).设所求圆柱的底面半径为r ,它的侧面积S 圆柱侧=2πrx.因为r R =H -x H ,所以r =R -R H ·x.所以S 圆柱侧=2πRx -2πR H·x 2. (2)因为S 圆柱侧的表达式中x 2的系数小于零,所以这个二次函数有最大值.这时圆柱的高x =H 2. 故当圆柱的高是已知圆锥的高的一半时,它的侧面积最大. 20.证明 方法一 如图所示,连接AN ,并延长交BE 的延长线于P ,连接CP.∵BE ∥AF , ∴FN NB =AN NP, 由AC =BF ,AM =FN 得MC =NB.∴FNNB =AM MC .∴AM MC =AN NP,∴MN ∥PC ,又PC ⊂平面BCE. ∴MN ∥平面BCE. 方法二 如图,作MG ⊥AB 于G ,连接GN ,转证面MNG ∥面CEB.∵MG ∥BC ,只需证GN ∥BE. ∵MG ∥BC ,∴AM AG =MC GB. 又AM =FN ,AC =BF ,∴AM AG =FN AG =NB GB.∴GN ∥AF ∥BE.∴面MNG ∥面BCE. 又MN ⊂面MNG ,∴MN ∥面BCE.21.解 (1)因为PA ⊥底面ABCD ,所以PA ⊥CD.又AD ⊥CD ,所以CD ⊥平面PAD ,从而CD ⊥PD.因为PD =22+22=23,CD =2,所以三角形PCD 的面积为12×2×23=2 3.(2)如图,取PB 中点F ,连接EF 、AF ,则EF ∥BC ,从而∠AEF(或 其补角)是异面直线BC 与AE 所成的角. 在△AEF 中,由EF =2,AF =2,AE =2知△AEF 是等腰直角 三角形,所以∠AEF =45°.因此,异面直线BC 与AE 所成的角的大小是45°.22.(1)证明 取PD 的中点E ,连接AE ,EN ,∵N 为中点, ∴EN 为△PDC 的中位线,∴EN 綊12CD ,又∵CD 綊AB ,M 为中点,∴EN 綊AM.∴四边形AMNE 为平行四边形,∴MN ∥AE. 又∵MN ⊄平面PAD ,AE ⊂平面PAD ,∴MN ∥平面PAD.(2)证明 ∵PA ⊥平面ABCD ,CD ⊂平面ABCD ,AD ⊂平面ABCD.∴PA ⊥CD ,PA ⊥AD.∵CD ⊥AD ,PA∩AD =A ,∴CD ⊥平面PAD.又∵AE ⊂平面PAD ,∴CD ⊥AE.∵∠PDA =45°,E 为PD 中点,∴AE ⊥PD.又∵PD∩CD =D ,∴AE ⊥平面PCD.∵MN ∥AE ,∴MN ⊥平面PCD ,又∵MN ⊂平面PMC ,∴平面PMC ⊥平面PCD.(3)解 V M —PCD =V P —CDM =13S △CDM ·PA =13×12×CD×AD×PA=13×12×2×1×1=13.。
立体几何证明(教师版)
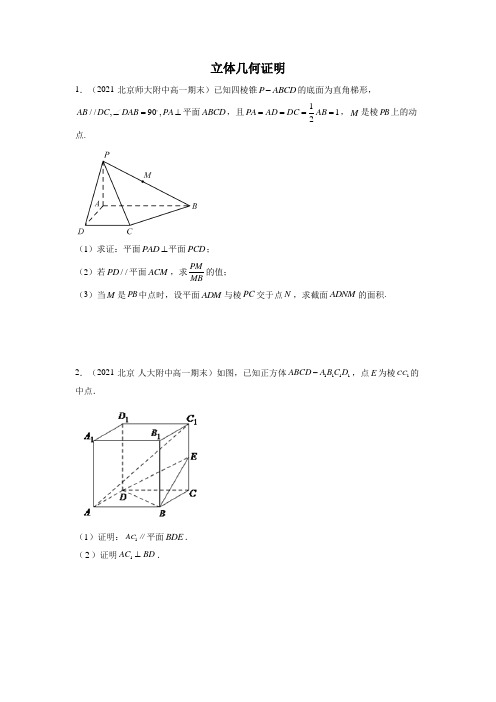
立体几何证明1.(2021·北京师大附中高一期末)已知四棱锥P ABCD -的底面为直角梯形,//,90,AB DC DAB PA ∠=⊥平面ABCD ,且112PA AD DC AB ====,M 是棱PB 上的动点.(1)求证:平面PAD ⊥平面PCD ;(2)若//PD 平面ACM ,求PM MB的值; (3)当M 是PB 中点时,设平面ADM 与棱PC 交于点N ,求截面ADNM 的面积.2.(2021·北京·人大附中高一期末)如图,已知正方体1111ABCD A B C D -,点E 为棱1CC 的中点.(1)证明:1AC ∥平面BDE .(2)证明1AC BD ⊥.3.(2021·北京·汇文中学高一期末)如图1,已知菱形AECD 的对角线AC ,DE 交于点F ,点E 为AB 的中点.将三角形ADE 沿线段DE 折起到PDE 的位置,如图2所示.(1)求证:DE PC ⊥;(2)试问平面PFC 与平面PBC 所成的二面角是否为90︒,如果是,请证明;如果不是,请说明理由;(3)在线段PD ,BC 上是否分别存在点M ,N ,使得平面//CFM 平面PEN ?若存在,请指出点M ,N 的位置,并证明;若不存在,请说明理由.4.(2021·北京·首都师范大学附属中学高一期末)如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,O ,M 分别为BD ,PC 的中点.设平面PAD 与平面PBC 的交线为l .(1)求证://OM 平面PAD ;(2)求证://BC l ;(3)在棱PC 上是否存在点N (异于点C ),使得//BN 平面PAD ?若存在,求出PN PC的值;若不存在,说明理由.5.(2021·北京·101中学高一期末)已知正四棱柱1111ABCD A B C D -中,M 是1DD 的中点.(1)求证:1//BD 平面AMC ;(2)求证:1AC BD ⊥;(3)在线段1BB 上是否存在点P ,当1BP BB λ=时,平面11//A PC 面AMC ?若存在,求出λ的值并证明;若不存在,请说明理由.6.(2021·北京师大附中高一期末)在正方体1111ABCD A B C D -中,E 为1CC 中点.(1)求证:1//BC 平面1AD E ;(2)求证:1A D ⊥平面11ABC D .7.(2021·北京·汇文中学高一期末)如图所示,在三棱锥A BCD -中,点M 、N 分别在棱BC 、AC 上,且//MN AB .(1)求证://MN 平面ABD ;(2)若MN CD ⊥,BD CD ⊥,求证:平面CBD ⊥平面ABD .8.(2019·北京师大附中高一期末)如图,在三棱柱111ABC A B C -中,1AA ⊥底面ABC ,90BAC ∠=,2AB AC ==,1AA ,M N 分别为1,BC CC 的中点,P 为侧棱1BB 上的动点(Ⅰ)求证:平面APM ⊥平面11BB C C ;(Ⅱ)若P 为线段1BB 的中点,求证:1//A N 平面APM ;(Ⅲ)试判断直线1BC 与平面APM 是否能够垂直.若能垂直,求PB 的值;若不能垂直,请说明理由9.(2019·北京师大附中高一期末)如图,已知四棱锥S ABCD-,底面ABCD是边长为2的菱形,60∠=,侧面SAD为正三角形,侧面SAD⊥底面ABCD,M为侧棱SB的中点,ABCE为线段AD的中点SD平面MAC;(Ⅰ)求证://⊥;(Ⅱ)求证:SE AC-的体积(Ⅲ)求三棱锥M ABC-中,PA⊥平面ABCD,底10.(2019·北京·101中学高一期末)如图,在四棱锥P ABCD部ABCD为菱形,E为CD的中点.(Ⅰ)求证:BD⊥平面PAC;(Ⅱ)若∠ABC=60°,求证:平面PAB⊥平面PAE;(Ⅲ)棱PB上是否存在点F,使得CF∥平面PAE?说明理由.11.(2019·北京·中央民族大学附属中学高一期末)在四面体ABCD 中,CB =CD ,AD BD ⊥,且E ,F 分别是AB ,BD 的中点,求证:(I )直线EF ACD 面;(II )EFC BCD ⊥面面.12.(2020·北京师大附中高一期末)如图,四棱锥P ABCD -的底面是正方形,侧棱PA ⊥底面ABCD ,E 是PA 的中点.(1)求证://CD 平面PAB ;(2)求证://PC 平面BDE ;(3)证明:BD CE ⊥.13.(2021·北京·人大附中高一期末)如图1,已知△ABD 和△BCD 是两个直角三角形,∠BAD =∠BDC =2π.现将△ABD 沿BD 边折起到1A BD 的位置,如图2所示,使平面1A BD ⊥平面BCD .(1)求证:平面1A BC ⊥平面1A CD ;(2)1A C 与BD 是否有可能垂直,做出判断并写明理由.14.(2020·北京·101中学高一期末)如图1,在△ABC 中,D ,E 分别为AB ,AC 的中点,O 为DE 的中点,AB AC ==4BC =.将△ADE 沿DE 折起到△1A DE 的位置,使得平面1A DE ⊥平面BCED ,F 为1A C 的中点,如图2.(1)求证://EF 平面1A BD ;(2)求证:平面1A OB ⊥平面1A OC ;(3)线段OC 上是否存在点G ,使得OC ⊥平面EFG ?说明理由.15.(2020·北京师大附中高一期末)如图,在多面体ABCDEF 中,底面ABCD 为矩形,侧面ADEF 为梯形,//AF DE ,DE AD ⊥,DC DE =.⊥;(Ⅰ)求证:AD CEBF平面CDE;(Ⅱ)求证://(Ⅲ)判断线段BE上是否存在点Q,使得平面ADQ⊥平面BCE?并说明理由.-中,平面16.(2020·北京·中国人民大学附属中学朝阳学校高一期末)在三棱锥P ABC⊥.设D,E分别为PA,AC中点.PAC⊥平面ABC,PA AC⊥,AB BCDE平面PBC;(Ⅰ)求证://(Ⅱ)求证:BC⊥平面PAB;(Ⅲ)试问在线段AB上是否存在点F,使得过三点D,E,F的平面内的任一条直线都与平面PBC平行?若存在,指出点F的位置并证明;若不存在,请说明理由.答案:1.(1)证明见解析;(2)12;【分析】 (1) 要证平面PAD ⊥平面PCD ,只需证明DC ⊥平面PAD ,利用线面垂直的判定可证DC ⊥平面PAD .(2) 根据题意,作出点M ,再利用相似三角形求PM MB的值 (3) 从四点共面角度出发,利用平面向量基本定理确定点N 的位置,再求截面面积.【详解】(1)证明:因为90DAB ∠=,所以AB AD ⊥,又//AB DC ,所以DC AD ⊥.因为PA ⊥平面ABCD ,DC ⊂平面ABCD ,所以PA DC ⊥.又AD ,PA 在平面PAD 内,且相交于点A ,所以DC ⊥平面PAD . 又DC ⊂平面PCD ,所以平面PAD ⊥平面PCD .(2)如图,连接AC ,BD 相交于点E ,过点E 作//EM PD ,交PB 于点M . 因为//EM PD ,PD ⊄平面ACM ,EM ⊂平面ACM ,所以//PD 平面ACM . 故上述所作点M 为使得//PD 平面ACM 的点M .如图在梯形ABCD 中,有//AB DC ,112AD DC AB === 令()22DE DB DA DC DA DC λλλλ==+=+, 因为A ,E ,C 三点共线,所以21λλ+=,13λ=.即13DE DB =,所以23BE DB =,12DE BE =. 因为//EM PD ,所以BME BPD ,12DE P MB BE M ==. (3)设PN PC μ=, 因为,,,A D N M 四点共面,所以存在实数m ,n ,使得AN mAD nAM =+. 因为()12AN AP PN AP PC AD AB AP μμμμ=+=+=++-,22n n mAD nAM mAD AB AP +=++, 又AD ,AB ,AP 为一组基底, 所以,,2212m n n μμμ⎧⎪=⎪⎪=⎨⎪⎪-=⎪⎩解得23m n ==. 所以2233AN AD AM =+.因为PA ⊥平面ABCD ,AD ⊂平面ABCD ,所以PA AD ⊥. 又AD AB ⊥,PA ,AB 在平面PAB 内,且相交于点A , 所以AD ⊥平面PAB ,又AM ⊂平面PAB ,所以AD AM ⊥. 在四边形AMND 中,AD AM ⊥,1AD =,AM = 因为2233AN AD AM =+,点N 到AM 的距离为2233AD =,点N 到AD的距离为23AM . 所以截面ADNM的面积1121223ADN AMNS S S =+=⨯+2.(1)见解析;(2)见解析【详解】试题分析:(1)连结AC 交BD 于F ,连结EF ,通过正方形对角线的性质以及三角形中位线可得112EF AC ,根据线面平行判定定理可得结果;(2)通过证明BD ⊥平面1ACC 可得结论.试题解析:(1)证明:连结AC 交BD 于F ,连结EF ,正方形ABCD 中,AC 与BD 互相平分,∴F 为AC 中点,在1ACC 中,∵E ,F 分别为1CC 与AC 中点,∴112EF AC ,∵EF ⊂平面BDE ,1AC ⊄平面BDE ,∴EF 平面BDE .(2)证明:在正方形ABCD 中,AC BD ⊥,在正方体1111ABCD A B C D -中, 1CC ⊥平面ABCD ,∵BD ⊂平面ABCD ,∴1CC BD ⊥,∵1AC CC C ⋂=,∴BD ⊥平面1ACC ,∵1AC ⊂平面1ACC ,∴1AC BD ⊥.3.(1)证明见解析;(2)平面PFC 与平面PBC 所成的二面角为90︒,证明见解析;(3)存在满足条件的,M N ,,M N 分别为,PD BC 中点,证明见解析. 【分析】(1)根据线面垂直的判定可证得DE ⊥平面PCF ,由线面垂直性质可证得结论; (2)根据平行关系可证得BC ⊥平面PCF ,由面面垂直的判定可证得两平面垂直,由此得到所成角为90︒;(3)利用平行四边形和三角形中位线性质可证得线线平行关系,由此证得线面平行和面面平行,从而确定存在满足条件的,M N . 【详解】(1)四边形AECD 为菱形,AC DE ∴⊥,即DE PF ⊥,DE CF ⊥, 又,PF CF ⊂平面PCF ,PFCF F =,DE ∴⊥平面PCF ,PC ⊂平面PCF ,DE PC ∴⊥.(2)平面PFC 与平面PBC 所成的二面角为90︒,证明如下:E 为AB 中点且四边形AECD 为菱形,//BE CD ∴,∴四边形BCDE 为平行四边形,//BC DE ∴,由(1)知:DE ⊥平面PCF ,BC ∴⊥平面PCF ,又BC ⊂平面PBC ,∴平面PCF ⊥平面PBC ,即平面PFC 与平面PBC 所成的二面角为90︒.(3)存在满足条件的,M N ,,M N 分别为,PD BC 中点,证明如下:由(2)知:四边形BCDE 为平行四边形,又,F N 分别为,DE BC 中点,//EF CN ∴,∴四边形EFCN 为平行四边形,//CF EN ∴,又EN ⊂平面PEN ,CF ⊄平面PEN ,//CF ∴平面PEN ;,M F 分别为,PD DE 中点,MF ∴为PDE △中位线,//MF PE ∴,又PE ⊂平面PEN ,MF ⊄平面PEN ,//MF ∴平面PEN ,又MFCF F =,,MF CF ⊂平面FCM ,∴平面//CFM 平面PEN .【点睛】本题考查立体几何中线线垂直关系、面面垂直与平行关系的证明问题,涉及到线面垂直的判定与性质、面面垂直的判定、线面平行与面面平行的判定等定理的应用,属于常考题型.4.(1)证明见解析;(2)证明见解析;(3)不存在,理由见解析. 【分析】(1)连接AC , 易知O 为AC 的中点,进而得//AP OM ,再结合线面平行的判定定理即可证明;(2)由题知//BC 平面PAD ,进而根据线面平行的性质定理即可证明//BC l ;(3))假设在棱PC 上存在点N (异于点C ),使得//BN 平面PAD ,进而在平面PDC 中,过点N 作PD 的平行线EN ,交DC 于E ,故平面//BEN 平面PAD ,进而得//BE AD ,另一方面,在平行四边形ABCD 中,BE 与AD 不平行,矛盾,故不存在. 【详解】解:(1)证明:连接AC ,因为底面ABCD 为平行四边形,O 为BD 的中点, 所以O 为AC 的中点,因为M 为PC 的中点, 所以在APC △中,//AP OM ,因为OM ⊄平面PAD ,AP ⊂平面PAD , 所以//OM 平面PAD(2)因为底面ABCD 为平行四边形, 所以//AD BC ,因为AD ⊂平面PAD ,BC ⊄平面PAD , 所以//BC 平面PAD ,因为平面PAD 与平面PBC 的交线为l ,BC ⊂平面PBC , 所以//BC l(3)假设在棱PC 上存在点N (异于点C ),使得//BN 平面PAD , 在平面PDC 中,过点N 作PD 的平行线EN ,交DC 于E , 因为EN ⊄平面PAD ,PD ⊂平面PAD ,所以//EN 平面PAD , 因为EN BN N ⋂=,所以平面//BEN 平面PAD , 因为BE ⊂平面BEN ,所以//BE 平面PAD ,又因为BE ⊂平面ABCD ,平面ABCD 平面PAD AD =,所以//BE AD 另一方面,在平行四边形ABCD 中,BE 与AD 不平行,矛盾, 所以在棱PC 上不存在点N (异于点C ),使得//BN 平面PAD .5.(1)证明见解析;(2) 证明见解析;(3)在线段1BB 上存在点P ,当12λ=时,平面11//A PC 平面AMC . 【分析】(1) 利用线面平行的判定定理证明1//BD 平面AMC ;(2) 利用线面垂直的判定定理证明AC ⊥平面11BB D D ,则有1AC BD ⊥; (3) 先确定λ的值,再根据面面平行的判定定理证明两平面平行. 【详解】因为四棱柱1111ABCD A B C D -是正四棱柱,所以底面ABCD 为正方形,侧棱垂直底面,侧面均为矩形.(1)证明:记AC 和BD 相交于点N ,因为ABCD 为正方形,所以N 为BD 的中点.又M 是1DD 的中点, 所以1//MN BD .又1BD ⊄平面AMC ,MN ⊂平面AMC , 所以1//BD 平面AMC .(2)证明:因为ABCD 为正方形,所以AC BD ⊥.因为1D D ⊥平面ABCD ,AC ⊂平面ABCD ,所以1D D AC ⊥. 又BD ,1D D 在平面11BB D D 内,且相交于点D , 所以AC ⊥平面11BB D D .又1BD ⊂平面11BB D D , 所以1AC BD ⊥.(3) 在线段1BB 上存在点P ,当12λ=,即112BP BB =时,平面11//A PC 面AMC . 理由如下:当112BP BB =时,P 为1BB 的中点. 取1CC 的中点G ,连接1PC ,GB ,则有1//PC GB .连接MG ,因为四边形11CC D D 是矩形,M 是1DD 的中点,G 是1CC 的中点, 所以//MG CD ,MG CD =.在正方形ABCD 中,有,//CD AB ,CD AB =.所以//MG AB ,MG AB =,四边形ABGM 为平行四边形. 有//BG AM ,又1//PC GB ,所以1//PC AM ,又1PC ⊄平面AMC ,AM ⊂平面AMC ,所以1PC //平面AMC . 同理可证:1//PA 平面AMC .又1PC ,1PA 在平面11A PC 内,且相交于点P , 所以平面11//A PC 平面AMC . 6.(1)证明见解析;(2) 证明见解析. 【分析】(1)先证明四边形11ABC D 为平行四边形,得到11//BC AD ,再利用线面平行的判定定理证明1//BC 平面1AD E ;(2)先证明11A D AD ⊥,再由线面垂直的性质得到1AB A D ⊥,最后由线面垂直的判定定理证明1A D ⊥平面11ABC D.(1)证明:在正方体1111ABCD A B C D -中, 有//AB CD ,11//CD C D ,所以11//AB C D .又11AB C D =,所以四边形11ABC D 为平行四边形,有11//BC AD . 又1BC ⊄平面1AD E ,1AD ⊂平面1AD E , 所以1//BC 平面1AD E(2)证明:因为1A D ,1AD 为正方形的对角线,所以11A D AD ⊥. 因为AB ⊥平面11AA D D ,1A D ⊂平面11AA D D ,所以1AB A D ⊥. 又1AD ,AB 在平面11ABC D 内,且相交于点A , 所以1A D ⊥平面11ABC D .7.(1)证明见解析;(2)证明见解析. 【分析】(1)由//MN AB ,利用直线与平面平行的判断定理,证明//MN 平面ABD .(2)推导出BA DC ⊥,DC BD ⊥,从而CD ⊥平面ABD ,由此能证明平面ABD ⊥平面BCD . 【详解】(1)∵在三棱锥A BCD -中,点M 、N 分别在棱BC 、AC 上,且//MN AB .MN ⊄平面ABD ,AB 平面ABD ,∴//MN 平面ABD(2)∵MN CD ⊥,//MN AB ,∴AB CD ⊥, ∵BD CD ⊥,ABBD B =∴CD ⊥平面ABD , ∵CD ⊂平面BCD ∴平面ABD ⊥平面BCD . 【点睛】本题考查的是空间中平行与垂直的证明,较简单.8.(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)直线BC 1与平面APM 不能垂直,详见解析 【分析】(Ⅰ)由等腰三角形三线合一得AM BC ⊥;由线面垂直性质可得1AM BB ⊥;根据线面垂直的判定定理知AM ⊥平面11BB C C ;由面面垂直判定定理证得结论;(Ⅱ)取11C B 中点D ,可证得1//A D AM ,//DN MP ;利用线面平行判定定理和面面平行判定定理可证得平面1//A DN 平面APM ;根据面面平行性质可证得结论;(Ⅲ)假设1BC ⊥平面APM ,由线面垂直性质可知1BC PM ⊥,利用相似三角形得到111C B PB MB BB =,从而解得BP 长度,可知满足垂直关系时,P 不在棱1BB 上,则假设错误,可得到结论.(Ⅰ)AB AC =,M 为BC 中点 AM BC ∴⊥1AA ⊥平面ABC ,11//AA BB 1BB ∴⊥平面ABC又AM ⊂平面ABC 1AM BB ∴⊥ 1,BB BC ⊂平面11BB C C ,1BB BC B = AM ∴⊥平面11BB C C又AM ⊂平面APM ∴平面APM ⊥平面11BB C C (Ⅱ)取11C B 中点D ,连接11,,,A D DN DM B C,D M 分别为11,C B CB 的中点 1//DM AA ∴且1DM AA = ∴四边形1A AMD 为平行四边形 1//A D AM ∴又1A D ⊄平面APM ,AM ⊂平面APM 1//A D ∴平面APM,D N 分别为111,C B CC 的中点 1//DN B C ∴又,P M 分别为1,BB CB 的中点 1//MP B C ∴ //DN MP ∴ 又DN ⊄平面APM ,MP ⊂平面APM //DN ∴平面APM 1,A D DN ⊂平面1A DN ,1A DDN D = ∴平面1//A DN 平面APM又1A N ⊂平面1A DN 1//A N ∴平面APM(Ⅲ)假设1BC ⊥平面APM ,由PM ⊂平面APM 得:1BC PM ⊥设PB x =,x ⎡∈⎣当1BC PM ⊥时,11BPM B C B ∠=∠ Rt PBM ∴∆∽11Rt B C B ∆ 111C B PB MB BB =∴由已知得:MB11C B =1BB=,解得:x ⎡=⎣ ∴假设错误 ∴直线1BC 与平面APM 不能垂直【点睛】本题考查立体几何中面面垂直、线面平行关系的证明、存在性问题的求解;涉及到线面垂直的判定与性质、线面平行的判定、面面平行的判定与性质定理的应用;处理存在性问题时,常采用假设法,通过假设成立构造方程,判断是否满足已知要求,从而得到结论. 9.(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)12【分析】(Ⅰ)连接BD ,交AC 于点O ;根据三角形中位线可证得//MO SD ;由线面平行判定定理可证得结论;(Ⅱ)由等腰三角形三线合一可知SE AD ⊥;由面面垂直的性质可知SE ⊥平面ABCD ;根据线面垂直性质可证得结论;(Ⅲ)利用体积桥的方式将所求三棱锥体积转化为14S ABCD V -;根据已知长度和角度关系分别求得四边形面积和高,代入得到结果. 【详解】(Ⅰ)证明:连接BD ,交AC 于点O四边形ABCD 为菱形 O ∴为BD 中点 又M 为SB 中点 //MO SD ∴MO ⊂平面MAC ,SD ⊄平面MAC //SD ∴平面MAC (Ⅱ)SAD ∆为正三角形,E 为AD 中点 SE AD ∴⊥平面SAD ⊥平面ABCD ,平面SAD ⋂平面ABCD AD =,SE ⊂平面SADSE ∴⊥平面ABCD ,又AC ⊂平面ABCD SE AC ∴⊥ (Ⅲ)M 为SB 中点 11112443M ABC M ABCD S ABCD ABCDV V V SSE ---∴===⨯⋅又2AB BC AD CD SA SD ======,60ABC ∠= 2AC ∴=,12222sin 60232ABCDABC SS ∆==⨯⨯⨯=由(Ⅱ)知,SE AD ⊥ SE ∴=11122M ABC V -=⨯∴ 【点睛】本题考查立体几何中线面平行、线线垂直关系的证明、三棱锥体积的求解问题;涉及到线面平行判定定理、面面垂直性质定理和判定定理的应用、体积桥的方式求解三棱锥体积等知识,属于常考题型. 10.(Ⅰ)见解析; (Ⅱ)见解析; (Ⅲ)见解析. 【分析】(Ⅰ)由题意利用线面垂直的判定定理即可证得题中的结论;(Ⅱ)由几何体的空间结构特征首先证得线面垂直,然后利用面面垂直的判断定理可得面面垂直;(Ⅲ)由题意,利用平行四边形的性质和线面平行的判定定理即可找到满足题意的点. 【详解】(Ⅰ)证明:因为PA ⊥平面ABCD ,所以PA BD ⊥; 因为底面ABCD 是菱形,所以AC BD ⊥; 因为PAAC A =,,PA AC ⊂平面PAC ,所以BD ⊥平面PAC .(Ⅱ)证明:因为底面ABCD 是菱形且60ABC ∠=︒,所以ACD ∆为正三角形,所以AE CD ⊥, 因为//AB CD ,所以AE AB ⊥;因为PA ⊥平面ABCD ,AE ⊂平面ABCD , 所以AE PA ⊥; 因为PA AB A = 所以AE ⊥平面PAB ,AE ⊂平面PAE ,所以平面PAB ⊥平面PAE .(Ⅲ)存在点F 为PB 中点时,满足//CF 平面PAE ;理由如下:分别取,PB PA 的中点,F G ,连接,,CF FG EG , 在三角形PAB 中,//FG AB 且12FG AB =;在菱形ABCD 中,E 为CD 中点,所以//CE AB 且12CE AB =,所以//CE FG 且CE FG =,即四边形CEGF 为平行四边形,所以//CF EG ; 又CF⊄平面PAE ,EG ⊂平面PAE ,所以//CF 平面PAE .【点睛】本题主要考查线面垂直的判定定理,面面垂直的判定定理,立体几何中的探索问题等知识,意在考查学生的转化能力和计算求解能力. 11.(I )证明见解析. (II )证明见解析. 【详解】证明:(I )E ,F 分别为AB ,BD 的中点EF AD ⇒}EF ADAD ACD EF ACD EF ACD⇒⊂⇒⊄面面面. (II )}}}EF ADEF BDAD BD CD CB CF BD BD EFCF BD EF CF F⇒⊥⊥=⇒⊥⇒⊥⋂=面为的中点,又BD BCD ⊂面,所以EFC BCD ⊥面面.12.(1)证明见解析;(2)证明见解析;(3)证明见解析. 【分析】(1)根据底面是正方形,得到CDAB ,再利用线面平行判定定理证明.(2)连结AC ,BD ,交于点O ,连结OE ,由中位线定理得到OE PC ∥,再利用线面平行判定定理证明.(3)根据底面是正方形,得到BD AC ⊥,由侧棱PA ⊥底面ABCD ,得到BD PA ⊥,从而BD ⊥平面ACE ,由此能证明BD CE ⊥. 【详解】(1)∵四棱锥P ABCD -的底面是正方形, ∴CDAB ,∵CD CD ⊄平面PAB ,AB 平面PAB ,∴CD ∥平面PAB . (2)如图所示:连结AC ,BD ,交于点O ,连结OE ,∵四棱锥P ABCD -的底面是正方形,∴O 是AC 中点,∵E 是PA 的中点.∴OE PC ∥,∵PC ⊄平面BDE ,OE ⊂平面BDE ,∴PC 平面BDE .(3)∵四棱锥P ABCD -的底面是正方形,侧棱PA ⊥底面ABCD ,∴BD AC ⊥,BD PA ⊥,∵AC PA A ⋂=,∴BD ⊥平面ACE ,∵CE ⊂平面ACE ,∴BD CE ⊥.【点睛】本题主要考查线面平行的判定定理,线面垂直的判定定理,还考查了转化化归的思想和逻辑推理的能力,属于中档题.13.(1)证明见解析;(2)1A C 与BD 不可能垂直,证明见解析.【分析】(1)证得1A B ⊥平面1A CD ,结合面面垂直的判定定理即可得出结论;(2)假设1A C 与BD 垂直,然后推出与已知条件11A B A D ⊥矛盾,即可得出1A C 与BD 不可能垂直.【详解】(1)因为平面1A BD ⊥平面BCD ,平面1A BD 平面BCD =BD ,CD ⊂平面BCD ,CD ⊥BD ,所以CD ⊥平面1A BD ,又因为1A B ⊂平面1A BD ,所以CD ⊥1A B ,又因为11A B A D ⊥,1A D CD D =,所以1A B ⊥平面1A CD ,且1A B ⊂平面1A BC ,所以平面1A BC ⊥平面1A CD ;(2)假设1A C 与BD 垂直,又因为CD ⊥BD ,且1AC CD C ⋂=,所以DB ⊥平面1A CD ,又因为1A D ⊂平面1A CD ,所以1DB A D ⊥,这与11A B A D ⊥矛盾,故假设不成立,即1A C 与BD 不可能垂直.23.(1)见解析;(2)见解析;(3)见解析【解析】试题分析:(1)取线段1A B 的中点H ,由三角形中位线性质以及平行四边形性质得四边形DEFH 为平行四边形,即得//EF HD .再根据线面平行判定定理得结论,(2)先根据等腰三角形性质得1A O DE ⊥.再根据面面垂直性质定理得1A O ⊥平面BCED ,即得1CO A O ⊥,根据勾股定理得CO BO ⊥,所以由线面垂直判定定理得 CO ⊥平面1A OB ,最后根据面面垂直判定定理得结论,(3)假设线段OC 上存在点G ,使得OC ⊥平面EFG ,则EO EC =,与条件矛盾.试题解析:解:(1)取线段1A B 的中点H ,连接HD ,HF .因为在△ABC 中,D ,E 分别为AB ,AC 的中点,所以 //DE BC ,12DE BC =. 因为 H ,F 分别为1A B ,1A C 的中点,所以 //HF BC ,12HF BC =, 所以 //HF DE ,HF DE =,所以 四边形DEFH 为平行四边形,所以 //EF HD . 因为 EF ⊄平面1A BD , HD ⊂平面1A BD ,所以 //EF 平面1A BD .(2)因为在△ABC 中,D ,E 分别为AB ,AC 的中点,所以 AD AE =.所以11A D A E =,又O 为DE 的中点,所以 1A O DE ⊥.因为平面1A DE ⊥平面BCED ,且1AO ⊂平面1A DE , 所以 1A O ⊥平面BCED ,所以 1CO A O ⊥.在△OBC 中,4BC =,易知 OB OC ==所以 CO BO ⊥,所以 CO ⊥平面1A OB ,所以 平面1A OB ⊥平面1A OC .(3)线段OC 上不存在点G ,使得OC ⊥平面EFG .否则,假设线段OC 上存在点G ,使得OC ⊥平面EFG ,连接 GE ,GF ,则必有 OC GF ⊥,且OC GE ⊥.在Rt △1A OC 中,由F 为1A C 的中点,OC GF ⊥,得G 为OC 的中点.在△EOC 中,因为OC GE ⊥,所以EO EC =,这显然与1EO =,EC =所以线段OC 上不存在点G ,使得OC ⊥平面EFG .14.(Ⅰ)见证明;(Ⅱ)见证明;(Ⅲ)见解析【分析】(I )由AD ⊥DE ,AD ⊥CD 可得AD ⊥平面CDE ,故而AD ⊥CE ;(II )证明平面ABF ∥平面CDE ,故而BF ∥平面CDE ;(III )取CE 的中点P ,BE 的中点Q ,证明CE ⊥平面ADPQ 即可得出平面ADQ ⊥平面BCE .【详解】(Ⅰ)由底面ABCD 为矩形,知AD CD ⊥.又因为DE AD ⊥,DE CD D ⋂=,所以AD ⊥平面CDE .又因为CE ⊂平面CDE ,所以AD CE ⊥.(Ⅱ)由底面ABCD 为矩形,知//AB CD ,又因为AB ⊄平面CDE ,CD ⊂平面CDE ,所以//AB 平面CDE .同理//AF 平面CDE ,又因为AB AF A ⋂=,所以平面//ABF 平面CDE .又因为BF ⊂平面ABF ,所以//BF 平面CDE .(Ⅲ)结论:线段BE 上存在点Q (即BE 的中点),使得平面ADQ ⊥平面BCE . 证明如下:取CE 的中点P ,BE 的中点Q ,连接,,AQ DP PQ ,则//PQ BC .由//AD BC ,得//PQ AD .所以,,,A D P Q 四点共面.由(Ⅰ),知AD ⊥平面CDE ,所以AD DP ⊥,故BC DP ⊥.在△CDE 中,由DC DE =,可得DP CE ⊥.又因为BC CE C ⋂=,所以DP ⊥平面BCE .又因为DP ⊂平面ADPQ所以平面ADPQ ⊥平面BCE (即平面ADQ ⊥平面BCE ).即线段BE 上存在点Q (即BE 中点),使得平面ADQ ⊥平面BCE【点睛】本题考查了线面垂直、面面垂直的判定与性质定理的应用,线面平行的判定,熟练运用定理是解题的关键,属于中档题.15.(Ⅰ)见证明;(Ⅱ)见证明;(Ⅲ)见解析.【分析】(Ⅰ)证明以DE ∥平面PBC ,只需证明DE ∥PC ;(Ⅱ)证明BC ⊥平面PAB ,根据线面垂直的判定定理,只需证明PA ⊥BC ,AB ⊥BC ;(Ⅲ)当点F 是线段AB 中点时,证明平面DEF ∥平面PBC ,可得平面DEF 内的任一条直线都与平面PBC 平行.【详解】(Ⅰ)证明:因为点E 是AC 中点,点D 为PA 的中点,所以//DE PC .又因为DE ⊄面PBC ,PC ⊂面PBC ,所以DE ∥平面PBC .(Ⅱ)证明:因为平面PAC ⊥面ABC ,平面PAC ∩平面ABC =AC ,又PA ⊂平面PAC ,PA ⊥AC , 所以PA ⊥面ABC ,因为BC ⊂平面ABC ,所以PA ⊥BC .又因为AB ⊥BC ,且PA ∩AB =A ,所以BC ⊥面PAB .(Ⅲ)当点F 是线段AB 中点时,过点D ,E ,F 的平面内的任一条直线都与平面PBC 平行. 取AB 中点F ,连EF ,连DF .由(Ⅰ)可知DE ∥平面PBC .因为点E 是AC 中点,点F 为AB 的中点,所以EF ∥BC .又因为EF ⊄平面PBC ,BC ⊂平面PBC ,所以EF ∥平面PBC .又因为DE ∩EF =E ,所以平面DEF ∥平面PBC ,所以平面DEF 内的任一条直线都与平面PBC 平行.故当点F 是线段AB 中点时,过点D ,E ,F 所在平面内的任一条直线都与平面PBC 平行.【点睛】本题考查线面平行,考查线面垂直,考查面面平行,考查学生分析解决问题的能力,掌握线面平行、线面垂直、面面垂直的判定定理是关键.16.(1)证明见解析;(2)证明见解析;(3)证明见解析.【分析】(1)根据底面是正方形,得到CD AB ,再利用线面平行判定定理证明.(2)连结AC ,BD ,交于点O ,连结OE ,由中位线定理得到OE PC ∥,再利用线面平行判定定理证明.(3)根据底面是正方形,得到BD AC ⊥,由侧棱PA ⊥底面ABCD ,得到BD PA ⊥,从而BD ⊥平面ACE ,由此能证明BD CE ⊥.【详解】(1)∵四棱锥P ABCD -的底面是正方形,∴CD AB ,∵CD ⊄平面PAB ,AB平面PAB , ∴CD ∥平面PAB .(2)如图所示:连结AC ,BD ,交于点O ,连结OE ,∵四棱锥P ABCD -的底面是正方形,∴O 是AC 中点,∵E 是PA 的中点.∴OE PC ∥,∵PC ⊄平面BDE ,OE ⊂平面BDE ,∴PC 平面BDE .(3)∵四棱锥P ABCD -的底面是正方形,侧棱PA ⊥底面ABCD ,∴BD AC ⊥,BD PA ⊥,∵AC PA A ⋂=,∴BD ⊥平面ACE ,∵CE ⊂平面ACE ,∴BD CE ⊥.【点睛】本题主要考查线面平行的判定定理,线面垂直的判定定理,还考查了转化化归的思想和逻辑推理的能力,属于中档题.。
立体几何经典试题(含答案)

1. 如图,三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA 1,D 是棱AA 1的中点的中点(I)证明:平面BDC 1⊥平面BDC(Ⅱ)平面BDC 1分此棱柱为两部分,求这两部分体积的比. 【解析】(Ⅰ)由题设知BC BC⊥⊥1CC ,BC ,BC⊥⊥AC AC,,1CC AC C Ç=,∴BC ^面11ACC A , , 又又∵1DC Ì面11ACC A ,∴1DC BC ^,由题设知01145A DC ADC Ð=Ð=,∴1CDC Ð=090,即1DC DC ^, 又∵DC BC C Ç=, , ∴∴1DC ⊥面BDC , , ∵∵1DC Ì面1BDC , ∴面BDC ⊥面1BDC ;(Ⅱ)设棱锥1B DACC -的体积为1V ,AC =1,由题意得,1V =1121132+´´´=12,由三棱柱111ABC A B C -的体积V =1,∴11():V V V -=1:1, ∴平面1BDC 分此棱柱为两部分体积之比为1:1. 2. 如图5所示,在四棱锥P ABCD -中,AB ^平面PAD ,//AB CD ,PD AD =,E 是PB 的中点,F 是CD 上的点且12DF AB =,PH 为△PAD 中AD 边上的高. (1)证明:PH ^平面ABCD ;(2)若1PH =,2AD =,1FC =,求三棱锥E BCF -的体积;的体积;(3)证明:EF ^平面PAB . B 1C B A D C 1A 1【解析】(1)证明:因为AB ^平面PAD ,所以PH AB ^。
因为PH 为△PAD 中AD 边上的高,边上的高, 所以PH AD ^。
因为AB AD A = ,所以PH ^平面ABCD 。
(2)连结BH ,取BH 中点G ,连结EG 。
立体几何综合题题型练习教师版

立体几何综合题题型练习例1:知识点交汇题型(1)如图1,在正方体ABCD-A 1B 1C 1D 1中,P 是侧面BB 1C 1C 内一动点,若点P 到直线BC 与直线C 1D 1的距离相等,则动点P 的轨迹所在的曲线是( )(A )直线 (B )圆 (C )双曲线 (D )抛物线分析:立体几何问题向平面几何转化是解决问题的一个途径.本题将立体几何中的“距离”与解析几何中的“轨迹”巧妙地组合起来,将解析几何问题转化为平面几何问题,揭示了不同数学分支之间的内在联系,令人倍感清新和谐、回味无穷.无独有偶,2004年重庆卷也有一道类似的高考题. (2)若三棱锥A-BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等,则动点P 的轨迹与△ABC 组成的图形可能是( ).分析:利用普性遍与特殊性的关系,首先考虑特殊图形,当AC ⊥平面BCD 时,问题化为点P 到AB 和BC 距离相等的点的轨迹.显然,点P 的轨迹是∠ABC 的平分线.如图2所示. 当AC 不垂直于平面BCD 时,如图3所示,设点P 到平面DBC 、到边BC 和到边AB 的距离分别为h 、d BC 、d AB ,设A -BC -D 的大小为θ,则AB BC BCd hd d=sin θ≤1,所以答案选D.【评注】 显然在这个相类似的问题中,重庆卷的题目比北京卷的要难一些.(3)如图5,动点P 在正方体ABCD-A 1B 1C 1D 1的对角线BD 1上.过点P 作垂直于平面BB 1D 1D 的直线,与正方体表面相交于M 、N .设BP=x ,MN=y ,则函数y=f(x)的图象大致是( )分析:本题给出了变量——自变量和因变量,给出了函数图象的选项,要求函数的大致图象.显然若能求出函数解析式,问题便解出,但却不是一件容易的事.改变研究视角是正确的选择:把MN 向平面ABCD 内作正投影,保持其长度不变,从而把空间问题转为平面问题,在平面内研究函数关系即可顺利完成.解:设正方体的棱长为a .由图形的对称性知点P 始终是MN 的中点,而且随着点P 从点B 向BD 1的中点滑动,y 的值逐渐增大到最大,再由BD 1的中点向点D 1滑动,y的值逐渐变小,(A )(B )(C ) (D )由此排除选项A 和C ,如图6,把MN 向平面ABCD 内正投影得''M N ,则''M N =MN=y ,由于1'BP BD BP BD ==,所以'BP =,所以当x ≤时,2'MN y BP x ===,为一次函数.故答案选B.. 【评注】MN 向平面ABCD 内作正投影是转化问题的关键. 例2:表面最短距离题型如图,在正三棱柱ABC A B C -111中,AB =3,AA 14=,M 为AA 1的中点,P 是BC 上一点,且由P 沿棱柱侧面经过棱CC 1到M 的最短路线长为29,设这条最短路线与CC 1的交点为N ,求: (I )该三棱柱的侧面展开图的对角线长; (II )PC 和NC 的长;(III )平面NMP 与平面ABC 所成二面角(锐角)的大小(用反三角函数表示)解:(I )正三棱柱ABC A B C -111的侧面展开图是一个长为9,宽为4的矩形,其对角线长为949722+=.(II )如图1,将侧面BB C C 11绕棱CC 1旋转120使其与侧成AA C C 11在同一平面上,点P 运动到点P 1的位置,连接MP 1,则MP 1就是由点P 沿棱柱侧面经过棱CC 1到点M 的最短路线.设PC x =,则P C x 1=,在Rt MAP ∆1中,由勾股定理得()322922++=x求得x =2.111242.,.55PC NC PC PC NC MA P A∴====∴= (III )如图2,连结PP 1,则PP 1就是平面NMP 与平面ABC 的交线,作NH PP ⊥1于H ,又CC 1⊥平面ABC ,连结CH ,由三垂线定理得,CH PP ⊥1.∴∠NHC 就是平面NMP 与平面ABC 所成二面角的平面角(锐角);在Rt PHC ∆中, ∠=∠=PCH PCP 12601,∴==CH PC21. 在Rt NCH ∆中,tg NHC NC CH ∠===45145,A故平面NMP 与平面ABC 所成二面角(锐角)的大小为arctg 45. 例3:折叠题型在直角梯形ABCP 中,AP ∥BC ,1,2,2AP AB AB BC AP D ⊥===是AP 的中点,E ,F ,G 分别为PC 、PD 、CB 的中点,将△PCD 沿CD 折起,使得PD ⊥平面ABCD ,如图2. (1)求证:AP ∥平面EFG ; (2)求二面角G-EF-D 的大小;解:(Ⅰ)证明:方法一)连AC ,BD 交于O 点,连GO ,FO ,EO.,E F 分别为,PC PD 的中点,EF∴12CD ,同理GO12CD ,EF∴GO∴四边形EFOG 是平行四边形,EO ∴⊂平面EFOG. ……………………3分又在三角形PAC 中,E ,O 分别为PC ,AC 的中点,PA ∴∥EO……………4分EO ⊂平面EFOG ,PA ⊄平面EFOG ,………………………………………………………5分PA ∴∥平面EFOG ,即PA ∥平面EFG.……………………………………………………6分(法二)如图以D 为原点,以DA ,DC ,DP,为方向向量建立空间直角坐标系D-xyz. 则有关点及向量的坐标为:P (0,0,2),C (0,2,0),G (1,2,0), E (0,1,1),F (0,0,1),A (2,0,0) (2,0,2),(0,1,0),(1,1,1)AP EF EG =-=-=-设平面EFG 的法向量为(,,)n x y z =0000n y x zx y z y n EF EG ⎧⎧-==⎪⎪⇒⎨⎨+-==⎪⎪⎩⎩⋅=∴⇒⋅=⎧⎨⎩. 取(1,0,1).n =……………………4分1(2)00120,,n AP n AP ⋅=⨯-+⨯+⨯=∴⊥…………………………………………5分又AP ⊄平面EFG.AP ∴∥平面EFG.…………………………………………………………6分(Ⅱ)连AC ,BD 交于O 点,连GO ,FO ,EO.,E F 分别为PC ,PD 的中点,EF∴12CD ,同理GE12PB又CD AB ,EF∴12AB,,EG EF E PB AB B ==∴ 平面EFG ∥平面PAB ,又PA ⊄平面PAB ,PA ∴∥平面EFG. 由已知底面ABCD 是正方形AD DC ∴⊥,又PD ⊥ 面ABCD AD PD ∴⊥ 又PD CD D =AD ∴⊥平面PCD ,∴向量DA是平面PCD 的一个法向量,(2,0,0)DA =……………8分又由(Ⅰ)知平面EFG 的法向量为(1,0,1)n =,……………………………………9分cos ,||||DA n DA n DA n ⋅∴〈〉===⋅……………………………………………10分 结合图知二面角G-EF-D 的平面角为45°.…………………………………12分 例4:探索题型在四棱锥P ABCD -中,AB //CD ,AB AD ^,4,2AB AD CD ===,PA ^平面ABCD ,4PA =. (Ⅰ)设平面PAB 平面PCD m =,求证:CD //m ; (Ⅱ)求证:BD ⊥平面PAC ;(Ⅲ)设点Q 为线段PB 上一点,且直线QC 与平面PAC,求PQ PB 的值.解答:(Ⅰ)证明: 因为AB //CD ,CD ⊄平面PAB ,AB ⊂平面PAB ,所以CD //平面PAB . ………………………………………2分 因为CD ⊂平面PCD ,平面PAB 平面PCD m =, 所以CD //m . ………………………………………4分(Ⅱ)证明:因为AP ^平面ABCD ,AB AD ^,所以以A 为坐标原点,AB ,AD ,AP 所在的直线分别为x 轴、y 轴、z 轴建立空间直角坐标系,则(4,0,0)B ,(0,0,4)P,D,C . ………5分所以(BD =-,AC = ,(0,0,4)AP =,所以(4)2000BD AC ⋅=-⨯+⨯=,(4)00040BD AP ⋅=-⨯++⨯=.所以BD AC ⊥,BD AP ⊥.因为AP AC A = ,AC ⊂平面PAC ,PA ⊂平面PAC ,所以 BD ⊥平面PAC . (Ⅲ)解:设PQPB λ=(其中01λ#),(,,)Q x y z ,直线QC 与平面PAC 所成角为θ.所以 PQ PB λ= .所以 (,,4)(4,0,4)x y z λ-=-.所以 4044x y z λλ=⎧⎪=⎨⎪=-+⎩即(4,0,44)Q λλ-+.所以(42,44)CQ λλ=---+. ………………………………………11分由(Ⅱ)知平面PAC的一个法向量为(BD =-.因为 sin cos ,CQ BDCQ BD CQ BDθ×=<>=×,所以3=,解得7[0,1]12λ=∈. 所以712PQ PB =. ……………………………………14分 例5:三视图为背景题型已知某几何体的直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形, 俯视图为直角梯形. (1)求证:BN 丄平面C 1B 1N ;(2)设M 为AB 中点,在BC 边上找一点P ,使MP//平面CNB 1,并求的值.解答.方法一1 1∵B 1C 1∥BC ,∴B 1C 1⊥平面ANBB 1 因此B 1C 1⊥BN 4分在直角梯形B 1BAN 中,过N 作NE ∥AB 交BB 1于E , 则B 1E = BB 1-AN = 4故△NEB 1是等腰直角三角形,∠B 1NE = 45° 6分又AB = 4,AN = 4,∴∠ANB = 45° 因此∠BNB 1 = 90°,即BN ⊥B 1N又B 1N ∩B 1C 1 = B 1,∴BN ⊥平面C 1B 1N . 8分 (2)解:过M 作MR ∥BB 1,交NB 1于R ,则8462MR +== 过P 作PQ ∥BB 1,交CB 1于Q ,则PQ ∥MR , 设PC = a ,则1284PQ PQ PC aPQ a BB BC =⇒=⇒=由PQ = MR 得:2a = 6,a = 310分此时,PMRQ 是平行四边形,∴PM ∥RQ , ∵RQ ⊂平面CNB 1,MP ⊄ 平面CNB 1, ∴MP ∥平面CNB 1,43133BP PC -==. 12分方法二(1)证:∵该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形, ∴BA 、BC 、BB 1两两互相垂直 2分以BA 、BB 1、BC 分别为x 轴、y 轴、z 轴建立空间直角坐标系,则 A (4,0,0),N (4,4,0),B 1(0,8,0), C 1(0,8,4),C (0,0,4),B (0,0,0)4分1(440)B N =- ,,,11(004)B C = ,, ∵1(440)(440)0BN B N ⋅=⋅-=,,,,, 11(440)(004)0BN B C ⋅=⋅=,,,, 6分∴BN ⊥B 1N ,BN ⊥B 1C 1,又B 1N ∩B 1C 1 = B 1 ∴BN ⊥平面C 1B 1N8分 (2)解:设P (0,0,a )为BC 上一点,∵M 为AB 的中点,∴M (2,0,0),故(20)MP a =-,, 设平面CNB 1的一个法向量为n = (x ,y ,z ),则有1NC NB ⊥⊥,n n , ∴()(444)04440()(440)0440x y z x y z x y ax y z x y x y ⋅--=--+=+=⎧⎧⎧⇒⇒⎨⎨⎨⋅-=-+==⎩⎩⎩,,,,,,,,∴平面CNB 1的一个法向量为n = (1,1,2)要使MP ∥平面CNB 1,只需MP ⊥n ,于是 0MP ⋅=n ,即(-2,0,a )·(1,1,2) = 0 解得:a = 1∵MP ⊄ 平面CNB 1,∴MP ∥平面CNB 1, 此时PB = a = 1,∴13BP PC = 例6:不规则几何体题型如图所示的多面体是由底面为ABCD 的长方体被截面1AEC F 所截面而得到的,其中4AB =,2BC =,13CC =,1BE =.(Ⅰ)求BF 的长;(Ⅱ)求点C 到平面1AEC F 的距离.解:(I )建立如图所示的空间直角坐标系,则(0,0,0)D ,(2,4,0)B1(2,0,0),(0,4,0),(2,4,1),(0,4,3)A C E C 设(0,0,)F z .∵1AEC F 为平行四边形,(II )设1n 为平面1AEC F 的法向量,显然1n 不垂直于平面ADF ,故可设1(,,1)n x y =由1100n AE n AF ⎧⋅=⎪⎨⋅=⎪⎩ ,得04102020x y x y ⨯+⨯+=⎧⎨-⨯+⨯+=⎩ 即410220y x +=⎧⎨-+=⎩,114x y =⎧⎪∴⎨=-⎪⎩又1(0,0,3)CC = ,设1CC 与1n的夹角为α,则 .333341161133||||cos 1111=++⨯=⋅=n CC α11,,(2,0,)(2,0,2),2.(0,0,2).(2,4,2).||AEC F AF EC z z F EF BF BF ∴∴=-=-∴=∴∴=--=由为平行四边形由得于是即的长为∴C 到平面1AEC F 的距离为.11334333343cos ||1=⨯==αCC d 例7:不常规放置题型3、如图,已知正三棱柱ABC —111C B A 的底面边长是2,D 是侧棱1CC 的中点,直线AD 与侧面11BB C C 所成的角为45 .(Ⅰ)求此正三棱柱的侧棱长; (Ⅱ) 求二面角C BD A --的大小; (Ⅲ)求点C 到平面ABD 的距离.解:(Ⅰ)设正三棱柱ABC —111C B A 的侧棱长为x .取BC 中点E ,连AE .ABC ∆ 是正三角形,AE BC ∴⊥.又底面ABC ⊥侧面11BB C C ,且交线为BC .AE ∴⊥侧面11BB C C .连ED ,则直线AD 与侧面11BB C C 所成的角为45ADE ∠=. 在AED Rt ∆中,tan 45AEED==,解得x =∴此正三棱柱的侧棱长为注:也可用向量法求侧棱长.(Ⅱ)解法1:过E 作EF BD ⊥于F ,连AF ,⊥AE 侧面,11C C BB ∴AF BD ⊥.AFE ∴∠为二面角C BD A --的平面角.在BEF Rt ∆中,sin EF BE EBF =∠,又1,sin 3CD BE EBF BD =∠===∴EF =又AE =∴在AEF Rt ∆中,tan 3AEAFE EF∠==. 故二面角C BD A --的大小为arctan 3. 解法2:(向量法,见后)(Ⅲ)解法1:由(Ⅱ)可知,⊥BD 平面AEF ,∴平面AEF ⊥平面ABD ,且交线为AF ,∴过E 作EG AF⊥AB D1A 1B 1C EF GHI于G ,则EG ⊥平面ABD .在AEF Rt ∆中,AE EFEG AF⨯===. E 为BC 中点,∴点C 到平面ABD的距离为2EG =. 解法2:(思路)取AB 中点H ,连CH 和DH ,由,CA CB =DA DB =,易得平面ABD ⊥平面CHD ,且交线为DH .过点C 作CI DH ⊥于I ,则CI 的长为点C 到平面ABD 的距离. 解法3:(思路)等体积变换:由C ABD A BCD V V --=可求. 解法4:(向量法,见后) 题(Ⅱ)、(Ⅲ)的向量解法:(Ⅱ)解法2:如图,建立空间直角坐标系xyz o -.则(0,1,0),(0,1,0),(,0)A B C D -.设1(,,)n x y z = 为平面ABD 的法向量.由1200n AB n AD ⎧⋅=⎪⎨⋅=⎪⎩得0y y ⎧=⎪-+=.取1()n =…………6分 又平面BCD 的一个法向量2(0,0,1).n =…………7分∴10101)3()6(1)1,0,0()1,3,6(,cos 222212121=+-+-⨯⋅--=⋅>=<n n n n n n . 结合图形可知,二面角C BD A --的大小为. (Ⅲ)解法4:由(Ⅱ)解法2,1(),n =(0,1CA =-∴点C 到平面ABD的距离d =2221)3()6()1,3,6()3,1,0(+-+---⋅-==10302. 例8:实验操作题型一个几何体的三视图如右图所示,其中正视图和侧视 图是腰长为6的两个全等的等腰直角三角形.(Ⅰ)请画出该几何体的直观图,并求出它的体积; (Ⅱ)用多少个这样的几何体可以拼成一个棱长为1正视图侧视图俯视图6的正方体ABCD —A 1B 1C 1D 1? 如何组拼?试证明你的结论;(Ⅲ)在(Ⅱ)的情形下,设正方体ABCD —A 1B 1C 1D 1的棱CC 1的中点为E , 求平面AB 1E 与平面ABC 所成二面角的余弦值.解:(Ⅰ)该几何体的直观图如图1所示,它是有一条 侧棱垂直于底面的四棱锥. 其中底面ABCD 是边长为6的 正方形,高为CC 1=6,故所求体积是 7266312=⨯⨯=V (Ⅱ)依题意,正方体的体积是原四棱锥体积的3倍, 故用3个这样的四棱锥可以拼成一个棱长为6的正方体, 其拼法如图2所示.证明:∵面ABCD 、面ABB 1A 1、面AA 1D 1D 为全等的正方形,于是D D AA C A ABB C ABCD C V V V 1111111---== 故所拼图形成立.(Ⅲ)方法一:设B 1E ,BC 的延长线交于点G , 连结GA ,在底面ABC 内作BH ⊥AG ,垂足为H , 连结HB 1,则B 1H ⊥AG ,故∠B 1HB 为平面AB 1E 与 平面ABC 所成二面角或其补角的平面角. 在Rt △ABG 中,180=AG ,则512180126=⨯=BH ,5182121=+=BB BH H B ,32cos 11==∠HB HB HB B ,故平面AB 1E 与平面ABC 所成二面角的余弦值为32±.方法二:以C 为原点,CD 、CB 、CC 1所在直线分别为x 、y 、z 轴建立直角坐标系(如图3),∵正方体棱长为6,则E (0,0,3),B 1(0,6,6),A (6,6,0). 设向量n =(x ,y ,z ),满足n ⊥1EB ,n ⊥1AB ,于是⎩⎨⎧=+-=+066036z x z y ,解得⎪⎩⎪⎨⎧-==z y zx 21.取z =2,得n =(2,-1,2).又=1BB (0,0,6),321812||||,cos 111==>=<BB n BB 故平面AB 1E 与平面ABC 所成二面角的余弦值为32±. BC DC 1图1BC DD 1A 1B 1C 1 图2。
高考大题训练(立体几何教师版)共31题王斌高考总复习高考最后冲刺

1.(2011湖南嘉禾一中)(本小题满分13 分)如图(1)是一正方体的表面展开图,MN 和PB 是两条面对角线,请在图(2)的正方体中将MN 和PB 画出来,并就这个正方体解决下面问题。
(1)求证:MN//平面PBD ; (2)求证:AQ ⊥平面PBD ; (3)求二面角P —DB —M 的大小.答案 1.解:M 、N 、Q 、B 的位置如右图示。
(正确标出给1分) (1)∵ND//MB 且ND=MB ∴四边形NDBM 为平行四边形 ∴MN//DB ………………3分∴BD ⊆平面PBD ,MN PBD 平面⊄∴MN//平面PBD ……………………4分(2)∵QC ⊥平面ABCD ,BD ⊂平面ABCD , ∴BD ⊥QC ……………………5分 又∵BD ⊥AC ,∴BD ⊥平面AQC …………………………6分∵AQ ⊂面AQC ∴AQ ⊥BD ,同理可得AQ ⊥PB , ∵BD PD=B ∴AQ ⊥面PDB ……………………………8分 (3)解法1:分别取DB 、MN 中点E 、F 连结 PE 、EF 、PF ………………9分 ∵在正方体中,PB=PB ∴PE ⊥DB ……………………10分 ∵四边形NDBM 为矩形 ∴EF ⊥DB∴∠PEF 为二面角P —DB —M 为平面角…………11分 ∵EF ⊥平面PMN ∴EF ⊥PF设正方体的棱长为a ,则在直角三角形EFP 中∵a PF a EF 22,== ∴22tan ==∠EF PF PEF 22arctan=∠PEF …………………………13分解法2:设正方体的棱长为a ,以D 为坐标原点建立空间直角坐标系如图: 则点A (a,0,0),P (a,0,a ),Q (0,a,a )…………9分 ∴),,(),0,,(a a a a a -=-=………………10分 ∵PQ ⊥面DBM ,由(2)知AQ ⊥面PDB∴,分别为平面PDB 、平面DBM 的法向量……………………12分∴,cos >=<363222=⋅=aa a∴22arctan,,22,tan >=<>=<PQ AQ PQ AQ ………………13分. 2.(2010辽宁理)(19)(本小题满分12分)已知三棱锥P -ABC 中,PA ⊥ABC ,AB ⊥AC ,PA=AC=½AB ,N 为AB 上一点,AB=4AN,M,S 分别为PB,BC 的中点.(Ⅰ)证明:CM ⊥SN ;(Ⅱ)求SN 与平面CMN 所成角的大小.证明:设PA=1,以A 为原点,射线AB ,AC ,AP 分别为x ,y ,z 轴正向建立空间直角坐标系如图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ABCD1A 1C 1B E科 目 数学 年级 高三 备课人 高三数学组第 课时9.2立体几何大题11、(2013新课标)如图,直棱柱111ABC A B C -中,,D E 分别是1,AB BB 的 中点,122AA AC CB AB ===. (Ⅰ)证明:1//BC 平面1A CD ; (Ⅱ)求二面角1D A C E --的正弦值.【答案】2、(2013湖南)如图5,在直棱柱1111//ABCD A BC D AD BC -中,,90,,1BAD AC BD BC ∠=⊥=,13AD AA ==.(I)证明:1AC B D ⊥; (II)求直线111B C ACD 与平面所成角的正弦值.【答案】解(Ⅰ) AC BB ABCD BD ABCDBB D C B A ABCD ⊥⇒⊂⊥∴-111111,面且面是直棱柱 D B AC BDB D B BDB AC B BB BD BD AC 11111,,⊥∴⊂⊥∴=⋂⊥,面。
面且又 . (证毕)(Ⅱ)。
的夹角与平面的夹角即直线与平面直线θ111111,////ACD AD ACD C B AD BC C B ∴ 轴正半轴。
为轴正半轴,为点,量解题。
设原点在建立直角坐标系,用向X AD Y AB A()BDAC y BD y AC y C y B D D A ⊥-== ),0,,3(),0,,1()0,,1(),0,,0(),3,0,3(),0,0,3(,00,01,则,设).3,0,3(),0,3,1(.30,003012==∴=⇒>=+-⇒=⋅AD AC y y y BD AC ),,(),,(的一个法向量平面则的法向量为设平面303,313-.0,111==⇒⎪⎩⎪⎨⎧=⋅=⋅AD n ACD AD n AC n n ACD7213733|,cos |sin 003,313-1=⋅=><=⇒==∴AD n AD n ACD θ),,(),,(的一个法向量平面72111夹角的正弦值为与平面所以ACD BD .3、(2013 北京)如图,在三棱柱ABC -A 1B 1C 1中,AA 1C 1C 是边长为4的正方形,平面ABC ⊥平面AA 1C 1C ,AB=3,BC=5.(Ⅰ)求证:AA 1⊥平面ABC ;(Ⅱ)求二面角A 1-BC 1-B 1的余弦值;(Ⅲ)证明:在线段BC 1存在点D,使得AD ⊥A 1B ,并求1BDBC 的值.【答案】解:(I)因为AA 1C 1C 为正方形,所以AA 1 ⊥AC.因为平面ABC⊥平面AA 1C 1C,且AA 1垂直于这两个平面的交线AC,所以AA 1⊥平面ABC.(II)由(I)知AA 1 ⊥AC,AA 1 ⊥AB. 由题知AB=3,BC=5,AC=4,所以AB⊥AC. 如图,以A 为原点建立空间直角坐标系A-xyz ,则B(0,3,0),A 1(0,0,4),B 1(0,3,4),C 1(4,0,4),设平面A 1BC 1的法向量为,,)x y z n =(,则1110A B A C ⎧⋅=⎪⎨⋅=⎪⎩n n ,即34040y z x -=⎧⎨=⎩,令3z =,则0x =,4y =,所以(0,4,3)n =.同理可得,平面BB 1C 1的法向量为(3,4,0)m =,所以16cos 25⋅==n m n,m |n ||m |. 由题知二面角A 1-BC 1-B 1为锐角,所以二面角A 1-BC 1-B 1的余弦值为1625. (III)设D (,,)x y z 是直线BC1上一点,且1BD BC λ=. 所以(,3,)(4,3,4)x y z λ-=-.解得4x λ=,33y λ=-,4z λ=.所以(4,33,4)AD λλλ=-. 由1·0AD A B =,即9250λ-=.解得925λ=. 因为9[0,1]25∈,所以在线段BC 1上存在点D, 使得AD⊥A 1B. 此时,1925BD BC λ==.4、(2013江苏)本小题满分10分.如图,在直三棱柱111A B C ABC-中,AC AB ⊥,2==AC AB ,41=AA ,点D 是BC 的中点(1)求异面直线B A 1与D C 1所成角的余弦值 (2)求平面1ADC 与1ABA 所成二面角的正弦值.【答案】本题主要考察异面直线.二面角.空间向量等基础知识以及基本运算,考察运用空间向量解决问题的能力.解:(1)以{}1,,AA AC AB 为为单位正交基底建立空间直角坐标系xyz A -,则)0,0,0(A )0,0,2(B ,)0,2,0(C ,)4,0,0(1A ,)0,1,1(D ,)4,2,0(1C ∴)4,0,2(1-=B A ,)4,1,1(1--=B A∴10103182018,cos 111111==∙>=<DC B AD C B A D C B A ∴异面直线B A 1与D C 1所成角的余弦值为10103 (2))0,2,0(=AC 是平面1ABA 的的一个法向量设平面1ADC 的法向量为),,(z y x m =,∵)0,1,1(=AD ,)4,2,0(1=AC 由1,AC m AD m ⊥⊥∴⎩⎨⎧=+=+0420z y y x 取1=z ,得2,2=-=x y ,∴平面1ADC 的法向量为)1,2,2(-=m设平面1ADC 与1ABA 所成二面角为θ∴32324,cos cos =⨯-=∙=><=mAC m AC m AC θ, 得35sin =θ ∴平面1ADC 与1ABA 所成二面角的正弦值为355、(2013年新课标1)如图,三棱柱ABC-A 1B 1C 1中,CA=CB,AB=A A 1,∠BA A 1=60°.(Ⅰ)证明AB ⊥A 1C;(Ⅱ)若平面ABC⊥平面AA 1B 1B,AB=CB=2,求直线A 1C 与平面BB 1C 1C 所成角的正弦值.【答案】(Ⅰ)取AB 中点E,连结CE,1A B ,1A E ,∵AB=1AA ,1BAA ∠=060,∴1BAA ∆是正三角形,∴1A E ⊥AB, ∵CA=CB, ∴CE⊥AB, ∵1CE A E ⋂=E,∴AB⊥面1CEA ,∴AB⊥1AC ;(Ⅱ)由(Ⅰ)知EC⊥AB,1EA ⊥AB,又∵面ABC⊥面11ABB A ,面ABC∩面11ABB A =AB,∴EC⊥面11ABB A ,∴EC⊥1EA ,∴EA,EC,1EA 两两相互垂直,以E 为坐标原点,EA 的方向为x 轴正方向,|EA |为单位长度,建立如图所示空间直角坐标系O xyz -, 有题设知A(1,0,0),1A (0,3,0),C(0,0,3),B(-1,0,0),则BC =(1,0,3),1BB =1AA =(-1,0,3),1A C =(0,-3,3),设n =(,,)x y z 是平面11CBB C 的法向量,则100BC BB ⎧∙=⎪⎨∙=⎪⎩n n ,即3030x z x y ⎧+=⎪⎨+=⎪⎩,可取n =(3,1,-1), ∴1cos ,A C n =11|A C A C ∙n |n ||105,∴直线A 1C 与平面BB 1C 1C 所成角的正弦值为1056、(2013江西)如图,四棱锥P ABCD-中,PA ,ABCD E BD ⊥平面为的中点,G PD 为的中点,3,12DAB DCB EA EB AB PA ∆≅∆====,,连接CE 并延长交AD 于F . (1) 求证:AD CFG ⊥平面;(2) 求平面BCP 与平面DCP 的夹角的余弦值.【答案】解:(1)在ABD ∆中,因为E 是BD 的中点,所以1EA EB ED AB ====,故,23BAD ABE AEB ππ∠=∠=∠=,因为DAB DCB ∆≅∆,所以EAB ECB ∆≅∆, 从而有FED FEA ∠=∠,故,EF AD AF FD ⊥=,又因为,PG GD =所以FG ∥PA . 又PA ⊥平面ABCD ,所以,GF AD ⊥故AD ⊥平面CFG . (3) 以点A 为坐标原点建立如图所示的坐标系,则33(0,0,0),(1,0,0),(,,0),(0,3,0)22A B C D ,(4)3(0,0,)2P ,故1333333(0),(,),(,,0)2222222BC CP CD ==--=-,,,设平面BCP 的法向量111(1,,)n y z =,则111130223330222y y z ⎧+=⎪⎪⎨⎪--+=⎪⎩ ,解得113323y z ⎧=-⎪⎪⎨⎪=⎪⎩,即132(1,,)33n =-. 设平面DCP 的法向量222(1,,)n y z =,则22233223330222y y z ⎧-+=⎪⎪⎨⎪--+=⎪⎩,解得2232y z ⎧=⎪⎨=⎪⎩,即2(1,3,2)n =.从而平面BCP 与平面DCP 的夹角的余弦值为1212423cos 41689n n n n θ⋅===⋅.【课后反思】。
