0的乘除法
有关0的运算

《有关0的运算》教学设计教学内容:人教版小学数学第四册P13。
●教材分析:《有关0的运算》是人教版小学数学四年级下册第一单元四则运算中的内容。
小学四年级孩子都已经认识了0,掌握了有关0的加、减、乘法计算,明白了这些加减法的含义。
在学习了乘除法后,学生进一步掌握了0在乘除法以及四则混合运算中的特性。
本节课是对0的运算知识系统化的总结和学习。
而本节课的难点是0不能做除数,这部分内容让学生理解和体验起来有一些困难。
因此,我根据学生的年龄特点及已有的知识经验,创设了一定的情境,让学生通过分析具体题目,自己验证并得出0不能做除数的结论,从而获得良好的知识体验。
●设计理念:本节课中0不能做除数的教学内容很重要,也很难理解。
针对这一难点我从四年级学生的认知水平和已有的知识经验出发,抓住新课标中“以学生的发展为本”的思想,精心设计了让学生动手操作、用眼观察、动口表达、用心思考等一系列合作学习活动。
通过充分利用材料,放手让学生独立思考、自主探索、合作交流,以培养学生的表达能力和合作探究能力,并在此基础上形成解决问题的步骤和方法。
●教学目标:1.整理和概括有关0在四则运算中的特性。
2.理解0不能做除数以及0为什么不能做除数的原因。
3.学生在解决问题时养成认真审题、合作交流以及学会归纳总结等学习习惯。
●重点、难点:1.0不能做除数,并理解0不能做除数的原因。
2.提高发现问题以及归纳总结的能力。
●教具准备:PPT课件。
●学具准备:铅笔、数学书、练习纸。
●教学过程:一、回顾旧知,承上启下同学们,前几节课我们学习了四则混合运算,老师这里有几道四则混合运算的题目想考考大家。
看看谁能算得又快又对!(请学生拿出练习纸计算,同时要求划出运算顺序)(出示课件第3页)600÷(42-40)(5+35)÷8 46+5×(27-7) 29+8÷2-12师:同学们算的都很棒,现在请同学们以四人小组为单位,说一说四则混合运算的顺序。
乘除法口诀表
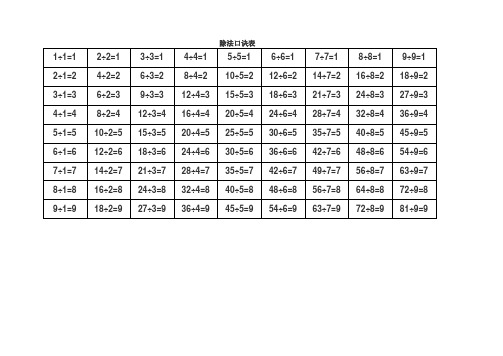
乘法口诀表
1×1=1
1×2=2 2×2=4
1×3=3 2×3=6 3×3=9
1×4=4 2×4=8 3×4=12 4×4=16
1×5=5 2×5=10 3×5=15 4×5=20 5×5=25
1×6=6 2×6=12 3×6=18 4×6=24 5×6=30 6×6=36
1×7=7 2×7=14 3×7=21 4×7=28 5×7=35 6×7=42 7×7=49
1×8=8 2×8=16 3×8=24 4×8=32 5×8=40 6×8=48 7×8=56 8×8=64
1×9=9 2×9=18 3×9=27 4×9=36 5×9=45 6×9=54 7×9=63 8×9=72 9×9=81
一一得一
一二得二二二得四
一三得三二三得六三三得九
一四得四二四得八三四十二四四十六
一五得五二五一十三五十五四五二十五五二十五
一六得六二六十二三六十八四六二十四五六三十六六三十六
一七得七二七十四三七二十一四七二十八五七三十五六七四十二七七四十九
一八得八二八十六三八二十四四八三十二五八四十六八四十八七八五十六八八六十四
一九得九二九十八三九二十七四九三十六五九四十五六九五十四七九六十三八九七十二九九八十一。
四年级上册关于0的乘除法计算

关于有“0”的乘除法计算专项训练
姓名:
1.关于有“0”的乘法(可以先不算“0”,算完再添上没算的“0”)
60×80=25×20=50×3=400×30=120×8=
6300÷70=479÷81≈602×39≈398÷21≈
478÷81≈ 396×41≈6294÷71≈
二、用竖式计算下面各题并验算。
128×25=816÷51=130×70=
2880÷64=301×36=230÷15=
560÷80=480÷40=960÷60=1600÷40=280÷20=
720÷90=300÷5=600÷50=630÷7=2400÷30=
一、直接写出得数。
60×8=24×30=96÷6=70×12=
0÷32 =540÷6=18×50=420÷70=
420÷70=390”的除法(可以同时划掉被除数和除数中相同个数的“0”,再计算)
例如:270÷30=9,(同时划掉被除数和除数一个“0”,可以算成27÷3。)
270÷3=90 (不能同时划掉被除数和除数一个“0”,因为除数是3,末尾没有“0”。)
4200÷60=70 (这道题,只能划掉被除数和除数一个“0”,因为除数只有一个“0”,被除数也划掉一个“0”,还剩一个“0”,可以算成420÷6=70。)
《0的认识》(教案)2023-2024学年数学一年级上册西师大版

《0的认识》(教案)20232024学年数学一年级上册西师大版在20232024学年数学一年级上册的教学中,我选择了西师大版的教材,本节课的主题是《0的认识》。
一、教学内容教材的第80页至第81页,主要内容包括0的概念,0的加减法,以及0在实际生活中的应用。
二、教学目标通过本节课的学习,使学生能够理解0的概念,掌握0的加减法,并能应用于实际生活。
三、教学难点与重点重点:0的概念,0的加减法。
难点:0的减法,以及0在实际生活中的应用。
四、教具与学具准备教具:黑板,粉笔,投影仪。
学具:练习本,铅笔。
五、教学过程1. 实践情景引入:通过一个实际生活中的例子,比如一个篮子里有0个苹果,然后学生依次把苹果放入篮子中,让学生感受到0的存在。
2. 教材讲解:讲解0的概念,0的加减法。
通过例题,讲解0的加法,比如0+1=1,0+2=2等等。
然后讲解0的减法,比如10=1,20=2等等。
3. 随堂练习:让学生在练习本上完成教材上的练习题,比如0的加减法,以及0的乘除法。
4. 例题讲解:通过例题,讲解0在实际生活中的应用,比如购物时,商品的价格为0元,表示免费。
5. 课堂互动:让学生分组讨论,讨论0的加减法,以及0在实际生活中的应用。
六、板书设计板书内容包括0的概念,0的加减法,以及0在实际生活中的应用。
七、作业设计1. 请用0和其它数字,组成一个加法算式,使结果为5。
答案:0+5=52. 请用0和其它数字,组成一个减法算式,使结果为3。
答案:52=33. 请举例说明0在实际生活中的应用。
答案:购物时,商品的价格为0元,表示免费。
八、课后反思及拓展延伸拓展延伸:让学生思考,除了在购物时,0还可以在其它场景中表示什么意思?重点和难点解析在20232024学年数学一年级上册的教学中,我选择了西师大版的教材,本节课的主题是《0的认识》。
在教学过程中,我发现有几个重点和难点需要特别关注。
一、0的概念0的概念是本节课的基础,学生需要理解0是一个数,它是自然数的一部分,表示没有数量。
0的乘除法运算法则

在数学中,0的乘除法运算法则是一个重要的概念。
首先,任何数与0相乘都等于0,即a×0=0,其中a是任意实数。
其次,0除以任何非零实数都等于0,即0÷b=0,其中b是任意非零实数。
这些运算法则的合理性可以从数学的角度进行证明。
例如,对于任何实数a,与0相乘等于0是因为任何数与空集的交集都是空集,而空集的任何函数值都等于0。
对于0除以任何非零实数等于0,可以理解为0个任何数相加仍然是0,因此除以一个非零实数相当于将0个该数相加,结果仍然是0。
这些运算法则在数学和物理学中有广泛的应用。
例如,在计算体积或面积时,如果某个维度为0(例如高度为0的圆柱体或长度为0的矩形),则该体积或面积必然为0。
此外,在概率论中,如果某个事件发生的概率为0,则该事件必然不会发生。
总之,0的乘除法运算法则是数学中的基本法则之一。
这些法则不仅在数学中有应用,也在其他学科中有广泛的应用。
(苏教版)五上“小数乘除法”竖式练习题

小数乘法练习题(一)一、一般乘法竖式计算题65×0.70.0016×130.65×0.170.62×5.2 0.65×7.372×0.038.7×0.927.65×8.53.7×0.016 5.76×1.3 3.83×2.6 1.28×0.04二、乘数中间有“0”的乘法56.2×4.08 2.02×3.6125×2.0423.5×1.02 2.5×20.18.81×1.0119.1×0.307 2.01×1.03三、积末尾有“0”的乘法1.6×0.850.35×8.042.25×2.40.15×2.80.25×0.44 3.15×1.80.025×36 1.25×0.8三、简便计算。
0.125×64 0.68×101 3.26×5.7-3.26×0.7 55.6×99+55.6 1.25×213×0.8 19.625-(4.379+9.625)3.42×5.7+4.3×3.42 8.75×11-8.75 9.9×202小数乘法练习题(二)一、一般乘法竖式计算题205×0.18305×0.14 2.03×0.1310.2×2.3 103×0.230.408×0.24 1.05×3.5 1.07×1.8 2.03×0.1420.4×2.6205×0.130.34×0.1260.32×0.14 2.4×0.96 0.5×0.15 0.36×2.3二、乘数中间有“0”的乘法518×3.070.131×202 4.15×1.03 2.42×1.051.25×8.08 1.02×2.15 1.02×20.6 2.05×4.6三、积末尾有“0”的乘法18.6×1.5 2.06×0.25 2.8×0.165 2.36×0.351.25×8.80.24×2.50.025×14 1.05×35三、简便计算。
小数乘除法计算法则

小数乘除法计算法则
小数乘法法则:先按照整数乘法的法则算出积,再看因数中一共有几位小数,就从积的末位起向左数出几位,点上小数点。
得数的小数部分末尾有 0,一般要把 0 去掉。
小数除法法则:先移动除数的小数点,使它变成整数,除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的在被除数末尾用 0 补足),然后按照除数是整数的除法法则进行计算。
在进行小数乘除法计算时,需要注意以下几点:
1. 小数点的位置:在乘法中,因数中的小数点决定了积的小数点的位置;在除法中,除数和被除数的小数点的移动决定了商的小数点的位置。
2. 数位对齐:在进行小数乘除法时,需要将因数或被除数、除数的数位对齐,从右往左依次进行计算。
3. 0 的处理:在小数乘法中,如果因数中有 0,则积的末尾也可能有 0,一般要把 0 去掉;在小数除法中,如果被除数中有 0,则商的末尾也可能有 0,一般要把 0 去掉。
4. 近似数的处理:在进行小数乘除法时,如果需要保留近似数,则需要根据四舍五入的原则进行处理。
总之,小数乘除法的计算法则与整数乘除法的计算法则类似,只是需要注意小数点的位置和数位对齐的问题。
在计算过程中,需要认真仔细,避免出现错误。
(完整版)乘除法的关系及运算律知识点整理

乘除法的关系及运算律【知识要点】(一)、乘除法各部分之间的关系:(1)乘法各部分之间的关系:因数×因数=积一个因数=积÷另一个因数(2)除法各部分之间的关系:①没有余数的除法:被除数=商×除数除数=被除数÷商商= 被除数÷除数②有余数的除法:被除数=商×除数 + 余数除数=(被除数-余数)÷商商= (被除数-余数)÷除数(3)乘、除法之间的关系:除法是乘法的逆运算 (注意:0不能作除数。
)(4)整除:a÷b(b≠0)=c则a能被b整除,b能整除a。
(二)乘法运算律1、乘法交换律:两个数相乘,交换因数的位置,它们的积不变。
这个规律叫做乘法交换律。
用字母表示为:a×b=b×a2、乘法结合律:三个数相乘,先把前两个数相乘再乘第三个数,或先将后两个数相乘再乘第一个数,它们的积不变。
这个规律叫做乘法结合律。
用字母表示为:(a×b)×c=a×(b×c)3、乘法分配律:两个数的和与一个数相乘,可以把这两个加数分别与这个数相乘,再把积相加。
这个规律叫做乘法分配律。
用字母表示为: (a+b)×c=a×c+b×c 或 a×c+b×c=(a+b)×c乘法分配律的拓展:两个数的差与一个数相乘,可以用这个数分别去乘相减的两个数,再把积相减。
用字母表示为: (a-b)×c=a×c-b×c a×c-b×c=(a-b)×c(三)减法简便运算:1、一个数连续减去两个数,可以用这个数减去这两个数的和。
用字母表示:a-b-c=a-(b+c)2、一个数连续减去两个数,可以用这个数先减去后一个数再减去前一个数。
用字母表示:a-b-c=a—c-b(四)除法简便运算:1、一个数连续除以两个数,可以用这个数除以这两个数的积。
关于教学_乘除法竖式书写中有关0的问题_的争论与思考

就不大了
的数, 柳 1 亿读写很方便, 而 6卯m 58 0 万的读数却让 人发蒙? 笔者再次查阅 数学 (人教版四年级上册)中
师 :谁能帮他们解决这两个问题?
生 3 :我觉得十位上余数是 O , 可以不写 , 直接把个 位上的0 落下来就可以了 师:你真聪明 , 一下就把两个问题 都解决了 ! 根据这 段对话 我们可 以知道 像
42 ] : 3 二 这道 题 的竖式 除 了我 们 的 ( 教材中提供 的写法 之外 还 可以 书写 为 如右 图 :
第六, 读法 中后者认为 改写后的数的读法 , 都
是先读出新得到的数 ,再加上 万 或 亿 , 笔者赞同这
一方法 , 前面已作了说明 , 这里不再赘述 只是后者所列举 的例子 2 7 ( )3 X (X ) 2 7 0.0 3 万,读 作 :二百七十点零三万 而没有读作二百七十万点零
千九百万七千五百八十个万 后 , 还是认为读作六千九
2 3 0 2 7 6
2 3
而不是把被除数 420 中的
2 7 6
O 落下来 所以这里的第二种做法不对 , 题还没有做
这位老师接着让学生讨论做法二和做法三中: 2 3
xr o 的积中 , 个位上的 0 写还是不写 时 , 耗了好长时 间也没有说明白为什么
开始, 我觉得学生乙的做法比较简便, 而学生甲的
述也不清楚 , 存在漏洞, 千位 十千(万)位是第二节 ,
三位一节 , 少 了一位 , 密位 百密位 是第三位 , 是 位 , 还是 节 , ? 并且也只有两位 笔者认为 自相矛 盾 表述不清 表述不妥的理由缺乏说服力
有理数的乘除法

1.4.1有理数的乘法
一、有理数的乘法法则
1.两数相乘,同号得正,异号得负,并 把绝对值相乘。 2.任何数与0相乘,都得0.
计算:
(3) 3 (1)
(3)2 (1)
(1) (3) (2)
2 (4) (4)
(6) 03
(2) 0 (5)
计算
5 1 2 ) 0 ( ) (3) ( 12 2 3
有理数乘法运算律:
1.乘法交换律: ab
ba
a(bc)
2.乘法结合律:(ab)c 3.分配律: a(b c)
ab ac ab ac a(b c)
计算:
4 1 (1) ( 5) 6 ( ) 5 4
1 1 (3) 15 ( ) 5 3
计算: 3
2 3 (1)( ) 3 1 ( ) 5 3 4
5 4 2 5 1 ( ) ( ) (2 ) 6 7 3 14 42
15 12 13 12 ( ) (17 ) ( ) (3)65 17 13 17 13 1 3 2 1 ) (4) ( 12 ) ( 3 10 5 6
9 2 2 (2) ( 54) ( ) ( ) 4 9 9
1 1 (3) ( 2) (3) (4) ( ) ( 4) 2 3
计算:
5 1 3 2 (1)( 48) (1 2 1 ) 8 6 4 3
4 5 3 5 5 3 ( ) 1 (2)( ) 5 13 5 13 13 5
多个非零有理数相乘:
(1) 2 3 4 (5)
(2 ) 2 3 (4) (5) (3 ) 2 (3) (4) (5)
数学0奥秘

数字“0”由来及神奇作用关于零的由来,还有一段令人气愤的故事。
大约在1500年前欧洲的数学家们是不知道用“0”的。
他们使用。
是用几个表示数的符号,按照一定规则,把它们组合起来表示不同的数目。
在这种数字的运用里,不需要“0”这个数字。
而在当时,有一位学者从印度记数法里发现了“0”这个符号。
他发现,有了“0”,进行数学运算方便极了,他非常高兴,还把使用“0”的方法向大家做了介绍。
过了一段时间,这件事被当时的罗马知道了。
当时是欧洲的中世纪,教会的势力非常大,罗马的权利更是远远超过皇帝。
非常恼怒,他斥责说,神圣的数是上帝创造的,在上帝创造的数里没有“0”这个怪物,如今谁要把它给引进来,谁就是亵渎上帝!于是,教皇就下令,把这位学者抓了起来,并对他施加了,用把他的十个手指头紧紧夹注,使他两手残废,让他再也不能握笔写字。
就这样,“0”被那个愚昧、残忍的罗马教皇令禁止了。
但是,虽然“0”被禁止使用,然而罗马的数学家们还是不管禁令,在数学的研究中仍然秘密地使用“0”,仍然用“0”做出了很多数学上的贡献。
后来“0”终于在欧洲被广泛使用,而却逐渐被淘汰了。
0是极为重要的数字,0的发现被称为人类伟大的发现之一。
0在我国古代叫做金元数字,意即极为珍贵的数字。
0这个数据说是由印度人在约公元5世纪时发明,在1202年时,一个商人写了一本算盘之书,在东方中由于数学是以运算为主(西方当时以几何和逻辑为主),由于运算上的需要,自然地引入了0这个数。
在中国很早便有0这个数字很多文献都有记载。
在1208年时将印度的阿拉伯数字引入本书,并在开头写了“印度人的9个数字,加上阿拉伯人发明的0符号便可以写出所有数字……”由于一些原因,在初时引入0这个符号到西方时,曾经引起西方人的困惑,因当时西方认为所有数都是正数,而且0这个数字会使很多算式,逻辑不能成立(如除以0),甚至认为是魔鬼数字,而被禁用。
直至约公元15,16世纪0和负数才逐渐给西方人所认同,才使西方数学有快速发展。
三年级-口算题-末位带0的乘除法-60题x50页
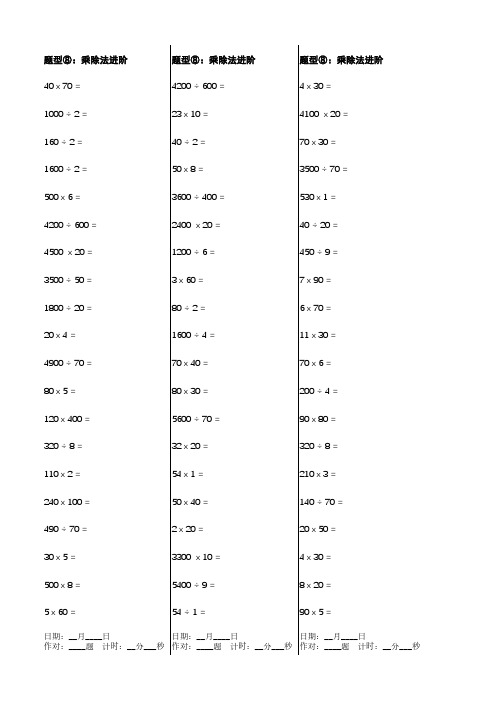
140 x 10 =
13 x 30 =
30 x 3 =
420 ÷ 60 =
1200 ÷ 3 =
60 x 30 =
2100 ÷ 70 =
8 x 90 =
1000 ÷ 500 =
50 x 9 =
31 x 1 =
480 ÷ 8 =
630 ÷ 90 =
60 x 4 =
70 x 40 =
40 x 90 =
6300 ÷ 90 =
3 x 50 =
32 x 20 =
200 x 3 =
4900 ÷ 70 =
400 x 2 =
8 x 80 =
300 ÷ 5 =
530 x 100 =
80 x 60 =
50 x 4 =
210 x 1 =
2400 ÷ 40 =
700 x 3 =
220 x 10 =
60 ÷ 30 =
2400 ÷ 40 =
3600 ÷ 400 =
530 x 1 =
4200 ÷ 600 =
2400 x 20 =
40 ÷ 20 =
4500 x 20 =
1200 ÷ 6 =
450 ÷ 9 =
3500 ÷ 50 =
3 x 60 =
7 x 90 =
1800 ÷ 20 =
80 ÷ 2 =
6 x 70 =
20 x 4 =
1600 ÷ 4 =
11 x 30 =
4900 ÷ 70 =
70 x 40 =
70 x 6 =
80 x 5 =
80 x 30 =
200 ÷ 4 =
120 x 400 =
5600 ÷ 70 =
小学除法中“0”的问题

小数除法中“0”的问题小数除法是在学生已经掌握了整数的相关运算,并且学习了小数乘法的基础上进行的学习。
是五年级上册小数计算教学中的一个重点难点。
这部分的计算是学生错误比较集中的地方,通过练习发现学生在计算小数除法时错误较多的题,主要是商“0”的问题。
【计算中存在的问题】1.扩大被除数末尾忘记添0。
如4.2÷0.02,有的学生通过商不变的规律进行扩大,除数扩大了100倍,但被除数只扩大了10倍,当成42÷2,于是得到了错误答案12.2.商中间的“0”不占位。
比如:23.12÷4,小数除法除到哪一位商应写在哪一位的上面,中间不够上商“1”时用“0”占位。
但学生在遇到不够除的时候急于把后一位移下来接着除,导致前一数位上的“0”未占位,得到7.3这个错误答案。
3.被除数整数部分不够除,就商“0”。
如2.88÷12,被除数的整数部分不够除,应用“0”占位。
有的学生用整数除法的方法计算,先看被除数第一位,不够除就直接看前两位,于是就用28除以12,得到错误的商2.4。
4.整数除以整数,但被除数小于除数,不够除就先商“0”。
如1÷5,有的学生直接在被除数末尾添个“0”就除,根本就不考虑商“0”的问题,于是得到错误商2。
5.被除数末尾“0”未移上去。
比如51.3÷0.27,除到被除数末尾0的前一位就已经整除了,这时候应该把末尾的一个“0”或者几个“0”移到商对应的末尾,但有的学生发现除尽后就停止了,不再补被除数末尾的“0”,得到错误答案16。
【出错原因的分析】1.口算基础不扎实20以内加减法、100以内加减法、表内乘除法是四则运算的基础,必须达到“不假思索,脱口而出”的程度。
如果口算基础不扎实,计算中必然会出现试商慢或试错商的情况。
2、数理不清楚数理是算法的前提,不管何种计算,都应讲清算理,明确算法。
老师们在引导学生理解算理时蜻蜓点水,很快就开始介绍计算程序,算理成了可有可无的事情。
小学数学知识归纳正数与负数的乘除法

小学数学知识归纳正数与负数的乘除法正数与负数的乘除法是小学数学中的重要内容,通过学习和掌握这些知识,能够帮助孩子更好地理解数学运算的规律和特点。
本文将对小学数学中正数与负数的乘除法进行归纳总结,以帮助学生更好地掌握这部分知识。
1. 正数与正数的乘法两个正数相乘,结果仍为正数。
例如:3 × 2 = 6,4 × 5 = 20。
这表示在数轴上,两个正数相乘的结果是从原点开始,向右侧移动的位置数。
2. 负数与负数的乘法两个负数相乘,结果也是正数。
例如:(-3) × (-2) = 6,(-4) × (-5) = 20。
这表示在数轴上,两个负数相乘的结果是从原点开始,向右侧移动的位置数。
3. 正数与负数的乘法一个正数与一个负数相乘,结果为负数。
例如:3 × (-2) = -6, 4 ×(-5) = -20。
这表示在数轴上,一个正数与一个负数相乘的结果是从原点开始,向左侧移动的位置数。
4. 正数与零的乘法一个正数与零相乘,结果仍为零。
例如:3 × 0 = 0, 4 × 0 = 0。
这表示在数轴上,一个正数与零相乘的结果仍停留在原点。
5. 负数与零的乘法一个负数与零相乘,结果仍为零。
例如:(-3) × 0 = 0, (-4) × 0 = 0。
这表示在数轴上,一个负数与零相乘的结果仍停留在原点。
6. 正数的除法正数除以正数,结果仍为正数。
例如:6 ÷ 3 = 2, 8 ÷ 2 = 4。
这表示在数轴上,一个正数除以另一个正数,相当于从原点开始,向右侧移动的位置数。
7. 负数的除法负数除以负数,结果仍为正数。
例如:(-6) ÷ (-3) = 2, (-8) ÷ (-2) = 4。
这表示在数轴上,一个负数除以另一个负数,相当于从原点开始,向右侧移动的位置数。
8. 正数除以负数正数除以负数,结果为负数。
关于0的乘除法知识

关于0的乘除法知识
嘿,朋友们!今天咱来好好唠唠关于 0 的乘除法知识。
你们想啊,0 这个数字可太特别啦!
先说说乘法。
0 乘以任何数都等于 0 哦!比如说 5 乘以 0,那结果就是0 嘛,就好像你有 5 个苹果,去乘以空无一物的 0,那可不就是啥都没有嘛,哈哈!那要是 0 乘以 0 呢,还是 0 呀,这不是很神奇吗?
再来看看除法。
0 可不能当除数哦!这就好比把一块蛋糕分给 0 个人,那根本没法分呀,这不是很荒谬吗?但是任何数除以 0 就没意义啦!大家想想,如果 8 除以 0,这要怎么算呀?算不出来吧!
“哎呀,那 0 在这些运算里可真是让人又爱又恨呀!”这时候小明可
能就会这么说了。
“可不是嘛!”小红也会跟着附和。
对呀对呀,0 的乘除法知识就是这么特别。
就像生活中的一些事情,有时候会给我们带来惊喜,有时候又会让我们有点抓耳挠腮呢!但正是因为有了这些特别之处,数学才变得这么有趣呀!所以呀,我们可不要小瞧了 0 在
乘除法里的这些规则哦,它们可是数学世界里很重要的一部分呢!一定要好好掌握呀,不然做题的时候可就要出岔子咯!这就是我关于 0 的乘除法知识的看法啦,你们觉得呢?。
