反比例函数专题复习
初三数学反比例函数知识点归纳-复习必备打印背熟

反比例函数是什么?反比例函数相关知识1:反比例函数是什么?反比例函数的定义域和值域因为x在分母上,所以x≠0,即自变量X的取值范围为非零实数。
而且常数k≠0,因此y≠0,即因变量y的`取值范围为非零实数。
反比例函数的图像及其性质形状:反比例函数的图象是两条双曲线,每一条曲线都无限向X轴Y轴延伸但不与坐标轴相交。
增减性:当k>0时,双曲线的两支分别位于第一、三象限,在每个象限内y随x的增大而减小;当k<0时,双曲线的两支分别位于第二、四象限,在每个象限内y随x的增大而增大。
对称性:反比例函数的图象既是轴对称图形,又是中心对称图形,它有两条对称轴y=x和y=-x,对称中心是坐标原点。
2:反比例函数知识点1、反比例函数的表达式X是自变量,Y是X的函数y=k/x=k?1/xxy=ky=k?x^(-1)(即:y等于x的负一次方,此处X必须为一次方)y=kx(k为常数且k≠0,x≠0)若y=k/nx此时比例系数为:k/n2、函数式中自变量取值的范围①k≠0;②在一般的情况下,自变量x的取值范围可以是不等于0的任意实数;③函数y的取值范围也是任意非零实数。
解析式y=k/x其中X是自变量,Y是X的函数,其定义域是不等于0的一切实数y=k/x=k?1/xxy=ky=k?x^(-1)y=kx(k为常数(k≠0),x不等于0)3、反比例函数图象反比例函数的图像属于以原点为对称中心的中心对称的双曲线(hyperbola),反比例函数图像中每一象限的每一支曲线会无限接近X轴Y轴但不会与坐标轴相交(K≠0)。
4、反比例函数中k的几何意义是什么?有哪些应用?过反比例函数y=k/x(k≠0),图像上一点P(x,y),作两坐标轴的垂线,两垂足、原点、P点组成一个矩形,矩形的面积S=x的绝对值_y的.绝对值=(x_y)的绝对值=|k|研究函数问题要透视函数的本质特征。
反比例函数中,比例系数k有一个很重要的几何意义,那就是:过反比例函数图象上任一点P作x轴、y轴的垂线PM、PN,垂足为M、N则矩形PMON的面积S=PM?PN=|y|?|x|=|xy|=|k|。
中考数学专题复习7反比例函数及其运用(解析版)

反比例函数及其运用复习考点攻略考点一 反比例函数的概念1.反比例函数的概念:一般地.函数ky x=(k 是常数.k ≠0)叫做反比例函数.反比例函数的解析式也可以写成1y kx -=的形式.自变量x 的取值范围是x ≠0的一切实数.函数的取值范围也是一切非零实数. 2.反比例函数k y x =(k 是常数.k ≠0)中x .y 的取值范围:反比例函数ky x=(k 是常数.k ≠0)的自变量x 的取值范围是不等于0的任意实数.函数值y 的取值范围也是非零实数. 【例1】下列函数中.y 与x 之间是反比例函数关系的是 A .xyB .3x +2y =0C .y =D .y =【答案】A考点二 反比例函数的图象和性质1.反比例函数的图象与性质(1)图象:反比例函数的图象是双曲线.它有两个分支.这两个分支分别位于第一、三象限.或第二、四象限.由于反比例函数中自变量x ≠0.函数y ≠0.所以.它的图象与x 轴、y 轴都没有交点.即双曲线的两个分支无限接近坐标轴.但永远达不到坐标轴.(2)性质:当k >0时.函数图象的两个分支分别在第一、三象限.在每个象限内.y 随x 的增大而减小.当k <0时.函数图象的两个分支分别在第二、四象限.在每个象限内.y 随x 的增大而增大.2kx 21x +表达式 ky x=(k 是常数.k ≠0) kk >0k <0大致图象所在象限 第一、三象限第二、四象限增减性在每个象限内.y 随x 的增大而减小在每个象限内.y 随x 的增大而增大反比例函数的图象既是轴对称图形.又是中心对称图形.其对称轴为直线y =x 和y =-x .对称中心为原点. 【注意】(1)画反比例函数图象应多取一些点.描点越多.图象越准确.连线时.要注意用平滑的曲线连接各点.(2)随着|x |的增大.双曲线逐渐向坐标轴靠近.但永远不与坐标轴相交.因为反比例函数ky x=中x ≠0且y ≠0. (3)反比例函数的图象不是连续的.因此在谈到反比例函数的增减性时.都是在各自象限内的增减情况.当k >0时.在每一象限(第一、三象限)内y 随x 的增大而减小.但不能笼统地说当k >0时.y 随x 的增大而减小.同样.当k <0时.也不能笼统地说y 随x 的增大而增大.【例2】一次函数与反比例函数在同一坐标系中的图象可能是( ) A . B .C .D .y ax a =-(0)ay a x=≠【答案】D【解析】当时..则一次函数经过一、三、四象限.反比例函数经过一 、三象限.故排除A.C 选项; 当时..则一次函数经过一、二、四象限.反比例函数经过二、四象限.故排除B 选项.故选:D .【例3】若点.在反比例函数的图象上.且.则的取值范围是( )A .B .C .D .或【答案】B【解析】解:∵反比例函数.∴图象经过第二、四象限.在每个象限内.y 随x 的增大而增大.①若点A 、点B 同在第二或第四象限.∵.∴a -1>a+1.此不等式无解;②若点A 在第二象限且点B 在第四象限.∵.∴.解得:; ③由y 1>y 2.可知点A 在第四象限且点B 在第二象限这种情况不可能. 综上.的取值范围是.故选:B .考点三 反比例函数解析式的确定1.待定系数法:确定解析式的方法仍是待定系数法.由于在反比例函数ky x=中.只有一个待定系数.因此只需要一对对应值或图象上的一个点的坐标.即可求出k 的值.从而确定其解析式.2.待定系数法求反比例函数解析式的一般步骤 (1)设反比例函数解析式为ky x=(k ≠0); (2)把已知一对x .y 的值代入解析式.得到一个关于待定系数k 的方程; (3)解这个方程求出待定系数k ;(4)将所求得的待定系数k 的值代回所设的函数解析式.【例4】点A 为反比例函数图象上一点.它到原点的距离为5.到x 轴的距离为3.若点A 在第二象限内.则这个函数的解析式为( )0a >0a -<y ax a =-(0)ay a x=≠0a <0a ->y ax a =-(0)ay a x=≠()11,A a y -()21,B a y +(0)ky k x=<12y y >a 1a <-11a -<<1a >1a <-1a >(0)ky k x=<12y y >12y y >1010a a -⎧⎨+⎩<>11a -<<a 11a -<<A.y=12xB.y=-12xC.y=112xD.y=-112x【答案】B【解析】设A点坐标为(x.y).∵A点到x轴的距离为3.∴|y|=3.y=±3.∵A点到原点的距离为5.∴x2+y2=52.解得x=±4.∵点A在第二象限.∴x=-4.y=3.∴点A的坐标为(-4.3).设反比例函数的解析式为y=.∴k=-4×3=-12.∴反比例函数的解析式为y=.故选B.考点四反比例函数中|k|的几何意义1.反比例函数图象中有关图形的面积2.涉及三角形的面积型当一次函数与反比例函数结合时.可通过面积作和或作差的形式来求解.(1)正比例函数与一次函数所围成的三角形面积.如图①.S△ABC=2S△ACO=|k|;(2)如图②.已知一次函数与反比例函数kyx=交于A、B两点.且一次函数与x轴交于点C.则S△AOB=S△AOC+S△BOC=1||2AOC y⋅+1||2BOC y⋅=1(||||)2A BOC y y⋅+;(3)如图③.已知反比例函数kyx=的图象上的两点.其坐标分别为()A Ax y,.k x 12 x-()B B x y ,.C 为AB 延长线与x 轴的交点.则S △AOB =S △AOC –S △BOC =1||2A OC y ⋅–1||2B OC y ⋅=1(||||)2A B OC y y ⋅-.【例5】如图.已知双曲线经过直角三角形OAB 斜边OB 的中点D .与直角边AB 相交于点C .若△OBC 的面积为9.则k =__________.【答案】6【解析】如图.过点D 作x 轴的垂线交x 轴于点E .∵△ODE 的面积和△OAC 的面积相等.∴△OBC 的面积和四边形DEAB 的面积相等且为9. 设点D 的横坐标为x .纵坐标就为. ∵D 为OB 的中点.∴EA =x .AB =. ∴四边形DEAB 的面积可表示为:(+)x =9;k =6. 故答案为:6.【例6】如图.A 、B 两点在双曲线y x=的图象上.分别经过A 、B 两点向轴作垂线段.已知1S =阴影.则12S S +=ky x=k x 2k x12k x 2k xA .8B .6C .5D .4【答案】B【解析】∵点A 、B 是双曲线y =上的点.分别经过A 、B 两点向x 轴、y 轴作垂线段.则根据反比例函数的图象的性质得两个矩形的面积都等于|k |=4.∴S 1+S 2=4+4-1×2=6.故选B .考点五 反比例函数与一次函数的综合1.涉及自变量取值范围型当一次函数11y k x b =+与反比例函数22k y x=相交时.联立两个解析式.构造方程组.然后求出交点坐标.针对12y y >时自变量x 的取值范围.只需观察一次函数的图象高于反比例函数图象的部分所对应的x 的范围.例如.如下图.当12y y >时.x 的取值范围为A x x >或0B x x <<;同理.当12y y <时.x 的取值范围为0A x x <<或B x x <.2.求一次函数与反比例函数的交点坐标(1)从几何角度看.一次函数与反比例函数的交点由k 值的符号来决定. ①k 值同号.两个函数必有两个交点;②k 值异号.两个函数可能无交点.可能有一个交点.也可能有两个交点;(2)从代数角度看.一次函数与反比例函数的交点主要取决于两函数所组成的方程组的解的情况.【例7】已知抛物线y =x 2+2x +k +1与x 轴有两个不同的交点.则一次函数y =kx ﹣k 与反比例函数y =在同一坐标系内的大致图象是( )4xA.B.C.D.【解析】∵抛物线y=x2+2x+k+1与x轴有两个不同的交点.∴△=4﹣4(k+1)>0.解得k<0.∴一次函数y=kx﹣k的图象经过第一二四象限.反比例函数y=的图象在第二四象限.故选:D.考点六反比例函数的实际应用解决反比例函数的实际问题时.先确定函数解析式.再利用图象找出解决问题的方案.特别注意自变量的取值范围.【例8】如图.△OAC和△BAD都是等腰直角三角形.∠ACO=∠ADB=90°.反比例函数y=k在第一象限的图象经过点B.若xOA2−AB2=12.则k的值为______.【解析】设B点坐标为(a,b).∵△OAC和△BAD都是等腰直角三角形.∴OA=√2AC.AB=√2AD.OC=AC.AD=BD.∵OA2−AB2=12.∴2AC2−2AD2=12.即AC2−AD2=6.∴(AC+AD)(AC−AD)=6.∴(OC+BD)⋅CD=6.∴a⋅b=6.∴k=6.故答案为:6..(其中mk≠0)图象交于【例9】如图.一次函数y=kx+b与反比例函数y=mxA(−4,2).B(2,n)两点.(1)求一次函数和反比例函数的表达式;(2)求△ABO的面积;(3)请直接写出当一次函数值大于反比例函数值时x 的取值范围.【解析】(1)∵一次函数y =kx +b 与反比例函数y =m x(mk ≠0)图象交于A(−4,2).B(2,n)两点.根据反比例函数图象的对称性可知.n =−4. ∴{2=−4k +b−4=2k +b .解得{k =−1b =−2.故一次函数的解析式为y =−x −2. 又知A 点在反比例函数的图象上.故m =−8. 故反比例函数的解析式为y =−8x ; (2)在y =−x −2中.令y =0.则x =−2. ∴OC =2.∴S △AOB =12×2×2+12×2×4=6; (3)根据两函数的图象可知:当x <−4或0<x <2时.一次函数值大于反比例函数值.第一部分 选择题一、选择题(本题有10小题.每题4分.共40分)1.下列函数:①2x y =;②2y x =;③12y x=-;④12y x -=中.是反比例函数的有( ) A .1个 B .2个 C .3个D .4个【答案】C【解析】①不是正比例函数.②③④是反比例函数.故选C .2.点A 为反比例函数图象上一点.它到原点的距离为5.则x 轴的距离为3.若点A 在第二象限内.则这个函数的解析式为( )A .y =12xB .y =-12xC .y =112xD .y =-112x【答案】C【解析】∵反比例函数y =-中.k =-6.∴只需把各点横纵坐标相乘.结果为-6的点在函数图象上.四个选项中只有C 选项符合.故选C . 3. 已知点A (1.m ).B (2.n )在反比例函数(0)ky k x=<的图象上.则( ) A .0m n << B .0n m << C .0m n >>D .0n m >>【答案】A【解析】∵反比例函数(0)k y k x =<.它的图象经过A (1.m ).B (2.n )两点.∴m =k <0.n =2k<0.∴0m n <<.故选A .4. 如图.等腰三角形ABC 的顶点A 在原点.顶点B 在x 轴的正半轴上.顶点C 在函数y =kx(x >0)的图象上运动.且AC =BC .则△ABC 的面积大小变化情况是( )A .一直不变B .先增大后减小C .先减小后增大D .先增大后不变【答案】A【解析】如图.作CD ⊥AB 交AB 于点D .则S △ACD =.∵AC =BC .∴AD =BD .∴S △ACD =S △BCD . ∴S △ABC =2S △ACD =2×=k .∴△ABC 的面积不变.故选A .6x 2k2k5.如图.点.点都在反比例函数的图象上.过点分别向轴、轴作垂线.垂足分别为点..连接...若四边形的面积记作.的面积记作.则( )A .B .C .D .【答案】C【解析】解:点P (m.1).点Q (−2.n )都在反比例函数y =的图象上. ∴m×1=−2n =4.∴m =4.n =−2.∵P (4.1).Q (−2.−2).∵过点P 分别向x 轴、y 轴作垂线.垂足分别为点M.N.∴S 1=4.作QK ⊥PN.交PN 的延长线于K.则PN =4.ON =1.PK =6.KQ =3. ∴S 2=S △PQK −S △PON −S 梯形ONKQ =×6×3−×4×1−(1+3)×2=3.∴S 1:S 2=4:3.故选:C .6. 已知一次函数y 1=kx +b 与反比例函数y 2=kx在同一直角坐标系中的图象如图所示.则当y 1<y 2时.x 的取值范围是( )(,1)P m (-2,)Q n 4y x=P x y M N OP OQ PQ OMPN 1S POQ △2S 12:2:3S S =12:1:1S S =12:4:3S S =12:5:3S S =4x121212A .x <-1或0<x <3B .-1<x <0或x >3C .-1<x <0D .x >3【答案】B【解析】根据图象知.一次函数y 1=kx +b 与反比例函数y 2=kx的交点是(-1.3).(3.-1).∴当y 1<y 2时.-1<x <0或x >3.故选B .7.如图.在平面直角坐标系xOy 中.函数()0y kx b k =+≠与()0my m x=≠的图象相交于点()()2,3,6,1A B --.则不等式mkx b x+>的解集为( )A .6x <-B 60x -<<.或2x >C .2x >D 6x <-.或02x <<8. 如图.直线l ⊥x 轴于点P .且与反比例函数y 1=1k x(x >0)及y 2=2k x (x >0)的图象分别交于点A .B .连接OA .OB .已知△OAB 的面积为2.则k 1-k 2的值为( )A .2B .3C .4D .-4【答案】C【解析】根据反比例函数k 的几何意义可知:△AOP 的面积为12k .△BOP 的面积为22k. ∴△AOB 的面积为12k −22k . ∴12k −22k =2.∴k 1–k 2=4.故选C . 9. 一次函数y =ax +b 与反比例函数a by x-=.其中ab <0.a 、b 为常数.它们在同一坐标系中的图象可以是( )A .B .C .D .【答案】C【解析】A .由一次函数图象过一、三象限.得a >0.交y 轴负半轴.则b <0.满足ab <0. ∴a −b >0.∴反比例函数y =a bx-的图象过一、三象限.所以此选项不正确; B .由一次函数图象过二、四象限.得a <0.交y 轴正半轴.则b >0.满足ab <0. ∴a −b <0.∴反比例函数y =a bx-的图象过二、四象限.所以此选项不正确; C .由一次函数图象过一、三象限.得a >0.交y 轴负半轴.则b <0.满足ab <0.∴a −b >0.∴反比例函数y =a bx的图象过一、三象限.所以此选项正确; D .由一次函数图象过二、四象限.得a <0.交y 轴负半轴.则b <0.满足ab >0.与已知相矛盾. 所以此选项不正确.故选C .10. 如图.一次函数与x 轴.y 轴的交点分别是A(−4,0).B(0,2).与反比例函数的图象交于点Q .反比例函数图象上有一点P 满足:①PA ⊥x 轴;②PO =√17(O 为坐标原点).则四边形PAQO 的面积为( )A. 7B. 10C. 4+2√3D. 4−2√3【答案】C【解析】∵一次函数y =ax +b 与x 轴.y 轴的交点分别是A(−4,0).B(0,2). ∴−4a +b =0.b =2. ∴a =12.∴一次函数的关系式为:y =12x +2. 设P(−4,n).∴√(−4)2+n 2=√17. 解得:n =±1.由题意知n =−1.n =1(舍去). ∴把P(−4,−1)代入反比例函数y =mx . ∴m =4.反比例函数的关系式为:y =4x .解{y =12x +2y =4x 得.{x =−2+2√3y =√3+1.{x =−2−2√3y =1−√3. ∴Q(−2+2√3,√3+1).∴四边形PAQO 的面积=12×4×1+124×2+12×2×(−2+2√3)=4+2√3. 故选:C .第二部分 填空题二、填空题(本题有6小题.每题4分.共24分)11.若正比例函数的图象与某反比例函数的图象有一个交点的纵坐标是2.则该反比例函数的解析式为________. 【答案】 【解析】令y=2x 中y=2.得到2x=2.解得x=1.∴正比例函数的图象与某反比例函数的图象交点的坐标是(1,2). 设反比例函数解析式为.将点(1,2)代入.得. ∴反比例函数的解析式为.故答案为:. 12.如图.直线y =x 与双曲线()0ky k x=>的一个交点为A .且OA =2.则k 的值为__________.【答案】2【解析】∵点A 在直线y =x 上.且OA =2.∴点A的坐标为把得.∴k=2.故答案为:2. 13. 已知(),3A m 、()2,B n -在同一个反比例函数图像上.则m n =__________.【答案】23-【解析】设反比例函数解析式为()0ky k x=≠.将(),3A m 、()2,B n -分别代入.得 3k m =.2k n =-. 2y x =2y x=2y x =ky x=122k =⨯=2y x =2y x=(22),(22),ky x=22=∴2332k m k n ==--. 故答案为:23-. 14.平面直角坐标系xOy 中.点A (a .b )(a >0.b >0)在双曲线y =上.点A 关于x 轴的对称点B 在双曲线y =.则k 1+k 2的值为__________. 【答案】0【解析】∵点A (a .b )(a >0.b >0)在双曲线y =上.∴k 1=ab ; 又∵点A 与点B 关于x 轴对称.∴B (a .–b ).∵点B 在双曲线y =上.∴k 2=–ab ;∴k 1+k 2=ab +(–ab )=0.故答案为:0. 15.如图.点A 是反比例函数图象上的一点.过点A 作轴.垂足为点C .D 为AC 的中点.若的面积为1.则k 的值是【答案】4【解析】点A 的坐标为(m.2n ).∴.∵D 为AC 的中点.∴D (m.n ). ∵AC ⊥轴.△ADO 的面积为1.∴. ∴.∴ 16. 如图.反比例函数y =24x(x >0)的图象与直线y =32x 相交于点A .与直线y =kx(k ≠0)相交于点B .若△OAB 的面积为18.则k 的值为______.【答案】41k x2k x1k x2k x y x=AC x ⊥AOD ∆2mn k =x ()ADO11121222S AD OC n n m mn =⋅=-⋅==2mn =24k mn ==【解析】:由题意得.{y =24xy =32x .解得:{x 1=4y 1=6.{x 2=−4y 2=−6(舍去). ∴点A(4,6).(1)如图1.当y =kx 与反比例函数的交点B 在点A 的下方. 过点A 、B 分别作AM ⊥x 轴.BN ⊥x 轴.垂足分别为M 、N . 设点B 坐标为(b,24b ).则ON =b .BN =24b.∴点A(4,6).∴OM =4.AM =6;∵S △AOB =S △AOM +S 梯形AMNB −S △BON =S 梯形AMNB . ∴18=12(6+24b)(b −4).解得.b 1=8.b 2=−2(舍去) ∴点B(8,3).代入y =kx 得. k =38; (2)如图2.当y =kx 与反比例函数的交点B 在点A 的上方. 过点A 、B 分别作AM ⊥y 轴.BN ⊥y 轴.垂足分别为M 、N . 设点B 坐标为(b,24b ).则ON =24b.BN =b .∴点A(4,6).∴OM =6.AM =4;∵S △AOB =S △AOM +S 梯形AMNB −S △BON =S 梯形AMNB . ∴18=12(b +4)(24b −6). 解得.b 1=2.b 2=−8(舍去) ∴点B(2,12).代入y =kx 得. k =6;故答案为:6或38.第三部分 解答题三、解答题(本题有6小题.共56分)17. 如图.已知A (–4.n ).B (2.–4)是一次函数y =kx +b 和反比例函数y =的图象的两个交点.(1)求一次函数和反比例函数的解析式; (2)求△AOB 的面积.【答案】(1)y =–x –2.y =–;(2)6【解析】(1)∵B (2.–4)在y =图象上. ∴m =–8.∴反比例函数的解析式为y =–. ∵点A (–4.n )在y =–图象上. ∴n =2. ∴A (–4.2).∵一次函数y =kx +b 图象经过A (–4.2).B (2.–4).∴.解得.∴一次函数的解析式为y =–x –2;(2)如图.令一次函数y =–x –2的图象与y 轴交于C 点.mx8xmx 8x8x4224k b k b -+=+=-⎧⎨⎩12k b =-=-⎧⎨⎩当x=0时.y =–2. ∴点C (0.–2). ∴OC =2.∴S △AOB =S △ACO +S △BCO =×2×4+×2×2=6. 18.如图.已知反比例函数y x=与一次函数y =x +b 的图象在第一象限相交于点A (1.-k +4). (1)试确定这两个函数的表达式;(2)求出这两个函数图象的另一个交点B 的坐标.并根据图象写出使反比例函数的值大于一次函数的值的x 的取值范围.【答案】(1).y =x +1;(2)B 的坐标为(-2.-1).x <-2或0<x <1 【解析】(1)∵已知反比例函数经过点A (1.-k +4). ∴.即-k +4=k . ∴k =2.∴A (1.2).∵一次函数y =x +b 的图象经过点A (1.2). ∴2=1+b .∴b =1.∴反比例函数的表达式为. 一次函数的表达式为y =x +1.12122y x=ky x=41kk -+=2y x=(2)由.消去y .得x 2+x -2=0. 即(x +2)(x -1)=0. ∴x =-2或x =1. ∴y =-1或y =2.∴或.∵点B 在第三象限. ∴点B 的坐标为(-2.-1).由图象可知.当反比例函数的值大于一次函数的值时.x 的取值范围是x <-2或0<x <1. 19.如图.一次函数的图象与反比例函数(为常数且)的图象相交于.两点.(1)求反比例函数的表达式;(2)将一次函数的图象沿轴向下平移个单位.使平移后的图象与反比例函数的图象有且只有一个交点.求的值.【答案】(1);(2)b 的值为1或9. 【解析】(1)由题意.将点代入一次函数得: 将点代入得:.解得 则反比例函数的表达式为; (2)将一次函数的图象沿轴向下平移个单位得到的一次函数的解析式为联立整理得: 12y x y x ⎧=+⎪⎨=⎪⎩21x y ⎧=-⎨=-⎩12x y ⎧=⎨=⎩5y x =+ky x=k 0k ≠(1,)A m -B 5y x =+y b (0)b >ky x=b 4y x=-(1,)A m -5y x =+154m =-+=(1,4)A -∴(1,4)A -ky x=41k =-4k =-4y x =-5y x =+y b 5y x b =+-54y x by x =+-⎧⎪⎨=-⎪⎩2(5)40x b x +-+=一次函数的图象与反比例函数的图象有且只有一个交点 关于x 的一元二次方程只有一个实数根此方程的根的判别式解得则b 的值为1或9.20.如图.一次函数y =kx +b (k 、b 为常数.k ≠0)的图象与x 轴、y 轴分别交于A 、B 两点.且与反比例函数y =(n 为常数.且n ≠0)的图象在第二象限交于点C .CD ⊥x 轴.垂足为D .若OB =2OA =3OD =12.(1)求一次函数与反比例函数的解析式;(2)记两函数图象的另一个交点为E .求△CDE 的面积; (3)直接写出不等式kx +b ≤的解集.【答案】(1)y =–2x +12;(2)140;(3)x ≥10.或–4≤x <0 【解析】(1)由已知.OA =6.OB =12.OD =4.∵CD ⊥x 轴.∴OB ∥CD .∴△ABO ∽△ACD . ∴=.∴=.∴CD =20. ∴点C 坐标为(–4.20).∴n =xy =–80. ∴反比例函数解析式为:y =–. 把点A (6.0).B (0.12)代入y =kx +b 得:.解得.∴一次函数解析式为:y =–2x +12; (2)当–=–2x +12时.解得x 1=10.x 2=–4; 当x =10时.y =–8.∴点E 坐标为(10.–8). ∴S △CDE =S △CDA +S △EDA =×20×10+×8×10=140; 5y x b =+-4y x=-∴2(5)40x b x +-+=∴2(5)440b ∆=--⨯=121,9b b ==nxnxOA AD OBCD 61012CD80x0612k b b =+=⎧⎨⎩212k b =-=⎧⎨⎩80x1212(3)不等式kx +b ≤.从函数图象上看.表示一次函数图象不高于反比例函数图象; ∴由图象得.x ≥10.或–4≤x <0. 21.如图.一次函数y =k 1x +b 的图象与反比例函数y=的图象相交于A 、B 两点.其中点A 的坐标为(–1.4).点B 的坐标为(4.n ).(1)根据图象.直接写出满足k 1x +b >的x 的取值范围; (2)求这两个函数的表达式;(3)点P 在线段AB 上.且S △AOP ∶S △BOP =1∶2.求点P 的坐标. 【答案】(1)x <–1或0<x <4;(2)y =–(3)P (.)【解析】(1)∵点A 的坐标为(–1.4).点B 的坐标为(4.n ).由图象可得:k 1x +b >的x 的取值范围是x <–1或0<x <4; (2)∵反比例函数y =的图象过点A (–1.4).B (4.n ). ∴k 2=–1×4=–4.k 2=4n .∴n =–1.∴B (4.–1). ∵一次函数y =k 1x +b 的图象过点A .点B .∴. 解得k =–1.b =3.∴直线解析式y =–x +3.反比例函数的解析式为y =–; (3)设直线AB 与y 轴的交点为C .∴C (0.3).∵S △AOC =×3×1=. ∴S △AOB =S △AOC +S △BOC =×3×1+×3×4=. n x2k x 2k xx 332k x2k x 11441k b k b -+=+=-⎧⎨⎩4x 12321212152∵S△AOP :S △BOP =1:2.∴S △AOP =×=. ∴S △COP =–=1.∴×3x P =1.∴x P =. ∵点P 在线段AB 上.∴y =–+3=.∴P (.).22.如图.反比例函数1k y x=和一次函数2y mx n =+相交于点()1,3A .()3,B a -. (1)求一次函数和反比例函数解析式;(2)连接OA.试问在x 轴上是否存在点P.使得OAP ∆为以OA 为腰的等腰三角形.若存在.直接写出满足题意的点P 的坐标;若不存在.说明理由.【答案】(1)22y x =+(2)见解析【解析】(1)∵反比例函数1k y x =和一次函数2y mx n =+相交于点()1,3A .()3,B a -. ∴k=1×3=3.∴13y x=. ∴-3a=3.解得:a=-1.∴B(-3.-1).∴331m n m n +=⎧⎨-+=-⎩.解得:12m n =⎧⎨=⎩. ∴22y x =+;(2)设P(t.0).∵()1,3A .∴222(1)(03)(1)9t t -+-=-+t 221310+. 15213525232122323732373∵OAP ∆为以OA 为腰的等腰三角形.∴OA=AP 或OA=OP.当OA=AP 时.22(1)9(10)t -+=.解得:1220t t ==,(不符合题意.舍去). ∴P(2.0);当OA=OP 时.t 10解得:10.∴10.0)或P(10.0).综上所述:存在点P.使OAP ∆为以OA 为腰的等腰三角形.点P 坐标为:(2.0) 或10.0)或(10.0).。
一次函数与反比例涵数的专题复习

一次函数与反比例函数专题复习第一部分 知识梳理考点一、平面直角坐标系 (3分) 1、平面直角坐标系在平面内画两条互相垂直且有公共原点的数轴,就组成了平面直角坐标系。
其中,水平的数轴叫做x 轴或横轴,取向右为正方向;铅直的数轴叫做y 轴或纵轴,取向上为正方向;两轴的交点O (即公共的原点)叫做直角坐标系的原点;建立了直角坐标系的平面,叫做坐标平面。
为了便于描述坐标平面内点的位置,把坐标平面被x 轴和y 轴分割而成的四个部分,分别叫做第一象限、第二象限、第三象限、第四象限。
注意:x 轴和y 轴上的点,不属于任何象限。
2、点的坐标的概念点的坐标用(a ,b )表示,其顺序是横坐标在前,纵坐标在后,中间有“,”分开,横、纵坐标的位置不能颠倒。
平面内点的坐标是有序实数对,当b a ≠时,(a ,b )和(b ,a )是两个不同点的坐标。
考点二、不同位置的点的坐标的特征 (3分) 1、各象限内点的坐标的特征(1) 点P(x,y)在第一象限0,0>>⇔y x(2)点P(x,y)在第二象限0,0><⇔y x (3)点P(x,y)在第三象限0,0<<⇔y x (4)点P(x,y)在第四象限0,0<>⇔y x 2、坐标轴上的点的特征(1)点P(x,y)在x 轴上0=⇔y ,x 为任意实数(2)点P(x,y)在y 轴上0=⇔x ,y 为任意实数(3)点P(x,y)既在x 轴上,又在y 轴上⇔x ,y 同时为零,即点P 坐标为(0,0) 3、两条坐标轴夹角平分线上点的坐标的特征(1)点P(x,y)在第一、三象限夹角平分线上⇔x 与y 相等(2)点P(x,y)在第二、四象限夹角平分线上⇔x 与y 互为相反数 4、和坐标轴平行的直线上点的坐标的特征(1)位于平行于x 轴的直线上的各点的纵坐标相同。
(2)位于平行于y 轴的直线上的各点的横坐标相同。
5、关于x 轴、y 轴或远点对称的点的坐标的特征(1)点P 与点p ’关于x 轴对称⇔横坐标相等,纵坐标互为相反数 (2)点P 与点p ’关于y 轴对称⇔纵坐标相等,横坐标互为相反数 (3)点P 与点p ’关于原点对称⇔横、纵坐标均互为相反数 6、点到坐标轴及原点的距离 (1)点P(x,y)到x 轴的距离等于y (2)点P(x,y)到y 轴的距离等于x (3)点P(x,y)到原点的距离等于22y x +考点三、函数及其相关概念 (3~8分) 1、变量与常量在某一变化过程中,可以取不同数值的量叫做变量,数值保持不变的量叫做常量。
反比例函数复习课件

知识点回顾1 1.什么是反比例函数?
一般地,函数 y k(k是常数, x
k≠0)叫做反比例函数.
2.解析式还有两种常见的表达形式。 y=kx-1(k≠0) xy = k (k≠0)
你一定能找对!
1.下列函数中哪些是反比例函数?
y = 3①x-1
y = 2x2
②y=
1 x
y = 23x③ ④
|k|的一半.
2.设x为一切实数,在下列函数中
,当x增大时,y的值总是减小的函
C
数是( )
(A) y = -5x -1 ( B) y=x2
(C) y=-2x+2; (D) y=4x.
3. 已知k<0,则函数 y1=kx,y2=
k x
在同一坐标系中的图像大致是
D
()
y
y
(A)
0
(B)
x
0
x
y
y
(C)
0
(D)
x
0
x
4. 已知k>0,则函数 y1=kx+k与kxy2=
在同一坐标系中的图像大致是 ( C)
y
y
(A)
(B)
0
x
0
x
y
y
(C)
(D)
0
x
0
x
5.设P(2,3)是反比例函数图像 上的一点,求△POA的面积。
y
P(2,3)
oA
x
y P(m,n)
oA
x
6.在平面直角坐标系内,从反比例函数
y=k/x(k>0)的图象上的一点分别作坐标轴 的垂线段,与坐标轴围成的矩形的面积是12,
8.已知:y=y1+y2,其中y1与x成正 比例,y2与x成反比例,当x=1时 ,y=4,当x=2时,y=5,求函数y 的解析式。
第二十六章反比例函数专题复习反比例函数中k的几何意义课件人教版数学九年级下册

模型二 两点一垂线或两点两垂线
3.如图,A,B 是函数 y=k) (k<0)的图象上关于原点 O 对称的任意两点,AC 平 x
行于 y 轴,BC 平行于 x 轴.若△ABC 的面积为 6,则 k 值为( B ) A.3 B.-3 C.-6 D.-12
第二十六章 反比例函数
专题 反比例函数中k的几何意义
模型一 一点两垂线或一点一垂线
1.如图,反比例函数 y=kx (x<0)的图象上有任意两点 P,Q,若将 S△OAP 记为 S1, S△OBQ 记为 S2,则( A )
A.S1=S2 B.S1>S2 C.S1<S2 D.无法判断
2.如图,A,B 两点在双曲线 y=4 上,分别经过 A,B 两点向坐标轴作垂线段, x
又∵点 D 与点 B 的纵坐标一样,且点 D 在反比例函数图象上,∴点 D 的坐标为 _(a3__,__3_ak__)_;
第三步:列方程:∵S 四边形 ODBE=S 四边形 ODBC-S△OCE=6,∴代入各点坐标后,解 得 k=___3____.
【对应训练】(重庆中考)如图,在平面直角坐标系中,矩形 ABCD 的顶点 A,B 在 x 轴的正半轴上,反比例函数 y=kx (k>0,x>0)的图象经过顶点 D,分别与对角线 AC,边 BC 交于点 E,F,连接 EF,AF.若点 E 为 AC 的中点,△AEF 的面积为 1, 则 k 的值为___3___.
4.(郴州中考)如图,点 A,C 分别是正比例函数 y=x 的图象与反比例函数 y=4 x
的图象的交点,过 A 点作 AD⊥x 轴于点 D,过 C 点作 CB⊥x 轴于点 B,则四边形 ABCD 的面积为__8___.
反比例函数复习讲义

反比例函数复习讲义知识点一:反比例函数的概念ﻫ 一般地,如果两个变量x 、y 之间的关系可以表示成k y x=(k为常数,)的形式,那么称y 是x 的反比例函数.注:(1)反比例函数k y x =中的k x 是一个分式,自变量x ≠0, k y x=也可写成1y kx -=或xy k =,其中k≠0;ﻫ (2)在反比例函数1y kx -=(k≠0)中,x 的指数是-1。
如,5y x=也写成:15y x -=;ﻫ (3)在反比例函数k y x=(k ≠0)中要注意分母x的指数为1,如21y x=就不是反比例函数。
ﻫ知识点二:反比例函数的图象反比例函数(0)ky k x=≠的图象是双曲线,它有两个分支,这两个分支分别位于第一、三象限或第二、四象限.它们关于原点对称,反比例函数的图象与x 轴、y 轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远不与坐标轴相交.ﻫ 注: (1)观察反比例函数(0)ky k x=≠的图象可得:x和y 的值都不能为0,并且图象既是轴对称图形,又是中心对称图形,它有两条对称轴,对称中心是坐标原点. (2)用描点法画反比例函数y=kx的图象时,应注意自变量x 的取值不能为0,一般应从1或-1开始对称取点.ﻫ (3)在一个反比例函数图象上任取两点P ,Q ,过点P ,Q分别作x 轴,y 轴的平行线,与两坐标轴分别围成的矩形面积为S 1,S2 则S 1=S 2. 知识点三:反比例函数的性质 1.图象位置与函数性质当k>0时,x 、y 同号,图象在第一、三象限,且在每个象限内,y 随x 的增大而减小;当k<0时,x 、y 异号,图象在第二、四象限,且在每个象限内,y 随x 的增大而增大.2.若点(a ,b)在反比例函数(0)ky k x=≠的图象上,则点(-a,-b )也在此图象上,故反比例函数的图象关于原点对称;正比例函数反比例函数解析式图 像直线 有两个分支组成的曲线(双曲线)位 置k>0,一、三象限; k<0,二、四象限 k >0,一、三象限 k <0,二、四象限增减性k>0,y 随x 的增大而增大 k<0,y 随x 的增大而减小k>0,在每个象限,y 随x的增大而减小ﻫk<0,在每个象限,y随x的增大而增大4.反比例函数y =kx 中k 的意义 反比例函数y = k x (k ≠0)中比例系数k 的几何意义,即过双曲线y = kx(k≠0)上任意一点引x轴、y 轴垂线,所得矩形面积为│k│.ﻫ知识点四:反比例函数解析式的确定ﻫ 反比例函数解析式的确定方法是待定系数法.由于在反比例函数关系式(0)ky k x=≠中,只有一个待定系数k,确定了k的值,也就确定了反比例函数,因此只需给出一组x 、y 的对应值或图象上点的坐标,代入(0)ky k x =≠中即可求出k 的值,从而确定反比例函数的解析式.ﻫ知识点五:应用反比例函数解决实际问题须注意以下几点1.反比例函数在现实世界中普遍存在,在应用反比例函数知识解决实际问题时,要注意将实际问题转化为数学问题。
初中数学反比例函数知识点总复习含解析

初中数学反比例函数知识点总复习含解析一、选择题1.如图,在平面直角坐标系中,点B在第一象限,BA⊥x轴于点A,反比例函数y=kx (x>0)的图象与线段AB相交于点C,且C是线段AB的中点,若△OAB的面积为3,则k的值为()A.13B.1 C.2 D.3【答案】D 【解析】【分析】连接OC,如图,利用三角形面积公式得到S△AOC=12S△OAB=32,再根据反比例函数系数k的几何意义得到12|k|=32,然后利用反比例函数的性质确定k的值.【详解】连接OC,如图,∵BA⊥x轴于点A,C是线段AB的中点,∴S△AOC=12S△OAB=32,而S△AOC=12|k|,∴12|k|=32,而k>0,∴k=3.故选:D.此题考查反比例函数系数k的几何意义,解题关键在于掌握在反比例函数y=kx图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.2.如图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上.反比例函数kyx=(x>0)的图象经过顶点B,则k的值为A.12 B.20 C.24 D.32【答案】D【解析】【分析】【详解】如图,过点C作CD⊥x轴于点D,∵点C的坐标为(3,4),∴OD=3,CD=4.∴根据勾股定理,得:OC=5.∵四边形OABC是菱形,∴点B的坐标为(8,4).∵点B在反比例函数(x>0)的图象上,∴.故选D.3.下列函数中,当x>0时,函数值y随自变量x的增大而减小的是()A.y=x2B.y=x C.y=x+1 D.1 yx =【解析】【分析】需根据函数的性质得出函数的增减性,即可求出当x >0时,y 随x 的增大而减小的函数.【详解】解:A 、y =x 2是二次函数,开口向上,对称轴是y 轴,当x >0时,y 随x 的增大而增大,错误;B 、y =x 是一次函数k =1>0,y 随x 的增大而增大,错误;C 、y =x+1是一次函数k =1>0,y 随x 的增大而减小,错误;D 、1y x=是反比例函数,图象无语一三象限,在每个象限y 随x 的增大而减小,正确; 故选D .【点睛】本题综合考查了二次函数、一次函数、反比例函数的性质,熟练掌握函数的性质是解题的关键.4.如图,点P 是反比例函数(0)k y k x=≠的图象上任意一点,过点P 作PM x ⊥轴,垂足为M . 连接OP . 若POM ∆的面积等于2. 5,则k 的值等于 ( )A .5-B .5C . 2.5-D .2. 5【答案】A【解析】【分析】 利用反比例函数k 的几何意义得到12|k|=2,然后根据反比例函数的性质和绝对值的意义确定k 的值.【详解】解:∵△POM 的面积等于2.5,∴12|k|=2.5, 而k <0,∴k=-5,故选:A .【点睛】本题考查了反比例函数系数k 的几何意义:在反比例函数y=k x 图象中任取一点,过这一个点向x 轴和y 轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.也考查了反比例函数的性质.5.如图,反比例函数11k y x=的图象与正比例函数22y k x =的图象交于点(2,1),则使y 1>y 2的x 的取值范围是( )A .0<x <2B .x >2C .x >2或-2<x <0D .x <-2或0<x <2【答案】D【解析】【分析】 先根据反比例函数与正比例函数的性质求出B 点坐标,由函数图象即可得出结论.【详解】∵反比例函数与正比例函数的图象均关于原点对称,∴A 、B 两点关于原点对称.∵A (2,1),∴B (-2,-1).∵由函数图象可知,当0<x <2或x <-2时函数y 1的图象在y 2的上方,∴使y 1>y 2的x 的取值范围是x <-2或0<x <2.故选D.6.如图,A ,B 是反比例函数y=4x在第一象限内的图象上的两点,且A ,B 两点的横坐标分别是2和4,则△OAB 的面积是( )A .4B .3C .2D .1【答案】B【解析】【分析】先根据反比例函数图象上点的坐标特征及A ,B 两点的横坐标,求出A (2,2),B (4,1).再过A ,B 两点分别作AC ⊥x 轴于C ,BD ⊥x 轴于D ,根据反比例函数系数k 的几何意义得出S △AOC =S △BOD =12×4=2.根据S 四边形AODB =S △AOB +S △BOD =S △AOC +S 梯形ABDC ,得出S △AOB =S 梯形ABDC ,利用梯形面积公式求出S 梯形ABDC =12(BD+AC )•CD=12×(1+2)×2=3,从而得出S △AOB =3.【详解】∵A ,B 是反比例函数y=4x在第一象限内的图象上的两点, 且A ,B 两点的横坐标分别是2和4,∴当x=2时,y=2,即A (2,2),当x=4时,y=1,即B (4,1),如图,过A ,B 两点分别作AC ⊥x 轴于C ,BD ⊥x 轴于D , 则S △AOC =S △BOD =12×4=2, ∵S 四边形AODB =S △AOB +S △BOD =S △AOC +S 梯形ABDC ,∴S △AOB =S 梯形ABDC ,∵S 梯形ABDC =12(BD+AC )•CD=12×(1+2)×2=3, ∴S △AOB =3,故选B .【点睛】本题考查了反比例函数()0k y k x=≠中k 的几何意义,反比例函数图象上点的坐标特征,梯形的面积,熟知反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S 与k 的关系为S=12|k|是解题的关键.7.给出下列函数:①y =﹣3x +2:②y =3x ;③y =﹣5x:④y =3x ,上述函数中符合条件“当x >1时,函数值y 随自变量x 增大而增大”的是( )A .①③B .③④C .②④D .②③【答案】B【解析】【分析】分别利用一次函数、正比例函数、反比例函数的增减性分析得出答案.【详解】解:①y =﹣3x +2,当x >1时,函数值y 随自变量x 增大而减小,故此选项不符合题意; ②y =3x,当x >1时,函数值y 随自变量x 增大而减小,故此选项不符合题意; ③y =﹣5x,当x >1时,函数值y 随自变量x 增大而增大,故此选项符合题意; ④y =3x ,当x >1时,函数值y 随自变量x 增大而增大,故此选项符合题意; 故选:B .【点睛】 此题考查一次函数、正比例函数、反比例函数,正确把握相关性质是解题关键. 8.若一个圆锥侧面展开图的圆心角是270°,圆锥母线l 与底面半径r 之间的函数关系图象大致是( )A .B .C .D .【答案】A【解析】【分析】根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长得到2πr=270180l π⋅⋅,整理得l=43r (r >0),然后根据正比例函数图象求解.【详解】 解:根据题意得2πr=270180l π⋅⋅,所以l=43r (r >0), 即l 与r 为正比例函数关系,其图象在第一象限.故选A .【点睛】本题考查圆锥的计算;函数的图象.9.如图,ABDC Y 的顶点,A B 的坐标分别是()(), 0,3 1, 0A B -,顶点,C D 在双曲线k y x=上,边BD 交y 轴于点E ,且四边形ACDE 的面积是ABE ∆面积的3倍,则k 的值为:( )A .6-B .4-C .3-D .12-【答案】A【解析】【分析】 过D 作DF//y 轴,过C 作//CF x 轴,交点为F ,利用平行四边形的性质证明,DCF ABO ∆≅∆利用平移写好,C D 的坐标,由四边形ACDE 的面积是ABE ∆面积的3倍,得到2,DB BE =利用中点坐标公式求横坐标,再利用反比例函数写D 的坐标,列方程求解k .【详解】解:过D 作DF//y 轴,过C 作//CF x 轴,交点为F ,则,CF DF ⊥ABDC QY ,,CDF BAO ∴∠∠的两边互相平行,,AB DC =CDF BAO ∴∠=∠,90,DFC BOA ∠=∠=︒Q,DCF ABO ∴∆≅∆,,CF BO DF AO ∴==设(,),k C m m由()(), 0,3 1, 0A B -结合平移可得:(1,3)k D m m++, Q 四边形ACDE 的面积是ABE ∆面积的3倍, 11()322BD BE DE CA h h BE ∴+=⨯⨯,,,BD BE h h AC BD ==Q3DE AC BE ∴+=,4,DE BD BE BE ∴++=2,DB BE ∴=(1,3),(1,0),0,E k D m B x m++=Q ∴ 由中点坐标公式知:110,2m ++= 2m ∴=- ,(1,)1k D m m ++Q , 3212k k ∴=+-+-, 6.k ∴=-故选A .【点睛】本题考查的是反比例函数的图像与性质,平行四边形的性质,平移性质,中点坐标公式,掌握以上知识点是解题关键.10.如图,二次函数2y ax bx c =++的图象如图所示,则一次函数y ax c =+和反比例函数b y x=在同平面直角坐标系中的图象大致是( )A .B .C .D .【答案】D【解析】【分析】直接利用二次函数图象经过的象限得出a ,b ,c 的值取值范围,进而利用一次函数与反比例函数的性质得出答案.【详解】∵二次函数y=ax 2+bx+c 的图象开口向下,∴a <0,∵二次函数y=ax 2+bx+c 的图象经过原点,∴c=0,∵二次函数y=ax 2+bx+c 的图象对称轴在y 轴左侧,∴a ,b 同号,∴b <0,∴一次函数y=ax+c ,图象经过第二、四象限,反比例函数y=b x图象分布在第二、四象限, 故选D .【点睛】此题主要考查了反比例函数、一次函数、二次函数的图象,正确把握相关性质是解题关键.11.如图,在平面直角坐标系中,等腰直角三角形ABC 的顶点A 、B 分别在x 轴、y 轴的正半轴上,90ABC ∠=︒,CA x ⊥轴,点C 在函数()0k y x x=>的图象上,若1AB =,则k 的值为( )A .1B .22C 2D .2【答案】A【解析】【分析】根据题意可以求得 OA 和 AC 的长,从而可以求得点 C 的坐标,进而求得 k 的 值,本题得以解决.【详解】Q 等腰直角三角形ABC 的顶点A 、B 分别在x 轴、y 轴的正半轴上,90ABC ∠=︒,CA ⊥x 轴,1AB =,45BAC BAO ︒∴∠=∠=, 2OA OB ∴==,2AC =, ∴点C 的坐标为2,22⎛⎫ ⎪ ⎪⎝,Q 点C 在函数()0k y x x=>的图象上, 2212k ∴=⨯=, 故选:A .【点睛】本题考查反比例函数图象上点的坐标特征、等腰直角三角形,解答本题的关键 是明确题意,利用数形结合的思想解答.12.如图所示,已知()121,,2,2A y B y ⎛⎫ ⎪⎝⎭为反比例函数1y x =图象上的两点,动点(),0P x 在x 轴正半轴上运动,当AP BP -的值最大时,连结OA ,AOP ∆的面积是 ( )A .12B .1C .32D .52【答案】D【解析】【分析】先根据反比例函数解析式求出A ,B 的坐标,然后连接AB 并延长AB 交x 轴于点P ',当P 在P '位置时,PA PB AB -=,即此时AP BP -的值最大,利用待定系数法求出直线AB 的解析式,从而求出P '的坐标,进而利用面积公式求面积即可.【详解】当12x=时,2y=,当2x=时,12y=,∴11(,2),(2,)22A B.连接AB并延长AB交x轴于点P',当P在P'位置时,PA PB AB-=,即此时AP BP-的值最大.设直线AB的解析式为y kx b=+,将11(,2),(2,)22A B代入解析式中得122122k bk b⎧+=⎪⎪⎨⎪+=⎪⎩解得152kb=-⎧⎪⎨=⎪⎩,∴直线AB解析式为52y x=-+.当0y=时,52x=,即5(,0)2P',115522222AOP AS OP y'∴=⋅=⨯⨯=V.故选:D.【点睛】本题主要考查一次函数与几何综合,掌握待定系数法以及找到AP BP-何时取最大值是解题的关键.13.如图,若直线2y x n=-+与y轴交于点B,与双曲线()2y xx=-<交于点(),1A m,则AOBV的面积为()A .6B .5C .3D .1.5【答案】C【解析】【分析】 先根据题意求出A 点坐标,再求出一次函数解析式,从而求出B 点坐标,则问题可解.【详解】解:由已知直线2y x n =-+与y 轴交于点B ,与双曲线()20y x x =-<交于点(),1A m ∴21m=-则m=-2 把A (-2,1)代入到2y x n =-+,得()122n =-⨯-+∴n=-3∴23y x =--则点B (0,-3)∴AOB V 的面积为132=32⨯⨯ 故应选:C【点睛】本题考查的是反比例函数与一次函数的综合问题,解题关键是根据题意应用数形结合思想.14.如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A 在反比例函数y=6x(x >0)的图象上,则经过点B 的反比例函数解析式为( )A .y=﹣6xB .y=﹣4xC .y=﹣2xD .y=2x【解析】【分析】直接利用相似三角形的判定与性质得出13 BCOAODSS= VV,进而得出S△AOD=3,即可得出答案.【详解】过点B作BC⊥x轴于点C,过点A作AD⊥x轴于点D,∵∠BOA=90°,∴∠BOC+∠AOD=90°,∵∠AOD+∠OAD=90°,∴∠BOC=∠OAD,又∵∠BCO=∠ADO=90°,∴△BCO∽△ODA,∵BOAO=tan30°=3,∴13BCOAODSS=VV,∵12×AD×DO=12xy=3,∴S△BCO=12×BC×CO=13S△AOD=1,∵经过点B的反比例函数图象在第二象限,故反比例函数解析式为:y=﹣2x.故选C.【点睛】此题主要考查了相似三角形的判定与性质,反比例函数数的几何意义,正确得出S△AOD=2是解题关键.15.若反比例函数()2221my m x-=-的图象在第二、四象限,则m的值是()A.-1或1 B.小于12的任意实数 C.-1 D.不能确定【解析】【分析】根据反比例函数的定义列出方程221m -=-且210m -<求解即可.【详解】解:22(21)m y m x -=-Q 是反比例函数,∴221m -=-,210m -≠,解之得1m =±.又因为图象在第二,四象限,所以210m -<, 解得12m <,即m 的值是1-. 故选:C .【点睛】 对于反比例函数()0k y k x=≠.(1)0k >,反比例函数图像分布在一、三象限;(2)k 0< ,反比例函数图像分布在第二、四象限内.16.当0x <时,反比例函数2y x=-的图象( ) A .在第一象限,y 随x 的增大而减小 B .在第二象限,y 随x 的增大而增大C .在第三象限,y 随x 的增大而减小D .在第四象限,y 随x 的增大而减小 【答案】B【解析】【分析】 反比例函数2y x =-中的20k =-<,图像分布在第二、四象限;利用0x <判断即可. 【详解】解:Q 反比例函数2y x=-中的20k =-<, ∴该反比例函数的图像分布在第二、四象限;又0x <Q ,∴图象在第二象限且y 随x 的增大而增大.故选:B .【点睛】 本题主要考查的是反比例函数的性质,对于反比例函数()0k y k x=≠,(1)0k >,反比例函数图像分布在一、三象限;(2)k 0< ,反比例函数图像分布在第二、四象限内.17.已知反比例函数2y x =-,下列结论不正确的是 A .图象必经过点(-1,2)B .y 随x 的增大而增大C .图象在第二、四象限内D .若x >1,则y >-2 【答案】B【解析】【分析】此题可根据反比例函数的性质,即函数所在的象限和增减性对各选项作出判断.【详解】解: A 、把(-1,2)代入函数解析式得:2=-21-成立,故点(-1,2)在函数图象上,故选项正确;B 、由k=-2<0,因此在每一个象限内,y 随x 的增大而增大,故选项不正确;C 、由k=-2<0,因此函数图象在二、四象限内,故选项正确;D 、当x=1,则y=-2,又因为k=-2<0,所以y 随x 的增大而增大,因此x >1时,-2<y <0,故选项正确;故选B .【点睛】本题考查反比例函数的图像与性质.18.如图,A 、C 是函数1y x=的图象上任意两点,过点A 作y 轴的垂线,垂足为B ,过点C 作y 轴的垂线,垂足为D .记Rt AOB ∆的面积为1S ,Rt COD ∆的面积为2S ,则1S 和2S 的大小关系是( )A .12S S >B .12S S <C .12=S SD .由A 、C 两点的位置确定【答案】C【解析】【分析】 根据双曲线的图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=12k|.【详解】由题意得:S1=S2=12|k|=12.故选:C.【点睛】本题主要考查了反比例函数y=kx中k的几何意义,即图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=12|k|,是经常考查的一个知识点;这里体现了数形结合的思想.19.如图,直线y=k和双曲线y=kx相交于点P,过点P作PA0垂直于x轴,垂足为A0,x 轴上的点A0,A1,A2,…A n的横坐标是连续整数,过点A1,A2,…A n:分别作x轴的垂线,与双曲线y=kx(k>0)及直线y=k分别交于点B1,B2,…B n和点C1,C2,…C n,则n nn nA BC B 的值为()A.11n+B.11n-C.1nD.11n-【答案】C【解析】【分析】由x轴上的点A0,A1,A2,…,A n的横坐标是连续整数,则得到点An(n+1,0),再分别表示出∁n(n+1,k),B n(n+1,kn1+),根据坐标与图形性质计算出A n B n=kn1+,B n∁n =k﹣kn1+,然后计算n nn nA BB C.【详解】∵x轴上的点A0,A1,A2,…,A n的横坐标是连续整数,∴An(n+1,0),∵∁n A n⊥x轴,∴∁n (n +1,k ),B n (n +1,k n 1+), ∴A nB n =k n 1+,B n ∁n =k ﹣k n 1+, ∴n n n n A B B C =11k n k k n +-+=1n . 故选:C .【点睛】考查了反比例函数与一次函数的交点问题,解题关键是抓住了反比例函数与一次函数图象的交点坐标满足两函数解析式.20.如图,,A B 是双曲线k y x=上两点,且,A B 两点的横坐标分别是1-和5,ABO -∆的面积为12,则k 的值为( )A .3-B .4-C .5-D .6-【答案】C【解析】【分析】 分别过点A 、B 作AD ⊥x 轴于点D ,BE ⊥x 轴于点E ,根据S △AOB =S 梯形ABED +S △AOD - S △BOE =12,故可得出k 的值.【详解】分别过点A 、B 作AD ⊥x 轴于点D ,BE ⊥x 轴于点E ,∵双曲线k y x=的图象的一支在第二象限 ∴k<0,∵A ,B 两点在双曲线k y x=的图象上,且A ,B 两点横坐标分别为:-1,-5, ∴A (-1,-k ),B (-5, 5k -) ∴S △AOB =S 梯形ABED +S △AOD - S △BOE =1||11||(||)(51)1||525225k k k k ⨯+⨯-+⨯⨯-⨯⨯=12||5k =12, 解得,k=-5故选:C .【点睛】 本题考查反比例函数系数k 的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|.本知识点是中考的重要考点,同学们应高度关注.。
中考数学备考专题复习反比例函数含解析

反比例函数一、单选题(共12题;共24分)1、(2016•龙东)已知反比例函数y= ,当1<x<3时,y的最小整数值是()A、3B、4C、5D、62、如果等腰三角形的底边长为x,底边上的高为y,则它的面积为定植S时,则x与y的函数关系式为()A、y=B、y=C、y=D、y=3、(2016•大庆)已知A(x1, y1)、B(x2, y2)、C(x3, y3)是反比例函数y= 上的三点,若x1<x2<x3, y2<y1<y3,则下列关系式不正确的是()A、x1•x2<0B、x1•x3<0C、x2•x3<0D、x1+x2<04、将一次函数y=x图象向下平移b个单位,与双曲线y=交于点A,与x轴交于点B,则OA2-OB2=( )A、-2B、2C、-D 、5、如图所示,点P(3a,a)是反比例函数y=(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为()A、y=B、y=C、y=D、y=6、如图,△AOB为等边三角形,点A在第四象限,点B的坐标为(4,0),过点C(4,0)作直线l交AO于D,交AB于E,且点E在某反比例函数y=(k≠0)图象上,当△ADE和△DCO的面积相等时,k的值为()A、-B、-C、-3D、-67、教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的()A、7:20B、7:30C、7:45D、7:508、(2015•玉林)如图,反比例函数y=的图象经过二次函数y=ax2+bx 图象的顶点(﹣,m)(m >0),则有()A、a=b+2kB、a=b﹣2kC、k<b<0D、a<k<09、如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=1,点A在函数y=﹣(x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y= (x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是()A 、B 、C 、D 、10、(2016•济宁)如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB= ,反比例函数y= 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于()A、60B、80C、30D、4011、(2016•湖北)一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为()A 、B 、C 、D 、12、(2016•天津)若点A(﹣5,y1),B(﹣3,y2),C(2,y3)在反比例函数y= 的图象上,则y1, y2, y3的大小关系是()A、y1<y3<y2B、y1<y2<y3C、y3<y2<y1D、y2<y1<y3二、填空题(共5题;共6分)13、如果函数y=x2m-1为反比例函数,则m的值是________.14、(2015•黄石)反比例函数y=的图象有一支位于第一象限,则常数a的取值范围是________ .15、(2016•宁波)如图,点A为函数y= (x>0)图象上一点,连结OA,交函数y= (x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为________.16、(2016•丽水)如图,一次函数y=﹣x+b与反比例函数y= (x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D两点,连结OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.(1)b=________(用含m的代数式表示);(2)若S△OAF+S四边形EFBC=4,则m的值是________.17、(2016•绍兴)如图,已知直线l:y=﹣x,双曲线y= ,在l上取一点A(a,﹣a)(a>0),过A作x轴的垂线交双曲线于点B,过B作y轴的垂线交l于点C,过C作x轴的垂线交双曲线于点D,过D作y轴的垂线交l于点E,此时E与A重合,并得到一个正方形ABCD,若原点O在正方形ABCD的对角线上且分这条对角线为1:2的两条线段,则a的值为________.三、解答题(共3题;共15分)18、当m 取何值时,函数是反比例函数?19、(2016•苏州)如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y= (x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.20、已知与是反比例函数图象上的两个点.(1)求m和k的值(2)若点C(-1,0),连结AC,BC,求△ABC的面积(3)根据图象直接写出一次函数的值大于反比例函数的值的的取值范围.四、综合题(共4题;共45分)21、(2016•曲靖)在平面直角坐标系中,把横纵坐标都是整数的点称为“整点”.(1)直接写出函数y= 图象上的所有“整点”A1, A2, A3,…的坐标;(2)在(1)的所有整点中任取两点,用树状图或列表法求出这两点关于原点对称的概率.22、(2015•广州)已知反比例函数y=的图象的一支位于第一象限.(1)判断该函数图象的另一支所在的象限,并求m的取值范围;(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值.23、(2016•枣庄)如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y= (k>0)的图象与BC边交于点E.(1)当F为AB的中点时,求该函数的解析式;(2)当k为何值时,△EFA的面积最大,最大面积是多少?24、(2016•雅安)已知直线l1:y=x+3与x轴交于点A,与y轴交于点B,且与双曲线y= 交于点C(1,a).(1)试确定双曲线的函数表达式;(2)将l1沿y轴翻折后,得到l2,画出l2的图象,并求出l2的函数表达式;(3)在(2)的条件下,点P是线段AC上点(不包括端点),过点P作x轴的平行线,分别交l2于点M,交双曲线于点N,求S△AMN的取值范围.答案解析部分一、单选题【答案】A【考点】反比例函数的性质【解析】【解答】解:在反比例函数y= 中k=6>0,∴该反比例函数在x>0内,y随x的增大而减小,当x=3时,y= =2;当x=1时,y= =6.∴当1<x<3时,2<y<6.∴y的最小整数值是3.故选A.【分析】根据反比例函数系数k>0,结合反比例函数的性质即可得知该反比例函数在x>0中单调递减,再结合x的取值范围,可得出y的取值范围,取其内的最小整数,本题得解.本题考查了反比例函数的性质,解题的关键是找出反比例函数y= 在1<x<3中y的取值范围.本题属于基础题,难度不大,解决该题型题目时,根据反比例函数的系数结合反比例函数的性质得出该反比例函数的单调性是关键.【答案】C【考点】根据实际问题列反比例函数关系式,三角形的面积【解析】【解答】∵S=xy,∴y=.故选C.【分析】考查列反比例函数关系式,得到三角形高的等量关系是解决本题的关键.三角形的面积= 1 2 底×高,那么高=,把相关数值代入即可求解.【答案】A【考点】反比例函数图象上点的坐标特征【解析】【解答】解:∵反比例函数y= 中,2>0,∴在每一象限内,y随x的增大而减小,∵x1<x2<x3, y2<y1<y3,∴点A,B在第三象限,点C在第一象限,∴x1<x2<0<x3,∴x1•x2<0,故选A.【分析】根据反比例函数y= 和x1<x2<x3, y2<y1<y3,可得点A,B在第三象限,点C在第一象限,得出x1<x2<0<x3,再选择即可.本题考查了反比例函数图象上点的坐标特征,解答此题的关键是熟知反比例函数的增减性,本题是逆用,难度有点大.【答案】B【考点】一次函数图象与几何变换,反比例函数与一次函数的交点问题【解析】【解答】∵平移后解析式是y=x+b,代入y=得:x+b=,即x2+bx=,y=x+b与x轴交点B的坐标是(-b,0),设A的坐标是(x,y),∴OA2-OB2=x2+y2+(-b)2=x2+(x+b)2-b2=2x2+2xb=2(x2+xb)=2×=2,故选B.【分析】本题考查了一次函数和反比例函数的交点问题的应用,主要考查学生的计算能力的能力.【答案】D【考点】反比例函数图象的对称性【解析】【解答】由于函数图象关于原点对称,所以阴影部分面积为圆面积,则圆的面积为10π×4=40π.因为P(3a,a)在第一象限,则a>0,3a>0,根据勾股定理,OP=于是π=40π,a=±2,(负值舍去),故a=2.P点坐标为(6,2).将P(6,2)代入y=,得:k=6×2=12.反比例函数解析式为:y=.故选D.【分析】根据P(3a,a)和勾股定理,求出圆的半径,进而表示出圆的面积,再根据圆的面积等于阴影部分面积的四倍,求出圆的面积,建立等式即可求出a的值,从而得出反比例函数的解析式.【点评】此题是一道综合题,既要能熟练正确求出圆的面积,又要会用待定系数法求函数的解析式.【答案】C【考点】反比例函数系数k的几何意义,待定系数法求反比例函数解析式,三角形的面积【解析】【解答】如图,连接AC,∵点B的坐标为(4,0),△AO B为等边三角形,∴AO=OB=4.∴点A的坐标为(2,-2).∵C(4,0),∴AO=OC=4,∴∠OCA=∠OAC.∵∠AOB=60°,∴∠ACO=30°.又∵∠B="60°." ∴∠BAC=90°.∵S△ADE=S△DCO, S△AEC=S△ADE+S△ADC, S△AOC=S△DCO+S△ADC,∴∴S△AEC=S△AOC =×AE•AC=•CO•2,即•AE•2=×2×2,∴E点为AB的中点(3,-).把E点(3,-)代入y=中得:k=-3故选C.【分析】连接AC,由B的坐标得到等边三角形AOB的边长,得到AO与CO,得到AO=OC,利用等边对等角得到一对角相等,再由∠AOB=60°,得到∠ACO=30°,可得出∠BAC为直角,可得出A的坐标,由三角形ADE与三角形DCO面积相等,且三角形AEC面积等于三角形AED与三角形ADC面积之和,三角形AOC面积等于三角形DCO面积与三角形ADC面积之和,得到三角形AEC与三角形AOC面积相等,进而确定出AE的长,可得出E为AB中点,得出E的坐标,将E坐标代入反比例解析式中求出k的值,即可确定出反比例解析式。
反比例函数整章知识点复习

在生物学中,反比例函数可用于描述种群数量与资 源之间的关系,如食物与捕食者数量等。
03
反比例函数的图像与性质
反比例函数的图像绘制
通过选择适当的x值,计算对应的y值 ,在坐标系上标出对应的点,连接各 点绘制出反比例函数的图像。
100%
经济问题
在经济学中,反比例函数可以用 来描述成本与产量的关系、供需 关系等。
80%
生态问题
在生态学中,反比例函数可以用 来描述种群数量与环境容量的关 系等。
05
反比例函数习题解析
基础题目解析
01
02
03
题目
已知点$P(x, y)$在反比例 函数$y = frac{k}{x}$的图 象上,若$x$与$y$的乘积 为$2k$,则$k$的值为 ____.
竞赛题目解析
01
k、a、b 的值;
02
k、a、b 的值;
03
k、a、b 的值;
04
k、a、b 的值;
THANK YOU
感谢聆听
反比例函数的计算方法
01
对于反比例函数
$f(x)
=
frac{k}{x}$,求值时只需将 $x$ 值
代入函数中即可。
02
若需要求 $f(x)$ 的导数或积分, 则需使用相应的微积分法则进行 计算。
反比例函数在实际问题中的应用
在物理学中,反比例函数可用于描述两个物理量之 间的反比关系,如电荷与电场强度、电流与电阻等 。
反比例函数的图像
图像特点
双曲线,分布在两个象限内,随着k的正负变化而分别分布在第一 、三象限或第二、四象限。
中考数学专题复习:反比例函数经典
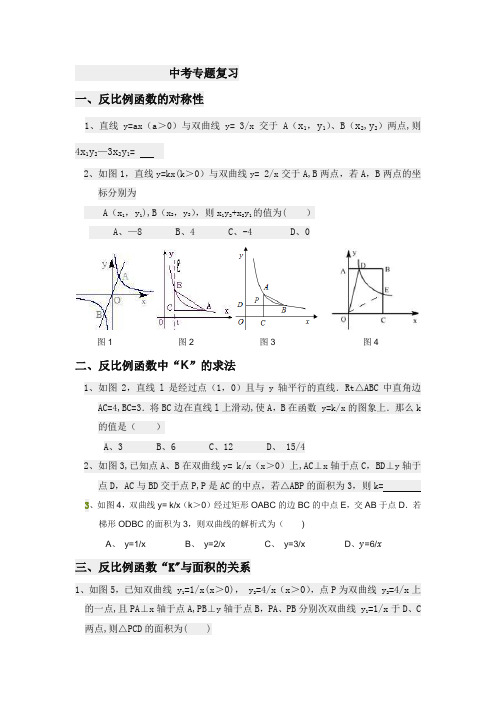
中考专题复习一、反比例函数的对称性1、直线y=ax(a>0)与双曲线y= 3/x交于A(x1,y1)、B(x2,y2)两点,则2、如图1,直线y=kx(k>0)与双曲线y= 2/x交于A,B两点,若A,B两点的坐标分别为A(x1,y1),B(x2,y2),则x1y2+x2y1的值为( )A、—8B、4C、-4D、0图1 图2 图3 图4二、反比例函数中“K”的求法1、如图2,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数 y=k/x的图象上.那么k 的值是()A、3B、6C、12D、 15/42、如图3,已知点A、B在双曲线y= k/x(x>0)上,AC⊥x轴于点C,BD⊥y轴于3、如图4,双曲线y= k/x(k>0)经过矩形OABC的边BC的中点E,交AB于点D.若梯形ODBC的面积为3,则双曲线的解析式为()A、y=1/xB、y=2/xC、y=3/xD、y=6/x三、反比例函数“K"与面积的关系1、如图5,已知双曲线 y1=1/x(x>0), y2=4/x(x>0),点P为双曲线y2=4/x上的一点,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别次双曲线y1=1/x于D、C 两点,则△PCD的面积为( )图5 图6 图72、如图6,直线l和双曲线 y=k/x(k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、0P,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则() A、S1<S2<S3B、S1>S2>S3C、S1=S2>S3D、S1=S2<S33、如图7,已知直线y=-x+3与坐标轴交于A、B两点,与双曲线 y=k/x交于C、D4、反比例函数y= 6/x 与y= 3/x在第一象限的图象如图8所示,作一条平行于x轴的直线分别交双曲线于A、B两点,连接OA、OB,则△AOB的面积为( )A、 3/2B、2C、3D、1图8 图9 图10 图115、如图9,已知梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,过点C的双曲线y=k/x交OB于D,且OD:DB=1:2,若△OBC的面积等于3,则k的值()A、等于2B、等于 3/4C、等于 24/5D、无法确定6、如图10,反比例函数y=k/x(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.若四边形ODBE的面积为6,则k的值为()A、1B、2C、3D、47、如图11,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交x轴于E(2,0),则四边形AOEC的面积为()A、根号3B、 3C、根号3-1D、根号3+18、如图,A、B是双曲线y= k/x(k>0)上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6.则k=图1 图2 图3四、反比例函数与一次函数综合:1、如图1,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y= 1/x(x>0)2、如图2,过y轴上任意一点P,作x轴的平行线,分别与反比例函数 y=—4/x和y=2/x 的图象交于A 点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积为( )A、3B、4C、5D、63、如图3,直线y=-x+b(b>0)与双曲线y= k/x(x>0)交于A、B两点,连接OA、OB,AM⊥y轴于M,BN⊥x轴于N;有以下结论:①OA=OB;②△AOM≌△BON;③若∠AOB=45°,则S△AOB=k;④当AB= 2时,ON—BN=1;其中结论正确的个数为()A、1B、2C、3D、44、如图4,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数 y=4/x(x>0)图象上位于直线下方的一点,过点P作x轴的垂线,垂足为点M,交AB于点E,过点P作y轴的垂线,垂足为点N,交AB于点F.则AF•BE=() A、8 B、6 C、4 D、 6倍根号2图4 图55、如图5,反比例函数 y=k/x(k>0)与一次函数 y=1/2x+b的图象相交于两点A(x1,y1),B(x2,y2),线段AB交y轴与C,当|x1-x2|=2且AC=2BC时,k、b的值分别为( )A、k= 1/2,b=2B、k= 4/9,b=1C、k= 1/3,b= 1/3D、k= 4/9,b= 1/3五、综合(函数与几何)1、如图,▱ABCD的顶点A、B的坐标分别是A(-1,0),B(0,—2),顶点C、D在双曲线y= k/x上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k=.2、如图,已知C、D是双曲线,y= m/x在第一象限内的分支上的两点,直线CD分别交x轴、y轴于A、B两点,设C、D的坐标分别是(x1,y1)、(x2,y2),连接OC、OD.(1)求证:y1<OC<y1+ m/y1;(2)若∠BOC=∠AOD=a,tana= 1/3,OC= 根号10,求直线CD的解析式;(3)在(2)的条件下,双曲线上是否存在一点P,使得S△POC=S△POD?若存在,请给出证明;若不存在,请说明理由.3、如图,将一矩形OABC放在直角坐际系中,O为坐标原点.点A在x轴正半轴上.点E 是边AB上的一个动点(不与点A、N重合),过点E的反比例函数y=k/x(x>0)的图象与边BC交于点F.(1)若△OAE、△OCF的而积分别为S1、S2.且S1+S2=2,求k的值;(2)若OA=2.0C=4.问当点E运动到什么位置时.四边形OAEF的面积最大.其最大值为多少?4、如图,已知直线l经过点A(1,0),与双曲线y= m/x(x>0)交于点B(2,1).过点P (p,p-1)(p>1)作x轴的平行线分别交双曲线y= m/x(x>0)和y=- m/x(x<0)于点M、N.(1)求m的值和直线l的解析式;(2)若点P在直线y=2上,求证:△PMB∽△PNA;(3)是否存在实数p,使得S△AMN=4S△AMP?若存在,请求出所有满足条件的p的值;若不存在,请说明理由.5、如图,四边形OABC是面积为4的正方形,函数y=k/x(x>0)的图象经过点B、E,F;(1)求k的值;(2)将正方形OABC分别沿直线AB、BC翻折,得到正方形MABC′、NA′BC.设线段MC′、NA′分别与函数y=k/x(x>0)的图象交于点E、F,求线段EF所在直线的解析式.。
中考数学复习----反比例函数之定义、图像与性质知识点总结与练习题(含答案解析)
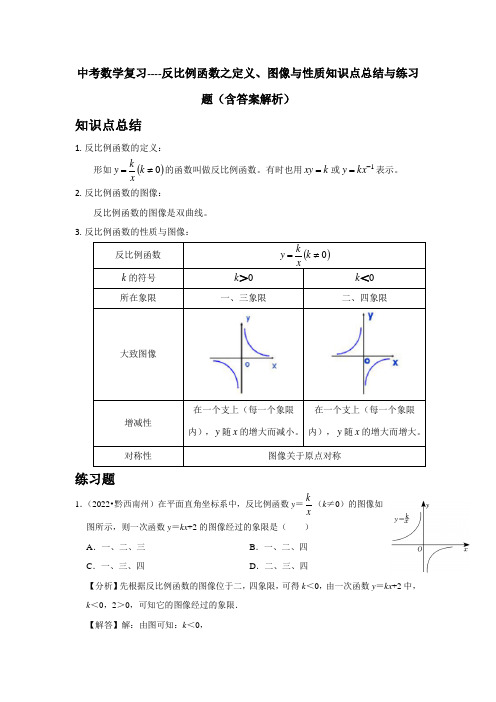
中考数学复习----反比例函数之定义、图像与性质知识点总结与练习题(含答案解析)知识点总结1. 反比例函数的定义:形如()0≠=k xky 的函数叫做反比例函数。
有时也用k xy =或1−=kx y 表示。
2. 反比例函数的图像:反比例函数的图像是双曲线。
3. 反比例函数的性质与图像:反比例函数()0≠=k xky k 的符号0>k0<k所在象限一、三象限二、四象限大致图像增减性在一个支上(每一个象限内),y 随x 的增大而减小。
在一个支上(每一个象限内),y 随x 的增大而增大。
对称性图像关于原点对称练习题1.(2022•黔西南州)在平面直角坐标系中,反比例函数y =xk(k ≠0)的图像如图所示,则一次函数y =kx +2的图像经过的象限是( ) A .一、二、三 B .一、二、四C .一、三、四D .二、三、四【分析】先根据反比例函数的图像位于二,四象限,可得k <0,由一次函数y =kx +2中,k <0,2>0,可知它的图像经过的象限. 【解答】解:由图可知:k <0,∴一次函数y =kx +2的图像经过的象限是一、二、四. 故选:B .2.(2022•上海)已知反比例函数y =xk(k ≠0),且在各自象限内,y 随x 的增大而增大,则下列点可能在这个函数图像上的为( ) A .(2,3)B .(﹣2,3)C .(3,0)D .(﹣3,0)【分析】根据反比例函数的性质判断即可.【解答】解:因为反比例函数y =(k ≠0),且在各自象限内,y 随x 的增大而增大, 所以k <0,A .2×3=6>0,故本选项不符合题意;B .﹣2×3=﹣6<0,故本选项符合题意;C .3×0=0,故本选项不符合题意;D .﹣3×0=0,故本选项不符合题意; 故选:B .3.(2022•广东)点(1,y 1),(2,y 2),(3,y 3),(4,y 4)在反比例函数y =x4图像上,则y 1,y 2,y 3,y 4中最小的是( ) A .y 1B .y 2C .y 3D .y 4【分析】根据k >0可知增减性:在每一象限内,y 随x 的增大而减小,根据横坐标的大小关系可作判断. 【解答】解:∵k =4>0,∴在第一象限内,y 随x 的增大而减小,∵(1,y 1),(2,y 2),(3,y 3),(4,y 4)在反比例函数y =图像上,且1<2<3<4, ∴y 4最小. 故选:D .4.(2022•云南)反比例函数y =x6的图像分别位于( ) A .第一、第三象限 B .第一、第四象限 C .第二、第三象限D .第二、第四象限【分析】根据反比例函数的性质,可以得到该函数图像位于哪几个象限,本题得以解决.【解答】解:反比例函数y =,k =6>0, ∴该反比例函数图像位于第一、三象限, 故选:A .5.(2022•镇江)反比例函数y =xk(k ≠0)的图像经过A (x 1,y 1)、B (x 2,y 2)两点,当x 1<0<x 2时,y 1>y 2,写出符合条件的k 的值 (答案不唯一,写出一个即可). 【分析】先根据已知条件判断出函数图像所在的象限,再根据系数k 与函数图像的关系解答即可.【解答】解:∵反比例函数y =(k ≠0)的图像经过A (x 1,y 1)、B (x 2,y 2)两点,当x 1<0<x 2时,y 1>y 2,∴此反比例函数的图像在二、四象限, ∴k <0,∴k 可为小于0的任意实数,例如,k =﹣1等. 故答案为:﹣1.6.(2022•福建)已知反比例函数y =xk的图像分别位于第二、第四象限,则实数k 的值可以是 .(只需写出一个符合条件的实数)【分析】根据图像位于第二、四象限,易知k <0,写一个负数即可. 【解答】解:∵该反比例图像位于第二、四象限, ∴k <0,∴k 取值不唯一,可取﹣3, 故答案为:﹣3(答案不唯一).7.(2022•成都)在平面直角坐标系xOy 中,若反比例函数y =xk 2−的图像位于第二、四象限,则k 的取值范围是 .【分析】根据反比例函数的性质列不等式即可解得答案. 【解答】解:∵反比例函数y =的图像位于第二、四象限,∴k ﹣2<0, 解得k <2, 故答案为:k <2.8.(2022•襄阳)二次函数y =ax 2+bx +c 的图像如图所示,则一次函数y =bx +c 和反比例函数y =xa在同一平面直角坐标系中的图像可能是( ) A . B .C .D .【分析】根据二次函数图像开口向下得到a <0,再根据对称轴确定出b ,根据与y 轴的交点确定出c <0,然后确定出一次函数图像与反比例函数图像的情况,即可得解. 【解答】解:∵二次函数图像开口方向向下, ∴a <0,∵对称轴为直线x =﹣>0,∴b >0,∵与y 轴的负半轴相交, ∴c <0,∴y =bx +c 的图像经过第一、三、四象限, 反比例函数y =图像在第二四象限, 只有D 选项图像符合. 故选:D .9.(2022•菏泽)根据如图所示的二次函数y =ax 2+bx +c 的图像,判断反比例函数y =xa与一次函数y =bx +c 的图像大致是( )A .B .C .D .【分析】先根据二次函数的图像,确定a 、b 、c 的符号,再根据a 、b 、c 的符号判断反比例函数y =与一次函数y =bx +c 的图像经过的象限即可. 【解答】解:由二次函数图像可知a >0,c <0, 由对称轴x =﹣>0,可知b <0,所以反比例函数y =的图像在一、三象限,一次函数y =bx +c 图像经过二、三、四象限. 故选:A .10.(2022•安顺)二次函数y =ax 2+bx +c (a ≠0)的图像如图所示,则一次函数y =ax +b 和反比例函数y =xc(c ≠0)在同一直角坐标系中的图像可能是( ) A . B .C .D .【分析】直接利用二次函数图像经过的象限得出a ,b ,c 的取值范围,进而利用一次函数与反比例函数的性质得出答案.【解答】解:∵二次函数y =ax 2+bx +c 的图像开口向上, ∴a >0,∵该抛物线对称轴位于y 轴的右侧, ∴a 、b 异号,即b <0. ∵抛物线交y 轴的负半轴,∴c <0,∴一次函数y =ax +b 的图像经过第一、三、四象限,反比例函数y =(c ≠0)在二、四象限. 故选:A .11.(2022•西藏)在同一平面直角坐标系中,函数y =ax +b 与y =axb(其中a ,b 是常数,ab ≠0)的大致图像是( )A .B .C .D .【分析】根据a 、b 的取值,分别判断出两个函数图像所过的象限,要注意分类讨论. 【解答】解:若a >0,b >0,则y =ax +b 经过一、二、三象限,反比例函数y =(ab ≠0)位于一、三象限,若a >0,b <0,则y =ax +b 经过一、三、四象限,反比例函数数y =(ab ≠0)位于二、四象限, 若a <0,b >0,则y =ax +b 经过一、二、四象限,反比例函数y =(ab ≠0)位于二、四象限, 若a <0,b <0,则y =ax +b 经过二、三、四象限,反比例函数y =(ab ≠0)位于一、三象限, 故选:A .12.(2022•张家界)在同一平面直角坐标系中,函数y =kx +1(k ≠0)和y =xk(k ≠0)的图像大致是( )A.B.C.D.【分析】分k>0或k<0,根据一次函数与反比例函数的性质即可得出答案.【解答】解:当k>0时,一次函数y=kx+1经过第一、二、三象限,反比例函数y=位于第一、三象限;当k<0时,一次函数y=kx+1经过第一、二、四象限,反比例函数y=位于第二、四象限;故选:D.13.(2022•绥化)已知二次函数y=ax2+bx+c的部分函数图像如图所示,则一次函数y=ax+b2﹣4ac与反比例函数y=xc ba++24在同一平面直角坐标系中的图像大致是()A.B.C.D.【分析】由二次函数y=ax2+bx+c的部分函数图像判断a,b2﹣4ac及4a+2b+c的符号,即可得到答案.【解答】解:∵二次函数y=ax2+bx+c的部分函数图像开口向上,∴a>0,∵二次函数y =ax 2+bx +c 的部分函数图像顶点在x 轴下方,开口向上, ∴二次函数y =ax 2+bx +c 的图像与x 轴有两个交点,b 2﹣4ac >0, ∴一次函数y =ax +b 2﹣4ac 的图像位于第一,二,三象限,由二次函数y =ax 2+bx +c 的部分函数图像可知,点(2,4a +2b +c )在x 轴上方, ∴4a +2b +c >0, ∴y =的图像位于第一,三象限,据此可知,符合题意的是B , 故选:B .14.(2022•贺州)已知一次函数y =kx +b 的图像如图所示,则y =﹣kx +b 与y =xb的图像为( )A .B .C .D .【分析】本题形数结合,根据一次函数y =kx +b 的图像位置,可判断k 、b 的符号;再由一次函数y =﹣kx +b ,反比例函数y =中的系数符号,判断图像的位置.经历:图像位置﹣系数符号﹣图像位置.【解答】解:根据一次函数y =kx +b 的图像位置,可判断k >0、b >0. 所以﹣k <0.再根据一次函数和反比例函数的图像和性质, 故选:A .15.(2022•广西)已知反比例函数y =xb(b ≠0)的图像如图所示,则一次函数y =cx ﹣a (c ≠0)和二次函数y =ax 2+bx +c (a ≠0)在同一平面直角坐标系中的图像可能是( )A .B .C .D .【分析】本题形数结合,根据反比例函数y =(b ≠0)的图像位置,可判断b >0;再由二次函数y =ax 2+bx +c (a ≠0)的图像性质,排除A ,B ,再根据一次函数y =cx ﹣a (c ≠0)的图像和性质,排除C .【解答】解:∵反比例函数y =(b ≠0)的图像位于一、三象限, ∴b >0;∵A 、B 的抛物线都是开口向下,∴a <0,根据同左异右,对称轴应该在y 轴的右侧, 故A 、B 都是错误的.∵C 、D 的抛物线都是开口向上,∴a >0,根据同左异右,对称轴应该在y 轴的左侧, ∵抛物线与y 轴交于负半轴, ∴c <0由a >0,c <0,排除C . 故选:D .16.(2022•滨州)在同一平面直角坐标系中,函数y =kx +1与y =﹣xk(k 为常数且k ≠0)的图像大致是( )A .B .C .D .【分析】根据一次函数和反比例函数的性质即可判断.【解答】解:当k >0时,则﹣k <0,一次函数y =kx +1图像经过第一、二、三象限,反比例函数图像在第二、四象限,所以A 选项正确,C 选项错误;当k <0时,一次函数y =kx +1图像经过第一、二,四象限,所以B 、D 选项错误. 故选:A .17.(2022•德阳)一次函数y =ax +1与反比例函数y =﹣xa在同一坐标系中的大致图像是( )A .B .C .D .【分析】根据一次函数与反比例函数图像的特点,可以从a >0,和a <0,两方面分类讨论得出答案.【解答】解:分两种情况:(1)当a >0,时,一次函数y =ax +1的图像过第一、二、三象限,反比例函数y =﹣图像在第二、四象限,无选项符合;(2)当a <0,时,一次函数y =ax +1的图像过第一、二、四象限,反比例函数y =﹣图像在第一、三象限,故B 选项正确. 故选:B .18.(2022•阜新)已知反比例函数y =x k (k ≠0)的图像经过点(﹣2,4),那么该反比例函数图像也一定经过点( )A .(4,2)B .(1,8)C .(﹣1,8)D .(﹣1,﹣8)【分析】先把点(﹣2,4)代入反比例函数的解析式求出k 的值,再对各选项进行逐一判断即可.【解答】解:∵反比例函数y =(k ≠0)的图像经过点(﹣2,4),∴k =﹣2×4=﹣8,A 、∵4×2=8≠﹣8,∴此点不在反比例函数的图像上,故本选项错误;B 、∵1×8=8≠﹣8,∴此点不在反比例函数的图像上,故本选项错误;C 、﹣1×8=﹣8,∴此点在反比例函数的图像上,故本选项正确;D 、(﹣1)×(﹣8)=8≠﹣8,∴此点不在反比例函数的图像上,故本选项错误. 故选:C .19.(2022•襄阳)若点A (﹣2,y 1),B (﹣1,y 2)都在反比例函数y =x2的图像上,则y 1,y 2的大小关系是( )A .y 1<y 2B .y 1=y 2C .y 1>y 2D .不能确定 【分析】根据反比例函数图像上点的坐标特征即可求解.【解答】解:∵点A (﹣2,y 1),B (﹣1,y 2)都在反比例函数y =的图像上,k =2>0,∴在每个象限内y 随x 的增大而减小,∵﹣2<﹣1,∴y 1>y 2,故选:C .20.(2022•海南)若反比例函数y =xk (k ≠0)的图像经过点(2,﹣3),则它的图像也一定经过的点是( )A .(﹣2,﹣3)B .(﹣3,﹣2)C .(1,﹣6)D .(6,1) 【分析】将(2,﹣3)代入y =(k ≠0)即可求出k 的值,再根据k =xy 解答即可.【解答】解:∵反比例函数y =(k ≠0)的图像经过点(2,﹣3),∴k =2×(﹣3)=﹣6,A 、﹣2×(﹣3)=6≠﹣6,故A 不正确,不符合题意;B 、(﹣3)×(﹣2)=6≠﹣6,故B 不正确,不符合题意;C 、1×(﹣6)=﹣6,故C 正确,符合题意,D 、6×1=6≠﹣6,故D 不正确,不符合题意.故选:C .21.(2022•武汉)已知点A (x 1,y 1),B (x 2,y 2)在反比例函数y =x6的图像上,且x 1<0<x 2,则下列结论一定正确的是( )A .y 1+y 2<0B .y 1+y 2>0C .y 1<y 2D .y 1>y 2 【分析】先根据反比例函数y =判断此函数图像所在的象限,再根据x 1<0<x 2判断出A (x 1,y 1)、B (x 2,y 2)所在的象限即可得到答案.【解答】解:∵反比例函数y =中的6>0,∴该双曲线位于第一、三象限,且在每一象限内y 随x 的增大而减小,∵点A (x 1,y 1),B (x 2,y 2)在反比例函数y =的图像上,且x 1<0<x 2,∴点A 位于第三象限,点B 位于第一象限,∴y 1<y 2.故选:C .22.(2022•天津)若点A (x 1,2),B (x 2,﹣1),C (x 3,4)都在反比例函数y =x8的图像上,则x 1,x 2,x 3的大小关系是( )A .x 1<x 2<x 3B .x 2<x 3<x 1C .x 1<x 3<x 2D .x 2<x 1<x 3 【分析】根据函数解析式算出三个点的横坐标,再比较大小.【解答】解:点A (x 1,2),B (x 2,﹣1),C (x 3,4)都在反比例函数y =的图像上, ∴x 1==4,x 2==﹣8,x 3==2. ∴x 2<x 3<x 1,故选:B .23.(2022•淮安)在平面直角坐标系中,将点A (2,3)向下平移5个单位长度得到点B ,若点B 恰好在反比例函数y =xk 的图像上,则k 的值是 .【分析】点A (2,3)向下平移5个单位长度得到点B (2,﹣2),代入y =利用待定系数法即可求得k 的值.【解答】解:将点A (2,3)向下平移5个单位长度得到点B ,则B (2,﹣2), ∵点B 恰好在反比例函数y =的图像上,∴k =2×(﹣2)=﹣4,故答案为:﹣4.24.(2022•北京)在平面直角坐标系xOy 中,若点A (2,y 1),B (5,y 2)在反比例函数y =xk (k >0)的图像上,则y 1 y 2(填“>”“=”或“<”). 【分析】先根据函数解析式中的比例系数k 确定函数图像所在的象限,再根据各象限内点的坐标特征及函数的增减性解答.【解答】解:∵k >0,∴反比例函数y =(k >0)的图像在一、三象限,∵5>2>0,∴点A (2,y 1),B (5,y 2)在第一象限,y 随x 的增大而减小,∴y 1>y 2,故答案为:>.。
反比例函数复习

第十一章 反比例函数复习一、反比例函数的概念:1、一般地,形如 的函数叫做反比例函数。
注意:(1)常数 k 称为比例系数,k 是非零常数;(2)解析式有三种常见的表达形式:(A ) (B ) (C ) 1.下列函数,①1)2(=+y x ②11+=x y ③21xy = ④x y 21-=⑤x y 2-=⑥x y 31=;其中是y 关于x 的反比例函数的有:_________________. 2.函数22)2(--=ax a y 是反比例函数,则a 的值是3.已知函数21y y y -=,其中1y 与x 成正比例, 2y 与x 成反比例,且当x =1时,y =1;x =3时,y =5.求:(1)求y 关于x 的函数解析式; (2)当x =2时,y 的值.二、反比例函数的图象和性质: 1.形状:图象是双曲线。
2.位置:(1)当k>0时,双曲线分别位于第________象限内. (2)当k<0时, 双曲线分别位于第________象限内。
3.增减性:(1)当k>0时,_________________, y 随x 的增大而________. (2)当k<0时,_________________,y 随x 的增大而______。
4.变化趋势:双曲线无限接近于x 、y 轴,但永远不会与坐标轴相交5.对称性:对于双曲线本身来说,它的两个分支关于直角坐标系原点____________. 1.若反比例函数()2212--=mx m y 的图象在第二、四象限,则m 的值是( )A 、 -1或1B 、小于12的任意实数 C 、-1 D、不能确定 2. 函数y =-ax +a 与xay -=(a ≠0)在同一坐标系中的图象可能是( )3.正比例函数2x y =和反比例函数2y x=的图象有 个交点. 4.正比例函数5y x =-的图象与反比例函数(0)ky k x=≠的图象相交于点A (1,a ),则a = .5.正比例函数y=k 1x(k 1≠0)和反比例函数y=2k x(k 2≠0)的一个交点为(m,n),则另一个交点为 .三、反比例函数中k 的几何意义是:1.过双曲线(0)ky k x=≠上任意引x 轴y 轴的垂线,所得矩形面积为 。
中考数学复习《反比例函数》专题练习-附带参考答案

中考数学复习《反比例函数》专题练习-附带参考答案一、选择题1.下列函数关系式中,y 是x 的反比例函数的是( )A .y =x +3B .y =x 3C .y =3x 2D .y =3x 2.若反比例函数y=6x 的图像经过点(﹣2,a ),则a 的值是( )A .6B .﹣2C .﹣3D .3 3.已知反比例函数y =−1x ,下列结论不正确...的是( ) A .该函数图象经过点(−1,1)B .该函数图象位于第二、四象限C .y 的值随着x 值的增大而增大D .该函数图象关于原点成中心对称 4.反比例函数(其中),当时,y 随x 的增大而增大,那么m 的取值范围是( ) A . B .C .D . 5.在同一直角坐标系中,函数y =−kx +k 与y =k x (k ≠0)的大致图象可能为( )A .B .C .D .6.反比例函数y =6x 图象上有三个点(x 1,y 1),(x 2,y 2),(x 3,y 3)其中y 1<y 2<0<y 3,则x 1,x 2,x 3的大小关系是( )A .x 1<x 2<x 3B .x 3<x 1<x 2C .x 2<x 1<x 3D .x 3<x 2<x 1 7.如图,A 、B 是第二象限内双曲线y =k x 上的点,A 、B 两点的横坐标分别是a ,3a ,线段AB 的延长线交x轴于点C ,S △AOC =12.则k 的值为( )A .﹣6B .﹣5C .﹣4D .﹣38.如图,矩形OABC与反比例函数y1=k1x(k1是非零常数,x>0)的图象交于点M,N,与反比例函数y2=k2x(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1﹣k2=()A.3 B.﹣3 C.32D.−32二、填空题9.已知点A(−3,2)在反比例函数y=kx的图象上,则k的值为.10.若点P1(﹣1,m),P2(﹣2,n)在反比例函数y=kx(k<0)的图象上,则m n.(填“>”,“<”或“=”)11.正比例函数y=k1x(k1≠0)和反比例函数y= k2x(k2≠0)的一个交点为(m,n),则另一个交点为12.如图,在平面直角坐标系中,点A是x轴上任意一点,BC∥x轴,分别交y=2x (x>0),y=kx(x<0)的图象于B,C两点,若△ABC的面积是3,则k的值为.13.如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y=4x的图象交于A,B两点,则四边形MAOB的面积为.三、解答题14.如图,一次函数的图象与反比例函数的图象在第一象限交于点,与轴的负半轴交于点,且.(1)求一次函数与反比例函数的表达式;(2)请直接写出不等式的解集.15.1896年,挪威生理学家古德贝发现,每个人有一条腿迈出的步子比另一条腿迈出的步子长的特点,这就导致每个人在蒙上眼睛行走时,虽然主观上沿某一方向直线前进,但实际上走出的是一个大圆圈!这就是有趣的“嗐转圈”现象.经研究,某人蒙上眼睛走出的大圆圈的半径y/米是其两腿迈出的步长之差x/厘米(x>0)的反比例函数,y与x之间有如表关系:请根据表中的信息解决下列问题:(1)求出y与x之间的函数解析式;(2)若某人蒙上眼睛走出的大圆圈的半径为35米,则其两腿迈出的步长之差是多少厘米?(k>0).16.如图,设反比例函数的解析式为y=3kx(1)若反比例函数与正比例函数y=2x的图象有一个交点的纵坐标为2,求k的值;(2)若反比例函数的图象与过点M (﹣2,0)的直线l :y =kx+b 的图象交于A 、B 两点,如图,当△ABO 的面积为12时,求直线l 的解析式.17.某医药研究所研制了一种新药,在试验药效时发现:成人按规定剂量服用后,检测到从第10分钟起每分钟每毫升血液中含药量增加0.3微克,第100分钟达到最高,接着开始衰退.血液中含药量y (微克)与时间x (分钟)的函数关系如图,并发现衰退时y 与x 成反比例函数关系.(1) ; (2)分别求出当和时,y 与x 之间的函数关系式; (3)如果每毫升血液中含药量不低于12微克时是有效的,求一次服药后的有效时间是多少分钟?18.如图,一次函数 y ax b =+ 的图象与反比例函数 k y x=的图象交于第一象限C ,D 两点,坐标轴交于A 、B 两点,连结OC ,OD (O 是坐标原点).(1)利用图中条件,求反比例函数的解析式和m 的值;(2)求△DOC 的面积.(3)双曲线上是否存在一点P ,使得△POC 和△POD 全等?若存在,给出证明并求出点P 的坐标;若不存在,说明理由.参考答案1.B2.C3.C4.A5.D6.C7.A8.B9.k=-610.>11.(-m,-n).12.−413.1014.(1)解:点在反比例函数的图象上反比例函数解析式为;OA=OB,点在轴负半轴上点.把点、代入中得解得:一次函数的解析式为;(2) 15.(1)解:设y 与x 之间的函数解析式为y =k x 将(2,7)代入得7=k 2∴k =14∴y 与x 之间的函数解析式为y =14x . (2)解:当y =35时,即14x =35,解得x =0.4∴某人蒙上眼睛走出的大圆圈的半径为35米,其两腿迈出的步长之差是0.4厘米.16.(1)解:∵反比例函数与正比例函数y =2x 的图象有一个交点的纵坐标为2 把y =2代入y =2x 求得x =1∴反比例函数与正比例函数y =2x 的图象交点的坐标为(1,2)把(1,2)代入y =3k x (k >0),得到3k =2 ∴k =23;(2)解:把M (﹣2,0)代入y =kx+b ,可得b =2k∴y =kx+2k解{y =3k x y =kx +2k 得{x =−3y =−k 或{x =1y =3k∴B (﹣3,﹣k ),A (1,3k )∵△ABO 的面积为12∴12•2•3k+12•2•k =12解得k =3∴直线l 的解析式为y =3x+6.17.(1)27(2)解:当时,设y 与x 之间的函数关系式为∵经过点 ∴解得:,∴解析式为;当时,y 与x 之间的函数关系式为∵经过点∴解得:∴函数的解析式为; (3)解:令解得:令,解得:∴分钟 ∴服药后能持续175分钟.18.(1)∵点C (1,2)在反比例函数 图象上 ∴k=2∴反比例函数解析式为 2y x= ∵点B (2,m )在反比例函数 图象上 ∴m= 22=1. (2)如图,过点C 作⊥OA 于E ,过点D 作DF ⊥OA 于 Fk y x =2y x =∵C (1,2),D (2,1)∴CE=2,DF=1∵C 、D 在一次函数 的图象上∴221a b a b +=⎧⎨+=⎩解得: 13a b =-⎧⎨=⎩∴一次函数解析式为y=-x+3当y=0时,x=3∴A 点坐标为(3,0)∴OA=3∴DOC S =S △AOC -S △AOD = 1122OA CE OA DF ⋅-⋅ = 11323122⨯⨯-⨯⨯ =1.5.(3)设点P 坐标为(n , 2n )∵C (2,1),D (1,2)∴OC=OD∵△POC 和△POD 全等∴PC=PD ∴222222(1)(2)(2)(1)n n n n -+-=-+-解得: 2n =∴P (, )或P ( 2 , ) ∴双曲线上存在一点P ,使得△POC 和△POD 全等,P ( , )或P ( , ). y ax b =+222-2222。
中考数学复习专题09反比例函数

反比例函数一、单选题1.(2021·山西)已知反比例函数6y x=,则下列描述不正确的是( ) A .图象位于第一,第三象限 B .图象必经过点34,2⎛⎫⎪⎝⎭C .图象不可能与坐标轴相交D .y 随x 的增大而减小【答案】D【分析】根据反比例函数图像的性质判断即可.【详解】解:A 、反比例函数6y x=,0k >,经过一、三象限,此选项正确,不符合题意;B 、将点34,2⎛⎫⎪⎝⎭代入6y x=中,等式成立,故此选项正确,不符合题意;C 、反比例函数不可能坐标轴相交,此选项正确,不符合题意;D 、反比例函数图像分为两部分,不能一起研究增减性,故此选项错误,符合题意;故选:D .【点睛】本题主要考查反比例函数图像的性质,熟知反比例函数的图像的性质是解题关键.2.(2021·四川达州市)在反比例函数21k y x+=(k 为常数)上有三点()11,A x y ,()22,B x y ,()33,C x y ,若1230x x x <<<,则1y ,2y ,3y 的大小关系为( )A .123y y y <<B .213y y y <<C .132y y y <<D .321y y y <<【答案】C【分析】根据k >0判断出反比例函数的增减性,再根据其坐标特点解答即可.【详解】解:∵210k +>,∴反比例函数图象的两个分支在第一、三象限,且在每个象限内y 随x 的增大而减小,∵B (x 2,y 2),C (x 3,y 3)是双曲线ky x=上的两点,且320x x >>,∴点B 、C 在第一象限,0<y 3<y 2,∵A (x 1,y 1)在第三象限,∵y 1<0,∴132y y y <<.故选:C .【点睛】本题考查了由反比例函数图象的性质判断函数图象上点的坐标特征,理解基本性质是解题关键.3.(2021·浙江杭州市)已知1y 和2y 均是以x 为自变量的函数,当x m =时,函数值分别为1M 和2M ,若存在实数m ,使得120M M +=,则称函数1y 和2y 具有性质P .以下函数1y 和2y 具有性质P 的是( )A .212y x x =+和21y x =--B .212y x x =+和21y x =-+C .11y x=-和21y x =-- D .11y x=-和21y x =-+ 【答案】A【分析】根据题中所给定义及一元二次方程根的判别式可直接进行排除选项. 【详解】解:当x m =时,函数值分别为1M 和2M ,若存在实数m ,使得120M M +=, 对于A 选项则有210m m +-=,由一元二次方程根的判别式可得:241450b ac -=+=>,所以存在实数m ,故符合题意;对于B 选项则有210m m ++=,由一元二次方程根的判别式可得:241430b ac -=-=-<,所以不存在实数m ,故不符合题意;对于C 选项则有110m m---=,化简得:210m m ++=,由一元二次方程根的判别式可得:241430b ac -=-=-<,所以不存在实数m ,故不符合题意;对于D 选项则有110m m--+=,化简得:210m m -+=,由一元二次方程根的判别式可得:241430b ac -=-=-<,所以不存在实数m ,故不符合题意;故选A . 【点睛】本题主要考查一元二次方程根的判别式、二次函数与反比例函数的性质,熟练掌握一元二次方程根的判别式、二次函数与反比例函数的性质是解题的关键. 4.(2021·天津)若点()()()1235,,1,,5,A y B y C y -都在反比例函数5y x=-的图象上,则123,,y y y 的大小关系是( )A .123y y y <<B .231y y y <<C .132y y y <<D .312y y y <<【答案】B【分析】将A 、B 、C 三点坐标代入反比例函数解析式,即求出123、、y y y 的值,即可比较得出答案.【详解】分别将A 、B 、C 三点坐标代入反比例函数解析式得:1515y =-=-、2551y =-=-、3515y =-=-.则231y y y <<.故选B . 【点睛】本题考查比较反比例函数值.掌握反比例函数图象上的点的坐标满足其解析式是解答本题的关键.5.(2021·四川乐山市)如图,直线1l 与反比例函数3(0)y x x=>的图象相交于A 、B 两点,线段AB 的中点为点C ,过点C 作x 轴的垂线,垂足为点D .直线2l 过原点O 和点C .若直线2l 上存在点(,)P m n ,满足APB ADB ∠=∠,则m n +的值为( )A.3B .3或32C .3或3D .3【答案】A【分析】根据题意,得()1,3A ,()3,1B ,直线2l :y x =;根据一次函数性质,得m n =;根据勾股定理,得PC =PA ,PB ,FB ,根据等腰三角形三线合一性质,得()2,2C ,OC AB ⊥;根据勾股定理逆定理,得90ABD ∠=︒;结合圆的性质,得点A 、B 、D 、P 共圆,直线2l 和AB 交于点F ,点F 为圆心;根据圆周角、圆心角、等腰三角形的性质,得2FC =;分PC PF FC =+或PC PF FC =-两种情况,根据圆周角、二次根式的性质计算,即可得到答案.【详解】根据题意,得3,33A ⎛⎫ ⎪⎝⎭,33,3B ⎛⎫ ⎪⎝⎭,即()1,3A ,()3,1B ∵直线2l 过原点O 和点C ∴直线2l :y x = ∵(,)P m n 在直线2l 上∴m n = ∴PC =连接PA ,PB ,FB ∴PA PB =,线段AB 的中点为点C ∴()2,2C ,OC AB ⊥ 过点C 作x 轴的垂线,垂足为点D ∴()2,0D∴AD ==,AB ==BD ==∴222AD AB BD =+ ∴90ABD ∠=︒∴点A 、B 、D 、P 共圆,直线2l 和AB 交于点F ,点F为圆心∴cos BD ADB AD ∠== ∵AC BC =,12FB FA AD ==∴12BFC AFB ∠=∠∵APB ADB ∠=∠,且12APB AFB ∠=∠ ∴APB ADB BFC ∠=∠=∠∴cos cos FC APB BFC FB ∠=∠===FC = ∴PC PF FC =+或PC PF FC =- 当PC PF FC =-时,APB ∠和ADB ∠位于直线AB 两侧,即180APB ADB ∠+∠=︒ ∴PC PF FC =-不符合题意∴22PC PF FC =+=+,且2m < ∴)2PC m ==-)2m -=∴32m =∴23m n m +==A .【点睛】本题考查了圆、等腰三角形、反比例函数、一次函数、三角函数、勾股定理、二次根式的知识;解题的关键是熟练掌握圆心角、圆周角、等腰三角形三线合一、三角函数、勾股定理的性质,从而完成求解.6.(2021·重庆)如图,在平面直角坐标系中,菱形ABCD 的顶点D 在第二象限,其余顶点都在第一象限,AB ∥X 轴,AO ⊥AD ,AO =A D .过点A 作AE ⊥CD ,垂足为E ,DE =4CE .反比例函数()0ky x x =>的图象经过点E ,与边AB 交于点F ,连接OE ,OF ,EF .若118EOFS=,则k 的值为( )A .73B .214C .7D .212【答案】A【分析】延长EA 交x 轴于点G ,过点F 作x 轴的垂线,垂足分别为H ,则可得△DEA ≌△AGO ,从而可得DE =AG ,AE =OG ,若设CE =a ,则DE =AG =4a ,AD =DC =DE +CE =5a ,由勾股定理得AE =OG =3a ,故可得点E 、A 的坐标,由AB 与x 轴平行,从而也可得点F 的坐标,根据EOFEOGFOHEGHF S SS S=+-梯形 ,即可求得a 的值,从而可求得k 的值.【详解】如图,延长EA 交x 轴于点G ,过点F 作x 轴的垂线,垂足分别为H ∵四边形ABCD 是菱形∴CD =AD =AB ,CD ∥AB ∵AB ∥x 轴,AE ⊥CD ∴EG ⊥x 轴,∠D +∠DAE =90゜∵OA ⊥AD ∴∠DAE +∠GAO =90゜∴∠GAO =∠D ∵OA =OD ∴△DEA ≌△AGO (AAS )∴DE =AG ,AE =OG设CE =a ,则DE =AG =4CE =4a ,AD =AB =DC =DE +CE =5a在Rt △AED 中,由勾股定理得:AE =3a ∴OG =AE =3a ,GE =AG +AE =7a ∴A (3a ,4a ),E (3a ,7a )∵AB ∥x 轴,AG ⊥x 轴,FH ⊥x 轴∴四边形AGHF 是矩形 ∴FH =AG =3a ,AF =GH∵E 点在双曲线()0ky x x =>上∴221ka =即221a y x=∵F点在双曲线221a y x=上,且F 点的纵坐标为4a ∴214a x =即214aOH =∴94a GH OH OG =-=∵EOFEOGFOHEGHF SSS S =+-梯形∴1191211137(74)4224248a a a a a a a ⨯⨯++⨯-⨯⨯= 解得:219a = ∴217212193k a ==⨯= 故选:A .【点睛】本题是反比例函数与几何的综合题,考查了菱形的性质,矩形的判定与性质,三角形全等的判定与性质等知识,关键是作辅助线及证明△DEA ≌△AGO ,从而求得E 、A 、F 三点的坐标.7.(2021·江苏扬州市)如图,点P 是函数()110,0k y k x x=>>的图像上一点,过点P 分别作x 轴和y 轴的垂线,垂足分别为点A 、B ,交函数()220,0k y k x x=>>的图像于点C 、D ,连接OC 、OD 、CD 、AB ,其中12k k >,下列结论:①//CD AB ;②122OCDk kS-=;③()21212DCPk k Sk -=,其中正确的是( )A .①②B .①③C .②③D .①【答案】B【分析】设P (m ,1k m),分别求出A ,B ,C ,D 的坐标,得到PD ,PC ,PB ,P A 的长,判断PD PB和PCPA 的关系,可判断①;利用三角形面积公式计算,可得△PDC的面积,可判断③;再利用OCD OAPB OBD OCA DPC S S S S S =---△△△△计算△OCD 的面积,可判断②.【详解】解:∵PB ⊥y 轴,P A ⊥x 轴,点P 在1k y x =上,点C ,D 在2ky x=上,设P (m ,1k m), 则C (m ,2k m ),A (m ,0),B (0,1k m ),令12k k m x =,则21k m x k =,即D (21k m k ,1k m), ∴PC =12k k m m -=12k k m -,PD =21k m m k -=()121m k k k -, ∵()121121m k k k k k PD PB m k --==,121211k k k k PC m k PA k m--==,即PD PCPB PA =,又∠DPC =∠BP A ,∴△PDC ∽△PBA ,∴∠PDC =∠PBC ,∴CD ∥AB ,故①正确; △PDC的面积=12PD PC ⨯⨯=()1212112m k k k k k m--⨯⨯=()21212k k k -,故③正确;OCDOAPB OBD OCA DPC S S S S S =---△△△△=()112221222112k k k k k k ----=()2121122k k k k k ---=()()21121112222k k k k k k k ---=()22112211222k k k k k k ---=221212k k k -,故②错误;故选B .【点睛】此题主要考查了反比例函数的图象和性质,k 的几何意义,相似三角形的判定和性质,解题关键是表示出各点坐标,得到相应线段的长度. 8.(2021·浙江宁波市)如图,正比例函数()1110y k x k =<的图象与反比例函数()2220k y k x=<的图象相交于A ,B 两点,点B 的横坐标为2,当12y y >时,x 的取值范围是( )A .2x <-或2x > B .20x -<<或2x > C .2x <-或02x << D .20x -<<或02x << 【答案】C【分析】根据轴对称的性质得到点A 的横坐标为-2,利用函数图象即可确定答案. 【详解】解:∵正比例函数与反比例函数都关于原点对称,∴点A 与点B 关于原点对称,∵点B 的横坐标为2,∴点A 的横坐标为-2,由图象可知,当2x <-或02x <<时,正比例函数()1110y k x k =<的图象在反比例函数()2220k y k x=<的图象的上方,∴当2x <-或02x <<时,12y y >,故选:C . 【点睛】此题考查正比例函数与反比例函数的性质及相交问题,函数值的大小比较,正确理解图象是解题的关键.9.(2021·浙江金华市)已知点()()1122,,,A x y B x y 在反比例函数12y x=-的图象上.若120x x <<,则( )A .120y y <<B .210y y <<C .120y y <<D .210y y <<【答案】B【分析】根据反比例函数的图象与性质解题. 【详解】解:反比例函数12y x=-图象分布在第二、四象限, 当0x <时,0y > 当0x >时,0y <120x x <<120y y ∴>>故选:B .【点睛】本题考查反比例函数的图象与性质,是重要考点,难度较易,掌握相关知识是解题关键.10.(2021·江苏连云港市)关于某个函数表达式,甲、乙、丙三位同学都正确地说出了该函数的一个特征.甲:函数图像经过点(1,1)-;乙:函数图像经过第四象限;丙:当0x >时,y 随x 的增大而增大.则这个函数表达式可能是( ) A .y x =- B .1y x =C .2y xD .1y x=-【答案】D【分析】根据所给函数的性质逐一判断即可.【详解】解:A .对于y x =-,当x =-1时,y =1,故函数图像经过点(1,1)-;函数图象经过二、四象限;当0x >时,y 随x 的增大而减小.故选项A 不符合题意; B .对于1y x =,当x =-1时,y =-1,故函数图像不经过点(1,1)-;函数图象分布在一、三象限;当0x >时,y 随x 的增大而减小.故选项B 不符合题意;C .对于2y x ,当x =-1时,y =1,故函数图像经过点(1,1)-;函数图象分布在一、二象限;当0x >时,y 随x 的增大而增大.故选项C 不符合题意;D .对于1y x=-,当x =-1时,y =1,故函数图像经过点(1,1)-;函数图象经过二、四象限;当0x >时,y 随x 的增大而增大.故选项D 符合题意;故选:D【点睛】本题考查的是一次函数、二次函数以及反比例函数性质,熟知相关函数的性质是解答此题的关键.11.(2021·浙江温州市)如图,点A ,B 在反比例函数k y x=(0k >,0x >)的图象上,AC x ⊥轴于点C ,BD x ⊥轴于点D ,BE y ⊥轴于点E ,连结AE .若1OE =,23OC OD =,AC AE =,则k 的值为( )A .2B .2C .94D .【答案】B【分析】设OD =m ,则OC =23m ,设AC =n ,根据213m n m =⨯求得32n =,在Rt △AEF中,运用勾股定理可求出m =2,故可得到结论. 【详解】解:如图,设OD =m ,∵23OC OD =∴OC =23m∵BD x ⊥轴于点D ,BE y ⊥轴于点E ,∴四边形BEOD 是矩形∴BD =OE =1∴B (m ,1)设反比例函数解析式为ky x=,∴k =m ×1=m 设AC =n ∵AC x ⊥轴∴A (23m ,n )∴23m n k m ==,解得,n =32,即AC =32 ∵AC =AE ∴AE =32在Rt △AEF 中,23EF OC m ==,31122AF AC FC =-=-=由勾股定理得,222321()()()232m =+ 解得,2m =2k = 故选:B 【点睛】此题考查了反比例函数的性质、待定系数法求函数的解析式.此题难度较大,注意掌握数形结合思想与方程思想的应用.12.(2021·浙江嘉兴市)已知三个点()11,x y ,()22,x y ,()33,x y 在反比例函数2y x=的图象上,其中1230x x x <<<,下列结论中正确的是( ) A .2130y y y <<< B .1230y y y <<< C .3210y y y <<< D .3120y y y <<< 【答案】A【分析】根据反比例函数图像的增减性分析解答.【详解】解:反比例函数2y x=经过第一,三象限,在每一象限内,y 随x 的增大而减小,∴当1230x x x <<<时,2130y y y <<<故选:A .【点睛】本题考查反比例函数的图像性质,掌握反比例函数的图像性质,利用数形结合思想解题是关键.13.(2021·重庆)如图,在平面直角坐标系中,矩形ABCD 的顶点A ,B 在x 轴的正半轴上,反比例函数(0,0)ky k x x=>>的图象经过顶点D ,分别与对角线AC ,边BC 交于点E ,F ,连接EF ,AF .若点E 为AC 的中点,AEF 的面积为1,则k 的值为( )A .125B .32C .2D .3【答案】D【分析】设D 点坐标为()k a a,,表示出E 、F 、B 点坐标,求出ABF 的面积,列方程即可求解.【详解】解:设D 点坐标为()ka a ,,∵四边形ABCD 是矩形,则A 点坐标为(0)a ,,C 点纵坐标为k a,∵点E 为AC 的中点,则E 点纵坐标为022kk a a+=,∵点E 在反比例函数图象上,代入解析式得2k ka x=,解得,2x a =,∴E 点坐标为(2)2k a a ,,同理可得C 点坐标为(3)ka a,,∵点F 在反比例函数图象上,同理可得F 点坐标为(3)3ka a,,∵点E 为AC 的中点,AEF 的面积为1, ∴2ACFS=,即122CF AB ⋅=,可得,1()(3)223k ka a a a--=,解得3k =,故选:D .【点睛】本题考查了反比例函数的性质和矩形的性质,解题关键是设出点的坐标,依据面积列出方程.14.(2021·四川自贡市)已知蓄电池的电压为定值,使用蓄电池时,电流O (单位:A )与电阻R (单位:Ω)是反比例函数关系,它的图象如图所示.下列说法正确的是( )A .函数解析式为13I R=B .蓄电池的电压是18VC .当10A I ≤时, 3.6R ≥ΩD .当6R =Ω时,4A I =【答案】C【分析】将将()4,9代入UI R=求出U 的值,即可判断A ,B ,D ,利用反比例函数的增减性可判断C . 【详解】解:设U I R=,将()4,9代入可得36I R =,故A 错误; ∴蓄电池的电压是36V ,故B 错误;当10A I ≤时, 3.6R ≥Ω,该项正确; 当当6R =Ω时,6A I =,故D 错误,故选:C .【点睛】本题考查反比例函数的实际应用,掌握反比例函数的图象与性质是解题的关键.15.(2021·浙江丽水市)一杠杆装置如图,杆的一端吊起一桶水,水桶对杆的拉力的作用点到支点的杆长固定不变.甲、乙、丙、丁四位同学分别在杆的另一端竖直向下施加压力 F F F F 丁乙甲丙、、、,将相同重量的水桶吊起同样的高度,若F F F F <<<甲丁丙乙,则这四位同学对杆的压力的作用点到支点的距离最远的是( )A .甲同学B .乙同学C .丙同学D .丁同学【答案】B【分析】根据物理知识中的杠杆原理:动力×动力臂=阻力×阻力臂,力臂越大,用力越小,即可求解.【详解】解:由物理知识得,力臂越大,用力越小,根据题意,∵ F F F F <<<甲丁丙乙,且将相同重量的水桶吊起同样的高度, ∴乙同学对杆的压力的作用点到支点的距离最远,故选:B .【点睛】本题考查反比例函数的应用,属于数学与物理学科的结合题型,立意新颖,掌握物理中的杠杆原理是解答的关键. 二、填空题1.(2021·浙江绍兴市)如图,在平面直角坐标系中,正方形ABCD 的顶点A 在x 轴正半轴上,顶点B ,C 在第一象限,顶点D 的坐标5(,2)2. 反比例函数k y x=(常数0k >,0x >)的图象恰好经过正方形ABCD 的两个顶点,则k 的值是_______.【答案】5或22.5【分析】先设一个未知数用来表示出B 、C 两点的坐标,再利用反比例函数图像恰好经过B 、C 、D 的其中两个点进行分类讨论,建立方程求出未知数的值,符合题意时进一步求出k 的值即可.【详解】解:如图所示,分别过B 、D 两点向x 轴作垂线,垂足分别为F 、E 点,并过C 点向BF 作垂线,垂足为点G ;∵正方形ABCD ,∴∠DAB =90°,AB =BC =CD =DA ,∴∠DAE +∠BAF =90°, 又∵∠DAE +∠ADE =90°,∠BAF +∠ABF =90°, ∴∠DAE =∠ABF ,∠ADE =∠BAF ,∴ADE ≌BAF ,同理可证△ADE ≌△BAF ≌△CBG ;∴DE =AF =BG ,AE =BF =CG ;设AE =m , ∵点D 的坐标 (52,2) ,∴OE=52,DE =AF =BG =2,∴B (92m +,m ),C (92,2m +), ∵5252⨯=,当()9252m +=时,809m =-<,不符题意,舍去;当952m m ⎛⎫+= ⎪⎝⎭时,由0m ≥解得m =,符合题意;故该情况成立,此时 5k =; 当()99222m m m ⎛⎫+=+ ⎪⎝⎭时,由 0m ≥解得3m =,符合题意,故该情况成立,此时()93222.52k =⨯+=; 故答案为:5或22.5.【点睛】本题综合考查了全等三角形的判定与性质、正方形的性质、反比例函数的图像与性质、解一元二次方程等内容,解题的关键是牢记相关概念与性质,能根据题意建立相等关系列出方程等,本题涉及到了分类讨论和数形结合的思想方法等.2.(2021·湖南)在反比例函数3m y x-=的图象的每一支曲线上,函数值y 随自变量x 的增大而增大,则m 的取值范围是________.【答案】m <3【分析】根据反比例函数的增减性,列出关于m 的不等式,进而即可求解. 【详解】解:∵在反比例函数3m y x-=的图象的每一支曲线上,函数值y 随自变量x 的增大而增大,∴m -3<0,即:m <3.故答案是:m <3.【点睛】本题主要考查反比例函数的性质,掌握反比例函数ky x=,在反比例函数的图象的每一支曲线上,函数值y 随自变量x 的增大而增大,则k <0,是解题的关键.3.(2021·湖北武汉市)已知点()1,A a y ,()21,B a y +在反比例函数21m y x+=(m是常数)的图象上,且12y y <,则a 的取值范围是__________. 【答案】10a -<<【分析】根据反比例函数的增减性解答.【详解】解:∵210m +>,∴图象经过第一、三象限,在每个象限内,y 随着x 的增大而减小,∵点()1,A a y ,()21,B a y +在反比例函数21m y x+=(m是常数)的图象上,且12y y <,1a a <+ ,∴010a a <⎧⎨+>⎩,∴10a -<<,故答案为:10a -<<.【点睛】此题考查反比例函数的性质:当0k >时,在每个象限内y 随着x 的增大而增大;当0k <时,在每个象限内y 随x 的增大而减小.4.(2021·湖南株洲市)点()11,A x y 、()121,B x y +是反比例函数ky x=图像上的两点,满足:当1>0x 时,均有12y y <,则k 的取值范围是__________. 【答案】k <0【分析】先分析该两点所在的图像的象限和增减性,最后确定k 的取值范围即可. 【详解】解:因为当10x >时,110x +>,说明A 、B 两点同时位于第一或第四象限, ∵当10x >时,均有12y y <,∴在该图像上,y 随x 的增大而增大, ∴A 、B 两点同时位于第四象限,所以k <0,故答案为:k <0.【点睛】本题考查了反比例函数的图像和性质,解决本题的关键是理解并牢记反比例函数的图像和性质,能根据点的坐标情况分析其图像特点等,涉及了数形结合的思想方法.5.(2021·陕西)若()11,A y ,()23,B y 是反比例函数2112m y m x -⎛⎫=< ⎪⎝⎭图象上的两点,则1y 、2y 的大小关系是1y ______2y (填“>”、“=”或“<”) 【答案】<【分析】先根据不等式的性质判断2-10m <,再根据反比例函数的增减性判断即可. 【详解】解:∵12m <∴1222m <⨯即2-10m <∴反比例函数图像每一个象限内,y 随x 的增大而增大∵1<3∴1y <2y 故答案为:<. 【点睛】本题考查反比例函数的增减性、不等式的性质、熟练掌握反比例函数的性质是关键.6.(2021·浙江宁波市)在平面直角坐标系中,对于不在坐标轴上的任意一点(),A x y ,我们把点11,B x y ⎛⎫⎪⎝⎭称为点A 的“倒数点”.如图,矩形OCDE 的顶点C 为()3,0,顶点E 在y 轴上,函数()20=>y x x的图象与DE 交于点A .若点B 是点A 的“倒数点”,且点B 在矩形OCDE 的一边上,则OBC 的面积为_________.【答案】14或32【分析】根据题意,点B 不可能在坐标轴上,可对点B 进行讨论分析:①当点B 在边DE 上时;②当点B 在边CD 上时;分别求出点B 的坐标,然后求出OBC 的面积即可.【详解】解:根据题意,∵点11,B x y⎛⎫⎪⎝⎭称为点(),A x y 的“倒数点”,∴0x ≠,0y ≠,∴点B 不可能在坐标轴上;∵点A 在函数()20=>y x x的图像上,设点A 为2(,)x x,则点B 为1(,)2x x ,∵点C 为()3,0,∴3OC =,①当点B 在边DE 上时;点A 与点B 都在边DE 上, ∴点A 与点B 的纵坐标相同,即22x x =,解得:2x =,经检验,2x =是原分式方程的解;∴点B 为1(,1)2,∴OBC 的面积为:133122S =⨯⨯=; ②当点B 在边CD 上时;点B 与点C 的横坐标相同,∴13x =,解得:13x =,经检验,13x =是原分式方程的解;∴点B 为1(3,)6, ∴OBC 的面积为:1113264S =⨯⨯=;故答案为:14或32. 【点睛】本题考查了反比例函数的图像和性质,矩形的性质,解分式方程,坐标与图形等知识,解题的关键是熟练掌握反比例函数的性质,运用分类讨论的思想进行分析.7.(2021·云南)若反比例函数的图象经过点()1,2-,则该反比例函数的解析式(解析式也称表达式)为_________.【答案】2y x=- 【分析】先设ky x=,再把已知点的坐标代入可求出k 值,即得到反比例函数的解析式.【详解】解:设反比例函数的解析式为ky x=(k ≠0), ∵函数经过点(1,-2),∴21k -=,得k =-2,∴反比例函数解析式为2y x=-,故答案为:2y x=-.【点睛】此题比较简单,考查的是用待定系数法求反比例函数的解析式,是中学阶段的重点. 三、解答题1.(2021·湖北随州市)如图,一次函数1y kx b =+的图象与x 轴、y 轴分别交于点A ,B ,与反比例函数2my x=(0m >)的图象交于点()1,2C ,()2,D n .(1)分别求出两个函数的解析式;(2)连接OD ,求BOD 的面积. 【答案】(1)22y x=,13y x =-+;(2)3 【分析】(1)将点C 、D 的横、纵坐标代入反比例函数的解析式,求得m 、n 的值,从而点D 纵坐标已知,将点C 、D 的横、纵坐标代入一次函数的解析式,求得k 、b 的值,从而两个函数解析式可求;(2)求出点B 的坐标,可知OB 的长,利用三角形的面积公式可求三角形BOD的面积.【详解】解:(1)∵双曲线2my x=(m >0)过点C (1,2)和D (2,n ), ∴212mm n ⎧=⎪⎪⎨⎪=⎪⎩,解得,21m n =⎧⎨=⎩.∴反比例函数的解析式为22y x =. ∵直线1y kx b =+过点C (1,2)和D (2,1),∴221k b k b +=⎧⎨+=⎩,解得,13k b =-⎧⎨=⎩.∴一次函数的解析式为13y x =-+.(2)当x =0时,y 1=3,即B (0,3).∴3OB =.如图所示,过点D 作DE ⊥y 轴于点E .∵D (2,1),∴DE =2.∴1132322BOD S OB DE ==⨯⨯=△.【点睛】本题考查了待定系数法求函数解析式、二元一次方程组、三角形的面积等知识点,熟知解析式、点坐标、线段长三者的相互转化是解题的关键. 2.(2021·湖北恩施州)如图,在平面直角坐标系中,Rt ABC 的斜边BC 在x 轴上,坐标原点是BC 的中点,30ABC ∠=︒,4BC =,双曲线ky x=经过点A .(1)求k ;(2)直线AC 与双曲线y =D .求ABD △的面积.【答案】(1)k =(2)ABD △的面积【分析】(1)过点A 作AE ⊥x 轴于点E ,由题意易得2,60AC ACB =∠=︒,进而可得1,==CE AE (A ,最后问题可求解;(2)由(1)可先求出直线AC 的解析式为y =+,然后联立直线AC 的解析式与反比例函数y =D 的坐标,最后利用割补法求解三角形的面积即可.【详解】解:(1)过点A 作AE ⊥x 轴于点E ,如图所示:∵30ABC ∠=︒,4BC =,90BAC ∠=︒, ∴122AC BC ==,60ACB ∠=︒,∴30EAC ∠=︒,∴112EC AC ==,∴在Rt △AEC 中,AE ==∵点O 是BC 的中点,∴OC =2,∴OE =1,∴(A,∴1k ==; (2)由(1)可得:(A ,()2,0C ,∴设直线AC 的解析式为y kx b =+,则把点A 、C代入得:20k b k b ⎧+=⎪⎨+=⎪⎩解得:k b ⎧=⎪⎨=⎪⎩,∴直线AC的解析式为y =+,联立y =+y =+=,解得:123,1x x ==-(不符合题意,舍去),∴点(3,D ,∴142ABDABCBCDSSS=+=⨯⨯=【点睛】本题主要考查反比例函数与几何的综合及含30°直角三角形的性质、勾股定理,熟练掌握反比例函数与几何的综合及含30°直角三角形的性质、勾股定理是解题的关键.3.(2021·四川广安市)如图,一次函数()1y kx b k 0=+≠的图象与反比例函数()2my m 0x=≠的图象交于()1,A n -,()3,2B -两点.(1)求一次函数和反比例函数的解析式;(2)点P 在x 轴上,且满足ABP △的面积等于4,请直接写出点P 的坐标.【答案】(1)124y x =-+,26y x=-;(2)(1,0)或(3,0)【分析】(1)根据点B 坐标求出m ,得到反比例函数解析式,据此求出点A 坐标,再将A ,B 代入一次函数解析式;(2)设点P 的坐标为(a ,0),求出直线AB 与x 轴交点,再结合△ABP 的面积为4得到关于a 的方程,解之即可.【详解】解:(1)由题意可得:点B (3,-2)在反比例函数2my x=图像上, ∴23m-=,则m =-6,∴反比例函数的解析式为26y x=-,将A (-1,n )代入26y x=-,得:661n =-=-,即A (-1,6),将A ,B 代入一次函数解析式中,得236k b k b -=+⎧⎨=-+⎩,解得:24k b =-⎧⎨=⎩,∴一次函数解析式为124y x =-+;(2)∵点P 在x 轴上,设点P 的坐标为(a ,0),∵一次函数解析式为124y x =-+,令y =0,则x =2,∴直线AB 与x 轴交于点(2,0),由△ABP 的面积为4,可得:()1242A B y y a ⨯-⨯-=,即18242a ⨯⨯-=,解得:a =1或a =3,∴点P 的坐标为(1,0)或(3,0).【点睛】本题考查一次函数和反比例函数相交的有关问题;通常先求得反比例函数解析式;较复杂三角形的面积可被x 轴或y 轴分割为2个三角形的面积和. 4.(2021·浙江杭州市)在直角坐标系中,设函数11ky x=(1k 是常数,10k >,0x >)与函数22y k x =(2k 是常数,20k ≠)的图象交于点A ,点A 关于y 轴的对称点为点B .(1)若点B 的坐标为()1,2-,①求1k ,2k 的值.②当12y y <时,直接写出x 的取值范围.(2)若点B 在函数33k y x=(3k 是常数,30k ≠)的图象上,求13k k +的值. 【答案】(1)①12k =,22k =;②1x >;(2)0【分析】(1)①根据点A 关于y 轴的对称点为点B ,可求得点A 的坐标是()1,2,再将点A 的坐标分别代入反比例函数、正比例函数的解析式中,即可求得12k =,22k =;②观察图象可解题;(2)将点B 代入33k y x=,解得3k 的值即可解题. 【详解】解(1)①由题意得,点A 的坐标是()1,2, 因为函数11k y x=的图象过点A ,所以12k =,同理22k =. ②由图象可知,当12y y <时,反比例函数的图象位于正比例函数图象的下方,即当12y y <时,1x >.(2)设点A 的坐标是()00,x y ,则点B 的坐标是()00,x y -,所以100k x y =,300k x y =-,所以310k k +=.【点睛】本题考查关于y 轴对称的点的特征、待定系数法求反比例函数、正比例函数的解析式等知识,是重要考点,难度较易,掌握相关知识是解题关键.5.(2021·山东临沂市)已知函数()()()31 31131x x y x x x x⎧≤-⎪⎪=-⎨⎪⎪≥⎩<< (1)画出函数图象;列表:描点,连线得到函数图象:(2)该函数是否有最大或最小值?若有,求出其值,若没有,简述理由; (3)设1122(,),(,)x y x y 是函数图象上的点,若120x x +=,证明:120y y +=. 【答案】(1)见解析;(2)有,当1x =时,最大值为3;当1x =-时,函数有最小值3-;(3)见解析【分析】(1)选取特殊值,代入函数解析式,求出y 值,列表,在图像中描点,画出图像即可;(2)观察图像可得函数的最大值;(3)根据120x x +=,得到1x 和2x 互为相反数,再分111x -<<,11x ≤-,11x ≥,分别验证120y y +=. 【详解】解:(1)列表如下:函数图像如图所示:(2)根据图像可知:当x =1时,函数有最大值3;当1x =-时,函数有最小值3-; (3)∵1122(,),(,)x y x y 是函数图象上的点,120x x +=,∴1x 和2x 互为相反数, 当111x -<<时,211x -<<,∴113y x =,223y x =,∴()1212123330y y x x x x +=+=+=; 当11x ≤-时,21x ≥,则()121212123330x x y y xx x x ++=+==;同理:当11x ≥时,21x ≤-,()121212123330x x y y xx x x ++=+==,综上:120y y +=.【点睛】本题主要考查正比例函数,反比例函数的图像和性质,描点法画函数图像,准确画出图像,理解120x x +=是解题的关键.6.(2021·安徽)已知正比例函数(0)y kx k =≠与反比例函数6y x=的图象都经过点A (m ,2).(1)求k ,m 的值;(2)在图中画出正比例函数y kx =的图象,并根据图象,写出正比例函数值大于反比例函数值时x 的取值范围.【答案】(1),k m 的值分别是23和3;(2)30x -<<或3x >【分析】(1)把点A (m ,2)代入6y x=求得m 的值,从而得点A 的坐标,再代入(0)y kx k =≠求得k 值即可;(2)在坐标系中画出y kx =的图象,根据正比例函数(0)y kx k =≠的图象与反比例函数6y x=图象的两个交点坐标关于原点对称,求得另一个交点的坐标,观察图象即可解答.【详解】(1)将(,2)A m 代入6y x=得62m =, 3m ∴=, (3,2)A ∴, 将(3,2)A 代入y kx =得23k =, 23k ∴=, ,k m ∴的值分别是23和3.(2)正比例函数23y x =的图象如图所示,∵正比例函数(0)y kx k =≠与反比例函数6y x =的图象都经过点A (3,2),∴正比例函数(0)y kx k =≠与反比例函数6y x=的图象的另一个交点坐标为(-3,-2),由图可知:正比例函数值大于反比例函数值时x 的取值范围为30x -<<或3x >. 【点睛】本题是正比例函数与反比例函数的综合题,利用数形结合思想是解决问题的关键.7.(2021·浙江)已知在平面直角坐标系xOy 中,点A 是反比例函数1(0)y x x=>图象上的一个动点,连结,AO AO 的延长线交反比例函数(0,0)ky k x x=><的图象于点B ,过点A 作AE y ⊥轴于点E .(1)如图1,过点B 作BF x ⊥轴于点F ,连结EF .①若1k =,求证:四边形AEFO 是平行四边形;②连结BE ,若4k =,求BOE △的面积.(2)如图2,过点E 作//EP AB ,交反比例函数(0,0)ky k x x=><的图象于点P ,连结OP .试探究:对于确定的实数k ,动点A 在运动过程中,POE △的面积是否会发生变化?请说明理由. 【答案】(1)①证明见解析,②1;(2)不改变,见解析【分析】(1)①计算得出AE OF a ==,利用平行四边形的判定方法即可证明结论;②证明AEO BDO ∽,利用反比例函数k 的几何意义求得212()2AO BO=,即可求解;(2)点A 的坐标为1()a a ,,点P 的坐标为()k b b,,可知四边形AEGO是平行四边形,由AEO GHP ∽,利用相似三角形的性质得到关于b a的一元二次方程,利用三角形的面积公式即可求解.【详解】(1)①证明:设点A 的坐标为1()a a,, 则当1k =时,点B 的坐标为1()a a--,,AE OF a ∴==, AE y ⊥轴,//AE OF ∴,∴四边形AEFO 是平行四边形;②解:过点B 作BD y ⊥轴于点D ,AE y ⊥轴,//AE BD ∴,AEO BDO ∴∽, 2()AEO BDOSAO SBO∴=, ∴当4k =时,则212()2AO BO=,即12AO BO =.21BOEAOES S∴==;(2)解 不改变. 理由如下:过点P 作PH x ⊥轴于点H PE ,与x 轴交于点G ,设点A 的坐标为1()a a,,点P 的坐标为()k b b,, 则1kAE a OE PH a b===-,,,OH =b ,由题意,可知四边形AEGO 是平行四边形,∴OG =AE =a ,∠HPG =∠OEG =∠EOA ,且∠PHG =∠OEA =90°,∴AEO GHP ∽, AE EOGH a b GH PH=--=,,即1a a k ab b=---, ∴1b a k ab+=,2()0b b k aa∴+-=,解得ba=。
反比例函数复习

2.过双曲线上任一点作x轴、y轴的垂线,所得矩形的 面积等于|k|.
课时训练
1.(2002年· 泸州市)如图所示,当k<0时,反比例函数 y=k/x和一次函数y=kx+2的图像大致是图 ( B )
课时训练
2.(2002年· 武汉市)若点(3,4)是反比例函数 m 2 + 2 m 1 的图像上一点,则此函数图像必经过点( A ) y
x
A.(2,6)
B.(2,-6)
C.(4,-3)
D.(3,-4)
3.如图所示,正比例函数y=kx (k>0) 与反比例函数y=1/x的图像相交于A、C 两点,过A作x轴的垂线交x轴于B, 连接BC.若△ABC面积为S,则 (A) A.S=1 B.S=2 C.S=3 D.不能确定
课时训练
4.已知:y=y1+y2,其中y1与x成反比,且比例系数是k1 ,y2与x2成正比,且比例系数是k2,若x=-1时,y=0, 则k1与k2的关系是( B ) A.k1+k2=0 B.k1-k2=0 C.k1· 2=1 k D.k1· 2=-1 k 5.如图所示,已知点P是反 比例函数y=k/x的图像在第 二象限内的一点,过P点分 别作x轴、y轴的垂线,垂 足为M、N,若矩形OMPN 的面积为5,则k= -5 .
k3 k1 k2 y ,y ,y 4.如图三个反比例函数 x x x
课前热身
在x轴上方的图像,由此观察得到的大小关系为( B ) A.k1>k2>k3 B.k2>k3>k1 C.k3>k2>k1 D.k3>k1>k2
课前热身
5.(2003年· 重庆市)如图所示.如果 函数y=-kx(k≠0)与y=-4/x的图像 交于A、B两点,过点A作AC垂直 于y轴,垂足为点C,则△BOC的 面积为 2 . 6.(2003年· 山西省)已知:反比例函数y=k/x(k≠0),当x <0时,y随x的增大而增大,那么一次函数y=kx-k的图 像经过( B ) A.第一、二、三象限 B.第一、二、四象限 C.第一、三、四象限 D.第二、三、四象限
高中数学-反比例函数专题复习

高中数学-反比例函数专题复习1.定义:一般地,如果两个变量x 、y 之间的关系表示成y=(k 为常数,k ≠0)的形式,那么称y 是x 的反比例函数,其中x 是自变量,y 是函数。
例如y =50x ;y =-8x ;y =m 2+1x(m 为常数)等。
提示:(1)y =k x 也可以写作y=kx -1的形式或xy=k 的形式(k为常数且k ≠0);(2)反比例函数的自变量x 不能为0;(3)k=xy 是反比例函数的另一种表示形式,即两变量的积是一个常数。
2.图像:反比例函数的图像属于双曲线。
反比例函数的图象既是轴对称图形又是中心对称图形。
有两条对称轴:直线y=x 和y=-x 。
对称中心是:原点。
3.性质:当k >0时双曲线的两支分别位于第一、第三象限,在每个象限内y 值随x 值的增大而减小;当k <0时双曲线的两支分别位于第二、第四象限,在每个象限内y 值随x 值的增大而增大。
xk4.|k|的几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积。
知识点:1·一般地,如果两个变量x、y之间的关系可表示成y=k x(K为常数,K≠0)的形式,那么称y是x的反比例函数。
反比例函数的自变量x不能为零。
2·反比例函数的图象及其画法反比例函数图象的画法——描点法:⑴列表——自变量取值应以0(但(x≠0)为中心,向两边取三对(或三对以上)互为相反数的数,再求出对应的y的值;⑵描点——先描出一侧,另一侧可根据中心对称点的性质去找;⑶连线——按照从左到右的顺序连接各点并延伸,注意双曲线的两个分支是断开的,延伸部分有逐渐靠近坐标轴的趋势,但永远不与坐标轴相交。
反比例函数y=kx的图象是由两支曲线组成的。
当k>0时,两支曲线分别位于第一、三象限内,当k<0时,两支曲线分别位于第二、四象限内。
小注:⑴这两支曲线通常称为双曲线。
⑵这两支曲线关于原点对称。
⑶反比例函数的图象与x轴、y轴没有公共点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反比例函数经典专题
知识点回顾
由于反比例函数解析式及图象的特殊性,很多中考试题都将反比例函数与面积结合起来进行考察。
这种考察方式既能考查函数、反比例函数本身的基础知识容,又能充分体现数形结合的思想方法,考查的题型广泛,考查方法灵活,可以较好地将知识与能力融合在一起。
下面就反比例函数中与面积有关的问题的四种类型归纳如下:
一、利用反比例函数中|k|的几何意义求解与面积有关的问题
设P为双曲线上任意一点,过点P作x轴、y轴的垂线PM、PN,垂足分别为M、N,则两垂线段与坐标轴所围成的的矩形PMON的面积为S=|PM|×|PN|=|y|×|x|=|xy|
∴xy=k 故S=|k| 从而得
结论1:过双曲线上任意一点作x轴、y轴的垂线,所得矩形的面积S为定值|k| 对于下列三个图形中的情形,利用三角形面积的计算方法和图形的对称性以及上述结论,可得出对应的面积的结论为:
结论2:在直角三角形ABO中,面积S=
结论3:在直角三角形ACB中,面积为S=2|k|
结论4:在三角形AMB中,面积为S=|k|
例题讲解
【例1】如右图,已知△P10A1,△P2A1A2都是等腰直角三角形,点P1、P2
都在函数y=4
x(x>0)
的图象上,斜边OA1、A1A2都在x轴上.则点A2的坐
标为 .
1、如例1图,已知△P1OA1,△P2A1A2,△P3A2A3…△P n A n-1A n都是等腰直角三角形,点P1、
P2、P3…P n都在函数y=4
x
(x>0)的图象上,斜边OA1、A1A2、A2A3…A n-1A n都在x轴上.则
点A10的坐标为
2、已知点A(0,2)和点B(0,-2),点P在函数y=
1
x
的图像上,如果△PAB的面积为6,
求P点的坐标。
【例2】如右图,已知点(1,3)在函数y=k
x
(x>0)的图像上,矩形ABCD的边BC在x轴
上,E是对角线BD的中点,函数y=k
x
(k>0)的图象又经过A,E两点,点E的横坐标
为m,解答下列各题
1.求k的值
2.求点C的横坐标(用m表示)
3.当∠ABD=45°时,求m的值112
1、已知:如图,矩形ABCD的边BC在x轴上,E是对角线AC、BD的交点,反比例函数y=2 x
(x>0)的图象经过A,E两点,点E的纵坐标为m.
(1)求点A坐标(用m表示)
(2)是否存在实数m,使四边形ABCD为正方形,若存在,请求出m的值;若不存在,请说明理由
2、如图1,矩形ABCD的边BC在x轴的正半轴上,点E(m,1)是对角线BD的中点,点A、
E在反比例函数y=k
x
的图象上.
(1)求AB的长;
(2)当矩形ABCD是正方形时,将反比例函数y=k
x
的图象沿y轴翻折,得到反比例函数y=
1
k
x
的图象(如图2),求k1的值;
(3)直线y=-x上有一长为2动线段MN,作MH、NP都平行y轴交在条件(2)下,第一
象限的双曲线y=k
x
于点H、P,问四边形MHPN能否为平行四边形(如图3)?若能,请求出
点M的坐标;若不能,请说明理由.
【例3】在平面直角坐标系中,已知A(1,0),B(0,1),矩形OMPN的相邻两边OM,ON分别在x,y轴的正半轴上,O为原点,线段AB与矩形OMPN的两边MP,NP的交点分别为E,F,△AOF∽△BOE(顶点依次对应)
(1)求∠FOE;
(2)求证:矩形OPMN的顶点P必在某个反比例函数图像上,并写出该函数的解析式。
如图,在平面直角坐标系中,直线y=-x+1分别交x 轴、y 轴于A ,B 两点,点P (a ,b )是反比例函数y=
1
2x
在第一象限的任意一点,过点P 分别作PM ⊥x 轴于点M ,PN ⊥y 轴于点N ,PM ,PN 分别交直线AB 于E ,F ,有下列结论:①AF=BE ;②图中的等腰直角三角形有4个;③S △OEF =
1
2
(a+b-1);④∠EOF=45°.其中结论正确的序号是②③④
【例4】已知:如右图,已知反比例函数y=2k
x
和一次函数y=2x-1,其中一次函数的图像经过(a ,b ),(a+1,b+k ). (1)求反比例函数的解析式;
(2)如图,已知点A 在第一象限,且同时在上述两个函数的图象上,求点A 的坐标; (3)利用(2)的结果,请问:在x 轴上是否存在点P ,使△AOP 为等腰三角形?若存在,把符合条件的P 点坐标都求出来;若不存在,请说明理
由
.
已知反比例函数y=
2k
x
和一次函数y=2x-1,其中一次函数的图象经过(a ,b ),(a+k ,b+k+2)两点. (1)求反比例函数的解析式;
(2)求反比例函数与一次函数两个交点A 、B 的坐标: (3)根据函数图象,求不等式
2k
x
>2x-1的解集; (4)在(2)的条件下,x 轴上是否存在点P ,使△AOP 为等腰三角形?若存在,把符合条件的P 点坐标都求出来;若不存在,请说明理由。
一、巩固练习:
解答题1、已知反比例函数y=k
x
图象过第二象限的点A(-2,m),作AB⊥x轴于B,Rt△AOB面积为
3;若直线y=ax+b经过点A,并且经过反比例函数y=k
x
的图象上另一点C(n,-1).
(1)反比例函数的解析式为y=-6
x
,m=3,n=6;
(2)求直线y=ax+b的解析式;
(3)设直线y=ax+b与x轴交于M,求AM的长;
(4)根据图象写出使反比例函数y=k
x
值大于一次函数y=ax+b的值的x的取值围。
2、已知如图:矩形ABCD 的边BC 在x 轴上,E 为对角线BD 的中点,点B 、D 的坐标分别为B (1,0),D (3,3),反比例函数y=
k
x
的图象经过A 点, (1)写出点A 和点E 的坐标; (2)求反比例函数的解析式;
3、如右图已知反比例函数y=
k
x
(k <0)的图像经过点A (3m ),过A 点作AB ⊥x 轴于点B,且△AOB 3
(1)求k 和m 的值
(2)若一次函数y=ax+1的图像经过点A ,并且与x 轴相交于点M,求∠AMO 和|AO|:|AM|的值
拓展训练
4、已知反比例函数y=
2k
x
和一次函数y=2x-1,其中一次函数的图象经过(a ,b )、(a+1,b+k )两点. (1)求反比例函数的解析式;
(2)若两个函数图象在第一象限的交点为A(1,m),请问:在x轴上是否存在点B,使△AOB为直角三角形?若存在,求出所有符合条件的点B的坐标;
(3)若直线y=-x+1
2
交x轴于C,交y轴于D,点P为反比例函数y=
2
k
x
(x>0)的图象上一点,过P作
y轴的平行线交直线CD于E,过P作x轴的平行线交直线CD于F,求证:DE•CF为定值.
过手练习
1、已知:如右图已知反比例函数y=12
x
的图像与一次函数y=kx-7的图像都经过P(m,2)
(1)求这个一次函数的解析式;
(2)如果等腰梯形ABCD的顶点A、B在这个一次函数的图象上,顶点C、D在这个反比例函数的图象上,两底AD、BC与y轴平行,且A和B的横坐标分别为a和a+2,求a的值.118
2.已知:如图,正比例函数y =ax 的图象与反比例函数x
k
y =
的图象交于点A (3,2). (1)试确定上述正比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限,当x 取何值时,反比例函数的值大于正比例函数的值; (3)M (m ,n )是反比例函数图象上的一动点,其中0<m <3,过点M 作直线MB ∥x 轴,交y 轴于点B ;过点A 作直线AC ∥y 轴交于点C ,交直线MB 于点D .当四边形OADM 的面积为6时,请判断线段BM 与DM 的大小关系,并说明理由.
3.如图,已知点A ,B 在双曲线)0(>=
x x
k
y 上,AC ⊥x 轴于点C ,BD ⊥y 轴于点D ,AC 与BD 交于点P ,P 是AC 的中点,若△ABP 的面积为3,求k 的值.
3(2010 )如图,已知直线12y x =与双曲线(0)k y k x =>交A ,B 两点,且点A 的横坐标为4.
(1)求k 的值; (2)若双曲线(0)k y k x =
>上一点C 的纵坐标为8,求△AOC 的面积;
(3)过原点O 的另一条直线l 交双曲线(0)k y k x
=>于P ,Q 两点(P 点在第一象限),若由点A ,B ,P ,Q 为顶点组成的四边形面积为24,求点P 的坐标.
4(2010 )如图13,在直角坐标系中,矩形OABC 的顶点
O 与坐标原点重合,顶点A ,C 分别在坐标轴上,顶点B 的坐标为 (4,2).过点D (0,3)和E (6,0)的直线分别与AB ,BC 交于 点M ,N .
(1)求直线DE 的解析式和点M 的坐标;
(2)若反比例函数x
m y =
(x >0)的图象经过点M ,求该 反比例函数的解析式,并通过计算判断点N 是否在该函数的图象上; (3)若反比例函数x m y =
(x >0)的图象与△MNB 有公共点,请直接..写出m 的取值围.。
