人教版数学八级下册压轴题含答案

合集下载

2021—2022学年人教版八年级下册数学期末动点最值压轴题

人教版八年级下册数学期末动点最值压轴题（答案）一、单选题1．如图，点A ，B 分别为x 轴、y 轴上的动点，2AB =，点M 是AB 的中点，点()0,3C ，()8,0D ，过C 作CE x ∥轴．点P 为直线CE 上一动点，则PD PM +的最小值为（）A 85B ．9C 89D ．325 2．如图，在平面直角坐标系中，O 为原点，点A ，C ，E 的坐标分别为（0，4），（8，0），（8，2），点P ，Q 是OC 边上的两个动点，且PQ ＝2，要使四边形APQE 的周长最小，则点P 的坐标为（）A ．（2，0）B ．（3，0）C ．（4，0）D ．（5，0） 3．如图，直线122y x =-+与x 轴、y 轴交于A 、B 两点，在y 轴上有一点C (0，4)，动点M 从A 点发以每秒1个单位的速度沿x 轴向左移动．当动到△COM 与△AOB 全等时，移的时间t 是（）A ．2B ．4C ．2或4D ．2或6 4．如图，在矩形ABCD 中，AB =4，△CAB =60°，点E 是对角线AC 上的一个动点，连接DE ，以DE 为斜边作Rt △DEF ，使得△DEF =60°，且点F 和点A 位于DE 的两侧，当点E 从点A 运动到点C 时，动点F 的运动路径长是（）A ．4B ．3C ．8D ．35．如图是甲、乙两个动点在某时段速度随时间变化的图象，下列结论错误的是（）A ．乙点前4秒是匀速运动，4秒后速度不断增加B ．甲点比乙点早4秒将速度提升到32cm/sC ．在4至8秒内甲的速度都大于乙的速度D ．甲、乙两点到第3秒时运动的路程相等6．如图，直线y ＝x ＋8分别与x 轴、y 轴交于点A 和点B ，点C ，D 分别为线段AB ，OB 的中点，点P 为OA 上一动点，当PC ＋PD 值最小时，点P 的坐标为（）A ．(－4，0)B ．(－3，0)C ．(－2，0)D ．(－1，0) 7．如图，点A ，B 在直线MN 的同侧，A 到MN 的距离8AC =，B 到MN 的距离5BD =，已知4CD =，P 是直线MN 上的一个动点，记PA PB +的最小值为a ，PA PB -的最大值为b ，则22a b -的值为（）A ．160B ．150C ．140D ．130 8．如图，在正方形ABCD 中，3AB =，E 是AD 上的一点，且1AE =，F ，G 是AB ，CD 上的动点，且BE FG =，BE FG ⊥，连接EF ，FG ，BG ，当EF FG BG ++的值最小时，CG 的长为（）A ．32B 10C ．125D ．65二、填空题9．如图，AB △CD ，AC 平分△BAD ，BD 平分△ADC ，AC 和BD 交于点E ，F ，G 分别是线段AB 和线段AC 上的动点，且AF =CG ，若DE =1，AB =2，则DF +DG 的最小值为______．10．如图，等腰BAC 中，120BAC ∠=︒，6BC =，P 为射线BA 上的动点，M 为BC 上一动点，则PM CP +的最小值为________．11．如图△，在△ABC中，△ACB＝90°，△A＝30°，点C沿BE折叠与AB上的点D重合，连接DE，请你探究：BCAB=______；请在这一结论的基础上继续思考：如图△，在△OPM中，△OPM＝90°△M＝30°，若OM＝2，点G是OM边上的动点，则12PG MG+的最小值为______．12．如图，在Rt△ABC中，△C＝90°，AC＝6，△B＝30°，点F在边AC上，并且CF＝2，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是_____．13．如图，F为正方形ABCD的边CD上一动点，AB＝2，连接BF，过A作AH△BF交BC于H，交BF于G，连接CG，当CG为最小值时，CH的长为_____．14．如图1，动点P从长方形ABCD的顶点A出发，沿A→C→D以1cm/s的速度运动到点D停止．设点P的运动时间为x（s），△P AB的面积为y（cm2）．表示y与x的函数关系的图象如图2所示，则长方形ABCD的面积为_____cm2．15．如图，Rt ABC中，2BC AC=D是斜边AB上一个动点，把ACD△沿直线CD 折叠，点A落在同一平面内的'A处，当'A D平行于Rt ABC的直角边时，AD的长为______．16．如图，在等腰三角形ABC中，AB＝AC＝13，BC＝10，D是BC边上的中点，AD ＝12，M，N分别是AD和AB上的动点，则BM+MN的最小值是_______．三、解答题17．如图1，在平面直角坐标系中，点A的坐标为（5，0），点B在第一象限内，且AB ＝4，OB＝3．(1)试判断△AOB的形状，并说明理由．(2)点P是线段OA上一点，且PB－P A＝1，求点P的坐标；(3)如图2，点C、点D分别为线段OB、BA上的动点，且OC＝BD，求AC＋OD的最小值．18．如图，在矩形ABCD中，AB=9，点E在边AB上，且AE=5．动点P从点A出发，以每秒1个单位长度，沿折线AD—DC运动，到达点C后停止运动．连接PE，作点A 关于直线PE的对称点F，设点P的运动时间为t秒（t＞0）．(1)如图1，在点P 的运动过程中，当F 与点C 重合时，求BC 的长；(2)如图2，如果BC=4，当点F 落在矩形ABCD 的边上时，求t 的值．19．已知：如图，△ABC 中，△C ＝90°，BC ＞AC ，点D 是AB 的中点，点P 是直线BC 上的一个动点，连接DP ，过点D 作DQ △DP 交直线AC 于点Q ．(1)如图△，当点P 、Q 分别在线段BC 、AC 上时（点Q 与点A 、C 不重合），过点B 作AC 的平行线交QD 的延长线于点G ，连接PG 、PQ ．△求证：PG ＝PQ ；△若BC ＝12，AC ＝9，设BP ＝x ，CQ ＝y ，求y 关于x 的函数表达式；(2)当点P 在线段CB 的延长线上时，依据题意补全图△，请写出线段BP 、PQ 、AQ 之间的数量关系，并说明理由．20．如图，直线24y x =-+与x 轴交于点A ，与y 轴交于点B ，点C 的坐标是()0,1-，P 为直线AB 上的动点，连接PO ，PC ，AC ．(1)求A ，B 两点的坐标．(2)求证：ABC 为直角三角形．(3)当PBC 与POA 面积相等时，求点P 的坐标．21．如图，P 为正方形ABCD 的边BC 上的一动点（P 不与B 、C 重合），连接AP ，过点B 作BQ △AP 交CD 于点Q ，将BCQ △沿着BQ 所在直线翻折得到BQE △，延长QE 交BA 的延长线于点M ．(1)探求AP 与BQ 的数量关系；(2)若3AB =，2BP PC =，求QM 的长．22．如图，在平面直角坐标系xOy 中，直线AP 交x 轴于点P （p ，0），与y 轴交于点A （0，a ），且a 、p 3a +（p ﹣1）2＝0．(1)求直线AP的解析式；(2)如图1，直线x＝﹣2与x轴交于点N，点M在x轴上方且在直线x＝﹣2上，若△MAP 的面积等于6，请求出点M的坐标；(3)如图2，已知点C（﹣2，4），若点B为射线AP上一动点，连接BC，在坐标轴上是否存在点Q，使△BCQ是以BC为底边的等腰直角三角形，直角顶点为Q，若存在，请求出点Q坐标；若不存在，请说明理由．参考答案：1．B解：如图，作D 关于CE 的对称点D ，连接D O '，交CE 于点P ，连接OM ，OM D M OD '+≥'，PM PD PM PD D M ''+=+≥，∴当,,,O M P D '共线时，PM 最短则PD PM +的最小值为OD 'OM -BOA △是直角三角形，点M 是AB 的中点，2AB =112OM AB ∴== 点()0,3C ，()8,0D ，(8,6)D '∴228610OD '∴+∴OD 'OM -1019=-=即PD PM +的最小值为9故选B2．C解：四边形APQE 的周长,AP PQ EQ AEPQ ＝2，0,4,8,2,A EAE PQ 是定值，所以四边形APQE 的周长最小，则AP EQ +最小，如图，把AP 沿x 轴正方向平移2个单位长度得,A Q 则2,4,A 则,A Q AP作E 关于x 轴的对称点,H 则8,2,H连接A H '交x 轴于,K 则,A K EK A H所以当,Q K 重合时，A Q QE 最小，即AP QE +最小，设A H '的解析式为：,y kx b =+24,82k b k b 解得：1,6k b 所以A H '的解析式为：6,y x =-+令0,y = 则6,x = 则6,0,K 即6,0,Q()4,0.P ∴故选C3．D 解：直线122y x =-+与x 轴、y 轴交于A 、B 两点，令0,x = 则2,y = 令0y =，则120,2x -+= 4,x ∴=如图，当1,M M 关于y 轴对称时，此时1,CM O ABO ≌此时112,246,OM OM AM6,t ∴=故选：D4．B解：当E 与A 点重合时，点F 位于点F '处，当E 与C 点重合时，点F 位于点F 处，如图，△F 的运动路径是线段FF '的长；△AB =4，△CAB =60°，△△DAC =△ACB =30°，△AC =2AB =8，AD =BC 22AC AB -3当E 与A 点重合时，在Rt △ADF '中，AD 3△DAF '=60°，△ADF '=30°，AF '=12AD 3△AF 'D =90°，当E 与C 重合时，△DCF =60°，△CDF =30°，CD =AB =4，△△FDF '=90°，△DF 'F =30°，CF =12CD =2， △△FDF '=△AF 'D =90°，DF 22CD CF -3△DF △AF '，DF =AF '=3△四边形FDAF '是平行四边形，△FF '= AD 3故选：B ．5．D【详解】A ．根据图象可得，乙前4秒的速度不变，为12米/秒，故A 正确，不合题意；B ．从图象可知，甲8秒时速度是32厘米/秒，乙12秒时速度是32厘米/秒，故B 正确，不符合题意；C ．在4至8秒内甲的速度图象一直在乙的上方，所以甲的速度都大于乙的速度，故C 正确，不合题意．D ．甲每秒增加的速度为：3284÷=（米/秒），3412⨯=（米/秒），甲前3秒的运动路程为481224++=（米)，乙前4秒的速度不变，为12米/秒，则行驶的路程为12336⨯=米，所以甲、乙两点到第3秒时运动的路程不相等，故D 错误，符合题意；故选：D ．6．C解：作点D 关于x 轴的对称点D ′，连接CD ′交x 轴于点P ，此时PC +PD 值最小，最小值为CD ′，如图．令y =x +8中x =0，则y =8，△点B 的坐标为（0，8）；令y =x +8中y =0，则x +8=0，解得：x =-8，△点A 的坐标为（-8，0）．△点C 、D 分别为线段AB 、OB 的中点，△点C （-4，4），点D （0，4）．△点D ′和点D 关于x 轴对称，△点D ′的坐标为（0，-4）．设直线CD ′的解析式为y =kx +b ，△直线CD ′过点C （-4，4），D ′（0，-4），△444k b b -+⎧⎨-⎩＝＝，解得：24k b -⎧⎨-⎩＝＝， △直线CD ′的解析式为y =-2x -4．令y =0，则0=-2x -4，解得：x =-2，△点P 的坐标为（-2，0）．故选：C ．7．A解：如图所示，作点A 关于直线MN 的对称点A '，连接A B '交直线MN 于点P ，则点P 即为所求点，过点A '作直线AE BD ⊥，△8AC =，5BD =，4CD =，△8A C '=，8+5=13BE =，==4A E CD '，在Rt A EB '中，根据勾股定理得， △22=+13+4=185A B BE A E ''即P A +PB 的最小值是185a如图所示，延长AB 交MN 于点P '，△P A P B AB ''-=，AB PA PB >-，△当点P 运动到P '点时，PA PB -最大，过点B 作BE AC ⊥，则4BE CD ==，△853AE AC BD =-=-=，在Rt AEB 中，根据勾股定理得，2222345AB AE BE ++=， △5PA PB -=，即5b =， △2222(185)5160a b -=-=，故选A ．8．A如图，过点G 作GT △AB 于T ，设BE 交FG 于R ．△四边形ABCD 是正方形，△AB =BC ，△A =△ABC =△C =90°，△GT △AB ，△△GTB =90°，△四边形BCGT 是矩形，△BC =GT ，△AB =GT ，△GF △BE ，△△BRF =90°，△△ABE +△BFR =90°，△TGF +△BFR =90°，△△ABE =△TGF ，在△BAE 和△GTF 中，A GTF AB GTABE TGF ∠=∠⎧⎪=⎨⎪∠=∠⎩， △△BAE △△GTF （ASA ），△AE =FT =1，△AB =3，AE =1，△BE 22AB AE +2231+10△GF =BE 10在Rt △FGT 中，FG 221310+△EF +FG 的值最小时，EF +FG +BG 的值最小，设CG =BT =x ，则EF +BG 22221(31)3x x +--+22221(2)3x x +-+ 22221(2)3x x +-+x 轴上寻找一点P （x ，0），使得点P 到M （0，3），N （2，1）的距离和最小．如图，作点M 关于x 轴的对称点M ′（0，-3），连接NM ′交x 轴于P ，连接PM ，此时PM +PN 的值最小．△N（2，1），M′（0，-3），△直线M′N的解析式为y=2x-3，△P（32，0），△x=3222221(2)3x x+-+故选：A．9．2解：连接BC，△AC平分△BAD，BD平分△ADC，AB△CD，△△DAC=△BAC，△ADB=△CDB，△AED=180°-180°÷2=90°，△AB△CD，△△DCA=△BAC，△△DCA=△DAC，△DA=DC，同理：DA=BA，△DC=AB，△AB△CD，△四边形ABCD是平行四边形，△DA=DC，△四边形ABCD是菱形．如图．在AC上取点B'，使AB'=AB，连接FB'，作点D关于AB的对称点D'，连接D'F、DD'．作B'H △CD 于点H ，作B'M △DD '于点M ．△DF =D 'F ，△AF =CG ，△B 'AF =△DCG ，AB '=AB =CD ，△△B 'AF △DCG （SAS ），△B 'F =DG ，△DF +DG =D 'F +B 'F ，△当B '、F 、D '三点在同一直线上时，DF +DG =D 'F +B 'F 取最小值为B 'D '． △DE =1，AD =AB =2，△△DAE =30°，△ADE =60°，△AC 33CB'32，△B'H =12B'C 31，CH 3=33△DH =DC -CH =2-（333，△四边形DHB′M 是矩形△DM =B'H 31，MB′=DH 31,△D 'M =DD '-DM 3-DM 331）3，△D 'B 2222(31)(31)22MB MD ''+-++=即DF +DG 的最小值为2 故答案为：2210．33解：作点C 关于BA 的对称点D ，连接BD ，点M 1是BC 上一点，连接DM 1，交AB 于点P ，连接CP ，作DM △BC 于M ，由对称可知，DP =CP ，△1PM CP PM DP DM +=+=当DM △BC 时，PM CP +最短，最小值为DM 长，△等腰BAC 中，120BAC ∠=︒，6BC =，△30ABC ACB ∠=∠=︒，由对称得，30ABD ∠=︒，6BC BD ==，△60CBD ∠=︒，30MDB ∠=︒， △132BM BD ==， 2233DM BD MB -= 故答案为：3311． 12 32解：△∵30A ∠=︒，∴60ABC ∠=︒，∵点C 沿BE 折叠与AB 上的点D 重合，∴BCE BDE ，∴BC BD =，30CBE DBE ∠=∠=°，90C BDE ∠=∠=︒，∴A DBE ∠=∠，∴AE BE =，AD BD =，∴12BD AB =， ∴12BC AB =，即12BC AB =； △如图所示：作射线MB ，使得30OMB ∠=︒，过点G 作GB MB ⊥，过点P 作PC MB ⊥交于点C ，连接PB ，在Rt POM 中，30PMO ∠=︒，2MO =， ∴112OP OM ==，223PM OM OP =- ∵30OMB ∠=︒，90GBM ∠=︒， ∴12GB GM =， ∴12PG GM PG GB PB PC +=+≥≥，即当P 、G 、B 三点共线时，12PG GM +取得最小值，在Rt PCM 中，∵30PMO ∠=︒，30OMB ∠=︒，90PCM ∠=︒，∴30CPM ∠=︒， ∴132CM PM ==2232PC PM CM =-， ∴12PG GM +的最小值为32；故答案为：△12；△32． 12．32解:如图，延长FP 交AB 于M ，当FP △AB 时，点P 到AB 的距离最小．△AC=6，CF=2，△AF=AC-CF=4，△△B＝30°，△ACB=90°△△A=60°△△AMF=90°，△△AFM=30°，△AM=1AF=2，2△FM22-3，AF FM△FP=FC=2，△PM=MF-PF32，△点P到边AB距离的最小值是32．故答案为:32．13．35解：如图，取AB的中点O，连接OG，OC.四边形ABCD是正方形，∴∠ABC=90°，AB=2，∴OB=OA=1，2222125OC OB BC ∴++AH △BF ，∴∠AGB =90°，AO =OB ，∴OG =12AB =1，CD OC OG ≥-，当O 、G 、C 共线时，CG 的值最小，最小值51，此时如图，OB =OG =1，∴∠OBG =∠OGB ，AB //CD ，∴∠OBG =∠CFG ，∠OGB =∠CGF ，∴∠CGF =∠CFG ，∴CF =CG 51，∠ABH =∠BCF =∠AGB =90°，∴△BAH +△ABG =90°,△ABG +△CBF =90°，∴△BAH =△CBF ，AB =BC ，∴△ABH ≌△BCF (ASA ) ，∴BH =CF 51，∴CH =BC -BH =2-51)=35 故答案为：3514．60解：由图象，结合题意可得AC=13cm，CD=25-13=12（cm），△AD2222AC CD--（cm），1312△长方形ABCD的面积为：12×5=60（cm2）．故答案为：60．15．222解：Rt△ABC中，BC＝AC2△AB＝2，△B＝△A′CB＝45°，△如图1，当A′D△BC，设AD＝x，△把△ACD沿直线CD折叠，点A落在同一平面内的A′处，△△A′＝△A＝△A′CB＝45°，A′D＝AD＝x，△△B＝45°，△A′C△AB，△BH2＝1，DH2A′D2x，△x2＋1＝2，△x＝22△AD＝22△如图2，当A′D△AC，△把△ACD沿直线CD折叠，点A落在同一平面内的A′处，△AD＝A′D，AC＝A′C，△ACD＝△A′CD，△△A′DC＝△ACD，△△A′DC＝△A′CD，△A′D＝A′C，△AD＝AC2综上所述：AD的长为：22216．120 13解：如图，作BH△AC，垂足为H，交AD于M′点，过M′点作M′N′△AB，垂足为N′，则BM′+M′N′为所求的最小值．△AB=AC，D是BC边上的中点，△AD是△BAC的平分线，△M′H=M′N′，△BM′+M′N′=BH，△BH是点B到直线AC的最短距离（垂线段最短），△AB =AC =13，BC =10，D 是BC 边上的中点，△AD △BC ，BD =12BC =5，在Rt △ABD 中，AB 2=AD 2+BD 2，△AD 22AB BD -22135-，△S △ABC =12AC •BH =12BC •AD ，△13•BH =10×12，解得：BH =12013，故答案为：12013． 17．解：△AOB 是以B 为直角顶点的直角三角形，理由如下：△A （5，0），△OA =5，△AB 2+OB 2=42+32=25=52=OA 2，△△AOB 是以OA 为斜边的直角三角形；(2)解：如图，作BE △OA 于E ，设P A =x ，则BP =x +1，△S △AOB ＝12BO •AB ＝12OA •BE ， △125OB AB BE OA ⋅==， △OE 2295OB BE -=， △PE =5-95-x =165-x ，在Rt △BEP 中，(x +1)2=(165-x )2+(125)2，解得x =2514△OP =5-2514=4514， △P (4514，0)； (3) 解：如图，过点O 作以OB 为腰，△BOH =90°的等腰直角三角形，△HO =BO ，△HOC =△OBD =90°，又△OC =DB ，在△HOC 和△OBD 中HO BO HOC OBD OC DB =⎧⎪∠=∠⎨⎪=⎩，△△HOC △△OBD （SAS ），△OD =HC ，△AC +OD =AC +HC ，△要使AC +OD 最小，则AC +CH 最小，△当A 、C 、H 三点共线时，AC +CH 最小，即AC +OD 有最小值为AH 的长，分别过点B ，H 作BE △x 轴于E ，HF △x 轴于F ，则OB =OH =3，△S △AOB ＝12BO •AB ＝12OA •BE ， △125OB AB BE OA ⋅==， △2295OE OB BE =+=， △△HFO =△HDB =△OEB =90°，△△HOF +△OHF =90°，△HOF +△BOE =90°，△△OHF =△BOE ，在△OHF 与△BOE 中，OFH BEO OHF BOE OH BO ∠=∠⎧⎪∠=∠⎨⎪=⎩，△△OHF △△BOE （AAS ），△OF =BE =125，HF =OE =95， △H 在第二象限，△H （-125，95）； △22129(5)()5855AH --+ 即AC +OD 5818．解：连接EC 、AP ，△F 与点C 重合，点A 与点F 关于直线PE 对称，连接EC 、AP ，△PE 是线段AC 的垂直平分线，△EC =AE =5，BE =AB -AE =4，△BC22EC BE-=3，△BC的长为3；(2)解：当点P在线段AD上，点F落在CD边上时，连接EF，过点F作FG△AB于点G，△矩形ABCD中，FG△AB，△四边形AGFD为矩形，△FG=AD=BC=4，△点A与点F关于直线PE对称，△PE是线段AC的垂直平分线，△EF=AE=5，△GE223EF FG-，△DF=AG=AE-GE=2，△t的值为4261+=(秒)；当点P在线段CD上，点F落在CD边上时，连接EF，过点F作FH△AB于点H，同理求得EH=3，BH=BE-EH=1=CF，△t的值为491121+-=(秒)；当点P在线段CD上，点F落在BC边上时，连接EF，同理求得FB =3，CF =BC -BF =1，△t 的值为491141++=(秒)；综上，t 的值为6秒或12秒或14秒．19．解：△证明：由题意知AD BD =△AC BG ∥△BGD AQD ∠=∠在BGD △和AQD 中BGD AQD BDG ADQ BD AD ∠=∠⎧⎪∠=⎨⎪=⎩△()BGD AQD AAS ≌△GD QD =△PD DQ ⊥△DP 垂直平分GQ△PG PQ =；△△PG PQ =△22PG PQ =；△由勾股定理知222222BG BP CQ C PG PQ P +===+ △ ()()2222912y x y x -+-+＝ △4732y x =- △y 关于x 的函数表达式为4732y x =-．(2)解：AQ 2＋BP 2＝PQ 2．补全图形，如图△：证明：作BG AC ∥，交QD 的延长线于点G ，连接PQ PG ，同（1）可证()BGD AQD AAS ≌△GD QD =△PD DQ ⊥△DP 垂直平分GQ△PG PQ =△22PG PQ =△由勾股定理知222222AQ PG PQ BG BP BP +=+== △222BP AQ PQ +=；补全图形，如图△：证明：作BG AC ∥，交QD 的延长线于点G ，连接PQ PG ，同（1）可证()BGD AQD AAS ≌△GD QD =△PD DQ ⊥△DP 垂直平分GQ△PG PQ =△22PG PQ =△由勾股定理知222222AQ PG PQ BG BP BP +=+== △222BP AQ PQ +=；综上所述，222BP AQ PQ +=．20．(1)△直线24y x =-+与x 轴交于点A ，与y 轴交于点B ， △令0y =，则240x -+=，解得2x =， △()2,0A ，令0x =，则4y =，△()0,4B .(2)△()0,4B ，()0,1C -，△5BC =，△在Rt ABO 中，222224220AB OB OA =+=+=，在Rt AOC △中，22222125AC OC OA =+=+=， △2220525AB AC +=+=，又△22525BC ==，△222AB AC BC +=，由勾股定理逆定理知，ABC 为直角三角形(3)设(),24P a a -+，△PBC 与POA 面积相等，则5224a a ⨯=⨯-+，△()5224a a =-+或()5224a a =--+，△89a =或8a =-， △820,99P ⎛⎫ ⎪⎝⎭或()8,20P -. 21．(1)△四边形ABCD 是正方形，△AB =BC ，△90ABQ CBQ ∠+∠=︒，△BQ △AP△90PAB QBA ∠+∠=︒，△PAB CBQ ∠=∠，在PBA △和BCQ △中，{PAB CBQAB BC ABP BCQ∠=∠=∠=，△()PBA QCB ASA ≌，△AP BQ =．(2)过点Q 作QH AB ⊥于H ，如图△四边形ABCD 是正方形，△QH =BC =AB =3，△BP =2PC ，△BP =2，PC =1， △22223213BQ AP AB PB =++△221392BH BQ QH =--，△四边形ABCD 是正方形，△DC //AB△CQB QBA ∠=∠，由折叠知识得EQB CQB ∠=∠，△QBA EQB ∠=∠，△MQ =MB ，设QM =x ，则有MB =x ，MH =x -2，在t R MHQ 中，根据勾股定理可得222(2)3x x =-+，解得x =134， △QM 的长为134． 22．(1)解：3a +（p ﹣1）2＝0．△a +3=0，p -1=0，解得a=-3，p =1，△P (1,0)，A (0,-3)，设直线AP 的解析式为y=kx+b ，△03k b b +=⎧⎨=-⎩，解得33k b =⎧⎨=-⎩， △直线AP 的解析式为y =3x -3；(2)解：过M 作MD AP ∥交x 轴于D ，连接AD ，△MD AP ∥，△MAP 的面积等于6，△△DAP 的面积等于6， △162A DP y ⋅⋅=，即1362DP ⋅⨯=， △DP =4，△D （-3，0）设直线DM 的解析式为y =3x+c ，则()330c ⨯-+=，△c=9，△直线DM 的解析式为y=3x +9，令x =-2，得y=3，△M （-2，3）；(3)解：存在设B （t ，3t -3），△当点Q 在x 轴负半轴时，过B 作BE △x 轴于E ，如图，△OE=t ，BE =3-3t ，△△BCQ是以BC为底边的等腰直角三角形，△BQ=CQ，△BQC=90°，△△BQE=90°-△NQC=△QCN，又△△BEQ=△QN C，△△BEQ△△QNC（AAS），△QN=BE=3-3t，QE=CN=4，△OQ=QE-OE=ON+QN，即4-t=2+3-3t，△t=12，△OQ=72，△Q（-72，0）；△当Q在y轴正半轴上时，过C作CF△y轴于F，过B作BG△y轴于G，如图，△BG=t，OG=3t-3，△△BCQ是以BC为底边的等腰直角三角形，△BQ=CQ，△BCQ=90°，△△CQF=90°-△BQG=△GBQ，又△△CFQ=△BGQ=90°，△△CQF△△QBG（AAS），△CF=QG=2，QF=BG=t，△O Q=OG-QG=OF-QF，即3t-3-2=4-t，△t=94，△OQ=4-t=74，△Q（0，74）；△当Q在y轴正半轴上时，过点C作CF△y轴于F，过B作BT△y轴于T，如图，△BT=t，OT=3t-3，同△可证△CFQ△△QTB（AAS），△CF=BT=t，QF=CF=2，△O Q=OT+QT=OF+QF，即3t-3+2=4+t，△t=52，△OQ=4+t=132，△Q（0，132）；综上，Q的坐标为（-72，0）或（0，74）或（0，132）．。

人教版八年级下册数学期末压轴题专题训练(含答案)

人教版八年级下册数学期末压轴题专题训练1．如图，已知长方形的边AD ＝8，AB ＝4，动点M 从点A 出发，以每秒2个单位长度的速度沿A →D →A 的路径匀速运动，同时，动点N 从点C 出发，沿C →B 方向以每秒1个单位长度的速度匀速运动，当其中一个动点到达终点时，另一点也随之停止运动，设运动时间为t 秒．(1)如（图一），当运动时间为1秒时，求MN 的长度；(2)当0≤t ≤4时，直接写出AMN 为直角三角形时的运动时间t 的值； (3)如（图二），当4＜t ＜8时，判断AMN 的形状，并说明理由．2．（1）感知：如图①，在正方形ABCD 中，E 为边AB 上一点（点E 不与点AB 重合），连接DE ，过点A 作AF DE ⊥，交BC 于点F ，证明：DE AF =．（2）探究：如图②，在正方形ABCD 中，E ，F 分别为边AB ，CD 上的点（点E ，F 不与正方形的顶点重合），连接EF ，作EF 的垂线分别交边AD ，BC 于点G ，H ，垂足为O ．若E 为AB 中点，1DF =，4AB =，求GH 的长．（3）应用：如图③，在正方形ABCD 中，点E ，F 分别在BC ，CD 上，BE CF =，BF ，AE 相交于点G ．若3AB =，图中阴影部分的面积与正方形ABCD 的面积之比为2：3，则ABG 的面积为______，ABG 的周长为______．3．如图．菱形ABCD的对角线AC，BD交于点O．尺规作图：过点A作直线BC的垂线（不写作法和证明，保留作图痕迹）．该垂线与BC交于点E，F为AD边上一点，DF=AE，连接OF，若OD=2AO，请猜想CE与OF的数量关系，并证明你的猜想．4．图1、图2分别是65的网格，网格中每个小正方形的边长均为1，线段AB的端点在小正方形的顶点上，请在图1、图2中各画一个图形，分别满足以下要求：(1)在图1中画一个以线段AB为一边的菱形（非正方形），所画菱形各顶点必须在小正方形的顶点上．(2)在图2中画一个以线段AB为一边的等腰三角形，所画等腰三角形各顶点必须在小正方形的顶点上，且所画等腰三角形的面积为52．5．如图，在▱ABCD中，对角线AC与BD相交于点O，点E，F分别为OB，OD的中点，延长AE至G，使EG＝AE，连接CG．(1)求证：△ABE≌△CDF；(2)当AB与AC满足什么数量关系时，四边形EGCF是矩形？请说明理由．⊥，垂6．如图，在ABCD中，E，F分别为AD，BC的中点，AG BD⊥，CH BD足分别为G，H，连接EG，EH，FG，FH．(1)求证：四边形GEHF是平行四边形；BC=，当BD=______时，GEHF是矩形．(2)若2AB=，37．如图1，在Rt△ABC中，∠ACB=90°，∠A=30°，BD是△ABC的角平分线，DE⊥AB 于E．(1)发现：如图1，连接CE，则△BCE的形状是_______________，∠CDB=____________°；(2)探索：如图2，点P为线段AC上一个动点，当点P在CD之间运动时，连接BP，作∠BPQ=60°，PQ交射线DE于Q，连接BQ，即△BPQ是等边三角形；思路：在线段BD上截取点H，使DH=DP，得等边△DPH，由∠DPQ=∠HPB，PD=PH，∠QDP=∠BHP，易证△PDQ≌△PHB（ASA），得PQ=PB，即△BPQ是等边三角形．试判断线段DQ、DP、AD之间的关系，并说明理由；(3)类比：如图3，当点P在AD之间运动时连接BP，作∠BPQ=60°，PQ交射线DE于Q，连接BQ．①试判断△BPQ的形状，并说明理由；②若AD=2，设AP=x，DQ=y，请直接写出y与x之间的函数关系式．8．下面是小东设计的“作平行四边形ABCD，使∠B＝45°，AB＝2cm，BC＝3cm”的作图过程．作法：如图，①画∠B＝45°；②在∠B的两边上分别截取BA＝2cm，BC＝3cm．③以点A为圆心，BC长为半径画弧，以点C为圆心，AB长为半径画弧，两弧相交于点D；则四边形ABCD为所求的平行四边形．根据小东设计的作图过程：(1)使用直尺和圆规，补全图形；（保留作图痕迹）(2)完成下面的证明．证明：∵AB＝，CB＝，∴四边形ABCD为所求的平行四边形（）（填推理的依据）．9．如图，已知菱形ABCD中，分别以C、D为圆心，大于1CD的长为半径作弧，两弧2分别相交于M、N两点，直线MN交CD于点F，交对角线AC于点E，连接BE、DE．(1)求证：BE＝CE；(2)若∠ABC＝72°，求∠ABE的度数．10．如图，四边形ABCD是一个正方形，E、F分别在AD、DC边上，且DE=CF，AF、BE交于O点，请说出线段AF和BE的关系，并证明你的结论．11．如图，在由边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，请按要求完成下列各题：(1)在网格中画出平行四边形ABCD；(2)线段AC的长为，CD的长为，AD的长为，△ACD为三角形，平行四边形ABCD的面积为．12．两个不全等的直角三角形ABC 和DEF 重叠在一起，其中∠A ＝60°，AC ＝1．固定△ABC 不动，将△DEF 进行如下操作：(1)如图（1），△DEF 沿线段AB 向右平移（D 点在线段AB 内移动），连接DC 、CF 、FB ，四边形CDBF 的形状在不断的变化，但它的面积不变化，请求出其面积；(2)如图（2），当D 点移到AB 的中点时，请你猜想四边形CDBF 的形状，并说明理由．13．如图，长方形ABCD 中，E 是AD 的中点，将ABE △沿BE 折叠后得到GBE ，且G 点在长方形ABCD 内部，延长BG 交DC 于点F ．(1)求证：GE DE =；(2)若9DC =，DF 2CF =，求AD 的长；(3)若DC n DF =⋅，求22AD AB 的值．14．在正方形ABCD 中，点E 是CD 边上任意一点．连接AE ，过点B 作BF ⊥AE 于F ．交AD 于H ．(1)如图1，过点D 作DG ⊥AE 于G ，求证：△AFB ≌△DGA ；(2)如图2，点E 为CD 的中点，连接DF ，求证：FH +FE ；(3)如图3，AB ＝1，连接EH ，点P 为EH 的中点，在点E 从点D 运动到点C 的过程中，点P 随之运动，请直接写出点P 运动的路径长．15．已知如图，四边形ABCD 是平行四边形．（1）尺规作图：作∠ABC 的角平分线交CD 的延长线于E ，交AD 于F （不写作法和证明，但要保留作图痕迹）．（2）请在（1）的情况下，求证：DE ＝DF ．16．如图，在Rt ABC ∆中，90ACB ∠=︒，CD 是斜边AB 上的中线，1AC CD ==，求直角边BC 的长．17．如图：正方形ABCD 中，点E 、F 分别在边BC 、CD 上，BE ＝CF ，连接AE ，BF 交于点O ，点M 为AB 中点，连接OM ，求证：12OM AB =．18．如图，在四边形ABCD 中，90ABD ACD ∠=∠=︒，E ，F 分别是BC 、AD 的中点．(1)若10AD =，求BF 的长； (2)求证：EF BC ⊥．19．如图，四边形ABDE 和四边形ACFG 都是正方形，CE 与BG 交于点M ，点M 在△ABC 的外部．(1)求证：BG ＝CE ； (2)求证：CE ⊥BG ； (3)求：∠AME 的度数．20．如图，△ABC中，D是AB边上任意一点，F是AC中点，过点C作CE//AB交DF 的延长线于点E，连接AE，CD．(1)求证：四边形ADCE是平行四边形；(2)若∠B＝30°，∠CAB＝45°，AC ，求AB的长．21．如图，△ABC中，∠C＝90°．(1)尺规作图：作边BC的垂直平分线，与边BC，AB分别交于点D和点E；（保留作图痕迹，不要求写作法）(2)若点E是边AB的中点，AC＝BE，求证：△ACE是等边三角形．22．已知：如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC 的平行线交BE的延长线于点F，且AF＝DC，连接CF．(1)求证：D是BC的中点；(2)如果AB＝AC，试判断四边形ADCF的形状，并证明你的结论．23．如图，四边形ABCD 是平行四边形．(1)尺规作图（不写作法，保留作图痕迹）；作出ABC ∠的角平分线BE ，交AD 于点E ；在线段BC 上截取BF BA =，连接EF ；(2)在（1）所作图中，请判断四边形ABFE 的形状，并说明理由．24．如图，矩形ABCD 中，E 、F 分别为边AD 和BC 上的点，BE ＝DF ，求证：DE ＝BF ．25．已知：在ABC 中，90BAC ∠=︒，AB AC =，点D 为直线BC 上一动点（点D 不与B 、C 重合）．以AD 为边作正方形ADEF ，连接CF ．(1)如图①，当点D 在线段BC 上时， ①求证：ABD △≌ACF ； ②ACF ∠的大小＝______°；③若8BC =，2CD =，则CF 的长＝______；(2)如图②，当点D 在线段BC 的延长线上时，其它条件不变，则CF 、BC 、CD 三条线段之间的关系是：CF =______；其它条件不变：①CF、BC、CD三条线段之间的关系是：CF ______；△的形状，并说明②若连接正方形的对角线AE、DF，交点为O，连接OC，探究AOC理由．26．已知：如图，▱ABCD中，延长BC至点E，使CE=BC，连接AE交CD于点O．(1)求证：CO=DO；(2)取AB中点F，连接CF，△COE满足什么条件时，四边形AFCO是正方形？请说明理由．参考答案：1．解：过点N作NR⊥AD于R．∵四边形ABCD是矩形，∴∠C=∠D=∠DRN=90°，∴四边形CDRN是矩形，∴RN=CD=4，CN=DR=1，∵AM=2，AD=8，∴RM=AD-AM-DR=8-2-1=5，∵∠MRN=90°，∴MN=(2)解：当0≤t≤4时，如果AM=BN，则△AMN是直角三角形，∴2t=8-t，∴t=83，当t=4时，点M与D重合，点N位于BC的中点，此时△AMN是等腰直角三角形，综上所述，当△AMN是直角三角形时，t的值为83或4．(3)解：∵当t=4时，△AMN是等腰直角三角形，∵点M的运动速度大于点N的运动速度，且M，N同时到达终点，即点M在点N的右侧，∴当4＜t＜8时，△AMN是锐角三角形．2．证明：∵四边形ABCD是正方形，∴AD AB =，90DAE ABF ∠=∠=︒，∵AF DE ⊥，∴90DAF BAF ∠+∠=︒，90DAF ADE ∠+∠=︒， ∴ADE BAF ∠=∠，在DAE △和ABF 中，ADE BAF AD AB DAE ABF ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴DAE △≌ABF （ASA ），∴DE AF =．探究：解：分别过点A 、D 作AN GH ∥，DM EF ∥，分别交BC 、AB 于点N 、M ，如图②所示：∵四边形ABCD 是正方形，∴AB CD ∥，AB CD =，90DAB B ∠=∠=︒，∴四边形DMEF 是平行四边形，∴1ME DF ==，DM EF =， ∵AN GH ∥，GH EF ⊥，∴DM GH ⊥，同理，四边形AGHN 是平行四边形，∴GH AN =，∵DM EF ∥，GH EF ⊥，∴AN DM ⊥，∴90DAN ADM ∠+∠=︒，∵90DAN BAN ∠+∠=︒，∴ADM BAN ∠=∠，在ADM △和BAN 中，90ADM BAN AD AB DAM ABN ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩，∴ADM △≌BAN （ASA ），∴DM AN =，∴EF GH DM AN ===，∵E 为AB 中点，∴122AE AB ==， ∴211AM AE ME =-=-=，∴DM ==∴GH =应用：解：∵AB ＝3，∴S 正方形ABCD ＝3×3＝9，∵阴影部分的面积与正方形ABCD 的面积之比为2：3，∴阴影部分的面积为：23×9＝6， ∴空白部分的面积为：9﹣6＝3，在△ABE 和△BCF 中，90BECF ABE BCF AB BC ，∴△ABE ≌△BCF （SAS ），∴∠BEA ＝∠BFC ，S △ABG ＝S 四边形CEGF ，∴S △ABG ＝12×3＝32，∠FBC +∠BEA ＝90°， ∴∠BGE ＝90°，∴∠AGB ＝90°，设AG ＝a ，BG ＝b ，则12ab ＝32， ∴2ab ＝6，∵a 2+b 2＝AB 2＝32，∴a 2+2ab +b 2＝32+6＝15，即（a +b ）2＝15，而0,a b +>∴a +bBG +AG∴△ABG，故答案为：323． 3．解：所作图形如图所示：结论：CE =OF ．理由：∵四边形ABCD 是菱形，∴AC ⊥BD ，OA =OC ，AD ∥BC ，∵AE ⊥BC ，OF ⊥AD ，∴AE ⊥AD ，∴∠AEC =∠DAE =∠AOD =∠DFO =90°，∴∠EAC +∠DAO =90°，∠FDO +∠DAO =90°，∴∠CAE =∠ODF ，∵OD =2AO ，AC =2AO ，∴AC =OD ，在△AEC 和△DFO 中，AEC DFO CAE ODF AC DO ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AEC ≌△DFO （AAS ），∴CE =OF ．4．解：所画菱形如图所示；(答案不唯一)(2)解根据勾股定理，AB = 所画等腰三角形的面积为52， ∴作以线段AB 为直角边的等腰直角三角形即可，所画三角形如图所示．5．证明：∵四边形ABCD 是平行四边形，∴AB =CD ，AB CD ∥，OB =OD ，OA =OC ，∴∠ABE =∠CDF ，∵点E ，F 分别为OB ，OD 的中点， ∴12BE OB =，12DF OD =， ∴BE =DF ，在△ABE 和△CDF 中，AB CD ABE CDF BE DF =⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△CDF(SAS).(2)解：当AC =2AB 时，可使四边形EGCF 为矩形；理由如下：∵△ABE ≌△CDF ，∴∠AEB =∠CFD ，∴∠AEO =∠CFO ，∴AE CF ∥，∵EA =EG ，OA =OC ，∴EO 是△AGC 的中位线，∴EO GC ∥，∴四边形EGCF 是平行四边形，∵AC =2AB ，AC =2AO ，∴AB =AO ，∵E 是OB 的中点，∴AE ⊥OB ，∴∠OEG =90°，∴平行四边形EGCF 是矩形．6．解：∵AG BD ⊥于G ，∴90AGD ∠=︒．∵在Rt AGD 中，E 为AD 的中点， ∴12EG ED AD ==，同理12HF BF BC ==． ∵在ABCD 中，AD BC =，∴EG FH =．∵在EGD 中，EG ED =，∴EDG EGD ∠=∠，同理在BFH △中，HBF FHB ∠=∠．∵在ABCD 中，AD BC ∥，∴EDG HBF ∠=∠．∴EGD FHB ∠=∠．∴EG FH ∥．又∵EG FH =，∴四边形GEHF 是平行四边形．(2)连接EF ，则EF =AB =CD =2，若四边形GEHF 是矩形，则EF =GH =2，在RtAGD 和Rt ΔCHB 中，41AGD CHB AD CB ∠=∠⎧⎪∠=∠⎨⎪=⎩， ΔAGD ≅ΔCHB （AAS )，∴DG =BH ；∴DG -GH =BH -GH ，即BG =DH ，设BG =DH =x ，在Rt △ABG 中，AG 2=AB 2-BG 2=4-x 2，在Rt △AGD 中，AG 2=AD 2-DG 2=9-DG 2=9－（2+x ）2，∴4-x 2=9-(2+x )2，解得x =14， ∴BD =BG +GH +HD =14+2+1452= ． 7．解：如图1，∵在Rt △ABC 中，∠ACB =90°，∠A =30°，∴∠ABC =60°，∵BD 是△ABC 的角平分线，∴∠ABD =∠CBD =12∠ABC =30°，∴∠ABD =∠A ，∠CDB =90°－∠CBD =60°，∴AD =BD ，又DE ⊥AB ，∴AE =BE =12AB ，又∠ACB =90°，∴CE =12AB =BE ，又∠ABC =60°，∴△BCE 是等边三角形，故答案为：等边三角形，60；(2)解：AD =DQ +DP ，理由为：在线段BD 上截取点H ，使DH =DP ，如图2，∵∠CDB =60°，∴△DPH 为等边三角形，∴DP =PH ，∠DPH =∠DHP =60°，又∠BPQ =60°，∴∠DPQ +∠QPH =∠HPB +∠QPH =60°，∠BHP =120°，∴∠DPQ =∠HPB ，∵∠A =30°，DE ⊥AB ，∴∠QDP =∠A +∠AED =30°+90°=120°，∴∠QDP =∠BHP ，在△PDQ ≌△PHB 中， DPQ HPB PD PHQDP BHP ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△PDQ ≌△PHB （ASA ），∴DQ =BH ，PQ =PB ，∵AD =BD ，∠BPQ =60°，∴△BPQ 为等边三角形，AD =BD =BH +DH =DQ +DP ，即AD =DQ +DP ；(3)解：①△BPQ 为等边三角形，理由为：延长BD 至F ，使DF =DP ，连接PF ，设DQ 和BP 相交于O ，如图3， ∵∠PDF =∠CDB =60°，∴△PDF 为等边三角形，∴PF =DP ，∠F =∠PDF =∠DPF =60°，∵∠A =30°，DE ⊥AB ，∴∠PDQ =90°－∠A =60°，∴∠F =∠PDQ =60°，∵∠DPF +∠DPB =∠BPQ +∠DPB ，又∠BPQ =60°，∴∠BPF =∠QPD ，在△PBF 和△PQD 中，F PDQ PF DPBPF QPD ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△PBF ≌△PQD （ASA ），∴PB =PQ ，BF =DQ ，又∠BPQ =60°，∴△BPQ 为等边三角形；②∵ DF =DP ，BF =DQ ，AD =BD ，∴DQ =BF =BD +DF =AD +DP ，∵AD =2， AP =x ，DQ =y ，∴y =2+2－x ，即y =－x +4．8．(1)补全图形如下，．(2)∵AB =CD ，CB =AD∴四边形ABCD 为所求的平行四边形（两组对边分别相等的四边形是平行四边形）．故答案为：CD ，AD ，两组对边分别相等的四边形是平行四边形．9．证明：∵四边形ABCD 是菱形，∴CB ＝CD ，∠ACB ＝∠ACD ，在△ECB 和△ECD 中，CE CE ECB ECD CB CD =⎧⎪∠=∠⎨⎪=⎩，∴△ECB ≌△ECD （SAS ），∴BE ＝DE ，由作图可知，MN 垂直平分线段CD ，∴EC ＝ED ，∴BE ＝CE ．(2)解：∵BA ＝BC ，∠ABC ＝72°，∴∠BAC ＝∠BCA ＝12（180°﹣72°）＝54°，∵EB ＝EC ，∴∠EBC ＝∠ECB ＝54°，∴∠ABE ＝∠ABC ﹣∠EBC ＝18°．10．解：AF⊥BE，AF=BE,证明如下：证明：∵正方形ABCD∴AB=AD=DC,∠D=∠BAD=90°∵CF=DE∴AE=AD-DE,DF=DC-CF∴AE=DF在△AEB和△AFD中AB=AD, ∠D=∠BAD, AE=DF∴△ABE≌△DAF（SAS）∴∠ABE=∠F AD，AF=BE∵∠BAD=90°∴∠ABE+∠AEB=90°∴∠F AD +∠AEB=90°∴∠AOE=90°，AF⊥BE．∴AF=BE，AF⊥BE．11．解：如图所示：平行四边形ABCD即为所求；(2)解：AC，CD =，5=AD ，∴222AC CD AD += ，∴△ACD 是直角三角形，∴平行四边形ABCD 的面积为122102ACD S=⨯ ． 12．解:过点C 作CG AE ⊥，垂足是点G ．由题可知，//CF AE ，CF AD BE ==，则四边形CDBF 是梯形．在直角ABC ∆中，90ACB ∠=︒，60A ∠=︒，1AC =，22AB AC ∴==，在直角ACG ∆中，90CGA ∠=︒，60A ∠=︒，1AC =，30ACG ∴∠=︒，1111222AG AC ==⨯=，CG ∴=．()()111122222CDBF S CE DB CG AD DB CG AB CG ∴=+⋅=+⋅=⋅=⨯=梯形； (2)证明：四边形CDBF 是菱形．理由如下：在直角ABC ∆中，D 是AB 的中点，AD DB CD ∴==，由（1）CF AD =，CF DB CD ∴==，又//CF AE ，∴四边形CDBF 是平行四边形．CD BD =，∴四边形CDBF 是菱形．13．证明∵GBE 是由ABE △折叠而成，∴△ABE ≌△GBE ，∴AE GE =，∵E 是AD 的中点，∴AE DE =，∴GE DE =；(2)解：连接EF ，∵DF 2CF =， ∴229633DF DC ==⨯=， ∴963CF DC DF =-=-=．∵四边形ABCD 是长方形，∴AD BC =，9AB DC ==，90A C D ∠=∠=∠=︒．∵△ABE ≌△GBE ，∴9BG AB ==，90A BGE FGE ∠=∠=∠=︒．在Rt EGF 和Rt EDF 中，∵GE DE =，EF EF =∴Rt △EGF ≌Rt △EDF (HL )，∴6GF DF ==．∴9615BF BG GF =+=+=，在Rt BCF 中，∵15BF =，3CF =，∴BC =．∴AD BC =＝(3)解：设DF a =，则AB DC n DF na ==⋅=，∴()1CF DC DF na a n a =-=-=-，又∵BG AB na ==，GF DF a ==，∴()1BF BG GF na a n a =+=+=+，在Rt BCF 中，∵()1BF n a =+，()1CF n a =-，∴ ()()22222222114BC BF CF n a n a na =-=+--=，∴ 2224AD BC na ==， ∴2222244AD na AB n a n==． 14．证明：∵四边形ABCD 是正方形，∴AB ＝AD ，∠BAD ＝90°∵DG ⊥AE ，BF ⊥AE∴∠AFB ＝∠DGA ＝90°∵∠F AB +∠DAG ＝90°，∠DAG +∠ADG ＝90°∴∠BAF ＝∠ADG在△AFB 和△DGA 中∵AFB DGABAF ADG AB AD∠=∠⎧⎪∠=∠⎨⎪=⎩∴△AFB≌△DGA（AAS）．(2)证明：如图2，过点D作DK⊥AE于K，DJ⊥BF交BF的延长线于J由题意知∠BAH＝∠ADE＝90°，AB＝AD＝CD∵BF⊥AE∴∠AFB＝90°∵∠DAE+∠EAB＝90°，∠EAB+∠ABH＝90°∴∠DAE＝∠ABH在△ABH和△DAE中∵BAH ADE AB ADABH DAE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABH≌△DAE（ASA）∴AH＝DE∵点E为CD的中点∴DE＝EC＝12CD∴AH＝DH∴DE＝DH∵DJ⊥BJ，DK⊥AE∴∠J＝∠DKE＝∠KFJ＝90°∴四边形DKFJ是矩形∴∠JDK ＝∠ADC ＝90°∴∠JDH ＝∠KDE在△DJH 和△DKE 中∵J DKE JDH KDE DH DE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△DJH ≌△DKE （AAS ）∴DJ ＝DK ，JH ＝EK∴四边形DKFJ 是正方形∴FK ＝FJ ＝DK ＝DJ∴DFFJ2FJ =∴FH +FE ＝FJ ﹣HJ +FK +KE ＝2FJDF ．(3)解：如图3，取AD 的中点Q ，连接PQ ，延长QP 交CD 于R ，过点P 作PT ⊥CD 于T ，PK ⊥AD 于K ，设PT ＝b由（2）得△ABH ≌△DAE （ASA ）∴AH ＝DE∵∠EDH ＝90°，点P 为EH 的中点∴PD ＝12EH ＝PH ＝PE∵PK ⊥DH ，PT ⊥DE∴∠PKD＝∠KDT＝∠PTD＝90°∴四边形PTDK是矩形∴PT＝DK＝b，PK＝DT∵PH＝PD＝PE，PK⊥DH，PT⊥DE ∴PT是△DEH的中位线∴DH＝2DK＝2b，DE＝2DT∴AH＝DE＝1﹣2b∴PK＝12DE＝12﹣b，QK＝DQ﹣DK＝12﹣b∴PK＝QK∵∠PKQ＝90°∴△PKQ是等腰直角三角形∴∠KQP＝45°∴点P在线段QR上运动，△DQR是等腰直角三角形∴QR DQ∴点P．15．解：（1）尺规作图如下：（2）四边形ABCD是平行四边形，,AB CE AD BC∴，,ABE E CBE DFE∴∠=∠∠=∠，BE平分ABC∠，ABE CBE∴∠=∠，E DFE ∴∠=∠，DE DF ∴=．16．解：在Rt △ABC 中，CD 是斜边AB 上的中线， ∴AB ＝2CD ＝2，由勾股定理得，BC ． 17．证明：∵四边形ABCD 是正方形，∴AB ＝BC ，∠ABE ＝∠BCF ＝90°，又BE ＝CF ，∴△ABE ≌△BCF （SAS ）．∴∠BAE ＝∠CBF ．∵∠ABO +∠CBF ＝90°，∴∠ABO +∠BAO ＝90°，即∠AOB ＝90°．在Rt △ABO 中，M 点是斜边AB 中点， ∴12OM AB =． 18．(1) 解： 90ABD ∠=︒， F 为AD 的中点，10,AD = 1 5.2BFAD (2) 证明：如图，连接,CF90ABD ACD ∠=∠=︒， F 是AD 的中点，11,,22CF AD BF AD ,CF BF ∴=E 是BC 的中点，.EF BC19．解：证明：在正方形ABDE 和ACFG 中，AB AE =，AC AG =，90BAE CAG ∠=∠=︒， BAE BAC CAG BAC ∴∠+∠=∠+∠，即CAE BAG ∠=∠，在ABG ∆和AEC ∆中，{AB AECAE BAG AC AG=∠=∠=，()ABG AEC SAS ∴∆≅∆，BG CE ∴=；(2)解：证明：设BG 、CE 相交于点N ，ABG AEC ∆≅∆，ACE AGB ∴∠=∠，9090180NCF NGF ACF AGF ∠+∠=∠+∠=︒+︒=︒，360()360(18090)90CNG NCF NGF F ∴∠=︒-∠+∠+∠=︒-︒+︒=︒， BG CE ∴⊥；(3)解：过A 作BG，CE 的垂线段交于点P ，Q ，ABG AEC ∆≅∆，,ABP AEQ AB AE ∴∠=∠=，90APB AQE ∠=∠=︒，()ΔΔABP AEQ AAS ∴≅，∴=AP AQ ，AM ∴是角平分线，45AMC ∴∠=︒，135AME ．20．证明：∵AB //CE ，∴∠CAD ＝∠ACE ，∠ADE ＝∠CED ．∵F 是AC 中点，∴AF ＝CF ．在△AFD 与△CFE 中，CAD ACE ADE CED AF CF ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝， ∴△AFD ≌△CFE （AAS ），∴DF ＝EF ，∴四边形ADCE 是平行四边形；(2)解：过点C 作CG ⊥AB 于点G ，∵∠CAB ＝45°，∴AG CG =，在△ACG 中，∠AGC ＝90°，∴222AG CG AC +=，∵AC=∴CG＝AG＝1，∵∠B＝30°,∴12CG BC=,∴2BC=,在Rt△BCG中，BG==，∴1AB AG BG=+=．21．解：如图所示，直线DE即为所求；，(2)证明：∵∠ACB=90°，点E是边AB的中点，∴AE=BE=CE=12 AB，∵AC=BE，∴AC=AE=CE，∴△ACE是等边三角形．22．证明：E是AD的中点，AE DE∴=，//AF BC∴，FAE BDE∴∠=∠，AFE DBE∠=∠．在AFE∆和DBE∆中，FAE BDEAFE DBE AE DE∠=∠⎧⎪∠=∠⎨⎪=⎩，()AFE DBE AAS ∴∆≅∆，AF BD ∴=．AF DC =，BD DC ∴=．即：D 是BC 的中点．(2)解：四边形ADCF 是矩形；证明：AF DC =，//AF DC ，∴四边形ADCF 是平行四边形，AB AC =，BD DC =，AD BC ∴⊥即90ADC ∠=︒，∴平行四边形ADCF 是矩形．23．(1)如图所示，BE 就是所求的ABC ∠的角平分线．BF BA =，(2)四边形ABFE 为菱形．理由如下：∵BE 是ABC ∠的平分线，∴∠ABE =∠FBE∵四边形ABCD 是平行四边形，∴AD ∥BC ，∴∠AEB =∠EBF ，∴∠ABE =∠AEB∴AB =AE∵BF BA =∴AE =BF∴四边形ABFE 为平行四边形，∵BF BA =，∴四边形ABFE 为菱形．24．证明：∵四边形ABCD 是矩形，∴AB ＝CD ，AD ＝BC ，∠A ＝∠D ＝90°，在Rt △ABE 和Rt △CDF 中，BE CF AB CD =⎧⎨=⎩， ∴Rt △ABE ≌Rt △CDF （HL ），∴AE ＝CF ，∴DE ＝BF ．25．（1）①证明：∵四边形ADEF 是正方形，∴AD AF =，90DAF ∠=︒，∵90BAC ∠=︒，∴BAD CAF ∠=∠，在ABD △和ACF 中，{AB ACBAD CAF AD AF=∠=∠=，∴ABD △≌ACF （SAS ）．②∵ABD △≌ACF ，∴ABD ACF ∠=∠，∵90BAC ∠=︒，AB AC =，∴45ABD ACB ∠=∠=︒，∴45ACF ∠=︒．故答案为：45．③∵ABD △≌ACF ，∴=CF BD ，∵826BD BC CD =-=-=．∴CF =6，故答案为：6．(2)（2）CF BC CD =+，由（1）同理可证ABD △≌ACF 得：CF BD BC CD ==+．故答案为：BC CD +．(3)（3）①由（1）同理可证ABD △≌ACF 得：CF BD CD BC ==-．故答案为：CD BC -．②AOC △为等腰三角形，理由如下：∵90BAC ∠=︒，AB AC =，∴18045135ABD ∠=︒-︒=︒，∵四边形ADEF 是正方形，∴AD AF =，90DAF ∠=︒，∴BAD CAF ∠=∠，同理可证BAD ≌CAF ，∴135ACF ABD ∠=∠=︒，∴90FCD ACF ACB ∠=∠-∠=︒，∴FCD 为直角三角形，∵正方形ADEF 中，O 为DF 的中点， ∴12OC DF =，12OA AE =，AE DF =， ∴OC OA =，∴AOC △是等腰三角形．26．证明：∵四边形ABCD 是平行四边形，∴AD=BC，AD//BC，∴∠DAE=∠E，∵CE=BC，∴CE=AD，又∵∠AOD=∠COE，∴△AOD≌△EOC（AAS），∴CO=DO；(2)解：当CO=EO，∠COE=90°时，四边形AOCF是正方形；理由如下：∵CO=DO，∴CO=1CD，2又∵F是AB的中点，∴AF=1AB，2∵四边形ABCD是平行四边形，∴AB=CD，AB//CD，∴AF=CO，AF//CO，∴四边形AFCO是平行四边形，∵△AOD≌△EOC，∴AO=EO，∵CO=EO，∴AO=CO，∴平行四边形AFCO是菱形，∵∠COE=90°，∴菱形AFCO是正方形．。

期末考试勾股定理与几何翻折压轴题专项训练—2023-2024学年八年级数学下学期(人教版)(解析版)

期末考试勾股定理与几何翻折压轴题专项训练【例题精讲】例1．（三角形翻折问题）如图，在Rt ABC △中，9086ABC AB BC ∠=︒==，，，分别在AB AC ，边上取点E F ，，将AEF △沿直线EF 翻折得到A EF '△，使得点A 的对应点A '恰好落在CB 延长线上，当60EA B '∠=︒时，AE 的长为，当A F AC '⊥时，AF 的长为．【答案】 32− 407【分析】由折叠的性质可得AE A E '=，先求出30A EB '∠=︒，从而可得1122A B A E AE ''==，再由勾股定理可得BE AE =，最后由AE BE AB +=，进行计算即可；令A F '交AB 于G ，连接CG ，由折叠的性质可得：A EA F '∠=∠，AFE A FE '∠=∠，AEF A EF '∠=∠，AF A F '=，由A F AC '⊥得出90A FA A FC ''∠=∠=︒，45AFE A FE '∠=∠=︒，证明()ASA A FC AFG '≌得到CF FG =，设CF FG x ==，则10AF x =−，AG ，根据1122ACG S AC FG AG BC =⋅=⋅建立方程，解方程即可得出CF 的长，即可求解．【详解】解：由折叠的性质可得：AE A E '=，90ABC ∠=︒，18090A BE ABC '∴∠=︒−∠=︒，60EA B '∠=︒，9030A EB EA B ''∴∠=︒−∠=︒，1122A B A E AE ''∴==，BE AE∴==，AE BE AB+=，8AE AE∴=，32AE∴=−如图，令A F'交AB于G，连接CG，A F AC'⊥，90A FA A FC''∴∠=∠=︒，由折叠的性质可得：A EA F'∠=∠，AFE A FE'∠=∠，AEF A EF'∠=∠，AF A F'=，90AFE A FE'∠+∠=︒，45AFE A FE'∴∠=∠=︒，设A EA Fα'∠=∠=，则45FEB AFEα∠=∠=+︒，180135AEF FEB A EFα'∴∠=︒−∠=︒−=∠，()13545902A EB A EF BEFααα''∴∠=∠−∠=︒−−︒+=︒−，902EA B A EBα''∴∠=︒−∠=，FA C EA B EA F Aα'''∴∠=∠−∠==∠，在A FC'和AFG中，CA F AA F AFA FC AFG∠=∠⎧⎪=⎨⎪∠=∠''⎩'，()ASAA FC AFG'∴≌，CF FG∴=，在Rt ABC△中，9086ABC AB BC∠=︒==，，，10AC∴，设CF FG x==，则10AF x=−，AG∴==1122ACGS AC FG AG BC=⋅=⋅，106x∴⋅=，整理得：271809000x x+−=，即29014400749x⎛⎫+=⎪⎝⎭，9012077x∴+=±，解得：307x=或30x=−（不符合题意，舍去），307CF∴=，30401077AF AC CF∴=−=−=，故答案为：32−407．【点睛】本题考查了折叠的性质、全等三角形的判定与性质、勾股定理、三角形的面积公式、等腰直角三角形的判定与性质、三角形外角的定义及性质、三角形内角和定理等知识，熟练掌握以上知识点，添加适当的辅助线是解此题的关键．例2．（坐标系中折叠问题）如图，在平面直角坐标系中，长方形ABCO的边OC OA、分别在x轴、y轴上，6AB=，点E在边BC上，将长方形ABCO沿AE折叠，若点B的对应点F 恰好是边OC的三等分点，则点E的坐标是．【答案】⎛−⎝⎭或(−【分析】本题主要考查了勾股定理与折叠问题，坐标与图形，由折叠的性质可得6AF AB==，BE EF=，90AFE B∠=∠=︒，再分当点F靠近点C时，24CF OF==，，当点F靠近点O 时，则42CF OF==，，两种情况利用勾股定理先求出OA的长，进而得到BC的长，设出CE 的长，进而得到EF的长，在Rt EFC△中，由勾股定理建立方程求解即可．【详解】解：在长方形ABCO 中，6CO AB ==，90BCO B AOC ∠=∠=∠=︒，由折叠的性质可得6AF AB ==，BE EF =，90AFE B ∠=∠=︒，F 恰好是边OC 的三等分点，∴当点F 靠近点C 时，24CF OF ==，，在Rt AFO V中，OA =，∴BC OA ==设CE x =，则BE EF x ==，在Rt EFC △中，由勾股定理得到222EF CF CE =+，∴()2222xx =+，解得x =，∴点E的坐标是⎛− ⎝⎭；当点F 靠近点O 时，则42CF OF ==，，在Rt AFO V中，OA ==∴BC OA ==设CE x =，则BE EF x ==，在Rt EFC △中，由勾股定理得到222CF CE =+，∴()2224x x =+，解得x =∴点E的坐标是(−；综上所述，点E的坐标是⎛− ⎝⎭或(−，故答案为：⎛− ⎝⎭或(−．例3．（四边形折叠问题）如图，已知矩形ABCD ，4AB =，5BC =，点P 是射线BC 上的动点，连接AP ，AQP △是由ABP 沿AP 翻折所得到的图形．(1)当点Q 落在边AD 上时，QC = ；(2)当直线PQ 经过点D 时，求BP 的长；(3)如图2，点M 是DC 的中点，连接MP 、MQ ．①MQ 的最小值为；②当PMQ 是以PM 为腰的等腰三角形时，请直接写出BP 的长．【答案】(2)2BP =或8BP =(3) 2.9BP =或4BP =或10BP =【分析】（1）根据折叠的性质和勾股定理进行求解即可；（2）分点P 在线段BC 上，点P 在线段BC 的延长线上，两种情况，进行讨论求解；（3）①连接AM ，勾股定理求出AM 的长，折叠求出AQ 的长，根据MQ AM AQ ≥−，求出最小值即可；②分PM MQ =和PM PQ =两种情况，再分点P 在线段BC 上，点P 在线段BC 的延长线上，进行讨论求解即可．【详解】（1）解：当点Q 落在边AD 上时，如图所示，∵矩形ABCD ，4AB =，5BC =，∴4,5CD AB AD BC ====，90BAD B BCD ADC ∠=∠=∠=∠=︒，∵翻折，∴4,90AQ AB AQP B ==∠=∠=︒，∴1DQ AD AQ =−=，在Rt CDQ △中，CQ ==（2）当直线PQ 经过点D 时，分两种情况：当点P 在线段BC 上时，如图：∵翻折，∴4AQ AB ==，90AQP B ∠=∠=︒，BP PQ =，∴90AQD ∠=︒，∴3DQ ==，设BP PQ x ==，则：5PC BC BP x =−=−，3DP DQ PQ x =+=+，在Rt PCD △中，222DP CP CD=+，即：()()222345x x +=+−，∴2x =；∴2BP =；②当P 在线段BC 的延长线上时：∵翻折，∴4,90AQ AB Q B ==∠=∠=︒，BP PQ =，∴3DQ ==，设BP PQ x ==，则：5PC BP BC x =−=−，3DP PQ DQ x =−=−，在Rt PCD △中，222DP CP CD =+，即：()()222345x x −=+−，∴8x =；∴8BP =；综上：2BP =或8BP =；（3）①连接AM ，∵M 是CD 的中点， ∴122DM CM CD ===，∴AM =∵翻折，∴4AQ AB ==，∵MQ AM AQ ≥−，∴当,,A Q M 三点共线时，MQ 的值最小，即：4MQ AM AQ =−=4；②当PM PQ =时，如图：∵翻折，∴BP PQ PM ==，设BP x =，则：,5PM x CP BC BP x ==−=−，在Rt PCM 中，222PM CM PC =+，即：()22225x x =+−，解得： 2.9x =，即： 2.9BP =；当PM QM =，点P 在线段BC 上时，如图：∵,QM PM DM CM ==，90D C ∠=∠=︒，∴()HL MDQ MCP ≌，∴CP DQ =，点Q 在AD 上，由（1）知：1DQ =，∴1CP DQ ==，∴4BP BC CP =−=；当点P 在BC 的延长线上时：如图：此时点M 在AP 上，连接BM ，∵翻折，∴BM MQ PM ==，∵MC BP ⊥，∴210BP BC ==；综上： 2.9BP =或4BP =或10BP =．质，综合性强，难度大，属于压轴题．利用数形结合和分类讨论的思想进行求解，是解题的关键．【模拟训练】1．如图，在长方形ABCD 中，点E 是AD 的中点，将ABE 沿BE 翻折得到FBE ，EF 交BC 于点H ，延长BF DC 、相交于点G ，若8DG =，10BC =，则DC = ．【答案】258【分析】本题考查了全等三角形的判定与性质，折叠的性质，勾股定理，连接EG ，根据点E 是AD 的中点得DE AE EF ==，根据四边形ABCD 是长方形得90D A ∠=∠=︒，根据将ABE 沿BE 翻折得到FBE 得90BFE D A ∠=∠=∠=︒，利用HL 证明Rt Rt EFG EDG △≌△，得8FG DG ==，设DC x =，则8CG DG DC x =−=−，8BG BF FG AB FG DC FG x =+=+=+=+，在Rt BCG V △中，根据勾股定理得，222CG BC BG +=，进行计算即可得．【详解】解：如图所示，连接EG ，∵点E 是AD 的中点，∴DE AE EF ==，∵四边形ABCD 是长方形，∴90D A ∠=∠=︒，∵将ABE 沿BE 翻折得到FBE ，∴90BFE D A ∠=∠=∠=︒在Rt EFG △和Rt EDG △中，EF ED EG EG =⎧⎨=⎩，∴()Rt Rt HL EFG EDG V V ≌，∴8FG DG ==，设DC x =，则8CG DG DC x =−=−，8BG BF FG AB FG DC FG x =+=+=+=+，在Rt BCG 中，根据勾股定理得，222CG BC BG +=，∴222(8)10(8)x x −+=+，解得258x =，故答案为：258．2．如图，在Rt ABC △中，90ACB ∠=︒，254AB =，154=AC ，点D 是AB 边上的一个动点，连接CD ，将BCD △沿CD 折叠，得到CDE ，当DE 与ABC 的直角边垂直时，AD 的长是．【答案】154或54【分析】本题考查了勾股定理，平行四边形的判定和性质，折叠的性质，全等三角形的判定和性质，分DE BC ⊥和DE AB ⊥两种情况进行求解即可得到答案，根据题意，正确画出图形是解题的关键．【详解】解：如图，当DE BC ⊥时，延长ED 交BC 于点F ，CE 与AB 相交于点M ，∵EF BC ⊥，∴90EFC EFB ∠=∠=︒，∴90E ECF ∠+∠=︒，由折叠得，B E ∠=∠，CE CB =，MCD FCD ∠=∠，∴90B ECF ∠+∠=︒，∴90CMB ∠=︒，即C M A B ⊥，∵90ACB ∠=︒，254AB =，154=AC ，∴5BC ==， ∵1122ABC S AC BC AB CM ==△，∴11512552424CM ⨯⨯=⨯⨯，解得3CM =，∴4BM =，∵90CFD CMD FCD MCD CD CD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩， ∴()AAS CFD CMD ≌，∴3CF CM ==，DF DM =，∴532BF BC CF =−=−=，设DF DM x ==，则4BD x =−，在Rt BFD 中，222DF BF BD +=，∴()22224x x +=−，解得32x =， ∴35422BD =−=， ∴25515424AD AB BD =−=−=；当DE AB ⊥时，如图，设DE 与AC 相交于点M ，由折叠可得，BCD ECD ∠=∠，DE DB =，ED BD =，5EC BC ==，∵DE AB ⊥，90ACB ∠=︒，∴DE BC ∥，∴EDC BCD ∠=∠，∴EDC ECD ∠=∠，∴5ED EC ==，∴5BD ED ==， ∴255544AD AB BD =−=−=；综上，AD 的长是154或54，故答案为：154或54．3．如图，等边三角形ABC 中，16AB BD AC =⊥，于点D ，点E F 、分别是BC DC 、上的动点，沿EF 所在直线折叠CEF △，使点C 落在BD 上的点C '处，当BEC '△是直角三角形时，BE 的值为．【答案】24−或323【分析】本题考查了翻折变换，等边三角形的性质，折叠的性质，熟练运用折叠的性质是本题的关键．由等边三角形的性质可得30DBC ∠=︒，分9090BEC BC E ''∠=︒∠=︒，两种情况讨论，由直角三角形的性质即可求解．【详解】解：ABC 是等边三角形，BD AC ⊥，30,DBC ∴∠=︒ 由折叠的性质可得：,CE C E '=若90,BEC ∠'=︒且30,C BE ∠'=︒,2,BE E B E C C ∴='''=16,BE CE BC +==16,CE +=8,E E C C ∴'==24BE ∴=−若90,30,E C B E C B ∠'=︒='∠︒2,,BE E B C E C ∴'''=16,BE CE BC +==16,3CE E C =='∴ 32.3BE ∴=故答案为∶ 24−323．4．如图，在ABC 中，120ACB ∠=︒，8AC =，4BC =，将边BC 沿CE 翻折，使点B 落在AB 上的点D 处，再将边AC 沿CF 翻折，使点A 落在CD 的延长线上的点A '处，两条折痕与斜边AB 分别交于点E 、F ，则线段FA '的长为．【答案】【分析】本题考查了折叠的性质，勾股定理，直角三角形的性质，添加恰当辅助线构造直角三角形是本题的关键．过点A 作AH BC ⊥交BC 的延长线于H ，由直角三角形的性质可求142HC AC ==，AH =AB 的长，由面积法可求CE 的长，由折叠的性质可求90BEC DEC ∠=∠=︒，BCE DCE ∠=∠，ACF DCF ∠=∠，然后再求解即可．【详解】解：如图，过点A 作AH BC ⊥，交BC 的延长线于H ，120ACB ∠=︒，ACB H HAC ∠=∠+∠，30HAC ∴∠=︒，142HC AC ∴==，AH ==，448BH ∴=+=，AB ∴1122ACB S BC AH AB CE =⨯⨯=⨯⨯，4CE ∴=，CE ∴，将边BC 沿CE 翻折，使点B 落在AB 上的点D 处，再将边AC 沿CF 翻折，90BEC DEC ∴∠=∠=︒，BCE DCE ∠=∠，ACF DCF ∠=∠，1602ECF ACB ∴∠=∠=︒，30CFE ∴∠=︒，EF ∴，在Rt BCE中，BE ===，AF AB EF BE ∴=−−==FA AF '∴==故答案为：5．如图，点D 是ABC 的边AB 的中点，将BCD △沿直线CD 翻折能与ECD 重合，若4AB =，2CD =，1AE =，则点C 到直线AB 的距离为．【答案】【分析】连接BE ，延长CD 交BE 于点G ，作CH AB ⊥于点H ，如图所示，由折叠的性质及中点性质可得AEB △为直角三角形，且G 为BE 中点，从而CG BE ⊥，由勾股定理可得BE的长，再根据2ABC BDC S S =△△，即11222AB CH CD BG ⋅=⨯⋅，从而可求得CH 的长．【详解】解：连接BE ，延长CD 交BE 于点G ，作CH AB ⊥于点H ，如图所示，由折叠的性质可得：BD ED =，CB CE =，∴CG 为BE 的中垂线， ∴12BG BE =，∵点D 是AB 的中点，4AB =，2CD =，1AE =， ∴122BD AD AB ===，CBD CAD S S =，AD DE =，∴DBE DEB ∠=∠，DEA DAE ∠=∠，∵180EDA DEA DAE ∠+∠+∠=︒，即22180DEB DEA ∠+∠=︒，∴90DEB DEA ∠+∠=︒，即90BEA ∠=︒，∴BE∴12BG BE ==， ∵2ABC BDCS S =△△， ∴11222AB CH CD BG ⋅=⨯⋅，∴422CH =⨯，∴CH ，∴点C 到直线AB 的距离为．故答案为：．【点睛】本题考查翻折变换，线段中垂线的判定，等腰三角形的性质，点到直线的距离，直角三角形的判定，勾股定理，利用面积相等求相应线段的长，解题的关键是得出CG 为BE 的中垂线，2ABC BDC S S =△△．6．如图，在ABC 中，90,A AB AC ∠=︒==D 为AC 边上一动点，将C ∠沿过点D 的直线折叠，使点C 的对应点C '落在射线CA 上，连接BC '，当Rt ABC '△的某一直角边等于斜边BC '长度的一半时，CD 的长度为．【答案】或【分析】由翻折得，12CD CC '=，分三种情况：①当点C '在边AC 上，且12AC BC ''=（即2BC AC ''=）时；②当点C '在CA 的延长线上，且12AC BC ''=（即2BC AC ''=）时；③当点C '在CA 的延长线上，且12AB BC '=（即2BC AB '==时，分别根据勾股定理求出AC '的长，再求出CC '的长即可【详解】解：由翻折得，12CD CC '=，分三种情况：①当点C '在边AC 上，且12AC BC ''=（即2BC AC ''=）时，90,A AB AC ∠=︒==∴由勾股定理得，222BC AC AB ''−=，即222(2)AC AC ''−=，AC '∴=CC '∴CD ∴；②当点C '在CA 的延长线上，且12AC BC ''=（即2BC AC ''=）时，同理得AC 'CC '∴CD ∴；③当点C '在CA 的延长线上，且12AB BC '=（即2BC AB '==由勾股定理得，222AC BC AB ''=−，即22218AC '=−=，AC '∴=CC '∴CD ∴=，0>，CD AB ∴>，此时点D 不在边AC 上，不符合题意，舍去，综上，当Rt ABC '△的某一直角边等于斜边BC '长度的一半时，CD 的长度为或．故答案为：或．【点睛】本题主要考查图形的翻折变换（折叠问题），勾股定理，等腰直角三角形的性质等知识，灵活运用折叠的性质及勾股定理是解答本题的关键，同时要注意分类思想的运用．7．如图，在ABC 中，90ACB ∠=︒，3AC =，4BC =，P 为斜边AB 上的一动点（不包含A ，B 两端点），以CP 为对称轴将ACP △翻折得到A CP '，连结BA '．当A P AB '⊥时，BA '的长为．【答案】【分析】当A P AB '⊥时，过点C 作CD AB ⊥于D ，可知125CD =，95AD =，得出PDC △为等腰直角三角形，得到PD CD =，求出PA '和BP 的长，利用勾股定理即可求出BA '的长．【详解】过点C 作CD AB ⊥于D ，在Rt ADC 中，90ACB ∠=︒，3AC =，4BC =，∴5AB = ∵1122AC BC AB CD ⨯=⨯，125CD ∴=，在Rt ADC 中，3AC =∴95AD ==，当A P AB '⊥时，如图由折叠性质可知12∠=∠，PA PA '=，又1290A PA '∠=∠+∠=︒145∠=∠2=︒∴，又2390∠+∠=︒，345∴∠=︒，23∴∠=∠，125PD CD ∴==，又PA PD AD =+，12921555PA ∴=+=，又PA PA '=，215PA '∴=，又BP AB PA =−，214555BP ∴=−=，在Rt BPA '△中，90BPA ∠='︒，222BP PA BA ∴='+，2224214575525BA ⎛⎫⎛⎫'∴=+= ⎪ ⎪⎝⎭⎝⎭，BA '∴=，故答案为：．【点睛】本题考查了勾股定理的应用，折叠问题，熟练掌握勾股定理是解题的关键．8．如图，在ABC 中，90ACB ∠=︒，AC BC =，D 为AB 上一点，连接DC ，将BDC 沿DC 翻折，得到EDC △，连接AE ，若AE CE =，4BC =，则D 到CE 的距离是．【答案】2【分析】本题考查等腰直角三角形中的折叠问题，涉及等边三角形判定与性质，勾股定理应用、面积法等知识．设BE 交CD 于G ，过E 作EF BC ⊥交BC 延长线于F ，根据将BDC 沿DC 翻折，得到EDC △，AC BC =，AE CE =，可得ACE △是等边三角形，即知60ACE ∠=︒，而90ACB ∠=︒，故150BCE ∠=︒，30ECF ∠=︒，可得75BCD ECD ∠=∠=︒，122EF CE ==，CF =BE =15CBE ∠=︒，可得90BGC ∠=︒，即CG BE ⊥，从而12BG BE GE ===，由勾股定理得CG ，在Rt BDG △中，DG ，即得CD DG CG =+，由面积法可得D 到CE 的距离是2．【详解】解：设BE 交CD 于G ，过E 作EF BC ⊥交BC 延长线于F ，如图：将BDC 沿DC 翻折，得到EDC △，4BC CE ∴==，BCD ECD ∠=∠，AC BC =，AE CE =，AC BC CE AE ∴===，ACE ∴是等边三角形，60ACE ∴∠=︒，90ACB ∠=︒，150BCE ∴∠=︒，30ECF ∠=︒，75BCD ECD ∴∠=∠=︒，122EF CE ==，CF =在Rt BEF △中，BE ==BCE 中，BC CE =，150BCE ∠=︒，15CBE ∴∠=︒，18090BGC BGC BCD ∴∠=︒−∠−∠=︒，即CG BE ⊥，12BG BE GE ∴==，CG ∴===，45ABC ∠=︒，15CBE ∠=︒，30DBG ∴∠=︒，在Rt BDG△中，DG =，CD DG CG ∴=+=，设D 到CE 的距离是h ，2DCE S CE h DC GE ∆=⋅=⋅，324DC GE h CE ⋅∴===，故答案为：2．9．在生活中、折纸是一种大家喜欢的活动、在数学中，我们可以通过折纸进行探究，探寻数学奥秘．【纸片规格】三角形纸片ABC ，120ACB ∠=︒，CA CB =，点D是底边AB 上一点．【换作探究】(1)如图1，若6AC =，AD =CD ，求CD 的长度；(2)如图2，若6AC =，连接CD ，将ACD 沿CD 所在直线翻折得到ECD ，点A 的对应点为点.E 若DE 所在的直线与ABC 的一边垂直，求AD 的长；(3)如图3，将ACD 沿CD 所在直线翻折得到ECD ，边CE 与边AB 交于点F ，且DE BC ∥，再将DFE △沿DF 所在直线翻折得到DFG ，点E 的对应点为点G ，DG 与CE 、BC 分别交于H ，K ，若1KH =，请直接写出AC 边的长．【答案】(1)(2)3或(3)3【分析】（1）作CE AB ⊥于E ，求得30A B ==︒∠∠，从而得出132CE AC ==，AE AC =进而得出DE AE AD =−=（2）当DE AB ⊥时，连接AE ，作CG AB ⊥于G ，依次得出45DAE DEA ∠=∠=︒，304575CAE CAD DAE ∠=∠+∠=︒+︒=︒，75CEA CAE ∠=∠=︒，30ACE ∠=︒，15ACD DCE ∠=∠=︒，45CDG CAB DAC ∠=∠+∠=︒，从而DG CG =，进一步得出结果；当ED AC ⊥时，设ED 交AC 于点W CE ，交AB 于V ，可推出90AVC ∠=︒，60ACE ∠=︒，从而30ACD DCE ∠=∠=︒，进一步得出结果；当DE BC ⊥时，可推出180ACB BCE ∠+∠=︒，从而90ACD DCE ∠=∠=︒，进一步得出结果；（3）可推出CKH 和CDH △及CHK 是直角三角形，且30HCK ∠=︒，30HDF ∠=︒，45DCH ∠=︒，进一步得出结果．【详解】（1）解：如图1，作CE AB ⊥于E ，90AEC ∴∠=︒，CA CB =，120ACB ∠=︒，30A B ∴∠=∠=︒，132CE AC ∴==，AE =，DE AE AD ∴=−==CD ∴=；（2）解：如图2，当DE AB ⊥时，连接AE ，作CG AB ⊥于G ，由翻折得：AD DE =，CAD CED =∠∠，AC CE =，45DAE DEA ∠∠∴==︒，304575CAE CAD DAE ∴∠=∠+∠=︒+︒=︒，75CEA CAE ∴∠=∠=︒，30ACE ∴∠=︒，15ACD DCE ∴∠=∠=︒，45CDG CAB DAC ∴∠=∠+∠=︒，DG CG ∴=，由（1）知：3CG =，AG =3AD AG DG ∴=−=；如图3，当ED AC ⊥时，设ED 交AC 于点W CE ，交AB 于V ，90E ACE ∴∠+∠=︒，E A ∠=∠，90A ACE ∴∠+∠=︒，90AVC ∴∠=︒，60ACE∴∠=︒，30ACD DCE∴∠=∠=︒，ACD A∴∠=∠，AD CD∴=，3CV =，CD∴=，AD CD∴==如图4，当DE BC⊥时，30E A∠=∠=︒，60BCE∴∠=︒，180ACB BCE∴∠+∠=︒，90ACD DCE∴∠=∠=︒，AD∴=，综上所述：3AD=或（3）解：如图5，∵DE BC ∥，30B C ∠=∠=︒，30BCF E ∴∠=∠=︒，30EDF B ∠=∠=︒，120ACB ∠=︒，90ACE ∴∠=︒，1452ECD ACD ACE ∴∠=∠=∠=︒，将DFE △沿DF 所在直线翻折得到DFG ，30GDF EDF ∴∠=∠=︒，60EDG ∴∠=︒，90CHK EHD ∴∠=∠=︒，DH CH ∴=1FH ∴==，1CF CH FH ∴=+，3AC ∴==．【点睛】本题考查了等腰三角形的判定和性质，直角三角形的性质等知识，解决问题的关键是正确分类，画出图形．10．如图，在ABC 中，90BAC ∠=︒，AB AC =，点D 为线段BC 延长线上一点，以AD 为腰作等腰直角DAF △，使90DAF ∠=︒，连接CF ．(1)请判断CF 与BC 的位置关系，并说明理由；(2)若8BC =，4CD BC =，求线段AD 的长；(3)如图2，在（2）的条件下，将DAF △沿线段DF 翻折，使点A 与点E 重合，连接CE ，求线段CE 的长．【答案】(1)CF BC ⊥，理由见解析(2)(3)【分析】（1）证明()SAS ABD ACF △≌△，则ADB AFC ∠=∠，如图1，记AD CF 、的交点为O ，根据180FAO AFO AOF DCO CDO COD ∠+∠+∠=︒=∠+∠+∠，AOF COD ∠=∠，可得90FAO DCO ∠=∠=︒，进而可得CF BC ⊥；（2）如图2，过A 作AH BC ⊥于H ，则142BH CH AH BC ====，6DH =，由勾股定理得，AD =（3）由翻折的性质可知，DE AD =，45EDF ADF ∠=∠=︒，90ADE ∠=︒，如图3，过A 作AM BC ⊥于M ，过E 作EN BC ⊥于N ，证明()AAS ADM DEN ≌，则46DN AM EN DM ====，，6CN =，由勾股定理得，CE =计算求解即可．【详解】（1）解：CF BC ⊥，理由如下：∵等腰直角DAF △，90DAF ∠=︒，∴AD AF =，又∵90BAC ∠=︒，∴BAC CAD DAF CAD ∠+∠=∠+∠，即BAD CAF ∠=∠，∵AB AC =，BAD CAF ∠=∠，AD AF =，∴()SAS ABD ACF △≌△，∴ADB AFC ∠=∠，如图1，记AD CF 、的交点为O ，∵180FAO AFO AOF DCO CDO COD ∠+∠+∠=︒=∠+∠+∠，AOF COD ∠=∠，∴90FAO DCO ∠=∠=︒，∴CF BC ⊥；（2）解：∵8BC =，4CD BC =，∴2CD =，如图2，过A 作AH BC ⊥于H ，∵ABC 是等腰直角三角形， ∴142BH CH AH BC ====，∴6DH =，由勾股定理得，AD =∴线段AD 的长为（3）解：由翻折的性质可知，DE AD =，45EDF ADF ∠=∠=︒，∴90ADE ∠=︒，如图3，过A 作AM BC ⊥于M ，过E 作EN BC ⊥于N ，∴90AMD DNE ∠=︒=∠，同理（2）可知，4AM =，6MD =，∵90ADM EDN EDN DEN ∠+∠=︒=∠+∠，∴ADM DEN ∠=∠，∵90AMD DNE ∠=︒=∠，ADM DEN ∠=∠，AD DE =，∴()AAS ADM DEN ≌，∴46DN AM EN DM ====，，∴6CN =，由勾股定理得，CE =，∴线段CE 的长为【点睛】本题考查了全等三角形的判定与性质，三角形内角和定理，勾股定理，折叠的性质，等腰三角形的性质．熟练掌握全等三角形的判定与性质，折叠的性质是解题的关键．11．如图1，在Rt ABC △中，90C ∠=︒，5AC =，12BC =，点D 为BC 边上一动点，将ACD 沿直线AD 折叠，得到AFD △，请解决下列问题．(1)AB =______；当点F 恰好落在斜边AB 上时，CD =______；(2)连接CF ，当CBF V 是以CF 为底边的等腰三角形时，请在图2中画出相应的图形，并求出此时点F 到直线AC 的距离；(3)如图3，E 为边BC 上一点，且4，连接EF ，当DEF 为直角三角形时，CD = ．（请写出所有满足条件的CD 长）【答案】(1)13，103(2)画图见解析，600169(3)52或或5或10【分析】（1）根据勾股定理可得AB 的长，再利用等积法求出CD 即可；（2）过点F 作FG AC ^，交CA 的延长线于G ，首先由等积法求出CH 的长，再根据勾股定理求出AH 的长，再次利用等积法可得FG 的长；（3）分90DEF ∠=︒或90EDF ∠=︒或90EFD ∠=︒分别画出图形，从而解决问题．【详解】（1）解：在Rt ABC △中，由勾股定理得，13AB ，当点F 落在AB 上时，由折叠知，CD DF =， ∴111222AC CD AB DF AC BC ⋅+⋅=⋅，51360CD CD ∴+=，103CD ∴=，故答案为：13，103；（2）过点F 作FG AC ^，交CA 的延长线于G ，BC BF =，AC AF =，AB ∴垂直平分CF ，由等积法得6013AC BC CH AB ⋅==，在Rt ACH 中，由勾股定理得，2513AH ===， 1122ACF S AC FG CF AH =⋅=⋅△，6025260013135169CF AH FG AC ⨯⨯⋅∴===；（3）当90DEF ∠=︒时，当点D 在CE 上时，作FH AC ⊥于H ，则4HF CE ==，5AF AC ==，3AH ∴=，2CH EF AC AH ∴==−=，设CD x =，则4DE x =−，在Rt EDF 中，由勾股定理得，222(4)2x x =−+，解得52x =，52CD ∴=，当点D 在EB 上时，同理可得538CH AC AH =+=+=，设CD DF x ==，则4DE x =−，在Rt EDF 中，由勾股定理得，222(4)8x x −+=，解得10x =，10CD ∴=，当90DFE ∠=︒时，由勾股定理得AE设CD DF x ==，则520x +=，x ∴，CD ∴=；当90FDE ∠=︒时，则45ADC ADF ∠=∠=︒，5CD AC ∴==，综上：52CD =或或5或10，故答案为：52或或5或10．【点睛】本题是三角形综合题，主要考查了翻折的性质，直角三角形的性质，勾股定理，等腰直角三角形的判定与性质等知识，利用等积法求垂线段的长是解题的关键．。

人教版八年级下册压轴题训练（含答案）

人教版八年级下册压轴题训练（含答案）压轴题训练01一．解答题（共3小题）1．如图①，已知抛物线y＝ax2+bx+c的图象经过点A（0，3）、B（1，0），其对称轴为直线l：x＝2，过点A作AC∥x轴交抛物线于点C，∠AOB的平分线交线段AC于点E，点P 是抛物线上的一个动点，设其横坐标为m．（1）求抛物线的解析式；（2）若动点P在直线OE下方的抛物线上，连结PE、PO，当m 为何值时，四边形AOPE 面积最大，并求出其最大值；（3）如图②，F是抛物线的对称轴l上的一点，在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由．【分析】（1）利用对称性可得点D的坐标，利用交点式可得抛物线的解析式；（2）设P（m，m2﹣4m+3），根据OE的解析式表示点G的坐标，表示PG的长，根据面积和可得四边形AOPE的面积，利用配方法可得其最大值；（3）存在四种情况：如图3，作辅助线，构建全等三角形，证明△OMP≌△PNF，根据|OM|＝|PN|，列方程可得点P的坐标；同理可得其他图形中点P的坐标．【解答】解：（1）如图1，设抛物线与x轴的另一个交点为D，由对称性得：D（3，0），设抛物线的解析式为：y＝a（x﹣1）（x﹣3），把A（0，3）代入得：3＝3a，a＝1，∴抛物线的解析式；y＝x2﹣4x+3；（2）如图2，∵△AOE的面积是定值，所以当△OEP面积最大时，四边形AOPE面积最大，设P（m，m2﹣4m+3），∵OE平分∠AOB，∠AOB＝90°，∴∠AOE＝45°，∴△AOE是等腰直角三角形，∴AE＝OA＝3，∴E（3，3），易得OE的解析式为：y＝x，过P作PG∥y轴，交OE于点G，∴G（m，m），∴PG＝m﹣（m2﹣4m+3）＝﹣m2+5m﹣3，∴S四边形AOPE＝S△AOE+S△POE，＝×3×3+PG?AE，＝+×3×（﹣m2+5m﹣3），＝﹣+，＝﹣（m﹣）2+，∵﹣＜0，∴当m＝时，S有最大值是；（3）分四种情况：①当P在对称轴的左边，且在x轴下方时，如图3，过P作MN⊥y 轴，交y轴于M，交l于N，∵△OPF是等腰直角三角形，且OP＝PF，易得△OMP≌△PNF，∴OM＝PN，∵P（m，m2﹣4m+3），则﹣m2+4m﹣3＝2﹣m，解得：m＝（舍）或，∴P的坐标为（，）；②当P在对称轴的左边，且在x轴上方时，如图3，同理得：2﹣m＝m2﹣4m+3，解得：m1＝（舍）或m2＝，③当P在对称轴的右边，且在x轴下方时，如图4，过P作MN⊥x轴于N，过F作FM⊥MN于M，同理得△ONP≌△PMF，∴PN＝FM，则﹣m2+4m﹣3＝m﹣2，解得：x＝或（舍）；P的坐标为（，）；④当P在对称轴的右边，且在x轴上方时，同理得m2﹣4m+3＝m﹣2，解得：m＝或（舍）P的坐标为：（，）；综上所述，点P的坐标是：（，）或（，）或（，）或（，）．【点评】本题属于二次函数综合题，主要考查了二次函数的综合应用，相似三角形的判定与性质以及解一元二次方程的方法，解第（2）问时需要运用配方法，解第（3）问时需要运用分类讨论思想和方程的思想解决问题．压轴题训练04一．解答题（共1小题）1．如图，已知直线l的解析式为y＝x﹣1，抛物线y＝ax2+bx+2 经过点A（m，0），B（2，0），D（1，）三点．（1）求抛物线的解析式及A点的坐标，并在图示坐标系中画出抛物线的大致图象；（2）已知点P（x，y）为抛物线在第二象限部分上的一个动点，过点P作PE垂直x轴于点E，延长PE与直线l交于点F，请你将四边形P AFB的面积S表示为点P的横坐标x的函数，并求出S的最大值及S最大时点P的坐标；（3）将（2）中S最大时的点P与点B相连，求证：直线l上的任意一点关于x轴的对称点一定在PB所在直线上．压轴题训练02参考答案与试题解析一．解答题（共1小题）1．如图，已知直线l的解析式为y＝x﹣1，抛物线y＝ax2+bx+2经过点A（m，0），B（2，0），D（1，）三点．（1）求抛物线的解析式及A点的坐标，并在图示坐标系中画出抛物线的大致图象；（2）已知点P（x，y）为抛物线在第二象限部分上的一个动点，过点P作PE垂直x轴于点E，延长PE与直线l交于点F，请你将四边形P AFB的面积S表示为点P的横坐标x的函数，并求出S的最大值及S最大时点P的坐标；（3）将（2）中S最大时的点P与点B相连，求证：直线l上的任意一点关于x轴的对称点一定在PB所在直线上．【分析】（1）根据待定系数法可求抛物线的解析式，再根据A （m，0）在抛物线上，得到0＝﹣m2﹣m+2，解方程即可得到m的值，从而得到A点的坐标；（2）根据四边形P AFB的面积S＝AB?PF，可得S＝﹣（x+2）2+12，根据函数的最值可得S的最大值是12，进一步得到点P的坐标为；（3）根据待定系数法得到PB所在直线的解析式为y＝﹣x+1，设Q（a，a﹣1）是y ＝x﹣1上的一点，则Q点关于x轴的对称点为（a，1﹣a），将（a，1﹣a）代入y ＝﹣x+1显然成立，依此即可求解．【解答】解：（1）∵抛物线y＝ax2+bx+2经过点B（2，0），D（1，），∴，解得a＝﹣，b＝﹣，∴抛物线的解析式为y＝﹣x2﹣x+2，∵A（m，0）在抛物线上，∴0＝﹣m2﹣m+2，解得：m1＝﹣4，m2＝2（舍去），∴A点的坐标为（﹣4，0）．如图所示：（2）∵直线l的解析式为y＝x﹣1，∴S＝AB?PF＝×6?PF＝3（﹣x2﹣x+2+1﹣x）＝﹣x2﹣3x+9＝﹣（x+2）2+12，其中﹣4＜x＜0，∴S的最大值是12，此时点P的坐标为（﹣2，2）；（3）∵直线PB经过点P（﹣2，2），B（2，0），∴PB所在直线的解析式为y＝﹣x+1，设Q（a，a﹣1）是y＝x﹣1上的一点，则Q点关于x轴的对称点为（a，1﹣a），将（a，1﹣a）代入y＝﹣x+1显然成立，∴直线l上的任意一点关于x轴的对称点一定在PB所在直线上．【点评】本题是二次函数的综合题型，其中涉及到的知识点有待定系数法求抛物线的解析式，待定系数法求直线的解析式，函数的最值问题，四边形的面积求法，以及关于x 轴的对称点的坐标特征．压轴题训练03姓名：班级；学号：一．解答题（共3小题）1．已知平面直角坐标系xOy（如图），双曲线y＝（k≠0）与直线y＝x+2都经过点A（2，m）．（1）求k与m的值；（2）此双曲线又经过点B（n，2），过点B的直线BC与直线y ＝x+2平行交y轴于点C，联结AB、AC，求△ABC的面积；（3）若（2）的条件下，设直线y＝x+2与y轴交于点D，在射线CB上有一点E，如果以点A、C、E所组成的三角形与△ACD相似，且相似比不为1，求点E的坐标．2．如图，在矩形OABC中，OA＝3，OC＝5，分别以OA、OC 所在直线为x轴、y轴，建立平面直角坐标系，D是边CB上的一个动点（不与C、B重合），反比例函数y＝（k ＞0）的图象经过点D且与边BA交于点E，连接DE．（1）连接OE，若△EOA的面积为2，则k＝；（2）连接CA、DE与CA是否平行？请说明理由；（3）是否存在点D，使得点B关于DE的对称点在OC上？若存在，求出点D的坐标；若不存在，请说明理由．3．已知如图，二次函数图象经过点A（﹣6，0），B（0，6），对称轴为直线x＝﹣2，顶点为点C，点B关于直线x＝﹣2的对称点为点D．（1）求二次函数的解析式以及点C和点D的坐标；（2）联结AB、BC、CD、DA，点E在线段AB上，联结DE，若DE平分四边形ABCD 的面积，求线段AE的长；（3）在二次函数的图象上是否存在点P，能够使∠PCA＝∠BAC？如果存在，请求出点P的坐标；若不存在，请说明理由．参考答案与试题解析一．解答题（共3小题）1．已知平面直角坐标系xOy（如图），双曲线y＝（k≠0）与直线y＝x+2都经过点A（2，m）．（1）求k与m的值；（2）此双曲线又经过点B（n，2），过点B的直线BC与直线y ＝x+2平行交y轴于点C，联结AB、AC，求△ABC的面积；（3）若（2）的条件下，设直线y＝x+2与y轴交于点D，在射线CB上有一点E，如果以点A、C、E所组成的三角形与△ACD相似，且相似比不为1，求点E的坐标．【解答】解：（1）∵直线y＝x+2都经过点A（2，m），∴m＝2+2＝4，则A（2，4），∵双曲线y＝（k≠0）经过点A，∴k＝2×4＝8；（2）∵双曲线经过点B（n，2），∴2n＝8，解得n＝4，∴B（4，2），由题意可设直线BC解析式为y＝x+b，把B点坐标代入可得2＝4+b，解得b＝﹣2，∴直线BC解析式为y＝x﹣2，∴C（0，﹣2），∴AC＝＝＝2，BC＝＝＝4，AB＝＝＝2，∴BC2+AB2＝AC2，∴△ABC是以AC为斜边的直角三角形，∴S△ABC＝AB?BC＝×2×4＝8；（3）∵直线y＝x+2与y轴交于点D，∴D（0，2），∴AD＝＝2，且AC＝2如图所示，∵AD∥CE，∴∠DAC＝∠ACE，若∠ACD＝∠EAC，则AE∥CD，四边形AECD为平行四边形，此时△ADC≌△CEA，不满足条件，∴∠ACD＝∠AEC，∴△ACD∽△CAE，∴＝，即＝，解得CE＝10，∵E点在直线BC上，∴可设E（x，x﹣2）（x＞0），又∵C（0，﹣2），∴CE＝＝x，∴x＝10，解得x＝10，∴E点坐标为（10，8）．2．如图，在矩形OABC中，OA＝3，OC＝5，分别以OA、OC 所在直线为x轴、y轴，建立平面直角坐标系，D是边CB上的一个动点（不与C、B重合），反比例函数y＝（k ＞0）的图象经过点D且与边BA交于点E，连接DE．（1）连接OE，若△EOA的面积为2，则k＝4；（2）连接CA、DE与CA是否平行？请说明理由；（3）是否存在点D，使得点B关于DE的对称点在OC上？若存在，求出点D的坐标；若不存在，请说明理由．【解答】解：（1）连接OE，如，图1，∵Rt△AOE的面积为2，∴k＝2×2＝4．（2）连接AC，如图1，设D（x，5），E（3，），则BD＝3﹣x，BE＝5﹣，＝，∴，又∵∠B＝∠B，∴△BDE∽△BCA，∴∠BED＝∠BAC，∴DE∥AC．（3）假设存在点D满足条件．设D（x，5），E（3，），则CD ＝x，BD＝3﹣x，BE＝5﹣，AE＝．作EF⊥OC，垂足为F，如图2，易证△B′CD∽△EFB′，∴，即＝，∴B′F＝，∴OB′＝B′F+OF＝B′F+AE＝+＝，∴CB′＝OC﹣OB′＝5﹣，在Rt△B′CD中，CB′＝5﹣，CD＝x，B′D＝BD＝3﹣x，由勾股定理得，CB′2+CD2＝B′D2，（5﹣）2+x2＝（3﹣x）2，解这个方程得，x1＝1.5（舍去），x2＝0.96，∴满足条件的点D存在，D的坐标为D（0.96，5）．3．已知如图，二次函数图象经过点A（﹣6，0），B（0，6），对称轴为直线x＝﹣2，顶点为点C，点B关于直线x＝﹣2的对称点为点D．（1）求二次函数的解析式以及点C和点D的坐标；（2）联结AB、BC、CD、DA，点E在线段AB上，联结DE，若DE平分四边形ABCD 的面积，求线段AE的长；（3）在二次函数的图象上是否存在点P，能够使∠PCA＝∠BAC？如果存在，请求出点P的坐标；若不存在，请说明理由．【解答】解：（1）∵二次函数经过A（﹣6，0），B（0，6），对称轴为直线x＝2，∴二次函数图象经过（2，0），设二次函数解析式为y＝a（x+6）（x﹣2），把B（0，6）代入得：6＝﹣12a，即a＝﹣，∴二次函数解析式为y＝﹣（x+6）（x﹣2）＝﹣x2﹣2x+6＝﹣（x+2）2+8，则C（﹣2，8），D（﹣4，6）；（2）如图1所示，由题意得：AB＝6，BC＝CD＝2，BD＝4，∵BD2＝CD2+BC2，∴∠DCB＝90°，∵直线AB的解析式为y＝x+6，直线DC解析式为y＝x+10，∴DC∥AB，∴四边形ABCD为直角梯形，若S梯形ABCD＝2S△ADE，即×2×（2+6）＝2××2×AE，解得：AE＝4；（3）如图2，在二次函数的图象上存在点P，使∠PCA＝∠BAC，直线CP与AB交于点G，可得GA＝GC，∵A（﹣6，0），C（﹣2，8），直线AB解析式为y＝x+6，设G （x，x+6），∴＝，两边平方得：2x2+24x+72＝2x2+8，移项合并得：24x＝﹣64，解得：x＝﹣，经检验是原方程的根且符合题意，∴G（﹣，），设直线CG解析式为y＝kx+b，把C与G坐标代入得：，解得：，∴直线CG解析式为y＝7x+22，联立得：，解得：或（经检验不合题意，舍去），∴P坐标为（﹣16，﹣90）；由（2）得到四边形ABCD为直角梯形，AB∥CD，∴∠DCA＝∠BAC，此时P与D重合，即P（﹣4，6），综上，满足题意P的坐标为（﹣16，﹣90）或（﹣4，6）．。

八年级下册数学压轴题(含答案)

八年级下压轴题1.如图，四边形OABC是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=15，OC=12，在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处．(1)求CE和OD的长；(2)求直线DE的表达式；(3)直线y=kx+b与AE所在的直线垂直，当它与矩形OABC有公共点时，求出b的取值范围．【答案】解：(1)依题意可知，折痕AD是四边形OAED的对称轴，∴在Rt△ABE中，AE=AO=15，AB=OC=12，BE=√AE2−AB2=√152−122=9，∴CE=15−9=6，在Rt△DCE中，DC2+CE2=DE2，又∵DE=OD，∴(12−OD)2+62=OD2，∴OD=7.5．(2)∵CE=6，∴E(6,12)．∵OD=7.5，∴D(0,7.5)，设直线DE的解析式为y=mx+n，∴{n=7.56m+n=12，解得{m =34n =152， ∴直线DE 的解析式为y =34x +152．(3)∵直线y =kx +b 与AE 所在的直线垂直，DE ⊥AE ，∴直线y =kx +b 与DE 平行，∴直线为y =34x +b ，∴当直线经过A 点时，0=34×15+b ，则b =−454，当直线经过C 点时，则b =12，∴当直线y =kx +b 与矩形OABC 有公共点时，−454≤b ≤12． 2. 如图，在平面直角坐标系中，直线l 1：y =34x 与直线l 2：y =kx +b(k ≠0)相交于点A(a,3)，直线l 2与y 轴交于点B(0,−5)．(1)求直线l 2的函数解析式；(2)将△OAB 沿直线l 2翻折得到△CAB ，使点O 与点C 重合，AC 与x 轴交于点D.求证：四边形AOBC 是菱形；(3)在直线BC 下方是否存在点P ，使△BCP 为等腰直角三角形？若存在，直接写出点P 坐标；若不存在，请说明理由．【答案】解：(1)∵直线l₁：y =34x 与直线l₂：y =kx +b 相交于点A(a,3)，∴A(4,3)，∵直线交l₂交y 轴于点B(0,−5)，∴y =kx −5，把A(4,3)代入得，3=4k −5，∴k =2，∴直线l 2的解析式为y =2x −5；(2)∵OA =√32+42=5，∴OA =OB ，∵将△OAB 沿直线l₂翻折得到△CAB ，∴OB =OC ，OA =AC ，∴OA=OB=BC=AC，∴四边形AOBC是菱形；(3)如图，过C作CM⊥OB于M，则CM=OD=4，∵BC=OB=5，∴BM=3，∴OB=2，∴C(4,−2)，过P1作P1N⊥y轴于N，∵△BCP是等腰直角三角形，∴∠CBP1=90°，∴∠MCB=∠NBP1，∵BC=BP1，∴△BCM≌△P1BN(AAS)，∴BN=CM=4，∴P1(3,−9)；同理可得，P2(7,−6)，P3(72,−112).综上所述，点P的坐标是(3,−9)或(7,−6)或P(72,−112).3.如图，在Rt△ABC中，∠C=90°，∠A=45°，AC=10cm，点D从点A出发沿AC方向以1cm/s的速度向点C匀速运动，同时点E从点B出发沿BA方向以√2cm/s的速度向点A匀速运动，当其中一个点到达终点时，另一个点也随之停止运动，设点D，E运动的时间是t(0<t≤10)s.过点E作EF⊥BC于点F，连接DE，DF．(1)用含t的式子填空；BE=______cm，CD=______cm．(2)试说明，无论t为何值，四边形ADEF都是平行四边形；(3)当t为何值时，△DEF为直角三角形？请说明理由．【答案】√2t t【解析】解：(1)由题意：BE=√2t(cm)，AD=t(cm)，故答案为√2t，t．(2)如图2中，∵CA=CB，∠C=90°，∴∠A=∠B=45°，∵EF⊥BC，∴∠EFB=90°，∴∠FEB=∠B=45°，∴EF=BF，∵BE=√2t，∴EF=BF=t，∴AD=EF，∵∠EFB=∠C=90°，∴AD//EF，∴四边形ADFE是平行四边形．(3)①如图3−1中，当∠DEF=90°时，易证四边形EFCD是正方形，此时AD=DE= CD，t=5．②如图3−2中，当∠EDF=90时，∵DF//AC，∴∠AED=∠EDF=90°，∵∠A=45°，∴AD=√2AE，∴t=√2(10√2−√2t)，，解得t=203③当∠EFD=90°，△DFE不存在．s.综上所述，满足条件的t的值为5s或2034.如图，在矩形ABCO中，点C在x轴上，点A在y轴上，点B的坐标是(−9,12).矩形ABCO沿直线BD折叠，使得点A落在对角线OB上的点E处，且直线BD与OA、x轴分别交于点D、F．(1)求线段BO的长；(2)求△OBD的面积；(3)在x轴上是否存在点M，使得以A、B、F、M为顶点的四边形是平行四边形？若存在，请求出满足条件的M点的坐标；若不存在，请说明理由．【答案】解：(1)∵四边形AB CO是矩形，∴∠BCO=90°．在Rt△BCO中，∵BO2=BC2+OC2，∴BO=√122+92=15．(2)设OD=x，∵四边形ABCO是矩形，∴∠BAD=90°．∵矩形ABCO沿直线BD折叠，使得点A落在对角线OB上的点E处，∴△BAD≌△BED，∴BE=BA=9，AD=ED=12−x，∠BED=∠BAD=90°，∴∠OED=90°，EO=BO−BE=15−9=6．在Rt△DEO中，OD2=OE2+DE2，∴x2=62+(12−x)2，解得x=152，即OD=152，∴S△OBD=12OD⋅AB=1354；(3)由(2)知，OD=152得D(0,152)，设直线BD的解析式为y=kx+b，∵B(−9,12)，D(0,152)，∴{−9k+b=12 b=152，解得{k =−12b =152， ∴直线BD 的解析式为y =−12x +152．当y =0时，x =15，∴OF =15．又∵AB =9，∴FM =9， ∴在x 轴上存在点M ，使得以A 、B 、F 、M 为顶点的四边形是平行四边形．满足条件的点M 的坐标为(6,0)或(24,0)．5. 如图，在平面直角坐标系中，O 为坐标原点，矩形OABC 的顶点A(12,0)、C(0,9)，将矩形OABC 的一个角沿直线BD 折叠，使得点A 落在对角线OB 上的点E 处，折痕与x 轴交于点D ．(1)线段OB 的长度为______；(2)求直线BD 所对应的函数表达式；(3)若点Q 在线段BD 上，在线段BC 上是否存在点P ，使以D ，E ，P ，Q 为顶点的四边形是平行四边形？若存在，请求出点P 的坐标；若不存在，请说明理由．【答案】解：(1)15；(2)如图，设AD =x ，则OD =OA −AD =12−x ，根据折叠的性质，DE =AD =x ，BE =AB =9，又OB =15，∴OE =OB −BE =15−9=6，在Rt △OED 中，OE 2+DE 2=OD 2，即62+x 2=(12−x)2，解得 x =92， ∴OD =12−92=152，∴点D(152,0)，设直线BD 所对应的函数表达式为：y =kx +b(k ≠0)，B(12,9)，则{12k +b =9152k +b =0，解得{k =2b =−15， ∴直线BD 所对应的函数表达式为：y =2x −15．(3)过点E 作EP//BD 交BC 于点P ，过点P 作PQ//DE 交BD 于点Q ，则四边形DEPQ 是平行四边形，再过点E 作EF ⊥OD 于点F ，由12⋅OE ⋅DE =12⋅DO ⋅EF ，得EF =6×92152=185，即点E 的纵坐标为185，又点E 在直线OB ：y =34x 上，∴185=34x，解得x=245，∴E(245,185)，由于PE//BD，所以可设直线PE：y=2x+n，∵E(245,185)在直线EP上，∴185=2×245+n，解得n=−6，∴直线EP：y=2x−6，令y=9，则9=2x−6，解得x=152，∴P(152,9)．6.如图，直线y=−12x+3与x轴、y轴分别相交于A，B两点，P是线段AB上的一个动点(不与AB两点重合)，点M的坐标为(4,0)，设P点的横坐标为x，设△OPM 的面积为S．(1)求点A，B的坐标；(2)求S关于x的函数解析式，并写出自变量x的取值范围；(3)当S=12S△AOB时，求点P的坐标；(4)画出函数S的图象．【答案】解：(1)针对于直线y=−12x+3，令x=0，∴y=3，∴B(0,3)，令y=0，∴−12x+3=0，∴x=6，∴A(6,0)；(2)∵点P在直线y=−12x+3上，且P点的横坐标为x，∴P(x,−12x+3)，∵M(4,0)，∴OM=4，∴S=S△OPM=12OM×|y P|=2y P=2(−12x+3)=−x+6(0<x<6)；(3)由(1)知，A(6,0)，B(0,3)，∴S△AOB=12OA×OB=9，由(2)知，S=−x+6(0<x<6)；当S=12S△AOB时，∴−x+6=92，∴x=32，∴y=−12x+3=94，∴P(32,94 )；(4)由(2)知，S=−x+6(0<x<6)，∴函数S的图象如图所示：7.如图，直线l1：y=kx+245与x轴、y轴分别相交于A、B两点，直线l2：y=−2x+b 与x轴、y轴、直线l1分别相交于点C、D、P.已知点A的坐标为(6,0)，点D的坐标为(0,6)，点M 是x 轴上的动点． (1)求k ，b 的值及点P 的坐标；(2)当△POM 为等腰三角形时，求点M 的坐标；(3)是否存在以点M 、O 、D 为顶点的三角形与△AOB 全等？若存在，请求出点M 的坐标；若不存在，请说明理由．【答案】解：(1)∵直线l 1：y =kx +245与x 轴相交于A(6,0)，∴6k +245=0，∴k =−45，∴直线l 1：y =−45x +245①∵直线l 2：y =−2x +b 与y 轴相交于点D(0,6)， ∴b =6，∴直线l 2：y =−2x +6②，联立①②解得，{x =1y =4，∴P(1,4)；(2)∵点M 是x 轴上的动点， ∴设M(m,0)， ∵P(1,4)，∴OP =√17，OM =|m|，MP =√(m −1)2+16， ∵△POM 为等腰三角形， ∴当OM =OP 时， ∴√17=|m|， ∴m =±√17， ∴M(−√17,0)或(√17,0)当OM=MP时，∴|m|=√(m−1)2+16，∴m=172，∴M(172,0)，当OP=MP时，∴√17=√(m−1)2+16，∴m=0(舍)或m=2，∴M(2,0)，即：点M的坐标为(−√17,0)或(√17,0)或(172,0)或(2,0)；(3)∵点A的坐标为(6,0)，点D的坐标为(0,6)，∴OA=OD=6，∵点M在x轴上，∴∠AOB=∠DOM=90°，∵以点M、O、D为顶点的三角形与△AOB全等，∴△AOB≌△DOM，∴OM=OB，∵直线l1：y=−45x+245与y轴相交于B，∴B(0,245)，∴OB=245，∴OM=245，∴M(245,0)或(−245,0)．8.在平面直角坐标系中，一次函数的图象与x轴交于点A，与y轴交于点B，且与正比例函数的图象交于点C(3，4)．(1)求、的值；(2)若D点是线段OC上的动点，过D作DE∥y轴交AC于点E．①设D点的横坐标为，线段DE的长为，则与的函数关系式为_______；②连接AD，若△AOD为等腰三角形，请求出点D的坐标；(3)在平面内是否存在点Q，使以O、A、C、Q为顶点的四边形是平行四边形？若存在，直接写出点Q的坐标；若不存在，请说明理由．【详解】（1）∵正比例函数的图象过点C（3，4），∴，解得：，∴正比例函数为，∵一次函数的图象过点C（3，4），∴，解得：，∴一次函数解析式为：；（2）①∵D在正比例函数上，∴ D点的纵坐标为：，∵E点在一次函数上，∴ E点的纵坐标为：，∴ DE ＝；②∵点A是一次函数与x轴的交点，∴ A（－3，2），即OA＝3，而D的坐标为（，），∵∠AOD是钝角，一定是等腰三角形的顶角，∴OD＝OA，∴OD＝，解得：，则，∴点D的坐标为（，）；（3）根据图象分析：①当OA作为平行四边形的边时，则CQ∥OA，CQ＝OA，此时Q（0，4），（6，4），②当OA作为平行四边形的对角线时，则OQ∥AC，OQ＝AC，此时Q（－6，－4），综上所述，存在，点Q的坐标为（0，4），（6，4），（－6，－4）．9.如图1，在平面直角坐标系xOy中，直线l1:y1=kx+b与l2: y2=kx+3相交于点C(1,2),直线l1与x轴交于点A (-1，0)、直线l2与x轴交于B点.(1) 求直线l1的解析式(表达式) ;(2)判断△ABC的形状并说明理由; (3)在x轴上是否存在点P，使△ACP为等腰三角形?若存在，请直接写出P 点的坐标;若不存在，请说明理由;(4) 如图2，设直线l2与y轴交于点D，点为线段BD上的一个动点，过点M 作ME⊥y轴于点E，作MF⊥x轴于点F，连接EF，问是否存在点M，使EF的值最小?若存在,求出此时EF 的值.10.如图，直线y=kx -3与x 轴、y 轴分别交于B ⎪⎭⎫ ⎝⎛0,23、C 两点，(1)求k 值；(2)若点A(x ，y)是直线y=kx -3上在第一象限内的一个动点，当点A 在运动过程中，试写出△AOB 的面积S 与x 的函数关系式；(不要求写出自变量的取值范围) (3)探究：①当A 点运动到什么位置时，△AOB 的面积为49，并说明理由； ②在①成立的情况下，x 轴上是否存在一点P ，使△AOP 是等腰三角形？若存在，请直接写出满足条件的所有P 点坐标；若不存在，请说明理由．答案解析（1）把B 的坐标代入y=kx -3，得：k -3=0，解得：k=2；（2）OB=，则S=×（2x -3）=x -；（3）①根据题意得：x -=，解得：x=3，则A 的坐标是（3，3）；②OA==3，当O是△AOP的顶角顶点时，P的坐标是（-3，0）或（3，0）；当A是△AOP的顶角顶点时，P与过A的与x轴垂直的直线对称，则P的坐标是（6，0）；当P是△AOP的顶角顶点时，P在OA的中垂线上，OA的中点是（，），与OA垂直的直线的斜率是：-1，设直线的解析式是：y=-x+b，把（，）代入得：=-+b，解得：b=，则直线的解析式是：y=-x+，令y=0，解得：x=，则P的坐标是（，0）．故P的坐标是：（-3，0）或（3，0）或（6，0）或（，0）．。

人教版八年级数学下册经典压轴题考点及例题解析

人教版八年级数学下册经典压轴题考点及例题解析例题1古希腊数学家把数 1 ， 3 ， 6 ， 10 ，15 ， 21 ，...... 叫做三角形数，它有一定的规律性。

若把第一个三角形数记为 a1 ，第二个三角形数记为 a2 ，......，第 n 个三角形数记为 an ，则 an + a(n+1) = ?答案：（n + 1）^2 。

例题2在平面直角坐标系中，对于平面内任意一点 P（a , b）若规定以下三种变换：① f（a , b）= （-a , b），如 f（2 , 5）= （-2 , 5）；② g（a , b） = （b , a）, 如 g（2 , 5）= （5 , 2）；③ h（a , b）= （-a , -b），如 h（2 , 5）= （-2 , -5）。

根据以上变换，那么 f（h（5 ， -3））等于多少？答案：（5,3）。

例题3如图，已知等腰直角△ABC 的直角边长为 1 ，以 Rt△ABC 的斜边 AC 为直角边，画第二个等腰 Rt△ACD ，在以 Rt△ACD 的斜边 AD 为直角边，画第三个等腰 Rt△ADE ， ... ，依次类推到第五个等腰 Rt△AFG ，则由这五个等腰直角三角形所构成的图形的面积是多少？答案：31/2 。

例题4如图所示，直线 OP 经过点 P（4,4√3），过 x 轴上的点 1、3、5、7、9、11 ......分别作 x 轴的垂线，与直线 OP 相交得到一组梯形，其阴影部分梯形的面积从左至右依次记为 S1 , S2 , S3 , ... , Sn , 则 Sn 关于 n 的函数关系式是？答案：Sn = 4√3 （2n - 1）。

例题5现将 1、√2、√3、√6 四个数按下列方式排列。

若规定（m , n）表示第 m 排从左到右第 n 个数，则（5 ， 4）与（15 ， 7）表示的两数之积是多少？答案：2√3 。

例题6现将一块直角三角形的花圃进行改造，已知两直角边长分别为 6 m 、8 m 。

人教版数学八年级下册压轴题含答案

1、如图11，已知正比例函数与反比例函数的图像都经过点M （－2，），且P （，－2）为双曲线上的一点，Q 为坐标平面上一动点，PA 垂直于x 轴，QB 垂直于y 轴，垂足分别是A 、B ．（1）写出正比例函数与反比例函数的关系式；（2）当点Q 在直线MO 上运动时，直线MO 上是否存在这样的点Q ，使得△OBQ 与△OAP 面积相等？假如存在，恳求出点的坐标，假如不存在，请说明理由；（3）如图12，当点Q 在第一象限中的双曲线上运动时，作以OP 、OQ 为邻边的平行四边形OPCQ ，求平行四边形OPCQ周长的最小值．y kx =12，所以正比例函数解析式为12x 同样可得，反比例函数解析式为2y x）当点Q 在直线设点Q 的坐标为1()2Q m m ，，于是211112224OBQ S OB BQ m m m △，而1(1)(2)12OAPS △，所以有，2114m ，解得2m =±所以点Q 的坐标为1(21)Q ，与2(21)Q ，（3）因为四边形OPCQ 是平行四边形，所以OP ＝CQ ，OQ图B A OP＝PC ，而点P （1-，2-）是定点，所以OP 的长也是定长，所以要求平行四边形OPCQ 周长的最小值就只需求OQ 的最小值．因为点Q 在第一象限中双曲线上，所以可设点Q 的坐标为2()Q n n，，由勾股定理可得222242()4OQ n nn n，所以当22()0nn即20nn时，2OQ 有最小值4，又因为OQ 为正值，所以OQ 与2OQ 同时获得最小值，所以OQ 有最小值2．由勾股定理得OP，所以平行四边形OPCQ 周长的最小值是2.已知：如图，正比例函数y ＝ax 的图象与反比例函数xk y=的图象交于点A (3，2)．(1)试确定上述正比例函数与反比例函数的表达式；(2)依据图象答复，在第一象限内，当x 取何值时，反比例函数的值大于正比例函数的值；(3)M (m ，n )是反比例函数图象上的一动点，其中0＜m ＜3，过点M 作直线MB ∥x 轴，交y 轴于点B ；过点A 作直线AC ∥y 轴交y 轴于点C ，交直线MB 于点D ．当四边形OADM 的面积为6时，请推断线段BM 与DM 的大小关系，并说明理由．解答：解：（1）将A（3，2）分别代入y=，y=ax中，得：2=，3a=2∴k=6，a=（2分）∴反比例函数的表达式为：y=（3分）正比例函数的表达式为y=x（4分）（2）视察图象，得在第一象限内，当0＜x＜3时，反比例函数的值大于正比例函数的值．（6分）（3）BM=DM（7分）理由：∵MN∥x轴，AC∥y轴，∴四边形OCDB是平行四边形，∵x轴⊥y轴，∴▱OCDB是矩形．∵S△OMB=S△OAC=×|k|=3，又S四边形OADM=6，∴S矩形OBDC=S四边形OADM+S△OMB+S△OAC=3+3+6=12，即OC•OB=12∵OC=3∴OB=4（8分）即n=4∴m=∴MB=，MD=3﹣=∴MB=MD（9分）．3.如图，直线y=x+b（b≠0）交坐标轴于A、B两点，交双曲线y=x2于点D ，过D作两坐标轴的垂线DC 、DE ，连接OD ．（1）求证：AD 平分∠CDE ；（2）对随意的实数b （b ≠0），求证BE ·OE 为定值；（3）是否存在直线AB ，使得四边形OBCD 为平行四边形？若存在，求出直线的解析式；若不存在，请说明理由．4.如图（1），直线122y x =-+交x 轴、y 轴于A 、B线AB 上第二象限内一点，且S △AOC =8，双曲线y=C（1）求k 的值（2）如图（2），过点C 作CM ⊥y 轴于M,反向延长CM 于H ，使CM=CH ，过H 作HN ⊥x 轴于N ，交双曲线y=xk于D ，求四边形OCHD 的面积（3）如图（3），点G 与点A 关于y 轴对称，P 为第二象限内双曲线上一个动点，过P 作PQ ⊥x 轴于Q ，分别交线段BG 于E,交射线BC 于F ，试推断线段QE+QF 是否为定值，若为定值，证明并求出定值；若不是定值，请说明理由。

八年级下册数学压轴题(含答案)

八年级下册数学压轴题(含答案)四边形AOBC的对角线互相平分，且相等，故为菱形；又因为OC经过翻折后落在AB上，且AC与x轴垂直，故OC垂直于AB，故AO=OC=OB=BC，故AOBC是一个菱形；3)设点P的坐标为(x,y)，则BPC为直角三角形，且BP=PC，又因为BP在y轴下方，故y<0，且BP与BC垂直，故BP的斜率为-2；设BP的解析式为y=-2x+b，且B点坐标为(0,-5)，则有b=-5；又因为BP=PC，故PC的解析式为y=2x+b，且C点坐标为(a,0)，代入得a=5；又因为XXX在BC下方，故y<0，代入得y=-2x-5；代入BP的解析式得x=5/3，代入得y=-25/3；故存在点P(5/3,-25/3)，使△BCP为等腰直角三角形。

题目：在平面直角坐标系中，已知点A(0,0)，B(5,0)，C(0,5√2)，D从A出发沿AC方向以1m/s的速度向C匀速运动，同时点E从B出发沿BA方向以√2m/s的速度向A匀速运动。

当其中一个点到达终点时，另一个点也随之停止运动。

设点D，E运动的时间是t(0<t≤10)秒。

过点E作EF⊥BC于点F，连接DE，DF。

1)求BE和CD的长度。

2)试说明，无论t为何值，四边形ADEF都是平行四边形。

3)当t为何值时，△DEF为直角三角形？请说明理由。

解法：1)由题意可知，BE=√2t，CD=t，故BE=√2t，CD=t。

2)如图所示，由题意可得，∠C=90°，∠A=45°，故∠B=45°。

又因为EF⊥BC，所以∠EFB=90°，∠FEB=45°，所以BE=EF。

又因为AE=√2t，DE=CD，所以DE=√2t。

因此，四边形ADEF的对角线相等，且相互平分，所以ADEF是平行四边形。

3)如图所示，当EF⊥BC时，由勾股定理可知，DE²=DF²+EF²，即(√2t)²=(t+BE)²+(5√2-BF)²。

(二)——2023-2024学年八年级数学下学期压轴题模拟训练(人教版)(解析版)

期末考试压轴题模拟训练（二）一、单选题1．已知a b <，且0ab ≠）A．−B．−C．D．【详解】解：a b <0,a b ∴<是（）A ．k 的值为2或－2B ．y 的值随x 的增大而减小C ．k 的值为1或－1D ．在22x −≤≤的范围内，y 的最大值为3 【答案】A【分析】本题考查了一次函数的图象与性质，熟练掌握一次函数的图象与性质是解题的关键．【详解】解：当2x =时，当2x =−时，21y k =−+当0k >时，y 随x 的增大而增大则由题意可得：21(21)8k k +−−+=2k ∴= 此时在22x −≤≤的范围内，y 的最大值为215k +=当0k <时，y 随x 的增大而减小则由题意可得：21(21)8k k −+−+=2k ∴=−此时在22x −≤≤的范围内，y 的最大值为215k −+=故选：A ．21y k =+3．如图，已知ABC 中，AB 的垂直平分线交BC 于点D ，AC 的垂直平分线交BC 于点E ，点M N ，为垂足，32BD =，2DE =，52EC =，则AC =（）A B C D∵2DE =，52EC =，∴592DC =+=，且满足3ABP ABO S S =，则a 的值为（）A ．2B ．2C ．2D ．2−∵点20A （-，），点()02B −，，点∴2,2,2,OA OB PD PC ===∵3ABP ABO SS =， ∴3AOP BOP AOB AOB SS S S ++=，的速度匀速前行乙比甲晚05h ．出发，并且在中途停留1h 后，按原来速度的一半继续前进．此过程中，甲、乙两人离A 地的路程s （km ）与甲出发的时间t （h ）之间的关系如图．下列说法：①A ，B 两地相距24km ；②甲比乙晚到B 地1h ；③乙从A 地刚出发时的速度为72km/h ；④乙出发17h 14与甲第三次相遇．其中正确的有（）A．1个B．2个C．3个D．4个乙比甲晚乙的第二个拐点时间为边向右作等边DEF，则AF DF+的最小值为（）A．4B．C．D．ABC和DEF都是等边三角形，2=AE BD∴=AH22(SAS∴≌CEF HDE+LF BF∴+AF BF=AB AC∴=AC LCA−，7．如图，在平面直角坐标系xOy中，直线AB与x轴负半轴，轴正半轴分别交于点1,0B ，在x 轴上取点()3,0C ，点D 是直线AB 上的一个动点，以CD 为边，在CD 的右侧作等边三角形CDF ，使得点F 落在第一象限，连接OF ．若60BAO ∠=︒，则OF CF +的最小值为（）A ．6B C ．8 D ，证明(SAS ACD MCF ≌∵()1,0A −，()3,0C ，∴134AC =−−=，∵60CAB ∠=︒，∴ACM △为等边三角形，∴4AM CM AC ===，ACM ∠∵MG AC ⊥，∵CDF 为等边三角形，CF CD =∴(SAS ACD MCF ≌同的ABC 有（）种．A ．2B ．3C ．4D ．5 【答案】C【分析】分ABC 是直角三角形、锐角三角形、钝角三角形，根据等腰三角形的判定与性质【详解】解：由题意知，符合条件形状不同的ABC 有4当ABC 是直角三角形，由直角三角形斜边上的中线等于斜边的一半可知，将ABC 分成两个等腰三角形；如图当ABC 是顶角为当ABC 是底角为将ABC 分成了两个等腰三角形，3；当ABC 中∠形，如图4．若6AC BC +=，空白部分面积为10.5，则AB 的长为（）ABCD证明(ASA FAM ABN ≌FAM ABN SS =，进而得到ABC S S =ABC S ，即：10.5ABC S =与ABN 中，90NAB =︒∴(ASA FAM ABN ≌FAM ABN SS =， ABC S =在ABC 中，22AC BC =＋10.5ABC S =10．如图，矩形纸片ABCD中，4AB=，8BC=，点E，F分别在AD，BC上，将纸片沿直线EF折叠，点C落在AD上的点H处，点D落在点G处，有以下四个结论：①四边形CFHE是菱形；②EC平分DCH∠；③线段BF的取值范围为34≤≤；④当点H与点ABF重合时，EF=）A．1个B．2个C．3个D．4个Rt ABF 中2AB BF =+11．若2021a a −=，则22021a −的值为．【答案】2022【分析】根据二次根式的被开方数的非负性，得a -2022≥0，进而化简绝对值，求解即可．12．如图，在平面直角坐标系中，直线1：与直线2：交于点，直线1与x 轴交于点B ，直线2l ：2y x b =−+过点()0,1，点C 是横轴上任意一点，满足：ABC 是等腰三角形的点C 坐标是．两点的坐标，再根据ABC 是ABC 是等腰三角形，则13．如图，直线43y x =−+交x 轴、y 轴于点A 、B ，点P 在第一象限内，且纵坐标为4．若点P 关于直线AB 的对称点P '恰好落在x 轴的正半轴上，则点P '的横坐标为．【详解】点点BP x 轴，=∠BPQ AP 又'=PQ P Q (BPQ AP Q ASA ∴'≌在直角OBP '中，2(6)m m −=上的动点，且BE FG =，BE FG ⊥，连接EF BG ，，当EF FG BG ++的值最小时，CG 的长为．【答案】3【分析】本题考查了轴对称最短问题，全等三角形的判定和性质，勾股定理，待定系数法求一次函数解析式，正方形的性质，过点G 作GT AB ⊥于T ，证明()ASA ABE TGF ≌，推出2AE FT ==，设CG BT x ==，则4AF AB FT BT x =−−=−，可得∵四边形ABCD 是正方形，∴AB BC =，A ABC ∠=∠∵CT AB ⊥，∴90GHB ∠=︒，∴(ASA ABE TGF ≌设直线M N '的解析式为y kx b =+，∵()4,2N ，()0,6M '−，246k b b=+⎧⎨−=⎩，解得26k b =⎧⎨=−⎩， ∴直线M N '的解析式为26y x =−，∴()3,0P ，∴3x =时，EF BG +的值最小，∵BE FG ==定值，∴当3CG =时，EF FG BG ++的值最小．故答案为：3．15．在等边三角形ABC 中，6AB =，BD AC ⊥于点D ，点E ，F 分别是BC ，CD 上的动点，CEF 沿EF 所在直线折叠后点C 落在BD 上的点'C 处，若'BEC 是等腰三角形，则'BC = ．【详解】解：在等边三角形CEF 沿CF C F '∴=∴'是等腰直角三角形，DC F2='CF C F三、解答题16．已知甲、乙两地相距10千米，小诚从乙地出发，匀速骑行至甲地，在甲地休息一段时间后，便以原速度的45匀速返回乙地．小诚从乙地出发10分钟后，小勤从甲地出发至乙地，小勤先匀速步行至两地中点，再从中点匀速慢跑至乙地，最后两人同时到达乙地．在运动过程中，小诚和小勤距甲地的距离y（千米）与小勤出发的时间x（小时）的关系如图所示，请结合图象信息解答下列问题：(1)小勤出发时，小诚骑行路程为______千米，小勤出发______小时后步行至甲、乙中点，小诚从乙地到甲地的骑行速度为______千米/小时，小勤的步行速度为______千米/小时；(2)写出小勤距甲地的距离y（千米）和x（小时）的关系式；(3)小勤出发多少小时后，两人在小勤未到达甲、乙中点前相距500米．17．在平面直角坐标系中，直线与y 轴交于点 B ，与x 轴交于点 C ，线段(),OB OC OB OC >的长是一元二次方程 29180x x −+=的两个根，直线 y x =交BC 于点A ．(1)求点A 的坐标；(2)在平面直角坐标系中有一点6,P m （），求AOP 的面积S 与m 的函数关系式；(3)M 为直线BC 上的动点，过点M 作y 轴的平行线，交直线OA 于点N ，点Q 在y 轴上，是否存在点M ，使MNQ △为等腰直角三角形？若存在，请直接写出点M 的坐标；若不存在，请说明理由．(12PEO PEA S S S −=当点P 在点E 上方时，即(12PEO PEA S S S −=综上所述：AOP 的面积（3）解：令直线AB 为1l (,26)M t t −+，则(,)N t t ，2636MN t t t ∴=−+−=−①如图1，若90MQN ∠=②如图2，图3，若QMN ∠则M MN x t ==，36t t ∴−=，32t ∴=或3t =，（1）如图1，在平面直角坐标系中，O 为坐标原点，四边形ABOC 为正方形，直线l 经过点A ，BE l ⊥于点E ，CF l ⊥于点F ，若点A 的坐标为(，3CF =，求EF 的长；【问题解决】（2）如图2，在平面直角坐标系中，O 为坐标原点，四边形ABOC 为菱形，直线l AC ⊥于点A 交OB 于点P ，BE AB ⊥交l 于点E ，点F 在AP 上，且ACF BAE ∠=∠，若AB =2EF =，求点E ，F 的坐标；【思维拓展】（3）如图3，在平面直角坐标系中，O 为坐标原点，四边形ABOC 为矩形，直线l 分BAC ∠为1:2两部分，BE l ⊥于点E ，CF l ⊥于点F ，若点F 的坐标为()1−−，直接写出点E 的坐标． ()AAS ACF BAE ≌，证明(ASA ACF BAE ≌BAE S =）四边形CF ∠BE ∴()AAS ACF BAE ≌）解：四边形l ∠∴(ASA ACF BAE ≌12BAE S =）解：四边形直线则33,1HF OH ==，BE l ⊥，CF l ⊥，BAE CAF CAF ∴∠+∠=∠+∠30BAE ACF ∴∠=∠=︒，OCF ∠=CFH ∴∠12ABE S =2CF HC =2AF CF +AG AE =同理可得：1,2CF AC AE ==33HF =，63CF ∴=，19．【发现问题】爱好数学的小强在做作业时碰到这样的一道题目：如图①，在ABC 中，8AB =，6AC =，E 为BC 中点，求AE 的取值范围．(1)小强经过多次的尝试与探索，终于得到解题思路：在图①中，作AB 边上的中点F ，连接EF ，构造出ABC 的中位线EF ，请你完成余下的求解过程．(2)如图②，在四边形ABCD 中，8AB =，6CD =，E 、F 分别为BC 、AD 中点，求EF 的取值范围．(3)变式：把图②中的A 、D 、C 变成在一直线上时，如图③，其它条件不变，则EF 的取值范围为_________．(4)如图④，在ABC 中，60A ∠=︒，8AB =，E 为BC 边的中点，F 是AC 边上一点且EF 正好平分ABC 的周长，则EF =______．平分ABC 的周长推得的直角三角形特征即可得到E 为BC8AB =，1又E 、F 分别为BC 、AD 12FG AB ∴=，12EG DC =8AB =，6CD =，4FG ∴=，又E 、F 分别为BC 、AD 中点，12FH AB ∴=，12EH DC =，8AB =，6CD =，4FH ∴=在HEF 中，17EF <<FM AF=∴∥，NE MC，FNFN AB∴∠=∠，∠FNM ABM∠=︒，A60EF正好平分ABC的周长，AB AF BE FM MC∴+=+⊥又NP EF∴∠=∠NFE20．已知长方形ABCO，O为坐标原点，B的坐标为8,6，点A，C分别在坐标轴上，P是=.线段BC上的动点，设PC m(1)已知点D 在第一象限且是直线26y x =+上的一点，设D 点横坐标为n ，则D 点纵坐标可用含n 的代数式表示为_________；(2)在（1）的条件下，此时若APD △是等腰直角三角形，求点D 的坐标；(3)直线2y x b =+过点()3,0，请问在该直线上，是否存在第一象限的点D 使APD △是等腰直角三角形？若存在，请直接写出这些点的坐标，若不存在，请说明理由. ，可证()AAS EDA FAP ≌，使APD 是等腰直角三角形，理由为：由直线APD 是等腰直角三角形，⊥轴，DE y∴∠=DEA在EDA和FAP中，∠=∠DEA AFP()∴≌EDA FAPAAS 四边形AFP∠=∴点DE y⊥轴，∴∠+∠EDA在EDA和△(AAS ∴≌EDA FPD∴四边形四边形在ABP和PFD中，∠=∠ABP PFD(AAS ABP PFD∴≌∴==−8,BP FD x AB∴B的坐标为四边形PFA∠=∴四边形在APF和DAE中，∠=∠APF DAE(AASAPF DAE∴≌=PC m6∴=AF是他从课本出发开展了如下探究：【课本再现】我们知道，如果一个四边形是平行四边形，那么它的任意一组对边平行且相等．反过来，一组对边平行且相等的四边形是平行四边形吗？小宁对此展开了探究．如图①，在四边形ABCD 中，已知AB CD ∥，AB CD =，求证：四边形ABCD 是平行四边形．小宁的思路如下：连接AC ，通过证明ABC ADC △≌△，得到BC DA =，最后可证得四边形ABCD 是平行四边形．请你根据小宁的思路将证明过程补充完整；【变式探究】如图②，在平行四边形ABCD 中，4AB BC ==，对角线AC =四边形ABCD 是正方形；【拓展应用】在图②的条件下，点E 是对角线AC 上一点，连接BE ，过点E 作EF BE ⊥交CD 于点F ，连接BF 交AC 于点G ，14AE AC =，2BG GF =，求CG 的长．在ABC 中，利用勾股定理的逆定理得到ABC 是直角三角形，且定定理、正方形的判定定理求证即可得到四边形ABCDAB在ABC和△=AB AB()∴≌SASABC ADC变式探究：证明：在ABC中，232AC=，即∴是直角三角形，且ABC□在ABCDABAC为对角线，∴平分AC⊥EN BC∴=EM ENEMC=∠∴四边形∠+∠FEI在BHE和△AC是正方形∴∠=BAHAEBGCI。

2020-2021学年人教版数学八年级下册期末压轴题专项复习卷(含答案)

2021年人教版数学八年级下册期末《压轴题专项》复习卷1.如图，点A的坐标是(－2，0)，点B的坐标是(6，0)，点C在第一象限内且△OBC为等边三角形，直线BC交y轴于点D，过点A作直线AE⊥BD，垂足为E，交OC于点F.(1)求直线BD的函数表达式；(2)求线段OF的长；(3)连接BF，OE，试判断线段BF和OE的数量关系，并说明理由．2.阅读下面材料：我们知道一次函数y=kx+b(k≠0，k、b是常数)的图象是一条直线，到高中学习时，直线通常写成Ax+By+C=0(A≠0，A、B、C是常数)的形式，点P(x0，y0)到直线Ax+By+C=0的距离可用公式d=计算．例如：求点P(3，4)到直线y=﹣2x+5的距离．根据以上材料解答下列问题：(1)求点Q(﹣2，2)到直线3x﹣y+7=0的距离；(2)如图，直线y=﹣x沿y轴向上平移2个单位得到另一条直线，求这两条平行直线之间的距离．3.已知正方形ABCD，AB=8，点E、F分别从点A、D同时出发，以每秒1m的速度分别沿着线段AB、DC向点B、C方向的运动，设运动时间为t．（1）求证：OE=OF．（2）在点E、F的运动过程中，连结AF．设线段AE、OE、OF、AF所形成的图形面积为S．探究：①S的大小是否会随着运动时间为t的变化而变化？若会变化，试求出S与t的函数关系式；若不会变化，请说明理由．②连结EF，当运动时间为t为何值时，△OEF的面积恰好等于的S．4.如图，在平面直角坐标系中，一次函数y=kx+b的图象与x轴交于点A（-3，0），与y轴交于点B，且与正比例函数的图象交点为C（m，4）．求：（1）一次函数y=kx+b的解析式；（2）若点D在第二象限，△DAB是以AB为直角边的等腰直角三角形，则点D的坐标为；（3）在x轴上求一点P使△POC为等腰三角形，请求出所有符合条件的点P的坐标．5.将正方形ABCD放在如图所示的直角坐标系中,A点的坐标为(4,0),N点的坐标为(3,0)，MN平行于y轴，E是BC的中点，现将纸片折叠，使点C落在MN上，折痕为直线EF.(1)求点G的坐标；(2)求直线EF的解析式；(3)设点P为直线EF上一点，是否存在这样的点P，使以P, F, G的三角形是等腰三角形?若存在，直接写出P点的坐标;若不存在，请说明理由.6.如图,已知直线y=kx+1经过点A(3,-2)、点B(a,2)，交y轴于点M.（1）求a的值及AM的长（2）在x轴的负半轴上确定点P，使得△AMP成等腰三角形，请你直接写出点P的坐标.（3）将直线AB绕点A逆时针旋转45°得到直线AC，点D（-3，b）在AC上，连接BD，设BE是△ABD 的高，过点E的射线EF将△ABD的面积分成2：3两部分，交△ABD的另一边于点F，求点F的坐标.7.阅读理解：运用“同一图形的面积相等”可以证明一些含有线段的等式成立，这种解决问题的方法我们称之为面积法．如图1，在等腰△ABC中，AB=AC，AC边上的高为h，点M为底边BC 上的任意一点，点M到腰AB、AC的距离分别为h1、h2，连接AM，利用S△ABC=S△ABM+S△ACM，可以得出结论：h=h1+h2．类比探究：在图1中，当点M在BC的延长线上时，猜想h、h1、h2之间的数量关系并证明你的结论．拓展应用：如图2，在平面直角坐标系中，有两条直线l1：y=0.75x+3，l2：y=﹣3x+3，若l2上一点M到l1的距离是1，试运用“阅读理解”和“类比探究”中获得的结论，求出点M 的坐标．8.如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,AB=3,AD=2,经过点C的直线y=x ﹣2与x轴、y轴分别交于点E、F．（1）求：①点D的坐标；②经过点D,且与直线FC平行的直线的函数表达式；（2）直线y=x﹣2上是否存在点P,使得△PDC为等腰直角三角形？若存在,求出点P 的坐标；若不存在,请说明理由．（3）在平面直角坐标系内确定点M,使得以点M、D、C、E为顶点的四边形是平行四边形，请直接写出点M的坐标．9.如图,在平面直角坐标系中,△AOB的顶点O为坐标原点,点A的坐标为（4,0）,点B的坐标为（0,1）,点C为边AB的中点,正方形OBDE的顶点E在x轴的正半轴上,连接CO,CD,CE．（1）线段OC的长为；（2）求证：△CBD≌△COE；（3）将正方形OBDE沿x轴正方向平移得到正方形O1B1D1E1，其中点O,B,D,E的对应点分别为点O1，B1，D1，E1，连接CD,CE,设点E的坐标为（a，0）,其中a≠2,△CD1E1的面积为S．①当1＜a＜2时,请直接写出S与a之间的函数表达式；②在平移过程中,当S=时,请直接写出a的值．10.如图，直线y=2x+m(m>0)与x轴交于点A(-2,0)直线y=-x+n(n>0)与x轴、y轴分别交于B、C 两点，并与直线y=2x+m(m>0)相交于点D，若AB=4．（1）求点D的坐标；（2）求出四边形AOCD的面积；（3）若E为x轴上一点，且△ACE为等腰三角形，直接写出点E的坐标．11.如图，直线l：交x、y轴分别为A、B两点，C点与A点关于y轴对称.动点P、Q分别在线段AC、AB上(点P不与点A、C重合)，满足∠BPQ=∠BAO.(1)点A坐标是， BC= .(2)当点P在什么位置时，△APQ≌△CBP，说明理由。

(一)——2023-2024学年八年级数学下学期压轴题模拟训练(人教版)(解析版)

期末考试压轴题模拟训练（一）一、单选题1．化简二次根式）ABCD【详解】2aaa+−A．10B．C D．【点睛】此题考查勾股定理的运用，在直角三角形中，已知两条边长时，可利用勾股定理求第三条边的长度.DC=：2，O点是BD的中点，连接AO并3．如图，在ABC中，D在AC边上，AD：1延长交BC于点E，则BE：EC=（）A．1：2B．1：3C．1：4D．2：3点∥OG BC∴:AG GC:AOBBOES SAO =2BOEAOBSS S S ==，，又点42ABD AODSS SS ==，，AD ：DC 28BDCABDS SS ∴==，7BDCBOESSS −=93AECAODABEAOBBOECDOE SS SS SS S S =+==+=四边形，，ABE AECSS=为（）A ．2.8B ．C ．2.4D ．3.5【答案】B【分析】延长BG 交CH 于点E ，根据正方形的性质证明△ABG ≌△CDH ≌△BCE ，可得GE=BE -BG=2，HE=CH -CE=2，∠HEG=90°，从而由勾股定理可得GH 的长．【详解】解：如图，延长BG 交CH 于点E ，∵四边形ABCD 是正方形， ∴∠ABC=90°，AB=CD=10， ∵AG=8，BG=6， ∴AG 2+BG 2=AB 2，5．如图，在平面直角坐标系中，点1,5,4,1,,,3,4A B C m m D m m −−−+，当四边形 ABCD 的周长最小时，则 m 的值为（）．A B ．32C ．2D ．3线BD 于点G ，连接AG ，若BE DF =，CEF α∠=，则AGB ∠=（）A ．αB ．32αC ．15α+︒D ．135α︒−()SAS ABE ADF ≌明(ASA GHE GDF ≌∵四边形ABCD 为正方形，∴ABE ADC ADF ∠=∠=∠在ABE 和ADF △中，90BE DF ABE ADF AB AD =⎧⎪∠=∠=︒⎨⎪=⎩， ∴(SAS ABE ADF ≌∴GHE GDF ∠=∠，GEH GFD ∠=∠， ∵四边形ABCD 为正方形， ∴45HBE ∠=︒，∴HBE 是等腰直角三角形，∴EH BE DF ==，在GHE △和GDF 中，GHE GDF HE DFGEH GFD ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴()ASA GHEGDF ≌， ∴GE GF =， ∴AG EF ⊥， ∴90AGE ∠=︒， ∴90AGB BGE ∠=︒−∠，∵45BGE FEC DBE a ∠=∠−∠=−︒， ∴()9045135AGB a a ∠=︒−−︒=︒−，故选：D ．7．如图，在平面直角坐标系xOy 中，平行四边形ABCO 的一边CO 在x 轴上，A ，B 在第二象限，C 在A 左侧，60AOC ∠=︒，5AC =，AO =ED 的解析式为5y x =−+，现将平行四边形沿x ED 恰好平分平行四边形ABCO 的面积时，此时的平移距离为（）A ．112B ．4+C ．8D ．5+【答案】A【分析】作AM OC ⊥于M ，解直角三角形求得Ａ、Ｃ的坐标，即可求得AC 中点的坐标，根据题意当直线ED 恰好平分平行四边形ABCO 的面积时，则ED 必经过AC 的中点，把中点的纵坐标答题直线5y x =−+求得横坐标，即可求得平移的距离．∠=AOC1(72−−−2D−在直线l：y＝kx＋8 8．如图，正方形ABCD的顶点A，B分别在x轴，y轴上，点6,2上．直线l分别交x轴，y轴于点E，F．将正方形ABCD沿x轴向左平移m个单位长度后，点B恰好落在直线l上．则m的值为（）A．2B．4C．6D．8将点B 向左平移m 个单位后坐标为（-m ，4）将（-m ,4）代入8y x =+，得：4=-m +8，解得：m =4．故选：B ．【点睛】本题考查了正方形的性质、全等三角形的判定与性质、点的平移以及点坐标与直线图像的关系等知识点，构造全等三角形求得求点B 坐标是解题的关键．二、填空题9．如图，在平行四边形OABC 中，()7,0A 、()3,4C ，若1OD =，直线l 经过D 点并且把平行四边形OABC 的面积分成相等的两部分，则直线l 的解析式是．10．如图，在平行四边形ABCD 中，5AD =，AB =D ∠是锐角，CE AD ⊥于点E ，F 是CD 的中点，连接BF ，EF ．若90EFB ∠=︒，则CE 的长为___________．(AAS BCF QDF ≌四边形DF FC =(AAS BCF QDF ∴≌EFB ∠=EF QB ∴⊥CE AD ⊥CE BC ∴⊥2CE DC =()2上，∠EDF=60°，若BF=3，CF=5，则AC边的长为．=BF CF3,∴=BC BFBDH∴是等边三角形∴∠=BDH点是ABC的中位线又BDF ∠+∠BDF ∴∠=∠()HDE BDF ASA ∴≅Rt ACD 中，【点睛】本题考查了直角三角形的性质、与性质、三角形的中位线定理等知识点，题关键．为边作等边三角形1ABA ，过点1A 作11A B x ∥轴，交直线l 于点1B ，以11A B 为边作等边三角形112A B A ，过点2A 作22A B x ∥轴，交直线l 于点2B ，以22A B 为边作等边三角形223A B A 以此类推，连接1AB ，与1A B 交于点1C ，连接12A B ，与21A B 交于点2C 则点2023C 的纵坐标是．1sin A A AB ∠A 垂线为y 轴建立直角坐标系，D E ，分别为线段AO 和线段AC 上一动点，且AD CE =．当BD BE +的值最小时，点E 的坐标为．，可证明()SAS ABD CFE ≌AO BC ⊥CF AO ∴∥AB AC =CAO ∴∠=AB CF =()SAS ABD CFE ∴≌AB AC =14．如图，直线AB ：2y x b =−+与坐标轴交于A 、B 两点，点C 为第一象限内一点，连接BC 且BC x ∥轴，交直线3x =于点E ，连接AC ，AE ，将ABC 沿着直线AB 翻折，得到ABD △，点D 正好落在直线3x =上，若26BDEACESS==，那么点C 的坐标为．BDES =6ACES =将ABC 沿着直线BD BC t ==BDES=26BDEACESS==，即3ACES=15．如图，在平面直角坐标系中，直线AB 交y 轴于点()0,2B ，现将直线AB 绕点()1,1A −按逆时针方向旋转45︒交x 轴于点C ，则点C 的坐标是．，再通过角度的和差，证明(AAS ABF BDE ≌ ∴(AAS ABF BDE ≌上，且12AE AB <，连接PE ，以PE 为边向右作等边PEF !，过点E 作EM AP ∥交FA 的延长线于点M ，点N 为MF 的中点，则四边形AEPN 的面积为．12APEAPNSSAE +=∵ABC 是边长为AB BC ==∴ABP 是等边三角形，点P 在AC 在GPE 和APF 中，∴()SAS GPE APF ≌在MEF 和△∴()ASA MEF AEP ≌12APEAPNSSAE +=17．某体育用品商店计划一共购进600套乒乓球拍和羽毛球拍进行销售，其中购进乒乓球拍的套数不超过250套，它们的进价和售价如下表：设购进乒乓球拍x （套），售完这批体育用品获利y （元）． (1)求y 与x 的函数关系式，并写出x 的取值范围；(2)该商店实际采购时，恰逢“双11”购物节，乒乓球拍的进价每套降低了()1015c c <<元，羽毛球拍的进价不变，若商店的售价不变，这批体育用品能够全部售完，请你利用函数的性质进行分析：如何购货才能获利最大？最大利润是多少（用含有c 的代数式表示）？（2）解：由题意，得：()()()()10075120806001524000y c x x c x =−++−−=−+， ∵1015c <<， ∴150c −<，∴y 随x 的增大而减小，∴当200x =时，此时600400x −=，y 取得最大值，最大值为：()152002400020021000c c −⨯+=+；答：购进乒乓球拍200套，羽毛球拍400套时，利润最大，为()20021000c +元．【点睛】本题考查一次函数的实际应用．根据题意，正确的列出函数关系式，是解题的关键． 18．如图，在四边形ABCD 中，90BC CD BAD BCD AB AD >∠=∠=︒=，，．(1)在图（1）中连接AC ，并证明CA 平分BCD ∠；(2)如图（2），连接对角线AC BD ，，若AC =BCD △的面积为3，求BD 的长； (3)如图（3），点E 在CB 的延长线上，且满足BE CD =，点F 是线段BC 的中点，连接AF DE ，，探究AF 与DE 的关系并说明理由． Rt Rt ABF DAE ≌，得AF 的面积为3，可得BC CD ⋅90BAD BCD ∠=∠=︒，180ABC ADC ∴∠+∠=︒，180ABC ABE ∠+∠=︒， ABE ADC ∴∠=∠， AE AC ⊥EAC ∴∠=EAC ∠=EAB ∴∠=AB AD =ABE ∴△≌△42AC =Q ，45ACE ∠=︒，4AE CE ∴==，BF CE AE ==,AD AB =，Rt Rt ABF DAE ∴△≌△，BCD的面积为1=DE CE∴⋅BC CD∠=∠=︒∠BAD DCB ABC90,∴∠=∠，ADC ABE==，AB AD DC BE,∴△≌△，ABE ADC∴是等腰直角三角形，AECM为CE中点，故AM⊥【点睛】此题考查了全等三角形的判定和性质，等腰三角形的性质，是四边形综合题，利用数形结合思想是解题关键．19．如图：直线3y kx =+与x 轴、y 轴分别交于A 、B 两点，43OA OB =，点(,)C x y 是直线3y kx =+上与A 、B 不重合的动点．(1)求直线AB 的解析式；(2)作直线OC ，当点C 运动到什么位置时，AOB 的面积被直线OC 分成1:2的两部分； (3)过点C 的另一直线CD 与y 轴相交于D 点，是否存在点C 使BCD △与AOB 全等？若存在，求出点C 的坐标；若不存在，说明理由．的位置时，AOB 的面积被直线若AOB CDB ≌时，分别求解即可．3kx +中，令0x =得43OA OB =）解：3OB =，AOB ∴的面积此时123AOC AOB S S D D ==， ∴122C OA y ⋅=，即142C y ⨯⨯= 此时243AOC AOB S S ∆∆==， ∴142C OA y ⋅=，即142C y ⨯⨯=的位置时，AOB 的面积被直线与AOB 全等，，5BD AB ∴==，3BC OB ==，(0,2)D ∴−，2AC AB BC =−=，设3,34C t t ⎛⎫−+ ⎪⎝⎭，则OH t =，AH 而222AH CH AC +=，223(4)344t t ⎛⎫∴−+−+= ⎪，若AOB CDB ≌时，如图： 3BD OB ∴==，90CDB AOB ∠=∠=︒，(0,6)D ∴，在334y x =−+中，令6y =得4x =−，(4,6)C ∴−，点(),4A m ，与x 轴交于点()4,0B −，直线AC 与x 轴交于点C ．(1)填空：b = ___________，m = ___________，k = ___________；(2)如图2，点D 为线段BC 上一动点，将ACD 沿直线AD 翻折得到AED △，线段AE 交x 轴于点F ．①当点E 落在y 轴上时，求点E 的坐标； ②若DEF 为直角三角形，求点D 的坐标．4①直线∴22222+===CG A8A GE AC当90EDF ∠=︒时，由翻折得：∴135ADO ADE EDF ∠=∠−∠=4AG =，∴4DG AG ==，当90DFE ∠=︒时，AE AC ==设DF x =，则DE DC FC ==在Rt DEF △中，由勾股定理得：解得：252x =−，【点睛】本题考查了一次函数，勾股定理，翻折的性质，直角三角形的判定于性质，解题的关键是作辅助线．21．在平面直角坐标系中，直线AB 与x 轴交于点A ，与y 轴交于点B ，且30OAB ∠=︒，9OA =．(1)如图1，点C 为线段AB 上一点，若AOC S =△C 的坐标；(2)如图2，点D 在线段OA 上，2,OD DA E F =、是直线AB 上的两个动点且EF =G 是x 轴上任意一点，连接DE GF 、，求DE EF FG ++的最小值；(3)在（2）的条件下，当DE EF FG ++取最小值时，M 为直线FG 上一动点，N 是平面内任意一点，当A B M N 、、、四点构成的四边形是以AB 为边的菱形时，请直接写出点N 的坐标．解：如图1，作CX OA⊥于X，由1932OA CX⋅=得，183183239CXOA===，作点D关于AB的对称点V，将点AB于F，作VT OA⊥于T，交AB 则DE EF FG++最小，最小为：2OD DA=，9OA=，3AD∴=，WRV∠=DV AD=9OA =，30OAB ∠=︒，∴12OB AB =，由勾股定理得63AB =，由（2）得：1322AT AD ==，2RV =339622OG ∴=−−=， A 、B 、(9,0)A ，决问题的关键是较强的计算能力．。

八年级下册数学期末压轴题(含答案)

八年级数学下册期末压轴题练习（含答案）一、填空题：1.如图，在矩形ABCD中，AD=6，AE⊥BD，垂足为E，ED=3BE，点P、Q分别在BD，AD上，则AP+PQ 的最小值为 .2.如图，Rt△ABC中，∠C=90°，以斜边AB为边向外作正方形ABDE，且正方形对角线交于点O，连接OC，已知AC=5，OC=6，则另一直角边BC的长为．3.如图，已知正方形ABCD边长为3，点E在AB边上且BE=1，点P，Q分别是边BC，CD的动点（均不与顶点重合），当四边形AE PQ的周长取最小值时，四边形AEPQ 的面积是．4.如图所示，现有一张边长为4的正方形纸片ABCD，点P为正方形AD边上的一点(不与点A．点D重合)将正方形纸片折叠，使点B落在P处，点C落在G处，PG交DC于H，折痕为EF，连接BP、BH.现给出以下四个命题（1）∠APB=∠BPH;（2）当点P在边AD上移动时，△PDH的周长不发生变化; （3）∠PBH=450 ; （4）BP=BH.其中正确的命题是．5.如图，正方形ABCD的边长为4，∠DAC的平分线交DC于点E，若点P、Q分别是AD和AE上的动点，则DQ+PQ的最小值是．二、综合题：6. (1)如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE.求证：CE=CF；(2)如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE=45°，请你利用(1)的结论证明：GE=BE+GD.(3)运用(1)(2)解答中所积累的经验和知识，完成下题：如图3，在直角梯形ABCD中，AD∥BC(BC＞AD)，∠B=90°，AB=BC，E是AB上一点，且∠DCE=45°，BE=4，DE=10，求直角梯形ABCD的面积.7.如图，已知等腰Rt△ABC和△CDE，AC=BC,CD=CE，连接BE、AD，P为BD中点，M为AB中点、N为DE中点，连接PM、PN、MN.（1）试判断△PMN的形状，并证明你的结论；（2）若CD=5，AC=12，求△PMN的周长.8.已知正方形ABCD和正方形AEFG有公共顶点A，将正方形AEFG绕点A旋转．（1）①当E点旋转到DA的延长线上时（如图1），△ABE与△ADG的面积关系是：．②当E点旋转到CB的延长线上时（如图2），△ABE与△ADG的面积关系是：（2）当正方形AEFG旋转任意一个角度时（如图3），（1）中的结论是否仍然成立？若成立请证明，若不成立请说明理由．（3）已知△ABC，AB=5cm，BC=3cm，分别以AB、BC、CA为边向外作正方形（如图4），则图中阴影部分的面积和的最大值是 cm2．9.一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动：将△MNK的直角顶点M放在△ABC的斜边AB的中点处，设AC=BC=a．（1）如图1，两个三角尺的重叠部分为△ACM，则重叠部分的面积为，周长为；（2）将图1中的△MNK绕顶点M逆时针旋转45°，得到图2，此时重叠部分的面积为，周长为；（3）如果将△MNK绕M旋转到不同于图1，图2的位置，如图3所示，猜想此时重叠部分的面积为多少？并试着加以验证．10.在正方形ABCD中，点E，F分别在边BC，CD上，且∠EAF=∠CEF=45°．（1）将△ADF绕着点A顺时针旋转90°，得到△ABG（如图①），求证：△AEG≌△AEF；（2）若直线EF与AB，AD的延长线分别交于点M，N（如图②），求证：EF2=ME2+NF2；（3）将正方形改为长与宽不相等的矩形，若其余条件不变（如图③），请你直接写出线段EF，BE，DF之间的数量关系．参考答案1.答案为：3.3.答案为：4.5．2.答案为：7；解法一：如图1所示，过O作OF⊥BC，过A作AM⊥OF，∵四边形ABDE为正方形，∴∠AOB=90°，OA=OB，∴∠AOM+∠BOF=90°，又∠AMO=90°，∴∠AOM+∠OAM=90°，∴∠BOF=∠OAM，在△AOM和△BOF 中，，∴△AOM≌△BOF（AAS），∴AM=OF，OM=FB，又∠ACB=∠AMF=∠CFM=90°，∴四边形ACFM为矩形，∴AM=CF，AC=MF=5，∴OF=CF，∴△OCF为等腰直角三角形，∵OC=6，∴根据勾股定理得：CF2+OF2=OC2，解得：CF=OF=6，∴FB=OM=OF﹣FM=6﹣5=1，则BC=CF+BF=6+1=7．故答案为：7．解法二：如图2所示，过点O作OM⊥CA，交CA的延长线于点M；过点O作ON⊥BC于点N．易证△OMA≌△ONB，∴OM=ON，MA=NB．∴O点在∠ACB的平分线上，∴△OCM为等腰直角三角形．∵OC=6，∴CM=ON=6．∴MA=CM﹣AC=6﹣5=1，∴BC=CN+NB=6+1=7．故答案为：7．4.答案为：（1）（2）（3）．5.答案为：2；解：作D 关于AE 的对称点D′，再过D′作D′P′⊥AD于P′，∵DD′⊥AE，∴∠AFD=∠AFD′，∵AF=AF，∠DAE=∠CAE，∴△DAF≌△D′AF，∴D′是D关于AE的对称点，AD′=AD=4，∴D′P′即为DQ+PQ的最小值，∵四边形ABCD是正方形，∴∠DAD′=45°，∴AP′=P′D′，∴在Rt△AP′D′中，P′D′2+AP′2=AD′2，AD′2=16，∵AP′=P′D'，2P′D′2=AD′2，即2P′D′2=16，∴P′D′=2，即DQ+PQ的最小值为2，6. (1)证明：∵四边形ABCD是正方形，∴BC=CD，∠B=∠CDF=90°，∵∠ADC=90°，∴∠FDC=90°.∴∠B=∠FDC，∵BE=DF，∴△CBE≌△CDF(SAS).∴CE=CF.(2)证明：如图2，延长AD至F，使DF=BE，连接CF.由(1)知△CBE≌△CDF，∴∠BCE=∠DCF.∴∠BCE+∠ECD=∠DCF+∠ECD，即∠ECF=∠BCD=90°，又∠GCE=45°，∴∠GCF=∠GCE=45°.∵CE=CF，GC=GC，∴△ECG≌△FCG.∴GE=GF，∴GE=GF=DF+GD=BE+GD.(3)解：如图3，过C作CG⊥AD，交AD延长线于G.在直角梯形ABCD中，∵AD∥BC，∴∠A=∠B=90°，又∵∠CGA=90°，AB=BC，∴四边形ABCG为正方形.∴AG=BC.…∵∠DCE=45°，根据(1)(2)可知，ED=BE+DG.…∴10=4+DG，即DG=6.设AB=x，则AE=x﹣4，AD=x﹣6，在Rt△AED中，∵DE2=AD2+AE2，即102=(x﹣6)2+(x﹣4)2.解这个方程，得：x=12或x=﹣2(舍去).…∴AB=12.∴S梯形ABCD=0.5(AD+BC)•AB=0.5×(6+12)×12=108.即梯形ABCD的面积为108.…7.解：（1）①∵正方形ABCD和正方形AEFG有公顶点A，将正方形AEFG绕点A旋转，E 点旋转到DA的延长线上，∴AE=AG，AB=AD，∠EAB=∠GAD，∴△ABE≌△ADG（SAS），∴△ABE的面积=△ADG的面积；②作GH⊥DA交DA的延长线于H，如图2，∴∠AHG=90°，∵E点旋转到CB的延长线上，∴∠ABE=90°，∠HAB=90°，∴∠GAH=∠EAB，在△AHG和△AEB中，∴△AHG≌△AEB，∴GH=BE，∵△ABE的面积=0.5EB•AB，△ADG的面积=0.5GH•AD，∴△ABE的面积=△ADG的面积；（2）结论仍然成立．理由如下：作GH⊥DA交DA的延长线于H，EP⊥BA交BA的延长线于P，如图3，∵∠PAD=90°，∠EAG=90°，∴∠PAE=∠GAH，在△AHG和△AEP中，∴△AHG≌△AEP（AAS），∴GH=BP，∵△ABP的面积=0.5EP•AB，△ADG的面积=0.5GH•AD，∴△ABP的面积=△ADG的面积；（3）∵AB=5cm，BC=3cm，∴AC==4cm，∴△ABC的面积=0.5×3×4=6（cm2）；根据（2）中的结论得到阴影部分的面积和的最大值=△ABC的面积的3倍=18cm2．故答案为相等；相等；18．8.解：（1）∵AM=MC=AC=a，则∴重叠部分的面积是△ACB的面积的一半为0.25a2，周长为（1+）a．（2）∵重叠部分是正方形∴边长为0.5a，面积为0.25a2，周长为2a．（3）猜想：重叠部分的面积为0.25a2．理由如下：过点M分别作AC、BC的垂线MH、MG，垂足为H、G 设MN与AC的交点为E，MK与BC的交点为F∵M是△ABC斜边AB的中点，AC=BC=a∴MH=MG=0.5a又∵∠HME+∠HMF=∠GMF+∠HMF，∴∠HME=∠GMF，∴Rt△MHE≌Rt△MGF∴阴影部分的面积等于正方形CGMH的面积∵正方形CGMH的面积是MG•MH=0.5a×0.5a =0.25a2,∴阴影部分的面积是0.25a2．9.（1）证明：∵△ADF绕着点A顺时针旋转90°,得到△ABG,∴AF=AG,∠FAG=90°，∵∠EAF=45°,∴∠GAE=45°，在△AGE与△AFE中，，∴△AGE≌△AFE（SAS）；（2）证明：设正方形ABCD的边长为a.将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM．则△ADF≌△ABG，DF=BG．由（1）知△AEG≌△AEF，∴EG=EF．∵∠CEF=45°，∴△BME、△DNF、△CEF均为等腰直角三角形，∴CE=CF，BE=BM，NF=DF，∴a﹣BE=a﹣DF，∴BE=DF，∴BE=BM=DF=BG，∴∠BMG=45°，∴∠GME=45°+45°=90°，∴EG2=ME2+MG2，∵EG=EF，MG=BM=DF=NF，∴EF2=ME2+NF2；（3）解：EF2=2BE2+2DF2．如图所示，延长EF交AB延长线于M点，交AD延长线于N点，将△ADF绕着点A顺时针旋转90°，得到△AGH，连结HM，HE．由（1）知△AEH≌△AEF，则由勾股定理有（GH+BE）2+BG2=EH2，即（GH+BE）2+（BM﹣GM）2=EH2又∴EF=HE，DF=GH=GM，BE=BM，所以有（GH+BE）2+（BE﹣GH）2=EF2，即2（DF2+BE2）=EF2。

八年级下压轴 50题(含答案及解析)

②当AB＝AE＝2，∠B＝60°时，将四边形ABCE向右平移a（a＞0）个单位后，恰有两个顶点落在反比例函数y＝的图象上，求k的值．
29．如图1，在平面直角坐标系中，直线y＝﹣ x+3与x轴、y轴相交于A、B两点，点C在线段OA上，将线段CB绕着点C顺时针旋转90°得到CD，此时点D恰好落在直线AB上，过点D作DE⊥x轴于点E．
（1）求证：∠BFC＝∠BEA；
（2）求证：AM＝BG+GM．
9．如图，正方形ABCD的对角线相交于点O．点E是线段DO上一点，连接CE．点F是∠OCE的平分线上一点，且BF⊥CF与CO相交于点M．点G是线段CE上一点，且CO＝CG．
（1）若OF＝4，求FG的长；
（2）求证：BF＝OG+CF．
10．（1）如图①，两个正方形的边长均为3，求三角形DBF的面积．
①当t＝秒时，以A、P、E、D、为顶点可以构成平行四边形．
②在P点运动过程中，是否存在以B、C、E、D为顶点的四边形是平行四边形？若存在，请求出t的值；若不存在，请说明理由．
23．如图，在平面直角坐标系中，直线y＝x+2与x轴，y轴分别交于A，B两点，点C（2，m）为直线y＝x+2上一点，直线y＝﹣ x+b过点C．
13．如图，菱形ABCD中，点E、M在AD上，且CD＝CM，点F为AB上的点，且∠ECF＝ ∠B．
（1）若菱形ABCD的周长为8，且∠D＝67.5°，求△MCD的面积；
（2）求证：BF＝EF﹣EM．
14．如图1，矩形OABC摆放在平面直角坐标系中，点A在x轴上，点C在y轴上，OA＝3，OC＝2，过点A的直线交矩形OABC的边BC于点P，且点P不与点B、C重合，过点P作∠CPD＝∠APB，PD交x轴于点D，交y轴于点E．

人教版八年级下册数学期末动点压轴题训练(带答案)

人教版八年级下册数学期末动点压轴题训练（带答案）1．如图，平面直角坐标系xOy 中，直线334y x =-+交x 轴于点A ，交y 轴于点B ，点P 是线段OA 上一动点（不与点A 重合），过点P 作PC AB ⊥于点C ．(1)当点P 是OA 中点时，求APC △的面积；(2)连接BP ，若BP 平分ABO ∠，求此时点P 的坐标；(3)BP 平分ABO ∠，在x 轴上有一动点H ，H 横坐标为a ，过点H 作直线l x ⊥轴，l 与线段PC 有交点，求a 的取值范围；(4)BP 平分ABO ∠，M 为x 轴上动点，CPM △为等腰三角形，求M 坐标．2．如图，直线l 1：y ＝kx +b 与y 轴交于点B （0，3），直线l 2：y ＝﹣2x ﹣1交y 轴于点A ，交直线l 1于点P （﹣1，t ）．(1)求k 、b 和t 的值； (2)求△ABP 的面积；(3)过动点D（a，0）作x轴的垂线与直线l1、l2，分别交于M、N两点，且MN＜4．①求a的取值范围；①当△AMP的面积是△AMB的面积的1时，求MN的长度．23．在平面直角坐标系中，坐标轴上的三个点A(a，0)，B(0，b)，C(c，0)(a＜0，b＞0)满足|c﹣1|+(a+b)2＝0，F为射线BC上的一个动点．(1)c的值为，①ABO的度数为．(2)如图（a），若AF①BC，且交OB于点E，求证：OE＝OC．(3)如图（b），若点F运动到BC的延长线上，且①FBO＝2①F AO，O在AF的垂直平分线上，求①ABF的面积．4．已知，长方形OABC在平面直角坐标系内的位置如图所示，点O为坐标原点，点A 的坐标为（10，0），点B的坐标为（10，8）．(1)直接写出点C的坐标为：C（，）；(2)已知Q（5，n）在直线AC；求n的值；(3)若动点P 从A 点出发，沿折线AO →OC 的路径以每秒2个单位长度的速度运动，到达C 处停止．求①OPQ 的面积S 与点P 的运动时间t （秒）的函数关系式．5．在①ABC 中，90ACB ∠=︒，60ABC ∠=︒，点D 是直线AB 上一动点，以CD 为边，在它右侧作等边①CDE ．(1)如图1，当E 在边AC 上时，直接判断线段DE ，EA 的数量关系______； (2)如图2，在点D 运动的同时，过点A 作AF CE ∥，过点C 作CF AE ∥，两线交于点F ，判断四边形AECF 形状，并说明理由；(3)若BC =AECF 为正方形时，直接写出AD 的值．6．已知在平面直角坐标系中，点()0,2A ，动点P 在x 轴正半轴上，作矩形OABP ，点C 为PB 中点，①ABC 沿AC 折叠后得到①ADC ，直线CD 与矩形OABP 一边交于点E ．(1)如图，当点E 与原点O 重合时， ①求证：OCP ADO ≌△△． ①求OP 长．(2)当5EC ED =，求点P 坐标．7．如图（1），在平面直角坐标系中点(),A x y ，()2,0B x 满足0x ，点C 为线段OB 上一个动点，以CA 为腰作等腰直角ACD △，且AC AD =．(1)求点A 、B 的坐标及AOB 的面积；(2)试判断CD 、OC 、BC 间的数量关系，并说明理由；(3)如图（2），若点C 为线段OB 延长线上一个动点，则（2）中的结论是否成立，并说明理由．8．如图，在平面直角坐标系中，直线4y x =+交y 轴于A 点，与直线BC 相交于点B (－2，m )，直线BC 与y 轴交于点C (0，－2)，与x 轴交于点D ；(1)求①ABC 的面积；(2)过点A 作BC 的平行线交x 轴于点E ，求点E 的坐标；(3)在（2）的条件下，点P 是直线AB 上一动点且在x 轴的上方，Q 为直角坐标平面内一点，如果以点D 、E 、P 、Q 为顶点的平行四边形的面积等于①ABC 面积，请求出点P 的坐标，并直接写出点Q 的坐标．9．如图，已知①ABC中，①B = 90°，AB = 8cm，BC = 6cm，P、Q是①ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．(1)出发2秒后，求PQ的长；(2)从出发几秒钟后，①PQB第一次能形成等腰三角形？(3)当点Q运动到CA上时，求能使①BCQ是等腰三角形时点Q的运动时间．10．如图1，四边形形ABCD是一个边长为2的正方形，点E是AB边上的一个动点（点E与点A，B不重合），连接CE，过点B作BF①CE于点G，交AD于点F．(1)求证：①ABF①①BCE；(2)如图2，当点E运动到AB中点时，①求BG的长；①连接DG，求证：DC＝DG．11．如图，在平面直角坐标系中，点O 为坐标原点，点A 、B 、C 的坐标分别为（0，6）、（-8，0）、（-3，0），10AB =，将ABC 沿着射线AC 翻折，点B 落到y 轴上点D 处．(1)求点D 的坐标；(2)动点P 以每秒1个单位长度的速度从点B 出发沿着线段BO 向终点O 运动，运动时间为t 秒，请用含有t 的式子表示PCA 的面积，并直接写出t 的取值范围； (3)在（2）的条件下，动点M 以每秒2个单位长度的速度从点A 出发沿着线段AO 向终点O 运动，动点N 以每秒a 个单位长度的速度从点O 出发沿着x 轴正方向运动，点P 、M 、N 同时出发，点M 停止时，点P 、N 也停止运动，当DOP MON △△≌时，求a 的值．12．如图，在平面直角坐标系中，一次函数21y x =--的图象分别交x 轴、y 轴于点A 和B ，已知点C 的坐标为（－3，0）．若点P 是x 轴上的一个动点．(1)求直线BC 的函数解析式；(2)过点P 作y 轴的平行线交AB 于点M ，交BC 于点N ，当点P 恰好是MN 的中点时，求出P 点坐标．(3)若以点B 、P 、C 为顶点的①BPC 为等腰三角形时，请直接写出所有符合条件的P 点坐标．13．如图所示，菱形ABCD 的顶点A B ，在x 轴上，点A 在点B 的左侧，点D 在y 轴的正半轴上．点C 的坐标为(4．动点P 从点A 出发，以每秒1个单位长度的速度，按照A D C B A →→→→的顺序在菱形的边上匀速运动一周，设运动时间为t 秒．(1)①点B 的坐标； ①求菱形ABCD 的面积；(2)当3t =时，问线段AC 上是否存在点E ，使得PE DE +最小，如果存在，求出PE DE +最小值；如果不存在，请说明理由．14．如图，①ABC 中，①C ＝90°，AC ＝8cm ，BC ＝6cm ，若动点P 从点C 开始，按C →A →B →C 的路径运动，且速度为每秒1cm ，设运动的时间为t 秒．(1)当t ＝秒时，CP 把①ABC 的面积分成相等的两部分，此时CP ＝ cm ；(2)当t 为何值时，①ABP 为等腰三角形．(3)若点P 在线段AC 上运动，点Q 是线段AB 上的动点，求PB +PQ 的最小值．15．已知等边①ABC 中，AB ＝8，点D 为边BC 上一动点，以AD 为边作等边①ADE ，且点E 与点D 在直线AC 的两侧，过点E 作EF //BC ，EF 与AB 、AC 分别相交于点F 、G ．(1)求证：四边形BCEF 是平行四边形；(2)设BD ＝x ，FG ＝y ，求y 关于x 的函数解析式，并写出定义域； (3)当AD 的长为7时，求线段FG 的长．16．如图，在平面直角坐标系中，点D 的横坐标为4，直线1l ：2y x =+经过点D ，与x 轴、y 轴分别交于A 、B 两点，直线2l ：y kx b =+经过点()1,0C 、点D 两点．(1)求直线2l 的函数表达式； (2)求ACD △的面积；(3)点P 为线段AD 上一动点，连接CP ． ①求CP 的最小值；①当ACP△为等腰三角形时，直接写出点P的坐标．17．如图，在矩形ABCD中，E是BC上一动点，将△ABE沿AE折叠后得到△AFE，点F在矩形ABCD内部，延长AF交CD于点G，AB＝3，AD＝4．(1)如图1，当①DAG＝30°时，求BE的长；(2)如图2，当点E是BC的中点时，求线段GC的长；(3)如图3，点E在运动过程中，当△CFE的周长最小时，直接写出BE的长．18．如图1，点A在y轴上，点B，点C在x轴上，点D在第一象限，且△ABC与△ADC均为等边三角形，点B坐标为（﹣3，0），点E为线段BC上一动点，点F为直线DC上一动点，且∠EAF＝60°，连接EF．(1)填空：写出点A、点D的坐标，点A；点D；(2)试判断△AEF的形状，并给予证明；(3)直接写出EF长度的最小值以及此时点F的坐标；(4)将条件改为“点E为CB延长线上一点”，其他条件不变，△AEF的形状是否发生变化？在图2中画全图形（不必证明），直接写出当点E坐标为（﹣5，0）时，EF的长度以及此时点F的坐标．19．如图，在平面直角坐标系中，直线y＝kx过点B（m，6），过点B分别作x轴和y轴的垂线，垂足分别为点A，C，①AOB＝30°．动点P从点O出发，以每秒2个单位C运长度的速度向点B运动，动点Q从点B动．点P，Q同时开始运动，当点P到达点B时，点P，Q同时停止运动，设运动时间为t秒．(1)求m与k的值；(2)设①PQB的面积为S，求S与t的关系式；(3)若以点P，Q，B为顶点的三角形是等腰三角形，请求出t的值．（温擎提示：在直角三角形中，30°的角所对的直角边等于斜边的一半）20．如图，在平面直角坐标系中，OA=OB=6，OD=1，点C为线段AB的中点．(1)直接写出点C的坐标为；(2)点P是x轴上的动点，当PB+PC的值最小时，求此时点P的坐标；(3)在平面内是否存在点F，使得以A、C、D、F为顶点的四边形为平行四边形？若存在，请求出点F的坐标；若不存在，请说明理由．参考答案：1．(1)解：如图，连接BP ，直线334y x =-+交x 轴于点A ，交y 轴于点B ，∴点()4,0A ，点()0,3B ， 4AO ∴=，3OB =，5AB ∴，点P 是OA 中点，2AP OP ∴==，1122ABP S AP OB AB CP =⨯⨯=⨯⨯， 65CP ∴=，85AC ∴==， 124225APC S AC PC ∴=⨯⨯=； (2)如图，连接BP ，BP 平分ABO ∠，OBP CBP ∴∠=∠，又BP BP =，90BOP BCP ∠=∠=︒，BOP ∴①()BCP AAS ，3BO BC ∴==，OP CP =，532AC AB BC ∴=-=-=，222AP PC AC =+，22(4)4OP OP ∴-=+，32OP ∴=， 3,02P ⎛⎫∴ ⎪⎝⎭； (3)过点C 作⊥CH x 轴于点H ．由()2得，OP CP =＝32，2AC =， 4AP ∴=－32＝52， ①65AC CP CH AP ⋅==,AH ∴85， OH OA AH ∴=-＝125， a ∴的取值范围31225a ≤≤； (4)设点(),0M x ，过点C 作⊥CH x 轴于点H ，则22222126()()55MC HM CH x =+=-+，同理可得：2239()24CP ==，223()2MP x =-，当MC CP =时，即221269()()554x -+=，解得3310x =或3(2舍去)；当MC MP =时，同理可得392x =；当CP MP =时，同理可得0x =或3，故点M 的坐标为33,010⎛⎫ ⎪⎝⎭或39,02⎛⎫ ⎪⎝⎭或()0,0或()3,0． 2．解：①点P （﹣1，t ）在直线直线l 2上，①t ＝﹣2×（﹣1）﹣1＝1，即P （﹣1，1），把B 、P 的坐标代入可得13k b b -+=⎧⎨=⎩，解得 23k b =⎧⎨=⎩， ①t ＝1，k ＝2，b ＝3；(2)解：①直线y ＝﹣2x ﹣1交y 轴于点A ，①A （0，﹣1），①P （﹣1，1），B （0，3）， ①1114222PAB SAB =⨯=⨯=； (3)解：①①MN ①y 轴，①M、N的横坐标为a，设M、N的纵坐标分别为ym和yn，由（1）可知直线l1的函数表达式为y＝2x+3，①ym＝2a+3，yn＝﹣2a﹣1，当MN在点P左侧时，此时a＜﹣1，则有MN＝yn﹣ym＝﹣2a﹣1﹣（2a+3）＝﹣4a﹣4，①MN＜4，①﹣4a﹣4＜4，解得a＞﹣2，①此时﹣2＜a＜﹣1；当MN在点P的右侧时，此时a＞﹣1，则有MN＝ym﹣yn＝2a+3﹣（﹣2a﹣1）＝4a+4，①MN＜4，①4a+4＜4，解得a＜0，①此时﹣1＜a＜0；当a＝﹣1时，也符合题意，综上可知当﹣2＜a＜0时，MN＜4；①由（2）可知S△APB＝2，由题意可知点M只能在y轴的左侧，当点M在线段BP上时，过点M作MC①y轴于点C，如图1①S△APM＝12S△AMB，①S△ABM＝23S△APB＝43，①12AB•MC＝43，即2MC＝43，解得MC＝23，①点M的横坐标为﹣23，即a＝﹣23，①MN＝4a+4＝﹣83+4＝43；当点M在线段BP的延长线上时，过点M作MD①y轴于点D，如图2，①S△APM＝12AMB S，①S△ABM＝2S△APB＝4，①12AB•MD＝4，即2MD＝4，解得MD＝2，①点M的横坐标为﹣2，①MN＝﹣4a﹣4＝8﹣4＝4（不合题意舍去），综上可知MN的长度为43．3．解：①|c﹣1|+(a+b)2＝0，①c＝1，a＝﹣b，①OA＝OB，①①ABO＝45°，故答案为：1，45°．(2)证明：①AF ①BC ，①①AOE ＝①BFE ＝90°，①①AEO ＝①BEF ，①①OBC ＝①OAE ，在①AOE 和①BOC 中，===OAE OBC AOE BOC OA OB ∠∠⎧⎪∠∠⎨⎪⎩， ①①AOE ①①BOC (AAS )，①OE ＝OC ；(3)解：连结OF ，过点F 作FG ①x 轴，垂足为点G ，设①F AO ＝x ，则①FBO ＝2①F AO ＝2x ，①O 在AF 的垂直平分线上，①AO ＝OF ，①①OAF ＝①OF A ＝x ，①①GOF ＝①OAF +①OF A ＝2x ，①①FBO ＝2①F AO ＝2x ，OB ＝OA ＝OF ，①①OFC ＝①OBF ＝2x ，①①BCO ＝①COF +①OFB ＝4x ，①①OBC +①OCB ＝90°，①6x ＝90°，解得x ＝15°，①①OBC ＝①GOF ＝2x ＝30°，①C (1，0)，①OC ＝1，①①BOC ＝90°，①OBC ＝30°，①BC ＝2OC ＝2，OB ，①OA ＝OF ＝OB，同理可得：FG = ，①=+AC AO OC ，①S △ABF ＝S △ACB +S △ACF ＝12×AC ×FG +12×AC ×OB ＝12＝94 4．(1)①四边形ABCO 是矩形①AB =OC ，AO =BC①A （10，0），B （10，8）①OC =OB =8①点C 的坐标为（0，8）故答案为：0，8(2)设直线AC 的解析式为y kx b =+把点A （10，0），B （0，8）代入y kx b =+得，1008k b b +=⎧⎨=⎩ 解得，458k b ⎧=-⎪⎨⎪=⎩ ①直线AC 的解析式为485y x =-+ 把点Q （5，n ）代入485y x =-+得， 45845n =-⨯+=； (3)①当05t ≤≤时，102OP OA AP t =-=-过点Q 作QD ①OA 于点D ，如图，①Q （5，4）①QD =4 ①1(102)42042S t t =-⨯=-； ①当59<≤t 时，OP = AP -AO =2t -10过点Q 作QE ①OC 于点E ，如图，①Q （5，4）①QE =5 ①1(210)55252S t t =-⨯=- 综上，204(05)=525(59)t t S t t -≤≤⎧⎨-<≤⎩5(1)①90ACB ∠=︒，60ABC ∠=︒①30A ∠=︒①CDE △为等边三角形①60DEC ∠=︒①DEC ∠是ADE 外角①DEC A ADE ∠=∠+∠①30ADE A ∠=︒=∠①DE EA =故答案为相等．(2)取AB 中点O ，连接OC 、OE①AF CE ∥, CF AE ∥①四边形AECF 是平行四边形①90ACB ∠=︒①OC OB OA ==①60ABC ∠=︒①①BCO 为等边三角形①①CDE 是等边三角形①60DCB OCE DCO ∠=∠=︒-∠①OC BC = CD CE =①BCD OCE ≌△△①60EOC B ∠=∠=︒①60EOA ∠=︒又①OE OE =，OA OC =①()OCE OAE SAS ≌△△①CE EA =①平行四边形AECF 是菱形(3)当点D 在AB 延长线上时，作CH AD ⊥于H ，当四边形AECF 为正方形时，45ACE BCE ∠=∠=︒，90AEC ∠=︒ ①60DCE ∠=︒①15DCB ∠=︒①60ABC ∠=︒①45CDH ∠=︒①BC =①AC ==①12CH AC =①AH ==①CDE △为等边三角形 ①CH DH ==①AD =当点D 在AB 上时作CH AB ⊥于H ，同理可得CDH △是等腰直角三角形，则AD AH DH =-=综上AD =6．解：①矩形OABP 中，()02A ，， AB OP ∴=，2BP OA ==，90AOP OAB ABC OPB ∠=∠=∠=∠=︒ ． ABC 沿AC 折叠后得到ADC ，90ADC ABC ∴∠=∠=︒，AD AB =，AD OP ∴=，当点E 与原点O 重合时，18090ADO ADC ∠=︒-∠=︒，90AOD COP AOP ∠+∠=∠=︒，90AOD OAD ∴∠+∠=︒，COP OAD ∴∠=∠．在OCP △和AOD △中，90OPC ADO COP OAD OP AD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩()OCP AOD AAS ∴≌；①①点C 为PB 的中点，112CP BC PB ∴===，由①知：OCP AOD ≌，2OC AO ∴==，在Rt COP 中，由勾股定理得OP ，即OP(2)解：当5EC DE =，则4CD DE =．ABC 沿AC 折叠后得到ADC ，1CD BC ∴==，90ADC ABC ∠=∠=︒，AD AB =，1144DE CD ∴==，90ADE ∠=︒，AD OP =， 554CE ED ∴==，设OP p =，则AD AB OP p ===，若点E 在OP 上，连接AE ，如下图，在Rt CPE △中，1CP =，34EP ∴=， 34OE OP PE p ∴=-=-，在Rt AOE 中，22222324AE OA OE p ⎛⎫=+=+- ⎪⎝⎭，在Rt ADE △中， 222221=4AE DE AD p ⎛⎫=++ ⎪⎝⎭， 222213+244p p ⎛⎫⎛⎫∴=+- ⎪ ⎪⎝⎭⎝⎭，即22139+416216p p p =+-+，解得3p =，此时，点P 的坐标为()30，；若点E 在OA 上，点D 在第一象限，过点E 作EF BC ⊥于F 点，如下图，则90EFP EFC ∠=∠=︒，90EOP OPF EFP ∴∠=∠=∠=︒，①四边形EFPO 是矩形，90CEF ECF ∠+∠=︒，EF OP ∴=，90OEF ∠=︒，AD EF ∴=，90CEF AED AEF ∠+∠=∠=︒，AED ECF ∴∠=∠．在AED 和ECF △中，AED ECF ADE EFC AD EF ∠=∠∠=∠=⎧⎪⎨⎪⎩，()AED ECF AAS ∴≌，54AE EC =∴=．在Rt ADE △中，AD ==OP AD ∴== 此时，点P的坐标为0⎫⎪⎪⎝⎭．若点E 在OA 上，点D 在第二象限时，过点C 作CF OA ⊥于F 点，如下图，则90AFC ∠=︒．①①F AB =①B =①AFC =90°，①四边形AFCB 是矩形，①AB =CF ，1AF BC ==ABC 沿AC 折叠后得到ADC ，①90ADC ABC ADE ∠=∠=∠=︒，AD AB OP CF ===，90ADE EFC ∴∠=∠=︒．在AED 和CEF △中，AED CEF ADE EFC AD CF ∠⎪∠⎧=∠∠=⎪⎨⎩=，()AED CEF AAS ∴≌，AE CE ∴=，DE EF =．5EC ED =，1AF AE EF BC =+==，15CE EF CE DE DE DE ∴+==+=+，16DE EF ∴==，556CE DE ==，在Rt EFC 中，CF =即OP ， ∴点P的坐标为⎫⎪⎪⎝⎭．综上所述，点P 坐标()30，或0⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭． 7．(1)①0x =，①(0x ≥0≥，①x y ==①A ，()B ，132AOB S =⨯=△． (2)结论：222CD OC BC =+．理由：连接，①OA AB ==OB =①222OA OB OB +=，①90OAB ∠=︒，45AOB ABO ∠=∠=︒，①OAB CAD ∠=∠，①OAC BAD ∠=∠，①AO AB ∠=，AC AD =，①OAC BAD △△≌，①OC BD =，45AOC ABD ∠=∠=︒，①90CBD ∠=︒，①222CD BC BD =+．①222CD OC BC =+．(3)（2）中的结论仍然成立理由：连接，①90OAB ∠=︒，45AOB ABO ∠=∠=︒，①OAB CAD ∠=∠，①OAC BAD ∠=∠，①AO AB =，AC AD =，①OAC BAD △△≌，①OC BD =，45AOC ABD ∠=∠=︒，①90OBD DBC ∠=∠=︒，①222CD BC BD =+，①222CD OC BC =+．8．(1)解：将点2()B m -，，代入4y x =+得24m ，解得2m =，①()22B -，，当0x =时，4y =，①()0,4A ， ①12662ABC S ∆=⨯⨯=． (2)解：设直线BC 的解析式为()20y kx k =-≠，将B 点坐标代入得222k --=，解得2k =-，①直线BC 的解析式为22y x =--，故设过点A 且平行于BC 的直线解析式为2y x b =-+，将A 点坐标代入得4b =，①过点A 且平行于BC 的直线解析式为24y x =-+，当0y =时，2x =，①()2,0E ．(3)解：由（2）可得()1,0D -，以点D 、E 、P 、Q 为顶点的平行四边形分两种情况求解： ①当DE 是平行四边形的边长时，则点Q 在x 轴上方，设(),4P m m +，①62DEPQ ABC DEP SS S ===， ①()1432DEP S DE m =⨯+=，解得2m =-，①()2,2P -，①PQ DE ∥，PQ DE =，①()5,2Q -；同理62DEQP ABC DEP S S S ===，①()2,2P -，①()1,2Q ；①当DE 是平行四边形的对角线时，则点Q 在x 轴下方，设(),4P m m +，同理62DQEP ABC DEP S S S ===，①()2,2P -，①D E 、的中点坐标为102，⎛⎫ ⎪⎝⎭， ①P Q 、的中点坐标为102，⎛⎫ ⎪⎝⎭， ①()3,2Q -；综上所述，P 点坐标为()2,2-，Q 的点坐标为()5,2- 或()1,2 或()3,2-．9．如图所示：BQ=2×2=4cm，BP=AB-AP=8- 2×1=6cm，①①B= 90°①PQ==；(2)当△PQB第一次形成等腰三角形时，BQ =BP，①BQ = 2t，BP= 8-t，①2t= 8-t，解得：t=83；(3)①①B = 90°，AB = 8cm，BC = 6cm，①AC10=cm，①当CQ= BQ时，如图则①C=①CBQ，①①ABC= 90°，①①CBQ +①ABQ = 90°，①①A+①C= 90°，①①A=①ABQ，①BQ= AQ，①CQ=AQ=5cm，①BC+ CQ = 11cm，①t= 11 ÷2= 5.5秒；①当CQ= BC时，如图2，则BC+CQ=12cm，①t= 12÷2= 6秒；①当BC = BQ时，如图3，过B点作BE①AC于点E，则BE=·6824105AB BCAC⨯==cm，①CE185=cm，①CQ= 2CE = 7.2cm，①BC+ CQ = 13.2cm，①t= 13.2÷2= 6.6秒；综上可知，当t为5.5秒或6秒或6.6秒时，△BCQ为等腰三角形．10．(1)证明：①BF ①CE ，①①CGB ＝90°，①①GCB +①CBG ＝90°，①四边形ABCD 是正方形， ①①CBE ＝90°＝①A ，BC ＝AB ， ①①FBA +①CBG ＝90°，①①GCB ＝①FBA ，在①ABF 和①BCE 中，A CBE AB BCABF BCF ∠=∠⎧⎪=⎨⎪∠=∠⎩， ①①ABF ①①BCE （ASA ）；(2)解:①由题意可知AB ＝CD ＝BC ＝2， ①点E 是AB 的中点，①EA ＝EB ＝12AB ＝1，①CE在Rt①CEB 中，12BG •CE ＝12CB •EB ， ①BG ＝CB EB CE⋅①证明：如图，过点D 作DH ①CE 于H ，由①可得CG = ①①DCE +①BCE ＝90°，①CBF +①BCE ＝90°，①①DCE ＝①CBF ，①CD ＝BC ，①CHD ＝①CGB ＝90°，①①CHD ①①BGC （AAS ），①CH ＝BG①GH ＝CG ﹣CH ＝CH ， ①CH ＝GH ，DH ①CE ，①DC ＝DG ；11．(1)解：①AD 是由AB 折叠得到，①10AD AB ==，①()0,4D -；(2)BP t =，当05t ≤<时，①()8,0B -，()3,0C -，①8OB =，3OC =， ①1163922ACO S OA OC =⋅=⨯⨯=△，8OP OB BP t =-=-， ①()116824322APO S OA OP t t =⋅=⨯-=-△，①2439153PCA APO ACO S S S t t =-=--=-△△△，当58t <≤时，()9243315PCA ACO APO S S S t t =-=--=-△△△，综上所述，PCA 的面积是153S t =-，（05t ≤<），或315S t =-，（58t <≤）．(3)①DOP MON △△≌，①OP ON =，OM OD =，由题意可知：BP t =，2AM t =，ON at =，4OD =①8OP OB BP t =-=-，62OM AO AM t =-=-，①624t -=，解得1t =，8t at -=，解得7a =，①a 的值是7．12．(1)解：①一次函数21y x =--的图象分别交x 轴，y 轴于点A 和B ，①点A （－12，0），点B （0，－1），设直线BC 的解析式y kx b =+代入B （0，－1），C （－3，0）．解得13k =-，1b =- ①直线BC 的函数解析式113y x =--． (2)①设点P （m ，0），则点M （m ，21m --），点N （m ，113m --）依题意可得PM ＝PN ①1210013m m ⎛⎫---=--- ⎪⎝⎭解得：67m =- ①点P （－67，0） (3)设(),0,P x 而0,1,3,0,B C22222223,1,3110,PC x PB x BC 当PC PB =时，2231,x x 解得：4,3x4,0.3P 当,PB BC2110,x解得：3,x =±当3x =-时，不合题意舍去，3,0.P当PC BC =时，2310,x 12310,310,x x 310,0P 或310,0.P综上：点P （3，03，0）或（3，0）或4,03⎛⎫- ⎪⎝⎭． 13．(1)①①(490C AOD ∠=︒，，①4DC AD DO ===，①2OA ==，①四边形ABCD 是菱形，①42AB AD OB AB OA ===-=，，①点B 的坐标(2)0，，故答案为：(2)0，①①在菱形ABCD 中，4DC AB OD ===，①菱形ABCD 的面积•4AB OD ==⨯(2)如图所示：当3t =时，3AP =,在菱形ABCD 中，点P 关于AC 的对称点为3P AP ''=，，连接DP '交AC 于点E ，连接PE ，①PE DE P E ED P D ''+=+=．①2OA OD ==，①1OP '=，在Rt DOP '中，①222DO P O P D ''+=，①P D'①PE DE+14．(1)解：在直角三角形ACB中，由勾股定理得AB10，①CP把△ABC的面积分成相等的两部分，①P为AB的中点，CP＝152AB=．①运动的路径长为AC＋AP＝8＋5＝13．运动的时间为13÷1＝13（秒）所以t＝13；CP＝5．(2)解：①ABP为等腰三角形，点P只能在AC上且P A＝PB，设CP＝t，则AP＝BP＝8﹣t，在Rt①BCP中，BC2＋CP2＝BP2，即62＋t2＝（8﹣t）2，解得，t＝74，①当t＝74时，①ABP为等腰三角形；(3)作点B关于AC的对称点B′，过点B′作AB的垂线段，交AC于点P，交AB于点Q，连接AB′，则垂线段B′Q即为所求的PB＋PQ的最小值，①S△ABB′＝12×BB′×AC＝12×12×8＝48，S△ABB′＝12×AB×B′Q，①B′Q＝485，即PB＋PQ最小值为485．15．(1)①①ABC 是等边三角形① AB ＝AC①60,BAC ABC ACB ∠=∠=∠=︒①①ADE 是等边三角形①AD ＝AE①60,DAE ∠=︒BAC DAC DAE DAC∠-∠=∠-∠ 即BAD CAE∠=∠ ①ABD ACE ∆≅∆ （SAS ）① BD ＝EC①60ACE B ∠=∠=︒①120,BCE ACB ACE ∠=∠+∠=︒①180,B BCE ∠+∠=︒①AB //EC①EF //BC①四边形BCEF 是平行四边形(2)①EF //BC①60CGE ACB ∠=∠=︒①60CGE ACE ∠=∠=︒①GE ＝EC①GE ＝EC ＝BD ＝x①FG FE GE =-①8(08)y x x =-<<(3)作AH ①BC ，垂足为H在Rt AHB ∆中，90,AHD ∠=︒222AH BH AB +=①22248AH +=①AH =在Rt ADH ∆中，90,AHD ∠=︒①222AH DH AD +=即(222(4)7x +-=，解得5x =或3x =； ① 8FG x =-①FG 的长为3或516．(1)将4x =代入2y x =+得：6y =①点D 的坐标为()4,6．将()1,0C ，()4,6D 代入y kx b =+得046k b k b +=⎧⎨+=⎩解得22k b =⎧⎨=-⎩ ①直线2l 的表达式为22y x =-．(2)过点D 作DE x ⊥轴于点E ，①()4,6D ，①6DE =将0y =代入2y x =+得2x =①()2,0A -，①3AC = ①192ACD S AC DE =⋅=△． (3)①由题可知：当CP AB ⊥时，CP 的值最小，由（2）可知6DE =，①点E 坐标为()4,0，①246AE AO OE =+=+=在Rt ADE △中，90AED ∠=︒．①AD ==①192ACD S AD CP =⋅=△①29CP AD ⨯=== ①①点P 在直线y =x +2上，①设点P （x ，x +2）,①A (-2，0)，C (1，0)①22[1(2)]9AC =--=，222(2)PA x =+，222(1)(2)PC x x =-++ （a ）当AP AC =时，即22AP AC =，则：22(2)=9x +解得，x =当x =y =x =时，y =①点P （b ）当AC PC =时，即22AC PC =，则：22(1)(2)9x x -++=解得，x =1或x =-2（舍去）当1x =时，3y =；①点P 的坐标为（13，）（c ）当AP PC =时，即22AP PC =，则：22()2x +22(1)(2)x x =-++ 解得，12x =- ①32y = ①点P 的坐标为（12-，32）综上，点P 的坐标为：13，）或（12-，32） 17(1)解：①四边形ABCD 是矩形，①①BAD ＝90°，①①DAG ＝30°，①①BAG ＝60°由折叠知，①BAE ＝12①BAG ＝30°，在Rt △BAE 中，①BAE ＝30°，AB ＝3，①BE(2)解：如图4，连接GE ，①E 是BC 的中点，①BE ＝EC ，①①ABE 沿AE 折叠后得到△AFE ，①BE ＝EF ，①EF ＝EC ，①在矩形ABCD 中，①①C ＝90°，①①EFG ＝90°，①在Rt △GFE 和Rt △GCE 中，EG EG EF EC =⎧⎨=⎩①Rt △GFE ①Rt △GCE （HL ），①GF ＝GC ；设GC ＝x ，则AG ＝3+x ，DG ＝3﹣x ，在Rt △ADG 中，42+（3﹣x ）2＝（3+x ）2，解得x ＝43． (3)解：如图1，由折叠知，①AFE ＝①B ＝90°，EF ＝BE ， ①EF +CE ＝BE +CE ＝BC ＝AD ＝4，①当CF 最小时，△CEF 的周长最小，①CF≥AC-AF ，①当点A ，F ，C 在同一条直线上时，CF 最小，由折叠知，AF ＝AB ＝3，在Rt △ABC 中，AB ＝3，BC ＝AD ＝4，①AC＝5，①CF＝AC﹣AF＝2，在Rt△CEF中，EF2+CF2＝CE2，①BE2+CF2＝（4﹣BE）2，①BE2+22＝（4﹣BE）2，①BE＝32．18．解：（1）∵△ABC是等边三角形，AO⊥BC，∴OB＝OC，∠BAO＝∠CAO＝30°，∵点B坐标为（﹣3，0），∴OB＝OC＝3，∴AB＝6，∴OA∴A（0，，∵△ABC和△ADC都是等边三角形，∴AD＝AC＝AB＝6，∠ACB＝∠ACD＝∠D＝60°，∴∠D+∠BCD＝180°，∴AD∥BC，∴D（6，，故答案为：（0，，（6，；（2）△AEF是等边三角形．证明：∵△ABC和△ADC都是等边三角形，∴AB＝AC，∠B＝∠ACD＝∠BAC＝60°，∵∠EAF＝60°，∴∠BAE＝∠CAF，∴△ABE≌△ACF（ASA），∴AE＝AF，∴△AEF是等边三角形．（3）由（2）知AE＝EF＝AF，当AE⊥BC时，AE取得最小值，∴AE＝OA＝过点F作FM⊥x轴于点M，∵∠FOM＝30°，OF＝∴FM=∴OM92 =，∴F（92，即EF的最小值为F（92；（4）由（2）可知△ABE≌△ACF（ASA），∵E（﹣5，0），OB＝3，∴BE＝2，∴BE＝CF＝2，CE＝8，∵∠ACD＝∠ACB＝60°，∴∠ECF＝60°，过点F作FN⊥BC于点N，如图3，∴CN 12=CF ＝1，∴NF∴EF∵OC ＝3，∴ON ＝OC ﹣CN ＝3﹣1＝2，∴F （2，．19．(1)解：BA OA ⊥，90BAO ∴∠=︒，30AOB ∠=︒，6(),B m ，OA m ∴=，6AB =，212OB AB ∴==，OA =m ∴=B 6)，直线y kx =过点B 6)，k ∴= (2)如图1，过点P 作PF BC ⊥于点F ，BQ ∴，2OP t =，则122PB t =-，30OBC ∠=︒，∴在Rt PFB ∆中，6PF t =-，()2162S t ∴=⨯-=+； (3)分三种情况：①当BQ BP =122t =-，解得24t =-①当PQ PB =时，如图2，过点P 作PM BQ ⊥于点M ，BM ∴，2)t -，解得4t =；①当OB QP =时，如图3，过点Q 作ON BP ⊥于点N ，则6BN t =-，6t ∴-=，解得125t =；综上所述，当PQB ∆为等腰三角形时，t 的值为24-4或125． 20．(1)解：过点C 作CN OA ⊥于点N ，过点C 作CM OB ⊥于点N ．①CN OA ⊥①//CN OB又①点C 为线段AB 的中点，OA = 6 ①132ON OA == 同理132OM OB == ①C (3,3)(2)作点B关于x轴的对称点B'，连接CB'交x轴于点P，此时PB+PC的值最小，由已知得，点B的坐标为（0，6），①点B关于x轴的对称点B'（0，﹣6），由（1）知，C（3，3），可设直线CB'的解析式为y=kx+b，①633bk b-=⎧⎨=+⎩解得36kb=⎧⎨=-⎩① 直线CB'的解析式为y=3x﹣6，令y=0，则3x﹣6=0，解得：x=2，① P（2，0）；(3)存在点F，使以A、C、D、F为顶点的四边形为平行四边形，设点F的坐标为（m，n）．分三种情况考虑，如图所示：当AC为对角线时，①A（6，0），C（3，3），D（1，0），①1632200322mn++⎧=⎪⎪⎨++⎪=⎪⎩，解得：83mn=⎧⎨=⎩，①点F1的坐标为（8，3）；①当AD为对角线时，①A（6，0），C（3，3），D（1，0），①3162230022mn++⎧=⎪⎪⎨++⎪=⎪⎩，解得：43 mn=⎧⎨=-⎩，①点F2的坐标为（4，-3）；①当CD为对角线时，①A（6，0），C（3，3），D（1，0），①6312203022mn++⎧=⎪⎪⎨++⎪=⎪⎩，解得：23mn=-⎧⎨=⎩，①点F3的坐标为（-2，3）．综上所述，点F的坐标是（8，3），（4，-3）或（-2，3）．。

人教版八年级下册数学压轴题及答案

人教版八年级下册数学压轴题及答案本页仅作为文档页封面，使用时可以删除八年级下数学压轴题1．已知，正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N，AH⊥MN于点H．（1）如图①，当∠MAN绕点A旋转到BM=DN时，请你直接写出AH与AB的数量关系：；（2）如图②，当∠MAN绕点A旋转到BM≠DN时，（1）中发现的AH与AB 的数量关系还成立吗？如果不成立请写出理由，如果成立请证明；（3）如图③，已知∠MAN=45°，AH⊥MN于点H，且MH=2，NH=3，求AH的长．（可利用（2）得到的结论）2．如图，△ABC是等边三角形，点D是边BC上的一点，以AD为边作等边△ADE，过点C作CF∥DE交AB于点F．（1）若点D是BC边的中点（如图①），求证：EF=CD；（2）在（1）的条件下直接写出△AEF和△ABC的面积比；（3）若点D是BC边上的任意一点（除B、C外如图②），那么（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．3．（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．求证：CE=CF；（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE=45°，请你利用（1）的结论证明：GE=BE+GD．（3）运用（1）（2）解答中所积累的经验和知识，完成下题：如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B=90°，AB=BC，E是AB上一点，且∠DCE=45°，BE=4，DE=10，求直角梯形ABCD的面积．4．如图，正方形ABCD中，E为AB边上一点，过点D作DF⊥DE，与BC延长线交于点F．连接EF，与CD边交于点G，与对角线BD交于点H．（1）若BF=BD=，求BE的长；（2）若∠ADE=2∠BFE，求证：FH=HE+HD．5．如图，将一三角板放在边长为1的正方形ABCD上，并使它的直角顶点P 在对角线AC上滑动，直角的一边始终经过点B，另一边与射线DC相交于Q．探究：设A、P两点间的距离为x．（1）当点Q在边CD上时，线段PQ与PB之间有怎样的数量关系？试证明你的猜想；（2）当点Q在边CD上时，设四边形PBCQ的面积为y，求y与x之间的函数关系，并写出函数自变量x的取值范围；（3）当点P在线段AC上滑动时，△PCQ是否可能成为等腰三角形？如果可能，指出所有能使△PCQ成为等腰三角形的点Q的位置．并求出相应的x值，如果不可能，试说明理由．6．Rt△ABC与Rt△FED是两块全等的含30°、60°角的三角板，按如图（一）所示拼在一起，CB与DE重合．（1）求证：四边形ABFC为平行四边形；（2）取BC中点O，将△ABC绕点O顺时钟方向旋转到如图（二）中△A′B′C′位置，直线B'C'与AB、CF分别相交于P、Q两点，猜想OQ、OP长度的大小关系，并证明你的猜想；（3）在（2）的条件下，指出当旋转角至少为多少度时，四边形PCQB为菱形（不要求证明）7．如图，在正方形ABCD中，点F在CD边上，射线AF交BD于点E，交BC 的延长线于点G．（1）求证：△ADE≌△CDE；（2）过点C作CH⊥CE，交FG于点H，求证：FH=GH；（3）设AD=1，DF=x，试问是否存在x的值，使△ECG为等腰三角形？若存在，请求出x的值；若不存在，请说明理由．8．在平行四边形ABCD中，∠BAD的平分线交直线BC于点E，交直线DC于点F．（1）在图1中证明CE=CF；（2）若∠ABC=90°，G是EF的中点（如图2），直接写出∠BDG的度数；（3）若∠ABC=120°，FG∥CE，FG=CE，分别连接DB、DG（如图3），求∠BDG的度数．9．如图，已知▱ABCD中，DE⊥BC于点E，DH⊥AB于点H，AF平分∠BAD，分别交DC、DE、DH于点F、G、M，且DE=AD．（1）求证：△ADG≌△FDM．（2）猜想AB与DG+CE之间有何数量关系，并证明你的猜想．10．如图，在正方形ABCD中，E、F分别为BC、AB上两点，且BE=BF，过点B作AE的垂线交AC于点G，过点G作CF的垂线交BC于点H延长线段AE、GH交于点M．（1）求证：∠BFC=∠BEA；（2）求证：AM=BG+GM．11．如图所示，把矩形纸片OABC放入直角坐标系xOy中，使OA、OC分别落在x、y轴的正半轴上，连接AC，且AC=4，（1）求AC所在直线的解析式；（2）将纸片OABC折叠，使点A与点C重合（折痕为EF），求折叠后纸片重叠部分的面积．（3）求EF所在的直线的函数解析式．12．已知一次函数的图象与坐标轴交于A、B点（如图），AE平分∠BAO，交x轴于点E．（2）求直线AE的表达式；（3）过点B作BF⊥AE，垂足为F，连接OF，试判断△OFB的形状，并求△OFB的面积．（4）若将已知条件“AE平分∠BAO，交x轴于点E”改变为“点E是线段OB上的一个动点（点E不与点O、B重合）”，过点B作BF⊥AE，垂足为F．设OE=x，BF=y，试求y与x之间的函数关系式，并写出函数的定义域．13．如图，直线l1的解析表达式为：y=﹣3x+3，且l1与x轴交于点D，直线l2经过点A，B，直线l1，l2交于点C．（1）求点D的坐标；（2）求直线l2的解析表达式；（3）求△ADC的面积；（4）在直线l2上存在异于点C的另一点P，使得△ADP与△ADC的面积相等，请直接写出点P的坐标．14．如图1，在平面直角坐标系中，O是坐标原点，长方形OACB的顶点A、B分别在x轴与y轴上，已知OA=6，OB=10．点D为y轴上一点，其坐标为（0，2），点P从点A出发以每秒2个单位的速度沿线段AC﹣CB 的方向运动，当点P与点B重合时停止运动，运动时间为t秒．（1）当点P经过点C时，求直线DP的函数解析式；（2）①求△OPD的面积S关于t的函数解析式；②如图②，把长方形沿着OP折叠，点B的对应点B′恰好落在AC边上，求点P的坐标．（3）点P在运动过程中是否存在使△BDP为等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．15．如图，在平面直角坐标系中，已知O为原点，四边形ABCD为平行四边形，A、B、C的坐标分别是A（﹣5，1），B（﹣2，4），C（5，4），点D在第一象限．（1）写出D点的坐标；（2）求经过B、D两点的直线的解析式，并求线段BD的长；（3）将平行四边形ABCD先向右平移1个单位长度，再向下平移1个单位长度所得的四边形A1B1C1D1四个顶点的坐标是多少？并求出平行四边形ABCD与四边A 1B1C1D1重叠部分的面积．16．如图，一次函数的图象与x轴、y轴交于点A、B，以线段AB 为边在第一象限内作等边△ABC，（1）求△ABC的面积；（2）如果在第二象限内有一点P（a，）；试用含有a的代数式表示四边形ABPO的面积，并求出当△ABP的面积与△ABC的面积相等时a的值；（3）在x轴上，是否存在点M，使△MAB为等腰三角形？若存在，请直接写出点M的坐标；若不存在，请说明理由．2018年06月17日梧桐听雨的初中数学组卷参考答案与试题解析一．解答题（共16小题）1．已知，正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N，AH⊥MN于点H．（1）如图①，当∠MAN绕点A旋转到BM=DN时，请你直接写出AH与AB的数量关系：AH=AB ；（2）如图②，当∠MAN绕点A旋转到BM≠DN时，（1）中发现的AH与AB 的数量关系还成立吗？如果不成立请写出理由，如果成立请证明；（3）如图③，已知∠MAN=45°，AH⊥MN于点H，且MH=2，NH=3，求AH的长．（可利用（2）得到的结论）【解答】解：（1）如图①AH=AB．（2）数量关系成立．如图②，延长CB至E，使BE=DN．∵ABCD是正方形，∴AB=AD，∠D=∠ABE=90°，在Rt△AEB和Rt△AND中，，∴Rt△AEB≌Rt△AND，∴AE=AN，∠EAB=∠NAD，∵∠DAN+∠BAN=45°，∴∠EAB+∠BAN=45°，∴∠EAN=45°，在△AEM和△ANM中，，∴△AEM≌△ANM．∴S△AEM =S△ANM，EM=MN，∵AB、AH是△AEM和△ANM对应边上的高，∴AB=AH．（3）如图③分别沿AM、AN翻折△AMH和△ANH，得到△ABM和△AND，∴BM=2，DN=3，∠B=∠D=∠BAD=90°．分别延长BM和DN交于点C，得正方形ABCD，由（2）可知，AH=AB=BC=CD=AD．设AH=x，则MC=x﹣2，NC=x﹣3，在Rt△MCN中，由勾股定理，得MN2=MC2+NC2∴52=（x﹣2）2+（x﹣3）2（6分）解得x1=6，x2=﹣1．（不符合题意，舍去）∴AH=6．2．如图，△ABC是等边三角形，点D是边BC上的一点，以AD为边作等边△ADE，过点C作CF∥DE交AB于点F．（1）若点D是BC边的中点（如图①），求证：EF=CD；（2）在（1）的条件下直接写出△AEF和△ABC的面积比；（3）若点D是BC边上的任意一点（除B、C外如图②），那么（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．【解答】（1）证明：∵△ABC是等边三角形，D是BC的中点，∴AD⊥BC，且∠BAD=∠BAC=30°，∵△AED是等边三角形，∴AD=AE，∠ADE=60°，∴∠EDB=90°﹣∠ADE=90°﹣60°=30°，∵ED∥CF，∴∠FCB=∠EDB=30°，∵∠ACB=60°，∴∠ACF=∠ACB﹣∠FCB=30°，∴∠ACF=∠BAD=30°，在△ABD和△CAF中，，∴△ABD≌△CAF（ASA），∴AD=CF，∵AD=ED，∴ED=CF，又∵ED∥CF，∴四边形EDCF是平行四边形，∴EF=CD．（2）解：△AEF和△ABC的面积比为：1：4；（易知AF=BF，延长EF交AD于H，△AEF的面积=•EF•AH=•CB•AD=••BC•AD，由此即可证明）（3）解：成立．理由如下：∵ED∥FC，∴∠EDB=∠FCB，∵∠AFC=∠B+∠BCF=60°+∠BCF，∠BDA=∠ADE+∠EDB=60°+∠EDB∴∠AFC=∠BDA，在△ABD和△CAF中，∴△ABD≌△CAF（AAS），∴AD=FC，∵AD=ED，∴ED=CF，又∵ED∥CF，∴四边形EDCF是平行四边形，∴EF=DC．3．（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．求证：CE=CF；（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE=45°，请你利用（1）的结论证明：GE=BE+GD．（3）运用（1）（2）解答中所积累的经验和知识，完成下题：如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B=90°，AB=BC，E是AB上一点，且∠DCE=45°，BE=4，DE=10，求直角梯形ABCD的面积．【解答】（1）证明：∵四边形ABCD是正方形，∴BC=CD，∠B=∠CDF=90°，∵∠ADC=90°，∴∠FDC=90°．∴∠B=∠FDC，∵BE=DF，∴△CBE≌△CDF（SAS）．∴CE=CF．（2）证明：如图2，延长AD至F，使DF=BE，连接CF．由（1）知△CBE≌△CDF，∴∠BCE=∠DCF．∴∠BCE+∠ECD=∠DCF+∠ECD，即∠ECF=∠BCD=90°，又∠GCE=45°，∴∠GCF=∠GCE=45°．∵CE=CF，GC=GC，∴△ECG≌△FCG．∴GE=GF，∴GE=GF=DF+GD=BE+GD．（3）解：如图3，过C作CG⊥AD，交AD延长线于G．在直角梯形ABCD中，∵AD∥BC，∴∠A=∠B=90°，又∵∠CGA=90°，AB=BC，∴四边形ABCG为正方形．∴AG=BC．…（7分）∵∠DCE=45°，根据（1）（2）可知，ED=BE+DG．…（8分）∴10=4+DG，即DG=6．设AB=x，则AE=x﹣4，AD=x﹣6，在Rt△AED中，∵DE2=AD2+AE2，即102=（x﹣6）2+（x﹣4）2．解这个方程，得：x=12或x=﹣2（舍去）．…（9分）∴AB=12．=（AD+BC）•AB=×（6+12）×12=108．∴S梯形ABCD即梯形ABCD的面积为108．…（10分）4．如图，正方形ABCD中，E为AB边上一点，过点D作DF⊥DE，与BC延长线交于点F．连接EF，与CD边交于点G，与对角线BD交于点H．（1）若BF=BD=，求BE的长；（2）若∠ADE=2∠BFE，求证：FH=HE+HD．【解答】（1）解：∵四边形ABCD正方形，∴∠BCD=90°，BC=CD，∴Rt△BCD中，BC2+CD2=BD2，即BC2=（）2﹣（BC）2，∴BC=AB=1，∵DF⊥DE，∴∠ADE+∠EDC=90°=∠EDC+∠CDF，∴∠ADE=∠CDF，在△ADE和△CDF中，∵，∴△ADE≌△CDF（ASA），∴AE=CF=BF﹣BC=﹣1，∴BE=AB﹣AE=1﹣（﹣1）=2﹣；（2）证明：在FE上截取一段FI，使得FI=EH，∵△ADE≌△CDF，∴DE=DF，∴△DEF为等腰直角三角形，∴∠DEF=∠DFE=45°=∠DBC，∵∠DHE=∠BHF，∴∠EDH=∠BFH（三角形的内角和定理），在△DEH和△DFI中，∵，∴△DEH≌△DFI（SAS），∴DH=DI，又∵∠HDE=∠BFE，∠ADE=2∠BFE，∴∠HDE=∠BFE=∠ADE，∵∠HDE+∠ADE=45°，∴∠HDE=15°，∴∠DHI=∠DEH+∠HDE=60°，即△DHI为等边三角形，∴DH=HI，∴FH=FI+HI=HE+HD．5．如图，将一三角板放在边长为1的正方形ABCD上，并使它的直角顶点P 在对角线AC上滑动，直角的一边始终经过点B，另一边与射线DC相交于Q．探究：设A、P两点间的距离为x．（1）当点Q在边CD上时，线段PQ与PB之间有怎样的数量关系？试证明你的猜想；（2）当点Q在边CD上时，设四边形PBCQ的面积为y，求y与x之间的函数关系，并写出函数自变量x的取值范围；（3）当点P在线段AC上滑动时，△PCQ是否可能成为等腰三角形？如果可能，指出所有能使△PCQ成为等腰三角形的点Q的位置．并求出相应的x 值，如果不可能，试说明理由．【解答】解：（1）PQ=PB，（1分）过P点作MN∥BC分别交AB、DC于点M、N，在正方形ABCD中，AC为对角线，∴AM=PM，又∵AB=MN，∴MB=PN，∵∠BPQ=90°，∴∠BPM+∠NPQ=90°；又∵∠MBP+∠BPM=90°，∴∠MBP=∠NPQ，在Rt△MBP≌Rt△NPQ中，∵∴Rt△MBP≌Rt△NPQ，（2分）∴PB=PQ．（2）∵S四边形PBCQ =S△PBC+S△PCQ，∵AP=x，∴AM=x，∴CQ=CD﹣2NQ=1﹣x，又∵S△PBC=BC•BM=•1•（1﹣x）=﹣x，S△PCQ=CQ•PN=（1﹣x）•（1﹣x），=﹣+，∴S=﹣x+1．（0≤x≤）．（4分）四边形PBCQ（3）△PCQ可能成为等腰三角形．①当点P与点A重合时，点Q与点D重合，PQ=QC，此时，x=0．（5分）②当点Q在DC的延长线上，且CP=CQ时，（6分）有：QN=AM=PM=x，CP=﹣x，CN=CP=1﹣x，CQ=QN﹣CN=x﹣（1﹣x）=x﹣1，∴当﹣x=x﹣1时，x=1．（7分）．6．Rt△ABC与Rt△FED是两块全等的含30°、60°角的三角板，按如图（一）所示拼在一起，CB与DE重合．（1）求证：四边形ABFC为平行四边形；（2）取BC中点O，将△ABC绕点O顺时钟方向旋转到如图（二）中△A′B′C′位置，直线B'C'与AB、CF分别相交于P、Q两点，猜想OQ、OP 长度的大小关系，并证明你的猜想；（3）在（2）的条件下，指出当旋转角至少为多少度时，四边形PCQB为菱形（不要求证明）【解答】（1）证明：∵△ABC≌△FCB，∴AB=CF，AC=BF．∴四边形ABFC为平行四边形．（2）解：OP=OQ，理由如下：∵OC=OB，∠COQ=∠BOP，∠OCQ=∠PBO，∴△COQ≌△BOP．∴OQ=OP．（3）解：90°．理由：∵OP=OQ，OC=OB，∴四边形PCQB为平行四边形，∵BC⊥PQ，∴四边形PCQB为菱形．7．如图，在正方形ABCD中，点F在CD边上，射线AF交BD于点E，交BC 的延长线于点G．（1）求证：△ADE≌△CDE；（2）过点C作CH⊥CE，交FG于点H，求证：FH=GH；（3）设AD=1，DF=x，试问是否存在x的值，使△ECG为等腰三角形？若存在，请求出x的值；若不存在，请说明理由．【解答】（1）证明：∵四边形ABCD是正方形，∴DA=DC，∠1=∠2=45°，DE=DE，∴△ADE≌△CDE．（2）证明：∵△ADE≌△CDE，∴∠3=∠4，∵CH⊥CE，∴∠4+∠5=90°，又∵∠6+∠5=90°，∴∠4=∠6=∠3，∵AD∥BG，∴∠G=∠3，∴∠G=∠6，∴CH=GH，又∵∠4+∠5=∠G+∠7=90°，∴∠5=∠7，∴CH=FH，∴FH=GH．（3）解：存在符合条件的x值此时，∵∠ECG＞90°，要使△ECG为等腰三角形，必须CE=CG，∴∠G=∠8，又∵∠G=∠4，∴∠8=∠4，∴∠9=2∠4=2∠3，∴∠9+∠3=2∠3+∠3=90°，∴∠3=30°，∴x=DF=1×tan30°=．8．在▱ABCD中，∠BAD的平分线交直线BC于点E，交直线DC于点F．（1）在图1中证明CE=CF；（2）若∠ABC=90°，G是EF的中点（如图2），直接写出∠BDG的度数；（3）若∠ABC=120°，FG∥CE，FG=CE，分别连接DB、DG（如图3），求∠BDG的度数．【解答】（1）证明：如图1，∵AF平分∠BAD，∴∠BAF=∠DAF，∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，∴∠DAF=∠CEF，∠BAF=∠F，∴∠CEF=∠F．∴CE=CF．（2）解：连接GC、BG，∵四边形ABCD为平行四边形，∠ABC=90°，∴四边形ABCD为矩形，∵AF平分∠BAD，∴∠DAF=∠BAF=45°，∵∠DCB=90°，DF∥AB，∴∠DFA=45°，∠ECF=90°∴△ECF为等腰直角三角形，∵G为EF中点，∴EG=CG=FG，CG⊥EF，∵△ABE为等腰直角三角形，AB=DC，∴BE=DC，∵∠CEF=∠GCF=45°，∴∠BEG=∠DCG=135°在△BEG与△DCG中，∵，∴△BEG≌△DCG，∴BG=DG，∵CG⊥EF，∴∠DGC+∠DGA=90°，又∵∠DGC=∠BGA，∴∠BGA+∠DGA=90°，∴△DGB为等腰直角三角形，∴∠BDG=45°．（3）解：延长AB、FG交于H，连接HD．∵AD∥GF，AB∥DF，∴四边形AHFD为平行四边形∵∠ABC=120°，AF平分∠BAD∴∠DAF=30°，∠ADC=120°，∠DFA=30°∴△DAF为等腰三角形∴AD=DF，∴CE=CF，∴平行四边形AHFD为菱形∴△ADH，△DHF为全等的等边三角形∴DH=DF，∠BHD=∠GFD=60°∵FG=CE，CE=CF，CF=BH，∴BH=GF在△BHD与△GFD中，∵，∴△BHD≌△GFD，∴∠BDH=∠GDF∴∠BDG=∠BDH+∠HDG=∠GDF+∠HDG=60°9．如图，已知▱ABCD中，DE⊥BC于点E，DH⊥AB于点H，AF平分∠BAD，分别交DC、DE、DH于点F、G、M，且DE=AD．（1）求证：△ADG≌△FDM．（2）猜想AB与DG+CE之间有何数量关系，并证明你的猜想．【解答】证明：（1）∵四边形ABCD是平行四边形，∴AB∥CD，AD∥BC，∴∠BAF=∠DFA，∵AF平分∠BAD，∴∠DAF=∠DFA，∴AD=FD，∵DE⊥BC，DH⊥AB，∴∠ADG=∠FDM=90°，在△ADG和△FDM中，，∴△ADG≌△FDM（ASA）．（2）AB=DG+EC．证明：延长GD至点N，使DN=CE，连接AN，∵DE⊥BC，AD∥BC，∴∠ADN=∠DEC=90°，在△ADN和△DEC中，，∴△ADN≌△DEC（SAS），∴∠NAD=∠CDE，AN=DC，∵∠NAG=∠NAD+∠DAG，∠NGA=∠CDE+∠DFA，∴∠NAG=∠NGA，∴AN=GN=DG+CE=DC，∵四边形ABCD是平行四边形，∴AB=CD，∴AB=DG+EC．10．如图，在正方形ABCD中，E、F分别为BC、AB上两点，且BE=BF，过点B作AE的垂线交AC于点G，过点G作CF的垂线交BC于点H延长线段AE、GH交于点M．（1）求证：∠BFC=∠BEA；（2）求证：AM=BG+GM．【解答】证明：（1）在正方形ABCD中，AB=BC，∠ABC=90°，在△ABE和△CBF中，，∴△ABE≌△CBF（SAS），∴∠BFC=∠BEA；（2）连接DG，在△ABG和△ADG中，，∴△ABG≌△ADG（SAS），∴BG=DG，∠2=∠3，∵BG⊥AE，∴∠BAE+∠2=90°，∵∠BAD=∠BAE+∠4=90°，∴∠2=∠3=∠4，∵GM⊥CF，∴∠BCF+∠1=90°，又∠BCF+∠BFC=90°，∴∠1=∠BFC=∠2，∴∠1=∠3，在△ADG中，∠DGC=∠3+45°，∴∠DGC也是△CGH的外角，∴D、G、M三点共线，∵∠3=∠4（已证），∴AM=DM，∵DM=DG+GM=BG+GM，∴AM=BG+GM．11．如图所示，把矩形纸片OABC放入直角坐标系xOy中，使OA、OC分别落在x、y轴的正半轴上，连接AC，且AC=4，（1）求AC所在直线的解析式；（2）将纸片OABC折叠，使点A与点C重合（折痕为EF），求折叠后纸片重叠部分的面积．（3）求EF所在的直线的函数解析式．【解答】解：（1）∵=，∴可设OC=x，则OA=2x，在Rt△AOC中，由勾股定理可得OC2+OA2=AC2，∴x2+（2x）2=（4）2，解得x=4（x=﹣4舍去），∴OC=4，OA=8，∴A（8，0），C（0，4），设直线AC解析式为y=kx+b，∴，解得，∴直线AC解析式为y=﹣x+4；（2）由折叠的性质可知AE=CE，设AE=CE=y，则OE=8﹣y，在Rt△OCE中，由勾股定理可得OE2+OC2=CE2，∴（8﹣y）2+42=y2，解得y=5，∴AE=CE=5，∵∠AEF=∠CEF，∠CFE=∠AEF，∴∠CFE=∠CEF，∴CE=CF=5，∴S=CF•OC=×5×4=10，△CEF即重叠部分的面积为10；（3）由（2）可知OE=3，CF=5，∴E（3，0），F（5，4），设直线EF的解析式为y=k′x+b′，∴，解得，∴直线EF的解析式为y=2x﹣6．12．已知一次函数的图象与坐标轴交于A、B点（如图），AE平分∠BAO，交x轴于点E．（1）求点B的坐标；（2）求直线AE的表达式；（3）过点B作BF⊥AE，垂足为F，连接OF，试判断△OFB的形状，并求△OFB的面积．（4）若将已知条件“AE平分∠BAO，交x轴于点E”改变为“点E是线段OB上的一个动点（点E不与点O、B重合）”，过点B作BF⊥AE，垂足为F．设OE=x，BF=y，试求y与x之间的函数关系式，并写出函数的定义域．【解答】解：（1）对于y=﹣x+6，当x=0时，y=6；当y=0时，x=8，∴OA=6，OB=8，在Rt△AOB中，根据勾股定理得：AB=10，则A（0，6），B（8，0）；（2）过点E作EG⊥AB，垂足为G（如图1所示），∵AE平分∠BAO，EO⊥AO，EG⊥AG，∴EG=OE，在Rt△AOE和Rt△AGE中，，∴Rt△AOE≌Rt△AGE（HL），∴AG=AO，设OE=EG=x，则有BE=8﹣x，BG=AB﹣AG=10﹣6=4，在Rt△BEG中，EG=x，BG=4，BE=8﹣x，根据勾股定理得：x2+42=（8﹣x）2，解得：x=3，∴E（3，0），设直线AE的表达式为y=kx+b（k≠0），将A（0，6），E（3，0）代入y=kx+b得：，解得：，则直线AE的表达式为y=﹣2x+6；（3）延长BF交y轴于点K（如图2所示），∵AE平分∠BAO，∴∠KAF=∠BAF，又BF⊥AE，∴∠AFK=∠AFB=90°，在△AFK和△AFB中，∵，∴△AFK≌△AFB，∴FK=FB，即F为KB的中点，又∵△BOK为直角三角形，∴OF=BK=BF，∴△OFB为等腰三角形，过点F作FH⊥OB，垂足为H（如图2所示），∵OF=BF，FH⊥OB，∴OH=BH=4，∴F点的横坐标为4，设F（4，y），将F（4，y）代入y=﹣2x+6，得：y=﹣2，∴FH=|﹣2|=2，=OB•FH=×8×2=8；则S△OBF（4）在Rt△AOE中，OE=x，OA=6，根据勾股定理得：AE==，=AE•BF=BE•AO（等积法），又BE=OB﹣OE=8﹣x，S△ABE∴BF==（0＜x＜8），又BF=y，则y=（0＜x＜8）．13．如图，直线l1的解析表达式为：y=﹣3x+3，且l1与x轴交于点D，直线l2经过点A，B，直线l1，l2交于点C．（1）求点D的坐标；（2）求直线l2的解析表达式；（3）求△ADC的面积；（4）在直线l2上存在异于点C的另一点P，使得△ADP与△ADC的面积相等，请直接写出点P的坐标．【解答】解：（1）由y=﹣3x+3，令y=0，得﹣3x+3=0，∴x=1，∴D（1，0）；（2）设直线l2的解析表达式为y=kx+b，由图象知：x=4，y=0；x=3，，代入表达式y=kx+b，∴，∴，∴直线l2的解析表达式为；（3）由，解得，∴C（2，﹣3），∵AD=3，∴S△ADC=×3×|﹣3|=；（4）△ADP与△ADC底边都是AD，面积相等所以高相等，△ADC高就是点C 到直线AD的距离，即C纵坐标的绝对值=|﹣3|=3，则P到AD距离=3，∴P纵坐标的绝对值=3，点P不是点C，∴点P纵坐标是3，∵y=﹣6，y=3，∴﹣6=3x=6，所以P（6，3）．14．如图1，在平面直角坐标系中，O是坐标原点，长方形OACB的顶点A、B分别在x轴与y轴上，已知OA=6，OB=10．点D为y轴上一点，其坐标为（0，2），点P从点A出发以每秒2个单位的速度沿线段AC﹣CB的方向运动，当点P与点B重合时停止运动，运动时间为t秒．（1）当点P经过点C时，求直线DP的函数解析式；（2）①求△OPD的面积S关于t的函数解析式；②如图②，把长方形沿着OP折叠，点B的对应点B′恰好落在AC边上，求点P的坐标．（3）点P在运动过程中是否存在使△BDP为等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．【解答】解：（1）∵OA=6，OB=10，四边形OACB为长方形，∴C（6，10）．设此时直线DP解析式为y=kx+b，把（0，2），C（6，10）分别代入，得，解得则此时直线DP解析式为y=x+2；（2）①当点P在线段AC上时，OD=2，高为6，S=6；当点P在线段BC上时，OD=2，高为6+10﹣2t=16﹣2t，S=×2×（16﹣2t）=﹣2t+16；②设P（m，10），则PB=PB′=m，如图2，∵OB′=OB=10，OA=6，∴AB′==8，∴B′C=10﹣8=2，∵PC=6﹣m，∴m2=22+（6﹣m）2，解得m=则此时点P的坐标是（，10）；（3）存在，理由为：若△BDP为等腰三角形，分三种情况考虑：如图3，①当BD=BP1=OB﹣OD=10﹣2=8，在Rt△BCP1中，BP1=8，BC=6，根据勾股定理得：CP1==2，∴AP1=10﹣2，即P1（6，10﹣2）；②当BP2=DP2时，此时P2（6，6）；③当DB=DP3=8时，在Rt△DEP3中，DE=6，根据勾股定理得：P3E==2，∴AP3=AE+EP3=2+2，即P3（6，2+2），综上，满足题意的P坐标为（6，6）或（6，2+2）或（6，10﹣2）．15．如图，在平面直角坐标系中，已知O为原点，四边形ABCD为平行四边形，A、B、C的坐标分别是A（﹣5，1），B（﹣2，4），C（5，4），点D 在第一象限．（1）写出D点的坐标；（2）求经过B、D两点的直线的解析式，并求线段BD的长；（3）将平行四边形ABCD先向右平移1个单位长度，再向下平移1个单位长度所得的四边形A1B1C1D1四个顶点的坐标是多少？并求出平行四边形ABCD与四边形A1B1C1D1重叠部分的面积．【解答】解：（1）∵B（﹣2，4），C（5，4），∴BC=5﹣（﹣2）=5+2=7，∵A（﹣5，1），∴点D的横坐标为﹣5+7=2，∴点D的坐标为（2，1）；（2）设直线BD的解析式为y=kx+b，将B（﹣2，4）、D（2，1）代入得：，解得，∴经过B、D两点的直线的解析式为y=﹣x+，过B点作AD的垂线，垂足为E，则BE=4﹣1=3，DE=2﹣（﹣2）=2+2=4，在Rt△BDE中，BD===5；（3）∵▱ABCD向右平移1个单位长度，再向下平移1个单位长度，∴A1（﹣4，0），B1（﹣1，3），C1（6，3）D1（3，0），∴重叠部分的底边长7﹣1=6，高为3﹣1=2，∴重叠部分的面积S=6×2=12．16．如图，一次函数的图象与x轴、y轴交于点A、B，以线段AB 为边在第一象限内作等边△ABC，（1）求△ABC的面积；（2）如果在第二象限内有一点P（a，）；试用含有a的代数式表示四边形ABPO的面积，并求出当△ABP的面积与△ABC的面积相等时a的值；（3）在x轴上，是否存在点M，使△MAB为等腰三角形？若存在，请直接写出点M的坐标；若不存在，请说明理由．【解答】解：（1）分别令y=0和x=0，得一次函数y=x+1的图象与x 轴．y轴的交点坐标分别是A（，0），B（0，1），即OA=，OB=1，∴AB==2∵△ABC为等边三角形，∴S△ABC=；（2）如图1，S△AOB =，S△AOP=，S△BOP=|a|•OB=﹣．∴S四边形ABPO =S△AOB+S△BOP=，而S△ABP =S四边形ABPO﹣S△APO，∴当S△ABP =S△ABC时，=，解得a=﹣；（3）如图2，满足条件的点M有4个：M1（﹣，0），M2（﹣2，0），M3（，0），M4（+2，0）．。

(完整)八年级下数学压轴题及答案.docx

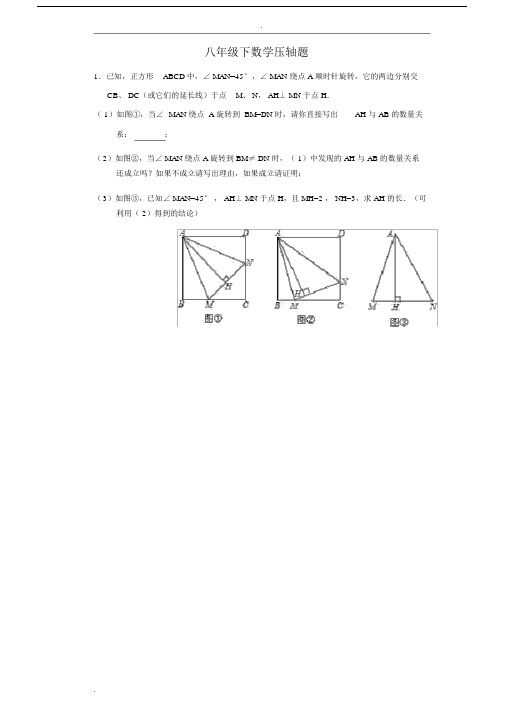
.八年级下数学压轴题1．已知，正方形ABCD中，∠ MAN=45°，∠ MAN 绕点 A 顺时针旋转，它的两边分别交CB、 DC（或它们的延长线）于点M、 N， AH⊥ MN 于点 H．（ 1）如图①，当∠MAN 绕点 A 旋转到 BM=DN 时，请你直接写出AH 与 AB 的数量关系：；（2）如图②，当∠ MAN 绕点 A 旋转到 BM≠ DN 时，（ 1）中发现的 AH 与 AB 的数量关系还成立吗？如果不成立请写出理由，如果成立请证明；（3）如图③，已知∠ MAN=45°， AH⊥ MN 于点 H，且 MH=2 ， NH=3，求 AH 的长．（可利用（ 2）得到的结论）.2．如图，△ ABC 是等边三角形，点 D 是边 BC上的一点，以AD 为边作等边△ADE，过点C 作 CF∥ DE交 AB 于点 F．（1）若点 D 是 BC边的中点（如图①），求证： EF=CD；（2）在（ 1）的条件下直接写出△ AEF和△ ABC的面积比；（3）若点 D 是 BC 边上的任意一点（除 B、 C 外如图②），那么（ 1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．.3．（ 1）如图 1，在正方形ABCD中， E 是 AB 上一点， F 是 AD 延长线上一点，且DF=BE．求证： CE=CF；（2）如图 2，在正方形 ABCD中， E 是 AB 上一点， G 是 AD 上一点，如果∠ GCE=45°，请你利用（ 1）的结论证明： GE=BE+GD．（3）运用（ 1）（ 2）解答中所积累的经验和知识，完成下题：如图 3，在直角梯形ABCD中， AD∥ BC（ BC＞ AD），∠ B=90°，AB=BC，E 是 AB 上一点，且∠ DCE=45°， BE=4， DE=10，求直角梯形ABCD的面积．.4．如图，正方形ABCD中， E 为 AB 边上一点，过点 D 作 DF⊥ DE，与 BC 延长线交于点F．连接 EF，与 CD边交于点 G，与对角线 BD 交于点 H．（1）若 BF=BD= ，求 BE 的长；（2）若∠ ADE=2∠ BFE，求证： FH=HE+HD．.5．如图，将一三角板放在边长为 1 的正方形ABCD上，并使它的直角顶点P 在对角线AC 上滑动，直角的一边始终经过点B，另一边与射线DC 相交于 Q．探究：设A、 P 两点间的距离为x．（1）当点 Q 在边 CD上时，线段 PQ 与 PB 之间有怎样的数量关系？试证明你的猜想；（2）当点 Q 在边 CD上时，设四边形 PBCQ的面积为 y，求 y 与 x 之间的函数关系，并写出函数自变量x 的取值范围；（ 3）当点 P 在线段 AC 上滑动时，△ PCQ是否可能成为等腰三角形？如果可能，指出所有能使△ PCQ成为等腰三角形的点Q 的位置．并求出相应的x 值，如果不可能，试说明理由．.6．Rt△ ABC与 Rt△FED是两块全等的含30°、60°角的三角板，按如图（一）所示拼在一起， CB 与 DE 重合．（ 1）求证：四边形ABFC为平行四边形；（ 2）取 BC 中点 O，将△ ABC 绕点 O 顺时钟方向旋转到如图（二）中△A′B′位C置′，直线 B'C'与 AB、 CF分别相交于 P、 Q 两点，猜想 OQ、 OP 长度的大小关系，并证明你的猜想；（ 3）在（ 2）的条件下，指出当旋转角至少为多少度时，四边形PCQB为菱形？（不要求证明）.7．如图，在正方形ABCD中，点 F 在 CD边上，射线AF 交 BD 于点 E，交 BC的延长线于点 G．（1）求证：△ ADE≌△ CDE；（2）过点 C 作 CH⊥ CE，交 FG于点 H，求证： FH=GH；（3）设 AD=1，DF=x，试问是否存在 x 的值，使△ ECG为等腰三角形？若存在，请求出x 的值；若不存在，请说明理由．.8．在平行四边形ABCD中，∠ BAD 的平分线交直线BC于点 E，交直线 DC 于点 F．（1）在图 1 中证明 CE=CF；（ 2）若∠ ABC=90°， G 是 EF的中点（如图2），直接写出∠ BDG 的度数；（ 3）若∠ ABC=120°，FG∥CE，FG=CE，分别连接DB、DG（如图 3），求∠ BDG的度数．.9．如图，已知 ?ABCD中， DE⊥ BC 于点 E，DH⊥ AB 于点 H，AF 平分∠ BAD，分别交 DC、DE、 DH 于点 F、 G、 M，且 DE=AD．（1）求证：△ ADG≌△ FDM．（2）猜想 AB 与 DG+CE之间有何数量关系，并证明你的猜想．.10．如图，在正方形 ABCD 中， E、 F 分别为 BC、 AB 上两点，且 BE=BF，过点 B 作 AE 的垂线交 AC 于点 G，过点 G 作 CF的垂线交 BC于点 H 延长线段 AE、GH 交于点 M．（1）求证：∠ BFC=∠ BEA；（2）求证： AM=BG+GM．.11．如图所示，把矩形纸片OABC 放入直角坐标系xOy 中，使OA、OC 分别落在x、 y 轴的正半轴上，连接AC，且 AC=4，（1）求 AC 所在直线的解析式；（2）将纸片 OABC折叠，使点 A 与点 C重合（折痕为 EF），求折叠后纸片重叠部分的面积．（3）求 EF所在的直线的函数解析式．.12．已知一次函数的图象与坐标轴交于A、B 点（如图），AE 平分∠ BAO，交x 轴于点 E．（1）求点 B 的坐标；（2）求直线 AE 的表达式；（3）过点 B 作 BF⊥ AE，垂足为 F，连接 OF，试判断△ OFB的形状，并求△ OFB的面积．（4）若将已知条件“AE平分∠ BAO，交 x 轴于点 E”改变为“点 E 是线段 OB上的一个动点（点 E 不与点 O、 B 重合）”，过点 B 作 BF⊥ AE，垂足为 F．设 OE=x， BF=y，试求 y 与 x 之间的函数关系式，并写出函数的定义域．.13．如图，直线l1的解析表达式为：y=﹣ 3x+3，且 l1与 x 轴交于点D，直线 l2经过点 A，B，直线 l1， l2交于点 C．（1）求点 D 的坐标；（2）求直线 l 2的解析表达式；（3）求△ ADC的面积；（ 4）在直线l 2上存在异于点 C 的另一点P，使得△ ADP 与△ ADC 的面积相等，请直接写出点 P 的坐标．.14．如图 1，在平面直角坐标系中，O 是坐标原点，长方形OACB的顶点 A、B 分别在 x 轴与 y 轴上，已知OA=6， OB=10．点 D 为 y 轴上一点，其坐标为（0， 2），点 P 从点 A 出发以每秒 2 个单位的速度沿线段 AC﹣ CB的方向运动，当点 P 与点 B 重合时停止运动，运动时间为 t 秒．（1）当点 P 经过点 C 时，求直线 DP 的函数解析式；（2）①求△ OPD的面积 S关于 t 的函数解析式；②如图②，把长方形沿着OP 折叠，点 B 的对应点B′恰好落在A C 边上，求点P的坐标．（ 3）点 P 在运动过程中是否存在使△BDP 为等腰三角形？若存在，请求出点P 的坐标；若不存在，请说明理由．.15．如图，在平面直角坐标系中，已知O 为原点，四边形ABCD为平行四边形，A、 B、C 的坐标分别是A（﹣ 5， 1）， B（﹣ 2， 4）， C（ 5， 4），点D 在第一象限．（ 1）写出 D 点的坐标；（ 2）求经过 B、 D 两点的直线的解析式，并求线段BD 的长；（ 3）将平行四边形 ABCD先向右平移 1 个单位长度，再向下平移 1 个单位长度所得的四边形 A1 1 1 1四个顶点的坐标是多少？并求出平行四边形ABCD与四边B C DA1B1C1D1重叠部分的面积．.16．如图，一次函数的图象与x 轴、 y 轴交于点A、B，以线段 AB 为边在第一象限内作等边△ABC，（ 1）求△ ABC 的面积；（ 2）如果在第二象限内有一点P（ a，）；试用含有a 的代数式表示四边形ABPO的面积，并求出当△ABP 的面积与△ ABC的面积相等时 a 的值；（ 3）在 x 轴上，是否存在点M，使△ MAB 为等腰三角形？若存在，请直接写出点M 的坐标；若不存在，请说明理由．..2018 年 06 月 17 日梧桐听雨的初中数学组卷参考答案与试题解析一．解答题（共16 小题）1．已知，正方形ABCD中，∠ MAN=45°，∠ MAN 绕点 A 顺时针旋转，它的两边分别交CB、 DC（或它们的延长线）于点M 、N，AH⊥ MN 于点 H．（ 1）如图①，当∠ MAN 绕点 A 旋转到 BM=DN 时，请你直接写出AH 与 AB 的数量关系：AH=AB；（2）如图②，当∠ MAN 绕点 A 旋转到 BM≠ DN 时，（ 1）中发现的 AH 与 AB 的数量关系还成立吗？如果不成立请写出理由，如果成立请证明；（3）如图③，已知∠ MAN=45°， AH⊥ MN 于点 H，且 MH=2 ， NH=3，求 AH 的长．（可利用（ 2）得到的结论）【解答】解：（ 1）如图① AH=AB．（ 2）数量关系成立．如图②，延长CB至 E，使 BE=DN．∵ ABCD是正方形，∴AB=AD，∠ D=∠ ABE=90°，在 Rt△ AEB和 Rt△ AND 中，，∴Rt△ AEB≌ Rt△AND，∴AE=AN，∠ EAB=∠NAD，∵∠ DAN+∠ BAN=45°，∴∠ EAB+∠ BAN=45°，∴∠ EAN=45°，∴∠ EAM=∠ NAM=45°，在△ AEM 和△ ANM 中，，.∵ AB、 AH 是△ AEM 和△ ANM 对应边上的高，∴AB=AH．（ 3）如图③分别沿AM 、AN 翻折△ AMH 和△ ANH，得到△ ABM 和△ AND，∴BM=2， DN=3，∠ B=∠ D=∠BAD=90°．分别延长 BM 和 DN 交于点 C，得正方形 ABCD，由（2）可知，AH=AB=BC=CD=AD．设AH=x，则MC=x﹣ 2， NC=x﹣ 3，在 Rt△ MCN 中，由勾股定理，得MN 2=MC2+NC2∴52=（ x﹣ 2）2 +（x﹣ 3）2（ 6 分）解得 x1=6， x2 =﹣ 1．（不符合题意，舍去）∴AH=6．2．如图，△ ABC 是等边三角形，点 D 是边 BC上的一点，以AD 为边作等边△ADE，过点C作 CF∥ DE 交 AB 于点 F．（ 1）若点 D 是 BC边的中点（如图①），求证： EF=CD；（ 2）在（ 1）的条件下直接写出△ AEF和△ ABC的面积比；（3）若点 D 是 BC 边上的任意一点（除 B、 C 外如图②），那么（ 1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．..【解答】（1）证明：∵△ ABC是等边三角形， D 是 BC的中点，∴ AD⊥ BC，且∠ BAD= ∠ BAC=30°，∵△ AED是等边三角形，∴AD=AE，∠ ADE=60°，∴∠ EDB=90°﹣∠ ADE=90°﹣ 60°=30°，∵ED∥CF，∴∠ FCB=∠ EDB=30°，∵∠ ACB=60°，∴∠ ACF=∠ ACB﹣∠ FCB=30°，∴∠ ACF=∠ BAD=30°，在△ ABD 和△ CAF中，，∴△ ABD≌△ CAF（ASA），∴AD=CF，∵ AD=ED，∴ED=CF，又∵ ED∥ CF，∴四边形 EDCF是平行四边形，∴EF=CD．（ 2）解：△ AEF和△ ABC的面积比为：1： 4；（易知AF=BF ，延长EF交AD于H，△AEF的面积..=?EF?AH= ? CB ?AD= ? ?BC?AD，由此即可证明）（3）解：成立．理由如下：∵ ED∥ FC，∴∠ EDB=∠FCB，∵∠ AFC=∠ B+∠ BCF=60°+∠ BCF，∠ BDA=∠ ADE+∠EDB=60°+∠ EDB ∴∠ AFC=∠ BDA，在△ ABD 和△ CAF中，∴△ ABD≌△ CAF（AAS），∴AD=FC，∵ AD=ED，∴ED=CF，又∵ ED∥ CF，∴四边形 EDCF是平行四边形，∴EF=DC．3．（1）如图 1，在正方形 ABCD中，E 是 AB 上一点， F 是 AD 延长线上一点，且 DF=BE．求证： CE=CF；（2）如图 2，在正方形 ABCD中， E 是 AB 上一点， G 是 AD 上一点，如果∠ GCE=45°，请你利用（ 1）的结论证明： GE=BE+GD．（3）运用（ 1）（ 2）解答中所积累的经验和知识，完成下题：如图 3，在直角梯形ABCD中， AD∥ BC（ BC＞AD），∠ B=90°， AB=BC，E 是 AB 上一点，且∠ DCE=45°， BE=4， DE=10，求直角梯形ABCD的面积．..【解答】（ 1）明：∵四形ABCD是正方形，∴BC=CD，∠ B=∠CDF=90°，∵∠ ADC=90°，∴∠FDC=90°．∴∠B=∠ FDC，∵BE=DF，∴△ CBE≌△ CDF（ SAS）．∴CE=CF．（2）明：如 2 ，延 AD 至 F，使 DF=BE，接 CF．由（ 1）知△CBE≌△ CDF，∴∠ BCE=∠ DCF．∴∠ BCE+∠ ECD=∠DCF+∠ ECD，即∠ ECF=∠ BCD=90°，又∠ GCE=45°，∴∠ GCF=∠ GCE=45°．∵CE=CF，GC=GC，∴△ ECG≌△ FCG．∴GE=GF，∴GE=GF=DF+GD=BE+GD．（3）解：如 3， C作 CG⊥ AD，交 AD 延于 G．在直角梯形ABCD中，∵ AD∥ BC，∴∠A=∠B=90°，又∵∠ CGA=90°， AB=BC，∴四形 ABCG正方形．∴AG=BC．⋯（ 7 分）∵∠ DCE=45°，根据（ 1）（ 2）可知， ED=BE+DG．⋯（ 8 分）∴10=4+DG，即 DG=6．AB=x， AE=x 4， AD=x 6，在Rt△ AED中，..∵DE2=AD2+AE2，即 102 =（ x 6）2+（x 4）2．解个方程，得： x=12 或 x= 2（舍去）．⋯（9 分）∴ AB=12．∴ S 梯形ABCD= （ AD+BC） ?AB= ×（ 6+12）× 12=108．即梯形 ABCD的面108．⋯（ 10 分）4．如，正方形 ABCD中， E AB 上一点，点 D 作 DF⊥ DE，与 BC 延交于点F．接 EF，与 CD 交于点 G，与角 BD 交于点 H．（1）若 BF=BD= ，求 BE 的；（2）若∠ ADE=2∠ BFE，求： FH=HE+HD．【解答】（ 1）解：∵四形ABCD正方形，∴∠ BCD=90°，BC=CD，∴Rt△ BCD中， BC2+CD2=BD2，即 BC2=（）2（ BC）2，∴BC=AB=1，∵DF⊥ DE，∴∠ ADE+∠ EDC=90°=∠EDC+∠ CDF，∴∠ ADE=∠ CDF，在△ ADE 和△ CDF中，∵，∴△ ADE≌△ CDF（ ASA），..∴ AE=CF=BF﹣ BC=﹣1，∴ BE=AB﹣ AE=1﹣（﹣1）=2﹣；（2）证明：在 FE 上截取一段 FI，使得 FI=EH，∵△ADE≌△CDF，∴ DE=DF，∴△ DEF为等腰直角三角形，∴∠ DEF=∠ DFE=45°=∠DBC，∵∠ DHE=∠ BHF，∴∠ EDH=∠ BFH（三角形的内角和定理），在△ DEH和△ DFI中，∵，∴△ DEH≌△ DFI（ SAS），∴DH=DI，又∵∠ HDE=∠BFE，∠ ADE=2∠BFE，∴∠ HDE=∠ BFE= ∠ ADE，∵∠ HDE+∠ ADE=45°，∴∠ HDE=15°，∴∠ DHI=∠ DEH+∠ HDE=60°，即△ DHI 为等边三角形，∴DH=HI，∴FH=FI+HI=HE+HD．5．如图，将一三角板放在边长为 1 的正方形ABCD上，并使它的直角顶点P 在对角线AC 上滑动，直角的一边始终经过点B，另一边与射线DC 相交于 Q．探究：设 A、 P 两点间的距离为x．（1）当点 Q 在边 CD上时，线段 PQ 与 PB 之间有怎样的数量关系？试证明你的猜想；（2）当点 Q 在边 CD上时，设四边形 PBCQ的面积为 y，求 y 与 x 之间的函数关系，并..写出函数自变量x 的取值范围；（ 3）当点 P 在线段 AC 上滑动时，△ PCQ是否可能成为等腰三角形？如果可能，指出所有能使△ PCQ成为等腰三角形的点Q 的位置．并求出相应的x 值，如果不可能，试说明理由．【解答】解：（ 1） PQ=PB，（1 分）过P 点作 MN ∥ BC分别交 AB、 DC于点 M、 N，在正方形 ABCD中， AC 为对角线，∴ AM=PM ，又∵ AB=MN，∴MB=PN，∵∠BPQ=90°，∴∠ BPM+∠ NPQ=90°；又∵∠ MBP+∠BPM=90°，∴∠ MBP=∠ NPQ，在Rt△ MBP≌Rt△ NPQ 中，∵∴Rt△ MBP≌Rt△ NPQ，（ 2 分）∴PB=PQ．（2）∵ S 四边形PBCQ=S△PBC+S△PCQ，∵AP=x，∴AM=x，∴CQ=CD﹣ 2NQ=1﹣ x，又∵ S△PBC= BC?BM= ?1?（ 1﹣x） =﹣x，S△PCQ= CQ?PN=（1﹣x） ?（ 1﹣x），..=﹣+，∴ S 四边形PBCQ=﹣x+1 ．（ 0≤ x≤）．（4分）（ 3）△ PCQ可能成为等腰三角形．①当点 P 与点 A 重合时，点Q 与点 D 重合，PQ=QC，此时， x=0．（ 5 分）②当点 Q 在 DC的延长线上，且CP=CQ时，（6 分）有：QN=AM=PM=x，CP=﹣x，CN=CP=1﹣x，CQ=QN﹣ CN=x﹣（ 1﹣x）=x﹣ 1，∴当﹣ x=x﹣ 1 时， x=1．（ 7 分）．6．Rt△ ABC 与 Rt△FED是两块全等的含30°、60°角的三角板，按如图（一）所示拼在一起， CB与 DE 重合．（ 1）求证：四边形ABFC为平行四边形；（ 2）取 BC 中点 O，将△ ABC 绕点 O 顺时钟方向旋转到如图（二）中△A′B′位C置′，直线B'C'与 AB、 CF分别相交于 P、Q 两点，猜想 OQ、OP 长度的大小关系，并证明你的猜想；（ 3）在（ 2）的条件下，指出当旋转角至少为多少度时，四边形PCQB为菱形？（不要求证明）..【解答】（ 1）证明：∵△ABC≌△ FCB，∴AB=CF， AC=BF．∴四边形ABFC为平行四边形．（2）解： OP=OQ，理由如下：∵OC=OB，∠ COQ=∠BOP，∠ OCQ=∠ PBO，∴△ COQ≌△ BOP．∴OQ=OP．（ 3）解： 90°．理由：∵ OP=OQ，OC=OB，∴四边形PCQB为平行四边形，∵BC⊥ PQ，∴四边形PCQB为菱形．7．如图，在正方形 ABCD中，点 F 在 CD 边上，射线 AF 交 BD 于点 E，交 BC 的延长线于点G．（1）求证：△ ADE≌△ CDE；（2）过点 C作 CH⊥ CE，交 FG 于点 H，求证： FH=GH；（3）设 AD=1，DF=x，试问是否存在 x 的值，使△ ECG为等腰三角形？若存在，请求出x的值；若不存在，请说明理由．【解答】（ 1）证明：∵四边形ABCD是正方形，∴DA=DC，∠ 1=∠ 2=45°，DE=DE，∴△ ADE≌△ CDE．..（2）证明：∵△ADE≌△CDE，∴∠ 3=∠4，∵ CH⊥ CE，∴∠ 4+∠5=90°，又∵∠ 6+∠ 5=90°，∴∠ 4=∠6=∠ 3，∵AD∥ BG，∴∠ G=∠3，∴∠ G=∠6，∴ CH=GH，又∵∠ 4+∠ 5=∠ G+∠7=90°，∴∠ 5=∠7，∴ CH=FH，∴ FH=GH．（ 3）解：存在符合条件的x 值此时，∵∠ ECG＞ 90°，要使△ ECG为等腰三角形，必须CE=CG，∴∠ G=∠8，又∵∠ G=∠ 4，∴∠ 8=∠4，∴∠ 9=2∠4=2∠ 3，∴∠ 9+∠3=2∠ 3+∠ 3=90°，∴∠ 3=30°，∴ x=DF=1× tan30 °=．8．在 ?ABCD中，∠ BAD 的平分线交直线BC于点 E，交直线DC于点 F．（1）在图 1 中证明 CE=CF；（2）若∠ ABC=90°，G 是 EF 的中点（如图 2），直接写出∠ BDG的度数；（3）若∠ ABC=120°， FG∥ CE， FG=CE，分别连接 DB、 DG（如图 3），求∠ BDG 的度数．..【解答】（ 1）证明：如图1，∵AF 平分∠ BAD，∴∠ BAF=∠ DAF，∵四边形 ABCD是平行四边形，∴ AD∥ BC，AB∥ CD，∴∠ DAF=∠ CEF，∠ BAF=∠F，∴∠ CEF=∠ F．∴CE=CF．（ 2）解：连接GC、 BG，∵四边形ABCD为平行四边形，∠ABC=90°，∴四边形ABCD为矩形，∵AF 平分∠ BAD，∴∠DAF=∠ BAF=45°，∵∠DCB=90°，DF∥ AB，∴∠DFA=45°，∠ ECF=90°∴△ ECF为等腰直角三角形，∵G 为 EF中点，∴EG=CG=FG， CG⊥ EF，∵△ ABE 为等腰直角三角形，AB=DC，∴BE=DC，∵∠ CEF=∠ GCF=45°，∴∠ BEG=∠DCG=135°在△ BEG与△ DCG中，∵，∴△ BEG≌△ DCG，∴BG=DG，..∵CG⊥ EF，∴∠ DGC+∠ DGA=90°，又∵∠ DGC=∠ BGA，∴∠ BGA+∠ DGA=90°，∴△ DGB为等腰直角三角形，∴∠ BDG=45°．（3）解：延长 AB、 FG交于 H，连接 HD．∵ AD∥ GF， AB∥ DF，∴四边形 AHFD 为平行四边形∵∠ABC=120°， AF 平分∠ BAD∴∠ DAF=30°，∠ ADC=120°，∠ DFA=30°∴△ DAF 为等腰三角形∴AD=DF，∴CE=CF，∴平行四边形AHFD为菱形∴△ ADH，△ DHF 为全等的等边三角形∴DH=DF，∠ BHD=∠ GFD=60°∵FG=CE， CE=CF，CF=BH，∴ BH=GF在△ BHD 与△ GFD中，∵，∴△ BHD≌△ GFD，∴∠ BDH=∠GDF∴∠ BDG=∠ BDH+∠HDG=∠GDF+∠ HDG=60°..9．如图，已知 ?ABCD中， DE⊥ BC于点 E，DH⊥ AB 于点 H，AF 平分∠ BAD，分别交 DC、DE、 DH 于点 F、G、 M，且 DE=AD．（1）求证：△ ADG≌△ FDM．（2）猜想 AB 与 DG+CE之间有何数量关系，并证明你的猜想．【解答】证明：（1）∵四边形ABCD是平行四边形，∴AB∥ CD，AD∥ BC，∴∠ BAF=∠ DFA，∵ AF 平分∠ BAD，∴∠ DAF=∠ DFA，∴AD=FD，∵DE⊥ BC， DH⊥ AB，∴∠ ADG=∠ FDM=90°，在△ ADG 和△ FDM 中，，∴△ ADG≌△ FDM（ ASA）．（2） AB=DG+EC．证明：延长GD 至点 N，使 DN=CE，连接 AN，∵DE⊥ BC， AD∥ BC，∴∠ ADN=∠DEC=90°，..在△ ADN 和△ DEC中，，∴△ ADN≌△ DEC（ SAS），∴∠ NAD=∠CDE， AN=DC，∵∠ NAG=∠NAD+∠ DAG，∠ NGA=∠ CDE+∠ DFA，∴∠ NAG=∠NGA，∴AN=GN=DG+CE=DC，∵四边形 ABCD是平行四边形，∴AB=CD，∴AB=DG+EC．10．如图，在正方形ABCD 中， E、 F 分别为 BC、 AB 上两点，且BE=BF，过点B 作 AE 的垂线交 AC 于点 G，过点 G 作 CF的垂线交BC于点 H 延长线段AE、 GH 交于点 M．（ 1）求证：∠ BFC=∠ BEA；（ 2）求证： AM=BG+GM．【解答】证明：（ 1）在正方形 ABCD中， AB=BC，∠ ABC=90°，在△ ABE和△ CBF中，，..∴△ ABE≌△ CBF（ SAS），∴∠ BFC=∠BEA；（2）连接 DG，在△ ABG 和△ ADG 中，，∴△ ABG≌△ ADG（ SAS），∴BG=DG，∠2=∠3，∵ BG⊥AE，∴∠ BAE+∠ 2=90°，∵∠ BAD=∠ BAE+∠4=90°，∴∠ 2=∠3=∠ 4，∵ GM⊥ CF，∴∠ BCF+∠ 1=90°，又∠ BCF+∠ BFC=90°，∴∠ 1=∠BFC=∠ 2，∴∠ 1=∠3，在△ ADG 中，∠ DGC=∠3+45°，∴∠ DGC 也是△ CGH 的外角，∴D、G、 M 三点共线，∵∠ 3=∠4（已证），∴AM=DM ，∵DM=DG+GM=BG+GM，∴ AM=BG+GM．11．如图所示，把矩形纸片OABC 放入直角坐标系xOy 中，使OA、OC 分别落在x、 y 轴的正半轴上，连接AC，且 AC=4，..（1）求 AC所在直线的解析式；（2）将纸片 OABC折叠，使点 A 与点 C 重合（折痕为 EF），求折叠后纸片重叠部分的面积．（3）求 EF所在的直线的函数解析式．【解答】解：（ 1）∵=，∴可设 OC=x，则 OA=2x，在Rt△ AOC中，由勾股定理可得 OC2+OA2=AC2，∴ x2+（ 2x）2=（4 ）2，解得 x=4（ x=﹣ 4 舍去），∴ OC=4， OA=8，∴A（ 8， 0）， C（0， 4），设直线 AC 解析式为 y=kx+b ，∴，解得，∴直线 AC 解析式为y=﹣x+4；（ 2）由折叠的性质可知AE=CE，设AE=CE=y，则 OE=8﹣ y，在Rt△ OCE中，由勾股定理可得 OE2+OC2=CE2，∴（ 8﹣ y）2+42=y2，解得 y=5，∴AE=CE=5，∵∠ AEF=∠CEF，∠ CFE=∠ AEF，∴∠ CFE=∠ CEF，∴CE=CF=5，∴S△CEF= CF?OC= × 5× 4=10，..即重叠部分的面积为10；（3）由（ 2）可知 OE=3， CF=5，∴ E（3 ，0）， F（ 5，4 ），设直线 EF的解析式为 y=k′x+b′，∴，解得，∴直线 EF的解析式为y=2x﹣ 6．12．已知一次函数的图象与坐标轴交于A、B 点（如图），AE 平分∠ BAO，交x 轴于点 E．（1）求点 B 的坐标；（2）求直线 AE 的表达式；（3）过点 B 作 BF⊥ AE，垂足为 F，连接 OF，试判断△ OFB的形状，并求△ OFB的面积．（4）若将已知条件“AE平分∠ BAO，交 x 轴于点 E”改变为“点 E 是线段 OB上的一个动点（点 E 不与点 O、B 重合）”，过点 B 作 BF⊥AE，垂足为 F．设 OE=x，BF=y，试求 y 与 x 之间的函数关系式，并写出函数的定义域．..【解答】解：（ 1）对于 y=﹣x+6，当x=0 时， y=6；当 y=0 时， x=8，∴ OA=6， OB=8，在 Rt△ AOB中，根据勾股定理得： AB=10，则 A（ 0， 6）， B（8，0）；（ 2）过点 E 作 EG⊥ AB，垂足为 G（如图 1 所示），∵ AE 平分∠ BAO， EO⊥AO，EG⊥ AG，∴ EG=OE，在 Rt△ AOE和 Rt△ AGE中，，∴Rt△ AOE≌Rt△ AGE（HL），∴AG=AO，设OE=EG=x，则有 BE=8﹣ x， BG=AB﹣ AG=10﹣ 6=4，在Rt△ BEG中， EG=x， BG=4， BE=8﹣ x，根据勾股定理得： x2+4 2=（ 8﹣ x）2，解得： x=3，∴E（3 ，0），设直线 AE 的表达式为 y=kx+b（ k≠ 0），将A（ 0， 6）， E（ 3，0）代入 y=kx+b 得：，解得：，则直线 AE 的表达式为y=﹣ 2x+6；（ 3）延长 BF 交 y 轴于点 K（如图 2 所示），..∵AE 平分∠ BAO，∴∠ KAF=∠ BAF，又BF⊥AE，∴∠ AFK=∠ AFB=90°，在△ AFK和△ AFB 中，∵，∴△ AFK≌△ AFB，∴FK=FB，即F 为KB 的中点，又∵△ BOK为直角三角形，∴OF= BK=BF，∴△ OFB 为等腰三角形，过点 F 作 FH⊥ OB，垂足为H（如图 2 所示），∵OF=BF， FH⊥ OB，∴OH=BH=4，∴F 点的横坐标为 4，设F（ 4， y），将 F（ 4， y）代入 y=﹣ 2x+6 ，得： y=﹣ 2，∴ FH=| ﹣2| =2，则 S△OBF= OB?FH= × 8× 2=8；（4）在 Rt△ AOE中， OE=x， OA=6，根据勾股定理得：AE==，又BE=OB﹣ OE=8﹣ x， S△ABE= AE?BF= BE?AO（等积法），∴ BF==（0＜x＜8），又BF=y，则 y=（0＜x＜8）．13．如图，直线l1的解析表达式为：y=﹣ 3x+3，且 l1与 x 轴交于点D，直线 l2经过点 A，B，直线 l 1， l2交于点 C．（1）求点 D 的坐标；（2）求直线 l2的解析表达式；..（3）求△ ADC的面积；（4）在直线 l 2上存在异于点 C 的另一点 P，使得△ ADP 与△ ADC 的面积相等，请直接写出点 P 的坐标．【解答】解：（ 1）由 y=﹣ 3x+3，令 y=0，得﹣ 3x+3=0，∴x=1，∴D（ 1，0）；（ 2）设直线l 2的解析表达式为y=kx+b，由图象知： x=4，y=0； x=3，，代入表达式y=kx+b，∴，∴，∴直线 l2的解析表达式为；（ 3）由，解得，∴ C（2，﹣ 3），∵ AD=3，∴ S△ADC=× 3× |﹣3| =；（ 4）△ ADP 与△ ADC 底边都是AD，面积相等所以高相等，△ADC 高就是点 C 到直线AD 的距离，即 C 纵坐标的绝对值=| ﹣ 3| =3，则 P 到 AD 距离 =3，∴ P 纵坐标的绝对值=3，点 P 不是点 C，∴点 P 纵坐标是3，∵ y=1.5x﹣6 ，y=3，..∴1.5x﹣ 6=3x=6，所以 P（ 6，3）．14．如图 1，在平面直角坐标系中，O 是坐标原点，长方形OACB的顶点 A、B 分别在 x轴与 y 轴上，已知OA=6， OB=10．点 D 为 y 轴上一点，其坐标为（0， 2），点 P 从点 A出发以每秒 2 个单位的速度沿线段AC﹣CB 的方向运动，当点 P 与点 B 重合时停止运动，运动时间为t 秒．（1）当点 P 经过点 C 时，求直线 DP 的函数解析式；（2）①求△ OPD 的面积 S关于 t 的函数解析式；②如图②，把长方形沿着 OP 折叠，点 B 的对应点 B′恰好落在 AC 边上，求点 P 的坐标．（ 3）点P 在运动过程中是否存在使△BDP 为等腰三角形？若存在，请求出点P 的坐标；若不存在，请说明理由．【解答】解：（ 1）∵ OA=6， OB=10，四边形OACB为长方形，∴C（ 6， 10）．设此时直线DP 解析式为y=kx+b，把（ 0，2 ）， C（6， 10）分别代入，得，解得则此时直线DP 解析式为y=x+2；（ 2）①当点P 在线段 AC 上时， OD=2，高为 6， S=6；当点 P 在线段 BC 上时， OD=2，高为 6+10﹣2t=16 ﹣2t ，S=× 2×（16﹣2t）=﹣2t+16；②设 P（ m， 10），则 PB=PB′=m，如图 2，∵OB′=OB=10， OA=6，∴ AB′==8，..∴B′C=10﹣ 8=2，∵ PC=6﹣ m，∴m2=22+（ 6﹣ m）2，解得 m=则此时点 P 的坐标是（，10）；（ 3）存在，理由为：若△ BDP为等腰三角形，分三种情况考虑：如图3，①当 BD=BP1=OB﹣ OD=10﹣ 2=8，在Rt△ BCP1中， BP1=8， BC=6，根据勾股定理得： CP1==2 ，∴AP1=10﹣ 2 ，即 P1（6， 10﹣ 2 ）；②当BP2 =DP2时，此时 P2（ 6，6）；③当DB=DP3=8 时，在 Rt△ DEP 中， DE=6，3根据勾股定理得：P3E==2，∴ AP3=AE+EP3=2+2，即 P3（ 6， 2+2），综上，满足题意的P 坐标为（ 6， 6）或（ 6， 2+2）或（ 6， 10﹣ 2）．..15．如图，在平面直角坐标系中，已知O 为原点，四边形ABCD为平行四边形，A、 B、C 的坐标分别是A（﹣ 5，1）， B（﹣ 2， 4），C（ 5， 4），点 D 在第一象限．（ 1）写出 D 点的坐标；（ 2）求经过B、D 两点的直线的解析式，并求线段BD 的长；（ 3）将平行四边形ABCD 先向右平移 1 个单位长度，再向下平移 1 个单位长度所得的四边形 A1B1C1 D1四个顶点的坐标是多少？并求出平行四边形ABCD与四边形 A1 B1 C1D1重叠部分的面积．【解答】解：（ 1）∵ B（﹣ 2， 4）， C（ 5， 4），∴BC=5﹣（﹣ 2） =5+2=7，∵ A（﹣ 5，1），∴点 D 的横坐标为﹣ 5+7=2，∴点D 的坐标为（ 2， 1）；（ 2）设直线 BD 的解析式为 y=kx+b，将 B（﹣ 2， 4）、D（ 2， 1）代入得：，解得，∴经过 B、 D 两点的直线的解析式为y=﹣x+，过 B 点作 AD 的垂线，垂足为E，则 BE=4﹣ 1=3，DE=2﹣（﹣ 2）=2+2=4，..在 Rt△ BDE中， BD===5；（ 3）∵ ?ABCD向右平移1 个单位长度，再向下平移 1 个单位长度，∴A1（﹣ 4， 0），B1（﹣ 1， 3）， C1（ 6，3） D1（ 3，0 ），∴重叠部分的底边长 7﹣ 1=6，高为 3﹣1=2，∴重叠部分的面积S=6× 2=12．16．如图，一次函数的图象与x 轴、 y 轴交于点A、B，以线段AB 为边在第一象限内作等边△ABC，（ 1）求△ ABC的面积；（ 2）如果在第二象限内有一点P（ a，）；试用含有a 的代数式表示四边形ABPO的面积，并求出当△ABP的面积与△ ABC的面积相等时 a 的值；（3）在 x 轴上，是否存在点 M，使△ MAB 为等腰三角形？若存在，请直接写出点 M 的坐标；若不存在，请说明理由．【解答】解：（ 1）分别令 y=0 和 x=0，得一次函数y=x+1 的图象与x 轴．y 轴的交点坐标分别是A（，0），B（0，1），即OA=，OB=1，∴ AB==2∵△ ABC为等边三角形，∴ S△ABC=；（ 2）如图 1， S△AOB=，S△AOP=，S△BOP=| a| ?OB=﹣．∴ S 四边形ABPO=S△AOB+S△BOP=，而 S△ABP=S 四边形ABPO﹣S△APO，..∴当 S△ABP=S△ABC时，=，解得 a=﹣；（ 3）如图 2，满足条件的点M 有 4 个：M 1（﹣，0），M 2（﹣ 2，0），M3（，0），M 4（+2，0）．.。

新人教版八年级下压轴题

初二期末复习题1.△ABC 、△ADE 都是正三角形，CD=BF. （1）、求证：△ACD ≌△CBF（2）、当D 运动至BC 边上的何处时，四边形CDEF 为平行四边形，且∠DEF=30°,并证明你的结论.分析 ⑴.证明△ACD ≌△CBF 已经有了CD=BF ，而△ABC 、△ADE 都是正三角形又可以给我们提供,CA CB ACD CBF 60=∠=∠=条件，根据“SAS ”判定方法可以证得△ACD ≌△CBF.⑵.根据⑴问的△ACD ≌△CBF 得出AD CF =,又△ADE 是正三角形的DE CF =,所以CF DE =;要使四边形CDEF 为平行四边形可以证CF DE .若四边形CDEF 为平行四边形，则FCD DEF 30∠=∠=；当EDB 30∠=时，就有FCD EDB ∠=∠,此时就能证得CF DE .由正△ADE 可以得出ADE 60∠=，则ADB 603090∠=+=,AD BC ⊥;由于等腰三角形具有“三线合一”的特征，所以当D 运动至BC 边上中点时，四边形CDEF 为平行四边形.2.D 为□ABCD 外一点，∠APC=∠BPD=90°.求证: □ABCD 为矩形分析：判定矩形的方法主要有三种.但在已知了四边形ABCD 是平行四边形的情况下，要判定ABCD 是矩形的途径有两条：其一、找一内角是直角；其二、找出对角线相等，即找出AC BD =.由于本题的另一主要条件是∠APC=∠BPD=90°，要根据题中条件和图形位置转换成四边形的内角为90°比较困难，所以本题我们先想办法找出对角线相等，即找出AC BD =.我们发现本题在APC Rt 和BPD Rt 的两斜边的交点O 恰好是平行四边形对角线的交点，根据平行四边形对角线互相平分可知：O 同时是AC BD 、的中点；所以自然联想到连结PO 这条两直角三角形公共的中线（见图）.根据以上条件，在APC Rt 和BPD Rt 中就有：AC 2PO = BD 2PO =,故AC BD =,由对角线相等的平行四边形是矩形，可判定ABCD 是矩形.3. △ABC 中，∠BAC=90°，BD 平分∠ABC ，AH ⊥BC 于H 交BD 于E,DF ⊥BC 于F,求证：四边形AEFD 是菱形分析：判定菱形方法主要有三种，三种方法都可以使本题获得解决.下面我们选择“四边都相等的四边形是菱形”这一途径来分析. 可以先根据角平分线的性质得出AD FD =,进而容易证明 ABD ≌AFD ,所以BA BF =;再证明ABE ≌AFE 可以得到EA EF =（也可以利用等腰三角形的“三线合一”）；利用等角的余角相等可以推出 ADE AED ∠=∠,所以EA DA =,于是AE EF FD DA ===,故四边形AEFD 是菱形.4、如图所示，在菱形ABCD 中，,AB 4BAD 120=∠=，AEF为正三角形，点E F 、分别在菱形的边BC CD 、上滑动，且E F 、不与B C D 、、重合． ⑴.证明不论E F 、在BC CD 、D 上如何滑动，总有BE CF =? ⑵.当点E F 、在BC CD 、上滑动时，探讨四边形AECF 的面积是否发生变化？如果不变，求出这个定值. 分析： FA B CABH D EF OBPA 321EH AB F⑴.先求证AB AC =，进而求证ABC ACD 、为等边三角形，得=BAC 60AC AB ∠=，进而求证ABE≌ACF ，即可求得BE CF = ⑵.根据ABE ≌ACF 可得ABE ACF SS =;根据S 四边形AECF =AEC S +ACF S=AEC S+BAE S=ABC S即可解得.⑴.证明：连接AC ，如下图所示.∵四边形ABCD 为菱形，BAD 120∠=∴,1EAC 602EAC 60∠+∠=∠+∠= ∴12∠=∠∵BAD 120∠=∴ABC 60∠=∴ABC 和ACD 都为等边三角形 ∴=460AC AB ∠=， ∴在ABE 和ACF 中，12AB AC ABC 3∠=∠⎧⎪=⎨⎪∠=∠⎩∴ABE ≌ACF ()ASA ∴BE CF =⑵.解：四边形AECF 的面积不变.理由：由⑴得ABE ≌ACF ，则ABE ACF S S =.故S 四边形AECF =AEC S +ACF S =AEC S +BAE S =ABC S 是定值.作AH BC ⊥于H 点，则BH 2=S四边形ABCD ＝SABC =11BC AH 22⋅=5、(1)在图25－1中，已知∠MAN ＝120°，AC 平分∠MAN ． ∠ABC ＝∠ADC ＝90°，则能得如下两个结论： ① DC = BC; ②AD+AB=AC.请你证明结论②；(2)在图25－2中，把（1）中的条件“∠ABC ＝∠ADC ＝90°”改为∠ABC ＋∠ADC ＝180°，其他条件不变，则(1)中的结论是否仍然成立？若成立，请给出证明;若不成立，请说明理由．5、（1）证明：∵∠MAN ＝120°，AC 平分∠MAN ． ∴∠DAC = ∠BAC =60 ∵∠ABC ＝∠ADC ＝90°，∴∠DCA ＝∠BCA ＝30°，在Rt △ACD 中，∠DCA ＝30°，Rt △ACB 中， ∠BCA ＝30°∴AC=2AD ， AC = 2AB ， ∴2AD=2AB∴AD=AB∴AD+AB=AC.（2）解：（1）中的结论① DC = BC; ②AD+AB=AC 都成立理由如下：如图24－2，在AN 上截取AE=AC ，连结CE ， ∵∠BAC =60°，∴△CAE 为等边三角形， ∴AC=CE ，∠AEC =60°， ∵∠DAC =60°， ∴∠DAC =∠AEC ， ∵∠ABC ＋∠ADC ＝180°∠ABCCNMD BAN M DC＋∠EBC ＝180°，∴∠ADC =∠EBC ， ∴ADC △≌△EBC ∴DC = BC ，DA = BE ， ∴AD+AB=AB+BE=AE ， ∴AD+AB=AC ．6如图所示，直线l ：y=-221与x 轴、y 轴分别交于A 、B 两点，在y 轴上有一点C （0，4），动点M 从A 点以每秒1个单位的速度沿x 轴向左移动．（1）求A 、B 两点的坐标；（2）求△COM 的面积S 与M 的移动时间 t 之间的函数关系式；（3）当t 为何值时△COM ≌△AOB ，并求此时M 点的坐标．A 、B 两点的坐标分别为A （4，0）、B （0，2）；（2）∵C（0，4），A （4，0）∴OC=OA=4，当0≤t≤4时，OM=OA-AM=4-t ，S △OCM = 1 2×4×（4-t ）=8-2t ；当t ＞4时，OM=AM-OA=t-4，S △OCM = 1 2×4×（t-4）=2t-8；（3）分为两种情况：①当M 在OA 上时，OB=OM=2，△COM≌△AOB．∴AM=OA -OM=4-2=2∴动点M 从A 点以每秒1个单位的速度沿x 轴向左移动2个单位，所需要的时间是2秒钟； M （2，0），②当M 在AO 的延长线上时，OM=OB=2，则M （-2，0），即M 点的坐标是（2，0）或（-2，0）． 7、如图，直线y=kx+6分别与x 轴、y 轴相交于点E 和点F ，点E 的坐标为（-8，0），点A 的坐标为（0，6）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1、如图11，已知正比例函数和反比例函数的图像都经过点M （－2，1），且P （1，－2）为双曲线上的一点，Q 为坐标平面上一动点，PA 垂直于x 轴，QB 垂直于y 轴，垂足分别是A 、B ．
（1）写出正比例函数和反比例函数的关系式；
（2）当点Q 在直线MO 上运动时，直线MO 上是否存在这样的点Q ，使得△OBQ 与△OAP 面积相等？如果存在，请求出点的坐标，如果不存在，请说明理由；
（3）如图12，当点Q 在第一象限中的双曲线上运动时，作以OP 、OQ 为邻边的平行四边形
OPCQ ，求平行四边形OPCQ 周长的最小值．
解：（1）设正比例函数解析式为y kx =，将点M （2-，1-）坐标代入得1
2
k ，所以正
比例函数解析式为1
2
y
x 同样可得，反比例函数解析式为2y
x
（2）当点Q 在直线DO 上运动时，设点Q 的坐标为1()2
Q m m ，，于是2
1
11
12224
OBQ S OB BQ m m m △，而1
(1)(2)12
OAP S △，
所以有，
2114
m ，解得2m =±
所以点Q 的坐标为1(21)Q ，
和2(21)Q ，（3）因为四边形OPCQ 是平行四边形，所以OP ＝CQ ，OQ ＝PC ，
而点P （1-，2-）是定点，所以OP 的长也是定长，所以要求平行四边形OPCQ 周长的最小值就只需求OQ 的最小值．
因为点Q 在第一象限中双曲线上，所以可设点Q 的坐标为2()Q n n
，，由勾股定理可得2
2
22
42()4OQ
n n
n n
，
图
所以当22()0n
n
即20n
n
时，2OQ 有最小值4，
又因为OQ 为正值，所以OQ 与2
OQ 同时取得最小值，所以OQ 有最小值2．
由勾股定理得OP ＝5，所以平行四边形OPCQ 周长的最小值是
2()2(52)254OP OQ ．
2.已知：如图，正比例函数y ＝ax 的图象与反比例函数x
k
y
的图象交于点A (3，2)． (1)试确定上述正比例函数和反比例函数的表达式；
(2)根据图象回答，在第一象限内，当x 取何值时，反比例函数的值大于正比例函数的值； (3)M (m ，n )是反比例函数图象上的一动点，其中0＜m ＜3，过点M 作直线MB ∥x 轴，交
y 轴于点B ；过点A 作直线AC ∥y 轴交y 轴于点C ，交直线MB 于点D ．当四边形OADM 的面积为6时，请判断线段BM 与DM 的大小关系，并说明理由．
解答：解：（1）将A （3，2）分别代入y=，y=ax 中，得：2=，3a=2 ∴k=6，a=（2分）
∴反比例函数的表达式为：y=（3分）正比例函数的表达式为y=x （4分）
（2）观察图象，得在第一象限内，当0＜x ＜3时，反比例函数的值大于正比例函数的值．（6分）
（3）BM=DM （7分）
理由：∵MN ∥x 轴，AC ∥y 轴， ∴四边形OCDB 是平行四边形， ∵x 轴⊥y 轴，
∴▱OCDB 是矩形．
∵S △OMB =S △OAC =×|k|=3，又S 四边形OADM =6， ∴S 矩形OBDC =S 四边形OADM +S △OMB +S △OAC =3+3+6=12，即OC •OB=12 ∵OC=3
∴OB=4（8分）即n=4 ∴m=
∴MB=，MD=3﹣= ∴MB=MD （9分）．
3.如图，直线y=x+b （b ≠0）交坐标轴于A 、B 两点，交双曲线y=
x
2
于点D ，过D 作两坐标轴的垂线DC 、DE ，连接OD ．（1）求证：AD 平分∠CDE ；（2）对任意的实数b （b ≠0），求证BE ·OE 为定值；
（3）是否存在直线AB ，使得四边形OBCD 为平行四边形？若存在，求出直线的解析式；
若不存在，请说明理由．
A B
C E O D
x
y
4.如图（1），直线1
22
y x =-
+交x 轴、y 轴于A 、B 两点，C 为直线AB 上第二象限内一点，且S △AOC =8，双曲线k
y x
=经过点C
（1）求k 的值
（2）如图（2），过点C 作CM ⊥y 轴于M,反向延长CM 于H ，使CM=CH ，过 H 作HN ⊥x 轴于N ，交双曲线y=
x
k
于D ，求四边形OCHD 的面积（3）如图（3），点G 和点A 关于y 轴对称，P 为第二象限内双曲线上一个动点，过P 作PQ ⊥x 轴于Q ，分别交线段BG 于E,交射线BC 于F ，试判断线段 QE+QF 是否为定值，若为定值，证明并求出定值；若不是定值，请说明理由
x
y
O
C
A
B M H
D N
图（2）
图（3）
y O
C A
B G P
F
E
Q
x
y
O
C
A
B 图(1)。

人教版数学八级下册压轴题含答案

2021—2022学年人教版八年级下册数学期末动点最值压轴题

人教版八年级下册数学期末压轴题专题训练(含答案)

最新2019-2020年人教版八年级数学下册期末压轴题练习卷(有答案)

期末考试勾股定理与几何翻折压轴题专项训练—2023-2024学年八年级数学下学期(人教版)(解析版)

人教版八年级下册压轴题训练（含答案）

八年级下册数学压轴题(含答案)

人教版八年级数学下册经典压轴题考点及例题解析

最新人教版数学八年级下册压轴题含答案名师优秀教案

人教版数学八年级下册压轴题含答案

八年级下册数学压轴题(含答案)

(二)——2023-2024学年八年级数学下学期压轴题模拟训练(人教版)(解析版)

2020-2021学年人教版数学八年级下册期末压轴题专项复习卷(含答案)

(一)——2023-2024学年八年级数学下学期压轴题模拟训练(人教版)(解析版)

八年级下册数学期末压轴题(含答案)

八年级下压轴 50题(含答案及解析)

人教版八年级下册数学期末动点压轴题训练(带答案)

人教版八年级下册数学压轴题及答案

(完整)八年级下数学压轴题及答案.docx

新人教版八年级下压轴题