初二数学图形辅助线常见做法

合集下载

初中数学常见辅助线的做法

初中数学常见辅助线的做法
初中数学常见辅助线的做法
在初中数学中，辅助线是解题过程中常用的工具。

通过适当地引入辅助线，可以使问题更加清晰明了，从而更容易解决。

本文将介绍几种常见的辅助线做法。

1.平移法
平移法是一种常用的辅助线做法。

它的基本思想是将图形沿某个方向平移，使得问题更加清晰。

例如，在解决一个三角形的问题时，我们可以平移其中的一条边，使得三角形更加规则，从而更容易解决问题。

2.垂线法
垂线法也是一种常用的辅助线做法。

它的基本思想是引入垂线，将原问题转化为更简单的问题。

例如，在解决一个三角
形的问题时，我们可以引入垂线，将三角形分成两个直角三角形，从而更容易解决问题。

3.对称法
对称法是一种常用的辅助线做法。

它的基本思想是通过引入对称轴，将原问题转化为更简单的问题。

例如，在解决一个图形的问题时，我们可以引入对称轴，将图形分成对称的两部分，从而更容易解决问题。

4.相似法
相似法是一种常用的辅助线做法。

它的基本思想是通过找到相似的图形，将原问题转化为更简单的问题。

例如，在解决一个三角形的问题时，我们可以找到一个相似的三角形，从而更容易解决问题。

总之，辅助线是解决初中数学问题的常用工具。

通过灵活运用各种辅助线做法，我们可以更加轻松地解决各种数学问题。

初中数学辅助线的做法总结

初中数学辅助线的做法总结一、加法与减法辅助线1.相差减一法：对于计算两个数之差的问题，我们可以使用相减法，即将两个数按位相减，并将每一位之差写在下方。

为了更加清晰，可以在个位上方画一条水平线，表示个位数。

例如：45-23，画线表示为：4-233—2.加减齐次法：当计算加法或减法的时候，两个数位数不同，我们可以借助辅助线将两数齐次，使问题更易解。

例如：34+20，可以在个位上方画一条辅助线，表示个位数相加得4，十位数不变。

+0-----3.补充法：当计算减法时，被减数小于减数，我们可以通过补充的方式，使被减数增加一个数位，将问题转化为一个正常的减法。

例如：36-47，可以在个位上方画一条辅助线，表示个位数不够减，需要向十位借1，并在个位上加10，即变成36+10=46-47，再进行减法运算。

-136+10-47-------1二、乘法与除法辅助线1.竖式计算法：对于较复杂的乘法运算，我们可以使用竖式计算法，将乘法运算拆分为多个小的乘法运算。

例如：36×25，可以将25拆分成20和5，然后依次与36相乘，最后相加。

36×20-----72+180-----9002.倍数计算法：当计算除法时，我们可以利用倍数的性质，将除法问题转化为乘法问题。

分为两种情况：一是被除数为倍数的情况，二是除数为倍数的情况。

例如：115÷5，可以找到被除数和除数都是5的倍数，115÷5=(100+10+5)÷5=20+2+1=233.分数的乘法与除法：对于计算分数的乘除法，我们可以利用分数的定义和简化规则，将计算转化为整数的运算。

例如：(8/5)×(7/3)，可以将其转化为整数相乘，然后再进行约分。

8×7=565×3=15所以结果为56/15，再进行约分。

三、几何问题的辅助线1.直角三角形辅助线：解决直角三角形的问题时，可以在直角处画一条垂线，以辅助解题。

初中数学做辅助线的方法总结

初中数学做辅助线的方法总结
在初中数学中，做辅助线是解题的重要方法之一。

以下总结了几
种常见的做辅助线的方法：
1. 对称性辅助线法：当一个图形或方程式具有对称性时，可以
画出一条对称轴或一些对称线，从而利用对称性来简化问题。

例如，
在求三角形的中线长度相等定理时，可以描绘出三角形的垂直平分线，并在中点处作垂线，得到两个相等的直角三角形。

2. 垂线辅助线法：当一个角、线段或线段的垂线很难直接操作时，可以画出一条垂线，将问题转化为一个直角三角形问题。

例如，
在求一条线段的垂线长度时，可以先画出一条垂线与该线段相交，并
组成一个直角三角形。

3. 平移辅助线法：当一个几何图形或方程式涉及到平移时，可
以通过向图形或方程式添加平移线或平移量来使问题变得简单。

例如，在证明平行四边形对角线平分的定理时，可以平移一个平行四边形，
使其成为一个重合的平行四边形，从而使问题变得简单。

4. 分割辅助线法：当一个图形或方程式很复杂时，可以通过将
其分解成几个简单的部分来解题。

例如，在求多边形面积时，可以将
多边形分割成几个三角形或梯形，并将它们的面积相加，从而得到多
边形的面积。

总之，做辅助线的方法不只有以上四种，还可以根据具体问题的
不同情况选用其他的方法。

需要注意的是，在使用辅助线时，要注意
画出清晰的图形，并理解各种辅助线的作用，才能有效地解决问题。

人教版八年级上册几何常用辅助线秘籍

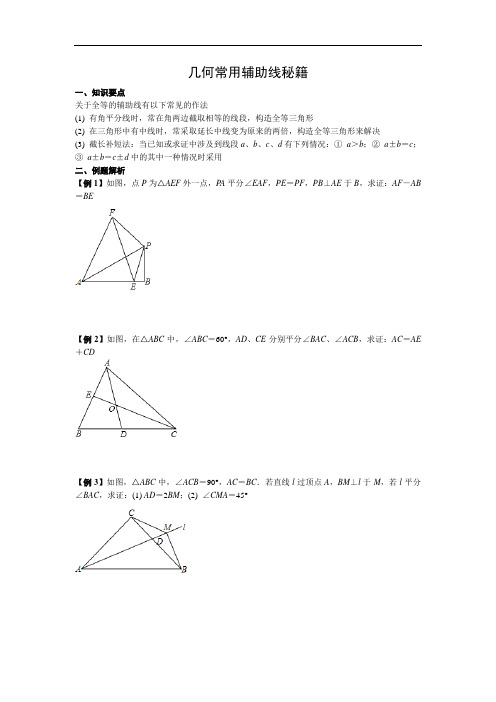
几何常用辅助线秘籍一、知识要点关于全等的辅助线有以下常见的作法(1) 有角平分线时，常在角两边截取相等的线段，构造全等三角形(2) 在三角形中有中线时，常采取延长中线变为原来的两倍，构造全等三角形来解决(3) 截长补短法：当已知或求证中涉及到线段a、b、c、d有下列情况：①a＞b；②a±b＝c；③a±b＝c±d中的其中一种情况时采用二、例题解析【例1】如图，点P为△AEF外一点，P A平分∠EAF，PE＝PF，PB⊥AE于B，求证：AF－AB ＝BE【例2】如图，在△ABC中，∠ABC＝60°，AD、CE分别平分∠BAC、∠ACB，求证：AC＝AE ＋CD【例3】如图，△ABC中，∠ACB＝90°，AC＝BC．若直线l过顶点A，BM⊥l于M，若l平分∠BAC，求证：(1) AD＝2BM；(2) ∠CMA＝45°【例4】如图，已知AD是△ABC的中线，BE交AC于点E，交AD于点F，且AE＝EF，求证：AC＝BF【例5】如图，在△ABC中，AB＝AC，延长AB到D，使BD＝AB，E为AB的中点，连结CE、CD，求证：CD＝2EC【例6】如图，△ABC中，∠C＝90°，BE⊥AB且BE＝AB，BD⊥BC且BD＝BC，CB的延长线交DE于F(1) 求证：点F是ED的中点(2) 求证：S△AB C＝2S△BEF【例7】如图，已知等腰Rt△ABC中，∠ACB＝90°，AC＝BC＝4，D为△ABC的一个外角∠ABF 的平分线上一点，且∠ADC＝45°，CD交AB于E(1) 求证：AD＝CD(2) 求AE的长三、课堂练习如图，△ABC中，CA＝CB，∠CAB＝∠CBA＝45°，点E为BC的中点，CN⊥AE交AB于N，求证：CN＋EN＝AE四、反馈练习1．如图，四边形ABCD中，AB＞AD，AC平分∠BAD，CE⊥AD于E点，若∠B＋∠ADC＝180°，求证；CD＝CB2．(1) 如图，△ABC中，若AD平分∠BAC，AB＋BD＝AC，求：∠C∶∠B (2) 如图，△ABC中，若AD平分∠BAC，∠B＝2∠C，求证：AB＋BD＝AC。

初中几何常用辅助线做法

常用辅助线做法➢考点考向1. 与角平分线有关的辅助线2. 与线段长度相关的辅助线3. 与等腰、等边三角形相关的辅助线4. 与中点相关的辅助线5. 构造一线三垂直（等角）6. 等面积法常见辅助线的作法总结1)遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变换中的“对折”．2)遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形，利用的思维模式是全等变换中的“旋转”．3)遇到角平分线，可以自角平分线上的某一点向角的两边作垂线，利用的思维模式是三角形全等变换中的“对折”，所考知识点常常是角平分线的性质定理或逆定理．4)过图形上某一点作特定的平分线，构造全等三角形，利用的思维模式是全等变换中的“平移”或“翻转折叠”。

5)截长法与补短法，具体做法是在某条线段上截取一条线段与特定线段相等，或是将某条线段延长，是之与特定线段相等，再利用三角形全等的有关性质加以说明．这种作法，适合于证明线段的和、差、倍、分等类的题目．6)构造等腰三角形或作等腰三角形的高利用“三线合一”性质。

7)作三角形的中位线。

8)引平行线构造全等三角形。

9）特殊方法：在求有关三角形的定值一类的问题时，常把某点到原三角形各顶点的线段连接起来，利用三角形面积的知识解答．（等面积法）10）构造三垂直模型。

✧考点一：与角平分线有关的辅助线（1）可向两边作垂线。

（2）可构造等腰三角形（3）在角的两边截取相等的线段，构造全等三角形【例1】已知：∠AOB＝90°，OM是∠AOB的平分线，将三角板的直角顶点P在射线OM上滑动，两直角边分别与OA、OB交于C、D，PC和PD有怎样的数量关系，请说明理由．✧考点二：与线段长度有关的辅助线（1）截长：证明某两条线段的和或差等于第三条线段时，经常在较长的线段上截取一段，使得它和其中的一条相等，再利用全等证明余下的等于另一条线段即可（2）补短：证明某两条线段的和或差等于第三条线段时，也可以在较短的线段上延长一段，使得延长的部分等于另外一条较短的线段，再利用全等证明延长后的线段等于那一条长线段即可（3）倍长中线：题目中如果出现了三角形的中线，方法是将中线延长一倍，再将端点连结，便可得到全等三角形。

初二数学辅助线常用做法及例题(含答案)

DCB A常见的辅助线的作法总论：全等三角形问题最主要的是构造全等三角形，构造二条边之间的相等，构造二个角之间的相等【三角形辅助线做法】图中有角平分线，可向两边作垂线。

也可将图对折看，对称以后关系现。

角平分线平行线，等腰三角形来添。

角平分线加垂线，三线合一试试看。

线段垂直平分线，常向两端把线连。

要证线段倍与半，延长缩短可试验。

三角形中两中点，连接则成中位线。

三角形中有中线，延长中线等中线。

1.等腰三角形“三线合一”法：遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题2.倍长中线：倍长中线，使延长线段与原中线长相等，构造全等三角形3.角平分线在三种添辅助线4.垂直平分线联结线段两端5.用“截长法”或“补短法”：遇到有二条线段长之和等于第三条线段的长，6.图形补全法：有一个角为60度或120度的把该角添线后构成等边三角形7.角度数为30、60度的作垂线法：遇到三角形中的一个角为30度或60度，可以从角一边上一点向角的另一边作垂线，目的是构成30-60-90的特殊直角三角形，然后计算边的长度与角的度数，这样可以得到在数值上相等的二条边或二个角。

从而为证明全等三角形创造边、角之间的相等条件。

8.计算数值法：遇到等腰直角三角形，正方形时，或30-60-90的特殊直角三角形，或40-60-80的特殊直角三角形,常计算边的长度与角的度数，这样可以得到在数值上相等的二条边或二个角，从而为证明全等三角形创造边、角之间的相等条件。

常见辅助线的作法有以下几种：最主要的是构造全等三角形，构造二条边之间的相等，二个角之间的相等。

1) 遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变换中的“对折”法构造全等三角形．2) 遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形，利用的思维模式是全等变换中的“旋转” 法构造全等三角形．3) 遇到角平分线在三种添辅助线的方法，（1）可以自角平分线上的某一点向角的两边作垂线，利用的思维模式是三角形全等变换中的“对折”，所考知识点常常是角平分线的性质定理或逆定理．（2）可以在角平分线上的一点作该角平分线的垂线与角的两边相交，形成一对全等三角形。

初二几何辅助线添加方法

初二几何辅助线添加方法几何辅助线是在解决几何问题时，通过添加额外的线段或线条来帮助我们更好地理解和解决问题。

在初二阶段的几何学中，辅助线的使用是非常重要的，可以帮助我们找到问题的关键点，简化问题的分析和解决过程。

下面将介绍几个常见的初二几何辅助线添加方法。

第一种方法是绘制垂直辅助线。

在解决一些关于垂直关系的问题时，我们可以通过添加垂直辅助线来辅助解题。

例如，在求两条平行直线之间的距离时，我们可以通过在两条直线上分别取一点，然后通过添加垂直辅助线来构建一个直角三角形，从而求出距离。

第二种方法是绘制平行辅助线。

在求两条直线平行或相交关系时，我们可以通过添加平行辅助线来辅助解题。

例如，在求两条平行线之间的距离时，我们可以通过添加一条与两条平行线相交的直线，然后构建一个平行四边形，从而求出距离。

第三种方法是绘制角平分线。

在解决涉及到角度的问题时，我们可以通过添加角平分线来辅助解题。

例如，在求一个角的角平分线时，我们可以通过画出这个角的两条边的延长线，然后通过它们的交点来构建角平分线。

第四种方法是绘制对称线。

在求对称形状或对称位置的问题时，我们可以通过添加对称线来辅助解题。

例如，在求一个图形的对称轴时，我们可以通过添加对称线来找到对称轴的位置。

除了上述介绍的四种常见的几何辅助线添加方法外，还有许多其他的方法。

例如，绘制中垂线来求三角形的垂心和外心，绘制角的角平分线来求多边形的内角和，等等。

每个问题都有其特定的解题方法和特定的辅助线添加方法。

总结起来，初二几何辅助线的添加方法是非常多样的。

通过合理地添加辅助线，可以帮助我们更好地理解和解决几何问题。

在解题过程中，我们应该根据问题的特点和要求，选择合适的辅助线添加方法。

同时，多进行几何练习，多掌握不同的辅助线添加方法，可以提高我们的解题能力和思维灵活性。

初中数学辅助线常用做法

初中数学辅助线常用做法1.三角形问题添加辅助线方法方法1：有关三角形中线的题目，常将中线加倍。

含有中点的题目，常常利用三角形的中位线，通过这种方法，把要证的结论恰当的转移，很容易地解决了问题。

方法2：含有平分线的题目，常以角平分线为对称轴，利用角平分线的性质和题中的条件，构造出全等三角形，从而利用全等三角形的知识解决问题。

方法3：结论是两线段相等的题目常画辅助线构成全等三角形，或利用关于平分线段的一些定理。

方法4：结论是一条线段与另一条线段之和等于第三条线段这类题目，常采用截长法或补短法，所谓截长法就是把第三条线段分成两部分，证其中的一部分等于第一条线段，而另一部分等于第二条线段。

2.平行四边形中常用辅助线的添法平行四边形（包括矩形、正方形、菱形）的两组对边、对角和对角线都具有某些相同性质，所以在添辅助线方法上也有共同之处，目的都是造就线段的平行、垂直，构成三角形的全等、相似，把平行四边形问题转化成常见的三角形、正方形等问题处理，其常用方法有下列几种，举例简解如下：（1）连对角线或平移对角线：（2）过顶点作对边的垂线构造直角三角形（3）连接对角线交点与一边中点，或过对角线交点作一边的平行线，构造线段平行或中位线（4）连接顶点与对边上一点的线段或延长这条线段，构造三角形相似或等积三角形。

（5）过顶点作对角线的垂线，构成线段平行或三角形全等.3.梯形中常用辅助线的添法在题目中若已知圆的直径，一般是作直径所对的圆周角，利用"直径所对的圆周角是直角"这一特征来证明问题。

（3）见切线作半径命题的条件中含有圆的切线，往往是连结过切点的半径，利用"切线与半径垂直"这一性质来证明问题。

（4）两圆相切作公切线对两圆相切的问题，一般是经过切点作两圆的公切线或作它们的连心线，通过公切线可以找到与圆有关的角的关系。

（5）两圆相交作公共弦对两圆相交的问题，通常是作出公共弦，通过公共弦既可把两圆的弦联系起来，又可以把两圆中的圆周角或圆心角联系起来。

初中几何辅助线大全(最全版)

三角形中作辅助线的常用方法举例一、延长已知边构造三角形：分析：欲证 AD ＝BC ，先证分别含有AD ，BC 的三角形全等，有几种方案：△ADC 与△BCD ，△AOD 与△BOC ，△ABD 与△BAC ，但根据现有条件，均无法证全等，差角的相等，因此可设法作出新的角，且让此角作为两个三角形的公共角。

证明：分别延长DA ，CB ，它们的延长交于E 点， ∵AD ⊥AC BC ⊥BD （已知） ∴∠CAE ＝∠DBE ＝90° （垂直的定义）在△DBE 与△CAE 中∵⎪⎩⎪⎨⎧=∠=∠∠=∠)()()(已知已证公共角AC BD CAE DBE E E∴△DBE ≌△CAE （AAS ）∴ED ＝EC EB ＝EA （全等三角形对应边相等） ∴ED －EA ＝EC －EB 即：AD ＝BC 。

（当条件不足时，可通过添加辅助线得出新的条件，为证题创造条件。

）二、连接四边形的对角线，把四边形的问题转化成为三角形来解决。

三、有和角平分线垂直的线段时，通常把这条线段延长。

分析：要证BD ＝2CE ，想到要构造线段2CE ，同时CE 与∠ABC 的平分线垂直，想到要将其延长。

证明：分别延长BA ，CE 交于点F 。

∵BE ⊥CF （已知）∴∠BEF ＝∠BEC ＝90° （垂直的定义）在△BEF 与△BEC 中，19-图DCBAEF 12ABCDE17-图O∵ ⎪⎩⎪⎨⎧∠=∠=∠=∠)()()(21已证公共边已知BEC BEF BE BE ∴△BEF ≌△BEC （ASA ）∴CE=FE=21CF （全等三角形对应边相等） ∵∠BAC=90° BE ⊥CF （已知）∴∠BAC ＝∠CAF ＝90° ∠1＋∠BDA ＝90°∠1＋∠BFC ＝90° ∴∠BDA ＝∠BFC在△ABD 与△ACF 中⎪⎩⎪⎨⎧∠=∠∠=∠)()()(已知＝已证已证AC AB BFC BDA CAF BAC∴△ABD ≌△ACF （AAS ）∴BD ＝CF （全等三角形对应边相等） ∴BD ＝2CE四、取线段中点构造全等三有形。

初中几何辅助线大全(很详细哦)

初中几何辅助线大全(很详细哦)初中几何辅助线―克胜秘籍等腰三角形1.作底边上的高，构成两个全等的直角三角形，这是用得最多的一种方法；2.作一腰上的高；3.将底边的一端作为底边的垂直线交叉，并与另一条腰部的延长线相交，形成直角三角形。

梯形1.垂直于平行边2.垂直于下底，将上底延伸为一条平行于两条斜边的腰部3的平行线4使两条垂直于底部的垂直线5延伸两条斜边，形成一个三角形菱形1.连接两对角2.做高平行四边形1.垂直于平行边2.按对角线将平行四边形分成两个三角形，高度为3-注意形状内外的矩形1.对角线2.作垂线很简单。

无论是哪一个主题，第一个都应该考虑主题的要求，例如Ab= AC+BD，这样的方法是找到另一个与AB长度相同的线段的方法，然后证明A+BD＝另一个AB。

三角形图中有角平分线，可向两边作垂线（垂线段相等）。

也可将图对折看，对称以后关系现。

角平分线平行线，等腰三角形来添。

角平分线加垂线，三线合一试试看。

线段垂直平分线，常向两端把线连。

要证线段倍与半，延长缩短可试验。

三角形的中点连接成一条中线。

三角形中有中线、延长中线和其他中线。

解几何题时如何画辅助线?① 在中点处看到中线，并将中线延长一倍在几何题中，如果给出中点或中线，可以考虑过中点作中位线或把中线延长一倍来解决相关问题。

② 在证明比例线段时，通常使用平行线。

作平行线时往往是保留结论中的一个比，然后通过一个中间比与结论中的另一个比联系起来。

③ 对于梯形问题，添加辅助线的常用方法有：1。

穿过上底的两个端点用作下底的垂直线；2.穿过上底的一个端点用作一条腰部的平行线；3.穿过上底部的一个端点用作对角线的平行线；4.穿过一根腰部的中点用作另一根腰部的平行线5、过上底一端点和一腰中点的直线与下底的延长线相交6、作梯形的中位线7、延长两腰使之相交四边形的平行四边形出现，对称中心等分点。

梯形里面作高线，平移一腰试试看。

平行移动对角线，补成三角形常见。

证相似，比线段，添线平行成习惯。

初中数学常见辅助线做法

初中数学常用辅助线一.添辅助线有二种情况:1按定义添辅助线:如证明二直线垂直可延长使它们,相交后证交角为90°;证线段倍半关系可倍线段取中点或半线段加倍;证角的倍半关系也可类似添辅助线。

2按基本图形添辅助线:每个几何定理都有与它相对应的几何图形,我们把它叫做基本图形,添辅助线往往就是具有基本图形的性质而基本图形不完整时补完整基本图形,因此“添线”应该叫做“补图”！这样可防止乱添线,添辅助线也有规律可循。

举例如下:(1)平行线就是个基本图形:当几何中出现平行线时添辅助线的关键就是添与二条平行线都相交的等第三条直线(2)等腰三角形就是个简单的基本图形:当几何问题中出现一点发出的二条相等线段时往往要补完整等腰三角形。

出现角平分线与平行线组合时可延长平行线与角的二边相交得等腰三角形。

(3)等腰三角形中的重要线段就是个重要的基本图形:出现等腰三角形底边上的中点添底边上的中线;出现角平分线与垂线组合时可延长垂线与角的二边相交得等腰三角形中的重要线段的基本图形。

(4)直角三角形斜边上中线基本图形出现直角三角形斜边上的中点往往添斜边上的中线。

出现线段倍半关系且倍线段就是直角三角形的斜边则要添直角三角形斜边上的中线得直角三角形斜边上中线基本图形。

(5)三角形中位线基本图形几何问题中出现多个中点时往往添加三角形中位线基本图形进行证明当有中点没有中位线时则添中位线,当有中位线三角形不完整时则需补完整三角形;当出现线段倍半关系且与倍线段有公共端点的线段带一个中点则可过这中点添倍线段的平行线得三角形中位线基本图形;当出现线段倍半关系且与半线段的端点就是某线段的中点,则可过带中点线段的端点添半线段的平行线得三角形中位线基本图形。

(6)全等三角形:全等三角形有轴对称形,中心对称形,旋转形与平移形等;如果出现两条相等线段或两个档相等角关于某一直线成轴对称就可以添加轴对称形全等三角形:或添对称轴,或将三角形沿对称轴翻转。

数学辅助线常用做法(八年级学生适用)

规律1.当两直线平行时，同位角的角平分线互相平行，内错角的角平分线互相平行，同旁内角的角平分线互相垂直.例：如图，以下三种情况请同学们自己证明.规律2. 有以线段中点为端点的线段时，常加倍延长此线段构造全等三角形.例：已知，如图，AD 为△ABC 的中线，且∠1 = ∠2，∠3 =∠4，求证：BE ＋CF ＞EF规律3. 在三角形中有中线时，常等倍延长中线构造全等三角形. 例：已知，如图，AD 为△ABC 的中线，求证：AB ＋AC ＞2AD规律4. 当已知或求证中涉及到线段a 、b 、c 、d 有下列情况之一时用截长补智短法： ①a＞b ②a±b = c ③a±b = c±d截长法：在较长的线段上截取一条线段等于较短线段；补短法：延长较短线段和较长线段相等. 这两种方法统称截长补短法. 例：已知，如图，在△ABC 中，AB ＞AC ，∠1 = ∠2，P 为AD 上任一点，求证：AB －AC ＞PB －PCMABC D E F12345 12E DC B AP12NCBAA B21PH G FE D B C A H GFE D B C A H GFE D BC AE F D C B A 练习：1.已知，在△ABC 中，∠B = 60o,AD 、CE 是△ABC 的角平分线,并且它们交于点O求证：AC = AE ＋CD 2.已知，如图，AB ∥CD ∠1 = ∠2 ,∠3 = ∠4.求证：BC = AB ＋CD规律5.在一个图形中，有多个垂直关系时，常用同角（等角）的余角相等来证明两个角相等.例：已知，如图Rt △ABC 中，AB = AC ，∠BAC = 90o，过A 作任一条直线AN ，作BD ⊥AN 于D ，CE ⊥AN 于E ，求证：DE = BD －CE规律6.连接四边形的对角线，把四边形问题转化成三角形来解决问题. 例：已知，如图，AB ∥CD ，AD ∥BC 求证：AB = CD练习：已知，如图，AB = DC ，AD = BC ，DE = BF ，求证：BE = DF规律7.有和角平分线垂直的线段时，通常把这条线段延长。

初中数学做辅助线的方法总结

初中数学做辅助线的方法总结初中数学中，辅助线是解题的一种重要方法，可以帮助我们清晰地理解题意和问题，并找到解题的思路。

下面是关于初中数学做辅助线的方法总结。

一、直线法1.作垂线：当题目中出现垂直关系时，我们可以通过作垂线来解决问题。

例如，求两个直线的垂直平分线、两个线段的中垂线等。

2.作平行线：当需要证明两条直线平行时，可以通过作一条与已知直线平行的辅助线，再应用平行线的性质进行证明。

二、角度法1.作角平分线：当需要求一个角平分线时，可以通过作一个角的辅助线将该角分成两个相等的角，进而求出角平分线。

2.作等角：当题目中需要证明两个角相等时，可以通过作一条等角的辅助线，将两个角变成等角，然后再应用等角的性质进行证明。

三、三角形法1.作高：当需要求一个三角形的高时，可以通过作条辅助线，形成一个矩形或直角三角形，从而利用高的性质求解。

2.作中线：当需要求一个三角形的中线时，可以通过作条辅助线，形成一个平行四边形或直角三角形，从而利用中线的性质求解。

3.作角平分线：当需要求一个三角形的角平分线时，可以通过作条辅助线，将该角分成两个相等的角，进而求出角平分线。

四、平行四边形法1.作对角线：当题目中出现平行四边形时，可以通过作对角线来将该平行四边形分成两个相等的三角形，进而利用三角形的性质进行求解。

五、轴对称法1.关于对称轴作对称点：当题目中出现轴对称图形时，可以通过作关于对称轴的对称点，将原图形和对称点所成的线段连结起来，形成对称图形，从而利用对称性进行求解。

六、相似三角形法1.作比例：当需要求解两个三角形相似的比例时，可以通过作条辅助线，形成相似三角形，并利用相似三角形的性质求解。

七、图形拓展法1.分割图形：当需要对一个复杂的图形进行分析时，可以通过作一些辅助线，将复杂图形分割成若干个简单的图形，进而分别求解。

总之，在初中数学中，辅助线是解题的有力工具，可以帮助我们合理分析题目，找到解题的思路，解决数学问题。

初中数学常见辅助线的做法

初中数学常见辅助线的做法一、中点模型的构造1.已知任意三角形一边上的中点，可以考虑：(1)倍长中线或类中线(与中点有关的线段)构造全等三角形.如图1、图2所示.(2)三角形中位线定理.2.已知直角三角形斜边中点，可以考虑构造斜边中线.3.已知等腰三角形底边中点，可以考虑与顶点连接用“三线合一二4.有些题目的中点不直接给出，此时需要我们挖掘题目中的隐含中点，例如：直角三角形中斜边中点, 等腰三角形底边上的中点，当没有这些条件的时候，可以用辅助线添加.二、角平分线模型的构造与角平分线有关的常用辅助线作法,即角平分线的四大基本模型.已知。

是4MON平分线上一点，(1)若以_L 0M于点4 ,如图1,可以过户点作PB1ON于点&则与二以.可记为“图中有角平分线, 可向两边作垂线”.(2)若点4是射线0M上任意一点，如图2,可以在ON上截取(用=0/1 ,连接/7人构造△()*?三△ /%.可记为“图中有角平分线，可以将图对折看，对称以后关系现二⑶若翼妆舔踹嚼鼠3耳以黠部交0N于点从周造A4 0H基尊健三角形/是底边4加勺中点.可记为“角平分线加垂线，三线合一试试看二(4)若过P点作PQ//0N交0M于点0,如图4,可以构造△P0Q是等腰三角形，可记为“角平分线+平行线，等腰三角形必呈现二三、轴对称模型的构造下面给出几种常见考虑要用或作轴对称的基本图形.(1 )线段或角度存在2倍关系的,可考虑对称.(2)有互余、互补关系的图形，可考虑对称.(3)角度和或差存在特殊角度的，可考虑对称.(4)路径最短问题，基本上运用轴对称，将分散的线段集中到两点之间，从而运用两点之间线段最短，来实现最短路径的求解.所以最短路径问题，需考虑轴对称.几何最值问题的儿种题型及解题作图方法如下表所示.四、圆中辅助线构造在平面几何中，解决与圆有关的问题时，常常需要添加适当的辅助线，架起题设和结论间的桥梁,从而使问题化难为易，顺其自然地得到解决，因此, 灵活掌握作辅助线的一般规律和常见方法，对.提高学生分析问题和解决问题的能力是大有帮助的。

初二几何题辅助线技巧

初二几何题辅助线技巧
初二的几何学习中，辅助线是一个重要的技巧。

它可以帮助我们更快地解决难题，节省时间，提高解题效率。

以下是一些关于初二几何题辅助线技巧的建议：
1.使用垂线和平行线
在解决三角形和四边形的问题时，我们可以使用垂线和平行线来辅助解题。

例如，当我们需要求一个三角形的高度时，我们可以通过画一条垂线，将三角形分割成两个直角三角形，然后应用三角函数求解。

同样，在解决四边形的问题时，我们可以使用平行线来构造相似三角形，然后应用相似三角形的性质来求解。

2.使用中垂线
在解决圆的问题时，我们可以使用中垂线来辅助求解。

中垂线是连接圆心与一个线段中点的线段。

当我们需要求一个线段的中点时，我们可以通过将两个圆心连接线段两端，然后连接两个圆心的中垂线来找到线段中点。

同样，在解决圆的切线问题时，我们可以使用中垂线来构造一个直角三角形，然后应用三角函数来求解。

3.使用角平分线
在解决角度问题时，我们可以使用角平分线来辅助求解。

角平分线将一个角分成两个相等的角。

当我们需要求一个角度的大小时，我们可以通过使用角平分线来构造一个直角三角形，然后应用三角函数来求解。

同样，在解决三角形相似性问题时，我们可以使用角平分线来构造相似三角形，然后应用相似三角形的性质来求解。

综上所述，初二几何题辅助线技巧是解决难题的有效方法。

通过熟练掌握这些技巧，我们可以更快地解决问题，提高解题效率。

(完整版)初二数学辅助线常用做法及例题(含答案)

也可将图对折看，对称以后关系现。

角平分线平行线，等腰三角形来添。

角平分线加垂线，三线合一试试看。

线段垂直平分线，常向两端把线连。

要证线段倍与半，延长缩短可试验。

三角形中两中点，连接则成中位线。

三角形中有中线，延长中线等中线。

从而为证明全等三角形创造边、角之间的相等条件。

常见辅助线的作法有以下几种：最主要的是构造全等三角形，构造二条边之间的相等，二个角之间的相等。

初中数学常用辅助线添加技巧

初中数学常用辅助线添加技巧初中数学常用辅助线添加技巧一.添辅助线有二种情况：1按定义添辅助线：如证明二直线垂直可延长使它们相交后证交角为90°;证线段倍半关系可倍线段取中点或半线段加倍;证角的倍半关系也可类似添辅助线。

2按基本图形添辅助线：每个几何定理都有与它相对应的几何图形，我们把它叫做基本图形，添辅助线往往是具有基本图形的性质而基本图形不完整时补完整基本图形，因此“添线”应该叫做“补图”!这样可防止乱添线，添辅助线也有规律可循。

举例如下：(1)平行线是个基本图形：当几何中出现平行线时添辅助线的关键是添与二条平行线都相交的等第三条直线(2)等腰三角形是个简单的基本图形：当几何问题中出现一点发出的二条相等线段时往往要补完整等腰三角形。

出现角平分线与平行线组合时可延长平行线与角的二边相交得等腰三角形。

(3)等腰三角形中的重要线段是个重要的基本图形：出现等腰三角形底边上的中点添底边上的中线;出现角平分线与垂线组合时可延长垂线与角的二边相交得等腰三角形中的重要线段的基本图形。

(4)直角三角形斜边上中线基本图形出现直角三角形斜边上的中点往往添斜边上的中线。

出现线段倍半关系且倍线段是直角三角形的斜边则要添直角三角形斜边上的中线得直角三角形斜边上中线基本图形。

(5)三角形中位线基本图形几何问题中出现多个中点时往往添加三角形中位线基本图形进行证明当有中点没有中位线时则添中位线，当有中位线三角形不完整时则需补完整三角形; 当出现线段倍半关系且与倍线段有公共端点的线段带一个中点则可过这中点添倍线段的平行线得三角形中位线基本图形;当出现线段倍半关系且与半线段的端点是某线段的中点，则可过带中点线段的端点添半线段的平行线得三角形中位线基本图形。

(6)全等三角形：全等三角形有轴对称形，中心对称形，旋转形与平移形等;如果出现两条相等线段或两个档相等角关于某一直线成轴对称就可以添加轴对称形全等三角形：或添对称轴，或将三角形沿对称轴翻转。