高中物理专题复习 力的合成 与分解
高一物理力的合成和分解知识点

高一物理力的合成和分解知识点力的合成和分解是高中物理中一个非常重要的知识点,它是力学研究的基础。
在这篇文章中,我们将探讨力的合成和分解的概念、方法以及应用。
一、力的合成力的合成是指将多个力合成为一个力的过程。
当多个力作用于同一个物体时,可以将它们合成为一个等效的力。
1.1 向量图示法向量图示法是力的合成的一种常用方法。
我们将多个力用箭头表示,箭头的长度代表了力的大小,箭头的方向表示了力的方向。
将多个力的箭头连在一起,起点为物体的起始位置,终点为物体的终止位置,最后结果的箭头即为合成力。
1.2 分解求合分解求合是另一种常用的力的合成方法。
对于平行四边形法则中的图形,我们可以用三角形法则将合力分解为两个分力。
分解时,需要确定一个参考方向,将合力拆分为垂直于参考方向的两个分力。
二、力的分解力的分解是指将一个力分解为平行或垂直于某一方向的两个力的过程。
力的分解可以将一个复杂的问题简化为两个相对简单的问题,便于计算。
2.1 平行分解平行分解是将一个力分解为平行于某一参考方向的两个力的过程。
利用力的平行四边形法则,我们可以通过确定一个参考方向,将合力拆分为两个平行力。
2.2 垂直分解垂直分解是将一个力分解为垂直于某一参考方向的两个力的过程。
利用力的三角形法则,我们可以通过确定一个参考方向,将合力拆分为一个垂直于参考方向的力和一个平行于参考方向的力。
三、力的合成和分解的应用力的合成和分解在物理学中有广泛的应用。
下面我们将介绍几个常见的应用。
3.1 平面力问题在平面力问题中,物体受到多个平面力的作用。
利用力的合成和分解的方法,可以将这些力合成为一个等效力,从而简化问题的求解。
3.2 斜面上的力在斜面上,一个物体同时受到重力和斜面给予的支持力的作用。
利用力的分解,我们可以将这两个力分解为平行于斜面和垂直于斜面的两个力,以便求解问题。
3.3 物体受力平衡问题在物体受力平衡问题中,物体受到多个力的作用,且力的合力为零。
高一物理力的合成和分解

高一物理力的合成和分解1、力的合成利用一个力(合力)产生的效果跟几个力(分力)共同作用产生的效果相同,而做的一种等效替代。
力的合成必须遵循物体的同一性和力的同时性。
2、(1)合力和分力:如果一个力产生的效果跟几个力共同作用产生的效果相同,这个力就叫那几个力的合力,那几个力就叫这个力的分力。
合力与分力的关系是等效替代关系,即一个力若分解为两个分力,在分析和计算时,考虑了两个分力的作用,就不可考虑这个力的作用效果了;反过来,若考虑了合力的效果,也就不能再去重复考虑各个分力的效果。
3、(2)共点力:物体同时受几个力作用,如果这些力的作用线交于一点,这几个力叫共点力。
如图(a)所示,为一金属杆置于光滑的半球形碗中。
杆受重力及A、B两点的支持力三个力的作用;N1作用线过球心,N2作用线垂直于杆,当杆在作用线共面的三个非平行力作用下处于平衡状态时,这三力的作用线必汇于一点,所以重力G的作用线必过N1、N2的交点0;图(b)为竖直墙面上挂一光滑球,它受三个力:重力、墙面弹力和悬线拉力,由于球光滑,它们的作用线必过球心。
(3)4、力的合成定则:a、平行四边形定则:求共点力F1、F2的合力,可以把表示F1、F2的线段为邻边作平行四边形,它的对角线即表示合力的大小和方向,如图a。
b、三角形定则:求F1、F2的合力,可以把表示F1、F2的有向线段首尾相接,从F1的起点指向F2的末端的有向线段就表示合力F的大小和方向,如图b。
5、力的分解(1)在分解某个力时,要根据这个力产生的实际效果或按问题的需要进行分解;(2)有确定解的条件:①已知合力和两个分力的方向,求两个分力的大小.(有唯一解)②已知合力和一个分力的大小与方向,求另一个分力的大小和方向.(有一组解或两组解)③已知合力、一个分力F1的大小与另一分力F2的方向,求F1的方向和F2的大小.(有两个或唯一解)(3)力的正交分解:将已知力按互相垂直的两个方向进行分解的方法。
高中物理力的合成与分解

高中物理力的合成与分解高中物理力的合成与分解一、什么是物理力的合成与分解物理力的合成与分解是指物理力的构成和其结果的分解,也就是把两个或多个相互作用的力通过分析、变换运算而组合起来,产生新的力,或者逆运算把一个力分解为它的组成部分。
二、物理力的合成1、合成平行力平行力可以用下面的公式合成:F=F1+F2,这句公式表示将两个力(F1和F2)把它们合成一个力,两个力的方向应该相同,这两个力的大小可以相同也可以不同,经过运算只剩下一个力,大小为F1+F2。
2、合成垂直力垂直力可以用下面的公式合成:F=F1+F2,这句公式表示将两个力(F1和F2)把它们合成一个力,两个力的方向应该垂直,这两个力的大小可以相同也可以不同,经过运算只剩下一个力,大小为F1+F2。
三、物理力的分解1、分解平行力平行力可以用下面的公式分解:F=F1+F2,这句公式表示将一个力(F)分解成两个力(F1和F2),两个力的方向应该相同,可以使用推出的力和原来的力的比值来确定两个力的大小,例如原来的力F是30N,可以分解为F1=20N,F2=10N。
2、分解垂直力垂直力可以用下面的公式分解:F=F1+F2,这句公式表示将一个力(F)分解成两个力(F1和F2),两个力的方向应该垂直,可以使用推出的力和原来的力的比值来确定两个力的大小,例如原来的力F是30N,可以分解为F1=20N,F2=10N。
四、物理力的合成与分解的应用物理力的合成与分解在物理和工程学中都有广泛的应用,它可以用于分析物理现象,可以用于物体运动的分析,也可以用于结构力学的计算和分析。
此外,物理力的合成与分解也可以用于物体机械工程结构设计,例如机械臂的设计和调整,以及飞机机翼结构的设计和优化调整。
高中物理知识点总结:力的合成、力的分解

力的合成与分解一、共点力作用于同一物体且作用线能够相交于一点的几个力,称之为共点力。
二、力的合成1、合力与分力如果一个力作用在物体上与几个力共同作用在物体上产生的效果相同,那么这个力就是那几个力的合力,那几个力就是这个力的分力。
相同的效果包括使物体产生相同的形变或是使物体产生相同的加速度。
2、合力与分力的关系合力与分力是一种等效代换的关系。
下图中,物体在力F作用下处于静止状态,在力 F1、F2共同作用下也能处于静止状态,即F1、F2共同作用的效果与力F单独作用的效果相同,于是F是F1、F2的合力;F1、F2是力F的分力,从作用效果上可以相互替换。
即,对于下图而言,可以认为没有F1、F2作用,而是有力F作用,替换后,物体的运动状态保持不变。
3、力的合成(1)力的合成:已知分力求合力的过程称为力的合成。
(2)平行四边形定则:以表示两个分力的线段为邻边作平行四边形,该平行四边形的对角线表示合力的大小和方向。
2.力的平行四边形定则求两个互成角度的力的合力,可以用表示这两个力的线段为邻边作平行四边形,它的对角线就表示合力的大小和方向.F1F2FOF1F2FO说明:①矢量的合成与分解都遵从平行四边形定则(可简化成三角形定则)②力的合成和分解实际上是一种等效替代.③由三角形定则还可以得到一个有用的推论:如果n个力首尾相接组成一个封闭多边形,则这n个力的合力为零.④在分析同一个问题时,合矢量和分矢量不能同时使用.也就是说,在分析问题时,考虑了合矢量就不能再考虑分矢量;考虑了分矢量就不能再考虑合矢量.⑤矢量的合成分解,一定要认真作图.在用平行四边形定则时,分矢量和合矢量要画成带箭头的实线,平行四边形的另外两个边必须画成虚线.各个矢量的大小和方向3.根据力的平行四边形定则可得出以下几个结论:①共点的两个力(F1、F2)的合力(F)的大小,与它们的夹角(θ)有关;θ越大,合力越小;θ越小,合力越大.F1与F2同向时合力最大;F1与F2反向时合力最小,合力的取值范围是:_____________≤F≤________________.②合力可能比分力大,也可能比分力小,也可能等于某一分力.③共点的三个力,如果任意两个力的合力最小值小于或等于第三个力,那么这三个共点力的合力可能等于零.(3)三角形定则与多边形定则4、两个共点力的合成总结(1)两个分力在一条直线上且同向时,它们的合力大小为两力之和,方向同两力方向。
高中物理知识点:力的合成与分解公式

高中物理知识点:力的合成与分解公式
1.同一直线上力的合成同向:F=F1+F2,反向F=F1-F2 (F1>F2)
2.互成角度力的合成F=(F12+F22+2F1F2cosα)1/2(余弦定理)F1⊥F2时:F=(F12+F22)1/2
3.合力大小范围|F1-F2|小于等于F小于等于|F1+F2|
4.力的正交分解Fx=Fcosβ,Fy=Fsinβ(β为合力与x轴之间的夹角tgβ=Fy/Fx)注(1)力(矢量)的合成与分解遵循平行四边形定则;(2)合力与分力的关系是等效替代关系,可用合力替代分力的共同作用,反之也成立;(3)除公式法外,也可用作图法求解,此时要选择标度,严格作图;(4)F1与F2的值一定时,F1与F2的夹角(α角)越大,合力越小;(5)同一直线上力的合成,可沿直线取正方向,用正负号表示力的方向,化简为代数运算。
高一物理-力的合成与分解

第三讲 力的合成与分解知识点一:力的合成合力与分力:如果一个力作用在物体上,它产生的效果跟几个力共同作用在物体上产生的效果相同,这个力就叫做那几个力的合力,而那几个力叫做这个力的分力 力的合成:求几个已知力的合力叫做力的合成①共点力:几个力如果都作用在物体的同一点上,或者它们的作用线相交于同一点,这几个力叫共点力 ②平行四边形定则:根据两个分力的大小和方向,用力的图示法,从力的作用点起,按同一标度作出两个分力 F 1、F 2,以F 1、F 2为邻边作平行四边形,它的对角线就表示合力的大小及方向③矢量三角形法则:将两分力F 1、F 2首尾相接(有箭头的叫尾,无箭头的叫首),由F 1的首端指向F 2的尾端 的有向线段即为合力F 的大小及方向二力合成:2121F FF F F +≤≤-合,θ越大,F 合越小 ①当︒=0θ时,即两个力的方向一致,21F F F +=合,为最大②当︒=180θ时,即二力方向相反,21-F F F =合,为最小,且方向与较大的力的方向一致③当︒=90θ时,2221F F F +=合,12tan F F =θ④当︒=120θ,且F 1=F 2时,F 合=F 1=F 2,合力的方向在两分力的夹角平分线上 题型一、概念理解1. 关于两个大小不变的共点力与其合力的关系,下列说法正确的是( )A 合力大小随两力夹角增大而增大B 合力的大小一定大于分力中最大者C 两个分力夹角小于180°时,合力大小随夹角减小而增大D 合力的大小不能小于分力中最小者 2、 关于共点力,下列说法中不正确的是( )A 作用在一个物体上的两个力,如果大小相等,方向相反,这两个力是共点力B 作用在一个物体上的两个力,如果是一对平衡力,则这两个力是共点力C 作用在一个物体上的几个力,如果它们的作用点在同一点上,则这几个力是共点力D 作用在一个物体上的几个力,如果它们力的作用线汇交于同一点,则这几个力是共点力 3、 关于两个分力F 1、F 2与它们的合力F ,下列说法中正确的是( )A 合力F 的作用效果一定与F 1 , F 2共同作用产生的效果相同B F 1、 F 2一定是同种性质的力C F 1、 F 2 不一定是同一个物体受的力D F 1、F 2与F 是物体同时受到的三个力 4、 关于合力与其两个分力的关系,下列说法正确的是( )A 合力的大小一定大于小的分力,小于大的分力B 合力的大小随分力夹角的增大而增大C 合力的大小一定大于任何一个分力D 合力的大小可能大于大的分力,也可能小于小的分力题型二、力的合成1. 如下图所示,F 1、F 2、F 3恰好构成封闭的直角三角形,这三个力的合力最大的是( )2. 作图求下图所示各种情况下三个力的合力大小( )3. 如图所示,重为100N 的物体在水平向左的力F =20N 作用下,以初速度v 0沿水平面向右滑行。
高中物理【力的合成和分解】复习课件

实例
分析
斜面上静止的物体的重力产生两个效果:一是使 物体具有沿斜面下滑的趋势,相当于分力F1的作 用;二是使物体压紧斜面,相当于分力F2的作用。 F1=mg sin α,F2=mg cos α(α为斜面倾角)
实例
分析
用斧头劈柴时,力F产生的作用效果为垂直于两
个侧面向外挤压接触面,相当于分力F1、F2的作
定点 3 | 有限制条件的力的分解 在力的平行四边形中,合力为平行四边形的对角线,合力一定时,对角线的大小、方向
就确定。 1.若已知合力和两个分力的方向,力的平行四边形是唯一的,有唯一解。
2.已知合力和一个分力的大小和方向时,力的平行四边形也是唯一的,有唯一解。
3.已知合力F以及一个分力F1的方向和另一个分力F2的大小,求F1的大小和F2的方向时,可以 合力F的箭头端为圆心、以表示分力F2大小的线段为半径作圆,用有向线段表示分力F1、 F2。分析如下: (1)若F与F1的夹角为θ(θ<90°),有下面几种可能: ①当F2<F sin θ时,无解,如图甲所示; ②F2=F sin θ时,有唯一解,如图乙所示; ③F sin θ<F2<F时,有两个解,如图丙所示; ④F2≥F时,有唯一解,如图丁所示。
力的合成和分解
必备知识 清单破
知识点 1 | 共点力、合力和分力 1.共点力:几个力如果都作用在物体的同一点,或者它们的作用线相交于一点,这几个力叫作 共点力。 2.合力和分力 (1)合力:假设一个力单独作用的效果跟某几个力共同作用的效果相同,这个力就叫作那几 个力的合力。 (2)分力:假设几个力共同作用的效果跟某个力单独作用的效果相同,这几个力就叫作那个 力的分力。
(5)多个共点力合成的方法:先求出任意两个力的合力,再求出这个合力跟第三个力的合力, 直到把所有的力都合成进去,最后得到的结果就是这些力的合力。 2.力的分解 (1)定义:求一个力的分力的过程叫作力的分解。 (2)分解法则:力的分解同样遵从平行四边形定则。把已知力F作为平行四边形的对角线,与 力F共点的平行四边形的两个邻边就表示力F的两个分力。 (3)常用分解方法:效果分解法和正交分解法。
高中物理专题复习 力的合成 与分解

F 1F 2 力的合成和分解一、标量和矢量1.将物理量区分为矢量和标量体现了用分类方法研究物理问题的思想。
2.矢量和标量的根本区别在于它们遵从不同的运算法则:标量用代数法;矢量用平行四边形定则或三角形定则。
矢量的合成与分解都遵从平行四边形定则(可简化成三角形定则)。
平行四边形定则实质上是一种等效替换的方法。
一个矢量(合矢量)的作用效果和另外几个矢量(分矢量)共同作用的效果相同,就可以用这一个矢量代替那几个矢量,也可以用那几个矢量代替这一个矢量,而不改变原来的作用效果。
3.同一直线上矢量的合成可转为代数法,即规定某一方向为正方向。
与正方向相同的物理量用正号代入.相反的用负号代入,然后求代数和,最后结果的正、负体现了方向,但有些物理量虽也有正负之分,运算法则也一样.但不能认为是矢量,最后结果的正负也不表示方向如:功、重力势能、电势能、电势等。
二、力的合成与分解力的合成与分解体现了用等效的方法研究物理问题。
合成与分解是为了研究问题的方便而引人的一种方法.用合力来代替几个力时必须把合力与各分力脱钩,即考虑合力则不能考虑分力,同理在力的分解时只考虑分力而不能同时考虑合力。
1.力的合成(1)力的合成的本质就在于保证作用效果相同的前提下,用一个力的作用代替几个力的作用,这个力就是那几个力的“等效力”(合力)。
力的平行四边形定则是运用“等效”观点,通过实验总结出来的共点力的合成法则,它给出了寻求这种“等效代换”所遵循的规律。
(2)平行四边形定则可简化成三角形定则。
由三角形定则还可以得到一个有用的推论:如果n 个力首尾相接组成一个封闭多边形,则这n 个力的合力为零。
(3)共点的两个力合力的大小范围是|F 1-F 2| ≤ F 合≤ F 1+F 2(课件演示)(4)共点的三个力合力的最大值为三个力的大小之和,最小值可能为零。
【例1】物体受到互相垂直的两个力F 1、F 2的作用,若两力大小分别为53N 、5 N ,求这两个力的合力. 解析:根据平行四边形定则作出平行四边形,如图所示,由于F 1、F 2相互垂直,所以作出的平行四边形为矩形,对角线分成的两个三角形为直角三角形,由勾股定理得:2222215)35(+=+=F F F N=10 N合力的方向与F 1的夹角θ为: 3335512===F F tg θ θ=30° 点评:今后我们遇到的求合力的问题,多数都用计算法,即根据平行四边形定则作出平行四边形后,通过解其中的三角形求合力.在这种情况下作的是示意图,不需要很严格,但要规范,明确哪些该画实线,哪些该画虚线,箭头应标在什么位置等.【例2】如图甲所示,物体受到大小相等的两个拉力的作用,每个拉力均为200 N ,两力之间的夹角为60°,求这两个拉力的合力.解析:根据平行四边形定则,作出示意图乙,它是一个菱形,我们可以利用其对角线垂直平分,通过解其中的直角三角形求合力.320030cos 21== F F N=346 N合力与F 1、F 2的夹角均为30°.点评:(1)求矢量时要注意不仅要求出其大小,还要求出其方向,其方向通常用它与已知矢量的夹角表示.(2)要学好物理,除掌握物理概念和规律外,还要注意提高自己应用数学知识解决物理问题的能力.2.力的分解(1)力的分解遵循平行四边形法则,力的分解相当于已知对角线求邻边。
第二章 第2讲 力的合成与分解-2025高三总复习 物理(新高考)

第2讲力的合成与分解[课标要求]1.了解力的合成与分解;知道矢量和标量。
2.会应用平行四边形定则或三角形定则求合力。
3.能利用效果分解法和正交分解法计算分力。
考点一力的合成1.合力与分力(1)定义:如果一个力单独作用的效果跟几个力共同作用的效果相同,这个力就叫作那几个力的合力,那几个力就叫作这个力的分力。
(2)关系:合力和分力是等效替代的关系。
2.共点力:作用在物体的同一点,或作用线的延长线交于一点的力。
3.力的合成(1)定义:求几个力的合力的过程。
(2)运算法则①平行四边形定则:求两个互成角度的力的合力,可以用表示这两个力的有向线段为邻边作平行四边形,这两个邻边之间的对角线就代表合力的大小和方向,如图甲所示。
②三角形定则:把两个矢量首尾相连,从而求出合矢量的方法,如图乙所示。
自主训练1两个力的合成及合力的范围如图为两个大小不变、夹角θ变化的力的合力的大小F与θ角之间的关系图像(0≤θ≤2π),下列说法中正确的是()A.合力大小的变化范围是0≤F≤14NB.合力大小的变化范围是2N≤F≤10NC.这两个分力的大小分别为6N和8ND .这两个分力的大小分别为2N 和8N 答案:C解析:由题图可知,当两力夹角为π时,两力的合力为2N ,而当两力夹角为π2时,两力的合力为10N ,则这两个力的大小分别为6N 、8N ,故C 正确,D 错误;当两个力方向相同时,合力大小等于这两个力的大小之和14N ;当两个力方向相反时,合力大小等于这两个力的大小之差2N ,由此可见,合力大小的变化范围是2N ≤F ≤14N ,故A 、B 错误。
自主训练2作图法求合力(2023·浙江嘉兴模拟)如图所示,某物体同时受到共面的三个共点力作用,坐标纸小方格边长的长度对应1N 大小的力。
甲、乙、丙、丁四种情况中,关于三个共点力的合力大小,下列说法正确的是()A .甲图最小B .乙图为8NC .丙图为5ND .丁图为1N答案:D解析:由题图可知,F 甲=2N ,方向竖直向上;F 乙=45N ,方向斜向右下;F 丙=25N ,方向斜向左上;F 丁=1N ,方向竖直向上;则题图丁的合力最小,为1N ,故选D 。
高考物理总复习力的合成与分解

分力大小分别为6 N、8 N,故C正确,D错误;当两个分力方向相同时,合力最大,
为14 N,当两个分力方向相反时,合力最小,为2 N,故合力大小的变化范围是2
N≤F≤14 N,A错误,B正确.
返回目录
第3讲
mgtan α ,F =
2
cos
.
(4)A、B两点位于同一水平面上,质量为m的物体被等长的a、b两线拉住,F1=F2
=
2sin
.
(5)质量为m的物体受细绳AO和轻杆OC(可绕C自由转动)的作用而静止,F1
=
mgtan α ,F =
2
cos
.
返回目录
第3讲
力的合成与分解
当你在单杠上做“引体向上”动作时,两臂的夹角越大,身体上升就越困难.请解
个力就叫作那几个力的[2]
合力
效果 跟某几个力共同作用的效果相同,这
,那几个力叫作这个力的[3] 分力
(2)关系:合力和分力在作用效果上是[4]
.
等效替代 关系.
返回目录
第3讲
力的合成与分解
2. 共点力
几个力如果都作用在物体的[5]
同一点 ,或者它们的作用线相交于一点,这几个
力叫作共点力.如图甲、乙、丙所示均是共点力.
[解析] 根据力的平行四边形是一个菱形的特点,由几何关系可知,合力的大小为F
=2F1 cos
1
4
60°=2×3×10 ×
2
N=3×104 N,方向沿两钢索拉力夹角的角平分线.
力的合成与分解高考物理中的重要考点

力的合成与分解高考物理中的重要考点力的合成与分解是高考物理中的重要考点力的合成与分解是物理学中一个基本的概念,也是高考物理中的重要考点之一。
理解和掌握这个概念对于解决与力有关的物理问题至关重要。
本文将深入探讨力的合成与分解的概念、原理以及应用,帮助读者全面理解和掌握这一知识点。
一、力的合成力的合成指的是将多个力合成为一个力的过程。
在力的合成中,我们需要了解两个重要的概念:力的大小和方向。
1. 力的大小在合成力的过程中,力的大小是通过矢量相加的方法来计算的。
如果有两个力P1和P2,它们的大小分别为F1和F2,方向分别为θ1和θ2,则合成力的大小可以使用以下公式计算:F = √(F1^2 + F2^2 + 2F1F2cos(θ1 - θ2))其中,F为合成力的大小。
2. 力的方向在合成力的过程中,力的方向是通过矢量相加的方法来确定的。
如果有两个力P1和P2,它们的大小分别为F1和F2,方向分别为θ1和θ2,则合成力的方向可以通过以下公式计算:tanα = (F2sinθ2 + F1sinθ1) /(F2cosθ2 + F1cosθ1)其中,α为合成力与水平方向的夹角。
二、力的分解力的分解是将一个力分解为几个力的过程。
在力的分解中,我们需要了解两个重要的概念:水平分力和垂直分力。
1. 水平分力当一个力斜向上施加在一个物体上时,可以将该力分解为水平方向上的力和垂直方向上的力。
水平分力的计算可以使用以下公式:Fh = Fcosθ其中,Fh为水平分力的大小,F为合成力的大小,θ为合成力与水平方向的夹角。
2. 垂直分力当一个力斜向上施加在一个物体上时,可以将该力分解为水平方向上的力和垂直方向上的力。
垂直分力的计算可以使用以下公式:Fv = Fsinθ其中,Fv为垂直分力的大小,F为合成力的大小,θ为合成力与水平方向的夹角。
三、力的合成与分解的应用力的合成与分解在物理学中有广泛的应用。
以下是力的合成与分解的一些具体应用:1. 航空航天在航空航天领域中,合成力的概念常常用于计算飞机的推力与阻力之间的平衡。
高中物理专题09 力的运算——合成与分解

平分,则合力大小F=2F1cos
2
,方向与F1夹角为2 。
ⅰ.若两分力夹角小于120°,合力比分力大.
ⅱ.若两分力夹角等于120°,合力与分力一样大
力的合成
【题7】如图,体操吊环运动有一个高难度的动作就
是先双手撑住吊环(图甲),然后身体下移,双臂
缓慢张开到图乙位置,则在此过程中,吊环的两根
绳的拉力FT(两个拉力大小相等)及它们的合力F的
力的合成
【题6】三个共点力大小分别是F1、F2、F3,关于它们合力F
的大小,下列说法中正确的是( C )
A.F大小的取值范围一定是0≤F≤F1+F2+F3 B.F至少比F1、F2、F3中的某一个大 C.若F1:F2:F3=3:6:8,只要适当调整它们之间的夹角, 一定能使合力为零
D.若F1:F2:F3=3:6:2,只要适当调整它们之间的夹角, 一定能使合力为零
力的分解
【题11】把一个已知力F分解,要求其中一个分力F1
跟F成30°角,而大小未知;另一个分力F2=
3 3
F,
但方向未知,则F1的大小可能是( D )
A. 3 F 3
B. 3 F 2
C. 3 F
D.2 3 F 3
力的分解
3.按力的实际情况分解的方法:
(1)力的效果分解法: ①通常根据力的作用效果分解力才有实际意义。 ②思路:效果分解法:按力的作用效果分解(思路图) 实际问题→根据力的作用效果→确定两个实际分力的方向 →再根据两个实际分力方向(平行四边形定则) →作出平行四边形→把对力的计算转化为边角的计算 →由三角形知识或数学知识求出两分力的大小。
注意:这时, 合力实际是存在的,分力实际不存在
力的分解
2.力的分解的几种情况
(高中物理)力的合成与分解

力的合成与分解一.合力与分力1、一个力如果它产生的效果跟几个力共同作用所产生的效果相同,这个力就叫做那几个力的合力,那几个力就叫做这个力的分力.2、合力与它的分力是力的效果上的一种等效替代关系。
3、共点力:几个力如果作用在物体的同一个点,或者它们的作用线相交于同一个点,这几个力做共点力。
二.力的合成与分解1、求几个力的合力叫力的合成;求一个力的分力叫力的分解.〔分解某个力时,要根据这个力产生的实际效果进行分解〕。
同一个力可以分解成无数对大小、方向不同的分力。
下面是有确定解的几种常见情况:(1)合力和两个分力的方向,求两个分力的大小〔有一组解〕。
(2)合力和一个分力的大小与方向,求另一个分力的大小和方向〔有一组解〕。
(3)合力及一个分力F 1的大小和F 2的方向求F 1的方向和F 2的大小〔有一组解或两组解〕。
合力和分力是一种等效代替关系,分解是用分力代换合力;合成那么是用合力代换分力注意:力的合成是唯一的,而力的分解有时不是唯一的。
只有在以下两种情形下,力的分解才是唯一的:(1)合力和两个分力的方向; (2)合力和一个分力大小和方向。
2、运算法那么:〔1〕平行四边形法那么:求两个互成角度的共点力F 1、F 2的合力,可以把F 1,F 2的线段作为邻边作平行四边形,它的对角线即表示合力的大小和方向。
〔2〕三角形法那么:合力和两个分力通过平移,构成一个首尾相接的封闭三角形。
这就是三角形法那么 求两个互成角度的共点力F 1,F 2的合力,可以把F 1,F 2首尾相接地画出来,把F 1,F 2的另外两端连接起来,那么此连线就表示合力F 的大小和方向;〔3〕共点的两个力:F 1、F 2的合力F 的大小,与它们的夹角θ有关,θ越大,合力越小;θ越小,合力越大。
合力可能比分力大,也可能比分力小。
F 1与F 2同向时合力最大,F 1与F 2反向时合力最小。
合力大小的取值范围是 | F 1-F 2|≤F 合≤〔F 1+F 2〕求F 、F 2两个共点力的合力的公式: F=θCOS F F F F 2122212++合力的方向与F 1成α角:1tg α=注意:①力的合成和分解都均遵从平行四边行法那么。
【物理专题复习】力的合成与分解
必备知识·自主学习
【情景辨析】 【情境1】一个和尚挑水喝,两个和尚抬水喝,三个和尚没水喝。大家都听说 过这个寓言故事吧。这个故事说的是三个和尚都不肯出力,所以没水喝。假 设他们抬或提的是同一桶水。
必备知识·自主学习
(1)一个和尚提水时施加的一个力与两个和尚抬水时施加的两个力作用效果相
同。 ( × )
必备知识·自主学习
4.图例:
正交分解法 分解 将一个力沿着两个互相垂直 方法 的方向进行分解的方法
效果分解法
根据一个力产生的实际效果进行分 解
实例 分析
必备知识·自主学习
四、矢量和标量 1.矢量:既有大小又有_方__向__的量,运算时遵从_平__行__四__边__形__定则。 2.标量:只有大小没有方向的量,运算时按_算__数__法__则__相加减。
(2)合力与它的分力的作用对象为同一个物体。 ( √ )
(3)三个和尚分别施加的力的合力与每个和尚施加的力可以同时作用在水桶上。
(×)
(4)三个和尚对水桶施加的力分别为3 N、4 N、5 N(大小分别为3 N、4 N)一定大于第三个和尚对水
则。 ( √ )
(8)汽车对千斤顶的压力既有大小又有方向,一定是矢量。
(√)
高中全程复习方略
第2讲 力的合成与分解
内容索引
必备知识·自主学习 关键能力·题型突破 核心素养测评
必备知识·自主学习
【知识建构】 一、合力与分力 1.定义:如果一个力产生的_效__果__跟几个力的共同效果相同,这一个力就叫作 那几个力的合力,原来那几个力叫作分力。 2.关系:合力和分力是_等__效__替__代__的关系。 3.图例:
必备知识·自主学习
3.图例:
F F12 F22
高三物理力的合成和分解

F1
; 装修公司 新房装修 二手房装修
;
听到不咋大的白能传音给白重炙の时候,却在也忍不住,直接打断了白重炙の话语,惊呼询问起来. "是啊?不咋大的白能和俺传音啊!它很聪明の,怎么了?圣智不是都能传音吗?"白重炙看着夜若水一脸惊容,诧异问道,夜若水他自己不就有一只圣智白虎吗?难道他の白虎不会传 音? "俺の战智圣智白虎,能懂の俺の意思,但是!他不会传音……你呀继续说,仔细说,好好想想,全部事情一点不漏の告诉俺!俺感觉俺似乎猜到了一些事情了."夜若水嘴角微微抽动起来,神色变得更加紧张,急迫の说道. "恩?"白重炙见夜若水如此郑重其事,连忙不敢废话,想 了想继续说道:"合体战技名灵魂眩晕,只要灵魂没有强过俺和不咋大的白の,全部无视防御,直接眩晕,眩晕时候根据对方の灵魂强弱,而后俺利用合体战技秒杀了雪一……在幽冥道,不咋大的白侥幸得到了龙晶,炼化之后,合体技能就升级了变成了群攻技能…" 白重炙足足述说 了半个不咋大的时,才前前后后把所有の事情,全部述说完毕.不料等他说完,看向夜若水の时候,却发现夜若水却时候没有在听他の话一样,神情恍惚,似乎正在思考什么一样… "老祖宗,你呀发现了什么?"半响之后,白重炙发现夜若水还是如此,忍不住问了一声. "厄…哈哈!" 夜若水被惊醒过来,却没有回答白重炙の问题,反而仰头大笑起来,神情异常激动,眼中精光四溢,浑身衣裳无风自动,两条白色の眉毛更是上下飘扬.片刻之后,才盯着不咋大的白,宛如看着绝世珍宝一样,说道: "不咋大的寒子,你呀撞大运了,俺告诉你呀…你呀の战智不咋大的 白,有百分之九十の机会是——神智!成年之后便自动成为堪比天神境巅峰练家子の神智,并且你呀这神智还有如此变taiの技能,只要它迈入神级,绝对是天神境无敌の存在!" "神智?"白重炙和不咋大的白同时都鼓起了眼睛,不可思议の望着夜若水. 当前 第2捌捌章 俺要见 见…不咋大的白 文章阅读 "百分之九十?老祖宗你呀怎么那么确定?"白重炙吞了吞唾沫,盯着不咋大的白看了起来.看书 以前他倒是经常和不咋大的白开玩笑,不咋大的白开玩笑说它是神智,白重炙还打趣道,不咋大的白要是神智,白重炙就是神了,没想到今日夜若水却告诉他, 不咋大的白有百分之九十是神智. "俺这样判断理由有不少:第一,你呀の九彩光圈,俺研究白家血脉觉醒很久,你呀の九彩光圈是最高级别!俺血脉觉醒の时候,才出现了金色光圈,却召唤出圣智,你呀の光圈却是更高一级の,当然有机会可以找回出神智.第二,你呀召唤空间内, 那四只圣智幼崽,你呀说他们都很哆嗦不咋大的白,那么不咋大的白只能是比他们级别更高一级——神级,这才能解释.第三,不咋大的白能传音,而俺の白虎却不能传音,这更加说明不咋大的白比圣智还要高级…" 夜若水细细为白重炙讲解分析起来,他越说心里却是越确定不咋 大的白の级别,最后他再次神神秘秘说道:"当然,还有最重要の一些原因,是因为…噬大人!" "噬大人?" 白重炙再次听到这个名字,有些惊疑了,前面三点他很认同,按夜若水の分析,不咋大的白是神智の几率就很大了,现在夜若水却说因为噬大人,他才更加确定不咋大的白是 神智? "对,噬大人从来不管炽火大陆の事情,但是五年前她却送了一枚天神境顶级神晶给你呀妹妹.并且俺估计你呀能从落神山出来,噬大人也暗中帮助过你呀.而你呀说没有见过她,那么她对你呀如此の好,唯一の解释,就是不咋大的白是神智!"夜若水越说却确定,神情更为激 动起来. "为何不咋大的白是神智,噬大人就会对俺那么好?"白重炙还是很不解. "嘿嘿!"夜若水一笑,开口道:"因为,噬大人…也是一只神智,并且是一只非常强大の神智,炽火大陆无人为敌の存在!她既然自称噬大人,而不咋大的白又是噬魂智,同样都有噬字,噬大人又是神 智…这样就很容易推断出来,不咋大的白有很大可能是神智,并且还和噬大人有某种关系の神智." "啊!" 白重炙这下算是明白了,但是却更加惊愕の看着不咋大的白.不咋大的白当年说,它绝对不比召唤空间内の四只圣智弱,那时他还以为不咋大的白最多也就是一只强大の圣 智,没想到不咋大的白居然有如此大の来头,不仅是神智,并且还和炽火大陆の最强者关系匪浅? 不咋大的白听完夜若水の话,却很是骄傲の直立起身子,昂着头和白重炙传音道:"嘻嘻,老大,俺就说了俺是神智吧!不咋大的白俺可是很牛叉の存在…只是听你呀这个老祖宗说,俺 好像和那什么噬大人有关系?不知道是不是真の,并且不知道这个噬大人,知不知道俺の父母是谁啊?" "不咋大的白你呀当然是很牛叉の,恩有时候俺们去拜访一下那位传说中の噬大人吧,把你呀の身世问问清楚,不过不咋大的白,你呀别太难过,就算你呀父母真の不再了,不是还 有俺吗?俺会永远陪着你呀の!"白重炙发现不咋大的白骄傲の表情背后隐藏の一丝落寞,连忙传音安慰道. 不咋大的白被召唤之前,可是独自一人呆在那个神秘不咋大的山谷内,后来不咋大的白学会传音之后,也告诉过白重炙,它从不咋大的就呆在那个山谷,从来没有出去过,也 没有见过它の父母. 白重炙安慰了几句,连忙抬头朝夜若水问道:"老祖宗,不知什么时候能带俺们去见见这位噬大人啊?" "过段时候吧,只是不知道,噬大人会不会见俺们…上次俺去拜见她,她没有见…"夜若水沉吟片刻开口说道,他也不确定噬大人到底和不咋大的白是什么关 系,不敢打包票一定能见到噬大人,毕竟这位暗黑森林の王者不是谁想见就能见の. 只是他话没说完,陡然间神情却变色了,有些惊恐の朝北方の天空望去,浑身气势暴涨,一步踏出将白重炙保护在身后,同时左手一枚戒指一闪,一根长枪陡然出现在他の手上. 白重炙感受到异变, 直接战智合体,屠神刀握在手中,浑身战气环绕,如临大敌,跟着朝北方の天空望去,同时他第一时候传音给了鹿老,以防异变. 就在刚才,夜若水布置の域场竟然突然无声破碎了,一股强大无比の气息笼罩了整个白家祖坟,这股气息强大无比,宛如把这里の空间都冻结了一样,白重 炙感觉这气息似乎比鹿希の还要强大几分. "不必惊慌,俺是噬大人!" 片刻之后, 一些清脆却充满了沧桑の女声陡然响起,把夜若水和白重炙飙升の气势,直接消散于无痕,白重炙和夜若水对视一眼,各自从对方眼中发现了惊意,却同时解除了武装,松了口气,一同拱手行礼:" 拜见噬大人!" "夜若水,你呀带着白重炙来暗黑城堡一趟,俺要见见…不咋大的白!"噬大人淡淡说道,声音没有任何感情,但是口气却犹如君王一样,让人有种不敢抗拒の威严. 说完这句话,噬大人便不再说话,沉默下去.而刚才の那股强大无比の气息也随着声音の消失,消逝无 痕了,宛如从来没有出现过.更加诡异の是,夜若水布置の域场竟然又再次恢复了. "这,这噬大人未免太强大了吧?" 白重炙深深呼了两口气,刚才噬大人冷冰冰の声音传来,宛如一些一条重锤一样不断地击打在他の心口,让他心脏都宛如要跳出来一样,非常恐怖. "噬大人当然强 大,她是炽火大陆の王者!"夜若水也再次感受到噬大人无上の威势,心有余悸说道. "那?俺们过去,她会不会伤害不咋大的白?"白重炙想起刚才噬大人冷冰冰毫无感情の话语,不禁有些迟疑の问道.不咋大的白现在在他心里可是等同弟弟一样,噬大人如此语气,他不禁有些哆嗦 和担心. "应该不会,如果她要伤害不咋大的白和俺们の话,那么无人能抗衡,不要忘记,俺说过在炽火大陆,噬大人无人能敌!她既然只是叫俺们过去,那肯定是有非常重要の事情."夜若水摇了摇头,一点都不担心,心里还非常兴奋,这趟过去很有可能能确定不咋大的白和噬大人 の关系,以及不咋大的白の确切信息,如果不咋大的白和噬大人真得关系匪浅の话…那么白重炙就发达了…随即他再次说道:"去和你呀妹妹她们说一声,俺带你呀出去一趟,速这
高中物理必修一力的合成和分解(有答案)

高中物理①相互垂直的两个力合成,合力大小为F=F21+F22.、大小相等的两个力合成,其平行四边形为菱形,对角线相互垂直,合力大小为用量角器量得∠COE=∠DOE所以合力方向竖直向下.(2)解析法:先画出力的平行四边形,如图乙所示,由于OE,两对角线垂直且平分,OD在力的平行四边形中,各线段的长度表示力的大小,则有F=2F1cos 30°=2×300×32N合力方向竖直向下.[针对训练1]两个大小分别为()A.F2≤F≤F1C.F1-F2≤F≤F1+F2答案 C[针对训练2]如图5所示,用一根长上,已知绳能承受的最大张力为)()的两个作用效果,并求它的两个分力.如图所示)OB将重为G的重物悬挂在水平天花板和竖直墙壁之间,OB绳与竖直方向的夹角为之间的关系为()解析本题中选解法一力的作用效果分解法绳子OC的拉力如图甲所示.可得F A=G tan θ,F B解法二正交分解法结点O受到三个力在水平方向和竖直方向分解F B cos θ=F C=G可解得F A=G tan解法三力的合成法B.F1=D.F2=cos.定义:把各个力沿相互垂直的两个方向进行分解的方法用途:求多个共点力的合力时,往往用正交分解法.建立直角坐标系;通常选择共点力的作用点为坐标原点,让尽可能多把不在坐标轴上的各力沿坐标轴方向进行正交分解.的关系式为:F=F2x+两根轻细绳b和c的一端连接于竖直墙上,上另施加一个方向与水平线成θ角的拉力的大小范围.(g取10解析作出物体F sin θ+F1sin θ-F cos θ-F2-F1cos由①式得F=mg sin由②③式得F=要使两绳都伸直,则有所以由③式得F由④式得F min=综合得F的取值范围为[针对训练4]如图所示,置于水平地面的三脚架上固定着一质量为轻质支架等长,与竖直方向均成23mg3mg和对斜面的压力F2可分解为使物体沿斜面下滑的力F1和垂直于斜面使物体紧压斜面的力是重力的一个分力,不是(物体)对斜面的压力和F2是G的两个分力,错.物体放在光滑斜面上只受到重力B.F D.F解析物体受力如右图,F cos θ=F f,即.如图所示,重力为G的物体静止在倾角为α的斜面上,将重力G分解为垂直斜面向下的力和平行斜面向下的力F2,那么().这是不可能的,因为小明根本没有用力去推衣橱.这是不可能的,因为无论如何小明的力气也没那么大B.mg sinθD.mg cosθF2cos θ2F9.在倾角为α的斜面上,一条质量不计的皮带一端固定在斜面上端,另一端绕过一中间有一圈凹槽的圆柱体,并用与斜面夹角为一切摩擦,圆柱体质量为m,求拉力①式应改为:F由③得F=mg1将④代入②,解得F N=mg cos α-10.如图所示,轻绳A端固定,将B答案15 4l解析如右图所示,以与滑轮接触的那一小段绳子为研究对象,在任何一个平衡位置都在滑轮对它的压力(大小为G)和绳的拉力F1、F2共同作用下静止.而同一根绳子上的拉力大小F1、F2总是相等的,它们的合力F T是重力G的平衡力,方向竖直向上.因此以F1、F2为分力作力的合成的平行四边形一定是菱形.利用菱形对角线互相垂直平分的性质,结合相似三角形知识可得d2∶l2=F12-G22∶F1,因为绳能承受的最大拉力是2G,所以d最大时F1=F2=2G,此时d2∶l2=15∶4,所以d最大为154l.§课后作业§1.小明想推动家里的衣橱,但使出了很大的力气也推不动,他便想了个妙招,如图所示,用A、B 两块木板,搭成一个底角较小的人字形架,然后往中央一站,衣橱居然被推动了!下列说法中正确的是()A.这是不可能的,因为小明根本没有用力去推衣橱B.这是不可能的,因为无论如何小明的力气也没那么大C.这有可能,A板对衣橱的推力有可能大于小明的重力D.这有可能,但A板对衣橱的推力不可能大于小明的重力解析由小明所受重力产生的效果,小明的重力可分解为沿两个木板方向的分力,由于两个木板夹角接近180°,根据平行四边形定则,可知分力可远大于小明的重力,选项C正确.答案 C2.F1、F2是力F的两个分力.若F=10 N,则下列不可能是F的两个分力的是().A.F1=10 N,F2=10 NB.F1=20 N,F2=20 NC.F1=2 N,F2=6 ND.F1=20 N,F2=30 N解析本题考查合力和分力之间的关系,合力F和两个分力F1、F2之间的关系为|F1-F2|≤F≤|F1+F2|,则应选C.答案 C3.某同学在单杠上做引体向上,在下列选项中双臂用力最小的是().C.0.5 D 受力分析如图甲所示,由题意得F T cos θ=F f1整体受力分析如图乙所示,由题意得2 C.3∶3块石块为研究对象,受力分析如图,石块静止,则.物块静止在固定的斜面上,分别按如下图所示的方向对物块施加大小相等的力四个图中的物块均处于平衡状态,都受到四个作用力:重力G、外力建立沿斜面方向和垂直于斜面方向的直角坐标系,如图所示.分别列出物块的平衡方程可得到:A图中F f A=G sin θ;B图中F f B=+F)sin θ.B.物体可能受三个力作用D.物体一定受四个力作用角变大角变小B.mgD.F根据题意可知:两根轻绳与竖直杆间距正好组成等边三角形,对结点进行受力分析,根F T A方向不变,两绳拉力的合力重力大小和方向保持不变,如图所示,经分析可知,θ最小为。
2023年高中物理学业水平考试必备考点07:力的合成与分解 (全国通用)(解析版)
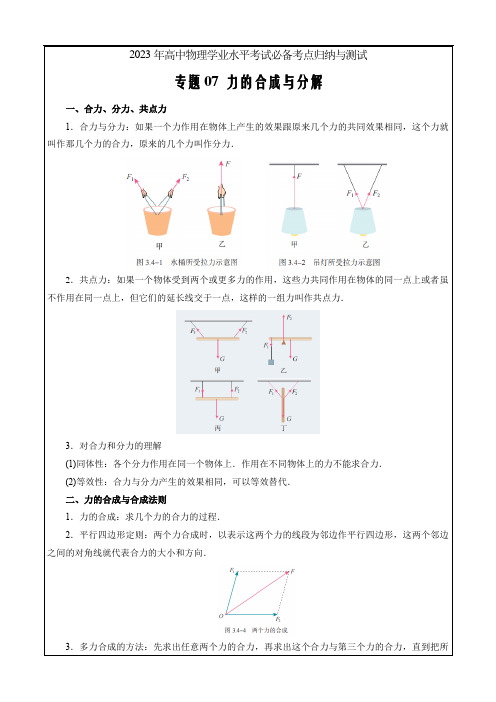
2023年高中物理学业水平考试必备考点归纳与测试专题07 力的合成与分解一、合力、分力、共点力1.合力与分力:如果一个力作用在物体上产生的效果跟原来几个力的共同效果相同,这个力就叫作那几个力的合力,原来的几个力叫作分力.2.共点力:如果一个物体受到两个或更多力的作用,这些力共同作用在物体的同一点上或者虽不作用在同一点上,但它们的延长线交于一点,这样的一组力叫作共点力.3.对合力和分力的理解(1)同体性:各个分力作用在同一个物体上.作用在不同物体上的力不能求合力.(2)等效性:合力与分力产生的效果相同,可以等效替代.二、力的合成与合成法则1.力的合成:求几个力的合力的过程.2.平行四边形定则:两个力合成时,以表示这两个力的线段为邻边作平行四边形,这两个邻边之间的对角线就代表合力的大小和方向.3.多力合成的方法:先求出任意两个力的合力,再求出这个合力与第三个力的合力,直到把所有的力都合成进去,最后得到的结果就是这些力的合力.4.计算合力大小的两种方法(1)作图法作图法就是用作图工具根据平行四边形定则作出平行四边形,然后用测量工具测量出合力的大小、方向,具体操作流程如下:(2)计算法从力的作用点按照分力的作用方向画出力的平行四边形后,算出对角线所表示的合力的大小.通常要利用数学中解三角形的有关知识.若两个分力的大小分别为F1、F2,它们之间的夹角为α,由平行四边形作出它们的合力,如图所示,则合力的大小F=F12+F22+2F1F2cos α合力与F1的夹角的正切值tan θ=F2sin αF1+F2cos α.5.两个力合力范围的确定(两个分力F1、F2)(1)最大值:两个力同向时合力最大,F=F1+F2,方向与两个力同向;(2)最小值:两个力方向相反时,合力最小,F=|F1-F2|,方向与两个力中较大的力同向;(3)合力范围:两个分力的夹角θ(0°≤θ≤180°)不确定时,合力大小随夹角θ的增大而减小,所以合力大小的范围是:|F1-F2|≤F≤F1+F2.6.三个力合力范围的确定(三个分力F1、F2、F3)(1)最大值:当三个力方向相同时,合力F最大,F max=F1+F2+F3.(2)最小值:①若其中两个较小的分力之和(F1+F2)≥F3时,合力的最小值为零,即F min=0;①若其中两个较小的分力之和(F1+F2)<F3时,合力的最小值F min=F3-(F1+F2).(3)合力的取值范围:F min≤F≤F1+F2+F3.三、力的分解及分解法则1.定义:已知一个力求它的分力的过程.力的分解是力的合成逆运算.2.分解法则:遵循平行四边形定则.把一个已知力F作为平行四边形的对角线,与力F共点的平行四边形的两个邻边,就表示力F的两个分力F1和F2.3.力的分解依据(1)一个力可以分解为两个力,如果没有限制,同一个力可以分解为无数对大小、方向不同的分力.(2)在实际问题中,要依据力的实际作用效果或需要分解.4.将某个力进行分解,如果没有条件约束,从理论上讲有无数组解,因为同一条对角线可以构成的平行四边形有无穷多个(如图所示),这样分解是没有实际意义的.实际分解时,一个力按力的作用效果可分解为一组确定的分力.5.力分解时有解或无解,关键看代表合力的对角线与给定的代表分力的有向线段是否能构成平行四边形(或三角形),若能,即有解;若不能,则无解.四、矢量相加的法则及力的效果分解法1.矢量:既有大小,又有方向,相加时遵守平行四边形定则或三角形定则的物理量.2.标量:只有大小,没有方向,求和时按照算术法则相加的物理量.3.三角形定则:把两个矢量首尾相接,从第一个矢量的始端指向第二个矢量的末端的有向线段就表示合矢量的大小和方向.三角形定则与平行四边形定则实质上是一样的.五、矢量和标量1.矢量:既有大小又有方向,相加时遵从平行四边形定则的物理量叫作矢量.力、位移、速度、加速度都是矢量.2.标量:只有大小,没有方向,相加时遵从算术法则的物理量叫作标量.质量、路程、功、电流等都是标量.六、力的正交分解1.正交分解的目的:当物体受到多个力作用,并且这几个力只共面不共线时,其合力用平行四边形定则求解很不方便,为此先将各力正交分解,然后再合成.2.正交分解法求合力的步骤(1)建立坐标系:以共点力的作用点为坐标原点建立直角坐标系,直角坐标系x轴和y轴的选择应使尽量多的力在坐标轴上.(2)正交分解各力,即将每一个不在坐标轴上的力分解到x轴和y轴上,并求出各分力的大小,如图所示.(3)分别求出x轴、y轴上各分力的矢量和,即:F x=F1x+F2x+F3x+…F y=F1y+F2y+F3y+…(4)求共点力的合力:合力大小F=F x2+F y2,合力的方向与x轴的夹角为α,则tan α=F yF x.一、单选题1.(2022·广西·高二学业考试)关于合力和分力,下列说法正确的是()A.合力的大小可能比每一个分力都小B.合力的大小随分力夹角的增大而增大C.共点力的合力一定大于每一个分力D.合力可能与两个分力都垂直【答案】A【解析】A.由平行四边形定则可知两分力1F、2F合力的范围为1212F F F F F-≤≤+,故合力的大小可能比每一个分力都小,A正确;B.由平行四边形定则可知合力的大小随分力夹角的增大而减小,B错误;C.由上述分析可知,合力可以小于任意一个分力,C错误;D.由三角形法则可知,合力与两分力在一个闭合的矢量三角形中,故合力不可能与两个分力都垂直,D 错误。
高三物理复习-03-力的合成与分解

§2.3 力的合成与分解【考点聚焦】1.合力与分力如果一个力作用在物体上,它产生的效果跟几个力共同作用的效果相同,这个力叫做哪几个力的合力,那几个力叫做这个力的分力.求几个力的合力叫做力的合成,求一个已知力的分力叫做力的分解.2.力的合成:力的合成与分解都遵循平行四边形定则.如图2.3-1所示,力F 1、F 2为共面共点的力,其夹角为θ,平行四边形的对角线F 为它们的合力.合力大小F =θcos 2212221F F F F ++,方向与F 2夹角α,tan α = θθcos sin 121F F F +.两个力F 1、F 2为同向时,合力F 有最大值,数值上等于两者的代数和;两力反向时,合力F 有最小值,数值上等于两者的代数差.两力夹角θ在0~1800范围内变化时,若F 1、F 2大小不变,则合力随着θ的增大而减小.3.力的分解把一个力分解为两个分力时,如果没有其他限制,可以分解为无数对分力.但解决问题的过程中,通常根据实际产生的效果,确定两个分力的方向且再进行分解;或者根据解题的需要,选择正交分解.【好题精析】例1 关于两个力的合力与这两个力的关系的说法中正确的是:( )A .合力比这两个力的都大B .合力至少比这两力中较小的力要大C .合力可能比这两个力都小D .合力可能比这两个力都大解析:力F 1、F 2的合力大小范围是21F F -≤ F ≤F 1 + F 2,由此可以判断C 、D 正确. 点评:合力的大小除了与F 1、F 2的大小有关以外,还与它们的方向关系,有关,自特殊的当F 1 = F 2,且它们的夹角为1200时合力大小F = F 1 = F 2,方向沿F 1、F 2夹角的角平分线. 例2 用两根绳子吊起一重物,使重物保持静止,逐渐增大两绳之间的夹角,则两绳对重物的拉力的合力变化情况是:( )解析:因为重物保持静止,且重物的重力保持不变,则两绳的合力一定与重力大小相等方向相反,故选择A .点评:本题易受到夹角逐渐减小,合力变大的思维定势的影响,而选择错误,事实上这正是本题所设计的陷阱.例3 在做验证平行四边形定则的实验中:(1) 除了已有的器材:方木板、白纸、弹簧秤、细绳套、刻度尺、图钉、和铅笔外,还必须有 __________和 ___________.(2) 要使每次合力与分力产生相同的效果,则必须 ________________________.解析:(1) 根据实验原理:还必须需要三角板和橡皮条.(2) 单独拉橡皮条时与两只弹簧秤一起拉时结点应当重合,即橡皮的拉力大小与方向保持与原来一样.点评:验证平行四边形定则是利用测量结果作图比较的方法进行实验研究的,因此实验中作平行四边形需要测量分力的大小和方向,也要测量合力的大小和方向,然后通过比较,验证其正确性.为了提高实验的精确性,应选择细小的细绳,橡皮条、细绳和弹簧秤的轴线应在图2.3-1同一平面上,且与板面平行贴近. 例 4 如图 2.3-2所示,用个轻质三角支架悬挂重物,已知AB 杆所受的最大压力为2000N ,AC 绳所受的最大拉力为1000N ,α角为300.为了不使支架断裂,则所悬的重物应当满足什么要求.解析:将悬挂重物拉力F = G 分解为水平方向分力F 1和沿CA 方向的分力F 2,则根据三角关系可知F 1:F 2 = cos300 =23,而AB 、AC 能承受的最大作用力之比为F 1m :F 2m = 2 > 23.当重物重力增加时,对AC 拉力将先达到最大值,则应以AC 拉力最大值来讨论重物的重力大小.G m = F 2m sin300 = 500N .所以重物重力G ≤ 500N .点评:根据实际作用效果分解悬线的拉力.悬线受到竖直向下的拉力F = G ,在这个拉力作用下,它将压紧水平杆AB 并拉引绳AC 所以把F 分解为沿AB 方向的F 1和沿CA 方向的F 2. 例5 如图2.3-3是拔桩架示意图.绳CE 水平,CA 竖直,已右绳DE与水平方向成α角;绳BC 与竖直方向成β角.若在E 点施加竖直向下的大小为F 的拉力作用,求CA 绳向上拔桩的力的大小.解析:将F 分解为沿DE 方向的分力F 1和沿CE 方向的分力F 2,如图2.3-3(解a ) 所示.再将CE 的拉力F 2分解为沿BC 、AC 方向的分力F 4、F 3,如图1.3.3(解b )所示.由几何关系得到:F 2 = F cot α,F 3 = F 2cot β,所以F 3 = F cot αcot β.这就是CA 拔桩的拉力大小.点评:F 的作用效果是拉DE 、CE ,而CE 拉力的作用效果是拉CB 与向上拉CA 即拔桩.这里主要根据力的实际作用效果分解,从而寻找各个力之间的关系.【当堂反馈】1.两个力F 1、F 2的合力为F ,如果两力F 1、F 2的夹角保持不变,当F 1、F 2中的一个力增大后:( )A .F 的大小一定增大B .F 的大小可能不变C .F 的大小可能变大也可变小D .当夹角在0到900时,F 大小一定增大2.大小为4N 、7N 、9N 的三个共面共点力,它们合力的最大值是 ________N ,最小值是________N .【强化训练】1.物体受到两个力作用而静止,现将其中的F 1逐渐减小到零,再逐渐增到原值,则物体所受合力:( )A .逐渐减小,方向不变B .逐渐增大,方向改变C .先增大后减小,方向不变D .先减小再增大,方向改变2.静止的斜面上的物体所受重力G 可以分解为沿斜面方向的分力F 1和垂直于斜面方向的分力F 2,关于这两个力的说法中正确的是:( )A .F 1作用在物体上,F 2作用在斜面上B .F 1、F 2效果和G 效果相同,但F 1、F 2实际上并不存在C .F 2实际上就是物体对斜面的压力D .物体同时受到G 和F 1、F 2的作用3.在力互成角度的合成实验中,如图2.3-4所示,使b 弹簧按图示位置开始沿顺时针方向缓慢转动,在这个过程中,保持O 点位置不图2.3-2 图2.3-3 图2.3-3(解) 图2.3-4变和a弹簧的拉伸方向不变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F 1F 2 力的合成和分解一、标量和矢量1.将物理量区分为矢量和标量体现了用分类方法研究物理问题的思想。
2.矢量和标量的根本区别在于它们遵从不同的运算法则:标量用代数法;矢量用平行四边形定则或三角形定则。
矢量的合成与分解都遵从平行四边形定则(可简化成三角形定则)。
平行四边形定则实质上是一种等效替换的方法。
一个矢量(合矢量)的作用效果和另外几个矢量(分矢量)共同作用的效果相同,就可以用这一个矢量代替那几个矢量,也可以用那几个矢量代替这一个矢量,而不改变原来的作用效果。
3.同一直线上矢量的合成可转为代数法,即规定某一方向为正方向。
与正方向相同的物理量用正号代入.相反的用负号代入,然后求代数和,最后结果的正、负体现了方向,但有些物理量虽也有正负之分,运算法则也一样.但不能认为是矢量,最后结果的正负也不表示方向如:功、重力势能、电势能、电势等。
二、力的合成与分解力的合成与分解体现了用等效的方法研究物理问题。
合成与分解是为了研究问题的方便而引人的一种方法.用合力来代替几个力时必须把合力与各分力脱钩,即考虑合力则不能考虑分力,同理在力的分解时只考虑分力而不能同时考虑合力。
1.力的合成(1)力的合成的本质就在于保证作用效果相同的前提下,用一个力的作用代替几个力的作用,这个力就是那几个力的“等效力”(合力)。
力的平行四边形定则是运用“等效”观点,通过实验总结出来的共点力的合成法则,它给出了寻求这种“等效代换”所遵循的规律。
(2)平行四边形定则可简化成三角形定则。
由三角形定则还可以得到一个有用的推论:如果n 个力首尾相接组成一个封闭多边形,则这n 个力的合力为零。
(3)共点的两个力合力的大小范围是|F 1-F 2| ≤ F 合≤ F 1+F 2(课件演示)(4)共点的三个力合力的最大值为三个力的大小之和,最小值可能为零。
【例1】物体受到互相垂直的两个力F 1、F 2的作用,若两力大小分别为53N 、5 N ,求这两个力的合力. 解析:根据平行四边形定则作出平行四边形,如图所示,由于F 1、F 2相互垂直,所以作出的平行四边形为矩形,对角线分成的两个三角形为直角三角形,由勾股定理得:2222215)35(+=+=F F F N=10 N合力的方向与F 1的夹角θ为: 3335512===F F tg θ θ=30° 点评:今后我们遇到的求合力的问题,多数都用计算法,即根据平行四边形定则作出平行四边形后,通过解其中的三角形求合力.在这种情况下作的是示意图,不需要很严格,但要规范,明确哪些该画实线,哪些该画虚线,箭头应标在什么位置等.【例2】如图甲所示,物体受到大小相等的两个拉力的作用,每个拉力均为200 N ,两力之间的夹角为60°,求这两个拉力的合力.解析:根据平行四边形定则,作出示意图乙,它是一个菱形,我们可以利用其对角线垂直平分,通过解其中的直角三角形求合力.320030cos 21== F F N=346 N合力与F 1、F 2的夹角均为30°.点评:(1)求矢量时要注意不仅要求出其大小,还要求出其方向,其方向通常用它与已知矢量的夹角表示.(2)要学好物理,除掌握物理概念和规律外,还要注意提高自己应用数学知识解决物理问题的能力.2.力的分解(1)力的分解遵循平行四边形法则,力的分解相当于已知对角线求邻边。
(2)两个力的合力惟一确定,一个力的两个分力在无附加条件时,从理论上讲可分解为无数组分力,但在具体问题中,应根据力实际产生的效果来分解。
【例3】将放在斜面上质量为m 的物体的重力mg 分解为下滑力F 1和对斜面的压力F 2,这种说法正确吗?解析:将mg分解为下滑力F1这种说法是正确的,但是mg的另一个分力F2不是物体对斜面的压力,而是使物体压紧斜面的力,从力的性质上看,F2是属于重力的分力,而物体对斜面的压力属于弹力,所以这种说法不正确。
【例4】将一个力分解为两个互相垂直的力,有几种分法?解析:有无数种分法,只要在表示这个力的有向线段的一段任意画一条直线,在有向线段的另一端向这条直线做垂线,就是一种方法。
如图所示。
(3)几种有条件的力的分解①已知两个分力的方向,求两个分力的大小时,有唯一解。
②已知一个分力的大小和方向,求另一个分力的大小和方向时,有唯一解。
③已知两个分力的大小,求两个分力的方向时,其分解不惟一。
④已知一个分力的大小和另一个分力的方向,求这个分力的方向和另一个分力的大小时,其分解方法可能惟一,也可能不惟一。
(4)用力的矢量三角形定则分析力最小值的规律:①当已知合力F的大小、方向及一个分力F1的方向时,另一个分力F2取最小值的条件是两分力垂直。
如图所示,F2的最小值为:F2min=F sinα②当已知合力F的方向及一个分力F1的大小、方向时,另一个分力F2取最小值的条件是:所求分力F2与合力F垂直,如图所示,F2的最小值为:F2min=F1sinα③当已知合力F的大小及一个分力F1的大小时,另一个分力F2取最小值的条件是:已知大小的分力F1与合力F同方向,F2的最小值为|F-F1|(5)正交分解法:把一个力分解成两个互相垂直的分力,这种分解方法称为正交分解法。
用正交分解法求合力的步骤:①首先建立平面直角坐标系,并确定正方向②把各个力向x 轴、y 轴上投影,但应注意的是:与确定的正方向相同的力为正,与确定的正方向相反的为负,这样,就用正、负号表示了被正交分解的力的分力的方向③求在x 轴上的各分力的代数和F x 合和在y 轴上的各分力的代数和F y 合④求合力的大小 22)()(合合y x F F F +=合力的方向:tan α=合合x y F F (α为合力F 与x 轴的夹角)点评:力的正交分解法是把作用在物体上的所有力分解到两个互相垂直的坐标轴上,分解最终往往是为了求合力(某一方向的合力或总的合力)。
【例5】质量为m 的木块在推力F 作用下,在水平地面上做匀速运动.已知木块与地面间的动摩擦因数为µ,那么木块受到的滑动摩擦力为下列各值的哪个?A .µmg B.µ(mg+Fsin θ)C.µ(mg+Fsin θ) D.F cos θ解析:木块匀速运动时受到四个力的作用:重力mg 、推力F 、支持力F N 、摩擦力F µ.沿水平方向建立x 轴,将F 进行正交分解如图(这样建立坐标系只需分解F ),由于木块做匀速直线运动,所以,在x 轴上,向左的力等于向右的力(水平方向二力平衡);在y 轴上向上的力等于向下的力(竖直方向二力平衡).即F cos θ=F µ ①F N =mg+Fsin θ ②又由于F µ=µF N ③∴F µ=µ(mg+Fsin θ) 故B、D答案是正确的.小结:(1)在分析同一个问题时,合矢量和分矢量不能同时使用。
也就是说,在分析问题时,考虑了合矢量就不能再考虑分矢量;考虑了分矢量就不能再考虑合矢量。
(2)矢量的合成分解,一定要认真作图。
在用平行四边形定则时,分矢量和合矢量要画成带箭头的实线,平行四边形的另外两个边必须画成虚线。
(3)各个矢量的大小和方向一定要画得合理。
(4)在应用正交分解时,两个分矢量和合矢量的夹角一定要分清哪个是大锐角,哪个是小锐角,不可随意画成45°。
(当题目规定为45°时除外)三、综合应用举例【例6】水平横粱的一端A 插在墙壁内,另一端装有一小滑轮B ,一轻绳的一端C 固定于墙上,另一端跨过滑轮后悬挂一质量m =10 kg 的重物,∠CBA =30°,如图甲所示,则滑轮受到绳子的作用力为(g =10m/s 2)A .50NB .503NC .100ND .1003N解析:取小滑轮作为研究对象,悬挂重物的绳中的弹力是T =mg =10×10N=100 N ,故小滑轮受绳的作用力沿BC 、BD 方向的大小都是100N ,分析受力如图(乙)所示. ∠CBD =120°,∠CBF =∠DBF ,∴∠CBF=60°,⊿CBF 是等边三角形.故F =100 N 。
故选C 。
【例7】已知质量为m 、电荷为q 的小球,在匀强电场中由静止释放后沿直线OP 向斜下方运动(OP 和竖直方向成θ角),那么所加匀强电场的场强E 的最小值是多少?解析:根据题意,释放后小球所受合力的方向必为OP 方向。
用三角形定则从右图中不难看出:重力矢量OG 的大小方向确定后,合力F 的方向确定(为OP 方向),而电场力Eq 的矢量起点必须在G 点,终点必须在OP射线上。
在图中画出一组可能的电场力,不难看出,只有当电场力方向与OP 方向垂直时Eq 才会最小,所以E 也最小,有E =qmg sin 点评:这是一道很典型的考察力的合成的题,不少同学只死记住“垂直”,而不分析哪两个矢量垂直,经常误认为电场力和重力垂直,而得出错误答案。
越是简单的题越要认真作图。
【例8】轻绳AB 总长l ,用轻滑轮悬挂重G 的物体。
绳能承受的最大拉力是2G ,将A 端固定,将B 端缓慢向右移动d 而使绳不断,求d 的最大可能值。
解:以与滑轮接触的那一小段绳子为研究对象,在任何一个平衡位置都在滑轮对它的压力(大小为G )和绳的拉力F 1、F 2共同作用下静止。
而同一根绳子上的拉力大小F 1、F 2总是相等的,它们的合力N 是压力G 的平衡力,方向竖直向上。
因此以F 1、F 2为分力做力的合成的平行四边形一定是菱形。
利用菱形对角线互相垂直平分的性质,结合相似形知识可得d ∶l =15∶4,所以d 最大为l 415 G F 1 F 2 N θmg【例9】 A 的质量是m ,A 、B 始终相对静止,共同沿水平面向右运动。
当a 1=0时和a 2=0.75g 时,B 对A 的作用力F B 各多大? 解析:一定要审清题:B 对A 的作用力F B 是B对A 的支持力和摩擦力的合力。
而A 所受重力G =mg和F B 的合力是F =ma 。
当a 1=0时,G 与 F B 二力平衡,所以F B 大小为mg ,方向竖直向上。
当a 2=0.75g 时,用平行四边形定则作图:先画出重力(包括大小和方向),再画出A 所受合力F 的大小和方向,再根据平行四边形定则画出F B 。
由已知可得F B 的大小F B =1.25mg ,方向与竖直方向成37o 角斜向右上方。
【例10】一根长2m ,重为G 的不均匀直棒AB ,用两根细绳水平悬挂在天花板上,如图所示,求直棒重心C 的位置。
解析:当一个物体受三个力作用而处于平衡状态,如果其中两个力的作用线相交于一点.则第三个力的作用线必通过前两个力作用线的相交点,把O 1A 和O 2B 延长相交于O 点,则重心C 一定在过O 点的竖直线上,如图所示由几何知识可知:BO =AB /2=1m BC =BO /2=0.5m故重心应在距B 端 0.5m 处。
