常用反三角函数公式
反三角函数公式大全

反三角函数公式大全三角函数的反函数,是多值函数。
它们是反正弦Arcsin x,反余弦Arccos x,反正切Arctan x,反余切Arccot x,反正割Arcsec x=1/cosx,反余割Arccsc x=1/sinx等,各自表示其正弦、余弦、正切、余切、正割、余割为x的角。
为限制反三角函数为单值函数,将反正弦函数的值y限在y=-π/2≤y≤π/2,将y为反正弦函数的主值,记为y=arcsin x;相应地,反余弦函数y=arccos x的主值限在0≤y≤π;反正切函数y=arctan x的主值限在-π/2<y<π/2;反余切函数y=arccot x的主值限在0<y<π。
反三角函数实际上并不能叫做函数,因为它并不满足一个自变量对应一个函数值的要求,其图像与其原函数关于函数y=x对称。
其概念首先由欧拉提出,并且首先使用了arc+函数名的形式表示反三角函数,而不是f-1(x).反三角函数主要是三个:y=arcsin(x),定义域[-1,1] ,值域[-π/2,π/2]y=arccos(x),定义域[-1,1] ,值域[0,π]y=arctan(x),定义域(-∞,+∞),值域(-π/2,π/2)sinarcsin(x)=x,定义域[-1,1],值域【-π/2,π/2】反三角函数公式:arcsin(-x)=-arcsinxarccos(-x)=∏-arccosxarctan(-x)=-arctanxarccot(-x)=∏-arccotxarcsinx+arccosx=∏/2=arctanx+arccotxsin(arcsinx)=x=cos(arccosx)=tan(arctanx)=cot(arccotx)当x∈〔—∏/2,∏/2〕时,有arcsin(sinx)=x当x∈〔0,∏〕,arccos(cosx)=xx∈(—∏/2,∏/2),arctan(tanx)=xx∈(0,∏),arccot(cotx)=xx〉0,arctanx=arctan1/x,arccotx类似若(arctanx+arctany)∈(—∏/2,∏/2),则arctanx+arctany=arctan(x+y/1-xy)。
高考数学必备公式:反三角函数公式

?反三角函数主要是三个:
y=arcsin(x),定义域[-1,1] ,值域[-π/2,π/2]图象用红色线条;
y=arccos(x),定义域[-1,1] , 值域[0,π],图象用蓝色线条;
y=arctan(x),定义域(-∞,+∞),值域(-π/2,π/2),图象用绿色线条;
sin(arcsinx)=x=cos(arccosx)=tan(arctanx)=cot(arccotx)
当x∈[—π/2,π/2]时,有arcsin(sinx)=x
当x∈[0,π],arccos(cosx)=x
x∈(—πLeabharlann 2,π/2),arctan(tanx)=x
x∈(0,π),arccot(cotx)=x
“师”之概念,大体是从先秦时期的“师长、师傅、先生”而来。其中“师傅”更早则意指春秋时国君的老师。《说文解字》中有注曰:“师教人以道者之称也”。“师”之含义,现在泛指从事教化工作或是传授学问技术也或是某方面有特长值得学习者。“老师”的原意并非由“老”而形容“师”。“老”在旧语义中也是一种尊称,隐喻年长且学识渊博者。“老”“师”连用最初见于《史记》,有“荀卿最为老师”之说法。渐渐“老师”之说也不再有年龄的限制,老少皆可适用。只是司马迁笔下的“老师”当然不是今日意义上的“老师”,其只是“老”和“师”的复合构词,所表达的含义多指对学问渊博者的一种尊称,虽能从其身上学以“道”,但其不肯定是学问的传播者。今日看来,“老师”的必要条件不光是拥有学问,更重于传播学问。若(arctanx+arctany)∈(—π/2,π/2),则arctanx+arctany=arctan(x+y/1-xy)
sin(arcsin x)=x,定义域[-1,1],值域 [-1,1] arcsin(-x)=-arcsinx
常用反三角函数公式
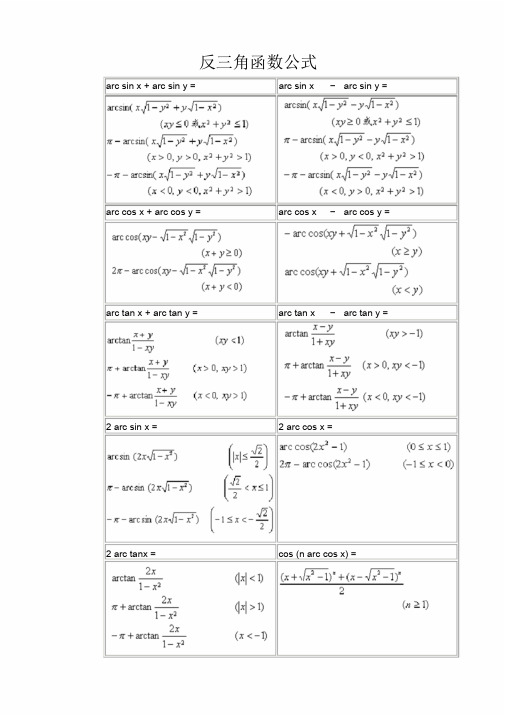
WORD格式专业分享反三角函数公式arc sin x + arc sin y = arc sin x –arc sin y = arc cos x + arc cos y = arc cos x –arc cos y = arc tan x + arc tan y = arc tan x –arc tan y = 2 arc sin x = 2 arc cos x =2 arc tanx = cos (n arc cos x) =WORD格式专业分享反三角函数图像与特征反正弦曲线图像与特征反余弦曲线图像与特征拐点( 同曲线对称中心) :拐点( 同曲线对称中心) :,该点切线斜率为 1,该点切线斜率为- 1 反正切曲线图像与特征反余切曲线图像与特征拐点:拐点( 同曲线对称中心) :,该点切线斜率为1,该点切线斜率为- 1渐近线:渐近线:WORD格式名称反正割曲线反余割曲线方程图像顶点渐近线反三角函数的定义域与主值范围函数主值记号定义域主值范围反正弦若,则反余弦若,则反正切若,则反余切若,则反正割若,则反余割若,则一般反三角函数与主值的关系为式中n为任意整数.专业分享反三角函数的相互关系arc sin x = arc cos x = arc tan x = arc cot x =sin x= x-x3/3!+x5/5!-...(-1)k-1* x2k-1/(2k-1)!+... (- ∞<x<∞)cos x= 1- x2/2!+ x4/4!-...(-1)k* x2k/(2k)!+... (- ∞<x<∞)arcsin x= x+ 1/2* x3/3 + 1*3/(2*4)* x5/5 + ... (|x|<1)arccos x= π- ( x+ 1/2* x3/3 + 1*3/(2*4)* x5/5 + ... ) (|x|<1)arctan x= x- x^3/3 + x^5/5 - ... (x≤ 1)ArcSin(x) 函数为Double。
常用反三角函数公式

反三角函数公式反三角函数图像与特征1,该点切线斜率为-:反三角函数的定义域与主值范围,则式中n为任意整数.反三角函数的相互关系sin x = x-x3/3!+x5/5!-...(-1)k-1*x2k-1/(2k-1)!+... (-∞<x<∞)cos x = 1-x2/2!+x4/4!-...(-1)k*x2k/(2k)!+... (-∞<x<∞)arcsin x = x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... (|x|<1)arccos x= π - ( x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... ) (|x|<1)arctan x = x - x^3/3 + x^5/5 - ... (x≤1)ArcSin(x) 函数功能:返回一个指定数的反正弦值,以弧度表示,返回类型为Double。
语法:ArcSin(x)。
说明:其中,x的取值范围为[-1,1],x的数据类型为Double。
程序代码:Function ArcSin(x As Double) As DoubleIf x >= -1 And x < -0.5 Then ArcSin = -Atn(Sqr(1 - x * x) / x) - 2 * Atn(1) If x >= -0.5 And x <= 0.5 Then ArcSin = Atn(x / Sqr(1 - x * x))If x > 0.5 And x <= 1 Then ArcSin = -Atn(Sqr(1 - x * x) / x) + 2 * Atn(1) End FunctionArcCos(x) 函数功能:返回一个指定数的反余弦值,以弧度表示,返回类型为Double。
语法:ArcCos(x)。
说明:其中,x的取值范围为[-1,1],x的数据类型为Double。
常用反三角函数公式表

反三角函数公式arc sin x + arc sin y = arc sin x – arc sin y = arc cos x + arc cos y = arc cos x – arc cos y = arc tan x + arc tan y = arc tan x – arc tan y = 2 arc sin x = 2 arc cos x =2 arc tanx = cos (n arc cos x) =反三角函数图像与特征反正弦曲线图像与特征反余弦曲线图像与特征拐点(同曲线对称中心):,该点切线斜率为1拐点(同曲线对称中心):,该点切线斜率为-1反正切曲线图像与特征反余切曲线图像与特征拐点(同曲线对称中心):,该点切线斜率为1拐点:,该点切线斜率为-1渐近线:渐近线:名称反正割曲线反余割曲线方程图像顶点渐近线反三角函数的定义域与主值范围函数主值记号定义域主值范围反正弦若,则反余弦若,则反正切若,则反余切若,则反正割若,则反余割若,则式中n为任意整数.反三角函数的相互关系arc sin x = arc cos x = arc tan x = arc cot x =sin x = x-x3/3!+x5/5!-...(-1)k-1*x2k-1/(2k-1)!+... (-∞<x<∞)cos x = 1-x2/2!+x4/4!-...(-1)k*x2k/(2k)!+... (-∞<x<∞)arcsin x = x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... (|x|<1)arccos x = π - ( x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... ) (|x|<1)arctan x = x - x^3/3 + x^5/5 - ... (x≤1)ArcSin(x) 函数功能:返回一个指定数的反正弦值,以弧度表示,返回类型为Double。
常用反三角函数公式

常用反三角函数公式-CAL-FENGHAI.-(YICAI)-Company One1反三角函数公式arc sin x + arc sin y = arc sin x – arc sin y = arc cos x + arc cos y = arc cos x – arc cos y = arc tan x + arc tan y = arc tan x – arc tan y = 2 arc sin x = 2 arc cos x =2 arc tanx = cos (n arc cos x) =反三角函数图像与特征反正弦曲线图像与特征反余弦曲线图像与特征拐点(同曲线对称中心):,该点切线斜率为1拐点(同曲线对称中心):,该点切线斜率为-1 ?反正切曲线图像与特征反余切曲线图像与特征拐点(同曲线对称中心):,该点切线斜率为1拐点:,该点切线斜率为-1渐近线:渐近线:?名称反正割曲线反余割曲线方程图像顶点渐近线反三角函数的定义域与主值范围函数主值记号定义域主值范围反正弦若,则反余弦若,则反正切若,则反余切若,则反正割若,则反余割若,则式中n为任意整数.反三角函数的相互关系arc sin x = arc cos x = arc tan x = arc cot x =sin x = x-x3/3!+x5/5!-...(-1)k-1*x2k-1/(2k-1)!+... (-∞<x<∞)cos x = 1-x2/2!+x4/4!-...(-1)k*x2k/(2k)!+... (-∞<x<∞)arcsin x = x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... (|x|<1)arccos x= π - ( x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... ) (|x|<1)arctan x = x - x^3/3 + x^5/5 - ... (x≤1)ArcSin(x) 函数功能:返回一个指定数的反正弦值,以弧度表示,返回类型为Double。
常用反三角函数公式表
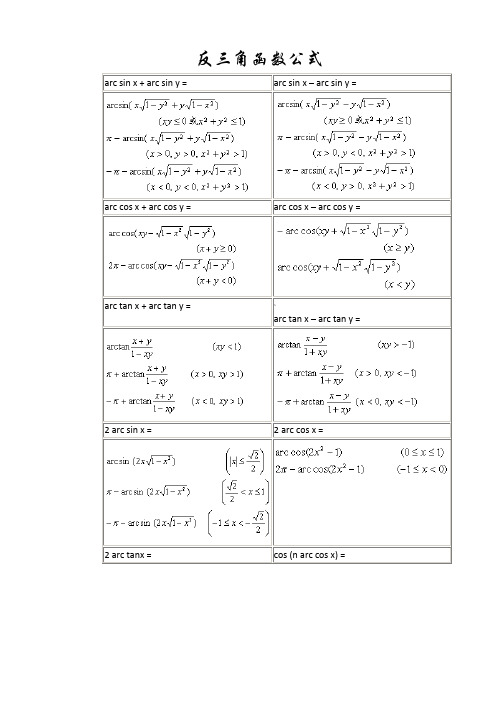
反三角函数公式arc sin x + arc sin y = arc sin x – arc sin y = arc cos x + arc cos y = arc cos x – arc cos y = arc tan x + arc tan y = ~arc tan x – arc tan y = 2 arc sin x = 2 arc cos x =2 arc tanx = cos (n arc cos x) =(反三角函数图像与特征反正弦曲线图像与特征反余弦曲线图像与特征拐点(同曲线对称中心):,该点切线斜率为1拐点(同曲线对称中心):,该点切线斜率为-1 |反正切曲线图像与特征反余切曲线图像与特征拐点(同曲线对称中心):,该点切线斜率为1拐点:,该点切线斜率为-1渐近线:—渐近线:名称反正割曲线反余割曲线方程图像、顶点渐近线反三角函数的定义域与主值范围函数、主值记号定义域主值范围反正弦若,则反余弦若,则|反正切若,则反余切若,则反正割…若,则反余割若,则式中n为任意整数.反三角函数的相互关系¥arc sin x = arc cos x = arc tan x = arc cot x =&{sin x = x-x3/3!+x5/5!-...(-1)k-1*x2k-1/(2k-1)!+... (-∞<x<∞)cos x = 1-x2/2!+x4/4!-...(-1)k*x2k/(2k)!+... (-∞<x<∞)arcsin x = x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... (|x|<1)arccos x = π - ( x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... ) (|x|<1)arctan x = x - x^3/3 + x^5/5 - ... (x≤1)~ArcSin(x) 函数功能:返回一个指定数的反正弦值,以弧度表示,返回类型为Double。
常用反三角函数公式表(完整资料).doc

此文档下载后即可编辑
反三角函数公式
arc sin x + arc sin y = arc sin x – arc sin y = arc cos x + arc cos y = arc cos x – arc cos y = arc tan x + arc tan y = arc tan x – arc tan y = 2 arc sin x = 2 arc cos x =
2 arc tanx = cos (n arc cos x) =
反三角函数图像与特征
反正弦曲线图像与特征反余弦曲线图像与特征
拐点(同曲线对称中心):,该点切线斜率为1
拐点(同曲线对称中心):
,该点切线斜率为-1 反正切曲线图像与特征反余切曲线图像与特征
拐点(同曲线对称中心):,该点切线斜率为1 拐点:
,该点切线斜率为-1
渐近线:
渐近线:
名称反正割曲线反余割曲线
方程
图像
顶点
渐近线
反三角函数的定义域与主值范围
函数主值记号定义域主值范围
反正弦若,则
反余弦若,则
反正切若,则
反余切若,则
反正割若,则
反余割若,则
式中n为任意整数.。
常用反三角函数公式

精品文档.反三角函数公式arc sin x + arc sin y =arc sin x – arc sin y =arc cos x + arc cos y =arc cos x – arc cos y =arc tan x + arc tan y =arc tan x – arc tan y =2 arc sin x =2 arc cos x =2 arc tanx =cos (n arc cos x) =精品文档.反三角函数图像与特征反正弦曲线图像与特征反余弦曲线图像与特征拐点(同曲线对称中心):,该点切线斜率为1拐点(同曲线对称中心):,该点切线斜率为-1反正切曲线图像与特征反余切曲线图像与特征拐点(同曲线对称中心):,该点切线斜率为1拐点:,该点切线斜率为-1渐近线:渐近线:精品文档. 名称反正割曲线反余割曲线方程图像顶点渐近线反三角函数的定义域与主值范围函数主值记号定义域主值范围反正弦若,则反余弦若,则反正切若,则反余切若,则反正割若,则反余割若,则式中n为任意整数.精品文档.反三角函数的相互关系arc sin x = arc cos x = arc tan x = arc cot x =sin x = x -x 3/3!+x 5/5!-...(-1)k-1*x 2k-1/(2k-1)!+... (-∞<x <∞) cos x = 1-x 2/2!+x 4/4!-...(-1)k*x 2k/(2k)!+... (-∞<x <∞) arcsin x = x + 1/2*x 3/3 + 1*3/(2*4)*x 5/5 + ... (|x |<1) arccos x = π - ( x + 1/2*x 3/3 + 1*3/(2*4)*x 5/5 + ... ) (|x |<1)arctan x = x - x ^3/3 + x ^5/5 - ... (x ≤1)ArcSin(x) 函数功能:返回一个指定数的反正弦值,以弧度表示,返回类型为Double 。
常用反三角函数公式表

,该点切线斜率为-1
渐近线:
渐近线:
名称
反正割曲线
反余割曲线
方程
图像
顶点
渐近线
反三角函数的定义域与主值范围
函数
主值记号
定义域
主值范围
反正弦
若 ,则
反余弦
若 ,则
反正切
若 ,则
反余切
若 ,则
反正割
若 ,则
反余割
若 ,则
一般反三角函数与主值的关系为
式中n为任意整数.
Ifx> 0.5 Andx<= 1 ThenArcSin= -Atn(Sqr(1 -x*x) /x) + 2 * Atn(1)
Ifx>= -0.5 Andx<= 0.5 Then ArcCos = -Atn(x/ Sqr(1 -x*x)) + 2 * Atn(1)
Ifx> 0.5 Andx<= 1 Then ArcCos = Atn(Sqr(1 -x*x) /x)
End Function
End Function
ArcCos(x) 函数
功能:返回一个指定数的反余Fra bibliotek值,以弧度表示,返回类型为Double。
语法:ArcCos(x)。
说明:其中,x的取值范围为[-1,1],x的数据类型为Double。
程序代码:
Function ArcCos(xAs Double) As Double
Ifx>= -1 Andx< -0.5 Then ArcCos = Atn(Sqr(1 -x*x)/x) + 4 * Atn(1)
2 arc cos x =
2 arc tanx =
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反三角函数公式
arc sin x + arc sin y = arc sin x – arc sin y = arc cos x + arc cos y = arc cos x – arc cos y = arc tan x + arc tan y = arc tan x – arc tan y = 2 arc sin x = 2 arc cos x =
2 arc tanx = cos (n arc cos x) =
反三角函数图像与特征
反正弦曲线图像与特征反余弦曲线图像与特征
拐点(同曲线对称中心):,该点切线斜率为1
拐点(同曲线对称中心):
,该点切线斜率为-1反正切曲线图像与特征反余切曲线图像与特征
拐点(同曲线对称中心):,该点切线斜率为1拐点:
,该点切线斜率为-1
渐近线:
渐近线:
名称反正割曲线反余割曲线
方程
图像
顶点
渐近线
反三角函数的定义域与主值范围
函数主值记号定义域主值范围
反正弦若,则
反余弦若,则
反正切若,则
反余切若,则
反正割若,则
反余割若,则
一般反三角函数与主值的关系为
式中n为任意整数.
反三角函数的相互关系
arc sin x = arc cos x = arc tan x = arc cot x =
sin x = x-x3/3!+x5/5!-...(-1)k-1*x2k-1/(2k-1)!+... (-∞<x<∞)
cos x = 1-x2/2!+x4/4!-...(-1)k*x2k/(2k)!+... (-∞<x<∞)
arcsin x = x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... (|x|<1)
arccos x= π - ( x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... ) (|x|<1)
arctan x = x - x^3/3 + x^5/5 - ... (x≤1)
ArcSin(x) 函数
功能:返回一个指定数的反正弦值,以弧度表示,返回类型为Double。
语法:ArcSin(x)。
说明:其中,x的取值范围为[-1,1],x的数据类型为Double。
程序代码:
Function ArcSin(x As Double) As Double
If x >= -1 And x < Then ArcSin = -Atn(Sqr(1 - x * x) / x) - 2 * Atn(1) If x >= And x <= Then ArcSin = Atn(x / Sqr(1 - x * x))
If x > And x <= 1 Then ArcSin = -Atn(Sqr(1 - x * x) / x) + 2 * Atn(1) End Function
ArcCos(x) 函数
功能:返回一个指定数的反余弦值,以弧度表示,返回类型为Double。
语法:ArcCos(x)。
说明:其中,x的取值范围为[-1,1],x的数据类型为Double。
程序代码:
Function ArcCos(x As Double) As Double
If x >= -1 And x < Then ArcCos = Atn(Sqr(1 - x * x) / x) + 4 * Atn(1) If x >= And x <= Then ArcCos = -Atn(x / Sqr(1 - x * x)) + 2 * Atn(1) If x > And x <= 1 Then ArcCos = Atn(Sqr(1 - x * x) / x)
End Function。
