半导体物理_第六章学习资料
合集下载
半导体物理基础 第六章 MOS
把
QS QB qNa xd
2 qNa xd S 2k s 0
（6-5）
和
（6-6）
6.2 理想MOS电容器
代入（6-44）式解出 x
d
Xd
kS 0 kS 0 2VG 1 C0 2 C0 C0 qkS 0 N a
2 0 12
（6-45）
C 2C 1 qN k VG C0 a S 0
6.2 理想MOS电容器
积累区（ VG <0）
MOS系统的电容C基本上等于绝缘体电容 C0。当负偏压的数值逐渐减少时，空间电 荷区积累的空穴数随之减少，并且 QS 随 C也就变小。 平带情况（ VG =0）
S
的变化也逐渐减慢， C S 变小。总电容
C FB C0
1 k 0 LD 1 k s x0
（6-1）
掌握载流子积累、耗尽和反型和强反型的概念。 正确画出流子积累、耗尽和反型和强反型四种情况的能带图。 导出反型和强反型条件
6.2 理想MOS电容器
6.2 理想MOS电容器
系统单位面积的微分电容
微分电容C与外加偏压 VG 的关系称为MOS系统的电容—电压特性。
dQM C dVG
（6-1）
S =半导体表面的电场
k0 =氧化物的相对介电常数
k S =半导体相对介电常数
xd =空间电荷区在半导体内部的边界亦即空间电荷区宽度。
外加电压 VG 为跨越氧化层的电压
V0和表面势 S 所分摊：
（6-2）
VG V0 S
6.1 理想MOS结构的表面空S结构内的电位分布
（6-22）
dV0 d s 1 dVG C dQM dQM dQM
QS QB qNa xd
2 qNa xd S 2k s 0
（6-5）
和
（6-6）
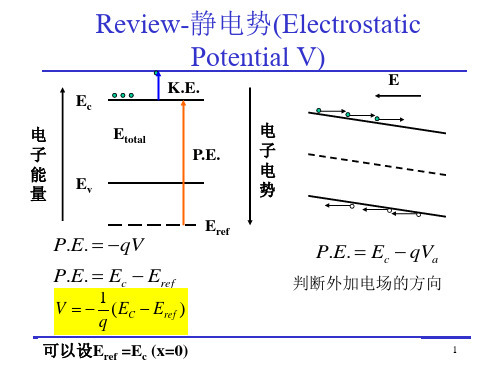
6.2 理想MOS电容器
代入（6-44）式解出 x
d
Xd
kS 0 kS 0 2VG 1 C0 2 C0 C0 qkS 0 N a
2 0 12
（6-45）
C 2C 1 qN k VG C0 a S 0
6.2 理想MOS电容器
积累区（ VG <0）
MOS系统的电容C基本上等于绝缘体电容 C0。当负偏压的数值逐渐减少时，空间电 荷区积累的空穴数随之减少，并且 QS 随 C也就变小。 平带情况（ VG =0）
S
的变化也逐渐减慢， C S 变小。总电容
C FB C0
1 k 0 LD 1 k s x0
（6-1）
掌握载流子积累、耗尽和反型和强反型的概念。 正确画出流子积累、耗尽和反型和强反型四种情况的能带图。 导出反型和强反型条件
6.2 理想MOS电容器
6.2 理想MOS电容器
系统单位面积的微分电容
微分电容C与外加偏压 VG 的关系称为MOS系统的电容—电压特性。
dQM C dVG
（6-1）
S =半导体表面的电场
k0 =氧化物的相对介电常数
k S =半导体相对介电常数
xd =空间电荷区在半导体内部的边界亦即空间电荷区宽度。
外加电压 VG 为跨越氧化层的电压
V0和表面势 S 所分摊：
（6-2）
VG V0 S
6.1 理想MOS结构的表面空S结构内的电位分布
（6-22）
dV0 d s 1 dVG C dQM dQM dQM
半导体物理_第六章_pn结
Jn dEF dx n n
qDp dEF J p p0 kT dx
电流密度与费米能级的关系 对于平衡的pn结，Jn, Jp均为零，因此，
Jp dEF dx p p
EF=常数
qDp dEF J p p0 kT dx
当电流密度一定时，载流子浓度大的地方， EF随 位置变化小，而载流子浓度小的地方， EF随位置 变化较大。
非平衡载流子的电注入：正向偏压使非平衡载流子进入半导 体的过程。
注入到p区的电子断与空穴复合，电子流不断转化 为空穴流，直到全部复合为止。
扩散电流〉漂移电流
根据电流连续性原理，通过pp’(或nn’)任何一个界 面的总电流是相等的。只是电子电流和空穴电流 的比例不同。 总电流=扩散电流+漂移电流
反向偏移下，非平衡状态 外加反向电场与内建势场方向一致。
1. pp’处注入的非平衡少数载流子浓度：
EFn Ei n p ni exp( ) k0T EFn EFP n p p p ni exp( ) k0T
2
p p ni exp(
Ei EFp k0T
)
在pp’边界处， x=-xp, qV=Efn-Efp,
qV n p ( x p ) p p ( x p ) ni exp( ) k0T
电子电势能-q V(x)由n到p不断升高 P区能带整体相对n区上移。n区能带整体相对p区下移。 直到具有统一费米能级 pn结费米能级处处相等标志pn结达到动态平衡，无扩散、 漂移电流流过。
动态平衡时
本征费米能级Ei的变化与-qV(x)一致
k0T n Dn q
k0T n Dn q
同理，空穴电流密度为：
qV x p ( ) 0 2. 加反向偏压下，如果qV>>k0T, e k0T
半导体物理学第六章解读
ND X D ND NA
1
Q=eND
Xn
2
0e
(
NDNA ND NA
)(VD
V
2 )
♦单边突变结:
XD
2
e
0
1
(VD V NB
)
2
♦势垒区主要在轻掺杂 一边
• 对p+-n结, NB代表ND • 对p-n+结, NB代表NA
xn X D
xp XD
P+-n结
3. 突变结的势垒电容
电势
图6-8
电子势能(能带)
6.1.5p-n载流子的分布 ♦ 当电势零点取x=-xp处,则有: EC (x) EC qV (x)
EV (x) EV qV ( x)
x x p , EC ( x) EC x xn , EC (x) EC qVD
♦势垒区的载流子浓度为:
EC qV ( x ) EF
• 反向偏压下的突变结势垒电容(单位面积):
1
CT A
dQ dV
2(
0eND NA
ND NA )(VD
V
)
2
CT 0
A XD
CT
(VD
1 V )1/ 2
• 几点说明:
① p-n结的势垒电容可以等效为一个平行
板电容器,势垒宽度即两平行极板的距离
② 这里求得的势垒电容, 主要适用于反向 偏置情况
xn
NAXD ND NA
, xp
ND X D ND NA
• 代入上式
VD
q
2 0
( NAND ND NA
)
X
2 D
♦则，平衡p-n结
1
XD
半导体物理课件 第六章(2015.11.20)
低空间电荷减少 ♦当pn结上外加的反向电压增加，势垒高度增
加空间电荷增加
26
偏压上升(含正负)： 变窄
P区
空穴补偿 电子补偿
n区
偏压下降(含正负) ： 变宽
P区
空穴释放 电子释放
n区
2015/12/26
Semiconductor Physics
27
②扩散电容 CD —当pn结上外加电压变化，扩散区的非平衡 载流子的积累相应变化所对应的电容效应. ♦当正向偏臵电压增加，扩散区内的非平衡载 流子积累很快增加 ♦在反向偏臵下，非平衡载流子数变化不大,扩 散电容 可忽略 pn结的势垒电容和扩散电容都随外加电压而变 化-- CT 和CD都是微分电容: C=dQ/dV
x xp
xn - x
eV ( x ) kT
n np 0
n nn0
eV ( x ) kT
p pp0
p pn0
n( x ) n p 0 e
p( x) p p 0e
12
平衡p-n结载流子浓度分布的基本特点: ♦ 同一种载流子在势垒区两边的浓度关系服 从玻尔兹曼关系 ♦ 处处都有n•p=ni2 ♦ 势垒区是高阻区(常称作耗尽层)
1. 热击穿
pn结的反向扩散流由平衡少子产生：
pno = ni２/ND
npo = ni２/ NA
产生电流正比于ni
反向电流密切依赖于本征载流子浓度。 |ＶR |
反向偏压
Pc
功 耗
Tj
结温
ni
IR
IR
击穿
ni２∝T3 exp(-Eg0/KT)
43
2. 隧道击穿
隧道效应---电子具有波动性，它可以一定几率穿过能量 比其高的势垒区，这种现象称作隧道效应。
微电子学 半导体物理学 第六章pn结
(N
2 x 2 + N D xn ) A p
x D = xn + x p N A x p = N D xn
NA ND xn = xD x p = xD NA + ND NA + ND
1/ 2
1/ 2
2ε 0ε r 2ε ε N + N D 代入 VD 得 x D = 0 r A VD = qN VD N AN D q eff q2 N A (x + x p )2 (-xp<x<0) EC ( x ) = EC ( p ) − 2ε 0ε r q2 N D ( x − xn )2 − 2011 EC ( x ) = E复旦大学半导体物理 -qV D (0<x<xn) + C ( p) 2ε 0ε r
复旦大学半导体物理 - 2011
14
平衡时的费米能级
J n = J n扩 + J n漂 = 0
dn 0 J n = qn 0 µ n E + qDn dx
dn0 1 dEi 1 dE F = − n0 + n0 dx k BT dx k BT dx dV ( x ) 1 dEi E=− = dx q dx
NDNA越大，VD越大；Eg越大，ni越小，VD越大。 NA=1017cm-3, ND=1015cm-3, Si的VD＝0.70V. 复旦大学半导体物理 - 2011
17
平衡时，
qVD = Ecp − Ecn = E g + ( EFn − Ec ) + ( Ev − EFp )
对于非简并半导体，势垒高度会大于禁带宽度Eg吗？
耗尽层近似
从N区到P区，随着电子势能的升高，电子浓度 迅速下降，由于Vd（~1V），在势垒区的大部 分范围内，电子极为稀少，可视为电子耗尽， N侧空间电荷区的电荷基本是由电离施主贡献 的。同理，P侧空间电荷区的电荷有电离受主 贡献。 认为，在空间电荷区载流子被耗尽了
精选半导体物理第六章资料
增大，从而导致半导体材料中电子和空穴浓度随着时 间而变化，直到最后达到新的平衡。
外部的光照，也会产生额外的电子－空穴对，从 而建立起一个非热平衡状态。
6.1.1 热平衡状态半导体的产生和复合
处于热平衡状态的半导体材料，其电子和空穴的浓度 不随时间发生变化，但实际这是一种动态平衡。在半 导体材料中仍然不断地存在着大量电子－空穴对的产 生过程，也存在着大量电子－空穴对的复合过程。
扩散方程的物理意义：
与时间相关的扩散方程描述过剩载流子浓度随着时间和 空间位置的变化规律。
§6.3 双极输运
在第5章中，导出的电子电流密度方程和空穴电流密 度方程中，引起漂移电流的电场指的是外加的电场。
如果在半导体材料中的某一处产生了过剩电子和过剩 空穴，若有外加电场存在，这些过剩电子和过剩空穴 就会在外加电场的作用下朝着相反的方向漂移。
由于
所以扩散方程中的电子和空穴的浓度包含了： 热平衡时的载流子浓度； 非热平衡条件下的过剩载流子浓度；
热平衡载流子浓度n0、p0不随时间和空间位置变 化，因此：
电子和空穴的扩散方程可进一步变换为下式：
上述两式就是在掺杂和组分均匀的条件下，半导体材 料中过剩载流子浓度随着时间和空间变化规律的方程。
如果半导体材料受到外部的激励(如温度的突然 升高），那么在原来热平衡浓度的基础上，会增加额 外的导带电子和价带空穴----非平衡过剩载流子，过 剩载流子是半导体器件工作的基础。
本章重点学习描述非平衡过剩载流子随空间位置 和时间变化状态---双极输运方程，这是研究分析PN 结和双极型晶体管特性的基础。
电子的产生率---Gn0 空穴热产生率---Gp0，
单位：cm-3·s-1。
对于导带与价带之间的的复合率--- Rn0 空穴的复合率--- Rp0
外部的光照，也会产生额外的电子－空穴对，从 而建立起一个非热平衡状态。
6.1.1 热平衡状态半导体的产生和复合
处于热平衡状态的半导体材料，其电子和空穴的浓度 不随时间发生变化，但实际这是一种动态平衡。在半 导体材料中仍然不断地存在着大量电子－空穴对的产 生过程，也存在着大量电子－空穴对的复合过程。
扩散方程的物理意义：
与时间相关的扩散方程描述过剩载流子浓度随着时间和 空间位置的变化规律。
§6.3 双极输运
在第5章中，导出的电子电流密度方程和空穴电流密 度方程中，引起漂移电流的电场指的是外加的电场。
如果在半导体材料中的某一处产生了过剩电子和过剩 空穴，若有外加电场存在，这些过剩电子和过剩空穴 就会在外加电场的作用下朝着相反的方向漂移。
由于
所以扩散方程中的电子和空穴的浓度包含了： 热平衡时的载流子浓度； 非热平衡条件下的过剩载流子浓度；
热平衡载流子浓度n0、p0不随时间和空间位置变 化，因此：
电子和空穴的扩散方程可进一步变换为下式：
上述两式就是在掺杂和组分均匀的条件下，半导体材 料中过剩载流子浓度随着时间和空间变化规律的方程。
如果半导体材料受到外部的激励(如温度的突然 升高），那么在原来热平衡浓度的基础上，会增加额 外的导带电子和价带空穴----非平衡过剩载流子，过 剩载流子是半导体器件工作的基础。
本章重点学习描述非平衡过剩载流子随空间位置 和时间变化状态---双极输运方程，这是研究分析PN 结和双极型晶体管特性的基础。
电子的产生率---Gn0 空穴热产生率---Gp0，
单位：cm-3·s-1。
对于导带与价带之间的的复合率--- Rn0 空穴的复合率--- Rp0
《半导体物理》胡礼中第六章 非平衡载流子
第六章 非平衡载流子处于热平衡状态的半导体在一定温度下载流子密度是一定的。
但在外界作用下，热平衡状态将被破坏，能带中的载流子数将发生明显改变，产生非平衡载流子。
在半导体中非平衡载流子具有极其重要的作用，许多效应都是由它们引起的，如晶体管电流放大，半导体发光和光电导等都与非平衡载流子密切相关。
在大多数情况下，非平衡载流子都是在半导体的局部区域产生的，这些载流子除了在电场作用下作漂移运动外，还要作扩散运动。
本章主要讨论非平衡载流子的运动规律及其产生和复合机理。
§6-1 非平衡载流子的产生和复合一．非平衡载流子的产生。
若用n 0和p 0分别表示热平衡时的电子和空穴密度，则当对半导体施加外界作用使之处于非平衡状态时，半导体中的载流子密度就不再是n 0和p 0了，要比它们多出一部分。
比平衡态多出的这部分载流子称过剩载流子，习惯上也称非平衡载流子。
设想有一块n 型半导体，若用光子能量大于其禁带宽度的光照射该半导体，则可将其价带中的电子激发到导带，使导带比热平衡时多出了一部分电子n ∆，价带多出了一部分空穴p ∆，从而有：0n n n -=∆ （6-1） 0p p p -=∆ （6-2） 且 n ∆=p ∆ （6-3） 式中，n 和p 分别为非平衡状态下的电子和空穴密度，n ∆称非平衡多子，p ∆称非平衡少子，对于p 型半导体则相反。
n ∆和p ∆统称非平衡载流子。
图6-1为光照产生非平衡载流子的示意图。
通过光照产生非平衡载流子的方法称光注入，如果非平衡载流子密度远小于热平衡多子密度则称小注入。
虽然小注入对多子密度的影响可以忽略，但是对少子密度的影响却可以很大。
光注入产生的非平衡载流子可以使半导体的电导率由热平衡时的0σ增加到σσσ∆+=0，其中，σ∆称附加电导率或光电导，并有：p n pe ne μμσ∆+∆=∆ （6-4） 若n ∆=p ∆，则 )(p n pe μμσ+∆=∆ （6-5） 通过附加电导率的测量可直接检验非平衡载流子是否存在。
半导体物理第六章PN结
二、PN结的反向电流
加反向偏压时，外加电场与内 建电场方向相同，增强了势垒区的 电场强度，势垒区加宽、增高，漂 移运动超过了扩散运动。n区中的空 穴（p区中的电子）一旦到达势垒区 边界处，就立即被电场扫向p区（n 区），构成了pn结的反向电流，方 向由n区到p区。
一、PN结的正向电流
多子电流与少子电流的转换
注入的非平衡少子在扩散过程中与多子相遇
中性区 势垒区 扩散区 扩散区 中性区 + p n
而不断复合，经过一个扩散长度后，复合基 本完毕，载流子浓度接近平衡数值。非平衡 少子边扩散边复合的区域称为扩散区，载流 子浓度接近平衡值的区域称为中性区 半导体中的电流主要由多子运载，然而pn结 正向电流是由电注入的非平衡少子引起的。 �非平衡少子被多子复合并非电流的中断， 因为与少子复合的多子是从n区的右边过来的 电子，所以它们的复合正好实现了少子电流 到多子电流的转换，如图c所示。
qV ) k0T
� pn结的正向电流随正向偏压呈指数规律增长。
一、PN结的正向电流
正偏压作用下的能带图
1、由于正偏压的作用，势垒高度下降， pn结不再处于平衡状态，在势垒区和扩散区，电子 准费米能级和空穴准费米能级不一致，而在中性区二者则趋于重合。 �说明通过势垒边界分别注入到两侧的非平衡载流子扩散一段距离后才复合完毕。而中性区 载流子的分布接近热平衡分布，故在中性区，两个准费米能级趋于汇合成统一的费米能级。
qα j x d 2V ( x ) ρ ( x) = − = − dx 2 ε sε 0 ε sε 0
xD 对上式积分，并利用边界条件 ε ⎛ ± ⎜ ⎝ 2
⎞ ⎟ = 0 , 得： ⎠
ε ( x) =
qα j
2ε sε 0x − Nhomakorabea2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
对小注入条件来说，τn0是一个常数，上式反 映了过剩少数载流子电子的衰减过程，因此τn0 也称为过剩少数载流子的寿命。微秒数量级
过剩少数载流子电子的复合率（通常其定义为 一个正值）则可以表示为：
对于带与带之间的直接复合过程来说，过剩多 数载流子空穴也将以同样的速率发生复合，即：
对于N型半导体材料，在小注入条件下，少数载 流子空穴的浓度将以时间常数τp0进行衰减。
在小注入的条件下，上述方程很容易求解。 对于非本征的N型半导体材料，通常n0>>p0；而对 于非本征的P型半导体材料，则有p0>>n0，小注入 条件也就是过剩载流子的浓度远远低于热平衡时 多数载流子的浓度。反之，大注入条件(接近或超 过)
对于P型半导体，在小注入条件下上述方程变为 此方程的解为一个指数衰减函数：
τp0称为过剩少数载流子的寿命。此时多数载流 子电子和少数载流子空穴的复合率也完全相等， 即：
一般而言，过剩载流子产生率通常与电子或空 穴的浓度无关。
讨论过剩载流子产生和复合过程常用的符号
3. 产生与复合过程 （1）带与带之间的产生与复合过程：
（2）通过复合中心的间接产生与复合过程：
（3）俄歇复合过程（三粒子过程）：
过剩电子和过剩空穴一般是由外界激发条件 而产生的，其产生率通常记为gn'和gp'，对于 导带与价带之间的直接产生过程来说，过剩电 子和过剩空穴也是成对产生的，因此有：
当有过剩载流子产生时，电子的浓度和空穴 的浓度就会高出热平衡时的浓度，即：
其中n0和p0分别是热平衡状态下导带电子和价带 空穴的浓度，δn和δp分别是过剩电子和过剩空 穴的浓度。
中电子和空穴的浓度不随时间发生变化。但是 这只是一种动态平衡，在半导体材料中仍然不 断地存在着大量电子－空穴对的产生过程，同 时也存在着大量电子－空穴对的复合过程。
假设电子和空穴的热产生率分别为Gn0和Gp0，其 单位为cm-3·s-1，对于导带与价带之间的产生 过程，电子和空穴都是成对产生的，因此有：
右图所示 就是由光 激发所引 起的过剩 电子和过 剩空穴的 产生过程
当有过剩载流子产生时，外界的激发作用就 已经打破了热平衡状态，电子和空穴的浓度也 不再满足热平衡时的条件，即：
和热平衡时一样，过剩电子也会不断地和过 剩空穴相复合。假设过剩电子和过剩空穴的复 合率分别为Rn'和Rp'，由于过剩电子和过剩空 穴也是成对复合掉的，因此有：
这两个电流密度公式中都分别包含了漂移电 流项和扩散电流项。如果我们将上述两式分别 除以电子的电量e，则可得到：
对上述两式求散度（此处即对x求导数），并 代回到电子和空穴的连续性方程中，即可得到：
由于电子和空穴的浓度中既包含热平衡时 的载流子浓度，也包含非热平衡条件下的过剩 载流子浓度，而热平衡时的载流子浓度n0、p0 一般不随时间变化，对于掺杂和组分均匀的半 导体材料来说，n0和p0也不随空间位置变化， 因此利用下述关系：
除了空穴粒子流的通量之外，空穴的产生率 和复合率同样也会影响微分体积元中空穴的浓度， 因此考虑空穴的产生和复合效应之后，单位时间 内微分体积元中空穴的净增量为：
其中p为空穴的浓度，上式右边第一项是由 于空穴粒子流的通量而引起的单位时间内空穴的 增加量，
第二项则是由于空穴的产生作用而引起的 单位时间内空穴的增加量，而第三项则是由于 空穴的复合作用而引起的单位时间内空穴的减 少量。上式中空穴的复合率表示为p/τpt，其中 τpt既包含热平衡载流子寿命，又包含过剩载流 子寿命。将上式两边分别除以微分体积元的体 积，则有：
能量守恒和动量守恒的考虑： 直接带隙半导体材料 间接带隙半导体材料
声子参与
§6.2 连续性方程
过剩载流子的产生率和复合率无疑是非常 重要的描述非平衡过剩载流子特性的参数，但 是在有电场和浓度梯度存在的情况下，过剩载 流子随着时间和空间位置的变化规律也具有同 样的重要性。
连续性方程： 考虑一个微分体积元，一个一维空穴粒子
上式即称为一维条件下的空穴连续性方程。
类似地可以得到一维条件下的电子连续性方程为：
式中Fn－为电子粒子流的通量，其单位也是 cm-2s-1，电子的复合率表示为n/τnt，其中τnt既 包含热平衡载流子寿命，也包含过剩载流子寿命。
在第五章中我们曾经推导出了空穴的电流密度 方程和电子的电流密度方程，它们分别为：
半导体物理_第六章
§6.1 载流子的产生与复合 所谓载流子的产生，即把一个价带电子激
发至导带，形成一对可以参与导电的电子－空 穴对的过程；所谓载流子的复合，即一个导带 电子跃迁至价带，使得一对本来可以参与导电 的电子－空穴对消失的过程。
1. 热平衡状态下的半导体材料 对于处于热平衡状态的半导体材料来说，其
与此类似，假设电子和空穴的复合率分别为Rn0 和Rp0，其单位也是cm-3·s-1，对于导带与价带之 间的直接复合过程来说，电子和空穴也是成对 复合掉的：
在热平衡状态下，电子和空穴的浓度不随时间 改变，即达到动态平衡，因此有：
2. 过剩载流子的产生与复合 当有外界激发条件（例如光照）存在时，
将会把价带中的一个电子激发至导带，从而产 生了一个电子－空穴对，这些额外产生出的电 子和空穴就称为过剩电子和过剩空穴。
流的通量在x处进入微分体积元，又在x+dx处离 开微分体积元。空穴粒子流的通量为Fpx+，其单 位是cm-2s-1，则有下式成立：
因此单位时间内由于x方向空穴粒子流的通 量而导致微分体积元中空穴的净增量为：
假如Fpx+(x)>Fpx+(x+dx)，则微分体积元中 净的空穴数量将随着时间而不断增加。如果我 们将上式推广到一般的三维情形，则上式变为：
下图所示为半导体材料中过剩载流子的复合过 程，如果撤掉外界作用，由于过剩载流子的复 合作用，非热平衡状态将会逐渐地向热平衡状 态恢复。
对于导带与价带之间的直穴的浓度成正比，因此有：
其中第一项αrni2为热平衡时的产生率。由于 过剩电子和过剩空穴总是成对产生的，即：
过剩少数载流子电子的复合率（通常其定义为 一个正值）则可以表示为：
对于带与带之间的直接复合过程来说，过剩多 数载流子空穴也将以同样的速率发生复合，即：
对于N型半导体材料，在小注入条件下，少数载 流子空穴的浓度将以时间常数τp0进行衰减。
在小注入的条件下，上述方程很容易求解。 对于非本征的N型半导体材料，通常n0>>p0；而对 于非本征的P型半导体材料，则有p0>>n0，小注入 条件也就是过剩载流子的浓度远远低于热平衡时 多数载流子的浓度。反之，大注入条件(接近或超 过)
对于P型半导体，在小注入条件下上述方程变为 此方程的解为一个指数衰减函数：
τp0称为过剩少数载流子的寿命。此时多数载流 子电子和少数载流子空穴的复合率也完全相等， 即：
一般而言，过剩载流子产生率通常与电子或空 穴的浓度无关。
讨论过剩载流子产生和复合过程常用的符号
3. 产生与复合过程 （1）带与带之间的产生与复合过程：
（2）通过复合中心的间接产生与复合过程：
（3）俄歇复合过程（三粒子过程）：
过剩电子和过剩空穴一般是由外界激发条件 而产生的，其产生率通常记为gn'和gp'，对于 导带与价带之间的直接产生过程来说，过剩电 子和过剩空穴也是成对产生的，因此有：
当有过剩载流子产生时，电子的浓度和空穴 的浓度就会高出热平衡时的浓度，即：
其中n0和p0分别是热平衡状态下导带电子和价带 空穴的浓度，δn和δp分别是过剩电子和过剩空 穴的浓度。
中电子和空穴的浓度不随时间发生变化。但是 这只是一种动态平衡，在半导体材料中仍然不 断地存在着大量电子－空穴对的产生过程，同 时也存在着大量电子－空穴对的复合过程。
假设电子和空穴的热产生率分别为Gn0和Gp0，其 单位为cm-3·s-1，对于导带与价带之间的产生 过程，电子和空穴都是成对产生的，因此有：
右图所示 就是由光 激发所引 起的过剩 电子和过 剩空穴的 产生过程
当有过剩载流子产生时，外界的激发作用就 已经打破了热平衡状态，电子和空穴的浓度也 不再满足热平衡时的条件，即：
和热平衡时一样，过剩电子也会不断地和过 剩空穴相复合。假设过剩电子和过剩空穴的复 合率分别为Rn'和Rp'，由于过剩电子和过剩空 穴也是成对复合掉的，因此有：
这两个电流密度公式中都分别包含了漂移电 流项和扩散电流项。如果我们将上述两式分别 除以电子的电量e，则可得到：
对上述两式求散度（此处即对x求导数），并 代回到电子和空穴的连续性方程中，即可得到：
由于电子和空穴的浓度中既包含热平衡时 的载流子浓度，也包含非热平衡条件下的过剩 载流子浓度，而热平衡时的载流子浓度n0、p0 一般不随时间变化，对于掺杂和组分均匀的半 导体材料来说，n0和p0也不随空间位置变化， 因此利用下述关系：
除了空穴粒子流的通量之外，空穴的产生率 和复合率同样也会影响微分体积元中空穴的浓度， 因此考虑空穴的产生和复合效应之后，单位时间 内微分体积元中空穴的净增量为：
其中p为空穴的浓度，上式右边第一项是由 于空穴粒子流的通量而引起的单位时间内空穴的 增加量，
第二项则是由于空穴的产生作用而引起的 单位时间内空穴的增加量，而第三项则是由于 空穴的复合作用而引起的单位时间内空穴的减 少量。上式中空穴的复合率表示为p/τpt，其中 τpt既包含热平衡载流子寿命，又包含过剩载流 子寿命。将上式两边分别除以微分体积元的体 积，则有：
能量守恒和动量守恒的考虑： 直接带隙半导体材料 间接带隙半导体材料
声子参与
§6.2 连续性方程
过剩载流子的产生率和复合率无疑是非常 重要的描述非平衡过剩载流子特性的参数，但 是在有电场和浓度梯度存在的情况下，过剩载 流子随着时间和空间位置的变化规律也具有同 样的重要性。
连续性方程： 考虑一个微分体积元，一个一维空穴粒子
上式即称为一维条件下的空穴连续性方程。
类似地可以得到一维条件下的电子连续性方程为：
式中Fn－为电子粒子流的通量，其单位也是 cm-2s-1，电子的复合率表示为n/τnt，其中τnt既 包含热平衡载流子寿命，也包含过剩载流子寿命。
在第五章中我们曾经推导出了空穴的电流密度 方程和电子的电流密度方程，它们分别为：
半导体物理_第六章
§6.1 载流子的产生与复合 所谓载流子的产生，即把一个价带电子激
发至导带，形成一对可以参与导电的电子－空 穴对的过程；所谓载流子的复合，即一个导带 电子跃迁至价带，使得一对本来可以参与导电 的电子－空穴对消失的过程。
1. 热平衡状态下的半导体材料 对于处于热平衡状态的半导体材料来说，其
与此类似，假设电子和空穴的复合率分别为Rn0 和Rp0，其单位也是cm-3·s-1，对于导带与价带之 间的直接复合过程来说，电子和空穴也是成对 复合掉的：
在热平衡状态下，电子和空穴的浓度不随时间 改变，即达到动态平衡，因此有：
2. 过剩载流子的产生与复合 当有外界激发条件（例如光照）存在时，
将会把价带中的一个电子激发至导带，从而产 生了一个电子－空穴对，这些额外产生出的电 子和空穴就称为过剩电子和过剩空穴。
流的通量在x处进入微分体积元，又在x+dx处离 开微分体积元。空穴粒子流的通量为Fpx+，其单 位是cm-2s-1，则有下式成立：
因此单位时间内由于x方向空穴粒子流的通 量而导致微分体积元中空穴的净增量为：
假如Fpx+(x)>Fpx+(x+dx)，则微分体积元中 净的空穴数量将随着时间而不断增加。如果我 们将上式推广到一般的三维情形，则上式变为：
下图所示为半导体材料中过剩载流子的复合过 程，如果撤掉外界作用，由于过剩载流子的复 合作用，非热平衡状态将会逐渐地向热平衡状 态恢复。
对于导带与价带之间的直穴的浓度成正比，因此有：
其中第一项αrni2为热平衡时的产生率。由于 过剩电子和过剩空穴总是成对产生的，即：