线性回归方程-高中数学知识点讲解
高三回归方程知识点汇总

高三回归方程知识点汇总回归方程是数学中重要的数学模型,用于描述变量之间的关系和进行预测。
在高三阶段,学生需要掌握回归分析的基本知识和技巧。
本文将对高三数学中回归方程的知识点进行全面汇总,并提供一些实例和应用场景供参考。
一、线性回归方程1.1 线性关系与线性回归方程线性关系指的是两个变量之间存在直线关系,可用一条直线来近似表示。
线性回归方程是线性关系的数学表达式,常用形式为 y = kx + b,其中 k 表示直线的斜率,b 表示直线在 y 轴上的截距。
1.2 最小二乘法最小二乘法是确定线性回归方程中斜率 k 和截距 b 的常用方法。
它通过最小化观测值与回归直线的拟合误差平方和,找到最佳的拟合直线。
1.3 直线拟合与误差分析直线拟合是利用线性回归方程将观测数据点拟合到一条直线上。
误差分析可以评估回归方程的拟合优度,常用指标有决定系数R²、平均绝对误差 MAE 等。
二、非线性回归方程2.1 非线性关系与非线性回归方程非线性关系指的是两个变量之间的关系不能用一条直线来近似表示,而是需要使用曲线或其他非线性形式进行描述。
非线性回归方程可以是多项式方程、指数方程、对数方程等形式。
2.2 最小二乘法拟合非线性回归方程与线性回归相似,最小二乘法也可以用于拟合非线性回归方程。
但由于非线性方程的复杂性,通常需要借助计算工具进行求解,例如利用数学软件进行非线性拟合。
2.3 模型选择和拟合优度检验在选择非线性回归模型时,需要综合考虑模型的拟合优度和实际应用的需求。
常见的方法包括比较不同模型的决定系数 R²、检验残差分布等。
三、应用实例3.1 人口增长模型以某地区的人口数据为例,通过拟合合适的回归方程,可以预测未来的人口增长趋势,为城市规划和社会发展提供决策依据。
3.2 经济增长模型回归方程可以用于分析经济数据,例如拟合国民生产总值与时间的关系,预测未来的经济增长态势,为政府制定经济政策提供参考。
3.3 科学实验数据分析在科学研究中,常常需要利用回归方程对实验数据进行拟合和分析。
高一数学必修线性回归分析知识点

⾼⼀数学必修线性回归分析知识点 分析按照⾃变量和因变量之间的关系类型,可分为线性回归分析和⾮线性回归分析。
下⾯是店铺给⼤家带来的⾼⼀数学必修线性回归分析知识点,希望对你有帮助。
⾼⼀数学线性回归分析知识点总结(⼀) 重点难点讲解: 1.回归分析: 就是对具有相关关系的两个变量之间的关系形式进⾏测定,确定⼀个相关的数学表达式,以便进⾏估计预测的统计分析⽅法。
根据回归分析⽅法得出的数学表达式称为回归⽅程,它可能是直线,也可能是曲线。
2.线性回归⽅程 设x与y是具有相关关系的两个变量,且相应于n组观测值的n个点(xi, yi)(i=1,......,n)⼤致分布在⼀条直线的附近,则回归直线的⽅程为。
其中 。
3.线性相关性检验 线性相关性检验是⼀种假设检验,它给出了⼀个具体检验y与x之间线性相关与否的办法。
①在课本附表3中查出与显著性⽔平0.05与⾃由度n-2(n为观测值组数)相应的相关系数临界值r0.05。
②由公式,计算r的值。
③检验所得结果 如果|r|≤r0.05,可以认为y与x之间的线性相关关系不显著,接受统计假设。
如果|r|>r0.05,可以认为y与x之间不具有线性相关关系的假设是不成⽴的,即y与x之间具有线性相关关系。
典型例题讲解: 例1.从某班50名学⽣中随机抽取10名,测得其数学考试成绩与物理考试成绩资料如表:序号12345678910数学成绩54666876788285879094,物理成绩61806286847685828896试建⽴该10名学⽣的物理成绩对数学成绩的线性回归模型。
解:设数学成绩为x,物理成绩为,则可设所求线性回归模型为, 计算,代⼊公式得 ∴所求线性回归模型为=0.74x+22.28。
说明:将⾃变量x的值分别代⼊上述回归模型中,即可得到相应的因变量的估计值,由回归模型知:数学成绩每增加1分,物理成绩平均增加0.74分。
⼤家可以在⽼师的帮助下对⾃⼰班的数学、化学成绩进⾏分析。
高中数学知识点精讲精析 线性回归分析 (2)
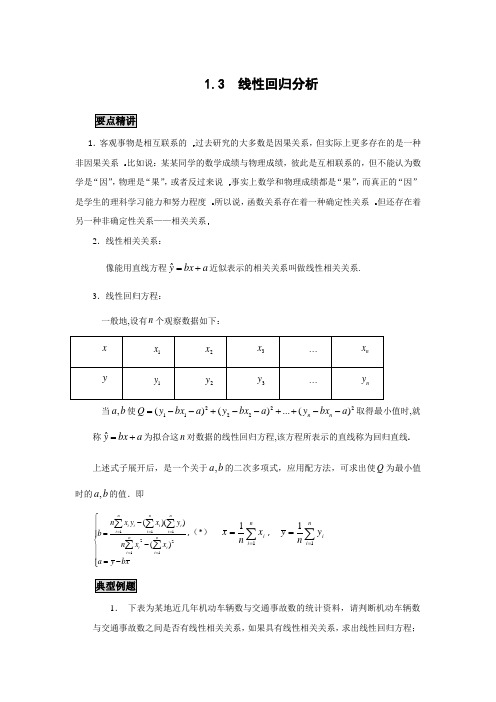
1.3 线性回归分析1.客观事物是相互联系的但实际上更多存在的是一种非因果关系 某某同学的数学成绩与物理成绩,彼此是互相联系的,但不能认为数学是“因”,物理是“果”,或者反过来说 “果”,而真正的“因”是学生的理科学习能力和努力程度 函数关系存在着一种确定性关系 2.线性相关关系:像能用直线方程ˆybx a =+近似表示的相关关系叫做线性相关关系. 3.线性回归方程:一般地,设有n 个观察数据如下:当,a b 使2221122()()...()n n Q y bx a y bx a y bx a =--+--++--取得最小值时,就称ˆybx a =+为拟合这n 对数据的线性回归方程,该方程所表示的直线称为回归直线. 上述式子展开后,是一个关于,a b 的二次多项式,应用配方法,可求出使Q 为最小值时的,a b 的值.即1112211()()()n n n i i i i i i i i i i i n x y x y b n x x a y bx=====⎧-⎪⎪=⎨-⎪⎪=-⎪⎩∑∑∑∑∑,(*) ∑==ni i x n x 11, ∑==n i i y n y 111. 下表为某地近几年机动车辆数与交通事故数的统计资料,请判断机动车辆数与交通事故数之间是否有线性相关关系,如果具有线性相关关系,求出线性回归方程;如果不具有线性相关关系,说明理由.【解析】在直角坐标系中画出数据的散点图,直观判断散点在一条直线附近,故具有线性相关关系.计算相应的数据之和:8888211111031,71.6,137835,9611.7ii i i i i i i i xy x x y ========∑∑∑∑,将它们代入(*)式计算得0.0774, 1.0241b a ≈=-,所以,所求线性回归方程为0.0774 1.0241y x =-.2.有10名同学高一(x )和高二(y )的数学成绩如下:⑴画出散点图;⑵求y 对x 的回归方程 【解析】 ⑴如图:⑵ 由已知表格的数据可得,,所以,又可查表中相应与显著性水平0.05和n -2的相关系数的临界值 因为可知,y 与x 具有相关关系. 因为y 与x 具有相关关系,设y=bx+a ,∴71,72.3x y ==101011710,723ii i i xy ====∑∑1010102211151467,50520,52541i ii i i i i x yx y ======∑∑∑10100.7802972i ix y x yr -⋅===∑0.050.632,r =0.05r r >1012110 1.22,14.3210i ii nii x y x yb a y bx xx==-⋅=≈=-≈--∑∑∴所求的回归方程为y=1.22x -14.32.3.下列两个变量之间的关系哪个不是函数关系( D ) A .角度和它的余弦值B.正方形边长和面积C .正n边形的边数和它的内角和 D.4.给出施化肥量对水稻产量影响的试验数据:(1)画出上表的散点图;(2)求出回归直线并且画出图形 【解析】(1)散点图(略).(2)表中的数据进行具体计算,列成以下表格 故可得到 2573075.43.399,75.430770002≈⨯-=≈⨯-=a b从而得回归直线方程是^4.75257y x =+.(图形略)5.一个工厂在某年里每月产品的总成本y (万元)与该月产量x (万件)之间由如下一组数据: 1)画出散点图;2)检验相关系数r 的显著性水平;3)求月总成本y 与月产量x 之间的回归直线方程.解析:=,==2.8475,=29.808,=99.2081,=54.243 1)画出散点图:2)r==在“相关系数检验的临界值表”查出与显著性水平0.05及自由度12-2=10相应的相关数临界值r0.05=0.576<0.997891, 这说明每月产品的总成本y(万元)与该月产量x(万件)之间存在线性相关关系。
高三线性回归方程知识点

高三线性回归方程知识点线性回归是数学中的一种方法,用于建立一个自变量与因变量之间的关系。
在高三数学中,线性回归方程是一个重要的知识点。
本文将介绍高三线性回归方程的基本概念、推导过程以及应用范围。
一、基本概念1. 线性回归方程线性回归方程,也叫作线性回归模型,表示自变量x和因变量y之间的关系。
它可以用如下的一般形式表示:y = β0 + β1x + ε其中,y表示因变量,x表示自变量,β0和β1表示模型中的参数,ε表示误差项。
2. 参数估计线性回归方程中的参数β0和β1需要通过观测数据进行估计。
常用的方法是最小二乘法,即通过最小化实际观测值和预测值之间的差异,来得到最优的参数估计值。
二、推导过程1. 求解参数通过最小二乘法,可以得到线性回归方程中的参数估计值。
具体推导过程包括以下几个步骤:(1)确定目标函数:将观测值和预测值之间的差异平方和作为目标函数。
(2)对目标函数求偏导:对目标函数分别对β0和β1求偏导,并令偏导数为0。
(3)计算参数估计值:根据求得的偏导数为0的方程组,解出β0和β1的值。
2. 模型拟合度评估在得到参数估计值之后,需要评估线性回归模型的拟合度。
常用的指标包括相关系数R和残差平方和SSE等。
相关系数R可以表示自变量和因变量之间的线性相关程度,取值范围在-1到1之间,越接近1表示拟合度越好。
三、应用范围线性回归方程在实际问题中有广泛的应用,例如经济学、统计学、社会科学等领域。
它可以用来分析自变量和因变量之间的关系,并预测未来的结果。
1. 经济学应用在线性回归模型中,可以将自变量设置为经济指标,例如GDP、通货膨胀率等,将因变量设置为某一经济现象的数值。
通过构建线性回归方程,可以分析不同经济指标对经济现象的影响,为经济决策提供参考依据。
2. 统计学应用线性回归方程是统计学中的一项重要工具。
通过对观测数据的拟合,可以得到参数估计值,并进一步分析自变量和因变量之间的关系。
统计学家可以利用线性回归分析建立统计模型,为实验数据的解释提供更为准确的结论。
高中数学:线性回归方程

高中数学:线性回归方程一、推导2个样本点的线性回归方程例1、设有两个点A(x1,y1),B(x2,y2),用最小二乘法推导其线性回归方程并进行分析。
解:由最小二乘法,设,则样本点到该直线的“距离之和”为从而可知:当时,b有最小值。
将代入“距离和”计算式中,视其为关于b的二次函数,再用配方法,可知:此时直线方程为:设AB中点为M,则上述线性回归方程为可以看出,由两个样本点推导的线性回归方程即为过这两点的直线方程。
这和我们的认识是一致的:对两个样本点,最好的拟合直线就是过这两点的直线。
上面我们是用最小二乘法对有两个样本点的线性回归直线方程进行了直接推导,主要是分别对关于a和b的二次函数进行研究,由配方法求其最值及所需条件。
实际上,由线性回归系数计算公式:可得到线性回归方程为设AB中点为M,则上述线性回归方程为。
二、求回归直线方程例2、在硝酸钠的溶解试验中,测得在不同温度下,溶解于100份水中的硝酸钠份数的数据如下0 4 10 15 21 29 36 51 6866.7 71.0 76.3 80.6 85.7 92.9 99.4 113.6 125.1描出散点图并求其回归直线方程.解:建立坐标系,绘出散点图如下:由散点图可以看出:两组数据呈线性相关性。
设回归直线方程为:由回归系数计算公式:可求得:b=0.87,a=67.52,从而回归直线方程为:y=0.87x+67.52。
三、综合应用例3、假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下统计资料:(1)求回归直线方程;(2)估计使用10年时,维修费用约是多少?解:(1)设回归直线方程为:(2)将x = 10代入回归直线方程可得y = 12.38,即使用10年时的维修费用大约是12.38万元。
高一数学知识点笔记

高一数学知识点笔记高一年级数学必修三知识点1、概念:(1)回归直线方程(2)回归系数2.最小二乘法3.直线回归方程的应用(1)描述两变量之间的依存关系;利用直线回归方程即可定量描述两个变量间依存的数量关系(2)利用回归方程进行预测;把预报因子(即自变量x)代入回归方程对预报量(即因变量Y)进行估计,即可得到个体Y值的容许区间。
(3)利用回归方程进行统计控制规定Y值的变化,通过控制x 的范围来实现统计控制的目标。
如已经得到了空气中NO2的浓度和汽车流量间的回归方程,即可通过控制汽车流量来控制空气中NO2的浓度。
4.应用直线回归的注意事项(1)做回归分析要有实际意义;(2)回归分析前,先作出散点图;(3)回归直线不要外延。
高一数学必修二重要知识点公理1:如果一条直线上的两点在一个平面内,那么这条直线上的所有的点都在这个平面内。
公理2:如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线。
公理3:过不在同一条直线上的三个点,有且只有一个平面。
推论1:经过一条直线和这条直线外一点,有且只有一个平面。
推论2:经过两条相交直线,有且只有一个平面。
推论3:经过两条平行直线,有且只有一个平面。
公理4:平行于同一条直线的两条直线互相平行。
等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等。
高一数学必修一第一章知识点第一:高考数学中有函数、数列、三角函数、平面向量、不等式、立体几何等九大章节。
主要是考函数和导数,这是我们整个高中阶段里最核心的板块,在这个板块里,重点考察两个方面:第一个函数的性质,包括函数的单调性、奇偶性;第二是函数的解答题,重点考察的是二次函数和高次函数,分函数和它的一些分布问题,但是这个分布重点还包含两个分析就是二次方程的分布的问题,这是第一个板块。
第二:平面向量和三角函数。
重点考察三个方面:一个是划减与求值,第一,重点掌握公式,重点掌握五组基本公式。
高中数学知识点:线性回归方程

高中数学知识点:线性回归方程
线性回归方程是高中数学中的一个重要知识点。
其中,回归直线是指通过散点图中心的一条直线,表示两个变量之间的线性相关关系。
回归直线方程可以通过最小二乘法求得。
具体地,可以设与n个观测点(xi,yi)最接近的直线方程为
y=bx+a,其中a、b是待定系数。
然后,通过计算n个偏差的平方和来求出使Q为最小值时的a、b的值。
最终得到的直线方程即为回归直线方程。
需要注意的是,只有在散点图大致呈线性时,求出的回归直线方程才有实际意义。
因此,在进行线性回归分析时,应先看其散点图是否成线性。
另外,求回归直线方程时,需要仔细谨慎地进行计算,避免因计算产生失误。
回归直线方程在现实生活与生产中有广泛的应用。
这种方程可以将非确定性问题转化为确定性问题,从而使“无序”变得“有序”,并对情况进行估测和补充。
因此,研究回归直线方程后,学生应更加重视其在解决相关实际问题中的应用。
注:原文已经没有格式错误和明显有问题的段落。
线性回归方程的知识要点

线性回归方程的知识要点1.回归直线如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线叫作回归直线。
2.回归直线方程ˆˆˆybx a =+ 对于一组具有线性相关关系的数据11(,)x y ,22(,)x y ,……,(,)n n x y ,其回归直线ˆˆˆybx a =+的截距和斜率的最小二乘法估计公式分别为: 121()()ˆ()niii nii x x y y bx x ==--=-∑∑,ˆˆay bx =- 其中表示数据x i (i=1,2,…,n )的均值,表示数据y i (i=1,2,…,n )的均值,表示数据x i y i (i=1,2,…,n )的均值.、的意义是:以为基数,x 每增加一个单位,y 相应地平均变化个单位. 要点诠释:①回归系数121()()ˆ()niii nii x x y y bx x ==--=-∑∑,也可以表示为1221ˆni ii nii x y nx ybxnx==-=-∑∑,这样更便于实际计算。
②12111()n i n i x x x x x n n===+++∑;12111()n i n i y y y y y n n===+++∑。
③(,)x y 称为样本中心点,回归直线ˆˆˆya bx =+必经过样本中心点(,)x y 。
④回归直线方程ˆˆˆya bx =+中的表示x 增加1个单位时的变化量,而表示不随x 的变化而变化的量。
3.求回归直线方程的一般步骤: ①作出散点图由样本点是否呈条状分布来判断两个量是否具有线性相关关系,若存在线性相关关系,进行第二步。
②求回归系数、 计算121()n x x x x n=+++,121()n y y y y n=+++,11221ni in n i x yx y x y x y ==++∑,2222121ni n i x x x x ==+++∑,利用公式1221ˆni ii nii x y nx ybxnx==-=-∑∑求出,再由ˆˆay bx =-求出的值; ③写出回归直线方程;④利用回归直线方程ˆˆˆya bx =+预报在x 取某一个值时y 的估计值。
高中数学 2.4《线性回归方程》素材 苏教版必修3

线性回归方程导学一、学法指导利用样本数据的情况估计总体数据的情况,这是统计的基本思想.线性回归方程是从样本中各个数据之间的相关关系入手,来分析验证样本中各个数据的特点规律,进而对总体数据的相关关系作出估计.因此学好线性回归方程,要在进一步体会统计的基本思想和方法的基础上,还要回忆我们已学过的两个变量之间存在的函数关系(即确定性关系).学习本节时,首先要知道变量相互关系有两种:一类是确定性的函数关系,如正方形的边长与面积的关系;另一类是变量确实存在关系,但又不具备函数关系所要求的确定性,它们的关系是带有随机性的.例如,某位同学的“物理成绩”与“数学成绩”之间的关系,我 们称它们为相关关系;其次是如何判断和分析具有相关关系的两个或多个变量,也就是如何寻找具有相关关系的两个变量中非确定性关系的某种确定性.本节的难点问题是建立回归直线方程的思想方法,其关键是如何用数学的方法来刻画“从整体上看各点与直线的距离最小”,即最贴近已知的数据点,最能代表变量x 与y 之间的关系,这就是“最小二乘法”的思想.另外还要注意,进行回归分析,通常先进行相关性检验,若能确定两个变量具有线性相关性,再去求其线性回归方程,否则所求方程毫无意义. 二、知识点概要 1.相关关系所谓相关关系是自变量取值一定时,因变量的取值带有一定的随机性. 对相关关系的理解应注意以下几点:(1)相关关系与函数关系不同.因为函数关系是一种非常确定的关系,而相关关系是一种非确定性关系,即相关关系是非随机变量与随机变量之间的关系.而函数关系可以看成是两个非随机变量之间的关系.因此,不能把相关关系等同于函数关系.(2)函数关系是一种因果关系,而相关关系不一定是因果关系,它也可能是伴随关系. (3)在现实生活中存在着大量的相关关系,如何判断和描述相关关系,统计学发挥着非常重要的作用.变量之间的相关关系带有不确定性,这需要通过收集大量的数据,对数据进行统计分析,发现规律,才能作出科学的判断. 2.回归分析对具有相关关系的两个变量进行统计分析的方法叫做回归分析.通俗地讲,回归分析就是寻找相关关系中非确定性关系的某种确定性. 3.散点图我们把一组具有相关关系的两个变量的数据()(123)i i x y i n ,,,,,对应的点(即样本点)画在坐标系内,得到的图形叫做散点图.利用散点图可以判断变量之间有无相关关系,所以判断两个变量之间是否存在某种关系时,必须从散点图入手.画出散点图,可以作出如下判断:(1)如果所有的样本点都落在某一函数曲线上,就用该函数来描述变量之间的关系,即说明变量之间具有函数关系;(2)如果所有的样本点都落在某一函数曲线附近,则说明变量之间具有相关关系;(3)如果所有的样本点都落在某一直线附近,则变量之间具有线性相关关系.4.正相关、负相关线性相关关系又分为正相关和负相关.正相关是指两个变量具有相同的变化趋势,即从整体上来看一个变量会随另一个变量变大而变大.从散点图可以看出因变量随自变量的增大而增大,图中的点分布在左下角到右上角的区域.负相关是指两个变量具有相反的变化趋势,即从整体上来看一个变量会随另一个变量变大而变小.负相关的散点图中的点分布在左上角到右下角的区域.由此,我们得出判断两个变量之间到底是不是具有线性相关关系,可以用“数据”说话,画出散点图更具有说服力.5.回归直线和回归直线方程如果散点图中的点的分布从整体上看大致在一条直线附近,就称这两变量之间具有线性相关关系.这条直线叫做这两个变量的回归直线,回归直线的方程叫做回归方程.这里注意,只有散点图中的点呈条状集中在某一直线周围的时候,才可以说两个变量之间具有线性相关关系,才有两个变量的正线性相关和负线性相关的概念,才可以用回归直线来描述这两个变量之间的关系.(1)求回归直线方程的思想方法观察散点图的特征,发现各点大致分布在一条直线的附近.类似图中的直线可画出不止一条,比如可以连接最左侧点和最右侧点得到一条直线,也可以让画出的直线上方的点和下方的点数目相等,……,但这些能保证各点与此直线在整体上是最接近的吗?它们虽然都有一定的道理,却总让人感到可靠性不强.那么,其中的哪一条直线最能代表变量x与y之间的关系呢?实际上求回归直线方程的关键是如何用数学的方法来刻画“从整体上看各点与此直线的距离最小”,即最贴近已知的数据点,最能代表变量x与y之间的关系.最能代表变量x与y之间关系的直线的特征是直线与这n个点的离差的平方和最小.(2)回归直线方程的求法根据最小二乘法的思想和公式,利用计算器或计算机,可以方便地求出回归方程.利用计算机求回归方程(Excel软件):在Excel的工作表中添加“图表”得到散点图后,用鼠标选中散点,单击鼠标右键,单击“添加趋势线”,在出现的对话框中单击类型标签,选择“线性”,单击“选项”标签,选中“显示公式”单选框,最后点击“确定”即可.利用科学计算器求回归方程:大多科学计算器都有回归计算(REG模式),但不同的计算器参数可能不同,这里不作详细介绍.一般在输入数据后按相应按键可直接得到a和b,这样就可以写出回归方程y bx a=+,非常简便,同学们在使用前一定要看懂计算器的使用说明书.回归直线方程在现实生活与生产中有广泛的应用.应用回归直线方程可以把非确定性问题转化成确定性问题,把“无序”变为“有序”,并且可根据情况进行估测、补充.因此,学过回归直线方程以后,应能积极应用回归直线方程解决一些相关的实际问题,并进一步体会回归直线的应用价值. (3)相关系数与相关性检验给定()(123)i i x y i n =,,,,,,只要123n x x x x ,,,,不全相等,就能求出一条回归直线,但它有无意义可是一个大问题.由于根据散点图看数据点是否大致在一直线附近主观性太强,为此可以利用样本相关系数来衡量两个变量之间线性关系的强弱. 样本相关系数:()()nii xx y y r --=∑叫做变量y 与x 之间的样本相关系数,简称相关系数,用它来衡量它们之间的线性相关程度.1r ≤,且|r|越接近于1,相关程度越高;r 越接近于0,相关程度越低.统计学认为,相关变量的相关系数: [10.75]r ∈--,时,两变量负相关很强; [0.751]r ∈,时,两变量正相关很强;(]0.750.3r ∈--,或[)0.30.75,时,两变量相关性一般;[0.250.25]r ∈-,时,两变量相关程度很弱.三、特别提示1.相关关系的理解.借助实例(如数学成绩与物理成绩之间的关系,粮食产量与施肥量之间的关系,吸烟与健康之间的关系,父母身高与子女身高之间的关系等)明确相关关系与函数关系不同,它是一种非确定性的关系,即一个变量取值一定时,另一个变量的取值带有一定的随机性.相关关系包括正相关和负相关.2.相关关系的研究方法:散点图法和写出回归直线方程y bx a =+,其中11112222111n n n n i i i i i i i i i i n n ni i i i i i n x y x y x y nx y b x nx n x x a y bx =======⎧⎛⎫⎛⎫--⎪ ⎪⎪⎝⎭⎝⎭⎪==⎪⎛⎫⎨-- ⎪⎪⎝⎭⎪⎪=-⎩∑∑∑∑∑∑∑,.3.线性回归思想:把相关关系(不确定性关系)转化为函数关系(确定性关系).当两个具有相关关系的变量近似满足一次函数关系时,所进行的回归分析又叫线性回归分析,所求的函数关系y bx a =+就是线性回归方程.4.求线性回归直线方程前应对数据进行线性相关分析,其关键是求a b ,,由于计算量大,因此计算过程要注意分层次、按步骤进行. 线性回归中的相关系数线性回归问题在生活中应用广泛,求解回归直线方程时,应该先判断两个变量是否是线性相关,若相关再求其直线方程,判断两个变量有无相关关系的一种常用的简便方法是绘制散点图;另外一种方法是量化的检验法,即相关系数法.下面为同学们介绍相关系数法. 一、关于相关系数法统计中常用相关系数r 来衡量两个变量之间的线性相关的强弱,当i x 不全为零,y i 也不全为零时,则两个变量的相关系数的计算公式是:()()nnii i ixx y y x ynx yr ---==∑∑r 就叫做变量y 与x 的相关系数(简称相关系数).说明:(1)对于相关系数r ,首先值得注意的是它的符号,当r 为正数时,表示变量x ,y 正相关;当r 为负数时,表示两个变量x ,y 负相关;(2)另外注意r 的大小,如果[]0.751r ∈,,那么正相关很强;如果[]10.75r ∈--,,那么负相关很强;如果(]0.750.30r ∈--,或[)0.300.75r ∈,,那么相关性一般;如果[]0.250.25r ∈-,,那么相关性较弱.下面我们就用相关系数法来分析身边的问题,确定两个变量是否相关,并且求出两个变量间的回归直线. 二、典型例题剖析77(1)对变量y 与x 进行相关性检验;(2)如果y 与x 之间具有线性相关关系,求回归直线方程; (3)如果父亲的身高为73英寸,估计儿子身高.解:(1)66.8x =,67y =,102144794i i x ==∑,102144929.22i i y ==∑,4475.6x y =,24462.24x =,24489y =,10144836.4i i i x y ==∑,所以10i ix ynx yr -=∑44836.4104475.6(4479444622.4)(44929.2244890)-⨯=--80.40.9882.04=≈≈, 所以y 与x 之间具有线性相关关系. (2)设回归直线方程为y a bx =+,则101102211010i ii i i x yxyb x x==-=-∑∑44836.4447560.46854479444622.4-=≈-,670.468566.835.7042a y bx =-=-⨯=.故所求的回归直线方程为0.468535.7042y x =+.(3)当73x =英寸时,0.46857335.704269.9047y =⨯+=, 所以当父亲身高为73英寸时,估计儿子的身高约为69.9英寸.点评:回归直线是对两个变量线性相关关系的定量描述,利用回归直线,可以对一些实际问题进行分析、预测,由一个变量的变化可以推测出另一个变量的变化.这是此类问题常见题型.例2 10其中x 为高一数学成绩,y 为高二数学成绩. (1)y 与x 是否具有相关关系;(2)如果y 与x 是相关关系,求回归直线方程. 解:(1)由已知表格中的数据,利用计算器进行计算得101710ii x==∑,101723i i y ==∑,71x =,72.3y =,10151467i i i x y ==∑.102150520ii x==∑,102152541i i y ==∑.1010i ix yx yr -=∑0.78=≈.由于0.78r ≈,由0.780.75>知,有很大的把握认为x 与y 之间具有线性相关关系. (2)y 与x 具有线性相关关系,设回归直线方程为y a bx =+,则1011022211051467107172.31.2250520107110i ii i i x yx yb x x==--⨯⨯==≈-⨯-∑∑, 72.3 1.227114.32a y bx =-=-⨯=-.所以y 关于x 的回归直线方程为 1.2214.32y x =-.点评:通过以上两例可以看出,回归方程在生活中应用广泛,要明确这类问题的计算公式、解题步骤,并会通过计算确定两个变量是否具有相关关系.方方面面评说回归直线方程一、回归分析对于线性回归分析,我们要注意以下几个方面:(1)回归分析是对具有相关关系的两个变量进行统计分析的方法.两个变量具有相关关系是回归分析的前提.(2)对于关系不明确的两组数据,可先作散点图,在图上看它们有无关系,关系的密切程度,然后再进行回归分析.(3)通过散点图的观察,一般地,若图中数据大致分布在一条直线附近,那么这两个变量近似成线性相关关系.(4)求回归直线方程,首先应注意到,只有在散点图大至呈线性时,求出的回归直线方程才有实际意义,否则,求出的回归直线方程毫无意义. 二、回归直线方程一般地,设x 与y 是具有相关关系的两个变量,且对应于n 组观测值的n 个点(()12)i i x y i n =,,,,,大致分布在一条直线的附近,求在整体上与这n 个点最接近的一条直线,记此直线方程为y a bx =+ (1)这里在y 的上方加记号“^”,是为了区分Y 的实际值y ,表示当x 取值(12)i x i n =,,,时,Y 相应的观察值为i y ,而直线上对应于i x 的纵坐标是i y a bx =+.(1)式叫做Y 对x 的回归直线方程,a ,b 叫做回归系数. 三、求回归直线方程的思想方法 在观察散点图特征时,我们会发现有时各点大致分布在一条直线的附近,且画出不止一条类似的直线,而最能代表变量x 与y 之间关系的直线的特征,即为n 个离差的平方和最小.设所求直线方程为y a bx =+,其中a ,b 是待定系数,则(12)i i y a bx i n =+=,,,. 于是得到各个离差()(12)i i i i y y y bx a i n -=-+=,,,. 显然,离差i i y y -的符号有正有负,若将它们相加会造成相互抵消,故采用n 个离差的平方和21()ni i i Q y bx a ==--∑,采用最小二乘法可求出使Q 为最小值时的a 和b .1122211()()()nnii i ii i nniii i xx y y x ynxyb xx xnx====---==--∑∑∑∑, a y bx =-,其中11n i i x x n ==∑,11ni i y y n ==∑.四、求回归直线方程的一般步骤(1)作出散点图,判断散点是否在一条直线附近;(2)如果散点在一条直线附近,用公式求出a ,b ,并写出回归直线方程.注:计算a ,b 时由于计算量较大,所以在计算时应借助技术手段(如计算器或计算机),认真细致,谨防计算中产生错误.例 在10年期间,某城市居民收入与某种商品的销售额之间的关系见下表.(1)画出散点图;(2)如果散点图中各点大致分布在一条直线的附近,求x 与y 之间的回归直线方程; (3)试预测居民年收入50亿元时这种商品的销售额.解题指导:只有散点图大致表现为线性时,求回归直线方程才有实际意义. 解:(1)散点图如图所示:(2)通过观察散点图可知各点大致分布在一条直线的附近.列出下表,利用计算器进行计算.序号 xy2x2yxy1 32.2 25.0 1036.84 625 805 2 31.1 30.0967.21900 933 3 32.9 34.0 1082.41 1156 1118.6 4 35.8 37.0 1281.64 1369 1324.6 5 37.1 39.0 1376.41 1521 1446.9 6 38.0 41.0 1444 1681 1558 7 39.0 42.0 1521 17645 1638 8 43.0 44.0 1849 1936 1892 9 44.6 48.0 1989.162304 2140.8 1046.0 51.0211626012346∑379.7 391 14663.67 15857 15202.91011022211015202.9379.739.1 1.447379.71014663.671010i ii ii x yx y b xx==--⨯==≈⎛⎫--⨯ ⎪⎝⎭∑∑。
高考线性回归方程总结

第二讲 线性回归方程一、相关关系:1、⎩⎨⎧<=1||1||r r 不确定关系:相关关系确定关系:函数关系2、相关系数:∑∑∑===-⋅---=ni ini ini iiy y x x y y x x r 12121)()())((,其中:(1)⎩⎨⎧<>负相关正相关00r r ;2相关性很弱;相关性很强;3.0||75.0||<>r r例题1:下列两个变量具有相关关系的是A.正方形的体积与棱长;B.匀速行驶的车辆的行驶距离与行驶时间;C.人的身高和体重;D.人的身高与视力;例题2:在一组样本数据),,,2)(,(),,(),,(212211不全相等n n n x x x n y x y x y x ≥的散点图中,若所有样本点),2,1)(,(n i y x i i =都在直线121+-=x y 上,则样本相关系数为 例题3:r 是相关系数,则下列命题正确的是:(1)]75.0,1[--∈r 时,两个变量负相关很强;2]1,75.0[∈r 时,两个变量正相关很强; (3))75.0,3.0[]3.0,75.0(或--∈r 时,两个变量相关性一般; (4)41.0=r 时,两个变量相关性很弱; 3、散点图:初步判断两个变量的相关关系;例题4:在画两个变量的散点图时,下列叙述正确的是 A.预报变量在x 轴上,解释变量在y 轴上; B.解释变量在x 轴上,预报变量在y 轴上; C.可以选择两个变量中的任意一个变量在x 轴上;D.可以选择两个变量中的任意一个变量在y 轴上; 例题5:散点图在回归分析过程中的作用是A.查找个体个数B.比较个体数据的大小C.研究个体分类D.粗略判断变量是否线性相关二、线性回归方程:1、回归方程:a x b yˆˆˆ+= 其中2121121)())((ˆxn xy x n yx x x y yx x bni ini ii ni ini ii--=---=∑∑∑∑====,x b y aˆˆ-=代入样本点的中心 例题1:设),(),,(),,(2211n n y x y x y x 是变量n y x 的和个样本点,直线l 是由这些样本点通过最小二乘法得到的线性回归直线过一、二、四象限,以下结论正确的是 A.直线l 过点),(y x B.当n 为偶数时,分布在l 两侧的样本点的个数一定相同 C.的和y x 相关系数在0到1之间 D.的和y x 相关系数为直线l 的斜率例题2:工人月工资y 元依劳动生产率x 千元变化的回归直线方程为x y9060ˆ+=,下列判断正确的是A.劳动生产率为1000元时,工资为150元;B.劳动生产率提高1000元时,工资平均提高150元;C.劳动生产率提高1000元时,工资平均提高90元;D.劳动生产率为1000元时,工资为90元;例题3:设某大学的女生体重)(kg y 与身高)(cm x 具有线性相关关系,根据一组样本数据)2,1)(,(n i y x i i =,用最小二乘法建立的回归方程为71.8585.0ˆ-=x y,则不正确的是 A.y 与x 具有正的线性相关关系; B.回归直线过样本点的中心),(y xC.若该大学某女生身高增加1cm,则其体重约增加D.若该大学某女生身高为170cm,则可断定其体重必为例题4:为了了解儿子的身高与其父亲身高的关系,随机抽取5对父子的身高数据如下:则y 对x 的线性回归方程为 A.1-=x y B.1+=x y C.x y 2188+= D.176=y 2、残差:(1)残差图:横坐标为样本编号,纵坐标为每个编号样本对应的残差; (2)残差图呈带状分布在横轴附近,越窄模型拟合精度越高; 3残差平方和∑=-ni i iyy12)ˆ(越小,模型拟合精度越高; 3、相关指数:∑∑==---=n i ini i iy yyyR 12122)()ˆ(1(1)其中:∑=-ni i iyy12)ˆ(为残差平方和;∑=-ni i y y 12)(为总偏差平方和; (2))1,0(2∈R ,越大模型拟合精度越高; 例题5:下列说法正确的是(1)残差平方和越小,相关指数2R 越小,模型拟合效果越差; (2)残差平方和越大,相关指数2R 越大,模型拟合效果越好; (3)残差平方和越小,相关指数2R 越大,模型拟合效果越好; (4)残差平方和越大,相关指数2R 越小,模型拟合效果越差; A.12 B.34 C.14 D.23例题6:关于回归分析,下列说法错误的是A.在回归分析中,变量间的关系若是非确定关系,则因变量不能由自变量唯一确定;B.线性相关系数r 可以是正的,也可以是负的C.样本点的残差可以是正的,也可以是负的D.相关指数2R 可以是正的,也可以是负的 例题7:下列命题正确的是(1)线性相关系数r 越大,两个变量的线性相关性越强,反之,线性相关性越弱; (2)残差平方和越小的模型,拟合的效果越好;(3)用相关指数2R 来刻画回归效果,2R 越小,说明模型的拟合效果越好; (4)随机误差e 是衡量预报精确度的一个量,但它是一个不可观测的量;(5)i eˆ表示相应于点),(i i y x 的残差,且0ˆ1=∑=ni ie;A.135B.245C.124D.23例题8:已知x 与y 之间的几组数据如下表:a xb yˆˆˆ+=;若某同学根据上表中的前两个数据)2,2(),0,1(求得的直线方程为a x b y '+'=,则下列结论正确的是A.a a b b'>'>ˆ,ˆ B.a a b b '<'>ˆ,ˆ C.a a b b '>'<ˆ,ˆ D.a a b b '<'<ˆ,ˆ 例题9:关于某设备的使用年限x年和所支出的维修费用y 万元有下表所示的资料:(1)线性回归方程a x b yˆˆˆ+=中的回归系数b a ˆ,ˆ; (2)残差平方和与相关指数2R ,作出残差图,并对该回归模型的拟合精度作出适当判断; (3)使用年限为10年时,维修费用大约是多少 三、非线性回归模型:例题1:如果样本点分布在某一条指数函数曲线bx ae y =的周围,其中a 和b 是参数,通过两边取自然对数的方法,把指数关系式变成对数关系式后,下列哪个变换结果是正确的 A.a bx y ln ln ⋅= B.a bx y ln ln += C.a bx y ln ln ln ⋅= D.a bx y ln ln ln += 例题2:下列回归方程中, 是线性回归方程; 是非线性回归方程;(1)27.3688.0ˆ+=x y28.1225.0ˆ2-=x y 3x e y 3.16.2ˆ= (4)x y5.14ˆ-= 5xe y 185.038.1ˆ-=例题3:某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x 单位:千元对年销售量y 单位:t 和年利润z 单位:千元的影响,对近8年的年宣传费和年销售量i=1,2,···,8数据作了初步处理,得到下面的散点图及一些统计量的值;表中w 1 w =1881i w=∑1Ⅰ根据散点图判断,y a bx =+与y c =+哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型给出判断即可,不必说明理由Ⅱ根据Ⅰ的判断结果及表中数据,建立y 关于x 的回归方程;Ⅲ以知这种产品的年利率z 与x 、y 的关系为z=;根据Ⅱ的结果回答下列问题:(i ) 年宣传费x=49时,年销售量及年利润的预报值是多少 (ii )年宣传费x 为何值时,年利率的预报值最大附:对于一组数据u 1 v 1,u 2 v 2…….. u n v n ,其回归线v=αβ+u 的斜率和截距的最小二乘估计分别为:四、独立性检验:例题1:下表是一个22⨯列联表:的值分别为 ;例题2:可以粗略的判断两个分类变量是否有关系的是 A.散点图 B.残差图 C.等高条形图 D.以上都不对例题3:在等高条形图中,下列哪两个比值相差越大,要推断的论述成立的可能性就越大A.d c c b a a ++与 B.d a c d c a ++与 C.c b c d a a ++与 D.ca cd b a ++与例题4:在判断两个分类变量是否有关系的常用方法中,最为精确的方法是 A.考察随机误差e B.考察线性相关系数r C.考察相关指数2R D.考察独立性检验中的2K例题5:在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是;①若2k 的观测值满足635.62≥k ,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有 99人患有肺病;②从独立性检验可知有99%的把握认为吸烟与患病有关系时,我们说某人吸烟,那么他有99&的可能患有肺病;③从统计量中得知有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推断出现错误;A.①B. ①③C. ③D. ②例题6:在调查学生数学成绩与物理成绩之间的关系时,得到如下数据人数:数学成绩与物理成绩之间有把握有关;A. B. C. D.。
高考线性回归知识点

高考线性回归知识点线性回归是高考数学中的一个重要知识点,它是一种统计学上常用的方法,用于分析两个变量之间的线性关系。
在高考中,线性回归经常被应用于解决实际问题和预测未知数据。
本文将介绍线性回归的基本概念、公式以及应用示例,帮助大家更好地理解和应用这一知识点。
一、线性回归的基本概念线性回归是建立一个自变量X和一个因变量Y之间的线性关系模型,通过最小化实际观测值与模型预测值之间的误差,来拟合和预测因变量Y的值。
线性回归的模型可以表示为:Y = β0 + β1*X + ε其中,Y是因变量,X是自变量,β0是截距,β1是斜率,ε是误差项,代表模型无法准确拟合数据的部分。
二、线性回归的公式1. 简单线性回归如果模型中只有一个自变量X,称为简单线性回归。
简单线性回归的公式为:Y = α + βX + ε其中,α表示截距,β表示斜率,ε为误差项。
我们利用给定的数据集,通过最小二乘法来估计α和β的值,从而得到一条最佳拟合直线。
2. 多元线性回归如果模型中有多个自变量X1、X2、X3...,称为多元线性回归。
多元线性回归的公式为:Y = α + β1*X1 + β2*X2 + β3*X3 + ... + ε同样,我们利用最小二乘法来估计α和每个β的值,从而得到一个最佳拟合的平面或超平面。
三、线性回归的应用示例线性回归在实际问题中有广泛的应用。
下面通过一个简单的例子来说明线性回归的具体应用过程。
例:某城市的房价与面积的关系假设我们要研究某个城市的房价与房屋面积之间的关系。
我们收集了一些房屋的信息,包括房屋的面积和对应的价格。
我们可以使用线性回归来建立一个房价和面积之间的模型,从而预测未知房屋的价格。
1. 数据收集首先,我们收集了一些房屋的面积和价格数据,得到一个数据集。
2. 模型建立根据数据集,我们可以建立一个线性回归模型:价格= α + β*面积+ ε通过最小二乘法,估计出α和β的值。
3. 模型评估为了评估模型的好坏,我们需要计算误差项ε。
高中数学:.《线性回归方程》课件(共10张PPT)

直线 yˆ bxa 与图中六个点的接近 程度,所以,设法取 a , b 的值,使 Q ( a , b )
达到最小值.这种方法叫做最小平方法 (又称最小二乘法) .
线性相关系:
像这样能用直线方程 yˆ bxa
近似表示的相关关系叫做线性相关关系.
问题:
某小卖部为了了解热茶销售量与气温
之间的关系,随机统计并制作了某6天 卖出热茶的杯数与当天气温的对照表:
气温 /0C
26
18
13
10
4
-1
杯数 20 24 34 38 50 64
如果某天的气温是-50C,你能根据这些
数据预测这天小卖部卖出热茶的杯数吗?
为了了解热茶销量与
气温的大致关系,我们
以横坐标x表示气温,
……………… 怎样的直线最好呢?
建构数学
1.最小平方法:
用方程为 yˆ bxa 的直线拟合散点图中
的点,应使得该直线与散点图中的点最接近
那么,怎样衡量直线 yˆ bxa 与图中六
个点的接近程度yˆ 呢?
我们将表中给出的自变量 x 的六个值
带入直线方程,得到相应的六个值:
2 6 b a , 1 8 b a , 1 3 b a , 1 0 b a , 4 b a , b a
2
选择怎样的直线近似地表示热茶销量与气
…y 3
y n 当a,b使
事实上数学和物理成绩都是
Q ( y b x a ) ( y b x a ) . . . ( y b x a ) 但还存在着另一种非确定
数据预测这天小卖部卖出热茶的杯数吗?
2
2
像这样能用直线方程1 1
高一数学(必修3):第四章线性回归方程Word版含解析

重点列表:重点详解:1.变量间的相关关系常见的两变量之间的关系有两类:一类是确定性的函数关系,另一类是________;与函数关系不同,相关关系是一种________关系,带有随机性. 2.两个变量的线性相关(1)如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有____________,这条直线叫________.(2)从散点图上看,如果点分布在从左下角到右上角的区域内,那么两个变量的这种相关关系称为________;如果点分布在从左上角到右下角的区域内,那么两个变量的这种相关关系称为________.※ (3)相关系数r =∑∑∑===----nj jn i ini iiy yx x y y x x 12121)()())((,当r >0时,表示两个变量正相关;当r <0时,表示两个变量负相关.r 的绝对值越接近________,表示两个变量的线性相关性越强;r 的绝对值越接近________,表示两个变量的线性相关性越弱.通常当r 的绝对值大于0.75时,认为两个变量具有很强的线性相关关系. 3.回归直线方程 (1)通过求Q =∑=--ni i ix y12)(βα的最小值而得出回归直线的方法,即使得样本数据的点到回归直线的距离的平方和最小的方法叫做____________.该式取最小值时的α,β的值即分别为,.(2)两个具有线性相关关系的变量的一组数据:(x 1,y 1),(x 2,y 2),…,(x n ,y n ),其回归方程为a x b yˆˆˆ+=,则 ⎪⎪⎪⎩⎪⎪⎪⎨⎧-=--=---=∑∑∑∑====.ˆˆ,)())((ˆ1221121x b y axn xy x n yx x x y y x x b ni ini ii n i i ni i i【答案】1.相关关系 非确定性2.(1)线性相关关系 回归直线 (2)正相关 负相关 (3)1 0 3.最小二乘法重点1:相关关系的判断 【要点解读】在研究两个变量之间是否存在某种关系时,必须从散点图入手.对于散点图,可以做出如下判断:(1)如果所有的样本点都落在某一函数曲线上,就用该函数来描述变量之间的关系,即变量之间具有函数关系.(2)如果所有的样本点都落在某一函数曲线附近,变量之间就有相关关系. (3)如果所有的样本点都落在某一直线附近,变量之间就有线性相关关系. 【考向1】确定性关系与随机关系【例题】下列变量之间的关系不是..相关关系的是( ) A .已知二次函数y =ax 2+bx +c ,其中a ,c 是已知常数,取b 为自变量,因变量是这个函数的判别式Δ=b 2-4ac B .光照时间和果树亩产量 C .降雪量和交通事故发生率 D .每亩施用肥料量和粮食亩产量解:由函数关系和相关关系的定义可知,A 中Δ=b 2-4ac ,因为a ,c 是已知常数,b 为自变量,所以给定一个b 的值,就有唯一确定的Δ与之对应,所以Δ与b 之间是一种确定的关系,是函数关系.B ,C ,D 中两个变量之间的关系都是相关关系.故选A .【评析】要注意函数关系与相关关系的区别:函数关系是确定性关系,而相关关系是随机的、不确定的.重点2:线性回归方程有关概念 【要点解读】样本中心点一定在回归直线上 【考向1】样本中心点【例题】为了考查两个变量x 和y 之间的线性关系,甲、乙两位同学各自独立做了10次和15次试验,并且利用线性回归方法,求得回归直线分别为l 1,l 2,已知两人得到的试验数据中,变量x 的平均值都等于s ,变量y 的平均值都等于t ,那么下列说法正确的是( ) A .直线l 1和l 2一定有公共点(s ,t ) B .直线l 1和l 2相交,但交点不一定是(s ,t ) C .必有直线l 1∥l 2 D .直线l 1和l 2必定重合【评析】回归方程一定通过样本点的中心(,y );中心相同的样本点的回归方程不一定相同.【考向2】线性回归直线的理解【例题】由一组样本数据(x 1,y 1),(x 2,y 2),…,(x n ,y n )得到回归直线方程a x b yˆˆˆ+=,那么下面说法错误..的是( ) A .直线a x b yˆˆˆ+=必经过点(,y ) B .直线a x b yˆˆˆ+=至少经过点(x 1,y 1),(x 2,y 2),…,(x n ,y n )中的一个点 C .直线a x b yˆˆˆ+=的斜率=∑∑==--ni ini ii xn xy x n yx 1221D .直线a x b y ˆˆˆ+=和各点(x 1,y 1),(x 2,y 2),…,(x n ,y n )的偏差∑=+-ni ii a x b y 12)]ˆˆ([是该坐标平面上所有直线与这些点的偏差中最小的重点3:散点图 【要点解读】根据散点图可以直观判断正负相关以及数据所对应的函数模型 【考向1】正相关与负相关【例题】(1)对变量x ,y 有观测数据(x i ,y i )(i =1,2,…,10),得散点图1;对变量u ,v 有观测数据(u i ,v i )(i =1,2,…,10),得散点图2.由这两个散点图可以判断( )图1图2A .变量x 与y 正相关,u 与v 正相关B .变量x 与y 正相关,u 与v 负相关C .变量x 与y 负相关,u 与v 正相关D .变量x 与y 负相关,u 与v 负相关解:由这两个散点图可以判断,变量x 与y 负相关,u 与v 正相关,故选C.【评析】点分布在从左下角到右上角的区域时,两个变量的相关关系为正相关;点分布在从左上角到右下角的区域时,两个变量的相关关系为负相关.(2)下面是一块田的水稻产量与施化肥量的一组观测数据(单位:kg): 施化肥量15 20 25 30 35 40 45 水稻产量 320 330 360 410 460 470 480 (Ⅰ)将上述数据制成散点图;(Ⅱ)你能从散点图中发现施化肥量与水稻产量近似成什么关系吗?水稻产量会一直随施化肥量的增加而增长吗? 解:(Ⅰ)散点图如下:(Ⅱ)从图中可以发现施化肥量与水稻产量具有线性相关关系,当施化肥量由小到大变化时,水稻产量由小变大.图中的数据点大致分布在一条直线的附近,因此施化肥量和水稻产量近似成线性相关关系,但水稻产量只是在一定范围内随着化肥施用量的增加而增长,不会一直随化肥施用量的增加而增长.【评析】任何一组数据(二元数据)都可以作出散点图,散点图可以直观地观察两个变量间的关系.【考向2】散点图的画法及相关关系识别【例题】(1)从左至右,观察下列三个散点图,变量x与y的关系依次为________(正相关记作①;负相关记作②;不相关记作③).(2)科研人员为了全面掌握棉花新品种的生产情况,查看了气象局对该地区年降雨量与年平均气温的统计数据(单位分别是mm,℃),并作了统计:(Ⅰ)试画出散点图;(Ⅱ)判断两个变量是否具有线性相关关系.解:(Ⅰ)作出散点图如图所示.(Ⅱ)由散点图可知,各点并不在一条直线附近,所以两个变量不具有线性相关关系.难点列表:求线性回归直线方程的步骤(1)用散点图或进行相关性检验判断两个变量是否具有线性相关关系;(2)求系数b ^:公式有两种形式,b ^=∑ni =1(x i -x -)(y i -y -)∑n i =1(x i -x -)2=∑n i =1x i y i -nx - y-∑ni =1x 2i -nx-2,根据题目具体情况灵活选用;(3)求a ^:a ^=y --b ^x -; (4)写出回归直线方程.说明:当数据较复杂时,题目一般会给出部分中间结果,观察这些中间结果可确定选用公式的哪种形式求b ^.难点1:求回归方程及用回归方程进行估计 【要点解读】(1)回归分析是对具有相关关系的两个变量进行统计分析的方法,只有在散点图大致呈线性时,求出的回归直线方程才有实际意义,否则无意义.(2)根据回归方程进行的估计仅是一个预测值,而不是真实发生的值.(3)用最小二乘法求回归方程,关键在于正确求出系数,,由于,的计算量大,计算时应仔细小心,分层进行(最好列出表格),避免因计算而产生错误. 【考向1】求线性回归方程【例题】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x (吨)与相应的生产能耗y (吨标准煤)的几组对照数据:(1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程;(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?(参考值3×2.5+4×3+5×4+6×4.5=66.5) 解:(1)散点图如下:(2)由系数公式可知,=4.5,y =3.5, =66.5-4×4.5×3.586-4×4.52=0.7, =3.5-0.7×4.5=0.35,所以线性回归方程为yˆ=0.7x +0.35. (3)x =100时,yˆ=0.7x +0.35=70.35,所以预测生产100吨甲产品的生产能耗比技术改造前降低19.65吨标准煤.【评析】牢记求线性回归方程的步骤:(1)列表;(2)计算,y ,∑=ni i i y x 1,∑=ni i x 12;(3)代入公式求,再利用x b y aˆˆ-=求,(4)写出回归方程. 【考向2】利用线性回归方程进行预测【例题】从某居民区随机抽取10个家庭,获得第i 个家庭的月收入x i (单位:千元)与月储蓄y i (单位:千元)的数据资料,算得∑=101i ix=80,∑=101i iy=20,∑=101i ii y x =184,∑=1012i ix=720.(1)求家庭的月储蓄y 对月收入x 的线性回归方程y =bx +a ; (2)判断变量x 与y 之间是正相关还是负相关;(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄. 附:线性回归方程y =bx +a 中,b =∑∑==--ni ini ii xn xy x n yx 1221,x b y a -=,其中,y 为样本平均值,线性回归方程也可写为y ^=b ^x +a ^.解:(1)由题意知n =10,=1n ∑=ni ix 1=8010=8, y =1n ∑=ni i y 1=2010=2,又∑=ni ix12- n 2 =720 -10×82=80,∑=ni ii y x 1-n y x =184-10×8×2=24,由此得b =2480=0.3,a =y -b =2-0.3×8=-0.4,故所求回归方程为y =0.3x -0.4.(2)由于变量y 的值随x 的值增加而增加(b =0.3>0),故x 与y 之间是正相关. (3)将x =7代入回归方程可以预测该家庭的月储蓄为y =0.3×7-0.4=1.7(千元). 难点2:非线性相关转化为线性相关 【要点解读】通过观察散点图,分析其函数模型,然后转化成线性相关 【考向1】非线性相关转化为线性相关【例题】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y (单位:t)和年利润z (单位:千元)的影响.对近8年的年宣传费x i 和年销售量y i (i =1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.(1)根据散点图判断,y =a +bx 与y =c +d x 哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型?(给出判断即可,不必说明理由)(2)根据(1)的判断结果及表中数据,建立y 关于x 的回归方程.(3)已知这种产品的年利润z 与x ,y 的关系为z =0.2y -x .根据(2)的结果回答下列问题: ①年宣传费x =49时,年销售量及年利润的预报值是多少? ②年宣传费x 为何值时,年利润的预报值最大?附:对于一组数据(u 1,v 1),(u 2,v 2),…,(u n ,v n ),其回归直线v =α+β u 的斜率和截距的最小二乘估计分别为β^=解题指导] 切入点:回归分析中对散点图的理解,回归方程的求法和应用;关键点:通过换元把非线性回归方程转化为线性回归方程求解.解] (1)由散点图可以判断,y =c +d x 适宜作为年销售量y 关于年宣传费x 的回归方程类型.(2)令w =x ,先建立y 关于w 的线性回归方程.c ^=y -d^ w =563-68×6.8=100.6, 所以y 关于w 的线性回归方程为y ^=100.6+68w , 因此y 关于x 的回归方程为y ^=100.6+68x . (3)①由(2)知,当x =49时,年销售量y 的预报值y^=100.6+6849=576.6, 年利润z 的预报值z ^=576.6×0.2-49=66.32. ②根据(2)的结果知,年利润z 的预报值z ^=0.2(100.6+68x )-x =-x +13.6x +20.12. 所以当x =13.62=6.8,即x =46.24时,z ^取得最大值.故年宣传费为46.24千元时,年利润的预报值最大.【趁热打铁】1.两个变量成负相关关系时,散点图的特征是( ) A .点分布在从左下角到右上角的区域B .散点图在某方形区域内C .散点图在某圆形区域内D .点分布在从左上角到右下角的区域2.对于给定的两个变量的统计数据,下列说法正确的是( ) A .都可以分析出两个变量的关系B .都可以用一条直线通过近似表示两者关系来估计总体的均值C .都可以作出散点图D .都可以用确定的表达式表示两者的关系 3.下列命题:①任何两个变量都具有相关关系; ②圆的周长与该圆的半径具有相关关系;③某商品的需求与该商品的价格是一种非确定性关系; ④根据散点图求得的回归直线方程可能是没有意义的;⑤两个变量间的相关关系可以通过回归直线把非确定性问题转化为确定性问题进行研究. 其中正确的命题为( )A .①③④B .②④⑤C .③④⑤D .②③⑤4.对四组数据进行统计,获得以下散点图,关于其相关系数比较,正确的是( )A .r 2<r 4<0<r 3<r 1B .r 4<r 2<0<r 1<r 3C .r 4<r 2<0<r 3<r 1D .r 2<r 4<0<r 1<r 35.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,根据收集到的数据(如下表),由最小二乘法求得回归方程y ^=0.67x +54.9.A .67B .68C .69D .706.变量X 与Y 相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5);变量U 与V 相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1).r 1表示变量Y 与X 之间的线性相关系数,r 2表示变量V 与U 之间的线性相关系数,则( )A .r 2<r 1<0B .0<r 2<r 1C .r 2<0<r 1D .r 2=r 17.某市物价部门对本市的5家商场的某商品的一天销售量及其价格进行调查,得到售价x (元)和销售量y (件)之间的一组数据如下表:yˆ=-3.2x +a ,则a =______.8.某数学老师身高176 cm ,他爷爷、父亲和儿子的身高分别是173 cm 、170 cm 和182 cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为________cm.9.假设关于某种设备的使用年限x (年)与所支出的维修费用y (万元)有如下统计资料:已知∑=512i ix=90,∑=51i ii y x =112.3.(1)求,y ;(2)如果x 与y 具有线性相关关系,求出线性回归方程; (3)估计使用年限为10年时,维修费用约是多少?10.某班主任为了对本班学生的月考成绩进行分析,决定从全班25名女同学,15名男同学中随机抽取一个容量为8的样本进行分析.(1)如果按性别比例分层抽样,应选男女生各多少人; (2)随机抽取8位同学的数学、物理分数对应如表:性相关性,求出线性回归方程(系数精确到0.01);如果不具有线性相关性,请说明理由.第四章1解:正确的只有D 选项.故选D.2解:任两个变量均可作出散点图,从散点图上看有相关关系的才具有分析的价值,无相关关系的则作不出什么结论.故选C.4解:由相关系数定义及散点图所表达含义可知r 2<r 4<0<r 3<r 1,故选A.5解:=15×(10+20+30+40+50)=30,由于y ^=0.67x +54.9必过点(,y ),∴y =0.67×30+54.9=75,因此图表中的模糊数据为75×5-(62+75+81+89)=68.故选B. 6解:对于变量Y 与X 而言,Y 随X 的增大而增大,故Y 与X 正相关;对于变量V 与U 而言,V 随U 的增大而减小,故V 与U 负相关,故r 2<0<r 1.故选C.7解:价格的平均数=9+9.5+10+10.5+115=10,销售量的平均数y =11+10+8+6+55=8,由yˆ=-3.2x +a 知b =-3.2,所以a =y -b =8+3.2×10=40.故填40. 8解:根据题中所提供的信息,可知父亲与儿子的身高的对应数据可列表如下:=173,y =176,∴=∑∑==---3121)())((i ii i ix xy y x x=3×6(-3)2+32=1,=y -=176-173=3. ∴回归直线方程为yˆ=x +3,从而可预测他孙子的身高为182+3=185(cm).故填185.10解:(1)按性别比例分层抽样,应选男生15×840=3(人),选女生25×840=5(人).(2)以数学成绩x 为横坐标,物理成绩y 为纵坐标作散点图如图所示.从散点图可以看出这些点大致分布在一条直线附近,并且在逐步上升,故物理与数学成绩线性正相关.设y 与x 的线性回归方程是yˆ=bx +a ,根据所给的数据,可以计算出≈0.65,≈34.5, 所以y 与x 的回归方程是yˆ=0.65x +34.5.。
高中数学知识点:线性回归方程

高中数学知识点:线性回归方程1.回归直线方程(1)回归直线:观察散点图的特征,发现各个大致分布在通过散点图中心的一条直线附近。
如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线叫做回归直线。
求出的回归直线方程简称回归方程。
2.回归直线方程的求法设与n 个观测点(,i ix y )()1,2,,i n =⋅⋅⋅最接近的直线方程为,y bx a =+,其中a 、b 是待定系数.则,(1,2,,)i i y bx a i n =+= .于是得到各个偏差(),(1,2,,)i i i i y y y bx a i n -=-+=. 显见,偏差i i y y -的符号有正有负,若将它们相加会造成相互抵消,所以它们的和不能代表几个点与相应直线在整体上的接近程度,故采用n 个偏差的平方和.表示n 个点与相应直线在整体上的接近程度.记21()n i i i Q y bx a ==--∑.上述式子展开后,是一个关于a 、b 的二次多项式,应用配方法,可求出使Q 为最小值时的a 、b 的值.即1122211()()()n n i i i i i i n n i i i i x x y y x y nx y b x x x nx a y bx ====⎧---⎪⎪==⎪⎨--⎪⎪=-⎪⎩∑∑∑∑, ∑==n i i x n x 11,∑==n i i y n y 11 相应的直线叫做回归直线,对两个变量所进行的上述统计分析叫做回归分析 上述求回归直线的方法是使得样本数据的点到回归直线的距离的平方和最小的方法,叫做最小二乘法。
要点诠释:1.对回归直线方程只要求会运用它进行具体计算a 、b ,求出回归直线方程即可.不要求掌握回归直线方程的推导过程.2.求回归直线方程,首先应注意到,只有在散点图大致呈线性时,求出的回归直线方程才有实标意义.否则,求出的回归直线方程毫无意义.因此,对一组数据作线性回归分析时,应先看其散点图是否成线性.3.求回归直线方程,关键在于正确地求出系数a 、b ,由于求a 、b 的计算量较大,计算时仔细谨慎、分层进行,避免因计算产生失误.4.回归直线方程在现实生活与生产中有广泛的应用.应用回归直线方程可以把非确定性问题转化成确定性问题,把“无序”变为“有序”,并对情况进行估测、补充.因此,学过回归直线方程以后,应增强学生应用回归直线方程解决相关实际问题的意识.。
2.4 线性回归方程

-1
杯数
20
24
34
38
50
64
如果某天的气温是-50C,你能根据这些数据预测这天小卖部卖处热茶 的杯数吗?
x
x1
x2
x3
…
xn
y
y1
y2
y3
…
yn
若上面数据满足线性相关关系,那么 y bx a
则称为这n个数据的线性回归方程.
其中
n
n
n
n
xi yi
xi
yi
b
i 1
i 1
i 1
n
n
i 1
20
10 -5 0
E DC
B A
5 15 25 35 x
答:都分布在同一条直线的附近.
象这样能用直线方程 y bx来表a示两个变量之间的相关关系我
们把它称为线性相关关系.
某小卖部为了了解热茶销售量与气温之间的系, 随机统计并制作了某6天卖出热茶的杯数与当天气 温的对照表:
气温
26
18
13
10
4
高中数学 必修3
思考下列问题:
两个变量之间的常见关系有几种?
(1)确定性的函数关系,变量之间的关系可以用函数表示. (2)相关关系,变量之间有一定的联系,但不能完全用函数来表示.
A 1.球的体积和球的半径具有( )
A.函数关系
B.相关关系
C.不确定关系
D.无任何关系
D 2.下列两个变量之间的关系不是函数关系的是( )
50
64
气 26 18 13 10 4 -1
温
y
杯 20 24 34 38 50 数
为了了解热茶销
售与气温的大致关系,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线性回归方程
1.线性回归方程
【概念】
线性回归是利用数理统计中的回归分析,来确定两种或两种以上变数间相互依赖的定量关系的一种统计分析方法之一,运用十分广泛.分析按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析.如果在回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析.如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析.变量的相关关系中最为简单的是线性相关关系,设随机变量与变量之间存在线性相关关系,则由试验数据得到的点将散布在某一直线周围.因此,可以认为关于的回归函数的类型为线性函数.
【实例解析】
例:对于线性回归方程푦=1.5푥+45,푥1∈{1,7,5,13,19},则푦=
解:푥=1+7+5+13+19
5
=
9,因为回归直线必过样本中心(푥,푦),
所以푦=1.5×9+45=13.5+45=58.5.
故答案为:58.5.
方法就是根据线性回归直线必过样本中心(푥,푦),求出푥,代入即可求푦.这里面可以看出线性规划这类题解题方法比较套路化,需要熟记公式.
【考点点评】
这类题记住公式就可以了,也是高考中一个比较重要的点.
1/ 1。
