衍射线方向的确定
X射线衍射方向材料分析

X射线衍射⽅向材料分析第⼆章X射线衍射⽅向X射线照射晶体,电⼦受迫振动产⽣相⼲散射;同⼀原⼦内各电⼦散射波相互⼲涉形成原⼦散射波。
由于晶体内各原⼦呈周期排列,因此各原⼦散射波间也存在固定的位相关系⽽产⽣⼲涉作⽤,在某些⽅向上发⽣相长⼲涉,即形成了衍射波。
由此,可知衍射的本质是晶体中各原⼦相⼲散射波叠加(合成)的结果。
衍射波的两个基本特征—衍射线(束)在空间分布的⽅位(衍射⽅向)和强度,与晶体内原⼦分布规律(晶体结构)密切相关。
X射线衍射分析是以X射线在晶体中的衍射现象作为基础的。
衍射可归结为两⽅⾯的问题,即衍射⽅向及衍射强度。
布拉格⽅程是阐明衍射⽅向的基本理论,⽽倒易点阵与爱⽡尔德图解则是解决衍射⽅向的有⼒⼯具。
晶体⼏何结构是更为基础的知识,在讨论上述内容之前应该有所了解。
有关点阵、晶胞、晶系以及晶向指数、晶⾯指数等在某些课程中可能已涉及,为适应衍射分析的需要,⼤家课前应该有所准备,这⾥不在重复。
⼀、劳厄⽅程:波长为λ的⼀束X射线,以⼊射⾓α投射到晶体中原⼦间距为a的原⼦列上(图1)。
假设⼊射线和衍射线均为平⾯波,且晶胞中只有⼀个原⼦,原⼦的尺⼨忽略不计,原⼦中各电⼦产⽣的相⼲散射由原⼦中⼼点发出,那么由图1可知,相邻两原⼦的散射线光程差为:若各原⼦的散射波互相⼲涉加强,形成衍射,则光程差必须等于⼊射X射线波长λ德整数倍:式中:H为整数(0,1,2…),称为衍射级数。
⼊射X射线的⽅向S0确定后,则决定各级衍射⽅向α/⾓可由下式求得:由于只要α/⾓满⾜上式就能产⽣衍射,因此,衍射线将分布在以原⼦列为轴,以α/⾓为半顶⾓的⼀系列圆锥⾯上,每⼀个H值对应于⼀个圆锥。
在三维空间中,设⼊射X射线单位⽮量S0与三个晶轴a,b,c的交⾓分别为α,β,γ。
若产⽣衍射,则衍射⽅向的单位⽮量S 与三个晶轴的交⾓α/,β/,γ/必须满⾜:a(COSα/-COSα)= Hλb(COSβ/-COSβ)= Kλc (COSγ/-COSγ)= Lλ式中H,K,L均为整数,a,b,c分别为三个晶轴⽅向的晶体点阵常数。
X射线的衍射方向

44
(3) 衍射线方向与晶体结构的关系
将立方、四方及斜方晶系的面间距公式代入布拉 格方程,得出以下公式:
立方晶系:sin2θ=λ2/4a2 (h2+k2+l2) 四方晶系: sin2θ= λ2/4[(h2+k2)/ a2+l2/c2] 斜方晶系: sin2θ= λ2/4(h2/ a2+k2/b2+l2/c2) 由以上三个公式可看出: ①波长选定后,不同晶系或同一晶系而晶胞大小 不同的晶体,其衍射线束的方向不同。因此,研究衍 射线束的方向,可以确定晶胞的形状和大小; ②衍射线束的方向与原子在晶胞中的位置和原子 种类无关。
第4章 X射线的衍射方向
§4.1 X射线衍射的概念 §4.2 劳埃方程式 §4.3 布拉格方程式 §4.4 衍射矢量方程和厄瓦尔德图解
§4.1 X射线衍射的概念
光 栅 对 可 见 光 的 衍 射
2
X射线在晶体中的衍射
X 射线通过晶体时会发生衍射现象,形成衍射花样。
X射线在晶体中产生的衍射示意图
3
αh。h称为劳埃第一干涉指数, αh为衍射线束与原子列 或行列的夹角。
7
衍射条件: a0( cosαh- cosα0)= h
该式称为劳埃第一方程式,可求出散射加强的 方向αh。h称为劳埃第一干涉指数, αh衍射线束与 原子列或行列的夹角。
劳埃第一干涉指数可取 0,1, 2, 3等整数, 但不是无限的。
劳埃方程从理论上解决了X射线在晶 体中衍射的方向。
20
劳埃方程的缺陷: 用劳埃方程描述X射线被晶体衍射的现象
时,入射线、衍射线与晶轴的6个夹角不易确 定,三个劳埃方程在使用上也不方便,即从实 用的角度来说,该理论有简化的必要。
X射线衍射方向(4)Ewald图解—雨课堂课件

k'
k
k
因此,O'B是一衍射线方向。B点为(hkl)面的倒易点。
第二章 X射线衍射
三、埃瓦尔德(Ewald)图解
由此可见,当X射线沿O'O方向入射的情况下,所有能发生衍射的晶面, 其倒易点都应落在以O'为球心,以1/λ为半径的球面上,从球心O'指向倒易 点的方向是相应晶面反射线的方向。以上求衍射线方向的作图法称爱瓦尔 德图解,它是解释各种衍射花样(包括电子衍射)的有力工具。
提交
单选题 1分
在下面的Ewald球中,(hkl)晶面衍射线方向是 ( )。 A AB B OB C O’B D O’O
提交
单选题 1分
若某立方系晶体的(111)、(220)、(311)、(222)面对应的倒易 点均落在爱瓦尔德球上。则这些面对应的衍射角(2θ)hkl大小 顺序为( )。
A (2θ)111 > (2θ)220 > (2θ)311 > (2θ)222
提交
The end
B (2θ)220 > (2θ)111 > (2θ)311 > (2θ)222 C (2θ)111< (2θ)220 < (2θ)222 < (2θ)311 D (2θ)111 < (2θ)220 < (2θ)311 < (2θ)222
提交
单选题 1分
立方系晶体的(111)、(220)、(311)、(222)面对应的倒易球半 径大小Rhkl大小顺序为( )。
4)连接爱瓦尔德球心与落在球 面上的倒易点方向,即为(hkl)晶 面衍射线方向。
第二章 X射线衍射
三、埃瓦尔德(Ewald)图解
思考: 如果是静置的单晶材料,某个(hkl)晶面的倒易点是否必然落到爱瓦尔
XRD衍射方向和强度

材料研究方法
x 射线衍射分析
特征X射线的波长
莫塞莱 (H. G. Moseley) 发现,特征 X 射线的波长与 原子序数 Z 的平方成反比关 系。
特征X射线的波长与管电 压无关,但其强度则与管电 压有关:
= I 标 K 3i (U − U K ) n
K3 均为常数。特征X射线的 UK 为临界激发电压,n、
二、布拉格方程的讨论
将衍射看成反射是布拉格方程的基础。但衍射是本质, 反射仅是为了使用方便的描述方式。 X射线只有在满足布拉格方程的θ角上才能发生反 射,亦称选择反射。 布拉格方程在解决衍射方向时是极其简单而明确的。 波长为λ的X射线,以角θ投射到晶体中间距为d的晶面 时,有可能在晶面的反射方向上产生反射(衍射)线, 其条件是相邻晶面的反射线的程差为波长的整数倍。但 是布拉格方程只是获得衍射的必要条件而非充分条件。 布拉格方程联系了晶面间距d、掠射角θ 、反射级 数n和X射线波长λ四个量。
1 1 1 − 2 )( Z − σ ) 2 n2 n1
λ
=
R(
强度:相对强度决定于电子在不同能级间的跃迁几率; 绝对强度随管电流和管电压的增大而增大。
= I 标 K 3i (U − U K ) n
用途:X射线衍射分析的主要光源;元素成分分析。
Intensity (%) 100 90 80 70 60 50 40 30 20 10 0 35 40
材料研究方法
x 射线衍射分析
X射线滤波片
在X射线衍射分析中常常要采用单色X光,因Kα 的强度较高,故一般是选择 Kα 作光源。但在 X 射线 管发出的X射线中有Kα时,必定伴有Kβ和连续X射线。 这对衍射分析是不利的。必须设法把 Kβ 和连续 X 射 线除去或将其减弱到最小程度。通常是用滤波片来 实现这一目的。
x射线衍射原理

s0 、 s 及R*HKL构成等 腰三角形, s0 的终点 是倒易原点, s 的终点
是R*HKL的终点,即倒 易点, s0 与 s 夹角为 2,为衍射角。
乙 Confidential
© 2012 乙 Corporation
- X射线衍射原理 第一节 衍射方向
厄瓦尔德图解步骤
具体步骤见书P.71。下图为某晶体(001)*倒易面 上倒易点与反射球相交截情形
为了通过衍射现象来分析晶体内部结构的各种问题,必须在 衍射现象与晶体结构之间建立关系。
乙 Confidential
© 2012 乙 Corporation
- X射线衍射原理
第一节 衍射方向 一、布拉格方程
反射线光程差: = ML +LN= 2dsin
干涉一致加强的条件为: = n
得到了“选择反射”的结 果
3、产生衍射的极限条件:由布拉格方程可知,晶体中只有满足d> /2的晶面才产生衍射,所以产生的衍射线时有限的,利用此条件可判 断出现衍射线条的数目。
4、布拉格方程反映晶体结构中晶胞大小及形状,而对晶胞中原子的 品种和位置并未反映,d相同, 相同。
乙 Confidential
© 2012 乙 Corporation
乙 Confidential
© 2012 乙 Corporation
- X射线衍射原理 第二节 X射线衍射强度
一、一个电子的散射强度
根据汤姆逊的工作,一个电子对入射
强度为I0的偏振X射线(电场矢量E0只沿 一个固定方向振动)的散射强度Ie为:
Ie
I0
e4 R 2m 2c4
sin2φ
对于非偏振X射线,将其电场矢量E0分解为垂直的两束偏振光,如 图,E0x和E0z,且 I0 = E02 = E0x2 + E0z2。对于完全非偏振光有: E= E0z,所以E0x2 = E0z2= E02 /2 ,即I0x=I0z= I0 /2。因而有:
第3节 X射线衍射原理

(a) 体心立方 a-Fe a=b=c=0.2866 nm
(b) 体心立方 W a=b=c=0.3165 nm
衢州学院化学与材料工程学院
Intensity (%) 100 90 80 70 60 50 40 30 20 10 0 35 40
1,1,0 (44.68,100.0)
b(cosβ2-cosα2)= Kλ 也可写成 a · ( S-S0)= Hλ b· ( S-S0)= Kλ
• 这表明构成平面的两列原子产生的衍射圆锥的交线才是衍射方向。
衢州学院化学与材料工程学院
• 三维劳厄方程——考虑三维晶体的衍射方向 劳厄方程 • 只有同时满 足三个方程 的方向上才 会出现衍射 a(cosβ1-cosα1)= Hλ b(cosβ2-cosα2)= Kλ c(cosβ3-cosα3)= Lλ 也可写成 a · (S -S0)= Hλ b· (S -S0)= Kλ c· (S -S0)= Lλ • 三个方向直线 点阵的衍射圆 锥交成衍射线 S ,衍射方向 由衍射指标 hkl表征。
任选两相邻面,反射线光程差
δ=ML+LN= 2dsinӨ 干涉一致加强的条件为: δ=nλ 即 2dsinӨ =nλ (布拉格方程)
式中:n-任意正整数,称反射级数。
布拉格方程 的导出
衢州学院化学与材料工程学院
布拉格方程( 2dsinӨ=nλ)的讨论
① 选择反射 • 衍射线的方向恰好是原子面 对入射线的反射,类似可见光镜 面反射的入射及反射束、反射 面法线均处于同一平面的特点。• 故借用镜面反射几何描述 X 射线 的衍射。
衢州学院化学与材料工程学院
衢州学院化学与材料工程学院
•
衍射方向理论小结
材料现代分析技术-2X射线衍射方向

±1,±2共5个值。用Mo Kα 线(λ = 0.711Α) H 可取0, ±1, ±2, ±3, ±4, ±5共11个值。
劳埃第二方程
二维衍射 原子的二维排列称为原子网,可视为由一系 列周期为b的平行的原子列所组成。与一维衍 射时类同,这些原子列产生的衍射束要能加 强,也须满足以下条件:
x射线有强的穿透能力,在x射线作用下晶体的散射线来自若 干层原子面,除同一层原子面的散射线互相干涉外,各原子 面的散射线之间还要互相干涉。这里只讨论两相邻原子面的 散射波的干涉。过A点分别向入射线和反射线作垂线,则SA 之前和TA之后两束射线的光程相同,它们的光程差为:
d = QA′Q′ -PAP′=SA′+A′ T= 2dsinθ
首先作晶体的倒易点阵,O*为倒易原点。入射线沿OO*方向 入射,且令OO* =S0/λ=K0。 以0为球心,以1/λ为半径画 一 球 , 称 反 射 球 。 若 球 面 与 倒 易 点 G 相 交 , 连 OG 则 有 OGS0/λ =O*G,这里O*G为一倒易矢量。因OO* =OG=1/λ,故 △OO*G为等腰三角形,OG是一衍射线方向。由此可见,当x 射线沿OO*方向入射的情况下,所有能发生反射的晶面,其 倒易点都应落在以O为球心。以1/λ为半径的球面上,从球 心O指向倒易点的方向是相应晶面反射线的方向。以上求衍 射线方向的作图法称爱瓦尔德图解,它是解释各种衍射花样 的有力工具。
复杂点阵晶胞中含有n个相同或不同种类的原子,它们除占 据单胞的顶角外,还可能出现在体心、面心或其他位置。
复杂点阵单胞的散射波振幅应为单胞中各原子的散射振幅的 矢量合成。由于衍射线的相互干涉,某些方向的强度将会加 强,而某些方向的强度将会减弱甚至消失。这种规律称为系 统消光。
X射线衍射图谱的分析

X射线衍射图谱的分析----------------------------------------------------------------------------------------------------------------------------------------------A 衍射峰的有无、位置B 衍射峰的强度C 衍射峰的峰形E 衍射测试实验条件选择F 其他相关知识----------------------------------------------------------------------------------------------------------------------------------------------A 衍射峰的有无、位置1、衍射方向取决于晶体的周期或晶胞的大小。
2、X射线入射到结晶物质上,产生衍射的充分必要条件是3、第一个公式确定了衍射方向。
在一定的实验条件下衍射方向取决于晶面间距d。
而d是晶胞参数的函数,;第二个公式示出衍射强度与结构因子F(hkl)的关系,衍射强度正比于F(hkl)模的平方,4、F(hkl)的数值取决于物质的结构,即晶胞中原子的种类、数目和排列方式,因此决定X射线衍射谱中衍射方向和衍射强度的一套d和I的数值是与一个确定的结构相对应的。
这就是说,任何一个物相都有一套d-I特征值,两种不同物相的结构稍有差异其衍射谱中的d和I将有区别。
这就是应用X射线衍射分析和鉴定物相的依据。
5、若某一种物质包含有多种物相时,每个物相产生的衍射将独立存在,互不相干。
该物质衍射实验的结果是各个单相衍射图谱的简单叠加。
因此应用X射线衍射可以对多种物相共存的体系进行全分析。
6、一种物相衍射谱中的(是衍射图谱中最强峰的强度值) 的数值取决于该物质的组成与结构,其中称为相对强度。
当两个样品的数值都对应相等时,这两个样品就是组成与结构相同的同一种物相。
X射线衍射方向

1、选择反射:X 射线在晶体中的衍射实质是晶体中各原子散射波之间的干涉结果。
只是由于衍射线的方向恰好相当于原子面对入射线的发射,所以可以借用镜面发射规律来描述X 射线的衍射,即将衍射看成反射,是布拉格方程的基础。
但衍射是本质,反射仅是为了使用方便的描述方式。
X 射线的晶面反射与可见光的镜画反射亦有所不同。
一束可见光以任意角度投射到镜面上都可以产生反射,但X 射线只有在满足布拉格方程的θ角上才能发生反射,是具有选择性的而非任意的,只有当d 、θ和λ满足布拉格方程时才能发生反射,。
因此,这种反射亦称选择反射。
一组面网只能在一定的角度上反射X 射线,级次越高,衍射角越大。
人们经常用“反射”这个术语来描述一些衍射问题,有时也把“衍射”和“反射”作为同义语混合使用,但其实质都是说明衍射问题;有两种几何学的关系必须牢记:①入射光束、反射面的法线和衍射光束一定共面;②衍射光束与透射光束之间的夹角等于2θ,这个角称为衍射角。
例1: Al ,面心立方,已知a=0.405nm用nm CuK 15416.0=α线照射,问(111)面网组能产生几条衍射线。
解: nm d 234.03405.0==04.315418.0234.02=⨯≤n n=1,2,3 能产生三条衍射线n=1 329.021sin 1==d λθ,12191︒=θ’n=2 659.022sin 2==d λθ,13412︒=θ’ n=3 988.023sin 3==dλθ,07813︒=θ’ 例2、Lu 2O 3,立方晶系,已知a=1.0390 nm 用nm CoK 17980.01=α线照射,问(400)面网组能产生几条衍射线。
解:2598.04039.1==d 89.21798.02598.02=⨯≤n 2,1=n2、反射级数:公式中的n称为反射级数。
由相邻两个平行晶面反射出的X射线束,其波程差用波长去量度所得的整份数在数值上就等于n。
在使用布喇格方程时,并不直接赋予n 以1、2、3等数值,而是采用另一种方式。
05-X射线衍射分析原理
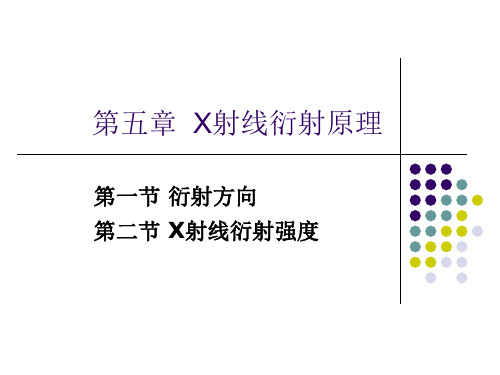
布拉格方程是X射线在晶体中衍射必须满
足的基本条件。它反映了衍射线的方向(用θ表 示)与晶体结构(用d代表)之间的关系。可通 过θ的测定,在λ已知的情况下,解出d。或者d已 )选择反射 X射线从原子面的反射与可见光的镜面反射 不同,前者是有选择的反射,其选择条件为布拉格 定律;而一束可见光以任意角度投射到镜面上时都 可以产生反射,即反射不受条件限制。 因此,X射线的晶面反射称为选择反射。
衍射方向决定于:
晶胞大小、形状及位向等因素。 衍射强度决定于: 晶胞中的原子种类、数量及其具体分布排列。 X射线的衍射方向描述方法:
劳埃方程、布拉格方程和衍射矢量方程。
二、布拉格方程式(Bragg) 晶体对X射线的衍射在形式上可看成是在 特定条件下晶体的面网对X射线的“反射”。 将衍射成反射,是导出布拉格方程的基 础。1912年,由英国物理学家布拉格提出。
C
O
1/λ
O*
可将上述描述拓宽至三维空间,假设存在 一个半径为1/λ的球面,令X射线沿球面的直径 方向入射,则球面上所有点均满足布拉格条件, 该球被命名为反射球。
该法由厄瓦尔德提出,故称为厄瓦尔德球, 该作图方法被称为厄瓦尔德图解。
四、劳埃方程式(Laue)
1、一维原子列对X射线的衍射 一维原子列的衍射线可看成一个行列对 X射线的衍射。如下图,点阵周期为a0
满足劳埃第一方程式,即可产生衍射, 衍射线与行列成αh角,即与行列夹角为αh的 方向都可产生衍射,因此衍射线的分布是 以原子列为轴、以αh为半径角的圆锥母线。
h每等于一个整数值(0,1, 2……),即形成一 个圆锥状衍射面。 因此一维原子列对X射线的的衍射为一套 圆锥。
如果用单色X射线垂直照射原子列 (α0=90)时: a0 cosα h = h, cosα h = h / a0
04 第三章 X射线衍射原理-衍射方向

3.3.2 布拉格方程
布拉格公式的推导
首先讨论一个 晶面的衍射: P
Q
P' Q'
q
q'
A
B
1 d(h k l) 2 d(h k l) 3
入射线在波阵面PQ处位相相同,它射向晶面1时,被原子散 射。如果原子A,B的散射线在波阵面P′Q′处是同位相的话, 便产生相干加强,形成衍射光束。 这要求:
PA AP QB BQ
材料分析测试技术
Materials Characterization
湘潭大学 材料科学与工程学院
第三章 X射线衍射分析原理
1. 概述
2. X射线物理学基础 3. X射线衍射方向 4. X射线衍射强度
2015/10/22
2
3.3 X射线的衍射方向
3.3.1 劳埃方程 3.3.2 布拉格方程 3.3.3 布拉格方程的讨论 3.3.4 衍射矢量方程 3.3.5 布拉格方程的厄瓦尔德图解 3.3.6 常见的衍射方法
cos 2 a cos 2 cos 2 1
四个方程解三个 未知数?
用单色X射线照射不 动的单晶体,一般 不能获得衍射!
必须增加一个变量: 1. 利用连续X射线,使波长为变量,晶体固定不动-劳埃法; 2. 利用单色的X射线,单晶体围绕某一主要晶轴转动,周转晶 体法。
2015/10/22
3.3.1 劳埃方程
Laue方程的讨论
测量时若晶体不动: a0,0,0一定; 用单色光: l一定;
a cos a cos a 0 H l b cos cos 0 K l c cos cos 0 Ll
对于特定的晶体和特定的方向: a,b,c,H,K,L一定. Laue 方程中只有 a ,, 是变量 , 又由于 a ,, 不是独立的变量 , 因此 一般得不到衍射图(三个变量四个方程)。
02 X射线的方向和强度

ra x Ia <ZIe
即电子波合成有所损耗 定义
Aa Ia 1 2 f= =( ) Ae Ie
即为原子对X射线散射 大小atomic scattering factor,称散射因子
i
-i
i 2
= Ae i Ae -i=A 2
• 晶胞中N个原子1,2,3……的坐标为u1v1w1, u2v2w2,u3v3w3…… unvnwn • 散射因子为f1,f2,f3……位相差:φ1 ,φ 2,φ3 ……φn • 合成振幅 n
i1 i2 in A b=A ( f e + f e +......+ f e )=A e f je e 1 2 n j=1
e
0 0
温度因子=
加热振动IT f =e-2m或 =e-m 静止振动I f0
6n 2 ( x) 1 sin 2 m= [ ] 2 m a k x 4
( x)德拜函数 查表
x=/T -特征温度平均值
粉末法的衍射线强度
3 e2 2 V 2 -2M I=I0 ( ) P F ( ) A ( ) e 32 R mc2 Vc2 R为观察试样距离, Vc-晶胞体积 V被照射体积
=f[1 eLeabharlann i(h+k)]
h,k同性数(都是奇数或者偶数)时:F=2f F2=4f2 h,k异性数(一个奇数一个偶数)时:F=0 消光
3)体心立方
F=fe
2 i(0)
fe
h k l 2 i( + + ) 2 2 2
衍射花样的标定步骤及技巧

1. 一般的物质衍射花样都是已知的物质,顶多也就是已知的几种里面的一个。
所以在确定哪几个物种之后,去找一下相关物质的PDF卡片,网上有一个软件PCPDFWIN,可以方便查讯电子版的PDF卡。
2. 找到了相应的PDF卡,那么就是要测量衍射花样了。
衍射花样的拍摄要严格按照操作规程来,尤其要注意在拍摄时样品聚焦尽量准确。
另外,无论底片拍摄还是CCD拍摄,一定要保证用标准样品做了校正。
3. 接下来就是测量衍射点对应的d值。
对于底片来说就是测量衍射点到中心透射斑的实际距离R,然后根据d = (L×电子波长)/R,其中L是相机常数,底片上写着,单位是cm,电子波长一般的电镜书上都有,200 kV电镜是0.00251 nm。
代入计算即可得到相应的d值。
选取两个相邻且最靠近中心斑点的衍射点,二衍射斑点以夹角接近或者等于90度为好。
选取测量d值之后,二者同中心斑点连线的夹角也要测量一下。
对于CCD相机拍摄的衍射花样,对应的都有标尺,d值测量就是量取衍射点到透射斑的距离后取倒数即可。
角度测量可以通过量取衍射点到中心斑连线对应control对话框的R值(角度),二者相减即得。
4. 将计算的d值和PDF卡相对应,看最接近哪个面的数值。
这个测量会有一定的误差,有相近值时,需要通过夹角来确定。
方法是,选取两个比较可能的面,然后代入相应晶系对应的公式,计算夹角,如果和测量值很接近,就算是找对了。
Ustb版主说过,计算值和测量值应该相差很小,0.1-0.2度的范围。
至于计算两个面夹角的公式,可以去找郭可信先生写的那本《电子衍射图在晶体学中的应用》,Page104-105上有具体的公式,其中的hkl值都是你要计算的面对应的值,abc是你确定晶相的晶胞参数,PDF卡上都有,r1*r2*分别指的是两个面的d值倒数。
5. 确定了两个方向的衍射点,那么接下来就是确定投射方向,也就是面的法线方向是什么带轴,这个querida朋友已经写了,我这里引用一下:“FFT后的一个斑点对应这正空间一族晶面,这一族晶面和这个斑点的矢量方向垂直,当一张图片上任意不在同一直线上的2个斑点知道后,那么入射电子束也就是带轴的方向就知道了,具体可用h1 | k1 l1 h1 k1 | l1h2 | k2 l2 h2 k2 | l2u v wu=k1l2-l1k2v=l1h2-h1l2w=h1k2-k1h2你可以适当化简达到互质的3个数。
晶体衍射原理

(4) 如需具体数学计算,仍要使用Bragg方程。
练习Exercise
•1) 试解释Bragg 方程。
explain the physical meaning of Bragg’s law
2 H
1/ C S0/
O
Sphere of reflection
Direction of direct beam
极限球
Limiting sphere
增大晶体产生衍射机率的方法
(3)改变波长, 使 Ewald球的数量增加, 球壁增厚(Laue法)
1/ C
hkl S/
S0/
O
增大晶体产生衍射机率的方法
而衍射则是一定厚度内
许多间距相同晶面共同
作用的结果。
1
2
A
C
B
1’ hkl
2’ dhkl
(2)入射线波长与面间距关系
sin /d1
2
所以要产生衍射,必须有
d > /2
这规定了X衍射分析的下限:
对于一定波长的X射线而言,晶体中能产生衍射 的晶面数是有限的。
对于一定晶体而言,在不同波长的X射线下,能 产生衍射的晶面数是不同的。
•2) 试简述X射线照射到固体物质上所产生 的物理信息。
explain the physical information occurring in solid struck by X-ray
• 3) 试解释下列术语:白色X射线;特征X 射线;段波限; Ewald 球;衍射矢量; 倒易球。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如图AS、BT为A、B两个原子为中 心所产生的衍射方向,在S、T处 为同相,AS、BT与点阵轴呈α角, 这时它们的程差应满足: δ=AD-BC=Hλ
式中H为整数(0,±1,±2……),即衍射级数 AD=acosα,BC=acosα0 δ=acosα-acosα0=a(cosα-cosα0)=Hλ
a(cos cos0 ) H
因此当掠射角α0一定时,在适合于下列 条件的方向,都可以找到衍射线束:
cos
cos0
H
a
衍射线的轨迹系在一个以点阵轴为轴,
ω≠0
r1
r2
r3
ω=0
R
当λ及α0一定时,衍射线级数有一定限制。因为cosα的绝对值不能大于1。Hλ/a 为最大的条件是cosa0=-1(a0=180°)及cosa=1(a=0°),这时Hλ/a=2。如果 λ/a>2,则不可能有衍射线产生(除去H为0,a=a0的情况,这时衍射线实际上是 入射线的继续)。倘使希望能发生衍射现象,则λ/a必须小于或等2 。下面举一个例
一系列不同α作为其半圆锥角。 当单色的X射线由与点阵轴(即衍射圆锥
的轴)垂直的方向射入,照相底片放在原子
列的后面和点阵轴平行时,由图可取看出,
其衍射花样为一系列双曲线(包括若干对双 曲线),即一系列衍射线圆锥和底片所成的
交线;如果照相底片和点阵轴垂直,则衍 射花样为一系列的同心圆。
式中的H必须为整数,否则将不会得到衍射线条(衍射线强度为0),可以证明如
X射线受二维点阵(原子平面,原子网)衍射的条件
如图所示,X及Y为二维点阵的两个晶轴,两者之间的夹角为γ,点阵常数为a 及b。入射的X射线自任何方向射入,与此二维点阵相遇,与X轴成a0角,与Y轴 成β0角。依上节所述加以推衍,由于X及Y两个原于列所发生的H级及K级衍射线 的轨迹分别是两个圆锥面,它们和X及Y轴分别成a及β角,当a+β>Y时,这两个 圆锥面相交于两个直线方向(衍射方向)。此时可以用下式表示二维点阵的衍射 条件:
晶体衍射的几何理论
在实验上观测到晶体的衍射花样之后,劳厄就面临着理论解释的问题。实 际所要求的就是将物理光学中的一维光栅理论公式推广到三维。在这方面劳 厄可算是驾轻就熟。他的博士论文是普朗克指导的,题目就是“平行平板干 涉现象的理论”,前两年又应索末非之邀,为《数理百科全书》第五卷撰写 了一篇“波动力学”的专论,其中包括将一维光栅的理论推广到二维光栅, 而现在面临的问题就是将二维光栅的衍射推广到三维。这样,就得到描述晶 体X射线衍射的劳厄方程。
子看看,当λ、a0及a为已知值时,究竟有多少级的衍射线条能够发生。 如果入射的X射是单色的,其波长为1.54Å(Cu-Kα辐射),原子列的点阵常数
a=5Å,入射X射线与原子列的夹角为α=90°,则衍射线与原子列的夹角α为:
cos
H
a
cos0
H
1.54 5
0.308H
因为|cosα| ≤1,所以H可以等于0,±1,±2及±3
以α角为半圆锥角的圆锥面上。同样,满 足此式的入射X射线可以由任何方向与点 阵相遇,只要其夹角等于α0可,这时入射 线的轨迹是在以点阵轴为轴,取α0为半圆 锥角的圆锥面上,而0级衍射线系在一个
共顶相对的同样圆锥面上。适合上式条件
的其他衍射线轨迹圆锥面都和入射线轨迹
圆锥共轴线及顶点,但以符合上式要求的
平行于原射线波前的公切线称为0极衍射线束的波前,顺次相差一个波长的球 面波前的公切线形成1极级衍射束波前.以此类推,可以得到2级、3级、4级……以 及-1、-2、-3、-4、……等级衍射线束的波前及其他传播方向。
劳厄方程的推导
X射线受一维点阵(原子列)衍射的条件 一列等距离排列的原子可以构成一个一一束X射线照射到晶体上时,被组成晶体的原子的电子所散射,电子的
散射波可近似地看作由原子中心发出。在入射X射线的照射下,可以把晶体中 的每个原子看成是一个新的散射源,它们都向空间辐射出与入射波同频率的 电磁波。由于这些散射波的相干作用,使得空间某些方向上的波始终保持互 相叠加,在这些方向上可以观察到强的衍射线条;而在另一些方向上由于始 终保持相互抵消,在这些方向不能观察到衍射线。
当H=1时,cosα=0.308,α=72.06° 当H=-1时,cosα= -0.308,α=107.94°
当H=2时,cosα=0.616,α=51.98° 当H=-2时,cosα= -0.616,α=128.02°
当H=3时,cosα=0.921,α=22.5° 当H=-3时,cosα= -0.921,α=157.07°
下:
如果由相邻两个原子1、2为中心所产生散射线的程差δ1-2,不是λ的整数倍,而 是: a(cosα-cosα0)=(H+ω)λ 其中的值为1>ω>0,那么由这些散射波所引的相差为:
1-2=2π(H+ω)=2πH+2πω=2πω 对于由1原子和3原子为中心所产生散射线的程差δ1-3为δ1-2的两倍,其相应的相差也 是两倍,即: 1-3=4πω
因此,X射线在晶体中的衍射现象的实质是大量原子散射波相互干 涉的结果。
如图表示当X射线束与一列等距离排列的质点相遇时,其相互平行的波前将在 每一个质点处产生一系列球面散射波,它们都和原X射线具有同样的波长和频率。 如果沿着这些球面波前作公切线,则这些公切线的法线方向即为散射波相互加强的 方向,这样就产生了衍射。
依同理推衍,
1-n=2(n-1)πω 一般点阵中原子数目极多,团此,纵然
ω极小,但只要它不等于零,出图可见看出, 共振幅的合成矢量R的长度与每一个单独振 幅矢量r的长度仍在同一数量级,如果这个 原子列上有一万个原子,而ω为零时,则R 的长度将为r长度的一万倍,因此可以认为 只有当H为整数时方能发生衍射。
