2016年安徽省中考数学试卷含答案

合集下载

2016-2017安徽省中考数学试题及解答

2016年XX省中考数学试卷一、选择题（本大题共10小题，每小题4分，满分40分）1．（4分）（2016•XX）﹣2的绝对值是（）A．﹣2 B．2 C．±2 D．2．（4分）（2016•XX）计算a10÷a2（a≠0）的结果是（）A．a5B．a﹣5C．a8D．a﹣83．（4分）（2016•XX）2016年3月份我省农产品实现出口额8362万美元，其中8362万用科学记数法表示为（）A．8.362×107 B．83.62×106 C．0.8362×108D．8.362×1084．（4分）（2016•XX）如图，一个放置在水平桌面上的圆柱，它的主（正）视图是（）A．B．C．D．5．（4分）（2016•XX）方程=3的解是（）A．﹣B．C．﹣4 D．46．（4分）（2016•XX）2014年我省财政收入比2013年增长8.9%，2015年比2014年增长9.5%，若2013年和2015年我省财政收入分别为a亿元和b亿元，则a、b之间满足的关系式为（）A．b=a（1+8.9%+9.5%）B．b=a（1+8.9%×9.5%）C．b=a（1+8.9%）（1+9.5%）D．b=a（1+8.9%）2（1+9.5%）7．（4分）（2016•XX）自来水公司调查了若干用户的月用水量x（单位：吨），按月用水量将用户分成A、B、C、D、E五组进行统计，并制作了如图所示的扇形统计图．已知除B组以外，参与调查的用户共64户，则所有参与调查的用户中月用水量在6吨以下的共有（）组别月用水量x（单位：吨）A 0≤x＜3B 3≤x＜6C 6≤x＜9D 9≤x＜12E x≥12A．18户B．20户C．22户D．24户8．（4分）（2016•XX）如图，△ABC中，AD是中线，BC=8，∠B=∠DAC，则线段AC的长为（）A．4 B．4C．6 D．49．（4分）（2016•XX）一段笔直的公路AC长20千米，途中有一处休息点B，AB长15千米，甲、乙两名长跑爱好者同时从点A出发，甲以15千米/时的速度匀速跑至点B，原地休息半小时后，再以10千米/时的速度匀速跑至终点C；乙以12千米/时的速度匀速跑至终点C，下列选项中，能正确反映甲、乙两人出发后2小时内运动路程y（千米）与时间x（小时）函数关系的图象是（）A．B．C．D．10．（4分）（2016•XX）如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为（）A．B．2 C．D．二、填空题（本大题共4小题，每小题5分，满分20分）11．（5分）（2016•XX）不等式x﹣2≥1的解集是．12．（5分）（2016•XX）因式分解：a3﹣a=．13．（5分）（2016•XX）如图，已知⊙O的半径为2，A为⊙O外一点，过点A作⊙O的一条切线AB，切点是B，AO的延长线交⊙O于点C，若∠BAC=30°，则劣弧的长为．14．（5分）（2016•XX）如图，在矩形纸片ABCD中，AB=6，BC=10，点E在CD上，将△BCE沿BE折叠，点C恰落在边AD上的点F处；点G在AF上，将△ABG沿BG折叠，点A恰落在线段BF上的点H处，有下列结论：①∠EBG=45°；②△DEF∽△ABG；③S△ABG=S△FGH；④AG+DF=FG．其中正确的是．（把所有正确结论的序号都选上）三、（本大题共2小题，每小题8分，满分16分）15．（8分）（2016•XX）计算：（﹣2016）0++tan45°．16．（8分）（2016•XX）解方程：x2﹣2x=4．四、（本大题共2小题，每小题8分，满分16分）17．（8分）（2016•XX）如图，在边长为1个单位长度的小正方形组成的12×12网格中，给出了四边形ABCD的两条边AB与BC，且四边形ABCD是一个轴对称图形，其对称轴为直线AC．（1）试在图中标出点D，并画出该四边形的另两条边；（2）将四边形ABCD向下平移5个单位，画出平移后得到的四边形A′B′C′D′．18．（8分）（2016•XX）（1）观察下列图形与等式的关系，并填空：（2）观察下图，根据（1）中结论，计算图中黑球的个数，用含有n的代数式填空：1+3+5+…+（2n﹣1）+（）+（2n﹣1）+…+5+3+1=．五、（本大题共2小题，每小题10分，满分20分）19．（10分）（2016•XX）如图，河的两岸l1与l2相互平行，A、B是l1上的两点，C、D是l2上的两点，某人在点A处测得∠CAB=90°，∠DAB=30°，再沿AB方向前进20米到达点E（点E在线段AB上），测得∠DEB=60°，求C、D两点间的距离．20．（10分）（2016•XX）如图，一次函数y=kx+b的图象分别与反比例函数y=的图象在第一象限交于点A（4，3），与y轴的负半轴交于点B，且OA=OB．（1）求函数y=kx+b和y=的表达式；（2）已知点C（0，5），试在该一次函数图象上确定一点M，使得MB=MC，求此时点M 的坐标．六、（本大题满分12分）21．（12分）（2016•XX）一袋中装有形状大小都相同的四个小球，每个小球上各标有一个数字，分别是1，4，7，8．现规定从袋中任取一个小球，对应的数字作为一个两位数的个位数；然后将小球放回袋中并搅拌均匀，再任取一个小球，对应的数字作为这个两位数的十位数．（1）写出按上述规定得到所有可能的两位数；（2）从这些两位数中任取一个，求其算术平方根大于4且小于7的概率．七、（本大题满分12分）22．（12分）（2016•XX）如图，二次函数y=ax2+bx的图象经过点A（2，4）与B（6，0）．（1）求a，b的值；（2）点C是该二次函数图象上A，B两点之间的一动点，横坐标为x（2＜x＜6），写出四边形OACB的面积S关于点C的横坐标x的函数表达式，并求S的最大值．八、（本大题满分14分）23．（14分）（2016•XX）如图1，A，B分别在射线OA，ON上，且∠MON为钝角，现以线段OA，OB为斜边向∠MON的外侧作等腰直角三角形，分别是△OAP，△OBQ，点C，D，E分别是OA，OB，AB的中点．（1）求证：△PCE≌△EDQ；（2）延长PC，QD交于点R．①如图1，若∠MON=150°，求证：△ABR为等边三角形；②如图3，若△ARB∽△PEQ，求∠MON大小和的值．2016年XX省中考数学试卷参考答案一、选择题1．B2．C3．A4．C5．D6．C7．D8．B9．A10．B二、填空题11．x≥312．a（a+1）（a﹣1）13．．14．解：∵△BCE沿BE折叠，点C恰落在边AD上的点F处，∴∠1=∠2，CE=FE，BF=BC=10，在Rt△ABF中，∵AB=6，BF=10，∴AF==8，∴DF=AD﹣AF=10﹣8=2，设EF=x，则CE=x，DE=CD﹣CE=6﹣x，在Rt△DEF中，∵DE2+DF2=EF2，∴（6﹣x）2+22=x2，解得x=，∴ED=，∵△ABG沿BG折叠，点A恰落在线段BF上的点H处，∴∠3=∠4，BH=BA=6，AG=HG，∴∠2+∠3=∠ABC=45°，所以①正确；HF=BF﹣BH=10﹣6=4，设AG=y，则GH=y，GF=8﹣y，在Rt△HGF中，∵GH2+HF2=GF2，∴y2+42=（8﹣y）2，解得y=3，∴AG=GH=3，GF=5，∵∠A=∠D，==，=，∴≠，∴△ABG与△DEF不相似，所以②错误；∵S△ABG=•6•3=9，S△FGH=•GH•HF=×3×4=6，∴S△ABG=S△FGH，所以③正确；∵AG+DF=3+2=5，而GF=5，∴AG+DF=GF，所以④正确．故答案为①③④．三、15．（﹣2016）0++tan45°=1﹣2+1=0．16．解：配方x2﹣2x+1=4+1∴（x﹣1）2=5∴x=1±∴x1=1+，x2=1﹣．四、17．解：（1）点D以与四边形ABCD另两条边如图所示．（2）得到的四边形A′B′C′D′如图所示．18．2n+1；2n2+2n+1．五、19．解：过点D作l1的垂线，垂足为F，∵∠DEB=60°，∠DAB=30°，∴∠ADE=∠DEB﹣∠DAB=30°，∴△ADE为等腰三角形，∴DE=AE=20，在Rt△DEF中，EF=DE•cos60°=20×=10，∵DF⊥AF，∴∠DFB=90°，∴AC∥DF，由已知l1∥l2，∴CD∥AF，∴四边形ACDF为矩形，CD=AF=AE+EF=30，答：C、D两点间的距离为30m．20．解：（1）把点A（4，3）代入函数y=得：a=3×4=12，∴y=．OA==5，∵OA=OB，∴OB=5，∴点B的坐标为（0，﹣5），把B（0，﹣5），A（4，3）代入y=kx+b得：解得：∴y=2x﹣5．（2）∵点M在一次函数y=2x﹣5上，∴设点M的坐标为（x，2x﹣5），∵MB=MC，∴解得：x=2.5，∴点M的坐标为（2.5，0）．六、21．解：（1）画树状图：共有16种等可能的结果数，它们是：11，41，71，81，14，44，74，84，17，47，77，87，18，48，78，88；（2）算术平方根大于4且小于7的结果数为6，所以算术平方根大于4且小于7的概率==．七、22．解：（1）将A（2，4）与B（6，0）代入y=ax2+bx，得，解得：；（2）如图，过A作x轴的垂直，垂足为D（2，0），连接CD，过C作CE⊥AD，CF⊥x 轴，垂足分别为E，F，S△OAD=OD•AD=×2×4=4；S△ACD=AD•CE=×4×（x﹣2）=2x﹣4；S△BCD=BD•CF=×4×（﹣x2+3x）=﹣x2+6x，则S=S△OAD+S△ACD+S△BCD=4+2x﹣4﹣x2+6x=﹣x2+8x，∴S关于x的函数表达式为S=﹣x2+8x（2＜x＜6），∵S=﹣x2+8x=﹣（x﹣4）2+16，∴当x=4时，四边形OACB的面积S有最大值，最大值为16．八、23．（1）证明：∵点C、D、E分别是OA，OB，AB的中点，∴DE=OC，∥OC，CE=OD，CE∥OD，∴四边形ODEC是平行四边形，∴∠OCE=∠ODE，∵△OAP，△OBQ是等腰直角三角形，∴∠PCO=∠QDO=90°，∴∠PCE=∠PCO+∠OCE=∠QDO=∠ODQ=∠EDQ，∵PC=AO=OC=ED，CE=OD=OB=DQ，在△PCE与△EDQ中，，∴△PCE≌△EDQ；（2）①如图2，连接RO，∵PR与QR分别是OA，OB的垂直平分线，∴AP=OR=RB，∴∠ARC=∠ORC，∠ORQ=∠BRO，∵∠RCO=∠RDO=90°，∠COD=150°，∴∠CRD=30°，∴∠ARB=60°，∴△ARB是等边三角形；②由（1）得，EQ=EP，∠DEQ=∠CPE，∴∠PEQ=∠CED﹣∠CEP﹣∠DEQ=∠ACE﹣∠CEP﹣∠CPE=∠ACE﹣∠RCE=∠ACR=90°，∴△PEQ是等腰直角三角形，∵△ARB∽△PEQ，∴∠ARB=∠PEQ=90°，∴∠OCR=∠ODR=90°，∠CRD=∠ARB=45°，∴∠MON=135°，此时P，O，B在一条直线上，△PAB为直角三角形，且∠APB=90°，∴AB=2PE=2×PQ=PQ，∴=．2017年XX 省初中学业水平考试数学（试题卷）注意事项：1.你拿到的试卷满分为150分，考试时间为120分钟。

2016年安徽省初中毕业学业考试数学试题及答案解析

2016年安徽省初中毕业学业考试数学试题(试题卷)注意事项：1. 你拿到的试卷满分为150分，考试时间为120分钟．2. 本试卷包括“试题卷”和“答题卷”两部分，“试题卷”共4页，“答题卷”共6页．3. 请务必在“答题卷”上答题，在“试题卷”上答题是无效的．4. 考试结束后，请将“试题卷”和“答题卷”一并交回．一、选择题(本大题共10小题，每小题4分，满分40分)每小题都给出A 、B 、C 、D 四个选项，其中只有一个是正确的．1. －2的绝对值是( )A. －2B. 2C. ±2D. 122. 计算a 10÷a 2(a ≠0)的结果是( )A. a 5B. a －5C. a 8D. a －83. 2016年3月份我省农产品实现出口额8362万美元．其中8362万用科学记数法表示为( )A. 8.362×107B. 83.62×106C. 0.8362×108D. 8.362×1084. 如图，一个放置在水平桌面上的圆柱，它的主(正)视图是( )5. 方程2x ＋1x －1＝3的解是( ) A. －45 B. 45C. －4D. 4 6. 2014年我国省财政收入比2013年增长8.9%，2015年比2014年增长9.5%.若2013和2015年我省财政收入分别为a 亿元和b 亿元，则a 、b 之间满足的关系式是( )A. b ＝a(1＋8.9%＋9.5%)B. b ＝a(1＋8.9%×9.5%)C. b ＝a(1＋8.9%)(1＋9.5%)D. b ＝a(1＋8.9%)2(1＋9.5%)7. 自来水公司调查了若干用户的月用水量x(单位：吨)，按月用水量将用户分成A 、B 、C 、D 、E 五组进行统计，并制作了如图所示的扇形统计图．已知除B 组以外，参与调查的用户共64户，则所有参与调查的用户中月用水量在6吨以下的共有( )组别月用水量x(单位：吨) A0≤x<3 B3≤x<6 C6≤x<9 D9≤x<12 E x ≥12第7题图A. 18户B. 20户C. 22户D. 24户8. 如图，△ABC 中，AD 是中线，BC ＝8，∠B ＝∠DAC ，则线段AC 的长为( )第8题图A. 4B. 4 2C. 6D. 4 39. 一段笔直的公路AC 长20千米，途中有一处休息点B ，AB 长15千米．甲、乙两名长跑爱好者同时从点A 出发．甲以15千米/时的速度匀速跑至点B ，原地休息半小时后，再以10千米/时的速度匀速跑至终点C ；乙以12千米/时的速度匀速跑至终点C.下列选项中，能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是( )10. 如图，Rt △ABC 中，AB ⊥BC ，AB ＝6，BC ＝4，P 是△ABC 内部的一个动点，且满足∠PAB ＝∠PBC.则线段CP 长的最小值为( )A. 32B. 2C. 81313D. 121313第10题图第13题图第14题图二、填空题(本大题共4小题，每小题5分，满分20分)11. 不等式x －2≥1的解集是________．12. 因式分解：a 3－a ＝________________．13. 如图，已知⊙O 的半径为2，A 为⊙O 外一点．过点A 作⊙O 的一条切线AB ，切点是B ，AO 的延长线交⊙O 于点C.若∠BAC ＝30°，则劣弧BC ︵的长为______．14. 如图，在矩形纸片ABCD 中，AB ＝6，BC ＝10.点E 在CD 上，将△BCE 沿BE 折叠，点C 恰落在边AD 上的点F 处；点G 在AF 上，将△ABG 沿BG 折叠，点A 恰落在线段BF 上的点H 处．有下列结论：①∠EBG ＝45°；②△DEF ∽△ABG ；③S △ABG ＝32S △FGH ；④AG ＋DF ＝FG. 其中正确的是______________．(把所有正确结论的序号都选上)三、(本大题共2小题，每小题8分，共16分)15. 计算：(－2016)0＋3－8＋tan45°.16. 解方程：x 2－2x ＝4.四、(本大题共2小题，每小题8分，满分16分)17. 如图，在边长为1个单位长度的小正方形组成的12×12网格中，给出了四边形ABCD 的两条边AB 与BC ，且四边形ABCD 是一个轴对称图形，其对称轴为直线AC.(1)试在图中标出点D ，并画出该四边形的另两条边；(2)将四边形ABCD 向下平移5个单位，画出平移后得到的四边形A ′B ′C ′D ′.第17题图18. (1)观察下列图形与等式的关系，并填空：(2)观察下图，根据(1)中结论，计算图中黑球的个数，用含有n的代数式填空：1＋3＋5＋…＋(2n－1)＋(________________)＋(2n－1)＋…＋5＋3＋1＝____________．五、(本大题共2小题，每小题10分，满分20分)19. 如图，河的两岸l1与l2相互平行，A、B是l1上的两点，C、D是l2上的两点．某人在点A 处测得∠CAB ＝90°，∠DAB ＝30°，再沿AB 方向前进20米到达点E(点E 在线段AB 上)，测得∠DEB ＝60°，求C 、D 两点间的距离．第19题图20. 如图，一次函数y ＝kx ＋b 的图象分别与反比例函数y ＝a x的图象在第一象限交于点A(4，3)，与y 轴的负半轴交于点B ，且OA ＝OB.(1)求函数y ＝kx ＋b 和y ＝a x的表达式； (2)已知点C(0，5)，试在该一次函数图象上确定一点M ，使得MB ＝MC.求此时点M 的坐标．第20题图六、(本题满分12分)21. 一袋中装有形状大小都相同的四个小球，每个小球上各标有一个数字，分别是1，4，7，8.现规定从袋中任取一个小球，对应的数字作为一个两位数的个位数；然后将小球放回袋中并搅拌均匀，再任取一个小球，对应的数字作为这个两位数的十位数．(1)写出按上述规定得到所有可能的两位数；(2)从这些两位数中任取一个，求其算术平方根大于4且小于7的概率．七、(本题满分12分)22. 如图，二次函数y＝ax2＋bx的图象经过点A(2，4)与B(6，0)．(1)求a，b的值；(2)点C是该二次函数图象上A，B两点之间的一动点，横坐标为x(2<x<6)．写出四边形OACB的面积S关于点C的横坐标x的函数表达式，并求S的最大值．第22题图八、(本题满分14分)23. 如图1，A，B分别在射线OM，ON上，且∠MON为钝角．现以线段OA，OB为斜边向∠MON的外侧作等腰直角三角形，分别是△OAP，△OBQ，点C，D，E分别是OA，OB，AB的中点．(1)求证：△PCE≌△EDQ；(2)延长PC，QD交于点R.①如图2，若∠MON＝150°，求证：△ABR为等边三角形；AB的值．②如图3，若△ARB∽△PEQ，求∠MON大小和PQ2016年安徽省初中毕业学业考试数学试题参考答案1. B 【解析】依据负数的绝对值是它的相反数求解．∵－2是负数，∴－2的相反数是2，∴－2的绝对值是2.2. C 【解析】根据同底数幂的除法运算法则：“底数不变，指数相减”计算即可．a 10÷a 2＝a 10－2＝a 8.3. A 【解析】∵1万＝104，8362＝8.362×103，∴8362万＝8.362×103×104＝8.362×107.4. C 【解析】该圆柱从正面看是一个宽与圆柱的底面直径相等，长与圆柱高相等的矩形．(注：该圆柱的主视图不包括水平桌面部分的主视图)5. D 【解析】将方程2x ＋1x －1＝3去分母，得2x ＋1＝3(x －1)，去括号，得2x ＋1＝3x －3，移项、合并同类项，得－x ＝－4.解得x ＝4.经检验x ＝4是原分式方程的根．6. C 【解析】∵2013年我省财政收入为a 亿元，2014年我省财政收入比2013年增长8.9%，∴2014年我省财政收入为a(1＋8.9%)亿元，又∵2015年我省财政收入为b 亿元，2015年比2014年增长9.5%，∴b ＝a(1＋8.9%)(1＋9.5%)．7. D 【解析】∵由扇形统计图可知，除B 组以外，其余四组在所有参与调查的用户中所占的比例为10%＋5%＋30%＋35%＝80%，且参与调查的用户共有64户，∴所有参与调查的总用户数为64÷80%＝80(户)．∵A 、B 两组用户所占的比例为10%＋(1－80%)＝30%，∴所有参与调查的用户中月用水量在6吨以下的共有80×30%＝24(户)．8. B 【解析】∵∠B ＝∠DAC ，∠C ＝∠C ，∴△ABC ∽△DAC.∴BC AC ＝AC DC ，即AC 2＝BC ·DC.∵AD 是中线，BC ＝8，∴DC ＝12BC ＝4.∴AC 2＝8×4，∴AC ＝4 2. 9. A 【解析】由题意可知：甲所跑路程分为3个时段：开始1小时，以15千米/时的速度匀速由点A 跑至点B ，所跑路程为15千米；第1小时至第32小时休息，所跑路程不变；第32小时至第2小时，以10千米/时的速度匀速跑至终点C ，所跑路程为5千米，即甲累计所跑路程为20千米时，所用时间为2小时，并且甲开始1小时内的速度大于第32小时至第2小时之间的速度．因此选项A 、C 符合甲的情况．乙从点A 出发，以12千米/时的速度匀速一直跑至终点C ，所跑路程为20千米，所用时间为53小时，并且乙的速度小于甲开始的速度但大于甲第3时段的速度．所以选项A 、B 符合乙的情况．故选A.10. B 【解析】如解图，∵∠PAB ＝∠PBC ，∠ABC ＝90°，∴∠BAP ＋∠PBA ＝90°，∴∠APB ＝90°，∴点P 始终在以AB 的中点O 为圆心，以OA ＝OB ＝OP ＝12AB ＝3为半径的圆上，由解图知，只有当在点P 在OC 与⊙O 的交点处时， PC 的长最小．在Rt △OBC 中，OC ＝OB 2＋BC 2＝32＋42＝5，∴P ′C ＝OC －OP ′＝5－3＝2，∴线段CP 长的最小值为2.第10题解图11. x ≥3 【解析】移项，得x ≥1＋2，合并同类项，得x ≥3.12 .a(a ＋1)(a －1)【解析】a 3－a 提取公因式a 得，a(a 2－1)，利用平方差公式分解因式得，原式＝a(a ＋1)(a －1)．13. 43π【解析】如解图，连接OB.∵AB 为⊙O 的切线，B 为切点，∴∠B ＝90°，又∵∠A ＝30°，∴∠AOB ＝60°，∴∠BOC ＝120°，∴劣弧BC ︵的长＝120×π×2180＝43π.第13题解图14. ①③④【解析】由折叠的性质得，∠CBE ＝∠FBE ，∠ABG ＝∠FBG ，∴∠EBG ＝∠FBE ＋∠FBG ＝12×90°＝45°，故①正确；由折叠的性质得，BF ＝BC ＝10，BA ＝BH ＝6，∴HF ＝BF －BH ＝4，AF ＝BF 2－BA 2∴AF ＝8，设GH ＝x ，则GF ＝8－x ，在Rt △GHF 中，x 2＋42＝(8－x)2，∴x ＝3，∴GF ＝5，∴AG ＝3，同理在Rt △FDE 中，由FD 2＝EF 2－ED 2得ED ＝83，EF ＝103，∴ED FD ＝43≠ABAG＝2，∴△DEF 与△ABG 不相似，故②不正确；S △ABG ＝12×3×6＝9，S △FGH ＝12×3×4＝6，S △ABG S △FGH＝96＝32，故③正确；∵AG ＝3，DF ＝AD －AF ＝2，FG ＝5，∴AG ＋DF ＝FG ＝5，故④正确．15. 解：原式＝1＋(－2)＋1 ＝0.16. 解：两边都加上1，得x 2－2x ＋1＝4＋1，即(x －1)2＝5，开平方，得x－1＝±5，∴原方程的解是x1＝1＋5，x2＝1－ 5.17. 解：(1)所求点D及四边形ABCD的另两条边AD、CD如解图所示；(2)所求四边形A′B′C′D′如解图所示．第17题解图18. 解：(1)42；n2；【解法提示】观察每一行图形变换，可以发现，当小球有4行时，小球的总个数＝4×4＝42(个)，∴第一个空填42；根据此规律可知，当小球有n行时，小球的总数＝n·n＝n2，∴第二个空填n2.(2)2n＋1；2n2＋2n＋1.【解法提示】在连续的奇数中，2n－1后边的数是2n＋1，∴第一个空填“2n＋1”；由第(1)小题的结论可知，在等式的左边的数中，“2n－1”前面的所有数之和等于n2，后面的所有的数之和也等于n2，∴总和＝n2＋(2n＋1)＋n2＝2n2＋2n＋1，∴等式的右边填“2n2＋2n＋1”．19. 解：∵∠DEB＝60°，∠DAB＝30°，∴∠ADE＝60°－30°＝30°，∴∠DAB＝∠ADE，∴DE＝AE＝20，如解图，过点D 作DF ⊥AB 于点F ，则∠EDF ＝30°， ∴在Rt △DEF 中，EF ＝12DE ＝10，∴AF ＝20＋10＝30， ∵DF ⊥AB ，∠CAB ＝90°， ∴CA ∥DF ，又∵l 1∥l 2，∴四边形CAFD 是矩形， ∴CD ＝AF ＝30，答：C 、D 两点间的距离为30米．第19题解图20. 【思路分析】(1)由点A 的坐标和OA ＝OB 可得点B 的坐标，用待定系数法即可求出一次函数的解析式；将点A 的坐标代入反比例函数解析式中即可求出反比例函数的解析式；(2)由题意可知，使MB ＝MC 的点在线段BC 的垂直平分线上，故求出线段BC 的垂直平分线和一次函数的交点即可．解：(1)∵点A(4，3)， ∴OA ＝42＋32＝5， ∴OB ＝OA ＝5， ∴B(0，－5)，将点A(4, 3)、点B(0, －5)代入函数y ＝kx ＋b 得，⎩⎪⎨⎪⎧4k ＋b ＝3b ＝－5，解得⎩⎪⎨⎪⎧k ＝2b ＝－5，将点A(4, 3)代入y ＝ax 得，3＝a 4， ∴a ＝12，∴所求函数表达式分别为y ＝2x －5和y ＝12x；(2) 如解图，∵点B 的坐标为(0, －5)，点C 的坐标为(0, 5)， ∴x 轴是线段BC 的垂直平分线， ∵MB ＝MC ， ∴点M 在x 轴上，又∵点M 在一次函数图象上，∴点M 为一次函数的图象与x 轴的交点，如解图所示，令2x －5＝0，解得x ＝52，∴此时点M 的坐标为(52， 0)．第20题解图21.解：(1)所有可能的两位数用列表法列举如下表：个位数十位数 1 4 7 8 111141718(2)由(1)知，所有可能的两位数共有16个，即16种等可能结果，其中算术平方根大于4且小于7即大于16且小于49的两位数共6种等可能结果：17，18，41，44，47，48，则所求概率P ＝616＝38.22.解：(1)∵二次函数y ＝ax 2＋bx 的图象经过点A(2，4)与B(6，0)． ∴⎩⎪⎨⎪⎧4＝4a ＋2b0＝36a ＋6b ，解得，⎩⎪⎨⎪⎧a ＝－12b ＝3； (2)如解图①，过点A 作x 轴的垂线，垂足为点D(2，0)，连接CD ，过点C 作CE ⊥AD ，CF ⊥x 轴，垂足分别为点E ，点F ，则S △OAD ＝12OD ·AD ＝12×2×4＝4，S △ACD ＝12AD ·CE ＝12×4×(x －2)＝2x －4，S △BCD ＝12BD ·CF ＝12×4×(－12x 2＋3x)＝－x 2＋6x ，则S ＝S △OAD ＋S △ACD ＋S △BCD ＝4＋(2x －4)＋(－x 2＋6x)＝－x 2＋8x. ∴S 关于x 的函数表达式为S ＝－x 2＋8x(2<x<6)． ∵S ＝－(x －4)2＋16，∴当x ＝4时，四边形OACB 的面积S 取最大值，最大值为16.第22题解图①【一题多解】解法一：由(1)知y ＝－12x 2＋3x ，如解图②，连接AB ，则S ＝S △AOB ＋S △ABC ，其中S △AOB ＝12×6×4＝12，设直线AB 解析式为y 1＝k 1x ＋b 1，将点A(2，4)，B(6，0)代入，易得，y 1＝－x ＋6，过C 作直线l ⊥x 轴交AB 于点D ， ∴C(x ，－12x 2＋3x)，D(x ，－x ＋6)，∴S △ABC ＝S △ADC ＋S △BDC ＝12·CD ·(x －2)＋12·CD ·(6－x)＝12·CD ·4＝2CD ，其中CD ＝－12x 2＋3x －(－x ＋6)＝－12x 2＋4x －6，∴S △ABC ＝2CD ＝－x 2＋8x －12，∴S ＝S △ABC ＋S △AOB ＝－x 2＋8x －12＋12＝－x 2＋8x ＝－(x －4)2＋16(2<x<6)，即S 关于x 的函数表达式为S ＝－x 2＋8x(2<x<6)，∴当x ＝4时，四边形OACB 的面积S 取最大值，最大值为16.第22题解图②解法二：∵点C 在抛物线上y ＝－12x 2＋3x 上，∴点C(x ，－12x 2＋3x)，如解图③，过点A 作AD ⊥x 轴，垂足为点D ，过点C 作CE ⊥x 轴，垂足为点E ，则点D 的坐标为(2，0)，点E 的坐标为(x ，0)，∴S ＝S △OAD ＋S 梯形ADEC ＋S △CEB ＝12×2×4＋12(4－12x 2＋3x)(x －2)＋12(6－x)(－12x 2＋3x)＝－x 2＋8x ，∵S ＝－x 2＋8x ＝－(x －4)2＋16(2<x<6)，∴当x ＝4时，四边形OACB 的面积S 取最大值，最大值为16.第22题解图③23.(1)证明：∵点C ，D ，E 分别是OA ，OB ，AB 的中点， ∴DE=OC ，DE ∥OC 且CE=OD ，CE ∥OD ， ∴四边形CEDO 是平行四边形，∴∠ECO ＝∠EDO ，又∵△OAP ，△OBQ 都是等腰直角三角形， ∴∠PCO ＝∠QDO ＝90°，∴∠PCE ＝∠PCO ＋∠ECO ＝∠QDO ＋∠EDO ＝∠EDQ ，又∵PC ＝12AO ＝OC ＝DE ，CE ＝12BO ＝OD ＝DQ ，∴△PCE ≌△EDQ ；(2)①证明：如解图①，连接OR ， ∵PR 与QR 分别为线段OA 与OB 的中垂线， ∴AR ＝OR ＝BR ，∠ARC ＝∠ORC ，∠ORD ＝∠BRD ，在四边形OCRD 中，∠OCR ＝∠ODR ＝90°，∠MON ＝150°， ∴∠CRD ＝30°，∴∠ARB ＝∠ARO ＋∠BRO ＝2∠CRO ＋2∠ORD ＝2∠CRD ＝60°.(9分) ∴∠ABR 为等边三角形；第23题解图①②解：如解图②，由(1)知EQ ＝PE ，∠DEQ ＝∠CPE ， ∴∠PEQ ＝∠CED －∠CEP －∠DEQ ＝∠ACE －∠CEP －∠CPE ＝∠ACE －∠RCE ＝∠ACR ＝90°，即△PEQ 为等腰直角三角形， ∵△ARB ∽△PEQ ， ∴∠ARB ＝90°，∴在四边形OCRD中，∠OCR＝∠ODR＝90°，∠CRD＝12∠ARB＝45°，∴∠MON＝360°－90°－90°－45°＝135°，又∵∠AOP＝45°，∴∠POD＝180°，即P、O、B三点共线，在△APB中，∠APB＝90°，E为AB中点，∴AB＝2PE，又∵在等腰直角△PEQ中，PQ＝2PE，∴ABPQ＝PEPE22＝ 2.第23题解图②。

年安徽省中考数学试卷及答案详解

2016年安徽省中考数学试卷一、选择题（本大题共１0小题，每小题４分，满分4０分)1.（4分）﹣2的绝对值是(）A．﹣2 B．2C．±２D．2.（4分）计算a10÷a２（a≠0)的结果是（)A．a5B.a﹣5C.a8D．a﹣８３.(４分）20１6年3月份我省农产品实现出口额8362万美元，其中8３62万用科学记数法表示为( ）A．8．３62×1０7B.８3.62×10６Ｃ．0．8362×10８D．8.3６2×108４.(4分）如图，一个放置在水平桌面上的圆柱,它的主(正）视图是（）A．Ｂ.C． D.5．（4分)方程＝3的解是(）Ａ．﹣Ｂ． C.﹣4 Ｄ．46．（4分）２０14年我省财政收入比20１３年增长8.９%，2015年比２014年增长9.5%，若20１3年和2015年我省财政收入分别为a亿元和ｂ亿元,则a、b之间满足的关系式为（)A.b＝a（1+８.9％+9.5%）Ｂ.b=ａ（1+8.９%×9．5％）C．b=a(1+8.9%)(1+９．5％）Ｄ.b=a（1+８.9％)2（1+９.5%)７.（4分)自来水公司调查了若干用户的月用水量ｘ(单位:吨），按月用水量将用户分成Ａ、B、C、D、E五组进行统计,并制作了如图所示的扇形统计图.已知除B组以外，参与调查的用户共64户，则所有参与调查的用户中月用水量在6吨以下的共有( )组别月用水量x（单位:吨）Ａ0≤x<3B 3≤x<6C ６≤x<９D 9≤x<１2 Ｅx≥1２A.18户B.２０户Ｃ．22户D．24户8.（4分)如图，△ＡBＣ中，AD是中线，BC＝8,∠B＝∠DAC,则线段ＡＣ的长为( )A.４B.4C.6D．49．（4分)一段笔直的公路ＡC长20千米，途中有一处休息点B,ＡＢ长１5千米，甲、乙两名长跑爱好者同时从点Ａ出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C；乙以１２千米/时的速度匀速跑至终点C，下列选项中,能正确反映甲、乙两人出发后２小时内运动路程y(千米)与时间ｘ(小时）函数关系的图象是( ）A.B．C． D.１0.（４分）如图,Rt△AＢC中,AB⊥BＣ,ＡB=6，ＢC＝4,P是△ABC内部的一个动点,且满足∠PAB=∠ＰBＣ，则线段ＣP长的最小值为(）A．B．2Ｃ. D.二、填空题(本大题共4小题，每小题5分，满分20分)１1.（５分）不等式x﹣２≥1的解集是.12．（5分)因式分解：ａ３﹣ａ=.13.(５分）如图,已知⊙O的半径为2，A为⊙O外一点,过点A作⊙Ｏ的一条切线AB，切点是Ｂ，AO的延长线交⊙Ｏ于点C，若∠BAＣ=3０°,则劣弧的长为．14.（5分)如图，在矩形纸片ABCD中,AB＝6,BＣ=10，点Ｅ在CD上，将△BCE沿BE折叠，点C恰落在边AD上的点F处；点G在AF上，将△ＡBＧ沿ＢＧ折叠，点Ａ恰落在线段ＢＦ上的点H处，有下列结论：①∠EＢG=４5°；②△DEF∽△ABG；③S△AＢＧ=S△FGH；④ＡG＋DF=FG．其中正确的是．（把所有正确结论的序号都选上）三、（本大题共2小题,每小题8分，满分16分）15．(8分）计算：(﹣2０1６)0++tan45°．16.（8分）解方程：ｘ２﹣2ｘ＝4.四、(本大题共2小题，每小题8分，满分1６分）17.（8分）如图，在边长为１个单位长度的小正方形组成的１2×12网格中,给出了四边形ABCD 的两条边AＢ与BC，且四边形ABCＤ是一个轴对称图形,其对称轴为直线AC.（1)试在图中标出点D，并画出该四边形的另两条边;（２)将四边形ABCD向下平移5个单位，画出平移后得到的四边形A′B′Ｃ′D′.18.（8分）(1)观察下列图形与等式的关系,并填空(2)观察下图,根据（1）中结论，计算图中黑球的个数,用含有ｎ的代数式填空:１+3+5＋…+（2n﹣１)＋( )＋(2n﹣1）+…+５+3+1= .五、(本大题共2小题，每小题10分，满分２0分)19．(10分）如图,河的两岸l1与ｌ2相互平行，A、B是ｌ1上的两点，C、D是l２上的两点，某人在点A处测得∠ＣAB＝90°，∠ＤＡB=3０°，再沿AB方向前进２0米到达点E(点E在线段ＡB 上）,测得∠ＤＥB＝60°,求C、D两点间的距离.２0.(1０分)如图,一次函数y=kｘ+ｂ的图象分别与反比例函数y=的图象在第一象限交于点A(4，3），与y轴的负半轴交于点B，且OＡ=OＢ.（１）求函数ｙ=kx+ｂ和y=的表达式；(２）已知点C(０,５），试在该一次函数图象上确定一点M,使得MB=MC，求此时点M的坐标.六、（本大题满分１2分)21.（１2分)一袋中装有形状大小都相同的四个小球，每个小球上各标有一个数字,分别是１，4,７,8．现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数；然后将小球放回袋中并搅拌均匀，再任取一个小球,对应的数字作为这个两位数的十位数.（１)写出按上述规定得到所有可能的两位数；（２）从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.七、(本大题满分１2分)２2.(１2分)如图，二次函数y=ａx2＋bx的图象经过点A(2，4)与B(6,0).(1）求ａ，ｂ的值；(2）点C是该二次函数图象上Ａ,B两点之间的一动点,横坐标为x（2＜ｘ＜6),写出四边形OACB 的面积Ｓ关于点C的横坐标x的函数表达式，并求S的最大值.八、(本大题满分14分）23.（14分)如图1，A,Ｂ分别在射线OM，ON上,且∠MON为钝角,现以线段OA，OＢ为斜边向∠MO Ｎ的外侧作等腰直角三角形，分别是△OＡP，△ＯBQ,点C,Ｄ，Ｅ分别是OA,ＯB，AB的中点．（1）求证：△ＰCE≌△EDQ;(2）延长PC，QＤ交于点R.①如图2,若∠MON=150°，求证：△ＡＢR为等边三角形;②如图3,若△ARB∽△PＥQ，求∠MＯN大小和的值．2016年安徽省中考数学试卷参考答案与试题解析一、选择题（本大题共1０小题,每小题4分,满分4０分)1.(4分)（201６•安徽)﹣2的绝对值是（）A．﹣2 Ｂ.2 C.±2 D.【分析】直接利用数轴上某个数与原点的距离叫做这个数的绝对值,进而得出答案.【解答】解:﹣2的绝对值是：2.故选:Ｂ.2.（4分）（2016•安徽）计算a1０÷a2（ａ≠０)的结果是()A．a5B．ａ﹣５Ｃ.a8D．a﹣8【分析】直接利用同底数幂的除法运算法则化简求出答案.【解答】解：ａ1０÷ａ2（a≠0)=a８．故选：C.3．(4分）（２016•安徽）201６年3月份我省农产品实现出口额８36２万美元,其中8３62万用科学记数法表示为(）A.8.3６2×107B．83.6２×106C.0.8３62×10８D．8．３62×10８【分析】科学记数法的表示形式为a×１0n的形式,其中1≤｜a|<１０，n为整数.确定ｎ的值时，要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,ｎ是负数.【解答】解:８362万=８362 ０00０=8.36２×１０7，故选：A．4．(4分）（2016•安徽)如图，一个放置在水平桌面上的圆柱,它的主（正）视图是( )A． B. C.D．【分析】根据三视图的定义求解．【解答】解:圆柱的主(正)视图为矩形.故选Ｃ.5．(４分）（2０１6•安徽)方程=3的解是( ）Ａ．﹣ B.C．﹣4 D．4【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值，经检验即可得到分式方程的解．【解答】解:去分母得:2ｘ+1=3ｘ﹣３，解得：x=4，经检验x=4是分式方程的解，故选D．６.(４分）（20１６•安徽)2０14年我省财政收入比2013年增长８．9%,２０15年比２014年增长9.5%，若20１３年和20１5年我省财政收入分别为a亿元和b亿元，则a、b之间满足的关系式为()A.ｂ=a（1+８．9%＋9.5％)B.b＝a（１+８．9%×9.5%)C．b=a(1＋８.9%)（1＋9.５％）Ｄ．b=ａ(1+８.9％)２(1+9．5%)【分析】根据201３年我省财政收入和2014年我省财政收入比2０1３年增长8.9%，求出2014年我省财政收入,再根据出2０1５年比20１4年增长9.５%，２01５年我省财政收为ｂ亿元，即可得出ａ、b之间的关系式.【解答】解:∵２0１3年我省财政收入为a亿元,2０1４年我省财政收入比２0１３年增长８．9%，∴２014年我省财政收入为a(1+8.９%)亿元,∵２０１5年比20１4年增长9.5%,２0１５年我省财政收为b亿元,∴2015年我省财政收为b=ａ（1+8.９%）(1＋9.5%）；故选Ｃ．7.(4分）（2016•安徽）自来水公司调查了若干用户的月用水量ｘ(单位：吨）,按月用水量将用户分成A、Ｂ、C、D、Ｅ五组进行统计,并制作了如图所示的扇形统计图．已知除B组以外,参与调查的用户共64户,则所有参与调查的用户中月用水量在6吨以下的共有（)组别月用水量x（单位:吨）Ａ0≤x<３B 3≤x<6Ｃ6≤ｘ<9D 9≤x<12E x≥12A.18户B.20户C．2２户D．24户【分析】根据除B组以外参与调查的用户共6４户及A、C、D、Ｅ四组的百分率可得参与调查的总户数及B组的百分率,将总户数乘以月用水量在6吨以下(A、B两组）的百分率可得答案.【解答】解：根据题意，参与调查的户数为:＝80（户），其中B组用户数占被调查户数的百分比为:１﹣10％﹣３5％﹣３0%﹣5%=2０%,则所有参与调查的用户中月用水量在６吨以下的共有：８0×(10%+20%）＝24(户），故选:D．8．(4分）(2016•安徽)如图,△ABC中,AD是中线，BC=8，∠B=∠DAC,则线段AC的长为（）Ａ．４Ｂ．4Ｃ．6 Ｄ．4【分析】根据AD是中线，得出CD=4,再根据AA证出△CBA∽△ＣAD,得出=,求出AC即可.【解答】解:∵BC=8，∴CD=4，在△ＣBA和△CAD中，∵∠Ｂ＝∠DＡＣ,∠C=∠C,∴△CBA∽△ＣAD,∴＝，∴AC2=CD•BC＝4×8＝３2,∴AＣ＝4；故选B．9．(4分)（2０16•安徽)一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点Ｃ;乙以１2千米/时的速度匀速跑至终点C，下列选项中，能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时）函数关系的图象是()A.Ｂ. C.Ｄ．【分析】分别求出甲乙两人到达Ｃ地的时间，再结合已知条件即可解决问题．【解答】解;由题意,甲走了1小时到了Ｂ地，在B地休息了半个小时，２小时正好走到C地，乙走了小时到了C地，在C地休息了小时.由此可知正确的图象是A．故选A．1０.(4分)（2016•安徽）如图,Rｔ△ABC中,ＡB⊥BC，AB=６,BC=4，Ｐ是△ABC内部的一个动点,且满足∠ＰAＢ=∠PＢC，则线段ＣP长的最小值为( ）Ａ． B.2C． D.【分析】首先证明点P在以AＢ为直径的⊙O上，连接OC与⊙Ｏ交于点P,此时PC最小，利用勾股定理求出ＯC即可解决问题.【解答】解:∵∠ABC＝90°，∴∠AＢP+∠ＰBＣ=90°，∵∠PAB=∠ＰＢC，∴∠BAＰ+∠ABP=９0°，∴∠APＢ＝90°,∴点P在以AB为直径的⊙O上，连接OC交⊙O于点P，此时PC最小，在RT△BＣO中,∵∠OBC＝９0°,BC＝4,OB=3，∴OC=＝5，∴PC=ＯC=OＰ＝5﹣3=２.∴PC最小值为2．故选B．二、填空题(本大题共４小题，每小题5分,满分20分)1１．（５分)(２0１６•安徽）不等式x﹣2≥1的解集是x≥3 ．【分析】不等式移项合并,即可确定出解集.【解答】解:不等式x﹣２≥1,解得：x≥3，故答案为:ｘ≥3１2.（5分)(2016•安徽)因式分解：a3﹣a＝a(a+１）(a﹣1) ．【分析】原式提取a，再利用平方差公式分解即可.【解答】解:原式＝a（a2﹣1)=ａ（ａ+１）（ａ﹣1)，故答案为:a（ａ+1）(a﹣１）1３.(5分)(2016•安徽)如图，已知⊙O的半径为2,Ａ为⊙Ｏ外一点，过点A作⊙O的一条切线ＡB,切点是B,ＡＯ的延长线交⊙O于点C,若∠BAC=30°，则劣弧的长为.【分析】根据已知条件求出圆心角∠BOC的大小,然后利用弧长公式即可解决问题．【解答】解：∵AB是⊙O切线，∴ＡB⊥OＢ，∴∠ＡBＯ=90°，∵∠A=30°，∴∠AＯB＝９０°﹣∠Ａ=6０°,∴∠BOC=１20°,∴的长为=.故答案为．14.(５分)（2０16•安徽)如图,在矩形纸片ABCD中，ＡB=6,BC=１０,点E在CD上，将△ＢCE沿BＥ折叠,点Ｃ恰落在边AD上的点F处;点G在AＦ上,将△ＡＢG沿BG折叠，点A恰落在线段BF上的点Ｈ处,有下列结论:①∠EBG=４5°;②△DＥF∽△AＢＧ;③S△ＡB G=S△FGＨ;④AＧ+DF=FＧ．其中正确的是①③④．(把所有正确结论的序号都选上)【分析】由折叠性质得∠1=∠2，CE=FE,ＢF=BC=10,则在Ｒt△ＡＢF中利用勾股定理可计算出A Ｆ=８,所以DF=AＤ﹣AF=2，设EF=x,则CE=x，DE=CD﹣CＥ=6﹣x，在Ｒt△DＥF中利用勾股定理得（６﹣ｘ)2＋２２=x２,解得ｘ=,即ＥD=;再利用折叠性质得∠３=∠4，BH=BA＝6，ＡG=HG,易得∠2＋∠3＝４5°，于是可对①进行判断;设AG＝y,则GＨ=y，GＦ=８﹣y，在Ｒt△HGF中利用勾股定理得到y2+4２＝（8﹣y)2，解得y=3，则AG=GH=3，GF=5,由于∠A＝∠D和≠,可判断△ABG与△DＥＦ不相似，则可对②进行判断；根据三角形面积公式可对③进行判断；利用AG=３,GＦ=5，DＦ=2可对④进行判断．【解答】解：∵△BCE沿BE折叠，点C恰落在边AD上的点Ｆ处,∴∠１＝∠2，ＣＥ＝FE，BF=BＣ=10,在Rt△ABF中，∵ＡB＝6,BF＝1０,∴ＡF＝=8，∴ＤＦ=AD﹣AF=１０﹣8＝2，设ＥF=x,则CＥ=ｘ,DＥ=CD﹣CE=6﹣x,在Rt△DＥF中,∵ＤＥ2+DF２＝EF２,∴（6﹣x）2+２２=x2,解得x=，∴ＥD=,∵△ABG沿BG折叠,点A恰落在线段BF上的点Ｈ处,∴∠3=∠4，BH=BA=6，AＧ＝HG,∴∠2＋∠3=∠AＢＣ=４５°，所以①正确;ＨF=BF﹣BH=10﹣6=4,设ＡG＝y,则ＧH=y，GF=8﹣y,在Rｔ△HGF中,∵ＧH2+ＨF２=GF2,∴y2+4２=（8﹣y)２,解得y=3，∴AG＝GH=3,GＦ=５，∵∠Ａ＝∠D,==，=,∴≠，∴△ABG与△DEF不相似,所以②错误;∵Ｓ△AＢG=•６•3=9,S△ＦGＨ＝•GH•HF=×３×4=６,∴S△AＢG＝Ｓ△ＦＧＨ,所以③正确;∵AG+DＦ=３+2=5，而ＧF=5,∴AG+ＤF=GF,所以④正确．故答案为①③④.三、（本大题共2小题,每小题8分,满分16分)15．（８分)（２016•安徽）计算：（﹣20１6）0＋+tan45°．【分析】直接利用特殊角的三角函数值以及立方根的性质分别化简求出答案.【解答】解：(﹣２016）0++ｔａn４5°=１﹣２+１＝0.16．（８分)（2０16•安徽)解方程:x2﹣２ｘ＝４．【分析】在方程的左右两边同时加上一次项系数一半的平方，左边就是完全平方式,右边就是常数,然后利用平方根的定义即可求解【解答】解:配方x２﹣2x+1=4+1∴（ｘ﹣1)２=5∴ｘ=1±∴x1=1+,x2=1﹣.四、(本大题共2小题,每小题８分，满分16分）17.（8分）（20１6•安徽)如图,在边长为1个单位长度的小正方形组成的１2×1２网格中，给出了四边形ＡＢCD的两条边AB与BC,且四边形ABCD是一个轴对称图形，其对称轴为直线AＣ. (1)试在图中标出点D，并画出该四边形的另两条边；（2）将四边形ABCD向下平移5个单位,画出平移后得到的四边形A′Ｂ′C′D′．【分析】（1)画出点B关于直线AC的对称点D即可解决问题.(2)将四边形ABＣD各个点向下平移5个单位即可得到四边形A′B′C′D′.【解答】解:（1）点D以及四边形ＡＢCD另两条边如图所示．(2)得到的四边形A′B′C′D′如图所示．1８.(8分）（２01６•安徽)（1)观察下列图形与等式的关系，并填空(2）观察下图,根据（1)中结论,计算图中黑球的个数，用含有ｎ的代数式填空:１+３+5+…+（2ｎ﹣１）+（2n+1 )+(2n﹣１)＋…+5+3＋1= 2n2+２n+1 ．【分析】(1）根据1+３+5+7=１6可得出１６=42；设第n幅图中球的个数为ａｎ，列出部分a n的值，根据数据的变化找出变化规律“aｎ﹣1＝1＋3+５+…+(2n﹣１)＝ｎ2”,依此规律即可解决问题；(2)观察（１)可将(２）图中得黑球分三部分,1到n行，第n+１行,n+２行到2ｎ+1行，再结合(１）的规律即可得出结论.【解答】解：（1)１＋３+5+７=16=42，设第n幅图中球的个数为a n，观察,发现规律:ａ1＝1+３=22，a2=1+３+5=3２,a3=1＋3＋5+７=42,…,∴aｎ﹣１=1+3＋５+…+（2n﹣1)=n2．故答案为:42；ｎ2．(2）观察图形发现：图中黑球可分三部分，1到n行，第n+1行,n+2行到2n+1行，即1+3＋5＋…+（２n﹣１）+[2(n+1）﹣１]+(2n﹣１)+…＋5+3+1,=１+3＋5+…+（2n﹣1）＋(２ｎ+１)＋（2n﹣1）+…+５+3+1，＝ａn﹣1＋（2n+1)+a n﹣1,=n２＋2n+1＋ｎ2,＝2n2+2n+1.故答案为:2ｎ+１；2n2+2n+1．五、（本大题共2小题,每小题10分,满分2０分)19．(１0分）（２016•安徽）如图，河的两岸l１与l2相互平行,A、Ｂ是ｌ１上的两点，C、Ｄ是l2上的两点，某人在点A处测得∠ＣAB=90°，∠DＡB=30°，再沿AB方向前进２０米到达点E（点E在线段AB上),测得∠DＥＢ=6０°，求C、D两点间的距离．【分析】直接利用等腰三角形的判定与性质得出DＥ=ＡE=2０，进而求出EＦ的长，再得出四边形ACDF为矩形，则CD=AF=AＥ+EF求出答案．【解答】解:过点D作l1的垂线，垂足为Ｆ,∵∠DEＢ＝6０°，∠DAB=30°，∴∠ＡＤE＝∠DEＢ﹣∠DAＢ=3０°，∴△ADＥ为等腰三角形，∴DE=ＡE=２0,在Rt△DEF中，EF＝DE•cos6０°＝20×=1０,∵DF⊥ＡF，∴∠ＤFB＝90°,∴ＡC∥DＦ,由已知l１∥ｌ２,∴CD∥AF，∴四边形ACDF为矩形，ＣＤ=AF=AＥ＋EF=30,答：C、Ｄ两点间的距离为30m.20.（1０分）(２01６•安徽）如图,一次函数y=kx+ｂ的图象分别与反比例函数y＝的图象在第一象限交于点A(4,3）,与y轴的负半轴交于点B，且OA=ＯＢ．（１）求函数y＝kx＋b和y=的表达式;(２)已知点C(0，5），试在该一次函数图象上确定一点M，使得MB=MC,求此时点Ｍ的坐标.【分析】(１)利用待定系数法即可解答；(2)设点Ｍ的坐标为(x，2x﹣5)，根据MB＝MC,得到,即可解答.【解答】解：（1)把点A（4，3）代入函数y=得：a=3×4=12，∴y=.OＡ==5,∵ＯA＝ＯB,∴ＯB=５,∴点Ｂ的坐标为（0,﹣5）,把B（0，﹣５),Ａ(4，3)代入y=kｘ＋b得:解得:∴ｙ=２ｘ﹣5.（2）∵点M在一次函数y＝2ｘ﹣5上，∴设点Ｍ的坐标为（x,2x﹣５)，∵MB＝MＣ，∴解得:ｘ=2．5,∴点M的坐标为(２.5,0).六、(本大题满分12分)21.(12分)（2016•安徽）一袋中装有形状大小都相同的四个小球，每个小球上各标有一个数字,分别是1，４,7，8．现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀，再任取一个小球,对应的数字作为这个两位数的十位数.（1）写出按上述规定得到所有可能的两位数；(2)从这些两位数中任取一个，求其算术平方根大于4且小于7的概率．【分析】（1）利用树状图展示所有16种等可能的结果数，然后把它们分别写出来;(２)利用算术平方根的定义找出大于16小于49的数，然后根据概率公式求解．【解答】解：(1)画树状图：共有16种等可能的结果数，它们是：11,4１,71,81，1４,44，74，８4，１７,47，77，87，18,48,78,88；（2）算术平方根大于4且小于7的结果数为6，所以算术平方根大于4且小于7的概率=＝．七、（本大题满分12分)22．（12分）（2０16•安徽）如图，二次函数y=ax2+bｘ的图象经过点A(2,4）与B（6,0)．(1）求ａ，b的值;（2)点C是该二次函数图象上A,B两点之间的一动点，横坐标为ｘ(2＜x<6）,写出四边形OACB 的面积S关于点Ｃ的横坐标x的函数表达式，并求Ｓ的最大值.【分析】(1)把A与B坐标代入二次函数解析式求出a与ｂ的值即可;(2）如图，过A作x轴的垂直，垂足为D（2,0),连接CD，过Ｃ作ＣE⊥AＤ,ＣF⊥x轴，垂足分别为E,F，分别表示出三角形OAD，三角形ACD,以及三角形BＣD的面积，之和即为S，确定出S 关于ｘ的函数解析式,并求出x的范围,利用二次函数性质即可确定出S的最大值,以及此时x的值．【解答】解：(1)将A(2，４）与B(6，0)代入y=ａx2+bｘ,得，解得:;(２）如图,过A作x轴的垂直，垂足为D(２,0）,连接CＤ，过C作CＥ⊥AＤ,CF⊥ｘ轴，垂足分别为E,F,S△OＡD=OD•AD=×２×４＝４；Ｓ△ＡＣD=AD•CＥ=×4×（ｘ﹣2)＝２x﹣4;S△ＢCＤ＝BD•ＣF=×４×(﹣x2+３ｘ）＝﹣x2+6x,则Ｓ=Ｓ△OAD＋S△ACＤ＋S△ＢCＤ＝4+2ｘ﹣4﹣x２+6ｘ＝﹣x2+8x,∴S关于x的函数表达式为S=﹣x2+8x(2＜x<6）,∵Ｓ=﹣x2+8ｘ=﹣（ｘ﹣4）2+１6,∴当x＝4时，四边形OＡCＢ的面积Ｓ有最大值，最大值为1６．八、（本大题满分14分)２３.(１４分）（201６•安徽)如图１，A，B分别在射线OＭ,ON上，且∠MON为钝角，现以线段OA，OＢ为斜边向∠MON的外侧作等腰直角三角形,分别是△OAＰ，△OBＱ,点Ｃ,D,E分别是OA,OＢ,AB的中点.（１)求证:△ＰCE≌△ＥＤＱ；（２）延长PC，ＱＤ交于点R．①如图2，若∠MON=１50°,求证：△AＢR为等边三角形;②如图3,若△ARＢ∽△ＰEQ,求∠MON大小和的值．【分析】（1）根据三角形中位线的性质得到DE＝OC，∥OＣ,CE=OD,CE∥ＯD,推出四边形ODEC 是平行四边形,于是得到∠OCE=∠ODE，根据等腰直角三角形的定义得到∠PCO=∠ＱDO＝９0°，根据等腰直角三角形的性质得到得到PC＝ED,CE＝DＱ,即可得到结论（2)①连接RＯ,由于ＰR与QR分别是ＯＡ,ＯB的垂直平分线，得到AＰ=OR=ＲＢ,由等腰三角形的性质得到∠ARC=∠ＯRＣ,∠OＲQ＝∠BRO,根据四边形的内角和得到∠CRD=30°，即可得到结论；②由（1)得,EQ=EP,∠DEＱ=∠CPE,推出∠PEQ=∠AＣR=9０°,证得△ＰEQ是等腰直角三角形，根据相似三角形的性质得到ARB=∠PEQ=９0°,根据四边形的内角和得到∠MＯN＝１３5°，求得∠APB=90°,根据等腰直角三角形的性质得到结论.【解答】(１）证明：∵点Ｃ、D、E分别是OＡ,OB,AB的中点，∴DE=OＣ,DE∥ＯC，CＥ=ＯD,CE∥ＯD,∴四边形ODEＣ是平行四边形，∴∠OCＥ=∠ODＥ，∵△ＯAP，△OBQ是等腰直角三角形，∴∠PCO=∠QDO=９0°，∴∠PCE=∠PCO＋∠OCＥ=∠ＱDO+∠EDO＝∠EＤQ，∵PC=ＡO＝ＯC＝ED，CE＝ＯD=ＯB=DQ，在△ＰCE与△EＤＱ中，，∴△ＰＣE≌△EDQ;(2)①如图2，连接RO,∵PR与QR分别是OA，OＢ的垂直平分线,∴AR=OR=RB，∴∠ARC＝∠ORC,∠ＯRQ＝∠ＢRO,∵∠ＲCO＝∠RＤO=９０°，∠ＣOＤ=150°，∴∠ＣＲD=30°，∴∠ＡRB＝6０°,∴△ARB是等边三角形；②由(1）得，ＥQ＝EP，∠DＥQ=∠CＰE,∴∠PEＱ=∠CＥD﹣∠CEP﹣∠DEQ=∠ＡＣＥ﹣∠ＣEP﹣∠CPE＝∠ＡCＥ﹣∠RCE=∠ACＲ=90°,∴△ＰEQ是等腰直角三角形,∵△ARB∽△PＥＱ,∴∠ARＢ=∠PEＱ=９0°，∴∠OCＲ=∠ＯＤＲ＝９0°,∠CＲＤ=∠ARB=45°,∴∠MON=135°，此时P,Ｏ,Ｂ在一条直线上,△ＰAB为直角三角形,且∠APB=９０°,∴ＡB=2PE=2×PＱ＝PQ,∴＝．。

安徽省中考数学真题试题(含答案)

21：2016年安徽省初中毕业学业考试数学注意事项：1. 你拿到的试卷满分为 150分，考试时间为120分钟。

2. 本试卷包括“试题卷”和“答题卷”两部分。

“试题卷”共4页，“答题卷”共6页。

3. 请务必在“答题卷”上答题，在“试题卷”上答题是无效的。

4. 考试结束后，请将“试题卷”和“答题卷”一并交回。

、选择题（本大题共 10小题，每小题4分，满分40分）每小题都给出 A B C 、D 四个选项，其中只有一个是正确的. 12的绝对值是7 6 8 8A . 8.362 10B . 83.62 10C . 0.8362 10D . 8.362 104.如图，一个放置在水平桌面上的圆柱，它的主（正）视图是7.自来水公司调查了若干用户的月用水量x （单位:吨），按月用水量将用户分成 A 、B C D E 五组进行统计，并制作了如图所示的扇形统计图.已知除B 组以夕卜，参与调查的用户共 64户，则A . — 2 B.2 C.2D1 • 22 .计算a 102a (a 0）的结果是A . a 5B5a iC8.aD.a3. 2016年3月份我省农产品实现出口额5.方程A .2x 1 x 14 5的解是6 . 2014年我省财政收入比 2013年增长8.9 %,2015我省财政收入分别为 a 亿元和 A. b =a （1+8.9 % +9.5 %） b 亿元和 B. 2014年增长了 9.5 % .若2013年和2015年比 b 亿元，则a 、b 之间满足的关系式是b =a (1+8.9 % 9.5 %) C. b =a (1+8.9 %) (1+9.5 %)D.b =a (1+8.9 %) 2(1+9.5 %)8362万美元.其中8362万用科学记数法表示为射洋僂:呦A 0 S z < 5BcD笫丁题图9•一段笔直的公路AC长为20千米，途中有一处休息点B, AB长为15千米•甲、乙两名长跑爱好者同时从点A出发•甲以15千米/时的速度匀速跑至点B,原地休息半小时后，再以10千米/时的速度匀速跑至终点C ；乙以12千米/时的速度匀速跑至终点C •下列选项中，能正确反映甲、乙两人出发后2小时内运动路程y （千米）与时间x （小时）函数关系的图像是、填空题（本大题共4小题，每小题5分，满分20分）11 •不等式x 2 1的解集是_____________12 .因式分解：a3 a _________________ •13.如图，已知O O的半径为2, A为。

2016年合肥市中考数学真题试题与答案

2016年合肥市中考数学试题与答案注意事项：1. 你拿到的试卷满分为150分，考试时间为120分钟。

2. 本试卷包括“试题卷”和“答题卷”两部分。

“试题卷”共4页，“答题卷”共6页。

3. 请务必在“答题卷．．．”上答题，在“试题卷”上答题是无效的。

4. 考试结束后，请将“试题卷”和“答题卷”一并交回。

一、选择题（本大题共10小题，每小题4分，满分40分）每小题都给出A 、B 、C 、D 四个选项，其中只有一个是正确的．1．－2的绝对值是A ．－2B ．2C ．2±D ．21 2．计算)0(210≠÷a a a的结果是 A ．5a B ．5-a C ．8a D ．8-a3． 2016年3月份我省农产品实现出口额8362万美元. 其中8362万用科学记数法表示为A ．710362.8⨯B ．61062.83⨯C ．8108362.0⨯D ．810362.8⨯4．如图，一个放置在水平桌面上的圆柱，它的主（正）视图是5．方程 3112=-+x x 的解是 A ．54- B ．54 C ．4- D ．4 6．2014年我省财政收入比2013年增长8.9％，2015年比2014年增长了9.5％.若2013年和2015我省财政收入分别为a 亿元和b 亿元和b 亿元，则a 、b 之间满足的关系式是A. b =a （1+8.9％+9.5％）B. b =a （1+8.9％⨯9.5％）C. b =a （1+8.9％）（1+9.5％）D. b =a （1+8.9％）2(1+9.5％）7．自来水公司调查了若干用户的月用水量x （单位：吨），按月用水量将用户分成A 、B 、C 、D 、E 五组进行统计，并制作了如图所示的扇形统计图.已知除B 组以外，参与调查的用户共64户，则所有参与调查的用户中用水量在6吨以下的共有A. 18户B. 20户C. 22户D. 24户8．如图，ABC ∆中，AD 是中线，DAC B BC ∠=∠=,8,则线段AC 的长为A ．4B ．24C ．6D ．34 9．一段笔直的公路AC 长为20千米，途中有一处休息点AB B ,长为15千米．甲、乙两名长跑爱好者同时从点A 出发．甲以15千米/时的速度匀速跑至点,B 原地休息半小时后，再以10千米/时的速度匀速跑至终点C ；乙以12千米/时的速度匀速跑至终点C ．下列选项中，能正确反映甲、乙两人出发后2小时内运动路程 y （千米）与时间 x （小时）函数关系的图像是10．如图，ABC Rt ∆中，P BC AB BC AB .4,6,==⊥是ABC ∆内部的一个动点，且满足.PBC PAB ∠=∠则线段CP 长的最小值为A ．23 B ．2 C ．13138 D ．131312二、填空题（本大题共4小题，每小题5分，满分20分）11．不等式12≥-x 的解集是． 12．因式分解：=-a a 3．13．如图，已知⊙O 的半径为2，A 为⊙O 外一点．过点A 作⊙O 的一条切线AB ，切点是B ． AO 的延长线交⊙O 于点C ．若︒=∠30BAC ，则劣弧的长为．14．如图，在矩形纸片ABCD 中，10,6==BC AB ．点E 在CD 上，将BCE ∆沿BE 折叠，点C 恰落在边AD 上的点F 处；点G 在AF 上，将ABG ∆沿BG 折叠，点A 恰落在线段BF 上的点H 处．有下列结论：其中正确的是．（把所有正确结论的序号都选上）三、（本大题共2小题，每小题8分，满分16分）15．计算：︒+-+-45tan 8)2016(30．16．解方程：422=-x x ．四、（本大题共2小题，每小题8分，满分16分）17．如图，在边长为1个单位长度的小正方形组成的1212⨯网格中，给出了四边形ABCD 的两条边AB 与BC ，且四边形ABCD 是一个轴对称图形，其对称轴为直线AC ．（1）试在图中标出点四边形D ，并画出该四边形的另两条边；（2）将四边形ABCD 向下平移5个单位，画出平移后得到的四边形．18．（1）观察下列图形与等式的关系，并填空：（2）观察下图，根据（1）中结论，计算图中黑球的个数，用含有n 的代数式填空： ()12(531+-+⋅⋅⋅+++n =+++⋅⋅⋅+-+135)12()n五、（本大题共2小题，每小题10分，满分20分）19．如图，河的两岸1l 与2l 相互平行，A 、B 是1l 上的两点，C 、D 是2l 上的两点．某人在点A 处测得︒=∠︒=∠30,90DAB CAB ，再沿AB 方向前进20米到达点E (点E 在线段AB 上)，测得︒=∠60DEB ，求C 、D 两点间的距离．20．如图，一次函数b kx y +=的图像分别与反比例函数xa y =的图像在第一象限交于点 )3,4(A ，与y 轴的负半轴交于点B ，且OB OA =．（1）求函数b kx y +=和xa y =的表达式；（2）已知点)5,0(C ，试在该一次函数图像上确定一点M ，使得MC MB =．求此时点M 的坐标．六、（本题满分12分）21．一袋中装有形状大小都相同的四个小球，每个小球上各标有一个数字，分别是1,4,7,8．现规定从袋中任取一个小球，对应的数字作为一个两位数的个位数；然后将小球放回袋中并搅拌均匀，再任取一个小球，对应的数字作为这个两位数的十位数．（1）写出按上述规定得到所有可能的两位数；（2）从这些两位数中任取一个，求其算术平方根大于4且小于7的概率．七、（本题满分12分）22．如图，二次函数bx ax y +=2的图象经过点)4,2(A 与)0,6(B ．（1）求b a ,的值；（2）点C 是该二次函数图象上B A ,两点之间的一动点，横坐标为)62(<<x x ．写出四边形OACB 的面积S 关于点C 的横坐标x 的函数表达式，并求S 的最大值．八、（本题满分14分）22．如图1，B A ,分别在射线ON OM ,上，且MON ∠为钝角．现以线段OB OA ,为斜边向MON ∠的外侧作等腰直角三角形，分别是OBQ OAP ∆∆,,点E D C ,,分别是AB OB OA ,,的中点．（1）求证：EDQ PCE ∆≅∆；（2）延长DQ PC ,交于点R ．① 如图2，若︒=∠150MON ，求证：ABR ∆为等边三角形；② 如图3，若ARB ∆∽PEQ ∆，求MON ∠大小和PQAB 的值．。

2016年安徽省中考数学试卷-答案

安徽省2016年初中毕业学业考试数学答案解析第Ⅰ卷一、选择题1.【答案】B【解析】2-的绝对值是：2，故选B.【提示】直接利用数轴上某个数与原点的距离叫做这个数的绝对值，进而得出答案.【考点】绝对值2.【答案】C【解析】10280a a a a ÷≠=（），故选C.【提示】直接利用同底数幂的除法运算法则化简求出答案.【考点】同底数幂的除法，负整数指数幂3.【答案】A【解析】783628362 00008.36210==⨯万，故选A.【提示】科学记数法的表示形式为10n a ⨯的形式，其中110a ≤＜，n 为整数.确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同.当原数绝对值1>时，n 是正数；当原数的绝对值1<时，n 是负数.【考点】科学记数法—表示较大的数4.【答案】C【解析】圆柱的主（正）视图为矩形，故选C.【提示】根据三视图的定义求解.【考点】简单几何体的三视图5.【答案】D【解析】去分母得：2133x x +=-，解得：4x =，经检验4x =是分式方程的解，故选D.【提示】分式方程去分母转化为整式方程，求出整式方程的解得到x 的值，经检验即可得到分式方程的解.【考点】分式方程的解6.【答案】C【解析】∵2013年我省财政收入为a 亿元，2014年我省财政收入比2013年增长8.9%，∴2014年我省财政收入为(18.9%)a +亿元，∵2015年比2014年增长9.5%，2015年我省财政收为b 亿元，∴2015年我省财政收为(18.9%)(19.5%)b a =++；故选C.【提示】根据2013年我省财政收入和2014年我省财政收入比2013年增长8.9%，求出2014年我省财政收入，再根据出2015年比2014年增长9.5%，2015年我省财政收为b 亿元，即可得出a 、b 之间的关系式.【考点】列代数式7.【答案】D 【解析】根据题意，参与调查的户数为：648010%35%30%5%=+++（户），其中B 组用户数占被调查户数的百分比为：110%35%30%5%20%----=，则所有参与调查的用户中月用水量在6吨以下的共有：8010%20%24⨯+=（）（户），故选D. 【提示】根据除B 组以外参与调查的用户共64户及A 、C 、D 、E 四组的百分率可得参与调查的总户数及B 组的百分率，将总户数乘以月用水量在6吨以下（A 、B 两组）的百分率可得答案.【考点】扇形统计图8.【答案】B【解析】∵8BC =，∴4CD =，在△CBA 和△CAD 中，∵B DAC C C ∠=∠∠=∠，，∴CBA CAD △∽△， ∴AC CD BC AC=， ∴2•4832AC CD BC ==⨯=，∴AC = B.【提示】根据AD 是中线，得出4CD =，再根据AAS 证出CBA CAD ∆∆∽，得出AC CD BC AC =，求出AC 即可.【考点】相似三角形的判定与性质9.【答案】A【解析】解：由题意，甲走了1小时到了B 地，在B 地休息了半个小时，2小时正好走到C 地，乙走了53小时到了C 地，在C 地休息了13小时.由此可知正确的图象是A ，故选A.【提示】分别求出甲乙两人到达C 地的时间，再结合已知条件即可解决问题.【考点】函数的图象10.【答案】B【解答】∵90ABC ∠=︒，∴90ABP PBC ∠+∠=︒，∵PAB PBC ∠=∠，∴90BAP ABP ∠+∠=︒，∴90APB ∠=︒，∴点P 在以AB 为直径的⊙O 上，连接OC 交⊙O 于点P ，此时PC 最小，在R t △BCO 中，∵9043OBC BC OB ∠=︒==，，，∴5OC ，∴532PC OC OP ====﹣. ∴PC 最小值为2，故选B .【提示】首先证明点P 在以AB 为直径的⊙O 上，连接OC 与⊙O 交于点P ，此时PC 最小，利用勾股定理求出OC 即可解决问题.【考点】点与圆的位置关系，圆周角定理二、填空题11.【答案】3x ≥【解析】不等式21x≥﹣ 解得：3x ≥故答案为：3x ≥【提示】不等式移项合并，即可确定出解集.【考点】解一元一次不等式12.【答案】(1)(1)a a a +-【解析】原式2(1)(1)(1)a a a a a ==+--，故答案为：(1)(1)a a a +-【提示】原式提取a ，再利用平方差公式分解即可.【考点】提公因式法与公式法的综合运用13.【答案】43π 【解析】∵AB 是⊙O 切线，∴AB OB ⊥，∴90ABO ∠=︒，∵30A ∠=︒，∴9060AOB A ∠=︒∠=︒﹣， ∴120BOC ∠=︒，∴BC 的长为120241803ππ=，故答案为43π.【提示】根据已知条件求出圆心角∠BOC 的大小，然后利用弧长公式即可解决问题.【考点】切线的性质，弧长的计算14.【答案】①③④【解析】∵△BCE 沿BE 折叠，点C 恰落在边AD 上的点F 处，∴12∠=∠，10CE FE BF BC ===，，在R t △A BF 中，∵610AB BF ==，，∴8AF ，∴1082DF AD AF =-=-=，设EF x =，则6CE x DE CD CE x ==-=-，，在Rt △DEF 中，∵222DE DF EF +=，∴22262x x -+=（），解得103x =， ∴83ED =， ∵△ABG 沿BG 折叠，点A 恰落在线段BF 上的点H 处，∴346BH BA AG HG ∠=∠===，，，∴2345ABC ∠+∠=∠=︒，所以①正确；1064HF BF BH =-=-=，设AG y =，则8GH y GF y ==-，，在Rt △HGF 中，∵222GH HF GF +=，∴22248y y +=-（），解得3y =，∴35AG GH GF ===，， ∵6133842AB AG A D DE DF ∠=∠=÷==，，， ∴AB AG DE DF≠， ∴△ABG 与△DE F 不相似，所以②错误； ∵16392ABG S ∆==，1134622FGH GH S HF ==⨯⨯= ∴32ABG FGH S S ∆∆=，所以③正确； ∵325AG DF +=+=，而5GF =，∴AG DF GF +=，所以④正确.故答案为①③④.【考点】相似形综合题三、解答题15.【答案】020********tan ︒=-+=（-）【提示】直接利用特殊角的三角函数值以及立方根的性质分别化简求出答案.【考点】实数的运算，零指数幂，特殊角的三角函数值16.【答案】配方22141x x +=+﹣∴215x =（﹣）∴1x =∴1211x x ==【提示】在方程的左右两边同时加上一次项系数一半的平方，左边就是完全平方式，右边就是常数，然后利用平方根的定义即可求解【考点】解一元二次方程-配方法，零指数幂17.【答案】（1）点D 以及四边形ABCD 另两条边如图所示.（2）得到的四边形A′B′C′D ′如图所示.【提示】（1）画出点B 关于直线AC 的对称点D 即可解决问题.（2）将四边形ABCD 各个点向下平移5个单位即可得到四边形A′B′C′D′.【考点】作图平移变换18.【答案】（1）21357164+++==，设第n 幅图中球的个数为a n ，观察，发现规律：222123132135313574a a a =+==++==+++=，，，…，∴2113521n a n n =+++⋯+=﹣（﹣）. 故答案为：24；2n .（2）观察图形发现：图中黑球可分三部分，1到n 行，第n +1行，n +2行到2n +1行，即：11222135(21)[2(1)1](21)531135(21)(21)(21)531(21)21221n n n n n n n n a n a n n n n n +++⋯+++++⋯+++=+++⋯+++++⋯+++=+++=+++=++﹣﹣﹣﹣﹣﹣﹣故答案为：21n +；2221n n ++.【提示】（1）根据135716+++=可得出2164=；设第n 幅图中球的个数为n a ，列出部分n a 的值，根据数据的变化找出变化规律2113521n a n n =+++⋯+=﹣（﹣），依此规律即可解决问题；（2）观察（1）可将（2）图中得黑球分三部分，1到n 行，第1n +行，2n +行到21n +行，再结合（1）的规律即可得出结论.【考点】规律型：图形的变化类19.【答案】过点D 作1l 的垂线，垂足为F ，∵6030DEB DAB ∠=︒∠=︒，，∴30ADE DEBDAB ∠=∠∠=︒﹣， ∴△ADE 为等腰三角形，∴20DE AE ==.在Rt △DEF 中，1•6020102EF DE cos =︒=⨯= ∵DF AF ⊥，∴90DFB ∠=︒，∴AC ∥DF.由已知1l ∥2l ，∴CD ∥AF .∴四边形ACDF 为矩形，30CD AF AE EF ==+=.答：C 、D 两点间的距离为30m.【提示】直接利用等腰三角形的判定与性质得出20DE AE ==，进而求出EF 的长，再得出四边形ACDF 为矩形，则CD AF AE EF ==+求出答案.【考点】两点间的距离20.【答案】（1）把点A (4,3)代入函数a y x =得：3412a =⨯=， ∴12y x=.5OA ==，∵OA OB =，∴5OB =.∴点B 的坐标为(0,5)-.把B (05)-，，A (4,3)代入y kx b =+得：543b k b =-⎧⎨+=⎩解得：25k b =⎧⎨=-⎩ ∴25y x =-.（2）∵点M 在一次函数25y x =-上，∴设点M 的坐标为(,25)x x -，∵MB MC ==解得：52x =，∴点M 的坐标为5(,0)2.【提示】（1）利用待定系数法即可解答；（2）设点M 的坐标为(,25)x x -，根据MB MC =答.【考点】反比例函数与一次函数的交点问题21.【答案】（1）画树状图：共有16种等可能的结果数，它们是：11，14，17，18，41，44，47，48，71，74，77，78，81，84，87，88；（2）算术平方根大于4且小于7的结果数为6，所以算术平方根大于4且小于7的概率63168P == 【提示】（1）利用树状图展示所有16种等可能的结果数，然后把它们分别写出来；（2）利用算术平方根的定义找出大于16小于49的数，然后根据概率公式求解.【考点】列表法与树状图法；算术平方根.22.【答案】（1）将A (2,4)与B (6,0)代入2y ax bx =+，得4243660a b a b +=⎧⎨+=⎩，解得：123a b ⎧=-⎪⎨⎪=⎩；（2）如图，过A 作x 轴的垂直，垂足为D (2,0)，连接CD ，过C 作CE AD ⊥，CF x ⊥轴，垂足分别为E ，F ，11•24422OAD S OD AD ∆==⨯⨯=； 11•422422ACD S AD CE x x ∆==⨯⨯-=-（）； 2211•43622BCD S BD CF x x x x ∆==⨯⨯+=-+（-），则2242468OAD ACD BCD S S S S xx x x x ∆∆∆=++=+-+=-+﹣. ∴S 关于x 的函数表达式为2826S x x x =-+（＜＜），∵228(x 4)16S x x =-+=--+.∴当4x =时，四边形OACB 的面积S 有最大值，最大值为16.【提示】（1）把A 与B 坐标代入二次函数解析式求出a 与b 的值即可；（2）如图，过A 作x 轴的垂直，垂足为D (2,0)，连接CD ，过C 作CE AD ⊥，CF x ⊥轴，垂足分别为E ，F ，分别表示出三角形OAD ，三角形ACD ，以及三角形BCD 的面积，之和即为S ，确定出S 关于x 的函数解析式，并求出x 的范围，利用二次函数性质即可确定出S 的最大值，以及此时x 的值.【考点】待定系数法求二次函数解析式，二次函数的最值23.【答案】（1）证明：∵点C 、D 、E 分别是OA ，OB ，AB 的中点，∴DE OC CE OD ==，，CE ∥OD∴四边形ODEC 是平行四边形，∴OCE ODE ∠=∠.∵△OAP ，△OBQ 是等腰直角三角形，∴90PCO QDO ∠=∠=︒.∴PCE PCO OCE QDO ODQ EDQ ∠=∠+∠=∠=∠=∠. ∵1122PC AO OC ED CE OD OB DQ ======，在△PCE 与△EDQ 中，PC DE PCE EDQ CE DQ =⎧⎪∠=∠⎨⎪=⎩∴PCE EDQ ∆∆≌.（2）①如图2，连接RO ，∵PR 与QR 分别是OA ，OB 的垂直平分线，∴AP OR RB ==，∴ARC ORC ORQ BRO ∠=∠∠=∠，.∵90150RCO RDO COD ∠=∠=︒∠=︒，，∴30CRD ∠=︒，∴60ARB ∠=︒.∴△ARB 是等边三角形.②由（1）得，EQ EP DEQ CPE =∠=∠，，∴90PEQ CED CEP DEQ ACE CEP CPE ACE RCE ACR ∠=∠-∠-∠=∠-∠-∠=∠-∠=∠=︒， ∴△PEQ 是等腰直角三角形.∵ARB PEQ ∆∆∽，∴90ARB PEQ ∠=∠=︒，∴9045OCR ODR CRD ARB ∠=∠=︒∠=∠=︒，.∴135MON ∠=︒.此时P ，O ，B 在一条直线上，△P AB 为直角三角形，且90APB ∠=︒.∴22AB PE ===，∴AB PQ=【考点】相似形综合题。

2016-2017安徽省中考数学试题及解答

2016年省中考数学试卷一、选择题〔本大题共10小题，每题4分，总分值40分〕1．〔4分〕〔2016•〕﹣2的绝对值是〔〕A．﹣2 B．2 C．±2 D．2．〔4分〕〔2016•〕计算a10÷a2〔a≠0〕的结果是〔〕A．a5B．a﹣5C．a8D．a﹣83．〔4分〕〔2016•〕2016年3月份我省农产品实现出口额8362万美元，其中8362万用科学记数法表示为〔〕A．8.362×107 B．83.62×106 C．0.8362×108D．8.362×1084．〔4分〕〔2016•〕如图，一个放置在水平桌面上的圆柱，它的主〔正〕视图是〔〕A．B．C．D．5．〔4分〕〔2016•〕方程=3的解是〔〕A．﹣B．C．﹣4 D．46．〔4分〕〔2016•〕2014年我省财政收入比2013年增长8.9%，2015年比2014年增长9.5%，假设2013年和2015年我省财政收入分别为a亿元和b亿元，那么a、b之间满足的关系式为〔〕A．b=a〔1+8.9%+9.5%〕B．b=a〔1+8.9%×9.5%〕C．b=a〔1+8.9%〕〔1+9.5%〕D．b=a〔1+8.9%〕2〔1+9.5%〕7．〔4分〕〔2016•〕自来水公司调查了假设干用户的月用水量x〔单位：吨〕，按月用水量将用户分成A、B、C、D、E五组进展统计，并制作了如下图的扇形统计图．除B组以外，参与调查的用户共64户，那么所有参与调查的用户中月用水量在6吨以下的共有〔〕组别月用水量x〔单位：吨〕A 0≤x＜3B 3≤x＜6C 6≤x＜9D 9≤x＜12E x≥12A．18户B．20户C．22户D．24户8．〔4分〕〔2016•〕如图，△ABC中，AD是中线，BC=8，∠B=∠DAC，那么线段AC的长为〔〕A．4 B．4C．6 D．49．〔4分〕〔2016•〕一段笔直的公路AC长20千米，途中有一处休息点B，AB长15千米，甲、乙两名长跑爱好者同时从点A出发，甲以15千米/时的速度匀速跑至点B，原地休息半小时后，再以10千米/时的速度匀速跑至终点C；乙以12千米/时的速度匀速跑至终点C，以下选项中，能正确反映甲、乙两人出发后2小时运动路程y〔千米〕与时间x〔小时〕函数关系的图象是〔〕A．B．C．D．10．〔4分〕〔2016•〕如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC部的一个动点，且满足∠PAB=∠PBC，那么线段CP长的最小值为〔〕A．B．2 C．D．二、填空题〔本大题共4小题，每题5分，总分值20分〕11．〔5分〕〔2016•〕不等式x﹣2≥1的解集是．12．〔5分〕〔2016•〕因式分解：a3﹣a=．13．〔5分〕〔2016•〕如图，⊙O的半径为2，A为⊙O外一点，过点A作⊙O的一条切线AB，切点是B，AO的延长线交⊙O于点C，假设∠BAC=30°，那么劣弧的长为．14．〔5分〕〔2016•〕如图，在矩形纸片ABCD中，AB=6，BC=10，点E在CD上，将△BCE 沿BE折叠，点C恰落在边AD上的点F处；点G在AF上，将△ABG沿BG折叠，点A 恰落在线段BF上的点H处，有以下结论：①∠EBG=45°；②△DEF∽△ABG；③S△ABG=S△FGH；④AG+DF=FG．其中正确的选项是．〔把所有正确结论的序号都选上〕三、〔本大题共2小题，每题8分，总分值16分〕15．〔8分〕〔2016•〕计算：〔﹣2016〕0++tan45°．16．〔8分〕〔2016•〕解方程：x2﹣2x=4．四、〔本大题共2小题，每题8分，总分值16分〕17．〔8分〕〔2016•〕如图，在边长为1个单位长度的小正方形组成的12×12网格中，给出了四边形ABCD的两条边AB与BC，且四边形ABCD是一个轴对称图形，其对称轴为直线AC．〔1〕试在图中标出点D，并画出该四边形的另两条边；〔2〕将四边形ABCD向下平移5个单位，画出平移后得到的四边形A′B′C′D′．18．〔8分〕〔2016•〕〔1〕观察以下图形与等式的关系，并填空：〔2〕观察以下图，根据〔1〕中结论，计算图中黑球的个数，用含有n的代数式填空：1+3+5+…+〔2n﹣1〕+〔〕+〔2n﹣1〕+…+5+3+1=．五、〔本大题共2小题，每题10分，总分值20分〕19．〔10分〕〔2016•〕如图，河的两岸l1与l2相互平行，A、B是l1上的两点，C、D是l2上的两点，某人在点A处测得∠CAB=90°，∠DAB=30°，再沿AB方向前进20米到达点E 〔点E在线段AB上〕，测得∠DEB=60°，求C、D两点间的距离．20．〔10分〕〔2016•〕如图，一次函数y=kx+b的图象分别与反比例函数y=的图象在第一象限交于点A〔4，3〕，与y轴的负半轴交于点B，且OA=OB．〔1〕求函数y=kx+b和y=的表达式；〔2〕点C〔0，5〕，试在该一次函数图象上确定一点M，使得MB=MC，求此时点M的坐标．六、〔本大题总分值12分〕21．〔12分〕〔2016•〕一袋中装有形状大小都一样的四个小球，每个小球上各标有一个数字，分别是1，4，7，8．现规定从袋中任取一个小球，对应的数字作为一个两位数的个位数；然后将小球放回袋中并搅拌均匀，再任取一个小球，对应的数字作为这个两位数的十位数．〔1〕写出按上述规定得到所有可能的两位数；〔2〕从这些两位数中任取一个，求其算术平方根大于4且小于7的概率．七、〔本大题总分值12分〕22．〔12分〕〔2016•〕如图，二次函数y=ax2+bx的图象经过点A〔2，4〕与B〔6，0〕．〔1〕求a，b的值；〔2〕点C是该二次函数图象上A，B两点之间的一动点，横坐标为x〔2＜x＜6〕，写出四边形OACB的面积S关于点C的横坐标x的函数表达式，并求S的最大值．八、〔本大题总分值14分〕23．〔14分〕〔2016•〕如图1，A，B分别在射线OA，ON上，且∠MON为钝角，现以线段OA，OB为斜边向∠MON的外侧作等腰直角三角形，分别是△OAP，△OBQ，点C，D，E分别是OA，OB，AB的中点．〔1〕求证：△PCE≌△EDQ；〔2〕延长PC，QD交于点R．①如图1，假设∠MON=150°，求证：△ABR为等边三角形；②如图3，假设△ARB∽△PEQ，求∠MON大小和的值．2016年省中考数学试卷参考答案一、选择题1．B2．C3．A4．C5．D6．C7．D8．B9．A10．B二、填空题11．x≥312．a〔a+1〕〔a﹣1〕13．．14．解：∵△BCE沿BE折叠，点C恰落在边AD上的点F处，∴∠1=∠2，CE=FE，BF=BC=10，在Rt△ABF中，∵AB=6，BF=10，∴AF==8，∴DF=AD﹣AF=10﹣8=2，设EF=x，那么CE=x，DE=CD﹣CE=6﹣x，在Rt△DEF中，∵DE2+DF2=EF2，∴〔6﹣x〕2+22=x2，解得x=，∴ED=，∵△ABG沿BG折叠，点A恰落在线段BF上的点H处，∴∠3=∠4，BH=BA=6，AG=HG，∴∠2+∠3=∠ABC=45°，所以①正确；HF=BF﹣BH=10﹣6=4，设AG=y，那么GH=y，GF=8﹣y，在Rt△HGF中，∵GH2+HF2=GF2，∴y2+42=〔8﹣y〕2，解得y=3，∴AG=GH=3，GF=5，∵∠A=∠D，==，=，∴≠，∴△ABG与△DEF不相似，所以②错误；∵S△ABG=•6•3=9，S△FGH=•GH•HF=×3×4=6，∴S△ABG=S△FGH，所以③正确；∵AG+DF=3+2=5，而GF=5，∴AG+DF=GF，所以④正确．故答案为①③④．三、15．〔﹣2016〕0++tan45°=1﹣2+1=0．16．解：配方x2﹣2x+1=4+1∴〔x﹣1〕2=5∴x=1±∴x1=1+，x2=1﹣．四、17．解：〔1〕点D以与四边形ABCD另两条边如下图．〔2〕得到的四边形A′B′C′D′如下图．18．2n+1；2n2+2n+1．五、19．解：过点D作l1的垂线，垂足为F，∵∠DEB=60°，∠DAB=30°，∴∠ADE=∠DEB﹣∠DAB=30°，∴△ADE为等腰三角形，∴DE=AE=20，在Rt△DEF中，EF=DE•cos60°=20×=10，∵DF⊥AF，∴∠DFB=90°，∴AC∥DF，由l1∥l2，∴CD∥AF，∴四边形ACDF为矩形，CD=AF=AE+EF=30，答：C、D两点间的距离为30m．20．解：〔1〕把点A〔4，3〕代入函数y=得：a=3×4=12，∴y=．OA==5，∵OA=OB，∴OB=5，∴点B的坐标为〔0，﹣5〕，把B〔0，﹣5〕，A〔4，3〕代入y=kx+b得：解得：∴y=2x﹣5．〔2〕∵点M在一次函数y=2x﹣5上，∴设点M的坐标为〔x，2x﹣5〕，∵MB=MC，∴解得：x=2.5，∴点M的坐标为〔2.5，0〕．六、21．解：〔1〕画树状图：共有16种等可能的结果数，它们是：11，41，71，81，14，44，74，84，17，47，77，87，18，48，78，88；〔2〕算术平方根大于4且小于7的结果数为6，所以算术平方根大于4且小于7的概率==．七、22．解：〔1〕将A〔2，4〕与B〔6，0〕代入y=ax2+bx，得，解得：；〔2〕如图，过A作x轴的垂直，垂足为D〔2，0〕，连接CD，过C作CE⊥AD，CF⊥x 轴，垂足分别为E，F，S△OAD=OD•AD=×2×4=4；S△ACD=AD•CE=×4×〔x﹣2〕=2x﹣4；S△BCD=BD•CF=×4×〔﹣x2+3x〕=﹣x2+6x，那么S=S△OAD+S△ACD+S△BCD=4+2x﹣4﹣x2+6x=﹣x2+8x，∴S关于x的函数表达式为S=﹣x2+8x〔2＜x＜6〕，∵S=﹣x2+8x=﹣〔x﹣4〕2+16，∴当x=4时，四边形OACB的面积S有最大值，最大值为16．八、23．〔1〕证明：∵点C、D、E分别是OA，OB，AB的中点，∴DE=OC，∥OC，CE=OD，CE∥OD，∴四边形ODEC是平行四边形，∴∠OCE=∠ODE，∵△OAP，△OBQ是等腰直角三角形，∴∠PCO=∠QDO=90°，∴∠PCE=∠PCO+∠OCE=∠QDO=∠ODQ=∠EDQ，∵PC=AO=OC=ED，CE=OD=OB=DQ，在△PCE与△EDQ中，，∴△PCE≌△EDQ；〔2〕①如图2，连接RO，∵PR与QR分别是OA，OB的垂直平分线，∴AP=OR=RB，∴∠ARC=∠ORC，∠ORQ=∠BRO，∵∠RCO=∠RDO=90°，∠COD=150°，∴∠CRD=30°，∴∠ARB=60°，∴△ARB是等边三角形；②由〔1〕得，EQ=EP，∠DEQ=∠CPE，∴∠PEQ=∠CED﹣∠CEP﹣∠DEQ=∠ACE﹣∠CEP﹣∠CPE=∠ACE﹣∠RCE=∠ACR=90°，∴△PEQ是等腰直角三角形，∵△ARB∽△PEQ，∴∠ARB=∠PEQ=90°，∴∠OCR=∠ODR=90°，∠CRD=∠ARB=45°，∴∠MON=135°，此时P，O，B在一条直线上，△PAB为直角三角形，且∠APB=90°，∴AB=2PE=2×PQ=PQ，∴=．2017年省初中学业水平考试数学〔试题卷〕考前须知：1.你拿到的试卷总分值为150分，考试时间为120分钟。

2016年安徽省中考数学试卷

2016年安徽省中考数学试卷一、选择题（本大题共10小题，每小题4分，满分40分）1．（4分）﹣2的绝对值是（）A．﹣2B．2C．±2D．2．（4分）计算a10÷a2（a≠0）的结果是（）A．a5B．a﹣5C．a8D．a﹣83．（4分）2016年3月份我省农产品实现出口额8362万美元，其中8362万用科学记数法表示为（）A．8.362×107B．83.62×106C．0.8362×108D．8.362×108 4．（4分）如图，一个放置在水平桌面上的圆柱，它的主（正）视图是（）A．B．C．D．5．（4分）方程＝3的解是（）A．﹣B．C．﹣4D．46．（4分）2014年我省财政收入比2013年增长8.9%，2015年比2014年增长9.5%，若2013年和2015年我省财政收入分别为a亿元和b亿元，则a、b之间满足的关系式为（）A．b＝a（1+8.9%+9.5%）B．b＝a（1+8.9%×9.5%）C．b＝a（1+8.9%）（1+9.5%）D．b＝a（1+8.9%）2（1+9.5%）7．（4分）自来水公司调查了若干用户的月用水量x（单位：吨），按月用水量将用户分成A、B、C、D、E五组进行统计，并制作了如图所示的扇形统计图．已知除B组以外，参与调查的用户共64户，则所有参与调查的用户中月用水量在6吨以下的共有（）组别月用水量x（单位：吨）A0≤x＜3B3≤x＜6C6≤x＜9D9≤x＜12E x≥12A．18户B．20户C．22户D．24户8．（4分）如图，△ABC中，AD是中线，BC＝8，∠B＝∠DAC，则线段AC的长为（）A．4B．4C．6D．49．（4分）一段笔直的公路AC长20千米，途中有一处休息点B，AB长15千米，甲、乙两名长跑爱好者同时从点A出发，甲以15千米/时的速度匀速跑至点B，原地休息半小时后，再以10千米/时的速度匀速跑至终点C；乙以12千米/时的速度匀速跑至终点C，下列选项中，能正确反映甲、乙两人出发后2小时内运动路程y（千米）与时间x（小时）函数关系的图象是（）A．B．C．D．10．（4分）如图，Rt△ABC中，AB⊥BC，AB＝6，BC＝4，P是△ABC内部的一个动点，且满足∠P AB＝∠PBC，则线段CP长的最小值为（）A．B．2C．D．二、填空题（本大题共4小题，每小题5分，满分20分）11．（5分）不等式x﹣2≥1的解集是．12．（5分）因式分解：a3﹣a＝．13．（5分）如图，已知⊙O的半径为2，A为⊙O外一点，过点A作⊙O的一条切线AB，切点是B，AO的延长线交⊙O于点C，若∠BAC＝30°，则劣弧的长为．14．（5分）如图，在矩形纸片ABCD中，AB＝6，BC＝10，点E在CD上，将△BCE沿BE 折叠，点C恰落在边AD上的点F处；点G在AF上，将△ABG沿BG折叠，点A恰落在线段BF上的点H处，有下列结论：①∠EBG＝45°；②△DEF∽△ABG；③S△ABG＝S△FGH；④AG+DF＝FG．其中正确的是．（把所有正确结论的序号都选上）三、（本大题共2小题，每小题8分，满分16分）15．（8分）计算：（﹣2016）0++tan45°．16．（8分）解方程：x2﹣2x＝4．四、（本大题共2小题，每小题8分，满分16分）17．（8分）如图，在边长为1个单位长度的小正方形组成的12×12网格中，给出了四边形ABCD的两条边AB与BC，且四边形ABCD是一个轴对称图形，其对称轴为直线AC．（1）试在图中标出点D，并画出该四边形的另两条边；（2）将四边形ABCD向下平移5个单位，画出平移后得到的四边形A′B′C′D′．18．（8分）（1）观察下列图形与等式的关系，并填空（2）观察下图，根据（1）中结论，计算图中黑球的个数，用含有n的代数式填空：1+3+5+…+（2n﹣1）+（）+（2n﹣1）+…+5+3+1＝．五、（本大题共2小题，每小题10分，满分20分）19．（10分）如图，河的两岸l1与l2相互平行，A、B是l1上的两点，C、D是l2上的两点，某人在点A处测得∠CAB＝90°，∠DAB＝30°，再沿AB方向前进20米到达点E（点E在线段AB上），测得∠DEB＝60°，求C、D两点间的距离．20．（10分）如图，一次函数y＝kx+b的图象分别与反比例函数y＝的图象在第一象限交于点A（4，3），与y轴的负半轴交于点B，且OA＝OB．（1）求函数y＝kx+b和y＝的表达式；（2）已知点C（0，5），试在该一次函数图象上确定一点M，使得MB＝MC，求此时点M的坐标．六、（本大题满分12分）21．（12分）一袋中装有形状大小都相同的四个小球，每个小球上各标有一个数字，分别是1，4，7，8．现规定从袋中任取一个小球，对应的数字作为一个两位数的个位数；然后将小球放回袋中并搅拌均匀，再任取一个小球，对应的数字作为这个两位数的十位数．（1）写出按上述规定得到所有可能的两位数；（2）从这些两位数中任取一个，求其算术平方根大于4且小于7的概率．七、（本大题满分12分）22．（12分）如图，二次函数y＝ax2+bx的图象经过点A（2，4）与B（6，0）．（1）求a，b的值；（2）点C是该二次函数图象上A，B两点之间的一动点，横坐标为x（2＜x＜6），写出四边形OACB的面积S关于点C的横坐标x的函数表达式，并求S的最大值．八、（本大题满分14分）23．（14分）如图1，A，B分别在射线OM，ON上，且∠MON为钝角，现以线段OA，OB 为斜边向∠MON的外侧作等腰直角三角形，分别是△OAP，△OBQ，点C，D，E分别是OA，OB，AB的中点．（1）求证：△PCE≌△EDQ；（2）延长PC，QD交于点R．①如图2，若∠MON＝150°，求证：△ABR为等边三角形；②如图3，若△ARB∽△PEQ，求∠MON大小和的值．2016年安徽省中考数学试卷参考答案与试题解析一、选择题（本大题共10小题，每小题4分，满分40分）1．（4分）﹣2的绝对值是（）A．﹣2B．2C．±2D．解：﹣2的绝对值是2．故选B．2．（4分）计算a10÷a2（a≠0）的结果是（）A．a5B．a﹣5C．a8D．a﹣8解：a10÷a2（a≠0）＝a8．故选C．3．（4分）2016年3月份我省农产品实现出口额8362万美元，其中8362万用科学记数法表示为（）A．8.362×107B．83.62×106C．0.8362×108D．8.362×108解：8362万＝8362 0000＝8.362×107，故选A．4．（4分）如图，一个放置在水平桌面上的圆柱，它的主（正）视图是（）A．B．C．D．解：圆柱的主（正）视图为矩形．故选C．5．（4分）方程＝3的解是（）A．﹣B．C．﹣4D．4解：去分母得2x+1＝3x﹣3，解得x＝4，经检验x＝4是分式方程的解，故选D．6．（4分）2014年我省财政收入比2013年增长8.9%，2015年比2014年增长9.5%，若2013年和2015年我省财政收入分别为a亿元和b亿元，则a、b之间满足的关系式为（）A．b＝a（1+8.9%+9.5%）B．b＝a（1+8.9%×9.5%）C．b＝a（1+8.9%）（1+9.5%）D．b＝a（1+8.9%）2（1+9.5%）解：∵2013年我省财政收入为a亿元，2014年我省财政收入比2013年增长8.9%，∴2014年我省财政收入为a（1+8.9%）亿元，∵2015年比2014年增长9.5%，2015年我省财政收为b亿元，∴2015年我省财政收为b＝a（1+8.9%）（1+9.5%）；故选C．7．（4分）自来水公司调查了若干用户的月用水量x（单位：吨），按月用水量将用户分成A、B、C、D、E五组进行统计，并制作了如图所示的扇形统计图．已知除B组以外，参与调查的用户共64户，则所有参与调查的用户中月用水量在6吨以下的共有（）组别月用水量x（单位：吨）A0≤x＜3B3≤x＜6C6≤x＜9D9≤x＜12E x≥12A．18户B．20户C．22户D．24户解：根据题意，参与调查的户数为＝80（户），其中B组用户数占被调查户数的百分比为1﹣10%﹣35%﹣30%﹣5%＝20%，则所有参与调查的用户中月用水量在6吨以下的共有：80×（10%+20%）＝24（户），故选D．8．（4分）如图，△ABC中，AD是中线，BC＝8，∠B＝∠DAC，则线段AC的长为（）A．4B．4C．6D．4解：∵BC＝8，∴CD＝4，在△CBA和△CAD中，∵∠B＝∠DAC，∠C＝∠C，∴△CBA∽△CAD，∴＝，∴AC2＝CD•BC＝4×8＝32，∴AC＝4；故选B．9．（4分）一段笔直的公路AC长20千米，途中有一处休息点B，AB长15千米，甲、乙两名长跑爱好者同时从点A出发，甲以15千米/时的速度匀速跑至点B，原地休息半小时后，再以10千米/时的速度匀速跑至终点C；乙以12千米/时的速度匀速跑至终点C，下列选项中，能正确反映甲、乙两人出发后2小时内运动路程y（千米）与时间x（小时）函数关系的图象是（）A．B．C．D．解；由题意，甲走了1小时到了B地，在B地休息了半个小时，2小时正好走到C地，乙走了小时到了C地，在C地休息了小时．由此可知正确的图象是A．故选A．10．（4分）如图，Rt△ABC中，AB⊥BC，AB＝6，BC＝4，P是△ABC内部的一个动点，且满足∠P AB＝∠PBC，则线段CP长的最小值为（）A．B．2C．D．解：∵∠ABC＝90°，∴∠ABP+∠PBC＝90°，∵∠P AB＝∠PBC，∴∠BAP+∠ABP＝90°，∴∠APB＝90°，∴OP＝OA＝OB（直角三角形斜边中线等于斜边一半），∴点P在以AB为直径的⊙O上，连接OC交⊙O于点P，此时PC最小，在RT△BCO中，∵∠OBC＝90°，BC＝4，OB＝3，∴OC＝＝5，∴PC＝OC﹣OP＝5﹣3＝2．∴PC最小值为2．故选B．二、填空题（本大题共4小题，每小题5分，满分20分）11．（5分）不等式x﹣2≥1的解集是x≥3．解：不等式x﹣2≥1，解得x≥3，故答案为x≥312．（5分）因式分解：a3﹣a＝a（a+1）（a﹣1）．解：原式＝a（a2﹣1）＝a（a+1）（a﹣1），故答案为a（a+1）（a﹣1）13．（5分）如图，已知⊙O的半径为2，A为⊙O外一点，过点A作⊙O的一条切线AB，切点是B，AO的延长线交⊙O于点C，若∠BAC＝30°，则劣弧的长为．解：∵AB是⊙O切线，∴AB⊥OB，∴∠ABO＝90°，∵∠A＝30°，∴∠AOB＝90°﹣∠A＝60°，∴∠BOC＝120°，∴的长为＝．故答案为．14．（5分）如图，在矩形纸片ABCD中，AB＝6，BC＝10，点E在CD上，将△BCE沿BE 折叠，点C恰落在边AD上的点F处；点G在AF上，将△ABG沿BG折叠，点A恰落在线段BF上的点H处，有下列结论：①∠EBG＝45°；②△DEF∽△ABG；③S△ABG＝S△FGH；④AG+DF＝FG．其中正确的是①③④．（把所有正确结论的序号都选上）解：∵△BCE沿BE折叠，点C恰落在边AD上的点F处，∴∠1＝∠2，CE＝FE，BF＝BC＝10，在Rt△ABF中，∵AB＝6，BF＝10，∴AF＝＝8，∴DF＝AD﹣AF＝10﹣8＝2，设EF＝x，则CE＝x，DE＝CD﹣CE＝6﹣x，在Rt△DEF中，∵DE2+DF2＝EF2，∴（6﹣x）2+22＝x2，解得x＝，∴ED＝，∵△ABG沿BG折叠，点A恰落在线段BF上的点H处，∴∠3＝∠4，BH＝BA＝6，AG＝HG，∴∠2+∠3＝∠ABC＝45°，所以①正确；HF＝BF﹣BH＝10﹣6＝4，设AG＝y，则GH＝y，GF＝8﹣y，在Rt△HGF中，∵GH2+HF2＝GF2，∴y2+42＝（8﹣y）2，解得y＝3，∴AG＝GH＝3，GF＝5，∵∠A＝∠D，＝＝，＝，∴≠，∴△ABG与△DEF不相似，所以②错误；∵S△ABG＝•6•3＝9，S△FGH＝•GH•HF＝×3×4＝6，∴S△ABG＝S△FGH，所以③正确；∵AG+DF＝3+2＝5，而GF＝5，∴AG+DF＝GF，所以④正确．故答案为①③④．三、（本大题共2小题，每小题8分，满分16分）15．（8分）计算：（﹣2016）0++tan45°．解：（﹣2016）0++tan45°＝1﹣2+1＝0．16．（8分）解方程：x2﹣2x＝4．解：配方x2﹣2x+1＝4+1∴（x﹣1）2＝5∴x＝1±∴x1＝1+，x2＝1﹣．四、（本大题共2小题，每小题8分，满分16分）17．（8分）如图，在边长为1个单位长度的小正方形组成的12×12网格中，给出了四边形ABCD的两条边AB与BC，且四边形ABCD是一个轴对称图形，其对称轴为直线AC．（1）试在图中标出点D，并画出该四边形的另两条边；（2）将四边形ABCD向下平移5个单位，画出平移后得到的四边形A′B′C′D′．解：（1）点D以及四边形ABCD另两条边如图所示．（2）得到的四边形A′B′C′D′如图所示．18．（8分）（1）观察下列图形与等式的关系，并填空（2）观察下图，根据（1）中结论，计算图中黑球的个数，用含有n的代数式填空：1+3+5+…+（2n﹣1）+（2n+1）+（2n﹣1）+…+5+3+1＝2n2+2n+1．解：（1）1+3+5+7＝16＝42，设第n幅图中球的个数为a n，观察，发现规律：a1＝1+3＝22，a2＝1+3+5＝32，a3＝1+3+5+7＝42，…，∴a n﹣1＝1+3+5+…+（2n﹣1）＝n2．故答案为42；n2．（2）观察图形发现：图中黑球可分三部分，1到n行，第n+1行，n+2行到2n+1行，即1+3+5+…+（2n﹣1）+[2（n+1）﹣1]+（2n﹣1）+…+5+3+1，＝1+3+5+…+（2n﹣1）+（2n+1）+（2n﹣1）+…+5+3+1，＝a n﹣1+（2n+1）+a n﹣1，＝n2+2n+1+n2，＝2n2+2n+1．故答案为2n+1；2n2+2n+1．五、（本大题共2小题，每小题10分，满分20分）19．（10分）如图，河的两岸l1与l2相互平行，A、B是l1上的两点，C、D是l2上的两点，某人在点A处测得∠CAB＝90°，∠DAB＝30°，再沿AB方向前进20米到达点E（点E在线段AB上），测得∠DEB＝60°，求C、D两点间的距离．解：过点D作l1的垂线，垂足为F，∵∠DEB＝60°，∠DAB＝30°，∴∠ADE＝∠DEB﹣∠DAB＝30°，∴△ADE为等腰三角形，∴DE＝AE＝20，在Rt△DEF中，EF＝DE•cos60°＝20×＝10，∵DF⊥AF，∴∠DFB＝90°，∴AC∥DF，由已知l1∥l2，∴CD∥AF，∴四边形ACDF为矩形，CD＝AF＝AE+EF＝30，答：C、D两点间的距离为30m．20．（10分）如图，一次函数y＝kx+b的图象分别与反比例函数y＝的图象在第一象限交于点A（4，3），与y轴的负半轴交于点B，且OA＝OB．（1）求函数y＝kx+b和y＝的表达式；（2）已知点C（0，5），试在该一次函数图象上确定一点M，使得MB＝MC，求此时点M的坐标．解：（1）把点A（4，3）代入函数y＝得a＝3×4＝12，∴y＝．OA＝＝5，∵OA＝OB，∴OB＝5，∴点B的坐标为（0，﹣5），把B（0，﹣5），A（4，3）代入y＝kx+b得解得∴y＝2x﹣5．（2）方法一：∵点M在一次函数y＝2x﹣5上，∴设点M的坐标为（x，2x﹣5），∵MB＝MC，∴解得x＝2.5，∴点M的坐标为（2.5，0）．方法二：∵B（0，﹣5）、C（0，5），∴BC＝10，∴BC的中垂线为直线y＝0，当y＝0时，2x﹣5＝0，即x＝2.5，∴点M的坐标为（2.5，0）．六、（本大题满分12分）21．（12分）一袋中装有形状大小都相同的四个小球，每个小球上各标有一个数字，分别是1，4，7，8．现规定从袋中任取一个小球，对应的数字作为一个两位数的个位数；然后将小球放回袋中并搅拌均匀，再任取一个小球，对应的数字作为这个两位数的十位数．（1）写出按上述规定得到所有可能的两位数；（2）从这些两位数中任取一个，求其算术平方根大于4且小于7的概率．解：（1）画树状图：共有16种等可能的结果数，它们是11，41，71，81，14，44，74，84，17，47，77，87，18，48，78，88；（2）算术平方根大于4且小于7的结果数为6，所以算术平方根大于4且小于7的概率＝＝．七、（本大题满分12分）22．（12分）如图，二次函数y＝ax2+bx的图象经过点A（2，4）与B（6，0）．（1）求a，b的值；（2）点C是该二次函数图象上A，B两点之间的一动点，横坐标为x（2＜x＜6），写出四边形OACB的面积S关于点C的横坐标x的函数表达式，并求S的最大值．解：（1）将A（2，4）与B（6，0）代入y＝ax2+bx，得，解得；（2）如图，过A作x轴的垂线，垂足为D（2，0），连接CD、CB，过C作CE⊥AD，CF⊥x轴，垂足分别为E，F，S△OAD＝OD•AD＝×2×4＝4；S△ACD＝AD•CE＝×4×（x﹣2）＝2x﹣4；S△BCD＝BD•CF＝×4×（﹣x2+3x）＝﹣x2+6x，则S＝S△OAD+S△ACD+S△BCD＝4+2x﹣4﹣x2+6x＝﹣x2+8x，∴S关于x的函数表达式为S＝﹣x2+8x（2＜x＜6），∵S＝﹣x2+8x＝﹣（x﹣4）2+16，∴当x＝4时，四边形OACB的面积S有最大值，最大值为16．八、（本大题满分14分）23．（14分）如图1，A，B分别在射线OM，ON上，且∠MON为钝角，现以线段OA，OB 为斜边向∠MON的外侧作等腰直角三角形，分别是△OAP，△OBQ，点C，D，E分别是OA，OB，AB的中点．（1）求证：△PCE≌△EDQ；（2）延长PC，QD交于点R．①如图2，若∠MON＝150°，求证：△ABR为等边三角形；②如图3，若△ARB∽△PEQ，求∠MON大小和的值．（1）证明：∵点C、D、E分别是OA，OB，AB的中点，∴DE＝OC，DE∥OC，CE＝OD，CE∥OD，∴四边形ODEC是平行四边形，∴∠OCE＝∠ODE，∵△OAP，△OBQ是等腰直角三角形，∴∠PCO＝∠QDO＝90°，∴∠PCE＝∠PCO+∠OCE＝∠QDO+∠EDO＝∠EDQ，∵PC＝AO＝OC＝ED，CE＝OD＝OB＝DQ，在△PCE与△EDQ中，，∴△PCE≌△EDQ；（2）①如图2，连接RO，∵PR与QR分别是OA，OB的垂直平分线，∴AR＝OR＝RB，∴∠ARC＝∠ORC，∠ORQ＝∠BRO，∵∠RCO＝∠RDO＝90°，∠COD＝150°，∴∠CRD＝30°，∴∠ARB＝60°，∴△ARB是等边三角形；②由（1）得，EQ＝EP，∠DEQ＝∠CPE，∴∠PEQ＝∠CED﹣∠CEP﹣∠DEQ＝∠ACE﹣∠CEP﹣∠CPE＝∠ACE﹣∠RCE＝∠ACR＝90°，∴△PEQ是等腰直角三角形，∵△ARB∽△PEQ，∴∠ARB＝∠PEQ＝90°，∴∠OCR＝∠ODR＝90°，∠CRD＝∠ARB＝45°，∴∠MON＝135°，此时P，O，B在一条直线上，△P AB为直角三角形，且∠APB＝90°，∴AB＝2PE＝2×PQ＝PQ，∴＝．。

安徽省2016年中考数学试题(word版)

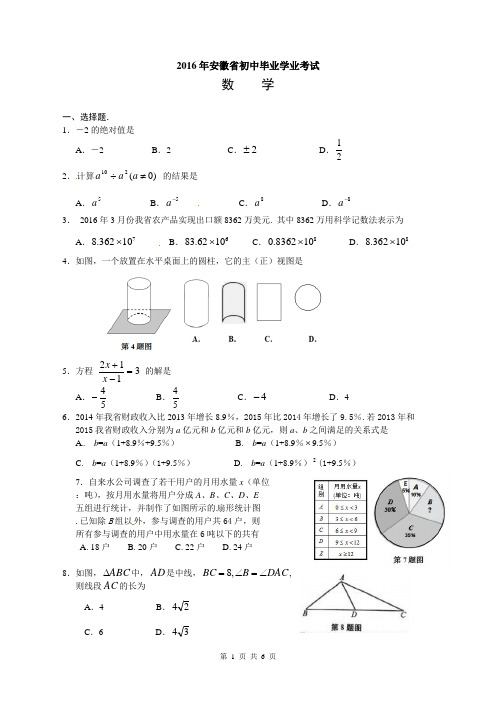
2016年安徽省初中毕业学业考试数学一、选择题．1．－2的绝对值是A ．－2B ．2C ．2±D ．21 2．计算)0(210≠÷a a a 的结果是A ．5aB ．5-aC ．8aD ．8-a3． 2016年3月份我省农产品实现出口额8362万美元. 其中8362万用科学记数法表示为A ．710362.8⨯B ．61062.83⨯C ．8108362.0⨯D ．810362.8⨯4．如图，一个放置在水平桌面上的圆柱，它的主（正）视图是5．方程 3112=-+x x 的解是 A ．54- B ．54 C ．4- D ．4 6．2014年我省财政收入比2013年增长8.9％，2015年比2014年增长了9.5％.若2013年和 2015我省财政收入分别为a 亿元和b 亿元和b 亿元，则a 、b 之间满足的关系式是 A. b =a （1+8.9％+9.5％） B. b =a （1+8.9％⨯9.5％）C. b =a （1+8.9％）（1+9.5％）D. b =a （1+8.9％）2(1+9.5％）7．自来水公司调查了若干用户的月用水量x （单位：吨），按月用水量将用户分成A 、B 、C 、D 、E 五组进行统计，并制作了如图所示的扇形统计图.已知除B 组以外，参与调查的用户共64户，则所有参与调查的用户中用水量在6吨以下的共有A. 18户B. 20户C. 22户D. 24户8．如图，ABC ∆中，AD 是中线，DAC B BC ∠=∠=,8,则线段AC 的长为A ．4B ．24C ．6D ．349．一段笔直的公路AC 长为20千米，途中有一处休息点AB B ,长为15千米．甲、乙两名长跑爱好者同时从点A 出发．甲以15千米/时的速度匀速跑至点,B 原地休息半小时后，再以10千米/时的速度匀速跑至终点C ；乙以12千米/时的速度匀速跑至终点C ．下列选项中，能正确反映甲、乙两人出发后2小时内运动路程 y （千米）与时间 x （小时）函数关系的图像是10．如图，ABC Rt ∆中，P BC AB BC AB .4,6,==⊥是ABC ∆内部的一个动点，且满足.PBC PAB ∠=∠则线段CP 长的最小值为A ．23B ．2C ．13138D ．131312二、填空题11．不等式12≥-x 的解集是．12．因式分解：=-a a 3 ．13．如图，已知⊙O 的半径为2，A 为⊙O 外一点．过点A 作⊙O 的一条切线AB ，切点是B ． AO 的延长线交⊙O 于点C ．若︒=∠30BAC ，则劣弧的长为．14．如图，在矩形纸片ABCD 中，10,6==BC AB ．点E 在CD 上，将BCE ∆沿BE 折叠，点C 恰落在边AD 上的点F 处；点G 在AF 上，将ABG ∆沿BG 折叠，点A 恰落在线段BF上的点H 处．有下列结论：其中正确的是．（把所有正确结论的序号都选上）三、解答题15．计算：︒+-+-45tan 8)2016(30．16．解方程：422=-x x ．17．如图，在边长为1个单位长度的小正方形组成的1212⨯网格中，给出了四边形ABCD 的两条边AB 与BC ，且四边形ABCD 是一个轴对称图形，其对称轴为直线AC ．（1）试在图中标出点四边形D ，并画出该四边形的另两条边；（2）将四边形ABCD 向下平移5个单位，画出平移后得到的四边形．18．（1）观察下列图形与等式的关系，并填空：（2）观察下图，根据（1）中结论，计算图中黑球的个数，用含有n 的代数式填空：()12(531+-+⋅⋅⋅+++n =+++⋅⋅⋅+-+135)12()n19．如图，河的两岸1l 与2l 相互平行，A 、B 是1l 上的两点，C 、D 是2l 上的两点．某人在点A 处测得︒=∠︒=∠30,90DAB CAB ，再沿AB 方向前进20米到达点E (点E 在线段AB 上)，测得︒=∠60DEB ，求C 、D 两点间的距离．19．如图，一次函数b kx y +=的图像分别与反比例函数x a y =的图像在第一象限交于点)3,4(A ，与y 轴的负半轴交于点B ，且OB OA =．（1）求函数b kx y +=和xa y =的表达式；（2）已知点)5,0(C ，试在该一次函数图像上确定一点M ，使得MC MB =．求此时点M 的坐标．21．一袋中装有形状大小都相同的四个小球，每个小球上各标有一个数字，分别是1,4,7,8．现规定从袋中任取一个小球，对应的数字作为一个两位数的个位数；然后将小球放回袋中并搅拌均匀，再任取一个小球，对应的数字作为这个两位数的十位数．（1）写出按上述规定得到所有可能的两位数；（2）从这些两位数中任取一个，求其算术平方根大于4且小于7的概率．22．如图，二次函数bx ax y +=2的图象经过点)4,2(A 与)0,6(B ．（1）求b a ,的值；（2）点C 是该二次函数图象上B A ,两点之间的一动点，横坐标为)62(<<x x ．写出四边形OACB 的面积S 关于点C 的横坐标x 的函数表达式，并求S 的最大值．22．如图1，B A ,分别在射线ON OM ,上，且MON ∠为钝角．现以线段OB OA ,为斜边向MON ∠的外侧作等腰直角三角形，分别是OBQ OAP ∆∆,,点E D C ,,分别是AB OB OA ,,的中点．（1）求证：EDQ PCE ∆≅∆；（2）延长DQ PC ,交于点R ．① 如图2，若︒=∠150MON ，求证：ABR ∆为等边三角形；② 如图3，若ARB ∆∽PEQ ∆，求MON ∠大小和PQAB 的值．数学试题卷第4页（共4页）。

2016年安徽蚌埠中考数学试题免费版含答案

2016年安徽省蚌埠市中考数学试题（免费版含答案）为了方便您的阅读请点击全屏查看一、选择题（本大题共10小题，每小题4分，满分40分）每小题都给出A 、B 、C 、D 四个选项，其中只有一个是正确的．1．－2的绝对值是A ．－2B ．2C ．2±D ．212．计算)0(210≠÷a a a 的结果是 A ．5a B ．5-a C ．8a D ．8-a3． 2016年3月份我省农产品实现出口额8362万美元. 其中8362万用科学记数法表示为A ．710362.8⨯B ．61062.83⨯C ．8108362.0⨯D ．810362.8⨯4．如图，一个放置在水平桌面上的圆柱，它的主（正）视图是5．方程 3112=-+x x 的解是A ．54-B ．54C ．4-D ．46．2014年我省财政收入比2013年增长8.9％，2015年比2014年增长了9.5％.若2013年和2015我省财政收入分别为a 亿元和b 亿元和b 亿元，则a 、b 之间满足的关系式是 A.b=a （1+8.9％+9.5％）B.b=a （1+8.9％⨯9.5％）C.b=a （1+8.9％）（1+9.5％）D.b=a （1+8.9％）2(1+9.5％）7．自来水公司调查了若干用户的月用水量x （单位：吨），按月用水量将用户分成A 、B 、C 、D 、E 五组进行统计，并制作了如图所示的扇形统计图.已知除B 组以外，参与调查的用户共64户，则所有参与调查的用户中用水量在6吨以下的共有A. 18户B. 20户C. 22户D. 24户数学试题卷第1页（共4页）8．如图，ABC ∆中，AD 是中线，DAC B BC ∠=∠=,8,则线段AC 的长为A ．4B ．24C ．6D ．349．一段笔直的公路AC 长为20千米，途中有一处休息点AB B ,长为15千米．甲、乙两名长跑爱好者同时从点A 出发．甲以15千米/时的速度匀速跑至点,B 原地休息半小时后，再以10千米/时的速度匀速跑至终点C ；乙以12千米/时的速度匀速跑至终点C ．下列选项中，能正确反映甲、乙两人出发后2小时内运动路程 y （千米）与时间 x （小时）函数关系的图像是10．如图，ABC Rt ∆中，P BC AB BC AB .4,6,==⊥是ABC ∆内部的一个动点，且满足.PBC PAB ∠=∠则线段CP 长的最小值为A ．23B ．2C ．13138D ．131312二、填空题（本大题共4小题，每小题5分，满分20分）11．不等式12≥-x 的解集是．12．因式分解：=-a a 3 ．13．如图，已知⊙O 的半径为2，A 为⊙O 外一点．过点A 作⊙O 的一条切线AB ，切点是B ． AO 的延长线交⊙O 于点C ．若︒=∠30BAC ，则劣弧的长为．14．如图，在矩形纸片ABCD 中，10,6==BC AB ．点E 在CD 上，将BCE ∆沿BE 折叠，点C 恰落在边AD 上的点F 处；点G 在AF 上，将ABG ∆沿BG 折叠，点A 恰落在线段BF上的点H 处．有下列结论：其中正确的是．（把所有正确结论的序号都选上）三、（本大题共2小题，每小题8分，满分16分）[来源:]15．计算：︒+-+-45tan 8)2016(30． 16．解方程：422=-x x ．数学试题卷第2页（共4页）四、（本大题共2小题，每小题8分，满分16分）17．如图，在边长为1个单位长度的小正方形组成的1212⨯网格中，给出了四边形ABCD 的两条边AB 与BC ，且四边形ABCD 是一个轴对称图形，其对称轴为直线AC ．（1）试在图中标出点四边形D ，并画出该四边形的另两条边；（2）将四边形ABCD 向下平移5个单位，画出平移后得到的四边形．18．（1）观察下列图形与等式的关系，并填空：（2）观察下图，根据（1）中结论，计算图中黑球的个数，用含有n 的代数式填空：()12(531+-+⋅⋅⋅+++n =+++⋅⋅⋅+-+135)12()n五、（本大题共2小题，每小题10分，满分20分）19．如图，河的两岸1l 与2l 相互平行，A 、B 是1l 上的两点，C 、D 是2l 上的两点．某人在点A 处测得︒=∠︒=∠30,90DAB CAB ，再沿AB 方向前进20米到达点E (点E 在线段AB 上)，测得︒=∠60DEB ，求C 、D 两点间的距离．数学试题卷第3页（共4页）19．如图，一次函数b kx y +=的图像分别与反比例函数x a y =的图像在第一象限交于点)3,4(A ，与y 轴的负半轴交于点B ，且OB OA =．（1）求函数b kx y +=和x a y =的表达式；（2）已知点)5,0(C ，试在该一次函数图像上确定一点M ，使得MC MB =．求此时点M 的坐标．[来源:Z§xx§]六、（本题满分12分）21．一袋中装有形状大小都相同的四个小球，每个小球上各标有一个数字，分别是1,4,7,8．现规定从袋中任取一个小球，对应的数字作为一个两位数的个位数；然后将小球放回袋中并搅拌均匀，再任取一个小球，对应的数字作为这个两位数的十位数．（1）写出按上述规定得到所有可能的两位数；（2）从这些两位数中任取一个，求其算术平方根大于4且小于7的概率．七、（本题满分12分）22．如图，二次函数bx ax y +=2的图象经过点)4,2(A 与)0,6(B ．（1）求b a ,的值；（2）点C 是该二次函数图象上B A ,两点之间的一动点，横坐标为)62(<<x x ．写出四边形OACB 的面积S 关于点C 的横坐标x 的函数表达式，并求S 的最大值．八、（本题满分14分）22．如图1，B A ,分别在射线ON OM ,上，且MON ∠为钝角．现以线段OB OA ,为斜边向MON ∠的外侧作等腰直角三角形，分别是OBQ OAP ∆∆,,点E D C ,,分别是AB OB OA ,,的中点．（1）求证：EDQ PCE ∆≅∆；（2）延长DQ PC ,交于点R ．① 如图2，若︒=∠150MON ，求证：ABR ∆为等边三角形；② 如图3，若ARB ∆∽PEQ ∆，求MON ∠大小和PQ AB的值．数学试题卷第4页（共4页）2016年安徽省蚌埠市中考数学中考试题答案解析。

2016年安徽中考数学试题(附含答案解析)

2016 年安徽省中考数学试卷C． b=a（ 1+8.9%）（ 1+9.5%）D． b=a2（ 1+8.9%）（ 1+9.5%）一、选择题（本大题共10 小题，每小题 47．（ 4 分）（2016?安徽）自来水公司调查了分，满分40 分）若干用户的月用水量 x（单位：吨），按月用1．（ 4 分）（ 2016?安徽）﹣2 的绝对值是（）水量将用户分成A、B、C、D、E 五组进行统A．﹣ 2B． 2C．±2 D．计，并制作了如图所示的扇形统计图．已知除 B 组以外，参与调查的用户共64 户，则102所有参与调查的用户中月用水量在6吨以下2．（ 4 分）（2016?安徽）计算 a÷a（a≠0）的结果是（）的共有（）A． a5B． a﹣5C． a8D． a﹣8组别月用水量 x（单位：吨）3．（ 4 分）（2016?安徽） 2016 年 3 月份我省A0≤x＜ 3农产品实现出口额8362 万美元，其中 8362B3≤x＜ 6万用科学记数法表示为（）C6≤x＜ 9A．8.362 ×10 7B．83.62 ×10 6D9≤x＜ 1288E x≥12C．0.8362 ×10D．8.362 ×104．（ 4 分）（2016?安徽）如图，一个放置在水平桌面上的圆柱，它的主（正）视图是（）A．B．C．D．5．（ 4 分）（2016?安徽）方程=3 的解是（）A．﹣B．C．﹣ 4D． 46．（ 4 分）（2016?安徽） 2014 年我省财政收入比2013 年增长8.9%，2015 年比2014 年增长 9.5%，若 2013 年和 2015 年我省财政收入分别为 a 亿元和 b 亿元，则 a、 b 之间满足的关系式为（）A． b=a（ 1+8.9%+9.5%）B． b=a（1+8.9%×9.5%）A．18 户 B．20 户 C．22 户 D． 24 户8．（ 4 分）（2016?安徽）如图，△ ABC 中，AD是中线， BC=8，∠ B=∠DAC，则线段 AC的长为（）A．4B．4 C ．6D． 49．（4 分）（2016?安徽）一段笔直的公路 AC长 20 千米，途中有一处休息点 B，AB长 15 千米，甲、乙两名长跑爱好者同时从点 A 出发，甲以 15 千米 / 时的速度匀速跑至点 B，原地休息半小时后，再以 10 千米 / 时的速度匀速跑至终点C；乙以12 千米/ 时的速度匀速跑至终点C，下列选项中，能正确反映甲、乙两人出发后 2小时内运动路程 y（千米）与时间 x（小时）函数关系的图象是（）A．B．11．（5 分）（2016?安徽）不等式x﹣2≥1的解集是．12．（5 分）（2016?安徽）因式分解：a3﹣a=．13．（ 5 分）（2016?安徽）如图，已知⊙O的半径为 2，A 为⊙O外一点，过点 A 作⊙O 的一条切线AB，切点是B，AO的延长线交⊙O于点 C，若∠ BAC=30°，则劣弧的长为．C．D．10．（4 分）（2016?安徽）如图，Rt△ABC中，AB⊥BC， AB=6， BC=4， P 是△ ABC内部的一个动点，且满足∠ PAB=∠PBC，则线段 CP长的最小值为（）A．B．2C．D．二、填空题（本大题共 4 小题，每小题 5 分，满分 20 分）14．（ 5 分）（2016?安徽）如图，在矩形纸片ABCD中，AB=6，BC=10，点 E 在 CD上，将△ BCE 沿 BE折叠，点 C 恰落在边 AD上的点 F 处；点G在AF上，将△ABG沿BG折叠，点A 恰落在线段 BF 上的点 H 处，有下列结论：①∠ EBG=45°；②△ DEF∽△ ABG；③S△ABG=S△FGH；④ AG+DF=FG．其中正确的是．（把所有正确结论的序号都选上）三、（本大题共 2 小题，每小题8 分，满分16分）15．（8 分）（2016?安徽）计算：（﹣ 2016 ）0++tan45 °．16．（8 分）（2016?安徽）解方程： x2﹣2x=4．四、（本大题共 2 小题，每小题8 分，满分16分）17．（ 8 分）（2016?安徽）如图，在边长为1个单位长度的小正方形组成的12×12 网格中，给出了四边形 ABCD的两条边 AB 与 BC，且四边形 ABCD是一个轴对称图形，其对称轴为直线AC．（1）试在图中标出点 D，并画出该四边形的另两条边；（2）将四边形 ABCD向下平移 5 个单位，画出平移后得到的四边形 A′B′C′D′．18．（ 8 分）（2016?安徽）（ 1）观察下列图形与等式的关系，并填空：（ 2）观察下图，根据（ 1）中结论，计算图中黑球的个数，用含有 n 的代数式填空：1+3+5+ +（ 2n﹣1）+（）+（ 2n ﹣ 1）+ +5+3+1=．五、（本大题共 2 小题，每小题10 分，满分20 分）19．（ 10 分）（2016?安徽）如图，河的两岸l 1与 l 2相互平行， A、B 是 l 1上的两点， C、D 是 l 2上的两点，某人在点 A 处测得∠CAB=90°，∠ DAB=30°，再沿AB方向前进 20 米到达点 E（点 E 在线段 AB 上），测得∠DEB=60°，求 C、 D 两点间的距离．20．（ 10 分）（2016?安徽）如图，一次函数y=kx+b 的图象分别与反比例函数y=的图象在第一象限交于点 A（ 4，3），与 y 轴的负半轴交于点 B，且 OA=OB．（1）求函数 y=kx+b 和 y= 的表达式；（2）已知点 C（ 0， 5），试在该一次函数图象上确定一点 M，使得 MB=MC，求此时点 M 的坐标．线段 OA，OB为斜边向∠ MON的外侧作等腰直角三角形，分别是△ OAP，△ OBQ，点C， D，E 分别是 OA， OB， AB 的中点．（ 1）求证：△ PCE≌△ EDQ；（ 2）延长 PC，QD交于点 R．①如图 1，若∠ MON=150°，求证：△ ABR 为等边三角形；②如图 3，若△ ARB∽△ PEQ，求∠ MON大小和的六、（本大题满分12 分）21．（ 12 分）（2016?安徽）一袋中装有形状值．大小都相同的四个小球，每个小球上各标有一个数字，分别是1，4，7，8．现规定从袋中任取一个小球，对应的数字作为一个两位数的个位数；然后将小球放回袋中并搅拌均匀，再任取一个小球，对应的数字作为这个两位数的十位数．（1）写出按上述规定得到所有可能的两位数；（2）从这些两位数中任取一个，求其算术平方根大于 4 且小于 7 的概率．七、（本大题满分12 分）22．（ 12 分）（2016?安徽）如图，二次函数2y=ax +bx 的图象经过点A（ 2， 4）与 B（ 6，0）．（1）求 a， b 的值；（2）点C 是该二次函数图象上A，B 两点之间的一动点，横坐标为x（2＜x＜6），写出四边形 OACB的面积 S 关于点 C 的横坐标 x的函数表达式，并求S 的最大值．八、（本大题满分14 分）23．（ 14 分）（2016?安徽）如图1， A， B 分别在射线OA，ON上，且∠ MON为钝角，现以2016 年安徽省中考数学试卷参考答案一、选择题1． B2． C3． A4． C5． D6． C7． D8． B9． A10． B二、填空题11．x≥312． a （ a+1）（ a﹣ 1）13．．14．解：∵△ BCE 沿 BE折叠，点 C恰落在边 AD 上的点 F 处，∴∠ 1=∠2， CE=FE，BF=BC=10，在 Rt△ABF 中，∵ AB=6， BF=10，∴AF==8，∴D F=AD﹣ AF=10﹣ 8=2，设 EF=x，则 CE=x， DE=CD﹣ CE=6﹣x，在 Rt △DEF中，∵ DE2+DF2=EF2，∴（ 6﹣ x）2+22=x2，解得 x=，∴E D= ，∵△ ABG沿 BG折叠，点 A 恰落在线段 BF 上的点 H处，∴∠ 3=∠4， BH=BA=6， AG=HG，∴∠ 2+∠3=∠ABC=45°，所以①正确；HF=BF﹣ BH=10﹣ 6=4，设 AG=y，则 GH=y， GF=8﹣ y，在 Rt△HGF中，∵ GH2+HF2=GF2，222∴y+4 =（ 8﹣ y），解得 y=3，∴AG=GH=3， GF=5，∵∠A=∠D，= =，=，∴≠，∴△ ABG与△ DEF 不相似，所以②错误；∵S=?6?3=9，△ABGS△FGH= ?GH?HF= ×3×4=6，∴S△ABG=S△FGH，所以③正确；∵A G+DF=3+2=5，而 GF=5，∴AG+DF=GF，所以④正确．故答案为①③④．三、15．（﹣ 2016）0++tan45 °=1﹣ 2+1=0．16．2解：配方x ﹣ 2x+1=4+1∴x=1±∴x1=1+，x2=1﹣．四、17．解：（ 1）点 D 以及四边形ABCD另两条边如图所示．（2）得到的四边形A′B′C′D′如图所示．18．2n+1； 2n2+2n+1．五、19．解：过点D作 l 1的垂线，垂足为F，∵∠ DEB=60°，∠ DAB=30°，∴∠ ADE=∠DEB﹣∠ DAB=30°，∴△ ADE为等腰三角形，∴D E=AE=20，在 Rt△DEF中， EF=DE?cos60°=20× =10，∵D F⊥AF，∴∠ DFB=90°，∴AC∥DF，由已知 l 1∥l2，∴CD∥AF，∴四边形 ACDF为矩形， CD=AF=AE+EF=30，答： C、 D两点间的距离为 30m．20．解：（ 1）把点 A（ 4， 3）代入函数y=得：a=3×4=12，∴y= ．OA==5，∴O B=5，∴点 B 的坐标为（ 0，﹣ 5），把 B（0，﹣ 5）， A（ 4， 3）代入 y=kx+b 得：解得：∴y=2x﹣ 5．（2）∵点 M在一次函数 y=2x ﹣ 5 上，∴设点 M的坐标为（ x， 2x﹣ 5），∵MB=MC，∴解得： x=2.5 ，∴点 M的坐标为（ 2.5 ， 0）．六、21．解：（ 1）画树状图：共有 16 种等可能的结果数，它们是： 11，41，71，81，14，44，74，84，17，47，77，87，18， 48， 78， 88；（ 2）算术平方根大于 4 且小于 7 的结果数为 6，所以算术平方根大于 4 且小于 7 的概率== ．七、22．解：（ 1）将 A（ 2，4）与 B（6，0）代入 y=ax 2+bx，得，解得：；（2）如图，过 A 作 x 轴的垂直，垂足为 D（2， 0），连接 CD，过 C作 CE⊥AD，CF⊥x轴，垂足分别为 E， F，S△OAD=OD?AD= ×2×4=4；∵OA=OB，S△ACD= AD?CE= ×4×（ x﹣ 2） =2x﹣ 4；S△BCD= BD?CF= ×4×（﹣x2+3x）=﹣ x2+6x，则 S=S△OAD+S△ACD+S△BCD=4+2x﹣ 4﹣x2+6x= ﹣x2+8x，∴S关于 x 的函数表达式为 S=﹣ x2+8x（ 2＜x ＜ 6），∵S=﹣ x2+8x=﹣（ x﹣ 4）2+16，∴当 x=4 时，四边形 OACB的面积 S 有最大值，最大值为 16．∴∠ ARB=60°，∴△ ARB是等边三角形；②由（ 1）得， EQ=EP，∠ DEQ=∠CPE，∴∠ PEQ=∠CED﹣∠ CEP﹣∠ DEQ=∠ACE﹣∠CEP﹣∠ CPE=∠ACE﹣∠ RCE=∠ACR=90°，∴△ PEQ是等腰直角三角形，∵△ ARB∽△ PEQ，∴∠ ARB=∠PEQ=90°，∴∠ OCR=∠ODR=90°，∠CRD= ∠ARB=45°，∴∠ MON=135°，此时 P， O， B 在一条直线上，△ PAB 为直角三角形，且∠ APB=90°，∴AB=2PE=2×PQ= PQ，∴=．八、23．（1）证明：∵点C、 D、 E 分别是 OA，OB，AB的中点，∴DE=OC，∥ OC， CE=OD，CE∥OD，∴四边形 ODEC是平行四边形，∴∠ OCE=∠ODE，∵△ OAP，△ OBQ 是等腰直角三角形，∴∠ PCO=∠QDO=90°，∴∠PCE=∠PCO+∠OCE=∠QDO=∠ODQ=∠EDQ ，∵P C= AO=OC=ED， CE=OD= OB=DQ，在△ PCE与△ EDQ中，，∴△ PCE≌△ EDQ；（2）①如图2，连接 RO，∵PR与 QR分别是 OA， OB的垂直平分线，∴AP=OR=RB，∴∠ ARC=∠ORC，∠ ORQ=∠BRO，∵∠ RCO=∠RDO=90°，∠ COD=150°，∴∠ CRD=30°，（素材和资料部分来自网络，供参考。

安徽省2016年中考数学试题(附解析)

1.【答案】B. 【解析】试题分析：根据绝对值的性质可得-2的绝对值是2，故答案选B. 考点：绝对值. 2.【答案】C.考点：同底数幂的除法. 3.【答案】A. 【解析】试题分析：科学计数法是指：a ×n10，且101 a ，n 为原数的整数位数减一.8362万=83620000=8.362×107.故答案选A. 考点：科学计数法.4.【答案】C.【解析】试题分析：几何体的主视图是从正面看到的图形，圆柱从正面看是一个矩形，故答案选C. 考点：几何体的三视图.5.【答案】D.考点：解方式方程.6.【答案】C.【解析】试题分析：由题意可得2014年的财政收入为a(1+8.9%),2015年的财政收入为a(1+8.9%)（1+9.5%），所以b=a(1+8.9%)（1+9.5%），故答案选C.考点：列代数式.7.【答案】D.考点：扇形统计图；用样本估计总体.8.【答案】B. 【解析】试题分析：已知AD 是直线，BC=8，所以CD=4，又因∠B=∠DAC,∠C 为公共角，可得△ACD ∽Rt △BCA ，根据相似三角形的性质可得AC CD BC AC =,即ACAC 48=,解得AC=42，故答案选B.考点：相似三角形的判定及性质.9.【答案】A. 【解析】试题分析：由题意可知，甲图中休息半个小时，可排除选项B 、D,由题意可以计算出乙35小时到达终点，甲1小时到达B 处，休息半小时后再用半个小时到达终点，符合要求的选项只有A ，故答案选A. 考点：函数图像.10【答案】B.考点：最短距离问题.11.【答案】x ≥3. 【解析】试题分析：解不等式可得x ≥3. 考点：解不等式. 12.【答案】a （a+1）（a-1）. 【解析】试题分析：先提公因式a 后再利用平方差公式分解即可，即原式=a （a 2-1）=a （a+1）（a-1）. 考点：因式分解. 13.【答案】34.考点：切线的性质；弧长公式. 14.【答案】①③④. 【解析】试题分析：由折叠的性质可得BC=BF=10，CE=EF,AB=BH=8,AG=GH,∠CBE=∠FBE,∠ABG=∠HBG,因∠CBE+∠FBE+∠ABG+∠HBG=90°，所以∠HBG+∠FBE=40°,即∠EBG=45°，故①正确；在Rt △ABF 中，由勾股定理求得AF=8，所以DF=AD-AF=2，在Rt △DEF 中，设CE=EF=x,则DE=6-x ，由勾股定理得22262x x =-+）（，解得x=310，即CE=EF=310，DE=38；在Rt △GHF 中，设AG=GH=y,则GF=8-y ，HF=10-6=4,由勾股定理得222)8(4y y -=+，解得y=3，即GF=5；因∠A=∠D=90°，DFAGDE AB ≠,所以△DEF 与△ABG 不相似，故②错误；因9632121=⨯⨯=⋅=∆AB AG S ABG ,6432121=⨯⨯=⋅=∆HF GH S FGH ,所以ABG S ∆=FGH S ∆23，故③正确；因AG+DF=FG=5，所以④正确.故正确答案为①③④.考点：四边形综合题.15.【答案】0.考点：零指数幂；立方根；特殊角的三角函数值. 16.【答案】51,5121-+==x x . 【解析】试题分析：用配方法解方程即可.试题解析：考点：一元二次方程的解法.17.【答案】(1)详见解析；（2）详见解析.考点：轴对称作图；平移变换作图.18.【答案】(1)24,2n ；（2）2n+1，1222++n n .【解析】试题分析：(1)观察图形，得出规律，即可得答案；（2）中间这个数为2n-1+2=2n+1；由（1）的规律可得，原式=2n +2n+1+2n =1222++n n .试题解析：(1)24,2n ；（2）中间这个数为2n-1+2=2n+1；由（1）的规律可得，原式=2n +2n+1+2n =1222++n n .考点：规律探究题.19.【答案】30米.考点：解直角三角形的应用.20.【答案】(1)x y 12,y=2x-5;(2)(25,0).考点：待定系数法求函数解析式.21.【答案】(1)11、14、17、18、41、44、47、48、71、74、77、78、81、84、87、88；（2）83. 【解析】试题分析：(1)按顺序直接列举出所有的两位数即可；（2）找出这16个数中算术平方根大于4且小于7的两位数的个数，根据概率公式即可求得答案. 试题解析：考点：用列举法求概率. 22.【答案】(1)21-=a ,b=3;(2))62(82 x x x S +-=,16.试题解析：考点：二次函数的综合题.23.【答案】(1)详见解析；（2）①详见解析；②135°，2.（2）①连接OR，由已知可得PR、RQ分别是线段OA、OB的垂直平分线，根据线段垂直平分线的性质可得RA=RO=RB,∠ARC=∠ORC，∠ORD=∠BRQ，在四边形RCOD中，根据四边形的内角和为360°可求得∠PRQ=30°，所以∠ARB=2∠PRQ=60°，再由AR=RB 即可判定△ABR为等边三角形；②由（1）得EQ=PE,∠DEQ=∠CPE，由四边形CODE是平行四边形可得∠CED=∠COD=∠ACE，所以∠PEQ=∠CED-∠CEP-∠DEQ=∠ACE-∠CEP-1∠CPE=∠ACE-∠ACR=90°，由△ARB∽△PEQ可得∠ARB=90°，由（2）可得∠PRQ=2∠ARB=45°，在四边形RCOD 中，根据四边形的内角和为360°可求得∠MON=135°，由此可得P 、O 、B 三点共线，△APB 为直角三角形，根据直角三角形斜边的中线等于斜边的一半可得AB=2PE,在Rt △PEC 中，由勾股定理可得PE=22PQ,所以22222=⨯==PQPQ PQPE PQ AB . 试题解析：考点：三角形与四边形的综合题.。

2016安徽省中考数学试题及答案解析

2016年安徽省初中毕业学业考试数学试题解析本试卷共8大题，计23小题，满分150分，考试时间120分钟。

一、选择题（本大题共10小题，每小题4分，满分40分）每小题都给出代号为A 、B 、C 、D 的四个选项，其中只有一个是正确的，请把正确选项的代号写在题后的括号内，每一小题选对得4分，不选、选错或选出的代号超过一个的（不论是否写在括号内）一律得0分.1.（2016安徽，1，4分）下面的数中，与-3的和为0的是 ………………………….（）A.3B.-3C.31 D.31- 1. 解析：根据有理数的运算法则，可以把选项中的数字和－3相加，进行筛选只有选项A符合，也可以利用相反数的性质，根据互为相反数的两数和为0，必选－3的相反数3．解答：A ．点评：本题考查了有理数的运算、及其概念，理解有关概念，掌握运算法则，是解答此类题目的基础.2. （2016安徽，2，4分）下面的几何体中，主（正）视图为三角形的是（）A. B. C. D.2. 解析：根据这几个常见几何题的视图可知：圆柱的主视图是矩形，正方体的主视图是正方形，圆锥的主视图是三角形，三棱柱的主视图是宽相等两个靠着的矩形．解答：C ．点评：此题是由立体图形到平面图形，熟悉常见几何体的三视图，如果要求画出几何体的三视图，要注意它们之间的尺寸大小，和虚实线.3. （2016安徽，3，4分）计算32)2(x -的结果是（） A.52x - B. 68x - C.62x - D.58x - 3. 解析：根据积的乘方和幂的运算法则可得．解答：解：6323328)()2()2(x x x -=-=- 故选B ．点评：幂的几种运算不要混淆，当底数不变时，指数运算要相应的降一级，还要弄清符号，这些都是易错的地方，要熟练掌握，关键是理解乘方运算的意义. 4. （2016安徽，4，4分）下面的多项式中，能因式分解的是（）A.n m +2B. 12+-m mC. n m -2D.122+-m m 4. 解析：根据分解因式的方法，首先是提公因式，然后考虑用公式，如果项数较多，要分组分解，本题给出四个选项，问哪个可以分解，对照选项中的多项式，试用所学的方法分解．就能判断出只有D 项可以.解答：解：22)1(12-=+-m m m 故选D ．得分评卷人点评：在进行因式分解时，首先是提公因式，然后考虑用公式，（两项考虑用平方差公式，三项用完全平方公式，当然符合公式才可以.）如果项数较多，要分组分解，最后一定要分解到每个因式不能再分为止.5. （2016安徽，5，4分）某企业今年3月份产值为a 万元，4月份比3月份减少了10％，5月份比4月份增加了15％，则5月份的产值是（）A.（a -10％）（a +15％）万元B. a （1-10％）（1+15％）万元C.（a -10％+15％）万元D. a （1-10％+15％）万元5. 解析：根据4月份比3月份减少10﹪，可得4月份产值是（1－10﹪）a , 5月份比4月份增加15﹪，可得5月份产值是（1－10﹪）（1+15﹪）a , 解答：A ．点评：此类题目关键是弄清楚谁是“基准”，把“基准”看作“单位1”，在此基础上增加还是减少，就可以用这个基准量表示出来了.6. （2016安徽，6，4分）化简xxx x -+-112的结果是（） A.x +1 B. x -1 C.—x D. x6. 解析：本题是分式的加法运算，分式的加减，首先看分母是否相同，同分母的分式加减，分母不变，分子相加减，如果分母不同，先通分，后加减，本题分母互为相反数，可以化成同分母的分式加减．解答：解：x x x x x x x x x x x =--=--=---=1)1(11122 故选D ．点评：分式的一些知识可以类比着分数的知识学习，分式的基本性质是关键，掌握了分式的基本性质，可以利用它进行通分、约分，在进行分式运算时根据法则，一定要将结果化成最简分式．7. （2016安徽，7，4分）为增加绿化面积，某小区将原来正方形地砖更换为如图所示的正八边形植草砖，更换后，图中阴影部分为植草区域，设正八边形与其内部小正方形的边长都为a ，则阴影部分的面积为（） A.22a B. 32a C. 42a D.52a7. 解析：图案中间的阴影部分是正方形，面积是a 2，由于原来地砖更换成正八边形，四周一个阴影部分是对角线为a 的正方形的一半，它的面积用对角线积的一半来计算．解答：解：222242121a a a =⨯⨯+故选A ．点评：本题考查了正多边形的性质，关键要找出正八边形和原来正方形的关系，尽量用所给数据来计算.8. （2016安徽，8，4分）给甲乙丙三人打电话，若打电话的顺序是任意的，则第一个打电话给甲的概率为（） A.61 B. 31 C.21 D.32 8. 解析：第1个打电话给甲、乙、丙（因为次序是任意的）的可能性是相同的，所以第一个打电话给甲的概率是31．解答：故选B ．9. （2016安徽，9，4分）如图，A 点在半径为2的⊙O 上，过线段OA 上的一点P 作直线，与⊙O 过A 点的切线交于点B ，且∠APB=60°，设OP=x ，则△PAB 的面积y 关于x 的函数图像大致是（）9. 解析：利用AB 与⊙O 相切，△BAP 是直角三角形，把直角三角形的直角边表示出来，从而用x 表示出三角形的面积，根据函数解析式确定函数的图象．解答：解：∵AB 与⊙O 相切，∴∠BAP=90°， OP=x ，AP=2－x,∠BPA=60°，所以AB=)2(3x -，所以△APB 的面积2)2(23x y -=，（0≤x ≤2）故选D ．点评：此类题目一般都是根据图形性质，用字母表示出这个变量，把运动变化的问题转化成静止的.再根据函数的性质解答.有时变化过程的有几种情况，注意它们的临界值. 10. （2016安徽，10，4分）在一张直角三角形纸片的两直角边上各取一点，分别沿斜边中点与这两点的连线剪去两个三角形，剩下的部分是如图所示的直角梯形，其中三边长分别为2、4、3，则原直角三角形纸片的斜边长是（）A.10B.54C. 10或54D.10或17210. 解析：考虑两种情况．要分清从斜边中点向哪个边沿着垂线段过去裁剪的. 解答：解：如下图，54)44()22(22=++⨯，1054)44()32(22=++⨯故选C ．点评：在几何题没有给出图形时，有的同学会忽略掉其中一种情况，错选A 或B ；故解决本题最好先画出图形，运用数形结合和分类讨论的数学思想进行解答，避免出现漏解．二、填空题（本大题共4小题，每小题5分，满分20分）11. （2016安徽，11，5分）2015年安徽省棉花产量约378000吨，将378000用科学计数法表示应是______________.11. 解析：科学记数法形式：a ×10n （1≤|a |＜10，n 为整数）中n 的值是易错点，由于378 000有6位，所以可以确定n =6﹣1=5，所以378 000=3.78×105 答案： 3.78×105 12. （2016安徽，12，5分）甲乙丙三组各有7名成员，测得三组成员体重数据的平均数都是58，方差分别为362=甲S ，252=乙S ，162=丙S ，则数据波动最小的一组是___________________.12. 解析：平均数是反映数据集中趋势的特征量，方差反映数据离散程度的特征量，由于平均数相等，方差越大，说明数据越离散，波动越大，方差越小，说明数据越集中，波动越小.丙组方差最小，波动最小. 答案：丙组13. （2016安徽，13，5分）如图，点A 、B 、C 、D 在⊙O 上，O 点在∠D 的内部，四边形OABC 为平行四边形，则∠OAD+∠OCD=_______________°.13. 解析：根据同圆中同弧所对的圆周角是圆心角的一半，所以∠AOC=2∠D ；又因为四边形OABC 是平行四边形，所以∠B=∠AOC ；圆内接四边形对角互补，∠B+∠D=180°，所以∠D= 60°，连接OD ，则OA=OD,OD=OC,∠OAD=∠ODA,∠OCD=∠ODC,即有∠OAD+∠OCD=60°. 答案：60．点评：本题是以圆为背景的几何综合题，在圆内圆周角和圆心角之间的关系非常重要，经常会利用它们的关系来将角度转化，另外还考查了平行四边形对角相等，圆内接四边形对角互补，以及等腰三角形的性质.解决此类题目除了数学图形的性质，还要学会识图，做到数形结合.14. （2016安徽，14，5分）如图，P 是矩形ABCD 内的任意一点，连接PA 、PB 、PC 、PD ，得到△PAB 、△PBC 、△PCD 、△PDA ，设它们的面积分别是S 1、S 2、S 3、S 4，给出如下结论： ①S 1+S 2=S 3+S 4 ② S 2+S 4= S 1+ S 3③若S 3=2 S 1，则S 4=2 S 2 ④若S 1= S 2，则P 点在矩形的对角线上得分评卷人其中正确的结论的序号是_________________（把所有正确结论的序号都填在横线上）. 14. 解析：过点P 分别向AD 、BC 作垂线段，两个三角形的面积之和42S S +等于矩形面积的一半，同理，过点P 分别向AB 、CD 作垂线段，两个三角形的面积之和31S S +等于矩形面积的一半. 31S S +=42S S +,又因为21S S =，则32S S +=ABCD S S S 2141=+,所以④一定成立答案：②④．点评：本题利用三角形的面积计算，能够得出②成立，要判断④成立，在这里充分利用所给条件，对等式进行变形.不要因为选出②，就认为找到答案了，对每个结论都要分析，当然感觉不一定对的，可以举反例即可.对于 ④这一选项容易漏选.三、（本大题共2小题，每小题8分，满分16分）15. （2016安徽，15，8分）计算：)2()1)(3(-+-+a a a a15. 解析：根据整式的乘法法则，多项式乘多项式时，用其中一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加；单项式乘多项式，可以按照乘法分配率进行．最后再根据合并同类项法则进行整式加减运算.解：原式=a 2－a+3a －3+a 2－2a =2a 2－3 16. （2016安徽，16，8分）解方程：1222+=-x x x16. 解析：根据一元二次方程方程的几种解法，本题不能直接开平方，也不可用因式分解法.先将方程整理一下，可以考虑用配方法或公式法.解：原方程化为：x 2－4x=1配方，得x 2－4x+4=1+4 整理，得（x －2）2=5∴x －2=5±,即521+=x ，522-=x .四、（本大题共2小题，每小题8分，满分16分）17. （2016安徽，17，8分）在由m ×n （m ×n ＞1）个小正方形组成的矩形网格中，研究它的一条对角线所穿过的小正方形个数f ，（1）当m 、n 互质（m 、n 除1外无其他公因数）时，观察下列图形并完成下表：mnm n +f1 2 3 2 1 3 4 3 2 3 5 4 2 4 7 3 5 7猜想：当m 、n 互质时，在m ×n 的矩形网格中，一条对角线所穿过的小正方形的个数f 与m 、n 的关系式是______________________________（不需要证明）；解：（2）当m 、n 不互质时，请画图验证你猜想的关系式是否依然成立， 17：解析：（1）通过题中所给网格图形，先计算出2×5，3×4，对角线所穿过的小正方形个数f ，再对照表中数值归纳f 与m 、n 的关系式.（2）根据题意，画出当m 、n 不互质时，结论不成立的反例即可. 解：（1）如表：f=m+n-1（2）当m 、n 不互质时，上述结论不成立，如图2× 42×418. （2016安徽，18，8分）如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC （顶点是网格线的交点）和点A1.（1）画出一个格点△A1B1C1，并使它与△ABC 全等且A 与A1是对应点；m n m n f 1 2 3 2 1 3 4 32 3 5 4 2 4 7 6 3 5 7 6（2）画出点B关于直线AC的对称点D，并指出AD可以看作由AB绕A点经过怎样的旋转而得到的.解:18.解析：（1）考查全等变化，可以通过平移、旋转、轴对称等来完成；（2）先作出图形，因为要回答旋转角度，利用方格纸算出AB、AD、BD的长度，再计算角度.解：（1）答案不唯一，如图，平移即可2(2)作图如上，∵AB=10，AD=10，BD=5∴AB2+AD2=BD2 新课标一网∴△ABD是直角三角形，AD可以看作由AB绕A点逆时针旋转90°得到的.点评：图形变换有两种，全等变换和相似变换，掌握每种变换的概念、性质是作图的基础，一般难度不大.五、（本大题共2小题，每小题10分，满分20分）2，求19. （2016安徽，19，10分）如图，在△ABC中，∠A=30°，∠B=45°，AC=3C45°30°ABAB 的长，解：19. 解析：本题在一个三角形中已知两个角和一边，求三角形的边.不是直角三角形，要利用三角函数必须构筑直角三角形，过点C 作CD ⊥AB 于D,利用构造的两个直角三角形来解答. 解:过点C 作CD ⊥AB 于D,在Rt △ACD 中，∠A=30°，AC=32 ∴CD=AC ×sinA=32×0.5=3，AD=AC ×cosA=32×23=3，在Rt △BCD 中，∠B=45°，则BD=CD=3， ∴AB=AD+BD=3+3点评：解直角三角形中，除了直角外，还知道两个元素（至少有一个是边），就能求出其余的边和角. 一般三角形中，知道三个元素（至少有一个是边），就能求出其余的边和角. 这时将三角形转化为直角三角形时，注意尽量不要破坏所给条件.20. （2016安徽，20，10分）九（1）班同学为了解2015年某小区家庭月均用水情况，随月均用水量x (t) 频数(户) 频率05x <≤ 6 0.12510x <≤ 0.241015x <≤ 16 0.321520x <≤ 10 0.20 2025x <≤ 4 2530x <≤ 2 0.04 请解答以下问题：（1）把上面的频数分布表和频数分布直方图补充完整；（2）若该小区用水量不超过15t 的家庭占被调查家庭总数的百分比；解：（3）若该小区有1000户家庭，根据调查数据估计，该小区月均用水量超过20t 的家庭大约有多少户？解：20. 本题考查了数据的统计中的频数分布表和不完整的频数分布直方图.所有的频数和就是样本容量，所有频率和等于1，且有n数据总数频数频率=，（1）数据总数5012.06===频率频数，50×0.24=12，4÷50=0.08，（2）用水量不超过15吨是前三组，（0.12+0.24+0.32）×100﹪=68﹪第20题图月用水量(t)（3）用样本来估计总体，根据抽取的样本超过20吨的家庭数，来估计该小区的情况.. 解：（1）统计中的频数分布表和不完整的频数分布直方图，补充如下（2）用水量不超过15吨是前三组，（0.12+0.24+0.32）×100﹪=68﹪ （3）1000×（0.04+0.08）=120（户）六、（本题满分12分）21. （2016安徽，21，12分）甲、乙两家商场进行促销活动，甲商场采用“慢200减100”的促销方式，即购买商品的总金额满200元但不足400元，少付100元；满400元但不足600元，少付200元；……，乙商场按顾客购买商品的总金额打6折促销。

2016安徽中考数学试题及答案大全_数学难易程度怎样

2016安徽中考数学试题及答案大全_数学难易程度怎样
2016安徽中考数学考试结束,中国教育在线在考试后及时公布安徽中考试题、答案和中考作文。

那么首先来看看2016安徽中考数学的试题以及答案吧，大家看看有没有难度。

2016年安徽省中考数学试题及答案
2016年安徽中考数学试卷难易程度调查合肥部分考生认为较难
今天上午，2016年安徽中考数学科目开考。

据悉，昨日的语文考试试卷整体不难，那么今天的数学考试试卷难吗?据合肥42中考点，提前交卷的个别考生透露，数学试卷较难。

小编做个小调查，今年中考数学试题难不难，欢迎来吐槽。

6月15日，中考进入第二天。

相比前一天的骄阳似火，昨天的天气算是相当“给力”，让等候在考场外的家长们也觉得轻松不少。

题目难易方面，考生们普遍觉得，数学大题有点难度，历史政治很轻松。

昨日下午，在合肥50中新区天鹅湖校区考点外，没有烈日，陪考的家长明显比第一天多不少。

上午11点左右，数学考试结束，不少考生一出大门就互相询问。

“最后一题做出来没有?”合肥宁溪中学考生王同学告诉记者，这次数学感觉有点难，尤其是最后一题。

“是一道几何解析题，关于正三角形的，我没有做出来。

”50中东区的李同学也表示，数学前面的题目还好，后面几道大题有点难度，自己没有全部答出来。

相比数学，下午的政治历史则让考生和家长轻松不少，走出考场的考生大部分是满面笑容。

“历史和政治都不难，政治有些大题要想一想，选择题也有难度。

”考生刘同学告诉记者，历史最后一道大题是关于外交政策的，不过自己正好复习到了，觉得答得还可以。

考生小秦则觉得历史比政治还要简单一些。