蒙特卡罗算法
蒙特卡洛启发式算法

蒙特卡洛启发式算法简介蒙特卡洛启发式算法(Monte Carlo Heuristic Algorithm)是一种基于随机模拟的优化算法,用于解决各种复杂问题。
它通过进行大量的随机采样和模拟,以得到问题的近似解。
蒙特卡洛启发式算法在许多领域都有广泛的应用,如计算机科学、统计学、物理学等。
原理蒙特卡洛启发式算法的原理是基于概率统计和随机采样。
它通过生成大量的随机样本,并对这些样本进行模拟运行,以得到问题的近似解。
这些样本通常是根据某种概率分布生成的,并且可以根据具体问题进行调整。
蒙特卡洛启发式算法通常包含以下步骤:1.建立模型:首先需要将问题转化为一个数学模型。
这个模型可以是一个数学函数、一个概率分布或者一个状态转移矩阵。
2.生成样本:根据建立的模型,生成大量的随机样本。
这些样本可以是从某个概率分布中抽取得到的,也可以是根据某种规则生成的。
3.模拟运行:对于每个生成的样本,进行模拟运行。
根据具体问题,可以进行一系列的计算、判断和决策,以得到问题的近似解。
4.统计结果:统计模拟运行得到的结果。
可以计算平均值、方差、置信区间等统计指标,以评估问题的解。
5.优化调整:根据统计结果,对模型进行优化调整。
可以调整概率分布的参数、改变模型结构或者调整采样策略等。
6.迭代循环:重复以上步骤,直到达到预定的停止条件。
通常情况下,蒙特卡洛启发式算法需要进行多次迭代才能得到较好的解。
应用领域蒙特卡洛启发式算法具有广泛的应用领域,以下是一些常见领域的应用示例:1. 计算机科学蒙特卡洛启发式算法在计算机科学领域有着广泛的应用。
例如,在人工智能中,可以使用蒙特卡洛树搜索(Monte Carlo Tree Search)来改进搜索算法,在图像处理中,可以使用蒙特卡洛积分(Monte Carlo Integration)来估计图像的属性。
2. 统计学蒙特卡洛启发式算法在统计学中具有重要的地位。
例如,在统计推断中,可以使用蒙特卡洛马尔可夫链(Markov Chain Monte Carlo)方法来进行参数估计和模型选择。
蒙特卡罗算法

蒙特卡洛算法算法简介:蒙特·卡罗方法(Monte Carlo method),也称统计模拟方法,是二十世纪四十年代中期由于科学技术的发展和电子计算机的发明,而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。
是指使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。
蒙特·卡罗方法的名字来源于摩纳哥的一个城市蒙地卡罗,该城市以赌博业闻名,而蒙特·卡罗方法正是以概率为基础的方法。
与它对应的是确定性算法。
蒙特·卡罗方法在金融工程学,宏观经济学,计算物理学(如粒子输运计算、量子热力学计算、空气动力学计算)等领域应用广泛。
背景知识:蒙特卡洛是摩纳哥公国第一大城市,与澳门、美国拉斯维加斯并称世界三大赌城。
位于地中海沿岸,首都摩纳哥之北,建于阿尔卑斯山脉突出地中海的悬崖之上。
景色优美,是地中海地区旅游胜地。
市内建有豪华的旅馆、俱乐部、歌剧院、商店、游泳池、温泉浴室、运动场等娱乐设施。
城内开设有蒙特卡洛大赌场。
赌场建于1865年,为双层楼建筑,上有钟楼、塔厅和拱形亭阁,还饰以若干人物雕塑,庭前棕榈树成行,还辟有花园,旁边有大酒店和酒吧间。
整个城市在旺季时,约有赌场70多个,约有赌室3500间左右。
蒙特卡罗赌场由国家经营。
当地的其他活动,许多也带有赌博色彩。
游客住的旅店房间,有抽奖的号码,中奖的免付部分房费。
早餐的牛奶麦片粥里,如遇上金属牌子,亦可领奖。
该城只有1万人口,但每天报纸销量可达100万份,因为报纸上都印有可能得奖的号码。
游客最后离境,购买的车票上也印有彩票号码,于离境前开彩。
经营赌业是摩纳哥的主要经济来源,每年都从赌业中收取高额外汇利润。
蒙特卡洛算法简单描述:以概率和统计理论方法为基础的一种计算方法。
将所求解的问题同一定的概率模型相联系,用计算机实现统计模拟或抽样,以获得问题的近似解。
比如,给定x=a,和x=b,你要求某一曲线f和这两竖线,及x轴围成的面积,你可以起定y轴一横线y=c 其中c>=f(a) and c>=f(b),很简单的,你可以求出y=c,x=a,x=b,及x轴围成的矩形面积,然后利用随机参生生大量在这个矩形范围之类的点,统计出现在曲线上部点数和出现在曲线下部点的数目,记为:doteUpCount,nodeDownCount,然后所要求的面积可以近似为doteDownCounts所占比例*矩形面积。
主元素问题蒙特卡洛算法

主元素问题蒙特卡洛算法1. 引言主元素问题是一个在计算机科学领域中常见的问题,涉及到数学和算法。
在一个包含n个元素的数组中,如果某个元素的出现次数超过n/2,那么这个元素就被称为主元素。
主元素问题的解决方法有很多,其中之一就是蒙特卡洛算法。
2. 蒙特卡洛算法概述蒙特卡洛算法是一种基于概率统计的算法,通过模拟重复实验来解决问题。
它通常使用随机数来进行模拟,通过大量的模拟实验来估计问题的概率或得到问题的近似解。
在主元素问题中,蒙特卡洛算法可以用来判断一个给定的元素是否为主元素。
3. 蒙特卡洛算法解决主元素问题3.1 算法思想蒙特卡洛算法解决主元素问题的思想很简单,就是随机选择数组中的元素并判断其是否为主元素,通过多次重复实验来得到一个概率估计。
具体步骤如下:1.随机选择数组中的一个元素;2.在数组中计算该元素的出现次数;3.判断该元素的出现次数是否超过n/2;4.重复上述步骤多次,取所有实验中判断为主元素的元素中出现次数最多的作为最终的估计结果。
3.2 算法实现下面是蒙特卡洛算法解决主元素问题的实现代码(使用Python语言):import randomdef monte_carlo_majority(arr):n = len(arr)experiments = 1000experiment_results = []for _ in range(experiments):random_index = random.randint(0, n-1)random_element = arr[random_index]count = arr.count(random_element)if count > n/2:experiment_results.append(random_element)if len(experiment_results) == 0:return Nonemax_count = 0majority_element = Nonefor element in experiment_results:count = arr.count(element)if count > max_count:max_count = countmajority_element = elementreturn majority_element4. 算法分析与复杂度4.1 算法正确性分析蒙特卡洛算法解决主元素问题的正确性可以通过概率统计的方法来进行分析。
马尔可夫链蒙特卡洛算法

马尔可夫链蒙特卡洛算法
马尔可夫链蒙特卡洛算法(Markov Chain Monte Carlo,
MCMC算法)是一类经典的统计模拟方法,用于从复杂的概
率分布中进行抽样,以求解各种统计问题。
MCMC算法的核心是利用马尔可夫链的性质进行概率抽样。
具体步骤如下:
1. 确定目标分布:首先需要确定所要抽样的目标分布,通常是在计算困难的概率模型中计算概率密度(或概率质量)函数的常数比例。
2. 构建马尔可夫链:构建一个马尔可夫链,使得其平稳分布等于目标分布。
常见的马尔可夫链包括Metropolis-Hastings算法、Gibbs采样等。
3. 进行迭代抽样:从适当的初始状态开始,根据马尔可夫链的转移规则进行迭代。
每次迭代都根据当前状态和转移规则生成一个新的候选状态,接受或者拒绝该状态作为下一步的状态,通过计算接受概率等条件转移概率来决定是否接受。
4. 收敛检验:经过充分迭代后,进行收敛检验,判断抽样结果是否已经达到平稳分布,通常使用自相关函数等进行检验。
5. 统计分析:使用抽样结果进行统计分析,例如估计分布的均值、方差等参数。
MCMC算法具有广泛的应用,如蒙特卡洛积分、贝叶斯统计、马尔可夫链模型参数估计等。
但是,MCMC算法的主要困难
在于如何构建合适的马尔可夫链、如何设置收敛准则以及如何处理高维空间中的抽样问题。
蒙特卡洛算法的应用及原理

蒙特卡洛算法的应用及原理简介蒙特卡洛算法(Monte Carlo algorithm)起初是由数学家冯·诺依曼(John von Neumann)和斯坦尼斯拉夫·乌拉姆(Stanislaw Ulam)在20世纪40年代末引入的一种计算方法,利用随机数模拟求解问题。
蒙特卡洛算法在物理学、金融学、计算机科学等领域被广泛应用,尤其在复杂的计算问题上具有较高的效率和准确度。
原理蒙特卡洛算法的核心思想是通过随机采样和统计分析获得问题的近似解,而不是通过解析求解等传统计算方法。
其基本流程如下: 1. 确定问题的范围和目标。
2. 设计合适的模型并确定输入参数。
3. 生成符合模型要求的随机数,并进行实验或模拟。
4. 统计实验或模拟结果,得到问题的近似解。
5. 根据需要,调整模型和参数,并重复上述步骤,直到达到预期的结果。
应用领域蒙特卡洛算法在各个领域得到了广泛应用,以下列举几个常见的应用场景。
1. 物理学蒙特卡洛算法在物理学领域的应用非常广泛。
例如,在计算粒子物理学中,科学家利用蒙特卡洛算法模拟高能粒子在加速器中的相互作用,以研究粒子的行为和性质。
此外,蒙特卡洛算法还可以用于计算电磁场、热传导和量子力学等问题。
2. 金融学在金融学中,蒙特卡洛算法被用于评估金融产品的风险和收益。
例如,在期权定价中,可以使用蒙特卡洛模拟来估计期权的价值和价格。
此外,蒙特卡洛算法还可以应用于投资组合优化、风险管理和股票价格预测等方面。
3. 计算机科学蒙特卡洛算法在计算机科学中也有广泛的应用。
例如,在人工智能领域,蒙特卡洛树搜索算法被用于博弈论和决策树的建模。
此外,蒙特卡洛算法还可以应用于随机算法设计、优化问题求解和机器学习等方面。
4. 统计学蒙特卡洛算法在统计学中被用于参数估计和假设检验。
通过生成服从特定分布的随机样本,可以对未知参数进行统计推断。
此外,蒙特卡洛算法还可用于模拟数据、计算置信区间和进行统计模型的评估等。
蒙特卡洛树算法 ucb1算法公式两项的含义

蒙特卡洛树算法ucb1算法公式两项的含义摘要:一、蒙特卡洛树算法(MCTS)简介二、UCB1算法原理及公式含义1.探索与利用的平衡2.公式推导与解释三、MCTS在实际应用中的优势与局限四、总结与展望正文:一、蒙特卡洛树算法(MCTS)简介蒙特卡洛树算法(Monte Carlo Tree Search,简称MCTS)是一种随机模拟算法,广泛应用于博弈、机器学习等领域。
它通过多次随机模拟进行搜索,逐步构建一颗搜索树,并根据搜索树的结果来选择最优策略。
MCTS算法在每一步都会重复进行多次随机模拟,对每个状态进行探索,并选择具有较高UCB1值的策略。
二、UCB1算法原理及公式含义1.探索与利用的平衡UCB1(Upper Confidence Bound 1)算法在MCTS中起到平衡探索与利用的作用。
探索是指尝试新的状态或策略,以发现更好的结果;利用则是对已有的状态或策略进行重复试验,以提高结果的准确性。
UCB1算法在每一步通过计算每个状态的期望回报,平衡探索与利用的关系。
2.公式推导与解释UCB1算法的核心公式如下:π_i = argmax_a (Q_i(a) + c * √(N_i(a) * log(N)))其中,π_i表示在第i次迭代时选择的动作;Q_i(a)表示状态i下选择动作a的期望回报;N_i(a)表示状态i下选择动作a的试验次数;N表示总的试验次数;c为调节探索与利用的参数。
公式中的第一部分Q_i(a)表示利用已有数据得到的期望回报,第二部分√(N_i(a) * log(N))表示探索部分,随着试验次数的增加,探索部分逐渐减小,以实现探索与利用的平衡。
三、MCTS在实际应用中的优势与局限1.优势:- 适用于大规模问题,因为MCTS可以在每次迭代中快速剪枝,减少计算量。
- 能应对动态环境,因为MCTS可以根据新数据不断更新策略。
- 具有较好的泛化能力,因为MCTS通过随机模拟进行搜索,能较好地处理不确定性问题。
蒙特卡洛算法及简单应用

蒙特卡洛算法及简单应用蒙特卡洛算法是一种随机模拟算法,起源于1950年代,在计算机模拟方面的应用非常广泛。
蒙特卡洛算法采用概率的方法通过重复随机抽样来解决问题,因此具有很强的泛化能力和普适性,适用于不同领域中的各种问题。
蒙特卡洛算法的基本思想是利用随机数模拟真实情况,通过模拟实验来获取实验结果,从而得到问题的解。
一般而言,蒙特卡洛算法分为三个步骤:1. 构造模型:将问题抽象成一个数学模型;2. 随机化:对模型进行随机化,生成随机数,使结果具有随机性;3. 收集结果:重复多次实验,得到多组随机结果,进行统计分析,得到最终的结果。
蒙特卡洛算法的原理非常简单,但其应用却是非常广泛、复杂和深入的,几乎涵盖了所有数学、物理、化学、生物等科学领域。
下面我们将分别介绍几个蒙特卡洛算法的简单应用,以便更好地理解蒙特卡洛算法的奥妙。
一、蒙特卡洛方法在积分计算中的应用在数学中,积分是一种非常重要的运算方式,它可以求出曲线下面的面积、弧长甚至是体积等。
对于复杂的积分,解析解不一定存在,因此需要采用数值积分方法求解,而蒙特卡洛算法就是其中之一。
通过蒙特卡洛方法进行积分计算的基本思路是:将积分问题转换成随机抽样问题,然后通过采样得到一组随机数值,利用该样本进行统计分析和计算,得到最终结果。
这种方法的优点在于可以精确、有效地解决复杂积分计算问题,避免了解析解无法求得时出现的问题。
二、蒙特卡洛方法在股票估价中的应用金融领域是蒙特卡洛方法的主要应用领域之一,其中股票价格的预测是蒙特卡洛算法的主要应用之一。
在股票交易中,涨跌幅度的大小是多变的,而且具有不确定性,因此用蒙特卡洛模拟方法模拟股票变化时,必须加入随机性,来反应真实的情况。
过程如下:首先需要对股票的走势模型建模,模型可以是布朗运动模型、几何布朗运动模型等;接着,根据模型和实际数据生成随机变量;最后,根据这些随机变量得到一个随机路径,并且对一段时期的随机路径进行平均计算,从而得到股价的预测范围。
蒙特卡洛(Monte Carlo)算法
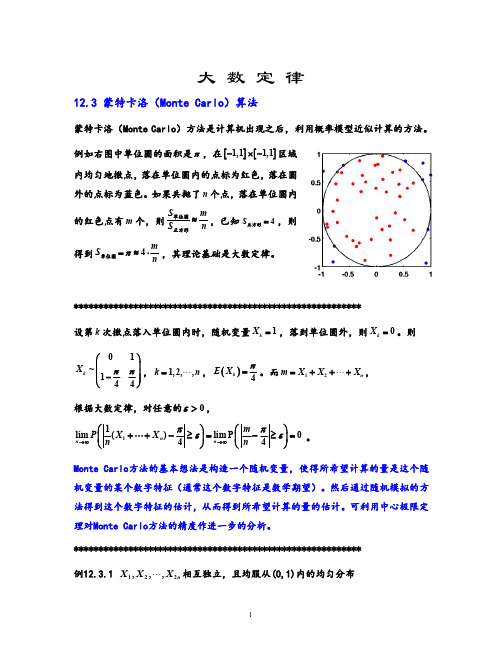
大数定律12.3蒙特卡洛(Monte Carlo)算法蒙特卡洛(Monte Carlo)方法是计算机出现之后,利用概率模型近似计算的方法。
例如右图中单位圆的面积是π,在[][]1,11,1-⨯-区域内均匀地撒点,落在单位圆内的点标为红色,落在圆外的点标为蓝色。
如果共抛了n 个点,落在单位圆内的红色点有m 个,则S mS n ≈单位圆正方形,已知4S =正方形,则得到4m S nπ=≈⋅单位圆,其理论基础是大数定律。
**********************************************************设第k 次撒点落入单位圆内时,随机变量1k X =,落到单位圆外,则0k X =。
则01~144k X ππ⎛⎫ ⎪ ⎪- ⎪⎝⎭,1,2,,k n = ,()4k E X π=。
而12n m X X X =+++ ,根据大数定律,对任意的0>ε,11lim ()lim P 044n n n m P X X n n ππεε→∞→∞⎛⎫⎛⎫++-≥=-≥= ⎪ ⎪⎝⎭⎝⎭。
Monte Carlo方法的基本想法是构造一个随机变量,使得所希望计算的量是这个随机变量的某个数字特征(通常这个数字特征是数学期望)。
然后通过随机模拟的方法得到这个数字特征的估计,从而得到所希望计算的量的估计。
可利用中心极限定理对Monte Carlo方法的精度作进一步的分析。
**********************************************************例12.3.1n X X X 221,,, 相互独立,且均服从(0,1)内的均匀分布⎩⎨⎧<+=-其他,01,422212k k k X X Y ,n k ,,2,1 =,(1)对任意给定的正整数n ,证明nY Y Y Y n +++= 21的期望为π;(2)用中心极限定理估计100n =时,()1.0<-πY P ;(3)用切比雪夫不等式估计,n 取多大时,可保证()9.01.0≥<-πY P 。
马尔可夫链蒙特卡洛算法

马尔可夫链蒙特卡洛算法简介马尔可夫链蒙特卡洛算法(Markov Chain Monte Carlo,MCMC)是一种基于马尔可夫链的随机模拟方法,用于解决概率统计中的各种问题。
它通过从概率分布中采样来近似计算数学期望、方差和其他统计量。
MCMC在统计学、物理学、机器学习等领域都有广泛应用。
马尔可夫链马尔可夫链是一种随机过程,具有无记忆性质。
在一个离散的时间序列中,每个状态的转移只依赖于前一个状态,而与其他状态无关。
这个性质被称为马尔可夫性质。
马尔可夫链可以用一个状态空间和一个转移矩阵来描述。
状态空间是所有可能的状态的集合,转移矩阵则描述了从一个状态转移到另一个状态的概率。
蒙特卡洛方法蒙特卡洛方法是一类基于随机采样的数值计算方法。
它通过生成大量随机样本来近似计算复杂问题的解。
蒙特卡洛方法通常具有简单易实现、适用范围广等优点。
MCMC算法马尔可夫链蒙特卡洛算法是一种基于马尔可夫链的蒙特卡洛方法。
它通过构建一个满足平稳分布的马尔可夫链,然后从该马尔可夫链中采样得到样本,从而近似计算目标分布的统计量。
MCMC算法的核心思想是通过马尔可夫链的状态转移来实现采样。
具体而言,我们需要定义一个接受概率函数,来决定当前状态是否接受转移到下一个状态。
这个接受概率函数通常与目标分布有关,可以通过贝叶斯定理得到。
MCMC算法的步骤如下: 1. 初始化:选择一个初始状态。
2. 迭代:根据当前状态和转移矩阵进行状态转移。
3. 接受:根据接受概率函数决定是否接受新状态。
4. 重复:重复步骤2和步骤3直到达到设定的迭代次数。
在迭代过程中,由于马尔可夫链具有无记忆性质,最终会收敛到平稳分布。
我们可以利用这个性质来近似计算目标分布的统计量。
应用举例MCMC算法在很多领域都有广泛应用。
以下是一些常见的应用举例:贝叶斯统计推断MCMC算法可以用于贝叶斯统计推断,通过从后验分布中采样来近似计算参数的分布。
这对于复杂的概率模型非常有用,因为往往无法直接求解后验分布。
metropolis 蒙特卡洛算法

metropolis 蒙特卡洛算法Metropolis蒙特卡罗算法是一种基于概率分布的随机采样算法,广泛应用于统计物理学、计算化学和机器学习等领域。
该算法通过赋予每个状态一个能量值,并随机采样生成下一个状态,根据采样出的新状态的能量和当前状态能量间的比较,以一定的概率接受或拒绝新状态,最终达到从概率分布中随机采样的目的。
以下是Metropolis蒙特卡罗算法的详细步骤:1. 定义问题:将问题转化为一个概率分布,设定初始状态首先需要将问题转化为一个概率分布,也就是定义系统状态的空间,并且给出每个状态的概率。
例如,在一个2D格点上,每个格点上可以有一个粒子或者没有粒子,我们可以定义一个概率分布,表示每个格点上粒子的存在概率。
接着,需要设定一个初始状态,也就是从哪个状态开始采样。
2. 采样新状态在设定好初始状态后,需要采样一个新的状态。
采样方式可以是随机的,也可以是根据某种采样规则生成,例如在格点系统中,可以随机选择一个粒子,随机将其移动到周围的一个格点上。
3. 计算新状态的能量在确定了新状态后,需要计算新状态的能量,并将其与当前状态比较。
这里,能量可以根据实际问题的物理特性定义。
在格点系统中,能量可以定义为粒子之间的相互作用能,或者粒子与外部势场的相互作用能。
4. 判断是否接受新状态在计算出新状态的能量之后,需要根据接受准则,决定是否接受新状态。
接受准则通常是基于Metropolis-Hastings算法的接受准则来定义的,即:设当前状态的能量为E,新状态的能量为E',则新状态被接受的概率为min(1, [P(E')/P(E)][Q(E|E')/Q(E'|E)])。
其中,P(E)表示当前状态的概率,P(E')表示新状态的概率,Q(E|E')表示给定新状态,接受状态为当前状态的概率,Q(E'|E)表示给定当前状态,接受状态为新状态的概率。
根据接受准则,当随机生成的数小于接受概率时,就接受新状态,否则拒绝新状态,继续沿用当前状态。
蒙洛卡特算法

蒙洛卡特算法蒙洛卡特算法是一种基于随机抽样技术的数值计算方法,广泛应用于风险评估、金融衍生品定价、物理模拟等众多领域。
本文将对蒙洛卡特算法的原理、应用以及优势进行介绍。
一、蒙洛卡特算法原理蒙特卡洛算法是一种随机化算法,基于随机抽样的方法获取样本来求解问题。
直接蒙特卡洛算法是一种非常原始的方法,将问题转化为一个期望值,使用随机抽样的方法进行估计。
而蒙洛卡特算法则是通过改进直接蒙特卡洛算法,使得随机抽样的效率更高。
具体来说,蒙洛卡特算法首先通过随机抽样的方法生成多个独立的随机数序列,这些序列称为样本。
然后,将这些样本输入到函数中进行计算,最后对计算结果进行统计分析得到估计值。
蒙洛卡特算法有以下几个特点:1. 独立性。
样本之间应该是相互独立的,这意味着每个样本都是完全独立于其他样本的,并且可以多次使用。
2. 随机性。
随机抽样的过程应该是完全随机的,这意味着每个样本的值应该是随机的,并且应该具有相同的概率分布。
3. 代表性。
样本应该是代表性的,这意味着样本的数量应该足够大,以及样本应该来自于整个概率分布的区域。
4. 收敛性。
当样本数量足够大时,蒙洛卡特算法会收敛于真值。
二、蒙洛卡特算法应用1. 风险评估。
用蒙洛卡特算法进行风险评估,可以帮助投资者更加准确地评估投资的风险。
2. 金融衍生产品定价。
蒙洛卡特算法可以帮助金融衍生产品的定价,例如期权、期货等。
3. 物理模拟。
使用蒙洛卡特算法可以模拟物理系统,例如量子场论、蒙特卡洛模拟等。
4. 优化模型。
蒙洛卡特算法可以用于优化模型,例如寻找一个函数的最小值或最大值。
三、蒙洛卡特算法优势1. 可分布计算。
蒙洛卡特算法允许在分布式计算环境下运行,这使得它能够利用并行计算的优势来提高计算效率。
2. 适应高维数据。
相比于其他的数值计算方法,蒙洛卡特算法在处理高维数据时表现更加优秀。
3. 不要求导数。
相比较于一些需要求导数的数值计算方法,例如最优化算法和差分方程算法,蒙洛卡特算法不需要对函数进行求导。
蒙特卡洛算法

蒙特卡洛算法主要用在求解最优化模型(多约束非线性规划问题)上,图像采样的问题,是以一系列随机数来模拟过程,解决问题的算法,但是求解时间很长。
以概率和统计理论方法为基础的一种计算方法。
将所求解的问题同一定的概率模型相联系,用计算机实现统计模拟或抽样,以获得问题的近似解。
步骤:Step1,根据提出的问题构造一个简单、适用的概率模型或随机模型,使问题的解对应于该模型中随机变量的某些特征(如概率、均值和方差等),所构造的模型在主要特征参量方面要与实际问题或系统相一致。
比如在多约束非线性规划问题问题中,采用的是unifrnd函数。
Step2,根据模型中各个随机变量的分布,在计算机上产生随机数,实现一次模拟过程所需的足够数量的随机数。
通常先产生均匀分布的随机数,然后生成服从某一分布的随机数,进行随机模拟试验。
Step3,根据概率模型的特点和随机变量的分布特性,设计和选取合适的抽样方法,并对每个随机变量进行抽样(包括直接抽样、分层抽样、相关抽样、重要抽样等)。
比如在多约束非线性规划问题问题中,采用的是循环随机抽样。
Step4,按照所建立的模型进行仿真试验、计算,求出问题的随机解。
Step5,统计分析模拟试验结果,给出问题的概率解以及解的精度估计。
(其精度检验需要手工来操作,因为涉及查表,但是需要在matlab 里面加入计算概率的语句。
)代码:《Matlab 在数学建模中运用》Test1.m 文件实现的是122/x x y ;例题:随机数生成方式:更为详细的在:/link?url=CF2pgipej6-j1p8V8IfxM_XDs2g RSsNBjUxgztOmfPP4d89txs0M06Yy__O48tTfY549WGn26_cW8o5jLuHdal O42KgjERnD8ZalfowTnWO/link?url=N5b5_BfgHTlzlA5OeFooJsyMJPZ PBgFddYfTo4X59iSy0JAgDw2riIHiivkxLmzsQS9BkxAxU9j4ABlGDQtcpEAgxPT6wYaX1Wc_2ytvJnaRand(n),,rand(n,m)Matlabbetarnd贝塔分布的随机数生成器binornd二项分布的随机数生成器chi2rnd卡方分布的随机数生成器exprnd指数分布的随机数生成器frndf分布的随机数生成器gamrnd伽玛分布的随机数生成器geornd几何分布的随机数生成器hygernd超几何分布的随机数生成器lognrnd对数正态分布的随机数生成器nbinrnd负二项分布的随机数生成器ncfrnd非中心f分布的随机数生成器nctrnd非中心t分布的随机数生成器ncx2rnd非中心卡方分布的随机数生成器normrnd正态(高斯)分布的随机数生成器poissrnd泊松分布的随机数生成器raylrnd瑞利分布的随机数生成器trnd学生氏t分布的随机数生成器unidrnd离散均匀分布的随机数生成器unifrnd连续均匀分布的随机数生成器weibrnd威布尔分布的随机数生成器Matlab自己产生的随机数:normrnd 可以生成一定均值和标准差的正态分布gamrnd 可以生成gamma分布的伪随机数矩阵chi2rnd 可以生成卡方分布的伪随机数矩阵trnd 可以生成t分布的伪随机数矩阵frnd 可以生成f分布的伪随机数矩阵raylrnd 可以生成rayleigh分布的伪随机数矩阵。
蒙特卡洛算法

随机点的产生 准随机算法
伪随机算法都存在差异性,不均匀性。因此,不要求新 的发生器模拟真实的均匀分布,而力求任意大小的样本(尤 其是小样本)都能满足低差异性。换言之,以牺牲随机性为 代价,换来均匀性的提高,称其为准随机模拟器。 目前有3种准随机序列可用来辅助生成均匀分布随机数,
分别是Halton序列、Sobol序列、Latin超立方体序列。
蒙特卡洛算法的介绍
算法简介
蒙特卡洛算法,也称统计模拟方法,是二十世纪四十年代中期 由于科学技术的发展和电子计算机的发明,而被提出的一种以概率统 计理论为指导的一类非常重要 数值计算方法,蒙特· 卡罗方法在金融 工程学,宏观经济学,计算物理学(如粒子输运计算、量子热力学计 算、空气动力学计算)等领域应用广泛。
//Halton序列的产生 // 以2 、3为基底产生序列 //使2和3产生的序列中元素的个数相同 //索引项 //x数组定义 //二维数组q定义 //二维数组d定义 //输入参数值,得到序列中的元素 // K.length=2
//给q,d赋值 //q[0]=63,q[1]=40 //d[0]=63,d[1]=40
随机点的产生 在二维中,0~1之间产生的点的序列就是(1/2, 1/3)(1/4,2/3)(3/4,1/9)(1/8,4/9) (5/8,7/9)(3/8,2/9)(7/8,5/9) (1/16,8/9)(9/16,1/27)….
核心代码分析
//把参数传给k
//这部分通过运算
double[] nextPoint() { 第二个点 index++; for(int i = 0; i < K.length; i++) { for(int j = 0; j < K[i]; j++) { d[i][j]++; x[i] += q[i][j]; if (d[i][j] < P[i]) { break; } d[i][j] = 0; x[i] -= (j == 0? 1.0: q[i][j-1]); } } return x; } }
蒙特卡罗算法(或蒙特卡洛方法)-MonteCarlomethod

蒙特卡罗算法(或蒙特卡洛⽅法)-MonteCarlomethod是以概率统计理论为指导的⼀类⾮常重要的数值计算⽅法。
是指使⽤(或更常见的)来解决很多计算问题的⽅法。
以和的理论、⽅法为基础的⼀种,将所求解的问题同⼀定的相联系,⽤电⼦计算机实现或,以获得问题的,故⼜称或。
蒙特卡洛⽅法的基本思想当所求解问题是某种出现的,或者是某个的时,通过某种“实验”的⽅法,以这种事件出现的估计这⼀随机事件的,或者得到这个的某些,并将其作为问题的解。
有⼀个例⼦可以使你⽐较直观地了解蒙特卡洛⽅法:假设我们要计算⼀个不规则图形的⾯积,那么图形的不规则程度和分析性计算(⽐如,积分)的复杂程度是成正⽐的。
蒙特卡洛⽅法是怎么计算的呢?假想你有⼀袋⾖⼦,把⾖⼦均匀地朝这个图形上撒,然后数这个图形之中有多少颗⾖⼦,这个⾖⼦的数⽬就是图形的⾯积。
当你的⾖⼦越⼩,撒的越多的时候,结果就越精确。
在这⾥我们要假定⾖⼦都在⼀个平⾯上,相互之间没有重叠。
蒙特卡洛⽅法的⼯作过程在解决实际问题的时候应⽤蒙特卡洛⽅法主要有两部分⼯作:1. ⽤蒙特卡洛⽅法模拟某⼀过程时,需要产⽣各种的。
2. ⽤统计⽅法把模型的估计出来,从⽽得到实际问题的数值解。
蒙特卡洛⽅法分⼦模拟计算的步骤使⽤蒙特卡洛⽅法进⾏分⼦模拟计算是按照以下步骤进⾏的:1. 使⽤产⽣⼀个随机的分⼦。
2. 对此分⼦构型的其中粒⼦坐标做⽆规则的改变,产⽣⼀个新的分⼦构型。
3. 计算新的分⼦构型的能量。
4. ⽐较新的分⼦构型于改变前的分⼦构型的能量变化,判断是否接受该构型。
若新的分⼦构型能量低于原分⼦构型的能量,则接受新的构型,使⽤这个构型重复再做下⼀次。
若新的分⼦构型能量⾼于原分⼦构型的能量,则计算玻尔兹曼因⼦,并产⽣⼀个随机数。
若这个随机数⼤于所计算出的,则放弃这个构型,重新计算。
若这个随机数⼩于所计算出的玻尔兹曼因⼦,则接受这个构型,使⽤这个构型重复再做下⼀次迭代。
5. 如此进⾏迭代计算,直⾄最后搜索出低于所给能量条件的分⼦构型结束。
蒙特卡洛算法

蒙特卡洛算法
蒙特卡洛算法是一种利用计算机模拟来解决复杂问题的方法,它被认为是一种博弈论算法,可以用于多种实际问题的数学解决方案,并且在许多工业领域得到广泛应用。
蒙特卡洛算法的基本思想是,它重复性地从概率分布中生成随机样本,使用这些样本来估算一个定义在概率分布领域上的数学函数。
这个数学函数是一个所谓的“期望”,所谓“期望”是指把采样概率分布的概率乘以所采样的值,然后求和的操作。
蒙特卡洛算法的核心思想是服从某一分布的随机实验,并经过数量规模放大来反映出大量样本的特性。
在实施蒙特卡洛算法时,我们需要先确定随机实验,并选择有利于解决问题的期望值,然后再收集尽可能多的样本,以此来估计期望值。
蒙特卡洛算法有许多优势,其中最重要的一点是它能够解决复杂的问题,不论问题的规模大小如何,只要有足够的样本量,就能够解决。
此外,蒙特卡洛算法不需要任何特定的先验知识,并且不像函数优化算法耗费大量时间,以及不像任何人工智能算法耗费大量计算开支,所以可以说,蒙特卡洛算法有着很高的效率。
蒙特卡洛算法的应用非常广泛,比如在金融领域,它可以用来评估风险、寻找投资机会、定义投资组合、进行盘活资产等。
在工业制造领域,它可用来设计优化工艺流程,解决配送问题。
此外,蒙特卡洛算法也可以在建模、机器学习、自然语言处理等领域得到应用。
总之,蒙特卡洛算法是一种相当有效的算法,能够被广泛应用于
各种实际问题的数学解决方案之中,且其优势明显。
因此,研究人员们希望能够不断提出新的蒙特卡洛算法,以更好地解决复杂的实际问题。
(完整版)蒙特卡洛算法详讲

(完整版)蒙特卡洛算法详讲Monte Carlo 法§8.1 概述Monte Carlo 法不同于前⾯⼏章所介绍的确定性数值⽅法,它是⽤来解决数学和物理问题的⾮确定性的(概率统计的或随机的)数值⽅法。
Monte Carlo ⽅法(MCM ),也称为统计试验⽅法,是理论物理学两⼤主要学科的合并:即随机过程的概率统计理论(⽤于处理布朗运动或随机游动实验)和位势理论,主要是研究均匀介质的稳定状态[1]。
它是⽤⼀系列随机数来近似解决问题的⼀种⽅法,是通过寻找⼀个概率统计的相似体并⽤实验取样过程来获得该相似体的近似解的处理数学问题的⼀种⼿段。
运⽤该近似⽅法所获得的问题的解in spirit 更接近于物理实验结果,⽽不是经典数值计算结果。
普遍认为我们当前所应⽤的MC 技术,其发展约可追溯⾄1944年,尽管在早些时候仍有许多未解决的实例。
MCM 的发展归功于核武器早期⼯作期间Los Alamos (美国国家实验室中⼦散射研究中⼼)的⼀批科学家。
Los Alamos ⼩组的基础⼯作刺激了⼀次巨⼤的学科⽂化的迸发,并⿎励了MCM 在各种问题中的应⽤[2]-[4]。
“Monte Carlo ”的名称取⾃于Monaco (摩纳哥)内以赌博娱乐⽽闻名的⼀座城市。
Monte Carlo ⽅法的应⽤有两种途径:仿真和取样。
仿真是指提供实际随机现象的数学上的模仿的⽅法。
⼀个典型的例⼦就是对中⼦进⼊反应堆屏障的运动进⾏仿真,⽤随机游动来模仿中⼦的锯齿形路径。
取样是指通过研究少量的随机的⼦集来演绎⼤量元素的特性的⽅法。
例如,)(x f 在b x a <<上的平均值可以通过间歇性随机选取的有限个数的点的平均值来进⾏估计。
这就是数值积分的Monte Carlo ⽅法。
MCM 已被成功地⽤于求解微分⽅程和积分⽅程,求解本征值,矩阵转置,以及尤其⽤于计算多重积分。
任何本质上属随机组员的过程或系统的仿真都需要⼀种产⽣或获得随机数的⽅法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
我们可产生一系列随机数 1,2 ,3,4 ,5,6 ,....... 可简单取3个随机数构成一个随机点,即
(1,2 ,3 ), (4 ,5,6 ),.......
相应地,
1 b 1 n a f ( x)dx n f ( xi ) ba i 1 d b 1 1 n c a f ( x, y)dxdy n f ( xi , yi ) (d c)(b a) i 1
据此,可得产生 X 的随机数的具体过程为:每产 生一个(0,1)区间上均匀分布随机数U ,若
P(n 1) U P(n)
则令 X 取值 x n .
26
例1:
离散型随机变量X有ቤተ መጻሕፍቲ ባይዱ下分布律: X 0 1 2 P(x) 0.3 0.3 0.4 设 U1 ,U2 ,,U N 是(0,1)上均匀分布的随机数,令
每个 xi j 有 m 种选择,所以向量 ( xi 1 , xi 2 ......xi -k ) 可以取 m
k -1
个不同的值,所以这样的随机数生成器
的最大周期可以达到 mk -1 1,大大提高了简单同余 生成器的周期。
22
算法实现
许多程序语言中都自带生成随机数的方法,如 c 中的 random() 函数,Matlab中的rand()函数等。 但这些生成器生成的随机数效果很不一样,比如 c 中的函数生成的随机数性质就比较差,如果用 c ,最好自己再编一个程序。Matlab 中的 rand() 函数,经过了很多优化。可以产生性质很好的随 机数,可以直接利用。
2147483399 2147483563
复杂一些的生成器
Multiple recursive generator
xi (a1 xi 1 a2 xi 2 ...... ak xi k ) mod m ui xi / m 需要选取种子(xk 1 , xk 2 .......x0 )
4
于是有: l p P( X sin ) 2 0
l sin 2
0
2 2l dxd a a
2l ap
若我们独立重复地作 n 次投针试验,记 n ( A) 为 A 发生的次数。 f n ( A) 为 A
ˆ 在 n 次中出现的频率。假如我们取 f n ( A) 作为 p P ( A) 的估计,即 p fn ( A) 。
16
乘同余法:
U(0,1)随机数的生成
xi 1 axi mod m ui 1 xi 1 / m
其中 xi , a, m 均为整数, x0 可以任意选取。
x0 称为种子,a 是乘因子,m是模数
17
一个简单的例子
当 x0 1 时,得到序列: 1,6,3,7,9,10,5,8,4,2,1,6,3......
将 {P(n)} 作为区间(0,1)的分点.若随机变量 U ~ U (0,1) ,有
P{P(n 1) U P(n)} P(n) P(n 1) pn , (n 1,2,)
25
令 {P(n 1) U P(n)} {X xn}
则有
P{X xn } pn
20
常用的线性同余生成器
Modulus m 2^31-1 =2147483647 Multiplier a 16807 39373 742938285 950706376 1226874159 40692 40014 Reference Lewis, Goodman, and Miller L’Ecuyer Fishman and Moore Fishman and Moore Fishman and Moore L’Ecuyer L’Ecuyer 21
23
从U(0,1)到其它概率分布的随机数
1.离散型随机数的模拟
2.连续型随机数的模拟
3.正态随机数的模拟
24
1.离散型随机数的模拟
设随机变量 X 的分布律为 令
P{X xi } pi
n i 1
(i 1,2,)
(n 1, 2 ,)
P(0) 0, P(n) pi ,
一般地,
A
f ( x)d (measure of A) (average of f over n random points in A)
8
Monte Carlo数值积分的优点
与一般的数值积分方法比较,Monte Carlo方法 具有以下优点:
1. 一般的数值方法很难推广到高维积分的情形,而 Monte Carlo方法很容易推广到高维情形
由定理 1 ,要产生来自 F ( x) 的随机数,只要先 产生来自U (0,1) 随机数 u ,然后计算 F 1 (u ) 即 可。具体步骤如下:
11
均匀分布随机变量X的取值具有”均匀性” 均匀性特点:均匀分布随机变量X落在(a,b)内 任意子区间的概率只与子区间的长度有关,而与 子区间的位置无关. 可假设有这种特性的随机变量服从均匀分布.
12
2. 正态分布 正态分布随机变量X的概率密度函数是
1 1 x 2 f ( x) exp[ ( ) ], x R 2 2
ˆ 然后取 2l a.s. ˆ 作为 的估计。根据大数定律,当 n 时, p f n ( A) p. af n ( A) 2l P 。这样可以用随机试验的方法求得 的估计。历史上 af n ( A)
ˆ 从而有
有如下的试验结果。
5
试验者
时间(年)
0, 0 U i 0.3 xi 1, 0.3 U i 0.6 2, 0.6 U i
则 x1 , x2 ,, xN 是具有X分布律的随机数.
27
2.连续型随机数的模拟
a.逆变换方法(常用) (Inverse Transform Method) b.舍取方法 (Acceptance-Rejection Method)
4.必要时,还应改进模型以降低估计方差和减少试验费 用,提高模拟计算的效率
10
回顾几种连续型分布
1.均匀分布U(a,b) 其概率密度函数为
1 ,a x b f ( x) b a 0 , 其他
有
cd P{c x d} , 其中(c, d ) (a, b) ba
定理: 设随机变量Y的分布函数F(y)是连续函数, 而U是在(0,1)上均匀分布的随机变量, 令 X F 1 (U ) , 则Y与X有相同的分布.
28
证明: 由 F 1 (U ) 的定义和均匀分布的分布函数可得: P( X x) P( F 1 (U ) x) P(U F ( x)) F ( x)
一般形式: xi 1 (axi c) mod m ui 1 xi 1 / m
1. c是非负整数.通过适当选取参数c可以改善 随机数的统计性质(独立性,均匀性).
2. 线性同余器可以达到的最长周期为 m 1 ,我们 可以通过适当的选择 m 和 a ,使无论选取怎样的 初值 x0 都可以达到最大周期(一般选取 m 为质数)
14
3. 指数分布 指数分布随机变量X的概率密度为
ex , x 0 f ( x) 0, x 0
指数分布常用来描述寿命问题.
15
二.随机数的生成
1.蒙特卡罗模拟的关键是生成优良的随机数。 2.在计算机实现中,我们是通过确定性的算法生成 随机数,所以这样生成的序列在本质上不是随机 的,只是很好的模仿了随机数的性质(如可以通过 统计检验)。我们通常称之为伪随机数(pseudorandom numbers)。 3.在模拟中,我们需要产生各种概率分布的随机数, 而大多数概率分布的随机数产生均基于均匀分布 U(0,1)的随机数。
Monte Carlo Simulation Methods (蒙特卡罗模拟方法)
主要内容: 一. M-C方法概述. 二. 随机数的生成. 三. 模拟训练. 四. 实验题目.
成信院数学与信息科学系 李胜坤
1
一.M-C方法概述
蒙特卡洛(Monte Carlo)方法,或称计算机 随机模拟方法,是一种基于“随机数”的计 算方法。这一方法源于美国在第二次世界大 战中研制原子弹的“曼哈顿计划”。该计划 的主持人之一、数学家冯· 诺伊曼用驰名世 界的赌城—摩纳哥的Monte Carlo—来命名 这种方法,为它蒙上了一层神秘色彩。
2
基本思想很早以前就被人们所发现和 利用。17世纪,人们就知道用事件发 生的“频率”来决定事件的“概率”。 19世纪人们用投针试验的方法来决定π。 高速计算机的出现,使得用数学方法 在计算机上大量模拟这样的试验成为 可能。
3
从Buffon(蒲丰)投针问题谈起
Buffon 投针问题:平面上画很多平行线,间距为 a.向此平面投掷长为 l ( l < a) 的 针,此针与任一平行线相交的概率 p。
xi1 6xi mod11, ui+1 xi1 /11 (a 6, m 11 )
如果令 a 3, x0 1 ,得到序列: 1,3,9,5, 4,1,3,9........ 如果令 a 3, x0 2, 得到序列: 2, 6, 7,10,8, 2, 6.......
针长 投针次数 相交次数
π的估计值
Wolf
1850
0.80
5000
2532
3.15956
Smith
1855
0.60
3204
1218
3.15665
Fox
1884
0.75
1030
489
3.15951
Lazzarini
1925
0.83
3408
1808
3.14159292
6
数值积分问题
