最新标准答案北京大学春季学期线性代数作业资料

合集下载

线性代数参考题1-6答案

线性代数参考题一答案：（注：为了大家共同的利益，我做了每一道题，希望你发现有做错处及时告诉我，谢谢，你的朋友冯国晨 gcfeng@ ）一. 填空题(每小题3分,满分30分)1．42342311a a a a 与44322311a a a a -；2.b a =；3.)(211E A A -=-；4.可逆阵或满秩阵或非奇异阵；5.特征根为0；6.1-=α；7.)()(T r A r =；8.3R ；9.负定；10.25≠t二. 陈治中版《线性代数》例题1.5.7（p.26）答案：nn bc ad D )(2-=三. 令⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛=130231,3512,343122321C B A 则⎪⎪⎪⎭⎫⎝⎛---=⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎭⎫⎝⎛----=--2115.053,2153,1115.235.123111X BA四. 令),,,(4321αααα=A ，则⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-→⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----==0000310020101013130631120140121),,,(4321ααααA 因而3)(=A r ，321,,ααα构成一个极大无关组，且321432αααα+-=五. 陈治中版《线性代数》习题4.6（p.121）答案：p.211 六. 将二次型f 化成矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=211121112A ，显然A 为实对称阵，可以正交对角化的，即由特征方程0||=-E A λ，得01=λ，33,2=λ当01=λ 对应的特征向量为T)1,1,1(1=α，标准化为T)1,1,1(311=η；当33,2=λ 对应的特征向量为T)0,1,1(2-=α和T)1,0,1(3-=α正交化T)0,1,1(22-==αβ，标准化为T)0,1,1(212-=ηT)1,1,0(,,2222333-=⋅><><-=ββββααβ，标准化T)1,1,0(213-=η因而),,(321ηηη=P ，且232233y y f += 七. 令αααααααααααααααβββββL n nn=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛+++++++=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=3213213212113211111111111............由 1||=L 以及n αα,,1 线性无关得n ββ,,1 线性无关。

(完整word版)线性代数习题集(带答案)

第一部分专项同步练习第一章行列式一、单项选择题1．下列排列是5阶偶排列的是 ( ）.（A) 24315 （B) 14325 （C ） 41523 (D)24351 2．如果n 阶排列n j j j 21的逆序数是k , 则排列12j j j n 的逆序数是（）. (A ）k (B ）k n - （C)k n -2! （D)k n n --2)1(3. n 阶行列式的展开式中含1211a a 的项共有( ）项。

(A) 0 （B ）2-n （C ） )!2(-n (D) )!1(-n4．=0001001001001000( ）。

(A ） 0 (B)1- (C) 1 （D) 25. =0001100000100100( ）.(A) 0 (B)1- (C ） 1 (D) 26．在函数100323211112)(x x x x x f ----=中3x 项的系数是( ）.(A) 0 （B ）1- (C) 1 （D) 27。

若21333231232221131211==a a a a a a a a a D ，则=---=323133312221232112111311122222 2a a a a a a a a a a a a D ( ）. (A ） 4 (B) 4- (C) 2 （D ） 2-8．若a a a a a =22211211，则=21112212ka a ka a ( ）。

（A)ka (B)ka - (C ）a k 2 (D)a k 2-9．已知4阶行列式中第1行元依次是3,1,0,4-, 第3行元的余子式依次为x ,1,5,2-，则=x （ )。

（A) 0 (B)3- (C) 3 (D) 210. 若5734111113263478----=D ,则D 中第一行元的代数余子式的和为( ). (A ）1- (B ）2- (C ）3- （D ）011. 若2235001011110403--=D ，则D 中第四行元的余子式的和为( ）。

线性代数参考答案(部分)

解：将行列式按第一列展开得
Dn = x (−1)1+1
x 0 0
y x 0
0 y 0
L L L
0 0 x
L L L L L
+ y (−1) n +1
y x 0
0 y 0
L L L
0 0 x
0 0 y
L L L L L
= x n + ( −1) n +1 y n
说明：请注意这种形式的行列式！ 2. 含参数行列式的计算
x
yபைடு நூலகம்
0
L
0
0
0 x y L 0 0 Dn = L L L L L L 0 y 0 0 0 0
3
L L
x 0
y x
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
1+ a 1 1 1 a + 10 a + 10 a + 10 a + 10 2 2+a 2 2 2 2+a 2 2 解： D4 = = 3 3 3+ a 3 3 3 3+ a 3 4 4 4 4+a 4 4 4 4+a
= ( a + 10) 1 1 2 2+a 3 4
3
1 2 3+ a 4
1 2 3 4+a
−2 λ +1 −2
2 λ +3
1 1
−2 −2
2 −k λ +3
=
k −4
− k = (λ − 1) 0 λ + 1
= (λ − 1) 0 λ + 1

北大版-线性代数第一章部分课后标准答案详解

北大版-线性代数第一章部分课后答案详解————————————————————————————————作者：————————————————————————————————日期：习题1.2：1 .写出四阶行列式中11121314212223243132333441424344a a a a a a a a a a a a a a a a 含有因子1123a a 的项解：由行列式的定义可知，第三行只能从32a 、34a 中选，第四行只能从42a 、44a 中选，所以所有的组合只有()()13241τ-11233244a a a a 或()()13421τ-11233442a a a a ，即含有因子1123a a 的项为11233244a a a a 和11233442a a a a2. 用行列式的定义证明11121314152122232425313241425152000000000a a a a a a a a a a a a a a a a =0 证明：第五行只有取51a 、52a 整个因式才能有可能不为0，同理，第四行取41a 、42a ，第三行取31a 、32a ，由于每一列只能取一个，则在第三第四第五行中，必有一行只能取0.以第五行为参考，含有51a 的因式必含有0，同理，含有52a 的因式也必含有0。

故所有因式都为0.原命题得证.。

3.求下列行列式的值：（1）01000020;0001000n n -L L M M M OM L L（2）00100200100000n n-L L M O M O M L L；解：（1）010000200001000n n -LLM M M OM LL=()()23411n τ-L 123n ⨯⨯⨯⨯L =()11!n n --（2）00100200100000n n-L LM OM O M L L=()()()()12211n n n τ---L 123n ⨯⨯⨯⨯L =()()()1221!n n n --- 4.设n 阶行列式：A=1111nn nna a a a LM OM L，B=11111212212221212n n nn n n n n nna ab a b a b a a b a b a b a -----L L MMOM L，其中0b ≠，试证明：A=B 。

《线性代数》课后习题答案

《线性代数》课后习题答案第一章行列式习题1.11. 证明：（1）首先证明)3(Q 是数域。

因为)3(Q Q ?，所以)3(Q 中至少含有两个复数。

任给两个复数)3(3,32211Q b a b a ∈++，我们有3)()3()3)(3(3)()()3()3(3)()()3()3(21212121221121212211212122 11b a a b b b a a b a b a b b a a b a b a b b a a b a b a +++=++-+-=+-++++=+++。

因为Q 是数域，所以有理数的和、差、积仍然为有理数，所以)3(3)()3()3)(3()3(3)()()3()3()3(3)()()3()3(2121212122112121221 121212211Q b a a b b b a a b a b a Q b b a a b a b a Q b b a a b a b a ∈+++=++∈-+-=+-+∈+++=+++。

如果0322≠+b a ，则必有22,b a 不同时为零，从而0322≠-b a 。

又因为有理数的和、差、积、商仍为有理数，所以)3(33)(3)3()3)(3()3)(3(332222212122222121222222112211Q b a b a a b b a b b a a b a b a b a b a b a b a ∈--+--=-+-+=++。

综上所述，我们有)3(Q 是数域。

（2）类似可证明)(p Q 是数域，这儿p 是一个素数。

（3）下面证明：若q p ,为互异素数，则)()(q Q p Q ?。

（反证法）如果)()(q Qp Q ?，则q b a p Q b a +=?∈?,，从而有q ab qb a p p 2)()(222++==。

由于上式左端是有理数，而q 是无理数，所以必有02=q ab 。

所以有0=a 或0=b 。

线性代数练习题库及答案

线性代数练习册答案第五章相似矩阵及二次型51ξ- 内积52ξ- 方阵的特征值与特征向量一．填空题：1.A 是正交矩阵，则A1A =± . 2.已知n 阶方阵A 的特征值为12,,,n λλλ⋅⋅⋅，则E A λ-= ()()()12n λλλλλλ--⋅⋅⋅- .3.已知3阶方阵A 的特征值为1,1,2-，则232B A A =-的特征值为 1,5,8 ；A = 2- ；A 的对角元之和为 2 .4.若0是A 的特征值，则A 不可逆（可逆，不可逆）.5.A 是n 阶方阵，A d =，则AA *的特征值是 ,,,d d d ⋅⋅⋅（共n 个） . 二．用施密特法把下列向量组规范正交化123111(,,)124139ααα⎛⎫⎪= ⎪ ⎪⎝⎭解：()111,1,1Tβα==[]()()()2122121,61,2,31,1,11,0,13TT Tαββαββ=-=-=- [][]313233122212,,αβαββαββββ=--()()()1481211,4,91,1,11,0,1,,32333TTTT⎛⎫=---=- ⎪⎝⎭故)1111,1,1T b ββ==，)2221,0,1T b ββ==-，)3331,2,1Tb ββ==-.三．求下列矩阵的特征值和特征向量1. 1221A ⎛⎫= ⎪⎝⎭2. 100020012B ⎛⎫⎪= ⎪ ⎪⎝⎭解：1. A 的特征多项式为12(3)(1)21A E λλλλλ--==-+-故A 的特征值为123,1λλ==-.当13λ=时，解方程()30A E x -=.由221132200rA E --⎛⎫⎛⎫-= ⎪ ⎪-⎝⎭⎝⎭:得基础解系111P ⎛⎫= ⎪⎝⎭，故1(0)kPk ≠是对应于13λ=的全部特征向量. 当21λ=-时，解方程()0A E x +=.由22112200r A E ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭:得基础解系211P -⎛⎫= ⎪⎝⎭，故2(0)kP k ≠是对应于21λ=-的全部特征向量.2. B 的特征多项式为2100020(1)(2)012B E λλλλλλ--=-=--- 故B 的特征值为1231,2λλλ===.当11λ=时，解方程()0B E x -=.由000011010010011000r B E ⎛⎫⎛⎫ ⎪ ⎪-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭:得基础解系1100P ⎛⎫⎪= ⎪ ⎪⎝⎭，故1(0)kP k ≠是对应于11λ=的全部特征向量. 当232λλ==时，解方程()20B E x -=.由1001002000000010010r B E -⎛⎫⎛⎫ ⎪ ⎪-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭:得基础解系2001P ⎛⎫ ⎪= ⎪ ⎪⎝⎭，故2(0)kP k ≠是对应于232λλ==的全部特征向量.四．证明下列各题1. x 为n 维列向量，且1T x x =，求证：2T H E xx =-是对称的正交阵.2. 设A 、B 为同阶正交阵，证明：AB 也是正交阵. 证明：1. ()()222TTTTT TT T H E xx H E xxE xx H =-⇒=-=-=故H 为对称阵.又()()()224444T T T T T T T T H H E xx E xx E xx x x x x E xx xx E =--=-+=-+=故H 为正交阵.2. 因,A B 为同阶正交阵，故,T T A A E B B E ==. 又()()TT T T T AB AB B A AB B EB B B E ====，故AB 为正交阵.五．A 是n 阶方阵，命题P 为：A 的特征值均不为0.请尽量多的列举与P 等价的命题.（如A 可逆.至少列举3个）解：等价命题：1P ：A 的列（行）向量组线性无关 2P ：0A ≠3P ：齐次线性方程组0Ax =只有0解 4P ：A 的秩为n53ξ- 相似矩阵54ξ- 实对称矩阵的相似矩阵一．填空题：1.若ξ是A 的特征向量，则 1P ξ- 是1P AP -的特征向量.2.若A 与B 相似，则A.3.20000101A x ⎛⎫ ⎪= ⎪ ⎪⎝⎭与20000001B y ⎛⎫ ⎪= ⎪ ⎪-⎝⎭相似，则x = 0 ，y = 1 .4.若λ是A 的k 重特征根，则必有k 个相应于λ的线性无关的特征向量，不对（对，不对），若A 是实对称的呢？对（对，不对）.二．多项选择题（选出全部正确的选项，可能不只一个）1.n 阶方阵A 相似于对角矩阵的充分必要条件是A 有n 个（ C ）（A ）互不相同的特征值；（B ）互不相同的特征向量；（C ）线性无关的特征向量；（D ）两两正交的特征向量；2.方阵A 与B 相似，则必有（ BD ）（A ）E A E B λλ-=-；（B ）A 与B 有相同的特征值；（C ）A 与B 有相同的特征向量；（D ）A 与B 有相同的秩； 3.A 为n 阶实对称矩阵，则（ ACD ）（A ）属于不同特征值的特征向量必定正交；（B ）0A >；（C ）A 必定有n 个两两正交的特征向量；（D ）A 的特征值均为实数；三．100021012A ⎛⎫ ⎪= ⎪ ⎪⎝⎭，试求一个可逆矩阵P 使得1P AP -为对角阵，并求m A .解：先求A 的特征值和特征向量.2100021(1)(3)012E A λλλλλλ--=-=--- 故A 的所有特征值为1233,1λλλ===.当13λ=时，解方程()30A E x -=.2001003011011011000rA E -⎛⎫⎛⎫⎪ ⎪-=-- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭:令1011P ⎛⎫⎪= ⎪ ⎪⎝⎭，则1P 即为对应于13λ=的特征向量. 当231λλ==时，解方程()0A E x -=.000000011011011000r A E ⎛⎫⎛⎫ ⎪ ⎪-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭:令23100,101P P ⎛⎫⎛⎫ ⎪ ⎪==- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，则23,P P 即为对应于231λλ==的特征向量.显然，123,,P P P 线性无关.令()123010,,101101P P P P ⎛⎫⎪==- ⎪ ⎪⎝⎭，则11110031313102211313022mm m m mm P AP A P P A P P ---⎛⎫ ⎪⎛⎫ ⎪+-+ ⎪⎪Λ==⇒=Λ⇒=Λ= ⎪⎪⎪ ⎪⎝⎭-++ ⎪⎪⎝⎭四．三阶实对称矩阵A 的特征值为0,2,2，又相应于特征值0的特征向量为1111P ⎛⎫ ⎪= ⎪ ⎪⎝⎭，求出相应于2的全部特征向量.解：因为A 为三阶实对称矩阵，故A 有三个线性无关的特征向量，且对应于不同特征值的特征向量两两正交.已知对应于10λ=的特征向量为1P ，设对应于232λλ==的特征向量为23,P P ，则12130,0T T P P P P ==.即23,P P 为齐次线性方程组10T P x =的两个线性无关的解.由10T P x =得1230x x x ++=.令2310,01x x ⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则11,1x =--.取23111,001P P --⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，则23,P P 即为对应于232λλ==的特征向量.令2233k P k P ξ=+（23,k k 不全为零），则ξ为对应于232λλ==的全部特征向量. 五．设3阶方阵A 的特征值为1231,0,1λλλ===-，对应的特征向量分别依次为1231222,2,1212P P P -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪==-=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，求A .解：因为123λλλ≠≠，故A 可对角化，且123,,λλλ所对应的特征向量123,,P P P 线性无关.显然()()112312323,,,,A P P P P P P λλλ⎛⎫⎪= ⎪ ⎪⎝⎭，令()123,,P PP P =，故1112311021001231220A P P P P λλλ---⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭.55ξ- 二次型及其标准形56ξ- 用配方法化二次型为标准形57ξ- 正定二次型一．填空题：1. 22(,)22f x y x xy y x =+++是不是二次型？答：不是 .2. 123121323(,,)422f x x x x x x x x x =-++的秩是 3 ；秩表示标准形中平方项的个数．3．21101000A k k ⎛⎫⎪= ⎪ ⎪⎝⎭,A 为正定矩阵,则k 满足大于1 .二．A 为实对称矩阵，选出全部的A 为正定矩阵的充分必要条件（ 12346 ） 1.对任意的列向量0x ≠，0x Ax '> 2.存在可逆方阵C ，使得A C C '= 3.A 的顺序主子式全部大于零 4.A 的主子式全部大于零 5.A 的行列式大于零 6.A 的特征值全部大于零三．212312331001(,,)(,,)300430x f x x x x x x x x ⎛⎫⎛⎫ ⎪⎪= ⎪⎪ ⎪⎪⎝⎭⎝⎭1.求二次型123(,,)f x x x 所对应的矩阵A ；2.求正交变换x Py =，将二次型化为标准形.解：1. 2112312331232123001(,,)(,,)300(,,)343043x x f x x x x x x x x x x x x x x ⎛⎫⎛⎫⎛⎫⎪⎪ ⎪== ⎪⎪ ⎪ ⎪⎪ ⎪+⎝⎭⎝⎭⎝⎭22212233343x x x x x =+++ 故二次型123(,,)f x x x 所对应的矩阵100032023A ⎛⎫⎪= ⎪ ⎪⎝⎭.2. 问题可转化为求正交矩阵P ，将A 化为对角形.21032(1)(5)023A E λλλλλλ--=-=--- 故A 的特征值为1231,5λλλ===.当121λλ==时，解方程()0A E x -=.000011022000022000r A E ⎛⎫⎛⎫⎪ ⎪-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭:.令1310,01x x ⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，得20,1x =-.取12100,101ξξ⎛⎫⎛⎫ ⎪ ⎪==- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，则12,ξξ即为对应于121λλ==的特征向量.显然，12,ξξ正交.将12,ξξ单位化得121212010,0P P ξξξξ⎛⎫ ⎪ ⎪⎛⎫⎪==== ⎪ ⎪⎝⎭⎪ ⎪⎝⎭当35λ=时，解方程()50A E x -=.4001005022011022000rA E -⎛⎫⎛⎫⎪ ⎪-=-- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭:.令31x =，得1201x x =⎧⎨=⎩.取3011ξ⎛⎫ ⎪= ⎪ ⎪⎝⎭，则3ξ即为对应于35λ=的特征向量.将3ξ单位化得3330P ξξ⎛⎫⎪ ⎪==. 令()123P P P P =，则1115P AP -⎛⎫⎪= ⎪ ⎪⎝⎭.故123(,,)f x x x 的标准形为2221235y y y ++.四．已知A 和B 都为n 阶正定矩阵，求证A B +的特征值全部大于零. 证明：因为,A B 都为n 阶正定矩阵，则对任意n 维列向量0x ≠，有()0,00T T T x Ax x Bx x A B x >>⇒+>.即A B +是正定矩阵. 故A B +的特征值全部大于零. 五．已知A 为n 阶正定矩阵，求证1A E +>.证明：因为A 为n 阶正定矩阵，则A 的n 个特征值12,,,n λλλ⋅⋅⋅全大于零且存在正交矩阵P ，使得112211n n P AP A P P λλλλλλ--⎛⎫⎛⎫⎪⎪⎪ ⎪=⇒= ⎪ ⎪⋅⋅⋅⋅⋅⋅⎪ ⎪⎝⎭⎝⎭. 由1122111n n A E P P PP P E P λλλλλλ---⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪⎪⎪ ⎪+=+=+ ⎪ ⎪ ⎪⋅⋅⋅⋅⋅⋅ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭121111n P P λλλ-+⎛⎫⎪+⎪= ⎪⋅⋅⋅ ⎪+⎝⎭，得()()()121121111111n n A E PP λλλλλλ-+++==++⋅⋅⋅+>⋅⋅⋅+六.求22:1L x xy y ++=围成的面积.解：设二次型()22112(,),112x f x y x xy y x y y ⎛⎫ ⎪⎛⎫=++=⎪ ⎪ ⎪⎝⎭ ⎪⎝⎭. 令112112A ⎛⎫ ⎪=⎪ ⎪ ⎪⎝⎭，则A 是对称矩阵且正定.设12,λλ为A 的特征值，可知存在正交矩阵P ，使得11200T P AP P AP λλ-⎛⎫== ⎪⎝⎭.由0E A λ-=，得1213,22λλ==. 因为正交变换不改变向量的长度，故可用正交变换12z x P z y ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，使得1221122T T T T X AX Z P APZ Z P APZ z z λλ-===+，其中12,z x X Z z y ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭. 综上可知，经过正交变换后，221213(,)22f x y z z =+.故L 的面积即为椭圆： 221213122z z +=的面积.面积S =.第五章复习题三、计算题1、设3阶对称阵A 的特征值为6，3，3，与特征值6对应的特征向量为()11,1,1Tp =，求A解：因为对称矩阵对应于不同特征值的特征向量是两两正交的，所以求对应于3的特征向量即为求与()1,1,1T正交的特征向量。

线性代数习题及解答完整版

线性代数习题及解答 HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】线性代数习题一说明：本卷中，A -1表示方阵A 的逆矩阵，r (A )表示矩阵A 的秩，||α||表示向量α的长度，αT表示向量α的转置，E 表示单位矩阵，|A |表示方阵A 的行列式. 一、单项选择题（本大题共10小题，每小题2分，共20分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

1．设行列式111213212223313233a a a a a a a a a =2，则111213313233213122322333333a a a a a a a a a a a a ------=（） A ．-6 B ．-3 C ．3D ．62．设矩阵A ，X 为同阶方阵，且A 可逆，若A （X -E ）=E ，则矩阵X =（） A ．E +A -1B ．E -AC ．E +AD ．E -A -13．设矩阵A ，B 均为可逆方阵，则以下结论正确的是（）A ．⎛⎫⎪⎝⎭A B 可逆，且其逆为-1-1⎛⎫⎪⎝⎭A B B ．⎛⎫⎪⎝⎭A B 不可逆 C ．⎛⎫⎪⎝⎭A B 可逆，且其逆为-1-1⎛⎫ ⎪⎝⎭B AD ．⎛⎫⎪⎝⎭A B 可逆，且其逆为-1-1⎛⎫⎪⎝⎭A B 4．设α1，α2，…，αk 是n 维列向量，则α1，α2，…，αk 线性无关的充分必要条件是（）A ．向量组α1，α2，…，αk 中任意两个向量线性无关B ．存在一组不全为0的数l 1，l 2，…，l k ，使得l 1α1+l 2α2+…+l k αk ≠0C ．向量组α1，α2，…，αk 中存在一个向量不能由其余向量线性表示D ．向量组α1，α2，…，αk 中任意一个向量都不能由其余向量线性表示5．已知向量2(1,2,2,1),32(1,4,3,0),T T+=---+=--αβαβ则+αβ=（） A ．（0，-2，-1，1）TB ．（-2，0，-1，1）TC ．（1，-1，-2，0）TD ．（2，-6，-5，-1）T6．实数向量空间V ={(x , y , z )|3x +2y +5z =0}的维数是（） A ．1B ．2C ．3D ．47．设α是非齐次线性方程组Ax =b 的解，β是其导出组Ax =0的解，则以下结论正确的是（）A ．α+β是Ax =0的解B ．α+β是Ax =b 的解C ．β-α是Ax =b 的解D ．α-β是Ax =0的解8．设三阶方阵A 的特征值分别为11,,324，则A -1的特征值为（） A ．12,4,3 B ．111,,243C ．11,,324D ．2,4,39．设矩阵A =121-，则与矩阵A 相似的矩阵是（）A ．11123--B ．01102C ．211- D ．121-10．以下关于正定矩阵叙述正确的是（） A ．正定矩阵的乘积一定是正定矩阵 B ．正定矩阵的行列式一定小于零 C ．正定矩阵的行列式一定大于零D ．正定矩阵的差一定是正定矩阵二、填空题（本大题共10小题，每空2分，共20分）请在每小题的空格中填上正确答案，错填、不填均无分。

线性代数习题册(答案)

线性代数习题册答案第一章行列式练习一班级学号姓名1．按自然数从小到大为标准次序，求下列各排列的逆序数：（1）τ(3421)= 5 ; （2）τ(135642)= 6 ;（3）τ(13…(2n-1)(2n)…42) = 2+4+6+…+（2 n-2）= n （n-1）.2．由数字1到9组成的排列1274i56j9为偶排列，则i= 8 、j= 3 .3．在四阶行列式中，项12233441a a a a 的符号为负 .4．00342215= －24 .5．计算下列行列式：（1）122212221-----= －1＋（－8）＋（－8）－（－4）－（－4）―（－4）= －5 或（2）111111λλλ---= －3λ＋1＋1－（－λ）－（－λ）―（－λ） = －3λ＋3λ+2=2(2)(1)λλ-+练习二班级学号姓名 1．已知3阶行列式det()ij a =1，则行列式det()ij a -= －1 . 3(1)11-⋅=-2． 1112344916= 2 .3．已知D=1012110311101254--,则41424344A A A A +++= —1 .用1，1，1，1替换第4行4．计算下列行列式：(1)111ab c a b c abc +++ = 13233110110011,0110111111r r r r c c a b c b ca b ca b c-----+-==++++++(2)xy x y y x y x x yxy+++(3)130602121476----(4)1214012110130131-5．计算下列n 阶行列式：(1)n x a aa x a D a a x=（每行都加到第一行，并提公因式。

）(2)131111n +(3)123123123n n n a ba a a a ab a a a a a a b+++练习三班级学号姓名1．设线性方程组123123123111x x x x x x x x x λλλ--=⎧⎪++=⎨⎪-++=⎩有惟一解，则λ满足的条件是什么？1,0,1λλλ≠-≠≠2. 求解线性方程组12341234123412345242235232110x x x x x x x x x x x x x x x x +++=⎧⎪+-+=-⎪⎨---=-⎪⎪+++=⎩3.已知齐次线性方程组123123123000x x x x x x x x x λλλ--=⎧⎪-++=⎨⎪--+=⎩有非零解，求λ的值。

线性代数课后习题答案全）习题详解

线性代数课后习题答案全）习题详解前言因能力有限，资源有限，现粗略整理了《工程数学线性代数》课后习题，希望对您的了解和学习线性代数有参考价值。

第一章行列式1.利用对角线法则计算下列三阶行列式：（1）381141102---；（2）b a c a c b c b a ; （3）222111c b a c b a ；（4）y x y x x y x yyx y x +++. 解（1）=---381141102811)1()1(03)4(2??+-?-?+?-?)1()4(18)1(2310-?-?-?-?-??-=416824-++-=4-（2）=ba c a cb cb a ccc aaa bbb cba bac acb ---++3333c b a abc ---=（3）=222111c b a c b a 222222cb ba ac ab ca bc ---++))()((a c c b b a ---=（4）yx y x x y x y yx y x +++yx y x y x yx y y x x )()()(+++++=333)(x y x y -+-- 33322333)(3x y x x y y x y y x xy ------+= )(233y x +-=2.按自然数从小到大为标准次序，求下列各排列的逆序数：（1）1 2 3 4；（2）4 1 3 2；（3）3 4 2 1；（4）2 4 1 3；（5）1 3 … )12(-n 2 4 … )2(n ；（6）1 3 … )12(-n )2(n )22(-n … 2.解（1）逆序数为0（2）逆序数为4：4 1，4 3，4 2，3 2 （3）逆序数为5：3 2，3 1，4 2，4 1,2 1 （4）逆序数为3：2 1，4 1，4 3 （5）逆序数为2)1(-n n ： 3 2 1个 5 2，5 4 2个 7 2，7 4，7 6 3个……………… …)12(-n 2，)12(-n 4，)12(-n 6，…，)12(-n )22(-n )1(-n 个（6）逆序数为)1(-n n3 2 1个 5 2，54 2个……………… …)12(-n 2，)12(-n 4，)12(-n 6，…，)12(-n )22(-n )1(-n 个4 2 1个 6 2，6 4 2个……………… …)2(n 2，)2(n 4，)2(n 6，…，)2(n )22(-n )1(-n 个3.写出四阶行列式中含有因子2311a a 的项.解由定义知，四阶行列式的一般项为43214321)1(p p p p t a a a a -，其中t 为4321p p p p 的逆序数．由于3,121==p p 已固定，4321p p p p 只能形如13□□，即1324或1342.对应的t 分别为10100=+++或22000=+++∴44322311a a a a -和42342311a a a a 为所求.4.计算下列各行列式：（1）7110025*********4；（2）-265232112131412；（3）---ef cf bf de cd bd ae ac ab ；（4）---d c b a100110011001解(1)7110025102021421434327c c c c --0100142310202110214---=34)1(143102211014+-?---=143102211014-- 321132c c c c ++1417172001099-=0(2)2605232112131412-24c c -2605032122130412-24r r -0412032122130412- 14r r -0000032122130412-=0(3)ef cf bf de cd bd ae ac ab ---=e c b e c b e c b adf ---=1 11111111---adfbce =abcdef 4(4)d c b a 100110011001---21ar r +dc b a ab 100110011010---+=12)1)(1(+--dc a ab 10111--+23dc c +010111-+-+cd c ada ab =23)1)(1(+--cdadab +-+111=1++++ad cd ab abcd5.证明: (1)1112222b b a a b ab a +=3)(b a -; (2)bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax +++++++++=y x z x z y z y x b a )(3 3+;(3)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a ;(4)444422221111d c b a d c b a d c b a ))()()()((d b c b d a c a b a -----=))((d c b a d c +++-?;(5)1221100000100001a x a a a a x x x n n n +-----n n n n a x a x a x ++++=--111 . 证明(1)00122222221312a b a b a a b a ab a c c c c ------=左边a b a b a b a ab 22) 1(22213-----=+21))((a b a a b a b +--= 右边=-=3)(b a(2)bz ay by ax z by ax bx az y bx az bz ay x a ++++++分开按第一列左边bzay by ax x by ax bx az z bxaz bz ay y b +++++++ ++++++002y by ax z x bx az y z bz ay x a 分别再分bz ay y x by ax x z bx az z y b +++zy x y x z xz y b y x z x z y z y x a 33+分别再分右边=-+=233)1(yx z x z y zy x b y x z x z y z y x a(3) 2222222222222222)3()2()12()3()2()12()3()2()12()3()2()12(+++++++++++++++ +=d d d d d c c c c c b b b b b a a a a a 左边964412964412964412964412241312++++++++++++---d d d d c c c c b b b b a a a a c c c c c c 964496449644964422222++++++++d d d d c c c c b b b b a a a a 分成二项按第二列964419644196441964412222+++++++++d d d c c c b b b a a a949494949464222224232423d d c c b b a a c c c c c c c c ----第二项第一项06416416416412222=+dd d c c c bb b a a a (4) 444444422222220001ad a c a b a ad a c a b a a d a c a b a ---------=左边=)()()(222222222222222a d d a c c a b b a d a c a b ad a c a b --------- =)11))()((222a d d a c c a b b a d a c ab a d ac a b ++++++--- =?---))()((ad a c a b )()()()()(00122222a b b a d d a b b a c c a b b bd b c a b +-++-++--+ =?-----))()()()((b d b c a d a c a b )()()()(112222b d a b bd d b c a b bc c ++++++++=))()()()((d b c b d a c a b a -----))((d c b a d c +++-(5) 用数学归纳法证明.,1,2212122命题成立时当a x a x a x a x D n ++=+-==假设对于)1(-n 阶行列式命题成立，即,122111-----++++=n n n n n a x a x a x D:1列展开按第则n D1110010001)1(11----+=+-x xa xD D n n n n 右边=+=-n n a xD 1 所以，对于n 阶行列式命题成立.6.设n 阶行列式)det(ij a D =,把D 上下翻转、或逆时针旋转 90、或依副对角线翻转，依次得n nn n a a a a D 11111 =， 11112n nn n a a a a D = ，11113a a a a D n nnn =，证明D D D D D n n =-==-32)1(21,)1(.证明 )det(ij a D =nnnn nn n nn n a a a a a a a a a a D 2211111111111)1(--==∴ =--=--nnn n nnn n a a a a a a a a 331122111121)1()1( nnn n n n a a a a 111121)1()1()1(---=--D D n n n n 2)1()1()2(21)1()1(--+-+++-=-= 同理可证nnn n n n a a a a D 11112)1(2)1(--=D D n n Tn n 2)1(2)1()1()1(---=-= D D D D D n n n n n n n n =-=--=-=----)1(2)1(2)1(22)1(3)1()1()1()1(7.计算下列各行列式（阶行列式为k D k ）：(1)aaD n 11=,其中对角线上元素都是a ，未写出的元素都是0；(2)xa a ax aa a x D n =; (3) 1111)()1()()1(1111n a a a n a a a n a a a D n n n nn n n ------=---+; 提示：利用范德蒙德行列式的结果． (4) n nn nn d c d c b a b a D000011112=; (5)j i a a D ij ij n -==其中),det(;(6)nn a a a D +++=11111111121 ,021≠n a a a 其中.解(1) aa a a a D n 000100000000 00001000 =按最后一行展开)1()1(1000000000010000)1(-?-+-n n n aa a)1)(1(2)1(--?-+n n n a a a(再按第一行展开)n n n nn a a a+-?-=--+)2)(2(1)1()1(2--=n n a a )1(22-=-a a n(2)将第一行乘)1(-分别加到其余各行，得ax x a ax x a a x x a aa a x D n ------=0000000 再将各列都加到第一列上，得ax ax a x aaa a n x D n ----+=000000000)1( )(])1([1a x a n x n --+=- (3) 从第1+n 行开始，第1+n 行经过n 次相邻对换，换到第1行，第n 行经)1(-n 次对换换到第2行…，经2)1(1)1(+=++-+n n n n 次行交换，得 nnn n n n n n n n a a a n a a a n a a aD )()1()()1(1111)1(1112)1(1-------=---++此行列式为范德蒙德行列式∏≥>≥++++--+--=112)1(1)]1()1[()1(j i n n n n j a i a D∏∏≥>≥+++-++≥>≥++-?-?-=---=111)1(2)1(112)1()][()1()1()]([)1(j i n n n n n j i n n n j i j i∏≥>≥+-=11)(j i n j i(4) nnn d c d c b a b a D 011112=nn n n n nd d c d c b a b a a 0000000011111111----展开按第一行0000)1(1111111112c d c d c b a b a b nn n n n nn ----+-+2222 ---n n n n n n D c b D d a 都按最后一行展开由此得递推公式：222)(--=n n n n n n D c b d a D即∏=-=ni i i iin D c b d22)(而 111111112c b d a d c b a D -==得∏=-=ni i i i i n c b d a D 12)((5)j i a ij -=432140123310122210113210)det( --------==n n n n n n n n a D ij n ,3221r r r r --0 432111111111111111111111 --------------n n n n ,,141312c c c c c c +++152423210222102210002100001---------------n n n n n =212)1()1(----n n n (6)nn a a D a +++=11111111121 ,,433221c c c c c c ---n n n n a a a a a a a a a a +-------100 00100010000100010001000011433221展开（由下往上）按最后一列))(1(121-+n n a a a a nn n a a a a a a a a a --------000 00000000000000000000000022433221 nn n a a a a a a a a ----+--000000000000000001133221 ++ nn n a a a a a a a a -------000000000000000001143322n n n n n n a a a a a a a a a a a a 322321121))(1(++++=--- )11)((121∑=+=ni in a a a a8.用克莱姆法则解下列方程组：=+++-=----=+-+=+++;01123,2532,242,5)1(4321432143214321x x x x x x x x x x x x x x x x=+=++=++=++=+.15,065,065,065,165)2(545434323212 1x x x x x x x x x x x x x上一页下一页。

数值线性代数北大版答案全

数值线性代数习题解答习题1１．求下三角阵的逆矩阵的详细算法。

[解] 设下三角矩阵L的逆矩阵为T我们可以使用待定法，求出矩阵T的各列向量。

为此我们将T按列分块如下：注意到我们只需运用算法1·1·1，逐一求解方程便可求得[注意]考虑到内存空间的节省，我们可以置结果矩阵T的初始状态为单位矩阵。

这样，我们便得到如下具体的算法：算法（求解下三角矩阵L的逆矩阵T，前代法）２．设为两个上三角矩阵，而且线性方程组是非奇异的，试给出一种运算量为的算法，求解该方程组。

[解]因，故为求解线性方程组，可先求得上三角矩阵T的逆矩阵，依照上题的思想我们很容易得到计算的算法。

于是对该问题我们有如下解题的步骤：（1）计算上三角矩阵T的逆矩阵，算法如下：算法1（求解上三角矩阵的逆矩阵，回代法。

该算法的的运算量为）（2）计算上三角矩阵。

运算量大约为.（3）用回代法求解方程组：.运算量为；（4）用回代法求解方程组：运算量为。

算法总运算量大约为：３．证明：如果是一个Gauss变换，则也是一个Gauss变换。

[解]按Gauss变换矩阵的定义，易知矩阵是Gauss变换。

下面我们只需证明它是Gauss变换的逆矩阵。

事实上注意到，则显然有从而有４．确定一个Gauss变换L，使[解] 比较比较向量和可以发现Gauss变换L应具有功能：使向量的第二行加上第一行的2倍；使向量的第三行加上第一行的2倍。

于是Gauss变换如下５．证明：如果有三角分解，并且是非奇异的，那么定理1·1·2中的L和U都是唯一的。

[证明]设，其中都是单位下三角阵，都是上三角阵。

因为A非奇异的，于是注意到，单位下三角阵的逆仍是单位下三角阵，两个单位下三角阵的乘积仍是单位下三角阵；上三角阵的逆仍是上三角阵，两个上三角阵的乘积仍是上三角阵。

因此，上述等将是一个单位下三角阵与一个上三角阵相等，故此，它们都必是单位矩阵。

即，从而即A的LU分解是唯一的。

北大版-线性代数部分课后答案详解

2•用行列式的泄义证明习题1.2：如如如如1 •写岀四阶行列式中幻I'2勺3"24含有因子的项“3】a 32 a 33a 34«41勺 2«43仙解：由行列式的泄义可知，第三行只能从@2、中选，第四行只能从厲2、中选，所以所有的组合只有（-l ）f （，324）如给角2知或（-1）"网 a H a 23a 34a 42，即含有因子勺］“23的项为一如吹32% 和 a H a 23a 34a 42证明：第五行只有取他「山2整个因式才能有可能不为°,同理，第四行取“42,第三行取①I 、©2，由于每一列只能取一个，则在第三第四第五行中，必有一行只能取0 •以第五行为参考，含有的因式必含有0,同理，含有的因式也必含有0“故所有因式都为0 •原命题得证・。

3 •求下列行列式的值:0 1 0♦ • ♦0 •… 0 1 00 02 ♦ • 00 ... 2 0 0(1)■ ■ ■ ■■ ；（2）• • ■ • • •0 00 • • ”一〃一 1 0 0 0n 0 0 • •• 00 …0 H0 1 0 ♦ • • 00 2• • • 0解：（1） ■ ■ ■■ ■ ■ ■■ ■/lX r(234...nl)=("1)Ix2x3x--•xn =(-1)*"1 n\0 0 ・•・//-In 0 0 • • • 0a 2l0 01 0 0 ■ …2 • •0 ■ 0 ■■ ”一• • …0 • 0 ■0 0 00 n=(-1)侶心5)» B= 如■ •“22 ■■f 1-n…5少…如尸■5肝・・・a nn证明:A=BoE (T 严•”%叫2…％沪Wi"叫z (T 严％%…讣A 叩2・・％和巾时2 ••叭和巾命题得证。

5•证明：如下2007阶行列式不等于61 2 …2006 200722 32 …20072 2OO82 D=33 • 43 • …20083 • • 20083■• ■■ •• • • •■ ■证明：最后一行元素，除去2007*”是奇数以外，其余都是偶数，故含2008^7的因式也都是偶数。

线性代数(含全部课后题详细答案)1第一章一元多项式习题及解答.docx

A 组1.判别Q (厉)二｛0 +勿亦|0,处0｝是否为数域？解是.2.设/(x) = x3 4-x2 4-x+l, g(兀)=兀2+3兀+ 2,求 /(兀)+ g(x)，/(x)-g(x), f(x)g(x). 解/(x) + g (x) = x3 4- 2x2 + 4x + 3 ,/(兀)-g(x)"-2x-l,f(x)g(x) = x5 +4x4 +6兀'+6兀$ +5x + 2 .3.设/(%) = (5x-4),993(4x2 -2x-l),994 (8x3 -1 lx+2)'995,求 /(%)的展开式中各项系数的和.解由于/(兀)的各项系数的和等于/⑴，所以/(I) = (5-4严3(4-2- 1尸94(8-11 + 2)1995 =-1.4.求g(兀)除以/(兀)的商q(x)与余式心).(1)f (x) —— 3%2— x — 1, g(兀)=3F - 2兀+1 ；(2)/(x) = x4 -2x4-5, g(x) = x2 -x + 2 .解（1）用多项式除法得到x 73x~ — 2x +13_93X + 3—x —x-i3 37 ° 14 7-- 无_+ —x --3 9 926 2-- X ---9 9所以'恥）十岭心）W（2）用多项式除法得到x4— 2x + 5兀4 —”丫" + 2 兀2— 2x~ — 2 兀+5 jy?—兀~ + 2 兀-x2-4x4-5-兀? + X - 2—5x + 7所以，q(x) = x2 +x-l, r(x) = -5x + 7 .5.设是两个不相等的常数，证明多项式/(兀)除以(x-a)(x-b)所得余式为af(b)_bg)a-b a-h证明依题意可设/(x) = (x - a)(x - b)q(x) + cx+d,则”(a) = ca + d,[f(b) = cb + d.解得F=(/a) --,\d = (af(b)-bf(a))/(a-b).故所得余式为a-b a-b6.问m,p,q适合什么条件时，/(兀)能被g(x)整除？(1) /(x) = x3 + px + q , g(x) = x2 + nvc-1；(2) f(x) = x4 + px2 +q , g(兀)=x2 + mx+l.解(1)由整除的定义知，要求余式r(x) = 0 .所以先做多项式除法,3x2 + mx -1x-in“+ “X + q3 2x + mx^ - x-mx1 +(〃 + l)x + g2 2一 mx_ — m^x + m°(# +1 + 加〜)兀 + (g —m)要求厂(x) = (/? + l +加2)兀+ (§ —加)=0 ,所以(“ + 1 +加2) = 0, q-m = 0.即p = -l-m2, q - m时, 可以整除.（2）方法同上.先做多项式除法，所得余式为厂（兀）=加（2 — ”一nr ）兀+ （1 + @ —卩一加〜），所以 m （2-p-/772） = 0, 1 + ^ - p - m 2= 0 ,即 m = 0, p = q + \ 或“二 2— 加［q = l 时，可以整除.7. 求/（兀）与gCr ）的最大公因式:(1) f (x) — x 4 + — 3%2 — 4x — 1, g (x)=兀彳 + — x — 1 ； (2) f(x) = x 4— 4x 3+ 1, g(x) = x 3— 3x 2+1 ；(3) /(x) = x 4 -10x 2 +1, g(x) = x 4 -4A /2X 3 +6X 2 +4A /2X +1 .解（1）用辗转相除法得到用等式写出來，就是所以(/(x),g(x)) = x + l ・（2）同样地,<8 4 / 3 3= -X + — — -X-—(3 344-2x 2-3x-l1 1 --- X 4——2 -- 4 X 3+ X 2- X - 1 x 4 + x 3- 3x 2- 4x- 11 2 3 , -2x 2 — 3兀—12 21 2 3 1 -- X ----- X ---—2兀~ — 2兀2 4 433-- X ----X -144一丄 184—X H - 3 3 0心宀丄兀2 24 3 2牙+牙-X - Xf(x) = xg(x)^(-2x 2-3x-l),g(x) =所以(/⑴,g (兀)) = 1.⑶ 同样用辗转相除法，可得(/(x),g(x)) = F —2血兀一1.8.求 w(x),仄兀)使 w(x) f\x) + v(x)g(ji) = (/(x), g(%))：(1) f (x) = %4 4- 2x^ — %2 — 4x — 2, (x) = %4 + x — x~ — 2x — 2 : (2) /(x) = 4x 4-2x 3-16x 2+5x4-9, g(x) = 2兀3-x 2-5x+4:(3) /(x) = x A-x 3-4x 2 +4x + l, g (兀)=x 2 -x-l.解(1)利用辗转相除法，可以得到/(x) = g (A ：) + (x 3-2x)'g (兀)=(x+l)(x 3 - 2x) + (x 2 -2),x — 2兀=x(^x~ — 2).因而，(/(x),g(x)) = x 2-2,并且(/(兀),g (兀))=/ 一 2 = g (兀)_ (兀+1)(疋 _ 2兀) =g (兀)一(X +1) (f(x) -g (兀))=(一兀一 1)/(兀)+ (兀+2)g(x),所以 u(x) = -x-\, v(x) = x + 21 10 -- X H --- 3 9x 3 - 3x 2x-13 1 2 2X H —X X 3 3 10 2 2~~'- ---- X H 兀+ 13 -- 3 10 ° 10 20 X --- 兀 3 9 916~~1T —X ------ 9 927 441 --------- X ---------------16 256-3x 2+—x1649一一539 兀+ --- 27 256(2)利用辗转相除法，可以得到/(x) = 2xg(x)-(6x 2 +3兀-9),(\ 1Ag(x) = —(6x_ + 3兀一9) ——% + — — (% — 1), —(6x - + 3x — 9) = —(x —1)(6% + 9).因而，(/⑴,g(Q) = x-1，并且(1 1 …厶— —X + _ f (x) + _兀_—x~\ I 3 3丿 (3 3丿] 1 2 7 2fi/f 以 W (X )= X H —, V (X )= — --- X — \ •3 3 3 3(3) 利用辗转相除法，可以得到fM = X —3)g(x) + (x — 2),g(x) = (x+l)(x-2) + l ・因而( f(x), g(x)) = 1 ,并且(/(兀),g(x)) = 1 = g(x) - (x+1)(兀一 2)=g (兀)-(兀+1)(/(兀)-(x 2 一3)gCr))—(—兀―1) f (x) + (兀'+ 兀2 — 3兀—2)g(x),所以u (兀)= -x-l, v(x) = x 3 +x 2 -3x-2.9.设/(x) = %3+ (14-t)x 2+ 2x + 2w, g(x)二F+zx + u 的最大公因式是一个二次多项式，求/，凤的值.解利用辗转相除法，可以得到/(%) = g(x) + (l + /)兀2 +(2-/)兀 + « ,(/(x), g(x)) = x-l = -(6x 2+ 3x-9)+ | _g(x)I d J J(I ] \= (/(x)-2xg(x)) --x+- -g(x)\ 3丿 <2 o 2 d ,、 U 3 广—---- 兀+ (1 + r t-2(l +r)2(尸 + r—w)(i+r) + (t— 2)~u[(l + t)2 — (r —2)]由题意，/(x)与g(Q的最大公因式是一个二次多项式，所以(广 + / —w)(l + /) + (f— 2)~(T H?皿(l + r)2-(r-2)] A ；=0,(l + O2解得u = o^t = -4.10.设(x —I)[(A/+ B F+I),求A和B.由题意要求知解用(兀一1)2 去除f\x) = Ar4 + Bx2 +1 ,得余式”(x) = (4A + 2B)兀+1 -3人一B,斤（兀）=0,即4A + 2B = 0,1-3A-B = O,解得A = l,B = -2.11.证明:如果(/(x),g(x)) = l, (/(x),/z(x)) = l,那么(/(x), g(x)/z(x)) = l. 证明由条件可知,存在络(兀)和片⑴ 使得旳(兀)/(兀)+岭⑴g(x) = l,存在如(兀)和卩2(兀)使得u2(x)f(x) + v2(x)h(x) = 1.用/?(兀)乘以第一式得坷(x)f(x)h(x) + V, (x)g(x)h(x) = h(x),代入第二式得u2(x)f(x) + v2 (x) [u t (x)f(x)h(x) 4-Vj (x)g(x)/z(x)] = 1, 即[w2(兀)+ u\ (x)v2(x)h(x)]f(x) + [v, (x)v2(x)]g(x)h(x) = 1,所以(/(x),g(x)/z(x)) = l.12.证明：如果/(x)与g(x)不全为零，且/心)/(兀)+ 咻)g(兀)=(/(%), g(Q)，证明由于w(x)/(x) + v(x)g(x) = (/(x),g(x)), /(X )与 g(x)不全为零，所以(/(x)，g(x))HO.两边同时除以(/(Hg(Q)HO,有所以(弘(兀),咻)) = 1 .13.证明：如果〃(兀)|/(兀),〃(兀)|g(x),且〃(兀)为/(兀)与g(x)的一个组合，那么〃(兀)是/G)与 g(x)的一个最大公因式.证明由题意知d(x)是/(X )与g(x)的公因式.再由条件设d(x) = w(x)/(x) + v(x)^(x) •又设h(x) 为/(x)与g(x)的任一公因式，即/z(x)|/(x), h(x)\g(x),则由上式有h(x)\d(x).故而”(兀)是/(兀)与 g(x)的一个最大公因式.14.证明：(.fO)/2(X ), gO)/2(X )) = (.f(X ), g(x))〃(x),其中力(兀)的首项系数为 1.证明显然(/(x), g(x))/?(x)是f{x)h{x)与g(x)h(x)的一个公因式.下面來证明它是最大公因式. 设 /心),v(x)满足 w(x)/(x) + v(x)g(x) = (/(x), g(X>),贝iJu(x)f(x)h(x) + v(x)g(x)h(x) = (/(x),g(x))/z(x).由上题结果知，(/(兀),g(X ))/7(X )是/(X )/?(X )与g(JC”7(X )的一个最大公因式，又首项系数为1,所以(/(x)A(x), ^(%)/?(%)) = (/(x), ^(x))/i(x)・/⑴ g (兀)、(/(兀),g (兀))’(f(x),g(x))丿证明设〃(兀)=(/(兀),g(x)),则存在多项式M (x), v(x),使d(x) = u(x)f(x) + v(x)g(x)・因为/(X )与g (尢)不全为零，所以d(x)HO.上式两边同时除以〃(兀)，有故 /(兀) _____________ g (x)l (/(x),g(x))‘(/(x),g(x))‘u(x) /(X ) (/(%), g(x)) + v(x) g(x) (y (x ),^(x ))15.设多项式/(x)与gS)不全为零，证明1 = u(x)/(兀)(/(兀),g(x))+咻)g(x) (/(兀),g(x))=1成立.16. 分别在复数域、实数域和有理数域上分解兀4+ 1为不可约因式之积.在有理数域上兀°+1是不可约多项式.否则，若+ +1可约，有以下两种可能.(1) 兀4+1有一次因式，从而它有有理根，但/(±1)工0,所以卍+1无有理根.(2) x 4+ 1 无一次因式，设x 4+1 = (x 2+处 +方)(F +cx + d),其中 a,b y c,cl 为整数.于是a + c = O, b+ 〃 + ac = O, cut + be = 0 , bd = \,又分两种情况：① b = d = \,又 a = —c,从而由 b + 〃 + ac = O,得 a 2=2,矛盾； ② b = d = — \,则 a 2= —2 ,矛盾.综合以上情况，即证.17. 求下列多项式的有理根： (1) /(x) = x 3-6x 2+15兀一 14 ；(2) ^(X ) = 4X 4-7X 2-5X -1；(3) /z(x) = x 5+ %4— 6x^ — 14x~ — 1 lx — 3 ・解(1)由于/(x)是首项系数为1的整系数多项式，所以有理根必为整数根，且为-14的因数.-14的因数有：±1, ±2, ±7, ±14,计算得到:/(D = -4, /(-1) = -36, /(2) = 0, /(-2) = -72,/(7) = 140, /(-7) = -756, /(14) = 1764, /(一 14) = —4144,故x = 2是/(兀)的有理根.再由多项式除法可知，x = 2是于(兀)的单根.⑵ 类似(1)的讨论可知，g(x)的可能的有理根为:故x = --是巩兀)的有理根.再由多项式除法可知，兀二-丄是/(劝的2重根.2 2⑶ 类似地，加兀)的可能的有理根为：±1,±3,计算得到解在实数域上的分解式为X4+ 1 = (X 2 + 1)2-2X 2 =(X 2+V2X + 1)(X 2-V2X +1).在复数域上的分解式为x + ----------1 2 2%4+ 1 = f亠迈亠近、X ---------- 12 2/±1, ±1 ±?计算得到g(l) = -9,g(-1) = 1, g(］、r 、171=-5, g —=0, g — 一 —‘ g —〔2< 264 ,4丿11A(l) = -28, /?(-l) = 0,(3) = 0,加一3) = -96.故x = -l, x = 3是//(兀)的有理根.再由多项式除法可知，x = -\是/z(x)的4重根，兀=3是//(兀)的单根.18.若实系数方程x34- px + q = 0有一根a + bi (a,b为实数，/?工0),则方程x3 + px-q = 0有实根2—证明设原方程有三个根不失一般性，令=a + bi,从而有a2 =a-bi,由根与系数的关系可知0 = $ + 冬 + 他=(° + 勿)+ (a - bi) + ,所以冬二-2d，即(-2a)‘ + /?(-2a) + g = 0，故(2a)' + p(2a)-q = 0.这说明x3 + /zr-g = 0有实根2a .19.证明：如果(%-i)|/(r),那么证明因为u-i)|/(z),所以/(r)= /(i)= 0.因此，令y(x)=(x-i)g(x),则有E =(*-i)g(;),即(伙-1)|/(疋).20.下列多项式在有理数域上是否可约？(1)土 (%) = F+1；(2)/；(X)= X4-8?+12X2+2；(3)人(x) = x" +『+1 ；(4)厶(无)=* + "； + 1,门为奇素数；(5)厶(兀)=兀°+4尬+ 1, A为整数.解(1) ./；(兀)的可能的有理根为：±1,而/(±1) = 2,所以它在有理数域上不可约.(2)由Eisenstein判别法，取素数p = 2,则2不能整除1,而2|(-8), 2|12, 2|2,但是2?不能整除2,所以该多项式在有理数域上不可约.(3)令x=y + l,代入厶(x) = P+x'+l有^(y) = ^(y + l) = / + 6/+15/+21/+18y24-9y4-3.取素数0 = 3,由Eisenstein判别法知，g(y)在有理数域上不可约，所以/(兀)在有理数域上不可约.(4)令兀= y_l,代入f4(x) = x p 4-px + 1,得g(y)=厶(y j) = -+ cy~2——C；-2y2 + (Cf* + p)y-p，取素数p,由Eisenstein判别法知，g(y)在有理数域上不可约，所以£(兀)在有理数域上不可约.(5)令x=y + l,代入农(兀)=兀4+4Ax+l,得g(.y)=厶(y +1) = y" + 4y‘ + 6y2 + (4k + 4)y + 4R + 2 ,収素数p = 2,由Eisenstein判别法知，g(y)在有理数域上不可约，所以点(兀)在有理数域上不可约.1•设/(X)，g(X)，加兀)是实数域上的多项式，(1)若/2U) = xg2(x) + x/z2(x),则/(x) = g(x) = h{x) = 0 .(2)在复数域上，上述命题是否成立？证明(1)当g(兀)=/2(兀)=0时，有严⑴=0,所以/(%) = 0 ,命题成立.如果g(x), /z(x)不全为零，不妨设g(x)H0・当h(x) = 0时，a(xg2(x) + x/i2U)) = l + 2a^(x)为奇数；当加兀)工0时，因为g(x),瓜兀)都是实系数多项式，所以Xg2(x)与兀胪(兀)都是首项系数为正实数的奇次多项式，于是也有d(xg2(x) + x/『(x))为奇数.而这时均有/2(x)^0 ,且df\x) = 2df(x)为偶数,矛盾.因此有g(兀)=力(兀) = 0,从而有f(x) = 0 .(2)在复数域上，上述命题不成立.例如，设f(x) = 0 , g(x) = x\ h(x) = ix,1,其中斤为自然数, 有/2 (x) = xg2 (x)xh2 (x),但g(x) / 0 ,力(兀)工0.2.设/(x), g(x)9 h(x)e P[x],满足(x2 4-l)h(x)4-(x-l)/(x) + (x+2)g(x) = 0,(x2 + l)/?(x) + (x+ l)/(x) + (x - 2)^(%) = 0.证明(X2+1)|(/U), g(X))・证明两式相加得到2(x2 + l)h(x) + 2x(/(x) + g(兀))=0.由(x2+l,兀)=1可知(x2 + l)|(/(x) + g(x)).两式相减得到-2f(x) + 4g(x) = 0, f(x) = 2g(x).故(x2 + l)|/(x), (x2+l)|g(x), BP(X2+1)|(/(X),g(x)).3・设gi(x)g2(x)\f{(x)f2(x),证明(1)若/(x)|g](x)，/(X)H0,则g2(x)\f2(x)；(2)若g2(x)|/；(x)/；(x),是否有g2(x)\f2(x)?解(1)因为gi(兀)g2(兀)庞(兀)£(兀)，/O)|gi(X)，故存在多项式h(x), h}(x)使得fl(x)f 2(x) = g](x)g 2(x)h(x\ g](兀)=Z (x)h }(x).于是/；(兀)£(兀)=/(兀)人(兀)g2(x)力(兀)•由于土(兀)工0,故有 f 2(x) = h l (x)g 2(x)h(x),即g 2(x)\f 2(x).(2)否•例如取 g {(x) = x-2 , ^2(X ) = X 2-1 , (x) = (x-l)(x-2), (x) = (x + l)(x4-2).虽然 gSx)g 2(x)\f^x)f 2(x)且 g 2(x)\f {(x)f 2(x),但 g 2(x)不能整除 f 2(x).4.当R 为何值时，/(x) = X 2 +伙+ 6)x + 4k + 2和g(x) = F+(£ + 2)x + 2R 的最大公因式是一次的？并求出此吋的最大公因式.解显然 g(x) = (x + £)(x+2).当(/(x),g(Q) = x + 2时'/(一2) = 4 — 2伙+ 6) + 4£ + 2 = 0‘ 则k = 3.当(于(兀),g(Q )=兀 + £ 时’/(一灯=k 2 - k(k + 6) + 4Z: + 2 = 0 ‘ 则 k = l.这时(/(x), g(x))=兀+1. 5.证明：对于任意正整数斤，都有(/(x),g(Q)"=(/"(x),g"(x))・证明由题意可知/(%)与&(兀)不全为零.令(/(x), g(x)) = d(x),Z 、” g(x) 、d(x)丿/心)/"(兀)+ 咚)g"(兀)=d\x).又由 d(x)\f(x), d(x)|g(x),有 d n (x) f l \x), d"(x) g"(x),因此 d"(x)是厂(x)与 g"(x)的首项系数为1的最大公因式，从而有(广(x),g"(x))= 〃"(兀)=(/(x),g(x))" •6.设 / (x) = af(x) + bg(x), g[ (x) = c/(x) + dg(x),且 ad - be H 0 ,证明(/(x),g(x)) = (/](x), g](X ))・证明设(/(x), g(x)) = d(x),则 d(x)\f(x\d(x)\g(x).由于 “所以对任意正整如，有爲J 寫〕"卜于是有u{x) +咻) 则〃(兀)工0,从而fi (兀)=妙(x) + bg(x) , g] (x) = (x) + dg (x),故d (x)| (x), d (x)|g t (x).又设h(x)\ (x), /z(x)|(x),由上式及ad-bc^O ,可得从而/?(x)|/(x), h(x)\g(x),于是h(x)\d(x),即〃(兀)也是/；(兀)和g|(x)的最大公因式，即(/(x), g(x)) = (/；(x),&(兀))・7.设 /(x) = t/(x)/(x), g(Q 二 dCr)g](x),且/O)与 gd)不全为零，证明〃(兀)是/O)与 gCO的一个最大公因式的充分必要条件是(/(劝,g|(x)) = 1.证明必要性.若〃(x)是/(兀)与g (兀)的一个最大公因式，则存在多项式w(x),v(x)使W (x)/(x) +v(x)g(x) = d(x),于是u(x)d(x)f t (x) + v(x)d(x)g l (x) = d(x).由/(力与g (兀)不全为零知如工0,因此有u(x)f l (x) + v(x)g l (x) = l f 即(土(兀),g©))i •充分性.若(f l (x),g l (x)) = l ,则存在多项式u(x),v(x),使 u(x)f l (x)+ v(x)g l (x) = l. 两边同吋乘〃(兀)有u(x)f(x) + v(x)g(x) = d(x)・由d(x)是/(x)与g(x)的一个公因式知，d(x)是f(x)与g(x)的一个最大公因式.8.设于(兀)和g(x)是两个多项式，证明(f(x), g(x)) = l 当且仅当(f(x)-l-g(x), f(x)g(x)) = l. 证明必要性.设(f(x)9g(x)) = l,若f(x) + g(x)与/⑴g(x)不互素，则有不可约公因式p(x), 使p(x)lf(x)g(x)f所以 p(x)| /(X )或 0(x)|g(x).不妨设 p(x)\ /(x),由 P (x)|(/(x) + g (兀))可知 p(x)|g(x),因此 P (兀)是 /(兀)和g“)的公因式,与/(%), g (x)互素矛盾,故蚀+g (兀)与蚀g (兀)互素.充分性.设(/(兀)+ gO) J(x)g (兀)) = 1,则存在w(x), v(x)使(/(兀)+ g (兀))心)+ /(x)g(x)v(x) = 1 , f(x)u(x) + g (兀)(臥兀)+d ad-be zw- h ad 一gi (兀)， g(x) -c ad -be a ad -be g](x)，/(x)v(x)) = 1, 上式说明(/(兀),g(兀)) = 1.9.如果(x2 +x + l)|/j(x3) + x/^(x3),那么(x-l)|/；(x), 0 — 1)|/；(兀)・T；®所以，^3=£23 = 1.证明X2+X + l的两个根为£\= 士护和£2=因为U2+x+l)|(/；(^3) + x/；(^3)),所以(兀一£|)(x - £2)|/；(X')+/(F)，故有y 窗)+ £/(郃)=0,［爪哥)+ £2£(哥)=0,即解得/(l) = /；(l) = o,从而(兀—1)|久(兀)，(x-1)|/；(%).10.若f(x)\f(x H),则/(x)的根只能是零或单位根.证明因为f(x)\f(x n),故存在多项式g(x),使/(x n) = /(x)^(x).设。

线性代数北邮版课后习题答案习题2

习题二（A 类）1. 1. 设A =121221211234⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，B =432121210101⎡⎤⎢⎥--⎢⎥⎢⎥--⎣⎦，（1）计算3A -B ，2A +3B ；（2）若X 满足A +X =B ，求X ；（3）若Y 满足（2A -Y ）+2（B -Y ）=0，求Y .解：（1）3A -B =3636636333912⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦-432121210101⎡⎤⎢⎥--⎢⎥⎢⎥--⎣⎦=1315828237913-⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。

2A +3B =242442422468⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦+1296363630303⎡⎤⎢⎥--⎢⎥⎢⎥--⎣⎦=14138725252165⎡⎤⎢⎥--⎢⎥⎢⎥⎣⎦。

（2）因A +X =B ，则X =B -A ，即X =432121210101⎡⎤⎢⎥--⎢⎥⎢⎥--⎣⎦-121221211234⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦=311140401335-⎡⎤⎢⎥--⎢⎥⎢⎥----⎣⎦。

（3）因为（2A -Y ）+2（B -Y ）=0，所以3Y =2A +2B ，即Y =23（A +B ）=23（432121210101⎡⎤⎢⎥--⎢⎥⎢⎥--⎣⎦+121221211234⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦）=55332020231133⎡⎤⎢⎥⋅⎢⎥⎢⎥⎣⎦=10102233440033222233⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦。

2. 计算下列矩阵的乘积.（1）[]11321023⎡⎤⎢⎥-⎢⎥-⎢⎥⎢⎥⎣⎦=；（2）500103120213⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦；（3） []32123410⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦；（4）()111213112321222323132333a a a x x x x a a a x a a a x ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦；（5） 111213212223313233100011001a a a a a a a a a ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦；（6） 12101031010101210021002300030003⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥-⎣⎦⎣⎦. 【解】(1) 32103210;64209630-⎡⎤⎢⎥--⎢⎥⎢⎥-⎢⎥-⎣⎦(2)531⎡⎤⎢⎥-⎢⎥⎢⎥-⎣⎦; (3) (10);(4)3322211122233312211213311323322311()()()ij i j i j a x a x a x a a x x a a x x a a x x a x x ==++++++++=∑∑(5)111212132122222331323233a a a a a a a a a a a a +⎡⎤⎢⎥+⎢⎥⎢⎥+⎣⎦; (6) 1252012400430009⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥-⎣⎦. 3. 设111111111⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦A ，121131214⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦B ，求(1)2-AB A ;(2) -AB BA ；(3) 22()()-=-A+B A B A B 吗?【解】(1) 2422;400024⎡⎤⎢⎥-=⎢⎥⎢⎥⎣⎦AB A (2) 440;531311⎡⎤⎢⎥-=--⎢⎥⎢⎥--⎣⎦AB BA(3) 由于AB ≠BA ,故(A +B )(AB )≠A 2B 2.4. 举例说明下列命题是错误的.(1) 若2=A O ，则=A O ； (2) 若2=A A ，则=A O 或=A E ；(3) 若AX =AY ，≠A O ，则X =Y . 【解】(1) 以三阶矩阵为例，取2001,000000⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦0A A ,但A ≠0(2) 令110000001-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦A ,则A 2=A ,但A ≠0且A ≠E(3) 令11021,=,0111210110⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=≠=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦A Y X 0则AX =AY ,但X ≠Y .5. 计算：（1）3010001000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦；（2）cos sin sin cos kθθθθ⎡⎤⎢⎥-⎣⎦（k 为正整数）；（3）101kλ⎡⎤⎢⎥⎣⎦（k 为正整数）. 解：（1）3010001000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦=010001000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦010001000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦010001000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦=001000000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦010001000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦ =33000000000⨯⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦O 。

(完整版)线性代数习题集带答案

第一部分专项同步练习第一章行列式一、单项选择题1．下列排列是5阶偶排列的是 ( ).(A) 24315 (B) 14325 (C) 41523 (D)243512．如果n 阶排列n j j j 21的逆序数是k , 则排列12j j j n 的逆序数是( ). (A)k (B)k n - (C)k n -2! (D)k n n --2)1(3. n 阶行列式的展开式中含1211a a 的项共有( )项.(A) 0 (B)2-n (C) )!2(-n (D) )!1(-n4．=0001001001001000( ).(A) 0 (B)1- (C) 1 (D) 25.=0001100000100100( ).(A) 0 (B)1- (C) 1 (D) 26．在函数1323211112)(x x xxx f ----=中3x 项的系数是( ).(A) 0 (B)1- (C) 1 (D) 27. 若21333231232221131211==a a a a a a a a a D ，则=---=323133312221232112111311122222 2a a a a a a a a a a a a D ( ). (A) 4 (B) 4- (C) 2 (D) 2- 8．若a a a a a =22211211，则=21112212ka a ka a ( ).(A)ka (B)ka - (C)a k 2 (D)a k 2-9．已知4阶行列式中第1行元依次是3,1,0,4-, 第3行元的余子式依次为x ,1,5,2-, 则=x ( ).(A) 0 (B)3- (C) 3 (D) 210. 若5734111113263478----=D ，则D 中第一行元的代数余子式的和为( ). (A)1- (B)2- (C)3- (D)011. 若2235001011110403--=D ，则D 中第四行元的余子式的和为( ). (A)1- (B)2- (C)3- (D)012. k 等于下列选项中哪个值时，齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x kx x kx x kx x x 有非零解.( )(A)1- (B)2- (C)3- (D)0二、填空题1. n 2阶排列)12(13)2(24-n n 的逆序数是.2．在六阶行列式中项261365415432a a a a a a 所带的符号是.3．四阶行列式中包含4322a a 且带正号的项是.4．若一个n 阶行列式中至少有12+-n n 个元素等于0, 则这个行列式的值等于.5. 行列式=100111010100111.6．行列式=-000100002000010n n .7．行列式=--001)1(2211)1(111n n n n a a a a a a .8．如果M a a a a a a a a a D ==333231232221131211，则=---=323233312222232112121311133333 3a a a a a a a a a a a a D .9．已知某5阶行列式的值为5，将其第一行与第5行交换并转置，再用2乘所有元素，则所得的新行列式的值为.10．行列式=--+---+---1111111111111111x x x x .11．n 阶行列式=+++λλλ111111111.12．已知三阶行列式中第二列元素依次为1,2,3, 其对应的余子式依次为3,2,1，则该行列式的值为.13．设行列式5678123487654321=D ，j A 4)4,3,2,1(=j 为D 中第四行元的代数余子式，则=+++44434241234A A A A .14．已知db c a cc a b b a b c a cb a D =， D 中第四列元的代数余子式的和为.15．设行列式62211765144334321-==D ，j A 4为)4,3,2,1(4=j a j 的代数余子式，则=+4241A A ，=+4443A A .16．已知行列式nn D001030102112531-=，D 中第一行元的代数余子式的和为.17．齐次线性方程组⎪⎩⎪⎨⎧=+-=+=++0020232121321x x x kx x x x kx 仅有零解的充要条件是.18．若齐次线性方程组⎪⎩⎪⎨⎧=+--=+=++0230520232132321kx x x x x x x x 有非零解，则k =.三、计算题1.cb a db a dc a dc bd c b a d c ba d cb a++++++++33332222; 2．yxyx x y x y y x y x +++；3．解方程0011011101110=x x xx ； 4．111111321321221221221----n n n n a a a a x a a a a x a a a a xa a a a x ；5. na a a a 111111111111210(n j a j ,,1,0,1 =≠)； 6. bn b b----)1(1111211111311117. n a b b b a a b b a a a b 321222111111111； 8．xa a a a x a a a a x a a a a x n nn 321212121;9.2212221212121111nn n nnx x x x x x x x x x x x x x x +++; 10. 21000120000021001210001211．aa a a a a aa a D ---------=110001100011000110001.四、证明题1．设1=abcd ，证明：011111111111122222222=++++dddd c c c c b b b b a a a a .2．3332221112333332222211111)1(c b a c b a c b a x c b x a x b a c b x a x b a c b x a xb a -=++++++.3．))()()()()()((111144442222d c b a c d b d b c a d a c a b d c b a d c b adc b a +++------=.4．∏∑≤<≤=----=nj i i jni innn nn nn n nna aa a a a a a a a a a a a a 1121222212222121)(111.5．设c b a ,,两两不等，证明0111333=c b a c ba 的充要条件是0=++cb a .参考答案一．单项选择题A D A C C D ABCD B B 二．填空题1.n ;2.”“-;3.43312214a a a a ;4.0;5.0;6.!)1(1n n --;7.1)1(212)1()1(n n n n n a a a ---; 8.M 3-; 9.160-; 10.4x ; 11.1)(-+n n λλ; 12.2-;13.0; 14.0; 15.9,12-; 16.)11(!1∑=-nk k n ; 17.3,2-≠k ; 18.7=k三．计算题1．))()()()()()((c d b d b c a d a c a b d c b a ------+++-； 2. )(233y x +-； 3. 1,0,2-=x ; 4.∏-=-11)(n k kax5.)111()1(00∑∏==-+-nk k nk k a a ; 6. ))2(()1)(2(b n b b ---+- ;7. ∏=--nk k kna b1)()1(; 8. ∏∑==-+nk k nk k a x a x 11)()(;9. ∑=+nk k x 11; 10. 1+n ;11. )1)(1(42a a a ++-. 四. 证明题 (略)第二章矩阵一、单项选择题1. A 、B 为n 阶方阵，则下列各式中成立的是( )。

北京大学《线性代数》六套试卷与答案

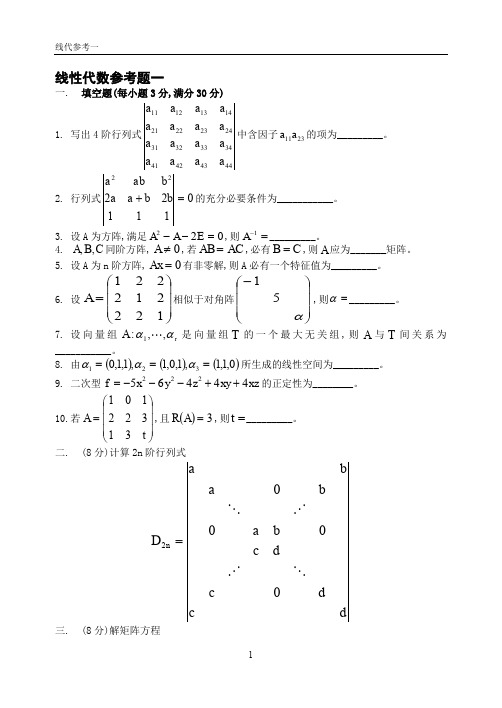
线性代数参考题一一. 填空题(每小题3分,满分30分)1. 写出4阶行列式44434241343332312423222114131211a a a a a a a a a a a a a a a a 中含因子2311a a 的项为_________。

2. 行列式01112222=+b b a a b ab a 的充分必要条件为___________。

3. 设A 为方阵,满足022=--E A A ,则=-1A _________。

4. C B A ,,同阶方阵,0≠A ,若AC AB =,必有C B =,则A 应为_______矩阵。

5. 设A 为n 阶方阵,0=Ax 有非零解,则A 必有一个特征值为_________。

6. 设⎪⎪⎪⎭⎫⎝⎛=122212221A 相似于对角阵⎪⎪⎪⎭⎫⎝⎛-α51,则=α_________。

7. 设向量组r A αα,,:1 是向量组T 的一个最大无关组,则A 与T 间关系为___________。

8. 由()()()0,1,1,1,0,1,1,1,0321===ααα所生成的线性空间为_________。

9. 二次型xz xy z y x f 44465222++---=的正定性为________。

10.若⎪⎪⎪⎭⎫⎝⎛=t A 31322101,且()3=A R ,则=t _________。

二. (8分)计算2n 阶行列式d cdc dc b a ba ba D n 0002=三. (8分)解矩阵方程⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛1302313512343122321X求?=X四. (10分)设向量组A:()()()()3,6,2,0,1,3,0,1,3,1,1,2,0,1,4,14321-=--=--==αααα求向量组A 的秩及一个最大无关组. 五. 12分)讨论方程组的解的情况⎪⎩⎪⎨⎧=++=++=++23213213211λλλλλx x x x x x x x x六. (16分)求正交变换PY X =,将二次型323121232221222222x x x x x x x x x f ---++=化为标准形,并写出其标准形.七. (8分)设n n ααβααβαβ++=+== 121211,,,且n αα,,1 线性无关, 证明:n ββ,,1 线性无关.八. (8分)A 为n 阶方阵,且A 与())1,,2,1(1-=-+n i iE A i均不可逆.则A 可否对角化?线性代数参考题二一、填空题(每小题3分,满分30分) 1．设B A ,都是5阶矩阵,且2,31=-=-B A ,则=A B2．已知0222=++I A A ,则=+-1)(I A (其中I 是n 阶单位阵)3． ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=12241031x A 设,已知矩阵A 的秩r(A)=2,则=x4．()814370122222632144-==⨯ija A 设,又ij A 是ij a 的代数余子式,则=+++44434241A A A A5．若一向量组只有唯一的极大无关组,则该向量组6．设3221232221321222),,(x tx x x x x x x x x f ++++=是正定二次型, 则t 的取值区间为7．设A 是n 阶正交矩阵,1-=A ,则()=*TA8．设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=20002121x A 相似于对角阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--211,则=x9．设非齐次线性方程组b AX =的两个解为)(,,2121ξξξξ≠A 的秩为1-n ,则 b AX =的一般解=ξ .10．已知向量组[][][]1,4,2,1,0,,0,2,1,1,2,1321--==-=αααt 的秩为2,则=t 二．(8分)计算n 阶行列式ba a a ab a a a a b a D n n n n ---=212121三．(8分)求矩阵X 满足⎥⎦⎤⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎦⎤⎢⎣⎡1041120112201117241X 四．(10分)设[][][][]10,2,1,2,4,1,5,1,3,6,3,11,5,5,10,2,3,2,1,24321-==-=-=αααα求向量组的秩及其一个极大无关组. 五. (12分)问常数b a ,各取何值时, 方程组()()⎪⎪⎩⎪⎪⎨⎧=+++++=++++=+-=+++,5853,34232,12,1432143214324321x a x x x b x x a x x x x x x x x x 无解,有唯一解,或有无穷多解,并在有无穷多解时写出其一般解. 六. (16分)求正交变换PY X =,将二次型()323121232221321222222,,x x x x x x x x x x x x f ---++=化为标准形,并写出其标准形.七. (8分)设向量432,,,1αααα线性无关,且43214432134321243211,,,ββββαββββαββββαββββα+---=-+--=--+-=---=证明向量组4321,,,ββββ线性无关.八. (8分)A 为n 阶方阵,且A 与())1,,2,1(1-=-+n i iI A i均不可逆。

线性代数习题参考答案

线性代数习题参考答案(总96页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面，使用请直接删除第一章行列式§1 行列式的概念1．填空(1) 排列6427531的逆序数为，该排列为排列。

(2) i = ，j = 时，排列1274i56j9为偶排列。

(3) n阶行列式由项的代数和组成，其中每一项为行列式中位于不同行不同列的n个元素的乘积，若将每一项的各元素所在行标按自然顺序排列，那么列标构成一个n元排列。

若该排列为奇排列，则该项的符号为号；若为偶排列，该项的符号为号。

(4) 在6阶行列式中，含152332445166a a a a a a的项的符号为，含324314516625a a a a a a的项的符号为。

2．用行列式的定义计算下列行列式的值(1)112223323300 0aa aa a解：该行列式的3!项展开式中，有项不为零，它们分别为，所以行列式的值为。

(2)12,121,21,11, 12,100000nn nn n n n n n n n n nnaa aa a aa a a a------解：该行列式展开式中唯一不可能为0的项是，而它的逆序数是，故行列式值为。

3．证明：在全部n 元排列中，奇排列数与偶排列数相等。

证明：n 元排列共有!n 个，设其中奇排列数有1n 个，偶排列数为2n 个。

对于任意奇排列，交换其任意两个元的位置，就变成偶排列，故一个奇排列与许多偶排列对应，所以有1n 2n ，同理得2n 1n ，所以1n2n 。

4．若一个n 阶行列式中等于0的元素个数比n n -2多，则此行列式为0，为什么 5．n 阶行列式中，若负项的个数为偶数，则n 至少为多少（提示：利用3题的结果） 6．利用对角线法则计算下列三阶行列式（1）21141183---（2）222111ab c a b c§2 行列式的性质1．利用行列式的性质计算系列行列式。

北理-线性代数-在线作业

若行列式主对角线上的元素全为0，则此行列式为0.()判断题10.0 错误未判断×.有非零解的齐次线性方程组的基础解系是唯一判断题10.0 错误未判断×单选题10.0 2 ×单选题10.0 3 ×1 / 58单选题10.0 4 ×单选题10.0 1 ×按定义，5阶行列式有项，其中带负号的有项.填空题10.0 120&60×填空题10.0 5&奇×填空题10.0 ×2 / 58填空题10.0&×本次作业总分值:100.0 得分:0.0 正确的题数：0 题目总数：10 正确率:0.0%单选题10.2 ×3 / 58单选题10.3 ×单选题10.3 ×单选题10.2 ×单选题10.1 ×4 / 585 / 58 填空题10.0 &×填空题10.正×填空题10.×填空题10.0 &×6 / 58 填空题10.0 &×本次作业总分值:100.0 得分:0.0 正确的题数：0 题目总数：10 正确率:0.0%判断题10.0 正确未判断×行阶梯形矩阵中非零行的个数就是它的秩判断题10.0 正确未判断×判断题10.0 正确未判断×单10.0 1 ×选题单10.0 4 ×选题单10.0 4 ×选题单10.0 2 ×选题填10.0 ×空题填10.0 E×空题7 / 58填空题10.0相等×本次作业总分值:100.0 得分:0.0 正确的题数：0 题目总数：10 正确率:0.0%判断题10.0 错误未判断×对于一个给定的向量组，不是线性相关就是线性无关；判断题10.0 正确未判断×.有非零解的齐次线性方程组的基础解系是唯一判断题10.0 错误未判断×单选题10.0 1 ×8 / 58单10.0 1 ×选题单10.0 1 ×选题单10.0 2 ×选题填10.0 ×空题填10.0 唯一×空题填10.0 ×空题9 / 58本次作业总分值:100.0 得分:0.0 正确的题数：0 题目总数：10 正确率:0.0%判断题10.0 正确特征多项式相同的矩阵相似. 判断题10.0 错误单选题10.0 3下面二次型中正定的是单选题10.0 2单选题10.0 310 / 58单10.0 2选题单10.0 1选题填10.0空题填10.0空题填10.0空题本次作业总分值:100.0 得分:0.0 正确的题数：0 题目总数：10 正确率:0.0%11 / 58判断题10.0 正判断题10.0 正判断题10.0 错单选题10.0 2下面二次型中正定的是单选题10.0 2单选题10.0 312 / 58单10.0 1选题填10.0空题填10.0空题填10.0空题本次作业总分值:100.0 得分:0.0 正确的题数：0 题目总数：10 正确率:0.0%13 / 58若行列式主对角线上的元素全为0，则此行列式为0.( ) 判断题10.0 错误错误√.有非零解的齐次线性方程组的基础解系是唯一判断题10.0 错误错误√单选题10.0 2 2 √单选题10.0 3 3 √14 / 58单选题10.0 4 4 √单选题10.0 1 1 √按定义，5阶行列式有120项，其中带负号的有______项. 填空题10.060*&*６０60 ×填空题10.05*&*奇5&奇×填空题10.0 0 零×填空10.0 正×15 / 58题本次作业总分值:100.0 得分:60.0 正确的题数：6 题目总数：10 正确率:60.000004%16 / 58判断题10.0错误错误√对于一个给定的向量组，不是线性相关就是线性无关；判断题10.0正确正确√.有非零解的齐次线性方程组的基础解系是唯一判断题10.0错误错误√单选题10.0 1 1 √单选题10.0 1 1 √单选10.0 1 1 √17 / 58题单选题10.0 2 ×填空题10.0 1 ×填空题10.0唯一×填空题10.0 n*s ×本次作业总分值:100.0 得分:60.0 正确的题数：6 题目总数：10 正确率:60.000004%18 / 58判断题10.0 正确未判断×特征多项式相同的矩阵相似. 判断题10.0 错误未判断×判断题10.0 错误未判断×单选题10.0 3 ×单选题10.0 2 ×单选题10.0 1 ×19 / 58单选题10.0 1 ×填空题10.0将A的第1列的1/a倍加到第2列×填空题10.0线性无关×填空题10.0 C'AC ×本次作业总分值:100.0 得分:0.0 正确的题数：0 题目总数：10 正确率:0.0%本次作业总分值:100.0 得分:70.0 正确的题数：7 题目总数：10 正确率:70.0%20 / 58单选题10.0 2 ×下列各项中，（）为某4阶行列式中带正号的项单选题10.0 4 ×单选题10.0 4 ×21 / 58单10.0 3 ×选题单10.0 4 ×选题填10.0 10 ×空题填10.0 -18 ×空题22 / 58填空题10.0-113×填空题10.0 -1 ×填空题10.0 192 ×本次作业总分值:100.0 得分:0.0 正确的题数：0 题目总数：10 正确率:0.0%23 / 58判断题10.0正确未判断×行阶梯形矩阵中非零行的个数就是它的秩判断题10.0正确未判断×判断题10.0正确未判断×单选题10.0 1 ×单选题10.0 4 ×单选题10.0 4 ×24 / 58单选题10.0 2 ×填空题10.0 1 ×填空题10.0 E ×填空题10.0相等×本次作业总分值:100.0 得分:0.0 正确的题数：0 题目总数：10 正确率:0.0%25 / 58判断题10.0错误未判断×判断题10.0错误未判断×判断题10.0错误未判断×单选题10.0 1 ×单选题10.0 1 ×单选题10.0 1 ×26 / 58单选题10.0 2 ×本次作业总分值:100.0 得分:90.0 正确的题数：9 题目总数：10 正确率:90.0%[复习建议][返回阶段列表]北京理工大学现代远程教育学院版权所有京ICP备05065315号Copyright©2000-2006 All right reserved. 填空题10.0 3 ×填空题10.0 -2 ×27 / 58填空题10.0 2 ×本次作业总分值:100.0 得分:0.0 正确的题数：0 题目总数：10 正确率:0.0%单选题10.0 2 ×下列各项中，（）为某4阶行列式中带正号的项单选题10.0 4 ×单选题10.0 4 ×28 / 58单10.0 3 ×选题单10.0 4 ×选题填10.0 10 ×空题填10.0 -18 ×空题29 / 58填空题10.0-113×填空题10.0 -1 ×填空题10.0 192 ×本次作业总分值:100.0 得分:0.0 正确的题数：0 题目总数：10 正确率:0.0%[复习建议][返回阶段列表]北京理工大学现代远程教育学院版权所有京ICP备05065315号Copyright©2000-2006 All right reserved.30 / 58判断题10.0 错误错误√对于一个给定的向量组，不是线性相关就是线性无关；判断题10.0 正确正确√.有非零解的齐次线性方程组的基础解系是唯一判断题10.0 错误错误√单选题10.0 1 1 √单选题10.0 1 1 √单选题10.0 1 1 √单选题10.0 2 2 √31 / 58填空题10.0 1 ×填空题10.0 唯一唯一√填空题10.0 n*s n*s √单10.0 2 ×选题32 / 58单选题10.0 3 ×单选题10.0 3 ×单选题10.0 2 ×单选题10.0 1 ×i=4,j=____ 填空10.0 j=7 ×33 / 58题填空题10.0 正×4阶行列式中含有因子a13a31的项是___填空题10.0-a13a22a31a44+a13a24a31a42×i=4,j=____填空题10.0 2 ×X3的系数是157。

（精选）线性代数课后作业及参考答案

（精选）线性代数课后作业及参考答案《线性代数》作业及参考答案一．单项选择题1.设行列式a aa a11122122=m，a aa a13112321=n，则行列式a a aa a a111213212223++等于（）A. m+nB. -(m+n)C. n-mD. m-n2.设矩阵A=100020003，则A-1等于（）A.130012001B.100120013C. 1 3 00 010 00 1 2D. 1 2 00 10013.设矩阵A=312101214---，A*是A的伴随矩阵，则A *中位于（1，2）的元素是（）A. –6B. 6C. 24.设A是方阵，如有矩阵关系式AB=AC，则必有（）A. A =0B. B≠C时A=0C. A≠0时B=CD. |A|≠0时B=C5.已知3×4矩阵A的行向量组线性无关，则秩（A T）等于（）A. 1B. 2C. 3D. 46.设两个向量组α1，α2，…，αs和β1，β2，…，βs均线性相关，则（）A.有不全为0的数λ1，λ2，…，λs使λ1α1+λ2α2+…+λsαs=0和λ1β1+λ2β2+…λsβs=0B.有不全为0的数λ1，λ2，…，λs使λ1（α1+β1）+λ2（α2+β2）+…+λs（αs+βs）=0C.有不全为0的数λ1，λ2，…，λs使λ1（α1-β1）+λ2（α2-β2）+…+λs（αs-βs）=0D.有不全为0的数λ1，λ2，…，λs和不全为0的数μ1，μ2，…，μs使λ1α1+λ2α2+…+λsαs=0和μ1β1+μ2β2+…+μsβs=07.设矩阵A的秩为r，则A中（）A.所有r-1阶子式都不为0B.所有r-1阶子式全为0C.至少有一个r阶子式不等于0D.所有r阶子式都不为08.设Ax=b是一非齐次线性方程组，η1，η2是其任意2个解，则下列结论错误的是（）A.η1+η2是Ax=0的一个解2η1+12η2是Ax=b的一个解C.η1-η2是Ax=0的一个解D.2η1-η2是Ax=b的一个解9.设n阶方阵A不可逆，则必有（）A.秩(A)<n< bdsfid="226" p=""></n<>B.秩(A)=n-1C.A=0D.方程组Ax=0只有零解10.设A是一个n(≥3)阶方阵，下列陈述中正确的是（）A.如存在数λ和向量α使Aα=λα，则α是A的属于特征值λ的特征向量B.如存在数λ和非零向量α，使(λE-A)α=0，则λ是A的特征值C.A的2个不同的特征值可以有同一个特征向量D.如λ1，λ2，λ3是A的3个互不相同的特征值，α1，α2，α3依次是A的属于λ1，λ2，λ3的特征向量，则α1，α2，α3有可能线性相关11.设λ0是矩阵A的特征方程的3重根，A的属于λ0的线性无关的特征向量的个数为k，则必有（）A. k≤3B. k<3C. k=3D. k>312.设A是正交矩阵，则下列结论错误的是（）A.|A|2必为1B.|A|必为1C.A-1=A TD.A的行（列）向量组是正交单位向量组13.设A是实对称矩阵，C是实可逆矩阵，B=C T AC.则（）A.A与B相似B. A与B不等价C. A与B有相同的特征值D. A与B合同15.设有矩阵Ａｍ×ｎ，Ｂｍ×ｓ，Ｃｓ×ｍ，则下列运算有意义的是（）。

标准答案北京大学春季学期线性代数作业

2016年春季学期线性代数作业一、选择题（每题2分，共36分）1.（教材§1.1）行列式（B）。

A.6B.5C.10D.72.（教材§1.1）行列式（A）。

A.B.C.0 D.3.（教材§1.2）行列式（D）。

A.40B.-40C.10D.-104.（教材§1.3）下列对行列式做的变换中，（A）会改变行列式的值。

A.将行列式的某一行乘以3B.对行列式取转置C.将行列式的某一行加到另外一行D.将行列式的某一行乘以3后加到另外一行5.（教材§1.3）行列式（2/9）。

(提示：参考教材P32例1.3.3)A.2/9B.2/3C.2/9D. 3/46.（教材§1.4）若线性方程组有唯一解，那么（B）。

A.2/3B.1C.-2/3D.1/37.（教材§2.2）矩阵2110231134411132⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦的秩是（D）。

A.1B.2C.3D.48.（教材§2.2）若线性方程组无解，则a的值为（C）。

A.-1B.-2C.-3D.09.（教材§3.1）已知向量，，，则向量（B）。

A.B. C. D.10.（教材§3.3）已知向量组线性相关，下面说法正确的是（C）。

A.如果，则必有;B.矩阵的秩等于向量的个数；C.元齐次线性方程组有非零解；D.向量组A 中任何一个向量都不能由其余的个向量线性表示。

11.（教材§3.3）下列向量组中，线性无关的是（C）。

A.B.C.D.12.（教材§3.3）下列向量组中，线性相关的是（D）。

A.B.C.D.13.（教材§4.1）已知矩阵，矩阵和矩阵均为n阶矩阵，为实数，则下列结论不正确的是（C）。

A. B.C. D.14.（教材§4.1）已知矩阵，矩阵，则（A）。

A. B.C. D.15.（教材§4.1）已知矩阵，为矩阵，矩阵为矩阵，为实数，则下列关于矩阵转置的结论，不正确的是（D）。