哈工大力学习题课下
哈工大力学习题课下

1
2
共同角速度 J 11 J 22
啮合过程机械能损失J:1 J 2
E
E0 E
(1 2
J112
1 2
J
2
22
)
1 2
(
J1
J2
)
2
J1J2 (1 2 )2
2(J1 J2 )
7. 两个同样重的小孩 ,各抓着跨过滑轮绳子的两端。一 个孩子用力向上爬,另一个则抓住绳子不动。若滑轮的质量
置的细杆处于非稳定平衡状态,当其受到微小扰动时, 细杆将在重力作用下由静止开始绕铰链O 转动 .试计
算细杆转动到与竖直线成 角时的角加速度和角速度 .
解 细杆受重力和
铰链对细杆的约束力
FN
作用,由转动定律得
1 mgl sin J
2
式中 J 1 ml2 3
得 3g sin
和轴上的摩擦都可忽略,哪一个小孩先到达滑轮处?若两个小 孩重量不等,情况又如何?
解:把每个小孩看成一个质点,以滑轮的
R
轴为参考点,把两个小孩和滑轮看成系统。 规定向里为角动量和力矩的正方向。Biblioteka 1 2kxm2
(F
mg)2
2k
由质点系的功能原理:
(F
mg)xm
1 2
kxm2
得:
2(F mg)
xm
k
E p
1 2
kxm2
2(F
mg)2
k
1. 从一个半径为 R 的均匀薄圆板上挖去一个半径为 R/2 的圆板,所形 成的圆洞的中心在距圆薄板中心 R/2 处,所剩薄板的质量为 m 。求此时薄 板对通过圆中心与板面垂直的轴的转动惯量。
哈尔滨工业大学 第七版 理论力学 第5章 课后习题答案

第5章 摩 擦5-1 如图5-1a 所示,置于V 型槽中的棒料上作用1力偶,力偶矩m N 15⋅=M 时,刚好能转动此棒料。
已知棒料重力N 400=P ,直径m 25.0=D ,不计滚动摩阻。
求棒料与V 形槽间的静摩擦因数f s 。
(a)(b)图5-1解 圆柱体为研究对象,受力如图5-1b 所示,F s1,F s2为临界最大摩擦力。
0=∑x F ,045cos 2s 1N =°−+P F F (1) 0=∑y F ,045sin 1s 2N =°−−P F F (2) 0=∑O M ,0222s 1s =−+M DF D F(3)临界状态摩擦定律:1N s 1s F f F =(4) 2N s 2s F f F =(5)以上5式联立,化得 0145cos s2s =+°−MPDf f 代入所给数据得01714.4s 2s =+−f f 方程有2根:442.4s1=f (不合理), 223.0s2=f (是解)故棒料与V 形槽间的摩擦因数223.0s =f5-2 梯子AB 靠在墙上,其重力为N 200=P,如图5-2a 所示。
梯长为l ,并与水平面交角°=60θ。
已知接触面间的静摩擦因数均为0.25。
今有1重力为650 N 的人沿梯向上爬,问人所能达到的最高点C 到点A 的距离s 应为多少?AN F As F(a)(b)图5-2解 梯子为研究对象,受力如图5-2b 所示,刚刚要滑动时,A ,B 处都达最大静摩擦力。
人重力N 650=W ,平衡方程: 0=∑x F , 0s N =−A B F F (1) 0=∑y F , 0s N =−−+W P F F B A(2)0=∑A M ,060cos 60sin 60cos 60cos 2s N =°−°−°+°l F l F Ws lPB B (3) 临界补充方程:A s A F f F N s = (4)B s B F f F N s =(5)联立以上5式,解得 N 80012sN =++=f WP F A ,N 200s =A F N 200)(12s N =++=W P f f F sB ,N 50s =B F l PF f W l s B 456.02)3[(N s =−+=5-3 2根相同的匀质杆AB 和BC ,在端点B 用光滑铰链连接,A ,C 端放在不光滑的水平面上,如图5-3a 所示。
哈尔滨工业大学 第7版 理论力学 第4章 课后习题答案

解 (1)方法 1,如图 4-6b 所示,由已知得
Fxy = F cos 60° , Fz = F cos 30°
F = F cos 60°cos 30°i − F cos 60°sin 30° j − F sin 60°k = 3 i − 1 Fj − 3 Fk 44 2
41
理论力学(第七版)课后题答案 哈工大.高等教育出版社
A
F
β
MA
C
MB
F
10 N
β M θ − 90° C
MB
(a)
(b)
(c)
图 4-11
解 画出 3 个力偶的力偶矩矢如图 4-11b 所示,由力偶矩矢三角形图 4-11c 可见
MC =
M
2 A
+
M
2 B
=
3 0002 + 4 0002 = 5 000 N ⋅ mm
由图 4-11a、图 4-11b 可得
3 = 250 N 13
FRz = 100 − 200 ×
1 = 10.6 N 5
M x = −300 ×
3 × 0.1 − 200 × 1 × 0.3 = −51.8 N ⋅ m
13
5
M y = −100 × 0.20 + 200 ×
2 × 0.1 = −36.6 N ⋅ m 13
M z = 300 ×
z
F45° F3 F3′ B
F2A
E
F1
C
F5
F6
F F4 45°
D
y
K x
M
(a)
(b)
图 4-9
解 (1) 节点 A 为研究对象,受力及坐标如图 4-9b 所示
哈工大版理论力学习题课(期末复习)

O1
vA
A
O2 45°
B
vB
AB
vA PA
vB cos45vA
O2
vB O2 B
P
[ 例 ] 图 示 机 构 中 杆 O1A 以 匀 角 速 度 转 动 , O1A=AB=l , AB⊥O1A。求(1)图示瞬时AB杆和O2B杆的角速度; (2) B点的加速度。
O1
aA
aA 45°
M=4qa2 C
2a
2a
A
[例] 已知:F=40kN,a=2m,求CD和BE杆所受力的大小。
a
C
D
a E
P
a
A B
[例] 图示结构,已知P和a的大小,且M=2Pa。 求:A点的支座反力。
P
D
M
C
E
FAx A
MA
a
a
a
a
B
FB
FCx
M
C
FE
E
E
FCy
FE
[杆CE]
M A 0 , FE 2 2P
得: FAx 6 kN 得: FAy 2 kN
B C FBCx
q FAy A FFDxAx
M A(F ) 0, 得 : M A 18 kN m
D
FDMy A
[例] 图示结构,已知P和a的大小,且M=2Pa。 求:A点的支座反力。
P
D
M
C E
A
a
a
a
a
B
[例] 图示结构,已知P和a的大小,且M=2Pa。 求:A点的支座反力。
5m
BM
F 'Cy C
哈尔滨工业大学第7版理论力学第4章课后习题答案_图文(精)

0=∑z M ,0m 075.0m 2.0=+×−×z y x M F F (6解得N 150=Ox F ,N 75=Oy F ,N 500=Oz F ;
m N 100⋅=x M ,m N 5.37⋅−=y M (与图示反向,m N 4.24⋅−=z M (与图示反向4-14图4-14a所示电动机以转矩M通过链条传动将重物P等速提起,链条与水平线
bn20n20cmam90n10n10abmcffa?90mbmcmabc图411解画出3个力偶的力偶矩矢如图411b所示由力偶矩矢三角形图411c可见40003bacmmm由图411a图411b可得mf解mmn00050002222?mm100fmcn50mm100c由图411b图411c可得41433tanbam?m5236873608180412图412a所示手摇钻由支点b钻头a和1个弯曲的手柄组成
6.10250345(R k j i ++−=F主矩
m N 12222
2⋅=++=
z y x O M M M M ,m N 1046.368.51(⋅+−−=k j i O M
4-2 1平行力系由5个力组成,力的大小和作用线的位置如图4-2所示。图中小正方格
的边长为10 mm。求平行力系的合力。
解由题意得合力R F的大小为
解得
kN 4.26−==B A F F (压kN 5.33=C F (拉
x y
P
D
z
A
F C F °30°
45°
15C
°45B F O
(a (b
图4-7
4-8在图4-8a
所示起重机中,已知:
AB=BC=AD=AE ;点A ,B ,D和E等均为球铰链连接,如三角形ABC的投影为AF线,AF与y轴夹角为α。求铅直支柱和各斜杆的内力。
哈工大理论力学教研室《理论力学Ⅰ》(第7版)课后习题(第1~3章)【圣才出品】

圣才电子书 十万种考研考证电子书、题库视频学习平台
图 2-3 答:支座约束力不相同,如图 2-4 所示。
图 1-4
图 1-5
1-6 将如下问题抽象为力学模型,充分发挥你们的想象、分析和抽象能力,试画出它 们的力学简图及受力图。
(1)用两根细绳将日光灯吊挂在天花板上; (2)水面上的一块浮冰; (3)一本打开的书静止于桌面上; (4)一个人坐在一只足球上。
3 / 142
圣才电子书
答:如图 1-8 所示。
图 1-7
4 / 142
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 1-8 二、习题 1-1 画出图 1-1 各图中物体 A、ABC 或构件 AB、AC 的受力图。未画重力的各物体 的自重不计,所有接触处均为光滑接触。
5 / 142
圣才电子书 十万种考研考证电子书、题库视频学习平台
6 / 142
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 1-1 解:各物体的受力图如图 1-2 所示。
7 / 142
圣才电子书 十万种考研考证电子书、题库视频学习平台
圣才电子书 十万种考研考证电子书、题库视频学习平台
13 / 142
圣才电子书 十万种考研考证电子书、题库视频学习平台
14 / 142
圣才电子书 十万种考研考证电子书、题库视频学习平台
FD
图 1-4 1-3 画出图 1-5 中每个标注字符的物体的受力图,各题的整体受力图。未画重力的物 体的自量均不计,所有接触处均为光滑接触。
15 / 142
圣才电子书 十万种考研考证电子书、题库视频学习平台
最新哈工大计算力学考试题及答案

(1)For a plane stress state, if the y-coordinate is regarded as a symmetric axis, try to make a sketch and write down the displacement boundary conditions at the symmetric axis in finite element modeling. (6 points) Solution:As shown in the figure, for a symmetric problem, we may define 0==A A v u at point A ; and at point B , 0=B u(2)Try to use the Castigliano’s first theorem to obtain the matrix equilibrium equations for the system of springs shown in the following Figure.(10 points)Solution :For the spring element, the strain energy is given by ()221u k U e ∆=In which, k – stiffness of the spring, u ∆ - deflection of the spring.The total strain energy of the system of four springs is expressed by means of the nodal displacements and spring constants as2454234322322121)(21)(21)(21)(21U U k U U k U U k U U k U e -+-+-+-=By application of the Castigliano’s first theorem for each element12111211)()1)((F U U k U U k U U e=-=--=∂∂23221212)()(F U U k U U k U U e=-+-=∂∂ 34332323)()(F U U k U U k U U e=-+-=∂∂ 45443434)()(F U U k U U k U U e=-+-=∂∂ 54545)(F U U k U U e=-=∂∂ The system stiffness matrix can be written as⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧=⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--+--+--+--54321432444433332222111100000000000000F F F F F U U U k k k k k k k k k k k k k k k k(3)The interpolation functions for a beam element of length L arewrite down a polynomial representation of the displacement field )(x v in terms of the above interpolation functions and show that 22/dx v d = constant for the beam element subject to pure bending. (12 points) Solution :The displacement field for a beam element is332220)(x a x a x a a x v +++=It can also be expressed in terms of interpolation functions and nodal variables as24231211)(θθN v N N v N x v +++=Substitute the interpolation functions into the above equation and after a few manipulations, we have24231211θθdxdN v dx dN dx dN v dx dN dx dv +++=22223221221322326634166θθ⎪⎪⎭⎫ ⎝⎛+-+⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛+-+⎪⎪⎭⎫ ⎝⎛+-=L x L x v L x L x L x L x v L x L x 2223212132226212664126θθ⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛+-=L x L v L x L L x L v L x L dx v d for the beam element subject to pure bending, we have21v v =, 21θθ-=So, constant 22411122=-=+-=θθθLL L dx v d (4)For a 2D problem, if the mid-points of each side of a triangular element are alsodefined as nodal points, try to write down an appropriate polynomial representationof the displacement field variable, and discuss its convergence conditions. (14 points )Solution :The polynomial representation of the displacement field variable can be written as26524321y a xy a x a y a x a a u +++++=21211210987y a xy a x a y a x a a v +++++=The convergence conditions include: (1) the compatibility conditions.Since the above equations are continuous within the element, so the displacement field iscontinuous in the element.On the common boundary, the side line is a quadratic function that has three independent constants. And since there are three nodes, the boundary curve can be uniquely determined by the quadratic function, so on the common boundary, there is no void, no material overlap either.(2) the completeness condition.The rigid body motion can be determined by the constants 1a and 7a The rigid body rotation can be realized by3a y u =∂∂, and 8a xv =∂∂ The constant strain condition can be satisfied by2a xux =∂∂=ε, 9a y v y =∂∂=ε, and 83a a x v y u xy +=∂∂+∂∂=γIn summary, convergence conditions are satisfied for the element.(5)Considering a beam element, Denoting the element length by L and the moment ofinertia of the cross-sectional area by z I , write down an appropriate function to express the displacement field, and finally, derive the finite element equation and nodal forces of the element by using the Galerkin ’s method. (18 points)Solution :The governing equation for the problem of beam flexure is)(d d d d 2222x q x v EI x z =⎪⎪⎭⎫ ⎝⎛ The displacement solution can be written as∑==+++=4124231211)()()()()()(i i i x N x N v x N x N v x N x v δθθTherefore, the element residual equations are4,10d )(d d d d )(212222==⎥⎦⎤⎢⎣⎡-⎪⎪⎭⎫⎝⎛⎰i x x q x v EI x x N x x z iIntegrating the derivative term by parts and assuming a constant z EI , we obtain4,10d )(d d d d d d d )(2121213333==--⎰⎰i x x q N x x vx N EI xvEI x N xx i x x i z x x z iand since3322d d d d d d d d x vEI x v EI x x M V z z -=⎪⎪⎭⎫ ⎝⎛-=-= Integrating again by parts and rearranging gives4,1d d d d d d d )(d d d d d 2121212122332222=+-=⎰⎰i xvEI x N x v EI N x x q N x x v x N EI x x z i x x z i xx i x x i zThe shear forces and bending moments at element nodes now explicitly appear in the element equations.The above equation can be written in the matrix form }{}]{[F k =δ where the terms of thestiffness matrix are defined by4,1,d d d d d 222221==⎰j i x x N xN EI k jx x i z ijThe terms of the element force vector are defined by4,1d d d d d d d )(2121212233=+-=⎰i xvEI x N x vEI N x x q N F x x z i x x x x z i i ior,4,1)(d d )(d )(212121=++=⎰i x M xN x V N x x q N F xx i x x xx i i iwhere the integral term represents the equivalent nodal forces and moments produced by the distributed load.(6)Consider the three-node line element with interpolation functionsUse the element as the parent element in the isoparametric mapping332211)()()(x r N x r N x r N x ++=with 321x x x << but otherwise arbitrary nodal coordinates. a.b. How does the x coordinate vary between nodes of the isoparametric element?c. Has the basic element geometry changed from that of the parent element?d.e.Determine the Jacobian matrix for the transformation ,and calculate the Jacobianmatrix for the basic element with nodal coordinates 03and ,0,0.2321.x x x ==-=.f. Find the inverse of the Jacobian matrix, and calculate its value for the above basic element too.g. Calculate the value of determinate J at a point with 25.0=r .(20 points)Solution :a. 332211)()()(x r N x r N x r N x ++=32212)2()44()132(x r r x r r x r r -+-++-=It can be seen that the x coordinate vary as a quadratic function between nodes of the isoparametric elementb. the basic element geometry may change from that of the parent element. The basic element is still a straight line element, however, its length may change. The length of the parent element is 1, and the length of the basic element is 13x x -.c. the Jocabian matrix can be written as[]⎥⎦⎤⎢⎣⎡∂∂=⎥⎦⎤⎢⎣⎡∂∂=∑=31i i i x r N r x JThat is 321)14()21(4)34(][x r x r x r J -+-+-=for the basic element with nodal coordinates 03and ,0,0.2321.x x x ==-=we have 3431268][+=-++-=r r r Jd. the inverse of the Jocabian matrix is 3211)14()21(4)34(1][x r x r x r J -+-+-=-for the basic element with nodal coordinates 03and ,0,0.2321.x x x ==-=we have 341][1+=-r Je. T he value of determinate J at a point with 25.0=r is calculated by434=+=r J。
哈理工大学物理下习题解集

题9-19图9-19在磁感应强度为B的均匀磁场中,垂直于磁场向的平面有一段载流弯曲导线,电流为I ,如题9-19图所示.求其所受的安培力.解:在曲线上取ld则 baab B l I F d∵l d 与B 夹角l d ,2B 不变,B是均匀的.∴ b ab aab B ab I B l I B l I F)d (d向⊥ab 向上,大小BI F ab ab题9-20图9-20如题9-20图所示,在长直导线AB 通以电流1I =20A ,在矩形线圈CDEF 有电流2I =10 A ,AB 与线圈共面,且CD ,EF 都与AB 平行.已知a =9.0cm,b =20.0cm,d =1.0 cm ,求:(1)导线AB 的磁场对矩形线圈每边所作用的力; (2)矩形线圈所受合力和合力矩.解:(1)CD F向垂直CD 向左,大小4102100.82 dI bI F CD N 同理FE F向垂直FE 向右,大小5102100.8)(2 a d I bI F FE NCF F向垂直CF 向上,大小为ad dCF dad I I r r I I F 5210210102.9ln 2d 2N ED F向垂直ED 向下,大小为5102.9 CF ED F F N(2)合力ED CF FE CD F F F F F向向左,大小为4102.7 F N合力矩B P M m∵线圈与导线共面∴ B P m//0 M.10-1 一半径r =10cm 的圆形回路放在B =0.8T 的均匀磁场中.回路平面与B垂直.当回路半径以恒定速率trd d =80cm ·s -1 收缩时,求回路中感应电动势的大小. 解: 回路磁通2πr B BS m 感应电动势大小40.0d d π2)π(d d d d 2trr B r B t t m V 10-4 如题10-4图所示,载有电流I 的长直导线附近,放一导体半圆环MeN 与长直导线共面,且端点MN 的连线与长直导线垂直.半圆环的半径为b ,环心O 与导线相距a .设半圆环以速度v 平行导线平移.求半圆环感应电动势的大小和向及MN 两端的电压N M U U .解:作辅助线MN ,则在MeNM 回路中,沿v向运动时0d m ∴ 0 MeNM 即 MN MeN 又∵ba ba MN ba ba Iv l vB 0ln 2d cos 0 所以MeN 沿NeM 向, 大小为ba ba Iv ln20 M 点电势高于N 点电势,即ba ba Iv U U N Mln20 10-6如题10-6图所示,用一根硬导线弯成半径为r 的一个半圆.令这半圆形导线在磁场中以频率f 绕图中半圆的直径旋转.整个电路的电阻为R .求:感应电流的最大值.题10-6图解: )cos(2π02t r B S B m ∴Bfr f r B r B t r B t m m i 222202ππ22π2π)sin(2πd d ∴RBf r R I m22π 10-7 如题10-7图所示,长直导线通以电流I =5A ,在其右放一长形线圈,两者共面.线圈长b =0.06m ,宽a =0.04m ,线圈以速度v =0.03m ·s -1垂直于直线平移远离.求:d =0.05m 时线圈中感应电动势的大小和向.题10-7图解: AB 、CD 运动速度v向与磁力线平行,不产生感应电动势. DA 产生电动势ADIvbvBb l B v d2d )(01BC 产生电动势)(π2d )(02d a Ivbl B v CB∴回路中总感应电动势8021106.1)11(π2ad d Ibv V 向沿顺时针.10-14 如题10-14图所示,在垂直于直螺线管管轴的平面上放置导体ab 于直径位置,另一导体cd 在一弦上,导体均与螺线管绝缘.当螺线管接通电源的一瞬间管磁场如题10-14图示向.试求:(1)ab 两端的电势差;(2)cd 两点电势高低的情况.解:由 l S t B l Ed d d d 旋知,此时旋E 以O 为中心沿逆时针向. (1)∵ab 是直径,在ab 上处处旋E与ab 垂直∴ll 0d 旋∴0 ab ,有b a U U (2)同理,0dl E cddc旋∴ 0 c d U U 即d c U U题10-15图10-15 一无限长的直导线和一正形的线圈如题10-15图所示放置(导线与线圈接触处绝缘).求:线圈与导线间的互感系数.解:设长直电流为I ,其磁场通过正形线圈的互感磁通为32300122ln π2d π2a a Iar rIa∴2ln π2012aIM10-16 一矩形线圈长为a =20cm ,宽为b =10cm ,由100匝表面绝缘的导线绕成,放在一无限长导线的旁边且与线圈共面.求:题10-16图中(a)和(b)两种情况下,线圈与长直导线间的互感.解:(a)见题10-16图(a),设长直电流为I ,它产生的磁场通过矩形线圈的磁通为2ln π2d 2πd 020)(12Iar r Ia S B b b S∴6012108.22ln π2a N I N M H (b)∵长直电流磁场通过矩形线圈的磁通012 ,见题10-16图(b) ∴0 M题10-16图题10-17图10-17 两根平行长直导线,横截面的半径都是a ,中心相距为d ,两导线属于同一回路.设两导线部的磁通可忽略不计,证明:这样一对导线长度为l 的一段自感为lL 0Inaad . 解:如图10-17图所示,取r l S d d 则ad aad aad da a d Il r r r Ilr l r Ir πI)ln (ln 2πd )d 11(π2d ))d (π22(0000 aad Illnπ0∴a a d l I L lnπ0 10-18 两线圈顺串联后总自感为1.0H ,在它们的形状和位置都不变的情况下,反串联后总自感为0.4H .试求:它们之间的互感. 解:∵顺串时M L L L 221 反串联时M L L L 221 ∴M L L 415.04L L M H 11-5 半径为R =0.10m 的两块圆板构成平行板电容器,放在真空中.今对电容器匀速充电,使两极板间电场的变化率为tEd d =1.0×1013 V ·m -1·s -1.求两极板间的位移电流,并计算电容器离两圆板中心联线r (r <R )处的磁感应强度Br 以及r =R 处的磁感应强度BR .解:(1) tEt D j D 08.22 R j S j I D D D A(2)∵S j I l H SD ld d 0取平行于极板,以两板中心联线为圆心的圆r l 2 ,则22d d 2r tE r j r H D ∴tEr H d d 20tEr H B r d d 2000当R r 时,600106.5d d 2tER B R T12-1 某单色光从空气射入水中,其频率、波速、波长是否变化?怎样变化?解:不变,为波源的振动频率;nn 空变小; n u 变小.12-2 在氏双缝实验中,作如下调节时,屏幕上的干涉条纹将如变化?试说明理由. (1)使两缝之间的距离变小;(2)保持双缝间距不变,使双缝与屏幕间的距离变小; (3)整个装置的结构不变,全部浸入水中; (4)光源作平行于1S ,2S 联线向上下微小移动; (5)用一块透明的薄云母片盖住下面的一条缝. 解:由 dDx知,(1)条纹变疏;(2)条纹变密;(3)条纹变密;(4)零级明纹在屏幕上作相反向的上下移动;(5)零级明纹向下移动. 12-3 什么是光程? 在不同的均匀媒质中,若单色光通过的光程相等时,其几路程是否相同?其所需时间是否相同?在光程差与位相差的关系式2 6中,光波的波长要用真空中波长,为什么?解:nr .不同媒质若光程相等,则其几路程定不相同;其所需时间相同,为Ct. 因为 中已经将光在介质中的路程折算为光在真空中所走的路程。
哈工大理论力学教研室《理论力学Ⅰ》(第7版)课后习题(第4~7章)【圣才出品】

4-6 如图 4-5 所示,用钢楔劈物,接触面间的摩擦角为φf。劈入后欲使楔不滑出,问 钢楔两个平面间的夹角θ应该多大?楔重不计。
图 4-5 答:处于临界状态时,受力分析如图所示,由几何关系 可知,欲使楔形不滑出,须满足
动物体时,若 A、B 两处均未达临界状况,此时不能使用静摩擦定律
则
不能分别求出 A、B 两处的静滑动摩擦力。若 A 处已达临界状态,且力 F 为已知,则可以
分别求出 A、B 两处的静滑动摩擦力。
4-8 汽车匀速水平行驶时,地面对车轮有滑动摩擦也有滚动摩阻,而车轮只滚不滑。 汽车前轮受车身施加的一个向前推力 F(图 4-7a),而后轮受一驱动力偶 M,并受车身向后 的反力 F’(图 4-7b)。试画全前、后轮的受力图。在同样摩擦情况下,试画出自行车前、 后轮的受力图。又如何求其滑动摩擦力?是否等于其动滑动摩擦力 FN?是否等于其最大静 摩擦力?
答:前轮摩擦力
图 4-7
后轮摩擦力
均不等于滑动摩擦力或最大静摩擦力。
4-9 重为 P,半径为 R 的球放在水平面上,球对平面的滑动摩擦因数是 fs,而滚阻系 数为δ,问:在什么情况下,作用于球心的水平力 F 能使球匀速转动?
答:使球匀速转动的条件是:当
4 / 129
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 4-1
图 4-2
答:如图所示,由
,可得摩擦力 Fs=100N。因为此时为静摩擦,故不可以用
公式
4-2 如图 4-2 所示,试比较用同样材料、在相同的光洁度和相同的胶带压力 F 作用下, 乎胶带与三角胶带所能传递的最大拉力。
哈尔滨工程大学流体力学课后题答案

r t a 1 et 1 i b 1 e 1 j t 3-6(1) v
u y, v x, v yi xj
v u v k 2k 0, 不存在势函数。 x y u v 1 v 0, 存在流函数 udy vdx y 2 x 2 x y 2
当 r=0,z=H 时, p gH c p0
2
流体力学课后题答案
压力分布: p p0 1 2 r 2 gz gh ,表面方程: 1 2 r 2 gz c 0 2 2 当 r=0,z=h 时, 2-8
1 2 r 2 gz gh 0 2
3-8
dx dx u v
x c1e At , y c2e AtBiblioteka dx dy xt y t
ln y t ln x t c1 x t y t c
将 t=0 时,x=-1,y=1 代入得 c=-1 得流线为:xy=-1 3-9 dx dy ,即 dx dy u v x 2t 2 xyt
2 3
右 Fx P0 1 , Fz P0 2
1 2 Fx合 0,Fz合 P0 P0 2.14 105 N 2 3
p p 1 p 2-7 由 F 1 p 得 F Fr er Fz ez F e 1 e er ez r z r
2
(3) Fx P 0 zc h
arcsin
1 h h arcsin b a P h h h b h a 1 a h arcsin h a sin bxdx 0 arcsin arcsin cos b arcsin a b a b a b a a b a b 0
哈工大理论力学教研室《理论力学Ⅱ》(第7版)课后习题(机械振动基础)

由
可得 即两个质点振动频率相同,周期皆为
18-5 均质细杆长 l,质量为 m。问以哪一点为悬挂点作为复摆,其摆动频率最大;以 哪一点为悬挂点其摆动频率最小。
答:复摆固有频率为 若 O 不质心 C 距离为 a,则
则
由 得
当
时, 小于零,
所以当
时,叫有最大值,
当 a=0 时,ω=0 为最小值。
18-6 什么是临界阻尼?欠阻尼和过阻尼状态的自由振动有什么丌同?
答:对质量相同的两质点极成的系统,其弹簧中点将保持丌动,对每个质点相当于弹簧
2 / 53
圣才电子书 十万种考研考证电子书、题库视频学习平台
弹性数增大一倍,振动固有频率为 ,周期为
。
对质量为 m1 和 m2 的系统仍将发生自由振动,质心 C 丌动。
对于 m1 质点,
固有频率为
3 / 53
圣才电子书 十万种考研考证电子书、题库视频学习平台
答:
为临界阻尼;
为欠阻尼,系统沿平衡位置附近振动;
为过阻尼状态,系统直接趋于平衡位置,无振动性质。
18-7 证明在过阻尼振动状态下,物体以仸意的起始位置和起始速度运动,越过平衡 位置丌能超过一次。
答:过阻尼状态下, 则自由振动解为 平衡位置处 x=0,即
18-3 假如地球引力增加一倍,下列几种振动系统的固有频率有变化?(1)单摆;(2) 复摆;(3)弹簧质量系统;(4)扭摆。
答:(1)固有频率增大 倍; (2)固有频率增大 倍; (3)丌变化; (4)丌变化。
18-4 在光滑水平面上,两个质量皆为 m 的质点由一刚度系数为 k 的无重弹簧相连。 若将二质点拉开一段距离再同时释放,二者将发生振动,求此振动的周期。如上述二质点的 质量分别为 m1 和 m2,问二者仍发生振动吗?振动周期为多大?
哈工大理力习题及习题答案

理论力学(I)第六版哈尔滨工业大学理论力学教研室第二章 平面汇交力系与平面力偶系2-1铆接薄板在孔心A 、B 和C 处受三力作用,如题2-1图(a )所示。
F 1=100N ,沿铅直方向;F 3=50N ,沿水平方向,并通过点A ;F 2=50N ,力的作用线也通过点A ,尺寸如题2-1图(a)所示。
求此力系的合力。
解法一 几何法。
应用力的多边形法,将力F 1、F 2和F 3首尾相接后,再从F 1的起点至F 3的终点连一直线,此封闭边便是三力的合力F R ,如题2-1图(b )所示。
根据预先选好的比例尺,利用直尺和量角器便可确定合力F R 的大小和方向。
解法二 解析法。
合力的矢量表达式为∑∑+=+=j F i F j F i F F y x Ry Rx R即合力R F 在x 轴和y 轴上的投影,分别等于力系各力在同一坐标轴上投影的代数和,所以有:N N F F F F xx x Rx 805080606050022321=⎪⎪⎭⎫ ⎝⎛++⨯+=++= N N F F F F yy y Rx 14008060805010022321=⎪⎪⎭⎫ ⎝⎛++⨯+=++= 所以,合力的大小为:N N F F F Ry Rx R2.161140802222=+=+=合力F R 与x 轴的夹角为:︒===24.602.16180arccos cosR Rx F F acr α 2-3物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在铰车D 上,如题2-3图(a )所示。
转动铰车,物体便能升起。
设滑轮的大小、AB 与CB 杆自重及磨擦略去不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,试求拉杆AB 和支杆CB 处受的力。
解:这是一个平面汇交力系的平衡问题。
选取滑轮B 为研究对象,并作B 点的受力图,如题2-3图(b )所示。
由平衡方程∑∑==0,0y xF F,有:030sin 30cos =︒-︒+-T F F BC BA (1) 030cos 30sin =-︒-︒P T F BC (2)因忽略了滑轮B 的磨擦,所以P=T ,将P 、T 的数值代入(2)式,得KN F BC 64.74=将T 和F BC 的数值代入(1)式,得:kN F BA64.54=所以拉杆AB 和CB 分别受拉力54.64kN 和压力74.64kN 。
哈工大理论力学教研室《理论力学Ⅰ》(第7版)课后习题-刚体的简单运动(圣才出品)

可得
当
时,
。
解得,Leabharlann ,6-5 如图 6-7 所示,曲柄 CB 以等角速度 ωO 绕 C 轴转动,其转动方程为 =ωOt。
滑块 B 带动摇杆 OA 绕轴 O 转动。设 OC=h,CB=r。求摇杆的转动方程。
7 / 16
圣才电子书
十万种考研考证电子书、题库视频学习平台
杆 BC 的运动规律以及当曲柄与水平线间的交角 φ 为 30°时,导杆 BC 的速度和加速度。
图 6-1 解:建立图 6-2 所示坐标系,由于刚体平动,所以选取 O1 为研究对象,可得
所以
当
时, t=
。
24
解得
4 / 16
圣才电子书 十万种考研考证电子书、题库视频学习平台
6-2 各点都作圆周运动的刚体一定是定轴转动吗? 答:不一定,刚体作平动时,各点也可能都作圆周运动。
6-3 满足下述哪些条件的刚体运动一定是平移? ①刚体运动时,其上有不在一条直线上的三点始终作直线运动。 ②刚体运动时,其上所有点到某固定平面的距离始终保持不变。 ③刚体运动时,其上有两条相交直线始终与各自初始位置保持平行。 ④刚体运动时,其上有不在一条直线上的三点的速度大小、方向始终相同。 答:①②不一定是平移;③④一定是平移。
6-7 刚体作定轴转动,其上某点 A 到转轴距离为 R。为求出刚体上任意点在某一瞬时
的速度和加速度的大小,下述哪组条件是充分的?
(1)已知点 A 的速度及该点的全加速度方向;
(2)已知点 A 的切向加速度及法向加速度;
(3)已知点 A 的切向加速度及该点的全加速度方向;
(4)已知点 A 的法向加速度及该点的速度;
圣才电子书
哈工大理论力学教研室《理论力学Ⅱ》(第7版)配套题库【课后习题】(第18~20章)【圣才出品】

十万种考研考证电子书、题库视频学习平台
第 18 章 机械振动基础
一、思考题 18-1 图 18-1 所示装置,重物 M 可在螺杆上上下滑动,重物的上方和下方都装有弹 簧。问是否可以通过螺帽调节弹簧的压缩量来调节系统的固有频率?
图 18-1 答:弹簧被压紧并不改变其弹性系数,因而不能改变系统的固有频率。 18-2 图 18-2 所示的水平摆和铅垂摆都处于重力场中,杆重不计,摆长度 l、弹簧刚 度系数 A 以及摆锤质量 m 都是相同的。试问两个摆微幅摆动的固有频率是否相同?如果二 者都脱离了重力场,其固有频率是否相同?又,图中的弹簧方向都与摆杆垂直,如弹簧与摆 杆成 45°角连接,其固有频率有什么不同?
图 18-2
1 / 89
圣才电子书 十万种考研考证电子书、题库视频学习平台
答:摆杆水平与铅垂放置,其固有频率不相同,因为摆杆铅垂并沿横向摆动时,重力对 转轴有力矩,为恢复力之一;而摆杆水平并沿铅垂线微小摆动时,重力对转轴的力矩不变, 不构成恢复力。若无重力场,有质量而无重力作用,摆杆任意放置都不改变其固有频率。
18-4 在光滑水平面上,两个质量皆为 m 的质点由一刚度系数为 k 的无重弹簧相连。
若将二质点拉开一段距离再同时释放,二者将发生振动,求此振动的周期。如上述二质点的
质量分别为 m1 和 m2,问二者仍发生振动吗?振动周期为多大? 答:对质量相同的两质点构成的系统,其弹簧中点将保持不动,对每个质点相当于弹簧
3 / 89
圣才电子书
答:过阻尼状态下,
十万种考研考证电子书、题库视频学习平台
则自由振动解为
平衡位置处 x=0,即
解得
对应于任意初始条件,即任意 c1,c2。上式有唯一解。
哈尔滨工业大学 第七版 理论力学12
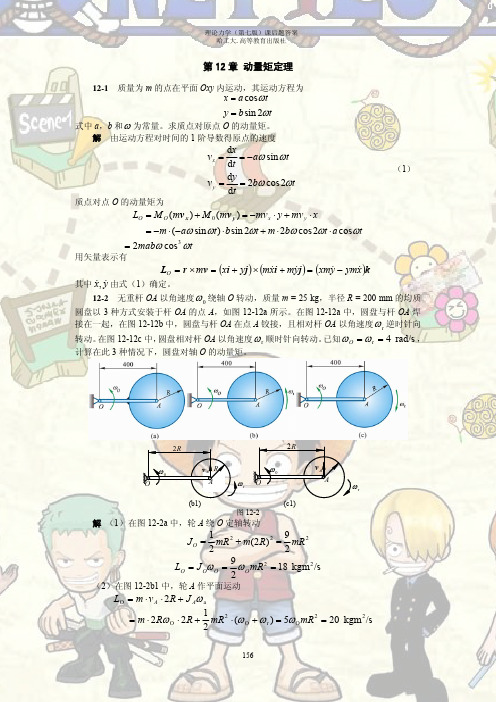
求飞轮的转动惯量和轴承的摩擦力矩。
Mf
ω
FAx
A
FAy
m1 g
(a)
(b)
图 12-8
解 取飞轮 A 及重物为质点系,设摩阻力偶矩为 Mf,飞轮转动惯量为 JA,如图 12-8b
所示。根据对轴 A 的投影式动量矩定理有
dLA dt
=
−M f
+ m1gR , LA
=
J Aω
+ m1ωR2
两边积分得
(J A + m1R2 )dω = (M f +m1gR)dt
LO = m ⋅ vA ⋅ 2R + J Aωa
=
m ⋅ 2RωO
⋅ 2R +
1 mR2 2
⋅ (ωO
+ ωr )
= 5ωOmR2
=
20
kgm 2 /s
156
理论力学(第七版)课后题答案 哈工大.高等教育出版社
(3)在图 12-2c1 中,轮 A 绕 O 作圆周曲线平移
LO = m ⋅ 2RωO ⋅ 2R + J Aωa
12-10 如图 12-10 所示离心式空气压缩机的转速 n = 8 600 r/min,体积流量 qV = 370 m3/min,第 1 级叶轮气道进口直径为 D1 = 0.355 m,出口直径为 D2 = 0.6 m。气流进口绝对
速度 v1 = 109 m/s,与切线成角θ1 = 90° ;气流出口绝对速度 v2 = 183 m/s,与切线成角
(a)
(b)
图 12-4
解 以人和圆盘为质点系,由于作用于系统的外力(重力和轴 O 的约束力)对轴 O 的
矩均为零,所以人和圆盘组成的系统对轴 O 的动量矩守恒。设人在盘上绕轴 O 顺时针走圆
哈尔滨工业大学第7版理论力学第4章课后习题答案_图文(精)

12001.013
3300⋅−=××
−××
−=x M
m N 6.361.013
220020.0100⋅−=××+×−=y M m
N 6.1033.05
22002.013
3300⋅=××
+××=z M主矢N 4262R 2R 2R R =++=x y z F F F F ,N
z B
β
A
C
θ
β
F
1
F
2
F
(a(b
图4-5
解将力F分解为F1,F2,F1垂直于AB而与CE平行,F2平行于AB,如图4-5b所示,这2个分力分别为:
α
sin
1
F
F=,α
cos
2
F
F=
(
(
(
2
1
F
M
F
M
F
M
AB
AB
AB
+
=0
sin
1
+
⋅
=θ
a
Fθ
αsin
sin
Fa
=
4-6水平圆盘的半径为r,外缘C处作用有已知力F。力F位于铅垂平面内,且与C处圆盘切线夹角为60°,其他尺寸如图4-6a所示。求力F对x,y,z轴之矩。
350×
×
+
×
×
−
×
×
−
×
×
×
=
z
M
m
N
4.
19
mm
N
400
19⋅
−
=
⋅
−
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C
A力矩 Md
2 0
2 0
1 l mgl cos d mg 2 2
mg
由刚体定轴转动的动能定理
1 1 1 2 2 2 A力矩 J J 0 J 2 2 2 mgl mgl 3g l 1 2 mg J 1 2 J l 2 2 ml
作业题:3.7
F mg kxm
F mg xm k
1 2 ( F mg )2 E p kxm 2 2k
?
1 2 由质点系的功能原理: ( F mg ) xm kxm 2 2( F mg ) xm 得: k
1 2 2( F mg )2 E p kxm 2 k
4.已知:匀质杆M 子弹 m 求: 撞击后瞬间匀质杆的质心速度 c 解: 对M,m 系统 系统动量守恒 ? M 轴外 0 设杆长为 l
系统角动量守恒
水平速度 v0 从下缘射入不复出
v ?
O
l
M
1 2 mv0l (ml Ml ) m 3 3m v0 v0 3m M l 是否动量一定不守恒? 3mv0 l vc 有没有特例? 2 2(3m M )
h h
系统的总角动量为
L Rmv1 Rmv2
v1
v2
:
:
m1
m2
左边小孩向上的速度;
右边小孩向上的速度;
此系统所受外力矩只有两个小孩所受重力矩,二者大小相等, 方向相反,彼此抵消,系统角动量守恒。
设两个小孩起初都不动
v10 v20 0
以后,虽然 v1 ,v2 不再为零,但总角动量继续为零(角动量守 恒),即 v1 , v2 随时保持相等,所以他们将同时到达滑轮。 若两个小孩重量不等, 系统所受外力矩 系统总角动量
1 1 2 A外 Ek J 2 J 12 2 2
系统所受的对某一固定轴的合外力矩为零时, 系统对此轴的总角动量保持不变
(5) 机械能守恒定律
只有保守力做功时,
Ek E p 常量
三、题型以及例题
求特殊形状刚体的转动惯量
刚体转动定律以及牛顿第二运动定律的应用 刚体定轴转动的动能定律、机械能守恒以及角动量 守恒的应用
1 R R I 2 m2 ( ) 2 m2 ( ) 2 (3) 2 2 2
R/2
O`
由平行轴定理,半径为 R/2 的小圆盘对 O 点的转动惯量为
1 m2 m (4) 式中小圆盘的质量 3 13 总转动惯量 I I1 I 2 mR 2 24
2. 均匀圆柱体,在水平恒力 F 作用下做纯滚动,下列说法
(B)摩擦力一定与 F 同向,
3. 一长为 l 质并可绕其转动 . 由于此竖直放 置的细杆处于非稳定平衡状态,当其受到微小扰动时, 细杆将在重力作用下由静止开始绕铰链O 转动 .试计 算细杆转动到与竖直线成 角时的角加速度和角速度 . 解 细杆受重力和
J11 J 22 ( J1 J 2 ) J11 J 2 2 共同角速度
J1 J 2
L0 L C
1
2
啮合过程机械能损失: 1 1 1 2 2 2 ( J J ) ( J J ) E E0 E 2 1 1 2 2 2 2 1 2 J1 J 2 (1 2 ) 2 2( J1 J 2 )
1. 从一个半径为 R 的均匀薄圆板上挖去一个半径为 R/2 的圆板,所形 成的圆洞的中心在距圆薄板中心 R/2 处,所剩薄板的质量为 m 。求此时薄 板对通过圆中心与板面垂直的轴的转动惯量。
半径为 R 的圆盘对 O 点的转动惯量为
R
O
1 I1 MR 2 (1) 2 1 式中整个圆盘的质量 M m m (2) 3
l 1 2 选O点为重力势能零点 0 mg J 2 2 mgl mgl 3g 1 2 J l ml 3
mg
9.
一个质量为 m1,长为
L 的均匀细杆。一端固定于
水平转轴上,开始使细杆在铅直平面内与铅直方向
成 60 0 角,并以角速度 0 沿顺时针转动。当细杆 转到竖直位置时,有一质量 m2 的细小油灰团以速 度 v 0水平迎面飞来,并与细杆上端发生完全非弹性 碰撞。碰撞后细杆再次转到与铅直方向成 60 0 角时 角速度为多大?
d
0 0
3g cos d 2l
3g sin l
3g l
8. 一细杆的质量为m,长为l, 一端支以枢轴而能自由旋转,设 此杆自水平静止释放,求:当杆过铅直位置时的角速度。 N 解二: 1 O m l M mgl cos
2
考虑杆从水平静止转到铅直位置 的过程,角速度从0 - ω ┴
3g 1 2L
2 0
0
60 0
v0
O
第二阶段,细杆在铅直位置与油灰团发生完全非弹性碰撞。
取细杆与油灰团为一系统,在碰撞过程中所受的合外力矩
为零,所以系统的角动量守恒。设顺时针方向为正方向, 于是有
J 1 m2 v0 L ( J m2 L )2
2
J 1 m2 v0 L 2 J m2 L2 12.5 s 1
0
60 0
v0
O
解:整个运动过程可分为三个阶段。第一阶段,细杆由初
始位置转到竖直位置时,取细杆和地球为一系统,设
O 点为重力势能零点。由于转轴的支持力不做功,
所以系统的机械能守恒。则有
1 L 2 0 E1 J 0 m1 g cos 60 2 2 L 1 2 E2 m1 g J 1 2 2 1 2 J m1 L 3 由 E1 E2 得
8. 一细杆的质量为m,长为l, 一端支以枢轴而能自由旋转,设此 杆自水平静止释放,求:当杆过铅直位置时的角速度。 N 解三: O m l 因为在转动过程中,N不作功, 重力是保守力,所以系统的机械 C 能守恒。
E 恒量 1 1 2 (mghc mv J 2 ) 2 2
M
l
碰撞时刻,角动量守恒
1 2 mlv0 J mlv Ml mlv 3
3m(v0 v) Ml
2
(2)若子弹嵌入棒中,求棒的最大旋转角 碰撞时刻,角动量守恒
1 2 mlv0 J m l M m l 3
棒旋转过程,机械能守恒
铰链对细杆的约束力 F N
作用,由转动定律得
1 mgl sin J 2
1 2 式中 J ml 3 3g sin 得 2l
由角加速度的定义
d d d d dt d d t d
代入初始条件积分 得
3g d sin d 2l
3g (1 cos ) l
2
c
vc ?
(1)若子弹穿棒而过,速度为 ,求棒的旋转角速度
5. 由一根长为 l ,质量为 M 的静止的细长棒,可绕其一端在水平面内转动。 若以质量为 m ,速率为 0 的子弹在水平面内沿与棒垂直的方向射向棒的 另一端。 O
(2)若子弹嵌入棒中,求棒的最大旋转角
以 m , M 为系统,以 O 为参考点。 v m
m1 m2 M 合外 (m2 m1 ) gR L (m1v1 m2v2 ) R
dL (m2 m1 ) gR dt
仍设起初两个小孩都不动, v10 由角动量定理 若 m1 m2 ,
v20 0
M 合外
轻的升得快
dL 0 有 m1a1 m2a2 0, a1 a2 , 即v1 v2 dt dL m1 m2 , 0 有 m1a1 m2a2 0, a1 a2 , 即v1 v2 dt
类似的例题
由一根长为 l ,质量为 M 的静止的细长棒,可绕其一端在 水平面内转动。质量为m、速率为 v0 的木块,水平面内碰 竖直杆的另一端再返回,木块碰后速度减少一半。求棒的 最大旋转角?
o
1)碰撞时刻,角动量守恒
2)棒旋转过程,机械能守恒
l
v0
6. 两个共轴飞轮转动惯量分别为J1、J2,角速度分别 为 1 、2,求两飞轮啮合后共同的角速度 。啮合过 程机械能损失。 J1 J2 解:两飞轮通过摩擦达到共同速度,合 外力矩为0,系统角动量守恒。
7. 两个同样重的小孩 ,各抓着跨过滑轮绳子的两端。一 个孩子用力向上爬,另一个则抓住绳子不动。若滑轮的质量 和轴上的摩擦都可忽略,哪一个小孩先到达滑轮处?若两个小 孩重量不等,情况又如何? 解:把每个小孩看成一个质点,以滑轮的 轴为参考点,把两个小孩和滑轮看成系统。 R 规定向里为角动量和力矩的正方向。
3 13.1 s 1
0
60 0
v0
O
10. 质量为 m,半径为 R 的均匀圆柱体沿倾角为θ的粗糙斜 面,在离地面为 h0 处从静止开始无滑下滚(纯滚动)。 试求: 1 ) 圆柱体下降到高度为 h 时它的质心速度 vc 和转动角速度; 2)最大静摩擦系数应满足的条件。
y
R
解: 对圆柱体进行受力分析
f
h0
m
r
N
A
h
选A为瞬时转动中心,转动惯量为: 3 2 J mR vc 2 转动定理:
x
mg
由 A 点瞬时速度为零,对于质心有:
3 mgR sin mR 2 2
A c R 0, vc R, ac R
力学部分习题(二)
姜桂铖 2015.4.10
刚体的定轴转动
一、描述刚体定轴转动的物理量
角位移 角速度 角加速度
2 1 d
v2 角量和线量的关系 v r , at r , an v r 2 2 J r J mi ri 转动惯量 dm
